Amaçlar
Bu üniteyi çalıştıktan sonra;
• fonksiyon
kavramını tanıyacak,
• bir fonksiyonun bire-bir ve örten olup olmadığını araştırabilecek,
• iki fonksiyonun bileşkesini bulabilecek,
• ters fonksiyon kavramını anlayacak,
• fonksiyon
grafiği kavramını öğrenip bazı fonksiyonların
gra-fiklerini çizebileceksiniz.
İçindekiler
• Giriş
83
• Fonksiyon Kavramı
83
• Fonksiyon Grafikleri
98
• Değerlendirme Soruları
116
ÜNİTE
3
Fonksiyon Kavramı
Yazar
• Yazarak
çalışınız
• Bir kavramı anlamadan diğerine geçmeyiniz
• Çözümleri size bırakılan soruları mutlaka çözünüz ve
cevapla-rınızı kontrol ediniz
• Grafikleri doğru çizebilmek için yanınızda kareli kağıt ve
cet-vel bulundurunuz
1. Giriş
Fonksiyon kavramı matematiğin en temel kavramlarından birisidir. Bu kavramı ta-nımlamadan önce birkaç örneği ele alalım.
i) Fiyatı 40 000 TL olan ekmekten x tane aldığımızda ödeyeceğimiz paraya y dersek
y = 40 000 x
yazabiliriz. Burada ödeyeceğimiz paranın aldığımız ekmeğin miktarına bağlı olduğu açıktır. Ekmek miktarı değiştikçe ödenecek para da değişecektir. İşte bu durumda ödenecek para alınan ekmek miktarının bir fonksiyonudur diyoruz. ii) Bir çemberde, Ç çevre uzunluğu, r yarıçap olmak üzere , Ç = 2πr olduğunu
biliyoruz. Burada da yarıçap değiştikçe çevre uzunluğu değişecek ve her bir ya-rıçap için çevre uzunluğu olarak tek bir sayı bulunacaktır. Bu durumda da çevre uzunluğu yarıçapın bir fonksiyonudur diyoruz.
iii) Hava direncinin olmadığı bir ortamda belirli bir yükseklikten serbest bırakı-lan bir cismin aldığı s yolu ile t zamanı arasında
bağıntısının varlığını fizik derslerinden biliyoruz. Burada da s yolu t zamanı-na bağlıdır. Yani t değiştikçe s de değişmektedir. Bu durumda da s yolu t zama-nının bir fonksiyonudur diyoruz.
2. Fonksiyon Kavramı
Yukarıdaki örneklerle sezdirmeye çalıştığımız fonksiyon kavramının kesin tanımı-nı verelim.
Boş kümeden farklı A ve B gibi iki küme verilsin. A kümesindeki her bir elemana B kümesinden bir ve yalnız bir eleman karşılık getiren bir eşlemeye A kümesinden B kümesine bir fonksiyon denir.
Bu eşleme genellikle bir kuralla verilir. Bu kural çoğu kez f, g,..., h gibi harflerle gösteri-lir. A kümesinden B kümesine f kuralı ile verilen fonksiyon f : A→ B şeklinde gös-terilir. Bu durumda A kümesine f fonksiyonunun tanım kümesi , B kümesine de de-ğer kümesi denir. A kümesinden alınan bir x elemanına B kümesinden f ile karşı geti-rilen elemana x in f altında görüntüsü denir ve bu eleman f(x) ile gösterilir. A
kü-s = 1 2 gt
mesindeki tüm elemanların f fonksiyonu altındaki görüntülerinin oluşturduğu kü-meye f fonksiyonunun görüntü kümesi denir ve f (A) ile gösterilir. Bazen, f : A→ B fonksiyonuna A üzerinde bir fonksiyon da denir.
Örneğin, A ve B kümeleri olarak Z tamsayılar kümesini alalım ve her tam sayıyı ka-resi ile eşleyen eşlemeyi düşünelim. Bu eşlemede her tam sayıya karşılık o sayının karesi olan bir tam sayı vardır ve bu tamsayı tektir. Bu nedenle bu eşlemeye bir fonk-siyondur diyebiliriz. Bu fonksiyon,
f : Z → Z, x → x2
veya
f : Z → Z, f (x) = x2
şeklinde gösterilir. Bu fonksiyon altında 0 ın görüntüsünün 0, - 1 ile 1 in görüntü-sünün 1, - 4 ile 4 ün görüntügörüntü-sünün 16 olduğunu şu şekilde ifade ederiz: f (0) = 0 , f (-1) = 1, f (1) = 1, f (- 4) = 16, f (4) = 16. Bu fonksiyonun tanım ve değer kümeleri Z tam sayılar kümesi iken her tam sayının karesi pozitif tam sayı veya 0 olduğundan görüntü kümesi, f (Z) = IN ∪ {0} dır. Bu fonksiyonu Venn şeması ile şöyle gös-terebiliriz.
Tanım kümesine ait her bir elemanın bir fonksiyon altındaki görüntüsü tek olmak zorundadır, ancak tanım kümesine ait farklı iki elemanın görüntüsü aynı olabilir. Örneğin yukarıdaki f fonksiyonunda f (-1) = f (1) = 1 dir.
Ünitenin başlangıcındaki birinci örneğimizde, alınan ekmek sayısı doğal sayılarla ifade edildiğinden tanım kümesi IN doğal sayılar kümesi, değer kümesi ise, satın alınan ekmek sayısı 40 000 katı ile eşlendiğinden o da IN olarak alınabilir. Buna göre bu fonksiyon şu şekilde ifade edilir:
g: IN→ IN, g (x) = 40 000x.
Burada değer kümesi, 40 000 den büyük doğal sayılar kümesini içeren herhangi bir küme de olabilir. Örneğin Z, Q veya IR alınabilir:
Z f Z 4 1 0 -1 -4 0 1 16 . . . . . . . . . . . . . . . . . .
h: IN→ Z, h (x) = 40 000x, k: IN → Q, k (x) = 40 000x, l: IN → IR, l (x) = 40 000x.
Ancak bu durumlarda fonksiyon doğal sayılar kümesinden doğal sayılar kümesine değil, doğal sayılar kümesinden sırasıyla tamsayılar, rasyonel sayılar veya gerçel sayılar kümesine tanımlanmış bir fonksiyon olur. Bu fonksiyonların görüntüleri ay-nıdır ve hepsinde 40 000 den büyük doğal sayılar kümesidir. İkinci ve üçüncü ör-neklerimizi bir fonksiyon olarak şöyle ifade edebiliriz:
t: IR + → IR , t (r) = 2πr,
burada yarıçapın herhangi bir pozitif gerçel sayı olabileceğine dikkat ediniz,
burada da her türlü kesirli zamanın ölçülebildiğini varsaymış bulunuyoruz. Bu son örneklerimizden de görüldüğü gibi, bir fonksiyonda tanım kümesinin elemanları x den farklı harflerle de gösterilebilir. Örneğin yukarıdaki f fonksiyonu, f : Z → Z, f (n) = n2, veya f : Z → Z, f (u)= u2 şeklinde de ifade edilebilir. Bir fonksiyonda
önemli olan,tanım ve değer kümelerinin elemanlarının, bunlar farklı harfle gösteril-mek koşuluyla, hangi harfle gösterildiği değil, tanım ve değer kümeleri ile bu kü-melere ait elemanların nasıl eşlendiği, yani kural önemlidir.
Alanı 10 birim olan dikdörtgeninin yüksekliğini x taban uzunluğunun fonksiyo-nu olarak yazınız.
Cevabınız
Örnek: Yukarıda verilen g , t, s fonksiyonlarına göre g (10), t (3) ve s (5) görüntü-lerini bulalım.
Çözüm: g : IN → IN, g (x) = 40 000x olduğundan g (10) = 40 000. 10 = 400 000 , buna göre 10 ekmeğin bedelinin 400 000 TL olduğu açıktır.
t: R + → IR , t (r) = 2πr olduğundan t (3) = 2π. 3 = 6 π ≅ 18,84 , buna göre,
yarıça-pı 3 cm olan bir çemberin çevresi yaklaşık olarak 18,84 cm dir.
buna göre, yeteri kadar yüksek bir yerden serbest düşmeye bırakılan bir cisim 5 sa-niyede 122,5 m yol alır.
s : IR+ → IR , s t = 1 2 gt 2 , s : IR+ → IR , s t = 1 2 gt 2 , g = 9,8 m / sn2 olduğundan s 5 = 1 2 9,8 . 5 2 = 4,9 . 25 = 122,5 ,
?
f x = 10 x olmalıdır.Örnek: A = {x| x Türkiye’de bir il}, B = IN olmak üzere, her ili trafikteki plaka numa-rasına gönderen bir fonksiyondan söz edebiliriz. Bu fonksiyona göre Eskişehir’ in görüntüsü 26, İstanbul’un görüntüsü 34 dür. Bu fonksiyona p dersek, p(Eskişehir) = 26, p(İstanbul) = 34 yazabiliriz.(Bu fonksiyonda 1 i 01, 2 yi 02,..., 9 u 09 şeklinde göste-riyoruz.)
Örnek: f:IR→ IR, f(x)= x2-2x fonksiyonu veriliyor. f(1) + f(-1) i bulunuz.
Çözüm: Fonksiyon tanım kümesinin her bir x elemanını bu elemanın karesi ile 2 ka-tının farkına göndermektedir. Yani x → x2-2x dir. Buna göre f(1)= 12 - 2.1= -1,
f(-1)= (-1)2 - 2.(-1)= 3 olduğundan f(1) + f(-1)= -1 + 3= 2 dir.
Örnek: f : IR → IR, f (x) = x3- 4x2 + 2x + 1 fonksiyonu veriliyor. Bu fonksiyon kuralına
göre her x gerçel sayısı x3 - 4x2 + 2x + 1 gerçel sayısı ile eşlenmektedir. Şimdi
f (0), f (1), f (-3), görüntülerini bulalım. Bunun için fonksiyonun kuralında x yerine ilgili sayıyı yazıp gerekli işlemleri yapacağız.
f (0) = 03- 4.02 + 2.0 + 1 = 1 , f (1) = 13 – 4.12 + 2.1 +1 = 1- 4 + 2 + 1 = 0 ,
f (-3) = (-3)3 – 4.(-3)2 + 2.(-3) + 1 = -27 – 36 – 6 + 1 = - 68 ,
f:IR →→→→ IR, f(x)= x2 - 2x fonksiyonu için f(π) ve f(-2) sayılarını bulunuz.
Cevaplarınız ≅ 3,58 ve 8 olmalıdır.
f : A → B fonksiyonu verildiğinde tanım kümesine ait bir x elemanının bu fonksiyon altındaki görüntüsünün f (x) şeklinde gösterildiğini yukarıda ifade etmiştik. f (x) de bazen y,z ..gibi harflerle gösterilir. Bir fonksiyonun tanım ve değer kümeleri açıkça biliniyor ve eşleme f (x) gibi bir kuralla ifade edilebiliyorsa, fonksiyon kısaca, y = f (x) şeklinde de gösterilir. Örneğin her gerçel sayıyı 2 katı ile eşleyen fonksiyon, f : IR → IR, f (x) = 2x gösterimi yerine, kısaca y = 2x biçiminde de gösterilmekte-dir. Ancak bu tür gösterimlerde tanım ve değer kümelerinin çok açık olarak bilini-yor olması gerekir. Burada x tanım kümesindeki tüm elemanları tararken y de x e bağlı olarak değişecektir. Bu nedenle x e bağımsız değişken y ye de bağımlı değiş-ken denir. Bir fonksiyonda tanım kümesi, IR gerçel sayılar kümesinin alt kümesi ise fonksiyona gerçel değişkenli fonksiyon denir.
f : A →A, f (x) = x fonksiyonuna A kümesinin birim fonksiyonu denir ve IA
şek-linde gösterilir. Sözle ifade edersek, bir kümenin her bir elemanını kendisiyle eşle-yen fonksiyona bu kümenin birim fonksiyonu denir.
f : A → B , f (x) = c , yani A kümesinin tüm elemanlarını B kümesinin tek bir c elemanı ile eşleyen fonksiyona sabit fonksiyon denir.
f 2
f 2 = 2 3 - 4 . 2 2 + 2 . 2 + 1 = 2 2 - 8 + 2 2 + 1 = 4 2 - 7 ≅ - 1,343 .
f : A → B, g : C → D fonksiyonları verilsin. Eğer aşağıdaki koşullar sağlanırsa bu iki fonksiyona eşittir denir ve f = g şeklinde gösterilir.
i) A = C, ii) B = D,
iii) her x ∈ A (= C ) için f (x ) = g (x).
Bir fonksiyonda asıl olanın tanım kümesi ve tanım kümesindeki her bir elema-nın ne ile eşlendiği diyorsanız, o zaman iki fonksiyonun eşitliği için değer küme-lerinin eşitliği koşulunu aramayabilirsiniz.
Örnek : A = {0,2}, B = {0,4} olmak üzere, f : A → B, f (x) = 2x, g: A → B , g (x) = x2
fonksiyonları yukarıdaki koşulları sağladığından bu iki fonksiyon eşittir.
Gerçel değişkenli bir fonksiyon, y = f (x) biçiminde verilip tanım kümesi açıkça verilmemişse, bu durumda tanım kümesi olarak fonksiyonun kuralının anlamlı olduğu en geniş gerçel sayılar kümesi fonksiyonun tanım kümesi olarak alınır.
Örnek: y = f (x) = fonksiyonunun tanım kümesi açıkça verilmemiştir. Bu
durumda ün anlamlı olduğu (yani bir gerçel sayı olduğu) en geniş gerçel sayılar kümesini bu fonksiyonun tanım kümesi olarak alacağız. ifadesinde x yerine 3 den farklı hangi sayıyı yazarsak yazalım bir gerçel sayı bulabiliriz. Ancak x = 3 için payda sıfır olur, bir sayının sıfıra bölümü ise tanımsızdır. Bu nedenle bu fonk-siyonun tanım kümesi olarak IR – {3} kümesini alacağız. Yani y = fonksiyo-nunu, f : IR – {3} → IR, f (x) = fonksiyonunun kısaca ifade edilmiş biçimi olarak kabul edeceğiz.
Örnek: y = fonksiyonunun tanım kümesini bulalım.
Çözüm: Bu fonksiyonun kuralı x → dir. Bu kuralın anlamlı olabilmesi
için 4 + x ≥ 0 olmalıdır. Bu eşitsizliğin çözüm kümesi, [- 4, ∞) olduğundan fonksi-yonun tanım kümesi [- 4, ∞) dır. Bu fonksiyonu da g : [- 4, ∞) → IR, g (x) = fonksiyonu olarak anlayacağız.
y = g (x) = fonksiyonunun tanım kümesini bulunuz.
y = h (x) = fonksiyonunun tanım kümesini bulunuz.
Birinci soruda cevabınız [-2,2] aralığı , ikinci soruda ise IR olmalıydı. Nedenlerini düşününüz.
Sayılarla yapılan bazı işlemler , fonksiyonlarla da yapılabilir. 4 - x2 4 - x2 3
?
?
1 x - 3 1 x - 3 1 x - 3 1 x - 3 1 x - 3 4 + x 4 + x 4 + xf : A→ IR, g : A → IR fonksiyonları verilsin. Her x ∈ A için x i f(x) + g (x) ile eşle-yen fonksiyona f ile g nin toplamı denir ve f+g ile gösterilir. Buna göre,
f + g : A → IR, (f + g) (x ) = f (x) + g (x). Benzer şekilde ,
f - g : A → IR, (f - g) (x ) = f(x) - g(x) fonksiyonuna f ile g nin farkı ,
f.g: A → IR, (f.g) (x) = f (x) .g (x) fonksiyonuna f ile g nin çarpımı,
fonksiyonuna da f ile g nin bölümü denir. Örnek: f: IR → IR, f (x) = -2 x2 + 3x - 4, g: IR → IR, g (x) = x2 +1 fonksiyonları veriliyor. i) (f + g) (2), (f - g) (2), (f . g) (2), (2) , ii) (f + g) (x), (f- g) (x), (f . g) (x), (x) değerlerini bulalım. Çözüm: i) (f + g) (2) = f (2) + g (2) = (-2.22 + 3.2 - 4) + (22 +1) = - 6 + 5 = -1, (f – g) (2) = f (2) - g (2) = (-2.22 + 3.2 - 4) - (22 +1) = - 6 - 5 = -11, (f.g) (2) = f (2).g (2) = (-2.22 + 3.2 - 4) . (22 +1) = - 6.5 = -30,
bulunur . Benzer şekilde, f g : A → IR , fg x = f x g x ( her x ∈ A için g x ≠ 0 ) f g f g f g 2 = f 2 g 2 = - 2 . 2 2 + 3 . 2 - 4 22 + 1 = -6 5
ii) (f + g) (x) = f (x) + g (x) = (-2x2 +3x - 4) + (x2 + 1) = -x2 +3x -3,
(f - g) (x) = f (x) – g (x) = (-2x2 +3x - 4) - (x2 + 1) = - 3x2 +3x -5,
(f.g) (x) = f (x) .g (x) = (-2x2 + 3x - 4) (x2 +1 ) = -2 x4 + 3x3 - 6x2 + 3x - 4,
(f + g) (2), (f – g) (2), (f . g) (2), ( 2) sayılarını son bulduğumuz kurallara
göre bulup, yukarıda bulunan değerlerle karşılaştırınız.
f(x)= x2 + 3x -5 ve g(x)= -x2 + 3x + 4 fonksiyonlarının toplamını ve farkını bulunuz.
Cevaplarınız 6x -1 ve 2x2 -9 olmalıdır.
Bire – bir fonksiyon
f: A → B fonksiyonu verilsin. Eğer her x1, x2 ∈ A ve x1 ≠ x2 için f (x1) ≠ f (x2) ise
f fonksiyonuna bire – bir (1-1) fonksiyon denir. Sözle ifade edersek, tanım kümesi-nin herhangi farklı iki elemanının görüntüleri farklı ise, fonksiyona bire – bir fonksi-yon denir.
Örnek: f : IN → IN , f (x) = 40 000 x fonksiyonu bire – birdir. Çünkü x1, x2 ∈ IN
ve x1 ≠ x2 için 40 000 x1 ≠ 40 000 x2 olduğundan f (x1) ≠ f (x2) dir.
Örnek: f: IR → IR , f (x) = x2 fonksiyonu bire – bir değildir. Örneğin -2 ≠ 2
oldu-ğu halde f (-2) = f (2) = 4 dür. Farklı iki elemanın görüntüsü eşit olduoldu-ğundan bu fonksi-yon bire – bir olamaz.
Örnek: f : IR → IR , f (x) = x2 - 6x + 7 fonksiyonunun bire – bir olup olmadığını
araştırınız.
Çözüm: Her x1 , x2 ∈ IR ve x1 ≠ x2 için f (x1) ≠ f (x2) olup olmadığını görmek
kolay görünmemektedir. Bu örnekte f(1) = 1- 6 + 7 = 2, f (5) = 25 - 30 +7 = 2 dir. Farklı iki elemanın görüntüleri eşit olduğundan bu fonksiyon bire - bir değildir. Sizde bu örnek için görüntüleri eşit başka sayılar bulabilirsiniz. Ancak her zaman bu kadar şanslı olmayabiliriz. Aşağıdaki önermeyi ispatladıktan sonra, fonksiyonların bire – bir olup olmadıklarını biraz daha kolay araştırabiliriz.
Önerme: f : A → B fonksiyonu verilsin. Eğer her x1, x2 ∈A ve f (x1) = f (x2) iken
x1= x2 oluyorsa, f fonksiyonu bire – birdir.
f g x = f x g x = -2x 2 + 3x - 4 x2 + 1 . f g
?
?
İspat: Bire – birliğin tanımına göre, her x1, x2 ∈ A ve x1 ≠ x2 için f (x1) ≠ f (x2)
olduğunu göstermeliyiz. En az bir x1 , x2 ∈ A , x1 ≠ x2 için f (x1) = f (x2) olamaz.
Çünkü, f (x1) = f (x2) olsaydı, hipoteze göre, x1= x2 olurdu. Bu ise x1 ≠ x2 ile
çelişirdi.
Bu önerme bire – birliğin ikinci tanımı olarak alınabilir. Buna göre,
her x1, x2 ∈∈∈∈ A ve f (x1) = f (x2) iken x1= x2 oluyorsa, f fonksiyonu bire – birdir diyebiliriz.
Örnek : Yukarıda en son verdiğimiz örneğin bire – bir olmadığını bir de bu önermeyi kullanarak görmeye çalışalım.
f: IR → IR , f (x) = x2 – 6x + 7 olduğundan f (x 1) = f (x2) ise x12 - 6x1 + 7 = x22 – 6x2 + 7 dır. Buradan x12 - 6x1 - x22 + 6x2 = 0, (x1 - x2) (x1 + x2 - 6) = 0, x1 = x2 veya x1 + x2 = 6
bulunur. Bu eşitliklerin manası tanım kümesi olan IR den alınan iki sayının f altında görüntüleri eşitse ya bu sayılar eşittir, ya da bu sayıların toplamı 6 dır. Tanım küme-si olan IR deki sayıların toplamı 6 ise bu sayılar eşit olmak zorunda olmadığından (örneğin 1 ile 5, 2 ile 4 ... gibi) fonksiyon bire – bir değildir.
Örnek: f: IR → IR, f (x) = 2x + 1 fonksiyonunun bire – bir olduğunu gösteriniz. Çözüm: Herhangi x1 , x2 gerçel sayıları için f (x1) = f (x2) ise x1 = x2 olduğunu
göstermeliyiz.
f (x1) = f (x2) ise 2x1 + 1= 2x2 +1 dir. Buradan 2x1 = 2x2, x1 = x2 elde edilir.
Dolayı-sıyla fonksiyon bire – birdir.
Örnek: f: IR+ ∪ {0} → IR , f (x) = x2 fonksiyonunun bire – bir olup olmadığını
araştırı-nız.
Çözüm: Herhangi x1 , x2 ∈ IR + ∪ {0} için f (x1) = f (x2) ise x12 = x22 dir.
Buradan x12 – x22 = 0, (x1 – x2) (x1 + x2) = 0 buradan da x1 - x2 = 0 veya x1 + x2 = 0
olmalıdır. Bu eşitliklerin birincisinden x1 = x2 , ikincisinden x1 = - x2 elde edilir. İkinci
eşitlik sadece x1= x2= 0 için doğrudur (x1 ≥ 0 , x2 ≥ 0 olduğunu hatırlayınız).
Bu nedenle x1 = x2 olmak zorundadır. Dolayısıyla fonksiyon bire – birdir.
IR üzerinde tanımlı f(x)= x2 fonksiyonunun bire – bir olmadığını göstermiştik. Bu
örnekle, fonksiyonun bire – birliğinin, fonksiyonun kuralı kadar tanım kümesine de bağlı olduğunu görmüş olduk.
f:IR →→→→ IR, f(x)= x3 -x fonksiyonunun bire-bir olmadığını gösteriniz. (f (0) ve f (1) değerlerini karşılaştırınız).
Bir fonksiyonun sadece kuralına bakarak bire – birliğine karar veremeyiz. Kural-la birlikte tanım kümesini de göz önüne almamız gerekir.
Örten fonksiyon
f : A → B fonksiyonu verilsin. Eğer f (A) = B ise yani değer kümesindeki herhangi bir eleman tanım kümesindeki en az bir elemanın görüntüsü ise, f fonksiyonuna ör-ten fonksiyon denir. Fonksiyonun örör-tenliğini şöyle de ifade edebiliriz. B değer kü-mesinden alınan herhangi bir b elemanına karşılık, f (a) = b olacak şekilde A tanım kümesinden en az bir a elemanı bulunabiliyorsa , f fonksiyonu örtendir denir.
Örnek: f : IR → IR , f (x) = 2x +1 fonksiyonunun örten olup olmadığını araştıralım. Çözüm: Fonksiyonun örten olduğunu görmek için her bir b ∈ IR için f (a ) = b olacak şekilde en az bir a ∈ IR nin varlığını görmeliyiz.
f (a) = b ise 2a + 1 = b
dir. Buradan bulunur. b gerçel sayısı için de bir gerçel sayıdır ve fonksiyonun tanım kümesinin elemanıdır. Böylece herhangi bir b sayısına karşılık f (a) = b koşulunu sağlayan bir a sayısı bulabildiğimizden fonksiyon örtendir.
Örnek: g: IR → IR, g (x) = x2 fonksiyonunun örten olmadığı açıktır. Çünkü
de-ğer kümesinden alacağımız herhangi bir negatif sayı, örneğin - 1 , hiçbir gerçel sayı-nın karesine eşit olamaz, dolayısıyla tanım kümesine ait hiçbir elemasayı-nın görüntüsü değildir.
Buna karşılık f : IR → IR + ∪ {0}, f (x) = x2 fonksiyonu örtendir. Çünkü değer
küme-sinden alınacak herhangi bir b değeri, hem hem de nin görüntüsüdür. Bir fonksiyonun sadece kuralına bakarak örten olup olmadığına karar vereme-yiz. Kuralla birlikte değer kümesini de göz önüne almamız gerekir.
Bir fonksiyonun tanım kümesi ve kuralı değiştirilmeden, fonksiyon örten bir fonk-siyona dönüştürülebilir. Bunun için değer kümesi olarak görüntü kümesini almak yeterlidir. Yani, f : A → f (A) fonksiyonu daima örten fonksiyondur.
Bir fonksiyonun bire-bir veya örten olmadığını göstermek için tanımlarla uyuş-mayan elemanlar (sayılar) bulmak yeterli iken bu özelliklerin varlığını görmek için genel ispat yapmamız gerektiğine dikkat ediniz.
a = b - 1 2 a = b - 1 2
?
- b bf:[-2, 3] →→→→ B, f(x)= x2 fonksiyonunun örten olması için B kümesi ne olmalıdır?
Cevabınız B= [0, 9] aralığı olmalıdır. Bileşke Fonksiyon
f :A → B, g : B → C fonksiyonları verilsin. Herhangi bir x∈A elemanını g (f (x)) ile eşleyen, yani x i f (x) in g altındaki görüntüsü ile eşleyen fonksiyona f ile g nin bi-leşkesi denir ve gof ile gösterilir.
Buna göre, gof : A → C , (gof) (x) = g (f (x)) dir.
gof fonksiyonunun tanım kümesinin f nin tanım kümesi olan A, değer kümesinin ise g nin değer kümesi olan C olduğuna dikkat ediniz.
Örnek : A = {-1, 2, 3}, B = {0,1,4,5}, C = {1,2} kümeleri veriliyor. Bu kümeler üzerinde, f : A → B , f (- 1) = 5, f (2) = 0, f (3) = 1,
g : B → C , g (0) = 1, g (1) = 1, g (4) = 2, g (5) = 2 fonksiyonları tanımlanıyor.
gof fonksiyonunu bulunuz. Çözüm: gof : A → C, (gof) (-1) = g (f (- 1)) = g (5) = 2, (gof) (2) = g (f (2)) = g (0) = 1, (gof) (3) = g (f(3)) = g (1) = 1 dir. A f B g C -1 2 3 0 1 4 5 1 2 A f B g C f(x) gof g(f(x)) x
?
Örnek: f: IR → IR, f (x) = 3x + 1, g : IR → IR , g (x ) = x2 – 4
fonksiyonları veriliyor. (gof) (1), (gof) (2), (gof) (x), (fog) (1), (fog) (2) ve (fog) (x) gö-rüntülerini bulalım.
Çözüm: (gof) (1) = g (f (1)) = g (3.1+1) = g (4) = 16 - 4 = 12, (gof) (2) = g (f (2)) = g (3.2 +1) = g (7) = 49 - 4 = 45, (gof) (x) = g (f (x)) = g ( 3x+1) = (3x +1 )2 - 4 = 9x2 + 6x -3.
Bu son eşitlikle gof fonksiyonunun kuralını bulmuş olduk. (gof) (1) ve (gof) (2) gö-rüntülerini bu kural yardımıyla da bulabileceğinizi görünüz. Diğer sorulara cevap vermeden önce şunu ifade edelim: gof tanımlı iken fog tanımlı olmayabilir. fog nin tanımlı olabilmesi için g nin görüntü kümesinin f nin tanım kümesinin bir alt kümesi olması gerektiğini görmeye çalışınız. Bu soruda bu koşul sağlanmaktadır. Bu ne-denle soru anlamlıdır.
(fog) (1) = f (g (1)) = f (12 - 4) = f (-3) = 3.(-3) +1 = - 8,
(fog) (2) = f ( g(2)) = f (22 -4) = f (0) = 3.0 +1 = 1,
(fog) (x) = f (g (x)) = f (x2 - 4) = 3 (x2 – 4) + 1 = 3x2 –11.
Bu örnekten de görüldüğü gibi, genel olarak gof ≠≠≠≠ fog dir. f : A →→→→ B, g: B →→→→ C, h : C →→→→ D fonksiyonları verildiğinde fo (goh) = (fog) oh dir. fonksiyonları verilsin. gof ve fog bileşke fonksiyonlarını bulunuz.
Cevaplarınız gof: IR+ ∪ { 0 } → IR , (gof) (x) = - x - 1 , fog ise "tanımsızdır" olmalıdır.
Örnek: f: IR→ IR, f (x) = x2 +1 olduğuna göre f (x - 2) yi bulunuz.
Çözüm: g (x) = f (x - 2) dersek, g fonksiyonu h (x) = x - 2 fonksiyonu ile f (x) = x2 + 1 fonksiyonunun bileşkesidir. Bu nedenle g (x) i bulmak için x2 + 1
ifadesin-de x yerine x – 2 yazmak yeterlidir. Buna göre,
f (x - 2) = (x - 2)2 + 1 = x2 - 4x + 5
bulunur.
g: IR →→→→ IR, g (x) = x3 – 4x + 2 olduğuna göre , g (x + 1) i bulunuz.
Cevabınız x3 + 3x2 - x -1 olmalıdır.
Ters fonksiyon
f: A → B fonksiyonu verildiğinde tanım kümesine ait herhangi bir elemanın gö-rüntüsünü, diğer bir deyişle x in resmini f(x) kuralı ile bulabiliyoruz. Acaba resmi bilirsek aslı bulabilir miyiz? Şimdi bu soruya cevap vermeye çalışacağız. f (A) gö-rüntü kümesinden alınan herhangi bir eleman, gögö-rüntü kümesinin tanımı gere-ği, tanım kümesinden en az bir elemanın görüntüsüdür. Bu nedenle herhangi bir b ∈ f (A) elemanına karşılık f (a) = b olacak şekilde en az bir a ∈ A elemanı bulabiliriz. Ancak fonksiyon bire – bir değilse b ye karşılık bulunan a birden fazla olabilir. Eğer f fonksiyonu bire – bir olursa, herhangi bir b ∈ f( A) için f (a) = b olacak şekilde tek bir a ∈ A bulunur ve dolayısıyla ters yönde bir eşlemeyle, yani f (A) dan A ya tanımlanan yeni bir fonksiyonla b ye karşı gelen a yı bulabiliriz. İşte bu eşlemeye f nin ters fonksiyonu denir.
f: A →→→→ B bire – bir fonksiyonu verilsin. f (A) görüntü kümesinden alınan
herhan-gi bir görüntüyü (resmi) A daki aslına gönderen fonksiyona f nin ters fonksiyonu denir ve f -1 ile gösterilir.
Buna göre,
f -1: f (A) → A, f-1 (b) = a ⇔ f (a) = b.
Örnek: A ={1,2,3,4}, B ={- 1, - 4, - 7, -10, - 15 } olmak üzere A dan B ye aşağıdaki Venn şeması ile verilen f fonksiyonu tanımlanıyor.
Bu f fonksiyonunun varsa ters fonksiyonunu bulalım.
f nin bire – bir olduğu açıkça görülmektedir. Bu nedenle f (A) = {- 1, - 4, - 7, - 10 } küme-sinden A kümesine f -1 tersi fonksiyonu vardır.
f -1 : {- 1, - 4, - 7, - 10 } → {1, 2, 3,4} ve
?
A f B 1 2 3 4 -1 -4 -7 -10 -15f (1) = -1 olduğundan f -1 (-1) = 1,
f (2) = - 4 “ f -1 (- 4) = 2,
f (3) = -7 “ f -1 (-7) = 3,
f (4) = -10 “ f -1 (- 10) = 4
dir. f–1 fonksiyonunun Venn şeması ile gösterimi aşağıdaki gibidir.
i) f: A →→→→ B fonksiyonunun ters fonksiyonu varsa, f -1: f (A) →→→→ A ters
fonksiyonunun bire – bir ve örten olduğuna dikkat ediniz.
ii) f fonksiyonu bire – bir ve örten ise, ters fonksiyonun değer kümesinden tanım kümesine tanımlandığına dikkat ediniz.
Örnek: f : IR+ ∪ {0} → IR, f (x) = x2 +1
fonksiyonunun varsa ters fonksiyonunu bulunuz.
Çözüm: Ters fonksiyonun olması için f nin bire – bir olması gerekir. Şimdi bunu araştıralım.
x1 , x2 ∈ IR+ ∪ {0} için f (x1) = f (x2) ise x1 = x 2 olduğunu görmeliyiz.
f (x1) = f (x2) ⇒ x12 +1 = x22 +1
(x1 – x2) (x1 + x2) = 0,
buradan da x1 = x2 veya x1 = - x2 bulunur. x1, x2 ∈ IR + ∪ {0} olduğundan x1 = - x2
eşitliği ancak x1= x2= 0 ise mümkündür, bunun dışında x1= -x2 olamaz. Bu nedenle
x1 = x2 olmalıdır, dolayısıyla fonksiyon bire – birdir. Fonksiyon bire – bir olduğundan
ters fonksiyonu vardır. Ters fonksiyonun tanım kümesi, f nin f ( IR + ∪ {0}) görüntü
kümesi olduğundan, bu görüntü kümesini bulalım (fonksiyon örten ise görüntü kümesinin değer kümesi olduğunu hatırlayınız).
f(A) f A -1 -4 -7 -10 -1 1 2 3 4 ⇒ x12 - x22 = 0,
Her x ∈ IR + ∪ (0} için x2 ≥ 0 olduğundan x2 + 1 ≥ 1 dır. Buna göre görüntü kümesi
[1, ∞ ) aralığı olabilir. Bu aralığın görüntü kümesi olduğunu görmek için, bu ara-lıktan alacağımız herhangi bir b sayısına karşılık f (a) = b olacak şekilde tanım kümesinde bir a elemanının varlığını görmeliyiz. a2 + 1 = b ise a2 = b – 1 dir .
b ∈ [1, ∞) olduğundan b–1 ≥ 0 dır. Buradan veya bulunur.
olmasına karşılık dır. Dolayısıyla aradığımız a
sayısı dir. Böylece [1, ∞ ) aralığına ait herhangi bir sayının tanım kümesine ait bir sayının görüntüsü olduğunu, yani [1, ∞ ) aralığının fonksiyonun görüntü kümesine eşit olduğunu göstermiş olduk. Buna göre,
f -1 : [1, ∞ ) → IR+ ∪ {0}
dır. Şimdi de ters fonksiyonun kuralını bulalım.
f : x x2 + 1= y
olduğundan
f -1 : y = x2 + 1 x
dir. f -1 fonksiyonu altında y değişkeni, x değişkenine dönüştüğünden x i y
tü-ründen ifade edersek, y ye karşı gelen x görüntülerini daha kolay bulabiliriz.
y = x2 + 1 , x2 = y – 1 buradan da bulunur. Burada
y >1 için
f -1 : [1, ∞ ) → IR + ∪ {0}, y ,
f -1 : [1, ∞ ) → IR + ∪ {0} ,
dir.
Genellikle fonksiyonlarda bağımsız değişkeni x ile gösterdiğimizden ve ileride gra-fik çiziminde de sorun yaratmamak amacıyla bu ters fonksiyonu şu şekilde ifade edeceğiz:
f -1 : [1, ∞ ) → IR + ∪ {0}, f -1 (x ) = .
y = f (x) fonksiyonunun ters fonksiyonunu bulmak için, önce y = f (x) eşitliğinden x değişkeni y türünden hesaplanır daha sonra x yerine y , y yerine x yazılır.
Örnek: f: R → R , f (x) = 3x + 5 fonksiyonunun varsa ters fonksiyonunu bulunuz. Çözüm: f fonksiyonunun bire-bir olduğunu kolayca görebiliriz. Bu nedenle fonksi-yonun ters fonksiyonu vardır. Ayrıca f örten olduğundan, f -1: IR → IR dir. Ters
x = y - 1 , x = - y - 1 - y - 1 ∉ R+ ∪ 0 dır. O halde, x = y - 1 f-1 y = y - 1 x - 1 a = - b - 1 a = b - 1 - b - 1∉ IR+ b - 1∈ IR+ ∪ 0 b - 1
fonksiyonun kuralını bulmak için, y = 3x + 5 ifadesinde x i y cinsinden çözüp x yerine y , y yerine x yazalım.
y = 3x + 5 , 3x = y – 5 buradan da bulunur. Şimdi x yerine y, y yerine x ya-zarsak, elde ederiz. Buna göre ters fonksiyon
f -1: IR → IR, y = f -1 (x) =
dir.
f : A → B bire – bir ve örten fonksiyon ise, aşağıdaki Venn şemasından görüldü-ğü gibi x ∈A için (f -1of) (x) = x dir. Dolayısıyla f -1of = I
A dir.
Benzer bir şema ile fof -1 = I
B olduğunu da siz gösteriniz.
Örnek: f : IR → IR , f (x) = x2 fonksiyonu bire – bir olmadığından ters fonksiyonu
yoktur. Buna karşılık,
g : IR + ∪ { 0} → IR , g (x) = x2 fonksiyonunun ters fonksiyonu vardır ve
g (IR + ∪ {0}) = R+ ∪ {0} olduğundan
g -1 : IR + ∪ {0} → IR+ ∪ {0} , g -1 (x) =
dir.
a ve b gerçel sayılar ve a≠ 0 olmak üzere f: IR →→→→ IR , f(x) = ax + b
fonksiyonu-nun ters fonksiyofonksiyonu-nunu bulunuz. Cevabınız f -1: IR → IR , f -1(x) =
h : IR →→→→ IR, h (x) = x3 fonksiyonunun ters fonksiyonunun var ve
h -1 : IR →→→→ IR , h -1(x) = olduğunu gösteriniz. A x f B A f(x) f of f (f(x)) = x f-1 -1 -1 x x 3
?
x = y - 5 3 y = x - 5 3 x - 5 3 x - b a olmalıdır.?
3. Fonksiyon Grafikleri
A ve B boş kümeden farklı iki küme olmak üzere, f : A → B fonksiyonu verildi-ğinde bu fonksiyonu
f = {(x , y)| y = f (x) , x ∈ A }
şeklinde bir ikililer kümesi olarak düşünebiliriz. Bu düşünce, analitik geometri bil-gilerimizle, fonksiyonları geometrik olarak temsil etme , fonksiyonun" resmini" çiz-me olanağı sağlamıştır. İnsanoğlu resmini çizebildiği soyut kavramları daha iyi an-layabilmekte ve bu tür kavramlar arasında daha kolay ilişki kurabilmektedir. Bu ne-denle resmini çizebildiğimiz ( bu resme fonksiyonun grafiği denir) fonksiyonların davranışlarını daha kolay anlayabilmekteyiz. Bir fonksiyonun grafiği konusuna geçmeden önce düzlemdeki kartezyen koordinat sistemini tanıtmaya çalışalım.
Düzlemde, sıfıra karşı gelen noktalarında birbirini dik olarak kesen yatay ve düşey doğrultuda iki sayı ekseni alalım. Bu sayı eksenlerinde yatay olanı soldan sağa , dü-şey olanı da aşağıdan yukarı doğru yönlendirelim. Yani, pozitif yön, yatay doğru üzerinde soldan – sağa, düşey doğru üzerinde ise aşağıdan – yukarıya doğru olsun. Böylece oluşturulan yatay eksene apsisler ekseni (x-ekseni), düşey eksene ordinat-lar ekseni (y-ekseni), bu iki eksenin oluşturduğu sisteme kartezyen koordinat sis-temi veya dik koordinat sissis-temi veya kısaca koordinat sissis-temi , eksenlerin kesiştik-leri noktaya da başlangıç noktası veya orijin denir. Düzlemde böyle bir koordinat sistemi belirlendikten sonra, düzlemin noktaları aşağıda açıklayacağımız şekilde adreslenebilmekte ve bu sayede birçok geometri problemleri cebirsel yöntemlerle çözülebilmektedir. Bu tür geometriye de analitik geometri denilmektedir. Bu dü-şünceyi ilk kez ünlü filozof Descartes ortaya attığından bu koordinat sistemine Des-cartes'in sistemi anlamında kartezyen koordinat sistemi denilmektedir.
Düzlemde bir kartezyen koordinat sistemi seçelim. Bu koordinat sistemi yardımıy-la düzlemin noktayardımıy-ları ile IR x IR = {(x,y): x,y ∈ IR } kartezyen çarpım kümesinin ele-manları arasında bire – bir eşleme kurmaya çalışacağız. Bunun için düzlemde bir P noktası alalım ve bu noktadan yatay ve düşey eksenlere birer dikme çizelim. Bu dik-melerin birer tane olduğunu Euclid (Öklid) geometrisi derslerinden bilmekteyiz. Yatay eksene çizilen dikmenin bu ekseni kestiği noktaya karşı gelen sayıya x, düşey eksene çizilen dikmenin bu ekseni kestiği noktaya karşı gelen sayıya ise y diyelim. Yatay ve düşey eksenler sayı doğrusu olduklarından her noktaya karşılık bir ve yal-nız bir gerçel sayı vardır. Bu nedenle böyle x ve y sayıları vardır ve bunlar tektir.
y 0
Böylece elde ettiğimiz x ve y sayıları ile sıraya da dikkat ederek, yani yatay eksenden bulduğumuz sayıyı birinci, düşey eksenden bulduğumuz sayıyı ikinci bileşen ala-rak, (x, y) sıralı ikilisini elde ederiz. Bu yolla düzlemdeki her bir P noktasına karşılık (x,y) gibi bir tek gerçel sayı ikilisi bulmuş oluruz. Tersine, (x,y) gibi bir gerçel sayı ikilisi verildiğinde, x sayısına yatay eksen üzerinde , y sayısına ise düşey eksen üze-rinde karşı gelen noktaları belirledikten sonra, bu noktalardan üzeüze-rinde bulunduk-ları eksenlere birer dik çizersek bu dikmeler P gibi bir noktada kesişirler. Bu P nokta-sını (x,y) gerçel sayı ikilisine düzlemde karşı gelen nokta olarak aldığımızda, gerçel sayı ikilileri ile düzlemin noktaları arasında bire-bir bir eşleme kurmuş oluruz. Bu eşleme nedeniyle düzlemdeki herhangi bir noktaya bir gerçel sayı ikilisi, tersine her-hangi bir gerçel sayı ikilisine de düzlemde bir nokta gözüyle bakabiliriz.
Düzlemde alınan herhangi bir P noktasına yukarıdaki eşleme ile karşı gelen gerçel sayı ikilisi (x, y) ise x e P noktasının apsisi, y ye P noktasının ordinatı, (x,y) ikilisine de P noktasının koordinatları denir ve P noktası, P = (x,y) veya P(x,y) şeklinde gösterilir.
Örnek: Düzlemde A (2,1); B (-1,3) ; C (0,-3); D (-3,-2); E (- 0,5 , 2); gerçel
sayı ikililerine karşı gelen noktaları işaretleyiniz.
Çözüm: Birinci bileşenlere yatay eksen üzerinde , ikinci bileşenlere düşey eksen üzerinde karşı gelen noktaları bulduktan sonra her bir noktadan üzerinde bulundu-ğu eksene birer dik çizersek, karşılıklı dikmelerin kesiştikleri noktalar aradığımız noktalar olacaktır.
Şimdi fonksiyonun grafiği konusuna dönelim.
P = (x, y) x y F 5 , 3 1 0,5 -1 2 3 E B F A -3 -2 -3 D C 5 2
•
A ⊂ IR ve B ⊂ IR olmak üzere f: A → B fonksiyonu verildiğinde, bu fonksiyonu f = {(x,y)| y = f (x), x ∈ A} şeklinde bir ikililer kümesi olarak düşünebileceğimizi yu-karıda ifade etmiştik. Bu ikililer kümesinin elemanı olan her bir ikili düzlemin bir noktası ile geometrik olarak temsil edilebilir. Böylece f kümesinin elemanı olan her-hangi bir (x,y) ikilisine düzlemin tek bir noktası karşılık getirilebilir. İşte f kümesi-nin elemanı olan (x,f (x)) ikililerine düzlemde karşı gelen noktaların kümesine f fonksiyonunun grafiği denir.
f : A →→→→ B fonksiyonu verilsin. f = {(x,y)| y = f (x), x ∈∈∈∈ A} kümesinin elemanla-rına düzlemde karşı gelen noktaların kümesine f fonksiyonunun grafiği denir.
Örnek: A = {-2, -1, - 0, 5, 0, 0, 5, 1, , 2} olmak üzere, f: A → IR , f (x) = 2x + 1 fonksiyonunun grafiğini çizelim.
Çözüm: f = {(-2, - 3),(-1, -1),(-0,5 , 0),(0,1),(0,5 , 2),(1,3), ( ),(2,5)} dir. Bu ikililere düzlemde karşı gelen noktaların kümesi fonksiyonun grafiği olacaktır.
2
2 , 2 2 + 1
f:{-2, -1, -0,5, 0, 0,5, 1, , 2} → IR, f(x )= 2x + 12 Şekil 3.1:
Fonksiyonun grafiği olarak bulduğumuz bu noktaların bir doğru üzerinde olduğu-nu bir cetvel yardımıyla kontrol edebiliriz. Burada tanım kümesinde az sayıda ele-man bulunduğundan grafiği oluşturan noktaları tek tek bulmak mümkündür. Ta-nım kümesinde eleman sayısı çok sayıda hatta sayılamaz sayıda olabilir, bu durum-larda grafiği, fonksiyonu oluşturan tüm ikilileri yazıp daha sonra bunlara karşı ge-len noktaları işaretleyerek bulamayız. Ancak tanım kümesine ait sonlu tane x1,
x2,...,xn değerleri seçilir ve fonksiyonun bu noktalardaki değerleri olan y1 = f
(x1), y2 = f (x2),...,yn= f (xn) bulunduktan sonra düzlemde (x1, y1),(x2, y2),....,(xn, yn)
ikililerine karşı gelen noktalar “düzgün” bir eğri ile birleştirilerek y = f (x) fonksiyo-nunun grafiği denilen eğri bulunur. Tanım kümesinden ne kadar çok ve ne kadar yaygın eleman seçilirse fonksiyonun gerçek grafiğine o kadar yakın bir eğri bulu-nur. Daha sonraki ünitelerde inceleyeceğimiz türev kavramından sonra fonksiyo-nun grafiği daha hassas ve gerçeğe yakın çizilebilecektir. Bazı durumlarda da grafik bilinen bir eğri olabilir, bu durumda bu eğriyi daha kolay çizebiliriz. Örneğin eğer fonksiyon
g : IR → IR , g (x) = 2x + 1
ise, bu fonksiyonun grafiğinin bir doğru olduğu ünite 4 de görülecektir. Bu doğru yukarıda bulduğumuz noktaları taşıyan doğrudur.
g:IR → IR , g(x)= 2x + 1 Şekil 3.2:
f: IR →→→→ IR , f (x) = x fonksiyonunun grafiğinin aşağıdaki doğru olduğunu görü-nüz.
Örnek: A = {-2, , -1, - 0,5, 0, 0,5, 1, , 2} olmak üzere, f:
A → IR, f (x) = x2 fonksiyonunun grafiğini çizelim.
Çözüm: f = {(-2, 4), (-1,1), (- 0,5, 0,25) , (0,0) , (0,5, 0,25) , (1,1),
(2,4)} dir. Fonksiyonu oluşturan ikililerde birinci bileşen x bağım-sız değişkenini gösterirken ikinci bileşen x in f altındaki görüntüsünü, diğer bir de-yişle x e karşı gelen y değerini ifade ettiğinden fonksiyonu oluşturan ikililer aşağı-daki tabloaşağı-daki gibi de verilebilir.
Bu ikililere düzlemde karşı gelen noktalar ve dolayısıyla fonksiyonun grafiği aşağı-daki gibidir. 2 , 3 - 3 , 3 , - 2 , 2 , 2 , 2 , 3 , 3 , f: IR → IR , f(x)= x Şekil 3.3: x y -2 4 3 2 -1 1 - 0,5 0,25 0 0 0,25 1 1 2 3 4 - 3 - 2 0,5 2 3 2
?
- 3 , - 2Eğer fonksiyon g: IR → IR, g (x) = x2 olsaydı onun grafiği yukarıda bulduğumuz
noktalardan geçen “düzgün” bir eğri olurdu. Bu eğriye parabol denir. f: -2 , - 3 , - 2 , -1 , -0,5 , 0, 0,5 , 1, 2 , 3 , 2 → IR , f x = x2
Şekil 3.4:
g: IR → IR , g(x)= x2
Eğer fonksiyon h : IR → IR , h (x) = - x2 olsaydı bu fonksiyonun grafiği bir önceki
g fonksiyonunun grafiğinin x-eksenine göre simetriği olurdu. Çünkü (x,y) ∈ g iken (x, -y) ∈ h dir.
Örnek : f: IR+∪ {0} →IR, f (x) = fonksiyonunun grafiğini çizelim.
Çözüm: Tanım kümesine ait bazı noktaların görüntülerini bulalım (tanım kümesi negatif olmayan sayılar kümesidir).
Bu tabloya göre, (0, 0), (0,25, 0,5), (0,5, 0, 707), (1, 1), (1,44, 2), (2, 1,41), (3, 1,73), (4, 2), (5, 2,24) ikililerine karşı gelen noktalar f nin grafiğine aittir (burada irrasyonel sayı-ların yaklaşık değerlerini aldığımıza dikkat ediniz).
Bu ikililere karşı gelen noktalar işaretlendikten sonra bu noktalar “düzgün” bir eğri ile birleştirilirse, bu fonksiyonun grafiği olan aşağıdaki eğri elde edilir.
h:IR → IR , h(x)= -x2 Şekil 3.6: x x y 0 0,25 0,5 1 1,44 2 3 4 5 0 0,5 0,707 1 1,2 1,41 1,73 2 2,24
Örnek: f: IR → IR , f (x) = 3 sabit fonksiyonunun grafiğini çiziniz.
Çözüm:Bu fonksiyonun grafiğini çizmek için tablo hazırlamaya gerek yoktur. Çünkü tüm x gerçel sayılarının görüntüsü 3 tür. Yani f = {(x,3): x ∈ IR} dir. Bu ne-denle fonksiyonun grafiği, şekilde görüldüğü gibi x- eksenine paralel bir doğrudur.
NOT:
i) Bazı fonksiyonların grafiğini çizmek mümkün değildir. Örneğin Dirichlet fonksiyonu dediğimiz, rasyonel sayıları 1 ile irrasyonel sayıları 0 ile eşleyen fonksiyonun grafiğini çizmek mümkün değildir.
ii) Bir fonksiyonun grafiği verildiğinde herhangi bir x0 değerinin bu fonksiyon
altındaki görüntüsünü bulabiliriz. Bunun için, x0 noktasından x-eksenine dik
bir doğru çizilirse bu doğrunun grafiği kestiği noktanın y0 ordinatı, x0 ın f
altın-daki görüntüsü olur. f: IR+ ∪ {0} → IR , f(x)= x Şekil 3.7: y 3 x x y 0 0 y x x0
Düzlemdeki herhangi bir eğri her zaman bir fonksiyon grafiği midir?
Eğer x-eksenine çizilen her dik doğru eğriyi en çok bir noktada kesiyorsa, bu eğri, uygun bir küme üzerinde tanımlanmış bir fonksiyon grafiği olarak düşünülebilir. Eğer x- eksenine çizilen dik doğrulardan bir tanesi dahi eğriyi iki veya daha çok nok-tada kesiyorsa bu eğri bir fonksiyon grafiği olamaz. Örneğin aşağıdaki şekildeki eğ-ri bir fonksiyon grafiği değildir.
Bir fonksiyonun grafiğini bilirsek , o fonksiyonun bire – bir olup olmadığına kolayca karar verebiliriz. Eğer apsisler eksenine paralel olarak çizilen her doğru grafiği en çok bir noktada keserse fonksiyon bire – birdir. Eğer apsisler eksenine paralel olarak çizilen doğrulardan bir tanesi dahi grafiği birden fazla noktada keserse fonksiyon bire – bir değildir.
f: A → B fonksiyonu bire – bir ise bu fonksiyonun, f -1: f (A) → A ters
fonksiyo-nunun varlığını biliyoruz. Bu durumda, x ∈ A, y ∈ f (A) olmak üzere, (x,y) ∈ f iken (y,x) ∈f -1 dir. Yani (x,y) ikilisine düzlemde karşı gelen nokta f nin
gra-fiğine ait bir nokta iken, (y,x) ikilisine karşı gelen nokta f-1 in grafiğine ait bir
nokta-dır. Bu iki nokta birinci ile üçüncü bölgenin açıortay doğrusuna göre simetrik oldu-ğundan f -1 in grafiği, f nin grafiğinin bu açıortay doğrusuna göre
simetriği-dir. Bu açıortay doğrusu h : IR → IR , h (x) = x fonksiyonunun grafiği olduğun-dan, bu doğru, y = x doğrusu olur. O halde,
?
y
x
0
x
Bire - bir fonksiyon Bire - bir olmayan fonksiyon
y c b a y y x
Aynı koordinat sisteminde f -1 ters fonksiyonunun grafiği, f fonksiyonunun
gra-fiğinin y = x doğrusuna göre simetriğidir diyebiliriz.
Örnek: f: IR → IR , f (x) = 2x fonksiyonunun ters fonksiyonunun
f -1: IR → IR , f -1 (x) = olduğunu biliyoruz. Şimdi bu iki fonksiyonun grafiklerini
aynı koordinat sisteminde çizelim.
f (x) = 2x fonksiyonunun grafiğine ait bazı noktaları bulalım.
y = 2x fonksiyonunun grafiği çizildikten sonra bu grafiğin y = x doğrusuna göre si-metriği de ters fonksiyonunun grafiğidir.
(x, y) y x x y (y, x) y= x 2 x 2 x y = 2x -3 -2 -1,5 -1 0 0,5 1 1,5 2 3 -6 -4 -3 -2 0 1 2 3 4 6 Şekil 3.8:
Örnek : f: IR → IR , f (x) = x3 fonksiyonunun ters fonksiyonunun
f -1: IR → IR , f -1 (x) = olduğunu yukarıda ifade etmiştik. Şimdi bu iki
fonksi-yonun grafiğini aynı koordinat siteminde görelim.
A ⊂ IR olmak üzere, f: A → IR fonksiyonu verilsin. f fonksiyonunun grafiği bilin-diğinde bu fonksiyon yardımıyla tanımlanan g: A → IR, g (x) = f (x) + a , (a ∈ IR), fonksiyonunun grafiği de bulunabilir. Bunun için f nin grafiğini y-ekseni doğrultusun-da, a pozitif ise yukarı doğru, a negatif ise aşağı doğru|a| birim kaydırmak yeterlidir. Çünkü, (x0 , y0) noktası f nin grafiğine ait bir nokta ise, (x0 , y0 + a) noktası da g nin
grafiğine ait bir noktadır. (x0 , y0 + a) noktası (x0 , y0) noktasının y-ekseni
doğrultu-sunda, a nın işaretine göre |a| birim kaydırılmışı olduğundan g nin grafiği f nin grafiği-nin y-ekseni doğrultusunda |a| birim kaydırılmışıdır.
x
3
Örnek: g: IR → IR g (x) = x2 + 2 fonksiyonunun grafiğini çizelim.
Çözüm: Bu fonksiyonda f (x) = x2 ve a = 2 alabiliriz. Buna göre, g nin grafiği f nin
grafiğinin y ekseninin pozitif yönünde (yukarı doğru) 2 birim kaydırılmışıdır. Şekil 3.10:
y = x3 - 1
fonksiyonunun grafiğini çiziniz. Cevabınız şu şekilde olmalıydı.
f fonksiyonunun grafiği bilindiğinde bu fonksiyon yardımıyla tanımlanan g (x) = f (x – a) , (a ∈ IR) fonksiyonunun grafiği bulunabilir. g nin grafiği, f nin grafiğinin x ekseni doğrultusunda |a| birim , a pozitif ise sağa doğru, a negatif ise sola doğru kaydırılmışıdır. Çünkü bir (x0 , y0) noktası f nin grafiğine ait ise y0 = f
(x0) demektir. Yani f nin x0 daki değeri y0 dır. g fonksiyonu aynı y0 değerini x0 +
a noktasında alır, çünkü g (x0 + a) = f (x0 + a – a ) = f(x0) dır. Buna göre, (x0 + a,
y0) noktası g nin grafiğine aittir. (x0 + a, y0) noktası (x0 , y0) noktasının x - ekseni
doğrultusunda a nın işaretine göre |a| birim kaydırılmışı olduğundan, g nin grafiği f nin grafiğinin x ekseni doğrultusunda |a| birim kaydırılmışıdır.
Örnek: a) y = (x-1)3
b) y = (x + 2)2
fonksiyonlarının grafiklerini çiziniz.
Çözüm: a) f (x) = x3 ve a = 1 alınabilir. Buna göre, y = (x-1)3 fonksiyonunun grafiği,
y = x3 fonksiyonunun grafiğinin x-ekseni doğrultusunda ve pozitif yönde (sağa
doğru) 1 birim kaydırılmışıdır.
?
b) f (x) = x2 ve a = -2 alınabilir. Buna göre y = (x + 2 )2 fonksiyonunun grafiği
aşağıda-ki gibidir.
Şekil 3.13:
f fonksiyonunun grafiği bilindiğinde bu fonksiyon yardımıyla tanımlanan g (x) = f (x -a) + b, ( a,b ∈ IR) fonksiyonunun grafiğini bulabiliriz. g fonksiyonu-nun grafiği, yukarıdaki iki kaydırma işlemi yardımıyla kolayca bulunabilir. Bufonksiyonu-nun için f nin grafiği önce x-ekseni doğrultusunda, yöne de dikkat ederek, |a| birim kay-dırılır, daha sonra elde edilen yeni grafik y- ekseni doğrultusunda yine yöne dikkat ederek |b| birim kaydırılır.
Örnek: g(x) = (x + 1)2 + 3 fonksiyonunun grafiğini çiziniz.
Çözüm: Burada f (x) = x2 , a = -1 , b = 3 alabiliriz. Bu nedenle y = x2
fonksiyonu-nun grafiği önce x-ekseni doğrultusunda sola doğru 1 birim kaydırılır, daha sonra yeni grafik y-ekseni doğrultusunda yukarı doğru 3 birim kaydırılırsa g nin grafiği elde edilir.
y = (x-2)2 - 1 fonksiyonunun grafiğini çiziniz.
Şekil 3.15:
Cevabınız aşağıdaki gibi olmalıdır.
f1: IR → IR ve f2 : IR → IR fonksiyonları verilsin.
gibi tanımlanan f: IR → IR fonksiyonuna parçalı tanımlı fonksiyon denir. Tanım-dan görüldüğü gibi f(x), x ın a ya kadar olan değerlerinde f1 (x) e, a dan sonraki
de-ğerlerinde ise f2(x) e eşittir. Parçalı tanımlı fonksiyonun grafiğini çizmek için x in
a ya kadar olan değerleri için y= f1 (x) in, x in a dan sonraki değerleri için ise y= f2
(x) in grafiğini çizmek gerekiyor.
Benzer yolla iki tane yerine, sonlu tane fonksiyonlarla belirlenen parçalı fonksiyon-lar tanımlanabilir.
Aşağıda tanımlarını vereceğimiz mutlak değer, tam değer ve işaret fonksiyonları parçalı fonksiyonlardır.
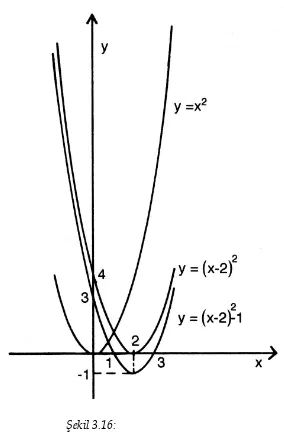
f: IR → IR , f(x)= |x| fonksiyonuna mutlak değer fonksiyonu denir. Şimdi mutlak değer fonksiyonunun grafiğini çizelim.
Şekil 3.16: f x = f1 x , x ≤ a ise f2 x , x > a ise veya f x = f1 x , x < a ise f2 x , x ≥ a ise f : IR → IR , f x = x = x , x ≥ 0 ise, -x , x < 0 ise,
yazılabilir. Bu yazıma göre, grafik, x ≥ 0 için y= x olduğundan y= x doğrusunun I. bölgedeki parçası ile, x < 0 için y= -x olduğundan y= -x doğrusunun ikinci bölgede-ki parçasından oluşur.
f: IR →→→→ IR , f(x)= |x - 2|, g: IR →→→→ IR , g(x)= - |x| + 2
fonksiyonlarının grafiklerinin aşağıdaki biçimde olduğunu görmeye çalışınız. f: IR → IR , f(x)= |x|
Şekil 3.17:
f: IR → IR , f(x)= |x - 2| Şekil 3.18:
Bir x ∈ IR sayısı verilsin. x den büyük olmayan (yani küçük veya eşit) en büyük tam sayıya x in tam değeri denir ve [x] biçiminde gösterilir. Örneğin [ 1, 5 ]= 1, [ 0, 9 ]= 0, [ π ]= 3, [ - π ]= - 4, [ 0 ]= 0, [ - 2 ]= - 2, [ 100 ]= 100. f: IR → IR , f(x)= [ x ] fonksiyonuna tam değer fonksiyonu denir. Bu fonksiyonu-nun grafiği sonsuz basamaklı bir merdivene benzer. Bufonksiyonu-nun hakkında bir fikir ver-mek için, g: [- 1, 2] → IR , g(x)= [ x ] fonksiyonunun grafiğini çizelim.
-1 ≤ x < 0 ise [ x ]= -1 olduğundan g(x)= -1 0 ≤ x < 1 ise [ x ]= 0 olduğundan g(x)= 0 1 ≤ x < 2 ise [ x ]= 1 olduğundan g(x)= 1 x= 2 ise [ x ]= 2 olduğundan g(x)= 2 dir. Buna göre g nin grafiği aşağıdaki gibidir.
Şekil 3.19: - 1 2 = - 1 , y 2 1 x 2 -1 1 -1 g: IR → IR , g(x)= -|x| + 2 Şekil 3.20: g: [-1, 2] → IR , g(x)= [ x ]
fonksiyonuna işaret fonksiyonu denir. Bu fonksiyonun grafiğinin aşağıdaki biçim-de olduğu kolayca görülebilir.
İşaret fonksiyonu f(x)= sgnx gibi de gösterilir.
Değerlendirme Soruları
1. Alanı 10 birim kare, bir taban uzunluğu 4 birim olan bir yamuğun yüksekliğini diğer tabanının x uzunluğunun bir fonksiyonu olarak yazımı aşağıdakilerden hangisidir? A. B. C. D. E.
2. Kenar uzunluğu x cm (x > 4) olan bir karenin her köşesinden, kenar uzun-lukları 2 cm olan küçük kareler kesilip çıkarılmış ve sonra kenarlar kıvrılarak üstü açık bir kutu yapılmıştır. Bu kutunun hacminin (cm3) x in fonksiyonu
olarak yazımı aşağıdakilerden hangisidir? A. 2x2 + 16x + 32 B. 2x2 + 32 C. 2x2 + 16x - 32 D. x2 + 16 E. 2x2 - 16x + 32 f : IR → IR , f x = 1 , x > 0 ise 0 , x = 0 ise -1 , x < 0 ise y 1 x -1 20 4 - x 4 + x 20 20 4 + x x 5 5 x
3.
fonksiyonunun tanım kümesi hangisidir? A. IR
B. C. IR+
D.
E. (- ∞, 1]
4. fonksiyonunun tanım kümesi hangisidir?
A. [-1, 1] B. [0, 1] C. D. (-1, 1) E. (-1, 0)
5. f: IR → IR , f(x) = x2 - 2x + 2 fonksiyonunun görüntü kümesi hangisidir?
A. IR B. [1, ∞) C. IR+ ∪ {0}
D. (- ∞, 1] E. (- ∞, 0]
6. f: IR → IR , f(x) = 2 - |x| fonksiyonu görüntü kümesi hangisidir? A. (- ∞, 2]
B. (- ∞, 2) C. IR D. IR+ ∪ {0}
E. IR- ∪ {0}
7. f: IR → IR , f(x) = x2 + x için f(x - 1) - f(-x) aşağıdakilerden hangisidir?
A. x B. 2 C. 2x D. 0 E. x - 1 f x = - 3x2 + 4x - 1 1 3 , 1 1 3 , 1 f x = 1 1 - x2 - 1 2 , 12
8. A. x B. 1 C. - x D. 0 E. x + 1
9. f: A → IR , f(x) = x2 - 2x fonksiyonu verilsin. A kümesi aşağıdakilerden
han-gisi olduğunda bu fonksiyon A üzerinde bire-birdir? A. [1/2, ∞)
B. IR+ ∪ {0}
C. [-1, ∞) D. [1, ∞) E. (- ∞, 2]
10. f: [-1, 2) → B, f(x)= x2 fonksiyonu verilsin. B kümesi aşağıdakilerden hangisi
olduğunda bu fonksiyon örtendir? A. [1, 4]
B. [0, 4] C. (1, 4) D. [0, 4) E. (0, ∞)
11. f: IR → IR , f(x) = x2 + 1 , g: IR → IR , g(x) = sgn x (işaret fonksiyonu)
veril-sin. (gof) (x) hangisidir? A. x
B. 1 C. 0 D. x2 + 1
E. x2
12. f(x) = x2 - 1 fonksiyonu için (fof) (-2) = ?
A. 0 B. 1 C. 3 D. 8 E. 9
13. fonksiyonunun tanım kümesi aşağıdakilerden hangisidir?
A. IR B. [1, ∞) C. (- ∞, 0) ∪ [1, ∞) D. (1, ∞) E. (0, ∞) f : IR - 0 → IR , f x = x + 1 x için f x - f 1x hangisidir? f x = x x
14. f: (- ∞, a] → IR , f(x) = (x - 1)2 fonksiyonu verilsin. f fonksiyonunun (- ∞, a]
üzerinde bire-bir olmasını sağlayacak en büyük a değeri hangisidir? A. - 2
B. - 1 C. 0 D. 1 E. 2
15. fonksiyonunun görüntü kümesi hangisidir?
A. (- ∞, 0) B. IR- {0} C. IR D. [-1, ∞) E. (- ∞, -1]
Değerlendirme Sorularının Yanıtları
1. C 2. E 3. B 4. D 5. B 6. A 7. D 8. D 9. D 10. D 11. B 12. D 13. C 14. D 15. A
f : IR - 0 → IR , f x = - 1 x2
![Şekil 3.19: - 1 2 = - 1 , y 2 1 x 2-11 -1 g: IR → IR , g(x)= -|x| + 2 Şekil 3.20: g: [-1, 2] → IR , g(x)= [ x ]](https://thumb-eu.123doks.com/thumbv2/9libnet/2733013.25/35.892.140.580.151.520/sekil-y-x-g-ir-ir-sekil-ir.webp)