LĠSE ÖĞRENCĠLERĠNĠN GEOMETRĠK DÖNÜġÜMLERLE ĠLGĠLĠ
MATEMATĠKSEL SÖYLEMLERĠNĠN GELĠġĠMĠNĠN
ĠNCELENMESĠ
Elçin Emre Akdoğan
DOKTORA TEZĠ
ORTAÖĞRETĠM FEN VE MATEMATĠK ALANLARI EĞĠTĠMĠ
ANA BĠLĠM DALI
GAZĠ ÜNĠVERSĠTESĠ
EĞĠTĠM BĠLĠMLERĠ ENSTĠTÜSÜ
i
TELĠF HAKKI ve TEZ FOTOKOPĠ ĠZĠN FORMU
Bu tezin tüm hakları saklıdır. Kaynak göstermek koĢuluyla tezin teslim tarihinden itibaren 12 ay sonra tezden fotokopi çekilebilir.
YAZARIN
Adı: Elçin
Soyadı: Emre Akdoğan
Bölümü: Ortaöğretim Fen ve Matematik Alanları Eğitimi Ġmza:
Teslim tarihi:
TEZĠN
Türkçe Adı: Lise öğrencilerinin Geometrik DönüĢümlerle ilgili Matematiksel Söylemlerinin GeliĢiminin Ġncelenmesi
Ġngilizce Adı: Exploring the Development of High School Students‟ Mathematical Discourses on Geometric Transformations
ii
ETĠK ĠLKELERE UYGUNLUK BEYANI
Tez yazma sürecinde bilimsel ve etik ilkelere uyduğumu, yararlandığım tüm kaynakları kaynak gösterme ilkelerine uygun olarak kaynakçada belirttiğimi ve bu bölümler dıĢındaki tüm ifadelerin Ģahsıma ait olduğunu beyan ederim.
Yazar Adı Soyadı: Elçin Emre Akdoğan
iv
v
TEġEKKÜR
Akademik hayatım boyunca geliĢimimi sağlayan ve desteğini hep yanımda hissettiğim hocam Prof. Dr. Ziya Argün‟e çok teĢekkür ederim.
Farklı bakıĢ açısı ile bana her zaman ilham veren ve tez çalıĢmam boyunca destek olan hocam Prof. Dr. Ahmet Arıkan‟a teĢekkür ederim.
Tez çalıĢmamın dönüm noktasında tanıĢtığım Yrd. Doç. Dr. Beste Güçler‟e, Massachusetts Dartmouth Üniversitesin‟de bulunduğum sürede ve sonrasında tezimin dayandığı Anna Sfard‟ın kuramını anlamamı ve baĢarıyla uygulamamı sağladığı için teĢekkür ederim. Kendisinin ABD‟de bana göstermiĢ olduğu dostluğu ve babamı kaybettiğim için Türkiye‟ye geri dönerken yapmıĢ maddi ve manevi desteği hiç unutmayacağım.
Tez konumla ilgili olarak kendisi ile sadece e-posta ile iletiĢim kursak da, sorularıma sabırla cevap veren ve bana araĢtırma problemimi öneren Prof. Dr. Anna Sfard‟ a teĢekkür ederim.
Tez çalıĢmam boyunca vakit ayırarak görüĢleri ile beni aydınlatan hocam Yrd. Doç. Dr. Ġffet Elif Yetkin Özdemir‟e teĢekkür ederim.
Akademik ve özel hayatımda bana her zaman destek olan, yaptığımız akademik tartıĢmalar ve etkinliklerle ufkumu geniĢleten ve ne zaman darda kalsam yanımda olan arkadaĢım Dr. Gönül Yazgan-Sağ‟a çok teĢekkür ederim.
Amerika‟da bulunduğum süre boyunca yaptığımız akademik konuĢmalarla bakıĢ açımın geniĢlemesini sağlayan, yurt dıĢında yabancı olmanın ortaklığını birlikte yaĢadığımız arkadaĢlarım Yenny Otalora Sevilla ve Claudia Carvalho‟ya, bir sene boyunca arabasıyla beni üniversite‟ye taĢıyan Dr. Sara Dalton‟a ve birlikte güzel paylaĢımlarda bulunduğumuz arkadaĢlarım Margaret French ve Heather Trahan-Martins‟e teĢekkür ederim.
vi
Tez çalıĢmamın en önemli aĢamalarından veri toplanmasında sabırla bana zaman ayıran ve yardımcı olan okuldaki matematik öğretmenine, Eda ve Okan isimli öğrencilere çok teĢekkür ederim.
Tezim son sürecinde hayatıma giren sevgili eĢim ve yardımcı danıĢmanım Dr. KurtuluĢ Erinç Akdoğan‟a, gergin ve çıkıĢsız hissettiğim anlarımda beni rahatlatıp doğru kararlar almamı sağladığı, tezimi ve makalelerimi gözden geçirdiği, ABD‟ye gitme fikri ve orada gösterdiği destek için teĢekkür ederim. Varlığıyla bana her zaman destek olan ve güç veren canım kardeĢim Erkin Emre‟ ye çok teĢekkür ederim. Azmi, çalıĢkanlığı ve yeniliklere açık tavrı ile bana her zaman örnek olan, sevgisi ve sıcaklığıyla çalıĢmam boyunca bana destek olan ve yüreklendiren sevgili annem Gönül Emre‟ye ne kadar teĢekkür etsem azdır.
Beni hep profesör kızım diye seven canım babacım, bu sürecin sonunu görmeni çok isterdim. Benimle her zaman gurur duyan, sevgisiyle beni saran ve destek olan canım babam Ali Emre, bol kahkahalı günlerimizi çok özlüyorum.
vii
LĠSE ÖĞRENCĠLERĠNĠN GEOMETRĠK DÖNÜġÜMLERLE ĠLGĠLĠ
MATEMATĠKSEL SÖYLEMLERĠNĠN GELĠġĠMĠNĠN
ĠNCELENMESĠ
(Doktora Tezi)
Elçin Emre Akdoğan
GAZĠ ÜNĠVERSĠTESĠ
EĞĠTĠM BĠLĠMLERĠ ENSTĠTÜSÜ
Aralık 2015
ÖZ
Bu araĢtırmanın amacı, lise öğrencilerinin dönüĢümler öğrenme alanı ile ilgili matematiksel söylemlerinin geliĢimini ve öğretimle olan iliĢkisini ortaya koymaktır. Durum çalıĢması desenine sahip olan araĢtırmanın katılımcıları iki 10. sınıf öğrencisi ve bir öğretmendir. AraĢtırmanın verileri, tarama soruları, öğretmen ve öğrencilerle yapılan klinik görüĢmeler ve sınıf gözlemleri aracılığıyla sekiz haftada toplanmıĢtır. Verilerin analizi ise Matematiksel BiliĢe ĠletiĢimsel YaklaĢım teorisine göre yapılmıĢtır. Öğrencilerin dönüĢümler öğrenme alanında geliĢimsel analizi ortaya çıkarmıĢtır ki, öğretmenin kullandığı söylem, öğrencilerin geliĢimsel seviyelerinin üstündedir. Bu sebeple öğretmen ve öğrencilerin söylemleri arasındaki farklılıkların sınıf içinde iletiĢimsel bozukluklara sebep olduğu gözlemlenmiĢtir. Öğretmenlerin sınıf içindeki iletiĢimsel bozuklukları önlemek için öğrencilerin söylemlerinin geliĢimsel süreçlerinin farkında olup desteklemeleri gerekmektedir.
viii Bilim Kodu:
Anahtar Kelimeler: Geometrik dönüĢümler, Matematiksel Söylemler, Lise seviyesi matematik eğitimi, Matematiksel BiliĢe ĠletiĢimsel YaklaĢım, Matematiksel söylem geliĢimi
Sayfa Adedi: 326
DanıĢman: Prof. Dr. Ziya Argün
ix
EXPLORING THE DEVELOPMENT OF HIGH SCHOOL
STUDENTS’ MATHEMATICAL DISCOURSES ON GEOMETRIC
TRANSFORMATIONS
(Ph.D Thesis)
Elçin Emre Akdoğan
GAZI UNIVERSITY
GRADUATE SCHOOL OF EDUCATIONAL SCIENCES
December 2015
ABSTRACT
The purpose of the study was to examine the development of high school students‟ mathematical discourses on geometric transformations in the context of a Turkish high school classroom through a discursive perspective. Participants of this case study were two tenth grade students and their teacher. Data consisted of surveys, clinical interviews with the students and teacher and classroom observations across eight weeks. Data was analyzed in terms of the components of the students‟ mathematical discourses, which are then compared to the teachers‟ discourse on transformations. Findings indicated that the teacher‟s discourse was at a higher level compared to the students‟ discursive levels. As a result, we observed differences between the students‟ and the teacher‟s discourses, suggesting miscommunication in the classroom. We conclude that teachers‟ awareness of their students‟ discursive development processes is critical to support students‟ mathematical development and prevent miscommunication in the classroom.
x Science Code:
Key Words: Geometric transformations, Mathematical discourses, Mathematics education at high school level, Commognitive framework, Development of mathematical discourse Page Number: 326
Supervisor: Prof. Dr. Ziya Argün
xi
ĠÇĠNDEKĠLER
ÖZ ... vii
ABSTRACT ... ix
TABLOLAR LĠSTESĠ ... xiv
ġEKĠLLER LĠSTESĠ ... xviii
SĠMGELER VE KISALTMALAR LĠSTESĠ... xx
GĠRĠġ ... 1
1.1.Problem Durumu ... 1
1.2.AraĢtırmanın Önemi ve Amacı ... 3
1.3.AraĢtırmanın Problemi ... 4
1.4. AraĢtırmanın Sınırlılıkları ve Varsayımları ... 4
1.5. Tanımlar ... 4
KAVRAMSAL ÇERÇEVE VE LĠTERATÜR TARAMASI... 7
2.1. DönüĢümlerin Kavramsal Yapısı ve Öğrenimi ... 7
2.1.1.DönüĢümler nedir? ... 7
2.1.2.DönüĢümlerin Öğretimi ... 9
2.1.3. DönüĢümler ile ilgili Yapılan ÇalıĢmalar ... 13
2.1.4. DönüĢümlerin Öğretim Programındaki Yeri ... 15
2.2. Teorik Çerçeve ... 16
xii
2.2.2. Matematiksel BiliĢe ĠletiĢimsel YaklaĢım... 17
2.2.3. Matematiksel BiliĢe ĠletiĢimsel YaklaĢım ile ilgili Yapılan ÇalıĢmalar ... 20
METODOLOJĠ ... 23
3.1.AraĢtırmanın Katılımcıları ve AraĢtırmanın Bağlamı ... 23
3.1.1.Okulun Seçimi... 24
3.1.2.Eda ve Okan ... 25
3.1.3.Öğretmen ... 28
3.1.4. AraĢtırmanın Bağlamı ... 29
3.2.Veri Kaynakları ve Veri Toplama Prosedürü ... 29
3.2.1.Sınıf Gözlemleri ... 31
3.2.2.GörüĢmeler ... 32
3.2.3.Öğretmenle Yapılan GörüĢme ... 37
3.3.Verilerin Analizi... 38
3.3.1.Verilerin Transkripti ... 38
3.3.2.Kodlama ... 39
BULGULAR VE YORUMLAR ... 47
4.1. Öteleme ile ilgili Matematiksel Söylemler ... 47
4.1.1. Öğretmenin Öteleme ile ilgili Matematiksel Söylemler ... 47
4.1.2. Öğrencilerin Ötelemeyle ilgili Matematiksel Söylemleri ... 65
4.1.3. Öğretmen ile Öğrencilerin Öteleme ile ilgili Söylemlerinin KarĢılaĢtırılması ... 103
4.2. Dönme ile ilgili Matematiksel Söylemler ... 108
4.2.1. Öğretmenin Dönme ile ilgili Matematiksel Söylemleri ... 108
4.2.2. Öğrencilerin Dönme ile ilgili Matematiksel Söylemlerinin GeliĢimi... 125
4.2.3. Öğretmen ile Öğrencilerin Dönme ile ilgili Matematiksel Söylemlerinin KarĢılaĢtırılması ... 167
xiii
4.3. Yansıma ile ilgili Matematiksel Söylemler ... 173
4.3.1. Öğretmenin Yansıma ile ilgili Matematiksel Söylemler ... 173
4.3.2. Öğrencilerin Yansıma ile ilgili Matematiksel Söylemlerinin GeliĢimi ... 195
4.3.3. Öğretmen ile Öğrencilerin Yansıma ile ilgili Matematiksel Söylemlerinin KarĢılaĢtırılması ... 233
SONUÇLAR VE ÖNERĠLER ... 241
5.1.1. Öteleme ile ilgili Sonuçlar ... 241
5.1.2. Dönme ile ilgili Sonuçlar ... 243
5.1.3. Yansıma ile ilgili Sonuçlar ... 245
5.2. TartıĢma ... 248
5.3. Öneriler ... 250
KAYNAKLAR ... 252
xiv
TABLOLAR LĠSTESĠ
Tablo 1. Veri Toplama Araçları………...30
Tablo 2. Veri Toplama Araçlarının Uygulanma Zamanları……….31
Tablo 3. Eda ve Okan‟la yapılan Klinik GörüĢmelerin Süresi……….33
Tablo 4. Eda ve Okan‟la Yapılan Klinik GörüĢmelerin Uygulama Zamanları…………....33
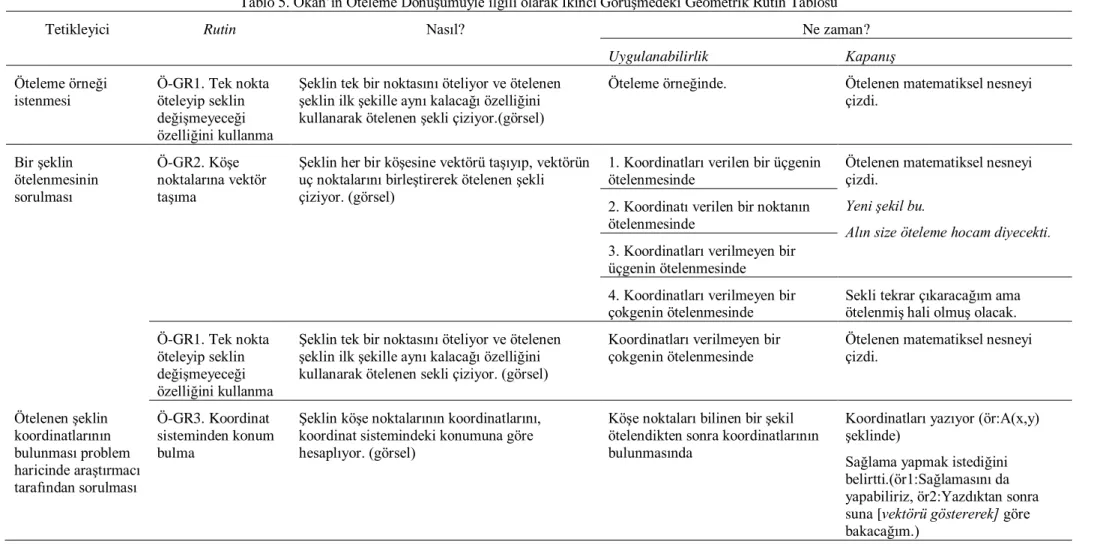
Tablo 5. Okan‟ın Öteleme DönüĢümüyle ilgili olarak Ġkinci GörüĢmedeki Geometrik Rutin Tablosu………...………...44
Tablo 6. Öğretmenin Rutin-bazlı, Tabir-bazlı, Nesne-bazlı Sözcük Kullanımlarına Örnekler...49
Tablo 7. Öğretmenin Ötelemeyle ilgili Ders Gözlemindeki Rutin Tablosu……….53
Tablo 8. Ötelemeyle ilgili GörüĢmede Sorulan Soruların Ġçerikleri………...…….56
Tablo 9. Öğretmenin Öteleme GörüĢmesindeki Cebirsel Rutin Tablosu ………....62
Tablo 10. Öğretmenin Öteleme Dersi Gözlemleri ile Öteleme GörüĢmesindeki Söylemlerinin KarĢılaĢtırılması………64
Tablo 11. Öğretmenin Öteleme ile ilgili Söylemleri………....64
Tablo 12. Ötelemeyle ilgili 1., 2. ve 3. GörüĢmede Sorulan Soruların Ġçerikleri…...…….65
Tablo 13. Okan‟ın Kullandığı Ö-GR2 Rutinine Örnek………....71
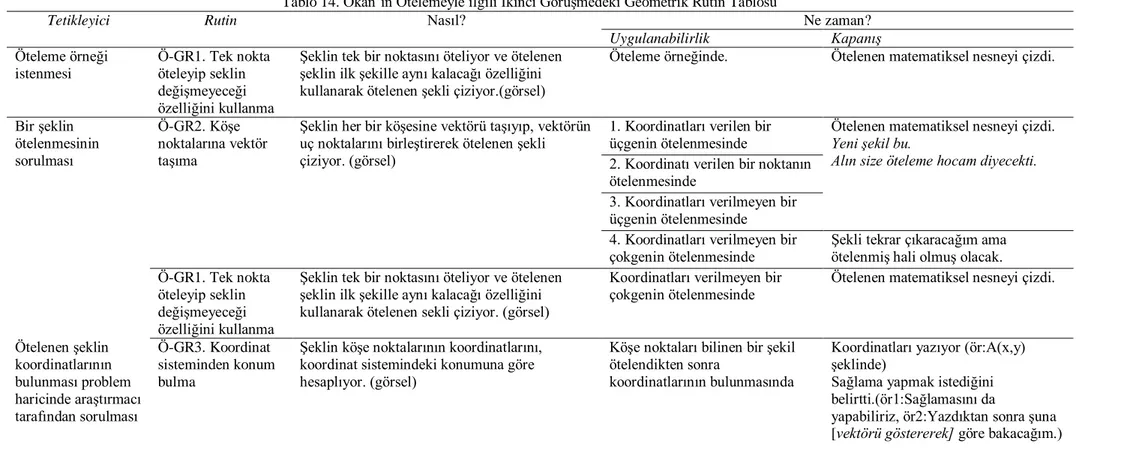
Tablo 14. Okan‟ın Ötelemeyle ilgili Ġkinci GörüĢmedeki Geometrik Rutin Tablosu…...73
Tablo 15. Okan‟ın Ötelemeyle ilgili Ġkinci GörüĢmedeki Cebirsel Rutin Tablosu.………74
Tablo 16. Okan‟ın Ġkinci GörüĢmede Kullandığı Geometrik ġekillerde oluĢan Görsel Aracıları………...………..…………...76
Tablo 17. Okan‟ın Ġkinci GörüĢmede Kullandığı Sembolik Notasyonlardan oluĢan Görsel Aracıları………...……….………...77
Tablo 18. Okan‟ın Ötelemeyle ilgili Üçüncü GörüĢmedeki Geometrik Rutinlerin Tablosu………..……...82
Tablo 19. Okan‟ın Öteleme ile ilgili Matematiksel Söylemlerinin GeliĢimi………...84
Tablo 20. Eda‟nın Anlatısını Tasdik eden Görsel Aracı………..…………..……..89
Tablo 21. Eda‟nın Öteleme ile ilgili Ġkinci GörüĢmedeki Geometrik Rutin Tablosu...95
Tablo 22. Eda‟nın Öteleme ile ilgili Ġkinci GörüĢmedeki Cebirsel Rutin Tablosu…...95
xv
Tablo 24. Eda‟nın Öteleme ile ilgili Matematiksel Söylemlerinin GeliĢimi………...…...103
Tablo 25. Öğretmenin ve Okan‟ın Öteleme ile ilgili Anlatıları………...104
Tablo 26. Öğretmen ile Okan‟ın Öteleme ile ilgili Söylemlerinin KarĢılaĢtırılması…….105
Tablo 27. Öğretmenin ve Eda‟nın Öteleme ile ilgili Anlatıları……….………107
Tablo 28. Öğretmen ile Eda‟nın Öteleme ile ilgili Söylemlerinin KarĢılaĢtırılması…….108
Tablo 29. Öğretmenin Dönmeyle ilgili Ders Gözlemlerindeki Rutin Tablosu…………..114
Tablo 30. Dönmeyle ilgili GörüĢmede Sorulan Soruların Ġçerikleri………....……..116
Tablo 31. Öğretmenin Dönmeyle ilgili GörüĢmedeki Geometrik Rutin Tablosu…...122
Tablo 32. Öğretmenin Dönme Dersi Gözlemleri ile GörüĢmedeki Söylemlerinin KarĢılaĢtırılması……….………124
Tablo 33. Öğretmenin Dönme ile ilgili Söylemleri………..…...125
Tablo 34. Dönme ilgili 1., 2. ve 3. GörüĢmede Sorulan Soruların Ġçerikleri…...……….126
Tablo 35. Okan‟ın Kullandığı D-GR1 Rutinine Örnek……….………....129
Tablo 36. Okan‟ın Dönmeyle ilgili Birinci GörüĢmedeki Geometrik Rutin Tablosu…..131
Tablo 37. Okan‟ın Kullandığı D-CR1 Rutinine Örnek……….………....135
Tablo 38. Okan‟ın Dönmeyle ilgili Ġkinci GörüĢmedeki Geometrik Rutin Tablosu………..137
Tablo 39. Okan‟ın Dönmeyle ilgili Ġkinci GörüĢmedeki Cebirsel Rutin Tablosu…...137
Tablo 40. Okan‟ın Kullandığı D-GR1 Rutinine Örnek………..………141
Tablo 41. Okan‟ın Dönmeyle ilgili Üçüncü GörüĢmedeki Geometrik Rutin Tablosu...143
Tablo 42. Okan‟ın Dönmeyle ilgili Üçüncü GörüĢmedeki Cebirsel Rutin Tablosu……….…...143
Tablo 43. Okan‟ın Dönme ile ilgili Matematiksel Söylemlerinin GeliĢimi………...145
Tablo 44. Eda‟nın Dönmeyle ilgili Birinci GörüĢmedeki Geometrik Rutin Tablosu...150
Tablo 45. Eda‟nın Dönmeyle ilgili Ġkinci GörüĢmedeki Geometrik Rutin Tablosu………...157
Tablo 46. Eda‟nın Dönmeyle ilgili Ġkinci GörüĢmedeki Cebirsel Rutin Tablosu………...157
Tablo 47. Eda‟nın Kullandığı D-CR1 Rutinine Örnek………..162
Tablo 48. Eda‟nın Kullandığı D-GR2 Rutinine Örnek……….….162
Tablo 49. Eda‟nın Dönmeyle ilgili Üçüncü GörüĢmedeki Cebirsel Rutin Tablosu …...164
Tablo 50. Eda‟nın Dönmeyle ilgili Üçüncü GörüĢmedeki Geometrik Rutin Tablosu...165
Tablo 51. Eda‟nın Dönme ile ilgili Matematiksel Söylemlerinin GeliĢimi…………...…167
Tablo 52. Öğretmenin ve Okan‟ın Dönme ile ilgili Anlatıları………...169
xvi
Tablo 54. Öğretmenin ve Eda‟nın Dönme ile ilgili Anlatıları………...…………....172 Tablo 55. Öğretmen ile Eda‟nın Dönme ile ilgili Söylemlerinin KarĢılaĢtırılması……...173 Tablo 56. Öğretmenin Yansımayla ilgili Ders Gözlemindeki Tabir ve Nesne-bazlı Sözcük Kullanımlara Örnek………..………...175 Tablo 57. Öğretmenin Yansımayla ilgili Ders Gözlemindeki Görsel Aracıya Örnek...176 Tablo 58. Öğretmenin Yansımayla ilgili Ders Gözlemindeki Y-GR1 Rutinine Örnek….178 Tablo 59. Öğretmenin Yansımayla ilgili Ders Gözleminde Kullandığı Y-CR1 Rutinine Örnek………..179 Tablo 60. Öğretmenin Yansımayla ilgili GörüĢmedeki Geometrik Rutin Tablosu...……182 Tablo 61. Öğretmenin Yansımayla ilgili GörüĢmedeki Cebirsel Rutin Tablosu ……….182 Tablo 62. Öğretmenin Yansıma Dersinde Kullandığı Yansıma DönüĢümü Tanımı...183 Tablo 63. Yansımayla ilgili GörüĢmede Kullanılan Soruların Ġçerikleri………..….…...185 Tablo 64. Öğretmenin Yansımayla ilgili GörüĢmedeki Nesne-bazlı ve Tabir-bazlı Sözcük Kullanımına Örnek………..………..186 Tablo 65. Öğretmenin Kullandığı Y-GR1 Rutinine Örnek……….…..189 Tablo 66. Öğretmenin Kullandığı Y-CR1 Rutinine Örnek………190 Tablo 67. Öğretmenin Yansımayla ilgili GörüĢmedeki Geometrik Rutin Tablosu ……..192 Tablo 68. Öğretmenin Yansımayla ilgili GörüĢmedeki Cebirsel Rutin Tablosu …….….192 Tablo 69. Öğretmenin Yansımayla ilgili Ders Gözlemleri ile GörüĢmedeki Söylemlerinin KarĢılaĢtırılması ………194 Tablo 70. Öğretmenin Yansıma ile ilgili Matematiksel Söylemleri………...…...195 Tablo 71. Yansıma ilgili 1., 2. ve 3. GörüĢmede Sorulan Soruların Ġçerikleri………..…196 Tablo 72. Okan‟ın Kullandığı Görsel Aracıya Örnek………..….199 Tablo 73. Okan‟ın Kullandığı Y-GR1 Rutinine Örnek……….200 Tablo 74. Okan‟ın Yansımayla ilgili Birinci GörüĢmedeki Geometrik Rutin Tablosu …201 Tablo 75. Okan‟ın Kullandığı Görsel Aracıya Örnek………204 Tablo 76. Okan‟ın Kullandığı Y-GR1 Rutinine Örnek………..205 Tablo 77. Okan‟ın Yansımayla ilgili Ġkinci GörüĢmedeki Geometrik Rutin Tablosu …..206 Tablo 78. Okan‟ın Tabir-bazlı ve Rutin-bazlı Sözcük kullanımına Örnek…………..…..208 Tablo 79. Okan‟ın Kullandığı Y-GR1 Rutinine Örnek……….….210 Tablo 80. Okan‟ın Yansımayla ilgili Üçüncü GörüĢmedeki Geometrik Rutin Tablosu ...211 Tablo 81. Okan‟ın Yansıma ile ilgili Matematiksel Söylemlerinin GeliĢimi……….213 Tablo 82. Eda‟nın Kullandığı Y-GR1 Rutinine Örnek………..……217 Tablo 83. Eda‟nın Yansımayla ilgili Birinci GörüĢmedeki Geometrik Rutin Tablosu …218 Tablo 84. Eda‟nın Nesne-bazlı ve Rutin-bazlı Sözcük Kullanıma Örnek……….220
xvii
Tablo 85. Eda‟nın Kullandığı Görsel Aracıya Örnek……….221 Tablo 86. Eda‟nın Kullandığı Y-GR1 Rutinine Örnek………...………...222 Tablo 87. Eda‟nın Yansımayla ilgili Ġkinci GörüĢmedeki Geometrik Rutin Tablosu …..224 Tablo 88. Eda‟nın Tabir-bazlı ve Rutin-bazlı Sözcük kullanımına Örnek………….…...226 Tablo 89. Eda‟nın Kullandığı Görsel Aracıya Örnek………....228 Tablo 90. Eda‟nın Kullandığı Y-GR1 Rutinine Örnek……….….229 Tablo 91. Eda‟nın Yansımayla ilgili Üçüncü GörüĢmedeki Geometrik Rutin Tablosu ...231 Tablo 92. Eda‟nın Yansıma ile ilgili Matematiksel Söylemlerinin GeliĢimi…………...233 Tablo 93. Öğretmenin ve Okan‟ın Yansıma ile ilgili Anlatıları……….235 Tablo 94. Öğretmen ile Okan‟ın Yansıma ile ilgili Söylemlerinin KarĢılaĢtırılması…….236 Tablo 95. Öğretmen ve Eda‟nın Yansıma ile ilgili Anlatıları………238 Tablo 96. Öğretmen ile Eda‟nın Yansıma ile ilgili Söylemlerinin KarĢılaĢtırılması…….239
xviii
ġEKĠLLER LĠSTESĠ
ġekil 1. Öğretmenin kullandığı cebirsel görsel aracıya bir örnek………..…...58
ġekil 2. Öğretmenin koordinat sistemi oluĢturduğu görsel aracılarına bir örnek………….59
ġekil 3: Öğretmenin koordinat sistemi oluĢturduğu görsel aracıya bir örnek…………...59
ġekil4. Öğretmenin kullandığı Ö-CR1 rutinine bir örnek………....61
ġekil 5. Okan‟ın birinci görüĢmede kullandığı görsel aracıya örnek………. 67
ġekil 6. Okan‟ın yansıma ve öteleme ile ilgili kafasının karıĢık olmasına örnek…………68
ġekil 7. Okan‟ın kullandığı Ö-GR1 rutinine örnek………..70
ġekil 8. Okan‟ın kullandığı Ö-GR3 rutinine örnek………..71
ġekil 9. Okan'ın Cebirsel Rutinine (Ö-CR1) Örnek………...72
ġekil 10. Okan‟ın anlatısını tasdik eden görsel aracıya örnek………...…..78
ġekil 11. Okan‟ın kullandığı görsel aracıya örnek………...80
ġekil 12. Eda‟nın vektörü doğru olarak çizdiği görsel aracıya örnek………..86
ġekil 13. Eda‟nın “hatalı soru çözümünün yer aldığı problem” de kullandığı görsel aracı.86 ġekil 14. Eda‟nın verdiği öteleme örneği ………88
ġekil 15. Eda‟nın yansıma ile öteleme hakkında kafasının karıĢık olduğu duruma örnek..90
ġekil 16. Eda‟nın “hatalı soru çözümünün yer aldığı problem”de kullandığı görsel aracı..90
ġekil 17. Eda‟nın Ö-GR1 rutine örnek……….93
ġekil 18. Eda‟nın kullandığı Ö-CR1 rutine örnek………94
ġekil 19. Eda‟nın kullandığı görsel aracıya örnek………...96
ġekil 20. Eda‟nın kullandığı görsel aracıya örnek………...99
ġekil 21. Eda‟nın kullandığı Ö-GR1 rutinine örnek………...…100
ġekil 22. Öğretmenin kullandığı görsel aracıya örnek………...120
ġekil 23. Öğretmenin kullandığı cebirsel notasyonları içeren görsel aracıya örnek……..120
ġekil 24. Öğretmenin kullandığı D-GR1 rutinine örnek………121
xix
ġekil 26. Okan‟ın cebirsel notasyonları kullandığı görsel aracıya örnek………...134
ġekil 27. Okan‟ın kullandığı görsel aracıya örnek……….140
ġekil 28. Eda‟nın kullandığı görsel aracıya örnek……….147
ġekil 29. Eda‟nın kullandığı görsel aracıya örnek……….148
ġekil 30. Eda‟nın kullandığı D-GR1 rutinine örnek………..149
ġekil 31.Eda‟nın kullandığı görsel aracıya örnek………..153
ġekil 32. Eda‟nın kullandığı görsel aracıya örnek……….154
ġekil 33. Eda‟nın kullandığı D-CR1 rutinine örnek………..155
ġekil 34. Eda‟nın kullandığı görsel aracıya örnek……….160
ġekil 35.Öğretmenin derste kullandığı görsel aracıya örnek……….177
ġekil 36. Öğretmenin kullandığı görsel aracıya örnek………..187
ġekil 37. Öğretmenin cebirsel notasyon olarak kullandığı görsel aracıya örnek………..188
ġekil 38. Okan‟ın kullandığı görsel aracıya örnek………209
ġekil 39. Eda‟nın kullandığı görsel aracıya örnek………....216
xx
SĠMGELER VE KISALTMALAR LĠSTESĠ
ÖT Öğretmen
O Okan E Eda
SC Sınıftan gelen cevaplar ÖG1 Öğrenci görüĢme protokolü 1 ÖGP2 Öğrenci görüĢme protokolü 2 ÖGP3 Öğrenci görüĢme protokolü 3 ÖGP4 Öğrenci görüĢme protokolü 4 ÖGP5 Öğrenci görüĢme protokolü 5
Ö-GR1 Ötelemede kullanılan birinci geometrik rutin Ö-GR2 Ötelemede kullanılan ikinci geometrik rutin Ö-GR3 Ötelemede kullanılan üçüncü geometrik rutin Ö-CR1 Ötelemede kullanılan birinci cebirsel rutin
D-GR1 Dönmede kullanılan birinci geometrik rutin D-GR2 Dönmede kullanılan ikinci geometrik rutin D-CR1 Dönmede kullanılan birinci cebirsel rutin Y-GR1 Yansımada kullanılan birinci geometrik rutin Y-CR1 Yansımada kullanılan birinci cebirsel rutin
1
BÖLÜM 1
GĠRĠġ
1.1.Problem Durumu
Geometrik dönüĢümler öğrencilerin örüntüleri ve basit isometrileri keĢfetmesine, genellemeler yapmalarına ve görsel becerilerini geliĢtirmelerine olanak sağlamaktadır (Clements, Battista, Sarama ve Swaminathan, 1997; Portnoy, Grundmeimer ve Graham, 2006). Ayrıca öğrencilerin fonksiyonlar, benzerlik, eĢlik gibi matematikle ilgili önemli kavramları düĢünmelerine ve muhakeme seviyelerini artırıp farklı temsil biçimlerini kullanmalarına yardımcı olmaktadır (Hollebrands, 2003). Bunlarla birlikte ilköğretimden liseye birçok geometri müfredatında, öğretim programında ve matematik eğitimi araĢtırmalarında dönüĢümler önemli bir yere sahiptir (Flagan, 2001; Jones, 2000; Mili Eğitim Bakanlığı [MEB], 2010, 2013; National Council of Teachers of Mathematics [NCTM], 2000; Yanik, 2006). Milli Eğitim Bakanlığı ortaöğretim geometri programı, 10. sınıfta yer alan öğrenme alanları aracılığı ile öğrencilerden “öteleme, dönme ve yansıma dönüĢümlerini analiz etme ve bu dönüĢümleri problem çözme sürecinde kullanma” kazanımını edinmeleri beklenmektedir (MEB, 2010). NCTM standartları ise lise öğrencilerinden (9.sınıf-12.sınıf) “öteleme, dönme ve yansımayı anlamalarını ve gösterimlemelerini, basit dönüĢümleri ve onların bileĢkelerine olan etkisini anlamalarına yardımcı olması için farklı temsilleri kullanmalarını” beklemektedir (NCTM, 2000).
DönüĢümler öğrenme alanı ile ilgili yapılan çalıĢmalar öğrenciler, öğretmen ve öğretmen adaylarının düĢüncelerini inceleyenler olmak üzere üç ana baĢlıkta toplanabilir. Yapılan çalıĢmaların sonucunda, öğrencilerin öteleme dönüĢümü ile karĢılaĢtıkları zorlukların
2
temelinde vektör kavramı olduğunu ortaya çıkarılmıĢtır (Hollebrands, 2004; Laborde, 2001). DönüĢümlerle ilgili öğrencilerin yaĢadığı bir diğer zorluk ise dönüĢümün sadece düzlem üzerindeki nesneye değil düzlemin bütün noktalarına uygulanmasıdır (Hollebrands, 2003; Sünker ve Zembat, 2012). DönüĢümleri matematiksel nesne yerine fiziksel bir hareket olarak algılama öğrencilerin karĢılaĢtığı bir diğer zorluktur (Hollebrands, 2003). Flagan (2001), araĢtırmasının sonucunda, öğrencilerin dönüĢümleri bir hareket olarak algılamasından ziyade bir fonksiyon olarak ele almasının oldukça önemli olduğunu vurgulamıĢtır. Sonuç olarak, araĢtırmalar öğrencilerin dönüĢümleri fiziksel hareket ve fonksiyon olmak üzere iki farklı Ģekilde öğrendiklerini özetlemiĢlerdir. Edwards (2003), dönüĢümleri fiziksel hareket olarak algılayan öğrencilerin fikirlerini Ģu Ģekilde özetlemektedir: “i) Düzlem boĢ ve görünmez bir arka plandır, ii) geometrik Ģekiller düzlemin üzerinde oturmaktadır ve iii) dönüĢümler düzlem üzerindeki geometrik Ģekillerin fiziksel hareketleridir. DönüĢümleri, fonksiyon olarak ele alan öğrencilerin ise düzlemin sonsuz sayıda noktadan oluĢtuğunu ve geometrik Ģekillerin bu noktaların alt kümesi olarak ele aldığını belirtmiĢtir (Edwards, 2003).
Yapılan bazı çalıĢmalar öğretmen ve öğretmen adaylarının dönüĢümler öğrenme alanı bağlamında karĢılaĢtıkları zorlukları araĢtırmıĢlardır (Portnoy, Grundmeimer, ve Graham, 2006; Thaqi, Giménez, ve Rosich, 2011; Yanik, 2006, 2011; Yanik ve Flores, 2009). Örneğin, öğretmenlerin dönüĢümlere yaklaĢımı geometrik nesnelerin hareketlerinin görselleĢtirmesi Ģeklinde ise öğretmenlerin dönüĢümlerle ilgili ortak özelliklerin soyutlanmasında zorluk yaĢadıkları tespit edilmiĢtir (Portnoy, Grundmeimer ve Graham, 2006; Thaqi, Giménez, ve Rosich, 2011).Vektörü simetri doğrusu olarak kullanma öğretmen adaylarının karĢılaĢtığı bir diğer zorluktur (Yanik, 2011; Yanik ve Flores, 2009). Harper (2002), öğretmen adaylarının dönüĢümler öğrenme alanı bağlamında kullandıkları dilin baĢlangıç seviyesinde olduğunu ortaya çıkarmıĢtır.
Öğretmen ve öğrencilerin dönüĢümler öğrenme alanı ile ilgili düĢüncelerinin ağırlıklı olarak biliĢsel ve yapılandırmacı yaklaĢıma göre incelendiği Ģimdiye kadar yapılan çalıĢmalarda görülmektedir. DönüĢümler bağlamında öğrencilerin geliĢimsel öğrenmelerini, öğretimi sosyo-kültürel bakıĢ açısından ve öğrenme ve öğretimi birlikte inceleyen çalıĢmalara ihtiyaç duyulduğu görülmektedir. Sonuç olarak, literatürde öğrencilerin dönüĢümler ile ilgili öğrenmelerinin geliĢimini ve öğrencilerin öğrenmelerini
3
öğretmenin öğretimi ile birlikte iletiĢimsel bakıĢ açısıyla inceleyen çalıĢmaların gerekliliği önem arz etmektedir.
1.2.AraĢtırmanın Önemi ve Amacı
Öğretmenin ve öğrencinin dönüĢümler öğrenme alanı ile ilgili düĢüncelerini inceleyen Ģimdiye kadar yapılan çalıĢmalar çoğunlukla biliĢsel ve yapılandırmacı yaklaĢımlara dayanmaktadır. Öğretmen ve öğretmen adaylarının düĢünmelerini biliĢsel ve yapılandırmacı teoriden inceleyen çalıĢmalar, öğretmenlerin dönüĢümler bağlamındaki matematiksel düĢünmelerini geliĢtirmek için daha dikkatli ve derinlemesine araĢtırmaların gerekliliğini vurgulamıĢlardır (Battista, Wheatley, ve Talsma, 1982; Harper, 2002; Laborde, 2001; Margolinas, Coulange, ve Bessot, 2005). Ayrıca, öğrenmenin ve öğretimin birlikte incelenmesinin önemine rağmen (Lerman, 2001); çok az çalıĢma öğrencilerin dönüĢümler ile ilgili öğrenmelerini ve bunun öğretimle iliĢkisini sosyo-kültürel teori perspektifinden incelemiĢtir (Yanık, 2011). Ayrıca öğrencilerin dönüĢümler üzerine öğrenmelerinin zaman içinde nasıl değiĢtiğini inceleyen araĢtırmaların gerekliliğini vurgulanmıĢtır (Yanık, 2011). Buna ek olarak, literatürde öğretmenin kullandığı dilin öğrencinin dönüĢümleri öğrenmesini nasıl etkilediğini derinlemesine inceleyen çalıĢmaların önemli olmasına rağmen az olduğu belirtilmiĢtir (Yanık, 2011). Öğrencilerin dönüĢümleri hareket olarak kavramalarından matematiksel nesne olarak kavramalarına geçiĢin nasıl olduğunun derinlemesine araĢtırılması oldukça önemlidir ve bu da öğrencilerin dönüĢümleri öğrenmelerinin zaman içinde nasıl değiĢtiğini sınıf ortamı içinde incelemeyi gerektirmektedir.
Bu araĢtırma, literatürün daha fazla araĢtırılması gereken konuları üzerine odaklanmaktadır. Öğrenmenin geliĢimini ve öğretimi birlikte ele alarak sosyo-kültürel teorinin perspektifinden incelemektedir. Bu bağlamda araĢtırmanın amacı, lise öğrencilerinin dönüĢümler öğrenme alanı ile ilgili matematiksel söylemlerinin geliĢimini ve öğretimle olan iliĢkisini ortaya koymaktır.
4
1.3.AraĢtırmanın Problemi
Bu araĢtırmanın temel sorusu “10. sınıf lise öğrencilerinin dönüĢümler öğrenme alanı bağlamındaki sınıf içindeki matematiksel söylemlerinin geliĢimi nasıldır? “ Ģeklinde formüle edilmiĢtir. Bu araĢtırma bu soruyu bir 10. sınıftaki öğrenci ve öğretmenlerine odaklanarak araĢtırmıĢtır. AraĢtırmanın alt soruları aĢağıda verilmiĢtir:
a. Bu sınıfta öğretmenin dönüĢümler öğrenme alanı bağlamında matematiksel söylemi nelerdir?
b. Bu sınıfta öğrencilerin dönüĢümler öğrenme alanı bağlamında matematiksel söylemlerinin geliĢimi nasıldır?
c. Bu sınıfta öğretmen ve öğrencilerin dönüĢümler öğrenme alanı bağlamındaki matematiksel söylemlerinin karĢılaĢtırılması nasıldır?
1.4. AraĢtırmanın Sınırlılıkları ve Varsayımları
AraĢtırmada sınıf ortamında doğal gözlemle ilgilendiği için sınıf ortamındaki matematiksel söylemler kayıt altına alınmıĢtır. Yapılan sınıf gözlemi sırasında sınıfın doğal bir ortam olduğu kabul edilmiĢtir. Bu araĢtırmada bahsedilmeyen sınıf ortamında farklı söylemler olmasına rağmen, burada sadece matematiksel söylemlere odaklanılmıĢtır. AraĢtırma sınıf ortamındaki matematiksel söylemlerin, iki 10.sınıf öğrencisi ve bir öğretmenle yapılan görüĢmelerin iletiĢimsel yaklaĢım aracılığıyla incelenmesi ile sınırlandırılmıĢtır. GörüĢmeye katılan öğrencilerin ve öğretmenin görüĢme esnasında sorulan sorulara samimi bir Ģekilde cevap verdikleri düĢünülmektedir.
1.5. Tanımlar
AĢağıda verilen tanımlar Sfard‟dan (2008) alınmıĢtır.
Matematiksel BiliĢe ĠletiĢimsel YaklaĢım (Commognition): Ġngilizce olarak, iletiĢim (communication) ve biliĢ (cognition) kelimelerinin birleĢiminden ortaya çıkan bir kavramdır.
5
ĠletiĢim: Toplu bir Ģekilde gerçekleĢtirilen bir bireyin gerçekleĢtirdiği eylem A nın, diğer bir bireyin gerçekleĢtirdiği eylem B ile takip edildiği örüntülü bir aktivitedir.
Matematiksel öğrenme: Matematiksel söyleme iĢtirak etme biçimde söylemdeki sürekli değiĢimdir.
Öğrenmedeki geliĢim: Söylemdeki değiĢimdir.
Söylem (Discourse): Özel bir iletiĢim biçimidir; her söylem kendi söylem topluluğunu tanımlar; söylemler, sözcük kullanımı, görsel aracılar, rutinler ve tasdik edilmiĢ anlatıları ile birbirilerinden ayırt edilebilirler.
Matematiksel Söylem: Kelimeleri matematikten gelen söylemlerdir (örneğin, sayılar, iĢlemler, geometrik Ģekiller).
Söylem topluluğu (Community of discourse): Söyleme katılan tüm bireyleri içeren topluluktur.
Sözcük Kullanımı (Word use): Katılımcıların söylemlerinde kullandıkları anahtar kelimelerdir.
Rutin (Routine): Katılımcıların matematiksel söylemlerinde kendini tekrarlayan üst seviyedeki kuralları kapsamaktadır.
Görsel Aracılar (Visual mediators): Matematiksel iletiĢim için oluĢturulmuĢ ve üzerinde iĢlem gerçekleĢtirdiğimiz tüm görsel araçlar (semboller, grafikler, geometrik Ģekiller, tablolar ve hatta matematiğin ifade edildiği lisandaki görsel simgeler (harfler, yazılı sözcükler).
Anlatılar (Narratives): Matematiksel nesneler, bu nesneler arasındaki iliĢkiler ve bu nesneler üzerinde uygulanan iĢlemler hakkında onaya veya redde açık tüm sözlü ifadeleri içermektedir.
7
BÖLÜM 2
KAVRAMSAL ÇERÇEVE VE LĠTERATÜR TARAMASI
2.1. DönüĢümlerin Kavramsal Yapısı ve Öğrenimi
2.1.1.DönüĢümler nedir?
Geometri baĢlangıçta düzlem ve uzaydaki Ģekillerin incelenmesini konu edinmiĢtir. Bu Ģekiller somut nesnelerden oluĢmalarına karĢın, geometri deneysel yöntemlerin kullanımını çok erken bırakmıĢtır. Babilliler ve Mısırlılarda önceleri ispat yokken sonrasında Thales (Ġ.Ö. 626-545) ve Öklid ‟le (Ġ.Ö. 300) birlikte geometride ispat önem kazanmaya baĢlamıĢ ve sonrasında geometri tümüyle ispatlanmıĢtır. Aksiyomlar ispatlanmamıĢ¸ önermeler olarak kabul edilmektedir. Öklid, çağdaĢları ve o çağlardaki geometri öğrencileri için aĢağıdaki aksiyomlar veya postulatlar hariç¸ bütün iddialar kanıtlanabilmiĢ¸ ve bu beĢ tanesi asırlar boyu ispatlanmadan doğru oldukları kabul edile gelmiĢlerdir.
1 Herhangi bir noktadan baĢka bir noktaya bir doğru çizilir.
2 Herhangi bir doğru üzerinde herhangi sonlu bir doğru devamlı elde edilebilir. 3 Bütün dik açılar birbirine eĢtir.
8
5 Bir doğru iki doğru ile kesiĢtiğinde oluĢan iç¸ ve aynı yöndeki açıların ölçüleri toplamı iki dik açının ölçüleri toplamından daima küçüktür, iki doğru uzatılarak oluĢan doğrular bir tarafta kesiĢirler ve kesiĢtikleri yöndeki açının ölçüsü iki dik açının ölçüleri toplamından daima küçüktür.
Geometri ile ilgili okul kitaplarının çoğunda yukarıdaki aksiyomlardan ilk dördü günümüz dilinde yeniden ifade edilmiĢlerdir ve 5. aksiyom yerine ise Öklid‟ in beĢinci aksiyomuna denk olan John Playfair‟ in ifadesi kullanılmaktadır. Bunlar Ģu Ģekilde yazılmaktadır: 1 Ġki nokta arasına bir doğru çizilebilir (iki nokta bir doğru ile bağlanabilir).
2 Herhangi bir doğruda herhangi bir uzunluğa sahip doğru parçası oluĢturulabilir.
3 Herhangi merkezli ve herhangi yarıçaplı bir çember çizilebilir.
Öklid dıĢı geometrilerin ortaya çıkıĢı geometride büyük bir devrime yol açmıĢtır. Sonrasında ise Felix Klein, Erlangen programı (1872) olarak isimlendirilen ünlü çalıĢmasında Öklid dıĢı geometrilerin sınıflandırılmasını önermiĢtir. Bugüne kadar kurulan her geometrik yapıda bu yapılara ait dönüĢümler altında değiĢmeyen bazı özellikler göze çarpmıĢ ve bunun sonucu olarak da her geometrik yapıya bir dönüĢüm grubu eĢlik ettirilmeye çalıĢılmıĢtır (Dönmez, 2002). Alman matematikçisi Felix Klein (1872) “S bir küme, G de S yi kendisine dönüĢtüren dönüĢümlerden meydana gelen bir grup olmak üzere, S kümesinin G nin elemanları olan dönüĢümler altında değiĢmez (invaryant) kalan özellikleri inceleyen bilim dalı” olarak yaptığı Geometri tanımı yukarıdaki ifadelerin bir sonucudur (Kaya, 2005).
ġimdi geometrinin bu tanımını açmaya çalıĢalım. Geometri, “Geometrik Ģekillerin özelliklerini inceleyen bir bilim dalıdır.” denildiğinde özellik kelimesinin genel bir karakteristiği vardır ve hiçbir Ģekilde Ģekillerin bütün özellikleri geometride çalıĢılmamaktadır. Örneğin, beyaz bir kâğıda ya da tahtaya çizilen bir üçgenin rengi geometrinin konusu değildir çünkü renk Ģeklin çizildiği kâğıdın özelliğidir, Ģeklin kendine ait bir özellik değildir. Bu noktada, geometrinin Ģekillerin hangi özelliklerini çalıĢtığına dair daha net bir matematiksel tanıma ihtiyaç vardır. Lobachevsky‟nin kurduğu öklidyen olmayan geometri, öklid geometrisinden baĢka geometrilerin varlığını gündeme getirmiĢ ve sezgisel bir Ģekilde tanımlanan geometrik özellikler daha net hale gelmiĢtir. Peki “bu geometrik özellikler nelerdir?” sorusu geometri kurulmadan geometrik özellikler de söz
9
konusu değildir, Geometri kelimesini kullanmadan geometrik özellikleri tanımlayabilmeliyiz.
Artık, Ģekillerin geometrik özelliklerini: “Bütün denk Ģekillerde aynı olan özelliklerdir” Ģeklinde tanımlayabiliriz. Bu durumda da, denk Ģekillerin ne anlama geldiğini ortaya koymamız gerekmektedir. Denk Ģekiller, hareketle birbiri üzerine çakıĢan Ģekiller olarak algılanmaktadır. Bu nedenle, Ģekillerin geometrik özellikleri demek, bütün denk Ģekillerde aynı olan ve Ģekilleri hareket ettirilmesiyle değiĢmeyen özelliklerdir. Sonuç olarak geometrinin yeni tanımı: “Hareketler altında değiĢmeyen geometrik Ģekillerin özelliklerini inceleyen bir bilim dalıdır.” ġimdi de hareketin anlamının ne olduğunun ortaya konulması gerekmektedir. ġekillerin hareket ettirilmesi düzlemdeki dönüĢümleri gündeme getirmektedir; çünkü Ģeklin ilk hali bu dönüĢümün tanım kümesi, Ģeklin hareket ettirildikten sonraki hali dönüĢümün görüntü kümesi olarak ele alınabilir. Daha da öte bu dönüĢümlerin birebir ve örten olması da kaçınılmaz gözükmektedir. Sebebi ise denk Ģekillerin hareket ettirilip birbirleri üzerine çakıĢtırıldığında her iki Ģekilde de boĢta kalan kısmın bulunmamasıdır. Ayrıca bu dönüĢümlerin uzaklıkları ve açılarının ölçülerini değiĢtirmemesi de beklenmektedir. Yapılan bu incelemeler ıĢığında geometri, hareket adı verilen dönüĢümler altında değiĢmeyen (invaryant) geometrik Ģekillerin özelliklerini inceleyen bir bilim dalı olarak tanımlanmıĢ ve halen bu tanım geçerliliğini sürdürmektedir (Yaglom, 1962).
2.1.2.DönüĢümlerin Öğretimi
Öklid geometrisinin de dönüĢümler altında değiĢmeyen özellikleri söz konusudur. Bu özelliklerin neler olduğundan ziyade, dönüĢümlerin neler olduğu açıklanmalıdır. Öklid geometrisindeki temel dönüĢümler: yansımalar, öteleme, dönme, homoteti ve simetridir. Bunlardan kısaca söz edelim.
Ġçinde yaĢadığımız uzayda her nesne belli bir hızda hareket halindedir. Bu hareketler ya doğrultuyu değiĢtirmeden veya dönerek, yansıyarak, kayarak, geniĢleyerek, büzülerek veya bunların belli bir sırada uygulanmasıyla gerçekleĢmektedir.
10
2.1.2.1. Öteleme Dönüşümü
Öteleme ile yapılan harekette nesneler belli bir doğrultuda yer değiĢtirirler. Doğrultularını vektörler belirlediğinden her vektöre bir öteleme, karĢıt olarak her bir ötelemeye de bir vektör karĢılık gelmektedir. Dolayısıyla 𝐸𝑛 de bir öteleme uygulandığında bütün noktalar ötelemeyi temsil eden vektör doğrultusunda ve vektörün boyu mesafesinde yer değiĢtirirler ve dolayısıyla ötelemeler altında bir cismin görüntüsü kendisi ile eĢ olmak durumundadır. Düzlemde öteleme dönüĢümünün formal tanımı aĢağıda verildiği gibidir:
Tanım: 𝑇: 𝐸2→ 𝐸2 ; 𝑇 𝑃 = 𝑃 + 𝑣 , (𝑃 ∈ 𝐼𝑅𝑛) Ģeklinde tanımlı T dönüĢümüne 𝑣 ∈ 𝐸𝑛 ile eĢleĢtirilmiĢ bir öteleme dönüĢümü adı verilir.
Öteleme dönüĢümünün matematiksel tanımı böyle yapılırken, pedagojik boyutunun da göz önüne alınması ve öğrencilerin karĢılaĢtıkları güçlüklerin irdelenmesi gerekmektedir. Öteleme dönüĢümü düzlemi düzleme dönüĢtüren bir dönüĢüm olduğu için düzlemdeki tüm noktaların ötelendiğinin anlaĢılması önemlidir. Bu dönüĢümün sabit noktası yoktur, birebir ve örtendir. Bu ise düzlemde pek çok noktanın, doğru parçaların ve düzlemsel Ģekillerin öteleme sonucundaki görüntülerinin belirlenmesi ve gözlemlenmesi ile fark edilir. Vektörlerin öteleme dönüĢümündeki rolünün fark edilmesi önemlidir. Bu rolü anlamada aĢağıdaki maddelerin kavramsallaĢtırılması temel teĢkil eder.
i) Öteleme dönüĢümünü temsil eden vektörün değiĢtirilmesi sadece noktaların görüntülerini, yani görüntü noktalarını etkiler;
ii) Vektörün büyüklüğünün değiĢtirilmesi düzlemdeki noktalar ile onların görüntüsü olan noktalar arasındaki mesafeyi etkiler;
iii) Vektörün yönünün değiĢtirilmesi görüntü noktalarının hareket yönünü etkiler; iv) Sıfır vektörünün temsil ettiği öteleme düzlemdeki bütün noktaları sabit tutar. Öteleme dönüĢümü uzaklığı ve bunun sonucu olarak açıları ve arada olmayı korur. Böylece doğrudaĢ noktalar yine doğrudaĢ noktalara dönüĢür ve böylece doğrular doğrulara, çokgenler çokgenlere, çemberler çemberlere dönüĢür. Ötelemenin geometrik nesnelere (doğru parçası, ıĢın, çember, doğru, vs.) uygulanabilirliğinin özümsenmesi oldukça önemlidir (Argün vd., 2014).
11
2.1.2.2. Dönme Dönüşümü
Hareketli bir nesnenin yaptığı temel hareketlerden biri dönmedir. DönüĢümler dönmeler kullanılarak da inĢa edilebilir. Dolayısıyla uzayda dönme dönüĢümleri, nesneleri verilen bir nokta etrafında (dönme merkezi) verilen bir açı ölçüsü kadar hareket ettirir. Buna göre, düzlemde dönmeyi iki tür veri ile tamamen belirleyebiliriz. Bunlar biri nokta ve diğeri açıdır. Saat yönünün ters yönünde döndürmek için pozitif yöndeki açılar, saat yönünde döndürmek için negatif yöndeki açılar kullanılır.
Dönme dönüĢümünün formal tanımı aĢağıda verildiği gibidir:
Tanım: 𝐸2 Öklid düzlemi, 𝑀(ℎ, 𝑘) ∈ 𝐸2 de sabit bir nokta ve 𝜃 bir açının esas ölçüsü olsun. P(x,y) düzlemin herhangi bir noktası olmak üzere,
𝑅𝜃 ,𝑀 𝑃 : = 𝑅𝜃,𝑀 𝑥, 𝑦 = 𝑥′, 𝑦′
= ( 𝑥 − ℎ 𝑐𝑜𝑠𝜃 − 𝑦 − 𝑘 𝑠𝑖𝑛𝜃 + ℎ, 𝑥 − ℎ 𝑠𝑖𝑛𝜃 + 𝑦 − 𝑘 𝑐𝑜𝑠𝜃 + 𝑘)
Ģeklinde tanımlı 𝑅𝜃 ,𝑀: 𝐸2 → 𝐸2 dönüĢümüne M(h,k) merkezli 𝜃 radyanlık bir dönme dönüĢümü denir.
Dönme dönüĢümünün tanımı böyle yapılırken pedagojik boyutunun da düĢünülmesi ve öğrencilerin yaĢadıkları zorlukların irdelenmesi gerekmektedir. Dönme dönüĢümü düzlemi düzleme dönüĢtüren bir dönüĢüm olduğu için düzlemdeki tüm noktaların ötelendiğinin öğrencilerce anlaĢılması önemlidir. Bu dönüĢümün tek sabit noktası dönmenin merkezidir ve dönme dönüĢümü birebir ve örtendir. Bu ise düzlemde pek çok noktanın, doğru
parçalarının ve düzlemsel Ģekillerin dönme sonucundaki görüntülerinin belirlenmesi ve gözlemlenmesi ile fark edilir.
Verilen açının dönme dönüĢümündeki rolünün anlaĢılması önemlidir. Bu rolü anlamada Ģu bileĢenlerin kavramsallaĢtırılması gerekmektedir.
i) Açının veya merkezin değiĢtirilmesi sadece değer kümesindeki noktaları, yani görüntü noktalarını etkiler.
ii) Açının ölçüsünün değiĢtirilmesi belirli noktalar ile görüntülerinin birbirlerine göre konumlarını etkiler.
iii) Vektörün yönünün değiĢtirilmesi görüntü noktalarının hareket yönünün etkiler. iv) Dönme açısının ölçüsü 0 olan dönme dönüĢümü düzlemdeki bütün noktaları
12
Dönme dönüĢümü uzaklığı koruduğundan açıları ve arada olmayı da korur. DoğrudaĢ noktalar yine doğrudaĢ noktalara dönüĢtüğünden doğrular doğrulara, çokgenler çokgenlere, çemberler çemberlere dönüĢür. Dönmenin geometrik nesnelere (doğru parçası, ıĢın, çember, doğru, vb.) uygulanabilirliğinin iyi anlaĢılması önem teĢkil etmektedir. Bunlar yapılırken aĢağıdaki adımlar dikkate alınmalıdır:
i) Bir doğru parçası ile dönme dönüĢümü altındaki görüntüsü eĢittir.
ii) Açının ölçüsü, yönü ve merkezi değiĢse bile ötelemeye uğratılan doğru parçasının ve görüntüsünün eĢliği bozulmaz.
iii) Doğru parçası üzerindeki tüm noktalar açı ölçüsünün büyüklüğüne ve merkeze bağlı olarak dönüĢüme uğrar.
iv) Doğru parçası üzerindeki tüm noktalar açı ölçüsünün büyüklüğüne merkeze bağlı olarak dönüĢüme uğrar.
v) Doğru parçası üzerindeki tüm noktalar açı ölçüsünün büyüklüğüne ve merkeze bağlı olarak dönüĢüme uğrar (Argün vd., 2014).
2.1.2.3. Yansıma Dönüşümü
Düz aynaya baktığımızda bir nesne aynaya hangi uzaklıkta ise, o nesnenin görüntüsünün aynaya uzaklığının da aynı olduğu görülür. Bunun anlamı, düzlemin her bir noktasını ayna rolünü oynayan bir doğruya göre yansıttığımızda o noktanın düzlemde bir görüntüsünü elde ederiz. Bu noktanın doğruya olan uzaklığı ne ise bu noktanın görüntüsünün de doğruya olan uzaklığı odur. Bu doğruya “yansıma doğrusu” adı verilmektedir. Noktaları böyle dönüĢtürmenin iki temel özelliği vardır. Bunlardan birincisi, yansıtılan nokta P ile onun görüntüsü P‟ nün oluĢturduğu 𝑃𝑃′ doğru parçasının yansıma doğrusuna dik
olmasıdır. Ġkincisi ise, P noktası yansıma doğrusuna ait olduğunda 𝑃 = 𝑃′ olmasıdır. Diğer
taraftan süsleme, kaplama, resim, tasarım ve sanat gibi gerçek hayatın hemen hemen her alanında kullanılan dönüĢümlerden biri yansımadır.
13
Tanım:
(1) 𝑆: 𝐼𝑅3→ 𝐼𝑅3 bir lineer dönüĢüm, d bir düzlem ve ℎ𝑒𝑟 𝑃 ∈ 𝐼𝑅3 için 𝑆 𝑃 = 𝑃′ olsun. Eğer düzlemi 𝑃 ∈ 𝐼𝑅3 𝑖ç𝑖𝑛 𝑃𝑃′ doğru parçasına dik ve 𝑃 𝑖𝑙𝑒 𝑆 𝑃 = 𝑃′ noktalarının d düzlemine uzaklıkları eĢit ise o zaman S dönüĢümüne d düzlemine göre yansıma dönüĢümü adı verilir.
(2) 𝑆: 𝐼𝑅3→ 𝐼𝑅3 bir lineer dönüĢüm, 𝑙 bir doğru ve her 𝑃 ∈ 𝐼𝑅3 için 𝑆 𝑃 = 𝑃′ olsun. Eğer 𝑙 doğrusu 𝑃 ∈ 𝐼𝑅3 için 𝑃𝑃′ doğru parçasına dik ve 𝑃 𝑖𝑙𝑒 𝑆 𝑃 = 𝑃′ noktalarının 𝑙 doğrusuna uzaklıkları eĢit ise o zaman S dönüĢümüne 𝑙 doğrusuna göre yansıma dönüĢümü adı verilir.
(3) 𝑆: 𝐼𝑅3→ 𝐼𝑅3 bir lineer dönüĢüm, 𝐼𝑅3 de bir nokta C olsun. 𝐼𝑅3 deki her P noktası için 𝑃𝑃′ doğru parçasının orta noktası C ise S dönüĢümüne C noktasına göre yansıma dönüĢümü adı verilir.
Yansıma dönüĢümünü tanıtırken, özel yansıma doğruları ile yansıma noktaları seçmek bu kavramın anlaĢılmasını kolaylaĢtırır. Bunun için yaygın seçimler yansıma doğruları için eksenler ve 𝑦 = 𝑥 𝑣𝑒 𝑦 = −𝑥 ile verilen doğrular; yansıma noktası için 0,0 , 𝑥, 0 ve (0, 𝑦) Ģeklindeki noktalardır. Örneğin, doğruya göre yansıma dönüĢümünün cebirsel ifadesinde 𝑥 = 0 doğrusu alınırsa 𝑎 = 1, 𝑏 = 0 ve 𝑐 = 0 olur ve bu durumda 𝑘 = 1 olacaktır. Buna göre yansıma dönüĢümü 𝑥′ = −𝑥, 𝑦′ = 𝑦 olarak ifade edilir. Benzer Ģekilde, 𝑦 = 0 doğrusuna göre yansıma dönüĢümü de 𝑥′ = 𝑥, 𝑦′ = −𝑦 olur (Argün vd., 2014).
2.1.3. DönüĢümler ile ilgili Yapılan ÇalıĢmalar
DönüĢümler öğrenme alanı ile ilgili yapılan çalıĢmalar incelendiğinde, kavramın öğretimini, öğretmen ve öğretmen adaylarının bilgilerini ve öğrencilerin ve öğretmen adaylarının öğrenmesini inceleyen çalıĢmalar olmak üzere üç ana baĢlıkta toplanabilir. Yapılan çalıĢmaların ağırlıklı olarak dönüĢümlerin öğretimi üzerine olduğu söylenebilir. Örneğin, literatürde dinamik geometrik programları kullanılarak (GSP, Cabri 3D, TI hesap makineleri) dönüĢümler ile ilgili verilen eğitimin ilköğretim, lise seviyesinde öğrencilerin ve öğretmen adaylarının öğrenmesine etkisinin araĢtırıldığı çalıĢmaların çoğunlukta olduğu tespit edilmiĢtir (Battista vd., 1982; Dixon, 2010; Edwards, 1991; Ernest, 1988; Flanagan,
14
2001; Harper, 2002; Hollebrands, 2003, 2007; Kordaki ve Potari, 1998; Laborde, 2001; Leong ve Tim-Teo, 2003; Sünker ve Zembat, 2012).
Flagan (2001), araĢtırmasının sonucunda, öğrencilerin dönüĢümleri bir hareket olarak algılamasından ziyade bir fonksiyon olarak ele almasının oldukça önemli olduğunu vurgulamıĢtır. Flagan (2001), fonksiyonlar kavramının dönüĢümler öğrenme alanının öğrenilmesinde temel bir öneme sahip olduğunu vurgulamıĢ ve dönüĢümlerin öğrenilmesinde fonksiyonlar dıĢında hangi matematiksel kavramların öğrenilmesinin önemli bir yere sahip olduğunu araĢtıran çalıĢmaların yapılmasını gerektiğini vurgulamıĢtır. Edwards (1991), Logo Microworld ile ortaokul öğrencileriyle yaptığı çalıĢmasında öğrencilerin bilgisayar ekranında dönüĢümler ile ilgili kavramsal değiĢimler yerine daha çok geometrik Ģeklin yönü ve konumu ile ilgili görsel değiĢikliklere odaklandıklarını bulmuĢtur. Mesela bir öğrenciye bir Ģeklin yansımasını sorduğunda, öğrenci Ģeklin dikey ve yatay hareketlerini göstermek yerine direk olarak en son halini çizmiĢtir. Logo Microworld ile yapılan çalıĢmalarda öğrencilerin ya görsel figürlere ya da sembolik temsillere odaklandıklarında ve bu ikisi arasındaki iliĢkiyi bazen keĢfedemediklerini belirtmiĢlerdir (Hoyles ve Noss, 1987; Edwards, 1991).
Öğretmen adaylarının ve öğretmenlerin dönüĢümler ile ilgili bilgilerini biliĢsel ve yapılandırmacı teoriler aracılığıyla inceleyen çalıĢmalar tespit edilmiĢtir (Law, 1991; Portnoy, Grundmeimer, ve Graham, 2006; Thaqi, Giménez, ve Rosich, 2011; Yanik ve Flores, 2009; Yanik, 2006, 2011). Ayrıca öğretmenin dönüĢümler ile ilgili bilgisini öğrencilerle olan etkileĢimi bağlamında inceleyen çalıĢmalar da yapılmıĢtır (Dekker ve Elshout-Mohr, 2004; Margolinas vd., 2005). Yapılan çalıĢmalar öğretmenlerin ve öğretmen adaylarının dönüĢümler ile ilgili yaĢadığı zorlukları ortaya koymuĢlardır (Portnoy, Grundmeimer, ve Graham, 2006; Thaqi, Giménez, ve Rosich, 2011; Yanik, 2006, 2011; Yanik, Flores, 2009). Örneğin, eğer öğretmenlerin dönüĢümler ile ilgili yaklaĢımları görsel ise onların dönüĢümlerin ortak özelliklerini soyutlamada zorluk yaĢadıkları ortaya çıkarılmıĢtır (Portnoy, Grundmeimer, ve Graham, 2006; Thaqi, Giménez, ve Rosich, 2011). Ötelemeyi matematiksel nesne yerine fiziksel bir hareket olarak ele alma öğretmen adaylarının karĢılaĢtığı bir diğer zorluk olduğu yapılan araĢtırmalar sonucu elde edilmiĢtir (Yanik ve Flores, 2009). Law (1991) ise öğretmen adaylarının dönüĢümler ile ilgili nesnelleĢtirilmiĢ soyut tanım yapmada zorluk çektiklerini belirtmiĢtir. Vektörü simetri doğrusu olarak alma öğretmen adaylarının yaĢadığı
15
zorluklardan bir diğeridir (Yanik, 2011; Yanik ve Flores, 2009). Harper (2002), yaptığı araĢtırmasında öğretmen adaylarının dönüĢümlerle ilgili kullandıkları kelimelerin oldukça basit olduğunu ortaya koymuĢtur. Ayrıca, öğretmen adaylarının öteleme vektörünü asıl Ģekil ve görüntüsü arasında konumlandırmada ve öteleme vektörünü Ģekil görüntüsünü bulurken kullanmada zorluk çektiklerini tespit etmiĢtir.
Öğrenme üzerine yapılan çalıĢmalar ise; öğrencilerin öğrenmelerini teknolojik ortamda inceleyenler (Edwards, 1997; Glass, 2001) ve teknolojik olmayan bir ortamda inceleyenler (Hollebrands, 2004; Xistouri ve Pitta-Pantazi, 2011) olmak üzere ikiye ayrılmaktadır. Yapılan araĢtırmalar, öğrencilerin öteleme dönüĢümünde yaĢadıkları zorlukların vektör kavramından kaynaklandığını vurgulamaktadır (Hollebrands, 2004; Laborde, 2001). DönüĢümlerin düzlemi düzleme dönüĢtüren bir dönüĢüm olduğu için düzlemin tüm noktalarına uygulanmasında öğrencilerin güçlük yaĢadığı tespit edilmiĢtir (Sünker ve Zembat, 2012; Hollebrands, 2003; Yanik ve Flores, 2009). Örneğin, ABC üçgeninin DE doğrusuna göre yansımasını ele alacak olursak, burada dönüĢüm sadece ABC üçgenine uygulanmaz aynı zamanda DE doğrusuna da uygulanır (Hollebrands, 2003). Ötelemeyi matematiksel nesne yerine fiziksel bir hareket olarak ele alma öğrencilerin karĢılaĢtığı bir diğer zorluk olarak yapılan araĢtırmalar sonucu elde edilmiĢtir (Glass, 2001; Hollebrands, 2003; Yanik ve Flores, 2009).
2.1.4. DönüĢümlerin Öğretim Programındaki Yeri
Türkiye'deki matematik öğretim programı sarmal bir yapıya sahiptir, yani öğrenciler geometrik dönüĢümleri ilköğretimde 6. ,7. ve 8. sınıf seviyesinde, lisede ise 9. ve 10. sınıf seviyesinde görmüĢlerdir (MEB, 2009, 2010). Ġlköğretim matematik öğretim programı dönüĢümleri düzlemdeki noktaları noktalara eĢleyen fonksiyon yerine fiziksel hareket olarak öğretilmesini önermektedir (Sünker ve Zembat, 2012). 9.sınıfta geometrik dönüĢümler çokgenler ve düzlemde kaplamalar ünitesi altında yer almaktadır; ilköğretim matematik öğretim programında olduğu gibi öğretim programı dönüĢümlerin fiziksel hareket olarak öğretilmesini önermektedir. 10. sınıfta ise ilköğretim ve 9. sınıf öğretim programının aksine dönüĢümlerin düzlemdeki noktaları noktalara eĢleyen fonksiyon olarak öğretilmesi önerilmektedir. Sonuç olarak, 10. sınıfta geometrik dönüĢümlerin öğretilmesi kritik bir öneme sahiptir, çünkü öğrencilerin öğrenmelerinin geliĢiminde dönüĢümleri
16
fiziksel hareket olarak algılamadan fonksiyon olarak algılamaya geçiĢ yapmaları gerekmektedir. Bu geliĢimsel süreçte öğrencilerin dönüĢümleri hareket yerine fonksiyon olarak öğrenmelerine geçiĢ yapmalarını sağlamak adına öğretmenler önemli bir role sahiptirler.
2.2. Teorik Çerçeve
2.2.1. Matematik Öğrenimine Sosyo-kültürel YaklaĢım
“Matematiksel BiliĢe ĠletiĢimsel YaklaĢım” teorisinin kökenleri sosyal kültürel teoriye dayanmaktadır. Vygotsky‟e (1978) göre, bireylerin kültürel geliĢimi iki seviyede görülür; öncelikle sosyal seviyede sonrasında bireysel seviyede; yani diğer bir deyiĢle bu kültürel geliĢim önce bireyler arasında (inter-psychological) ve sonra da bireyin içinde (intra-psychological) gerçekleĢir. Vygotsky (1978), bireyin diğerleriyle iletiĢim kurmak için kullandığı konuĢmanın, yüksek seviyedeki zihinsel süreçlerini içselleĢtirdiği içsel konuĢmasından önce geldiğini belirtmektedir. DüĢünme, bireyler arası iletiĢimin bireyselleĢtirilmiĢ biçimi olarak karĢımıza çıkmaktadır. Yüksek seviyedeki zihinsel süreçler genel konuĢmadan (public speech) içsel konuĢmaya (inner private speech) doğru içselleĢtirilmiĢ süreçler olarak araçlarla gerçekleĢtirilir (Vygotsky, 1986). Matematiksel BiliĢe ĠletiĢimsel YaklaĢım teorisi ise düĢünmeyi kiĢinin kendisiyle olan iletiĢimi olarak tanımlayarak Vygotsky‟ ye göre bireysel seviyede gerçekleĢen düĢünmeyi iletiĢim gibi sosyal bir olgu olarak ele almaktadır (Güçler, baskıda).
Sosyal kültürel teori üzerine çalıĢan teorisyenler uzun yıllardan beri üzerine çalıĢmalar yapılan bireysel biliĢten uzaklaĢtırıp, öğrenme ve düĢünmeyi iletiĢim ve farklı etkinliklere katılım aracılığıyla incelememizi sağlamaktadırlar. Bunun yanında bu teorisyenler biliĢsel teorisyenlerin yöntem ve bulgularını reddetmemektedirler, sadece öğrenmeye farklı bir perspektiften bakmaktadırlar. Kökenleri Vygotsky‟ nin çalıĢmasına dayanan sosyal kültürel teori, bireyin zihinsel faaliyetlerini bağlamsal olarak anlamayı hedeflemektedir (Wertsch, 1990).Bu bağlamda sınıf içi yapılacak araĢtırmalarda bize iyi bir perspektif sağlayacağı düĢünülen teorilerden biri de sosyal kültürel teoridir çünkü sosyal kültürel teori öğrenmeyi bağlamıyla birlikte incelemektedir. Bunun için bireyin zihinsel faaliyetleri
17
ile bunların gerçekleĢtiği kültürel, tarihsel, kurumsal durumlar/ortamlar arasındaki iliĢkiyi açıklamak önemlidir (Wertsch vd.,1995). Bireyin zihinsel faaliyetlerini bağlamsal olarak anlamakla birlikte, zihinsel faaliyetler bireyler arası iletiĢimin bireyselleĢtirilmesinden doğar ve böylece öğrenme iletiĢim yoluyla oluĢan değiĢikliktir (Ben-Yehuda vd., 2005). Özellikle, matematiği öğrenme, matematiksel söylemlerin daha açık ve net hale gelmesi olarak görülür (Sfard, 2001). Özetle, bu araĢtırmada lise öğrencilerinin dönüĢümler öğrenme alanı ile ilgili matematiksel söylemlerinin geliĢimini incelerken sosyal kültürel teoriden faydalanacaktır.
2.2.2. Matematiksel BiliĢe ĠletiĢimsel YaklaĢım
Matematiksel BiliĢe ĠletiĢimsel YaklaĢım teorisi düĢünmeyi kiĢinin kendisiyle olan iletiĢimi olarak tanımlayarak düĢünme ile iletiĢim arasındaki ikilem ortadan kalkmaktadır. (Sfard, 2008). Sfard‟ a (2008) göre söylem, kiĢisel veya kiĢilerarası bir iletiĢim Ģeklidir, sözel olabilir veya olmayabilir ve konuma bağlı değiĢir. Matematiksel kelimeleri günlük hayatımızda da kullanıyorsak (limit gibi), ona günlük dile ait söylemler içinde günlük konuĢma dilini kullanmak denilir. Böylece matematiksel düĢünmenin mekanizmasını keĢfetmek için öğrencilerin günlük hayatta ve matematikte kullandıkları söylemler önemlidir; çünkü öğrenciler düĢünme süreçlerini açıklamaya alıĢkın olmayabiliriler, fakat ne bildiklerini söylerler. Sfard (2008), matematiksel öğrenmeyi matematiksel söyleme iĢtirak etme biçimdeki sürekli değiĢim olarak ele almaktadır (Güçler, baskıda). Özellikle, matematiği öğrenme, matematiksel söylemlerin (mathematical discourse) daha açık ve net hale gelmesi olarak görülür (Sfard, 2001).
Özetle, öğrencilerin ve öğretmenin matematiksel söylemlerini incelerken, dönüĢümler öğrenme alanı bağlamında, matematiksel iletiĢim için kullandıkları simgeler, temsiller, kelimeler, diyagramlar ve sembollerin yer aldığı cümlelere farklı zamanlarda odaklanılmıĢtır. Bunun nedeni ise matematiksel öğrenmenin ortama bağlı olarak bireysel veya bireyler arasındaki iletiĢimin değiĢimiyle gerçekleĢtiği düĢünülmektedir. Bunun için matematiksel söylemlerin dört bileĢeni göz önünde bulundurulmuĢtur: sözcük kullanımı (word use), görsel aracılar (visiual mediators), rutinler (routines), tasdik edilmiş anlatılar (endorsed narratives) (Sfard, 2008).
18
2.2.2.1. Sözcük Kullanımı
Söylemlerin ayırıcı özelliklerinden biri kullandıkları anahtar kelimelerdir (Sfard, 2008). Matematikte kelimeler sadece miktarı ve Ģekilleri belirtmezler. Günlük dilde kullandığımız söylemlerde birçok sayıyla iliĢkili kelimeler karĢımıza çıkar. Fakat okulda veya akademik ortamda kullanılan matematiksel söylemlerde bu sözcüklerin kullanımı kullanılan alana özgüdür. Sözcük kullanımı oldukça önemlidir, çünkü kullanılan sözcük baĢka anlamlarıyla eĢdeğer olabilir, bu bireyin kelimeyi hangi anlamda kullandığıyla ilgilidir. Sözcük kullanımı matematiksel iletiĢimin ya da iletiĢim bozukluğunun en temel göstergesidir; çünkü sözcük kullanımında konuĢma, eylem, yazılanlar, çizilenler ve doğru kabul edilen her Ģey vardır. Bu verilen bileĢenlerle iletiĢim kuvvetlenebilir ya da iletiĢimle ilgili sorunlar çıkabilir. GeliĢimsel olarak verilen sözcük kullanımının hiyerarĢik aĢamaları örnekleriyle birlikte aĢağıdaki gibi özetlenmiĢtir.
Bu geliĢim dört hiyerarĢik aĢamadan oluĢmaktadır: edilgen kullanım (passive use), rutin-bazlı kullanım (routine-driven use), tabir-bazlı kullanım (phrase-driven use), ve nesne-bazlı kullanım (object-driven use) (Sfard, 2008). Edilgen kullanım aĢamasında öğrenciler matematiksel sözcükleri sözel olarak dile getirememelerine rağmen, o sözcükleri baĢkalarından duyduklarında belli rutinleri uygulamaya baĢlayabilirler...Edilgen sözcük kullanımı özellikle küçük yaĢtaki öğrencilerde daha net bir Ģekilde gözlemlenebilir. Bu aĢamada, öğrenci “toplam” kelimesini cümle içinde kullanamamaktadır. Rutin-bazlı sözcük kullanımında öğrenci belli matematiksel kelimeleri söyleminde kullanmaya baĢlamıĢtır, ancak bu kullanım sadece belirli eylemsel rutinlerle sınırlıdır. Mesela bir öğrenci “toplam” kelimesini söyleminde kullanabiliyor fakat bu kelimeyi her duyduğu ve gördüğü durumda otomatikleĢmiĢ bir sayma eylemi baĢlatıyorsa, bu öğrenci “toplam” kelimesini rutin-bazlı kullanmaktadır. BaĢka bir deyiĢle, bu öğrenci için “toplam” kelimesi sayma eylemiyle sınırlıdır. Tabir-bazlı sözcük
kullanımı matematiksel sözcüklerden ziyade o sözcüklerin içinde bulunduğu tabirler öğrencinin
söyleminde baskın bir hal almaktadır. Bu aĢamadaki öğrenciler, matematiksel kelimeleri uyguladıkları rutinler yerine belirli tabirlerle eĢleĢtirmektedirler. Mesela bir öğrenci “toplam nedir?” sorusuna “ (sayma eylemini yapmadan) toplam dendiği zaman çeĢitli nesneleri grupluyoruz”... gibi cevaplar veriyorsa, toplam kelimesini tabir-bazlı kullanmaktadır. Matematiksel sözcük kullanımının son aĢaması olan nesne-bazlı kullanımda, öğrenci sözcükleri isim olarak kullanabilmektedir. Bu aĢamada matematiksel kelimeler nesneleĢtirilmiĢ ve kendi içlerinde anlam taĢıyan somut matematiksel birimlere ve kavramlara dönüĢtürülmüĢtür (Güçler, baskıda, s. 631-632).
2.2.2.2. Görsel Aracılar
ĠletiĢim sürecinin bir parçasını harekete geçiren öğelerden biri de görsel nesnelerdir (Sfard, 2008). Günlük dile ait olan söylemler, söylemler içinde yer alan materyallerin resimleri ile iliĢkilendirilirken, bilimsel matematiksel söylemler daha çok iletiĢimin bir parçasında üretilen sembolik notasyonlarla iliĢkilendirilirler. Görsel aracılar üzerindeki iĢlemlerle ilintili iletiĢim; otomatikleĢmiĢ ve somutlaĢtırılmıĢtır. Matematiksel söylemde görsel
19
aracılar, matematiksel iletiĢim için yazılı ve sözlü olarak kullandığımız tüm görsel araçları kapsamaktadır. Semboller, grafikler, geometrik Ģekiller, tablolar ve hatta matematiğin ifade edildiği lisandaki görsel simgeler (harfler, yazılı sözcükler) görsel aracılara birer örnektir. Matematiksel söylem analizinde söyleme katılan bireylerin hangi görsel aracıları kullandığını listelemek yeterli değildir. Analizin tamamlanması için, bu görsel aracıları katılımcıların nasıl kullandığı (rutinler), bu aracıları kullanma aĢamasındaki sözcük tercihleri ve bu görsel aracıları hangi matematiksel anlatıları tasdik etmek için kullandıklarının araĢtırılması oldukça önemlidir (Güçler, baskıda).
2.2.2.3. Rutinler
Matematiksel söyleme katılan bireylerin sürekli tekrarlayan eylemleridir (Sfard, 2008). Bu eylemler matematiksel söylemin diğer öğeleri üstü kapalı veya açık etkiler. Özel olarak, bu eylemler; matematiksel kelimeler ya da sayılar ve geometrik Ģekillerle ilgili süreçler olarak görülebilir. Bu örüntüler, katılımcıların eylemleri ile matematiksel söylemlerindeki diğer öğeleri yönlendirir. Rutinler, söylem içindeki kelimeler veya eylemler arasında tutarlılık var mı ya da iletiĢimsel bozukluk var mı yok mu onu ortaya çıkarmamızı sağlıyor. Eğer biz söylem analizinde sadece kelime kullanımına baksaydık bu durum bizi sınırlandırırdı, söylem analizinde eylemleri incelemek bize farklı perspektifler sunmaktadır. Rutinlerin incelenmesi, katılımcıların eylemlerinin analizi sonucunda mümkün olmaktadır ve rutinlerin analizinin içerikleri aĢağıda verilmektedir/
Sfard‟ın teorisine göre rutin analizinin ilk aĢaması rutinlerin ortaya çıkmasına ve kullanımına neden olan tetikleyici durumları (prompts) saptamaktır. Bu teori bir rutinin nasıl ve ne zaman uygulandığının incelenmesini gerekli görmektedir. Rutinin nasıl uygulandığı, rutin uygulanırken kullanılan yöntemi ve eylemi içermektedir. Rutinin ne zaman uygulandığı ise katılımcıların bir rutinin kullanımını hangi matematiksel koĢullarda uygun gördüklerini içerir.
Rutinlerin ne zaman kullanıldığını iki ayrı terim kapsamında ele alınmaktadır: uygulanabilirlik
(applicability) ve kapanış (closure). Uygulanabilirlik, bir katılımcının hangi durumlarda belirli bir rutini uygulayacağının altını çizerken, kapanış katılımcının hangi durumlarda uyguladığı