Fibonacci dizisi ve altın oran'ın müzikte kullanımının incelenmesi

T.C.

SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ

FİBONACCİ DİZİSİ ve ALTIN ORAN’IN MÜZİKTE KULLANIMININ İNCELENMESİ

Sümeyye BAKIM YÜKSEK LİSANS Matematik Anabilim Dalı

Mayıs-2014 KONYA Her Hakkı Saklıdır

Sümeyye Bakım tarafından hazırlanan “Fibonacci Dizisi ve Altın Oran’ın Müzikte Kullanımın İncelenmesi” adlı tez çalışması …/…/… tarihinde aşağıdaki jüri tarafından oy birliği / oy çokluğu ile Selçuk Üniversitesi Fen Bilimleri Enstitüsü Matematik Anabilim Dalı’nda YÜKSEK LİSANS TEZİ olarak kabul edilmiştir.

Jüri Üyeleri İmza

Başkan

Unvanı Adı SOYADI ………..

Danışman

Prof. Dr. Durmuş BOZKURT ………..

Doç. Dr. Seyit YÖRE ………..

Üye

Unvanı Adı SOYADI ………..

Üye

Unvanı Adı SOYADI ………..

Üye

Unvanı Adı SOYADI ………..

Yukarıdaki sonucu onaylarım.

Prof. Dr. Aşır Genç FBE Müdürü

Bu tezdeki bütün bilgilerin etik davranış ve akademik kurallar çerçevesinde elde edildiğini ve tez yazım kurallarına uygun olarak hazırlanan bu çalışmada bana ait olmayan her türlü ifade ve bilginin kaynağına eksiksiz atıf yapıldığını bildiririm.

DECLARATION PAGE

I hereby declare that all information in this document has been obtained and presented in accordance with academic rules and ethical conduct. I also declare that, as required by these rules and conduct, I have fully cited and referenced all material and results that are not original to this work.

Sümeyye BAKIM Tarih:

iv

ÖZET

YÜKSEK LİSANS

FİBONACCİ DİZİSİ ve ALTIN ORAN’IN MÜZİKTE KULLANIMININ İNCELENMESİ

Sümeyye BAKIM

Selçuk Üniversitesi Fen Bilimleri Enstitüsü Matematik Anabilim Dalı

Danışman: Prof. Dr. Durmuş BOZKURT Doç. Dr. Seyit YÖRE

2014, 47 Sayfa Jüri

Danışman Prof. Dr. Durmuş BOZKURT Doç. Dr. Seyit YÖRE

Prof. Dr. Hasan ŞENAY Doç. Dr. Yıldıray KESKİN

Bu çalışmada kısaca matematiksel sayı dizileri tanımlandıktan sonra Fibonacci Dizisi ve Altın Oran’ın özellikleri verilmiştir. Genel olarak matematik ve müzik arasındaki ilişki değerlendirilerek, Fibonacci Dizisi ve Altın Oran’ın müzikle ilişkisine geçilmiştir. Bazı Avrupa sanat müziği/çoksesli müzik bestecilerinin eserlerinden seçilen örnekler üzerinde bu zamana kadar yapılmış olan çalışmalardaki ön kabuller matematiksel ve müziksel doğrular çerçevesinde tartışılmıştır.

Anahtar Kelimeler: Altın Oran, Fibonacci Dizisi, Fibonacci Sayıları, Lucas Sayıları, Matematik, Müzik

v

ABSTRACT

MS THESIS

EXAMINATION OF THE USE OF FIBONACCI SEQUENCE AND GOLDEN PROPORTION IN MUSIC

Sümeyye BAKIM

THE GRADUATE SCHOOL OF NATURAL AND APPLIED SCIENCE OF SELÇUK UNIVERSITY

THE DEGREE OF MASTER OF SCIENCE IN MATHEMATICS Advisor: Prof. Dr. Durmuş BOZKURT

Assoc. Prof. Dr. Seyit YÖRE 2014, 47 Pages

Jury

Advisor Prof. Dr. Durmuş BOZKURT Assoc. Prof. Dr. Seyit YÖRE

Prof. Dr. Hasan ŞENAY Assoc. Prof. Dr. Yıldıray KESKİN

In this study, after defining mathematical number sequences, the properties of Fibonacci Sequence and Golden Ratio have been presented. The relationship between mathematics and music has generally been evaluated and then proceeded into the relationship of Fibocacci Sequence and Golden Ratio with music. Pre acceptances on the studies applied to the chosen examples of some European art music/multi-vocal composers up to now have been discussed within the framework of mathematical and musical facts.

Keywords: Golden Proportion, Fibonacci Sequence, Fibonacci Numbers, Lucas Numbers, Mathematics, Music

vi SİMGELER VE KISALTMALAR n F :n . Fibonacci sayısı. n L : n . Lucas sayısı.

 : Phi, Türkçe okunuşuyla ‘fi’, Altın Oran’ı ifade eden simge. : : Reprise, yineleme, tekrar anlamına gelir.

Ö. : Ölçü. AO: Altın Oran.

: Bemol, sesleri kalınlaştırmaya yarayan işaret.

: Diyez, sesleri inceltmeye yarayan işaret.

vii

TANIMLAR

12 Ses sistemi (Twelve tone system): Do, Do♯, Re, Re♯, Mi, Fa, Fa♯, Sol, Sol♯, La,

La♯, Si notalarından oluşan ses sistemi ve 12 sesin 4 farklı çevrimine dayalı bir matematiksel bestecilik tekniğidir.

Akor (chord): İngilizce bir kelimedir. İki veya daha fazla notanın dikey olarak

eşzamanlı bir şekilde seslendirilmesidir.

Akord (tuning): İngilizce bir kelimedir. Çalgılarda teller arasında belirlenmiş ses

aralıklarının ayarıdır.

Allegro: İtalyanca bir kelimedir. Bir müzik eserinin hızlı tempoda seslendirileceğini

ifade eder.

Aralık: Müzikte seslerin arasındaki çeşitli matematiksel oranlardır. Küçük üçlü, büyük

altılı, sekizli vb. gibi terimlerle ifade edilir.

Armoni (harmony): İngilizce bir kelimedir. Müzikte akorların uyumlu olarak kendi

arasında nasıl bağlanacağını belirleyen kurallardır.

Arya (aria): İtalyanca bir kelimedir. Opera ve Oratoryo gibi müzikli sahne eserlerinde

bir veya daha fazla solistin orkestra eşliğinde söylediği kendi içinde bütünlüğü olan bir şarkı formudur.

Diyatonik dizi (diatonic): İngilizce bir kelimedir. Aynı anda tam, yarım, eksik ve artık

ses aralıklarından oluşan bir ses dizisi çeşitidir.

Doruk noktası (climax): İngilizce bir kelimedir. Bir müzik eserinde en yoğun ve

duygusal noktadır.

Forte: İtalyanca bir kelimedir. Müzik eserinin belirli bir yerinin kuvvetli bir şekilde seslendirilmesi demektir.

Fortissimo: İtalyanca bir kelimedir. Forte’den daha kuvvetli bir seslendirme demektir. Fugato: İtalyanca bir kelimedir. Bir füg formu çeşitidir.

Füg (Fugue): Fransızca bir kelimedir. Çoksesli müzikte bir formdur.

İkincil (Ara) Tema: Bir müzik eserinin birincil (ana) temasından sonra gelen

viii

Kantat (cantata): İtalyanca bir kelimedir. Orkestra, koro ve solistler için bestelenen bir

çoksesli müzik formudur.

Koda (coda): İtalyanca bir kelimedir. Bir bestenin sonuna konan bitiş bölümüdür. Kodetta (codetta): İtalyanca bir kelimedir. Koda’nın daha kısa şeklidir.

Konçerto (concerto): İngilizce bir kelimedir. Orkestra ve solist olan bir müzik aleti için

bestelenen bir çoksesli müzik formudur.

Kromatik dizi (chromatic): İngilizce bir kelimedir. Yarım ses aralıklardan oluşan bir

ses dizisi çeşitidir. Kromatik dizide temelde on iki yarım ses aralığı vardır.

Motif (motif): Fransızca bir kelimedir. Bir müzik eserinin en küçük/kısa temel fikridir

ve eser bu fikir üzerine kurulur.

Nakarat (chorus): İngilizce bir kelimedir. Bir müzik eserinin/şarkının tekrar kısmıdır. Oktav (octave): İngilizce bir kelimedir. Yedi sesten meydana gelen diziye (do, re, mi,

fa, sol, la, si) ve müzikte sekizli aralığa bu ad verilir.

Ostinato: İtalyanca bir kelimedir. Bir müzik eserinin tamamında veya bir kısmında aynı

şekilde tekrar eden kısa melodik veya ritmik yapıdır.

Ölçü (measure): İngilizce bir kelimedir. Bir müzik eserinin en küçük metrik kesitini

ifade eder. Ölçüler dikey çizgilerle birbirinden ayrılır. Bunlara ölçü çizgisi denir.

Pentatonik dizi (pentatonic): İngilizce bir kelimedir. Beş sesli (do, re, mi, sol, la) dizi

demektir.

Prelüd (prelude): İngilizce bir kelimedir. Giriş, başlangıç anlamına gelir ve müzik

eserlerinde giriş müziği olarak kullanılmasının yanı sıra kendi başına kısa bir formdur.

Resitatif (recitativo): İtalyanca bir kelimedir. Opera, oratoryo ve kantat gibi müzikli

sahne eserlerinde konuşma şeklindeki şarkı formudur.

Ritim (rhythm): İngilizce bir kelimedir. Müzik seslerinin belirli matematiksel (birlik,

ikilik, dörtlük, sekizlik vd.) sürelere bölünmesidir.

Senfoni (symphony): İngilizce bir kelimedir. Genellikle üç veya dört bölüm içeren ve

büyük orkestralar için bestelenen bir çoksesli müzik formudur.

Sonat (sonata): İtalyanca bir kelimedir. Bir veya birden fazla çalgı için bestelenen bir

ix

Sonat-allegro (sonata-allegro): İngilizce bir kelimedir. Bir sonatın veya sonattan

oluşan konçerto ve senfoni gibi formların ilk bölümüdür.

Sonat-rondo (sonata-rondo): İngilizce bir kelimedir. Hem sonat hem de rondo

formlarının özelliklerini taşıyan formdur.

Tema ve çeşitleme (theme and variations): İngilizce bir kelimedir. İlk olarak ana

temayı gösteren ve sonrasında gelen ifadelerle değişen ve gelişen bir çoksesli müzik formudur.

Tema (theme): İngilizce bir kelimedir. Bir müzik eserinin kurulduğu ana ezgidir. Tokkata (toccata): İtalyanca bir kelimedir. Özellikle org ve diğer çalgılar için

bestelenen bir çoksesli müzik formudur.

Vivo: İtalyanca bir kelimedir. Bir müzik eserinin tamamının veya belirli bir kısmının

daha canlı ve hareketli bir şekilde çalınmasını ifade eder.

Vuruş (beat): İngilizce bir kelimedir. Müzikte belirli sürelere bölünmüş ritmik

x İÇİNDEKİLER ÖZET ... iv ABSTRACT ...v SİMGELER VE KISALTMALAR ... vi TANIMLAR ... vii İÇİNDEKİLER ...x 1. GİRİŞ ...1 1.1. Tezin Amacı ...1 1.2. Tezin Önemi ...1

1.3. Matematiksel Diziler ve Fibonacci Dizisi ...2

1.4. Fibonacci Dizisi ve Altın Oran ...3

1.5. Matematik ve Müzik İlişkisi ...9

1.6. Fibonacci Dizisi ve Altın Oran’ın Müzikle İlişkisi ... 12

2. KAYNAK ARAŞTIRMASI ... 17

3. MATERYAL VE YÖNTEM ... 19

4. ARAŞTIRMA BULGULARI VE TARTIŞMA ... 20

4.1. İki ve Üç Bölümlü Form ... 20

4.2. Chopin’in Prelüdleri ... 21

4.3. Mozart’ın Piyano Sonatları ... 22

4.5. Bartók’un İki Piyano ve Vurmalı Çalgı Sonatı ... 27

4.6. Bach’ın Kromatik Fantezisi ... 34

5. SONUÇLAR VE ÖNERİLER... 37

5.1. Sonuçlar ... 37

5.2. Öneriler ... 38

KAYNAKLAR ... 39

xi

1. GİRİŞ

1.1. Tezin Amacı

Ortaçağ’ın en önemli İtalyan matematikçilerinden biri olan Leonardo Fibonacci (1170-1250) özgün bir teori geliştirmiştir ki Fibonacci Dizisi veya Sayıları olarak anılan teorideki sayıların ve bunlara bağlı olarak oluşan Altın Oran’ın doğal bilimler ve müzikte kullanıldığına dair dünyada birçok çalışma yapılmıştır. Fibonacci Dizisi ve Altın Oran’ın müzikteki varlığına dair çalışmalar, Avrupa sanat müziği/çoksesli müzik bestecilerinin eserlerinde bu sayıların kullanıldığının kanıtlanmaya çalışılması şeklindedir. Ancak, bu çalışmaları yapanların çoğunlukla Fibonacci Dizisi ve Altın Oran’ın müzikteki varlığını baştan kabul ettikleri, doğrudan bu sayıları bulmaya yöneldikleri, ancak bu sayıların müzik kuramıyla örtüşüp örtüşmediğine bakmadıkları ve incelenen bestecilerin bu sayıları bilinçli olarak kullanıp kullanmadıklarını sorgulamadıkları görülmüştür. Bu durumlar, Fibonacci Dizisi ve Altın Oran’ın müzikteki varlığına ilişkin bir problem ortaya çıkarmış, ilgili sayıların uluslararası müzik kuramına uymadığı, dolayısıyla yapılan çalışmalarda hatalar olduğu tespit edilmiştir.

Bu çalışmada, Fibonacci Dizisi ve Altın Oran’ın Avrupa sanat müziği eserlerinde olup olmadığını çeşitli yöntemlerle ifade eden kaynakların incelenmesi ve doğruluğunun tartışılması amaçlanmaktadır.

1.2. Tezin Önemi

Fibonacci Dizisi ve Altın Oran’ın müzikteki varlığını baştan kabul eden, doğrudan bu sayıları bulmaya yönelen, ancak bu sayıların müzik kuramıyla örtüşüp örtüşmediğini ve ilgili bestecilerin bu sayıları bilinçli olarak kullanıp kullanmadığını sorgulamayan çalışmaların doğrulunun tartışılmasıyla uluslararası alanda hatalı bir yaklaşımın düzeltilmesi ve bundan sonra Fibonacci Dizisi ve Altın Oran’ın müzikteki varlığına ilişkin yapılacak çalışmaları doğru bir şekilde yönlendirmek bu çalışmanın önemini oluşturur.

1.3. Matematiksel Diziler ve Fibonacci Dizisi

Tanım kümesi IN doğal sayılar kümesi, değer kümesi ise IR gerçel sayılar kümesi olan bir fonksiyona dizi denir.

x x x

1, 2, 3,

...

sayılarına dizinin terimleri, n ye

bağlı bir ifade olan

x

n ye ise dizinin genel terimi denir. Diziler ya

x x x

1, 2, 3,

...

gibi veya n

x

genel terimi x_n veya

 

x_n gibi gösterilebilir. Dizi sonlu ya da sonsuz olabilir. Pozitif tam sayılar



1, 2, 3, 4,...



sonsuz diziye örnek olarak verilebilir.



1, 2, 3, 4



dizisi ise sonlu bir dizidir. Sonsuz dizilerin bazı türleri bir sınır değerine yaklaşabilir. Sözgelimi 1,1/ 2,1/ 3,...,1/ ,...n dizisinde n sonsuza yaklaştıkça sıfır sınırına ulaşılır. Bir dizinin limiti önemli bir matematiksel kavramdır. Aritmetik diziler de sonsuz dizinin bir örneğidir. 1, 2, 3,..., ,... 2, 5, 8,..., 2 ( 1).3,... n u u u u n     

dizisinde n . terimin formülü, 2 ( 1).3

n

u   n

şeklindedir. Bir diziyi belirtmenin diğer bir yolu da dizinin ilk terimini belirlemektir: 2 1  u ve formül, n1 ve n   için 3 1   _n n u u (1)

şeklindedir. Bu tanıma tekrarlı tanım ve formüle tekrar formülü veya tekrarlı formül denir. İlk iki terimi,

1 ,

1 ₂

1  u 

u

ve tekrar formülü, n2ve n   için

2 1     _{n n} n u u u şeklinde belirlenirse, 1,1, 2,3,5,8,13,...

dizisi elde edilir. Bu diziye, on üçüncü yüzyıl İtalyan matematikçisi Leonardo Fibonacci’nin soyadını alan, Fibonacci Dizisi ve terimlerine de Fibonacci Sayıları adı verilir. n . Fibonacci Sayısı F ile gösterilirse, _n

1 1, 2 1, 3 2, 4 3, 5 5, 6 8,...

F  F  F  F  F  F 

olur. Bu dizi ile ilgili detaylı bilgi, bir sonraki bölümde verilecektir.

(1) formülü kullanılarak ve dizideki ilk iki terim için farklı sayılar seçilerek birçok farklı dizi belirlenebilir. Mesela, u₁ 1 ve u₂ 3 ve alınırsa aynı tekrar formülü ile,

1, 3, 4, 7, 11, 18, 29,...

şeklinde, on dokuzuncu yüzyıl Fransız matematikçisi F. Édouard Lucas’ın (1842-1891) soyadını alan, Lucas Dizisi elde edilir. Lucas dizisinin sayılarına, Lucas Sayıları denir ve n . Lucas sayısı için L gösterimi kullanılır. Lucas sayıları, Fibonacci sayıları ile _n yakından ilişkilidir (Hoggatt, 1969).

Genel olarak, (1) ile tanımlanan dizinin ilk iki terimi için rasgele tamsayılar olan p ve q alınırsa, yani u ₁ p ve u ₂ qiçin,

, , , 2 , 2 3 , 3 5 ,...

p q pq p q p q p q

Genelleştirilmiş Fibonacci Dizisi elde edilir (Hoggatt, 1969).

1.4. Fibonacci Dizisi ve Altın Oran 1.4.1. Tavşan problemi

Leonardo Pisano Bigollo veya Leonardo Bonacci olarak da anılan Leonardo Fibonacci (1170-1250), Liberabaci (Hesaplama Kitabı) (1202) adlı eserinde, sonradan gelecek olan matematikçilerin Altın Oran’ı anlaması için anahtar niteliğinde olan matematiksel bir bulmaca kurmuştur (Marie, 2012). Bu bulmaca tavşan problemidir. Bu problem, Ergin bir tavşan çiftinin her ay yeni bir yavru çifti verdiği ve yeni doğan bir çiftin 1 ay zarfında tam ergenliğe eriştikleri varsayımıyla, bir tavşan çiftinden başlayıp 1 yılda oluşan toplam tavşan çifti sayısını sormaktadır.

Fibonacci’nin bu problemi aşağıdaki şekilde özetlenebilir:

2. Bu çift Şubat ayının birinci günü ve sonrasında gelen her ayın birinci gününde bir çift tavşan oluşturur.

3. Her yeni çift bir ayda olgunlaşır ve ömrünün üçüncü ayından itibaren her ayın birinci günü bir çift oluşturur ve hiç tavşan ölmez.

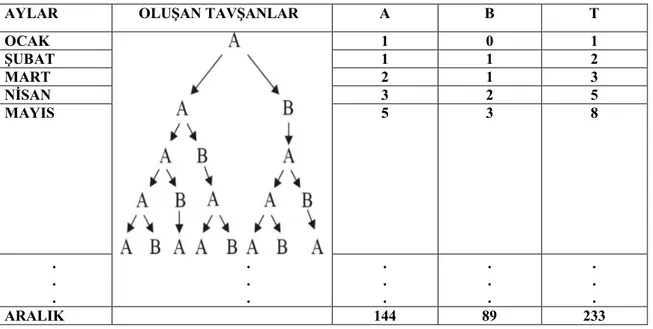
Tavşan çiftlerini kolayca hesaplamak için bu oluşumu çizelge ile göstermek daha yararlı olacaktır. Yetişkin çiftler A, yavru çiftler B, toplam tavşan sayısı T ile gösterilirse:

Çizelge 1.1: Bir yıl içinde oluşan tavşan çiftlerinin sayısı

AYLAR OLUŞAN TAVŞANLAR A B T

OCAK 1 0 1 ŞUBAT 1 1 2 MART 2 1 3 NİSAN 3 2 5 MAYIS 5 3 8 . . . . . . . . . . . . . . . ARALIK 144 89 233

Hem yetişkin, hem yavru hem de toplam çift sayısının bulunmasını sağlayan çizelge elde edilir.

“A’ların sayısı” sütunundaki diziyi belirtmek için ilk iki terim, 1

1 

u ve u₂ 1

ve tekrar formülü, u2 için u_n u_n1u_n2

yazıldığında, beklenildiği gibi, 1, 1, 2, 3, 5, 8, 13, 21, 34,...

dizisi bulunur. “B’lerin sayısı” sütunu için, u₁ 0 ve u₂ 1 ve aynı tekrar formülü ile, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34,...

dizisi elde edilir. “Toplam çiftlerin sayısı” sütunu için, u₁ 1 ve u₂ 2 ve dizi, 1, 2, 3, 5, 8, 13, 21, 34,...

bulunur. Tavşan probleminden dolayı 1, 2, 3, 5, 8, 13, 21, 34,...

dizisine Fibonacci Dizisi ve terimlerine Fibonacci Sayıları denir. n. Fibonacci sayısı Fn şeklinde gösterilir. Dolayısıyla,

1 , 1 ₂ 1  F  F F₃ 2, F₄ 3 F₅ 5,F₆ 8 yazılır. Dahası, 1 2 1  F  F , F_n F_n1F_n2, n2 veya 1 2 1  F  F , F_n1 F_n F_n1, n1 veya 1 2 1  F  F , F_n2 F_n1F_n, n1

alternatif formları da yazılabilir.

Artık Fibonacci’nin tavşan probleminin daha biçimli ifadesi verilebilir. Bütün n pozitif tamsayıları için, n . ayın ilk günü için;

An= A’ların sayısı (yetişkin tavşan çiftleri)

Bn= B’lerin sayısı (yavru tavşan çiftleri)

Tn= Toplam tavşan çiftlerinin sayısı = An+Bn

olsun. n. ayın ilk günü sadece A’lar (n+1). ayın ilk günü B’leri oluşturacağından, n1 için

n

n A

B _1

olur. Şekil 1’den de görülebileceği gibi A₁ 1 ve A₂ 1 dir. Dolayısıyla A₁,A₂,A₃,.... dizisi bir Fibonacci dizisidir ve n1 için

n

n F

A  ,

n n A B _1 olduğundan,n2 için 1 1     _{n n} n A F B

bulunur. Son formül için n1 alınırsa,

0 1 F

B 

olur. F_n1 F_n F_n1 formülü için n1 alınırsa,

0 1 2 F F F   veya 0 1 1 1 2 0 F F    F

bulunur. Bu da Şekil 1’deki B₁ 0 değerini doğrular. Böylece F da tanımlanmış olur. ₀ Sonuç olarak n. aydaki toplam çift sayısı 233 bulunur (Hoggatt, 1969).

1.4.2. Altın oran ve Fibonacci kuadratik denklemi

Bir AB doğru parçası alıp C noktasından iki bölüme ayrıldığında C noktasının

AB doğru parçasını,

AB AC

AC  CB

orantısını verecek şekilde bölmesi halinde, C’ye AB ’nin ‘Altın Bölümü’, bu orantıyı oluşturan AB / AC ve AB /CB oranlarına da Altın Oran denir.

Şekil 1.1: Altın bölüm

C noktasından bölünmüş olan AB doğru parçası üzerinde AC x ve CB 1olsun

1 1 x x x  

şeklinde yazılabilir. Bu da,

2 1 x x  veya 0 1 2 _{ x } x

şeklinde ikinci dereceden bir denklem verir. Bu kuadratik denklemin köklerini bulmak için ax2 bxc0 biçimindeki denklemlerin çözümünde kullanılan

a ac b b x 2 4 2 2 , 1    

kuadratik formül kullanılırsa kökler,

1 1 5 1, 61803... 2 x    2 1 5 0, 61803... 2 x   

olarak bulunur. x₁ 1,61803... değeri Altın Oran’ın beş basamaklı değeridir. Kısaca, 1,618 olarak kabul edilir. x₂ 0,61803... ise Altın Oran’ın ters değeridir.

Altın Oran’ın 1,618 değeri ile 0,618 ters değeri karşılaştırıldığında, ilginç bir özelliğin farkına varılır. 1,618 sayısı, kendisinden 1 çıkarıldığında kendi tersine eşit olan yegâne sayıdır. Yani,

618 , 0 618 , 1 1 1 618 , 1   

dir. Bir diğer özellik:

618 , 1 1 1 618 , 1   olduğuna göre, 1 618 , 1 ) 618 , 1 ( 618 , 1   1 618 , 1 ) 618 , 1 ( 2  

618 , 2 ) 618 , 1 ( 2 

olup, demek ki Altın Oran, kendisine 1 eklendiğinde kendi karesini vermektedir. Bu da aynı şekilde başka hiçbir sayıda olmayan bir niteliktir (Bergil, 1993). Aynı zamanda dizideki herhangi bir sayının 2,618 katı, iki sonraki sayıyı (89 1, 618 223), herhangi bir sayının 0,382 katı ise iki önceki sayıyı (89 0,382 34) verir. 0,382 değeri F_n/F_n2 oranının, 2,618 değeri F_n2/F_n oranının limitidir (bkz Ek-4).

Ardışık Fibonacci sayılarının oranlarının (F_n1/F_n veya F_n/F_n1) dizisi ile ilgili ne söylenebilir? Yakınsar mı? Öyle ise limiti nedir? Eğer limiti varsa geometrik anlamı var mıdır? Bu soruların cevapları için öncelikle ilk 15 Fibonacci sayısının F_n1/F_n ve

1

/ n n

F F_ oranları incelenmelidir.

Çizelge 1.2: İlk 15 Fibonacci sayılarının oranları (Lehmann ve Posamentier, 2007)

n n F F _1 1  n n F F 000000000 . 1 1 1  1.000000000 1 1  000000000 . 2 1 2  0.500000000 1 2  500000000 . 1 2 3  0.666666667 3 2  666666667 . 1 3 5  0.600000000 5 3  600000000 . 1 5 8  0.625000000 8 5  625000000 . 1 8 13  0.615384615 13 8  615384615 . 1 13 21  0.619047619 21 13  619047619 . 1 21 34  0.617647059 34 21  617647059 . 1 34 55  0.618181818 55 34  618181818 . 1 55 89  0.617977528 89 55  617977528 . 1 89 144  0.618055556 144 89  618055556 . 1 144 223  0.618025751 233 144 

618025751 . 1 233 377  0.618037135 377 233  618037135 . 1 377 610  0.618032787 610 377  618032787 . 1 610 987  0.618034448 987 610 

n sayısı arttıkça F_n1/F_n ve F_n/F_n1 değerleri birer limite yaklaşır. Yaklaşık olarak 0,61803 ve 1,61803 değerlerine. x2  x10 kuadratik denkleminin pozitif kökü olan 1,61803 ve bunun tersi olan 1 0, 61803

1, 61803 değerleriyle aynı olduğuna dikkat edilir. Oranın limiti matematikte en meşhur sayılardan biridir. Bu oranı göstermek için, eserlerinde Altın Oran’ı sıklıkla kullanması dolayısıyla ünlü Antik Yunan heykeltraşı Phidios’un (MÖ 490-430) adının ilk harfi olan Yunan alfabesinin 21. Harfi  (Phi: Türkçe okunuşuyla ‘fi’) kullanılmaya başlanmıştır (Bergil, 1993).

1, 61803...    1 veya 1 1, 61803...  1 1    

1.5. Matematik ve Müzik İlişkisi

Matematik ve müzik ilişkisinin kökeni Antik Yunan filozofu Pisagor (Pythagoras) (MÖ 570-495) ile milattan önce altıncı yüzyıla kadar dayanır. Birçok kişi onu geometri ve trigonometri ile ilişkili Pisagor Teoreminden bilmesine rağmen bu onun ünlü olmasının tek sebebi değildir. Pisagor aynı zamanda müzikle ilgilenmiş ve ses perdeleri arasındaki aritmetik ilişkileri ortaya çıkarmıştır. Onun sayı ve ses arasındaki ilişkiyi keşfettiği söylenir. Pisagor, sayıların evrenin idari prensibi olduğuna inanıyordu. İnsanların kulakları sesi sayısal olarak analiz edemediğinden, sesi titreşen tellere dönüştürerek tellerin ve perdelerin uzunluklarını incelemiş ve notalarda bağdaşan basit oranlar bulmuştur. Müziksel akord sistemi bu buluş üzerine temellenmiştir (Hammond, 2011).

Bu güne kadar diyatonik ve kromatik dizi (standart ve standart olmayan), aralıklar, ritim, ölçü, form, melodi, akorlar, dizi, oktav eşdeğerliği, doğuşkanlar, tını,

akustik, eşit aralıklı ses sistemi ve akordun alternatif yöntemleri gibi bazı müziksel kavramların matematiksel olarak izahı yapılmıştır (Wright, 2009).

Matematik ve müzik ilişkisini incelemeye, iki alanın da tanımları ile başlamak gerekirse, matematik için: sayılar, geometrik şekiller, fonksiyonlar, uzaylar gibi soyut varlıkların özelliklerini ve birbirleri ile olan ilişkileri inceleyen bilim, müzik için: birtakım duygu ve düşünceleri belli kurallar çerçevesinde uyumlu seslerle anlatma sanatı denilebilir. Çizelge 1.3’te görülen sınıflandırma, günümüzden yaklaşık 26 yüzyıl önceki Pisagor okulunun müfredatını gösteriyor. Burada, müzik göreceli olan niceliklerle, geometri sabit duran, astronomi ise hareketli büyüklüklerle ilişkili olarak sınıflandırılmıştır. Acaba müziği neden matematiğin dalı olarak sınıflandırmışlardı; bu hiç yerinde olmayan bir sınıflandırma mıydı yoksa mantıklı yanları mı vardı? Bu sorunun yanıtını düşünürken müziği en küçük, temel bileşeninden en üst düzeydeki yapılarına kadar gözden geçirerek anımsamak matematik–müzik ilişkisini aydınlatmaya yardımcı olacaktır (Bora, 2002).

Çizelge 1.3: Dört ilim (Quadrivium) ve bileşenleri DÖRT İLİM Matematik (Değişmez'in Bilimi) Aritmetik (Mutlak) Müzik (Göreceli) Geometri (Sabit) Astronomi (Hareketli)

Müziksel sesleri gürültüden ayıran özellik, müziksel seslerin ayırt edilebilir bir perde verebilme özelliğinin olmasıdır. Perde, sesin tizlik derecesine ilişkin bilgiyi taşıyan parametresidir. Yani sesin temel frekansına bağlı bir tizlik (incelik) derecesi (perde) algılanıyor. Bir sese ilişkin bir perdenin algılanabilmesinin ölçütü ise, o sesin periyodik (süreli) olma derecesidir. Müziksel bir ses, zamana bağlı bir periyodik fonksiyon olarak düşünülebilir. Yani,   t ve mZ için formül

0

( ) ( )

g tmT g t

Şekil 1.2: Periyodik bir g(t) fonksiyonu

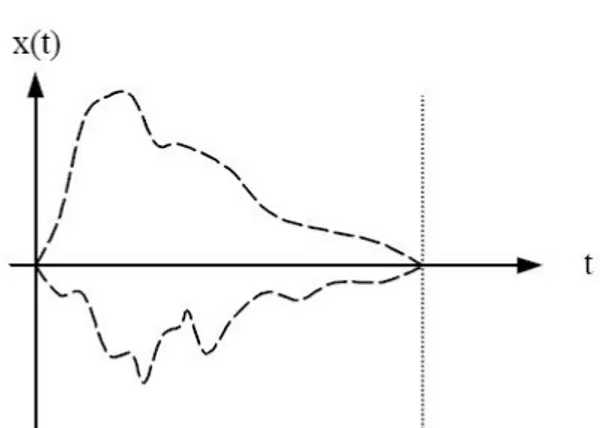
Şekil 1.3: Doğal bir müziksel ses zarfı örneği

Şekil 1.2’de periyodu T olan periyodik bir ses yer alıyor, dikey eksen de ₀ şiddetini gösteriyor. Ancak doğal kaynaklı müziksel seslerin sınırlı bir süresi vardır ve yarı periyodik özelliktedirler (Şekil 1.3). Müziksel seslerin belirleyici özellikleri arasında ‘perde’, ‘şiddet’ ve ‘süre’nin yanı sıra bir de ‘tını’, yani örneğin keman, flüt ve piyano seslerinin birbirinden ayrılmasını sağlayan özellik bulunmaktadır. Tını, ‘sesin dokusu’ olarak adlandırılabilir. Doğal müziksel ses zarfı örneğini gösteren şekilde (Şekil 1.3), sesin şiddetindeki yükselme ve alçalmalar, o sese ilişkin tınıyı belirleyen özellikler arasındadır (Bora, 2002).

Bir efsaneye göre, Pisagor ellerinde çekiçlerle çalışan bazı demircilere rastlar. Çekiçlerden çıkan sesler birbiriyle çok uyumlu tınlamaktadır. Pisagor çekiçleri tarttığında ağırlıklarının (12:9:8:6) oranında olduğunu fark eder. Çekiç ağırlıklarıyla seslerinin temel frekansları arasında matematiksel bir ilişki kurmak pek olası değil; ama gergin bir telin boyu ile sesinin temel frekansı arasında kesin bir ilişki bulunuyor (Şekil 1.4). Pisagorcular (12:9:8:6) oranlarından Şekil 1.5’teki gibi türettikleri (2:1), (3:2), (4:3) ve (9:8) oranlarını müzikteki esas aralıklar olarak kabul etmişlerdir. Bu oranlar, tamsayı katlardaki frekansların tek bir oktav (başlangıç frekansı ile onun iki katı olan frekans arasındaki oktav) içine aktarıldığında başlangıç frekansına oranlarını

belirtmektedir. Şekil 1.4’te görülen ‘monokord’ kullanılarak, telin boyunu değiştirmek yoluyla bu ‘bağıl frekanslar’ kolayca hesaplanabilmektedir (Bora, 2002).

Şekil 1.4: Monokord

Şekil 1.5: Pisagorculara göre ‘esas aralıklar’

1.6. Fibonacci Dizisi ve Altın Oran’ın Müzikle İlişkisi

Fibonacci sayıları müzikle ilişkilidir. Bu ilişki matematik profesörü Tom Zerger tarafından da incelenmiştir.

 İngilizce ‘Music’ kelimesi İngiliz alfabesinin on üçüncü ve yirmi birinci harfleri ile başlamaktadır. Sekizinci, on üçüncü ve yirmi birinci harfler ile ‘Hum’ (şarkı) kelimesi oluşturulabilir.

 Amerika Kongre Kütüphanesi’nde (The Library of Congress) müzik için sınıflandırma sayısı M, on üçüncü harftir.

 Dewey Ondalık (Decimal) Sistem’de müzik için sınıflandırma sayısı 780’ dir. 780 = 2.2.3.5.13, Fibonacci sayılarının çarpımıdır.

 Piyanolar saniyede 440 devir standardına göre akort edilir. 440 = 8.55. 8 ve 55 birer Fibonacci sayısıdır (Koshy, 2001).

Yukarıdaki ifadelerde müzikle Fibonacci sayıları ilişkilendirilmeye çalışılmış ve rastlantı sonucu elde edilen sayılarla varsayım ispatlanmaya çalışılmıştır. Özellikle ilk

2:1→ oktav (sekizli) 3:2→ tam beşli

9:8→ tam ses (büyük ikili) 4:3→ tam dörtlü

maddede İngilizce ‘music’ kelimesinden yola çıkılarak ve yine İngilizce ‘hum’ (şarkı) kelimesi türetilerek Fibonacci sayıları ve müzik ilişkisine evrensellik dışı bir yaklaşımla bakılmış olduğu ortaya çıkmaktadır. O halde aynı mantıkla şu sonuç çıkarılabilir: Fibonacci sayılarından 13, 21, 34 ve 55 alınır ve bunların her biri asal çarpanlarına ayrılırsa, (13), (7, 3), (2, 17) ve (5, 11), sırası ile yazıldığında: 2, 3, 5, 7, 11, 13, 17 olur ve bunlar ilk yedi asal sayıdır. Üstelik çarpımları olan 510 da Dewey Ondalık (Decimal) sınıflandırmasında matematik için kullanılan sayıya tekabül eder. Bu ve buna benzer ifadeler müzik ve Fibonacci sayıları arasında ilişki kurmaya çalışan yazarlar tarafından birçok internet sitesinde ve kaynakta mevcut olmasına rağmen maalesef kurulmaya çalışılan ilişki ile ilgili anlamlı bir hiçbir şey ifade etmemektedir (Lehmann ve Posamentier, 2007).

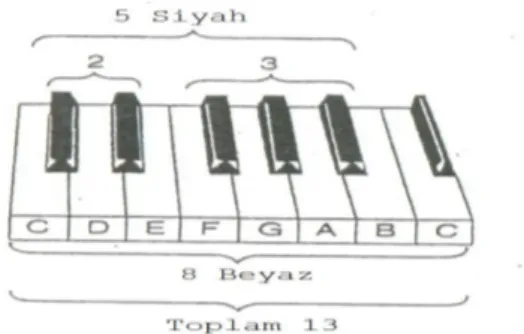
Piyano tuşları da Fibonacci sayıları ve müzik arasındaki bağlantının büyüleyici görsel açıklamasına olanak sağlar. Klavyedeki bir oktav, biri diğerinden daha yüksek olan iki nota arasındaki müziksel aralığı temsil eder. Yüksek olan notanın frekansı, düşük olanın iki katıdır. Klavyede bir oktav, 5 siyah ve 8 beyaz tuş olacak şekilde bölünür, toplamda 13 tuş (Şekil 1.6) vardır. Beş siyah tuş biri ikili biri üçlü olmak üzere iki gruba ayrılır. 2, 3, 5, 8 ve 13 birer Fibonacci Sayısıdır.

Şekil 1.6: Piyano tuşlarının bir oktavındaki Fibonacci sayıları

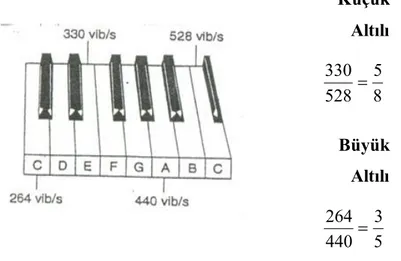
Oktav formundaki on üç nota Batı müziğindeki en popüler aralıklar olan kromatik diziyi oluşturur. Kromatik dizi, 5 notalı pentatonik dizi ve 8 notalı diyatonik diziden önce gelir. Mary Had a Little Lamb ve Amazing Grace gibi popüler şarkılarda pentatonik dizi kullanılmışken, Row row your boat gibi melodilerde diyatonik dizi vardır. Büyük altılı ve küçük altılı kulağa en hoş gelen müziksel aralıktır. Mesela, büyük altılı, sırasıyla Do ve La notalarından oluşur, saniyede 264 ve 440 titreşim yaparlar (Şekil 1.7). Dikkat edilmelidir ki 264/440 = 3/5 bir Fibonacci oranıdır (Koshy, 2001).

Küçük Altılı 8 5 528 330  Büyük Altılı 5 3 440 264 

Şekil 1.7: Müziksel aralıklardaki Fibonacci oranları

Bir küçük altılı aralığı, bir örnek olarak sırasıyla Mi ve Do notalarından oluşur ve saniyede 330 ve 528 titreşim yaparlar. Bunların oranı da Fibonacci oranıdır: 330/528 = 5/8 (Koshy, 2001).

Yukarıdaki örneklerde olduğu gibi Fibonacci sayılarının varlığını ortaya koymak üzere verilen 8 notalı dizilerle ilgili yazılanlar tamamen hatalıdır. Diyatonik diziler sekiz değil yedi notaya sahiptir. Çünkü sekizinci nota, birinci notanın tekrarıdır ve sayısal olarak bir sonraki oktava hareket eder. Bu durumda tuşlarla ilgili bir dizi yazılacaksa 2, 3, 5, 7, 12 yazılmalıdır ki bu da Fibonacci Dizisi değildir. Gerçek şu ki piyanodaki siyah tuşların ikili ve üçlü ayrılmış olmasının Fibonacci dizisi ile hiçbir ilgisi yoktur. Zaten iki ya da üç, hangisinin önce geldiğini söylemek imkansızdır. Çünkü kendilerini ayıran beyaz tuşlardan başka hiçbir şeyle bağı yoktur. Fibonacci sayıları ile müzik ilişkisi kurmak adına büyük altılı ve küçük altılının örnek verilmesi de yanıltıcıdır ki bunların da Fibonacci dizisi ile ilgisi yoktur. Çünkü bunlar, büyük üçlü (5:4) ve küçük üçlü (6:5) gibi müziğin zengin armonik özüne katkı sağlayan bir yığın orandan birkaçıdır (Lehmann ve Posamentier, 2007).

Müzikteki birçok yapı, malzeme ve eserde bilinçli olarak yapılanlar dışında çoğunlukla tesadüfi olarak Fibonacci Dizisinde yer alan sayılara rastlanabilir. Ancak bunların hepsinin Fibonacci Dizisi ile ilişkilendirilmenin herhangi bir anlamı, mantığı ve önemi yoktur. Asıl olan doğrudan Fibonacci Dizisi kullanılarak oluşturulmuş müziksel yapılar veya eserlerdir. Aşağıda verilen örneklerde olduğu gibi Fibonacci Dizisindeki bazı rakamlar, birlikte veya ayrı ayrı çeşitli müziksel yapılar içerisinde varolabilir.

Fibonacci dizisindeki bazı rakamlar ses aralıklarının oranlarını oluştursa da bu oranlar ortaya çıktığında Fibonacci dizisi bilinmemekteydi.

1:1 Birli 2:1 Sekizli 2:3 Dörtlü 2:5 Artık Beşli 3:2 Tam Beşli 3:5 Küçük Üçlü 3:8 Tam Beşli 5:2 Üçlü 5:3 Büyük Altılı 5:8 Üçlü 8:3 Dörtlü 8:5 Küçük Altılı 21:13 Küçük Altılı 13:8 Küçük Altılı

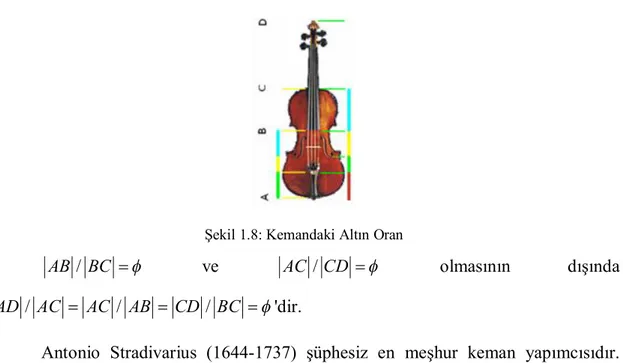
Müzik aletleri de çoğunlukla  sayısı temel alınarak yapılır. Keman tasarımında olduğu gibi yüksek kalitedeki ses telinin tasarımında da Fibonacci Sayıları

ve  kullanılmıştır. Şekil 1.8’de müzik aletlerinden biri olan keman üzerindeki Altın

Şekil 1.8: Kemandaki Altın Oran

/

AB BC  ve AC / CD  olmasının dışında

/ / /

AD AC  AC AB  CD BC 'dir.

Antonio Stradivarius (1644-1737) şüphesiz en meşhur keman yapımcısıdır. Yaptığı çalgılar günümüzde hala kullanılan standartlara sahiptir. Çalgılarının oranları, bileşenleri ve kurulumu, rahatça çalınan ve konser salonunun tamamına ulaşabilecek benzer bir alet yapmak isteyenler tarafından taklit edilmiştir (Lehmann ve Posamentier, 2007).

Birçok ünlü bestecinin (Mozart, Beethoven, Bach, Chopin, Béla Bartók, ... ) eserlerinde Fibonacci Dizisi ve Altın Oran’ı kullandığı varsayılmış ve ispat edilmeye çalışılmıştır. Bunun yanında, Fibonacci dizisini bilinçli olarak kullanan ve bunu belirten besteciler de bulunmaktadır.

2. KAYNAK ARAŞTIRMASI

Bu bölümde bu tez çalışmasına ışık tutan kaynaklar hakkında kısa bir bilgi verilecektir.

A. Yıldırım ve H. Şimşek, “Sosyal Bilimlerde Nitel Araştırma Yöntemleri” adlı bu alanda etraflıca yazılmış ve örneklerle somutlaştırılmış çalışmalarında, okuyucuda iz bırakan ve nitel araştırma nedir? Nasıl yapılır? Nereden başlanır ve geliştirilir? Nasıl raporlaştırılır? sorularına açık cevaplar vermişlerdir. Kitabın başlığında her ne kadar Sosyal Bilimler ifadesi bulunsa da kitapta yer alan örneklerin hemen tamamının eğitim-öğretim faaliyetlerine, ilişkilerine ve durumlarına değin örnekler olduğu göz önüne alındığında, bu kitabın eğitim-öğretim alanında yer alan öğrenciler ile bu alanda ürün verme gayretinde olan araştırmacıların çok daha fazla ilgisini çekeceği rahatlıkla söylenebilir.

D. Wright, “Mathematics and Music” adlı çalışmasında, matematik ve müzik arasındaki karşılıklı ilişkiyi araştırmıştır. Her iki alanda da bazı temel kavramları gözden geçirmiş ve karşılaştırmıştır.

H. A. Simons, “Béla Bartók’s Sonata for Two Pianos and Percussion” adlı çalışmasında, Bartók’un 1937’de bestelediği Sonata for Two Pianos and Percussion (İki Piyano ve Vurmalı Çalgı Sonatı) adlı eserini kapsamlı birşekilde incelemiştir. Çalışma, müzik araştırmasının tarihsel, analitik ve estetik üç alanı ile bestecinin tarihsel profili, ortaya çıkardığı çeşitli ve seçmeli düzensel etkilerin kronolojik tartışmasının yanı sıra biyografik bilgi de içermektedir. Adı geçen çalışmada, sayısız düzensel etkilerin genel olarak Bartók’un olgun stiline ve özel olarak da Sonata for Two Pianos and Percussion eserine nasıl etki ettiği tartışılmıştır.Çalışmanın detaylı analizi, kendine özgü müziksel örnekler verilerek her ayrı bölümün yanı sıra, eserin tamamının incelenmesini de içermektedir. Şekilsel tasarım, Altın Oran’ın baz alındığı önceden tasarlanmış Batı modellerinin yapısal karışımı açısından tartışılmıştır. Düzensel sistemin kullanımı, özel olarak Altın Oran, Fibonacci Dizisi ve akustik sistem üzerinde durularak tarif edilmiştir. J. K. Hammond, “Mathematics of Music” adlı çalışmasında, matematik tarihinin müzik ve temel ses fiziği ile bağlantılar içerdiğini ve şu anda müzikte ve modern akord sisteminde bulunan oran ve aralıkların bunun doğal oluşumu olduğunu ifade ederek matematik ve müzik ilişkisini bu fikirler çerçevesinde incelemiştir.

M. S. Bergil, “Doğada/ Bilimde/ Sanatta Altın Oran” adlı çalışmasında, Altın Oran’ın ne olduğuna ve doğada, sanatta ve bilimde nasıl kullanıldığına dair bilgilerin geniş kapsamlı bir derlemesini yapmıştır. Geçmişe Altın Oran gözlüğüyle nasıl bakılabileceğini örnekleyen bir çalışma ile Altın Oran’ın görsel yaratım alanında günümüze de kazandırılabileceğine işaret eden yorumlarda bulunmuştur.

N. Karasar, “Bilimsel Araştırma Yöntemi” adlı çalışmasında, araştırma eğitimi konusunda uygun bir bakış açısı geliştimek amacıyla, aşağıdaki soruları cevaplandırmaya çalışmıştır;

 Araştırma eğitimi nedir? Hangi düzeyde yapılır? Araştırma bilimcisi eğitimi ile farkı nedir?

 Araştırma eğitiminin amaçları nelerdir?

 Araştırma eğitiminin içeriğini oluşturan temel bilgi alanları nelerdir?

 Araştırma eğitiminin öğretim yöntemi nasıl olmalıdır?

 Lisans-üstü eğitimde araştırma eğitiminin yeri, önemi ve amaçları nedir? Bu tür yaralanabilme koşulları nelerdir?

 Tabii ve sosyal bilim dalları arasında, araştırma eğitimine ilişkin sorular bakımından ayrılıklar var mıdır? Varsa, nelerdir?

T. Power, “J. S. Bach and the Divine Proportion” adlı çalışmasında, Johann Sebastian Bach’ın Altın Oran’ı bildiğini ve eserlerinin ölçü ve formlarını tasarlarken bunu kullandığını düşünerek inceleme yapmıştır. Çalışmada, orantılı yapıların bütünleşmiş yapısı ve uyumu dolayısıyla bestecinin büyük olasılıkla Altın Oran’ı bilerek eserini tasarladığı sonucuna ulaşılmaktadır.

U. Bora, “Bilim ve Sanatın Kesiştiği Temel Bir Nokta: Matematik ve Müzik İlişkisi” adlı çalışmasında, sesin yapısından diziler, melodi, ritim, armoni gibi konulara uzanan müzik öğeleriyle matematiğin ilişkisini incelemiştir. Perde, tını, aralıklar, Pisagor koması, eşit aralıklı ses sistemi gibi kavramların matematiksel açıklamaları, ayrıca tematik dönüşümler ve armonik uzaklık hesaplamaları ile ilgili çalışmalara örnekler vermiştir.

V. E. Hoggatt, “Fibonacci and Lucas Numbers” adlı çalışmasında, Fibonacci ve Lucas sayılarının bazı ilginç özelliklerine bir giriş sunmaktadır. Burada matematiksel genellemelerin bazı basit kavramlarla türemesi incenlenmiştir.

3. MATERYAL VE YÖNTEM

Bu tez çalışması, nitel araştırma yöntemine dayalı betimsel düzende durum saptamaya yönelik olarak “durum/örnek olay tarama modeli” ve bu modelde yer alan “bütüncül tek durum deseni” ile gerçekleştirilecektir. Örnek olay tarama modelleri, evrendeki belli bir ünitenin (birey, aile, okul, dernek vb. nin), derinliğine ve genişliğine, kendisini ve çevresi ile olan ilişkilerini belirleyerek, o ünite hakkında bir yargıya varmayı amaçlayan tarama düzenlemeleridir. Bunlara ‘monografi’ çalışmaları da denir (Tütengil, 1975; Aktaran: Karasar, 2002). “Tarama modellerinde amaçların ifade edilişi genellikle soru cümleleri ile olur. Bunlar: Ne idi? Nedir?, Ne ile ilgilidir? ve Nelerden oluşmaktadır gibi sorulardır” (Karasar, 2002). “Var olan kaynak ve belgeleri inceleyerek veri toplamaya belgesel/literatür tarama denir. Belgesel/literatür taraması, araştırma probleminin seçilerek anlaşılmasına ve araştırmanın tarihsel bir perspektife oturtulmasına yardımcı olur” (Karasar, 2002). Bütüncül tek durum deseninin kullanılma durumları şöyledir: “Eğer ortada iyi formüle edilmiş bir kuram varsa, bunun teyit edilmesi veya çürütülmesi amacıyla, genel standartlara pek uymayan aşırı, aykırı veya kendine özgü durumların çalışılmasında, daha önce hiç kimsenin çalışmadığı veya ulaşamadığı durumlar, bütüncül tek durum deseni kullanılarak çalışılabilir” (Yıldırım ve Şimşek, 2005).

Konuyla ilgili bu zamana dek hazırlanmış yüksek lisans ve doktora tezleri, basılı kitaplar, bitirme ödevleri ve hakemli dergilerde yayınlanmış olan çalışmalar araştırmanın temel materyallerini oluşturur. Bu materyaller tezin amacı doğrultusunda matematiksel ve müziksel doğrulara göre değerlendirilerek Fibonacci Dizisi ve Altın Oran’ın müzikteki varlığı tartışılmıştır.

4. ARAŞTIRMA BULGULARI VE TARTIŞMA 4.1. İki ve Üç Bölümlü Form

Bünyesinde iki bölüm içeren müziğe ikili veya iki bölümlü (AB) form adı verilir. ‘Eşit ve eşit olmayan’ iki çeşit ikili form vardır: Müziksel ölçü sayıları bakımından eşit olan ikili formda eser, birbirine eşit iki parçaya bölünür. Eşit olmayan ikili formda genellikle ikinci bölüm, birinci bölümden belirgin şekilde daha büyüktür, yani daha fazla ölçü sayısına sahiptir. İki bölüm birbirini dengelediğinden dolayı besteciler eşit ikili formu kullanmanın sonuçlarından oldukça memnun olmuşlardır. Çünkü, iki yarımın da birbirini dengelediği görülmüştür. Aynı şekilde başarılı olabilen eşit olmayan ikili formu kullandıklarında ise her iki tarafın birbirine oranı sorusu ortaya çıkmıştır. Büyük bestecilerin genellikle çatı katında yalnız başına oturup mum ışığında uzak esintilerden gelen ilhamlarını dillendirdiği düşünülür. Eserlerinin, düşlerinin sonucu olduğu hayal edilir. Ancak birçoğunun yaptığı gayet akılcı ve planlı bir iştir. Besteleme sürecinde içlerindeki sesleri dinlediklerinde bu ses kendilerine olağan dışı birşey yapmalarını söyler. Çoğu zaman onlar, kendilerini geliştiren ve ‘dinlenilebilen’ müziği yapmalarını sağlayan yılların getirdiği eğitim ve tecrübe ile hüner sahibi olurlar. Besteciyi zorlayan şey, eserin unsurlarını kontrol etmektir ki mantığı sürdürmenin yanı sıra, hala eserin anın dürtüsü üzerine yapıldığının hissini vermesidir. En önemlisi müzik, dinleyiciyi eğlendirmeli, pürüzsüz ve akıcı bir sunuma sahip olmalıdır. Birkaç istisna dışında çoğu besteci, becerilerini geliştiren ve hünerlerini arttıran zeki insanlardır. Kağıdın üzerine kalemi koyduklarında, müziğe ait masallarını anlatan sesler ve sessizlikler dizisinin seçimlerini ölçüp tartarak yapmaktadırlar. Besteleme süreci oyuna benzer özellikler taşır. Bu oyunun bazı kuralları, o eserin stilinden türer ve kendine has özellikler taşır. Besteciler sadece besteci ve armonici değil aynı zamanda oyuncudurlar (Lehmann ve Posamentier, 2007).

Bu yüzden eserlerini bestelerken kullandıkları malzemeler kimi zaman doğrudan içten gelen duyguya ve bilinçaltına, kimi zamanda bilinçli düşünmeye dayanır. Böylece besteciler, bazen birbirlerine eşit bazen de eşit olmayan ve kendi dönemlerinin dışındaki istisna müziksel yapılar ile eserlerini yaratırlar. Bu da eserlerde tesadüfi veya bilinçli matematiksel yapılar ortaya çıkarabilir ki aslında müziğin analitik yapısı fizik ve matematiğe dayanmaktadır. Bu yüzden eserlerde bestecinin bilinçlice yapmış oldukları dışında ortaya çıkan tesadüfi matematiksel kuramlar her zaman olabileceğinden önemli bir değer ifade etmez, müziksel açıdan önemli olan eserin bütüncül değeridir. Böylece,

aynı bestecinin kullandığı belirli bir form kimi zaman eşit kimi zaman eşit olmayan bölümlerden oluşabilir ki müzik tarihinde bu şekilde çok örnek bulunmaktadır. Bunlar dışında, Çağdaş dönem müziğindeki 12 Ses Sistemi gibi ancak bilinçli bir şekilde matematiksel özelliklerle yaratılıp aynı zamanda bir estetik değere de sahip eserler bu farklı özelliğiyle önem kazanabilir. Bunun dışındakiler her biri ayrı değeri olan olağan eserlerdir (Lehmann ve Posamentier, 2007).

İkili form dışında baştaki bölümü tekrar eden (ABA) veya etmeyen (ABC) üçlü veya üç bölümlü formlar da vardır. Bazı kuramcılar baştaki bölümü tekrar eden formu ikili form olarak niteleseler de baştaki bölümü tekrar etmeyen yani her bölümü özgün olan (ABC) form üç bölümlü ise baştaki bölümü tekrar eden (ABA) form da üç bölümlüdür. Temel ikili (AB) ve üçlü (ABA, ABC) müzik formları bu şekilde belirlenir (Cangal, 2004).

4.2. Chopin’in Prelüdleri

Ondokuzuncu yüzyılın piyano eserlerinden biri Frederic Chopin’in (1810-1849) Op. 28 Preludes’üdür1. Bu albüm, en müstesna müziksel minyatürlerin yirmi dört tanesini içerir. Bunlardan ilki Chopin’in kendi kendine oynadığı bir oyun üzerine kuruludur. Şekil 4.1’de sağ elin gerekli melodik hareketlerinin görülebileceği basitleştirilmiş bir çizim vardır. Her ölçü (son altısı hariç), biri sol ele eşlik eden (içi boş nota), diğeri etmeyen (siyah nota), birbirine birer adım uzakta iki nota içerir. Yaklaşık yarım dakika süren bu eser, farklı ölçülerde iki belirgin bölüm olarak kurulmuştur. Melodi Sol ve La notaları ile başlayıp 5. ölçüde Mi-Re notalarına kadar çıkmakta, üç ölçü devam etmekte ve sonra 9. ölçüde tekrar Sol-La notalarına inmektedir. Buradan sonra melodi daha fazla yükselip 21. ölçüde Re-Do notalarında doruk noktalarına ulaşmaktadır. Sonra 25. ölçüde Sol-La notalarına inişe geçmektedir. Burada iki kez Mi-Re notalarına atlamakta ve sonra aşağısında Sol-La nota çiftleri ile birlikte olan Do’lu ölçülere gelmektedir. Bu eserin doruk noktası, 34 ölçünün Altın Oran’ı olan 21. ölçüye tekabül etmektedir. 21 ve 34 birer Fibonacci sayısıdır ve 34 0, 618 21’dir. Doruk noktasının aynı Altın Oran’a yerleştirilmesi Prelude Op. 28 No.92 adlı eserde de vardır. Bu eser 12 ölçü uzunluğundadır ve 48 vuruş içermektedir. Doruk noktası, tam olarak 29. vuruşta (48 0, 618 29), 8.ölçünün başında ortaya çıkmaktadır. Doruk noktasının

1

Bkz. https://www.youtube.com/watch?v=8wegyayhHcU

2

yeri her zaman matematiksel bir formüle uymak zorunda değildir. Bazı durumlarda Altın Oran’a yaklaşık bir değere ulaşılmaktadır. Prelude’lerin birçoğu Altın Oran’a uygun değildir. Belki de Chopin, Fi’nin kullanımının müziksel başarıyı garantilemek için gerekli olmadığını düşünmüş olabilir (Lehmann ve Posamentier, 2007).

Şekil 4.1: Chopin: Prelüd No. 1, C Major

Şekil 4.2, Şekil 4.1’in grafiksel eşdeğeridir ve doruk noktasının Altın Oran değerini perde dizisi içinde göstermektedir.

Şekil 4.2: Chopin: Prelüd No. 1, C Major

4.3. Mozart’ın Piyano Sonatları3

Bazı ünlü besteciler tarafından eserin formunu belirlemede oynanan oyunlardan biri, Altın Oran’ın kullanımı ile ilişkilidir. Wolfgang Amadeus Mozart (1756-1791), sayıları ve her çeşit oyunu sevdiğinden bu uygulamaya düşkünlüğü ile bilinmektedir. Piyano sonatlarını yazmak üzere oturduğunda, kafasında her zaman aynı plan vardı: Altın Oran’ı kullanarak biçimsel zerafet ve dengeyi yaratmaya çalışmak. Mozart zamanında, solo klavye sonatı üç bölümden oluşmaktaydı. Bölümlerden ilki, güçlü ve

3 Bkz. https://www.youtube.com/watch?v=QtFZC658RP8 S es P erd es i Zaman

enerjik, ikincisi yavaş ve şiirsel, üçüncüsü en yüksek hızdadır. Bu hızla sonata heyecanlı bir son getirilmektedir (Lehmann ve Posamentier, 2007).

On sekizinci yüzyılın sonlarının müziğe en belirgin katkılarından biri, ‘sonat-allegro’ formu olarak adlandırılan müzik formunun geliştirilmesidir. Bu isim, tamamı sonatın bir formu olarak hesaba katılabilen, hemen hemen tüm büyük çalgısal formların (oda müziği, senfoni, konçerto gibi) ilk bölümlerinde kullanılması durumundan türemiştir. Örneğin, iki keman, bir viyola ve bir çellodan oluşan bir dörtlü oda müziği çalgı topluluğu için bestelenen eser bir sonattır. Bir konçerto, bir solist ve bir orkestra için bestelenen bir sonattır. Senfoni ise, bir büyük orkestra için bestelenen bir sonattır. Yani, sonat-allegro’su bir sonatın veya sonattan oluşan konçerto ve senfoni gibi formların ilk bölümüdür. Bu yüzden sonat -allegro’nun içindeki sergi, gelişme ve sergi tekrarı’na alt bölüm denir. Sonat-allegro formunun kendisinde olduğu gibi, senfoni de üç temel alt bölümden oluşur ve her biri kendi içinde ve arasında tekrar eder. Sergi (exposition) adı verilen ilk alt bölümde eserin müziksel malzemeleri sunulur. Bu alt bölüm kendi içinde tekrarlanır böylece herşey tekrardan duyulabilir. Sergi’nin tekrarından sonra sırasıyla ‘gelişme’ (development) ve ‘sergi tekrarı’ (reexposition) alt bölümlerine geçilir.

Gelişme alt bölümü, serginin malzemelerinin değiştiği ve karıştığı yerdir. Çoğu zaman coşku ve heyecan vericidir. Burada gerilimin yükselmesi, bu bölümü doruk noktasına ulaştırır. Şiddet azaldıkça, bu bölümün başına dönülür. İşte bu ‘sergi tekrarı’ ile özetleme demektir. Bu nokta çalgıda en çok el becerisinin olduğu noktadır. Eğer dikkat edilmiyorsa, sergi alt bölümünün tekrarının duyulduğu zannedilebilir, fakat tekrar değildir. Bu alt bölümde çokça değişiklik yapılmasına rağmen, ustaca olduğu için fark edilmez (Lehmann ve Posamentier, 2007; Cangal, 2004).

Barok dönemde (1600-1750) birçok müzik türü, özellikle dans formları, eşit ikili formdadır. Her alt bölüm yaklaşık olarak aynı büyüklükte olup, benzer müzikler içerir ve genellikle tekrar edilir. Klasik dönemin (1750-1825) bestecilerine kadar bu form şu an ‘sonat-allegro’ formu olarak bilinen form haline getirilir. Bu şekline başa dönüşlü form adı verilir. Çünkü bu alt bölümün sonunda, ki aslında üçüncü alt bölümde, başlangıç kısmına dönüş yapılır. Şuna benzer: : A : : A : (Lehmann ve Posamentier, 2007).

Mozart on sekiz piyano eseri yazmıştır. Bunlardan biri dışında hepsinde sonat-allegro formu kullanılmıştır. Kalan bir tanesinde ‘tema ve çeşitleme’ formu kullanılmıştır. Çizelge 4.1’de görülebileceği gibi, on yedi eserden altı tanesi (%35) tam olarak Altın Oran’a bölünebilmektedir. Bunlar, ölçü sütununda ‘altın’ kelimesi ile belirtilmiştir. Sekiz tanesi (%47) Altın Oran’a çok yakındır ve bunlar ölçü sütununda -3 ile +4 arasında değişen hata oranlarıyla gösterilmiştir. Bu rakamlar, Altın Oran olmadığının göstergesidir. Kalan üç tanesi (%18), 6, 8 ve 12 değerleri çok yüksek olduğundan, değerlendirmeye alınma konusunda Altın Oran’a yeteri kadar yakın değillerdir. İstatistiksel olarak, bu örneklerden yola çıkılarak Altın Oran’ın Mozart için önemli olduğu sonucuna ulaşılır (Lehmann ve Posamentier, 2007).

Çizelge 4.1: Mozart’ın piyano sonatları

Mozart Sonatı Anahtar Uzunluk Sergi Sergi /Uzunluk 1-1/’den

sapma (%)

No. 1. K. 279 C major 100 38 0.38 Altın

No. 2. K. 280 F major 144 56 0.389 Altın

No. 3. K. 281 Bb major 109 40 0.367 -2

No. 4. K. 282 Eb major 36 15 0.417 1

No. 5. K. 283 G major 120 53 0.442 8

No. 6. K. 284 D major 127 51 0.402 3

No. 7. K. 309 C major 156 59 0.378 Altın

No. 8. K. 310 A minor 133 49 0.368 -1

No. 9. K. 311 D major 112 9 0.348 -3

No. 10 K. 330 C major 149 57 0.383 Altın

No. 11. K. 331 A major 135 55 Tema 

Çeşitleme

No. 12. K. 332 F major 229 93 0.406 6

No. 13. K. 333 Bb major 170 63 0.371 -1

No. 14. K. 457 C minor 185 74 0.4 4

No. 15. K. 545 C Major 73 28 0.384 Altın

No. 16. K. 570 Bb major 209 79 0.378 Altın

No. 17. K. 576 D major 160 58 0.363 -2

No. 18. K. 533 F major 240 103 0.429 12

‘Altın’ kelimesi ile belirtilen altı eserden bir tanesi olan Sonata No.1 (K279)4 adlı eserin sergi alt bölümü, 38. ölçüde sona eren ve tamamı 100 ölçüden oluşan bir

4

eserdir ki aralarında Altın Oran’a en yakın olanı budur. Şekil 4.3’teki gibi gösterilebilir (Lehmann ve Posamentier, 2007).

Şekil 4.3 : Mozart’ın Piyano Sonatı No.1 (K279)

Franz Joseph Haydn’ın (1732-1803) piyano sonatlarında Altın Oran’ı kullanıp kullanmadığı değerlendirilirse, Haydn’ın  ’ye bağlılığının Mozart ile kıyaslanamayacağı sonucuna varılır. Rastgele seçilen aynı sayıdaki piyano sonatları incelendiğinde, sonat-allegro formlarının sadece %18’inde (3/17) tam olarak Altın Oran, %53’ünde ise (9/17), Altın Oran’a yakınlık görülmektedir. Kalan %29’u (5/17) ise, Altın Oran’la ilgisi olmadığından hesaba katılmamaktadır (Lehmann ve Posamentier, 2007).

Çizelge 4.2: Haydn’ın piyano sonatları5

Haydn Sonatı Anahtar Uzunluk Sergi Sergi /Uzunluk 1-1/’den

sapma(%)

No. 14. 1767 E major 100 84 30 -2

No. 15. 1767 D major 144 110 36 -6

No. 16. 1767 Bb major 109 116 38 -6

No. 17. 1767 D major 36 103 42 2

No. 19. 1773 C major 120 150 57 Altın

No. 21. 1773 F major 127 127 46 -3 No. 25. 1776 G major 156 143 57 2 No. 26. 1776 Eb major 133 141 52 -2 No. 27. 1776 F major 112 90 31 -4 No. 31. 1778 D major 149 195 69 -6 No. 32. 1778 E minor 135 127 45 -4 No. 33. 1780 C major 229 172 68 2 No. 34. 1780 C # minor 170 100 33 -5

No. 35. 1780 D major 185 103 40 Altın

No. 42. 1786 G minor 73 77 30 Altın

No. 43. 1786 Ab major 209 112 38 -5

No.49. 1793 Eb major 160 116 43 -1

5

Bkz. https://www.youtube.com/watch?v=0kEQx2juCSo&list=PL2B7B03DC5CF1DBC9

Sergi Gelişme Tekrarı

62 ÖLÇÜ

Mozart’ın eserlerindeki Altın Oran’larının ortalaması 0,388 ve Haydn’ın eserlerinin Altın Oran’larının ortalaması 0,364 olarak hesaplanır. Mozart’ın ölçüleri yerleştirmesi  ’ye oranla -3 ile +12 aralığında bulunurken, Haydn’ınki ise sadece -6 ile +2 arasında yer almaktadır. Müziğin kalitesinin ve estetik değerinin bu sayılarla bir ilgisi yoktur. Bunu test etmek için bir Mozart ve bir Haydn’dan değerlendirmeye alınan 34 eser dinlendiğinde, hangisinin Altın Oran’a daha yakın olduğu sonucuna varılamasa da çokça güzel müzik eserleri dinlenilmiş olur (Lehmann ve Posamentier, 2007).

4.4. Beethoven’ın Beşinci Senfonisi6

Şekil 4.4 : Beethoven’ın beşinci senfonisinin ilk bölümü

Op. 67 numaralı bu senfoninin Allegro con brio (neşeli gösterişle) tempolu ilk bölümünün başlangıcındaki beş ölçü, belki de klasik müzikte evrensel olarak en çok bilinen müziksel ifadedir. Bu eserin formu, Mozart ve Haydn’ın sonat ve senfonilerinden farklıdır. Ludwig van Beethoven’ın (1770-1827) beşinci senfonisinde, sergi, gelişme ve sergi tekrarı alt bölümleri yaklaşık olarak aynı uzunluktadır. Böylece bu üç alt bölümde Altın Oran engellenmiştir. İlk alt bölümü sonuca götürmek yerine, daha önceki müzisyenlerde görülmeyen şekilde, sergi tekrarı kodaya dönüştürülerek yeni (ikinci) bir gelişme alt bölümü meydana getirilir. Kodaya bir de kodetta eklendiğinde oluşan birleşmede, anlamlı ve benzersiz bir beşinci alt bölüm meydana getirilmiş olur. Dolayısıyla 124 ile 128 ölçüden oluşan dört değil beş alt bölümle eserin bu bölümü sona erer. Bu form, yeni bir sonat-allegro formu çeşidir. Şekil 4.4’te görülebileceği gibi, bu yeni geliştirilmiş sonat-allegro formu, üç Altın Oran alt bölümü içerir. İlk olarak, serginin tekrarı, 372. ölçüdedir ve bu tüm bölümün Altın Oran’ıdır. Kodetta olmadan bu bölümün uzunluğu 602 ölçüdür ve Altın Oran’ı: 602 0, 618 372’dir. Sergi alt bölümünün tekrarının son kesiti (124 2 248ölçü),

6

Bkz. https://www.youtube.com/watch?v=6z4KK7RWjmk

Gelişme Tekrar Koda Kodetta

125/249 182/306 248/372 268/392 374/498 478/602 502/626

Obua Durgusu

Ayrım Sergi

hemen hemen tüm bölümün Altın Oran’ıdır (248 626 0,389). Serginin sonundaki iki ölçü de çıkarılırsa Altın Oran’a daha çok yaklaşılır (244 626 0,389) (Lehmann ve Posamentier, 2007).

Bu eserde oran üzerine iki biçimsel olay meydana gelir. İlki; dört notalı motifin önce iki, sonra bire ayrıldığı gelişme alt bölümünde gerçekleşir. Bu dört notalı motifin dağılımı 306. ölçüdedir ve bu, 498. ölçüdeki tekrar bölümünün sonuna kadar olan kısmın Altın Oran’ıdır (306 498 0, 614). Tüm senfoninin en önemli anlarından biri, 392. ölçüde tekrar bölümünde, obua (oboe) dışında tüm orkestranın durduğu andır. Obuanın çaldığı kısa durgunun hiçbir örneği yoktur ve sonat-allegro formunu bilenler için olağan dışıdır. Bu solo, tüm bölümün Altın Oran’ına sadece altı ölçü uzaklıkta gerçekleşir (626 0, 618 386). Beethoven’ın bu özel anı Altın Oran’a göre planlayıp planlamadığı asla bilinemez. Fakat sonuç, Altın Oran’a yakındır.

4.5. Bartók’un İki Piyano ve Vurmalı Çalgı Sonatı

Béla Bartók’un (1881 - 1945) 1937’de bestelemiş olduğu Sonata for Two Pianos

and Percussion7 (İki Piyano ve Vurmalı Çalgı Sonatı) adlı eseri üç bölümden

oluşmaktadır. Bu bölümlerin her biri, biçimsel olarak parçalara ayrılmış ve bu parçaların birbirlerine oranlarının Altın Oran’la ilişkisi incelenmiştir.

4.5.1. Birinci bölüm

Çizelge 4.3: Bölümün biçimsel planı BÖLÜM 1: BİÇİMSEL TASLAK (PLAN)

1.Ölçü Giriş Allegro’yu önceden belirtir

32. Ölçü Allegro/Sergi

İlk tematik grup

Do notasında bölümün başlangıcı Tema 1 (Ana tema)

43. Ölçü İlk tematik grup Tema 2

84-101.Ölçü Ara tema

105.Ölçü Kodetta

161. Ölçü Sonuç Ara temaya ilişkin

175. Ölçü Geçiş Dörtlüler tabakası

195. Ölçü Gelişme a) Mi notasında ana tema grubunun ikinci temasını ana

tema altında benzeterek ostino olarak kullanır.

217. Ölçü b) Kısa ara fasıl.

232. Ölçü c) Sol diyezde sırası değiştirilmiş ostinato.

274. Ölçü Sergi Tekrarı

332. Ölçü Koda Fugato başlangıcı; kapanış teması üzerine kurulmuştur.

443. Ölçü Son

7

Birinci bölümün biçimsel ayrımı, hem uzun hem de kısa olan kesitlerde Altın Oran ilkelerine uymaktadır. Bu bölümde Altın Oran’ı incelemek için biçimsel ayrımlar, uzunluk olarak hesaplanmış ve Altın Oran’ın 0,618 ters değeri veya 0,382 değeri ile çarpılmıştır. Girişin birinci ölçüsünden itibaren, sergi ve tematik malzemenin son ölçüsü olan 171. ölçüye kadar olan birleşmenin uzunluğu, 170 ölçüdür. Öncesindeki 171. ölçüyü de dahil ederek ‘geçiş’ kesiti ve 274. ölçüye kadar olan ‘gelişme’ alt bölümünün birleşmesinden oluşan uzunluk, 104 ölçüdür. Birinci bölümün tamamının Altın Bölümü, ‘sergi tekrarı’ nın başı olan 274. ölçüde gözlenir (443 0, 618 274). Bölümün kalan kısmı 274. ölçüden itibaren 169 ölçüdür. 169’un Altın Oran’ı 169 0, 618 104, 44  olur. Bu da, Bartók’un birinci bölümle ilgili tüm planının, Altın Oran’a sadık kalarak simetrik bir tasarım yapmak olduğunu göstermektedir (Simons, 2000).

Öncesindeki 171. ölçüyü de dahil ederek geçiş kesiti ve 274. ölçüye kadar olan gelişme alt bölümünün birleşmesinden oluşan uzunluk 104 değil, 103’tür. Bölümün kalan kısmı 274. ölçüden itibaren 169 değil, 170 ölçüdür. Dolayısıyla hesaplama 170 0, 618 105, 06  şeklinde olmalıdır. Bunun ise, 103’le bir ilgisi yoktur. Bu durumda ortaya konan Altın Oran iddiası yanlış olur.

Şekil 4.5: İlk bölümün biçimsel ayrımı. Üstteki rakamlar büyük kısımlardaki ölçü sayısı, alttaki rakamlar, küçük kısımlardaki ölçü sayısıdır

Daha küçük ölçülü Altın Oran’lar da bu biçimsel taslak dahilinde görülebilmektedir. Örneğin, giriş alt bölümündeki yapısal ayrımlar, ayrı kanonik kısımlarla birlikte, Altın Oran’a bağlı yapısal özellikler göstermektedir (Şekil 4.5). İlk kanonik (giriş) bölümdeki 55 vuruşun Altın Oran’ı, 6. ölçüde veya 34. vuruşta ortaya çıkan fortissimo (çok güçlü) çıkışı ile vurgulanmaktadır (55 0, 618 33,99). 8. ölçüdeki es (sus), 55 vuruşun 52. sindedir ve ilk iki kanonik alt bölümün birleşiminin Altın Oran’ına tekabül eder: Toplam 84 vuruş0, 61851,912. Aynı zamanda ilk dört kanonik alt bölüm iki eşit kısımdan oluşur. Her biri 55 vuruşluk bir alt bölümün ardından, 26 vuruşluk tematik malzeme alt bölümü ile devam eder. Birinci ve üçüncü alt

170.ö 169.ö 104.ö Giriş Sergi 195 175 32 Ölçü 1 171 274 329 332

bölümlerdeki 55 vuruşun Altın Oran’ı 26,01’dir ve bu da ikinci ve dördüncü alt bölümlerdeki tematik malzemenin 26 vuruşudur (Şekil 4.6) (Simons, 2000).

Burada 55 sayısının Altın Oran’ı yanlış hesaplanmıştır. Birinci ve üçüncü alt bölümlerdeki 55 vuruşun Altın Oran’ı 26,01 değil, 55 0,382 21, 01’dir. Bu da ikinci ve dördüncü bölümlerdeki tematik malzemenin 26 vuruşuna karşılık gelmemektedir. Dolayısıyla iddia edilen Altın Oran söz konusu değildir.

Şekil 4.6: Birinci bölümün girişten 32. ölçüye kadar Altın Oran’ları. En üsttekiler; kanonik bölümlerin sayısı, ortadakiler; saniyedeki vuruş sayıları, alttakiler; vuruşlar

32. ölçüde serginin başından, 101. ölçüdeki ikincil (ara) temanın sonuna kadar 70 ölçü vardır. 70’in Altın Oran’ı (70 0, 618 ) 43,2’dir. Bu rakam, sayısal olarak 43. ölçüdeki ilk tematik grubun 2. temasına denk gelmektedir (Şekil 4.7).

Şekil 4.7: Sergiden geçişe, Birinci bölümün Altın Oran’ları. Alttakiler, kısımların toplam ölçü sayıları

Yukarıdaki bölünmede küçük ölçülü başka Altın Oran’ları da gözlemlemek mümkündür. Örneğin, sergi alt bölümünün ilk tematik grubunun (84 32 52) Altın Oran’ı (52 0, 618 32,13), bu alt bölümün başlamış olduğu ölçüye tekabül eder. Aynı zamanda, kodettadan vivo (canlı)ya kadar olan kısmın (28 ölçü) Altın Oran’ı hesaplandığında, 28 0, 618 17,304  , ikincil (ara) temanın uzunluğu bulunur. Kodetta’nın sonuç alt bölümüne kadar olan uzunluğunun Altın Oran’ı (55 0, 618 33,99), sonuç alt bölümü ile geçiş kesitinin birleşmesinden meydana gelen ölçü uzunluğu olan 34 ile ilişkilidir. Böylece, kodetta ile geçiş kesitinin sonuna kadar olan kısmın ölçü sayısının Altın Oran’ı (89 0, 618 55,02), kodettanın 161. ölçüdeki sonuç alt bölümüne olan uzaklığına eşittir. Bu rakamlar, giriş alt bölümünün

Sergi Tema 1

(A.O.) Vivo Tema 2 Ara Tema Kodetta

Kodetta Sonuç Geçiş Ölçü 32 43 84 101 105 133 161 175 195 (12 Ö.) (51 Ö.) (21 Ö.) (55 Ö.) (14 Ö.) (21 Ö.) 55 26 55 26 89 IV I II III V VURUŞ 1 34 52 56 82 _{85 140} 166 176 265