7. SINIF MATEMATİK DERSİ ÇOKGENLER ALT ÖĞRENME
ALANININ KAVRAM HARİTASI KULLANILARAK ÖĞRETİMİNİN
AKADEMİK BAŞARIYA ETKİSİ VE ÖĞRENCİ GÖRÜŞLERİ
Neslihan Biçer
YÜKSEK LİSANS TEZİ
MATEMATİK EĞİTİMİ ANABİLİM DALI
GAZİ ÜNİVERSİTESİ
EĞİTİM BİLİMLERİ ENSTİTÜSÜ
i
TELİF HAKKI VE TEZ FOTOKOPİ İZİN FORMU
Bu tezin tüm hakları saklıdır. Kaynak göstermek koşuluyla tezin teslim tarihinden itibaren bir (1) ay sonra tezden fotokopi çekilebilir.
YAZARIN
Adı: Neslihan Soyadı: BİÇER
Bölümü: Matematik ve Fen Bilimleri Eğitimi İmza:
Teslim Tarihi:
TEZİN
Türkçe Adı: 7. Sınıf Matematik Dersi Çokgenler Alt Öğrenme Alanının Kavram Haritası Kullanılarak Öğretiminin Akademik Başarıya Etkisi ve Öğrenci Görüşleri
İngilizce Adı: The Impact of Using Concept Maps on Academic Achievement in The Sub-Learned Area of Polygons in 7th Grade Maths and Intervews of Student
ii
ETİK İLKELERE UYGUNLUK BEYANI
Tez yazma sürecinde bilimsel ve etik ilkelere uyduğumu, yararlandığım tüm kaynakları kaynak gösterme ilkelerine uygun olarak kaynakçada belirttiğimi ve bu bölümler dışındaki tüm ifadelerin şahsıma ait olduğunu beyan ederim.
Yazar Adı Soyadı: Neslihan BİÇER İmza:
iii
JÜRİ ONAY SAYFASI
Neslihan BİÇER tarafından hazırlanan "7. Sınıf Matematik Dersi Çokgenler Alt Öğrenme Alanının Kavram Haritası Kullanılarak Öğretiminin Akademik Başarıya Etkisi ve Öğrenci Görüşleri" adlı tez çalışması aşağıdaki jüri tarafından oy birliği ile Gazi Üniversitesi Matematik Eğitimi Anabilim Dalı' nda Yüksek Lisans tezi olarak kabul edilmiştir.
Danışman: Doç. Dr. Devrim ÇAKMAK
Matematik Eğitimi Anabilim Dalı, Gazi Üniversitesi ...
Başkan: Prof. Dr. Ahmet IŞIK
Matematik Eğitimi Anabilim Dalı, Kırıkkale Üniversitesi ...
Üye: Prof. Dr. Ahmet ARIKAN
Matematik Eğitimi Anabilim Dalı, Gazi Üniversitesi ...
Tez Savunma Tarihi: 06/04/2017
Bu tezin Matematik Eğitimi Anabilim Dalı' nda Yüksek Lisans tezi olması için şartları yerine getirdiğimi onaylıyorum.
Prof. Dr. Ülkü ESER ÜNALDI
iv
v
TEŞEKKÜR
Tez sürecine başladığım andan itibaren çalışma konusunu belirlememde bana yardım eden, tecrübelerini ve bilgilerini benimle paylaşan, yardımlarını benden esirgemeyen ve değerli insanlarla tanışmamı sağlayan saygıdeğer danışmanım Doç. Dr. Devrim ÇAKMAK' a teşekkürlerimi sunarım. Ayrıca Gazi Üniversitesi İlköğretim Ana Bilim Dalı Matematik Eğitimi Bölüm Başkanı olan Prof. Dr. Cengiz ÇINAR' a, Arş. Gör. Sezin KAYAGİL SEÇİR' e ve bölümdeki değerli Öğretim Elemanları ve Öğretim Üyelerine ve tezim hakkında tecrübeleri ve bilgileri ışığında değerlendirme ve önemli eleştirilerde bulunan değerli jüri üyeleri Prof. Dr. Ahmet ARIKAN ve Prof. Dr. Ahmet IŞIK' a teşekkür ederim. Araştırmam devam ederken bana özverili bir biçimde yardımcı olan öğrencilerime, bu süreçte bana destek olan tüm öğretmen arkadaşlarıma ve manevi desteğini üzerimden eksik etmeyen Özlem BAŞAY' a teşekkür ediyorum.
Yüksek lisans eğitimimde beni cesaretlendiren ve her aşamasında yanımda olan ablam Yasemin BİÇER' e ve hayatımın ilk öğretmenleri olan anneme ve babama sonsuz şükran ve minnet duygularımı sunarım.
vi
7. SINIF MATEMATİK DERSİ ÇOKGENLER ALT ÖĞRENME
ALANININ KAVRAM HARİTASI KULLANILARAK ÖĞRETİMİNİN
AKADEMİK BAŞARIYA ETKİSİ VE ÖĞRENCİ GÖRÜŞLERİ
(Yüksek Lisans Tezi)
Neslihan Biçer
GAZİ ÜNİVERSİTESİ
EĞİTİM BİLİMLERİ ENSTİTÜSÜ
Nisan 2017
ÖZ
Bu araştırma, kavram haritası kullanımının öğrencilerin Çokgenler alt öğrenme alanındaki başarına etkilerini incelemek amacıyla 2015-2016 eğitim öğretim yılında, Çankırı ili Çerkeş ilçesinde bir devlet okulunda yapılmıştır. Deney grubunda 25 öğrenci, kontrol grubunda 25 öğrenci bulunmaktadır. Çalışmada 7. sınıf şubelerinden biri deney ve biri kontrol grubu olarak öntest başarı puanları ortalamalarının denkliğine göre rastgele seçilmiştir. Çalışma 4 hafta süresince devam etmiş olup kontrol grubuna mevcut programdaki etkinliklerle öğretim ile deney grubuna ise kavram haritası kullanılarak öğretim yapılmıştır. Araştırmada karma yöntem kullanılmış olup nicel ve nitel veri toplama yöntemleri birlikte kullanılmıştır. Araştırmada veri toplama aracı olarak, Çokgenler Başarı Testi (ÇBT) ve yarı yapılandırılmış görüşme soruları kullanılmıştır. 23 soruluk çokta seçmeli ÇBT, Ön test , son test ve kalıcılık testi olarak kullanılmıştır. Verilerin analizi için SPSS programı kullanılmıştır. Yapılan analizler sonucunda deney ve kontrol grubunun son test puanları ortalamaları arasında ortalama olarak deney grubu lehine artış olsa da istatistiksel açıdan anlamlı bir fark bulunmamıştır. Ayrıca kalıcılık testinde elde edilen
vii
verilerin analiz sonuçlarına bakıldığında deney ve kontrol grubu arasında istatistiki açıdan anlamlı bir fark olduğu görülmüştür. Ayrıca deney grubuyla yapılan görüşme verilerinin analizi sonucunda kavram haritası kullanımının öğretimde yararlı olduğunu, konunun daha kalıcı olmasını sağladığı ve iyi bir özetleyici olduğu gibi görüşler ortaya çıkmıştır. Araştırma sonucunda, kavram haritalarının anlamlı öğrenmede ön örgütleyici olarak kullanılabildiği gibi konu öğretimi sırasında ve sonrasında iyi bir özetleyici, eski ve yeni bilgileri sentezleyici olduğunu destekler bulgulara ulaşılmıştır. Kavram haritası kullanılarak yapılan öğretimin öğrenci başarısını ve kalıcılığı olumlu yönde etkilediği ortaya çıkmıştır.
Anahtar Kelimeler: Kavram Haritaları, Matematik Eğitimi, Anlamlı Öğrenme, Çokgenler Alt Öğrenme Alanı, Akademik Başarı.
Sayfa Adedi: 155
viii
THE IMPACT OF USING CONCEPT MAPS ON ACADEMIC
ACHIEVEMENT IN THE SUB-LEARNED AREA OF POLYGONS IN
7TH GRADE MATHS AND INTERVIEWS OF STUDENT
(M.S. Thesis )
Neslihan Biçer
GAZI UNIVERSITY
GRADUATE SCHOOL OF EDUCATIONAL SCIENCES
April 2017
ABSTRACT
This research was conducted in a public school in Çankırı, Çerkeş province in the academic year of 2015-2016 in order to examine the effects of using concept mapping on the success of students in polygon sub-learning. There are both 50 students in the experiment and control group. Experiment and control group were selected according to the average of the achievement averages. Application period is 4 weeks. The control group was taught with the activities in the current program and the experimental group was taught using the concept map. In this study, to collect and resolve the data, quantitative and qualitative methods were used together. Therefore, the carried out study is a mixed methods research. Polygon Success Test (ÇBT) consists of 23 multiple choice questions related to the polygon. The same test was used as pretest, posttest and permanence test.
ix
Analysis of the data was done in SPSS. In the collection of qualitative data, semi-structured interview form is used. As a result of the analyzes made, statistically significant difference wasn't found between the mean of the post test scores of the experimental and control groups. There was a statistically significant difference between the experimental group and the control group in the permanence test. Findings revealed that the mathematics instruction which was enriched by concept maps has a significant effect on seventh grade students' academic achievement and permanence of this achievement related to measurement and polygon sub-learning areas. Also, according to the analysis of the opinion forms of the experimental group, it is found out that most of the students want to learn mathematics through concept maps and they think the use of concept mapping is useful, it makes the subject more permanent and is a good summarizer.
Key Words: Concept Maps, Mathematics Education, Meaningful Learning, Polygons Sub-learned Area, Academic Achievement.
Page Number: 155
x
İÇİNDEKİLER
İÇİNDEKİLER ... vi
TABLOLAR LİSTESİ... xiv
ŞEKİLLER LİSTESİ ... xvi
SİMGELER VE KISALTMALAR LİSTESİ ... xvii
BÖLÜM I. ... 1 GİRİŞ ... 1 1.1. Problem Durumu... 1 1.2. Problem Cümlesi ... 3 1.2.1. Alt Problemler ... 3 1.3. Araştırmanın Amacı ... 4 1.4. Araştırmanın Önemi ... 4 1.5. Varsayımlar ... 5 1.6. Sınırlılıklar ... 5 BÖLÜM II. ... 7
KURAMSAL ÇERÇEVE ve İLGİLİ ARAŞTIRMALAR ... 7
2.1. Kuramsal Çerçeve ... 7
2.1.1. Matematik ve Matematik Öğretimi ... 7
2.1.2. Kavram: ... 8
xi
2.1.4. Kavram Haritaları ... 9
2.1.5. Kavram Haritalarının Kullanım Amaçları ... 11
2.1.6. Kavram Haritalarının Çizimi ... 14
2.1.7. Kavram Haritası Türleri ... 15
2.1.8. Kavram Haritasının Yararları ... 18
2.1.9. Kavram Haritası Kullanımında Karşılaşılan Zorluklar ... 19
2.2. İlgili Araştırmalar ... 20
2.2.1. Kavram Haritaları ile İlgili Yapılan Araştırmalar ... 20
2.2.2. Çokgenler Alt Öğrenme Alanı ile İlgili Yapılan Araştırmalar ... 27
BÖLÜM III ... 31
YÖNTEM... 31
3.1. Araştırmanın Modeli ... 31
3.2. Çalışma Grubu ... 32
3.3. Uygulama Öncesi Hazırlık ... 33
3.4. Uygulamanın Yapılışı ... 34
3.5. Kavram Haritaları Kullanılarak Yapılan Öğretimin Uygulanışı ... 34
3.6. Veri Toplama Araçları ve Veri Toplama Araçlarının Oluşturulma Süreci ... 36
3.6.1. "Çokgenler" Alt Öğrenme Alanı İle İlgili Başarı Testi ... 36
3.6.2. Pilot Uygulama Süreci ve Madde Analiz İstatistikleri ... 37
3.7. Başarı Testi Sorularının Bloom' un Bilişsel Alan Aşamalarına göre Dağılımları ... 41
3.8. Yarı Yapılandırılmış Görüşme Formunun Hazırlanması... 43
3.9. Verilerin Analizi ... 46
BÖLÜM IV. ... 47
xii
4.1. Birinci Alt Probleme İlişkin Bulgular ve Yorumlar ... 49
4.2. İkinci Alt Probleme İlişkin Bulgular ve Yorumlar ... 49
4.3. Üçüncü Alt Probleme İlişkin Bulgular ve Yorumlar ... 50
4.4. Dördüncü Alt Probleme İlişkin Bulgular ve Yorumlar ... 51
4.5. Beşinci Alt Probleme İlişkin Bulgular ve Yorumlar ... 52
4.6. Altıncı Alt Probleme İlişkin Bulgular ve Yorumlar ... 53
4.7. Yedinci Alt Probleme İlişkin Bulgular ve Yorumlar ... 54
4.8. Sekizinci Alt Probleme İlişkin Bulgular ve Yorumlar ... 55
BÖLÜM V... 74
TARTIŞMA, SONUÇLAR VE ÖNERİLER ... 74
5.1. Tartışma ve Sonuçlar ... 74
5.1.1. Akademik Başarıya İlişkin Elde Edilen Sonuçlar... 74
5.1.2. Kalıcılığa İlişkin Elde Edilen Sonuçlar ... 76
5.1.3. Öğrenci Görüşlerine İlişkin Elde Edilen Sonuçlar ... 77
5.2. Öneriler ... 79
KAYNAKLAR ... 81
EKLER... 94
EK 1. Kavram Haritası Destekli Öğretim Ders Planı 1 ... 95
EK 2. Kavram Haritası Destekli Öğretim Ders Planı 2 ... 101
EK 3. Kavram Haritası Destekli Öğretim Ders Planı 3 ... 110
EK 4. Çokgen nedir? Çokgenlerin genel özellikleri nelerdir? İle İlgili Kavram Haritası... 108
Ek 5. Çokgenlerin elemanları nelerdir? İle İlgili Kavram Haritası ... 109
Ek 6. n kenarlı bir çokgendeki iç açıların toplamı, dış açıların toplamı ile ilgili hesaplamalar nelerdir? İle İlgili Kavram Haritası ... 110
xiii
Ek 7. Düzgün çokgen nedir ve özellikleri nelerdir? İle İlgili Kavram Haritası ... 111 Ek 8. Düzgün çokgenlerde bir iç açı ve bir dış açı ile ilgili hesaplamalar nelerdir? İle İlgili Kavram Haritası ... 112 Ek 9. Çokgenlerde köşegenlerle ilgili hesaplamalar nelerdir? İle İlgili Kavram Haritası... 113 Ek 10. Özel dörtgenlerden paralelkenarın tanımı nedir? Genel özellikleri nelerdir? Alanı ve çevresi ile ilgili hesaplamalar nelerdir? İle İlgili Kavram Haritası... 114 Ek 11. Özel dörtgenlerden karenin tanımı nedir? Genel özellikleri nelerdir? Alanı ve çevresi ile ilgili hesaplamalar nelerdir? İle İlgili Kavram Haritası ... 115 Ek 12. Özel dörtgenlerden dikdörtgenin tanımı nedir? Genel özellikleri nelerdir? Alanı ve çevresi ile ilgili hesaplamalar nelerdir? İle İlgili Kavram Haritası... 116 Ek 13. Özel dörtgenlerden eşkenar dörtgenin tanımı nedir? Genel özellikleri nelerdir? Alanı ve çevresi ile ilgili hesaplamalar nelerdir? İle İlgili Kavram Haritası... 125 Ek 14. Özel dörtgenlerden yamuğun tanımı nedir? Yamuk çeşitleri ve onların genel özellikleri nelerdir? Alanı ve çevresi ile ilgili hesaplamalar nelerdir? İle İlgili Kavram Haritası ... 126 Ek 15. Kavram Haritalarının Öğrenci Uygulaması... 130 Ek 16. Çokgenler Başarı Testi' nin Ön Test, Son Test ve Kalıcılık Testi Olarak Kullanılan Hali ... 132 Ek 17. Çokgenler Başarı Testi Cevap Anahtarı ... 136 Ek 18. Yarı Yapılandırılmış Görüşme Formu' nun Uygulama İçin Kullanılan Hali ... 137 Ek 19. İzin Belgeleri ... 139
xiv
TABLOLAR LİSTESİ
Tablo 1. TIMSS 2011 8. Sınıflar Uluslararası Matematik Yeterlik Düzeylerinin Tanımı ... 2
Tablo 2. Ön test ve Son test Kontrol Gruplu Desen ... 32
Tablo 3. Deney ve Kontrol Gruplarındaki Örneklem Sayıları ... 32
Tablo 4. Çokgenler Alt Öğrenme Alanı Kazanım Tablosu ... 33
Tablo 5. Kazanımlar ve Kullanılan Kavram Haritaları ... 35
Tablo 6. 25 Sorudan Oluşan Çokgenler Başarı Testi' nde Her Maddenin Güçlük İndeksi (p) ve Ayırıcılık İndeksi (r) Değerleri ... 39
Tablo 7. Kazanıma İlişkin Sorular ... 41
Tablo 8. Bloom un Bilişsel Alan Aşamaları ... 43
Tablo 9. Deney ve Kontrol Grubundaki Öğrencilerin Testlere göre Yaptıkları Doğru Sayıları ve Ortalamaları ... 48
Tablo 10.Deney ve Kontrol gruplarının Ön Test Başarı Puanlarının Karşılaştırılması... ... 49
Tablo 11. Deney Grubunun Ön test ve Son Test Başarılarının Karşılaştırılması ... 50
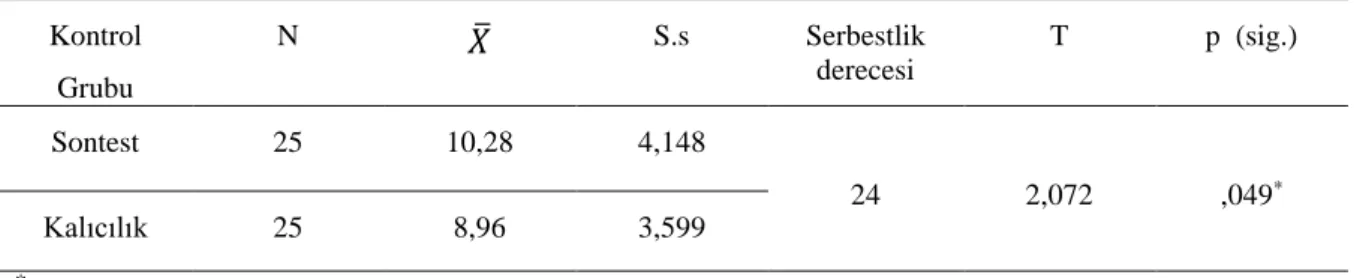
Tablo 12. Kontrol Grubunun Ön Test ve Son Test Başarılarının Karşılaştırılması ... 51
Tablo 13. Deney ve Kontrol Gruplarının Son Test Başarı Puanlarının Karşılaştırılması .. 52
Tablo 14. Deney Grubunun Son Test ve Kalıcılık Testi Başarı Puanlarının Karşılaştırılması ... 53
Tablo 15. Kontrol Grubunun Son Test ve Kalıcılık Testi Başarı Puanlarının Karşılaştırılması ... 54
xv
Tablo 16. Deney ve Kontrol Gruplarının Kalıcılık Testi Başarı Puanlarının
Karşılaştırılması...55
Tablo 17. Öğrencilerin Soru 1 e Verdikleri Yanıtların Analizi ... 56
Tablo 18. Deney Grubu Öğrencilerinin Soru 1 e ait Görüşleri ... 57
Tablo 19. Öğrencilerin Soru 2 ye Verdikleri Yanıtların Analizi ... 58
Tablo 20. Deney Grubu Öğrencilerinin Soru 2 ye Ait Görüşleri ... 59
Tablo 21. Öğrencilerin Soru 3 e Verdikleri Yanıtların Analizi ... 60
Tablo 22. Deney Grubu Öğrencilerinin Soru 3 e Ait Görüşleri ... 61
Tablo 23. Öğrencilerin Soru 4 e Verdikleri Yanıtların Analizi ... 62
Tablo 24. Deney Grubu Öğrencilerinin Soru 4 e Ait Görüşleri ... 63
Tablo 25. Öğrencilerin Soru 5 e Verdikleri Yanıtların Analizi ... 64
Tablo 26. Deney Grubu Öğrencilerinin Soru 5 e Ait Görüşleri ... 65
Tablo 27. Öğrencilerin Soru 6 ya Verdikleri Yanıtların Analizi ... 66
Tablo 28. Deney Grubu Öğrencilerinin Soru 6 ya Ait Görüşleri ... 67
Tablo 29. Öğrencilerin Soru 7 ye Verdikleri Yanıtların Analizi ... 68
Tablo 30. Deney grubu Öğrencilerinin Soru 7 ye Ait Görüşleri ... 69
xvi
ŞEKİLLER LİSTESİ
Şekil 1. Kavram Haritasının Kavram Haritası ... 13
Şekil 2. Örümcek kavram haritası örneği ... 15
Şekil 3. Zincir kavram haritası örneği ... 16
Şekil 4. Hiyerarşik kavram haritası örneği ... 17
Şekil 5. Balık kılçığı haritası örneği ... 18
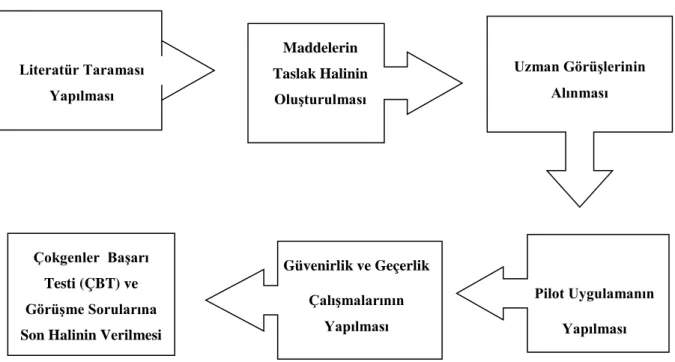
Şekil 6. ÇBT ve Görüşme sorularının hazırlanma süreci ... 36
xvii
SİMGELER VE KISALTMALAR LİSTESİ
MEB Milli Eğitim Bakanlığı
TTKB Talim ve Terbiye Kurulu Başkanlığı
ÇBT Çokgenler Başarı Testi
F Frekans
1
BÖLÜM I.
GİRİŞ
Bu bölümde problem durumu, problem cümlesi, alt problemler, araştırmanın önemi, araştırmanın amacı, varsayımlar ve sınırlılıklar üzerinde durulmuştur.
1.1.Problem Durumu
Matematik dersi çok fazla korkuya, önyargıya sebep olan derslerden biridir. Bunlar, matematik dersinde başarısızlığı getiren sebeplerden bazılarıdır. Ancak matematiği ezberden kurtarıp anlamanın yolunu keşfeden bireylerin matematiği çok sevdikleri görülmektedir. Sertöz (2003), "Birçok insan için matematik, hayatını zehir eden derslerden, içine korku salan sınavlardan ve okulu bitirir bitirmez kurtulacağı bir kâbustan ibarettir. Bazıları içinse matematik, hayatı anlamanın ve sevmenin bir yolu olabilmiştir. Çünkü sevmenin yolu, her şeyde olduğu gibi anlamaktan geçer." ifadeleriyle konu hakkındaki düşüncelerini belirtmiştir.
Ayrıca, TIMSS (Trends in International Mathematics and Science Study- Uluslararası Matematik ve Fen Araştırmaları Sınavı) ve PISA (Program for International Student Assessment - Uluslararası Öğrenci Değerlendirme Sınavı) gibi uluslararası sınavların sonuçları irdelediğinde Türkiye açısından geometri başarısının düşük olduğu görülmektedir. Örneğin, TIMMS nihai raporuna göre Türkiye matematik alanında 39 ülke arasında 24. sırada yer almaktadır. Matematik alanında Singapur 621 puanla birincidir. Uluslararası ortalama 500 puan iken Türkiye’nin ortalaması 458 puandır. TIMSS matematik başarısı bir önceki döneme göre 6 puan artarak 458 olmuştur. Türkiye de 8.
2
sınıflarda matematiğin alt boyutlar açısından ortalamaları incelendiğinde ise veri ve olasılık 466 puan, cebir 460 puan, sayılar 447 puan ve geometri 463 puandır (TIMSS, 2015). Türkiye' nin aldığı puanlara göre bulunduğu düzey Tablo 1 e göre belirlenmiştir. Tablo 1 e göre Türkiye alt düzeyde bulunmaktadır. Bu bilgiden yola çıkarak öğrencilerin bazı temel bilgilere sahip olduğu görüşüne ulaşılmaktadır. Diğer taraftan PISA sonuçlarına göre Türkiye sınava katılan 65 ülke içinde matematik alanında 44. sırada yer almaktadır. Bu sınavda matematikte Şangay- Çin 613 puanla birinci olurken Türkiye 448 puan almıştır. Türkiye’nin alt boyutlara göre ortalaması incelendiğinde belirsizlik ve veri (olasılık) 447 puan, değişim ve ilişkiler (cebir) 448 puan, uzay ve şekil 443 puan ve sayısal (aritmetik, çokluk) 442 puandır (PISA, 2012). Bu puanlardan da anlaşılacağı gibi Türkiye TIMMS sınavında en çok geometri alt boyutunda, PISA sınavında ise sayısal alt boyutundan sonra en çok uzay ve şekil boyutunda başarısız olduğu görülmektedir (Bal, 2012).
Tablo 1
TIMSS 2011 8. Sınıflar Uluslararası Matematik Yeterlik Düzeylerinin Tanımı
625 ve üstü İleri Düzey
Öğrenciler bilgiyle akıl yürütebilir, sonuç çıkarabilir, genelleme yapabilir ve doğrusal eşitlikleri çözebilir.
550- 625 altı Üst Düzey
Öğrenciler bilgi ve anlamalarını çeşitli değişkenlikteki göreceli olarak karmaşık durumlara uygulayabilir.
475- 550 altı Orta Düzey
Öğrenciler temel matematik bilgilerini değişik durumlara uyarlayabilirler.
400- 475 altı Alt Düzey
Öğrenciler tüm sayılar, ondalıklar, işlemler ve temel grafiklerle ilgili bazı bilgilere sahiptirler.
3
Matematik dersi için sahip olunan kaygıları azaltmak için, matematik dersini daha eğlenceli hale getirerek sevdirmek ve matematik öğretiminde daha etkili öğretim yolları bulabilmek için yapılan çalışmalar büyük önem taşımaktadır. Ayrıca üst düzey bilişsel davranışları kazanabilmek, problem çözme, ilişkilendirme, akıl yürütme gibi matematiksel biliş kazanabilmek için farklı öğretim metotlarının etkililiği üzerinde çalışmalar yapılmalıdır. Uluslararası sınavlarda daha yüksek başarılar elde edebilmek için matematik eğitimi ve öğrenimi üzerine çalışmalar yapılmalıdır. Matematiksel biliş kazanabilmek, ulusal alanda ülkemizi daha iyi temsil edebilmek gibi sebeplerden dolayı ülkemizde matematik öğretimiyle ilgili çalışmalara büyük oranda ihtiyaç vardır.
1.2. Problem Cümlesi
Kavram haritası kullanımının ortaokul 7. sınıf öğrencilerinin matematik dersi çokgenler alt öğrenme alanındaki akademik başarılarına ve bilgilerinin kalıcılık düzeylerine etkisi nedir?
1.2.1. Alt Problemler
1. Çokgenler alt öğrenme alanında, kavram haritası kullanılarak öğretim yapılan deney grubu ile kontrol grubunun matematik ön test başarı puan ortalamaları arasında istatistiki açıdan anlamlı bir farklılık var mıdır?
2. Çokgenler alt öğrenme alanında, kavram haritası kullanılarak öğretim yapılan deney grubunun ön test ve son test matematik başarı puan ortalamaları arasında istatistiki açıdan anlamlı bir farklılık var mıdır?
3. Çokgenler alt öğrenme alanında, kontrol grubunun matematik ön test ve son test matematik başarı puan ortalamaları arasında istatistiki açıdan anlamlı bir farklılık var mıdır?
4. Çokgenler alt öğrenme alanında, deney grubu ile kontrol grubunun son test başarı puan ortalamaları arasında istatistiki açıdan anlamlı bir farklılık var mıdır?
5. Çokgenler alt öğrenme alanında deney grubunun son test ile kalıcılık testi puanlarının ortalamaları arasında anlamlı bir farklılık var mıdır?
4
6. Çokgenler alt öğrenme alanında kontrol grubunun son test ile kalıcılık testi puanlarının ortalamaları arasında istatistiki açıdan anlamlı bir farklılık var mıdır?
7. Çokgenler alt öğrenme alanında, kontrol grubu ile deney grubunun kalıcılık testi puanların ortalamaları arasında istatistiki açıdan anlamlı bir farklılık var mıdır?
8. Çokgenler alt öğrenme alanında, kavram haritası kullanılarak öğretim yapılan deney grubu öğrencilerinin uygulama sonrasındaki görüşleri nelerdir?
1.3. Araştırmanın Amacı
Bu çalışma ile Çankırı ili Çerkeş ilçesinde bulunan bir devlet okulunda öğrenim gören 7. sınıf öğrencilerinde Çokgenler alt öğrenme alanında kavram haritası destekli öğretimin matematik dersindeki başarı ve kalıcılığa ne derece etki ettiğinin ölçülmesi hedeflenmiştir. Bu çalışma ile aynı zamanda araştırma problemine ve alt problemlerine cevap bulmak da hedeflenmiştir. Matematik öğreniminde ve değerlendirme aşamasında kullanılan kavram haritalarının öğrenci başarısına ve bilgilerinin kalıcılığına nasıl etki ettiği çalışma sonunda elde edilen veriler kapsamında değerlendirilmesi amaçlanmaktadır.
1.4. Araştırmanın Önemi
Kavram haritası destekli matematik dersi öğretimi, anlamlı öğrenme noktasında önemli bir yer teşkil etmektedir. Öğrencilerin anlamlı öğrenmeleri bilgiyi farklı ortamda uygulayabilmeleri, kavramlar arasındaki ilişkiyi kurabilmeleri, bilgiyi çeşitli temsil biçimlerine dönüştürebilmeleriyle yakından ilgilidir (MEB, 2005). Tüm yapıyı bir bütün olarak önünde gören öğrenci kavramlar arasında ilişki kurabilir ve kavramsal yapıyı daha iyi anlayabilir.
Anlamlı öğrenmenin sağlanabilmesi için ön örgütleyicilerden kavram haritalarının etkili bir şekilde kullanılması gerekmektedir. Bu sayede zor olarak bilinen matematik dersi hem etkili bir şekilde öğrenilebilir hem de derse yönelik olumsuz tutuma sahip olan öğrencilerin duygu ve davranışları olumlu yönde değişebilir.
Ayrıca, kavram haritasının derse yönelik tutum geliştirmede etkili olup olmadığının incelendiği çalışmalar ele alındığında bu çalışmaların fen bilimleri ve sosyal bilimler
5
alanları ile sınırlı kaldığı görülmüştür (Altınok ve Açıkgöz, 2006; Canbolat, 2008; Çolak, 2010; Güçlüer, 2006; Horton vd., 1993; Kavak, 2009; Kendirli, 2008; Kılıç, 2009; Olugbemiro, Folusho ve Okebukola, 1990; Vurkaya, 2010; Yener, 2006). Artık son zamanlarda matematik öğreniminde kavram haritaları çalışmalarına da yer verilmektedir. Matematik eğitimi ve öğreniminde yapılan kavram haritaları ile ilgili çalışmalara "İlgili Literatür" kısmında yer verilmiştir.
Bu çalışmada, Çokgenler alt öğrenme alanı ile ilgili kavramların, kavram haritası ile öğreniminin öğrencilerdeki akademik başarı ve kalıcılık üzerine etkisi test edilmiştir. Bu amaçla, kavram haritası destekli öğretimin ortaokul 7. sınıf öğrencilerinin Çokgenler alt öğrenme alanında öğrenme başarılarına, kalıcılığa etkisi mevcut programdaki etkinliklerle öğretimle karşılaştırılarak incelenmiş ve sonuçları desteklemek için öğrenciler ile yarı yapılandırılmış görüşmeler yapılmıştır. Böylelikle yapılan bu çalışmanın literatüre katkıda bulunacağı düşünülmektedir.
1.5. Varsayımlar
Araştırmada,
1. Araştırmaya katılan öğrencilerin uygulanacak etkinliklere ve görüşmelere samimiyetle ve ciddiyetle cevap vereceği,
2. Dışsal etkilerin deney ve kontrol grubunu eşit düzeyde etkileyeceği varsayılmıştır.
1.6. Sınırlılıklar
Araştırma,
1. Çankırı ili Çerkeş ilçesinde bulunan bir devlet okulunun öğrencileri sınırlandırılmıştır.
2. 7. sınıf öğretim programında bulunan "Çokgenler" alt öğrenme alanı kazanımlarının öğretimi ile sınırlandırılmıştır.
3. MEB' in "Çokgenler" alt öğrenme alanı için belirlediği ders süresi ile sınırlandırılmıştır.
6
4. Başlangıçta kavram haritası oluşturmak için yeterli bilgiye sahip olmamam, ancak akademik anlamda araştırma ve pratik yaparak kendimi geliştirmem uygulamaya başlamak adına beni sınırlandırmıştır.
5. MEB tarafından verilen izinler için beklenen süresi araştırma uygulamalarına başlama zamanını sınırlandırmıştır.
7
BÖLÜM II.
KURAMSAL ÇERÇEVE VE İLGİLİ ARAŞTIRMALAR
Bu bölümde problem durumu ile ilgili olarak kuramsal çerçeveye, kavram haritaları ve "Çokgenler" alt öğrenme alanı ile ilgili yapılan araştırmalara yer verilmiştir.
Araştırmalar yapılmış oldukları tarih sıralarına dikkat edilerek verilmiştir.
2.1. Kuramsal Çerçeve
2.1.1. Matematik ve Matematik Öğretimi
Matematik, ardışık soyutlama ve genellemeler süreci olarak geliştirilen yapılar ve bağlantılardan oluşan bir sistem olarak ifade edilmektedir. Bu tanımda üç husus dikkat çekmektedir. Bunlardan biri matematiğin sistem olduğu, diğeri yapılardan ve bağıntılardan oluştuğu, üçüncüsü de bu yapıların ardışık soyutlamalar ve genellemeler süreci ile oluştuğudur. Buna göre matematiği insan tarafından zihinsel olarak yaratılan bir sistem olarak ifade etmek mümkündür. Bu durum matematiği soyut hale getirir (Baki, 2006, s. 46- 47).
İnsanların matematiği nasıl gördükleri şu maddelerle ifade edilebilir:
• Matematik, günlük hayattaki problemleri çözmede kullanılan sayma ve hesaplamadır.
8
• Matematik, insanda mantıklı düşünmeyi geliştiren bir sistemdir.
• Matematik, dünyayı anlamada ve yaşadığımız çevreyi geliştirmede başvurulan bir yardımcıdır (Baykul, 2002, s. 32).
Matematik öğretiminin amacı ise genel olarak şu şekilde söylenebilir: Kişiye günlük hayatta ihtiyacı doğrultusunda matematik bilgisi ve becerisi kazandırmak, ona problem çözmeyi öğretmek ve herhangi bir olayla karşılaştığı zaman nasıl davranacağı, bu problemi nasıl çözeceği yaklaşımı içinde olan bir düşünme biçimi kazandırmaktır (Altun, 2001).
Matematiğin yapısına uygun bir öğretim,
1. Öğrencilerin matematikle ilgili kavramları anlamaları, 2. Matematikle ilgili işlemleri anlamaları,
3. Kavramların ve işlemlerin arasındaki bağları kurmaları
şeklinde belirtilen amaçlara uygun olmalıdır (Van de Wella, 2004' ten aktaran Baykul, 2005).
İlişkisel anlama olarak adlandırılan bu üç amaç, matematikteki yapıları anlama, sembollerle ifade etme ve bunun kolaylıklarından yararlanma, matematikteki işlemlerin tekniklerini anlama ve bunları sembollerle ifade etme, metotlar, semboller ve kavramlar arasındaki bağıntılar ya da ilişkileri kurma olarak açıklanabilir (Baykul, 2005).
2.1.2. Kavram:
Kavram, bir nesnenin zihindeki soyut ve anlaşılabilen kısmının genel tasarımıdır. Yani kavram, ortak özelliklerin nesne, olay, fikir ve davranışların oluşturduğu sınıflamaların soyut temsilcisidir (Fidan, 1986, s. 13).
Kavramlar zihinde oluşturulan şeylerdir. Dış dünyada değil insanın düşünce sisteminde yer alan kavramlar eşyayı, olayları, insanları ve düşünceleri benzerliklerine göre gruplandırıldığında gruplara verilen isimlerdir (Kabaca, 2003, s. 1).
9
2.1.3. Matematik Öğretiminde Kavram Öğretimi
Matematik, birçok temel kavrama sahiptir ve bu kavramlar genel olarak soyut kavramlardır. Soyut kavramların kazanılmasının zor olmasından dolayı, matematiği öğrenmenin öğrencilere zor geldiği de bilinmektedir. Bu sebeple matematik öğretimi için kolaylaştırıcı yöntemlerin üzerinde durulması gerekir (Alakoç, 2003). Matematik öğretiminde kavramların öğrenci zihninde oluşmasını sağlamak için kavram öğretimi yapılmalıdır. Bir matematik konusuna ait öğretim yapılırken, o konunun temel kavramları tam olarak kazandırılmadan alıştırma ya da uygulama çalışmaları yapmak ezberci öğretime neden olabilir.
Piaget, matematiksel kavramların ilköğretim düzeyindeki çocuklar tarafından kavranması için birçok tecrübe yaşayabilecekleri materyallere ve çizimlere ihtiyaç olduğunu ifade etmektedir. Matematiği günlük hayatla ilişkilendirmeyi sağlayacak materyaller geliştirerek kavram öğrenimi sağlanmalıdır (Gürbüz, 2006).
Kavram öğretimi yapılırken sembolik ve matematiksel dile çok fazla yer vermeden öğrencilerin anlayacağı sade bir dil kullanmak gerekir. Örnekler değişse de kavramların özellikleri aynı kaldığı için bu durumun öneminin öğrencilere kazandırılması gerekir (Özdemir, 2015, s. 13). Sonuç olarak, kavramsal yolu benimseyen öğrenci matematiği anlamada daha geçerli bir yol izlemiş olur, bu da öğrenmeleri daha fonksiyonel ve kalıcı hale getirir (Baki, 2006, s. 198- 199).
2.1.4. Kavram Haritaları
Bilişsel psikolojinin üzerinde çalıştığı temel konulardan biri de bireyin bilgiyi nasıl organize edip yapılandırdığıdır. Beynin verimli olarak nasıl çalıştığı ve kavramların insan zihninde nasıl organize edildiğine dair pratik uygulamalar bilişsel stratejiler olarak ele alınmaktadır. Bilişsel öğrenme konusunda yapılan araştırmalar (Erdoğan, 2000; Merrienboer, 2001), bilginin yapılandırılması sırasında çerçevelendirme, sınıflandırma, zihinsel canlandırma, sembolleştirme gibi birçok bilişsel stratejiler geliştirildiğini ortaya koymaktadır. Öğrenci bir konu ile ilgili kavram haritası hazırlaması sırasında bu stratejilerden yararlanmaktadır. Bu da öğrencinin bilgi organizasyonu süreci ile ilgili doğrudan ve hızlı bir şekilde analitik veri elde edilmesini sağlar (Hoeft vd., 2003). Bu
10
nedenle, bireysel yapılandırmaların, organizasyonların ortaya çıktığı kavram haritaları öğrenme-öğretme etkinliklerinin planlanmasında ve değerlendirilmesinde sıklıkla kullanılmaktadır.
Kavram haritalarının ortaya çıkışının dayandığı temel noktalardan biri Ausubel' in anlamlı öğrenme modelindeki yeni kavramların özümsenmesinin ancak eski kavramlar üzerine inşasıyla mümkün olduğu fikridir (Batdı, 2014). Yapılandırmacılık yaklaşımına göre, bilgi hazır olarak alınmaz, aksine yeni bilgiler eski bilgilerin üzerine inşa edilerek "bilişsel yapı" oluşturulur. Ausubel' e göre anlamlı öğrenme, yeni bilgilerin bilişsel yapıya bağlanmasıyla meydana gelir (Ausubel, 1968).
Ausubel (1968)' e göre insanların çoğu, yeni bilgileri var olan bilgilerini kullanmadan öğrenmeye çalışır ve anlamlı öğrenmeden uzaklaşır. Asıl olan eski bilgilerle yeni bilgiler arasında anlamlı bağlantılar oluşturabilmektir. Öğrenciler yeni bir kavramla karşılaştıklarında o kavrama ait deneyimlerini düşünmeye başlar. Bu deneyimlerle öğrenci bilgiyi yapılandıracak, diğer bilgilerle ilişki kuracak ve yeni kavramın öğrenilmesi tamamlanacaktır. Bu aşamalar öğrenciye kazandırılırsa anlamlı öğrenmelerin sağlanacağı görülecektir. Ausubel' e göre eski ve yeni bilgi arasında bağlantı kurulabilmesi için "ön örgütleyici" lere ihtiyaç vardır. Bunlar sesli materyal, resim, grafik vb. olabilir. Ausubel' e göre öğrenme yukarıdan aşağı doğru veya tümdengelim ile gerçekleşir (Kılınç, 2007). Ausubel' in teorisine göre bilişsel yapının oluştuğu, yeni bilgilerin öğrenilmesi için eski bilgilere ihtiyaç duyulduğu anlamlı öğrenmeye bağlı kalarak ilk defa 1970' li yıllarda Novak ve Cornell Üniversitesi öğrencileri tarafından kavram haritaları geliştirilmiştir. Novak ve öğrencilerinin fen eğitimi alanında kavramların daha kolay öğretilebilmesi ile ilgili bir araştırma projesi kapsamında yapılan çalışmaların sonucunda ortaya çıkmıştır (Novak ve Gowin, 1984). Novak' a göre haritalar hiyerarşik bir düzen içinde olmalıdır. Bilginin bir yapısı varsa, bu bilginin birtakım alt birimlere ayrılarak gösterilebileceğini savunmuşlardır (Kaşlı vd., 2002).
1990’dan beri kavram haritası farklı konu alanlarında yapılan araştırmalarda kullanılmıştır. Barenholz ve Tamir (1992), Trowbridge ve Wandersee (1994) kavram haritasını fen öğretiminin değerlendirmesinde kullanmışlardır. Hegarty-Hazel ve Prosser (1991), McClure, Sonak ve Suen (1999)’in çalışmaları ise daha çok kavramsal öğrenmeler ile çalışma yöntemleri arasındaki ilişkileri ortaya koymaya yöneliktir. Bütün bu araştırmalarda
11
bir öğretim metodu olarak kavram haritasının geçerlik, güvenirlik ve uygulanabilirliği kanıtlanmıştır (Duru ve Gürdal, 2002).
Aynı zamanda Novak (1991), kavram haritalarının uygulanamayacağı hiçbir bilim dalı olmadığını vurgulamıştır. Literatürü incelediğimizde Novak' ı destekleyen çalışmalardan bazılarına örnek olarak; Hsu ve Hsieh (2005), Gul ve Boman (2006) hemşirelik eğitiminde, Köse (2007), Altınok ve Açıkgöz (2006), Kaya (2003) fen eğitiminde, Kırkkılıç, Maden, Şahin ve Girgin (2011) Türkçe eğitiminde, Çoban, Devecioğlu ve Coşkuner (2008) beden eğitimi ve spor alanında, Bektüzün (2013), Sakiyo ve Waziri (2015), Patankar ve Marutirao (2016) biyoloji eğitiminde, Singh (2015) kimya eğitiminde, Oğraş ve Bozkurt (2011), Mwakapenda (2003), Müjdeci (2009), Laçin (2014), Özdemir (2015) matematik eğitimde ve daha bir çok araştırmacı farklı eğitim alanlarında öğretimi etkili kılmak için kavram haritası yöntemini kullanmıştır.
Matematikte kavramlar ve işlemler arasındaki ilişkinin kurulması, kavramların ve ilişkilerin anlamlı hale geldiğini gösterir. Çünkü kavramlar ve ilişkiler tek başlarına kullanıldıklarında matematiksel olarak bir anlam içermezler. Kavram haritaları matematiksel bilgi organizasyonlarının değerlendirilmesi amacıyla kullanılabilir (Hiebert ve Carpenter, 1992). Aynı zamanda içsel süreçlerin ortaya çıkarılmasında kullanılan (Pearson ve Somekh, 2003) kavram haritalarının eğitimsel uygulamaları, bir öğrenme stratejisi ve çeşitli alanlarda bir değerlendirme aracı olma özelliğini taşıması nedeniyle öğrencilerin yanlış anlamalarını tespit etmede de etkili olarak kullanılır (Bartels, 1995; Novak, 1991). Yani, kavram haritaları öğrenme-öğretme sürecinde kullanılan bir teknik olmasının yanı sıra ölçme ve değerlendirme sürecinde de kullanılan bir tekniktir (RuizPrimo ve Shavelson, 1996, 2005; Vanides, Yin, Tomita& Ruiz, 2005, 2011).
2.1.5. Kavram Haritalarının Kullanım Amaçları
Gaines (2002), kavram haritalarının kullanım amaçlarını aşağıda verildiği gibi sıralamıştır:
1. Yaratıcılık amacı: Aynen beyin fırtınasında olduğu gibi öğrenci kavramları seçmede ve
bağlantı kelimelerini bulmada tamamen özgürdür. Bu arada yeni kavram ve ilişkilerin keşfi kolaylaşır.
12
2. Büyük metinleri tasarlama amacı: Özellikle bilgisayar yazılımları sayesinde karmaşık
bir konu haritalandırılır.
3. İletişim amacı: Öğrenci kendi kavramlarını diğer arkadaşlarıyla paylaşır. Kavram
haritası tüm bir grubun görüşlerini de taşıyor olabilir. Kavramlar ve bağlantılar tartışılır, böylece işbirlikli öğrenme sağlanır.
4. Öğrenme amacı: Novak’ ın ana amacı kavram haritalarının bir öğrenme aracı olarak
kullanılmasıdır. Yapılandırmacı öğrenme yeni bilginin eskilerine entegre edilmesini öngörür. Kavramlar arasındaki ilişkilere dikkat çekilir. Deneyimlerle öğrenilen kavramlar kavram haritaları ile şekillenir. Ayrıca öğrencilerin en iyi düşünme becerileri burada geliştirilir (Jonassen ve Grabowski, 1993).
5. Problem çözme amacı: Eğitimdeki problem çözme yollarından birisidir. Alternatif
yollar kullanarak problem çözme becerilerini yükseltir. Problem çözme, eğitimde genelde küçük gruplarda başarılı olurken kalabalık gruplarda bu stratejinin kavram haritalarının içinde kullanımı ile verim arttırılır.
6. Değerlendirme amacı: Öğrenciler bir sınavda kendi kavram haritalarını çıkarır veya
boşlukları doldurur. Tek başına uygulanmasındansa diğer değerlendirme araçlarıyla birlikte zenginlik içinde sunulmasının faydalı olduğu düşünülür.
13
Kavram Haritaları
Düzenlenmiş Bilgi
Yapı ile İlişki
İlgili Duygu ve İzlenim Etkili Öğretme Çapraz Bağlantılar Etkili Öğrenme Kavramlar Normal Durumlar Durumlar Belirlenmiş Hiyerarşik olarak yapılandırılmış
Olaylar Nesneler Semboller Kelimeler Yaratıcılık sunar. oluşur. oluşur. oluşur. oluşturur/ içerir. içerir. için gereklidir. içerir. olan dır. dır. içindeki ile teşvik eder. bazen Karşılıklı İlişkiler Farklı Harita Katmanları Yeni Oluşumlar ile başlar. görmeyi gerektirir. ile başlar. gösterir. arasındaki
Şekil 1. Kavram Haritasının Kavram Haritası (Novak, J. D. (1984). The theory underlying
concept maps and how to construct them. Cambridge University.
14
Ayrıca kavram haritasının kullanım alanlarına bakacak olursak,
"Kavram haritasının öğretmen tarafından çizilmesi ise iki şekilde olabilir:
a. Konu anlatılırken adım adım kavram haritası çizilir. Bu arada öğrencinin ana kavramlara, farklılıklara dikkat etmesi sağlanır.
b. Konu anlatımı bittikten sonra kavram haritası adım adım çizilerek konunun özeti yapılır." (Yaman, 2006, s.56).
2.1.6. Kavram Haritalarının Çizimi
Kavram haritası çiziminde izlenmesi gereken bazı yollar vardır. Cunningham ve Turgut'un (aktaran Yaman, 2006, s. 59) belirttiğine göre bir kavram haritası geliştirmede ilgili aşamalar aşağıdaki şekilde sıralanabilir:
1. Bir kâğıda öğretilecek kavramlar listelenir. Kavramlarla ilgili açıklamalara, ilkelere, kavramlar arası ilişkilere yer verilmez.
2. Bir başka yere özel örnekler, öğrenciler için önemli olaylar not edilir.
3. Kavramlar listesinden en genel kavram, ayrı bir kâğıdın başına yazılır. Bundan sonra öğretilmek istenen ilişkili kavramlar aşamalı bir düzende kâğıda yerleştirilir. Birincil kavramdan sonra ikincil kavramlarla bağlantıyı sağlayan kavramlara koordinat kavramlar denir. Düşey düzenlemede genel kavramlar üstte, eşit genellikteki kavramlar aynı satırda yer almalıdır.
4. Her kavram, haritada yalnız bir kere yer almalıdır. Kavramlar, haritadaki diğer sözcüklerden kolayca ayırt edebilmek için kutu içine alınmalıdır. Haritada yer alan iki kavram arası ilişkiyi göstermek için iki kutu çizgi ile bağlanır. Bazı durumlarda ilişkinin yönü önemli olduğu için, yön oklarla gösterilir.
5. Kavramlar arası ilişkiler, ilişki çizgilerinin üzerine birkaç sözcük ile yazılır (Çakmak & Kalaycı, 2000).
15
2.1.7. Kavram Haritası Türleri
Jones, Palincsar, Ogle ve Carr (1987)' e göre örümcek, zincir, hiyerarşi ve balık kılçığı olmak üzere dört çeşit kavram haritası tanımlanmıştır:
2.1.7.1. Örümcek Kavram Haritası
Örümcek kavram haritasının, örümceğin vücudu ve bacaklarında olduğu gibi, bir merkezi ve bu merkezden çıkan dalları vardır. Merkezde bir nesne ya da kavram, dallarda onun başlıca parçaları ya da özellikleri yer alabilir. Bazen merkezde bir düşünce, dallarda onun kanıtları; merkezde bir problem, dallarda onun çözümleri yer alabilir (Üzel' den aktaran Bektüzün, 2013, s. 21). Örümcek kavram haritası ile ilgili örnek Şekil 2' de gösterilmiştir.
HARİTA TÜRLERİ ZİNCİR G TİPİ F TİPİ HİYERARŞİ ÖRÜMCEK KARMA
Şekil 2. Örümcek kavram haritası örneği (Kabaca, M. (2003). Kavram haritalarının matematik
öğretiminde ölçme ve değerlendirme aracı olarak kullanımının incelenmesi. Yüksek Lisans Tezi. Marmara Üniversitesi Eğitim Bilimleri Enstitüsü. İstanbul.)
16 2.1.7.2. Zincir Kavram Haritası
Zincir kavram haritaları, yukarıdan aşağı birbirini izleyen kavramların bağlantı kelimeleri veya ekleri ile ilişkilendirilmesi sonucu oluşturulur. Bu tür kavram haritaları herhangi bir olayın işlem basamaklarını, olay sırasını ve sonuçlarını açıklamak amacıyla kullanılır (Bayırdır, 2006, s. 42). Zincir kavram haritası ile ilgili örnek Şekil 3' te gösterilmiştir.
Şekil 3. Zincir kavram haritası örneği (Erdoğan, Y. (2000). Bilgisayar Destekli Kavram Haritalarının Matematik Öğretiminde Kullanılması. Doktora Tezi. Marmara
Üniversitesi, Fen Bilimleri Enstitüsü. İstanbul.). İÇERİĞİ PLANLAMA MATERYALİN SEÇİMİ KAVRAMLARIN TESPİT EDİLMESİ KAVRAMLARIN DÜZENLENMESİ İLİŞKİLERİN BELİRLENMESİ İLİŞKİLERİN ÇİZİLMESİ
17 2.1.7.3. Hiyerarşik Kavram Haritası
Genel bir kavramın altında hiyerarşik bir şekilde oluşturulmuş haritalardır (Bektüzün, 2013, s. 23). Hiyerarşik kavram haritalarında yeni kavramlar, kendisi ile ilişkili olan daha kapsamlı kavramların altına eklenir (Özdemir, 2015, s. 23). Hiyerarşik kavram haritası ile ilgili örnek Şekil 4' te gösterilmiştir.
Şekil 4. Hiyerarşik kavram haritası örneği (Kurada, K. (2006). Lise II tarih dersinin öğretiminde kavram haritası kullanımının öğrenmeye etkisi. Yüksek Lisans Tezi. Marmara
18 2.1.7.4. Balık Kılçığı Haritası
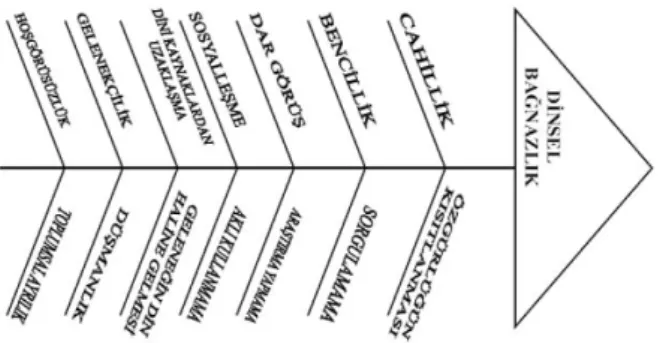
Karmaşık bir olayın nedenlerini ve sonuçlarını ortaya koymak için kullanılır. Kılçığın üst tarafında olaylar, alt tarafında da olayların nedenleri gösterilir. Aslında olayların neden- sonuç ilişkileri harita ile gösterilmiş olur (Bayındır, 2006, s. 41). Balık kılçığı kavram haritası ile ilgili örnek Şekil 5' te gösterilmiştir.
Şekil 5. Balık kılçığı haritası örneği (Tosun, C. ve Doğan, R. (2005). Din kültürü ve ahlak bilgisi öğretiminde kavram haritaları. Ankara: Pegem.)
2.1.8. Kavram Haritasının Yararları
Kavram haritası kullanımının yapılan araştırmalar sonucunda sağladığı yararlar,
1. Öğrenilenlerin kalıcı olmasını sağlar.
2. Öğrenme güçlüğü çeken öğrencilere yardımcı olur.
3. Öğrencilerin karmaşık yapıları bir bütün olarak algılamalarını sağlar.
4. Öğretmene bir konu alanında öğrencilerin sahip olduğu bilgileri gözlemleme ve hangi öğrencinin daha çok yardıma ihtiyacı olduğunu ayırt edebilme şansı tanır.
5. Anlam uzlaşmalarına yardımcı olur.
6. Öğrenci portföyünden gelişimin takip edilmesinde etkilidir (Anderson-Inman & Ditson, 1999).
7. Öğrencilerin kavram haritası yoluyla öğrendikleri yeni bilgilerini kolayca yapılandırabilmelerine imkan verir (Foster, 2001).
19
8. Bilgilerin anlamlı öğrenilmesini destekleyen kavram haritaları öğrencilerin bilgilerini organize etmelerine yardım ettiği gibi kavram yanılgılarının da ortaya çıkarılmasına yardımcı olur (Kaptan ve Korkmaz, 2001).
9. Bütün kavramların özet halinde haritada bulunmasından dolayı tüm kavramlara aynı anda ulaşabilmeyi mümkün kılar (Hagemans, Meij ve Jong, 2013, s. 3).
10. Öğrenciler kavram haritalarıyla öğrenme sürecinde daha fazla bilgi hatırlar (Nesbit ve Adesope, 2011, s. 210).
2.1.9. Kavram Haritası Kullanımında Karşılaşılan Zorluklar
Kavram haritası kullanılmasının yararlarının yanı sıra yapılan araştırmalarda, araştırmacılar aşağıda belirtildiği gibi birtakım zorluklarla karşılaşmışlardır:
1. Uzun kavram haritaları söz dizimine uygun okunmadığında öğrencilerde karmaşaya yol açabilir.
2. Kavram haritası uygulamaları bir ders saatine sığdırılamayabilir. 3. Küçük yaş gruplarına uygulanırsa anlam karmaşalarına yol açabilir. 4. Öğretmen yöntemi doğru uygulayamayabilir.
5. Mevcudu fazla olan sınıflarda disiplin problemleri oluşabilir.
6. Kavram haritaları okunurken söz dizimine uygun okunmadığından öğrencide anlam karmaşasına yol açabilir (Bektüzün, 2013, s. 25).
7. Kısıtlı öğrenme zamanları olan öğretmenler için kavram haritalarını yapılandırmak ve değerlendirmek bir zaman kaybı olarak görülebilir (Uzuntiryaki, 1998).
Çokgenler ve kavram haritaları ile ilgili olarak yapılan araştırmalara "İlgili Araştırmalar" kısmında yer verilecektir.
20
2.2. İlgili Araştırmalar
2.2.1. Kavram Haritaları ile İlgili Yapılan Araştırmalar
Kavram haritaları, 70’li yılların başında Joseph Novak ve arkadaşları tarafından Cornell Üniversitesi’nde bir öğretim aracı olarak geliştirilmiştir (Novak ve Gowin, 1984).
Schmind ve Telaro (1990), biyoloji eğitimde öğretim stratejisi olan kavram haritalarının başarıya etkisini incelemiştir. Kavram haritalarıyla öğrencilerin anlamlı bir örgütsel ağ içinde kavramları ve bunların karşılıklı etkileşim planlarını oluşturmalarını gerektiren, belirli bir müfredatla farklı sözel yeteneklere sahip öğrencilerin etkileşimi test edilmiştir. Öğretmenler, Farklı öğrenme kabiliyet düzeylerine sahip olanlara tekniğin öğretilmesi ve uygulanması sürecini yerleştirme ve eşlenen içeriğin analiz ve uygulama düzeylerini ölçen testi kullanarak haritalama için olumlu bir tepki yaratabilir ve bilgilerin kalıcılığını kolaylaştırabilirler. Araştırmaları sonunda etkinlikleri kullanarak ve küçük gruplar halinde çalışarak öğrencilerin motivasyonlarını ve kavram haritası kullanma yeterliklerinin büyük ölçüde arttığını gözlemlemişlerdir.
Erdoğan (2000), çalışmasında bilgisayar tabanlı kavram haritaları ile kağıt tabanlı kavram haritalarının matematik öğretiminde kullanımı arasındaki farkı ve bu yöntemlerin geleneksel yöntemle arasındaki ilişkiyi incelemiştir. Aynı zamanda matematik öğretimi ile cinsiyet arasındaki ilişkiyi, mezun oldukları okul türleri gibi değişkenlerin matematik başarısına etkisini incelemiştir. Araştırma sonunda geleneksel yönteme göre matematik başarısında kavram haritası yöntemi lehine anlamlı bir farklılık bulunmuştur. Bununla birlikte bilgisayar tabanlı kavram haritaları ile kağıt tabanlı kavram haritaları arasında akademik başarıya etkisine yönelik anlamlı bir fark bulunmamıştır. Cinsiyetin, matematik başarısına etkisi konusunda da anlamlı bir fark bulunmamıştır.
Şahin (2002), çalışmasında Fen Bilgisi eğitiminde öğretmenlerin öğrencilerin zihinlerinde bilgiyi nasıl yapılandırdıklarını öğrenmede kavram haritalarının etkilerini araştırmıştır. Ayrıca bu çalışmada kavram haritaları bir değerlendirme aracı olarak kullanılmıştır. Araştırma sonucunda kavram haritasının anlamlı ve ezbere öğrenenleri birbirinden ayırabildiği sonucuna ulaşılmıştır.
21
Kazancı, Bora, Atılboz ve Altın (2003), çalışmalarında Biyoloji eğitiminde kavram haritası yönteminin genetik konusunda öğrenme başarısına etkisini geleneksel yöntemle karşılaştırarak incelemişlerdir. Çalışma sonunda kavram haritası yöntemi ile öğrenim gören grubun geleneksel yöntemle öğrenim gören gruba göre daha başarılı olduğu saptanmıştır. Kabaca (2003), çalışmasında kavram haritalarını bir ölçme değerlendirme aracı olarak ele almıştır. Ülkemizdeki eğitim sisteminde matematik öğretiminde kullanılan yazılı sınav ve test türü sınavlara verilen puanlar ile kavram haritalarına verilen puanlar arasındaki ilişkiyi analiz etmiştir. Ayrıca kavram haritalarını kullanarak matematik başarısını ölçse de kavram haritalarının özelliklerinden dolayı sözel ilişkilendirme kabiliyetine de ihtiyaç duyduğundan edebiyat dersi notları ile kavram haritası notları arasındaki ilişkiyi de ölçmüştür. Çalışmasının sonunda kavram haritaları ile güvenilir bir ölçme yapılacağını tespit etmiştir.
Hsu ve Hsieh (2005), çalışmasında hemşirelik eğitiminde öğrenme stratejisi olarak kavram haritalamayı uygulamak ve senaryoya dayalı kavram haritalarını oluşturarak öğrencilerin öğrenmelerindeki gelişimi değerlendirmek istemiştir. Öğrenciler ilk kavram haritalarında düşük puanlara sahipken daha sonrakilerde anlamlı bir şekilde gelişme göstermişlerdir. Çalışmanın sonucunda öğrenciler başlangıçta kavram haritalarını hiyerarşik bir şeklinde oluştururken, sonunda öğrencilerin kavramlar arası ilişkileri yüksek oranda kurarak kavram haritası oluşturduklarını gözlemlemiştir. Öğrenciler süreçte çalışmanın zaman alıcılığından şikayet etseler de verileri organize ederek, kavramlar arası ilişkiyi kurarak problem çözme ve eleştirel düşünme becerileri kazanmışlardır.
Safayeni ve Derbentseva (2005), çalışmalarında kavramlar ve ihtiyaçlar üzerinden döngüsel kavram haritalarını incelemişlerdir. Oluşturulan kavram haritalarının kavramlar arası ilişkileri organize eden araçlar olarak düşünülmüştür. Ayrıca döngüsel kavram haritaları, bir kavramdaki değişikliğin diğer kavramları nasıl etkilediği konusu, dinamik bir sistem olarak düşünülmesi gerektiğini ortaya koymuştur.
Bolte (2006), çalışmasında kavram haritalarının çeşitli matematik derslerinde nasıl kullanılacağına ve geometri dersinde Van Hiele düzeyinde öğrencilerin geometrik kavram geliştirmelerinin sınıflandırmalarına ilişkin derin düşünmeye ilişkin bilgi vermiştir. Çoğu öğrenci projeyi faydalı olarak dikkate almış, matematik anlamalarını derinleştirmiş ancak
22
yine de bazı öğrenciler daha sayısal, daha az açık uçlu ödevler tercih etmeye devam etmişlerdir.
Gul ve Boman (2006), çalışmalarında hemşirelik eğitiminde öğretim stratejisi olan kavram haritasının bir değerlendirme aracı olarak kullanımını incelemişlerdir. Anlamlı öğrenme yoluyla bilgi edinimini kolaylaştıran kavram haritalarını eleştirel düşünmeyi teşvik etmek ve değerlendirmek amacıyla kullanmışlardır. Kavram haritalarının not almaya, kavramlar arası yapıları incelemeyi, kavramları eşlemede karmaşık önemli yolları basit biçimde gerçekleştirmeyi öğrenmelerine katkı sağladığını gözlemlemişlerdir.
Gürbüz (2006), çalışmasında kendisi tarafından geliştirilen somut öğretim nesneleri, çalışma yaprakları ve bir kavram haritası ile gerçekleştirilen öğretimin olasılık konusundaki kavramsal gelişime etkisini araştırmıştır. Araştırma sonunda geleneksel öğretim yöntemleriyle sezgisel düşünmeden yararlanılmadığı ortaya çıkmıştır. Buna karşın öğrencilerin somut nesneleri kullanarak deneyler yaptıkları, çalışma yapraklarıyla bilgiyi kendilerinin düzenleyebildikleri ve kavram haritalarıyla kavramlar arası ilişkileri muhakeme edebildikleri sonucuna ulaşmıştır.
Altınok ve Açıkgöz (2006), çalışmalarında işbirlikli kavram haritalama, bireysel kavram haritalama ve geleneksel öğretim yöntemlerinin öğrencilerin Fen Bilgisi dersine yönelik tutumları üzerindeki etkilerini incelemişlerdir. İşbirlikli kavram haritalama yöntemi öğrencilerin Fen Bilgisi dersine yönelik tutumlarını hem bireysel kavram haritalama hem de geleneksel öğretim yöntemlerine göre daha olumlu etkilediğini gözlemlemişlerdir. Kılınç (2007), çalışmasında kavram haritalarının oluşturulması, tarihi temelleri, öğrenme basamakları, öğrenciye sağladığı faydaları, geleneksel yöntemlerle kıyaslanmasını, karşılaşılan sorunları vb. ile ilgili bilgilere yer vermiştir.
Köse (2007), çalışmasında difüzyon ve ozmos kavramlarına ilişkin kavram yanılgılarının belirlenmesi ve kavram haritalarıyla öğretimin kavram yanılgılarını ortadan kaldırmaya etkisini incelemiştir. Araştırma sonunda kavram haritalarına dayalı öğretim geleneksel öğretimden daha etkili bulunmuştur.
Ahlberg ve Ahoranta (2008), çalışmalarında öğrencilerin öğrenme ve zihin yapılarının incelenmesinde kavram haritaları ve kısa cevap testlerinin etkilerini incelemişlerdir. Öğretmen tarafından ortaya koyulan kavram haritalarından ziyade öğrencilerin yapıları
23
oluşturmaları istenmiştir. Sonunda öğretmen yönlendirmeleriyle ve teşvikiyle öğrencilerin hem kavram haritalarını kullanırken hem de kısa cevaplı testleri kullanırken zihinsel olarak üst bilişsel davranışları gösterdiklerini gözlemlemişlerdir.
Çoban, Devecioğlu ve Coşkuner (2008), çalışmalarında kavram haritalarının beden eğitimi ve spor alanında kullanılmasına örnek teşkil edecek şemalar oluşturmuşlardır.
İngeç (2008), çalışmasında kavram haritalarının Fizik öğretiminde bir değerlendirme aracı olarak nasıl kullanılacağını araştırmıştır. "Sıfır harita yap" türü kavram haritası tekniğini kullanılmıştır yani çocuklardan konu ile ilgili zihinlerinde olan bilgileri kullanmaları, kaynak kullanmamalarını istemiştir. Bu teknik kullanımı sonucunda elde edilen kavram haritalarının puanlarının ortalaması, başarı testi puanlarının ortalamasından düşük bulunmuştur. Çünkü öğretmen adaylarının çokça kavram bilmelerine rağmen kavramlar arası ilişkileri kuramadıkları görülmüştür.
Müjdeci (2009), çalışmasında Matematik öğretiminde alternatif bir ölçme değerlendirme aracı olarak kavram haritasının kullanılmasını incelemiştir. Araştırmasında, öğrencilerin klasik yazılı, test ve Türkçe sınavlarından aldıkları puanlar ile yaptıkları kavram haritalarından aldıkları puanları karşılaştırmıştır. Klasik yazılı ile kavram haritaları puanları arasında anlamlı bir ilişki bulmuştur. Aynı zamanda test puanları ile kavram haritaları puanları arasında anlamlı bir ilişki bulmuştur. Araştırmacının çalışmasında Türkçe sınavı puanlarına bakmasındaki amaç kavram haritası oluşturmanın sözel olarak düşünme ve düşündüklerini ifade edebilme kabiliyeti ile paralel olmasıdır. Araştırma sonucuna göre Türkçe puanları ile kavram haritası puanları arasında anlamlı bir ilişki bulunmuştur. Ayrıca araştırmacı, kavram haritası başarısı ile anne ve babanın eğitim düzeyleri ve sosyo-ekonomik durumları arasındaki ilişkileri incelemiştir, sonuçlar anlamlı çıkmamıştır. Elde edilen verilere göre kavram haritalarının matematik derslerinde güvenilir bir ölçme değerlendirme aracı olarak kullanılabileceği sonucuna ulaşılmıştır.
Özdemir (2009), çalışmasında ilköğretim 6.sınıf matematik dersi kesirler konusunun öğretiminde kavram haritası kullanımının öğrenci başarısına etkisini araştırmıştır. Çalışmada kontrol grubuna geleneksel öğretim yöntemi ile deney grubuna ise kavram haritası destekli öğretim yöntemi ile ders işlenmiştir. Araştırmaya göre kavram haritası kullanımının, matematik dersi sayılar öğrenme alanının kesirler alt öğrenme alanına ilişkin öğrenci başarısını artırmada daha etkili olduğu sonucuna ulaşılmıştır.
24
Tzeng (2009), çalışmasında Öz yeterliliğin ve performansın bilgisayar tabanlı kavram haritalama ile öğrenmeye etkisini incelemiştir. Farklı öz yeterlilik algısına sahip kişilerde farklı performanslar sergilendiğini gözlemlemiştir. Öğrencilere uygulama sonrasında motivasyon anketi uygulamıştır. Motivasyon anketini katılımcıların kavram eşleme stratejisini bilgisayar tabanlı kavram haritalarını kullanırken motivasyonun öğrenmelerini kolaylaştırıp kolaylaştırmadığını ölçmek amacıyla kullanmıştır. Uygulama öncesinde çoğu öğrenci kavram haritası oluşturmanın zorluğunu hafife alarak sürekli kavramlar arasındaki ilişkileri tahmin etme eğilimine gitmiş, ancak yaptıkları yanlışlar artınca uygulamayı dikkatli bir şekilde takip etmeye başladıklarını gözlemlemiştir. Kavram haritalarını oluşturmaya başladıktan sonra performansı artan öğrencilerin motive olduklarını belirttiklerini gözlemlemiştir.
Çakmak (2010), çalışmasında öğretmen adayları tarafından oluşturulan öğretmen rollerine ilişkin hazırlanan kavram haritalarını incelemiştir. Öğretmen adaylarına kavram haritasının tanımı yapılmış ve örnek çalışmalar verildikten sonra onlardan öğretmen rollerine ilişkin kavram haritası oluşturmaları istemiştir. Sonuç olarak, birçok öğrenci kavram haritası hazırlama ilkelerini ihmal etmiş ve bu durum öğretmen adaylarının haritaları hazırlarken teorik bilgileri uygulamakta zorlandıklarını göstermiştir.
Haugwitz, Nesbit ve Sandmann (2010), çalışmalarında biyoloji eğitiminde kavram haritalarının işbirlikli öğrenmeye katkısını araştırmışlardır. Çalışmalarında kavram haritası stratejisinin yalnızca bilişsel öğrenme düzeyi yüksek olan öğrenciler için avantajlı olduğunu görmüşlerdir. Düşük bilişsel öğrenme düzeyine sahip olan öğrenciler yüksek düzeye sahip olan öğrencilerle eşleştirerek onların gelişimine katkı sağlayıp sağlamadığını incelemişlerdir. Araştırma sonunda kavram haritaları oluşturma etkinliklerinin işbirlikli öğrenme faaliyetlerine yönelttiğini, kavramları birbirine eşleme görevinde bilişsel düzeyi düşük öğrencilerin başarı sağladıkları sonucuna ulaşmışlardır.
Jin ve Wong (2010), çalışmalarında ikinci kademe öğrencilere geometriyle ilgili kavram haritaları oluşturmanın birçok yolunu vermişler ve anlatımda değişik öğretim metotları denemişlerdir. Haftada 40 dakikadan 3'er ders kavram haritalama hakkında uygulamalı öğretim yapmışlardır. Ancak bu sürenin yeterli olmadığına ve basit bir ifade hakkında bile her öğrencinin farklı bir harita geliştirdiğini gözlemlemişlerdir. Farklı seviyelerdeki
25
öğrencilerle öğretim metotlarının daha dikkatli incelenmesi gerektiği sonucuna ulaşmışlardır.
Buldu (2010), çalışmasında Birleşik Arap Emirlikleri’nde öğretmen eğitimi programlarında süreç değerlendirmesi olarak kavram haritalarının kullanışlılığı ve öğretmen adaylarının kavram haritalarına ilişkin memnuniyetlerini incelemiştir. Kavram haritalarının eğitimciler için açıklayıcı bir araç olduğu ve öğretmen adaylarının öğrenmelerinin gelişiminde ve öğrenme süreçlerinin farkına varmalarında etkili olduğu sonucuna ulaşmıştır.
Ata ve Adıgüzel (2011), çalışmalarında aşamalı kavram haritası tekniği ile aşamalı olmayan kavram haritası tekniğini karşılaştırılarak hangisinin öğrencilerin akademik başarısını artırdığı ve kavram haritası yapabilme düzeyi üzerinde daha etkili olduğunu incelemişlerdir. Aşamalı kavram haritası tekniğinde öğrencilerden direkt konular ile ilgili kavram haritası çizmelerini istemişler, aşamalı olmayan kavram haritası tekniğinde ise belli yerlerde boşluk bırakılarak oluşturulan kavram haritasında belli kavramlarla bu boşlukların öğrenciler tarafından doldurulmasını istemişlerdir. Elde edilen verilere göre aşamalı olmayan kavram haritası tekniğinin akademik başarıyı artırdığını gözlemlemişlerdir.
Oğraş ve Bozkurt (2011), çalışmalarında çember ve daire konusu ile ilgili üst bilişsel öğrenme aracı olarak nitelendirilen kavram haritaları ve Vee diyagramı kullanımının öğrenci başarısı üzerindeki etkisini araştırmışlardır. Kavram haritası ve Vee diyagramının eski ve yeni öğrenmelerini ilişkilendirmeleri bakımından öğrencilere fırsat verdiğinden başarı üzerinde etkili olduğunu görmüşlerdir.
Kırkkılıç, Maden, Şahin ve Girgin (2011), çalışmalarında Türkçe eğitiminde kavram haritalarının okuduğunu anlama ve kalıcılık üzerine etkisini araştırmışlardır. Araştırma sonunda kavram haritalama tekniğinin kullanıldığı deney grubu lehine anlamlı sonuçlara ulaşmışlardır.
Kurnaz ve Pektaş (2013), çalışmalarında Fen ve Teknoloji öğretmenlerinin ölçme ve değerlendirme aracı olarak kavram haritası kullanım durumlarını incelemişlerdir. Araştırma sonucunda, öğretmenlerin kavram haritalarını etkili bir teknik olarak gördükleri ve derslerinde sıkça kullandıklarını gözlemleseler de ölçme ve değerlendirme sürecinde etkili olarak kullanamadıklarını gözlemlemişlerdir.
26
Bektüzün (2013), çalışmasında kavram haritaları ile öğretimin öğrencilerin biyoloji dersindeki başarı ve tutumları üzerine etkilerini incelemiştir. Araştırma sonuçlarına göre, ortaöğretim biyoloji dersinde başarıyı artırmak ve biyoloji dersine karşı olan tutumu iyileştirmek için kavram haritası ile yapılan öğretimi daha etkili bulmuştur. Ayrıca araştırmacı, bu yöntemle öğrencilerin derse olan ilgilerinin arttığını gözlemlediğini belirtmiştir.
Laçin (2014), çalışmasında kavram haritası ve Vee diyagramının ilköğretim 8.sınıf istatistik ve olasılık konusunda öğrenci başarısına ve tutumuna etkisini incelemiştir. Araştırmadan elde edilen bulgulara göre matematik öğretiminde kavram haritası ve Vee diyagramı ile öğretimin geleneksel öğretim yönteminden daha etkili olduğu sonucuna varmıştır. Araştırmacı elde ettiği verilere göre Ausubell' in geliştirdiği anlamlı öğrenmede öğrencilerin kavram haritası, Vee diyagramı gibi ön örgütleyicilerin kullanılması yeni bilgilerin eski bilgilerle ilişkilendirilmesinde ve kavramlar arası ilişkilerin kolay kurulmasında yardımcı olduğunu vurgulamıştır.
Batdı (2014), çalışmasında kavram haritası tekniği ile geleneksel öğretim yönteminin kullanılmasının öğrencilerin başarıları, bilgilerinin kalıcılığı ve tutumlarına etkisini içeren bir meta analiz çalışması yapmıştır. Kavram haritası kullanımının öğrencilerin tutumlarına olumlu etki ettiğini saptamıştır. Aynı zamanda kavram haritası tekniğine yönelik öğretim ortamında yapılan uygulamaların, geleneksel öğretim yöntemine göre öğrencilerin kalıcılık puanları açısından daha etkili olduğunu saptamıştır.
Gündüz (2015), çalışmasında öğretmenlerin okuduğu fakülte, cinsiyet gibi bazı değişkenler açısından kavram haritasının kullanım alanlarına yönelik görüşlerinin farklılaşıp farklılaşmadığını belirlemeye çalışmıştır. Cinsiyet değişkeni açısından öğretmenler arasında anlamlı bir farklılık bulmamıştır. Ancak mezun olduğu fakültenin kullandığı kavram haritası düzeyi bakımından bir farklılık oluşturduğunu gözlemlemiştir.
Polat ve Doğan (2015), çalışmalarında ölçme araçlarından Vee diyagramı, tanılayıcı dallanmış ağaç ve kavram haritalarının matematik dersindeki tutum ile başarıya etkilerini incelemişlerdir. Araştırmanın sonucunda bu yöntemler kullanılarak işlenen derste öğrencilerin tutumlarında bir artış gözlemlemişlerdir. Bunun yanında başarıya ilişkin en yüksek puanları Vee diyagramından elde etmişlerdir.