İLKOKUL 4. SINIF ÖĞRENCİLERİNİN FARKLI PROBLEM
KURMA DURUMLARINA YÖNELİK ORTAYA KOYDUKLARI
PROBLEMLERİN İNCELENMESİ
İLKNUR ÇARKCI
YÜKSEK LİSANS TEZİ
SINIF EĞİTİMİ ANA BİLİM DALI
GAZİ ÜNİVERSİTESİ
EĞİTİM BİLİMLERİ ENSTİTÜSÜ
i
TELİF HAKKI VE TEZ FOTOKOPİ İZİN FORMU
Bu tezin bütün hakları saklıdır. Kaynak göstermek koşuluyla tezin teslim tarihinden itibaren (24) ay sonra tezden fotokopi çekilebilir.
YAZARIN
Adı : İlknur
Soyadı : ÇARKCI
Bölümü : Sınıf Eğitimi Bilim Dalı
İmza :
Teslim tarihi :
TEZİN
Türkçe Adı : İlkokul 4. Sınıf Öğrencilerinin Farklı Problem Kurma Durumlarına
Yönelik Ortaya Koydukları Problemlerin İncelenmesi
İngilizce Adı :Investigation of The ProblemsEncountered by 4th Grade Primary Students in Different Problem Posing Situations
ii
ETİK İLKELERE UYGUNLUK BEYANI
Tez yazma sürecinde bilimsel ve etik ilkelere uyduğumu yararlandığım tüm kaynakları kaynak gösterme ilkelerine uygun olarak kaynakçada belirttiğimi ve bu bölümler dışındaki tüm ifadelerin şahsıma ait olduğunu beyan ederim.
Yazarın Adı Soyadı: İlknur ÇARKCI İmza :
iii
JÜRİ ONAY SAYFASI
İlknur ÇARKCI tarafından hazırlanan “İlkokul 4. Sınıf Öğrencilerinin Farklı Problem Kurma Durumlarına Yönelik Ortaya Koydukları Problemlerin İncelenmesi” adlı tez çalışması aşağıdaki jüri tarafından oy birliği / oy çokluğu ile Gazi Üniversitesi Sınıf Eğitimi Anabilim Dalı’nda Yüksek Lisans tezi olarak kabul edilmiştir.
Danışman:Doç. Dr. Neşe TERTEMİZ
(Sınıf Eğitimi Anabilim Dalı, Gazi Üniversitesi) ………
Başkan: (….) ……… Üye: (….) ……… Üye: (….) ……… Üye: (….) ………
Tez Savunma Tarihi: …./…./………
Bu tezin Gazi Üniversitesi Sınıf Eğitimi Anabilim Dalı’nda Yüksek Lisans tezi olması için şartları yerine getirdiğini onaylıyorum.
Prof. Dr. Tahir ATICI
iv
v
TEŞEKKÜR
Tüm çalışmam sürecinde bana eleştiri ve görüşleri ile ışık tutan, yol gösteren, cesaretlendiren, sürecin her aşamasında katkısı ve desteğiyle bana yardımcı olan tez danışmanım ve değerli hocam Doç. Dr. Neşe TERTEMİZ’e,
Tüm hayatım boyunca olduğu gibi tez dönemimde de benimle sevinen benimle üzülen, her daim yanımda olan canım annem ve babama,
Hayatının bir ayını çaldığım canım kızım Öyküme,
Hiçbir zaman desteğini esirgemeyen, karamsarlığa kapıldığım her anda beni yeniden umutlandıran eşim Özgür ÇARKCI’ya,
Sınıf Öğretmenliği Anabilim dalında aynı odayı paylaştığım bütün araştırma görevlisi arkadaşlarıma, Arş. Gör. Dr. A. Selcen BİNGÖL-ARSLANGİLAY’a, Arş. Gör. Ayşe YILMAZ’a, Arş. Gör. Aysun ÖZTÜRK’e,
Araştırmamı gerçekleştirmek üzere okullarında bulunduğum Okul müdürü İbrahim GÜRSOY’a, bu okulda araştırmamı yürütmeme vesile olan okul öğretmenlerinden Emine ÇETİN‘e, tezimin uygulama aşamasında benden desteklerini esirgemeyen okul öğretmenlerinden Suna FINDIK ve Tülay İSKAR’a,
Ayrıca Eğitim Bilimleri Enstitüsü çalışanlarına,
Ve tez sürecinde emeği geçen ve ismini sayamadığım herkese sonsuz teşekkürler…
vi
İLKOKUL 4. SINIF ÖĞRENCİLERİNİN FARKLI PROBLEM
KURMA DURUMLARINA YÖNELİK ORTAYA KOYDUKLARI
PROBLEMLERİN İNCELENMESİ
(Yüksek Lisans Tezi)
İlknur ÇARKCI
GAZİ ÜNİVERSİTESİ
EĞİTİM BİLİMLERİ ENSTİTÜSÜ
Şubat, 2016
ÖZ
Bu araştırmanın amacı, ilkokul 4. sınıf öğrencilerinin farklı problem kurma durumlarına yönelik ortaya koydukları problemlerin incelenmesidir. Öğrencilerin problem kurma becerileri; oluşturulan problemlerin verilen duruma uygunluğu ve problemler kurulurken hangi dört işlem becerisine yönelik olarak yazılmış olduğu açılarından değerlendirilmiştir. Araştırmada 4. sınıf öğrencilerinin farklı problem kurma durumları içeren doğal sayılarla dört işlem becerisine yönelik kurdukları problemler nasıldır?” sorusuna yanıt aranmıştır. Araştırmada nitel araştırma türlerinden durum (örnek olay) çalışması kullanılmıştır. Araştırmanın çalışma grubunu, Ankara ili Keçiören ilçesinde bulunan bir devlet ilkokulunun 2015-2016 eğitim-öğretim yılında 4. sınıfa devam eden 31 öğrenci oluşturmaktadır. Çalışma grubunun oluşturulmasında kolay ulaşılabilir durum örneklemesinden yararlanılmıştır. Veri toplama aracı olarak; öğrencilere toplam 10 sorudan oluşan problem kurma görevi verilmiştir. Öğrencilere verilen problem kurma görevleri oluşturulurken, Stoyanova ve Ellerton (1996) tarafından ortaya konulan serbest, yarı-yapılandırılmış ve yapılandırılmış problem kurma stratejileri ile Christou ve arkadaşları (2005) tarafından öne sürülen problem kurma yönteminde yer alan kavrama, aktarma, düzenleme ve seçme alt boyutları benimsenmiştir. Araştırmada kullanılan problem kurma görevleri oluşturulurken, asıl uygulama öncesinde oluşturulan 14 problem durumunun en uygun olanlarının asıl uygulamada kullanılması için 3 farklı uzman görüşü alınmıştır. Uzman görüşlerinin değerlendirilmesi sonucunda 10 sorunun çalışmanın amacına en iyi şekilde hizmet ettiğine
vii
karar verilmiştir. Daha sonra hazırlanan soruların anlaşılırlığını ve uygunluğunu kontrol etmek amacıyla aynı okulda başka bir 4.sınıfa devam eden 33 öğrenciye ön deneme amacıyla uygulanarak ölçme aracına son hali verilmiştir. Çalışmanın başında belirlenen ana kategoriler çerçevesinde öğrenciler tarafından kurulan problemler içerik analizine tabii tutulmuştur. Verilerin analizinde bir araştırmacıdan yardım alınarak kodlayıcılar arası güvenirlik çalışması yapılıp iki kodlayıcı arasındaki uyum yüzdesi %89 olarak hesaplanmıştır. Araştırma sonucunda öğrencilerin serbest problem kurmaları istendiğinde bu görevleri başarıyla gerçekleştirdiği ve kurdukları problemlerin çoğunun sözel alıştırma problemi olduğu görülmüştür. Yarı- yapılandırılmış problem durumlarında yöneltilen resim ve grafiğe dayalı problemler kurmaları istendiğinde ise, öğrencilerin yarısının ve yarısından biraz fazlasının başarılı olduğu ve daha çok sözel hikâye problemi kurdukları görülmüştür. Bu kategoriler bir temsil biçiminin başka bir temsil biçiminde ifadesini içerdiğinden öğrenciler bu kategoride problem kurmada sıkıntısı yaşamışlardır. Yapılandırılmış problem kurma durumlarında, matematiksel işleme yönelik problem kurma ve bir sözel hikâye problemine istenen yazılmasına yönelik problem kurmaları istenmiştir. Öğrenciler bu problem durumlarının daha az işlem gerektiren I. Problem durumlarında daha başarılı olurken, II. problem durumlarında öğrencilerin sadece yarısının başarılı olduğu görülmüştür. Araştırma sonucunda öğrencilerin farklı problem kurma durumlarıyla ilk kez karşılaştıkları ve daha çok dört işlemde (en fazla toplama işleminde) sonuç bilinmeyene yönelik problem ifadesi yazdıkları görülmüştür. Öğrencilerin kurdukları yanlış problemlerde ifadelerin yetersiz olduğu, istenenin olmadığı, birimin unutulduğu ve anlaşılamayan ifadelerin olduğu durumlara rastlanmıştır. Araştırma sonucunda öğrencilerin farklı durumlara yönelik problem kurma konusunda sıkıntı yaşadıkları söylenebilir.
Anahtar Kelimeler : Problem kurma, matematik eğitimi, 4. Sınıf öğrencileri Sayfa Adedi : 127
viii
INVESTIGATION OF THE PROBLEMS ENCOUNTERED BY 4
THGRADE PRIMARY STUDENTS IN DIFFERENT PROBLEM POSING
SITUATIONS
(M.S. Thesis)
İlknur ÇARKCI
GAZİ UNIVERSITY
INSTITUTE OF EDUCATIONAL SCIENCES
February, 2016
ABSTRACT
This study has been conducted in order to investigate the problems the 4th grade primary
students’ exhibit in problem posing situations. The problem posing skills of the students has been evaluated in terms of convenience to the given situation, on the other hand in terms of which four operations they are written towards. For this aim, the students have been given the task of problem posing that is composed of a total of 10 questions. The problem posing tasks given to the students have been formed by adopting the free, semi structured and
structured problem posing study developed by Stoyanova and Ellerton (1996) and the sub
dimensions of comprehending, translating, editing and selecting that are placed in the model that has been put forward by Christou and friends (2005) and according to this classification. During the formation of the problem posing tasks, 3 different expert views have been taken for the 14 problem situations that have been formed before the real application in order to be used in the real application process. Experts have reviewed the questions in terms of convenience to the student level, reflection of the categories and etc. and finally 10 questions have been decided as serving the best for the aim of the study. The data collection tool has been finalized by applying it to the 33 students attending the same school same grade for the aim of controlling the convenience and comprehensibility of the questions. The study group of the research is composed of 31 students attending 4th grade in a state primary school in
ix
easy reachable situation sampling has been used. As the research has been conducted with the aim of investigating the problems of primary school 4th grade students towards different
problem posing situations, among the types of qualitative research types case study has been used. In the study the answer to the question “how are the problems the 4th grade students
pose towards four operation skills including natural numbers?” has been sought. In the framework of the main categories determined at the beginning of the study, problems posed by the students have been analyzed via content analysis. In the data analysis process with the help of a researcher reliability among the coders have been made and the coherence between the two coders have been calculated as 89%. At the end of the research it has been seen that when the students are asked to pose free problems they fulfill these tasks successfully and most the problems they pose are story problems. When they were asked to pose problems based on pictures and graphics in the case of semi-structured problem situations, it has been seen that half and more than half of the students have been successful and they usually posed story problems. Because these categories included the expression of a representation form in another representation form, students have had difficulties in posing problems in this category. In structured problem posing situations, they were asked to pose problems towards mathematical operation and writing to a story problem. Students have been more successful in the I. problem situations which require less operation whereas only the half of the students have been successful in the II. Problem situations. At the end of the research it has been seen that the students have confronted with some of the problem situations they pose towards different problem posing situations for the first time. It has also been seen that previously they posed problems just changing the data in the problems; they had difficulties in problem posing and they could write problem statements more often on addition results on the unknown. Situations in which the expressions of the students in the wrong problems they posed are inadequate and incomprehensible expressions have been come across.
KeyWords : Problem posing, mathematics education, 4thgradestudents.
PageNumber : 127
x
İÇİNDEKİLER
TELİF HAKKI VE TEZ FOTOKOPİ İZİN FORMU ... i
ETİK İLKELERE UYGUNLUK BEYANI ... ii
JÜRİ ONAY SAYFASI ... iii
TEŞEKKÜR ... v
ÖZ ... vi
ABSTRACT ... viii
TABLOLAR LİSTESİ... xiii
ŞEKİLLER LİSTESİ ... xv
SİMGELER VE KISALTMALAR LİSTESİ ... xvi
BÖLÜM I ... 17 GİRİŞ ... 17 1.1. Problem Durumu... 17 1.2. Araştırmanın Amacı ... 19 1.3. Araştırmanın Önemi ... 20 1.4. Sayıltılar ... 21 1.5. Sınırlılıklar ... 21 1.6. Tanımlar ... 22 BÖLÜM II ... 23 KAVRAMSAL ÇERÇEVE ... 23 2.1. Problem Nedir? ... 23 2.2. Problemin Özellikleri ... 24 2.3. Problemlerin Sınıflandırılması... 26
xi
Kapalı Problemler ... 26
Açık Uçlu Problemler ... 27
Matematiksel Araştırmalar ve Projeler ... 28
2.4. Problem Çözme ... 28
Problemin Anlaşılması ... 29
Çözümle İlgili Stratejinin Seçilmesi (Çözüm İçin Plan Yapma) ... 30
Seçilen stratejinin uygulanması ... 31
Çözümün değerlendirilmesi ... 31
2.5. Problem Kurma ... 32
2.6. Problem Kurma Stratejileri ... 36
2.7. Matematiğin Çoklu Temsil Biçimleri ... 38
BÖLÜM III ... 43 İLGİLİ ARAŞTIRMALAR ... 43 BÖLÜM IV ... 55 YÖNTEM... 55 4.1. Araştırmanın Modeli... 55 4.2. Çalışma Grubu ... 56
4.3. Veri Toplama Araçlarının Geliştirilmesi ve Verilerin Toplanması... 57
Farklı Problem Kurma Durumları İçeren Ölçme Aracının Geliştirmesi ... 57
Verilerin Toplanması ... 59
Araştırma Kapsamında Kullanılan Farklı Problem Durumlarına Yönelik Problem İfadeleri ... 61
4.4. Verilerin Analizi ... 62
BÖLÜM V... 64
BULGULAR VE YORUM ... 64
5.1. Araştırmanın Birinci Alt Problemine İlişkin Bulgular ve Yorum ... 64
xii
5.3. Araştırmanın Üçüncü Alt Problemine İlişkin Bulgular ve Yorum ... 90
BÖLÜM VI ... 102
SONUÇ, TARTIŞMA VE ÖNERİLER ... 102
6.1. Araştırmanın Birinci Alt Problemine İlişkin Sonuç ve Tartışma ... 102
6.2. Araştırmanın İkinci Alt Problemine İlişkin Sonuç ve Tartışma ... 105
6.3. Araştırmanın Üçüncü Alt Problemine İlişkin Sonuç ve Tartışma ... 108
6.4. Öneriler ... 110
KAYNAKLAR ... 113
EKLER... 122
EK 1. Farklı Problem Kurma Durumları İçeren Ölçme Aracı ... 123
xiii
TABLOLAR LİSTESİ
Tablo 1. Pilot Çalışma ve Uygulamalarda Yer Alan Öğrenci Sayıları ve Cinsiyetleri ... 57 Tablo 2. Betimsel Analizde Kullanılacak Olan Temalar ve Öğrencilere Verilecek Problem
Kurma Görevlerine Örnekler ... 59
Tablo 3. Öğrencilerin Problem Durumu I ’ e İlişkin Kurdukları Problem İfadelerinin
Analizi ... 65
Tablo 4. Öğrencilerin Doğru Kurdukları Problemlere Dört İşlem Becerisi Açısından
Yükledikleri Anlamlar ... 66
Tablo 5. Öğrencilerin Problem Durumu II’ ye İlişkin Kurdukları Problem İfadelerinin
Analizi ... 69
Tablo 6. Öğrencilerin Doğru Kurdukları Problemlere Dört İşlem Becerisi Açısından
Yükledikleri Anlamlar ... 70
Tablo 7. Öğrencilerin Problem Durumu I ’ e İlişkin Kurdukları Problem İfadelerinin
Analizi ... 73
Tablo 8. Öğrencilerin Doğru Kurdukları Problemlere Dört İşlem Becerisi Açısından
Yükledikleri Anlamlar ... 74
Tablo 9. Öğrencilerin Problem Durumu II ’ ye İlişkin Kurdukları Problem İfadelerinin
Analizi ... 77
Tablo 10. Öğrencilerin Doğru Kurdukları Problemlere Dört İşlem Becerisi Açısından
Yükledikleri Anlamlar ... 78
Tablo 11. Öğrencilerin Problem Durumu I ’ e İlişkin Kurdukları Problem İfadelerinin
Analizi ... 82
Tablo 12. Öğrencilerin Doğru Kurdukları Problemlere Dört İşlem Becerisi Açısından
Yükledikleri Anlamlar ... 83
Tablo 13. Öğrencilerin Problem Durumu II’ ye İlişkin Kurdukları Problem İfadelerinin
xiv
Tablo 14. Öğrencilerin Doğru Kurdukları Problemlere Dört İşlem Becerisi Açısından
Yükledikleri Anlamlar ... 88
Tablo 15. Öğrencilerin Problem Durumu I ’ e İlişkin Kurdukları Problem İfadelerinin
Analizi ... 91
Tablo 16. Öğrencilerin Problem Durumu II ’ye İlişkin Kurdukları Problem İfadelerinin
Analizi ... 94
Tablo 17. Öğrencilerin, Yapılandırılmış Problem Kurma Durumu Seçme Alt Boyutu
Problem Durumu I’ e İlişkin Tamamladıkları İfadelerin Analizi ... 98
Tablo 18. Öğrencilerin, Yapılandırılmış Problem Kurma Durumu Seçme Alt Boyutu
xv
ŞEKİLLER LİSTESİ
Şekil 1. Matematiksel problemler için sınıflandırma şeması ... 26
Şekil 2. Beyaz eşya mağazası problem durumuna yönelik resim ... 72
Şekil 3. Manav problem durumuna yönelik resim ... 76
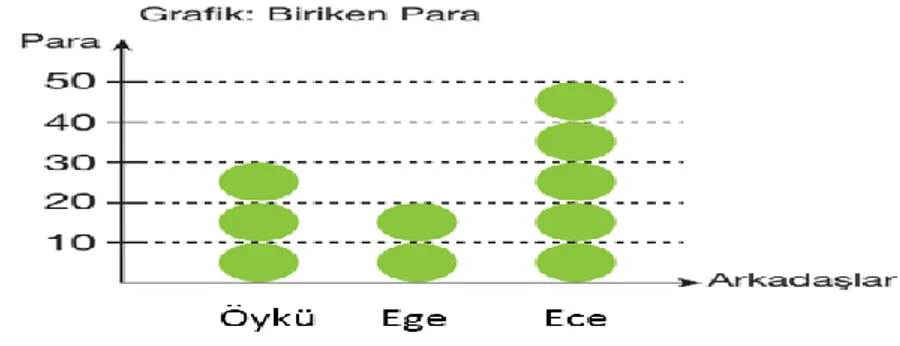
Şekil 4. Biriken para miktarı problem durumuna yönelik resim ... 81
xvi
SİMGELER VE KISALTMALAR LİSTESİ
MEB Milli Eğitim Bakanlığı
17
BÖLÜM I
GİRİŞ
Bu bölümde, ilgili literatür çerçevesinde çalışma konusu olarak ele alınan problemin, araştırmanın amacının, araştırmanın öneminin, araştırmanın sınırlılıklarının, araştırmanın varsayımlarının ve araştırmaya ait tanımların neler olduğu ortaya konulmuştur.
1.1. Problem Durumu
Matematik eğitiminin önemli etkinliklerinden biri olan problem kurma, öğrencilerin matematiksel düşünmesini geliştirmektedir. Ulusal matematik öğretmenleri konseyi (National Council of Teachers of Mathematics [NCTM], 1989), Matematik sınıflarında öğrencilere kendi problemlerini kurmalarını ve var olan problemi kendi deneyimlerine göre değiştirip yeni bir problem kurmayı vurgulamaktadır.
Literatürde problem kurma farklı kişiler tarafından farklı şekillerde tanımlanmıştır. Leung (1993), problem kurmayı verilen bir problemin yeniden düzenlenmesi şeklinde tanımlamıştır. Silver (1994), ise problemi hem yeni problemler üretme, hem de var olan problemi düzenleme olarak tanımlamıştır. Benzer şekilde, NCTM‘de problem kurmanın yeni bir problem oluşturma olduğunu vurgulamıştır. Gonzales (1998), ise problem kurmayı Polya’nın (1957) problem çözme adımlarının sonuncusu olarak tanımlamıştır. Tüm bu tanımlar incelendiğinde problem kurma ile ilgili ortak noktanın problem üretme olduğu söylenebilir.
Problem kurma çalışmaları ile ilgili farklı sınıflamalar yapılmıştır. Bu sınıflamalardan en bilineni Stoyanova ve Ellerton (1996) tarafından ortaya konmuştur. Stoyanova ve Ellerton
18
(1996) problem kurma durumlarını serbest, yapılandırılmış ve yarı yapılandırılmış durumlar olmak üzere 3’ e ayrılmıştır:
Serbest problem kurma etkinliğinde, öğrencilere herhangi bir problem sunulmadan öğrencilerden olabildiğince yaratıcı bir problem kurmaları istenir.
Yapılandırılmış problem kurma etkinliğinde öğrencileri bir resim, bir hikâye, bir tablo veya bir çözüm sunulduktan sonra öğrencilerden bu veri ya da verileri kullanarak yeni bir problem kurmaları istenir.
Yarı yapılandırılmış problem kurma etkinliğinde öğrencilere açık uçlu bir durum sunulduktan sonra, öğrencilerden bilgi beceri ve deneyimlerini kullanarak yeni bir problem kurmaları istenir.
Christou, Mousoulides, Pittalis, Pitta- Pantazi ve Sriraman (2005)’da problem kurmayı 4 kategoride ele almıştır.
Editing (Düzenleme) problem kurma etkinliğinde, öğrencilerden problem kurma sırasında dikkate alacakları üzerinde sayıların olduğu günlük hayattan alınan resimleri kullanarak hiçbir kısıtlama olmaksızın problemdeki verileri kullanarak problem kurmaları istenir.
Selecting (Seçme) problem kurma etkinliğinde, öğrencilere belli bir hikâye durumu ve kuracakları problemin sonucu verilir verilen cevaba uygun bir problem kurmaları istenir.
Comprehending (Kavrama) problem kurma etkinliğinde öğrencilerden bütün sayıları, işlem basamakları ve sonucu belli bir eşitlik verilerek problem kurmaları istenir.
Translatimg ( Aktarma) problem kurma etkinliğinde öğrencilerden verilen grafik veya tabloya uygun problem kurmaları istenir.
Problem kurma ile ilgili alan yazın incelendiğinde, problem kurmanın öğrencilerin muhakeme becerilerini geliştirdiği, kavramsal öğrenmeyi arttırdığı (Akay,2006; Crespo &Sinclair,2008; English, 2003; Tolluk- Uçar,2009) görülmüştür. Ayrıca problem kurma öğrencilerin günlük yaşamda karşılaştıkları matematiği fark etmelerini de sağlamaktadır (Abu-Elwan,2002). Problem kurma deneyimi sayesinde öğrenciler, problemlerde geçen kavramları daha iyi anlamakta (Dickerson,1999); neler yaptıklarının farkında olmaktadır (Whiten,2004). Ayrıca öğretmenlerin problem kurmayı bir ölçme aracı olarak kullanabileceklerini ifade edilmektedir (Whiten,2004). Benzer şekilde Silver ve Cai (1996) de öğrencilerin aritmetiksel işlem becerilerinin değerlendirilmesinde problem kurmanın
19
kullanılabileceğini ifade etmiştir. Problem kurmanın öğrencilerin matematiğe yönelik tutumlarını olumlu anlamda etkilediğini savunan araştırmalarda bulunmaktadır (Akay & Boz, 2008; 2010; Barlow & Cates,2010).
İlkokul düzeyinde problem kurma becerisinin matematik dersinin önemli bir bileşeni ve hedefi olarak kabul edildiği (Milli Eğitim Bakanlığı [MEB], 2009) dikkate alındığında ve her sınıf düzeyinde tüm öğrenme alanlarına ilişkin son kazanımda yer alan “… problemleri
çözer ve kurar” ifadesiyle yer alan kazanımlarla tüm öğrenme alanlarında problem kurmanın
önemine işaret edilmiştir. Hatta 2015 yılında en son çıkan ilkokul matematik programında da aynı ifadelerin yer alması problem kurmaya problem çözme kadar önem verildiğini göstermektedir. Programda problem çözme becerisi öğrenciler kazandırılırken problem çözme etkinliklerinin gerçek hayatla ilişkilendirilmesine; konu edilen problem durumlarının gerçek hayattan seçilmesine ve matematik dünyası içinde ulaşılan çözümlerin tekrar gerçek hayat bakımından yorumlanmasına özellikle önem verilmesine vurgu yapılmaktadır (MEB, 2015). Bu durum konunun önemini ve üzerinde daha çok çalışmaya duyulan ihtiyacı ortaya
koymaktadır. Literatür incelendiğinde Türkiye’ de yapılan çalışmaların genellikle problem çözme üzerine olduğu, problem kurma konusundaki çalışmaların genellikle öğretmen adaylarıyla ve daha üst sınıf düzeylerine yönelik yapılmış olduğu görülmektedir. Mevcut araştırmada, tüm bu düşünce ve ihtiyaçlardan yola çıkarak ilkokul 4. sınıf öğrencilerinin verilen farklı problem kurma durumları çerçevesinde kurdukları problemlerin incelenmesine odaklanılmıştır.
1.2. Araştırmanın Amacı
Bu çalışma tüm bu düşünce ve ihtiyaçlardan yola çıkarak 4. sınıf öğrencilerinin Christou vd. (2005)’nin ortaya koyduğu yapılandırılmış model çerçevesinde kurdukları problemlerin incelenmesine yöneliktir. Araştırmanın amacı “İlkokul 4. sınıf öğrencilerinin farklı problem kurma durumlarını içeren doğal sayılarla dört işlem becerisine yönelik kurdukları problemler nasıldır?” sorusuna cevap aramaktır. Bu amaç doğrultusunda, araştırmanın alt amaçları şunlardır:
1) İlkokul 4.sınıf öğrencilerinin, serbest problem kurma durumunda: a) Öğrencilerin kendilerine bir konu verilmeden,
kurdukları problemler nasıldır?
20
b) Öğrencilerin kendilerine bir konu verilerek, kurdukları problemler nasıldır?
kurdukları doğru problemlere yükledikleri anlamlar nasıldır?
2) İlkokul 4.sınıf öğrencilerin, yarı-yapılandırılmış problem kurma durumunda:
a) Öğrencilerin düzenleme gerektiren durumda, kurdukları problemler nasıldır?
kurdukları doğru problemlere yükledikleri anlamlar nasıldır? b) Öğrencilerin aktarma gerektiren durumda,
kurdukları problemler nasıldır?
kurdukları doğru problemlere yükledikleri anlamlar nasıldır?
3) İlkokul 4. sınıf öğrencileri, yapılandırılmış problem kurma durumunda:
a)Öğrencilerin kavrama gerektiren durumda, kurdukları problemler nasıldır? b) Öğrencilerin seçme gerektiren durumda
kurdukları problemler nasıldır?
1.3. Araştırmanın Önemi
Ülkemizde yapılan problem kurma ile ilgili çalışmalara bakıldığında, problem kurma konusunun 2005 yılında uygulanmaya başlanan ilköğretim matematik dersi öğretim programlarında adının geçmesiyle birlikte yer alması nedeniyle bu konuda az sayıda araştırma yapıldığı görülmüştür. İlgili literatür incelendiğinde yapılan bu çalışmaların daha çok öğretmen adaylarına yönelik olduğu ve ilkokul düzeyinde yapılmış birkaç çalışmadan öteye gidilmediği görülmüştür. Bu tez çalışması söz konusu alanda yaşanan eksikliği gidermek adına bir katkı sunmaktadır. Eldeki çalışmada ilkokul 4. sınıf öğrencilerinin doğal sayılarla dört işlem becerisine yönelik problem kurma becerileri nitel yöntem kullanılarak derinlemesine incelenmektedir. Bu çalışmada özellikle ilkokul 4. Sınıf öğrencileriyle çalışılmaktadır. Bu araştırmanın ilkokul 4. Sınıf öğrencileriyle yapılmasının iki nedeni vardır.
21 Bunlar;
İlkokul düzeyinde 4 sınıf düzeyinin bulunması,
4. Sınıf düzeyinde yapılan bu çalışmanın ilkokulun son yılına kadar yapılan problem kurma çalışmalarını deneyimleyen öğrencilerin ilkokul düzeyinde matematik problemi kurma konusundaki yeterlilikleri hakkında genel bir çerçeve ortaya koyacağının düşünülmesidir.
Bu nedenle, araştırmadan elde edilen bulguların ve ulaşılan sonuçların ilkokulun son sınıfında öğrenim gören öğrencilerin bu konudaki yeterlilikleri hususunda aydınlatıcı bilgiler ortaya koyduğunu söyleyebiliriz. Çalışmadan elde edilen bulgu ve sonuçlar ışığında ilkokul öğrencilerinin problem kurma yeterliliklerinin artırılması, problem kurma konusunda nelerin yapılabileceği ve problem kurma konusunun sınıf içi uygulamalarına yönelik öneriler getirilmektedir ki bu açılardan da eldeki çalışma alan yazınına katkı sağladığı düşünülebilir.
1.4. Sayıltılar
Bu araştırmanın temelinde aşağıdaki sayıltılar yer almaktadır:
1. Kapsam geçerliği için kendilerine başvurulan 3 “Doç. Dr.” ünvanlı sınıf eğitimi matematik alan uzmanı ve 2 ilkokul dördüncü sınıf öğretmeninin görüşleri yeterlidir.
2. Öğrenciler kendilerine uygulanan ölçme aracına içten cevap vermişlerdir.
1.5. Sınırlılıklar
Bu araştırma;
1. 2015-2016 eğitim- öğretim yılı ve aynı yıl uygulamada olan İlköğretim Matematik Dersi Öğretim Programı (1-5.sınıflar) (2005) belirtilen sınırlılıklar ve kazanımlar çerçevesinde 4.sınıf düzeyinde doğal sayılar öğrenme alanına yönelik dört işlem becerisi gerektiren problem durumlarıyla,
2. Problem kurma durumları; Stoyanova ve Ellerton (1996) tarafından geliştirilen, serbest, yarı–yapılandırılmış ve yapılandırılmış problem kurma çalışması ve Christou vd. (2005) tarafından öne sürülen modelde yer alan kavrama, aktarma, düzenleme ve seçme alt boyutları ile sınırlıdır.
22
1.6. Tanımlar
Problem Kurma: Problem kurma, yeni bir problem oluşturmak veya verilen bir problemin
yeniden düzenlenmesidir. Problem kurma, denildiğinde 3 farklı matematiksel aktiviteden bahsedilebilir. Bunlardan bir tanesi verilen bir durumdan orijinal bir problem oluşturmak, bir diğeri daha önceden çözülmüş bir problemin yeniden düzenlenmesi veya düzeltilmesi şeklinde olurken, sonuncusu henüz çözülen bir problemin, amacı veya koşulları değiştirilerek yeni bir problem oluşturmak şeklindedir (Silver, 1994). Bu çalışmada, öğrencilerden verilen bir durumdan orijinal bir problem oluşturmaları istenmiştir.
Dört İşlem Becerisine Yönelik Problem: Bu çalışmada öğrencilerden kurmaları istenen
problemler doğal sayılar öğrenme alanında ve çözümünde toplama, çıkarma, çarpma ve bölme işlemi gerektiren problemlerdir.
23
BÖLÜM II
KAVRAMSAL ÇERÇEVE
Bu bölümde araştırmanın konusuyla ilgili olarak; problem kavramının anlamına, problemlerin özelliklerine, problemlerin sınıflandırılmasına, problem çözme ve problem kurma süreçlerine ve matematiğin farklı temsil biçimlerine yer verilmiştir. Öncelikle problem kavramının anlamlarına bu çalışmada yer verilen anlamına değinilmiş, ardından problemlerin taşıdıkları özelliklerin neler olduğu açıklanmıştır. Daha sonra problem çözme ve problem kurma süreçlerinden bahsedilmiş ve problem çözme ve problem kurma ilişkisi ele alınmıştır. En son olarak matematiğin çoklu temsil biçimlerine değinilmiştir.
2.1. Problem Nedir?
Problem sözcüğü hem günlük hayatta, hem de matematiksel bir terim olarak farklı anlamlarda kullanılmasına rağmen bu tanımların belli ortak noktalarının olduğu görülmektedir. Alan yazında problem tanımlarından bazıları şöyledir:
Davis’e göre problem, organizmanın karşılaştığı ve hazır tepkisinin bulunmadığı uyarıcı durumu olduğunu söylerken (Demirel’den aktaran Tertemiz, 1994), John Dewey problemi, “insan zihnini karıştıran, ona meydan okuyan ve inancını belirsizleştiren her şey” olarak tanımlamıştır (Dewey’ den aktaran Baykul, 2003). Blum ve Niss’e (1991) göre problem belirli açık sorular taşıyan, kişinin ilgisini çeken ve kişinin bu soruları cevaplayacak doğru yöntem, prosedür ve algoritma bilgisine sahip olmadığı bir durumdur. Foong (2002, s.4) ise problemi bireyin onun için hâlihazırda çözümü olmayan bir durumla karşılaştığında bu durumun üstesinden gelmeye karar vererek problem için düşünmesi ve akıl yorması olarak tanımlamıştır.
24
Tanımlardan anlaşıldığı gibi bir durumun problem olarak adlandırılabilmesi için insan zihninde bir belirsizlik oluşturması, bireyin önceki yaşamında karşılaşmamış olması ve üzerinde çalıştığında bir çözümünün olması gerekir (Van De Walle,2012, s.27). Schoenfeld (1992) problemlerin zor, şaşırtıcı ve öğrenciyi özgün düşünmeye yönlendiren sorular olduğunu vurgulamaktadır. Farklı kişilerin problem tanımlarında ortak olan durum problemin ilk karşılaşıldığında insan zihnini bulanıklaştırması, öğrenciyi düşünmeye sevk etmesi olarak özetlenebilir.
2.2. Problemin Özellikleri
Bir durumun problem olması için insanın zihnini karıştırması, karşılaşılan bu durumun yeni olması yani bireyin bu durumla daha önce hiç karşılaşmamış olması gerektirir. Bu duruma göre, bir birey için problem olan durum başka biri için problem olmayabilir; çünkü bir durumla, bazı bireyler daha önce karşılaşmış oldukları halde bazıları karşılaşmamış olabilir. 2000‘li yılların başlarından itibaren matematik içeriğinin gün geçtikçe soyut teorik matematiğin kazandırılması görüşünden ziyade, hayatla matematiğin iç içe olduğu görüşü kabul görmüştür. Bütün bunlar ışığında hem gerçek hayat ortamında matematik kullanılarak öğrencinin karşılaştığı problemlerin üstesinden gelmesi, hem de gerçek hayat koşullarında oluşturulan modellemelerle matematiksel bilginin gelişimi amaçlanmıştır. Buna göre; öğretmenlerin matematik derslerinde kullandıkları problemlerin aşağıdaki nitelikleri taşıyor olması oldukça önemlidir.
1. Problemler, çocuğun kendi yaşantısından ev, aile, okul ve sınıf hayatından, çevredeki ve yurdun çeşitli alanlarındaki işlerinden alınmalıdır.
2. Problemler, çocuğun istekle yapacağı canlı ve ilgi çekici nitelikte olmalıdır.
3. Öğretmen, problemlerde daima çocukların günlük yaşantılarını göz önünde tutmalı ve onun gerektirdiği işlerin, o zamana kadar öğrenilenlerden olmasına dikkat etmelidir.
4. İşlemlerin kavratılması amacı ile verilen problemler çok basit olmalı, konu sonlarındaki problemler, kolaydan zora doğru sıralanmalıdır.
5. Öğrencilere verilen problemlerde, onların gelişim durumları ve problemlerin o zamana kadar öğrenilenlerle çözülebilir olmasına dikkat edilmelidir (Yıldızlar, 2001, s. 8).
Marton’a göre iyi bir problemde bulunması gereken özellikler aşağıda açıklanmıştır:
Gerçekçilik: Problem gerçekçi olmalıdır. Öğrenci için gerçek nedir? Öğrenci için gerçek,
onun yaşantısıdır. İlk problem örnekleri öğrencilerin içinde bulunduğu ortamdan, karşılaştığı veya karşılaşabileceği olaylar arasından seçilmelidir. Böylelikle problem daha inandırıcı olur. Özellikle ilköğretimin 1., 2., 3. sınıflarında gerçek hayat problemlerine yer verilmelidir. Problemin öğrenci seviyesine uygunluğu tam olmalıdır.
25
Amaç: Her problemin amacı olmalıdır. Herhangi bir problemin amacı şu sorularla daha
anlaşılır olabilir. Problem ile öğrencilere kazandırılmak istenen nedir?, Hangi bilgi ve becerinin uygulanması isteniyor?, Problem niçin soruluyor?, Problemde amaç yok ise o problemin etkililiği tartışılır.
İlgi: Çocuk çevresinin ürünüdür. Çocukların çevresinde olup biten olaylara karşı ilgileri
daha fazladır. Çözülecek problemlerin konusu öğrencilerin çevresinden seçilmelidir. Bu sayede öğrenciler problemle daha çok ilgileneceklerdir ve böylece problemi ve çözümünü anlamaları daha kolay olacaktır.
Dil: Problem kurmada dikkat edilmesi gereken hususlardan biri de kullanılacak ifade
şeklidir. Problemlerde kullanılacak ifade şekli (yani problemin dili) öğrencinin anlayabileceği dilden olmalıdır. Problemde verilen, istenen her öğrencinin anlayacağı şekilde ifade edilmeli, anlaşılamayan, birden çok anlam ifade eden sözcükler kullanılmamalıdır (Marton’ dan aktaran Albayrak, 2010).
Bir sorunun problem olabilmesi için verilen durumla öğrencinin ilk defa karşılaşmış olması gerekir. Öğretmenin sınıfta çözdüğü ve ders kitaplarında bulunan daha önce çözülmüş olan bir soru öğrenci için yeni bir durum olmadığından problem değildir sadece öğrencilerin o zamana kadar kazandıkları bilgi ve becerilerle cevaplayabilecekleri, ilk defa karşılaştıkları sorular problemlerdir. Sınıf ortamında öğrencilere sunulan bir durum, bir öğrenci için problem olsa da başka bir öğrenci için problem olmayabilir (Tertemiz, 1994).
Yukarıda bir problemde olması istenen özellikler ifade edilmiştir. Buna göre; bir durumun problem olabilmesi için, durumun yeni olması, çözümün birey tarafından bilinmiyor olması ve önceden geçirdiği yaşantılarla çözülebilmesi gerekmektedir. İyi bir problemin özellikleri ise, bir gerçek hayat durumunu içermesi, bir amacının olması, öğrencinin dikkatini çekmesi ve anlaşılabilmesi şeklinde özetlenebilir. Öğrencilerden farklı problem kurma durumlarına yönelik problem kurmalarını istenilen bu çalışmada bir problemde bulunması gereken özellikleri taşıyan ve problem durumunu yansıtan problem ifadelerini “doğru problem” olarak nitelendirilmiştir.
26
2.3. Problemlerin Sınıflandırılması
Foong (2002) problemlerin sınıflamasını farklı kaynaklardan yararlanarak aşağıdaki gibi şemalaştırmıştır.
Şekil 1. Matematiksel problemler için sınıflandırma şeması
Foong, P. Y. (2002). Roles of problems to enhance pedagogical practices in the Singapore classrooms. The Mathematics Educator, 6 (2), pp 8.
Kapalı Problemler
Tek bir doğru cevabın bazı basit yollarla belirlenebildiği ve gerekli bilgilerin problem ifadesinde verilmiş olduğu, açıkça formüle edilmiş ve görevler yönünden “iyi yapılandırılmış” (well- structured) olan problemlerdir. Kapalı problemler, özel içerikli rutin ve çok adımlı problemleri kapsadığı gibi, rutin olmayan heuristik tabanlı problemleri de kapsar.
Bu problemler çözülürken, problem çözücü basit hatırlatmalardan çok, yaratıcı düşünme yoluyla çözüm metodu içinde çok önemli adımlar üretmeli ve bu süreçte kabiliyetlerini geliştirmelidir. Literatürde “meydan okuyan problemler (challenge problems)” olarak bilinen bu problemler, özel bir konudaki problemleri çözmek, öğretimdeki asıl rolünü
PROBLEMLER Kapalı Tipler (ders kitaplarındaki alıştırmalar haricindekiler) Rutin Problemler 1.Özel konulular 2. Çok adımlı olanlar
Rutin Olmayan Problemler (heuristik problem
çözme stratejileri kullanılır)
Açık Uçlu Tipler
Kavramsal anlama için ders kitaplarındaki alıştırmaların açık uçlu
problemlere dönüştürülmesi
Eksik Bilgi (Missing Data)
Problem Kurma (Problem Posing)
Kavramları açıklayan, kural veya hatalar Gerçek hayat içerikli uygulamalı problemler
Matematiksel Araştırmalar ve
27
vurgulamak ve öğrencilerin ileri düzeyde analitik düşünme kabiliyetlerini ortaya çıkarmak için kullanılmaktadır (Foong, 2002).
Kapalı problemler; rutin ve rutin olmayan problemler olarak iki sınıfa ayrılabilir.
a. Rutin (Dört İşlem) Problemler:
Bunlar matematik ders kitaplarında çokça yer alan ve dört işlem problemleri olarak bilinen problemlerdir. Yabancı literatürde word problem ya da story problem olarak adlandırılırlar. Rutin problemler bir ya da çok işlemli olabilirler. “Ali 212 sayfalık bir kitabın birinci gün
30, ikinci gün 42 sayfasını okudu. Üçüncü gün kitabın yarısına geldiğine göre üçüncü gün kaç sayfa okumuştur?” bu türden bir problemdir. Dört işlem problemlerinin öğretiminin
amacı, çocukların günlük hayatta çok gerekli olan işlem becerilerini geliştirmeleri, problem hikâyesinde geçen bilgileri matematik eşitliklere aktarmayı öğrenmeleri, düşüncelerini şekillerle anlatmaları, yazılı ve görsel yayınları anlamaları ve problem çözmenin gerektirdiği temel becerileri kazanmalarıdır (Altun, 2014).
b. Rutin Olmayan (Gerçek) Problemler:
Rutin olmayan problemlerin çözümleri işlem becerilerinin ötesinde, verileri organize etme, sınıflandırma, ilişkileri görme gibi becerilere sahip olmayı ve bir takım aktiviteleri arka arkaya yapmayı gerektirir (3). Örneğin; “Bir adam bir oyundan bir tilki, bir ördek ve bir
çuval mısır kazanıyor. Bunlarla birlikte bir nehrin bir kıyısından öbür kıyısına geçmek zorunda fakat bir kayık var ve çok küçük. Adamla birlikte bu kayık ancak birini alabiliyor. Mısırı geçirse tilki ördeği yiyebilir, tilkiyi geçirse ördek mısırı. Hiçbir zayiat olmadan bunları karşıya nasıl geçirebilir?” sorusu bu türden bir problemdir. Bu problemler ya gerçek
hayatta karşılaşılmış ya da karşılaşılabilecek bir durumun ifadesidirler. Bundan ötürü bunlara gerçek hayat problemleri de denir. (Altun, 2014)
Açık Uçlu Problemler
Bu kategorideki problemler çoğu zaman “iyi yapılandırılmamış (ill-structured)”olarak isimlendirilir. Eksik bilgi ve kabullerin olduğu, doğru ve tam bir çözümü garantileyen basit bir işlemin, açık bir formülasyonunun olmadığı problemler açık uçlu problemlerdir. Açık uçlu problemler, tek bir cevabı olmayan ve günlük yaşantıdaki problemleri kapsayan problemlerdir (Foong, 2002).
28
Matematiksel Araştırmalar ve Projeler
Açık uçlu matematiksel araştırmalar ve projelerde, genellikle öğrencilerin bağımsız çalışmaları üzerinde kendi yaratıcılıklarını, yeteneklerini ve matematiksel bilgi ve becerilerini ayrıntılı raporlar şeklinde sergilemeleri gerekir. Bu tür araştırmalar genellikle yüksek düzeyde matematik bilgisi olan öğrencilerle yapılan çalışmalarda ve matematiğin kuramsal temelli çalışmalarında kullanılır.
Araştırmamızda da bahsi geçen dört işlem problemlerinin öğretiminin amacı, çocukların günlük hayatta çok gerekli olan işlem becerilerini geliştirmelerinde yardımcı olmak, problem hikâyesinde geçen bilgileri matematik eşitliklere aktarmayı öğrenmeleri, matematiksel bir eşitliği sözel bir problem cümlesine dönüştürebilmeleri, düşüncelerini farklı temsil biçimleriyle anlatmaları, yazılı ve görsel yayınları anlamaları ve problem çözmenin gerektirdiği temel becerileri kazanmalarıdır.
Problem çözme öğretimi, genel hedeflerimiz arasında olan kendi kendine güçlüklerin üstesinden gelebilen insanın yetiştirilmesinde de büyük önem taşımaktadır. Bu bakımdan problem çözme öğretimi önemlidir. Eğitim öğretim faaliyetlerinde problem çözme sadece bir matematik konusu olarak ele alınıp sonra terk edilmemeli, bütün eğitimin odak noktası olmalıdır. Yani öğretimde problem çözme yaklaşımı, en temel yaklaşım olarak benimsenmelidir.
2.4. Problem Çözme
Günlük hayatta kullanımının gerekliliği ve diğer bilimlerle olan ilişkisi nedeniyle öğrencilerin matematiği öğrenmesi ve bu öğrendiklerini günlük hayata transfer edebilmesi büyük önem taşımaktadır. Matematik öğretiminin genel amaçlarının da kişiye günlük hayatın gerektirdiği matematik becerilerini kazandırmak, problem çözmeyi öğretmek ve olayları problem çözme yaklaşımı içinde ele alan bir düşünme biçimi kazandırmak olduğu söylenebilir (Altun, 2010).
Problem çözme “Ne yapılacağının bilinmediği durumlarda yapılması gerekeni bilmektir.” Problem çözme tek bir doğru sonuç bulma olarak algılansa da daha geniş bir zihinsel süreci ve becerileri kapsayan bir eylemdir (Altun, 2002). Başka bir tanıma göre problem çözme bir amaca erişmekte karşılaşılan güçlükleri yenme sürecidir (Polya, 1957), bu da bilgiyi kullanarak ve buna orijinallik, yaratıcılık ya da hayal gücünü ekleyerek çözüme ulaşma
29
süreci olarak açıklanabilir. Bu anlamda problem çözmenin yüksek düzeyde bilişsel bir süreç olduğu söylenebilir (Roth’den aktaran Tertemiz &Çakmak, 2003).
Birey bir problemle karşılaştığı zaman, birey tarafından problemin anlaşılması oldukça önemlidir. Çünkü birey anlamadığı bir problem için çözüm öneremez, çözümü için herhangi bir strateji tespit edip, bu stratejiyi uygulayamaz bu nedenle “problem çözme süreci, net olarak tasarlanan fakat hemen ulaşılamayan bir hedefe varmak için kontrollü etkinliklerle araştırma yapma” şeklinde açıklanabilir (Altun, 2014).
Problem çözmede pek çok model vardır. Bunlardan en bilineni George Polya’nın (1957) dört adımdan oluşan problem çözme modelidir. Bu dört adım; problemi anlama, plan yapma, planı uygulama ve değerlendirmedir. Bahsedilen dört adım doğrudan öğrenilecek bir bilgi olmaktan ziyade modellerle desteklenen, öğretmen soruları ile yönlendirilen bir süreçtir. Problem çözme sürecinin bu dört adımı, bir yandan problem çözme sırasında izlenecek yolu gösterirken, diğer yandan öğrencilere bilimsel düşünme yöntemi kazandırmayı amaçlar. Problem çözme etkinlikleri sırasında hem matematiksel becerilerin gelişimi desteklenir hem de akıl yürütmenin sistematiği kazandırılmaya çalışılır.
Polya (1997) 4 aşamalı bir süreç geliştirerek problemin çözüm sürecini sistematikleştirmiştir. Bu sürecin basamakları şu şekildedir:
1. Problemin anlaşılması
2. Çözümle ilgili stratejinin seçilmesi
3. Seçilen stratejinin uygulanması 4. Çözümün değerlendirilmesi
Polya’nın (1957) ortaya koymuş olduğu basamakların bilinmesi problemle karşılaşan kişinin problemde ne istenildiğini bilmesine ve problemin çözümde hangi stratejinin kullanacağı kişiye bağlı olması nedeniyle problemi çözmez ancak problemin çözümünü kolaylaştırır.
Problemin Anlaşılması
Bu basamakta veriler nelerdir, koşullar nelerdir ve bilinmeyen nedir? Şeklindeki iki temel soruya cevap aranmalıdır. Eğer öğrenci bu sorulara tam olarak cevap verebiliyorsa problemi anlamış demektir. Problemi anlamanın başka göstergeleri de vardır:
30
2. Problemde eksik ya da fazla bilgi varsa bunları bulabiliyor mu? 3. Problemden ne tür bilgiler elde edileceğini görebiliyor mu?
4. Problemdeki olaylara ve ilişkilere uygun şekil ya da diyagram çizebiliyor mu? 5. Problemi kısımlarına (alt problemlere) ayırabiliyor mu? (Altun, 2000).
Çözümle İlgili Stratejinin Seçilmesi (Çözüm İçin Plan Yapma)
Problemde verilenler ile bilinmeyenler arasındaki ilişkilerin araştırıldığı safhadır. Eğer hemen bir ilişki bulunamıyor ise, benzer problemler ve onların çözümleri göz önüne alınmalıdır. Bu girişimlerin sonunda çözüm için bir plan ortaya çıkar. Bunun için öğrenci kendine şu soruları sormalıdır:
Buna benzer, daha önce bir problem çözdüm mü? Orada ne yaptım? Çözümde işe yarayacak bir bağıntı biliyor muyum?
Bu problemi çözemiyorsam, buna benzer daha basit bir problem ifade edip çözebilir miyim?
Tasarladığım çözümde bütün bilgileri kullanmış oluyor muyum?
Bu problemin cevabını tahmin edebiliyor muyum? Cevap hangi değerler arasında olabilir?
Problemi parça parça çözebilir miyim? Her seferinde çözüme ne kadar yaklaşmaktayım?
Çözüm planı, temelde çözüme uygun bir stratejinin seçilmesine bağlıdır. Bir problemin çözümünde bazen bir, bazen birkaç strateji birlikte kullanılır. Bazen de aynı problemin çözümüne farklı stratejiler uygun düşebilir. Problem çözmede kullanılan stratejilerin bazıları şunlardır ( Altun, 2010; Tertemiz & Çakmak, 2003):
Sistematik Liste Yapma Tahmin ve Kontrol Diyagram Çizme
Bağıntı Bulma ( Veriler arasında ilişki arama) Eşitlik Yazma
Tahmin Etme
Benzer Problemlerin Çözümünden Faydalanma Geriye Doğru Çalışma
31 Tablo Yapma
Muhakeme Etme
Problem çözme ile ilgili yapılan bazı araştırmalarda (Kılıç, 2013; Yaman & Dede, 2004) ortaya konulan sonuçlara bakıldığında problem çözme stratejileri öğrenilebilmekte ve öğrenciler bu stratejileri kullanabilmektedir. Her strateji tüm problemlerin çözümüne uygun değildir. Bazı stratejiler diğerlerine göre daha çok kullanılmaktadır. Ayrıca bir problemin çözümünün değişik basamaklarında değişik stratejilere ihtiyaç duyulabilmektedir. Değişik stratejilerin öğrenilmesi, öğrencilere karşılaşacakları değişik problemler için bir alışkanlık ve yatkınlık sağlamaktadır. Öğrencilerin stratejileri etkili kullanabilmeleri için, strateji tanıtılmadan doğrudan problemle karşılaştırılmalı, alternatif yaklaşımları denemeleri için onlara fırsat verilmelidir. Problem çözme stratejilerinin kazanılması ve kullanılması, öğrencinin gelişmişlik seviyesiyle ilgilidir. Öğretimde stratejilerin güçlük düzeyleri dikkate alınmalıdır.
Seçilen stratejinin uygulanması
Seçilen stratejinin kullanılması ile problem adım adım çözülmeye çalışılır. Her basamakta yapılan işlemler kontrol edilir. Çözülemez ise problemin birinci veya ikinci adımına dönülerek bu stratejide ısrar edilir. Yine çözülemez ise strateji değiştirilir.
Çözümün değerlendirilmesi
Çözümün değerlendirilmesi daha çok “sonuçların doğruluğunun kontrolü” olarak anlaşılmaktadır. Problemin çözümünün değerlendirilmesi safhası problem çözme yeteneğinin geliştirilmesi ile ilgili birçok etkinlik içerir. Değerlendirme bir anlamda süreçle ilgili bir aydınlanma safhasıdır. Nerede ne yaptık? Niçin yaptık?
Bu safhaların temel eylemleri şunlardır:
Sonuçların doğruluğunu ve çözümde yürüttüğün mantığı kontrol et. Problemi varsa başka yollardan çöz.
Problemin değişik şekillerini ifade et ve bu durumda çözümün nasıl olacağını düşün.
32
Bu sorularla, değerlendirme basamağında sonuçların doğruluğu ve anlamlılığı kontrol edilir, başka bir çözüm yolu varsa o denenir. Hepsinden önemlisi çözülen problem değişik şekillerde ifade edilir ve her bir durumda problemin nasıl çözüleceği tartışılır (Altun, 2010).
Problem çözme ve kurma, matematiğin gerçek hayatla olan ilişkisinin anlaşılmasında, öğrencilerin düşünce biçimleri hakkında bilgiler edinilmesinde ve sonuca değil sürece odaklanıldığından güven duygusunun gelişmesinde oldukça önemli bir işleve sahiptir. Bu nedenle problem çözme etkinliklerinin mutlaka gerçek hayatla ilişkilendirilmesine; konu edilen problem durumlarının gerçek hayattan seçilmesine ve matematik dünyası içinde ulaşılan çözümlerin tekrar gerçek hayat bakımından yorumlanmasına özellikle önem
verilmelidir (MEB, 2015).
2.5. Problem Kurma
Pek çok bilim insanı özellikle problem kurmanın, var olan problemi çözmek kadar önemli olduğunu vurgulamıştır. Einstein ve İnsfeld, matematiksel ve deneysel durumlarda problemin oluşturulmasının (kurulmasının formulation) çoğu zaman problemin çözümünden daha önemli olduğunu ifade etmiştir ( Einstein &İnsfeld’ den aktaran Cai & Hwang, 2003). Literatürde problem kurma farklı kişiler tarafından farklı şekillerde tanımlanmıştır. Leung (1993), problem kurmayı verilen bir problemin yeniden düzenlenmesi şeklinde tanımlamıştır. Silver (1994) ise problemi hem yeni problemler üretme, hem de var olan problemi düzenleme olarak tanımlamıştır. Benzer şekilde, NCTM (2000) de problem kurmanın yeni bir problem oluşturma olduğunu vurgulamıştır. Gonzales (1998) ise problem kurmayı Polya’nın (1957) problem çözme adımlarının sonuncusu olarak tanımlamıştır. Tüm bu tanımlar incelendiğinde problem kurma ile ilgili ortak noktanın problem üretme olduğu söylenebilir.
Problem kurma son yıllarda pek çok araştırmacı tarafından yeni bir problem oluşturmak veya verilen bir problemin yeniden düzenlenmesi olarak tanımlanmıştır. Problem kurma, denildiğinde 3 farklı matematiksel aktiviteden bahsedilebilir. Bunlardan bir tanesi verilen bir durumdan orijinal bir problem oluşturmak, bir diğeri daha önceden çözülmüş bir problemin yeniden düzenlenmesi veya düzeltilmesi şeklinde olurken, sonuncusu henüz çözülen bir problemin, amacı veya koşulları değiştirilerek yeni bir problem oluşturmak şeklindedir (Silver, 1994).
33
Silver (1994) problem kurmanın problem çözmenin farklı aşamalarında uygulanabileceğini belirtmiştir. Silver (1995; 2004)’e göre problem kurma problem çözme sürecinde, öncesinde veya sonrasında bulunabilir. Bunlar aşağıdaki gibi ifade edilebilir:
a) Çözüm öncesi problem kurma: Sunulan matematiksel ya da uyarıcı bir durumdan orijinal problemler üretilmesi.
b) Çözüm içerisinde problem kurma: Çözümü yapılmış bir problemin yeniden formülasyonu veya oluşturulması.
c) Çözüm sonrası problem kurma: Yeni problemler üretmek için çözümü mevcut olan bir problemin amaçlarının ve şartlarının modifikasyonudur.
İlkokul Matematik dersi programında; (MEB, 2015) öğrencilerin, matematik derslerinde önceden kurgulanmış problem durumlarıyla karşılaştırmayı içeren etkinliklerin yanında, öğrencilerin kendi problemlerini kurmalarının sağlanmasına özellikle değinilmiştir. Programda problem kurmanın, yeni bir problem durumu kurgulamayı ya da verilen bir problem durumunu yeniden düzenlemeyi gerektiren bir beceri olduğu belirtilmiştir. Öğrenciden günlük hayatta karşılaşacağı bir problemi çözmek için matematiksel olarak modelleme yapması, problemi matematik terimleriyle ifade etmesi veya verilen bir problemde çözüm için eksik bırakılan ögeleri belirleyerek problem kurması çalışmalarını yapabilmesi istenmiştir.
Problem kurma, problem çözmeyi bir başka yönden ele almaktır ve bu bakımdan çok önemlidir. Öğrencinin daha önce çözdüğü problemdeki ilişkileri içeren bir problemi kurması o problemdeki ilişkilerin kavradığını işaret eder. Problemin cevaptan kurulduğu durumlarda öğrenci cevabı bildiği için çözüm yollarını, hangi işlemlere niçin yer verildiğini kolayca anlar. Bu durum yeni karşılaştıkları bir problemi çözmede onlara yardımcı olur.
Altun’a (2002sayfa???) göre problem kurma etkinlikleri şunlardır:
Verilen bir matematiksel ifadeye uygun problem söyleme
“( +3) x 4 = 16 ifadesine uygun bir problem yazınız.” gibi.
Böyle bir soruya verilen cevaplar çeşitlilik gösterir ve bu çeşitlilikte yarar vardır. Öğrencilerin çeşitlilik gösteren doğru cevapları sınıfta tartışılır. Eksik verilen cevaplar (öğrencinin eksikliğini fark edebilmesi için) ipuçları vermek suretiyle giderilir
Şemaya uygun problem söyleme
İkinci maddede probleme uygun şemanın nasıl çizileceği anlatıldı. Burada yapılan onun tam tersidir. Şema verilir problem istenir. Öğrencilerin cevaplarının doğruluğunu birbirlerine kontrol ettirmek suretiyle çalışmalardaki çeşitlilik artırılır.
34
"Bir sayının 5 katının 3 eksiği 32 ediyor. Bu sayı kaçtır?" gibi.
Burada öğrenci 7 olan cevabı zihninde tutmuş, 5 katının 3 eksiğinin 32 ettiğini arkadaşına söylemiştir.
Öğrencilerin kendi problemlerini kurmaları istenirken verilen bir matematiksel ifadeye uygun problem söyleme, şemaya uygun problem söyleme ve cevabı zihinde tutarak sayı ilişkilerine dayanan problemler söyleme etkinliklerinden faydalanılabilir.
Problem kurma çalışmalarına sayıların büyük, ilişkilerin karmaşık olduğu durumlarda da başvurulur. Önce basit, benzer bir problem kurup onun üzerinde çalışılır. Daha sonra kurulması istenen asıl probleme geçilir.
Örnek: Üç kardeşin üçünün kumbaralarından çıkan paranın toplamı 7.375 TL' dır. Birincinin
parası ikincininkinden 75 TL fazla, ikincininki üçüncününkinden 125 TL fazladır. Her birinin parasını bulunuz.
Çözüm için öğrencilerin hangi yolu kullanacaklarını bulmalarına yardımcı olmak amacıyla bu problemdeki sayılar küçük ve yuvarlak seçilerek; "İki kardeşin
kumbaralarından çıkan paraların toplamı 100 lira olsun. İkincisinin parası birincinin parasından 10 lira fazla ise her birinin parasını bulunuz." şeklinde ifade edilir.
Verilen problemdeki ilişkilerin karmaşık olduğu durumlarda öğretmenden beklenen seri problem kurabilmesidir. Bunun için öğretmenin problem kurarken şöyle bir yol izlemesi uygun olur: Düşünülen problemin öğrencilerce bulunacak cevabı öğretmen tarafından zihinde tutulur, sonra diğer sayısal ilişkiler göz önüne alınarak öğrencilere verilecek sayısal bilgiler söylenir. Yani öğretmen problemi cevaptan hareket ederek kurmalıdır (Altun, 2002) Öğretmen, 5 ve 8 yaşlarındaki iki kardeşin yaşları üzerinde bir problem kurmak ve çözdürmek istiyor olsun. "Çocuklar, iki kardeşin yaşları toplamı 13,farkları 3' tür. Bunların
yaşlarını bulunuz," diyebilir.
Bunlar yapıldığı takdirde sonuçlar problemin doğasına ve problemdeki olaylara uygun çıkar. Ayrıca öğretmen problemin verilenlerini ve istenenlerini bildiği için öğrenci çözümlerine daha iyi rehberlik eder.
Moses, Bjork ve Goldenberg (1993) öğrencilerinin problem kurmalarını sağlamak için öğretmenlere dört kural sunmuşlardır. Bu kurallar şu biçimde sıralanmaktadır:
1. Öğrencilerin dikkatlerini bilinene, bilinmeyene ve şartlara toplamalarını sağlayın.
Daha sonra öğrencilerin şu sorular hakkında düşünmelerini sağlayın: “Bilinen ve
bilinmeyenler değiştiğinde ne olur?”, “Eğer şartlar değiştirilirse ne olur?”: Problemlerin zenginleştirilmesini sağlamak için “Nasıl çözerim?” sorusu yerine ilk olarak “Bu problem ne anlatıyor?” sorusu sorulmalıdır. Bu kural öğrencinin,
35
problemin ne hakkında olduğunu araştırmasını sağlar ve yeni bir problem yaratmak için bir yol gösterir.
2. Alışılagelen matematiksel durumlarla bağlayın: Öğrencileri cesaretlendirme ve öğretmenin model olması ile bilinen durumlarla başlamak öğrencilerin problemin özelliklerini belirlemelerine ve problemin sınırlarını değiştirmelerine olanak sağlayabilir. Bu tür bir yaklaşıma, problem kurma davranışını oluşturmak için küçük yaşlardan itibaren başlanmalıdır.
3. Yeni sorular ve problemler yaratmaları için öğrencileri belirsizlikleri kullanmaya
cesaretlendirin: Burada önemli olan sadece belirsizliği yakalamak değil üretici bir
biçimde kullanmaktır. Belirsiz durumlar öğrencilerin kendi düşüncelerini üretmede merak uyandırarak hayal gücünü kullanmayı sağlayabilir. Bu açıdan belirsiz durumları başarısızlık olarak nitelendirmekten çok kullanışlı duruma getirmek önemlidir.
4. Öğrencileri, küçük yaşlardan itibaren matematiksel nesnelerin yer aldığı
oyunlardaki parçaları değiştirerek oynamaları için cesaretlendirin: Oyunlar,
sınırlayıcı kurallara yaratıcı gözle bakmayı sağlayabilir. Aynı oyunu farklı parçalarla oynamak öğrencilerin farklı matematik nesneleri keşfetmelerini sağlamak için bir fırsat yaratabilir (Aktaran: Turhan, 2011).
Yapılan araştırmaların birçoğunda problem kurmanın, matematiksel etkinliklerin merkezinde ve matematik öğretim programlarının önemli bir bileşeni olduğuna işaret edilmiştir (Brown & Walter, 1993; Mose, Bjork & Goldenberg, 1990; NCTM, 2000; Silver, 1994). Matematik eğitimi araştırmacılarından bazıları, problem kurmanın öğrencilerin matematik eğitimleri ile ilgili yönlerini geliştirmede önemli fırsatlar sağladığını vurgulamışlar; bu bağlamda matematik derslerinde problem kurma etkinliklerinin düzenlenmesini önermişlerdir (Silver & Cai, 1996; Nakano, Murakami, Hirashima & Takeuchi, 2002; Korkmaz & Gür, 2006 ). Bu araştırmacılardan Lavy ve Bershadsky (2003), öğretmen adaylarının geometri etkinlikleri ile ilgili kurmuş oldukları problem çeşitleri üzerine bir araştırma yapmış ve öğretmenlerin formel genelleştirmeyi içeren problem etkinlikleri kurmada yetersiz olduklarına dikkat çekmiştir. Nicolaou ve Philippou (2007) problem kurma ile matematiksel başarı arasında güçlü bir ilişki olduğuna vurgu yapmış ve beşinci ve altıncı sınıf öğrencilerinin problem kurma yetenekleri arasında önemli farklılıklar olduğuna işaret etmiştir.
36
English(1997), beşinci sınıf öğrencileri için problem çözme becerileri ve sayı algılamaları içeren bir problem-kurma programı tasarlamış ve bu problem kurma programının, öğrencilerin problem yapılarını tanımlama ve kullanmada, öğrencilerin farklı problem çeşitlerini algılamalarında ve öğrencilerin farklı matematiksel düşünceler geliştirmelerinde yaralı olduğunu belirtmiştir. Akay, Soybaş ve Argün (2006), matematik öğretiminde kısa açık uçlu soruların ve problem kurma yaklaşımının kullanılmasının matematiksel kavramları anlamaya ve öğrenmeye olan etkisini araştırmıştır. Problem kurma becerisinin, öğrencilere matematiksel muhakemeyi öğretme, matematiksel durumları keşfetme ve matematiksel durumları düzgün bir şekildeş özlü veya yazılı olarak ifade edebilme özelliğini kazandırdığına işaret etmiştir.
Öğrenciler problem kurma yoluyla, deneyimleri ile matematiksel bir dil geliştirebilmekte, matematiksel kavram ve işlemleri ilişkilendirebilmekte, temsil biçimlerine anlam yükleyebilmekte ve çözüm için gerekli olan adımlar arasındaki bağlantıları kurabilmektedir (Abu-Elwan, 2002; Akay, 2006; Cai, 2003; Crespo & Sinclair, 2008; English, 1997; Işık, Işık & Kar, 2011; Lowrie, 2002; Toluk-Uçar, 2009). English (1998) öğrencilerin sembolik matematiksel ifadeleri tanımlayabilme ve günlük yaşam durumları ile ilişkilendirebilme becerilerinin, problem kurma etkinlikleri ile değerlendirilip geliştirilebileceğini belirtirken, Dickerson (1999) öğrencilerin kendi problemlerini kurduklarında, problemlerin yapısının altında yatan anlamları ve yaklaşımları fark edebileceklerini, kavramlar ve sayılar arasındaki ilişkileri oluşturabileceklerini belirtmiştir.
2.6. Problem Kurma Stratejileri
Problem kurma ile ilgili literatür incelendiğinde çeşitli problem kurma stratejilerinin olduğu görülmüştür. Öğretmenlerin, öğrencilerinin problem kurmalarını desteklemek için kullanabilecekleri problem kurma stratejileri şunlardır:
Brown ve Walter (1990) “olmaz ise ne olur? (what-if not)” stratejisini öne sürmüşlerdir. Yapılandırılmış problem kurma durumlarında yer alan bu strateji, verilen bir problemin özelliklerinin değiştirilerek yeni ve ilginç problemler üretmeyi temel almaktadır (Lavy & Shriki, 2007). “Olmaz ise ne olur?” stratejisi, matematikte öğrencilerin kendi problemlerini kurmaları için bilindik matematiksel sistemler ile başlamasına, niteliklerin ya da öğelerin listelenmesine ve daha sonra bu niteliklerin reddedilerek bilinmeyen sistemlerin denendiğinde ne olacağının belirlenmesine dayanır. Bu bilinmeyen sistemler araştırılarak
37
bilindik sistemlerle bir ilişkisinin olup olmadığı belirlenir. Kısacası öğrenciler başlangıç sistemleriyle yeni sistemler oluştururlar (Goldenberg, 1993). Bu strateji, öğrencilerin, tek doğru yolu olan ve esnek olmayan öğretim biçiminden uzaklaşmalarına olanak sağlar. Bu problem kurma stratejisini kullanarak, öğrencilerin çeşitli düşünceleri tartışmalarını sağlamanın yanı sıra problemleri sadece çözmeye odaklanan öğrencilerin problem denildiğinde zihinlerinde çözmeye odaklanılan anlamının yanında farklı anlamlar taşıdığını fark etmelerini de sağlar (Lavy & Shriki, 2007).
Ambrus (1997) ise öğrencilere problem kurma becerisini kazanmaya yönelik 5 temel strateji önermiştir. Bu stratejiler şunlardır:
1. Eğer… ise… Değildir stratejisi (“Eğer… ise… dir”) 2. Verilen bir probleme birden fazla çözüm üretme
3. Analoji kullanma 4. Genelleme
5. Bir problemin çözümü için farklı temsiller kullanma (Ambrus’ dan aktaran Yaman & Dede, 2005)
Stoyanova ve Ellerton’da (1996; aktaran Stoyanova, 2003) üç farklı problem kurma stratejisinden bahsetmektedir: bu stratejiler serbest, yarı-yapılandırılmış ve yapılandırılmış problem kurma durumlarıdır.
Serbest Problem Kurma: Serbest problem kurma durumlarında öğrencilere herhangi bir
problem verilmez. Serbest problem kurma durumlarında öğrenciler, okul içindeki ya da dışındaki günlük yaşamdaki bir durumu kullanarak ve birtakım sorular üreterek yeni bir problem düzenlerler. Öğrenciler, “istediğin bir problemi üret”, “matematik yarışmaları veya testler için uygun bir problem düzenle” veya “kolay veya zor problem yaratmak” şeklinde teşvik edilerek yeni bir problem düzenlemeleri istenir. Problem derleme durumları kapsamında, günlük hayat durumları serbest problem derleme, istediğin bir problem, matematik yarışmaları için problemler, bir arkadaş için yazılan problemler ve zevk için üretilmiş problemler gibi etkinliklerden biri ya da birkaçı olabilir (Stoyanova, 2003).
Yarı-yapılandırılmış Problem Kurma: Yarı-yapılandırılmış problem kurma durumlarında,
öğrencilere açık uçlu bir durum verilir ve öğrencilerden bilgilerini, yeteneklerini, kavramları ve önceki matematiksel deneyimlerindeki ilişkileri kullanarak bu durumu inceleyip araştırmaları istenir (Stoyanova & Ellerton, 1996). Problem durumları, açık-uçlu problemler
38
(matematiksel araştırmalar), verilen problemlere benzer problemler, benzer durumdaki problemler, çok özel kuramlarla ilgili problemler, verilen resimlerden çıkarılan problemler ve kelime problemleri tiplerinden oluşmaktadır (Abu-Elwan, 1999).
Yapılandırılmış Problem Kurma: Yapılandırılmış problem kurma durumlarında, herhangi
bir matematik problemi bilinen verilerden oluşmaktadır. Öğretmen, bilineni değiştirip yeni bir problem düzenleyebilir ya da verilen veriyi sabit tutarak gereksinim duyulanı değiştirebilir (Stoyanova & Ellerton, 1996).
Constantinos, Nicholas, Marios, Demetra ve Bharath (2005) ise bu sınıflandırmadan farklı olarak öğrencilerin problem kurma sürecinde nasıl düşündüklerini dikkate alan yeni bir problem kurma modeli geliştirmişlerdir. Öğrencilerin problem kurarken, mevcut duruma nicel bilgi ekleyebileceğini (editing quantitative information) söylediği ekleme kategorisinde, verilen bilgi veya hikâye durumuna hiçbir sınırlama getirmeden problem kurulmasını, nicel bilgiyi seçebileceğini (selecting quantitative information) söylediği seçme kategorisinde, bir durum ya da verilen çözüme uygun problem kurulmasını, nicel bilgiyi kavrayıp organize edebileceğini (comprehending and organizing quantitative information) söylediği anlama kategorisinde matematiksel denklem ya da işlemlere uygun problem kurulmasını ve son olarak nicel bilgiyi bir formdan başka bir forma dönüştürebileceğini (translating quantitative informationfrom one form to another) söylediği dönüştürme kategorisi ise verilen grafik, diyagram ya da tablolara uygun problemlerin kurulmasını gerektirdiğini belirtmiştirler. Yapılan bu tür bir sınıflandırma, Stoyanova’nın (1998) yapmış olduğu sınıflamadaki yapılandırılmış ve yarı-yapılandırılmış problem kurma durumlarına karşılık geldiği söylenebilir. Constantinos, Nicholas, Marios, Demetra ve Bharath (2005) bu tür bir sınıflandırmayı toplama ve çıkarma ile ilişkili problemler için önermişler, ayrıca bu modellerin cebir, geometri ve ölçme gibi matematiğin diğer alanlarındaki konulara ve farklı yaş gruplarına da uygulanabileceğini belirtmişlerdir (Işık & Kar, 2012)
2.7. Matematiğin Çoklu Temsil Biçimleri
İlkokul 4. sınıf öğrencilerinin farklı problem kurma durumlarına yönelik oluşturdukları doğal sayılarla dört işlem becerisine yönelik problemleri incelediğimiz bu çalışmada; farklı problem durumlarından kastedilen farklı temsil biçimlerinden (resimler, grafikler, tablolar, cebirsel ve sözel ifadeler, gerçek hayat durumları) birini kullanarak oluşturulan problem durumlarına yönelik olarak öğrencilerin söz konusu temsil biçimini sözel temsil biçimine