5. SINIF MATEMATİK DERSİNDE GERÇEKÇİ MATEMATİK
EĞİTİMİ DESTEKLİ ÖĞRETİMİN ÖĞRENCİ BAŞARISINA,
TUTUMUNA VE MATEMATİK ÖZ BİLDİRİMİNE ETKİSİ
Ali Özkaya
DOKTORA TEZİ
İLKÖĞRETİM ANA BİLİM DALI
GAZİ ÜNİVERSİTESİ
EĞİTİM BİLİMLERİ ENSTİTÜSÜ
i
TELİF HAKKI VE TEZ FOTOKOPİ İZİN FORMU
Bu tezin tüm hakları saklıdır. Kaynak göstermek koşuluyla tezin teslim tarihinden itibaren 12(on iki) ay sonra tezden fotokopi çekilebilir.
YAZARIN
Adı : Ali Soyadı : ÖzkayaBölümü : İlköğretim Matematik Öğretmenliği İmza :
Teslim tarihi :27/12/2016
TEZİN
Türkçe Adı: 5. Sınıf Matematik Dersinde Gerçekçi Matematik Eğitimi Destekli Öğretimin Öğrenci Başarısına, Tutumuna ve Matematik Öz Bildirimine Etkisi
İngilizce Adı: The effects of Realistic Mathematics Education on Student’s Achivements, Attitudes and Self reports in 5.th grades Mathematics Lesson.
ii
ETİK İLKELERE UYGUNLUK BEYANI
Tez yazma sürecinde bilimsel ve etik ilkelere uyduğumu, yararlandığım tüm kaynakları kaynak gösterme ilkelerine uygun olarak kaynakçada belirttiğimi ve bu bölümler dışındaki tüm ifadelerin şahsıma ait olduğunu beyan ederim.
Yazarın Adı Soyadı: Ali ÖZKAYA
iii
JÜRİ ONAY SAYFASI
Ali Özkaya tarafından hazırlanan “5. Sınıf Matematik Dersinde Gerçekçi Matematik Eğitimi Destekli Öğretimin Öğrenci Başarısına, Tutumuna Ve Matematik Öz Bildirimine Etkisi” adlı tez çalışması aşağıdaki jüri tarafından oy birliği ile Gazi Üniversitesi İlköğretim Anabilim Dalı İlköğretim Matematik Eğitimi Bilim Dalı’nda Doktora tezi olarak kabul edilmiştir.
Danışman: Doç. Dr. Sebahat YETİM KARACA ……….…….
Matematik Eğitimi Anabilim Dalı, Gazi Üniversitesi
Başkan: Doç. Dr. Cem Oktay GÜZELLER ……….…..…….
Gastronomi ve Mutfak Sanatları Bölümü, Akdeniz Üniversitesi
Üye: : Prof. Dr. Cengiz ÇINAR ………..………..
Matematik Eğitimi Anabilim Dalı, Gazi Üniversitesi
Üye: Yrd. Doç. Dr. Hasan ES ……….………
Matematik Eğitimi Anabilim Dalı, Gazi Üniversitesi
Üye: Doç. Dr. Hesna KABADAYI ………….………
Matematik Bölümü, Ankara Üniversitesi
Tez Savunma Tarihi:27/12/2016
Bu tezin İlköğretim Anabilim Dalı’nda Doktora tezi olması için şartları yerine getirdiğini onaylıyorum.
Eğitim Bilimleri Enstitüsü Müdürü
iv
TEŞEKKÜR
Tez çalışmam süresince bana yol gösteren ve ilgisini eksik etmeyen, tez danışmanım Sayın Doç. Dr. Sebahat YETİM KARACA’ya emekleri ve sabrı için saygılarımı ve teşekkürlerimi sunarım.
Doktora Eğitimimin her aşamasında değerli düşüncelerini, zamanlarını ve bilgilerini benimle paylaşan Yrd. Doç Dr. Hasan ES’e, Doç. Dr. Hesna KABADAYI’ya, Yrd. Doç. Dr. Dursun SOYLU’ya saygılarımı ve teşekkürlerimi sunarım.
Tezimin uygulama aşamasının sorunsuz bir şekilde yürütülmesinde desteklerini esirgemeyen Antalya İl Milli Eğitim Müdürlüğüne ve ilköğretim kurumlarının yöneticilerine ve öğretmenlerine teşekkür ederim.
Son olarak, benim için maddi ve manevi her türlü fedakârlığı yapan ve benden hiçbir zaman yardımlarını esirgemeyen eşime sevgi, anlayış ve sabrı için sonsuz teşekkür ediyorum.
v
5. SINIF MATEMATİK DERSİNDE GERÇEKÇİ MATEMATİK
EĞİTİMİ DESTEKLİ ÖĞRETİMİN ÖĞRENCİ BAŞARISINA,
TUTUMUNA VE MATEMATİK ÖZ BİLDİRİMİNE ETKİSİ
(Doktora Tezi)
Ali Özkaya
GAZİ ÜNİVERSİTESİ
EĞİTİM BİLİMLERİ ENSTİTÜSÜ
ARALIK 2016
ÖZ
Bu tez çalışmasının amacı 5. Sınıf Sayılar ve İşlemler Ünitesinde, Gerçekçi Matematik Eğitimi Destekli Öğretimin, öğrencilerin Akademik Başarılarına, Matematik Tutumlarına ve Öz bildirimlerine etkisini incelemektir. Bu amaçla; rastgele iki sınıf belirlenmiş, Grup Denkliği Başarı testi (GDBT) ile grupların denk olduğu görüldükten sonra sınıflara Öğrenme Alanı Başarı Testi (ÖABT), Matematik Tutum Ölçeği (MTÖ) ve Matematik Öz Bildirim Envanteri (MÖBE) uygulanmış ve ünite öncesi, öğrenme alanıyla ilgili grupların düzeyleri ölçülmüştür. Daha sonra uygulamaya geçilmiş, 7 hafta boyunca Deney grubu Gerçekçi Matematik Eğitimine göre hazırlanmış etkinliklerle, Kontrol grubu ise Milli Eğitim Bakanlığı (MEB) programına uygun etkinliklerle Üniteyi işlemişlerdir. Ünite bitiminde Gruplara Öğrenme Alanı Başarı Testi (ÖABT), Matematik Tutum Ölçeği (MTÖ) ve Matematik Öz Bildirim Envanteri (MÖBE) tekrar uygulanmış ve grupların uygulama öncesi verileri ile karşılaştırılmıştır. Bu karşılaştırma sonucu, Doğal Sayılarla İşlemler konusunu Gerçekçi Matematik Eğitimi ile öğrenen öğrencilerin Akademik Başarılarının, Matematik Tutum ve Öz Bildirimlerinin Klasik yöntemle öğrenen öğrencilere göre daha yüksek olduğu sonucuna varılmıştır.
Anahtar Kelimeler: Gerçekçi Matematik Eğitimi, Matematik Tutumu, Matematik Öz Bildirimi, Akademik Başarı, Matematik Eğitimi
Sayfa Adedi: 125
vi
THE EFFECTS OF REALISTIC MATHEMATICS EDUCATION ON
STUDENT’S ACHIVEMENTS, ATTITUDES AND SELF REPORTS IN 5
TH GRADES MATHEMATICS LESSON
(Ph.D Thesis)
Ali ÖZKAYA
GAZI UNIVERSITY
GRADUATE SCHOOL OF EDUCATIONAL SCIENCES
DECEMBER, 2016
ABSTRACT
The aim of this research is to analyse the effects of realistic mathematics education on student achievement, attitudes towards mathematics and self-report on the unit ‘numbers and operations’ for the 5th grades. For this reason two classes were randomly identified. After seeing that the groups were equivalent using the Achievement test of Group Equvialency, Learning Area Achievement Test, Scale of Attitudes towards Mathematics and the Inventory of Mathematics Self-Report were applied to both groups. Afterwards the application was conducted, for 7 weeks the experimental group was taught the unit using the Realistic Mathematics Education activities. On the other hand, the control group was taught the topic using the activities suggested by the Ministry of Education. Learning Area Achievement Test, Scale of Attitudes towards Mathematics and the Inventory of Mathematics Self-Report were conducted again as post-tests, and the results were evaluated by comparing them with the pre-test results. After this comparison, it was seen that the Academic Achievement, the attitudes of students and self report of the students who were taught in accordance with the Realistic Mathematics Education was higher than the students who were taught by classical methods.
Key Words: Realistic Mathematics Education, Mathematics Attitude Scale, Mathematics Self Report Scale, Academic Achievement, Maths Education
Page Number:125
vii
İÇİNDEKİLER
ÖZ ... v ABSTRACT ... vi İÇİNDEKİLER ... vviii TABLOLAR LİSTESİ ... xŞEKİLLER LİSTESİ ... xiii
SİMGELER VE KISALTMALAR LİSTESİ ... xiiii
BÖLÜM 1 ... 1 GİRİŞ ... 1 1.1 Problem Durumu ... 1 1.2 Araştırmanın Amacı ... 5 1.3 Araştırmanın Önemi... 6 1.4 Problem Cümlesi ... 7 1.5 Sayıltılar ... 8 1.6 Sınırlılıklar ... 8 1.7 Tanımlar ... 8 BÖLÜM 2 ... 10 KAVRAMSAL ÇERÇEVE ... 10
2.1 Matematik ve Matematik Eğitimi ... 10
2.2 Matematik Öğretiminde Karşılaşılan Sorunlar ... 13
2.3 Matematik Öğretiminde Yapılandırmacılık ... 14
2.3.1 Bilişsel Yapılandırmacılık - Jean Piaget ... 15
2.3.2 Sosyal Yapılandırmacılık - L. S. Vygotsky ... 16
2.3.3 Radikal Yapılandırmacılık - E. Von Glasersfeld ... 18
2.4 Gerçekçi Matematik Eğitimi (GME) ... 18
2.4.1 Gerçekçi Matematik Eğitimi (GME) Nedir? ... ...24
2.4.2 Matematikleştirme ... 24
2.5 Gerçekçi Matematik Eğitimi (GME)’nin Temel Özellikleri ... 26
viii
2.5.2 Modellerin Kullanımı... 28
2.5.3 Öğrencilerin Kendi Ürün ve Yapılarını Kullanımı…..…….……….…29
2.5.4 Etkileşim ... 30
2.5.5 İç İçe Geçmiş Öğrenme İplikçikleri………..……….30
2.6 Geçekçi Matematik Eğitimi (GME)’nin Temel İlkeleri ... 31
2.6.1 Aktivite İlkesi... 31
2.6.2 Gerçeklik İlkesi ... 31
2.6.3. Seviye İlkesi ... 32
2.6.4 Birbiriyle İlişki İlkesi ... 32
2.6.5 Etkileşim İlkesi ... 32
2.6.6 Rehberlik İlkesi ... 33
2.7 Gerçekçi Matematik Eğitimi (GME)’ne Uygun Matematik Ders Planının Hazırlanması ... 33
2.7.1 Sınıf Düzeyi ... 33
2.7.2 Ders Düzeyi ... 34
2.7.3 Kuramsal Düzey... 34
2.8 Gerçekçi Matematik Eğitimi (GME)’ne Dayalı Ders Planının Öğeleri... 34
2.8.1 Hedefler... 34
2.8.2 Materyaller ... 35
2.8.3 Aktiviteler ... 35
2.8.4 Değerlendirme... 36
2.9 Gerçekçi Matematik Eğitimi (GME)’de Öğretmenin Rolü ... 37
2.10 Gerçekçi Matematik Eğitimi (GME) ve Yapılandırmacı Yaklaşımın karşılaştırılması ... 37
2.10.1 GME ile Yapılandırmacı Yaklaşımın Benzer Yönleri ... 38
2.10.2 GME ile Yapılandırmacı Yaklaşımın Farklı Yönleri... 39
2.11 İlgili Literatür ... 40
BÖLÜM 3 ... 51
YÖNTEM ... 51
3.1 Araştırmanın Modeli ... 51
3.2 Araştırma Grubu ... 52
3.3 Veri Toplama Araçları ... 53
ix
3.3.1.1 Grup Denkliği Başarı Testi……….…..53
3.3.1.2 Öğrenme AlanıBaşarı Testi………..………….53
3.3.2 Matematik Tutum Ölçeği (MTÖ) ... 55
3.3.3 Matematik Öz-Bildirim Envanteri (MÖBE) ... 56
3.4 Verilerin Elde Edilmesi... 57
3.5 Verilerin Analizi ... 58
BÖLÜM 4 ... 60
BULGULAR ... 60
4.1 Araştırmanın Birinci Alt Problemine İlişkin Bulgular... 60
4.2 Araştırmanın İkinci Alt Problemine İlişkin Bulgular ... 62
4.3 Araştırmanın Üçüncü Alt Problemine İlişkin Bulgular ... 65
BÖLÜM 5 ... 74
SONUÇ VE ÖNERİLER ... 74
5.1 Sonuçlar ... 74
5.1.1 Beşinci Sınıf Matematik Dersinde Gerçekçi Matematik Eğitimi Destekli Öğretimin Öğrenci Başarısına Etkisine Yönelik Sonuçlar ... 74
5.1.2 Beşinci Sınıf Matematik Dersinde Gerçekçi Matematik Eğitimi Destekli Öğretimin Öğrenci Tutumuna Etkisine Yönelik Sonuçlar ... 75
5.1.3 Beşinci Sınıf Matematik Dersinde Gerçekçi Matematik Eğitimi Destekli Öğretimin Öğrenci Öz Bildirimine Etkisine Yönelik Sonuçlar ... 76
5.2 Öneriler ... 79
5.2.1 Uygulamaya Yönelik Öneriler ... 79
5.2.2 Araştırmacılara Yönelik Öneriler ... 81
KAYNAKLAR ... 83
x
TABLOLAR LİSTESİ
Tablo 2.1 Matematik Öğretiminin Dört Çeşidi ……….………..…….……25 Tablo 3.1 Araştırmanın Deneysel Deseni: Öntest - Sontest Kontrol Gruplu Desen ...51 Tablo 3.2 Grupların 4.Sınıf Matematik Notlarının Denkliğine İlişkin t-testi Sonuçları …..…52 Tablo 3.3 Grup Denkliği Başarı Testine İlişkin t-testi Sonuçları ….………..……….53 Tablo 3.4 Matematik Öz-Bildirim Envanterine İlişkin Betimleyici İstatistikler ....……….….57 Tablo 4.1 Deney ve Kontrol Grubu Ön-Test Akademik Başarı Puanlarının
Karşılaştırılması ……….………..…... 60 Tablo 4.2 Deney ve Kontrol Grubu Son-Test Akademik Başarı Puanlarının
Karşılaştırılması ………..….…………61 Tablo 4.3 Deney Grubu Ön Test – Son Test Akademik Başarı Puanlarının
Karşılaştırılması ………..………...………..……61 Tablo 4.4 Kontrol Grubu Ön Test – Son Test Akademik Başarı Puanlarının
Karşılaştırılması …………..………..…………..…….……62 Tablo 4.5 Deney ve Kontrol Grubu Ön-Test Tutum Puanlarının Karşılaştırılması ..….…….63 Tablo 4.6 Deney ve Kontrol Grubu Son-Test Tutum Puanlarının Karşılaştırılması ...….…63 Tablo 4.7 Deney Grubu Ön Test – Son Test Tutum Puanlarının Karşılaştırılması …...…....64 Tablo 4.8 Kontrol Grubu Ön Test – Son Test Tutum Puanlarının Karşılaştırılması ...….…64 Tablo 4.9 Deney ve Kontrol Grubu Ön-Test İlgi Değeri Puanlarının Karşılaştırılması ..…...65 Tablo 4.10 Deney ve Kontrol Grubu Son-Test İlgi Değeri Puanlarının Karşılaştırılması .….65 Tablo 4.11 Deney Grubu Ön Test – Son Test İlgi Değeri Puanlarının Karşılaştırılması …...66 Tablo 4.12 Kontrol Grubu Ön Test – Son Test İlgi Değeri Puanlarının Karşılaştırılması ….66 Tablo 4.13 Deney ve Kontrol Grubu Ön-Test Kullanışlık Değeri Puanlarının
Karşılaştırılması ………...………..………..…67 Tablo 4.14 Deney ve Kontrol Grubu Son-Test Kullanışlık Değeri Puanlarının Karşılaştırılması ……….………..………..…………..……67 Tablo 4.15 Deney Grubu Ön Test – Son Test Kullanışlık Değeri Puanlarının
xi
Tablo 4.16 Kontrol Grubu Ön Test – Son Test Kullanışlık Değeri Puanlarının Karşılaştırılması ………...……….…………..….………69 Tablo 4.17 Deney ve Kontrol Grubu Ön-Test Başarı Değeri Puanlarının
Karşılaştırılması ………...………68 Tablo 4.18 Deney ve Kontrol Grubu Son-Test Başarı Değeri Puanlarının
Karşılaştırılması ……….………..70 Tablo 4.19 Deney Grubu Ön Test – Son Test Başarı Değeri Puanlarının
Karşılaştırılması ………..…..………...…70 Tablo 4.20 Kontrol Grubu Ön Test – Son Test Başarı Değeri Puanlarının
Karşılaştırılması ………...………71 Tablo 4.21 Deney ve Kontrol Grubu Ön-Test Kişisel Değer Puanlarının
Karşılaştırılması ………..……….………71 Tablo 4.22 Deney ve Kontrol Grubu Son-Test Kişisel Değer Puanlarının
Karşılaştırılması ………..……….…………72 Tablo 4.23 Deney Grubu Ön Test – Son Test Kişisel Değer Puanlarının
Karşılaştırılması ………...………72 Tablo 4.24 Kontrol Grubu Ön Test – Son Test Kişisel Değer Puanlarının
xii
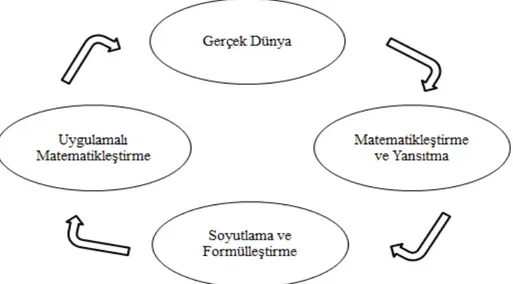
ŞEKİLLER LİSTESİ
Şekil 2.1 GME’ye göre öğrenme döngüsü………22 Şekil 2.2 Yatay ve dikey matematikleştirme………...…….………24 Şekil 2.3 Gerçek dünyadaki matematiksel kavramları ve fikirleri geliştirme süreci olan kavramsal matematikleştirme………..……….………27 Şekil 2.4 Modelleme aşamaları……….29
xiii
SİMGELER VE KISALTMALAR LİSTESİ
MEB Milli Eğitim Bakanlığı GME Gerçekçi Matematik Eğitimi GDBT Grup Denkliği Başarı Testi ÖABT Öğrenme Alanı Başarı Testi MTÖ Matematik Tutum Ölçeği
BÖLÜM 1
GİRİŞ
Bu bölümde araştırmanın; problem durumu, amacı, önemi, problem cümlesi, varsayımları, sınırlılıkları ve tanımlarına yer verilmiştir.
1.1 Problem Durumu
Matematik, insanoğlunun eski çağlardan günümüze kadar birebir veya dolaylı yollardan kullandığı bir olgudur. En basit günlük hayat durumlarından, en karışık problemlere kadar yapılan tüm çözümler matematik sayesinde gerçekleşmiştir. Bu durum da toplumlar için matematiğin ne kadar önemli olduğunu göstermektedir (Altaylı, 2012).
Matematiği önemli kılan hususlardan ilki bireyin yaşam sürecini garanti altına aldıktan sonra daha kaliteli yaşamak istemesidir. İkincisi, mevcut olan doğal varlık ve olayların kararlı bir yapıda olması ve bu kararlılıklarının ancak matematik sayesinde açıklanabilmesidir. Üçüncüsü ise, matematiğin insanın düşünme muhakeme etme ve tartışma yeteneklerini geliştirmesidir. Dolayısıyla, matematiğin birey tarafından nasıl öğrenildiğinin bilinmesi, matematik eğitiminde gelişme sağlamanın önemli bir yoludur (Skemp, 1987).
De Corte (2004)’un belirttiği üzere “Günümüzde matematik, öğrenilmesi gereken soyut kavramların ve becerilerin bir koleksiyonu değil, gerçeğin modellemesini temel alan, problem çözme ve anlamlandırma süreci ile oluşan bilgi ve bu süreçte geliştirilen beceriler olarak algılanmaktadır. Buna göre; matematik öğrenmenin hedefi, matematik yatkınlık kazandırmak olmuştur” (De Corte, 2004). Burada sözü edilen matematiksel yatkınlık; iyi organize edilmiş öğretim içeriğiyle birlikte öğrencinin matematik ve problem çözmeye ilişkin inançları, bilişsel ve duyuşsal olarak kendini düzenleme becerilerinin geliştirilmesi gerekliliğini ifade eder (Üzel, 2007). Dolayısıyla, günlük yaşamda gerekli olan; iletişim kurabilme, yaratıcı ve bağımsız düşünebilme, genelleştirme yapabilme ve çözümleyebilme gibi üst düzey davranışları geliştirebilen matematiğin öğretilmesi kaçınılmazdır (Aşkar,
2
1986). Bu öneminden dolayı matematikle ilgili davranışlar ilköğretimin ilk yıllarından itibaren yükseköğretim programlarına kadar her düzeyde ve her alanda yer alır (Üzel, 2007).
Matematik eğitiminin amacı, bireylerin günlük hayatlarında karşılarına çıkabilecek problemlerinde akıl yürütme yoluyla eleştirel düşünebilen, bunun için kullanılacak matematiksel kavramların ve işlemlerin arasındaki bağı kurabilen bireyler olarak yetişmelerini sağlayacak bilgi ve becerileri kazanmalarına yardımcı olmaktır (Yazıcı, 2004). Buna göre; matematik dersi öğretim programlarında; günlük hayatta matematiği kullanabilen, problem çözebilen, çözümlerini ve düşüncelerini paylaşabilen, ekip çalışması yapabilen, matematikte kendine güvenen ve matematiğe yönelik olumlu tutum geliştiren bireyler yetiştirilmesinin önemli olduğu görüşü benimsenmiştir (Altaylı, 2012). Milli Eğitim Bakanlığı Matematik Eğitimi programının genel amaçları da:
1. Matematik programı, “Her çocuk matematiği öğrenebilir.” ilkesine
dayanmaktadır.
2. Programda; günlük hayatında matematiği kullanabilen, problem çözebilen ve
çözümlerini paylaşabilen, ekip çalışmasına önem veren, matematikte öz güven duyabilen ve matematiğe yönelik olumlu tutum geliştiren bireylerin yetiştirilmesi büyük önem taşımaktadır.
3. Matematikle ilgili kavramları ve bu kavramlar arasındaki ilişkileri, işlemlerin
altında yatan anlamları ve işlem becerilerinin kazandırılması vurgulanmaktadır.
4. Öğrencilerin somut deneyimlerinden, sezgilerinden matematiksel anlamları
oluşturmalarına ve soyutlama yapabilmelerine yardımcı olmak amaçlanmıştır. Bu yaklaşımla; matematiksel kavramların geliştirilmesi ve bazı önemli becerilerin geliştirilmesi de hedeflenmiştir. Bu beceriler; problem çözme, iletişim kurma, akıl yürütme ve ilişkilendirmedir.
5. Programda öğrencilerin araştırma ve keşif yapabilecekleri, problem
çözebilecekleri, çözüm ve yaklaşımlarını paylaşıp tartışabilecekleri ortamların sağlanması vurgulanmıştır. Bu anlamda matematiğin eğlenceli ve estetik yönünün ortaya çıkarılması ve öğrencilerin etkinliklerinde matematikle uğraştıklarının farkında olmaları önem taşımaktadır (MEB, 2009).
Öğrenci merkezli anlayışı temele alan ve yapılandırmacı öğrenme yaklaşımına uygun olarak hazırlanan ilköğretim matematik programları, her ne kadar yukarıda yazılan amaçlar doğrultusunda ülkemiz eğitim sisteminde uygulanmaya çalışılsa da bazı eksiklikler,
3
imkânsızlıklar ve geleneksel matematik eğitiminin getirdiği kısıtlamalardan dolayı yeterince uygulanamamaktadır.
Bahsedilen kısıtlamalar neticesinde öğrenciler; kendi düşüncelerini çoğunlukla ifade edememekte, bu yüzden derslerde güçlük çektikleri noktalar kolaylıkla belirlenememekte, yerinde ve zamanında düzeltmeler yapılamamaktadır. Bununla birlikte öğrenciler, öğretmen tarafından aktarılan bilgiyi not alırken bu bilginin doğruluğunu yeterince sorgulamamakta, konu hakkında derinlemesine düşünmemektedirler. Böylelikle en iyi öğrencilerin düşünceleri bile pasifleşebilmektedir (Ünal, 2008). Bu nedenle, son yıllarda matematiğin öğretim şekli çok tartışılmaya başlanmıştır. Okullardaki matematik öğretiminin gerçek hayatta karşılaşılan sorunlarla bağdaşmaması, öğrencilerin okulda aldıkları bilgi ve becerileri gerçek hayatta kullanmada yetersiz kalmaları, karşılaşılan problemler üzerinde düşünmek ve çözüm stratejileri üretmek yerine, işlemlerde hızlı bir şekilde sonuca gitmeye çalışmaları, bu konulardaki alan araştırmalarının yoğunlaşmasına yol açmıştır.
Ayrıca araştırmalar, gerekli ön bilgi ve becerileri almış olmalarına rağmen öğrencilerin orta güçlükteki problemleri bile çözmede zorlandığını (Fitzpatrick, 1994; Schoenfeld, 1988), matematikte iyi olanların bile matematik ve matematik öğrenmeye karşı olumsuz tutum (Altun, 2006) geliştirdiklerini rapor etmiştir (Arseven, 2010). Bu nedenle, matematik eğitiminin amaçları ve beklentilerine ulaşmayı sağlayacak yenilikçi eğitim yaklaşımlarına ihtiyaç duyulmuştur (Ünal, 2008).
Bu bağlamda Yapılandırmacılık (constructivism) matematik öğretiminde önemli bir yer sahibi olmuş, bununla beraber Gerçekçi Matematik Eğitimi (GME) gibi yeni yaklaşımlar ortaya konmuştur. Yapılandırmacılık ve GME yaklaşımlarının temel ilkeleri paralellik göstermektedir (Olkun ve Toluk 2003).
Günümüz eğitiminde etkisini hissettiğimiz Yapılandırmacı Öğrenme Kuramı’nın temel dayanağı “bilginin dış dünyada bireyden bağımsız olarak var olmadığı ve bilginin bireyin zihnine birileri tarafından aktarılmadığı, bunun aksine kendisi tarafından yapılandırıldığı” (Doolittle, 1999) düşüncesidir. Özünde bilgi edinmeyle ilgili bir kuram olarak geliştirilmiş, öğrenme olayına olan yakın ilgisi nedeniyle zaman içinde bir öğrenme kuramı olarak da belirmiştir (Nelissen ve Tomic, 1998; Demirel, 2005). Matematik eğitiminin iyileştirilmesi ve geliştirilmesi amacıyla ortaya koyulan Gerçekçi Matematik Eğitimi Yaklaşımı’nda ise; matematik öğrenme bir anlamlandırma süreci olarak düşünülmektedir (Nelissen ve Tomic, 1998). Matematik öğretiminin gerçek hayattan alınan problemler ve olgular için çözüm
4
arayışı şeklinde gerçekleşmesi yani matematik yapma şeklinde olması gerektiği ifade edilmektedir (Freudenthal, 1973). Buna bağlı olarak da; bireyin bilgiyi nasıl yapılandırdığı, yapılandırma sürecinde nelerin etkili olduğu, hangi koşulların bilginin niteliğini arttırabileceği gibi hususlar, öğrenme alanının önemli araştırma konuları haline gelmiştir (Memnun, 2011).
Gerçekçi Matematik Eğitimi (GME), Hollanda’da Utrecht Üniversitesine bağlı Freudental Enstitüsünde 1971 yılında, Hollandalı matematikçi ve eğitimci Hans Freudenthal tarafından geliştirilen matematik öğretimi yaklaşımıdır (Çakır, 2013).
Freudenthal, tarihte matematiğin gerçek hayat problemleri ile başladığını, gerçek hayatın matematikleştirildiğini, daha sonra formal sisteme geçildiğini belirterek, önce formal matematik bilgiyi verip ardından uygulamaya geçme şeklindeki öğrenmenin anti didaktik olduğunu ifade etmiştir. Freudenthal’e göre; “çocuk için matematik, anlamlandırma ile başlar ve gerçek matematik yapmak için her safhada anlamlandırmanın esas alınması gerekir.” Freudental’e göre matematik bir insan aktivitesidir, keşfedilmez, icat edilir (Altun, 2006).
Gerçekçi Matematik Eğitimine (GME) göre matematik, çocuklara yakın ve günlük yaşamdaki durumlarla ilişkili olmak zorundadır. Fakat “gerçekçi (realistic)” kelimesi tam olarak gerçek dünya ile bağlantıyı işaret etmemektedir. Gerçekçilik, öğrencilerin zihinlerindeki gerçek problem durumlarına işaret etmektedir. Masalların fantastik dünyası kadar matematiğin formal dünyası öğrencilerin zihninde gerçek olduğu kadarıyla bir problem için uygun içerik sunabilir (Demirdöğen ve Kaçar, 2010).
GME yöntemi ile öğrencilerin güncel yaşam problemleri üzerinde düşünmeleri, olası çözümleri tartışmaları ve akılcı çözüm önerileri geliştirmeleri ile matematiksel kavramlara ulaşmaları, dolayısıyla bu kavramları zihinlerinde yapılandırmaları sağlanmaktadır. Kaygı duyulan bir ders olan matematik dersinin bu şekilde matematiksel bir etkinliğe dönüşmesi ile öğrencilerin, matematik dersine yönelik daha olumlu bir tutum içinde olacakları ve matematik başarılarını artıracakları düşünülmektedir.
Öğrenme süreçlerinin etkileyen önemli faktörlerden biride motivasyondur. Motivasyon, organizmayı davranışa iten, bu davranışların süreklilik ve düzenliğini belirleyen, davranışa amaç ve yön veren çeşitli iç ve dış etkenler ile bunların işleyişini sağlayan mekanizmalar olarak tanımlanır (Aydın, 2001). Bireyler, yeterli olma, problem çözme, bir işi başarmak, kendisini ve çevresini anlamak ve sorunları ile başa çıkmak için güdülenirler.
5
İlköğretim okullarında öğretmenlerin öğrencilere, konuları onların ilgisini çekecek şekilde uygun yöntem ve teknik kullanarak anlatması öğrencilerin motivasyonunu yükseltecek ve istenilen düzeyde kavramların kazandırılmasına yardımcı olacaktır (Cavallo, Miller ve Saunders, 2002). Öğrencinin öğrenmeye ve başarmaya yönelik motivasyonu, profesyonel eğitim programlarında önemi çoğu zaman ihmal edilen bir faktördür. Oysaki öğrencilerin motivasyonu eğitim programlarının en kritik unsurudur. İyi tasarlanmış ve uygulanmış olan eğitim programlarının başarısız olmasındaki nedenlerden biri olarak, programı alan öğrencilerin düşük motivasyonundan kaynaklandığı belirtilmektedir (Gökcül, 2007). Araştırmalar matematikle ilgili motivasyonun matematik başarısı üzerinde büyük bir etkisinin olduğunu göstermesine rağmen bu alandaki deneysel araştırmaların öğrencilerin matematik tutumu ve motivasyonundan çok matematik başarısına dikkat çektiği görülmektedir.
1.2 Araştırmanın Amacı
Birçok ülkede matematik derslerinde öğretim yöntemi olarak uygulanan GME’nin, ülkemizde de uygulanabileceği ve bu yaklaşımın, MEB tarafından matematik dersi öğretim programları için öngörülen özellikleri gerçekleştirdiği düşünülmektedir (Demirdöğen, 2007). Matematik dersi öğretim programlarında, öğrencilerin eleştirel düşünme, bilimsel araştırma, yaratıcı düşünme, iletişim ve girişimcilik gibi becerileri kazanmaları amaçlanmaktadır. Bu amaçların gerçekleşmesi için matematik derslerinin öğrenme-öğretme sürecinde, öğrencilere; işlem ve hesap yapabilme becerilerinden ziyade problem çözme, akıl yürütme ve tahminde bulunma gibi daha üst düzey becerilerin kazandırılacağı yöntemler tercih edilmelidir (Arseven ve Yağcı, 2010; Olkun ve Toluk, 2003). Özellikle, uluslararası sınavlarda ve ülkemizde düzenlenen sınavların sonuçlarına göre; öğrencilerimizin matematik alanında başarısız olduğu (Arseven ve Yağcı, 2010) düşünüldüğünde, öğrencilerin muhakeme yapma becerilerini geliştiren öğrenme-öğretme yöntemleri tercih edilebilir. Bunun yanı sıra program, öğrencilerin matematiği yaşam boyu kullanmalarını ve matematiğe karşı olumlu tutum geliştirmelerini amaçlamaktadır. Eğer öğrenciler matematiğe gereken önemi vermiyorsa, programın işlevselliğinden söz etmek mümkün değildir (Luttrell, Callen, Allen, Wood, Deeds ve Richard, 2010). Bu nedenle öğrencilerin matematikten beklentilerini ve matematiğe verdikleri değeri öğrenmek, matematik eğitiminde çok büyük önem taşımaktadır.
6
Bu bağlamda araştırmanın genel amacı; ortaokul 5. Sınıf matematik dersinde Gerçekçi Matematik Eğitimine uygun hazırlanan etkinliklerin öğrencilerin matematik dersine yönelik başarısına, tutumuna ve matematik öz bildirimine etkisini incelemektir.
1.3 Araştırmanın Önemi
Tün dünyada, her düzeydeki okullarda matematik öğrenimi ve öğretiminin gerekliliği tartışılmaz bir şekilde kabul edilmektedir. İlköğretimin temel amacı; bireyleri hayata ve üst öğrenime hazırlamaktır. Her iki amacın gerçekleşmesi için gerekli zihinsel beceriler; etkili akıl yürütme, eleştirel düşünme ve problem çözmedir. Bu becerilerin gerçekleştirilmesinde ilköğretim programında bulunan tüm derslerin içerisinde matematik dersi oldukça önemlidir (Özsoy, 2002). Özellikle ilköğretim döneminde çocuklar için soyut kavramların ve süreçlerin anlaşılması oldukça zordur. Somut araç-gereçler kullanılarak bu problemin bir ölçüde çözülmesi ve öğretimin daha iyi olması sağlanabilir. Soyut olarak algılanan, anlaşılmasının zor olduğu söylenen ve birçok öğrenenin yaşamı boyunca problem olarak gördükleri derslerin biri de matematik olmuştur. Matematik dersindeki başarısızlık, bu derse karşı olumsuz tutumlar gelişmesine yol açmaktadır. İlköğretim döneminde matematik dersinde öğrenme hedefleme, öğrenci özelliklerine uygun somut yaşantılar sunan gerçek objelerin, modellerin kullanıldığı eğitim durumlarına yer verilmesi bu problemlerin çözümünde düşünülebilecek bir konudur (Arsal, 2002).
2009 yılı İlköğretim Matematik Dersi Programı’nda, matematik ile ilgili bilgilerin kavramsal temellerinin oluşturulmasına daha çok zaman ayırma, böylece kavramsal ve işlemsel bilgi ve beceriler arasında ilişkiler kurmanın önemsendiği görülmektedir. Dolayısıyla öğrencilerin somut deneyimlerinden, sezgilerinden yararlanarak matematiksel anlamları oluşturmalarına ve soyutlama yapabilmelerine yardımcı olma amaçlanmıştır (MEB, 2009). Bu bağlamda araştırmada, Gerçekçi Matematik Eğitimi kuramlarına uygun olarak düzenlenen öğrenme ortamlarında öğrencilerin bilgiyi elde etme süreçlerinin incelenmesi, ilköğretim ders programlarının uygulamalarında öğrencilerin bilgi oluşturmalarının nasıl gerçekleşeceğinin tespit edilmesi konusunda örnek teşkil edebilir. Bu araştırmadan elde edilecek sonuçlar, farklı matematik konularının öğreniminde öğrencilerin bilgi oluşumu için izlenecek yolları belirleme açısından önem arz etmektedir. İlköğretim matematiğinin birinci kademesinde genellikle doğal sayılar ve doğal sayılarla yapılan işlemlerle uğraşılır. Doğal sayılar kümesinde karşılaşılan matematik kavramları, doğal sayılarla yapılan işlemlerinin öğretimi ve diğer sayı kümelerinin öğretimi için temel teşkil eder (Olkun ve Toluk, 2007). Verschaffel, de Corte ve Viersraete (1999)’e göre;
7
ilköğretim öğrencilerinin, sıra sayıları içeren ve standart olmayan, sözel toplumsal problemleri çözme ve modellemedeki başarıları oldukça düşüktür. Ayrıca, öğrencilerin büyük sayılar içeren problemler çözme başarıları, küçük sayıları içerenlere göre daha düşük bulunmuştur. Bu durumun bir nedeni, öğrencilerin rutin olmayan sözel problemlerin çözümünde modelleme yapmasının gerekli olduğu, modellemenin de büyük sayılarda hata yapmaya daha elverişli olmasıdır. Ayrıca öğrenciler, küçük sayılar içeren problemleri çözerken doğrudan işlem yapmak yerine saymaya dayalı stratejiler kullanarak çözüme gitmeyi deneyebilmektedir. Öğrenciler, küçük sayılar içeren problemler için kullandıkları bir kuralı büyük sayılı problemlere de uygulayabilmektedirler (Arseven, 2010). Burada modelleme yapmanın bir amacı da genelleme yapmaktır. (Olkun, Şahin, Akkurt, Dikkartın ve Gülbağcı, 2009). Büyük sayılar diye adlandırılan altı ve daha fazla basamaklı sayıların öğretiminde Gerçekçi Matematik Eğitimi yaklaşımının etkisini araştırmanın konuyla ilgili literatüre katkı sağlayacağı öngörülmektedir.
Bu araştırmada aynı zamanda ortaokulda öğrenim gören öğrenciler için başarı güdüsüne dayalı beklenti-değer kuramını temel alarak matematik öz bildirimlerini ortaya koyan ölçme aracının (Akın, 2011) uygulanması sağlanmıştır. Bu yönü ile araştırma öğrencilerin matematiğe olan bakış açılarını göstermekle birlikte, mevcut matematik programının işlevselliği hakkında bilgi vermesi bakımından önem teşkil etmektedir.
1.4 Problem Cümlesi
Araştırmanın problem konusu “5. Sınıf matematik dersi Doğal Sayılar ve İşlemler konusunun Gerçekçi Matematik Eğitimi Yöntemiyle işlenmesinin öğrenci başarısına, matematik dersine yönelik tutumuna ve matematik öz bildirimine etkisi var mıdır?” şeklinde belirlenmiştir.
Bu bağlamda araştırmada aşağıda ki alt problemlere cevap aranmıştır:
1. 5. Sınıf matematik dersi Doğal Sayılar ve İşlemler konusunda Gerçekçi
Matematik Eğitimine göre hazırlanan ders etkinliklerinin kullanıldığı deney grubundaki öğrenciler ile mevcut programa yönelik uygulamaların yapıldığı kontrol grubu öğrencilerinin akademik başarıları arasında anlamlı bir fark var mıdır?
2. 5. Sınıf matematik dersi Doğal Sayılar ve İşlemler konusunda Gerçekçi
Matematik Eğitimine göre hazırlanan ders etkinliklerinin kullanıldığı deney grubundaki öğrenciler ile mevcut programa yönelik uygulamaların yapıldığı
8
kontrol grubu öğrencilerinin matematik dersine yönelik tutumları arasında anlamlı bir fark var mıdır?
3. 5. Sınıf matematik dersi Doğal Sayılar ve İşlemler konusunda Gerçekçi
Matematik Eğitimine göre hazırlanan ders etkinliklerinin kullanıldığı deney grubundaki öğrenciler ile mevcut programa yönelik uygulamaların yapıldığı kontrol grubu öğrencilerinin matematik öz bildirimleri arasında anlamlı bir fark var mıdır?
1.5 Sayıltılar
1. Araştırmanın uygulama sürecinde, deney ve kontrol grubu öğrencilerinin
kontrol altında alınamayan dışsal etkenlerden eşit düzeyde etkilenecekleri düşünülmektedir.
2. Öğrenciler ölçme araçlarını içten ve dürüst bir şekilde cevaplandırmışlardır. 3. Araştırmada deney ve kontrol grubundaki öğrencilerin veri toplama araçlarına
verdikleri cevapların gerçeği yansıttığı varsayılmıştır.
1.6 Sınırlılıklar
1. Araştırmanın çalışma grubu, 2014-2015 eğitim öğretim yılı, Antalya ili
Muratpaşa ilçesi Özel Antalya Doğa Ortaokulu’nda öğrenimlerine devam eden toplam 45 beşinci sınıf öğrencisinden oluşmaktadır. Seçilen iki şubeden biri deney (n=23), diğeri kontrol (n=22) grubu olarak seçkisiz yolla atanmıştır.
2. Araştırma, 5. Sınıf Matematik dersinin 1. Ünitesi (Doğal Sayılar ve Doğal
Sayılarla İşlemler) ile yürütülmüş ve diğer üniteler araştırma kapsamına alınmamıştır.
3. Araştırma, Öğrenme Yöntemlerinden “Gerçekçi Matematik Eğitimi” ile
sınırlıdır. Diğer öğrenme yöntemleri araştırma kapsamına alınmamıştır. Seçilen bağımsız değişkenler; akademik başarı, matematik tutumu ve matematik öz bildirimi ile sınırlıdır.
1.7 Tanımlar
Gerçekçi Matematik Eğitimi (GME): Gerçekçi Matematik Eğitimi (GME), matematik
öğretimi ve öğreniminde ihtiyaç duyulan reformu gerçekleştirmek amacıyla, Hollandalı matematikçi ve eğitimci olan Hans Freudenthal tarafından temeli atılan bir matematik
9
öğretimi yaklaşımı ve alana özel (domain-specific) bir eğitim teorisidir (Freudenthal, 1973).
Matematik Öz-Bildirim Envanteri (MÖBE): Ortaokulda öğrenim gören öğrenciler için
başarı güdüsüne dayalı beklenti değer kuramı temel alınarak hazırlanan, matematik okur-yazarlığı ile ilgili algılanan görev değeri ve beklenti inançlarını ölçen ve ilgi değeri, kullanışlık değeri, başarı değeri, kişisel değer ve başarı değeri faktörlerini içeren ölçme aracıdır (Akın, 2011).
Matematik Tutum Ölçeği (MTÖ): Öğrencilerin matematik dersine ilişkin tutum
düzeylerini belirlemek için kullanılan likert tipi ölçektir. Baykul (1990) tarafından geliştirilen “Matematik Dersine Yönelik Tutum Ölçeği (MTÖ)” bu araştırmada kullanılmak üzere seçilmiştir. Ölçek 30 maddeden oluşmaktadır. Araçta yanıtlayıcılar için beşli derecelendirme ölçeği kullanılmıştır. Tek faktörle açıklanabilen ölçek 15 olumlu (1, 2, 5, 6, 10, 11, 12, 16, 17, 18, 23, 25, 26, 27) ve 15 olumsuz (3, 4, 7, 8, 9, 13, 14, 15, 19, 20, 21, 22, 24, 28, 29, 30) maddeden oluşmaktadır. Ölçekten alınabilecek en yüksek puan 150 iken en düşük puan 50’dir. Ölçekten alınacak yüksek puan öğrencilerin matematik dersine ilişkin olarak olumlu bir tutum içinde olduğunu gösterir.
10
BÖLÜM 2
KAVRAMSAL ÇERÇEVE
2.1 Matematik ve Matematik Eğitimi
Matematik günlük hayatımızın bir parçası olmasına rağmen, matematik sözcüğünün kesin bir tanımı bulunmamaktadır (Ersoy, 2013). Matematiğin aritmetik, cebir, geometri gibi sayı ve ölçüleri temel alan niceliklerin özelliklerini inceleyen bilimlerin genel adı olmasının yanında; sayı ve ölçüyü temel almayan matematiğin de varlığı unutulmamalıdır. Ayrıca matematik yalnızca niceliklerin özelliklerini değil sistemlerin de özelliklerini inceler. Bu durum matematiğin bir tanım cümlesi içine sığdırmanın zor olduğunu göstermektedir (Alkan ve Altun, 1998).
Milli Eğitim Bakanlığı Öğretim Programı’na göre matematik, örüntülerin ve düzenlerin bilimidir. Başka bir deyişle matematik; sayı, şekil, büyüklük, uzay ve bunlar arasındaki ilişkilerin bilimidir. Aynı zamanda matematik, sembol ve şekiller üzerine kurulmuş evrensel bir dildir. Matematik; bilgiyi işlemeyi (düzenleme, analiz etme, yorumlama ve paylaşma) üretmeyi, tahminlerde bulunmayı ve bu dili kullanarak problem çözmeyi içerir. Kavramlar arasında anlamlı ilişkiler bulunan, kendine özgü sembolleri ve terminolojisi olan evrensel bir dildir (MEB, 2009).
Matematik, soyut olması, diğer bilimlerden farklı bir bilim oluşu, sayı bilimi diye de ifade edilebilmesi ve hayatın her alanını kuşatması dolayısı ile herkesin her zaman karşılaşmak zorunda kaldığı ve uygun yöntemler ile herkesin severek çalışabileceği düşünülen çok geniş bir sistemdir (Ersoy, 2013).
Peki, insanoğlu niçin matematik öğrenmek zorundadır? Çünkü insanoğlunun karakteristik vasfı, düşünen ve akıl yürüten bir varlık olmasıdır. İnsanoğlunun yaşam süreci, sadece canlılığını devam ettirme çabasından daha ileri bir şeydir ve merak, araştırma, düşünme, akıl yürütme ve öğrenme üzerine kuruludur (Arseven, 2010). Buna bağlı olarak ülkeler de okulda verilen matematik ile öğrenciye istenilen matematik kültürü verilerek ve matematiksel düşünme yeteneğini geliştirerek, toplumun ihtiyaç duyduğu teknisyen,
11
mühendis ve bilim adamlarını yetiştirmesini bekler. Kısaca, toplumun okullarda verilen eğitimden beklediği: “Bütün öğrenciler matematikte belli seviyede yetişme fırsatı bulmalı, hayatımızın bir parçası olan teknolojiyi anlayabilecek şekilde bilgilendirilmelidir.” Bu amaç, okul matematiğine her ülkede büyük sorumluluklar yüklemiştir (Baki, 2014).
Matematik öğretiminin, eğitimin her basamağında en iyi şekilde gerçekleştirilebilmesi için, matematik öğretiminin amaçlarının en iyi şekilde belirlenmiş olması ve matematik öğrenmenin gereğinin açıklanması gerekmektedir (Ünal, 2008). Ülkemizde, T. C. Mili Eğitim Bakanlığı Talim Terbiye Kurulu (2013) tarafından yenilenen Ortaokul Matematik Dersi Öğretim Programı’nda “Matematiği öğrenmek; temel kavram ve becerilerin kazanılmasının yanı sıra matematikle ilgili düşünmeyi, genel problem çözme stratejilerini kavramayı ve matematiğin gerçek yasamda önemli bir araç olduğunu takdir etmeyi de içermektedir. Yenilenen matematik dersi programı ile hayatında matematiği kullanabilen, problem çözebilen, çözümlerini ve düşüncelerini paylaşabilen, ekip çalışması yapabilen ve matematiğe yönelik olumlu tutum geliştiren bireylerin yetiştirilmesi amaçlanmıştır.” ifadesi yer almaktadır. Verilen ifadeye göre İlköğretim Matematik eğitiminin genel amaçlarına bakıldığında öğrenci;
1. Matematiksel kavramları anlayabilecek, bunlar arasında ilişkiler kurabilecek, bu
kavram ve ilişkileri günlük hayatta ve diğer disiplinlerde kullanabilecektir.
2. Matematikle ilgili alanlarda ileri bir eğitim alabilmek için gerekli matematiksel
bilgi ve becerileri kazanabilecektir.
3. Problem çözme sürecinde kendi düşünce ve akıl yürütmelerini ifade
edebilecektir.
4. Matematiksel düşüncelerini mantıklı bir şekilde açıklamak ve paylaşmak için
matematiksel terminoloji ve dili doğru kullanabilecektir.
5. Tahmin etme ve zihinden işlem yapma becerilerini etkin kullanabilecektir. 6. Problem çözme stratejileri geliştirebilecek ve bunları günlük hayattaki
problemlerin çözümünde kullanabilecektir.
7. Kavramları farklı temsil biçimleri ile ifade edebilecektir.
8. Matematiğe yönelik olumlu tutum geliştirebilecek, özgüven duyabilecektir. 9. Sistemli, dikkatli, sabırlı ve sorumlu olma özelliklerini geliştirebilecektir. 10. Araştırma yapma, bilgi üretme ve kullanma becerilerini geliştirebilecektir
12
Ortaokul matematik öğretim programında matematiksel kavramların kazandırılmasının yanı sıra, matematiği etkili öğrenmeye ve kullanmaya yönelik bazı temel becerilerin geliştirilmesi de hedeflenmektedir (MEB, 2013). Bu beceriler şöyle sıralanmaktadır:
1. Problem çözme
2. Matematiksel süreç becerileri: - İletişim - Akıl yürütme - İlişkilendirme 3. Duyuşsal beceriler
4. Psikomotor beceriler
5. Bilgi ve iletişim teknolojileri (BİT)
Ortaokul matematik dersi öğretim programında “Sayılar ve İşlemler”, “Cebir”, “Geometri ve Ölçme”, “Veri İşleme” ve “Olasılık” olmak üzere 5 öğrenme alanı bulunmaktadır. Bazı sınıf seviyelerinde bu öğrenme alanlarından tümü yer alırken, bazılarında hepsine yer verilmemiştir. Olasılık öğrenme alanı sadece 8. sınıfta yer alırken, cebir öğrenme alanı 5. sınıf hariç tüm sınıflarda yer almaktadır. Sayılar ve İşlemler, Geometri ve Ölçme ve Veri İşleme öğrenme alanları tüm sınıf düzeylerinde mevcuttur (MEB, 2013).
İlköğretim matematik öğretim programının içeriğinin yapılandırılmasında “Sayılar ve İşlemler” öğrenme alanı, en büyük oranda yer almaktadır. Sayılarla ilgili kavram ve işlem bilgileri, ayrıca geliştirilecek çok sayıda beceriler vardır. Her öğrencinin Türkçe okuryazar olması kadar sayıları kavramaları ve günlük yaşamlarında problem çözmede kullanmaları, kısaca varlıkları ve nesneleri nicel özellikleriyle betimlemeleri, sayı bilgisi okuryazarı olmaları beklenmektedir. Sayılarla ilgili tüm bilgi ve beceriler, ön şartlık ilkesi gözetilerek konu ve kazanımlar bakımından bir takım başlıklar altında yeniden öbekleştirilerek programın içeriği sarmal bir yapı içerisinde ele alınarak, yalnızca sayılarla ilgili bilgiler ve beceriler değil, örneğin problem çözme becerileri ve iletişim becerileri de geliştirilebilir (Ersoy, 2006).
Sayılar ve İşlemler öğrenme alanı, tüm sınıf seviyelerinde yer almaktadır. 5. Sınıfta öğrencilerden doğal sayıları okuyup yazmaları ve doğal sayılarda dört işlem yapmaları beklenmektedir. Bu sınıf seviyesinde öğrencilerin tam sayılı ve bileşik kesirleri anlamlandırmaları, dönüşüm yapmaları, paydaları eşit veya birbirinin katı olan kesirleri sıralamaları, bu kesirlerde toplama-çıkarma işlemlerini yapmaları ve bu işlemleri anlamlandırmaları beklenmektedir. Ondalık gösterimlere de yer verilerek, öğrencilerin ondalık gösterimleri verilen sayıları sıralamaları, sayı doğrusunda göstermeleri ve bu sayılarda toplama-çıkarma işlemlerini yapmaları amaçlanmaktadır. Sayılar ve İşlemler
13
öğrenme alanında yüzde kavramına da yer verilerek, yüzde kavramının kesir ve ondalık gösterimlerle ilişkilendirilmesi beklenmektedir (MEB, 2013).
2.2 Matematik Öğretiminde Karşılaşılan Sorunlar
Genel olarak, ülkemizde problem çözme başarılarının düşük, mekanik işlemlerdeki başarının akıl yürütmeyi gerektiren davranışlara oranla daha yüksek olduğu gözlenmektedir. Bunun sebebi, matematik eğitiminde, matematiğin yapısına uygun öğretim stratejilerinin kullanılmamasıdır. Ezberci öğretimden uzaklaşılması gerekmektedir (Baykul, 2003). Matematik öğretiminde uygulanan yöntemlerin soyutluğu, tekdüzeliği ve ezberi gerektiren bir yapıda oluşu, matematiğin yasamdaki gerçek yerinin, mantıksal yapısının sezilmesini zorlaştırmaktadır. Öte yandan, çeşitli sınavlara yönelik düşünmeden çözüme götüren pratik yolların öğretilmesi, öğrencilerin düşünme becerileri kullanmalarını ve matematiğin mantıksal yapısını kavramalarını engellemektedir (Abdik, 2002).
Matematiğin, günlük yaşamda önemli bir yeri olmasına rağmen dünyanın her yerinde öğretilmesinin güçlüğü yanında, öğrenilmesi de “zor” olarak kabul edilmektedir. Aslında matematiğin zorluğu yapısından olduğu kadar ona karşı geliştirilen önyargıdan, korkudan ve kaygıdan da kaynaklanmaktadır (Şahin, 2004).
Matematiğin zor olarak düşünülmesi ve matematikten korkulmasının sebeplerinden biri, matematikle ilgili kavramların doğası gereği soyut nitelikte olmasıdır. 7-12 yaş somut işlemler döneminde bulunan derslerdeki soyut kavramların, somut materyallerle desteklenerek işlenmesi özellikle bu öğretim düzeyinde büyük önem taşımaktadır (Erden ve Akman, 2002). Bir diğeri ise; öğrencilerin matematik dersinde öğrendikleriyle gerçek hayat arasında bağ kuramamasıdır. Matematik konularının gerçek hayatla arasında bağ kurularak öğrencilere verilmesi matematiğin daha anlamlı olarak algılanmasını sağlayacaktır. Matematik gibi soyut bir dersin ilköğretim basamağındaki çocuklara öğretiminde istenen hedeflere ulaşabilmek için, konuyu çeşitli araç ve gereçlerle somutlaştırarak ve gerçek hayatla bağlantı kurarak işlemek gerekmektedir (Bıldırcın, 2012).
Matematiğe karşı oluşturulan olumsuz tutumlar nedeniyle matematiğin tüm gerçeklerini yaşamda görebilmek olanaksızdır. Bireylerin zihinlerinde oluşturdukları dünyalarında, kendi yaklaşımları ile matematik bilgisine ulaşmaları beklenmektedir (Yeşildere ve Türnüklü, 2004). Bu bağlamda Yapılandırmacılık (constructivism) matematik öğretiminde
14
önemli bir yer sahibi olmuş, bununla beraber Gerçekçi Matematik Eğitimi (GME) gibi yeni yaklaşımlar ortaya konmuştur (Ünal, 2008).
2.3 Matematik Öğretiminde Yapılandırmacılık
Teorik temelleri J. Piaget, T. Khun ve L.S. Vygotsky tarafından ortaya atılan, kökleri felsefe ve psikolojiye dayanan Yapılandırmacılık (Constructivism) bir öğrenme kuramıdır. Özü, öğrencilerin aktif bir şekilde deneyimlerinden yararlanarak bilgi ve anlamalarını inşa etmeleridir (Baker ve Piburn, 1997; Doolittle, 1999). Başlangıçta öğrencilerin bilgiyi nasıl öğrendiklerine ilişkin bir kuram olarak gelişmişse de zaman içinde bilgiyi nasıl yapılandırdıklarına yönelik bir yaklaşım haline dönüşmüştür (Demirel, 2005).
Yapılandırmacı yaklaşımda öğrenen birey, öğrenme-öğretme sürecinde aktif bir role sahiptir. Bu sebeple yapılandırmacı sınıf ortamı, sadece bilgilerin aktarıldığı yer değil; öğrencinin etkin katılımının sağlandığı, problemlerin çözüldüğü, sorgulama ve araştırmaların yapıldığı bir ortamdır. Sınıf içi etkinlikler, öğrencilere zengin öğrenme yaşantıları geçirmelerini sağlayacak şekilde düzenlenmelidir. Yapılandırmacı yaklaşımı temel alan eğitim uygulamalarında süreç ağırlıklı değerlendirme söz konusudur. Dolayısıyla ürüne değil, süreç değerlendirmelerine ağırlık verilmelidir (Arseven, 2010). Yapılandırmacı eğitim uygulamalarında dikkate alınması gereken temel ilkeler Lebow (1993) tarafından geliştirilmiş olmakla birlikte, yapılandırmacı öğrenme kuramcıları tarafından yeniden yorumlanmış ve genişletilip derinleştirilmiştir (Yurdakul, 2004).
Yapılandırmacılığın öğrenme-öğretme sürecindeki temel ilkeleri şunlardır:
1. Tüm öğrenme etkinlikleri geniş bir görev ya da probleme bağlıdır.
2. Öğrenenlerin özgün bilgi yapılarını kendilerinin oluşturacakları yaşantılar
düzenlenmeli ve bu yaşantılarla öğrenme sorumluluğu öğrencilere bırakılmalıdır.
3. Yeni öğrenmeleri oluşturmada önbilgiler dikkate alınmalıdır. 4. Öğrenme sürecinde sosyal etkileşim sağlanmalıdır.
5. Anlamlı öğrenmeyi gerçekleştirmek üzere özgün öğrenme görevleri
tasarlanmalı ve gerçek yaşamın karmaşıklığını yansıtacak öğrenme ortamı oluşturulmalıdır.
6. Çoklu gerçeklikler açığa çıkarılarak bilişsel çelişkiler yaratılmalı ve bireysel
15
7. Bilgiyi yapılandırma sürecinin farkına varılmasını desteklemek üzere nasıl
öğrenildiğinin yansıtılmasını sağlayacak yaşantılar düzenlenmelidir.
8. Öğrenme için tehlikesiz ve güvenli bir ortam yaratılmalıdır.
9. Öğrenenin düşüncelerinin desteklendiği bir öğrenme ortamı yaratılmalıdır.
Yapılandırmacı öğrenme planları incelendiğinde ise; genellikle şu aşamaları izlediği görülmektedir: Dersin başında öğrencilerin dikkati çekilmekte, problem durumu sunulmakta ve öğrenenlerin önbilgileri açığa çıkarılmaktadır. Daha sonra işbirliği içinde problemleri incelemekte olan öğrenciler, bilgi kaynaklarına ulaşmak için hipotezler üretmekte, problemlere çözüm önerileri geliştirmekte, görülerini arkadaşlarıyla paylaşmakta, diğer görüşleri eleştirmekte ve kendi fikirlerini gözden geçirmektedir. Son aşamada ise, öğrenciler kendi bilgi yapılarını değerlendirmekte ve geliştirmek için neler yapması gerektiğine karar vermektedir. Bu süreçte öğretmenin rolü öğrenciye rehberlik etmek, yönlendirmek ve düşünmelerine yardımcı olmaktır (Çelik, 2006).
Yapılandırmacılığın matematik eğitiminde kullanılan 3 türü vardır:
1. Bilişsel Yapılandırmacılık 2. Sosyal Yapılandırmacılık 3. Radikal Yapılandırmacılık
2.3.1 Bilişsel Yapılandırmacılık - Jean Piaget
Piaget, bilginin doğasıyla ilgili üç terim kullanmaktadır. Bunlar şema, kavram ve yapıdır. Şema hem fiziksel, hem de zihinsel olabilmekte ve bir öğrenci tarafından amaca ulaşmak ya da bir problemi çözmek için tekrar kullanılan süreçleri veya hareketleri ifade etmektedir. Gelişimde şemaların rolünü çalışmanın yanında, zaman, uzay, sayı, korunum ve sınıflar gibi değişik kavramlara da odaklanan Piaget, kavramların olabildiğince anlamayı sağladığını ve bu yönüyle şemalardan ayrıldığını ifade etmektedir. Piaget, kavramların ortaya çıkışının zamanla olacağını ve yavaş yavaş gelişeceğini savunmaktadır. Piaget’in şema ve kavramın yanında bilgiyi tanımlamak için kullandığı üçüncü terimi yapı ise; bilginin şekli ve fikirlerin organize edilmesini sağlamaktadır (Marlowe ve Page, 1998; Byrnes, 2001).
Bilişsel Yapılandırmacılık, yapısalcı bütünün bir sonunu ya da sınırını temsil eder ve özgün olarak bilgi işlemeyle ve bilişin tamamlayıcı işlemleri üzerine bağlantılıdır. Öyle ki bilgi edinme uyarlanmış bir süreçtir ve öğrenen tarafından aktif bilme ile sonuçlanır (Doolittle, 1999).
16
Bununla birlikte Bilişsel Yapılandırmacılık ve onun bilgi süreciyle olan tarihsel işbirliği; çoklu kuram, öğrenme ve hafızanın hesaplama modelleri ve beyin fonksiyonlarının sinirsel modellerine örnek teşkil eder. Ayrıca bu teorik gelişmelerin her biri; kavram haritaları, okuma stratejilerinin ve problem çözme stratejilerinin kullanımı; başarılı öğretim uygulamalarına birer örnektir (Doolittle, 1999).
Bilişsel Yapılandırmacılığın eğitsel çıkarımları ise aşağıdaki gibi özetlenebilir (Byrnes, 2001; Sternberg ve Williams, 2002).
1. Zihinsel yapıların yaratılması için öğrencilerin öncelikle tekrar yapması ve
şemalarını içselleştirmeleri gereklidir. Öğrencilerin hedeflere ulaşmalarına yardımcı olan eylemlerini defalarca uygulamalarını sağlayan olanaklar yaratılmalıdır.
2. Öğrencilerin bilişsel gelişim düzeyleri dikkate alınmalı, öğrencilerden
gelişimsel olarak yapamayacağı beklentiler oluşturulmamalıdır.
3. Öğrencilere sonraki fikirlerinin öncüsü olarak hizmet edebilecek yardımcı
fikirler, mevcut yanlış anlamalarıyla çatışan deneyimler ve öğrencilerin kavrayıp uygulayabilecekleri alternatifler sunularak düşüncelerinde gelişim sağlanmalıdır.
4. Öğrencilerin doğuştan getirdiği bilimsel özelliği yansıtmalarına yardımcı
olunmalı, bu bağlamda doğal merakın açığa çıkışı teşvik edilmelidir.
5. Yanlışlara ve nedenlerine karşı duyarlı olunmalı ve yanlışı vurgulamak yerine
yanlışın altında yatan nedenler araştırılmalıdır.
6. Yeni bilişsel yapıların eskilerinin üzerine yapılandırıldığı unutulmayarak
öğrenme sürecinde öğrenenlerin önbilgileri dikkate alınmalıdır.
2.3.2 Sosyal Yapılandırmacılık - L. S. Vygotsky
Bilişsel Yapılandırmacılık yaklaşımından farklı olarak bilginin elde edilmesi sürecinde sosyal etkileşimin, dilin ve kültürün önemini vurgulayan bir yaklaşımdır. Sosyal Yapılandırmacı yaklaşıma göre bilgi insan ürünüdür ve birikim sonucu sosyal ve kültürel olarak oluşur (Altun, 2006). Bununla beraber Sosyal Yapılandırmacılık, Bilişsel ve Radikal Yapılandırmacılık arasında yer alır. Sosyal Yapısalcılar genellikle bilginin zihinsel yapılanmasını önemsemez ve anlamanın sosyal etkinlik içerisinde yapılanmasını vurgular (Doolittle, 1999).
17
Sosyal Yapılandırmacılar öğrenmeyi açıklamada, Vygotsky’ in görüşlerini kullanır. Vygotsky öğrenmenin Piaget’ in öne sürdüğü gibi kişinin sadece kendi başına gerçekleştirdiği bir süreç olmadığını, öğrenmede sosyal etkileşimin ve dilin de önemli yeri bulunduğunu öne sürmüştür Vygotsky’e göre, sosyal yaşantılar düşünme ve dünyayı yorumlama yollarını şekillendirmektedir. Ona göre çocuklar problemlerini kendi bilişsel gelişim seviyelerinden ziyade, yetişkinlerin veya akran gruplarının yardımını alarak çözmektedir ve bundan dolayı sosyal etkileşim bilişin gelişmesinde temel bir rol oynar (Özden, 2003). Yetişkin, bilgisi ve rehberliği sayesinde öğrencinin potansiyelini artırmasını sağlar. Akran ise; işbirlikli çalışmalarda problem çözerken arkadaşına yardımcı olabilir, model olabilir, cesaretlendirebilir veya gerekli bazı açıklamalarla rehberlik edebilir (Henson, 2003). Öğrenme için çevreye gereksinim vardır. Bu bakımdan öğrenme ortamının ve o ortamdaki bireylerle iletişim kurmanın bilgi edinmede büyük bir payı vardır (Özden, 2003).
Sosyal Yapılandırmacılığın eğitsel çıkarımları ise aşağıda verildiği gibi özetlenebilir (Jaramillo, 1996; Byrnes, 2001; Sternberg ve Williams, 2002):
1. Öğrenenlerin dışsal diyalogları içselleştirerek öğrendikleri dikkate alınmalıdır.
Öğrenenler çevrelerini gözleyerek daha iyi öğrenirler ve eleştirel düşünebilirler. Bu süreçte öğretmen ve diğer öğrenenler model olmalıdır.
2. Öğretmenler, öğrenenlerin kendi başlarına ilerlemelerine yardım etmek için
yeterince rehberlik sağlayan bir destekleyici olarak davranmalıdır.
3. Öğretim, öğrenenin o anki bilgi seviyesinden her zaman ileri düzeyde olmalıdır. 4. Öğrenenlerin bir beceriyi içselleştirebilmeleri için, öğretim dört aşamada
gerçekleşmelidir. İlk aşamada öğretmenler, beceriye dair örnekler vermeli, ne yaptıklarına ve niçin yaptıklarına ilişkin sözel açıklamalar getirmelidirler. İkinci aşamada öğrenenler, öğretmen ne yaptıysa onu taklit etmeye çalışmalıdırlar. Üçüncü aşamada öğrenenler, beceriler üzerinde daha fazla hâkimiyet sağladıkça, öğretmenler yavaş yavaş geriye çekilmelidirler. Son olarak öğrenenler, beceriyi içselleştirmek için yeterince uygulama yapmalıdırlar.
5. Öğrenenler içsel kavramların daha doğru ve genel olması için bilimsel
18
2.3.3 Radikal Yapılandırmacılık - E. Von Glasersfeld
Radikal Yapılandırmacılık her bireyin deneyim ve çevresi farklı olacağından bilgisinin de farklı olacağını savunur. Yani, bilgi bireysel olarak yapılandırılır. Birey için anlam ifade etmeyen, algılanamayan gerçeklikler o birey için bilgi değildir (Altun, 2006).
Von Glasersfeld (1995)’e göre, kavramlar basit bir şekilde öğretmenlerden öğrenenlere aktarılamamaktadır. Bir şeyi bilme yolu yoktur. Var olmanın anlamı sadece tecrübeler dünyasının içerisinde tanımlanabilir. Bu nedenle, bu kurama göre matematik öğrenme ve öğretiminin etkililiğini değerlendirmek için betimleyici durum çalışmaları, deneysel ve kontrol edilen şartları içeren çalışmalardan daha önemlidir (Skemp, 1987).
Yapısalcılıkta “gerçeklik” sözcüğünün kullanılabileceğini açıklayan Von Glasersfeld; gerçekliği, bireyin yaşantılarında güvendiği şeyler ve ilişkiler ağından meydana gelen bir olgu olarak görmektedir. Piaget’in “Bilgi uyarlanabilir bir etkinliktir.” görüşüne katılan Von Glasersfeld, bu bağlamda, dış dünyanın gerçeklik kavramının, artık yaşanabilirlik fikri ile değiştiğini ileri sürmektedir (Von Glasersfeld, 1995).
Radikal Yapılandırmacılığa göre hiçbir bilgi eşsiz, değişmez ve tek yol değildir. Bir problemin çözümü çok başarılı ve kullanışlı gözükebilir ancak bu çözümün tek olası çözüm olarak ilan edilmesi doğru değildir. Öğrenciler, yaratıcı ve eleştirel düşünmelerinde ilerleme sağlayabilmeleri için birden fazla çözüm yolunun bulunduğu problemler ile karşı karşıya bırakılmalı, hatta öğrencilere birden fazla doğru cevabın olabildiği problemlerin de olabileceği gösterilmelidir (Yeşildere ve Türnüklü, 2004).
Yukarıda özetlenen yapılandırmacı kuramlarının üçü de nesnel gerçekliği reddetmektedir. Bilişsel Yapılandırmacılığa göre nesnel gerçeklik bilişsel yapılarla şekillendirilirken, Sosyal Yapılandırmacılıkta nesnel gerçekliğin, dile ve kültüre bağımlı olduğu vurgulanmaktadır. Radikal Yapılandırmacılık ise; nesnel gerçekliğin bilinemeyeceği çünkü gerçekliğin kişiyi öznelleştirdiği belirtmektedir (Akkaya, 2010).
2.4 Gerçekçi Matematik Eğitimi (GME)
Geçmişte mutlak bir bilim olarak ele alınan matematiğin tartışılamaz, sabit kural ve bilgiler bütünü olduğu; bunların da ezberlenerek öğrenilebileceği fikri benimsenmekteydi. Matematiksel bilginin bir kez edinildiğinde, sonsuza kadar devam ettiği; her noktada birbirleriyle anlaşan bilginler tarafından keşfedildiği ve mevcut bilgiye eklendiği fikri hâkimdi. Bu düşüncelerin yanı sıra, “Matematik en iyi şekilde nasıl öğretilebilir? Öğrencilerin matematiğe olan ilgileri nasıl artırabilir? Öğrenciler matematiği gerçekte nasıl
19
öğrenirler? Matematiğin önemi nedir?” gibi sorular neticesinde bilginin pasif bir şekilde alınamayacağı, öğrenenlerin kendi etkinlik ve çabalarının sonucu olduğu anlaşılmaya başlanmıştır. Bu doğrultuda matematik eğitim ve öğretiminde yeni yaklaşımlar ortaya çıkmıştır (Nelissen 1999).
Matematik, genelde soyut ve formal bir okul bilgisi olarak görüldüğünden, soyut matematiği somutlaştırarak öğretme yoluna gidilmiştir. Ancak Freudenthal (1983) bu görüşe karşı çıkararak, matematiğin etrafımızdaki somut olayları gözlemleyerek keşfedilebileceğini belirtmiştir. Bu nedenle öğretimin, öğrencinin aşina olduğu somut olgular (diyagramlar, modeller, sayı doğrusu ve abaküs gibi sınıflandırma teknikleri) üzerine oturtulması gerektiğini savunmuştur. Çocukların cesaretlerini kıracak formal matematiksel formüllerle yüzleştirmekten kaçınılmalı, öğretim, çocukların kendi etraflarından algılayabilecekleri matematiksel açıdan zengin yapılara dayandırılmalıdır. Böylelikle matematik öğrenciler için anlamlı hale gelir ve kendi deneyimlerini yansıtarak öğrenirler. 1970’lerde, bu yeni bakış açısı neticesinde matematik insan etkinliği olarak ele alınmaya başlanmış, bunun sonucunda da “Gerçekçi” olarak adlandırılan yeni bir matematik eğitimi teorisi doğmuştur (Nelissen 1999).
Araştırmacılar, Hollanda’da Freudenthal Enstitüsünde Gerçekçi Matematik Eğitimi (GME) olarak bilinen, eğitim biliminde 30 yıldan fazla süredir bir teori olarak kabul edilen matematik programı geliştirmişlerdir. Bu eğitim programı çocukların matematiksel gelişimlerine yardımcı olacak gerçekçi konular kullanmaktadır ve şu anda birçok okulda da bu programdan yaygın olarak faydalanılmaktadır. Hollanda, bugün dünyada matematik eğitimi alanında en başarılı ülkeler arasında bulunmaktadır (Dickinsonn ve Eade, 2005).
2.4.1 Gerçekçi Matematik Eğitimi (GME) Nedir?
Gerçekçi Matematik Eğitimi - GME (Realistics Mathematics Education-RME) ilk olarak Hollanda’da Utrecht Üniversitesi’ne bağlı Freudental Enstitüsünde araştırma ve geliştirme ekipleri tarafından 1971’li yıllarda matematik öğretim/öğreniminde ihtiyaç duyulan reformu gerçekleştirmek amacıyla, Hollandalı matematikçi ve eğitimci Hans Freudenthal tarafından temeli atılan bir matematik öğretimi yaklaşımı ve alana özel bir eğitim teorisidir (Freduenthal, 1973). Hollanda’da uzun yıllardır başarı ile uygulanmaktadır. Bu teori daha sonraları İngiltere, Danimarka, Almanya, İspanya, ABD ve Japonya gibi dünyanın birçok ülkesinde de kabul görmüştür (De Lange, 1996).
20
Freudenthal matematik öğrenmenin bir anlamlandırma süreci olduğunu ileri sürerek, düşüncesini “çocuk için matematik anlamlandırma ile başlar ve gerçek matematik yapmak için her yeni safhada anlamlandırmanın esas alınması gerekir.” (Nelissen ve Tomic, 1998) şeklinde ifade etmiştir.
Freudenthal’a göre matematik bir insan aktivitesidir, keşfedilmez icat edilir. İnsan çevresindeki olayları kontrol altında tutmak için onları sayar, ölçer, sınıflar ve sıralar. Örneğin boyutları a ve b olan dikdörtgenin alanını A= a.b ile temsil ederiz. Bu bir ölçme eylemidir ve kendi icat ettiğimiz bir şeydir. Geleneksel öğretime bir meydan okuma olarak ortaya çıkmış olan bu yaklaşıma göre, matematik yapma gereksinimi öğretimin ana ilkesi olmalıdır ve matematik öğretimi gerçek hayat problemleri ile başlamalıdır (Gravemeijer, 1994). Bu durumda, matematik eğitiminin gerçekçi durumlara dayandırılması ve öğrenenin gerçek dünyasından yola çıkılması gerektiği belirtilir. GME, zihinde soyut olan şeyleri gerçek yapabilme üzerinde durur. Yani öğrencilerin zihninde gerçek olarak algıladıklarını kasteder. Bunun anlamı, problemin içeriğinde gerçek dünyadan durum ve olayların olabilmesi gibi masalların fantastik dünyası, hatta matematiğin formal dünyasında da öğrencilerin zihninde gerçek olduğu kadarıyla uygun bir problem içeriğinin sunulabilmesidir (Van den Heuvel-Panhuizen, 2000).
GME yaklaşımı, gerçek yaşam problemiyle başlar. Freudenthal, gerçek hayat problemlerinden başlayarak matematiksel kavrama ulaşma şeklinde işleyen bu sürece “matematikleştirme” adını vermiştir. Öğretimde matematikleştirme anahtar süreçtir ve bu durumun iki temel nedeni vardır. Birincisi; matematikleştirme sadece matematikçilerin değil her bireyin işidir. İkincisi ise; yeniden keşfetme ile ilgilidir. Matematikte formal bilgiye ulaşma en son basamak olmalıdır. Öğrencinin çalışabileceği ve denemeler yapabileceği bir ortamın hazırlanması gerekir. Öğrenme şekli sürecin, birey tarafından keşfi şeklinde olmalıdır (Altun, 2006).
GME’nin matematikleştirme için önerdiği üç temel ilke vardır (Gravemeijer, 1994):
1- Yönlendirilmiş Keşfetme: Yönlendirilmiş keşfetme, matematikleştirmeyi geliştirme ile
ilgilidir. Bu ilkeye dayanarak öğrencilere, matematiğin keşfedilmesi ve icat edilmesini sağlayan bir yöntemi ya da çalışmayı denemeleri için fırsat tanınmalıdır. Bunun için esin kaynağı olarak matematik tarihi kullanılabilir. Yönlendirilmiş keşif ilkesi, informal çözümlerden yola çıkılarak uygulanabilir. Öğrencilerin informal stratejilerinin yorumu, formal stratejilere giden bir yol olarak belirlenebilir. İlkenin iyi kullanımı için, gelişmiş matematikleştirmeye ulaşacak şekilde çevresel problemlerin bulunmasına ihtiyaç vardır.
21
2- Çevre problemlerinin uyarıcı olması ve bir kavramın yeniden keşif süreciyle kazanılması (Didaktik fenomoloji): Didaktik fenomonoloji matematik kavramların
analizini yapmak suretiyle onun nasıl oluştuğunu açıklayabilmektedir. Eğer ki biz matematiğin, tarihsel olarak pratik problemlerin çözümlerinden elde edildiğini anlarsak, günümüzdeki uygulamalardan da bu yaklaşım sayesinde matematik üretebileceğimizi umabiliriz. Çevre problemleri uyarıcı olmakta ve kavram, sürecin yeniden keşfi ile kazanılmaktadır. Didaktik fenomonolojiye göre matematik konuların öğrenilmesinde öğretim için tasarlanmış konuların ve uygulamaların matematikleştirmeye uygunluğu önemlidir. Sonra bize düşen iş genelleştirilebilecek durumlar için yatay matematikleştirmeye uygun problem durumları bulmak, sonra da dikey matematikleştirmeyi sağlayacak öğrenme ortamları yaratmaktır. Toplama öğretimi üzerinde bu durumu örnekleyecek olursak, 5+3 için 5 elma ve 3 elma daha kaç elma eder? Sorusu açıkça toplama yapılması gerektiğini bildirmektedir. Bunun yerine, toplama yapılmasının gerektiğinin açıkça belli olmadığı bir durumdan yararlanmak gerekir. Örneğin, benim 5 elmam var, Efe’nin benden 3 daha fazla, Efe’nin elmaları kaç tanedir? gibi. Bu ikinci durumda matematiksel uyarım daha yüksektir ve bu durumda toplama bir ihtiyaç olarak hissedilmektedir (Üzel, 2007).
3- İnformal bilgi ile formal bilgi arasında köprü görevi görecek modellere yer verilmesi: Burada sözü edilen modeller hazır materyallerden ziyade çocuğun kendi
informal aktivitelerinden geliştirilebilecek matematiksel modellerdir. Öğrencinin informal aktiviteleri adım adım geliştirilerek formal matematiksel muhakemeye ulaşılır. Burada birçok aşama sırayla yaşanır ve bu durum bir anlamlandırma zinciri olarak görülebilir. Anlamlandırmanın en temel iki safhası sırayla hedef kavram için informal bilginin matematikleştirilmesine uygun modelin seçimi, ikincisi bu başlangıçtan formal bilgi için uygun bir modele varmadır. Yani önce öğrencinin kendi hayatından onun anlamlandırabileceği, informal bilgisinin iyi değerlendirilebileceği bir model seçilir sonra bu model dayandığı spesifik durumlardan kopar ve (matematiksel gerçekleri içerecek şekilde) geliştirilerek formal matematik için bir model haline gelir. Modeller öğrencinin kendi hayatından seçildiği ve öğrenci tarafından anlamlandırıldığı için öğrenci tarafından kolay kavranır. Örneğin; ilköğretim matematik ders kitaplarında sayı doğrusunun öğretimi doğruda şekli çizilerek tanıtılmakta, bazen günlük hayatta kullanılan basit nesneler vb. modeller referans alınmaktadır. Freudenthal’a göre, tüm bu matematiksel kavramlar, insanın gerçek hayatı matematikleştirmesi suretiyle ortaya çıkmıştır (Gravemeijer, 1999).