Düzgün Da ılım Fonksiyonlarına Sahip Da ılımlar Ailesi çin Majorant Vektörler Kullanılarak En Dar nvaryant Güven Aralı ının Elde Edilmesi

Düzgün Da ılım Fonksiyonlarına Sahip Da ılımlar Ailesi çin Majorant

Vektörler Kullanılarak En Dar nvaryant Güven Aralı ının Elde Edilmesi

1

Bu ra SARAÇO LU2_{, Mehmet Fedai KAYA}2

Özet: Kaya ve ark. tarafından yapılan çalı mada düzgün da ılım fonksiyonları ailesi için sıra istatistikleri ve majorant vektörler yardımıyla olu turulan _{[ ] [ ]}

= = n i i i n i i iX b X a 1 1 , rasgele aralı ının = − + − + = n i i i a b i n n 1 ₁( 1)( ) 1

α

seviyeli ana kitleyi kapsayan invaryant güven aralı ı oldu u gösterilmi ti [1]. Bu çalı mada, invaryant güven aralı ının seviyesi

α

=

0

.

90

olacak biçimde _{[ ] [ ]}

= = − n i i i n i i iX a X b 1 1 de erini en küçük yapan b

a ve majorant vektörler arasındaki ili kinin elde edilebilmesi için bir optimizasyon modeli kurulmu ve bu modelin çözümü bilgisayar programı yardımıyla bulunmu tur. Anahtar Sözcükler: Sıra istatistikleri, nvaryant güven aralıkları, Majorant vektörler

Obtaining The Narrowest Invariant Confidence Interval For The Family Of

Uniform Distribution Functions Using By Majorant Vectors

Abstract: A random interval _{[ ] [ ]}

= = n i i i n i i iX b X a 1 1

, that is constructed by order statistics and majorant vectors, was shown as invariant confidence intervals containing main mass for the family of uniform distribution with level

= − + − + = n i i i a b i n n 1 ₁( 1)( ) 1

α

given in the study by [1]. In this study, an optimization model is consructed for the relationship between a andb majorant vectors which

minimizes _{[ ] [ ]} = = − n i i i n i i iX a X b 1 1

such that

α

=

0

.

90

and this model is solved via computer programme.

Key words: Order Statistics, Invariant Confidence Intervals, Majorant Vectors

1

Bu makale Yüksek Lisans tezinin bir parçasıdır.

2

1. Giri .

{

∈Θ

}

= _θ,

θ

P P parametrik da ılım fonksiyonlarının bir ailesi, X1,X2,...,Xn , Pθ ∈P da ılımına sahip bir örneklem, f₁ ve f₂ ;

) ,..., , ( ) ,..., , ( için ) ,..., , (x₁ x₂ x_n ∈Rn f₁ x₁ x₂ x_n ≤ f₂ x₁ x₂ x_n ∀ (1.1)

ko uluna sahip iki borel ölçülebilir fonksiyon, Xn+1, X1,X2,...,Xn örnekleminden ba ımsız ve aynı P

∈

θ

P da ılımına sahip yeni bir rasgele de i ken olmak üzere; ∀

θ

∈Θ için,

(

)

(

)

(

)

{

X f X X X f X X X

}

R

Pθ n+1∈ 1 1, 2,..., n , 2 1, 2,..., n =

α

,

α

∈ (1.2)

oluyorsa

(

f1

(

X1,X2,...,X_n

)

,f2

(

X1,X2,...,X_n

)

)

rasgele aralı ına P sınıfı için

α

güven seviyesine

sahip ana kitleyi kapsayan invaryant güven aralı ı denir.

(

a₁,a₂,...,a_n

)

Rn, b

(

b₁,b₂,...,b_n

)

Rn

a= ∈ ∀ = ∈

∀ için D+ =

{

(

u₁,u₂,...,u_n

)

:u₁≥u₂ ≥...≥u_n

}

biçiminde tanımlanan bir küme olsun. a_{[ ]1} ≥a_{[ ]2} ≥...≥a_{[ ]n} veb_{[ ]1} ≥b_{[ ]2} ≥...≥b_{[ ]n} ; n n R b R

a∈ ve ∈

vektörlerinin elemanlarının büyüklük sırasına göre dizilmi hallerini göstermek üzere;

[ ] [ ] [ ] [ ] 1,2, ,n 1 . 2 . 1 1 1 1 1 − = ≤ = = = = = Κ k b a b a k i i k i i n i i n i i (1.3)

ko ulları sa lanıyorsa a ve b vektörlerine majorant vektörlerdir denir ve a πb biçiminde gösterilir [2].

b

a ve vektörlerinin birbirleriyle majorant olmaları için gerek ve yeter ko ul;

(

₁,...,

)

∈ +için = ∀u u un D ; = = ≤ n i i i n i i iu bu a 1 1 olmasıdır [2].

2. Düzgün Da ılım Fonksiyonlarına Sahip Da ılımlar Ailesi için nvaryant Güven Aralıkları Teorem 2.1. X1,X2,...,Xn;F(x)∈ < < = − − = = c x d F x x c d c x x F x F( ): ( ) , , ( ) P

da ılımına sahip bir örneklem, Xn+₁, bu örneklemden ba ımsız ve aynı F(x) da ılımına sahip

yeni bir rasgele de i ken ve a πb olmak üzere;

(

)

(

)

(

)

= _{[ ] [ ]} = = n i i i n i i i n n f X X X a X b X X X X f 1 1 2 1 2 2 1 1 , ,.., , , ,.., ,

rasgele aralı ını göz önüne alalım.

(

)

(

)

(

)

{

}

_{[ ] [ ]}

α

≡ = − + − + = ∈ = ∈ = = = + + ) ,..., ; ,..., ) 1 . 2 ( ) )( 1 ( 1 1 , ,.., , , ,.., , 1 1 1 1 1 1 2 1 2 2 1 1 1 n n n i i i n i i i n i i i n n n n b b a a a b i n n X b X a X P X X X f X X X f X P dır. Yani, [ ] [ ] = = n i i i n i i iX b X a 1 1

spat.

(

)

{

x₁,x₂...,x ,x ₁ :x ₁

(

f₁

(

x₁,x₂...,x

) (

,f₂ x₁,x₂...,x

)

)

, c x x ₁ ... x₁ d} G= _{n n+ n+} ∈ _{n n} < _n < _n− < < < olmak üzere;

(

)

(

)

(

)

{

X 1 f1 X1,X2,..,X ,f2 X1,X2,..,X

}

P

{

X1,X2,..,X ,X 1 G} P n+ ∈ n n = n n+ ∈

(

)

( )

( ) ( )

( )

(

)

(

)

(

(

)

)

[

] ( )

( )

[ ] [ ]

( )

( )

= = = = = + − + − + = − − − − − − = − = − = = − − − − n i i i n n d c x c x c n i i i n i i i d c x c x c n n i i i n i i i d c x c x c n n n d c x c x c n x x f x x f n a b i n n dx dx dx c d c d c x a c d c x b n x dF x dF X a F X b F n x dF x dF x x x f F x x x f F n x dF x dF x dF n n n n n n n 1 1 2 1 1 1 1 1 1 2 1 1 2 1 2 ,... ,... 1 1 ) )( 1 ( 1 1 ... ) 1 ( ) ( ) ( ... ! ... ... ! ... ,..., , ,..., , ... ! ... ! ... 1 1 1 1 1 1 1 1 2 1 1 1 dır.

2.1. Düzgün Da ılım Fonksiyonlarına Sahip Da ılımlar Ailesi çin ααα=0.90 Seviyesinde α En Dar nvaryant Güven Aralı ının Elde Edilmesi

Bilindi i gibi büyük bir güven katsayısında güven aralı ı ne kadar dar olursa tahmin o ölçüde güvenilir olur. Dolayısıyla

α

güven katsayısının 1 de erine çok yakın seçilmesi durumunda,

[ ] [ ] = = n i i i n i i iX b X a 1 1

, rasgele aralı ının olabildi ince dar olması için bi veai ’ ler arasındaki fark

minimum olmalıdır. 90 , 0 =

α

seçilmesi durumunda a ve b majorant vektörler olmak üzere (1.3) ’ deki ko ul altında amaç fonksiyonu:

= − = n i i i a b f 1 min ve kısıtları: = ∈ = − + − + = ≤ ≤ = = = = = n i R b a a b i n n b a n k b a i i n i i i n i i n i i k i i k i i ,..., 2 , 1 , , 90 . 0 ) )( 1 ( 1 1 , 1 1 1 1 1 (2.2)

eklinde olan bir optimizasyon problemi kar ımıza çıkar. Bu problem tümevarımsal yöntemler kullanılarak a a ıdaki ekilde çözülmü tür.

2 = n için model; = ∈ = − − + = + ≥ − = = = 2 , 1 , , 90 . 0 ) 3 )( ( 3 1 min 2 1 2 1 2 1 1 1 2 1 i R b a i a b a a b b a b a b f i i i i i i i i (2.3)

eklindedir. Bu modelin çözümü Tablo 1’ de verilmi tir. 3 = n için model; = ∈ = − − + + = + + + ≥ + ≥ − = = = 3 , 2 , 1 , , 90 . 0 ) 4 )( ( 4 1 min 3 1 3 2 1 3 2 1 2 1 2 1 1 1 3 1 i R b a i a b a a a b b b a a b b a b a b f i i i i i i i i (2.4)

biçimindedir. Bu modelin çözümü Tablo 2’ de verilmi tir. 4 = n için model; = ∈ = − − + + + = + + + + + ≥ + + + ≥ + ≥ − = = = 4 , 3 , 2 , 1 , , 90 . 0 ) 5 )( ( 5 1 min 4 1 4 3 2 1 4 3 2 1 3 2 1 3 2 1 2 1 2 1 1 1 3 1 i R b a i a b a a a a b b b b a a a b b b a a b b a b a b f i i i i i i i i (2.5)

biçimindedir. Bu modelin çözümü de Tablo 3’ te verilmi tir.

Çe itli n de erleri verildi inde (2.2) modelinin çözümü bilgisayar programı yardımıyla bulunmu tur. Sonuçlar Tablo 4 ve Tablo 5’ deki gibi elde edilmi tir.

Tablo 1. (2.3) modelinin çözümü 1 1 a b − b −2 a2 minf 2.7 -2.7 5.4 Tablo2. (2.4) modelinin çözümü 1 1 a b − b −2 a2 b −3 a3 min f 1.8 0 -1.8 3.6 Tablo 3. (2.5) modelinin çözümü 1 1 a b − b −2 a2 b −3 a3 b −4 a4 minf 1.5 0 0 -1.5 3

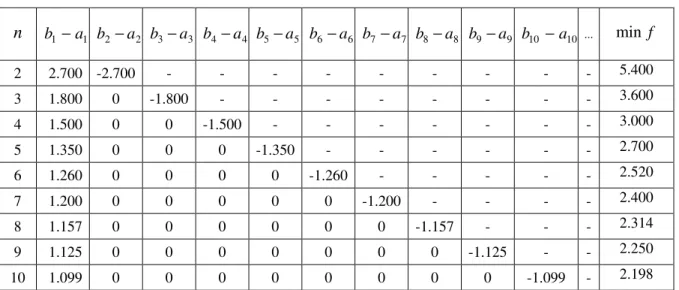
Tablo 4. Çe itli n=2,...,10 de erleri için (2.2) modelinin çözümü

n

b −₁ a₁ b −2 a2 b −3 a3 b −4 a4 b −5 a5 b −6 a6 b −7 a7 b −8 a8 b −9 a9 b10 −a10 ... min f 2 2.700 -2.700 - - - 5.400 3 1.800 0 -1.800 - - - 3.600 4 1.500 0 0 -1.500 - - - 3.000 5 1.350 0 0 0 -1.350 - - - 2.700 6 1.260 0 0 0 0 -1.260 - - - 2.520 7 1.200 0 0 0 0 0 -1.200 - - - - 2.400 8 1.157 0 0 0 0 0 0 -1.157 - - - 2.314 9 1.125 0 0 0 0 0 0 0 -1.125 - - 2.250 10 1.099 0 0 0 0 0 0 0 0 -1.099 - 2.198

Tablo 5. Çe itli n=15,20,25,50,100 de erleri için (2.2) modelinin çözümü

n

b −₁ a₁ b −2 a2 ... b −15 a15 ... b20−a20 ... b25−a25 ... b50−a50 ... b100−a100 min f 15 1.029 0 0 -1.029 - - - 2.058 20 0.995 0 0 0 0 -0.995 - - - 1.990 25 0.975 0 0 0 0 0 0 -0.975 - - - - 1.950 50 0.937 0 0 0 0 0 0 0 0 -0.937 - - 1.874 100 0.919 0 0 0 0 0 0 0 0 0 0 -0.919 1.838

3. Sonuç ve Öneriler < < − − = = c x d c d c x x F x F( ): ( ) ,

P düzgün da ılım fonksiyonlarına sahip da ılımlar

sınıfı olmak üzere majorant vektörler yardımıyla _{[ ] [ ]}

= = i n i i i n i iX b X a 1 1 , rasgele aralı ının = − + − + = n i i i a b i n n 1 ) )( 1 ( 1 1

α

seviyeli ana kitleyi kapsayan invaryant güven aralı ı oldu u [1] tarafından gösterilmi tir.

Bu güven aralı ı kullanılarak yapılacak testlerin gücünün yüksek çıkması için bu aralı ın olabildi ince dar olması gerekir. Bu da

b

_i ve

a

_i ’ ler arasındaki farkın en küçük olması ile sa lanır. Bu çalı mada a1 ≥...≥a_n veb1 ≥...≥b_n, a πb majorant vektörler ve

α

=0.90 olmak üzere;

= ∈ = − + − + = ≤ ≤ − = = = = = = = n i R b a a b i n n b a n k b a a b f i i n i i i n i i n i i k i i k i i n i i i ,..., 2 , 1 , , 90 . 0 ) )( 1 ( 1 1 , min 1 1 1 1 1 1

eklinde bir optimizasyon modeli ile kar ıla ılmı ve bu modelin çözümü Tablo 4 ve Tablo 5 ’ deki gibi elde edilmi tir. Majorant vektörler arasındaki ili ki bilgisayar programı yardımıyla tespit edilmi tir. Bu ili kiyi sa layan her majorant vektörü kesin çözüm olarak kabul edebiliriz. Bu vektörler yardımıyla olu turulan invaryant güven aralı ı bir kitlenin da ılımının düzgün da ılımdan gelip gelmedi ini test etmek amacıyla kullanılabilir. Bununla ilgili çalı malar devam etmektedir.

Kaynaklar

[1] Kaya, M.F., Saraço lu, B., Ku , C. Düzgün Da ılım Fonksiyonları Ailesi çin nvaryant Güven Aralıkları, statistik Ara tırma Dergisi, 2, 47-55, A ustos 2003, D E, Ankara.

[2] Marshal, A.W., Olkin, I. Inequalities. Theory of Majorizations and It’s Applications. Academic Press. - (1979).