ORTAOKUL 7. SINIF MATEMATĠK DERSĠ DÖNÜġÜM GEOMETRĠSĠ VE ÖRÜNTÜ-SÜSLEMELER ALT ÖĞRENME ALANLARININ GÖRSEL SANATLAR DERSĠ ĠLE DESTEKLENMESĠNĠN ÖĞRENCĠ BAġARILARI
VE TUTUMLARINA ETKĠSĠ
TUĞBA YÜKSEL
DOKTORA TEZĠ
ĠLKÖĞRETĠM MATEMATĠK EĞĠTĠMĠ ANABĠLĠM DALI
GAZĠ ÜNĠVERSĠTESĠ
EĞĠTĠM BĠLĠMLERĠ ENSTĠTÜSÜ
i
TELĠF HAKKI ve TEZ FOTOKOPĠ ĠZĠN FORMU
Bu tezin tüm hakları saklıdır. Kaynak göstermek koĢuluyla tezin teslim tarihinden itibaren 2 yıl (24) ay sonra tezden fotokopi çekilebilir.
YAZARIN
Adı : Tuğba Soyadı : YÜKSEL
Bölümü : Ġlköğretim Matematik Eğitimi Anabilim Dalı Ġmza :
Teslim tarihi : …../07/2015
TEZĠN
Türkçe Adı: Ortaokul 7. Sınıf Matematik Dersi DönüĢüm Geometrisi ve Örüntü Süslemeler Alt Öğrenme Alanlarının Görsel Sanatlar Dersi Ġle Desteklenmesinin Öğrenci BaĢarıları ve Tutumlarına Etkisi
Ġngilizce Adı: Effects of visual art support on secondary school seventh (7th) year math class sub learning fields transformation geometry and pattern – tesselation to students‘ achievements and attitudes
ii
ETĠK ĠLKELERE UYGUNLUK BEYANI
Tez yazma sürecinde bilimsel ve etik ilkelere uyduğumu, yararlandığım tüm kaynakların kaynak gösterme ilkelerine uygun olarak kaynakçada belirttiğimi ve bu bölümler dıĢındaki tüm ifadelerin Ģahsıma ait olduğunu beyan ederim.
Yazar Adı Soyadı : Tuğba YÜKSEL Ġmza :
iii
Jüri Onay Sayfası
Tuğba YÜKSEL tarafından hazırlanan ―Ortaokul 7. Sınıf Matematik Dersi DönüĢüm Geometrisi ve Örüntü Süslemeler Alt Öğrenme Alanlarının Görsel Sanatlar Dersi Ġle Desteklenmesinin Öğrenci BaĢarıları ve Tutumlarına Etkisi‖ adlı tez çalıĢması aĢağıdaki jüri tarafından oy birliği / oy çokluğu ile Gazi Üniversitesi Eğitim Bilimleri Enstitüsü Ġlköğretim Matematik Eğitimi Anabilim Dalı‘nda Doktora tezi olarak kabul edilmiĢtir.
DanıĢman: (Unvanı Adı Soyadı)
(Anabilim Dalı, Üniversite Adı) ………
BaĢkan: (Unvanı Adı Soyadı)
(Anabilim Dalı, Üniversite Adı) ………
Üye: (Unvanı Adı Soyadı)
(Anabilim Dalı, Üniversite Adı) ………
Üye: (Unvanı Adı Soyadı)
(Anabilim Dalı, Üniversite Adı) ………
Tez Savunma Tarihi: …../…../……….
Bu tezin Ġlköğretim Matematik Eğitimi Anabilim Dalı‘nda Doktora tezi olması için Ģartları yerine getirdiğini onaylıyorum.
Prof. Dr. Servet KARABAĞ
iv
TEġEKKÜR
Doktora eğitimim süresince ilgi ve desteğini esirgemeyen, araĢtırmamda fikirleri ile çalıĢmalarıma rehberlik eden değerli danıĢmanım Yrd. Doç. Dr. Mine AKTAġ‘a teĢekkürlerimi sunuyorum.
2211-A Genel Yurt Ġçi Doktora Burs Programı (2011-3) kapsamında 2011 yılından itibaren bursiyeri olduğum TÜBĠTAK‘a maddi desteğinden ötürü teĢekkür ederim.
Bu çalıĢmanın uygulanmasında ve yürütülmesinde bana yardımcı olan çalıĢmakta olduğum Boğaziçi Ortaokulu Müdürü Azmi YILMAZ‘a, ders içi aktivitelere istekle katılan sevgili öğrencilerime teĢekkür ederim.
Hayatım boyunca hep yanımda olan ve desteklerini hiç esirgemeyen çok değerli annem ve babama, bu zor süreçte bana yardımcı olan ve beni motive eden canım kardeĢlerim Kerem ve Ahmet‘e, ailemize yeni katılan gelinimiz Burcu‘ya binlerce kez teĢekkürler.
Son olarak doktora eğitimimin bana kazandırdığı en kıymetli kiĢiye, sevgili niĢanlım Bahadır KILCAN‘a desteği, sabrı, yardımı ve her aĢamada yanımda olduğu için çok teĢekkür ederim.
Tuğba YÜKSEL Temmuz, 2015
v
ORTAOKUL 7. SINIF MATEMATĠK DERSĠ DÖNÜġÜM
GEOMETRĠSĠ VE ÖRÜNTÜ - SÜSLEMELER ALT ÖĞRENME
ALANLARININ GÖRSEL SANATLAR DERSĠ ĠLE
DESTEKLENMESĠNĠN ÖĞRENCĠ BAġARILARI VE
TUTUMLARINA ETKĠSĠ
(Doktora Tezi)
Tuğba Yüksel
GAZĠ ÜNĠVERSĠTESĠ
EĞĠTĠM BĠLĠMLERĠ ENSTĠTÜSÜ
Temmuz, 2015
ÖZ
Bu çalıĢma 7. sınıf matematik dersi öğretim programında bulunan ―DönüĢüm Geometrisi‖ ve ―Örüntü-Süslemeler‖ alt öğrenme alanlarını görsel sanatlar dersi ile desteklemenin öğrenci baĢarı ve tutumlarında farklılaĢmaya sebep olup olmadığını ortaya koymak için 2013–2014 eğitim öğretim yılının bahar döneminde Ankara ilinin Mamak ilçesinde yer alan bir ortaokulda yapılmıĢtır. Öntest-sontest kontrol gruplu yarı deneysel desen kullanılarak gerçekleĢtirilmiĢ olan çalıĢmada veri toplama aracı olarak, araĢtırmacı tarafından geliĢtirilen ve güvenirliği test edilen baĢarı testi ile katılımcıların matematik dersine karĢı tutumlarını belirlemek için Milli Eğim Bakanlığı tarafından hazırlanan matematik dersine yönelik tutum ölçeği kullanılmıĢtır. Verilerin analizinde aritmetik ortalama, standart sapma ve t-testi kullanılmıĢtır. AraĢtırma sonucunda görsel sanatlar dersi ile desteklenerek ders iĢlenmenin, öğrencilerin akademik baĢarılarını ve tutumlarını artırmada, yapılandırmacı yaklaĢım ile ders iĢlemeye göre daha etkili olduğu görülmüĢtür.
Bilim Kodu :
Anahtar kelimeler : DönüĢüm geometrisi, örüntü, süsleme, görsel sanatlar, disiplinlerarası. Sayfa Adedi :
vi
EFFECTS OF VISUAL ART SUPPORT ON SECONDARY SCHOOL
SEVENTH (7th) YEAR MATH CLASS SUB LEARNING FIELDS
TRANSFORMATION GEOMETRY AND PATTERN –
TESSELATION TO STUDENTS’ ACHIEVEMENTS AND
ATTITUDES
(Ph.D Thesis)
Tuğba Yüksel
GAZI UNIVERSITY
INSTITUTE OF EDUCATION SCIENCES
July, 2015
ABSTRACT
This study has been executed at a secondary school which is located at Ankara Mamak during 2013-2014 spring term for observing the differentiation on student achievements and attitudes with supporting Secondary School Seventh Year Lectures sub learning fields ‗‘Tranformation Geometry‘‘ and ‗‘Pattern-Tesselation‘‘ by visual arts. During the study which is completed by using Quasi-experimental design with pretest-posttest control group, for data collection, achievement test developed by researcher and tested for reliability with attitude scale prepared by National Education Ministry for defining participants‘ attitude against math class have been used. Arithmetic mean, standard deviation and t- test have been used for analyzing of data. As a result of this study, it has been observed that teaching lesson with support of visual arts is more effective than teaching lesson by using constructivist approachment.
Science Code:
Key Words: Transformation Geometry, Pattern, Tesselation, Visual Arts, Interdisciplinary. Page Number:
vii
ĠÇĠNDEKĠLER
TELĠF HAKKI ve TEZ FOTOKOPĠ ĠZĠN FORMU ... i
ETĠK ĠLKELERE UYGUNLUK BEYANI ... ii
Jüri Onay Sayfası ... iii
TEġEKKÜR ... iv ÖZ ... v ABSTRACT ... vi ĠÇĠNDEKĠLER ... vii TABLOLAR LĠSTESĠ... x ġEKĠLLER LĠSTESĠ ... xi BÖLÜM I GĠRĠġ ... 1 1.1. Problem Durumu ... 1 1.2. Problem Cümlesi ... 3 1.3. Alt Problemler ... 3 1.4. AraĢtırmanın Amacı ... 4 1.5. AraĢtırmanın Önemi ... 4 1.6. Sınırlamalar ... 5 1.7. AraĢtırmanın Varsayımları ... 6 1.8. Tanımlar ... 6 BÖLÜM II KAVRAMSAL ÇERÇEVE ... 9 2.1. Matematik Öğretimi ... 9 2.2. DönüĢüm Geometrisi ... 12 2.3. Örüntü ve Süslemeler ... 14 2.4. Matematik ve Sanat ... 18
2.5. Matematik ve Görsel Sanatlar ... 45 BÖLÜM III
viii
YÖNTEM... 51
3.1. AraĢtırma Modeli ... 51
3.2. ÇalıĢma Grubu... 53
3.3. Veri Toplama Araçları ... 53
3.3.1. Matematik BaĢarı Testi OluĢturma Süreci ... 54
3.4. Uygulama... 57
3.4.1. Renkli Fotoğraflar ... 58
3.4.2. ÇalıĢma Yaprakları ... 59
3.4.3. Ġp Baskısı: ... 66
3.4.4. Sulu Boya Baskısı: ... 68
3.4.5. Kes-YapıĢtır ... 68
3.4.6. Maket ... 70
3.5. Verilerin analizi ... 73
BÖLÜM IV BULGULAR ... 75
4.1. Akademik BaĢarıya ĠliĢkin Bulgular ... 75
4.1.1. Görsel Sanatlar Dersi ile Desteklenen Matematik Eğitiminin Yapıldığı Deney Grubu ile Geleneksel Öğrenme Ortamında Eğitim Yapılan Kontrol Grubunun Ön–Test Puanlarına ĠliĢkin Bulgu ve Yorumlar ... 76
4.1.2. Görsel Sanatlar Dersi ile Desteklenen Matematik Eğitiminin Yapıldığı Deney Grubunun Ön–Test ve Son–Test Puanlarına ĠliĢkin Bulgu ve Yorumlar ... 76
4.1.3. Geleneksel Öğrenme Ortamında Eğitim Yapılan Kontrol Grubunun Ön-Test ve Son-Test Puanlarına ĠliĢkin Bulgu ve Yorumlar ... 77
4.1.4. Görsel Sanatlar Dersi ile Desteklenen Matematik Eğitiminin Yapıldığı Deney Grubu ile Geleneksel Öğrenme Ortamında Eğitim Yapılan Kontrol Grubunun Son-Test Puanlarına ĠliĢkin Bulgu ve Yorumlar... 78
4.2. Matematik Tutumlarına ĠliĢkin Bulgular ... 79
4.2.1. Görsel Sanatlar Dersi ile Desteklenen Matematik Eğitiminin Yapıldığı Deney Grubu ile Geleneksel Öğrenme Ortamında Eğitim Yapılan Kontrol Grubu Öğrencilerinin Matematik Dersine Yönelik Tutum Ölçeği Ön-Test Puanlarına ĠliĢkin Bulgu ve Yorumlar ... 80
ix
4.2.2. Görsel Sanatlar Dersi ile Desteklenen Matematik Eğitiminin Yapıldığı Deney Grubunun Matematik Dersine Yönelik Tutum Ölçeği Ön-Test ve
Son-Test Puanlarına ĠliĢkin Bulgu ve Yorumlar ... 80
4.2.3. Geleneksel Öğrenme Ortamında Eğitim Yapılan Kontrol Grubunun Matematik Dersine Yönelik Tutum Ölçeği Ön-Test ve Son-Test Puanlarına ĠliĢkin Bulgu ve Yorumlar ... 81
4.2.4. Görsel Sanatlar Dersi ile Desteklenen Matematik Eğitiminin Yapıldığı Deney Grubu ile Geleneksel Öğrenme Ortamında Eğitim Yapılan Kontrol Grubu Öğrencilerinin Matematik Dersine Yönelik Tutum Ölçeği Son-Test Puanlarına ĠliĢkin Bulgu ve Yorumlar ... 82
BÖLÜM V SONUÇ, TARTIġMA VE ÖNERĠLER ... 85
5.1. Sonuçlar ve TartıĢma ... 85
5.1.1. Akademik BaĢarıya ĠliĢkin Sonuçlar ve TartıĢma ... 85
5.1.2. Tutuma ĠliĢkin Sonuçlar ve TartıĢma ... 86
KAYNAKLAR ... 89
x
TABLOLAR LĠSTESĠ
Tablo 1. Süsleme ÇeĢitleri ... 15
Tablo 2. Düzgün Çokgenler ve Escher Resimleri ... 23
Tablo 3. Logolar ve Altın Oran... 44
Tablo 4. Sanatsal Öğrenme AĢamaları ... 48
Tablo 5. Renklerin Psikolojik Etkileri ... 48
Tablo 6. Matematik ve Görsel Sanatlar Dersinde Kullanılan Ortak Kavramlar.. ... 49
Tablo 7. Sınıf Geometri Öğrenme Alanına Ait Kazanımlar ... 54
Tablo 8. 7. Sınıf BaĢarı Testi Soru Analizi ... 56
Tablo 9. Deney ve Kontrol Grubunun Matematik Dersine Yönelik Ön-Test t-Testi Sonuçları ... 76
Tablo 10. Deney Grubunun Matematik Dersine Yönelik Ön-Test ve Son-Test t-Testi Sonuçları ... 77
Tablo 11. Kontrol Grubunun Matematik Dersine Yönelik Ön-Test ve Son-Test t-Testi Sonuçları ... 78
Tablo 12. Deney ve Kontrol Grubunun Matematik Dersine Yönelik Son-Test t-Testi Sonuçları ... 79
Tablo 13. Deney ve Kontrol Grubunun Matematik Dersine Yönelik Tutum Ölçeği Ön-Test Puanlarının Farklılığı Ġçin t-Testi Sonuçları ... 80
Tablo 14. Deney Grubunun Matematik Dersine Yönelik Tutum Ölçeği Ön-Test ve Son-Test Puanlarının Farklılığı Ġçin t-Son-Testi Sonuçları ... 81
Tablo 15. Kontrol Grubunun Matematik Dersine Yönelik Tutum Ölçeği Ön-Test ve Son-Test Puanlarının Farklılığı Ġçin t-Son-Testi Sonuçları ... 81
Tablo 16. Deney ve Kontrol Grubunun Matematik Dersine Yönelik Tutum Ölçeği Son-Test Puanlarının Farklılığı Ġçin t-Son-Testi Sonuçları ... 82
xi
ġEKĠLLER LĠSTESĠ
ġekil 1. Dönme simetrisi ―A‖ harfi örneği ... 13
ġekil 2. Düzenli süsleme örneği ... 16
ġekil 3. Düzgün beĢgenler ... 16
ġekil 4. Düzgün yedigenler ... 17
ġekil 5. Yarı düzenli süsleme örneği ... 17
ġekil 6. KarmaĢık desenli süsleme... 18
ġekil 7. Metamorfoz... 20
ġekil 8. Balık / KuĢ ... 21
ġekil 9. Çember limit ... 22
ġekil 10. Ġslami süsleme örneği ... 24
ġekil 11. Sekizgen kullanarak oluĢturulan yıldız figürleri... 25
ġekil 12. Dama tahtası süsleme figürü ... 25
ġekil 13. Selçuklu zamanı süsleme örneği-1, Kayseri - Aksaray Sultan Hanı, 1229 ... 26
ġekil 14. Selçuklu zamanı süsleme örneği-2, Sivas - Ġzzettin Keykavus Kümbeti, 1217 ... 26
ġekil 15. Selçuklu zamanı süsleme örneği-3, Ġspanya - El Hamra Sarayı, 1338-90 ... 27
ġekil 16. Selçuklu zamanı süsleme örneği-4, Amasya - Halifet Gazi Türbesi, 1145 ... 27
ġekil 17. El Hamra Sarayından düzlemsel ve hiperbolik süsleme örnekleri ... 28
ġekil 18. ―Y‖ figürünün kullanıldığı düzlemsel ve hiperbolik süsleme örnekleri ... 29
ġekil 19. Selçuklu zamanı süsleme örneği-5, Konya - AkĢehir, Seyyid Mahmut Hayrani Türbesi, 1268 ... 29
ġekil 20. Selçuklu zamanı süsleme örneği-6, Amasya, Gök Medrese, 1276... 30
ġekil 21. Selçuklu zamanı süsleme örneği-7, Karaman, Ġbrahim Bey Ġmareti, 1433, Karaman Beyliği... 30
ġekil 22. Süleymanname süsleme örneği, 1517... 31
ġekil 23. Edirne, Selimiye Camii süsleme örneği-1, 1568-1574 ... 31
ġekil 24. Edirne, Selimiye Camii süsleme örneği-2, 1568-1574 ... 31
xii
ġekil 26. 12 kenarlı yıldızı oluĢturma aĢamaları ... 32
ġekil 27. Özbekistan‘da bulunan bir camiinin süslemesi ... 33
ġekil 28. 1310‘da çizilen Kur‘an-ı Kerim süslemesi ... 34
ġekil 29. Yer karosu örneği-1 ... 35
ġekil 30. Yer karosu örneği-2 ... 35
ġekil 31. AraĢtırmacı tarafından çizilen desen - 1 ... 36
ġekil 32. AraĢtırmacı tarafından çizilen desen - 2 ... 36
ġekil 33. Kar tanesi ... 37
ġekil 34. Altın oran ... 38
ġekil 35. Fibonacci dikdörtgenleri ... 38
ġekil 36. Ġnsan kolu ve altın oran... 39
ġekil 37. Parmak yapısı ve altın oran... 40
ġekil 38. Deniz kabuğu ve altın oran ... 40
ġekil 39. Çam kozalağı ve altın oran ... 41
ġekil 40. Salyangoz kabuğu ve altın oran ... 41
ġekil 41. Mona Lisa tablosu ve altın oran... 42
ġekil 42. Piet Mondrian dikdörtgenleri ve altın oran ... 43
ġekil 43. Süleymaniye Camii ve altın oran ... 43
ġekil 44. Deneysel modelin simgesel gösterimi ... 51
ġekil 45. AraĢtırma deseninin aĢamaları ... 52
ġekil 46. Simetri ekseni için hazırlanan fotoğraflar ... 58
ġekil 47. Simetri ekseni için hazırlanan fotoğraflar ve simetri eksenleri ... 59
ġekil 48. Doğru simetrisi çalıĢma yaprağı (çöp adam) ... 60
ġekil 49. ÇalıĢma yaprağı uygulanan bir öğrenci ... 61
ġekil 50. Öğrenci tarafından çizilen simetrik resim... 61
ġekil 51. Doğru simetrisi çalıĢma yaprağı ... 62
ġekil 52. Doğru simetrisi çalıĢma yaprağı (trafik iĢaretleri) ... 63
ġekil 53. Yansıma ve dönme simetrisi çalıĢma yaprağı (mozaikler) ... 64
ġekil 54. Simetri çalıĢma yaprağı (logo tasarlama) ... 65
ġekil 55. Dönme simetrisi çalıĢma yaprağı (salyangoz) ... 66
ġekil 56. Ġp baskısı etkinliğine katılan bir öğrenci ... 66
ġekil 57. Öğrencilerin yaptığı ip baskısı örnekleri ... 67
xiii
ġekil 59. Sulu boya baskısı etkinliği ... 68
ġekil 60. Kes-yapıĢtır etkinliği ... 68
ġekil 61. Kes-yapıĢtır etkinliğinden örnekler ... 69
ġekil 62. Dönme merkezi etkinliği ... 70
ġekil 63. Dönme simetrisine sahip çokgenlerin belirlenmesi ... 70
ġekil 64. Dönme merkezi (90o‘lik dönme) ... 71
ġekil 65. Dönme merkezi (180o‘lik dönme) ... 71
ġekil 66. Dönme simetrisine sahip çokgenler (eĢkenar üçgen) ... 72
xiv
SĠMGELER VE KISALTMALAR LĠSTESĠ
MEB Milli Eğitim Bakanlığı
NCTM National Council of Teachers of Mathematics TDK Türk Dil Kurumu
1
BÖLÜM I
GĠRĠġ
Bu bölümde; araĢtırmanın problem durumu, amacı, önemi, varsayımları, sınırlılıkları ve araĢtırmaya ait gerekli tanımlar yer almaktadır.
1.1. Problem Durumu
Matematik, okulöncesi eğitim kademesinden baĢlamak üzere ilkokul ve ortaokul öğretim programlarının her aĢamasında yer alan bir derstir. Ġnsanlar tarafından iyi bir yaĢamın ve iyi bir kariyerin kapı açıcısı olarak görülen matematik, aynı zamanda hayatın ve dünyanın anlaĢılması ve bunlar hakkında fikirler üretilebilmesi için yardımcı bir eleman olarak da görülmektedir (Yenilmez ve Uysal, 2007). Matematik ve matematiksel düĢünme, günlük yaĢamda kapladığı büyük yere karĢın dünyanın her yerinde "zor" kabul edilir ve öğretiminde genellikle güçlük çekilir. Matematiğin zorluğu yapısından olduğu kadar ona karĢı geliĢtirilen önyargı ve korkudan da kaynaklanmaktadır (Umay, 1996). Bu sebeple ilk önce öğrencilerin matematiğe karĢı olan bu ön yargılarını yıkmak gerekmektedir.
Eğitimde belirlenen hedeflere ulaĢmada en önemli öğelerden biri öğrenme sürecini iyi organize etmektir. Özellikle öğrenenin ilgisini çekecek ve sürece daha fazla motive olmasını sağlayacak yöntem ve tekniklerin kullanılması bu sürece olumlu katkı sağlayarak sürecin daha verimli geçmesini sağlayabilir (Öner, Yıldırım ve Bars, 2014). Bu organizeyi iyi yapabilmek için matematik programlarının da çok dikkatli bir Ģekilde hazırlanması gerekmektedir. National Council of Teachers of Mathematics [NCTM] (2000)‘ye göre bütün matematik programları öğrencilerin;
● Yaratma ve organize etme için gösterimler kullanma, kaydetme ve matematiksel fikirlerini iletme,
2
● Model için, gösterimler (simgelemeler) yapma ve fiziksel, sosyal ve matematiksel doğayı yorumlama becerilerini geliĢtirecek Ģekilde düzenlenmelidir (Turğut ve Yılmaz, 2012).
Geleneksel yöntem olarak isimlendirilen ve öğretmenin aktif, öğrencinin pasif rol aldığı öğretme-öğrenme sürecinde öğrenciler ezbere yönelmektedir. Schoenfeld (1983), matematik öğretiminde geleneksel yaklaĢımın sınırlılıklarını iki önemli faktöre bağlamıĢtır. Bunlar öğretmen merkezli öğretimin sınırlılıkları ve matematiksel bilgilerin öğrencilere basmakalıp, hazır Ģekilde sunulmasıdır. Johnson, Johnson ve Smith (1995), bu eski öğretim yönteminin John Locke‘ın, eğitilmemiĢ öğrenci zihni, öğretmenin üzerine bir Ģeyler yazmasını bekleyen boĢ bir kâğıda benzer sanısına dayandığını ve bu gibi sanılar sebebiyle öğretmenlerin öğretim hakkındaki düĢüncelerinin Ģu etkinliklerdeki terimlerle sınırlı olduğunu ifade etmiĢlerdir:
1. Bilginin öğretmenden öğrenciye aktarılması: Öğretmen bilgiyi verir, öğrenci ise alır. Öğretmen, öğrencilerin hatırlayacağını umarak bilgiyi aktarır.
2. Pasif boĢ kutuların bilgiyle doldurulması: Öğrenciler bilginin pasif alıcılarıdır. Öğretmenler, öğrencilerin hatırlayıp geri çağıracakları bilginin sahibidir.
3. Öğrencilerin sınıflandırılması: Bilgi seviyelerine bakılarak öğrenciler sınıflandırılır. 4. Öğrenciler kategorilere ayrılır: Öğrencilerin; mezun olmak, üniversiteye gitmek ve iyi bir iĢe sahip olmak gibi ihtiyaçları karĢılayıp karĢılamadıklarına karar verilerek öğrenciler kategorilere ayrılır.
5. Öğrencilerin kendi aralarında ve öğretmenlerle öğrenciler arasında kiĢisel olmayan iliĢkiler içerisinde eğitimin yönlendirilmesi: Taylor‘ın endüstriyel organizasyon modeline dayanarak, öğrenci ve öğretmenlere ―eğitim makinesi‖ içinde değiĢtirilebilir ve yerleri doldurulabilir parçalar oldukları hissettirilir.
6. Rekabetçi örgütsel bir yapının sürdürülmesi: Öğrenciler sınıf arkadaĢlarından, öğretmenler de meslektaĢlarından daha iyisini yapmak için çalıĢırlar.
7. Alanında uzman olan kiĢilerin eğitim almadan öğretebileceğinin sanılması: Alan uzmanlarının gerekli yetiye ve eğitime sahip olmadan öğretme eylemini gerçekleĢtirebileceğinin düĢünülmesidir (Çırakoğlu, 2009).
Öğrencilerin bu basmakalıp öğrenme anlayıĢından ve ezberden kurtulabilmeleri için öğretimde somut deneyimler kullanılmalı ve yapılandırmacı aktivitelerle öğrencilerin
3
bilgiye kendilerinin ulaĢmaları sağlanmalıdır. Öğrencilerin matematiğe karĢı pozitif tutum geliĢtirmeleri için matematiğin önemini anlamaları sağlanmalı ve motivasyonlarını üst düzeyde tutmak için farklı teknikler kullanılmalıdır (AltıntaĢ ve Görgen, 2014).
1.2. Problem Cümlesi
Ortaokul 7. sınıf matematik dersinde dönüĢüm geometrisi ve örüntü-süslemeler alt öğrenme alanlarının görsel sanatlar dersi ile desteklenerek iĢlenmesi öğrenci baĢarısını ve tutumunu etkilemekte midir?
1.3. Alt Problemler
1) Görsel sanatlar dersi ile desteklenen matematik eğitiminin yapıldığı deney grubu ile geleneksel öğrenme ortamında eğitim yapılan kontrol grubunun ön-test puanları arasında anlamlı bir fark var mıdır?
2) Görsel sanatlar dersi ile desteklenen matematik eğitiminin yapıldığı deney grubunun ön-test ve son-test puanları arasında anlamlı bir fark var mıdır?
3) Geleneksel öğrenme ortamında eğitim yapılan kontrol grubunun ön-test ve son-test puanları arasında anlamlı bir fark var mıdır?
4) Görsel sanatlar dersi ile desteklenen matematik eğitiminin yapıldığı deney grubu ile geleneksel öğrenme ortamında eğitim yapılan kontrol grubunun son-test puanları arasında anlamlı bir fark var mıdır?
5) Görsel sanatlar dersi ile desteklenen matematik eğitiminin yapıldığı deney grubu ile geleneksel öğrenme ortamında eğitim yapılan kontrol grubu öğrencilerinin matematik dersine yönelik tutum ölçeği ön-test puanları arasında anlamlı bir fark var mıdır?
6) Görsel sanatlar dersi ile desteklenen matematik eğitiminin yapıldığı deney grubunun matematik dersine yönelik tutum ölçeği ön-test ve son-test puanları arasında anlamlı bir fark var mıdır?
7) Geleneksel öğrenme ortamında eğitim yapılan kontrol grubunun matematik dersine yönelik tutum ölçeği ön-test ve son-test puanları arasında anlamlı bir fark var mıdır?
8) Görsel sanatlar dersi ile desteklenen matematik eğitiminin yapıldığı deney grubu ile geleneksel öğrenme ortamında eğitim yapılan kontrol grubu öğrencilerinin matematik dersine yönelik tutum ölçeği son-test puanları arasında anlamlı bir fark var mıdır?
4
1.4. AraĢtırmanın Amacı
Matematiğin temel amacı bireyin hayatında çok büyük öneme sahip olan düĢünce yapısını geliĢtirmek; bireye düĢünme, olaylar arasında bağ kurma, akıl yürütme, tahminlerde bulunma, problem çözme gibi önemli destekler sağlamaktır. Bu nedenledir ki matematik eğitimi temel eğitimin önemli yapı taĢlarından birini oluĢturur (Bulut, 2009).
Bu çalıĢmada, ortaokul 7.sınıfta geometri öğrenme alanının dönüĢüm geometrisi ve örüntü-süslemeler alt öğrenme alanları konu olarak seçilmiĢtir. Öğrencilerin, görsel sanatlar dersi ile desteklenen yapılandırmacı öğrenme ortamında iĢlenen ders süreci sonunda dönüĢüm geometrisini kavrayabilmeleri, alt öğrenme alanlarına ait kazanımları görsel sanatlara ve dolayısı ile günlük hayata uygulayabilmeleri, görsel sanatlarda kullanılan matematiği fark edebilmeleri ve matematiğe karĢı olumlu tutum geliĢtirmeleri amaçlanmıĢtır.
1.5. AraĢtırmanın Önemi
Matematik hayatın hemen hemen her aĢamasında karĢımıza çıkmasına rağmen bir o kadar da zor ve soyut kabul edilir. Özellikle ortaokuldan itibaren ağırlık kazanan geometri öğrenme alanı öğrenciler için daha karıĢık gelmektedir.
Ġlkokul 1. sınıfta okuma-yazma bilmeyen öğrencilere matematik ve geometri verilmektedir. Bu yaĢtaki öğrenciler somut iĢlemler döneminde olduğundan daha çok somut modellerden ve Ģekillerden faydalanılır. 7.sınıfta yer alan dönüĢüm geometrisine ait kazanımlar da öğrencilere soyut gelebilmektedir. Öğrencilerin matematiği sevmesi ve baĢarılı olabilmesi için öğretimde değiĢiklikler yapmak ve yeni öğretme ve öğrenme modellerine yönelmek gerekmektedir (Gür ve Seyhan, 2006). Birinci sınıfta uygulanan yönteme benzer olarak bu sınıf seviyesinde de görsel sanatlar dersindeki etkinliklerden faydalanılabilir. Renkler, Ģekiller, resimler ve birçok teknik kullanarak matematiğin uygulamaları öğrenciler tarafından birebir yapılabilmektedir. Böylece sayılar ve formüllerden ibaret görülen matematiğin görsel sanatlar dersi ile iliĢkilendirilerek eğlenceli tarafı fark ettirilebilir. Yaparak ve yaĢayarak öğrenen öğrencinin matematiğe karĢı önyargısı ve olumsuz tutumu da ortadan kaldırılabilir.
Matematiğin birçok tanımı vardır. Yapılan her bir tanım matematiğin farklı bir uygulamasına ya da yapısına dikkat çekmektedir. Hemen hemen herkesin hemfikir olduğu Ģey ise matematiğin bir düĢünme eylemi olduğudur. Yani matematikle uğraĢan insan, düĢünen insandır. DüĢünen insanın gündelik zihni ihtiyaçlarına nazaran matematik, Ģekil,
5
miktar ve hareketin en soyut seviyede incelenmesi eylemine ve bu eylem neticesinde vücut bulan bilgi birikimine verilen isimdir (Tezer, 2003). Ferri (2003), matematiksel düĢünme süreç tarzlarını ise üç gruba ayırmıĢtır;
1) Görsel (Resimler, grafikler, çizelgeler, Ģekillerle düĢünme). 2) Analitik (Sembolik düĢünme).
3) Kavramsal (Soyut düĢünme, sınıflama yapma).
Görsel sanatlarla iliĢkilendirilen matematik dersinde Ferri‘nin gruplandırmasında birinci sırada yer alan ―resimler, grafikler ve Ģekillerle düĢünme‖ süreci ağırlıklı olarak kullanılabilir.
Genelde ergenlik çağındaki öğrencilerin oluĢturduğu ortaokul öğrencilerinin eğitiminin, çocuk ve yetiĢkinlerin eğitimine oranla daha ayrı bir ustalık gerektirdiği bilinmektedir (Uysal, 2005). Matematik dersi ile görsel sanatlar dersi iliĢkilendirilerek bu çağdaki öğrencilerin daha fazla duyusuna hitap edilerek ders somutlaĢtırılabilir, daha eğlenceli hale getirilebilir ve yaparak-yaĢayarak öğrenme sürecine aktif katılan öğrencinin öğrenmedeki kalıcılığı artacağı düĢünülebilir.
Bunun yanı sıra yapılan literatür taramasında, dönüĢüm geometrisi ve örüntü-süslemeler alt öğrenme alanlarında matematik dersi ile görsel sanatlar dersinin iliĢkilendirilerek disiplinlerarası böyle bir çalıĢma yapılmadığı saptanmıĢtır. Bununla birlikte matematik programlarında yapılan bu çalıĢmanın yol gösterici olabileceği düĢünülmektedir.
1.6. Sınırlamalar
Yapılan bu araĢtırma,
1. Uygulamanın yapıldığı Ankara ilinde bulunan bir ortaokuldaki iki 7.sınıf Ģubesi,
2. 7. sınıfların matematik dersi dönüĢüm geometrisi ve örüntü-süslemeler alt öğrenme alanları,
3. Uygulamanın yapıldığı tarihler, Nisan 2014 – Mayıs 2014, 4. Yurt içi ve yurt dıĢı literatür taramasından elde edilen kaynaklar ile sınırlıdır.
6
1.7. AraĢtırmanın Varsayımları
AraĢtırmada kullanılan varsayımlar Ģunlardır;
1. AraĢtırmanın uygulamasına katılan deney ve kontrol grubu öğrencilerinin kontrol altına alınamayan dıĢsal etkenlerden eĢit düzeyde etkilendikleri varsayılmıĢtır.
2. Görsel sanatlar dersi ile desteklenerek matematik dersinin iĢlendiği deney grubunda kullanılan araç-gereçler ve materyaller için baĢvurulan uzman görüĢlerinin yeterli düzeyde olduğu varsayılmıĢtır.
3. AraĢtırma sürecinde yer alan öğrencilerin uygulamalara içtenlikle katıldıkları varsayılmıĢtır.
4. AraĢtırma süresince deney ve kontrol grubunda bulunan öğrencilerin, sınıf dıĢından yardım almadıkları ve bu öğrencilerle herhangi bir ek çalıĢma yapılmadığı varsayılmıĢtır. 5. AraĢtırmada kullanılan ölçeklerin kapsam geçerliliği için baĢvurulan uzmanların görüĢlerinin yeterli olduğu varsayılmaktadır.
1.8. Tanımlar
DönüĢüm Geometrisi: Yansıma, öteleme ve dönme hareketlerinden bir ya da birkaçının
Ģekil ya da noktaya uygulanmasıdır (Milli Eğitim Bakanlığı [MEB], 2012, s. 85).
Örüntü: Olay veya nesnelerin düzenli bir biçimde birbirini takip ederek geliĢmesidir
(Türk Dil Kurumu [TDK], 2014). Matematikte örüntü ise belirli olan bir kurala göre düzenli bir Ģekilde tekrarlanan ya da geniĢleyen Ģekil veya sayı dizisine örüntü ismi verilmektedir.
Süsleme: Bir düzlemin boĢluk kalmadan ve Ģekiller üst üste gelmeden örüntü oluĢturacak
Ģekilde döĢenmesidir (MEB, 2012, s. 94). Her süsleme aynı zamanda örüntüdür.
Görsel Sanatlar: Heykel, mimari, resim, fotoğraf ve sinema, tiyatro, bale, opera gibi alt
dallara ayrılan görsel sanatlar; güzel sanatların bir alt koludur (Kılıçkan, 1999, s. 6).
Disiplinlerarası: Metodoloji ve dili birden fazla disiplinden alıp merkezde bulunan
konuyu, sorunu, baĢlığı ya da deneyimi incelemek için bilinçli Ģekilde uygulayan bir bilgi bakıĢ açısı ve müfredat yaklaĢımı bir problemi farklı disiplinler açısından değerlendirmek
7
ve bu perspektifleri genel sonuçlara bakarak bir senteze dönüĢtürmektir. Ġçeriği ve kavramları diğer alanlarla yakınlaĢtırırken bu konunun geleneksel sınırlarını korumaktır (Özkök, 2004).
Deneysel Yöntem: Deneysel yöntem, problemlerin kontrol edilmiĢ denel koĢullar altında
9
BÖLÜM II
KAVRAMSAL ÇERÇEVE
2.1. Matematik Öğretimi
Matematiğin temel amacı bireyin hayatında çok büyük öneme sahip olan düĢünce yapısını geliĢtirmek; bireye düĢünme, olaylar arasında bağ kurma, akıl yürütme, tahminlerde bulunma, problem çözme gibi önemli destekler sağlamaktır. Bu nedenledir ki matematik eğitimi temel eğitimin önemli yapı taĢlarından birini oluĢturur (Bulut, 2009). Matematik öğretimi, matematikte, amaçlanan hedef davranıĢların sağlıklı ve kalıcı olacak Ģekilde kazandırılması iĢidir (Acar, 2005). Bu sebeple matematik öğretiminin amacının genel olarak, kiĢiye günlük hayatın gerektirdiği matematik bilgi ve becerileri kazandırmak, ona problem çözmeyi öğretmek ve olayları problem çözme atmosferi içinde ele alan bir düĢünme biçimi kazandırmak olduğu söylenebilir (Yenilmez ve Girit, 2013).
Birçok insan için matematik, hayatını zehir eden derslerden, içine korku salan sınavlardan ve okulu bitirir bitirmez kurtulacağı bir kâbustan ibarettir. Bazıları içinse matematik, hayatı anlamanın ve sevmenin bir yolu olabilmiĢtir. Çünkü sevmenin yolu, her Ģeyde olduğu gibi anlamaktan geçer (Sertöz, 2003). Öğrenciler anladıkları Ģeyleri öğrenmeye daha fazla istek duyarlar. Bu da onların anlama kapasitelerini arttırır. Bu yüzden matematik öğretmeni dersi anlamlı hale getirerek öğrencilerin öğrenmelerini kolaylaĢtırmalıdır. ĠĢte bu sebeple matematik, öğrencilerin anlamalarına fırsatlar oluĢturan, öğrenciyi merkeze alan ve onun özgürlüklerini kısıtlamayan, tam tersine geliĢtirmesine yardımcı olan bir eğitim sistemine gereksinim duyan alanların baĢında gelmektedir. Tüm bunlar dikkate alınarak matematik eğitiminde aĢağıdaki yaklaĢımlar önerilmektedir;
● Amaç, öğrencinin geliĢtirilmesi olduğuna göre, her Ģeyden önce eğitimin temelinde öğrencinin olması sağlanmalıdır.
10
● Öğrenci esnek, huzurlu ve renkli bir ortamda, düĢüncelerini korkusuzca söyleyebilmelidir.
● Doğru yaklaĢımlar kadar yapılan yanlıĢların da değerli olduğu unutulmamalıdır. ● Eğitim bir süreçtir ve okul bittiğinde kesilmez.
● Matematikte ezbere yer olmamalıdır (Umay, 1996).
Bir matematik öğretmeni matematik konularını defalarca öğrencilerine sunmuĢ olabilir, ancak matematik öğretmeni alanındaki yeni geliĢmeleri örneklerle zenginleĢtirerek sunmazsa öğrencilerini monotonluktan kurtaramaz. Matematik dersini zor ve anlaĢılmaz bir ders olmaktan çıkaramaz (Dursun ve Peker, 2003). Bunu engellemek için dersin amacına ve grubun özelliklerine uygun Ģekilde yöntem ve teknikler belirlenerek uygulanmalıdır. Matematik öğretiminde en sık kullanılan yöntemler aĢağıda sıralanmıĢtır;
► Düz Anlatım Yöntemi
► BuluĢ Yoluyla Öğretim Yöntemi ► Senaryo ile Öğretim Yöntemi ► Gösterip Yaptırma Yöntemi ► Analizle Öğretim Yöntemi ► Oyunlarla Öğretim Yöntemi
► Deneysel Etkinliklerle Öğretim Yöntemi ► Kurallar Yardımıyla Öğretim Yöntemi
► AraĢtırma – Ġnceleme Yoluyla Öğretim Yöntemi ► Tanımlar Yardımıyla Öğretim Yöntemi
Sıralanan yöntemler dıĢında matematik öğretimde pek çok teknik de kullanılmaktadır. Tüm bu teknik ve yöntemlerin ortak amaçlarından biri de matematiksel düĢünme becerisini geliĢtirmektir. Matematiksel düĢünmeyi geliĢtirmek için Ģu 5 varsayım sıralanabilir:
i) Matematiksel düĢünebilirsiniz.
ii) Matematiksel düĢünme problemler üzerinde derinlemesine düĢünerek ve farklı problemlerle uğraĢarak geliĢtirilebilir.
11
iv) Matematiksel düĢünme sorgulayarak, derinlemesine düĢünerek ve meydan okuyarak desteklenebilir.
v) Matematiksel düĢünmenin desteklenmesi dünyayı ve çevremizi anlamamızın artmasına yardımcı olur (Mason, Burton ve Stacey‘den aktaran Bulut, 2009).
Öğrencilerin matematik dersi ile ilgili duygularından ortaya çıkan matematiğe karĢı tutumları, matematik eğitiminde çok önemlidir (Aydın, 2011). Yeni Zelanda‘da 11 yaĢ grubundaki öğrencilerin seçtikleri dersler hakkında bir araĢtırmada öğrencilere, velilere ve okuldaki öğretmenlere bu yaĢ grubu için almaları gereken dersler sorulmuĢtur. AraĢtırma sonucunda her üç grubun da üzerinde özellikle durdukları dersler matematik ve Ġngilizce olmuĢtur. Öğrencilere dersleri seçmedeki önemli faktörler sorulduğunda eğlenceli olması, daha önce o dersten aldıkları güzel notlar, baĢarmayı istemek, iyi bir iĢ sahibi olmak cevapları alınmıĢtır. En az etkili faktörler ise kariyer planlayıcısının ve ailelerin önerisi olarak belirlenmiĢtir (Hipkins ve Vaughan, 2002). Bu araĢtırma, öğrencilerin ders seçimlerinde eğlenceli olma kriterinin öncelikli olduğunu göstermiĢtir.
Hayatın hemen hemen her aĢamasında karĢımıza çıkmasına rağmen matematik, okulda korkulan dersler sıralamasında ön sıralarda yer almaktadır. Matematik korkusu ve kaygısı, öğrenmeyle iliĢkilidir ve öğrenciliğin ilk yıllarından itibaren baĢlamaktadır (ġahin, 2004). YaĢadıkları korku ve endiĢe öğrencilerin akademik baĢarılarını da olumsuz etkileyebilmektedir. Bu yüzden bu korkuyu ortadan kaldıracak ya da en aza indirecek Ģekilde ders iĢlenmelidir. Öğrenciler, renkler ve Ģekillerle beraber matematik dersi iĢlendiğinde, matematiğe karĢı olan korku ve endiĢeden belki de farkında olmadan kurtulma imkânı bulacaklardır. Sadece sayı ve formüllerle değil; kesip yapıĢtırabilecekleri, boyama yapabilecekleri zihinsel aktivitelerle birlikte psikomotor becerilerini de kullanabilecekleri, görsel sanatlarla desteklenmiĢ bir matematik dersi özellikle ortaokul seviyesindeki öğrenciler için çok daha istekli katılacakları bir ders ortamı oluĢturacaktır. Matematiğe gönül vermiĢ insanların çoğu matematiği bir sanat olarak görmektedirler. Onlara göre matematikte önemli olan yapılan iĢin derinliği, kullanılan yöntemlerin estetik değeri ve matematiğin kendi içinde bir iĢe yaramasıdır (Bilim Teknik, 2007). Bu tanımı kabul eden insanlar matematiği seven ve bu yüzden de matematiğin güzel yönlerini görenlerdir.
12
2.2. DönüĢüm Geometrisi
Ortaokul matematik öğrenme programında yer alan öğrenme alanları; sayılar ve iĢlemler, cebir, geometri ve ölçme, veri iĢleme ve olasılıktır (MEB, 2013, s. 10). Yenilenen ilköğretim matematik programında, özellikle geometri alanında, bazı konular ilk kez daha çok öne çıkarılmıĢtır. Örneğin, örüntü ve süslemeler, fraktallar, dönüĢüm geometrisi (öteleme, dönme, yansıma, ötelemeli yansıma) ve izdüĢüm (perspektif) matematik programı içinde geometri alanında daha çok ön plana çıkan kavramlar arasındadır (Faydacı ve Zimbat, 2012).
Bu araĢtırmanın yapıldığı 7. Sınıf seviyesinde dönüĢüm geometrisi alt öğrenme alanında öteleme ve yansıma dönüĢümleri derinlemesine incelenmektedir. DönüĢüm geometrisi dönme kavramı ile devam etmektedir (MEB, 2013, s. 93).
Uygulandığında Ģeklin özelliklerini değiĢtirmeyen dönüĢüm, simetri olarak tanımlanmaktadır (Leikin, Berman ve Zaslavsky, 1997). Aynı zamanda düzlemdeki tüm noktaları yine düzlemde noktalara dönüĢtüren ve simetri doğrusuna göre noktalar arasındaki uzaklığı koruyan bir dönüĢüm olarak da belirtilebilen yansıma, birebir ve örten bir fonksiyon olarak da tanımlanabilir (Zembat, 2007). Köse ve ÖzdaĢ (2009), simetri kavramı ile ilgili yaptıkları çalıĢmada, öğrencilerin simetri doğrusu ile ilgili cevaplarını incelemiĢlerdir. Öğrencilerin, ―uyum‖, ―aynılık‖, ―yansıma‖, ―aynısını tekrarlama‖, ―birbirine benzeme‖, ―ters dönmüĢ halleri‖ gibi çeĢitli sözel ifadeler kullanmalarının yanı sıra― ortadan böldüğümüzde, katladığımızda‖, ―bir Ģekli ortadan ikiye böldüğümüzde iki tarafta da aynı Ģekillerin olması ve eĢit Ģekillerin olması‖ gibi açıklamalarda bulunmaları onların simetri doğrusunun farkında olduklarının bir göstergesi kabul edilmiĢtir.
Simetri kavramında öğrencileri en çok zorlayan, simetri doğrusunun konumu değiĢtiğinde Ģeklin simetrisini almaktır. Sekizinci sınıf öğrencilerinin, dikey ve yatay konumda olan bir doğruya göre Ģeklin simetriğini, eğik konumdaki doğruya göre daha yüksek bir oranda doğru bir biçimde aldıkları görülmüĢtür. Aynı çalıĢmada öğrencilerin simetriyi öteleme gibi algılayıp dönüĢümü buna göre yaptıkları için zorluk çektikleri de tespit edilmiĢtir (Köse, 2012).
Öteleme konusunda çok fazla problem yaĢamayan öğrenciler dönme kavramında zorlanmaktadırlar. Kaplan ve Öztürk‘ün (2014) yaptıkları araĢtırma, dönme simetrisinde öğrencilerin karĢılaĢtıkları zorlukları ortaya koymuĢtur. Yapılan araĢtırmada öğrencilerin Ģekli bir bütün olarak döndürmeye çalıĢtıkları, döndürmede bir referans noktası belirleyip
13
bu noktaya göre Ģekli döndüremedikleri tespit edilmiĢtir. ġeklin bütünlüğünü koruyamayıp dönmede geometrik Ģeklin iç açısını dönme açısı olarak algılayan öğrencilerin, dönmede dönme yönünü Ģekle göre belirlemek gibi bir yanılgı içerisinde oldukları görülmüĢtür. Öğrencilerin dönme sonucu oluĢan Ģekli, bütün noktalarını taĢıyıp doğru parçalarıyla birleĢtirmek yerine tek noktaya göre taĢıyıp sonra Ģekli çizmekten kaynaklı hatalar yaptıkları gözlemlenmiĢtir.
ġekil 1‘de dekoratif biçimde yazılan ―A‖ harfinin saat yönünde ve saat yönünün tersinde belli açılarla döndürülerek elde edilen simetrileri gösterilmiĢtir.
ġekil 1. Dönme simetrisi ―A‖ harfi örneği (Field ve Golubitsky, 2009, s. 46)
Simetri dendiğinde çoğunlukla yansımayı düĢünen öğrenciler, dönme simetrisi kavramını anlamakta ve uygulamakta zorluk yaĢadıklarından yukarıdakine benzer etkinliklerde
14
verilen Ģekli istenilen açılarda döndürememektedir. Bunun en büyük sebeplerinden biri de kareli kağıt ya da koordinat sistemi kullanılmadığından öğrencilerin yönü ve açıyı algılayamamalarıdır.
2.3. Örüntü ve Süslemeler
Geometri, günlük hayatta kullanılarak birçok yarar sağlamasına rağmen ilkokuldan itibaren öğrenciler geometriyi sevmemekte, geometriden korkmakta ve bu derste baĢarısız olmaktadırlar (Karadeniz ve Akar, 2014). Bu korkuyu ve buna bağlı baĢarısızlığı ortadan kaldırmak için öğrencilerin matematiksel düĢünce biçimlerini bilerek buna göre yaklaĢımlar geliĢtirmek gerekmektedir. Matematiksel olayları açıklamada olduğu gibi anlamada da birçok yol bulunmaktadır. Örneğin bazı insanlar taslak ya da grafiği çizerek; bazıları yapılar, örüntüler ve formüller arasındaki iliĢkiyi araĢtırıp uygulayarak öğrenir. Bu da bize birden fazla düĢünme Ģekli olduğunu göstermektedir. Matematiksel düĢünme biçimlerini Burton (1999) aĢağıdaki gibi sınıflandırmıĢtır.
Stil A: Görsel (resimlerde veya canlı düĢünme)
Stil B: Analitik (sembolik veya kurallaĢtırıcı düĢünme) Stil C: Kavramsal (kavramsal düĢünmek veya sınıflandırma)
Bu düĢünce stillerinden özellikle stil A ve stil B matematiksel düĢünme biçimleri, geometri öğrenme alanının alt öğrenme alanı olan örüntü ve süslemeler de kullanılabilmektedir. Süsleme ve örüntü birbirinden farklı kavramlardır. Belirli bir kuralı takip eden Ģekil veya sayı dizileri örüntü olarak adlandırılırken; süsleme, Ģekiller arasında hiç boĢluk kalmayacak ya da kullanılan Ģekiller üst üste binmeyecek biçimde Ģekillerin tekrar etmesiyle bir yerin ya da yüzeyin kaplanması olarak tanımlanmaktadır (Billstein, Libeskind ve Lott, 2004). Süslemeler, geometrik Ģekillere dönüĢüm geometrisi alt öğrenme alanında verilen öteleme, dönme, yansıma ve ötelemeli yansıma hareketlerinden biri ya da birkaçı kullanılarak oluĢturulmaktadır. Süsleme, ilköğretim düzeyinde geometrik Ģekillerden yararlanılarak gerçekleĢtirilmektedir. Bu nedenle, öncelikle süsleme yardımı ile geometrideki estetiğin öğrenciler tarafından fark edilmesi amaçlanmaktadır (Kılıç, Köse, TanıĢlı ve ÖzdaĢ, 2007). Süslemeler, kullanılan çokgen çeĢitlerine göre düzenli, yarı düzenli ve düzensiz süslemeler olmak üzere üç gruba ayrılmaktadır. Tablo 1‘de süsleme çeĢitleri, özellikleri ve bu süsleme çeĢitlerine birer örnek gösterilmiĢtir.
15 Tablo 1. Süsleme ÇeĢitleri
Süsleme ÇeĢidi Özelliği Örnek
Düzenli Süsleme
Sadece kare, eĢkenar üçgen ve düzgün altıgen olmak üzere üç düzgün çokgenden
yalnız biri kullanılarak oluĢturulabilir.
Yarı Düzenli Süsleme
Birden fazla farklı düzgün çokgenler bir arada kullanılarak oluĢturulabilir.
Düzensiz Süsleme
Düzgün olmayan çokgenler (kenar uzunlukları ve iç
açıları eĢit olamayan) kullanılarak oluĢturulabilir.
Düzgün çokgenler kullanılarak oluĢturulan düzenli ya da yarı düzenli süslemelerin kodları bulunmaktadır. Bu kodlama, her köĢede birleĢen düzgün çokgen sayısı ile bunların kenar sayıları kullanılarak yapılmaktadır. Bir süslemenin kodu, köĢe noktası etrafındaki istenilen bir çokgenden baĢlanarak çokgenlerin kenar sayılarının arasına ―;‖ konularak gösterilmektedir. Süsleme yapılabilmesi için her bir köĢede oluĢan açıların ölçüleri toplamının 360o
16
ġekil 2. Düzenli süsleme örneği
ġekil 2‘de gösterilen düzenli süsleme, eĢkenar üçgenler kullanılarak oluĢturulmuĢtur. Seçilen nokta etrafında toplam 6 üçgen olduğundan bu süslemenin kodu (3; 3; 3; 3; 3; 3) Ģeklinde gösterilmektedir. Her bir üçgenin iç açısı 60o
olduğundan gösterilen köĢede birleĢen çokgenlerin açıları toplamı 60o
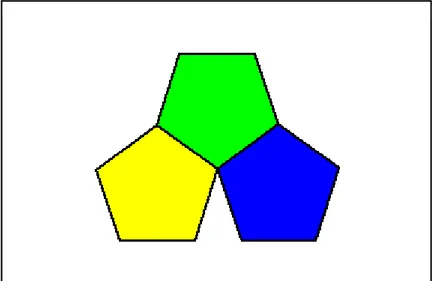
+ 60o+ 60o+ 60o+ 60o+ 60o=360o olmaktadır. Her düzgün çokgenle düzenli süsleme oluĢturmak mümkün değildir. AĢağıdaki Ģekilde düzgün beĢgenler süsleme oluĢturmak için bir araya getirilmiĢtir. Her birinin iç açısı 108o olduğundan köĢedeki açıların toplamı 360o
değil 324o olmaktadır. Verilen bir örüntünün süsleme olabilmesi için arada boĢluk kalmaması gerekmektedir. ġekil 3‘te gösterildiği gibi düzgün beĢgen kullanılarak düzenli süsleme oluĢturulamaz.
17
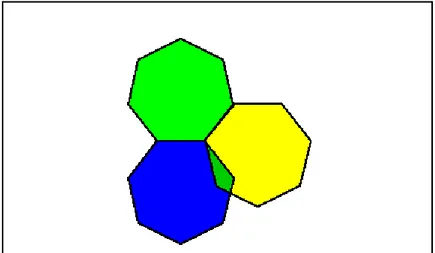
Benzer Ģekilde düzgün yedigenler kullanılarak da düzenli bir süsleme oluĢturmak mümkün değildir. ġekil 4‘de görüldüğü gibi Ģekiller üst üste bindiği için süslemeden bahsedilemez.
ġekil 4. Düzgün yedigenler
ġekil 5‘te gösterilen yarı düzenli süsleme, eĢkenar üçgen ve düzgün altıgen kullanılarak oluĢturulmuĢtur. Bir süslemenin kodu seçilen nokta etrafındaki istenilen çokgenden baĢlanarak bulunabilmektedir. Altıgenden baĢlanarak kod (6; 3; 6; 3) veya üçgenden baĢlanarak (3; 6; 3; 6) olarak gösterilebilmektedir. EĢkenar üçgenin bir iç açısı 60o
ve düzgün altıgenin bir iç açısı 120o
olduğundan gösterilen köĢede birleĢen çokgenlerin açıları toplamı 60o
+ 120o+ 60o+ 120o=360o olmaktadır.
18
ġekil 6‘da gösterildiği gibi çokgenler dıĢında farklı Ģekiller kullanılarak da süsleme yapılabilmektedir. Ancak 7. sınıf matematik öğretim programındaki kazanımlar ―çokgensel bölge modelleriyle bir bölgeyi döĢeyerek süsleme yapar‖ ve ―düzgün çokgensel bölge modelleriyle oluĢturulan süslemelerdeki kodları belirler‖ Ģeklinde olduğundan bu araĢtırmada sadece çokgenler kullanılarak oluĢturulan süslemeler ele alınmıĢtır.
ġekil 6. KarmaĢık desenli süsleme (Field ve Golubitsky, 2009, s. 45)
2.4. Matematik ve Sanat
Tarihte gerçek hayat tanımlanırken matematik ve sanat zıt kutuplarda bulunan iki alan olmasına rağmen hem matematikçiler hem de sanatçılar kullanıĢsız, ilginç ve alıĢılmadık Ģeylerle uğraĢan garip insanlar olarak görülüyordu. Ancak eski yunan tarihine bakıldığında sanat eserlerinde matematiğin kullanıldığı dikkati çekmektedir (Velichova, 2010). G. H. Hardy‘nin Bir Matematikçinin Savunması ve Jerry P. King‘in Matematik Sanatı isimli kitaplarında matematiğin aslında bilimden çok sanata yakın olduğuna vurgu yapılmaktadır (Kum, 2003).
Sanat, en basit tanım ve deyimle; bir form meydana getirebilme yetenek ve becerisidir. Sonsuz sayıda değiĢik ve değiĢen formlar üreten doğa karĢısında insan, yetenek ve becerisi ile değer kazanabilmekte ve bir ölçüde de yaratıcı olabilmektedir (Üstüner, 2007).
19
Matematik ve sanat arasındaki iliĢki bundan 30-35 yüzyıl öncesi buzul çağından baĢlamaktadır aslında. O dönemde yaĢayan insanlar, mağara duvarlarına çizdikleri hayvan figürleri ve çeltiklerle sayı grupları oluĢturarak saymadan çoklukları ayırt edebilmiĢlerdir. Buzul çağının ardından M.Ö. 3000-2000 yılları arasında Mezopotamya‘da Nil Nehri‘nin sularının taĢmasıyla insanların tarlaları arasındaki sınırlar kaybolmaktaydı. O zamanlar için çok kıymetli olan bu arazilerde sınırları tekrar tekrar belirlemek çok zor ve zahmetliydi. Her su taĢkınından sonra sınırları belirlemekle görevli insanlar gelir ve gerekli ölçümleri yaptıktan sonra sınırları tekrar çizmekteydi. Heredot‘a göre geometri, bu ölçümler sonucunda oluĢmaya baĢlamıĢtır (Özder, 2008). M.Ö. 596-500 yılları arasında yaĢayan ve sayıların babası olarak anılan Pisagor, döneminde yaptığı birçok matematiksel çalıĢma ile hala tüm dünyada saygın matematikçiler arasında gösterilmektedir. Pisagor teoreminin sahibi olan matematikçi, adını kendi öğrencilerini yetiĢtirdiği okula da vermiĢtir. Matematik, fizik, felsefe, astronomi ve müzik alanında yenilikler yapmak isteyen Pisagor‘un okulu, dönemin dini inanç ve siyasetine ters düĢtüğü iddiası ile halk ayaklandırılarak yakılmıĢtır. Okulun yakılmasıyla Pisagor ve öğrencilerinin yaptığı birçok Ģey yanarak yok olmuĢtur. Ancak matematikçinin müziğe olan ilgisi bilinmektedir. Bir gün demirciler çarĢısından geçerken, demircilerin çıkardıkları sesler dikkatini çeker. Dikkatli bir Ģekilde sesleri dinlediğinde bir sesin tüm ahengi bozduğunu fark eder. Demircilerle konuĢarak demir dövdükleri çekiçleri alıp diğerlerinden farklı ses çıkararak ahengi bozan çekici bulmak ister. Eve getirdiği çekiçleri tek tek tarttığında, tüm çekiçlerin ağırlıklarının belli bir düzene göre arttığını, ağırlıklarının bir sayı örüntüsü oluĢturduğunu bulur. Ahengi bozan sesi çıkaran çekicin ağırlığı, bu sayı örüntüsüne de uymamaktadır. Bu matematiksel buluĢu müzik için önemli bir adım olmuĢtur. Telli çalgılarda tellerin uzunluğu ile çıkan sesleri inceleyerek matematik ile müziği birleĢtiren çalıĢmalar yapmıĢtır (Türkmen, 2008). Tüm bunlar matematik ile sanat arasındaki iliĢkinin çok eski zamanlara dayandığını ve aslında bu iliĢkinin doğal olarak var olduğunu göstermektedir.
Hickman ve Huckstep (2003), matematik ve sanatın etkileĢim içerisinde olduğunu söylemektedir. Geometri, topoloji, olasılık, mantık baĢta olmak üzere matematiğin pek çok dalı sanat çalıĢmalarında doğal olarak kullanılmakta, sanatçıya yol göstermektedir. Genel olarak matematiğin felsefesi ve evrendeki yaĢama yaklaĢımı da tüm sanatların baĢlı baĢına temelini oluĢturmaktadır. Bu da, matematiğin bağımsız olarak bir sanat gibi değerlendirilebileceği sonucunu ortaya çıkarmaktadır (Cereci, 2012).
20
Son yıllarda özellikle fraktallar konusu sanatta büyük ilgi görmekte ve bilgisayar tabanlı çizimlerde kullanılmaktadır. Maurits Cornelis Escher (1898-1972) algoritmik resimler yapan ama bunları bilgisayar kullanarak değil el ile oluĢturan geleneksel bir sanatçıdır (Velichova, 2010). Mimarlık eğitiminin ardından grafik eğitimi alan Escher, eğitiminin ardından Ġtalya‘ya gidip burada evlenmiĢtir. Ġspanya seyahatine çıkan sanatçı, Al-Hamra Sarayından çok etkilendiği için eĢi ile birlikte sarayı sık sık gezerek saray ile ilgili çalıĢmalar yapmıĢtır. BaĢta Al-Hamra Sarayı ve Ġslam sanatı olmak üzere, Ġtalyan sanatından çok etkilenen Escher, incelediği eserlerdeki çini ve fayansların çizimlerini yaparak çalıĢmıĢtır. Matematiğin; topoloji, permütasyon teorisi, geometri, stereometri (katıların hacim ve boyutlarını ölçme bilimi) gibi özel alt dalları ile uygulanması son derece zor olan çeĢitli baskı tekniklerini kullanarak ortaya çıkardığı eserlerinde, evrene bakıĢ açısını izleyebildiğimiz nadir sanatçılardan olan M. C. Escher, baskı ressamları ve özellikle matematikçiler için bir ekoldür. Escher, bir hikâye anlatmak için resimleri ―Metamorfoz‖ serilerinde kullanmıĢtır. Bu tasarımlar, Escher‘in birçok yeteneğini bir araya getirmekte ve yumuĢak geçiĢler serisinin düzlem üzerindeki düzenli bir objeye uygulanması ile baĢka bir objeye dönüĢmesini göstermektedir (Ġlter, 2003).
ġekil 7. Metamorfoz (Escher, 1937)
Escher tüm zamanların entelektüel açıdan en önemli uyarıcı çizimlerin yaratıcısıdır. Bunların çoğunun kaynağında paradoks, yanılsama ya da çifte anlam vardır. Escher‘in çizimlerinin hayranları arasında ilk sırayı matematikçiler alır; çizimleri çoğunlukla simetri veya örüntü gibi matematik ilkelerine dayandıkları için bu oldukça anlaĢılabilir durumdur (Portakal, 2011).
Programa eklenen geometri öğrenme alanındaki örüntü ve süslemeler ile eĢlik ve benzerlik alt öğrenme alanları, programda belirtilen ―matematik ve sanat iliĢkisini kurabilecek, estetik duygular geliĢtirebilecektir‖ Ģeklindeki matematiğin genel amaçlarına hitap etmektedir (Delil ve GüleĢ, 2007). Aynı zamanda öğrencilerin matematiğe karĢı
21
tutumlarını olumlu yönde geliĢtireceği de düĢünülen bu öğrenme alanlarında Escher‘in çalıĢmalarından faydalanılabilir. Bilindiği gibi çokgenler kullanılarak süsleme oluĢturulabildiği gibi çokgenler dıĢında farklı Ģekiller kullanılarak da süslemeler oluĢturulabilmektedir. ġekil 8‘de gösterilen resimde Escher, çokgensel bölgeleri kullanarak elde ettiği balık ve kuĢ figürleri ile düz bir zemini hiç boĢluk kalmayacak Ģekilde döĢemiĢtir. Kullanılan Ģekiller üst üste binmediği için bu resim, matematikte çokgenler dıĢında baĢka Ģekiller kullanılarak oluĢturulan süslemelere örnektir.
ġekil 8. Balık / KuĢ (Escher, 1967)
Escher 1923 yılında, Haag adlı bir Alman matematikçinin kaleme aldığı bir makale üzerinde yaptığı çalıĢmalarla; düzlemin düzenli bölüntülenmesinin matematikçiler tarafından nasıl tanımlandığı ve bir dıĢbükey yüzeyin küçük çemberlerin yardımı ile düzenli motiflerle nasıl bölüntüleneceği hakkında önemli bilgilere ulaĢmıĢtır. Edindiği bu
22
bilgilerin ıĢığı altında yaptığı çalıĢmalarda önemli aĢama kaydettiği görülen sanatçı bir süre sonra matematikte ulaĢtığı yeni kapı aracılığıyla kristalografiye giriĢ yapmıĢtır (Kızıltepe, 2011).
ġekil 9. Çember limit IV (Escher, 1960)
Escher, düzgün çokgenlerin üzerine motifleri çizerek eserlerini oluĢturmuĢtur. Genelde üçgen, kare ve altıgen kalıpları kullanan sanatçı, iki boyutlu süslemelerden 3 boyutlu
23
resimler ortaya çıkarmıĢtır. Tablo 2‘de Escher‘in kullandığı kalıplar ve oluĢturduğu resimler gösterilmiĢtir.
Tablo 2. Düzgün Çokgenler ve Escher Resimleri
(EĢkenar Üçgen)
(Düzgün Altıgen)
(Kare)
Escher gibi matematik ve sanatı birlikte kullanan pek çok sanatçı, sanat içinde matematiğin matematik içinde de sanatın olduğunu göstermiĢtir.
24
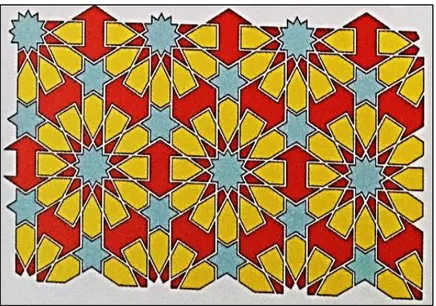
Ġslam dininde insan ve hayvan tasvirinin geçmiĢte yasaklanmıĢ olması, ayrıca hendese (geometri) bilimine verilen önem, süsleme sanatında geometrik Ģekillerin ağırlıklı olarak kullanılmasına yol açmıĢtır (Arık ve Sancak, 2007, s. 91). Abas (2001) yaptığı çalıĢmada Ġslami sanat eserlerinde bulunan simetri örneklerini incelemiĢtir. Ġslami süslemelerde genelde geometrik Ģekiller tercih edildiğini söyleyen Abas, bunlar arasında yıldız figürünün çok önemli bir değere sahip olduğunu belirtmiĢtir. Yapılan bu araĢtırmada, En‘am Suresi 97. ayet (O, karanın ve denizin karanlıklarında yolunuzu bulmanız için size yıldızları yaratandır. Bilen bir kavim-topluluk için Biz ayetleri geniş geniş (yeterince) açıkladık) ıĢığında, birçok cami çini ve halılarında yıldız figürünün kullanıldığı örneklerle gösterilmiĢtir. ġekil 10‘da Ġslami süslemelere ait bir örnek verilmiĢtir. Yıldız figürünün kullanıldığı bu süslemede, yansıma simetrisi ve dönme simetrisinin kullanıldığı görülmektedir.
ġekil 10. Ġslami süsleme örneği
Kaplan (2000), çalıĢmasında Ġslami süslemelerde kullanılan figürleri incelemiĢtir. ġekil 11‘de sekizgen kullanılarak oluĢturulabilen yıldız figürleri gösterilmiĢtir.
25
ġekil 11. Sekizgen kullanarak oluĢturulan yıldız figürleri
Sekizgen dıĢında düzgün bir çokgen olan kare kullanılarak da süsleme oluĢturulduğunu gösteren Kaplan (2000), özellikle ahĢap üzerinde kabartma Ģeklinde duran süslemeleri incelemiĢtir. ġekil 12‘de aynı taslak kullanılarak oluĢturulan bir süslemenin aĢamaları gösterilmiĢtir. Bunlardan son figür, 3 boyutlu bir görünüme sahiptir.
ġekil 12. Dama tahtası süsleme figürü
Arık ve Sancak (2007, s. 91)‘ın belirttiği üzere ―Orta Asya‘dan Türkler tarafından getirilmiĢ geometrik Ģekillerle, Ġslam kültürünün birleĢimi sonucu ortaya çıkan Selçuklu yapılarındaki geometrik süslemeler, zamanına göre çok ileri ve etkileyici güzelliktedir‖. ġekil 13‘te Selçuklu zamanında tek karo kullanılarak yapılan süslemelere örnekler gösterilmiĢtir. Yan yana gelen karoların aynı renkte olmaması için iki ya da üç rengin yeterli olduğu bu süslemelerde geometrik motifler dikkat çekmektedir.
Düz Ana
26
ġekil 13. Selçuklu zamanı süsleme örneği-1, Kayseri - Aksaray Sultan Hanı, 1229 (Arık ve Sancak, 2007, s. 92)
Yukarıdaki Ģekilde Kayseri – Aksaray Sultan Hanı‘nda yer alan süsleme örneği verilmiĢtir. Sadece tek bir karo kullanılarak öteleme, yansıma ve dönme simetrileri uygulanarak Ģekildeki süsleme elde edilmiĢtir. ġekil 14‘te 1217 yılında Sivas‘ta yapılan Ġzzettin Keykavus Kümbetinden alınan süsleme örneği gösterilmiĢtir. Üç farklı renk kullanılarak süsleme renklendirilmiĢ böylece yan yana gelen karoların aynı renk olması engellenmiĢtir.
ġekil 14. Selçuklu zamanı süsleme örneği-2, Sivas – Ġzzettin Keykavus Kümbeti, 1217 (Arık ve Sancak, 2007, s. 92)
27
Arık ve Sancak (2007, s. 94)‘ın belirttiği üzere, ―Selçuklu döneminde tek karo kullanılarak süslemeler yapılmıĢtır. Beni Nasr ya da Beni Ahmer Devleti (1232-1492) olarak bilinen Ġspanya‘daki Ġslam devleti zamanında yapılmıĢ olan El Hamra Sarayı‘nda kullanılan bu tür geometrik süslemelerle Selçuklu döneminde kullanılmıĢ olan geometrik süslemeler büyük benzerlik göstermektedir‖. ġekil 15‘te gösterilen ilk süsleme Ġspanya‘daki El Hamra Sarayı‘ndan, ikinci süsleme ise Amasya‘da bulunan Halifet Gazi Türbesi‘nden alınmıĢtır. Ġki süslemenin birbirine benzerliği dikkat çelmektedir.
ġekil 15. Selçuklu zamanı süsleme örneği-3, Ġspanya – El Hamra Sarayı, 1338-90 (Arık ve Sancak, 2007, s. 94)
ġekil 16. Selçuklu zamanı süsleme örneği-4, Amasya – Halifet Gazi Türbesi, 1145 (Arık ve Sancak, 2007, s. 94)
28
Dunham (2001), araĢtırmasında Ġspanya‘nın Granada kentinde bulunan El Hamra Sarayı‘nın süslemelerini incelemiĢtir. Saraydaki Ġslami süsleme örneklerini Euclidean (Öklidyen) düzleme uygulayarak yeni süslemeler elde etmiĢtir. Düzlemsel bir bölgeden küresel bir bölgeye uygulanan süsleme örnekleri ġekil 17‘de gösterilmiĢtir.
ġekil 17. El Hamra Sarayından düzlemsel ve hiperbolik süsleme örnekleri
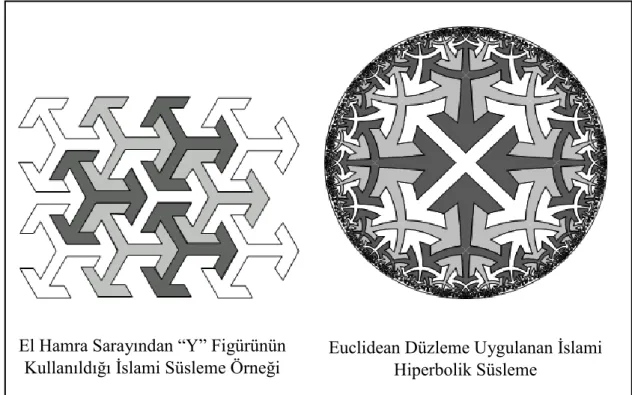
Ġslami süslemelerde genellikle spiral, anahtar, yıldız ve ―Y‖ figürlerinin sürekli tekrarlanarak kullanıldığını belirten Dunham (2001), bu süslemeleri ―tekrarlayan örüntüler‖ olarak isimlendirmiĢtir. Sürekli tekrar eden geometrik Ģekle motif diyen araĢtımacı, Ġslami süslemelerde geometrik Ģekiller dıĢında çiçek ve asma gibi arabesk desenlerin de kullanıldığını söylemiĢtir. ġekil 18‘de El Hamra Sarayı‘nada alınan ―Y‖ figürünün kullanıldığı süsleme örneği ve bunun hiperbolik düzlemdeki uygulaması gösterilmiĢtir.
El Hamra Sarayından Ġslami Süsleme Örneği
Euclidean Düzleme Uygulanan Ġslami Hiperbolik Süsleme
29
ġekil 18. ―Y‖ figürünün kullanıldığı düzlemsel ve hiperbolik süsleme örnekleri Ġslam ve Selçuklu süsleme sanatında çok kollu yıldızlar en fazla kullanılan geometrik Ģekillerdendir. Çok kollu yıldızlar ve bunları birbirine bağlayan diğer karolar kullanılarak pek çok süsleme yapılmıĢtır (Arık ve Sancak, 2007, s. 96). AĢağıdaki Ģekillerde Selçuklu zamanında yapılan eserlerde kullanılan süslemeler gösterilmiĢtir.
ġekil 19.Selçuklu zamanı süsleme örneği-5, Konya – AkĢehir, Seyyid Mahmut Hayrani Türbesi, 1268 (Arık ve Sancak, 2007, s. 94)
El Hamra Sarayından ―Y‖ Figürünün Kullanıldığı Ġslami Süsleme Örneği
Euclidean Düzleme Uygulanan Ġslami Hiperbolik Süsleme
30
ġekil 20. Selçuklu zamanı süsleme örneği-6, Amasya, Gök Medrese, 1276 (Arık ve Sancak, 2007, s. 94)
ġekil 21. Selçuklu zamanı süsleme örneği-7, Karaman, Ġbrahim Bey Ġmareti, 1433, Karaman Beyliği (Arık ve Sancak, 2007, s. 94)
Sanat eserlerinin süslenmesinde Osmanlı da geometrik Ģekilleri çok sık kullanmıĢtır. AĢağıdaki Ģekillerde, Selçukludan kalan süsleme tekniğini miras kabul edip geliĢtiren Osmanlı Ġmparatorluğu zamanında yapılan eserlerde kullanılan süslemelere örnekler gösterilmiĢtir.
31
ġekil 22. Süleymanname süsleme örneği, 1517 (Arık ve Sancak, 2007, s. 100)
ġekil 23. Edirne, Selimiye Camii süsleme örneği-1, 1568-1574 (Arık ve Sancak, 2007, s. 100)
ġekil 24. Edirne, Selimiye Camii süsleme örneği-2, 1568-1574 (Arık ve Sancak, 2007, s. 100)
32
ġekil 25. 12 ve 15 kenarlı yıldız içeren süsleme örneği
ġekil 25‘te gösterilen süslemede 12 ve 15 kenarlı yıldızlar kullanılmıĢtır. Ġslami süslemelerde çok sık karĢılaĢılan bu süsleme örneğindeki 12 kenarlı yıldızı oluĢturma aĢamalarını Aljamali ve Banissi (2004), ġekil 26‘daki gibi görselleĢtirmiĢlerdir.
ġekil 26. 12 kenarlı yıldızı oluĢturma aĢamaları
1. AĢama 2. AĢama 4. AĢama 5. AĢama
Grid-1: Dörtgenler
Grid-2: Altıgenler
33
Ġslami eserlerde benzer desenlerin sürekli kullanıldığı görülmektedir. ġekil 27‘de Özbekistan‘da bulunan bir camiinin süslemesi gösterilmiĢtir. Ana çerçevesini sekizgenin oluĢturduğu süslemede yıldız figürleri dikkat çekmektedir (Field ve Golubitsky, 2009, 85).
ġekil 27. Özbekistan‘da bulunan bir camiinin süslemesi (Field ve Golubitsky, 2009, s. 85)
Field ve Golubitsky (2009, s. 86)‘ın belirttiği üzere ―Ġslami eserlerde kullanılan simetrik örüntülere en güzel örnekler özellikle Kur‘an-ı Kerim‘de bulunan dekoratif sayfalarda dikkat çekmektedir‖. ġekil 28‘de 1310 yılında Ali ibn Muhammed ibn Zayd ‗Alavı al-‗Husayni tarafından çizilen, Kur‘an-ı Kerim‘in ön sayfasında yer alan süsleme gösterilmiĢtir. Süslemede altıgen kafesler kullanılarak oluĢturulan karıĢık desenler yer almaktadır.
34
ġekil 28. 1310‘da çizilen Kur‘an-ı Kerim süslemesi (Field ve Golubitsky, 2009, s. 86) Yapılan bu araĢtırmalar, günlük hayatta karĢımıza süsleme olarak çıkan dekoratif motiflerin aslında matematik kullanılarak oluĢturulduğunu göstermektedir. Matematik ve günlük hayat arasındaki iliĢkiyi gösteren örneklerden biri de çok sık karĢılaĢtığımız yer ya da duvar karolarıdır. Yan yana dizilerek süslemeye güzel örnekler oluĢturan karolarda simetrinin hemen hemen her çeĢidine rastlamak mümkündür. AĢağıda Ģekil 29 ve Ģekil 30‘da bu karo örnekleri gösterilmiĢtir.
35
ġekil 29. Yer karosu örneği-1 (Field ve Golubitsky, 2009, s. 80)
ġekil 30. Yer karosu örneği-2 (Field ve Golubitsky, 2009, s. 80)
Bir çok tarihi eserin üzerinde, camilerde ya da sarayların duvarlarında bulunan süslemeler, rastgele oluĢturulmuĢ motifler değil, matematiğin sanat ile iç içe olduğunu gösteren somut
36
örneklerdir. Birçok kiĢinin eğitim almadan dahi oluĢturabildiği pekçok resim, simetri çeĢitlerini içinde barındıran ve sık karĢılaĢtığımız çalıĢmalardır. ġekil 31 ve Ģekil 32‘de keçeli kalemler ve tahta kalemi kullanılarak araĢtırmacı tarafından çizilen iki farklı desen örneği gösterilmiĢtir. Bu desenler yansıma simetrisi, öteleme simetrisi ve dönme simetrisi içermektedir.
ġekil 31. AraĢtırmacı tarafından çizilen desen - 1
37
Matematiğin sanat üzerindeki bir çok uygulaması ―matematik ne iĢime yarayacak?‖ sorusuna da verilebilecek en güzel cevaplardandır. Bu soruya verilecek cevaplara doğada da rastlamak mümkündür. Sadece dört iĢlmeden ibaret olmayan matematiğin karĢımıza çıkan en güzel örneklerinden biri de bir fotoğraf sanatçısının objektifinden yansıyan kar tanesinin fotoğrafıdır. ġekil 33‘te gösterilen fotoğrafta, dönüĢüm geometirisi alt öğrenme alanının kazanımlarından olan öteleme simetrisi, yansıma simetrisi ve döndürme simetrisini görmek mümkündür.
38
2.4.1. Altın Oran
Altın oran, özellikle çeĢitli bilim dallarında, mimari ve sanatsal alanlarda yararlanılan, belirli bir tutarlılık üzerine kurulu parçalar arasındaki uyumu yansıtan geometrik ve sayısal değerlere verilen isimdir. Ġlk kez Mısırlılar ve Yunanlar tarafından mimari yapılarda, heykellerde ve diğer sanatsal alanlarda kullanılmıĢtır. Temel olarak bölünen bir bütünün yan yana getirilen iki parçasının diğer büyük parçayı oluĢturması prensibine dayanan altın oranın sayısal değeri 1,618'dir (Duru ve ĠĢleyen, 2005).
ġekil 34. Altın oran
Altın Oran, varlığı kayıtlı tarihe göre M.Ö. 8000‘lere kadar uzanan, bilimsel olarak günümüzden yaklaĢık 2300 yıl önce ele alınmıĢ, bugünkü adı ile de yaklaĢık 1500 yıldır anılan bir fenomendir. Tarih, geçen bunca zaman boyunca bilinçli ve bilinçsiz kullanımlarına Ģahit olmuĢ, fakat 16. yüzyıldan itibaren üzerinde bilimsel nitelikli araĢtırmalar ve gözlemler yapılmaya baĢlanmıĢtır (Mutver, 2007).
Sanattan doğaya, insan vücudundan mimari eserlere kadar birçok alanda karĢımıza çıkan altın oran, Fibonacci Dikdörtgenleri olarak da bilinen altın dikdörtgende de vardır ve altın oranın hesaplanmasında kullanılmaktadır.