İLKÖĞRETİM 5. SINIF
MATEMATİK DERSİNDE ÖĞRENCİLERİN PROBLEM KURMA
ÇALIŞMALARININ PROBLEM ÇÖZME BAŞARISINA ETKİSİ
YÜKSEK LİSANS TEZİ
Hazırlayan Sema FİDAN
İLKÖĞRETİM 5. SINIF
MATEMATİK DERSİNDE ÖĞRENCİLERİN PROBLEM KURMA
ÇALIŞMALARININ PROBLEM ÇÖZME BAŞARISINA ETKİSİ
YÜKSEK LİSANS TEZİ
Hazırlayan Sema FİDAN
Tez Danışmanı
Yrd. Doç. Dr. Neşe TERTEMİZ
JÜRİ ve ENSTİTÜ ONAY SAYFASI
Sema FİDAN’ ın “İlköğretim 5. Sınıf Matematik Dersinde Öğrencilerin Problem Kurma Çalışmalarının Problem Çözme Başarısına Etkisi” başlıklı tezi, 19/06/2008 tarihinde jürimiz tarafından İlköğretim Anabilim Dalı, Sınıf Öğretmenliği Bilim Dalı’nda YÜKSEK LİSANS TEZİ olarak kabul edilmiştir.
Jüri Üyeleri İmza
Üye (Danışman) Yrd. Doç. Dr. Neşe TERTEMİZ
Başkan Yrd. Doç. Dr. Leyla ERCAN
ÖNSÖZ
Matematik öğretiminde problem çözme öğretiminin yanında, matematiksel düşünmenin merkezi olarak ifade edilen problem kurma becerilerinin geliştirilmesi de önemlidir. Bu çalışmada, matematik öğretiminde problem kurma çalışmaları yapılmasının, öğrencilerin problem çözme ve problem çözme adımlarındaki (problemi anlama, plan yapma, planı uygulama, kontrol) başarılarına olan etkisi araştırılmıştır.
Araştırmamın başından sonuna kadar değerli görüş ve fikirlerinden yararlandığım, danışman hocam sayın, Yrd. Doç. Dr. Neşe Tertemiz’ e teşekkürü bir borç bilirim.
Araştırmamda bilgi ve görüşlerinden yararlandığım Dr. Mustafa Başaran ve Arş. Gör. Bülent Akbaba’ ya, istatistik çalışmalarında yardımcı olan, ölçme değerlendirme uzmanı Tülin Acar’a, Gazi Üniversitesi Sınıf Öğretmenliği Anabilim Dalı değerli öğretim üyelerine teşekkürlerimi sunarım.
Çalışmamın uygulama aşamasında yardımcı olan değerli eşim Ömer Faruk Fidan’ a, her zaman yanımda olan ve desteğini esirgemeyen anneme, babama ve kardeşim İbrahim Arpa’ ya şükranlarımı sunuyorum.
Sema FİDAN Ankara-2008
ÖZET
İLKÖĞRETİM 5. SINIF
MATEMATİK DERSİNDE ÖĞRENCİLERİN PROBLEM KURMA ÇALIŞMALARININ PROBLEM ÇÖZME BAŞARISINA ETKİSİ
FİDAN, Sema
Yüksek Lisans Tezi ,İlköğretim Sınıf Öğretmenliği Bilim Dalı Tez Danışmanı: Yrd. Doç. Dr. Neşe TERTEMİZ
Haziran -2008
Bu araştırmada, ilköğretim 5. sınıfta problem kurma çalışmaları yapılmasının, öğrencilerin problem çözme başarısı üzerindeki etkisi araştırılmıştır. Araştırmada, problem kurma çalışmalarının Polya’nın problem çözme adımlarındaki (problemi anlama, plan yapma, planı uygulama, kontrol) başarıya etkisi de belirlenmeye çalışılmıştır.
Araştırma 2007-2008 eğitim-öğretim yılında, ön test-son test kontrol gruplu deneysel desen modelinde gerçekleştirilmiştir. Araştırmada veri toplama aracı olarak, araştırmacı tarafından hazırlanan, 20 maddeden oluşan, Problem Çözme Testi kullanılmıştır.
Araştırma Afyonkarahisar ili Emirdağ ilçesindeki bir ilköğretim okulunda, iki farklı sınıfta okuyan toplam 48 5. sınıf öğrencisi ile yürütülmüştür. Araştırmada problem çözme ve kurma çalışmaları etkinlikleri, toplam 10 hafta deney grubu öğrencilerine (n=24) uygulanırken, kontrol grubunda (n=24) ise, deney grubuna uygulanan problemler çözdürülmüştür. Deney grubu öğretmeni, problem kurma uygulamaları ile yapılan matematik öğretimi konusunda sözel olarak ve öğretmen bilgilendirme dosyası hazırlanarak bilgilendirilmiştir. Araştırmanın sonucunda elde edilen verilerin analizinde t testi kullanılmıştır.
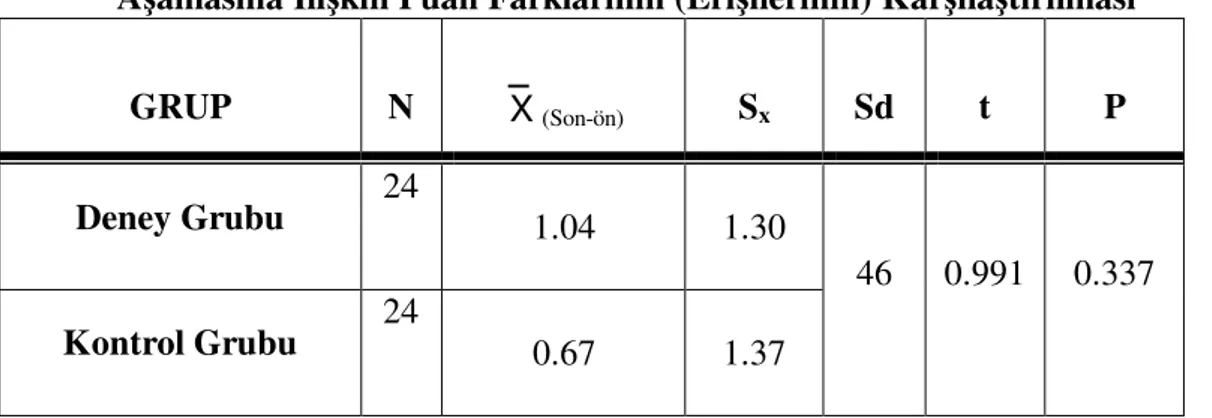
Araştırma sonucunda, deney ve kontrol grubu öğrencilerinin Problem Çözme Testi son test puan ortalamalarının, ön test puan ortalamalarından yüksek olduğu görülmektedir. Deney ve kontrol grubu ön test- son test fark puanları (erişi) karşılaştırıldığında ise deney grubu örencilerinin başarılarındaki artışın kontrol grubu öğrencilerine göre daha yüksek olduğu görülmektedir. Deney ve kontrol grubu öğrencilerinin Polya’nın problem çözme adımlarındaki erişilerinin karşılaştırılmasında ise gruplar arasında anlamlı bir farklılık görülmemiştir.
Sonuçlara bakıldığında, problem çözme ve kurma çalışmaları yapılmasının, öğrencilerin problem çözme başarılarını pozitif yönde, anlamlı düzeyde artırdığı görülmektedir.
Anahtar Kelimeler: Problem, Problem Çözme, Problem Çözme Öğretimi, Problem Kurma.
ABSTRACT
THE EFFECT OF STUDENTS’ PROBLEM POSING STUDIES ON THE SUCCESS OF SOLVING THE PROBLEMS IN MATHEMATICS LESSON AT
THE 5 th GRADE OF PRIMARY SCHOOL FİDAN, Sema
Master Thesis, Department of Primary Education Thesis Counselor: Yrd. Doç. Dr. Neşe TERTEMİZ
June-2008
In this study, the effect of the teaching method through problem posing, which is being taught at primary school 5th grade, on the success of the students in problem solving is researched. In the study, also the effect of problem solving applications on the success of problem solving in Polya’s problem solving steps ( understanding the problem, planning, application of the plan and control) was tried to be determined.
The research was realized in 2007-2008 educational year with experimental design method that has primary test - conclusion test control groups. In the study as the data collection tool, which consists of 20 questions, Problem Solving Scale which is prepared by the researcher was used.
The study was executed with totally 48 5th grade students being educated in a primary school in two different classes in Afyonkarahisar City Emirdağ district. While problem solving and design application activities were applied to the experiment group students totally for 10 weeks (n=24), to the control group (n=24), the problems which were applied to the experiment group were solved. The experiment group teacher was informed verbally and by a specially prepared information file about the mathematics teaching which is done with problem posing. In the conclusion of the study, during the analysis of the obtained data t test was used.
As the result of the study, it is seen that the Problem Solving Test-conclusion test average points of the experiment and control group students is higher than the primary test average point. When the primary test and conclusion test differences of the experiment and the control group are compared, it is seen that success progress of the experiment group is higher to those in the control group. In the comparison of the experiment and the control group difference in the problem solving steps of Polya, there could not be determined a meaningful difference between the groups.
When the results are viewed it is seen that the studies of problem solving and posing increase the problem solving success of the students at a meaningful level in a positive manner.
Key Words: Problem, Problem Solving, Teaching Problem Solving, Problem Posing.
İÇİNDEKİLER
JÜRİ ve ENSTİTÜ ONAY SAYFASI ...i
ÖNSÖZ ...ii
ÖZET ...iii
ABSTRACT ...iv
İÇİNDEKİLER ...v
TABLOLAR LİSTESİ ...vii
ŞEKİLLER LİSTESİ ...ix
BÖLÜM I 1. GİRİŞ ...1 1.1. Problem durumu...1 1.2. Problem Cümlesi...3 1.3. Alt Problemler...3 1.4. Araştırmanın Amacı...4 1.5. Önem...4 1.6. Varsayımlar...5 1.7. Sınırlılıklar...5 1.8. Tanımlar...6 1.9. Kısaltmalar...6 BÖLÜM II 2. KAVRAMSAL ÇERÇEVE ...7 2.1. Problem Nedir? ...7
2.2. Matematik Dersinde Problemler...8
Sıradan (Rutin) Problemler...8
Sıradışı (Rutin Olmayan) Problemler ...9
2.3. Problem Çözme...11
2.4. Problem Çözmenin Öğretimi...15
2.6. Problem Kurma ve Problem Çözme...23
2.7. Matematik Öğretiminde Problem Kurmanın Önemi...29
2.8. Polya’ nın Problem Çözme Adımları ve Problem Kurma...30
BÖLÜM III 3. İLGİLİ ARAŞTIRMALAR...32 BÖLÜM IV 4. YÖNTEM ...39 4.1. Araştırmanın Modeli ...39 4.2. Çalışma Grubu ...40
4.3. Veri Toplama Araçları ...42
4.4. Veri Toplama Sürecinde Yapılan Uygulamalar...43
4.5. Toplanan Verilerin Analizi ...45
BÖLÜM V 5. BULGULAR ve YORUM ...46
5.1. Birinci Alt Probleme İlişkin Bulgular ve Yorum ...46
5.2. İkinci Alt Probleme İlişkin Bulgular ve Yorum ...47
5.3. Üçüncü Alt Probleme İlişkin Bulgular ve Yorum ...48
5.4. Dördüncü Alt Probleme İlişkin Bulgular ve Yorum ...49
5.5. Beşinci Alt Probleme İlişkin Bulgular ve Yorum ...50
5.6. Altıncı Alt Probleme İlişkin Bulgular ve Yorum ...51
5.7. Yedinci Alt Probleme İlişkin Bulgular ve Yorum ...51
BÖLÜM VI 6. SONUÇ VE ÖNERİLER ...53 6.1. Sonuçlar...53 6.2. Öneriler ...56 KAYNAKÇA...57 EKLER...63
Ek-1: Uygulama İzin Yazısı (a)...64
Ek-2: Uygulama İzin Yazısı (b)...65
Ek-3: Problem Çözme Testi ...66
Ek-4: Problem Çözme Testi Belirtke Tablosu ve Cevap Anahtarı...75
Ek-5: Öğretmen Bilgilendirme Dosyası ...76
Ek-6: Problem Çözme ve Kurma Etkinliği Çalışma Kağıdı Örn(Deney Grubu)....84
Ek-7: Problem Çözme Etkinliği Çalışma Kağıdı Örn(Kontrol Grubu)...89
Ek-8: Çalışma Kağıtlarında Yer Verilen Problemlere Örnekler...94
TABLOLAR LİSTESİ
Tablo 1 : Araştırma Modeli...39
Tablo 2: Çalışma Grubunda Yer Alan Öğrencilerin Dağılımı... 40
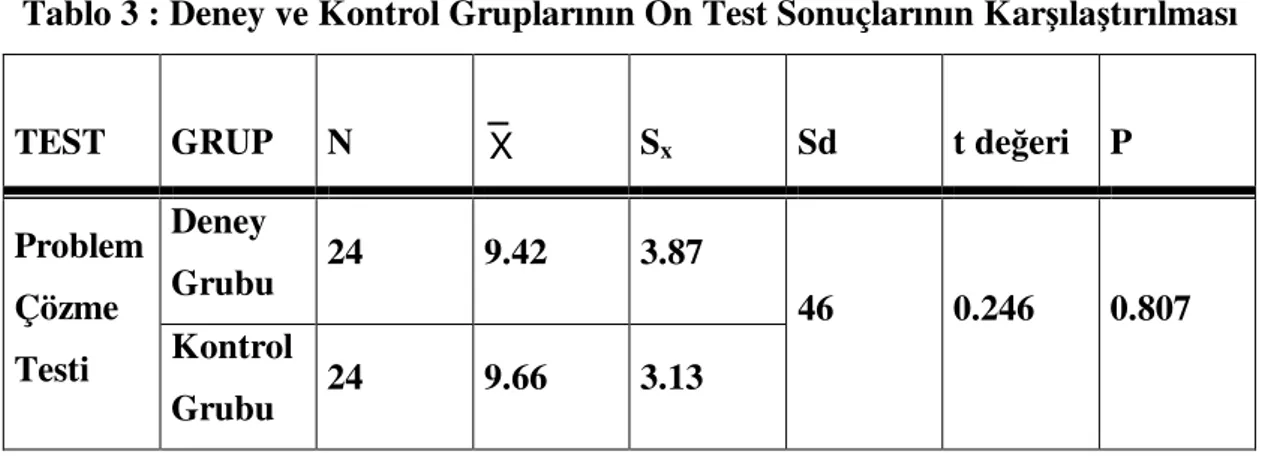
Tablo 3: Deney ve Kontrol Gruplarının Ön Test
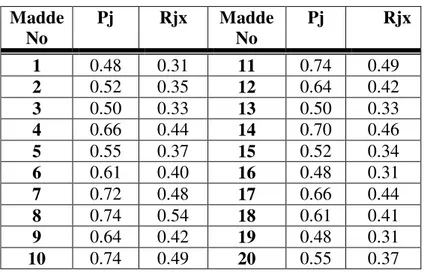
Sonuçlarının Karşılaştırılması...41 Tablo 4: Problem Çözme Testi
Madde Analizi Sonuçları...43
Tablo 5: Problem Kurma Çalışmaları Yapılan (Deney Grubu) Öğrencilerin
Problem Çözme Testi Ön Test İle Son Test Puanlarının Karşılaştırılması...46
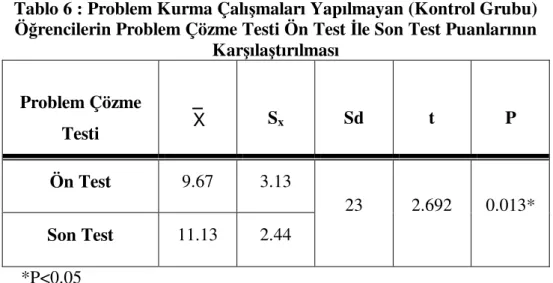
Tablo 6: Problem Kurma Çalışmaları Yapılmayan (Kontrol Grubu) Öğrencilerin Problem Çözme Testi Ön Test İle Son Test Puanlarının Karşılaştırılması...47
Tablo 7: Deney ve Kontrol Gruplarındaki Öğrencilerin, Problem Çözme
Testi Öntest – Sontest Puan Farklarının (Erişilerinin) Karşılaştırılması ... 48
Tablo 8: Deney ve Kontrol Gruplarının Problem Çözmenin “Problemi Anlama” Aşamasına İlişkin Puan Farklarının (Erişilerinin) Karşılaştırılması ...49
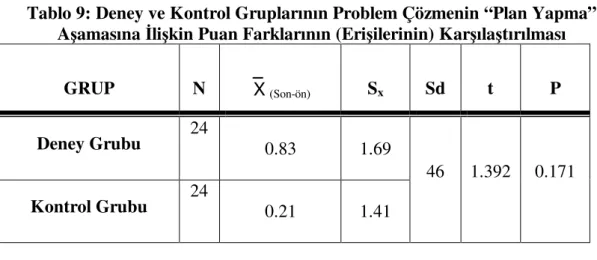
Tablo 9: Deney ve Kontrol Gruplarının Problem Çözmenin “Plan Yapma”
Aşamasına İlişkin Puan Farklarının (Erişilerinin) Karşılaştırılması ...50
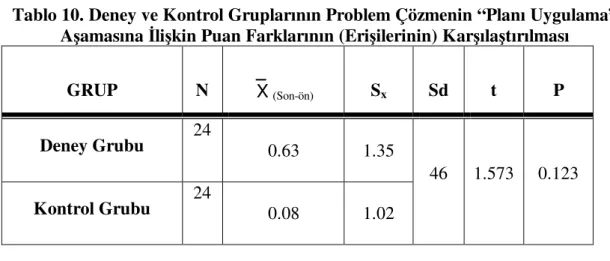
Tablo 10: Deney ve Kontrol Gruplarının Problem Çözmenin “Planı Uygulama” Aşamasına İlişkin Puan Farklarının (Erişilerinin) Karşılaştırılması ...51
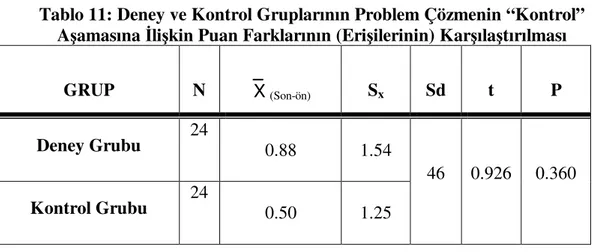
Tablo 11: Deney ve Kontrol Gruplarının Problem Çözmenin “Kontrol”
ŞEKİLLER LİSTESİ
Şekil 1: Farklı Tipten Problemlerin Bir Sınıflandırılması...10
I.BÖLÜM
GİRİŞ
Bu bölümde araştırmanın; problem durumu, problem cümlesi, alt problemler, amacı, önemi, varsayımlar, sınırlılıklar, araştırmada kullanılan kavramların tanımı ve kısaltmalar ele alınmaktadır.
1.1. Problem Durumu
Bazı insanlar için matematik, hayatı anlamanın ve sevmenin bir yolu olabilmiştir. Çünkü sevmenin yolu, her şeyde olduğu gibi burada da anlamaktan geçer. Ancak anlayabildiğimiz şeyleri severiz. Anlamadıklarımıza karşı ise olumsuz bir tutum sergileriz. İnsanlar matematiği tam olarak anlayamadıklarından dolayı bu derse karşı olumsuz tutum sergilemektedirler. Matematiğe karşı duyulan bu olumsuz tutumların sebeplerinden biri de, bireyin problem çözme yeteneği konusundaki kendine duyduğu güven ile yakından ilgilidir . Bu nedenle matematik derslerinde problem çözme oldukça önemlidir (Yıldızlar, 2001).
Problem çözmenin matematik programlarının merkezinde olması, bu konuya matematik eğitimcilerinin ayrı bir önem vermesine neden olmuştur. Çünkü matematiksel bilgiyi anlama ve bu bilgiler arasındaki ilişkiyi oluşturma, problem çözme sürecinde meydana gelmektedir. Bundan dolayı matematik eğitimcileri, öğrencilerin problem çözme becerilerinin geliştirilmesi ve eğitimin öncelikli amacı olması konusunda fikir birliğindedirler (Karataş ve Güven, 2004).
Öğrencilerde problem çözme becerisini geliştirmek, matematik eğitiminin önemli amaçlarından birisidir. İçinde bulunduğumuz çağa damgasını vuran problem çözme yalnızca matematik dersinin amaçları arasında değil, bütün derslerin amaçları arasında yer almaktadır. Bu nedenle problem ve problem çözmenin yapısı ile
problem çözmede başarının artırılması, pek çok eğitimci ve psikolog tarafından üzerinde çalışılan bir konudur (Kılıç ve Samancı, 2005).
Son yıllarda, öğrencilerin problem çözme becerilerinin geliştirilmesinin yanında, verilen durumlardan hareketle yeni problemler üretme veya var olan problemlerin içeriğinde bazı değişiklikler yaparak kendine özgü yeni problemler oluşturmayı ifade eden problem kurma becerilerinin geliştirilmesine de önem verilmektedir. “Çünkü problem çözme becerisi, hazır ve kalıplaşmış problemler üzerinde olduğunda, öğrenciler kitaba veya diğer kaynaklara bağımlı kalmakta ve problemin çözümü için farklı çözüm stratejileri geliştirmeye gerek duymamaktadırlar. Bu durumda, öğrencilerin açık uçlu ve daha önce öğrendiklerinden farklı bir problemle karşılaştıklarında nasıl davranacaklarını bilememelerine neden olmaktadır. Bu yüzden öğrencilerin problem kurma becerilerini de kazanmaları gereklidir”(Dede ve Yaman,2005:42).
Problem kurma matematiksel araştırmaların anahtar bileşenlerinden biridir. Yapılan bilimsel araştırmalara göre, problemin formulize edilmesi problemin çözümünün bulunmasından çoğu zaman daha önemli bir iştir (Einstein, Infeld, 1938; Cai, 2003). Bundan başka, öğrencilerin problemleri nasıl kurduklarına odaklanmak, öğrencilerin problemleri nasıl çözdüğü üzerindeki çalışmalardan neler öğrenilebileceğine ışık tutmaya yardımcıdır (NCTM, 2000; Cai, 2003). Problem kurmada öğrencilerin daha aktif öğrenenler oldukları yapılan araştırmalar ile ortaya konmaktadır.
Temel işlemsel beceriler ile karmaşık problem çözme becerileri ve problem kurma becerileri arasında sıkı bir ilişki vardır. Temel işlemsel becerilerinde eksik olan öğrenciler, başarılı problem çözücü olamazlar, problem çözmeyi başaramayanlar da başarılı problem kurucu olamazlar (Korkmaz, 2003).
Problem kurma aktivitelerinde bulunan öğrencilerin, daha girişken, yaratıcı ve aktif öğrenenler oldukları araştırmacılar tarafından ifade edilmektedir. Ayrıca öğrenciler bilişsel yeteneklerine göre ilgi alanlarıyla ilgili oluşturdukları problemlerle vakit geçirme şansına sahiptirler. Araştırmalar, problem kurmanın öğrencilerin
matematik kaygısını azalttığını ve matematiğe karşı tutumlarını geliştirdiğini ve onları öğrenmeye karşı daha sorumlu hale getirdiğini göstermektedir (Brown,1984;Abu-Elwan,1999,2006).
1.2.Problem Cümlesi
Araştırmanın problem cümlesi: “İlköğretim 5. sınıfta dört işlem problemlerini çözdürme sürecinde problem kurma çalışmaları yapılmasının, öğrencilerin problem çözme ve problem çözme adımlarındaki (problemi anlama, plan yapma, planı uygulama, kontrol) başarıları üzerinde etkisi var mıdır?” Araştırmanın problemine cevap bulabilmek amacı ile aşağıdaki alt problemler oluşturulmuştur.
1.3. Alt Problemler
1. Problem kurma çalışmaları yapılan (deney grubu) öğrencilerin, Problem Çözme Testi ön test ve son test puan ortalamaları arasında anlamlı bir fark var mıdır?
2. Problem kurma çalışmaları yapılmayan (kontrol grubu) öğrencilerin, Problem Çözme Testi ön test ve son test puan ortalamaları arasında anlamlı bir fark var mıdır?
3. Problem kurma çalışmaları yapılan (deney grubu) öğrencilerle, yapılmayan öğrencilerin (kontrol grubu) , Problem Çözme Testi öntest – sontest puan farklarının (erişi) ortalamaları arasında anlamlı bir fark var mıdır?
4. Problem kurma çalışmaları yapılan (deney grubu) öğrencilerle, yapılmayan öğrencilerin (kontrol grubu), Problem Çözme Testi “problemi anlama” aşamasına ilişkin ölçülen öntest – sontest puan farklarının (erişi) ortalamaları arasında anlamlı bir fark var mıdır?
5. Problem kurma çalışmaları yapılan (deney grubu) öğrencilerle, yapılmayan öğrencilerin (kontrol grubu), Problem Çözme Testi “plan yapma” aşamasına ilişkin ölçülen öntest – sontest puan farklarının (erişi) ortalamaları arasında anlamlı bir fark var mıdır?
6. Problem kurma çalışmaları yapılan (deney grubu) öğrencilerle, yapılmayan öğrencilerin (kontrol grubu), Problem Çözme Testi “planı uygulama” aşamasına ilişkin ölçülen öntest – sontest puan farklarının (erişi) ortalamaları arasında anlamlı bir fark var mıdır?
7. Problem kurma çalışmaları yapılan (deney grubu) öğrencilerle, yapılmayan öğrencilerin (kontrol grubu), Problem Çözme Testi “kontrol” aşamasına ilişkin ölçülen öntest – sontest puan farklarının (erişi) ortalamaları arasında anlamlı bir fark var mıdır?
1.4.Araştırmanın Amacı
Bu araştırmada, dört işleme dayalı problem çözme öğretiminde problem kurma çalışmaları yapılmasının, öğrencilerin problem çözme başarılarını yükseltmede etkili olup olmayacağının belirlenmesi amaçlanmıştır. Aynı zamanda, problem kurma çalışmaları yapılmasının; problem çözmenin problemi anlama, plan yapma, planı uygulama ve kontrol adımlarındaki başarıyı etkileyip etkilemediği sorusuna cevap aranmıştır.
1.5.Önem
Çağımızda eğitimin en önemli amaçlarından bir tanesi de bireylere problem çözme becerisi kazandırmaktır. Öğrencilerin hayatlarında ve derslerde karşılaştıkları problemleri çözme yeterlikleri kazandırılmak istenmektedir. Bu bağlamda, matematik dersinde ve diğer derslerde problem çözme öğretimine yer verilmesi önemlidir. Ancak, öğrencilerin sadece problem çözme becerisine sahip olması yeterli değildir. Bunun yanında, matematiksel düşünmenin merkezi olarak tanımlanan
problem kurma becerilerinin üzerinde de durulmadır. Çünkü yapılan araştırmalarda, öğrencilerin problem kurmada daha aktif öğrenenler oldukları ifade edilmektedir.
Problem ortaya atma, problem üretme, problem oluşturma şeklinde de ifade edilen problem kurma ile ilgili yapılan araştırmaları incelediğimizde ülkemizde sınırlı sayıda da olsa, öğrencilerin ve öğretmen adaylarının problem kurma becerilerinin belirlenmesine yönelik çalışmalar yapıldığı görülmektedir. Problem kurma çalışmaları yapılmasının öğrencilerin problem çözme başarıları üzerindeki etkisi ise yalnızca üniversite düzeyinde araştırılmıştır. İlköğretim düzeyinde problem kurma çalışmalarının, öğrencilerin problem çözme ve problem çözme adımlarındaki (problemi anlama, plan yapma, planı uygulama, kontrol) başarılarına etkisini belirleme amaçlı bir çalışma yapılmamıştır. Araştırma bu yönüyle özgündür.
Bu araştırma ile öğrencilere problem kurma uygulamaları yapılmasının, problem çözme başarısı üzerindeki etkisi belirlenerek, problem kurma çalışmalarının matematik öğretiminde uygulanmasının önemi ortaya konmaya çalışılacaktır. Bu bakımdan araştırmanın, problem kurma çalışmaları ile problem çözme başarısını geliştirme ile ilgili yapılan çalışmalara katkılar sağlaması beklenmektedir.
1.6.Varsayımlar
1. Araştırmada kullanılan Problem Çözme Testi öğrencilerin problem çözme başarılarını belirlemek için yeterli olmuştur.
2. Araştırma için belirlenen uygulama süresi yeterlidir.
3. Deney ve kontrol gruplarındaki öğrenciler araştırmanın uygulama sürecinde kontrol altına alınamayan dışsal etkenlerden etkilenmemiştir.
1.7.Sınırlılıklar
1. Afyonkarahisar ili, Emirdağ ilçesinde bir merkez ilköğretim okulunda 2007-2008 eğitim öğretim yılında öğrenime devam eden 5. sınıf öğrencileri ile sınırlıdır.
2. Problem çözme başarısı, Polya’nın problem çözme adımlarındaki problemi anlama, plan yapma, planı uygulama, kontrol adımlarındaki başarı ile sınırlıdır.
3. Araştırmada konu edilen problem kurma çalışmaları, çözüm sonrası problem kurma durumu ile sınırlıdır.
4. Problem kurma çalışmaları, araştırmacı tarafından hazırlanan problem çözme ve kurma etkinlikleri ile sınırlıdır.
1.8.Tanımlar
Problem Kurma:
Verilen bir durum hakkında incelenecek veya keşfedilecek soruları ve yeni problemler üretmeyi içine alan problem çözme aktivitesidir. Problem çözme süreci boyunca, problemin yeniden formülasyonu ve örüntü aramayı da ihtiva eder (Argün ve diğerleri;2006).
Problem Çözme:
Problem çözme, istenilen hedefe varabilmek için etkili ve yararlı olan araç ve davranışları türlü olanaklar arasından seçme ve kullanmadır (Bingham, 1983;Akt. Aksu, 1993).
Erişi:
Öğrencilerin Problem Çözme Testi son test puanlarının, ön test puanlarından farkıdır.
1.9.Kısaltmalar
NCTM : Ulusal Matematik Öğretmenleri Konseyi (National Council of Teachers of Mathematics).
II. BÖLÜM
KAVRAMSAL ÇERÇEVE
Bu bölümde, araştırmanın kuramsal yapısı açıklanarak; araştırmanın yapılandırılmasında problem kurma ve problem çözmenin nasıl ele alındığı açıklanmıştır.
2.1.Problem Nedir?
Problem, sonucu bilinmeyen ya da zor olan bir durumdur. Problemin önemi, keşfedilecek, tartışılacak ya da düşünülecek bir soru olmasındadır. Problem aynı zamanda giderilmek istenen bir güçlük olarak da tanımlanabilir (Van De Walle, 1980;Akt. Tertemiz ve Çakmak, 2007).
Problem, temelde bireyin bir hedefe ulaşmada engelleme ile karşılaştığı bir çatışma durumudur (Morgan, 1995: 130;Akt. Soylu ve Soylu, 2006). Olkun ve Toluk (2004: 44), problemi kişide çözme arzusunu uyandıran ve çözüm prosedürü hazırda olmayan fakat kişinin bilgi ve deneyimlerini kullanarak çözebileceği durumlar olarak tanımlamaktadır.
Polya’ ya göre problem, kişinin belli bir amaca en uygun yoldan ulaşması için eylemlerin bilinçli olarak araştırılmasıdır. Zihindeki bir durum herhangi bir güçlükle karşılaşmadan belli hareketlerle ortadan kaldırılabiliyorsa bir problemin varlığından bahsedilmez. Eğer, bu durumu ortadan kaldırmak için hangi hareketlerin yapılacağı belli değilse çözülmesi gereken bir problemin varlığından söz edilebilir (Akt; Sertsöz, 2003).
Klaas'a göre Dewey problemi, insan zihnini karıştıran, ona meydan okuyan ve inancı belirsizleştiren her şey olarak tanımlamaktadır. Aksu’da (1985) problemi benzer biçimde tanımlamakta, ek olarak problem durumunda bireyin bir durumla etkileşmesinin önemini de vurgulamaktadır.
Problem için verilen tanımlar analiz edildiğinde, bir durumun problem olması için insan zihnini karıştırması gerektiği sonucuna varılır. Bu, karşılaşılan durumun yeni olmasını; bireyin bu durumla daha önce hiç karşılaşmamış olmasını gerektirir. Bu nedenle, bir birey için problem olan bir durum başka bir birey için problem olmayabilir. Konu belirtilen koşullar altında bir çözüm gerektiriyorsa, kişi konuyu anlıyor, ama çözüm için stratejiyi hemen göremiyorsa araştırmaya motive ediliyorsa o bir problemdir. (Gür ve Korkmaz, 2003).
2.2. Matematik Dersinde Problemler
Matematikte bir problem, ifade veya ifadelerden (yazılı, sözel, sembolik veya grafik olabilir), bilinen ve bilinmeyen değişkenlerden, bilinmeyenler ve verilen veriler arasındaki ilişkiyi açıklayan koşulların bir kümesinden ve bir konudan oluşur (Gür ve Korkmaz, 2003).
Matematik derslerinde problem denince ilk akla sözel problemler gelmektedir. Bunun en önemli sebeplerinden birisi, problemlerin çoğunlukla sözel formda olmasıdır. Sözel problemlerin öğrencilerde dil oluşumunda, akıl yürütmede ve matematiksel gelişimde önemli bir yeri vardır (Aydoğdu ve Oklun 2004: 27–38; Soylu ve Soylu,2006). Buna rağmen yapılan araştırmalar göstermiştir ki, çoğunlukla cebirsel sözel problemler çözümleri zor bulunan problemler olarak algılanmaktadır (Stacey ve MacGregor 2000;Akt. Dede, 2004).
Altun’ a (2002) göre matematik derslerinde kullanılan problemler iki şekilde sınıflandırılabilir.
Sıradan (Rutin) Problemler
Bunlar matematik ders kitaplarında yer alan ve dört işlem becerileri ile çözülebilen problemlerdir. Sıradan problemler bir ya da birden çok işlemli olabilirler. “Ali 212 sayfalık bir kitabın birinci gün 30, ikinci gün de 42 sayfasını okudu. Üçüncü gün kitabın yarısına geldiğine göre üçüncü günde kaç sayfasını okumuştur?” problemi çok işlemli sıradan bir problemdir. Sıradan problemlerin öğretimi günlük
hayatta çok gerekli olan işlem becerilerini geliştirmek, çocukların problem hikayesinde geçen bilgileri matematik eşitliklere aktarmayı öğrenmeleri ve problem çözmenin gerektirdiği diğer becerileri kazanmaları bakımından önemlidir.
Sıradışı (Rutin Olmayan ) Problemler
Sıradışı problemler bir veya birkaç işlemin doğru seçilmesiyle hemen çözülememeleri bakımından sıradan problemlerden farklıdır. Çözümleri işlem becerilerinin ötesinde, verileri organize etme, sınıflandırma, ilişkileri görme gibi becerilere sahip olmayı ve bir takım eylemleri arka arkaya yapmayı gerektirir. Örneğin; “Bir adam bir oyundan bir tilki, bir ördek ve bir çuval mısır kazanıyor. Bunlarla birlikte bir nehrin kıyısından öbür kıyısına geçmek zorunda, ancak birini alabiliyor. Mısırı geçirirse tilki ördeği yiyebilir, tilkiyi geçirirse ördek mısırı. Hiçbir zaiyat olmadan bunları karşıya nasıl geçirebilir?”. Sıradışı problemlerin konusu çoğunlukla çevresel veya çevrede rastlanabilecek bir olaydır. Bundan ötürü bunlara gerçek problem veya gerçek hayat problemi denir. Böylelikle öğrencilerin hem problem çözme becerileri gelişir hem de matematiğe karşı olumlu tutum geliştirirler (Altun, 2002: 85-86).
Rutin olmayan problemler, “iyi problem” kriterlerine uyduğu ve problem çözme öğretiminde çok önemli bir yer kapladığı bir gerçektir. Polya , öğrencilere rutin problemler dışında başka tür problem çözdürmemenin “affedilemez bir hata” olduğunu, böyle yapmanın öğrencileri “düş gücü ve yargı”dan mahrum bıraktığını belirterek rutin olmayan problemlere verdiği önemi göstermektedir (Yazgan ve Bintaş, 2005:211).
Matematik dersinde seçilen problemler, öğrencilerin günlük yaşamında gereksinim duyduğu konular ve okulda yaptığı etkinliklerle ilgili ve ilginç olmalıdır. Bu durumda öğrencilerin kazandıkları matematiksel bilgi ve beceriler daha anlamlı olacak ve bu bilgiyi farklı durumlara uygulamaları kolaylaşacaktır (İlköğretim Matematik Programı 1-5. Sınıflar, 2005: 11). Yapılan araştırmalarda, gerek matematik ders kitaplarında gerekse öğretmenlerin ders işleyişlerinde genelde tek bir doğru cevabı olan problemler kullanıldığı görülmektedir. Kitap hazırlarken veya ders
hazırlıkları yaparken tek doğru cevabı olan soruların yanı sıra öğrencilere ilginç ve şaşırtıcı gelecek olan aşağıdaki tür sorulara da yer verilmelidir.
• Çözümsüz (çözümü olmayan) • Birden çok çözümü olan • Eksik ya da fazla bilgi içeren • Sayısal veri içermeyen
• Gerçek hayatın uygulamasını konu edinen (Altun, 2001 ). Şekil 1. Farklı Tipten Problemlerin Bir Sınıflandırılması
PROBLEMLER Kapalı Tipler (Ders Kitaplarındakiler, Alıştırmalar)
Açık Uçlu Tipte Olanlar
Matematiksel Alıştırmalar ve
Projeler
(Kaynak: Foong, 1990, Akt. Yenilmez ve Yaşa,2007) Rutin Problemler 1. Özel konular içerenler 2. Çok adımlı olanlar Rutin Olmayan Problemler (Heuristik adımlarla problem çözme stratejileri kullanılır.) Kavramsal anlama için açık uçlu problem içeren ders kitapları Gerçek hayatı yansıtan uygulamalı problemler Eksik Bilgili Olanlar Problem
Kurma Kavramları açıklayanlar; kural veya hatalar
Şekil 1’ de Foong’un (1990) problem çözümü ve problemlerin kullanımı üzerine yaptığı sistematik bir literatür taramasına dayanarak 21. yüzyıl matematik sınıflarında teşvik edilen farklı tipten problemlerin bir sınıflandırılması yapılmıştır (Akt. Yenilmez ve Yaşa,2007).
Argün, Akay ve Soybaş’ a (2006) göre öğrencileri şaşırtıcı matematik problemleri ile karşı karşıya getirmek muhakeme yeteneklerini geliştirmekte, düşündüklerine deliller sağlamakta, matematiksel düşüncelerini ortaya koyarak iletişimde bulunabilmelerine ve matematiğin gerçek hayatla bağlantılar kurabilmelerini sağlamaktadır.
2.3. Problem Çözme
Problem çözme, insanlar için en eski zihinsel beceri ya da zihinsel ustalık olarak bilinir (Hacısalihoğlu, Mirasyedioğlu ve Akpınar,2003:33). Problem çözme, istenilen hedefe varabilmek için etkili ve yararlı olan araç ve davranışları türlü olanaklar arasından seçme ve kullanmadır (Aksu, 1993).
Problem çözme bir amaca erişmekte karşılaşılan güçlükleri yenme sürecidir, bu da bilgiyi kullanarak ve buna orijinallik, yaratıcılık ya da hayal gücünü ekleyerek çözüme ulaşma süreci olarak açıklanabilir. Bu anlamda problem çözme yüksek düzeyde bilişsel bir süreçtir (Roth, 1990; Akt. Tertemiz ve Çakmak, 2007:12).
Skemp’e göre (1986), problem çözme yeteneği insanın varlığını sürdürebilmesi için gerekli en temel yeteneklerden biridir. Her alandaki zorluklarla başa çıkmadaki rolünden dolayı, okul matematik programlarının ana hedeflerinden biri, bu yeteneğin geliştirilmesi ile ilgilidir. Çocuklar fiziksel büyümelerine katkı veren fiziksel aktivitelerden hoşlandıkları kadar, zihinsel gelişmelerine katkı veren zihinsel aktivitelerden de hoşlanırlar ve hoşlandıkları için gelişirler (Akt. Altun, Dönmez, İnan, Taner ve Özdilek, 2001). Problem çözme etkinlikleri, bu zihinsel aktivitelerin başında gelir. Bu açıdan bakıldığında problem çözme, zihinsel gelişmenin tamamlanabilmesi için bir ihtiyaçtır (Altun ve diğerleri ,2001).
Kabadayı (1992:32), problem çözme sürecinin hem zihinsel bir faaliyet ya da beceri hem de eğitimde teknik ya da yöntem olduğunu belirtmiş ve problem çözme sürecinin eğitimde alabileceği boyutları değerlendirmiştir. Ona göre problem çözme;
a. Bilişsel bir özellik ya da davranış, b. Duyuşsal özellik,
c. Bir yöntem, bir yaşantıdır.
Bu tanım bizlere, problem çözmenin bilişsel, duyuşsal ve davranışsal boyutları olan karmaşık bir süreç olduğunu göstermektedir.
Lester’e göre (1994:662), bireylere gelecekte karşılaşabilecekleri problemlerin üstesinden gelebilecek becerileri kazandırmak eğitimin öncelikli hedefidir. Öğrencilere bu becerileri kazandırmak ancak problem çözmenin, eğitimin merkezinde olmasıyla mümkün olabileceği düşünülmektedir. Bu düşünce son yıllarda genelde eğitimde, özelde ise matematik eğitiminde köklü değişiklikler olmasına neden olmuştur. Birçok matematik eğitimcisi; problem çözmenin, eğitimin hedeflerine ulaşılmasında çok önemli olduğu ve eğitimin her kademesinde matematik eğitiminin öncelikli amacı olması gerektiği konusunda fikir birliğindedirler(Charles ve Lester, 1985 :18; Akt. Karataş ve Güven,2004).
İlköğretim için problem çözme yeteneğinin taşıdığı önem aşağıdaki sebeplere dayandırılabilir(Dursun, 1999:48).
a. İlköğretimin ilk 5 yılı, çocukların zihin gelişiminin hızlı olduğu yıllardır. Problem çözme ile ilgili beceriler bu yıllarda, uygun yaklaşımlarla, daha hızlı bir şekilde geliştirilebilir.
b. Problem çözme becerisi, matematik becerileri arasında önemli bir yer tutar. c. İlköğretimin en önemli görevi, bireyleri hayata hazırlamaktır. Günlük hayatta
her gün çeşitli problemlerle karşılaşılmaktadır. Birey, bu problemleri ilköğretimde aldığı matematik bilgisi çerçevesinde çözmeye çalışır.
Baykul (1999) ise Dursun’la (1999) benzer olarak, ilköğretimde problem çözme becerilerinin geliştirilmesinin önemini şu şekilde açıklamaktadır:
a. Problem çözme becerisi, matematik becerileri arasında önemli bir yer tutar. b. İlköğretim çağı, çocukların zihin gelişiminin hızlı olduğu yıllara rastlar.
Problem çözme ile ilgili beceriler bu yıllarda uygun yaklaşımlarla daha hızlı bir şekilde geliştirilebilir.
c. İlköğretimin iki görevinden biri, bireyi hayata, diğeri üst öğrenime hazırlamaktır. Günlük hayatta her gün çeşitli problemlerle karşılaşılmaktadır. Ülkemizdeki ilköğretim okulları mezunlarının bir kısmının üst öğrenime devam etmeyerek hayata atıldıkları düşünülürse, bu yeteneğin ilköğretim okulunda en iyi şekilde geliştirilmesi, bireylerin hayattaki başarılarının artmasına, dolayısıyla mutluluklarına önemli katkı sağlar.
d. Problem çözme becerisi, ilköğretimi izleyen öğretim kademelerinde ve bilimsel çalışmalarda vazgeçilmez bir özelliktir. İlköğretimden sonraki öğretim kademelerinde ve bütün alanlarda matematiğin kendisi, matematiksel mantık ve akıl yürütme yanında problem çözme becerisini gerektirir. Günümüzde sosyal bilimler alanında öğretim yapan yükseköğretim kurumlarındaki öğrenci seçmede problem çözme becerisinin yoklamasına önem verilmektedir.
NCTM' nin Okullarda matematik öğretimi ve eğitimi ile ilgili başvuru kaynaklarından "Principles and Standards for School Mathematics" (Okul Matematiği için İlkeler ve Ölçütler) adlı kaynak yapıtta, önceki çalışmalara atıf yapılarak tüm öğrenciler için problem çözmeyi aşağıda açıklandığı biçimde belirlemektedir. Okul öncesinden K-12 (lise son sınıfa) kadar öğretim programlarında tüm öğrenciler:
• Yeni matematik bilgileri, baştan sona problem çözmeyle inşa edilmelidir; • Matematik ve diğer bağlamlarda görünen problemleri çözmeliler;
• Problem çözmek için çok çeşitli uygun stratejileri uygulayabilmeli ve uyarlayabilmeli;
• Problem çözme sürecini izleyebilmeli ve yansıtabilmelidir (Akt. Ersoy,2004). Matematikte başarılı olmanın yolu, iyi problem çözmeyle doğrudan ilgilidir. Bu anlamda matematik dersinin öğretiminde ve öğrenilmesinde problem çözme sürecinin nasıl işlediği oldukça önemlidir. Problem çözme aynı zamanda bilimsel bir yöntem olduğundan, eleştirel düşünmeyi, yaratıcı ve yansıtıcı düşünmeyi, analiz ve sentezleme becerilerinin de kullanımını gerektirir. Öğrencilerde problem çözme becerisini geliştirmek matematik eğitiminin önemli amaçlarından birisidir (Reusser ve Stebler,1997:39–27;Akt. Soylu ve Soylu, 2006).
Çocuk düşünmeyi problem çözmeyle birleştirince hayattaki başarının anahtarını elde etmiş olacaktır. Problem çözme etkinlikleri çocuğun düşünme ve sorgulama becerilerini geliştirecektir. Sonuca ulaşmak çocukta kendine güven ve kabiliyetin gelişmesine yardımcı olacaktır. Kendi yeterliliğinin farkına varan çocuk fikirlerini diğerleriyle paylaşmaya başlayacak ve başkalarıyla etkili çalışmanın temelleri atılmış olacaktır (Yenilmez ve Yaşa, 2007).
İlköğretim (1-5. Sınıflar) Matematik Programı’nda (2005) ise öğrencilere problem çözme becerisi kazandırılırken aşağıdaki becerilerinde geliştirilmesi hedeflendiği belirtilmiştir.
1) Problemi çözmeyi, matematiksel kavramları anlama ve irdeleme için kullanma.
2) Matematiksel ve günlük yaşam durumlarını kullanarak problem kurma. 3) Çözümlerin probleme uygunluğunu ve akla yatkınlığını kontrol etme ve yorumlama.
4) Matematiği anlamlı bir şekilde kullanmak için öz güven ve olumlu tutum geliştirebilme.
5) Değişik problemleri çözebilmek için farklı problem çözme stratejileri kullanabilme.
• Deneme yanılma
• Şekil, resim, tablo vb. kullanma • Materyal (malzeme) kullanma • Sistematik bir liste oluşturma • Örüntü arama
• Geriye doğru çalışma • Tahmin ve kontrol etme • Varsayımları kullanma
• Problemi başka bir biçimde ifade etme • Problemi basitleştirme
• Problemin bir bölümünü çözme • Benzer bir problem çözme • Akıl yürütme
• İşlem seçme.
Öğrencilere problem çözme becerilerini kazandırma da, İlköğretim Matematik Programı’nda (2005) belirtilen problem çözme sürecinin önemli bir öğesi olan problem çözme stratejilerinin öğretilmesi önemlidir. Problem çözme stratejileri Dhillon’a (1998) göre problem çözme sürecinde gösterilen problem çözme davranışlarının genel bir planı olarak görülebilir. Problem çözme davranışı, problem çözmede öğrencinin yaptığı etkinlikleri içerir. Her etkinlik bir strateji ya da bir stratejinin uygulanmasından oluşur. Her bir strateji bir davranış ya da davranışlar serisini içerir ve bir davranış ile yorumlanır(Akt. Çalışkan, Selçuk ve Erol,2006).
2.4. Problem Çözmenin Öğretimi
Problem çözümünün etkin öğretimi, stratejilerden ziyade, problem çözme deneyimleri ile öğrencilerin kendilerini rahat hissetmelerini sağlayacak teknikleri içermektedir (Suydam, 1982;Akt. Hacısalihoğlu ve diğerleri, 2003). Hacısalihoğlu ve diğerlerine göre (2003) bu süreçte öğretmenin kullanabileceği anahtar ilkeler aşağıdaki gibi listelenebilir:
1. Problemler dikkatlice seçilip, zorluk düzeylerine özel dikkat ve ilgi gösterilmeli,
2. Öğrenciler küçük gruplara ayrılmalı, problem çözme sürecinde birlikte çalışmaları sağlanmalı,
3. İstenen, verilen ve ihtiyaç duyulan bilgiler tanımlanmalı,
4. Problem açık bir yolla ifade edilip öğrencilerin anlaması sağlanmalı, 5. Problem geniş bir hedef içinde sunulmalı,
6. Problemler sık sık sunulmalı,
7. Öğrencilerin problemi analiz edip yapılandırmasına fırsat verilmeli, 8. Öğrencilere aynı stratejilerle farklı problemleri çözme şansı verilmeli, 9. Öğrencilere belirli problem için uygun strateji seçme fırsatı verilmeli, 10. Öğrencilerin problem hakkında ayrıntıları tanımalarına yardımcı olunmalı, 11. Öğrencilere, problem çözme sürecindeki yansımalar ve sonuçları tartışmak
için zaman verilmeli,
12. Öğrencilerin çözümlerine nasıl ulaştıkları ve elde ettikleri sonuçları uygulamalı bir biçimde açıklamalarına fırsat verilmeli,
13. Problemlerin daha farklı biçimde nasıl çözülebileceği tartışılmalıdır.
Yukarıdaki ilkeler öğretmenler tarafından matematik öğretiminde uygulandığında öğrencilerin problem çözme başarısının artması beklenmektedir. Ancak, sadece bu ilkelerin göz önünde bulundurulması yeterli değildir. Yapılan araştırmalar, öğrencilere problem çözmenin öğretiminde belli adımlar olması gerektiğini göstermektedir.
Polya’ya (1957) göre bir problemi çözme, açık olarak düşünüleni elde etmenin çözümünü araştırmaktır. Problem çözme, sadece bir üründen ziyade bir süreçtir. Bir problemi çözmek, yeni ve sıradan (rutin) olmayan yol ile birlikte bilgiyi kullanmanın bir süreci ve yöntemidir. Öğrencilere problemleri çözmeleri için, Polya'nın (1957) 4 adımlı yöntemi tanıtılır.
Bu Adımlar Şunlardır:
1. Problemin Anlaşılması
2. Problemin Çözümü İçin Bir Plan Yapılması 3. Çözüm Planının Uygulanması
4. Sonucun Doğru Olup Olmadığının Kontrol Edilmesi
Problemin Anlaşılması:
Problemi çözmede ilk adım problemde ne sorulduğunun dikkatlice belirlenmesidir. Karmaşık gibi görülen problemin çözümü çok kolay olabilir, burada önemli olan problemdeki verileri görmektir. Önce tüm veriler yazılmalı, önemli ve önemsizler belirlenmelidir. Gerekirse tablo, şema ve benzeri çizilmelidir (Tertemiz ve Çakmak,2007: 28).
Özellikle bir problemin anlaşılabilmesi için: Neler verilmiştir? ve Neler istenmektedir? sorularına tam olarak cevap verilebilmesi için problemin anlaşılmış olması gerekir. Bunu anlayabilmek için de şu noktalara dikkat edilmelidir.
1. Öğrenci vurgu düzeyine uygun okuyabiliyor mu? 2. Problemde eksik ya da fazla bilgi var mıdır? 3. Problemden ne tür bilgiler elde edilmektedir?
4. Problemdeki olaylara ve ilişkilere uygun şekil ya da diyagram çizebiliyor mu?
5. Problemi parçalara (alt problemlere) ayırabiliyor mu? (Altun, 2000).
Problemin özetlenmesi, verilenlerin ve istenilenlerin kısaltılarak veya sınıf seviyesine göre sembol kullanılarak yazılmasıdır. O halde problemi anlama ile ilgili kritik davranışlar;
1. Problemde verilenlerin ve istenilenlerin neler olduğunun yazılması; 2. Problemi, öğrencinin kendi ifadesiyle söylemesi
3. Probleme uygun (onu açıklayan) bir şekil çizilmesi
4. Problemin özet olarak yazılması olarak belirtilebilir (Baykul, 2002).
Problemin Çözümü İçin Bir Plân Yapılması:
Altun’a göre (2002), bu aşamanın temel işlevi bazı sorular yöneltilerek öğrencilerin problemi çözmede uygun stratejileri seçmelerini sağlamaktır. Bu aşamada şu sorular sorulabilir.
a. Bu problemde neyin bulunması isteniyor?
b. Hangi bilgiler verilmiştir? Neyi biliyorsun, hatırla?
c. Buna benzer, daha önce başka bir problem çözdün mü? Orada ne yaptın, hatırla?
d. Bu problemi çözemiyorsan, buna benzer daha basit bir problem ifade edip çözebilir misin?
e. Tasarladığın çözümde bütün bilgileri kullanabiliyor musun?
f. Bu problemin yanıtını tahmin edebiliyor musun? Hangi değerler arasındadır? Bu adım, problemde verilenler ve istenenlerle ilgili matematik kavramlarına sahip olunmasını, bunlardan problemle ilgili olanların seçilmesini ve seçilen bu bilgi yardımıyla verilenlerle istenenler arasında matematiksel ilişkilerin kurulmasını gerektirir. Bu adımın kendisi bir kritik davranıştır (Baykul, 2002).
Bu aşamada problemin içindeki gizli ipuçlarını görebilmek “Tablo çizmek yaralı olur mu?”, “Daha önce buna benzer bir durumla karşılaştım mı?”, “Onu nasıl çözmüştüm?”, “Belki şu yoldan gidersem çözebilirim.” gibi çeşitli sorular üzerinde düşünmek yaralı olabilir (Tertemiz ve Çakmak, 2007:29).
Çözüm Plânının Uygulanması:
Bu aşamada seçilen stratejiyi dikkatlice uygulamak, işlemlerde dikkatli olmak ve işlemleri doğru yapmak önemlidir (Tertemiz ve Çakmak,2007:29).Ayrıca plânı
doğru olarak uygulayabilen kimse, problemin sonucunu belli bir yaklaşıklıkla tahmin edebilir. Bu bakımdan, üçüncü basamağın kritik davranışları;
1. İşlem sonuçlarının tahmin edilmesi
2. Problemin çözümünde kullanılacak plânın gerçekleştirilmesi veya işlemlerin yapılması olarak belirtilebilir (Baykul, 2002).
Sonucun Doğruluğunun Kontrol Edilmesi:
Bu aşamada elde edilen sonucun doğru olup olmadığına, kullanılan stratejinin uygun olup olmadığına, başka bir çözüm yolunun olup olmadığına bakılır. Kullanılan stratejinin neden seçildiği açıklanır (Altun, 2002).
Bu aşamanın kritik davranışları;
1. Problemin çözümünde kullanılan işlemlerin sağlamasının yapılması, 2. Sonucun tahminle karşılaştırılması,
3. Problemin başka yolla çözümünün araştırılması,
4. Benzer problem yazılması, şeklinde belirtilebilir (Tertemiz ve Çakmak,2007:29).
Yukarıdaki açıklamaların ışığında matematik problemlerini çözmede başvurulan adımlardaki kritik davranışlar aşağıdaki gibi listelenebilir:
• Problemde verilenlerin ve istenenlerin neler olduğunun yazılması, • Problemin özetlenmesi,
• Probleme uygun bir şekil veya şemanın çizilmesi,
• Problemin çözümü için bir plân yapılması veya dört işlem problemlerinde gerekli matematik cümlesinin veya çözümde başvurulacak işlem veya işlemlerin yazılması,
• Problemin sonucunun tahmin edilmesi,
• Plânın uygulanarak veya işlemlerin yapılarak çözümün elde edilmesi, • Bulunan sonucun tahmin sonucu ile karşılaştırılması.
• Verilen verilere uygun bir problem yazılması (Baykul, 2002).
Araştırmacılar tarafından, problem çözme basamakları farklı şekillerde belirlenmiştir. Bu araştırmada ise, matematik öğretiminde kullanılan Polya’nın (1957) problem çözme adımları esas alınacaktır.
2.5.Problem Çözmeyi Değerlendirme
Öğrencilere problem çözme becerilerini kazandırmak kadar, öğrencilerin bu becerilere hangi düzeyde sahip olduğunu belirlemek de önemlidir. Çünkü, becerilerin değerlendirilmesi ile hem öğrencilerin matematik bilgisi hakkında, hem de öğretim programlarına yön verebilecek ipucu niteliğinde bilgiler elde edilmiş olacaktır (Charles, Lester ve O’Daffer, 1988, 10;Akt. Karataş,2002, 15).
Van De Walle (1980:41;Akt. Özsoy,2002)’ye göre sınıf içi problem çözme çalışmalarını değerlendirme, karmaşık bir problemdir ve çaba gerektirir. Öğrencilerin problemin doğru cevabını bulmaları, onların problem çözme becerilerine sahip oldukları anlamına gelmeyebilir. Bazı öğrenciler doğru cevabı bulmalarına rağmen çözüme yanlış yoldan gitmiş olabilirler. Bazıları ise çözüm için mükemmel stratejiler geliştirip basit işlem hataları ile yanlış sonuca ulaşabilirler. Problem çözme süreci, tüm aşamalarında düşünmeyi gerektirir (Çakmak, 2003).
Geleneksel öğretim yönteminde öğretmenler öğrencilerin problem çözme becerilerini değerlendirmede yalnızca sonuca ulaşılıp ulaşılmadığına dikkat etmektedirler. Hâlbuki problem çözmeyi değerlendirmede doğru sonuca ulaşmak kadar öğrencinin sonuca ulaşıncaya kadar ki davranışları, yani süreçte önemlidir.
Bu bağlamda öğretmenler, öğrencilerin problem çözme süreci boyunca yaptıkları davranışlara odaklanmalıdır. Reys ve diğerleri (1998) problem çözme becerilerinin değerlendirilmesinde aşağıdaki hususların göz önüne alınması gerektiğini ifade etmiştir;
• Problemi dikkatli okuduğunu gösteren bulgu var mı?
• Bir strateji uyguluyorlar mı? Yoksa öğrendikleri en son yöntemi mi uyguluyorlar?
• İlk stratejileri başarısızlık ile sonuçlandığında başka bir yöntem kullanıyorlar mı?
• Bir stratejiyi uygulamada ne kadar kararlı ve ısrarlılar?
• Dikkatsiz hatalar yapıyorlar mı? Yapıyorlarsa ne zaman ve niçin? • Bir problemi çözmede ne kadar istekli davranıyorlar ve uğraşıyorlar? • Probleme ne kadar konsantre oluyorlar?
• Ne kadar sıklıkta yardım istiyorlar?
• Her bir öğrencinin en çok kullandığı stratejiler nedir? • Görsel materyaller kullanıyorlar mı? Nasıl?
• Öğrencilerin davranışları ve yüzündeki ifadeler, ilgilerini ve katılımlarını ortaya koyuyor mu? (Akt. Karataş ve Güven, 2003).
Çakmak (2003) ise problem çözmeyi değerlendirmede kullanılabilecek ipuçlarını aşağıdaki gibi ifade etmektedir.
Duyuşsal Nedenler (Aşağıda bunlara ilişkin örnek davranışlar verilmektedir):
Öğrencilerin problem çözme için gönüllülük göstermeleri, problem çözme yeteneklerinde kendine güven göstermeleri, gelişim yavaş bile olsa problem çözme girişimlerinde sabırlı olmaları, problem çözmeden hoşlanmaları, problemleri çözerken gruplarla birlikte işbirliği içinde çalışmaları.
Problemi Anlama (Aşağıda bunlara ilişkin örnek davranışlar verilmektedir):
Öğrencilerin problem için gerekli bilgiye karar verebilmeleri, problemde aranılana açıkça işaret edebilmeleri, problemde bilinmeyen kelimeler ya da belirsiz durumlara açıklık getirebilmeleri, çalışmaya başlamadan önce alt problemleri ya da istenilenleri tanımlamaları, bazı alternatif çözüm önerileri geliştirebilmeleri.
Bilgi Stratejisi ve Seçimi (Aşağıda bunlara ilişkin örnek davranışlar verilmektedir):
Öğrencilerin problemde kullanması için verilen bir stratejiyi uygun bir biçimde kullanabilmeleri, sıklıkla farklı stratejileri kullanmaları, verilen problem kullanılarak uygun stratejiyi belirleyebilmeleri.
Problemler Üzerinde Çalışma (Aşağıda bunlara ilişkin örnek davranışlar verilmektedir):
Öğrencilerin çalışmalarına gösterdikleri dikkat, sürecin gelişimini kendi kendine izleyebilmeleri,takıldıkları yerleri fark edebilmeleri ve gerektiğinde diğer bir yaklaşımı seçebilmeleri.
Geriye Bakma (Aşağıda bunlara ilişkin örnek davranışlar verilmektedir):
Öğrencilerin probleme verdikleri ve çözüm sürecindeki cevapları değerlendirebilmeleri, kullanılan problem çözme stratejilerini tanımlayabilmeleri.
Yukarıda belirtilen hususlar dikkate alındığında problem çözmenin değerlendirilmesinde öğrencilerin sorulara verdikleri cevaplardan ziyade, daha çok öğrencilerin problem çözme sürecinde gösterdikleri davranışların değerlendirilmesine çalışıldığı görülmektedir.
Bu anlamda, problem çözmeyi süreç olarak değerlendirmenin faydaları şu şekilde belirtilebilir.
• Problem çözmenin ne şekilde ve ne yönde olduğunu, hangi çözüm yollarının kullanıldığını, sonucun nasıl yorumlanabileceğini gösterir.
• Matematiksel düşünme ve muhakeme yeteneğinin ne ölçüde kullanıldığını gösterir.
• Yazılı, sözlü ve görsel biçimlerde matematiksel bağlantıların nasıl kullanıldığını gösterir.
• Öğrencilere matematiksel düşünme, muhakeme yapma ve ilişkiler kurma imkanı tanır (Lappan,1994:95; Akt. Özsoy,2002).
2.6.Problem Kurma ve Problem Çözme
Geleneksel matematik eğitimi anlayışında, matematiksel bilgiler küçük beceri parçacıklarına ayrılmış halde öğretmen tarafından öğrencilere sunulur. Öğrencilerin de bu bilgileri verilen alıştırmalarla tekrar etmeleri beklenir. Soruların önceden belirlenmiş belirli yanıtlama yöntemi veya yöntemleri ve tek bir cevabı vardır. Böyle bir anlayış ortamında, öğrenciler pasif alıcılar durumundadırlar. Bir nedene dayandırılamayan bir sürü bağıntı, kural ve simgeler öğrencilere verilir. Öğrenciler ezbere dayalı öğrenmeye sevk edilir. Sonuç olarak, öğrenciler gösterilmeyen bir problemi çözemez hale gelirler (Olkun ve Toluk, 2004).
Problem kurmada ise öğrencilerin karmaşık bir durum veya olay ile karşı karşıya kalması, durum veya olaydan sorumlu olma rolünü hissetmesi söz konusu olduğu için, problem çözmeyi beceremeyen öğrenciler problem kurmada başarılı olamazlar (Korkmaz, 2003).
Problem kurma , matematik disiplininin ve matematik düşünmenin merkezidir. Problem kurma, verilen bir problemin çözümünden çok verilen durumlardan veya olaylardan hareketle yeni problemler üretebilme becerisidir (English, 2001;Akt. Dede ve Yaman,2005). Verilen bir durum hakkında incelenecek veya keşfedilecek soruları ve yeni problemler üretmeyi içene alan bir problem çözme aktivitesi olan problem kurma aynı zamanda problem çözme süreci boyunca, problemin yeniden formülasyonu ve örüntü aramayı da ihtiva eder (Argün ve diğerleri,2006).
Öğrencilerin matematiksel gelişiminin önemli bir bileşeni olarak tanımlanan problem kurmanın aslında öğrenmenin içe dönük bir aktivitesi olduğu vurgulanmaktadır (NCTM,1991;Silver, 1994).
Problem çözme ve problem kurma arasında güçlü bir ilişki olduğunu söyleyen Cai ve Hwang (2002), öğrencilerin problem çözme becerilerinin gelişmesi ile problem kurma becerilerinin de gelişeceğini belirtmişlerdir. Cai (1997) de, bu iki kavram arasında önemli bir ilişki olduğunu belirtmiş ve öğrencilerin problem kurma becerilerinin geliştirilmesi için farklı çözüm stratejilerinin üzerinde durulmasının önemli olduğunu vurgulamıştır. (Akt. Dede ve Yaman,2005).
Cai (2003), öğrencilere uygulanan problem çözme testlerinin, öğrencilerin çözüm stratejilerini ve çözüm yöntemini anlamamıza yardımcı olacağını belirtmiştir. Öğrencilerin kurdukları problemleri sunuş yollarında birbirine benzeyen örneklerin olup olmadığını görmek için matematiksel problem kurma durumlarını sınayabiliriz. Bu yüzden problem kurma, öğrencilerin farklı perspektiften düşünmeleri üzerine odaklanır.
Silver (1994) problem kurmanın şu nedenlerden dolayı ilginç olduğunu ifade etmiştir.
• Yaratıcılık ve olağanüstü matematik yeteneğiyle ilişkisi bakımından • Öğrencilerin problem çözmesini geliştirmesi bakımından
• Öğrencilerin matematiği anlamalarına açılan bir pencere olarak • Öğrencilerin matematik yönündeki mizacını geliştiren bir yol olarak
• Öğrencilerin otonom (özerk) öğrenenler olmalarına yardım eden bir yol olarak.
Öğrenciler çoğunlukla problemlerini, matematik öğretmeninden veya ders kitaplarından hazır olarak alırlar, nadiren öğrencilerden kendi problemlerini oluşturmaları istenir. Matematik eğitimi araştırmacıları, öğrenciler tarafından problem kurmanın eğitimsel değerinin önemini vurgulamışlardır. Okullarda matematik dersleri içerisinde problem kurma aktivitelerini kullanmayı önermişlerdir (Leung ve Silver,1997;Akt. Korkmaz,2003).
Öğrencilerin problem kurma becerilerinin geliştirilmesi için problem kurma etkinliklerinin düzenlenmesi zorunludur. Bu amaca yönelik olarak English (1997) problem kurma etkinliklerinde aşağıda belirtilen soruların sorulmasını önermiştir:
a. Bu problemdeki önemli fikirler nelerdir?
b. Bu problemdekine benzer fikirleri nerelerde görebiliriz?
c. Problemi farklı bir biçimde çözmek için bu bilgiyi kullanabilir miyiz? d. Problemi çözmek için yeterli bilgimiz var mı?
e. Farklı bir problem üretmek için bu bilgilerin hepsine ihtiyaç var mı?
f. Bu bilgilerin bazılarını değiştirebilir miyiz? Bu durumda, problemin yeni hali nasıl olur? (Akt. Dede ve Yaman,2005).
İlköğretim (1-5.Sınıf) Matematik Programı’nda (2005) öğrencilere problem çözme becerileri kazandırılırken geliştirilecek beceriler arasında problem kurma becerileri şu şekilde ifade edilmektedir.“Matematiksel ve günlük yaşam durumlarını kullanarak problem kurma.” Müfredattaki önemine rağmen problem kurma, matematik eğitimi topluluğundan gereken ilgiyi toplayamamıştır. Öğrencilerin problem çözme yeteneği üzerine oldukça fazla bir araştırma olmasına rağmen; öğrencilerin hem sayısal hem de sayısal olmayan bağlamlarda kendi problemlerini yaratma yeteneği veya bu yeteneklerin problem çözmedeki yeterlikle bağlantılı olan boyutu hakkında az şey bilinmektedir (English,1998).
Silver (1995;2004)’e göre problem kurma problem çözme sürecinde, öncesinde veya sonrasında bulunabilir. Bu aşağıdaki şekilde ifade edilebilir:
a. Çözüm öncesi problem kurma:
Sunulan matematiksel yada uyarıcı bir durumdan orijinal problemler üretilmesi. b. Çözüm içerisinde problem kurma:
Çözümü yapılmış bir problemin yeniden formülasyonu veya oluşturulması. c. Çözüm sonrası problem kurma:
Yeni problemler üretmek için çözümü mevcut olan bir problemin amaçlarının ve şartlarının modifikasyonu ( Silver, Cai, 1996).
Verilen bir problemin değişik bir biçimini ortaya atma için bazı yararlı teknikler vardır. Bu teknikler tek başına kullanılabildiği gibi, birkaç teknik birleştirilerek de kullanılır.
• Verilen ve istenilen bilgiyi ters çevirme, • Yeni bilgi ekleme,
• Koşulları ve konuyu değiştirmeyip, verilen verilerin değerlerini değiştirme, • Verilen verileri ve koşulları değiştirmeyip, konuyu değiştirme,
• Verilen verileri ve konuyu değiştirmeyip, koşulları değiştirme, • Bağlamı veya problemin kuruluşunu değiştirme ,
• Verilen bir ifadenin bir veya daha fazla parçasının çelişmesi (Lave ve Smith ve Butler 1989;Ersoy,2004).
Tilley, English ve Cudmore (1998;Akt. Kormaz,2003) çalışmasında, problem kurma ve problem kritik etme aktivitelerini yürütürken birkaç adımın takip edilmesi gerektiğini belirtmişlerdir:
• Öğrenciler problemlerini bireysel olarak tamamlar.
• Daha sonra problemleri için bir çözüm yazarlar. Problemi ve çözümünü öğretmene gösterirler. Eğer gerekirse, bu adım bir ev ödevi düzenlemesi olarak verilir.
• Bir sonraki derste, öğretmen öğrencilerin ürettiği problemlerin hepsini toplar, ama çözümleri almaz. Daha sonra öğrencileri çiftlere ayırır. Üretilen problemler için, öğretmen öğrencilere bir eleştiri kağıdı verir.
• Öğrenciler eleştiri kağıdının arkasında aldıkları probleme dair çalışmalarını gösterirler. Problemi bitirdikten sonra eleştiri kağıdını doldururlar. Eleştiri kağıdı öğretmen tarafından görülür ve problem yazarına döner. Öğrenciler daha sonra ya diğer bir arkadaşın ürettiği problemi seçmede ya da kendi problemlerinin ileri seviyesinde başka bir probleme başlamak için serbesttirler.
• Problem yazarları, problemleri gözden geçirenler tarafından sağlanan cevapları kontrol ederler ve onların dönütlerini dikkate alırlar. Uygun
gördükleri yerde, orijinal problemleri düzeltmek ve genişletmek için dönütlere göre hareket ederler.
Albayrak ve Erkal’a (2003) göre problem kurmada dört aşama vardır. Problemin: 1. Amacı olmalıdır,
2. Gerçekci olmalıdır, 3. İlgi uyandırmalıdır, 4. Diline dikkat edilmelidir.
Ders kitaplarındaki problemler, dili ve anlatımı bakımından öğrenciler için yetersiz kalabilmektedir. Bu gibi durumlarda, öğrencilerin ve öğretmenlerin; amacı olan, ilgi uyandıran, sade bir dile sahip, gerçekçi problemler kurması gerekmektedir. Bu bağlamda, problem kurma uygulamaları, öğretmenin ve öğrencilerin ders kitaplarına olan bağlılığını azaltması bakımından da önem arz etmektedir.
Bir beceri, geliştirilen bir yetenek olduğu için, iyi organize eden bir öğretmen tarafından dikkatli bir planlama sayesinde geliştirilebilir. Bir öğretmen, bir öğrencinin problem oluşturma yeteneğini geliştirmek için ihtiyaç duyulan becerileri nasıl oluşturabilir? Sorusunun cevabı etraflıca araştırılması önem arz etmektedir. Öğretmen, daha etkili bir öğrenme için sorular oluşturmanın, bu sorulara cevap bulmanın ve problemle ilgili bütün düşüncelerini kaydetmenin üzerinde durmalıdır(Akay, 2006).
Çocuklar için çok miktarda pratik yapmadan, özel talimatlar veya kılavuzlu sorgulamalar olmadan problem oluşturmak zordur (Ellerton,1986; Silver,2004). Bu yüzden eğitimcilerin, öğrencilerin problem kurma becerilerini geliştirmek amacı ile gerekli aktiviteleri yapması gerekmektedir.
İyi bir problem düzenleme durumlarını sağlayan öğretme-öğrenme koşullarını sağlamak için, (Lowrie,1999;Akt. Akay,2006) matematik öğretmenlerine aşağıdaki tavsiyelerde bulunmuştur:
• Problem üretmede yetenekli hale gelinceye kadar, öğrencilerinizi, kendi seviyelerinde ya da seviyelerine yakın arkadaşları için problemler düzenlemelerini teşvik etme.
• Öğrencilerinizin tasarladıkları problemler hakkında bir dönüt alabilmeleri için problemleri çözerken işbirlikçi olarak çalışmaları sağlayınız.
• Öğrencilerinizden, arkadaşları problemi çözmeden önce, problemin başarılı bir şekilde çözülebilmesi için gerekli olan stratejileri anlatmalarını isteyiniz. • Problem çözmek için gruptaki öğrencilerin problemleri ne derecede zor,
karışık, motive edici ve düşündürücü olduklarını birbiriyle tartışmalarına olanak sağlayınız.
• Seviyesi düşük olan öğrencilerin bu öğrencileri daha üst düzeyde düşünmesine teşvik edecek arkadaşlarıyla çalışmasını sağlayan imkanları oluşturunuz.
• Öğrencilerinizi klasik kelime problemlerin dışında, açık-uçlu ve gerçek hayatla bağlantılı problemler tasarlamaya teşvik ediniz.
• Öğrencilerinizi matematiksel düşüncelerini geliştirebilmelerine yardımcı olacak teknolojik (hesap makinesi, bilgisayar, CD, vb.) araçları kullanmaya teşvik ediniz. Böylece, öğrencileriniz teknolojiyi kullanarak yeni problem durumları tasarlayabilirler.
Öğrenciler ilk zamanlarda problem kurmada zorluk çekebilirler. Zorluğun sebebi, problem için gerekli olan veriyi toplayamamak veya verileri düzene koyamamaktan kaynaklanır. Öğretmen örnek olması bakımından zaman zaman problem için gerekli olan verileri tahtaya yazmak suretiyle öğrencilere rehberlik edecek şekilde problemin nasıl kurulduğu üzerinde durursa, problem kurmada öğrencilerin yaşayacakları zorlukları ortadan kaldırabilir (Albayrak ve Erkal, 2003).
2.7. Matematik Öğretiminde Problem Kurmanın Önemi
Problem kurma becerisi, öğrencilere matematiksel muhakemeyi öğretme, matematiksel durumları keşfetme ve matematiksel durumları düzgün bir şekilde sözlü veya yazılı olarak ifade edebilme özelliğini kazandırır. Problem kurma yaklaşımının öneminin bilincinde, temel bilgi ve becerilerle donanmış öğretmenlerin yetiştirilmesi gereklidir. Alışılmış öğretim modeli yerine, problem kurmanın matematik müfredatlarındaki bütünleyici önemini kavrayarak öğrencilere kendi problemlerini kurmaları için fırsatlar verilmesinin öğretime büyük bir katkıda bulunacağı düşünülmektedir (Argün ve diğerleri,2006).
Problem kurmanın faydaları, sınıfta onu kullanarak ve geliştirilerek kazanılır. Böyle bir çevrenin esas pekiştiricilerinden birisi de, muhtemelen problem durumlarını keşfetmeleri ve kişisel olarak araştırmanın hatlarını izlemeleri için bütün çocuklara izin verilmesidir. Böyle bir atmosfer, daha üretici ve hoşa giden bir matematiksel öğrenme için içerik yaratır. Daha özel olarak problem kurma,
• Meraklılığa teşvik edebilir, daha farklı ve esnek düşünme meydana getirebilir.
• Çocukları, öğrenmeleri için daha fazla sorumluluk almalarında cesaretlendirebilir.
• Hem öğretmenleri hem de öğrencileri, anlam karmaşasında ve kavram yanılgılarında uyarabilir.
• Çocukların problem çözmelerini arttırabilir. Aynı zamanda temel kavramları pekiştirebilir ve zenginleştirebilir.
• Matematiğin doğası üzerine olan yanlış/hatalı görüşleri kaldırabilir.
• Matematik öğrenme hakkındaki ortak korkuları ve kaygıları dağıtabilir (Brown ve Wolter,1993;Silver,1994;English, 1997).
English (1997) ise, problem kurmanın faydalarını şu şekilde ifade etmiştir. Problem kurma aktivitelerinin teşvik edilmesinin birçok faydası vardır. Problem kurma, öğrencilerin zor olan problemleri çözmede farklı ve esnek düşünmelerini sağladığı gibi, bununla beraber temel matematik düşüncelerini (kavram)
zenginleştirmiş ve güçlendirmiştir. Problem kurma aktiviteleri problem kurgucusunun tutum, kabiliyet ve düşüncesini geliştirmiş ve böylece güçlü bir karar aracı olmuştur (English,1997;Lowrie,1999;Silver,2004).
2.8. Polya’ nın Problem Çözme Adımları ve Problem Kurma
Şekil 2’ de problem çözmenin yapısı görülmektedir. Uzun yıllardır Georgia Üniversitesi’nde, problem çözme derslerinde bu yapı kullanılmaktadır. Oklar problem çözme süreci boyunca öğrenci etkinliklerini göstermektedir (Wilson, Fernandez ve Hadaway, 1993;Akt. Korkmaz,2003).
Şekil 2. Problem Çözme Süreci
(Kaynak: Wilson, Fernandez, Hadaway, 1993; Akt. Korkmaz, 2003)
Problem çözmedeki etkinlikler, ilgili bir problem ortaya atma için bir geçiş aşaması olarak kullanılır. Gonzales (1998;Akt. Ersoy,2004), Polya'nın (1945) dört adımlı yöntemine beşinci adımı ekler: ilgili bir problem ortaya atma. Öğrencilere çözdükleri problemleri yeniden gözden geçirmeleri ve verilen bir problem ifadesinin bir değişik biçimini veya daha kapsamlısını üreterek her bir probleme beşinci bir adım eklemeleri öğretilir. Öğrencilerden çözümledikleri problemlerin değişik biçimlerini üretmeleri istenir. Örneğin, öğrenciler verilen verinin değerlerini değiştirerek, verilen ve istenilen bilgiyi ters çevirerek veya özgün problemin içeriğini değiştirerek ilgili bir problem ortaya atmış olurlar (Ersoy,2004).
Problem Ortaya Atma Problemi Anlama Plan Yapma Planı Uygulama Geriye Bakış