T.C.
SELÇUK ÜNĠVERSĠTESĠ FEN BĠLĠMLERĠ ENSTĠTÜSÜ
AÇIK ATÖLYE ÇĠZELGELEME PROBLEMLERĠNĠN PARALEL KANGURU
ALGORĠTMASI ĠLE ÇÖZÜMÜ Taha DURMAZ
YÜKSEK LĠSANS TEZĠ Endüstri Mühendisliği Anabilim Dalı
Temmuz-2011 KONYA Her Hakkı Saklıdır
TEZ KABUL VE ONAYI
Taha DURMAZ tarafından hazırlanan ―AÇIK ATÖLYE ÇİZELGELEME PROBLEMLERİNİN PARALEL KANGURU ALGORİTMASI İLE ÇÖZÜMÜ‖ adlı tez çalışması 15/07/2011 tarihinde aşağıdaki jüri üyeleri tarafından oy birliği ile Selçuk Üniversitesi Fen Bilimleri Enstitüsü Endüstri Mühendisliği Anabilim Dalı’nda YÜKSEK LİSANS TEZİ olarak kabul edilmiştir.
Jüri Üyeleri Ġmza
BaĢkan
Doç. Dr. Orhan ENGİN ……….
DanıĢman
Yrd. Doç. Dr. M. Emin BAYSAL ……….
Üye
Yrd. Doç. Dr. Tamer EREN ……….
Yukarıdaki sonucu onaylarım.
Prof. Dr. Bayram SADE FBE Müdürü
TEZ BĠLDĠRĠMĠ
Bu tezdeki bütün bilgilerin etik davranış ve akademik kurallar çerçevesinde elde edildiğini ve tez yazım kurallarına uygun olarak hazırlanan bu çalışmada bana ait olmayan her türlü ifade ve bilginin kaynağına eksiksiz atıf yapıldığını bildiririm.
DECLARATION PAGE
I hereby declare that all information in this document has been obtained and presented in accordance with academic rules and ethical conduct. I also declare that, as required by these rules and conduct, I have fully cited and referenced all material and results that are not original to this work.
Taha DURMAZ Tarih: 15.07.2011
iv ÖZET
YÜKSEK LĠSANS TEZĠ
AÇIK ATÖLYE ÇĠZELGELEME PROBLEMLERĠNĠN PARALEL KANGURU ALGORĠTMASI ĠLE ÇÖZÜMÜ
Taha DURMAZ
Selçuk Üniversitesi Fen Bilimleri Enstitüsü Endüstri Mühendisliği Anabilim Dalı DanıĢman: Yrd. Doç. Dr. Mehmet Emin BAYSAL
2011, 47 Sayfa Jüri
Yrd. Doç. Dr. Mehmet Emin BAYSAL Doç. Dr. Orhan ENGĠN
Yrd. Doç. Dr. Tamer EREN
Açık atölye çizelgeleme problemi, pek çok işletmede özellikle benzer ürün gruplarının üretiminde görülen bir çizelgeleme problemidir. Esası itibarı ile her işin her bir makinede işlem görmesi gereken sadece bir işleminin bulunduğu ve işlem sırasının önemli olmadığı bir çizelgeleme türüdür. Bu çalışmada açık atölye çizelgeleme problemi, maksimum tamamlanma zamanının minimizasyonuna yönelik, rassal zıplama tekniği ile işleyen Paralel Kanguru algoritması ile ele alınmıştır. Paralel Kanguru Algoritması sürekli daha iyi çözümlere ulaşmaya çalışan metasezgisel bir algoritmadır. Literatürdeki Taillard’ın (1993) ve Guéret ile Prins’in (1999) açık atölye çizelgeleme örnekleri vahşi ve evcil iki operatörün(kangurunun) paralel çalıştırıldığı bir yaklaşımla çözülmüştür. Daha sonra algoritma üzerinde bir dizi iyileştirme çalışması yapılarak etkinliği artırılmıştır. Elde edilen sonuçlar literatürdeki en iyi sonuçlarla karşılaştırılmış ve Paralel Kanguru Algoritmasının performansı ortaya konulmuştur.
v ABSTRACT MS THESIS
PARALLEL KANGAROO ALGORITHM FOR OPEN SHOP SCHEDULING PROBLEMS
Taha DURMAZ
THE GRADUATE SCHOOL OF NATURAL AND APPLIED SCIENCE OF SELÇUK UNIVERSITY
THE DEGREE OF MASTER OF SCIENCE IN INDUSTRIAL ENGINEERING
Advisor: Assist. Prof. Dr. Mehmet Emin BAYSAL 2011, 47 Pages
Jury
Assist. Prof. Dr. Mehmet Emin BAYSAL Assoc. Prof. Dr. Orhan ENGĠN
Assist. Prof. Dr. Tamer EREN
Open shop scheduling problem is a fruquently seen scheduling problem, particularly in firms that are manufacturing similar types of product groups. In its basic it is a scheduling type that each job has only one operation to be processed on each machine and processing order is not necessary. In this study open shop scheduling problem, is used in order to minimize the total makespan with Parallel Kangaroo algorithm which runs by random jumping method. Parallel Kangaroo Algorithm is a meta heuristic algorithm which continuously tries to reach better solutions. The open shop scheduling instances of Taillard(1993) and Guéret and Prins(1999) in the literature, are solved with an approach in which wild and tame operators(kangaroos) are operated in a parallel manner. Then the efficiency is increased by application of a series of enhancement studies on the algorithm. The yielded results are copmared with the best results in the literature and the performance of the Parallel Kangaroo Algorithm is introduced.
vi ÖNSÖZ
Açık Atölye Çizelgeleme(AAÇ), çizelgeleme alanında zorluğu ve en iyi çözümlere ulaşmadaki harcanan çaba nedeniyle göreceli olarak daha az çalışılmış bir alandır. AAÇ problemlerinin çözümünde çoğu zaman genetik algoritmalar, tavlama benzetimi, karınca kolonileri vb. metasezgisel yöntemler kullanılmaktadır. Doğal olarak bu tezde de çözüm yöntemi yine bir metasezgisel olan Paralel Kanguru Algoritması seçilmiştir. Bu seçimde etkili olan temel neden, diğer metasezgisellerden farklı olarak Paralel Kanguru Algoritmasının bu alanda uygulaması olamayan bir algoritma olmasıdır.
Öncelikle hayatta farkında olduğum ve olmadığım sayısız nimetleri veren yüce Yaratıcımıza, çalışmam süresince değerli destek ve katkılarından dolayı danışmanım sayın Yrd. Doç. Dr. Mehmet Emin BAYSAL’a, sayın Doç. Dr. Orhan ENGİN ve sayın End. Müh. Mustafa Kerim YILMAZ’a, desteklerini hiç bir zaman esirgemeyen aileme, Türksat A.Ş.’deki yöneticilerime, arkadaşlarıma ve dostlarıma teşekkürlerimi sunarım.
Taha DURMAZ KONYA – 2011
vii ĠÇĠNDEKĠLER ÖZET ... iv ABSTRACT ... v ÖNSÖZ ... vi ĠÇĠNDEKĠLER ... vii
SĠMGELER VE KISALTMALAR ... viii
1. GĠRĠġ ... 1
2. KAYNAK ARAġTIRMASI ... 2
2.1. Açık Atölye Çizelgeleme ... 2
2.2. Paralel Kanguru Algoritması ... 9
3. MATERYAL VE YÖNTEM ... 12
3.1. Materyal ... 12
3.1.1. Açık Atölye Çizelgeleme ... 12
3.2. Yöntem ... 14
3.2.1. Kanguru Algoritması ... 14
3.2.2. Paralel Kanguru Algoritması ... 15
3.2.3. Parametrelerin Belirlenmesi ... 17
4. ARAġTIRMA BULGULARI VE TARTIġMA ... 25
4.1. Hesaplama Ortamı ... 25 4.2. Uygulama Tekniği ... 25 4.3. Bulgular ... 27 4.4. Değerlendirme ... 34 5. SONUÇLAR VE ÖNERĠLER ... 35 KAYNAKLAR ... 36 ÖZGEÇMĠġ ... 39
viii
SĠMGELER VE KISALTMALAR Kısaltmalar
AAÇ Açık Atölye Çizelgeleme ATÇ Akış Tipi Çizelgeleme BEÇ Bilinen en iyi çözüm
GA Genetik Algoritma
KA Kanguru Algoritması
KKO Karınca kolonisi optimizasyonu
NP Polinomal olmayan
PKA Paralel Kanguru Algoritması PSO Parçacık Sürü Optimizasyonu TA Tabu Araştırması
1. GĠRĠġ
Artan rekabet ve gelişen teknoloji, verimlilik beklentilerinin hızla yükselmesine neden olmuştur. Kaynakların daha verimli kullanılması ve gelecek öngörülerinin daha tutarlı yapılabilmesi ancak başarılı bir planlama ile mümkündür. Çizelgeleme, tüm sektörler için üretim planlamanın önemli bir unsurudur. Endüstriyel üretim süreçlerinin modellenmesinde sıklıkla kullanılan çizelgeleme problemleri, araştırmacılar tarafından artan bir ilgi görmektedirler (Liaw ve ark., 2002).
Açık atölye çizelgeleme problemi, m makinelik bir sette işlenmesi gereken n adet işin bulunduğu, her bir işin farklı bir makinede gerçekleştirilmesi gereken m adet işlemden oluştuğu bir çizelgeleme problemidir. İşlemler herhangi bir sıra ile gerçekleştirilebilir, takip edilmesi gereken bir işlem sırası yoktur. Herhangi bir zamanda bir makinede en fazla bir işlem gerçekleştirilebilir ve yine herhangi bir zamanda bir işin en fazla bir işlemi gerçekleştirilebilir.
Açık atölye çizelgeleme problemlerinin çözümü çok fazla çaba ve zaman gerektirdiğinden, bu problemler için sezgisel yöntemler çözüm sürecinde etkin olarak kullanılmaktadır. Harcanan çaba ve zaman tasarrufu açısından önemli faydalar sağlayan bu yöntemler tekil olarak kullanılabildikleri gibi, özellikle algoritmanın zayıf yönlerini gidermeye yönelik melezlemeler, paralel uygulamalar veya öncül/ardıl işlemlerle daha etkili biçimlerde de kullanılmışlardır.
Çalışmada, kanguru zıplayışından esinlenerek rassal zıplamalar ile arama yapan ve iyi sonuçlar üzerinden daha iyilerine ulaşmaya çalışan Kanguru algoritmasının açık atölye çizelgeleme problemleri üzerindeki başarımı incelenmiştir. Algoritmanın daha etkin bir hali olarak; evcil kanguru ile yerel çözüm alanlarının keşfedilmesini, vahşi kanguru ile düşük başarılı çözüm alanlarında takılmamayı hedefleyen ve belirli bir iterasyona ulaşıldığında aynı noktada buluşan paralel kanguru yöntemi tercih edilmiştir.
Çalışma şu şekilde organize edilmiştir: Girişten sonraki ikinci bölümde AAÇ ve PKA üzerine güncel literatür bilgisi verilmiştir. Üçüncü bölümde ele alınan problem ve çözüm yöntemi ayrıntılı bir şekilde sunulmuştur. Dördüncü bölümde yapılan uygulama anlatılmıştır. Elde edilen bulgular üzerinde performans ölçütlerine göre değerlendirmeler yapılmıştır. Beşinci ve son bölümde sonuç ve öneriler yer almaktadır.
2. KAYNAK ARAġTIRMASI
Kaynak araştırması, literatürde yer alan Açık Atölye Çizelgeleme problemleri ve Kanguru Algoritması uygulamaları ayrımıyla iki ana başlıkta gerçekleştirilmiştir.
2.1. Açık Atölye Çizelgeleme
AAÇ problemleri üzerine hem farklı çizelgeleme modelleri hem de farklı çözüm yöntemleri içeren geniş bir literatür bulunmaktadır. İncelenen çalışmalarda yer alan farklı AAÇ modelleri şöyledir:
- Öncelikli AAÇ: Bu modelde standart AAÇ’den farklı olarak bazı işlemlerin aynı anda birden çok makinede işlem görmesi gerekir.
- Eş-zamanlı AAÇ: Standart AAÇ’nin biraz daha esnek hale getirilmiş bu versiyonunda bir işin herhangi iki işlemi farklı makinelerde aynı anda gerçekleştirilebilmektedir.
- Yığın AAÇ: İşlerin gruplar halinde ele alındığı AAÇ tipidir. Benzer yapıdaki işler gruplanarak, hazırlık, sökme gibi işlem sürelerinden fayda sağlanmaya çalışılır.
- Zaman kısıtlı AAÇ: Atıl zaman, taşıma zamanı, teslim tarihi gibi zaman kısıtlarına sahip modeller.
Makine sayısı m≥3 için NP(Polinomal olmayan) zor olarak bilinen (Gonzalez ve Sahni, 1976) açık atölye çizelgeleme problemlerinin çözümünde çoğu NP zor problemin çözümünde olduğu gibi ağırlıkla meta sezgiseller tercih edilmiştir. Çözüm kalitesi ise seçilen yöntemin başarılı yönleri, olumsuz yönleri ve kullanılan parametrelere bağlıdır. En iyi çözüm veren parametreler, problemlerin yapısına göre de değişmektedir.
Çalışmada incelenen AAÇ problemlerine ilişkin çalışmalar Çizelge 2.1’de sunulmaktadır.
Çizelge 2.1. Açık Atölye Çizelgeleme ile ilgili yapılan çalışmalar
Yıl Yazar AraĢtırma
2010 Zhang ve Velde
Maksimum tamamlanma zamanı minimizasyonu amaçlı, çevrimiçi iki makineli bir AAÇ çözümünde doyumsuz algoritma kullanmıştır.
2010 Naderi ve ark.
Maksimum tamamlanma süresi minimizasyonu amaçlı AAÇ problemini, farklı bir permutasyon listesi tekniği ile
çözülmüştür.
2010 Akgöbek ve ark.
AAÇ için literatürde ilk paralel doyumsuz algoritma kullanımında ulaşılmış en iyi çözüme %1 sapma ile yaklaşılmıştır.
2009 Low ve Yeh
Hazırlık, işlem ve sökme zamanları ayrıştırılmış AAÇ problemleri için genetik algoritma temelli sezgiseller geliştirilmiştir.
2009 Sedeño-Noda ve ark.
Performans maliyeti ve tamamlanma zamanı amaçlı, çift kriterli AAÇ problemlerinin çözümünde ağ algoritması kullanılmıştır.
2008 Werra ve ark. Çok işlemcili öncelikli AAÇ çözümü için polinomiyel zaman algoritmaları kullanılmıştır.
2008 Mosheiov ve Oron
Minimum tamamlanma zamanı ve minimum akış zamanı amaçlı bir açık atölye yığın çizelgelemesi üzerinde çalışılmıştır.
2008 Lin ve ark.
Tüm süreç aşamaları için toplam işlem süresinin minimizasyonunu amaçlayan, hareket edebilen atanmış makinelerden oluşan beklemesiz bir AAÇ çözümünde iki aşamalı sezgisel algoritmalar kullanılmıştır.
2008 Brasel ve ark. Anlamlı akış zamanı minimizasyonu amaçlı AAÇ çözümünde yapısal sezgisel algoritmalar sınanmıştır.
2008 Sha ve Hsu
AAÇ problemlerinin çözümünde yeni bir PSO (Parçacık Sürü Optimizasyonu) tekniği kullanılmış ve bazı çözülmemiş problemler için en iyi sonuçlara ulaşılmıştır.
2006 Gribkovskaia ve ark.
Doğrusal zaman diliminde optimal bir üç yığınlı çizelgeye ulaşmak için araştırmacılardan De Werra’nın geliştirdiği açık atölye algoritması uygulanmıştır.
2006 Sedeno-Noda ve ark.
Zaman pencereli öncelikli AAÇ problemleri için ağ akışı yaklaşımları uygulanmıştır.
2006
Senthilkumar ve
Shahabudeen
AAÇ problemleri için tamamlanma zamanı minimizasyonu amaçlı genetik algoritma temelli bir sezgisel geliştirilmiştir.
2006 Shabtay ve Kaspi
Konveks kaynak tüketim fonksiyonuna sahip AAÇ
problemlerinde tamamlanma zamanı minimizasyonu üzerine çalışılmış, iki makine için verimli bir algoritma geliştirilmiştir.
Çizelge 2.1. (devam) Açık Atölye Çizelgeleme ile ilgili yapılan çalışmalar
2005 Blum AAÇ problemlerinde ışın taraması ve karınca kolonisi optimizasyonu melez tekniği kullanılmıştır.
2004 Mosheiov ve Yovel
―Bir kritik makine ve her bir iş için iki işlem içeren akış tipi ve AAÇ‖ makalesi üzerine yorum ve değerlendirmelerde
bulunulmuştur.
2003 NG ve ark. Geciken işlerin ağırlıklandırılmış sayısını azaltma amaçlı eş-zamanlı AAÇ üzerine çalışılmıştır. 2002 Liaw İki makineli öncelikli AAÇ problemi için verimli bir tabu
araştırması yaklaşımı üzerinde çalışılmıştır.
Zhang ve Velde (2010), maksimum tamamlanma zamanı minimizasyonu amaçlı çevrimiçi iki makineli bir AAÇ çözümünü doyumsuz algoritma ile gerçekleştirmişlerdir. Çalışmada ilk işlemin tamamlanması ile ikinci işlemin başlangıcı arasında kalan sürelerin atıl zamanı oluşturduğu kabul edilmektedir. Bu durumda doyumsuz algoritmanın, algoritma kalitesini ifade eden rekabet oranının 2 olduğu ve en uzun aranın herhangi bir işlemin en kısa gerçekleştirilme süresinden kısa olması halinde bu oranın 5/3’e indirilebildiği gösterilmektedir. Aynı zamanda hiçbir beklemesiz paralel algoritmanın, √2’den daha iyi bir rekabet oranı veremeyeceği ispatlanılmıştır.
Naderi ve ark. (2010), permutasyon listesi tekniğinin farklı bir uygulamasını maksimum tamamlanma süresi minimizasyonu amaçlı AAÇ problemine, uyarlamışlardır. Permutasyon listesi, tüm operatörlere yüksek uyarlanabilirlik, kavramsal basitlik ve kolay uygulanma gibi önemli avatajlara sahiptir. Bununla birlikte getirdiği yükler nedeniyle özellikle büyük hacimli örnekler için elverişsiz olması bir dezavantajdır. Bu dezavantajın nedenine inilerek, eksikliklerin giderilmesine odaklanan dört teorem ile optimal sonuçlara %95 azalan sürelerle ve %2,5 sapmayla yaklaşılabildiği ifade edilmektedir.
Akgöbek ve ark. (2010), AAÇ problemlerinin çözümünde paralel doyumsuz meta sezgisel algoritmanın kullanımını, literatürde ilk olarak incelemişlerdir. Üzerinde çalıştıkları beş iş, beş makineli örnek üzerinde ulaşılmış en iyi çözüme %1 sapma ile yaklaşmışlardır. Çalışmada optimum çizelgelemeye ulaşmanın oldukça zor bir iş olduğu, AAÇ problemlerinde paralel doyumsuz algoritma kullanılarak parametrelerin optimizasyonu yardımıyla oldukça başarılı sonuçlara ulaşılabileceği ifade edilmektedir.
Low ve Yeh (2009), toplam iş gecikmesi minimizasyonu amaçlı, bağımsız hazırlık zamanı ve bağımlı sökme zamanı kısıtlamalı AAÇ problemininin literatürde ilk defa olarak 0–1 tam sayı programlama modeli ile optimal çözümünü elde etmişlerdir. Ardından bazı melez genetik sezgiseller kullanarak çözüm süresini kabul edilebilir sürelere indirgemişlerdir. Bu sezgisellerin adaptasyon elverişliliğini göstermek için, matematiksel programlama modelinden veya genetik algoritma, tavlama benzetimi ve TA gibi klasik meta sezgisellerden elde edilen sonuçlarla karşılaştırmışlardır. Elde edilen sonuçlar, melez genetik temelli sezgisellerin, özellikle de çiftli genetik algoritmanın, biraz daha fazla hesaplama gerektirse de başarılı olarak kabul edilebilir olduklarını göstermiştir. İş sayısının 10’un üzerinde olması durumunda uyguladıkları melez genetik temelli sezgisellerin, alışılmış meta sezgisellerden daha başarılı hesaplama sürelerine sahip olduğu ifade edilmektedir.
Sedeño-Noda ve ark. (2009), performans maliyeti ve tamamlanma zamanı amaçlı, çift kriterli AAÇ problemlerinin çözümünde Pareto optimal noktalar yaklaşımına dayanan bir ağ algoritması kullanmaktadırlar. İşleri zaman pencereleriyle ifade ederek geliştirdikleri yaklaşımlarının, inceledikleri problemlerin geçici polinomiyel zaman dilimleri içinde çözülmesine imkan sağladığını ifade etmektedirler. Çift kriterli AAÇ problemlerinin karmaşıklığı, çözüm alanında mevcut Pareto optimal tamsayı nokta sayısına bağlıdır. Yaklaşım, hizmet birimlerinde personel zaman çizelgeleri, kalite kontrol faaliyetlerinin çizelgelenmesi gibi gerçek hayat problemlerinde duyarlılık analizi yapmayı sağlamaktadır.
Werra ve ark. (2008), öncelikli AAÇ probleminin genelleştirilmiş bir halini ele almışlardır. Çalışmada işlemciler iki gruba ayrılarak her bir işlemin tek bir işlemcide veya bir işlemci grubunun tüm işlemcilerinde aynı anda gerçekleştirilmesini sağlamışlardır. Önceliğin belirli kesikli noktalarda veya tam sayı değerlerde olduğu iki farklı varyasyon üzerinde durulmuştur. Kesikli problemin doğrusal programlama ile çözüm süresi polinomiyel sürelere indirgenmiş, tam sayılı problemin kısıtlı bir hali ise yuvarlama tekniğiyle çözülmüştür.
Mosheiov ve Oron (2008), minimum tamamlanma zamanı ve minimum akış zamanı amaçlı bir açık atölye yığın çizelgelemesi üzerinde çalışmışlardır. Çalışmalarında her bir işe özel süreler; iş, makine ve sıralamadan bağımsız hazırlık zamanları ve yığın esnekliği kabulleri yaparak, minimum tamamlanma zamanı problemini sabit sürede çözmüşlerdir. Ayrıca en uygun yığın sayısının makine sayısına
eşit çıktığı ve minimum akış zamanı probleminin karmaşıklık düzeyinin bilinmediği ifade edilmiştir.
Lin ve ark. (2008), çalışmalarında günlük hayatta karşılaşılan gaz, su, telefon hattı döşeme gibi işlemleri de içeren yol yapımı işinin çizelgelenmesi sorununu ele almışlardır. Problem hareketli makinelerden oluşan çok işlemcili çok aşamalı AAÇ karakteristiklerini taşımaktadır. Amaç, bütün aşamalardaki işlem zamanlarını minimize ederek minimum toplam işlem zamanına ulaşmaktır. Problemin çözümü için iki aşamalı bir sezgisel algoritma önerilmiştir. Sonuçlar küçük çaplı problemler için algoritmaların etkin çalıştığını göstermekte, optimal veya optimale yakın sonuçlara ulaşıldığı ifade edilmektedir. Ayrıca, gerçek hayat verileri ile yapılan denemeler sezgiselin çizelgeleme problemlerinin çözümünde etkin bir şekilde kullanılabilme potansiyeli olduğu gösterilmektedir. Uygulamanın 360 test probleminin yaklaşık % 89’unda; ortalamada % 0,25, maksimum ise % 6,67 hata oranı verdiği belirtilmektedir.
Brasel ve ark. (2008), ortalama akış zamanının minimizasyonuna yönelik AAÇ çözümünde yapısal sezgisel algoritmaları denemişlerdir. 50 iş ve 50 makineye kadar farklı AAÇ modelleri üzerinde çalışan araştırmacılar, bir AAÇ probleminin çözümünde önerilmesi gereken yapısal sezgiselin, iş sayısı/makine sayısı oranı ile ilgili olduğunu ifade etmektedirler. Ayrıca, ortalama akış zamanı minimizasyonuna yönelik AAÇ problemi için uygun bir yapısal çözüm prosedürü seçiminin, işlem zamanlarından ziyade iş sayısı ve makine sayısı ilişkisine bağlı olduğu sonucuna ulaşılmıştır.
Sha ve Hsu (2008), AAÇ problemlerinin çözümünde yeni bir PSO tekniği kullanmışlardır. Geliştirilen algoritma, orijinal PSO ile karşılaştırıldığında, parçacık konumunun gösterimi öncelikler yardımıyla, parçacık hareketi ise bir ekleme operatörü vasıtasıyla değiştirilmiştir. Ayrıca bir parçacığın konumunu çizelgeye yüklemek için, değiştirilmiş parametreli bir aktif çizelge oluşturma algoritması kullanılmıştır. Bu algoritma ile izin verilen maksimum bekleme zamanı kontrol edilerek, beklemesiz çizelge ile aktif çizelge arasındaki arama alanı küçültülüp, büyütülebilmektedir. Daha sonra yöntem ışın taraması ile melezlenmiştir. Çalışmada Taillard, Brucker, ve Guéret ile Prins'in AAÇ test problemleri kullanılmıştır. Hesaplama sonuçları, yöntemin pek çok çözülmemiş problemin yeni en iyi değerlerinin elde edildiğini göstermektedir.
Gribkovskaia ve ark. (2006), optimal bir üç yığınlı çizelgelemeye doğrusal zamanda ulaşmak için araştırmacılardan De Werra’nın geliştirdiği açık atölye algoritmasını kullanmışlardır. İki makineli bir açık atölye yığın probleminde tamamlanma süresinin minimizasyonu amaçlı bir optimal çizelgenin her makinede bir,
iki veya üç yığına sahip olması gerektiği ve iki yığınlı bir optimal çizelge bulmanın NP zor olduğu belirtilmiştir. Sonuç olarak bir veya üç yığın için optimal bir çizelge varsa bunlara doğrusal bir zamanda ulaşılabildiği, lakin iki yığın için optimal bir çizelge varsa bu problemin NP zor olduğu ifade edilmiştir.
Sedeno-Noda ve ark. (2006), zaman pencereli öncelikli AAÇ problemleri üzerinde çalışmışlardır. Uygunluğu kontrol eden bir ağ akışı yaklaşımı ve tamamlanma zamanının minimizasyonunu amaçlayan maksimum akış parametreli bir algoritma geliştirmişlerdir. İlgili uyunluk ve optimizasyon algoritmalarının hesaplama karmaşıklıkları değerlendirilmiş, geliştirilen yöntemin polinomiyel yapıda ve zaman pencereli öncelikli AAÇ problemleri için önemli bir algoritma olduğu ifade edilmiştir. Yöntemin uygulanması sonucu elde edilen sonuçlar, algoritmanın güçlü bir algoritma olduğunun delili olarak sunulmuştur.
Senthilkumar ve Shahabudeen (2006), AAÇ problemleri için tamamlanma zamanı minimizasyonuna yönelik genetik algoritma temelli bir sezgisel geliştirmişlerdir. Genetik algoritma operatörleri uygunluğu sağlayacak biçimde değiştirilmiştir. Üzerinde çalışılan örnekler 2x3 ile 4x4 aralığındadır. Elde edilen sonuçlar daha önceki çalışmalarda sunulmuş sonuçlarla istatistiki olarak karşılaştırılmıştır. Ulaşılan sonuçların geçmiş çalışmalara göre açık şekilde daha başarılı olduğu ifade edilmiştir.
Shabtay ve Kaspi (2006), işlem sürelerinin sınırlı ve yenilenemeyen ortak bir kaynağın konveks azalan fonksiyonuna bağlı olduğu AAÇ problemleri üzerinde çalışmışlardır. Çizelgelemenin amacı tamamlanma zamanını minimize edecek şekilde, her bir makine için en uygun iş sıralamasını ve her bir işlem için en uygun kaynak atamasını gerçekleştirmektir. Çalışmada problemin NP zor olduğunun ıspatlanıldığı, bununla birlikte iki makine problemine özel olarak verimli bir optimizasyon algoritması sağlanıldığı ifade edilmektedir. Ayrıca öncelikli problemlerin çözümü için tam polinomiyel bir yakınsama tablosu da sunulmuştur. Bu yapının gerçek hayatta örnekleri bulunsa da, literatürde benzeri bir çalışma bulunmadığı ifade edilmektedir. Ayrıca kontrol edilebilir işlem sürelerine sahip çizelgeleme problemlerinin çözümünde eşit yükleme yönteminden kaynaklanan geniş bir kullanım alanı olduğu da belirtilmektedir.
Blum (2005)’un çalışmasında AAÇ problemlerinin çözümü için ışın taraması ile KKO (Karınca kolonisi optimizasyonu/Ant colony optimization) yöntemleri melezlenilmiştir. KKO, zor kombinatoryal optimizasyon problemlerinin çözümünde kullanılan bir meta sezgisel yaklaşımdır. KKO’nun temel bileşeni, olasılığa dayalı bir
çözüm mimarisi mekanizmasıdır. Yapısal doğasından dolayı KKO, bir ağaç arama yöntemi olarak değerlendirilebilir. Bu gözleme dayanılarak, KKO’nun çözüm mimarisi mekanizması, iyi bilinen bir ağaç arama yöntemi olan ışın taraması ile melezlenilmiştir. Işın-KKO (Beam-ACO) adı verilen bu yaklaşım AAÇ üzerinde kullanılarak işe yaradığı gösterilmiştir. Çalışma literatürdeki pek çok mukayese çalışmasında kullanılmış yöntemlerle karşılaştırıldığında, Işın-KKO’nun AAÇ problemlerinin çözümünde yeni bir yöntem olduğu görülmüştür.
Mosheiov ve Yovel (2004) tarafından yapılan çalışmada, n işin her birinin en fazla iki işlemle sınırlı olduğu ve bu işlemlerden birinin tüm işler için ortak olduğu bir akış tipi çizelgeleme problemini konu alan geçmiş bir makale [Eur. J. Operat. Res. 127 (2000) 120] hakkında algoritmanın doğruluğuna, karmaşıklığına, optimallik ıspatına ve muhtemel açılımlarına dair bazı çıkarımlarda bulunulmuştur.
NG ve ark. (2003), bir işin farklı makinelerdeki herhangi iki işleminin aynı anda yapılabildiği, AAÇ problemlerinin daha esnek bir tipi olan eş-zamanlı AAÇ üzerine çalışmışlardır. Bir işin tamamlanma süresinin, o işin işlemlerinin maksimum tamamlanma süresine eşit olduğu belirtilen çalışmada amaç, işlem gerçekleştirme sürelerinin 0-1 ve d’nin ortak tamamlanma tarihi olduğu durumda, geciken işlerin ağırlıklandırılmış sayısının azaltılmasıdır. Problemin NP zor olduğu ve problem için bir (1+d)-yakınsama algoritması geliştirildiği ifade edilmektedir.
Liaw (2002), iki makineli öncelikli AAÇ problemi için etkin bir TA yaklaşımı üzerine çalışmıştır. Amaç toplam gecikmenin minimizasyonunudur ve problem NP zordur. İşlerin tamamlanma sürelerinin, verilen iş tamamlanma sıralamasına uygun olmasını sağlayacak bir optimal zaman algoritması sunulmuştur. Ardından iş tamamlanma çizelgeleri ve nihai çizelgeleri oluşturmak üzere optimal zaman algoritmasına bir TA yaklaşımı uygulanılmıştır. Tabu araştırmasına bir başlangıç çözümü elde etmek için etkin bir sezgisel geliştirilmiştir. Algoritmayı güçlendirmek için çeşitlendirme ve kuvvetlendirme stratejileri incelenilmiştir. Son olarak değinilen yaklaşımın performasını göstermek için hesaplamalar sunulmuştur. Sonuçlarla geliştirilen bu tabu araştırması yaklaşımının, mantıklı süreler içinde yüksek kalitede sonuçlara ulaştığı gösterilmiştir.
2.2. Paralel Kanguru Algoritması
Literatürde PKA veya KA’nın çeşitli çizelgeleme problemlerinin çözümünde, yalın veya farklı yöntemlerle melez olarak kullanım örnekleri bulunmaktadır. Yapılan çalışmalarda PKA’nın, geçmiş çalışmalara nazaran işlem zamanı ve başarımında fayda sağladığı kaydedilmektedir. Çizelge 2.2’de PKA ve KA ile ilgili yapılan son çalışmalar özetlenilmiştir:
Çizelge 2.2. Kanguru Algoritması ile ilgili yapılan çalışmalar
Yıl Yazar ÇalıĢma
2010 Yılmaz ve ark. Çift amaçlı akış tipi çizelgeleme için PKA uygulaması yeni bir ağırlık birleşim yaklaşımıyla gerçekleştirmiştir.
2010 Yılmaz ve ark. PKA ile beklemesiz akış tipi çizelgeleme problemlerinin çözümü üzerine çalışılmıştır. 2010 Kökçam ve
Engin
Bulanık proje çizelgeleme problemlerinin meta sezgisel yöntemlerle çözümü üzerine çalışılmıştır.
2007 Minzu ve Beldiman
Bir paralel melez meta sezgiselin uygulamasına dair bazı yönleri incelenmiştir.
2007 Serbencu ve ark.
Tek makine çizelgeleme probleminin çözümünde karınca kolonisi sistemi temelli bir meta sezgisel önerilmiştir. 2003 Teske Paralel kanguru yöntemi ile kesikli logaritmaların çözümü üzerine çalışılmıştır. 2001 Stein ve Teske Gerçek kuadratik fonksiyon alanlarında paralelleştirilmiş
Pollard kanguru yönteminin kullanımı incelenmiştir. 2001 Jellouli ve
Chatelet
Tedarik zincirinde belirsiz talep ve dağıtım zamanları çözümlemesinde, Monte Carlo simulasyonu, TA ve KA kullanılmıştır.
2000 Pollard Değer aralığı belirli, isteğe bağlı bir devir grubu içindeki kesikli bir logaritma, kesin işlem süresi içinde hesaplanmıştır.
Yılmaz ve ark. (2010), çift amaçlı akış tipi çizelgeleme için PKA uygulamasını yeni bir ağırlık birleşim yaklaşımıyla gerçekleştirmişlerdir. Çalışmada tamamlanma zamanı ve toplam gecikme olmak üzere iki ana minimizasyon hedefine odaklanılmıştır. Birleştirilmiş iki amaçlı akış tipi çizelgeleme probleminin çözümü için bir PKA geliştirilmiştir. Geliştirilen algoritmanın etkinliği, rassal oluşturulan örnekler üzerinde bilgisayar ortamında yapılan çalışmalarla sunulmuştur. Çalışmada geliştirilen yöntem ile daha gerçekçi ve dengeli sonuçlara ulaşıldığı ifade edilmektedir.
Yılmaz ve ark. (2010), iki makineli beklemesiz akış tipi çizelgeleme problemlerini, PKA ile çözmüşlerdir. NP zor olduğu ifade edilen çalışmanın amacı tamamlanma zamanının minimizasyonu üzerinedir. PKA’nın etkinliğinin belirlenebilmesi için örneklerin gruplama yöntemiyle de çözüldüğü ve başarılı sonuçlara ulaşıldığı ifade edilmiştir. PKA’nın literatürde son dönemlerde başarılı kullanımları bulunan bir meta sezgisel olduğu ve beklemesiz akış tipi çizelgeleme problemleri için literatürdeki ilk kullanımının bu çalışma olduğu belirtilmiştir.
Kökçam ve Engin (2010), bulanık proje çizelgeleme problemlerinin meta sezgisel yöntemlerle çözümü üzerine yaptıkları çalışmalarında PKA’ya geniş yer verilmiştir. Çalışmada güncel proje çizelgeleme ihtiyaçlarının kesin çözüm veren yöntemlerle çözülmesinin gerçekçilik ve çözüm süresi açılarından mümkün olmadığı ve bu durum için en doğal yöntemin bulanık küme teorisi olduğu belirtilmiştir. Çalışmada proje çizelgeleme, temel unsurları, teknikleri, bulanık proje çizelgeleme, bulanık küme teorisi, kesin çözüm veren doğrusal yöntemler (doğrusal programlama, tam sayılı programlama, dal sınır yöntemi) ve meta sezgisellerin kullanımına literatürden örnekler verilmiştir. Ayrıca PKA ile bulanık proje çizelgeleme örneği sunulmuştur.
Minzu ve Beldiman (2007), GA (Genetik Algoritma) ve PKA melez kullanımını, bir kesikli optimizasyon çözümünde uygulamışlardır. Belirledikleri meta sezgiselin kullanımı ile iki temel imalat problemini çözmüşlerdir. Geliştirdikleri melez sistemin uygulanmasında avantaj bulunan bazı yaklaşımları vurgulamışlardır. Bilgisayar ortamına aktarılan yöntemin ilgi çekici bir işleyişi ve çok iyi bir uygulama karmaşıklık düzeyi sunduğu; elde edilen sonuçların yalın bir GA ile karşılaştırıldığında çok etkin olduğu, makul süreler ve atama sayıları için optimal çözümler sunduğu ifade edilmiştir.
Serbencu ve ark. (2007), çalışmalarında tek makine çizelgeleme problemini, karınca kolonisi ve paralel kanguru optimizasyonunun kullanıldığı bir melez yöntem ile çözmüşlerdir. Kurdukları döngüde karınca kolonisinden elde edilen sonuçları PKA süreçlerinden geçirmişlerdir. Sonuçta KA’nın geçmiş çalışmalarda yer alan yerel arama algoritmalarından daha basit ve verimli olduğu, yalın bir karınca kolonisi sistemiyle karşılaştırıldığı ve melez yapının daha etkin olduğu, iterasyon sayısı ve genel iterasyon sayısının problemin hacmine göre düzenlenmesi gerektiği, makul zaman ve iterasyon sayısında çok iyi sonuçlar bulunduğu, çalıştırma süresinin artışının kabul edilebilir olduğu ifade edilmektedir.
Teske (2003), kesikli logaritmaları Paralel Kanguru yöntemiyle rasgele seçilmiş devir grupları dahilinde hesaplamıştır. Seri sürümünün çok az hafıza kullandığı,
doğrusal bir hız artışıyla paralelleştirilebildiği ve paralel sürümünün hafıza gereksiniminin etkin olarak izlenebildiğini ifade etmişler, bu durumun da kanguru yöntemini kesikli logaritma problemlerinin çözümünde en güçlü yöntem kıldığını belirtmişlerdir. Çalışmada uygulamanın en etkin kullanımı için tecrübeye ve teoriye dayalı çeşitli yönler tartışılmıştır.
Stein ve Teske (2001), gerçel karesel fonksiyon alanlarında sabitlerin hesaplanmasında, paralelleştirilmiş Pollard Kanguru yöntemi kullanımını incelemişlerdir. Çalışmada özellikle bu mimariye kanguru yönteminin nasıl uygulanacağı anlatılmıştır. Bununla birlikte iki yolla hesaplama süresinin nasıl hızlandırıldığı gösterilmiştir.
Jellouli ve Chatelet (2001), olasılıklı talep ve teslim sürelerine sahip bir tedarik zinciri üzerinde çalışmışlardır. Amaçları, memnun müşteri oranıyla ilişkili olan başarılı performans değerlerine ulaşmayı sağlayacak optimal parametreleri bulmaktır. Bu amaçla Monte Carlo simulasyonu ve iki meta sezgisel kullanılmıştır. Ardından kısa ve uzun dönem stratejileri değerlendirilmiştir. Bu yöntemin, olasılıklı parametreler ve tahmin hataları göz önünde bulundurularak sistemin optimize edilmesini sağladığı ifade edilmiştir. Monte Carlo simulasyonundan elde edilen sonuçlarla kıyaslama için istatistiki testler kullanılmıştır.
Pollard (2000), değer aralığı belirli, isteğe bağlı bir devir grubu içindeki kesikli bir logaritmayı, kesin işlem süresi içinde hesaplamıştır. Çalışmada işlem süresi analiz edilmiştir. Bu nedenle programlar seri ve paralel bilgisayarlar için geliştirilmiştir. İşlem sürelerindeki farklılaşma, kanguruların zıplamalarıyla ilişkilendirilmiştir. Kruskal algoritmasına dayanan bir kart oyunu ve bazı tekel oyunları üzerinden yöntem örneklendirilmiştir.
3. MATERYAL VE YÖNTEM
Çalışmada literatürde yer alan AAÇ test problemleri kullanılmıştır. Bu test problemleri metasezgisel yöntemlerden PKA ile ele alınmıştır.
3.1. Materyal
Çalışmada, http://mistic.heig-vd.ch/taillard/problemes.dir/ordonnancement.dir/ ordonnancement.html ve http://www.mines-nantes.fr/en/Media/Elements-Sites-Persos/ Christelle-Gueret/Open-shop/HardOSInstances internet adreslerinden temin edilen Taillard (1993) ile Guéret ve Prins’in (1999) Açık Atölye Çizelgeleme test problemleri kullanılmıştır.
3.1.1. Açık Atölye Çizelgeleme
İş çizelgeleme problemleri, üretim başta olmak üzere günlük yaşamda sıklıkla karşılaşılan problemlerdendir. Literatüre bakıldığında AAÇ problemleri üzerinde, ATÇ (Akış Tipi Çizelgeleme) ve Atölye Çizelgeleme problemlerinden daha az çalışıldığı görülmektedir (Türkeli, 2010). ATÇ problemlerinde bir işin tamamlanması için belirli makine veya makine gruplarında gerçekleştirilmesi gereken işlemlerin, belirli bir sırası vardır. AAÇ problemlerinde ise işlem sırası önemsiz yani serbesttir. AAÇ mimarisi, Çizelge 3.1’de sunulmuştur.
Çizelge 3.1. Açık Atölye Çizelgeleme Modeli
İş Makine / İşlem 1 2 - j - m 1 t11 t12 - t1j - t1m 2 t21 t22 - t2j - t2m - - - - i ti1 ti2 - tij - tim - - - - n tn1 tn2 - tnj - tnm n: iş sayısı m: makine sayısı
tij: i işinin j makinesindeki işlem süresi
AAÇ problemlerinde, her işin her makinede gerçekleştirilmesi gereken, sırası önemsiz birer farklı işlemi bulunmaktadır. Meyve ve ekmek almak için ilgili
reyonlarında birer çalışanı bulunan bir markete giden iki müşterinin durumu; 2 iş, 2 makinelik bir AAÇ problemine uymaktadır. A ve B müşterilerinin meyve ve ekmek reyonlarında birer işlemi vardır, her bir işlemin birbirinden bağımsız işlem süreleri bulunmaktadır. İşlerin tamamlanması için belirli bir işlem sırası yoktur. Bir çalışan aynı anda bir müşteriye hizmet verebilmekte, bir müşteri aynı anda bir işlem gerçekleştirebilmektedir. İşlerin tamamlanabilmesi için ilk olarak bu 4 işlemden 1’i, ardından kalan 3 işlemden 1’i, onun ardından kalan 2 işlemden 1’i ve son olarak kalan işlem, makine sayısı ve müsaitlik durumlarına göre gerçekleştirilir. Yani 2 makine 2 işten oluşan bir AAÇ probleminin çözümünde 4! = 24 farklı işlem sırası izlenebilir.
Her bir işlem xij notasyonunuyla ifade edilirse; i iş numarasını, örneğimiz
üzerinde müşteri numarasını, j makine numarasını, örneğimiz üzerinde hangi reyon olduğunu ifade etmektedir. Müşterilerin meyve alımı için harcadıkları zamanlar sırasıyla 3 ve 5 birim zaman, ekmek alım süreleri ise 2 ve 4 birim zaman olarak alınırsa işlem süreleri; x11 = 3, x12 = 2, x21 = 5 ve x22 = 4 birim zaman olur. x11 → x12 → x21 →
x22 işlem sıralaması ile bu problemin çözüm süresi 12 birim zamandır. Zaman çizelgesi
Çizelge 3.2’de verilmiştir.
Çizelge 3.2. Örnek Zaman Çizelgesi
Meyve satın alma x11 (3) x21 (5)
Ekmek satın alma x12 (2) X22 (4)
Müşteri 1 Müşteri 2
İlgili işlem sıraları zaman çizelgesi üzerinde incelendiğinde, paralel çalışma imkanı nedeniyle bazı dizilimlerin aynı zaman çizelgesine sahip olduğu görülmektedir. Çok boyutlu bir sıralama çizelgeleme sistemi için girilecek hesaplama zorluğu yerine, az sayıdaki tekrar ile yapılan çözümün hesaplama süresini düşük oranda uzatması tercih edilmektedir.
Buradaki asıl sorun, tamamlanma süresini en aza indirmek için hangi sıralamanın seçilmesi gerektiğidir. Çalışmada literatürde geçen 3 x 3 ile 20 x 20 boyut aralığındaki makine sayısının işlem sayısına eşit olduğu NP zor olarak değerlendirilen AAÇ test problemleri kullanılmıştır. Örneklerin işlem sayıları 9–400, sıralama alternatifleri 9! adet ile 400! adet aralığındadır.
3.2. Yöntem
Literatürde yer alan açık atölye çizelgeleme problemlerinin çözümünde kullanılmış yöntemler kısaca aşağıdaki gibi sıralanabilir:
- Genetik algoritmalar - Tabu araştırması - Tavlama benzetimi - Pareto optimizasyonu - Permutasyon listesi - Yakınsama - Doyumsuz algoritma
- Özel algoritmalar (De Werra gibi)
Çalışma için seçilen PKA’nın, literatürde AAÇ problemleri çözümünde uygulamasına rastlanılmamıştır. PKA’nın kullanıldığı diğer çizelgeleme problemlerini çözmekteki başarısı yöntem seçiminde etkili olmuştur.
3.2.1. Kanguru Algoritması
KA, adından da anlaşıldığı gibi zıplayarak hareket eden Kanguru’lardan esinlenilerek geliştirilmiş bir algoritmadır. KA, literatürde ―Pollard’ın Kangurusu‖, ―Pollard’ın Rho algoritması‖ veya ―Pollard’ın Lambda algoritması‖ olarak da bilinmektedir. Kanguru algoritmasını ilk defa 1978 yılında Pollard ortaya atmıştır (Kökçam ve Engin, 2010).
Serbencu ve ark. (2007), Kanguru algoritmasının tavlama benzetimine benzeyen, lakin daha farklı bir arama tekniği kullanan rassal kökenli bir yakınsama tekniği olduğunu ifade etmektedirler. Kanguru yöntemi, minimizasyon amaçlı bir f(u) fonksiyonunun tekrarlı sürecine yerleştirilerek uygulanır. Eldeki çözüm u’yu rastsal seçimle belirlenen ve daha iyi bir çözüm olan komşusu N(u) ile değiştirir. Tekrarlama sayısı A, algoritmanın bir parametresidir. Çözüm sürecinde iyileşme olmuyorsa, zıplama yapılarak yerel minimumun çekim alanından uzaklaşılmaya çalışılır. Kısa sürede karşılaşılabilse de eldeki çözümden daha iyiye ulaşılması, bu safhada beklenmemektedir. N’(u) gibi farklı bir komşuluk tanımı kullanılabilir. Durma kriteri, maksimum iterasyon sayısı veya amaç fonksiyonunun alt sınırı olabilir.
Minzu ve Beldiman (2007), KA uygulamasının N(u) komşuluğu tarzında işlediğini; i ile i+1 konumundaki işlerin yer değiştirmesi ile u’dan elde edilen u' çözüm kümesine ulaştığını ifade etmektedirler. Örneğin; eğer u = [1 4 3 2 5] ise;
N(u) = { [4 1 3 2 5], [1 3 4 2 5], [1 4 2 3 5], [1 4 3 5 2], [5 4 3 2 1] } değerini almaktadır.
3.2.2. Paralel Kanguru Algoritması
Teske (2003), Kanguru yönteminin aynı zamanda lambda yöntemi olarak da bilindiğini, fakat rho yönteminin paralelleştirilmesinin popülerleşmesiyle birlikte, rho yönteminin lamda yöntemi olarak ifade edildiğini ve yöntemlerin birbirine karıştırıldığını belirtmektedir. Pollard’ın kesikli logaritmaların çözümü için geliştirdiği rho yönteminde, G içinde bir sıralama ( yk ) oluşturulur. Başlangıç terimi y0 є G seçilir,
takip eden kural şöyledir: yk+1 = F(yk), k є N, F: G → G. Bu periyodik sıralama, boş bir
kağıt üzerine çizilirse, alt köşeden başlayıp bir daireyle sonlanarak Yunan alfabesindeki rho karakterinin şeklini alır (Şekil 3.1 (a)).
Kanguru yöntemi kağıt üzerine aktarılırsa; evcil kanguru sol alttan, vahşi kanguru sağ alttan başlar ve yolları bir süre sonra kesişir. Bu grafik de Yunan alfabesindeki lambda karakteriyle aynıdır (Şekil 3.1 (b)).
Parallelleştirilmiş rho yönteminde, farklı rho sıralamaları bulunur ve bunların kesiştiği yerlerde lambda görünümü oluşur (Şekil 3.1 (c)). Bu durum fonksiyonların çalışma benzerliğini de gösterir.
ġekil 3.1 (a) Rho, (b) Kanguru ve (c) Paralel rho yöntemleri
Paralel kanguru algoritmasında adından da anlaşılabileceği gibi aynı zaman diliminde birbirinden bağımsız zıplayan iki operatör (kanguru) bulunmaktadır. Evcil kanguru küçük adımlarla zıplayarak daha lokal aramalar sağlar. Vahşi kanguru ise daha büyük adımlara sahiptir ve farklı çözüm bölgelerine ulaşmaya çalışır. Uygulamamızda her iki kanguru hareketlerine aynı anda, farklı başlangıç sıralamaları ile başlarlar ve hedef değere ulaşıncaya kadar veya maksimum iterasyon sayısına ulaşıncaya kadar zıplamaya devam ederler. Her bir zıplayışın ardından hesaplama fonksiyonu tekrar çağrılır, elde edilen sonuç öncekinden daha iyiyse yeni sıralama üzerinden devam edilir. Maksimum iterasyon sayısına ulaşıldığında, evcil ve vahşi kangurunun hangisinin ulaştığı sonuç daha iyiyse, diğer kanguru da sıradaki iterasyon grubuna o dizilim ile başlar. Bu süreç hedef değere veya maksimum iterasyon grubu sayısına ulaşılıncaya kadar devam eder.
Uygulama, parametrelerin seçimi ve algoritmanın işleyişi olarak iki bölümde ele alınırsa:
1. Parametrelerin seçimi a. İterasyon sayısı b. İterasyon grubu sayısı
c. Evcil ve vahşi kangurular için bağımsız adım aralıkları d. Evcil ve vahşi kanguru için başlangıç iterasyonları e. Zıplama yönteminin seçilmesi
2. Algoritmanın işleyişi
a. Vahşi kanguru başlangıç iterasyonu için amaç fonksiyonu değeri hesaplanır
b. Vahşi kanguru, adım büyüklüğünü kendisi için belirlenmiş aralık içinden rastsal olarak seçer ve belirli yönteme göre zıplar
c. Vahşi kanguru için amaç fonksiyon değeri tekrar hesaplanır, ulaşılan değer öncekiyle aynı veya daha iyiyse bu iterasyon üzerinden, değilse önceki iterasyon üzerinden devam edilir.
d. b ve c adımları, hedef değere ulaşılıncaya kadar, ulaşılmazsa iterasyon sayısına ulaşılıncaya kadar tekrarlanır
e. İlk 4 adım, evcil kanguru için kendi parametreleriyle tekrarlanır f. Böylece bir iterasyon grubu tamamlanır, vahşi ve evcil kangurudan
sonucu daha iyi olanın dizilimi sonraki turda hem vahşi hem evcil kanguru için başlangıç iterasyonu kabul edilir
g. Hedef değere, ulaşılmazsa maksimum tur sayısına ulaşılıncaya kadar b, c, d, e, f adımları tekrarlanır.
PKA, bu şekilde iyi çözümlerden daha iyilerine zıplayarak en iyi çözüm kümesine yaklaşmayı hedefleyen, paralelliği kullanarak aynı anda hem yerel hem daha geniş alanda arama yapan bir yöntemdir.
3.2.3. Parametrelerin Belirlenmesi
Deney tasarımı için tam faktoriyel tasarım tekniği kullanılmıştır. Test için tüm örnek hacimlerinden birer örnek alınmış, her bir parametre için beşer defa tekrarlı olarak KA ile çözülmüştür. Böylece test algoritmamız 14 test problemi için toplamda 184.560 kez çalıştırılmış ve ulaşılan değerler kayıt altına alınmıştır. Problemlerin çözümünde kullanılan nihai sabitlere, yapılan testlerin sonuçları doğrultusunda karar verilmiştir. Parametrelerin detaylı analizleri aşağıda yer almaktadır. Analizlerin yüzdelik ve bindelik hassasiyetteki değerleri bütün olarak Ek-1’de sunulmuştur.
3.2.3.1. Zıplama Yöntemi
İki zıplama yöntemi incelenmiştir;
1. Araya girmeli zıplama: yi elemanının j adım büyüklüğünde zıplayarak yi+j ile
yi+j+1 elemanlarının arasına girdiği zıplama yöntemidir.
2. Yer değiştirmeli zıplama: yi elemanının j adım büyüklüğünde zıplayarak yi+j
elemanıyla yer değiştirdiği zıplama yöntemidir.
İşlem sürelerine bakıldığında yer değiştirmeli zıplamanın %3 daha fazla süre gerektirdiği ve sonuç başarılarına bakıldığında araya girmeli zıplamanın yer değiştirmeli zıplamaya göre amaç fonksiyonundan %6 daha uzak değerler verdiği görülmüştür. İşlem sürelerindeki farkın az olması nedeniyle uygulamada yer değiştirmeli zıplama yöntemi tercih edilmiştir. İlgili değerler Çizelge 3.3, 3.4, Şekil 3.2 ve 3.3’te sunulmuştur:
ġekil 3.2. Zıplama yöntemleri için ortalama işlem süreleri grafiği Çizelge 3.3. Zıplama yöntemleri için ortalama işlem süreleri tablosu
Test problemi Araya girmeli zıplama Yer değiştirmeli zıplama
gp_3_0 0,087 0,084 gp_4_0 0,156 0,157 gp_5_0 0,244 0,246 gp_6_0 0,372 0,365 gp_7_0 0,519 0,506 gp_8_0 0,700 0,689 gp_9_0 0,920 0,906 gp_10_0 1,193 1,164 taillard_4_0 0,281 0,284 taillard_5_0 0,435 0,449 taillard_7_0 0,923 0,935 taillard_10_0 2,050 2,124 taillard_15_0 5,771 5,884 taillard_20_0 11,317 11,941 Genel Ortalama 3,005 3,106 Mukayese 1,000 1,033
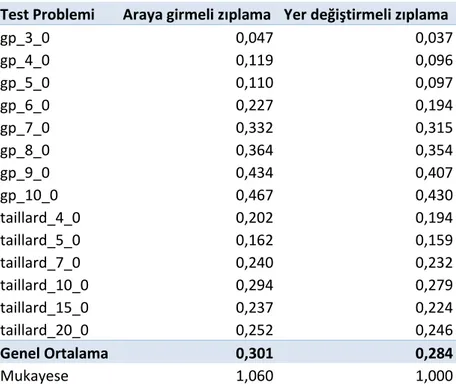
ġekil 3.3 Zıplama yöntemleri için ortalama sapma grafiği Çizelge 3.4. Zıplama yöntemi için ortalama sapma tablosu
Test Problemi Araya girmeli zıplama Yer değiştirmeli zıplama
gp_3_0 0,047 0,037 gp_4_0 0,119 0,096 gp_5_0 0,110 0,097 gp_6_0 0,227 0,194 gp_7_0 0,332 0,315 gp_8_0 0,364 0,354 gp_9_0 0,434 0,407 gp_10_0 0,467 0,430 taillard_4_0 0,202 0,194 taillard_5_0 0,162 0,159 taillard_7_0 0,240 0,232 taillard_10_0 0,294 0,279 taillard_15_0 0,237 0,224 taillard_20_0 0,252 0,246 Genel Ortalama 0,301 0,284 Mukayese 1,060 1,000 3.2.3.2. BaĢlangıç Ġterasyonu
Büyükten küçüğe, karışık ve küçükten büyüğe olmak üzere üç tip başlangıç iterasyonu, sonuç başarımı yönünden incelenmiştir. Elde edilen sonuçların ortalaması alındığında karışık sıralamalı başlangıç iterasyonunun diğerlerinden %5 - %6 aralığında daha başarılı olduğu, bununla birlikte bazı örnek gruplarında büyükten küçüğe ve
küçükten büyüğe sıralamalı başlangıç iterasyonlarının daha başarılı oldukları görülmüştür. Uygulamada, bu analizler doğrultusunda vahşi kanguru için karışık sıralamalı, evcil kanguru için büyükten küçüğe sıralamalı başlangıç iterasyonları tercih edilmiştir. İlgili değerler Çizelge 3.5 ve Şekil 3.4’te sunulmuştur:
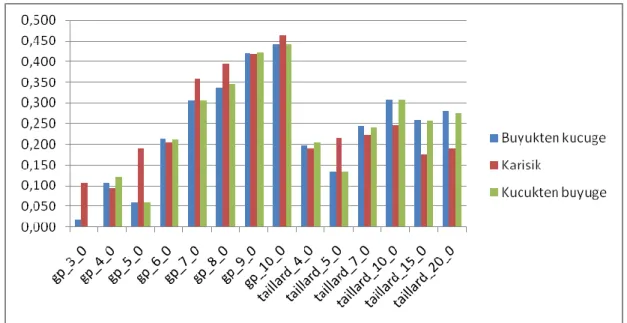
ġekil 3.4 Başlangıç iterasyonları için ortalama sapma grafiği Çizelge 3.5. Başlangıç iterasyonları için ortalama sapma grafiği
Test Problemi Büyükten küçüğe Karışık Küçükten büyüğe
gp_3_0 0,018 0,108 0,000 gp_4_0 0,108 0,094 0,121 gp_5_0 0,060 0,191 0,060 gp_6_0 0,213 0,206 0,212 gp_7_0 0,306 0,359 0,305 gp_8_0 0,337 0,395 0,345 gp_9_0 0,421 0,418 0,421 gp_10_0 0,441 0,464 0,441 taillard_4_0 0,198 0,191 0,205 taillard_5_0 0,133 0,215 0,133 taillard_7_0 0,244 0,222 0,241 taillard_10_0 0,307 0,247 0,307 taillard_15_0 0,258 0,174 0,257 taillard_20_0 0,281 0,191 0,276 Genel Ortalama 0,298 0,282 0,297 Mukayese 1,055 1,000 1,054
3.2.3.3. Ġterasyon Sayısı
Test sonucunda, tüm örnekler için sonuç başarımıyla iterasyon sayısı arasında tek yönlü bir ilişki olduğu görülmüştür. Bu anlamda en yüksek iterasyon sayısı denemesi 1000, kendine en yakın olan 750’den % 0,3, 500’den % 1, 250’den % 4 kadar daha başarılı sonuçlar vermiştir. İşlem sürelerinde de, olumsuz yönde benzer bir ilişki bulunduğu, doğru orantıya sahip oldukları tespit edilmiştir. Uygulamada en iyi sonuçları veren iterasyon sayısı 1000 tercih edilmiştir. İlgili değerler Çizelge 3.6, 3.7, Şekil 3.5 ve 3.6’da sunulmuştur:
ġekil 3.5 İterasyon sayıları için ortalama işlem süreleri grafiği Çizelge 3.6. İterasyon sayıları için ortalama işlem süreleri tablosu
Test Problemi 10 25 50 100 250 500 750 1000 gp_3_0 0,003 0,007 0,014 0,026 0,064 0,126 0,189 0,252 gp_4_0 0,005 0,013 0,024 0,048 0,117 0,233 0,348 0,464 gp_5_0 0,008 0,019 0,038 0,074 0,183 0,364 0,546 0,727 gp_6_0 0,012 0,029 0,056 0,111 0,274 0,548 0,821 1,094 gp_7_0 0,017 0,039 0,077 0,153 0,381 0,763 1,145 1,527 gp_8_0 0,023 0,054 0,106 0,209 0,517 1,033 1,549 2,065 gp_9_0 0,031 0,071 0,139 0,274 0,679 1,357 2,036 2,715 gp_10_0 0,040 0,092 0,179 0,353 0,877 1,752 2,629 3,506 taillard_4_0 0,014 0,027 0,048 0,089 0,212 0,418 0,624 0,830 taillard_5_0 0,015 0,035 0,068 0,134 0,330 0,658 0,985 1,313 taillard_7_0 0,031 0,073 0,142 0,280 0,694 1,382 2,071 2,759 taillard_10_0 0,071 0,164 0,320 0,629 1,557 3,104 4,651 6,197 taillard_15_0 0,198 0,458 0,891 1,755 4,347 8,668 12,990 17,313 taillard_20_0 0,399 0,918 1,782 3,507 8,680 17,298 25,915 34,533 Genel Ortalama 0,104 0,241 0,467 0,921 2,280 4,545 6,811 9,077 Mukayese 1,000 2,307 4,481 8,826 21,854 43,570 65,292 87,014
ġekil 3.6 İterasyon sayıları için ortalama sapma grafiği Çizelge 3.7. İterasyon sayıları için ortalama sapma tablosu
Test Problemi 10 25 50 100 250 500 750 1000 gp_3_0 0,0585 0,0422 0,0400 0,0394 0,0394 0,0394 0,0394 0,0394 gp_4_0 0,1845 0,1260 0,0985 0,0909 0,0904 0,0904 0,0904 0,0904 gp_5_0 0,1351 0,1165 0,1036 0,0966 0,0943 0,0943 0,0943 0,0943 gp_6_0 0,2963 0,2635 0,2285 0,1952 0,1759 0,1746 0,1746 0,1746 gp_7_0 0,4378 0,3900 0,3501 0,3113 0,2786 0,2735 0,2733 0,2733 gp_8_0 0,4451 0,4079 0,3762 0,3503 0,3266 0,3218 0,3216 0,3216 gp_9_0 0,5415 0,4909 0,4530 0,4160 0,3771 0,3627 0,3604 0,3600 gp_10_0 0,6179 0,5403 0,4803 0,4327 0,3914 0,3774 0,3742 0,3737 taillard_4_0 0,2679 0,2120 0,1903 0,1833 0,1829 0,1829 0,1829 0,1829 taillard_5_0 0,1813 0,1671 0,1597 0,1558 0,1550 0,1550 0,1550 0,1550 taillard_7_0 0,3049 0,2748 0,2502 0,2254 0,2090 0,2074 0,2074 0,2074 taillard_10_0 0,3596 0,3236 0,3003 0,2816 0,2633 0,2565 0,2554 0,2551 taillard_15_0 0,2886 0,2601 0,2440 0,2294 0,2133 0,2045 0,2011 0,1995 taillard_20_0 0,2883 0,2731 0,2619 0,2511 0,2381 0,2298 0,2258 0,2235 Genel Ortalama 0,3769 0,3381 0,3098 0,2857 0,2640 0,2566 0,2547 0,2540 Mukayese 1,484 1,331 1,220 1,125 1,039 1,010 1,003 1,000 3.2.3.4. Adım Büyüklüğü
Minimum adım büyüklüğü tüm örnekler için 1 birimdir. Maksimum adım büyüklüğü ise örnek hacminin büyüklüğüne bağlıdır. n x n’lik bir örnekte n2 adet işlem bulunmaktadır. Bir kangurunun maksimum adım büyüklüğü ise n2 – 1’dir. Testte yer
alan en büyük örnek 20 x 20 büyüklüğündedir. Dolayısıyla en büyük adım aralığı 399’dur. 399 parametreye kadar 14 örnek için 5’er defa çözüm yapmak iş yükünü önemli ölçüde arttıracağı için, 100 – 225 adım aralığında sadece çift sayılar, 225’in üstünde ise 4’ün katları alınarak hafifletilmiştir. Elde edilen sonuçlar incelendiğinde ortalama değerlere göre en küçük ve en büyük hacimlerde birbirine yakın sonuçlara ulaşılabildiği, orta gruplarda ise amaç fonksiyonunun yönünden daha ayrık olunduğu görülmüştür. Bununla birlikte her örneğin kendi özelinde daha iyi sonuçlar veren değerler de gözlemlenmiştir. 200’ün üstünde sütunun yer aldığı tablonun analizini daha kolay hale getirmek için içlerinden her bir örnek için en iyi değerlere ulaşılan adım büyüklükleri Çizelge 3.14’te listelenmiştir. Bu analizler doğrultusunda örneğe has elde edilebilecek başarımları kaçırmamak için adım büyüklükleri kanguru niteliğine dikkat edilerek belirli aralıklar dahilinde rassal olarak tespit edilmiştir. Aralık değerleri şöyle seçilmiştir:
Evcil Kanguru: 1 – 9 birim adım aralığı
Vahşi Kanguru: 10 – ( 0,9 x işlem sayısı ) birim adım aralığı İlgili değerler Çizelge 3.8 ve Şekil 3.7’de sunulmuştur:
Çizelge 3.8. Adım Büyüklükleri için ortalama sapma tablosu Test Problemi 5 8 10 11 13 22 23 28 35 37 52 67 68 80 88 128 gp_3_0 0,03 0,06 gp_4_0 0,08 0,04 0,07 0,08 0,12 gp_5_0 0,10 0,08 0,08 0,09 0,07 0,11 0,14 gp_6_0 0,21 0,20 0,18 0,19 0,18 0,14 0,14 0,15 0,31 gp_7_0 0,34 0,31 0,32 0,33 0,32 0,31 0,32 0,29 0,30 0,28 gp_8_0 0,39 0,37 0,33 0,35 0,34 0,34 0,35 0,37 0,34 0,32 0,31 gp_9_0 0,47 0,43 0,42 0,42 0,40 0,40 0,40 0,41 0,40 0,41 0,39 0,38 0,40 0,62 gp_10_0 0,51 0,48 0,44 0,44 0,45 0,45 0,46 0,44 0,43 0,45 0,41 0,40 0,39 0,43 0,48 taillard_4_0 0,19 0,18 0,15 0,16 0,20 taillard_5_0 0,15 0,15 0,15 0,14 0,15 0,17 0,18 taillard_7_0 0,23 0,22 0,23 0,22 0,21 0,23 0,22 0,24 0,20 0,23 taillard_10_0 0,30 0,30 0,29 0,29 0,29 0,27 0,28 0,27 0,28 0,28 0,27 0,28 0,28 0,28 0,29 taillard_15_0 0,25 0,25 0,23 0,23 0,22 0,22 0,22 0,22 0,22 taillard_20_0 0,26 0,25 0,25 0,25 0,24 0,24 0,24 Genel Ortalama 0,25 0,24 0,24 0,25 0,25 0,26 0,28 0,29 0,32 0,33 0,31 0,35 0,31 0,36 0,31 0,23
4. ARAġTIRMA BULGULARI VE TARTIġMA
4.1. Hesaplama Ortamı
Hesaplamalar, Intel Core 2 Duo P8600 modeli 2,4 GHz işlemcili 2 GB belleğe sahip bir bilgisayarda, işlemcinin tek çekirdeği kullanılarak gerçekleştirilmiştir. Windows XP işletim sistemi üzerine kurulan EasyPHP yazılım paketi ile gelen kurulum içinden; işlem için PHP dili, arayüz için Apache ve verileri kaydetmek için MySQL veritabanı kullanılmıştır. Doğrudan çalıştırılabilir program dillerine göre daha yavaş kalmasına rağmen, sunum kolaylığı nedeniyle yazılım dili olarak PHP dili tercih edilmiştir. Bu nedenle işlem süreleri değerlendirilirken, tek çekirdek kullanımı ve dil seçimi unsurları göz ardı edilmemelidir.
İstenilen değer, diğer bir deyişle döngüyü sonlandıracak amaç fonksiyon değeri olarak; en yakın güncel çalışma olan Sha ve Hsu’nun (2008) çalışmalarında yer alan BEÇ (Bilinen en iyi çözüm / Best Known Solution) değerleri göz önüne alınmıştır.
4.2. Uygulama Tekniği
Algoritmanın belirlenen başlangıç parametreleriyle, özellikle küçük hacimli örneklerde daha başarılı olduğu gözlemlenmiştir. Bunun üzerine bazı iyileştirme çalışmaları yapılmıştır.
Yüksek iterasyon sayılarına rağmen, daha iyi sonuca ulaşılamaması doğru bir çözüm alanında olunmadığını göstermektedir. Bu alandan çıkmak için tek bir zıplayış yeterli olmamaktadır, bu nedenle böyle bir bölgeye gelindiğinde çoklu zıplamalar gerekebilecektir. Bu nedenle başarısızlıkta belli bir sayıda takılma olursa, çoklu zıplamaların çoğalacak biçimde başlatılmasının daha başarılı sonuçlar vereceği açıktır. Bununla birlikte toplu zıplama sayısının iterasyon sayısına kadar çoğalarak gitmesi de anlamsız bir karmaşaya neden olabilecektir. Bu sayının belirli bir maksimumda durması veya belirli bir periyod içinde tekrar azalıp çoğalması faydalı görülmüştür. Bu mantık doğrultusunda algoritmaya şu ilave yapılmıştır: Her bir zıplama sonrasında daha iyiye gidilemediyse hafızada tutulan başarısızlık sayısı bir yükseltilir ve eşik değerinin aşılıp aşılmadığı kontrol edilir. Daha iyi değere ulaşılan zıplamalarda ise başarısızlık değeri sıfırlanır. Başarısızlık tekrarı eşik değerinin ilk aşılışında amaç fonksiyon değeri
hesaplanmadan önce kanguru ilave olarak bir kez daha zıplatılır. Başarısızlık hala devam ediyorsa ilave zıplama sayısı her seferinde bir arttırılır. İlave zıplamaların anlamsız derecede fazlalaşmaması için belirlenen belirli bir döngü sayısı mod alınarak ilave zıplama sayısı bu değere ulaştığında tekrar sıfırlanır. Uygulamada çoklu zıplamayı başlatan başarısızlık tekrarı eşik değeri 25, çoklu zıplama maksimum döngü değeri 100 seçilmiştir.
Kanguruların her bir zıplama sonrasında, bulunulan noktadan mı (y’), önceki konumdan mı (y) devam edileceğinin seçiminde iki kabul kullanılabilmektedir; f(y’) < f(y) veya f(y’) ≤ f(y). İkinci yol, özellikle büyük örnek hacimlerinde daha çok alanı taramaya imkan sağlamakta ve ilkine göre daha kısa sürede daha başarılı sonuçlar vermektedir. İkinci yol seçildiğinde, eşitlik de başarı olarak görüldüğü için başarısızlık eşik değerine ulaşmak daha da zor hale gelecektir. Bu katkıdan mahrum olmamak için eşik değeri ise ilk olarak 7’ye düşürülmüştür.
Kangurunun iyiden daha iyiye ulaşmayı sağlayan faydasının indirgenmemesi, bununla birlikte yapılan iyileştirmelerin faydalarından da mahrum kalınmaması için zıplama sonrası öncekiyle aynı amaç fonksiyon değeri elde edilmişse hemen bu değer kabul edilmeyip, aynı değere ulaşma durumu tekrarlı bir şekilde devam ediyorsa, belirli bir ısrar değerinin ardından bu konum kabul edilip devam edilmiştir. Eşit değerdeki sıralamanın kabulü daha iyi bir değere ulaşma anlamına gelmediği için bu durum da başarısızlık sayacının ilerlemesine imkan verir hale getirilmiştir. Bu nedenle algoritmanın bu halindeki başarısızlık tekrarı eşik değeri 25 olarak korunmuştur. Aynı sonuçtaki yeni konumun kabulünü sağlayacak ısrar değeri ise 3 veya 2 olarak alınmıştır. Programın bu iyileştirilmiş halinin ekran görüntüsü Şekil 4.1’de sunulmuştur.
Ulaşılan en başarılı dizilimlerin yakın alanlarında olabilecek daha iyi dizilimlerin gözden kaçırılmaması için, BEÇ’ye ulaşamamış örneklerin en başarılı 5 dizilimleri için lokal arama gerçekleştirilmiştir. Lokal arama, n elemandan oluşan bir dizilimde, her bir yi elemanının yi+1 konumundan yn konumuna kadar, ve y0
konumundan yi-1 konumuna kadar tüm alternatif konumlara getirilerek amaç fonksiyon
değerinin hesaplanmasıyla gerçekleştirilmiştir. Lokal arama tekli, ikili, üçlü, dörtlü ve beşli eleman grupları halinde uygulanmıştır.
ġekil 4.1. Program arayüzü 4.3. Bulgular
Literatürde AAÇ problemlerinin çözüm tekniklerinin mukayesesinde çok defa kullanılmış olan Guéret ve Prins’in (1999) çalışmalarında yer alan onar adet 3, 4, 5, 6, 7, 8, 9 ve 10’lu n iş n makine AAÇ test problemleri ve Taillard’ın (1993) çalışmasında yer alan yine onar adet 4, 5, 7, 10, 15 ve 20’li n iş n makine AAÇ test problemleri kullanılmıştır.
Fonksiyonu sonlandıracak hedef değer olarak en güncel çalışmalarda (Sha ve Hsu, 2008) kullanılan BEÇ’ler kullanılmıştır. Belirlenen maksimum iterasyon grubu sayısına ulaşılmadan bu değerlere ulaşılırsa fonksiyon sonlandırılmıştır.
Sonuç veritabanında işlem süresi, sonuca ulaşmak için gerçekleştirilen iterasyon grup sayısı, iterasyon sayısı, BEÇ’ye ulaşıldıysa hangi kanguru ile ulaşıldığı, kayıt tarihi ve varsa diğer parametre bilgileri tutuldu. Ulaşılan sonuçların BEÇ’lere göre sapma yüzdeleri şu formülasyonla belirlendi:
Sapma Yüzdesi = ( ( Ulaşılan Sonuç – BEÇ ) / BEÇ ) *100
Bu yöntemle ulaşılan en iyi sonuçlar Çizelge 4.1 ve Çizelge 4.2’de sunulmuştur. Sonuçların analizini kolaylaştıran bazı grafikler Şekil 4.2, Şekil 4.3 ve Şekil 4.4’te sunulmuştur.
Çizelge 4.1. Guéret ve Prins (1999) AAÇ örnekleri ile elde edilen sonuçlar
Örnek Sonuç BEÇ Sha&Hsu
(2008)
Sapma
Yüzdesi İşlem süresi (sn)
gp_3_0 1168 1168 1168 0,00 0,003 gp_3_1 1170 1170 1170 0,00 0,016 gp_3_2 1168 1168 1168 0,00 0,011 gp_3_3 1166 1166 1166 0,00 0,010 gp_3_4 1170 1170 1170 0,00 0,003 gp_3_5 1169 1169 1169 0,00 0,009 gp_3_6 1165 1165 1165 0,00 0,009 gp_3_7 1167 1167 1167 0,00 0,009 gp_3_8 1162 1162 1162 0,00 0,009 gp_3_9 1165 1165 1165 0,00 0,011 gp_4_0 1281 1281 1281 0,00 0,692 gp_4_1 1270 1270 1270 0,00 3,598 gp_4_2 1288 1288 1288 0,00 1,439 gp_4_3 1261 1261 1261 0,00 1,234 gp_4_4 1289 1289 1289 0,00 10,336 gp_4_5 1269 1269 1269 0,00 1,200 gp_4_6 1267 1267 1267 0,00 11,090 gp_4_7 1259 1259 1259 0,00 17,655 gp_4_8 1280 1280 1280 0,00 29,243 gp_4_9 1263 1263 1263 0,00 8,695 gp_5_0 1245 1245 1245 0,00 0,989 gp_5_1 1247 1247 1247 0,00 0,318 gp_5_2 1265 1265 1265 0,00 4,428 gp_5_3 1258 1258 1258 0,00 48,546 gp_5_4 1280 1280 1280 0,00 39,225 gp_5_5 1269 1269 1269 0,00 3,476 gp_5_6 1269 1269 1269 0,00 0,574 gp_5_7 1287 1287 1287 0,00 0,689 gp_5_8 1262 1262 1262 0,00 2,788 gp_5_9 1254 1254 1254 0,00 46,988 gp_6_0 1264 1264 1264 0,00 33,860 gp_6_1 1285 1285 1285 0,00 13,378 gp_6_2 1255 1255 1255 0,00 72,589 gp_6_3 1275 1275 1275 0,00 72,689 gp_6_4 1299 1299 1299 0,00 14,444 gp_6_5 1284 1284 1284 0,00 70,634 gp_6_6 1290 1290 1290 0,00 134,935 gp_6_7 1265 1265 1265 0,00 20,754 gp_6_8 1243 1243 1243 0,00 73,351 gp_6_9 1254 1254 1254 0,00 20,134
Çizelge 4.1. (devam) Guéret ve Prins (1999) AAÇ örnekleri ile elde edilen sonuçlar
Örnek Sonuç BEÇ Sha&Hsu
(2008)
Sapma
Yüzdesi İşlem süresi (sn)
gp_7_0 1159 1159 1159 0,00 84,624 gp_7_1 1185 1185 1185 0,00 8,137 gp_7_2 1237 1237 1237 0,00 51,382 gp_7_3 1167 1167 1167 0,00 105,459 gp_7_4 1157 1157 1157 0,00 15,491 gp_7_5 1193 1193 1193 0,00 103,542 gp_7_6 1185 1185 1185 0,00 98,004 gp_7_7 1180 1180 1180 0,00 44,910 gp_7_8 1220 1220 1220 0,00 102,009 gp_7_9 1270 1270 1270 0,00 10,300 gp_8_0 1139 1130 1133 0,80 145,109 gp_8_1 1135 1135 1135 0,00 140,047 gp_8_2 1120 1110 1110 0,90 149,597 gp_8_3 1153 1153 1153 0,00 147,381 gp_8_4 1218 1218 1218 0,00 149,073 gp_8_5 1135 1115 1115 1,79 144,086 gp_8_6 1127 1126 1126 0,09 138,257 gp_8_7 1152 1148 1148 0,35 144,569 gp_8_8 1124 1114 1114 0,90 141,009 gp_8_9 1161 1161 1161 0,00 136,423 gp_9_0 1143 1129 1129 1,24 202,597 gp_9_1 1117 1110 1112 0,63 189,461 gp_9_2 1116 1116 1117 0,00 186,867 gp_9_3 1166 1130 1130 3,19 198,566 gp_9_4 1180 1180 1180 0,00 197,535 gp_9_5 1101 1093 1093 0,73 185,574 gp_9_6 1126 1091 1091 3,21 196,174 gp_9_7 1131 1106 1108 2,26 189,788 gp_9_8 1123 1123 1126 0,00 180,046 gp_9_9 1121 1112 1122 0,81 192,307 gp_10_0 1113 1093 1093 1,83 259,016 gp_10_1 1124 1097 1097 2,46 267,552 gp_10_2 1113 1081 1084 2,96 277,538 gp_10_3 1145 1083 1083 5,72 283,610 gp_10_4 1107 1073 1082 3,17 273,084 gp_10_5 1152 1071 1071 7,56 252,713 gp_10_6 1100 1080 1081 1,85 272,426 gp_10_7 1144 1095 1097 4,47 281,943 gp_10_8 1142 1115 1123 2,42 281,943 gp_10_9 1126 1092 1092 3,11 267,109
Çizelge 4.2. Taillard (1993) AAÇ örnekleri ile elde edilen sonuçlar
Örnek Sonuç BEÇ Sha&Hsu Yüzdesi Sapma süresi (sn) İşlem
taillard_4_0 193 193 193 0,00 0,202 taillard_4_1 236 236 236 0,00 8,039 taillard_4_2 271 271 271 0,00 6,706 taillard_4_3 250 250 250 0,00 1,166 taillard_4_4 295 295 295 0,00 1,937 taillard_4_5 189 189 189 0,00 0,048 taillard_4_6 201 201 201 0,00 0,994 taillard_4_7 217 217 217 0,00 0,032 taillard_4_8 261 261 261 0,00 1,518 taillard_4_9 217 217 217 0,00 25,791 taillard_5_0 301 300 300 0,33 163,108 taillard_5_1 262 262 262 0,00 164,906 taillard_5_2 328 323 323 1,55 48,910 taillard_5_3 311 310 310 0,32 48,710 taillard_5_4 326 326 326 0,00 49,479 taillard_5_5 312 312 312 0,00 49,134 taillard_5_6 305 303 303 0,66 49,436 taillard_5_7 300 300 300 0,00 49,808 taillard_5_8 353 353 353 0,00 49,178 taillard_5_9 326 326 326 0,00 49,330 taillard_7_0 442 435 435 1,61 151,900 taillard_7_1 447 443 443 0,90 18,476 taillard_7_2 475 468 468 1,50 481,936 taillard_7_3 463 463 463 0,00 41,319 taillard_7_4 422 416 416 1,44 104,761 taillard_7_5 454 451 451 0,67 105,579 taillard_7_6 431 422 422 2,13 635,439 taillard_7_7 427 424 424 0,71 525,457 taillard_7_8 460 458 458 0,44 107,530 taillard_7_9 399 398 398 0,25 107,284 taillard_10_0 651 637 637 2,20 884,113 taillard_10_1 595 588 588 1,19 249,771 taillard_10_2 610 598 598 2,01 474,080 taillard_10_3 580 577 577 0,52 241,163 taillard_10_4 653 640 640 2,03 246,941 taillard_10_5 538 538 538 0,00 80,460 taillard_10_6 621 616 616 0,81 236,415 taillard_10_7 601 595 595 1,01 618,250 taillard_10_8 595 595 595 0,00 247,025 taillard_10_9 602 596 596 1,01 249,026