TÜREVLERİ FARKLI TÜRDEN KONVEKS FONKSİYONLAR İÇİN
HERMİTE-HADAMARD TİPLİ İNTEGRAL EŞİTSİZLİKLER VE UYGULAMALARI
Abdullah YARADILMIŞ Yüksek Lisans Tezi Matematik Anabilim Dalı Yrd. Doç. Dr. Mustafa GÜRBÜZ
2016
AĞRI İBRAHİM ÇEÇEN ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
YÜKSEK LİSANS TEZİ
TÜREVLERİ FARKLI TÜRDEN KONVEKS FONKSİYONLAR
İÇİN HERMİTE-HADAMARD TİPLİ İNTEGRAL EŞİTSİZLİKLER
VE UYGULAMALARI
Abdullah YARADILMIŞ
MATEMATİK ANABİLİM DALI
AĞRI 2016 Her hakkı saklıdır
i
ÖZET
Yüksek Lisans Tezi
TÜREVLERİ FARKLI TÜRDEN KONVEKS FONKSİYONLAR İÇİN HERMİTE-HADAMARD TİPLİ İNTEGRAL EŞİTSİZLİKLER VE
UYGULAMALARI
Abdullah YARADILMIŞ Ağrı İbrahim Çeçen Üniversitesi
Fen Bilimleri Enstitüsü Matematik Anabilim Dalı
Danışman: Yrd. Doç. Dr. Mustafa GÜRBÜZ
Bu tezde, ikinci mertebeden ve genel olarak 𝑛 . mertebeden türevlenebilen fonksiyonlar incelenerek yeni integral eşitsizlikler elde edilmiştir. İlk bölüm giriş niteliğinde olup, bu bölümde konveks fonksiyonlar ve Eşitsizlik Teorisi’nin tarihsel gelişimini içermekte olup literatürde mevcut çalışmalar ile ilgili bilgiler verilmiştir. İkinci bölümde tezde kullanılan konveks fonksiyon kavramları, bunlar arasındaki hiyerarşi ve bazı teoremler verilmiştir. Üçüncü bölümde literatürde mevcut ikinci mertebeden ve genel olarak 𝑛. mertebeden türevlenebilen fonksiyonlar ile ilgili bazı integral eşitsizlikler verilmiştir. Dördüncü bölümde ise ikinci mertebeden türevlenebilen konveks fonksiyonlar için yeni bir lemma elde edilmiş olup bu lemma kullanarak bazı yeni eşitsizlikler elde edilmiş ve bu eşitsizliklerden elde edilen sonuçlarla da uygulamalar verilmiştir. Ayrıca 𝑛 . mertebeden türevlenebilen fonksiyonlar için literatürde mevcut bir lemmaya bazı konvekslik sınıfları uygulanarak yeni eşitsizlikler elde edilmiştir. Elde edilen sonuçların literatürü desteklediği gözlemlenmiştir.
2016, 69 sayfa
Anahtar Kelimeler: Hermite-Hadamard tipli eşitsizlikler, Hölder eşitsizliği,
ii
ABSTRACT
Master Thesis
HERMITE-HADAMARD TYPE INTEGRAL INEQUALITIES AND THEIR APPLICATIONS FOR FUNCTIONS WHOSE DERIVATIVES ARE IN
DIFFERENT TYPES OF CONVEXITY
Abdullah YARADILMIŞ Ağrı İbrahim Çeçen University
Graduate School of Natural and Applied Sciences Department of Mathematics
Supervisor : Asst. Prof. Dr. Mustafa GÜRBÜZ
In this thesis, new integral inequalities were gathered by investigating second degree and nth degree, in general, differentiable functions. The first part was introductory part which included the historical developments of convex functions and Inequality Theory, as well as, information related to studies in literature. In the second part, concepts of convex functions used in the thesis, the hierarchy between them, and some theorems were given. In the third part, some integral inequalities related to second degree and nth degree, in general, differentiable functions in literature were given. In the fourth part, on the other hand, a new lemma for second degree differentiable convex functions was found and some new inequalities were gathered by using this lemma and some applications were given with the results gathered from these inequalities. In addition, new inequalities were gathered by applying some convex function classes to a lemma in the literature for nth degree differentiable functions. It was observed that the obtained results were supported by the literature.
2016, 69 pages
Keywords: Hermite-Hadamard type inequalities, Hölder inequality, Power-mean
iii
TEŞEKKÜR
Yüksek lisans eğitimi boyunca, tez konumu belirleyip bu konuda çalışmamı sağlayan, çalışmalarımda bilgi ve deneyimleriyle bana rehberlik eden, çalışmalarımın tamamlanması için her türlü şartı sağlayan saygıdeğer danışman hocam;
Sayın Yrd. Doç. Dr. Mustafa GÜRBÜZ’e;
teşekkür ve şükranlarımı sunarım.
Öğrenim hayatım boyunca kendilerinden görmüş olduğum destek ve güvenden dolayı aileme ve sevgili eşim Pınar YARADILMIŞ’a sonsuz teşekkürlerimi sunarım.
Yüksek lisans eğitimim sürecinde ve önceki öğrenimlerimde emeği geçen çok değerli hocalarıma teşekkürü bir borç bilir, ayrıca yüksek lisans eğitimim sürecinde bana desteklerinden dolayı arkadaşım sayın Faruk SAYKAL’a teşekkür ederim.
Abdullah YARADILMIŞ Ocak 2016
iv İÇİNDEKİLER ÖZET... i ABSTRACT ... ii TEŞEKKÜR ... iii SİMGELER DİZİNİ... vi ŞEKİLLER DİZİNİ ... vi 1. GİRİŞ ... 1 2. KURAMSAL TEMELLER ... 6 2.1. Genel Kavramlar ... 6
2.2. Bazı Konveks Fonksiyon Sınıflarının Hiyerarşisi ... 20
3. MATERYAL ve YÖNTEM.. ... 24
3.1. Konveks Fonksiyonlar İçin Bazı Eşitsizlikler ... 24
3.2. İkinci Mertebeden Türevlenebilen Fonksiyonlar İçin Bazı Eşitsizlikler ... 26
3.3. 𝑛. Mertebeden Türevlenebilen Fonksiyonlar İçin Bazı Eşitsizlikler ... 28
4. ARAŞTIRMA BULGULARI.. ... 30
4.1. İkinci Mertebeden Türevlenebilen Fonksiyonlar İçin Elde Edilen Bazı İntegral Eşitsizlikler ... 30
4.2. 𝑛. Mertebeden Türevlenebilen Fonksiyonlar İçin Elde Edilen Bazı İntegral Eşitsizlikler ... 46
4.3. Elde Edilen Teoremlere Dair Bazı Uygulamalar ... 62
5. TARTIŞMA ve SONUÇ ... 66
KAYNAKLAR ... 67
v
SİMGELER DİZİNİ
𝐶(𝐼) Konveks Fonksiyonlar Sınıfı 𝐷(𝑓) 𝑓 Fonksiyonunun Tanım Kümesi
𝑓′ 𝑓 Fonksiyonunun Birinci Mertebeden Türevi
𝑓′′ 𝑓 Fonksiyonunun İkinci Mertebeden Türevi
𝐼 ℝ’de Bir Aralık
𝐼° 𝐼’nın İçi 𝐽(𝐼) Jensen-Konveks Fonksiyonların Sınıfı 𝐽𝑄𝐶(𝐼) Jensen-Quasi-Konveks Fonksiyonların Sınıfı 𝐾𝑚(𝑏) 𝑚 −Konveks Fonksiyonların Sınıfı 𝐾𝑚𝛼(𝑏) (𝛼, 𝑚) −Konveks Fonksiyonların Sınıfı 𝐾𝑛(𝑏) 𝑛 −konveks Fonksiyonlar Sınıfı
𝐾𝑠2 İkinci Anlamda 𝑠 −Konveks Fonksiyonların Sınıfı 𝐿(𝐼) 𝐿𝑜𝑔 −Konveks Fonksiyonlar sınıfı
𝐿1[𝑎, 𝑏] [𝑎, 𝑏] Aralığında İntegrallenebilen Fonksiyonların Kümesi ℒ𝑟(𝑥, 𝑦) Genelleştirilmiş Logaritmik Ortalaması
𝑀𝑟(𝑥, 𝑦; 𝜆) Kuvvet Ortalaması Max Maksimum Min Minimum 𝑃(𝐼) 𝑃 −Fonksiyonlar Sınıfı 𝑄(𝐼) Godunova-Levin Fonksiyonlar Sınıfı 𝑄𝐶(𝐼) Quasi-Konveks Fonksiyonlar Sınıfı 𝑆𝑉(ℎ, 𝐼) ℎ −Konkav Fonksiyonlar Sınıfı 𝑆𝑋(ℎ, 𝐼) ℎ −Konveks Fonksiyonların Sınıfı
vi
ŞEKİLLER DİZİNİ
Şekil 2.1. Konveks küme ... 6
Şekil 2.2. Konveks olmayan küme ... 7
Şekil 2.3. Aralıklar üzerinde konveks fonksiyon ( f(x) = |x|) ... 8
Şekil 2.4. Konveks fonksiyon ... 9
Şekil 2.5. Doğrusal 𝑚 −Konveks fonksiyonlar ... 12
Şekil 2.6. İkinci dereceden 𝑚 −Konveks polinom fonksiyonlar ... 12
Şekil 2.7. Godunova-Levin, 𝑃 −fonksiyon, Quasi-Konveks fonksiyon, Konveks fonksiyon ve 𝐿𝑜𝑔 −Konveks fonksiyon sınıflarının ilişkisi ... 21
Şekil 2.8. Konveks fonksiyon, 𝑚 −Konveks fonksiyon, 𝑛 −Konveks fonksiyon ve Starshaped fonksiyon sınıflarının ilişkisi ... 22
1. GİRİŞ
Konvekslik, M.Ö. 250 yılında Archimedes’in ünlü 𝜋 değerini hesaplamasına kadar uzanan basit ve bilinen bir kavramdır. Buna rağmen matematikte yer alması 19. yüzyıl sonu 20. yüzyıl başını bulmaktadır. “Konvekslik” kavramı ilk olarak Hermite tarafından Ekim 1881’de elde edilen bir sonucun, 1883 yılında Mathesis adlı dergide yayınlanmasıyla ortaya çıkmıştır. Hadamard’ın 1893 yılındaki çalışmasında konveksliğe rastlansa da konveks fonksiyonların sistematik olarak çalışılması 1905-1906 yıllarında J.L.W.V. Jensen ile başlar.
Konveksliğin tanımı eşitsizlikle ifade edildiğinden ve matematik bir bakıma karşılaştırma olduğundan Konveks Fonksiyonlar Teorisinde eşitsizliklerin önemli bir yeri vardır. Hardy, Littlewood, Pόlya, Beckenbach, Bellman, Mitrinović, Pachpatte, Pečarić ve Fink gibi matematikçiler Konveks Fonksiyonlar ile Eşitsizlikler Teorisi’ni bir arada inceleyerek çeşitli kitaplar ve çok sayıda makaleler yayınlamışlardır. Bu tür eşitsizlikleri konu alan ilk temel çalışma 1934’te Hardy, Littlewood ve Pόlya tarafından yazılan “Inequalities” adlı kitaptır (Hardy et al. 1952). İkinci çalışma ise E.F. Beckenbach ve R. Bellman tarafından 1961’de yazılan 1934-1960 yılları arasında elde edilen yeni eşitsizliklerin sonuçlarını içeren ve yine “Inequalities” adı verilen kitaptır (Beckenbach and Bellman 1961). Bunu Mitrinović’in 1970 yılında yayınladığı ve ilk iki kitapta bulunmayan farklı konulara da yer verdiği “Analytic Inequalities” isimli kitabı takip eder (Mitrinović 1970). Bu temel kaynakların yanı sıra “Inequalities Involving Functions and Their Integrals and Derivatives” (Mitrinović et al. 1991), “Classical and New Inequalities in Analysis” (Mitrinović et
al. 1993), “Mathematical Inequalities” (Pachpatte 2005) ve “Convex Functions and
Their Applications” (Niculescu and Persson 2006) literatürde mevcut olan diğer kaynaklardır.
Konveks Fonksiyonlar Teorisi ile ilişkili olan Eşitsizlik Teorisi C.F. Gauss, A.L. Cauchy ve P.L. Čebyšev ile gelişmeye başlamıştır. 19.-20. yy’da bulunan eşitsizliklerin bir kısmı konveks fonksiyonlarla ilişkilendirilerek temel eşitsizlikler haline gelmiştir. Bunların en önemlileri 1881 yılında Hermite tarafından elde edilen
Hermite-Hadamard eşitsizliği ve 1938 yılında Ostrowski tarafından elde edilen Ostrowski eşitsizliğidir. Hermite-Hadamard eşitsizliği ile ilgili çalışmaların büyük bir kısmı S.S. Dragomir ve C.E.M. Pearce tarafından 2000 yılında yazılmış olan “Selected Topics on Hermite-Hadamard Inequalities and Applications” isimli kaynakta bir araya getirilmiştir (Dragomir and Pearce 2000).
Konveks fonksiyonlar için eşitsizlikler üzerine yoğun çalışan diğer matematikçiler M.E. Özdemir, U.S. Kırmacı, R. Agarval, G. Anastassiou, G.V. Milovanovic, A.M. Fink, A.W. Roberts, D.E. Varberg, N.S. Barnett, H. Yıldırım, M.Z. Sarıkaya, N. Ujević, S. Varošanec, P.S. Bullen, P. Cerone, G. Toader, M. Alomari, F. Qi, C.E.M. Pearce, M. Darus, M.K. Bakula, J. Pečarić, E. Set, A.O. Akdemir, H. Kavurmacı Önalan, M. Avcı Ardıç, M. Gürbüz, A. Ekinci, Ç. Yıldız, M. Tunç şeklinde sıralanabilir. Bu konu üzerine yazılan birçok kitabın dışında literatürde doktora ve yüksek lisans çalışmalarına da rastlanmaktadır.
“Inequalities and Applications” başlıklı doktora tezinde integral eşitsizlikleri üzerine uygulamalar yazılmış ve ortalamalar üzerine farklı sonuçlar elde edilmiştir. Bunun yanında Cauchy-Schwartz, Bessel ve Jensen eşitsizlikleri üzerine çalışmalar yapılmıştır (Rooin 2003).
“Solving Methods of Linear Functional Equation and Stability of 𝑡 −Convex Functions” başlıklı doktora tezinde eşitsizlikler yardımıyla lineer fonksiyonel denklemlerin çözüm yöntemleri incelenmiş, ve 𝑡 −konveks fonksiyonların kararlılığı incelenirken yine bazı eşitsizlikler kullanılmış ve yenileri elde edilmiştir (Hazy 2005).
“Inequalities and Applications” başlıklı yüksek lisans tezinde ortalamalar üzerine yeni eşitsizlikler elde edilmiş, yeni fonksiyon sınıfları ortaya atılmıştır (Bagdasar 2006).
“Bazı Farklı Türden Konveks Fonksiyonlar İçin İntegral Eşitsizlikleri” başlıklı doktora tezinde 𝐸 −konveks ve 𝐸 − 𝑚 −konveks fonksiyonlar ile birlikte farklı türden 𝐸 −konveks ve 𝐸 − 𝑚 −konveks fonksiyonlar için Hermite-Hadamard
tipli ve diğer bazı farklı türden konveks fonksiyonlar olan 𝑚 − konveks, (𝛼, 𝑚) − konveks, 𝑙𝑜𝑔 − konveks, 𝑞𝑢𝑎𝑠𝑖 − konveks, 𝑠 − konveks, 𝑟 − konveks ve ℎ −konveks fonksiyonlar için yeni integral eşitsizlikleri verilmiştir. Bunların yanı sıra bazı genelleştirmeler de elde edilmiştir (Set 2010).
“Bazı Konveks Fonksiyonlar İçin Hermite-Hadamard Tipli Eşitsizlikler Ve Uygulamaları” başlıklı doktora tezinde konveks ve farklı tip konveks fonksiyon sınıfları için Hermite-Hadamard tipli eşitsizlikler elde edilmiştir. Daha sonra elde edilen eşitsizlikler için özel uygulamalar ve sonuçlar verilmiştir (Tunç 2011).
“Several Inequalities of Hermite-Hadamard, Ostrowski and Simpson Type for 𝑠 −Convex, 𝑄𝑢𝑎𝑠𝑖 −Convex and 𝑟 −Convex Mappings and Applications” başlıklı doktora tezinde 𝑠 −konveks, 𝑞𝑢𝑎𝑠𝑖 −konveks ve 𝑟 −konveks fonksiyon sınıfları kullanılarak Hermite-Hadamard, Ostrowski ve Simpson tipli integral eşitsizlikleri elde edilmiştir ve bu eşitsizlikler için uygulamalar verilmiştir (Alomari 2011).
“Quasi Konveks Fonksiyonlar İçin Eşitsizlikler Ve Uygulamaları” başlıklı yüksek lisans tezinde 𝑞𝑢𝑎𝑠𝑖 −konveks fonksiyonlar için yapılan geniş bir literatür taramasının yanısıra, 𝑞𝑢𝑎𝑠𝑖 − konveks fonksiyonlar için Hermite-Hadamard, Ostrowski ve Simpson tipli eşitsizlikler elde edilmiştir. Daha sonra elde edilen eşitsizlikler için sonuçlar ve bu sonuçlara bağlı özel uygulamalar verilmiştir (Yıldız 2011).
“Bazı Farklı Türden Konveks Fonksiyonlar İçin Ostrowski ve Hermite-Hadamard Tipli İntegral Eşitsizlikler” başlıklı doktora tezinde farklı türden konveks fonksiyon sınıfları kullanılarak yeni baskın konveks fonksiyon kavramları tanımlanmış, bu yeni fonksiyon sınıfları için Hermite-Hadamard tipli integral eşitsizlikleri edilmiştir. Konveks fonksiyonlar için Hermite-Hadamard tipli; konveks ve konveks fonksiyonlar için Ostrowski tipli yeni integral eşitsizlikleri elde edilmiştir ve elde edilen bazı eşitsizlikler için uygulamalar verilmiştir(Kavurmacı 2012).
“Farklı Türden Konveks Fonksiyonların Çarpımı Üzerine İntegral Eşitsizlikleri Ve Uygulamaları” başlıklı doktora tezinde farklı türden konveks
fonksiyonlar kullanılarak yeni tanımlamalar, örneklemeler yapılmış olup bu türden konveks fonksiyonlar ve literatürde bulunan bazı konveks fonksiyonların çarpımı üzerine integral eşitsizlikleri elde edilmiştir (Gürbüz 2013).
“ 𝑛 . mertebeden türevlenebilen konveks fonksiyonlar için integral eşitsizlikleri’’ başlıklı doktora tezinde Fejér eşitsizliği kullanılarak yeni teoremler ispatlanmış, 𝑔 ’ nin özel değerleri için yeni sonuçlar elde edilmiştir. Ayrıca 𝑛 . mertebeden türevlenebilen fonksiyonlar için Lemmalar yazılmış ve bu Lemmalar kullanılarak yeni genelleştirmeler yapılmıştır(Yıldız 2014).
Neden Matematiksel Eşitsizlikler?
1978 yılında Richard Bellman, Almanya’da 2. Uluslararası Matematik Eşitsizlikler Konferansı’nda bu soruya şu şekilde cevap vermiştir. Eşitsizlik çalışmak için üç neden vardır. Bunlar:
1. Pratik Nedenler 2. Teorik Nedenler 3. Estetik Nedenler dir.
Pratik açıdan bakıldığında, birçok araştırmada bir niceliği diğer bir nicelikle sınırlandırmak karşımıza çıkmaktadır. Klasik eşitsizlikler de bu şekilde ortaya çıkmıştır. Teorik açıdan bakıldığında çok basit sorular sorularak tüm temel teoremler oluşturulabilir. Örneğin, negatif olmayan bir niceliğin ne zaman bir diğerini kapsadığı sorulabilir ve bu basit soru ile Pozitif Operatörler Teorisi ve Diferansiyel Eşitsizlikler Teorisi kurulur. Son olarak estetik açıdan bakıldığında genel olarak resim, müzik ve matematiğin bazı parçalarının uyumlu olduğu görülür. Elde edilen eşitsizliklerin göze hitap etmesi de eşitsizlikleri çekici hale getirir.
Bu çalışmada, farklı türden konveks fonksiyonlar detaylı olarak incelenmiştir. Bu amaçla çalışmanın ikinci bölümünde matematikte yer alan bazı temel tanım ve teoremler, bazı konveks fonksiyon sınıfları arasındaki hiyerarşi verilmiştir. Üçüncü
bölümünde literatürde mevcut ikinci mertebeden ve 𝑛. mertebeden türevlenebilen fonksiyonlar için bazı integral eşitsizlikler verilmiştir. Dördüncü bölümünde ilk olarak ikinci mertebeden türevlenebilen konveks fonksiyonlar için elde edilen yeni lemma kullanılarak yeni eşitsizlikler elde edilmiş, daha sonra 𝑛 . mertebeden türevlenebilen konveks fonksiyonlarla ilgili verilen lemmada integraller için mutlak değer özelliği, Hölder, Power-mean eşitsizlikleri kullanılarak teoremler ispatlanmıştır. Bu çalışmada elde edilen sonuçlardan bir çoğunun literatürü desteklediği gözlemlenmiştir.
2. KURAMSAL TEMELLER 2.1. Genel Kavramlar
Bu bölümde, araştırmada kullanılacak bazı temel tanım, teorem ve örnekler verilecektir.
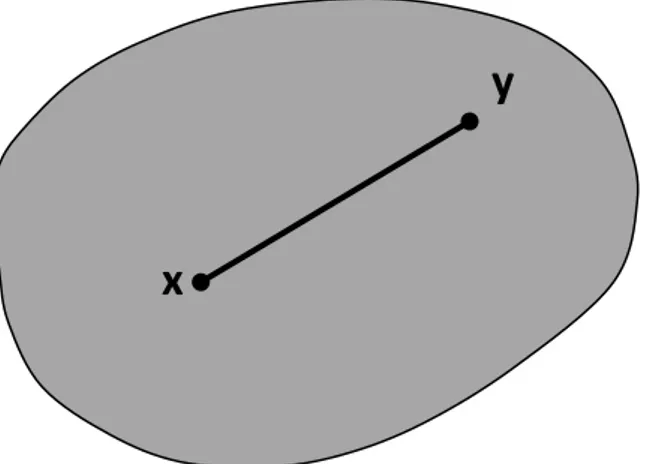
Tanım 2.1.1. (Konveks Küme): 𝐿 bir lineer uzay 𝐴 ⊆ 𝐿 ve 𝑥, 𝑦 ∈ 𝐴 keyfi olmak
üzere
𝐵 = {𝑧 ∈ 𝐿: 𝑧 = 𝛼𝑥 + (1 − 𝛼)𝑦, 0 ≤ 𝛼 ≤ 1} ⊆ 𝐴
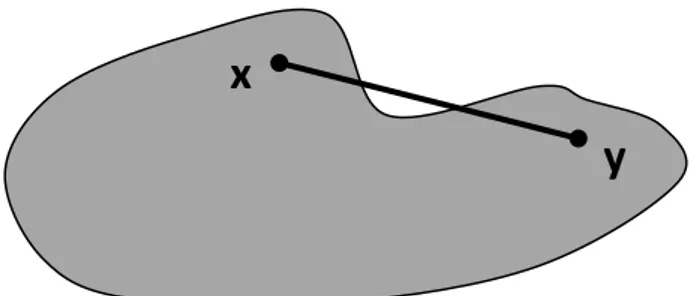
ise 𝐴 kümesine konveks küme denir. Eğer 𝑧 ∈ 𝐵 ise 𝑧 = 𝛼𝑥 + (1 − 𝛼)𝑦 eşitliğindeki 𝑥 ve 𝑦 ’nin katsayıları için 𝛼 + (1 − 𝛼) = 1 bağıntısı her zaman doğrudur. Bu sebeple konveks küme tanımındaki 𝛼, 1 − 𝛼 yerine 𝛼 + 𝛽 = 1 şartını sağlayan ve negatif olmayan 𝛼, 𝛽 reel sayıları alınabilir. Geometrik olarak 𝐵 kümesi uç noktaları 𝑥 ve 𝑦 olan bir doğru parçasıdır. Bu durumda sezgisel olarak konveks küme, boş olmayan ve herhangi iki noktasını birleştiren doğru parçasını ihtiva eden kümedir (Bayraktar 2000).
Şekil 2.1. Konveks küme
x
Şekil 2.2. Konveks olmayan küme
Örneğin aralıklar reel eksen üzerindeki konveks kümelerdir.
Tanım 2.1.2. (𝑱 −Konveks Fonksiyon): 𝐼,ℝ’de bir aralık olmak üzere her 𝑥, 𝑦 ∈ 𝐼
için
𝑓 (𝑥 + 𝑦 2 ) ≤
𝑓(𝑥) + 𝑓(𝑦) 2
şartını sağlayan 𝑓 fonksiyonuna 𝐼 üzerinde Jensen anlamında konveks veya 𝐽 −konveks fonksiyon denir (Mitrinović 1970).
Tanım 2.1.3. (Kesin 𝑱 −Konveks Fonksiyon): Her 𝑥, 𝑦 ∈ 𝐼 ve 𝑥 ≠ 𝑦 için
𝑓 (𝑥 + 𝑦 2 ) <
𝑓(𝑥) + 𝑓(𝑦) 2
oluyorsa 𝑓 fonksiyonuna 𝐼 üzerinde kesin 𝐽 −konveks fonksiyon denir (Mitrinović 1970).
Tanım 2.1.4. (Konveks Fonksiyon): 𝐼, ℝ’de bir aralık ve 𝑓: 𝐼 → ℝ bir fonksiyon
olmak üzere her 𝑥, 𝑦 ∈ 𝐼 ve 𝛼 ∈ [0,1] için,
𝑓(𝛼𝑥 + (1 − 𝛼)𝑦) ≤ 𝛼𝑓(𝑥) + (1 − 𝛼)𝑓(𝑦) (2.1)
x
şartını sağlayan 𝑓 fonksiyonuna konveks fonksiyon denir. Eğer (2.1) eşitsizliği 𝑥 ≠ 𝑦 ve 𝛼 ∈ (0,1) için kesin ise bu durumda 𝑓 fonksiyonuna kesin konvekstir denir (Pečarić et al. 1992).
Sonuç 2.1.1. Her konveks fonksiyon 𝐽 −konveks fonksiyondur.
Sonuç 2.1.2. 𝐼 ⊂ ℝ olmak üzere, bir 𝑓 fonksiyonunun 𝐼 ’da konveks olması için
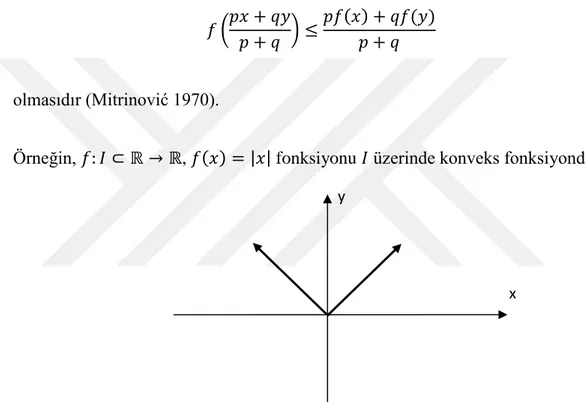
gerek ve yeter şart, her 𝑥, 𝑦 ∈ 𝐼 ve her 𝑝, 𝑞 > 0 reel sayıları için
𝑓 (𝑝𝑥 + 𝑞𝑦 𝑝 + 𝑞 ) ≤
𝑝𝑓(𝑥) + 𝑞𝑓(𝑦) 𝑝 + 𝑞 olmasıdır (Mitrinović 1970).
Örneğin, 𝑓: 𝐼 ⊂ ℝ → ℝ, 𝑓(𝑥) = |𝑥| fonksiyonu 𝐼 üzerinde konveks fonksiyondur.
Şekil 2.3. Aralıklar üzerinde konveks fonksiyon (𝑓(𝑥) = |𝑥|)
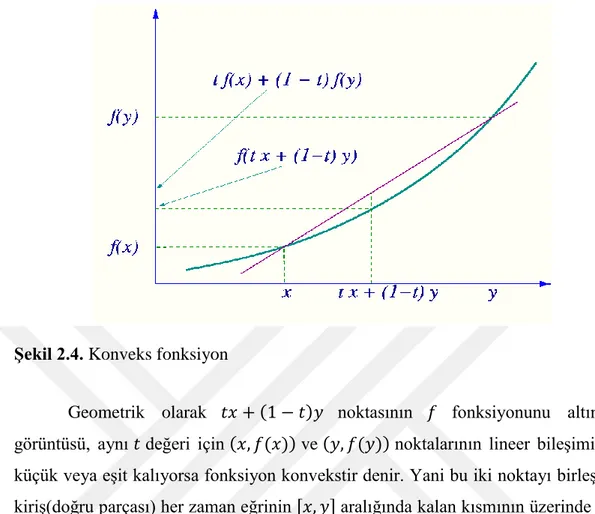
Konveks fonksiyonun geometrik anlamı aşağıdaki gibidir: x y
Şekil 2.4. Konveks fonksiyon
Geometrik olarak 𝑡𝑥 + (1 − 𝑡)𝑦 noktasının 𝑓 fonksiyonunu altındaki görüntüsü, aynı 𝑡 değeri için (𝑥, 𝑓(𝑥)) ve (𝑦, 𝑓(𝑦)) noktalarının lineer bileşiminden küçük veya eşit kalıyorsa fonksiyon konvekstir denir. Yani bu iki noktayı birleştiren kiriş(doğru parçası) her zaman eğrinin [𝑥, 𝑦] aralığında kalan kısmının üzerinde veya üstündedir. Konkav fonksiyon için kiriş 𝑓 fonksiyonunun grafiğinin [𝑥, 𝑦] aralığında kalan kısmının üzerinde veya altındadır.
Eğer 𝑓 fonksiyonu [𝑎, 𝑏] aralığında tanımlı, [𝑎, 𝑏] aralığında konveks (konkav) ve 𝑥0
noktasında diferensiyellenebilen bir fonksiyon ise 𝑥 ∈ (𝑎, 𝑏) için
𝑓(𝑥) − 𝑓(𝑥0) ≤ (≥)𝑓′(𝑥
0)(𝑥 − 𝑥0) (2.2)
eşitsizliği yazılır. Yani (𝑎, 𝑏) aralığında diferensiyellenebilen konveks fonksiyon (2.2) eşitsizliğini sağlar (Roberts and Varberg 1973)
Tanım 2.1.5. (Süreklilik): 𝑓: 𝑆 ⊆ ℝ → ℝ, 𝑥0 ∈ 𝑆 ve 𝜀 > 0 verilmiş olsun.
𝑥 ∈ 𝑆 ve |𝑥 − 𝑥0| < 𝛿 için |𝑓(𝑥) − 𝑓(𝑥0)| < 𝜀
Teorem 2.1.1. 𝑓 fonksiyonu [𝑎, 𝑏] aralığında konveks ise
a. 𝑓, (𝑎, 𝑏) aralığında süreklidir ve
b. 𝑓, [𝑎, 𝑏] aralığında sınırlıdır (Azpeitia 1994).
Tanım 2.1.6. (Artan ve Azalan Fonksiyonlar): 𝑓, 𝐼 aralığında tanımlı bir fonksiyon
ve 𝑥1, 𝑥2 de 𝐼’da iki nokta olsun. Bu durumda
(a) 𝑥2 > 𝑥1 iken 𝑓(𝑥2) > 𝑓(𝑥1) ise 𝑓 fonksiyonu 𝐼 üzerinde artandır,
(b) 𝑥2 > 𝑥1 iken 𝑓(𝑥2) < 𝑓(𝑥1) ise 𝑓 fonksiyonu 𝐼 üzerinde azalandır,
(c) 𝑥2 > 𝑥1 iken 𝑓(𝑥2) ≥ 𝑓(𝑥1) ise 𝑓 fonksiyonu 𝐼 üzerinde azalmayandır,
(d) 𝑥2 > 𝑥1 iken 𝑓(𝑥2) ≤ 𝑓(𝑥1) ise 𝑓 fonksiyonu 𝐼 üzerinde artmayandır
denir (Adams and Essex 2010).
Teorem 2.1.2. 𝐽 açık bir aralık ve 𝐽 ⊆ 𝐼 olmak üzere 𝑓 , 𝐼 üzerinde sürekli ve 𝐽 üzerinde diferensiyellenebilir bir fonksiyon olsun. Bu durumda
(a) Her 𝑥 ∈ 𝐽 için 𝑓′(𝑥) > 0 ise 𝑓 fonksiyonu 𝐼 üzerinde artandır.
(b) Her 𝑥 ∈ 𝐽 için 𝑓′(𝑥) < 0 ise 𝑓 fonksiyonu 𝐼 üzerinde azalandır.
(c) Her 𝑥 ∈ 𝐽 için 𝑓′(𝑥) ≥ 0 ise 𝑓 fonksiyonu 𝐼 üzerinde azalmayandır.
(d) Her 𝑥 ∈ 𝐽 için 𝑓′(𝑥) ≤ 0 ise 𝑓 fonksiyonu 𝐼 üzerinde artmayandır. (Adams and Essex 2010).
Aşağıdaki konveks fonksiyonların türevleri ile artanlık (azalanlık) arasındaki ilişkiyi içeren sonuç ve teoremler verilmiştir.
Sonuç 2.1.3. 𝑓, 𝑔 konveks fonsiyonlar ve 𝑔 aynı zamanda artan ise 𝑔 ∘ 𝑓 fonksiyonu
konvekstir (Roberts and Varberg 1973).
Teorem 2.1.3. Eğer 𝑓: 𝐼 → ℝ tanımlı konveks (kesin konveks) bir fonksiyon ise 𝑓+′(𝑥) ve 𝑓
−′(𝑥) var ve bu fonksiyon 𝐼°’de artandır (kesin artandır) (Pečarić et al.
Teorem 2.1.4. 𝑓 fonksiyonu (𝑎, 𝑏) aralığında diferensiyellenebilir bir fonksiyon olsun. Bu durumda 𝑓 fonksiyonunun konveks olması için gerek ve yeter şart 𝑓′ fonksiyonunun artan (kesin artan) olmasıdır (Pečarić et al. 1992).
Teorem 2.1.5. 𝑓 fonksiyonunun 𝐼 açık aralığında ikinci türevi varsa, 𝑓 fonksiyonunun bu aralık üzerinde konveks olması için gerek ve yeter şart 𝑥 ∈ 𝐼 için
𝑓′′(𝑥) ≥ 0 olmasıdır (Mitrinović 1970).
Tanım 2.1.7. ( 𝒎 − Konveks Fonksiyon): 𝑓: [0, 𝑏] → ℝ ve 𝑏 > 0 olsun. Her
𝑥, 𝑦 ∈ [0, 𝑏], 𝑡 ∈ [0,1] ve 𝑚 ∈ [0,1]için
𝑓(𝑡𝑥 + 𝑚(1 − 𝑡)𝑦) ≤ 𝑡𝑓(𝑥) + 𝑚(1 − 𝑡)𝑓(𝑦)
şartı sağlanıyorsa 𝑓 fonksiyonuna 𝑚 −konvekstir denir (Toader 1984).
−𝑓 fonksiyonu 𝑚 −konveks ise bu takdirde 𝑓 fonksiyonu 𝑚 −konkavdır. Ayrıca 𝑓(0) ≤ 0 için [0, 𝑏] aralığında tanımlı tüm 𝑚 −konveks fonksiyonların sınıfı 𝐾𝑚(𝑏) ile gösterilir.
Örnek 2.1.1. 𝑟 > 0, 𝑓: [0, 𝑟] → ℝ, 𝑥 ∈ [0, 𝑟] olmak üzere 𝑓(𝑥) = 𝑎𝑥 + 𝑏 şeklindeki
(𝑎, 𝑏 ∈ ℝ; 𝑎 ≠ 0) doğrusal fonksiyonlar 𝑏 ≤ 0 için 𝑚 − konveks fonksiyondur (Gürbüz 2013).
Şekil 2.5. Doğrusal 𝑚 −konveks fonksiyonlar (Gürbüz 2013).
gibi görsel olarak örneklendirilebilir. Yani, grafiği 𝑦 ekseninin pozitif kısmını kesmeyen her doğrusal fonksiyon 𝑚 −konvekstir.
Örnek 2.1.2. 𝑟 > 0, 𝑓: [0, 𝑟] → ℝ, (𝑎, 𝑏, 𝑐 ∈ ℝ) olmak üzere 𝑓(𝑥) = 𝑎𝑥2+ 𝑏𝑥 + 𝑐,
𝑎, 𝑐 ≤ 0 şeklindeki 2. dereceden polinom fonksiyon 𝑚 −konvekstir (Gürbüz 2013).
Görsel olarak; grafiği 𝑦 −ekseninin pozitif kısmını kesmeyen ve konkav olan her 2. dereceden polinom fonksiyon 𝑚 −konveks fonksiyondur.
Şekil 2.6. 𝑚 −konveks olan ikinci dereceden polinom fonksiyonlar
Tanım 2.1.8. ((𝜶, 𝒎) −Konveks Fonksiyon): 𝑓: [0, 𝑏] → ℝ ve 𝑏 > 0 olsun. Her
𝑥, 𝑦 ∈ [0, 𝑏], 𝑡 ∈ [0,1] ve (𝛼, 𝑚) ∈ [0,1]2 için
𝑓(𝑡𝑥 + 𝑚(1 − 𝑡)𝑦) ≤ 𝑡𝛼𝑓(𝑥) + 𝑚(1 − 𝑡𝛼)𝑓(𝑦)
şartı sağlanıyorsa 𝑓 fonksiyonuna (𝛼, 𝑚) −konveks fonksiyon denir (Miheşan 1993).
𝑓(0) ≤ 0 için [0, 𝑏] aralığında tanımlı tüm (𝛼, 𝑚) −konveks fonksiyonların sınıfı 𝐾𝑚𝛼(𝑏) ile gösterilir. Burada (𝛼, 𝑚) ∈ {(0,0), (𝛼, 0), (1,0), (1, 𝑚), (1,1), (𝛼, 1)}
alındığında sırasıyla artan, 𝛼 − starshaped, starshaped, 𝑚 − konveks, konveks ve 𝛼 −konveks fonksiyon sınıfları elde edilir. 𝑓(0) ≤ 0 olmak üzere 𝐾11(𝑏), sınıfında sadece 𝑓: [0, 𝑏] → ℝ tanımlı konveks fonksiyonlar yer alır. Yani 𝐾11(𝑏) . [0, 𝑏] üzerinde tanımlı tüm konveks fonksiyonlar sınıfının uygun bir alt sınıfıdır.
Tanım 2.1.9. (𝒉 −Konveks Fonksiyon): ℎ: 𝐽 → ℝ negatif olmayan bir fonksiyon ve
ℎ ≢ 0 olsun. 𝑓: 𝐼 → ℝ negatif olmayan fonksiyonu her 𝑥, 𝑦 ∈ 𝐼 ve 𝛼 ∈ (0,1) için
𝑓(𝛼𝑥 + (1 − 𝛼)𝑦) ≤ ℎ(𝛼)𝑓(𝑥) + ℎ(1 − 𝛼)𝑓(𝑦)
eşitsizliğini sağlıyorsa 𝑓 fonksiyonuna ℎ −konveks fonksiyon veya 𝑆𝑋(ℎ, 𝐼) sınıfına aittir denir (Varošanec 2007).
Bu eşitsizlik yön değiştirirse, bu durumda 𝑓’ye ℎ −konkav fonksiyon veya 𝑆𝑉(ℎ, 𝐼) sınıfına aittir denir. Eğer ℎ(𝛼) = 𝛼 alınırsa, bu takdirde tüm negatif olmayan konveks fonksiyonlar 𝑆𝑋(ℎ, 𝐼) sınıfına ve tüm negatif olmayan konkav fonksiyonlar 𝑆𝑉(ℎ, 𝐼) sınıfına aittir. ℎ(𝛼) = 1
𝛼 alınırsa, 𝑆𝑋(ℎ, 𝐼) sınıfı 𝑄(𝐼) sınıfını;
ℎ(𝛼) = 1 alınırsa, 𝑃(𝐼) sınıfını ve ℎ(𝛼) = 𝛼𝑠, 𝑠 ∈ (0,1) alınırsa, 𝐾𝑠2 sınıfını
içereceği açıktır.
Örnek 2.1.3. ℎ fonksiyonu her 𝛼 ∈ (0,1) için ℎ(𝛼) ≥ 𝛼 şartını sağlayan negatif
özelliğe sahiptir). 𝑓 fonksiyonu 𝐼 üzerinde negatif olmayan konveks fonksiyon ise; 𝑥, 𝑦 ∈ 𝐼, 𝛼 ∈ (0,1) için,
𝑓(𝛼𝑥 + (1 − 𝛼)𝑦) ≤ 𝛼𝑓(𝑥) + (1 − 𝛼)𝑓(𝑦) ≤ ℎ(𝛼)𝑓(𝑥) + ℎ(1 − 𝛼)𝑓(𝑦) yazılabilir. Bu, 𝑓 ∈ 𝑆𝑋(ℎ, 𝐼) anlamına gelir. Benzer şekilde ℎ fonksiyonu, 𝛼 ∈ (0,1) için ℎ(𝛼) ≤ 𝛼 şartını sağlıyorsa 𝑓 negatif olmayan konkav fonksiyonu 𝑆𝑉(ℎ, 𝐼) sınıfına ait olur (Varošanec 2007).
Örnek 2.1.4. 𝑥 > 0, 𝑘 < 0 olmak üzere ℎ𝑘(𝑥) = 𝑥𝑘 verilsin. Bu durumda;
𝑓: 𝐼 = [𝑎, 𝑏] → ℝ, 𝑓(𝑥) = {
1, 𝑥 ≠𝑎 + 𝑏 2 21−𝑘, 𝑥 =𝑎 + 𝑏
2 fonksiyonu konveks değildir ama ℎ𝑘−konvekstir (Varošanec 2007).
Tanım 2.1.10. ((𝒉, 𝒎) −Konveks Fonksiyon): ℎ: 𝐽 ⊆ ℝ → ℝ negatif olmayan bir
fonksiyon olsun. ∀𝑥, 𝑦 ∈ [0, 𝑏], 𝑚 ∈ [0,1] ve 𝛼 ∈ [0,1] olacak şekilde 𝑓: [0, 𝑏] → ℝ tanımlı negatif olmayan 𝑓 fonksiyonu
𝑓(𝛼𝑥 + 𝑚(1 − 𝛼)𝑦) ≤ ℎ(𝛼)𝑓(𝑥) + 𝑚ℎ(1 − 𝛼)𝑓(𝑦)
şartını sağlıyorsa 𝑓 fonksiyonuna (ℎ − 𝑚) −konveks fonksiyon denir (Özdemir et al. 2011).
Tanım 2.1.11. (Birinci Anlamda 𝒔 −Konveks Fonksiyon): 𝛼, 𝛽 ≥ 0, 𝛼𝑠+ 𝛽𝑠 =
1 ve 𝑠 ∈ (0,1] olmak üzere tüm 𝑢, 𝑣 ∈ ℝ+ için 𝑓: ℝ+ → ℝ fonksiyonu
eşitsizliğini sağlıyorsa 𝑓 ’ye birinci anlamda 𝑠 − konveks fonksiyon denir. Bu fonksiyonların sınıfı 𝐾𝑠1 ile gösterilir. Eşitsizlik yön değiştirirse 𝑓 fonksiyonu birinci
anlamda 𝑠 −konkav fonksiyon olarak adlandırılır (Orlicz 1961).
Tanım 2.1.12. (İkinci Anlamda 𝒔 −Konveks Fonksiyon): 𝛼, 𝛽 ≥ 0, 𝛼 + 𝛽 = 1 ve
𝑠 ∈ (0,1] olmak üzere tüm 𝑢, 𝑣 ∈ ℝ+ için 𝑓: ℝ+→ ℝ fonksiyonu eğer
𝑓(𝛼𝑢 + 𝛽𝑣) ≤ 𝛼𝑠𝑓(𝑢) + 𝛽𝑠𝑓(𝑣)
eşitsizliğini sağlıyorsa 𝑓 ’ye ikinci anlamda 𝑠 − konveks fonksiyon denir. Bu fonksiyonların sınıfı 𝐾𝑠2 ile gösterilir. Eşitsizlik yön değiştirirse 𝑓 fonksiyonu ikinci
anlamda 𝑠 −konkav fonksiyon olarak adlandırılır (Breckner 1978).
Yukarıda verilen her iki 𝑠 − konvekslik tanımı 𝑠 = 1 için bilinen konveksliğe dönüşür.
Örnek 2.1.5. 𝑠 ∈ (0,1) ve 𝑎, 𝑏, 𝑐 ∈ ℝ olsun. 𝑓: [0, ∞) → ℝ fonksiyonu
𝑓(𝑡) = {𝑎, 𝑡 = 0 𝑏𝑡𝑠 + 𝑐, 𝑡 > 0 olarak tanımlansın. Bu takdirde
(i) 𝑏 ≥ 0 ve 0 ≤ 𝑐 ≤ 𝑎 ise 𝑓 ∈ 𝐾𝑠2 dir.
(ii) 𝑏 > 0 ve 𝑐 < 0 ise 𝑓 ∉ 𝐾𝑠2 dir (Hudzik and Maligranda 1994).
Tanım 2.1.13. (Quasi-Konveks Fonksiyon): 𝑓: 𝑆 → ℝ bir fonksiyon ve 𝑆 ⊂ ℝ
boştan farklı konveks küme olsun. ∀𝑥, 𝑦 ∈ 𝑆 ve 𝜆 ∈ [0,1] için
𝑓(𝜆𝑥 + (1 − 𝜆)𝑦) ≤ 𝑚𝑎𝑥{𝑓(𝑥), 𝑓(𝑦)}
Eğer
𝑓(𝜆𝑥 + (1 − 𝜆)𝑦) < 𝑚𝑎𝑥{𝑓(𝑥), 𝑓(𝑦)}
ise 𝑓’ye strictly 𝑞𝑢𝑎𝑠𝑖 −konveks fonksiyon denir. Aynı şartlar altında
𝑓(𝜆𝑥 + (1 − 𝜆)𝑦) ≥ 𝑚𝑎𝑥{𝑓(𝑥), 𝑓(𝑦)}
ise 𝑓’ye 𝑞𝑢𝑎𝑠𝑖 −konkav fonksiyon ve
𝑓(𝜆𝑥 + (1 − 𝜆)𝑦) > 𝑚𝑎𝑥{𝑓(𝑥), 𝑓(𝑦)}
ise 𝑓’ye strictly 𝑞𝑢𝑎𝑠𝑖 −konkav fonksiyon denir (Dragomir and Pearce 1998).
Tanım 2.1.14. 𝑓 hem 𝑞𝑢𝑎𝑠𝑖 − konveks hem de 𝑞𝑢𝑎𝑠𝑖 − konkav ise 𝑓 ’ye
𝑞𝑢𝑎𝑠𝑖 −monotonik fonksiyon denir (Greenberg and Pierskalla 1970).
Sonuç 2.1.4. Herhangi bir konveks fonksiyon 𝑞𝑢𝑎𝑠𝑖 −konveks fonksiyondur. Fakat
tersi her zaman doğru değildir. Yani 𝑞𝑢𝑎𝑠𝑖 − konveks olup konveks olmayan fonksiyonlar vardır. Örneğin 𝑔: [−2,2] → ℝ,
𝑔(𝑡) = { 1, 𝑡 ∈ [−2, −1] 𝑡2, 𝑡 ∈ (−1, 2]
fonksiyonu [−2,2] aralığında konveks değildir. Fakat 𝑔 fonksiyonu [−2,2] aralığında 𝑞𝑢𝑎𝑠𝑖 −konveks fonksiyondur (Ion 2007).
Tanım 2.1.15. (Godunova-Levin Fonksiyonu): 𝑓: 𝐼 → ℝ negatif olmayan
fonksiyonu 𝑥, 𝑦 ∈ 𝐼, 𝜆 ∈ (0,1) olmak üzere
𝑓(𝜆𝑥 + (1 − 𝜆)𝑦) ≤ 𝑓(𝑥)
𝜆 +
𝑓(𝑦) 1 − 𝜆
eşitsizliğini sağlıyorsa 𝑓 ’ye Godunova-Levin fonksiyonu veya 𝑄(𝐼) sınıfına aittir denir.
Bu tanıma denk olarak; 𝑓 ∈ 𝑄(𝐼) ve 𝑥, 𝑦, 𝑧 ∈ 𝐼 ise, bu takdirde
𝑓(𝑥)(𝑥 − 𝑦)(𝑥 − 𝑧) + 𝑓(𝑦)(𝑦 − 𝑥)(𝑦 − 𝑧) + 𝑓(𝑧)(𝑧 − 𝑥)(𝑧 − 𝑦) ≥ 0 eşitsizliği sağlanır (Godunova and Levin 1985).
Tanım 2.1.16. (𝑷 −Fonksiyonu): 𝑓: 𝐼 → ℝ negatif olmayan fonksiyonu 𝑥, 𝑦 ∈ 𝐼,
𝜆 ∈ [0,1] olmak üzere
𝑓(𝜆𝑥 + (1 − 𝜆)𝑦) ≤ 𝑓(𝑥) + 𝑓(𝑦)
eşitsizliğini sağlıyorsa 𝑓’ye 𝑃 − fonksiyonu veya 𝑃(𝐼) sınıfına aittir denir (Dragomir
etal. 1995).
Tanımlardan açıkça görüleceği üzere, tüm negatif olmayan konveks fonksiyonlar 𝑄(𝐼) sınıfına aittir. Ayrıca 𝑄(𝐼) ⊃ 𝑃(𝐼) ve 𝑃(𝐼) sınıfından fonksiyonlar negatif olmayan konveks ve Quasi-konveks fonksiyonları içermektedir.
Tanım 2.1.17. (Logaritmik Konveks Fonksiyon): 𝐼, ℝ’de bir aralık 𝑓: 𝐼 → [0, ∞)
bir fonksiyon olsun. Her 𝑥, 𝑦 ∈ 𝐼 ve 𝛼 ∈ [0,1] için,
𝑓(𝛼𝑥 + (1 − 𝛼)𝑦) ≤ [𝑓(𝑥)]𝛼[𝑓(𝑦)](1−𝛼)
eşitsizliği sağlanırsa, 𝑓 fonksiyonuna 𝑙𝑜𝑔 − konvekstir denir. 𝑓 = 𝑒𝑥𝑝 (𝑙𝑜𝑔𝑓) olduğundan 𝑙𝑜𝑔 − konveks fonksiyon konvekstir. Fakat tersi her zaman doğru değildir (Pečarić et al. 1992).
Tanım 2.1.18. (Starshaped Fonksiyon): 𝑏 > 0 olmak üzere 𝑓: [0, 𝑏] → ℝ
𝑓(𝑡𝑥) ≤ 𝑡𝑓(𝑥)
şartını sağlıyorsa bu fonksiyona starshaped fonksiyon denir (Toader 1984).
Tanım 2.1.19. (Bazı Özel Ortalamalar):
Bu kısımda 𝑎, 𝑏 gibi pozitif iki reel sayı için bazı ortalamalar verilecektir (Bullen et al. 1988; Bullen 2003);
(1) Aritmetik ortalama: 𝐴 = 𝐴(𝑎, 𝑏) ≔𝑎 + 𝑏 2 , (2) Geometrik ortalama: 𝐺 = 𝐺(𝑎, 𝑏) ≔ √𝑎𝑏, (3) Harmonik ortalama: 𝐻 = 𝐻(𝑎, 𝑏) ≔ 2𝑎𝑏 𝑎 + 𝑏 (4) Logaritmik ortalama: ℒ = ℒ(𝑎, 𝑏) ≔ { 𝑎, 𝑎 = 𝑏 𝑏 − 𝑎 𝑙𝑛𝑏 − 𝑙𝑛𝑎, 𝑎 ≠ 𝑏 (5) Identric ortalama: 𝐼 = 𝐼(𝑎, 𝑏) ≔ { 𝑎, 𝑎 = 𝑏 1 𝑒( 𝑏𝑏 𝑎𝑎) 1 𝑏−𝑎 , 𝑎 ≠ 𝑏
𝐻 ≤ 𝐺 ≤ ℒ ≤ 𝐼 ≤ 𝐴.
Tanım 2.1.20. (Ağırlıklı Aritmetik Ortalama): 𝑥𝑖 ∈ [𝑎, 𝑏] , 𝑝𝑖 > 0 ve 𝑃𝑛 ≔ ∑𝑛𝑖=1𝑝𝑖 > 0 (𝑖 = 1,2, … , 𝑛) olmak üzere 𝐴𝑛(𝑥, 𝑝) ≔ 1 𝑃𝑛 ∑ 𝑝𝑖𝑥𝑖 𝑛 𝑖=1
şeklindeki ifadeye 𝑥𝑖 (𝑖 = 1,2, … , 𝑛) sayılarının 𝑝𝑖 (𝑖 = 1,2, … , 𝑛) ağırlıklı aritmetik ortalaması denir (Mitrinović et al. 1993).
Tanım 2.1.21. (Gama ve Beta Fonksiyonu):
Euler, gamma fonksiyonunun integral temsilini
𝛤(𝑥) = ∫ 𝑒−𝑡𝑡𝑥−1𝑑𝑡, 𝑥 > 0
∞
0
olarak ifade eder (Kannappan 2009). Beta fonksiyonu;
𝛽(𝑥, 𝑦) = ∫ 𝑡𝑥−1(1 − 𝑡)𝑦−1𝑑𝑡, 𝑥, 𝑦 > 0 1
0
şeklindedir (Dragomir et al. 2000). Bu eşitlik Euler tipli Beta fonksiyonu ya da birinci çeşit Euler integrali olarak adlandırılır. Bu fonksiyonların,
i) 𝛽(𝑥 + 1, 𝑦) = 𝑥 𝑥+𝑦𝛽(𝑥, 𝑦), 𝑥, 𝑦 > 0 ii) 𝛽(1, 𝑦) = 1 𝑦 , 𝑦 > 0 iii) 𝛽(𝑥, 𝑦) = ∫ 𝑡𝑥−1(1 − 𝑡)𝑦−1𝑑𝑡 = ∫ 𝑡 𝑥−1 (1+𝑡)𝑥+𝑦 ∞ 0 𝑥, 𝑦 > 0 1 0 iv) 𝛽(𝑥, 𝑦) =𝛤(𝑥)𝛤(𝑦) 𝛤(𝑥+𝑦) , 𝑥, 𝑦 > 0 v) 𝛽(𝑥, 𝑦) = 𝛽(𝑦, 𝑥), 𝑥, 𝑦 > 0
vi) 𝛽(𝑥, 𝑥) = 21−2𝑥𝛽 (𝑥,1
2) , 𝑥 > 0
gibi özellikleri vardır (Jeffrey and Dai 2008).
Literatürden bilinir ki gama ve beta fonksiyonları sırasıyla (0, ∞) ve (0, ∞)2’de logaritmik konveks fonksiyonlardır.
Teorem 2.1.6. (Üçgen Eşitsizliği): Herhangi 𝑥, 𝑦 reel sayıları için
|𝑥 + 𝑦| ≤ |𝑥| + |𝑦|,
||𝑥| − |𝑦|| ≤ |𝑥 − 𝑦|,
||𝑥| − |𝑦|| ≤ |𝑥 + 𝑦|
ve tümevarım metoduyla
|𝑥1+ ⋯ + 𝑥𝑛| ≤ |𝑥1| + ⋯ + |𝑥𝑛|
eşitsizlikleri geçerlidir (Mitrinović et al. 1993).
Teorem 2.1.7. (Üçgen Eşitsizliğinin İntegral Versiyonu): 𝑓, [𝑎, 𝑏] aralığında sürekli reel değerli bir fonksiyon olsun. Bu takdirde
|∫ 𝑓(𝑥)𝑑𝑥 𝑏 𝑎 | ≤ ∫ |𝑓(𝑥)|𝑑𝑥 𝑏 𝑎 (𝑎 < 𝑏)
eşitsizliği geçerlidir (Mitrinović et al. 1993).
2.2. Bazı Konveks Fonksiyon Sınıflarının Hiyerarşisi
Fonksiyonlar teorisi çalışmalarında yeni sonuçlar ve genelleştirmeler elde etmek için kimi zaman fonksiyonun şartlarında bazı kısıtlamalar yapmak gerekirken
kimi zamanda fonksiyona ek özellikler katmak gerekir. Çünkü fonksiyonlar aynı anda birçok özelliği sağlayabilir veya bir fonksiyon sınıfı başka bir fonksiyon sınıfıyla bazı özellikleri itibariyle benzerlik gösterebilir. Çalışmalarımızda farklı türden konveks fonksiyonlar için çeşitli integral eşitsizlikleri ispatlarken, bu eşitsizliklerin belli özel durumlar için başka konvekslik sınıfları içinde sağlandığını açıkça görebiliriz. Dolayısıyla buradan konveks fonksiyonlar arasında özellikleri açısından bir hiyerarşi olduğu gerçeğine ulaşılır. Fakat bu hiyerarşide tüm konvekslik sınıflarını beraber değerlendirmek oldukça güç olduğu için aralarındaki ilişki, tanımları ve özellikleri yardımıyla şu şekilde oluşturulabilir;
Teorem 2.2.1. 𝐼 ⊆ ℝ olmak üzere, 𝐿𝑜𝑔 − Konveks fonksiyonlar sınıfı, (negatif olmayan) Konveks fonksiyonlar sınıfı, (negatif olmayan) Quasi-konveks fonksiyonlar sınıfı, 𝑃 −fonksiyonlar sınıfı ve Godunova-Levin fonksiyonlar sınıfı sırasıyla 𝐿(𝐼), 𝐶(𝐼), 𝑄𝐶(𝐼), 𝑃(𝐼), 𝑄(𝐼) ile gösterilirse;
𝐿(𝐼) ⊂ 𝐶(𝐼) ⊂ 𝑄𝐶(𝐼) ⊂ 𝑃(𝐼) ⊂ 𝑄(𝐼) olduğu görülür (Kavurmacı 2012).
Şekil 2.7.Godunova-Levin, 𝑃 −fonksiyon, Quasi-konveks fonksiyon, Konveks fonksiyon ve 𝑙𝑜𝑔 −konveks fonksiyon sınıflarının ilişkisi
Lemma 2.2.1. Eğer 𝑓 fonksiyonu 𝑚 − konveks fonksiyonlar sınıfına ait ise 𝑓 fonksiyonu starshaped fonksiyondur (Toader 1988).
Godunova-Levin fonksiyon P-fonksiyon Quasi-konveks fonksiyon Konveks fonksiyon 𝐿𝑜𝑔 −konveks fonksiyon
Lemma 2.2.2. Eğer 𝑓 fonksiyonu 𝑚 −konveks fonksiyon ve 0 ≤ 𝑛 < 𝑚 ≤ 1 ise 𝑓 fonksiyonu 𝑛 − konveks fonksiyondur (Toader 1988). Yukarıdaki lemmalar yardımıyla; 0 ≤ 𝑛 ≤ 𝑚 ≤ 1 olmak üzere, konveks fonksiyonlar sınıfı, 𝑚 −konveks fonksiyonlar sınıfı, 𝑛 −konveks fonksiyonlar sınıfı ve starshaped fonksiyonlar sınıfı sırasıyla 𝐾(𝑏), 𝐾𝑚(𝑏), 𝐾𝑛(𝑏), 𝑆∗(𝑏) ile gösterilirse;
𝐾(𝑏) ⊂ 𝐾𝑚(𝑏) ⊂ 𝑆∗(𝑏)
olduğu görülür (Toader 1988).
Şekil 2.8.Konveks fonksiyon, 𝑚 −konveks fonksiyon, 𝑛 −konveks fonksiyon ve starshaped fonksiyon sınıflarının ilişkisi
ℎ − konveks fonksiyon tanımından açıkça görülebilir ki; eğer ℎ(𝑡) = 𝑡 seçilirse negatif olmayan konveks fonksiyonlar veya eşitsizliğin yön değiştirmesinde negatif olmayan konkav fonksiyonlar, ℎ(𝑡) = 1
𝑡 seçilirse fonksiyon 𝑄(𝐼) sınıfından,
eğer ℎ(𝑡) = 1 sabit fonksiyonu olarak seçilirse 𝑃(𝐼) sınıfından fonksiyon, eğer ℎ(𝑡) = 𝑡𝑠 seçilirse burada 𝑠 ∈ (0,1) olmak üzere 𝐾𝑠2 sınıfından konveks bir fonksiyon elde edileceği aşikârdır. Bu bilgiler ışığında ℎ(𝑡) fonksiyonun bazı özel değerleri için; 𝐶(𝐼) ⊂ 𝑆𝑋(ℎ, 𝐼), 𝑃(𝐼) ⊂ 𝑆𝑋(ℎ, 𝐼), 𝐾𝑠2 ⊂ 𝑆𝑋(ℎ, 𝐼) Starshaped fonksiyon 𝒏 −konveks fonksiyon 𝑷 −fonksiyon 𝒎 −konveks fonksiyonQuasi-Konveks fonksiyon Konveks fonksiyon
yazılabilir. Burada ℎ fonksiyonu negatif olmayan fonksiyon olduğu için negatif olmayan konveks fonksiyonlar 𝑆𝑋(ℎ, 𝐼) sınıfının alt kümesidir.
3. MATERYAL ve YÖNTEM
3.1. Konveks Fonksiyonlar İçin Bazı Eşitsizlikler
Teorem 3.1.1.(Hermite-Hadamard Eşitsizliği):𝐼, ℝ’de bir aralık, 𝑎, 𝑏 ∈ 𝐼 ve 𝑎 < 𝑏 olmak üzere 𝑓: 𝐼 ⊆ ℝ → ℝ konveks bir fonksiyon olsun. Bu takdirde
𝑓 (𝑎 + 𝑏 2 ) ≤ 1 𝑏 − 𝑎∫ 𝑓(𝑥)𝑑𝑥 ≤ 𝑓(𝑎) + 𝑓(𝑏) 2 𝑏 𝑎
eşitsizliği literatürde Hermite-Hadamard eşitsizliği olarak bilinir (Pečarić et al. 1992).
Birçok klasik eşitsizlik, yukarıdaki eşitsizliğin bir sonucudur.
Teorem 3.1.2. (Hölder Eşitsizliği): 𝑎 = (𝑎1, … , 𝑎𝑛) ve 𝑏 = (𝑏1, … , 𝑏𝑛) reel veya kompleks sayıların iki 𝑛 −lisi olsun. Bu takdirde
1 𝑝+ 1 𝑞= 1 olmak üzere (a) 𝑝 > 1 ise, ∑ 𝑎𝑘𝑏𝑘≤ (∑|𝑎𝑘|𝑝 𝑛 𝑘=1 ) 1 𝑝 (∑|𝑏𝑘|𝑞 𝑛 𝑘=1 ) 1 𝑞 𝑛 𝑘=1 , (b) 𝑝 < 0 veya 𝑞 < 0 ise, ∑ 𝑎𝑘𝑏𝑘 ≥ (∑|𝑎𝑘|𝑝 𝑛 𝑘=1 ) 1 𝑝 (∑|𝑏𝑘|𝑞 𝑛 𝑘=1 ) 1 𝑞 𝑛 𝑘=1
eşitsizlikleri geçerlidir (Mitrinović 1970).
Teorem 3.1.3. (İntegraller için Hölder Eşitsizliği): 𝑝 > 1 ve 1
𝑝+ 1
𝑞= 1 olsun. 𝑓 ve 𝑔,
[𝑎, 𝑏] aralığında tanımlı reel fonksiyonlar, |𝑓|𝑝 ve |𝑔|𝑞 , [𝑎, 𝑏] aralığında
integrallenebilir fonksiyonlar ise
∫ |𝑓(𝑥)𝑔(𝑥)| 𝑏 𝑎 𝑑𝑥 ≤ (∫ |𝑓(𝑥)|𝑝𝑑𝑥 𝑏 𝑎 ) 1 𝑝 (∫ |𝑔(𝑥)|𝑞𝑑𝑥 𝑏 𝑎 ) 1 𝑞
eşitsizliği geçerlidir (Mitrinović et al. 1993).
Ayrıca Hölder eşitsizliğinin bir sonucu olan power-mean eşitsizliği de aşağıdaki gibi ifade edilir.
Sonuç 3.1.1. (Power Mean Eşitsizliği): 𝑞 ≥ 1 olsun. 𝑓 ve 𝑔, [𝑎, 𝑏] aralığında tanımlı
reel fonksiyonlar, |𝑓| ve |𝑔|𝑞, [𝑎, 𝑏] aralığında integrallenebilir fonksiyonlar ise
∫ |𝑓(𝑥)𝑔(𝑥)| 𝑏 𝑎 𝑑𝑥 ≤ (∫ |𝑓(𝑥)|𝑑𝑥 𝑏 𝑎 ) 1−1𝑞 (∫ |𝑓(𝑥)||𝑔(𝑥)|𝑞𝑑𝑥 𝑏 𝑎 ) 1 𝑞 eşitsizliği geçerlidir.
Teorem 3.1.4. (Ostrowski Eşitsizliği): 𝑓: 𝐼 ⊂ [0, ∞) → ℝ , 𝐼𝑜 üzerinde
diferensiyellenebilen bir fonksiyon, 𝑓′ ∈ 𝐿[𝑎, 𝑏] ve 𝑎, 𝑏 ∈ 𝐼 için 𝑎 < 𝑏 olsun. Eğer |𝑓′(𝑥)| ≤ 𝑀 ise |𝑓(𝑥) − 1 𝑏 − 𝑎∫ 𝑓(𝑡)𝑑𝑡 𝑏 𝑎 | ≤ 𝑀 𝑏 − 𝑎[ (𝑥 − 𝑎)2+ (𝑏 − 𝑥)2 2 ]
Teorem 3.1.5. (Simpson Eşitsizliği): 𝑓: [𝑎, 𝑏] → ℝ , (a,b) üzerinde dördüncü mertebeden türevi sürekli olan bir fonksiyon ve ‖𝑓(4)‖
∞ = 𝑠𝑢𝑝𝑥∈(𝑎,𝑏)|𝑓 (4)(𝑥)| < ∞ olsun. Bu durumda |1 3[ 𝑓(𝑎) + 𝑓(𝑏) 2 + 2𝑓 ( 𝑎 + 𝑏 2 )] − 1 𝑏 − 𝑎∫ 𝑓(𝑥)𝑑𝑥 𝑏 𝑎 | ≤ 1 2880‖𝑓 (4)‖ ∞(𝑏 − 𝑎) 4
eşitsizliği elde edilir. Bu eşitsizlik literatürde Simpson Eşitsizliği olarak bilinmektedir (Dragomir et al. 2000).
3.2. İkinciMertebeden Türevlenebilen Fonksiyonlar İçin Bazı Eşitsizlikler
Lemma 3.2.1. 𝐼 ⊂ ℝ bir açık aralık, 𝑎, 𝑏 ∈ 𝐼 ve 𝑎 < 𝑏 olsun. 𝑓: 𝐼 → ℝ ikinci mertebeden diferensiyellenebilen bir fonksiyon ve 𝑓′′, 0 ≤ 𝜆 ≤ 1 için integrallenebilir ise (𝜆 − 1)𝑓 (𝑎 + 𝑏 2 ) + 𝜆 𝑓(𝑎) + 𝑓(𝑏) 2 + 1 𝑏 − 𝑎∫ 𝑓(𝑥)𝑑𝑥 𝑏 𝑎 = (𝑏 − 𝑎)2∫ 𝑘(𝑡)𝑓′′(𝑡𝑎 + (1 − 𝑡)𝑏) 1 0 𝑑𝑡
eşitliği geçerlidir. Burada
𝑘(𝑡) = { 𝑡(𝑡 − 𝜆)/2, 0 ≤ 𝑡 ≤ 1 2 (1 − 𝑡)(1 − 𝜆 − 𝑡)/2, 1 2≤ 𝑡 ≤ 1
fonksiyonudur (Sarıkaya ve Aktan, 2011).
Teorem 3.2.1. 𝐼 ⊂ ℝ bir açık aralık, 𝑎, 𝑏 ∈ ℝ ve 𝑎 < 𝑏 olsun. 𝑓: 𝐼 → ℝ ikinci mertebeden diferensiyellenebilen bir fonksiyon, 𝑓′′, 0 ≤ 𝜆 ≤ 1 için integrallenebilir ve |𝑓′′|, [𝑎, 𝑏] üzerinde konveks fonksiyon ise
|(𝜆 − 1)𝑓 (𝑎 + 𝑏 2 ) + 𝜆 𝑓(𝑎) + 𝑓(𝑏) 2 + 1 𝑏 − 𝑎∫ 𝑓(𝑥)𝑑𝑥 𝑏 𝑎 |
≤ { (𝑏 − 𝑎)2 12 [ (𝜆4+ (1 + 𝜆)(1 − 𝜆)3+5𝜆 − 3 4 ) |𝑓 ′′(𝑎)| + (𝜆4+ (2 − 𝜆)𝜆3+1 − 3𝜆 4 ) |𝑓 ′′(𝑏)| ] , 0 ≤ 𝜆 ≤ 1 2 (𝑏 − 𝑎)2(3𝜆 − 1) 48 [|𝑓 ′′(𝑎)| + |𝑓′′(𝑏)|], 1 2≤ 𝜆 ≤ 1 eşitsizliği elde edilir (Sarıkaya ve Aktan, 2011).
Teorem 3.2.2. 𝐼 ⊂ ℝ bir açık aralık, 𝑎, 𝑏 ∈ ℝ ve 𝑎 < 𝑏 olsun. 𝑓: 𝐼 → ℝ ikinci mertebeden diferensiyellenebilen bir fonksiyon, 𝑓′′, 0 ≤ 𝜆 ≤ 1 için integrallenebilir ve |𝑓′′| , [𝑎, 𝑏] üzerinde konveks fonksiyon ise 𝑞 ≥ 1 için
|(𝜆 − 1)𝑓 (𝑎 + 𝑏 2 ) − 𝜆 𝑓(𝑎) + 𝑓(𝑏) 2 + 1 𝑏 − 𝑎∫ 𝑓(𝑥)𝑑𝑥 𝑏 𝑎 | ≤ { (𝑏 − 𝑎)2 2 ( 𝜆3 3 + 1 − 3𝜆 24 ) 1−1𝑞 × {([𝜆 4 6 + 3 − 8𝜆 3. 26 ] |𝑓′′(𝑎)|𝑞+ [ (2 − 𝜆)𝜆3 6 + 5 − 16𝜆 3. 26 ] |𝑓′′(𝑏)|𝑞) 1 𝑞 + ([(1 + 𝜆)(1 − 𝜆) 3 6 + 48𝜆 − 27 3. 26 ] |𝑓′′(𝑎)|𝑞+ [ 𝜆4 6 + 3 − 8𝜆 3. 26 ] |𝑓′′(𝑏)| 𝑞 ) 1 𝑞 } , 0 ≤ 𝜆 ≤ 1 2 için (𝑏 − 𝑎)2 2 ( 3𝜆 − 1 24 ) 1−1 𝑞 {(8𝜆 − 3 3. 26 |𝑓 ′′(𝑎)|𝑞+16𝜆 − 5 3. 26 |𝑓 ′′(𝑏)|𝑞) 1 𝑞 + (16𝜆 − 5 3. 26 |𝑓 ′′(𝑎)|𝑞+8𝜆 − 3 3. 26 |𝑓 ′′(𝑏)|𝑞) 1 𝑞 } , 1 2≤ 𝜆 ≤ 1 için
eşitsizliği elde edilir (Sarıkaya ve Aktan, 2011).
3.3. 𝒏. Mertebeden Türevlenebilen Fonksiyonlar İçin Bazı İntegral Eşitsizlikler
Lemma 3.3.1. 𝑛 ≥ 1 için, 𝑓: 𝐼 ⊂ ℝ → ℝ tanımlı 𝑛. mertebeden türevlenebilen bir fonksiyon olsun. 𝑎, 𝑏 ∈ 𝐼 ve 𝑓(𝑛)∈ 𝐿[𝑎, 𝑏] için
∫ 𝑓(𝑥)𝑑𝑥 = ∑ ( 1 + (−1) 𝑘 2𝑘+1(𝑘 + 1)!) (𝑏 − 𝑎)𝑘+1𝑓(𝑘) 𝑛−1 𝑘=0 𝑏 𝑎 (𝑎 + 𝑏 2 ) +(𝑏 − 𝑎)𝑛+1∫ 𝑀 𝑛(𝑡)𝑓(𝑛)(𝑡𝑎 + (1 − 𝑡)𝑏)𝑑𝑡 1 0
eşitliği mevcuttur. Burada 𝑀𝑛(𝑡): [0,1] → ℝ
𝑀𝑛(𝑡) = { 𝑡 𝑛 𝑛!, 𝑡 ∈ [0, 1 2] (𝑡 − 1)𝑛 𝑛! , 𝑡 ∈ ( 1 2, 1] fonksiyonudur.
Teorem 3.3.1. 𝑎, 𝑏 ∈ 𝐼 ve 𝑎 < 𝑏 olmak üzere 𝑓: 𝐼 ⊂ ℝ → ℝ tanımlı ve (𝑎, 𝑏) aralığında 𝑛. mertebeden türevlenebilen bir fonksiyon olsun. Eğer 𝑓(𝑛)∈ 𝐿[𝑎, 𝑏](𝑛 ≥
1) ve |𝑓(𝑛)|, [𝑎, 𝑏] aralığında konveks ise
|∫ 𝑓(𝑡)𝑑𝑡 − ∑ ( 1 + (−1) 𝑘 2𝑘+1(𝑘 + 1)!) (𝑏 − 𝑎)𝑘+1𝑓(𝑘) 𝑛−1 𝑘=0 𝑏 𝑎 (𝑎 + 𝑏 2 )| ≤ (𝑏 − 𝑎) 𝑛+1 2𝑛(𝑛 + 1)!( |𝑓𝑛(𝑎)| + |𝑓𝑛(𝑏)| 2 )
Teorem 3.3.2. 𝑎, 𝑏 ∈ 𝐼 ve 𝑎 < 𝑏 olmak üzere 𝑓: 𝐼 ⊂ ℝ → ℝ tanımlı ve (𝑎, 𝑏) aralığında 𝑛. mertebeden türevlenebilen bir fonksiyon olsun. Eğer 𝑓(𝑛)∈ 𝐿[𝑎, 𝑏] (𝑛 ≥
1) ve |𝑓(𝑛)|𝑞, [𝑎, 𝑏] aralığında konveks ise
|∫ 𝑓(𝑥)𝑑𝑥 − ∑ ( 1 + (−1) 𝑘 2𝑘+1(𝑘 + 1)!) (𝑏 − 𝑎) 𝑘+1𝑓(𝑘) 𝑛−1 𝑘=0 𝑏 𝑎 (𝑎 + 𝑏 2 )| ≤(𝑏 − 𝑎) 𝑛+1 2𝑛+1𝑛! ( 1 𝑛𝑝 + 1) 1 𝑝 × {(|𝑓 𝑛(𝑎)|𝑞+ 3|𝑓𝑛(𝑏)|𝑞 4 ) 1 𝑞 + (3|𝑓 𝑛(𝑎)|𝑞+ |𝑓𝑛(𝑏)|𝑞 4 ) 1 𝑞 }
eşitsizliği elde edilir. Burada 1
𝑝+ 1
𝑞= 1 dir.
Teorem 3.3.3. 𝑎, 𝑏 ∈ 𝐼 ve 𝑎 < 𝑏 olmak üzere 𝑓: 𝐼 ⊂ ℝ → ℝ tanımlı ve (𝑎, 𝑏) aralığında 𝑛. mertebeden türevlenebilen bir fonksiyon olsun. Eğer 𝑓(𝑛)∈ 𝐿[𝑎, 𝑏](𝑛 ≥
1), |𝑓(𝑛)|𝑞, [𝑎, 𝑏] aralığında konveks ve 𝑞 ≥ 1 ise
|∫ 𝑓(𝑥)𝑑𝑥 − ∑ ( 1 + (−1) 𝑘 2𝑘+1(𝑘 + 1)!) (𝑏 − 𝑎)𝑘+1𝑓(𝑘) 𝑛−1 𝑘=0 𝑏 𝑎 (𝑎 + 𝑏 2 )| ≤ (𝑏 − 𝑎) 𝑛+1 2𝑛+1(𝑛 + 1)!{( 𝑛 + 1 2𝑛 + 4|𝑓 𝑛(𝑎)|𝑞+ 𝑛 + 3 2𝑛 + 4|𝑓 𝑛(𝑏)|𝑞) 1 𝑞 + (𝑛 + 3 2𝑛 + 4|𝑓 𝑛(𝑎)|𝑞+ 𝑛 + 1 2𝑛 + 4|𝑓 𝑛(𝑏)|𝑞) 1 𝑞 }
4. ARAŞTIRMA BULGULARI
4.1. İkinci Mertebeden Türevlenebilen Fonksiyonlar İçin Elde Edilen İntegral Eşitsizlikler
Bu bölümde ikinci mertebeden türevlenebilen fonksiyonlar için yeni bir lemma elde edildi ve bu lemma yardımıyla bazı integral eşitsizlikler ispatlandı.
Lemma 4.1.1 𝑎, 𝑏 ∈ 𝐼, 𝑎 < 𝑏 ve 𝐼 ⊂ ℝ olmak üzere 𝑓: 𝐼 → ℝ fonksiyonu, 𝐼° üzerinde
iki kez türevlenebilen bir fonksiyon ve 𝛼, 𝜆 ∈ [0,1] olsun. 𝑓, 𝑓′𝑓′′ ∈ 𝐿[𝑎, 𝑏] olmak
üzere (𝑏 − 𝑎) (𝛼 −1 2) 𝑓 ′((1 − 𝛼)𝑏 + 𝛼𝑎) − 1 𝑏 − 𝑎∫ 𝑓(𝑥) 𝑏 𝑎 𝑑𝑥 +(1 − 𝜆) 𝑓((1 − 𝛼)𝑏 + 𝛼𝑎) + 𝜆(𝛼𝑓(𝑎) + (1 − 𝛼)𝑓(𝑏)) =(𝑏 − 𝑎) 2 2 ∫ 𝑘(𝑡)𝑓 ′′(𝑡𝑏 + (1 − 𝑡)𝑎) 1 0 𝑑𝑡
eşitliği geçerlidir. Burada
𝑘(𝑡) = { 2𝛼𝜆𝑡 − 𝑡
2, 0 ≤ 𝑡 ≤ 1 − 𝛼
(1 − 𝑡)(𝑡 − 1 + 2𝜆(1 − 𝛼)), 1 − 𝛼 ≤ 𝑡 ≤ 1 fonksiyonudur.
İspat: Verilen şartlar altında;
𝐼 = ∫ 𝑘(𝑡)𝑓′′(𝑡𝑏 + (1 − 𝑡)𝑎) 1 0 𝑑𝑡 = ∫ (2𝛼𝜆𝑡−𝑡2)𝑓′′(𝑡𝑏 + (1 − 𝑡)𝑎) 1−𝛼 0 𝑑𝑡 + ∫ (1 − 𝑡)(𝑡 − 1 + 2𝜆(1 − 𝛼))𝑓′′(𝑡𝑏 + (1 − 𝑡)𝑎)𝑑𝑡 1 1−𝛼
ifadesine kısmi integrasyon uygulanırsa 𝐼 = (2𝛼𝜆𝑡−𝑡2)𝑓 ′(𝑡𝑏 + (1 − 𝑡)𝑎) 𝑏 − 𝑎 | 0 1−𝛼 − ∫ (2𝛼𝜆 − 2𝑡) 1−𝛼 0 𝑓′(𝑡𝑏 + (1 − 𝑡)𝑎) 𝑏 − 𝑎 𝑑𝑡 + ((1 − 𝑡)(𝑡 − 1 + 2𝜆(1 − 𝛼))𝑓 ′(𝑡𝑏 + (1 − 𝑡)𝑎) (𝑏 − 𝑎) )| 1−𝛼 1 − ∫ 2(1 − 𝑡 − 𝜆(1 − 𝛼)) 1 1−𝛼 𝑓′(𝑡𝑏 + (1 − 𝑡)𝑎) 𝑏 − 𝑎 𝑑𝑡 = (2𝛼𝜆𝑡(1 − 𝛼) − (1 − 𝛼)2)𝑓 ′((1 − 𝛼)𝑏 + 𝛼𝑎) 𝑏 − 𝑎 − (𝛼(−𝛼 + 2𝜆(1 − 𝛼)))𝑓 ′((1 − 𝛼)𝑏 + 𝛼𝑎) 𝑏 − 𝑎 − 2 𝑏 − 𝑎{∫ (𝛼𝜆 − 𝑡)𝑓 ′(𝑡𝑏 + (1 − 𝑡)𝑎) 1−𝛼 0 𝑑𝑡 + ∫ (1 − 𝑡 − 𝜆(1 − 𝛼))𝑓′(𝑡𝑏 + (1 − 𝑡)𝑎)𝑑𝑡 1 1−𝛼 }
elde edilir. Gerekli işlemler yapılırsa
𝐼 = (2𝛼 − 1)𝑓 ′((1 − 𝛼)𝑏 + 𝛼𝑎) 𝑏 − 𝑎 − 2 𝑏 − 𝑎{(𝛼𝜆 − 𝑡) 𝑓(𝑡𝑏 + (1 − 𝑡)𝑎) 𝑏 − 𝑎 | 0 1−𝛼 − ∫ −𝑓(𝑡𝑏 + (1 − 𝑡)𝑎) 𝑏 − 𝑎 1−𝛼 0 𝑑𝑡 + (1 − 𝑡 − 𝜆(1 − 𝛼))𝑓(𝑡𝑏 + (1 − 𝑡)𝑎) 𝑏 − 𝑎 | 1−𝛼 1 − ∫ −𝑓(𝑡𝑏 + (1 − 𝑡)𝑎) 𝑏 − 𝑎 𝑑𝑡 1 1−𝛼 } = (2𝛼 − 1)𝑓 ′((1 − 𝛼)𝑏 + 𝛼𝑎) 𝑏 − 𝑎
− 2 𝑏 − 𝑎{(𝛼𝜆 − 1 + 𝛼) 𝑓((1 − 𝛼)𝑏 + 𝛼𝑎) 𝑏 − 𝑎 − 𝛼𝜆𝑓(𝑎) 𝑏 − 𝑎 + ( −𝜆(1 − 𝛼)𝑓(𝑏) 𝑏 − 𝑎 ) −(𝛼 − 𝜆(1 − 𝛼))𝑓((1 − 𝛼)𝑏 + 𝛼𝑎) 𝑏 − 𝑎 + ∫ 𝑓(𝑡𝑏 + (1 − 𝑡)𝑎) 𝑏 − 𝑎 𝑑𝑡 1 0 } = (2𝛼 − 1)𝑓 ′((1 − 𝛼)𝑏 + 𝛼𝑎) 𝑏 − 𝑎 + 2 (𝑏 − 𝑎)2{(1 − 𝜆)𝑓((1 − 𝛼)𝑏 + 𝛼𝑎) +𝜆(𝛼𝑓(𝑎) + (1 − 𝛼)𝑓(𝑏)) − ∫ 𝑓(𝑡𝑏 + (1 − 𝑡)𝑎)𝑑𝑡 1 0 }
bulunur. 𝑥 = 𝑡𝑏 + (1 − 𝑡)𝑎 değişken değiştirmesi yapılıp, eşitliğin her iki tarafı
(𝑏−𝑎)2
2 çarpılırsa lemma elde edilir.
Teorem 4.1.1. 𝑓: 𝐼 ⊂ ℝ → ℝ, 𝐼° üzerinde iki kez türevlenebilen fonksiyon, 𝑓, 𝑓′, 𝑓′′ ∈
𝐿[𝑎, 𝑏], 𝑎, 𝑏 ∈ 𝐼 ile 𝑎 < 𝑏 olsun. |𝑓′′| fonksiyonu, [𝑎, 𝑏] aralığında konveks fonksiyon ise 𝛼, 𝜆 ∈ [0,1] için, 𝛾1 =8 3(𝛼𝜆) 4+ (1 − 𝛼)3(1 − 𝛼 4 − 2𝛼𝜆 3 ) 𝛾2 = 8 3(𝛼𝜆) 3(1 − 𝛼𝜆) + (1 − 𝛼)2[1 − 𝛼 3 − 𝛼𝜆 − (1 − 𝛼)2 4 + 2𝛼𝜆(1 − 𝛼) 3 ] 𝛾3 = 2𝛼𝜆(1 − 𝛼) 3 3 − (1 − 𝛼)4 4 𝛾4 = (1 − 𝛼)2[𝛼𝜆 −1 − 𝛼 3 − 2𝛼𝜆(1 − 𝛼) 3 + (1 − 𝛼)2 4 ] ve
𝜇1= 4 3(1 − 𝛼) 3𝜆3(1 − 𝜆(1 − 𝛼)) − 1 12(𝛼 − 2𝜆(1 − 𝛼)) 2 [𝛼(3𝛼 − 4) − 4𝜆(1 − 𝛼)2(1 − 𝜆)] 𝜇2= 4 3(1 − 𝛼) 4𝜆4+ 1 12(𝛼 − 2𝜆(1 − 𝛼)) 2 [𝛼2(4𝜆2− 4𝜆 + 3) + 4𝛼𝜆(1 − 2𝜆) + 4𝜆2] 𝜇3= 4 3(1 − 𝛼) 3𝜆3(1 − 𝜆(1 − 𝛼)) + 1 12(𝛼 − 2𝜆(1 − 𝛼)) 2 [𝛼(3𝛼 − 4) − 4𝜆(1 − 𝛼)2(1 − 𝜆)] 𝜇4 = 4 3(1 − 𝛼) 4𝜆4− 1 12(𝛼 − 2𝜆(1 − 𝛼)) 2 [𝛼2(4𝜆2− 4𝜆 + 3) + 4𝛼𝜆(1 − 2𝜆) + 4𝜆2] olmak üzere |(𝑏 − 𝑎) (𝛼 − 1 2) 𝑓 ′((1 − 𝛼)𝑏 + 𝛼𝑎) − 1 𝑏 − 𝑎∫ 𝑓(𝑥)𝑑𝑥 𝑏 𝑎 +(1 − 𝜆)𝑓((1 − 𝛼)𝑏 + 𝛼𝑎) + 𝜆(𝛼𝑓(𝑎) + (1 − 𝛼)𝑓(𝑏)) | ≤ { (𝑏 − 𝑎)2 2 {(𝛾1+ 𝜇1)|𝑓 ′′(𝑏)| + (𝛾 2+ 𝜇2)|𝑓′′(𝑎)|}, 2𝛼𝜆 ≤ 1 − 𝛼 ≤ 1 − 2𝜆(1 − 𝛼) (𝑏 − 𝑎)2 2 {(𝛾1+ 𝜇3)|𝑓 ′′(𝑏)| + (𝛾 2+ 𝜇4)|𝑓′′(𝑎)|}, 1 − 𝛼 ≥ 𝑚𝑎𝑥{2𝛼𝜆, 1 − 2𝜆(1 − 𝛼)} (𝑏 − 𝑎)2 2 {(𝛾3+ 𝜇1)|𝑓 ′′(𝑏)| + (𝛾 4+ 𝜇2)|𝑓′′(𝑎)|}, 1 − 𝛼 ≤ 𝑚𝑖𝑛{2𝛼𝜆, 1 − 2𝜆(1 − 𝛼)} (𝑏 − 𝑎)2 2 {(𝛾3+ 𝜇3)|𝑓 ′′(𝑏)| + (𝛾 4+ 𝜇4)|𝑓′′(𝑎)|}, 1 − 2𝜆(1 − 𝛼) ≤ 1 − 𝛼 ≤2𝛼𝜆
eşitsizliği elde edilir.
İspat: Lemma 4.1.1’den ve integraller için mutlak değer özelliğinden
|(𝑏 − 𝑎) (𝛼 − 1 2) 𝑓 ′((1 − 𝛼)𝑏 + 𝛼𝑎) − 1 𝑏 − 𝑎∫ 𝑓(𝑥)𝑑𝑥 𝑏 𝑎 +(1 − 𝜆)𝑓((1 − 𝛼)𝑏 + 𝛼𝑎) + 𝜆(𝛼𝑓(𝑎) + (1 − 𝛼)𝑓(𝑏)) | ≤(𝑏 − 𝑎) 2 2 ∫ |𝑘(𝑡)| |𝑓 ′′(𝑡𝑏 +(1 − 𝑡)𝑎)| 1 0 𝑑𝑡
= (𝑏 − 𝑎) 2 2 {∫ 𝑡|2𝛼𝜆 − 𝑡||𝑓 ′′(𝑡𝑏 + (1 − 𝑡)𝑎)|𝑑𝑡 1−𝛼 0 + ∫ (1 − 𝑡)|1 − 2𝜆(1 − 𝛼) − 𝑡||𝑓′′(𝑡𝑏 + (1 − 𝑡)𝑎)|𝑑𝑡 1 1−𝛼 }
elde edilir. |𝑓′′| fonksiyonu, [𝑎, 𝑏] aralığında konveks olduğundan
|(𝑏 − 𝑎) (𝛼 − 1 2) 𝑓 ′((1 − 𝛼)𝑏 + 𝛼𝑎) − 1 𝑏 − 𝑎∫ 𝑓(𝑥)𝑑𝑥 𝑏 𝑎 +(1 − 𝜆)𝑓((1 − 𝛼)𝑏 + 𝛼𝑎) + 𝜆(𝛼𝑓(𝑎) + (1 − 𝛼)𝑓(𝑏)) | ≤ (𝑏 − 𝑎) 2 2 {∫ 𝑡|2𝛼𝜆 − 𝑡|(𝑡|𝑓 ′′(𝑏)| + (1 − 𝑡)|𝑓′′(𝑎)|)𝑑𝑡 1−𝛼 0 + ∫ (1 − 𝑡)|1 − 2𝜆(1 − 𝛼) − 𝑡|(𝑡|𝑓′′(𝑏)| + (1 − 𝑡)|𝑓′′(𝑎)|)𝑑𝑡 1 1−𝛼 } ≤ (𝑏 − 𝑎) 2 2 {∫ |2𝛼𝜆 − 𝑡|(𝑡 2|𝑓′′(𝑏)| + 𝑡(1 − 𝑡)|𝑓′′(𝑎)|)𝑑𝑡 1−𝛼 0 + ∫ |1 − 2𝜆(1 − 𝛼) − 𝑡|(𝑡(1 − 𝑡)|𝑓′′(𝑏)| + (1 − 𝑡)2|𝑓′′(𝑎)|)𝑑𝑡 1 1−𝛼 }
eşitsizliği elde edilir. Burada gerekli integral işlemleri yapılırsa,
∫ |2𝛼𝜆 − 𝑡|(𝑡2|𝑓′′(𝑏)| + 𝑡(1 − 𝑡)|𝑓′′(𝑎)|)𝑑𝑡 1−𝛼 0 = {𝛾1|𝑓 ′′(𝑏)| + 𝛾 2|𝑓′′(𝑎)|, 2𝛼𝜆 ≤ 1 − 𝛼 𝛾3|𝑓′′(𝑏)| + 𝛾 4|𝑓′′(𝑎)|, 2𝛼𝜆 ≥ 1 − 𝛼 olur. Burada
𝛾1 =8 3(𝛼𝜆) 4+(1 − 𝛼)4 4 − 2𝛼𝜆(1 − 𝛼)3 3 𝛾2 = 8(𝛼𝜆)4−16 3 (𝛼𝜆) 3(1 + 2𝛼𝜆)+ 8(𝛼𝜆)3 −(1 − 𝛼) 4 4 + (1 − 𝛼)3 3 (1 + 2𝜆𝛼)− 𝛼𝜆(1 − 𝛼) 2 𝛾3 = 2𝛼𝜆(1 − 𝛼) 3 3 − (1 − 𝛼)4 4 𝛾4 = 𝛼𝜆(1 − 𝛼)2−(1 − 𝛼) 3 3 − 2𝛼𝜆(1 − 𝛼)3 3 + (1 − 𝛼)4 4 dır. Diğer taraftan ∫ |1 − 2𝜆(1 − 𝛼) − 𝑡|(𝑡(1 − 𝑡)|𝑓′′(𝑏)| + (1 − 𝑡)2|𝑓′′(𝑎)|)𝑑𝑡 1 1−𝛼 = {𝜇1|𝑓 ′′(𝑏)| + 𝜇 2|𝑓′′(𝑎)|, 1 − 𝛼 ≤ 1 − 2𝜆(1 − 𝛼) 𝜇3|𝑓′′(𝑏)| + 𝜇4|𝑓′′(𝑎)|, 1 − 𝛼 ≥ 1 − 2𝜆(1 − 𝛼) olup, burada 𝜇1= − (1 − 2𝜆(1 − 𝛼))4 6 + (1 − 2𝜆(1 − 𝛼))3 3 − (1 − 𝛼)4 4 + (1 − 𝛼)3(2 − 2𝜆(1 − 𝛼)) 3 −(1 − 2𝜆(1 − 𝛼))(1 − 𝛼) 2 2 − (1 − 2𝜆(1 − 𝛼)) 6 + 1 12 𝜇2 = (1 − 2𝜆(1 − 𝛼)) 4 6 − 2(1 − 2𝜆(1 − 𝛼))3 3 + (1 − 2𝜆(1 − 𝛼)) 2 −(1 − 2𝜆(1 − 𝛼)) 3 3 + 1 12+ (1 − 𝛼)4 4 − (1 − 𝛼)3(3 − 2𝜆(1 − 𝛼)) 3
+(1 − 𝛼) 2(3 − 4𝜆(1 − 𝛼)) 2 − (1 − 2𝜆(1 − 𝛼))(1 − 𝛼) 𝜇3= − 1 − 2𝜆(1 − 𝛼) 6 + 1 12+ (1 − 𝛼)4 4 − (1 − 𝛼)3(2 − 2𝜆(1 − 𝛼)) 3 +(1 − 2𝜆(1 − 𝛼))(1 − 𝛼) 2 2 𝜇4 = −1 − 2𝜆(1 − 𝛼) 3 + 1 12− (1 − 𝛼)4 4 + (1 − 𝛼)3(3 − 2𝜆(1 − 𝛼)) 3 −(1 − 𝛼) 2(3 − 4𝜆(1 − 𝛼)) 2 + (1 − 2𝜆(1 − 𝛼))(1 − 𝛼)
yazılabilir. İfadeler düzenlenirse Teorem 4.1.1’de verilen 𝛾𝑖 ve 𝜇𝑖 (𝑖 = 1,2,3,4)
katsayıları elde edilir. Böylece ispat tamamlanır.
Teorem 4.1.2. 𝑓: 𝐼 ⊂ ℝ → ℝ, 𝐼° üzerinde iki kez türevlenebilen fonksiyon, 𝑓, 𝑓′, 𝑓′′ ∈
𝐿[𝑎, 𝑏], 𝑎, 𝑏 ∈ 𝐼 ile 𝑎 < 𝑏 olsun. |𝑓′′|𝑞, [𝑎, 𝑏] aralığında konveks fonksiyon olmak
üzere; 𝑞 ≥ 1, 𝛼, 𝜆 ∈ [0,1] için, 𝜏1 = 8 3(𝛼𝜆) 3+ (1 − 𝛼)2(1 − 𝛼 3 − 𝛼𝜆) 𝜏2 = (1 − 𝛼)2(𝛼𝜆 −1 − 𝛼 3 ) 𝑧1 = 4 3(1 − 𝛼) 3𝜆3+1 3(𝛼 − 2𝜆(1 − 𝛼)) 2 (𝛼(1 − 𝜆) + 𝜆) 𝑧2 =4 3(1 − 𝛼) 3𝜆3−1 3(𝛼 − 2𝜆(1 − 𝛼)) 2 (𝛼(1 − 𝜆) + 𝜆) ve
Teorem 4.1.1’de tanımlanan 𝛾𝑖 ve 𝜇𝑖 (𝑖 = 1,2,3,4) katsayıları için, |(𝑏 − 𝑎) (𝛼 − 1 2) 𝑓 ′((1 − 𝛼)𝑏 + 𝛼𝑎) − 1 𝑏 − 𝑎∫ 𝑓(𝑥)𝑑𝑥 𝑏 𝑎 +(1 − 𝜆)𝑓((1 − 𝛼)𝑏 + 𝛼𝑎) + 𝜆(𝛼𝑓(𝑎) + (1 − 𝛼)𝑓(𝑏)) | ≤ { (𝑏 − 𝑎)2 2 [ 𝜏11− 1 𝑞 (𝛾1|𝑓′′(𝑏)|𝑞+ 𝛾2|𝑓′′(𝑎)|𝑞) 1 𝑞 𝑧11− 1 𝑞 (𝜇1|𝑓′′(𝑏)|𝑞+ 𝜇2|𝑓′′(𝑎)|𝑞) 1 𝑞 ] , 2𝛼𝜆 ≤ 1 − 𝛼 ≤ 1 − 2𝜆(1 − 𝛼) (𝑏 − 𝑎)2 2 [ 𝜏11− 1 𝑞 (𝛾1|𝑓′′(𝑏)|𝑞+ 𝛾2|𝑓′′(𝑎)|𝑞) 1 𝑞 𝑧21− 1 𝑞 (𝜇3|𝑓′′(𝑏)|𝑞+ 𝜇4|𝑓′′(𝑎)|𝑞) 1 𝑞 ] , 1 − 𝛼 ≥ 𝑚𝑎𝑥{2𝛼𝜆, 1 − 2𝜆(1 − 𝛼)} (𝑏 − 𝑎)2 2 [ 𝜏21− 1 𝑞 (𝛾3|𝑓′′(𝑏)|𝑞+ 𝛾 4|𝑓′′(𝑎)|𝑞) 1 𝑞 𝑧11− 1 𝑞 (𝜇1|𝑓′′(𝑏)|𝑞+ 𝜇 2|𝑓′′(𝑎)|𝑞) 1 𝑞 ] , 1 − 𝛼 ≤ 𝑚𝑖𝑛{2𝛼𝜆, 1 − 2𝜆(1 − 𝛼)} (𝑏 − 𝑎)2 2 [ 𝜏21− 1 𝑞 (𝛾3|𝑓′′(𝑏)|𝑞+ 𝛾4|𝑓′′(𝑎)|𝑞) 1 𝑞 𝑧21− 1 𝑞 (𝜇3|𝑓′′(𝑏)|𝑞+ 𝜇4|𝑓′′(𝑎)|𝑞) 1 𝑞 ] , 1 − 2𝜆(1 − 𝛼) ≤ 1 − 𝛼 ≤ 2𝛼𝜆
eşitsizliği elde edilir.
İspat: Lemma 4.1.1’de integraller için mutlak değer özelliği ve Power-mean eşitsizliği
kullanılırsa |(𝑏 − 𝑎) (𝛼 − 1 2) 𝑓 ′((1 − 𝛼)𝑏 + 𝛼𝑎) − 1 𝑏 − 𝑎∫ 𝑓(𝑥)𝑑𝑥 𝑏 𝑎 +(1 − 𝜆)𝑓((1 − 𝛼)𝑏 + 𝛼𝑎) + 𝜆(𝛼𝑓(𝑎) + (1 − 𝛼)𝑓(𝑏)) | ≤(𝑏 − 𝑎) 2 2 ∫ |𝑘(𝑡)| |𝑓 ′′ (𝑡𝑏 +(1 − 𝑡)𝑎)| 1 0 𝑑𝑡 = (𝑏 − 𝑎) 2 2 {∫ 𝑡|2𝛼𝜆 − 𝑡||𝑓 ′′(𝑡𝑏 + (1 − 𝑡)𝑎)|𝑑𝑡 1−𝛼 0
+ ∫1 (1 − 𝑡)|1 − 2𝜆(1 − 𝛼) − 𝑡||𝑓′′(𝑡𝑏 + (1 − 𝑡)𝑎)|𝑑𝑡 1−𝛼 } ≤ (𝑏 − 𝑎) 2 2 [{(∫ |2𝛼𝜆𝑡 − 𝑡 2|𝑑𝑡 1−𝛼 0 ) 1−𝑞1 (∫1−𝛼|2𝛼𝜆 − 𝑡2||𝑓′′(𝑡𝑏 + (1 − 𝑡)𝑎)|𝑞𝑑𝑡 0 ) 1 𝑞 } + {(∫ |(1 − 𝑡)(1 − 2𝜆(1 − 𝛼) − 𝑡)|𝑑𝑡 1 1−𝛼 ) 1−𝑞1 × (∫ |(1 − 𝑡)(1 − 2𝜆(1 − 𝛼) − 𝑡)||𝑓′′(𝑡𝑏 + (1 − 𝑡)𝑎)|𝑞𝑑𝑡 1 1−𝛼 ) 1 𝑞 }]
eşitsizliği elde edilir. |𝑓′′|𝑞
fonksiyonu, [𝑎, 𝑏] aralığında konveks ve 𝑡 ∈ [0,1] olduğundan
|𝑓′′(𝑡𝑏 + (1 − 𝑡)𝑎)|𝑞≤ 𝑡|𝑓′′(𝑏)|𝑞+ (1 − 𝑡)|𝑓′′(𝑎)|𝑞
eşitsizliği yazılır. Dolayısıyla
|(𝑏 − 𝑎) (𝛼 − 1 2) 𝑓 ′((1 − 𝛼)𝑏 + 𝛼𝑎) − 1 𝑏 − 𝑎∫ 𝑓(𝑥)𝑑𝑥 𝑏 𝑎 +(1 − 𝜆)𝑓((1 − 𝛼)𝑏 + 𝛼𝑎) + 𝜆(𝛼𝑓(𝑎) + (1 − 𝛼)𝑓(𝑏)) | ≤(𝑏 − 𝑎) 2 2 [{(∫ 𝑡|2𝛼𝜆 − 𝑡|𝑑𝑡 1−𝛼 0 ) 1−1𝑞 × (∫ |2𝛼𝜆 − 𝑡|(𝑡2|𝑓′′(𝑏)|𝑞+ 𝑡(1 − 𝑡)|𝑓′′(𝑎)|𝑞𝑑𝑡) 1−𝛼 0 ) 1 𝑞 }
+ {(∫ (1 − 𝑡)|(1 − 2𝜆(1 − 𝛼) − 𝑡)|𝑑𝑡 1 1−𝛼 ) 1−1 𝑞 × (∫ |(1 − 2𝜆(1 − 𝛼) − 𝑡)| (𝑡(1 − 𝑡)|𝑓′′(𝑏)|𝑞+ (1 − 𝑡)2|𝑓′′(𝑎)|𝑞)𝑑𝑡 1 1−𝛼 ) 1 𝑞 }] olur. Burada ∫ 𝑡|2𝛼𝜆 − 𝑡|𝑑𝑡 1−𝛼 0 = {𝜏1, 2𝛼𝜆 ≤ 1 − 𝛼 𝜏2, 2𝛼𝜆 ≥ 1 − 𝛼 olmak üzere 𝜏1 =8 3(𝛼𝜆) 3+ (1 − 𝛼)2(1 − 𝛼 3 − 𝛼𝜆) 𝜏2 = (1 − 𝛼)2(𝛼𝜆 − 1 − 𝛼 3 ) ve ∫ (1 − 𝑡)|(1 − 2𝜆(1 − 𝛼) − 𝑡)|𝑑𝑡 1 1−𝛼 = {𝑧1, 1 − 2𝜆(1 − 𝛼) ≥ 1 − 𝛼 𝑧2, 1 − 2𝜆(1 − 𝛼) ≤ 1 − 𝛼 olmak üzere 𝑧1 = 4 3(1 − 𝛼) 3𝜆3+1 3(𝛼 − 2𝜆(1 − 𝛼)) 2 (𝛼(1 − 𝜆) + 𝜆) 𝑧2 = 4 3(1 − 𝛼) 3𝜆3−1 3(𝛼 − 2𝜆(1 − 𝛼)) 2 (𝛼(1 − 𝜆) + 𝜆)
∫ |2𝛼𝜆 − 𝑡|(𝑡2|𝑓′′(𝑏)|𝑞+ 𝑡(1 − 𝑡)|𝑓′′(𝑎)|𝑞𝑑𝑡) 1−𝛼 0 = { 𝛾1|𝑓 ′′(𝑏)|𝑞+ 𝛾 2|𝑓′′(𝑎)|𝑞, 2𝛼𝜆 ≤ 1 − 𝛼 𝛾3|𝑓′′(𝑏)|𝑞+ 𝛾 4|𝑓′′(𝑎)|𝑞, 2𝛼𝜆 ≥ 1 − 𝛼 ve ∫ |(1 − 2𝜆(1 − 𝛼) − 𝑡)|(𝑡(1 − 𝑡)|𝑓′′(𝑏)|𝑞+ (1 − 𝑡)2|𝑓′′(𝑎)|𝑞)𝑑𝑡 1 1−𝛼 = { 𝜇1|𝑓′′(𝑏)|𝑞+ 𝜇 2|𝑓′′(𝑎)|𝑞, 1 − 2𝜆(1 − 𝛼) ≥ 1 − 𝛼 𝜇3|𝑓′′(𝑏)|𝑞+ 𝜇 4|𝑓′′(𝑎)|𝑞, 1 − 2𝜆(1 − 𝛼) ≤ 1 − 𝛼
ifadelerindeki katsayılar Teorem 4.1.1’ de belirtildiği şekildedir. 𝜏𝑖 ve 𝑧𝑖 (𝑖 = 1,2) ve 𝛾𝑖 ve 𝜇𝑖 (𝑖 = 1,2,3,4) katsayıları düzenlenirse ispat tamamlanmış olur.
Teorem 4.1.3. 𝑓: 𝐼 ⊂ ℝ → ℝ, 𝐼° üzerinde iki kez türevlenebilen fonksiyon, 𝑓, 𝑓′, 𝑓′′ ∈
𝐿[𝑎, 𝑏], 𝑎, 𝑏 ∈ 𝐼 ile 𝑎 < 𝑏 olsun. 𝑝, 𝑞 ≥ 1 , 1
𝑝+ 1
𝑞= 1 ve |𝑓
′′|𝑞 , [𝑎, 𝑏] aralığında
konveks fonksiyon ise 𝛼, 𝜆 ∈ [0,1] için,
𝜑1 = (2𝛼𝜆)𝑝+1+ (1 − 𝛼(1 + 2𝜆))𝑝+1 𝑝 + 1 𝜑2 = (2𝛼𝜆)𝑝+1− (−1)𝑝+1(1 − 𝛼(1 + 2𝜆))𝑝+1 𝑝 + 1 𝜓1 = (2𝜆(1 − 𝛼)) 𝑝+1 + (𝛼 − 2𝜆(1 − 𝛼))𝑝+1 𝑝 + 1 𝜓2 = (2𝜆(1 − 𝛼)) 𝑝+1 − (−1)𝑝+1(𝛼 − 2𝜆(1 − 𝛼))𝑝+1 𝑝 + 1