Kesirli türevlere sahip diferansiyel denklemler ve pantograf denklemlerin diferensiyel dönüşüm yöntemi ile çözümlerinin incelenmesi

FEN BİLİMLERİ ENSTİTÜSÜ

KESİRLİ TÜREVLERE SAHİP DİFERANSİYEL DENKLEMLER VE

PANTOGRAF DENKLEMLERİN

DİFERANSİYEL DÖNÜŞÜM YÖNTEMİ İLE ÇÖZÜMLERİNİN İNCELENMESİ

Mehmet Eyüp KİRİŞ Doktora Tezi Matematik Anabilim Dalı

iii T.C

SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ

KESİRLİ TÜREVLERE SAHİP DİFERANSİYEL DENKLEMLER VE

PANTOGRAF DENKLEMLERİN

DİFERANSİYEL DÖNÜŞÜM YÖNTEMİ İLE ÇÖZÜMLERİNİN İNCELENMESİ

Mehmet Eyüp KİRİŞ DOKTORA TEZİ

MATEMATİK ANABİLİM DALI KONYA, 2007

Bu tez 27/08/2007 tarihinde aşağıdaki jüri tarafından oybirliği / oyçokluğu ile kabul edilmiştir.

Doç. Dr. Galip OTURANÇ (Danışman)

Prof. Dr. Şefik BİLİR Prof. Dr. Durmuş BOZKURT

(Üye) (Üye)

Yrd.Doç.Dr. Fatma AYAZ Yard.Doç.Dr.Ayşe NALLI

iii ÖZET

Doktora Tezi

Kesirli Türevlere Sahip Diferansiyel Denklemler ve Pantograf Denklemlerin Diferansiyel Dönüşüm Yöntemi İle Çözümlerinin İncelenmesi

Mehmet Eyüp KİRİŞ

Selçuk Üniversitesi Fen Bilimleri Enstitüsü Matematik Anabilimdalı

Danışman: Doç. Dr. Galip OTURANÇ II. Danışman: Yrd. Doç. Dr. Aydın KURNAZ

Bu tez çalışmasında; kesirli türevlere sahip diferansiyel denklemler ve kesirli türevlere sahip diferansiyel denklem sistemleri ile fonksiyonel diferansiyel denklemlerin özel bir sınıfı olarak bilinen Pantograf denklemlerin çözümlerinin diferansiyel dönüşüm yöntemi ile çözümleri irdelenmiştir. Öncelikli olarak diferansiyel dönüşüm yönteminin tanımı ve özellikleri verilmiş; daha sonrasında da yöntemin kesirli türevlere sahip diferansiyel denklemler için genelleştirilmiş hali olan kesirli diferansiyel dönüşüm yöntemi tanımlanmıştır. Bu yöntem, pantograf denklemlere uygulanarak konuyla ilgili bazı diferansiyel denklemlerin çözümleri karşılaştırmalı olarak yapılmıştır.

Birinci bölümde; genel bir literatür özeti verilmiştir. Metodun ortaya çıkış tarihi oldukça yakın bir tarih olup son dönemlere kadar pek fazla ilgi görmemiş

iv

olması da dikkate alınırsa konu ile ilgili yayınların çoğunluğu ayrıntılı biçimde incelenmiştir.

İkinci bölümde ise; tezimizin genelinde sıklıkla başvurulacak olan genel tanım ve teoremler yer almaktadır.

Üçüncü bölümde; öncelikle bir boyutlu daha sonrada n boyutlu diferansiyel

dönüşüm yönteminin tanımları yapılarak diferansiyel dönüşüm metodunun özellikleri birçoğu ispatları ile birlikte verilmiştir.

Dördüncü bölümde; kesirli Diferansiyel dönüşüm tanımı verilerek kesirli diferansiyel denklemlere uygulanışına ait örnekler verilmiştir. Bununla birlikte kesirli diferansiyel dönüşüm kesirli diferansiyel denklem sistemlerine uygulanarak çözümlü örnekler verilmiştir.

Beşinci bölümde; pantograf denklemler tanımlanarak diferansiyel dönüşüm yöntemi uygulanmış konu ile ilgili çözümlü örneklere yer verilmiştir.

Altıncı bölümde; tezimizde kullandığımız örneklerin Mapple 10 program kodlarına yer verilmiştir.

En son olarak çalışmamızda elde edilen sonuçlar yorumlanıp öneriler sunularak yararlanılan kaynaklar verilmiştir.

Anahtar Kelimeler: Diferansiyel Dönüşüm metodu, Diferansiyel denklemlerin yaklaşık çözümleri, nümerik metodlar, Pantograf denklemler, Gecikmeli diferansiyel denklemler, Kesirli türevli diferansiyel denklemler.

v ABSTRACT

Ph.D. Thesis

Research of the Fractional Differential Equations and Pantograph Equations Solutions with Differential Transformation Method

Mehmet Eyüp KİRİŞ

Selçuk University

Graduate School of Natural and Applied Sciences Department of Mathematicsı

Supervisor: Assoc. Prof. Dr. Galip OTURANÇ Co- Supervisor: Asist. Prof. Dr. Aydın KURNAZ

In the present thesis; the solutions of the fractional differential equations, systems of the fractional differential equations and pantograph equations which are known a special class of functional differential equations by the generalized differential transform method were presented. Firstly, we give definition and properties of the differential transform method. Then, the generalization of the method for the fractional differential equations which is called the fractional differential transform method was investigated. Finally, the differential transform method has been applied to some examples and results have been compared with those of other methods.

vi

In the first section, a general literature about this method were summarized in detail. Historically this method was uphold at near past and limited number of studies were published in the relevant literature. Therefore it was so easy to obtain the most of the studies those were related to this subject.

Section two begins with some definitions and theorems those were used in this thesis. Thus, it was aimed to establish a relationship between the sections of this thesis.

Section three reviews the definition and some proporties of the differential transform method for different dimensions.

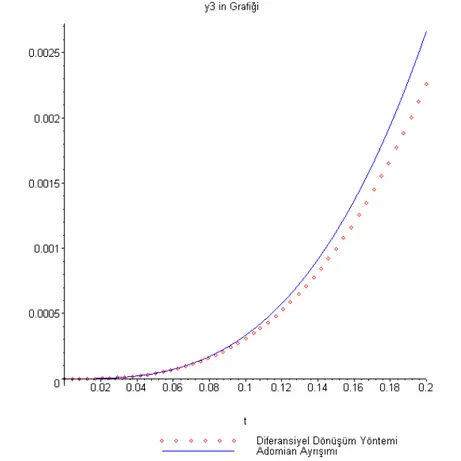
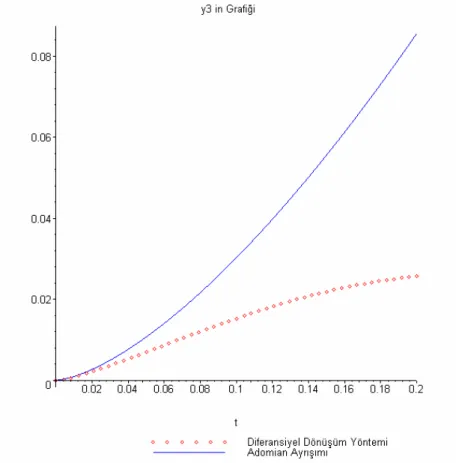
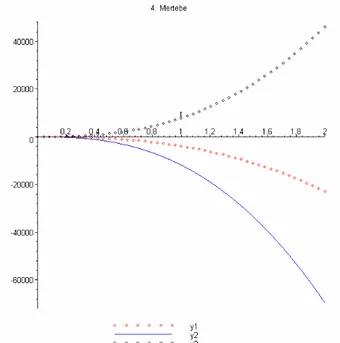
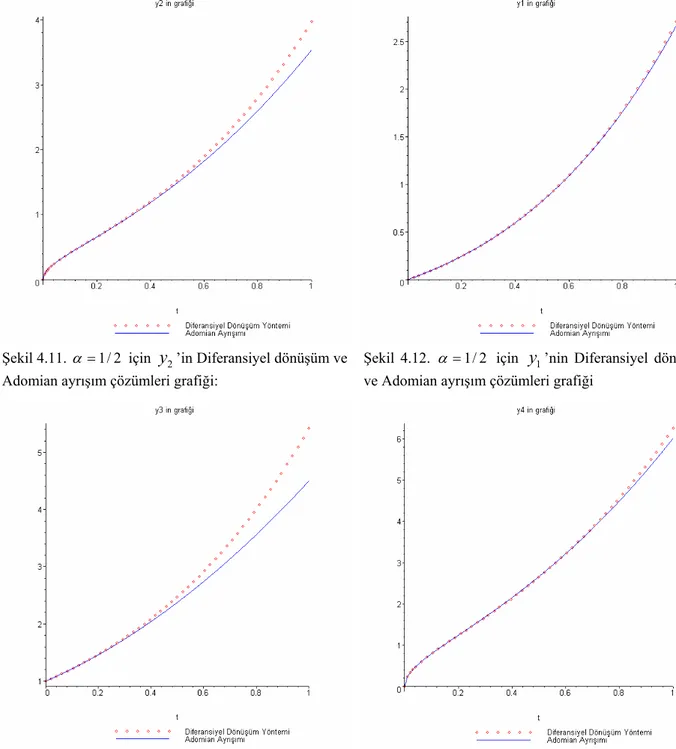
In section four, we define the fractional differential transformation and apply this method to the fractional differential equations, systems of fractional differential equations and multi order fractional differential equations. The numerical results of the problems are compared with those of the known methods and comparisons are shown by graphical representations and tables.

In section five, differential transformation has been applied to pantograph equations and results of the solution has been compared with exact solutions and other methods.

In section six, the algorithmic scheme of the method for the Mapple 10 software which is used to calculate numerical results of given problems has been presented.

In the last section, findings of this investigation and discussions of the results have been summarized. Additionally some recommendations for future studies have been drawn.

Keywords: Diferential Transformation Method, Approximate solutions of the differential equations, Numerical Methods, Pantograph equations, Delayed differential equations, Fractional differential equations.

vii ÖNSÖZ

Bu tez Selçuk Üniversitesi Fen Edebiyat Fakültesi Matematik Bölümü öğretim üyeleri; Sayın Doç. Dr. Galip OTURANÇ ve Yrd. Doç. Dr. Aydın KURNAZ danışmanlıklarında hazırlanarak Selçuk Üniversitesi Fen Bilimleri Enstitüsüne Matematik Ana Bilim Dalında Doktora tez çalışması olarak sunulmuştur.

Yapılan çalışmada; Diferansiyel dönüşüm metodunun bazı genel özellikleri ile birlikte Kesirli diferansiyel denklemlerin çözümünde kullanılması amacıyla Kesirli diferansiyel dönüşüm tanımlanmıştır. Bununla birlikte diferansiyel dönüşüm metodunun, özel bir sınıf gecikmeli diferansiyel denklem olan Pantograf denklemlerin çözümü için uygulanmasına yer verilmiştir.

Doktora çalışması olarak bu tezin hazırlanmasında beni yönlendirerek değerli tecrübe ve bilgi birikimlerini benimle paylaşan öncelikle çok değerli hocam sayın Doç. Dr. Galip OTURANÇ ve ikinci danışmanım olarak Yrd. Doç. Dr. Aydın KURNAZ’a sonsuz teşekkürlerimi ve saygılarımı sunarım. Bununla birlikte yapmış olduğu katkılardan dolayı, değerli arkadaşım Arş. Grv. Yıldıray KESKİN’e, Selçuk Üniversitesi Uygulamalı Matematik araştırma merkezinde görevli kıymetli tüm arkadaşlarıma, göstermiş oldukları sabır ve destek için, eşim Fatma KİRİŞ, çocuklarım Hasan Eren ve Osman Emir’e ve bana olan güvenlerinden dolayı sevgili Anne ve Babama teşekkürlerimi sunarım.

viii İÇİNDEKİLER Özet iii Abstract v Önsöz viii I. BÖLÜM 1 1. GİRİŞ 1 II. BÖLÜM 14 2. BÖLÜM: TANIM VE TEOREMLER. 14 III. BÖLÜM 19 3. BÖLÜM: DİFERANSİYEL DÖNÜŞÜM YÖNTEMİ 19

3.1.1 Bir Boyutlu Diferansiyel Dönüşüm 19 3.1.2 n-Boyutlu Diferansiyel Dönüşüm 22 3.2. Diferansiyel Dönüşüm Yönteminin Özellikleri 24

IV. BÖLÜM 39

4. DİFERANSYEL DÖNÜŞÜM YÖNTEMİ İLE KESİRLİ

DİFERANSİYEL DENKLEM VE KESİRLİ DİFERANSİYEL DENKLEM SİSTEMLERİNİN ÇÖZÜMLERİ

39

4.1.1. Kesirli Difreansiyel Dönüşüm Yöntemi 39

4.2. Kesirli Difreansiyel Denklemlere Yöntemin Uygulanması 45 4.2.1. Dαy+ f₍t₎y=g₍t_), t>_0, m−₁<α ≤m _{başlangıç değer problemi 45}

4.2.2. Dmy₊aDαy₊by₌g₍t₎ t_>0, m_{−1<α ≤}m _{başlangıç değer}

problemi 48

4.3. Yöntemin Kesirli Diferansiyel Denklem Sistemlerine Uygulanması 56 4.4. Lineer Çok Terimli Kesirli Difreansiyel Denklemler ₆₃

ix

V. BÖLÜM 71

5. BÖLÜM: PANTOGRAF DENKLEMLERİN DİFERANSİYEL

DÖNÜŞÜM YÖNTEMİ İLE ÇÖZÜMÜ 71

5.1.1 Diferansiyel Dönüşüm Yönteminin Pantograf Denklemlere

Uygulanışı 73

VI. BÖLÜM 80

6. PROBLEMLERİN ÇÖZÜMLERİNDE KULLANILAN MAPPLE 10

PROGRAM KODLARI 80

SONUÇ VE ÖNERİLER 88

1. GİRİŞ

Yapmış olduğumuz doktora tez çalışmasında, Diferansiyel Dönüşüm (Differential Transform, DT) metodu kullanılarak, özel bir sınıf fonksiyonel diferansiyel denklem olan pantograf denklemlerin, mertebesi kesirli olan türevlere sahip bazı diferansiyel denklemlerin ve kesirli türevlere sahip diferansiyel denklem sistemlerinin nümerik ve analitik çözümlerinin bulunması amaçlanmıştır. Genel olarak, çeşitli mühendislik bilimleri, doğa bilimleri (fizik, kimya v.b), ekonomi problemleri ve matematik ana bilim dalında araştırılan problemlerin matematiksel modellemelerinde karşılaşılan problemlerin çözümlenebilmesi için; diferansiyel denklemler ve problemin doğasına uygun olarak verilen şartlar altındaki çeşitli türlerinin çözülmesi problemi ile karşılaşılmaktadır.

Herhangi bir diferansiyel denklemin çözümünün yapılabilmesi için bir çok farklı yöntem geliştirildiği bilinmektedir. Bununla birlikte problemin çözümünün varlık ve tekliği ile çözümlerinin davranışları için verilen teoremler yardımıyla kolaylıkla bulunabilir. Son yıllarda bu tür problemlerin teorik çözümlerinin bulunmasına ilaveten, bu çözümlerin teknolojide kullanılabilir olması çok daha büyük bir önem kazanmıştır. Bu ise diferansiyel denklem problemlerinin çözümünün; aşikâr formunda bulunması sorununu veya herhangi bir başka yöntem kullanarak nümerik çözümlerinin bulunması problemini ortaya çıkarmıştır. Yukarıda anlatıldığı gibi zincirleme biçimde birbirlerini etkileyen yeni gereksinimler, problemlerin çözülebilmesi için nümerik ve yaklaşık çözüm yöntemlerinin geliştirilmesinin gerekliliği kaçınılmaz biçimde ortaya çıkmıştır.

Son yıllarda çeşitli bilim dallarında araştırılan problemlerin matematiksel modellemelerinde; problemlerin daha doğru kurulabilmeleri için lineer (doğrusal) problemlerden ziyade lineer olmayan problemler olarak kurulması gerekliliği sonucuna varılmıştır. Bu ise; bu şekilde kurulan diferansiyel denklemlerin çözümlerinin analitik biçimde verilmesini daha da zorlaştırmaktadır. Bu sorun

nümerik ve yaklaşık çözüm yöntemlerinin geliştirilmesini daha da önemli kılmaktadır.

Nümerik yöntemler son zamanlarda teorinin pratikte uygulanabilirliği bakımından çok önemli rol oynamaktadır. Hızlı bilgisayarların varlığı, mühendislik dallarında ortaya çıkan karmaşık problemlerin nümerik yöntemlerle daha hızlı ve daha iyi tamlığa sahip olacak şekilde çözülmesine imkan vermektedir. Bugüne kadar birbirlerinden farklı birçok nümerik metot kurulmuştur. Bunlardan biri; Euler (1768) tarafından verilen türevin sonlu fark yaklaşımı ile ifade edildiği metottur. Euler yöntemi olarak adlandırılan bu yöntem, bir boyutlu sistemlerin sonlu fark metodu ile çözümleri için kullanılmıştır. İki boyutlu sistemlerin sonlu fark metodu ile çözümleri için gerekli olan yöntem ise Runge (1908) tarafından verilmiştir. Daha sonraları bu metod farklı araştırmacılar tarafından istenen amaç doğrultusunda farklı yönlerde geliştirilmiştir. Bu çalışmalardan biri Liebmann (1918)’ın adıyla anılmakta olup bir adımlı iterasyon yönteminin kurucusu olarak bilinir. Kısmi türevli diferansiyel denklemlerin modern nümerik çözümler teorisinin kurucuları ise Courant, Friedrichs, Lewy (1928) olarak kabul edilmektedir. Sonlu fark yöntemlerinin algoritmaları bazı iterasyon yöntemleri ile birlikte çok daha iyi sonuçlar vermektedir. Bu tür yöntemler 1950’li yıllardan itibaren bilgisayar teknolojisinin baş döndürücü bir hızla gelişmesi ile birlikte bilgisayar ortamında uygulanabilirliği ile doğru orantılı olarak gelişmiş ve bu gelişimini hâlâ sürdürmektedir. Bu yüzden son dönemlerde daha çok; basit, kolay bir şekilde algoritması oluşturulabilen ve dolayısıyla da programlanabilen, çok daha hızlı sonuçlanan, hem lineer hemde nonlineer problemlerin çözümünde kullanılabilen metotlara ihtiyaç duyulmaktadır. Son dönemlerde bu tür özellikleri taşıyan ve en çok çalışılan yöntemlerden bazıları şu şekilde sıralanabilir: Laplace yöntemi, Fourier yöntemi, Adomian decomposition metot, Wawelet Galerkin yöntemi, Runge-Kutta yöntemi, Newton yöntemi ve Diferansiyel Dönüşüm metodu (Differential Transformation Method: DT).

Hazırlanan bu tez çalışmasında yukarıda adı geçen metotlardan, Diferansiyel Dönüşüm metodu özel bir tip gecikmeli diferansiyel denklem sınıfı olan, p xl( ) ve

( )

x

f ’ler analitik fonksiyonlar, α_l, β_l,λ_l’lar ise reel veya kompleks sabitler olmak üzere

( )

( )

_∑

−

( )

( )

(

) ( )

= + + = 1 0 m l l l l l m _{x p x y x f x} y α β ( )

_{( )}

_{0 = , l=0,1,...,m−1} yl _λl biçiminde ifade edilebilen, lineer fonksiyonel argümanlar içeren genelleştirilmiş pantograf denklemler olarak adlandırılan ve özel olarak elektrikle çalışan bir trenin en öndeki baş kısmının hareketinin modellemesi olarak karşımıza çıkan denklemlerin çözümleri için ve _{f t}( ) _Cn₁

−

∈ olmak üzere bir f(t) reel değerli fonksiyonu için

1 ( ) * * 1 ( ) ( ) , 1 , , 0 ( ) ( ) ( ) ( ) , t n n n a a a t a n n t u f u du n n n t n D f t I D f t d f t n dt α α α α α α α − − −  − − < < ∈ > Γ −  = =   ₌ 

∫

`

biçiminde tanımlanan ve Caputo anlamında kesirli türev olarak bilinen türevlere sahip fonksiyonları içeren diferansiyel denklemlerin çözümleri için uygulanmıştır.

Hızla gelişen bilgisayar dünyasının ve yeni dönem teknolojilerinin daha basit algoritmalarla daha hızlı ve daha az bir hata miktarı ile sonuca ulaşan çözüm yöntemlerine ihtiyaç duyduğu göz önüne alınırsa yukarıda bahsettiğimiz özelliklerdeki yöntemlerin ve daha başka yeni yöntemlerin çalışılması ve ortaya çıkarılması kaçınılmazdır.

İlk olarak Zhou (1986) tarafından ortaya atılan diferansiyel dönüşüm yönteminin en önemli avantajlarından birisi, verilen bir adi veya kısmi diferansiyel denklemi sade ve basit bir dönüşüm yardımıyla cebirsel bir denkleme dönüştürüyor olmasıdır. Laplace ve Fourier gibi diğer yöntemler dikkate alındığında bu yöntemlerde de cebirsel bir denkleme dönüştürme olmakla birlikte bunun için kullanılan dönüşümlerde özellikle denklemin mertebesi ile de alâkalı olarak son derece karmaşık integraller ile karşılaşılabilmektedir. Diferansiyel dönüşüm yönteminde ise cebirsel bir denklem elde etmek için kullanılan dönüşüm de yalnızca türev ifadeleri olduğundan algoritmasında hem daha hızlı sonuç vermekte hem de çok daha basit hesaplamalar gerektirmektedir. Bununla birlikte geriye sadece cebirsel denklem çözümü yapmak kalmaktadır. Yöntemin en büyük avantajlarından bir diğeri ise, lineer veya nonlineer problemlere rahatlıkla uygulanabilmesinde yatmaktadır.

Zhou (1986) çalışmasında ilk olarak bu yöntemi, elektrik devre analizlerinde otaya çıkan lineer ve nonlineer başlangıç değer problemlerini çözmek için ortaya koymuştur.

Chen, C.K., Ho, S.H.; “Application of differential transformation to eigenvalue problems. Applied Mathematics and Computation; 79, 1996, 179-188”. İsimli çalışmalarında, diferansiyel dönüşüm metodunu, özdeğer problemlerine uygulamışlardır. Özdeğerlerin ve özfonksiyonların bulunmasında kullanılan en çok bilinen yöntemler olan Ritz ve Galerkin yöntemlerinde, i≥2 için i . özdeğerin bulunması oldukça güç olup Chen ve Ho yaptıkları çalışmada diferansiyel dönüşüm metodu ile özdeğerleri ve özfonksiyonları elde etmişlerdir.

Jang, M.J., Chen, C.L.; “Analysis of the response of a strongly nonlinear damped system using a differential transform method. Applied Mathematics and Computation; 88, 1997, 137-151”. İsimli çalışmalarında, güçlü lineer olmayan sönümlü bir sistemin tepkisinin analizinde diferansiyel dönüşüm yöntemi kullanılmış olup elde edilen sonuçlarla, sistemin Runge-Kutta yöntemi ile çözülmesiyle elde edilen sonuçlar karşılaştırılarak diferansiyel dönüşüm yöntemi ile elde edilen sonuçların daha hassas olduğunu ifade etmişlerdir.

Yu, L.T, Chen, C-K.; “The solution of the blasius equation by the differential transform method. Math. Comput. Modelling, 28, 1998, 101-111”. İsimli çalışmalarında, Blasius diferansiyel denklemi olarak bilinen ve üçüncü mertebeden nonlinear bir adi türevli diferansiyel denklem olan denklemin diferansiyel dönüşüm yöntemi ile çözümünü yapmışlardır.

Chen, C.L., Liu, Y.C.; “Differential transformation technique for steady nonlinear heat conduction problems. Applied Mathematics and Computation; 95, 1998, 155-164”. İsimli çalışmalarında, diferansiyel dönüşüm yardımıyla lineer olmayan ısı kondüksiyon problemlerinin çözümü ile birlikte analitik çözümün spektrumunun elde edilebilmesi için bir prosedür geliştirilmiş olup çözüm Taylor serileri yardımıyla ifade etmişlerdir.

Chen, C.K., Ho, S.H.; “Transverse vibration of a rotating twisted timoshenko beams under axial loading using differential transform. Intenational Journal of Mechanical Science; 41-11, 1999, 1339-1356”. İsimli çalışmalarında, dönerek

bükülmüş Timoshenko kirişinin serbest vibrasyon problemini çözmek için diferansiyel dönüşüm yöntemi kullanılmış, çözümler ise analitik formda ifade edilmiştir.

Chen, C.K., Ho, S.H.; “Solving partial differential equations by two dimensional differential transform method. Applied Mathematics and Computation; 106, 1999, 171-179”. İsimli çalışmalarına kadar yalnızca adi türevli diferansiyel denklemler için uygulanabilen diferansiyel dönüşüm metodu, bu çalışmayla birlikte ilk olarak kısmi türevli diferansiyel denklemlere genişleterek iki boyutlu diferansiyel dönüşümü tanımlamışlardır.

Jang, M.J., Chen, C.L., Liu, Y.C.; “On the solving initial value problems using the differtential transform method. Applied Mathematics and Computation; 115, 2000, 145-160”. İsimli çalışmalarında, ilk olarak lineer ve nonlineer başlangıç değer problemleri gridler yardımıyla diferansiyel dönüşüm yöntemi kullanılarak çözülmüştür. Nümerik yöntemlerde sıklıkla gridlerden faydalanılmasına rağmen, ilk olarak böyle bir çalışmada dikkate alınmış olmakla birlikte hem daha iyi sonuçlar elde edilmiş hem de çözümün global hatası kontrol altına alınmıştır.

Abdel- Halim Hassan, I.H.; “On solving eigenvalue problems by using a differential transformation. Applied Mathematics and Computation; 127, 2002, 1-22”. İsimli çalışmasında, diferansiyel dönüşüm yöntemi yardımıyla, sturm-liouville özdeğer problemi için özdeğer ve normalleştirilmiş özdeğer fonksiyonu elde edilmiştir. Bununla birlikte özdeğerlerin yakınsaklığı incelenmiş ve bilinen analitik sonuçlar ile elde edilen sonuçlar karşılaştırılmıştır.

Abdel- Halim Hassan, I.H.; “Different Applications for the differential transformation in differential equations, Applied Mathematics and Computation; 129, 183-221, 2002”. İsimli çalışmasında ise yazar, bir boyutlu diferansiyel dönüşüm yöntemini ikinci ve dördüncü mertebe diferansiyel denklemlerin özdeğer ve normalleştirilmiş öz fonksiyonlarının bulunmasında kullanmıştır. Bununla birlikte iki boyutlu diferansiyel dönüşüm yardımıyla sabit katsayılı birinci ve ikinci mertebe kısmi türevli diferansiyel denklemlerin çözümleri elde edilmiş elde edilen sonuçlar, aynı problemlerin fark denklemleri yardımıyla elde edilen sonuçları ve analitik sonuçlar karşılaştırılmıştır.

Jang, M.J., Wang, J-S., Liu, Y.C.; “Applying differtential transform method to parameter identification problems. Applied Mathematics and Computation; 139, 2-3, 2003, 491-502”. İsimli çalışmda, parametre tanımlama probleminde maksimum ihtimal değerlerinin bulunması için diferansiyel dönüşüm yönteminden faydalanılmıştır. Bu parametrelerin tanıtım kriterleri fonksiyonu Diferansiyel dönüşüm yardımıyla kurulmuştur. Böylece; sistem modelinin spektrumunun bilinmeyen parametre ve önceden belirlenmiş değişkenin başlangıç değeri yardımıyla bulunuyor olması, singülerlik ve duyarlılık probleminin ters probleme gerek olmadan çözülebilmesi, çözülen problemin iterasyonla yapılıyor olması ve kolaylıkla nümerik hesaplamalara dönüşmesi ve hem lineer, hem de nonlineer problemler için farklı yöntemlere gerek kalmadan aynı yöntemle çözülmesi problemin çözümünde diferansiyel dönüşüm yönteminin tercih edilmesindeki en önemli etkenler olarak dikkati çekmektedir.

Ayaz, F.; “On the two dimensional differential transform method. Applied Mathematics and Computation; 143, 2003, 361-374”. Bu çalışmada, iki boyutlu diferansiyel dönüşüm için bazı teoremler verilmiş ve bununla birlikte lineer ve lineer olmayan kısmi türevli başlangıç değer problemleri çözülmüştür.

Ayaz, F.; “Applications of differential transform methods to differential algebric equations. Appl. Maths Comput.; 152, 2004, 649-657”. İsimli çalışmada lineer cebirsel-diferansiyel denklemlerin çözümü diferansiyel dönüşüm metodu ile incelenerek konuyla ilgili örneklerden elde edilen sonuçlar analitik çözümlerle karşılaştırılmıştır.

Chen, C.K., Ju, S-P.; “Application of differential transformation to trasient advective-dispersive transport equation. Applied Mathematics and Computation; 155, 2004, 25-38”. İsimli çalışmalarında, süreksiz adjective dispersive taşınım denkleminin çözümü diferansiyel dönüşüm metodu ile bulmuşlardır. Ayrıca bu çalışmanın bir özelliği de hem sonlu fark metodu hem de diferansiyel dönüşüm metodunun birlikte kullanılmış olmasıdır ki bu durum sonuçların daha hassas elde edilmesi ile önemini ortaya koymuştur.

Arikoğlu, A., Özkol I.; “Solution of boundry value problems for integro-differential equations by using integro-differential transform method. Applied Mathematics

and Computation; 168, 2, 2005, 1145-1158”. İsimli çalışmada, integral denklemler için diferansiyel dönüşüm teorisi verilerek nadiren analitik çözümleri bulunabilen bu denklemler için analitik çözümleri bilinen bir takım lineer ve lineer olmayan integro diferansiyel denklemlerin çözümleri araştırılmış, aynı zamanda literatürde değişik çalışmalarda wavelet-galerkin ve Adomian Decomposition yöntemleri ile çözülen bu örnekler için karşılaştırma yapma olanağı sağlanmıştır.

Chen, C.K., Chen, S-S.; “Application of the differential transformation method to a non linear conservative system. Applied Mathematics and Computation; 154, 2004, 431-441”. İsimli çalışmada, lineer olmayan serbest conservative sistemin çözümü diferansiyel dönüşüm yöntemi ile incelenmiş, elde edilen sonuçlar Runge-Kutta Yönteminden elde edilenlerle karşılaştırılmış ve daha iyi sonuçlar verdiği gözlemlenmiştir.

Kurnaz A., Oturanç, G.; “The differential transform approximation fort he system of ordinary differential equuation. International Journal of Computer Mathematics; 82, 6, 2005, 709 – 719”. İsimli çalışmada; diferansiyel dönüşüm metodu çözümün arandığı aralıktaki çözüm fonksiyonu gridlere bölünerek sistemlere uygulanmış böylece çözüm fonksiyonu her bir alt aralık için bulunarak çözüme yaklaşılmıştır. Bununla birlikte hata kontrolü yapılarak hata için sisteme girilen üst sınıra bağlı olarak, alınması gereken minimum grid sayısı tesbit edilmiştir.

Bildik, N., Konuralp, A., Bek, F.O., Küçükarslan, S.; “Solution of different type of partial differential equation by differential transform method and adomian’s decomposition method. Applied Mathematics and Computation; 172, 2006, 551-567”. İsimli çalışmada, farklı türlerdeki kısmi türevli diferansiyel denklemlerin çözümü hem diferansiyel dönüşüm metodu ile hem de Adomian decomposition yöntemi ile yapılmış olup elde edilen sonuçlar karşılaştırılmıştır.

Kurnaz A., Oturanç G., Kiriş M.E.;“n dimensional differential transformation method for solving PDE’s. International Journal of Computer Mathematics; 82, 2005, 369-380. İsimli çalışmada, kısmi türevli diferansiyel denklemlerin çözümü için genelleştirme yapılmış ve n boyutlu DT metodu tanımlanmıştır. Sonuçlar bazı lineer ve lineer olmayan kısmi türevli diferansiyel denklemler çözülerek test edilmiştir.

Özkan O., Keskin Y.; “An application of the differential transform Method to the boundary value problems of the system of integro differential equations. Selçuk Journal of Applied Mathematics, 6, 2005, 43-53”. İsimli çalışmada, integro-diferansiyel denklem sistemlerinin çözümleri belirli sınır şartları için incelenmiştir.

Ertürk V. S., Momani S., Odibat Z.; “Application of generalized differential transform method to multi-order fractional differential equations. Communications in Nonlinear Science and Numerical Simulation, Baskıda, Corrected Proof, Available online 24 February 2007”. İsimli çalışma, caputo anlamında türevlere sahip çoklu mertebeli lineer ve lineer olmayan kesirli diferansiyel denklemlerin sayısal çözümleri için Diferansiyel dönüşüm yönteminin uygulanmasını ve konuyla ilgili çözülmüş örnekleri içermektedir.

Jafari H., Daftardar-Gejji V.; “Solving a system of nonlinear fractional differential equations using Adomian decomposition. Journal of Computational and Applied Mathematics, 196, 2, 2006, 644-651”. İsimli çalışma, lineer olmayan kesirli diferansiyel denklemlerin sayısal çözümleri için Adomian decomposition yöntemi kullanılmıştır.

Jafari H., Daftardar-Gejji V.; “Analysis of a system of nonautonomous fractional differential equations involving Caputo derivatives. Journal of Mathematical Analysis and Applications, 328, 2, 2007, 1026-1033”. Bu çalışmada ise caputo anlamındaki türevlere sahip lineer olmayan kesirli diferansiyel denklem sistemlerinin çözümlerinin varlık, teklik ve kararlılıkları incelenmiştir.

Momani S., Odibat Z.; “Numerical comparison of methods for solving linear differential equations of fractional order. Chaos, Solitons & Fractals, 31, 5, 2007, 1248-1255”. Bu çalışmada lineer kesirli diferansiyel denklemlerin çözümleri için kesirli fark yöntemi, Adomian decomposition yöntemi ve varyasyonel iterasyon teknikleri kullanılarak farklı tip problemler için çözümler elde edilerek elde edilen sonuçlar ile analitik sonuçlar karşılaştırılmıştır.

Kumar P., Agrawal O. P.; “An approximate method for numerical solution of fractional differential equations. Signal Processing, 86, 10, 2006, 2602-2610”. Bu çalışmada kesirli diferansiyel denklemlerin bir sınıfı için nümerik çözüm şeması ortaya konmuştur. Yine bu çalışmada caputo anlamındaki türevler dikkate alınmıştır.

Burada Caputo türevinin, kesirli diferansiyel denklemlerin Volterra integral denklemi içine dönüştürülebilmesi özelliğinden faydalanılarak Volterra integral denklemi için geliştirilen birçok nümerik şemanın kesirli diferansiyel denklemlerin çözümünün bulunmasında da kullanılabileceği gösterilmiş ve bununla ilgili örnekler verilmiştir.

Momani S., Shawagfeh N.; “Decomposition Method for solving fractional Riccati differential equations. Applied Mathematics and Computation, 182, 2007, 1083-1092”. Bu çalışmada kesirli Riccati diferansiyel denkleminin çözümü için Adomian decmposition metodu kullanılmıştır.

Momani S., Noor M. A.; “Numerical methods for fourth-order fractional integro- differential equations. Applied Mathematics and Computation, 182, 2006, 754-760”. Bu çalışmada ise caputo anlamındaki türev yardımıyla 4. mertebeden lineer ve lineer olmayan kesirli integro-diferansiyel denklemlerin sınır değer problemlerinin çözümleri için Adomian decomposition metodu uygulamıştır.

Jafari H., Daftardar-Gejji V.; “Revised Adomian decomposition method for solving systems of ordinary and fractional differential equations. Applied Mathematics and Computation, 181, 1, 2006, 598-608”. Bu çalışmada ise caputo anlamındaki türevlere sahip lineer olmayan kesirli diferansiyel denklem sistemlerinin çözümlerinin varlık, teklik ve kararlılıkları incelenmiştir.

Momani S., Odibat Z.; “Numerical methods for nonlinear partial differential equations of fractional order. Applied Mathematics and Computation, Baskıda, Corrected Proof, Available online 20 December 2006”. Bu çalışmada lineer olmayan kesirli kısmi türevli diferansiyel denklemlerin çözümleri için Adomian decomposition yöntemi ve varyasyonel iterasyon teknikleri kullanılarak farklı tip problemler için çözümler elde edilmiş, elde edilen sonuçlar ile analitik sonuçlar karşılaştırılmıştır.

Jafari H., Daftardar-Gejji V.; “Solving a multi-order fractional differential equation using adomian decomposition. Applied Mathematics and Computation, Baskıda, Corrected Proof, Available online 12 January 2007”. Bu çalışmada caputo anlamında türevlere sahip çoklu mertebeli bir kesirli diferansiyel denklemin α mertebeli bir kesirli diferansiyel denklemler sistemine dönüştürülmesi için adomian decomposition algoritması ve bu algoritmanın uygulanışını gösteren örnekler verilmiştir.

Oturanç G., Kurnaz A., Keskin Y.; “A new Analytical Approximate Method for the Solution of Fractional Differential Equation. International Journal of Computer Mathematics; Baskıda, 2007”. Bu çalışmada kesirli türevli diferansiyel denklemlerin çözümlerine yönelik yeni bir yaklaşık analitik metod sunulmuştur. Bu yöntemle ilgili tanım ve teoremler verilip lineer veya lineer olmayan denklemler için çözümler incelenmiştir.

Odibat Z., Shawagfeh N. T.; “Generalized Taylor’s Formula. Applied Mathematics and Computation, 186, 1, 2007, 286-293”. Bu çalışmada mertebesi

0< ≤α 1 biçiminde olan, caputo anlamında türevler içeren, klasik Taylor frmülünden elde edilen yeni bir genelleştirilmiş Taylor formülü kurulmuştur..

Ertürk V. S., Momani S., Odibat Z. “Generalized differential transform method: Application to differential equations of fractianal order. Appl. Math. Comput., Baskıda, Accepted Manuscript, Available online 2 August 2007”. Bu çalışma caputo anlamında türevlere sahip kesirli diferansiyel denklemlerin sayısal çözümleri için Diferansiyel dönüşüm yönteminin bir genelleştirilmesi sunulmuş ve bununla ilgili çeşitli örnekler çözülmüştür. Sonuç olarak literatürde var olan sonuçlarla oldukça uyumlu, güzel sonuçların elde edildiğini gösterilmiştir.

Daftardar-Gejji V., Babakhani A.; “Analysis of a system of fractional differential equations. Journal of Mathematical Analysis and Applications, 293, 2, 2004, 511-522”. Bu çalışmada kesirli diferansiyel denklem sistemleri için bir analiz sunulmuştur. Bu analizde kesirli diferansiyel denklemlerin başlangıç değer problemleri için varlık ve teklik teoremleri ile kararlılık kriterleri verilmiştir.

Jafari H., Daftardar-Gejji V.; “Adomian decomposition: a tool for solving a system of fractional differential equations. Journal of Mathematical Analysis and Applications, 301, 2, 2005, 508-518”. Bu çalışma kesirli diferansiyel denklemlerin tam çözümleri ele alınarak lineer kesirli diferansiyel denklemler için Adomian decomposition yöntemi geliştirilmiştir.

Brunner H.; “On the discretization of differential and Volterra integral equations with variable delay. BIT Numerical Mathematics, 37, 1, 1997, 1-12”. Bu çalışmada, m-basamak mertebeli implicit (kollokasyon-tabanlı) Runge-Kutta metodları, ikinci tip değişken gecikmeli diferansiyel denklemler ve Volterra integral denklemleri için uygulanmıştır. Bununla birlikte gecikmesiz veya sabit gecikmeli

diferansiyel denklemler için Gauss –Legendre noktalarındaki kollokasyonun bir kazanç sağlamayacağı görülmüştür.

Ishiwata E.; “On the attainable order of collocation methods for the neutral Functional differential equations with propotional delays. Computing, 64, 2000, 207-222”. Bu çalışmada, H. Brunner 1997’de oransal gecikmeli diferansiyel denklemler ve oransal gecikmeli Volterra integral denklemleri için elde edilen sonuçlar, Nötral fonksiyonel diferansiyel denklemlere ve gecikmeli Volterra integro diferansiyel denklemleri genişletilmiştir. Bunun için, t=h ilk ağ noktasında Nötral fonksiyonel diferansiyel denklemlerin bir v t

( )

kollokasyon (eşyerleşim) çözümünün bulunabilmesi için m. mertebeden kapalı Runge-Kutta yöntemleri kullanılmış ve kollokasyon polinomlarının varlığı araştırılmıştır.

Bellen A.; “One-Step Collocation for delay differential equations. Journal of Computational and Applied Mathematics, 10, 275-283, 1984”. Bu çalışmada, sınırlı gecikmeli diferansiyel denklemler için kollokasyon noktaları, Gauss-Legendre noktaları tarafından belirlenmiş, _p* _{=2m olacak şekilde m. Basamak mertebeli}

Runge-Kutta yöntemi ile sonuçlar elde edilmiştir.

Liu M. Z., Dongsong L.; “Properties of analytic solution and numerical solution of multi-pantograph equation. Applied Mathematics and Computation, 155, 3, 2004, 853-871”. Bu çalışmada, Multi Pantograf denklemlerin analitik çözümünün varlığı ve tekliği ile Drichlet seri çözümleri ortaya konulmuş, analitik çözümün asimptotik kararlılığı için yeter şart elde edilmiştir.

Muroya Y., Ishiwata E., Brunner H.; “On the attainable order of collocation methods for pantograph integro-differential equations. Journal of Computational and Applied Mathematics, 152, 1-2, 2003, 347-366”. Bu çalışmada, oransal gecikmeli homojen olmayan terimler içeren pantograf integro-diferansiyel denklemler için t=h ilk ağ noktasında m. mertebeden kapalı Runge-Kutta yöntemleri dikkate alınmış, kollokasyon polinomları için şartlar verilmiştir.

Keskin Y., Kurnaz A., Kiriş, M.E., Oturanç, G.; “Approximate solution of Generalized Pantograph Equations by the differential transform method. International Journal of Nonlinear Sciences and Numerical Simulation; 8, 2, 2007, 159-164”. Bu çalışmada, genelleştirilmiş pantograf denklemlerin çözümü için

diferansiyel dönüşüm yöntemi uygulanmış, konuyla ilgili örnekler ortaya konulmuştur.

Li D., Liu M. Z.; “Runge–Kutta methods for the multi-pantograph delay equation. Applied Mathematics and Computation, 163, 1, 2005, 383-395”. Bu çalışmada, multi pantograf diferansiyel denklemler için değişken adım aralıklı Runge- Kutta metodlarının asimptotik kararlılığını garantileyen şartlar verilmiştir.

Sezer M., Akyüz-Daşcıoğlu A.; “A Taylor method for numerical solution of generalized pantograph equations with linear functional argument. Journal of Computational and Applied Mathematics, 200, 1, 2007, 217-225”. Bu çalışmada, lineer fonksiyonel argümanlar içeren ve pantograf denklem olarak bilinen fonksiyonel diferansiyel denklem için bir genelleştirme yapılmış ve bu tür denklemlerin çözümleri için Taylor polinomları üzerine kurulmuş yaklaşık bir yöntem sunulmuştur.

Marshall J.C., Van-Brunt B., Wake G.C.; “A natural boundary for solutions to the second order pantograph equation. Journal of Mathematical Analysis and Applications, 299, 2004, 314-321”. Bu çalışmada, genellikle doğal sınırlara sahip pantograf denklemlerin çözümleri gösterilmiş, bu çözümlerin özel bir kümesi üzerinde çalışılmıştır.

Toshiyuki K.; “Stability of Runge-Kutta methods for the generalized pantograph equation. Numerische Mathematik, 84, 2, 1999, 233-247”. Bu çalışmada, genelleştirilmiş pantograf denklemi adı verilen değişken gecikmeli bir otonom gecikmeli diferansiyel denkleminden değişkenlerin değiştirilmesi yöntemi ile elde edilen sabit gecikmeli otonom olmayan bir gecikmeli diferansiyel denkleme uygulanan Runge-Kutta metodlarının kararlılık özelliği incelenmiştir.

Evans D. J., Raslan K. R.; “The Adomian decomposition method for solving delay differential equation. International Journal of Computer Mathematics, 82, 1, 2005, 49 – 54”. Bu çalışmada, gecikmeli diferansiyel denklemlerin yaklaşık çözümleri için Adomian decomposition yöntemi kullanılmıştır ve elde edilen algoritma başlangıç değer problemlerine uygulanmıştır.

Derfel G., Iserles A. “The pantograph equation in the complex plane. J. Math. Anal. Appl., 213, 1997, 117-132”. Bu çalışmada, ilerletilmiş veya genelleştirilmiş pantograph denklem tanımı yapılarak, kompleks düzlem üzerinde tanımlanan pantograph denklemlerin çözümlerinin varlık ve tekliği ile birlikte çözümlerinin asimptotik davranışları incelenmiştir.

II. BÖLÜM

2. TANIM VE TEOREMLER

Mühendislik, Fizik ve Ekonomi gibi uygulamalı bilim dallarında eldeki problemin özelliklerini açıklayan matematiksel modellerin kurulabilmesi oldukça önemlidir. Bir matematiksel modelin ortaya konulmasında bir veya daha çok değişkene bağlı fonksiyonlar ve bunların değişik mertebelerde türevlerini ihtiva eden denklem veya denklem sistemleri ile karşılaşılmaması neredeyse imkansızdır. Elde edilen fonksiyon, bir bağımsız değişken içeriyorsa bu fonksiyonun türevlerini de içeren denkleme adi türevli diferansiyel denklem, bu tip denklemlerin oluşturduğu sisteme de adi türevli diferansiyel denklem sistemi adı verilir. Eğer fonksiyon, birden çok bağımsız değişken içeriyorsa denkleme kısmi türevli diferansiyel denklem adı verilir ve kısmi türevli diferansiyel denklemlerden oluşan bir sisteme de kısmi türevli diferansiyel denklem sistemi denir. Bir denklemin mertebesi adi türevli bir diferansiyel denklem için, içerdiği en yüksek mertebeli türevin mertebesi, kısmi türevli diferansiyel denklemler için ise, denklemde görülen en yüksek mertebeden kısmi türevin mertebesi olarak tanımlanır.

Bu bölüm tezimizin içerisinde sıklıkla geçen bazı tanım ve teoremlere ayrılmıştır. Burada yer verilen teoremlerin ispatları, literatürde ayrıntılı bir şekilde verildiği için ayrıca ispatları yapılmayacaktır.

Tanım 2.1. a_0,a₁,",a_m ve Q , x’in verilmiş fonksiyonları ve a₀

( )

x ≠0 olmak üzere,

( )

_{x y}( ) _a

( )

_{x y}( ) _a

( )

_{x y a}

( )

_{x y Q}

( )

_x a m ₊ m _{+ + m ′+ m =} − − 1 1 1 0 "

denklemine m. mertebeden lineer diferansiyel denklem denir.

Tanım 2.2. _{\ ,} n _{n-boyutlu reel Euclid uzayı, F fonksiyonu;}

1

: nm nm n

F \ ×\ − × ×" \ × × →\ U \ ve u U: → \ bilinmeyen fonksiyon olmak üzere,

( )

( )

( ) ( )

(

D u x D u x Du x u x x

)

(

x U

)

F m _, m−1 _{,", , , =0 ∈ (2.1)}

biçiminde ifade edilen bir denkleme, m. mertebeden kısmi türevli diferansiyel denklem denir. Bu denklemin çözümü, ∂U, U’nun sınırı olmak üzere belirli sınır şartları sağlayan fonksiyonlar arasından (2.1) denklemini sağlayan tüm u’ların bulunması olarak tanımlanabilir [Evans, 1998]. Bundan sonraki tanım ve teoremlerde

1 ≥

m biçiminde belirli bir tam sayı ve _{U ⊂ \ olacak biçimdeki bir açık alt küme} n olarak dikkate alınacaktır.

Tanım 2.3. k ≤m olmak üzere, verilen ak ve f fonksiyonu için (2.1)

denklemi;

( )

x D u f

( )

x a m k k k =

∑

≤ (2.2) formunda yazılabilir ise, denkleme Lineer Diferansiyel Denklem denir. Bununla birlikte eğer, f ≡0 ise bu taktirde denkleme Homojendir denir [Evans, 1998].

Tanım 2.4. Eğer, (2.1) denklemi;

( )

(

1 , , , ,

)

0 0 = + − =

∑

a x D u a Dm u Du u x m k k k " (2.3) formunda yazılabilir ise, kısmi türevli diferansiyel denkleme Semi-Lineer Diferansiyel Denklem denir [Evans, 1998].

Tanım 2.5. Eğer, (2.1) denklemi;

( )

(

, , , ,

)

(

1 , , , ,

)

0 0 1 ₊ − ₌ = −

∑

a x D u Du u x D u a Dm u Du u x m k k m k " " (2.4)

formunda yazılabilir ise, kısmi türevli diferansiyel denkleme Quasilineer Denklem denir [Evans, 1998]. Tanım 2.6.F fonksiyonu; 1 : nm nm n F A × A − × × A × A× →U A \ \ " \ \ \ ve _{u:U →ℜ}A_,u=

(

_u1_,u2_{," u,} A

)

_{bilinmeyen fonksiyon olmak üzere,}

( )

( )

( ) ( )

(

D u x D u x Du x u x x

)

(

x U

)

F m _, m−1 _{,", , , =0 ∈ (2.5)}

biçiminde ifade edilen bir denklem sistemine, m. mertebeden kısmi türevli diferansiyel denklem sistemi denir [Evans, 1998].

Tanım 2.7. i=1 ",2, ,n için α_i’ler negatif olmayan tamsayılar olmak üzere

(

α αn

)

α = ₁,", biçiminde ifade edilen vektöre Multiindex adı verilir. Verilen bir α multiindex’i için,

( )

( )

n n x x x x u x u D _{α α α} α α ∂ ∂ ∂ ∂ = " 2 1 2 1 olarak tanımlanır. Bununla birlikte, k ≥0 ve k∈ ] için, k. Mertebeden bütün kısmi türevli diferansiyel denklemlerin ailesi, α =α₁+α₂ +"+α_n olmak üzere,

( )

x

{

D u

( )

x k

}

u

Dk ₌ α _{: α = (2.6)}

biçiminde gösterilir [Evans, 1998].

Tanım 2.8. x−x₀ <r olmak üzere,

( )

=

_∑

(

−

)

k k k x x f x f ₀ (2.7) olacak şekilde bir r>0 ve

{ }

f_k sabitleri var ise :_{f \}n _{→\ biçiminde tanımlanan} f fonksiyonuna x₀ civarında analitik fonksiyon denir [Evans, 1998]. Buradaki toplamın k’nın tüm multiindexleri üzerinden alındığına ve k=

(

k₁,k₂,",k_n

)

multiindexi için

(

kn

)

n k k k _{x x x} x 1, 2, , 2 1 "

= olarak tanımlandığına dikkat edilmelidir. Eğer f fonksiyonu x₀ noktası civarında analitik ise, bu fonksiyona _C ∞

sınıfındandır veya C∞ diferansiyellenebilirdir denir. Bununla birlikte f_k sabitleri, ! ! ! ! k₁ k₂ k_n k = " olmak üzere,

( )

! 0 k x f D f k k = biçiminde hesaplanabilir. Bu durumda (2.7) eşitliği düzenlenirse,

( )

=

_∑

( )(

−

)

k k k _{f x x x} D k x f _{0 0} ! 1 (2.8) yazılabileceğinden f fonksiyonu kendisinin x₀ noktasındaki Taylor seri açılımına eşittir [Evans, 1998].

Uyarı 2.1. _{U ⊂ \ açık bölgesi üzerinde tanımlı (2.4)} n _{m. mertebeden} quasilineer kısmi türevli diferansiyel denklemini dikkate alalım. Kabul edelim ki Γ ;

noktasındaki birim normal v

( )

x0 ₌v₌

(

v₁,v₂,_",v_n

)

_{olsun. u’nun x}0_∈Γ

noktasındaki .j normal türevi,

n n n k n j k k k k n k j j k k k j j v v x x u uv D v u " " "

∑

∑

= + + = ∂ ∂ = = ∂ ∂ 1 1 1 1 1 biçiminde tanımlanır. Buna göre, verilen m tane g g₀, , ,₁" g_m−1:Γ →\ fonksiyonları için; Γ ’ da,

1 0, 1, , 1 1 m m m u u u g g g v v − − − ∂ ∂ = = = ∂ " ∂ (2.9) sınır şartlarına bağlı olarak, (2.4) m. mertebeden quasilineer kısmi türevli diferansiyel denklemini çözen bir u fonksiyonunu bulma problemine Cauchy Problemi denir [Evans, 1998].

(2.4), (2.9) denklemleri ile verilen sınır şart probleminde; Γ , Γ ⊂

{

x_n =0

}

biçiminde verilen hiperdüzlemin bir alt kümesi olmak üzere, (2.4), (2.9) problemi yeniden düzenlenirse

( )

(

1

)

(

1

)

0 1 1 1 , , , , , , , , 0 , , , 0 , ve 0 için m k m k k m k n k n n a x D u Du u x D u a D u Du u x x r u u u g x r x x x − − = − −  + = <   _{∂ ∂}  = = = ′ < = ∂ ∂ 

∑

" " " (2.10)

biçiminde verilebilir. Buradaki pozitif r daha sonra bulunacak olup, a_k( k =m)

ve a analitik fonksiyonlar ve ₀ x=

(

x x₁, , ,₂ " x_n−1

)

olarak alınmıştır. Bu durumda (2.10) probleminin varlığı ile ilgili teorem aşağıdaki gibi verilebilir.

Teorem 2.1. (2.10) problemi için öyle bir r>0 ve analitik reel bir fonksiyon vardır ki, bu sınır değer probleminin çözümü

k k k

u=

∑

u x (2.11) biçimindedir [Evans, 1998]. Bu teorem literatürde Cauchy-Kovalevskaya teoremi olarak bilinmektedir.

Tanım 2.9. 0 n n a ∞ =

∑

ve 0 n n b ∞ =

∑

serileri verilmiş olsun.

0 n n k n k k c a b₋ = =

∑

olmak üzere, 0 n n c ∞ =

∑

yakınsak serisine 0 n n a ∞ =

∑

ve 0 n n b ∞ =

∑

serilerinin Cauchy çarpımı denir [Gleason, 1966].

n n n

a =c z ve n n n

b =d z biçiminde dikkate alındığında Cauchy çarpımı,

0 0 0 0 k n n k n n k i i n n k i c z d z c d z ∞ ∞ ∞ − = = = =   _⋅ ₌         

∑

 

∑



∑ ∑

  (2.12) biçiminde yazılabilir. Bu şekilde kuvvet serileri için Cauchy çarpımı ifade edilmiş olur. Teorem 2.2.

( )

1 n n u x ∞ =

∑

serisi bir S kümesi üzerinde tanımlı u x

( )

fonksiyonuna düzgün yakınsıyor ve her u x_n

( )

, ,

[ ]

a b ⊆S de integrallenebiliyorsa

( )

u x ’te

[ ]

a b, ⊆S de integrallenebilirdir ve

( )

( )

( )

1 1 b b b n n n n a a a u x dx ∞ u x dx ∞ u x dx = = =

∑

=

∑

∫

∫

∫

(2.13) yazılabilir [Brabanec, 1990].

III. BÖLÜM

3. DİFERANSİYEL DÖNÜŞÜM YÖNTEMİ

Bu bölümde, Diferansiyel Dönüşüm (DT) yönteminin tanımı ve genel özellikleri ifade edilecektir. Daha önce de belirtildiği gibi yöntem diferansiyel denklemlerin cebirsel denklemlere dönüştürülerek çözülmesini içermektedir. Yine, önceki bölümlerde ifade edildiği gibi, diferansiyel denklemleri cebirsel denklemlere dönüştürerek çözen diferansiyel dönüşüm yönteminden başka yöntemler de mevcut olmakla birlikte çalışmalar göstermiştir ki, diferansiyel dönüşüm yöntemi bu yöntemlere nazaran çok daha iyi sonuçlar vermektedir. İlk olarak Zhou (1986) tarafından ortaya konulan diferansiyel dönüşüm yöntemi, diferansiyel denklemin içerdiği bağımsız değişken sayısına göre şekillenmektedir. Daha iyi anlaşılabilmesi için öncelikle bir tek bağımsız değişken içeren diferansiyel denklemler için bir boyutlu diferansiyel dönüşüm tanıtılacaktır.

3.1.1. Bir Boyutlu Diferansiyel Dönüşüm

Bir I =

( )

a b, ⊂ \ üzerinde tanımlı u I: → \ analitik fonksiyonu dikkate alındığında, Tanım 2.8’ den herhangi bir x ∈ noktası için I u x

( )

fonksiyonu x₀ noktası civarında

( )

(

0

)

k k k u x =

∑

∞ C x x− (3.1) biçiminde kuvvet serisine açılabilir. Bu serinin x₀ noktası civarında düzgün yakınsak olduğu söylenebilir. Analitik bir fonksiyon sonsuz diferansiyellenebilir olması ve Taylor serilerinin diferansiyellenebilmesi teoreminden C_k katsayıları,

( )

_{( )}

0 ! k k u x C k = olarak elde edilir. Bu C_k değerleri (3.1) eşitliğinde yerine yazıldığında,

( )

( )

( ) (

0

)

0 0 ! k k k u x u x x x k ∞ = =

∑

− (3.2) bulunur. Bununla birlikte, K , negatif olmayan tamsayıların bir kümesi ve k∈K

olmak üzere,

(

)

( )

( )

( )

_{( )}

(

)

0 0 0, ! ! k k x x u x u x U x k k k = = = (3.3) biçiminde seçilir ve (3.3) eşitliği (3.2) de yerine yazılırsa,

( )

(

) (

0

)

0, _! k k x x u x U x k k ∞ − =

∑

(3.4) elde edilir. Buradan elde edilen sonuçla birlikte analitik fonksiyonların yalnız bir şekilde seriye açılabilmesinden dolayı, herhangi bir analitik u x

( )

fonksiyonu için,

0

x noktası civarında

( )

{

(

0,

)

}

_{k 0}

u x ↔ U x k ∞₌ biçiminde birebir bir eşlemenin olduğu söylenebilir.

Genel olarak, M k

( )

, k ya bağlı bir reel sayı ve q x

( )

≠0 olmak üzere

( )

,

q x I da tanımlı herhangi bir fonksiyon olmak üzere,

(

)

( ) ( ) ( )

(

)

( ) 0 0, , 0,1, 2,... k x x U x k M k q x u x k = = ⋅ =

biçiminde kabul edilirse, u x

( )

analitik fonksiyonu;

( )

_{( )}

(

_{( )}

0

)

(

0

)

0 , 1 ! k k U x k x x u x q x M k k ∞ = − =

∑

(3.5) yazılabilir. Burada

( )

1,

( )

1 ! q x M k k = = olarak seçilirse,

( )

(

0

)(

0

)

0 , k k u x ∞ U x k x x = =

∑

− (3.6) bulunur.

Tanım 3.1. I =

( )

a b, ⊂ \ üzerinde tanımlı u I: → \ analitik fonksiyonu dikkate alındığında,

{

(

₀

)

}

0

, k

noktasındaki spektrumu denir. Yani; analitik bir u x

( )

fonksiyonunun seri açılımında karşılaşılan ve (3.3) teki gibi tanımlanan

{

(

₀

)

}

0

, k

U x k ∞₌ katsayılarına u x

( )

fonksiyonunun spektrumu olarak adlandırılmaktadır. Buradaki spektrum tanımı ile Fonksiyonel Analizdeki spektrum tanımı karıştırılmamalıdır. Ayrıca

{

(

₀

)

}

0

, k U x k ∞₌ ailesinin her bir elemanına da spektra adı verilir.

Tanım 3.2. I =

( )

a b, ⊂ \ üzerinde tanımlı u I: → \ analitik fonksiyonunun

(

)

{

U x k0,

}

_{k 0} ∞

= spektrum ayrışımına Diferansiyel Dönüşüm (DT) denir. Burada u x

( )

orijinal fonksiyon,

{

(

₀

)

}

0

, k

U x k ∞₌ fonksiyonu ise dönüşmüş fonksiyon olarak tanımlanır.

Tanım 3.3.

{

(

₀

)

}

0

, k

U x k ∞₌ fonksiyonunun ters diferansiyel dönüşümü, (3.6) ile verilen

( )

(

0

)(

0

)

0 , k k u x ∞ U x k x x = =

∑

− biçiminde tanımlanır.

Herhangi bir u x

( )

analitik fonksiyonu için,

( )

_{( )}

1

(

_{( )}

0,

)

(

0

)

! k N k N U x k x x R x q x M k k ∞ = − =

∑

olarak alınırsa diferansiyel dönüşüm tanımı ve Taylor seriye açılımından söylenebilir ki,

( )

_{( )}

(

_{( )}

0

)

(

0

)

0 , 1 ! k N k U x k x x u x q x = M k k − =

∑

tir. Buradan da açıkça görülmektedir ki, diferansiyel dönüşüm tanımı Taylor seri açılımından çıkarılmaktadır.

3.1.2. n-Boyutlu Diferansiyel Dönüşüm

Burada n değişkenli fonksiyonlar için n-boyutlu diferansiyel dönüşümü tanımlanacaktır. Bu genelleştirmede n=2 ve n=3 alınacak olursa, sırasıyla iki ve üç değişkenli fonksiyonlar için iki boyutlu ve üç boyutlu diferansiyel dönüşümler elde edilebilir.

n

\ ’ de herhangi bir nokta x=

(

x x₁, ,...,₂ x_n

)

, k ₌

(

k k₁, ,...,₂ k_n

)

, k_{i∈ ]}+

multiindeks,

(

₁, ₁

) (

₂, ₂

)

(

,

)

n , 1

n n

D= a b × a b × ×" a b ⊆\ n≥ n boyutlu dikdörtgen ve u x

( )

fonksiyonu da D bölgesinde analitik bir fonksiyon olsun. Multiindeks tanımından k =k₁+k₂ + +... k_n yazılabileceğine dikkat edelim. Bu durumda, n -boyutlu uzayda tanımlı analitik u x

( )

fonksiyonu;

( )

(

)

₁

( )

0

(

0

)

1 2 0 1 1 , , , ! i n k k n i i n k k k n i i x x u x u x u x x x x x k ∞ = = − ∂ = = ∂ ∂

∑

∏

" " (3.7)

kuvvet serisi biçiminde yazılabilir. Burada

(

)

1 2

0 0 0 0 , ,..., n

x = x x x dır. Bu seri de tek boyutlu diferansiyel dönüşümde olduğu gibi x noktası civarında ₀ u x

( )

’e düzgün yakınsar. Analitik fonksiyonun ve Taylor serisinin sonsuz diferansiyellenebilir olmasından,

(

)

( )

(

)

(

(

)

(

)

)

( )

1 0 1 0 0 1 2 1 0 0 0 0 1 2 1 2 1 1 , , ... ! 1 , , , , , , , , ! n n k n k k n _{x x} k n n k k n _{x x} u x U x k k k k k k x x u x U x k U x x x k k k k x x = = ∂ = ⋅ = + + + ∂ ∂ ∂ = = ⋅ ∂ ∂ " " " " (3.8)

yazılabilir. (3.8) ifadesi (3.7)’de yerine yazılırsa,

( )

(

)

(

0

)

0 0 1 , n ki i i k i u x ∞ U x k x x = = =

∑

∏

− (3.9) elde edilir.

(3.9) sonucu ve analitik fonksiyonların yalnız bir şekilde seriye açılabilmesinden dolayı, u x

( )

analitik fonksiyonu için, x= noktası civarında x₀

( )

{

(

0,

)

}

_{k 0}

u x ↔ U x k ∞₌ biçiminde birebir bir eşlemenin olduğu söylenebilir.

Genel olarak, M k

( )

, k ya bağlı bir reel sayı ve q x

( )

≠0 olmak üzere

( )

,

q x D de tanımlı herhangi bir fonksiyon olmak üzere,

(

)

( )

(

( ) ( )

₁

)

0 0 1 , n k k k n _{x x} q x u x U x k M k x x = _{∂ ⋅}    =  ∂ ∂   " 

biçiminde kabul edilirse, u x

( )

analitik fonksiyonu;

( )

_{( )}

(

_{( )}

0

)

(

0

)

0 1 , 1 ! i k n i i k i i x x U x k u x q x M k k ∞ = =  ₋    =    

∑

∏

(3.10) yazılabilir. Burada, x noktası civarında ₀

( )

( )

1 2 1 1, ! ! _n! q x M k k k k = = ⋅ ⋅ ⋅" olarak seçilirse,

( )

(

0

)

(

0

)

0 1 , i n k k i u x ∞ U x k x x = =   = _ − _  

∑

∏

(3.11) elde edilir.

Tanım 3.4. D bölgesi üzerinde tanımlı u

( )

x bir analitik fonksiyon olmak üzere

{

U

(

x₀,k

)

}

∞_{k =0} gösterimine u

( )

x fonksiyonunun n-boyutlu spektrumu denir.

Tanım 3.5. D bölgesi üzerinde analitik herhangi bir u

( )

x fonksiyonunun n-boyutlu spektrum ayrışımına n-boyutlu diferansiyel dönüşüm olarak adlandırılır. Burada u

( )

x orijinal fonksiyon,

{

U

(

x₀,k

)

}

∞_{k =0} ise dönüşmüş fonksiyon olarak tanımlanır.

Tanım 3.6.

{

U

(

x₀,k

)

}

∞_{k =0}’ dönüşmüş fonksiyonunun ters diferansiyel dönüşümü,

( )

_∑

∞

(

)

_∏

(

)

= =                 − = 0 1 0 0, k k n i i i i x x k x U x u (3.12) biçiminde tanımlanır.

Şimdi diferansiyel dönüşüm yöntemi ile ilgili bazı teorem ve sonuçları vermeden önce verilecek özelliklerde genelleme olması için _{D⊂ \ ’de tanımlı} n fonksiyonlar dikkate alınacağı ve aksi söylenmedikçe küçük harflerle orijinal fonksiyonların, büyük harflerle de dönüşmüş fonksiyonların gösterileceği ifade edilmelidir.

3.2. Diferansiyel Dönüşüm Yönteminin Özellikleri

Bu bölümde verilecek olan özellikler öncelikle n=1 ve n=2 için sırasıyla bir ve iki boyutlu uzaylar için bir boyutlu ve iki boyutlu diferansiyel dönüşümlere ait özellikler ispatsız olarak, daha sonrada bu teoremlerin n-boyutlu uzaydaki karşılıkları ispatlı olarak verilecektir.

Teorem 3.3.1. Bir I =

( )

a b, ⊂ \ üzerinde tanımlı tek değişkenli u v ve y , analitik fonksiyonları dikkate alındığında, y x

( )

=u x

( ) ( )

±v x biçiminde ifade edilebiliyor ise bu durumda sırasıyla u ve v fonksiyonlarının diferansiyel dönüşümleri U ve V ile gösterilmek üzere, y fonksiyonunun diferansiyel dönüşümü,

(

0,

)

(

0,

)

(

0,

)

Y x k =U x k ±V x k (3.13) biçimindedir [Chen-Ho, 1996].

Teorem 3.3.2. n=2 için bir _{D⊂ \ üzerinde tanımlı iki değişkenli ,}2 _{u v ve}

w analitik fonksiyonları dikkate alındığında, w x y

( )

, =u x y

( ) ( )

, ±v x y, biçiminde ifade edilebiliyor ise bu durumda sırasıyla u ve v fonksiyonlarının diferansiyel dönüşümleri U ve V ile gösterilmek üzere, w fonksiyonunun diferansiyel dönüşümü,

(

) ( )

(

0, 0 , ,

)

(

(

0, 0

) ( )

, ,

)

(

(

0, 0

) ( )

, ,

)

W x y k h =U x y k h ±V x y k h (3.14) biçimindedir [Chen-Ho, 1999].

Teorem 3.3.3. Bir _{D⊂ \ üzerinde tanımlı , ,}n _{u v ve w analitik fonksiyonları} dikkate alındığında, w x

( )

=u x

( ) ( )

±v x biçiminde ifade edilebiliyor ise bu durumda

sırasıyla u v fonksiyonlarının diferansiyel dönüşümleri , , U ve V ile gösterilmek üzere, w fonksiyonunun diferansiyel dönüşümü,

(

0,

)

(

0,

)

(

0,

)

W x k =U x k ±V x k (3.15) biçimindedir.

İspat. u ve v _{D⊂ \ üzerinde tanımlı analitik fonksiyonlar olduklarından,} n

( )

(

)

( )

(

)

(

)

(

)

( )

(

)

( )

(

)

(

)

(

)

1 1 0 0 0 1 2 0 0 1 1 0 1 0 0 0 1 2 0 0 1 1 0 1 , , , , ! , , , , ! i i n i i n k k _{n n} k i i n k k i i k n i i k i k k _{n n} k i i n k k i i k n i i k i x x u x u x u x x x U x k x x k x x x x v x v x v x x x V x k x x k x x ∞ ∞ = = = = ∞ ∞ = = = = − ∂ = = = − ∂ ∂ − ∂ = = = − ∂ ∂

∑

∏

∑

∏

∑

∏

∑

∏

" " " "

yazılabilir. Bu ifadeler, w x

( )

=u x

( ) ( )

±v x eşitliğinde yerine yazılırsa,

( )

( ) ( )

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

0 0 0 0 0 1 0 1 0 0 0 0 1 , , , , i i i n _k n _k i i i i k i k i n _k i i k i w x u x v x U x k x x V x k x x U x k V x k x x ∞ ∞ = = = = ∞ = = = ± = − ± − = ± −

∑

∏

∑

∏

∑

∏

olup

(

0,

)

(

0,

)

(

0,

)

W x k =U x k ±V x k elde edilir. İspatlanan bu teorem [Kurnaz, Oturanç, Kiriş, 2005] tarafından ispatsız olarak verilmiştir.

Teorem 3.3.4. α∈ \ olmak üzere, bir I =

( )

a b, ⊂ \ üzerinde tanımlı tek değişkenli u ve y analitik fonksiyonları dikkate alınsın. Eğer, y x

( )

=αu x

( )

biçiminde ifade edilebiliyor ise bu durumda y fonksiyonunun diferansiyel dönüşümü,

(

0,

)

(

0,

)

Y x k =αU x k (3.16) biçimindedir [Chen-Ho, 1996].

Teorem 3.3.5. α bir sabit olmak üzere, n=2 için bir _{D⊂ \ üzerinde} 2

tanımlı iki değişkenli u ve w analitik fonksiyonları dikkate alınsın. Eğer,

( )

,

( )

,

w x y =αu x y biçiminde ifade edilebiliyor ise bu durumda w fonksiyonunun diferansiyel dönüşümü,