İki katlı kamal dönüşümü metodu ve telgraf denkleminin çözümüne uygulanması

T.C.

SELÇUK ÜNĠVERSĠTESĠ FEN BĠLĠMLERĠ ENSTĠTÜSÜ

ĠKĠ KATLI KAMAL DÖNÜġÜMÜ METODU VE TELGRAF DENKLEMĠNĠN ÇÖZÜMÜNE

UYGULANMASI

Fatma TEZCAN HOġDAVRAN YÜKSEK LĠSANS TEZĠ

Matematik Anabilim Dalı

Ağustos - 2019 KONYA Her Hakkı Saklıdır

ii

TEZ KABUL VE ONAYI

Fatma TEZCAN HOŞDAVRAN tarafından hazırlanan “İki Katlı Kamal Dönüşümü Metodu ve Telgraf Denkleminin Çözümüne Uygulanması” adlı tez çalışması 23/08/2019 tarihinde aşağıdaki jüri tarafından oy birliği ile Selçuk Üniversitesi Fen Bilimleri Enstitüsü Matematik Anabilim Dalı’nda YÜKSEK LİSANS olarak kabul edilmiştir.

Jüri Üyeleri Ġmza

BaĢkan

Doç. Dr. Bilge PEKER ………..

DanıĢman

Dr. Öğr. Üyesi Haldun Alpaslan PEKER ……….. Üye

Prof. Dr. Kemâl AYDIN ………..

Yukarıdaki sonucu onaylarım.

Prof. Dr. Mustafa YILMAZ FBE Müdürü

iii

TEZ BĠLDĠRĠMĠ

Bu tezdeki bütün bilgilerin etik davranış ve akademik kurallar çerçevesinde elde edildiğini ve tez yazım kurallarına uygun olarak hazırlanan bu çalışmada bana ait olmayan her türlü ifade ve bilginin kaynağına eksiksiz atıf yapıldığını bildiririm.

DECLARATION PAGE

I hereby declare that all information in this document has been obtained and presented in accordance with academic rules and ethical conduct. I also declare that, as required by these rules and conduct, I have fully cited and referenced all material and results that are not original to this work.

Fatma TEZCAN HOŞDAVRAN

iv ÖZET

YÜKSEK LĠSANS TEZĠ

ĠKĠ KATLI KAMAL DÖNÜġÜMÜ METODU VE TELGRAF DENKLEMĠNĠN ÇÖZÜMÜNE UYGULANMASI

Fatma TEZCAN HOġDAVRAN Selçuk Üniversitesi Fen Bilimleri Enstitüsü

Matematik Anabilim Dalı

DanıĢman: Dr. Öğr. Üyesi Haldun Alpaslan PEKER

2019, ix+35 Sayfa Jüri

Dr. Öğr. Üyesi Haldun Alpaslan PEKER Prof. Dr. Kemal AYDIN

Doç. Dr. Bilge PEKER

Bir integral dönüşümü olan Kamal dönüşümü Abdelilah Kamal tarafından 2016 yılında bulunmuştur. Bu tezde öncelikle Kamal dönüşümü ele alınıp Kamal dönüşümünün literatürdeki adi ve kısmi diferensiyel denklemlere uygulanması incelenmiştir. Daha sonra iki katlı Kamal dönüşümünü tanımlayıp birinci ve ikinci mertebeden kısmi türevlerin iki katlı Kamal dönüşümü formüllerini elde ettik. Sonra iki katlı Kamal dönüşümünü telgraf denklemine uyguladık.

Anahtar Kelimeler: Diferensiyel Denklem, İki Katlı Kamal Dönüşümü, Kamal Dönüşümü, Kısmi Diferensiyel Denklem, Telgraf Denklemi, Ters Kamal Dönüşüm

v ABSTRACT

MS THESIS

DOUBLE KAMAL TRANSFORM METHOD AND ITS APPLICATION FOR SOLVING TELEGRAPH EQUATION

Fatma TEZCAN HOġDAVRAN

THE GRADUATE SCHOOL OF NATURAL AND APPLIED SCIENCE OF SELÇUK UNIVERSITY

THE DEGREE OF MASTER OF SCIENCE IN MATHEMATICS

Advisor: Asst. Prof. Dr. Haldun Alpaslan PEKER 2019, ix+35 Pages

Jury

Asst. Prof. Dr. Haldun Alpaslan PEKER Prof. Dr. Kemâl AYDIN

Assoc. Prof. Dr. Bilge PEKER

The Kamal transform, an integral transform, was found by Abdelilah Kamal in 2016. In this thesis, the application of Kamal transformation to ordinary and partial differential equations in the literature was examined. We then defined the double Kamal transformation and obtained the double Kamal transformation formulas for first-and second-order partial derivatives. Then we applied the double Kamal transformation to the Telegraph equation.

Keywords: Differential Equation, Double Kamal Transformation, Inverse Kamal Transformation, Kamal Transform, Partial Diffrerential Equation, Telegraph Equation

vi ÖNSÖZ

İki katlı Kamal dönüşümü metodu ve telgraf denkleminin çözümüne uygulanması üzerine yaptığım bu çalışma sırasında başta hayatım boyunca her anımda desteklerini esirgemeyen ailem ve eşim olmak üzere, lisansüstü eğitimim boyunca bana karşı daima olumlu tutumu ve bilimsel bir çalışma yapılırken dikkat edilmesi gereken temel hususlar konusunda vermiş olduğu bilgiler, gerek mesai saatleri içerisinde gerekse mesai saatleri dışarısında sürekli ilgi ve alakasından dolayı Selçuk Üniversitesi Fen Fakültesi Matematik Bölümü öğretim üyesi Dr. Öğr. Üyesi Haldun Alpaslan PEKER’e en samimi şükranlarımı sunmayı bir borç bilirim.

Fatma TEZCAN HOŞDAVRAN KONYA-2019

vii ĠÇĠNDEKĠLER ÖZET ... iv ABSTRACT ... v ÖNSÖZ ... vi ĠÇĠNDEKĠLER ... vii

SĠMGELER VE KISALTMALAR ... viii

ÇĠZELGELER VE ġEKĠLLER ... ix 1. GĠRĠġ ... 1 1.1. Literatür Özeti... 2 2. ĠNTEGRAL DÖNÜġÜMLERĠ ... 4 2.1. Laplace DönüĢümü ... 4 2.2. Kamal DönüĢümü ... 4

2.3. Adi Diferensiyel Denklemlerin Kamal DönüĢümü ile Çözümü ... 10

2.4. Bazı Kısmi Türevlerin Kamal DönüĢümü ... 17

3. ĠKĠ KATLI KAMAL DÖNÜġÜMÜ ... 24

3.1. Bazı Kısmi Türevlerin Ġki Katlı Kamal DönüĢümü ... 25

3.2. Ġki Katlı Kamal DönüĢümünün Telgraf Denklemine UygulanıĢı ... 30

4. SONUÇLAR ... 33

KAYNAKLAR ... 34

viii

SĠMGELER VE KISALTMALAR

Simgeler

K : Kamal Operatörü

2

K : İki Katlı Kamal Operatörü _{: Ters Kamal Operatörü} L : Laplace Operatörü

ix

ÇĠZELGELER VE ġEKĠLLER Çizelgeler

Çizelge 2.1. Kamal dönüşümü s:7

Çizelge 2.2. Kamal ve Laplace dönüşümü s:8

Çizelge 2.3. Ters Kamal dönüşümü s:9

ġekiller

1. GĠRĠġ

Bir veya daha fazla bağımsız değişkene göre bilinmeyen fonksiyonun türevlerini bulunduran denkleme diferensiyel denklem denir. Diferensiyel denklemlerin kulllanıldığı matematiksel modellere nüfus oranının hesabında, faiz hesaplarında, ekonomi ve işletme hesaplarında, mühendislik alanlarındaki birçok uygulamanın hesabında oldukça sık rastlanır (Bronson ve Costa, 2013). aralığında tanımlanan bir fonksiyonun “İntegral Dönüşümü”

 

{ ( )}f x F k

∮

(1.1) ile gösterilir ve

 



  

{ ( )} K , b a f x F k 



x k f x dx

∮

(1.2)

ile belirtilir. Burada K x k ile verilen fonksiyonda x ve k bilinmeyenleri dönüşümün

 

, değişkenleri olarak adlandırılır.

∫ işlemcisi genellikle “İntegral Dönüşüm İşlemcisi” veya basitçe “İntegral Operatörü” şeklinde adlandırılır (Yaşar, 2003).

İntegral hesabının kullanımının aslında on dokuzuncu yüzyılın ilk çeyreğinde, keşfiyle başladığı düşünülebilir. Fakat sembolik metot fikrini ilk öne süren G.W.Leibnitz (1646-1716) dır. Sonradan J.L.Lagrange (1736-1813) ve P.S.Laplace (1749-1827) sembolik metot için önemli yazılar yazmıştır. İlk sistematik integral kullanımının gelişimi için temel adım J.Fourier (1768-1830) ve A.L.Cauchy (1789-1853) tarafından kullanılmıştır. Genel kanı, integral dönüşümü kavramının Fourier integral teoremi tarafından türetildiğiydi (Yaşar, 2003).

Diferensiyel denklemler, uygulamalı matematiğin her alanında önemli olmuştur. İntegral dönüşümleri, yüzyıllar boyunca diferensiyel ve integral denklemleri çözmek için kullanılmış matematiksel araçlardır (Khan ve ark., 2018). Bu nedenle, uygulamalarda karşılaşılan denklemlerin incelenmesi ve analizi derin matematiksel problemlere yol açtı. Diferensiyel denklemlerin analitik ve yaklaşık olarak çözümlerinin incelenmesi için pek çok yöntem bulunmuştur ve diferensiyel denklemleri çözmek için kullanılan yöntemlerden biri integral dönüşümleridir (Sedeeg ve Mahamoud, 2017).

Tipik olarak, Fourier, Sumudu, Elzaki, Aboodh ve Mahgoub integral dönüşümleri diferensiyel denklemlerin çözümü için uygun matematiksel araçlardır. Kamal dönüşümü son zamanlarda kullanılan yeni bir integral dönüşümüdür. 2016 yılında Abdelilah Kamal tarafından bulunmuştur. Bu dönüşüm Laplace, Aboodh ve Mahgoub dönüşümleriyle bağlantılıdır (Kamal ve Sedeeg, 2016). Bu tezde amacımız Kamal dönüşümünün uygulamalarını inceleyip iki katlı Kamal dönüşümünü araştırmaktır.

1.1. Literatür Özeti

Laplace dönüşümü bir integral dönüşümü olup, fizik, mekanik, mühendislik, tıp ve bazı diğer bilim dallarında kullanılan önemli bir yöntemdir. Bu yöntem, diferensiyel denklemlerin çözümünde büyük kolaylıklar sağladığı gibi, fiziğin matematiksel denklemlerinin çözümünde de yararlanılabilen bir yöntemdir (Yaşar, 2005).

Laplace dönüşümleri, Doğrusal diferensiyel denklem sistemlerin yani aynı sayıdaki bilinmeyen fonksiyonla iki yada daha fazla diferensiyel denklem setinin çözümünde kullanışlıdır. Sistemdeki her bir diferensiyel denklemin Laplace dönüşümü alınır, elde edilen ardışık denklemler setinden dönüşmüş bilinmeyen fonksiyonlar cebirsel olarak belirlenir ve ters Laplace dönüşümü yardımıyla hesaplanır (Bronson ve Costa, 2013).

Bir tür integral dönüşümüdür. Kamal ve Sedeeg (2016) yılındaki çalışmasında yeni bir integral dönüşümü olan “Kamal Dönüşümü” çalışmasını yapmıştır. Diferensiyel denklem, uygulamalı matematiğin her alanında her zaman merkezi rol oynamıştır. Bu nedenle, uygulamalarda kullanılan denklemlerin incelenmesi ve analizi çok derin matematiksel problemlere yol açtı. Diferensiyel denklemleri çözmek için çok sayıda farklı teknik vardır. Ama integral dönüşümü en yaygın kullanılanıdır (Sedeeg ve Mahamoud, 2017). Kamal dönüşümü, klasik integral dönüşümüdür ve bazı temel özellikleri diferensiyel denklemleri geliştirmek için kullanılır (Kamal ve Sedeeg, 2016). İntegral dönüşümleri, yüzyıllar boyunca diferensiyel ve integral denklemleri çözmek için kullanılmış matematiksel araçlardır (Khan ve ark., 2018). Burada amacımız bu ilginç dönüşümün uygulanabilirliği ve problemlerin çözümünde etkisini göstermektedir. Bu çalışmada, kısmi türevlerin Kamal dönüşüm formülünü kullanıyoruz ve bazı başlangıç değerlerinin çözümünde uygulayabiliyoruz (Sedeeg ve Mahamoud, 2017).

Kamal ve Sedeeg (2016) da yeni bir integral dönüşümü olan “Kamal Dönüşümü” çalışmasını yapmıştır. Kamal dönüşümünü sabit katsayılı doğrusal adi diferensiyel denklemlere uygulamışlardır.

Sedeeg ve Mahamoud (2017) de bu dönüşümün uygulanabilirliği ve problemlerin çözümünde etkisini göstermişlerdir. Kamal dönüşümünü, kısmi diferensiyel denklemlere uygulamışlardır.

Khan ve ark. (2018) de değişken katsayılı doğrusal adi diferensiyel denklemleri çözmek için Kamal dönüşümünü uygulamıştır.

2. ĠNTEGRAL DÖNÜġÜMLERĠ

2.1. Laplace DönüĢümü

Tanım: f t

 

, 0  t için tanımlı olsun ve s bir reel değişkeni göstersin.

 

f t nin L{f(t)} veya F(s) ile gösterilen Laplace dönüşümü, genelleştirilmiş integralin yakınsadığı tüm s değerleri için

 





 

 

0 st L f t F s e f t dt    

_

(2.1)

ile verilir. Yakınsama,

 

0 lim R st R e f t dt  



(2.2)

limiti var olduğunda elde edilir. Eğer limit yoksa genelleştirilmiş integral ıraksar ve f(t) nin Laplace dönüşümü yoktur (Bronson ve Costa, 2013).

2.2. Kamal DönüĢümü

 

1 2

 

 





{ : , , 0, j 1 0, } t j k A f t M k k  f t M e t    (2.3)

olarak tanımlanan kümedeki fonksiyonları göz önünde bulunduracağız.

A kümesinde verilen bir fonksiyon için sabit olan M sayısı sonlu sayıda olmalıdır. sonlu veya sonsuz olabilir. K operatörü tarafından elde edilen Kamal dönüşümü,

 

 

 

/ 0 t v K f t G v f t e dt        



, t0 , k₁ v k₂ , , k k_{1 2} 0 (2.4)

Her f t fonksiyonunun Kamal dönüşümü bulunamamaktadır. Şu halde hangi

 

şart altında integral yakınsak olmaktadır. Bunun için gerekli şart

 

0 k t v_{f t dt}

e





nin her k 0 için tanımlı olmasıdır. Bunun olabilmesi içinde f nin

 

0, k aralığındaki her pozitif k için “düzgün sürekli” olması gerekir. Şimdi bu tanımı verelim:

Tanım 2.2.1. (Parçalı Süreklilik)

 

f t fonksiyonu

 

a b aralığında parçalı süreklidir, şayet her bir ,



a t,1



,



tj1,tj



ve



t tn, b



açık aralıklarında f fonksiyonu, sürekli ve

 

lim t a f t   , tlimj

 

f t   , tlimj

 

f t   ve limt b

 

f t   (2.5)

şeklindeki tek taraflı limitler sonlu olacak şekilde a   t₁ t₂ t_n b noktaları vardır. Bu tanım nin, [a,b] aralığındaki sonlu sayıdaki nokta hariç sürekli olduğu bu noktalardaki sağ ve sol limitler birbirinden farklı ya da aynı olsa bile nin değerine eşit olmadığını ifade etmektedir. Bu noktalardaki süreksizlik, sıçrama süreksizliği olarak adlandırılmaktadır (Pala, 2006).

Mesela Şekil 1.1. deki fonksiyon noktaları hariç [0, a] aralığında süreklidir. Bu iki noktada sıçrama süreksizliğine sahiptir (Pala, 2006).

Eğer f fonksiyonu [ ] aralığında parçalı sürekli ise, o taktirde _etv_{f t}

 

_ve

 

0 k t v e f t dt



mevcuttur. Ancak,

 

0 k t v e f t dt



nin her k varlığı

 

0 lim k t v k e f t dt  



nin

varlığını garantilemez. Mesela _t2

e [ ] nın her aralığında süreklidir. Fakat

2 0 t t v e e dt  _ 



bütün reel ler için ıraksaktır. Şu halde Kamal dönüşümünün yakınsaklığı için daha başka bir şarta ihtiyacımız vardır. O da şudur: Şayet, M ve b sayıları için

 

bt

f t Me oluyorsa bu takdirde vb için

 

t 1 1 t v b v e f t Me       _ _  (2.6) dir. Oysa 1 1 b v için 0 1 1 v b t Me dt     _{ }   



integrali M b v b v  

 ye yakınsar. Şu halde₀

 

t v e f t dt 



ve

 

0 t v e f t dt 



ifadesi yakınsar (Pala, 2006).

Bazı fonksiyonların Kamal dönüşümünü bulalım,

olursa, Kamal dönüşümünün tanımına göre

 

 

/ / 0 0 1 lim[ ] b t v t v b K G v e dt e dt      







/ lim[ 0 ] | t v b b ve    (2.7) [ ]

olarak bulunur. alınırsa o zaman, Kamal dönüşümünün tanımına göre

 

 

/ 0 t v K t G v te dt    



= / 0 lim[ ] b t v b te dt  



= / / 0 lim[ ( ) | ] 0 b t v t v b b t v e v e dt   



(2.8)

=lim[ _/ | 2 0 ] t v b b t v v e    = 2 v

 

2 K t v olarak bulunur. n { } için, 1 n ! n

K t  _{ } n v  olur (Kamal ve Sedeeg, 2016).

2.2.2 Bazı fonksiyonların Kamal dönüĢümü

Bazı fonksiyonların Kamal dönüşümü tablosu Khan ve ark. (2018) makalesinde aşağıdaki Çizelge 2.1. deki gibi verilmiştir.

Çizelge 2.1. Kamal dönüşümü

f (t)

[ ]

1 t n! _{⁄ ⁄} ⁄ Sin(at) ⁄ Cos(at) ⁄ Sinh(at) ⁄ Cosh(at) ⁄

2.2.3 Kamal ve Laplace dönüĢümü

K operatörü tarafından elde edilen Kamal dönüşümü,

 

 

 

/ 0 t v K f t G v f t e dt        



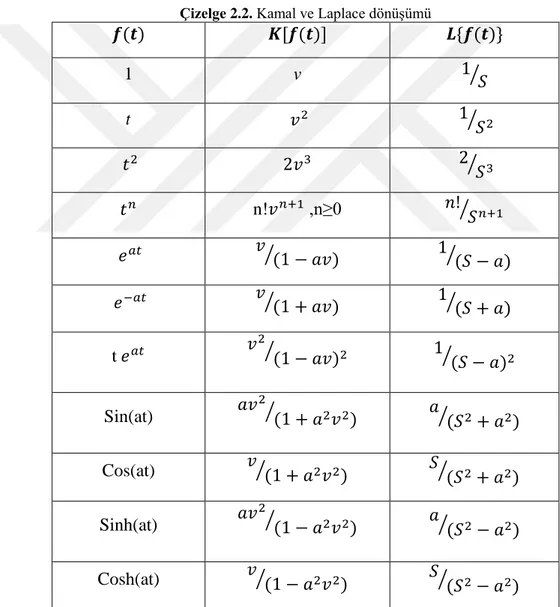
t0 , k₁ v k₂ , , k k_{1 2} 0 eşitliği kullanılarak elde edilir. (Kamal ve Sedeeg, 2016).

Aşağıdaki Çizelge 2.2. de bazı fonksiyonlar için Kamal ve Laplace dönüşümleri gösterilmiştir (Khan ve ark., 2018; Bronson ve Costa, 2013).

Çizelge 2.2. Kamal ve Laplace dönüşümü

[ ] { } 1 v ⁄ t ⁄ ⁄ n! _,n≥0 ⁄ _⁄ ⁄ _⁄ ⁄ t ⁄ ⁄ Sin(at) ⁄ ⁄ Cos(at) ⁄ ⁄ Sinh(at) ⁄ ⁄ Cosh(at) ⁄ ⁄

2.2.4 Ters Kamal dönüĢümü

K[f(t)] = G(v) ise f(t), G(v) nin ters Kamal dönüşümüdür ve matematiksel olarak _{[ ] ile ifade edilir (Aggarwal ve ark., 2018).}

Aşağıdaki Çizelge 2.3. de bazı fonksiyonların ters Kamal dönüşümleri verilmiştir (Aggarwal ve ark., 2018).

Çizelge 2.3. Ters Kamal dönüşümü

G(v) [ ] v 1 _{, n≥0} ⁄ ⁄ ⁄ ⁄ Sin(at) ⁄ Cos(at) ⁄ Sinh(at) ⁄ Cosh(at)

2.3. Adi Diferensiyel Denklemlerin Kamal DönüĢümü ile Çözümü

Aşağıdaki örnekler Kamal dönüşümünün adi diferensiyel denklemler tarafından açıklanan belirli başlangıç değer problemlerinin çözümünde kullanımını göstermektedir. Teorem 2.1.

G(v), f(t) nin Kamal dönüşümü olsun yani, K[y(t)] = G(v). Bu durumda,

i. K y

 

 v K y1

 

 –  0y

 

(2.9) ii.

 

 

 

 

2 1 K 0 0 K y v y v y y (2.10) iii.    

_{ }

1 1  

_{ }

0 K 0 n n n k n k k K y v y v y           



(2.11)

olur (Kamal ve Sedeeg, 2016).

Şimdi birinci mertebeden bir diferensiyel denklem düşünelim;

dx

px

dt  = f t

 

, t0, x

 

0 a, (2.12)

denkleminde her iki tarafın Kamal dönüşümü alınırsa,

 

 

dx K K px K f t dt     _ _     (2.13)

 

 

dx K pK x K f t dt     _ _     [dx] [ ] K K x dt   ve

 

 

 

1 0 K x v K x x

 

 

 

 

1 0 v K x x pK x  K f t_ _

x(0) = a başlangıç koşulunu denklemde yerine koyarsak ve [ ] yazılırsa

 

 

 

1

 



1



 

K x v p G v a

 

1

 

K x p G v a v  _ _{ }    

 

1 vp

 

K x G v a v   _{  }     o zaman,

 

 

 

1 ₁ G v a vG v av K x vp _vp v    _  

olur (Kamal ve Sedeeg, 2016).

Şimdi ikinci mertebeden bir diferensiyel denklem düşünelim; ve reel sabitler olmak üzere,

 

 

 

2 2 2 , 0 , 0 d y dy p qy f x y a y b dx  dx     (2.14) başlangıç şartları ile verilen denklemin her iki tarafının Kamal dönüşümü alınırsa;

 

 

2 2 2 d y dy K K p K qy K f x dx dx  _  _{   }   _ _    

 

 

2 2 2 d y dy K pK qK y K f x dx dx  _  _{   }    _{ }     (2.15)

 

 

 

 

2 2 1 2 0 0 d y K K y v K y v y y dx               (2.16)

 

1

 

 

0 dy K K y v K y y dx   _{  }     _ (2.17) (2.16) ve (2.17) eşitlikleri (2.15) de yerine yazılırsa,

 

 

 



 

 



 

 

2 1 1

0 0 2  –  0        

v K y v y y  p v K y y qK y G v (2.18) elde edilir. Bu denkleme, y

 

0 , a y

 

0 b başlangıç koşullarını uygulayalım.

 



 



 

 

2 1 1 2 v K y v a b   p v K y  a qK y G v (2.19)

 

 

 

 

2 a 2p  _– 2         v K y b K y pa qK y G v v v  _{    }

 

2

 

1 2 2 p a K y q G v b pa v v v  _{ } _{   }    

 

2 2

 

2 1 2pv qv v G v a bv pav K y v v             

 

2

 

2 2 2





2 1 2 1 2 1 2 1 2 v G v bv av pv K y pv qv pv qv pv qv          

elde edilir (Kamal ve Sedeeg, 2016). Örnek 2.1

:

dy y 0,y

 

0 1

dx   başlangıç değer problemini çözelim.

Çözüm: Verilen denklemin her iki tarafın Kamal dönüşümünü alalım.

 

0 dy K K y dx        

 

 

0 K y K y 

 

 

 

1   _{–  0     0} v K y y K y 

y(0) = 1 başlangıç değerini yerine yazalım.

 

1

 

1 1 1 v K y K y v v  _{  } _   _  

Her tarafın ters Kamal dönüşümünü alalım.

 

1 1 1 v K K y K v  _{  }      _{ } _

y x

 

ex olarak bulunur (Kamal ve Sedeeg, 2016).

Örnek 2.2

:

y 4y12 , t y

 

0 0, y

 

0 7 başlangıç değer probleminin çözümünü bulunuz.

Çözüm:

4 12

y  y t

denkleminde her tarafın Kamal dönüşümünü alırsak,



4



 

12 K y  y K t

 

4

 

1 2

 

K y  K y  K t

 

 

2 4 1 2 K y  K y  v

 

 

 

 

2  _– 1 _{0  – 0   4   12} 2 v K y v y y  K y  v

elde edilir. Bu denklemde başlangıç değerleri yerine yazılırsa,

 

 

2 2 4 1 2 7 v K y  K y  v 

 

2 2 1 4 1 2 7 K y v v   _  _   

 

2 2 12 7 1 4 v K y v    _     

 





2 2 2 12 7 4 1 v v K y v     ⇒

 

 

 

2 2 2 2 2 2 4 2 3 3 2 2 1 2 1 v v K y v v v v      

Her tarafın ters Kamal dönüşümü alınırsa,

⇒

 

 

2 1 1 2 2 2 3 2 2 1 v K K y K v v  _{  }  _{ } _   _{  }   ⇒y t

 

3 2 t sin t2 olarak elde edilir (Kamal ve Sedeeg, 2016).

Örnek 2.3:y  y 0 , 0 y

 

 y

 

0 1 başlangıç değer problemini çözünüz. Çözüm:y  y 0 denkleminde her tarafın kamal dönüşümü alınırsa

 

0 K y_  y K _

 

 

 

 

2 1 0 0 0 v K y v y y K y 

 



2



1 1 1 K y v v  _{  }

 

22 1 1 v v K y v v   _     

 

22 1 v v K y v   

 

22 2 1 1 v v K y v v    

bulunur. Her tarafın ters Kamal dönüşümü alınırsa,

 

2 1 1 2 2 1 1 v v K K y K v v  _{  }   _      _{ }    y t

 

sint cost 

olarak bulunur (Kamal ve Sedeeg, 2016).

Teorem 2.2.

K[f(t)] = G(v) tarafından verilen f(t) fonksiyonunun Kamal dönüşümü ise o zaman,

i.

 

2 1

 

 

0 d K tf t v G v f dv v          _ _ (2.20)

ii.

 

 

 

 

 

2 2 4 3 2 1 1 0 2 0 d d K t f t v G v f v G v f dv v dv v              _ _ _ _ (2.21) iii. K tf”

 

t v2 d 1₂ G v

 

1 f

 

0 f

 

0 dv v v          _  _ (2.22) iv.

 

 

 

 

 

 

 

2 2 4 3 2 2 2 1 1 1 1 0 0 2 [ 0 0 d d K t f t v G v f f v G v f f dv v v dv v v       _           (2.23)

formülleri elde edilir (Khan ve ark., 2018).

Örnek 2.4:t y  



1 2t y



2 0 , y y

 

0 1 ,  y

 

0 2 başlangıç değer problemini hesaplayınız. Çözüm:



1 2



2 0 t y  t y y

 

 

2

 

2

 

0 t y t y t  ty t  y t  Her tarafın Kamal dönüşümü alınırsa,

[ ( )] [ ( )] 2 [ ( )] 2 [ ( )] 0

K ty t K y t  K ty t  K y t 

[ ( )], [ ( )], [ ( )]

K ty t K y t K ty t eşitlikleri yerine yazılırsa,

 

 

 

   

   

 

2 2 2 1 1 1 1 0 0 0 2 0 2 0 d d v G v y y G v y v G v y G v dv v v v dv v  _{ } _{  }  _ _{ }         

y(0) = 1 , yerine yazılırsa,

 

 

 

 

2 2 2 1 1 1 1 2 1 2 1 2 0 d d v G v G v v G v G v dv v v v dv v  _{ } _{  }  _{ } _        

 

2

_{ }

 

_{ }

2 2 2 2 1 1 2 2 0 G v v v G v v d d v G v v G v dv v v dv v                    

 



 



_{ }





 

_{ }

' 2 2 2 2 4 2 ( 1 4 ) 2 2 _{1 ( 1)} 1 2 2 0 G v v v v G v v v _{G v v G v v} v G v v G v v v v        _{    }      _{ }        _

 

 

_{ }

_{ }

_{ }

_{ }

2 2 3 2 3 2 4 2 2 4 1 1 2 2 2 2 2 0 v G v v v vG v v v G v vG v v G v v G v v v               

 

 

_{ }

_{ }

2 2 2 2 1 1 2 0 v G v v vG v G v vG v v v              

 

2

 

1

 

 

1 1 2 0 G v G v G v vG v v v        

 

 





1 1 2 0 G v G v v v     

işlemlere devam edersek,

 





1

 

1 2 G v v G v v   

 

 



1 21



G v G v v v   →

 

 

d



1 21



G v v dv G v v v   





 





( ) (1 2 )

 

ln G v ln v ln  v ln c

 





( ) 1 2 v ln G v ln c v  

 

1 2 v G v c v  

Her tarafın Kamal dönüşümü alınırsa,

 

1 1 1 2 v K G v K c v  _{  }      _{ } _

y(0) =1 başlangıç değerini yerine yazarsak, ⇒

2.4. Bazı Kısmi Türevlerin Kamal DönüĢümü

Bu bölümde bazı kısmi türevlerin Kamal dönüşümünü göstereceğiz

 

K f t_ _ = ∫ =G(v) , t ,

eşitliği kullanılarak bazı kısmi türevlerin Kamal dönüşümü aşağıdaki şekilde elde edilir (Sedeeg ve Mahamoud, 2017).

Örnek 2.5:

 

 

/ 0 , , t v f x t f x t K e dt t t         _  _

 



eşitliğini elde edelim

Çözüm: Kısmi integral uygulanırsa _{ve ∫} ∫ = /

 

 

/ 0 1 lim[ , | , ] 0 t v t v b b e f x t f x t e dt v     



=

 

 

 

1 lim b , , 0 , b e f x b f x _vG x v     =f x

 

, 0 v G x v1

 

,

 

, 1

_{   }

, , 0 f x t K v G x v f x t        _    olarak bulunur. 

 

,

_{ }

, f x t d K G x v x dx        _      

 

 

2 2 2 2 , , f x t d K G x v x dx       _  _{ }   

 

,

 

, n n n n f x t d K G x v x dx       _  _{ }  

Örnek 2.6:

 

 

2 2 , , f x t f x t K K t t t            _  _  _    

    denklemini elde edelim.

( f x t

 

, g x t

 

, t t     _    _  _ diyelim.) =K



g x t

 

,



t         

 





 

/ 0 , , t v g x t g x t K e dt t t              



Kısmi integral uygulanırsa, _ve



g x t

 

,



_{dt dv} t   





1 t/ v e dt du v   _

 

 

/ / 0 1 lim[ g , | ] g , 0 t v t v b b e x t e x d v t t      



 



,



_{ }

1

_{ }

, 0 , g x t K g x v K g x t t          _{ }     

 

 

, , f x t g x t t    olduğundan,

 

,

 

, 0 1

 

, t f x t f x f x t K v K t t t    _ _   _  _  _  _         düzenlenirse

 

 

_{   }

2 1 1 2 , , 0 , , 0 t f x t f x K v v G x v f x t            _  _{  }   o zaman

 

_{ }

_{ }

 

2 2 1 2 , , 0 , , 0 f x t f x K v G x v v f x t t          _  _  

Örnek 2.7:

 

 

0 , t , v f x t f x t K e dt x x  _       _  _

 



eşitliğini elde edelim.

 

0 , t v e f x t dt x  _   



 

,

_

_{ }

_

_{ }

, , f x t d K G x v G x v x dx        _   

olarak elde edilir (Sedeeg ve Mahamoud, 2017). Örnek 2.8:

 

 

2 2 2 2 0 , , tv f x t f x t K e dt x x  _      _  _  



=

 

2 2 0 , tv f x t dt x e    



=



 



2 2 , d G x v dx

 

_

_{ }

_

_{ }

2 2 2 2 , , , f x t d K G x v G x v x dx        _  

olarak bulunur (Sedeeg ve Mahamoud, 2017).

Örnek 2.9: , x , u(x,0) = birinci mertebeden başlangıç değer probleminin çözümünü bulalım. Çözüm:

her tarafın Kamal dönüşümü alınırsa,

 

 

 

 

[ _x , 2 [ _t , , K u x t _ K u x t K u x t _ (2.24)

 

,

_

_{ }

_

, x t d K G x v x dx      _    (2.25)

 

,

 

, K u x t_ _G x v (2.26)

 

, 1

_{   }

, , 0 x t K v G x v u x t        _    (2.27)

(2.25-27) eşitlikleri (2.24) de yerine yazılırsa,

 

1

   

 

, 2 , , 0 ,

G x v  _v G x v u x _G x v

 

_{, 2} 1

 

_{, 2}

   

_{, 0 ,}

G x v  v G x v  u x G x v

) = _{başlangıç değerini yerine yazarsak,}

 

1

 

3

 

, 2 , 2 x , G x v  v G x v  e G x v denklem düzenlenirse,

 

_{, 2} 1

 

_{,  –} 

 

_{,      2} 3x G x v  v G x v G x v  e o zaman,

 

2

 

3 , 1 , 2 x G x v G x v e v    _    _   2 2 1 d 1 x x v v e e

_    _    _{integral çarpanı olarak bulunur. O zaman çözüm,}

 

2 1 3 , 1 x x v v G x v e ce v    _{ }      

 

2 1 1 1 3 1 , [ 1 ] x x v v K G x v K e cK e v      _{ }    _      _{ } _

G(x,v) sınırlı olduğundan olmalı. O zaman çözüm,

 

3 2

, x t u x t  e 

olarak bulunur (Sedeeg ve Mahamoud, 2017).

Örnek 2.10: x t, 0 olmak üzere,

 

 

0, , 0 0, , 0

xx tt t

u u  u x  u x cosx

şeklindeki homojen Laplace denklemini çözelim.

Çözüm: Denkleminde her iki tarafın Kamal dönüşümü alınırsa,

 

_xx [ _tt] 0 K u K u 

 

2

 

1

 

 

, , 0 , 0 tt t K u v G x v v u x u x ve K u

 

_xx G x v

 

, olarak alınırsa;

 

 

2

 

 

, 2 , , , 0 tt t xx u x t  u x t  u x t  G x v 

u( x, 0) = 0 ve başlangıç değerleri yerine yazılırsa,

_{= 0}

_{+ = 0}

2.mertebeden diferensiyel denklemini çözersek;

 

, 2 2 1 v cosx G x v v  

Her tarafın ters Kamal dönüşümü alınırsa,





2 1 1 2 , 1 v cosx K G x v K v  _{ }        _  

 

,



 



u x t  sinht  cosx

olarak bulunur (Sedeeg ve Mahamoud, 2017).

Örnek 2.11: u_t u_xx , u x

 

, 0 sin x l 

 , u

   

0, 1, 0t u t  kısmi diferensiyel denklemini çözelim.

Çözüm: ut uxx Denkleminde her tarafın Kamal dönüşümü alınırsa;

 

t

 

xx K u K u

 

_xx

 

, K u G x v ve K u[ ]_t v G x v1

   

, u x, 0 alınırsa;

 

_xx [ ]_t 0 K u K u 

 

1

   

, ( , , 0 ) 0 G x v  v G x v u x 

 

_, 1

   

_{, , 0 0} G x v v G x v u x 

 

, 0 sin u x x l 

 başlangıç koşulunu yerine koyarsak;

 

1

 

, , G x v v G x v sin x l      

olur. Bu denklem ikinci mertebeden adi diferensiyel denklemdir. Bu denklemin sahip olduğu özel çözüm ise,

 

2 2 sin sin , 1 ₁ x x l l G x v D v _{l v}         _{ }  _{ }          _{  }  



,



2 1 vsin x l G x v v l           → 1

 

, 1 ₂ 1 vsin x l K G x v K v l                _{ }     _{ }   

 

2 , t l u x t e sin x l  _     _{ } 

3. ĠKĠ KATLI KAMAL DÖNÜġÜMÜ

Kamal dönüşümü, bir tür integral dönüşümü yöntemidir. Kamal ve Seedeg, (2016) yılındaki çalışmasında yeni bir integral dönüşümü olan “Kamal dönüşümü” çalışmasını yapmıştır. Diferensiyel denklem uygulamalı matematiğin her alanında merkezi rol oynamıştır. Diferensiyel denklemleri çözmek için çok sayıda farklı teknik vardır. Ama integral dönüşümü en yaygın kullanılanıdır (Seedeg ve ark., 2017). Laplace, Fourier, Mellin, Sumudu, Elzaki ve Aboodh gibi dönüşümlerle ilgili birçok problem çözüldü. Ayrıca bu problemler diferensiyel dönüşüm metodu ile çözülmüştür (Thangavelu ve ark., 2018). Bu makalede Thangavelu ve ark., (2018) ve Aboodh ve ark., (2017) makalelelerinden yola çıkarak iki katlı Kamal dönüşümünü tanımladık. Daha önce iki katlı Sumudu, iki katlı Elzaki, iki katlı Mahgoub, iki katlı Laplace ve iki katlı Aboodh dönüşümleri için çalışmalar yapılmıştır (Perveen ve ark., 2018; Eltayeb ve Kiliçman, 2010; Eltayeb ve Kiliçman, 2013). Bu çalışmada, iki katlı Kamal dönüşümü ilk kez tanımlanmıştır ve fonksiyonun kısmi türevlerinin iki katlı Kamal dönüşümleri elde edilmiştir. Daha sonra iki katlı Kamal dönüşümünü telgraf denklemine uyguladık.

Tanım 3.1.

olmak üzere, f x t yakınsak sonsuz bir seri olarak ifade edilebilen bir

 

, fonksiyon olsun. Bu durumda, için f x t fonksiyonunun iki katlı Kamal

 

, dönüşümü, K₂_f x t

 

, _ ile gösterilmek üzere,

 

 

2 0 0 , , x t u v K f x t e f x t dxdt      _{ }       



(3.1)

şeklinde tanımlanır (Tezcan ve Peker, 2019). Teorem 3.1.







2 1 1 ax bt uv K e au bv       _{ } (3.2) ifadesi geçerlidir.

Ġspat: 2 0 0 1 1 0 0 1 1 0 0 1 0 1 0 1 1 1 t x ax bt v u ax bt x a t b u v t b x a v u t b v t b v K e e e dxdt e e dxdt e e dx dt u e dt au u e dt au u au                    _{ }   _{ }          _{  }  _{  }              _{ }        _{ }        _ _      _{ }       _{ } _     _    













1 v bv    _    elde edilir.

3.1. Bazı Kısmi Türevlerin Ġki Katlı Kamal DönüĢümü

Teorem 3.1.1.

Birinci ve ikinci mertebeden kısmi türevlerin iki katlı Kamal dönüşümü aşağıdaki şekildedir: i) K₂ f 1G u v

 

, G

 

0,v x u       _   (3.3) ii)

 

 

 

2 2 2 2 1 1 , 0, _x 0, f K G u v G v G v x u u  _{  } _    (3.4) iii) K₂ f 1G u v

 

, G u

 

, 0 t v       _   (3.5) iv)

 

 

 

2 2 2 2 1 1 , , 0 _t , 0 f K G u v G u G u t v v  _{  } _    (3.6)

v)

 

 

 

 

2 2 1 1 1 , , 0 0, 0, 0 x t f K G u v G u G v f uv u v  _{   } _{ }    _(3.7) Ġspat: i.

 

 

2 0 0 0 0 , , t x v u t x v u f x t f K e dxdt x x f x t e e dx dt x      _{ }    _  _    _{ } _  _       _{ }   







burada

 

0 , x u f x t I e dx x     



yazılır ve I ya kısmi integrasyon uygulanırsa,

    0 1 , 0, x u I f t u e f x t dx     

_

elde edilir. I yerine yazılırsa,

 

 

0 0 , 1 0, t x v u e e f x x u t t d f t d   _{   }    _  







 

 

0 0 0 1 0, , x t t u v v e f t dt e f x t dxdt u    _{   }      









burada

 

 

0 0 , , x t u v e f x t dxdt G u v    _  _  _   _



ve

 

 

0 0, 0, t v e f t dt G v  _ 



yazılırsa,

 

 

2 1 0, , f K G v G u v x u        _   elde edilir.

ii.

 

 

2 2 2 2 2 0 0 2 2 0 0 , , t x v u t x v u f x t f K e dxdt x x f x t e e dx dt x      _{ }    _  _   _ _  _       _{ }   







burada

 

2 2 0 , x u f x t I e dx x  _{ }  



yazılır ve I ya kısmi integrasyon uygulanırsa,

    0 0, 1 x_u , f t I x t u f x e dx x         

_

elde edilir. I yerine yazılırsa,

 

 

0 0 , 0, 1 t x v u f x t e f e dx dt x t x u  _{ }  _{  }  _ _    







 

 

0 0 0 0, 1 , t x v f t u f x t e dt e dxdt x u x           









burada

 

 

 

0 0 , 1 0, , x u f x t e dx G v G u t v x d u        





yazılırsa,

 

1

 

1

 

0, 0, , x G v G v G u v u u      _  _  

 

 

 

2 2 2 2 1 1 0, 0, , x G v G v G u f K u x   u v   _     elde edilir.

iii.

 

 

2 0 0 0 0 , , t x v u x t u v f x t f K e dxdt t t f x t e e dt dx t      _{ }    _  _       _{ }       _{ }   







burada

 

0 , t v f x t I e dt t     



yazılır ve I ya kısmi integrasyon uygulanırsa,

 

 

0 1 , , 0 t v I f x v e f x t dt     



elde edilir. I yerine yazılırsa,

 

 

0 0 , 1 , 0 x t u v e e f x t v x x d f t d   _{   }    _  







 

 

0 0 0 1 , 0 , x t x u v u e f x dx e f x t dxdt v    _{  }        









burada

 

 

0 0 , , x t u v e f x t dxdt G u v    _  _  _   _



yazılırsa,

 

 

2 1 , 0 , f K G u G u v t v        _   elde edilir. iv.

 

 

2 2 2 2 2 0 0 2 2 0 0 , , t x v u x t u v f x t f K e dxdt t t f x t e e dt dx t      _{ }    _  _   _ _  _       _{ }   







burada

 

2 2 0 , t v f x t I e dt t  _{ }  

    0 1 , , 0 t v f x I t t v f x e dt t         

_

elde edilir. I yerine yazılırsa,

 

 

0 0 , , 0 1 x t u v f x t e f e dt dx t x t v  _{ }  _{  }  _ _    







 

 

0 0 0 , 1 , 0 x t x u v u f f x t e x dx e dxdt t v t    _  _{ }           









burada

 

₂

 

 

0 0 , 1 u, 0 , x t u v f x t e dxdt t f K G G u v t v    _{ }          _  _     





yazılırsa,

 

 

2

 

1 1 , 0 , 0 , t G u G u G u v v v      _  _  

 

 

2

 

2 2 2 1 1 , 0 , 0 , t G u G u t v K f G u v v   _       elde edilir. v.

 

 

2 2 2 0 0 0 0 , , t x v u x t t x v u f x t f K e dxdt x t f x t e e dx dt t x      _ _  _  _     _{ }  _{ }        _{ }    







Kısmi integrasyon uygulanırsa

 

 

0 0 0 , 1 , t x t x v u f x t v u f x t e e dx e e dx dt x v x              _{ }  _  _







 

 

 

0 0 , 1 1 0, , t t x v v u f x t e f t G u v e e dxdt u v x          _  _   



 

1

 

1 1

 

 

0, 0 G , 0 G , G 0, f u u v v u v u      _  _   olur. Buradan,

 

 

 

 

2 2 1 1 1 , , 0 0, 0, 0 x t f K G u v G u G v f uv u v  _{   } _{ }    elde edilir.

3.2. Ġki Katlı Kamal DönüĢümünün Telgraf Denklemine UygulanıĢı

Bu bölümde, iki katlı Kamal dönüşümünü genel doğrusal telgraf denklemine uygulayacağız. Verilen bir kısmi diferensiyel denklemi iki katlı Kamal dönüşümü ile çözmek için Thangavelu ve ark. nın (2018) yılında yapmış oldukları çalışmada iki katlı Mahgoub dönüşümü için kullanılan adımlarının benzerini aşağıdaki şekilde uygulayacağız.

i. Verilen kısmi diferensiyel denkleminin iki katlı Kamal dönüşümü alınır. ii. Verilen denklemin koşullarının tek Kamal dönüşümü alınır.

iii. Koşulların Kamal dönüşümü i) de bulunan denklemin Kamal dönüşümünde yerine yazılır.

iv. Çözümü elde etmek için Kamal dönüşümünün iki katlı tersi alınır.

Örnek 3.1: Genel doğrusal telgraf denklemini düşünelim, 2 c u_xx u_tt au_tbu (3.8) Başlangıç ve sınır koşulları,

 

0, 1

 

, x

 

0, 1

 

u t  f t u t g t (3.9)

 

, 0 2

 

, t

 

, 0 2

 

u x  f x u x g x (3.10)

olan genel doğrusal telgraf denklemini çözelim.

 

 

 

 

 

 

 

 

 

2 2 2 1 1 1 1 , 0, 0, , , 0 , 0 1 , , 0 , x t c G u v G v G v G u v G u G u u u v v a G u v G u bG u v v  _{ } _{  }        _  _   (3.11)

bulunup, (3.9) ve (3.10) un tek Kamal dönüşümü alınarak, elde edilen,

 

0, 1

 

, x

 

0, 1

   

, , 0 2

 

, t

 

, 0 2

 

G v F v G v G v G u F u G u G u eşitlikleri (3.11) de yerine yazılırsa,

 

 

 

 

 

 

 

 

 

2 1 1 2 2 2 2 2 1 1 1 1 , , 1 , , c G u v F v G v G u v F u G u u u v v a G u v F u bG u v v  _{ } _{  }        _  _  

 

2 2

 

2

 

 

 

1 1 2 2 2 2 1 1 , c a c G u v b c G v F v G u F u u v v u v             

 

2 2 2 1

 

2 2 1

 

2 2 2

 

2 2

 

2 2 2

 

2 2 2 2 2 2 , c u v G v c uv F v u v G u u vF u u v aF u G u v c v u avu bu v         elde edilir.

Thangavelu ve ark., (2018) makalesinden yola çıkarak genel doğrusal telgraf denkleminin (3.1) formundaki çözümünü elde etmek için ters iki katlı Kamal dönüşümü

alınırsa,

 

1

 

 

2 , , , u x t K  _G u v _G x t elde edilir. Örnek 3.2: Başlangıç ve sınır koşulları,

 

, 0 x , _t

 

, 0 x u x e u x  e (3.12)

 

0, t , _x

 

0, t u t e u t e (3.13)

Çözüm u_xx u_tt u_t udenkleminde her tarafın iki katlı Kamal dönüşümü alınırsa

 

 

 

 

 

 

 

 

 

 

2 2 1 1 1 1 , 0, 0, , , 0 , 0 1 1 , , 0 , , x t G u v G v G v G u v G u G u u u v v G u v G u G u v G u v v v          (3.14)

bulunup, (3.12) ve (3.13) ün tek Kamal dönüşümü alınarak,

 

, 0 ,

 

, 0 ,

 

0, ,

 

0, 1 t 1 1 x 1 u u v v G u G u G v G v u u v v     _{ }        

elde edilir. Bu bulunanlar, denklem (3.14) de başlangıç ve sınır değerler yerine yazılırsa,

 

 

 

 

2 2 1 1 1 1 1 , , , , 1 1 1 1 1 v v u u u G u v G u v G u v G u v u u v v v v u  uv  u

 

2 2

_

_{ }

_

1 1 1 , 1 1 1 1 v v u G u v u v v v u v v u  _{   } _{ }   _{  }  

 

2 2 2 22 2 2







_

2

_

2



2

_





1 1 , 1 1 u uv v u v v u vu u v G u v u v uv u v             _{ }  

    

, 1 1 1 1 uv u v G u v u v u v        olur.

Doğrusal telgraf denkleminin çözümünü elde etmek için iki katlı ters Kamal dönüşümü alınırsa, u x t

 

, e ex tolup telgraf denkleminin çözümü elde edilir.