ORTAOKUL 5. SINIF MATEMATĠK DERSĠ GEOMETRĠK CĠSĠMLER ÖĞRETĠMĠNDE, MATEMATĠK OYUNLARI KULLANIMININ ÖĞRENCĠ
BAġARISI VE TUTUMUNA ETKĠSĠ
DÖNDÜ YILMAZ
YÜKSEK LĠSANS TEZĠ ĠLKÖĞRETĠM ANA BĠLĠM DALI
MATEMATĠK ÖĞRETMENLĠĞĠ BĠLĠM DALI
GAZĠ ÜNĠVERSĠTESĠ
EĞĠTĠM BĠLĠMLERĠ ENSTĠTÜSÜ
TELĠF HAKKI ve TEZ FOTOKOPĠ ĠZĠN FORMU
Bu tezin tüm hakları saklıdır. Kaynak göstermek koĢuluyla tezin teslim tarihinden itibaren …..(….) ay sonra tezden fotokopi çekilebilir.
YAZARIN
Adı : Döndü
Soyadı : Yılmaz
Bölümü : Ġlköğretim Matematik Öğretmenliği
Ġmza :
Teslim tarihi :
TEZĠN
Türkçe Adı : Ortaokul 5. Sınıf Matematik Dersi Geometrik Cisimler Öğretiminde, Matematik Oyunları Kullanımının Öğrenci BaĢarısı Ve Tutumuna Etkisi
Ġngilizce Adı : Effects Of Using Math Games On Student‟s Achievement And Attitudes
At Geometric Objects Teaching At Secondary School 5th GradeETĠK ĠLKELERE UYGUNLUK BEYANI
Tez yazma sürecinde bilimsel ve etik ilkelere uyduğumu, yararlandığım tüm kaynakları kaynak gösterme ilkelerine uygun olarak kaynakçada belirttiğimi ve bu bölümler dıĢındaki tüm ifadelerin Ģahsıma ait olduğunu beyan ederim.
Yazar Adı Soyadı: ………..
i
JÜRĠ VE ENSTĠTÜ ONAY SAYFASI
Döndü YILMAZ tarafından hazırlanan “Ortaokul 5. sınıf matematik dersi geometrik
cisimler öğretiminde, matematik oyunları kullanımının öğrenci baĢarısı ve tutumuna etkisi” adlı tez çalıĢması aĢağıdaki jüri tarafından oy birliği / oy çokluğu ile Gazi Üniversitesi Ġlköğretim Anabilim Dalı, Matematik Öğretmenliği Bilim Dalı‟nda Yüksek Lisans Tezi olarak kabul edilmiĢtir.
DanıĢman: Yrd. Doç. Dr. Gülay KORU YÜCEKAYA
Ġlköğretim Anabilim Dalı, Gazi Üniversitesi ………. BaĢkan: ………. Üye: ………. Üye: ………. Üye: ……….
Tez Savunma Tarihi: …../…../……….
Bu tezin Ġlköğretim Anabilim Dalı, Matematik Öğretmenliği Bilim Dalı‟nda Yüksek Lisans tezi olması için Ģartları yerine getirdiğini onaylıyorum.
……….
Eğitim Bilimleri Enstitüsü Müdürü ………..
ii
TEŞEKKÜR
Bu çalıĢma Ortaokul 5. Sınıflar Matematik Dersi „Geometrik Cisimler ve Yüzey Alanları‟ alt öğrenme alanlarının oyunla öğretiminin akademik baĢarı ve tutuma olan etkisini araĢtırmak amacıyla yapılmıĢtır.
AraĢtırmaya baĢladığım andan itibaren desteğini, bilgisini ve düĢüncelerini benden esirgemeyen, akademik bilgileri ile bana yol gösteren değerli danıĢmanım ve hocam Yrd. Doç. Gülay KORU YÜCEKAYA‟ya, araĢtırmamın test kısmını geliĢtirmeme yardımcı olan Ölçme ve Değerlendirme Uzmanı Ergün ĠÇÖZ „e, araĢtırmamın uygulama kısmında
kullanılan oyunları hazırlamama etkinlikler kısmını geliĢtirmeme yardımcı olan Pınar Eğitim Kurumları Matematik Zümresi Öğretmenlerine en derin teĢekkürlerimi ve Ģükranlarımı sunarım.
Ayrıca eğitim hayatım boyunca ve bugünlere gelmem için emek sarf eden anneme, babama ve aileme sonsuz teĢekkürlerimi sunarım.
Döndü YILMAZ Ankara-2014
iii
ORTAOKUL 5. SINIF MATEMATĠK DERSĠ GEOMETRĠK CĠSĠMLER ÖĞRETĠMĠNDE, MATEMATĠK OYUNLARI KULLANIMININ ÖĞRENCĠ
BAġARISI VE TUTUMUNA ETKĠSĠ
Yüksek Lisans Tezi Döndü YILMAZ GAZĠ ÜNĠVERSĠTESĠ EĞĠTĠM BĠLĠMLERĠ ENSTĠTÜSÜ
Aralık -2014
ÖZ
Bu araĢtırma; Ortaokul 5. sınıf matematik dersi geometrik cisimler öğretiminde, matematik oyunları kullanımının öğrenci baĢarısı ve tutumuna etkisini incelemek amacıyla yapılmıĢtır. ÇalıĢma 2013–2014 Eğitim-Öğretim yılı Ankara Ġli Çankaya Ġlçesindeki bir ortaokulda okuyan 48 öğrenci üzerinde yapılmıĢtır. AraĢtırmada ön-test, son-test kontrol gruplu deneysel yöntem uygulanmıĢtır. AraĢtırmanın deney grubunda 24, kontrol grubunda ise 24 öğrenci bulunmaktadır. Deney grubunda oyunla öğretim yöntemi, kontrol grubunda ise geleneksel öğretim yöntemi kullanılmıĢtır. Veri toplama aracı olarak araĢtırmacı tarafından hazırlanan baĢarı testi kullanılmıĢtır. BaĢarı testi deney ve kontrol grubuna uygulama öncesinde (ön-test), uygulama sonrasında (son-test) olarak toplam iki kez kullanılmıĢtır. Ayrıca kontrol ve deney grubuna EARGED tarafından geliĢtirilen „Matematik Dersine Yönelik Tutum Ölçeği‟ uygulanmıĢtır. Tutum Ölçeği uygulama öncesinde (ön-test), uygulama sonrasında (son-test) olarak toplam iki kez kullanılmıĢtır. Elde edilen veriler SPSS 20.0 programı ile analiz edilmiĢtir. Verilerin analizi sonucunda, oyun ile öğretim yönteminin kullanıldığı deney grubu ile geleneksel öğretim yönteminin kullanıldığı kontrol grubunun akademik baĢarı ve matematik dersine yönelik tutumları arasında deney grubu lehine anlamlı farklılık bulunmuĢtur. Sonuç olarak geometrik cisimler öğretiminde matematik oyunları kullanımının 5.sınıf öğrencilerin matematik baĢarısını arttırdığı ve derse yönelik tutumu olumlu etkilediği görülmüĢtür. Oyun ile öğretimin matematik derslerinde kullanılması önerilmiĢtir.
Anahtar Kelimeler: Matematik Öğretimi, Oyunla Öğretim, Tutum Sayfa Adedi: 81
iv
EFFECTS OF USING MATH GAMES ON STUDENT’S
ACHIEVEMENTANDATTITUDES AT GEOMETRIC OBJECTS TEACHING AT
SECONDARY SCHOOL 5TH GRADE MATHEMATICS LESSON
MASTER THESIS Döndü YILMAZ GAZĠ UNIVERSITY EDUCATION FACULTY December -2014 Abstract
This research was carried out to investigate the effect of using math games on students‟ achievement and attitudes at geometric objects teaching at secondary school 5th grade mathematics lesson. This study was conducted on 48 students studying at a secondary school of Çankaya district of Ankara Province in 2013-2014 academic year. In this study, experimental methods containing pre-test, post-test control group have been applied. There are 24 students in the experimental group and in the control group, there are 24 students. Teaching with games method was used on the experimental group. In the control group, traditional teaching method was applied. Achievement test prepared by the researcher was used as a means of data collection. Achievement test was applied two times on experimental and control groups as prior to application (pre-test) and after the application (post-test). In addition, 'Attitudes Toward Mathematics Scale‟ developed by EARGED was used on the experimental and control groups. The obtained data were analyzed with SPSS 20.0 program. As a result of data analysis, between the experimental group that teaching with games method was used on and the control group that traditional teaching method was used on , there is a significant difference in favor of experimental group as a means of academic achievement and attitudes towards mathematics.
As a result, it has been shown that the use of math games in teaching of geometric objects increased the 5th grade students‟ achievement in Math and positively affects the attitude towards the course.
Keywords: Mathematics Teaching, Teaching with Games, Attitude Number of Pages: 81
v
ĠÇĠNDEKĠLER
JÜRĠ VE ENSTĠTÜ ONAY SAYFASI ... i
TEġEKKÜR ... ii
ÖZ ... iii
ABSTRACT ... iv
ĠÇĠNDEKĠLER ... v
TABLOLAR LĠSTESĠ... viii
BÖLÜM I ... 1 GĠRĠġ ... 1 1.1. Problem Durumu ... 1 1.2. AraĢtırmanın Amacı ... 3 1.3. AraĢtırmanın Önemi ... 3 1.4. AraĢtırmanın Varsayımları... 4 1.5. AraĢtırmanın Sınırlılıkları ... 4 1.6. Tanımlar ... 4 BÖLÜM II ... 6 KAVRAMSAL ÇERÇEVE ... 6 2.1. Matematik Öğretimi ... 6
2.2.Matematik Öğretimi ve Kuramlar ... 9
2.3.Matematik Öğretimi ve Öğretim Yöntemleri ... 11
2.4. Matematik Öğretimi ve Oyun ... 14
2.5. Matematik Öğretimi ve Tutum... 16
vi
BÖLÜM III ... 23
YÖNTEM... 23
3.1 AraĢtırmanın Modeli ... 23
3.2. Evren ve Örneklem ... 24
3.3. Veri Toplama Araçları ... 24
3.4. Veri Çözümleme Teknikleri ... 27
BÖLÜM IV ... 28
BULGULAR VE YORUMLAR ... 28
4.1. Birinci Alt Probleme ĠliĢkin Bulgular ... 28
4.2. Ġkinci Alt Probleme ĠliĢkin Bulgular ... 28
4.3. Üçüncü Alt Probleme ĠliĢkin Bulgular ... 29
4.4. Dördüncü Alt Probleme ĠliĢkin Bulgular ... 30
4.5. BeĢinci Alt Probleme ĠliĢkin Bulgular ... 30
4.6. Altıncı Alt Probleme ĠliĢkin Bulgular ... 31
4.7. Yedinci Alt Probleme ĠliĢkin Bulgular ... 31
4.8. Sekizinci Alt Probleme ĠliĢkin Bulgular ... 32
BÖLÜM V... 33
SONUÇLAR, TARTIġMA VE ÖNERĠLER ... 33
5.1. Sonuçlar ... 33
5.2. TartıĢma ... 35
5.3. Öneriler ... 38
KAYNAKÇA ... 40
EKLER... 45
EK-1: Matematik BaĢarı Testi ve Cevapları ... 46
EK-2: Matematik BaĢarı Testi Belirtke Tablosu ... 53
EK-3:Matematik Dersine Yönelik Tutum Ölçeği ... 56
vii
EK-5: Ortaokul 5. Sınıf Geometrik Cisimler ve Yüzey Alanları Alt Öğrenme
Alanlarına Ait Eğitim Programı ... 68 EK-6: Oyun Malzemeleri ... 70
viii
TABLOLAR LĠSTESĠ
Tablo 1. AraĢtırmanın Deneysel Deseni ... 23
Tablo 2 AraĢtırmada Kullanılan Deney Deseni ... 24
Tablo 3. Deney ve Kontrol Grubundaki Öğrencilerin Cinsiyet Dağılımı ... 24
Tablo 4. Ön-test Sonuçlarının Gruplara Göre U Testi Sonuçları ... 28
Tablo 5. Son-test Sonuçlarının Gruplara Göre U Testi Sonuçları ... 29
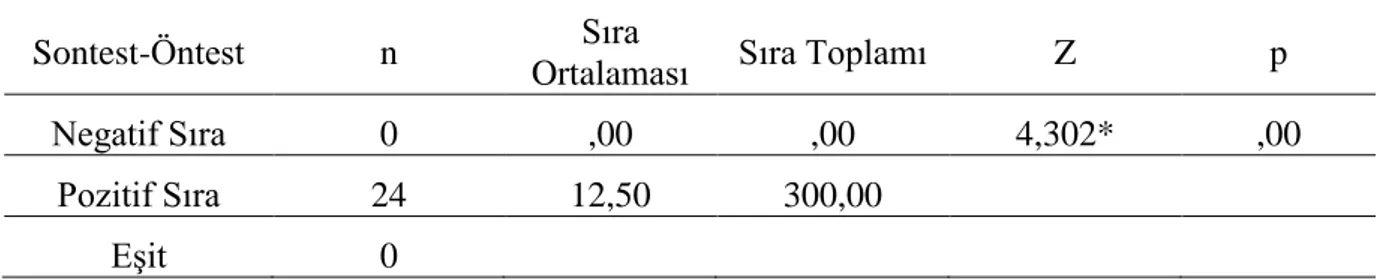
Tablo 6. Deney Grubu BaĢarı Testi Ön ve Son Test Uygulamalarına ĠliĢkin Wilcoxon ĠĢaretli Sıralar Testi Sonuçları ... 29
Tablo 7. Kontrol Grubu BaĢarı Testi Ön ve Son Test Uygulamalarına ĠliĢkin Wilcoxon ĠĢaretli Sıralar Testi Sonuçları ... 30
Tablo 8. Tutum Ölçeği Ön Uygulama Sonuçlarının Gruplara Göre U Testi Sonuçları .. 30
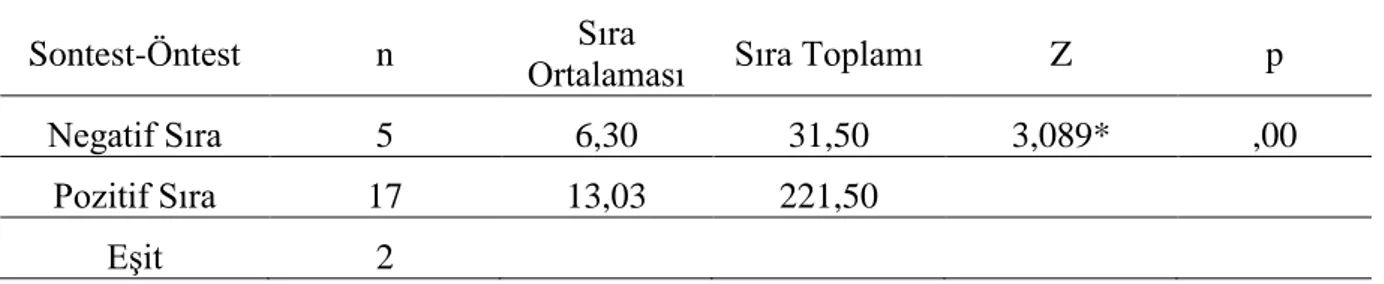
Tablo 9. Tutum Ölçeği Son Uygulama Sonuçlarının Gruplara Göre U Testi Sonuçları . 31 Tablo10. Deney Grubu Tutum Ölçeği Ön ve Son Test Uygulamalarına ĠliĢkin Wilcoxon ĠĢaretli Sıralar Testi Sonuçları ... 31
Tablo 11. Kontrol Grubu Tutum Ölçeği Ön ve Son Test Uygulamalarına ĠliĢkin Wilcoxon ĠĢaretli Sıralar Testi Sonuçları ... 32
1
BÖLÜM I
GĠRĠġ
1.1. Problem Durumu
Ġnsan varoluĢundan bu yana doğayı, evreni ve sırlarını keĢfetme ve kontrol altına alma çabası içerisinde olmuĢtur. Merak ve araĢtırma dürtüleri dinmek bilmeyen insan öğrendiklerini bir yandan kendinden sonra gelenlere aktarabilmek bir yandan da her yeni öğrenme çabasında aynı zorlukları yaĢamamak için bilgilerini sistematikleĢtirme yolunu seçmiĢtir. Bilgilerin sistematikleĢmesi, onlar üzerinde tartıĢabilme ve yorumlamalar yapabilmeyi beraberinde getirmiĢtir. ġüphe götüren ikna edici olmayan ya da herkes için aynı Ģeyi ifade etmeyen noktalarda kesinliği arayan insanoğlu tüm bilimlerin kraliçesi olan matematiğin doğmasını sağlamıĢ ve bu nefes kesici uzun soluklu serüven baĢlamıĢtır (Uğurel, 2003).
DoğuĢundan bu yana matematik bilim ve teknolojiyi yakından etkilemiĢ ve halen etkilemektedir. Bu nedenle bilimin vazgeçilmez bir kaynağıdır. Matematiğin bu kadar önem kazanması aynı zamanda matematik öğretiminin de önemini arttırmıĢtır. Matematik öğretiminde yaĢanan zorlukları aĢmak adına birçok çalıĢma yapılmıĢtır. Geleneksel matematik öğretimi öğrencileri derste sıkmakta, derse karĢı olumsuz tutum sergilemelerine neden olmaktadır. Bu durum öğrencilerin matematik derslerinde baĢarısız olmasına, matematik yapabilme becerisini kazanamamasına neden olmaktadır. Matematik öğretiminde baĢarılı olmanın ve zorlukların aĢılmasında öğrenci yaklaĢımı ve bakıĢ açısı önemli bir yere sahiptir. Öğrenciler kendilerini ifade edemedikleri ve içinde var olmadıkları bir konuyu öğrenmekte zorluk yaĢamaktadırlar (Uğurel, 2003).
Ortaokul düzeyindeki öğrenciler kendilerini oyunla ifade etmeyi tercih ederler. Oyun öğrencilerin çocuk kimliklerinde önemli bir yer tutmaktadır. Hayatlarını bir oyun olarak
2
algılayan öğrencilere matematik tutkusu aĢılamak için matematik oyunlarını yaĢamlarının bir parçası haline getirmek gerekir (Baykul, 2003).
Tutum, en geniĢ anlamda bir bireyin belirli bir objeye veya bir kimseye karĢı zihinsel açıdan hazır oluĢ durumu veya belirli bir biçimdeki vaziyet alıĢıdır (Allport, 1935). BaĢka bir deyiĢle, bireylerin belirli objelere karĢı, geçirdiği çeĢitli deneyimler sonucu düzenli bir tavır alıĢları, davranıĢ biçimleridir ( Baykul, 2003).
Öğrencilerin matematik dersinde olumlu ya da olumsuz tutum oluĢturmalarında öğretim yöntemi önemli bir paya sahiptir. Dolayısıyla, kullanılan matematik öğretim yöntemi öğrencinin matematik dersindeki baĢarısını ve tutumunu etkileyecektir ( Baykul, 2003). Öğrencinin öğretim sürecinde aktif olarak yer alamsı, kendini ifade edebilmesi derse olan tutumunu olumlu yönde etkilemektedir. Oyun ise çocukların kendilerini özgürce ifade edebildikleri bir alandır ( Baykul, 2003). Bu alanın matematik öğretiminde kullanılması ile öğrencilerin derste baĢarı durumlarındaki değiĢim ve derse yönelik tutumlarında oluĢan farklılık bu çalıĢmanın ana konusudur.
Bu konu çerçevesinde, Ortaokul 5. Sınıf matematik dersi geometrik cisimler öğretiminde matematik oyunları kullanımının öğrenci baĢarısı ve tutumuna etkisinin belirlenmesi bu araĢtırmanın problemini teĢkil etmektedir.
Ayrıca çalıĢmanın alt problemleri aĢağıdaki gibidir.
1- Oyun ile matematik öğretiminin yapıldığı deney grubu ile geleneksel öğrenme ortamında öğretim yapılan kontrol grubunun ön test puanları arasında manidar bir fark var mıdır?
2- Oyun ile matematik öğretiminin yapıldığı deney grubu ile geleneksel öğrenme ortamında öğretim yapılan kontrol grubunun son test puanları arasında manidar bir fark var mıdır?
3- Oyun ile matematik öğretiminin yapıldığı deney grubu ön test ve son test puanları arasında manidar bir fark var mıdır?
4- Geleneksel öğrenme ortamında öğretim yapılan kontrol grubu ön test ve son test puanları arasında manidar bir fark var mıdır?
5- Ortaokul 5. sınıf matematik dersi geometrik cisimler öğretiminde matematik oyunları kullanımıyla iĢlenen dersler sonucunda öğrencinin matematik dersine yönelik
3
6- Oyun ile matematik öğretiminin yapıldığı deney grubu ile geleneksel öğrenme ortamında öğretim yapılan kontrol grubu öğrencilerinin öğretim öncesinde matematik dersine yönelik tutumları arasında manidar bir fark var mıdır?
7- Oyun ile matematik öğretiminin yapıldığı deney grubu öğrencilerinin matematik dersine yönelik tutum ön test ve son test puanları arasında manidar bir fark var mıdır?
8- Geleneksel öğretiminin yapıldığı kontrol grubu öğrencilerinin matematik dersine yönelik tutum ön test ve son test puanları arasında manidar bir fark var mıdır?
1.2. AraĢtırmanın Amacı
Bu araĢtırmanın amacı,“Ortaokul 5. sınıf matematik dersi geometrik cisimler öğretiminde, matematik oyunları kullanımının öğrenci baĢarısı ve tutumuna etkisi” hakkında bilgi edinmektir.
Bu araĢtırmanın amacına yönelik, “Oyun yoluyla iĢlenen matematik dersleri sonucunda öğrencilerin matematik dersindeki baĢarılarında nasıl değiĢim oluĢmuĢtur? Oyun yoluyla iĢlenen matematik dersleri sonucunda öğrencilerin matematik dersine yönelik tutumlarında nasıl bir değiĢim gözlenmiĢtir?” sorularının cevapları araĢtırılmıĢtır ve oyunla öğretimin matematik derslerindeki baĢarıya katkısına ve derse yönelik tutuma etkisi araĢtırılmıĢtır.
1.3. AraĢtırmanın Önemi
Bu çalıĢma matematik oyunları ile yapılan matematik öğretiminin Ortaokul 5. sınıf öğrencilerinin matematik tutum ve becerileri üzerine etkisi hakkında fikir edinilmesine katkı sağlayacaktır.
Ülkemizde bu alanda araĢtırmalar yapılmasına karĢın henüz istenilen seviyeye ulaĢılamamıĢtır. Bu nedenle ülkemizde matematik öğretimi alanında yapılan her çalıĢmanın ayrı bir önemi vardır. Bu çalıĢma matematik öğretiminde yaĢanan sıkıntıların giderilmesi ve matematik öğretiminin geliĢimine destek olması açısından önemlidir.Bu açıdan önemlilik arz etmektedir.
4
1.4. AraĢtırmanın Sınırlılıkları
1) AraĢtırma zaman açısından 2012-2013 öğretim yılı ile sınırlıdır.
2) AraĢtırma ekonomik zorluklar, zaman sınırlılığı, ulaĢım zorluğu ve uygulama ile ilgili sorunlar nedeniyle; örneklem açısından Türkiye‟de rastgele seçilen Ankara ili Özel Çankaya Pınar Ortaokulu 5. Sınıf A ve B Ģube öğrencileri ile sınırlıdır.
3) AraĢtırma öğrencilerin Geometrik Cisimler Testi ve Matematik Dersine Yönelik Tutum Ölçeği‟nden elde edilen puanları ile sınırlıdır.
1.5. AraĢtırmanın Varsayımları
AraĢtırmada aĢağıdaki varsayımlar kabul edilmiĢtir.
1) AraĢtırmada kullanılan yöntem ve testler araĢtırmanın amacına ve konusuna uygundur. 2) AraĢtırma sonucu elde edilen veriler araĢtırmayı desteklemektedir.
3) AraĢtırmanın örneklemi evreni temsil etmektedir.
4) Öğrenciler ölçek ve test sorularına samimi cevap vermiĢlerdir.
5) Testteki her yanlıĢ cevap yanlıĢ bilgi sahibi olmayı, boĢ cevap bilgi sahibi olmamayı ifade etmektedir.
1.6. Tanımlar
Bu araĢtırmada kullanılacak olan terimler aĢağıda tanımlanmıĢtır.
Eğitim: Bireyde kendi yaĢantısı yoluyla kalıcı istendik davranıĢ değiĢikliği meydana
getirme sürecidir.
Öğretim: Eğitimin okulda planlı ve programlı yürütülen kısımdır.
Öğrenme: KiĢinin çevre ile etkileĢimi sonucunda meydana gelen kalıcı davranıĢ
değiĢiklikleridir.
5
Öğretim Yöntemi: Bir sorun çözmek, bir deneyi sonuçlandırmak, bir konuyu öğrenmek ya
da öğretmek gibi amaçlara ulaĢmak için bilinçli olarak seçilen ve izlenen düzenli yol[dur] (Hesapçıoğlu, 1992, s.134)
Oyun: Bir ya da birden fazla kiĢinin belli kurallara uyarak, rekabet ederek ya da iĢbirliği
yaparak belli hedefe ulaĢmak için eylemde bulunmasıdır ( Uğurel,2003).
Tutum: Belirli nesne, durum, kavram ya da değer, insanlara karĢı öğrenilmiĢ, olumlu ya da
6
BÖLÜM II
KAVRAMSAL ÇERÇEVE VE ĠLGĠLĠ ARAġTIRMALAR
2.1. Matematik ve Öğretimi
Literatürde matematiğin birden fazla tanımına rastlanmaktadır. Birçoğu matematiğin bir takım özelliklerini ve matematiksel bilginin kullanım alanlarını içermektedir. Tanımların çoğunun tam anlamıyla matematiğin bütününü içermemesinin sebebi matematiğin anlam ve içerik bakımından sınırsız olmasıdır.
“Matematiğin tanımı, kiĢilerin matematiği kullanma amaçlarına, kullanılan matematik konularına, tecrübelerine, matematiğe yönelik tutumlarına ve matematiğe olan ilgilerine göre değiĢiklik göstermektedir.”( Baykul,2000,s.32)
Bu durumda birbirinden farklı matematik tanımının çıkması kaçınılmaz bir durumdur. Belli baĢlı matematik tanımları Ģöyle sıralanabilir.
Matematik bir düĢünceler serüvenidir (Strunk,2002,s.15).
Matematik doğanın insana armağan ettiği ölümsüz tacın yani aklın en göz alıcı pırlantasıdır (Aslan, 2000;99).
Matematik bir toplumda fen, mühendislik ve teknolojinin kullandığı ortak dildir. Bilim ve teknolojinin temelidir ( Ersoy,2000,s.235).
Matematik diziliĢ ve iç uyum ile karakterize edebilen bir sanattır (Pesen,2008,s.2).
Galileo matematiği Ģöyle tanımlar” doğanın büyük kitabı yalnızca onun yazıldığı dili bilenler tarafından okunabilir; o dil matematiktir” ( Uğurel, 2003,s.3).
Baykul‟un matematik için yaptığı tanım grubu Ģöyledir:
1. Matematik problem çözmede kullanılan sayma, hesaplama, ölçme ve çizmedir. 2. Matematik semboller kullanılan bir dildir.
7
3. Matematik, mantıklı düĢünmeyi geliĢtiren bir sistemdir.
4. Matematik, dünyayı anlamamıza, yaĢadığımız çevreyi geliĢtirmemize yardımcıdır. Matematiğin kendine özgü özellikleri vardır. Bu özellikleri bilmek matematiği anlamaya yardımcı olacaktır.
Alkan ve Altun‟a (1998) göre matematik soyuttur ve özgün bir dile sahiptir. Matematik kesin ve Ģüphe götürmez bilgiler ortaya koyan matematik ardıl bir bilimdir ve kendini geliĢtirir.
Matematiğin baĢlıca öğeleri; mantık, sezgi, çözümleme, genellilik, yapı kurma ve estetiktir (Alkan ve Altun,1998, s.5).
Ġlkçağlardan itibaren farklı Ģekillerde tanımı yapılan matematik biliminin öğretimine gelmiĢ geçmiĢ tüm uygarlıklar büyük önem vermiĢtir. Bu nedenle her ülke eğitim programında matematik öğretimi için geniĢ bir yer ayırmıĢtır. Matematik öğretimini etkin hale getirmek isteyen birçok ülkede bu alanda çeĢitli çalıĢmalar ve araĢtırmalar yapılmıĢtır. Ġnsanoğlu var olduğundan bu zamana kadar doğayı anlama, açıklama ve kontrol edebilme adına ürettiği bilim ve teknolojinin geliĢimi için matematiğe ihtiyaç duymuĢtur. Bu nedenle matematiğin önemi iyice kavranmıĢ ve matematik öğretimine daha çok önem verilmiĢtir (Tural, 2005, s. 30-31).
Matematik bilgisi olmayan bir toplum modern bir dünyada söz sahibi olmaz. Çağımızda söz sahibi olmak için matematiğin ve öğretiminin önemi büyüktür ( Blair‟den aktaran Gökaydın,2002).
Matematik bilimlerin temeli olmanın yanı sıra geliĢmiĢliğinde göstergesidir. Matematik alanında iyi olan toplum bilim ve teknolojide ilerlemiĢ toplumlardır. ĠlerlemiĢ toplumların matematik öğretimindeki geliĢmeleri yakından takip etmesi ve özümsemesi kaçınılmaz bir yaklaĢımdır (Rıza‟dan aktaran Tural,2005).
Baykul‟a(2003) göre matematiğin yapısına uygun öğretimin üç ana amacı olmalıdır.
Bunlar; öğrencilerin matematiksel kavramları anlamalarını, matematik iĢlemlerini anlamalarını ve kavramlar ile iĢlemler arasında bağlar kurabilmelerini sağlamaktır.
Matematik öğretiminin genel ve özel amaçları vardır. Öğretim sonunda bu amaçlara ulaĢmak hedeflenmektedir. Talim ve Terbiye Kurulu 2009‟da yayınladığı programda matematik öğretiminin genel amaçları aĢağıdaki Ģekildedir:
8 1. Mantıksal düĢünme becerisi geliĢtirme, 2. Günlük hayatta problemleri çözebilme,
3. Gerekli durumlarda bilgiyi nicel verilerle ortaya koyma alıĢkanlığı kazandırma, 4. SoyutlaĢtırma becerisi kazandırma ve yaratıcığı geliĢtirme,
5. Sezgisel düĢünce becerisini arttırma,
6. Analiz ve sentez yapma becerisini geliĢtirme,
7. Bir problem karĢısında birden fazla çözüm yöntemi kullanabilme, 8. AraĢtırma yapma ve bilgi üretip kullanabilme,
9. Matematik ve sanat arasında iliĢki kurabilme ( TTK, 2009,s. 9-10). Matematiğin genel amaçlarını 5 ana grupta incelemek mümkündür. Toplumsal Amaç: Herkes matematik kullanabilmelidir.
Kültürel Amaç: Matematiğin kültüre katkısının anlaĢılabilmesidir. Teknik Amaç: Matematikçilerin yetiĢtirilmesidir.
Estetik Amaç: Matematiğin özelliklerinin ve güzelliğinin anlaĢılmasıdır ( Ersoy‟dan aktaran Tural, 2005).
Baykul‟a (2003) göre bireyin ortaokul sonunda matematik öğretimi açısından ulaĢması gereken genel amaçlar vardır. Ortaokul matematik öğretimi açısından ulaĢılması gereken genel hedefler Ģu Ģekilde sıralanabilir.
1. Matematik dersine karĢı olumlu tutum geliĢtirebilme, 2. Matematik ve öğretiminin önemini kavrayabilme,
3. Matematik elemanları arasındaki temel iliĢkileri kavrayabilme, 4. Zihinden hesaplama ve dört iĢlem yapabilme,
5. Problem kurabilme ve çözebilme,
6. Ölçü, grafik, plan, çizelge ve cetvel gibi malzemelerden yararlanabilme, 7. Matematik dersinde edinilen bilgi ve becerileri diğer alanlarda kullanabilme,
8. Geometrik Ģekiller arasındaki iliĢkileri kavrayabilme ve alan ve hacimlerini hesaplayabilme,
9. Basit cebirsel ifadeleri yapabilme, 1. Ve 2. dereceden denklem sistemlerini çözebilme,
10. Ġstatistik, olasılık, kombinasyon konularını kavrayabilme, 11. Tümevarım ve tümden gelim yöntemlerini uygulayabilme,
9
12. Yaratıcı düĢünme, akıl yürütme, açık fikirli olma gibi becerileri edinebilme (MEB,2009, s.9-25).
Birçok ülkede olduğu gibi ülkemizde de 1950‟li ve 1960‟lı yılların öğretmen merkezli ve geleneksel öğrenme yöntemi kullanılarak yapılan matematik öğretiminin öğrencilerde problem çözme, analitik düĢünme, akıl yürütme, düĢüncelerini savunma ve ispatlama gibi üst düzey becerileri geliĢtirmediği fark edilmiĢtir. Bu yönde birçok çalıĢma yapılarak öğretmen merkezli öğretimden öğrenci merkezli öğretime geçilmiĢtir (MEB, 2009, s. 12). Bu geçiĢle matematik öğretiminde önemli geliĢmeler olmuĢ ve birçok özel öğretim teknikleri ile öğrenci baĢarıları arttırılmıĢtır. Matematik dersine yönelik olumlu tutum oluĢturulması hedeflenmiĢtir. Matematik öğretimini daha ileri düzeye taĢımak için kuramlardan faydalanılarak birçok öğretim yöntemi kullanılmıĢtır.
2.2. Matematik Öğretimi ve Kuramlar
Ġnsanoğlu çevresi ile etkileĢim içindedir. Bu etkileĢim sayesinde öğrenme gerçekleĢtirilir. Özden‟e göre (1998) öğrenme çevre ile etkileĢim sonucu bireyde oluĢan davranıĢ, düĢünce ve duyuĢ değiĢikliğidir. Öğrenmenin nasıl gerçekleĢtiğine yönelik yapılan araĢtırmalar sonucu kuramlar ortaya çıkmıĢtır. Alkan ve Altun (1998) öğrenmenin iyi tanımlanmasının, öğrenme modellerinin kullanılmasının öğrenmeyi etkili kılacağına belirtmiĢlerdir.
Öğrenme kuramları temel farklılıklarına göre davranıĢçılık, biliĢselcilik, duyuĢsalcılık ve yapısalcılık olmak üzere 4 ana baĢlıkta toplanmaktadır. Bu kuramlar kısaca aĢağıdaki gibidir:
1. DavranıĢçılık kuramı; öğrenmenin uyarıcı ile davranıĢ arasında bir bağ kurularak geliĢtiğini ve pekiĢtirme yoluyla davranıĢ değiĢtirmenin gerçekleĢtiğini kabul eder ( Özden, 1998, s.22).
Geleneksel davranıĢçılar, Aristo‟nun, Descartes‟in, Lock‟un ve Rousseau‟nun öğrenme ile ilgili görüĢlerini temel alarak, Ģartlanan davranıĢı ve istenen tepkiyi oluĢturmak için çevre değiĢimini vurgulamaktadır (Demirel, 2000,s.33).
Bu kuramın baĢlıca temsilcileri Watson, Thorndike ve Skinnerdır. Bu kuramın ilkeleri aĢağıdaki gibidir (Fidan ve Erden‟den aktaran Uğurel, 2003,s.30).
10
2. Öğrenmede pekiĢtirme ve güdüleme önemlidir.
3. Kalıcı öğrenme ve beceri kazanılmasında tekrar önemlidir.
2. BiliĢselcilik kuramına göre öğrenme; gözlenemeyen zihinsel bir süreçtir (Özden, 1998,s.25). BiliĢsel kuram daha çok anlama, düĢünme, duyuĢ ve yaratma gibi kavramlara önem vermektedir. DavranıĢçıların aksine biliĢsel akımın öncüleri öğrencilerin zihinlerinde durumlara göre ilkeler kazandırmayı tercih etmektedirler.
Piaget, Glaser,Bruner ve Bloom bu alanda çalıĢmalar yapmıĢ ünlü bilim adamlarıdır.
BiliĢsel kuramın Öğretim ilkeleri aĢağıdaki gibidir (Fidan ve Erden‟den aktaran Uğurel, 2003,s.30).
1. Yeni bilgiler eski bilgiler üzerine inĢa edilir. Bu nedenle öğretmen ve öğrenciler eski bilgilerin farkında olmalıdır.
2. Öğrenme anlam yüklemek demektir. Bu nedenle konunun detaylarını ve özünü öğrenmeye yönelik düzenlemeler yapılmalıdır.
3. Öğrenciye öğrendiklerini uygulama fırsatı verilmelidir. 4. Öğretmen otoriteden ziyade rehber rolünü üstlenmelidir.
Yukarıdaki maddeler ve açıklamalar göz önünde bulundurulduğunda, matematik zihinsel bir olgu olduğu için matematik öğretiminin en çok etkilendiği kuram olması kaçılmazdır. 3. DuyuĢsalcılık kuramı duyuĢ ve zihin değiĢimine göre öğrenmeyi kiĢinin kendisi yeniden yaratması olarak görmektedir. Öğrenmenin doğasından ziyade sonuçları ile ilgilenmektedir. Benlik ve ahlak geliĢimine önem verir (Özden, 1998,s.29)
DuyuĢsal kuramın baĢlıca öğretim ilkeleri aĢağıda verilmiĢtir:
1. Öğretimin öğrenin özgüvenini arttırması, akademik baĢarı beklentisine sahip olmasını sağlamalıdır (Özden,1998).
2. Öğrenicinin özsaygı geliĢimine yardımcı olmalıdır (Rogers‟tan aktaran Özden, 1998).
3. Öğrenci zayıf ve güçlü yanlarını öğrenmelidir. Benlik tasarımı oluĢturmada öğrenciye yardımcı olmalıdır (Özden,1998).
Yukarıdaki ilkeler düĢünüldüğünde matematik dersine yönelik geliĢtirilen öğrenci tutumu matematik öğretiminde önemli bir yer tutmaktadır. Öğrenci matematik öğretimi sırasında özgüveni desteklenir ve baĢarıları takdir edilirse derse karĢı olumlu tutum sergileyecektir (Özden,1998).
11
4. Yapısalcılık kuramı; bireyin bilgiyi aktarma ve baĢkasının aktardığı bilgiyi olduğu gibi kaydetmekten öte bilgiyi yapılandırmayı vurgulayan bir yaklaĢımdır (Özden,1998).
“Parçaların bir araya getirilerek bir yapının inĢa edilmesi olarak ifade edilen yapısalcılık, bilginin doğası, nasıl kurulduğu bireyin neyi bilip neyi bilemeyeceği konuları üzerinde durur”( Baki ve Bell‟den aktaran Uğurel, 2005, s.60).
Bu yaklaĢımda, öğrenci öğretimin merkezinde bulunurken öğrenci sadece rehber görevi üstlenmektedir. Bu kuramda yeni bilgiler eski bilgilerin üzerine inĢa edilir. Bu yaklaĢımda ön bilgileri harekete geçirme, geliĢime dikkat etme, etkili iletiĢim, uygulama öğrenme sürecinde önemli yer tutmaktadır. BaĢlıca savunucusu Vygotskydir.
BaĢlıca öğrenme ilkeleri aĢağıda verilmiĢtir:
1. Öğrenme aktif bir süreçtir. Bu süreçte öğrenci anlamlı öğrenme gerçekleĢtirir. 2. Anlamlı öğrenme için etkin bir öğrenme dili gereklidir.
3. Öğrenme sosyaldir, bağlamsaldır.
2.3. Matematik Öğretimi ve Öğretim Yöntemleri
Öğretim sürecinde etkili öğretimin gerçekleĢmesi farklı yöntem ve tekniklerin ortaya çıkmasına neden olmuĢtur. Yöntem belli bir amaca ulaĢmak için tutulan yol kullanılan iĢlem olarak tanımlanmaktadır ( Yıldırım‟dan aktaran Uğurel,2005).
Altun (2002); öğretim yöntemini öğretim etkinliklerinde amaca ulaĢmak için kullanılan yol olarak tanımlamıĢtır. Altun (2002)‟a göre yöntemden beklenen; sonuca götürücü, az maliyetli ve tam öğrenmeyi sağlamasıdır. Öğretim yöntemleri bazı kesimlerde strateji ya da teknik olarak adlandırılırken bazı kesimlerde teknik yöntemin alt baĢlığı olarak verilmektedir. Bu durum karıĢıklığa neden olmaktadır (Uğurel, 2005).
Matematik öğretiminde kullanılan yöntemlerden bazıları aĢağıda verilmiĢtir (Altun,2002, s.25-26).
1.Düz anlatım ile öğretim yöntemi: Öğretmen merkezli bir yöntemdir. Öğretmenin bildiklerini karĢı tarafa aktarması suretiyle öğrencilere bilgi vermesidir (Altun, 2002, s. 25). Öğrenci pasiftir. Kalabalık gruplarda etkin kullanılır. Kısa zamanlı bilgi aktarımında, bir konuya dikkat çekerken ve ara özetlerde kullanılabilir. Bu yönteme baĢvurulduğunda uzun konuĢmalardan kaçınılmalıdır. Öğrencilerin kendilerini ifade etmelerine izin verilmeli, açıklamalar net ve anlaĢılır yapılmalıdır (Altun, 2002, s.25).
12
2.Soru- Cevap ile öğretim yöntemi: Öğrencinin aktif olduğu bu yöntemde öğretmen ve öğrenci karĢılıklı iletiĢim içindedir. Bu yöntem ile öğrenciye akıl yürütme becerisi kazandırmak istenmektedir. Bu yöntem kullanılırken, öğretmen soruyu önce sınıf geneline sormalı, daha sonra seçilen bir öğrenciye sormalıdır. Soru seviyesi her düzeyde olmalı, sorunun zorluk derecesine göre cevap süresi verilmelidir. Öğrencinin seviyesine uygun soru seçilmeli ve açık ve anlaĢılır olmasına dikkat edilmelidir. Cevaplar yetersiz ya da yanlıĢ olduğunda düzeltilmeli ve olumlu dönütler verilmelidir ( Altun, 2002,s. 28).
3.BuluĢ yoluyla öğretim yöntemi: Öğretmenin sadece rehber görevi gördüğü öğrenci merkezli bir yöntemdir. Bu yöntemde bir kavram ile ilgili bir bilgi kazandırılırken kavramın tanımı yapılmadan, kavramla alakalı ya da alakasız örnekler bir arada verilir, bu örneklerden kavrama ulaĢmaları beklenir ( Altun, 2002,s. 28).
Bu yöntemin uygulanması esnasında amaçlar ve hedefler açık olmalı, örnekler konuya, öğrenci seviyesine uygun olmalı ve zaman iyi kullanılmalıdır.
4.TartıĢma ile öğretim yöntemi: Öğrencilerin kendi arasında veya öğretmenle belli bir konu hakkında bir amaca ulaĢmak için yaptıkları konuĢmadır. Bu yöntem öğrencilerin dinleme, konuĢma, bir düĢünceyi savunma, yargıya varma, analiz ve sentez yapabilme becerilerini geliĢtirmede faydalıdır ( Altun,2002,s.30).
Öğretim yöntemi kullanılırken uygun tartıĢma ortamı oluĢturmalı, konudan uzaklaĢılmamalıdır. Diğer tekniklerle birlikte rahat kullanılabilen bir yöntemdir ( Altun, 2002,s. 30).
5.Analiz ile öğretim yöntemi : Altun (2002) bu yöntemi bir konuyu bütün basamaklarını sırayla inceleyerek ele alarak anlamayı amaçlayan yöntem olarak tanımlamaktadır.
Teoremlerin ve kuramların öğretiminde kullanılır. Matematiksel yapıları kolay anlaĢılmasına, model oluĢturulmasına, teorem ve kuramların ispatlanmasına yardımcı olur. Yöntem esnasında basamaklar tek tek yapılmalı, her basmakta gerekli açıklamalar yapılmalı, öğrenci seviyesine uygun matematik dili kullanılmalıdır. Öğrencilere uygulama yapma Ģansı verilmelidir ( Altun, 2002,s. 32).
6.Modüller ile öğretim yöntemi : Bir dersin alt konularının uzmanlar tarafından belli bir zaman aralığında iĢlenecek Ģekilde ünitelendirilmesi ile öğretimin sağlanmasını amaçlayan yöntemdir. Konular modüllere ayrılmıĢtır ve her modül sonunda değerlendirme yapma Ģansı
13
vardır. Grup çalıĢması için uygun bir yöntemdir. Uzman tarafından yapıldığında daha etkilidir( Altun, 2002,s. 32).
7.Gösterip yaptırma ile öğretim yöntemi: Bu yöntemde öncelikle ilgili konu, iĢlem veya kazanıma yönelik açıklama ve örnekleme öğretmen tarafından yapılır. Açıklama ve örneklemeden sonra öğrencilerin araĢtırma ve uygulamalar yapması sağlanır. Özellikle matematik ve geometri öğretiminde kullanılırken öğretmen iĢlenen konu, iĢlemi araç gereçlerle beĢ duyu organına hitap edecek Ģekilde örneklemelidir. Uygulamalar sırasında öğrenciye yeterince zaman verilmelidir (Altun, 2002,s. 32).
8.Senaryo ile öğretim yöntemi: Bilgi beceri kazandırmak için gerçek veya hayali ortamlar oluĢturup bu ortamda rol yardımıyla yapılan öğretimdir. Bu öğretimde senaryonun konuya öğrenci seviyesine uygun olmasına, rollerin dikkatli dağıtılmasına, senaryonun uygun olmasına dikkat edilmelidir ( Altun, 2002,s. 32).
9.Proje ile öğretim yöntemi: Herhangi bir konuda bilgi, araç gereç ve benzeri Ģeyleri bir araya getirerek bunlardan yeni bir Ģey oluĢturmayı amaçlayan planlı ve amaçlı çalıĢmadır. Bu çalıĢmalar, araĢtırma yapma, veri toplama bilgileri bir araya getirme ve mantıklı bir sonuç çıkarma alıĢkanlıkları kazandırabilir. Yöntemin kullanımında konu seçimine, öğrenci seviyesine, araç ve gereç seçimine dikkat edilmelidir ( Altun, 2002,s. 33).
10. ĠĢbirlikçi öğrenme yöntemi: Ortak bir amaç için gruplar halindeki öğrencilerin yardımlaĢarak yaptıkları çalıĢmalardır. Her öğrencinin bir görevi vardır. Böylece hem grup olarak hem de bireysel olarak öğrencilere çalıĢma imkânı sunulmuĢtur. Üst düzeyde iletiĢim kurulduğu için tartıĢarak, soru sorarak bilgi alıĢ veriĢi yapıla bilmektedir. Öğrenci aktiftir ve her türlü sınıf ortamında uygulanabilmektedir ( Hacısalihoğlu ve Mirasyedioğlu, 2004,s.27-28).
11.Problem çözme yöntemi: Bu yöntem öğrencilerin analiz, sentez ve genelleme gibi fonksiyonları kullanıp, geliĢtirmesini sağlayarak birer problem çözücü olmalarını hedeflemektedir ( Pesen, 2008,s.66-67).
Polya‟ya göre problem çözmek dört adımdan oluĢmaktadır; problemi anlama, çözüm planı yapma, problem çözme ve çözümü kontrol etme (Pesen,2008,s.69).
Öğrenciler bu yöntemle bağımsız düĢünme, analiz etme, araĢtırma gibi beceriler kazanmaktadır. Bu yöntem uygulanırken problem niteliğine, düzeye uygunluğuna dikkat edilmelidir (Altun, 2002,s.30).
14
12. Oyun ile öğretim yöntemi: Konunun bir takım oyunlar ile eğlenerek, yarıĢarak öğrenilmesini sağlayan yöntemdir. Bu yöntem her seviyeye uygulanabilir. Uygulamalar konuya, süreye ve amaca bağlı olarak bireysel, gruplar halinde yapılabilir. Öğretmen oyun esnasında matematik bilgilerinin yeterli kullanımına dikkat etmelidir. Oyunların kullanılmadan iyi planlanması, konuya göre oyunun hazırlanması, oyunun aĢamalarının belirlenmesi oyunun uygulanmasında kolaylık sağlayacaktır (Uğurel, 2005,s.80).
2.4. Matematik Öğretimi ve Oyun
Oyun “ fiziksel ve zihinsel yeteneklerle, sosyal uyum ve duygusal olgunluğu geliĢtirmek için yapılan kurallı, belli yer ve zaman içinde süregelen eğlenceli etkinliktir”.(Tamer‟den aktaran Tural, 2005;65). Eğitimciler oyunu farklı Ģeklerde tanımlamıĢlardır. Çocuklar oyunlarda kültürel geliĢimini yaĢamaktadır (Yavuzer‟den aktaran Tural, 2005,s.100). Gross‟a göre oyun olgunluk için ön denemelerdir (Özdoğan,2000,s.101). Sel (1985) e göre oyun çocuğun dünyayı tanıma, öğrenme, bir Ģeyler oluĢturma aracıdır, baĢka bir deyiĢle yaĢam tarzıdır. Ünlü düĢünür Monteigne “çocukların oyunu oyun değil, onların en ciddi uğraĢıdır” diyerek oyunun çocuk dünyasındaki önemini vurgulamıĢtır (Tural, 2005,s.68). YetiĢkinlere göre, oyunlar eğlenceli ama amaçsız bir uğraĢtır. Aslında, çocuklar oyunda hareket ve biliĢ düzeylerini ortaya koymaktadırlar (Gander ve Gardiner , 2004, s.278-279).
Oyun, çocukların kendini ifade etme yöntemlerinden biridir. Çocuk dünyayı anlamak, kavramak ve incelemek için oyunu kullanır. Bu sebeple oyun bir öğrenme aracıdır ve çocukların evrensel dilidir. ( Mure ve Kattman‟dan aktaran Tural, 2005).
Çocuğun hayatında önemli bir yere sahip oyunun çocuğun geliĢimine önemli katkıları vardır. Oyun, çocuğun dil, sosyal, duygusal ve zihinsel becerilerini geliĢtirebileceği en önemli durumdur. Oyun aktif ve doğal bir öğrenme ortamıdır (Özdoğan,2000,s.101).
Özbey (2004)‟ e göre oyun çocukların için eğlenceli bir uğraĢtır ve bu nedenle psikolojik, zihinsel geliĢimi sağlamada önemli bir role sahiptir.
Oyun ile öğrenme ile ilgili yapılan bir araĢtırmada, bir grubun problemle ilgili malzemelerle uğraĢması sağlanırken diğer gruba sadece çözüm için yönergeler verilmiĢtir. AraĢtırma sonucunda deney grubunun problemi daha rahat çözdüğü gözlenmiĢtir (Gander ve Gardiner, 2004).
15
Matematik öğretimi ilginç ve eğlenceli olmalıdır. Köroğlu ve YeĢildere (2002)‟ye göre öğrenciler matematik derslerini sevdikleri zaman öğrenme ve motivasyonları artmaktadır. Oyun ile en ilgisiz öğrenciler bile derse katılmaktadır. Öğretim amaçlarından uzaklaĢmadan, öğretimde oyuna yer vermek öğrencinin ilgisini çekecek ve derse tutumunu olumlu etkileyecektir (Tural,2005).
Ġlkokul ve ortaokul çağındaki çocuklar için oyun çok önemlidir. Çünkü oyunlar çocuklara hayal gücünü geliĢtirme fırsatı vermektedir. Genel düĢüncenin aksine oyun derslerden engelleyici değil aksine eğer iyi uyarlanırsa derse ilgi arttırıcıdır. Sonuç olarak çocuk oyunla geliĢir. GeliĢim aĢamasında, öğretim esnasında oyun kullanmak çocuğun geliĢimini arttıracaktır. Oyunun öğretim alanında kullanılması öğretimi daha etkili kılacaktır (Tural,2005).
Öğretimde kullanılan baĢlıca oyunlar Ģunlardır:
Tek baĢına oyun Paralel oyun ĠĢbirliğine dayalı oyun
AlıĢtırmalı oyun Taklit oyunu Kurallı oyun
Sportif oyun Bilgisayar oyunu Yap-boz oyunu
Kart oyunu Lego-tangram oyunu Zekâ- mantık oyunu
Sözcük oyunu Matematik oyunu
Matematik oyunları, matematik derslerinde kullanılan ders için özel geliĢtirilmiĢ oyunlardır. Matematik derslerinin sunulması, kavratılması, pekiĢtirilmesi ve değerlendirilmesi için kullanılmaktadır. Öğretimde kullanılan birçok oyun matematik öğretimi içinde kolaylıkla kullanılabilmektedir (Tural,2005).
Çocuğun hayatında önemli yere sahip oyuna maalesef öğretim sürecinde fazla yer verilmemektedir. Bunun baĢlıca nedenleri fiziki ortam, zaman yetersizliği ve öğretmenlerin oyunun önemini kavramaması ve oyun malzemelerinin yetersizliğidir (Tural,2005).
Oyun için gerekli malzemelerin bulunması, uygun sınıf ortamı sağlanması ve öğretmenlerin gerekli eğitimi almasıyla oyunlar öğretimde etkin bir Ģekilde kullanılabilmektedir. Oyun iyi bir öğretim aracı olup, ilköğretimde bütün alanlarda hem metot hem de öğretim aracı olarak kullanılabilmektedir. Oyunla öğretimin amacı, oyunun zevk ve yarıĢma duygusundan faydalanarak oyuna katılanların fiziksel ve zihinsel yeteneklerini geliĢtirmektir. Ortaokulda
16
öğrenciler düĢünerek değil deneyimlerine dayanarak öğrenmektedir. Oyunla öğretim sonucunda, öğrenilenler hafızada daha iyi kalır, öğrencinin mukayese ve karar verme becerisi artmaktadır. Öğrenci davranıĢları olumlu yönde etkilenmektedirler. ( Aracı‟dan aktaran Tural,2005,s. 89).
Oyunla öğretim öğrencinin dikkatini kolayca ders toplamasında faydalı olmaktadır. Matematik derslerinde öğrenciler konudan çabucak uzaklaĢmakta yapamayacakları bir konu olduğunda zihinlerini baĢka Ģeylerle meĢgul etmektedir. Böylelikle dersten tamamen kopmaktadır. Oyun ile matematik öğretiminde öğrenci derste dikkatini daha rahat toplayabilmektedir (Tural,2005).
2.5. Matematik Öğretimi ve Tutum
Tutum ile ilgili birçok görüĢ mevcuttur, bunlardan bazıları aĢağıda verilmiĢtir:
Özgüven (2011) „e göre tutum “bireylerin belirli bir kiĢiyi, grubu veya düĢünceyi kabul ya da reddetmesi Ģeklinde gözlenen, duygusal hazır oluĢ hali ve eğilimidir”.
Tutum, beyindeki zihinsel bir durumdur, olaylara zihnen bakıĢtır (Özgüven, 2011).
Allport‟a göre tutum; birey bir nesne ve duruma verdiği tepki üzerinde yönlendirici etkisi bulunan deneyimler sonucu oluĢmuĢ ve ĢekillenmiĢ zihinsel ve sinirsel hazır bulunma durumudur ( Bilgin, 1996).
Bireyler, çevrelerinde meydana gelen olaylara bir anlam yüklerler. Bu anlamlar bireysel deneyimler olarak yansıtılır. Bu deneyimler sonucunda inançlar ve yaklaĢımlar oluĢur. Bu yaklaĢım ve inançların tümü tutumdur ( Yenilmez ve Özabacı, 2003).
Tutum birbiri ile uyumlu düĢünce, duygu ve davranıĢ öğelerinden oluĢmaktadır. DuyuĢsal öğe, kiĢinin tutum konusunda gösterdiği duygusal tepkilerdir. Derse mutlu veya mutsuz gelme, derse katılmada istek veya isteksizlik örnek olarak verilebilir. BiliĢsel öğe, kiĢinin tutum konu hakkında oluĢturduğu inançlardır. Matematik dersinin zor olduğuna, öğretmenin düĢük not verdiğine dair inançlar örnek olabilir. DavranıĢsal öğe, tutum konusuna yönelik hareketlerdir. Derse devamsızlık yapma, ödev yapmama gibi davranıĢlar örnek verilebilir. (Tural,2005).
Tutumun bazı özellikleri vardır:
17
Tutumlar doğrudan gözlemlenemez, davranıĢlardan çıkarım yapılabilir.
Tutum süreklilik göstermektedir.
Tutum hem sosyal hem de kiĢisel özelliğe sahiptir ( TavĢancıl,2002).
Bireylerin tutumlarını doğrudan gözlemlemek mümkün değildir. Thurstone (1929) tutumların kanılar aracılığıyla ölçülebildiğini belirtmiĢtir. Bireylerin davranıĢlarının tutumlardan kaynaklandığı düĢünülmektedir. Bu kanı tutumların ölçülebileceğini göstermektedir ( Özgüven, 2011).
Tutum doğrudan ölçülemez, davranıĢlardan çıkarılabilir. Soru cevaplama sözel bir davranıĢtır. Bu amaçla geliĢtirilen baĢlıca ölçme tekniği tutum ölçekleridir (Çetin, 2003). Tutum ölçeklerinin baĢlıca kullanım amaçları aĢağıdaki gibidir (TavĢancıl,2002):
Bireylerin belirli bir tutum ve değerlerinin belirlenmesi,
Bireylerde gözlemlenen tutum ve değer yargılarını etkileyen aile ve çevre faktörlerinin incelenmesidir.
AraĢtırmada kullanılan Likert Tipi ölçek olduğu için bu ölçek tipi hakkında kısaca bilgi verilmiĢtir.
Rensis Likert tarafından geliĢtirilen ölçekte, tutumları ölçülen bireylerin tepkide bulunacakları ifadeler yer almaktadır. Bu ölçekte birey benimsediği ifadeyi benimsemek yerine her ifadeye ne ölçüde katıldığını derecelerle belirlemektedir ( TavĢancıl, 2002). Her bir derece belli bir puana sahiptir ve ölçek puanı bu derece puanlarının toplanmasıyla oluĢur. Bu ölçekte bir objeye ait tutumlarla ilgili olumlu ve olumsuz cümleler yer almaktadır. En pratik olanı beĢli ölçektir ve bu araĢtırmada beĢli ölçek kullanılmıĢtır ( TavĢancıl, 2002).
Matematik dersine yönelik tutum “ matematiği sevme ya da sevmeme, matematiksel faaliyetlere katılma veya onlardan kaçma eğilimi, matematikte iyi veya kötü olacağına dair inancın toplam ölçüsü” olarak tanımlanmaktadır ( Neale‟den aktaran Akgün,2002).
Bloom(1998)‟ a göre bir öğrencinin bir konuyu iyi bir Ģekilde öğrenebilmesi için öğrenmeye karĢı istek duyması gerekmektedir. Öğrencinin matematik dersine yönelik olumlu tutumu olmadığı sürece matematik dersinde baĢarılı olması güçtür. Matematik dersinde ilerleyen öğrencilerin, öğrenim hayatlarının baĢından itibaren derse karĢı olumlu tutum sergiledikleri, dersi sevdikleri ortaya çıkmıĢtır ( TavĢancıl, 2002).
18
2.6. Ġlgili AraĢtırmalar
Uğurel (2003)‟ in yaptığı çalıĢmada ortaöğretimde oyun ve etkinliklerle matematik öğretimine iliĢkin öğretmen adaylarının ve öğretmenlerinin görüĢleri araĢtırılmıĢtır. ÇalıĢma 2002-2003 eğitim öğretim yılında Dokuz Eylül Üniversitesi Buca Eğitim Fakültesi Ortaöğretim Matematik Öğretmenliği bölümünde öğrenim görmekte olan 226 matematik öğretmen adayı ve Ġzmir ili merkez ilçelerinde farklı sosyo-ekonomik yapıya sahip liselerde görev yapmakta olan 44 matematik öğretmeni üzerinde yapılmıĢtır. Anket, gözlem, görüĢme ve doküman analizi yöntemleriyle araĢtırmanın verileri toplanmıĢtır. AraĢtırmanın sonuçları ile ortaöğretim matematik öğretmen adayları ve öğretmenlerinin matematik öğretiminde oyun ve etkinlik kullanımı hakkındaki görüĢleri ortaya çıkarılmıĢtır.
Çuha (2004) „nın çalıĢmasında ilköğretim 6. sınıf matematik dersi “Kesirler” ünitesinin iĢleniĢinde eğitsel oyun destekli öğretimin; baĢarı, akademik benlik, baĢarı güdüsü ve kalıcı izli davranıĢ değiĢikliği üzerine etkisi araĢtırılmıĢtır. AraĢtırmada deneysel yöntemin kontrol gruplu ön test- son test deseni kullanılmıĢtır. Kontrol grubunda geleneksel öğretim sürdürülürken; deney grubunda eğitsel oyun destekli öğretim uygulanmıĢtır. AraĢtırmada baĢarı testi, akademik benlik kavramı ölçeği ve baĢarı güdüsü ölçeği kullanılarak veriler toplanmıĢtır. AraĢtırma sonucunda ilköğretim 6. sınıf matematik dersinde eğitsel oyun destekli öğretimin uygulanmasının öğrencinin baĢarı durumunun olumlu etkilendiği bulunmuĢtur. Yapılan ön test ve son test ortalamaları farkları göz önünde bulundurulduğunda Ġlköğretim 6. sınıf matematik dersinde eğitsel oyun destekli öğretimin öğrencinin baĢarı güdüsünü arttırdığı ve öğretimin daha kalıcı olduğu bulunmuĢtur.
Tural (2005) araĢtırmasında ilköğretim matematik öğretiminde oyun ve etkinliklerle öğretimin, geleneksel öğretime göre, öğrencilerin eriĢleri ve matematik dersine iliĢkin tutumları üzerine etkisini araĢtırmıĢtır. AraĢtırmada ön test son test modeli kullanılmıĢtır. AraĢtırma 2004- 2005 öğretim yılı bahar döneminde beĢ hafta boyunca Ġzmir ili Buca Ġlçesi Kaynaklar Ġlköğretim okulu 3. sınıflarda “ritmik saymalar, doğal sayılar, toplama, çıkarma, çarpma ve bölme” konularında yapılmıĢtır. AraĢtırma sonucunda elde edilen bulgulara göre Oyun ve Etkinliklerle Öğretim‟in uygulandığı deney grubu ile Geleneksel Öğretim‟in uygulandığı grubun eriĢi düzeyleri ve matematik dersine iliĢkin tutumları arasında deney grubu lehine anlamlı farklar bulunmuĢtur.
19
Altunay (2004)‟ın yaptığı araĢtırmanın amacı oyunla desteklenmiĢ matematik öğretiminin, öğrencilerin Matematik dersindeki baĢarılarına ve öğrenilenlerin kalıcılığına etkisini belirlemektir. 2002-2003 öğretim yılında Ankara ili Keçiören ilçesinde 23 Nisan ilköğretim Okulu‟nda öğrenim gören öğrenciler arasından 36 sı deney grubu, 31 i kontrol grubu olmak üzere 67 öğrenci seçilmiĢtir. 4. Sınıf Matematik Dersi Programı VII ve VIII Üniteleri geometri konularına iliĢkin hedef ve davranıĢların öğretimi sırasında, konular öğretmen tarafından açıklanmıĢ ve oyunlarla desteklenmiĢtir. AraĢtırmada ön test son test modeli kullanılmıĢtır. AraĢtırma sonucunda, oyunla desteklenmiĢ matematik öğretiminin öğrencilerin matematik baĢarılarında etkili olduğu ve öğrenilenlerin kalıcılığını olumlu yönde etkilediği sonuçlarına ulaĢılmıĢtır.
Songur (2006) tarafından yapılan araĢtırmadaoyun ve bulmacalarla iĢlenen matematik dersinin ilköğretim 8. sınıf öğrencilerinin baĢarı ve kalıcılık düzeylerine etkisi araĢtırılmıĢtır. AraĢtırma 2005-2006 eğitim öğretim yılında Ġstanbul ili GaziosmanpaĢa Ġlçesi Boğazköy okuyan tüm 8. sınıf öğrencileriyle yapılmıĢtır. AraĢtırmada öğrencilerin 8. sınıf matematik derslerinde harfli ifadeler ve denklemler konularında oyun ve bulmacalarla öğretim yönteminin akademik baĢarıya ve hatırlamaya etkisi ile oyun ve bulmacalarla öğretim yönteminin öğrencilerin matematik dersine karĢı tutumunu nasıl etkilediği araĢtırılmıĢtır. Ayrıca çalıĢmanın bitiminde 6 hafta sonra kalıcılık testi uygulanmıĢ ve yapılan etkinliklerin baĢarıya, matematik tutumuna ve kalıcılığa etkisi değerlendirilmiĢtir. Bu araĢtırmada elde edilen bulgulara dayanarak Ģu sonuçlar çıkarılmıĢtır: Ġlköğretim 8. sınıf matematik öğretiminde oyun ve bulmacalarla öğretim yöntemiyle iĢlenen matematik dersi ile düz anlatım yöntemiyle iĢlenen arasında, oyun ve bulmacalarla öğretim yöntemiyle iĢlenen matematik dersi lehine anlamlı bir farklılık bulunmuĢtur. Oyun ve bulmacalarla öğretim yönteminin uygulandığı deney grubu ile düz anlatım yönteminin uygulandığı kontrol grubu öğrencilerinin hatırlama düzeyleri arasında yapılan t testi sonuçlarında deney grubu lehine anlamlı bir fark olduğu belirlenmiĢtir. Ġlköğretim 8. sınıf matematik öğretiminde oyun ve bulmacalarla öğretim yöntemiyle iĢlenen matematik dersleri öğrencilerin matematiğe karĢı tutumlarını olumlu yönde etkilemektedir. Ġlköğretim 8. sınıf matematik öğretiminde oyun ve bulmacalarla öğretim yöntemiyle iĢlenen matematik dersleri öğrencilerin matematikte algılanan baĢarı düzeylerini artırmıĢtır. Ġlköğretim 8. sınıf matematik öğretiminde oyun ve bulmacalarla öğretim yöntemiyle iĢlenen matematik dersleri öğrencilerin matematiğin algılanan yararları üzerinde etkili olmuĢtur. Ġlköğretim 8. sınıf matematik öğrencilerinin matematik dersindeki akademik baĢarıları cinsiyete göre değiĢiklik göstermemektedir.
20
Altınsoy (2007)‟un deneysel çalıĢmasında takım- oyun turnuvaları tekniğinin ilköğretim dördüncü sınıf matematik dersinde öğrencilerin akademik baĢarıları ve derse iliĢkin tutumları üzerine etkisi olup olmadığı araĢtırılmıĢtır. Takım- oyun tekniği araĢtırmanın bağımsız değiĢkeni olurken matematik baĢarısı ve matematik dersine iliĢkin tutum ise bağımlı değiĢkenleri oluĢturmaktadır. AraĢtırma ön test ve son test kontrol gruplu deneme modelinde tasarlanmıĢtır. Nitel verilerin toplanmasında deney grubunda yer alan öğrencilerin sürece iliĢkin görüĢlerini belirlemeye yönelik yarı yapılandırılmıĢ görüĢme formu kullanılmıĢtır. GörüĢme formunda elde edilen veriler nitel araĢtırmalarda kullanılan içerik analizi yöntemiyle çözümlenmiĢtir. AraĢtırmada sonunda elde edilen verilere göre, baĢarı testi ve tutum ölçeği son test puanları açısından deney grubu lehine istatistiksel olarak anlamlı bir fark bulunmamıĢtır. BaĢarı testi ve tutum testi ölçeği kalıcılık puanları açısından da deney grubu lehine anlamlı bir fark bulunmamıĢtır.
Kılıç (2007) çalıĢmasında oyunla öğretim yönteminin, ödülle birlikte uygulandığı durumlarda öğrencilerin 1. sınıf matematik dersindeki baĢarı düzeylerinde olabilecek etkilerin incelenmesi araĢtırılmıĢtır. Bu amaçla Ġstanbul Özel Sevgi Çiçeği Anafen Ġlköğretim Okulunun 1. sınıflarından iki sınıf, deney ve kontrol grubu olacak Ģekilde seçkisiz olarak belirlenmiĢtir. Örneklem grubunu oluĢturan toplam öğrenci sayısı 48‟dir. Bu araĢtırmada elde edilen bulgulara dayanarak ortaya çıkan sonuçlar Ģunlardır. Oyunla matematik öğretimi geleneksel yöntemlere göre daha yüksek matematik baĢarısı getirebilmektedir. Oyunla matematik öğretiminde ödüller olumlu rol oynamaktadır.
Dinçer (2008)‟in yaptığı çalıĢmanın amacı; ilköğretim ikinci sınıfların matematik dersinde, müziklendirilmiĢ matematik oyunlarıyla yapılan öğretimin akademik baĢarı ve tutuma etkisinin ne olduğunu belirlemektir. AraĢtırmada örneklem ve kontrollü, ön test ve son test modeli kullanılmıĢtır. AraĢtırma, Bolu ili Merkez okullarından 60. Yıl Ġlköğretim okulunun 58 öğrencisi üzerinde yapılmıĢtır. AraĢtırmada geleneksel matematik öğretimine göre müziklendirilmiĢ matematik oyunlarıyla yapılan matematik dersinin öğrenci baĢarısı açısından daha etkili olduğu, matematik dersinde müziklendirilmiĢ matematik oyunlarıyla yapılan öğretimin öğrencilerin derse iliĢkin tutumlarını arttırmada, geleneksel öğretime göre daha etkili olduğu sonucuna varılmıĢtır.
Gökçen (2009) tarafından yapılan araĢtırmanın amacı, ilköğretim 6. sınıf matematik dersinde oyun ile öğretim yönteminin öğrencinin matematik baĢarısına olan etkisini belirlemektir. Bu temel amaç çerçevesinde Ortak Katlar ve Bölenler konusu oyun temelli yöntemle iĢlenmiĢ ve bu yöntemin geleneksel yöntemle arasındaki baĢarı ve kalıcılık yönünden farkı
6
7
21
incelenmiĢtir. ÇalıĢma evrenini 2008-2009 eğitim- öğretim yılında Çanakkale ili Eceabat ilçesindeki Alçıtepe ve Köprülü Hamdi Bey Ġlköğretim okulu 6. sınıf öğrencileri (40 kiĢi) oluĢturmaktadır. AraĢtırmada elde edilen verilerin analizi sonucunda oyun ile öğretim yönteminin akademik baĢarı ile elde edilen kazanımların kalıcılığı üzerine olumlu bir etkisi olduğu görülmüĢtür.
Kılıç (2010)‟ın çalıĢmasında “1. sınıf matematik dersindeki iĢlem becerilerinin kazandırılmasında oyunla öğretimin baĢarıya etkisi” araĢtırmıĢtır. ÇalıĢma, Ġzmir ili Çiğli ilçesi Büyük Çiğli Ġlköğretim Okulu 1. sınıf öğrencilerinin katılımıyla gerçekleĢtirilmiĢtir. ÇalıĢma, deneysel bir çalıĢma olup kontrol gruplu ön-test, son-test deneysel desen kullanılmıĢtır. ÇalıĢmanın örneklemini 46 öğrenci oluĢturmaktadır. ÇalıĢmada elde edilen verilere dayanarak Ģu sonuçlara ulaĢılmıĢtır. Oyunla öğretimin uygulandığı deney grubu ile geleneksel öğretim yaklaĢımının uygulandığı kontrol grubu öğrencilerinin baĢarı testi puanları arasında anlamlı farklılık vardır. Oyunla öğretimin uygulandığı deney grubu öğrencilerinin baĢarı düzeylerinde geleneksel yönteminin kullanıldığı kontrol grubu öğrencilerine göre artma gözlenmiĢtir.
Aksoy (2010) tarafından yapılan araĢtırmada; ilköğretim 6. sınıf matematik dersi kesirler ünitesinin oyun destekli öğrenme yaklaĢımı ile öğretiminin öğrenci baĢarısına ve tutumuna etkisi incelenmiĢtir. ÇalıĢma, 2009- 2010 eğitim-öğretim yılında Ankara Ġli Sincan Ġlçesi‟nde bulunan bir ilköğretim okulunda öğrenim gören toplam 70 öğrenci ile gerçekleĢtirilmiĢtir. AraĢtırmada ön-test, son-test ve kalıcılık testi olmak üzere üç tekrarlı ölçüm üzerine kurulu kontrol gruplu deneysel araĢtırma modeli kullanılmıĢtır. AraĢtırma sonucunda; oyun destekli öğrenmelerin öğrencilerin kazanımlara iliĢkin baĢarılarını, öz-yeterlilik algılarını ve matematik dersine yönelik tutumlarındaki geliĢimleri etkilediği görülmüĢtür. Bununla birlikte baĢarı geliĢimleri ile tutum, öz- yeterlik geliĢimleri arasında istatiksel olarak anlamlı iliĢki olduğu görülmüĢtür.
GüneĢ (2010)‟in çalıĢması; ilköğretimin ikinci kademesinde matematik öğretimi sürecinde oyun ve etkinlik kullanımının, öğretmenlerin görüĢleri ıĢığında olumlu ve olumsuz yönlerini ortaya koymak, uygulamadaki aksaklıkları tespit ederek buna uygun çözüm önerileri sunmak amacıyla yapılmıĢtır. Bu çalıĢmanın örneklemini 2009-2010 eğitim öğretim yılında Kars Ġl Milli Eğitim Müdürlüğü‟ne bağlı ilköğretim okullarının ikinci kademesinde matematik derslerine giren 43 bayan, 42 erkek olmak üzere 85 öğretmen oluĢturmaktadır. AraĢtırma; öğretmenlerin ilköğretim ikinci kademe matematik derslerinde oyun ve etkinliklerin kullanımını uygun bulduklarına ancak bazı sorunlarla karĢılaĢtıklarına iĢaret
22
etmektedir. Bulgular aynı zamanda gösteriyor ki, öğretmenler okul imkânlarının ve müfredatın oyun ve etkinlik kullanımına uygun hale getirilmesi, hizmet içi eğitim alınması gibi düzenlemelerle bu yöntemin çok daha verimli hale geleceğini de düĢünmektedirler. ÇalıĢmanın sonucunda birtakım öneriler sunulmuĢtur.
Kavasoğlu (2010)‟nun çalıĢmasında ilköğretim 6,7 ve 8. sınıf matematik dersinde olasılık konusunun oyuna dayalı öğretiminin öğrenci baĢarısına etkisini incelemek amaçlanmıĢtır. ÇalıĢma 2008-2009 eğitim öğretim yılında beĢ hafta boyunca Ankara Ġli Çubuk Ġlçesi‟nde bulunan bir merkez ilköğretim okulunda öğrenim gören toplam 200 öğrenci ile gerçekleĢtirilmiĢtir. AraĢtırmada kontrollü ön test ve son test deneysel araĢtırma modeli kullanılmıĢtır. AraĢtırma sonucunda elde edilen bulgulara göre, oyuna dayalı öğretimin uygulandığı deney grubu lehine anlamlı farklar bulunmuĢtur.
HoĢgör (2010)‟ün çalıĢmasında “Ġlköğretim 1. sınıf öğretmenlerinin matematik derslerinde oyun etkinliklerinin kullanımına iliĢkin görüĢleri” incelenmiĢtir. AraĢtırma nitel bir araĢtırma olup veri toplamak için görüĢme tekniği kullanılmıĢtır. ÇalıĢma grubunu Adana Ġli merkez ilçelerinde (Çukurova, Yüreğir) Milli Eğitim Bakanlığı‟na bağlı resmi ilköğretim okullarının birinci sınıfında görev yapan 20 sınıf öğretmeni oluĢturmuĢtur. Veriler, araĢtırma kapsamında geliĢtirilen yarı yapılandırılmıĢ görüĢme formlarının incelenmesi ile toplanmıĢtır. AraĢtırmalardan elde edilen bulgular göre, öğretmenlerin hepsi matematik öğretiminde oyunları kullanmaktadır. Ayrıca öğretmenlerin matematik dersinde oyun kullanımına iliĢkin olumlu görüĢleri olduğu ancak, uygulama sırasında bazı sorunlar yaĢadıkları görülmüĢtür. AraĢtırmanın sonunda bu sorunların giderilmesine yönelik önerilere de yer verilmiĢtir.
23
BÖLÜM III
YÖNTEM
Bu bölümde araĢtırmanın modeli, evren ve örneklemi, veri toplama teknikleri, uygulama, verilerin toplanması ve verilerin analizi açıklanmıĢtır.
3.1. AraĢtırmanın Modeli
Ortaokul matematik öğretiminde oyun ile öğretim uygulamalarının matematik dersindeki baĢarıya ve tutuma etkisini belirlemenin amaçlandığı bu araĢtırma deneysel yöntemle yürütülmüĢtür. AraĢtırma var olan bir durumu doğal koĢulları içerisinde betimlemektir. Söz konusu durum hakkında genel bir yargıya varabilmek amacıyla evreni temsil ettiği düĢünülen bir örneklem üzerinde çalıĢılmıĢtır. AraĢtırmanın modeli kontrollü ön-test son-test deneysel araĢtırma modeli olarak ifade edilebilir. Bu modelde, yansız atama ile oluĢturulmuĢ iki grup bulunmaktadır. Bu gruplardan biri deney, diğeri kontrol grubu olarak atanmıĢtır. Grupların her ikisinde de deney öncesi ve deney sonrası ölçmeler yapılmıĢtır. Modelde uygulanan ön-testler, grupların benzerlik derecelerinin belirlemesine ve son-testler sonuçlarının buna göre düzeltilmesine yardım eder. Modelin simgesel görünümü Tablo 1 ve Tablo 2‟de verilmiĢtir ( Karasar, 2002,s.97).
Tablo 1. AraĢtırmanın Deneysel Deseni G1 R O 1.1 X O1.2
G2 R O2.1 O2.2
Tablo 2. AraĢtırmada Kullanılan Deney Deseni
Gruplar Ön test Deneysel ĠĢlem Son test
24
3.2. Evren ve Örneklem
Bu araĢtırmada, kuramsal bir öğretim modelini desteklemek için deneysel desen kullanıldığından Ankara Ġli Çankaya Ġlçesindeki Ortaokulları çalıĢma evreni olarak kabul edilmiĢtir. AraĢtırma örneklemi Ankara Ġli Çankaya Ġlçesi‟nde özel bir okulun 5. Sınıf öğrencileri oluĢturmaktadır. Bu araĢtırma, 2013-2014 eğitim öğretim yılının ikinci yarısında 4 haftalık dönem boyunca 48 öğrenci ile matematik derslerinde yürütülmüĢtür. Tablo 3‟te öğrenci sayıları verilmiĢtir.
AraĢtırma, öğrencilerin bir önceki ders yılı not ortalamaları ve cinsiyetleri göz önüne alınarak, baĢarı, cinsiyet ve sayı yönünden birbirine denk iki grup oluĢturulmuĢtur. Yansız atama ile bu iki gruptan biri deney diğeri ise kontrol grubu olarak seçilmiĢtir
.
Tablo 3.Deney ve Kontrol Grubu Öğrencilerinin Cinsiyetlerine Göre Sayıları
Gruplar Kız Erkek Toplam
Deney 12 12 24
Kontrol 12 12 24
3.3. Veri Toplama Araçları
AraĢtırma denenicilerinin sınanması için gerekli olan veriler, araĢtırmacı tarafından geliĢtirilen dört seçenekli çoktan seçmeli “ Geometrik Cisimler Konulu Matematik BaĢarı Testi” ve EARGED tarafından geliĢtirilmiĢ “ Matematik Dersine Yönelik Tutum Ölçeği” ile elde edilmiĢtir.
BaĢarı testi, ön-test ve son-test olmak üzere, deneysel iĢlemin baĢında ve sonunda öğrencilere iki kez kullanılmıĢtır. BaĢarı testinin hazırlanması, geliĢtirilmesi ve uygulanması sürecinde göz önünde bulundurulan ilkeler ve yapılan iĢlemler aĢağıda belirtilmiĢtir:
Ortaokul 5. Sınıf matematik dersi geometrik cisimler konusu ile ilgili hedef davranıĢlar gözden geçirilmiĢtir.
25
Ölçülmek istenen her kazanım ve davranıĢın yoklanabilmesi için çoktan seçmeli en az dört soru seçilerek ön deneme formu hazırlanmıĢtır
Ön deneme testi toplam 45 sorudan oluĢmaktadır. Soru sayısı bir derste cevaplamak için fazla olduğundan test 25 soru ve 20 soru olmak üzere iki bölüme ayrılıp bu Ģekilde farklı ders saatlerinde uygulanmıĢtır. Uygulama esnasında testin güvenirliğini düĢürecek etkiler kontrol altına alınmaya çalıĢılmıĢtır. Öğrencilerin tek oturmasına ve öğretmenin denetlemesine dikkat edilmiĢtir.
Ön deneme testi 2012-2013 Eğitim Öğretim Yılı I. Döneminde Ankara Ġli Sincan Ġlçesi Mehmet Akif Ersoy Ortaokulu‟nda okuyan toplam 225 altıncı sınıf öğrencilerine uygulanmıĢtır.
Ön denemeden elde edilen sonuçlar bilgisayar ortamına aktarılmıĢ ve SPSS programı kullanılarak çözümlenmiĢtir. Yapılan istatistiksel çözümler sonucunda, madde güçlük indeksleri, madde ayırıcılık indeksleri, testin ortalaması ve güvenirlik katsayısı (KR-20) hesaplanmıĢtır. Testin güvenirlik katsayısı.90 olarak bulunmuĢtur.
Ön denemeden elde edilen verilere göre, testin son formuna alınacak maddeler ölçme ve değerlendirme uzmanı ve deneyimli matematik öğretmenleri ile görüĢülerek belirlenmiĢtir.
Ayırıcılıkdeğeri .20‟nin altında olan maddeler atılmıĢ, .30‟un üstünde olan maddeler teste bırakılmıĢtır. Bunun sonucunda 20 maddelik “ Geometrik Cisimler Konulu Matematik BaĢarı Testi” oluĢturulmuĢtur. Ek 1 „ de verilmiĢtir.
AraĢtırmada kullanılan “Matematik Dersine Yönelik Tutum Ölçeği” EARGED (2006) tarafından geliĢtirilen likert tipi tek boyutlu tutum ölçeğidir. Bu ölçek MEB matematik ders kitaplarında kullanılan, geçerliliği ve güvenirliği belirlenmiĢ bir ölçektir. Bu ölçekte 12 olumlu ve 8 olumsuz olmak üzere toplam 20 madde bulunmaktadır. Tutum ölçeği Ek-3‟ te verilmiĢtir.
Test ve tutum ölçeğinin hazırlanmasından sonra uygulamaya baĢlanmıĢtır. Uygulama aĢamalarında önce uygulamanın yapılacağı okul idaresi ile görüĢülmüĢ ve gerekli izin alınmıĢtır. Veri toplama araçları olan baĢarı testi ve tutum ölçeği araĢtırmada kullanılmak üzere yeterli sayıda çoğaltılmıĢtır. Deney ve kontrol grubu olarak atanan öğrencilerden iki ayrı sınıf düzeni kurulmuĢtur. Deneysel çalıĢma yapılacak gruba çalıĢmadan yaklaĢık bir ay öncesinden oyunla öğretim ve matematik oyunları hakkında bilgi verilmiĢ, yöntemin temel ilkeleri ve yöntemin uygulanması sırasında uyulması gereken kurallar açıklanmıĢtır. Deney grubunda kullanılacak oyunların üretilmesi esnasında uygulama yapılan okulun matematik