T.C.
GAZİ ÜNİVERSİTESİ EĞİTİM BİLİMLERİ ENSTİTÜSÜ
İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ ANABİLİM DALI
5E ÖĞRENME DÖNGÜSÜ MODELİNE DAYALI ÖĞRETİM
ETKİNLİKLERİNİN İLKÖĞRETİM 7. SINIF ÖĞRENCİLERİNİN MATEMATİK DERSİ BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ DENKLEMLER
KONUSUNDAKİ AKADEMİK BAŞARILARINA ETKİSİ
YÜKSEK LİSANS TEZİ
Hazırlayan Burcu HİÇCAN
Tez Danışmanı
Yrd. Doç. Dr. Devrim ÇAKMAK
Etkinliklerinin İlköğretim 7. Sınıf Öğrencilerinin Matematik Dersi Birinci Dereceden Bir Bilinmeyenli Denklemler Konusundaki Akademik Başarılarına Etkisi” başlıklı tezi 02.05.2008 tarihinde jürimiz tarafından İlköğretim Matematik Öğretmenliği Anabilim Dalında Yüksek Lisans Tezi olarak kabul edilmiştir.
Adı Soyadı İmza
Üye (Tez Danışmanı) : Yrd. Doç. Dr. Devrim ÇAKMAK …..………..
Üye : Yrd. Doç. Dr. Dursun SOYLU …..………..
Üye : Yrd. Doç. Dr. Melek ÇAKMAK …..………..
Bu tez çalışması Gazi Üniversitesi Bilimsel Araştırma Projeleri Birimi tarafından 04/ 2007 – 13 numaralı proje kodu ile desteklenmiştir.
i
ÖNSÖZ
Çalışmaya başladığım ilk günden bugüne kadar her konuda destek ve yardımlarını gördüğüm, idealistliği ile örnek aldığım danışmanım Yrd. Doç. Dr. Devrim ÇAKMAK’a, çalışmanın her aşamasında bana yardımcı olan, çalışmalarımda cevaplarını aradığım soruları titizlikle inceleyerek her zaman olumlu katkılarda bulunan hocalarım Yrd. Doç. Dr. Ebru KILIÇ ÇAKMAK ve Yrd. Doç. Dr. Nusret KAVAK’a, çalışmamın istatistiksel analizleri sırasında bana yol gösterip yardımcı olan hocam Yrd. Doç. Dr. Mustafa SARIKAYA’ya, candan tavırları ile beni sürekli destekleyerek yüreklendiren hocalarım Yrd. Doç. Dr. Melike ÖZER KESKİN ve Yrd. Doç. Dr. Melek ÇAKMAK’a teşekkürü bir borç bilirim.
Hayatımın her anında bana özveriyle destek olan, en sancılı dönemlerde varlığıyla beni yüreklendiren sevgili anneme, canım teyzeme, bitanecik kardeşime, uzaklarda bir yerde olduğu halde, aldığım her nefeste, sevgisini ve sıcaklığını yanımda hissettiğim sevgili babama teşekkür ederim. Ayrıca doğduğum ilk günden beri bana emeği geçen ve yetişmemde hiçbir fedakârlığı esirgemeyen sevgili babaannem, büyükbabam, amcam, anneannem ve dedeme sonsuz sevgi ve teşekkürlerimi sunarım.
ÖZET
5E ÖĞRENME DÖNGÜSÜ MODELİNE DAYALI ÖĞRETİM
ETKİNLİKLERİNİN İLKÖĞRETİM 7. SINIF ÖĞRENCİLERİNİN MATEMATİK DERSİ BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ DENKLEMLER
KONUSUNDAKİ AKADEMİK BAŞARILARINA ETKİSİ HİÇCAN, Burcu
Yüksek Lisans Tezi, İlköğretim Matematik Öğretmenliği Anabilim Dalı Tez Danışmanı: Yrd.Doç.Dr.Devrim ÇAKMAK
2008
Bu araştırmada, 5E öğrenme döngüsü modeline dayalı öğretim etkinliklerinin 7. sınıf öğrencilerinin birinci dereceden bir bilinmeyenli denklemler konusundaki akademik başarılarına etkisi araştırılmıştır. Araştırmanın evrenini 2006 - 2007 eğitim-öğretim yılında Kırıkkale ili Milli Eğitim Müdürlüğü’ne bağlı Nuran-Refik Altaş İlköğretim okulunda öğrenim görmekte olan 7. sınıf öğrencileri, örneklemini ise aynı okulda öğrenim gören 24 öğrenci oluşturmaktadır. Araştırma nitel ve nicel araştırma yöntemleri kullanılarak iki aşamada gerçekleştirilmiştir.
Araştırmanın nicel verilerinin toplanmasında, araştırmacı tarafından geliştirilen 20 sorudan oluşan iki aşamalı başarı testi kullanılmıştır. Birinci aşama çoktan seçmelidir. İkinci aşama ise öğrencinin işaretlediği seçeneği işaretleme nedenini belirttiği kısımdır. Dersler, araştırmacı tarafından geliştirilen 5E öğrenme döngüsü modeline dayalı etkinliklerle hazırlanan ders planları kullanılarak işlenmiştir.
Verilerin çözümlenmesinde, Excel ve SPSS programlarından yararlanılmıştır. Öğrencilerin her soruya vermiş oldukları yanıtların frekans ve yüzde dağılımları çıkarılmıştır. Test sonuçları incelendiğinde, öğrencilerin sontest puanlarının öntest puanlarına göre anlamlı düzeyde yüksek olduğu görülmüştür. Sontestin uygulanmasından bir ay sonra iki aşamalı başarı testi öğrencilere tekrar uygulanarak bilgilerin kalıcılığına bakılmıştır. Kalıcılık testi sonuçlarının, öntest sonuçlarından yüksek ancak sontest sonuçlarından düşük olduğu belirlenmiştir.
iii
Araştırmanın nitel kısmında ise örneklemdeki beş öğrenci ile yarı yapılandırılmış mülakatlar gerçekleştirilerek öğrencilerin birinci dereceden bir bilinmeyenli denklemler konusunda geçen matematiksel kavramları nasıl anlamlandırdıkları incelenmiştir. Öğrencilerin görüşlerinden elde edilen veriler kategorilere ayrılarak yorumlanmıştır.
Araştırmada, 5E öğrenme döngüsü modeline dayalı olarak hazırlanan ders etkinlikleri ile işlenen derslerin, hem kavramsal hem de işlemsel düzeyde, birinci dereceden bir bilinmeyenli denklemler konusunun öğretiminde anlamlı düzeyde etkili olduğu sonucuna varılmıştır. 5E öğrenme döngüsü modeline dayalı olarak işlenen derslerin, öğrencilerin derse olan ilgilerini, motivasyonlarını ve derse katılımlarını arttırdığı da ulaşılan sonuçlar arasındadır.
Anahtar Kelimeler: Yapılandırmacı Öğrenme Kuramı, 5E Öğrenme Döngüsü
ABSTRACT
THE INFLUENCE OF TEACHING ACTIVITIES WITH RESPECT TO 5E LEARNING CYCLE MODEL ON ACADEMIC ACHIEVEMENTS IN MATHEMATICS LESSON OF 7th GRADE STUDENTS IN PRIMARY SCHOOL
ABOUT LINEAR EQUATIONS IN ONE VARIABLE HİÇCAN, Burcu
M.S. Thesis,The Department of Mathematics Education Advisor: Asst. Professor Dr. Devrim ÇAKMAK
2008
In this research, it was investigated that influence of teaching activities with respect to 5E learning cycle model on academic achievements in mathematics lesson of 7th grade students in primary school about linear equations in one variable. Universe of the research was composed of 7th grade students who studied Nuran-Refik Altaş primary education school subsidiary to Public Education Directorate of Kırıkkale in 2006-2007 and sampling unit was composed of 24 students who were educated in the same school. Research was realized in two steps with qualitative and quantitative research methods.
In the gathering of quantitative datas of the research, two phased success test composed of 20 questions and developed by researcher, was used. Second step was the section that why student pointed out his choice. Classes were done by utilizing curriculum prepared activities based upon 5E learning cycle model which was developed by the researcher.
Excel and SPSS programmes were benefitted in analyzing the datas and percentage distribution of answers were drawn for every question by students. When test results were reviewed, it was found that the last test scores were more meaningful than preliminary test scores of students. After one month from the application of the last test, two phased success test was applied to students again so as to monitor stability of their knowledge. Stability test scores were determined higher than preliminary test scores and lower than the last test scores.
v
In qualitative section of the research, it was reviewed that how the students gave meaning to mathematical concepts about linear equations in one variable in accordance with interviews with five students carried out. The datas gained by views of the students were commented by dividing into categories.
In this research, it was concluded that classes perpetrated by class activities prepared with respect to 5E learning cycle model was meaningfully effective on teaching linear equations in one variable. It was among to attained results that classes perpetrated with respect to 5E learning model increased interests, motivations and participations in classes of students.
Key Words: Constructivist Learning Theory, 5E Learning Cycle Model,
İÇİNDEKİLER Sayfa No ÖNSÖZ………... ÖZET……….. i ii ABSTRACT……… iv İÇİNDEKİLER………... vi TABLOLAR LİSTESİ……….... ix ŞEKİLLER LİSTESİ……….. x BÖLÜM - I GİRİŞ……….……….…… 1
1.1. Matematik ve Matematik Eğitimi …….………...………….…….. 2
1.1.1. Matematik Eğitiminde Cebir Öğretimi………...…... 3
1.1.1.1. Birinci dereceden bir bilinmeyenli denklemler konusunun öğretimi ve karşılaşılan öğrenme zorlukları………….……….. 4
1.1.2. Matematik Eğitiminde Kavramların Rolü ………....…. 8
1.2. Yapılandırmacılık (Constructivism)……….... 11 1.2.1. Öğrenme Döngüsü Modeli………. 16 1.2.2. 5E Öğrenme Döngüsü Modeli………..………..……... 18 1.3. Problem Cümlesi……….. 1.4. Alt Problemler……...………... 25 26 1.5. Araştırmanın Amacı………. 26 1.6. Araştırmanın Önemi………. 26 1.7. Sayıltılar………... 27 1.8. Sınırlılıklar………... 28 1.9. Tanımlar………...……… 28
vii
BÖLÜM - II
İLGİLİ ARAŞTIRMALAR ………. 29
2.1. 5E Öğrenme Döngüsü Modeli İle İlgili Araştırmalar……….. 29
2.1. Cebir Öğretimi İle İlgili Araştırmalar……….. 33
BÖLÜM - III YÖNTEM………... 37
3.1. Araştırma Modeli …..……….. 37
3.2. Evren ve Örneklem……….. 39
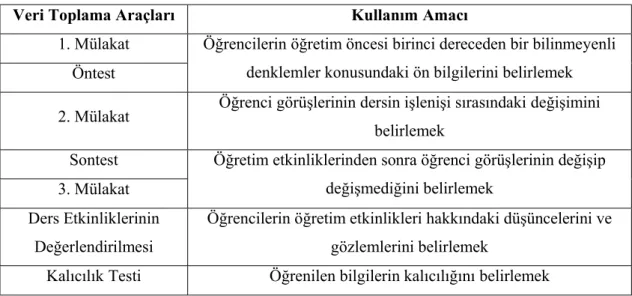
3.3. Veri Toplama Araçları………. 40
3.3.1. Konu Başarı Testi………..………. 40
3.3.2. Kalıcılık Testi……… 43
3.3.3. Mülakatlar..……… 43
3.3.4. Gözlem………... 3.3.5. Ders Etkinliklerinin Değerlendirilmesi……….. 45 45 3.4. Derslerin İşlenişine Hazırlık Süreci………. 46
3.5. Araştırmanın Uygulama Süreci……… 47
3.5.1. Derslerin İşleniş Süreci……….. 49
3.6.Verilerin Analizi………... 53
3.6.1. Konu Başarı Testi İle Elde Edilen Verilerin Analizi...……….. 53
3.6.2. Mülakatlardan Elde Edilen Verilerin Analizi……… 54
BÖLÜM - IV BULGULAR VE YORUM………. 55
4.1. Öğrencilerin İki Aşamalı Başarı Testine Verdikleri Cevaplara İlişkin Bulgu ve Yorumlar……….. 55
4.2.Araştırmanın Alt Problemlerine İlişkin Bulgu ve Yorumlar…………... 65
4.2.1. Birinci Alt probleme ilişkin Bulgular ve Yorumlar ……….. 65
4.2.2. İkinci Alt probleme ilişkin Bulgular ve Yorumlar ……… 66
4.3. Öğrencilerle Gerçekleştirilen Mülakatlar Sonucunda Elde Edilen Verilere İlişkin Bulgu ve Yorumlar ………... 67
4.4. Öğrencilerin 5E Modeli Hakkındaki Görüşlerinden Elde Edilen Verilere İlişkin Bulgu ve Yorumlar……… 93
BÖLÜM - V SONUÇLAR VE ÖNERİLER……… 100 5.1. Sonuçlar ……….…………. 100 5.2. Öneriler………..……….. 105 KAYNAKÇA………. 107 EKLER……….. 120
EK- 1: Birinci Dereceden Bir Bilinmeyenli Denklemler Konusuna İlişkin Hedef ve Davranışlar EK- 2: İki Aşamalı Başarı Testi……… 121 123 EK- 3: Yarı Yapılandırılmış Mülakat Soruları……….………… 130
EK- 4: 5E öğrenme Döngüsü Modeline Dayalı Olarak Geliştirilen Örnek Bir Ders Planı..………... 132
ix
TABLOLAR LİSTESİ
Tablo No Sayfa No
Tablo 1.1. Rodger Bybee’nin 5E modeli………. 23
Tablo 3.1. Araştırmanın Deneysel Deseni………... 38
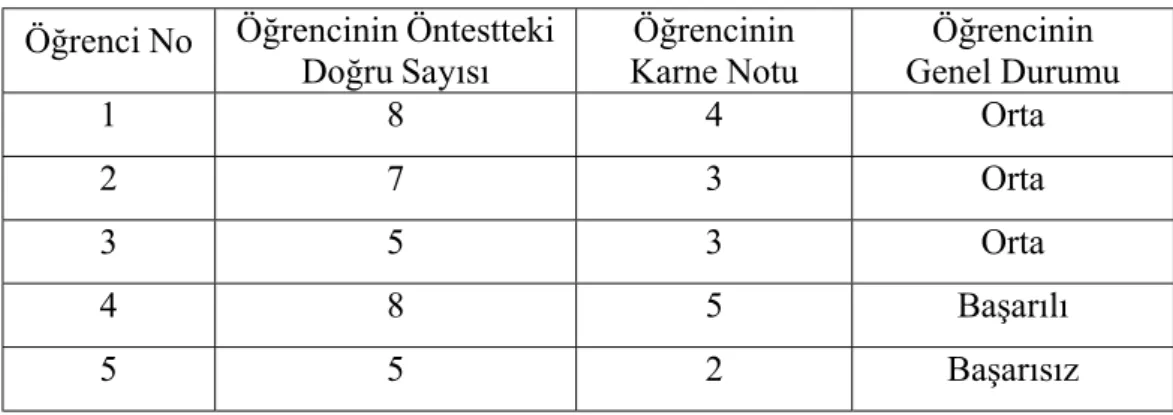
Tablo 3.2. Mülakat Yapılan Öğrencilere Ait Kişisel Bilgiler……… 39
Tablo 3.3. Veri Toplama Araçlarının Kullanım Amaçları……….. 46
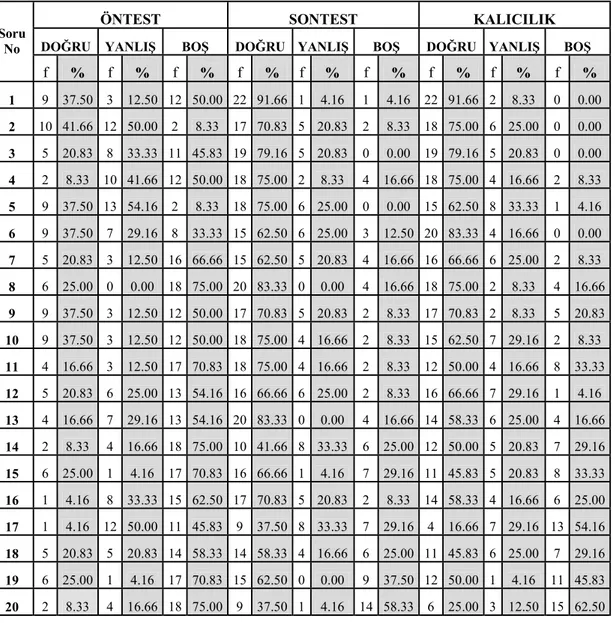
Tablo 4.1. Öğrencilerin Konu Başarı Testine Verdikleri Cevapların Öntest, Sontest ve Kalıcılık Testi Frekans ve Yüzde Dağılımları……….. 56
Tablo 4.2. Öğrencilerin Öntest - Sontest Puanlarına İlişkin Bağımlı Gruplar t-Testi Sonuçları ………...………. 65
Tablo 4.3. Öğrencilerin Sontest - Kalıcılık Testi Puanlarına İlişkin Bağımlı Gruplar t-Testi Sonuçları ……….. 66
Tablo 4.4. 1. Soruya Verilen Cevapların Analizi..……….. 68
Tablo 4.5. 2. Soruya Verilen Cevapların Analizi……… 72
Tablo 4.6. 3. Soruya Verilen Cevapların Analizi……… 75
Tablo 4.7. 4. Soruya Verilen Cevapların Analizi……… 79
Tablo 4.8. 5. Soruya Verilen Cevapların Analizi……… 81
Tablo 4.9. 6. Soruya Verilen Cevapların Analizi……… 83
Tablo 4.10. 7. Soruya Verilen Cevapların Analizi……… 87
Tablo 4.11. 8. Soruya Verilen Cevapların Analizi……… 89
Tablo 4.12. 9. Soruya Verilen Cevapların Analizi……… 91
Tablo 4.13. Öğrencilerin 5E Öğrenme Döngüsü Modeli Hakkındaki Görüşlerinin Toplandığı Kategorilerin Frekans ve Yüzde Dağılımları………. 99
ŞEKİLLER LİSTESİ
Şekil No Sayfa
Şekil 1.1. 5E Öğrenme Döngüsü Modeli………...……… 22 Şekil 3.1. 5E Modeli Keşfetme Aşamasında Gerçekleştirilen Etkinlik Resmi 50
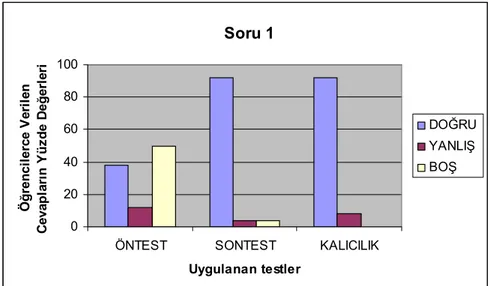
Şekil 4.1. Öntest, Sontest ve Kalıcılık Testi 1. Soruda Öğrencilerce Verilen
Cevapların Yüzde Değerleri………...… 58
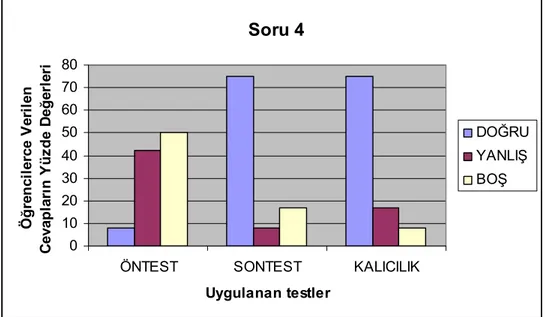
Şekil 4.2. Öntest, Sontest ve Kalıcılık Testi 4. Soruda Öğrencilerce Verilen
Cevapların Yüzde Değerleri………... 59
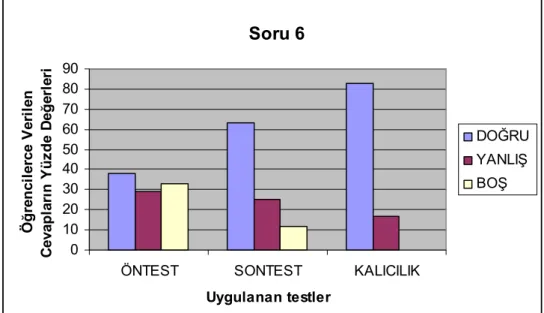
Şekil 4.3. Öntest, Sontest ve Kalıcılık Testi 6. Soruda Öğrencilerce Verilen
Cevapların Yüzde Değerleri………... 60
Şekil 4.4. Öntest, Sontest ve Kalıcılık Testi 14. Soruda Öğrencilerce Verilen
Cevapların Yüzde Değerleri……….. 61
Şekil 4.5. Öntest, Sontest ve Kalıcılık Testi 13. Soruda Öğrencilerce Verilen
Cevapların Yüzde Değerleri……….………. 62
Şekil 4.6. Öntest, Sontest ve Kalıcılık Testi 17. Soruda Öğrencilerce Verilen
Cevapların Yüzde Değerleri……….………. 63
Şekil 4.7. Öntest, Sontest ve Kalıcılık Testi 20. Soruda Öğrencilerce Verilen
BÖLÜM - I GİRİŞ
21. yüzyılın yaşandığı günümüzde her şey hızla değişmektedir. Teknoloji, insanların yaşam tarzları, beklentileri, hayat standartları değişmekte; kendini yenilemektedir. Hızla gelişen ve ilerleyen bilim çağına ayak uydurmak ancak iyi ve kaliteli eğitim almış bireylerin varlığıyla mümkündür.
Eğitim, çağdaşlaşmanın itici gücünü, yani kalkınmanın gerektirdiği niteliklere sahip insan gücünü yetiştirmekle görevlidir. Bu görev kendisine diğer tüm, toplumsal sistemler tarafından verilmiştir (Bilen, 2002:3).
Titiz’e göre (2000) eğitim, değişen durumların gerektirdiği bilgi ve becerileri kişisel çaba ile öğrenebilme ve bunları yaşamın özel durumlarına uygulayabilme sanatının kazanılmasıdır.
Ülkemizde yaygın olarak kullanılan tanıma göre; “Eğitim, bireyin davranışlarında kendi yaşantıları yoluyla kasıtlı olarak, istendik değişiklik meydana getirme sürecidir” (Ertürk, 1993).
Umay’a göre (2002) eğitimin amacı, bireyleri toplumla uyumlu hale getirmek ve toplumun gereksinim duyduğu niteliklerde insan gücü yetiştirmektir. Bu amaç doğrultusunda eğitimin yeni hedefi; bilgiyi nasıl ve nerede kullanacağını bilen, kendi öğrenme yöntemlerini tanıyıp etkili bir biçimde kullanan ve yeni bilgiler üretmede önceki bilgilerinden yararlanan bir insan modeli yaratmadır (Abbott, 1999:68). Bu da ancak nasıl öğreneceğini öğrenen, araştırmacı ve yaratıcı bireylerle mümkündür.
1.1. Matematik ve Matematik Eğitimi
Bireyin yaşamını dengeli ve verimli biçimde sürdürebilmesi için, yaşadığı çağa ve topluma, yapıcı ve yaratıcı bir üye olarak katkıda bulunması gerekmektedir. Günümüzde bilgili, özgür ve yaratıcı düşünen, zihinsel olarak analiz ve sentez yapmaya hazır, çağın koşullarına uygun bireylere gereksinim vardır. Bunun gerçekleşmesi için de, etkili akıl yürütme, eleştirici düşünme ve problem çözme önemli zihinsel becerilerdir. Bu becerilerin geliştirilmesinde matematiğin önemli bir yeri vardır.
Matematik; bireyleri doğruya, kesin bilgiye götüren düşünme yöntemidir (Yıldırım, 1996). Matematik, yalnız bilim insanlarının veya mühendislerin gereksinim duyduğu ortak iletişim dili ve etkin bir araç değil aynı zamanda bilimde olduğu kadar günlük yaşamımızdaki problemlerin çözülmesinde de kullandığımız önemli araçlardan biridir.
Matematik, pek çok yetişkin ve iş gören için edinilmesi gereken temel ve zorunlu bilgiler, bir takım beceriler içerir; ayrıca, bireylerin günlük yaşamlarını sürdürmede çok önemli işlevleri vardır. Özellikle zorunlu eğitimin ilk basamağı olan ilköğretim okullarındaki matematik derslerinde yer alan kavramlar, kurallar ve işlem bilgileri, demokratik ülkelerde her yurttaş için gerekli olduğundan bu konularda herkesin okuryazar olması ve matematikte güçlenmesi gerekmektedir (Ersoy, 1997).
Matematik i yi b i r eğitimin vazgeçilmez yapı t a ş ı d ı r. Çünkü matematik eğitimi, öğrencilerde yaratıcı düşünceyi erken yaşlardan başlayarak geliştirmeye olanaklar ve fırsatlar sunar (Çıkla ve Ersoy, 2001:121).
Bireylerin b e l i r l i düzeyde matematik eğitimi alması gerektiği i çi n tüm dünyada matematik zorunlu ders olarak okutulmaktadır. Hatta birçok ülkenin i l k ve ortaöğretim okul programlarında, ü l k e n i n ana d i l i n d e n sonra en fazla matematiğe yer verildiği bilinmektedir (Ersoy, 1997).
3
Matematik ilköğretim programlarında çekirdek derslerden b i r i n i oluşturmaktadır (Çakmak, 2000:127). Matematik dersi birinci sınıftan başlayarak bütün öğretim yılları boyunca temel ve ağırlıklı bir ders olarak varlığını sürdürmeye devam etmektedir.
Bireylerin, toplumların, bilimin ve teknolojinin gelişiminde önemli bir disiplin olan matematik kendi içinde belli bölümlere ayrılmıştır. Bu bölümlerden biri de cebirdir. Cebir; genel olarak, sayı ve sembolleri kullanarak eldeki incelenen ilişki veya ilişkileri genelleştirilmiş denklemlere dönüştüren bir matematik dalıdır. Cebirin konusu, aritmetik işlemlerde sayılar yerine semboller kullanarak değişik ve basit çözüm yolları ortaya koymaktır (Aktaran: Akkaya, 2006).
1.1.1. Matematik Eğitiminde Cebir Öğretimi
İnsanlar günlük hayatta bilgileri analiz ederken cebir ve cebirsel düşünmeyi kullanmaktadırlar. Ama çoğu zaman bunun farkında değildirler (Davidenko, 1997). Günlük hayatta karşılaşılan problemlerin değişkenleri arasındaki ilişkileri belirlemek ve problemlere farklı çözüm yolları üretmek cebirle mümkündür (Aktaran: Akkaya, 2006).
Cebir öğretimi öğrencilerin matematiksel gelişimi için de oldukça önemlidir. Cebir adeta köprü mahiyetinde bir derstir; çünkü hem ilk seviyedeki bir matematik öğrencisi için hem de yüksek matematik eğitimi alan bir öğrenci için başlama noktasıdır (Weaver, 2004). Cebir, öğrencilere soyut düşünmenin ve mantıksal çıkarım yapmanın kapılarını açmaktadır (MacGregor ve Stacey, 1996). Lacampagne (1995) cebir için;
“Cebir matematiğin dilidir. O, tam manasıyla öğrenilmesi durumunda, ileri matematiksel konular için kapılar açar. O, öğrenilememesi durumunda üniversite ve teknolojiye dayalı kariyer kapılarını kapatır…” demiştir (Aktaran: Dede, 2003).
Bu nedenle cebir, birçok ülkenin matematik programında çok önemli bir yere sahiptir. Öyle ki cebire matematik ve diğer derslerde başarılı olmak için anahtar bir rol verilmiştir. İleri matematik öğretimi ve yüksek öğretime devam edebilmek için cebir öğrenmek şarttır (Ersoy, 1997).
Lacampagne (1995) cebiri matematiğin dili olarak tanımlamıştır. Ona göre de temel cebirsel kavramların tam öğrenilmesi, ileri matematiksel konuların öğrenilmesini kolaylaştıracaktır (Aktaran: Dede, 2003).
Matematik ve öğretimi açısından bu kadar önemli olan cebir öğretimi üzerindeki çalışmalar son yıllarda büyük artış göstermiştir. Cebir öğretimi ile ilgili öğrenme ve öğretme güçlükleri yıllar boyunca fark edilmiş ancak tam anlamıyla anlaşılamamıştır. Bugün bile öğrencilerin pek çoğunun yeterli düzeyde cebir bilgilerinin ve becerilerinin olmadığı görülmektedir. Oysa, çağdaş öğretim programları amaç, içerik ve beklentiler yönünden incelendiğinde, cebirle ilgili olarak erişilecek hedefler sayıca giderek artmakta ve seviye yükselmekte, ve buna bağlı olarak da her ülkede daha çok sayıda kişinin daha derinlemesine cebirsel bilgi ve beceriler edinerek yetkinleşmesi gerekmektedir (Ersoy ve Erbaş, 2002).
Özellikle ilköğretim çağında öğrencilerin cebir konuları ile ilgili kazanımları günlük yaşamlarında önemli rol oynamaktadır. Öğrencilerdeki temel cebirsel kavramların oluşumu ve cebirsel düşüncenin gelişimi, ilköğretim çağında verilen cebir eğitimiyle yakından ilişkilidir.
1.1.1.1. Birinci dereceden bir bilinmeyenli denklemler konusunun öğretimi ve karşılaşılan öğrenme zorlukları
İlköğretimde verilen birinci dereceden bir bilinmeyenli denklemler konusu cebirin önemli konularından biridir. Sözel problemleri denklem haline dönüştürmek ve çözümlerini bulmak aritmetikten cebire geçişin en temel kısmıdır. Dolayısıyla birinci dereceden bir bilinmeyenli denklemler konusu, cebir öğretiminin temel
5
konularından biridir. Öğrencilerin ileriki cebir konularında başarılı olmaları için temel konuları iyi öğrenmeleri gerekmektedir.
Yapılan birçok çalışma, öğrencilerin temel cebir kavramlarını (eşitlik çözümü, cebirsel ifadelerin kullanımı, problem çözme, değişken vb.) anlama ile ilgili güçlükleri, ortak yanlışları ve yanılgıları olduğunu göstermiştir (MacGregor ve Stacey, 1997; Baki ve Kartal, 1998; Erbaş, 1999; Ersoy ve Erbaş, 2002; Ergöz, 2000; Dede, 2003). Öğrenciler, birinci dereceden bir bilinmeyenli denklemler konusunun öğrenilmesi sırasında da bir takım zorluklarla karşılaşmakta ve bu konunun öğrenilmesi zor bir konu olduğunu düşünmektedirler.
Birinci dereceden bir bilinmeyenli denklemler konusunda geçen bilinmeyen kavramı özellikle öğrencilerce öğrenilmesi kolay olmayan bir kavram olarak görülmektedir(Macgregor ve Stacey, 1997; Rosnick, 1981; Davidenko, 1997).
Hersovics ve Kieran (1980) kullanılan bilinmeyene dair bazı kavramsal güçlükler belirlemişlerdir. Öğretmen ve öğrenciler denklemlerdeki bilinmeyeni her zaman aynı şekilde yorumlayamamaktadırlar. Örneğin öğrenciler bilinmeyen değerin yerine harflerin kullanılmasını algılayamamaktadırlar.(Aktaran: Dede,2003)
Matematikte harflerin farklı kullanımlarının olması, öğrencilerin bilinmeyen kavramını anlamalarını zorlaştırmaktadır. Örneğin birinci dereceden bir bilinmeyenli denklemler konusunda 2x ifadesinde x yerine 3 konulduğunda cebirsel olarak 2 x 3 anlamına gelirken aritmetiksel açıdan bakıldığında ise 2x ifadesi x yerine 3 konulduğunda 23 sayısı anlamına gelmektedir.
Sleeman (1984) yaptığı çalışmada, yapılan birçok yanlışın, “yanlış kurallama” dan dolayı gerçekleştiğini belirtmiştir. Sleeman (1984) öğrencilerin hatalarını dört grup altında incelemektedir: beceri hataları, ayrıştırma hataları, yazı hataları ve tesadüfî hatalar. (Akt: Ergöz, 2000).
Hilling (1976) tarafından yapılan araştırmada ise öğrencilerin, aritmetiksel terimlerle ifade edilen durumları anlayabilirken, cebirsel ifadelerle gösterilen durumları anlayamadıkları görülmüştür. Öğrenciler harfleri nesnelerin etiketi olarak düşünmektedirler. “e” harfinin elmayı, “m” harfinin muz ya da metreyi ifade ettiğini düşünmektedirler. x harfini ise herhangi bir nesne ile eşleştiremediklerinden bu harfe bir anlam yükleyememektedirler (Akt: Ergöz, 2000).
Öğrencilerin birinci dereceden bir bilinmeyenli denklemler konusunda zorlandıkları bir diğer noktada sözel ifadeleri cebirsel ifadelere dönüştürmek ve sözel ifadelere uygun denklemi kurmaktır. MacGregor ve Stacey (1997) tarafından yapılan bir araştırmada öğrencilerin sözel problemleri cebirsel ifadelere dönüştürme başarılarının beklenenin oldukça altında olduğu görülmüştür. Bu araştırmaya göre öğrencilerin denklem kurmayı anlamada zorlandıkları görülmüştür. Rosnick (1981)’e göre de sözlü cümlelerden eşitliklere dönüşüm ya da İngilizce’den matematiğe dönüşüm, her yaştaki öğrenci için karmaşa yaratmaktadır.
National Council of Teachers of Mathematics (NCTM)’ye göre, 6-8. sınıftaki öğrenciler, problemleri çözmek için sembol kullanabilme yeteneğine sahip olmalıdırlar (Aktaran:Dede, 2003). Başka araştırma sonuçları da NCTM’nin bu görüşünü destekler niteliktedir. Bu araştırmaların sonuçları, 7. sınıf öğrencilerinin denklemlerdeki nicelikleri anladıkları zaman denklemlerin temel mantığını anladıklarını, problemlerin çözümü için cebirsel mantığı kullandıklarını ortaya çıkarmıştır (Carraher ve diğerleri, 1998).
Öğrencilerin birinci dereceden bir bilinmeyenli denklemler konusunda zorlanmalarının bir diğer nedeni de onların aritmetiksel işlemlerde yeterince deneyime sahip olmamalarıdır (MacGregor ve Stacey, 1997). Birinci dereceden bir bilinmeyenli denklemler konusu öğrencilerin diğer matematiksel deneyimleri üzerine inşa edildiğinden ötürü, onların aritmetiksel işlem yeteneklerinin güçlü olmaları gerekmektedir.
7
Birinci dereceden bir bilinmeyenli denklemler konusu aritmetiğin devamı niteliğinde olsa da aritmetikten bir takım farklılıklar da göstermektedir. Örneğin eşittir işareti, aritmetikte sonuç belirtirken, birinci dereceden bir bilinmeyenli denklemlerde denklik belirtmektedir. Öğrencilerce bu farkın anlaşılamaması birinci dereceden bir bilinmeyenli denklemler konusunun öğrenilmesinde zorluklar yaşanmasına neden olmaktadır. Yapılan birçok araştırmada çocukların eşittir işaretini ilişkisel bir sembol değil de eylem belirten bir sembol olarak gördüklerini ortaya koymuştur (Falkner ve diğerleri, 1999; Yaman ve diğerleri, 2003).
Falkner, Levi ve Carpenter (1999) yaptıkları araştırmada öğrencilere 7+5=….+4 gibi sorular yöneltmişlerdir. Öğrencilerin verdikleri yanıtlar araştırmacılarca aşağıdaki gibi maddeleştirilmiştir:
1. Eşit işaretinden sonra her zaman cevap geleceğini düşünen öğrenciler boş bırakılan kısma 12 yazmışlardır.
2. Bütün sayıların toplanacağını düşünen öğrenciler boş bırakılan yere 16 yazmışlardır.
3. Bazı öğrenciler işlemi 7+5=12+4=16 şeklinde yapmışlardır.
4. Bazı öğrenciler ise her iki taraftaki sayıların toplamlarının eşit olması gerektiğini düşünerek boş bırakılan kısma 8 yazmışlardır.
Araştırma sonuçlarına bakıldığında öğrencilerin eşitlik çözümünde bir takım kavram yanılgılarına ve yanlış öğrenmelere sahip oldukları görülmektedir (Aktaran: Dede, 2003).
Araştırmalarda görüldüğü gibi birinci dereceden bir bilinmeyenli denklemler konusunun öğretimi sırasında hem işlemsel bilgi hem de kavramsal bilgi önemli rol oynamaktadır. Matematiğin yapısına uygun bir öğretim, aşağıdaki üç amaca yönelik olarak gerçekleştirilmelidir (Van de Wella, 1989):
1. Öğrencilerin matematikle ilgili kavramları anlamalarına, 2. Matematikle ilgili işlemleri anlamalarına,
Bu nedenle matematik öğretmenlerinin, temel kavramların öğrenilmesine de en az matematiksel işlemleri anlamalarına verdikleri önem kadar önem vermeleri, anlaşılması ve öğrenilmesi zor olan kavramları öğrencilere daha dikkatli bir şekilde kavratmaları gerekmektedir.
1.1.2. Matematik Eğitiminde Kavramların Rolü
İyi bir matematik eğitimi, bilginin temel taşları olan kavramlar düzeyinde ele alınarak sağlanabilir. Kavramlar, bireyin düşünmesini sağlayan zihinsel araçlar olarak çok kapsamlı bilgileri kullanılabilir birimler haline getirirler (Senemoğlu, 2001:93). İnsanlar, çocukluktan başlayarak düşüncenin birimleri olan kavramları ve onların adları olan sözcükleri öğrenirler (Turgut ve diğerleri, 1997). Kavramları sınıflar, aralarındaki ilişkileri bulur, böylece bilgilerine anlam kazandırır, yeniden düzenler, hatta yeni kavramlar ve bilgiler yaratırlar (Kaptan, 1998). Anlamlı öğrenme, eski bilgilerle yeni bilgiler arasında bağıntılar kurulduğu zaman gerçekleşir. Temel kavramlar anlaşılmadıkça konuyla ilgili ileri düzeydeki diğer kavramların anlaşılamayacağı bilinmektedir.
İlköğretim öğrencilerinin matematikle ilgili ilkeleri öğrenebilmeleri ve karşılarına çıkabilecek matematiksel problemleri çözebilmeleri için temel kavramları çok iyi anlamaları gerekmektedir. Bu yüzden, öğretilecek kavramların açık bir şekilde ifade edilmesi, belirsiz cümlelerden sakınılması, kavramın doğru bir şekilde anlaşılması için çok önemlidir. Öğretmenlerin, matematiksel kavramları kullanırken yanlış anlamaları en aza indirgemek için göz önünde tutması gereken hususlardan bazıları aşağıdaki gibidir:
9 Matematiksel kavramlar, farklı içeriklerde farklı anlamlara gelebilir, 9 Öğrencilerin, öğretilen kavramı anlayıp anlamadıklarını,
9 Öğrenilen kavramı öğrencilerin kendi ifadeleri ile tanımlamalarına imkan vererek değerlendirmek,
9 Öğretilecek kavram ile öğrencilerin geçmiş bilgilerinin uyumunu sağlayacak ortamların hazırlanması (Lansdell, 1999).
9
Yukarıdaki hususlar dikkate alınmadığında işlemsel bilgi ile kavramsal bilgi arasındaki ilişkiyi kuramayan öğrenciler, matematiksel kavramları yanlış algılamakta ve öğrencilerde öğrenme sürecini olumsuz yönde etkileyen kavram yanılgıları oluşmaktadır. Kavram yanılgısı ifadesi öğrencilerin kendi öznel anlamaları olarak düşünülebilir. Öğrencilerin kavramlara kendilerine özgü biçimde anlam vermeleri ile oluşan kavram yanılgıları, anlamlı öğrenmeyi engelleyen bir faktör olarak görülmektedir. Bu anlamda “kavram yanılgıları, hem yeni öğrenilen bilginin tekrar yapılandırılmasına ket vurduğu, hem de kavramlar arasında anlam bütünlüğünü bozduğu için, bir elektrik devresinde kısa devreye yol açan iletken tellere benzer” şeklinde tanımlanmaktadır (Bahar, 2003). Öğretim boyunca kazanılan kavram yanılgılarının temelinde, kavram bilgisi ve matematik işlem bilgilerinin birbirini tamamlayacak biçimde öğrenilmemesi / öğretilmemesi, öğrencilerin problem çözmeyle ilgili gerekli bilgi ve becerileri yeterli düzeyde edinememeleri bulunmaktadır. Uygulanan testlerde yapılan ortak yanlışlar incelendiğinde ise öğrencilerin yanlış kurallar kullanma, sürçmeler ve dikkatsiz işlem yapma gibi yetersizlikleri olduğu görülmüştür (Ersoy ve Ardoğan, 2003).
Matematik eğitiminde yapılan son zamanlardaki araştırmalarda öğrencilerin herhangi bir kavram yanılgısı oluşturmalarını engelleyecek bir yolla öğretim yapmanın imkânsız olduğu, öğrencilerin doğru olmayan bazı genellemeler yaptıkları ve öğretmenlerin bunları açığa çıkarmak için özel bir çaba harcamadıkça bunların gizli kalacağı belirtilmiştir. Bu yüzden kavram yanılgılarını tartışan ve açığa çıkaran öğretim stillerini kullanarak kavram yanılgıları sınırlandırılabilir.
Mirasyedioğlu’na (1998:6) göre “Matematiksel kavramların her zaman soyut doğası vardır. Bu nedenle konuların, matematiğin doğal yapısı içinde geliştirilerek stratejilerle ilişki kurmayı, düşünmeyi ve oluşturmayı içeren etkinlikler aracılığında öğrencilere sunulması gerekir”. Bu etkinlikler günlük yaşamda karşılaşılabilecek sorunlarla ilgili olmalı ve somut materyaller kullanılmalıdır.
MacGregor ve Stacey (1996), öğrencilerin basit cebirsel ifadeleri nasıl algıladıklarını ve onlar tarafından yapılan hata ve yanlış anlamaların neler oldukları
incelenmiştir. Araştırma sonuçlarına bakıldığında öğretme yaklaşımlarının bir kısmının öğrencilerde yanlış anlamalara neden olduğu sonucuna varılmıştır.
Black ve Ammon’a (1992) göre ilgili deneyimler sonucunda elde elden bilgi başkalarından elde edilen bilgiden daha fazladır. Bu da öğrencinin ön bilgilerini dikkate alan ve öğrencinin bilgiye kendisinin ulaşmasına olanak sağlayan, yani öğrencilerin öğrenme sürecine aktif olarak katıldıkları ve öğrenmede sorumluluk aldıkları yöntemlerin uygulanmasının gerekliliğini ortaya koymaktadır.
Son yıllarda ülkemizde fen ve matematik eğitimi alanında yapılan çalışmalar, çeşitli öğrenme yaklaşımlarının öğrencilerin öğrenmeleri üzerindeki etkilerinde yoğunlaşmaktadır. Bu anlamda çağdaş yaklaşımlar olarak değerlendirilen çok sayıda öğretim yaklaşımı uygulamaya konulmuştur. Bunlar aşağıdaki şekilde özetlenebilir:
1. Sunuş ve aktarma modelleri (Direct Teaching) 2. Buluş yoluyla öğretim modeli ( Discovery Teaching) 3. Araştırma yoluyla öğretim modelleri (Inquiry Teaching) 4. Problem Çözme modeli (Problem Solving Model)
5. Zihinde yapılanma kuramına dayanan modeller (Costructivist Models) 6. Gruplarda işbirliğiyle öğretim modelleri (Collaborative Learning Models)
dir (Turgut ve diğerleri, 1997).
Bunlar içerisinde öğrencilerin bilgiyi aktif olarak yapılandırdıkları ve birlikte çalıştıkları öğrenme yaklaşımlarının daha çok ön plana çıktığı göze çarpmaktadır. Öğrenciler, öğrenmenin merkezinde ve bilgi ile bağlantıda olduklarında daha üst düzeydeki düşünme basamaklarına daha kolay ulaşmaktadırlar. Böylece öğrenciler, Bloom’un (1956) da vurguladığı gibi ezberlemekten öte, kavrama, uygulama, analiz, sentez ve değerlendirme basamaklarına çıkabilmekte ve bilgi birikimlerini daha işlevsel olarak kullanabilmektedirler.
Çağdaş yaklaşımlar, öğrencinin bireysel farklılıklarını ve öğrenme özelliklerini dikkate alarak onların öğrenmesini temel alan öğrenci merkezli bir
11
öğretimi vurgulamaktadır. “Öğretmen öğretir, öğrenci öğrenir.” anlayışının yerini “Öğretmen öğrenmeyi sağlar, öğretmen ve öğrenci birlikte öğrenir ve paylaşırlar.” anlayışı almaktadır. Öğrenciler, öğrenme sürecinde pasif ve bilgileri alan değil, öğrenme sürecinde etkin olan ve bilgileri yapılandıran bireylerdir, öğretimdeki yeni yaklaşımlar, çok bilen ve çok fazla yanıt veren değil düşünen, araştıran, sorgulayan ve üreten bireyler yetiştirmeyi temel almaktadır.
Bu yaklaşımlardan biri olan zihinde yapılanma kuramına dayanan yapılandırmacılığın son yıllarda etkililiği artmıştır. Bunun nedenleri arasında öğrenci merkezli öğrenmeyi savunması ve yüksek düzeydeki öğrenci motivasyonunu ve düşünme becerilerini artırmaya katkı sağlayarak etkili bir öğrenme ortamı sağlaması sayılabilir (Boddy ve diğerleri, 2003).
1.2. Yapılandırmacılık (Constructivism)
Yapılandırmacılık insanın nasıl öğrendiği ve bilginin doğası konuları üzerine geliştirilmiş bir yaklaşımdır (Noddings, 1990). Bu nedenle yapılandırmacılıkta öğretimden çok öğrenme üzerinde durulur. Bu yaklaşım, öğrenenlerin bilgiyi nasıl öğreneceklerine ilişkin bir kuram olarak gelişmiş ve zaman içinde öğrenenlerin bilgiyi nasıl yapılandırdıklarına ilişkin bir yaklaşım biçimine dönüşmüştür (Demirel, 2001:132).
Yapılandırmacılık, öğrenenlere öğrenmeyi öğretmekte ve onlar için bilgiyi anlamlı kılmaktadır. Eğitimin yeni hedefi, bilgiyi nasıl ve nerede kullanacağını bilen, kendi öğrenme yöntemlerini tanıyıp etkili bir biçimde kullanan ve yeni bilgiler üretmede önceki bilgilerinden yararlanan bir insan modeli yaratmadır. Bu hedefe ulaşmada yapılandırmacı yaklaşım önemli bir rol oynamaktadır (Abbott, 1999: 68).
Yapılandırmacı eğitim ortamında hedef, öğrenenin bilgiyi temelden kurmasıdır. Öğrenenler sınıfa yaşantılarıyla gelirler ve öğrenmeye etkin katılarak bilgiyi zihinlerinde yapılandırırlar. Bu bağlamda öğrenenler kendi düşünce ve
yorumlarını geliştirirler. Öğrenme, aktarılan belirli bir bilgi kümesini almayı değil öğrenenlerin etkili düşünme, usa vurma, sorun çözme ve öğrenme becerilerini kazanmasını içerir (Alkan ve diğerleri, 1995: 57).
Piaget’e göre, insanlar çevreleriyle etkileşimde bulunarak, bu etkileşimden o anki bilgilerine göre anlamlar çıkarıp şemalar oluşturarak ve bilgiyi işleyerek öğrenir. Piaget, bu durumu uyma (accomodation) ve özümseme (assimilation) süreçlerinden oluşan bir adaptasyon (adaptation) ile açıklar. Buna göre, birey yeni bir durumla karşılaştığında eski bilgilerinden faydalanarak yeni durumu anlamlandırmaya çalışır. Dışarıdan alınan bilgi bireyin daha önce öğrendiği bilgilerle çelişmiyor ve zihinde belli bir şemaya yerleşiyorsa, bilgi belleğe kaydedilir. Dışarıdan alınan bilgi zihindeki yapılara uymuyor ve belli bir şema içine yerleşmiyorsa, birey bir takım yeni düzenlemeler yapar (Turgut ve diğerleri, 1997). Böylece yeni durumu anlamlandırmaya çalışır. Anlamlandırma sürecinden sonra birey, yeni durumu özümseyerek onunla ilgili bilgisini oluşturur.
Yapılandırmacılığa göre bilgi öğrenenin zihninde yapılandırılır (Bodner ve diğerleri, 2001). Bu bağlamda yapılandırmacı kurama göre öğrenme, bireyin zihninde oluşan bir iç süreçtir; ezberlemeye değil öğrenenin bilgiyi transfer etmesine, var olan bilgiyi yeniden yorumlanmasına ve yeni bilgiyi oluşturmasına dayanır (Perkins, 1999:8). Birey, dış uyaranların edilgen bir alıcısı olmayıp onların özümleyicisi ve davranışlarının etkin oluşturucusudur (Fidan, 1986:65). Bu düşünceye göre öğrenci yeni kazandığı bilgileri eski bilgileri ile karşılaştırarak zihninde yeniden yapılandırır ve böylece etrafındaki dünyayı anlamlandırır.
Yapılandırmacı yaklaşımda bilginin her bir öğrenen tarafından bireysel olarak yapılandırıldığı ve öğrenmede bireyin ön bilgilerinin ve kişisel özelliklerinin son derece önemli olduğu vurgulanmaktadır. Bu yaklaşım temelde öğrencilerin mevcut bilgilerini kullanarak yeni bilgi edinmelerini, öğrenmeyi ve kendine özgü bilgi oluşturmayı açıklamaya çalışmaktadır (Hand ve Treagust, 1991; Turgut ve diğerleri, 1997). Öğrenciler yeni düşünceler ya da olaylarla eski bilgileri arasında bağ kurma sonucunda bilgiyi oluştururlar.
13
Yapılandırmacı öğrenme kuramına yönelik en önemli felsefi bakışlar, Von Glesersfeld’in radikal yaklaşımı ve Vygotsky’nin desteklediği sosyal yaklaşımdır (Keser, 2003). Radikal yapılandırmacı görüşte, bilginin bireysel öğrenme ile biçimlendirilip geliştiği düşüncesi hâkimken, sosyal yapılandırmacı görüşte ise paylaşılan bilgilerin gelişiminin sosyal etkileşim ile sağlanabileceği düşüncesi hâkimdir. Bu görüşe göre; öğrencilerin sosyal bir ortamda tartışma ve karşılıklı fikir alış verişi ile ortak bir anlamı yapılandırdıkları kabul edilmektedir. Yürütülen tartışmalar sırasında öğrencilerin kendi fikirlerini ortaya koyabilecekleri, arkadaşlarının fikirlerini farkına varabilecekleri, karşılıklı eleştirilerde bulunabilecekleri, kendi fikirlerini yeniden düzenleyebilecekleri ve sonuçta paylaşılan ortak anlam üzerinde uzlaşabileceklerine dikkat çekilmektedir (Küçüközer, 2004).
Yapılandırmacılığı etkileyen eğitimciler, felsefeciler ve psikologların ortak görüşleri aşağıdaki şekilde özetlenebilir (Marlowe ve Page, 1998) :
9 Öğrenenler, kendi öğrenmelerine etkin olarak katıldıklarında bilgi kalıcı olur.
9 Öğrenenler, bilgiyi araştırıp keşfederek, yaratarak, tekrar yaratarak, yorumlayarak ve çevre ile etkileşim kurarak bireysel bilgilerini yapılandırırlar.
9 Öğrenme etkin olarak, eleştirel düşünme ve problem çözmeye dayanır.
9 Etkin öğrenme ile öğrenenler, içerik ve süreci aynı zamanda öğrenirler.
Yapılandırmacılık yaklaşımında amaç, öğrenenlerin ne yapacaklarını önceden belirlemek değil, bireylere araçlar ve öğrenme materyalleri ile öğrenmeye kendi istekleri doğrultusunda yön vermeleri için fırsat vermektir (Erdem, 2001:58).
Yapılandırmacılıkta birey ne yapıyor olacağını bilmektedir. Algılamanın, sebep bulmanın, sonuç çıkarmanın ve hatırlamanın farkındadır. Kavrayarak öğrenme, bireyin öğrendiklerini problem çözme aracı olarak kullanmasına öncülük eder.
Bunun için bireyin uyaranları algılaması, yorumlaması, aralarında ilişki kurması, onları zihninde yeniden örgütlemesi gerekir (Ülgen, 1994:172).
Yapılandırmacılığa göre,
• Bilgi, birey tarafından aktif bir şekilde yapılandırılır, çevreden pasif olarak alınmaz.
• Birey, sahip olduğu eski bilgilerle yeni bilgiler arasında etkileşim kurarak bilgiyi yapılandırır. Bireylerin ön bilgileri farklı olduğu için her birey bilgiyi kendine özgü bir biçimde yapılandırır.
• Öğrencilerin öğrenmelerinde tecrübeleri, inançları, tutumları ve kültürleri etkilidir.
• Öğrenme, hem bireysel hem de sosyal bir süreçtir. Bilgi, bireyin diğer insanlarla olan iletişimi neticesinde yapılandırılır.
• Öğrenme, öğrencilerin öğrendiklerini başka problemlere de uygulayabilme becerisi kazanmalarını gerektirir (Smerdon, Burkam ve Lee, 1999).
Yapılandırmacı öğrenme kuramı, bilgiyi bireye olduğu gibi sunmak yerine, çevresiyle etkileşimi sonucu kişinin kendi bilgisini zihinde kendisinin yapılandırması gerektiğini savunmaktadır.
Yapılandırmacı öğrenme ortamlarının temel öğesi öğrencidir. Anlamlı öğrenmenin gerçekleşmesi ve bilginin yapılandırılması için öğrencinin öğrenmeye etkin olarak katılması gerekir. Bu ortamlarda öğrencilerin sorumluluk almaları ve etkin olmaları gerekmektedir. Öğrencilerin zengin öğrenme yaşantıları geçirmelerine ve çevreleri ile etkileşimde bulunmalarına olanak sağlayacak etkinliklere yer
15
verilmesi önemlidir. Zengin eğitsel yaşantıları içeren ortamlar yoluyla öğrenciler, daha önce zihinlerinde yapılandırdıkları bulguların doğruluğunu sınama ya da yanlışlarını düzeltme olanağı elde ederler (Yaşar, 1998:70).
Öğrencilerin aktif olduğu öğrenci merkezli bir eğitim ortamında öğretmen rehber görevindedir. Böyle bir ortamda öğrenciler, birbirleriyle etkileşimde bulunur, sorunlarını ve bilgilerini paylaşır, araştırır, düşünür ve keşfederler (Açıkgöz, 2003:39).
Yapılandırmacı öğrenmede ölçme-değerlendirme, öğrenme sürecinin içine alınmıştır. Sonuçtan çok, öğrencinin yaşadığı öğrenme süreci değerlendirilir. Ölçme-değerlendirme etkinlikleri de birer öğrenme etkinliğidir (Piburn ve Baker, 1997).
Yapılandırmacı yaklaşımı diğer yaklaşımlardan ayıran temel özelliklerden biri, öğretmen ve öğrencilerin sorumlulukları birlikte paylaşmalarıdır. Etkin öğrenme, sosyal öğrenme ve yaratıcı öğrenme sağlayan yapılandırmacılıkta, öğrenciler yalnızca dinleme, okuma ve rutin uygulamalarla çalışmak yerine tartışarak, hipotezler oluşturup incelemeler yaparak farklı bakış açıları kazanırlar. Bireyler, bilgi ve anlayışları bireysel olarak değil, diğer bireylerle iletişim içinde birlikte yapılandırırlar (Demirel, 2001:133).
Bu teorinin uygulanması ile gerçekleştirilen çeşitli araştırmalarda öğrencilerin yorum yapma, öğrendiklerini başka alanlara uygulama gibi yeteneklerinin geliştiği, öğrenmeye aktif olarak katıldıkları, öğrenme sürecinde daha fazla sorumluluk aldıkları ve kalıcı öğrenmeler gerçekleştirdikleri yönünde sonuçlar ortaya konulmuştur (Hand ve Treagust, 1991).
Sequeira, Leite ve Duarte (1993), öğretmenlerin öğretimlerini yapılandırmacı bir açıdan gerçekleştirmeleri ve öğrencilerin kavramalarını dikkate alan öğretim yöntemlerini kullanmaları gerektiğini ileri sürmektedirler.
Öğrencilerin daha önceki deneyimlerinden ve ön bilgilerinden yararlanarak yeni karşılaştıkları durumlara anlam verdiklerini ve özümsediklerini savunan yapılandırmacı öğrenme yaklaşımının kullanımına yönelik olarak farklı öğretim modelleri geliştirilmiştir (Duit, 1994).
Son zamanlarda eğitim-öğretim sürecinde yapılandırmacı öğrenme yaklaşımına dayalı bu modellerden birisi de öğrenme döngüsü modelidir. Bu model, Amerika’da ilköğretimde yeni müfredat geliştirme programı kapsamında Ulusal Bilim Vakfı (National Science Foundation) tarafından desteklenen proje sonunda ortaya çıkmıştır (Aktaran: Ergin, 2006).
1.2.1. Öğrenme Döngüsü Modeli
Öğrenme döngüsü modeli, öğrencilerin kavramsal gelişim yoluyla kazandıkları bilgilerin sınıfta tartışılması esasına dayanır (Lawson, 1995). İlk kez 1960’lı yılların başında Robert Karplus ve arkadaşları tarafından geliştirilen bu yaklaşım sınıf ortamında üç aşamada uygulanmaktadır (Ayas, 1995):
1. Keşif (Exploration)
2. Kavram Tanıtımı (Concept Introduction) 3. Kavram Uygulaması (Concept Application)
Öğrenme döngüsü modelinin keşif aşaması, öğrencileri somut deneyimlere yöneltmekte ve bu somut deneyimler öğrencilerin yeni fikirler üretmesini sağlamaktadır. Bu aşama aynı zamanda bilgilerin toplanılması, kavramların araştırılması aşaması olarak da bilinir. Öğrenme döngüsü modelinin ikinci aşaması olan kavramların tanımlanmasında, öğrenciler araştırma aşaması boyunca topladıkları bilgileri paylaşır ve tartışırlar, bilgilerin yorumlanması ile kavramların aslını öğrenirler. Son aşama olan kavram uygulamada ise öğrencilerin günlük hayattaki tecrübelerini kullanarak kavramları geliştirmeleri ve genişletmeleri sağlanır. (Özden, 2003:73).
17
Piaget’nin zihinsel çalışma modeli, öğrenme döngüsü modeli ile iç içedir. Öğrenme döngüsü modelinin keşif aşaması, yapılan etkinliklerle yeni bilginin özümsenmesini sağlar (Renner, Abraham ve Birnie, 1986) ve bu dönemde dengesizlik (disequilibrium) başlar. Kavram tanıtma aşamasında, birey kavram ile ilgili kendi tanımını yapar. Bireyin bunu yapması için de eski tecrübelerin ışığı altında yapmış olduğu etkinliklerden yararlanarak yeni bilgiyi özümsemesi gerekir. Genellikle özümseme sınıf içindeki bireyler arası veya gruplar arası tartışmalar sonucu oluşur. Kavram uygulama aşamasında, yapılan ilave deneyler, etkinlikler ve geziler sonucunda yeni bilgi genişletilir, uygulama alanları büyütülür ve gerçek hayatla bağdaşabilir hale getirilir. Birey yeni bilgiyi kendi hayatına adapte eder ve böylece organize bir şekilde hayatında kullanmaya başlar.
Öğrenme döngüsü modeli birçok araştırmada geleneksel öğretim metotlarıyla karşılaştırılmıştır. Fabian (1999) öğrenme halkası modelinin geleneksel metotlardan farklılığını şöyle aktarmaktadır:
“Öğrenme döngüsü modeli ilk olarak ezberciliği azaltarak anlamayı arttırır, ikinci olarak öğrenciler, öğrenme süreçlerinde daha fazla yer alırlar. Ayrıca öğrenme döngüsü modeli sınıfı sürekli canlı tutar.”
Tüm elde edilen bulgular, öğrenme döngüsü modelinin, modern ülkelerin eğitim standartlarıyla uyumlu olduğunu göstermiştir. Bu model ile bireye bilgi aktarımı değil, bilimsel süreç ve üstün beceriler kazandırma esas alındığı ifade edilmiştir (Türkmen, 2006).
Yapılandırmacı öğrenme teorisine dayalı birçok öğrenme döngüsü modeli tasarlanmıştır. Bu modellerde, aşamaların isimleri değişmesine rağmen modelin özü aynı kalmıştır (Beaudin ve Quick, 1995).
Öğrenme döngüsü modeli uygulamaları ve araştırmaları incelendiğinde, araştırmacılar, yıllar içerisinde bu üç aşamalı halkayı beş aşamaya dönüştürmüşlerdir. Böylece 5E öğrenme döngüsü modeli oluşmuştur. Bu model,
Biological Science Curriculum Study (BSCS)’nin öncü isimlerinden Rodger Bybee tarafından 1967 yılında geliştirilmiş ve kullanılmıştır (MMS, 2002).
1.2.2. 5E Öğrenme Döngüsü Modeli
Öğrenme döngüsünün Karplus modelindeki aşamaları, BSCS tarafından geliştirilen 5E modelinin ortasındaki üç bölüme eşdeğerdir. 5E öğrenme döngüsü modeli, öğrenme olayını beş ayrı safhadan oluşturur. Bu safhalar, Girme (Enter/Engage), Keşfetme (Explore), Açıklama (Explain), Derinleştirme (Elaborate) ve Değerlendirme (Evaluate) dir (Turgut ve diğerleri,1997; Çepni, Akdeniz & Keser, 2002). Bu modele 5E öğretim döngüsü modeli denmesinin nedeni beş aşamanın her birinin İngilizce adının E harfi ile başlamasıdır. Son zamanlarda 5E’nin girme ve derinleştirme basamaklarını ikiye ayıran yedi basamaklı bir model olan 7E modeli geliştirilmiştir. Bu model teşvik etme, keşfetme, açıklama, genişletme, kapsamına alma, değiştirme ve inceleme şeklinde yedi aşamadan oluşmaktadır (Çepni ve diğerleri, 2001). Basamak sayısının fazla olmasından dolayı araştırmanın olumsuz etkileneceği düşünüldüğünden bu araştırma 5E modeli ile yürütülecektir.
5E öğrenme döngüsü modelinde öğrenme deneyimleri belli bir sırada olur. Burada öğrencilerin kavramlar hakkındaki bilgisini yapılandırabilmesi için zamana gereksinimi vardır ve onlara bu fırsat verilir. 5E öğrenme döngüsü modelinin aşamalarını aşağıdaki gibi kısaca açıklayabiliriz (Turgut ve diğerleri, 1997; Çepni ve diğerleri, 2000).
Girme (Enter/ Engage) aşaması, giriş evresi olarak da kabul edilir. Burada öğrencilerin konu hakkındaki ön bilgilerinin neler olduğu tespit edilerek, karşılaşılacak olan yeni kavramla ilgili öğrencilerin güdülenmesi sağlanır. Bu güdülenme ilginç bir hikâye okunarak, ilginç sorular ve bulmacalar sorarak ya da dikkat çekici ilgili başka aktivitelerle sağlanabilir. Bu evre, ilgi ve merak uyandırmak, sorular ortaya koymak ve öğrencilerin konuyla ilgili bilgilerini tanımlamalarına yardımcı olmak için tasarlanmıştır. Önemli olan öğrencilerin doğru
19
cevabı bulmaları değil, değişik fikirler ileri sürerek soru sormalarını teşvik etmektir. Yaşamsal olayları, öğrencilerin ihtiyaçları ve ilgileriyle birleştirerek öğretimde başarılı bir öğrenim sağlanabilir (Trowbridge ve diğerleri, 2000). Bu aşamada iki amaç vardır: Birincisi öğrencilerin dikkatini çekmek, ikincisi konu ile ilgili önceki bilgileri hakkında fikir sahibi olmaktır.
Öğretmen ön bilgi, becerileri ve yeni kazanılacak bilgi/becerileri birbirine bağlayan, öğrenciler için ilginç, motive edici ve anlamlı etkinlikler hazırlar. Bu etkinlikler bir soru, belirlenen bir problem veya öğrencilerin ön bilgileriyle açıklamaya çalışıp fakat açıklamakta zorlanacağı bir olay olabilir. Öğrencinin, sorun ile mevcut bilgi ve becerileri arasında ilişki kurması ve konuya odaklanması sağlanır (Turgut ve diğerleri, 1997). Soru sormak, bir problemi tanımlamak, ilginç bir olayı anlatmak, öğrencinin dikkatini çekmekte ve öğrenme görevine odaklanmasına yardımcı olmaktadır (Koç, 2002). Yapılan etkinliğin sonunda öğrenci, dersin amaçları doğrultusunda ne yapacağı konusunda bir fikir sahibi olur. Bu tanıtıcı aktiviteler öğretmene, öğrencinin temel bilgilerini kontrol etme olanağı sunmalı ve deneyimler için sistem oluşturmalıdır.
Girme aşamasında öğrencilerin konuya ilgileri ve öğrenme istekleri oluşturulduktan sonra keşfetme (Explore) aşamasına geçilir. Keşfetme evresi öğrenci merkezlidir. Bu evre öğrencilerin kendilerine sağlanan materyallerle özgürce düşündüğü, hipotezler kurduğu bir dönemdir. Öğrenme her zaman nesneler, olaylar ve durumlar üzerinden gerçekleşir (Trowbridge ve diğerleri, 2000). Öğrencilerin, kavramlar ve konular hakkında araştırmalar yaptığı bu kısım 5E öğrenme döngüsü modelinin en önemli, en kapsamlı ve muhtemelen en eğlendirici evresidir. Öğrenciler, etkinlikleri birlikte yaparak kavramları keşfederler. Onlar, önceden sahip oldukları bilgilerden hareket ederek daha genel düşüncelere ulaşmak, yeni sorular keşfetmek, olası çözüm yolları bulmak ve sorgulamaya dayanan bir öğretim gerçekleştirebilmek için aktiviteleri yaparken işbirliği içinde çalışırlar. Keşfetme aşaması, işbirlikçi öğrenmeyi geliştirmek için en mükemmel zamanı sunar. Grupla çalışırken, paylaşmayı ve iletişimi sağlayan ortak yaşantılar gerçekleşmektedir (Koç, 2002). Böylelikle öğrenciler birlikte temel bilgiyi oluşturmaya başlarlar. Keşfetme
aşamasında öğretmenin görevi, öğrencilerine bu basamakta rehberlik yaparak gözlemlerde bulunmak ve onların kendi aralarında yapmış oldukları konuşmaları dinlemektir. Öğretmen, öğrencilerin yardıma gereksinimi olduğunda derinleştirici ve yönlendirici sorular sorarak, öğrencilerde kavramların oluşmasına katkı sağlar. Ancak direkt bilgi vermekten uzak durur. Öğrenciler yeni öğrendikleri kavramları ve olayları, önceden öğrendikleri kavramlarla ilişkilendirerek bilgilerini inşa etme fırsatı bulurlar.
Açıklama (Explain) aşaması ise birinci ve ikinci evrede öğrencilerin aktif katılımlarıyla ulaştıkları bilgileri, değişkenler arasındaki ilişkileri veya yeni keşifleri ifade eden kavramları adlandırma evresidir. Yeni ilişkileri veya kavramları öğrencilerin adlandırması güç olduğu için, sonrasında öğretmen, öğrencilerin eksik bilgilerini tamamlamalarına veya yanlış bilgilerini yenisiyle değiştirmelerine yardımcı olur. Bu evre 5E öğrenme döngüsü modelinin en öğretmen merkezli kısmıdır. Öğretmen bu süreci anlatım yöntemiyle veya tartışma, simülasyon (benzetim), video gibi yöntemleri kullanarak yürütebilir. Bu şekilde öğrencilerin deneyimlerini bir araya getirmelerinde, onların elde ettikleri sonuçları açıklamalarına ve yeni kavramlar yaratmalarında onlara yardımcı olunur. Bu kısım dersin öz kısmıdır. Bu kısımda öğretmen, daha önceki basamaklarda oluşan kavramları öğretmek amacı ile öğrencilere yaptıkları gözlem ve değerlendirmeleri açıklamaları için sorular sorar. Öğrencilerin dikkatlerini, girme ve keşfetme basamaklarında yaşadıkları deneyimlere, etkinliklere yöneltir, onlara kendi kavramlarıyla anlatımlarını kullanabilecekleri bir ortam sağlar. Öğrenciler kendi anladıkları kavramları anlatır, kendi yeteneklerini kullanır ve kendi yaklaşımlarını ifade ederler (Ergin, 2006). Öğretmen, onların açıklamalarını dinler, daha sonra yeni kavram ve becerileri tanıtır (Lorsbach, 2006; Turgut ve diğerleri, 1997). Bu kısımda soruların mantıksal bir şekilde birbirini takip etmesi son derece önemlidir. Bu basamak, öğrenme basamaklarının yansıtıldığı, kavramların oluştuğu ve bilinenlerden yeni durumlara geçişin olduğu kısımdır. Öğretmen, konuyu günlük hayattan verdiği örneklerle bağdaştırırken bir yandan da öğrencilerin kavram yanılgılarını tespit eder. Öğrencilerin sahip olduğu kavram yanılgılarını değiştirmeye çalışır. Böylece yanlış kavramlar doğrusuyla değiştirilir. Açıklama aşaması belki de en kısa aşamalardan
21
biridir. Çünkü bundan sonra gelen diğer aşamalar, öğrencilerin bilgileri yeniden yapılandırmalarını ve kavramları biraz daha genişletmelerini amaçlamaktadır.
Derinleştirme (Elaborate) aşaması, öğrencilerin kazandıkları kavramsal bilgileri geliştirmesi ve derinleştirmesi için gerekli evredir. Bu basamak, öğrenciye daha çok deneyim sunmaktadır. Bu aşamada, öğrencilere ilave etkinlikler yaptırılarak bir önceki evrede yeni edindikleri fikirleri benzer durumlarda uygulama ve kullanma fırsatı verilip yeni kazanılan bilgi ve becerilerin pekiştirilmesi amaçlanır. Öğrenciler pek çok genelleme etkinliği yaparlar. Bu evrede ayrıca öğrenciler, yeni öğrenilen kavramları doğru bir şekilde ifade etmeye ve tanımlamaya özendirilirler. Öğrenciler birbirleriyle tartışmaya, birbirlerinden bilgi isteyen aktiviteler içine girerler. Grup tartışmaları ve işbirlikçi öğrenme durumları öğrencilere nesneleri kendi anladıkları oranda anlatma fırsatı verir ve diğer öğrencilerden geri bildirim almalarını sağlar. Derinleştirme aşamasında öğrencilerin yeni durumlar ve yeni problemlerle karşılaşmaları, benzer açıklamalar gerektiren yeni problemlere cevap bulmaları sağlanmalıdır (Ergin, 2006). Bu basamak, öğrencilerin, öğrendikleri kavramları genişlettiği, diğer ilgili kavramlarla ilişki kurduğu ve bilgisini gerçek yaşamda kullandığı bir aşamadır (Koç, 2002). Etkinlikler, öğrencilerin mücadele etmesini, yeni durumlarla başa çıkmayı başarmasını, yeni durumla ilgili fikir yürütmesini ve yeni deneyimler kazanmasını sağlamalıdır (Trowbridge ve diğerleri, 2000). Derinleştirme evresi, öğretmen öğrenci rollerini, bundan öncekilere göre daha çok dengeler. Öğretmen, öğrencilerin yeni durumlarda anlayışlarını sergilemelerini teşvik eder (Turgut ve diğerleri,1997). Öğrencilerin neler öğrendiklerini sözlü olarak ifade edebilmeleri çok faydalıdır. Öğretmen, öğrenciler tarafından yeni öğrenilen bilgileri daha önceki bilgileri ile bağlantı kurmalarına, öğrenilen parça halindeki bilgileri bir bütün haline getirmeleri konusunda onlara yardımcı olur. Böylece yeni bilgi daha çok özümsenmiş olup daha sonra gerektiğinde kolayca kullanılabilir bilgi haline gelmiş olur.
Değerlendirme (Evaluate) aşaması, eğitim ile ilgili hedeflenen kazanımlara hangi oranda ulaşıldığını belirlemek amacıyla öğrencilerden düşüncelerini sergilemelerinin beklendiği evredir. Öğretmen, problem çözerken öğrencileri izler ve
onlara açık uçlu sorular sorar. Bu sorularla öğrencilerin kendi gözlemleri, kanıtları ve verdikleri cevaplar irdelenir. Bu basamak öğretmen açısından öğrencilerin gelişimini değerlendirmeleri ve öğretim amaçlarının sağlanıp sağlanmadığını görmeleri bakımından önemlidir. Değerlendirme aşaması, aynı zamanda yeni kavram ve becerileri öğrenmede, öğrencilerin kendi gelişmelerini değerlendirdikleri dönemdir. (Lorsbach,2006). Öğrenciler kendi açıklamalarının yeterliliğini de sorgularlar (Trowbridge ve diğerleri, 2000). Değerlendirme yapmak için dersin bitmesi beklenmez. Ders süresince de değerlendirme işlemi yapılabilir (Şekil 1.1).
GİRME
AÇIKLAMA
Şekil 1.1. 5E Öğrenme Döngüsü Modeli
Değerlendirme, devam eden bir süreç olup öğretim sürecinin her aşamasında yer almaktadır. Öğretmen, gözlemlerini, öğrenci görüşmelerini, öğrenci dosyalarını, proje ve probleme dayalı öğrenme ürünlerini bu aşamada kullanılır (Koç, 2002). Ancak değerlendirmenin amacı ve yapılış şekli aşamadan aşamaya değişebilir.
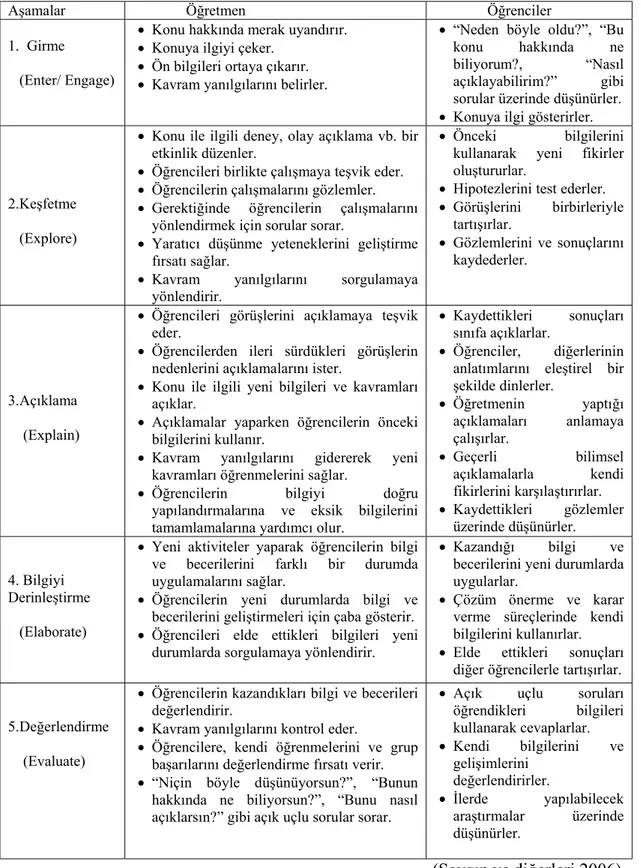
Rodger Bybee’nin 5E modelinin aşamaları öğretmen ve öğrenci görevleri dikkate alınarak, Lawson (1995), Lord (1999) ve Bybee (2002)’nin çalışmalarındaki esaslar doğrultusunda düzenlenip Tablo 1.1’de verilmiştir.
DEĞERLENDİRME
23
Tablo 1.1. Rodger Bybee’nin 5E Modeli
Aşamalar Öğretmen Öğrenciler 1. Girme
(Enter/ Engage)
• Konu hakkında merak uyandırır. • Konuya ilgiyi çeker.
• Ön bilgileri ortaya çıkarır. • Kavram yanılgılarını belirler.
• “Neden böyle oldu?”, “Bu konu hakkında ne biliyorum?, “Nasıl açıklayabilirim?” gibi sorular üzerinde düşünürler. • Konuya ilgi gösterirler.
2.Keşfetme (Explore)
• Konu ile ilgili deney, olay açıklama vb. bir etkinlik düzenler.
• Öğrencileri birlikte çalışmaya teşvik eder. • Öğrencilerin çalışmalarını gözlemler. • Gerektiğinde öğrencilerin çalışmalarını
yönlendirmek için sorular sorar.
• Yaratıcı düşünme yeteneklerini geliştirme fırsatı sağlar.
• Kavram yanılgılarını sorgulamaya yönlendirir.
• Önceki bilgilerini kullanarak yeni fikirler oluştururlar.
• Hipotezlerini test ederler. • Görüşlerini birbirleriyle tartışırlar. • Gözlemlerini ve sonuçlarını kaydederler. 3.Açıklama (Explain)
• Öğrencileri görüşlerini açıklamaya teşvik eder.
• Öğrencilerden ileri sürdükleri görüşlerin nedenlerini açıklamalarını ister.
• Konu ile ilgili yeni bilgileri ve kavramları açıklar.
• Açıklamalar yaparken öğrencilerin önceki bilgilerini kullanır.
• Kavram yanılgılarını gidererek yeni kavramları öğrenmelerini sağlar.
• Öğrencilerin bilgiyi doğru yapılandırmalarına ve eksik bilgilerini tamamlamalarına yardımcı olur.
• Kaydettikleri sonuçları sınıfa açıklarlar.
• Öğrenciler, diğerlerinin anlatımlarını eleştirel bir şekilde dinlerler. • Öğretmenin yaptığı açıklamaları anlamaya çalışırlar. • Geçerli bilimsel açıklamalarla kendi fikirlerini karşılaştırırlar. • Kaydettikleri gözlemler üzerinde düşünürler. 4. Bilgiyi Derinleştirme (Elaborate)
• Yeni aktiviteler yaparak öğrencilerin bilgi ve becerilerini farklı bir durumda uygulamalarını sağlar.
• Öğrencilerin yeni durumlarda bilgi ve becerilerini geliştirmeleri için çaba gösterir. • Öğrencileri elde ettikleri bilgileri yeni
durumlarda sorgulamaya yönlendirir.
• Kazandığı bilgi ve becerilerini yeni durumlarda uygularlar.
• Çözüm önerme ve karar verme süreçlerinde kendi bilgilerini kullanırlar.
• Elde ettikleri sonuçları diğer öğrencilerle tartışırlar.
5.Değerlendirme (Evaluate)
• Öğrencilerin kazandıkları bilgi ve becerileri değerlendirir.
• Kavram yanılgılarını kontrol eder.
• Öğrencilere, kendi öğrenmelerini ve grup başarılarını değerlendirme fırsatı verir. • “Niçin böyle düşünüyorsun?”, “Bunun
hakkında ne biliyorsun?”, “Bunu nasıl açıklarsın?” gibi açık uçlu sorular sorar.
• Açık uçlu soruları öğrendikleri bilgileri kullanarak cevaplarlar. • Kendi bilgilerini ve gelişimlerini değerlendirirler. • İlerde yapılabilecek araştırmalar üzerinde düşünürler. (Saygın ve diğerleri,2006)
Araştırmalar, öğrenilen bilginin bellekte kalma oranının öğrenme biçimi ile yakından ilgili olduğunu göstermektedir. Öğrenme şekline göre öğrenilen bilginin zihinde kalma oranlarının okuma ile öğrenme % 10, açıklamayı dinlemek suretiyle öğrenme % 20, bir yandan dinlerken bir yandan tahta veya tepegözle izleme halinde % 30, birinin yaptığını izleme ve açıklamayı dinleme halinde % 50 olduğu belirtilmektedir. Bütün bunlar ve öğrenmenin psikolojik temelleri, öğrencinin çalışmanın merkezinde olması ve etkinlikleri kendisinin yapması gerekliğini ortaya koymaktadır. Bu durum çağdaş öğrenme durumlarına “etkinlik yapma” şekliyle yansımıştır. Her etkinlik bir problem olmak zorunda değildir. Bazen bir bilginin pratik hayattaki uygulaması üzerinde çalışmak, bazen bir oyun, bilinen bir bağıntının geometrik bir uygulamasını yapmak birer etkinliktir (Altun, 2001). 5E öğrenme döngüsü modeli tüm basamaklarında öğrencilerin etkinlik yaparak kendilerinin bilgiyi fark etmelerini, keşfetmelerini ve bilgiyi anlamlandırarak farklı durumlara uygulayabilmelerini temel alır.
5E öğrenme döngüsü modeli kararlı, istekli yapılandırmacı bir eğitim ve öğretim düşüncesidir. Deneyimsel öğrenmeyi bilerek teşvik eder, bunu öğrencileri motive ederek ve ilgilerini çekerek yapar. Öğrenciler teşvik edildikçe üst düzey düşünme sürecine katılırlar (Ergin, 2006).
5E öğrenme döngüsü modeline uygun öğrenme ortamlarının tasarlanması öğretmene, sürekli olarak öğrencinin önceki bilgilerini tanıma ve yeni kavramlar oluşturma olanakları verir. Ayrıca bu model, öğrencilere mevcut yanlış kavramlarını düzeltebilecekleri öğrenme deneyimleri sağlar. Bu yüzden, özellikle kavram yanılgıları tespit edilen konularda, 5E öğrenme döngüsü modeline uygun ders etkinliklerin hazırlanması, yanlış bilgilerinin doğrularla yer değiştirmesi ve bu olayı aynı ders saati içerisinde yaşamaları kendilerini daha iyi hissetmelerine, bu nedenle de öğrenmeye karşı motivasyonlarının artmasına neden olabilir.
5E öğrenme döngüsü modeline dayalı öğretim etkinliklerinin öğrenmeye etkisi birçok araştırmacı tarafından araştırılmış; kavramsal anlamayı ve bilimsel süreç becerilerini geliştirdiği saptanmıştır (Cavallo ve Laubach, 2001; Odom ve
25
Kelly, 2001). Araştırmalar 5E öğrenme döngüsü modeline dayalı öğretim etkinliklerinin başarısını, öğrencinin öğrenme sürecine aktif katılımına ve öğrencilerin sistemli bir şekilde birbirleriyle ve öğretmen ile etkileşimde bulunmasına bağlamaktadır.
Slavin (1990), eğitim ortamının öğrencilerin zihinsel olarak aktif katılım sağladıkları, bilgiyi zihin süzgecinden geçirerek içselleştirdikleri, düşünceleri birleştirebildikleri ve fikirleri test edebildikleri ortamlar olması gerektiğini vurgulamaktadır. 5E öğrenme döngüsü modeli öğrencilere böyle bir ortam oluşturarak, öğrencilerin yeni kavramları keşfetmelerine ve onları önceki bilgileriyle kaynaştırmalarını hedef alır. Bu model öğrencileri, düşüncelerini açmaya ve genişletmeye götüren, zaman harcayarak düşünmeye teşvik eden, birbirleriyle etkileşmelerini isteyen, yansıtma ve önceden kestirmeyi teşvik eden, açık uçlu öğretmen soruları düşünmeye yardım eder. Öğrenciler, dinleyici ve okuyucunun da üzerinde olan bir konumdadırlar. Bu model ile öğrenciler, yeteneklerini analiz etme, verileri değerlendirme, becerilerini ve deneyimlerini geliştirme fırsatı bulurlar. Bütün birikimlerini, anlayışlarını birbirleriyle paylaşırlar ve konuşurlar. Öğrenciler, soru sorarlar, gözlem yaparlar, analiz ederler, açıklamalar yaparlar, çıkarımlarda bulunurlar ve yeni sorular üretirler. Bu sorgulama temelli deneyimler, sonuçta öğrencilerin hem sınama yapma becerilerini hem de mantıksal ve eleştirel düşünce becerilerini geliştirir.
Bu çalışmada 5E öğrenme döngüsü modeline dayalı etkinliklerin 7. sınıf öğrencilerinin birinci dereceden bir bilinmeyenli denklemler konusundaki etkililiği incelenmiştir.
1.3. Problem Cümlesi
5E öğrenme döngüsü modeline dayalı öğretim etkinliklerinin ilköğretim 7. sınıf öğrencilerinin matematik dersi birinci dereceden bir bilinmeyenli denklemler konusundaki akademik başarılarına etkisi var mıdır?
1.4. Alt Problemler
1. 5E Öğrenme Döngüsü Modeli ile öğrenim gören öğrencilerin öntest ve sontest puanları arasında anlamlı bir fark var mıdır?
2. 5E Öğrenme Döngüsü Modeli ile öğrenim gören öğrencilerin sontest ve kalıcılık test puanları arasında anlamlı bir fark var mıdır?
3. 5E Öğrenme Döngüsü Modeli ile öğrenim gören öğrencilerin birinci dereceden bir bilinmeyenli denklemler konusunu algılamaları nasıl değişmiştir?
1.5. Araştırmanın Amacı
Bu araştırmanın genel amacı, 5E öğrenme döngüsü modeline dayalı öğretim etkinliklerinin ilköğretim 7. sınıf öğrencilerinin matematik dersi birinci dereceden bir bilinmeyenli denklemler konusundaki akademik başarılarına etkisini ortaya koymaktır.
1.6. Araştırmanın Önemi
Nitelikli insan gücü, ülkelerin kalkınması için en önemli öğelerden biridir. Nitelikli insan gücünün oluşması iyi matematik eğitimi almış bireylerle sağlanabilir. Matematik alanında yapılan çalışmalarda, öğrencilerin anlamakta en çok zorlandıkları bölümler arasında cebir konuları yer almaktadır. Oysaki cebir öğrenimi günlük yaşam problemlerini çözmede sıklıkla kullanılan ve matematikte ileriki öğrenmelere temel teşkil eden önemli bir alandır. Birinci dereceden bir bilinmeyenli denklemler konusu cebir alanının temelini oluşturmaktadır. Özellikle temel kavramların edinilmesi ileriki öğrenmeler için ön şart niteliğinde olduğundan birinci dereceden bir bilinmeyenli denklemler konusunu anlamak önemlidir. Öğrencilerin birinci dereceden bir bilinmeyenli denklemler konusunu kapsamlı ve düzgün bir
27
şekilde anlamaları için görsel tekniklerin geliştirilmesine ihtiyaç duyduklarına inanılmaktadır (Silver, 2000). Bundan dolayı görsel teknikleri içeren yeni öğrenme ve öğretim modellerinin kullanılması ve bu modellere uygun yöntemler geliştirilmesi büyük önem taşımaktadır. Bu anlamda son yıllarda yürütülen çalışmalarda önemli bir yere sahip olan yapılandırmacı öğrenme kuramına dayalı olarak geliştirilen ve görsel teknikler kullanan öğrenme modellerinden birisi de 5E öğrenme döngüsü modelidir.
5E öğrenme döngüsü modeline göre gerçekleştirilen öğretimle bilgi toplumunun gerektirdiği yaratıcı düşünen, sorumluluk alan, karar veren, problem çözme becerisine sahip, eleştirel düşünebilen, ekip çalışmasına yatkın, bilgiye ulaşan, kullanan ve paylaşan insan nitelikleri ön plana çıkmaktadır. Bu nedenle, 5E öğrenme döngüsü modeli matematik derslerinde kullanım alanı bulabilecek önemli bir model olarak görülmektedir.
Bu araştırma, ilköğretim 7.sınıf birinci dereceden bir bilinmeyenli denklemler konusunun doğru öğrenilmesini sağlayacak alternatif bir öğrenme modelinin etkililiğini değerlendireceği için önemlidir. Ayrıca bu araştırma, sunmuş olduğu 5E öğrenme döngüsü modeli ile birinci dereceden bir bilinmeyenli denklemler konusunun öğretiminde ülkemizde ilk olması, öğrencilerin yaptıkları hata ve yanlış anlamaları bir sistematik halinde sunarak konunun öğretiminde öğretmenlere yardımcı olması, 5E öğrenme döngüsü modelinin bir öğretim ortamında nasıl uygulanabileceğini göstermesi açısından önemlidir.
1.7. Sayıltılar
1. Hazırlanan veri toplama araçları, öğrencilerin konuyla ilgili bilgilerini ölçebilecek niteliktedir.
2. Araştırmaya katılan öğrenciler, kullanılan veri toplama araçlarındaki sorulara dikkatli, doğru ve samimi bir şekilde cevap vermişlerdir.