Selçuk J. Appl. Math. Selçuk Journal of Special Issue. pp. 39-53, 2010 Applied Mathematics
An Investigation of Effects on Hierarchical Clustering of Distance Measurements
Murat Eri¸so˘glu, Sadullah Sakallıo˘glu
Department of Statistics, Faculty of Science and Letters, Çukurova University, 01330 Adana, Türkiye
e-mail: m erisoglu@ cu.edu.tr,sadullah@cu.edu.tr
Presented in 2National Workshop of Konya Ere˘gli Kemal Akman College, 13-14 May 2010.
Abstract. Clustering is an important tool for a variety of applications in data mining, statistical data analysis, data compression, and vector quantization. The goal of clustering is to group data into clusters such that the similarities among data members within the same cluster are maximal while similarities among data members from different clusters are minimal. There are a number of distance measures that have been used as similarity measures. Distance mea-sures play an important role in cluster analysis. The choice of distance measure is extremely important and should not be taken lightly. In this study, the effects of the distance measurements on hierarchical clustering will be investigated. For this purposes 8 different data sets commonly used in the literature and 2 data sets generated from multivariate normal distribution will be used.
Key words: Hierarchical Clustering, Distance Measures, Cophenetic Correla-tion, Wilks’ Lambda, Mixture Distance, Geometric Distance.
Mathematics Subject Classification: 62H30, 6207. 1. Introduction
Cluster Analysis is a multivariate statistical analysis that reveals latent clus-ters within the data set by accumulating the similar units in × dimensional data set without prior information regarding the cluster structure. There are many of different kinds of clustering algorithms. However we may catego-rize them into two major types: hierarchical and non-hierarchical (partitioning) approaches[1,2,3,6,7].
Hierarchical clustering methods are those which are aimed at forming clusters consecutively by summing up the units at different stages and determining at
what similarity level the units to fall within these clusters are the cluster el-ements[8,14]. The dendrogram obtained from the hierarchical clustering tech-niques and the combined cluster pairs along with the distance between them can be observed[13].
Anderberg(1973) states that hierarchical clustering methods are quite appropri-ate ones in some cases where the researcher does not know at first sight how many groups there are in the data set he studies and that the method is use-ful since it gives the researcher the chance to discover the formerly unobserved relations and principles in the data set which he studies.
Every clustering algorithm is based on the index of similarity between units (data points). Similarity is concerned with the distance or the relation between two units. When similarity is verbalized with distance, the similarity measures used are named as distance similarity measures. In this, the smaller the distance between two units, the more similar these two units become. Distances play an important role in cluster analysis. If there is no measure of distance between pairs of units, then no meaningful cluster analysis is possible. Various similarity and dissimilarity measures have been discussed by Sokal and Sneath (1973), Legendre and Legendre (1983), Anderberg (1973), Gordon (1999), and Brian Everitt et al. (2001).
In this study, we will be investigated on clustering in hierarchical clustering methods which single linkage, complete linkage, average linkage, weighted aver-age linkaver-age, centroid linkaver-age, median linkaver-age and ward linkaver-age methods effects of seven different distance measures that two newly distance measures and Euclid-ean, standardized EuclidEuclid-ean, .Mahalanobis, Manhattan, Minkowski distance for = 3 and = 4.
The rest of the paper is organized in the following way. Section 2 introduces dis-tance measures that used to for numerical data sets in cluster analysis. Section 3 presents hierarchical clustering methods. Section 4 defines comparison criteria which Wilks’ lambda test statistic and cophenetic correlation. In Sections 5, the effects of the distance measurements on hierarchical clustering analysis will be investigated. Conclusions are given in Section 6
2. Distance Measures
Let be a data set. A distance function on a data set X is defined to satisfy the following conditions: For ∈ ,
1. Symmetry ( ) = ( ) 2. Non-negativity ( ) ≥ 0 3. Identity ( ) = 0
4. Reflexivity ( ) = 0 if and only if = 5. Triangle inequality ( ) ≤ ( ) + ( )
also hold, it is called a metric. If only the triangle inequality is not satisfied, the function is called a semimetric[4,11].
2.1. Euclidean Distance
Euclidean distance is probably the most common distance we have ever used for numerical data. For two data points and in d-dimensional space, the Euclidean distance between them is defined to be
(1) ( ) = v u u t X =1 (− )2
where and are the values of the th attribute of and , respectively.
Euclidean distance satisfies all the conditions and therefore is a metric. Also, Euclidean distance are invariant to translations and rotations in the feature space[10].
2.2. Standardized Euclidean Distance
Standardized Euclidean distance is also called “Karl Pearson distance” and is defined to be each variable in the sum of squares is inverse weighted by the sample variance of that variable. It is defined by
(2) ( ) = v u u t X =1 1 2 (− )2
where 2 is, sample variance of th variable. 2.3. Mahalanobis Distance
Mahalanobis distance can alleviate the distance distortion caused by linear com-binations of attributes. It is defined by
(3) ( ) = ( − )0−1( − )
where is the covariance matrix of the data set defined. Therefore, this distance applies a weight scheme to the data. Another important property of the Maha-lanobis distance is that it is invariant under all nonsingular transformations[4]. However, the calculation of the inverse of may cause some computational burden for high-dimensional data.
2.4. Manhattan (City-Block) Distance
Manhattan distance is also called “city block distance” and is defined to be the sum of the distances of all attributes. That is, for two data points and in dimensional space, the Manhattan distance between them is
(4) ( ) = X =1 |− | 2.5. Minkowski Distance
The Euclidean distance, and Manhattan distance, are two particular cases of the Minkowski distance defined by
(5) ( ) = ⎛ ⎝ X =1 |− | ⎞ ⎠ 1 ≥ 1
is called the order of the above Minkowski distance. Note that if we take = 2, = 1 we get the Euclidean distance, and Manhattan distance, respectively. If the data set has compact or isolated clusters, the Minkowski distance works well; otherwise the largest-scale attribute tends to dominate the others. To avoid this, we should normalize the attributes or use weighting schemes [6]. 2.6. The Newly Distances
2.6.1. Geometric Distance
In order to reduce the effect of outliers within the data set on the distance between the units, a distance measurement based on a geometric mean can be used. For two data points and in dimensional space, the geometric distance between them is defined as follows:
(6) ( ) = ⎛ ⎝ Y =1 (|− | + 1) ⎞ ⎠ 1 − 1 2.6.2. Mixture Distance
Euclidean distance and Pearson correlation coefficient can be used together in clustering. Mixture distance between the units and for variables is defined as follows :
(7) ( ) = v u u t X =1 (−)2+ (1 − ) Ã 1− ¯ ¯ ¯ ¯ ¯ =1(−¯)(−¯) =1(−¯)2 =1(−¯)2 ¯ ¯ ¯ ¯ ¯ !
where is the mixture weight and 0 ≤ ≤ 1. A small value of mixture distance between units means they are similar.
3. Hierarchical Methods
An important group of clustering methods is hierarchical clustering. All hi-erarchical clustering methods proceed algorithmically through steps to either successively merge or divide groups. There are two main types of hierarchical clustering methods, agglomerative and divisive. An agglomerative hierarchical method begins with each individual as one group. It then merges the most similar groups together until the entire set of data becomes one group. On the contrary, a divisive hierarchical method starts with one big group and works backwards to eventually divide the group into separate groups for each indi-vidual in the set. In this study, the focus will be merely on agglomerative hierarchical clustering methods.
3.1. The Single Linkage Method
Single linkage is perhaps the method used most often in agglomerative clus-tering, which produces the hierarchical clustering. Single linkage is also called nearest neighbor, because the distance between two clusters is given by the smallest distance between objects, where each one is taken from one of the two groups. Let , , and be three observation vectors in data set. Then the distance between and ∪ can be obtained according the single linkage method
(8) ( { }) = min(( ) ( )) where ( )and ( )are a distance between two units. 3.2. The Complete Linkage Method
Complete linkage is also called the furthest neighbor method, since it uses the largest distance between observations, one in each group, as the distance be-tween the clusters. Then the distance bebe-tween and ∪ can be obtained according the complete linkage method
Complete linkage is not susceptible to chaining, but it does tend to impose a spherical structure on the clusters. In other words, the resulting clusters tend to be spherical, and it has difficulty recovering non-spherical groups. Like single linkage, complete linkage does not account for cluster structure.
3.3. The Average Linkage Method
The average linkage method is also referred as UPGMA, which stands for “un-weighted pair group method using arithmetic averages”. The average linkage method defines the distance between clusters as the average distance from all observations in one cluster to all points in another cluster. In other words, it is the average distance between pairs of observations, where one is from one cluster and one is from the other. Thus, we have the following distance
(10) ( { }) = ( ) + ( ) 2
This method tends to combine clusters that have small variances, and it also tends to produce clusters with approximately equal variance.
3.4. The Weighted Average Linkage Method
The weighted average linkage method is also referred to as the “weighted pair group method using arithmetic average”. Similar to UPGMA, the average link-age is also used to calculate the distance between two clusters. The difference is that the distances between the newly formed cluster and the rest are weighted based on the number of data points in each cluster. In this case,
(11) ( { }) = ( ) + ( ) +
where is the number of the observations in the th cluster, and is defined
similarly.
3.5. The Centroid Linkage Method
Another type, called centroid linkage, requires the raw data, as well as the distances. It measures the distance between clusters as the distance between their centroids. Their centroids are usually the mean, and these change with each cluster merge. We can write the distance between clusters, as follows
(12) ( ) = (¯ ¯)
where ¯is the average of the observations in the th cluster, and ¯is defined
3.6. The Median Linkage Method
The median linkage method is also referred to as the “weighted pair group method using centroids” or the “weighted centroid” method [6]. It was first proposed by Gower (1967) in order to alleviate some disadvantages of the cen-troid method. In the cencen-troid method, if the sizes of the two groups to be merged are quite different, then the centroid of the new group will be very close to that of the larger group and may remain within that group [2]. In the median method, the centroid of a new group is independent of the size of the groups that form the new group. In the median linkage method, the distances between newly formed groups and other groups are computed as
(13) ( { }) =( ) + ( )
2 −
( ) 4 3.7. The Ward Linkage Method
Ward linkage method, also known as the minimum variance method. Cluster membership is assigned by calculating the total sum of squared deviations from the mean of a cluster. The criterion for fusion is that it should produce the smallest possible increase in the error sum of squares. Ward linkage method joins the two clusters and that minimize the increase in SSE , defined as
(14) =
+
(¯− ¯)0(¯− ¯)
The distance between two clusters using Ward’s method is given by
(15) ( { }) = (+ )( ) + (+ )( ) − ( ) + +
4. Comparison Criteria
In this study we are going to analyze the effect of distance measurement on hierarchical clustering methods within the clustering according to cophenetic correlation coefficient and Wilks’ lambda test statistics. When the literature is analyzed, it is understood that comparison is common in terms of classification accuracy rate except for these criteria[4, 13, 14]. From the data sets being dis-cussed, a comparison for the Iris data will also be made in terms of classification accuracy rate.
4.1. Wilks’ Lambda Test Statistic Wilks’ Lambda test statistic is given by
(16) = | | | + |
where is the within sum of .squares and products matrix and + is the total sum of squares and products matrix. Differences between clusters are significant for small values of Wilks’ lambda test statistics .
4.2. Cophenetic Correlation Coefficient
A Cophenetic correlation coefficient () is an index used to validate hierarchical clustering structures. Given the similarity matrix = () of ,
Cophe-netic correlation coefficient measures the degree of similarity between and the cophenetic matrix = (), whose elements record the similarity level
where pairs of data points are grouped in the same cluster for the first time. Let ¯ and ¯ be the means of and , i.e., Cophenetic correlation coefficient is defined as[12] (17) = P (− ¯)(− ¯) P (− ¯)2P(− ¯)2
The value of cophenetic correlation coefficient lies in the range of [-1,1], and an index value close to 1 indicates a significant similarity between and and a good fit of hierarchical to the data.
5. Application
In this study the effects of the distance measurements on hierarchical clustering will be analyzed with 8 different data sets commonly used in literature and 2 data sets generated from multivariate normal distribution. The features regarding the data sets is shown in Table 1. The real data sets seen in Table 1 are retrieved from the link, http://archive.ics.uci.edu/ml/datasets.html [15].
Table 1. The data sets and features.
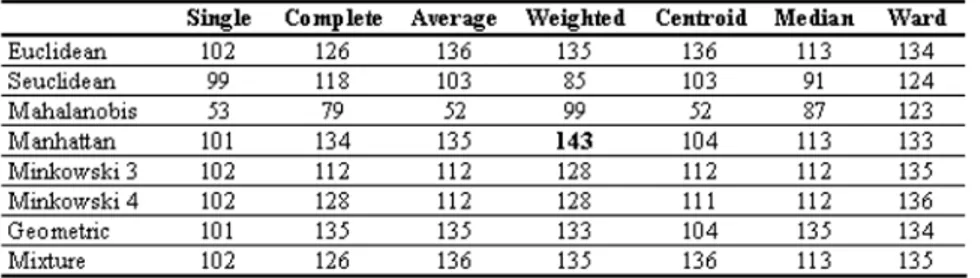
Firstly, number of classification accuracy units calculated for Iris data set are given Table 2.
Table 2. The accurately classified for Iris data.
When Table 2 is investigated, it is understood that the accurately classified unit number changes according to the selected distance measurement and clustering technique. For instance, when single linkage clustering is chosen as a clustering technique, the accurately classified unit number is 102 by using Euclidean dis-tance, whereas the number drops down to 53 with Mahalanobis distance. From the two suggested distance measurements, the unit number accurately classified at a geometric distance is 101, while 102 units are accurately classified at a mix-ture distance. In the Iris data, the highest accurately classified unit number is reached when Manhattan is used as a distance measurement in weighted average linkage clustering. With this combination, 143 units out of 150 are accurately classified.
Considering the classification accuracy rate while evaluating the clustering per-formance is, in fact , in contrast with clustering analysis logic; for, in clustering analysis, the actual cluster memberships are unknown. Seeing that the actual purpose in clustering is acquiring clustering where the change within the cluster
is at minimum and the change inter-clusters is at maximum, it will be more appropriate to use Wilks’ lambda test statistics which is a multivariate test in evaluating the clustering analysis performance. Separately, in evaluating the hierarchical clustering techniques, the cophenetic correlation coefficient based on the correlation between the pre-clustering distances and post-clustering dis-tances is a suitable criterion for the evaluation of clustering performance. The dendrogram acquired by using different distance measures of Iris data in single linkage method according to cophenetic correlation coefficient and the values in Wilks’ lambda test statistics are as follows
Figure 1. Dendrogram by different distance measures and the single linkage method for Iris data set
In accordance with the cophenetic correlation coefficient, the distance measure-ment where the best clustering is acquired is Minkowski distance, = 4. The distance where the worst clustering is acquired is, on the other hand, Maha-lanobis distance. In order to make an evaluation according to Wilks’ lambda test statistics, a single linkage clustering technique is applied to constitute the units into three clusters. According to Wilks’ lambda test statistics, the cluster-ing acquired by Euclidean, , = 3 and Minkowski distance, = 4 and mixture distances are the most successful clustering. Again according to Wilks’ lambda test statistics, the worst clustering performance is acquired with Mahalanobis distance as in cophenetic correlation coefficient. When the dendrograms in Fig-ure 1 are investigated, it is clearly seen that the clustering changes according to the selected distance measurement
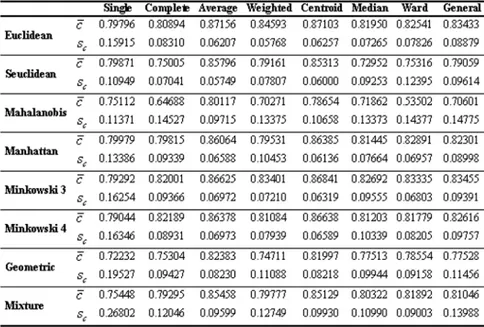
Considering the distance measurements, the general evaluation of the cluster-ing performance accordcluster-ing to the cophenetic correlation coefficient is shown on Table 3.
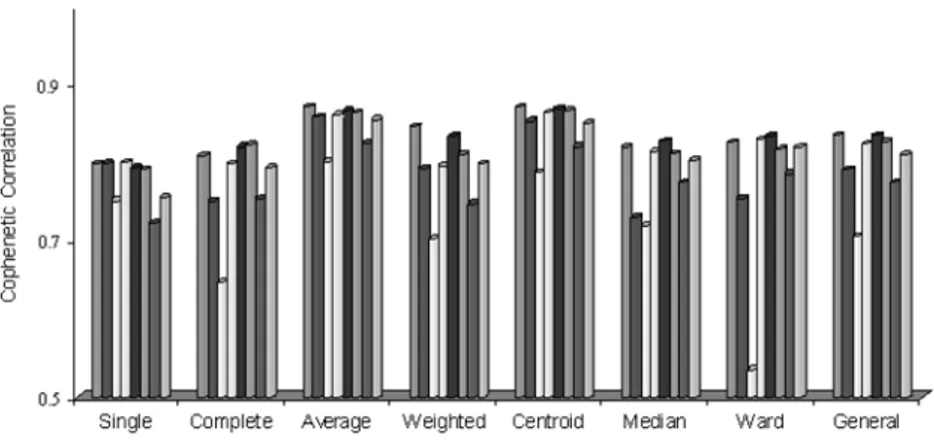
Table 3. The clustering performance according to cophenetic correlation. The best distance measurement according to cophenetic correlation coefficient without taking into consideration any clustering techniques is Euclidean Dis-tance. While the average cophenetic correlation coefficient obtained with the Euclidean distance is 0.83, with the latest identified distance measurements, this value is 0.77 at a geometric distance and 0.81 at a mixture distance. In the clustering of the data sets analyzed, the worst resulting distance measurement is Mahalanobis distance. The bar graph to be of use in interpreting Table 3 is shown in Figure 2.
Figure 2. Bar graph for the average cophenetic correlation values.
The new identified distance measurements, mixture and geometric distances have performed their best in weighted average linkage clustering and central linkage clustering techniques in accordance with the cophenetic correlation co-efficient. When Figure 2 is analyzed, it has been understood that the geometric distance in single linkage clustering has been the worst distance measurement having the worst performance according to the cophenetic correlation coefficient. The evaluation of the clustering performance according to Wilks’ lambda test statistics is given on Table 4. When clustering performances are evaluated in accordance with Wilks’ lambda test statistics without taking into consideration any clustering technique.
Mixture and geometric distances have performed their best in weighted average linkage clustering and central linkage clustering techniques in accordance with the cophenetic correlation coefficient. When Figure 2 is analyzed, it has been understood that the geometric distance in single linkage clustering has been the worst distance measurement having the worst performance according to the cophenetic correlation coefficient. The evaluation of the clustering performance according to Wilks’ lambda test statistics is given on Table 4.
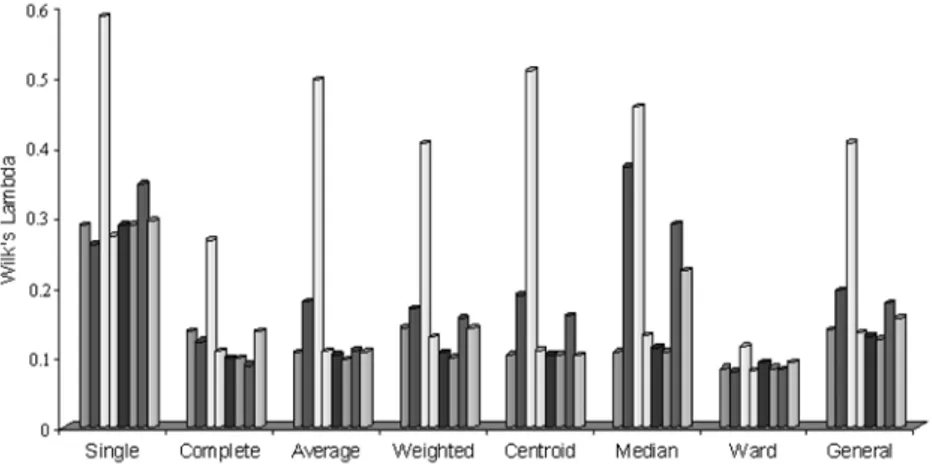
When clustering performances are evaluated in accordance with Wilks’ lambda test statistics without taking into consideration any clustering technique, Minkowski distance which is = 4 is the most successful distance measurement. And according to this criterion, the distance measurement having the worst per-formance is Mahalonobis distance. The bar graph obtained for making the interpretations from the results on Table 4 easier is given in Figure 3.
Table 4. The clustering performance according to Wilks’ lambda test statistics. When clustering performances are evaluated in accordance with Wilks’ lambda test statistics without taking into consideration any clustering technique, Minkowski distance which is = 4 is the most successful distance measurement. And according to this criterion, the distance measurement having the worst per-formance is Mahalonobis distance. The bar graph obtained for making the interpretations from the results on Table 4 easier is given in Figure 3.
According to Figure 3, the newly identified distance measurements, geometric and mixture distances have performed the best in Ward clustering technique. However, the other distance measurements also have had the best performance in Ward clustering technique in accordance with Wilks’ lambda test statistics. According to this statistics, geometric distance has been the most successful dis-tance measurement among the disdis-tance criteria in complete linkage clustering. Geometric and mixture distances, according to the same statistics, have had the worst performance in single linkage clustering. It is clearly seen in Figure 3 that Mahalanobis distance has been the worst performing distance measurement among all the other clustering techniques.
6. Conclusions
The results obtained from our empirical study that to investigate the effective-ness on hierarchical clustering of distance measurements can be summarized as follows.
1. The clustering performance changed according to the selected distance measurement and hierarchical clustering method.
2. The best distance measurement according to cophenetic correlation co-efficient without taking into consideration any clustering techniques is Euclidean distance.
3. When clustering performances are evaluated in according to Wilks’ lambda test statistics without taking into consideration any clustering tech-niques, Minkowski distance which is = 4 is the most successful distance mea-surement.
4. Mixture and geometric distances have performed their best in weighted average linkage clustering and central linkage clustering techniques in accor-dance with the cophenetic correlation coefficient.
5. The distance measurement having the worst performance is Mahalonobis distance according to each two criterion.
6. When clustering performances are evaluated in according to cophenetic correlation coefficient, weighted average linkage and centroid linkage methods which is the most successful hierarchical clustering methods..
7. According to Wilks’ lambda test statistics, geometric distance has been the most successful distance measurement among the distance criteria in com-plete linkage clustering.
8. Geometric and mixture distances, according to the Wilks’ lambda test statistics, have had the worst performance in single linkage clustering.
9. The newly identified distance measurements, geometric and mixture distances have performed the best in Ward clustering technique according to Wilks’ lambda test statistic.
7. Acknowledgements
The authors thank editors and anonymous referee for his or her careful reading and valuable comments on improving the original manuscript. This work is
supported by Çukurova University Scientific Research Project Unit (No. FEF 2008D15 LTP).
References
1. Anderberg, M. R. (1973), Cluster Analysis for Applications, Academic Press Inc., London.
2. Brian Everitt, Sabine Landau, Morven Leese (2001), Cluster Analysis, Fouth Edi-tion, Arnold Publishers.
3. Charles Romesburg (2004), Cluster Analysis For Researchers, Lulu Pres.
4.Gan Guojun, Ma Chaoqun, Wu Jianhong (2007), Data Clustering: Theory, Algo-rithms, and Applications, Society For Industrial & Applied Mathematics,U.S. 5. Gordon, A. (1999), Classification, 2nd edition, Boca Raton, FL: Chapman & Hall/CRC.
6. Jain, A. K. and Dubes, R. C. (1988) Algorithms for Clustering Data, Prentice Hall, New Jersey.
7.Kaufman, L. and Rousseeuw, P. J. (2005), Finding Groups in Data: An Introduction to Custer Analysis, John Wiley & Sons, New York.
8. Legendre, L. and Legendre, P. (1983), Numerical Ecology, New York: Elsevier Scientific.
9. Mark S. Aldenderfer, Roger K. Blashfield (1984), Cluster Analysis, Sage University Paper, London.
10.Martinez Wendy L. and Martinez Angel R. (2005), Exploratory Data Analysis with Matlab§, Chapman & Hall//CRC Series in Computer Science and Data Analysis. 11.Michel Marie Deza and Elena Deza (2006), Dictionary of Distances, Elsevier. 12. Rencher Alvin C. (2002), Methods of Multivariate Analysis, Second Edition, John Wiley&Sons Inc. Publication, Canada.
13. Rui Xu and D.C. Wunsch II (2009), Clustering, John Wiley.
14. Sokal, R. and Sneath, P. (1973), Numerical Taxonomy: The Principles and Practice of Numerical Classification, San Francisco: W.H. Freeman.