Kesirli diferensiyel denklemlerin çözüm yöntemleri

(1)

T.C.

SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ

KESİRLİ DİFERANSİYEL DENKLEMLERİN ÇÖZÜM YÖNTEMLERİ

CEMİLE SOYTAŞ

YÜKSEK LİSANS TEZİ MATEMATİK ANABİLİM DALI

(2)

T.C.

SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ

KESİRLİ DİFERANSİYEL DENKLEMLERİN ÇÖZÜM YÖNTEMLERİ

CEMİLE SOYTAŞ YÜKSEK LİSANS TEZİ MATEMATİK ANABİLİM DALI

Bu tez 08/09/2006 tarihinde aşağıdaki jüri tarafından oybirliği / oyçokluğu ile kabul edilmiştir.

Yrd.Doç.Dr. Galip OTURANÇ (Danışman)

Prof.Dr. Şefik BİLİR Yrd.Doç.Dr. Hasan KÖSE (Üye) (Üye)

(3)

ÖZET Yüksek Lisans Tezi

KESİRLİ DİFERANSİYEL DENKLEMLERİN ÇÖZÜM YÖNTEMLERİ

Cemile SOYTAŞ

Selçuk Üniversitesi Fen Bilimleri Enstitüsü Matematik Anabilim Dalı

Danışman :Yrd.Doç.Dr.Galip OTURANÇ 2006

Jüri:Prof.Dr. Şefik BİLİR

Yrd.Doç.Dr. Galip OTURANÇ Yrd.Doç.Dr. Hasan KÖSE

Bu çalışmada Kesirli Türev, Kesirli İntegral ve Adomian’ın Ayırma Yöntemi ile lineer olmayan bir diferansiyel denklemin çözümü verilmiştir. Kesirli türev formülüyle verilen bir fonksiyonun istenilen keyfi mertebeden kesirli türevi hesaplanabilir. Ayrıca verilen bir lineer olmayan kesirli diferansiyel denklemin çözümü Adomian’ın ayırma yöntemi ile yapılabilir.

Anahtar Kelimeler: Kesirli Türev, Kesirli İntegral, Lineer Olmayan Kesirli Diferansiyel Denklemler,Ayırma Metodu.

(4)

ABSTRACT

FRACTIONAL DIFFERENTIAL EQUATIONS AND SOLUTIONS METHODS

Cemile SOYTAŞ Selçuk University

Graduate School of Natural and Applied Sciences Department of Mathematics

Supervisior:Asst.Prof.Dr.Galip OTURANÇ 2006,

Jury:Prof.Dr.Şefik BİLİR

Asst.Prof.Dr.Galip OTURANÇ Asst.Prof.Dr. Hasan KÖSE

In this study we explained fractional derrivative, fractional integral and an nonlinear differential equation’s soluation with Adomian’s seperation method. If we choose a function that is given with fractional derrivative formüla, we can calculate it’s fractional derrivative form arbitrary order. Besides nonlinear fractional differential equation can be solved with Adomian’s seperation method.

Key words: Fractional Derivative, Fractional Integral, Nonlinear Fractional Differential Equations, Seperation Method.

(5)

İÇİNDEKİLER 1.GİRİŞ………1 1.1. Amaç ve Kapsam………..1 1.2. Literatür Özeti………...1 2. TEMEL KAVRAMLAR………..3 2.1. Gamma Fonksiyonu………...………...3 2.2.Hata Fonksiyonu………5 2.3.Anger Fonksiyonu………..5 2.4.Kesirli İntegral………...6 2.5.Kesirli Türev…………...………...6

3.KESİRLİ TÜREV VE İNTEGRALLER………...7

3.1.Grunwald - Letnikov Kesirli Türevleri…………..………7

3.2. Riemann - Liouville Kesirli Türeveri………16

3.3.Ardışık Kesirli Türevler………...22

3.4. Kesirli Türevlerin Özelikleri……….………...23

4.KESİRLİ TÜREVLER İÇİN GENELLEMELER VE UYGULAMALAR………24

4.1.Kesirli Türev………...24

4.2. Polinom Fonksiyonlar için Kesirli Türevin Formülü………..24

4.3.Örnekler………...24

5.ADOMİANIN AYIRMA METODU İLE LİNEER OLMAYAN KESİRLİ DİFERANSİYEL DENKLEMLERİN ÇÖZÜMLERİ…………..……… 36

5.1 Ayırma Metodu………...36

5.2.Uygulamalar………...……….38

6. GENEL SONUÇ VE ÖNERİLER………..49

7. TABLO 2.………...50

(6)

ÖNSÖZ

Kesirli diferansiyel denklemler, özellikle kesirli türev ve kesirli integraller teorik ve pratik bakımdan büyük önem taşımakta ve bütün fen ve mühendislik bilim dallarında çok geniş bir uygulama yeri bulunmaktadır.

Bu çalışmada kesirli türev, kesirli integral ve Adomian’ın ayırma yöntemi ile lineer olmayan bir diferansiyel denklemin çözümü verilmiştir. Kesirli türev formülüyle verilen bir fonksiyonun istenilen keyfi mertebeden kesirli türevi hesaplanabilir. Ayrıca verilen bir lineer olmayan kesirli diferansiyel denklemin çözümü Adomian’ın ayırma yöntemi ile yapılabilir.

Tez konusunun seçimi ve yürütülmesi konusundaki yardımları ve yakın ilgisinden dolayı sayın hocam Yrd.Doç.Dr. Galip OTURANÇ’a ve Arş.Gör. Yıldıray KESKİN’ e teşekkürlerimi sunarım.

Cemile SOYTAŞ Konya, 2006

(7)

1.GİRİŞ

1.1. Amaç ve Kapsam

Bu çalışmada Kesirli Türev, Kesirli İntegral ve Kesirli Diferansiyel Denklemlerin çözümlerine yer verilmiştir. Kesirli diferansiyel denklemlerin çözümleri için kesirli türev ve kesirli integral hesaplamalarının bilinmesi gerekir. Lineer olmayan kesirli diferansiyel denklemlerin çözümleri için Adomian’ın ayırma yöntemi uygulanmıştır. Bunun için kesirli türev ve kesirli integral hesaplarının bilinmesi gerekir. Bu yüzden öncelikle bunlara yer verilmiştir.Ayrıca kesirli türev sık bağımlı sıkıştırılmış metaryellerin hareketleri, bir Newton akışkanındaki ince geniş tabaka halindeki viskoelastik metaryellerin sürünme ve gevşeme fonksiyonları ve dinamik sistem ve benzerlerinin kontrolcüsü için PI Dλ μ kontrolcüsü gibi bir çok fiziksel problemde yer almaktadır.

Elektromanyetik, akustik, viskoelastik, elektrokimya ve madde bilimlerindeki fenomenlerde kesirli diferansiyel denklemleri kullanılmaktadır. Kesirli türev içeren diferansiyel denklemlerin çözümleri oldukça karışıktır. Bunun için önce kesirli türevin bilinmesi gerekir.

Kesirli türevler ve kesirli integraller lineer olmayan kesirli diferansiyel denklemlerin çözümlerinde kullanılmıştır. Kesirli diferansiyel denklemlerinin çözümleri ayırma yöntemi üzerinden elde edilmiştir.Genel olarak lineer olmayan kesirli diferansiyel denklemlerden tam çözüme ulaşılabilir bir yöntem yoktur. Sadece yaklaşık çözümler türetilmiştir.

1.2.Literatür Özeti

Podlubny, I. 1999, Fractional Differential Equations, Academic Pres.Bu çalışmada diferensiyel ve integralin notasyonlarının genelleştirilmesi için birkaç yaklaşım ele alınmıştır.İstenilen keyfi mertebeden kesirli türev ve kesirli integraller ve bunların özelliklerine yer verilmiştir. Ayrıca kesirli diferansiyel denklemler bu çalışmada bilhassa ele alınmıştır. Ray S.S., Bera R.K. 2004, An approximate solution of a

(8)

nonlinear fractional equation by adomian decomposition method, Applied mathematicsand Computation, Volume 165, Issue 2, 15 June 2005, Pages 473-483. Mevcut olan analizlerin amacı lineer olmayan kesirli diferansiyel denklemlerin çözümleri için Adomian’ın ayırma metodunu uygulamaktır. Sonuç olarak ayırma metoduyla elde edilen çözüm sayısal açıdan değerlendirilir ve truncated metoduyla elde edilen sonuçlar kıyaslanır. Sonuçlar arasında iyi bir uyum gözlemlenmiştir. Davis,H.D. 1936, The Theory of Linear Operators, Principial Press, Blommington, Indiana. Bu çalışmada lineer operatörlerin teoremleri ve gösterimlerinden bahsedilmiştir. Ayrıca kesirli türev ve kesirli integrallerin gösterimine yer verilmiştir.

(9)

2.TEMEL KAVRAMLAR

Mühendislikte, fiziki bilimlerde, sosyal bilimlerde ve daha birçok bilim dalında çok sayıda problemi çözmek için önce bu problemleri matematiksel ifadelerle formüle etmek ve sonra da bunlarla ilgili bazı sınır şartları ve başlangıç şartlarını kullanarak problemlerin çözümlerini oluşturan fonksiyonlar bulmak gerekir. Bilinen bir problemi formüle eden bu matematiksel ifadeleri bazen aranan fonksiyonun kesirli mertebeden, birinci mertebeden veya daha yüksek mertebeden türevlerini içermektedir.İşte bu şekilde bir matematiksel ifadeye içindeki türevlerin mertebesine göre diferansiyel denklem veya kesirli diferansiyel denklem denir.

2.1.Gamma Fonksiyonu

Tanım:

Γ( )x ile göstereceğimiz gamma fonksiyonu

1 0 ( ) x t x t e dt ∞ − − Γ =

_∫

(2.1) genelleştirilmiş integrali ile tanımlanır.

Aynı zamanda eşitlik (2.1.) den 0 ! n t n t e d ∞ − =

∫

t dt ) n

integraline geçiş yapmak mümkündür. Buradan da görüleceği üzere, Gamma fonksiyonuna faktöriyel fonksiyonuda denir.

1 0 ( ) n t n t e ∞ − − Γ =

_∫

genelleştirilmiş integrali yardımıyla n!= Γ + = Γ(n 1) n (

(10)

Gamma fonksiyonunun grafiği aşağıdaki gibidir (bkz şekil 1).

Şekil 1.

Çalışmanın ileri aşamalarında kullanılacak Gamma fonksiyonuna ilişkin rakamsal değerler Tablo 1’de verilmiştir.

Tablo 1:Gamma fonksiyonunun bazı rakamsal değerleri

(0) Γ _Tanımsız 1 ( ) 2 Γ π (1) Γ 1 ) 2 3 ( Γ 1 2 π (2) Γ 1 ) 2 5 ( Γ π 2 3 (3) Γ 2 ( ) Γ ∞ ∞

(11)

2.2.Hata Fonksiyonu (erf)

Tanım:

erf(x) ile gösterilen hata fonksiyonu 2 0 2 ( ) x t erf x e dt π − =

∫

(2.2) şeklinde tanımlanır.

Söz konusu fonksiyona ilişkin aşağıdaki eşitlik ve değerler mevcuttur. i) erf(x)=1-erfc(x)

ii) erf(-x)=-erf(x) iii) erf(0)=0 iv) erf(∞)=1

erf(x) in grafiği Şekil 2 de verilmiştir.

Şekil 2.

2.3. Anger Fonksiyonu (AngerJ) [Mapple 9]

Tanım:

AngerJ(v,x) fonksiyonu homojen olmayan bessel denkleminin çözümüdür.

xy xy (x v y) (x v)sin(vπ)

π

−

′′+ ′+ − = (2.3) burada x ve v ye verilen değerlere göre AngerJ(x.,v) fonksiyonu hesaplanabilir.

(12)

2.4. Kesirli İntegral

Tanım:[23]

Literatürde, Kesirli sıra integralinin en sık karşılaşılan açıklaması, kesirli sıra integralinin aşağıda verilen Riemann-Liouville integralidir.

₁ 0 ( ) 1 ( ) ( ) ( ) x q q d f x f t dt dx q x t − − =_Γ

∫

₋ −q (2.4) burada q( q>0 ve q∈R ) ve n-1≤ q ≤ n n∈Z dir . 2.5. Kesirli Türev Tanım:[23] Kesirli türev ₁ 0 ( ) 1 ( ) ( ) ( ) x q n q n d f x d f t dt dx =Γ −n q dx

∫

x t− − +n q (2.5)

(13)

3.KESİRLİ TÜREV VE İNTEGRALLER

Literatür [7] den bu çalışmada gösterim olarak;

_aDα_t f t( ) (3.1) (3.1) kullanılacaktır. Bu gösterim a ve t kesirli diferansiyelleme işleminin limit değerleri olmak üzere keyfi mertebeden türevler için “kesirli türev” gösterimidir. “Kesirli integral” keyfi mertebeden integraller anlamındadır veα ’ nın negatif değerine bağlıdır. Kesirli integraller için bir bölme notasyonu kullanılacaktır.

0

α > için

_aDt−α f t( ) (3.2)

gösterimi keyfi mertebeden integraller için “kesirli integral” gösterimidir. Kesirli diferansiyel denklem kesirli türev içeren bir denklemdir.

3.1.Grunwald-Letnikov Kesirli Türevleri

Teorem 3.1.1. [23]

f(t) fonksiyonu alınırsa a ve t’ler limit değerleri olmak üzere 0 ₀ ( ) lim ( 1) ( , ) ( ) n p p r a t h r nh t a D f t h− C p r f t rh → ₌ = − =

∑

− −

eşitliğinde p = m ise m. mertebeden türev ve eğer p=-m ise m katlı integral olur. İspat: [23]

Kesirli türev ve kesirli integral için bir yaklaşım tanımlanmıştır.

Bunlar klasik analizden bağımsız olarak verilmiştir. n tam sayılı mertebeden türev ve n katlı integraller olarak alınmıştır.

y=f(t) sürekli fonksiyonu alınırsa f(t) fonksiyonunun birinci türevi; f t'( )=df dt = 0 ( ) ( ) lim h f t f t h h → − − (3.3) dır. (3.3) iki kere uygulanırsa

(14)

2 2 2 ₀ 0 2 0 ( ) ( ) ( ) lim 1 ( ) ( ) ( ) ( 2 ) lim ( ) 2 ( ) ( 2 ) lim h h h d f f t f t h f t d t h f t f t h f t h f t h h h h f t f t h f t h h → → → ′ − ′ − ′′ = = − − − − − ⎧ ⎫ = _⎨ − _⎬ ⎩ ⎭ − − + − = (3.4) ikinci mertebeden türevi elde edilir. (3.3) ve (3.4) kullanılarak

3 3 ₀ 3 ( ) 3 ( ) 3 ( 2 ) ( 3 ) ( ) lim h d f f t f t h f t h f t h f t dt → h − − + − − − ′′′ = = (3.5)

elde edilir. Bu indiksiyonla genellenecek olursa 0 ₀ 1 ( ) lim ( 1) ( , ) ( ) n n n r n _h n r d f f t C n dt → h ₌ = =

∑

− r f t−rh

)

(3.6) olur. Burada

(

! ( , ) ! ! n C n r r n r = − (3.7) olarak ifade edilir. (3.3) - (3.6) daki kesirlerin genel ifadesi;

0 1 ( ) ( 1) ( , ) ( ) n p r h p r f t C p r f h = =

∑

− t−rh (3.8)

dır. Burada p keyfi bir tam sayı n de bir tam sayıdır. Açıkca p≤ n için ( ) ( ) 0 lim ( ) ( ) p p p h p h d f f t f t dt → = =

elde edilir. p nin negatif değeri alınırsa

( 1 ( , ) ! p r C p r r )! + + =

ile ifade edilir. Buradan;

C(-p,r)= ( 1)r ( , ) C p r −

dır. (3.8) deki p -p ile değiştirilirse; ( ) 0 ( ) n ( , ) ( ) p p h r f − t h C p r f t rh = =

∑

−

(15)

Eğer n sabit ise, ( p)_{( )} h

f − t nin iken limitinin 0’a gitmesi doğaldır. Sıfır

olmayan bir limite ulaşmak iken olmak zorundadır. 0 h→ 0 h→ h→ ∞ h t a n − =

alınabilir. Burada a bir reel katsayı ve ( p)_{( )} h

f − t nin limit değeri sonlu veya sonsuzdur.

( ) 0 lim p ( ) h h nh t a f − t → = − = p ( ) t aD f t − ile gösterilecektir.

Burada fonksiyonu üzerinde bir işlemdir, a ve t’ler limit değerleridir.

( ) , ( )

p

aDt f t f t −

Şimdi birkaç özel durum ele alınırsa ( ) 0 1 ( ) ( ) n p h p r f t f t h − = =

(

)

(

)

(

)

1 1 0 0 1 0 0 1 0 0 ( ) lim 1, ( ) lim 1, ( ) lim 1, ( ( 1) ) n p p t h r nh t a n p h r nh t a n p h r nh t a D f t h C p r f t rh h C p r f t rh h C p r f t r h − − + → ₌ = − → ₌ = − → ₌ = − = + − = + − − + −

∑

+ olur.

(

p+1,r

) ( ) (

= p r, + p+1,r− (3.11) 1

)

olur. Burada C p

(

+ − =1, 1

)

0 olmalıdır.

(3.11) i (3.10) daki toplama uygulamak için ikinci toplamdaki r ile r-1 yer değiştirilirse;

(

)

(

)

(

)

(

)

(

)

1 1 1 0 ₀ 0 ₀ 1 1 0 1 1 ₀ 1 1 1 ( ) lim , ( ) lim 1, 1 ( ) lim 1, 1 ( ) ( ) lim 1, ( ( 1) ) 1 ( ) ( ) lim 1, ( n n p p p t h h r r nh t a nh t a n p h r nh t a p p a t _h nh t a p p a t _n p D f t h C p r f t rh h C p r f t rh h C p r f t rh D f t h C p n f t n h t D f t t a C p n f a n − − → ₌ → ₌ = − = − + → ₌ = − − → = − − →∞ = − + + − − + − − = − + − + − = − − + −

∑

− ) a n elde edilir. 1 lim ( ) 0 n t a f a n →∞ − − = dır.

(

)

1 ( 1)( 2)...( ) 1 lim 1, lim ! ( p p n n p p p n C p n h n n →∞ →∞ _p ₁₎ + + + + = = Γ + olur. Burada 1 1 1 1 1 ( ) ( ) ( ) ( ) ( 1)! 1 ( ) ( ) ! t p p p a t a t a t p a D f t D f t t f d p t f d p τ τ τ τ τ τ − − ₌ − ₌ ₋ − − = −

∫

olur. Bu ise (3.9) un indiksiyon ile doğruluğunu gösterir. (3.9.) formülünün p-katlı integrali

(17)

(

)

1 2 1 ( ) ( ) ( ) ( ) ( 2)! t p p a t a t a d D f t t f d D f t dt p τ τ τ − ₌ ₋ − ₌ −

∫

p − + t − olup, buradan;

(

)

∑

−

eşitliğinde; eğer p = m ise m. mertebeden türev ve eğer p=-m ise m katlı integral olur.

Bu çalışma p nin reel değerleri ile sınırlanacaktır.

Tanım 3.1.2. [23]

[a,b] aralığında f t′( ) türevi sürekli ise (3.9) dan

( )( ) 1 ( ) ( ) ( ) ( 1) ( 1) t p p p a t a f a t a D f t t f d p p τ τ τ − ₌ − ₊ ₋ _′ Γ + Γ +

∫

(3.13)

olur ve eğer f(t) fonksiyonu m+1 sürekli türeve sahip ise buradan ( 1) 0 ( )( ) 1 ( ) ( ) ( ) ( 1) ( 1) t k p k m p p m m a t k a f a t a D f t t f d p k p k τ τ τ + − + + = − = + − Γ + + Γ + +

∑

∫

(18)

elde edilir. Burada p ( )’ nın t=a’ da asimtotik olduğu görülür. aDt f t

−

Tanım 3.1.3. [23]

f(t) sürekli fonksiyonunun p mertebeden kesirli türevi ( ) ( ) 1 0 0 ( )( ) 1 ( ) lim ( ) ( ) ( ) ( 1) ( 1) t k p k m p p m p m a t _h h k a nh t a f a t a D f t f t t f d p k p m τ τ τ − + − + → ₌ = − − = = + − Γ − + + Γ − + +

∑

∫

olarak tanımlanır. p>0 olsun, burada; ( ) 0 ( ) n ( 1) ( , ) ( ) p p r h r f t h− C p r f t rh = =

∑

− − (3.14) olmak üzere (3.15) 0 ( ) lim ( ) p a t h h nh t a D f t f t → = − = p

limiti değerlendirilecektir. (3.15) limitini değerlendirmek için aşağıdaki dönüşüm yapılır

C(p,r)=C(p-1,r)+C(p-1,r-1) olduğu biliniyor. Buradan

∫

(3.18) elde edilir.

[ ]

a t, ’ de sürekli f( )k ( ) (t k=1, 2, ...,m+ türevlerinin kabulünden ve 1)

’i sağlayan m tamsayısının varlığından (3.18) formülü elde edilir. m’nin en küçük değeri için m<p<m+1 dır.

1 m> −p

Teorem 3.1.4. [23]

( ) (f t = −t a)ν olmak üzere f(t) nin kesirli türevi ( 1) ( ) ( ) ( 1) p p aD tt a t a p ν ν ν ν − Γ + − = − Γ − + eşitliği sağlanır.

(20)

İspat: [23]

( ) (f t = −t a)ν ise -p mertebeden kesirli integrali alınırsa (3.9) formülü kullanılarak ₍ ₎ 1 ₍ ₎ 1₍ ₎ ( ) t p p a t a D t a t r a d p ν _τ − − ν _τ − = − − Γ −

∫

(3.19)

yazılır. Farzedelim ki integralin yakınsaması için ν>-1 olsun;

( a t a) τ = +ξ − dan, ₍ ₎ 1 ₍ ₎ ₍ ₎ 1 ( ) t p p a t a D t a t a t d p ν ν− ξν ξ −p ξ − = − − Γ −

∫

− = 1 ( , 1)( ) ( ) p B p t a p ν ν − − + − Γ − ( 1) ( ) ( 1) p t a p ν ν ν − Γ + = Γ − + − (p<0,ν>-1) (3.20) elde edilir, burada 0<m<p<m+1 dır.

Teorem 3.1.5. [23]

Tamsayı mertebeden türevler ile kesirli türevlerin bileşkesi; n

n d

dt tam sayı mertebeden türev, p kesirli türev ve

aDt ( ) 0 k f a = (k=0, 1, 2,…) olmak üzere ( ) ( ( )) ( ) ( n n p p p n a t a t a t n n d d f t D f t D D f t dt dt + = = ) eşitliği sağlanır. İspat: [23]

(3.18) deki m için sınırlama yapılarak m>p-1 olursa ve m yerine s yazarak (3.18) yazılırsa yani m<p<m+1 olmak koşuluyla

( ) 1 0 ( )( ) 1 ( ) ( ) ( 1) ( 1) t k p k s p s p s a t k a f a t a D t p k p s τ f τ τd − + − + = − = + − Γ − + + Γ − + +

∑

_∫

(3.21) olur.

(21)

(3.21) deki p mertebeden kesirli türevin n tamsayı mertebesinin türevini alınırsa, burada s=m+n-1 alınır. Sonuçta

(

)

( ) 0 ( 1) ( )( ) ( ) ( 1) 1 ( ) ( ) ( 1) ( ) n s k p n k p a t n k t s p n s a p n a t d f a t a D f t dt p n k t f p n s D f t d τ τ τ − − + = − − + + − = Γ − − + + + − Γ − − + + =

∫

elde edilir .(3.23) ve (3.24) ten ( ) 1 0 ( ) ( )( ) ( ( )) ( ) ( 1 n n n k p n k p p a t a t n n k d d f t f a t D f t D dt dt p n k ) a − − + − = − = + Γ − − + +

∑

(3.25)

elde edilir. (3.24) ve (3.25) den n

n d

dt ve işlemleri değişmelidir. Böylece t=a (k=0, 1, 2, …) olmak koşuluyla p aDt ( ) 0 k f a = ( ( )) ( ( )) ( n n p p p n a t a t a t n n d d f t D f t D D f t dt dt + = = )

(22)

elde edilir.

Teorem 3.1.6 [23]

0≤ ≤ ≤ +m p m 1 ve 0≤ ≤ ≤ +n q n 1 ve f t( )

olmak üzere ve diferansiyellerinin birleşimi ( )k _{( ) 0 , (} _0,1,..., ₁₎ f a = k= r− p aDt q aDt q( p ( )) p( q ( )) p q ( ) (3.26) aDt aD f tt aDt aD f tt aDt f t + = = (3.26) daki gibidir.

3.2. Riemann –Liouville Kesirli Türevleri

Literatür [23] de Riemann –Liouville kesirli türevleri Grünwald-Letnikov kesirli türevlerinin kesirli mertebeden geri farkının limiti olarak tanımlanır. (3.18) in özel bir durumu altında integral-diferansiyel açıklaması

1 ( ) ( ) ( ) , 1 m t p m p a t a d D f t t f d m p m dt τ τ τ + − ⎛ ⎞ =_⎜ _⎟ − ≤ ≤ ⎝ ⎠

∫

+ (3.27)

dır. (3.27) de verilen kesirli türev tanımı “Riemann-Liouville” tanımıdır.

Teorem 3.2.1. [23]

Tamsayı mertebeden kesirli türevlerin ve integrallerin bileşimi; k>n ise f(t) sürekli fonksiyonunun (k-n). türevi ( )_{( )} 1 ₍ ₎ 1 _{( )} ( ) t k n k n a f t D t f n τ τ τd − ₌ ₋ Γ

∫

− _(3.28) olmak üzere (3.28) k 0 ise k defa integrasyon, k>0 ise k defa diferansiyel ifade etmektedir.

k

D ≤

İspat: [23]

f( )τ her (a,t) sonlu aralığında sürekli ve integrallenebilir olsun ( )

f t fonksiyonu τ = noktasında r<1 mertebeden bir integrale sahip olsun. a lim( )r ( ) ( 0)

a a f t const

(23)

dır. Burada,

1_{( )} _{( )} t a

f− t =

∫

f τ τd

integrali vardır ve sonlu bir değere sahiptir.

Yani t→ a iken 0’a eşittir. Gerçekten τ = +a y t( −a) ve ε = − dan t a

1 1

0

lim ( ) lim ( ) lim( ) ( ( ))

t−τ f τ τd

genel durumda indiksiyon formülüyle Cauchy formülü _{( )} 1 ₍ ₎ 1 _{( )} ( ) t n n a f t t f n τ τ τd − ₌ ₋ Γ

∫

− _(3.30) elde edilir. n≥1 ve k≥0 tamsayısı alınırsa

(

( )

)

( ) p q p q aDt aDt f t a Dt f − − ₌ − − t

ve bunun ispatı aşağıdaki gibidir.

(

k− ≤ ≤1 p k (3.35)

yani f(t) fonksiyonunun kesirli türevi

( ) 1 ( ₁ ( ) ( ) t k p a t k k a d f d D f t k p dx t ) p τ τ τ − + = Γ −

∫

− k− ≤ ≤1 p k (3.36) olarak tanımlanır.

Riemann-Liouville kesirli türevlerinin bazı özellikleri alınacak olursa en önemlisi olarak p>0 ve t>a için Riemann-Liouville kesirli türevi için

p

(

p ( )

)

( )

aDt aDt f t f t

− ₌ _(3.37) özeliğidir. Yani Riemann-Liouville kesirli diferansiyel oparatörü aynı p mertebeden Riemann-Liouville kesirli integrasyonunun bir sol tersidir.

Diğer bir özelik p ( ) , ( 1 )

aD f tt k− ≤ <p k kesirli türev ise f t( ) fonksiyonu integrallenebilirdir. Buradan,

(

)

1 ( ) ( ) ( ) ( ) ( 1 p j k p p p j a t a t a t _{t a} j t a D D f t f t D f t p j − − − = = − ⎡ ⎤ = − _⎣ _⎦ ) Γ − +

∑

(3.38)

elde edlir. (3.37) ye benzer bir özelik olarak genel durumun özel hali p

(

q ( )

)

p q ( )

aDt aDt f t aDt f t

− ₌ − _(3.39) olup, burada f(t) sürekli kabul edilir ve eğer p≥ ≥q 0 iseaDtp qf t( ) türevi vardır.

-Teorem 3.2.4. [23]

f(t)=(t−a)βolmak üzere f(t) fonksiyonunun kesirli türevi (1 ) ( ) ( ) (1 ) p p aD tt a t a p β ν β ν − Γ + − = − Γ + − eşitliğinden elde edilebilir.

İspat: [23]

β∈R olmak üzere kuvvet fonksiyonunun ,

Riemann-Liouville kesirli türevini hesaplamak için

β ) ( ) (t t a f = − _aD f t_tp ( ) p _{( )} n

(

(n p) _{( ) , (}

)

₁ ₎ a t n a t d D f t D f t n p n dt − − = − ≤ < (3.40)

(26)

eşitliğini alalım. Bu fonksiyonun α = −n p mertebesinden kesirli integrali (3.40) da yazılırsa (1 ) ( ) ( ) (1 ) aDt t a t a α β ν β α ν α − ₋ ₌ Γ + ₋ + Γ + + den (1 ) ( ) ( ) (1 ) p p aD tt a t a p β ν β ν − Γ + − = − Γ + −

elde edilir ve burada ( ) (f t = −t a)β tek sıra integrallenebilmesi için β > −1 olmalıdır.

Teorem 3.2.5. [23]

Tamsayı mertebeden türevlerin birleşimi; t=a kesirli diferansiyelin en düşük noktası ve ( )k _{( )} _{0 (} _{0,1, 2,...,} ₁₎ olmak üzere

f a = k= n

-(

( )

)

∑

elde edilir.

Riemann-Liouville kesirli türev operatörü p’ nın aDt

n n d

dt ile birleştiğini görürüz. Öyleki t=a, kesirli diferansiyelin en düşük noktası, ( için

olup 0,1, 2,..., 1) k= n -( )k _{( )} ₀ f a =

(

( )

)

( ) ( ) n n p p p n a t a t a t n n d d D f t D f t D f t dt dt + ⎛ ⎞ = _⎜ _⎟= ⎝ ⎠ (3.43) elde edilir. Teorem 3.2.6. [23] p , ( 1 ) aDt m− ≤ <p m ve , ( 1 ) q

aDt n− ≤ <q n olmak üzere kesirli türevlerin birleşimi p

(

q ( )

)

q

(

p ( )

)

p q ( ) aDt aD f tt a Dt aD f tt a Dt f t + = = (3.44) (3.44) deki gibidir.

(28)

İspat:[23]

(

)

{

( )

(

)

}

1 1 ( ) ( ) ( ) ( ) ( ) (1 ) ( ) ( ) ( ) (1 ) m p q m p q a t a t m a t a t m n m p q m q j a t a t m _{t a} j q j n p q q j a t a t _{t a} j d D D f t D D f t dt d t D f t D f t dt m p j t a D f t D f t q j − − − − + − − = = − − + − = = = ⎧ _⎡ _⎤ − ⎫ = _⎨ − _⎣ _⎦ _⎬ Γ + − − ⎩ ⎭ − ⎡ ⎤ = − _⎣ _⎦ Γ − −

∑

p j a (3.45) elde edilir. p ve q nun yer değiştirmesiyle

(

-3.3. Ardışık Kesirli Türevler

Literatür [23] den bir fonksiyonun ardışık kesirli türevi 1 2 3 ... n

α α α α= + + + α

olmak üzere

_{D f t}α ( )=_Dα α α1+ + +2 3 ...αn _{f t}( )=_{D D D}α1 α2 α3..._Dαn _{f t}( ) (3.48)

(29)

3.4. Kesirli Türevlerin Özelikleri Lemma 3.4.1. [23] λ₁,λ₂∈R olmak üzere p( ₁ ( ) ₂ ( )) ₁ p ( ) ₂ ( (3.49) aDt λ f t +λ g t =λ aD f tt +λ aD g tt ) p ) rh −

(3.49) eşitliğinde görüldüğü üzere kesirli türevlerin lineerlik özeliği vardır.

∑∏

_⎝ _⎠ r r (3.51) (3.51) deki gibidir.

(30)

4. KESİRLİ TÜREVLER İÇİN GENELLEMELER VE UYGULAMALAR

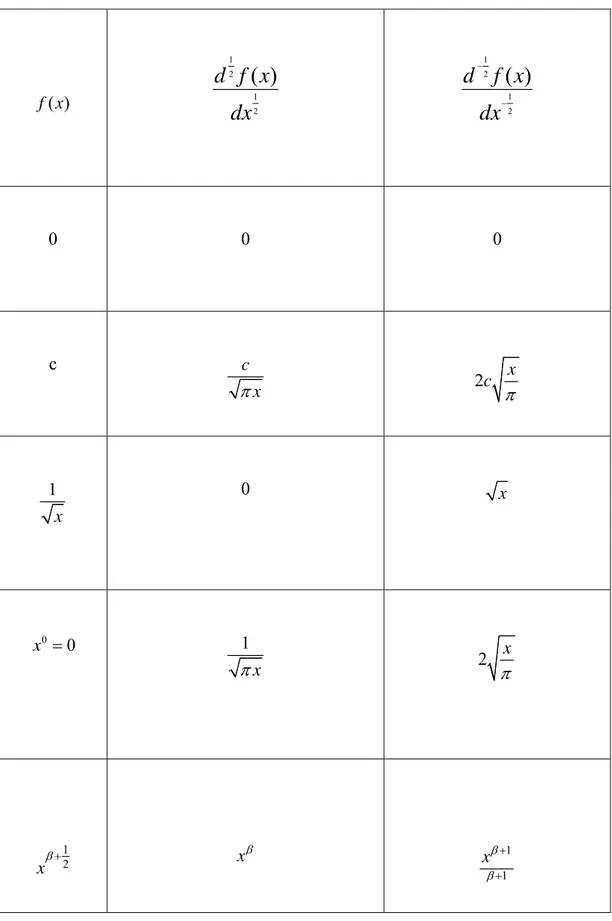
4.1. Kesirli Türev

Tanım 4.1.1.

Literatür [24] den f x( ) sürekli fonksiyon olmak üzere

₁ 0 ( ) 1 ( ) ( ) ( ) x q n q n d f x d f t dt dx =Γ −n q dx

∫

x t− − +n q (4.1) (4.1) n diferansiyel adımı göstermek üzere kesirli türevin tanımını gösterir burada

oparatörü

( 0

q q> veq∈ )R n− ≤ ≤1 q n’ye karşılık gelen tam sayıdır.Bu bölümdeki

uygulamalarda (4.1) den yararlanılmıştır.

4.2. Polinom Fonksiyonlar için Kesirli Türevin Formülü

Tanım 4.2.1.

( ) k f x =x

olmak üzere literatür [23] den polinom fonksiyonunun kesirli türevi ! ( )! a k k a d k a x x dx k a − = − dir. Bu gamma fonksiyonu ile

( 1) ( 1) a k a d k k a x x dx k a − Γ + = Γ − + (4.2) olarak tanımlanır. 4.3.Örnekler Örnek 4.3.1 f x( )= x fonksiyonunun 1. 2 türevini bulalım.

(31)

Çözüm:

Türev tanımındaki formülden (4.1) de işlem yapılırsa 0 1 2 ≤ ≤ 1 n=1 1 2 1 1 1 1 0 2 2 1 1 (1 ) ₍ ₎ 2 x d x d tdt dx dx x t − + = Γ −

∫

₋ 1 2 1 1 0 2 2 1 1 ( ) ₍ ₎ 2 x d x d tdt dx dx x t = Γ

∫

₋ tablo1 den 1 2 π ⎛ ⎞ Γ_{⎜ ⎟}=

⎝ ⎠ olduğu dikkate alınırsa

1 1 2 2 1 2 2 d x x dx π =

elde edilir. Diğer taraftan (4.2) formülünde 1

2 a= k=1 yerlerine yazılırsa 1 1 1 2 ₁ 2 2 1 2 (1 1) (2) 1 3 (1 1) ( ) 2 2 d x x x dx − Γ + Γ = = Γ − + Γ 1 1 2 2 1 2 ( ) 2 d f x x dx π =

elde edilir. Buda eşitlik (4.1) in eşitlik (4.2) ile aynı sonucu verdiğini gösterir.

Örnek 4.3.2.

( ) x

f x = fonksiyonunun e 1.

2 mertebeden türevini bulalım

Çözüm:

(32)

1 0 ( ) 1 ( ) ( ) ( ) x q n q n d f x d f t dt dx = Γ −n q dx

∫

x t− − +n q

idi. n-1<q<n olduğundan burada ( ) t

f t = , n=1, e 1

2 q=

bu veriler yerine yazılırsa 1 2 1 _{1 1} 1 0 2 2 1 1 (1 ) ₍ ₎ 2 x x t d e d e dt dx dx x t − + = Γ −

∫

₋

elde edilir, bu eşitlik düzenleyecek olursa

1 2 1 1 0 2 2 1 1 ( ) ₍ ₎ 2 x x t d e d e dt dx dx x t = Γ

∫

₋ olur. tablo1 den ( )1 2 π

Γ = olduğunun biliyoruz. Biz burada önce ₁ 0 ₍ ₎2 x t

e dt x t−

∫

integralini Mapple 9 programı yardımıyla hesaplayacak olursak

₁ 0 ₍ ₎2 x t e dt x t−

∫

= x

( )

e xerf x elde edilir. Bunun x e göre türevi alınırsa

( )

1 x x d e xerf x e erf x dx = x + π

( )

1 2 1 2 1 x x d e e erf x x dx π = +

olarak bulunur. Buradaki türev ve integral işlemlerinde Mapple 9 programından yararlanılmıştır.

Örnek 4.3.3.

f x( ) cos= x fonksiyonunun 1.

(33)

Çözüm:

(4.1) deki kesirli türev formülü

∫

x t− − +n q

idi. n-1<q<n olduğundan burada n=1

q=1

2

f t( ) cos= t

bu veriler yerine yazarsak 1 2 1 _{1 1} 1 0 2 2 cos 1 cos 1 (1 ) ₍ ₎ 2 x d x d tdt dx dx x t − + = Γ −

∫

₋

olur. Bu eşitlik düzenlenirse 1 2 1 1 0 2 2 cos 1 cos 1 ( ) ₍ ₎ 2 x d x d td dx dx x t = Γ

∫

₋ t

Mapple 9 proğramı yardımıyla işlemler yapılırsa;

1 2 1 2 1 ( , ) cos 1 1 1 1 ₂ 2 ( , ) 2 ( , ) 2 4 2 2 1 ( , ) 1 1 1 1 ₂ 1 2 ( , ) 2 ( , ) 4 2 4 2 2 1 1 1 1 2 2 ( , ) 2 ( , ) 4 2 4 2 3 2 2 AngerJ x d x AngerJ x x AngerJ x x x dx AngerJ x x AngerJ x x AngerJ x x x AngerJ x x AngerJ x x π π π π π ⎛ ₋ ⎞ ⎜ ⎟ = − + _⎜− + _⎟ ⎜ ⎟ ⎝ ⎠ ⎛ ₋ ⎞ ⎜ ⎟ + − + _⎜− − _⎟ ⎜ ⎟ ⎝ ⎠ ⎛ ₊ ₋ ⎞ ⎜ ⎟ ⎝ ⎠ − elde edilir.

(34)

Örnek 4.3.4.

f x( ) sin= x fonksiyonunun 1.

2 mertebeden türevini bulalım..

Çözüm: 1 2 1 1 0 2 2 sin 1 sin 1 ( ) ₍ ₎ 2 x d x d td dx dx x t = Γ

∫

₋ t

Mapple 9 proğramı yardımıyla işlemler yapılırsa;

1 2 1 3 2 2 1 1 1 1 2 2 ( , ) 2 ( , ) cos 4 2 4 2 2 1 ( , ) 1 1 1 3 ₂ 2 2 ( , ) 2( ( , )) 4 2 4 2 2 x AngerJ x x AngerJ x d x dx x AngerJ x AngerJ x x AngerJ x 1 x x x π π π ⎛ ₋ ₋ ⎞ ⎜ ⎟ ⎝ ⎠ = − ⎛ ⎞ ⎜ ⎟ + − + − ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ + 1 ( , ) 1 1 1 1 ₂ 2 ( , ) 2( ( , )) 4 2 4 2 2 AngerJ x AngerJ x x AngerJ x 1 x x x π − − − − − − + elde edilir. Örnek 4.3.5. _{( )} 3 ₃ 2 ₁ f x =x + x + + fonksiyonunun x 1.

2 mertebeden türevini bulalım.

Çözüm:

Kesirli türevler için lemma 3.4.1. den lineerlik özeliği olduğu biliniyor; (4.1) deki polinom fonksiyonlar için kısa kesirli türev formülünde 3_{, , ,1}2

(35)

kesirli türevleri bulunup ara işlemler yazılırsa 1 2 1 2 ( ) d f x dx bulunur. ( 1) ( 1) a k k a d k a x x dx k a − Γ + = Γ − + 1 1 5 3 2 ₃ 2 2 1 2 (3 1) (4) 1 7 (3 1) ( ) 2 2 d x x x dx − Γ + Γ = = Γ − + Γ 1 5 3 2 2 1 2 16 5 d x x dx π = 1 1 3 2 2 ₂ 2 2 1 2 (2 1) (3) 1 5 (2 1) ( ) 2 2 d x x x dx − Γ + Γ = = Γ − + Γ 1 3 2 2 2 1 2 8 3 d x x dx π = 1 1 1 2 ₁ 2 2 1 2 (1 1) (2) 1 3 (1 1) ( ) 2 2 d x x x dx − Γ + Γ = = Γ − + Γ 1 1 2 2 1 2 2 d x x dx π = 1 1 1 2 ₀ 2 2 1 2 1 (1 0) (1) 1 1 (0 1) ( ) 2 2 d x x dx − − Γ + Γ = = Γ − + Γ 1 1 2 2 1 2 1 d x x dx π − =

(36)

1 5 3 1 3 2 2 2 2 2 1 2 3 1 16 8 2 1 3 5 3 d x x x 1₂ x x x dx π π π π − + + + ₌ ₊ ₊ ₊ x 5 3 1 2 2 2 16 8 2 1 5 1 2 x x x π π π π x − = + + + (4.3)

bulunur. Kesirli türev formülünde aynı fonksiyon uygulanırsa;

1 3 2 2 1 1 0 2 2 ( ) 1 ( 3 1) 1 ( ) ₍ ₎ 2 x d f x d x x x dt dx dx x t + + + = Γ

∫

₋ 5 3 1 2 2 2 16 8 2 1 5 1 2 x x x π π π π x − = + + + (4.4)

bulunur. (4.3) ve (4.4) deki sonuçların aynı olduğu görülür.

Örnek 4.3.6.

_{( )} 3

f x =x fonksiyonunun kısa yoldan ve uzun yoldan 1.

2 mertebeden türevini

bulalım.

Çözüm:

1

2

a= k=3 değerlerini (4.1) de yerine yazarsak

1 1 2 ₃ 3 2 1 2 (3 1) 1 (3 1) 2 d x x dx − Γ + = Γ − + 5 2 (4) 7 ( ) 2 x Γ = Γ 5 2 16 5 π x = (4.5) Aynı şekilde temel formülden

(37)

1 3 3 2 1 1 0 2 2 1 1 (1 ) ₍ ₎ 2 x d x d t dt dx dx x t = Γ −

∫

₋ 5 2 16 5 π x = (4.6) elde edilir.Görüldüğü üzere (4.5) ile (4.6) dan elde edilen sonuçlar aynıdır.

Örnek 4.3.7.

_{( )} 3 f x =x ün 3.

Çözüm: ( 1) ( 1) a k a d k k a x x dx k a − Γ + = Γ − + formülünü kullanılırsa 3 2 a= , k = 3 3 3 2 ₃ 3 ₂ 3 2 (3 1) 3 (3 1) 2 d x x dx − Γ + = Γ − + 3 2 (4) 5 ( ) 2 x Γ = Γ 3 2 8 x π = (4.7)

(4.1) deki kesirli türev formülünde _{( )} 3 f x =x ün 3

2. mertebeden kesirli türevi

∫

x t− − +n q denkleminde 3 2

(38)

3 2 3 3 2 3 2 3 2 _{1 2} 0 2 1 1 ( ) ₍ ₎ 2 x d x d t dt dx dx x t − + = Γ

∫

₋ 3 2 3 2 3 2 3 1 2 0 2 1 1 ( ) ₍ ₎ 2 x d x d t dt dx dx x t = Γ

∫

₋ 3 2 8 x π = (4.8) olarak elde edilir. Böylece (4.7) ile (4.8) de bulunan sonuçların aynı olduğu görülür.

Örnek 4.3.8.

f x( )= x fonksiyonunun iki kere 1.

Çözüm: f( )x =x 1 1 2 ₁ 2 1 2 (1 1) 1 (1 1) 2 d x x dx − Γ + = Γ − + 1 2 (2) 3 ( ) 2 x Γ = Γ 1 2 2 x π =

aynı şekilde bulduğumuz bu fonksiyonun bir kez daha aynı mertebeden türevi alınırsa 1 1 1 1 2 2 2 2 1 1 1 2 2 2 ( ) 2 d d f x d x dx dx dx π ⎡ ⎤ ⎢ _{⎥ =} ⎢ ⎥ ⎢ ⎥ ⎣ ⎦

(39)

1 1 2 2 1 (1 ) 2 ₂ 1 1 ( 1) 2 2 x π − Γ + = Γ − + 0 3 ( ) 2 ₂ (1) x π Γ = Γ 1 2 2 ₁ 1 π π = =1 (4.9) elde edilir. Diğer taraftan

1 1 1 1 2 2 2 2 1 1 1 1 2 2 2 2 ( ) ( ) ( ) [ ] d d f x d f x df x dx dx dx dx d x dx + + = = = =1 (4.10) olur. (4.9) ve (4.10) daki sonuçların aynı olması Teorem 3.1.6. ile Teorem 3.2.6. nın doğruluğunu gösterir. Örnek 4.3.9. f x( )= x fonksiyonunun için ( ( )) ( ) 2 ( ) 3 2 1 1 2 1 x f D x f D x f D dx d t a t a t a = = + eşitliğinin doğruluğunu gösterelim. Çözüm:

f x( )= x olduğuna göre önce

1 2 (_a _t ( d D f x dx )) hesaplanırsa;

(40)

1 2 1 1 0 2 2 3 2 1 1 ( ) ₍ ₎ 2 1 4 [ ] 3 1 2 2 2 1 x d x d tdt dx dx x t d x dx x x d x dx x π π π π π = Γ ₋ = = = ⎡ _{⎤ =} ⎢ ⎥ ⎣ ⎦

∫

buradan 1 2 (_a _t ( )) d D f x dx = 1 (4.11) p x

olarak elde edilir. Diğer taraftan 3 2 _{( )} aD f x hesaplanırsa t 3 2 2 3 2 1 0 2 2 3 2 2 2 1 1 ( ) ₍ ₎ 2 1 4 [ ] 3 1 1 [ 2 ] x d x d tdt dx dx x t d x dx d x dx π π π = Γ ₋ = =

∫

ve böylece 3 2 3 2 1 d x x dx π = (4.12)

olarak elde edilir. Buradan (4.11) ile (4.12) nin aynı olması verilen eşitliğin doğruluğunu gösterir. Böylece Teorem 3.1.5. ile Teorem 3.2.5. in doğruluğu gösterilmiş olur.

(41)

5.ADOMİANIN AYIRMA METODU İLE LİNEER OLMAYAN KESİRLİ DİFERANSİYEL DENKLEMLERİN ÇÖZÜMLERİ

5.1. Ayırma Metodu

Tanım 5.1.1.

Literatür [24] den Adomian ayırma metodu kısa bir biçimde ele alınırsa; L

nin tersi doğrusal oparatör, R kalan lineer parça, lineer olmayan oparatör

olduğunda

N

Lu+Ru+Nu=g (5.1)

(5.1) formunda bir eşitlik yazılabilir. Ayrışımla denklemlerin genel çözümleri 0 n n u ∞ = =

∑

u (5.2) olarak tanımlanır.

Burada u₀ Lu=g nin genel çözümüdür. (5.1) den Lu= −g Ru−Nu

yazılabilir. 1

L− in tersi vardır. Her tarafı L−1 ile çarpılırsa 1 1 1 1

L Lu− =L g− −L Ru− −L Nu− olur.

Başlangıç değer problemi için 1 L− i n n d L dt

≡ 0 dan t ye kadar n katlı integrasyon oparatörü olarak tanımlanır.

Örneğin 2 2 d L dt ≡ oparatörü için 1 ₍₀₎ ₍₀₎ L Lu− = −u u −tu′ böylece ₍₀₎ ₍₀₎ 1 1 1 (5.3) u=u +u′ +L g− −L Ru− −L Nu− elde edilir.

Sınır değer problemleri kesin olmayan integrasyonlar kullanılarak ve sabit verilerden yola çıkarak değerlendirilir.

1 1 1 (5.4) u= +A Bt+L g− −L Ru− −L Nu−

(42)

olarak yazılabilir. u yu çözmek için (5.3) ve (5.4) deki eşitlikler varsayılan ayrışımla da belirlenir. 0 n n u ∞ = =

∑

u u₀

Literatür [1,2] den sonuç olarak özel lineer olmayan Nu= f u( ) için özel polinom

serileri yazılabilir. ( ) 0 n n Nu A ∞ = =

∑

u u u_{0, 1, 2}...u_n

Bu Adomian tarafından oluşturulmuştur. Tabiki bu polinomlarının lineer olmayışına dayanır. Bu ler aşağıda verilmiştir.

n A n A A₀ = f u( )₀ 0 1 1 0 ( ) df u A u du = 2 2 0 1 0 2 2 2 0 0 ( ) ( ) 2! df u u d f u A u du du = + 2 3 3 0 0 1 3 3 1 2 2 3 0 0 ( ) ( ) ( ) 3! df u d f u u d f u A u u u du du du = + + 0 0 1 − n g M

∑

(5.5) = = n v v n C v n f u A 1 0 ) ( ₍ ₎ ) , (

Burada C(v,n), u nun v li kombinasyonudur.

Son dönemde Adomian çözümleme metodu tekrar gözden geçirilmiştir ve Adomian polinomlarının matematiksel modeli sunulmuştur.

Böylece genel formül

1 (5.6) 0 0 n n u u L R u L Nu ∞ − = = −

∑

− 1 1 (5.7) 0 0 0 n n n u L R u L A ∞ ∞ − − = = = −

∑

−

∑

olur. Burada 1 ve 0 u = ∅ +L− L∅ = (0 Lu=g) (5.8) dır. Böylece (5.9) sonucu ortaya çıkar.

1 1

n n

(43)

Bilinen kullanılarak bütün bileşenler kullanılabilir. (5.9) eşitliği kullanılarak u₀ benzerleri bulunabilir. u u u_{0, 1, 2}...un (5.2) de yerine konularak u elde edilir.

5.2. Uygulamalar Örnek 5.2.1. [8] 2 10 , (0) 1 dy y y dt = =

adi diferansiyel denklemini Adomian ayırma metodu ile çözelim.

Çözüm: d L dt ≡ olduğu varsayılırsa 2 10 dy y

dt = eşitliğinin her iki tarafında

1

L− ile işlem yapılırsa 1dy 1₁₀ 2 L L y dt − ₌ − 1 1 n n y ₊ =L− A

Burada An ler Adomian polinomlarıdır.

2 0 0 1 1 0 0 1 2 2 1 2 2 0 0 2 10 20 20 (20 ) 20 20 10 2 A y A y y y y y 1 A y y y y y = = = = + = +

şeklinde hesaplanabilir. Böylece,

2 0 0 y =c A =c 1 1 1 2 2 1 0 10 n n y L A n y L c − + − = = = = 10c t

(44)

3 1 1 3 3 2 2 3 2 2 2 4 4 2 1 1 4 4 4 3 3 2 200 1 200 100 20 (100 ) 10(10 ) 3000 2 3000 1000 A c t n y L c t c t A c c t c t c t n y L A L c t c t − − − = = = = = + = = = = =

olmak üzere y y t y t y t değerleri ₀, ( ), ( ), ( )₁ ₂ ₃

0 1 2 3 ( ) ( ) ( ) ( ) ( ) ... y t = y t +y t +y t +y t + da yazılırsa 2 3 2 4 3 ( ) 10 100 1000 ... y t = +c c t+ c t + c t + elde edilir. Burada y(0)= =c 1 olduğundan

2 3 ( ) 1 10 100 1000 ... y t = + t+ t + t + sonucuna ulaşılır. Diğer taraftan 2 10 , (0) 1 dy y y dt = =

denkleminin analitik çözümünden, 2 2 10 10 dy dt y y dy− dt = = ve 1 10 (0) 1 y c t y = − = ise, c=1 olur. 1 1 10 y t = −

elde edilir. Bu fonksiyonunun seri açılımı

_{( ) 1 10} ₁₀₀ 2 ₁₀₀₀ 3 _... y t = + t+ t + t + dır. Bu da Adomian çözümünün doğruluğunu gösterir.