SELÇUK ÜNİVERSİTESİ
SOSYAL BİLİMLER ENSTİTÜSÜ
İŞLETME ANABİLİM DALI
MUHASEBE-FİNANSMAN BİLİM DALI
PARÇACIK SÜRÜ OPTİMİZASYONU YAKLAŞIMI İLE
PORTFÖY OPTİMİZASYONU ve İMKB’DE BİR
UYGULAMA
Melih KUTLU
YÜKSEK LİSANS TEZİ
Danışman
Doç. Dr. Ali ALAGÖZ
T.C.
SELÇUK ÜNİVERSİTESİ Sosyal Bilimler Enstitüsü Müdürlüğü
BİLİMSEL ETİK SAYFASI
Ö ğ re n c in in
Adı Soyadı MELİH KUTLU
Numarası 104227031002
Ana Bilim / Bilim Dalı
İŞLETME ANABİLİM DALI/ MUHASEBE FİNANSMAN BİLİM DALI
Programı Tezli Yüksek Lisans Doktora
Tezin Adı
PARÇACIK SÜRÜ OPTİMİZASYONU YAKLAŞIMI İLE PORTFÖY OPTİMİZASYONU ve İMKB’DE BİR UYGULAMA
Bu tezin proje safhasından sonuçlanmasına kadarki bütün süreçlerde bilimsel etiğe ve akademik kurallara özenle riayet edildiğini, tez içindeki bütün bilgilerin etik davranış ve akademik kurallar çerçevesinde elde edilerek sunulduğunu, ayrıca tez yazım kurallarına uygun olarak hazırlanan bu çalışmada başkalarının eserlerinden yararlanılması durumunda bilimsel kurallara uygun olarak atıf yapıldığını bildiririm.
Önsöz
Tez çalışmama katkılarından dolayı değerli hocam ve danışmanım Sayın Doç. Dr. Ali Alagöz’e, tez süresince desteklerini esirgemeyen Prof. Dr. Osman Okka, Doç. Dr. Yunus Ceran, Doç. Dr. Mikail Altan ve Yrd. Doç. Dr. Melek Acar Boyacıoğlu’na ve Muhasebe-Finansman Bilim Dalı Öğretim Üyelerine teşekkürü bir borç bilirim.
Ayrıca bu çalışmamda benden desteğini esirmeyen aileme ve arkadaşlarıma teşekkürlerimi sunarım.
Melih KUTLU
T.C.
SELÇUK ÜNİVERSİTESİ Sosyal Bilimler Enstitüsü Müdürlüğü
Ö ğ re n c in in
Adı Soyadı MELİH KUTLU
Numarası 104227031002
Ana Bilim / Bilim Dalı
İŞLETME ANABİLİM DALI/ MUHASEBE FİNANSMAN BİLİM DALI
Programı Tezli Yüksek Lisans Doktora Tez Danışmanı DOÇ. DR. ALİ ALAGÖZ
Tezin Adı PARÇACIK SÜRÜ OPTİMİZASYONU YAKLAŞIMI İLE PORTFÖY OPTİMİZASYONU ve İMKB’DE BİR UYGULAMA
ÖZET
Optimizasyon teorisi alternatifler arasından en iyisini seçmek için matematiksel bir model kurmayı ve bu modelin çözümlenmesini içermektedir. Doğrusal programlama, tam sayılı programlama, stokastik programlama, popülasyon tabanlı teknikler gibi birçok optimizasyon tekniği geliştirilmiştir.
Parçacık Sürü Optimizasyonu popülasyon tabanlı bir tekniktir. Kuş ve balık sürülerinden sosyal davranış benzetim yoluyla algoritmalar elde etmek için kullanılır. Parçacık Sürü Optimizasyonu doğrusal olmayan problemlerin çözümüne yönelik geliştirilmiştir. Bu çalışmada Optimizasyon ve Parçacık Sürü Optimizasyonu’nun teorik yapısını incelenecek ve Parçacık Sürü Optimizasyonu tekniğinin uygulama alanlarından biri olan portföy optimizasyonu konusunda bir uygulama yapılacaktır.
Bu uygulamanın sonuçları ile optimum portföy yapısı ve etkin sınır elde edilmeye çalışılmıştır.
Anahtar Kelimeler: Optimizasyon, Parçacık Sürü Optimizasyonu, Portföy Optimizasyonu
T.C.
SELÇUK ÜNİVERSİTESİ Sosyal Bilimler Enstitüsü Müdürlüğü
Ö ğ re n c in in
Adı Soyadı MELİH KUTLU
Numarası 104227041002
Ana Bilim / Bilim Dalı
İŞLETME ANABİLİM DALI/ MUHASEBE FİNANSMAN BİLİM DALI
Programı Tezli Yüksek Lisans Doktora Tez Danışmanı DOÇ. DR. ALİ ALAGÖZ
Tezin İngilizce Adı
USING PARTICLE SWARM OPTIMIZATION METHOD IN PORTFOLİO OPTIMIZATION AND A SAMPLE OF APPLICATION IN IMKB
SUMMARY
Optimization theory to establish a mathematical model to select the best among the alternatives and the resolution of this model includes. Many optimization techniques such as linear programming, integer programming, stochastic programming, population based techniques have been developed.
Particle Swarm Optimization is a technique that population based on. Flocks of birds and fish through the simulation algoritms are used to achieve social behavior. Particle Swarm Optimization has been developed fort he solution of nonlinear problems. This study examined the structure of Optimization and Particle Swarm
Optimization and Particle Swarm Optimization technique of theoretical practice in the application will be made in one of its portfolio optimization. The results of this application was attempted to obtain the optimal structure and efficient frontier.
İÇİNDEKİLER
BİLİMSEL ETİK SAYFASI ... i
YÜKSEK LİSANS TEZİ KABUL FORMU ... ii
Önsöz ... iii ÖZET ... iv SUMMARY ... vi İÇİNDEKİLER ... viii Kısaltmalar ... xiv Şekil Listesi ... xv
Tablo Listesi ... xvi
Giriş ... 1 BİRİNCİ BÖLÜM: PARÇACIK SÜRÜ OPTİMİZASYONU ... 3 1.1. Optimizasyon ... 4 1.1.1. Optimizasyon Kavramı ... 4 1.1.2. Optimizasyonun Önemi ... 4 1.1.3. Optimizasyon Uygulamaları ... 5
1.1.3.1.Üretim Planlaması Problemi ... 5
1.1.3.2.Depo Yeri Seçim Problemi ... 5
1.1.3.3.Gezgin Satıcı Problemi ... 5
1.1.3.5.Sistem Güvenirliliği Problemi ... 6
1.1.4. Optimizasyon Metotlarının Sınıflandırılması ... 6
1.1.4.1.Klasik Optimizasyon Teorisi ... 7
1.1.4.1.1.Kısıtlanmamış Problemler ... 7
1.1.4.1.1.1.Tek Değişkenli Fonksiyonlar ... 7
1.1.4.1.1.2.İki Değişkenli Fonksiyonlar ... 9
1.1.4.1.2.Kısıtlanmış Problemler ... 11
1.1.4.1.2.1.Eşitlik Kısıtları ... 11
1.1.4.1.2.2.Eşitsizlik Kısıtları ... 12
1.1.4.2.Sayısal Optimizasyon Teknikleri ... 13
1.1.4.2.1.Doğrusal Programlama ... 13
1.1.4.2.1.1.Doğrusal Programlama Kavramı ve Unsurları ... 13
1.1.4.2.1.2.Doğrusal Programlamanın Dayandığı Varsayımlar ... 15
1.1.4.2.1.3.Doğrusal Programlama Probleminin Özellikleri ... 16
1.1.4.2.1.4.Doğrusal Programlama Probleminin Çözümüne İlişkin Tanımlar 17 1.1.4.2.1.5.Doğrusal Programlama Çözüm Metotları ... 17
1.1.4.2.1.5.1.Grafik Çözüm Metodu ... 17
1.1.4.2.1.5.2.Simpleks Metodu ... 20
1.1.4.2.1.5.3.Dualite ... 22
1.1.4.2.2.Tam Sayılı Programlama ... 23
1.1.4.2.2.1.Tam Sayılı Programlama Kavramı ... 23
1.1.4.2.2.3.Tam Sayılı Programlamada Çözüm Yaklaşımları ... 24
1.1.4.2.3.Doğrusal Olmayan Programlama ... 25
1.1.4.2.3.1.Doğrusal Olmayan Programlama Kavramı ... 25
1.1.4.2.3.2. Doğrusal Olmayan Programlamanın Özellikleri ... 26
1.1.4.2.3.2.1.Temel Kavramlar ... 26
1.1.4.2.3.2.2.Gradiyant Kavramı... 27
1.1.4.2.3.2.3.Hessian Matrisi ... 27
1.1.4.2.3.2.4.Dışbükey (Konveks) ve İçbükeylik (Konkav) ... 28
1.1.4.2.4.Kuadratik Programlama(Kareli Biçimler) ... 30
1.1.4.2.5.Dinamik Programlama ... 31
1.1.4.2.5.1.Dinamik Programlama Kavramı ... 31
1.1.4.2.5.2.Richard Bellman Teoremi ... 32
1.1.4.2.5.3.Dinamik Programlama Sınıflandırılması ... 32
1.1.4.2.5.3.1.Belirli Dinamik Programlama ... 32
1.1.4.2.5.3.2.Belirsiz (Olasılıklı) Dinamik Programlama ... 33
1.1.4.2.6.Stokastik Programlama ... 34
1.1.4.2.6.1.Stokastik Programlama Kavramı ... 34
1.1.4.2.6.2.Stokastik Programlama Teknikleri ... 34
1.1.4.2.6.2.1.Şans Kısıtlı Programlama ... 34
1.1.4.2.6.2.2.Çok Aşamalı Programlama ... 35
1.1.4.2.7.Yapay Zeka Uygulamaları (Popülasyon Tabanlı Teknikler) . 35 1.1.4.2.7.1.Zeka Kavramı ... 35
1.1.4.2.7.2.Yapay Zeka Teknikleri ... 36
1.1.4.2.7.3.Genetik Algoritma ... 36
1.1.4.2.7.3.1.Genetik Algoritma Kavramı ... 36
1.1.4.2.7.3.2.Genetik Algoritma Özellikleri ... 37
1.1.4.2.7.4.Bulanık Mantık ... 38
1.1.4.2.7.5.Tabu Araştırma ... 38
1.1.4.2.7.6.Karınca Algoritması... 39
1.1.4.2.8.Parçacık Sürü Optimizasyonu ... 39
1.1.4.2.8.1.Parçacık Sürü Optimizasyonu Kavramı ... 39
1.1.4.2.8.2.Sürü Zekası... 45
1.1.4.2.8.2.1.Biyolojik Temeller ve Evrimsel Süreç ... 45
1.1.4.2.8.2.2.Sürü Zekası Kavramı ... 47
1.1.4.2.8.2.3.Sürü Zekası Özellikleri ... 48
1.1.4.2.8.2.4.Sürü Zekası ve Optimizasyon ... 49
1.1.4.2.8.2.5.Sosyal Davranışların Benzetimi ... 49
1.1.4.2.8.2.6.Komşuluk Topolojisi... 50
1.1.4.2.8.3.Parçacık Sürü Optimizasyonu Algoritması ... 52
1.1.4.2.8.3.1.En Yakın Komşu Hızıyla Karşılaştırma ve Anlamsız Hareket Etme ... 52
1.1.4.2.8.3.2.Mısır Tarlası Vektörü ... 52
1.1.4.2.8.3.3.Sürekli Parçacık Sürü Optimizasyonu ... 54
İKİNCİ BÖLÜM: PARÇACIK SÜRÜ OPTİMİZASYONU YAKLAŞIMI İLE
PORTFÖY OPTİMİZASYONU ... 56
2.1.Portföy Yönetimi ... 56
2.2. Beklenen Getiri ve Risk ... 57
2.2.1.Beklenen Getiri ... 57
2.2.2.Risk ... 58
2.2.2.1. Sistematik Risk ... 58
2.2.2.2. Sistematik Olmayan Risk ... 59
2.3. Fayda Fonksiyonu... 59
2.4.Portföy Getirisinin ve Riskinin Hesaplanması ... 60
2.4.1.Portföy Getirisi ... 60
2.4.2.Portföy Riski ... 60
2.5. Portföy Çeşitlendirmesi ... 62
2.6.Etkin Portföyler ve Etkin Sınır ... 64
2.7.Sermaye Pazarı Teorisi ... 65
2.7.1.Endeks Modeller ... 66
2.7.1.1.Tekli Endeks Modeli ... 66
2.7.1.2.Çoklu Endeks Modeli ... 67
2.7.2.Sermaye Varlıklarını Fiyatlandırma Modeli ... 67
2.7.2.1.Risk Primi ... 68
2.7.2.3.Sermaye Varlıklarını Fiyatlandırma Modelinin Alternatif
Formları……… ... 69
2.7.2.3.1.Sıfır Betalı SVFM ... 70
2.7.2.3.2.Çok Dönemli SVFM... 70
2.7.2.3.3.Çok Betalı SVFM ... 70
2.8.Parçacık Sürü Optimizasyonu Yaklaşımı ile Portföy Optimizasyonu.... 70
ÜÇÜNCÜ BÖLÜM: PARÇACIK SÜRÜ OPTİMİZASYONU YAKLAŞIMI İLE İMKB UYGULAMASI ... 73
3.1.Uygulamanın Amacı ve Kapsamı ... 73
3.2.Uygulamanın Yöntemi ... 73 3.2.1.Beta Katsayısı ... 74 3.2.2.MATLAB ... 75 3.3.Bulgular... 75 3.4.Yorum ... 84 Sonuç ... 85 Kaynakça ... 88
Kısaltmalar
DP: Doğrusal Programlama
İMKB: İstanbul Menkul Kıymetler Borsası
OVM: Ortalama Varyans Modeli
PSO: Parçacık Sürü Optimizasyonu
Şekil Listesi
Şekil 1: Stasyoner Noktalar Civarında Teğet Eğimlerinin Değişimi ... 8
Şekil 2: Global ve Lokal Maksimum-Minimum Noktalar ... 9
Şekil 3: İki Bağımsız Değişkenli Fonksiyonla Oluşturulan Mutlak Maksimum Yüzey Alanı ... 10
Şekil 4: İki Bağımsız Değişkenli Fonksiyonla Oluşturulan Mutlak Minimum Yüzey Alanı ... 10
Şekil 5: Eşitlik Kısıtları ... 12
Şekil 6: Dışbükey ve Dışbükey Olmayan Şekiller ... 16
Şekil 7: Grafik Çözüm Metodu ... 19
Şekil 8: Xo’ın R’deki Komşuluğu ... 26
Şekil 9: Hessian Matrisi ... 28
Şekil 10: Tek Boyutlu Konveks Fonksiyon ... 29
Şekil 11: Yukarı Doğru Konkav ve Aşağı Doğru Konkav ... 30
Şekil 12: Belirli (Deterministik) Dinamik Programlama ... 33
Şekil 13: Belirsiz (Olasılıklı) Dinamik Programlama ... 33
Şekil 14: İki Olası Komşuluk Topolojisi’nin Şematik Gösterimi ... 51
Şekil 15: Risk Karşısında Yatırımcı Tipleri ... 60
Şekil 16: İki Menkul Kıymetin Getirileri ... 62
Şekil 18: Ortalama Varyans Modeli ile Hesaplanan Portföyün Veri Girişi
... 76
Şekil 19: Markowitz Modeli İle Hesaplanan Portföyün Ağırlıkları ... 77
Şekil 20: Markowitz Modeli İle Hesaplanan Portföyün Getirileri ... 78
Şekil 21: Markowitz Modeli İle Hesaplanan Portföyün Riskleri... 78
Şekil 22: Parçacık Sürü Optimizasyonu Tekniği ile Elde Edilen Sonuçlar ... 80
Şekil 23: Hisse Senetlerinin Portföy İçindeki Ağırlıkları ... 81
Şekil 24: AEFES ve ENKAI Hisseleri İle Oluşturulan Etkin Sınır Çevresinde Parçacık Hareketi ... 82
Şekil 25: AEFES ve CIMSA Hisseleri İle Oluşturulan Etkin Sınır Çevresinde Parçacık Hareketi ... 83
Şekil 26: ENKAI ve CIMSA Hisseleri İle Oluşturulan Etkin Sınır Çevresinde Parçacık Hareketi ... 84
Tablo Listesi Tablo 1: Optimizasyon Tekniklerinin Sınıflandırılması ... 7
Tablo 2: Simpleks Tablo ... 22
Tablo 3: Parçacık Sürü Optimizasyonuna İlişkin Çalışmalar ... 40
Tablo 4: Hisselerin Beta Katsayıları ... 74
Tablo 5: Portföyün Kapsadığı Hisse Senetlerinin Getirileri ve İşlem Gördükleri Endeksler ... 75
Tablo 6: Markowitz Modeli ve Parçacık Sürü Optimizasyon Tekniği ile Elde Edilen Portföy Verilerinin Karşılaştırılması ... 81
Giriş
Günümüzdeki işletmeler, kaynaklarını etkin bir şekilde kullanmak, fon fazlalıklarını değerlendirmek gibi amaçlarını gerçekleştirebilmek için karar verme sistemlerini güçlendirmek zorundadır. Küreselleşme ile hızlı bir şekilde değişen iş ve ekonomi çevresine uyum sağlayabilmenin yolu, karar vericilerin karar verme sistemlerini geliştirmesinden geçmektedir.
Matematiksel bir model, bir işlemi veya olayı matematiksel terimlerle açıklayan formüller dizisidir. Gerçek dünyayı matematik eşitliklerle tarif etmeyi amaçlar. Bir problemi çözmede modellemeni kullanılmasının birçok nedeni vardır. Bir akarsu veya denizdeki balık sayısının belirlenmesi örneği gibi, problemin çözümünü bulmak için deneysel yöntemlere başvurmanın maliyeti çok yüksek olabilir. Yerçekiminin sıfır olduğu bir ortamda cisimlerin nasıl hareket ettiklerinin ortay konulması gibi, deneysel yollara başvurmak olanaksız olabilir. Gerçek dünyanın deneysel olarak ele alınmasında zorlukların olduğu her durumda sistemlerin nasıl davranacağını öngörebilmek amacıyla matematiksel modellemeye başvurulmaktadır.
İkinci Dünya Savaşı sonrasında gelişen piyasalarda karar vermenin zorluğu, bu alana yönelik bazı tekniklerin geliştirilmesine yol açmıştır. Bu tekniklere genel olarak optimizasyon teknikleri denilir. Optimizasyon teknikleri en iyileme çalışmaları olarak tanımlanabilir. Bu çalışmalar bize birçok değişken arasından en iyiyi sunmakta, zaman ve maliyet açısından tasarruf sağlamaktadır. Alternatifler arasından yapılan seçimlerin deneyimlere değil, matematiksel modellere göre yapılması daha sağlıklı neticeler vermektedir. Optimizasyon konusunda sayısal yöntemler olarak nitelendirilen tekniklerden Doğrusal Programlama bu konuda geliştirilen ilk tekniktir. Ancak gerçek hayatta birçok problemin doğrusal olmayan bir yapı sergilemesi diğer birçok tekniğin daha geliştirilmesine sebep olmuştur.
Matematiksel olarak geliştirilen modellerin zaman içerisinde gerçek hayat ile uyum probleminin ortaya çıkması, araştırmacıları doğanın içerisindeki yaşam kalıplarını incelemeye yöneltmiştir.
Bu yönelim sonucunda popülasyon tabanlı teknikler ortaya çıkmıştır. Bu tekniklerde kuş, karınca, arı vb. birçok koloni incelenmiş ve bu teknikler sosyal benzetim yolu ile birçok değişik alana uygulanmıştır.
Parçacık Sürü Optimizasyonu (PSO) tekniği kuş veya balık sürülerinin sosyal davranışlarından esinlenerek geliştirilmiştir. Birbirleriyle ve çevresiyle etkileşim içerisinde olan bireylerin davranışları incelenerek geliştirilmiştir. Bu kavram parçacık zekası olarak da isimlendirilmektedir. PSO’da parçacık olarak isimlendirilen potansiyel çözümler, mevcut en iyi çözümleri takip ederek problem uzayında gezinirler. PSO, fonksiyon optimizasyonu, çizelgeleme, yapay sinir ağlarının eğitimi, bulanık mantık sistemleri, görüntü işleme, portföy optimizasyonu vb. pek çok alanda yaygın olarak kullanılmaktadır.
Parçacık Sürü Optimizasyonun temel mantığı belirli bir alanda, sadece bir bölgede yiyecek olduğu, bir kuş grubunun bu alanda yiyecek aradığı ve başlangıçta yiyeceğin nerede olduğunu bilmediği kabul edilir ise, yiyecek bulmak için en iyi çözüm ne olabilir sorusuna yanıt aramaktır.
Bu çalışmada Parçacık Sürü Optimizasyonu tekniğinin portföy optimizasyonu için kullanıldığında ne gibi sonuçlar ortaya koyacağı ve bu sonuçların yorumlarına yer verilecektir. Parçacık Sürü Optimizasyonu tekniği ile optimum risk ve getiri dengesi ile portföy ağırlığı elde edilmeye çalışılacaktır.
Çalışmanın birinci bölümünde Parçacık Sürü Optimizasyonu teorisi ve bu teorinin temelini oluşturan optimizasyon teorisi anlatılacaktır. İkinci bölümde popülasyon tabanlı optimizasyon tekniği olan Parçacık Sürü Optimizasyonunun portföy yönetimi alanındaki uygulamasında bahsedilerek, üçüncü bölümde yapılacak olan Parçacık Sürü Optimizasyonu ile portföy yönetimi uygulaması için temel oluşturulacaktır. Üçüncü bölümde yapılacak uygulama ile birlikte optimum portföy yapısı ve etkin sınır elde edilmeye çalışılacaktır.
BİRİNCİ BÖLÜM: PARÇACIK SÜRÜ OPTİMİZASYONU
Karar verme sistemleri açısından en iyi çözüme ulaşmak önemlidir. Karar verici olarak insan, mantığı ve deneyimleri ölçüsünde en iyi çözüme ulaşmaya çalışmıştır. Ancak karmaşık sistemlerde karar vermenin zorluğu ve matematiğin gelişimi, en iyi çözüme ulaşmak için matematiksel uygulamaların ortaya çıkmasına neden olmuştur. Matematiksel uygulamalardan biri olan optimizasyon yönetim, ekonomi, planlama, mühendislik gibi birçok alanda en iyi çözümü sunan yöntemleri içermektedir.
1947 öncesinde, Fourier (1826) öncülüğündeki matematikçiler doğrusal eşitsizlik sistemlerini ve değişkenler hesabının klasik teorisi içerisinde yer alan eşitsizlik kısıtlarıyla birlikte (Bolza 1914; Valentine 1937) sistemlerin koşullarını optimal yapmaya çalışırlardı. George Dantzig (1947) tarafından Doğrusal Programlamaya ilişkin yapılan araştırmalar yeni optimizasyon teknikleri konusunda yapılan ilk çalışmalardır. Bu çalışmalarında Simpleks modeli geliştirilmiş ve optimizasyon için yeni teknikler geliştirilmesinin yolu açılmıştır.
Dinamik Programlama R. Bellman (1950) tarafından geliştirmiştir ve Doğrusal Programlamanın statik yapısını dinamik bir hale dönüştürmüştür. Dinamik Programlama da hesaplamalar yinelenerek yapılmaktadır. Diğer taraftan M. Frank ve P. Wolfe (1956) amaç fonksiyonu kareli biçimde olan Kuadratik Programlama üzerine araştırma yapmışlardır.
R.Gomory (1958) yaptığı çalışmada Tam Sayılı Programlama modelini geliştirmiştir. A. Charnes ve W. Cooper (1959) Şans Kısıtlı Programlama modellerini geliştirmişlerdir. Hedef Programlama A. Charnes ve W. Cooper (1965) tarafından geliştirildi. Hedef Programlama ile amacın önceliklerine göre optimal çözüm elde edilmeye çalışılmıştır. N. Karmarkar (1984) Doğrusal Programlama için alternatif bir çözüm algoritması olan iç nokta algoritmasını geliştirdi.
J.H. Holland (1992) tarafından bir sezgisel optimizasyon tekniği olarak kabul edilen Genetik Algoritmayı geliştirdi. Genetik Algoritma doğal seçim ilkelerine dayanan bir arama ve optimizasyon yöntemidir J.Kennedy ve R.C. Eberhart tarafından (1995) popülasyon tabanlı Parçacık Sürü Optimizasyonu tekniği geliştirmişler ve kuş sürülerinin hareketlerini gözlemleyerek modelleme yapmaya çalışmışlardır.
Çalışmanın bu bölümünde optimizasyonun tanımı yapılarak optimizasyonun temel bileşenlerinden bahsedildikten sonra optimizasyon metotlarının sınıflandırılması üzerinde durulacaktır. Daha sonra Parçacık Sürü Optimizasyon Tekniği’nin teorik yapısına geçilecektir.
1.1. Optimizasyon
1.1.1. Optimizasyon Kavramı
İnsanlar her zaman eniyileme bir diğer değişle optimizasyon uygulamalarına yönelmiştir. Değişkenler içerisinde bulunan alternatifler arasından en iyisini seçmek için gerekli olan optimizasyon, çözümlerin modellemesinin yapılmasını sağlayarak gerçek hayat ile ilişkilendirilmesine olanak vermektedir.
Optimizasyon, istenen en iyi sonuca ulaşabilmek ve bu sonucu elde edebilmek için durumlar setinin bulunma işlemidir (Okka, 2006: 38). Ayrıca Allaire (2007) göre optimizasyon, değişkenler hesabı, yöneylem araştırması(yönetim optimizasyonu veya karar süreçleri) ve optimum kontrol’e değinen çok geniş bir konudur.
Optimizasyonda modelleme ve çözümleme iki önemli bileşen olarak nitelendirilmektedir. Modelleme gerçek yaşamda karşılaşılan problemin matematiksel olarak ifade edilmesi; çözümleme ise bu modeli sağlayan en iyi çözümün elde edilmesini kapsamaktadır. Optimizasyon teknolojisinin gelişiminde araştırmacılar öncelikli olarak modellemeyle ilgilenmişlerdir (Türkay, 2006).
1.1.2. Optimizasyonun Önemi
Optimizasyon için doğrusal programlama, hedef programlama, dinamik programlama, tam sayılı programlama gibi teknikler geliştirilmiş sonrasında bu
tekniklere genetik algoritma, karınca kolonisi, parçacık sürüsü gibi popülasyon tabanlı teknikler eklenmiştir. Tüm bu modeller matematiksel bir temelde kurulmaktadır. Bu yüzden matematiksel programlama ve optimizasyon eşanlamlı olarak kullanılabilmektedir.
Tedarik, üretim, portföy yönetimi gibi birçok işletme uygulamasında getiri ve risk kavramlarının en iyileştirilmesi çalışmaları optimizasyon teknikleri ile daha verimli olarak yapılabilmektedir. Karar vericilerin bu teknikler sayesinde ortaya çıkan en iyi çözümü kullanmaları zaman ve maliyet açısından avantajlar sağlamaktadır.
1.1.3. Optimizasyon Uygulamaları
Optimizasyon teknikleri birçok işletme problemine uygulanabilmektedir. Aşağıda bu problemlerden birkaçı anlatılacaktır.
1.1.3.1.Üretim Planlaması Problemi
Doğrusal programlamanın en yaygın kullanıldığı alanlardan birisi her türlü üretim işlevli şirketlerin en karlı ve en düşük maliyetli üretim bileşimini belirlemede kullanılmaktadır (Öztürk, 2004: 45). Doğrusal programlama makine, hammadde, para ve insan gücünün en verimli bir şekilde kullanımını sağlar(Tekin, 2004: 47).
1.1.3.2.Depo Yeri Seçim Problemi
Tamsayılı karar modellerinin önemli bir uygulama alanı olan yer seçimi yani kuruluş yeri problemleridir. Genelde 0-1 tamsayılı karar modeli olarak karşılaşılan kuruluş yeri belirleme problemleri, özel durumların göz önüne alınmasıyla karma tamsayılı modellere dönüşebilir(Kara, 1986: 105).
1.1.3.3.Gezgin Satıcı Problemi
Gezgin satıcı problemi (GSP) verilen N düğüm (şehir) için, her düğüme bir kez uğramak şartıyla tekrar başlangıç düğümüne geri dönen en kısa (en az maliyetli) rotayı bulma problemidir. Tanımlaması son derece kolay fakat çözümü doğrusal olmayan zor bir problemdir. Bir eniyileme problemi olan bu problemde bir çizge üzerine yerleştirilmiş noktalar ve aralarındaki maliyetler göz önüne alınarak her
düğüme yalnız bir kere uğramak şartıyla en uygun maliyetle çizgedeki tüm düğümlerin dolaşılması olarak tanımlanabilir (Aytekin ve Kalaycı, 2010: 1).
1.1.3.4.Portföy Seçimi Problemi
Serbest piyasa ekonomisinde, yatırımcılar ellerindeki nakit paralarını, borsa, hazine bonosu ve bankaların yatırım fonlarına veya faize yatırarak paralarını değerlendirmek isterler. Yatırımcı için önemli olan elindeki paranın ne kadarını hangi yatırım aracına yatırmasıyla elindeki paranın en iyi şekilde değerlendirilmesidir(Öztürk, 2004: 72). Doğrusal Programlama ile çözülebilen portföy seçimi problemi, doğrusal olmayan modeller ile daha iyi neticeler vermektedir.
1.1.3.5.Sistem Güvenirliliği Problemi
Bir sistemin güvenilirliği, belirli koşullar altında belirli bir zaman aralığında sistemin başarılı olarak çalışma olasılığı olarak tanımlanmaktadır. Çoğu sistem, çeşitli işlemlerde kritik bir role sahiptir ve eğer sistemde arıza olursa sonuçları oldukça ciddi olmaktadır. Bu alanda optimizasyon, etkisiz parçaların sisteme en iyi şekilde tahsis edilebilme veya yararlanabilme yolunu bulmayı içermektedir. Parçalara, güvenilirliklerinin etkin olarak ölçülebilmesi için olasılıklar atanmaktadır. Bu konuda; Painton ve Campbell’in 1995’de, Sasaki, Gen ve Yamashiro’nun 1995’de, Coit ve Smith’in 1996’da, Dengiz, Altıparmak ve Smith’in 1997 ve 2000’de yayınlanmış çalışmaları bulunmaktadır (Emel ve Taşkın, 2002:145).
1.1.4. Optimizasyon Metotlarının Sınıflandırılması
Optimizasyon Metotlarını Klasik Optimizasyon Teorisi ve Sayısal Optimizasyon Teknikleri olarak iki ana başlıkta toplamak mümkündür. Bu başlıklar altında incelenecek olan konular Tablo 1’de sunulmuştur.
Tablo 1: Optimizasyon Tekniklerinin Sınıflandırılması
Klasik Optimizasyon Teorisi
-Kısıtlanmamış Problemler -Tek Değişkenli Fonksiyonlar -İki Değişkenli Fonksiyonlar -Kısıtlanmış Problemler -Eşitlik Kısıtları -Eşitsizlik Kısıtları
Sayısal Optimizasyon Teknikleri
-Doğrusal Programlama -Tam Sayılı Programlama
-Doğrusal Olmayan Programlama -Dinamik Programlama
-Stokastik Programlama -Yapay Zeka Teknikleri
1.1.4.1.Klasik Optimizasyon Teorisi
Neden özelleşmiş optimizasyon tekniklerine ihtiyaç duyduğumuzu anlamak için maksimum ve minimum noktaları içeren problem hesaplama uygulamalarının olduğu optimizasyon teorisinin klasik bakış açısını gözden geçirmek gerekir. Parçalı sürekli ve diferansiyel fonksiyonların optimizasyonu için hesaplama kullanımının kısıtlı olduğu görülecektir(Gottfriend ve Weisman, 1973: 26).
Değişken bir miktarın maksimum ve minimum değerleri, uygulama alanı çok olan değerlerdir. Verilen bir hacimde depo yapılabilmesi için minimum miktarda malzemeye gerek görülmesi; bir merminin ulaşacağı en büyük yüksekliğin bulunması gibi sorulara verilecek cevaplar bu gibi problemlerin çözümü ile elde edilecektir(Karadeniz, 2003: 99). Klasik Optimizasyon Teorisi’ni Kısıtlanmamış ve Kısıtlanmış Problemler olmak üzere iki alt başlıkta incelemek mümkündür.
1.1.4.1.1.Kısıtlanmamış Problemler
Bir fonksiyon yalnız bir değişkene bağlı ise tek değişkenli fonksiyon, birden fazla değişkene bağlı ise iki, üç,…, çok değişkenli fonksiyon adını alır (Karadeniz, 2003: 7). Kısıtlanmamış problemleri tek değişkenli ve çift değişkenli olarak incelemek mümkündür.
1.1.4.1.1.1.Tek Değişkenli Fonksiyonlar
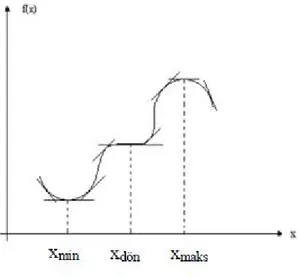
Tek değişkenli bir fonksiyona ait eğri Şekil 1 de gösterilmiştir. Fonksiyonun maksimum olduğu nokta civarında soldan sağa giderken teğetin eğimi sürekli azalır Diğer bir ifade ile fonksiyonun türevi x = xmaks noktasında negatif olur. Buna karşılık
fonksiyonun minimum olduğu nokta civarında soldan sağa giderken teğetin eğimi sürekli olarak artar. Bu nedenle x = xmin noktasında fonksiyonun ikinci türevi sıfır olur. Yatay dönem noktası civarında ise soldan sağa gittikçe teğetin eğimi önce artar, x = xmin noktasında sıfır olur, daha sonra azalmaya başlar(Akgün, 1987: 7).
Şekil 1: Stasyoner Noktalar Civarında Teğet Eğimlerinin Değişimi
Kaynak: Akgün, 1987: 8
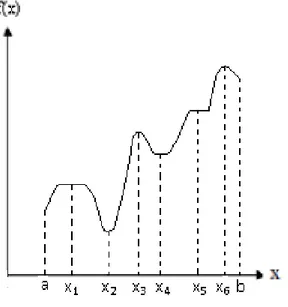
Şekil 2 de, [ a, b] aralığı boyunca f(x) tek değişkenli fonksiyonunun maksimum ve minimumunu göstermektedir. x1, x2, x3, x4, x5, x6 , f(x)’in tüm uç noktalarıdır. Bunlar x1, x3, x6 maksimum x2 ve x4 minumum uç noktalarını içerir.
f(x6) = maks { f(x1) f(x3) f(x6) }
olduğundan , f(x6) global veya mutlak maksimum, f(x1) ile f(x3) lokal veya görece maksimum diye adlandırılır. Benzer şekilde, f(x4) lokal minumum, f(x2)de global minimumdur. x1 maksimum nokta olmasına rağmen diğer lokal maksimumlardan ayrılır çünkü x1’in komşuluğunda en az bir noktadaki f değeri f(x1)’e eşittir (Taha, 2000: 737-738).
Şekil 2: Global ve Lokal Maksimum-Minimum Noktalar
Kaynak: Taha; 2000: 738
1.1.4.1.1.2.İki Değişkenli Fonksiyonlar
Çift değişkenli fonksiyonlarla tanımlanan yüzeyler üzerindeki stasyoner noktalardan eksenler doğrultusunda çizilen teğetlerin eğimi sıfır olur.
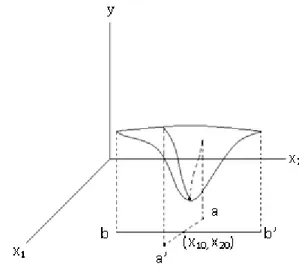
Görselleştirmenin sadeliği için, iki bağımsız değişkenli fonksiyonla oluşturulan yüzey alanı göz önünde bulundurulacaktır; örneğin, y = y(x1, xx). Şekil 3 ve Şekil 4 de sürekli fonksiyon için bir mutlak maksimum ve bir mutlak minimum noktası gösterilmiştir (Gottfriend ve Weisman, 1973: 32-33).
Şekil 3: İki Bağımsız Değişkenli Fonksiyonla Oluşturulan Mutlak Maksimum Yüzey Alanı
Kaynak: Gottfriend ve Weisman, 1973: 33
Şekil 4: İki Bağımsız Değişkenli Fonksiyonla Oluşturulan Mutlak Minimum Yüzey Alanı
1.1.4.1.2.Kısıtlanmış Problemler
Birçok kısıtlı optimizasyon probleminin yapısı aşağıdaki gibidir:
minimize f(x) x ∈ Rn
(1.1)
koşul ci (x) = 0 i ∈ E (1.2)
ci (x) ≥ 0 i ∈ I.
f(x) amaç fonksiyonu, kısıtlılık fonksiyonları ci (x), i=1,2,…p. E denklemlerin veya eşitlik kısıtlarının indeks kümesi, I eşitsizlik kısıtlarının kümesidir ve her iki kümede sınırlıdır.(Fletcher, 1987: 139-140).
1.1.4.1.2.1.Eşitlik Kısıtları
Kısıtlanmış türevler (Jakobiyen) yönteminde;
Min. Z=f(x) Kısıtlar: g(x) = 0 (1.3)
Burada X = (x1,x2,…,xn) g = (g1,g2,…,gn)T (1.4)
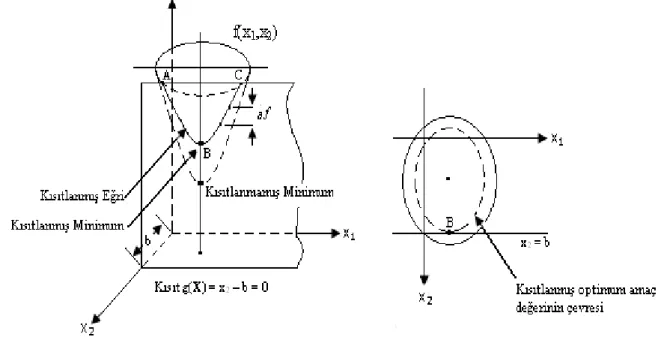
f(X) ve gi(X) fonksiyonları i=1,2,…,m için ikinci dereceden sürekli diferansiyel fonksiyonlar olarak varsayılsın. Kısıtlanmış türevlerin kullanılması düşüncesi g(X) = = kısıtının sağlandığı tüm noktalarda f(X)’in birinci kısmi türevinin kapalı formda ifadesini bulmaya dayanır. Buna karşılık gelen sabit noktalar, bu kısmi türevlerin sıfıra eşit olduğu noktalar olarak tanımlanır. Şekil 5 de f(x1,x2) fonksiyonu g1(x1,x2) = x2 – b = 0 kısıtı ile minimum kılınır. b sabittir, A,B,C gibi üç noktadan geçen eğri verilen kısıtı her zaman sağlayan f(x1,x2) değerlerini gösterir. Kısıtlanmış türevler yöntemi ABC eğrisi üzerindeki herhangi bir noktada f(x1,x2)’nin gradyanını tanımlar(Taha, 2000: 745).
Şekil 5: Eşitlik Kısıtları
Kaynak: Taha, 2000: 746 1.1.4.1.2.2.Eşitsizlik Kısıtları
Lagranj yöntemi Jakobiyen yöntemden geliştirilebilir.
Maks. Z= f(X) (1.5)
Kısıtlar: gi(X) ≤ 0, i=1,2,…,m (1.6)
probleminin verildiğini varsayalım. Negatif olmayan X ≥ 0 kısıtları, eğer varsa m kısıta dâhildir. Lagranj prosedürünün genişletilmesindeki genel düşünce şudur.: f(X)’in kısıtlanmamış optimumu tüm kısıtları karşılamıyorsa, kısıtlanmış optimum çözüm uzayının sınır noktasında ortaya çıkmaktır. Bu da m kısıtın bir veya birden fazla denklem formunda sağlamak zorundadır anlamına gelir.
1.1.4.2.Sayısal Optimizasyon Teknikleri
Klasik optimizasyon teorisi kısıtlanmış ve kısıtlanmamış fonksiyonların maksimum ve minimum (uç) noktalarını belirlemek için diferansiyel hesabı kullanır. Yöntemler etkin sayısal hesaplamalar için uygun olmayabilir. Bununla birlikte, bu teorinin temeli en çok doğrusal olmayan programlama algoritmalarının geliştirilmesidir(Taha, 2000: 737).
Maksimum ve minimum değerlerin belirlenmesi problemleriyle genelde matematiğin çeşitli dalları ilgilenmekte birlikte, bu tür problemlere ekonomik uygulamalarda da rastlanmaktadır. Mesela işletmelerin karlarını maksimize veya maliyetini minimize etmeye, sosyal planlamacıların toplumun refahını maksimize etmeye çalışmaları yanında, tüketicilerin gelirlerinden maksimum tatmini sağlayacak şekilde harcama yapma arzusunda oldukları gözlenir(Serper ve Gürsakal, 1982: 4).
Sayısal optimizasyon teknikleri:
Doğrusal Programlama Tamsayılı Programlama
Doğrusal Olmayan Programlama Dinamik Programlama
Stokastik Programlama Yapay Zeka Teknikleri
olarak sayılabilir.
1.1.4.2.1.Doğrusal Programlama
1.1.4.2.1.1.Doğrusal Programlama Kavramı ve Unsurları
II.Dünya Savaşı’nda büyük askeri ve sivil harekat her şeyden daha çok bu faaliyetlerin sistematik planlamasını ve koordinasyonunu gerektiriyordu. Bunun sonucu olarak “ihtiyaçlar keşfin anasıdır” değer yargısı burada bir defa daha doğrulanmış oldu. Nitekim Leontief’in temelde sektörler arası ekonomik ilişkileri açıklayan fakat optimizasyon gibi bir amacı olmayan girdi-çıktı modelinin rehberliğinde doğrusal programlama konusu araştırılmaya başlandı. Söz konusu
araştırmalar A.B.D. Hava Kuvvetleri’nde yapılan planlama çalışmaları içinde yürütülmüş ise de 1947 yılına kadar programlama problemlerinin genel formülasyonunu yapmak mümkün olmamıştır (Serper ve Gürsakal, 1982: 5).
A.B.D. Hava Kuvvetleri’nde matematikçi olarak Dantzig, 1947 yılında planlamakta olduğu lojistik faaliyet ve problemlerin, bugün bizim Doğrusal Programlama dediğimiz şekli aldığına dikkat etmiş ve bu özelliği, henüz saptanmamış matematiksel bir yapı olarak yorumlamıştır(Karakoyunlu, 1973: 51-52).
Doğrusal Programlama, sınırlı kaynakların kullanımını optimum kılmak için tasarlanmış bir matematiksel modelleme yöntemidir (Taha, 2000: 11). Bugün endüstriyel ve ekonomik analizlerde yaygınca kullanılan doğrusal programlama, tüm nicel teknikler arasında en geniş etki alanı olanıdır. Doğrusal programlama firmanın, ulaşım, üretim, finansman, dağıtım ve reklamcılık gibi pek çok faaliyetlerinde kullanılabilir (Öztürk, 2004: 23).
DP problemleri, bilinmeyenler içinde herhangi birinin eşitlik veya eşitsizlik olabileceği doğrusal kısıtlara bağlı bir şekilde amaç fonksiyonu olarak adlandırılan doğrusal bir fonksiyonun optimizasyonunu içermektedir (Goldfarb ve Todd, 1989: 73). Doğrusal programlama probleminin üç önemli unsuru vardır (Esin, 1981: 26-28):
-Amaç fonksiyonu,
-Kısıtlayıcı fonksiyonlar,
-Pozitif kısıtlama.
Doğrusal Programlama modelinden beklenen sonucun alınabilmesi için amacın açık olarak bilinmesi ve nicel olarak yazılımı gereklidir. Genellikle amaç, karların en büyüklenmesi veya maliyetlerin en küçüklenmesi yönündedir (Öztürk, 2004: 25).
Doğrusal Programlama problemini denklemler halinde gösterecek olursak(Sezginman, 2001: 1): a11x1 + a12x2 + … + a1mxm + … + a1nxn = b1 a21x1 + a22x2 + … + a2mxm + … + a2nxn = b2 (1.7) am1x1 + am2x2 + … + ammxm + … + amnxn = bm x1 ≥ 0, x2 ≥ 0, … , xm ≥ 0, … , xn ≥ 0 (1.8) kısıtları altında z = c1x1 + c2x2 + … + cmxm + … + cnxn (1.9)
amaç fonksiyonunu minimum (ya da maksimum) yapan x1, x2, …,xm, … xn bilinmeyenlerini (değişkenlerini) belirtmek doğrusal programlama problemidir.
1.1.4.2.1.2.Doğrusal Programlamanın Dayandığı Varsayımlar
Bir modelin Doğrusal Programlama yaklaşımı ile çözülebilmesi için aşağıdaki şartlara sahip olması gerekir ( Tekin, 2004: 51):
a. Modeldeki değişkenlerin rakamlarla gösterilmesi ve bölünebilir özellikte olması gerekir. Doğrusal Programlama rakamlarla gösterilemeyen modellerin çözümünde kullanılmaz.
b. Değişkenler arasında alternatif seçim olanağı olmalıdır. Örneğin; yalnızca bir makineye veya insan emeğine ihtiyaç gösteren üretime, Doğrusal Programlama uygulanmaz.
c. Değişkenler arasındaki ilişkilerin doğrusal olması gerekir. Doğrusallık modelde kullanılan bütün eşitlik veya eşitsizliklerin birinci dereceden olması anlamına gelmektedir.
d. Doğrusal Programlamanın uygulanacağı işletme problemleri kısa dönemlidir. Çünkü; Doğrusal Programlamanın en önemli koşulu olan doğrusallık, ancak kısa dönemde gerçekleşebilir.
1.1.4.2.1.3.Doğrusal Programlama Probleminin Özellikleri
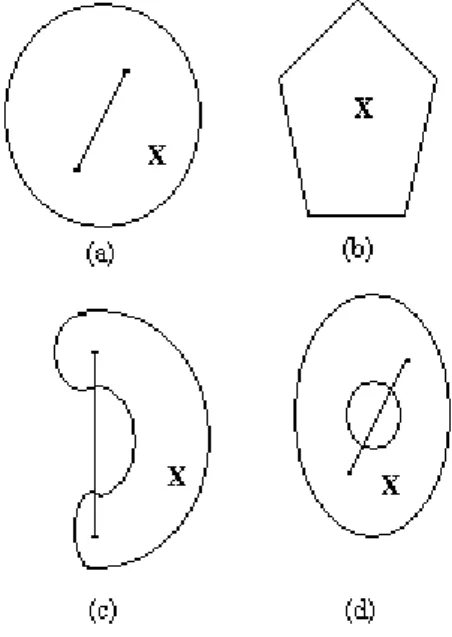
Özellik 1: Doğrusal karar modelinin uygun çözüm alanı dışbükey kümedir(Kara, 2000: 38).
Şekil 6: Dışbükey ve Dışbükey Olmayan Şekiller
-a ve b dışbükey, c ve d dışbükey olmayan şekillerdir.
Kaynak: Wismer ve Chattergy, 1978: 5
Özellik 2: Amaç fonksiyonu f(x) = c(x) olan bir doğrusal programlama modelinde (Kara, 2000: 40);
a. Eğer modelin en iyi çözümü varsa, bu nokta uygun çözüm alanının bir uç noktasıdır.
b. Amaç fonksiyonu en iyi değerini birden fazla uç noktada alıyorsa bu noktaların her dışbükey bileşimi de en iyi çözümdür.
1.1.4.2.1.4.Doğrusal Programlama Probleminin Çözümüne İlişkin Tanımlar Doğrusal programlama probleminin çözümünde kullanılan tanımları şöyle sıralayabiliriz(Öztürk, 2004: 24-25):
a. Uygun Çözüm: Çözüm doğrusal programlama probleminin tüm kısıtlayıcılarını doyurursa uygun çözüm olur.
b. Optimal Çözüm: Doğrusal programlama probleminin çözümünde birkaç uygun çözüm olabilir. Oysa tüm uygun çözümler arasından en iyi olanı optimal çözümdür.
c. Temel Çözüm: Amaç fonksiyonu ve negatif olmama koşulu dışında, problem m sayıda sınırlayıcılı ve n değişkenli ise tek bir temel çözüm vardır.
d. Bozulan Çözüm: Cari temel çözümün bir veya birkaç temel değişkenin değeri sıfırsa bozulan çözüm vardır.
1.1.4.2.1.5.Doğrusal Programlama Çözüm Metotları
Doğrusal Programlama değişik şekillerde çözümlenebilir. Bu çözüm yollarının en basit şekli, kayıtlayıcı ilişkilerinin ikili eksenler üzerinde doğrular olarak çizilmesi ve uygun çözüm alanının saptanmasıdır. Doğrusal Programlama çözümlerinin en mükemmel şekli olan Simpleks metot her tip Doğrusal Programlama çözümlerinde kullanılabilir(Karakoyunlu, 1973: 56).
1.1.4.2.1.5.1.Grafik Çözüm Metodu
Doğrusal programlama problemlerinin çözümünde grafik yönteminden yararlanabilmek için, söz konusu problemlerin en fazla üç değişken ihtiva etmesi gerekir. Çünkü üç boyuttan daha fazlası için grafik çizimi yapılamamaktadır(Serper ve Gürsakal, 1982: 7). Grafik yöntemde iki temel adım vardır (Taha, 2000:15):
1.Modelin tüm kısıtlarının sağlandığı uygun çözümleri içeren çözüm uzayının belirlenmesi,
2.Belirlenen bu uygun çözüm uzayındaki bütün noktalar arasından optimum çözümün belirlenmesi.
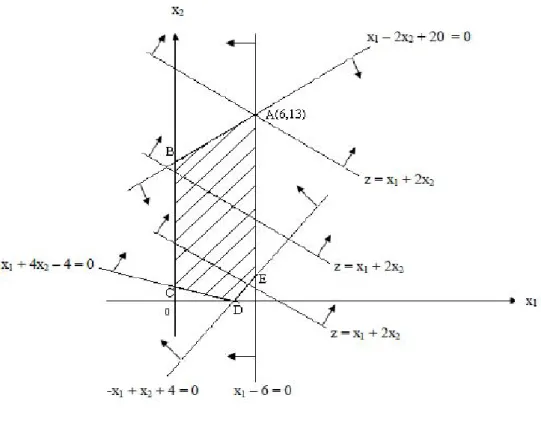
Grafik çözüme ilişkin bir örnek ile konuya açıklık getirmeye çalışalım(Sezginman, 2001:8): x1 + 4x2 – 4 ≥ 0 -x1 + x2 + 4 ≥ 0 (1.10) x1 – 6 ≤ 0 x1 – 2x2 + 20 ≥ 0 x1 ≥ 0 (1.11) x2 ≥ 0 Maks z = x1 + 2x2 (1.12)
Şekil 7: Grafik Çözüm Metodu
Kaynak: Sezginman, 2001: 8 Grafik çözümde:
1.(1.10) ve (1.11) koşullarının sağlandığı ABCDE bölgesi saptanır.
2.z bir parametre olarak düşünülürse z = x1 + 2x2 paralel doğru parametredir.
z nin bir değerine bu demetin bir tek doğrusu ve bu demetin bir doğrusuna da z nin bit tek değeri karşı gelir. En önemli husus z = x1 + 2x2 doğrusu hangi yönde ötelenirse z nin artacağının saptanmasıdır.
z = x1 + 2x2 de x2 nin katsayısı pozitif olduğundan (ya da x2 – ekseni kestiği noktaların koordinatlarından) z = x1 + 2x2 doğruları x2 – ekseni yönünde ötelediği zaman z nin artacağı görülür. Tabii x1 in katsayısının pozitif olması nedeniyle, x1 ekseni yönündeki öteleme de z yi artırır. Bunlara dayanarak (1.10) ve (1.11) koşullarının sağlandığı A(6,13) noktasından geçen z = x1 + 2x2 doğrusunda z nin maksimum değeri alacağı söylenebilir.
Şu halde optimum çözüm:
x1 = 6 x2 =13 X =(6,13); Maks z = 6 + 2.(13) = 32 dir.
1.1.4.2.1.5.2.Simpleks Metodu
Simpleks yöntemi tekrarlı bir hesaplama yöntemdir. Diğer bir ifade ile, bu yöntemde temel hesaplama işlemleri sürekli olarak tekrarlanmaktadır. Bu işlemlere en iyi çözüm bulununcaya kadar devam edilir. Tekrarlama sayısı sabit değildir. Tecrübeler göstermiştir ki, tekrarlama sayısı ile modeldeki eşitsizliklerin sayısı hemen hemen eşittir. Bu kural tam anlamıyla doğru olmamasına rağmen, tekrarlamaların sayısı hakkında bir bilgi verir(Serper ve Gürsakal, 1982: 15).
Problemlerin Doğrusal Programlama şeklinde formüle edilerek Simpleks Metoduna göre çözümlenebilmesi için aşağıdaki işlemlerin sırasıyla izlenmesi gerekir(Tekin, 2004:57):
1.Sınırlayıcı şartlara ve amaç fonksiyonuna göre Simpleks tablosu düzenlenir. Sınırlayıcı şartların sağ taraf değerleri, pozitif değerler olarak çözüme girmelidir.
2.≤ Şeklindeki sınırlayıcı şartlar için pozitif değişkenler ilk çözüm tablosunda yer alır. ≥ Şeklindeki sınırlayıcı koşullar için negatif boş değişkenler ilk çözüm tablosunda yer alırlar. ≥ ve = şeklindeki sınırlayıcı şartlar için yapay değişkenler ilk çözüm tablosunda yer alır.
3.Bu metodun ilk safhası amaç fonksiyonuna bakılmaksızın yapay değişkenleri elimine etmektir (çözümden çıkarmaktır). Yapay değişkenler ilk çözüm tablosunda yer alırlar.
4.Çözümün optimal olup olmadığı belirlenir. Temel olmayan değişkenlerin her birinin katsayısı bulunarak amaç fonksiyonundan temel değişkenler çıkarılır.
5.Z deki artışa neden olan temel değişkenlerin seçimine göre, temel olmayan değişkenler çözüme girer. Amaç fonksiyonunda en büyük artışı sağlayan temel olmayan değişken katsayısı seçilir. K çözüme giren temel değişken sayısını gösterir.
6.Çözüme giren temel değişkenlerden sıfır değerini alan ilk temel değişken çözümden çıkarılır, bj/cj oranı sıfırdan büyük olanı alınır. Çözümden çıkan temel değişkenlerden bj/cj oranı sıfırdan büyük olanı alınır. Çözümden çıkan temel değişkenlerden bj/cj oranı en küçük olanı seçilir.
7.Yeni temel uygun çözüm bulunur. Satır işlemlerinde temel olmayan değişkenler temel değişkenler için çözülür. Tamamlanan tabloda amaç satırı oluşturur.
Bu işlemler yapıldıktan sonra; optimal, sınırlı ya da temel uygun bir çözümün olup olmadığı tespit edilir.
Bir doğrusal programlama problemini tablo halinde de gösterebiliriz ve bu tabloya Simpleks Tablo denir (Okka, 2006: 805):
n max j j j =1 n ij j i 1 j = 1 j i Z = C X (1.13) K.S. a X + S =b i = 1,2,...,m (1.14) X 0 j = 1,2,...,n S 0
Tablo 2: Simpleks Tablo
Kaynakça: Okka, 2006: 806
Burada Zj değeri temel olmayan değişkenler satırında bir değişiklik yapıldığında birim başına K.S.’deki kaybı gösterir.
Cj - Zj değeriyse; bu satırdaki elemanın ilişkili bulunduğu değişkenden bir birim daha üretildiğinde sağlayacağı kazanç artışını (minimizasyon problemlerindeyse maliyet azalışını) gösterir(Okka, 2006: 806).
1.1.4.2.1.5.3.Dualite
Daha önceki bölümlerde incelenen Doğrusal Programlama problemlerinin çözümünde kullanılan model primal model olarak isimlendirilmektedir. Primal modelin değişik bir şekilde oluşturulması ile dual model meydana gelmektedir. Primal ve dual modelde değişken ve sınırlayıcı koşul sayılarının farklı olması, birinin çözümünün, diğerinden kolay olmasını sağlar. Primal modelde amaç fonksiyonu maksimizasyon ise, dual modelde amaç fonksiyonu minimizasyon biçiminde
olmaktadır. Primal modelde amaç fonksiyonu minimizasyon ise dual modelde amaç fonksiyonu maksimizasyon olmaktadır(Tekin, 2004: 79).
Kanonik şekilde verilen bir doğrusal programlama problemi şöyle yazılabilir(Okka, 2006: 822): n max j j j =1 n ij j i j = 1 j Z = C X , (1.15) S.S. a X b , j = 1,2,3...,n (1.16) X 0 i = 1,2,3,...,m
Böyle bir problemin duali şöyle yazılabilir:
m min i i i=1 m ij i j i = 1 i Y = b Y , (1.17) S.S. a Y C , j = 1,2,3...,n (1.18) Y 0 i = 1,2,3,...,m
1.1.4.2.2.Tam Sayılı Programlama
1.1.4.2.2.1.Tam Sayılı Programlama Kavramı
Gerçek hayatta karşılaşılan çoğu karar problemlerinde problemin yapısı gereği, karar değişkenlerinin tamamı ya da bir kısmı tamsayı değer almak zorundadır. Bazı problemlerde karar modeli geliştirme evresinde tamsayı değer alması öngörülen ara değişkenler kullanılır. Belirtilen durumlarla ilgili, yani karar değişkenlerinin tamsayılı olması gereken problemlerin modellemesi ve çözümüne ilişkin kavram ve teknikler “Tamsayılı Programlama” başlığı altında incelenmektedir(Kara, 194:1).
1.1.4.2.2.2.Tam Sayılı Karar Modeli
Tam sayılı karar modelinin genel yazılımı(Kara, 1984:2)
gi (x) = bi , i=1, 2, 3, ..., m (1.19)
xj tamsayı, j=1, 2, …, n (1.20)
kısıtları altında
en iyi f(x) şeklindedir.
Kara modelinin kıtları ve anaç fonksiyonu doğrusal fonksiyonlar ise; A teknik katsayılar matrisi, b sağtaraf sabitleri vektörü ve C katkı vektörü olmak üzere, model;
AX =b (1.21)
xj ≥ 0 ve tamsayı (1.22)
kısıtları altında,
en iyi f(X) = CX (1.23)
şeklinde yazılır ve modele “Tamsayılı Doğrusal Programlama Modeli” denir.
1.1.4.2.2.3.Tam Sayılı Programlamada Çözüm Yaklaşımları
Tamsayılı doğrusal programlama modelini çözmek için doğrusal programlama modelinin çözümde olduğu gibi genel bir teknik yoktur. Belirli bir tür problemden hareketle geliştirilen bir dizi çözüm yaklaşımları vardır. Bunlar ((Doğan, 1995:144-145):
1.Yuvarlama: Ax=b, X≥0 ve tamsayı, en iyi z=CX modeli önce Ax=b, X≥0, eniyi z=CX olarak çözülür. Eniyi çözümde karar değişkenleri tamsayı değer almışsa ilk modelin eniyi çözümü elde edilir. Değilse temel değişkenler, uygun çözüm koşulu bozulmadan, tamsayı değere(yuvarlama) dönüştürülerek yaklaşık eniyi çözüm bulunabilir.
2.Sayımlama Yöntemleri: Bu yaklaşım açık ya da kapalı olarak verilen modlein tamsayı tüm uygun çözümlerini göz önüne alarak, en iyi çözümü aramaktadır.
3.Kesme Düzlemi Teknikleri: Ax=b, X=0, en iyi z=CX modelinin eniyi çözüme erişildikten sonra, tamsayı çözüm elde edildikten sonra, tamsayı çözüm elde edilene kadar, her ardıştırmada modele tamsayı değer alacak değişkenlerden hareketle yeni kısıt eklenerek işlemlere devam ettirilmesi şeklindedir.
4.Ayrışımlı Algoritmalar: Karma tamsayılı modeli, tamsayılı modellerden hareketle verilen modelin eniyi çözümüne geçiş şeklindeki yaklaşımlardır.
5.Grup teorisi Algoritmaları: Gomory, x≥0 koşulu göz önüne alınmadığında, tamsayı değişkenlerle ilgili özel kıtılar altındaki tamsayılı programlama modelinin, bir grup üzerindeki tanımlanmış enküçükleme problemi şeklinde ele alınabilir olduğunu göstermiştir.
1.1.4.2.3.Doğrusal Olmayan Programlama
1.1.4.2.3.1.Doğrusal Olmayan Programlama Kavramı
Doğrusal programlama problemlerinde sınırlayıcı eşitlik veya eşitsizlikler ile amaç fonksiyonu lineer idi. Böyle bir doğrusal programlama problemini çözen etkin çözüm yöntemlerinin olduğunu biliyoruz. Gerçek hayatta karşılaşılan çoğu problem için geliştirilen karar modellerinin kısıtlarında ve amaç fonksiyonunda doğrusal ilişkileri gözlemek zordur. Karar modelinin kısıtlarından en az biri ve amaç fonksiyonunun doğrusal olmadığı durumlar için geliştirilen kavram ve teknikler Doğrusal Olmayan Programlama başlığı altında incelenmektedir (Doğan, 1995:193). Doğrusal olmayan programlama problemleri yalnızca diferansiyel fonksiyonlar üzerine kurulabilir (Wismer ve Chattergy, 1978:15).
Doğrusal Olmayan Programlama Probleminin standart hali(Pedregal, 2004:68):
x ∈ Rn olmak üzere (1.24)
1.1.4.2.3.2. Doğrusal Olmayan Programlamanın Özellikleri 1.1.4.2.3.2.1.Temel Kavramlar
Xo ∈ S iken Xo’in komşuluğu,
A = {X| |X- Xo| ≤ , X ∈ S} şeklinde gösterilir. S=R ise, Xo’ın komşuluğu şekil deki gibi çizilir (Kara, 1986: 2).
Şekil 8: Xo’ın R’deki Komşuluğu
Kaynak: Kara, 1986: 2
X bir vektör olmak üzere, f(x)’in tanım kümesi S ve Xo ∈ S için, Xo’in komşuluğu A olsun (Doğan, 1995: 194-195):
a. A’daki tüm X’ler için f (Xo) ≤ f(x) ise, f(x) x=x0 da yerel en küçük (local min.),
b. S’deki tüm X’ler için f(X0) ≤ f(x) ise, f(x) x=xo da bütünsel en küçük (Global min., Mutlak min.),
c. A’daki tüm X’ler için f (Xo) ≥ f(x) ise, f(x) x=x0 da yerel en büyük (local max.),
d. S’deki tüm X’ler için f(X0) ≤ f(x) ise, f(x) x=xo da bütünsel en büyük (Global maks., Mutlak maks.)
1.1.4.2.3.2.2.Gradiyant Kavramı
Z= f(x1, x2, …, xn) fonksiyonunun xj’ye göre kısmı türevi,
Z f xj xj (1.25) olup, , ,..., 1 2 f f f f x x xn (1.26)
sütun vektörüne f’in gradiyantı denir. Gradiyant f’in verilen bir X noktasındaki değeri ∇ ( ) şeklinde gösterilir. f(x)’in xj göre türevi,
1 2,, ...,
f gj x x xn x j (1.27)şeklinde bir fonksiyon olduğundan, bunların her birinin değişkenlere göre tekrar kısmı türevleri olabilir. Birinci kısmi türevlerin her birinin n kadar ikinci kısmi türevi söz konusu olabileceğinden, f’nin ikinci kısmi türevleri n2 kadardır (Kara,1986: 3-4-5).
1.1.4.2.3.2.3.Hessian Matrisi
Eğer verilen bir noktada f(x)’in ikinci kısmi türevleri var ve f(x) bu noktalarda sürekli ise, bütün i ve j ler için;
2f 2f x xi j xj xi (1.28) gerçeklenir.
İkinci kısmı türevleri içeren nxn boyutunda 2 f H f x x i j nxn (1.29)
matrisini yazabiliriz ki bu Hessian Matrisi olarak adlandırılır. Ve yukarıda belirtilen özelliğinde dolayı Hessian Matrisi simetriktir (Doğan, 1995: 197-198).
Şekil 9: Hessian Matrisi
2 2 2 2 1 2 1 1 2 2 2 2 2 1 2 2 2 2 2 2 1 2 f f f x x x xn x f f f H f x x x x xn f f f xn x xn x xn nxn Kaynak: Doğan, 1995: 198
1.1.4.2.3.2.4.Dışbükey (Konveks) ve İçbükeylik (Konkav) Bazı fonksiyonlar düzgün karakterli özelliktedirler:
y{ax1 + (1 – a)x2 } ≤ ay(x1) + (1 – a)y(x2), 0 < a < 1 (1.30)
Başka bir ifadeyle x1 ve x2 olmak üzere iki nokta alırsak belli bir orta noktada [ax1 + (1 – a)x2 ]fonksiyonun değeri y(x1) ve y(x2)’in ağırlıklı aritmetik ortalamasından daha az veya eşittir. Eğer denklem x1 ve x2 nin tüm noktalarını içeriyorsa fonksiyon y(x)’in konveks fonksiyon olduğu söylenir(Gottfriend ve Weisman, 1973: 10-11).
Şekil 10: Tek Boyutlu Konveks Fonksiyon
Kaynak: Gottfriend ve Weisman, 1973: 12
F(x) verilen bir kümede tanımlıyken bu kümeye ait olan ve birbirinden farklı her x1, x2 noktaları ve λ ∈ [0,1] için
F (λx1 + (1 – λ) x2 ) ≥ λ f (x1) + (1 – λ)f(x2) bağıntısı varsa f(x) içbükey(konkav) fonksiyon adı verilir(Doğan, 1995:203).
y = f(x) fonksiyonunu eğrisini göz önüne alalım. Eğer eğri üzerindeki bir x0 noktasından komşuluğunda x0 noktasındaki teğetin tamamı eğrinin altında kalıyorsa, eğriye yukarı konkav, x0 noktasının komşuluğunda bu noktadaki teğeti eğrinin üst kısmında kalıyorsa aşağı doğru konkav denir (Bozkurt vd., 2004: 250).
Şekil 11: Yukarı Doğru Konkav ve Aşağı Doğru Konkav
Kaynak: Bozkurt vd., 2004: 250
1.1.4.2.4.Kuadratik Programlama(Kareli Biçimler)
Amaç fonksiyonu kuadratik, yani kareli terimler içeren bir fonksiyon ve kısıt fonksiyonları da birer lineer fonksiyon olan bir matematiksel programlama problemi kuadratik programlama problemi olarak adlandırılır. C, amaç fonksiyonundaki doğrusal terimlerin katsayılarını ifade eden n-boyutlu satır vektörü ve Q, amaç fonksiyonundaki kareli terimlerin katsayılarını gösteren (nxn) boyutlu simetrik bir matris olmak üzere, genel olarak bir kuadratik programlama problemi aşağıdaki gibi yazılır( Erdoğan ve Alptekin, 2006:125).
Maksimum f(X) = cX + ½ XTQX (1.31)
Kısıtlar AX ≤ b (1.32)
Matris gösterimi (Kara, 1986: 18): 11 1 1 12 1 2 1 1 1 21 2 1 12 2 2 2 2 1 1 1 1 2 2 2
( )
n n n n n ij i j i j n n n nn n na x x
a x x
a x x
a x x
a x x
a x x
f x
a x x
a x x
a x x
a x x
şeklinde ise, f(x)’e bir kareli fonksiyon ya da f(x) kareli biçimdedir(quadratic form) denir.
1.1.4.2.5.Dinamik Programlama
1.1.4.2.5.1.Dinamik Programlama Kavramı
Dinamik Programlama, problemleri çözmek için bir ilişkiler arası kararlar serisi içeren nicelikli bir tekniktir. Temel olarak tam fayda sağlayabilecek bir zaman dilimi üzerinden optimal kararların bir kombinasyonunu bulma ile ilgilidir(Doğan, 1995:511).
Dinamik Programlama da hesaplamalar yinelenerek yapılır, bu bakımdan bir alt problemin optimum çözümü bir sonraki alt problemin girdisidir. Son alt problemi çözdüğümüze, problemin tamamı optimum çözümüne ulaşmış oluruz. Yinelenen hesaplamaların uygulanma biçimi orijinal problemi nasıl ayrıştırdığımıza bağlıdır. Özellikle, alt problemler bazı ortak kısıtlarla normalde birbirleriyle ilişkilendirilmişlerdir. Bir alt problemin bir sonrakine ilerledikçe bu kısıtların uygunluğuna dikkat etmek zorundadır (Taha, 2000:403).
1.1.4.2.5.2.Richard Bellman Teoremi
Dinamik Programlamaya adını veren R. Bellman’dır. Doğrusal Programlama statik karakterde olduğu halde Dinamik Programlama dinamiktir (Akalın, 1979: 399).
Teorem uygulamaya gayet basit bir işlem şeklinde girmekte ve her türlü probleme uygulanabilmektedir. Her optimal politika, alt optimal politikalardan meydana gelir. Teorem uygulandığı alanlarda, uygulamanın konusu bölümler halinde parçalanmasını sağlamakta ve her bir parçanın, parçalandığı en yakın kısıma bağlı olduğu ve en uygun hallerde ise, bu parçanın bir önceki veya bir sonraki parçaya bağlı bulunduğu açıklanmaktadır(Gülçür, 1966:542).
1.1.4.2.5.3.Dinamik Programlama Sınıflandırılması
Dinamik Programlama zaman itibariyle, süreç değişkenlerinin zamana göre tanımı yansıtan kesikli zaman ve proses değişkenlerinin zaman içinde süreli olduğu durumlara ilişkin sürekli zaman olmak üzere ikiye ayrılır. Süreçte belirsizlik yoksa deterministik, belirsizlik varsa olasılıklı olmak üzere belirlilik durumuna göre de ayrılabilir. Dinamik Programlamada prosesin zamanın mutlak değerine bağlı olup olmadığına göre duralar-duralamaz olmak üzere de bir ayrım yapılabilir(Akalın, 1979: 405-406-407). Üzerinde durmak istediğimiz ayırım belirlilik durumuna göre dinamik programlama sınıflandırılmasıdır.
1.1.4.2.5.3.1.Belirli Dinamik Programlama
Belirli dinamik programlama da şu an ki durumdan bir sonraki durum anlaşılabilir. Belirli dinamik programlama diyagram olarak aşağıdaki şekildeki gibi tanımlanabilir (Doğan, 1995:529).
Şekil 12: Belirli (Deterministik) Dinamik Programlama
Kaynak: Doğan, 1995: 529
1.1.4.2.5.3.2.Belirsiz (Olasılıklı) Dinamik Programlama
Olasılıklı dinamik programlamada her aşamadaki durumlar ve getiriler olasılıklıdır, bu nedenle deterministik dinamik programlamadan farklıdır. Olasılıklı dinamik programlamada özellikle stokastik stok problemlerinin ve Markov Süreçlerinin çözümünde sıkça kullanılır.(Taha, 2000:561).
Şekil 13: Belirsiz (Olasılıklı) Dinamik Programlama
1.1.4.2.6.Stokastik Programlama
1.1.4.2.6.1.Stokastik Programlama Kavramı
Stokastik programlama kavramına rastgele verilerin olduğu bazı optimizasyon problemlerinde başvurulur. Doğrusal programlama, tamsayılı programlama veya doğrusal olmayan programlamanın alt konusu olarak ele alınabilir. Önemli olan durum stokastik doğrusal programlama olduğudur. (Cornuejols ve Tütüncü, 2007: 6)
Stokastik programlama matematiksel programlama çerçevesinde stokastik bileşenlerin birleşimiyle ile ilgilenir. Stokastik bileşenler farklı biçimler alabilir, örneğin tahmini parametreler, risk önleme veya rastgele karar. Bunlar modele farklı basamaklarda girebilirler örneğin amaç fonksiyonu, kısıtlılıklar veya karar vektörü. Matematiksel programların modellemesi bile farklı biçimlerde olabilir örneğin, doğrusal programlama modeli, farklı veya diferansiyel eşitlikler içindeki doğrusal-kuadratik kontrol modeli veya kısıtlı çok oyunculu oyun modeli (Sengupta, 1982:1).
1.1.4.2.6.2.Stokastik Programlama Teknikleri
Stokastik programlama teknikleri çok aşamalı programlama ve şans kısıtlı programlama olmak üzere ikiye ayrılır. Şans kısıtlı stokastik programlar ilk olarak Charnes ve Cooper (1959) tarafından modellenmiştir. Symonds (1967), çalışmasında şans kısıtlı programlama problemleri için deterministik çözümler sunmuştur. Sengupta (1970), şans kısıtlı doğrusal programlamanın bazı dağılımlar açısından genelleştirilmesi üzerinde çalışmıştır. Hulsurkar, Biswal ve Sinha (1997), çok amaçlı stokastik doğrusal programlama problemlerinin bulanık programlama yaklaşımının bir uygulamasını çalışmışlardır (Atalay ve Apaydın, 2010:1).
1.1.4.2.6.2.1.Şans Kısıtlı Programlama
Şans kısıtı adı, her kısıtın 1 – ai minimum olasılığıyla gerçekleştirilmesinden
gelmektedir. Burada 0 < ai < 1’dir. Tüm aij ve bi’lerin rastgele değişkenler olduğu
varsayılır. Üç durum söz konusudur: İlk iki durum aij ve bi’lerin rastgele
değişkenlerinin ayrı ayrı ele alınmasına karşılık gelir. Üçüncü durum aij ve bi’nin
parametrelerin bilinen ortalama ve sapmalarla normal dağıldığı varsayılmaktadır(Taha, 2000: 799).
1.1.4.2.6.2.2.Çok Aşamalı Programlama
Statik problemlerde sonuç mevcut zamanda verilen kararlara bağlıdır, ancak dinamik problemlerde sonuç daha fazla bilginin var olabileceği sonraki aşamalardan da önemli ölçüde etkilenmektedir. Dinamik problemlerde karar aşamaları genellikle içsel bağımlıdır, böylece kararlar sonuç ele alınırken eşzamanlı olarak verilmektedir. Belirsizlik altında dinamik karar problemleri oldukça karmaşıktır; çünkü daha sonraki aşamaların kararları, birinci asamadan sonra ortaya çıkan bilgi altında verilmektedir. Sonraki aşamaların kararları belirsiz faktörlerin fonksiyonlarıdır, böylece genel karar problemi fonksiyonlar olarak karar değişkenlerini içermektedir. Örneğin yatırım problemleri planlanan süreçte yatırım portföyü güncellenebildiği zaman dinamik hale gelmektedir(Çakmak, 2008: 5-6).
1.1.4.2.7.Yapay Zeka Uygulamaları (Popülasyon Tabanlı Teknikler) 1.1.4.2.7.1.Zeka Kavramı
Her insan doğuştan belirli bir zekaya sahiptir. Zeka, belirli bir konuda çalışarak, öğretilerek, eğitilerek, edinilen bilgi ve birikimlerle, deneyimlere dayalı becerilerle geliştirilebilir. İlk kez karşılaşılan ya da ani olarak gelişen bir olaya uyum sağlayabilme, anlama, öğrenme, analiz yeteneği, beş duyunun, dikkatin ve düşüncenin yoğunlaştırılması zeka ile gerçekleştirilebilmektedir (Elmas, 2003: 21). Yapay Zeka konusunda ilk çalışma McCulloch ve Pitts tarafından 1940’lı yıllarda yapılmıştır.1943 yılında bu araştırmacılar tarafından yapay sinir sisteminin ilk matematiksel modeli geliştirilmiştir. 1949 yılında Hebb öğrenme için matematiksel bir yaklaşım geliştirmiştir. Sinir hücreleri arasındaki bağlantıların şiddetlerini değiştirmeden oluşan bu yaklaşım ile, öğrenebilen sinir ağları gerçekleştirmesi kolaylaştırmıştır. 1965’de, Zadeh tarafından önerilen bulanık mantık teorisi ise Yapay Zeka’ya yeni bir bakış açısı kazandırmıştır (Sağıroğlu vd., 2003:7-8).
1.1.4.2.7.2.Yapay Zeka Teknikleri
Yapay zeka araştırmacıların baştan beri ulaşmak istediği ideal, insan gibi düşünen ve davranan sistemler yaratmaktadır. Fakat buna ulaşmanın güçlüğü anlaşılınca çalışmanın yönü rasyonel düşünen ve davranan sistemlerin tasarlanmasına çevrilmiştir (Sağıroğlu vd., 2003:11)
1.1.4.2.7.3.Genetik Algoritma
1.1.4.2.7.3.1.Genetik Algoritma Kavramı
Genetik algoritmalar, doğal seçim ilkelerine dayanan bir arama ve optimizasyon yöntemidir. Temel ilkeleri John Holland tarafından ortaya atılmıştır. Temel ilkelerinin ortaya atılmasından sonra, genetik algoritmalar hakkında bir çok bilimsel çalışma yayınlanmıştır. Ayrıca, genetik algoritmaların teorik kısmı ve uygulamaları hakkında bir çok uluslararası konferans da düzenlenmektedir. Genetik algoritmaların, fonksiyon optimizasyonu, çizelgeleme, mekanik öğrenme, tasarım, hücresel üretim gibi alanlarda başarılı uygulamaları bulunmaktadır (Emel ve Taşkın, 2002, 130). Genetik Algoritma temel kavramları ( Tuğrut vd., 2002: 1174):
Kromozom (Chromosome) bir yada daha fazla genin bir araya gelmesi ile oluşan ve problemin çözümü için gerekli tüm bilgiyi üzerinde taşıyan genetik yapıdır. Örneğin, 100011101 genleri 4, 3, 5 birim uzunluklara sahip olan üç doğru parçasına ait uzunluk bilgisinin ikilik düzende kodlandığı bir kromozomu göstermektedir.
Çaprazlama (Crossover) iki kromozomun bir araya gelerek genetik bilgi değişimi yapmasıdır. Örneğin, 100011101 ve 010110001 kromozomları üzerinde 4. genden başlayarak tek noktalı çaprazlama yapıldığında, 100110001 ve 010011101 kromozomları elde edilmektedir.
Evrim (Evolution) genetik bilgi taşıyan bir topluluk üzerine genetik işlemlerin uygulanması sürecidir.
Gen (Gene) kendi başına anlamlı genetik bilgi taşıyan en küçük genetik yapıdır.
Genetik Programlama (GP, Genetic Programming) genlerinde program parçacıklarının kodlandığı kromozomlar üzerinde çalışan bir genetik algoritma yoluyla istenilen işi yapan bir programın geliştirilmesidir. Tersinme (Inversiyon) bir kromozomu ulaştıran genlerden ardışık bir
grubun kendi içerisinde birbirleri ile yer değiştirerek ters dizilmeleridir. Örneğin, 011110101 kromozomu 5. ve 8. gen konumları arasında tersindiğinde ortaya 011101011 kromozomu çıkmaktadır.
Eşleme (Mating) iki kromozomun çaprazlama amacıyla seçilmesidir. Değişim (Mutasyon) bir kromozomun taşıdığı genetik bilgide bir
nedene bağlı olmaksızın rastgele değişim olmasıdır. Örneğin, 100110000 kromozomunun 3. geninde değişim olması sonucunda, 101110000kromozomu oluşmaktadır.
Çoğalma, Kopyalama (Reproduction) bir kromozomun kendisi ile aynı genetik bilgiyi taşıyan bir kopyasının oluşturulmasıdır. Örneğin, 100111011 kromozumu çoğaltıldığında 100111011 ve 100111011 kromozomları elde edilmektedir.
Seçme (Selection) bir kromozom havuzundaki kromozomlardan hangilerinin yeni oluşturulacak havuza aktarılacağının, kromozomların başarı değerlerini dikkate alarak belirlenmesidir.
1.1.4.2.7.3.2.Genetik Algoritma Özellikleri
Çeşitli problemlerin çözümünde kullanılan genetik algoritmalar aşağıdaki özellikleri taşırlar (Özçakar, 1998: 70):
a. Uygun çözümler için bir veya daha fazla “popülasyon” mümkündür.
b. Önceden bilinen çoklu çözümlerin özelliklerini bir araya getirerek, yeni uygun çözümler üreten bir mekanizmaya sahiptir.
c. Önceden bilinen bir çözümün düzenini rastgele (tesadüfi) bir şekilde değiştirerek, yeni bir uygun çözüm üreten mekanizmaya sahiptir.
d. Popülasyon içinden, önceden vererek, ayrı çözümleri seçen bir mekanizmaya sahiptir.