Marshall-olkin iki değişkenli dağılımları ve istatistiksel sonuç çıkarımı

T.C.

SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ

MARSHALL-OLKİN İKİ DEĞİŞKENLİ DAĞILIMLARI VE İSTATİSTİKSEL SONUÇ

ÇIKARIMI Umut ÖKSÜZ YÜKSEK LİSANS İstatistik Anabilim Dalını

Nisan-2014 KONYA Her Hakkı Saklıdır.

TEZ BİLDİRİMİ

Bu tezdeki bütün bilgilerin etik davranış ve akademik kurallar çerçevesinde elde edildiğini ve tez yazım kurallarına uygun olarak hazırlanan bu çalışmada bana ait olmayan her türlü ifade ve bilginin kaynağına eksiksiz atıf yapıldığını bildiririm.

DECLARATION PAGE

I hereby declare that all information in this document has been obtained and presented in accordance with academic rules and ethical conduct. I also declare that, as required by these rules and conduct, I have fully cited and referenced all material and results that are not original to this work.

Umut ÖKSÜZ Tarih:

iv

ÖZET

YÜKSEK LİSANS TEZİ

MARSHALL-OLKIN İKİ DEĞİŞKENLİ DAĞILIMLARI VE

İSTATİSTİKSEL SONUÇ ÇIKARIMI Umut ÖKSÜZ

Selçuk Üniversitesi Fen Bilimleri Enstitüsü İstatistik Anabilim Dalı

Danışman: Doç. Dr. Coşkun KUŞ 2014, 51 Sayfa

Jüri

Doç. Dr. Coşkun KUŞ Doç.Dr.Murat ERİŞOĞLU Yrd.Doç.Dr.İsmail KINACI

Bu tez çalışmasında, Sahran ve Apaloo (2013) tarafından önerilen Genelleştirilmiş Chen dağılımı ve Marshall ve Olkin (1967) nin yöntemi kullanılarak İki değişkenli Marshall-Olkin Genelleştirilmiş Chen dağılımı önerilmiştir. Bu dağılımın olasılık yoğunluk fonksiyonu, dağılım fonksiyonu ve yaşam fonksiyonu gibi dağılımsal özellikleri incelenmiştir. ML tahmin edicileri Nelder-Maid yöntemiyle elde edilmiştir. EM algoritması da geliştirilerek ML tahminlerine ulaşılmıştır. Önerilen iki değişkenli dağılımın modelleme yeteneği gerçek örnek verilerek gösterilmiştir.

Anahtar Kelimeler: Genelleştirilmiş Chen dağılımı, Marshall-Olkin iki değişkenli dağılım, EM algoritması, En çok olabilirlik tahmin edicisi

v

ABSTRACT MS THESIS

BIVARIATE MARSHALL-OLKIN DISTRIBUTIONS AND

STATISTICAL INFERERNCE Umut ÖKSÜZ

THE GRADUATE SCHOOL OF NATURAL AND APPLIED SCIENCE OF SELÇUK UNIVERSITY

THE DEGREE OF MASTER OF SCIENCE IN DEPARTMENT OF STATISTICS

Advisor: Doç. Dr. Coşkun KUŞ 2014, 51 Pages

Jury

Doç. Dr. Coşkun KUŞ Doç.Dr.Murat ERİŞOĞLU Yrd.Doç.Dr.İsmail KINACI

In this thesis, Bivariate Marshall-Olkin generalized Chen distribution is obtained with generalized Chen distribution introduced by Sahran ve Apaloo (2013) using the same approach as was adopted to obtain the Marshall-Olkin bivariate exponential distribution. Some distributional properties such as probability density function, cumulative distribution function and survival function are investigated. Maximum likelihood estimates (MLEs) are obtained using Nelder-Maid method. EM algorithm is also provided to get the MLEs. A real example is also given to show the ability of the moddeling of new introduced distribution.

Keywords: Generalized Chen distribution, Bivariate Marshall-Olkin distribution, EM algorithm, Maximum likelihood estimate.

vi

ÖNSÖZ

Çalışmamın not için değil, öğrenmek için olduğunu idrak ettiren ve aramızda mesafeler olmasına rağmen benden yardımlarını, desteğini, sabrını ve bilgisini esirgemeyen değerli danışman hocam Doç.Dr. Coşkun KUŞ’a, bu tez çalışmasında bana her zaman destek olan, komutanlarım Binbaşı Serkan ERDOĞMUŞ ve Albay Adil SARAÇ’a, sevgili Anneme ve Havva'ya teşekkürlerimi sunarım.

Umut ÖKSÜZ KONYA–2014

vii İÇİNDEKİLER ÖZET ... iv ABSTRACT...v ÖNSÖZ ... vi İÇİNDEKİLER ... vii 1. GİRİŞ...1 2. TEMEL KAVRAMLAR ...3 2.1. Olasılık Teorisi ...3

2.2. İki Değişkenli Dağılım Fonksiyonları ...4

2.3 Literatürdeki Yeni Dağılımlar ...17

2.3.1 İki Değişkenli Üstelleştirilmiş Doğrusal Bozulma Oranlı Dağılım...17

2.3.2 İki Değişkenli Genelleştirilmiş Üstel Dağılım ...18

2.4. Asimptotik Normallik ...19

2.5. Olabilirlik Fonksiyonu ...20

2.6. Fisher Bilgi Matrisi...20

2.7. En Çok Olabilirlik Tahmin Edicileri ...21

2.8. Asimptotik Güven Aralıkları...21

3. İKİ DEĞİŞKENLİ ÜSTELLEŞTİRİLMİŞ CHEN DAĞILIMI ...23

4. PARAMETRE TAHMİNİ ...27

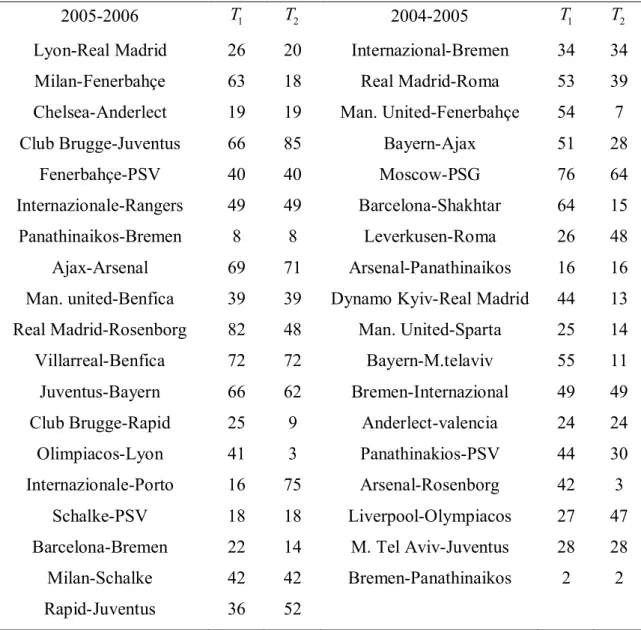
5. UYGULAMA...32

5.1. Gerçek Örnek Üzerinde İstatistiksel Sonuç Çıkarımı...32

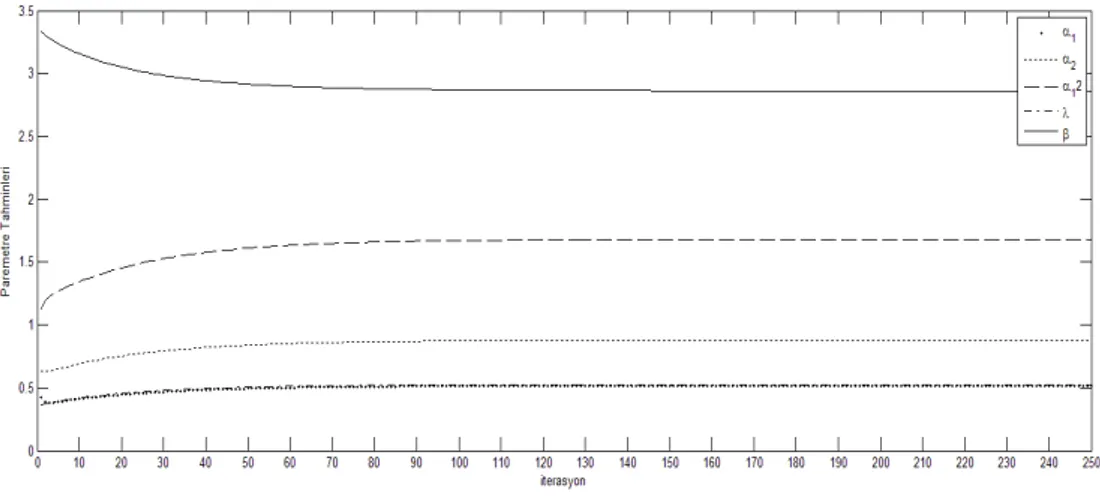
5.2. MOBEC Dağılımından Üretilen Veri İçin İstatistiksel Sonuç Çıkarımı ...36

6. SONUÇ VE ÖNERİLER...39

EKLER ...43

1. GİRİŞ

İki parametreli Chen dağılımı Chen (2000) tarafından önerilmiştir ve bu dağılım yaşam zamanı verilerini modellemede kullanılmaktadır. Sahran ve ark.(2012), Rastogi ve Tripathi (2012) Chen dağılımını reel datayı modellemede kullanmışlar ve Weibull, üstel ve genelleştirilmiş üstel gibi popular dağılımlara aday olabileceğini göstermişlerdir. Wu ve ark. (2011) ve Wu (2008), ilerleyen tür tip-II sansürlü örnekleme dayalı parametrelerin güven aralıklarını ve hipotez testlerini önermişleridir. Rastogi ve ark. (2012), ilerleyen tür tip-II sansürlü örnekleme dayalı ML ve Bayes tahmin edicilerini elde etmişler.

2013 yılında Sahran ve Apaloo (2013) Chen dağılımını genelleştirerek Genelleştirilmiş Chen dağılımını elde etmiş, dağılımsal özellikleri incelemiş ve parametre tahmini problemi üzerinde çalışmıştır. Reel data üzerinde de dağılımın modellemede başarılı olduğunu göstermiştir.

1960 lı yıllarda Olkin (1967), iki değişkenli üstel marjinalli Marshall-Olkin (MOBE) dağılımı önermişlerdir. Son zamanlarda, Marshall ve Marshall-Olkin’in MOBE dağılımını elde etme yöntemi kullanılarak yeni iki değişkenli dağılımlar önerilmiştir. Kundu ve Gupta (2009), iki değişkenli genelleştirilmiş üstel marjinalli Marshall-Olkin dağılımı, Sahran ve ark. (2011) iki değişkenli genelleştirilmiş linear failure rate marjinalli Marshall-Olkin dağılımını önermişlerdir.

Bu tez çalışmasında, Sahran ve Apaloo (2013) tarafından önerilen Genelleştirilmiş Chen dağılımı ve Marshall ve Olkin (1967) nin yöntemi kullanılarak İki değişkenli Marshall-Olkin Genelleştirilmiş Chen dağılımı önerilmiştir. Bu dağılımın oyf, df ve yaşam fonksiyonu gibi dağılımsal özellikleri incelenmiştir. ML tahmin edicileri Nelder-Maid yönetmiyle elde edilmiştir. EM algoritması da geliştirilerek ML tahminlerine ulaşılmıştır. Önerilen iki değişkenli dağılımın modelleme yeteneği, reel ve simulatif bir örnek verilerek gösterilmiştir.

Bu tez çalışmasının 1. Bölümü giriş kısmından oluşmaktadır. 2. Bölümde, temel kavramlar verilmiştir. 3. Bölümde, Genelleştirilmiş Chen dağılımı kullanılarak İki değişkenli Marshall-Olkin Genelleştirilmiş Chen dağılımı önerilmiştir. Bu dağılımın oyf, df ve yaşam fonksiyonu gibi dağılımsal özellikleri incelenmiştir. 4. Bölümde ise, ML tahmin edicileri Nelder-Maid yöntemiyle elde edilmiştir. EM algoritması da geliştirilerek ML tahminlerini ulaşılmıştır. Bölüm 5’de, elde edilen sonuçlar için

örnekler verilmiş ve sonuçlar yorumlanmıştır. 6. Bölüm’de ise sonuç ve önerilere yer verilmiştir.

2. TEMEL KAVRAMLAR

Bu bölümde iki değişkenli rasgele vektörler, iki değişkenli dağılım fonksiyonları,bazı olasılık teorisi kavramları ve literatürdeki bazı dağılımlara yer verilmiştir. Bu bölümdeki verilen Tanımlar ve Teoremler tezde kullanıldığı için Öztürk (1993) ve Rohatgi ve Ehsanes Saleh (2001) den derleme olarak verilmiştir.

2.1. Olasılık Teorisi

Tanım 2.1: W ¹ Æ olmak üzere , B₁,B₂,_K,B_n ÌW

(

nÎN

)

kümeleri

n j i B B B j i i n i £ < £ = Ç W = = 1 , , 1 f

U

_(2.1)

olacak biçimde belirlendiğinde B₁,B₂,K,B_n 'lere W 'nın bir parçalanması denir.

Teorem 2.1 ÝI,U, PÞ olasılık uzayı, B₁,B₂,K,B_n ler W 'nın bir parçalanması ve 0

) (B_i >

P

(

B_iÎU i, 1, 2,...,= n

)

olmak üzere A UÎ için ) ( ) | ( ) ( 1 i i n i B P B A P A P

å

= = (2.2) eşitliği yazılır.

İspat B B₁, ₂, ,_K B_n 'ler W 'nın bir parçalanması olduğundan

i n i B

U

₌₁ = W (2.3) yazılabilir. Buradan

ì A V I = A V

4

i=1 n Bi ì PÝAÞ = P

4

i=1 n AV Bi ì PÝAÞ =

>

i=1 n PÝA_{V B}iÞ ì PÝAÞ =

>

i=1 n PÝA|BiÞPÝBiÞ (2.4) şeklinde ispat tamamlanır.

2.2. İki Değişkenli Dağılım Fonksiyonları

ÝI,U, PÞ tanımlı bir X rasgele vektörü iki değişkenli olduğunda X rasgele

vektörünün dağılım fonksiyonu F aşağıda verilen teoremlerdeki özellikleri sağlar.

Teorem 2.2

( )

,

0£FX Y x y, £1 (2.5)

Teorem 2.3 X=

(

X Y,

)

¢, ÝI,U, PÞ olasılık uzayında tanımlı F x_X

( )

ve F y_Y

( )

marjinalli FX Y_,

( )

x y, dağılım fonksiyonuna sahip 2 boyutlu rasgele vektör olmak

üzere;

( )

(

)

( )

, , lim _{X Y} , _{X Y} , _Y x®¥F x y =F ¥ y =F y (2.6) ve

( )

(

)

( )

, , lim _{X Y} , _{X Y} , _X y®¥F x y =F x ¥ =F x (2.7) dir.

İspat lim_n®¥F_{X Y,}

( )

n y, =F y_Y

( )

eşitliğinin doğruluğu, lim_x®¥F_{X Y,}

( )

x y, =F y_Y

( )

eşitliğinin doğru olduğunu gösterir. Bu düşünceden hareketle

(

)

{

:

( )

}

, 1, 2, n A = X £n = w X w £n n= _K (2.8) ve

(

)

{

:

( )

}

B= Y £ y = w Y w £y (2.9) için A₁ÌA₂ Ì_{L olup} 1 lim _{n n} n A n A ¥

®¥ = U= = W olduğu göz önüne alındığında (2.6)

( )

(

)

( )

( )

{

}

(

)

(

)

(

)

(

)

(

)

(

)

(

)

( )

( )

{

}

(

)

(

)

( )

, lim , lim , lim : , lim lim lim : X Y n n n n n n n n n Y F n y P X n Y y P X n Y y P A B P A B P A B P B P B P Y y P Y y F y w w w w w ®¥ ®¥ ®¥ ®¥ ®¥ ®¥ = £ £ = £ £ = Ç = Ç = Ç = W Ç = = £ = £ = (2.10)

şeklinde gösterilebilir. Yukarıdaki düşünce ile lim_y®¥F_{X Y,}

( )

x y, =F x_X

( )

eşitliği kolayca gösterilebilir.

Teorem 2.4 X=

(

X Y,

)

¢, ÝI,U, PÞ olasılık uzayında tanımlı F_{X Y,}

( )

x y, dağılım fonksiyonuna sahip 2 boyutlu rasgele vektör olmak üzere

( )

, lim _{X Y} , 0 x®-¥F x y = (2.11) ve

( )

, lim _{X Y} , 0 y®-¥F x y = (2.12) dır.

İspat lim_n®¥F_{X Y,}

(

-n y,

)

=0 eşitliğinin doğruluğu, lim_x®-¥F_{X Y,}

( )

x y, =0 eşitliğinin doğru olduğunu gösterir. Bu düşünceden hareketle

(

)

{

:

( )

}

, 1, 2, n A = X £ - =n w X w £ -n n= _K (2.13) ve

(

)

{

:

( )

}

B= Y £ y = w Y w £y (2.14) için A₁ÉA₂ É_{L olup} 1 lim _{n n} n n A ¥ A ®¥ =

I

₌ = Æ (2.15)

(

)

(

)

( )

( )

{

}

(

)

(

)

(

)

(

)

(

)

(

)

(

)

( )

, lim , lim , lim : , lim lim lim 0 X Y n n n n n n n n n F n y P X n Y y P X n Y y P A B P A B P A B P B P w w w ®¥ ®¥ ®¥ ®¥ ®¥ ®¥ - = £ - £ = £ - £ = Ç = Ç = Ç = Æ Ç = Æ = (2.16)

şeklinde gösterilebilir. Yukarıdaki düşünce ile limy®-¥FX Y_,

( )

x y, =0 eşitliği kolayca

gösterilebilir.

Teorem 2.5 X=

(

X Y,

)

¢, ÝI,U, PÞ olasılık uzayında tanımlı FX Y,

( )

x y, dağılım

fonksiyonuna sahip 2 boyutlu rasgele vektör olmak üzere

( )

, , lim _{X Y} , 1 x y®¥F x y = (2.17) dır. İspat lim _{X Y,}

( )

, 1

n®¥F n n = eşitliğinin doğruluğu, x ylim, ®¥FX Y,

( )

x y, = eşitliğinin doğru 1

olduğunu gösterir. Bu düşünceden hareketle

(

)

{

:

( )

}

, 1, 2, n A = X £n = w X w £n n= _K (2.18) ve

(

)

{

:

( )

}

, 1, 2, n B = Y £n = w Y w £n n= _K (2.19) için A₁ÌA₂ Ì_{L olup} 1 lim _{n n} n n A A ¥ ®¥ =

U

₌ = W (2.20) ve B₁ÌB₂ Ì_{L olup} 1 lim _{n n} n n B ¥B ®¥ = =

U

= W (2.21)

( )

(

)

( )

( )

{

}

(

)

(

)

(

)

(

)

(

)

(

)

( )

, lim , lim , lim : , lim lim lim lim 1 X Y n n n n n n n n n n n n n F n n P X n Y n P X n Y n P A B P A B P A B P P w w w ®¥ ®¥ ®¥ ®¥ ®¥ ®¥ ®¥ = £ £ = £ £ = Ç = Ç = Ç = W Ç W = W = (2.22) şeklinde gösterilebilir.

Teorem 2.6 X=

(

X Y,

)

¢, ÝI,U, PÞ olasılık uzayında tanımlı F_{X Y,}

( )

x y, dağılım fonksiyonuna sahip boyutlu rasgele vektör olmak üzere F x y

( )

, , x ’e ve y 'ye göre sağdan süreklidir. Yani

(

)

(

)

( )

0 lim , , , h +F x h y F x y F x y + ® + = = (2.23) ve

(

)

(

)

( )

0 lim , , , h +F x y h F x y F x y + ® + = = (2.24) dir. İspat _lim

(

1_,

)

( )

_, n®¥ F x+n y =F x y eşitliğinin doğruluğu,

(

)

(

)

( )

0

lim_h® + F x h y+ , =F x y+, =F x y, eşitliğinin doğru olduğunu gösterir. Bu düşünceden hareketle

( )

1 lim , , n®¥F x n y F x y æ ₊ ö₌ ç ÷ è ø (2.25)

olduğu gösterildiğinde F x y

( )

, in x 'e göre sağdan sürekli olduğu gösterilmiş olur.

( )

1 lim , , 0 n®¥F x n y F x y æ ₊ ö_{- =} ç ÷ è ø (2.26)

( )

1 lim , , 0 n®¥ F x n y F x y ì æ ₊ ö_- ü₌ í ç_è ÷_ø ý î þ (2.27)

olup (2.25) eşitliğinin doğruluğu (2.27) eşitliğinin doğruluğunu gerektirir. (2.25) eşitliği

( )

(

)

1 1 lim , , lim , , 1 lim , n n n F x y F x y P X x Y y P X x Y y n n P x X x Y y n ®¥ ®¥ ®¥ ì æ ₊ ö_- ü₌ ì æ _{£ + £} ö_{- £ £} ü í ç ÷ ý í ç ÷ ý è ø è ø î þ î þ ì æ öü = _{í ç} < £ + £ _÷ý è ø î þ (2.28)

şeklinde yazılabilir.

( )

1 1 : n A x X x x X x n w w n æ ö ì ü =_ç < £ + _÷=_í < £ + _ý è ø î þ (2.29) ve

(

)

{

:

( )

}

B= Y £ y = w Y w £y (2.30) için A₁ÉA₂ É_{L olup} 1 lim _{n n} n n A ¥ A ®¥ =

I

₌ = Æ (2.31)

dir. (2.27) eşitliği kullanılarak

( )

(

)

(

)

(

)

(

)

(

)

(

)

( )

1 1 lim , , lim , lim lim lim 0 n n n n n n n n F x y F x y P x X x Y y n n P A B P A B P A B P B P ®¥ ®¥ ®¥ ®¥ ®¥ ì æ ₊ ö_- ü₌ ì æ _{< £ + £} öü í ç_è ÷_ø ý í ç_è ÷_øý î þ î þ = Ç = Ç = Ç = Æ Ç = Æ = (2.32)

elde edilir. Burada gösterilmiş oldu ki

( )

( )

( )

1 lim , , 0 1 lim , ,

, in x e göre sağdan süreklidir n n F x y F x y n F x y F x y n F x y ®¥ ®¥ ì æ ₊ ö_- ü₌ í ç_è ÷_ø ý î þ æ ö Þ _ç + _÷= è ø Þ

Yukarıdaki düşünce ile lim_{h 0}+ F x y h

(

,

)

F x y

(

,

)

F x y

( )

,

+

® + = = eşitliği yani

( )

,

F x y in y 'ye göre sağdan sürekli olduğu kolayca gösterilebilir.

(

1 1

)

( )

lim_n®¥F x+_n,y+_n =F x y, eşitliğinin doğruluğu,

(

)

(

)

( )

0

lim_h + F x h y h, F x y, F x y,

+ +

® + + = = eşitliğinin doğru olduğunu gösterir. Bu

düşünceden hareketle

( )

1 1 lim , , n®¥F x n y n F x y æ _{+ +} ö₌ ç ÷ è ø (2.33)

olduğu gösterildiğinde F x y

( )

, in x 'e ve y 'ye göre sağdan sürekli olduğu gösterilmiş olur.

( )

1 1 lim , , n®¥F x n y n F x y æ _{+ +} ö₌ ç ÷ è ø

( )

1 1 lim , , 0 n®¥F x n y n F x y æ ö Þ _ç + + _÷- = è ø (2.34)

( )

1 1 lim , , 0 n®¥ F x n y n F x y ì æ ö ü Þ _{í ç} + + _÷- _ý= è ø î þ (2.35)

olup (2.33) eşitliğinin doğruluğu (2.35) eşitliğinin doğruluğunu gerektirir. (2.33) eşitliği

( )

(

)

1 1 lim , , 1 1 lim , , 1 1 lim , n n n F x y F x y n n P X x Y y P X x Y y n n P x X x y Y y n n ®¥ ®¥ ®¥ ì æ _{+ +} ö_- ü í ç_è ÷_ø ý î þ ì æ ö ü = _{í ç} £ + £ + _÷- £ £ _ý è ø î þ ì æ öü = _{í ç} < £ + < £ + _÷ý è ø î þ (2.36) şeklinde yazılabilir.

( )

1 1 : , 1,2, n A x X x x X x n n w w n æ ö ì ü =_ç < £ + _÷=_í < £ + _ý = è ø î þ K (2.37) ve

( )

1 1 : , 1, 2, B y Y y y Y y n n w w n æ ö ì ü =_ç < £ + _÷=_í < £ + _ý = è ø î þ K (2.38) için A₁ÉA₂ É_{L olup} 1 lim _{n n} n n A ¥ A ®¥ =

I

₌ = Æ (2.39) ve B₁ÉB₂ É_{L olup} 1 lim _{n n} n n B ¥ B ®¥ =

I

₌ = Æ (2.40)

dir. (2.35) ve (2.36) eşitlikleri kullanılarak

( )

(

)

(

)

(

)

(

)

(

)

( )

1 1 1 1 lim , , lim , lim lim lim lim 0 n n n n n n n n n n n n F x y F x y P x X x Y y n n n n P A B P A B P A B P P ®¥ ®¥ ®¥ ®¥ ®¥ ®¥ ì æ _{+ +} ö_- ü₌ ì æ _{< £ + £ +} öü í ç ÷ ý í ç ÷ý è ø è ø î þ î þ = Ç = Ç = Ç = Æ Ç Æ = Æ = (2.41)

elde edilir. Burada gösterilmiş oldu ki lim n¸K F x + 1n ,y + 1 n ? FÝx, yÞ = 0 ì lim n¸KF x + 1n ,y + 1 n = FÝx, yÞ

ì FÝx, yÞ in x e ve y ye göre sağdan süreklidir Teorem 2.7 X=

(

X Y,

)

¢, ÝI,U, PÞ olasılık uzayında tanımlı F_{X Y,}

( )

x y, dağılım fonksiyonuna sahip 2 boyutlu rasgele vektör olmak üzere F x y

( )

, , x 'e ve y 'ye göre azalmayandır. Yani " Î ve y R x₁<x₂ için

(

1,

)

(

2,

)

F x y £F x y (2.42) R x " Î ve y₁<y₂ için

(

, 1

)

(

, 2

)

F x y £F x y (2.43) dir.

İspat. Gerçekten x1 < x2 için

(

) (

) (

) (

)

(

)

(

)

(

)

(

)

1 2 1 2 1 2 1 2 , , , , , , X x X x X x Y y X x Y y P X x Y y P X x Y y F x y F x y £ Ì £ Þ £ £ Ì £ £ Þ £ £ £ £ £ Þ £ (2.44)

olup F x y

( )

, , x 'e göre azalmayandır. Yukarıdaki düşünce ile y₁< y₂ için

(

, 1

)

(

, 2

)

F x y £F x y olduğu yani F x y

( )

, 'in y 'e göre azalmayan olduğu kolayca gösterilebilir.

Teorem 2.8 (Frechet Sınırları) X=

(

X Y,

)

¢, ÝI,U, PÞ olasılık uzayında tanımlı

( )

X

F x ve F yY

( )

marjinalli FX Y,

( )

x y, dağılım fonksiyonuna sahip p boyutlu

rasgele vektör olmak üzere F_{X Y,}

( )

x y,

( )

( )

{

}

( )

{

( ) ( )

}

max F xX +F yY -1,0 £F x y, £min F x F xX , Y (2.45)

eşitsizliğini sağlar. (http://mathworld.wolfram.com/FrechetBounds.html)

İspat. A=

(

X £x

)

ve B=

(

Y £ y

)

olaylar olmak üzere

(

)

( )

( )

(

)

1

P A BÈ =P A +P B -P A BÇ £ (2.46)

ifadesi göz önüne alındığında

(

)

( )

( )

(

)

(

)

(

)

( )

( )

( )

1 , 1 , _{X Y} 1 P A B P A P B P X x Y y P X x P Y y F x y F x F y Ç ³ + -Þ £ £ ³ £ + £ -Þ ³ + (2.47) elde edilir.

( )

( )

1 _X

( )

_Y

( )

1 P A +P B - =F x +F y - (2.48)

ifadesinin pozitif olup olmadığı belli olmadığından (ki negatif çıkabilir), Kolmogorovun .i aksiyomu gereği

( )

( )

{

}

max F xX +F yY -1, 0 (2.49)

dir. Diğer taraftan

(

)

( )

P A BÇ £P A (2.50) ve

(

)

( )

P A BÇ £P B (2.51) olduğundan

(

,

)

(

)

( )

, X

( )

P X £x Y £ y £P X £ x ÞF x y £F x (2.52) ve

(

,

)

(

)

( )

, Y

( )

P X £x Y £ y £P Y £ y ÞF x y £F y (2.53) olup buradan

( )

, min

{

_X

( )

, _Y

( )

}

F x y £ F x F x (2.54) yazılabilir.

Teorem 2.9 X=

(

X Y,

)

¢, ÝI,U, PÞ olasılık uzayında tanımlı F x_X

( )

ve F yY

( )

marjinalli FX Y,

( )

x y, dağılım fonksiyonuna sahip p boyutlu rasgele vektör olmak

üzere x₁<x₂ için

(

1 2,

)

(

2,

)

(

1,

)

P x < X £x Y £ y =F x y -F x y (2.55)

dir.

İspat

(

X £x Y₂, £ y

) (

= X £x Y₁, £ y

) (

È x₁< X £x Y₂, £y

)

(2.56)

eşitliği kullanılarak (2.55) eşitliği

(

)

(

) (

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)(

)

2 1 1 2 2 1 1 2 2 1 1 2 1 2 2 1 , , , , , , , , , , , , P X x Y y P X x Y y x X x Y y P X x Y y P X x Y y P x X x Y y F x y F x y P x X x Y y P x X x Y y F x y x y Þ £ £ = £ £ È < £ £ Þ £ £ = £ £ + < £ £ Þ = + < £ £ Þ < £ £ = (2.57) şeklinde gösterilebilir.

Teorem 2.10

(

X Y,

)

¢ rasgele vektörünün dağılım fonksiyonu F x y

( )

, olmak üzere her x₁<x₂ ve y₁< y₂ için

(

1 2, 1 2

)

(

2, 2

)

(

2, 1

)

(

1, 2

)

(

1, 1

)

P x <X £x y < £Y y =F x y -F x y -F x y +F x y (2.58) eşitliği vardır. İspat 2.10.1 A=

(

X £x1

)

, B=

(

X £x2

)

, C=

(

Y £y1

)

, D=

(

Y £ y2

)

olaylar olmak üzere

(

1 2, 1 2

)

{

(

) (

)

}

P x <X £x y < £Y y =P B A- Ç D C- (2.59)

olarak yazılabilir. Buradan

(

1 2, 1 2

)

{

(

)

(

)

}

P x < X <x y < <Y y =P Bé_ë Ç D C- ù é_{û ë}- AÇ D C- ù_û (2.60) yazılabilir. Burada BÉ A olduğundan BÇ

(

D C-

)

É ÇA

(

D C-

)

'dır. Böylece (2.59) eşitliğinden

(

) (

)

{

}

{

(

)

(

)

}

(

)

{

}

{

(

)

}

P B A D C P B D C A D C P B D C P A D C - Ç - = é_ë Ç - ù é_{û ë}- Ç - ù_û = Ç - - Ç - (2.61) yazılabilir. Buradan

(

)

{

}

{

(

)

}

P BÇ D C- -P AÇ D C- = P B

{

Ç - ÇD B C

} {

-P A D A CÇ - Ç

}

(2.62) yazılabilir. Burada DÉC olduğundan BÇ É Ç ve A DD B C Ç É Ç 'dir. A C Böylece

(

1 2, 1 2

)

P x <X £x y < £Y y = P B

(

ÇD

)

-P B C

(

Ç

)

-P A D

(

Ç

)

+P A C

(

Ç

)

(2.63) elde edilir. Yukarda tanımlanan A B C D olaylarının eşiti cd5 eşitliğinde yazılırsa , , ,

(

1 2, 1 2

)

(

2, 2

)

(

2, 1

)

(

1, 2

)

(

1, 1

)

P x <X £x y < £Y y =F x y -F x y -F x y +F x y (2.64)

eşitliği elde edilir.

İspat 2.10.2 :

(

x1< X £x Y2, £y2

) (

= x1< X £x Y2, £ y1

) (

È x1< X £x y2, 1< £Y y2

)

(2.65) eşitliğinde

(

1 2, 2

)

(

1 2, 1

)

(

1 2, 1 2

)

P x <X £x Y £ y =P x < X £x Y £ y +P x < X £ x y < £Y y (2.66)

yazılabilir. Teorem 2.10 (2.58) eşitliğine uygulandığında

(

2, 2

)

(

1, 2

)

(

2, 1

)

(

1, 1

)

(

1 2, 1 2

)

F x y -F x y =F x y -F x y +P x < X £x y < £Y y (2.67) olup buradan

(

1 2, 1 2

)

(

2, 2

)

(

2, 1

)

(

1, 2

)

(

1, 1

)

P x <X £x y < £Y y =F x y -F x y -F x y +F x y (2.68) elde edilebilir.

Sonuç: Olasılık ölçüsünün tanımı ve Teorem 2.10'dan

(

2, 2

)

(

2, 1

)

(

1, 2

)

(

1, 1

)

0

F x y -F x y -F x y +F x y ³ (2.69)

dır.

Bu özellik Poincar´e's Teoremi(içerme dışlama prensibi) kullanılarak 3 ve daha büyük boyutlu rasgele vektörlerin ortak dağılım için genelleştirilebilir.

Teorem 2.11

(

X Y,

)

¢, ÝI,U, PÞ olasılık uzayında tanımlı F x_X

( )

ve F yY

( )

marjinalli FX Y,

( )

x y, dağılım fonksiyonuna sahip p boyutlu rasgele vektör olmak

üzere her Ýx, yÞ 5 §2 için

{

,

}

( )

, 1 _X

( )

_Y

( )

( )

,

P X >x Y > y =F x y = -F x -F y +F x y (2.70) eşitliği vardır.

İspat A=

(

X £x

)

ve B=

(

Y £ y

)

olaylar olmak üzere

{

,

}

(

c c

)

P X >x Y > y =P A ÇB

yazılabilir. Eşitlik (2.70) ve daha sonra De Morgan kanunu uygulanırsa

{

}

(

(

)

)

(

)

( )

( )

(

)

(

)

(

)

(

)

( )

( )

( )

, 1 1 1 1 , 1 , c c c X Y P X x Y y P A B P A B P A P B P A B P X x P Y y P X x Y y F x F y F x y > > = - Ç = - È = -é_ë + - Ç ù_û = - £ - £ + £ £ = - - + (2.71)

ispat tamamlanır. İkinci bir yol olarak, ortak dağılım fonksiyonu için verilen 2. özellik ve Teorem 2.10' dan

{

}

(

)

(

)

(

)

(

)

( )

( )

( )

( )

, , , , , , 1 _{Y X} , P X x Y y P x X y Y F F y F x F x y F y F x F x y > > = < < ¥ < < ¥ = ¥ ¥ - ¥ - ¥ + = - - + (2.72)

ispat kolayca yapılabilir.

Teorem 2.12 F , _{R de tanımlı iki boyutlu bir fonksiyon olsun.} 2 _{F X ve Y ,}

rasgele değişkenlerinin ortak dağılım fonksiyonudur ancak ve ancak

1. F azalmayan ve her değişken için sağdan sürekli 2. lim_x®-¥F x y

( )

, =0, lim_y®-¥F x y

( )

, =0 ve lim_{x y, ®¥}F x y

( )

, =1 3. x₁< x₂ ve y₁< y₂ için

(

2, 2

)

(

2, 1

)

(

1, 2

)

(

1, 1

)

0

F x y -F x y -F x y +F x y ³

Yukarıdaki iki boyutlu dağılım fonksiyonu ile ilgili elde edilen sonuçlar p> 2 boyutlu dağılım fonksiyonlar için de kolayca genelleştirilebilir.

1. 0_{£F x}

( )

_£1, _{x RÎ} p 2. limF x

( )

F

(

, , ,

)

1 ®¥ = ¥ ¥ ¥ = x K 3. En az bir x için _i i=1,2, ,_K p lim

( )

0 i x®-¥F x =

4. F fonksiyonu sağdan süreklidir, yani

(

1 1 2 2

)

( )

1,2, , lim , , , i p p h i p F x h x h x h F x ®-¥ = + + + = K K (Öztürk, 1993).

5. F azalmayandır, yani x₁£ x₂ için F x

( )

1 £F x

( )

2 'dir. Bir başka deyişle

F , x 'in her bir elemanına göre azalmayandır.

Örnek 2.1 : İki değişkenli

FÝx, yÞ =

0 , x < 0 veya x + y < 1 veya y < 0

1 , diğer yerlerde

fonksiyonu ele alınsın. F x y

( )

, 1-5 özelliklerini sağlar.

1 1

1, 1

3 3

Pæ_ç <X £ < £Y ö_÷

è ø

olasılığı, Teorem 2.10' dan

(

1 2, 1 2

)

(

2, 2

)

(

2, 1

)

(

1, 2

)

(

1, 1

)

P x <X <x y < <Y y =F x y -F x y -F x y +F x y

( )

1 1 1 1 1 1 1, 1 1,1 , 1, ,1 3 3 3 3 3 3 1 0 1 1 1 0 Pæ_ç <X £ < £Y _÷ö=F +F_çæ ö_÷-Fæ_ç ö_÷-Fæ_ç ö_÷ è ø è ø è ø è ø = + - - = - <

olduğundan F x y

( )

, dağılım fonksiyonu değildir. (Rohatgi, V.K. 1976, syf:106: An Introduction to Probability Theory and Mathematical Statistics)

Not: F x x

(

1, , ,2 K xn

)

ortak dağılım fonksiyonundan F x1

( ) ( )

1 ,F x2 2 , ,K F xn

( )

n

marjinal dağılım fonksiyonlar tek biçimde belirlenir. Fakat tersi doğru değildir. Yani, aynı marjinal dağılım fonksiyonları farklı ortak dağılım fonksiyonunu verebilir.

Örnek 2.2: Aşağıda tanımlanan f ve ₁ f olasılık yoğunluk fonksiyonlar ₂ farklı olmasına rağmen aynı marjinallere sahiptir.

( ) {

1 , 1 , 0 , 1 f x y = <x y<

( )

{

(

)(

)

2 , 1 2 1 2 1 , 0 , 1, 1 1 f x y = +a x- y- <x y< - < <a

Sonuç: Örnek 2.1 ve Örnek 2.2 den görüldüğü gibi aynı marjinallere sahip birden çok ortak dağılım fonksiyonu olabilir.

2.3 Literatürdeki Yeni Dağılımlar

2.3.1 İki Değişkenli Üstelleştirilmiş Doğrusal Bozulma Oranlı Dağılım

Doğrusal Bozulma Oranlı Dağılımın (Linear Failure Rate Distribution, LFR) dağılım fonksiyonu

(

)

0, 0 2 exp 1 , ; 2 _{> >} þ ý ü î í ì_- -= b g b g g b x x x F_LFR (2.79) şeklinde tanımlanır.

Sahran ve Kundu (2009) bu dağılımı genelleştirmişlerdir. Sahran ve Kundu (2009)’un önerdiği dağılım olan Üstelleştirilmiş Doğrusal Bozulma Oranlı Dağılımın (GLFR) dağılım ve olasılık yoğunluk fonksiyonu, sırasıyla,

(

)

0, 0, 0 2 exp 1 , , ; 2 _{> > >} ÷÷ ø ö çç è æ þ ý ü î í ì_- -= b g a b g g b a a x x x F_GLFR (2.80)

(

) (

)

, 0, 0, 0 2 exp 1 , , ; 1 2 2 2 > > > ÷÷ ø ö çç è æ þ ý ü î í ì_- -+ = -÷ ø ö ç è æ ₊ -g b a g b g b a g b a a g b x x e x x f_GLFR x x (2.81)

şeklindedir. X ~ GLFR

(

a ,,b g

)

ile gösterilir.

İki Değişkenli Üstelleştirilmiş Doğrusal Bozulma Oranlı Dağılımı (Bivariate Generalized Linear Failure Rate, BGLFR) için; U₁,U₂veU₃ bağımsız 3 rasgele değişken ve her biri GLFR dağılımına sahip olsun. Burada

(

1 3

)

2

(

2 3

)

1 maxU ,U ve X maxU ,U

X = =

dönüşümleri tanımlansın. Bu durumda

(

X₁, X₂

)

¢ BGLFR dağılımının, dağılım fonksiyonu, olasılık yoğunluk fonksiyonu ve marjinal olasılık yoğunluk fonksiyonları sırasıyla aşağıda verilmiştir.

(

X₁,X₂

)

¢ ~BGLFR

(

a₁,a₂,a₃,b,g

)

olmak üzere

(

X₁, X₂

)

¢nin dağılım fonksiyonu aşağıdaki gibi yazılabilir. (Sarhan ve ark.)

(

)

(

)

∏

3

(

)

1 = 2 2 1 1 2 1 = ≤ ≤ = 2 1 i GLFR i i X , X x ,x P X x ,X x F x;α ,β,γ F , x₃ =min

{

x₁,x₂

}

(2.82)

(

X₁, X₂

)

¢ nin olasılık yoğunluk fonksiyonu aşağıdaki gibi yazılabilir:

(

)

(

(

)

)

( )

ï î ï í ì ¥ < = = < ¥ < < < ¥ < < < = x x x x f x x x x f x x x x f x x f_{X X} 2 1 0 2 1 2 1 2 2 1 2 1 1 2 1 , 0 0 , 0 , , 2 1 (2.83) , burada

(

)

(

)

(

)

(

)

(

)

(

)

( )

(

a a a b g

)

a a a a l b a a g b a l b a g b a a , , ; , , ; , , ; , , , ; , , ; , 3 2 1 3 2 1 3 0 3 2 2 1 1 2 1 2 2 2 3 1 1 2 1 1 + + + + = + = + = x f x f x f x f x x f x f x f x x f GLFR GLFR GLFR GLFR GLFR (2.84) 2 1veX

X 'nin marjinal dağılım fonksiyonları sırasıyla GLFR

(

α₁+α₃,β,γ

)

ve

(

α α ,β,γ

)

GLFR ₂ + ₃ şeklindedir.

2.3.2 İki Değişkenli Genelleştirilmiş Üstel Dağılım

Tek değişkenli genelleştirilmiş üstel dağılımın dağılım fonksiyonu ve olasılık yoğunluk fonksiyonu, sırasıyla, aşağıdaki gibidir:

(

)

(

_λx

)

α GE x;α,λ e F _{= 1-} - _(2.85)

(

)

_-

(

_-x

)

-1 e -1 = λx λ α GE x;α,λ αλe f (2.86)

(

a ,l

)

, ~

(

a ,l

)

~

(

a ,l

)

~ _{1 2 2 3 3} 1 GE U GE veU GE U birbirinden bağımsız

değişkenler olduğu varsayılsın ve aşağıdaki dönüşüm tanımlansın.

(

1 3

)

2

(

2 3

)

1 maxU ,U ve X maxU ,U

X = =

Buna göre,

(

X₁,X₂

)

¢~BVGE

(

a₁,a₂,a₃

)

olmak üzere İki değişkenli genelleştirilmiş üstel dağılımın ortak dağılım fonksiyonu x₁>0,x₂ >0 için ve

{

_{1 2}

}

=min x ,x

(

)

(

₁

) (

1 ₂

) ( )

2 3 2 1 -2 1 , , 1- 1- 1 -a a a _{x z} x X X x x e e e F = (2.87)

şeklindedir. (Kundu ve Gupta, 2009).

(

X1,X2

)

~BVGE

(

a1,a2,a3

)

olmak üzere İki değişkenli genelleştirilmiş üstel

dağılımın olasılık yoğunluk fonksiyonu x₁>0,x₂ >0 için ve z=min

{

x₁,x₂

}

olmak üzere aşağıdaki gibidir:(Kundu ve Gupta, 2009)

(

)

(

) (

)

(

)

(

-1

)

1+3-1

(

2

)

2-1 -1-2 2 3 1 2 2 3 1 1 2 1 1 -1 -1 + = + = x x α x α α x GE GE e e e α α α α ; x f α α ; x f x , x f (2.88)

(

)

(

)

(

)

(

)

(

-1

) (

1-1 -2

)

2+3-1 -1-2 1 3 2 3 2 2 1 1 2 1 2 -1 -1 + = + = x x α α x α x GE GE e e e α α α α α ; x f α ; x f x , x f (2.89) ( )

(

)

(

x

)

α α α x GE e e α α α α ; x f α α α α x f -1 -+ + -3 3 2 1 3 2 1 3 0 3 2 1 -1 = + + + + = (2.90)

(

X1,X2

)

~BVGE

(

a1,a2,a3

)

olmak üzere iki değişkenli genelleştirilmiş üstel

dağılımın marjinal dağılımları X₁~GE

(

a₁+a₃

)

ve X₂ ~GE

(

a₂+a₃

)

şeklindedir (Kundu ve Gupta, 2009).

(

X1,X2

)

~BVGE

(

a1,a2,a3

)

olmak üzere iki değişkenli genelleştirilmiş üstel

dağılımın ortak yaşam fonksiyonu aşağıdaki gibidir (Kundu ve Gupta, 2009):

(

_{1 2}

)

( )

₁

( )

₂

(

_{1 2}

)

2 1 2 1 2 1 x ,x =1-F x -F x +F x ,x S_{X ,X X X X,X} (2.91) 2.4. Asimptotik Normallik

( )

X rasgele değişkenlerin bir dizisi , n Z , standart normal dağılıma sahip bir

rasgele değişken ve _¾¾d_{® , dağılımda yakınsamayı göstermek üzere,} d n n n X a Z b - _¾¾®

olacak şekilde reel sayıların

( )

a ve pozitif reel sayıların _n

( )

b dizileri varsa, _n

( )

X _n dizisine asimptotik normal veya daha açık olarak “a ortalaması” ve “_n 2

n

asimptotik normal dizisi denir ve _~

(

_, 2

)

n n

n AN a b

X biçiminde gösterilir. Buradaki a _n sayısı X ’in beklenen değeri ve _n 2

n

b sayısı X nin varyansı olmayabilir. Bu değerler _n sırasıyla X ’in asimptotik ortalama ve asimptotik varyans değerleridir (Öztürk 2010). _n

2.5. Olabilirlik Fonksiyonu

n

X X

X₁, ₂,..., örneklemi, olasılık (yoğunluk) fonksiyonu ( ; ),_{f x γ γΡ olan} p

kitleden alınan n birimlik bir örneklem olsun. Örneklemin ortak olasılık yoğunluk fonksiyonu

( ; ), n

f x γ xΡ

olmak üzere bu fonksiyona parametrenin bir fonksiyonu gözü ile bakıldığında

( )

;

( )

; , p

L γ x = f x γ γÎ G Ì¡ (2.92)

şeklinde tanımlanan fonksiyona X₁,X₂,...,X_n örneklemine dayalı olabilirlik fonksiyonu

denir. Burada x=

(

x x₁, , ,₂ K x ¢_n

)

ve γ=

(

g g₁, , ,₂ K g_n

)

¢ şeklinde olup G parametre uzayıdır. Olabilirlik fonksiyonu L γ x

( )

; in logaritması alınarak

( )

log

(

( )

;

)

, p

L

= Î G Ì

γ γ x γ

l ¡ (2.93)

şeklinde elde edilen fonksiyona log-olabilirlik fonksiyonu denir.

2.6. Fisher Bilgi Matrisi

n

X X

X₁, ₂,..., örneklemi, olasılık (yoğunluk) fonksiyonu ( ; ),_{f x γ γΡ olan} p

kitleden alınan n birimlik bir örneklem olsun. Bu örneklem için Fisher bilgi matrisi(Fisher information matrix)

(

)

(

)

( )

( ) log ; I E L E ìæ ¶ öü = - íç_¶ ÷ý è ø î þ ìæ ¶ öü = - íç_¶ ÷ý è ø î þ γ γ X γ γ γl

( )

( )

( )

( )

( )

( )

( )

( )

( )

2 2 2 2 1 1 2 1 2 2 2 2 2 1 2 2 2 2 2 2 1 2 p p p p p g g g g g g g g g g g g g g g æ¶ ¶ ¶ ö ç _{¶ ¶ ¶ ¶ ¶} ÷ ç ÷ ç_{¶ ¶ ¶} ÷ ç ÷ ç ÷ = - ¶ ¶ ¶ ¶ ¶ ç ÷ ç ÷ ç_{¶ ¶ ¶} ÷ ç ÷ ç_{¶ ¶ ¶ ¶ ¶} ÷ è ø γ γ γ γ γ γ γ γ γ l l _L l l l _L l M M O M l l _L l (2.94)

şeklinde tanımlanır, burada L γ X

(

;

)

ve l

( )

γ sırasıyla eşitlik (2.92) ve (2.93) de verilen olabilirlik ve log-olabilirlik fonksiyonlarıdır (Wu ve Kuş, 2009).

2.7. En Çok Olabilirlik Tahmin Edicileri

Olabilirlik veya log-olabilirlik fonksiyonunu maksimum yapan γ değeri

( )

(

)

(

( )

)

ˆ arg max= L ; =arg max

γ γ x l γ (2.95)

γ nın en çok olabilirlik tahmin edicisi (Maximum Likelihood Estimator, MLE) olarak

adlandırılır.

2.8. Asimptotik Güven Aralıkları

Eşitlik (1.17) de tanımlanan en çok olabilirlik tahmin edicisi ˆγ bazı düzgünlük

şartları altında

(

_ˆ

)

d

(

_0, 1

( )

)

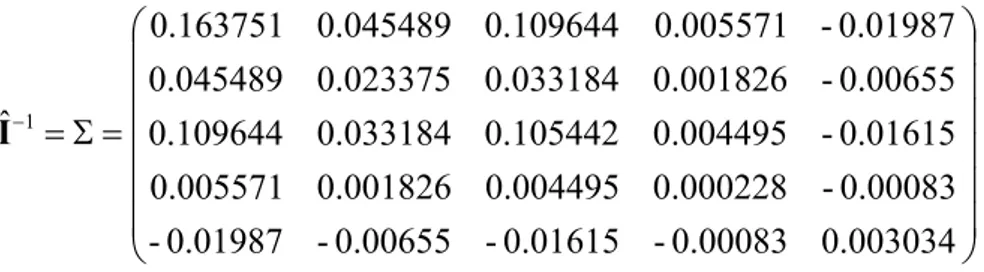
n _{γ γ- ¾¾®}N I- _γ

olmak üzere asimptotik normaldir, burada _I-1

( )

_{γ , (2.94) eşitliğinde tanımlı Fisher Bilgi}

Bu matrisin bilinmesi, büyük örneklemler için g gˆ ˆ₁, , ,₂ K tahmin edicilerinin ayrı ayrı gˆ_n asimptotik varyanslarının bilinmesi anlamına gelmektedir. _I-1

( )

_{γ nın tutarlı bir tahmin}

edicisi

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

1 2 2 2 2 1 1 2 1 2 2 2 1 ₂ 2 1 2 2 2 2 2 2 1 2 _ˆ p p p p p I g g g g g g g g g g g g g g g g g -= æ¶ ¶ ¶ ö ç _{¶ ¶ ¶ ¶ ¶} ÷ ç ÷ ç_{¶ ¶ ¶} ÷ ç ÷ ç ÷ = - ¶ ¶ ¶ ¶ ¶ ç ÷ ç ÷ ç_{¶ ¶ ¶} ÷ ç ÷ ç_{¶ ¶ ¶ ¶ ¶} ÷ è ø γ γ γ γ γ γ γ γ γ γ l l _L l l l _L l $ M M O M l l _L l (2.95a)

dır (Adamidis ve Loukas 1998). Buradan ,g_i i=1, 2, ,_{K için ˆ}p g ’ya dayalı asimptotik _i güven aralığı 1 1 2 2 ˆ_{i ii i} ˆ_{i ii} 1 P g z _a V g g z _a V a - -æ ö - < < + @ -ç ÷ è ø (2.95b)

şeklinde oluşturulabilir. Burada V , eşitlik (2.95a)’da verilen matrisin _ii .i diogonal elemanıdır ve aÎ

( )

0,1 için z , standart normal dağılımın _a a kuantilidir (Wu ve Kuş . 2009).

3. İKİ DEĞİŞKENLİ ÜSTELLEŞTİRİLMİŞ CHEN DAĞILIMI

,

X üstelleştirilmiş Chen yani EC

(

a l b dağılımına sahip olduğunda , ,

)

olasılık yoğunluk fonksiyonu ve dağılım fonksiyonu sırasıyla

( )

1

(

(

)

)

(

{

(

)

}

)

1 exp 1 x 1 exp 1 x EC f x =albxb- l -e b +xb - l -e b a- (3.1)

( )

(

1 exp

{

(

1 x

)

}

)

EC F x = - l -e b a (3.2)

olarak verilir. (Sarhan ve Apaloo, 2013).

1, 2, 12

X X X bağımsız ve sırasıyla EC

(

a l b ₁, ,

)

, EC

(

a l b ₂, ,

)

veEC

(

a l b dağılımına sahip rasgele değişkenler olsun. Burada ₁₂, ,

)

T1 = maxÝX1, X12Þ ve T2 = maxÝX2, X12Þ dönüşümleri tanımlansın. 1 2 T T æ ö = ç ÷ è ø

T rasgele vektörüne Marshal-Ollkin iki değişkenli üstelleştirilmiş Chen dağılımı denilecektir ve T~MOBEC

(

a a a l b1, 2, 12, ,

)

ile

gösterilecektir.

Teorem 3.1: T~MOBEC

(

a a a l b1, 2, 12, ,

)

T ve 1 T 'nin marjinal dağılım 2

fonksiyonlar sırasıyla EC

(

a a l b₁+ ₁₂, ,

)

ve EC

(

a₂+a l b₁₂, ,

)

olacaktır.

İspat.

( ) (

)

(

(

)

)

( ) (

)

( ) (

) (

)

( )

(

{

( )

}

)

(

{

( )

}

)

( )

(

{

( )

}

)

1 12 1 12 1 1 1 1 exp 1 1 exp 1 . 1 exp 1 , , max 1 1 1 1 1 12 1 1 1 1 1 12 1 1 1 1 1 12 1 1 1 1 1 a a a a b b b l l l + -= -= < < = < < = < = < = t t t e t F e e t F t X P t X P t F t X t X P t F t X X P t T P t F

( ) (

)

(

(

)

)

( ) (

)

( ) (

) (

)

( )

(

{

( )

}

)

(

{

( )

}

)

( )

(

{

( )

}

)

2 12 2 12 2 2 2 1 exp 1 1 exp 1 1 exp 1 , , max 2 2 2 2 2 12 2 2 2 2 2 12 2 2 2 2 2 12 2 2 2 2 2 a a a a b b b l l l + -= -= < < = < < = < = < = t t t e t F e e t F t X P t X P t F t X t X P t F t X X P t T P t F

Teorem 3.2 : T~MOBEC

(

a a a l b₁, ₂, ₁₂, ,

)

ise a) T 'nin dağılım fonksiyonu

( )

3

(

)

1 EC i, , ,i , i F F x a l b = = Õ T t (3.3)

burada x₃ =min

{

x x₁, ₂

}

'dir

b) T_i ~ EC

(

a_i+a₃,l,b

)

'dır. (Kundu ve Gupta, 2009) İspat.

(

)

(

(

)

(

)

)

(

) (

)

(

)

(

)

(

) (

) (

)

(

₁1 ₁1

) (

₂2 ₂2

) (

₁₂12 ₂1

)

1_{2 1}2 1 2 2 12 2 2 1 1 2 1 1 12 2 2 1 1 2 12 2 2 1 12 1 1 2 2 1 1 2 12 2 1 12 1 2 2 1 1 < ≤ ≤ ≤ = < ≤ ≤ ≤ = < ≤ ≤ ≤ = < ≤ ≤ ≤ = ≤ ≤ ≤ ≤ = ≤ ≤ ≤ ≤ = ≤ ≤ t t , t X P . t X P . t X P t t, t X P . t X P . t X P t t, t X , t X , t X P t t, t X , t X , t X P t X , t X , t X , t X P t T , t T P t X , X max , t X , X max P t T , t T P (3.4)

Sonuç 3.1: T 'nin dağılım fonksiyonu

( )

(

(

)

)

(

)

1 1 3 2 2 1 2 1 1 2 2 3 2 1 1 2 3 1 2 , ( , ) , 0 , ( , ) , 0 , , , 0 EC EC EC EC EC F t F t t t F F t F t t t F t t t t a a a a a a a a a + < < < ¥ ì ï =_í + < < < ¥ ï _{+ + < = = < ¥} î T t (3.5)

olup eşitlik (3.2) kullanılarak

( )

(

)

{

}

(

)

(

{

(

)

}

)

(

)

{

}

(

)

(

{

(

)

}

)

(

)

{

}

(

)

1 3 2 1 2 1 2 3 1 2 1 2 3 1 2 2 1 1 2 1 exp 1 1 exp 1 , 0 1 exp 1 1 exp 1 , 0 1 exp 1 , 0 t t t t t e e t t F e e t t e t t t b b b b b a a a a a a a a a l l l l l + + + + ì _{- - - - < < < ¥} ï ï ï =_í - - - - < < < ¥ ï ï - - < = = < ¥ ï î T t (3.6) şeklinde de yazılabilir.

Sonuç 3.2 : T 'nin yaşam fonksiyonu teorem 2.11 gereği

(

1, 2

)

1

( )

1

( )

2

(

1, 2

)

S t t = -F tT₁ -FT₂ t +F t t (3.7)

eşitliği kullanılarak açık bir biçimde ifade edilebilir.

Sonuç 3.3 : T'nin olasılık yoğunluk fonksiyonu

( )

(

(

)

)

( )

1 1 2 1 2 2 1 2 2 1 0 1 2 , , 0 , , 0 , , 0 f t t t t f f t t t t f t t t t < < < ¥ ì ï =_í < < < ¥ ï _{< = = < ¥} î T t (3.8) burada

(

)

(

)

(

)

(

)

(

)

(

)

( )

(

)

1 1 2 1 1 3 2 2 2 1 2 1 1 2 2 3 3 0 1 2 3 1 2 3 , ; , , ; , , , ; , , ; , , ; , , EC EC EC EC EC f t t f t f t f t t f t f t f t f t a a l b a l b a l b a a l b a _{a a a l b} a a a = + = + = + + + + (3.9) olup burada

(

)

(

)

( )

(

(

)

)

(

(

)

)

(

)

{

}

(

)

(

{

(

)

}

)

(

)

(

)

( )

(

(

)

)

(

(

)

)

(

)

{

}

(

)

(

{

(

)

}

)

( )

1 2 1 3 2 1 2 1 2 1 2 3 1 2 1 2 2 1 1 2 2 1 3 1 2 1 2 1 1 1 2 2 2 1 2 1 2 3 1 2 1 2 1 1 1 0 3 , exp 1 exp 1 1 exp 1 1 exp 1 , exp 1 exp 1 1 exp 1 1 exp 1 exp 1 t t t t t t t t t f t t t t e t e t e e f t t t t e t e t e e f t t e b b b b b b b b b _{b b} a a a b _{b b} a a a b a a a l b l l l l a a a l b l l l l a lb l -+ - -- + -= + - + - + ´ - - - -= + - + - + ´ - - - -=

(

(

- b

)

_+tb

)

(

1 exp_-

{

_l

(

1_-etb

)

}

)

a a a1+ + -2 3 1 (3.10) dır.

Teorem 3.2 T~MOBEC

(

a a a l b1, 2, 12, ,

)

ise max

( )

T T1, 2 ~EC

(

a a a l b1+ 2+ 12, ,

)

Teorem 3.3

(

T T₁, ₂

)

~EC

(

a a a l b₁, ₂, , ,₃

)

ise aşağıdaki eşitlik yazılabilir:(Kundu ve Gupta, 2009)

(

)

1 2

(

)

3

(

)

1 2 1 2 1 2 1 2 3 1 2 3 , _a , _s , , F t t a a F t t a F t t a a a a a a + = + + + + + 1 2 T ,T (3.11) burada z=min

{ }

t t₁, ₂ ,

(

)

(

{

(

)

}

)

1 2 3 1, 2 1 exp 1 z s F t t = - l -e b a a a+ + (3.12) ve

(

)

(

{

(

)

}

)

(

{

(

)

}

)

(

)

{

}

(

)

(

{

(

)

}

)

1 2 1 2 3 1 2 3 1 2 3 1 2 1 2 3 1 2 , 1 exp 1 1 exp 1 1 exp 1 1 exp 1 t t a z z F t t e e e e b b b b a a a a a a a a a _{l l} a a a l l a a + + + + = - - - -+ ´ - - - - -+ (3.13) dır.

4. PARAMETRE TAHMİNİ 1 11 21 2 12 22 , , , n , n T T T T T T æ ö æ ö æ ö ç ÷ ç ÷ ç ÷

è ø è ø K è ø MOBEC

(

a a a l b dağılımından bağımsız 1, 2, 12, ,

)

n

birimlik bir örneklem olsun. Bu örnekleme dayalı log-olabilirlik fonksiyonu

(

)

(

)

(

)

( )

1 2 0 1, 2, , ,3 ln 1 i1, 2i ln 2 i1, 2i ln 0 i i I i I i I f t t f t t f t a a a l b Î Î Î =

å

+

å

+

å

l (4.1) ve buradan

(

) (

)

{

( )

( )

}

( )

(

)

(

)

(

) (

)

(

{

(

)

}

)

(

)

(

{

(

)

}

)

( )

(

)

(

)

(

{

(

)

}

)

(

)

(

{

(

)

}

)

1 1 2 1 2 1 1 2 2 2 1 2 3 1 2 0 1 2 1 1 3 1 2 1 3 2 2 1 2 2 3 1 2 3

, , , , 2 2 log log log log

1 log 1 log 1 exp 1

1 1 exp 1 log log

1 log 1 exp 1 1 log 1 exp 1 i i i i t i i i I I i l t i l t i l t i l n n n n n t t e e n n e e b b b b a a a l b l b a a a b a a l a l a a a a l a a l Î È Î Î Î Î = + + + + + + + - + + - - -+ - - - + + + + - - -+ + - - - +

å

å

å

å

å

l

( )

(

)

(

{

(

)

}

)

(

)

( )

(

)

(

)

(

)

0 1 2 0 1 2 1 2 0 1 2 1 2 0 0 3 1 2 3 1 2 log 1 log 1 exp 1 1 log 1 1 1 i i i i t i l t t t i i I i I I i I I i I i i i i I I i I I i l n e t e e e t t t b b b b b b b a a a a l b l Î Î Î È Î È Î Î È Î È Î + + + - - -æ ö + - + ç_ç - + - + - ÷_÷ è ø + + +

å

å

å

å

å

å

å

å

(4.2) şeklinde yazılabilir, burada

{

}

{

}

{

}

{

}

1 1 2 2 1 2 0 1 2 0 1 2 ; ; ; 1, 2, , i i i i i i i I i t t I i t t I i t t t I I I I n = < = > = = = = È È = _K ve 0 0 , 1 1 , 2 2 n = I n = I n = I 'dır.

Bilinmeyen parametrelerin MLE'leri (4.2) maksimize edilerek elde edilebilir. Bu beş boyutlu bir optimizasyon problemidir. MLE'leri hesaplamak için aynı anda 5 tane non-lineer denklem çözümüne ihtiyaç olacaktır.