Dokuzuncu sınıf öğrencilerinin fonksiyon kavramı ile ilgili kavram tanımı ve imajları üzerine bir durum çalışması

ORTAÖĞRETĠM FEN VE MATEMATĠK ALANLARI EĞĠTĠMĠ

MATEMATĠK ÖĞRETMENLĠĞĠ BĠLĠM DALI

DOKUZUNCU SINIF ÖĞRENCĠLERĠNĠN FONKSĠYON KAVRAMI

ĠLE ĠLGĠLĠ KAVRAM TANIMI VE ĠMAJLARI ÜZERĠNE BĠR

DURUM ÇALIġMASI

YÜKSEK LĠSANS TEZĠ

Hazırlayan Vedat SÜZER

Ankara Mayıs, 2011

ORTAÖĞRETĠM FEN VE MATEMATĠK ALANLARI EĞĠTĠMĠ

MATEMATĠK ÖĞRETMENLĠĞĠ BĠLĠM DALI

DOKUZUNCU SINIF ÖĞRENCĠLERĠNĠN FONKSĠYON KAVRAMI

ĠLE ĠLGĠLĠ KAVRAM TANIMI VE ĠMAJLARI ÜZERĠNE BĠR

DURUM ÇALIġMASI

YÜKSEK LĠSANS TEZĠ

Vedat SÜZER

DanıĢman: Doç. Dr. AyĢe UYAR

Ankara Mayıs, 2011

Vedat SÜZER‟in “

DOKUZUNCU

SINIF

ÖĞRENCĠLERĠNĠN

FONKSĠYON KAVRAMI ĠLE ĠLGĠLĠ KAVRAM TANIMI VE

ĠMAJLARI ÜZERĠNE BĠR DURUM ÇALIġMASI” baĢlıklı tezi

ORTAÖĞRETĠM FEN

VE

MATEMATĠK

ALANLARI

EĞĠTĠMĠ

MATEMATĠK

ÖĞRETMENLĠĞĠ BĠLĠM DALI‟nda Yüksek Lisans Tezi olarak kabul edilmiĢtir.

Adı- Soyadı Ġmza BaĢkan ... ... Üye(Tez DanıĢmanı) ... ... Üye: ... ... Üye: ... ... Üye: ... ...

i TEġEKKÜR

AraĢtırmanın gerçekleĢmesinde görüĢleriyle yardımcı olan ve çalıĢma boyunca yol gösteren tez danıĢmanım Doç. Dr. AyĢe UYAR‟ a en derin saygılarımla teĢekkür ederim.

AraĢtırma boyunca sorduğum tüm sorulara samimiyetle cevap vererek tezimi okuma-eleĢtirme zahmetine katlanan Öğr. Gör. Dr. Handan DEMĠRCĠOĞLU‟ na,

Matematik öğretmenliği okumaya baĢladığım ilk günden beri ve yüksek lisans eğitimim boyunca tüm bilgi ve tecrübelerini benden esirgemeyen, her zaman destek olarak görüĢlerini benimle paylaĢan hocalarım Prof. Dr. Ziya ARGÜN‟ e, Prof. Dr. Ahmet ARIKAN‟ a, Prof. Dr. Hasan Hüseyin UĞURLU‟ ya,

AraĢtırma süresince gereken her durumda severek çalıĢmaya dâhil olduklarını hissettiğim on öğrenciye, onların matematik öğretmenine ve derse giren tüm öğrencilere,

Fikirleriyle bana yön veren, maddi ve manevi olarak desteklerini hiç esirgemeyen, hayatımdaki tüm güzelliklerin altında imzası olan ağabeyim Dr. Tamercan MORKOÇ ve ablam Ecz. Ümmügülsüm MORKOÇ‟a,

Tüm eğitim hayatım boyunca maddi ve manevi desteklerini esirgemeyen babam Erol SÜZER, Annem Adalet SÜZER ve biricik kardeĢim BüĢra SÜZER‟ e,

Tez çalıĢmam boyunca anlayıĢ gösterip her türlü fedakârlıktan kaçınmayan eĢim Ümran SÜZER‟ e içtenlikle teĢekkür ederim.

ii ÖZET

DOKUZUNCU SINIF ÖĞRENCĠLERĠNĠN FONKSĠYON KAVRAMI ĠLE ĠLGĠLĠ KAVRAM TANIMI VE ĠMAJLARI ÜZERĠNE BĠR DURUM ÇALIġMASI

SÜZER, Vedat

Yüksek Lisans, Matematik Öğretmenliği Ana Bilim Dalı Tez DanıĢmanı: Doç. Dr. AyĢe UYAR

Mayıs -2011, 97 Sayfa

Bu araĢtırmanın amacı; dokuzuncu sınıf öğrencilerin fonksiyon kavramı ile ilgili kavram tanım ve imajını ortaya çıkarmak ve konu ile ilgili bir durum tespiti yapmaktır. Katılımcılar bir orta öğretim kurumunun 2010-2011 eğitim öğretim yılında 9.sınıfında okuyan toplam on öğrenciden oluĢmaktadır. Öğrencilerin 8‟i bayan, 2‟si erkektir. GörüĢmeye seçilen bu öğrenciler amaçlı örneklem tekniğine (Patton, 1990) göre seçilmiĢ ve çalıĢmaya gönüllü olarak katılmıĢlarıdır. Veriler; görüĢmeler, öğrencilerin yazılı dokümanları (uygulama sınavı- yazılılar ) ile sınıf gözlemlerinden elde edilmiĢtir. Yapılan analizde özel olarak, katılımcıların verdikleri cevaplar doğrultusunda sahip oldukları kavram imajlarını teĢhis etmek üzere, görüĢme sorularına odaklanılmıĢtır. Elde edilen verilerin tamamı genel olarak Tall ve Vinner(1981) tarafından geliĢtirilen kavram imajı ve kavram tanımı yapısı esas alınarak analiz edilmiĢtir.

Toplanan bu veriler ve yapılan bu analizlerin ıĢığı altında Ģu açıklamalar yapılabilir: öğrencilerin 9. Sınıfta yeni bir kavram olarak öğrendikleri fonksiyon kavramına ait kavram imajları çok zayıf kalmaktadır. Bu yapılan görüĢmelerden anlaĢılmaktadır. Birçok öğrenci öğretmenin derste kurduğu tanımların örneklerin dıĢına çıkamamaktadır. Birçok öğrencide fonksiyon kavramı küme çizerek tanımlamaktan öteye geçememektedir.

Bu araĢtırmada elde edilen diğer bir bulgu ise öğretmenlerin fonksiyon tanımına ait kavram imajı ile öğrencilerin fonksiyon tanımına ait kavram imajı doğrudan birbirini etkilemektedir. Öğrenci öğretmeninin kavram imajı çerçevesinde bir kavram imajı oluĢturmaktadır.

AraĢtırmada ayrıca bulgular çerçevesinde, bu konularda çalıĢma yapmak isteyen araĢtırmacılara ve eğitimcilere yönelik önerilerde bulunulmuĢtur.

iii

ABSTRACT

A CASE STUDY ON CONCEPT DEFINITIONS AND IMAGES OF NINTH GRADE STUDENTS ABOUT THE CONCEPT OF FUNCTION

SÜZER, Vedat

Post Graduate, Department of Mathematics Teaching Thesis Advisor: Associate Prof. AyĢe UYAR

May -2011, 97 Pages

The aim of this research is to determine the concept definitions and images of ninth grade students about the concept of function and to make assessment. Participants consist of 10 students attending ninth grade in a secondary educational intuition in 2010-2011 educational year. 8 of the students are female, and 2 are male. Students chosen for interview are chosen according to aimed sample technique (Patton,1990) and participated voluntarily. Data are obtained from interviews, written documents of students (practical exams, exams) and classroom observations. In analysis, to define the concept images they have according to their answers, interview questions are especially focused. All of the data obtained are analyzed by concept image and concept definition structure developed by Tall and Vinner (1981).

These explanations can be made in the light of data collected and analysis: Concept images of ninth grade students about the concept of function they have learned as a new concept are quite weak. This can be conducted from the interviews. Most students cannot step out of the definitions and examples set by teacher. And most students cannot go beyond drawing sets to define function.

Another finding of this research is that, concept images of teacher and students about function definition affect each other directly. Student establishes a concept image within the concept image of the teacher.

In the research, within the findings, suggestions are made for researchers and educators who wish to study about these issues.

iv ĠÇĠNDEKĠLER TEġEKKÜR ... i ÖZET ... ii ABSTRACT ... ii ĠÇĠNDEKĠLER ... iv TABLOLAR LĠSTESĠ ... vi

ġEKĠLLER LĠSTESĠ ... vii

1. GĠRĠġ ... 1

1.1. Problemin Durumu ... 1

1.1.1. Öğrencilerde ve bu öğrencilerin öğretmenlerinde fonksiyon kavram tanımı ve imajını incelemek için gerekçeler... 1

1.2. AraĢtırmanın Problemi ve Alt Problemler ... 3

1.3. AraĢtırmanın Amacı ve Önemi ... 3

1.4. AraĢtırmanın Sınırlılıkları ... 5

1.5. AraĢtırmanın Varsayımları ... 5

1.6. Tanımlar ... 5

2. KAVRAMSAL ÇERÇEVE ... 7

2.1. Kavram Öğrenme ... 7

2.2. Kavram Tanımı ve Kavram Ġmajı ... 9

2.3. Fonksiyon Kavramı ... 17

2.4. Ġlgili AraĢtırmalar ... 24

2.4.1 Fonksiyon Kavramı ile Ġlgili Yapılan AraĢtırmalar ... 24

2.4.2. Kavram Ġmajı Ġle Ġlgili Yapılan AraĢtırmalar ... 30

3. YÖNTEM ... 33

v

3.2. AraĢtırmanın Modeli ... 34

3.3 AraĢtırmanın Uygulanması ... 34

3.3.2 AraĢtırmacının rolü ve araĢtırma süresi ... 35

3.4. Verileri Toplama Teknikleri ... 36

3.3. Geçerlilik ÇalıĢmaları ... 38

3.6 Verilerin Analizi ... 40

3.6.1. Ön hazırlık ... 40

3.6.2. Durum ÇalıĢması (Case Study) Yöntemi ve Kategorilerin OluĢturulması ... 40

4. BULGULAR VE YORUMLAR ... 43

4.1. Öğrenciler ile Yapılan Durum ÇalıĢmasının Bulguları ve Yorumları ... 43

4.1.1. Öğrencilere Uygulanan Açık Uçlu Sınavın Değerlendirilmesi ... 43

4.1.2. Öğrencilerle Yapılan GörüĢmelerin Değerlendirilmesi ... 58

5. SONUÇLAR VE ÖNERĠLER ... 67

5.1. Sonuçlar ... 67

5.2. Öneriler ... 69

KAYNAKÇA ... 70

EKLER ... 77

Ek 1. Uygulama Sınav Soruları ... 77

EK 2. GörüĢme Soruları ... 80

Ek 3. Uygulama Sınavına Öğrencilerin Verdikleri Cevapların Sınıflar Bazında Analizi ... 82

vi

TABLOLAR LĠSTESĠ

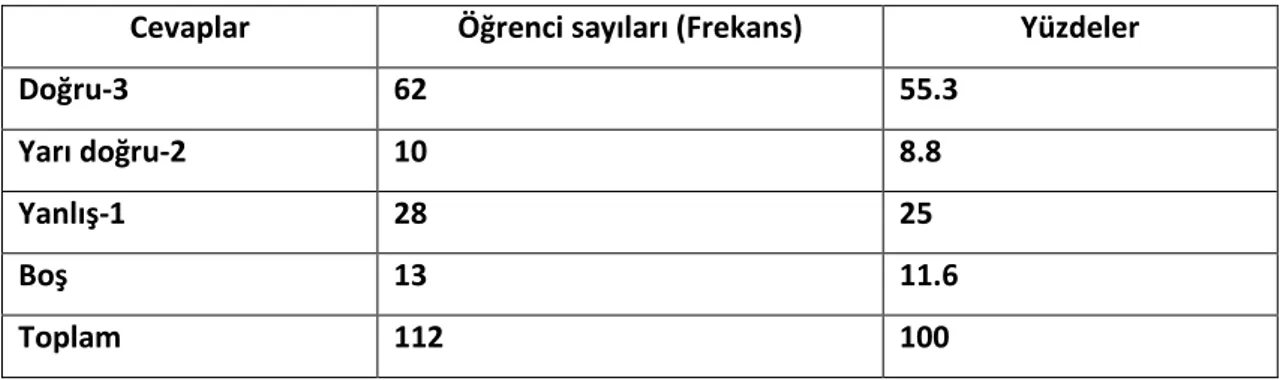
Tablo 1. Öğrencilerin fonksiyon kavramına verdikleri cevapların analizi ... 44

Tablo 2. Öğrencilerin Fonksiyon Kavramını AnlayıĢ Biçimleri ... 45

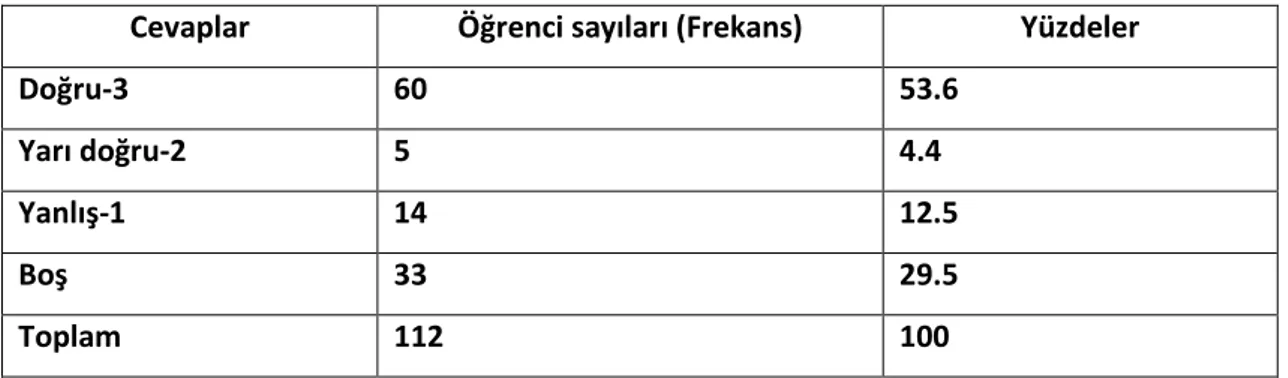
Tablo 3. Öğrencilerin soru 2‟ ye verdikleri cevapların Analizi ... 46

Tablo 4. Öğrencilerin soru 3‟ e verdikleri cevapların Analizi ... 48

Tablo 5. Öğrencilerin soru 4‟ e verdikleri cevapların Analizi ... 49

Tablo 6. Öğrencilerin soru 5‟ e verdikleri cevapların Analizi ... 51

Tablo 7. Öğrencilerin soru 6‟ ya verdikleri cevapların Analizi ... 52

Tablo 8. Öğrencilerin soru 7‟ ye verdikleri cevapların Analizi ... 54

Tablo 9. Öğrencilerin soru 8‟ e verdikleri cevapların Analizi ... 56

vii

ġEKĠLLER LĠSTESĠ

ġekil 1. Kavram OluĢum Süreci ... 13

ġekil 2. Kavram OluĢum Süreci ... 13

ġekil 3. Tanım ile Ġmaj Arasındaki Olması Beklenen Bağlantı ... 14

ġekil 4. Tamamen Formal Öğretim ... 15

ġekil 5. Sezgisel DüĢünce Ġle Öğretim ... 15

ġekil 6. Sezgisel YaklaĢım ... 16

ġekil 7. Uygun Olmayan Kavram Ġmajının, Ġmaj ġekillenmesine Etkisi ... 17

ġekil 8. Bir arazinin yandan topografiksel resmi ... 23

ġekil 9. BeĢgensel Model ... 25

ġekil 10. Fonksiyon Kavramına Matematiksel Perspektif ... 25

ġekil 11. Fonksiyon Kavramına Bilimsel (Sistematik) Perspektif ... 26

ġekil 12. Öğrenci A-22 nin soru-2 ye ait çizimi ... 48

ġekil 13. Öğrenci B-2 ün soru-2 ye ait çizimi ... 48

ġekil 14. Öğrenci D-2 nin soru-2 ye ait çizimi ... 49

ġekil 15. Öğrenci B-24 ün soru-6 ya ait çizimi ... 57

ġekil 16. Öğrenci A-22 nin soru-6 ya ait çizimi ... 57

ġekil 17. Öğrenci D-14 ün soru-6 ya ait çizimi ... 58

ġekil 18. Öğrenci D-14 ün soru-7 ye ait çizimi ... 60

ġekil 19. Öğrenci D-11 in soru-7 ye ait çizimi ... 61

ġekil 20. Öğrenci C-12 nin soru-7 ye ait çizimi ... 67

ġekil 21. Öğrenci-8 in görüĢmede sorulan 2.soruya ait çizimi ... 67

ġekil 22. Öğrenci-9 un görüĢmede sorulan 2.soruya ait çizimi ... 67

ġekil 23. Öğrenci-5 in görüĢmede sorulan 2.soruya ait çizimi ... 68

ġekil 24. Öğrenci-3 ün görüĢmede sorulan 3.soruya ait çizimi ... 69

ġekil 25. Öğrenci-9 un görüĢmede sorulan 3.soruya ait çizimi ... 69

ġekil 26. Öğrenci-10 nun görüĢmede sorulan 3.soruya ait çizimi ... 70

ġekil 27. Öğrenci-9 un görüĢmede sorulan 8.soruya ait çizimi ... 71

ġekil 28. Öğrenci-6 nın görüĢmede sorulan 8.soruya ait çizimi ... 71

ġekil 29. Öğrenci-1 in görüĢmede sorulan 10.soruya ait çizimi ... 72

ġekil 30. Öğrenci-9 un görüĢmede sorulan 10.soruya ait çizimi ... 72

Bu bölümde problemin durumu, araĢtırmanın problemi ve alt problemler, araĢtırmanın amacı ve önemi, araĢtırmanın varsayımları ile sınırlılıkları ele alınacaktır.

1.1. Problemin Durumu

Bu araĢtırma dokuzuncu sınıf öğrencilerinin fonksiyon kavramı ile ilgili kavram tanımı ve imajları üzerine bir durum çalıĢması olarak planlanmıĢtır. Bu plan doğrultusunda bir devlet lisesinde 9.sınıfta öğrenim gören öğrenciler ile birlikte bir çalıĢma yapılmıĢtır.

1.1.1.Dokuzuncu Sınıfta Öğrenim Gören Öğrencilerde Fonksiyon Kavram Tanımını ve Ġmajını Ġncelemek Ġçin Gerekçeler

Neden fonksiyon?

Tarihsel olarak bakıldığında fonksiyon kavramı matematiğin en temel kavramlarından biridir. Birçok ülkede olduğu gibi bizim ülkemizde de ortaöğretim matematik programında fonksiyon kavramı önemli bir yer kaplamaktadır.

Matematik dersinde öğrencilerin öğrenmekte zorlandığı ve kavram yanılgılarına düĢtükleri bazı konuların olduğu bilinmektedir. Fonksiyonlar konusu bu konulardan biridir. Literatürde fonksiyonlar konusunun cebir müfredatı için çok önemli olduğu ve matematik için önemli kavramları içerdiğine dair yapılan pek çok çalıĢma bulmak mümkündür (Dubinsky, 1992; NCTM, 1989). Yine yapılan bazı çalıĢmalarda, fonksiyon kavramın oldukça karmaĢık ve soyut düzeyde olduğunu, öğrencilerin anlamakta zorluk çektikleri, problem çözümlerinde fonksiyon kavramını unuttukları, göz ardı ettikleri veya bilgilerini uygulamaya geçirmede zorlandıkları ortaya çıkmaktadır (Aydın, 2000; Selden, 1992; Kieran, 1990; Dreyfus, 1990; Tall & Winner, 1981).

Neden kavram imajı?

Tall ve Vinner (1981) kavram imajını kavramla birlikte anılan tüm biliĢsel yapı olarak tanımlar. Bu yapı tüm zihinsel resimleri ve çağrıĢım yapan özellikleri ve yöntemleri içerir. O halde herhangi kavrama ait kavram imajı, kavramla bağlantılı her Ģeyi içerdiğinden (Tall & Vinner,1981) kavramla ilgili kısmen doğru olan yapılar ve kavram yanılgıları da kavram imajının içinde yer alır. Tall ve Vinner (1981)‟ in ortaya koyduğu Concept Image and Concept Definition (Kavram imajı ve Kavram tanımı) yapısı öğrencilerin zihinsel imajları ile kavramları nasıl anladıklarını belirlememizi sağlayabilecektir.

Kavram kelimesinin sözlük anlamı “nesnelerin veya olayların ortak özelliklerini kapsayan ve bir ortak ad altında toplayan genel tasarım, mefhum kavrayıĢ” ile “bir nesnenin veya düĢüncenin zihindeki soyut ve genel tasarımı” Ģeklinde verilir. (http://tdkterim.gov.tr/bts/)

Bir kavramın tanımından çok zihinde oluĢturduğu imaj kuĢkusuz o kavramı öğrenmede daha önemlidir. Eğitim bilimi açısından, kavram imajı ve kavram tanımı yapısı, öğretenin, öğrenenlerin kavramsal temellerini anlamasında etkin rol oynamaktadır (Cottrill, 2003).

Kavramlar bireylerin algılamaları ile alakalıdır. Bu yüzden bireyden bireye farklılık gösterebilir. Aynı zamanda kullanılan dilin zenginliğine göre anlam ve özellikler kazanabilir, hem soyut hem de somut özellikleri ayrı veya birlikte taĢıyabilirler. Kavramlar farklı kültürler içinde farklı anlamlar taĢıdığı gibi, aynı kültür içindeki bireyler arasında bile yaĢantılara bağlı anlam farklılıkları gösterebilir (Beydoğan,1998). Paulos(1993)‟ e göre kavramın ne olduğunu anlatmadan, uygulamaya geçen bir sistem eleĢtirel düĢünceyi öğretmemektedir.

Bireyin kavram ile iliĢkilendirdiği her Ģeyi içeren kavram imajları ile ilgili birçok çalıĢma bulunmaktadır. Fakat bu çalıĢmaların birçoğu kavram yanılgıları ve kavram algılamaları üzerinedir. Ayrıca araĢtırmacı tarafından yapılan literatür taramasında fonksiyon kavram ile imajının karĢılaĢtırılmasından ziyade, fonksiyon kavram görüntüleri, fonksiyon kavram yanılgıları, kavram algılamalarındaki güçlükler üzerinde durulduğu gözlemlenmiĢtir.

1.2. AraĢtırmanın Problemi ve Alt Problemler

AraĢtırmanın problemini “Dokuzuncu sınıf öğrencilerinin fonksiyon kavramı ile ilgili kavram tanımı ve imajları nasıldır?” soru cümlesi oluĢturmaktadır. Belirlenen bu temel problem ıĢığında bazı alt problemler oluĢturulmuĢtur.

1) Dokuzuncu sınıf öğrencilerinin fonksiyon kavramı ile ilgili kavram tanımları nasıldır?

2) Dokuzuncu sınıf öğrencilerinin fonksiyon kavramı ile ilgili kavram imajları nasıldır?

1.3. AraĢtırmanın Amacı ve Önemi

Bu araĢtırma ile dokuzuncu sınıfta öğrenim gören öğrencilerin fonksiyon kavramına ait kavram tanımları ve kavram imajları tespit edilmek istenmiĢtir.

Kavram yanılgılarının yanlıĢ anlamlara dayalı olduğunu (Powell, 1983) söylemektedir. Bundan dolayı kavram yanılgıları üzerinde çalıĢmak bizi ister istemez kavram tanımı ve bu tanıma ait olan kavram imajı üzerinde çalıĢmaya iter. Ġstenilen imaj olmaksızın kavram yanılgılarının doğru bir Ģekilde yeniden düĢünülmesi ya da çok derin bir matematik anlayıĢının kazanılabilmesi mümkün görünmemektedir. (Aktaran: Eraslan, 2005)

Birçok araĢtırmada bazı kavramlarda karĢılaĢılan zıtlıklar ortaya çıkarılmıĢtır. Bunlardan bazıları; teğetin eğriyi iki noktada kesmesi (Orton, 1977), ondalıklı sayılardaki sözlü yada diğer zorluklar (Tall, 1977), geometrik kavramlar (Vinner ve Hershkowist, 1980), fonksiyon kavramı (Vinner, 1983), limit ve süreklilik (Tall ve Vinner, 1981), dizilerin limiti (Robert, 1982), fonksiyonların limiti (Ervynck, 1983), sonsuzluk kavramı (Fischbein et al, 1979), diferansiyel kavramı (Artigue, 1986), ve fonksiyon kavramının çoklu temsillerinin çağrıĢtırdığı kavram görüntüleri (Akkoç, 2006).

Fonksiyon kavram tanımı, fonksiyon kavram yanılgıları, fonksiyon kavramına ait anlama zorlukları ile ilgili birçok araĢtırma öğretmen adayları, öğretmenler veya öğrenciler gibi değiĢik örneklem gruplarına yapılmıĢtır fakat kavram tanımını ve kavram imajını aynı anda inceleyen çalıĢmalara yaptığımız literatür taramasında çok

fazla karĢılaĢmadık. Bu araĢtırma bu konudaki eksikliği kısmen gidermek adına yapılmıĢtır.

Günlük hayatta her çeĢit insanın, bilerek veya bilmeyerek kullandığı fonksiyon kelimesinin öğrenciler tarafından nasıl algılandığının oldukça önemi vardır. Bu algılama sonucu olarak oluĢan, bir öğrencinin öğrenim ve tecrübeleriyle ortaya çıkan kavram imajlarını her yönüyle ortaya koymak, öğrencinin zihninde kavramla ilgili bütün bağlantıları ortaya çıkarmak gerekli görülmüĢtür. Böylelikle imajı belirlenen bir kavramın ne derece doğru yapılandığı, hangi eksiklerin saptandığı, öğrenim hayatı devamında kullanıĢlılığı gibi birçok özelliğin açıklığa kavuĢacağı söylenebilir.

Fonksiyon kavram tanımı ve kavram imajı ile ilgili birçok çalıĢma olmasının yanında, çalıĢmanın uygulanacağı gruplar açısından oldukça önemli bir araĢtırmadır. Çünkü dokuzuncu sınıfta öğrenim gören öğrencilerde fonksiyon kavram ve imajını incelemek bundan sonraki ders anlatma veya sunma durumlarında öğretmenlere bir fikir verebilir ve yardımcı olabilir. Çünkü bu sayede bu araĢtırmayı inceleyen bir öğretmen tarafından uygulanan öğretim yönteminde gerekli değiĢiklikler yapılabilir ve karĢılaĢılan kavram yanılgılarının önüne geçilebilir.

Fonksiyon kavramı matematiğin en temel kavramlarından biridir. Matematiğin her seviyesinde birçok konuya teĢkil eder. Lise seviyesinde reel ve tek değiĢkenli fonksiyonlar, üniversite seviyesinde sürekli ve türevlenebilir fonksiyonlar analizin merkezi kavramıdır (Vinner,1992). Bu yüzden öğrencilerin matematiğin temel kavramlarından olan fonksiyon kavramı ile ilgili kavram tanım ve imaj incelenmesi ve bu kavramı anlamada ve algılamada yaĢadıkları zorlukları tespit edilmesi ve doğrudan giderilmeye çalıĢılması açısından yine çok önemlidir.

Yine benzer Ģekilde eğitim öğretim sahasındaki öğretmelere fonksiyon kavram tanımını öğretirken zorlandıkları ve anlaĢılmadıkları noktaları tespit açısından önemli bir çalıĢma olabilir.

Tüm bunların yanında bu çalıĢma öğretmen adaylarının yetiĢtirilmesinde ve orta öğretim kurumlarında okutulan öğretim programları içinde yardımcı nitelik taĢıyabilir. Hem öğretmen adayları hem de okullarında bulunan öğretmenler bu çalıĢmanın sonucundan faydalanılabilir.

1.4. AraĢtırmanın Sınırlılıkları

1) Bu araĢtırma sadece 3 ay süren bir öğretim süresi ile sınırlıdır.

2) Bu araĢtırma yapılacak olan görüĢmeler, yazılı dokümanlar ve sınıf gözlemleri ile sınırlı olacaktır.

3) Bir diğer önemli sınırlılık ise sesli düĢünmenin getireceği sınırlılıktır. Öğrencilerin sesli düĢünme metodunu kullanırken bazı düĢüncelerini tam olarak net bir Ģekilde ifade edemeyeceği durumlar olabilir. Bu durum pilot çalıĢmalar ve ilk baĢta alıĢtırma çalıĢmaları ile aĢılmaya çalıĢılacaktır.

4) AraĢtırmaya konu olarak sadece fonksiyon kavramı tanımı ve temel yapıları dahil edilmiĢtir.

1.5. AraĢtırmanın Varsayımları

AraĢtırmada aĢağıdaki durumlar varsayım olarak kabul edilmiĢtir.

1) GörüĢme yapılan öğrencilerin görüĢme formundaki soruları ciddiyetle yanıtlayacakları, sorulara samimiyetle ve açık cevaplar verecekleri varsayılmıĢtır.

1.6. Tanımlar

Kavram: Bir nesnenin veya düĢüncenin zihindeki soyut ve genel tasarımı, mefhum fehva, konsept, nosyon.

Kavram Tanımı (Concept Definition): Bir kavramın formal (biçimsel) tanımıdır.

Kavram Ġmajı (Concept Image): Bir kavramın kiĢiden kiĢiye değiĢebilen informal (sezgisel) tanımıdır.

Fonksiyon: A ve B boĢ olmayan iki küme olmak üzere; A‟nın her elemanını, B‟nin yalnız bir elemanına eĢleyen; A‟dan B‟ye bir f bağıntısına, A‟dan B‟ye fonksiyon denir.

A‟dan B‟ye tanımlı bir f fonksiyonu:

1. A‟nın tüm elemanlarını, B‟nin elemanlarına eĢler.

2. A‟nın her elemanını, B‟nin yalnız bir elemanına eĢler. x ∈A ve y ∈B olmak üzere; A‟dan B‟ye bir f fonksiyonu, x‟i y‟ye eĢliyorsa;

2.1. Kavram Öğrenme

Kavramlar, toplumsal olarak kabul edilmiĢ sözcüklerin anlamı olarak ifade edilebilecekleri gibi ortak özellikleri olan nesne, olay, fikir ve davranıĢların oluĢturduğu sınıflamaların soyut temsilcisi olarak da ifade edilebilir. DoğuĢtan getirilen herhangi bir kavram yoktur. Bazı kavramların kolay öğrenilebilmesine karĢın bazı kavramların öğrenilmesi zordur ve zihinsel geliĢimle yakından iliĢkilidir.

Kavramlar isimlendirme ve tanımlama özelliklerine sahiptirler. Bu özellikleri nedeniyle de öğrenmenin vazgeçilmez ve temel elemanlarından biridir. Kavramlara ait çıkarılabilen bazı özellikleri aĢağıdaki gibi sıralanabilir:

 Kavramlar bireylerin algılamalarına dayalı olduğu için bireyden bireye farklılık gösterebilir.

 Kavramlar var olduğu dilin özelliklerine bağlı olarak dilin zenginliğine göre ve kültüre göre anlam ve özellikler kazanabilir.

 Kavramlar hem soyut hem de somut özellikleri ayrı veya birlikte taĢıyabilirler.  Kavramlar farklı kültürler içinde farklı anlamlar taĢıdığı gibi, aynı kültür içinde yer alan bireyler arasında bile yaĢantılara bağlı anlam farklılıkları gösterebilir. YaĢları, geliĢim düzeyleri ve hatta içinde bulundukları ortam aynı özelliklere sahip olmasına rağmen çocukların sahip oldukları kavramlar, hem kapsam hem de tür açısından aynı değildir. Çünkü çocuklarda kavram geliĢimini etkileyen pek çok faktör vardır. Bunlardan bazıları; duyu organları, fiziksel mekanlar, zekâ, cinsiyet faktörü, kiĢilik, yaĢantılar, öğrenme fırsatları, çocuklara sağlanan rehberlik düzeyi, yanlıĢ anlamalardır.

Eğer bir öğrenci, gördüğü bir objenin adını söyleyebilirse, bu öğrencinin kavramı kendi zihninde yapılandırdığı anlamına gelmez. O , mekanik olarak obje ya da olay ile onlara verilen ad arasında bağ kurmuĢ olabilir ( Ülgen, 1996). Clements ve Battissa (1992) ye göre öğrenme birden bire gerçekleĢmez ve belirli bir süre gerektirir. Bu yüzden, etkili bir öğrenmenin olabilmesi için bilgilerin tekrar gözden geçirilmesi, üzerinde etraflıca düĢünülmesi, tecrübe edilmesi ve kullanılması gerekmektedir. Bütün bunlar belirli bir süreç içerisinde gerçekleĢir. (Clements ve Battissa, 1992).

Vinner (1991)‟e göre kavram öğrenme doğrudan kavram imajını biçimlendirme anlamına gelmektedir. Kavram tanımının bilinmesi bireyin kavramı anlamıĢ olduğu anlamına gelmez. Bireyin kavramı anlamıĢ olması onun kavram imajına sahip olduğu anlamına gelir. Örneğin „bilmek‟, verilen bir fonksiyonun tanım kümesine bağlı olarak görüntü kümesini oluĢturabilmek olarak düĢünülürse, „anlamak‟, verilen fonksiyona ve tanım kümesine bağlı olarak görüntü kümesini oluĢturabilmektir. Görüntü kümesi imajı bazı kümelerin görüntü kümelerinin ne olduğunun hatırlanmasını içermektedir.

Ülgen (1996)‟a göre kavram öğrenme hangi yöntemle olursa olsun, iki aĢamada gerçekleĢir. Ġlk aĢama kavram yapılandırmadır. Kavram oluĢturmada genelleme yapmak vardır. Bireyler kendilerini uyaranların benzer ve farklı yönlerini ortaya koyar ve benzerliklerine göre genelleme yapar. Bireyler kontrollü denemelerle kavram kazanma konusunda beceri kazanabilirler. Kavram geliĢtirme ise bireyin oluĢturduğu ya da kazandığı kavramın nitelik açısından olumlu yönde artıĢ kaydetmesine iĢaret eder.

Kavram öğrenmesi gerçekleĢtikten sonra elde edilen ürünlere bakılacak olursa; öğrenme ürünleri üç açıdan incelenebilir. DavranıĢçı yaklaĢıma göre bireyin doğrudan gözlenebilen ve sözel olarak ifade edilen davranıĢlarını esas alır. Bir kavramı öğrenen öğrenci; kavramla ilgili öğrendiklerini sözleriyle bütünleĢtirir kavramın adını söyler ve tanımını yapar. Öğrendiği kavrama benzeyen bir kavramla karĢılaĢtığı zaman yeni kavramı tanır ve kendi sözcükleriyle tanımlar. BiliĢsel yaklaĢıma göre kavramın öğrenilmesi ise; bellek sürecinden daha önce öğrenilen ilgili bilgilerin hatırlanarak esnek algılarla yeniden yapılandırılması iĢidir. Esas kavram öğrenme ürünü bilgilerin transferidir ve problem çözebilmedir (Ülgen, 1996). Üçüncü olarak Posner (1982)‟ e göre de; kavramsal değiĢim kiĢinin bilgi yapısındaki köklü değiĢimler olarak da tanımlanabilir. Fakat bu bilgi yapısındaki köklü değiĢimler aniden ortaya çıkmaz, yavaĢ yavaĢ ve kademeli olarak gerçekleĢir. Öğrencinin karĢılaĢtığı yeni kavramı hemen ve anlaĢılır bir Ģekilde algılaması pek olası değildir.

Bu araĢtırmada öğrenciler ve bu öğrencilerin öğretmenlerinin fonksiyon kavram tanımı ve kavram imajı incelenmeye çalıĢılacaktır.

2.2. Kavram Tanımı ve Kavram Ġmajı

Öğrencilerin matematiksel düĢüncelerini keĢfetmek amacıyla araĢtırmacılar, özellikle farklı bakıĢ açılardan kavram imajını merkeze alan birçok analizler yapmaktadır. Matematiğin öğrenimi ve öğretiminde araĢtırmalar odak noktalarını, davranıĢçı perspektiften yapısalcı perspektife kaydırmıĢtır. AraĢtırmacılar için öğrencilerin kavramlara ait tanımlarının imajlarının ortaya çıkarılması büyük merak konusu olmuĢtur. Önceki yıllarda öğrencilerin değerlendirmesinde esas olan “sonucu doğru bulma ya da istenen cevabı söyleyebilme” iken; son yıllarda “süreci nasıl oluĢturduğu” ve “kavrama ait imajın ne olduğu” esas alınmaya baĢlamıĢtır. Yapısalcı yaklaĢım penceresi ile öğrenme sürecinde, öğrenci düĢünmeleri ve stratejileri merkez olmaya baĢlamıĢtır.

Tall ve Vinner tarafından 1981 yılında ortaya atılan kavram tanımı ve kavram imajı yapısı da öğrencilerin matematiksel düĢünmelerini incelemek için etkili bir yapı olarak görülmektedir. Kavram tanımı ve kavram imajı yapısı öğrencilerin matematiksel kavramlara ait kazanımlarını açıkça ortaya koymaktadır. Bu yüzden kavram tanımı ve kavram imajı yaklaĢımını baz alarak yapılan birçok matematik eğitimi araĢtırması bulunmaktadır. Ondalıklarla ilgili sözlü ve diğer zorluklar (Tall, 1977), geometrik kavramlar (Vinner ve Hershkowitz, 1980), fonksiyon fikri (Vinner, 1983), limit ve süreklilik (Tall ve Vinner, 1981), serilerin yakınsaklığı (Robert, 1982), fonksiyonların limitleri (Ervynck, 1983), eğim (Vinner, 1983; Tall, 1987), sonsuzluk hissi (Fischbein, 1979), diferansiyelin anlamı (Artigue, 1986) Fonsiyon öğretiminde kavramsal zorluklar (Ural, 2006) bunlardan bir kaçıdır.

80‟li yılların baĢında kavram imajı yapısı ilk defa öğrencilerin geometrik kavramlarını analiz eden bir çalıĢma eĢliğinde Vinner ve Hershkowitz tarafından ortaya konulmuĢtur. Bu sıralarda, Tall öğrencilerin limit ve süreklilik kavramlarını öğrenirken karĢılaĢtıkları zorlukları içeren bir çalıĢma yapmıĢtır. Ġki araĢtırmacı daha sonra ellerindeki verileri birleĢtirerek 1981 yılında “Limit ve Süreklilik Özel Referansı ile Kavram imajı ve Kavram tanımı” adını taĢıyan ve sonraki çoğu araĢtırmaya kaynak teĢkil edecek olan çalıĢmayı ortaya koymuĢlardır (Gülkıllık, 2008).

“Kavram imajı” ve “kavram tanımı” terimleri, bireyin kavramsal yapısında ne denli önemli olduğunu göstermek için, Vinner ve Herskowitz (1980) de tanıtılmıĢ ve sonra Tall ve Vinner (1981) tarafından Ģu Ģekilde tanımlanmıĢtır:

“Biz kavram imajı tanımını kavramla birlikte anılan tüm bilişsel yapı olarak tanımlayacağız. Bu yapı tüm zihinsel resimleri ve çağrışım yapan özellikleri ve yöntemleri içerir. Kavram imajı geliştikçe her zaman tutarlı olması gerekmez. Belirli bir zamanda aktif olan kavram imajına uyandırılmış (evoked) kavram imajı diyeceğiz. Farklı zamanlarda çelişkili görünen imajlar uyandırılabilir. Sadece çelişkili görüntüler kendiliğinden uyandırıldığında anlaşmazlık ve karışıklığın herhangi gerçek bir hissi olabilir.

Diğer taraftan kavram tanımı bu kavramı özelleştirmek için kullanılan kelimeler bütünüdür.” (Tall ve Vinner, 1981)

Fonksiyon kavramı gibi güçlü bir matematiksel kavram analiz edildiğinde, açık bir biçimde beliren bu kavramın biliĢsel karmaĢıklığıdır. Bir fonksiyonun kavram tanımı “A‟nın her bir elemanının, B‟nin yalnız bir elemanına eşleyen, A ve B kümeleri arasındaki ilişki” Ģeklinde verilebilir, fakat kavramın deneyimi diğer birçok yöne sahip olabilir. Örneğin bu deneyim A kümesinin her bir x elemanını B kümesinin bir f(x) elemanına karĢılık getiren bir olay, bir grafik veya bir değerler tablosu olarak görülebilir. Kavram imajını detaylı bir Ģekilde incelemek için bazı özelleĢtirmeler de yapılmıĢtır:

“… Biz, kavram imajı veya kavram tanımının başka bir parçasıyla çelişen bir parçasını potansiyel çelişki faktörü olarak adlandırabiliriz. Bu faktörler, bilişsel çatışmaya yol açan durumlarda kesinlikle uyandırılmamalıdır, fakat bunlar böyle uyandırılmışsa, ilgili faktörler bilişsel çatışma faktörü olarak adlandırılacaktır. Onlar sadece kendiliğinden uyandırıldıklarında bilişsel çatışma faktörü haline gelirler. Kesin durumlarda, tedirginliğin belirsiz hissi ile kendi kendini sadece açıkça belli eden çelişki ile bilişsel çatışma faktörleri bilinçsizce uyandırılabilir.” (Tall ve Vinner, 1981).

Kavram imajına ait potansiyel çatıĢma faktörünün nasıl durumlarda daha ciddi sorunlar ortaya çıkaracağı da Ģu Ģekilde belirtilmiĢtir:

“ … potansiyel çelişki faktörünün daha ciddi bir çeşidi, kavram imajının başka bir çeşidiyle olan değil de formal kavram tanımının kendisiyle olan kavram imajının içinde olanıdır. Bu faktörler formal teorinin öğrenilmesini ciddi olarak engelleyebilir, onlar formal kavram tanımı daha sonra bilişsel bir çatışmayla sonuçlanabilecek bir kavram imajı geliştirmedikçe gerçek bilişsel çatışma haline gelemezler. Kavram imajlarında böyle potansiyel çelişki faktörü olan öğrenciler, göz önüne alınan fikirlerin kendilerine ait gösterimlerde güvende hissedip formal teoriye işlevsiz ve fazla gereksiz gibi basitçe bakarlar.” (Tall ve Vinner, 1981).

Tall ve Vinner (1981), öğrencilerin yeni bir ortamda eski bir kavramla karĢılaĢmaları durumunda, önceki durumlardan özetlenen tüm dolaylı (örtülü) varsayımlarla birlikte, duruma cevap verenin kavram imajı olduğunu belirtir. Bu da öğrencinin bir problemle karĢılaĢtığında, kavram tanımını geri plana iterek kavram imajını kullanmaya eğilimli olduğunun göstergesidir.

Ayrıca yine yapılan bu çalıĢmada, kavram imajının formal tanımla çatıĢan deneyimler üzerine inĢa edilmesi halinde, formal teoriye uymayan cevapların ortaya çıkabileceği de vurgulanmaktadır. AraĢtırmada aynı zamanda Howson ve Austin, 1980 yılında yaptığı

“İngiltere‟de geleneksel lise eğitimi formal tanım üzerine, ilk ve ortaokullarda ise resmi olmayan veya görünüşe ait tanımlara dayanır.”

gözleminin de bu tespiti desteklediği belirtilmektedir.

AraĢtırmaya göre; gelenekler farklı ülkelere göre değiĢse bile, ilköğretimin ikinci basamağı iki üst yaĢ dönemi arasındaki geçiĢ basamağı, tanımların daha teknik bir hisle kullanılmaya baĢlandığı zamandır. Bilimsel çatıĢma üzerinde yapılan araĢtırmalar, öğrencilerden bireysel kavram imajlarının müdahale etmesini ummadan kavram tanımlarını mantıklı bir Ģekilde tartıĢmalarını beklemenin, çok akla uygun olmadığını gösterir.

Bir fonksiyonun kavram tanımını iĢaret ederek, Vinner (1983) Ģunları iddia etmektedir:

1. Kavramları incelemek için, birinin kavram tanımına değil de bir kavram imajına ihtiyacı vardır.

2. Kavram tanımları (kavram bir tanım ile birlikte bireye tanıtıldığında) pasif kalabilir, hatta unutulabilir. DüĢüncede hemen her zaman kavram imajı uyandırılacaktır.

BaĢka araĢtırmada da Vinner (1991), öğrencilerin matematiksel kavramlara ait düĢüncelerini belirlemek için kavram tanımı ile kavram imajı arasındaki iliĢki ve etkileĢimleri ortaya çıkarmaktadır.

Vinner (1991)‟ a göre, eğer bir fikir diyagramlar halinde sunulmak isteniyorsa, biliĢsel yapıda iki „hücre‟ye baĢvurulur. Birinci „hücre‟ kavram tanımı ve ikinci „hücre‟ de kavram imajı hücresidir. Ġlk hücre ve hatta bazen ikisi de boĢ olabilir. (Kavram imajı hücresi, herhangi bir anlamlandırma ile kavram ismi birleĢmemiĢse boĢ olarak düĢünülebilir. Kavram tanımı anlamsız bir yolla hatırlandıysa bu durum oluĢabilir.) Bu iki hücre arasında belli bir iliĢki olmasına rağmen bu iliĢki bağımsız olarak ĢekillendirilmiĢtir. Bir öğrenci, çeĢitli durumlarda birçok grafik görmek suretiyle koordinat sistemi hakkında kavram imajı oluĢturabilir. Bu kavram imajına göre, verilen iki eksen birbirini dik keser. Matematik öğretmenleri, koordinat sistemini birbirini dik kesen iki düz çizgi olarak tanımlayabilir. Bunun sonucunda 3 durum ortaya çıkabilir:

1. Kavram imajı, koordinat sisteminin eksenleri arasında dik açı yokmuĢ gibi değiĢebilir. (Yeniden yapılandırma – uyum / reconstructivism-accommodation) 2. Kavram imajı olduğu gibi kalabilir. Kavram tanımı hücresi bir süreliğine

öğretmenin tanımlamasını içerir fakat kısa bir süre sonra unutulabilir ve öğrenciden koordinat sistemini tanımlaması istendiğinde, öğrenci eksenlerin arasındaki dik açıdan bahsedebilir. (Formal tanım özümsenmemiĢ durumdadır.) 3. Ġki hücre de olduğu gibi kalabilir. Öğrenciye sunulduğunda öğretmenin tanımını

tekrardan söyleyebilir fakat bütün diğer durumlarda öğrenciler, birbirine dik iki ekseni düĢünürler (Vinner, 1991).

Benzer bir süreç, kavramla ilk defa o kavramın tanımı yardımı ile karĢılaĢıldığında gerçekleĢir. Burada kavram imajı hücresi boĢtur. Birçok örnekten ve açıklamadan sonra, bu hücre tamamen dolar. Ama bu tamamen kavram tanımını yansıtmaz. Benzer senaryolar 1 den 3 e yaĢanır.

Vinner(1991), kavram oluĢum süresince kavram tanımı ile kavram imajı arasında var olan etkileĢimi göstermek için aĢağıdaki Ģekli kullanmaktadır.

ġekil 1. Kavram OluĢum Süreci

ġekil–1 de kavram oluĢumunun uzun süreli bir süreci gösterilmiĢtir. Bu da gösterir ki bazı öğretmenler orta öğretim seviyesindeki (secondary ve collegiate level) öğrencilere, bu sürecin tek yönünü yaĢatmaktadırlar. Bu durum ġekil–2 de gösterilmiĢtir. Öğretmenler, kavram imajının kavram tanımından Ģekillendiğini ve tamamen onun tarafından kontrol edildiğini düĢünmektedirler (Vinner, 1991).

ġekil 2. Kavram OluĢum Süreci

Kavram imajının içeriğini kavram tanımının kontrol ettiğini kabul edersek, kavramın istenildiği gibi yapılandığını varsayabiliriz. Vinner ve Dreyfus (1989), kavram imajının genellikle kavram tanımı tarafından değil de, tipik örneklerle oluĢtuğuna iĢaret etmektedir. Bu yüzden; kavramın örnekleri olarak düĢünülen matematiksel objelerle oluĢturulan kavram imajı ile kavram tanımı tarafından tanımlanan matematiksel objeler tarafından oluĢturulan kavram imajı illa ki aynı değildir. Geleneksel öğretimin yapıldığı sınıflarda özellikle geometrik kavramlarda kavramlarla ilgili verilen örnekler genellikle kavram imajını oluĢturan matematiksel deneyimler olarak sunulmaktadır (Gülkıllık, 2008).

Ayrıca öğretmenler, problem çözme esnasında kavram tanımı ve kavram imajı arasında karĢılaĢtırılabilir tek yönlü bir iliĢkinin var olduğunu düĢünmektedir. Ne var ki Vinner (1991), problem çözme sürecinde kavram tanımının öğrenciler tarafından baz

Kavram Tanımı Kavram İmajı

alınmadığını söylemektedir. Tanım ile imaj arasında olması gereken bağlantı ġekil 3 ile verilmektedir.

ġekil 3. Tanım ile Ġmaj Arasındaki Olması Beklenen Bağlantı

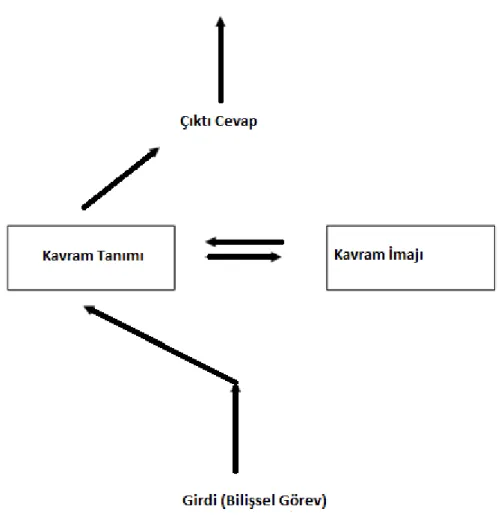
ġekil 4 ve ġekil 5 te ise öğrenciye biliĢsel bir görev verildiğinde ortaya çıkan süreçler gösterilmektedir. Teknik içerikli bir problemle karĢılaĢıldığında bilgileri birleĢtirme sisteminin nasıl çalıĢtığı ile ilgili bir sorun yoktur; kavramın tanımına baĢvurmadan önce çözüme bir formül bulmak gerekmez. Bu tabiî ki istenilen bir süreçtir. Aksi takdirde uygulama farklıdır. BiliĢsel sistemin doğasına aykırı olacak Ģekilde geliĢtirmek zordur ve hem kavram imajını Ģekillendirirken hem de biliĢsel bir iĢ üzerinde çalıĢırken tanımlara baĢvurmaya sevk etmek zordur. AĢağıda, uygulamada daha çok kullanılabilecek bir model görülmektedir: (Vinner, 1991).

ġekil 4. Tamamen Formal Öğretim

ġekil 4 te görüldüğü gibi öğrenciler formal bir durumunun benimsendiği öğretim ortamında problem çözerken kavram tanımını esas almaktadırlar.

ġekil 5 te görüldüğü gibi öğrenciler sezgiler düĢünceleri ile problem çözerken önce kavram imajına daha sonra ise kavram tanımına baĢvurarak iĢlem yapmaktadırlar. ġekil 6 da ise problem durumuna sezgisel yaklaĢan öğrencinin hangi süreçten geçtiğini açıklayan bir durum vardır.

ġekil 6. Sezgisel YaklaĢım

“Burada kavram tanımı hücresine, problem çözme sürecinde hiç başvurulmamıştır. Günlük yaşamdaki düşünce alışkanlıklarımız formal tanıma başvurmaya ihtiyaç duyduğumuzu fark etmeden, idareyi ele almıştır. Kavram imajına başvurmak genelde işe yarar, bu da insanların kavram tanımına başvurmalarını gerekli kılmaz. Belirli bilişsel işlerde kavram imajı ile bağlantı kurarız fakat farklı durumlarda aynı imajın tekrar canlanabileceğini söylemiyoruz. Analizciler, bilişsel sistemin sadece bir kısmını anlatmaktadırlar ki bu kısım, bir bilişsel iş üzerinde çalışırken aktif hale geçmektedir. Şu da açıktır ki teknik içerikli durumlarda kavram majı kendi başına yeterli olmayabilir.” (Vinner, 1991).

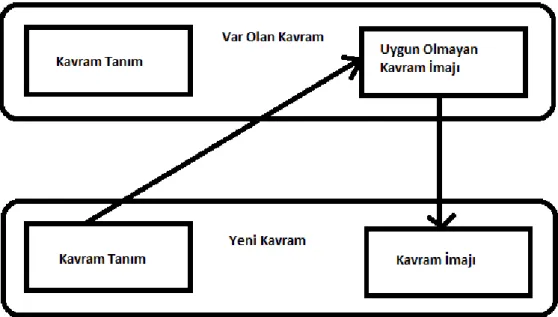
ġekil 7. Uygun Olmayan Kavram Ġmajının, Ġmaj ġekillenmesine Etkisi

ġekil 7 de kavram imajını Ģekillendirme esnasında etkin durumda olan uygun olmayan kavram imajının, kavram tanımı ile mücadele ettiği görülmektedir. Kavramla ilgili yeni bir durum söz konusu olduğunda tanımla ilgili özellikler, kavramla ilgili var olan kavram imajına baĢvurup yeni bir kavram imajı geliĢtirilmesine sebep olmaktadır.

2.3. Fonksiyon Kavramı

“…Fonksiyon kavramı matematikte önemli bir birleştirici kavramdır. İki küme arasında özel bir eşleme olan fonksiyon tüm müfredata yayılmıştır. Aritmetikte, fonksiyonlar sayı ikililerini tek bir sayıya eşleyen işlemlerdir (sayı ikililerindeki sayılann toplamı gibi); cebirde, fonksiyonlar sayılan temsil eden değişkenler arasındaki bağıntılardır; geometride, fonksiyonlar öteleme ve döndürme gibi hareketlerle nokta kümelerini görüntülerine eşler; olasılıkta, fonksiyonlar olayları olayların olma olasılıklarına eşlerler. Fonksiyon kavramı, teknolojik gelişmelerin sonucu olarak da ortaya çıkan ve gerçek dünyadaki birçok girdi-çıktı durumlarım temsil eden matematiksel ilişkiler olması açısından da önemlidir. Bunun bir örneği olarak hesap makinesi üzerindeki..√2 tuşu verilebilir.” (NCTM, 1989).

Fonksiyon kavramı matematiğin en temel kavramlarından biridir. 1960'lı yıllarda "yeni matematik" akımının etkisiyle fonksiyonlar, küme teorisi temel alınarak Bourbaki'nin sıralı ikili tanımı ile müfredatlarda yer almıĢtır. Günümüzde Amerika BirleĢik Devletlerinde, NCTM standartları fonksiyon kavramını müfredattaki diğer birçok kavramın üst kavramı olarak ifade eder ( Akkoç , 2006).

Fonksiyon kavramı, matematiğin temel ve birleĢtirici bir fikridir (Brieske, 1973) ve çoğu matematikçi ve matematik öğretmeni de bu fikre katılır (Selden ve Selden, 1992). NCTM (1989; 2000) tarafından matematikte birleĢtirici kavramların önemi vurgulanarak; fonksiyon kavramı, orta ve yüksek öğretim matematik müfredatı için merkezi ve diğer kavramları organize edici bir konu olarak görülmüĢtür. Sajka (2003) fonksiyon kavramının gösteriminin ve yorumunun çeĢitliliğiyle matematiğin temel kavramlarından biri olduğunu belirtmiĢtir. Biehler, Scholz ve Winkelman‟e (1993) göre fonksiyon kavramı matematik müfredatının tamamını etkileyen ve baĢka matematiksel kavramların öğretiminde kullanılan bir kavramdır. Matematik dersi diğer derslere göre daha güçlü bir sıralı yapıya sahip olduğundan Altun (1998), fonksiyonu tam olarak kavrayamayan bir öğrencinin fonksiyon kavramının önĢart olduğu baĢka bir kavramı da kavramasının zor olacağını belirtmiĢtir. Breidenbach (1992), Even (1990), Moschkovich (1993), Schwarz&Yerushalmy (1992) ve Sfard (1992) fonksiyonları iĢlem ve kavram açısından tanımlamıĢlar ve bu kavramların ikisinin de cebir öğreniminde önemli olduğunu belirtmiĢlerdir (Moschkovich, 2004). Breslich (1928), nicelikler arasındaki iliĢkileri ele alan fonksiyonel düĢünme olmadan matematiği anlamanın ve değerini bilmenin mümkün olamayacağını belirtmiĢtir.

1450 ve 1650 yılları arasında fonksiyon kavramına temel teĢkil edecek çeĢitli geliĢmeler olmuĢtur. Bunlar; reel sayıları ve hatta karmaĢık sayıları kapsayan sayı kavramının geniĢlemesi, sembolik bir cebirin geliĢtirilmesi, bilimin temel problemlerinden olan hareket araĢtırmalarının yapılması ve cebir ile geometrinin buluĢmasıdır . Fakat 18. yy‟ın baĢlarına kadar fonksiyon notasyonlarının henüz yayılmamıĢ olmasında, reel sayıların kontinyumu (continiuum) ve sembolik notasyonların geliĢimi gibi gerekli olan cebirsel yapıların oluĢmaması ve fonksiyonun soyut notasyonun tanımlanmasını gerektirecek ihtiyacın ortaya çıkmamasından kaynaklı isteklendirme yetersizliği baĢlıca nedenler olarak gösterilmiĢtir (Kleiner, 1989).

Vinner (1983), fonksiyon gösterimin fonksiyonun kuralının karakteristiğiyle sınırlanmaması gerektiğini, çünkü kuralın fonksiyonların farklı açılardan düĢünülebilir olma özelliğiyle çeliĢtiğini belirtmiĢtir. Sierpinska (1992) fonksiyon gösterimi, insanların dünyadaki gözlenen ve yaĢanan değiĢimlere uyum sağlama çabasının bir sonucu olarak görmektedir. Sierpinska, değiĢen objeleri x ve y sembolleriyle göstererek; f sembolünü, objeleri baĢka objelere dönüĢtüren bir iĢlem veya değiĢimler arasındaki bir bağıntı olarak vermiĢtir.

Schaaf (1930), fonksiyon kavramının geometrik, cebirsel ve girdi-çıktı makinesi (fonksiyon makinesi) olarak zihinsel görüntülerinin olduğunu söylemiĢtir. Schaaf (1930), fonksiyon kavramının geometrik ve cebirsel iki zihinsel imaj arasında bir rekabete neden olduğunu, ardından bu rekabete fonksiyonun bir girdi-çıktı makinesinin zihinsel imajı ile benzerliğinin yarattığı yeni bir kavramın da katıldığını ve böylece fonksiyonun geometrik kavramının gittikçe terk edilmeye baĢlandığını ve yeni rekabetin ussal (soyut, farazi, postulatlara dayalı) fonksiyon kavramı ile eski cebirsel (somut, analitik, yapısal) fonksiyon kavramı arasında olacağını ifade etmiĢtir.

Fonksiyonlar, anlaĢılmasında zorlukların olduğu bir kavramdır (Hauge, 93; Gaea, Orit ve Kay, 1990; Iaderosa ve Malara, 1999). Bunlar arasında en belirgin olanları Sierpinska (1992) tarafından belirlenen ve açıklanan bilgi felsefesi tarafından olaĢan zorluklardır. Bu zorluklar bir yandan matematiğin felsefesiyle, matematiksel metotlarla ve bilinçsiz yapılan düĢünme stratejileriyle, diğer yandan da fonksiyon kavramı ve iliĢkili olduğu terimlerle (fonksiyonun tanım kümesi, değer kümesi, görüntü kümesi, fonksiyonun tersi, değiĢken kavramı, bağımlı ve bağımsız değiĢkenler, koordinatlar, fonksiyonun grafiği, tablosu, fonksiyonun kuralı gibi) ilgilidir (Aktaran: Sajka, 2003).

Fonksiyonlar matematiğin temel kavramlarından biri olmakla beraber (Davis, 1984), (Tall & Vinner, 1981) öğrencilerin çoğu ne yazık ki fonksiyon kavramını çok basit ve ilkel bir Ģekilde anlayıp, kökleĢmiĢ kavram yanılgılarına sahiptirler (Meel, 2003). Buna çözüm üretme açısından öğrencilerin fonksiyon kavramını anlama seviyelerini tanımlamak için çok sayıda giriĢimler olmuĢtur. Dyrszlag (1978), Bergeron ve Herscovics (1982) ve Vollrath (1984) tarafından böyle seviyeler bulunmaya çalıĢılmıĢtır. Sierpinska (1992) tarafından yapılan bir çalıĢmada öğrencilerin fonksiyon kavramıyla ilgili yaptıkları aktiviteler ve belli baĢlı anlama kategorileri Ģu Ģekilde tanımlanmıĢtır:

1. Fonksiyonu sayısal denklemler ve bilinmeyenler olarak düĢünme,

2. Fonksiyonu yeni bir iĢleme veya düĢünmeye baĢlama noktası olarak görme (bir denklemi belirtme baĢlangıcı olarak görme). Böylece fonksiyonu bir denklemi çözmeyle iliĢkilendirme,

3. Fonksiyonu bir formül olarak değerlendirme,

4. Fonksiyonu bir iĢlem süreci olarak görme (Bir sayı verildiğinde yeni bir sayı bulma)

5. Grafik çizmeye yarayan bir çeĢit formül olarak görme.

Fonksiyon yapısal olarak bir kavramı, iĢlemsel olarak ise bir iĢlem sürecini ifade eder ve fonksiyonların farklı iki yolla anlaĢılması fonksiyon öğreniminde bir zorluk yaratır (Sfard, 1991). Kuratowski ve Mostowski (1966) fonksiyonunun yapısal açıdan bir sıralı ikililer kümesi olduğunu, Skemp (1971) iĢlemsel olarak da bir hesaplama süreci veya iyi tanımlı bir sistemden bir baĢka sistem oluĢturma metodu olduğunu belirtmiĢtir (Aktaran: Sajka, 2003). Sfard‟a (1991) göre biri diğerine baskın gelmeyen bu iki anlama yolu aslında birbirini tamamlamakta ve tutarlı bir bütünlük oluĢturmaktadır.

Fonksiyon gösterimi bir baĢka açıdan da birden fazla anlama gelir. Sierpinska (1992) fonksiyonları anlamada esnekliğin gerekli olduğunu vurgulamıĢtır. Örneğin f(x) sembolü bir fonksiyonun adını ve aynı zamanda da f fonksiyonunun değerini gösterir. Sierpinska yorumun içeriğe bağlı olduğunu ancak bu durumun ileri seviyede olmayan bir öğrencinin kafasını karıĢtırabileceğini belirtmiĢtir.

Even (1993), fonksiyonun günümüzde kullanılan tanımını Ģu Ģekilde vermiĢtir: Tanım: A ve B verilen iki küme olmak üzere, A B kartezyen kümesinin özel bir Ģartı sağlayan bir alt kümesine, A kümesinden B kümesine bir f fonksiyonu denir. Bu özel Ģart; A‟daki her eleman için B‟nin sadece bir b elemanı vardır öyle ki (a,b) ∈ f dir. Burada, A‟ya f fonksiyonunun tanım kümesi ve B‟ye değer kümesi denir. Bu tanım formal Drichlet-Bourbaki tanımı ile tutarlıdır. Bir çok araĢtırmacı, öğrencilerin bu tanımı problem çözerken pek kullanmadıklarını belirtmiĢtir (Dreyfus ve Eisenberg, 1983; Even, 1993; Ferini, Mundy ve Graham, 1991; Markovits, Eylon ve Bruckheimer, 1983, 1986; Marnyanskii, 1975; Vinner, 1983; Vinner ve Dreyfus, 1989) (Aktaran: Meel, 2003).

Vinner ve Dreyfus (1989) tarafından yönetilen bir çalıĢmada, öğrencilerin fonksiyonu tanımlamaları istenmiĢ ve alınan cevaplar altı kategoride toplanmıĢtır.

1) Formal Drichlet-Bourbaki tanımı,

2) Ġki değiĢken arasındaki bir bağımlılık bağıntısı, 3) Belirli bir ölçüde düzenlilik gerektiren bir kural, 4) Bir iĢlem veya iĢlem süreci,

5) Bir formül, cebirsel ifade veya denklem,

6) Bir grafik veya sembolik formdaki bir gösterim.

Öğrenciler genellikle fonksiyonu taĢıma eylemiyle iliĢkilendirerek bir formül olarak algılarlar (Graham, Ferini ve Mundy, 1990; Breidenbach, Dubinsky, Hawks ve Nichols, 1992). Bunun bir sebebinin, derslerde fonksiyonlarla ilgili problemlerin büyük bir kısmında öğrencilerin fonksiyonu bir formül olarak ele almalarının olabileceği belirtilmiĢtir (Even, 1993; Vinner ve Dreyfus, 1989).

Böyle bir bakıĢ fonksiyon kavramının yapısal temelde anlaĢılmasını Ģüphesiz sınırlı tutacaktır.

Leinhard (1990) ve Vinner&Dreyfus (1989), öğrencilerin bağıntıları fonksiyon olup olmamalarına göre sınıflamaları esnasında yaptıkları hataların çoğunun Dirichlet-Bourbaki tanımının kabul görmesindeki yetersizliğin bir sonucundan meydana gelmediğini vurgulamıĢlardır. Öğrencilerin Dirichlet-Bourbaki fonksiyon tanımını kabul ettikleri fakat fonksiyonları sınıflamaları istendiğinde neredeyse fonksiyonun eski tanımlarına oldukça benzeyen kiĢisel deneyimlerine daha fazla güvendikleri belirtilmiĢtir. Fonksiyonun eski tanımları Ģu Ģekildedir: “iki değiĢken öyle iliĢkilidir ki birindeki değiĢim diğerinde de değiĢim yaratır, bu durumda ikinci değiĢkene birincinin bir fonksiyonu denir” veya “x değiĢkenini içeren ve x‟e bir sayı verildiğinde net bir değer alan matematiksel bir ifadeye x in bir fonksiyonu denir” (Hight, 1968). Bu yüzden, yapılan hataların bir kavram yanılgısının sonucundan kaynaklanmadığı daha çok uygulamada öğrencilerin yanlıĢ kavram bilgisiyle hareket etmelerinden kaynaklandığı vurgulanmıĢtır (Meel, 2003).

Carlson (1998), çoğu öğrencinin cebirsel tanımlı bir fonksiyonu ve denklemi ayrı tutmada zorluk yaĢadığını söylemiĢtir. Carlson ve Oehrtman‟a (2005) göre eĢitlik iĢaretinin çeĢitli kullanımları olduğu ve çoğu eğitimcinin bir denklem gibi formül kullanmayı tercih ettikleri düĢünüldüğünde bu ĢaĢırtıcı değildir. Öğrenciler için denklem kelimesinin belirsiz ve çeĢitli Ģekillerde kullanımı, öğrencilerin iki değiĢen nicelik arasındaki bir iliĢkiyi temsil etmede kullanılan eĢittir iĢaretinin kullanımı ile iki ifadenin eĢitliğini ifade etmede kullanılan eĢitlik iĢaretinin kullanımını ayırt etmelerinde zorluk yaĢamalarına sebep olmaktadır (Ural, 2006).

Carlson ve Oehrtman (2005) öğrencilerin fonksiyonu; girdi değerlerinin kümesini, çıktı değerlerinin kümesine eĢleme Ģeklinde kavramamalarının sonucunda, fonksiyonun grafiğini sabit bir nesne gibi gördüklerini söylemiĢtir. Carlson ve Oehrtman‟a (2005) göre öğrenciler, bir fonksiyonun grafiğini düzlemde bir eğri veya sabit bir obje olarak düĢünürler ve girdi değerlerinin kümesini çıktı değerlerinin kümesine bir eĢleme olarak göz önüne almazlar. Bu durum, öğrencilerin bir fonksiyonun grafiğini çözümlemelerini ve yorumlamalarını Ģüphesiz engellemektedir.

Breidenbach‟a (1992) göre, öğrencilerin çoğu fonksiyonun tek bir cebirsel formülle tanımlanabilir olduğuna inanmaya eğilimlidirler ve bu yüzden bir fonksiyonun kuralı parçalı olarak verildiğinde kafaları karıĢır. Bu eğilimleri öğrencilerin, fonksiyonlar hakkında geniĢ düĢünmelerini engeller ve bütün fonksiyonların her zaman düzgün bir Ģekilde davrandıkları Ģeklinde hatalı bir bilgiye sahip olmalarına yol açar. Öğrenciler örneğin f1(n) = n2 ve f2(n) =

1

(2 1) n

k

k aynı fonksiyonu temsil eden farklı

formül kullanımlarını kavramada güçlük çekerler (Carlson ve Oehrtman, 2005).

Diğer taraftan, Schwarz ve Hershkowitz (1999) çoğu öğrencinin fonksiyonları lineer (1. dereceden) veya kuadratik (2. dereceden) olduğunu varsayma eğilimde olduğunu belirtmiĢtir. Carlson ve Oehrtman (2005) bu durumun nedenini fonksiyonların tipik olarak okul müfredatlarında çoğu zaman lineer veya kuadratik olarak tanıtılmasına bağlamaktadır. Örneğin öğrenciler rasyonel veya köklü ifadeleri fonksiyon olarak değerlendirmeyebilirler.

Öğrencilerin fonksiyonlarda yaĢadığı bir baĢka zorluk ise fiziksel bir olayın görsel nitelikleri ile olayı modelleyen bir fonksiyonun grafiğinin benzer niteliklerini karıĢtırmalarıdır. Bir fonksiyonun grafiğini, girdi değerlerinin bir kümesinden çıktı değerlerinin bir kümesine bir dönüĢüm olarak düĢünmekten ziyade konu olan fiziksel

durumun bir resmi olarak görürler. Reel yaĢamda somut durumları modellemede fonksiyonları kullanırken sık sık tomografiksel yapılar kullanılır ve öğrenciler bir fonksiyonel iliĢkinin grafiğini çizerken bu topografiksel Ģeklin belirgin özelliklerinden etkilenebilirler. Böylece öğrencilerin yapabileceği çeĢitli hata tipleri ortaya çıkar (Carlson, 1998; Monk, 1992; Monk ve Nemirovsky, 1994). Örneğin ġekil 1‟de iniĢli-çıkıĢlı bir arazinin yandan grafiksel bir resmi verilmiĢtir. Bu arazide bisikletli bir sürücünün hız-konum grafiğini çizerken öğrenciler çizecekleri grafiğe verilen arazi Ģeklinin özelliklerini yansıtabilirler (Monk, 1992).

ġekil 8. Bir arazinin yandan topografiksel resmi

Öğrencilerin fonksiyonlarla çalıĢırken yaĢadığı bir diğer yaygın biliĢsel zorluk, fonksiyon gösterimini kullanabilmeleriyle ilgilidir. Gösterimler geniĢ çapta bir bilgiyi özetler nitelikte olduğu için anlamakta zorluk çekerler. Örneğin Carlson (1998) öğrencilere, s‟yi t‟nin bir fonksiyonu olarak göstermeleri istendiğinde hangisinin bağımlı hangisinin bağımlı ve bağımsız değiĢken olduğu veya bunun nasıl yazılacağı konusunda zorluklar yaĢadığını belirtmiĢtir.

Öğrenciler ters fonksiyon kavramıyla ilgili olarak da öğrenme zorluğu yaĢarlar. Girdi ve çıktıların genel bir görüntüsü olmaksızın öğrenciler bir fonksiyonu ters çevrilebilir bir iĢlem süreci olarak düĢünemezler. Fakat sadece x ve y değiĢkenlerinin yerlerini değiĢtirerek x‟i çözme veya fonksiyonun grafiğini y=x doğrusuna göre simetriğini alma gibi iĢlemlerle ters alma iĢlemlerini pratik olarak yapabilirler ve ters fonksiyon kavramını anlamaları bu kadarla sınırlıdır. Eğer bu yaptıklarının mantığını anlayamazlarsa bu iĢlemsel yaklaĢım öğrenciler için gerçek bir anlam taĢımaz veya çok az bir anlam taĢır (Carlson, Oehrtman, 2005). Carlson, Oehrtman ve Engelke (2005) tarafından iki bin öğrenci üzerinde yapılan bir araĢtırmada, fonksiyonun bazı değerlerine ait bir tablo verildiğinde, öğrencilerin sadece %17‟sinin verilen bir değer için fonksiyonun tersinin değerine karar verebildikleri belirlenmiĢtir.

Diğer bir zorluk ise öğrencilerin bir durumu veya modeli açıklayıcı bir fonksiyona ait tabloyu tamamlamaya çalıĢmalarında ortaya çıkmaktadır. Ayrıca öğrenciler fonksiyonel değiĢkenler olan sembolleri tablodan denkleme dönüĢtürürken de

zorluk yaĢarlar (Herscovics, 1989). Kieran (1992) öğrencilerin denklemlerden ve tablolardan hareketle grafik çizmede ve grafiği yorumlamada da zorluklar yaĢadıklarını belirtmiĢtir ( Olsen, 1995).

Diğer taraftan, öğrenciler fonksiyonel değiĢkenleri göstermek için seçilen harflerin keyfiyetinin de farkında değildirler. Onlar literatürde kullanılan bir sembolü değiĢtirmenin bir fonksiyon tablosunun değerlerinde bir değiĢikliğe neden olabileceğine inanırlar (Herscovics, 1989). Öğrenciler fonksiyonu genellikle f(x), g(x) gibi sembollerle öğrendiklerinden ϕ(σ)=2σ+k gibi bir ifadeyi fonksiyon olarak algılamakta güçlük çekerler.

2.4. Ġlgili AraĢtırmalar

2.4.1 Fonksiyon Kavramı ile Ġlgili Yapılan AraĢtırmalar

Fonksiyon kavramı ile ilgili araĢtırmaların bazılarını aĢağıda verilmiĢtir.

Fonksiyon kavramı bağıntısal anlamda, girdilerin kümesi ile çıktıların kümesi arasında neden sonuç iliĢkilerini kapsayan bir bağıntı olarak tanımlanacağı gibi, temel düĢünce olarak bir niceliğin bir ya da daha fazla nicelikle olan bağıntısı olarak da tanımlanabilir (Hedrick, 1938).

Malik‟e (1980) göre fonksiyon fikri öğrencilere üç farklı aĢamada sunulmalıdır. Öncelikle öğrencilere değiĢken kavramı öğretilmelidir. Daha sonra ilgili problemlerde değiĢim fikrini tecrübe etmeleri sağlanmalı ve son olarak da iki küme arasında iliĢki kurma fikri verilmelidir.

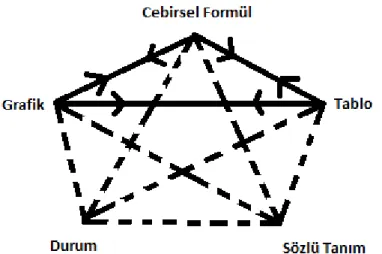
Janvier (1987), matematiksel fonksiyon kavramını öğrenmede tasarladığı pentagonal modeli bir çatı olarak sunmaktadır (Akt: Bowman, 1993) (ġekil 9). Pentagon modelin beĢ çizgisi matematiksel fonksiyonun beĢ yaygın gösterimini belirtmektedir; grafik, tablo, cebirsel formül, sözlü tanım ve durum (içerik). KöĢegenler, gösterimler arasındaki geçiĢi, tek yönlü geçiĢler ise kaynak-hedef geçiĢlerini göstermektedir.

ġekil 9. BeĢgensel Model

Matematiksel fonksiyon kavramı Dirichlet-Bourbaki küme-teorik tanımına dayalı matematiksel perspektiften (Vinner ve Dreyfus, 1989) veya fonksiyonun değiĢken büyüklükler arasındaki bir bağıntı olarak sunulduğu bilimsel perspektiften (Sierpinska, 1992) verilebilir. Matematiksel perspektif; cebirsel formüllere, tablolara, grafiklere ve bu üç gösterim arasındaki iliĢkisel dönüĢüme odaklanır (ġekil 10). Matematiksel perspektifte; bir fonksiyon boĢ kümeden farklı A ve B kümeleri arasında, A‟nın her bir elemanını B‟nin yalnızca bir elemanına eĢleyen bir iliĢkidir.

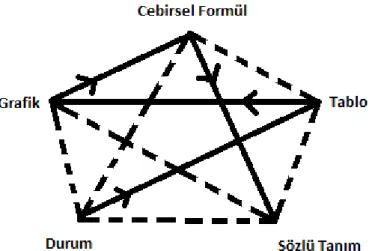
Bir kavramın ortaya çıkmasının temelinde çoğu zaman mevcut yaĢanan problemlerin yattığı düĢünüldüğünde, fonksiyon kavramına daha bilimsel (sistematik, rasyonel) bir perspektiften yaklaĢılabilir. Bilimsel perspektifte tüm bu beĢ gösterimi ve durumdan tabloya, tablodan grafiğe, grafikten cebirsel formüle ve cebirsel formülden sözlü ifadeye geçiĢler de dahil edilir (Ģekil 11) (Aktaran: Bowman, 1993). Sierpinska (1992), bir kavramın anlamının ona kaynağını veren problemlerde ve sorularda yattığı varsayıldığında, öğrencilerin fonksiyonu kavramaları için bilimsel perspektifin oldukça mantıklı göründüğünü belirtmektedir.

ġekil 11. Fonksiyon Kavramına Bilimsel (Sistematik) Perspektif

BeĢgensel modelin çatısındaki bu iki perspektif kıyaslandığında, fonksiyonun çeĢitli gösterimleriyle ve fonksiyon kavramının geniĢ çapta ve derinlemesine anlaĢılmasını sağlamasıyla ilgili problemler sadece matematiksel fonksiyonun öğretilmesi yollarına özgü olarak görülebilir. Ancak bu model;

(a) Müfredat tasarlama ve öğretimsel uygulamalardaki eksiklikleri belirlemede, (b) Matematiksel fonksiyon kavramını öğretme ve öğrenme araĢtırmalarını tasarlama ve yorumlamada da kullanılabilir. BeĢgensel modelin ayrıca,

(a) Matematiksel fonksiyonu öğrenme ve öğretme üzerine yapılmıĢ araĢtırmaları yeniden analiz etmede,

(b) Matematiksel fonksiyon kavramlarını daha güçlü biçimlendirmek için öğrenenlerin çeĢitli gösterimleri nasıl bağladıklarını anlamamızdaki eksiklikleri doldurmaya yönelik araĢtırmalar için ortak bir eylem planı çatısı kurmada ve

(c) Eğitim araĢtırmacıları, öğretim programı uzmanları ve sınıf öğretmenleri arasında iletiĢim için bir model araç olarak kullanılabileceği önerilmektedir (Bowman,1993).

Vinner (1983) öğrencilerin fonksiyonlarla ilgili kavram görüntülerini incelemiĢtir ve aĢağıda belirtilen kavram görüntülerini gözlemlemiĢtir:

. Bir fonksiyon bir tek kuralla verilmelidir. Ġki kural varsa, iki ayrı fonksiyon vardır. . Bir fonksiyonun "makul (düzgün)" bir grafiği olmalıdır.

. Fonksiyon tanımını bire-bir olma ile karıĢtırma. . Her fonksiyon birebirdir.

. ĠĢaret ve tam değer fonksiyonları için, fonksiyon olma koĢullarını dikkate almama. .Cebirsel olarak ifade edilmeyen fonksiyonları, özel olarak adlandırılmadıkları takdirde, fonksiyon olarak kabul etmemek.

Vinner (1983), ayrıca öğrencilerin çoğunun, fonksiyon kavramına çok özel ve kiĢisel anlamlar yükleyerek, kiĢisel kavram tanımlarını kullandıklarını bulmuĢtur. Akkoç (2002, 2005) ise, çeĢitli fonksiyon temsilleri için lise 3 öğrencilerinin tanımsal özellikleri nasıl kullandıklarını incelemiĢ ve öğrencilerin bazı temsillerde diğerlerine göre daha baĢarılı olduklarını gözlemlemiĢtir.

Even (1990) yapmıĢ olduğu çalıĢmada, öğretmen adaylarının fonksiyonlar konu-sundaki alan bilgilerini incelemiĢ ve birçok eksiklikler tespit etmiĢtir. Örneğin, katı-lımcıların büyük bir çoğunluğu bir fonksiyonun tanım kümesindeki her elemanı değer kümesinde bir ve yalnız bir elemana eĢlemesi gerektiği (univalence condition) kuralını bilmekle beraber bu özelliğin neden ve niçin önemli olduğu gibi sorulara mantıklı cevaplar verememiĢlerdir. Even, bu durumu ciddi bir eksiklik olarak görmekte ve bunun sebebi olarak da öğretmen yetiĢtirme programlarında alan bilgisinin iki temel özeliğinden biri olan sözdizimsel bilgilere yeterince önem verilmemiĢ olmasını gös-termektedir. Aynı çalıĢmada, katılımcıların çok büyük bir kısmı

, ( ) 0, . x x rasyonel sayıise g x x irrasyonel sayıise

ifadesini fonksiyon olarak kabul ederken, bu fonksiyonun grafiksel formunu reddetmiĢlerdir. Gerekçe olarak da, fonksiyon grafiğinin düzgün artan veya azalan sürekli bir eğri veya doğru olmayıĢını belirtmiĢlerdir. Bu durum ise öğretmen

adaylarının kavram tanımları ve kavram imajları arasında ciddi farklılıkların olduğunu göstermektedir.

Norman‟ın (1992) yapmıĢ olduğu nitel çalıĢmanın sonuçları ise lise öğretmenlerinin hem fonksiyon kavramını derinlemesine anlamada hem de fonksiyonlar konusunun izahında kullanılan temsilleri (grafikler, cebirsel ifadeler v.s.) ve sembolleri anlama ve kullanmada yetersiz olduklarını göstermiĢtir. Örneğin katılımcıların çoğu, bir fonksiyonu temsil için kullanılan „f‟ sembolü ile x gibi bir değiĢkenin bu fonksiyon altındaki görüntüsünü temsil için kullanılan f(x) sembolü arasındaki içeriksel farkı anlamakta yetersiz kalmıĢlardır. Bayazit‟in (2006) çalıĢması ise meslekte uzun yıllar çalıĢmıĢ tecrübeli öğretmenlerin bile kendilerini tek tür temsile (cebirsel ifadelere) kısıtladıklarını ve fonksiyonların cebirsel ve grafiksel formları arasında iliĢkilendirme yapmakta oldukça zorlandıklarını ortaya koymuĢtur.

Carlson ve Oehrtman (2005) fonksiyonlara iĢlem perspektifinden veya girdi-çıktı süreci perspektifinden yaklaĢılmasını Ģu Ģekilde kategorize etmiĢtir:

ĠĢlem Perspektifinden Girdi-Çıktı Süreci Perspektifinden 1)Bir fonksiyon özel bir kurala, formüle

veya hesaplamaya bağlıdır. Özel

hesaplamaları veya adımları

gerçekleĢtirmeyi gerektirir.

1) Bir fonksiyon girdi değerlerinin kümesinden çıktı değerlerinin kümesine bir eĢleme tanımlayan genelleĢtirilmiĢ bir girdi-çıktı iĢlemidir.

2) Bir öğrenci her bir eylemi yapmalı veya düĢünmelidir.

2) bir öğrenci her bir eylemi yapması gerekmeden tüm süreci düĢünebilir. (çıktı kümesini fonksiyonun alacağı

değerleri tek tek bulmadan

düĢünebilir.)

3) Cevap formüle bağlıdır. 3) Süreç formülden bağımsızdır.

4) Bir öğrenci girdi veya çıktı olarak sadece tek bir değer düĢünebilir.(örneğin x, belirli bir değeri simgeler.)

4) Öğrenci tüm girdilerin kümesini düĢünebilir, onun için girdiler süreklilik arz eder.

5) Ters alma iĢlemi hemen hemen cebirseldir ( x ve y’yi yer değiĢtirip x’i bulma ) veya geometriktir ( grafiğin y=x doğrusuna göre simetriğini bulma).

5) Bir fonksiyonun tersini bulma; çıktı değerlerinin kümesinden girdi değerlerinin kümesine bir eĢleme tanımlayan ters çevrilebilir bir süreçtir.

6) Tanım ve görüntü kümelerini bulma bir cebir problemi gibi düĢünülür (payda sıfır olamaz, kökün içi negatif olamaz gibi).

6) Tanım ve görüntü kümeleri, tüm olası girdi ve çıktıların kümesi üzerinde

iĢlem ve yansıtma yapılarak

oluĢturulur.

7) Fonksiyonlar statik olarak düĢünülür. 7) Fonksiyonlar dinamik olarak düĢünülür.

8) Bir fonksiyonun grafiği geometrik bir Ģekildir

8) Bir fonksiyonun grafiği girdilerin kümesinden çıktıların kümesine belirli bir eĢleme olarak düĢünülür.