SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
a2 + ab + b2 BİNARİ KUADRATİK FORMUNUN BAZI ELEMANTER ÖZELLİKLERİ VE a2 + ab + b2 BİNARİ KUADRATİK FORMLARI
İLE TAMSAYI KENARLI ÜÇGENLER ARASINDAKİ İLİŞKİLER ÜZERİNE
Nuran GÜZEY YÜKSEK LİSANS TEZİ MATEMATİK ANABİLİM DALI
T.C.
SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
a2 + ab + b2 BİNARİ KUADRATİK FORMUNUN BAZI ELEMANTER ÖZELLİKLERİ VE a2 + ab + b2 BİNARİ KUADRATİK FORMLARI
İLE TAMSAYI KENARLI ÜÇGENLER ARASINDAKİ İLİŞKİLER ÜZERİNE
Nuran GÜZEY
YÜKSEK LİSANS TEZİ MATEMATİK ANABİLİM DALI
Bu tez 15 /08/ 2006 tarihinde aşağıdaki jüri tarafından oybirliği ile kabul edilmiştir.
Yrd. Doç. Dr. Ahmet CİHANGİR Yrd. Doç. Dr. Süleyman SOLAK (DANIŞMAN) (JÜRİ)
Öğr. Gör. Dr. Ahmet DOĞAN (JÜRİ)
i ÖZET Yüksek Lisans Tezi
a2 + ab + b2 BİNARİ KUADRATİK FORMUNUN BAZI ELEMANTER ÖZELLİKLERİ VE a2 + ab + b2 BİNARİ KUADRATİK FORMLARI İLE TAMSAYI KENARLI ÜÇGENLER ARASINDAKİ İLİŞKİLER ÜZERİNE
Nuran GÜZEY Selçuk Üniversitesi Fen Bilimleri Enstitüsü Matematik Anabilim Dalı
Danışman : Yard. Doç. Dr. Ahmet CİHANGİR 2006, v + 46 Sayfa
Jüri : Yard. Doç. Dr. Ahmet CİHANGİR
Bu çalışmada; ilk olarak, a, b tamsayıları için a2 + b2 biçiminde iki değişkenli ikinci dereceden ifadelerin bazı özelliklerine yer verilmiştir. Daha sonra, negatif olmayan ve a ≥ b şartını sağlayan a, b tamsayıları için, a2 + ab + b2 biçiminde iki değişkenli ikinci dereceden ifadelerin bazı özellikleri verilerek bunlar ile diğer ikinci dereceden ifadelerin karşılaştırılması verilmiştir. Son bölümde ise, kenarları a, b, c tamsayıları olan ve a2 + ab + b2 = c2 denklemini sağlayan üçgenlerin, yani tamsayı kenarlı özel üçgenlerin cebirsel ve geometrik özellikleri incelenmiştir.
ii
ABSTRACT M. Sc. Thesis
SOME ELEMENTARY PROPERTIES OF a2 + ab + b2 BINARY QUADRATIC
FORM AND THE RELATIONSHIPS BETWEEN a2 + ab + b2 BINARY
QUADRATIC FORMS AND TRIANGLES HAVING INTEGER SIDES
Nuran GÜZEY Selçuk Üniversity
Graduate School of Natural and Applied Science Department of Mathematics
Supervisor : Asist. Prof. Dr. Ahmet CİHANGİR 2006, v + 46 Pages
Jury : Asist. Prof. Dr. Ahmet CİHANGİR
In this study, some properties of a2 + b2 second-degree two-variable expressions are discussed for the integers of a and b. In addition, presenting some of
the properties of the second-degree two – variable expressions in the form of a2 + ab + b2 for integers a and b that are not negative and satisfying the condition of
a ≥ b, the comparison of these with the other second degree expressions are given. In the last section, the algebraic and geometric properties of the triangles whose sides are a, b and c integers and verifying the a2 + ab + b2 = c2 equation that is to say the special triangles having integer sides are examined.
iii ÖNSÖZ
Günümüze kadar matematik alanında sayısız çalışma yapılmış ve insanlığın yükselmesi için kurulan merdivene birer basamak daha ilave edilmiştir.
Matematiğin de gelişen dünya koşullarında değişmeden, gelişmeden durması düşünülemez. Bütün bilimlerde olduğu gibi matematik de asırlardır çok değişik alanlarda gelişim göstermiştir. Ayrıca matematiğin gelişiminin büyülü yönlerinden biri de sayılar teorisi ile geometri arasındaki ilişkilerdir.
Bu çalışma, Beauregard ve Suryanarayan (1999) ın “ Integral Triangles ” ve Nair (2004) in “Elemantary Results on the Binary Quadratic Form a2 + ab + b2 ” başlıklı makaleleri üzerine kurulmuştur. Diğer kaynaklara da dayanılarak; a2 + b2 biçiminde yazılabilen tamsayıların bazı özellikleri ile a2 + ab + b2 biçiminde yazılabilen tamsayıların özellikleri verilerek, bu iki çeşit sayı gösterimi karşılaştırılmıştır. Ayrıca a2 + ab + b2 biçimindeki tamsayıların bir kareye eşit olması (yani a2 + ab + b2 = c2) durumunda bu denklem ile geometride bir tamsayı kenarlı özel üçgenler temsil edilebildiğinden bu tip üçgenler incelenmiştir. Bu bağlamda bu tip üçgenlerin birçok geometrik ve cebirsel özellikleri ile üretilmesi için formüller verilmiştir.
“a2 + ab + b2 Binari Kuadratik Formunun Bazı Elemanter Özellikleri ve a2 + ab + b2 Binari Kuadratik Formları ile Tamsayı Kenarlı Üçgenler Arasındaki İlişkiler Üzerine” adlı tez konusunun tespitinde ve hazırlanması sırasında yardımlarını esirgemeyen danışman hocam Yard. Doç. Dr. Ahmet CİHANGİR’ e teşekkür ederim. Ayrıca her zaman yanımda olan ve yardımlarını esirgemeyen eşime ve aileme teşekkürü bir borç bilirim.
Nuran GÜZEY Temmuz 2006
iv KULLANILAN SEMBOLLER
Z : Tamsayılar kümesi.
Z+: Pozitif tamsayılar kümesi.
Z*: Negatif olmayan tamsayılar kümesi. Q : Rasyonel sayılar kümesi
Q*: Negatif olmayan rasyonel sayılar kümesi R : Reel sayılar kümesi,
a
p p , a yı böler.
N(n): Bir n doğal sayısının iki tamsayının kareleri toplamı olarak farklı gösterimleri sayısı,
v İÇİNDEKİLER ÖZET ... i ABSTRACT ... ii ÖNSÖZ ...iii SEMBOLLER ... iv İÇİNDEKİLER ... v 1.GİRİŞ ... 1 1.1. Kaynak Araştırması ... 2 1.2. Ön Bilgiler ... 4 2. a2 + b2 BİÇİMİNDE İKİ DEĞİŞKENLİ İKİNCİ DERECEDEN İFADELER ... 10 3. a2 + ab + b2 BİÇİMİNDE İKİ DEĞİŞKENLİ İKİNCİ DERECEDEN İFADELER ... 15 3.1. Giriş ... 15
3.2. Bazı Bilinen Sonuçlar... 15
3.3. Özdeşlikler ... 16
3.4. B – Asallarının Esas Formu ... 17
3.5. B – Sayılarının Çarpanları ... 24
3.6. Bir B – Sayısının Genel Formu ... 26
3.7. Rasyonel Sayı Bileşenli B – Sayıları ... 26
3.8. a2 – ab + b2 Formu İle Karşılaştırma ... 27
3.9. ka2 + kab + kb2 ye Denk Olan Formlar İle Karşılaştırma ... 28
3.10. a2 + b2 Gösterimi ile Karşılaştırma ... 28
3.11. Sonuç ... 30
4. TAM SAYI KENARLI ÖZEL ÜÇGENLER ... 31
4.1 Giriş ... 31
4.2. Tamsayı Kenarlı Özel Üçgenlerin Yarı Grubu ... 32
4.3 Üçlülerin Grubu ... 36
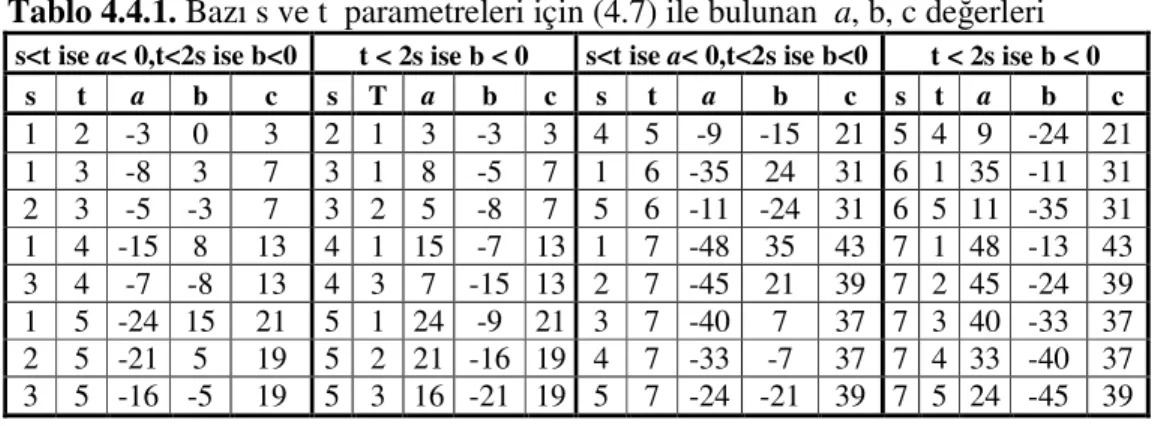
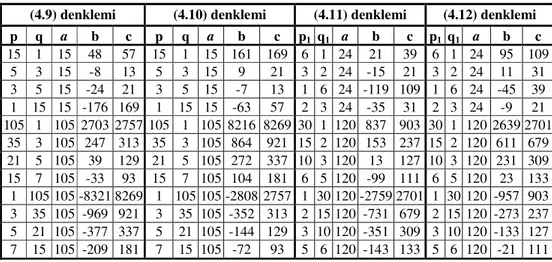
4.4 Üçlülerin Parametrik Gösterimi ... 37
4.5. Tamsayı Kenarlı Özel Üçgenlerin Bileşenlerinin Yapısı ... 39
4.6 Pythagorean Tamsayı Kenarlı Özel Üçgenler ... 44
1. GİRİŞ
Herhangi a, b tamsayıları için a2 ± ab + b2 ifadesine n dersek, n in de bir tamsayı olduğu açıktır. Acaba bu n tamsayısı hangi cebirsel özelliklere sahiptir? Ayrıca n bir tam kare, yani c∈ Z için n = c2 olması durumunda, a2 ± ab + b2 = c2 olacağından, bu ifade bize “a, b, c reel sayıları, herhangi bir üçgenin kenar uzunlukları olmak üzere a2 + b2 – 2 a.b.cos C = c2 dir.” biçiminde verilen ve kosinüs teoremi olarak bilinen özdeşliği hatırlatır. Bu durum ise; “a2 ± ab + b2 = c2 ifadesinin
hangi geometrik özellikleri vardır?” sorusunu akla getirir.
Üç yüzyıldan fazla zamandır, iki değişkenli ikinci dereceden ifadeler ve onların asal çarpanları üzerine kapsamlı araştırmalar yapılmaktadır. Bu konuyla ilgili ilk kapsamlı araştırma Lagrange tarafından yapılmıştır. Daha sonraları Legendre, Euler, Gauss gibi bir çok matematikçi bu konu üzerinde çalışmış ve halen bu konu çalışılmaya devam edilmektedir (Dickson 1999).
Herhangi a, b, x, y tamsayıları için ax2 + bxy + cy2 biçiminde ifade edilen ve daha çok Binary kuadratik form olarak bilinen; iki değişkenli ikinci dereceden ifadelerin genel teorisi üzerinde yapılan çalışmalar son dönemlerde özel modelleri üzerinde yönelmiştir. Çalışmamız, x2 + xy + y2 ifadesi ile ilgili olduğundan, bundan sonra ifademiz a2 + ab + b2 olarak alınacaktır. Örneğin A2 ± kB2 biçimindeki özel temsilleri göz önüne alalım. Bu ifadede k nın alacağı kare olmayan değerlere karşılık, bir çok farklı iki değişkenli ikinci dereceden ifadeler elde edilebilir. Gerçekten de a2 +ab + b2 = (a + b/2)2 + 3(b/2)2 olduğundan, çalışma konusuna bu A2 ± kB2 ifadesinin k = 3 için özel bir durumu olarak bakılabilir. Bu ifadelere bağlı bir çok asal sayı için temsil modelleri oluşturulmaktadır (Cox 1989).
Dickson (1999); tamsayı kenarlı üçgenlerin tarih boyunca birçok matematikçinin ilgisini çektiğini belirterek bu tip üçgenler hakkında ayrıntılı bilgiler vermiştir. Bu çalışmada, tamsayı kenarlı üçgenlerin özel bir modeli olan; kenarları a, b, c tamsayıları ve c kenarı karşısındaki açısının ölçümü tamsayı ve bu açının kosinüsü rasyonel değere sahip olan tamsayı kenarlı özel üçgenler ile ilgilenilmiştir. Bu alanda, zamanına kadarki çalışmaları eserinde özetleyen Dickson (1999), eserini ve bu konu ile ilgili diğer eserlerin incelenmesi sonucunda tamsayı kenarlı üçgenlerin çok etkileyici özelliklerini ortaya koymuştur. Örneğin tamsayı kenarlı üçgenlerin
sınırladığı alanının da tamsayı olması isteniyorsa, o zaman tamsayı kenarlı özel üçgenlerin özel bir modeli olan Heron üçgenlerine ulaşılır.
Bu çalışma dört bölümden oluşmaktadır. Birinci bölümde, çalışmayla ilgili kaynak araştırması, temel tanımlar ve ilgili temel teoremler asıl kaynaklarından alınarak verilmiştir. İkinci bölümde; iki değişkenli ikinci dereceden ifadelerin özel bir durumu olan, a ve b iki tamsayı olmak üzere a2 + b2 biçiminde yazılabilme anlamına gelen, iki tamsayının kareleri toplamının bazı özellikleri verilmiştir. Üçüncü bölümde ise ,negatif olmayan a, b tam sayıları için, a2 + ab + b2 biçiminde iki değişkenli ikinci dereceden ifadelerin özellikleri ve bu yapı ile diğer benzer yapıların karşılaştırmaları verilmiştir. Son bölümde de, kenarları a, b, c tamsayıları olan ve a2 + ab + b2 = c2 denklemini sağlayan üçgenlerin yani tamsayı kenarlı özel üçgenlerin cebirsel ve geometrik özellikleri incelenmiştir.
1.1. Kaynak Araştırması
Sierpinski(1962), Pythagorean Triangles isimli çalışmasında, tamsayı kenarlı üçgenlerin özel çeşidi olan Pythagorean üçgenlerini alan, kenar, çevre v.b. yönüyle incelemiştir. Bu, Pythagorean üçgenleri ile ilgili olarak yazılmış ilk çalışmasıdır.
Dickson(1999), eserinin ikinci cildinde Diophantine denklemlerini anlatmış, on üçüncü bölümünde de ax2 + bxy +cy2 = n ve ax2 + bxy +cy2 = dz2 biçimindeki ifadeler hakkında zamanına kadar yapılmış olan araştırmaların geniş bir özetini vermiştir. Ayrıca a, b, c ve d sayılarının özel durumlarına ilişkin olarak da geniş bir malumat vardır.
Heichelheim (1976), Edward Mcardle ve George Berzsenyi’ nin makalelerinden faydalanılarak; a2 + ab + b2 = c2 denkleminin genel çözümlerini gösteren iki teorem vermiştir.
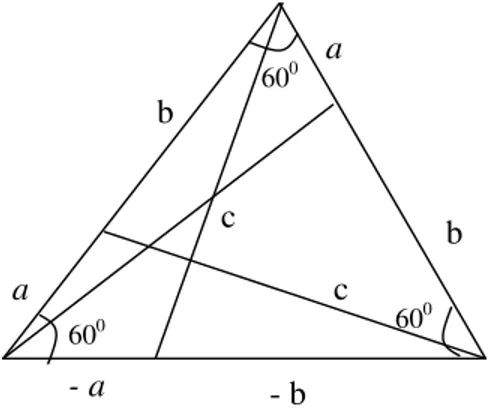
Gilder(1982), bir açısı 60o olan tam sayı kenarlı üçgenlerin kenarlarının iki parametreye bağlı olarak üretilmesini gösteren formüller vermiştir.
Selkirk (1983), 120o açılı tamsayı kenarlı üçgenleri kosinüs teoreminden faydalanılarak iki parametreye bağlı üretimlerini veren teoremler vermiştir.
Sierpinski (1988), ikinci bölümünde Diophantine denklemlerinin analizinin ele alındığı kitabının on birinci bölümünde de, doğal sayıların iki kare, üç kare ve
dört kare toplamı biçiminde gösterimleri verilmiş ve daha genel olarak diğer negatif olmayan k. kuvvetlerin toplamları olarak gösterimi geniş bir şekilde incelemiştir.
Adler ve Coury (1995), eserlerinin her bir bölümünde konuların anlatımını kısa tutarak, her bölüm sonunda konuyla ilgili önce çözülmüş ve sonra da çözülecek alıştırmalar vermiştir.
Elemanları tamsayılardan oluşan aritmetik diziden bir Heron üçgeninin kenar uzunlukları alınıyorsa bu üçgen aritmetik üçgen olarak isimlendirilir. Ayrıca bu aritmetik dizideki ardışık herhangi iki eleman arasındaki fark d ise üçgene d – aritmetik üçgen denir. Beauregard, Suryanarayan (1997), d - aritmetik üçgenleri inceleyerek; Pythagorean üçgenlerinden d – aritmetik üçgeninin nasıl elde edilebileceğini göstermişlerdir.
Hintli bir astronom ve matematikçi olan Brahmagupta (M.S. 598’de doğdu); yedinci yüzyılda ardışık tam sayı kenarlı Heron üçgenleri üzerine çalışmış ve primitif olan ilk sekiz tanesini tespit etmiştir. Beauregard ve Suryanarayan (1998) de Brahmagupta’ nın 1400 üncü doğum yılı anısına yayınladıkları makalelerinde bu tip üçgenlerin Pell denklemine bağlı olarak nasıl üretildiğini ortaya koymuşlardır.
Beauregard, ve Suryanarayan (1999), a2 + ab + b2 = c2 eşitliğini sağlayan a, b, c üçlülerinden oluşan tamsayı kenarlı üçgenlerin oluşturduğu kümenin yarı grup yapısını, parametrik biçimlerini, bileşenlerin yapısını ve pythagorean üçlüleriyle ilişkilerini incelemişlerdir.
Davenport (1999), eserinde sayılar teorisinin birçok konusunu verdikten sonra, ax2 + bxy + cy2 biçiminde verilen ikinci dereceden ifadeleri (Kuadratik formları) a, b, c tamsayılarının durumlarına göre ayrıntılı olarak incelemiştir.
Nair (2004); a2 + ab + b2 biçimindeki iki değişkenli ikinci dereceden ifadeler olarak gösterilebilen tamsayıların ilginç bazı özelliklerinin elemanter ispatlarını vermiştir. Ayrıca a2 + ab + b2 = p biçimindeki asalların k bir tamsayı olmak üzere 6k+1 biçiminde olduğunu göstermiştir.
MacLeod (2005); Kenarları tamsayı olan ve çevrel çemberinin yarıçapı olan R ile iç teğet çemberinin yarıçapı olan r nin oranı
r R
= N biçiminde tamsayı olan üçgenlerin oldukça az sayıda olduğunu ortaya koymuştur.
1.2. Ön Bilgiler
Bu kısımda daha sonraki bölümlerde kullanılacak tanım ve teoremler verilmiştir.
Tanım 1.1. Boştan farklı G kümesi üzerinde o : GxG → G biçiminde tanımlanan o ya G de bir ikili işlem veya kısaca işlem denir Ayrıca (G, o) sistemine de bir cebirsel yapı denir (Bozkurt, 2001).
Tanım 1.2. Bir cebirsel yapı üzerinde tanımlanan işlemin birleşme özelliği varsa bu cebirsel yapıya yarı grup denir (Bozkurt, 2002).
Tanım 1.3. Eğer (G, o) cebirsel yapısı birleşme, birim eleman ve ters eleman özelliklerine sahipse (G, o) cebirsel yapısına bir grup denir ve kısaca G grubu diye isimlendirilir. (Bozkurt, 2001).
Tanım 1.4. G, G′′′′ iki grup olmak üzere ϕ: G → G′ dönüşümü verilsin. Eğer ϕ dönüşümü, ∀ a, b∈ G için;
ϕ(ab) = ϕ(a)ϕ(b)
şartını sağlıyorsa bu dönüşüme grup homomorfizmi veya kısaca homomorfizm denir (Bozkurt, 2001).
Tanım 1.5. ϕ: G → G′ içine bir grup homomorfizmi olsun. Eğer ϕ homomorfizmi birebir ise ϕ ye bir izomorfizm denir (Bozkurt, 2001).
Tanım 1.6. Eğer bir ϕ grup homomorfizmi, birebir ve örten ise o zaman G ve G′ gruplarına izomorfik gruplar denir (Bozkurt, 2001).
Tanım 1.7. Sabit ve sıfırdan farklı bir m tamsayısı a ve b gibi herhangi iki tamsayının a – b farkını bölüyorsa (m|(a – b) ise) a, b ye m modülüne göre kongrüenttir denir ve bu a ≡ b(mod m) biçiminde belirtilir (Şenay, 1989).
Tanım 1.8. Bir kare matrisin esas köşegeninin üzerindeki elemanları dışındaki bütün elemanları sıfır ise bu matrise köşegen matris denir (Bozkurt ve Türen, 2002).
Tanım 1.9. z = a + bi karmaşık sayısının modülü veya mutlak değeri
2 2 b a bi a z = + = + şeklindedir (Sierpinski, 1988).
Tanım 1.10. Bir pozitif tamsayının 1 den büyük hiçbir kare çarpanı yoksa bu tamsayıya kare çarpansız (square – free) sayı denir. Başka bir deyişle onun asal çarpanlara ayrılışında bütün çarpanlarının kuvvetleri 1 ise bu sayılara kare çarpansız (square – free) sayı denir (Sierpinski, 1988).
Teorem 1.1. (Wilson teoremi). Herhangi bir p asalı için (p – 1)! ≡ – 1 (mod p) dir (Şenay, 1989).
İspat. Eğer p asal ise
xp – 1 – 1 ≡ (x – 1).(x – 2)…(x – p+1) (mod p)
dir. Burada x yerine sıfır yazılırsa o zaman her iki tarafın sabit terimleri elde edilir ki bu
– 1 ≡ ( p– 1)! (mod p) olmasını gerektirir (Şenay, 1989).
Teorem 1.2. p herhangi bir asal ve (p, c) = 1 olmak üzere x2 + y2 = c.p
olacak şekilde x ve y tamsayıları varsa, o zaman a2 + b2 = p
olacak şekilde de a ve b tamsayıları vardır (Bozkurt, 2001).
Teorem 1.3 (Fermat). Eğer a tamsayı, p asal ve p |/ a ise o zaman ap – 1 ≡
1(mod p) dir (Şenay, 1989).
Teorem 1.4 (Lagrange). Herhangi bir p asalı, a1, a2 , . . . , an – 1 tamsayıları ve an ≡/ 0 (mod p) şartını sağlayan an tamsayısı için f(x) polinomu
f(x) = anxn + an – 1xn– 1 + ... + a1x + a0 = ∑ = − n k k n kx a 0
şeklinde n dereceden bir polinom ise f(x)≡0 (mod p) kongrüans denkleminin en fazla n tane kökü vardır.
İspat. İspat n üzerinde tümevarımla yapılsın. n = 1 için; f(x) ≡ 0 (mod p) kongrüansı a0x + a1 ≡ 0 (mod p) şeklinde ve a0 ≡/0(mod p) olduğundan bu kongrüansın tam
olarak bir kökü vardır. Şimdi derecesi n – 1 olan her kongrüansın en fazla n – 1 tane kökünün olduğunu varsayarak; teoremin n için doğru olduğunu gösterelim. Eğer f(x) in derecesi n ve f(x0) ≡ 0 (mod p) ise f(x) ≡ (x – x0).g(x) ≡ 0 (mod p) olur. Burada
g(x) in derecesinin en fazla n – 1 olduğuna ilgi çekilmelidir. Bu durumda f(x) in herhangi bir kökü ya x0 veya g(x) in bir köküdür. Tümevarım hipotezinden dolayı
g(x) in kökleri x1, x2, …, xr olup burada r ≤ n – 1 dir. Eğer c, f(x) ≡ 0 (mod p)
kongrüansını gerçekleyen herhangi bir sayı ise bu durumda (c – x0).g (c) ≡ 0 (mod p)
olur. Bu ise c ≡ x0 (mod p) veya g(c) ≡ 0 (mod p) olmasını gerektirir. Buradan
1 ≤ i ≤ r aralığında kısıtlanan i ler için c = xi elde edilir. Başka bir deyişle f(x) ≡ 0 (mod p) kongrüans denkleminin r + 1 ≤ n tane kökü bulunmuş olur. Bu da f(x) in en fazla n tane kökünün bulunduğunu gösterir (Şenay, 1989).
Teorem 1.5 (Legendre). Eğer p asal ve d, p – 1 in bir böleni ise xd ≡1 (mod p)
kongrüansının tam olarak d tane farklı kökü vardır.
İspat. dp – 1 olduğundan, g(x) derecesi p – 1 – d olan bir polinom olmak üzere xp – 1 – 1 ≡ (xd – 1).g(x) (mod p)
dir. Lagrange teoremine göre
g(x) = xp – 1 – d + xp – 1 – 2d +…+ xd + 1
polinomunun en fazla n – 1 –d tane kökü vardır. Fermat teoreminden xp – 1≡ 1(mod p) kongrüansının en fazla p – 1 tane farklı kökü vardır. Bunlardan biri u ise
up – 1 – 1 = (ud – 1).g(u) ≡ 0 (mod p)
olmalıdır. Buradan ud – 1 ≡ 0(mod p) veya g(u) ≡ 0 (mod p) elde edilir. Lagrange teoremine göre bu denklemlerin kök sayıları da sırasıyla d ve p – 1 – d den fazla değildir. Buna göre
xd ≡ 1(mod p)
kongrüansının en az p – 1 – (p – 1 – d ) = d tane farklı kökü bulunmalıdır. Bunlardan daha fazla kök bulunmadığından bu kongrüansın tam olarak d tane kökü bulunacaktır (Şenay, 1989).
Tanım 1.11. Herhangi bir p asalı ve (a, p) = 1 olacak şekilde bir a tamsayısı için x2 ≡ a(mod p) şeklinde bir kongrüans verilsin.
Eğer bu kongrüansı sağlayan bir x tamsayısı varsa; yani denklem çözülebilirse, o zaman a ya p modülüne göre bir ikinci dereceden kalan denir ve aRp ile gösterilir.
Eğer bu kongrüansı sağlayan hiç bir x tamsayısı yoksa; yani denklem çözülemezse, o zaman a ya p modülüne göre bir ikinci dereceden olmayan kalan denir ve aNp ile gösterilir (Şenay, 1989).
Tanım 1.12. Eğer p asal ve (a, p) = 1 ise p a
şeklinde gösterilen Legendre sembolü
− = ise Np , 1 , 1 a ise aRp p a
olarak tanımlanır. Ek olarak pa ise p a = 0 dır (Şenay, 1989).
Tanım 1.13. Herhangi a, b ve c tamsayılar ve x ile y aralarında asal iki tamsayı temsil edendeğişkenler olmak üzere
ax2 + bxy + cy2 (*)
biçiminde iki değişkenli ikinci dereceden ifadesi verilsin. Bu durumda ∆ = b2 – 4ac eşitliğine (*) ifadesinin diskriminantı denir (Davenport, 1999).
Tanım 1.14. Diskriminantı eşit olan iki ikinci dereceden ifadeye denktir denir (Davenport, 1999).
Teorem 1.6 (Euler Kriteri). Herhangi bir p asalı ve (a, p) = 1 olacak şekilde bir a tamsayısı için x2 ≡ a (mod p) şeklinde bir kongrüans denklemi verilsin. Bu kongrüans denkleminin çözülebilir (yani a tamsayısının bir ikinci dereceden kalan) olması için gerek ve yeter şart
1 2 1 ≡ − p a (mod p)
kongrünsının doğru olmasıdır. İspat. Eğer aRp ise, x2
≡ a (mod p) nin x1, p – x1 gibi iki çözümü bulunduğundan
1, 2, …, p – 1 sayıları; x1 ve p – x1 çözümleri ile beraber birbirlerine eşit olmayan
2 1
(p – 3) sayıda ilgili çiftlere ayrılabilir. Bu durumda herhangi x, x´ ilgili çifti için x.x´≡ a (mod p)
iken x1 ve p – x1 çözümleri için
x1(p – x1) ≡ – x12 ≡ – a (mod p)
∏ ≡ − ≡− = − − = − − 1 1 2 1 2 3 1 1( ) )! 1 ( p x p p a a x p x x p (mod p) (1.1) elde edilir.
Öte yandan eğer aNp ise; 1, 2, 3, …, p – 1 sayıları (p – 1)/2 sayıda ilgili çiftlere ayrılabilir. Böylece ∏ ≡ = − − = − 1 1 2 1 )! 1 ( p x p a x p (mod p) (1.2)
elde edilir. Burada tanım 1.10 ile verilen Legendre sembolünü kullanacak olursak;
( )
2 1 )! 1 ( − − = − p p a a p (mod p) (1.3)toplu sonucu elde edilmiş olur.
Burada a = 1 ve
( )
1p = 1 olacak şekilde x2 ≡ 1 (mod p) kongrüansının çözümünün x = 1 olduğu göz önüne alınırsa (p – 1)! ≡ – 1 (mod p) sonucuna varılır. Bu (1.3) de kullanılacak olursa;( )
2 1 1 ≡ − p p a a (mod p)elde edilir ki burada
( )
pa = ± 1 olduğundan( )
2 1 − ≡ p p a a (mod p)elde edilir. Bu da ispatı istenendir (Şenay, 1989).
Teorem 1.7. – 1 sayısı, 4k + 1 biçimindeki asallar için bir ikinci dereceden kalandır. Yani; p, 4k + 1 şeklinde bir asalsa, o zaman z2 + 1 ≡ 0 (mod p) kongrüans denklemini sağlayan bir z pozitif tamsayısı vardır. Ayrıca – 1 sayısı, 4k + 3 biçimindeki asallar için bir ikinci dereceden olmayan kalandır.
İspat. Euler kriterinden (a, p) = 1 olmak üzere
2 1 ) 1 ( − − ≡ p p a (mod p) olduğundan burada a = – 1 alırsak,
2 1 ) 1 ( 1 − − ≡ − p p (mod p)
elde edilir. Burada – 1 sayısının ikinci dereceden kalan olması 2 1 − p sayısının çift
tamsayı olmasına bağlıdır. Yani 2 1 − p = 2k ⇒ p = 4k +1 olup − p 1 = (– 1)2k = 1 elde edilir. Ayrıca z = 1.2… 2 1 − p
olsun. 4n = p – 1 olduğundan z ifadesindeki çarpım sayısı çift olacaktır. Bunun sonucu olarak
z = (– 1)(– 2)…( 2
1 − − p )
olacaktır. Burada p – m ≡ – m (mod p) olduğu göz önüne alınırsa z2 = − 2 1 ... 2 . 1 p − − − − 2 1 )... 2 )( 1 ( p = − 2 1 ... 2 . 1 p + ...( −2)( −1) 2 1 p p p = (p – 1)!
bulunur. Teorem 1.1 e (Wilson teoremine) göre (p – 1)! ≡ – 1 (mod p) olduğundan istenen elde edilmiş olur.
– 1 sayısının 4k + 3 biçimindeki asallar için bir ikinci dereceden olmayan kalan olduğunun ispatı da benzer şekilde yapılır (Şenay, 1989).
Teorem 1.8. Bir tek asal p olsun. – 3 sayısının ikinci dereceden bir kalan olması için gerek ve yeter şart p ≡ 1 (mod 6) olmasıdır (Adler and Coury(1995)).
Tanım 1.15. A bir n boyutlu kare matris, I, n boyutlu birim matris ve λ reel sayı olmak üzere
det (λI – A) = ∆A( λ) = λn + a1.λn – 1 + a2.λn – 2 + ...+ an – 1.λ + an
polinomuna A matrisinin karakteristik polinomu denir (Bozkurt ve Türen, 2002). Tanım 1.16. ∆A (λ) = 0 denklemine A matrisinin karakteristik denklemi denir
(Bozkurt ve Türen, 2002).
Tanım 1.17. ∆A(λ) = 0 denkleminin köklerine A matrisinin öz değerleri veya
karakteristik değerleri denir (Bozkurt ve Türen, 2002).
Tanım 1.18. G bir değişmeli grup ise G nin sonlu mertebeden elemanlarının oluşturduğu H alt grubuna G nin torsiyon alt grubu denir.H nin elemanlarına da G nin torsiyon elemanları denir (Cohn,1995).
2. a2
+ b2 BİÇİMİNDE İKİ DEĞİŞKENLİ İKİNCİ DERECEDEN İFADELER ÜZERİNE
Bu bölümde iki değişkenli ikinci dereceden ifadelerin özel bir durumu olan, a ve b iki tamsayı olmak üzere a2 + b2 biçiminde yazılabilme anlamına gelen, iki tamsayının kareleri toplamının bazı özellikleri verilecektir.
Teorem 2.1. Herhangi iki tam sayının her biri iki kare toplamı şeklindeyse bunların çarpımları da iki kare toplamı şeklindedir.
İspat. Bunun için a, b, c, d tamsayılar olmak üzere u ve v tamsayılarının her birinin iki kare toplamı biçiminde olduğunu kabul edelim. Yani;
u = a2 + b2, v = c2 + d2 olsun. Bu durumda u.v = (a2 + b2)(c2 + d2) = a2 c2+ b2 c2 + a2 d2 + b2 d2 = a2 c2 + 2abcd + b2d2 + a2d2 – 2abcd + b2c2 = (ac + bd)2 + (ad – bc)2
elde edilir ki bu u.v tamsayısının da iki kare toplamı biçiminde olduğunu gösterir. Örnek 2.1. u = 13 = 22
+ 32, v = 25 = 32 + 42 olduğundan u.v = 25.13 = 325 = 152 + 102
yazılabilir. Bu ise u.v tamsayısının da iki kare toplamı biçiminde olduğunu gösterir.
Teorem 2.2. Eğer k bir tamsayı olmak üzere p asalı, 4k + 1 biçiminde ise o zaman p = a2 + b2 olacak şekilde a, b tamsayıları sayıları vardır.
İspat. Eğer p, 4k + 1 biçiminde bir asal ise x2 ≡– 1 (mod p) kongrüansı çözülebilir
olduğundan 0 ≤ x ≤ p – 1 olacak şekilde x2 ≡ – 1 (mod p) kongrüansının bir x çözümü vardır. Çünkü x sayısı p ile bölündüğünde kalan yine 0 ≤ x ≤ p – 1 aralığına düşecektir. Bundan dolayı x için x ≤
2 p
olarak kabul edebiliriz. Eğer x > 2 p
ve x2 + 1, p nin bir katı olacak şekilde kabul edebiliriz. O zaman x2 + 1 = c.p olacak şekilde bir c tam sayısı bulunur. Buradan c.p = x2 + 1 ≤
4
2
p
bulunur. Bu ise p |/ c demektir. Böylece Teorem 1.2 den dolayı p = a2 + b2 olacak şekilde a, b tamsayıları vardır.
Örnek 2.2.1. p = 29 asalı 29 = 4.7 + 1 olarak yazılabildiğinden, 4k + 1 biçimindedir. O halde 29 asalı iki tamsayının kareleri toplamı biçiminde yazılabilmelidir. Gerçekten 29 = 22 + 52 olarak yazılır.
Teorem 2.3. m = a2
+ b2 = n.k olsun. Eğer k iki kare toplamı değilse, n iki kare toplamı olmayan bir asal çarpana sahiptir.
İspat. m = n.k olsun. Eğer k iki kare toplamı biçiminde değilse, o zaman n nin n = p1.p2…px… biçiminde asal çarpanları bulunsun. Bütün pi lerin hepsinin iki kare toplamı biçiminde yazılabildiğini kabul edelim(i = 1, 2, …, x). O zaman Teorem 2.1. den dolayı
1
p m
tam sayısı bir iki kare toplamı,
2 1. p
p m
tam sayısı bir iki kare toplamı
ve bu şekilde devam edilirse
x p p p m ... . 2. . 1
t tam sayısı da bir iki kare toplamı olur ve
sonuçta k bir iki kare toplamı olur. Bu ise hipotezle çelişir. O halde bütün pi ler iki
kare toplamı olamaz. Örnek 2.3.1. 12789 = 1052
+ 422 = 1827.7 olur. Burada 7 iki kare toplamı olarak yazılamaz. 1827 = 609.3 olarak yazılabildiğinden, 3 sayısı da kare toplamı olarak yazılamaz.
Teorem 2.4. Bir n doğal sayısının iki tamsayının kareleri toplamı biçiminde olması için gerek ve yeter şart, n in asal çarpanlarına ayrılışında 4k+3 formundaki herhangi bir asal çarpanının tek kuvvete sahip olmamasıdır.
İspat. ⇒ (Gerek Şart); n nin,
n = a2 + b2 (2.1)
biçiminde iki tamsayının kareleri toplamı şeklinde temsil edilebildiğini kabul edelim. n nin asal çarpanlarına ayrılışı
s s q q q q n= 1α1 α22 α33... α (2.2)
biçiminde verilsin. Ayrıca p, n sayısının 4k + 3 biçiminde bir asal böleni olsun. d = (a, b) yazarsak, bu durumda (a1, b1) = 1 için a = da1, b = db1 olur. (2.1) den
dolayı d2n ve sonuçta bir n1 doğal sayısı için n = d 2
ayrılışta p nin kuvvetinin tek olduğunu kabul edelim. O zaman n = d2n1 olduğundan
pn1 = a12 +b22 elde ederiz. Bu da teorem 2.2 ile çelişir. Böylece teoremin gerek
şartını ispatlamış olduk. ⇐
⇐ ⇐
⇐ (Yeter şart); 1 = 12 + 02 olduğundan, n yi 1 den büyük kabul etmemiz genelliği bozmaz. (2.2) ifadesinin n nin asal çarpanlarına ayrılışı olduğunu kabul edelim. O zaman ya k = 1 veya k, 4t + 3 biçiminde olmayan farklı asalların çarpımı olmak üzere n = m2k olur. O halde 2 = 12 + 12 olduğundan bu asalların her biri iki doğal sayının kareleri toplamıdır. Ayrıca
(a2 + b2).(c2 + d2) = (ac± bd)2 + (adm bc)2
özdeşliği bize; iki tamsayının karesinin toplamı biçiminde olan iki doğal sayının çarpımı da yine iki tamsayının kareleri toplamı biçiminde olduğunu gösterir. Sonuçta
k iki tamsayının kareleri toplamıdır. Böylece k = u2 + v2 olduğundan dolayı n = m2k = (mu)2 + (mv)2 elde edilir. Bu ise yeter şartın ispatını tamamlar.
Böylece teoremin ispatı tamamlanmış olur.
Örnek 2.4.1. Örnek 2.3.1 de verilen 12789 sayısını göz önüne alalım. 12789 sayısı 12789 = 1052 + 422 = (3.5.7)2 + (2.3.7)2 = 32.72.(52 + 22) = 32. 72. 29
biçiminde yazılır. O halde 12789 sayısının asal çarpanlarına ayrılışında; 4k + 3 biçimindeki bütün asalların kuvvetleri çifttir.
Teorem 2.5. 4k – 1 biçimindeki bir asal, aralarında asal iki sayının kareleri toplamını bölemez.
İspat. İddiamızın aksine; a, b aralarında asal iki tamsayı olmak üzere a2
+ b2 ifadesini bir p tek asalı bölsün. Yani pa2 + b2 olsun. O zaman a2 ≡ – b2 (mod p) olur
ki, bu ifadenin 2
1 −
p
inci kuvvetini alırsak; 2 ( 1) 1 ) 1 ( ( 1) − − − ≡ − p p p b a (mod p) elde
edilir. Burada, (a, b) = 1 olduğundan, a, b sayıları p ile bölünemediğinden ve Fermat
teoreminden a(p – 1) ≡ b(p – 1) (mod p) olur. Sonuçta ( 1) 2 1 1
≡ −
−
p
(mod p) elde edilir ki burada p > 2 olduğundan bu
2 1 −
p
nin çift olduğunu gösterir. Bundan dolayı p, 4k+ 1 biçiminde olmalıdır. O halde p iki tamsayının kareleri toplamı biçiminde bir tek asal
değilse, yani 4k – 1 biçiminde bir tek asalsa p iki tamsayının kareleri toplamını bölemez.
Örnek 2.5.1. Aralarında asal 15 ve 16 doğal sayılarını alalım. O zaman 162 + 152 = 481 = 13.37
bulunur ki 13 ve 37 sayıları 4k + 1 biçiminde asallardır. Yani 481 in 4k + 3 biçiminde hiç bir asal böleni yoktur. Ayrıca 481 in asal çarpanları olan 13 ile 37 de iki kare toplamı biçiminde yazılabildiğinden
481 = (32 + 22).(62 + 12) = (3.6 ± 2.1)2 + (3.1 m 6.2)2 = (18 ± 2)2 + (3 m 12)2 bulunur. Buradan
481 = 202 + 92 = 162 + 152
olur. Bu ise bize 481 in iki kare toplamı biçiminde birden fazla temsilinin olduğunu gösterir.
Teorem 2.6. Eğer bir doğal sayı, iki tamsayının karelerinin toplamı biçiminde değilse o zaman bu doğal sayı iki rasyonel sayının karelerinin toplamı biçiminde de değildir.
İspat. Eğer n doğal sayısı iki tamsayının karelerinin toplamı biçiminde değilse o zaman teorem 2.4 den dolayı, n yi bölen ve kuvveti tek sayı olan 4k + 3 formunda bir
p asalı vardır. m ile m1 doğal sayıları ve l ile l1 tamsayıları için
2 1 2 + = m l m l n
olduğunu kabul edelim. O zaman (mm1) 2
n = (lm1) 2
+ (l1m) 2
elde edilir. Fakat eşitliğin sol tarafının çarpanlara ayrılışında p nin bir tek kuvveti bulunması gerektiğinden dolayı bu eşitliğin sağ tarafı için doğru olamaz. Bu ise Teorem 2.4 ile çelişir. O halde n yi bölen 4k + 3 biçimindeki asalın kuvveti çift olamaz. Bu da ispatı tamamlar.
Son olarak bir doğal sayının iki tamsayının kareleri toplamı olarak farklı temsillerinin sayısını hesaplayan teoremi ispatsız verelim.
Teorem 2.7. Herhangi n doğal sayının iki tamsayının kare toplamı olarak yazılabildiğini kabul edelim. Ayrıca pi ler, 4k + 1 biçiminde asallar; qj ler 4k + 3 biçiminde asallar; a, ai, pozitif tamsayılar ve bj ler çift pozitif tamsayılar olmak üzere n doğal sayısı n =2aCpiaiCqajj biçiminde verilsin. O zaman N(n) = 4C(ai+1) olur. Özel olarak; p, 4k + 1 biçiminde bir asal ise o zaman N(pm) = 4(m + 1) dir.
Örnek 2.7.1. p = 61 = 4. 15 + 1 olduğundan 61 asalı iki kare toplamı biçiminde yazılabilirdir. Gerçekten 61 = 62 + 52 olur ki buradan
61 = 62 + 52 = (– 6)2 + 52 = 62 + (– 5)2 = (– 6)2 + (– 5)2 = 52 + 62 = (– 5)2 + 62 = 52 + (– 6)2 = (– 6)2 + (– 5)2
elde edilir ki N(61) = 8 bulunur. Diğer bir deyişle N(61) = 4.(1+1) = 8 olur. Örnek 2.7.2. n = 2025 = 52
.13.37 ve 25 = 52 = 4.1 + 1, 13 = 4.3 + 1, 37 = 4.9 + 1 olduğundan N(12025) = 4.(2+1).(1+1)(1+1) = 48 olur. Yani 12025 sayısı 48 farklı şekilde iki tamsayının kareleri toplamı olarak yazılabilirdir.
Not. p = a2
+ b2 gösteriminde a, b tamsayılarının her ikisini de pozitif olarak alır ve sıra değişikliğini dikkate almazsak, p asalının iki doğal sayının kareleri toplamı biçiminde yazılımı tek türlü olur.
3. a2 + ab + b2 BİÇİMİNDE İKİ DEĞİŞKENLİ İKİNCİ DERECEDEN
İFADELER ÜZERİNE
3.1.Giriş
Bu bölümde negatif olmayan a, b tam sayıları için, a2 + ab + b2 biçiminde iki değişkenli ikinci dereceden ifadelerin; yani a2 + ab + b2 biçiminde temsil edilebilen tamsayıların özellikleri incelenecektir. Çünkü;
7 = 22 + 2.1 + 12 = 32 – 3.1 + 12, 13 = 32 + 3.1 + 12 = 42 – 4.1 + 12, 19 = 32 + 2.3 + 22 = 52 – 5.2 + 22 = 52 – 5.3 + 32, 31 = 52 + 5.1 + 12 = 62 – 6.1 + 12 = 62 – 5.6 + 52, 91 = 7.13 = 52 + 5.6 + 62 = 92 + 9.1 + 12 = 102 – 10.1 + 12 = . . . …
olduğundan bu şekilde temsil edilebilen sonsuz sayıda tamsayı vardır.
Tanım 3.1. Herhangi a, b ∈ Z* ve a ≥ b için a2 + ab + b2 ifadesine B – gösterimi denir.
Tanım 3.2. Eğer a ≠ c veya b ≠ d ise a2
+ ab + b2 ve c2 + cd + d2 biçimindeki B – gösterimleri birbirinden farklıdır(Nair, 2004).
Tanım 3.3. Eğer bir tam sayının en az bir B – gösterimi varsa bu sayıya bir B –sayısı denir(Nair, 2004).
Tanım 3.4. Eğer bir B – sayısı asal sayı ise bu sayıya bir B – asalı denir(Nair, 2004).
3.2. Bazı Bilinen Sonuçlar
Aşağıdaki teoremlerin ispatı tanımlarından hemen elde edilir.
Teorem 3.1. a, b ∈ R iken a2 ± ab + b2 formundaki bir sayı asla negatif olamaz. İspat. │a│≥│b│ olduğunu kabul edersek a2
>│ab│olur. Burada a2 –│ab│ve b2 negatif olmadığından onların toplamı da negatif değildir. Bu da a2 + ab + b2 ve a2 – ab + b2 sayılarının negatif olmadığını gösterir(Nair, 2004).
Teorem 3.2. Herhangi a, b ∈ Z* için p = a2 + ab + b2 olacak şekildeki p ve a nın değerleri için bir tek b değeri bulunur(Nair, 2004).
İspat. p = a2
+ ab + b2⇒ b2 + ab + a2 – p = 0 olacağından ve a ile p verildiğinden b nin değerinin b = 2 3 4p a2 a± − −
biçiminde olacağı açıktır. Burada b negatif olamayacağından b nin pozitif değerini alırız.
Teorem 3.3. Eğer bir n tam sayısı, a, b ∈ Z için n = a2
+ ab + b2 formundaysa, o zaman n bir B – sayısıdır. Yani c, d ∈ Z* için n = c2 + cd + d2 dir(Nair, 2004). İspat. Burada üç durumu göz önüne alalım.
1) Eğer a ve b nin her ikisi de negatif değilse tanım gereği n bir B sayısıdır.
2) Eğer a ve b nin her ikisi de negatif ise, c, d ∈ Z* için c = – a, d = – b alırsak; n = c2 + cd + d2 olur.
3) Eğer a ve b den biri negatif, diğeri negatif değilse o zaman a > 0 ve b< 0 olarak kabul edilebilir.
Eğer a > – b ise c = a + b, d = – b
olarak veya diğer durumda c = – (a + b),d = a olarak alalım. O zaman c, d ∈ Z* için n = c2 + cd + d2
bulunur ki ispat biter.
Not. Teorem 3. 3 ten dolayı B gösterimindeki a ve b yi Z den de alabiliriz. Ancak biz yine de a ve b sayılarını Z* dan alacağız.
3.3 Özdeşlikler
c2(a2 + ab + b2) – a2(c2 + cd + d2) = (bc + ad + ac)(bc – ad) (3.1a) c2(a2 + ab + b2) – b2(c2 + cd + d2) = (ac + bd + bc)(ac – bd) (3.1b) d2 (a2 + ab + b2) – a2(c2 + cd + d2) = (bd + ac + ad)(bd – ac) (3.1c) d2(a2 + ab + b2) – a2(c2 + cd + d2) = (ad + bc + bd)(ad – bc) (3.1d) Yukarıdaki özdeşliklerin geçerli olduğu kolaylıkla gösterilebilir.
Şimdi (3.1a) özdeşliğinin geçerli olduğunu gösterelim.
(bc + ad + ac)(bc – ad) = b2c2 – abcd + abcd – a2d2 + abc2 – a2cd
b2c2 – abcd + abcd – a2d2 + abc2 – a2cd + a2c2 – a2c2 = c2(a2+ab+b2) – a2(c2+cd+d2) olarak bulunur.
Benzer şekilde diğerleri de gösterilebilir. Teorem 3.4. a, b∈ Z* için, m = a2
+ab +b2, n = c2 +cd +d2 ve k=m.n olarak verilsin. O zaman;
a) α, β∈ Z* olmak üzere, k = α2 + αβ + β2 denkleminin çözümleri;
− = + + = > − = + + = ) ( ), ( ) ( ), ( mlarda diger duru ac bd bc ad ac ise bd ac eger bd ac bd bc ad β α β α (3.2a) − = + + = > − = + + = ) ( ), ( ) ( ), ( mlarda diger duru ad bc bd ac ad ise bc ad eger bc ad bc bd ac β α β α (3.2b) biçiminde verilir.
b)α, β∈ Z* olmak üzere; k = α2 + αβ + β2 denkleminin çözümleri;
− = + + = < − = + + = ) ( ), ( ) ( ), ( mlarda diger duru bd ac bc ad ac ise bd ac eger ac bd bd bc ad β α β α (3.3a) − = + + = < − = + + = ) ( ), ( ), ( ), ( mlarda diger duru ad bc bd ac ad ise bc ad eger ad bc bc bd ac β α β α (3.3b)
α = (ad + bc + bd), β = (ad + bc + ac) (3.3c) α = (ac + bd + bc), β = (ac + bd + ad) (3.3d) biçimindedir(Nair, 2004).
İspat. Bu eşitliklerin varlığı yukarıdaki özdeşliklerden kolaylıkla gösterilir.
Negatif olmayan α ve pozitif olmayan β( – β yerine kullanabiliriz.) için k = α2 + αβ + β2 denkleminin çözümleri olan (3.3a) – (3.3b) özdeşlikleri denktir. Benzer şekilde pozitif olmayan α ve β için k = α2 + αβ + β2 nin çözümleri olan (3.3c) – (3.3d) özdeşlikleri de denktir. Aynı durum α ve β yerine – α ve – β kullanılırsa da geçerlidir.
3.4. B – Asallarının Esas Formu
Bu kesimde bir asalın B – gösterimleri için gerek ve yeter şartları ve bu B – temsilinin tekliğini göstereceğiz.
7, 13, 19, 31, 37, 43, 61, 67, 73, 79, 97, 103, 109, 127, 139, 151, 157, 163, 181, 193, 199, 211, 223, 229, 241, 271, 277, 283, 301, 307, 313, 331, 337, 349, 367, 373, 379, 397, 409, 421, 433, 439, 457, 463, 487, 499, 523, 541, 547, 571, 577, 601, 607, 613, 619, 631, 643, 661, 673, 691, 709, 727, 733, 739, 751, 757, 769, 787, 811, 823, 829, 853, 859, 877, 883, 919, 937, 967, 991, 997, 1009
Teorem 3.5. 3 dışındaki bir asalın a2
+ ab + b2şeklinde bir gösteriminin olabilmesi için gerek ve yeter şart bu asalın 6k + 1 şeklinde olmasıdır ve bu gösterim tektir (Nair, 2004).
Bu Teorem’ den,
i) Bir B – asalı, tek bir B – gösterimine sahiptir.
ii) 3 ün dışındaki bütün B – asalları 6k + 1 biçimindedir. iii) 6k+1 şeklindeki bütün asallar B – asalıdır.
durumları ortaya çıkar. Teorem 3.5 in ispatlanabilmesi için bu 3 durumun ayrı – ayrı ispatlanması gerekir. Şimdi bu durumları sırasıyla ispatlayalım.
Bunun için önce i) durumunun ispatını verelim.
Teorem 3.6. Her bir B – asalının tek bir B – gösterimi vardır(Nair, 2004). İspat. a, b, c, d ∈ Z+
için,
p = a2 + ab + b2 = c2 + cd + d2 (3.4) biçiminde p asalının 2 farklı B gösterimi olsun. Eğer a > c kabul edersek ac > bd olur. (3.1d) ve (3.1b) özdeşlikleri kullanılırsa;
p(d2 – b2) = (ad – bc)(ad + bc + bd) (3.5a) ve
p(c2 – b2) = (ac – bd)(ac + bd + bc) (3.5b) bulunur. Burada p asal olduğundan ve (3.5a) dan dolayı (ad + bc + bd) ve (ad – bc) den en az birini böler. Şimdi her bir durumu ayrı – ayrı inceleyelim.
Eğer p|(ad + bc + bd) ise: ac > bd olduğundan, (3.2a) nın kullanılmasıyla p2 = (ad + bc + bd)2 + (ad + bc + bd)(ac – bd) + (ac – bd)2
elde edilebilir. Burada ad + bc + bd > 0 olduğundan, p = ad + bc + bd ve ac = bd olur. Sonra (3.5b) den c2 – b2 = 0 olacağından c = b ve Teorem 3.2 den dolayı a = d edilir ki bu p nin B – gösteriminin tek olduğunu gösterir.
Eğer ad > bc ise; (3.2b) den,
p2 = (ad + bc + bd)2 + (ad + bc + bd)(ac – bd) + (ac – bd)2
ve p asal olduğundan ac + bd + bc yi bölmeliydi. Öte yandan ac + bd + bc > 0 olduğundan p = ac + bd + bc bulunur ki bu bizi ad = bc sonucuna götürür.
Eğer ad ≥≥≥≥ bc ise; benzer bir yolla (3.2b) nin kullanılmasıyla p = ad + ac + bd olduğu ve böylece ad = bc olduğu görülür.
Her iki durumda da ad = bc olduğunu gösterdik. Sonra (3.5a) dan; d2 – b2 = 0 elde edilir ki buradan d = b ve Teorem 3.2 den de a = c elde edilir. Bu ise p nin B – gösteriminin tek olduğunu gösterir.
Böylece p nin B – gösteriminin her iki durumda da tek olduğu gösterilmiş olur.
Şimdi ii) nin ispatını kongrüansların özelliklerinden faydalanarak gösterelim. Teorem 3.7. 3 ün dışındaki bütün B – asalları 6k + 1 formundadır(Nair, 2004). İspat. p = a2
+ ab + b2 biçiminde bir asal olsun. Ayrıca a ≡ m (mod 6), b ≡ n (mod 6) ve a2 + ab + b2 ≡ z (mod 6) olarak verilsin. Sonra kongrüanslığın temel özellikleri kullanıldığında m2 + mn + n2 ≡ z (mod 6) olur. m = 0, 1,…, 5 ve n = 0, 1,…, 5 için z yalnız 0, 1, 3, 4 değerlerini alabileceğinden p de 6k, 6k + 1, 6k + 3 ve 6k + 4 değerlerini alır. Burada 6k ve 6k + 4 daima birleşik sayılardır. 6k + 3 de k = 0 için p = 3 olduğundan, k ≠ 0 için birleşik sayıdır. Böylece p asalının değerleri yalnızca 3 veya 6k + 1 dir.
Şimdi de iii) nin ispatını verelim. Bu ispatı 4 adımda yapabiliriz.
(1) Eğer B – sayısı, bir B – asalı ile bölünürse, diğer bir B – sayısı elde edilir. Bu durum Teorem 3.8 ile verilecektir.
(2) Önceki sonuç kullanılarak; eğer bir B – sayısının, B – sayısı olmayan bir çarpana sahip böleni mevcutsa, o zaman bölümün en az bir asal çarpanının B – asalı olmadığı durumu Teorem 3.9 ile verilecektir.
(3) Sonra a ile b aralarında asal olmak üzere a2 + ab + b2 biçimindeki bir B – sayısının her bir B – çarpanının bir B – sayısı olduğunu gösterelim. Buna bir çarpanının B – sayısı olmadığının kabulü ile başlayalım. Sonra bu özelliklere sahip herhangi bir sayıdan hareketle, kendinden daima küçük bir sayı bulabileceğimizi
ispatlayalım. Sonsuz iniş prensibinden dolayı böyle bir sayı bulunamaz. Bu durumu Teorem 3.10 ile vereceğiz.
(4) Son olarak da iyi bilinen sonuçlar kullanılarak; 6k + 1 formunda her bir asalın a∈ Z+ için a2 + a + 1 biçiminde bir sayıyı böldüğünü göstereceğiz. Burada a2 + a + 1 bir B – sayısı ve a ile 1 de aralarında asal olduğundan önceki sonuç bu asalın bir B – asalı olmasını gerektirecektir. Bu durum Teorem 3.12 ile verilecektir.
Şimdi bu durumları açıklayan teoremleri ve ispatlarını sırasıyla verelim. Teorem 3.8. Eğer bir B – sayısı olan n in, p gibi bir B – asal çarpanı varsa o zaman (n/p) sayısı bir B – sayısıdır(Nair, 2004).
İspat. a, b, c, d ∈ Z* için p = c2 + cd + d2 olmak üzere
n = a2 + ab + b2 (3.6)
ve n = pq olarak verilsin. Bu durumda q sayısının B – sayısı olduğunu göstermeliyiz. (3.la) özdeşliğini göz önüne alalım. p, (3.1a) nın sol tarafını böldüğünden sağ tarafını da böler. Burada p asal olduğundan, (3.1a) nın sağ tarafındaki (bc + ad + ac) ve (bc – ad) çarpanlarından en az birini böler. Bu iki durumu ayrı ayrı inceleyelim.
1. Durum: p(bc + ad + ac) olsun.
Bu durumda bölünebilme tanımı gereği bc + ad + ac = rp olacak şekilde r∈Z vardır. x, y ∈ Z olmak üzere a = rd + y ve b = rc + x alalım. Bunları birleştirirsek;
r(c2 + cd + d2) + cx + dy + cy = rp olur ki buradan
cx + cy + dy = 0 (3.7)
elde edilir. Sonra (3.6) da a ile b yerine a = rd + y ve b = rc + x koyar ve (3.7) yi kullanırsak;
n = r2(c2 + cd + d2) + x2 + xy + y2 + r(cx + dx + dy) (3.8) buluruz. Buradan (3.7) yi
c(x + y) + dy = 0
biçiminde yeniden yazarsak, (c, d) = 1 olduğundan c y yi böler. Burada w∈Z olmak üzere y = – cw alırsak, x = (c + d)w olur. x ile y nin bu değerlerini (3.8) de yerine yazar ve sadeleştirirsek,
n = (c2 + cd + d2)(r2 + rw + w2)
2.Durum: p(bc – ad) olsun. Bu durumda r ∈ Z olmak üzere bc – ad = rp olacaktır. Herhangi x, y ∈ Z için a = – rd + y ve b = rc + x olarak alalım. Bunları birleştirirsek; rc2 + cx – dy + rd2 = rc2 + rcd + rd2 olur. Bunun anlamı
rcd + dy – cx = 0 (3.9)
olmasıdır. Sonra (3.6) da a yerine a = y – rd ve b yerine b = x + rc yi koyar ve (3.9) u kullanırsak;
n = r2(c2 + cd + d2) + (x2 + xy + y2) + r(cy – dx) (3.10) buluruz. Burada (3.9);
c(x – rd) = dy
biçiminde yeniden yazıldığında ve (c, d) = 1 olduğundan cy elde edilir. Ayrıca w ∈ Z için y = cw koyarsak x = (r + w)d bulunur. x ile y nin bu değerlerini (3.10) da yerine koyar ve düzenlersek,
n = (c2 + cd + d2)(r2 + rw + w2)
elde edilir ki bu ise q = r2 + rw + w2 olması demektir. Böylece, her iki durumda da r, q∈ Z için q = r2 + rw + w2 olarak elde edilir. Bu ise teorem 3.3 den (n/p) nin bir B – sayısı olduğunu ortaya koyar.
Örnek 3.3.1. 148 = 82 + 8.6 + 62 olarak yazılabildiğinden 148 bir B – sayısı olur. Öte
yandan 148 = 37.22 ⇒ 148 / 22 = 37 olup, 37 = 42 + 4.3 + 32 olduğundan 37 bir B asalıdır. Ayrıca 148/37 = 4 = 22 + 2.0 + 02 olduğundan 148/37 sayısı da bir B sayısıdır.
Teorem 3.9. Eğer bir B – sayısı olan n, B – sayısı olmayan bir m çarpanına sahipse o zaman (n/m) sayısı, B – sayısı olmayan en az bir asal çarpana sahiptir.
İspat. n = m.k olarak verilsin. k çarpanının k = p1.p2…px biçiminde asal çarpanları
bulunsun. Bütün pi.s lerin (i = 1, 2,…, x), B – asalı olduğunu kabul edelim. O zaman Teorem 3.8 den dolayı n/p1 bir B – sayısıdır ve böylece n/(p1.p2) bir B –
sayısıdır ve bu şekilde devam edilirse n/(p1.p2…px) bir B – sayısı olur ki sonuçta m
bir B – sayısı olur. Bu ise hipotezle çelişir. O halde bütün pi ler B – asalları olamaz. Teorem 3.10. Eğer (a, b) = 1 olmak üzere n = a2
+ ab + b2 ise o zaman n in her bir çarpanı B – sayısıdır(Nair, 2004).
İspat. n nin B – asalı olmayan bir p çarpanının bulunduğunu kabul edelim. α, β ∈ Z ve – p/2 < α, β ≤ p/2 olmak üzere a = x.p + α ve b = y.p + β olarak verilsin. p, a2 + a.b + b2 yi böldüğünden p sayısı α2 + α.β + β2 yi de bölmelidir. Bu durumda α2
+ α.β + β2 = p.q olarak kabul edelim. Teorem 3.1 den dolayı α 2 + α.β + β2 ≥ 0 olup, buradan pq ≥ 0 ve sonuçta q ≥ 0 dır. Ayrıca α2 + α.β + β2 ≤ 3p2/4 olduğundan q ≤ 3p/4 < p bulunur.
(α, β) = γ olsun. Hem de u = α/γ ve v = β/γ olarak verilsin. Buradan u2 + uv + v2 =
2 γ
pq
elde edilir. Burada γ, p yi bölmediğinden(diğer durumda γ, a ile b nin her ikisini de böler), γ2 q yi böler. k = (q/γ2) olsun. O zaman
u2 + uv + v2 = pk
elde edilir. p, bir B – sayısı olmadığından Teorem 3.9 den dolayı k nin B – asalı olmayan bir r asal çarpanı bulunmalıdır. Çünkü r ≤ k ≤ q < p ⇒ r < p dir.
Bu nedenle B – sayısı olmayan bir p ≥ 0 sayısı ile başladık. Ancak p bir B – sayısının çarpanıdır ve kendinden daha küçük bir r sayısı bulduk. Bu r sayısı da B – sayısı değildir ve r ≥ 0 dır (aynı özelliğe sahip). Sonsuz iniş prensibinden dolayı bu imkansızdır. O halde p ler B – sayısı olmalıdır.
Örnek 3.3.3. (9, 4) = 1 olduğundan 92
+ 9.4 + 42 = 133 = 7.19 bulunur ki buradan 7.19 = (22 + 2.1 + 12).(32 + 3.2 + 22) olarak elde edilir.
Eğer (a, b) = k ise, a2 + a.b + b2 = k2x2 + kx.ky + k2y2 = k2(a2 + a.b + b2) dir. Eğer a2 + a.b + b2 kare çarpan bulundurmuyorsa ve (a, b) = 1 ise B – sayısıdır. Bu da bizi şu sonuca ulaştırır.
Sonuç 3.10.1. Kare çarpan ihtiva etmeyen bir B – sayısı, B – asallarının çarpımıdır (Nair, 2004).
Örnek 3.3.4. 252 + 25.23 + 232 = 1729 olduğundan 1729 sayısı bir B – sayısıdır.
Ayrıca 1729 = 7.13.19 ve 7, 13 ve 19 asalları 7 = 22 + 2.1 + 12, 13 = 32 + 3.1+ 12 ve 19 = 22 + 2.3+ 32 biçiminde yazılabildiğinden bu sayılar B – asallarıdır.
Teorem 3.11. 6k + 1 biçimindeki her bir p asalı için z2
+ z + 1 ≡ 0 (mod p) olacak şekilde z < p/2 şartını sağlayan bir tek z pozitif tamsayısı vardır(Nair, 2004).
İspat. Teorem 1.3 (Fermat teoremi) den
xp – 1 – 1 ≡ 0 (mod p) (3.11)
elde edilir. Hipotezde p asalı, 6k + 1 biçiminde bir asal olduğundan (p – 1)/2 = 3k olur ki burada xp – 1 – 1 = (x3k + 1)(x3k – 1) olacağından (3.11) kongrüans denkleminin çözümleri;
x3k + 1 ≡ 0 (mod p) (3.12a)
x3k – 1 ≡ 0 (mod p) (3.12b)
denklemlerinin çözümleri ile verilir. Teorem 3.4 den dolayı (3.12b) kongrüans denkleminin – p/2 ile p/2 arasında tam olarak 3k tane çözümü vardır. (3.12b) nin bu çözümleri
xk – 1 ≡ 0 (mod p) (3.13a)
ve
x2k + xk + 1 ≡ 0 (mod p) (3.13b)
kongrüans denklemlerinin çözümlerinden elde edilir. Burada (3.13a) denkleminin – p/2 < x < p/2 aralığında tam olarak k tane çözümü olduğundan, (3.13b) kongrüans denkleminin 2k tane çözümü sahip olabilir. Bu 2k çözümden herhangi birisini y = xk ile gösterirsek, bu çözüm;
y2 + y + 1 ≡ 0 (mod p) (3.14)
denkleminin de bir çözümü olur. Buradan hareketle herhangi bir k ∈ Z için, w = y + kp olarak seçilirse w tamsayısı da (3.14) denkleminin bir çözümüdür. Ayrıca – p/2 < u < p/2 olacak şekilde u² + u + 1 ≡ 0 (mod p) denklemini sağlayan bir u sayısı bulunabilecektir. Burada v = – (u + 1) alınırsa v² + v + 1 = u² + u + 1 olacağından v² + v + 1 ≡ 0 (mod p) elde edilir. Eğer u < 0, 0 < v < p/2 veya tersi geçerli ise o zaman en az iki tane çözüm vardır ki bunlar – p/2 den büyük ve p/2 den küçük olduğundan bunlardan birisi negatif diğeri de pozitiftir. Ancak, Lagrange teoreminden (3.14) kongrüans denkleminin – p/2 < y < p/2 aralığında en fazla iki çözümü vardır. Bundan dolayı p tek ve p > 1 olduğundan, (3.14) kongrüans denkleminin – p/2 ve p/2 aralığında tam olarak iki tane çözümü vardır ki bunlardan birisi p/2 den küçük pozitif bir tamsayı, diğeri de – p/2 den büyük negatif bir tamsayıdır. Bu pozitif tamsayı aranan çözümdür.
Örnek 3.3.5. p = 19 için 72
+ 7 + 1 = 57 ≡ 0 (mod 19) olup 7 <
2
19 şartı sağlanır.
Ayrıca p = 37 için 102 + 10 + 1 = 111 ≡ 0 (mod37) olup 10 <
2
37 şartı sağlanır.
Teorem 3.12. Eğer bir asal sayı 6k + 1 biçiminde ise o zaman bu bir B – asalıdır (Nair, 2004).
İspat. p = 6k + 1 biçiminde bir asal olsun. Teorem 3.11 den dolayı z2
+ z + 1 ≡ 0 (mod p) olacak şekilde pozitif bir z tam sayısı vardır. Bunun anlamı z2 + z + 1 = mp olacak şekilde bir z pozitif tamsayısı vardır. (z, 1) = 1 olduğundan (Teorem 3.10 ten dolayı) z² + z + 1 biçimindeki her bir çarpan bir B –sayısı olduğundan dolayı p bir B – asalıdır.
Böylece Teorem 3.5 in ispatı Teorem 3.6, Teorem 3.7 ve Teorem 3.11 in ispatlarından elde edilmiş olur.
Örnek 3.3.6. p = 433 olsun. 433 = 6.72 + 1 olduğundan 433, 6k + 1 biçiminde bir asaldır. 433 asalı 6k + 1 biçiminde olduğundan dolayı 433 = 132 + 13.11 + 112 olarak yazılır ki 433 aynı zamanda bir B – asalıdır.
3.5. B – Sayılarının Çarpanları
Bu kesimde B – sayılarının çarpanlarının bazı özellikleri verilecektir.
Teorem 3.13. Negatif olmayan herhangi bir tamsayının a² + ab + b² biçiminde olması için gerek ve yeter şart, bu tamsayının 3 den büyük ve 6k + 1 biçiminde olmayan bütün asal çarpanlarının kuvvetlerinin çift olmasıdır(Nair, 2004).
Yeter şart kısmının ispatı için şu teoremi verelim.
Teorem 3.14. Eğer bir sayının asal çarpanlarına ayrılışında 3 ve 6k + 1 formunda olmayan bütün asalların kuvvetleri çift ise bu sayı B sayısıdır(Nair, 2004).
İspat. (3.2a) dan B – sayılarının her hangilerinin çarpımları da bir B – sayısıdır. Özel olarak B – asallarının çarpımlarının da bir B – sayısı olduğunu biliyoruz. Her bir kare bir B – sayısı olduğundan, bir B – sayısı bir kare ile çarpıldığında bir B – sayısı olacaktır. Böylece B – asallarının çarpımı ile bir karenin çarpımı da bir B – sayısı olacaktır.
(1) Eğer bir B – sayısı bir kare çarpan ile bölünebiliyorsa, yani böyle bir sayı varsa, bölüm bir B – sayısıdır. (Teorem 3.15)
(2) Sonra, Sonuç 3.10.1 i kullanılarak istene sonuca ulaşılır. Teorem 3.15. Eğer m, k pozitif tamsayıları için, m.k2
bir B – sayısı ise o zaman m bir B – sayısıdır(Nair, 2004).
İspat. Her hangi a, b tamsayıları için,
k2.m = a2 + ab + b2 (3.15) olarak alalım. s2, m nin en büyük kare çarpanı olsun. Yani n = m/s2 olarak verilsin. Yalnız n nin bir B – sayısı olduğunu göstermeye ihtiyacımız var. Çünkü bu durumda m iki tane B – sayısının çarpımı olacaktır. Sonra p = ks olarak tanımlarsak, n tamsayısı 1 den büyük bir kare çarpan ihtiva etmemek üzere (3.15) ifadesi
a2 + ab + b2 = p2.n
biçimine dönüşür. g = (a, b) olarak alırsak; c = a/g, d = b/g olacağından g2(c2 + cd + d2) = p2.n veya c2 + cd + d2 = 2 2 g p .n
bulunur. Eğer g > 1 ise g2, n i bölemeyeceğinden p/g bir tam sayı olmalıdır. Sonra Teorem 3.10 dan dolayı son eşitliğin sol tarafındaki her bir çarpan bir B – sayısı olduğundan dolayı, n in her bir çarpanı bir B – sayısı olur. Sonuçta n tamsayısı B – sayılarının bir çarpımı olduğundan bir B – sayısıdır.
Örnek 3.4.1. 700 = 102
+ 10.20 + 202 olduğundan 700 bir B – sayısıdır. Ayrıca 700 = 102.(12 + 1.2 + 22) = 102.7 olduğundan
2 10 700
= 7 olup 7 bir B – asalıdır. Teorem 3.16. Bir B – sayısının asal çarpanlarına ayrılışında; B – asalı olmayan her bir asal çarpanının kuvveti çifttir(Nair, 2004).
İspat. Herhangi B – sayısı n ve s2 de n in en büyük kare çarpanı olsun. Teorem 3.15 den dolayı (n/s2) kare çarpan ihtiva etmeyen bir B – sayısıdır ki bu durumda Sonuç 3.10.1 den dolayı (n/s2) sayısı B – asallarının çarpımıdır. Böylece B – asalı olmayan bütün çarpanlar s2 de kapsanacağından, B – asalı olmayan bütün çarpanların kuvvetleri çift olur.
Böylece Teorem 3.13 nın ispatı, Teorem 3.14 ve Teorem 3.15 un ispatlarının yapılmasıyla tamamlanmış olur.
Örnek 3.4.2. 148 = 62
+ 6.8 + 82 olduğundan 148 bir B – sayısıdır. Ayrıca 148 = 22.37 olup 22 bir kare çarpan ve 37 = 6.6+1 olduğundan 37 bir B – asalıdır.
3.6. Bir B – Sayısının Genel Formu
Yukarıda ispat edilen teoremlerden bir B – sayısının genel formunu
n = x2.3y.aα.bβ.cγ … (3.16) biçiminde verebiliriz. Bu gösterimde ;
x: Z* da herhangi bir sayı olup, k∈ Z+ için 6k+1 şeklinde olmayan bir asal çarpandır. y: Z* da herhangi bir sayıdır.
a, b, c, … : k ∈ Z* için 6k + 1 formundaki asallardır. α, β, γ, … : Z* da herhangi bir sayıdır.
Bir sayının B – sayısı olması için gerek ve yeter şart o sayının (3.16) biçiminde gösterilebilmesidir.
Konjektür 3.1. (3.16) biçiminde verilen bir B – sayısının farklı B – gösterimlerinin sayısı, a = b ve a ile b den herhangi biri sıfır olması durumları dışında;
(
)
+ + + + + + + durumlarda diger )..., 1 )( 1 )( 1 ( 2 1 ise çift lar ,... , , bütün , )... 1 )( 1 )( 1 ( 1 2 1 γ β α γ β α γ β α (3.17) biçiminde verir.Bir sayının iki kare toplamı olarak farklı gösterimlerinin sayısını veren formül Teorem 2.7 ile verildi. Eğer bir B – sayısını (3.16) biçiminde seçersek; bu sayının farklı B – gösterimlerinin sayısını veren formül de (3.17) ile verilir. Bu (3.17) ifadesinin uygulaması biçiminde olup da farklı tanımlamaları da bulunabilir.
Bu konjektürün ispatı ile bu çalışmada uğraşılmadı.
3.7. Rasyonel Sayı Bileşenli B – Sayıları
Aşağıda vereceğimiz Teorem 3.17, a ve b için daha önce verilen teoremlerin Z*
Teorem 3.17. Eğer α ve β pozitif rasyonel sayılar olmak üzere bir n sayısı α2
+ α.β + β2şeklinde ifade edilebiliyorsa o zaman n bir B – sayısıdır(Nair, 2004). İspat. α = b a , β = d c olsun. Buradan n = α2 + α.β + β2 = 2 2 + + d c d c b a b a = 2 2 2 2 2 2 d b c b abcd d a + +
elde edileceğinden
n.(bd)2 = (ad)2 + (ad).(bc) + (bc)2
bulunur. O zaman Teorem 3.15 den dolayı n bir B – sayısıdır.
Örnek 3.7.1.α ile β rasyonel sayılarını α = 3/5 ve β = 5/13 alalım. Bu durumda
n = 2 2 13 5 13 5 5 3 5 3 4225 3121 + + = 2 2 13 . 5 5 . 5 13 . 13 . 5 . 5 5 . 5 . 13 . 3 13 . 5 13 . 3 + + = + + = 13 . 13 . 5 . 5 ) 5 . 5 ( 5 . 5 . 13 . 3 ) 13 . 3 ( 2 2 2 2 13 . 5 3121 = olup 52.132. 2 2 13 . 5 3121 = 392 + 39.25 + 252
olduğundan n sayısı bir B – sayısıdır. Ayrıca 3121 sayısı da bir B – sayısıdır.
3.8 a2
– ab + b2 Formu İle Karşılaştırma
Başka bir iki değişkenli ikinci dereceden aynı diskriminantlı gösterim olan a2 – ab + b2 temsili, a2 + ab + b2 gösterimi ile birçok ortak özelliği paylaşır. 3 ve 6k + 1 formundaki bütün asallar a2 – ab + b2şeklinde gösterilebilir, fakat bu gösterim tek türlü değildir.
Genellikle eğer n ∈ Z* için n = a2 + ab + b2 şeklinde ise o zaman x = a, y = a + b ve x = b, y = a + b alınarak n in x2 – xy + y2 biçimde iki farklı gösterimi verilebilir. Sadece tek temsil a = b hali için geçerlidir ki bu durumda n = 3a2 olacağından 3 sayısı bu özellikteki tek asaldır.
Örnek 3.8.1. 19 sayısı bir B – asalı olduğundan 19 = 32
+ 2.3 + 22 biçiminde bir tek B – gösterimi vardır. Ancak 19 asalının
19 = 52 – 5.2 + 22 = 52 – 5.3 + 32
Benzer şekilde a ≥ b şartı altında n = a2 – ab + b2 olduğu zaman x = a – b, y = b alınarak n sayısı x2 + xy + y2 biçiminde gösterilebilir. Bu karşılık getirmelerden dolayı bu çalışmada verilen Teorem 3.5, Teorem 3.6 ve Teorem 3.14 dışındaki bütün sonuçlar a2 – ab + b2 gösterimi için de geçerlidir.
3.9. ka2
+ kab + kb2 ye Denk Olan Formlar İle Karşılaştırma
Bu çalışmada verilen bir çok sonuç; k∈Z+ için ka2 + kab + kb2 biçimindeki bir çok ikinci dereceden iki değişkenli gösterimler için de geçerli olduğu ispatlanabilir.
Örneğin Euler (1763), 2a2 + 2ab + 2b2 gösterimine denk olan a2 + 3b2 gösterimi için aşağıdakilerin geçerli olduğunu ispatladı (Dickson 1999).
(1) Bir p asalının a2 + 3b2 biçiminde temsil edilebilmesi için gerek ve yeter şart p = 3 veya p ≡ 1 (mod 6) olmasıdır (Teorem 3.5). Bu temsilin tek olduğu da ilk kez Goring (1874) tarafından ispatlandı (Teorem 3.6).
(2) a ve b aralarında asal olmak üzere a2 + 3b2 formundaki bir sayının her bir asal böleni de(2 den hariç) bu formdadır (Teorem 3.10).
Benzer kıyaslama ka2 + kab + kb2 ye denk olan a2 + ab + 7b2, a2 + 12b2, 3a2 + 4b2, a2 + ab + 19b2, 3a2 + 3ab + 7b2 ifadeleri içinde bulunabilir.
Verilen ka2 + kab + kb2denklemi için ∆ = k2 – 4k2 = –3k2 olduğundan kıyaslamaları aşağıdaki örneklerle açıklayalım.
Örnek 3.8.1. k = 3 için 3a2 + 3ab + 3b2 ⇒ ∆ = – 3.9 = – 27 dir. Ayrıca a2 + ab + 7b2 ⇒ ∆ = 1 – 4 (1.7) = – 27 olduğundan ∆ lar eşittir. O halde 3a2 + 3ab + 3b2 ve a2 + ab + 7b2 gösterimleri denktir.
Örnek 3.8.2. k = 4 için 4a2
+ 4ab + 4b2 ⇒ ∆ = 3.16 = 1 – 48 dir. Ayrıca a2 + 12b2 ⇒ ∆ = 0 – 4.(12) = – 48 olduğundan ∆ lar eşittir. O halde 4a2 + 4ab + 4b2 a2 + 12b2 gösterimleri denktir.
Örnek 3.8.3. k = 5 için 5a2
+ 5ab + 5b2 ⇒ ∆ = –3.52 = – 75 dir. Ayrıca a2 + ab + 19b2 ⇒ ∆ = 1 – 4.(19) = – 75 olduğundan ∆ lar eşittir.
Ek olarak; 3a2 + 3ab + 7b2 ⇒ ∆ = 32 – 4.3.7 = 9 – 84 = – 75 bulunur. Yani 5a2 + 5ab +5b2 ile a2 + ab + 19b2, 3a2 + 3ab + 7b2 gösterimleri denktir.