Matematiksel problem kurma stratejilerinin 5. sınıf öğrencilerinin problem kurma başarılarına etkisi

MATEMATİKSEL PROBLEM KURMA STRATEJİLERİNİN 5.

SINIF ÖĞRENCİLERİNİN PROBLEM KURMA

BAŞARILARINA ETKİSİ

Ayşe İslamiye YALÇIN

YÜKSEK LİSANS TEZİ

İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ ANA BİLİM

DALI

GAZİ ÜNİVERSİTESİ

EĞİTİM BİLİMLERİ ENSTİTÜSÜ

i

TELİF HAKKI VE TEZ FOTOKOPİ İZİN FORMU

Bu tezin tüm hakları saklıdır. Kaynak göstermek koşuluyla tezin teslim tarihinden itibaren 12 (on iki) ay sonra tezden fotokopi çekilebilir.

YAZARIN

Bölümü : İlköğretim Matematik Öğretmenliği İmza :

Teslim tarihi: 04/05/2017

TEZİN

Türkçe Adı : Matematiksel Problem Kurma Stratejilerinin 5. Sınıf Öğrencilerinin Problem Kurma Başarılarına Etkisi

İngilizce Adı : Effect Of Mathematical Problem Posing Strategies On Problem Posing Achievement Of 5th Grade Students

ii

ETİK İLKELERE UYGUNLUK BEYANI

Tez yazma sürecinde bilimsel ve etik ilkelere uyduğumu, yararlandığım tüm kaynakları kaynak gösterme ilkelerine uygun olarak kaynakçada belirttiğimi ve bu bölümler dışındaki tüm ifadelerin şahsıma ait olduğunu beyan ederim.

Yazar Adı Soyadı: Ayşe İslamiye YALÇIN İmza: ………..

iii

JÜRİ ONAY SAYFASI

Ayşe İslamiye YALÇIN tarafından hazırlanan “Matematiksel Problem Kurma Stratejilerinin 5. Sınıf Öğrencilerinin Problem Kurma Başarılarına Etkisi” adlı tez çalışması aşağıdaki jüri tarafından oy birliği ile Gazi Üniversitesi İlköğretim Matematik Öğretmenliği Anabilim Dalı’nda Yüksek Lisans olarak kabul edilmiştir.

Danışman: Prof. Dr. Yüksel DEDE

Matematik Öğretmenliği ABD, Gazi Üniversitesi ……….. Başkan: Prof. Dr. Safure BULUT

Matematik Öğretmenliği ABD, Orta Doğu Teknik Üniversitesi ……… Üye: Doç. Dr. İhsan Seyit ERTEM

Sınıf Öğretmenliği ABD, Gazi Üniversitesi ………..

Tez Savunma Tarihi: 04/05/2017

Bu tezin İlköğretim Matematik Öğretmenliği Anabilim Dalı’nda Yüksek Lisans tezi olması için şartları yerine getirdiğini onaylıyorum.

iv

TEŞEKKÜR

Bu çalışmanın tamamlanmasında onlarca insana özel bir teşekkür borçluyum.

Öncelikle araştırmanın gerçekleşmesi sürecinin başından sonuna kadar desteğini esirgemeyen, değerli görüş ve fikirleriyle bana yol gösteren, yardımlarıyla bana güç veren danışman hocam sayın Prof. Dr. Yüksel Dede’ye şükranlarımı sunarım.

Araştırmanın gerçekleştirilmesinde önemli rol oynayan 2015-2016 eğitim öğretim yılında beşinci sınıfta öğrenim gören canım öğrencilerime çok teşekkür ederim.

Yüksek lisans eğitimim süresince sağladığı maddi desteklerden ötürü Türkiye Bilimsel ve Teknolojik Araştırma Kurumu’na teşekkürlerimi sunarım.

Yaşamım boyunca beni yalnız bırakmayan, desteklerini ve sevgilerini hiç esirgemeyen canım anneme ve babama çok teşekkürler. Ayrıca sevecenlikleri ve şakaları ile beni zaman zaman güldüren, manevi olarak desteklerini her zaman hissettiğim kardeşlerim Büşra Nur, Muhammet Abdullah ve Huzeyfe Özdemir’e teşekkür ederim.

Tanıdığım andan itibaren her zaman yanımda olan, bana her daim destek olan, beni anlayan, benimle aynı duyguları paylaşan can dostum Zuhal Burçak’a çok teşekkürler…

Son olarak her zaman yanımda olan, beni hiçbir zaman yalnız bırakmayan, benimle aynı heyecanı paylaşan, başaramayacağımı düşündüğüm her an bana moral veren ve çalışmalarımla ilgili her konuda bana yardımcı olan sevgili eşim Mehmet Tufan Yalçın’a ve ailemize katılarak bana anne olma duygusunu tattıran ve varlığından güç aldığım canım kızım Fatma Betül’e sonsuz teşekkürlerimi sunarım.

v

MATEMATİKSEL PROBLEM KURMA STRATEJİLERİNİN 5.

SINIF ÖĞRENCİLERİNİN PROBLEM KURMA

BAŞARILARINA ETKİSİ

Ayşe İslamiye YALÇIN

GAZİ ÜNİVERSİTESİ

EĞİTİM BİLİMLERİ ENSTİTÜSÜ

Mayıs, 2017

ÖZ

Bu araştırmada, matematiksel problem kurma stratejilerinin 5. sınıf öğrencilerinin problem kurma başarılarına etkisi Matematik Uygulamaları dersi çerçevesinde incelenmiştir. Araştırma 2015-2016 eğitim öğretim yılında, öntest-sontest kontrol gruplu gerçek deneme modelinde gerçekleştirilmiştir. Araştırmada veri toplama aracı olarak Matematik Uygulamaları öğretim materyalinden araştırmacı tarafından seçilen etkinlikler, problem kurma çalışma kâğıtları ve araştırmacı tarafından hazırlanan problem kurma başarı testi kullanılmıştır. Araştırma Ankara ilindeki bir ortaokulda, iki farklı sınıfta okuyan 30 deney, 22 kontrol grubu olmak üzere toplam 52 5. sınıf öğrencisi ile yürütülmüştür. Araştırmada Matematik Uygulamaları dersi etkinlikleri ve problem kurma çalışmaları, toplam 6 hafta deney grubu öğrencilerine uygulanırken, kontrol grubuna herhangi bir ek çalışma yapılmamıştır. Araştırmanın sonucunda elde edilen veriler t-testi, ANCOVA, Mann Whitney U testi ve Wilcoxon işaretli sıralar testi kullanılarak analiz edilmiştir. Araştırma sonucunda deney grubunda bulunan öğrencilerin problem kurma başarı testi öntest ve sontest puan ortalamaları arasında anlamlı bir artış görülürken, kontrol grubu öğrencilerinin sonuçlarında istatistiksel olarak anlamlı bir farklılık bulunmamıştır. Öte yandan, deney ve kontrol grubu

vi

öğrencilerinin problem kurma başarı testi öntest puan ortalamaları kontrol edildiğinde gruplararası sontest puan ortalamaları arasında deney grubu lehine istatistiksel olarak anlamlı bir farklılık belirlenmiştir. Araştırmanın diğer bir sonucu olarak çalışmaya katılan öğrencilerin problem kurma stratejilerine göre grup içi problem kurma başarı testi öntest ve sontest puan ortalamaları arasında anlamlı bir farklılık gözlenmemiştir. Ancak, deney grubu öğrencilerinin serbest problem kurma stratejisiyle oluşturulan soruları çözmeye daha eğilimli oldukları belirlenmiştir. Ayrıca deney ve kontrol grubu öğrencilerinin problem kurma stratejilerine göre problem kurma başarı testi sontest puan ortalamaları arasında anlamlı bir farklılık belirlenmemiştir. Sonuç olarak, 5.sınıf düzeyinde Seçmeli Matematik Uygulamaları dersi kapsamındaki etkinliklere ve problem kurma çalışmalarına dayalı öğrenme ortamının öğrencilerin problem kurma başarısını arttırdığı görülmüştür.

Anahtar Kelimeler: Problem kurma, problem kurma stratejileri, Matematik Uygulamaları dersi

Sayfa adedi: 129

vii

EFFECT OF MATHEMATICAL PROBLEM POSING STRATEGIES

ON PROBLEM POSING ACHIEVEMENT OF 5

GRADE

STUDENTS

(Master Thesis)

Ayşe İslamiye Yalçın

GAZI UNIVERSITY

GRADUATE SCHOOL OF EDUCATIONAL SCIENCES

May, 2017

ABSTARCT

In this study, effect of Mathematical problem posing strategies on problem posing achievement of 5th grade students has been investigated in scope of Mathematics Applications Lesson. The study has been conducted with true experimental model by pretest – posttest including a control group in 2015-2016 academic year. The data has been gathered from the activities selected by the researcher from Mathematics Applications teaching material, the problem posing worksheets and the problem posing achievement test implemented by the researcher. The study has been conducted with the participation of 52 5th grade students from one of the secondary schools in Ankara. The students are from two separated class. Experimental group of the study consists of 30 students and the control group consists of 22 students. The activities of Mathematics Applications Lesson and the problem posing practices have been carried out for six weeks to experiment group students and the control group students have not been received any of these practices. The data of the study has been analyzed by t-test, ANCOVA, Mann Whitney U test and Wilcoxon signed rank test. The results of the study have showed that the post-test scores of the experimental group are significantly higher than the pre-test scores. On the other hand, control group

viii

students’ pre-test and post-test scores are not significantly different. The experimental group’s post-test mean scores of the problem posing achievement test are statistically different and higher than the control group's post-test scores. The other notable result is that the pre-test and the post-test scores of the problem posing strategies are not statistically different within groups. However, the experimental group is more likely to respond the questions which are prepared as unconstrained problem posing strategies. Moreover, the experimental and the control groups’ problem posing achievement post-test mean scores has no significant difference in terms of the problem posing strategies. Consequently, it has been observed that the learning environment based on problem posing activities and activities conducted within the scope of 5th grade Mathematics Applications Lesson has increased the students' problem posing achievement.

Key Words: Problem posing, problem posing strategies, Mathematics Applications Lesson Page Number: 129

ix

İÇİNDEKİLER

ETİK İLKELERE UYGUNLUK BEYANI ... ii

JÜRİ ONAY SAYFASI ... iii

TEŞEKKÜR ... iv

ÖZ ... v

İÇİNDEKİLER ... ix

TABLOLAR LİSTESİ ... xiii

ŞEKİLLER LİSTESİ ... xv

BÖLÜM 1 ... 1

GİRİŞ ... 1

Problem Durumu... 1

4+4+4 Eğitim Sistemi ve Seçmeli Dersler ... 2

Matematik Uygulamaları Dersi ... 3

Problem Kurma ... 4

Araştırmanın Amacı ... 5

Araştırma Problemleri ve Alt Problemleri ... 5

Araştırmanın Önemi ... 6 Araştırmanın Sınırlılıkları ... 8 Araştırmanın Varsayımları ... 8 Tanımlar ... 8

BÖLÜM 2 ... 9

KURAMSAL ÇERÇEVE ... 9

Seçmeli Ders ... Hata! Yer işareti tanımlanmamış. Seçmeli Ders Genelgesi ... Hata! Yer işareti tanımlanmamış. Matematik Uygulamaları Dersi ... 25

x

Matematik Uygulamaları Dersinin Amacı ... 25

Matematik Uygulamaları Dersi ve Öğrencilerin Gelişim Özellikleri ... 26

Matematik Uygulamaları Dersinin İçeriği ... 27

Matematik Uygulamaları Dersinde Ölçme ve Değerlendirme ... 29

Matematik Uygulamaları Dersinin Kazanımları ... 30

Neden Matematik Uygulamaları Dersi ... 32

Problem Nedir? ... 10

Problemlerin Sınıflandırılması... 11

Matematiksel Problem Çözme ve Süreci ... 12

Matematiksel Problem Çözme Öğretiminin Amaçları ... 13

Matematiksel Problem Çözmenin Basamakları ... 14

Matematiksel Problem Çözme Öğretiminin Değerlendirilmesi... 16

Problem Çözme ve Problem Kurma Arasındaki İlişki ... 16

Problem Kurma ... 17

Problem Kurmanın Öğrencilerin Öğrenmeleri Üzerindeki Etkisi ... 20

Problem Kurma Stratejileri ... 20

Problem Kurmanın Değerlendirilmesi ... 22

İlgili Araştırmalar ... Hata! Yer işareti tanımlanmamış. Problem Kurma İle İlgili Yapılan Çalışmalar ... Hata! Yer işareti tanımlanmamış. Seçmeli Matematik Uygulamaları Dersiyle İlgili Yapılan Çalışmalar ... Hata! Yer işareti tanımlanmamış.

BÖLÜM 3 ... 40

YÖNTEM ... 40

Araştırmanın Modeli... 40

Çalışma Grubu ... 41

Veri Toplama Araçlarının Geliştirilmesi ... 41

1. Matematik Uygulamaları Dersi Etkinlikleri... 42

2. Problem Kurma Çalışma Kâğıtları ... 42

3. Problem Kurma Başarı Testi ... 43

Geçerlik Güvenilirlik Çalışması ... 44

Verilerin Toplanma Süreci ve İşlem ... 47

Geçerlik ve Güvenilirliğe Yönelik Tehditler ... 50

1. İç Tehditler... 50

xi

Verilerin Analizi ... 53

BÖLÜM 4 ...

57

BULGULAR VE YORUM ... 57

Birinci Probleme İlişkin Bulgular ve Yorumları ... 57

Birinci Alt Probleme İlişkin Bulgular ve Yorumları ... 57

İkinci Alt Probleme İlişkin Bulgular ve Yorumları ... 60

Üçüncü Alt Probleme İlişkin Bulgular ve Yorumları ... 60

Dördüncü Alt Probleme İlişkin Bulgular ve Yorumları ... 61

İkinci Probleme İlişkin Bulgular ve Yorumları ... 63

Birinci Alt Probleme İlişkin Bulgular ve Yorumları ... 64

İkinci Alt Probleme İlişkin Bulgular ve Yorumları ... 64

Üçüncü Alt Probleme İlişkin Bulgular ve Yorumları ... 65

Dördüncü Alt Probleme İlişkin Bulgular ve Yorumları ... 66

BÖLÜM 5 ... 68

SONUÇ VE TARTIŞMA ... 68

Sonuçlar... 68

Öneriler ... 72

Araştırma Sonuçlarına İlişkin Öneriler ... 72

Araştırma Sürecinde Yaşanan Sıkıntılara İlişkin Öneriler ... 73

KAYNAKLAR ... 75

EKLER ... 85

Ek 1. Milli Eğitim Müdürlüğü Araştırma İzin Belgesi ... 86

Ek 2. Futbol Turnuvası Etkinliği ... 87

Ek 3. Futbol Turnuvası Etkinliği Problem Kurma Çalışma Kâğıdı ... 88

Ek 4. Antik Mısır Matematiği Etkinliği ... 89

Ek 5. Antik Mısır Matematiği Etkinliği Problem Kurma Çalışma Kâğıdı... 92

Ek 6. Kutup Kırlangıçları Etkinliği ... 93

Ek 7. Kutup Kırlangıçları Etkinliği Problem Kurma Çalışma Kâğıdı ... 94

Ek 8. Seyahat Seçenekleri Etkinliği ... 95

Ek 9. Seyahat Seçenekleri Etkinliği Problem Kurma Çalışma Kâğıdı ... 97

Ek 10. Bardak Dizme Etkinliği ... 98

Ek 11. Bardak Dizme Etkinliği Problem Kurma Çalışma Kâğıdı ... 99

xii

Ek 13. Kuledeki Askerler Etkinliği Problem Kurma Çalışma Kâğıdı

... 101

xiii

TABLOLAR LİSTESİ

Tablo 1. Araştırma Modeli ... 41

Tablo 2. Ders Esnasında Uygulanan Etkinliklerin Sınıflandırılması ... 43

Tablo 3. Problem Kurma Testi Sorularında Kullanılan Problem Kurma Stratejileri ve İlgili Olduğu Alt Öğrenme Alanı ... 43

Tablo 4. Belirtke Tablosu ... 45

Tablo 5. Problem Kurma Başarı Testi Madde Analizi Sonuçları ... 46

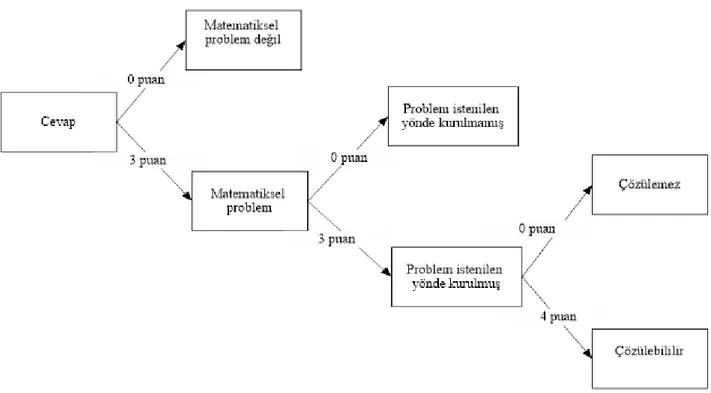
Tablo 6. 5. Maddeye İlişkin Puanlama Yönergesinin Uygulanışı ... 54

Tablo 7. Deney ve Kontrol Grupları Uygulama Öncesi Problem Kurma Başarıları Verilerinin Normalliği ... 57

Tablo 8. Deney ve Kontrol Grupları Uygulama Sonrası Problem Kurma Başarıları Verilerinin Normalliği ... 58

Tablo 9. Deneklerin Problem Kurma Başarı Testi Öntest Puanlarının Ortalamaları ... 59

Tablo 10. Kontrol Grubu Öğrencilerinin Problem Kurma Başarı Testine Yönelik Öntest ve Sontest Puanlarının Ortalamaları ... 60

Tablo 11. Deney Grubu Öğrencilerinin Problem Kurma Başarı Testine Yönelik Öntest ve Sontest Puanlarının Ortalamaları ... 61

Tablo 12. Problem Kurma Başarı Testi Puanlarının Gruplara Göre Betimsel İstatistikleri ... 62

Tablo 13. Öntest Problem Kurma Başarı Testine Göre Düzeltilmiş Puanlarının Gruba Göre ANCOVA Sonuçları ... 62

xiv

Tablo 14. Problem Kurma Başarı Testindeki Soruların Problem Kurma Stratejilerine Göre Öntest Puanlarının Gruplararası Mann Whitney U- Testi Sonuçları ... 64 Tablo 15. Kontrol Grubunun Problem Kurma Başarı Testindeki Soruların Problem Kurma Stratejilerine Göre Öntest-Sontest Wilcoxon İşaretli Sıralar Testi Sonuçları... 65 Tablo 16. Deney Grubunun Problem Kurma Başarı Testindeki Soruların Problem Kurma Stratejilerine Göre Öntest-Sontest Wilcoxon İşaretli Sıralar Testi Sonuçları... 66 Tablo 17. Problem Kurma Başarı Testindeki Soruların Problem Kurma Stratejilerine Göre Sontest Puanlarının Gruplararası Mann Whitney U- Testi Sonuçları ... 67

xv

ŞEKİLLER LİSTESİ

Şekil 1.A tipi uygulama problemi ... 28

Şekil 2. B tipi uygulama problemi... 28

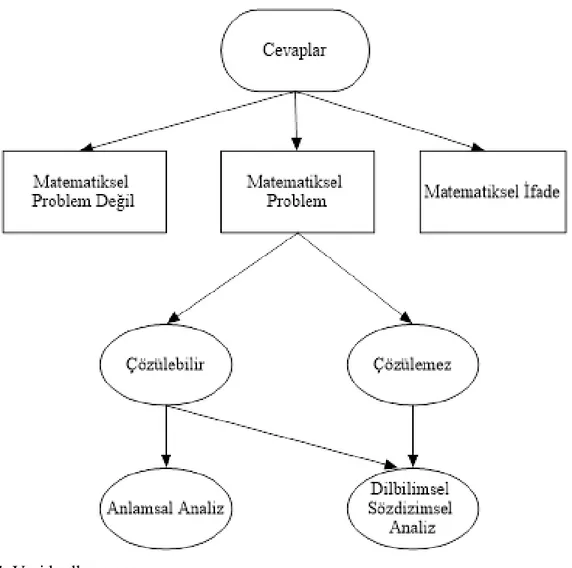
Şekil 3. Veri kodlama şeması ... 23

xvi

SİMGELER VE KISALTMALAR LİSTESİ

MEB Milli Eğitim Bakanlığı

TTKB Talim ve Terbiye Kurulu Başkanlığı

PISA Uluslararası Öğrenci Değerlendirme Programı

TIMSS Uluslararası Matematik ve Fen Eğilimleri Araştırması ERG Eğitim Reformu Girişimi

OECD Ekonomik Kalkınma ve İşbirliği Örgütü TEOG Temel Eğitimden Ortaöğretime Geçiş NCTM Matematik Öğretmenleri Ulusal Konseyi

1

BÖLÜM 1

GİRİŞ

Bu bölümde araştırmaya ilişkin problem durumu, problem cümlesi, araştırmanın önemi, sınırlılıkları, araştırmayla ilişkili kavramlar ve tanımlar üzerinde durulacaktır.

Problem Durumu

İçinde yaşadığımız, küresel değerleri ön plana çıkaran ve sürekli değişimin yaşandığı dönem bilgi toplumu olarak isimlendirilmektedir. Yaşanılan hızlı değişim ve meydana gelen gelişmeler toplumsal yapının değişmesine ve yeniden şekillenmesine neden olmaktadır. Küreselleşen dünyada ulusal ve uluslararası rekabeti ve üstünlüğü sağlayan; geçerli bilginin üretimi ve yeni alanlara uygulanmasıdır. Artık günümüzde toplumların başlıca zenginlik kaynağı bilgidir (Çalık & Sezgin, 2005). Zenginlik kaynağı olan bilginin üretimi ve kullanımı da ülkelerin eğitim sistemiyle çok yakından ilişkilidir.

İçinde bulunduğumuz bilgi toplumunda insan hayatta kalabilmek, varlığını sürdürebilmek ve küreselleşen dünyada rekabet edebilir düzeye gelmek için geçerli bilgiye ulaşabilmeli, bilgiyi kullanabilmeli ve bilgiye sahip olmalıdır (Aydın, 2003). Bilgi çağındaki eğitimin temel amacı yaratıcı ve yenilikçi insanlar yetiştirmektir. Bugün bilginin bireye doğrudan aktarılması değil, bireyin ihtiyaç duyduğu bilgilere nasıl ulaşacağının öğretilmesi önem kazanmıştır (Çalık & Sezgin, 2005). Ülkeler de bu bağlamda gelecekte ihtiyaç duyduğu insan tipini yetiştirmek ve küreselleşen dünyada ulusal ve uluslararası rekabet ve üstünlük sağlayabilmek için eğitim sistemlerinde değişim ve yenilikler yapmaktadırlar. Eski astronot ve senatör John Gleen’in liderliğinde hazırlanan Gleen Komisyon Raporu, “ 21. Yüzyılın

2

erken dönemlerindeki yeni mesleklerin %60’ının, günümüz iş gücünün sadece %20’sinin sahip olduğu becerileri gerektireceğini ifade etmiştir (Amerika Birleşik Devletleri Eğitim Bakanlığı’ndan aktaran Dede, 2013). Bu istatistiğin uluslararası alanda rekabet edebilmek için yetiştirilmesi gereken insan özelliklerinin ve niteliğinin önemine ilişkin ipuçları verdiği söylenebilir.

Ülkemiz küreselleşen dünyada bilgi toplumuna uyum sağlayabilmek ve rekabet edebilir bireyler yetiştirmek amacıyla 2005 yılında ilköğretim okulları için hazırlanan öğretim programları yapılandırmacı öğretim anlayışı doğrultusunda değiştirilmiştir. Yapılandırmacı yaklaşımda bireysellik ön plandadır, öğrenme sürecinin merkezinde öğrenci vardır, öğretimde öğrenme süreci çok önemlidir, öğretimin amacı öğrencide davranış değişikliği oluşturmak değil bir anlayış oluşturmaktır (Özdemir, Yalın ve Sezgin, 2012). Bu anlayışa göre hazırlanan yeni programlar etkinliklerle zenginleştirilerek öğrenci merkezli hale getirilmiştir. Dolayısıyla bilgi toplumunda ihtiyaç duyulan bireylerin yetiştirilmesi konusunda eğitimin niteliği açısından önemli bir adım atıldığı söylenebilir. Atılan bu adım önemli olsa da bilgi toplumunun eğitim anlayışı öğrencilerdeki bireysel farklılıklara cevap veren esnek programların uygulanmasını gerektirmektedir. Programda ortak zorunlu derslerle birlikte öğrencilerin ilgi, yetenek ve ihtiyaçlarına yönelik seçmeli derslerin bulunması, her öğrenciye özel ayrı bir programın yapılmasını gerektirmektedir (Kuzgun vd., 1997). Eğitim sistemimize 2012 yılında yenilik olarak gelen 4+4+4 değişikliğiyle seçmeli dersler konusunda önemli düzenlemeler yapılmıştır.

4+4+4 Eğitim Sistemi ve Seçmeli Dersler

Ortaöğretim kurumları yönetmeliğinde seçmeli dersler öğrencilerin hedefledikleri ve yöneldikleri alanda gelişmelerine veya ilgi ve istekleri doğrultusunda çeşitli programlarda ilerlemelerine, kişisel yeteneklerini geliştirmelerine imkân sağlayan dersler olarak tanımlanmıştır. Öğrencilerin ilgi, istek ve yeteneklerine uygun seçmeli derslerin getirilmiş ve ders seçiminde öğrenci ve velinin isteği göz önünde bulundurulmuştur (Eğitim Reformu Girişimcileri [ERG] ,2014; Milli Eğitim Bakanlığı [MEB], 2012a).

Seçmeli dersler Din, Ahlak ve Değerler, Dil ve Anlatım, Yabancı Dil, Fen Bilimleri ve Matematik, Sanat ve Spor ve Sosyal Bilimler olarak belirlenen altı (6) farklı alanda tanımlanmıştır. Fen ve matematik alanındaki seçmeli dersler Matematik Uygulamaları,

3

Bilim Uygulamaları, Çevre ve Bilim ve Bilişim teknolojileri ve yazılım dersleridir (MEB, 2012a).

Değişen ve gelişen dünya öğrencilere ne öğretilmesi gerektiğini etkilemektedir ve geleceğimiz olan öğrencilere muhtemelen günümüzde olmayan meslekler hazırlamaktadır. Ayrıca sadece basit hesaplamalar yapabilen insanlar için çok az mesleğin olduğu da bilinmektedir. Bu nedenle öğrencilere yeni problemlere çeşitli yollarla yaklaşabilmeyi, tahminler yapmak için algoritmalar düzenlemeyi ve karmaşık verileri yorumlamayı gerektirecek meslekler öngörülerek eğitim verilmelidir (Dede, 2013). Bu kapsamda mevcut araştırmada öğrenciler tarafından en çok tercih edilen seçmeli ders olan Matematik Uygulamaları dersi üzerine çalışılmıştır.

Matematik Uygulamaları Dersi

Ülkemizde matematik dersinin zor olduğuna dair yaygın bir inanış gözlemlenmektedir. Türkiye’de matematik öğretimi, çoğunlukla öğrenciler üzerinde bir baskıya dönüşerek matematik korkusunun yerleşmesine neden olmaktadır (Şahan, 2006). Öğrencilerde yer alan bu kaygı ve kendini yetersiz görme ulusal ve uluslararası sınavların sonuçlarında da kendini göstermektedir. Ülkemiz Uluslararası Öğrenci Değerlendirme Programı (PISA) sınavları açısından değerlendirildiğinde ne yazık ki çok parlak sonuçlar elde etmediği görülmektedir. PISA sınavlarında ölçülen temel yeterlik okuryazarlık başlığıdır. Matematik özelinde bu yeterlik gerçek bağlamda verilen bir problemi matematiksel olarak kurgulama, matematiksel bilgi, işlem ve muhakeme ile matematiksel problemi çözme ve elde edilen sonucun gerçek yaşama uygunluğuna karar verme boyutları ile ele alınmaktadır. PISA 2012 uygulamasında ilk kez öğrencilere sunulan öğrenim olanakları matematik özelinde ele alınmıştır. Bu amaçla öğrencilere bazı soru örnekleri gösterilerek bu sorular veya benzerleri ile derslerde ne kadar karşılaştıkları sorulmuştur. Öğrencilere sunulan öğrenim olanakları 3 boyutta ele alınmıştır. Bu boyutlardan birisi de Uygulamalı Matematik boyutudur. Bu boyutta öğrenciler kendilerine sunulan problemleri günlük yaşamda ne sıklıkla kullanabildiklerini ifade etmişlerdir. 2012 PISA sonuçlarında Türkiye’nin düzey 1 ve altı öğrenci oranı azalmasına rağmen, bu oran diğer Ekonomik İşbirliği ve Kalkınma Örgütü (OECD) ortalamasındaki düzey 1 ve altı öğrenci oranının yaklaşık 2 katıdır (MEB, 2013). Ülkemizde yapılan ulusal sınavlar incelendiğinde durum matematik açısından yine çok farklılık göstermemektedir.b2015-2016 eğitim öğretim yılında yapılan Temel Eğitimden

4

Ortaöğretime Geçiş (TEOG) sınavında 1. Dönem 42,90, 2. Dönem ise 42,05 ile ortalamasıyla en düşük ders Matematik dersi olmuştur (MEB, 2016b, 2016d). Derslerin ortalama güçlük düzeyine bakıldığında da 1. Dönem 0,428 ve 2. Dönem 0,42 ile en düşük güçlük düzeyine sahip olan ders yine matematiktir (MEB, 2016a, 2016c).

Tüm bu bilgiler ve sonuçlar göz önüne alındığında ülkemiz matematik öğretimi etkililiğinde sorunlar olduğu göze çarpmaktadır. 4+4+4 eğitim sistemiyle gelen Seçmeli Matematik Uygulamaları dersinin bu sorunların giderilmesi açısından önem taşıdığı düşünülmektedir. Çünkü bu dersin amaçları arasında öğrencilerin matematiksel bilgi ve becerilerini geliştirmek, düzeylerine uygun matematiksel uygulamalar yapma fırsatı vermek, matematiği sevdirmek ve matematiğe karşı olumlu tutum geliştirmek yer almaktadır. Ayrıca Matematik Uygulamaları dersi öğrencilerin matematiksel bilgi ve becerilerini geliştirirken aynı zamanda öğrencilerin iyi birer problem çözücü ve problem kurucu bireyler olmasını amaçlar. Bu bağlamda araştırma diğer bir boyutta problem kurmayla ilişkilendirilmiştir.

Problem Kurma

Problem kurma bir durumdan veya bir deneyimden yola çıkılarak bir problem oluşturma veya bir problemden yeni bir problem üretmedir (Silver’den aktaran Stoyanova 2003). Problem kurma son yıllarda problem çözme ile birlikte sıklıkla anılmaktadır. Öğrencilerin problem çözme becerilerinin yanında problem kurma becerilerinin geliştirilmesi de oldukça önemli görülmektedir. Ayrıca problem kurma PISA sınavlarında başarımızı artırmak açısından da önem taşımaktadır. Çünkü PISA’nın okuryazarlık başlığı altında yer alan gerçek bağlamda verilen bir problemi matematiksel problem olarak kurgulama (formulasyon) problem kurma ile yakından ilgilidir. English (1998), öğrencilerin sembolik matematiksel ifadeleri tanımlayabilme ve günlük yaşamdaki durumlar ile bağlantı kurabilme becerilerinin, problem kurma etkinlikleri ile geliştirilebileceğini belirtmiştir. Bu da problem kurmanın PISA’daki başarımızı önemli ölçüde artıracağının göstergesi olabilir. Ayrıca 21. yy bilgi toplumları, bireylerde temel becerilerin dışında bazı yeterliliklere sahip bireylere ihtiyaç duymaktadır. Bu nedenle eğitim sistemlerinde değişim ve yeniliklere gitmektedirler. Bilgi toplumları artık sadece bilen değil, sahip olduğu bilgiyi hayata uygulayabilen; karşılaştığı problemlere çözümler üreten bireyler istemektedirler. Bu amaçla son zamanlarda matematik eğitimi de yeni bir yapılanmaya giderek problem çözme, problem kurma ve öğrenci merkezli bir bakış açısıyla yeniden düzenlenmiştir. Ersoy (2006), İlköğretim

5

Matematik Öğretim Programındaki yenilikleri incelediği çalışmasında öğrencilere problem çözme becerisi kazandırılırken bazı becerilerinde geliştirilmesi gerektiğini ifade etmiştir. Matematiksel ve günlük yaşam durumlarını kullanarak problem kurma ve problemi başka bir biçimde ifade etme de geliştirilmesi gereken beceriler arasında yer almaktadır. Tüm bu bilgiler de problem çözme ve problem kurmanın önemini göz önüne sermektedir.

Yukarıda açıklamalar doğrultusunda bu araştırmanın amacı, problem cümlesi, önemi, sınırlılıkları ve varsayımları aşağıda açıklanmıştır.

Araştırmanın Amacı

Bu araştırmanın amacı ortaokullarda okutulan Seçmeli Matematik Uygulamaları dersinin “Problem çözümünü takiben yeni matematiksel problemleri kurar” kazanımından yola çıkarak, matematiksel problem kurma stratejilerinin öğrencilerinin problem kurma başarılarına etkisini incelemektir.

Araştırma Problemleri ve Alt Problemleri

Bu çalışmada aşağıdaki problemlere ve alt problemlere cevap aranmıştır.

1. Matematik Uygulamaları dersi etkinliklerinin ve problem kurma çalışmalarının öğrencilerin problem kurma başarı testinden aldıkları ortalama puanlar üzerinde anlamlı bir etkisi var mıdır?

1.1. Deney ve kontrol gruplarının problem kurma başarı testi öntest ortalama puanları arasında istatistiksel olarak anlamlı bir fark var mıdır?

1.2. Kontrol grubunun problem kurma başarı testi öntest ve sontest ortalama puanı arasında istatistiksel olarak anlamlı bir fark var mıdır?

1.3. Deney grubunun problem kurma başarı testi öntest ve sontest ortalama puanı arasında istatistiksel olarak anlamlı bir fark var mıdır?

1.4. Deney ve kontrol gruplarının problem kurma başarı testi öntest ortalama puanları kontrol edildiğinde sontest ortalama puanları arasında istatistiksel olarak anlamlı bir fark var mıdır?

6

2. 5. sınıf öğrencilerinin problem kurma stratejilerine (yapılandırılmış, yarı yapılandırılmış, serbest) göre problem kurma başarı testinden aldıkları puanlar arasında anlamlı bir farklılık var mıdır?

2.1. Deney ve kontrol gruplarının problem kurma stratejilerine (yapılandırılmış, yarı yapılandırılmış, serbest) göre problem kurma başarı testi öntest puan ortalamaları arasında istatistiksel olarak anlamlı bir farklılık var mıdır?

2.2. Kontrol grubunun problem kurma stratejilerine (yapılandırılmış, yarı yapılandırılmış, serbest) göre problem kurma başarı testi öntest-sontest ortalama puanı arasında istatistiksel olarak anlamlı bir fark var mıdır?

2.3. Deney grubunun problem kurma stratejilerine (yapılandırılmış, yarı yapılandırılmış, serbest) göre problem kurma başarı testi öntest-sontest ortalama puanı arasında istatistiksel olarak anlamlı bir fark var mıdır?

2.4. Deney ve kontrol gruplarının problem kurma stratejilerine (yapılandırılmış, yarı yapılandırılmış, serbest) göre problem kurma başarı testi sontest puan ortalamaları arasında istatistiksel olarak anlamlı bir farklılık var mıdır?

Araştırmanın Önemi

4+4+4 eğitim sistemi ile birlikte ortaokullara ve imam-hatip ortaokullarına getirilen seçmeli derslerden biri Matematik Uygulamaları dersidir. Talim ve Terbiye Kurulu Başkanlığı (TTKB, 2013b) şimdiye kadar matematiğin soyut taraflarını gören öğrencilerin, bu ders ile matematiğin günlük hayattaki kullanımını görerek öğrencilerin matematik öğrenmelerinin kolay ve zevkli hale geleceğini belirtmiştir. Matematik Uygulamaları dersi yeni bir ders olması sebebiyle birtakım yenilikleri de beraberinde getirmiştir. Öğrencilerin zorunlu matematik dersinin desteklenmesi ve ileri matematiksel problem çözme becerilerinin geliştirilmesi amacıyla Matematik Uygulamaları dersi geliştirilmiştir. Milli Eğitim Bakanlığı tarafından hazırlanan Ortaokul ve İmam-Hatip Ortaokulu Matematik Uygulamaları 5. Sınıf Öğretmenler İçin Ders Materyali kitabındaki etkinliklerden bir kısmı Ek 2, Ek 4, Ek 6, Ek 8, Ek 10 ve Ek 12’de verilmiştir. İleri matematiksel problem çözme ve problemlerin günlük hayatla ilişkisi açısından bu etkinlikler incelenebilir. Daha ileri problem çözme deneyimleri yaşamak için problem kurma çalışmalarının etkisi kaçınılmazdır. Ayrıca literatüre bakıldığında problem kurma ile ilgili birçok çalışma yapılmış olmasına rağmen Matematik Uygulamaları dersinin

7

problem kurmaya etkisini içeren bir çalışmaya rastlanmamıştır. Bu çalışma yeni bir ders olan Matematik Uygulamaları dersinin geliştirilme sebebi olan ileri problem çözme becerisine etkisi olacağı düşünülen problem kurma çalışmalarının etkisinin belirlenmesi açısından önemlidir. Aynı zamanda problem kurmanın öğrencilerin öğrenmeleri üzerinde önemli etkileri olduğu bilinen bir gerçektir. Matematik derslerinde yapılan problem kurma çalışmalarının öğrencilerin problem çözme başarılarını anlamlı düzeyde artırdığı (Fidan, 2008), matematiğe yönelik görüşlerinde anlamlı farklılıklar oluşturduğu, niteliksel akıl yürütme becerilerini geliştirdiği ve dolayısıyla da problemi anlama başarılarını üst düzeye çıkardığı (Cankoy & Darbaz, 2010), eleştirel düşünme becerisi, akıl yürütme, muhakeme yapma ve bilgileri organize edebilme becerisini geliştirdiği (Arıkan & Ünal, 2013; Gür & Korkmaz,2003; Işık & Kar, 2012) görülmüştür. Ayrıca Türkiye’nin PISA ve TIMSS gibi sınavlardaki başarısı pek iç açıcı değildir. TIMSS 2011’de hem 4. sınıf hem de 8. sınıf öğrencilerinin %25’i temel düzeydeki yeterliklere bile sahip olmadığı ve ülkemizin her iki sınıf düzeyinde de belirlenen ölçek ortalamasının altında kaldığı görülmüştür. PISA 2012 sonuçlarında da Türkiye’nin düzey 1 ve altı öğrenci oranı 2003 yılına oranla azalmasına rağmen, bu oran diğer OECD ortalamasındaki düzey 1 ve altı öğrenci oranının yaklaşık 2 katıdır. Ayrıca PISA 2012 Türkiye ortalaması da OECD ortalamasının altındadır (MEB, 2013). PISA ve TIMSS sınavlarında ortalamaların altında kalmamız nedeniyle matematik eğitiminde birtakım değişikliklere gidilmiştir. Bu amaçla ilk olarak matematik dersine ayrılan haftalık ders saati 1 saat arttırılmıştır. Ardından 4+4+4 eğitim sistemiyle birlikte Seçmeli Matematik Uygulamaları dersi getirilmiştir. Yapılan bu değişikliklerle PISA ve TIMSS başarımızın artacağı öngörülmektedir.

Matematik Uygulamaları dersi 5, 6, 7, ve 8. Sınıflara kademeli olarak getirilmiştir. Araştırmanın yapıldığı 2015-2016 eğitim öğretim yılında sadece 5. sınıflar için Matematik Uygulamaları dersine ait öğretim materyali vardır. Bu nedenle araştırmada 5. sınıflar üzerinde çalışılmıştır. 5. sınıflara yönelik yapılan bu çalışmanın 6, 7 ve 8. sınıflar için hazırlanacak öğretim materyallerine yol gösterip fikir vermesi açısından önemli olduğu düşünülmektedir. Ayrıca Matematik Uygulamaları dersi yeni bir ders olduğundan bu alanda yapılan çalışmalar çok yeni ve sınırlıdır. Literatürdeki eksikliğin tamamlanması açısından bu araştırma önemlidir. Araştırmanın aynı zamanda Matematik Uygulamaları dersini veren öğretmenlere de faydalı olacağı düşünülmektedir.

8 Araştırmanın Sınırlılıkları

Bu araştırma Ankara İlindeki orta sosyo-ekonomik düzeye sahip bir imam-hatip ortaokulunda 2015-2016 eğitim öğretim yılında iki sınıfta öğrenim gören öğrenciler ile sınırlıdır. Araştırmanın yapıldığı okul imam-hatip ortaokulu olduğundan karma eğitim verilmemektedir. Matematik Uygulamaları dersini alıp almama durumuna göre araştırmacının elinde olmayan nedenler sebebiyle deney grubu tamamen erkek öğrencilerden, kontrol grubu ise tamamen kız öğrencilerden oluşmaktadır.

Araştırmanın Varsayımları

Yapılan çalışmada öğrencilerin verilen sorulara samimi bir şekilde cevap verdiği, grupların birbirlerinden etkilenmedikleri ayrıca deney ve kontrol gruplarının araştırma için yeterli olduğu varsayılmıştır.

Tanımlar

Problem: Daha önce karşılaşmadığımız, bizi rahatsız eden zorluklar ve engellerdir. Problem Çözme: Önümüze çıkan engelleri aşmak için gösterilen çaba.

Problem Kurma: Bir durumdan veya bir problemden yola çıkılarak yeni problemler üretme.

Strateji: Bir amaca ulaşmak için belirlenen yolların ve uygulanan yöntemlerin tamamı. Problem Kurma Stratejisi: Problem kurma başarı testindeki soruların oluşturulmasında kullanılan stratejiler.

9

BÖLÜM 2

KURAMSAL ÇERÇEVE

Bu bölümde araştırmanın kavramsal çerçevesine, araştırmayla ilgili olduğu düşünülen temel kavram ve terimlerin açıklamalarına yer verilmiştir.

2012-2013 eğitim öğretim yılı itibariyle ülkemiz 4+4+4 olarak ifade edilen bir eğitim sistemine geçiş yapmıştır. Bu sistemle ilkokul ve ortaokul kısımları birbirinden ayrılmış; 5. sınıf öğrencileri ortaokul kısmına kaydırılmıştır. Bu doğrultuda da ortaokul öğretim programları 5, 6, 7 ve 8. sınıfları kapsayacak şekilde yeniden düzenlenmiştir. Bu uygulamanın neticesinde “Ortaokul Matematik Dersi Öğretim Programı” da yenilenmiştir. Yenilenen matematik dersi öğretim programında öğrencilerin aktif katılımcı olmaları vurgulanırken, öğretmenlerin de öğrencilere yol gösteren bir rehber gibi davranması istenmektedir.

Türkiye’de daha önce matematik eğitimi çoğunlukla öğretmeni merkeze alan bir yaklaşımla uygulanmaktaydı. Derslerde öğrencilere sıradan alıştırmalar ve uygulamalar yaptırılıp, çoktan seçmeli, kısa-uzun cevaplı sorulardan oluşan yazılı sınavlar yapılmaktaydı (Akay, Soybaş & Argün, 2006). Ancak günümüzdeki programa bakıldığında öğrenciyi merkeze alan bir yaklaşımın benimsendiği söylenebilir. Bu bağlamda matematik eğitimin davranışsal kuramdan yapılandırmacı kurama doğru bir yönelime girmiş olduğu söylenebilir. Ayrıca programda problem çözme ve problem kurma üzerinde önemle durulmuştur. Nitekim programda öğrencilere kazandırılmak istenen beceriler arasında en başta problem çözme gelmektedir (TTKB,2013a). Öğrencilere bu becerinin kazandırılması sürecinde vurgu yapılan bir başka terim de problem kurmadır. Öğrencilerden problemin çözümünün tamamlanmasının ardından bu probleme benzer veya özgün bir problem kurmaları istenerek

10

problem kurma becerilerinin geliştirilmesi amaçlanmaktadır. Tüm bu bilgiler ışığında öğretim programında üzerinde durulan problem, problem çözme ve problem kurma ile ilgili ayrıntılı bilgiler aşağıda açıklanmaya çalışılmıştır.

Problem Nedir?

Matematik denilince akla gelen ilk kavramlardan birisi de problemdir. İlgili literatür incelendiğinde birçok farklı problem tanımıyla karşılaşılmaktadır. Bu tanımlardan bir kısmı şu şekildedir.

Adair (2000)’ e göre problem önümüze atılmış ve bizi engelleyen bir şeydir.

Kneeland (2001) problemi bir şeyin olması gerektiği durum ile şu anda olan durum arasındaki fark veya olayların şu anda bulunduğu yeri ile onların olmasını istediğiniz yer arasındaki fark olarak tanımlamıştır.

Dewey (1910) problemi, insanın zihnine meydan okuyan ve onu bulandıran aynı zamanda inancı belirsizleştiren bir olgu olarak tanımlamıştır.

Morgan (1999)’a göre problem kişinin bir hedefe ulaşmasında karşılaştığı engelle çatışma durumudur.

Aksoy (2003)’e göre bir kimsenin istenilen bir amaca varmak maksadıyla topladığı mevcut güçlerinin karşısına dikilen engele problem denir.

Akay (2006) bir durum veya olayın problem olabilmesini, insana birtakım zorluklar getirmesine ve rahatsızlık vermesine bağlamıştır.

Problem, insan zihnini karıştıran, ona meydan okuyan ve inancı belirsizleştiren her şey olarak tanımlanmaktadır (Baykul, 1999).

MEB (2013a) ise problemi çözüm yolu önceden bilinmeyen ve çözümü aşikâr olmayan sorular olarak tanımlamıştır.

Bütün bu tanımlar incelendiğinde problemi tanımlarken ortak bir takım noktalar olduğu görülmektedir. Bu bağlamda problem daha önce karşılaşmadığımız, bizi rahatsız eden zorluklar ve engeller olarak tanımlanabilir.

Bu araştırmada Matematik Uygulamaları dersindeki problemlere en yakın tanım olan MEB (2013a)’in tanımı benimsenmiştir.

11

Problemin ne anlama geldiği, ne tür soruların problem olarak tanımlanabildiği yukarıda açıklanmıştır. Problemin ne anlama geldiğinin yanında ne tür bir sınıflandırılmaya tâbi tutulacağı da dikkate değer bir noktadır. Aşağıda değişik yaklaşımlara dayanarak yapılan bazı sınıflandırmalara yer verilmiştir.

Problemlerin Sınıflandırılması

Problemler genel hatlarıyla ele alındığında yapı olarak iki sınıfa ayrıldığı görülmektedir.

a) İyi Yapılandırılmış Problemler: Bu tür problemlerin genelde tek bir doğru cevabı vardır ve belirli stratejiler problemin doğru cevabını bulmayı sağlar. Mesela matematik problemleri, fizik ve kimya deneyleri ve bulmacalar (Kalaycı, 2001, s. 10)

b) İyi Yapılandırılmamış Problemler: Tek bir doğru yanıtın olmadığı, günlük hayatta karşılaştığımız problemleri kapsayan problem türüdür. Bu konuda özelikle Kohlberg’in yapmış olduğu çalışmalar dikkat çekmektedir (Senemoğlu, 2001, s. 70). Problem kavramı ele alındığında matematiksel problemin akla gelmemesi neredeyse imkânsızdır. Altun (2005) matematiksel problemleri sıradan (rutin) ve sıradışı (rutin olmayan) problemler olmak üzere ikiye ayırmıştır.

Rutin problemler: Bunlar, Matematik ders kitaplarında yer alan ve dört işlem becerileri ile çözülebilen problemlerdir (Altun, 2005, s.83).

Rutin olmayan problemler: Rutin olmayan problemlerin çözümünde işlem becerilerinin ötesinde, verileri organize etme, sınıflandırma ve ilişkileri görme gibi beceriler ve bir takım aktivitelerin arka arkaya yapılması önemlidir. Bu problemler gerçek hayatta karşılaşılmış veya karşılaşılabilecek durumlardır. Bundan ötürü bu problemlere gerçek hayat problemleri de denir (Altun, 2000).

Bir durum problem olarak belirlenip, bir sınıflandırmaya tâbi tutulduktan sonra çözüm aşamasına geçilmelidir. Problem çözülüp sorun ortadan kalktığı zaman bir anlam kazanır. Aşağıda problem çözme ve bu sürecin nasıl işlediği açıklanmaya çalışılmıştır.

12 Matematiksel Problem Çözme ve Süreci

Altun (2000) problem çözmeyi ne yapılacağının bilinmediği durumlarda yapılacak olanı bilmektir şeklinde tanımlamıştır. Problem çözme matematik dersinin ayrılmaz bir parçasıdır (MEB, 2008, s. 12). Problem çözmek test çözmek değildir. Yani problem çözme soru çözme değil sorun çözmektir (Olkun &Toluk Uçar, 2012, s. 41)

Problem çözmek sadece matematik öğrenmenin bir amacı değil aynı zamanda onun temel aracıdır. Problem çözme matematik öğrenmenin temel bir parçasıdır ve bu yüzden matematik programından ayrı ele alınmamalıdır (National Counsil of Teachers of Mathematics [NCTM], 2000). Yani matematik müfredatı öğrencilere matematiksel beceriler kazandırırken yeni problem çözme fırsatları da sunmalıdır (NCTM, 1989).

Morgan (1999), problem çözmeyi bireyin karşısına çıkan engelleri aşmasının en iyi yolunu bulması olarak tanımlamıştır. Schunk (2009) bireylerin otomatik bir çözümlerinin olmadığı bir sorun karşısında bir hedefe ulaşmak için gösterdiği çabaya problem çözme demiştir. Problem çözme bir sorunu çözmek için önceki yaşantılar yoluyla öğrenilen kuralların basit biçimde uygulanmasının ötesine giderek yeni çözüm yolları bulabilmektir (Korkut, 2002). Problem çözme bireyi engelleyen durumlarla başa çıkma, probleme çözüm üretme sürecidir (Şimşek, 2012).

Problem çözme süreci net olarak tasarlanan fakat hemen ulaşılamayan bir hedefe varmak için kontrollü etkinliklerle araştırma yapmadır (Altun, 2005, s. 83)

Hayat boyu bireylerin karşılaşacağı engeller ve ihtiyaç duyacağı şeyler önceden bilinmemektedir. Bu nedenle insanlar yaşadıkları çevreye uyum sağlayabilmek için problem çözmeyi öğrenmelidirler (Senemoğlu, 2011). Çağdaş eğitim de karşılaştığı engelleri kendi kendine aşabilen insan yetiştirmek istemektedir. Problem çözmede bilgi kendi başına işe yaramaz. Problem çözme yeteneği gelişmiş insan, bilgiyi etkili bir biçimde kullanabilir. Problem çözme yeteneği gelişmemiş bireyler ise bilginin sadece taşıyıcılığını yapar. Bu nedenle problem çözme ve onun öğretimi önemlidir (Altun, 2005).

Hayatları boyunca bireyler birtakım problemlerle karşı karşıya kalırlar. Bu problemler çözülebildiği sürece huzurlu ve mutlu bir yaşam sürdürülür. Bu nedenle problem çözme her birey için ayrı bir öneme sahiptir.

13

İlköğretimin temel amacı, bireyleri bir üst kademeye ve hayata hazırlamaktır. Bu bağlamda hedeflenen, yaşam boyu karşılaşabileceği problemlerin üstesinden gelebilen bireyler yetiştirmektir. Bu durum, matematik eğitiminin temel amaçları arasında problem çözmenin olması sonucunu doğurmuştur (Şimşek, 2012, s. 16). Nitekim Talim ve Terbiye Kurulu tarafından yayımlanan Ortaokul Matematik dersi öğretim programında problem çözmenin altı çizilmiştir. Öğretim programında Matematiği etkili öğrenmeye ve kullanmaya yönelik bazı temel becerilerin geliştirilmesi hedeflenmektedir. Bu temel becerilerden birisi de problem çözmedir. Bu bağlamda matematik eğitiminin genel amaçları arasında “Problem çözme sürecinde kendi düşünce ve akıl yürütmelerini ifade edebilecektir.” maddesi yer almaktadır (TTKB, 2013a).

Matematik eğitiminin genel amaçları arasında yer alan problem çözme ve öğretiminin amaçlarının ne olduğunun bilinmesi de gereklidir. Aşağıda problem çözme öğretiminin amaçları açıklanmaya çalışılmıştır.

Matematiksel Problem Çözme Öğretiminin Amaçları

Altun (2005) problem çözme öğretiminin amaçlarını özel ve genel amaçlar olmak üzere iki başlık altında toplamıştır.

Özel Amaçlar: Özel amaçlar işlem becerisini geliştirme, sayı ve şekillerle uğraşmaya alışma, veri toplama ve tasnif etme, problem metnine uygun şekil ve şema çizme, düşünceleri matematik diliyle anlatma, yazılı ve görsel yayınlarda kullanılan matematiksel ifadeleri anlamadır (Altun, 2005, s. 85).

Genel Amaçlar: Problem çözme öğretiminin genel amacı, öğrencilerin problem çözme yeteneğinin gelişmesini sağlamaktır. Problem çözme yeteneği, bir sorunla baş başa kalındığında onun özünü kavrama ve problemi anlama, çözümüne ilişkin stratejiyi seçme, bu stratejiyi kullanma ve çözüme ilişkin sonuçları yorumlama becerilerini kapsar (Altun, 2005, s. 86).

Problemin çözüm sürecinde hangi işlemlerin olduğu, problem çözmenin nasıl olduğu ve bu sürecin hangi parçalardan oluştuğu kesin olarak bilinememektedir. Ancak bazı kuramlar ve

14

yapılan araştırmalarla problem çözmenin bazı adımları ayırt edilebiliyor ve bunlara dayalı olarak problem çözme becerisinin geliştirilmesi hedefleniyor (Baykul, 1999).

Altun (2000) bütün problemlerin çözümünde kullanılan belirli bir yol ya da yöntemin olmadığını, eğer böyle bir yöntem olsaydı sorunun kökünden halledileceğini belirtmiştir. Öğrenciler bir sorunla karşılaştıklarında çoğu kez bu durumda kullanılabilecek bir kural bulmaya çalışırlar. Bu çözüme ulaşmak iyi bir yol değildir. Çünkü problem çözme kurallara göre değil bir sistematiğe göre çalışır.(Altun, 2005). Bu sistematikte de belirli basamaklar bulunmaktadır. Matematiksel problem çözme basamakları başlığı altında bu aşamalar açıklanmıştır.

Matematiksel Problem Çözmenin Basamakları

Polya (1957) tarafından yapılan çalışmalar, matematik problemlerinin çözümünde bazı aşamaların olduğunu ortaya koymuştur. Bu aşamalar şu şekildedir:

1. Problemin anlaşılması

2. Problemin çözümü için bir plan yapılması 3. Çözüm planının uygulanması

4. Sonucun doğru olup olmadığının kontrol edilmesi

Baykul (1999) bu adımların aynı zamanda öğrencilerin problemleri başarıyla çözebilmeleri için geliştirilmesi gereken yetenekleri gösterdiğini ifade etmektedir.

Birinci aşama olan problemin anlaşılması aşamasında, problem çözücü problemde nelerin var olduğu ve nelerin istendiğini açık bir şekilde görmeye çalışır. Kişinin bilinmeyen nedir, bilinen veriler nedir ve durum nedir yani bilinen ve bilinmeyenler arasındaki matematiksel ilişkiler nelerdir sorularına yanıt aradığı aşamadır (Olkun & Toluk Uçar, 2012).

İkici aşama olan problemin çözümü için bir plan yapılması aşaması bireyi problemin çözümüne götüren en önemli adımdır. Bu adım problemin anlaşılmasına bağlıdır. Problem anlaşılmadan bu adım gerçekleştirilemez (Baykul, 1999). Altun(2000) bu safhada öğretmenin rolünün bazı sorular yönelterek öğrencilerin uygun stratejileri seçmelerini sağlamak olduğunu belirtmiştir ve kullanılabilecek bazı soruları şu şekilde sıralamıştır:

 Bu problemde neyin bulunması isteniyor?

15

 Buna benzer, daha önce başka bir problem çözdün mü? Orada ne yaptın, hatırla.  Bu problemi çözemiyorsan, buna benzer daha basit bir problem ifade edip çözebilir

misin?

 Tasarladığın çözümde bütün bilgileri kullanabiliyor musun?

 Bu problemin cevabını tahmin edebiliyor musun? Hangi değerler arasındadır? Üçüncü aşama olan çözüm planının uygulanması aşamasının kritik davranışları işlem sonuçlarının tahmin edilmesi ve problemin çözümünde kullanılacak planın gerçekleştirilmesi veya işlemlerin yapılmasıdır (Baykul, 1999).

Dördüncü aşama olan sonucun doğruluğunun kontrol edilmesi aşamasında, hem işlemlerin doğru yapılıp yapılmadığı hem de sonucun tahmine uygun olup olmadığı kontrol edilir (Baykul, 1999). Ayrıca bu aşamada problemin bireye kattıkları da gözden geçirilir (Olkun & Toluk Uçar, 2012). Altun(2005), bu aşamanın temel eylemlerini sonuçların doğruluğunun ve uygunluğunun kontrol edilmesi, problemin başka çözüm yollarından çözülmesi, problemin değişik şekillerde ifade edilmesi ve bu durumda çözümün nasıl olacağının düşünülmesi biçiminde ifade etmiştir.

Matematik kitaplarındaki problemlere ilişkin çözümleri, bu dört basamağın başlı başına bir uygulamasından ibaret değildir. Bu basamaklar daha çok onların uygulama aşamasında gerekli olan temel becerilerin kazandırılmasıyla ilgilidirler. Çocuklar ilk yıllarda sıradan problemlerle daha çok meşgul edilerek zamanla gerçek problemlerle yüz yüze getirilmelidir (Altun, 2005).

Gonzales (1998) ise Polya’nın dört aşamalı olan problem çözme sürecinin beşinci basamağını problem kurma olarak nitelendirmiştir. Burada öğrenciler çözdükleri problemlere bakarak probleme eklemeler yaparak veya problemi değiştirerek problem kuracaklardır. Problem kurma ve problem çözme arasındaki ilişki hakkında araştırmanın ilerleyen kısımlarında daha ayrıntılı olarak bilgi verilmiştir.

Problem kurma sürecinin sağlıklı bir şekilde tamamlanmasının ardından bu sürecin etkili ve verimli bir şekilde değerlendirilmesi büyük önem taşır. Etkili ve verimli bir değerlendirme süreçte yaşanan sıkıntıların azalmasını ve başarıya ulaşmasını kolaylaştıracaktır. Aşağıda problem çözme öğretimin değerlendirilmesi açıklanmaya çalışılmıştır.

16

Matematiksel Problem Çözme Öğretiminin Değerlendirilmesi

Problem çözme sürecinin önemli bir adımı da bu sürecin değerlendirilmesidir. Bir problemin cevabını doğru bulan her öğrenci problemi doğru çözmüş sayılmaz. Bazı öğrenciler işlemlerde ardışık hatalar yaparak ya da yanlış bir akıl yürütme ile sonuca ulaşabilirler. Problem çözme davranışlarından bazıları henüz oluşmamış öğrencilerde problem çözmede başarısızlık oluşturmaktadır. Problem çözme sürecinde öğrenilebilir davranışlar gösterilmektedir. Problem çözmedeki başarının artırılması için eksik davranışlar belirlenmeli ve giderilmelidir. Böylece problem çözme başarısında artış sağlanabilir (Baykul, 1999).

Problem çözme öğretimini değerlendirmek için gözlem ve görüşme teknikleri de kullanılabilir. Gözlem, problem çözme sürecinde öğretmenin en sık kullanabileceği tekniklerden biri olabilir. Gözlem sırasında öğretmenler tarafından kullanılabilecek gözlem formları daha önceden hazırlanmalıdır. Yine, öğrencilerle problem çözme sürecinde yapacakları görüşmeler onları daha iyi tanıma konusunda önemli ipuçları verebilir (Çakmak, 2005, s. 45).

Özetle, problem çözme öğretiminde problem çözme sürecinin değerlendirilmesi de önemlidir. Bu süreçte sadece problemin sonucuna bakılmamalı, bireylerin hangi aşamaları kullanarak sonuca ulaştıkları belirlenmelidir. Daha sonra eksikler belirlenerek başarının artırılması sağlanmalıdır.

Problem Çözme ve Problem Kurma Arasındaki İlişki

Son yıllarda dünyada yaşanan değişimler ve ortaya çıkan bilgi toplumunun gerektirdiği insan tipinin yetiştirilmesinde problem çözebilen bireylerin yetiştirilmesi önemli görülmektedir. NCTM (2000), matematik öğretiminde öğrencilere özellikle problem çözme ve kurmaya yönelik çalışmalar yaptırılmasının altını çizmektedir. Hayatta karşılaştığımız problemler çözülmek içindir. En iyi çözüme giden yol da problemi anlamak ve bu verilen duruma uygun yeni ve benzer problemler üretmekten geçer. Problemi kuran kişinin çözümü de en iyi kendisinin yapması beklenir (Bunar, 2011). Yapılan araştırmalar problem çözme ve kurmanın birbirine bağlı olduğunu ve birbirini desteklediğini gösterir niteliktedir (Akay, 2006; Cankoy & Darbaz, 2010; Lowrie, 2002; Silver, 1994; Styonova, 2005; Turhan, 2011).

17

Özellikle matematikte problem çözme uygulamaları popüler olsa dason yıllarda problem kurma kavramı da ön plana çıkmaktadır. Çünkü problem çözme, hazır ve kalıplaşmış problemler üzerinde olduğundan öğrenciler farklı çözüm ve stratejileri üretip geliştirmeye gerek duymamaktadır. Böyle bir durumda da öğrenciler yeni bir problemle karşılaştığında nasıl davranacağına karar verememektedir. Öğrencilerde bu eksikliğin giderilmesi için problem çözme becerisinin yanında problem kurma becerisini de kazanmaları gereklidir (Yaman & Dede, 2005).

Temel işlemsel beceriler ile karmaşık problem çözme becerileri ve problem kurma becerileri arasında sıkı bir ilişki vardır. Temel işlemsel becerileri eksik olan öğrenciler ne iyi problem çözücü ne de iyi problem kurucu olamazlar. Öğretmenler öğrencilerin hem problem çözme hem de problem kurma becerilerini geliştirmelidir. Bunun için de daha etkili bir öğrenme için sorular oluşturmanın, bu sorulara cevap bulmanın ve problemle ilgili bütün düşüncelerin kaydedilmesi üzerinde durulmalıdır (Akay, 2006).

Gonzales (1998), Polya’nın dört aşamalı problem çözme basamaklarına beşinci adım olarak problem kurmayı eklemiştir. Öğrencilere çözdükleri problemleri yeniden gözden geçirmeleri ve problemin değişik bir biçimini ortaya atmaları veya kendilerine verilen bir durumdan hareketle yeni problemler üretmeleri öğretilmelidir. Problem kurma, problem çözme ile ilişkili olduğundan problem çözme basamaklarına beşinci adım olarak eklenmiştir. Ayrıca problem kurma her zaman yeni bir problem kurmayı gerektirmez. Var olan problemler veya önceden belirlenmiş problemlerde de problem kurmadan söz edilebilir. Buradan hareketle problem çözme ve problem kurmanın birbirini tamamladıklarını söyleyebiliriz.

Araştırmanın bundan sonraki kısmında problem kurmanın tanımına yer verilecek problem kurmanın öğrenciler üzerindeki etkisi ve problem kurma stratejilerinden bahsedilecektir.

Problem Kurma

Problem kurma matematik dersi öğretim programlarının önemli bir standardı olarak kabul görmektedir (Akay, 2006). Silver’den aktaran Stoyanova (2003) bir durumdan veya bir deneyimden yola çıkılarak bir problem oluşturma veya bir problemden yeni bir problem üretmeyi problem kurma olarak tanımlamıştır. Duncker’dan aktaran Stoyanova (2003) ise problem kurmayı yeni bir sorunun üretilmesi veya belirli bir sorunun yeniden formüle

18

edilmesi olarak tanımlamıştır. Bu tanıma benzer olarak ortaokul matematik dersi öğretim programında öğrencilerin problem çözme becerilerini geliştirmeye yönelik yapılan çalışmalarda “çözümü genelleme ve benzer/özgün problem kurma” sürecinin gözetilmesi gerektiği vurgulanmıştır. Ayrıca problem çözme sürecinde beklenen göstergeler arasında “eldeki bilgilere uygun gerçekçi problemler oluşturma” ifadesine yer verilmiştir (TTKB, 2013a). Akay (2006), problem kurmanın müfredatta önemli olmasına rağmen, matematik eğitimi topluluğundan gerekli ilgiyi göremediğini, çocukların kendi problemlerini oluşturma yetenekleri hakkında veya bu yeteneklerin problem çözmedeki yeterlikle bağlantılı olan boyutu hakkında çok az şey bilindiğini ve bu konunun çok yönlü araştırılması gerektiğini belirtmiştir.

Problem kurma, öğrencilerin matematiksel gelişiminin önemli bir bileşeni olarak tanımlanır ve problem kurmanın alan yazınında öğrenmelerin özüne dönük etkinlik olduğu belirtilmektedir (NCTM, 1991; Silver, 1994). Problem kurma verilen bir durum hakkında incelenecek veya keşfedilecek soruları ve yeni problemler üretmeyi içerir. Aynı zamanda problem çözme süreci boyunca, problemi yeniden formüle etmeyi de içermektedir (Akay, 2006).

Problem kurma, bir durumdan, bir deneyimden yola çıkılarak bir problem yaratma ya da verilen bir problemden yeni bir problem üretme olarak tanımlanmaktadır (Silver’den aktaran Stoyanova, 2003). Problem kurma eleştirel olarak düşünme ve öğrencilerin yaşamlarını analitik olarak yansıtma yetenekleri hakkında düşünmenin bir yolu olup, sınıftaki diyalogu düzenleyen ve şekillendiren tümevarımsal bir sorgulama sürecidir (Akay, 2006, s. 81). Problem kurma matematiksel keşfin anahtarlarından biridir ve bilimsel araştırmalarda problem kurmak, probleme çözümler bulmaktan daha önemlidir (Cai, 2003, s. 721).

Problem kurma dinamik, katılımcı ve bireye yetki veren bir uğraşıdır. Öğrencilere eleştirel olarak nasıl düşünüleceğini ve yaşadıkları dünyayı analitik olarak incelemeyi öğreten bir bakışla bireye güç kazandırır; yönlendiriciliği olanaklaştırır. Problem kurma, ayrıca, eleştirel düşünme becerilerini geliştirme ve kuvvetlendirme için bir araçtır; eleştirel olarak düşünmenin öğrenmedeki önemini gösterir (Gür & Korkmaz, 2003).

Son yıllarda öğrencilerin iyi problem çözücü olmalarının yanında, onlardan verilen durumdan hareketle yeni problemler üretmeleri veya var olan problemlerde bazı değişiklikler yaparak kendilerine özgü yeni problemler oluşturmaları beklenmektedir. Bu şekilde bir yaklaşım öğrencilerin hem problem çözme becerilerine katkı sağlayacak hem de

19

eğlenceli olduğu kadar zihinsel gelişimlerinin de artmasını sağlayacaktır. Ayrıca öğrencilerin kurdukları problemler kendi ürünleri olduğu için matematik ve fen derslerine yönelik motivasyonlarını da artıracaktır (Yaman & Dede, 2005).

Bir problemi çözebilen kişi, her zaman problemi tam olarak anlayamaz. Problemi daha derin bir şekilde anlamak için, problemin çözüm yöntemi ile çözülebilen problemler kurması önemlidir (Korkmaz & Gür, 2006). Öğrencilerin kendi deneyimleri yoluyla problem kurma ve çözme çalışmaları yapmaları yapılandırmacı yaklaşımın önemli unsurlarındandır. Bu çalışmalar öğrenilen bilgilerin kullanımına ve kalıcılığına katkıda bulunur (Kar, Özdemir, İpek ve Albayrak, 2010).

NCTM (2000) öğrencilerin kendi problemlerini kurmalarına imkân tanıyacak öğrenme ortamlarının oluşturulmasını desteklemektedir. Bu ortamların oluşturulmasında öğretmenlere büyük görev düşmektedir. Gonzales (1996), öğrencilerin problem kurmaya yönelik belirlenen kazanımlara ulaşması sürecinde öğretmenin köprü görevi üstlendiğini belirtmiştir. Problem kurma noktasında bu denli önemli bir göreve sahip olan öğretmenlerin henüz göreve başlamadan bu konuda eğitilmesi büyük önem arz etmektedir. Korkmaz ve Gür (2006) de bu konuda öğrencilerin problem kurma becerilerinin gelişmesi için öğretmen adaylarının problem kurma becerilerinin geliştirilmesi gerektiğini belirtmiştir.

Silver, problem kurmanın aşağıda belirtilen nedenlerden dolayı ilginç olduğunu belirtmiştir: • Yaratıcılık ve olağanüstü matematik yeteneğiyle ilişkisi bakımından

• Öğrencilerin problem çözmesini geliştirmesi bakımından • Öğrencilerin matematiği anlamalarına açılan bir pencere olarak • Öğrencilerin matematik yönündeki mizacını geliştiren bir yol olarak

• Öğrencilerin otonom (özerk) öğrenenler olmalarına yardım eden bir yol olarak (Silver, 1994).

Problem kurma çalışmalarının öğrenciler üzerindeki etkisinin belirlenmesi amacıyla birçok araştırma yapılmıştır. Bu araştırmaların öğrencilerin öğrenmeleri üzerindeki etkileri aşağıda açıklanmıştır.

20

Problem Kurmanın Öğrencilerin Öğrenmeleri Üzerindeki Etkisi

Yapılan bilimsel araştırmalar problem kurmanın öğrencilerin öğrenmeleri üzerinde olumlu etkisinin olduğunu göstermektedir. Matematik derslerinde yapılan problem kurma çalışmalarının öğrencilerin problem çözme başarılarını anlamlı düzeyde artırdığı (Fidan, 2008), matematiğe yönelik görüşlerinde anlamlı farklılıklar oluşturduğu, niteliksel akıl yürütme becerilerini geliştirdiği ve dolayısıyla da problemi anlama başarılarını üst düzeye çıkardığı (Cankoy & Darbaz, 2010), matematiksel durumları sözlü veya yazılı olarak ifade edebilme özelliği kazandırdığı (Akay, Soybaş & Argün, 2006; Gür & Korkmaz, 2003), eleştirel düşünme becerisi, akıl yürütme, muhakeme yapma ve bilgileri organize edebilme becerisini geliştirdiği (Arıkan & Ünal, 2013; Gür & Korkmaz,2003; Işık & Kar, 2012), öğrencilerin standart bir konuyu yeni bir bakış açısıyla görmelerine yardımcı olduğu, yaşamda yer alan sorunları fark etmelerini sağladığı (Turhan, 2011) görülmüştür. Ayrıca, problem kurmayı başarabilen öğrencilerde matematiğe karşı sempati artar, korku azalır ve öğrenciler problemleri gözlerinde büyütmezler (Altun, 2005, s. 100).Öğrenciler üzerinde bu kadar etkili olan problem kurma çalışmaları belli stratejilere dayalı olarak yapılmaktadır. Bu stratejiler aşağıda açıklandığı gibidir.

Problem Kurma Stratejileri

Stoyanova ve Ellerton’dan aktaran Stoyanova (2003) üç farklı problem kurma stratejisinden bahsetmektedir. Bunlar serbest problem kurma, yarı yapılandırılmış problem kurma ve yapılandırılmış problem kurmadır.

1. Yapılandırılmış Problem Kurma: Yapılandırılmış problem kurma durumlarında, iyi yapılandırılmış bir problem veya problem çözümü verilir; öğrenciden verilen problem veya çözümüyle ilişkili problem inşa etmesi beklenir (Stoyanova, 2003).

2. Yarı Yapılandırılmış Problem Kurma: Sorun oluşturan bir durum öğrencilere açık bir şekilde verildiğinde yarı yapılandırılmış olarak alınacaktır ve öğrencilerden daha önceki matematiksel bilgi, beceri, kavram ve ilişkileri kullanarak verilen soruna çözüm getirmeleri istenecektir (Stoyanova, 2003). Verilen bir şekli kullanarak problem oluşturma veya yarım bırakılmış bir problemden yola çıkarak problem

21

kurma söz konusudur. Bu durumda öğrenciler bilgi, beceri ve deneyimlerini kullanarak açık uçlu durumlardan hareketle problem kurarlar (Kazak, 2012). Yapılan araştırmalarda yarı yapılandırılmış problem kurma durumlarında bir resim, grafik veya tablonun sunulduğu görsel temsillere, verilen bir veya daha fazla işlem basamağını içeren sözel temsillere, günlük hayatta karşılaşılabilecek sözel açık uçlu hikâyelere yer verildiği görülmüştür (Arıkan & Ünal 2013; Çelik & Özdemir, 2011; Işık & Kar, 2012).

3. Serbest Problem Kurma: Öğrencilere herhangi bir problem kurma durumu verilmez. Öğrenciler günlük yaşamlarındaki bir durumu kullanarak yeni bir problem düzenler (Stoyanova, 2003). Öğrencilerden kolay veya zor bir problem oluşturmaları, matematik yarışmaları veya testler için uygun problem düzenlemeleri ya da istedikleri bir problemi üretmeleri istenir (Zehir, 2013).

Ambrus’dan aktaran Yaman ve Dede (2005) ise öğrencilere farklı şekillerde problem kurma becerisinin kazandırılabilmesi için bazı problem kurma stratejileri önermiştir. Bu stratejiler aşağıdaki gibidir:

1. “Eğer … ise … dir”, “ Eğer … ise … değildir.” stratejisi 2. Verile bir probleme çoklu çözüm üretme

3. Anoloji kullanma 4. Genelleştirme

5. Bir problemin çözümü için farklı gösterimler kullanma

Silver ve Cai (1996) problem kurmanın üç farklı süreçte uygulanabildiğini belirtmiştir. Bunlar çözüm öncesi problem kurma, çözüm içerisinde problem kurma ve çözüm sonrası problem kurmadır.

1. Çözüm Öncesi Problem Kurma: Verilen matematiksel durumdan farklı ve orijinal problemler oluşturma.

2. Çözüm Esnasında Problem Kurma: Çözülmüş bir problemin yeniden ifade edilmesi.

22

3. Çözüm Sonrası Problem Kurma: Yeni problemler oluşturmak için çözülmüş problemin amaçlarının ve şartlarının değiştirilerek yeni durumlar oluşturmak (Silver & Cai, 1996).

Problem kurma çalışmalarının belli stratejilere dayalı olarak yaptırılmasının ardından, bu çalışmaların değerlendirme süreci çalışmaların etkililiğinin belirlenmesi ve çalışmalar sürecindeki eksikliklerin giderilmesi açısından önemlidir. Bu çalışmada Stoyanova ve Ellerton’ın problem kurma stratejileri kullanılmıştır. Aşağıda yapılan literatür çalışmaları sonucunda kullanılan birtakım değerlendirme yöntemleri açıklanmıştır.

Problem Kurmanın Değerlendirilmesi

Problem kurma çalışmalarının etkililiğinin incelenebilmesi için problem kurma sürecinin ve ürünlerin değerlendirilmesi gerekmektedir. Problem kurmayı değerlendirmenin eğitimdeki yeri araştırılırken ilgili alan yazında temel bir değerlendirmeye rastlanmamıştır. İncelenen araştırmalarda birçok farklı değerlendirme türü vardır. Bu noktada öğretmenler, öğrencilerin kurdukları problemleri değerlendirmeden önce problemleri hangi yönden değerlendireceğini belirledikten sonra kendi ölçütlerini oluşturmalılar veya yapılan araştırmalarda kullanılan değerlendirme yöntemlerini kullanabilirler. Aşağıda bazı araştırmalar ve kullandıkları değerlendirme araç ve yöntemlerine yer verilmiştir.

Fetterly (2010), problem kurmanın sınıf öğretmeni adaylarının matematiksel yaratıcılıkları, inanç ve kaygılarına etkisini incelediği çalışmasında problem kurmasını istediği her bir madde için bir havuz oluşturmuştur. Her bir adayın toplam test puanının oluşturulması için maddeler orijinallik yönünden puanlanmıştır. Puanlama sürecinde her bir madde için oluşturulan havuzdaki cevaplardan farklılık bakımından %5 ‘in altında kalan problemler orijinal olarak değerlendirilmiştir.

Silver ve Cai (2005) yaptıkları çalışmada özellikle aritmetiksel işlemlere yönelik kurulan matematiksel problemlerin nicelik ve orijinallik yönünden analiz dilebileceğini belirtmişlerdir. Verilen duruma yönelik kurulan farklı türdeki problemlerin sayısı niceliği temsil etmektedir. Bu durumda çalışmanın uygulandığı grubun kurduğu problemler bir havuzda toplanır. Bu havuzda farklılık açısından bazı problemler daha az görülürken bazıları daha fazla görülecektir. Daha az görülen problemler orijinal olarak değerlendirilmektedir.