ÇANKAYA UNIVERSITY
GRADUATE SCHOOL OF SOCIAL SCIENCE DEPARTMENT OF MANAGEMENT
MASTER THESIS
FUZZY RULE-BASED MODELING IN QUEUING SYSTEMS
FARZANEH GHOLAMI ZANJANBAR
Title of the Thesis: Fuzzy Rule-Based Modeling in Queuing Systems
Submitted by: Farzaneh Gholami Zanjanbar
Approval of the Graduate School of Social Sciences, Çankaya University
Prof. Dr. Taner ALTUNOK.
Director I certify that this thesis satisfies all the requirements as a thesis for the degree of Master of Science.
Prof. Dr. Öznur YÜKSEL. Head of Department This is to certify that we have read this thesis and that in our opinion it is fully adequate, in scope and quality, as a thesis for the degree of Master of Science.
Asst. Prof. Dr. Đnci ŞENTARLI Supervisor
Examination Date : 20- 9- 2012 Examining Committee Members
Prof. Dr. Đsmail Burhan Türkşen (TOBB univ.) .
Prof. Dr. Hasan Işın DENER (Çankaya Univ.) .
iii
STATEMENT OF NON PLAGIARISM
I hereby declare that all information in this document has been obtained and presented in accordance with academic rules and ethical conduct. I also declare that, as required by these rules and conduct, I have fully cited and referenced all material and results that are not original to this work.
Name and Surname : Farzaneh Gholami Zanjanbar
Date : 20-9-2012
iv
ABSTRACT
FUZZY RULE-BASED MODELING IN QUEUING SYSTEMS
Farzaneh GHOLAMI ZANJANBAR M.S, Social Sciences
Supervisor: Asst. Prof. Dr. Đnci ŞENTARLI
September 2012, 60 pages
In this thesis, a new hard clustering method is proposed to provide objective knowledge for the fuzzy queuing systems. In this method, locally linear controllers are extracted and translated into the first-order Takagi-Sugeno rule based fuzzy model. In this extraction process, the region of fuzzy subspaces of available inputs corresponding to different implications is used to obtain the clusters of outputs of the queuing system. Then, the multiple regression functions associated with these separate clusters are used to interpret the performance of queuing systems. Some applications of the proposed method including calculations of performances and cost analysis with some comparisons are presented and the results are discussed.
Keywords: queuing system, fuzzy rule base, clustering, linear controller,
v
ÖZ
KUYRUK SĐSTEMLERĐNDE BULANIK KURAL TABANLI MODELLEME
GHOLAMI ZANJANBAR, Farzaneh Yükseklisans Tezi, Sosyal Bilimler Tez Yöneticisi: Asst. Prof. Dr. Đnci ŞENTARLI
Eylül 2012, 60 sayfa
Sistemlerin kontrol uygulamarında bulanık mantığın kullanıldığı tipdekı problemlerde büyük başarı ve beğeni kazanılmıştır. Dolayısıyla, gerçek yaşamlarda, kuyruk sistemlerinin bulanık kavramı ile tasarımı ve kontrolü daha gerçekçi ve uygulanabilir olacaktır.
Bu tez çalışmasında, bulanık kuyruk sistemleri için nesnel bilgi sağlamaya yönelik yeni bir sabit kümeleme yöntemi önerilmiştir. Bu yöntemde, yerel doğrusal denetleyicileri ayıklanıp birinci dereceden bulanık kural tabanlı Takagi-Sugeno modeline dönüştürülmektedir. Bu ayıklama işleminde, kuyruk sisteminin çıktı kümelerini elde etmek için farklı yansımalara karşılık gelen varolan girdilerin bulanık altuzayları bölgesi kullanılır. Daha sonra, bu ayrı kümeler ile ilişkili çoklu regresyon fonksiyonları kuyruk sistemlerinin performansını değerlendirmek için kullanılmıştır. Önerilen yöntem ile performanslar ve maliyet analizi hesaplamalarını içine alan bazı uygulamalar sunulmuştur ve sonuçlar tartışılmıştır.
Anahtar Kelimeler: kuyruk sistemi, bulanık kural tabanı, kümeleme, lineer
vi
ACKNOWLEDGEMENTS
The work of this thesis as well as my scientific growth and maturation was inspired, supported and encouraged by my advisor Asst. Prof. Dr. Đnci Şentarlı. She is being always available to stimulating discussions with a very friendly attitude made my work much easier and pleasant.
Some special thanks are also due to the members of my committee, Prof. Dr. Đsmail Burhan Türkşen in the department of Industrial Engineering at TOBB University and Prof. Dr. Hasan Işın DENER in the department of Management at the Çankaya University.
I would also like to thank Prof. Dr. Kenan Taş in the department of Mathematics and Computer, Yrd. Doç. Dr. Ulaş Beldek in the department of Electronic and Communication Engineering at Çankaya University and Doç.Dr. Özlem Müge Aydın in the department of Statistic at Başkent University, for spending valuable time and providing advice.
The biggest thanks are for the persons that made all this possible, those to whom I owe for being what I am now and to whom I dedicate this study: my parents. My father Mohammad Ali and my mother Mahin inspired my desire for thorough and supported all my endeavors confirming the fact that I can always count on them.
I want to thank Hatice and Burcu Unal and friendly people around me made everything much easier while performing my research work.
I would like to add a very special thanks to my daughter Yasmin and my husband Majid for their unconditional love and support.
vii
TABLE OF CONTENTS
STATEMENT OF NON PLAGIARISM...iii
ABSTRACT... iv
ÖZ... ... v
ACKNOWLEDGEMENTS ... vi
TABLE OF CONTENTS... vii
LIST OF TABLES ... ix
LIST OF FIGURERS... xi
CHAPTERS: INTRODUCTION ... 1
CHAPTER I 1.FUZZY LOGIC ESSENTIALS ... 4
1.1. BENEFITS OF FUZZY LOGIC... 4
1.2. FUZZY SETS ... 5
1.3. MEMBERSHIP FUNCTIONS ... 6
1.4. FUZZY SET OPERATIONS... 7
1.5. FUZZY SYSTEMS... 7
1.5.1. Fuzzy Inference... 8
1.5.1.1.Defuzzification... 8
1.5.2. Practical Relevance of Fuzzy Modeling ... 9
1.6. RULE-BASED FUZZY MODELS ... 11
1.6.1. Linguistic Fuzzy Model ... 11
viii
1.7. QUEUING SYSTEM WITH INFINITE CAPACITY (M/M/S) ... 13
1.8. FUZZY QUEUING SYSTEM WITH INFINITE CAPACITY FM/FM/S... 13
1.9. FUZZY N-POLICY QUEUING SYSTEM BASED UPON α-CUT MODEL14 CHAPTER II 2.PROPOSED RULE BASED FUZZY MODEL IN QUEUING SYSTEMS ... 18
2.1. KNOWLEDGE-BASED DESIGN FOR BUILDING PROPOSED FUZZY MODEL ... 18
2.2 FIRST-ORDER TSK RULE BASED FUZZY MODEL... 18
2.2.1 The Linguistic Terms in Premises... 20
2.2.2 Implication Numbers Identification ... 22
2.2.3 Consequence Parameters Identification ... 23
2.3 HARD CLUSTERING METHOD ... 24
2.3.1 Application of Interval Function to Evaluation of Consequence Parameters .. 25
CHAPTER III 3.APPLICATION OF THE PROPOSED MODEL IN FUZZY CONTROL AND DISCUSSION OF THE RESULTS ... 30
3.1. APPLICATION IN PERFORMANCE CALCULATIONS USING THE PROPOSED FUZZY MODEL ... 30
3.1.1. Computations of the Expected Length of Queue in the FM/FM/s Queuing System ... 30
3.1.2. Computations of the Expected Waiting Time in Queue in the FM/FM/s Queuing System ... 36
3.2. COMPARISON OF THE PROPOSED MODEL AND THE FUZZY N-POLICY QUEUING SYSTEM BASED UPON
α
-CUT MODEL ... 423.2.1. Expected Waiting Time in the Queue using the Fuzzy N-Policy Queue Model Based upon α-Cut ... 42
ix
3.2.3. Comparison of New Proposed Model and Fuzzy Model Based upon
α-cut
Method ... 46 3.3. APPLICATION IN FUZZY COST ANALYSIS IN QUEUING SYSTEMS . 46 3.3.1. The Cost Relationships in Queuing Systems Analysis ... 46 3.3.1.1.Queuing System Costs and Quality Service... 47 3.3.2. Conventional Economic Analysis in Queuing Systems... 48 3.3.3. Fuzzy Economic Cost Analysis of Queuing Systems Using the Proposed Model ... 49 CONCLUSIONS... 57 REFERENCES... 58 APPENDICES:x
LIST OF TABLES
Table 1.1 Crisp and fuzzy data in some system descriptions...8 Table 2.1 Linguistic terms, interval arrival rates set and its fuzzy subsets...20 Table 2.2 Linguistic terms, interval service time rates set and its fuzzy subsets...20
Table 3.1 The expected lengths of queue for all pairs(
λ
i,µ
i), regarding to the related linear membership function. (Shown in bold)...32Table 3.2 Calculation of the expected waiting time in a fuzzy FM/FM/s queuing
system...33
Table 3.3 The expected waiting time in queue for all pairs(
λ
i,µ
i), according to the related linear membership functions. (Shown in bold)………38Table 3.4 Calculations of the expected waiting time in queue in a fuzzy FM/FM/s
queuing system……...39
Table 3.5 The membership function of the expected waiting time in queue for the
fuzzy N-policy queue model based upon α-cut………43
Table 3.6 Results of the economic cost analysis of a queuing system design using the
conventional method……….……….48
Table 3.7 Linguistic terms and interval cost of waiting time set and its fuzzy
subsets………...………..49
Table 3.8
w ,
iy
icalculations and the corresponding total cost in the queuing system with 2 servers...52Table 3.9
w ,
iy
icalculations and the corresponding total cost in the queuing system with 3 servers...53Table 3.10
w ,
iy
icalculations and the corresponding total cost in the queuing system with 4 servers...54xi
LIST OF FIGURERS
Figure 1.1 Classic sets...5
Figure 1.2 Fuzzy sets...6
Figure 1.3 Types of membership functions...7
Figure1.4Takagi–Sugeno fuzzy model resembled by pieces of linear approximations of a nonlinear function ………..………...12
Figure 2.1 The first order Takagi-Sugeno-Kang fuzzy rule based model...19
Figure 2.2 ‘‘Crowded’’ and ‘’NotCrowded’’ arrival rates per hour...21
Figure 2.3 ‘’fast’’ and ‘’slow’’ service time rates per hour...21
Figure 2.4 The little inputs produce small values and big inputs produce large values on the fuzzy queuing system performances...22
Figure 2.5 A fuzzy system includes the hard clustering method...23
Figure 2.6 The proposed fuzzy model as a clarified piece-by-piece linearization of a nonlinear performance function...24
Figure 2.7 Crisp, interval and fuzzy arguments for evaluation of a crisp, interval and fuzzy function ...25
Figure 2.8 Evaluation of interval performance function with interval arrival and service time rates in the M/M/s queuing system...26
Figure 2.9 Matrix Y(m×n)is divided to(A×B)clusters...27
Figure 2.10 (a) The hard clustering model, (b) the function valued data points and their interpolation linear functions...29
Figure 3.1 Clusters of the function-valued results and the corresponding linear interpolation for the expected length of queue as crisp data points in the M/M/s queuing system……...31
Figure 3.2 Input-output data of the length of queue in the crisp M/M/s queuing system...32
xii
Figure 3.3 The comparison of the final output results of the proposed fuzzy model
and the conventional approach for the expected length of queue ……...34
Figure 3.4 The input-output data using the proposed fuzzy model to interpret the expected length of queue...35
Figure 3.5 Darker squares correspond to bigger values for the expected length of queue in the fuzzy system...35
Figure 3.6 Input-output the expected waiting time in queue in the crisp M/M/s queuing system...36
Figure 3.7 Clusters of the function-valued and their interpolation linear functions crisp data points of expected waiting time in the M/M/s queuing system...37
Figure 3.8 The comparison of the final output results of the proposed fuzzy model and the conventional approach for the expected waiting time ……...40
Figure 3.9 The input-output data of the proposed fuzzy model to interpret the expected waiting time in queue...41
Figure 3.10 Darker squares correspond to bigger values for the expected waiting time in queue in the fuzzy system...41
Figure 3.11 The trapezoidal membership function of the expected waiting time in the queue using the fuzzy N-policy queue model based upon α-cut...42
Figure 3.12 Prediction of the expected waiting time in a queuing system using proposed model...45
Figure 3.13 The cost relationship in queuing system analysis...47
Figure 3.14 ‘‘low cost’’ and ‘’high cost’’ waiting cost per customer...50
Figure 3.15 Total cost with 2 servers computed using the new model...51
Figure 3.16 Total cost with 3 servers computed using the new model...55
Figure 3.17 Total cost with 4 servers computed using the new model………….….55
1
INTRODUCTION
In this thesis, a new hard clustering method is presented to provide objective knowledge for the fuzzy queuing systems. In many literatures, probability distributions estimate the arrival times and service times. On the other hand, in many real-world applications there are the linguistic terms, such as “Crowded” arrivals, “Fast” or “Slow” services that describe the arrival and service patterns instead of the probability distributions. As you know in most of practical applications, both arrival times and service times are possibilistic. Therefore, design and control of the queuing system with fuzzy concept is more realistic and applicable. Controlling the queues occupy is an important place in our lives where control applications in decision making and management based on fuzzy logic has had the highest success.
With using the Zadeh’s extension principle (Zadeh, 1978), the possibility concept, and fuzzy Markov chain (Stanford, 1982), the problem of fuzzy queues has been inquired by Li & Lee (1989), Buckley (1990), Negi & Le (1992) and so on. Aydın & Apaydin (2008) the fuzzy queuing control parameters with different membership functions are considered. Wang & Yang and Li. (1999) the fuzzy queues are transformed to a group of crisp queues by using the
α
−
cut
method and Zadeh’s extension principle.Three key features of control systems are: inputs, outputs, and control parameters or, control actions (Timothy, 2004). For instance, priority dicipline machine for entering customers to different queues in the banks is a control mechanism where inputs are arrival and service time rates of customers, outputs are the length of the queues, and the control actions are the altering the queue disipline, capacity and etc.
Consider to a wide-range of real-world practical applications, description of dynamic systems with available input-output data is a critical moot point of the scientific research. Usually the input and output relationship of a process in fuzzy logic controller is expressed by “if-then rules”, as:
2
Since many real systems are innately nonlinear, the conventional systems can not identify these systems by linear models (Ljung, 1987). Currently, there are many capable studies to improve the nonlinear system identification methods using available data. The TSK (Takagi, Sugeno, & Kang) method was proposed in generating fuzzy rules using available input-output data set (Takagi and Sugeno, 1985; Sugeno and Kang, 1988). In the TSK rule based fuzzy model, a linear membership function in each implication is formed to describe the real relation of input-output in the system. Comparisons of clustering algorithms in the identification of Takagi-Sugeno model (Fazel Zarandi, 2012; Abonyi, 2000; Johansen, 2000) are presented by Vernieuwe (2006).
In recent researches, clustering technique is being utilized for extracting fuzzy rule consequences which requires the user to identify structure of the knowledge or the rule base. Clustering is a method of classification of patterns or data item or observations into clusters or groups and is helpful in constructing fuzzy rules from data (Timothy, 2004). The clustering algorithm needs the user to define the initial location of the cluster. Every cluster represents a set of typical data points covering the range of data behavior. There are various clustering algorithms using optimization techniques to identify the antecedents of a system in some literatures such as Gath-Geva clustering algorithm (1989), modified Gath–Geva fuzzy clustering algorithm (Abonyi, 2002), the Gustafson-Kessel clustering algorithm ( 1979), the subtractive clustering algorithm (Chiu, 1994).
This thesis shows a new hard clustering method in identification and simulation of fuzzy queuing systems just only using available input data set (Şentarlı and G. Zanjanbar, 2013). We proposed estimated an output data set and develop a mathematical approach in generating a rule based fuzzy model using a given input and the virtual output data sets. A crisp output data set is produced, using arrival and service rate data sets and the queuing system performance expression function. The calculated output data set is separated into few clusters due to the region of fuzzy subspaces of available inputs. Each cluster generates approximate linear membership function for related implication. In this thesis, a computer source code is provided for the new mathematical approach which derives the linear membership functions to
3
explain the real input and calculated output relation of the queuing system performances based on human interpretable information.
This thesis consists of 3 chapters. In the next section, we have a glance on the basic knowledge about fuzzy theory and the classical and fuzzy queuing systems with infinite capacity. Chapter 2 will be devoted to define the proposed new method of clustering to develop the first-order Takagi-Sugeno rule based fuzzy model on field of multi server queuing systems, using input data. In chapter 3, the realistic examples are illustrated the applicability of proposed approach. In this chapter, a cost analysis of a queuing system via new method and the comparisons of the proposed method with the conventional method are presented. The comparisons between new proposed model and the fuzzy N-Policy queuing system based upon α-cut method results on predicting performances in a queuing system are presented, too. Conclusions are provided at the end of this study.
4
CHAPTER I
FUZZY LOGIC ESSENTIALS 1.1. BENEFITS OF FUZZY LOGIC
Fuzzy logic is a technique that systematically and mathematically attempts to analyze human reasoning and decision making. Fuzzy logic provides engineers with a clear and intuitive way to implement control systems, decision-making and diagnostic systems in various branches of industry (Babuska, 1997). So that, fuzzy logic allows exploiting engineers’ empirical knowledge represented in the “if/then” rules and transfer it to a function. Fuzzy logic algorithms can be used for advanced applications in industrial automation such as:
• Intelligent control systems: Fuzzy control solutions are especially useful for
complex systems where standard control fails. Fuzzy logic is an advantage in conventional analytical-process models which are too involved. Fuzzy logic can be easily combined with conventional controllers and mainly improved their functionality, that, it is another advantage of fuzzy logic. For instance, fuzzy rules interpolate between a sets of locally linear controllers and plan improvements of a system controller based on changing operating conditions. So fuzzy rules do not necessarily have to displace conventional control methods, but rather develop their potentialities.
• Process diagnostics, fault detection: If an analytical process model is not
accessible or is too compound to be run in real-time, empirical knowledge can be used to classify process conditions and early detect faults.
• Decision-making and expert systems: Fuzzy rules can analyze an
experienced human operator in real time, e.g. select appropriate ingredients, components or machines according to specific situations in the manufacturing process.
5
1.2. FUZZY SETS
Prof. Lotfi Zadeh introduced the concept of fuzzy sets in 1965. Since then, the theory has been developed by many researchers and application engineers.
In classical set theory, a membership function define a set that assigns each element a degree of membership (0 or 1) so that, 0 means the element is not member of the set and 1 means the element is member of the set. The classical (crisp) Fuzzy sets include the degree of memberships in which are any values in the real unit interval [0, 1].
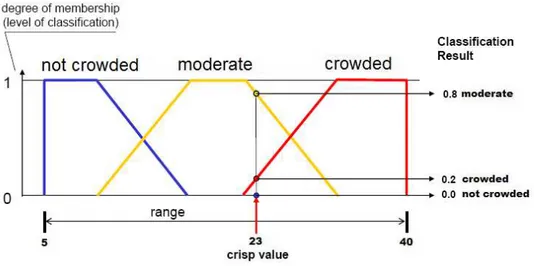
Let’s assume that we have defined three classical sets “Not Crowded“, “Moderate“ and “Crowded“ for variable arrival rate (see Figure. 1.1). If we want to classify (evaluate degree of membership) for example for value 23 to these sets, we get value 1 for set “Moderate“ and 0 for sets “Not Crowded“ and “Crowded“. Vague classification will be more realistic and thus closer to human reasoning, because no sharp distinction usually exists between moderate and crowded arrival rates, as one arrival rate reading can be moderate to some extent (0.8) and crowded to another one (0.2), see Figure. 1.2.
6
Figure 1.2 Fuzzy sets.
1.3. MEMBERSHIP FUNCTIONS
A function-theoretic form maps fuzzy set elements to a universe of membership values. In this text, a set symbol with a tilde above strike, denote a fuzzy set; for example, à is the fuzzy set A. each element of a fuzzy set à is assigned to a real number value on the interval 0 to 1 with a membership function.
If x is a member of fuzzy set Ã, then this mapping is extracted by ~
(
x
)
∈
[ ]
0
,
1
A
η
.In our particular example, the variable x is the arrival rate, X is the range [5, 40], Ã is e.g. “moderate” and for x=23 we get ~
(
23
)
=
0
.
8
A
η
.The variable x is called the linguistic variable and corresponding fuzzy sets defined on the range are called linguistic terms described by membership function. For example, the linguistic variable arrival rate has terms “Not Crowded”, “Moderate” and “Crowded”. The process of classification of a particular value of the variable x to corresponding fuzzy sets is called fuzzification.
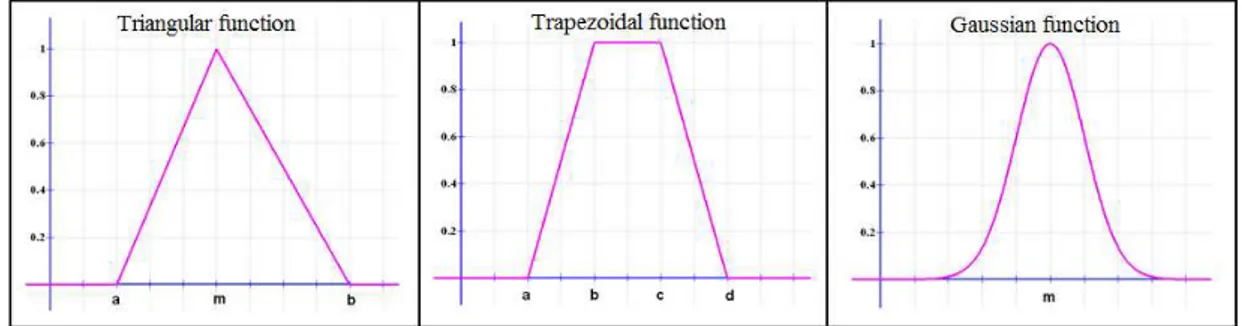
The most commonly used membership functions are in Figure 1.3. Singleton, whose degree of membership is 1 just for a single value c and 0, otherwise, is used just for output linguistic variables.
7
Figure 1.3 Types of membership functions.
1.4. FUZZY SET OPERATIONS
Suppose two fuzzy sets
A
~
andB
~
on the universe X. For∀
x
∈
X
, the following union, intersection, and complement function operations are denoted forA
~
andB
~
on X: Union(
)
~(
)
~(
)
) ~ ~ (A Bx
η
Ax
η
Bx
η
U=
∨
Intersection(
)
~(
)
~(
)
) ~ ~ (A Bx
η
Ax
η
Bx
η
I=
∧
Complement ~(
x
)
1
A~(
x
)
Aη
η
=
−
1.5. FUZZY SYSTEMSA fuzzy system is a static or dynamic system which utilizes fuzzy sets or fuzzy logic. To involve the fuzzy sets in a system, there are some ways (Babuska, 1997), such as:
• In the explanation of the system: A number of if-then rules or fuzzy relations with fuzzy means can explain a system. For instance, the relationship between the arrival rate and the length of queue in a queuing system is described by a fuzzy rule as :
If the arrival rate is crowded then the expected length of queue will be long
• In the system’s parameters specification: An algebraic or differential equation can explain a fuzzy system, where the parameters are fuzzy numbers, not real numbers.
8
• The fuzzy input sets and system state variables: Vague information related to human linguistic terms can extract fuzzy inputs, such as fast, slow, etc. Fuzzy systems can process the information of this type of data, which is not usable with conventional (crisp) systems.
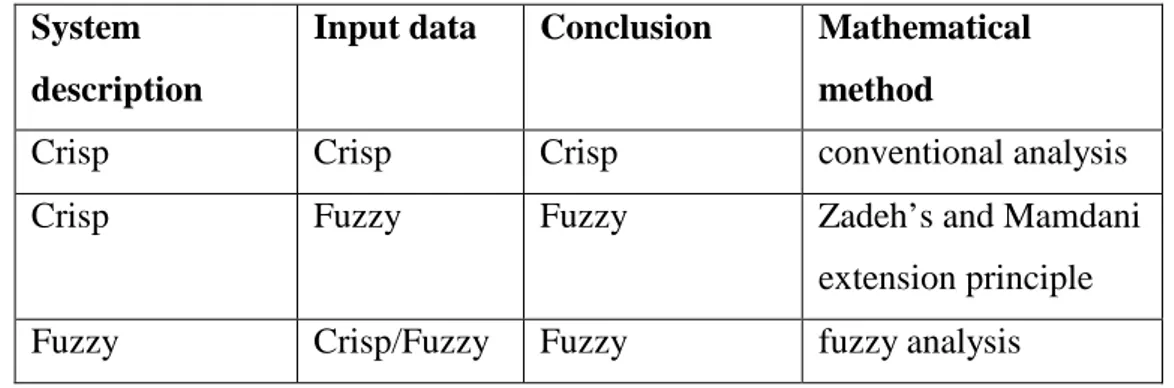
Some of the above properties can be included in a fuzzy system. Table 1.1 presents the relationships in fuzzy and crisp system descriptions (Babuska, 1999).
Table 1.1 Crisp and fuzzy data in some system descriptions. System
description
Input data Conclusion Mathematical
method
Crisp Crisp Crisp conventional analysis
Crisp Fuzzy Fuzzy Zadeh’s and Mamdani
extension principle
Fuzzy Crisp/Fuzzy Fuzzy fuzzy analysis
1.5.1. Fuzzy Inference
A fuzzy inference is a mechanism for evaluation of the fuzzy system, i.e. computing output values from input values. The fuzzy analysis consists of the following steps:
1. Fuzzification: Inputs are classified to corresponding linguistic terms to get premises membership functions.
2. Fuzzy rules evaluation: The membership function term of conclusions are calculated from premise membership function terms and logical operations. 3. Defuzzification: Output linguistic terms are converted to a real crisp value
according to their membership functions.
1.5.1.1.Defuzzification
In the most of processes, to analyze the output result of a fuzzy inference, we need a single scalar amount instead of a fuzzy set. Just as fuzzification is the alteration of an exact amount to a fuzzy amount, defuzzification is the alteration of a fuzzy amount to an exact amount. Recently, in many literatures, weighted average
9
• Weighted average method: The output is computed with weighted average of the each output of the set of rules, based on knowledge of the system. This type of defuzzification method is defined as:
∑
∑
= = = n i i n i i i w y w Y 1 1where Y is the defuzzified output,
y
i is the membership function of the output of each rule, andw
i is the weight of each rule. This fast and easy computable method gives adequately precise conclusion. In this thesis, this method has been first summarized and then illustrated in examples.• α – cut method: The study begin by considering a fuzzy set
A
~
, then definean α -cut set,
A
α , where 0 ≤ α≤ 1.The setA
α is a crisp set called the (α)-cutset of the fuzzy set
A
~
,whereA
α=
{
x
µ
~(
x
)
≥
α
}
A . Note that the α -cut
set
A
~
does not have a tilde above score; it is a crisp set derived from itsparent fuzzy set,
A
~
. Whereas an infinite number of values α in the interval [0, 1], every fuzzy setA
~
can be translated into an infinite number of α -cut sets. Any elementx
∈
A
α associates toA
~
with a grade of membership that is greater than or equal to the value α.1.5.2. Some Practical Relevancy of Fuzzy Modeling
• Lacking or Ambiguous knowledge about systems. The system behaviors can be described by conventional system theory just using crisp mathematical methods. For instance, mathematical models of queuing systems can be achieved with algebraic equations. In the most of systems, the comprehensions’ of the fundamental phenomenon’s is incompletely and crisp conventional methods can not be analyzed or too complex. The
10
biotechnology, finance, chemical, sociology, ecology are examples of such systems. The knowledge of human expert’s is available as a useful part of information about these systems. Explanation of this ambiguous and uncertain knowledge may be too difficult for crisp conventional methods. On the other hand, it seems often possible to define the behavior of systems in the form of if-then rules, by terms of natural language. “Fuzzy rule-based systems can be used as knowledge-based models constructed by using knowledge of experts in the given field of interest “(Pedrycz, 1990; Yager and Filev, 1994). Hence, fuzzy systems are very much alike to intelligence systems researched widely in the “symbolic” artificial intelligence (Buchanan and Shortliffe, 1984; Patterson, 1990).
• Imprecise information processing. Crisp exact numerical results with conventional mathematical methods only can be extracted with the correctly known parameters and input data. A modeling framework is required the processable data and associated uncertainty. Dealing with uncertainty is a usual way in stochastic approach. However, the stochastic framework cannot deal all types of uncertainty. Fuzzy logic and set theory is one of various alternative approaches which have been proposed (Smets, 1988).
• Fuzzy modeling and identification. Today’s, in scientific researches, identification of dynamic systems from input data are an important matter. Linear models used in conventional system identification, cannot extract many nonlinear real systems (Ljung, 1987). Newly, the nonlinear system methods are developed successfully from available data. Mathematical approaches in fuzzy systems can approximate other approaches or functions flexibility with a wanted precision. This effect is called “general function approximation” (Kosko, 1994; Wang, 1994; Zeng and Singh, 1995). In comparison to other well-known techniques like artificial neural networks, fuzzy systems provide a more clear description of the system according to the possible linguistic reasoning by the structure of implications. The logical structure of the rules makes the analysis of the model easier and close to human linguistics.
11
1.6. RULE-BASED FUZZY MODELS
The relationships between input-output data in rule-based fuzzy models are described by means of fuzzy if–then rules as form of:
If antecedent proposition then consequent proposition.
The type “
x
is Ô is always a fuzzy antecedent proposition wherex
is a linguistic variable and à is a linguistic term. The degree ofx
in fuzzy set à is a real number between zero and one. Two main types of rule-based fuzzy models are specified based on the form of the consequent:• Linguistic fuzzy model: the fuzzy propositions are composed of the antecedent as well as the consequent
• Takagi–Sugeno (TS) fuzzy model: The only fuzzy proposition is antecedent and the consequent is in the form of a crisp function.
Notice to the explanation of these two different fuzzy models in the following subsections in detailed meaning.
1.6.1. Linguistic Fuzzy Model
Available qualitative knowledge in this model (Zadeh, 1973; Mamdani, 1977), translates into the form of if–then rules:
:
i
R
Ifx
isA
~
i theny
isB
~
i i=1, 2, ..., n.In this expression, x denotes the antecedent input variable, and
A
~
i resembles the antecedent linguistic terms. Alike, y denotes the consequent output variable andi
B
~
resembles the consequent linguistic terms. The crisp x or y are defined in the regions of their universe base variable sets:x
∈
X
andy
∈
Y
. The membership functions of the antecedent and consequent fuzzy sets are:η
(x):X →[ ]
0,1 ,[ ]
0,1 :) (y Y →
η
. Fuzzy domains are defined by fuzzy setsA
~
i in the antecedent space, depending on the related consequent space. The linguistic termsA
~
iandB~i are usually chosen from sets of terms, such as “Slow”, “Fast”, etc. By meaning of these sets byA
~
andB
~
, we haveA
~
i⊂
A
~
and
B
~
i⊂
B
~
12
{
R
i
n
}
R
i,...,
2
,
1
=
=
and the constitute of the setsA
~
and B~, make available the basic knowledge consider to the linguistic model.1.6.2. Takagi–Sugeno (TS) Fuzzy Model
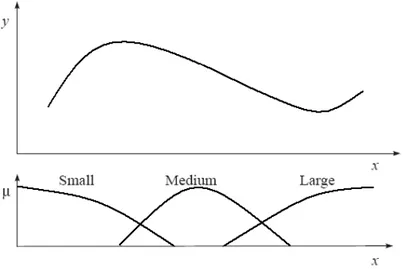
The linguistic model explains a given system behaviors by means of linguistic if-then rules with the fuzzy antecedents and fuzzy consequents using Zadeh’s extension principle. On the contrary, instead of fuzzy consequent, the crisp consequent functions are used in the TS fuzzy rule based model. Therefore, there is a relation between linguistic and mathematical regression equation where the fuzzy domains are defined by antecedents according to the input space in which consequent equations are valid. The TS rules are produced as:
i
R
: Ifx
isA
~
ithenyi = fi(x), i=1, 2…, n (1.1) In most cases, a vector-valued function if is extracted from a nonlinear function.
The functions f have the same structure with the different parameters in each rule. i
Simple and practically useful linear parameterizations in the rules have the form:
i
R
: If x isA
~
i theny
i=
a
iTx
+
b
i, i=1, 2… n (1.2) wherea
i is a parameter vector andb
iis a scalar offset.Figure 1.4 Takagi–Sugeno fuzzy model resembled by pieces of linear approximations of a nonlinear function.
13
1.7. QUEUING SYSTEM WITH INFINITE CAPACITY (M/M/S)
In this thesis, a multi servers M/M/s queuing system with infinite capacity is considered. In this system, following assumptions are supposed:
• There is a single server in each waiting line.
• The frequencies of arrival rate are resembled by a Poisson distribution (λ).
• The service times obey an exponential probability distribution.
• There is first-come, first-served (FCFS) discipline in the queue.
• There is no balking or reneging.
Various arrival and service time stochastic processes within the system are assumed to be independent of each other. Here, Lq and Wqresemble the expected number of customers in the queue and the expected waiting time in the queue, respectively. Consider the two system performances
L
q and Wq can easily be derived by a Markov chain approach. It follows that0 2
Pr
)
/
1
(
!
)
/
(
)
/
(
µ
λ
µ
λ
µ
λ
s
S
s
L
S q−
=
(1.3) where ) ( ) / ( ! / 1 ) / ( ! / 1 1 1 0 0Pr
λ
µ
µ
µ
λ
µ
λ
− + =∑
− = s s S n S S n nλ
q qL
W
=
(1.4)For the steady-state conditions, we have 0 < λ /µ < 1 and sµ >λ.
1.8. FUZZY QUEUING SYSTEM WITH INFINITE CAPACITY FM/FM/S
A fuzzy multi server queuing system with infinite capacity is considered with following assumptions:
• The frequencies of fuzzy arrival rate are resembled by a Poisson distribution
λ
~.14
• The fuzzy service times obey an exponential probability distribution..
•
λ
~and µ~ are uncertain.•
λ
~and µ~ by the convex fuzzy sets are represented.• η~(λ)
λ andηµ~(µ)define the trapezoidal membership functions of
λ
~
andµ~ , respectively.
For this FM/FM/s queue model we have:
{
η
λ
}
λ
~
=
(
x
,
λ~(
x
))
x
∈
{
η
µ
}
µ
~
=
(
x
,
µ~(
x
))
x
∈
where λand µ consists of the crisp sets of the arrival and service rates, respectively as:
{
λ
λ
λ
m}
λ
=
1,
2,
K
,
,µ
=
{
µ
1,
µ
2,
K
,
µ
n}
1.9. FUZZY N-POLICY QUEUING SYSTEM BASED UPON
α
-CUT MODELIn this part, we consider to present an FM/FM/1 N-policy fuzzy queuing model with infinite capacity based upon α-cut model. This fuzzy queuing model is developed by the N-policy M/M/1 queuing system utilizing the fuzzy set theory. The fuzzy arrival rate and the fuzzy service rate values are used to develop the membership function using a mathematical approach of the system performance. The fuzzy queues are translated to a group of crisp queues based on the α-cut model and Zadeh’s extension principle.
Let W define the expected waiting time in the queue. q W can be simply derived q
by a Markov chain approach. It is:
) ( 2 1
λ
µ
µ
λ
λ
+ − − = N Wq (1.5)where 0 < λ /µ < 1 since we have the steady-state condition.
Suppose f(x,y)define the system performances. Since
λ
~andµ
~ are fuzzy numbers, f(λ
~,µ
~) is also a fuzzy number. With Zadeh’s extension principle (Zadeh, 1978 and Zimmermann, 2001), the membership function of the system performance f(λ
~,µ
~) is obtained as:15
{
( ), ( ) ( , )}
min sup ) ( ~ ~ ) ~ , ~ ( z x y z f x y f = = Ω λ µ µ λ η η η (1.6) where Ω={
x∈X,y∈Y x〉0,y〉0}
In the N-policy M/M/1 queuing system, when the arrival rate x and the service rate y are crisp values, the crisp expected waiting time in the queue is such as: ) ( 2 1 x y y x x N Wq − + − = (1.7)
The membership functions of W~q as a result, become:
− + − = Ω 2 ( ) 1 ) ( ), ( min sup ) ( ~ ~ ~ x y y x x N y x z q W
η
λη
µη
(1.8)For practical use, the membership function in equation (1.8) is not explained in the typical forms and inferring the shapes of the related membership function with
q
W~ is too difficult. Therefore, the α-cuts of Wq
~
can be derived by applying the Zadeh’s extension principle to solve this problem. Consider to above explains, let us define the α-cuts of
λ
~and µ~ as follows:{
η α}
α λ( )= x∈X λ~(x)≥ (1.9){
η α}
α µ( )= y∈Y µ~(y)≥ (1.10)λ
~ resembles the fuzzy arrival rate and µ~ resembles the fuzzy service rate of the N-policy FM/FM/1 system. Hence, consider to equations (1.9) and (1.10), the crisp α-cut sets ofλ
~and µ~ can be redefined in such as:[
]
[
{
η
α
} {
η
α
}
]
α
λ
( )= xα,xα = min∈ x∈X λ~(x)≥ ,max∈ x∈X λ~(x)≥ X x X x U L (1.11)[
]
{
} {
}
∈ ≥ ∈ ≥ = = ∈ ∈η
α
η
α
α
µ
( ) yα,yα min y Y µ~(y) ,max y Y µ~(y) Y y Y y U L (1.12)“From equations (1.11) and (1.12), it indicates that
λ
~andµ
~ are lying the range of[
L U]
xxα, α and
[
yαL,yαU]
, respectively, at a possible level α” (Yin Wang, 2010). As you see, the N-policy FM/FM/1 queue decreases to a group of crisp N-policy D/D/1 queue with different α-level sets{
λ
(α
)0<α
<1}
and{
µ
(α
)0<α
<1}
. The upper and16
lower bounds of
λ
~and µ~ can be presented as functions of α as maxη
~1(α
)λ αU = − x , ) ( min
η
~1α
λ αL = −x , yαU =max
η
µ~−1(α
)and yαL =minη
µ~−1(α
) by the principal property ofconvex fuzzy numbers (Zimmermann, 2001). Since, α is the parameter of the membership function W~q therefore, the α-cuts approaches are used to develop the membership function W~q.
The membership function of the expected waiting time in the queue ~ (z)
q
W
η is
the minimum of ~(x) λ
η andηµ~(y)that is derived based on the Zadeh’s extension principle.
By solving the corresponding parametric nonlinear program the lower(Wq)αL and U
q
W )α
( upper limiting values of α-cuts of Wq
~
can be found as: ) ) ( 2 1 ( min ) ( x y y x x N Wq L − + − = Ω α , (1.13) s.t. xαL ≤x≤xαU and yαL ≤ y≤ yαU and ) ) ( 2 1 ( max ) ( x y y x x N Wq U − + − = Ω α (1.14) s.t. L U x x xα ≤ ≤ α and L U y y yα ≤ ≤ α .
The optimal solution changing’s are characterized by mathematical approaches in this model withxαL,xαU,yαL and yαU when value of α modifies between 0 and 1 . This model is a part of parametric NLP (Gal, 1979).
According to equations (1.10) and (1.11), we can replace x∈λ(α) and )
(α
µ
∈
y byx∈
[
xαL,xαU]
andy∈[
yαL,yαU]
, respectively. It is worthy of mention that α-cuts of x and y form an embedded structure based upon α (Zimmermann, 2001). Considering the two possibility levelsα
1andα
2 , we have[
L U] [
L U]
x x x x 2 2 1 1, α α , α α ∈ and[
yαL1,yαU1] [
∈ yαL2,yUα2]
17 where 0 <
α
2 <α
1 ≤ 1. Thus, as α increase forL q L q W W 2 1 ( ) ) ( α ≥ α , (Wq)αLincreases and for q U U q W W 2 1 ( ) )
( α ≤ α ,(Wq)αU decreases. Therefore, the membership function
η
w~q(z)will be computable. Defining an ascending function q L L
q W
W )α:
α
( )α( → and a
descending function(Wq)αU:
α
→(Wq)αU help us to explain the membership function ~ (z)q
w
η
, with invertible the both (W )q L and(W )q U, based upon α such as: ≤ ≤ ≤ ≤ ≤ ≤ = = = = = = = U q U q U q L q L q L q w W z W z R W z W W z W z L z q 0 1 1 1 1 0 ~ ) ( ) ( ), ( ) ( ) ( , 1 ) ( ) ( ), ( ) ( α α α α α α
η
(1.15)where the left shape functionL(z)is
[
(Wq)L]
−1 and the right shape function R(z)is[
]
1)
(Wq U − . In section 3.2.1, an example shows the alteration of the membership grade of the system performances at a different α level.
18
CHAPTER II
PROPOSED RULE BASED FUZZY MODEL IN QUEUING SYSTEMS
In this chapter, the new rule based fuzzy model in the field of queuing system is investigated making use of the Takagi-Sugeno-Kang (TSK) first-order rule based fuzzy model.
2.1 KNOWLEDGE-BASED DESIGN FOR BUILDING PROPOSED FUZZY MODEL
Generally, a fuzzy model according to available expert knowledge is designed as the following steps:
1) Choose variables resembling the input and output, the form of the rules, and the deduction, and methods to defuzzify the solutions.
2) Determine the required amount of linguistic terms for each rule and determine the related functions resembling the membership.
3) Translate the knowledge possessed using the fuzzy if-then rules.
4) Approve the model. If the expected performance is not visible, repeat the above steps.
2.2 FIRST-ORDER TSK RULE BASED FUZZY MODEL
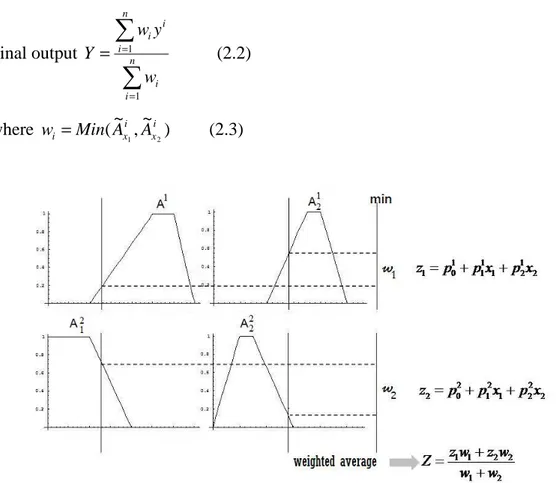
The TSK first-order rule based fuzzy model a given system is described by means of linguistic if-then rules with two inputs and an output. A fuzzy system is represented by first-order TSK model as form of the following implications:
1 R : If x1 is 1 1 ~ x A and x2 is 1 2 ~ x A then 1 y M M n R : If x1 is Axn 1 ~ and x2 is Axn 2 ~ then y (2.1) n where
19
i
y Output linear membership functions in the consequences.
2 1, x
x Crisp variables in the premises.
2 1, x
x A
A Membership functions of the fuzzy sets in the premises.
2 1 0,P,P
P Parameters of linear membership functions in the consequences.
n The number of implications (rules).
The crisp final output of the system is obtained via a weighted average defuzzification, as shown in Figure 2.1.
Final output
∑
∑
= = = n i i n i i i w y w Y 1 1 (2.2) where (~ ,~ ) 2 1 i x i x i Min A A w = (2.3)Figure 2.1 The first order Takagi-Sugeno-Kang fuzzy rule based model.
After above explanations, the proposed fuzzy model is denoted by a queuing system in detail in the next sections.
20
2.2.1 The Linguistic Terms in Premises:
A fuzzy queuing system process involving two fuzzy input sets is analyzed; arrival rate
λ
~and service rate µ~ to predict crisp performances as expected length of queue, L , and expected waiting time in queue, q W . qIn the form of TSK fuzzy rule based model in a queuing system, in order to model (2.1), we have:
i
R : If λ is
λ
~iand µisµ
~ theni y , i=1, 2…, n (2.4) iWhere
λ
~iandµ
~ are the premise linguistic terms. The linguistic terms iλ
~iandµ
~ are i selected from sets of human linguistic terms, such as crowded, slow, fast and etc. The fuzzy setsλ
~iandµ
~ are defined in their regions over their respective crisp i interval variables λandµ
. Fuzzy setsλ
~iandµ
~ define fuzzy regions in the iantecedent space, according to the respective consequent propositions. By denoting these sets by
λ
~andµ
~ respectively, we haveλ
~i ⊂λ
~andµ
~i ⊂µ
~.Example 3.1: Suppose that the crisp interval arrival rate set is λ= [1, 2, 3, 4]
per hour and the interval service rate set is µ= [11, 12, 13, 14] per hour as premise values.
The linguistic terms “Crowded” and “Not Crowded” fuzzy subsets of arrival rate and “Fast” and “Slow” fuzzy subsets of service rate set show in Table 2.1 and Table 2.2. Table 2.1 Linguistic terms, interval arrival rates set and its fuzzy subsets.
Domain element
linguistic term 1 2 3 4
Crowded 0 0 0.67 1
NotCrowded 1 1 0 0
Table 2.2 Linguistic terms, interval service time rates set and its fuzzy subsets. Domain element
linguistic term 11 12 13 14
Fast 0 0 0.67 1
21
Trapezoidal membership functions define the meaning of the linguistic terms, as you see in Figure 2.2 and Figure 2.3.
Figure 2.2 ‘‘Crowded’’ and ‘’NotCrowded’’ arrival rates per hour.
Figure 2.3 ‘’Fast’’ and ‘’Slow’’ service time rates per hour.
Remember that there is not universal way to define the linguistic terms. The numerical variables are selected arbitrarily.
As you see in Figure 2.4 when we use a “Crowded λ~2“ arrival rate and “slow
µ
~1“ service rate, we get out of the process large values of performances in queue; when we input “Not Crowded λ~1“and “ Fastµ
~2“ into the system, the performances reach to small values; when we input “Not Crowded 1~
λ“ and “ Slow
µ
~1“ or “Crowded 2~
λ “ and “ Fast
µ
~2“ into the system, the performances reach22
Figure 2.4 The little inputs produce small values and big inputs produce large values on the fuzzy queuing system performances.
2.2.2 Implication Numbers Identification:
In the rule based fuzzy method, the behavior of system translates to some implications. The fuzzy sets
λ
~iandµ
~ are defined in their regions over their i respective crisp interval variables λand µ.If the number of fuzzy subspacesλ
~iis “A” and the number of fuzzy subspaces µ~ is “B”, (Sugeno, 1985) each model i consists of (A×B)implications. Hence, a queuing system represented by some implications as: × × × × then ~ is and ~ is if : then ~ is and ~ is if : ) ( ) ( ) ( ) ( 1 1 1 1 B A B A k B A k B A k k y R y Rµ
µ
λ
λ
µ
µ
λ
λ
M M (2.5)The rule set R=
{
Rii=1,2,K,(A×B)}
and the knowledge base of the linguistic model is constituted with the sets λ and µ.Example 3.2:
As you see in Example 3.1,
λ
~is divided into two fuzzy subspaces “Crowded” and “Not Crowded”, and µ~ is divided into two fuzzy subspaces, “Fast” and “Slow”.23
Therefore, this model consists of (2×2)implications. If the y is the expected length i
of queue, implications having the form such as:
long is L then ) ~ slow( is and ) ~ crowded( is if : R moderate high is L then ) ~ fast( is and ) ~ crowded( is if : R moderate low is L then ) ~ slow( is and ) ~ ( NotCrowded is if : R short is L then ) ~ fast( is and ) ~ ( NotCrowded is if : R q 1 2 4 q 2 2 3 q 1 1 2 q 2 1 1 µ µ λ λ µ µ λ λ µ µ λ λ µ µ λ λ
2.2.3 Consequence Parameters Identification:
Suppose f(x,y)define the system performance and let redefine an FM/FM/s queue system in order to model (2.4) by following rules as:
i
R : If λ is
λ
~iand µ isµ
~ theni yi = fi(λ
,µ
), i=1, 2…, n (2.6)where the functions of fi(
λ
,µ
) is a clarified piece by piece linearization of a nonlinear function with different parameters in each rule consequence. Commonly, the fuzzy clustering techniques can estimate these parameters from the available data.In this thesis, for the purpose of to be able to use the linguistic terms to estimate vector-valued function i(
λ
,µ
)f , an output data is produced with available input and expression performance system function. Using the new hard clustering
method, we divide the computed output to some clusters and derive the fi(
λ
,µ
)of the queuing system performance for every implication that related to each cluster.24
In the rule based model (2.6), fi(
λ
,µ
)is a vector-valued function with parameterization as form fi(λ,µ)= p1iT.λ+ p2iT.µ+ p0iwhere p1i,p2i are parameters of vector and p0iis a scalar offset.
The inference formula of the TSK model is a straightforward extension of the (2.2):
∑
∑
= = + + = n i i T i T i T i n i i w p p p w Y 1 0 2 1 1 ) . . ( λ µThe proposed rule based fuzzy model in a queuing system can be observed as a clarified piece-wise approximation of the interval performance function, depicted in Figure 2.6.
Figure 2.6 The proposed fuzzy model as a clarified piece-by-piece linearization of a nonlinear performance function.
The line yidisplays the linear function in the consequence of implicationRi. The equation in a consequence is extracted to define a law based on the fuzzy subspace definition in premise and its calculated output in a consequence.
The utilization of hard clustering method to extract the linear consequences is presented in the next subsection completely.
2.3 HARD CLUSTERING METHOD
Suppose a data universe Y with n data members. Clustering identifies the
number of c clusters in Y where (2 ≤ c < n). For algebraic data, the member values of
25
clusters. To clustering identification we must determine the similarity between observations and classify the partitions.
2.3.1 Application of Interval Function to Evaluation of Consequence Parameters
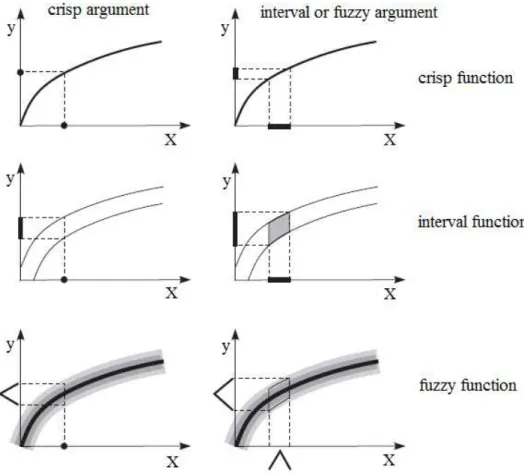
Fuzzy systems are inferred from descriptions of crisp interval-valued systems, which are crisp systems in general. Figure 2.7 illustrated this with an example of a function and its interval and fuzzy forms. In this figure, the evaluation of the function for crisp, interval and fuzzy data is depicted too. Remember that a function
f
:
X
→
Y
is a relation that can be observed as a subset of the Cartesian productX
×
Y
. As you see in the Figure 2.7, the vertical dashed lines show the extension of the given input into the product spaceX
×
Y
. After finding the intersection of this extension with the relation, this intersection is projected ontoY
that is shown with horizontal dashed lines.Since the function and the data (crisp, interval, fuzzy) are independent, this function evaluation makes clear up the use of fuzzy relations for inference in fuzzy modeling.
26
Fuzzy systems can supply various aims, such as data analysis, modeling, forecasting or decision making. In this research, a new fuzzy rule-based system is studied, for simplicity, attentive to its realized eventual purpose in field of queuing systems.
To introduce the evaluation interval function, we define a sample set of )
(m×n data that we wish to classify:
= mn m n y y y y Y L M M M L 1 1 11 (2.7)
defined by f :λ×µ →Y where f is a binary function which takes two inputs λ
with m factors and µ with n factors,
where
λ
=[
λ
1λ
2 Lλ
m]
T,µ
=[
µ
1µ
2 Lµ
n]
and Y is the calculated outputset.
It is noted that
λ
1<λ
2<L<λ
mandµ
1<µ
2<L<µ
n.The evaluated membership functions fi(
λ
,µ
) for a given input (arrival and service rates) of each implication are depicted in Figure 2.8.
Figure 2.8 Evaluation of interval performance function with interval arrival and service time rates in the M/M/s queuing system.
To evaluate the interval performance function in each implication, we have to determine the related region (partition) in the calculated outputY .
27
When a hard clustering approach is used, it is required to divide the data into different and unique clusters, where each data element exists exactly in one cluster. Based on the similarity between members within a cluster, we consider the similarity in value components of every member of each cluster. This means, every member in each cluster is calculated with same pair(λi,µj) of same sub interval values of
λandµ. Hence, interval inputsλandµ are divided to A subsets λi and B subsets
i
µ
in order toλ
~iandµ
~ fuzzy subset numbers (2.2.2 section definition). We i haveλ
i⊂
λ
andµ
i⊂
µ
.In general, there seems no theoretical approach available for the number of divisions.
Let L and K are vectors of orders (A−1)and (B−1) respectively:
[
1, 2,..., −1]
= l l lA
L andK =
[
k1,k2,...,kB−1]
(2.8)where l anda k represent the division space points (b ylakb) in matrix Y.
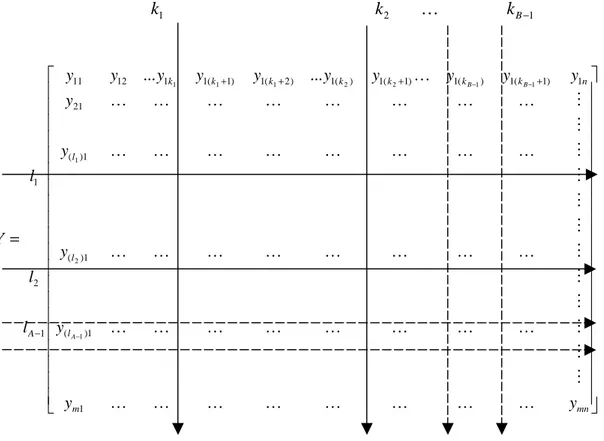
Therefore, the Y(m×n)matrix is divided into (A×B)clusters so that the crisp data of every cluster are related to an implication as you see in Figure 2.9.
1 k k K 2 kB−1 = − − − + + + + − mn m l l l n k k k k k k k A y y y y y y y y y y y y y y y y l l l Y A B B K K K K K K K K M M M K K K K K K K K M M M K K K K K K K K M M M M K K K K K K K K M M K K K K K K K K K 1 1 ) ( 1 ) ( 1 ) ( 21 1 ) 1 ( 1 ) ( 1 ) 1 ( 1 ) ( 1 ) 2 ( 1 ) 1 ( 1 1 12 11 1 2 1 1 2 1 1 1 2 2 1 1 1 ... ...
28
Define a family of clusters {Clakb, a = 1, 2, . . . , A-1 , b=1,2,...,B-1 } as a
hard c-partition of Y, where c=(A×B) is the number of clusters(2 ≤ c < (m×n)). The following set-theoretic forms apply to these partitions:
Y C A a B b k la b = = =
UU
1 1 for all l ,a kb (2.9)φ
=I
a b b ak l k l C C for all (la,kb)≠(la,kb) (2.10) Y Clakb ⊂ ⊂φ
for all l ,a kb (2.11)Equation (2.9) expresses the fact that the set of all clusters exhausts the universe of data sample. Equation (2.10) indicates that none of the clusters overlap in the sense that a data sample can belong to more than one cluster. Equation (2.11) expresses that a class cannot be empty and it cannot contain all the data samples.
Consequently, we define a hard cluster for Y as the following matrix set:
{
} {
}
{
}
{
}
{
} {
}
= = = × − < ≤ < ≤ < ≤ × = = = × = + + + + + + + + − − − − − − − − c r B j A i c r B j A i r j i C n k k T m l l k k k T l l l k T l ij r B B A A j j j i i i , , ), ,..., , ( ) ,..., , ( 1 2 , 1 , 1 ), ,..., , ( ) ,..., , ( 1 , 1 , 1 , ,..., , ( ) ,..., , ( 2 1 2 1 ) 2 ( ) 1 ( ) 2 ( ) 1 ( 2 1 2 1 1 1 1 1 1 1 1 1 1 1 µ µ µ λ λ λ µ µ µ λ λ λ µ µ µ λ λ λ (2.12) ) ( ij Clakb yχ is defined as the hard membership function-theoretic expression which resembles the regression of all datay in ij Clakbcluster.
For simplicity in notation, our membership assignment of the (i× j)th data point in the rthClakb cluster of data universe Y, is defined to be
j r i r r ij C ij Crlakb y
χ
r y p pλ
pµ
χ
( )≡ ( )= 0 + 1. + 2 . (2.13) where P0,P1,P2are the linear function constant parameters.In this sense, our system is inferred from descriptions of crisp interval-valued systems.
29
Figure 2.10 (a) The hard clustering model, (b) the function valued data points and their interpolation linear functions.
As you see in Figure 2.10, our model can be observed as a relation among the input data in premise and the parameters of a linear system as a consequence.
Therefore, using (2.5) and (2.13), the implications of queuing system have the form:
+ + = + + = × × × × × × × j ) ( 2 i ) ( 1 ) ( 0 ) ( ) ( ) ( ) ( j 1 2 i 1 1 1 0 1 1 1 1 . P . P ) , ( f n the ~ is and ~ is if : . P . P ) , ( f n the ~ is and ~ is if : µ λ µ λ µ µ λ λ µ λ µ λ µ µ λ λ B A B A B A B A B A k B A k B A j i P R P R M M
The step-by-step procedures in this hard clustering method are summarized into six steps:
1. Calculate matrix Y with crisp interval input data sets λandµ.
2. Divide λandµcrisp sets into desired parts and initialize A and B values: ) (A B c= × Then, do r = 1, 2... 3. Initialize L=
[
l1,l2,...,lA−1]
andK =[
k1,k2,...,kB−1]
4. DetermineCrlakb(yij). 5. Obtain C yij pr pr i p r j rλ
µ
χ
( )= 0 + 1. + 2 . 6. If r=c,Stop; otherwise set r = r + 1 and return to step 4.