1. Introduction
We live on a spherical Earth rather than on a Euclidean 3- space R3. We must
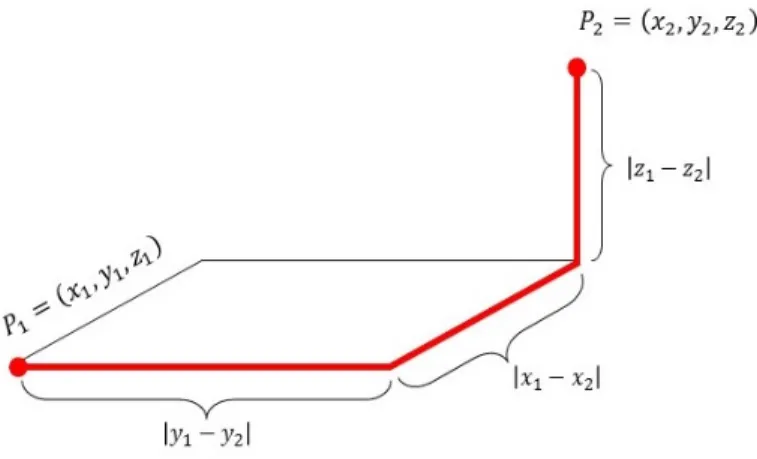
think of the distance as though a car would drive in the urban geography where physical obstacles have to be avoided. So, one had to travel through horizontal and vertical streets to get from one location to another. In this sense, the taxicab geometry was …rst introduced by K. Menger [4] and has developed by E. F. Krause [2]. Let P1= (x1; y1; z1) and P2= (x2; y2; z2) be two points in the R3; Z. Akca and
R. Kaya [14] de…ne the taxicab distance in R3 as follow d
T(P1; P2) = jx1 x2j +
jy1 y2j + jz1 z2j . Also, the paths of taxicab distance dT from P1to P2as shown
in Figure 1.
Although Euclidean geometry is convenient, taxicab geometry is a better model than Euclidean geometry for urban world.
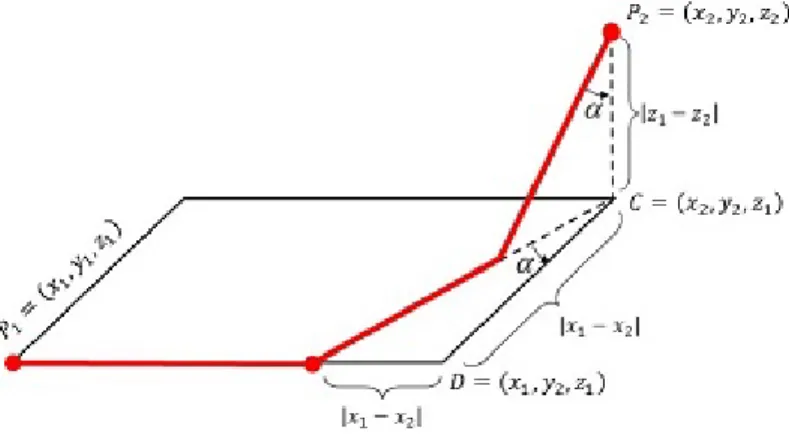
Researchers give alternative distance functions of which paths are di¤erent from path of Euclidean metric in the two or three dimensional analytic space. For ex-ample, G. Chen developed Chinese checker distance in the R2 of which paths are
similar to the movement made by Chinese checker [3]. Afterwards, Ö. Geli¸sgen et. al. [12] de…ned Chinese checker distance in the R3 of which paths from P
1 to P2
as shown in Figure 2. If P1= (x1; y1; z1) and P2= (x2; y2; z2) be any two points in
the R3, then Chinese checker distance is de…ned by dCC(P1; P2) = dL(P1; P2) +
p
2 1 dS(P1; P2) Received by the editors: April 04, 2016, Accepted: April 30, 2016.
2010 Mathematics Subject Classi…cation. 51K05, 51K99, 51B20 and 51F25.
Key words and phrases. Metric Geometry, distane geometry, metric, spherical coordinates, isometry group.
c 2 0 1 6 A n ka ra U n ive rsity C o m m u n ic a tio n s d e la Fa c u lté d e s S c ie n c e s d e l’U n ive rs ité d ’A n ka ra . S é rie s A 1 . M a th e m a t ic s a n d S t a tis tic s .
Figure 1. The Paths of Taxicab Distance dT
Figure 2. The Paths of Chinese Checker Distance dCC.
where
dS(P1; P2) = min fjx1 x2j + jy1 y2j ; jy1 y2j + jz1 z2j ; jz1 z2j + jx1 x2jg
and dL(P1; P2) = max fjx1 x2j ; jy1 y2j ; jz1 z2jg :
S. Tian [13] gave a family of metrics, metric (alpha metric) for 2 [0; =4], which includes the taxicab and Chinese checker metrics as special cases. Then, Ö. Geli¸sgen and R. Kaya extended the distance to three and n dimensional spaces in [11, 10], respectively. Afterwards, H. B. Çolako¼glu [6] extended the metric for 2 [0; =2) : For ( ) = (sec - tan ), d (P1; P2) = dL(P1; P2) +
p
2 1 dS(P1; P2) the paths of alpha metric d from P1to P2as shown in Figure
3.
Later, H. B. Çolako¼glu and R. Kaya [5] give the generalized m metric Rn which includes the taxicab, Chinese checker, maximum, and alpha metrics. It is the most important property of generalized m metric that its paths are not parallel to the coordinate axes in n-dimensional analytical space. Finally, H. G. Park et. al. [7] de…ne the polar taxicab distance dP T in the R2 of which paths composed of arc in
circle and line segments. The polar taxicab metric has very important applications in urban geography beacuse cities formed not only linear streets but also curvilinear streets (Figure 4).
Figure 4. (a) Sun city in Arizona (b) Square of the Star in Paris When we examine the common features of the metrics dM; dT; dCC; d and
dP T; we see that these metrics were …rst de…ned in a planar surface. Considering
Figure 5
travels are made through the interior of spherical Earth which is impossible [8]. Using the idea given in [7], we have de…ned a new alternative metric on spherical surfaces due to disadvantage and disharmony of Euclidean distance on earth’ s surface. This metric composed of arc of circle on sphere and line segments will be denoted dCL. Also another alternative metric on sphere was de…ned by A. Bayar
and R. Kaya [1].
2. An Alternative Metric In The R3
Let’s remember spherical coordinates, before de…nition of alternative metric is given. The Cartesian coordinate of x; y; z of a point can be expressed in terms of r; ; as shown in the Figure 5 (x = r sin cos ; y = r sin sin ; z = r cos ).
Now, we de…ne the distance function dCLin the three dimensional analytic space
as follows.
De…nition 1. Let P1 = (r1; 1; 1) and P2 = (r2; 2; 2) be two any points in the
spherical coordinates and the angle\P1OP2is denoted 'P1P2. The distance function
dCLis de…ned by
dCL(P1; P2) = r'P1P2 min fr1; r2g + jr1 r2j ; 0 'P1P2 2
1+ r2 ; 2 < 'P1P2
where
shortest arc length joining these points can be denoted by dCL(A; Br1) ; dCL(Br1; Cr1)
and dCL(A; Cr1) in terms of De…nition 1. Using the fact that the triangle inequality
is valid for the spherical triangles, we exactly write dCL(A; Br1) + dCL(Br1; Cr1)
dCL(A; Cr1) :
To show distance function dCL is the metric, we have proved following axioms
for dCLholds such that for all A; B and C 2 R3
i ) dCL(A; B) 0; (dCL(A; B) = 0 () A = B)
ii ) dCL(A; B) = dCL(B; A)
iii ) dCL(A; B) + dCL(B; C) dCL(A; C)
Note that dCL(A; B) 0 since absolute values, each of r1 and r2 and 'AB are
non-negative. Thus (i ) for distance dCL holds. If A = B, then 'AB = 0 and
r1= r2, so this means dCL(A; B) = 0. On the other hand, if dCL(A; B) = 0; then
there are two cases;
Case 1: For 0 'AB 2;
dCL(A; B) = 'AB min fr1; r2g + jr1 r2j = 0 ; each of two terms 'AB
min fr1; r2g and jr1 r2j must be zero; 'AB min fr1; r2g = 0 and jr1 r2j = 0.
So, jr1 r2j = 0 ) r1 = r2 and 'AB min fr1; r2g = 0 ) 'AB = 0 since
min fr1; r2g 0: So, A = B is obtained.
Case 2: For 2 < 'AB ;
dCL(P1; P2) = r1+ r2= 0; since min fr1; r2g 0; r1= r2= 0. Thus, A = B:
It is clearly that dCL(A; B) = dCL(B; A) : That is dCLis symmetric.
As for …nal axiom (iii ), is known as Triangle Inequality, we have to show that dCL(A; B) + dCL(B; C) dCL(A; C) for all A; B and C 2 R3:
Case 1: Let the angles 'AB; 'BC, 'AC be in [0; 2], then dCL(A; B) = dCL(A; Br1) + r2 r1;
dCL(A; Cr1) : Therefore, dCL(A; B)+dCL(B; C) dCL(A; C) = dCL(A; Br1) + dCL(B; Cr2) dCL(A; Cr1) dCL(A; Br1) + dCL(Br1; Cr1) dCL(A; Cr1) dCL(A; Cr1) dCL(A; Cr1) = 0:
Namely, dCL(A; B) + dCL(B; C) dCL(A; C) :
Case 2: Let the angles 'AB; 'BC be in [0; 2] and 'AC be in (2; ] ; then dCL(A; B) + dCL(B; C) = dCL(A; Br1) + dCL(B; Cr2) + r3 r1
dCL(A; Br1) + dCL(Br1; Cr1) + r3 r1
dCL(A; Cr1) + r3 r1
r3+ r1
= dCL(A; C) :
Namely, dCL(A; B) + dCL(B; C) dCL(A; C) :
Case 3: Let the angles 'AB and 'AC be in [0; 2] ; 'BC be in (2; ] ; then dCL(A; B) + dCL(B; C) = dCL(A; Br1) + r2 r1+ r2+ r3
dCL(A; Br1) + 2r2+ dCL(A; C) dCL(A; Cr1) :
Therefore,
dCL(A; B) + dCL(B; C) dCL(A; C) = dCL(A; Br1) dCL(A; Cr1) + 2r2
dCL(A; Br1) + 2r2
0: Namely, dCL(A; B) + dCL(B; C) dCL(A; C) :
Case 4: Let the angles 'AB be in [0; 2] ; 'BC and 'AC be in (2; ] ; then dCL(A; B) + dCL(B; C) = dCL(A; Br1) + r2 r1+ r2+ r3
dCL(A; Br1) + 2r2+ r3
dCL(A; Br1) + r1+ r3
= dCL(A; Br1) + dCL(A; C)
dCL(A; C) :
r3+ r1
= dCL(A; C) :
Namely, dCL(A; B) + dCL(B; C) dCL(A; C) :
Case 7: Let the angles 'AB and 'BC be in (2; ] ; 'AC be in [0; 2] ; then dCL(A; B) + dCL(B; C) = r1+ r2+ r2+ r3
= 2r2+ r3+ r1
r3+ r1
dCL(A; C) :
Thus, dCL(A; B) + dCL(B; C) dCL(A; C) :
Case 8: Let the angles 'AB; 'BC, 'AC be in (2; ], then dCL(A; B) + dCL(B; C) = r1+ r2+ r2+ r3
= 2r2+ r3+ r1
r3+ r1
= dCL(A; C) :
Thus, dCL(A; B) + dCL(B; C) dCL(A; C) : Therefore dCL holds the triangle
inequality for all cases. Consequently dCLis a metric.
3. Isometries of R3 CL
For the sake of simplicity, R3furnished by the metric d
CLis denoted R3CLin the
rest of the article.
A linear transformation T from Rn to Rn is called orthogonal if it preserves
the length of vectors. Also, we know that an orthogonal transformation preserves angles between vectors. For example, the re‡ection about the plane that passing the origin is a example of orthogonal transformations.
Suppose A = (r1; 1; 1) and B = (r2; 2; 2) are two any points in the spherical
dCL(A; B) = 'AB min fr1; r2g + jr1 r2j
= ' (A) (B) min fr1; r2g + jr1 r2j
= 'A B min fr1; r2g + jr1 r2j
= dCL(A ; B ) :
Namely, we obtain that the equality dCL(A; B) = dCL(A ; B ) for 0 'AB 2.
Similarly, the equality dCL(A; B) = dCL(A ; B ) can be easily shown for 2 <
'AB : Consequently, we have proved the following theorem.
Theorem 3. The re‡ection about the plane passing through the origin is an isometry in the R3
CL:
Orthogonal transformations in two or three-dimensional Euclidean space are rigid rotations, re‡ections, or combinations of rotations and re‡ections (also known as rotary re‡ection, rotary inversion and inversion). A rotation can be written as the composition of two distinct re‡ections about intersecting planes. That is, a rotation R about axis l is de…ned by where l is line of intersection between planes and : It is known that the rotation R = is an orthogonal transformation such that two planes and pass through the origin. Therefore, following Theorem 4 can be given similar to Theorem 3. A rotary re‡ection is an transformation which is the combination of a rotation about an axis and a re‡ection in a plane. That is, a rotary re‡ection is de…ned by such that and are two intersecting planes each perpendicular to plane . Also, a rotary re‡ection = is an orthogonal transformation if the planes , and pass through the origin. A inversion according to the origin O can be written as the O(X) = Y such that O
is the midpoint of X and Y for X ; Y 2 R3. Also the inversion
O is an orthogonal
transformation. Finally, rotary inversion is the combination of a rotation and an inversion in a point. That is, a rotary inversion ' is de…ned by OR where R is
a rotation transformation and O is a inversion according to the origin O: Also a
rotary inversion ' = OR is a example of orthogonal transformations. In the light
of above explanation, the following theorems can be proven similar to Theorem 3. Theorem 4. A rotation R with axis l through the origin is an isometry in the R3
CL:
Theorem 5. Let the planes , and pass through the origin. A rotary re‡ection = where and are two intersecting planes each perpendicular to plane
is an isometry in the R3 CL:
Isometries, Math. Commun. Vol. 16 (2011), 21 - 35.
[6] H. B.Colakoglu, Concerning the alpha distance, Algebras Groups Geom. 8 (2011),1-14. [7] H. G. Park, K. R. Kim, I. S. Ko, B. H. Kim, On Polar Taxicab Geometry In A Plane, J.
Appl. Math. & Informatics, 32 (2014), 783-790.
[8] J. J. Mwemezi, Y. Haung, Optimal Facilitiy Location On Spherical Surfaces: Algorithm And Application, New York Science Journal, 4(7) (2011), 21-28.
[9] Ö. Geli¸sgen, R. Kaya, Alpha(i) Distance in n-dimensional Space, Applied Sciences, Vol.10 (2006), 88-93.
[10] Ö. Geli¸sgen, R. Kaya, Generalization of -distance to n dimensional space, KoG. Croat. Soc. Geom. Graph. 10 (2006), 33-35.
[11] Ö. Geli¸sgen, R. Kaya, On Alpha-Distance in Three Dimensional Space, Applied Sciences, 8(2006), 65-69.
[12] Ö. Geli¸sgen, R. Kaya, M. Özcan, Distance Formulae in Chinese Checker Space, IJPAM, 26(1) (2006), 35-44.
[13] S. Tian, Alpha Distance-A Generalization of Chinese Checker Distance and Taxicab Dis-tance, Missouri Journal of Mathematical Sciences, 17(1) (2005), 35-40.
[14] Z. Akça, R. Kaya, On the Distance Formulae In three Dimensional Taxicab Space, Hadronic Journal, 27 (2006), 521-532.
Current address : Temel ERM ·I¸S :Eskisehir Osmangazi University, Faculty of Art and Sciences, Deparment of Mathematics and Computer Sciences, 26480 Eskisehir, TURKEY
E-mail address : termis@ogu.edu.tr
Current address : Özcan GEL·I¸SGEN: Eskisehir Osmangazi University, Faculty of Art and Sciences, Deparment of Mathematics and Computer Sciences, 26480 Eskisehir, TURKEY