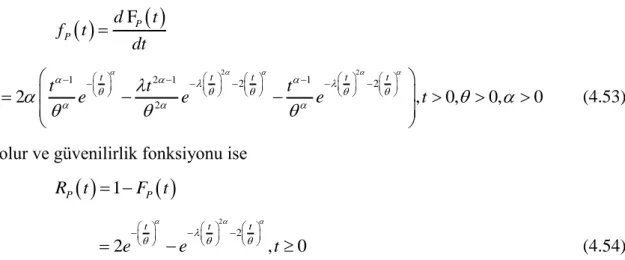T.C.
SELÇUK ÜNĠVERSĠTESĠ FEN BĠLĠMLERĠ ENSTĠTÜSÜ
YER DEĞĠġTĠRĠLEBĠLĠR BĠLEġENLĠ SĠSTEMLERĠN GÜVENĠLĠRLĠK
ÖZELLĠKLERĠ
Hatice SATILMIġOĞLU YÜKSEK LĠSANS TEZĠ Ġstatistik Anabilim Dalını
Ağustos-2018 KONYA Her Hakkı Saklıdır
iv ÖZET
YÜKSEK LĠSANS TEZĠ
YER DEĞĠġTĠRĠLEBĠLĠR BĠLEġENLĠ SĠSTEMLERĠN GÜVENĠLĠRLĠK ÖZELLĠKLERĠ
Hatice SATILMIġOĞLU
Selçuk Üniversitesi Fen Bilimleri Enstitüsü Ġstatistik Anabilim Dalı
DanıĢman: Doç. Dr. Ġsmail KINACI
2018, 71 Sayfa Jüri
Doç. Dr. Ġsmail KINACI Dr. Öğr. Üyesi Aydın KARAKOCA
Dr. Öğr. Üyesi Yunus AKDOĞAN
Bu çalıĢmada yer değiĢtirebilir bağımlı bileĢenlerden oluĢan seri ve paralel sistemler için bazı güvenilirlik özellikleri incelenmiĢtir. BileĢenlerin yaĢam zamanlarının üstel ve Weibull dağılımlarına sahip oldukları ve bağımlılık yapısının ise Marshall-Olkin ve Gumbel-Barnett kopula ile ifade edildiği varsayılmıĢtır. Bu düĢünceler altında seri ve paralel sistemler için sistemlerin yaĢam zamanlarına iliĢkin olasılık yoğunluk fonksiyonu, dağılım fonksiyonu, güvenilirlik fonksiyonu, hazard fonksiyonu ve ortalama kalan ömür fonksiyonu elde edilmiĢ ve bazı grafikler verilmiĢtir.
Anahtar Kelimeler: Gumbel-Barnett kopula, Güvenilirlik, Marshall-Olkin kopula, Sistemler, Yer DeğiĢtirilebilirlik.
v ABSTRACT
MS THESIS
RELIABILITY PROPERTIES OF SYSTEMS WITH EXCHANGEABLE COMPONENTS
Hatice SATILMIġOĞLU
THE GRADUATE SCHOOL OF NATURAL AND APPLIED SCIENCE OF SELÇUK UNIVERSITY
THE DEGREE OF MASTER OF SCIENCE / DOCTOR OF PHILOSOPHY IN MECHANICAL ENGINEERING
Advisor: Assoc.Prof.Dr. Ġsmail KINACI 2018, 71 Pages
Jury
Doç. Dr. Ġsmail KINACI Dr. Öğr. Üyesi Aydın KARAKOCA
Dr. Öğr. Üyesi Yunus AKDOĞAN
In this study, some reliability properties are investigated for serial and parallel systems consist of dependent and exchangeable components. It is assumed that the marginal distribution of the components are exponential and Weibull distributions and dependency structures of the components are Marshall-Olkin and Gumbel-Barnett copulas. Under these considerations, the probability density function, distribution function, reliability function, hazard function and mean residual life function for the lifetimes of the serial and parallel systems are obtained and some plots of these functions are given.
vi ÖNSÖZ
Bu tez çalıĢmasında benden yardımlarını hiç esirgemeyen çok değerli hocam sayın Doç. Dr. Ġsmail KINACI’ya teĢekkürü bir borç bilirim. Ayrıca bu süreçte bana destek olan sayın hocalarım Prof. Dr. CoĢkun KUġ’a, Dr. Öğr. Üyesi Yunus AKDOĞAN’a, Dr. Öğr. Üyesi Demet SEZER’e, ArĢ. Gör. Aynur ġAHĠN’e, ArĢ. Gör. Öznur ÖZALTIN, ArĢ. Gör. Kadir KARAKAYA, ArĢ. Gör. Caner TANIġ’a, ArĢ. Gör. Muslu Kazım Körez’e ve ArĢ. Gör. Harun YONAR’a ve Ġstatistik Bölüm Sekteri Yasemin GÜLVEREN ÇELĠK’e çok teĢekkür ederim.
Hayatımın her döneminde olduğu gibi bu tez çalıĢmasında da maddi manevi her türlü destekleriyle beni yalnız bırakmayan aileme çok teĢekkür ederim.
Hatice SATILMIġOĞLU KONYA-2018
vii ĠÇĠNDEKĠLER ÖZET ... iv ABSTRACT ... v ÖNSÖZ ... vi ĠÇĠNDEKĠLER ... vii 1. GĠRĠġ ... 1 2. KAYNAK ARAġTIRMASI ... 3 3. TEMEL KAVRAMLAR ... 9 3.1. Güvenilirlik ... 9 3.2. Sistem Güvenilirliği ... 11
3.2.1. Seri sistemin güvenilirliği ... 11
3.2.2. Paralel sistemin güvenilirliği ... 12
3.3. Bazı YaĢam Zamanı Dağılımları ... 13
3.3.1. Üstel dağılım ... 13
3.3.2. Weibull dağılımı ... 15
3.4. Yer değiĢtirilebilir Rasgele DeğiĢkenler ... 16
3.5. Kopulalar ... 17
3.5.1. Gumbel-Barnett Kopula ... 17
3.5.2. Marshall-Olkin Kopula ... 18
4. GUMBEL-BARNETT KOPULAYA D AYALI ĠKĠ YERDEĞĠġTĠRĠLEBĠLĠR BĠLEġENLĠ SĠSTEMLERĠN GÜVENĠLĠRLĠĞĠ ... 19
4.1. Üstel BileĢenli Sistemlerin Güvenilirliği ... 19
4.1.1. Seri sistemler ... 21
4.1.2. Paralel sistemler ... 25
4.2. Weibull BileĢenli Sistemlerin Güvenilirliği ... 29
4.2.1. Seri sistemler ... 31
4.2.2. Paralel sistemler ... 34
5. MARSHALL-OLKIN KOPULAYA DAYALI ĠKĠ YERDEĞĠġTĠRĠLEBĠLĠR BĠLEġENLĠ SĠSTEMLERĠN GÜVENĠLĠRLĠĞĠ ... 38
5.1. Üstel BileĢenli Sistemlerin Güvenilirliği ... 38
5.1.1. Seri sistemler ... 40
5.1.2. Paralel sistemler ... 44
5.2. Weibull BileĢenli Sistemlerin Güvenilirliği ... 48
5.2.1. Seri sistemler ... 50
viii
6. ARAġTIRMA SONUÇLARI VE TARTIġMA ... 57
7. SONUÇLAR VE ÖNERĠLER ... 58
7.1 Sonuçlar ... 58
7.2 Öneriler ... 58
KAYNAKLAR ... 60
1. GĠRĠġ
Gerçek hayatta rasgelelik içeren olgular olasılık dağılımları ile modellenebilmektedir. Bu olgular bazen basit bir yapıda olmasına rağmen bazen de oldukça karmaĢık bir yapıda olabilmektedir. Bu sebeple literatürde farklı türden olguları modelleyebilmek amacıyla çok sayıda olasılık dağılımı önerilmiĢtir. Olasılık dağılımlarının en yaygın olarak kullanıldığı sahalardan biri güvenilirlik sahasıdır. Burada bir parçanın, bileĢenin, canlının, sistemin vs. ömrü bir olasılık dağılımı ile modellenmeye çalıĢılmakta ve model yardımıyla yaĢam zamanına iliĢkin sonuçlar çıkarılmaya çalıĢılmaktadır. Özellikle sistem güvenilirliği konusunda genellikle sistemi oluĢturan bileĢenlerin bağımsız oldukları varsayılmaktadır. Bağımsızlık durumunda her bir bileĢenin yaĢam zamanına iliĢkin olasılık dağılımı hakkında bilgi sahibi olmak sistemin yaĢam zamanına iliĢkin olasılık dağılımı hakkında bilgi sahibi olunması için yeterli olmaktadır. Ancak bazı durumlarda sistemi oluĢturan bileĢenler bağımlı olabilmekte ve bu durumda her bir bileĢenin yaĢam zamanına iliĢkin olasılık dağılımından sistemin yaĢam zamanına iliĢkin olasılık dağılımı elde edilememektedir. Bununla birlikte bileĢenlerin bağımlılık yapıları hakkında bir bilgi verilmesi durumunda sistemin yaĢam zamanı dağılımı elde edilebilmektedir. Bu bağımlılık yapıları kopula olarak adlandırılan çeĢitli fonksiyonel yapılardır. Bu çalıĢmada yer değiĢtirebilir rasgele değiĢkenler, seri ve paralel sistemler, güvenilirlik, bağımlı rasgele değiĢkenler ve kopulalar konusu üzerinde durulmuĢtur ve üçüncü bölümde bu konular hakkında temel bilgiler verilmiĢtir. Dördüncü bölümde Gumbel-Barnett kopulaya dayalı iki yer değiĢtirebilir bileĢenden oluĢan sistemler için güvenilirlik özellikleri incelenmiĢtir. Öncelikli olarak bileĢenlerin yaĢam zamanlarının üstel dağılıma sahip olduğu durum için bileĢenlerin yaĢam zamanlarının ortak dağılımı Gumbel-Barnett kopulasına dayalı olarak elde edilmiĢ ve bu bileĢenlerden oluĢturulacak seri ve paralel sistemlerin yaĢam zamanlarına iliĢkin olasılık yoğunluk fonksiyonu, dağılım fonksiyonu, güvenilirlik fonksiyonu, hazard fonksiyonu ve ortalama kalan ömür fonksiyonları elde edilmiĢ ve bu fonksiyonlara iliĢkin bazı grafikler verilmiĢtir. Bu bölümde ayrıca bileĢenlerin yaĢam zamanlarının Weibull dağılımına sahip olduğu durum da ele alınmıĢ ve üstel dağılım durumunda elde edilen sonuçlar Weibull için de elde edilmiĢtir. BeĢinci bölümde ise Marshall-Olkin kopulaya dayalı iki yer değiĢtirebilir bileĢenden oluĢan sistemler için güvenilirlik özellikleri incelenmiĢtir. Yine öncelikli olarak bileĢenlerin yaĢam zamanlarının üstel dağılıma sahip olduğu durum için bileĢenlerin yaĢam zamanlarının
ortak dağılımı Marshall-Olkin kopulasına dayalı olarak elde edilmiĢ ve bu bileĢenlerden oluĢturulacak seri ve paralel sistemlerin yaĢam zamanlarına iliĢkin olasılık yoğunluk fonksiyonu, dağılım fonksiyonu, güvenilirlik fonksiyonu, hazard fonksiyonu ve ortalama kalan ömür fonksiyonları elde edilmiĢ ve bu fonksiyonlara iliĢkin bazı grafikler verilmiĢtir. Bu bölümde ayrıca bileĢenlerin yaĢam zamanlarının Weibull dağılımına sahip olduğu durum da ele alınmıĢ ve üstel dağılım durumunda elde edilen sonuçlar Weibull için de elde edilmiĢtir.
2. KAYNAK ARAġTIRMASI
Gerçek hayatta rasgelelik içeren olgular olasılık dağılımları ile modellenebilmektedir. Bu olgular bazen basit bir yapıda olmasına rağmen bazen de oldukça karmaĢık bir yapıda olabilmektedir. Bu sebeple literatürde farklı türden olguları modelleyebilmek amacıyla çok sayıda olasılık dağılımı önerilmiĢtir. Hawkes (1972), yakın tarihte Downton (1970) tarafından önerilen iki değiĢkenli üstel dağılımı güvenilirlik konusu içerisinde ele almıĢtır. Bu çalıĢma ile, uygulamalarda bazı avantajlara sahip olabilecek daha genel bir dağılım önerilmiĢtir (Hawkes, 1972). O’Cinneide ve Raftery (1989), iki değiĢkenli üstel dağılım için bir güvenilirlik modelini çok değiĢkenli duruma geniĢletmiĢlerdir ve bu çok değiĢkenli üstel dağılımı daha sonra çok değiĢkenli faz (phase) tipi olarak göstermiĢlerdir (O'Cinneide ve Raftery, 1989). Raftery (1984), tüm korelasyon yapısını modelleyebilen ve iki değiĢkenli durumda Frechet sınırlarına ulaĢabilen sürekli bir çok değiĢkenli üstel dağılımı tanıtmıĢtır. Bu dağılımın simüle edilmesinin kolay olduğunu, Ģoklara dayalı bozulmalar durumunda güvenilirlik için bir model olarak ortaya çıktığını ve çok değiĢkenli normal dağılıma benzediğini vurgulamıĢtır. Bu dağılımın modelleme yeteneğini gösterebilmek amacıyla iki örnek vermiĢtir (Raftery, 1984). Lai, Xie ve Murthy (2003), küvet eğrisi bozulma oranı fonksiyonunu modelleme yeteneğine sahip olan yeni bir yaĢam zamanı dağılımı önermiĢlerdir. Weibull dağılımının baĢka bir 3 parametreli genellemesi olarak düĢünülebilecek bu model, bütünleĢik Beta modelinin limit durumundan elde edilmiĢtir ve özel durumlar olarak Weibull dağılımı ve Tip-I uç değer dağılımlarını kapsamaktadır (Lai ve ark., 2003). Marshall ve Olkin (1967), çok değiĢkenli üstel dağılımın çok sayıda formunun önerildiğini, fakat bu dağılımların uygulanabilirliklerine dair yeterli çalıĢmaların yapılmadığını vurgulamıĢlardır. Bu çalıĢmada da, çok değiĢkenli üstel dağılımın bazı kullanıĢlı versiyonları incelenmiĢtir. Bu modellerin ikisi Ģok modellerine dayanmaktadır ve biri kalan ömrün yaĢtan bağımsız olması gerekliliğine dayanmaktadır. Bu dağılım için moment çıkaran fonksiyon elde edilmiĢtir, bağımsızlık durumu için karĢılaĢtırma yapılmıĢtır, minimumun dağılımı tartıĢılmıĢtır ve çeĢitli diğer özellikler incelenmiĢtir (Marshall ve Olkin, 1967). Mutairi, Ghitany ve Kundu (2011), son zamanlarda Gupta ve Kundu (2009)’nun ağırlıklandırılmıĢ üstel dağılım sınıfını tanıttıklarını ve önerilen ağırlıklandırılmıĢ üstel dağılımın çok esnek olduğunu ve çarpık veri analizinde oldukça etkili kullanılabileceğini vurgulamıĢlardır. Bu çalıĢmada,
ağırlıklandırılmıĢ üstel marjinaller ile yeni bir iki değiĢkenli dağılım önerilmiĢtir. Bu yeni iki değiĢkenli dağılımın farklı özellikleri araĢtırılmıĢtır. Bu yeni aile 3 bilinmeyen parametreye sahiptir ve bilinmeyen parametrelerin en çok olabilirlik tahmin edicilerinin (MLE) tek boyutlu bir optimizasyon problemini çözerek elde edilebildiği görülmüĢtür. En çok olabilirlik tahmin edicilerinin asimptotik dağılımı elde edilmiĢtir. En çok olabilirlik tahmin edicilerinin davranıĢlarını görmek için küçük simülasyon deneyleri gerçekleĢtirilmiĢ ve bir veri analizi örnek amaçlı sunulmuĢtur. Son olarak önerilen modelin çok değiĢkenli bir genellemesi tartıĢılmıĢtır (Al-Mutairi ve ark., 2011). Das (2008), bir hücresel üretim sisteminin (CMS) tasarlanmasında Weibull ve üstel dağılım yaklaĢımlarına dayalı olarak makine güvenilirliği konusunu ele almıĢtır. Bu çalıĢmada artan azalan veya sabit bozulma oranı gibi farklı bozulma özelliklerinin modellenme yeteneği üzerinde durulmuĢtur. Modelin uygulanabilirliğini göstermek için örnek bir problem çözümüne de yer verilmiĢtir (Das, 2008). Gómez-Déniz (2018), üstel dağılımın bir genelleĢtirmesi üzerinde çalıĢmıĢtır. Bu dağılım, üstel aileye ait olduğundan dolayı, değiĢen örnek büyüklükleri için sabit boyutlu yeterli istatistiğe sahiptir. Bu dağılımın özellikleri ve bundan elde edilen iki parametreli Weibull dağılımının bir genelleĢtirilmesi de sunulmuĢtur (Gómez-Déniz, 2018). Azad, Rasul, Alam, Ameer Uddin ve Mondal (2014), BangladeĢ’deki Hatiya adasının rüzgar enerjisi dönüĢümü özelliklerini bulup çıkarmak için Weibull dağılımını kullanarak rüzgar hız verilerini istatistiksel olarak analiz etmiĢlerdir (Azad ve ark., 2014). Rong-Tsorng Wang (2007), bağımlı bileĢenlerden oluĢan bir sistemin ölüm oranlarını tanımlamak için bir sayım süreci yaklaĢımı düĢünmüĢtür (Wang, 2007). Kundu ve Gupta (2013), bu makalede iki değiĢkenli Marshall-Olkin Weibull dağılımının Bayes analizi ele alınmıĢtır. (Kundu ve Gupta, 2013). Downton (1970), iki değiĢkenli üstel dağılımı, güvenilirlik bağlamında dikkate almıĢ ve güvenilirlik teorisi ile motive edilen farklı iki değiĢkenli üstel model için Marshall ve Olkin tarafından elde edilenlerle karĢılaĢtırılmıĢtır (Downton, 1970). Kayid ve Izadkhh (2015), bu makalede k bağımsız rasgele ömürlerin konvolüsyonu ve sıra istatistikleri rasgele zamanlar olarak göz önüne alınmıĢtır (Kayid ve Izadkhah, 2015). Awad (2016), güvenilirliği geliĢtirme testi (RGT), otomotiv, havacılık ve petrol ve gaz endüstrisi gibi birçok endüstride karmaĢık sistemlerin güvenilirliğini değerlendirmek için yaygın olarak kullanıldığını vurgulamıĢtır (Awad, 2016). Alexander ve Balakrishnan (1994), daha yüksek beklenen değere sahip iki uzak gözlem var olduğunda beklenen değerin etkin tahmin edicisinin seçilmesi problemini ele almıĢlardır. Ortalamanın tahmini için tekrarlı bir iĢlem sağlanmıĢ ve yöntem bir örnek
ile gösterilmiĢtir (Alexander ve Balakrishnan, 1995). Okasha, El-baz, Tarabia, Basheer (2017), yaĢam verilerini modellemek için daha esnek bir dağılım sunan ters Weibull dağılımının bir uzantısını tanıtmıĢlardır. Ters Weibull dağılımı Marshall-Olkin yöntemi (MOEIW) ile geniĢletilmiĢtir. Kuantiller, momentler ve güvenilirlik gibi MOEIW’ın bazı istatistiksel özellikleri araĢtırılmıĢtır (Okasha ve ark., 2017). Lee (1979), X1, ,X n rasgele değiĢkenlerinin keyfi ölçeklendirmeden sonra minimumlarının Weibull dağılımına sahip olduğunu vurgulamıĢ, bu sınıfın bazı özelliklerini incelemiĢtir (Lee, 1979). Karagiannidis, Zogas ve Kotsopoulos (2003), yıllar önce Blumenson ve Miller tarafından sunulan teoremin ispatından yararlanarak, üstel olarak korelasyonlu n değiĢkenli Nakagami-m olasılık yoğunluk fonksiyonu için kullanıĢlı bir kapalı formül önermiĢlerdir (Karagiannidis ve ark., 2003). Balakrishnan ve Shiji (2014), mutlak sürekli iki değiĢkenli üstel dağılımın bir sınıfını birinci dereceden otoregresif bir model kullanarak düzenlemiĢlerdir (Balakrishna ve Shiji, 2014). Wang ve Shi (2013), bu makalede üstel bir ailenin bir sınıfı için parametrelerin, yaĢam ve hazard fonksiyonlarının tahminini ele almıĢlardır (Wang ve Shi, 2013). Franco, Vivo ve Balakrishnan (2011), karma Weibull dağılımının birçok uygulamalı problemde dikkate alındığını vurgulamıĢlar ve negatif karıĢım ağırlıklarına da izin vererek bir genelleĢtirme yapmıĢlardır (Franco ve ark., 2011). Lu ve Bhattacharyya (1990), iki bileĢenli bir sistemin bileĢenlerinin bozulma davranıĢları düĢünerek iki değiĢkenli Weibull modellerinin inĢası için çeĢitli yaklaĢımlar geliĢtirmiĢlerdir (Lu ve Bhattacharyya, 1990). Cherubini ve Mulinacci (2017), üstel dağılımlı ömürler için Ģok varıĢ süreleri arasında bir miktar bağımlılığa izin veren Marshall-Olkin dağılımının bir genellemesini sunmuĢlardır (Cherubini ve Mulinacci, 2017). Haq, Usman, Hashmi ve Al-Omeri (2017), Marshall-Olkin geniĢlik tabanlı üstel dağılım olarak adlandırılan bir dağılım önermiĢlerdir. Önerilen modelin istatistiksel özellikleri tartıĢılmıĢ ve modelin parametrelerinin en çok olabilirlik tahmin edicileri elde edilmiĢtir (ul Haq ve ark., 2017).
Olasılık dağılımlarının en yaygın olarak kullanıldığı sahalardan biri güvenilirlik sahasıdır. Burada bir parçanın, bileĢenin, canlının, sistemin vs. ömrü bir olasılık dağılımı ile modellenmeye çalıĢılmakta ve model yardımıyla yaĢam zamanına iliĢkin sonuçlar çıkarılmaya çalıĢılmaktadır. Son zamanlarda güvenilirlik ile ilgili yapılan bazı çalıĢmalar Ģu Ģekildedir. Benkamra, Terbeche ve Tlemcani (2013), paralel-seri sistemin
güvenilirliğinin tahmini üzerinde durmuĢlardır ve bileĢenlerin güvenilirlikleri için bir beta-binom modeli seçmiĢlerdir (Benkamra ve ark., 2013). Ding ve Zhang (2018), sistem yapısının koherent sistemin göreceli yaĢlanma özellikleri üzerindeki etkisini, artan hazard oranı bakımından geniĢ bir Ģekilde incelemiĢlerdir. Bu makalede, paralel ve seri sistemlerin bileĢenleri arasındaki bağımlılığın ve farklılığın göreceli yaĢlanma üzerindeki etkileri incelenmiĢtir (Ding ve Zhang, 2018). Sharma, Agarwal ve Sen (2011), çok durumlu seri-paralel güvenilirlik yapıları içerisindeki güvenilirlik sınırlaması ve tüketici yük talebine cevap veren sistem modelinin toplam maliyetini minimize etmeyi amaçlamıĢlardır (Sharma ve ark., 2011). Navarro ve Sarabia (2013), koĢullu hazard fonksiyonlarının özelliklerine dayalı iki değiĢkenli koĢullu dağılımların iki sınıfı için güvenilirlik özellikleri üzerinde çalıĢmıĢlardır (Navarro ve Sarabia, 2013).
Özellikle sistem güvenilirliği konusunda genellikle sistemi oluĢturan bileĢenlerin bağımsız oldukları varsayılmaktadır. Bağımsızlık durumunda her bir bileĢenin yaĢam zamanına iliĢkin olasılık dağılımı hakkında bilgi sahibi olmak sistemin yaĢam zamanına iliĢkin olasılık dağılımı hakkında bilgi sahibi olunması için yeterli olmaktadır. Ancak bazı durumlarda sistemi oluĢturan bileĢenler bağımlı olabilmekte ve bu durumda her bir bileĢenin yaĢam zamanına iliĢkin olasılık dağılımından sistemin yaĢam zamanına iliĢkin olasılık dağılımı elde edilememektedir. Bununla birlikte bileĢenlerin bağımlılık yapıları hakkında bir bilgi verilmesi durumunda sistemin yaĢam zamanı dağılımı elde edilebilmektedir. Bu bağımlılık yapıları kopula olarak adlandırılan çeĢitli fonksiyonel yapılardır. Literatürde kopulalar ile ilgili çalıĢmaların bazıları Ģu Ģekildedir. Fernández ve González-López (2013), bu makalede kamu politikası içinde ilginin iki değiĢken arasındaki bağımlılığı modellemek için yeni bir Bayesci yaklaĢım uygulanmıĢtır: "100000 nüfus baĢına Gonore oranları" ve az sayıda eĢleĢtirilmiĢ gözlem ile " % 400 federal yoksulluk düzeyi ve üstü " (her ABD eyaleti için bir çift). Zayıf ve negatif bağımlılığı olan durumları temsil etmek için uygun bir Gambell-Barnett Kopula kullanılmıĢtır (Fernández ve González-López, 2013). Martinez ve Achcar (2014), yaĢam zamanlarının ortak dağılımını FGM, Clayton ve Gumbel-Barnett kopula fonksiyonlarını kullanarak elde etmiĢlerdir (Martinez ve Achcar, 2014). Cuadras (2009), iki kopulanın ağırlıklandırılmıĢ aritmetik ortalamasının yine bir kopula olduğunu ve bazı durumlarda geometrik ve harmonik ortalamaların da kopula olma özelliğini sağladığını belirtmiĢtir. AğırlıklandırılmıĢ geometrik ortalamalar kullanılarak FGM ve Ali-Mikhail-Haq kopulaları birleĢtirilmiĢtir. Gumbel-Barnett kopula da düĢünülmüĢ ve
iki kopulanın ağırlıklandırılmıĢ geometrik ortalamasına dayalı yeni bir kopula önerilmiĢtir (Cuadras, 2009). Lin, Lai ve Govindaraju (2016), ilk olarak iki değiĢkenli Marshall-Olkin üstel dağılımının temel özelliklerini ve sonra korelasyon yapısını incelemiĢlerdir. Ġki değiĢkenli üstel dağılımın korelasyonunun parametrelere bakılmaksızın her zaman kopuladan daha küçük olduğu gösterilmiĢtir (Lin ve ark., 2016). Bernhart, Anel, Mai ve Scherer (2013), Archimedean ve Levy-kırılgan kopula modellerinin bir birleĢimini önermiĢlerdir (Bernhart ve ark., 2013). Lin ve Li (2014), özel durumları Marshall-Olkin türü dağılımlar ve Marshall-Olkin üstel dağılımı olan çok değiĢkenli genelleĢtirilmiĢ Marshall-Olkin dağılımları üzerinde çalıĢmıĢlardır (Lin ve Li, 2014). Kundu, Franco ve Vivo (2014), çok değiĢkenli oransal ters hazard modelini önermiĢlerdir. Dahası, önerilen çok değiĢkenli oransal ters hazard modeli Marshall-Olkin kopuladan elde edilebileceği gözlenmiĢtir. Çok değiĢkenli oransal ters hazard modelleri de tekil bir bileĢene sahiptir ve marjinalleri orantısal olarak ters hazard dağılımlarına sahiptir. Çok değiĢkenli yaĢlanma ve bağımlılık özellikleri ayrıntılı olarak tartıĢılmıĢtır. Ayrıca iki değiĢkenli durum için özel olarak bazı bağımlılık ölçüleri de önerilmiĢtir (Kundu ve ark., 2014). Mesfioui, Quessy ve Toupin (2009), kopulaların parametrik aileleri için bir uyum iyiliği testi önermiĢlerdir (Mesfioui ve ark., 2009). Gıjbels, Omelka ve Sznajder (2010), iki rasgele değiĢken arasındaki pozitif kuadrant bağımlılığın (PQD) testi üzerinde durmuĢlardır. Önerilen test prosedürlerinin ana metodolojisi, bir kopulanın nonparametrik bir tahmini ve PQD özelliğine sahip olan kopulaların tüm kümesi ile referans bir durum olarak hizmet eden bağımsızlık kopulası arasındaki mesafeye dayanmaktadır (Gijbels ve ark., 2010). Mai ve Scherer (2011), yer değiĢtirilebilir Marshall-Olkin yaĢam kopulalarının [J.-F. Mai and M. Scherer, Lévy-Frailty copulas, J. Multivariate Anal. 100 (2009), pp. 1567–1585] 'de çalıĢılan kopulaların parametrik bir ailesine ait olduğunu göstermiĢlerdir (Mai ve Scherer, 2011). Durante, Omladič, Oražem ve Ružić (2017), kopulaların yeni bir sınıfını önermiĢlerdir (Durante ve ark., 2017). Omladič ve Ružić (2016), 1959’daki Sklar’ın teoreminden beri kopulaların rasgele değiĢkenlerin bağımlılığını modelleyen ana araçlardan biri olduğunu vurgulamıĢlardır. Burada iki bileĢenli bir sistemin model ömrüne tipik olarak uygulanan ünlü Marshall kopulaların (Marshall-Olkin Kopulaların bir uzantısı) bir benzeri düzenlenerek kopulalar inĢa edilmesi amaçlanmıĢtır (Omladič ve Ružić, 2016). Huillet (2018), kopulalar hiperküp tarafından desteklenen rasgele değiĢkenlerin bağımlılık yapısını tanımlamak için birçok genel araç sunduğunu vurgulamıĢtır. Biyolojideki tür bolluklarının problemlerinden esinlenerek kopulaların önemli bir rol oynadığı üç ayrı
model üzerinde çalıĢmıĢtır (Huillet, 2018). Li (2008), çok değiĢkenli Marshall-Olkin yaĢam kopulasının kuyruk bağımlılığının açık bir ifadesi türetmiĢ ve iki Marshall-Olkin yaĢam kopulasının kuyruk bağımlılıklarının karĢılaĢtırılabileceği koĢulları elde etmiĢtir (Li, 2008). Eryilmaz (2011), sistemin yaĢam zamanı verilerinden bileĢenlerin yaĢam zamanları dağılımının ortak bir parametresinin tahmin edilmesi probleminin, güvenilirlik mühendisliğinde ilgi ve öneme sahip olduğunu vurgulamıĢtır. BileĢenlerin dağılımının ortak ortalamalı üstel olması durumunda bileĢenlerin ortak yaĢam
zamanlarının Archimedian kopula yardımıyla üretildiği durum üzerinde çalıĢmıĢtır. Özellikle Clayton ve Ali-Mikhail-Haq kopulaları için 'nün moment tahmin edicisini elde etmiĢtir (Eryilmaz, 2011).
3. TEMEL KAVRAMLAR 3.1. Güvenilirlik
Bir parçanın ya da bir sistemin bozuluncaya (ölünceye) kadar geçen zamanı (dayanma süresi) T ile gösterilsin. Bu durumda
, 0R t P T t t (3.1)
Ģeklinde tanımlanan R t fonksiyonuna güvenilirlik (yaĢam) fonksiyonu denir. Bir
sistemin t anındaki güvenilirliği R t , bu parçanın t anında hala çalıĢıyor olması
olasılığıdır. Yani güvenilirlik
0,1 arasında bir sayıdır.
0 | lim , 0 t P t T t t T t h t t t (3.2)Ģeklinde tanımlanan h t fonksiyonuna bozulma oranı ya da hazard fonksiyonu denir. t
anına kadar yaĢayan (hala ölmediği bilinen) bir parçanın hemen ondan sonraki bir andaki bozulma oranıdır, yani h t bir olasılık değil, orandır.
T rasgele değiĢkeninin olasılık yoğunluk fonksiyonu f t , dağlım fonksiyonu
F t ve güvenilirlik fonksiyonu R t olmak üzere bu fonksiyonlar birbiri cinsinden
1 R t P T t P T t 1 F t
(3.3)
1
dF t f t dt d R t dt dR t
dt (3.4) Ģeklinde yazılabilir.Bir parçanın ortalama ömrü (ortalama bozulma zamanı, ortalama yaĢam zamanı) (MTTF, Mean Time to Failure) ise
MTTFE T
0 tf t dt
(3.5)Ģeklinde tanımlanır. Burada f t
dR t
dt ifadesi integralde yerine yazılırsa
0 E T tR t dt
(3.6)olarak yazılabilir ve kısmi integrasyon uygulanırsa
0
0 E T tR t R t dt
(3.7)elde edilir. Burada ilgilenilen parçaların ömürleri sonlu kabul edildiğinden R a( ) değeri a 'nın 'a yaklaĢmasından daha hızlı bir bir Ģekilde 0'a yaklaĢır. Bundan dolayı
0 lim
0
0 0 a tR t aR a R (3.8) olacağından
0 E T R t dt
(3.9)olarak elde edilir. Yani,
0 1 E T F t dt
(3.10)Ģeklinde yazılabilir. Ancak bu sonuç sadece pozitif değerler alan sürekli rasgele değiĢenler için geçerlidir.
YaĢam zamanı T olan bir parçanın herhangi bir t anında hala çalıĢtığını düĢünelim. t anına kadar kullanılan bu parçanın en az bir x kadar daha yaĢaması olasılığı
| | R x t P T t x T t P T t x P T t
R t x R t (3.11)Ģeklinde ifade edilir. Burada R x t fonksiyonu, t anına kadar kullanılmıĢ bir parçanın
| koĢullu güvenilirlik fonksiyonu ya da koĢullu yaĢam fonksiyonu olarak adlandırılır. Buna göre t anına kadar kullanılan bir parçanın ortalama kalan ömrü (MRL, Mean Residual Life)
0 0 0 | 1 MRL t R x t dx R t x dx R t R t x dx R t
1 t R t dt R t
(3.12)Ģeklinde tanımlanır. Açıktır ki MRL
0 E T
'dir. 3.2. Sistem GüvenilirliğiĠçinde birden fazla bileĢen bulunan yapılara sistem denir. Sistemi oluĢturan bileĢenler genelde birbirlerine seri ya da paralel bağlı olmakla birlikte bazen her iki türden bağlılığı da içerebilmektedir. Ayrıca k-out of n sistemler gibi sistemin yaĢamının sağlam bileĢen sayısına bağlı olduğu sistemler de bulunmaktadır. Burada seri ve paralel sistemler için güvenilirlik özellikleri ele alınacaktır.
3.2.1. Seri sistemin güvenilirliği
Birbirlerine seri olarak bağlı bileĢenlerden oluĢan bir sistemin ömrü ilk bozulan bileĢenin ömrü kadar olacaktır. Sistemin en az x kadar yaĢayabilmesi için tüm bileĢenlerin en az x kadar yaĢayabilmesi gerekmektedir. Seri sistemlerde sistemin güvenilirliği sistemi oluĢturan her bir bileĢenin güvenilirliğinden daha düĢüktür. Buna göre yaĢam zamanları X X1, 2, ,Xn rasgele değiĢkenleri ile ifade edilen n tane
bağımsız bileĢenden oluĢan bir sistemin ömrü XS min
X X1, 2, ,Xn
Ģeklinde ifadeedilebilir. Her bir bileĢenin güvenilirlik fonksiyonları R x R x1
, 2 , ,Rn
x olan bir seri sistemin güvenilirlik fonksiyonu
1 2 1 2 1 2 min , , , , , , s s n n n R x P X x P X X X x P X x X x X x P X x P X x P X x R x R x1
2 Rn
x (3.13) Ģeklinde bulunur.Eğer bileĢenler özdeĢ ise yani her bir bileĢenin güvenilirlik fonksiyonu R x( ) ise bu durumda sistemin güvenilirlik fonksiyonu
n sR x R x (3.14)
Ģeklinde olacaktır.
BileĢenlerin bağımlı olması durumunda bir seri sistemin güvenilirlik fonksiyonu ise
1 2 1 2 min , , , , , , s s n n R x P X x P X X X x P X x X x X x
1, 2, , n 1, 2, , 1 2 X X X n n x x x f x x x dx dx dx
(3.15) Ģeklinde bulunur.3.2.2. Paralel sistemin güvenilirliği
Birbirlerine paralel olarak bağlı bileĢenlerden oluĢan bir sistemin ömrü en son bozulan bileĢenin ömrü kadar olacaktır. Paralel sistemin en az x kadar yaĢayabilmesi için bileĢenlerden en az birinin en az x kadar yaĢaması gerekmektedir. Buna göre yaĢam zamanları X X1, 2, ,Xn rasgele değiĢkenleri ile ifade edilen n tane bağımsız
bileĢenden oluĢan bir sistemin ömrü XS max
X X1, 2, ,Xn
Ģeklinde ifade edilebilir. Paralel sistemlerde sistemin güvenilirliği sistemi oluĢturan her bir bileĢenin güvenilirliğinden daha büyüktür. Her bir bileĢenin güvenilirlik fonksiyonları
1 , 2 , , n
R x R x R x olan bir paralel sistemin güvenilirlik fonksiyonu
1 2 1 2 1 2 1 2 1 2 max , , , 1 max , , , 1 , , , 1 1 n P s n n n n X X X R x P X x P X X X x P X X X x P X x X x X x P X x P X x P X x F x F x F x 1
1R1
x
1R2
x
1Rn
x
(3.16) Ģeklinde bulunur.Eğer bileĢenler özdeĢ ise yani her bir bileĢenin güvenilirlik fonksiyonu R x( ) ise bu durumda sistemin güvenilirlik fonksiyonu
1 1
nP
Ģeklinde olacaktır.
BileĢenlerin bağımlı olması durumunda bir paralel sistemin güvenilirlik fonksiyonu ise
1 2 1 2 1 2 max , , , 1 max , , , 1 , , , P s n n n R x P X x P X X X x P X X X x P X x X x X x
1, 2, , 1 2 1 2 0 0 0 1 , , , n x x x X X X n n f x x x dx dx dx
(3.18) Ģeklinde bulunur.3.3. Bazı YaĢam Zamanı Dağılımları 3.3.1. Üstel dağılım
Üstel dağılım, üstel aileye ait sürekli bir dağılımdır ve yaĢam analizlerinde oldukça büyük öneme sahiptir. Üstel dağılıma sahip olan bir X rasgele değiĢkeninin olasılık yoğunluk fonksiyonu
1 , 0, 0 x f x e x (3.19)Ģeklindedir ve X Üstel
Ģeklinde gösterilir. Burada parametresi, ölçek (scale) parametresidir.X rasgele değiĢkeninin beklenen değeri
E X (3.20) varyansı
2 Var X (3.21) Ģeklindedir. parametreli üstel dağılıma sahip X rasgele değiĢkeninin dağılım fonksiyonu
F x P X x 1 , 0, 0 x e x (3.22)
1 1 1 x R x P X x F x e , 0 x e x (3.23)ve bozulma oranı (hazard) fonksiyonu
f x
h x R x 1 1 x x e e (3.24) olarak verilir.Burada dikkat edilirse üstel dağılım için bozulma oranı fonksiyonu h x( ), x 'e bağlı değildir yani sabittir. Üstelik tüm sürekli dağılımlar arasında bu özelliğe sahip olan tek dağılım üstel dağılımdır. Bozulma oranının sabit olması, bileĢenin zaman içerisinde hiç yıpranmadığı, çalıĢır durumda olduğu sürece hep yeni kaldığı anlamına gelmektedir.
x anına kadar kullanılmıĢ bir parçanın en az bir t kadar daha yaĢaması olasılığı, baĢka bir deyiĢle parçanın koĢullu güvenilirlik fonksiyonu
| | x t x R t x P X x t X x P X x t P X x R x t R x e e t e (3.25)Ģeklinde elde edilir. Burada dikkat edilirse R t x
| R t
olarak elde edilmiĢtir. Bu da hiç kullanılmamıĢ olan yeni bir parça ile x anında yaĢadığı bilinen kullanılmıĢ bir parçanın güvenilirlik fonksiyonları aynı demektir. Yani, yeni bir parça ile x anına kadar kullanılmıĢ ve hala sağlam olan bir parçanın bir t zaman kadar yaĢaması olasılıklarıeĢittir. BaĢka bir ifadeyle, parçaların yaĢam zamanlarının üstel dağılıma sahip olmaları durumunda kullanılmıĢ bir parça ile yeni bir parça arasında hiçbir farklılık yoktur. Bu durum üstel dağılımın belleksizlik özelliği olarak adlandırılmaktadır.
Üstel dağılıma sahip olan ve x anına kadar kullanılmıĢ bir parçanın ortalama kalan ömrü
0 | MRL x R t x dt
(3.26)eĢitliği elde edilir. Bu ifadede, üstel dağılımın belleksizlik özelliğinden, R t x
| R t
olacağından
0 MRL x R t dt E X
(3.27) olacaktır. 3.3.2. Weibull dağılımıĠlk olarak 1927'de Frechet tarafından tanımlanmıĢ ve ilk olarak 1933'de Rosin&Rammler tarafından bir parçacık büyüklüğü dağılımının tanımlamasında uygulanmasına rağmen 1951'de detaylı olarak tanımlayan Ġsveçli matematikçi Waloddi Weibull'un adını almıĢtır. Weibull dağılımı güvenilirlik analizinde yaĢam zamanı dağılımı olarak kullanılan en popüler dağılımlardan biridir. Bu dağılım, üstel dağılıma göre oldukça esnek bir dağılımdır.
Bozulma zamanı X olan bir parçanın olasılık yoğunluk fonksiyonu
1 , 0, 0, 0 x f x x e x (3.28) dağılım fonksiyonu
1 , 0 x F x P X x e x (3.29)Ģeklinde ise X , ve parametreli Weibull dağılımına sahiptir denir ve
,
X Weibull Ģeklinde gösterilir. Burada Ģekil (shape) parametresi, ise ölçek (scale) parametresidir.
X rasgele değiĢkeninin beklenen değeri
1 1 E X (3.30)varyansı
2 2 1 2 1 1 Var X (3.31) Ģeklindedir.Weibull dağılımına sahip olan bir X rasgele değiĢkeninin güvenilirlik fonksiyonu
1
R x F x , 0 x e x (3.32)ve bozulma oranı (hazard) fonksiyonu
f x
h x R x x 1;x 0 (3.33)olarak verilir. Bozulma oranı, 1 olduğunda sabit, 1 olduğunda artan ve 0 1 olduğunda ise azalan olacaktır. 2 olduğunda Rayleigh dağılımı olarak adlandırılır. Buradan da anlaĢılabileceği gibi Weibull dağılımı azalan, artan ya da sabit bozulma oranına sahip parçaların yaĢam zamanlarının modellenmesinde kullanılabilmektedir.
Weibull dağılımına sahip olan X rasgele değiĢkeninin ortalama kalan ömrü
0 1 1 t R t x MRL t dx R t R t R t dt R t
1 t t t e dt e
(3.34) olacaktır (Öztürk ve Özbek, 2015).3.4. Yer değiĢtirilebilir Rasgele DeğiĢkenler
1, 2, , n
X X X rasgele değiĢkenlerinin ortak dağılımı, içerisinde yer alan
1, 2, , n
x x x değerlerinin kendi aralarında yer değiĢtirmelerinden etkilenmiyorsa bu rasgele değiĢkenlere yer değiĢtirilebilir rasgele değiĢkenler denir. Örneğin, X ve 1 X 2
rasgele değiĢkenleri yer değiĢtirilebilir ise
1, 2 1, 2 1, 2 2, 1X X X X
gösterilmektedir. X X1, 2, ,Xn rasgele değiĢkenlerinin bağımsız ve aynı dağılıma sahip olmaları durumunda bu rasgele değiĢkenler aynı zamanda yer değiĢtirilebilirdir. Örneğin; bağımsız ve aynı dağılımlı X ve Y rasgele değiĢkenleri için ortak dağılım fonksiyonu
, ,
X Y X Y
F x y F x F y (3.35)
Ģeklinde yazılır. DeğiĢkenler yer değiĢtirdiğinde
, ,
X Y Y X
F y x F y F x (3.36)
olacaktır. EĢitlik 3.35, eĢitlik 3.36'ya eĢit olduğundan bağımsız ve aynı dağılıma sahip olan rasgele değiĢkenler yer değiĢtirilebilirdir (Eryilmaz, 2012).
3.5. Kopulalar
Kopulalar iki ya da daha çok rasgele değiĢkenin bağımlılığını modellemek için kullanılan bir araçtır. Sklar'ın çalıĢmasında kopula terimi ilk kez kullanılmıĢtır (Sklar, 1959). Latincede bağlamak ya da birleĢtirmek anlamına gelen 'copulare'den türetilmiĢtir. Benzer Ģekilde Hoeffding zaten 1940'larda 'ölçeğin keyfi değiĢimleri' adı altında dağılımları çalıĢmıĢtır. Bir kopulanın asıl amacı bağımlılık yapısını marjinallerden çözmektir.
Bu çalıĢmada Gumbel-Barnett Kopula ve Marshall-Olkin Kopulalar üzerinde çalıĢılarak bilgiler verilmiĢtir.
3.5.1. Gumbel-Barnett Kopula
Ġlk olarak Gumbel (1960a,b) tarafından üstel marjinal durumu için önerilmiĢtir. Bu kopulanın Gumbel-Barnett kopula olarak adlandırılmasının sebebi ise Barnett (1980)'in düzgün marjinaller durumu bu kopulayla ilk çalıĢan olmasıdır.
Gumbel-Barnett kopulanın dağılım fonksiyonu 0 1 olmak üzere
log 1 log 1, 1 1 1 u v
C u v u v u v e (3.37) olasılık yoğunluk fonksiyonu
log 1 log 1 , 1 log 1 1 log 1 u v c u v u v e (3.38) ve yaĢam fonksiyonu
log 1 log 1 , 1 1 u v C u v u v e (3.39)3.5.2. Marshall-Olkin Kopula
Marshall-Olkin kopulanın dağılım fonksiyonu
1 1
1 , 1 , , min , , u v u v C u v u v uv u v (3.40) ve yaĢam fonksiyonu
, 1
1
min 1
, 1
C u v u v u v
1 1
min 1 u 1 v , 1 u 1 v (3.41)4. GUMBEL-BARNETT KOPULAYA D AYALI ĠKĠ YERDEĞĠġTĠRĠLEBĠLĠR BĠLEġENLĠ SĠSTEMLERĠN GÜVENĠLĠRLĠĞĠ
Burada iki bileĢenli seri ve paralel sistemler için sistemi oluĢturan bileĢenlerin yaĢam zamanlarının üstel ve Weibull dağılımına sahip oldukları düĢünülmüĢtür. Burada öncelikli olarak üstel marjinaller durumunda Gumbel-Barnett kopula ile elde edilen iki değiĢkenli dağılımın özellikleri incelenmiĢtir. Ayrıca sistemi oluĢturan iki bileĢenin yaĢam zamanlarının bağımlı olduklarını ve bağımlılık yapısının Gumbel-Barnett kopula ile ifade edildiğini varsayarak seri ve paralel sistemler için güvenilirlik özellikleri incelenmiĢtir.
4.1. Üstel BileĢenli Sistemlerin Güvenilirliği
Gumbel-Barnett kopulada yer alan u , X rasgele değiĢkeninin dağılım fonksiyonu; v , Y rasgele değiĢkeninin dağılım fonksiyonu olarak alınır.
X rasgele değiĢkeninin marjinal yoğunluk fonksiyonu
1 1 1 1 , 0, 0 x X f x e x (4.1) ve dağılım fonksiyonu
1 1, 0 x X u F x e x (4.2)Ģeklinde, benzer Ģekilde Y rasgele değiĢkeninin marjinal yoğunluk fonksiyonu
2 2 2 1 , 0, 0 y Y f y e y (4.3) ve dağılım fonksiyonu
1 2, 0 y Y v F y e y (4.4) Ģeklinde alınsın.Sistemi oluĢturan iki bileĢenin yaĢam zamanları X ve Y'nin Gumbel-Barnett kopula bağımlılık yapısına sahip olması durumunda seri ve paralel sistemlerin güvenilirliğine geçmeden önce bileĢenlerin yaĢam zamanları X ve Y rasgele değiĢkenlerinin ortak dağılımına iliĢkin bazı sonuçlara yer verilecektir. Gumbel-Barnett kopula altında
X Y rasgele vektörünün ortak dağılım fonksiyonu ,
1 2 1 2 1 2 , , 1 ; 0, 0 x y x y xy X Y F x y e e e x y (4.5)
1 1 22 2 1 2 1 2 1 2 , 2 2 1 2 1 2 , ; 0, 0, 0, 0 y x xy X Y y x xy f x y e x y (4.6)olarak elde edilir.
X Y vektörüne iliĢkin ortak yaĢam fonksiyonu ise ,
1 2 1 2 , , , 0, 0 x y xy X Y R x y e x y (4.7)Ģeklinde elde edilmektedir. Fakat burada X ve Y rasgele değiĢkenleri yer değiĢtirilebilir değildir. Bu rasgele değiĢkenlerin yer değiĢtirilebilir olabilmesi için
1 2
alınması gerekmektedir ve bundan sonra 1 2 olduğu kabul edilecektir. Bu durumda X rasgele değiĢkeninin marjinal olasılık yoğunluk fonksiyonu
1 , 0, 0 x X f x e x (4.8) dağılım fonksiyonu
1 , 0 x X F x e x (4.9)ve benzer Ģekilde Y rasgele değiĢkeninin marjinal olasılık yoğunluk fonksiyonu
1 , 0, 0 y Y f y e y (4.10) dağılım fonksiyonu
1 , 0 y Y F y e y (4.11) Ģeklinde olacaktır.Yer değiĢtirilebilir olan X ve Y değiĢkenlerine bağlı olarak elde edilen
X Y ,
vektörünün ortak dağılım fonksiyonu
2 , , 1 , 0, 0 x y xy x y X Y F x y e e e x y (4.12)iken olasılık yoğunluk fonksiyonu
2 2 2 2 , , 4 , 0, 0, 0 x y xy X Y y x xy f x y e x y (4.13) ve güvenilirlik fonksiyonu
2 , , , 0, 0 x y xy X Y R x y e x y (4.14) Ģeklinde bulunur.4.1.1. Seri sistemler
Seri sistemi oluĢturan X ve Y bileĢenlerinin bağımlı, aynı dağılımlı ve her birinin Üstel
olduğu ve bu bağımlılığın Gumbel-Barnett kopula olduğu düĢünülsün. Bu durumda sistemin yaĢam zamanı T min
X Y,
rasgele değiĢkeninin dağılım fonksiyonu
1 ,
, S X Y t t F t f x y dydx
2 2 1 , 0 t t e t (4.15)Ģeklinde bulunurken ortak olasılık fonksiyonu
FS
S d t f t dt
2 2 2 2 , 0, 0 t t t e t (4.16)olur ve güvenilirlik fonksiyonu ise
,
, S X Y t t R t f x y dydx
2 2 , 0 t t e t (4.17)dir. Burada yukarıda elde edilen fS
t ve F t fonksiyonlarının çeĢitli parametre S
değerleri için grafikleri sırasıyla ġekil 4.1 ve ġekil 4.2’de verilmiĢtir.0 0.5 1 1.5 2 0 1 2 3 4 =0.3 f S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 1 2 3 4 =0.5 f S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 1 2 3 4 =0.7 f S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 1 2 3 4 =0.9 f S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5
ġekil 4.1. Gumbel-Barnett Kopulada üstel dağılımın parametre değerlerinin değiĢimine ait seri sistemin
olasılık yoğunluk fonksiyonu değiĢimi
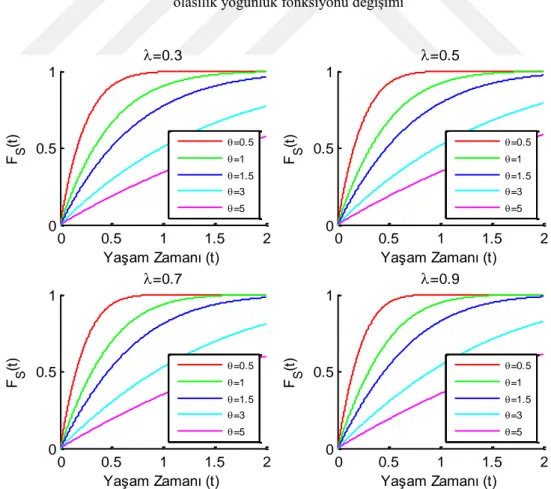
0 0.5 1 1.5 2 0 0.5 1 =0.3 F S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 0.5 1 =0.5 F S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 0.5 1 =0.7 F S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 0.5 1 =0.9 F S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5
ġekil 4.2. Gumbel-Barnett Kopulada üstel dağılımın parametre değerlerinin değiĢimine ait seri sistemin
T rasgele değiĢkeninin hazard (bozulma oranı) fonksiyonu
S S S dR t dt h t R t 2
t2
,t 0 (4.18)Ģeklinde iken ortalama kalan ömür fonksiyonu
t S
S S R t dt MRL t R t
2 2 1 1 2 t t erf e (4.19) ve ortalama ömür fonksiyonu
0 S S E T tf t dt
1 1 1 1 2 erf e (4.20) Ģeklindedir. Burada
2 0 2 x t erf x e dt
(4.21) Ģeklinde tanımlanır.Burada h t ve S
MRL t fonksiyonlarının çeĢitli parametre değerleri için S
grafikleri sırasıyla ġekil 4.3 ve ġekil 4.4’de verilmiĢtir.0 0.5 1 1.5 2 0 5 10 =0.3 h S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 5 10 15 =0.5 h S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 5 10 15 20 =0.7 h S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 5 10 15 20 =0.9 h S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5
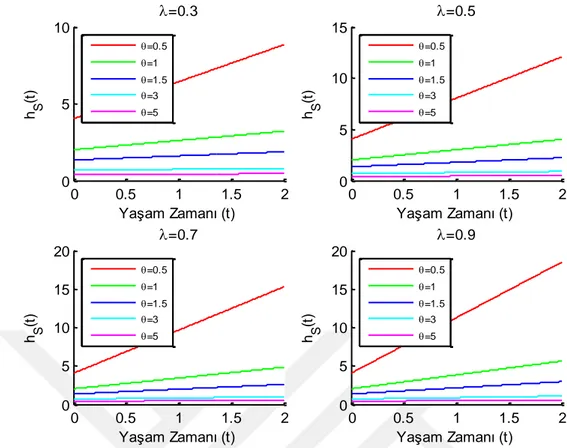
ġekil 4.3. Gumbel-Barnett Kopulada üstel dağılımın parametre değerlerinin değiĢimine ait seri sistemin
hazard fonksiyonunun değiĢimi
0 0.5 1 1.5 2 0 1 2 3 =0.3 M R L S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 1 2 3 =0.5 M R L S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 1 2 3 =0.7 M R L S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 0.5 1 1.5 2 =0.9 M R L S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5
ġekil 4.4. Gumbel-Barnett Kopulada üstel dağılımın parametre değerlerinin değiĢimine ait seri sistemin
4.1.2. Paralel sistemler
Paralel sistemi oluĢturan X ve Y bileĢenlerinin bağımlı, aynı dağılımlı ve her birinin Üstel
olduğu ve bu bağımlılığın Gumbel-Barnett kopula olduğu düĢünülsün. Bu durumda sistemin yaĢam zamanı T max
X Y,
olursa bu T rasgele değiĢkeninin dağılım fonksiyonu
,
0 0 , t t P X Y F t
f x y dydx 2 2 2 2 2 1 2 , 0 t t t t t t e e e t (4.22)iken olasılık yoğunluk fonksiyonu
FP
P d t f t dt 2 2 2 2 2 , 0, 0 t t t t e t e t (4.23)olur ve güvenilirlik fonksiyonu ise
1
P P R t F t 2 2 2 2 1 , 0 t t t t e e t (4.24)dir. Burada fP
t ve F t fonksiyonlarının çeĢitli parametre değerleri için grafikleri P
sırasıyla ġekil 4.5 ve ġekil 4.6’da verilmiĢtir.0 0.5 1 1.5 2 0 0.2 0.4 0.6 0.8 1 =0.3 f P (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 0.2 0.4 0.6 0.8 1 =0.5 f P (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 0.5 1 1.5 =0.7 f P (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 0.5 1 1.5 =0.9 f P (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5
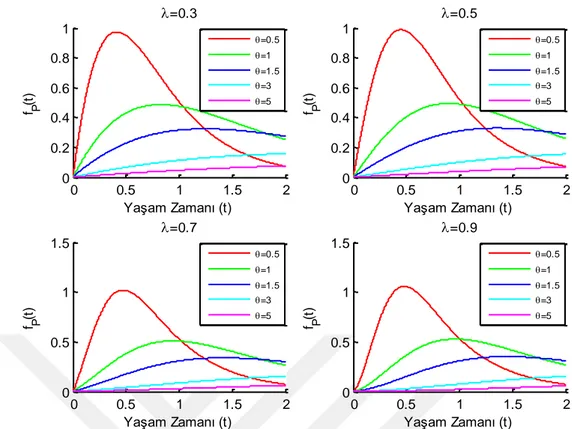
ġekil 4.5. Gumbel-Barnett Kopulada üstel dağılımın parametre değerlerinin değiĢimine ait paralel
sistemin olasılık yoğunluk fonksiyonunun değiĢimi
0 0.5 1 1.5 2 0 0.5 1 =0.3 F P (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 0.5 1 =0.5 F P (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 0.5 1 =0.7 F P (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 0.5 1 =0.9 F P (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5
ġekil 4.6. Gumbel-Barnett Kopulada üstel dağılımın parametre değerlerinin değiĢimine ait paralel
T rasgele değiĢkeninin hazard (bozulma oranı) fonksiyonu
P P P dR t dt h t R t 2 2 2 2 , 0 2 1 t t t t e t t e (4.25)Ģeklinde iken ortalama kalan ömür fonksiyonu
t P
P P R t dt MRL t R t
2 2 4 1 2 2 t t t t t t t erf e e e e e (4.26) ve ortalama ömür fonksiyonu
0 P P E T tf t dt
1 1 1 4 1 2 e erf e (4.27)Ģeklindedir. Burada hP
t ve MRLP
t fonksiyonlarının çeĢitli parametre değerleri için0 0.5 1 1.5 2 0 0.5 1 1.5 2 =0.3 h P (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 0.5 1 1.5 2 =0.5 h P (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 0.5 1 1.5 2 =0.7 h P (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 0.5 1 1.5 2 =0.9 h P (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5
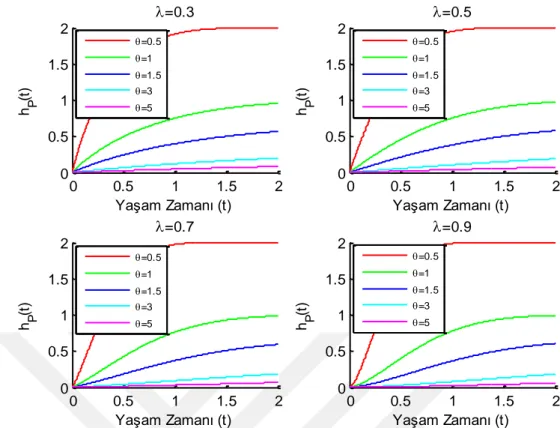
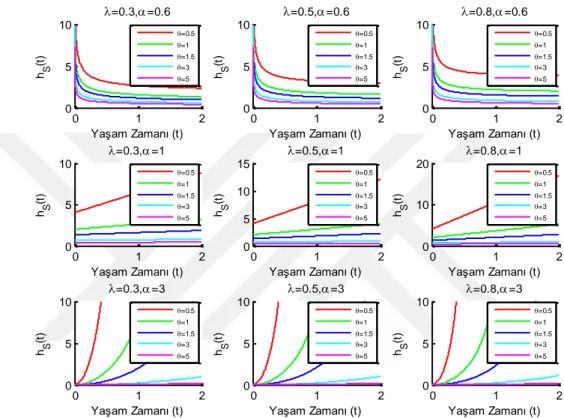
ġekil 4.7. Gumbel-Barnett Kopulada üstel dağılımın parametre değerlerinin değiĢimine ait paralel
sistemin hazard fonksiyonunun değiĢimi
0 0.5 1 1.5 2 0 5 10 =0.3 M R L P (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 5 10 =0.5 M R L P (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 5 10 =0.7 M R L P (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 5 10 =0.9 M R L P (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5
ġekil 4.8. Gumbel-Barnett Kopulada üstel dağılımın parametre değerlerinin değiĢimine ait paralel
4.2. Weibull BileĢenli Sistemlerin Güvenilirliği
Gumbel-Barnett kopulada yer alan u , X rasgele değiĢkeninin dağılım fonksiyonu; v , Y rasgele değiĢkeninin dağılım fonksiyonu olarak alındığını daha önce belirtmiĢtik.
X rasgele değiĢkeninin marjinal yoğunluk fonksiyonu
1 1 1 1 1 1 1 1 1 , 0, 0, 0 x X x e f x x (4.28) ve dağılım fonksiyonu
1 1 1 , 0 x X u F x e x (4.29)Ģeklinde, benzer Ģekilde Y rasgele değiĢkeninin marjinal yoğunluk fonksiyonu
2 2 2 2 1 2 2 2 2 , 0, 0, 0 y Y y e f y y (4.30) ve dağılım fonksiyonu
2 2 1 , 0 y Y v F y e y (4.31) Ģeklinde alınsın.Sistemi oluĢturan iki bileĢenin yaĢam zamanları X ve Y'nin Gumbel-Barnett kopula bağımlılık yapısına sahip olması durumunda seri ve paralel sistemlerin güvenilirliğine geçmeden önce bileĢenlerin yaĢam zamanları X ve Y rasgele değiĢkenlerinin ortak dağılımına iliĢkin bazı sonuçlara yer verilecektir. Gumbel-Barnett kopula altında
X Y rasgele vektörünün ortak dağılım fonksiyonu ,
1 2 1 2 1 2 1 2 1 2 1 2 , , 1 , 0, 0 x y x y x y X Y F x y e e e x y (4.32)Ģeklinde bulunurken ortak olasılık yoğunluk fonksiyonu
1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 1 2 1 1 , 1 2 2 1 2 1 2 , 1 x y x y X Y x y x y f x y e 1 2 1 2 1 2 1 2 1 2 1 2 2 1 2 1 1 2 1 2 2 2 2 1 2 1 2 , 0, 0, 0, 0, 0, 0 x y x y x y (4.33)
1 2 1 2 1 2 1 2 , , , 0, 0 x y x y X Y R x y e x y (4.34)Ģeklinde elde edilmektedir. Fakat burada X ve Y rasgele değiĢkenleri yer değiĢtirilebilir değildir. Bu rasgele değiĢkenlerin yer değiĢtirilebilir olabilmesi için
1 2
ve 1 2 alınması gerekmektedir. Bundan sonraki iĢlemlerde
1 2
ve 1 2 kabul edilecektir. Bu durumda X rasgele değiĢkeninin marjinal olasılık yoğunluk fonksiyonu
1 , 0, 0, 0 x X x e f x x (4.35) dağılım fonksiyonu
1 , 0 x X F x e x (4.36)ve benzer Ģekilde Y rasgele değiĢkeninin marjinal yoğunluk fonksiyonu
1 , 0, 0, 0 y Y y e f y y (4.37) ve dağılım fonksiyonu
1 , 0 y Y F y e y (4.38) Ģeklinde olacaktır.Yer değiĢtirilebilir olan X ve Y değiĢkenlerine bağlı olarak elde edilen
X Y ,
vektörünün ortak dağılım fonksiyonu
, , 1 , 0, 0 x y x y x y X Y F x y e e e x y (4.39)iken ortak olasılık yoğunluk fonksiyonu
2 2 2 1 2 1
2 1 1 1 2 1
, , 4 3 X Y x y x y x y f x y
1 1 2 1 , 0, 0, 0, 0 x y x y x y e x y (4.40) ve güvenilirlik fonksiyonu
, , , 0, 0 x y x y X Y R x y e x y (4.41) Ģeklinde bulunur.4.2.1. Seri sistemler
Seri sistemi oluĢturan X ve Y bileĢenlerinin bağımlı, aynı dağılımlı ve her birinin Üstel
olduğu ve bu bağımlılığın Gumbel-Barnett kopula olduğu düĢünülsün. Bu durumda sistemin yaĢam zamanı T min
X Y,
rasgele değiĢkeninin dağılım fonksiyonu
1 ,
, S X Y t t F t f x y dydx
2 2 2 1 , 0 t t e t (4.42) Ģeklinde bulunurken
FS
S d t f t dt 2 2 2 2 1 1 2 2 , 0, 0, 0 t t t t e t (4.43)olur ve güvenilirlik fonksiyonu ise
,
, S X Y t t R t f x y dydx
2 2 2 , 0 t t e t (4.44)dır. Burada fS
t ve F t fonksiyonlarının çeĢitli parametre değerleri için grafikleri S
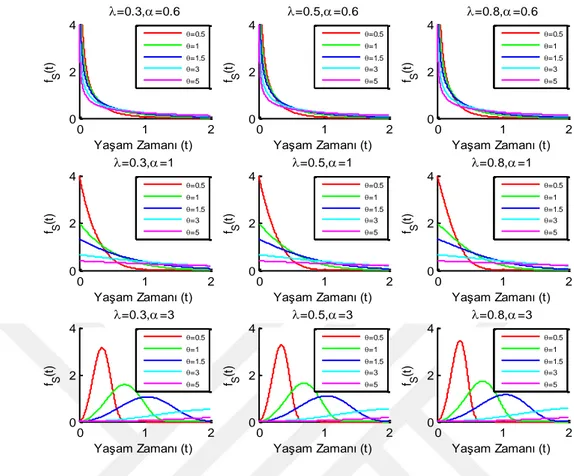
0 1 2 0 2 4 =0.3,=0.6 f S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 1 2 0 2 4 =0.5,=0.6 f S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 1 2 0 2 4 =0.8,=0.6 f S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 1 2 0 2 4 =0.3,=1 f S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 1 2 0 2 4 =0.5,=1 f S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 1 2 0 2 4 =0.8,=1 f S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 1 2 0 2 4 =0.3,=3 f S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 1 2 0 2 4 =0.5,=3 f S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 1 2 0 2 4 =0.8,=3 f S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5
ġekil 4.9. Gumbel-Barnett Kopulada weibull dağılımın parametre değerlerinin değiĢimine ait seri
sistemin olasılık yoğunluk fonksiyonunun değiĢimi
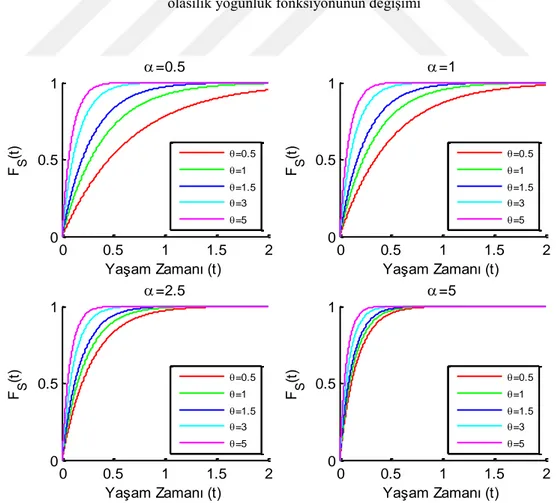
0 0.5 1 1.5 2 0 0.5 1 =0.3,=0.6 F S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 0.5 1 =0.8,=0.6 F S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 0.5 1 =0.3,=1 F S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5 0 0.5 1 1.5 2 0 0.5 1 =0.8,=1 F S (t ) Yaşam Zamanı (t) =0.5 =1 =1.5 =3 =5
ġekil 4.10. Gumbel-Barnett Kopulada weibull dağılımın parametre değerlerinin değiĢimine ait seri