Kararlılık üzerine Allee etkisi

(1)

T.C.

SELÇUK ÜNĠVERSĠTESĠ FEN BĠLĠMLERĠ ENSTĠTÜSÜ

KARARLILIK ÜZERĠNE ALLEE ETKĠSĠ

Öğrencinin Adı Soyadı Özlem AK GÜMÜġ

DOKTORA TEZĠ Matematik Anabilim Dalı

(2)

(3)

TEZ BĠLDĠRĠMĠ

Bu tezdeki bütün bilgilerin etik davranış ve akademik kurallar çerçevesinde elde edildiğini ve tez yazım kurallarına uygun olarak hazırlanan bu çalışmada bana ait olmayan her türlü ifade ve bilginin kaynağına eksiksiz atıf yapıldığını bildiririm.

DECLARATION PAGE

I hereby declare that all information in this document has been obtained and presented in accordance with academic rules and ethical conduct. I also declare that, as required by these rules and conduct, I have fully cited and referenced all material and results that are not original to this work.

Öğrencinin Adı SOYADI Özlem AK GÜMÜŞ Tarih: 29.09.2011

(4)

iv ÖZET DOKTORA TEZĠ

KARARLILIK ÜZERĠNE ALLEE ETKĠSĠ Öğrencinin Adı SOYADI

ÖZLEM AK GÜMÜġ

Selçuk Üniversitesi Fen Bilimleri Enstitüsü Matematik Anabilim Dalı

DanıĢman: YRD. DOÇ. DR. HASAN KÖSE 2011, 77 Sayfa

Jüri

Yrd. Doç. Dr. Hasan KÖSE Prof. Dr. Aşır GENÇ Prof. Dr. Durmuş BOZKURT Doç. Dr. Hüseyin YILDIRIM Doç. Dr. Galip OTURANÇ

Bu tezin konusunu genel olarak gecikmeli fark popülasyon modellerinin kararlılığı ve kararlılık üzerine Allee etkisi araştırması oluşturmuştur.

Öncelikle, bir boyutlu avcı etkisi içeren fark ve sürekli zaman popülasyon modelleri tanıtılmış, daha sonra gecikme ile fark popülasyon modelleri incelenmiştir. Bu modeller için ilgili kararlılık teoremlerine, sonuçlara ve nümerik similasyonlara yer verilmiştir. Bu doğrultuda ele aldığımız farklı modellerin kararlılığı araştırılmış ve Allee etkisinin popülasyon üzerindeki etkisine bağlı olarak kararlılık kriterleri yeniden elde edilmiştir. Ayrıca, kararlılık karşılaştırması yapılmıştır. İlk incelenen model için denge noktası değerlerinin daha net görülmesini sağlayan tabloya yer verilmiştir. Her bir ele alınan modelin zamana bağlı olarak popülasyon yoğunluğu değişimi, gerekli bilgilerin ardından grafiklerle verilmiş, hem Allee etkisi ile hem de Allee etkisiz olan modeller arasında kararlılık karşılaştırılması grafik ile gözlemlenmiştir.

(5)

v ABSTRACT

Ph.D THESIS

ALLEE EFFECT ON THE STABĠLĠTY

Özlem AK GÜMÜġ

THE GRADUATE SCHOOL OF NATURAL AND APPLIED SCIENCE OF SELÇUK UNIVERSITY

MATHEMATICS

Advisor: Asst. Prof. Dr.HASAN KÖSE 2011, 77 Pages

Jury

Asst. Prof. Dr. Hasan KOSE Prof. Dr. Durmuş BOZKURT

Prof. Dr. Aşır GENÇ

Assoc. Prof. Dr. Hüseyin YILDIRIM Assoc. Prof. Dr. Galip OTURANÇ

The subject of this thesis is the investigation of the stability of generally delayed difference population models and the impact of Allee effect on stability.

First of all, discrete and continuous time population models with one-dimension predator effect were described, later delay discrete population models were examined. Stability theorems related with these models, results and numeric simulations were also given. The stability of different models which we discussed in line with this was investigated and new stability criteria were established depending on the impact of Allee effect on population. Besides, stability comparison was made. For the first model examined, a table which provides more clear visibility of equilibrium point values. After some necessary information is provided, for each model dealt with the change in population in time was given via graphics and stability comparisons between the models both with Allee and without Alleee effect were observed with graphics.

(6)

vi ÖNSÖZ

Bu çalışma Selçuk Üniversitesi Fen Fakültesi Matematik Bölümü Öğretim Üyesi Yrd. Doç. Dr. Hasan KÖSE yönetiminde yapılarak Selçuk Üniversitesi Fen Bilimleri Enstitüsüne Doktora tezi olarak sunulmuştur.

Bu süre içinde çalışmamı destekleyen sevgili aileme ve saygıdeğer hocalarım Yrd. Doç. Dr. Hasan KÖSE’ye, Doç. Dr. Hüseyin MERDAN’a, Prof. Dr. Saber ELAYDİ’ye ve Yrd. Doç. Dr. Halife KODAZ’a en içten teşekkür ve saygılarımı sunarım.

Özlem AK GÜMÜŞ KONYA-2011

(7)

vii ĠÇĠNDEKĠLER ÖZET ... iv ABSTRACT ... v ÖNSÖZ ... vi ĠÇĠNDEKĠLER ... vii 1. GĠRĠġ ... 1 2. KAYNAK ARAġTIRMASI ... 2 3. TEORĠK ESASLAR ... 4

4. ARAġTIRMA SONUÇLARI VE TARTIġMA ... 10

4.1. Birinci Mertebeden Fark Popülasyon Modelinin Kararlılığı ... 10

4.2. Avcı Faktörü İçeren Genel Fark-Zamanlı Popülasyon Modelinin Kararlılık Analizi ve Allee etkisi ... 13

4.2.1. (4.13) modelinin kararlılık analizi ... 13

4.2.2. (4.13) modeli üzerine Allee etkisi ... 14

4.2.3. Nümerik similasyon ... 16

4.3. Avcı Sayısına Bağlı Sürekli Popülasyon Modelinin Kararlılık Analizi ve Allee Etkisi ... 18

4.3.1 (4.24) modelinin kararlılık analizi ... 18

4.3.2. Nümerik similasyon ... 19

4.4. Gecikmeli Popülasyon Dinamiklerinin Kararlılığı Üzerine Allee Etkisi ... 20

4.4.1 T=1 için (4.28) modelinin kararlılık analizi... 21

4.4.2. (4.29) gecikmeli fark modeli üzerine Allee etkisi ... 21

5. OLUġTURULAN FARK POPÜLASYON MODELLERĠ VE KARARLILIK . 24 5.1. Avcı Sayısının Değişimine Bağlı Olarak Fark Popülasyon Modelinin Kararlılığı ve Allee Etkisi ... 24

5.1.1. N₀ 0.4 ve belirli bir değerine göre popülasyon hareketi ... 24

5.1.2. Artan değerine göre popülasyon hareketi ... 26

5.1.3. Belirli değeri ve artan Allee sabitine göre popülasyon hareketi ... 27

5.1.4. Grafik yardımıyla karşılaştırma ... 29

5.2. Avcı Sayısı Değişimine Bağlı Olarak Sürekli Popülasyon Modelinin Kararlılığı ve Allee Etkisi ... 33

5.2.1. (5.4) ve (5.5) modelleri için ve sabitlere göre popülasyon hareketi ... 33

5.2.2 . Modellerin karşılaştırılması ... 35

5.3. Gecikmeli Popülasyon Modelinin Kararlılığı ve Allee Etkisi ... 36

5.3.2. (5.6) modeli üzerine Allee etkisi ... 40

5.4. İki Değişkenli Fonksiyon İçeren 2. Dereceden Gecikmeli Popülasyon Modelinin Kararlılık Analizi ve Allee Etkisi ... 53

(8)

viii

5.5. İki Değişkenli Fonksiyon İçeren 3. Dereceden Gecikmeli Popülasyon Modelinin Kararlılık Analizi ve Allee Etkisi ... 62

6. SONUÇLAR VE ÖNERĠLER ... 75

6.1. Sonuçlar ... 75

6.2. Öneriler ... 76

KAYNAKLAR ... 77

(9)

ix SĠMGELER

t

N : t zamandaki popülasyon yoğunluğu )

(N_t

f : popülasyon üyeleri arasındaki ilişki

K : popülasyonun bulunduğu ortamın taşıma kapasitesi

*

N : popülasyonun denge noktası

*

: normalize edilmiş büyüme oranı

0

N : popülayondaki başlangıç noktası T : organizmanın yeniden üreme zamanı

J : Jacobian matris

: popülasyondaki birim kare başına düşen büyüme oranı )

,

( ba : açık aralık )

,

[ ba : yarı açık aralık

N f

f : f fonksiyonunun türevi )

(N : t zamanda Allee fonksiyonu _t

(N : t zamanda Allee fonksiyonunun türevi _t) )

(N*

f :N noktasında f fonksiyonunun mutlak değeri *

A : A matrisinin determinantı log f : f fonksiyonunun logaritması

) (

lim_N _a f N : f fonksiyonunun a noktasındaki limiti )

(

(10)

1. GĠRĠġ

Dünyadaki yaşam bir denge içerisinde ilerler. Bu sebeple herhangi bir canlı grubundaki sayısal değişim, diğer canlı gruplarını etkiler. O halde, birbirine bağlı olan bu ekosistemde, hiçbir popülasyon tamamen yok olmamalıdır. Bu durumu kontrol altında tutmak, popülasyonun yaşamı hakkında bilgi sahibi olmaya bağlıdır. Genel itibariyle bu o kadar kolay değildir. Yine de gerçeğe yakın yaklaşımlar oluşturulabilir mi? sorusu akla gelir. Bu ve buna benzer yaklaşımlar bize matematiksel modellemenin önemini vurgular. Bir popülasyon yaşamının modellenmesi, o popülasyonun dinamikliği hakkında bize bilgi verir. Bu model sayesinde bir veya daha fazla faktörün popülasyona etkisi matematiksel yolla incelenebilir. Burada bahsedilen matematiksel modeller diferansiyel ve fark modelleri ile verilir. Biyolojik varsayımlardan elde edilen, popülasyonu etkileyen faktörler ise Allee etkisi olarak tanımlanır. Örneğin, eş bulmadaki zorluk, küçük popülasyon büyüklüğündeki sosyal bozukluk, çiftleşme depresyonu, yiyecek sömürüsü ve avcıdan savunma durumu gibi faktörler bu etkiye sebep olabilir. Biyolojik olayların matematiksel olarak değerlendirilmesi, kararlılık incelemesini gerektirir. Düşük yoğunlukta popülasyonun yok olması genelde beklenen bir durumdur. Bunun haricinde, popülasyon kararlı, kararsız ya da kaos durumunda bulunur. Allee etkisi, kararlılığı olumlu ya da olumsuz yönde etkileyebilir. Bu sonuçlar, üzerinde çalışılan konu için önem arz eder.

Bu çalışmada amacımız, çalışılan modellerden farklı olarak bir model sunmak ve kararlılığın Allee etkisiyle değişimini incelemektir. Öncelikle bir boyutlu fark ve sürekli popülasyon modellerinin kararlılığı incelenmiş ve kararlılık üzerindeki Allee etkisi araştırılmıştır. Bu yaklaşımla, popülasyonun gelişimini kontrol eden yeni fark modelleri oluşturulmuştur. Esas olarak bir boyutlu gecikmeli fark denklemler üzerine yoğunlaşılmıştır. Parametre değişimlerinin, modelin kararlılığı üzerindeki etkileri de incelenmiştir. Allee etkili ve Allee etkisiz modelin kararlılık şartları elde edilmiş ve kararlılıkları karşılaştırılmıştır. Kararlılık davranışları grafik çizimleri ile görsel olarak da doğrulanmıştır. Böylece incelenen modelin düşük yoğunluk altında, denge noktası civarındaki popülasyonun hareketi de gözlemlenmiştir. Bu uygulamalar gelecekte popülasyon durumunu daha net görmemize olanak sağlar. Bu durum, popülasyon hakkında bize bilgi vermesinin yanı sıra dengenin korunması açısından da önem arz etmektedir.

Genel itibariyle bu çalışma, popülasyon dinamikleri ile ilgili çalışmalara destek vermek amacıyla hazırlanmıştır.

(11)

2. KAYNAK ARAġTIRMASI

Ludwing ve ark. (1978) de, spruce budworm (böcek türü) ve balsam fir (bitki türü) modelini tanımlayan sistemin kaliteli analizi için bir prosedür tanımlamışlardır. Bu hızlı ve yavaş katagorilerde durum değişimini ayıran bir oluşumdur. İlk olarak hızlı değişken dinamikler ve sonra yavaş değişken dinamiklerin uzun dönem davranışlarını analiz ettiler.

Scheuring (1999) çalışmasında, bir popülasyondaki fark denkleminin dinamikliğini sunan N_t ₁ N_tf(N_t) bir boyutlu fark denkleminin kararlılığını araştırmıştır. Fark denklemini Allee etkisi ile birlikte ele alarak, Allee etkisinin kararlılığı artırdığı sonucuna ulaşmıştır. Ayrıca, artan parametresi ile denklemin kararlılığının azaldığını göstermiştir.

Cunningham ve ark. (2001) de, pozitif başlangıç şartları ve negatif olmayan parametreler ile, ikinci dereceden lineer olmayan fark denklemlerini ele almışlardır. Lineerleştirilmiş kararlılık teoremini kullanarak fark denklemlerin kararlılık sınırını vermişlerdir.

Fowler ve Ruxton (2001) de, , a, b pozitif sabitler ve _b

t t aN N f ) 1 ( ) (

olmak üzere N_t ₁ N_tf(N_t) fark denkleminin denge noktasının kararlılığını araştırmışlardır. Ele alınan fonksiyonda ; maksimum yeniden üreme potansiyeli, a; habitatın taşıma kapasitesine bağlı popülasyon büyüklüğü oranı, b; rekabetin kuvvetini tanımlayan parametredir. arttığında buna bağlı olarak b değeri de artar. Bu durum popülasyonda artan periyodik döngüler öncülüğünde kaosa sebep olmuştur. Bu sebeple f fonksiyonu Allee faktörü ile modifiye edilerek popülasyon artımı düşürülmüştür. Böylece, Allee etkisinin modelin kararlılığını artırdığını göstermişlerdir.

Çelik ve ark. (2006) da, N_t ₁ N_t f(N_t ₁) düşük popülasyon yoğunluğunda gecikmeli fark popülasyon modelinin kararlılık incelemesini yapmışlardır. Modele farklı zamanlardaki Allee faktörünün eklenmesi ile kararlılık şartlarını araştırmışlardır.

Merdan ve Duman (2007) de, N_t ₁ N_t N_t f(N_t) N_tg(N_t) düşük popülasyon yoğunluğunda avcı etkisi içeren genel fark popülasyon modelinin kararlılığı üzerinde çalışmışlardır. Allee etkisi ve Allee etkisiz denge noktasının lokal kararlılık şartlarını vermişlerdir. Allee faktörünün denge noktasının kararlılığını artırdığı sonucuna ulaşmışlardır.

(12)

Duman ve Merdan (2009) da, t _t ( _t) _t ( _t) N g N N f N dt dN düşük popülasyon yoğunluğunda avcı etkisi içeren, sürekli zaman dinamik popülasyon modelinin kararlılık analizi üzerinde durmuşlardır. Allee etkisinin kararlılığı geciktirdiği sonucuna ulaşmışlardır.

(13)

3. TEORĠK ESASLAR

Popülasyon dinamikleri; insanlar, hayvanlar ve bitkiler gibi canlı organizmaların bilimsel çalışmasını içeren bir alandır. Bu alan, zamana bağlı olarak popülasyonun yaş ve büyüklüğündeki değişim çalışmalarını kapsar. Biyolojik ve çevresel değişimler popülasyonu etkiler. Örneğin, ölüm oranları, göç olayı gibi faktörler popülasyonu etkileyen önemli çevresel unsurlardır. Ayrıca tezimizde önemli bir yere sahip olan Allee etkisi ise popülasyonu etkileyen bir biyolojik faktördür.

Popülasyon modelleri ise popülasyon dinamiklerini incelemek için oluşturulan matematiksel modellerdir. Bu sayede popülasyonu etkileyen faktörlerin ne olduğu ve ne oranda popülasyona etki ettiği daha net olarak araştırılabilir. O halde, çalışmanın daha iyi anlaşılması açısından gerekli tanım ve bilgileri verelim.

Tanım 3.1. Düşük yoğunlukta, popülasyonun büyüme oranı çok küçük olduğunda ortaya çıkan olay Allee etkisi olarak adlandırılır (Allee, 1931).

Allee faktörü ilk olarak 1931’de Warder Clyde Allee tarafından tanıtıldı. Allee etkisi, nüfus yoğunluğu ve birim kare başına büyüme oranı arasındaki bağıntı ile ifade edilen biyolojide bir olaydır. Bu etki bitkilerde, omurgalı ve omurgasız olan farklı organizmalar üzerinde gözlemlenir. Allee etkisi, düşük nüfus yoğunluğunda popülasyonu daha çok etkilerken, bu etki türlerin çoğalma potansiyelinin giderek artmasıyla kaybolur. Böylece popülasyon, çevrenin organizmayı destekleme kapasitesine kadar artmaya devam edecektir. Su, yiyecek ve canlının yaşadığı doğal ortam bu artmayı sınırlandıracaktır. Bu faktörler, farklı canlı türlerinde farklı etkilere sahiptir. İşte ekolojik popülasyon modelleri, fiziksel çevre etkisiyle organizmaların kendi türüyle ya da diğer türlerle etkileşiminin formülasyonudur. Burada canlının yaşadığı doğal ortam, bu ortamdaki organizmanın davranışı, sistemin değişimine sebep olabilir.

Bu çalışmada bir boyutlu lineer olmayan fark ve diferansiyel denklemlerin kararlılığını araştırdığımızdan bunun için gerekli kavramları verelim.

Tanım 3.2. a_i,i 1,2,...,n katsayılar, g(t); t’nin bir fonksiyonu ya da sabit ve x x(t) (t=zaman) olmak üzere,

) ( ) ( ) ( ... ) ( ₁ ₁ 1 1 a t x g t dt dx t a dt x d t a dt x d n n n n n n (3.1)

denklemine n mertebeli lineer diferansiyel denklem denir. Öte yandan g(t), x fonksiyonu veya x fonksiyonunun herhangi bir türevine bağlı ise (3.1) denklemi lineer

(14)

olmayan diferansiyel denklem olarak adlandırılır. (3.1) denklemi lineer ve g(t) 0 ise (3.1) denklemine homojen diferansiyel denklem denir. Bu denklem

0 ) , / ,..., / , / , (xdx dt d2x dt2 d x dt t

f n n şeklinde yazılabilir. Bu diferansiyel denklem

eğer t değerine bağlı değilse otonom diferansiyel denklem, t değerine bağlı ise otonom olmayan diferansiyel denklem olarak ifade edilir (Allen, 2007).

Tanım 3.3. x x(t) (t=zaman) ve j 1,2,...,k için a durum değişkenlerinden farklı _j olarak sabit veya t değerine bağlı olmak üzere

t t k t k k t k t ax a x a x b x ₁ ₁ ... ₁ ₁ , t 0,1,... (3.2) denklemine k mertebeli lineer fark denklemi denir. Aksi halde lineer olmayan fark denklemi olarak adlandırılır. (3.2) denklemi lineer ve tüm t'ler için b_t 0 ise o zaman denklem homojendir. f fonksiyonu, t ve x_t _k boyunca, x reel değişkenlerine bağlı reel _t değerli bir fonksiyon olmak üzere k mertebeli lineer fark denklemi

0 ) , , ..., , (x x ₁ x ₁ x t f _t _k _t _k _t _t , t 0,1,... (3.3) şeklinde verilebilir (Allen, 2007).

Tanım 3.4. Birinci mertebeden x_t ₁ f(x_t) fark denkleminde x f(x) sağlayan x sabit çözümüne denge noktası adı verilir. Benzer şekilde, dx/dt f(x_t) diferansiyel denkleminde dx/dt f(x) olacak şekilde x çözümü, birinci mertebeden diferansiyel denklemin denge noktası’dır (Allen, 2007).

Teorem 3.1. x_t ₁ f(x_t) denkleminin bir denge noktası x ve x ’yi içeren açık bir I aralığında f sürekli fonksiyon olsun. Eğer,

1 ) (x

f (3.4) ise x denge noktası lokal asimtotik kararlıdır. f (x) 1 ise x kararsızdır denir (Allen, 2007).

Teorem 3.2. dx/dt f(x_t) denkleminin bir denge noktası x ve x ’yi içeren açık bir I aralığında f sürekli fonksiyon olsun. Eğer,

0 ) (x

f (3.5) ise x denge noktası lokal asimtotik kararlıdır. f (x) 0 ise x kararsızdır denir (Allen, 2007).

(15)

Teorem 3.3. (Ortalama Değer Teoremi) f ; (a,b) açık aralığında türevi alınabilir ve [a,b] aralığında sürekli bir fonksiyon olsun. O zaman en azından bir c ( ba, ) sayısı vardır ki a b a f b f c f ( ) ( ) ( )

dır (Berkey and Blanchard, 1992).

Tanım 3.5. [a,b] aralığında tüm x1, x2 değerleri için x1 x2 olduğunda f(x1) f(x2)

ise f fonksiyonuna [a,b] aralığında artan fonksiyondur denir. a x₂ x₁ b sayıları için f(x₁) f(x₂) ise f , [a,b] aralığında azalan fonksiyondur denir (Thomas and Finney, 1952).

Tanım 3.6. T , organizmanın yeniden üreme zamanı olmak üzere, ), , ( 1 t t T t f x x x (3.6) fark denklemine gecikmeli fark denklemi denir (Allen, 2007).

Teorem 3.4. (Linerleştirilmiş Kararlılık) I, reel sayıların bir aralığı, x I ve I I I f : olmak üzere, ), , ( ₁ 1 n n n f x x x n 0,1,... (3.7) fark denklemini göz önüne alalım. x denge noktasında değerlendirilen f( vu, )’nin kısmi türevlerini, ) , (x x u f p ve (x,x) v f q

olarak tanımlayalım. O zaman, ,

1

1 n n

n py qy

y n 0,1,...

denklemi x denge noktası civarında (3.7)’nin lineerleştirilmiş denklemi olarak adlandırılır.

(a) 2 p q 0 (3.8) denkleminin kökleri 1 olacak şekilde açık birim disk içinde ise (3.7) denkleminin

x denge noktası lokal asimtotik kararlıdır.

(b) (3.8) denkleminin köklerinden en az birinin mutlak değeri 1’den büyükse, o zaman (3.7) denkleminin x denge noktası kararsızdır.

(c) (3.8) denkleminin her iki kökünün 1 olacak şekilde açık birim disk içinde olması için gerek ve yeter şart

(16)

2 1 q

p (3.9) olmasıdır (Cunningham ve ark., 2001).

Tanım 3.6. a ; reel sayılar olmak üzere, (3.3) denklemini gözönüne alalım. (3.3)’den _i elde edilen

0 )

( k a₁ k 1 a_k

p  (3.10) denklemine karakteristik denklem denir. , karakteristik denklemin kökleri veya sıfırlarıdır. (3.10) denklemi, A (a_ij) olmak üzere k boyutlu matrisinden de elde edilebilir. Bunun için A I 0 olmalıdır. O halde, (3.3) denkleminin asimtotik kararlı olması için gerek ve yeter şart | | 1 olmasıdır (Elaydi, 2006).

Teorem 3.5. (Schur-Cohn Kriteri) (3.10) ile verilen p( ) polinomunun sıfırlarının birim çember içine düşmesi için gerek ve yeter şart

(i) p(1) 0, (ii) ( 1)kp( 1) 0, (iii) (k 1) (k 1) matrisinin 2 3 1 3 4 1 1 3 2 3 1 1 0 0 0 0 0 0 1 0 1 0 1 0 0 1 a a a a a a a a a a a a a a a B k k k k k k k k k k              

pozitif iç matrislere sahip olmasıdır (Elaydi, 2006). )

(b_ij

B matrisinin iç matrisleri, matrisin kendisi ile birlikte, bu matrisin birinci ve son satırı ile birinci ve son sütununun aynı anda çıkarılmasıyla, elde edilen tüm matrislerdir. Eğer B matrisinin, iç martislerinin tümünün determinantı pozitif ise B matrisi pozitif iç matrislere sahiptir denir. Örneğin, aşağıda verilen farklı mertebeden A matrislerini ele alalım.

3 3

B matris B₄ ₄ matris B₅ ₅ matris

55 54 53 52 51 45 44 43 42 41 35 34 33 32 31 25 24 23 22 21 15 14 13 12 11 44 43 42 41 34 33 32 31 24 23 22 21 14 13 12 11 33 32 31 23 22 21 13 12 11 , , b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b

(17)

3 3

B matrisinin determinantı pozitif ve b₂₂ 0 B₃₃ matrisi pozitif içlere sahip bir matris, B₄ ₄ matrisinin determinantı pozitif ve 0

33 32 23 22 b b b b 4 4 B matrisi pozitif içlere sahip bir matris ve son olarak; B₅ ₅ matrisinin determinantı pozitif,

0 0 44 43 42 34 33 32 24 23 22 b b b b b b b b b

ve b₃₃ 0 B₅₅ matrisi pozitif içlere sahip bir matrisdir denir.

(3.10)’da verilen denklemde k 3 için, . ) ( 2 3 2 1 3 a a a p (3.11)

elde edilen denklemin asimtotik kararlı olması için gerek ve yeter şart, |a₁ a₃| 1 a₂ ve | a2 a1a3| 1 a32 olmasıdır (Elaydi, 2006).

O halde, lineer olmayan yüksek mertebeli polinomlar (3.10)’da verilen k. mertebeden lineer polinomlara dönüşüm yoluyla indirgenebilir. Bu durum sistemler için de geçerlidir.

Tanım 3.7. i 1,2,...,k olmak üzere, ) ), ( ),..., ( ), ( ( ) 1 (t f x₁ t x₂ t x t t x_i _i _k (3.12) sistemine birinci mertebeden k boyutlu fark sistemi denir (Allen, 2007).

Tanım 3.8. f ve g sürekli fonksiyonlar olmak üzere,

) , ( ) , ( 1 1 t t t t t t y x g y y x f x (3.13) sistemine iki boyutlu birinci mertebeden fark sistemi denir. (3.13) sisteminin lineerleştirilmişi

t

t JX

X ₁ (3.14) olmak üzere, (3.14)’ de verilen

x y x g x y x g y y x f x y x f J / ) , ( / ) , ( / ) , ( / ) , ( matrisine Jacobian matrisi adı verilir (Allen, 2007).

Tanım 3.9. f fonksiyonu, x a noktasında türev değerleri mevcut olan bir fonksiyon olmak üzere, ... ) ( ! 3 ) ( ) ( ! 2 ) ( ) )( ( ) ( ) ( ! ) ( 2 3 ) ( 0 a x a f a x a f a x a f a f a x k a f k k k (3.15) serisine f fonksiyonunun Taylor seri açılımı ve

(18)

... ! 3 ) ( ! 2 ) 0 ( ) 0 ( ) 0 ( ) 0 ( ! ) 0 ( ₂ ₃ ) ( 0 x a f x f x f f x k f k _k k

(19)

4. ARAġTIRMA SONUÇLARI VE TARTIġMA

Bu bölümde daha önce çalışılmış olan fark popülasyon modellerinin kararlılık durumu ve bu kararlılık durumuna Allee faktörünün etkisini inceleyeceğiz.

4.1. Birinci Mertebeden Fark Popülasyon Modelinin Kararlılığı

Scheuring, 1999 da ki çalışmasında, Allee etkisinin kararlılığı artırdığını göstermiştir. Yine (Fowler and Ruxton, 2002) çalışması da aynı sonucu destekler niteliktedir. N ; t zamandaki yoğunluk, _t ; popülasyonun birim kare başına büyüme oranı, f N ; popülasyon üyeleri arasındaki ilişkiyi (etkileşim gücünü) tanımlayan ( _t) fonksiyon olmak üzere,

1 ( ) ( , )

t t t t

N N f N F N (4.1) bir popülasyonun dinamikliğini sunan fark denklemini göz önüne alalım.

Burada, f N fonksiyonu yoğunluk artarken sürekli bir şekilde azalan fonksiyondur. ( _t) Bu durum matematiksel olarak;

e1) N 0, , f N( ) 0. e2) 0 f(0)

şeklinde ifade edilebilir.

Bu modelde öncelikle; verilen parametresinin, popülasyonun kararlılığını nasıl etkilediğini görelim.

1 2 olduğu varsayımından, (4.1) denkleminin 1 ve 2 parametrelerine

karşılık gelen (1)

N ve N(2) denge noktaları

(1) (2)

1 2

1 f N( ) , 1 f N( ) (4.2) denklemlerinin çözülmesiyle elde edilir. (4.2)’den (1) (2)

( ) ( )

f N f N yazılabilir. f fonksiyonu kesin bir şekilde monoton azalan olmasından dolayı N(1) N(2) ifadesi açıktır. (4.1) denkleminin her iki tarafının türevi alınırsa,

( ) ( ) ( ) ( )

( ,i i ) i ( i ) i i ( i )

F N f N N f N (4.3) ifadesi elde edilir. Bu eşitlikten

( ) ( ) ( ) ( ) ( ) ( , ) 1 ( ) i i i i i f N F N N f N (4.4)

(20)

yazılabilir. (4.1) denkleminin lokal kararlı olması için yeter şart ( )

( ,_i i ) 1

F N

olmasıdır. Bu eşitsizlikten ve (4.4) ifadesinden,

( ) ( ) ( ) ( ) 2 0 ( ) i i i f N N f N bulunur. ( ) 0, i 0 f N ve (1) (2)

N N olduğu da göz önüne alınırsa,

(1) (2) (1) (2) (1) (2) ( ) ( ) ( ) ( ) f N f N N N f N f N (4.5) eşitsizliği elde edilir. Bu sonuçtan, artan değeri ile denge noktasının kararlılığının azaldığı görülür. Bazı hesaplamalar sonucunda (4.5) eşitsizliğinin

( 2 )

(1)

(log ) 0

N

N f dN şeklinde de gösterilebileceği açıktır. O halde şimdiye kadar olan bilgilerden hareketle, popülasyonun uzun süreli kararlılığı için kişi başına büyüme oranı küçük olmalıdır.

Diferansiyellenebilir ve sürekli olan ( )N ’in e3) N 0ise ( )N 0

e4) N (0, ) ise (N) 0 e5) lim_N ( ) 1N

şartlarını sağladığı varsayımıyla, (4.1) denklemine Allee faktörü eklenmesi ile,

1 ( ) ( ) ( , )

t t t t t

N N N f N F N (4.6)

denklemi elde edilir.

(4.1) ve (4.6) denklemlerinin sıfır olmayan denge noktaları sırasıyla,

*

1 f N( ) (4.7.a)

** **

1 (N ) (f N ) (4.7.b) olup (4.7.b) denklemi en çok 2 çözüme sahipken, (4.7.a) denklemi en çok 1 çözüme sahiptir. e3) ve e5)’den ( ) 1N olduğu sonucuna varırız. Sonuç olarak; ( )N olup Allee etkili popülasyon modelinin gerçek büyüme oranı, daima Allee etkisiz popülasyon modelindekinin büyüme oranından daha azdır. (4.6) denkleminde

* *

(N ) olacak şekilde, * seçelim. Böylece her iki modelde aynı N denge * noktasına eğilimlidir.

(4.1) ve (4.6) denklemlerinin kararlılıklarını karşılaştıralım. (4.1) ve (4.6) denklemleri denge noktasında, türevleri alınarak değerlendirildiğinde,

(21)

* * * * ( ) ( , ) 1 ( ) f N F N N f N (4.8.a) ) ( ) ( ) ( ) ( 1 ) , ( _* * * * * * * N f N f N N N N F (4.8.b) ifadelerine ulaşılır. Yukarıdaki türevlerin mutlak değerleri 1’den küçükse denge noktası lokal asimtotik kararlıdır. (i) varsayımından, 1 için *

( , ) 1

F N ve * *

( , ) 1

F N

olmalıdır. Sonuç olarak denge noktasının kararsız olabilmesi için gerek ve yeter şart

*

( , ) 1

F N ve F( *,N*) 1 olmasıdır. (4.6) denkleminin iki denge noktasına sahip olduğu varsayımını göz önüne alarak, N _cr f fonksiyonun maksimum noktası olsun. (0) 0 ve f(0) sonlu olduğu için N 0 iken ( ) ( )N f N 0 dır.

cr

N N ise e1) ve e4)’den ( ) ( )N f N 0 olduğu kolayca görülebilir. Buna denk bir şekilde, * * * * ( ) ( ) 0 , (0, ) ( ) ( ) cr N f N eğer N N N f N (4.9.a) * * * * ( ) ( ) 0 , , , ( ) ( ) cr N f N eğer N N N f N (4.9.b) dir. Küçük olan N denge noktası, (0,₁* N_cr) arasında ve büyük olan N denge noktası ₂* ise N_cr, arasındadır. (4.8.b) ve (4.9.a)’dan N ’ın daima kararsız olduğu görülebilir. ₁* (4.9.b) durumu ele alındığında, (4.8.a) ve (4.8.b) denklemleri için

* * *

( , ) ( , )

F N F N (4.10) yazılır. (4.10), (4.8.a) ve (4.8.b)’den,

* * * ( ) ( ) f N N f N * * * * * ( ) ( ) ( ) ( ) N f N N N f N (4.11)

eşitsizliği elde edilir. (4.11) sadeleştirilirse,

* * * * * ( ) 0 (log ( )) ( ) N N N N N (4.12) elde edilebilir. N denge noktasının pozitifliğinden biz son eşitsizliğin daima doğru *

olduğu sonucunu çıkarabiliriz. Sonuç olarak Allee etkisi bizim model sınıfımızda denge noktasının lokal asimtotik kararlılığını artırır. Allee etkili popülasyon daha kararlıdır.

(22)

4.2. Avcı Faktörü Ġçeren Genel Fark-Zamanlı Popülasyon Modelinin Kararlılık Analizi ve Allee etkisi

Merdan ve Duman (2007) yaptıkları çalışmada, g N avcı fonksiyonu içeren ( _t) bir popülasyon modeli çalışmışlardır. (f N ve (_t) g N fonksiyonlarının, _t)

(f1) (0)f 0, pozitif sınırlı bir sayıdır. (f2) N (0, ) için f N( ) 0

(f3) ( )f N en azından bir pozitif köke sahiptir. (g1) g(0)=0 ve N (0, ) için 0 g N( ) (g2) lim_N g N( ) 0

(g3) g N( _c) 0 , N_c (0, )’da tek bir kritik değere sahiptir.

özelliklerini sağladığını kabul edelim. ve N bilinen parametreler olmak üzere, _t

1 ( ) ( ) ( , )

t t t t t t t

N N N f N N g N F N (4.13) popülasyon modelini göz önüne alalım. Birinci mertebeden lineer olmayan fark

denklemi ile ifade edilen (4.13) modeli (4.1) denkleminden daha karmaşık bir davranış sergiler. Ayrıca (g N fonksiyonunun grafiği, _t)

ġekil 4.1. g(N_t) fonksiyonunun grafiği

şeklindedir. Şimdi (4.13) denkleminin kararlılığını inceleyelim. 4.2.1. (4.13) modelinin kararlılık analizi

Burada, (4.13) denkleminin pozitif denge noktasının lokal kararlılığı üzerine şartlar elde edilmiştir.

Teorem 4.2.1.1. (Merdan ve Duman, 2007) (4.13) denkleminin pozitif denge noktası

* N olsun. O zaman, 0 ) ( ) ( ) ( ) ( ) ( 2 * * * * * * N g N g N f N f N g

N eşitsizliği doğru ise denge

(23)

Ġspat: (Merdan ve Duman, 2007) (4.13) denkleminde *

N bir pozitif denge noktası

olduğundan, * *

( ) ( )

f N g N yazılır. (g1) şartı ve 0 olduğu için f N( *) 0 olduğu sonucuna ulaşırız. Buradan,

* * ( ) ( ) g N f N (4.14) eşitliği elde edilir. *

N denge noktasında (4.13) denkleminin her iki tarafının türevi alınırsa,

* * * * * * *

( , ) 1 ( ) ( ) ( ) ( )

F N f N N f N g N N g N (4.15) denklemine sahip oluruz. (4.14)’de verilen değeri (4.15)’de yerine yazılırsa,

* * * * * * * ( ) ( , ) 1 ( ) ( ) ( ) g N F N N f N N g N f N bulunur. *

N pozitif bir değer ve (g1) şatından N*g(N*) 0 olmak üzere, *

N denge noktasının kararlı olması için gerek ve yeter şart

* * * * * * ( ) 2 ( ) ( ) 0 ( ) f N N g N N g N f N

olmasıdır. Buradan da,

* * * * * * 2 ( ) ( ) 0 ( ) ( ) ( ) f N g N N g N f N g N

eşitsizliği yazılabilir ki bu istenen durumdur.

Sonuç 4.2.1.1. (Merdan ve Duman, 2007) (4.13) denkleminin *

N pozitif denge noktası için, *

c

N N , N* N ve _c N* N durumlarını göz önüne alalım. Bu koşullarda, _c

sırasyla *

N ’ın kararsız olması için gerek ve yeter şart

* * * * * * ( ) ( ) 2 ( ) ( ) ( ) f N g N f N g N N g N , * * * * ( ) 2 ( ) ( ) f N f N N g N ve * * * * * * ( ) ( ) 2 ( ) ( ) ( ) f N g N f N g N N g N ( yada * * * * ( ) ( ) ( ) ( ) f N g N f N g N ) olmasıdır.

Şimdi (4.13) denkleminin Allee etkisiyle kararlılığını araştıralım.

4.2.2. (4.13) modeli üzerine Allee etkisi

Bu bölümde Allee etkisi ile birlikte (4.13) modelinin lokal kararlılık şartlarını vereceğiz. _*

(N ) ile tanımlanan normalize edilmiş büyüme oranı

*

(24)

fonksiyonu ( ) ( )f₁ f , ₃ g N fonksiyonu ( _t) ( ) (g₁ g ve ₃) (N ; e3)-e5) şartlaını _t) sağlayan fonksiyonlar olmak üzere,

* *

1 ( ) ( ) ( ) ( , )

t t t t t t t t

N N N N f N N g N F N (4.16) Allee etkisi ile lineer olmayan popülasyon modelini ele elalım. Bu denklemde ( )N _t

fonksiyonu, t zamanda N popülasyon yoğunluğunda Allee etkisi olarak ifade edilir. _t Biyolojik olaylar (N fonksiyonuna ulaşmada bize kılavuzluk eder. _t)

Teorem 4.2.2.1. (Merdan ve Duman, 2007) (4.16) denkleminin N pozitif bir denge *

noktası olsun. O halde,

* * * * * * * * 2 ( ) ( ) ( ) 0 ( ) ( ) ( ) ( ) N f N g N N g N N f N g N ise * N lokal kararlıdır.

Ġspat: (Merdan ve Duman, 2007) (4.16) denkleminin denge noktası *

N olduğuna göre, denge noktası tanımından

* * * *

(N ) (f N ) g N( ) (4.17) denklemine sahip oluruz. (4.16) denkleminin her iki tarafının türevi alınırsa,

) ( ) ( ) ( ) ( 1 ) , ( N* * N* f N* *N* N* f N* F (4.18) ) ( ) ( ) ( * * * * * * N g N N f N N

ifadesine ulaşırız. (4.17)’deki *

değeri (4.18) de yazılırsa, * * * * * * * * * * * * ( ) ( ) ( , ) 1 ( ) ( ) ( ) ( ) ( ) N f N F N N g N N g N N g N N f N (4.19) denklemini elde etmiş oluruz. *

N denge noktası için, lokal kararlılık tanımından

0 ) ( ) ( ) ( ) ( ) ( ) ( ) ( 2 _* * * * * * * * * * N g N N f N f N g N N N N g

N elde edilir ki her iki taraf

) ( *

*

N g

N değerine bölünürse istenen durum elde edilir.

Aşağıdaki sonuç ile, (4.13) ve (4.16) denklemlerinin kararlılık karşılaştırmalarını verelim.

Sonuç 4.2.2.1: (Merdan ve Duman, 2007) *

(0, c]

N N , (4.13) denkleminin denge

noktası olsun. *

N denge noktasının kararsız olması için gerek ve yeter şart

* ( , ) 1 F N olmasıdır. Burada, * * ( ) ( ) N

N daima pozitif olduğundan (4.15) ve (4.18) denklemleri karşılaştırılırsa,

* * *

( , ) ( , )

(25)

sonucuna ulaşılır.

Sonuç 4.2.2.2. (Merdan ve Duman, 2007) *

c

N N olduğunda (4.16) denklemindeki

Allee etkisi (4.13) denklemindeki *

N denge noktasının kararlılığını artırır.

Bu bölümde şimdiye kadar elde edilen sonuçların doğruluğunu nümerik similasyon ile görelim.

4.2.3. Nümerik similasyon

Bu bölümde, önceki bölümde elde edilen analitik sonuçları destekleyen örnekler vereceğiz. Bu hesaplamalar için Matlab programı kullanılmıştır. K; taşıma kapasitesi,

; Allee sabiti ve ; Allee etkisinin kuvveti olmak üzere,

K N N f t t) 1 ( , 2 1 ) ( t t t N N N g ve t t t N N N ) _

( olarak tanımlansın. Bu fonksiyonlara bağlı olarak (4.13) ve (4.16) denklemleri, 2 1 (1 ) 2 1 t t t t t t N N N N N K N (4.21) ve 2 2 * 1 (1 ) 2 1 t t t t t t t N N N N N N K N . (4.22)

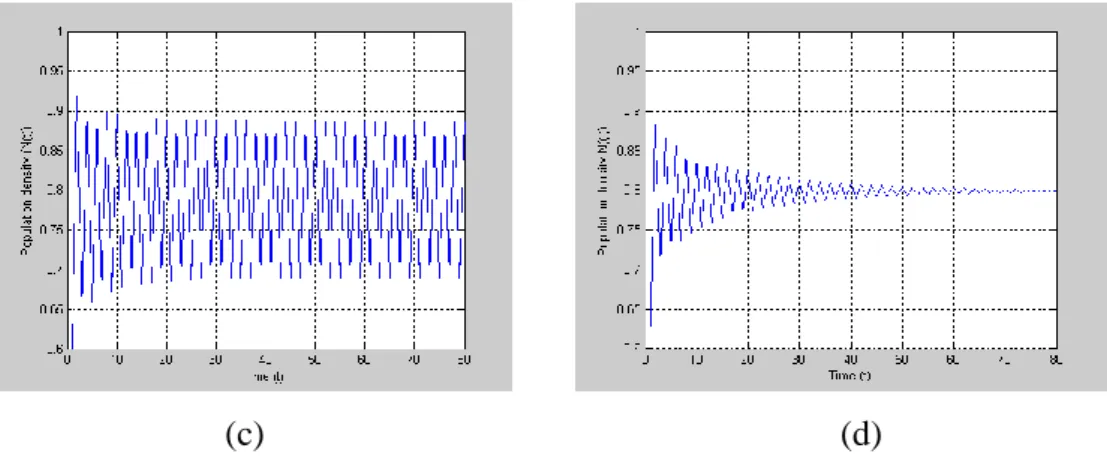
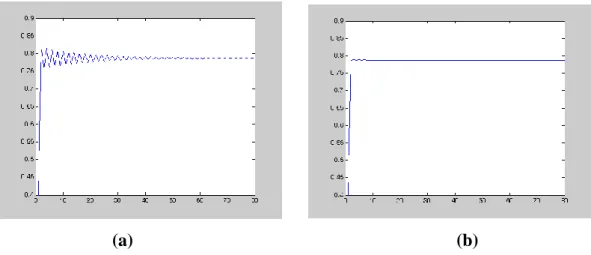
formundadır. (4.21) denklemi (Ludwing ve ark., 1978) çalışmasında tanımlanan Spruce Budworm modelinin fark versiyonudur. (4.21) denkleminde K 1 alalım. N pozitif * denge noktası * * * 2 (1 ) 1 ( ) N N N (4.23) denklemini sağlar. (4.21) ve (4.22) popülasyon modellerinin çözümlerinin yoğunluk-zaman grafiklerini verelim.

(26)

(c) (d)

ġekil 4.2. (a) 2.33 için (4.21) modelinin yoğunluk-zaman grafiği

(b) * 2.9190 için (4.22) modelinin yoğunluk-zaman grafiği

(c) 2.43 için (4.21) modelinin yoğunluk-zaman grafiği

(d) * 3.0380 için (4.22) modelinin yoğunluk-zaman grafiği

g fonksiyonunun N kritik noktası 1 olmak üzere, _c 2 1 * 1

2 N Nc eşitsizliği doğrudur. K=1 taşıma kapasitesi, N₀ 0.6 başlangıç şartı ve =0.2 Allee sabitidir. 2.33 büyüme oranına karşılık, (4.21) denkleminin denge noktası N* 0.7912 ve normalize edilen büyüme oranı *

2.9190 ’dır. Aynı zamanda, 2.43 değerine karşılık, (4.21) denkleminin denge noktası *

0.7993

N ve * 3.0380 olarak

hesaplanmıştır. Popülasyonun Allee etkisi ile denge noktasına daha hızlı bir şekilde yaklaştığı görülmüş olur.

Şimdi farklı Allee sabitleri seçimi ile (4.22) modelinin davranışını inceleyelim.

(27)

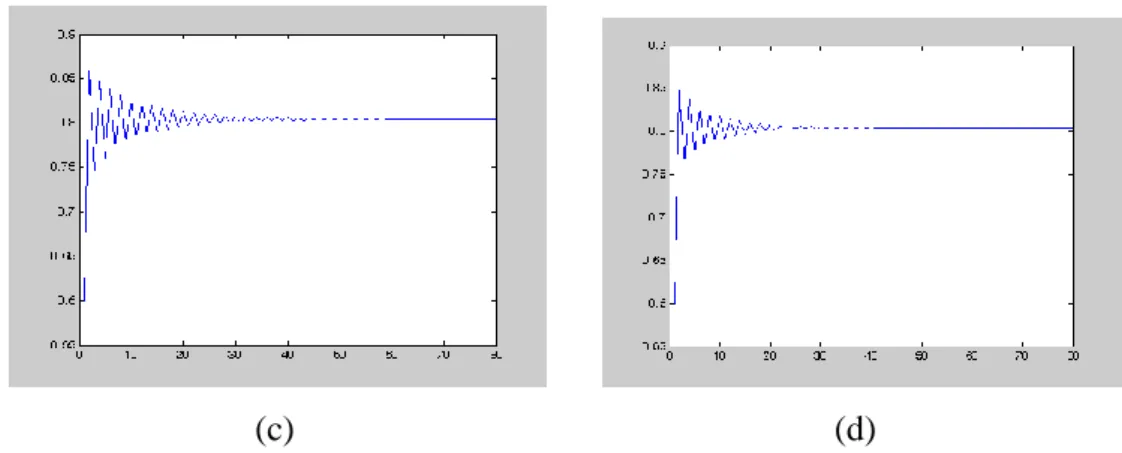
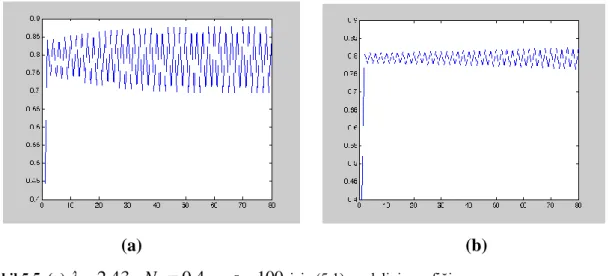
(c) (d)

ġekil 4.3. (a) 0.2ile (4.22) modelinin yoğunluk-zaman grafiği

(b) 0.4ile (4.22) modelinin yoğunluk-zaman grafiği

(c) 0.6ile (4.22) modelinin yoğunluk-zaman grafiği (d) 0.8 ile (4.22) modelinin yoğunluk-zaman grafiği

0 0.6

N başlangıç şartlı ve 2.5 değerlerine karşılık hesaplanan denge noktası

*

0.8046

N olmak üzere, Allee etkisi artımı (4.22) denkleminin denge noktasının lokal kararlılığını artırır.

4.3. Avcı Sayısına Bağlı Sürekli Popülasyon Modelinin Kararlılık Analizi ve Allee Etkisi

(Merdan ve Duman, 2008) yaptıkları çalışmada, düşük yoğunlukta g(N_t) avcı fonksiyonuna bağlı, ) ( ) ( _t _t _t t t N g N N f N dt dN (4.24) ) ( ) ( ) ( * t t t t t N g N N f N N dt dN (4.25) genel diferansiyel popülasyon modellerinin kararlılığını araştırmışlardır. Bu çalışmada

f fonksiyonu, fonksiyonu ve * değeri daha önceki modellerde olduğu gibi aynı özelliklere sahiptir.

Şimdi (4.24) ve (4.25) denklemlerinin kararlılık şartlarını verelim

4.3.1 (4.24) modelinin kararlılık analizi

Teorem 4.3.1.1. (Merdan ve Duman, 2008) (4.24) denkleminin pozitif N denge *

noktası için ) ( ) ( ) ( ) ( * * * * N g N g N f N f

eşitsizliği sağlanırsa o zaman, N denge noktası lokal * kararlıdır.

(28)

Ġspat: (Merdan ve Duman, 2008) Teorem 4.2.1.1’in ispatına benzer şekilde yapılır.

Teorem 4.3.1.2. (Merdan ve Duman, 2008) (4.25) denkleminde pozitif N denge *

noktası için ) ( ) ( ) ( ) ( ) ( ) ( * * * * * N g N g N f N f N N

eşitsizliği sağlanırsa N denge noktası lokal * kararlıdır.

Ġspat: (Merdan ve Duman, 2008) Teorem 4.2.2.1’in ispatına benzer şekilde yapılır. Sonuç 4.3.1.1 : (Merdan ve Duman, 2008) (4.24) ve (4.25) denklemleri ve 0

) ( ) ( * N N

durumu göz önüne alındığında, F ( ,N*) F ( ,N*) olduğu kolayca görülebilir. Diferansiyel denklemler için lokal kararlılık tanımından, Allee etkisi (4.24) modelinin

*

N denge noktasının lokal kararlılığını azalttır.

Elde edilen sonuçları nümerik similasyonla doğrulayalım.

4.3.2. Nümerik similasyon

Burada, teorik olarak ulaşılan sonuçları desteklemek için örnek vereceğiz. Hesaplamalar için Matlab ODE programı kullanılmıştır. K, taşıma kapasitesi ve , Allee etkisinin kuvvetini tanımlayan fonksiyon ve * normalize edilmiş büyüme oranı olmak üzere,

K N N f t t) 1 ( , ₂ 1 ) ( t t t N N N g ve t t t N N N ) _ ( fonksiyonlarını alalım. Bu fonksiyonlara bağlı olarak, (4.24) ve (4.25) denklemleri,

1 ) 1 ( ₂ 2 N N K N N dt dN (4.26) ve 1 ) 1 ( ₂ 2 2 * N N K N N N dt dN (4.27) şeklinde yazılabilir. (4.26) ile verilen denklem (Ludwing ve ark., 1978) de tanımlanan Spruce Budworm model versiyonudur.

(29)

(a)

(b)

ġekil 4.4. a) 2,N₀ 0.05 için (4.26) modelinin grafiği

b) '' 2.526873,N₀ 0.05 ve 0.2 için (4.27) modelinin grafiği

2 ve N₀ 0.05; parametre değerlerine karşılık sistemin denge noktası 759196

. 0 ~

*

N . 0.2; Allee sabitine karşılık normalize edilen büyüme oranı 526873

. 2

*

olarak bulunur. Yukarıda çizilen grafiklerden görüldüğü gibi Allee etkisi sisteme eklendiğinde, sistem daha yavaş bir şekilde denge noktasına yaklaşım göstermektedir.

4.4. Gecikmeli Popülasyon Dinamiklerinin Kararlılığı Üzerine Allee Etkisi

(Çelik ve ark. 2006) da , N bilinen değerleri ve T; organizmanın yeniden _t üreme zamanı olmak üzere,

) ( ) , , ( 1 t t T t t T t F N N N f N N (4.28) genel lineer olmayan fark denkleminin kararlılığını çalıştılar. Allee etkisinin modelin kararlılığı üzerindeki rolünü incelediler. Ayrıca, f(N_t _T) yeniden üreme olgunluğuna gelmiş bireyler arasındaki etkileşimi (rekabet) tanımlayan foksiyondur. Bu fonksiyon daha önceden verildiği gibi azalan bir fonksiyondur.

(30)

Şimdi (4.28) modelinin kararlılık şartlarını verelim.

4.4.1 T=1 için (4.28) modelinin kararlılık analizi f azalan bir fonksiyon olmak üzere,

0 ), , , ( ) ( ₁ ₁ 1 t t t t t N f N F N N N (4.29) lineer denklemini göz önüne alalım. (4.29) denkleminin kararlılık şartını verelim.

Teorem 4.4.1.2. (Çelik ve ark. 2006) N , (4.29) denkleminin pozitif bir denge noktası * olsun. O zaman N denge noktasının lokal kararlı olması için gerek ve yeter şart *

1 ) ( ) ( * * * N f N f N olmasıdır.

Ġspat: (Çelik ve ark. 2006) (4.29) denklemi lineerleştirildiğinde, 0 ) ( * * 2 N f

N 2. dereceden lineer bir denklem elde edilir. p 1 ve ) ( * * N f N

q alınırsa ve lineerleştirilmiş kararlılık teoreminden faydalanılırsa q 1 olduğu kolay bir şekilde görülür..

değeri arttıkça, (4.29) denkleminin kararlılık değişimini aşağıdaki teoremle ifade ederiz.

Teorem 4.4.1.3. (Çelik ve ark. 2006) 1 < 2 olacak şekilde, 1 ve 2’ye karşılık gelen

pozitif denge noktaları (1)

N ve N(2) olsun. O halde, [ (log ( )) 0

) 2 ( ) 1 ( dN N f N N N sağlanırsa, (2)

N denge noktasının lokal kararlılığı N(1) denge noktasından daha zayıftır. Allee etkisinin modelin kararlılığına etkisini inceleyelim.

4.4.2. (4.29) gecikmeli fark modeli üzerine Allee etkisi

Bu kısımda farklı Allee etkisi ile (4.29) denkleminin denge noktasının kararlılık analizini verelim.

4.4.2.1. t-1 zamanda Allee etkisi

(4.29) denkleminin t 1 zamanlı Allee etkisi ile gecikmeli lineer olmayan fark denklemi 0 ), , ; ( ) ( ) ( ₁ ₁ ( ) ₁ * * 1 t t t t t t N N f N F N N N (4.30)

(31)

şeklindedir. (4.30) denklemi en çok iki pozitif denge noktasına sahiptir. Varsayalım ki bu model N <₁* N olacak şekilde iki denge noktasına sahip olsun. Bu model ₂*

) ( ) ( ) (

1 * N f N h N denklemini sağlar ve h(N₁*) h(N₂*) 1’dir. Ortalama değer teoreminden, h(N_c) 0 ve N₁* N_c N₂* olacak şekilde N bir kritik nokta _c mevcuttur. O halde aşağıdaki teoremler elde edilir.

Teorem 4.4.2.1.1. (Çelik ve ark. 2006) (4.30) denkleminin * 1

N denge noktası kararsızdır. *

2

N denge noktasının kararlı olması için gerek ve yeter şart

1 ) ( ) ( ) ( ) ( * 2 * 2 * 2 * 2 * 2 N f N f N N N olmasıdır.

Teorem 4.4.2.1.2. (Çelik ve ark. 2006) Allee etkisi lokal kararlılığı artırır. Yani (4.30) denkleminin denge noktasının lokal kararlılığı (4.29) denkleminin lokal kararlılığından daha güçlüdür.

Ġspat: (Çelik ve ark. 2006) Her bir i=1,2 için ’nın tanımından 0 ) ( ) ( * 2 * 2 * 2 N N N elde ederiz. Bu durumda, ) ( ) ( ) ( ) ( ) ( ) ( * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 N f N f N N N N f N f N (4.31) yazılabilir. (4.31) göz önüne alınırsa, teoremin doğruluğu açıktır.

Sonuç 4.4.2.1.1. (Çelik ve ark. 2006) (4.30) denklemi için kararlı olan nokta (4.29) denklemi için kararsızdır.

4.4.2.2. t zamanda Allee etkisi

t zamanlı Allee etkisi ile birlikte (4.29) fark modeli ) , ; ( ) ( ) ( ₁ ₁ ( ) ₁ 1 t t t t t t N N f N F N N N (4.32)

seklindedir. (4.32) denkleminin N ve ₁* N iki denge noktası olduğundan ilgili teoremi ₂* takip edelim.

Teorem 4.4.2.2.1. (Çelik ve ark. 2006) (4.32) denkleminin * 1

N denge noktası kararsızdır. *

2

1 ) ( ) ( * 2 * 2 * 2 N f N f N olmasıdır.

(32)

Sonuç 4.4.2.2.1. (Çelik ve ark. 2006) (4.32) denkleminin *

N denge noktasının kararlı olması için gerek ve yeter şart, (4.29) denklemi içinde kararlı denge noktası olmasıdır.

4.4.2.3. t ve t-1 zamanda Allee etkisi

(4.29) modelinin t ve t 1 zamanlı Allee etkisi ile birlikte ) , ; ( ) ( ) , ( ₁ ₁ ( ) ₁ 1 , t t t t t t t N N N f N F N N N (4.33)

gecikmeli fark modelini alalım.

(4.33) denkleminin N ve ₁* N iki denge noktası olmak üzere ilgili teoremi verelim. ₂* Teorem 4.4.2.3.1. (Çelik ve ark. 2006) (4.33) denkleminin N denge noktası ₁* kararsızdır. *

2

1 ) ( ) ( ) , ( ) , ( * 2 * 2 * 2 * 2 * 2 * 2 * 2 1 N f N f N N N N N Nt olmasıdır.

Sonuç 4.4.2.3.1. (Çelik ve ark. 2006) (4.33) denkleminin *

N denge noktasının kararlı olması için gerek ve yeter şart, (4.29) denklemi içinde kararlı denge noktası olmasıdır.

4.4.2.4. Nümerik similasyon 1

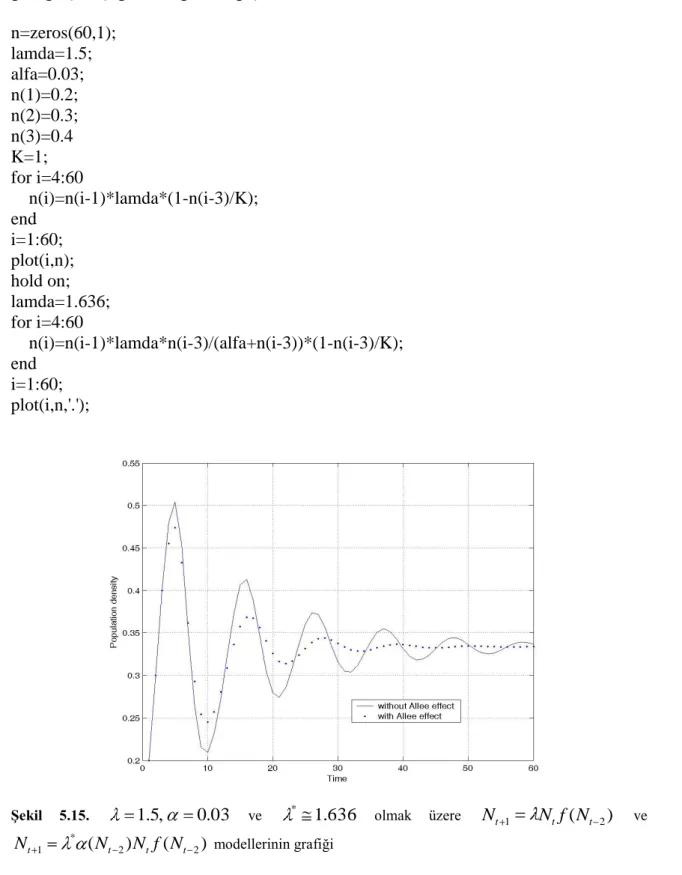
t zamanda Allee etkisinin popülasyon üzerindeki etkisini incelemek için yoğunluk-zaman grafiğini çizelim.

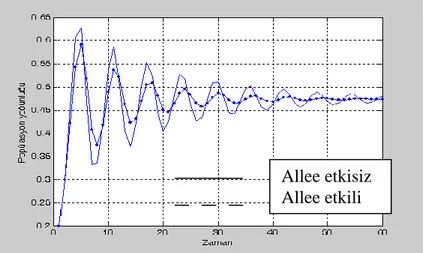
ġekil 4.5.K=1, 1.9, 0.03, * (N*)ve N ₁ 0.2veN₀ 0.3 başlangıç şartları

ileN_t ₁ N_t(1 N_t ₁/K) ve ( 1)(1 1/ )

*

1 N N N K

Nt t t t modellerinin yoğunluk-zaman

grafikleri.

Bu grafik 1.9, 0.03 ve N ₁, N başlangıç şartları olmak üzere her ₀ t zamanda popülasyon yoğunluğunu gösterir.

Allee etkisiz Allee etkili

(33)

5. OLUġTURULAN FARK POPÜLASYON MODELLERĠ VE KARARLILIK Bu bölümde, farklı modeller oluşturarak bu modellerin kararlılık şartlarını vereceğiz ve kararlılık üzerine Allee etkisini araştıracağız.

5.1. Avcı Sayısının DeğiĢimine Bağlı Olarak Fark Popülasyon Modelinin Kararlılığı ve Allee Etkisi

(4.2)’de verilen fark modelinde avcı sayısı değişiminin model üzerindeki etkilerini inceleyelim. (g2) ve (g3) şartları ile birlikte, s [1, ) için

s g(0) 1 ve

(0, )

N için 1 g(N) alalım. Buna göre,

s N N N N g t t t t 1 1 ) ( ₂

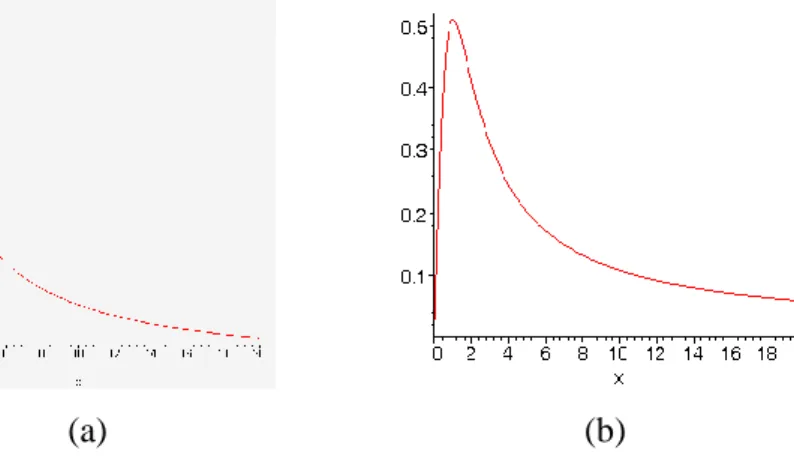
fonksiyonunu seçelim. s 1 ve s 100 değerleri için, g(N_t)fonksiyonunun grafikleri,

(a) (b)

ġekil 5.1. (a) s=1 içing(N_t) fonksiyonunun genel şekli

(b) s=100 için g(N_t) fonksiyonunun genel şekli

şeklindedir.

Şimdi s ’nin bu iki değeri için popülasyon davranışını inceleyelim. 5.1.1. N₀ 0.4 ve belirli bir değerine göre popülasyon hareketi

) ( ** * * N olarak verilen * *

parametresi normalize edilmiş büyüme oranı,

K N N f t t) 1 ( , t t t N N N ) _

( ve s 1 değeri ile yeni g(N_t) fonksiyonuna bağlı olarak, (4.13) ve (4.16) modelleri,

(34)

1 1 ) 1 ( ₂ 2 1 t t t t t t t t N N N N K N N N N (5.1) ve 1 1 ) 1 ( ₂ 2 2 * * 1 t t t t t t t t t N N N N K N N N N N (5.2) yazılabilir. 4 . 0 0

N başlangıç şartı altında K 1, 2.33 ve 0.05 alalım. Bu değerlere karşılık bulunan denge noktası N** 0.54187’dır.

(5.1) modeli için aşağıdaki algoritmayı yazabiliriz. n=zeros(80,1); n(1)=0.4; lamda=2.33; K=1; s=1; for i=1:79 n(i+1)=n(i)+lamda*n(i)*(1-n(i)/K)-n(i)^2/(1+n(i)^2)-n(i)/(n(i)+s); end i=1:80; plot(i,n);

Benzer şekilde (5.2) modeli için aşağıdaki algoritma verilebilir. n=zeros(80,1); n(1)=0.4; lamda_normalize=2.5450; K=1; alfa=0.05; s=1; for i=1:79 n(i+1)=n(i)+lamda_normalize*n(i)^2/(alfa+n(i))*(1-n(i)/K)-n(i)^2/(1+n(i)^2)-n(i)/(n(i)+s); end i=1:80; plot(i,n);

(35)

Bu algoritmalara bağlı olarak Matlab programı ile sırasıyla (5.1) ve (5.2) modellerine göre popülasyon değişim grafikleri aşağıdaki gibidir.

(a) (b)

ġekil 5.2. (a) 2.33, N₀ 0.4 ve s 1 değerleri için (5.1) modelinin grafiği

(b) * 2.5450, N₀ 0.4, s 1 ve 0.05 değerleri için (5.2) modelinin grafiği

Şimdi s=100 değeri için (5.1) ve (5.2) model hareketini gözlemleyelim.

(a) (b)

Şekil 5.3. (a) 2.33, N₀ 0.4 ve s 100 değerleri için (5.1) modelinin grafiği

(b) * 2.478, N₀ 0.4, s 100 ve 0.05değerleri için (5.2) modelinin grafiği

Dikkat edilecek olursa s değerleri arttıkça kararlılık azalmaktadır. Allee etkisinin kararlılığı hızlandırdığı gözlemlenir.

Şimdi artımı ile popülasyon davranışını inceleyelim.

5.1.2. Artan değerine göre popülasyon hareketi

Bu değişimi 2.43 alarak modeldeki popülasyon sayısının değişim durumunu inceleyelim.

(36)

(a) (b)

ġekil 5.4. (a) 2.43, N₀ 0.4 ve s 1 için (5.1) modelinin grafiği

(b) * 2.64667, N₀ 0.4, s 1 ve 0.05 için (5.2) modelinin grafiği

(a) (b)

ġekil 5.5. (a) 2.43, N₀ 0.4 ve s 100 için (5.1) modelinin grafiği

Birim kare başına büyüme oranı arttıkça, s 1 için denge noktasına yakınsama olurken, 100

s değerinde belirli döngülü titreşimler sözkonusudur. Allee etkisinin popülasyonu olumlu yönde etkilediği daha kolay bir şekilde gözlemlenmektedir. Denge noktasına doğru yaklaşım artırmıştır.

Şimdi de artan Allee etkisi ile popülasyon davranışını gözlemleyelim.

5.1.3. Belirli değeri ve artan Allee sabitine göre popülasyon hareketi 5

.

2 alalım. 0.2, 0.4 ve 0.6 Allee sabitleri için s değerleri ve zamana göre popülasyon değişimini inceleyelim.

(37)

(a) (b)

(c) (d)

ġekil. 5.6. (a) 2.5, N₀ 0.4 ve s 1 için (5.1) modelinin grafiği

(c) * 4.24471, N₀ 0.4, s 1 ve 0.4 için (5.2) modelinin grafiği

(d) * 5.117056, N₀ 0.4, s 1 ve 0.6 için (5.2) modelinin grafiği

(a) (b)

(38)

ġekil.5.7. (a) 2.5, N₀ 0.4 ve s 100 için (5.1) modelinin grafiği

(c) * 3.748652, N₀ 0.4, s 100 ve 0.4 için (5.1) modelinin grafiği

(d) 4.37298 0 0.4

*

N s 100 ve 0.6 için (5.2) modelinin grafiği

Her iki s değerine göre, Allee sabiti arttıkça popülasyonun da kararlılığa yaklaşım hızı artmaktadır.

(4.2) de verilen modellerin, avcı sayısı değişimine bağlı olarak, popülasyon davranışlarını karşılaştıralım.

5.1.4. Grafik yardımıyla karĢılaĢtırma )

(N_t

g değişiminin, popülasyonun davranışı üzerindeki etkisinin bir karşılaştırmasını verelim. İlk olarak, bu durumu farklı değerleri için inceleyelim.

(a) (b)

(c) (d)

ġekil. 5.8. (a) 2.33, N₀ 0.6 ve s 1 için (5.1) modelinin grafiği

(c) 2.33, N₀ 0.6 için (4.21) modelinin grafiği

(39)

(a) (b)

(c) (d)

ġekil.5.9. (a) 2.43, N₀ 0.6 ve s 1 için (5.1) modelinin grafiği

(b) * 3.296663, N₀ 0.6 ve s 1 için (5.2) modelinin grafiği

(c) 2.43 ve N₀ 0.6 için (4.21) modelinin grafiği

(d) 3.0380, N₀ 0.6 ve 0.2 için (4.22) modelinin grafiği

(5.1)-(5.2) ve (4.21)-(4.22) modellerini aynı değerler üzerinden karşılaştırdığımızda avcı sayısı artımı ile daha iyi sonuçlar aldığımızı görmekteyiz. Bu durumda, küçük parametre değişimlerinin, popülasyonlar üzerinde büyük bir etkiye sahip olduğu sonucuna varırız.

Şimdi de farklı Allee sabitleri alarak bu karşılaştırmayı yapalım.

(a) (b)

(40)

(c) (d)

ġekil. 5.10. (a) * 3.37235, N₀ 0.6, 0.2 ve s 1 için (5.2) modelinin grafiği

(c) N₀ 0.6 ve 0.2 için (4.22) modelinin grafiği

(d) N₀ 0.6 ve 0.4 için (4.22) modelinin grafiği

(a) (b)

(c) (d)

ġekil.5.11. (a) * 5.117056, N₀ 0.6, 0.6 ve s 1 için (5.2) modelinin grafiği

(b) * 5.98941, N₀ 0.6, 0.8 ve s 1 (5.2) modelinin grafiği

(c) N₀ 0.6 ve 0.6 (4.22) modelinin grafiği

(41)

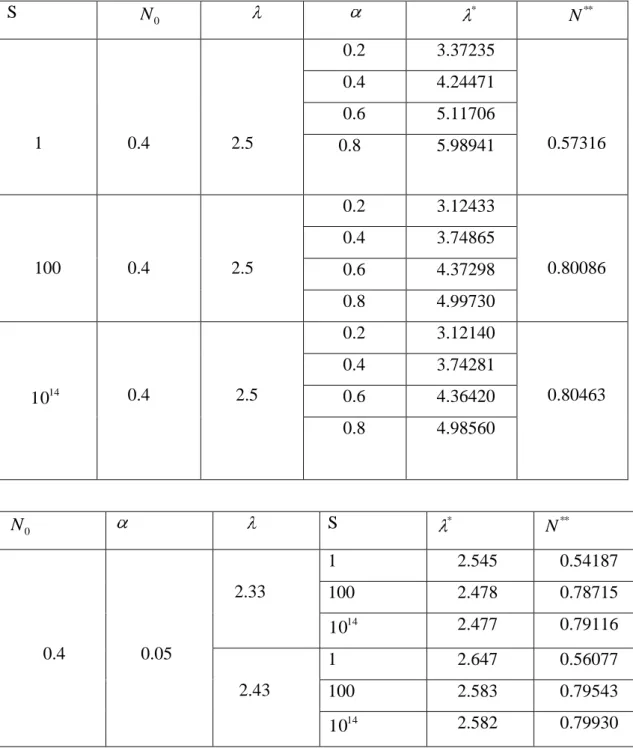
Modellerdeki kararlılık üzerindeki etkiyi benzer şekilde Allee sabitlerini artırarak gözlemledik. Şimdi bu çalışmada kullanılan değerleri daha açık görmek için aşağıdaki çizelgeye bakalım.

Çizelge 4.1. değerlerine karşılık gelen denge noktaları ve diğer kullanılan değerler S N ₀ * N ** 1 0.4 2.5 0.2 3.37235 0.57316 0.4 4.24471 0.6 5.11706 0.8 5.98941 100 0.4 2.5 0.2 3.12433 0.80086 0.4 3.74865 0.6 4.37298 0.8 4.99730 10 14 0.4 2.5 0.2 3.12140 0.80463 0.4 3.74281 0.6 4.36420 0.8 4.98560 0 N S * ** N 0.4 0.05 2.33 1 2.545 0.54187 100 2.478 0.78715 14 10 2.477 0.79116 2.43 1 2.647 0.56077 100 2.583 0.79543 14 10 2.582 0.79930

(42)

0 N S * N ** N * 0.6 0.2 2.33 1 3.190 0.54187 0.7912 100 2.922 0.78715 10 14 2.919 0.79116 2.43 1 3.297 0.56077 0.7993 100 3.041 0.79543 10 14 3.038 0.79930

Bu kısımdaki çalışma, The first İnternational Conference on Mathematics and Statistic, 2010 isimli konferansta sunulmuştur. Tam metin basım için Selcuk Journal of Applied Mathematics dergisine gönderilmiştir.

5.2. Avcı Sayısı DeğiĢimine Bağlı Olarak Sürekli Popülasyon Modelinin Kararlılığı ve Allee Etkisi

Bu bölümde amacımız, g(N_t) avcı fonksiyonunu

1 1 1 ) ( ₂ t t t t N N N N g (5.3) alarak 1 1 ) 1 ( ₂ 2 N N N N K N N dt dN (5.4) 1 1 ) 1 ( ₂ 2 2 * * N N N N K N N N dt dN (5.5) sürekli popülasyon modellerinin dinamikliğini incelemektir. Ayrıca bu modellerle, (4.26) ve (4.27) ile verilen modelleri karşılaştırarak, davranış değişimlerini gözlemlemektir.

5.2.1. (5.4) ve (5.5) modelleri için ve sabitlere göre popülasyon hareketi

2 ve K=1 olmak üzere (5.4) ve (5.5) ile verilen modelin popülasyon hareketini gözlemleyelim.

(43)

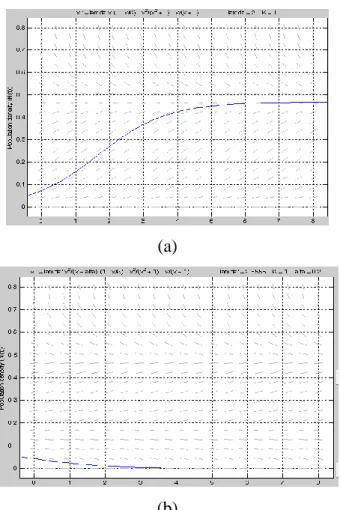
(a)

(b)

ġekil 5.12. (a) 2 K, 1 ve N₀ 0.05için (5.4) modelinin grafiği

(b) 2,K 1,N₀ 0.05 ve 0.2 için (5.5) modelinin grafiği

(5.4) modelinde belli bir zaman sonra popülasyon, denge noktasına ulaşmaktadır. Allee etkisiyle popülasyonun yok olduğu gözlemlenmektedir. Başlangıç noktasının çok küçük seçilmesi bu durumun oluşmasında etkilidir.

(5.5) modeli farklı başlangıç şartlarına göre yeniden incelenirse, popülasyon hareketi için Şekil 5.13 elde edilir.

ġekil 5.13. 2 K, 1, 0.2 ve N₀ :0.05:0.13:0.14:0.15:0.18:0.22 için (5.5) modeli

(44)

Görüldüğü gibi popülasyonda belli bir eşik noktası vardır ki bu değerin altında popülasyon yokoluşa sürüklenir. Bu popülasyon uygun bir başlangıç noktası seçimi ile hayatta kalabilir.

5.2.2 . Modellerin karĢılaĢtırılması

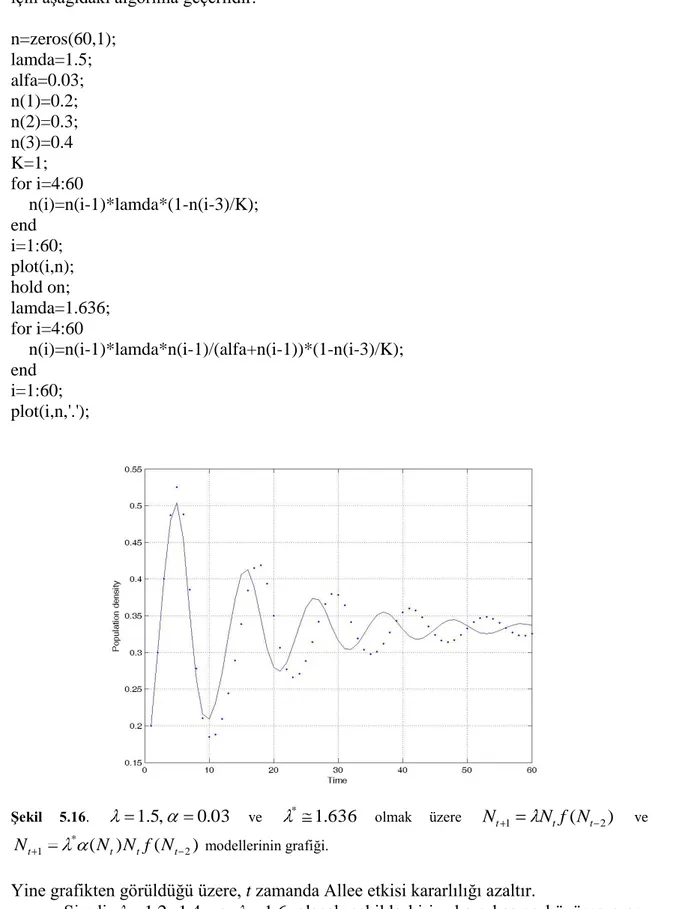
(4.26) ve (4.27) daha önce incelenen modellerle, (5.4) ve (5.5) modellerinin davranışını belirli değerler altında gözlemleyelim.

(a) (b) (c) (d) (e) (f) ġekil 5.14