Journal of Physics and Chemistry of Solids 137 (2020) 109214
Available online 24 September 2019
0022-3697/© 2019 Elsevier Ltd. All rights reserved.
Polarizability and electric field gradient of two-electron quantum dots
Yusuf Yakar
a,*, Bekir Çakır
b,**, Ayhan €Ozmen
baPhysics Department, Faculty of Arts and Science, Aksaray University, Campus, 68100, Aksaray, Turkey bPhysics Department, Faculty of Science, Selcuk University, Campus, 42031, Konya, Turkey
A R T I C L E I N F O Keywords:
Static polarizability Oscillator strength Electric field gradient
Helium/ helium-like quantum dots
A B S T R A C T
The energy levels of the quantum dots are evaluated by using Quantum Genetic Algorithm procedure and Hartree-Fock Roothaan method. Based on the calculated energies and wave functions, static dipole polarizability, oscillator strength and electric field gradient of helium/helium-like quantum dots are calculated as a perturbative calculation. It is worth to note that impurity charge and dot radius have a strong effect on the dipole polariz-ability, the oscillator strength and the electric field gradient. In small dot radii, since the spatial confinement effect is dominant, the polarizability of system is very weak. The polarizability increases monotonically with the increase of dot radius and then reaches a saturation value in large dot radii. On the other hand, the electric field gradient increases as dot radius decreases.
1. Introduction
Low dimensional structures are taking attention as being an inter-esting study subject in both physics and chemistry. The charge carriers in such structures are spatially trapped in an external potential. The spatial confinement effect causes drastic changes in observable proper-ties such as impurity energy, localization of electron(s), optical prop-erties, energy spectrum, polarizability, etc. [1]. Another important property is the impurity charge that causes remarkable changes in the energy states and optical properties. The performance features of mi-croelectronic and optoelectronic devices can be modified significantly by the presence of impurity charges. Besides, the impurity property leads to significant alterations in the energy distribution [2]. The nanostructures such as quantum dots (QDs) have shell structure and discrete energy levels, like real atoms, and they attract a considerable attention because of their potential applications in nanotechnology. Thus, in the past decade, binding energies [3–7], optical properties [8–17] and other properties [18–21] of QDs are studied by many researchers.
External perturbations such as electric and magnetic fields can pro-vide us with extremely useful information about quantum systems. Electric field leads to a shift (stark effect) in the impurity energy levels, and it also causes a polarization of the charge cloud. Such effects in the energy spectra are important to control and regulate the output of op-toelectronic devices [22]. The static dipole polarizability (SDP)
describes the distortion of charge cloud and it is associated with many physical properties such as the dielectric constant and the refractive index [23]. Using variational method, Dutt et al. [24] calculated the SDP of hydrogen atom inside a spherical box. Corella-Madue~no [25] carried out the ground state energy, pressure and SDP of He and Liþinside boxes
with paraboloidal walls using the variational method. Waugh et al. [26] studied SDP and hyper polarizabilities of a confined helium atom uti-lizing density-functional theory. For the ground state, Marin and Cruz [27] performed SDP and Fermi contact term of one- and two-electron atomic systems within spherical confining barriers. The optical proper-ties like polarizability and oscillator strength were carried out for a hydrogenic impurity by solving Schrodinger equation numerically [28]. Çakır et al. [29] studied the electric field effects on energy states of QDs and they are carried out some optical properties. In a GaAs quantum wire, the magnetic field effects on the SDP and binding energy of a shallow donor were studied by Zounoubi et al. [30]. The calculations of SDP for a confined hydrogen atom were reported by Sen et al. [31] by using the Sternheimer perturbation-numerical procedure. Holka et al. [32] calculated SDP for the ground state of QD with parabolic potential using coupled-cluster CCSD method. In very recently, Ghosh et al. [33] carried out the polarizability and electric dipole moment of GaAs QD in terms of spatially-varying effective mass and spatially-varying dielectric constant. The magnetic field effects on optical properties were investi-gated in detailed by our group [34]. For the ground state, the SDP of helium/helium-like dots were computed by Melono et al. [35] using * Corresponding author.
** Corresponding author.
E-mail addresses: yuyakar@yahoo.com (Y. Yakar), bcakir@selcuk.edu.tr (B. Çakır).
Contents lists available at ScienceDirect
Journal of Physics and Chemistry of Solids
journal homepage: http://www.elsevier.com/locate/jpcshttps://doi.org/10.1016/j.jpcs.2019.109214
variational approach. All of the studies mentioned above on polariz-ability have been performed for the ground state of one- and two-electron QDs. There are a few studies on SDP, oscillator strength and electric field gradient in two-electron QDs. Therefore, to better understand the electronic structure of QDs, studies in this field are still important for both theoretical and practical applications of QDs.
In this article, studies made by us in the past studies [29,34] are extended to two-electron QDs and calculated the wave functions and the singlet and triplet energy states 1s2 (1S), 1s2s (1,3S), 1s2p (1,3P), 1s3d (1, 3D) and 1s4f (1,3F) confined of H , He, Liþand Beþþdots. Energies and
wave functions of QDs are obtained by using a modified variational approach based mainly on Quantum Genetic Algorithm (QGA) and Hartree–Fock–Roothaan (HFR) method. Calculations of the physical parameters such as the energy states, the static polarizability, the oscillator strength and the electric field gradient are closely related to the number of electrons of QDs, and their calculations are a little com-plex and difficult for many-electron systems. These parameters are important for the optical studies of QDs. We have calculated the electric field gradient. Besides, we have investigated the polarizability as a function of dot radius and impurity charge in two-electron QDs. For the polarizability calculation, the Kirkwood αK, Unsold αU and αγ formulas
have been used.
2. Theory
In the effective-mass approximation, in atomic units (au), the Hamiltonian of two-electron QD inside an infinite potential well is expressed as follows
H ¼ H1þH2þ
1
εr12
þVCðr1;r2Þ; (1)
in which Hi is the one-electron Hamiltonian ði ¼ 1; 2Þ and it is given
by Hi¼ r2i 2m*i Z εri ; (2)
where r2 is the Laplacian operator, m* is the effective mass of electron,
Z and ε are impurity charge and dielectric constant. In Eq. (1), the term
VCðr1;r2Þis the confining potential, and it has the following form: VCðr1; r2Þ ¼∞ when r1 and r2�R and VCðr1;r2Þ ¼0 when r1 and r2<R, in which R is dot radius.
The Schr€odinger equation for two-electron QD is given by
HΨðq1;q2Þ ¼EΨðq1;q2Þ; (3)
in which E and Ψ are the energy eigenvalues and the eigenfunctions of Hamiltonian operator, and qi denotes the coordinates of ith electron.
Polarizability is a measure of how easily an electron cloud is dis-torted by an electric field. SDP has an important place in theoretical definition of interatomic interactions, investigation of optical properties of materials and studies of pressure effects on atoms. The sensitive calculation of SDP depends largely on the behavior of the wave function. SDP can be determined analytically from the second order energy correction of the perturbation theory [36]. SDP can be calculated from the formula [28]. αγ¼X f 6¼γ Pγf Ef Eγ �2; (4)
where fðγÞ shows higher (lower) energy states, and γ also indicates the level, at which polarization is calculated. Here, the summation is over all the bound and continuum states. The computation of the static polar-izability using sum-over states needs accurate evaluation of wave functions and energies of the system. The accurate evaluation of the integrals over all continuum states is very complex for the present nu-merical capability [1]. For the 1s polarizability, the transition from
one-shell to three shell does not change the polarizability. This is due to the fact that the major contribution to the 1s polarizability comes from the 1s2→1s2p transition and it is not significantly modified by
appear-ance of new p states in additional shells, owing to the great value of the energy difference between the ground state and the first excited state [36]. The term Pγf is oscillator strength, which is a dimensionless
quantity that expresses the probability of absorption or emission of electromagnetic radiation in optical transitions between energy states of QD. The oscillator strength is an important physical quantity in the study of optical properties and it can be defined as follows
Pγf¼ 2m* ℏ2 � ��Mγ→f���2 Ef Eγ � ; (5)
where Mγ→f is the dipole transition matrix element defined in Ref. [29].
The calculation of SDP is also evaluated from the Kirkwood formula [37, 38] as follows αK¼ 4 9a0 X2 i¼1 � r2 i �2 ; (6)
where a0 is Bohr radius. On the other hand, the SDP is carried out from
the formula suggested by Unsold [24].
αU¼ 2 3ΔE X2 i¼1 � r2 i � ; (7)
in which ΔE ¼ Ef Eγ is the energy difference.
The electric field gradient (EFG), which is existing at the impurity and arising from the electrostatic fields of the electron(s), depends sensitively on the asymmetry of the electron charge, and EFG gives useful information about the confined systems. EFG arises from the non- spherical charge distribution of the open-shell configuration. EFG has a critical importance in investigation of the local electronic environment. EFG can be measured with the nuclear magnetic resonance, nuclear quadrupole resonance or M€ossbauer spectroscopy and it has great practical relevance in spectroscopy studies [39]. In spherical coordinate, the z-component of EFG is given by [40,41].
Vzz¼ * Ψ � � � � �q X2 i¼1 3cos2θ i � r 3 i � � � � �Ψ + (8) 3. Computational method
One-electron atomic wave functions are constructed from a linear combination of Slater-type orbitals (STOs). STOs are preferred in the quantum mechanical analysis of atoms, molecules and the confined systems because of the fact that they represent the correct behavior of the electronic wave functions. In order to calculate the energy eigen-values and the wave functions of impurity states, we have used a modified variational method which is a combination of QGA procedure and HFR method.
QGA method is based on three basic genetic operations: reproduc-tion, crossover, and mutation. The method starts with an initial random population of possible solutions of the problem. A fitness value is assigned to each individual in the population. In the reproduction pro-cess, the individuals of current population are copied to the next gen-eration according to their fitness values. Therefore, in performing reproduction process, a selection procedure is necessary to choose the individuals to be copied to the next generation. In the crossover oper-ation, two individuals randomly selected from the present are combined to obtain two new individuals of the next generation population. Another operation in QGA, the mutation process, plays an important role in getting out of local minima and is implemented at lower proba-bilities than other operations. In this process, the genetic information is changed randomly. In application of this process, an individual is randomly selected and its value is randomly changed by a small increase
and decrease. The orbital exponents and expansion coefficients of a STO are considered as the genetic code of the corresponding individual, these parameters are chosen randomly for the initial population, provided that they satisfy the appropriate boundary conditions. The orbital set of each individual are orthonormalized using the Gram-Schmidt procedure. Here, we have given only the outline of the procedure. The details of the QGA used in this study are given in our previous work [42]. On the other hand, to speed up our calculations, Gaunt coefficients used into the analytical expressions of Eqs. (5) and (8) were calculated by the method presented in Ref. [43] using generalized binomial coefficients, which were recursively evaluated and stored in a small array.
4. Results and discussion
This work is devoted to investigate the static polarizability and EFG of two electron QDs in a spherical cavity. We have computed the wave functions and the energy states corresponding to the configurations 1s2
(1S), 1s2s (1,3S), 1s2p (1,3P), 1s3d (1,3D) and 1s4f (1,3F). The results are
expressed in terms of au (Rydberg).
We have calculated the ground state 1s-SDP for helium dot from three different formulas and the results are listed in Table 1 for different values of R. In Table 1, when R < �1, this region is known as the strong electron confinement region, the value of SDP is very weak since the electron cloud cannot be further deformed due to the strong spatial confinement effect. As the dot radius increases, the value of SDP starts to increase due to the fact that electron can be more easily distorted or polarized by EFG. It can be said that this behavior is closely related to the binding energy of the electron. That is, the farther the electron from the impurity (nucleus) is, the weaker the binding energy is, and so SDP of system reaches the highest value due to the maximum deformation. For the ground state, in larger R values, it is seen that the SDP of helium dot approaches to corresponding polarizability of the helium atom, which is 1.38376 au [44]. In Table 1, when R� 3 , the results are in good
agreement with literature [23]. However, when R>3 , there are small discrepancies between the results due to structural differences between of these three formulas.
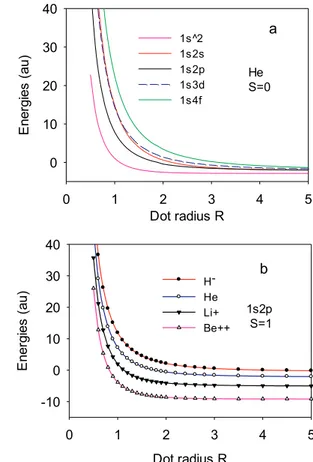
Fig. 1 displays the singlet and the triplet energy states of helium/ helium-like dots as a function of dot radius. As seen from the energy curves that the energies decreases when the dot radius increases. When the dot radius is large enough, the results approach to the corresponding energies of helium/helium-like atoms. For example, in (a), we have calculated the singlet energy values at R ¼ 7 as 2.8617au for 1s2, -
2.0702 au for 1s2s, 2.0782 au for 1s2p, 1.9035 au for 1s3d and 1.7222 au for 1s4f, respectively. Patil et al. [45] calculated the singlet energy values as - 2.0749 au for 1s2s, 2.0812 au for 1s2p. Similarly, in (b), we have calculated the triplet energy values at R ¼ 10 of helium-like dots as 0.4029 au for H , 5.1954au for Liþ, 9.1713 au for Beþþ. Flores-Riveros et al. [46] calculated the energy values as 0.40539 au for H , 5.02464au for Liþ. It is seen that these results are in agreement with the literature data. On the other hand, as it will be seen in (b), the impurity charge has a strong effect on the energy states. As the impurity charge increases, the total energy of the system goes further negative, as expected.
We have plotted the 1s-SDP from three different formula as a func-tion of R in Fig. 2 for helium dot. According to the SDP curves, when R < �1.3, the SDP is very weak. When 1:5 � R � 3 ,which is the medium confinement region, the SDP increases monotonically with the increase of dot radius. When R> 3, as known as the weak confinement region, the SDP increases until a certain dot radius and reaches a saturation value. More after, it goes to a constant value while the dot radius goes further. It may be said that, when R < �1.5, the charge distribution is less sen-sitive to the applied field since the electron cloud is much more local-ized. Whereas, when R> 3, the charge distribution starts to be more sensitive to the applied field. Thus, the polarizability of system in-creases. As seen in Fig. 2, the formulas in Eqs. (4), (6) and (7) give
Table 1
Some numerical values for the ground state static polarizability of helium dot at various dot radii. All values are given in au (R*
y). e-x means 10 x
Rða0Þ αK αU αγ Refs.
0.5 3.6924e-3 3.6286e-3 3.6168e-3 3.450e-3a
0.6 7.3361e-3 7.1630e-3 7.1473e-3 6.829e-3 a
0.7 0.0130 0.0126 0.0126 - 0.8 0.0212 0.0205 0.0205 1.958e-2 a 0.9 0.0323 0.0311 0.0311 2.981e-2 a 1.0 0.0469 0.0450 0.0449 4.309e-2 a 4.3e-2 b 1.2 0.0874 0.0834 0.0832 8.03e-2 a 8.0e-2 b 1.4 0.1441 0.1377 0.1370 1.31e-1 b 1.6 0.2167 0.2081 0.2061 - 1.8 0.3033 0.2937 0.2890 - 2.0 0.4002 0.3933 0.3830 0.371 a 0.374 b 2.2 0.5031 0.5030 0.4842 - 2.4 0.6074 0.6207 0.5885 - 2.6 0.7080 0.7419 0.6885 - 2.8 0.8017 0.8643 0.7845 - 3.0 0.8847 0.9835 0.8750 0.878 a 0.934 b 3.5 1.0473 1.2584 1.0374 - 4.0 1.1598 1.4777 1.1097 1.220 a 1.392 b 4.5 1.2240 1.6486 1.1187 - 5.0 1.2665 1.7717 1.1069 1.351 a 1.641 b 5.5 1.2676 1.8666 1.0781 - 6.0 1.2739 1.9387 1.0345 1.3844 a 1.763 b aRef. [35].
approximately similar results in the strong confinement region. How-ever, in the weak confinement regions, there are some discrepancies in the values of SDP. For the 1s-SDP, the numerical values computed from the Kirkwood formula gives the best prediction for the polarizability, which is corresponding the polarizability of helium atom. When the results obtained from αK and αγ formulas are compared with the
liter-ature ones, they are in good agreement with the polarizability curve (dashed line) drawn from the reference data [35]. On the other hand, in large dot radii, the results obtained from the Unsold formula are slightly higher than the other results. This case is originated from the formula structure.
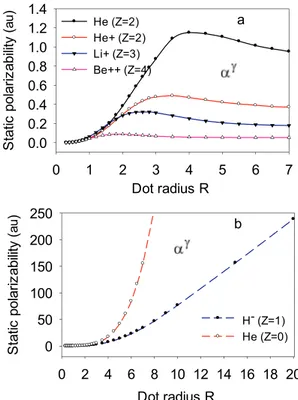
In Fig. 3, we have shown the 1s-SDP of two electron QD as a function of dot radius for the three different values of Z ¼ 2,3 and 4. Here, the SDP values are calculated from the Kirkwood formula. As it will be seen in the SDP curves, as the impurity charge increases, the polarizability de-clines with the increase of dot radius. In (a), in large dot radii, it is worth to note that the SDP value of neutral helium dot is higher than the
others, because the electron cloud is deformed easily by the applied field. On the other hand, while the impurity charge increases, the polarizability decreases since the charge cloud cannot be easily deformed. In other words, the binding energies of electrons increase because of the fact that electrons get closer to impurity. As a result of this, the polarizability of the system reduces while the binding energy increases. The opposite is also true. In (b), in the case of H dot, the electron cloud can be deformed easily by the external field since the impurity charge pulls electrons toward itself with a weaker force. In the case of HeðZ ¼ 0Þ, the impurity attraction energy is eliminated. As a result of this, the deformation of the system becomes much easier and the polarizability increases rapidly. In Fig. 3 (a), at R ¼ 4, we have calculated the SDP as 1.1398 au for He dot, 0.1761 au for Liþ dot and
4.78E-2 au for Beþþdot, respectively. For the H ðZ ¼ 1Þ and HeðZ ¼ 0Þ,
at R ¼ 4, the SDP are calculated as 8.3892 au and 21.9743 au. Fig. 4 shows the ground 1s-SDP of helium/helium like dots as a function of dot radius. Here, the polarizability is calculated from the αγ
formula, which depends on the dipole transition matrix element be-tween two levels, in which f indicates 1s2p (1P) level and γ demonstrates 1s2 level. Similar behaviors are observed here and the above-mentioned
definitions are also valid here. In Fig. 4, at R ¼ 4, we have obtained the polarizability values as 1.1597 au for He dot, 0.2119 au for Liþ dot,
5.47E-2 au for Beþþdot, 7.4414 au for H ðZ ¼ 1Þ dot and 17.4576 au for HeðZ ¼ 0Þ dot, respectively. The literature results are 1.220 au for He dot, 0.190 au for Liþ, 5.107E-2 au for Beþþ, 7.323 au for H ðZ ¼ 1Þ and
17.51 au for HeðZ ¼ 0Þ, respectively [35]. According to these results, there are small discrepancies originated from the used method among our results with the literature ones. However, when compared Fig.4 (b) to Fig. 3(b), it is found that the polarizability values calculated from αγ is
slightly different from αK, especially in large dot radii. For example, at
R ¼ 4, for H and HeðZ ¼ 0Þ, we have calculated the polarizability values as 7.4414 au and 17.4576 au in Fig. 4(b) and as 8.3892au and 21.9743 au in Fig. 3(b), respectively. Melono et al. have calculated the polarizability values as 7.323 au and 17.515 au for H . As a conse-quently, while the results obtained from the formulas αγ and αK are
qualitatively consistent with each other in neutral dot, there are slightly Fig. 2. Geound stste static polarizability of helium dot as a function of dot
radius. αγ* denotes the polarizability curve drawn from the reference data [35].
Fig. 3. Ground state static polarizability of helium/helium-like dots as a
differences in non-neutral dot.
In Fig. 5, we have displayed the SDP of the excited state 1s2s (1S) of
helium/helium–like dots by using the Kirkwood’s formula. Similar curves are also obtained here. That is, as the impurity charge increases, the SDP value decreases. On the other hand, as seen in Fig. 5, for H ðZ ¼ 1Þ; the value of SDP increases very rapidly. Here, the electrons are located considerably far away from each other. Thus, the total attractive potential between the electrons and the impurity charge be-comes weaker (or the binding energy bebe-comes weaker) and so the polarizability increases.
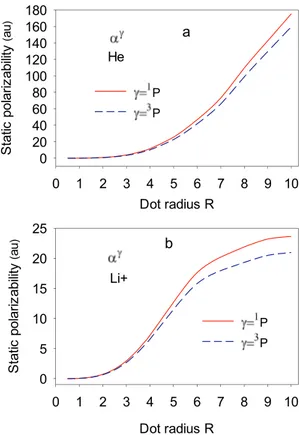
The SDPs of the singlet and triplet excited states of He and Liþdots
are shown in Fig. 6 as a function of dot radius. Here, we have utilized the Kirkwood approximation and considered the 1s2p (1,3P) and 1s3d (1,3D)
levels. The singlet and triplet polarizability curves exhibit the similar behaviours, but the polarizability values of He dot are larger than Liþdot
due to the impurity charge effect. As seen in the SDP curves, in the strong confinement region, the singlet and triplet polarizability values are almost the same and very weak. In this region, the spherical symmetry of the system is maintained due to strong spatial limitation. Thus, the polarizability of system becomes weaker. In the medium confinement regions, there exists a competition between spatial confinement and field confinement. As for in the weak confinement regions, the SDP in-creases monotonically. After a certain dot radius, the polarizability of the system reaches a saturation point. In this region, we can say that the external field effect on the electron cloud is more dominant than the spatial effect. As seen in Fig. 6, when R >� 5, the polarizabilities of singlet and triplet states begin to separate from each other, and the separation continues to increase with the increase of dot radius. As is known, the electric field has no effect on the spin polarization of elec-trons. This is originated from the change in energy difference between the levels. When compared (a) to (b), it is clearly seen that the polar-izability is reaching a critical value (saturation point) in shorter values of R due to the impurity effect. We could not compare our results since we were not able to find a similar result in literature.
In Fig. 7, we have plotted the oscillator strengths for permitted transitions between the singlet states (1s2) and (1s2p) of helium/helium-
like dots. The oscillator curves show similar behaviors. In Fig. 7, im-purity charge and dot radius effects are clearly seen on oscillator strength. As dot radius increases, first the oscillator strength increases and then reaches a maximum value. After it continues to decrease monotonically until reaching a minimum value, and then it goes to a constant value in very large dot radii. It is worthwhile to note that as the impurity charge increases, the oscillator peak positions shift toward smaller R values.
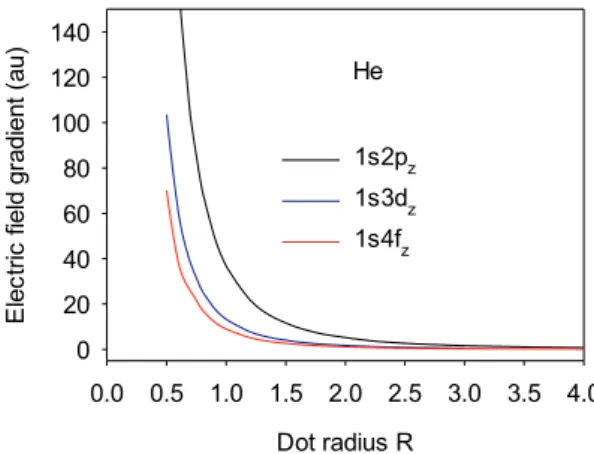
In order to investigate the EFG existing at the impurity and arising primarily from the electrostatic field of the electron in 2p, 3d and 4f orbitals, we have presented the z-component of EFG in Fig. 8 as a
function of R. In very large dot radii, the value of EFG is very weak and EFG increases monotonically as dot radius decreases. When the electron is close to the impurity, the value of EFG increases. As seen in Fig. 8, the EFG existing of the electron in higher levels is smaller than the level with small l. The reason is that when the electron is far away from the im-purity, the EFG creating at the impurity of the electron becomes very weak.
5. Conclusions
In this work, we have calculated the SDP for the ground and low lying excited states of helium/helium-like QDs. For the calculation of 1s- SDP, we have used the formulas αK, αU and αγ. In addition, the oscillator
strength and EFG of two electron QDs are calculated as a function of dot radius and impurity charge. The results show that both dot radius and Fig. 5. Excited state static polarizability of helium-like dots as a function of dot
radius from Kirkwood formula αK.
Fig. 6. Static polarizability for the singlet and triplet excited state (1s2p) of helium and Liþdots as a function of dot radius.
Fig. 7. Oscillator strengths of helium/helium-like dots as a function of dot radius.
impurity charge have a great influence on polarizability, oscillator strength and EFG of the system. While the polarizability is very weak due to the strong spatial confinement in small dot radii, it increases monotonically in large dot radii. For the ground state, it is seen that the approximation of Kirkwood gives good results. In addition, the electrons that are close to impurity charge create larger EFG, except for s-elec-trons. It is observed that the electrons which are close to impurity create larger EFG.
This work has been supported by Research Fund of Aksaray Uni-versity- Project Number: 2018-006.
References
[1] H.E. Montgomery Jr., K.D. Sen, Phys. Lett. A 376 (2012) 1992. [2] Z. Xiao, J. Zhu, F. He, J. Appl. Phys. 79 (1999) 9181.
[3] (a) Y. Yakar, B. Çakır, A. €Ozmen, Int. J. Quantum Chem. 111 (2011) 4139–4149;
(b) Y. Yakar, B. Çakır, A. €Ozmen, Philos. Mag. 95 (2015) 311–325;
(c) B. Çakır, Y. Yakar, A. €Ozmen, Chem. Phys. Lett. 684 (2017) 250. [4] S.A.A. Kohl, A.A. Simon, R.L. Restrepo, M.E. Mora-Ramos, C.A. Duque, Physica
Status Solidi B-Basic Solid State Phys. 252 (2015) 786.
[5] (a) J. Ganguly, S. Saha, A. Bera, M. Ghosh, Opt. Commun. 387 (2017) 166;
(b) S. Saha, S. Pal, J. Ganguly, M. Ghosh, Superlattice Microstruct. 88 (2015) 620. [6] (a) J.H. Yuan, J.S. Huang, M. Yin, Q.J. Zeng, J.P. Zhang, Opt. Commun. 283
(2010) 3529;
(b) P. Sujanah, A.J. Peter, C.W. Lee, Phase Transitions 90 (2017) 21.
[7] (a) M. Kırak, S. Yılmaz, M. Gençaslan, J. Microelectron. Optoelectron. 5 (2010) 1;
(b) F.K. Boz, B. Nisancı, S. Aktas¸, S.E. Okan, Appl. Surf. Sci. 387 (2016) 76. [8] S.M. Arif, A. Ghosh, A. Bera, M. Ghosh, Photonics Nanostruct. Fundam. Appl. 31
(2018) 8.
[9] M. Amini, M. Soleimani, M.H. Ehsani, Superlattice Microstruct. 112 (2017) 680. [10] (a) B. Çakır, Y. Yakar, A. €Ozmen, Physica B 458 (2015) 138–143.(b), B. Çakır, Y.
Yakar, A. €Ozmen, 510 (2017) 86.
[11] (a) A. Zamani, T. Azargoshasb, E. Nikname, Superlattice Microstruct. 110 (2017) 221;
(b) A. Zamani, T. Azargoshasb, E. Nikname, E. Mohammadhosseini, Optik 142 (2017) 273.
[12] E. Kasapoglu, C.A. Duque, M.E. Mora-Ramos, R.L. Restrepo, F. Ungan, U. Yesilgul, H. Sarı, I. Sokmen, Mater. Chem. Phys. 154 (2015) 170.
[13] (a) E.C. Niculescu, D. Bejan, Philos. Mag. 97 (2017) 2089;
(b) A.R. Jafari, Y. Naimi, S. Davatolhagh, Opt. Quant. Electron. 45 (2013) 517. [14] (a) Z.H. Zhang, G.C. Zhuang, K.X. Guo, J.H. Yuan, Superlattice Microstruct. 100
(2016) 440;
(b) S. Saho, K.X. Guo, Z.H. Zhang, N. Li, C. Peng, Superlattice Microstruct. 48 (2010) 541.
[15] (a) E. Ghazi, A. Jorio, L. Zorkani, Opt. Commun. 331 (2014) 73;
(b) E. Ghazi, A. Jorio, L. Zorkani, J. Optoelectron. Adv. Mater. 16 (2014) 1242. [16] (a) G. Safarpour, M. Novzari, M.A. Izadi, S. Yazdanpanahi, Physica E 66 (2015)
148;
(b) G. Safarpour, M.A. Izadi, N. Khajehei, M. Dialameh, Superlattice Microstruct. 76 (2014) 186.
[17] E. Sadeghi, M. Moradi, Chin. J. Phys. 54 (2016) 773.
[18] (a) Y. Yakar, B. Çakır, A. €Ozmen, J. Lumin. 134 (2013) 778–783;
(b) A. €Ozmen, B. Çakır, Y. Yakar, J. Lumin. 137 (2013) 259–268.
[19] V.I. Boichuk, I.V. Bilynskyi, R.Y. Leshko, L.M. Turyanska, Physica E 44 (2011) 476. [20] (a) B. Çakır, Y. Yakar, A. €Ozmen, Comput. Phys. Commun. 188 (2015) 88–93;
(b) B. Çakır, Ü. Atav, Y. Yakar, A. €Ozmen, Chem. Phys. 457 (2016) 61–68. [21] (a) Y. Naimi, A.R. Jafari, Physica B 420 (2013) 81;
(b) A.R. Jafari, Y. Naimi, J. Comput. Electron. 12 (2013) 36.
[22] A.L. Morales, A. Montes, S.Y. Lopez, N. Raigoza, C.A. Duque, Phys. Status Solidi C 0 (2003) 652.
[23] S.A. Ndengu�e, O. Motapon, R.L.M. Melono, A.J. Etindele, J. Phys. B At. Mol. Opt. Phys. 47 (2014), 015002.
[24] R. Dutt, A. Mukherjee, Y.P. Varshni, Phys. Lett. A280 (2001) 318.
[25] A. Corella- Madue~no, R.A. Rosas, J.L. Marin, R. Riera, Int. J. Quantum Chem. 77 (2000) 509.
[26] S. Waugh, A. Chowdhury, B. Banerjee, J. Phys. B At. Mol. Opt. Phys. 43 (2010) 225002.
[27] J.L. Marin, S.A. Cruz, J. Phys. B At. Mol. Opt. Phys. 25 (1992) 4365. [28] S. Lumb, S. Lumb, V. Prasad, Eur. Phys. J. Plus 130 (2015) 149. [29] B. Çakır, Y. Yakar, A. €Ozmen, Opt. Commun. 311 (2013) 222.
[30] A. Zounoubi, K. El Messaoudi, I. Zorkani, A. Jorio, Superlattice Microstruct. 30 (2001) 189.
[31] K.D. Sen, J. Garza, R. Vargas, N. Aquino, Phys. Lett. 295 (2002) 299.
[32] F. Holka, P. Neogrady, V. Kell€o, M. Urban, G.H.F. Diercksen, Mol. Phys. 103 (2005) 2747.
[33] (a) A. Ghosh, M. Ghosh, J. Phys. Chem. Solids 112 (2018) 252;
(b) A. Bera, M. Ghosh, Physica B 515 (2017) 18.
[34] (a) Y. Yakar, B. Çakır, A. €Ozmen, Chem. Phys. Lett. 708 (2018) 138;
(b) Y. Yakar, B. Çakır, A. €Ozmen, Chem. Phys. 513 (2018) 213.
[35] R.L.M. Melono, C.F. Lukong, O. Motopan, J. Phys. B At. Mol. Opt. Phys. 51 (2018) 205005.
[36] O. Motopan, S.A. Ndengue, K.D. Sen, Int. J. Quantum Chem. 111 (2011) 4425. [37] J.G. Kirkwood, Phys. Z. 33 (1932) 57.
[38] A.D. Sa~nu-Ginarte, L. Ferrer-Galindo, R.A. Rosas, A. Corella-Madue~no, Ri Betancourt-Riera, L.A. Ferrer-Moreno, R. Riera, J. Phys. Commun. 2 (2018) 015001.
[39] J. Autschbach, D. Peng, M. Reiher, J. Chem. Theory Comput. 8 (2012) 4239. [40] P.W. Fowler, Chem. Phys. Lett. 156 (1989) 494.
[41] T.M. Ho, T.C. Chang, Int. J. Quantum Chem. 57 (1996) 229.
[42] (a) B. Cakır, A. Ozmen, U. Atav, H. Yuksel, Y. Yakar, Int. J. Mod. Phys. C 18 (2007) 61;
(b) B. Cakır, A. Ozmen, U. Atav, H. Yuksel, Y. Yakar, Int. J. Mod. Phys. C 19 (2008) 599.
[43] Y. Yakar, A. Ozmen, B. Cakır, H. Yuksel, J. Chin. Chem. Soc. 54 (2007) 1139. [44] J. Mitroy, M.S. Safronova, C.W. Clark, J. Phys. B At. Mol. Opt. Phys. 43 (2010)
202001.
[45] S.H. Patil, Y.P. Varshni, Can. J. Phys. 82 (2004) 647.
[46] A. Flores-Riveros, A. Rodrίguez-Contreras, Phys. Lett. A 372 (2008) 6175. Fig. 8. z-component of electric field gradient for the excited states 1s2p, 1s3d