D O I: 1 0 .1 5 0 1 / C o m m u a 1 _ 0 0 0 0 0 0 0 7 6 6 IS S N 1 3 0 3 –5 9 9 1
SPECIAL SMARANDACHE CURVES IN R3
1
NURTEN (BAYRAK) GÜRSES, ÖZCAN BEKTA¸S, AND SALIM YÜCE
Abstract. In this study, we determine TN-Smarandache curves whose posi-tion vector is composed by Frenet frame vectors of another regular curve in Minkowski 3-space R3
1. Then, we present some characterisations of
Smaran-dache curves and calculate Frenet invariants of these curves. Moreover, we classify TN; TB; NB and TNB-Smarandache curves of a regular curve para-metrized by arc length by presenting a brief table with respect to the causal character of . Also, we will give some examples related to results.
1. Introduction
In di¤erential geometry, there are many important consequences and properties of curves studied by some authors [1, 2, 3]. Researchers always introduce some new curves by using the existing studies. Special Smarandache curves are one of them. Smarandache curve is de…ned as a regular curve whose position vector is composed by Frenet frame vectors of another regular curve in Minkowski spacetime in [4]. Special Smarandache curves have been studied by some authors [4, 5, 6]. M. Turgut and S. Y¬lmaz have identi…ed a special case of such curves and called them TB2-Smarandache curves in the space R41[4]. They have dealt with a special Smarandache curve which is de…ned by the tangent and second binormal vector …elds. Besides, they have computed formulae of this kind of curves by the method expressed in [4]. A. T. Ali has introduced some special Smarandache curves in the Euclidean space [5]. Special Smarandache curves such as TN1, TN2, N1N2 and TN1N2-Smarandache curves according to Bishop frame in Euclidean 3-space have been investigated by Çetin and Tunçer [6]. Furthermore, they have studied di¤erential geometric properties of these special curves and they have calculated the …rst and second curvature (natural curvatures) of these curves. Also, they have found the centres of the curvature spheres and osculating spheres of Smarandache curves.
Received by the editors: March 28, 2016, Accepted: May 24, 2016.
2010 Mathematics Subject Classi…cation. 53A35, 51B20.
Key words and phrases. Minkowski space, Frenet invariants, Smarandache curves.
c 2 0 1 6 A n ka ra U n ive rsity C o m m u n ic a tio n s d e la Fa c u lté d e s S c ie n c e s d e l’U n ive rs ité d ’A n ka ra . S é rie s A 1 . M a th e m a t ic s a n d S t a tis t ic s .
In addition, special Smarandache curves according to Darboux frame in Euclid-ean 3-space have been introduced in [7]. They have investigated special Smaran-dache curves such as Tg; Tn; gn and Tgn-SmaranSmaran-dache curves. Furthermore, they have found some properties of these special curves and calculated normal curvature, geodesic curvature and geodesic torsion of these curves.
In this study, we …rstly mention the fundamental properties and Frenet invari-ants of curves in R3
1. Then, we give the de…nition of TN; TB; NB and TNB-Smarandache curves of a regular curve parametrized by arc length in R3
1. In sections 2-4, we investigate and calculate Frenet invariants of TN-Smarandache curves of a timelike, spacelike and null curves in R3
1. In section 5, we obtain the characterisations of TN; TB; NB and TNB-Smarandache curves of a regular curve parametrized by arc length by presenting a brief table. We classify general results of these Smarandache curves with respect to the causal character of . Also, we present some examples.
2. Preliminaries
The Minkowski 3-space R31 is the real vector space provided with the standard ‡at metric given by
<; >= dx21+ dx22+ dx23;
where (x1; x2; x3) is a rectangular coordinate system of R31. An arbitrary vector v= (v1; v2; v3) in R31 can have one of three Lorentzian causal characters; it can be spacelike if hv; vi > 0 or v = 0; timelike if hv; vi < 0 and null (lightlike) if hv; vi = 0 and v 6= 0. Similarly, an arbitrary curve = (s) can be locally spacelike, timelike or null (lightlike) if all of its velocity vectors 0(s) are spacelike, timelike or null (lightlike), respectively. We say that a timelike vector is future pointing or past pointing if the …rst component of the vector is positive or negative, respectively. Also, the vector product of any vectors x = (x1; x2; x3) and y = (y1; y2; y3) in R31is de…ned by x y= e1 e2 e3 x1 x2 x3 y1 y2 y3 = (x2y3 x3y2; x1y3 x3y1; x2y1 x1y2) ; where e1 e2= e3; e2 e3= e1; e3 e1= e2: Let = (s) be a regular curve parametrized by arc length in R3
1and fT; N; B; ; g be its Frenet invariants, where fT; N; Bg ; and are moving Frenet frame, cur-vature and torsion of (s), respectively. The Frenet formulae of = (s) are described with respect to the causal character of 0(s). For an arbitrary timelike
curve (s) in the Minkowski space R3
1, the following Frenet formulae are given as follows ([8]): 8 < : T0= N N0= T + B B0= N; (2.1) where hT; Ti = 1; hN; Ni = hB; Bi = 1; hT; Ni = hT; Bi = hN; Bi = 0. Then, we write Frenet invariants in this way: T(s) = 0(s), (s) = jjT0(s)jj, N(s) = T0(s)= (s), B(s) = T(s) N(s) and (s) = hN(s)0, B(s)i.
For an arbitrary spacelike curve (s) in the space R3
1, the Frenet formulae are given as below ([8]): 8 < : T0= N N0= " T + B B0= N; (2.2) where " = 1. If " = 1, then (s) is a spacelike curve with spacelike principal normal N and timelike binormal B. Also, hT; Ti = hN; Ni = 1; hB; Bi = 1 and hT; Ni = hT; Bi = hN; Bi = 0. If " = 1 , then (s) is a spacelike curve with timelike principal normal N and spacelike binormal B. Besides, hT; Ti = hB; Bi = 1; hN; Ni = 1 and hT; Ni = hT; Bi = hN; Bi = 0. We de…ne Frenet invariants for spacelike curves in this way: T(s) = 0(s); (s) =p" < T0(s); T0(s) >; N(s) = T0(s)= (s); B(s) = T(s) N(s) and (s) = " < N0(s); B(s) >.
In addition, the Frenet formulae for a null curve parametrized by distinguished parameter (s) in R31, are given as follows:
8 < : T0= B N0= B B0= T+ N; (2.3) where hT; Ti = hN; Ni = hT; Bi = hN; Bi = 0; hB; Bi = 1; hT; Ni = 1 and T B= T, T N= B; B N= N. In this state, T and N are null vectors and B is a spacelike vector. We describe Frenet invariants T(s) = 0(s); (s) = jjT0(s)jj; N(s) = ((1= )( T + (1= )0T0+ (1= )T00))(s); B(s) = ((1= )T0)(s) and
(s) =(1=2)[(1= 3)jjT00jj2 ((1= )0)2 ](s) ([9]).
De…nition 2.1([4]). Let = (s) be a regular curve parametrized by arc length in R3
1 with its Frenet frame fT; N; Bg. Then, TN; TB; NB and TNB-Smarandache curves of are de…ned, respectively, as follows:
T N = 1 p 2(T+N) ; T B= 1 p 2(T + B) ; N B= 1 p 2(N + B) ;
T N B= 1 p
3(T + N + B) :
In the following sections, we investigate special TN-Smarandache curves for a given regular curve in R3
1. We consider Frenet invariants fT; N; B; ; g and fT ; N ; B ; ; g for and its TN-Smarandache curve T N, respectively.
3. TN-Smarandache curves of a timelike curve in R3 1
De…nition 3.1. Let the curve = (s) be a timelike curve parametrized by arc length in R3
1. Then, TN-Smarandache curves of can be determined by the Frenet vectors of such as:
T N = 1 p
2(T + N) ; (3.1)
where T is timelike, N and B are spacelike.
Let us investigate the causal character of TN-Smarandache curve T N: By dif-ferentiating Equation (3.1) with respect to s and using Equation (2.1), we get
0 T N = d T N ds = 1 p 2( T + N + B) ; (3.2) and h 0T N; 0 T Ni = 2 2 :
Therefore, there are two possibilities for the causal character of T N under the conditions 6= 0 and = 0. Because of the fact that 22 6= 1 for at least one 2 R, we know that s is not arc-length of T N. Assume that s is arc-length of T N: Case 3.1. If 6= 0; then TN-Smarandache curve T N is a spacelike curve.
If we rearrange Equation (3.2), we obtain the tangent vector of T N as below:
T = 1 j j( T + N + B) ; (3.3) where ds ds = j j p 2: (3.4)
i) Let T N be a spacelike curve with timelike binormal. If we di¤erentiate Equation (3.3) with respect to s, we obtain
dT ds ds ds = 1 2( 1T+ 2N+ 3B) ; (3.5) where 8 < : 1= 0 0 2 0 2= 2 0 0 0 + 2 0 3= 0 02 :
Substituting Equation (3.4) with Equation (3.5), we gain _ T = p 2 j 3j( 1T+ 2N+ 3B) :
According to the de…nition of the Frenet invariants of a spacelike curve with timelike binormal, we can calculate the curvature and principal normal vector …elds of T N such as: = p 2 j 3j q ( 2 1+ 22+ 23) and N = p 2 1 1+ 22+ 23 ( 1T+ 2N+ 3B) ; respectively. Furthermore, we have
B = T N = 1 j jp 2 1+ 22+ 23 T N B 1 2 3 :
Based upon this calculation, the binormal vector of T N is
B = 1 j jp 2 1+ 22+ 23 ( 1T+ 2N+ 3B) ; where 8 < : 1= 3 2 2= 1+ 3 3= 2+ 1:
So, the torsion of T N is given as below:
= 3 1 2+ 3 2( 1+ 3 ) 2 3( 3 2+ 1 0 1+ 2 0 2) 2 3( 3( 1 3 ) + 3 0 2+ 2 0 3) 2 2( 3 2+ 1 0 1+ 3 0 3) + 21( 3 2+ 2( 1 3 ) 2 0 2 3 0 3) + 1( 22 2+ 2( 2 0 1+ 1 0 2+ 3( 3 2+ 3 0 1+ 1 0 3)) j j ( 2 1+ 22+ 23)2 : ii) Let T N be a spacelike curve with timelike principal normal, then the
T = 1 j j( T + N + B) ; N = p 2 1 1 22 23 ( 1T+ 2N+ 3B) ; B = 1 j jp 2 1 22 23 ( 1T+ 2N+ 3B) ; = p 2 j 3j q ( 2 1+ 22+ 23); = 3 1 2+ 3 2( 1 3 ) + 2 3( 3 2+ 1 0 1+ 2 0 2) + 2 3( 3( 1 3 ) + 3 0 2+ 2 0 3) + 22( 3 2+ 1 0 1 3 0 3) + 2 1( 3 2+ 2( 1 3 ) + 2 0 2 3 0 3) 1( 22 2+ 2( 2 0 1+ 1 0 2+ 3( 3 2+ 3 0 1+ 1 0 3)) j j ( 2 1+ 22+ 23)2 : Case 3.2. If = 0, then TN-Smarandache curve T N is a null curve.
If we di¤erentiate Equation (3.1) with respect to s, the tangent vector of T N can be written namely:
T = p1 2
ds
ds (T + N): (3.6)
By di¤erentiating Equation (3.6), we obtain _ T = p1 2 (T + N); where = d 2s ds 2 + ds ds 2 0+ 2 ! :
From the calculations of Frenet invariants of a null curve, we …nd that the curvature of T N is equal to zero. So, there is no calculation for N and B in this case.
4. TN-Smarandache curves of a spacelike curve in R3 1
4.1. TN-Smarandache curves of a spacelike curve with timelike binormal. De…nition 4.1. Let the curve = (s) be a spacelike curve parametrized by arc length with timelike binormal in R3
1. Then, TN-Smarandache curves of can be de…ned by the frame vectors of such as:
T N = 1 p
2(T + N) ; (4.1)
Let us analyze the causal character of T N: By di¤erentiating Equation (4.1) with respect to s, we have
0 T N = 1 p 2( T+ N + B) ; and h 0T N; 0 T Ni = 2 2 2 2 :
In this situation, there are three possibilities for the causal character of T N under the circumstances 2 2 2< 0; 2 2 2> 0 andp2j j = j j. Because of the fact that 2 2 2
2 6= 1 for at least one or , we know that s is not arc-length of T N: Suppose that s is arc-length of T N.
Case 4.1. If 2 2 2< 0; then TN-Smarandache curve
T N is a timelike curve. If we di¤erentiate Equation (4.1) with respect to s, we obtain the tangent vector of T N as given below: T =p 1 j2 2 2j( T+ N + B) ; (4.2) where ds ds = p j2 2 2j p 2 : (4.3)
By di¤erentiating Equation (4.2) with respect to s, we have dT ds ds ds = 1 q j2 2 2j3 ( 1T+ 2N+ 3B) ; (4.4) where 8 < : 1= 4 2 0+ 2 0 2 2 2 ( 2+ 0) 2= 4 2 0 2 0 2 2 2 ( 2+ 0+ 2) 3= 4 0 2 2 0 2 2 2 ( + 0):
Substituting Equation (4.3) with Equation (4.4), we gain _
T =
p 2
(2 2 2)2( 1T+ 2N+ 3B) :
By using the de…nition of Frenet invariants of a timelike curve, the curvature and principal normal vector …elds of T N are
= T_ = p 2 (2 2 2)2 q ( 2 1+ 22 23) and N = p 2 1 1+ 22 23 ( 1T+ 2N+ 3B) ;
respectively. Additionally, we gain B = T N = p 2 p j2 2 2jp 2 1+ 22 23 T N B 1 2 3 :
From this calculation, the binormal vector of T N is
B = p 2 p j2 2 2jp 2 1+ 22 23 ( 1T+ 2N+ 3B) ; where 8 < : 1= 3 2 2 = 3 1 3= ( 1+ 2): So, the torsion of T N is given by:
= 3 1 2+ 32( 1+ 3 ) 23( 3 2+ 1 0 1+ 2 0 2 3 3 0 3) + 2 3( 3( 1+ 3 ) 2 3 0 2 2 2 03) 2 2( 3 2+ 1 0 1 3 03+ 2 2 0 2) + 21( 3 2 + 2( 1+ 3 ) + 2 0 2+ 1 0 1) + 1( 22 2 23 2+ 2 2 0 1+ 2 2 1 0 2 3( 3 0 1+ 2 1 0 3)) j2 2 2j ( 2 1+ 22 23)2 : Case 4.2. If 2 2 2> 0; then TN-Smarandache curve
T N is a spacelike curve. i) Let T N be a spacelike curve with timelike binormal, then the Frenet
in-variants of T N are given as below:
T = p 1 2 2 2( T+ N + B), N =p 1 2 1+ 22 23 ( 1T+ 2N+ 3B), B =p p2 2 2 2p 2 1+ 22 23 ( 1T+ 2N+ 3B), = (2 2p2 2)2 p ( 2 1+ 22 23), = 3 1 2+ 32( 1+ 3 ) 23( 3 2+ 1 0 1+ 2 0 2 3 3 0 3) + 2 3( 3( 1+ 3 ) 2 3 0 2 2 2 03) 2 2( 3 2+ 1 0 1 3 03+ 2 2 0 2) + 21( 3 2 + 2( 1+ 3 ) + 2 0 2+ 1 0 1) + 1( 22 2 23 2+ 2 2 0 1+ 2 2 1 0 2 3( 3 0 1+ 2 1 0 3)) j2 2 2j( 2 1+ 22 23)2 : ii) Let T N be a spacelike curve with timelike principal normal, then the
T = p 1 2 2 2( T+ N + B), N =p 21 1 22+ 23 ( 1T+ 2N+ 3B), B =p p2 2 2 2p 2 1 22+ 23 ( 1T+ 2N+ 3B), = p2 (2 2 2)2 p ( 2 1 22+ 23), = 3 1 2+ 32( 1+ 3 ) 23( 3 2+ 1 0 1+ 2 0 2 3 3 0 3) + 2 3( 3( 1+ 3 ) 2 3 0 2 2 2 03) 2 2( 3 2+ 1 0 1 3 03+ 2 2 0 2) + 21( 3 2 + 2( 1+ 3 ) + 2 0 2+ 1 0 1) + 1( 22 2 23 2+ 2 2 0 1+ 2 2 1 0 2 3( 3 0 1+ 2 1 0 3)) j2 2 2j( 2 1+ 22 23)2 : Case 4.3. If p2j j = j j, then TN-Smarandache curve T N is a null curve.
The tangent vector of T N and its derivative with respect to s are obtained, respectively, 8 > > < > > : T = p1 2 ds ds ( T+ N + B) _ T = p1 2( 1T+ 2N+ 3B); where 8 > > > > > < > > > > > : 1= d 2s ds 2( ) + dsds 2 0 2 2= d 2 s ds 2( ) + dsds 2 0 2 + 2 3= d 2s ds 2( ) + dsds 2 ( 0+ ) :
Based upon these calculations, the Frenet invariants of T N are namely:
N = (( 3)2+ 2 1 2)( p 2 ds ds + 1) [ 1 3( 3)0+ ( 1)2( 2)0+ ( 1)0 2 1])T +(( 3)2+ 2 1 2)( p 2 ds ds + 2) [ 2 3( 3)0+ ( 1)0( 2)2+ ( 2)0 2 1)])N +(( 3)2+ 2 1 2)( p 2 2 dsds + 3) [( 3) 2 ( 3)0+ ( 1)0 2+ 3 2 1+ 3])B (( 3)2+2 1 2) 3 2 ; B = p 1 ( 3)2+2 1 2 1 T+ 2N+ 3B; =p1 2 p ( 3)2+ 2 1 2; = (( 3)2+2 1 2)3( 3+2 1 2) 4( 3( 3)0+ 1( 2)0+( 1)0 2)2 8p2(( 1)2+2 1 2) 3 2 :
4.2. TN-Smarandache curves of a spacelike curve with timelike principal normal.
De…nition 4.2. Let the curve = (s) be a spacelike curve parametrized by arc length with timelike principal normal in R31. Then, TN-Smarandache curves of can be de…ned by the Frenet vectors of such as:
T N = 1 p
2(T + N) ; (4.5)
where N is timelike, T and B are spacelike.
Let us search the causal character of T N: If we di¤erentiate Equation (4.5) with respect to s, we get 0 T N = 1 p 2( T + N + B) : Then, we can obtain
h 0T N; 0T Ni = 2 2 :
Hence, there are two possibilities for the causal character of T N under the condi-tions 6= 0 and = 0. Because of the fact that 22 6= 1 for at least one 2 R, we suppose that s is arc-length of T N.
Case 4.4. If 6= 0, then TN-Smarandache curve T N is a spacelike curve. i) Let T N be a spacelike curve with timelike binormal, then the Frenet
invariants of T N are given as follows:
T = 1 j j( T + N + B) ; N = q 1 2 1 22+ 23 ( 1T+ 2N+ 3B) ; B = p 2 j j q 2 1 2 2+ 2 3 (!1T+!2N+ !3B) ; = p 2 j 3j q 2 1 22+ 23 ; = 3 1 2+ 3 2( !1+ 3 ) + 2 3( 3!2 !1 0 1+ !2 0 2) 2 3( 3( !1+ !3 ) + !3 0 2+ !2 0 3)+ 2 2( 3!2+ !1 0 1+ !3 0 3) + 21( 3!2 + 2( !1+ !3 ) !2 0 2+ !3 0 3) + 1( 22 2+ 2( 2 0 1 !1 0 2+ 3( 3!2 !3 0 1+ !1 0 3)) j j 21 2 2+ 2 3 2 ;
where 8 < : 1= 0+ 0j j + 2j j 2= 0+ 0 j j + 2j j + 2j j 3= 0+ j j + 0j j and 8 < : !1= 3 2 !2= 1+ 3 !3= 1 2:
ii) Let T N be a spacelike curve with timelike principal normal, then the Frenet invariants of T N are as follows:
T = 1 j j( T + N + B) ; N = p 1 q 2 1+ 22 23 ( 1T+ 2N+ 3B) ; B = p 2 j j q 2 1+ 22 23 (!1T+!2N+ !3B) ; = p 2 j 3j 2 1+ 2 2 2 3 ; = 3 1!2 32( !1+ !3 ) 23( 3!2 !1 0 1+ !2 0 2) + 2 3( 3( !1+ !3 ) + !3 0 2+ !2 0 3)+ 2 2( 3!2 !1 0 1 !3 0 3) 21( 3!2 + 2( !1+ !3 ) !2 0 2+ !3 0 3) + 1( 22!2+ 2( !2 0 1+ !1 0 2 3( 3!2 !3 0 1+ !1 0 3)) j j 21 2 2+ 2 3 2 : Case 4.5. If = 0, then TN-Smarandache curve T N is a null curve.
If we di¤erentiate Equation (4.5) with respect to s, we obtain the tangent vector of T N as below: T = p1 2 ds ds (T + N): (4.6) Then, we get _ T = p1 2 ds ds (T + N); where = d 2s ds 2 + ds ds 2 0+ 2 !
From the calculations of Frenet invariants of a null curve, the curvature of T N is equal to zero. So, there is no calculation for N and B in this case.
5. TN-Smarandache curves of a null curve in R3 1
De…nition 5.1. Let the curve = (s) be a null curve parametrized by pseudo arc length in R31. Then, TN-Smarandache curves of can be de…ned by the Frenet vectors of such as:
T N = 1 p
2(T + N) ; (5.1)
where T and N are null and B is spacelike.
Let us investigate the causal character of T N. By di¤erentiating Equation (5.1) with respect to s, we have
0 T N = d T N ds = 1 p 2( )B; and h 0T N; 0 T Ni = ( )2 2 :
In this state, there are two possibilities for the causal character of T N under the condition 6= and = . Since ( 2 )2 6= 1, for at least one or , we know that s is not arc-length of T N: Let s be arc-length of T N.
Case 5.1. If 6= ; then TN-Smarandache curve T N is a spacelike curve. If we di¤erentiate Equation (5.1) with respect to s; we obtain the tangent vector of T N as follows:
T = p1 2
ds
ds ( )B: (5.2)
i) Let T N be a spacelike curve with timelike binormal. If we di¤erentiate Equation (5.2) with respect to s, we obtain
_ T = p1 2( 1T+ 2N+ 3B); where 8 > < > : 1= dsds 2 ( + 2) 2= dsds 2 ( 2 ) 3= d 2 s ds 2 + ( ) dsds 2 ( 0+ 0) :
Then, Frenet invariants of T N are as follows: N = 1Tq+ 2N+ 3B 2 3+ 1 2 ; B = p1 2 ds ds 1 q 2 3+ 1 2 ( )( 2T+ 1N); = p1 2 q ( 23+ 1 2); = p1 2 ds ds ( ) " 2 1 22 2 23+ 1 2 2 2 3 03+ 01 2+ 1 02 + " 1 2 3+ 1 2 2 02 2 3 + 01 3 #
ii) Let T N be a spacelike curve with timelike principal normal. Then, Frenet invariants of T N are given below:
T = p1 2 ds ds ( )B; N = 1Tq+ 2N+ 3B 2 3 1 2 ; B = p1 2 ds ds 1 q 2 3 1 2 ( )( 2T+ 1N); = p1 2 q ( 23 1 2); = p1 2 ds ds ( ) " 2 1 22 2 23+ 1 2 2 2 3 03+ 01 2+ 1 02 + 2 1 3+ 1 2 2 02+ 2 3 01+ 3 #
Case 5.2. If = ; then TN-Smarandache curve T N is a null curve. In this case, there is no calculation of Frenet invariants of T N.
6. General results and examples
In this section, we will obtain the characterisations of TN; TB; NB and TNB-Smarandache curves of a regular curve parametrized by arc length in a brief table given in the following without calculations. The calculations can be done by
using the similar way giving in Section 2-5. We will classify general results of these Smarandache curves with respect to the causal character of . Also, we will give some examples related to Table 6.1.
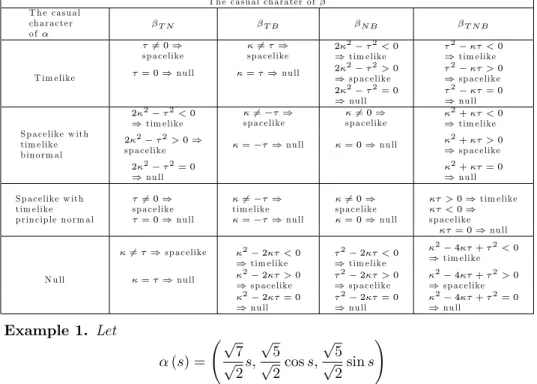
TABLE 6.1. The characterisations of Smarandache curves in Minkowski Space
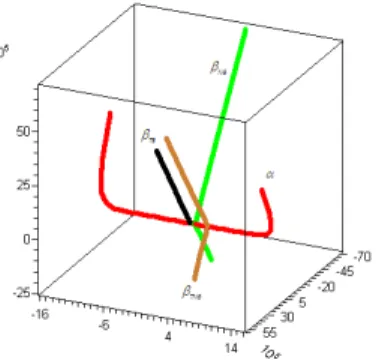
T h e c a s u a l ch a ra t e r o f T h e c a s u a l ch a ra c te r o f T N T B N B T N B 6= 0 ) s p a c e like s p a c e like6= ) 2 2 2< 0 ) tim elike 2 < 0 ) tim elike T im e like = 0) nu ll = ) nu ll 2 2 2> 0 ) sp a celike 2 > 0 ) sp a celike 2 2 2= 0 ) nu ll 2 = 0 ) nu ll 2 2 2< 0 ) tim elike 6= ) s p a c e like s p a c e like6= 0 ) 2+ < 0 ) tim elike S p a c e like w ith t im e like b in o rm a l 2 2 2> 0) s p a c e like = ) nu ll = 0) nu ll 2+ > 0 ) sp a celike 2 2 2= 0 ) nu ll 2+ = 0 ) nu ll S p a c e like w ith t im e like p rin c ip le n o rm a l 6= 0 ) s p a c e like = 0) nu ll 6= ) t im e like = ) nu ll 6= 0 ) s p a c e like = 0) nu ll > 0) tim elike < 0) s p a c e like = 0) nu ll 6= ) sp a celike 2 2 < 0 ) tim elike 2 2 < 0 ) tim elike 2 4 + 2< 0 ) tim elike N u ll = ) nu ll 2 2 > 0 ) sp a celike 2 2 > 0 ) sp a celike 2 4 + 2> 0 ) sp a celike 2 2 = 0 ) nu ll 2 2 = 0 ) nu ll 2 4 + 2= 0 ) nu ll Example 1. Let (s) = p 7 p 2s; p 5 p 2cos s; p 5 p 2sin s !
a timelike curve parametrized by arc length.
From the calculating of the Frenet invariants of a spacelike curve with timelike principal normal, we get = p5=2 > 0 and = p7=2 6= 0. Hence, it follows that 6= , 2 2 2> 0 and 2 > 0. From Table 6.1, under this conditions all of TN; TB; NB and TNB-Smarandache curves of are spacelike curves. Indeed, they can be given by using De…nition 2.1 respectively, as follows:
T N(s) = 1 2
p
7; p5 sin s +p2 cos s ;p5 cos s p2 sin s T B(s) = p 7 +p5 (1; sin s; cos s) N B(s) = 1 2 p
5; p2 cos s +p7 sin s ; p2 sin s +p7 cos s T N B(s)
=p1 6
p
It is obvious that all of the above curves are spacelike curves. They are shown in Figure 1. Example 2. Let (s) = p1 5sinh s; 1 p 5cosh s; p 6 p 5s !
a spacelike curve parametrized by arc length with timelike binormal.
If we calculate Frenet invariants of a timelike curve, we get = 1=p5 6= 0 and = p6=5. Hence, we have 2 2 2 < 0, 6= < 0 and 2+ < 0. From Table 6.1, TN; TNB-Smarandache curves of are timelike curves, and TB; NB-Smarandache curves of are spacelike curves given as below:
T N(s) = p110 cosh s + p
5 sinh s; sinh s +p5 cosh s;p6 T B(s) = 1 p 6 p 10 (cosh s; sinh s; 1) N B(s) = p110 p
5 sinh s p6 cosh s;p5 cosh s p6 sinh s; 1
T N B(s) = p1
15 1
p
6 cosh s +p5 sinh s; 1 p6 sinh s +p5 cosh s;p6 1 They are shown in Figure 2.
Example 3. Let (s) = p 3 2 cosh s; p 3 2 sinh s; s 2 !
be a nonplanar spacelike curve parametrized by arc length with timelike principal normal.
From the calculating of Frenet invariants of a timelike curve, we have =p3=2 6= 0 and = 1=2 6= 0. Hence, it follows that 6= , < 0. Thus, from Table 6.1, TN; NB and TNB-Smarandache curves of are spacelike curves and TB Smarandache curve of is a timelike curve given as below:
T N(s) = 2p12 p
3 + 2 sinh s + cosh s;p3 cosh s + 2 sinh s; 1 T B(s) = 2p12
p
3 1 sinh s; p3 1 cosh s;p3 + 1 N B(s) = 2p12 2 cosh s sinh s; 2 sinh s cosh s;
p 3 T N B(s) = 2p13
p
3 1 sinh s + 2 cosh s; p3 1 cosh s + 2 sinh s;p3 + 1 : They are indicated in Figure 3.
Example 4. Let
(s) = (cosh s; sinh s; 1)
be a planar spacelike curve parametrized by arc length with timelike principal nor-mal.
Frenet invariants of this curve can be calculated namely: = 1 6= 0 and = 0. Hence, it follows that 6= and = 0. From Table 6.1 TB-Smarandache curve is timelike curve, NB-Smarandache curve is spacelike curve and TN; TNB-Smarandache curves are null curves such that:
T N(s) = p12(cosh s + sinh s; cosh s + sinh s; 0) T B(s) = p12(sinh s; cosh s; 1)
N B(s) = p12(cosh s; sinh s; 1)
T N B(s) = p13(cosh s + sinh s; cosh s + sinh s; 1)
They are illustrated in Figure 4. Example 5. Let
(s) = (sinh s; s; cosh s) be a null curve.
Frenet invariants of the above null curve can be obtained such that: = 1 6= 0
and = 1=2. Thus, we have 6= , 2 2 = 0, 2 2 < 0 and 2
4 + 2< 0. By using these conditions, it is obvious from Table 6.1, NB; TNB-Smarandache curves are timelike, TN-TNB-Smarandache curve is spacelike curve and TB-Smarandache curve is null curve such that:
T N(s) = 2p12(cosh s; 3; sinh s)
T B(s) = p12(cosh s + sinh s; 1; cosh s + sinh s)
N B(s) = 2p12( cosh s + 2 sinh s; 1; sinh s + 2 cosh s) T N B(s) = 2p13(cosh s + 2 sinh s; 3; sinh s + 2 cosh s) They are indicated in Figure 5.
References
[1] M.P. Do Carmo, Di¤erential Geometry of Curves and Surfaces, Prentice Hall, Englewood Cli¤s, NJ, 1976.
[2] B. O’Neill, Elementary Di¤erential Geometry , Academic Press Inc. New York, 1966. [3] B. O’Neill, Semi-Riemannian Geometry, Academic Press, New York, 1983.
[4] M. Turgut, S. Y¬lmaz, Smarandache Curves in Minkowski Space-time, International Journal of Mathematical Combinatorics, 3 (2008) 51–55.
[5] A. T. Ali, Special Smarandache Curves in the Euclidean Space, International Journal of Math-ematical Combinatorics, 2 (2010) 30–36.
[6] M. Çetin, Y. Tunçer, M. K. Karacan, Smarandache Curves According to Bishop Frame in Euclidean 3- Space, General Mathematics Notes, 20 (2) 2014 50–66
[7] Ö. Bekta¸s, S. Yüce, Special Smarandache Curves According to Darboux Frame in Euclidean 3- Space, Romanian Journal of Mathematics and Computer Science, 3 (2013) 48–59. [8] R. Lopez, Di¤erential Geometry of Curves and Surfaces in Lorentz-Minkowski Space,
Interna-tional Electronic Journal of Geometry, 7 (1) (2014) 44–107
[9] K. L. Duggal, A. Bejancu, Lightlike Submanifolds of Semi Riemannian Manifolds and Appli-cations, Kluwer Academic Publishers, Dordrecht, 1996.
Current address : Nurten (BAYRAK) GÜRSES :Faculty of Art and Sciences, Department of Mathematics, Y¬ld¬z Technical University, 34220, ISTANBUL, TURKEY
E-mail address : nbayrak@yildiz.edu.tr
Current address : Özcan BEKTA¸S: Faculty of Art and Sciences, Department of
Mathemat-ics,Recep Tayyip Erdogan University, 53100, RIZE, TURKEY E-mail address : ozcan.bektas@erdogan.edu.tr
Current address : Salim YÜCE: Faculty of Art and Sciences, Department of Mathematics, Y¬ld¬z Technical University, 34220, ISTANBUL, TURKEY