T.C.
SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
HARİTA PROJEKSİYONLARINDA DEFORMASYON ANALİZLERİ
Osman Sami KIRTILOĞLU YÜKSEK LİSANS TEZİ
HARİTA MÜHENDİSLİĞİ ANABİLİM DALI KONYA, 2010
T.C.
SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
HARİTA PROJEKSİYONLARINDA DEFORMASYON ANALİZLERİ
Osman Sami KIRTILOĞLU
YÜKSEK LİSANS TEZİ
HARİTA MÜHENDİSLİĞİ ANABİLİM DALI KONYA 2010
Bu tez 04/01/ 2010 tarihinde aşağıdaki jüri tarafından oybirliği ile kabul edilmiştir.
Yrd.Doç.Dr. İ. Bülent GÜNDOĞDU Prof. Dr. Cevat İNAL
(Danışman) (Üye)
Doç.Dr. İ. Öztuğ BİLDİRİCİ
ÖZET
YÜKSEK LİSANS TEZİ
HARİTA PROJEKSİYONLARINDA DEFORMASYON ANALİZLERİ
Osman Sami KIRTILOĞLU
Selçuk Üniversitesi Fen Bilimleri Enstitüsü Harita Mühendisliği Anabilim Dalı
Danışman: Yrd. Doç. Dr. İsmail Bülent GÜNDOĞDU 2010, 92 Sayfa
Jüri: Yrd. Doç. Dr. İ. Bülent GÜNDOĞDU Prof. Dr. Cevat İNAL
Doç. Dr. İ. Öztuğ BİLDİRİCİ
Bu çalışmada öncelikle harita projeksiyonu teorisi, projeksiyonlardan kaynaklanan deformasyonlar ve bu deformasyonların analizi ve görselleştirilmesi konuları detaylı olarak ele alınmıştır. Deformasyon analizlerinin gerçekleştirilmesi için yapılan uygulamada, deformasyonların miktarının hesaplanabilmesi için MATLAB yazılımında yardımcı bir program geliştirilmiştir. Deformasyon değerlerinin hesaplanmasında yeryüzünün tamamının gösterildiği projeksiyonlar üzerinde durulmuş ve hesaplamalarda bu projeksiyonlara ait eşitlikler kullanılmıştır. Bu amaçla yeryüzü küre olarak kabul edilmiş ve hesaplamalarda kolaylık açısından
yarıçapı 1 birim olarak değerlendirmeye alınmıştır. Uygulamaya konu olan noktalar orijinal yüzeydeki coğrafi ağın kesişim noktaları olarak seçilmiştir. Görsel analizlerin sağlıklı bir şekilde yapılabilmesi için 5⁰x5⁰ coğrafi ağ kesişim noktaları değerlendirmeye alınmıştır. Bu noktaların her birine ait projeksiyon koordinatları ve deformasyon değerleri program yardımıyla hesaplanmıştır. Hesaplanan deformasyon değerleri, noktadaki maksimum uzunluk deformasyonu , noktadaki minimum uzunluk deformasyonu , meridyen boyunca uzunluk deformasyonu , paralel boyunca uzunluk deformasyonu , maksimum açı deformasyonu ω ve alan deformasyonunun değeri p, şeklindedir. Projeksiyonlara ait deformasyon değerleri hesaplandıktan sonra bu değerlerin öncelikle niceliksel olarak nasıl analiz edileceği incelenmiştir. Daha sonra deformasyon değerlerinin görsel olarak analizi detaylıca ele alınmıştır. Bu kapsamda Tissot endikatrisi, eşdeformasyon eğrileri metodu, renk metodu ve grid ağının deformasyon analizinde kullanımı incelenerek seçilen projeksiyonlara uygulanmıştır. Elde edilen sonuçlarla seçilen projeksiyonlar detaylı bir karşılaştırmaya tabi tutulmuştur. Yapılan karşılaştırmalar sonucunda yeryüzünün tamamının gösterildiği projeksiyonların, hangi amaçlar için daha uygun olduğu incelenmiştir.
Uygulamada ele alınan silindirik projeksiyonlar yerkürenin tamamının gösteriminde, gerek kutup bölgelerinde meydana gelen deformasyon miktarları, gerekse dış meridyenlerin doğru parçaları olarak gösterilmesi ve Dünyayı kapalı bir dikdörtgen şekli ile temsil etmesi nedeni ile pek kullanışlı değildir. Yerkürenin tamamının gösterildiği haritaların üretiminde, tüm loksodrom hatlarını düz hatlar olarak gösteren, denizcilik, havacılık ve yeryüzünde hareketlerin yönlendirilmesi için kullanılan Mercator projeksiyonu gibi özel amaçlar haricinde, en uygun projeksiyonlar bu amaç için özellikle oluşturulan gerçek anlamda olmayan azimutal ve silindirik projeksiyonlardır. Bu gibi projeksiyonlarda kutup bölgelerinde meydana gelen deformasyon miktarları ve dış meridyenlerin yeryüzünün şeklini anımsatması amacıyla karmaşık eğriler olarak oluşturulması nedeni ile gerçek anlamlı projeksiyonlara nazaran daha kullanışlıdır.
Anahtar Kelimeler: Kartografya, Harita Projeksiyonları, Harita Projeksiyon Deformasyonları, Tissot Endikatrisi, Deformasyon Analizleri, Deformasyonların Kartografik Gösterimi
ABSTRACT
Master Thesis
DISTORTION ANALYSIS OF MAP PROJECTIONS
Osman Sami KIRTILOĞLU
Selcuk University
Graduate School of Natural and Applied Sciences Department of Geomatic Engineering
Supervisor: Assist. Prof. Dr. İsmail Bülent GÜNDOĞDU 2010, 92 Papers
Jury: Yrd. Doç. Dr. İ. Bülent GÜNDOĞDU Prof. Dr. Cevat İNAL
Doç. Dr. İ. Öztuğ BİLDİRİCİ
In this study, first of all, map projection theory, map projection distortion, analysis and visualization of these distortions have been discussed in detail. For the realization of the deformation analysis in practice, an auxiliary program was developed by MATLAB programme, to calculate the amount of distortion. At the stage of the calculation of distortion the world map projections have been focused on and equations of these projections have been used. For this purpose, the Earth has been adopted as a globe and its radius were evaluated as 1 unit for convenience in calculations. The points of interest were chosen as the intersection points of the
geographic network of the original surface. 5⁰x5⁰ geographic network intersection points were taken into consideration for the visual analysis can be performed in a consistent way. The projection coordinates and distortion values for each point were calculated with the help of the program. The calculated distortion values are; the maximum linear distortion at any point , the minimum linear distortion at any point
, linear distortion along the parallel , linear distortion along the meridian , maximum angular distortion ω and the areal distortion value p. After calculating the distortion values how to analyze of these quantitative values has been primarily examined, then, the visual analysis of the distortion values are discussed in detail. In this context, Tissot indicatrix, isograms method, color method and the use of graticule in analysis have been discussed and implemented to selected projections. A detailed comparison of selected projections has been carried out with the obtained results. As a result of the comparisons, which world map projection is more appropriate for the purposes has been examined.
In practice, the considered cylindrical projections is not very useful for representation of entire globe because of both occurring distortion quantity in polar regions and show the world in a closed rectangular shape with straight buondary meridians. For special purposes such as all loksodrom lines are straight lines, the most suitable projections created especially for this purpose are pseudo-azimutal and pseudo-cylindrical projections. In these projections the amount of deformation occurring in polar regions and the shape of boundary meridians are complex curves as a reminder of the real shape of the earth, are more useful than cylindrical projections.
Keywords: Cartography, Map Projections, Map Projection Deformations, Tissot Indicatrix, Deformation Analysis, Cartographic Representations of Map Projection Deformations
TEŞEKKÜR
Bu tezin hazırlanmasında her türlü desteğini esirgemeyen, beni her zaman anlayışla karşılayan ve tez danışmanlığımı üstlenerek beni onurlandıran sayın hocam İsmail Bülent GÜNDOĞDU’ya,
Tez çalışmam sırasında yardımlarını esirgemeyen Arş. Gör. Serkan DOĞANALP’e,
Teşkkürü borç bilirim…
Osman Sami KIRTILOĞLU Konya, 2010
İÇİNDEKİLER
1 GİRİŞ ... 1
2 HARİTA PROJEKSİYONU TEORİSİ ... 5
2.1 Yeryüzünün Şekli ve Harita Üretiminde Kullanılan Referans Yüzeyleri ... 5
2.2 Coğrafi Koordinat Sistemi ... 7
2.3 Harita Projeksiyonu Kavramı ... 8
2.4 Harita Projeksiyonlarının Matematiği Hakkında Bazı Temel Prensipler ... 9
2.5 Harita Projeksiyonlarının Özellikleri ... 10
2.6 Harita Projeksiyonlarının Sınıflandırılma Sistemleri ... 11
2.6.1 Geometrik model ve konum ... 12
2.6.2 Geometrik özellikler... 13
2.7 Gerçek Anlamda Olmayan Projeksiyonlar... 14
3 HARİTA PROJEKSİYONLARINDA DEFORMASYONLAR ... 15
3.1 Uzunluk Deformasyonu ... 18
3.2 Referans Yüzeyinden Projeksiyon Yüzeyine Dönüşüm ... 20
3.3 Gauss’un Temel Büyüklükleri ... 24
3.4 Tissot Teoremi ve Ana Yönler ... 25
3.4.1 Deformasyon elipsi ... 26
3.5 Alan Deformasyonu ... 29
3.6 Maksimum Açı Deformasyonu ... 29
3.7 Konform Özellik (Açı Koruma) ... 30
3.8 Alan Koruma ... 31
3.9 Uzunluk Koruma ... 32
3.10 Sıfır Deformasyonlu Hatlar ve Noktalar ... 33
4 HARİTA PROJEKSİYONLARINDA DEFORMASYON ANALİZLERİ ... 34
4.1 Nicel Analizler ... 34
4.2.1 Grid ağının deformasyon analizinde bir görsel araç olarak kullanımı
... 36
4.3 Tissot Endikatrisi ... 41
4.4 Grid Kareler Metodu ... 43
4.5 Eşdeformasyon Eğrileri ... 44
4.6 Renk Metodu ... 45
4.7 Bilinen Şekiller Metodu ... 46
4.8 Deformasyonların Analizi ve Görselleştirilmesi Konusunda Yapılan Çalışmalar ... 48
5 UYGULAMA ... 51
5.1 Projeksiyon Seçimi ... 51
5.2 Deformasyon Analizleri İçin Kullanılan Deformasyon Parametreleri ... ... 55
5.3 Deformasyon Değerlerinin Belirlenmesi ve Analizinde Kullanılan Yazılımlar ... 55
5.4 Değerlendirme ... 57
5.4.1 Konform özelliğe sahip silindirik projeksiyon (Mercator) ... 57
5.4.2 Alan koruyan silindirik projeksiyon (Lambert) ... 61
5.4.3 Sinüsoidal projeksiyon ... 65
5.4.4 Eckert VI projeksiyonu ... 69
5.4.5 Hammer-Aitoff projeksiyonu ... 73
5.4.6 Mollweide projeksiyonu... 77
5.4.7 Wagner VII projeksiyonu ... 80
5.4.8 Eckert V projeksiyonu ... 83
6 TARTIŞMA ... 87
7 SONUÇ VE ÖNERİLER ... 90
TABLO LİSTESİ
Tablo 3.1 Küre üzerindeki dört nokta ... 22
Tablo 4.1 Silindirik alan koruyan (Lambert) bir projeksiyona ait uzunluk deformasyonları ve deformasyon değerleri ... 34
Tablo 5.1 Uygulamada kullanılan projeksiyonlar ... 54
Tablo 5.2 Mercator projeksiyonu deformasyon değerleri (özet) ... 59
Tablo 5.3 Alan koruyan silindirik projeksiyon deformasyon değerleri (özet) ... 63
Tablo 5.4 Sinüsoidal projeksiyon deformasyon değerleri (özet) ... 67
Tablo 5.5 Eckert VI projeksiyonu deformasyon değerleri (özet) ... 71
Tablo 5.6 Hammer-Aitoff projeksiyonu deformasyon değerleri (özet) ... 75
Tablo 5.7 Mollweide projeksiyonu deformasyon değerleri (özet) ... 79
Tablo 5.8 Wagner VII projeksiyonu deformasyon değerleri (özet) ... 82
Tablo 5.9 Eckert V projeksiyonu deformasyon değerleri (özet) ... 85
Tablo 6.1 Alan koruyan projeksiyonlarda maksimum açı deformasyonu değerlerinin birlikte gösterimi ... 87
Tablo 6.2 Açı deformasyonlarının tüm projeksiyon yüzeyi alanındaki oranı (%) ... 88
ŞEKİL LİSTESİ
Şekil 2.1 Küresel yüzeyden düzleme dönüşüm... 9
Şekil 2.2 Düzleme açılabilen üç yüzeyin projeksiyonu: Silindir, koni ve düzlem .... 12
Şekil 2.3 Harita projeksiyon konumları: Normal, eğik ve transversal ... 13
Şekil 3.1 Küresel bir yüzeyin düzleme açılabilmesi için bazı paraleller boyunca kesilmesi ve bu paralellerin iki kere gösterilmesi durumu (Maling, 1992) ... 15
Şekil 3.2 Haritanın kesilmeden sürekli bir yapıya sahip olması durumunda küresel yüzeyin düzleme açılabilmesi için paralel ve meridyenlerin deformasyona uğraması durumu.(Maling, 1992) ... 16
Şekil 3.3 Açısal ve alansal yönden uzunluk deformasyonunun etkisinin gösterilmesi. İlk durumda P noktasının koordinatları (10,10) şeklindedir ... 17
Şekil 3.4 Açısal ve alansal yönden uzunluk deformasyonunun gösterilmesi. ... 17
Şekil 3.5 Sonsuz derecede küçük küresel dörtgen ... 20
Şekil 3.6 Sonsuz derecede küçük olan Şekil 3.5'de verilen dörtgenin düzlem dönüşümü ... 21
Şekil 3.7 Küresel yüzey üzerinde sonsuz derecede küçük daire ... 26
Şekil 3.8 Tissot endikatrisi ya da diğer adıyla distorsiyon elipsi. Şekil 20 de gösterilen sonsuz derecede küçük dairenin düzleme dönüştürülmesi sonucu bir elipse dönüşmesi. ... 27
Şekil 3.9 Teğet ve kesen silindir. ... 33
Şekil 3.10 Teğet ve kesen koni ... 33
Şekil 4.1 Bazı yaygın kullanılan projeksiyonların grid ağları... 37
Şekil 4.3 Paralel aralıklarının ekvatordan uzaklaştıkça azalması ve meridyenlerin
kutuplarda aynı aralıkta kalması durumu. ... 40
Şekil 4.4 Aynı iki paralel çizgi arasında paralel–meridyen hücrelerinin aynı boyda olmaması durumu. ... 40
Şekil 4.5 Paralel–meridyen hücrelerinin boyutlarının kutuplara gidildikçe değişmemesi durumu. ... 41
Şekil 4.6 Sinusoidal projeksiyonda Tissot endikatrisi ... 42
Şekil 4.7 Lambert konform konik projeksiyonda Tissot endikatrisi ... 42
Şekil 4.8 Grid kareler metodu ... 43
Şekil 4.9 Hammer-Aitoff projeksiyonunda maksimum açısal deformasyonun eşdeformasyon eğrileri ile gösterimi ... 44
Şekil 4.10 Bonne projeksiyonuna ait maksimum açı deformasyonu değerlerinin renk metodu uygulaması ... 46
Şekil 4.11 Bilinen şekiller metodu Plate Carree (a), Sinüsoidal (b) ve Miller Silindirik (c) projeksiyonu ... 47
Şekil 4.12 Mollweide projeksiyonunda çizilmiş bir insan kafası figürünün alan koruyan silindirik projeksiyon ve Mercator projeksiyonundaki görünümü ... 47
Şekil 5.1 Projeksiyon hesapları için geliştirilen programa ait örnek görüntü ... 56
Şekil 5.2 Mercator projeksiyonu grid ağı (15⁰x15⁰) ... 58
Şekil 5.3 Mercator projeksiyonu alan deformasyonu ... 60
Şekil 5.4 Mercator projeksiyonu Tissot endikatrisi ... 61
Şekil 5.5 Alan koruyan silindirik projeksiyon grid ağı ... 62
Şekil 5.7 Alan koruyan silindirik projeksiyon Tissot endikatrisi ... 64
Şekil 5.8 Sinüsoidal projeksiyon grid ağı ... 66
Şekil 5.9 Sinüsoidal projeksiyonda maksimum açı deformasyonu ... 68
Şekil 5.10 Sinüsoidal projeksiyonda Tissot endikatrisi ... 68
Şekil 5.11 Eckert VI projeksiyonu grid ağı ... 70
Şekil 5.12 Eckert VI projeksiyonunda maksimum açı deformasyonu ... 72
Şekil 5.13 Eckert VI projeksiyonu Tissot endikatrisi ... 72
Şekil 5.14 Hammer Aitoff projeksiyonu grid ağı ... 74
Şekil 5.15 Hammer Aitoff projeksiyonu maksimum açı deformasyonu ... 76
Şekil 5.16 Hammer Aitoff projeksiyonu maksimum açı deformasyonu eşdeformasyon eğrileri ... 76
Şekil 5.17 Hammer Aitoff projeksiyonu Tissot endikatrisi ... 77
Şekil 5.18 Mollweide projeksiyonu grid ağı ... 78
Şekil 5.19 Mollweide projeksiyonu maksimum açı deformasyonu ... 79
Şekil 5.20 Mollweide projeksiyonu Tissot endikatrisi ... 80
Şekil 5.21 Wagner VII projeksiyonu grid ağı ... 81
Şekil 5.22 Wagner VII projeksiyonu maksimum açı deformasyonu ... 83
Şekil 5.23 Eckert V projeksiyonu grid ağı ... 84
Şekil 5.24 Eckert V projeksiyonu maksimum açı deformasyonu ve alan deformasyonunun birlikte gösterimi ... 85
SEMBOLLER
φ
: Enlemλ : Boylam
: Orta meridyen
R : Referans küre yarıçapı
: Meridyen boyunca uzunluk deformasyonu : Paralel boyunca uzunluk deformasyonu
: Maksimum uzunluk deformasyonu
: Minimum uzunluk deformasyonu
ω : Maksimum açı deformasyonu
1 GİRİŞ
Harita, yeryüzünün tümünün ya da bir parçasının belirli oranlarda küçültülüp işaretleştirilerek bir düzlem üzerinde gösterimidir. Harita üzerinde gösterilen çeşitli özelliklerin, birbirleri ile sahip oldukları ilişkilerin yaklaşık olarak aynı kalması beklenir. Bu işlemdeki başarı, haritanın oluşturulması için seçilen harita projeksiyonunun özelliklerine bağlıdır. Yeryüzü düzleme açılamayan kapalı bir şekil olduğundan küçültme ile birlikte harita projeksiyonları kullanılarak düzleme izdüşüm işlemi de yapılır.
Fiziksel yeryüzünün düzleme açılamayan, eğri ve düzensiz bir yapıya sahip olan bu yüzeyinin üzerinde bulunan noktalar arasındaki ilişkilerin belirlenmesi, düzlem geometri kuralları ile gerçekleştirilemez. Harita projeksiyonlarının amacı, yeryüzü için tanımlanmış bir referans yüzeyi üzerinde belirlenmiş bir koordinat sistemine göre tanımlı noktaları düzlem üzerine ya da düzleme açılabilen yüzeylere belirli matematiksel bağıntılara göre aktarmaktır. Yeryüzü için referans yüzeyi olarak haritanın amacına ya da ölçeğine göre küre ya da dönel elipsoit kullanılır (Uçar ve ark. 2004).
Elipsoit veya küre gibi eğri yüzeyler doğrudan doğruya düzleme açılamazlar. Bu nedenle referans yüzeyine indirgenmiş yeryüzü bilgileri matematiksel ya da geometrik kurallar uygulanarak ya doğrudan doğruya ya da düzleme açılabilen silindir ve koni gibi ara yüzeylere aktarılırlar. Harita projeksiyonunda yararlanılan düzlem ya da düzleme açılabilen koni ve silindir gibi yardımcı yüzeylere “Projeksiyon yüzeyi” adı verilir.
Dünya üzerinde yer alan ve harita yapımına konu olan bilgiler arasında uzunluk, alan ve şekil bakımından daima bir ilişki vardır. Bu bilgiler bir projeksiyon yüzeyine aktarıldığında aralarında bulunan ilişkilerin esas yüzeydeki gibi kalması beklenemez ve ilişkilerde bazı değişmeler ve bozulmalar olur. Projeksiyonda ortaya çıkan kaçınılmaz değişime ve bozulmalara “Deformasyon” denir. Projeksiyon yöntemlerinde deformasyonların hesaplanabilme olanağı vardır. (Koçak 1999)
Orijinal yüzeydeki özelliklerin değişime uğramadan projeksiyon yüzeyine aktarılması olanaksızdır. Ancak orijinal yüzeydeki bazı büyüklüklerin (uzunluk, alan ve açı) korunarak düzleme aktarılması mümkündür. Öte yandan projeksiyonu yapılan yüzeyin değişik elemanlarının deformasyonlarının bilinmesi, haritadan alınan büyüklüklerin orijinal değerlerinden farklılığının bilinmesi bakımından önemlidir. (Uçar ve ark. 2004)
Farklı projeksiyonlar, dönüşüm sonrasında farklı deformasyonlarla sonuçlanır. Bazı projeksiyonlar verilerin bir veya iki özelliğinde meydana gelen deformasyonları minimum seviyede tutmak için tasarlanmıştır. Herhangi bir projeksiyon, bir objenin alanını koruyabilir ancak bu durumda da orijinal yüzeydeki objenin şekli projeksiyon düzlemine aktarıldıklarında değişime uğramaktadır. Harita projeksiyonları özel amaçlar için tasarlanmıştır. Bir projeksiyon, sınırlı bir alanda, büyük ölçekli verilerde kullanılmak zorunda iken, bir diğeri dünyanın tamamının küçük ölçekli verisinde kullanmak zorunda olabilir. Küçük ölçekli veriler için tasarlanmış projeksiyonlar genellikle elipsoidal koordinatlardan ziyade küresel coğrafi koordinat sistemlerine dayandırılmaktadır. Bu bilgilerden hareketle yeryüzünün düzleme aktarılması işleminde orijinal yüzeydeki objelerin nasıl ve ne derece bir deformasyona uğrayacağı, bu deformasyonların miktarının belirlenmesi ve çalışmaları nasıl etkileyeceğinden haberdar olmak, bir projeye başlarken uygun projeksiyon seçim işlemi açısından oldukça önemlidir. Mevcut projeksiyonlar arasında, barındırdıkları deformasyonların yapısı ve dağılımı bakımından oldukça büyük bir sayıda farklılıklar mevcuttur.
Bir kartografın hazırlanacak harita için uygun projeksiyonun seçimi ile karşılaştığında, haritanın hangi amaç için kullanılacağını ve ne gibi özellikler aranacağını, açı, alan koruyan özellikleri, belirli hatların uzunluklarının korunması, paralel ve meridyenlerin şekli, sınırlandırıcı eğrilerin şekillerini, göz önünde bulundurması gerekmektedir. Ancak bu düşüncelerden sonra bu koşullardan bazılarını yerine getiren ve projeksiyonu yapılacak bölge için mümkün olan en küçük deformasyonları veren projeksiyon yöntemi seçilir.
Haritası yapılacak bölgenin ve haritanın amacının göz önünde bulundurulmasına ek olarak, üretilecek haritanın ölçeği de uygun harita
projeksiyonu seçimi için önemli bir kriterdir. Büyük ölçekli haritalarda meydana gelen deformasyonlar yerkürenin alanı ile karşılaştırıldığında oldukça küçüktür. Ancak, haritanın ölçeği küçüldükçe yeryüzünün küreselliğinden kaynaklanan hatalar oldukça büyük değerlerde gerçekleşmektedir ve düzleme aktarılan bilgilerin büyük ölçüde sapmasına neden olabilmektedir.
Harita projeksiyonlarını, barındırdıkları deformasyonların miktarı ve bu deformasyonların dağılımı bakımından birçok karşılaştırmaya tabi tutmak mümkündür. Bazı karşılaştırmalar tamamıyla grafik anlamda olup deformasyonların büyüklüklerini görselleştirme olanağı sunar. Diğer karşılaştırmalar matematiksel anlamda yapılır ve deformasyon miktarlarının hesabını içerir. Genellikle deformasyonların niceliksel olarak görselleştirilmesi kullanılmaktadır.
Bir küre, yapısı gereği düzgün bir şekle sahiptir. Bu düzgün şekil üzerinde konumların belirlenmesi için enlem ve boylamlarla ifade edilen grid ağı kullanılır. Kartografik amaçlı haritaların yapımı için uygulanan projeksiyonlarda öncelik, coğrafi koordinat ağını oluşturan paralel ve meridyen yaylarının gösterilmesidir.
Bu çalışmada yerkürenin tamamının gösterilmesi amacıyla kullanılan projeksiyonlar üzerinde durulacaktır. Bu projeksiyonlara ait deformasyon parametrelerinin hesaplanması ve elde edilen bu parametreler kullanılarak ilgili projeksiyonlara ait deformasyon analizleri detaylıca incelenerek yeryüzünün tamamının gösterimi için hangi projeksiyonun en uygun özellikleri taşıdığı tartışılacaktır.
Harita projeksiyonları için yöntemler incelenirken, yeryüzündeki ayrıntı noktalarının çizimine değinilmeden sadece paralel ve meridyen yaylarının projeksiyon yüzeyine geçirilmesi üzerinde durulacaktır. Deformasyon değerlerin yorumunun yapılmasında önemli bir yere sahip olan deformasyonların analiz işlemlerinin nicelik ve nitelik bakımından nasıl yapıldığı ve bu konuda çalışanlara hangi faydaları sağladığı, harita projeksiyonlarından kaynaklanan deformasyonlar, bu deformasyonların nasıl analiz edilebileceği ve yorumlanacağı konusu detaylıca ele alınmıştır.
2. bölümde harita projeksiyonları teorisi detaylıca ele alınmış, 3. bölümde projeksiyonlardan kaynaklanan deformasyonlar ve bu deformasyon değerlerinin nasıl hesaplandığı detaylıca ele alınmış ve 4. bölümde hesaplanan bu deformasyon değerlerinin nasıl analiz edileceği incelenmiştir. Teori olarak ele alınan bu konuların pratikte nasıl yapıldığını örneklemek açısından 5. bölümde sayısal bir uygulama gerçekleştirilerek açıklanan analiz yöntemlerine göre uygulama kapsamında seçilen projeksiyonlara ait deformasyon analizleri detaylıca ele alınmıştır. Daha sonra elde edilen sonuçlar tartışılarak deformasyon değerlerine göre projeksiyonların bir karşılaştırılması yapılmıştır.
2 HARİTA PROJEKSİYONU TEORİSİ
2.1 Yeryüzünün Şekli ve Harita Üretiminde Kullanılan Referans Yüzeyleri
Jeodezi, geometrik anlamda ve Dünyanın şeklinin mevcut düzensizliklerinin tanımlanmasında, gravite gibi belirli fizik kurallarını kullanan, Dünyanın şekli ve boyutları ile ilgilenen bir bilimdir. Bu konu, aynı zamanda, ölçme ve kartografya ile yakından ilgilidir. Yeryüzünün şekli ve boyutları hakkındaki verilerin büyük bir kısmı ölçümlere dayanmaktadır. Aslında bazı Avrupa dillerinde ‘jeodezi’ kelimesi kısmen ‘ölçme’ kelimesi ile aynı anlamda kullanılmaktadır. Bu anlatılanlardan yola çıkarak, yeryüzünün haritası oluşturulmak isteniyorsa, şekli ve boyutları hakkında bilgiye sahip olunması gerekmektedir.
Dünyanın, üzerinde bulunan denizler, dağlar ve vadiler tarafından oluşturulan düzensizlikleri ile beraber, neredeyse küre şeklinde bir gezegen olduğu bilinmektedir. Bununla birlikte bu topografik düzensizliklerin Dünyanın pürüzsüz görünümüne az da olsa bir etkisi vardır. Yeryüzünün yarıçapının yaklaşık olarak 6371 km olmasından ve ana kabartma (rölyef) elemanlarının deniz seviyesinin 9 km yukarısı ve 11 km aşağısından fazla olmamasından dolayı, bir golf topu üzerindeki çukurluklardan daha az bir öneme sahiptir. Eğer Dünya, bu sayfaya sığabilecek en büyük boyut olan 6cm yarıçapında bir daire olacak şekilde bir ölçekle çizilirse, Everest Tepesi ve Mariana Çukuru, gözün ayırt edebileceği çizgi kalınlığı olan 0.2 mm değerinden daha küçük olacaktır.
17. yüzyılın sonlarına doğru Newton, bir gerçek küresel yeryüzü kavramının, okyanus yüzeyinin dengesini tanımlamada yetersiz olduğunu öne sürmüştür. O, Dünyanın dönen bir gezegen olduğunu ve bu nedenle yüzeyinde bulunan sıvıların bu dönmenin etkisiyle ekvatora doğru zorlanma eğiliminde olduğunu savunmuştur. Basit bir teorik modelle ekvatoral yarıçapın kutupsal yarıçaptan uzun olması ile yüzeydeki hidrostatik dengenin korunabileceğini kanıtlamıştır. Bu kanıt ise Dünyanın kutuplardan basık bir şekle sahip olduğu anlamına gelmektedir. Yerin
kendine özgü bu biçimine “Geoid” adı verilir. Geoid bir denge yüzeyidir. Durgun deniz yüzeyi Geoidi belirler ve bu yüzeyin karaların altından da devam ettiği kabul edilir.
Fiziksel bir yüzey olması nedeni ile geoidi harita yapımında referans yüzeyi kabul etmek olanaksızdır. Bunun yerine dünya için geoide en uygun şekilde dönel bir elipsoit referans yüzeyi olarak seçilir. Dönel elipsoit, yarı eksenleri a ve b olan bir elipsin b küçük yarı ekseni etrafında dönmesinden oluşan geometrik bir yüzeydir.
Dönel elipsoit projeksiyon hesaplamalarında kullanmak açısından karmaşık bir yapıya sahiptir. Oluşturulacak haritalardan beklenen hassasiyeti etkilemeyeceği yerlerde daha kolay hesaplamaların yapılamasını sağlayan yüzey olarak küre yüzeyi kullanılabilmektedir. Bir haritanın ölçeği, harita üzerindeki bir uzunluğun yeryüzünde buna karşılık gelen uzunluğa oranı şeklinde tanımlanmaktadır. Eğer haritası oluşturulacak alanın boyutu yerin eğriliğini ihmal edebilecek derece küçükse harita ölçeği tüm harita boyunca sabit bir değer olarak alınabilir. Ancak haritası oluşturulacak bölgenin boyutları büyükse veya tüm Dünyanın haritasının yapılması isteniyorsa bu durumda bir küre ya da elipsoitten düzleme aktarma anlamına gelen bir harita projeksiyonu kullanmak gerekmektedir. Projeksiyonlar da doğası gereği deformasyonlara sahiptirler ve harita ölçeğinden artık sabit olarak bahsetmek de mümkün olmayacaktır. Bu nedenle yerel ölçek kavramını tanımlamak gerekmektedir. Yerel ölçek, harita üzerinde bir noktada sonsuz derecede küçük bir uzunluk elemanının yeryüzü üzerinde bu uzunluğa karşılık gelen sonsuz derecede küçük uzunluk elemanına oranıdır. Yerel ölçek harita üzerinde konuma ve doğrultuya bağlı olarak farklılık göstermektedir. Bunun yanı sıra yeryüzünün eğriliğinin ihmal edilebileceği derecede küçük alanların haritaların yapımında yeryüzünü düzlem olarak kabul eden ve ölçeğin tüm harita boyunca sabit olduğu durumlarda kullanılan ölçeğe de temel ölçek denmektedir.
Temel ölçek olarak tanımlanabilir ve harita projeksiyonlarından kaynaklanan deformasyon da bunun katları şeklinde değerlendirilebilir.
2.2 Coğrafi Koordinat Sistemi
Enlem ve boylam değerlerinin kullanıldığı coğrafi koordinat sistemi, yeryüzü için temel konumsal referans sistemidir. Bu sistem kartografya ve navigasyon gibi diğer tüm temel konum belirleme işlemlerinde daima kullanılmaktadır. Diğer bir sistem ise dik koordinat sistemidir. Genellikle 1:500 000 ve daha küçük ölçekli haritalarda coğrafi koordinatlar kullanılır. Düzlem dik koordinatlar daha büyük ölçeklerde kullanılırlar ve jeodezik projeksiyonlara göre üretilmiş haritaların pafta ağlarından birini oluştururlar, (Uçar ve ark. 2004). Coğrafi koordinat sistemi yeryüzü üzerindeki her bir detayın eşsiz bir konum bilgisine sahip olması amacıyla geliştirilmiştir. Yeryüzünün dönme ekseninin yeryüzünü kestiği noktalarda bulunan kuzey ve güney kutup noktaları, sistemin temel başlangıç noktalarıdır. Yeryüzü üzerinde bir konumun tanımlanması için ekvatordan olan kuzey güney açısal mesafeye karşılık gelen enlem ve bir başlangıç meridyenine olan doğu batı açısal mesafeye karşılık gelen boylama ihtiyaç vardır. Dünyayı kuzey ve güney yarımküreler olmak üzere ikiye ayıran ekvator düzlemine paralel düzlemlerin yerküre ile arakesit eğrileri “paralel daireleri”ni oluşturur. Ekvatorun kuzeyinde kalan dairelere kuzey paralelleri, güneyinde kalan dairelere güney paralelleri denir. Yeryüzü üzerinde aynı paralel daire üzerinde bulunan tüm noktaların enlemleri aynıdır. Ekvatoru dik olarak kesen, kutuplardan ve yerin merkezinden geçen düzlemlerin yerküre ile arakesit eğrileri “Meridyen Daireleri”ni belirler. Londra’da Greenwich gözlemevinde bulunan gök dürbününün ekseninden geçtiği varsayılan meridyen yayı, başlangıç meridyeni olarak seçilmiştir. Başlangıç meridyeninin doğusunda bulunanlara doğu meridyeni, batısında bulunanlara batı meridyeni denir. Aynı meridyen yayı üzerinde bulunan tüm noktaların boylamları aynıdır.
Küre üzerinde, kürenin merkezinden geçen düzlemlerin küre ile arakesitine büyük daire adı verilmektedir. Bu tanımdan hareketle tüm meridyenler birer büyük dairedir denebilir. Paralel dairelerden de yalnızca ekvator bir büyük daire özelliğine sahiptir. Kürenin merkezinden geçmeyen düzlemlerin küre ile arakesitine de küçük daireler denmektedir. Ekvator haricinde diğer tüm paralel daireler küçük dairelerdir.
Paralel daireler ve meridyenlerin oluşturdukları varsayılan sanal ağa da “coğrafi grid ağı” denmektedir.
Bir noktadan geçen paralel dairenin ekvatora olan açısal uzaklığına o noktanın enlemi denir. Enlem, o noktadan geçen meridyen düzlemi içinde ölçülür ve (φ) simgesi ile gösterilir. Bir noktadan geçen meridyen düzlemi ile başlangıç meridyeni düzlemi arasında kalan açıya o noktanın boylamı denir. Boylam, bu iki düzlem arasındaki en büyük ölçek açıdır, o noktanın paralel düzlemi içinde ya da ekvator düzlemi içinde ölçülür. Bir noktanın boylamı (λ) simgesi ile gösterilir. φ ve λ değer çiftine ilgili yeryüzü noktasının “Coğrafi Koordinatları” denir (Koçak 1999).
2.3 Harita Projeksiyonu Kavramı
Harita projeksiyonu en temel anlamda, fiziksel yeryüzü üzerindeki doğal ve yapay her türlü özellik ve tesislerin bir düzlem üzerine yani haritaya aktarılabilmesi problemi ile ilgilenir. Harita projeksiyonlarında, orijinal yüzeydeki tüm ayrıntıların projeksiyon düzlemine aktarılmasında öncelik coğrafi koordinatlar yardımıyla meridyen ve paralel daire yaylarının harita düzleminde çizilebilmesini sağlamaktır. Projeksiyon düzleminde oluşturulan dik koordinat sistemiyle diğer ayrıntılar yine coğrafi koordinatlara bağlı olarak aktarılır.
Maling (1992) harita projeksiyonunu şu şekilde tanımlamıştır:
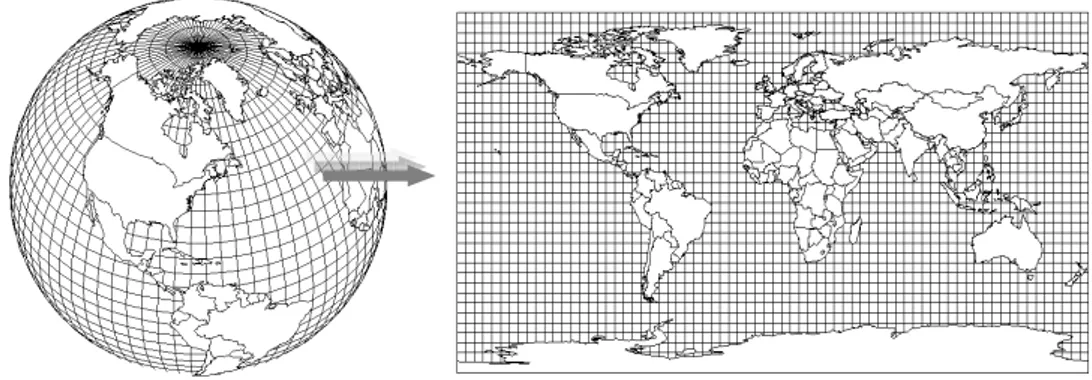
“Meridyenler ve paralellerin, küre veya elipsoidin küresel yüzeyini bir düzlem
Şekil 2.1 Küresel yüzeyden düzleme dönüşüm
Snyder (1987) :
“Bir harita projeksiyonu küresel bir cismin, özellikle Dünyanın, yüzeyinin tüm parçalarının, bir düzlem üzerinde sistematik olarak gösterimidir. Bu genellikle bir harita projeksiyonunun tanımlanmasında gerek duyulduğu gibi, meridyenler ve paraleller olarak isimlendirilen çizgileri içerir.”
Koçak (1999), harita projeksiyonu kavramını, referans yüzeyine indirgenmiş yeryüzü bilgilerinin bir harita düzlemine aktarılmasını sağlayan matematiksel kuralları ve yöntemleri inceler, şeklinde özetlemektedir.
2.4 Harita Projeksiyonlarının Matematiği Hakkında Bazı Temel Prensipler
Her projeksiyon kendine has bir koordinat gösterim formuna sahiptir ve bu gösterimlerde kartezyen ya da kutupsal koordinatlar kullanabilir. Başka bir ifadeyle, yeryüzü üzerinde coğrafi koordinatlarla (φ,λ) temsil edilen her bir nokta, düzlemde ya (x,y) ya da (r, θ) ile gösterilebilmektedir.
Bu ifade fonksiyonel bağıntıların genelleştirilmiş bir şekli ile belirtilecek olursa;
, (2.1)
ya da
, (2.3)
, (2.4)
şeklindedir.
Her bir harita projeksiyonu, kendini tanımlayacak ve oluşturacak olan x ve y ya da r ve θ için bir eşitliğe sahiptir. x ve y (ya da r ve θ) enlem ve boylamın birer fonksiyonudur, ifadesi, küre üzerinde coğrafi koordinatları , ile belli olan bir noktanın harita üzerinde (x,y) ile (ya da r ve θ) temsil edildiğini ifade etmektedir. Başka bir ifadeyle harita ve yeryüzü arasında bire-bir eşleşme söz konusudur. Yeryüzü üzerindeki tüm noktaların harita üzerinde birer karşılığı mutlaka vardır. Bazı istisnai durumlarda bu ifade geçerli olmayabilir. Bunun sebebi coğrafi kutupların bazı projeksiyonlarda nokta yerine çizgilerle gösterilmesidir veya yeryüzünün bazı kısımlarının projeksiyon üzerinde gösterilememesidir. Adı geçen bu istisnai durumlar genellikle projeksiyonların sınır bölgelerinde oluşur ve mutlaka istisnai durumlar olarak değerlendirilmelidirler. Bunlar dışında kalan projeksiyonlar içerisinde yeryüzüne ait noktalar yalnızca tek bir nokta ile ifade edilir.
Yeryüzü noktalarının harita üzerindeki noktalarla ilişkilerin doğruluğu kesin değildir. İlk olarak bazı ölçek değişimleri ortaya çıkabilir, çünkü yeryüzünün 1:1 lik bir ölçekte tasvir edilebilmesi fiziksel olarak olanaksızdır. Diğer bir etken de yeryüzünün sahip olduğu eğri yüzeyinin düzleme açılamaması gerçeğidir. Bunu gerçekleştirmek istediğimizde gerilme ve yırtılma (ya da sünme) anlamına gelen bazı deformasyonlarla karşılaşılması kaçınılmazdır.
2.5 Harita Projeksiyonlarının Özellikleri
Yeryüzünü temsil etmek üzere kabul edilen referans yüzeyleri (küre ya da elipsoit) düzleme açılabilen yüzeyler olmadıklarından, yeryüzünü deformasyonsuz olarak harita düzlemine aktarmak mümkün değildir. Ancak belli özelliklerin korunması mümkündür. Projeksiyonlarda ya belli doğruların uzunlukları, ya alanlar,
ya da diferansiyel anlamda açılar korunabilir. Bu üç özelliğin üçünün de sağlanması ya da tüm doğruların uzunluklarının korunması mümkün değildir (Uçar ve ark. 2004). Bu ifadeden de anlaşılacağı gibi, projeksiyon dönüşümlerinde oluşan deformasyonların tamamıyla önüne geçilemez. Projeksiyon yüzeyinde korunması mümkün olan üç özellik;
Açı Koruma (Konform Özellik) Alan Koruma
Uzunluk Koruma şeklinde sıralanabilir.
2.6 Harita Projeksiyonlarının Sınıflandırılma Sistemleri
Projeksiyon sistemleri birçok farklı yöntemle sınıflandırılmıştır. Bu metotlardan en yaygın olarak kullanılanları, geometrik modele, geometrik özelliklere ve parametrik sınıflandırmaya dayalı yöntemlerdir. Bunlara ek olarak, projeksiyon konumu ve grid ağı harita projeksiyonlarının sınıflandırılması ya da tanımlanmasına yardımcı olarak kullanılmaktadır. Sınıflandırma sistemleri mevcut olan yüzlerce harita projeksiyonunu organize etmeyi sağlayan bir yöntemdir.
Geometrik modele ve geometrik özelliklere dayalı sınıflandırma sistemleri aynı zamanda bir projeksiyonun temel özelliklerini ilk bakışta anlamada kolaylık sağlayan tanımlayıcı bir kelime hazinesi sağlamaktadır. Canters ve Decleir (1989) yayınlarında bu tanımlayıcı yöntemi tüm dünya projeksiyonları için kullanmışlardır. Terimlerinin oldukça tanımlayıcı olmasına karşın bazen aynı projeksiyonun çoklu isimlerle gösterilmesi gibi durumlarla sonuçlanan karmaşıklıkların da artmasına neden olmuştur. Harita projeksiyonlarının sınıflandırılmasına çok farklı bir yaklaşım da Tobler’in (1962) dört grup parametrik sınıflandırması ve Maling’in (1992) bu sistemi genişleterek elde ettiği sistemdir.
2.6.1 Geometrik model ve konum
Mevcut olan yüzlerce projeksiyonun bir çoğunu, sanal bir ara yüzeye dayanan üç temel kategoriden birine dahil etmek mümkündür. Bu yüzeyler Merkator projeksiyonu ile örneklenebilecek silindir; Lambert Konform Konik projeksiyonu ile örneklenebilecek koni ve Azimutal Uzunluk koruyan projeksiyonla örneklenebilecek düzlem yüzeylerdir.
Silindir
Koni
Düzlem
Şekil 2.2 Düzleme açılabilen üç yüzeyin projeksiyonu: Silindir, koni ve düzlem
Şekil 2.2 incelendiğinde; düzleme açılabilen yüzeylerden bir tanesi küreyi, tepe noktası kutup noktası üzerinde bulunan bir koni ile saran şekilde düşünülebilir. Eğer küre üzerindeki elemanlar koni yüzeyine dönüştürülebilirse, koni daha sonra, harita elemanlarını başka deformasyonlara maruz bırakmadan iki boyutlu bir harita oluşacak şekilde düzleme açılabilecektir. Sonuçta, Şekil 2.2’de koni olarak isimlendirilen projeksiyon oluşacaktır. Gerçekte harita projeksiyonları genellikle matematiksel fonksiyonlardır, ancak, geometrik model kavramı harita projeksiyonlarının sınıflandırılmasında oldukça faydalıdır ve önemli bir öğrenme aracıdır (Clarke ve Mulcahy 1995).
Konum, kesin bir sınıflandırma yöntemi olmamasına karşın, projeksiyon düzleminin grid ağına göre nasıl yöneltildiğini tanımlamada kullanılır. Bir projeksiyonun konumu, özel bir harita için mümkün olan minimum deformasyon parametrelerinin elde edilmesine yardımcı olmak amacıyla sıklıkla değiştirilebilmektedir. Wray (1974) bir projeksiyonun olası yedi adet konuma sahip
olabileceğini tanımlamasına karşın, tüm durumları için yeterli olan üç temel konum bulunmaktadır. Bunlar: Şekil 2.3’de gösterildiği gibi, normal konum (kutup konumlu), transversal (ekvator konumlu) konum ve eğik konumlardır.
Transversal
Normal Eğik
Şekil 2.3 Harita projeksiyon konumları: Normal, eğik ve transversal
Normal konum, her geometrik model için geometrik açıdan en basit olanıdır. Normal konumlu azimutal bir projeksiyonda projeksiyon düzlemi kutup noktası ile çakışıktır. Transversal konumlu azimutal projeksiyonda, projeksiyon düzlemi ekvator üzerindedir ve ekvatoral konumlu da denir. Son olarak eğik konumlu bir projeksiyon ise ekseni ekvator ve kutup noktasından faklı bir noktada bulunan projeksiyonlara verilen isimdir. Konum seçimi öncelikli olarak grid ağının görünümünü değiştirmektedir. Geleneksel metotlarla belirlenen deformasyon modelleri aynı kalır. Bir sınıflandırma sistemi olarak geometrik model, olası tüm projeksiyonları benzersiz olarak tanımlamak için kendi içerisinde yeterli değildir.
2.6.2 Geometrik özellikler
Geometrik özelliklerle sınıflandırma yöntemi genellikle bir projeksiyonun tam anlamıyla tanımlanması amacıyla geometrik model sınıflandırma sistemi ile birleştirilerek kullanılır. Temel amaç, sonuç projeksiyonda hangi geometrik özelliklerin, konform olma (açı koruma), alan ya da uzunluk, korunduğunu
belirlemektir. Geometrik model kavramında olduğu gibi, bu sistemde de tüm projeksiyonları tam anlamıyla tanımlayamama dezavantajı bulunmaktadır.
2.7 Gerçek Anlamda Olmayan Projeksiyonlar
Yeryüzünün ortaya çıkan geometrik yapıdan yararlanılarak düzlem, silindir, koni gibi aracı yüzeylere aktarılmadan sadece matematik bağıntılar kullanılarak harita düzlemine izdüşürüldüğü projeksiyonlara “gerçek anlamda olmayan” (pseudo, sözde) projeksiyonlar adı verilir. Gerçek olmayan projeksiyonların düzlem, silindir, koni gibi aracı yüzeylerle bir ilişkisi olmamasına rağmen azimutal, silindirik ve konik projeksiyonlardan elde edildikleri için gerçek anlamda olmayan azimutal, silindirik ve konik projeksiyonlar olarak da sınıflandırılırlar (Uçar ve ark. 2004).
3 HARİTA PROJEKSİYONLARINDA DEFORMASYONLAR
Yeryüzünün orijinal yüzeyi yerine seçilen küre incelendiğinde, sahip olduğu eğri yüzeyin düzleme tam olarak açılamayacağı anlaşılabilmektedir. Bir portakal kabuğunun yarısının kesilerek düzlem bir yüzey üzerinde düzleştirmeye çalışıldığında kabuğun yırtıldığını görülür. Aynı şekilde kürenin de yüzeye açılabilmesi için bazı paralel ve meridyenler boyunca kesilmesi gerekmektedir. Eğer küresel yüzey kesilirse bu şekilde neredeyse düzleme tam olarak açılabilecektir. Ancak bu işlem bazı enlemlerdeki paralellerin iki kere gösterilmesine ve bu paraleller arasında Şekil 3.1’de de gösterildiği üzere, haritanın sürekliliğini bozan büyük boşlukların oluşmasına neden olacaktır. Eğer haritanın tüm yüzeyi Şekil 3.2’deki gibi kesintisiz bir şekilde gösterilmesi isteniyorsa, bu durumda bu paraleller germe işlemi ile çakıştırılmalıdır.
Şekil 3.1 Küresel bir yüzeyin düzleme açılabilmesi için bazı paraleller boyunca kesilmesi ve
Şekil 3.2 Haritanın kesilmeden sürekli bir yapıya sahip olması durumunda küresel yüzeyin
düzleme açılabilmesi için paralel ve meridyenlerin deformasyona uğraması durumu.(Maling, 1992) Şekil 3.2’de gösterilen sürekli yapıya sahip bir haritanın oluşturulmasında tanımlanan deformasyon, uzunluk deformasyonudur ve meridyen doğrultusundadır. Grafiksel olarak elde edilen sonuç ise herhangi iki paralel arasındaki mesafenin haritanın ortasından sınırlara doğru gidildikçe artıyor olmasıdır. Diğer bir yandan, ardışık meridyenler arasındaki mesafeler sadece enlemlere göre değişmektedir. Eğer herhangi bir paralel boyunca meridyenler arasındaki mesafe dikkate alınacak olursa neredeyse sabit ve boşluklar birleştirilmeden önceki haline eşit olduğu görülür. Bu durum mevcut projeksiyondaki uzunluk deformasyonunun bir yönde gerçekleştiğini, diğer yönde gerçekleşmediğini göstermektedir. Bunun, harita üzerindeki açılar ve alanları açıkça etkileyeceği muhtemeldir. Etki, basit bir diyagram çizilerek gösterilebilir.
Şekil 3.3 Açısal ve alansal yönden uzunluk deformasyonunun etkisinin gösterilmesi. İlk
durumda P noktasının koordinatları (10,10) şeklindedir
Şekil 3.3’de noktasının merkezli bir sistemde ölçülen koordinatları 10,10 görülmektedir. Bundan hareketle açısının 45⁰olduğu söylenebilir ve karesinin alanı da 100 birim karedir. Şekil 3.4’de ordinat yönündeki ölçek iki katına çıkarılmış ancak buna rağmen apsis yönündeki ölçek değiştirilmeden korunmuştur. Burada (10,20) olmaktadır.
açısı 30⁰ ve dikdörtgeninin alanı 200 birim kare olmuştur. Açıda meydana gelen değişim, - açısına “açısal deformasyon” ya da “açı deformasyonu”, alanda meydana gelen değişim, - “alan deformasyonu” olarak isimlendirilmektedir. Açısal deformasyon ve alansal deformasyonun her ikisi de uzunluk deformasyonuna bağlıdır ve bu sebeple uzunluk deformasyonu ile tanımlanabilir. Sonuç olarak uzunluk deformasyonu harita projeksiyonları açısından oldukça öneme sahip olan ve herhangi bir doğrunun uzunluğunda meydana gelen değişimdir.
3.1 Uzunluk Deformasyonu
Bir haritanın ölçeği kesirli olarak ifade edilen ölçeğinden bilindiği zaman üç yönden bu ölçeğin sabit olduğu düşünülebilir.
1- Kesirli ifade ile gösterilen ölçeğin oranı harita üzerinden ölçülen tüm uzunluklara uygulanabilir. Örneğin haritanın ölçeği 1:25000 ise harita üzerindeki 40mm lik bir uzunluğun arazide 1km lik bir mesafeye denk gelmesi beklenir. Benzer şekilde 80mm lik bir uzunluğun 2km lik bir mesafeye ve 400mm lik bir uzunluğun da arazide 10km uzunluğa denk gelmesi beklenir. Bu nedenle kesirli ifade ile kurulan bağıntının, haritanın düzenli doğruları içerisinde devam edebilen herhangi bir uzunluğun lineer ölçümü için sabit olduğu varsayılabilir. Üstelik dünyanın hangi bölümünü temsil ettiği dikkate alınmaksızın aynı bağıntının tüm haritlar için geçerli olduğu düşünülebilir.
2- Kesirli ifade ile oluşturulan bağıntının haritanın tüm bölümleri için geçerli olması düşünülebilir. Bu nedenle haritada 40mm olarak ölçülen bir uzunluğun haritanın orta kısmında ya da sınır çizgisinin yakınlarında 1km lik mesafeye karşılık geldiği düşünülür.
3- Bağıntının doğrultudan bağımsız olduğu düşünülebilir. Bu sebeple 1/25000 ölçeğinde 40mm lik mesafenin kuzey-güney ya da doğu-batı veya bunların arasında bir doğrultuda ölçüldüğünü dikkate almadan 1km lik mesafeye karşılık geldiği düşünülebilir.
Bu üç varsayım, birçok harita kullanımı için doğru gibi gözükmektedir. Ancak tüm uzunluklar için, tüm bölgelerde ve tüm doğrultularda ölçeğin sabit olması varsayımı gerçeği yansıtmamaktadır. Eğer temel ölçeği tüm doğrultularda ve düzlem yüzeyin her yerinde korumak mümkün olabilseydi, oluşturulan harita küresel yüzeyin kusursuz bir gösterimi olabilirdi. Küresel bir yüzeyin doğasından ötürü, düzleme dönüşüm esnasında yukarıda açıklanan üç tanımlamanın bazılarında ya da hepsinde, ölçekte bazı değişimler meydana gelmektedir.
Verilen 1/25000 ölçeğindeki sayısal örnek 100-200 km2 alanı muhtemelen doğru olarak temsil etmektedir. Yeryüzünün bu gibi küçük bir bölümünün içerisinde ölçek değişimleri oldukça küçüktür. Ölçek değişimleri o kadar küçüktür ki ihmal edilebilir ve ölçeğin sabit olduğu varsayılabilir. Hatalar da gözün ayırt edebileceğinden daha küçüktür ve kağıt üzerinde nem ve sıcaklıktan kaynaklanan değişimlerden bile daha küçüktür. Ancak daha büyük alanlarda meydana gelebilecek ölçek değişimleri hataları dikkate değer bir boyuta taşıyacaktır.
Deformasyonları araştırmak için ilk olarak orijinal yüzeydeki ve projeksiyon yüzeyindeki sonsuz küçük iki uzunluk elemanının oranı ele alınmalıdır. Bu iki elemanın oranı uzunluk deformasyonunu vermektedir.
/ (3.1)
Buradan anlaşıldığı üzere uzunluk deformasyonu bir oran olup, sadece noktadan noktaya değişmemekte, aynı zamanda bir noktada çeşitli yönlerde de değişmektedir. Başka bir ifade ile, uzunluk deformasyonu hem noktanın konumuna, hem de yöne bağlıdır. Orijinal yüzey üzerinde böyle bir s uzunluk elemanı bir nokta etrafında döndürülürse sonsuz küçük bir daire oluşur. Buna karşılık uzunluk elemanının projeksiyon yüzeyindeki izdüşümü bir daire çizmez. Burada uzunluk deformasyonu sonsuz değişik değer alabilir. Ancak bunlardan bazılar önemlidir (Uçar ve ark., 2004).
3.2 Referans Yüzeyinden Projeksiyon Yüzeyine Dönüşüm
Dönüşümü yapılacak olan şekillerin boyutlarını, sonsuz derecede küçük hale gelecek kadar küçültmek oldukça önem kazanmaktadır. Bu durumun iki önemli neticesi olarak;
Birbirinin hem küre hem de düzlem üzerinde karşılığı olan şekillerin çizgileri birbirine çok ama çok yakın derecede denktir.
Çizgi çiftlerinin kesişimi ile oluşan açılar değişmeden kalmaktadır.
Buradan hareketle, meridyen ve paralellerin dik açı ile kesiştiği küresel bir dörtgen, dönüşüm sonrasında düz çizgilerden oluşan ve dört açısı da dik özelliğini koruyan bir şekle dönüşür. Yani Şekil 3.5’de bir dikdörtgendir.
Şekil 3.5 Sonsuz derecede küçük küresel dörtgen
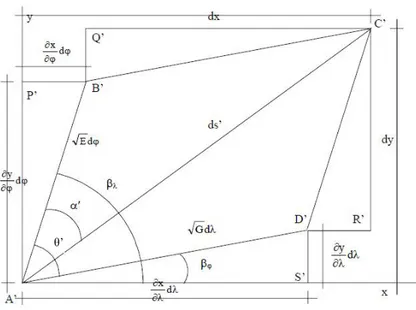
Harita üzerinde şeklinin kenarları ve köşegeni düz çizgilere dönüşmektedir, ancak, Ω gibi açılar korunmaktadır. Şekil 3.6’da bu dönüşümün genişletilmiş bir hali gösterilmektedir. ve noktalarının konumları aynı şekilde tahsis edilmiştir. Enlemde, boylamda, x ve y’de meydana gelen artan değişimler sırasıyla, , , ve şeklinde gösterilmektedir.
Şekil 3.6 Sonsuz derecede küçük olan Şekil 3.5'de verilen dörtgenin düzlem dönüşümü
Bu gösterim, sonsuz derecede küçük artışların gösterilmesinde kullanılan geleneksel bir ifade şeklidir. Sonuç olarak küre üzerindeki dört nokta Tablo 3.1’de gösterilmektedir. Yay uzunluğu hesabından, A noktasında meridyen elemanının uzunluğu;
. (3.2)
şeklindedir. Burada R, kürenin yarıçapını ifade etmektedir. Aynı şekilde paralel elemanının uzunluğu da;
. . (3.3)
şeklinde ifade edilebilmektedir. Ayrıca, dörtgeninin köşelerindeki açıların dik açılar olmasından dolayı, köşegen elemanının uzunluğunu pisagor bağıntısından hesaplanabilir. Bu sebeple;
(3.4)
. . . (3.5)
eşitliği yazılabilir. θ’
Tablo 3.1 Küre üzerindeki dört nokta
Düzlemde, , noktası ve , ’dir. Farklı yorumlara yardımcı olması bakımından eksenine paralel olarak
, , , hatları oluşturulmuştur. Aynı zamanda eksenine paralel , , hatları da oluşturulmuştur. Şekilde gösterilen her bir çizgi sembolik olarak kısmi türev sembolü ile gösterebilen bir geometrik ifadeye sahiptir. Bu sebeple , noktasından olan meridyen yayını, ve de aynı noktadan olan paralel yayını temsil etmektedir. , noktasından olan meridyen yayı ile açısını yapan herhanbir yayı temsil etmektedir. Oluşturulan diğer çizgiler aşağıdaki değişkenleri temsil etmektedir.
, enlemdeki kadar değişimden kaynaklanan ekseni yönündeki değişimi göstermektedir.
/ (3.6)
, enlemdeki aynı değişiminin neden olduğu ekseni yönünde artışı göstermektedir.
/ (3.7)
, boylamdaki kadar değişimden kaynaklanan ekseni yönündeki değişimi göstermektedir.
/ (3.8)
, boylamdaki kadar değişimden kaynaklanan ekseni yönündeki değişimi göstermektedir.
Nokta Enlem Boylam A
B C D
/ (3.9)
Şekil 3.6’dan da görülebileceği gibi arasındaki artışı, iki lineer elemanın, ve , birleşiminden oluşmaktadır.
(3.10)
Bu lineer elemanlarla uyuşan terimlerle yerleri değiştirilirse;
/ / (3.11)
şeklinde yazılabilir. Hesaplamalarda bu ’in toplam diferansiyeli olarak anılır. Benzer şekilde ve arasındaki ’nin toplam diferansiyeline eşit olan, toplam artışı da iki lineer elemanın, ve , olduğu görülebilmektedir.
(3.12)
/ / (3.13)
Pisagorun dik açılı üçgenler için geliştirdiği teoremden hareketle dörtgeninin kenarları ve köşegeni şu şekilde ifade edilebilir;
(3.14)
(3.15)
(3.16)
(3.17)
Gerekli işlemler yapılıp birbiri cinsinden yazılarak eşitliklerden köşegen yayının değeri;
/ / / / (3.18)
3.3 Gauss’un Temel Büyüklükleri
Gauss’un temel eşitlikleri kullanılarak, eşitliklerde bazı basitleştirmeler yapılabilmektedir.
/ / (3.19)
/ . / / . / (3.20)
/ / (3.21)
Bu tanımlar eşitlikleri daha kullanılır hale getirmektedir.
. 2 . . . (3.22)
Bu eşitliklerden yola çıkılarak noktasını ilgilendiren özel uzunluk deformasyonlarının tanımlamalarını yapmak mümkün olacaktır.
(1) Meridyen Yönündeki Uzunluk Deformasyonu
Oran şöyledir; / (3.23) (3.24) / / (3.25) olduğundan, √ . (3.26)
yay elemanı daha önce tanımlandığı üzere,
√ . / . (3.27)
√ / (3.28)
√ (3.29)
şeklinde meridyen yönündeki ölçek tanımlanabilir.
(2) Paralel Yönündeki Uzunluk Deformasyonu
Oran şöyledir; / (3.30) (3.31) / / (3.32) olduğundan, √ . (3.33)
yay elemanı daha önce tanımlandığı üzere,
√ . / . . (3.34)
√ / . (3.35)
ya da 1 kabulü ile,
√ / (3.36)
şeklinde paralel yönündeki ölçek tanımlanabilir.
3.4 Tissot Teoremi ve Ana Yönler
Harita projeksiyonlarının analizlerinin büyük bir kısmı 19. Yüzyılın başlarında Gauss tarafından gerçekleştirilmiştir. Harita projeksiyonlarının matematiksel teorisindeki bir diğer temel gelişme ise 1850’li yıllarda N. A. Tissot tarafından gerçekleştirilmiştir. Adını taşıyan teoremini ve Tissot Endikatrisi olarak bilinen deformasyon elipsi kavramını geliştirmiştir.
3.4.1 Deformasyon elipsi
Deformasyon elipsi kavramı, “küre yüzeyinde sonsuz derecede küçük bir daire, düzleme aktarıldığında, yarı eksenleri ana yönler boyunca uzanan sonsuz derecede küçük bir elipse dönüşmektedir” şeklinde özetlenebilir. Teorem, Reignier (1957), Fiala (1957), Richardus ve Adler (1972) tarafından detaylıca açıklanmaktadır.
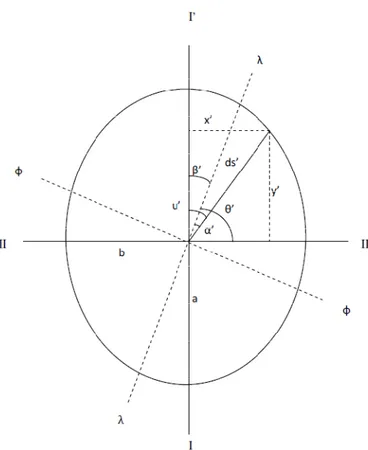
Şekil 3.7 Küresel yüzey üzerinde sonsuz derecede küçük daire
Şekil 3.7 küre üzerindeki coğrafi koordinatları , olan bir noktasını
göstermektedir. , Şekil 3.6’daki ’nin karşılığı olan sonsuz derecede küçük bir yayı, ’i göstermektedir. Kürenin eğri yüzeyi üzerinde ölçeğin sabit olması ve her yerde temel ölçeğe eşit olması nedeniyle, gibi tüm noktaların geometrik yeri bir daireyi çevreleyen çemberi merkezi ve yarıçapı ile keser. Temel ölçeğin 1 kabulunden sonra 1 eşitliğinden bahsetmek uygun olacaktır. Şekil 3.8 düzlem üzerinde daireye karşılık gelen şekli göstermektedir. ve , noktasındaki ana yönleri göstermektedir, yay elemanının doğrultuya bağlı olarak sürekli değişiyor olmasından ötürü, ya da başka bir ifadeyle ’ya bağlı olarak, gibi noktaların geometrik yerleri elipsi çevreleyen hattı keserler.
Şekil 3.8 Tissot endikatrisi ya da diğer adıyla distorsiyon elipsi. Şekil 20 de gösterilen sonsuz
derecede küçük dairenin düzleme dönüştürülmesi sonucu bir elipse dönüşmesi. Elipsin iki yarı ekseninin uzunlukları şu şekilde ifade edilebilir.
/ (3.37)
/ (3.38)
buradan
. (3.39)
. (3.40)
elde edilir. Ayrıca
. (3.41)
. (3.42)
. (3.44)
bu ifadeler birbirleri ile ilişkilendirilirse,
. . (3.45)
. . (3.46)
(3.47)
halini alır.
noktasındaki iki özel uzunluk deformasyonundan meridyen ve paralel yönündeki uzunluk deformasyonu olarak bahsedilebilir. Eğer açısı, noktasında, ana yönlerden biri olan ve meridyeni arasındaki açı ise, haritadaki karşılığı olan
açısı ile;
(3.48)
(3.49)
denebilir. Alt alta toplanıp sadeleştirme yapılırsa,
(3.50)
olur.
Bu eşitlikler, herhangi bir harita projeksiyonunun deformasyon karakteristiğinin analizinde, bilinen , ve değerlerinden ve ’nin hesaplanmasında önemli bir değere sahiptir. Buradan;
2 . 2 . (3.51)
ve,
2 . . / (3.52)
3.5 Alan Deformasyonu
gibi küçük bir dörtgenin alanı Şekil 3.8’den hareketle . . şeklinde tanımlanabilir. Bu nedenle
. . (3.53)
yazılabilir. Sonuç olarak aynı zamanda
. (3.54)
de yazılabilir. Buradaki parametresi özel uzunluk deformasyonları ile aynı birimde tanımlanır, bu nedenle alansal ölçek ya da alan deformasyonu olarak ifade edilir.
3.6 Maksimum Açı Deformasyonu
ve arasındaki farktan yola çıkılarak her ikisinin de aynı doğrultuya ait olmaları nedeniyle hattının doğrultusundaki değişimi aşağıdaki gibi değerlendirmek mümkündür; / . (3.55) ve / (3.56) sin / . / (3.57) şeklinde gösterilebilir ve sin / . / (3.58) sin sin (3.59)
Bu eşitlik sin 1 olduğunda maksimum değer alır ki bu da
yönlerle tanımlı dört adet doğrultu bulunacaktır. Eğer bir açı bu gibi iki doğrultunun kesişiminde bulunuyorsa, açının her iki kenarı da maksimum sapmaya uğruyor demektir ve bir noktadaki “maksimum açı deformasyonu”nu, , tanımlayan bir eşitlik yazılacak olursa;
sin /2 / (3.60)
eşitliği elde edilir ve bu eşitlik bir harita projeksiyonunda herhangi bir noktadaki parametrenin saptanmasında en yaygın olarak kullanılan eşitliktir.
3.7 Konform Özellik (Açı Koruma)
Konform özelliğe sahip bir haritada tüm noktalarda;
(3.61)
eşitliği sağlanmaktadır. Eğer bu koşul sağlanırsa, küre üzerindeki sonsuz derecede küçük bir dairenin düzlemdeki karşılığı her zaman bir boyutu farklı yani daha büyük ya da daha küçük bir daireyi gösterecektir. Ayrıca, maksimum açısal deformasyon değeri 3.60 eşitliğinden elde edilebileceği hatırlanacak olursa, ve birbirine eşit olduğu durumlarda 0 ’ye eşit olacaktır. Buradan, konform özelliğe sahip bir harita projeksiyonunun diferansiyel anlamda açısal deformasyona maruz kalmadığı, ya da başka bir ifadeyle diferansiyel anlamda açıların korunduğu sonucu çıkarılabilir. Bu, tüm konform projeksiyonların temel ve en önemli özelliklerinden biridir. Açıların ölçülmesi için kullanılacak bir harita için olmazsa olmaz bir özelliktir. Bu nedenle konform projeksiyonlar, navigasyon haritaları ve askeri haritalar için baz olarak kullanılırlar.
Küre üzerinde sonsuz derecede küçük bir dairenin, harita üzerinde daire olan şeklini devam ettirmesi, aynı zamanda bu özelliğe sahip projeksiyonlarda obje şekillerinin de korunduğunu göstermektedir. Bununla birlikte, bu ifade yalnızca bazı koşullarda geçerli olmaktadır. şeklinde ifade edilen eşitliğin 1 olmadığına dikkat edilmelidir. Konform özellik, tüm doğrultularda meydana gelen artışın aynı olduğunu göstermektedir. Bunun anlamı, alansal ölçeğin, özel ölçeğin
karesi ile orantılı olarak arttığı şeklindedir. Sonuç olarak sıfır deformasyonlu bir nokta üzerinde bulunan bir daire, haritanın sınır bölgesine yakın bir bölgede daire olan şeklini devam ettirecek, ancak alanı, dikkate değer bir şekilde büyümüş olacaktır. Bu sebeple, konform özelliğe sahip bir projeksiyonun tüm noktalarda küçük alana sahip objeleri iyi bir şekilde göstermesine rağmen, sıfır deformasyonlu noktalardan uzaklaştıkça uzunluk deformasyonlarında meydana gelen hızlı artış, bu projeksiyonları, okyanuslar ve kıtalar gibi büyük alana sahip objeleri göstermede uygunsuz bir hale getirmektedir.
0 değerine sahip olan herhangi bir projeksiyonda, tüm paralel–meridyen kesişimleri ortogonaldir. Bu, çoğunlukla kompleks eğri yapısına sahip meridyen ve paralellerin doğasına bakılmaksızın doğru olmak zorundadır. Eğer bir konform projeksiyon eğri meridyenler ve paralellerden oluşuyorsa, kesişim noktalarında bu her iki hatta çizilen teğetleri göz önüne getirmek oldukça önemlidir. Bu iki teğet birbirine diktir. Tersi durumla pek karşılaşılmaz. Bu nedenle tüm paralel ve meridyenleri dik kesişiyor diye bir projeksiyonun konform özellik taşıması şart değildir.
3.8 Alan Koruma
Alan koruyan bir projeksiyonda;
. 1 (3.62)
eşitliği sağlanmaktadır. Bu aynı zamanda
1/ (3.63)
veya
1/ (3.64)
anlamına gelmektedir. Yani maksimum ve minimum uzunluk deformasyonları birbirinin tersidir. Buradan, deformasyon elipsinin dikkate değer bir elipslik göstermesine rağmen alanlarının 1 birim olduğu sonucu çıkarılabilir.
Alan koruyan projeksiyonlar, istatistiksel değişkenlerin dağılımını gösteren haritaların üretilmesi bakımından oldukça büyük bir öneme sahiptir. Örneğin, nüfus, tarımsal ve endüstriyel istatistikler harita üzerinde gösterilmek isteniyorsa, bu olay, her biri değişkenin belli bir sayısını ifade eden noktalar gibi işaretlerin kullanılması ile gerçekleştirilir.
3.9 Uzunluk Koruma
Bir üçüncü önemli matematiksel özellik de, bir uzunluğun harita boyunca korunduğu durumdur. Genellikle bu meridyen yönündeki uzunluktur ve buradan hareketle;
1.0 (3.65)
yazılabilir. Dolayısıyla tüm paralellerin tüm meridyenleri, küredeki paraleller arasındaki yay uzunluğu ile eşit aralıkta kestiği bir projeksiyon oluşturulabilir. Bu durumun alternatifi olarak harita boyunca 1 yapılabilir. Bu özellik, bazı harita projeksiyonlarının türetilmesinde isteğe bağlı olarak ortaya çıkar, ancak, bu özellik, büyük daire yayları boyunca temel ölçeğin korunmasından daha az bir öneme sahiptir.
Yalnızca bir yöndeki uzunluğun korunmasından dolayı, uzunluk koruma, konformluk ve alan koruma özelliklerinin her ikisi ile de uyuşmamaktadır. Uzunluk koruma özelliği, hem alan koruma hem de konform özellikten daha az bir öneme sahiptir. Çünkü, bir haritanın yalnızca bir doğrultuda ölçülen uzunlukları korumasının istenmesi nadir rastlanan bir istektir. Uzunluk koruyan bir haritanın maksimum açısal deformasyonu, alan koruyana göre çok daha yavaş artış göstermektedir. Sonuç olarak, uzunluk koruyan haritalar genellikle atlaslarda, stratejik planlama haritalarında ve diğer özelliklerin korunmasının temel amaç olmadığı, yeryüzünün büyük parçalarının gösterildiği haritalarda kullanılır.
3.10 Sıfır Deformasyonlu Hatlar ve Noktalar
Ölçeği belirli hatlar boyunca ya da belirli noktalarda korumak mümkündür. Bu hatlar boyunca (ya da bu noktalarda) ölçek sabittir ve uzunluk deformasyonu değeri de 1.0 değerine eşittir. Sonuç olarak deformasyon meydana gelmez. Buradan hareketle aşağıdaki sonuçlar çıkarılabilir;
1. Bir harita projeksiyonu üzerindeki sıfır deformasyona sahip hatlar, uzunluğun bu hat boyunca korunduğu ve küre üzerinde belirli büyük dairelere ya da küçük dairelere karşılık gelen hatlardır.
2. Sıfır deformasyon değerine sahip bir nokta ise, harita projeksiyonu üzerinde temel ölçeğin korunduğu noktadır.
Bu durumlar Şekil 3.9 ve Şekil 3.10’da gösterilmektedir.
Şekil 3.9 Teğet ve kesen silindir.
Şekil 3.10 Teğet ve kesen koni
Projeksiyon yüzeyinin orijinal yüzeye teğet olduğu noktaya “standart nokta” ya da “merkez noktası”, teğet ya da kestiği hatlara da “standart hatlar” ya da durumlarına göre “standart paraleller” denmektedir.
4 HARİTA PROJEKSİYONLARINDA DEFORMASYON ANALİZLERİ
Harita projeksiyonlarındaki deformasyonların miktarı ve dağılımı açısından karşılaştırılabileceği birçok yöntem bulunmaktadır. Bazı karşılaştırmalar tümüyle grafik anlamda olup, deformasyonların alanının ve miktarının görsel olarak gösterimini sağlamaktadır. Diğerleri ise, matematik tabanlı olup deformasyonların miktarlarını nicelik olarak değerlendirmektedirler. Genellikle pratikte, deformasyonların niceliksel değerlerinin görsel modeli kullanılmaktadır.
4.1 Nicel Analizler
Bir harita projeksiyonunun deformasyon değerleri hesaplandıktan sonra bu değerleri yorumlamak, projeksiyonun deformasyon karakteristiğini anlamada ve buna bağlı olarak uygun projeksiyon seçimi aşamasında oldukça önemli bir yere sahiptir.
Tablo 4.1 Silindirik alan koruyan (Lambert) bir projeksiyona ait uzunluk deformasyonları ve
deformasyon değerleri
Enlem DeformasyonlarıÖzel Uzunluk DeformasyonuAlan
Maksimum Açısal Deformasyon φ k=a h=b p ω 0 1.0000 1.0000 1.0000 0⁰ 15 1.0353 0.9659 1.0000 3⁰58′ 30 1.1547 0.8660 1.0000 16⁰25′ 45 1.4142 0.7071 1.0000 38⁰57′ 60 2.0000 0.5000 1.0000 73⁰44′ 75 3.8637 0.2588 1.0000 121⁰57′ 90 ∞ 0.0000 1.0000 180⁰
Tablo 4.1’de silindirik alan koruyan (Lambert) bir projeksiyona ait uzunluk deformasyonları ve deformasyon değerleri gösterilmektedir. Bu değerler kullanılarak deformasyon değerlerinin yorumlanması aşamasında dikkat edilmesi gereken hususlar maddeler halinde yorumlanacak olursa;
(1) Sıfır deformasyonlu noktalar ya da hatların konumları hakkında kanıt aranmalıdır. Temel ölçeğin genel olarak 1.0 şeklinde ifade edilmesinden dolayı uzunluk deformasyonu kolonlarında bu değere eş olan değerlere bakılmalıdır. Tablo 4.1’de 0 olduğu 1. satırda her iki ölçeğin de birim değere eşit olduğu görülmektedir. Aynı zamanda 1.0000 ve 0 olduğu görülmektedir. Bu durum temel ölçeğin ekvator boyunca korunduğunu ve aynı zamanda sıfır deformasyonlu hat olduğunu kanıtlamaktadır. Başka herhangi bir yerde özel uzunluk deformasyonlarının birim değere eşit olmadığı görülmektedir. Sonuç olarak, bu projeksiyonda ekvator, sıfır deformasyona sahip tek hattır denebilir.
(2) Projeksiyon özellikleri hakkında kanıt aranmalıdır. Bu, tüm projeksiyon
için kurulmuş bir bağıntı olmak zorundadır. Daha önce anlatılan bölümlerde bu bağıntılar, , 1/ , 1.0000 veya 1.0000 şeklinde olabilir. Bir konform haritada 0 ve alan koruyan bir haritada 1.0000 olacaktır. Tablo 4.1’de 4. kolondaki 1.0000 değerlerinden hareketle, bu projeksiyonun alan koruyan bir projeksiyon olduğu söylenebilir. Bir projeksiyonun isimlendirilmesinde kullanılan alan-koruyan ya da konform ifadeleri, o projeksiyonun özelliği hakkında yeterli bilgiyi barındırmak zorundadır. Bazı projeksiyonlar genellikle bu gibi bilgileri barındırmayan, sadece özel isimlerle veya başlıklarla anılır (Mercator Projeksiyonu, Bonne Projeksiyonu ya da Twilight Projeksiyonu gibi).
(3) Ana yönlerle ilişkili kanıt aranmalıdır. Bu özel örnekte paralel ve
meridyenler ortogonal bir ağ oluşturmaktadır ve bu nedenle ana yönler grid ağı ile çakışıktır. Bu nedenle, ve ’dir. Böylesine bir projeksiyonla çalışmak, ana yönleri paralel ve meridyenlerle çakışmayan bir projeksiyonla çalışmaktan çok daha kolaydır.
(4) Sıfır ya da sonsuz değerine sahip istisnai noktalar hakkında kanıt
Burada ∞, 0.0000, hesaplanamaz değerde ve maksimum açısal deformasyon değeri de 180 ’dir. Tüm bu ipuçları bizlere, coğrafi kutuplarda bire bir uyum sağlanamadığı göstermektedir.
4.2 Görsel Analizler
Harita projeksiyonlarında deformasyonların gösterimi, projeksiyonları anlamak açısından oldukça önemli bir konudur. Görselleştirme metotları, harita projeksiyonlarındaki deformasyonların analitik olarak değerlendirilmesi ile elde edilen sonuçların görselleştirilmesini kapsamaktadır. Bu yöntemler, harita projeksiyonlarındaki deformasyonların karakteristiğini ortaya çıkararak, projeksiyon hakkında genel anlamda bir fikir edinmek amacıyla kullanılmaktadır.
4.2.1 Grid ağının deformasyon analizinde bir görsel araç olarak kullanımı
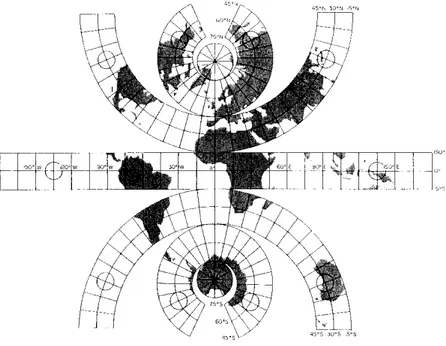
Grid ağı, yeryüzünün kavramsal olarak canlandırılmasında oldukça kullanışlı bir araçtır. Projeksiyonlar bazen basit anlamda, enlem ve boylamların grid ağının görünümlerine dayanarak değerlendirilmektedir. Gridler harita projeksiyonlarının deformasyonlarının anlaşılması ve bilinmeyen projeksiyonların tanımlanabilmesi için uzun süredir bir analitik araç olarak kullanılmaktadır. Şekil 4.1’de bazı projeksiyonlara ait grid ağlarının görünümleri gösterilmektedir.
Alan Koruyan Silindirik Eckert V
Eckert VI Sinusoidal
Plate Carreé Mollweide
Şekil 4.1 Bazı yaygın kullanılan projeksiyonların grid ağları
Bazen basılmış bir haritanın üzerinde herhangi bir projeksiyon bilgisi bulunmamasından dolayı projeksiyonunun tanımlanmasının neredeyse imkansız olması nedeniyle haritalardan, daima oluşturuldukları projeksiyon hakkında bir bilgi barındırması beklenmektedir. Kullanılan harita projeksiyonu tanımlanırken, eğer mümkünse, herhangi bir ölçüm yapmadan harita üzerindeki grid ağının görünümüyle, kullanılan projeksiyonun konik, silindirik, azimutal ya da diğer sınıflara ait bir projeksiyon olup olmadığı konusunda kullanıcıda bir ön yargının oluşması önemlidir. Projeksiyon sınıfı tanımlanabilirse haritanın sahip olduğu deformasyon karakteristikleri hakkında yorum yapılabilir. (Burgayevskiy ve Snyder 1995)
Harita grid ağının analizi, meridyen ve paralellerin projeksiyon düzlemi üzerindeki yerleşiminin incelenmesi ile başlamaktadır. Orta meridyen boyunca paralellerin dağılımı ve ekvator ya da başlangıç paraleli boyunca da meridyenlerin