Carnot grupları üzerindeki afin kontrol sistemlerinin kontrol edilebilirliği

i

YILDIZ TEKNİK ÜNİVERSİTESİ

FEN BİLİMLERİ ENSTİTÜSÜ

CARNOT GRUPLARI ÜZERİNDEKİ

AFİN KONTROL SİSTEMLERİNİN

KONTROL EDİLEBİLİRLİĞİ

Memet KULE

FBE Matematik Anabilim Dalı Matematik Programında Hazırlanan

DOKTORA TEZİ

Tez Savunma Tarihi : 26 Aralık 2008

Tez Danışmanı : Doç. Dr. Ayşe KARA (YTÜ) Jüri Üyeleri : Prof. Dr. Ulviye BAŞER (İTÜ)

: Prof. Dr. A. Göksel AĞARGÜN (YTÜ) : Prof. Dr. Ömer GÖK (YTÜ)

: Doç. Dr. Meral TOSUN (GSÜ)

ii

İÇİNDEKİLER

Sayfa

ÇİZELGE LİSTESİ ...iii

ÖNSÖZ ...iv ÖZET ... v ABSTRACT ...vi 1. GİRİŞ... 1 2. GENEL KAVRAMLAR ... 2 2.1 Manifold ... 2 2.2 Lie Grupları ... 5 2.3 Lie Cebiri... 6

3. GENEL KONTROL SİSTEMLERİ... 8

3.1 R üzerindeki Afin Kontrol Sistemleri ... 10 n 4. LİE GRUPLARI ÜZERİNDEKİ AFİN KONTROL SİSTEMLERİ ... 12

4.1 Carnot Grubu ... 13

4.1.1 Dilation Etkisi... 13

4.1.2 Carnot Grubunun Örnekleri... 14

4.1.3 Carnot Grubu Otomorfizmaları ... 15

5. BAZI LİE CEBİRLERİ İÇİN HESAPLAMALAR ... 19

6. SONUÇLAR ve ÖNERİLER ... 42

KAYNAKLAR... 43

iii

ÇİZELGE LİSTESİ

Sayfa

Çizelge 5.1 2.Dereceden Nilpotent Lie Grupları ... 39

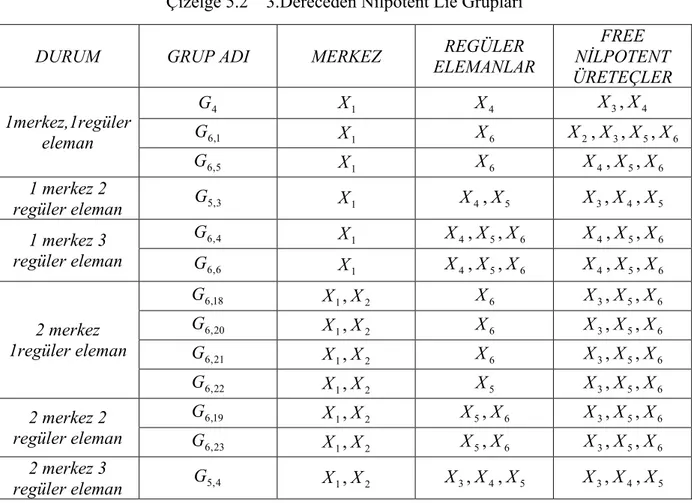
Çizelge 5.2 3.Dereceden Nilpotent Lie Grupları ... 40

Çizelge 5.3 4.Dereceden Nilpotent Lie Grupları ... 40

iv

ÖNSÖZ

Bu doktora çalışması sırasında desteğini hiçbir zaman esirgemeyen bilgisi ile çalışmamı yönlendiren Sayın hocam Doç.Dr. Ayşe KARA’ ya teşekkürlerimi sunarım.

Doktora tez izleme komitesinde görev alarak çalışmalarıma katkı sağlayan Prof.Dr. Ulviye BAŞER ve Prof.Dr. A. Göksel AĞARGÜN’e şükranlarımı sunarım.

v

ÖZET

CARNOT GRUPLARI ÜZERİNDEKİ AFİN KONTROL SİSTEMLERİNİN KONTROL EDİLEBİLİRLİĞİ

Memet KULE

Matematik Bölümü, Doktora Tezi

G basit bağlantılı nilpotent bir Lie grubu ve L(G) de onun Lie cebiri olsun. Eğer L(G) ‘nin

vektör alanları 1≤ j<r için

[

V₁,V_j

]

=V_j+1 ve

[

V₁,V_r

]

=0 şeklinde V₁, L(G) ‘nin tümünü üretiyorsa G ‘ye Carnot grubu denir. Bu grup üzerinde tanımlanmış afin kontrol sistemlerinin kontrol edilebilmesi için sistemin tekil noktalarının varlığı ve afin sisteme ilişik olan bilineer kısmının kontrol edilebilirliği ile olan ilişkisi karakterize edilmiştir.

Ayrıca 6. boyuta kadar bütün nilpotent Lie cebirlerinin merkezleri, regüler elemanları ve free nilpotent üreteçleri hesaplanmış ve tablo halinde sınıflandırılmıştır.

vi

ABSTRACT

CONTROLLABILITY OF AFFINE CONTROL SYSTEMS ON CARNOT GROUPS

Memet KULE

Dept. Of Maths., Ph.D. Thesis

Let G be a simply connected nilpotent Lie group and L(G) be its Lie algebra. If vector fields of L(G) produce the algebra such that for 1≤ j<r,

[

V₁,V_j

]

=V_j+1 and

[

V₁,V_r

]

=0, then G is called a Carnot group. For the controllability of affine control systems defined on this group, connections of existence singular points of the system and controllability of associated bilinear part has been characterized.

Moreover; centers, regular elements and free nilpotent generators of all nilpotent Lie algebras of up to dimension 6 has been calculated and listed in tables.

1. Giriş

Bu tez çalışmasının asıl amacı diferansiyel geometrik bakış açısından, topolojik ve cebirsel yaklaşımlar ile Lie gupları üzerindeki afin kontrol sistemlerinin kontrol edilebilirliği için genel bir sonuç elde etmektir. Bu problem ve yaklaşım ile ilgili, ilk olarak yayınlanmış (Jurdjevic ve Sallet, 1984) sonuçları mevcuttur. Daha sonra yapılan bazı çalışmalar takip edildiğinde, en son varılan genel durumun Genelleştirilmiş Heisenberg Lie Grubu üzerinde olduğu görülmektedir.

Lie grupları üzerinde yapılmış ilk kontrol edilebilirlik çalışması ise (Brockett, 1972)’a aittir. Daha sonra (Jurdjevic ve Sussmann, 1972) yayınladıkları makale ile Lie Grupları üzerindeki kontrol sistemlerinin sistematik matematiksel çalışmasını başlatmışlardır.

Bu çalışmanın amacı, daha genel bir durum uzayı üzerinde kontrol edilebilirlik problemi için genel bir sonuç elde etmektir. Bu amaçla, Carnot grupları üzerindeki afin kontrol sistemleri incelenmiştir. Ayrıca, 6. boyuta kadar bütün nilpotent Lie cebirlerinin merkezleri, regüler elemanları ve free nilpotent üreteçleri hesaplanmıştır.

Bu çalışma 4 bölümden oluşmaktadır. İlk bölüm de konu hakkında genel kavramlar verilmektedir. II. bölüm de genel kontrol tanımı verilip, ayrıca (Jurdjevic ve Sallet, 1984)‘ın

n

R üzerinde yapmış oldukları afin sistemlerin kontrol edilebilirlik karakterizasyonu

incelenmektedir. III. bölüm de Carnot grubu tanımı ve dilation etkisi verilip Carnot grubu üzerin de ki afin sistemlerin kontrol edilebilirlik karakterizasyonu elde edilmektedir. IV. bölümde de 3-boyutlu Heisenberg Lie grubu üzerindeki afin sistem örneği gözönüne alınmış ve bu amaçla 6. boyuta kadar bütün nilpotent Lie cebirlerinin merkezleri, regüler elemanları ve free nilpotent üreteçleri hesaplanmıştır.

2. GENEL KAVRAMLAR

Bu bölümde, tez çalışmasının temel kavramları olan manifold, Lie grubu ve Lie cebiri gibi bazı temel kavramlar yer almaktadır.

2.1 Manifold

Tanım : n boyutlu M yerel Öklid uzayı, her bir noktasının komşuluğu _{R Öklid uzayının} n açık alt kümesine homeomorfik olan Hausdorff topolojik uzayıdır.

Eğer ϕ, bağlantılı açık U ⊂M alt kümesinden _{R nin açık bir alt kümesi üzerine bir} n homeomorfizma ise, ϕ ‘ye koordinat tasviri, x_i =r_{i o}ϕ fonksiyonlarına koordinat fonksiyonları ve

(

U,ϕ

)

çiftine koordinat sistemi denir. Burada, r Rn R

i: → fonksiyonu,

(

)

(

n

)

n R a a

a= ₁,..., ∈ olmak üzere r_i

( )

a = şeklinde tanımlıdır. a_i

Tanım : M yerel Öklid uzayı üzerindeki _C ∞ _{sınıfından bir F diferansiyellenebilir yapısı} aşağıdaki üç şartı sağlayan

(

U_α,ϕ_α

)

,α∈I, koordinat sistemlerinin bir topluluğudur;

i) U M I = ∈

U

α α ii) _{ϕ ϕ}− ∈C∞ ∀_{α β}∈I β α o 1 , ,

iii) F topluluğu maksimaldir, yani,

(

U,ϕ

)

koordinat sistemi ∀α∈I için −1

α ϕ ϕ_o ve ∞ −1_{∈ C} ϕ ϕ_{α o} ’ yi sağlıyorsa,

(

U,ϕ

)

∈F dir. ∞

C sınıfından n boyutlu diferansiyellenebilir manifold, C sınıfından bir F ∞

diferansiyellenebilir yapısı ile birlikte M yerel Öklid uzayını içeren (M,F) çiftidir.

Örnek : _R n _{Öklid uzayı diferansiyellenebilir manifold yapısına sahiptir. R} n _üzerindeki standart diferansiyellenebilir F yapısı

( )

Rn_{, koordinat sistemini içeren maksimum} i

topluluktur. Burada, _i:Rn _→Rn _{ye birim tasvirdir.}

Örnek : _S1 ₌

{

( )

_x,_{y ∈R}2 :_x2 _+y2 ₌1

}

_{kümesini göz önüne alalım. S kümesi} 1 _{R de} 2 merkezi orjinde yarıçapı 1 birim olan çemberdir. _{S , 1-boyutlu yerel Öklid uzayıdır.} 1

( )

{

, 1: 0

}

1 = x y ∈S y> U (2.1)

( )

{

, 1: 0

}

2 = x y ∈S y< U (2.2)

( )

{

, 1: 0

}

3 = x y ∈S x> U (2.3)

( )

{

, 1: 0

}

4 = x y ∈S x<

U (2.4)

Kümelerini göz önüne alalım. Bu kümeler _{S in açık alt kümeleridir.} 1 4 3 2 1 1 _{U U U U} S = ∪ ∪ ∪ (2.5) R

I =(−1,1)⊂ açık aralığını göz önüne alalım. I

U₁ → 1:

ϕ (2.6)

( )

x,y _a x fonksiyonunu göz önüne alalım. x

y x, )= ( 1

ϕ fonksiyonu sürekli, bire-bir ve örten bir fonksiyondur.

1 1 1 :I →U − ϕ (2.7)

(

_{x, 1 x}2

)

x_a −

(

2

)

1 1− = x, 1−x

ϕ fonksiyonu da sürekli bire-bir ve örtendir. Dolayısıyla, ϕ₁ fonksiyonu bir homeomorfizmadır. Benzer şekilde,

I U₁ → 1: ϕ (2.8)

( )

x,y _a x I U₂ → 2 : ϕ (2.9)

( )

x,y _a x I U₃ → 3: ϕ (2.10)

( )

x,y _a y I U₄ → 4 : ϕ (2.11)

( )

x,y _a y

izdüşüm fonksiyonları da birer homeomorfizmadır.

(

) (

) (

) (

)

{

U₁,ϕ₁ , U₂,ϕ₂ ,U₃,ϕ₃ ,U₄,ϕ₄

}

F = topluluğu için i)

_U

4 1 1 = = i i U S dir.

1 3 1

−

ϕ

ϕ _o in C olup olmadığını inceleyelim. (2.8) alalım ve (2.10) nun ters fonksiyonu ∞

3 1 3 :I →U − ϕ (2.13)

(

y y

)

y 1₋ 2, a

olan fonksiyonu alalım o taktirde 1 3 1 − ϕ ϕ _o bileşkesi I U U I⎯⎯→3−1 ∩ ⎯⎯→1 1 3 ϕ ϕ _(2.14)

(

1_−y2,_y

)

1_−y2,

(

_y>0

)

y_{a a}

şeklinde olur. Dolaysıyla, ∞ −1 _{y −y}2 _∈C 3

1oϕ : a 1

ϕ , yani sürekli türetilebilirdir. Benzer şekilde, 4∀ ji, =1,2,3, için − _{∈ C}∞

j i ϕ 1

ϕ _o dur.

iii) F topluluğu maksimumdur. Gerçekten, (ii) koşulunu sağlayacak

(

U₅,ϕ₅

)

koordinat sistemi yoktur.

Sonuç olarak,

(

S ,1 F

)

_{yapısı 1-boyutlu diferansiyellenebilir bir manifolddur.}

Tanım : f,g_∈C∞(M) _{için X :C}∞_{(M)→R tasviri aşağıdaki şartları sağlarsa p∈M} noktasında bir tanjant vektörüdür;

i) X(f + )g = X

( )

f +X

( )

g

ii) X

( )

fg (p)= X

( )

f g(p)+ f

( ) ( )

p X g

M

p∈ noktasındaki tanjant vektörlerin kümesi MT_p ile gösterilir ve p∈M noktasındaki tanjant uzayı (teğet uzayı) denir. Ayrıca )dim(T_pM)=dim(M dir.

Tanım : TM ile gösterilen tanjant demeti

_U

M p pM T TM ∈

= şeklinde tanımlıdır. Tanjant demeti bir manifold olup dim(TM)=2dim(M) dir.

Tanım : M bir manifold olmak üzere dom(X)⊂M açık alt kümesinden TM tanjant demetine tanımlı olan X :dom(X)⊂M →TM sürekli fonksiyonuna vektör alanı denir. ∀p∈dom(X) için X_p ∈T_pM dir.

üzerinde bir fonksiyon olup p∈dom(X) ‘deki değeri X

( )

f (p)= X_p(f) dir.

Tanım : X ve Y , M üzerinde diferansiyellenebilir vektör alanları olsun.

[

X ,Y

]

de bir diferansiyellenebilir vektör alanı olup buna X ve Y nin Lie parantezi denir ve

[

X,Y

]

_m(f)= X_m(Yf)−Y_m(Xf) (2.15)

şeklinde tanımlanır. Burada, f ∈C∞_,m∈M _dir. Lie Parantezinin Özellikleri :

1.

[

X,X

]

=0

2.

[

X,Y

] [

=−Y,X

]

3.

[

X,

[ ]

Y,Z

]

+

[

Z,

[

X,Y

]

]

+

[

Y,

[

Z,X

]

]

=0 (Jakobi Özdeşliği)

Tanım :

1. M ve N birer manifold olmak üzere, eğer

) ( ) (U 1 V N M U f f ψ ϕ ψ ϕ ϕ ψ_{⎯ →⎯⎯} ⎯ ↓ ↓ ⎯→ ⎯ ⊂ − o o ve _{ψ ϕ}−1 o

o f ϕ( p) ‘de diferansiyellenebilecek şekilde, p için

(

U,ϕ

)

ve f(p) için

(

V,ψ

)

koordinat sistemleri varsa f :M →N fonksiyonu p∈M de diferansiyellenebilirdir denir.

2. M ile N iki manifold ve f :M →N diferansiyellenebilir bir fonksiyon olsun. f nin türevi olan df :TM →TN tasviri,

(

g f

)

X g X df( )( )= _o , ∀X ∈TM ve her bir g_∈C∞(N) şeklinde tanımlıdır. 2.2 Lie Grupları

Lie grubu hem manifold hemde grup yapısına sahip bir kümedir.

Tanım : G diferansiyellenebilir bir manifold ve grup yapısını sağlayan bir küme olmak üzere

( )

_, 1

, −

→

×G G σ τ _aστ

G tasviri diferansiyellenebilir ise G ‘ye Lie grubu denir.

Örnek : _S1 ₌

{

( )

_x,_{y ∈R}2 :_x2 _{+ y}2 ₌1

}

_{birim çemberi karmaşık sayılardaki çarpma işlemi} altında bir Lie grubudur.

Tanım : σ∈G olmak üzere,

G G l_σ : → (2.16) στ τ σ( )=

l tasvirine σ ‘nın sol ötelemesi denir. l ‘_σ nın türevi dl_σ :TG→TG şeklindedir ve

G T G T

dl_σ( _τ )⊂ _στ dir.

Tanım : X bir vektör alanı olmak üzere, ∀σ∈G için, X _ol_σ =dl_{σ o}X eşitliği sağlanıyorsa,

X vektör alanına G üzerinde sol invaryanttır denir.

Tanım : G bir Lie grubu ve L(G) G ‘nin sol invaryant vektör alanlarının bir kümesi olsun. O taktirde, L(G) reel vektör uzayıdır ve

G T G L( )→ _e : α (2.17) e X X)= (

α şeklinde tanımlı tasvir bir izomorfizmadır. Sonuç olarak,

G G T G L( ) dim _e dim dim = = dir. 2.3 Lie Cebiri

Tanım : L(G), K cismi üzerinde (K=R,C) bir vektör uzayı olsun. ) ( ) ( ) (G L G L G L × → (2.18)

(

X,Y

)

_a

[

X,Y

]

tasviri aşağıdaki şartları sağlıyorsa, L(G) ye Lie cebiri denir;

i) K cismi üzerinde bilineerdir, yani; ∀α₁,α₂∈K ve ∀X,X₁,X₂,Y,Y₁,Y₂ ∈L(G) için

[

α₁X₁ +α₂X₂,Y

]

=α₁

[

X₁,Y

]

+α₂

[

X₂,Y

]

ve

[

X,α1Y1+α2Y2

]

=α1

[

X,Y1

]

+α2

[

X,Y2

]

dir.

ii) Ters simetriktir, yani;

[

X,Y

] [

=−Y,X

]

iii)

[

X,

[ ]

Y,Z

]

+

[

Z,

[

X,Y

]

]

+

[

Y,

[

Z,X

]

]

=0 Jakobi özdeşliğini sağlar.

Lie cebirinin önemi, kendisine ilişik Lie grubunda özelliklerinin yansıyor olmasıdır.

G Lie grubunun L(G) Lie cebiri, G üzerindeki tüm sol(sağ)-invaryant vektör alanlarının kümesi olarak düşünülebilir. Bunun dışında, G’ nin L(G) Lie cebirini birimdeki tanjant uzayı

) (G

Örnek:3- boyutlu Heisenberg grubu, ⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ ∈ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = y x y z R z x G , , 1 0 0 1 0 1 şeklindedir. R t∈ ∀ için G t t ∈ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = 1 0 0 0 1 0 0 1 ) (

γ olup γ(t), G üzerinde γ(0)=I =e olacak şekilde bir eğridir. G T X t = ∈ _e ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = ⇒ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = • • 0 0 0 0 0 0 0 1 0 ) 0 ( 0 0 0 0 0 0 0 1 0 ) ( γ γ olur. R t∈ ∀ için t t ∈G ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = 1 0 0 1 0 0 0 1 ) (

α olup α(t), G üzerinde α(0)= I =e olacak şekilde bir eğridir. G T Y t = ∈ _e ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = ⇒ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = • • 0 0 0 1 0 0 0 0 0 ) 0 ( 0 0 0 1 0 0 0 0 0 ) ( α α olur. R t∈ ∀ için G t t ∈ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = 1 0 0 0 1 0 0 1 ) (

β olup β(t), G üzerinde β(0)=I =e olacak şekilde bir eğridir. G T Z t = ∈ _e ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = ⇒ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = • • 0 0 0 0 0 0 1 0 0 ) 0 ( 0 0 0 0 0 0 1 0 0 ) ( β β olur.

{

X Y Z

}

span G

T_e = , , olur. Burada, bunların Lie parantezlerine bakacak olursak

[

X,Y

]

=Z ,

[

X,Z

]

=0 ve

[ ]

Y,Z =0 dır. Buradan, G Heisenberg grubunun L(G) Lie cebiri L(G)≅T_eG

3. GENEL KONTROL SİSTEMLERİ

M diferansiyellenebilir bir manifold olmak üzere M’ nin açık alt kümeleri üzerinde tanımlı

tüm pürüzsüz (C veya analitik) vektör alanlarının topluluğunu ∞ X(M) ile gösterelim. X(M) ‘nin her bir elemanı M üzerindeki yerel difeomorfizmaların bir 1-parametreli grubunu tanımlar. Dolayısıyla, eğer )X∈X(M ise, manifoldlar üzerinde vektör alanları vasıtasıyla üretilmiş adi diferansiyel denklemlerin varlık ve teklik teoreminden dolayı, olanaklı her bir

R t∈ için, M M X dom X_t : ( _t)⊂ → (3.1)

bir yerel difeomorfizmadır. Bundan başka, eğer )_γ X(., x _{, x noktasındaki vektör alanının} integral eğrisi ise, o taktirde

) , ( ) (x t x X X t =γ (3.2)

dir. X yerel difeomorfizması aşağıdaki özelliklere sahiptir : _t

i) X_{t o}X_s = X_t+s , ∀ ,t s∈R

ii) ₍X_t)−1 = X_{−t , ∀t∈R}

iii) X₀ =Id.

Tanım : Bir ∑ kontrol sistemi ∑=(M,D) şeklindeki bir ikili olarak tanımlıdır. Burada, M diferansiyellenebilir bir manifold ve D, X(M) ‘in bir alt topluluğudur.

M ‘ye ∑ ’nın durum uzayı denir. D’ nin elemanları sistemin stratejileri ve ∑ kontrol sisteminin kontrolleridirler.∑ kontrol sistemi;

{

X X X X D t R r N

}

G r j _j t t t r ∈ ∈ ∈ = ∑ 11 o 22 o...o | , , (3.3)

sözde (pseudo) grubunu tanımlar ve ∑ tarafından M ‘de x ’in yörüngesi

{

∑

}

∑ x = x ∈G

G ( ) ϕ( )|ϕ (3.4)

x ’de G ’ nın etkisi ile verilir . _∑

Tanım: Bir ∑ kontrol sistemi, eğer x∈M olmak üzere G_∑(x)=M sağlanıyorsa, x ‘de geçişlidir denir.

) (

~ y y G x

olacak şekilde G_∑(x)⊂M üzerinde tanımlı “~” bağıntısı bir denklik bağıntısıdır. ∑ kontrol sistemi geçişli ise, ∀x∈M için,G_∑(x)=M ’dir.

Ayrıca ∑ ile birleşmiş,

{

X X X X D t r N

}

S r j _j t t t r ∈ ≥ ∈ = ∑ 11o 22 o...o | , 0, (3.6)

sözde yarı (pseudo-semi) grubu elde edilir. S x’ den _∑ ∑ ’nın ulaşılabilirlik (accesibility) kümesi olan ∑ ile M’ deki x’ in pozitif yörüngesi S_∑(x)=

{

ϕ(x)|ϕ∈S_∑

}

‘yı verir. Genel olarak, ∀x∈M için, S_∑(x)⊆G_∑(x)⊆M dir.

) (

~ y y S x

x ⇔ ∈ _∑ ile tanımlı S_∑(x)⊂M üzerindeki “~” bağıntısı, t > 0 olmak üzere M

x∈

∀ için X_−t(x)’ nin S_∑(x)’ e ait olması gerekmediğinden, simetrik bir bağıntı değildir. Kontrol Teorinin temel problemlerinden kontrol edilebilirlik problemi, S_∑(x)=Molacak şekilde M, D ve x∈Müzerindeki koşulları bulmaktır. Problemin amacı bir x başlangıç noktasından başlayarak ∑ ’ nın D negatif olmayan stratejileri ile M’in her noktasına ulaşmaktır.

Genel olarak, S_∑(x)⊆G_∑(x)⊆M olduğundan, ∑ ’nın geçişliliği bu problemi çözmek için gerekli bir koşuldur ancak yeterli değildir. Örneğin;

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ = ∑ dx d

R, sistemini göz önüne alalım. S =

[

∞

)

⊂G_∑ =R

≠

∑(1) 1, (1) dir.

Tanım: ∑=(M,D) bir kontrol sistemi ve x∈M olsun. ∑ ’ ya eğer S_∑(x)=M ise , x’ de kontrol edilebilirdir denir.

Eğer ∑ kontrol sistemi M ‘nin her noktasında kontrol edilebilir ise, kontrol edilebilirdir denir.

Teorem: (Yörünge Teoremi, (Sussman, 1973)) ∑=(M,D) bir kontrol sistemi ve x∈Mise, )

(x

G_∑ yörüngesi bir diferansiyellenebilir manifold yapısına sahiptir.

Teorik açıdan önemli bir sonuç olan Yörünge Teoremi (Sussmann, 1973) sistemin dinamiğinin tüm özelliklerini koruyarak, M’deki herhangi bir başlangıç koşulu için durum uzayının yörüngesine indirgenmesine olanak vermektedir.

3.1

Rn üzerindeki Afin Kontrol Sistemleri

n

R üzerindeki afin sistemlerin kontrol edilebilirlik karakterizasyonunu Jurdjevic ve Sallet

(1984) göstermişlerdir.

Bir afin reel uzay _{R n-boyutlu Öklid uzayı olmak üzere, bu uzay üzerindeki tüm} n endomorfizmaların uzayını _{EndR ve tüm lineer otomorfizmaların uzayını da} n _{AutR ile} n gösterirsek _AfRn _{= AutR}n _⊗Rn_{, R ’nin afin grubunu tanımlar ve grubun Lie cebiri de} n

n n n _{EndR R}

afR = ⊗ şeklindedir. _A∈EndRn _{ve a∈R}n _{için X(x)= Ax+a vektör alanına} afin vektör alanı denir.

n

R üzerinde tXexp ’ in etkisi _{R üzerindeki difeomorfizmaların bir 1-parametreli grubuna} n neden olur ve onun sonsuz küçük üreteci X(x)= Ax+a afin vektör alanıdır.

m

X X

X₀, ₁,..., afin vektör alanlarının herhangi bir sonlu topluluğu, X_i(x)= A_ix+a_i ;

i=0,1,…,m olmak üzere bir kontrol sistemi tanımlar.

∑

∑

= = + + + = + = m i i i i i m i i t X x A x a u t Ax a u x X dt dx 1 0 0 1 0( ) ( ) ( ) ( ) ( )( ) (3.7)

şeklindeki kontrol parametreli diferansiyel denklemler _R n _{üzerindeki afin sistemin} dinamiğini oluşturur. Burada, n

i U R

u ∈ ⊂ kontrollerle ilgili keyfi fonksiyonlar, A₀,A₁,...,A_m n

n× ’lik matrisler ve a₀,a₁,...,a_m ‘de _R n _{içindeki sütun vektörlerdir.}

F afin sistem olmak üzere, ∀X ∈F ve _∀x∈Rn _{için X(x)≠0 oluyorsa F afin ailesine} tekil noktası yoktur denir.

Teorem : (Jurdjevic, 1997)

Vektör alanlarının bir F afin ailesi eğer 1. F hiçbir tekil noktaya sahip değilse ve

2. Fr ; Rⁿ-{0} üzerinde kontrol edilebilir ise

F afin ailesi, Rⁿ üzerinde kontrol edilebilirdir denir. Burada, Fr F afin ailesinin bilineer

Teoremin ilk koşulu tekil noktaların var olmaması ile ilgilidir, kontrol edilebilirlik için gerekli bir koşuldur. Eğer tekil nokta olursa o noktada ki ulaşılabilirlik kümesi tek noktadan meydana gelen sabit bir noktadır. Teorem aşağıdaki gibi de ifade edilebilir:

1. i=0,1,…,m için A_ix+a_i =0 olacak şekilde _x∈Rn _{noktası yoktur,}

2.

∑

= + = m i i i t Ax u x A dt dx 1

0 ( ) biliner sistem Rn −

{ }

0 üzerinde kontrol edilebilirdir. Teoremin ispatında _{R üzerinde v merkezli,} n _{λ >0 oranlı ( ) ( )}

, x v x v

h_λv = +λ − homoteti fonksiyonu kullanılmaktadır. Böylece, F afin sistemi bu dönüşüm sayesinde Fr biliner sistemine dönüşür. Fr biliner sistemi Rⁿ-{0} üzerinde kontrol edilebilir olduğundan biliner sistemin ulaşılabilirlik kümesi açık bir kümedir. Buradan ters dönüşüm sayesinde F afin sisteminin ulaşılabilirlik kümesinin açık bir küme olduğu gösterilir ve böylece ispat tamamlanır.

4. LİE GRUPLARI ÜZERİNDEKİ AFİN KONTROL SİSTEMLERİ

Kompakt bağlantılı ve kompakt olmayan semi-simple Lie grupları üzerindeki afin sistemlerin kontrol edilebilirlik karakterizasyonunu (Ayala ve San Martin, 2000) yapmışlardır.

Daha sonra (Kara ve San Martin, 2006) Genelleştirilmiş Heisenberg Lie Grupları üzerinde afin sistemlerin kontrol edilebilirlik karakterizasyonunu elde etmişlerdir.

G bağlantılı bir Lie grubu ve L(G) de onun Lie cebiri olmak üzere, G' nin )Af(G afin grubu

G ile Aut(G)' nin semi-direkt çarpımıdır, yani: Af(G)= Aut(G)⊗G.

(

φ,g₁

) (

⋅ ϕ,g₂

) (

= φ_oϕ,g₁φ(g₂)

)

(4.1)

) (G

Af (4.1) işlemiyle grup yapısına sahiptir. Aut(G)‘ nin birim elemanını 1 ile ve G’ nin birim elemanını da e ile gösterirsek. Af(G) ‘nin birim elemanı (1,e) ve

( )

φ,g ∈Af(G) ‘nin tersi

(

_φ−1,_φ−1(_g−1)

)

_∈Af(_G) _dir.

) (G

Af ' nin Lie cebiri de af(G)=aut(G)⊗L(G) dir. Burada, aut(G), Aut(G)' nin Lie cebirini göstermektedir.

Bir G⊂Af(G) Lie grubu üzerindeki bir afin kontrol sistemi ∑=( DG, )

g d j j j j g u t Y D D X g ( ) ( )( ) 1 .

∑

= + + + = (4.2)

şeklindeki diferansiyel denklemlerin ailesi ile belirlidir. Burada, g∈ , G

) ( ,..., , ,_Y1 _Y2 _{Y L G} X d _{∈ , D,D}1_,D2_,...,Dd _∈aut(G)ve j u kontrolleridirler. O taktirde dinamik ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ∈ + + + =

∑

= d j d j j j t D Y u R u X D D 1 ) )( ( (4.3)

ile verilir. Eğer G basit bağlantılı ise Aut(G)≅ AutL(G) dir. Burada, AutL(G)grubu ile

L(G)’ nin otomorfizma gurubunu gösterelim. AutL(G) Lie grubunun Lie cebiri de

[

] [

] [

]

{

( ) , ( ) , ( ), , ( )

}

) (G D EndL G X Y L G D X Y D X Y X D Y L = ∈ ∀ ∈ ∴ = + ∂ (4.4)

şeklinde tanımlı ve Lie cebir işlemi de

(

) (

)

[

D1,X1 , D2,X2

] [

=

(

D1,D2

]

,D1X2 −D2X1+

[

X1,X2

]

)

(4.5)

Afin kontrol sistemleri genel olarak lineer ve bilineer kontrol sistemlerinden daha geniş bir sınıfı temsil ederler. Afin kontrol sistemlerinde Lie cebirinden gelen vektör alanları sıfır vektörü olarak alındığında sistem bilineer kontrol sistemine dönüşmektedir.

Ayrıca, afin kontrol sistemleri Abelyen Lie grupları üzerinde göz önüne alındığında sistem lineer kontrol sistemine dönüşmektedir.

4.1 Carnot Grubu

G basit bağlantılı nilpotent bir Lie grubu ve L(G) de onun Lie cebiri olsun. Eğer L(G) ‘nin vektör alanları 1≤ j <r için

[

V₁,V_j

]

=V_j+1 ve

[

V₁,V_r

]

=0 şeklinde V₁, L(G) ‘nin tümünü üretiyorsa G ‘ye Carnot grubu denir. Carnot grubunun Lie cebiri

r V V V G L( )= ₁⊕ ₂ ⊕...⊕ (4.6)

şeklinde ifade edilebilir.(Buliga, 2002)

4.1.1 Dilation Etkisi

G bir Carnot grubu ve L(G) ‘de onun Lie cebiri olsun. δ_ε :L(G)→L(G) tasviri, her i=1,...,m için X_i∈ ve V_i ε >0olmak üzere,

∑

∑

= = = → = m i i i m i i X X X X 1 1 ε δ_ε (4.7)

şeklinde tanımlı ise, dilation etkisidir. Burada, m sayısına grubun basamağı denir.(Buliga,2002)

Yardımcı Teorem : δ_ε dilation etkisi otomorfizmadır.

İspat : Öncelikle homomorfizma olduğunu gösterelim. L(G)’ nin herhangi iki elemanı

∑

= = m i i X X 1 ve

∑

= = m j j X Y 1 için,

[

]

[

]

∑∑

∑ ∑

∑

∑

∑

∑

= = + + = = + = = = = = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = = = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = m i m j m i m j j i j i j i j i m j j j m i i i m j j m i i Y X X X X X X X X X Y X 1 1 1 1 1 1 1 1 , , , , , ε ε ε ε ε ε ε δ δ δ ε ε ε δ δ δ δ (4.8)

dir. Buradan, δ_ε :L(G)→L(G) tasvirinin bir homomorfizma olduğu görülür.

(

)

X X X m X X i i m i i i i m i i i ⎟= = = ⎠ ⎞ ⎜ ⎝ ⎛ =

∑

∑

∑

= = = − 1 1 1 1 1 ε ε ε δ δ δ_{ε o ε ε} (4.9)

(

)

X X X m X X i i m i i i i m i i i _{⎟= = =} ⎠ ⎞ ⎜ ⎝ ⎛ =

∑

∑

∑

= = = − − 1 1 1 1 1 ε ε ε δ δ δ_{ε o ε ε} (4.10)

(4.9) ve (4.10) eşitliklerinden 1-1 ve örten olduğu sonucu elde edilir. Dolayısıyla, δ_ε izomorfizmadır. Tanım kümesi ile değer kümesi aynı olduğundan otomorfizmadır.

Sonuç :δ_ε dilation etkisi Lie cebir otomorfizmasının 1-parametreli grubunu tanımlar.

4.1.2 Carnot Grubunun Örnekleri (Buliga, 2002)

1)_Rn _{toplama işlemi altında değişmeli bir Carnot grubudur.}

2) Heisenberg grubu trivial olmayan ilk örnektir. )) , ( 2 1 , ( ) , )( , (x x_ y _y = x+ y x_+y_+ w x y (4.11) işlemi ile H

( )

n ₌R2n _×R _{grup yapısına sahiptir. Burada w, R}2n _{üzerinde standart simplektik} formdur. Lie parantezi

)) , ( , 0 ( ) , ( ), , (x x_ y _y _⎥⎦⎤= w x y ⎢⎣ ⎡ (4.12)

şeklindedir. Grubun cebirinin direkt toplam ayrışımı:

{ }

0 2 _× =_R n

V ve Z = 0

{ }

×R olmak üzere H

( )

n =V +Z şeklindedir. Burada, Z cebirin merkezidir ve grup 2.basamaktan nilpotent Lie grubudur.

3) H-tipi gruplar. Z Lie cebirinin merkezi olmak üzere, Z

V

N = + (4.13)

ortogonal direkt toplam ayrışımından meydana gelecek şekilde bir (·,·) iççarpım ile donatılmış 2.basamaktan nilpotent N Lie grubu alınsın.

( )

V End Z

J : → ,

(

J_zx,x′

)

=

(

z,

[ ]

x,x′

)

(4.14) fonksiyonu tanımlansın. Eğer ∀z∈Z için

I z J

J_{z o z} =− 2 (4.15)

4) n×n üst üçgen matrislerin grubu (n-1). basamaktan nilpotent olup aynı zamanda Carnot grubudur. Herhangi bir Carnot grup üst üçgen matrislerin bir grubunun bir alt grubuna izomorf olması nedeniyle bu örnek Carnot gruplarında önemli bir yeri vardır.

4.1.3 Carnot Grubu Otomorfizmaları

1. _G=RN _{Carnot grubunu alalım. Lie cebirinin} RN = RN1×RN2 ×...×RNr şeklinde bir

ayrışımı vardır.

( )

_x =δ

(

_x1_,x2_,...,xr

) (

= ε_x1_,ε2_x2_,...,εr_xr

)

_;xj ∈_RNj

δ_{ε ε} (4.16)

şeklinde tanımlı

( )

δ_{ε ε>0} dilation etkisi G’nin otomorfizmasıdır.

2. L(G) herhangi bir Lie cebiri olsun. ε >0 ve _{X∈ için V}i

( )

X _εiX

δ_ε = (4.17)

şeklinde tanımlı tasvir Lie cebiri üzerinde tanımlı grup otomorfizmasıdır. Özel olarak Heisenberg grubu ele alındığında

(

X_,Y_,Z

)

(

_εX_,εY_,ε2Z

)

δ_ε = (4.18)

L(G) Lie cebirinin otomorfizmasıdır.

3. δ_ε G’nin dilation etkilerinin 1-parametreli ailesi (δ_st =δ_{s o}δ_t ve δ₁ =id)

( ) ( )

(

x y

)

d

( )

x y x y G

d δ_ε ,δ_ε =ε , ; , ∈ (4.19)

ε

δ , G’nin kendisi üzerine bir otomorfizmaya neden olur.

Tanım: S, G üzerindeki vektör alanlarının bir ailesi olmak üzere, boş kümeden farklı G

A⊂ için, eğer ∀t∈R, ∀X∈S ve ∀x∈A için X_t(x) tanımlı olacak şekilde X_t(x)∈A

ise A’ya S-invaryant denir.

Teorem: G tıkız olmayan bağlantılı bir Lie grubu ve L(G) onun Lie cebiri olsun. O taktirde, eğer G üzerindeki kontrol sistemi invariant ise, G ‘nin tıkız altkümeleri G -invaryant _∑

değildir.

İspat: Her x∈G, her X∈L(G) ve her t∈R için, δ_X(.,x):(a,b)⊂R →G diferansiyellenebilir eğrisi )δ_X(t,x)= X_t(x şeklinde tanımlıdır. K ⊂G altkümesinin tıkız ve

∑

G -invaryant bir altküme olduğunu kabul edelim. Her X∈L(G) vektör alanı tam bir vektör alanıdır. K’ nın herhangi bir Λ =

{

U_ii∈Z+

}

açık örtüsünü göz önüne alalım. O halde, her

K

x∈ için X_t(x) olduğundan, her i için δ_X(t,U_i) K ‘nın açık örtüsüdür. K tıkız olduğundan, Λ_δ =

{

δ_X(t,U_i)i∈Z+

}

açık örtüsünün sonlu bir alt örtüsüne sahiptir. Böylece,

δ

Λ ’nın elemanlarının ters görüntüleri de R ‘yi örtmelidir. Buda R’ nin tanımıyla çelişir.

Yardımcı Teorem : ∑=(G,D), G bağlantılı Lie grubu üzerinde bir afin kontrol sistemi olsun. Sistemin her bir pozitif yörüngesi açık ise, o taktirde sistem kontrol edilebilirdir.

İspat : Eğer kontrol sisteminin her bir S_∑(x) pozitif yörüngesi açık ise, o taktirde = ∑( ) * _x S

{

1 2 ... | 0

}

2 1 X X −t > X r t t

t o o o r kümesi de açıktır. G ‘nin topolojisinden dolayı,

) (x

S

G = _∑ dir.

Teorem: Bir G Carnot grubu üzerindeki

(

)

⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ∈ ∂ ∈ ∈ + + + = ℑ

∑

= d i d d d i i i D X u R D D D L G X X X L G u X D 1 1 1_{, ( ); , , , ( )} , ; : _{L L} (4.20)

dinamiği ile verilen bir ∑ =

(

G,ℑ

)

afin kontrol sistemi, eğer ∑ tekil noktaya sahip değilse ve dinamiği ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ _{+ ∈ ∈∂} = ℑ

∑

= d i d d i i b D u D u R D D D L G 1 1_{, ( )} , ; : _L (4.21)

şeklinde olan ilişik bilineer kontrol sistemi ∑_b =

(

G,ℑ_b

)

G üzerinde kontrol edilebilirse, G üzerinde kontrol edilebilirdir.

İspat: Öncelikle, kontrol sistemleri için herhangi bir tekil noktaya sahip olmamak, sabit bir noktadan ulaşılabilir noktaların kümesinin tek bir noktadan meydana gelmesi, yani;

x x

G_∑( )= olması nedeniyle kontrol edilebilirlik için gerekli bir koşuldur.

(

)

( )

:Id δ_ε D X ξ D X D δ_ε X

ξ × = + → + = + olacak şekilde ξ:af(G)→af(G) şeklinde bir otomorfizma tanımlayalım. ∀X ∈L(G) için

∑

∑

= = = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = n j j j n j j X X X 1 1 ) ( δ ε δ_{ε ε} olduğundan 0 →

ε için δ_ε(X)→0 olur. Öyleyse ε →0 için ξ(ℑ)→ℑ_b dir.

(

b

)

b = G ℑ

∑ , bilineer kontrol sisteminin x’ten ulaşılabilirlik kümesini A_b(x) ile ve

(

ℑ

)

=

∑ G, afin kontrol sisteminin de x’ten ulaşılabilirlik kümesini A(x) ile gösterelim. Bir y∈ ve B(y) kapalı birim yuvarı göz önüne alınsın. Burada, B(y)={x:d(x,y) 1G ≤ } dir. S(y), bu yuvarın sınırını göstersin.

Tam kontrol edilebilirlik küçük pertürbasyonlarda korunur, (Sussman, 1976). Dolayısıyla, )

( )

(y A x

S ⊂ _b dir. Yeteri kadar küçük ε değeri için, S(y)⊂ξ_ε(A(x)) olur. u,z∈S(y) noktalarını alalım. S(y)⊂ξ_ε(A(x)) olduğundan, z ‘den u ‘ya normal olarak ulaşılabilirdir. Dolayısıyla, x ‘den ulaşılabilir küme u ‘nun bir açık komşuluğunu kapsar. δ_ε(u)⊂ξ_ε(A(x)) elde edilir. O halde, u₁∈δ_ε(u) , u₁∉S(y) ve u₁∈B(y)olacak şekilde bir u elemanı ₁

vardır. z ‘den u ‘e normal ulaşılabilir olduğundan, ₁ δ_ε(u₁)⊂ξ_ε(A(x)) elde edilir. Benzer şekilde, B(y) ‘nin tümü u ’lerin açık komşulukları tarafından örtülür. _i

)) ( ( ) ( ) ( 1 u A x y B _i i δε ⊂ξε ∪ ⊂ ∞

= dir ve B(y) tıkız olduğundan, B(y) 1 (ui) (A(x)) n

i δε ⊂ξε ∪

⊂ = dir ve böylece, B(y)⊂ξ_ε(A(x)) elde edilir.

Ters dönüşüm kullanılarak ξ_ε−1(B(y)) ⊂ξ_ε−1ξ_ε(A(x))=A(x) olduğundan, ∑ ’nın pozitif yörüngesi boştan farklı bir içe sahiptir. Dolayısıyla, ∑ x’den normal olarak ulaşılabilirlik özelliğine sahiptir. x keyfi olduğundan ∑ ,∀ x’den normal olarak ulaşılabilirlik özelliğine sahiptir. O halde, ∑ =

(

G,ℑ

)

G üzerinde kontrol edilebilirdir, (Sussmann, 1976 4.2 ve 4.3). Örnek: G, 3- boyutlu Heisenberg grubu, yani

⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ ∈ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = y x y z R z x G , , 1 0 0 1 0 1 (4.22)

olsun. G’nin Lie cebiri

L(G)={X,Y,Z} (4.23) z y x X ∂ ∂ − ∂ ∂ = 2 1 (4.24) z x y Y ∂ ∂ + ∂ ∂ = 2 1 (4.25) z Z ∂ ∂ = (4.26)

[

X,Y

]

=Z (4.27) şeklin de tanımlansın

⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = 1 0 0 0 0 0 0 0 1 1 D ve ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = 0 0 0 0 0 1 0 1 0 2 D D₁,D₂∈∂g (4.28)

olmak üzere G üzerinde ki afin dönüşüm

(

) (

)

[

D₁,X , D₂,Y

] [

=

(

D₁,D₂

]

,D₁Y −D₂X +

[

X,Y

]

)

(4.29) ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = 1 0 0 2 1 0 1 0 0 0 0 0 1 0 1 0 2 11 0 1 0 0 0 0 0 0 0 1 , 0 0 0 0 0 1 0 1 0 , 1 0 0 0 0 0 0 0 1 y x (4.30) ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − = 1 0 0 0 1 0 2 10 0 , 0 0 0 0 0 1 0 1 0 x (4.31) ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ + − ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − = 1 2 1 1 0 , 0 0 0 0 0 1 0 1 0 x _⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − = 0 0 0 1 0 0 1 2 1 0 0 , 0 0 0 0 0 1 0 1 0 x (4.32) ε δ otomorfizmi ) , , ( ) , , ( ) (_{g δ X Y Z εX εY ε}2_Z δ_ε = _ε = (4.33) ) ( ) ( :af G → af G ξ (4.34)

(

)

( ) :Id δ_ε D₁ X ξ D₁ X D₁ δ_ε X ξ × = + → + = + (4.35) g D ∈∂ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = 1 0 0 0 0 0 0 0 1 1 ve ( ) 2 1 0 1 G L y X ∈ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − = (4.36)

(

)

⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = + → + y X D X D 2 0 1 0 0 0 0 0 0 0 1 : _{1 1} ε ε ξ ξ (4.37)

0 → ε için ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = 1 0 0 0 0 0 0 0 1 1 D kalır

(

D + X

)

→ D + X − 1 1 1 _:ξ ξ (4.38)

(

)

X D X D X D Id δ_{ε ε} ξ δ_{ε ε ε} ξ− × − = +∂ → − + = + ∂− ∂ o 1 1 1 1 1 1 1_{: ( ) ( ( )) (4.39)} ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − + ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = − − y 2 . 0 . 1 0 0 0 0 0 0 0 1 1 1 ε ε ε ε X D y y + = ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ₋ + ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = ₁ 2 1 0 1 0 0 0 0 0 0 2 1 1 0 1 0 0 0 0 0 0 0 1 (4.40)

5. BAZI LİE CEBİRLERİ İÇİN HESAPLAMALAR

3-boyutlu Heisenberg Lie Grubu üzerindeki afin sistem örneği incelendiğinde Lie cebirinin dinamiğinin elemanları olan X ve Y’nin hem regüler hem de free nilpotent üreteçler olduğu gözlemlenmiştir. Heisenberg Lie Cebirin de merkez dışında ki elemanlar regüler olduğundan cebir seviyesinde merkez çıkarılarak (merkezin yörüngesini çıkarıyoruz) regüler elemanların oluşturduğu dinamiğin yörüngesi grup içersinde yoğun ve açık bir alt küme olur. Bu yörünge kontrol edilebilirse uzayın tamamı kontrol edebilirdir, (Kara ve San Martin, 2006). Bu fikirden yola çıkarak, bu bölümde 6 boyuta kadar bütün nilpotent Lie cebirlerinin merkezleri, regüler elemanları ve free nilpotent üreteçleri hesaplanmıştır. Bu hesaplamalar yapılırken (Nielsen, 1983) Lie cebir örnekleri kullanılmıştır.

Tanım: ς(X)=

{

∀Y∈g∴

[

X,Y

]

=0

}

ise g Lie cebirinin merkezi X’tir denir. i pozitif tamsayı olmak üzere Z(X ) ile Lie cebirinin merkezleyicisini gösterelim. _i

Tanım: Bir Lie Cebirinin bir elemanının merkezleyicisinin boyutu Lie cebirinin tüm elemanlarının merkezleyicileri arasında minimum ise bu elemana Lie cebirinin regüler elemanı denir.

Tanım: Lie cebirinin bazı elemanlarının olası tüm Lie parantezleri alınarak cebirin tamamı üretilebiliyorsa, o taktirde bu elemanlara Free Nilpotent üreteçler denir.

Hesaplamalar :

1) X₁, X₂, X vektör alanlarının oluşturduğu aşağıdaki 2.dereceden nilpotent Lie cebirini ₃

gözönüne alalım.

[X ,₃ X₂]=X₁ ve diğer Lie parantezleri 0 olacak şekilde tanımlı g=RX₁+RX₂+RX ₃

nilpotent Lie cebiri ve onun nilpotent Lie grubuda G olsun. ₃ X₁,X₂, X₃∈g ve

1 1 X X ∂ ∂ = , 2 1 3 2 x _{X X} X ∂ ∂ + ∂ ∂ = , 3 3 _X X ∂ ∂

= ; Z

( )

X_i ile X 'nin merkezleyicisini gösterirsek: _i

Z(X₁)={X₁,X₂, X } ₃

Z(X₂)={X₁,X₂}

Z(X )={₃ X₁, X } elde ederiz. ₃

Dolayısıyla, g Lie cebirinin regüler elemanları X₂ ve X , merkezi ise ₃ X₁'dir. Lie cebirinin Free nilpotent üreteçleri X₂,X tür. ₃

2) [X₄,X ]=₃ X₂ , [X₄,X₂]=X₁ ve diğer Lie parantezleri 0 olacak şekilde tanımlı g=RX₁+RX₂+RX +R₃ X₄ nilpotent Lie cebiri ve onun nilpotent Lie grubu G₄ olsun.

1 X ,X₂,X ,₃ X₄∈g ve 1 1 X X ∂ ∂ = , 2 1 4 2 X X x X ∂ ∂ + ∂ ∂ = , 3 2 4 1 2 4 3 2 1 X X x X x X ∂ ∂ + ∂ ∂ + ∂ ∂ = , 4 4 X X ∂ ∂

= ; Z

( )

X_i ile X 'nin merkezleyicisini gösterirsek. _i

Z(X₁)={X₁,X₂,X ,₃ X₄} Z(X₂)={X₁,X₂,X } ₃

Z(X )={₃ X₁,X₂,X } ₃

Z(X₄)={X₁,X₄}

Dolayısıyla, g Lie cebirinin regüler elemanı X₄ , merkezi ise X₁'dir. Lie cebirinin Free nilpotent üreteçleri X ,₃ X₄ tür.Bu örnekteki Lie cebiri 3.dereceden nilpotent bir Lie cebiridir.

3) [X ,₅ X₄]=X₁ , [X ,₃ X₂]=X₁ ve diğer Lie parantezleri 0 olacak şekilde tanımlı g=RX₁+RX₂+RX +R₃ X₄+RX nilpotent Lie cebiri ve onun nilpotent Lie grubu ₅ G olsun. _5,1

1 X ,X₂,X ,₃ X₄,X₅∈g ve 1 1 _X X ∂ ∂ = , 2 1 3 2 x _{X X} X ∂ ∂ + ∂ ∂ = , 3 3 X X ∂ ∂ = , 4 1 5 4 X X x X ∂ ∂ + ∂ ∂ = , 5 5 X X ∂ ∂

= ; Z

( )

X_i ile X 'nin merkezleyicisini gösterirsek. _i

Z(X₁)={X₁,X₂,X ,₃ X₄,X } ₅

Z(X₂)={X₁,X₂,X₄,X } ₅

Z(X )={₃ X₁,X ,₃ X₄,X } ₅

Z(X₄)={X₁,X₂,X ,₃ X₄} Z(X )={₅ X₁,X₂,X ,₃ X } ₅

Dolayısıyla, g Lie cebirinin regüler elemanları X₂,X ,₃ X₄,X dir ve merkezi ise ₅ X₁'dir. Lie cebirinin Free nilpotent üreteçleri X₂,X ,₃ X₄,X dir. Buradaki Lie cebiri 2.dereceden ₅

4) [X ,₅ X₄]=X₂ , [X ,₅ X ]=₃ X₁ ve diğer Lie parantezleri 0 olacak şekilde tanımlı g=RX₁+RX₂+RX +R₃ X₄+RX nilpotent Lie cebiri ve onun nilpotent Lie grubu ₅ G _5,2

olsun. X₁,X₂,X ,₃ X₄,X₅ ∈g ve 1 1 X X ∂ ∂ = , 2 2 X X ∂ ∂ = , 3 1 5 3 X X x X ∂ ∂ + ∂ ∂ = , 4 2 5 4 X X x X ∂ ∂ + ∂ ∂ = , 5 5 X X ∂ ∂

= ; Z

( )

X_i ile X 'nin merkezleyicisini gösterirsek. _i

Z(X₁)={X₁,X₂,X ,₃ X₄,X } ₅

Z(X₂)={X₁,X₂,X ,₃ X₄,X } ₅

Z(X )={₃ X₁,X₂,X ,₃ X₄} Z(X₄)={X₁,X₂,X ,₃ X₄} Z(X )={₅ X₁,X₂,X } ₅

Dolayısıyla, g Lie cebirinin regüler elemanı X , merkezleri ise ₅ X₁ ve X₂'dir. Lie cebirinin Free nilpotent üreteçleri X ,₃ X₄,X dir. Bu örnekteki Lie cebiri 2.dereceden nilpotent bir Lie ₅

cebiridir.

5) [X ,₅ X₄]=X₂ , [X ,₅ X₂]=X₁ , [X₄,X ]=₃ X₁ ve diğer Lie parantezleri 0 olacak şekilde tanımlı g=RX₁+RX₂+RX +R₃ X₄+RX nilpotent Lie cebiri ve onun nilpotent Lie grubu ₅

3 , 5 G olsun. X₁,X₂,X ,₃ X₄,X₅∈g ve 1 1 X X ∂ ∂ = , 2 1 5 2 X X x X ∂ ∂ + ∂ ∂ = , 3 1 4 3 X X x X ∂ ∂ + ∂ ∂ = , 4 2 5 1 2 5 4 2 1 X X x X x X ∂ ∂ + ∂ ∂ + ∂ ∂ = , 5 5 X X ∂ ∂ = ; Z

( )

X_i ile X 'nin _i merkezleyicisini gösterirsek. Z(X₁)={X₁,X₂,X ,₃ X₄,X } ₅ Z(X₂)={X₁,X₂,X ,₃ X₄} Z(X )={₃ X₁,X₂,X ,₃ X } ₅ Z(X₄)={X₁,X₂,X₄} Z(X )={₅ X₁,X ,₃ X } ₅

Dolayısıyla, g Lie cebirinin regüler elemanları X₄veX dir ve merkezi ise ₅ X₁ dir. Lie cebirinin Free nilpotent üreteçleri X ,₃ X₄,X dir. Bu örnekteki Lie cebiri 3.dereceden ₅

nilpotent bir Lie cebiridir.

6) [X ,₅ X₄]=X , [₃ X ,₅ X ]=₃ X₂ , [X₄,X ]=₃ X₁ ve diğer Lie parantezleri 0 olacak şekilde tanımlı g=RX₁+RX₂+RX +R₃ X₄+RX nilpotent Lie cebiri ve onun nilpotent Lie grubu ₅

4 , 5 G olsun. X₁,X₂,X ,₃ X₄,X₅∈g ve 1 1 _X X ∂ ∂ = , 2 2 _X X ∂ ∂ = , 3 2 5 1 4 3 X X x X x X ∂ ∂ + ∂ ∂ + ∂ ∂ = , 4 3 5 2 2 5 1 5 4 4 2 1 X X x X x X x x X ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ = , 5 5 X X ∂ ∂ = ;

( )

X_i

Z ile X 'nin merkezleyicisini gösterirsek. _i

Z(X₁)={X₁,X₂,X ,₃ X₄,X } ₅

Z(X₂)={X₁,X₂,X ,₃ X₄,X } ₅

Z(X )={₃ X₁,X₂,X } ₃

Z(X₄)={X₁,X₂,X₄} Z(X )={₅ X₁,X₂,X } ₅

Dolayısıyla, g Lie cebirinin regüler elemanları X ,₃ X₄,X dir ve merkezleri ise ₅ X₁ ve 2

X 'dir. Lie cebirinin Free nilpotent üreteçleri X ,₃ X₄,X dir.Buradaki Lie cebiri ₅

3.dereceden nilpotent bir Lie cebiridir.

7) [X ,₅ X₄]=X , [₃ X ,₅ X ]=₃ X₂ , [X ,₅ X₂]=X₁ ve diğer Lie parantezleri 0 olacak şekilde tanımlı g=RX₁+RX₂+RX +R₃ X₄+RX nilpotent Lie cebiri ve onun nilpotent Lie grubu ₅

5 , 5 G olsun. X₁,X₂,X ,₃ X₄,X₅∈g ve 1 1 X X ∂ ∂ = , 2 1 5 2 X X x X ∂ ∂ + ∂ ∂ = , 3 2 5 1 2 5 3 2 1 X X x X x X ∂ ∂ + ∂ ∂ + ∂ ∂ = , 4 3 5 2 2 5 1 3 5 4 2 1 6 1 X X x X x X x X ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ = , 5 5 X X ∂ ∂ = ;

( )

Xi

Z ile X_i'nin merkezleyicisini gösterirsek. Z(X₁)={X₁,X₂,X₃,X₄,X₅}

Z(X₂)={X₁,X₂,X₃,X₄} Z(X₃)={X₁,X₂,X₃,X₄}

Z(X₄)={X₁,X₂,X₃,X₄} Z(X₅)={X₁,X₅}

Dolayısıyla, g Lie cebirinin regüler elemanı X₅ dir ve merkezi ise X₁ dir. Lie cebirinin Free nilpotent üreteçleri X₄,X₅ dir. Bu örnekteki Lie cebiri 4.dereceden nilpotent bir Lie cebiridir.

8) [X₅,X₄]=X₃ , [X₅,X₃]=X₂ , [X₅,X₂]=X₁ , [X₄,X₃]=X₁ ve diğer Lie parantezleri 0 olacak şekilde tanımlı g=RX₁+RX₂+RX₃+RX₄+RX₅ nilpotent Lie cebiri ve onun nilpotent Lie grubu G_5,6 olsun. X₁,X₂,X₃,X₄,X₅ ∈g ve

1 1 X X ∂ ∂ = , 2 1 5 2 X X x X ∂ ∂ + ∂ ∂ = , 3 2 5 1 2 5 4 3 ) 2 1 ( X X x X x x X ∂ ∂ + ∂ ∂ + ∂ ∂ + = , 4 3 5 2 2 5 1 3 5 5 4 4 2 1 ) 6 1 ( X X x X x X x x x X ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + = , 5 5 X X ∂ ∂

= ; Z

( )

X_i ile X_i'nin merkezleyicisini gösterirsek. Z(X₁)={X₁,X₂,X₃,X₄,X₅}

Z(X₂)={X₁,X₂,X₃,X₄} Z(X₃)={X₁,X₂,X₃} Z(X₄)={X₁,X₂,X₄} Z(X₅)={X₁,X₅}

Dolayısıyla, g Lie cebirinin regüler elemanı X₅ dir ve merkezi ise X₁ dir. Lie cebirinin Free nilpotent üreteçleri X₄,X₅ dir. Buradaki Lie cebiri 4.dereceden nilpotent bir Lie cebiridir.

9) [X₆,X₅]=X₄ , [X₆,X₄]=X₁ , [X₃,X₂]=X₁ ve diğer Lie parantezleri 0 olacak şekilde tanımlı g=RX₁+RX₂+RX₃+RX₄+RX₅+RX₆ nilpotent Lie cebiri ve onun nilpotent Lie grubu G olsun. _6,1 X₁,X₂,X₃,X₄,X₅, X₆∈g ve 1 1 X X ∂ ∂ = , 2 1 3 2 X X x X ∂ ∂ + ∂ ∂ = , 3 3 X X ∂ ∂ = , 4 1 6 4 X X x X ∂ ∂ + ∂ ∂ = , 5 4 6 1 2 6 5 2 1 X X x X x X ∂ ∂ + ∂ ∂ + ∂ ∂ = , 6 6 X X ∂ ∂ = ; Z

( )

X_i ile i

X 'nin merkezleyicisini gösterirsek. Z(X₁)={X₁,X₂,X₃,X₄,X₅,X₆}

Z(X₂)={X₁,X₂,X₄,X₅,X₆} Z(X₃)={X₁,X₃,X₄,X₅,X₆} Z(X₄)={X₁,X₂,X₃,X₄,X₅} Z(X₅)={X₁,X₂,X₃,X₄,X₅} Z(X₆)={X₁,X₂,X₃,X₆}

Dolayısıyla, g Lie cebirinin regüler elemanı X₆ dır ve merkezi ise X₁'dir. Lie cebirinin Free nilpotent üreteçleri X₂,X₃,X₅,X₆ dır. Buradaki Lie cebiri 3.dereceden nilpotent bir Lie cebiridir.

10) [X₆,X₅]=X₄ , [X₆,X₄]=X₃ , [X₆,X₃]=X₁ , [X₅,X₂]=X₁ ve diğer Lie parantezleri 0 olacak şekilde tanımlı g=RX₁+RX₂+RX₃+RX₄+RX₅+RX₆ nilpotent Lie cebiri ve onun nilpotent Lie grubu G_6,2 olsun. X₁,X₂,X₃,X₄,X₅, X₆∈g ve

1 1 X X ∂ ∂ = , 2 1 5 2 X X x X ∂ ∂ + ∂ ∂ = , 3 1 6 3 X X x X ∂ ∂ + ∂ ∂ = , 4 3 6 1 2 6 4 2 1 X X x X x X ∂ ∂ + ∂ ∂ + ∂ ∂ = , 5 4 6 3 2 6 1 3 6 5 2 1 6 1 X X x X x X x X ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ = , 6 6 X X ∂ ∂

= ; Z

( )

X_i ile X_i'nin merkezleyicisini gösterirsek. Z(X₁)={X₁,X₂,X₃,X₄,X₅,X₆} Z(X₂)={X₁,X₂,X₃,X₄,X₆} Z(X₃)={X₁,X₂,X₃,X₄,X₅} Z(X₄)={X₁,X₂,X₃,X₄,X₅} Z(X₅)={X₁,X₂,X₃,X₄,X₅} Z(X₆)={X₁,X₂,X₆}

Dolayısıyla, g Lie cebirinin regüler elemanı X₆ dır ve merkezi ise X₁'dir. Lie cebirinin Free nilpotent üreteçleri X₂,X₅,X₆ dır. Bu örnekteki Lie cebiri 4.dereceden nilpotent bir Lie cebiridir.