Konveks fonksiyonlar ve matris eşitsizlikleri

T.C.

SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ

KONVEKS FONKSİYONLAR VE MATRİS EŞİTSİZLİKLERİ

Vildan BACAK YÜKSEK LİSANS TEZİ Matematik Anabilim Dalı

Temmuz-2012 KONYA Her Hakkı Saklıdır

iv ÖZET

YÜKSEK LİSANS TEZİ

KONVEKS FONKSİYONLAR VE MATRİS EŞİTSİZLİKLERİ

Vildan BACAK

Selçuk Üniversitesi Fen Bilimleri Enstitüsü Matematik Anabilim Dalı

Danışman: Doç. Dr. Ramazan TÜRKMEN 2012, 106 Sayfa

Jüri

Doç. Dr. Ramazan TÜRKMEN Prof. Dr. Hasan ŞENAY Prof. Dr. Durmuş BOZKURT

Bu tezde öncelikle konveks, konkav, matris konveks, matris monoton fonksiyonlar ve majorizasyon için temel tanım ve teoremler verildi. Daha sonra majorizasyon ve konveks fonksiyonlarla ilgili bilinen sonuçlardan bahsedildi ve bilinen bazı Hermite-Hadamard tipi eşitsizlikler ele alındı. Son olarak, operatör (matris) konveks fonksiyonlar için elde edilen Hermite-Hadamard tipi eşitsizlikler ve integral eşitsizlikleri verildi.

Anahtar Kelimeler: Hermite-Hadamard eşitsizliği, Hermityen matris, konkav fonksiyonlar, konveks fonksiyonlar, majorizasyon, matris konveks fonksiyonlar, matris monoton fonksiyonlar, öz değer.

v ABSTRACT MS THESIS

CONVEX FUNCTIONS AND MATRIX INEQUALITIES

Vildan BACAK

THE GRADUATE SCHOOL OF NATURAL AND APPLIED SCIENCE OF SELÇUK UNIVERSITY

THE DEGREE OF MASTER OF SCIENCE IN MATHEMATICS

Advisor: Assoc. Prof. Dr. Ramazan TÜRKMEN 2012, 106 Pages

Jury

Assoc. Prof. Dr. Ramazan TÜRKMEN Prof. Dr. Hasan ŞENAY

Prof. Dr. Durmuş BOZKURT

In this thesis firstly, the definitions and theorems for convex, concave, matrix convex, matrix concave functions and majorization were given. Later, we mentioned about the well known results of majorization and convex functions and we examined known Hermite-Hadamard inequalities for convex functions. Finally, Hermite-Hadamard’s type inequalities and integral inequalities for operator (matrix) convex functions were given.

Keywords: Concave functions, convex functions, eigenvalue, Hermite - Hadamard inequality, Hermitian matrix, majorization, matrix convex functions, matrix monoton functions.

vi ÖNSÖZ

Bu tez çalışması, Selçuk Üniversitesi Fen Fakültesi Matematik Bölümü Öğretim Üyesi Doç. Dr. Ramazan Türkmen danışmanlığında hazırlanarak, Selçuk Üniversitesi Fen Bilimleri Enstitüsü’ne yüksek lisans tezi olarak sunulmuştur.

Bu çalışma 8 bölümden oluşmaktadır. Tezin 1. bölümü Giriş ve Kaynak Araştırması’na ayrılmıştır. 2. bölümde tez içerisinde kullanılacak genel bilgilere yer verilmiştir. 3. bölümde konveks fonksiyonlar ve konveks kümeler tanıtılmıştır. 4. bölümde majorizasyon kavramı üzerinde durulmuştur. Majorizasyon ve konveks fonksiyonlar arasındaki ilişki ele alınmıştır. 5. bölümde matris monoton ve matris konveks fonksiyonların genel tanım ve teoremlerine ve bazı örneklere yer verilmiştir. 6. bölümde konveks fonksiyonlar için bilinen Hermite-Hadamard ve integral eşitsizlikleri verilmiştir. 7. bölümde araştırma sonuçlarına yer verilmiştir. Bu bölümde operatör konveks fonksiyonlar için elde edilen Hermite-Hadamard eşitsizlikleri ve integral eşitsizlikleri verilmiştir. Daha önceki çalışmalarla aralarındaki fark açıklanmıştır. 8. bölüm sonuçlar ve önerilerden oluşmaktadır.

Yüksek lisans eğitimim boyunca bilgileriyle ve tecrübesiyle bana yol gösteren danışmanım Sayın Doç. Dr. Ramazan Türkmen’e, Selçuk Üniversitesi Fen Fakültesi Matematik Bölümü’nün saygıdeğer öğretim elemanlarına ve benden desteğini hiç esirgemeyen, her zaman iyi niyetiyle yanımda olan sevgili arkadaşım Ayşegül Özcan’a ve aileme teşekkürlerimi sunarım.

Vildan BACAK KONYA-2012

vii İÇİNDEKİLER ÖZET ...iv ABSTRACT ... v ÖNSÖZ ...vi İÇİNDEKİLER ... vii

SİMGELER VE KISALTMALAR... viii

1. GİRİŞ VE KAYNAK ARAŞTIRMASI ... 1

2. GENEL KAVRAMLAR ... 3

3. KONVEKS FONKSİYONLAR VE KONVEKS KÜMELER ... 9

3.1. Konveks Kümeler ...9

3.2. Konveks Fonksiyonlar ... 10

4. MAJORİZASYON VE KONVEKS FONKSİYONLAR ... 22

4.1.Temel Gösterimler ... 22

4.2. Konveks ve Monoton Fonksiyonlar İçin Majorizasyon ... 27

4.4. Log-Konveks Fonksiyonlar İçin Eşitsizlikler ... 34

5. MATRİS MONOTON VE MATRİS KONVEKS FONKSİYONLAR... 39

5.1.Tanımlar ve Basit Örnekler ... 39

5.2.Temel Teoremler ... 43

6. HERMİTE-HADAMARD TİPİ EŞİTSİZLİKLER ... 48

7. ARAŞTIRMA SONUÇLARI VE TARTIŞMA ... 65

7.1. Operatör Konveks Fonksiyonlar İçin Eşitsizlikler ... 65

7.2. Tartışma ... 102 8. SONUÇLAR VE ÖNERİLER ... 103 8.1. Sonuçlar ... 103 8.2. Öneriler ... 103 KAYNAKLAR ... 104 ÖZGEÇMİŞ ... 106

viii

SİMGELER VE KISALTMALAR Simgeler

0

A  : A pozitif yarı tanımlı 0

A  : A pozitif tanımlı

AB : A B pozitif yarı tanımlı

A : A 



A A*



1/ 2

 : Kompleks sayılar kümesi

n

 : Kompleks sayılar üzerinde n bileşenli vektörlerin kümesi ( )A

 : A matrisinin spektrumu

H : Hilbert uzay

I : Reel sayılar kümesinin bir aralığı

0

I : Reel sayılar kümesinin 0 içermeyen bir aralığı

n

 : Hermityen matrisler kümesi

n

M : n n kompleks matrislerin kümesi

n

 : n n pozitif tanımlı matrislerin kümesi  : Reel sayılar kümesi

n

 : Reel sayılar kümesi üzerinde n bileşenli vektörlerin kümesi



 : Negatif olmayan reel sayılar kümesi

n 

 : Reel sayılar kümesi üzerinde bileşenleri negatif olmayan n bileşenli vektörlerin

kümesi

n 

 : Reel sayılar kümesi üzerinde bileşenleri pozitif olan n bileşenli vektörlerin

kümesi

m n

 : Elemanları reel sayılar olan m n matrislerin kümesi

n

 : n n pozitif yarı tanımlı matrislerin kümesi

x _{: Negatif koordinatların 0 ile yer değiştirmesiyle x’ten elde edilen vektör} x : Tüm koordinatların mutlak değeri alınarak elde edilen vektör

x y : x, y tarafından majorize edilmiştir

w

x y : x, y tarafından zayıf majorize edilmiştir

w

x y : x, y tarafından süper majorize edilmiştir

x y : x y (x y_{1 1},...,x y_{n n}) Kısaltmalar

det : Determinant

exp : Eksponansiyel (üstel) fonksiyon köş : Köşegen matris

1. GİRİŞ VE KAYNAK ARAŞTIRMASI

Konvekslik; kökeni  ’nin değerini tahmin etmesi dolayısıyla, Arşimed’e dayanan basit ve doğal bir kavramdır. Arşimed, konveks bir şeklin çevre uzunluğunun onu çevreleyen diğer bir konveks şeklin çevre uzunluğundan daha küçük olduğunu fark etmiştir.

Konvekslik, hayatımızın birçok evresinde karşımıza çıkmaktadır. Bunun en basit örneği ayakta dik duruş pozisyonumuzdur. Ayaklarımızın kapladığı konveks alanın içinde, ağırlık merkezimizin dik izdüşümü boyunca dengemizi korumaktayız. Konveks fonksiyonlar teorisi, matematiğin hemen hemen tüm dallarında önemlidir. Ayrıca endüstri, ticaret, tıp ve sanat gibi dalların nümerik uygulamalarında ve şans oyunlarının dengesinin sağlanmasında da kullanılmaktadır.

Konveks fonksiyonların başlangıcı, Johan Ludwig William Valdemar Jensen’e (1859-1925) dayanmaktadır. Fakat konveks fonksiyonlarla ilk uğraşan kişi Jensen değildir. Jensen’ den önce çalışanlar arasında Ch. Hermite, O. Hölder ve O. Stolz vardır. 20. yüzyıl boyunca geometrik fonksiyonel analizde, matematiksel ekonomide, konveks analizde ve lineer olmayan optimizasyonda yoğun araştırma faaliyetleri ve önemli sonuçlar gerçekleştirilmiştir. G.H. Hardy, J.E. Littlewood ve G. Polya’nın 1934 yılında basılan “Inequalities, Cambridge University Press, Great Britain” adlı kitabı konveks fonksiyonlar konusunun popüler olmasında önemli rol oynamıştır.

Eşitsizlikler, matematiğin tüm dallarında geniş çalışma alanına sahip, sürekli gelişmekte olan bir konudur. Bu konu, son yıllarda çok sayıda araştırmacının dikkatini çekmektedir. Jensen, Hadamard, Hilbert, Hardy, Opial, Poincaré, Sobolev, Levin ve Lyapunov isimleriyle özdeşleşmiş birçok eşitsizlik tipi arasında derin kökler vardır ve bu eşitsizlik tipleri matematiğin farklı dallarında kullanılmaktadır. Eşitsizlikler teorisinin gelişmesinde yukarıda bahsettiğimiz isimleriyle özdeşleşmiş eşitsizlikler üzerine çalışmalar yapan araştırmacıların artmasıyla; çalışma alanlarının yenilenmesi ve mevcut çalışma alanlarının genişlemesi bu teorinin cazibesini de arttırmaktadır.

Son yıllarda Hermite-Hadamard tipi eşitsizliklere ve integral eşitsizliklerine ilgi artmıştır. S.S. Dragomir, B.G. Pachpatte, G. Zabandan gibi araştırmacıların bu alanda yapılmış çalışmaları mevcuttur. B.G. Pachpatte 2003’te “On some inequalities for convex functions, RGMIA Res. Rep. Coll., 6(E)” makalesinde elemanter işlemler kullanarak konveks fonksiyonlar için eşitsizlikler vermiştir. M. Tunç 2011’de “On some new inequalities for convex functions, Turk J Math, 35,1-7” makalesinde Pachpatte’nin sonuçlarına benzer eşitsizlikler vermiştir. S.S. Dragomir 2011’de

“Hermite–Hadamard’s type inequalities for operator convex functions, Applied

Mathematics and Computation, 218, 766-772” makalesinde konveks fonksiyonlar için

var olan bir eşitsizliğin operatör konveks fonksiyonlar için de sağlandığı göstermiştir. G. Zabandan 2009’da “A new refinement of the Hermite-Hadamard inequality for convex functions, JIPAM, vol. 10, iss. 2, art.45” makalesinde Dragomir’in konveks fonksiyonlar için kullandığı eşitsizliğin bir genellemesini yapmıştır. Bu tezde yukarıda belirtilen araştırmacıların eşitsizliklerinden daha genel eşitsizlikler elde edilmiştir.

Matris monoton fonksiyonlar, ilk olarak K. Löwner (C. Loewner) tarafından 1934 yılında “Über monotone Matrixfunktionen, Math. Z. 38, 177-216” makalesinde incelenmiştir. Daha sonra 1951’de Heinz, “Beitrage zur Strörungstheorie der Spektralzerlegung, Math. Ann., 123, 415-438” makalesinde matris monotonluğu kullanmıştır.

Matris konveks fonksiyonlar, ilk olarak F. Kraus tarafından 1936’da “Über konvexe Matrixfunktionen, Math. Z.,41, 18-42” makalesinde incelenmiştir.

J.Bendat ve S.Sherman 1955’te “Monotone and convex operator functions,

Trans. Amer. Math. Soc., 79, 58-71” makalesinde Löwner ve Kraus’un teoremleri

üzerine yeni bir perspektif sağlamışlardır.

F. Zhang 2011’de “Matrix theory: Basic results and techniques, second ed.,

Springer, New York” kitabında matris teori üzerine bir çok tanım ve teorem vermiştir.

Ayrıca majorizasyon ve konveks fonksiyonlar için eşitsizlikler vermiştir.

J.S. Aujla ve F.C. Silva2003’te “Weak majorization inequalities and convex functions, Linear Algebra and its Appl., 369, 217-233” makalelerinde konveks fonksiyonlar için majorizasyon eşitsizlikleri vermişlerdir.

R.Bhatia 1997’de “Matrix analysis, Springer-Verlag, New York” kitabında matris teori üzerine tanımlar, teoremler, problemler vermiştir. Ayrıca, operatör konveks fonksiyonlar kavramına yer vermiş, tanım ve teoremler vermiştir.

Pecaric ve arkadaşları 1992’de “Convex functions, partial orderings and statistichal applications, Mathematics in Science and Engineering, vol 187, Academic

Press Inc, USA” kitabında konveks fonksiyonlara, konveks fonksiyonlarla ilişkili

2. GENEL KAVRAMLAR

Tanım 2.1.AM_n olmak üzere A’nın karakteristik polinomu P( ) det(IA) ile verilir. det( I A) denklemine 0 A’nın karakteristik denklemi ve karakteristik denklemin köklerine de A’nın öz değerleri denir. ( I A x)  denkleminde 0  _i

(1 i n) için karşılık gelen x vektörüne _i A’nın öz vektörü denir.

Tanım 2.2.A’nın tüm öz değerlerinin kümesine A’nın spektrumu denir ve ( )A ile gösterilir.

Tanım 2.3.AaijMn olmak üzere A’nın köşegen elemanlarının toplamına A’nın

izi denir ve 1 ( ) n ii i iz A a  



ile gösterilir.

Teorem 2.4.A B, M_n,   olmak üzere aşağıdaki ifadeler vardır: i) iz(A)iz A( )

ii) iz A B(  )iz A( )iz B( ) iii) iz AB( )iz BA( )

iv) _{S M ’de tersinir matris olmak üzere} , _n iz S AS( 1 )iz A( )’dır. v) iz(0)0, iz I( )n vi) 1 ( ) n i i iz A   

_

, ( )A 

_

₁,...,n

_

Tanım 2.5.A_a_ij_M_n olmak üzere A’nın transpozu AT _{  }a_ji ve A’nın adjointi

* ji

A _{  }a ’dir. Adjoint aşağıdaki özelliklere sahiptir:

Teorem 2.6.A B, M_n,  olmak üzere aşağıdaki ifadeler vardır: i)

 

A* *  A

ii)

_

AB

_

* A*B*

iii)



A



*A*

iv)



AB



*B A* *

v) det

 

A* det( )A

vii) ’nın A’nın bir öz değeri olması için gerek ve yeter şart ’nın A ’ın bir öz *

değeri olmasıdır. Yani,

 

*

_{ }





: ( )

A A A

     ’dır.

viii) A’nın tersinir olması için gerek ve yeter şart A ’ın tersinir olmasıdır. Yani, *

 

* 1



1



*

A   A dır.

Tanım 2.7. |A|



A A*



1/ 2 matrisinin öz değerlerine A’nın singüler değerleri denir ve singüler değerler, s A( )



s A s A₁( ), ( ),..., ( )₂ s A_n



ile gösterilir ve azalan sırada sıralanırlar: s A₁( )s A₂( ) ... s A_n( ) . 0

Tanım 2.8.A_a_ij_M_n olmak üzere

i) i olmak üzere j a ij 0 ise A köşegen matris, ii) i olmak üzere j a _ij 0 ise A üst üçgen matris, iii) AT  A ise A simetrik matris,

iv) A* A ise A Hermityen matris, v) A A* AA* ise A normal matris, vi) A A*  AA*  ise I A üniter matris, vii) A AT  AAT  ise I A ortogonal matristir. Not 2.9.

i) AaijMn olmak üzere A’nın Hermityen olması için gerek ve yeter şart

, 1, 2,...,

i j n için a_ij a_ji olmasıdır. Eğer A Hermityen ise A’nın köşegen elemanları reeldir.

ii) Hermityen iki matrisin toplamı Hermityendir.

iii) Hermityen iki matrisin çarpımının Hermityen olması için gerek ve yeter şart matrislerin değişmeli olmasıdır.

iv) AM_n Hermityen ise AA A A A*, * , A* Hermityendir.

v) A Hermityen ise k 1, 2,... için A Hermityendir. Eğer k A tersinir ise A1

Hermityendir.

Teorem 2.10 (Weyl Monotonluk Teoremi). A B   olmak üzere , _n _i( ), ( )A _i B ve (_i A B ) öz değerleri azalan sırada dizilsinler. Yani, ₁( )A ₂( )A _n( )A ,

1( )B 2( )B n( )B

   ve ₁(A B )₂(A B )_n(A B )’dir. Bu durumda her bir k1, 2,...,n için

1

( ) ( ) ( ) ( ) ( )

k A B k A B k A n B

      (2.1)

eşitsizliği vardır. (Bhatia,1997)

Tanım 2.11. Her satır ve sütununda bir tane 1 elemanı içeren ve diğer elemanları 0 olan matrise permütasyon matris denir.

Tanım 2.12. AM_n matrisinin determinantı sıfırdan farklı ise matrise düzgün (regüler)

matris, determinantı sıfır ise matrise tekil (singüler) matris denir.

Tanım 2.13. V , K cismi üzerinde bir vektör uzayı ve : ( , ) ( , ) , f V V K u v f u v u v     fonksiyonu; i) a b, K ve u v w V, ,  için au bv w , a u w, b v w, , ii) u v,  v u, , iii) u u  (, 0 u u, 0u0)

özelliklerini sağlıyorsa f fonksiyonuna, V vektör uzayı üzerinde bir iç çarpım ve V

uzayına da iç çarpım uzayı denir. V üzerinde tanımlanan bir iç çarpım, V üzerinde

,

u  u u (2.2)

ile verilen bir norm ve

( , ) ,

d u v  u v  uv uv (2.3)

Tanım 2.14. Üzerindeki iç çarpımla tanımlı metriğe göre tam olan iç çarpım uzayına

Hilbert uzayı denir.

Tanım 2.15. A Hermityen bir matris olmak üzere her x   içinn Ax x, x AxT 0 ise

A matrisine pozitif yarı tanımlı matris denir. Her x   içinn Ax x , 0 ise A

matrisine pozitif tanımlı matris denir.

A ve B Hermityen matrisler olmak üzere AB pozitif yarı tanımlı ise A B

ve pozitif tanımlı ise A B yazılır. Burada “  ”, Hermityen matrisler kümesi üzerinde kısmi bir sıralamadır ve kısmi Löwner sıralaması olarak bilinir ve aşağıdaki özellikleri sağlar:

i)  A n için A A’dır.

ii) AB ve B A ise AB’dir. iii) AB ve BC ise AC’dir.

Pozitif tanımlı ve pozitif yarı tanımlı matrisleri karakterize eden birçok durum vardır. Bunlardan birkaçı aşağıda listelenmiştir:

i) A ’nın pozitif yarı tanımlı olması için gerek ve yeter şart A’nın Hermityen

olması ve tüm öz değerlerinin negatif olmamasıdır. A ’nın pozitif tanımlı olması için gerek ve yeter şart A’nın Hermityen olması ve tüm öz değerlerinin pozitif olmasıdır. ii) A ’nın pozitif yarı tanımlı olması için gerek ve yeter şart Hermityen olması ve

tüm esas minörlerinin negatif olmamasıdır. A ’nın pozitif tanımlı olması için gerek ve yeter şart A’nın Hermityen olması ve tüm esas minörlerinin pozitif olmasıdır.

iii) A ’nın pozitif yarı tanımlı olması için gerek ve yeter şart bazı B matrisleri için

*

AB B olmasıdır. A ’nın pozitif tanımlı olması için gerek ve yeter şart A’nın Hermityen olması ve B ’ninregüler olmasıdır.

iv) A ’nın pozitif yarı tanımlı olması için gerek ve yeter şart üst üçgen T matrisleri

için AT T* olmasıdır.

v) A ’nın pozitif yarı tanımlı olması için gerek ve yeter şart bazı B matrisleri için

2

AB olmasıdır. Burada B bir tanedir. BA1/ 2 yazılır ve A ’nın pozitif kare kökü denir. A ’nın pozitif tanımlı olması için gerek ve yeter şart B ’nin pozitif tanımlı olmasıdır. (Bhatia,2007)

Teorem 2.16.AM_n olsun. Bu takdirde U V, M_n üniter matrisleri ve

1

( ( ),..., _n( ))

Dköş s A s A için A UDV * yazılabilir ki, bu ifadeye singüler değer

ayrışımı denir.

Teorem 2.17 (Spektral Ayrışım).AM_n ve A’nın öz değerleri ₁,..., olsun. Bu _n

takdirde A’nın normal olması için gerek ve yeter şart A’nın üniter olarak köşegenleştirilmesi, yani





*

1,..., n

U AU köş   (2.4)

olacak şekilde bir U üniter matrisinin olmasıdır. f I   aralığında tanımlı reel , değerli bir fonksiyon olsun. Bu durumda





*

1 2

( ) ( ( ), ( ),..., ( _n))

f A U köş f  f  f  U

şeklinde tanımlanır. Özel olarak A’nın Hermityen olması için gerek ve yeter şart  öz _i

değerlerinin reel olması ve A’nın pozitif yarı tanımlı olması için gerek ve yeter şart  _i

öz değerlerinin negatif olmamasıdır.

Tanım 2.18. A B, M_n için  :M_n   fonksiyonu aşağıdaki aksiyomları sağlıyorsa

matris norm denir:

i) A 0 ve A 0  A  0

ii) Kompleks cskalerleri için cA  c A dır. iii) AB  A  B

iv) AB  A B

Tanım 2.19. U V, üniter matrisleri için

|||A||| ||| UAV ||| (2.5)

Not 2.20. ||| .||| üniter invaryant bir norm için ||| |||A değeri A ’nın singüler değerlerinin

bir fonksiyonudur: U V, üniter matrisleri ve  matrisi için A s UAV( )s A( )’dır. Singüler değer eşitsizlikleri, kısmi Löwner sıralama eşitsizliklerinden daha zayıf ve üniter invaryant norm eşitsizliklerinden daha güçlüdür. Yani,

( ) ( ) ||| ||| ||| |||

j j

A  B s A s B  A  B (2.6)

dır.

Bazı özel matris norm türleri aşağıdadır:

i) Frobenius norm (veya Hilbert- Schmidt norm) :

 





1/ 2 1/ 2 2 2 2 1 || || ( ) j n F j A A s A iz A     _{ }  



 (2.7)

ii) Spektral norm (veya operatör norm):

1( )

A s A (2.8)

iii) 1 p  için Schatten p norm :

 





1/ 1/ 1 || || ( ) p n p p p p j j A s A iz A    _{ }  



 (2.9)

iv) k 1, 2,...,n için Ky- Fan k  norm :

( ) 1 || || ( ) k k j j A s A  

_

(2.10)

3. KONVEKS FONKSİYONLAR VE KONVEKS KÜMELER

3.1. Konveks Kümeler

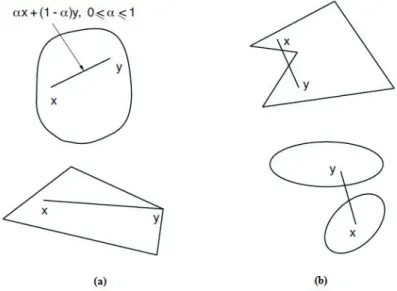
Tanım 3.1.1. C  n _{kümesi üzerindeki herhangi iki noktayı birleştiren doğru parçası}

üzerindeki noktalar, aynı kümede kalıyorsa C’ye konveks küme ya da afin denir. Yani, 0  olmak üzere 1 x x₁, ₂C için

1 (1 ) 2

x x C

    (3.1)

ise C   kümesi konveks bir kümedir. n

Aşağıda konveks kümelere ve konveks olmayan kümelere örnekler verilmiştir:

Şekil 3.1. (a) Konveks kümeler, (b) Konveks olmayan kümeler Teorem 3.1.2.C C  ₁, ₂ n konveks iki küme olsun. Bu durumda i) _{1 2} { _{1 2}| _{1 1}, _{2 2}} n

C C  x x x C x C   konveks kümedir. ii)   için C₁ konvekstir.

iii) C₁C₂ konvekstir.

iv) Boş küme, konveks küme olarak düşünülür.

v) Herhangi sayıda (sonlu, sayılabilir ya da sayılamaz) konveks kümelerin kesişimi yine konveks bir kümedir. (Rockafellar,1970)

3.2. Konveks Fonksiyonlar

Tanım 3.2.1.x y,    ve I 0  için 1







1



  

1



( )

f x  y f x   f y (3.2)

ise _{f I   fonksiyonuna konveks fonksiyon denir.}: 1

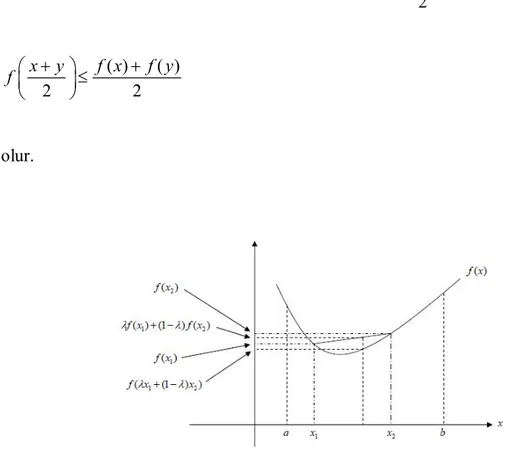
2   durumunda ( ) ( ) 2 2 x y f x f y f _  _    (3.3) olur.

Şekil 3.2. Konveks fonksiyon

Örnek 3.2.2 (  Üzerindeki Konveks Fonksiyon Örnekleri).

 Afin: Herhangi a b  , _için f x

 

ax b_{ fonksiyonu  üzerinde konveks bir}

fonksiyondur.

 Eksponansiyel: Herhangi a   için f x 

 

eax _{fonksiyonu  üzerinde} konveks bir fonksiyondur.

 Kuvvet: t  veya 1 t  için 0 f x

 

xt fonksiyonu pozitif reel sayılar kümesi (0, )

  

 Mutlak değer kuvveti: p 1 için xp _{fonksiyonu  üzerinde konveks bir}

fonksiyondur.

 Negatif entropi: f x( )xlogx fonksiyonu  üzerinde konveks bir _ fonksiyondur.

Tanım 3.2.3.x y,  ve I 0 için 1







1



  

1



( )

f x  y f x   f y (3.4)

ise _{f I   fonksiyonuna kesin konveks fonksiyon denir.} :

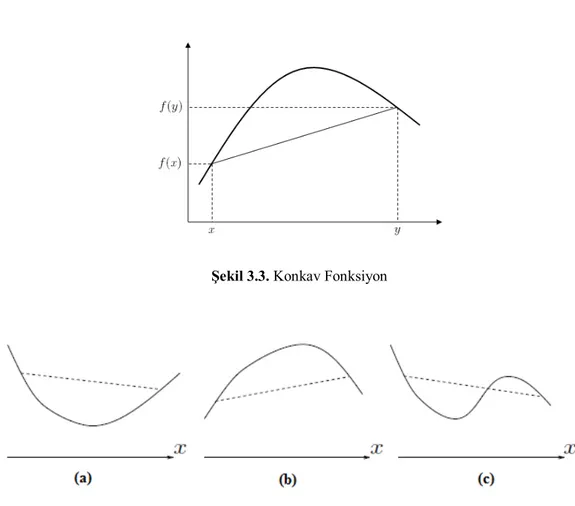
Tanım 3.2.4.f _{fonksiyonu konveks ise} f I   fonksiyonuna konkav fonksiyon : denir.

Tanım 3.2.5.f _{fonksiyonu kesin konveks ise} f I   fonksiyonuna kesin konkav :

fonksiyon denir.

Şekil 3.3. Konkav Fonksiyon

Şekil 3.4. (a) grafiği konveks bir fonkiyon, (b) grafiği konkav bir fonksiyon ve (c) grafiği ne konveks ne de konkav bir fonksiyondur

Örnek 3.2.6. (  Üzerindeki Konkav Fonksiyon Örnekleri)

 Afin: Herhangi a b  , _{için  üzerinde} f x

 

ax b konkav bir fonksiyondur.

 Kuvvet: 0  için pozitif reel sayılar kümesi t 1  üzerinde _ f x

 

xt

konkav bir fonksiyondur.

 Logaritma:  üzerinde logx konkav bir fonksiyondur. _ Teorem 3.2.7.

i) f I :  ve :g I  fonksiyonları konveks ve 0 ise f g ve

f

 fonksiyonları da I aralığında konvekstir.

ii) f I :  ve :g I  fonksiyonları konveks ve g artan ise g f

bileşkesi konvekstir.

iii) f I :  ve g I :  fonksiyonları konveks, negatif olmayan, azalan (veya artan) ise h x( ) f x g x( ) ( ) fonksiyonu da bu özellikleri sağlar.

iv) Eğer f_n :I , sonlu bir f limit fonksiyonuna yakınsayan konveks

fonksiyonların bir dizisi ise f de konvekstir.(Roberts ve Varberg, 1973)

İspat:

i) Konveks fonksiyon tanımından kolayca görülebilir. ii) x y,  ve I 



0,1



olsun.

























(1 ) ( ) (1 ) ( ) ( ) (1 ) ( ) ( )( ) (1 ) ( )( ) g f x y g f x f y g f x g f y g f x g f y                   _ _  _ _      (3.5) dir. iii) x y,  ve I 



0,1



olsun.



( ) ( )



( ) ( )



0 xy f x  f y g y g x  (3.6) dır ve (3.6)’dan

( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )

f x g y  f y g x  f x g x  f y g y (3.7)

elde edilir. Eğer  0 ise



 

















2 2 2 2 2 2 (1 ) (1 ) ( ) (1 ) ( ) ( ) (1 ) ( ) ( ) ( ) (1 ) ( ) ( ) ( ) ( ) (1 ) ( ) ( ) ( ) ( ) (1 ) ( ) ( ) ( ) ( ) (1 ) ( ) ( ) ( ) ( ) (1 ) ( ) ( ) (1 ) (1 ) f x y g x y f x f y g x g y f x g x f x g y f y g x f y g y f x g x f x g x f y g y f y g y f x g x f y g y                                                 _   _ _    _ f x g x( ) ( ) (1 ) ( ) ( )f y g y (3.8)

eşitsizliği elde edilir.

iv) x y,  ve I 



0,1



olsun.













(1 ) lim (1 ) lim ( ) (1 ) ( ) ( ) (1 ) ( ) n n n n n f x y f x y f x f y f x f y                      (3.9) dir.

Örnek 3.2.8 ( Üzerindeki Örnekler). Afin fonksiyonlar, n  üzerinde hem konveks n hem de konkav fonksiyonlardır. Tüm normlar  üzerinde konvekstir. n

 Afin: Herhangi _{a b x   için} , , n

 

T

f x a x b fonksiyonu, hem konveks hem konkav bir fonksiyondur.

 Normlar: l_p norm: p 1 _için

1/ 1 p p p i p i x x       





, l_ norm: x _ max_i x_i gibi normlar konveks fonksiyonlardır.

Örnek 3.2.9 (m×n Üzerindeki Örnekler). Afin fonksiyonlar, m n üzerinde hem konveks hem de konkav fonksiyonlardır. Normlar, m n üzerinde konveks fonksiyonlardır.

 Afin: A X,  m n _{ve b   için} 1 1 ( ) ( ) m n T ij ij i i f X iz A X b a x b     





fonksiyonu hem konveks hem de konkav fonksiyondur.

 Spektral (en büyük singüler değer) norm: _max, n n bir matrisin en büyük öz değerini belirtsin. Bu takdirde X m n olmak üzere

1/2 max

2

( ) ( ( T ))

f X  X   X X fonksiyonu konveks fonksiyondur. Tanım 3.2.10. f :n  bir fonksiyon olmak üzere f ’nin grafiği

{( , ( )) |x f x x n} (3.10)

şeklinde tanımlanır. Tanım 3.2.11.

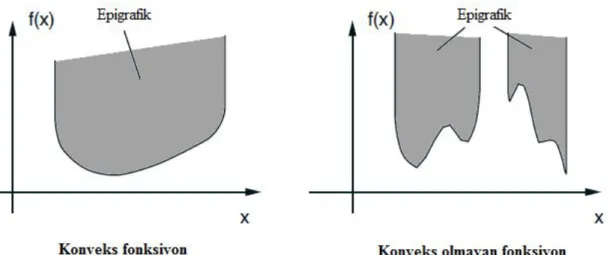
i) dom f {xn: ( )f x  } kümesine f ’nin tanım kümesi denir.

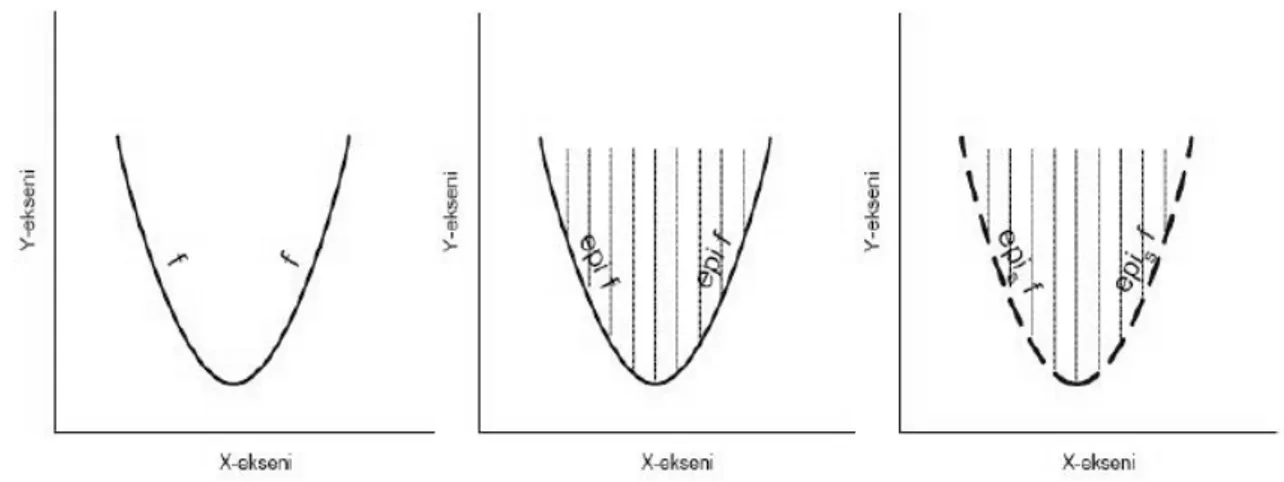
ii) f :n bir fonksiyon olmak üzere f ’nin epigrafiği (kesin epigrafiği)

 



( , ) n | ( )



,



epi_s( )f



(x t, ) n | (f x)





epi f  x t   f x t    t

(3.11)

şeklindedir.

f _{bir konveks fonksiyondur } epi f bir konveks kümedir.

 

iii) ( ) { n: ( ) }

t

S f  x f x t ile tanımlanan kümeye f nin bir alt düzey kümesi

denir.

( , )x t epi f  x S f_t( ) olduğu açıktır.

Şekil 3.6. Bir fonksiyonun epigrafiği ve kesin epigrafiği

Şekil 3.7. f x( )x2 fonksiyonunun S₂₅( )f {xn:x225}alt düzey kümesi

Not 3.2.12.

( ) ( ) px qy pf x qf y f p q p q            (3.12) ifadesine denktir.

ii) (3.2)’nin basit geometrik yorumu,



x f x,

 



ve



y f y,

 



noktaları arasındaki doğrunun grafiğin üzerinde olmasıdır.



x f x,

 



ve



y f y,

 



noktalarını birleştiren doğrunun denklemi ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) f y f x f s f x y x s x f y f x f s f x s x y x            (3.13)

şeklinde belirtilir. sty(1t x) noktasında hesaplanırsa,









( ) ( ) ( (1 ) ) ( ) ( ) ( ) ( ) ( ) ( ) (1 ) ( ) f y f x f ty t x f x t y x f x t f y f x y x tf y t f x              elde edilir.

iii) x₁x₂ x₃ olacak şekilde x x x ₁, ₂, ₃ I  ’de üç nokta ise (3.2) ifadesi

1 1 2 2 3 2 1 1 3 2 2 1 3 3 3 ( ) 1 ( ) 1 ( ) ( ) ( ) ( ) ( ) ( ) 0 ( ) 1 x f x x f x x x f x x x f x x x f x x f x        (3.14) ifadesine denktir. Bu da 2 3 1 2 2 1 3 1 3 1 3 ( ) x x ( ) x x ( ) f x f x f x x x x x       (3.15)

3 1 2 1 2 1 3 2 3 2 1 3 1 3 2 ( ) ( ) ( ) 0 ( )( ) ( )( ) ( )( ) f x f x f x x x x x  x x x x  x x x x  (3.16) ifadesine denktir.

iv) Köşeleri ( , ( )), ( , ( )), ( , ( ))x f x_{1 1} x₂ f x₂ x f x_{3 3} olan üçgenin alanı

1 1 2 2 3 3 ( ) 1 1 ( ) 1 2 ( ) 1 x f x P x f x x f x  (3.17) ile verilir.

v) (3.15)’in diğer bir yazılışı

2 3 1 2 1 3 1 3 2 1 2 2 3 ( ) ( ) ( ) ( ) , ( , ) f x f x f x f x x x ve x x x x x x x        (3.18)

şeklindedir. Böylece aşağıdaki sonuç geçerlidir: Her c   noktası için I f x( ) f c( )

x c



 fonksiyonu I aralığında artan ise f fonksiyonu konvekstir. (xc)

vi) (3.18)’i kullanarak aşağıdaki sonucu kolayca ispatalayabiliriz: f , I  

aralığında konveks bir fonksiyon ve x₁ y x₁, ₂  y₂, x₁x₂, y₁ y₂ ise aşağıdaki eşitsizlik geçerlidir: 2 1 2 1 2 1 2 1 ( ) ( ) ( ) ( ) . f x f x f y f y x x y y      (3.19) (Pecaric ve ark.1992)

( ) ( ) 2 2 x y f x f y f _  _    (3.20)

eşitsizliği geçerliyse f :



a b   foksiyonuna ,





a b üzerinde Jensen anlamda ,



konveks veya J -konveks denir. J -konveks bir f fonksiyonuna her ( , ),x y x y nokta çiftleri için (3.20)’de daha sıkı eşitsizlik sağlanırsa kesin J -konveks denir.

Konveks fonksiyonlar için Jensen eşitsizliği, matematik ve istatistikte çok önemli eşitsizliklerden biridir. Diğer birçok eşitsizlik bu eşitsizlikten elde edilebilir. Teorem 3.2.14 (Jensen Eşitsizliği). I , ’de bir aralık , f I  : konveks fonksiyon,

1,..., n

x x I ve ₁₂..._n  olmak üzere 1  ₁, ₂,...,  olsun. Bu durumda _n 0





1 1 ( ) n n i i i i i i f  x  f x   





(3.21)

eşitsizliği geçerlidir. Eğer f kesin konveks ise (3.21) ifadesi x₁...x_n olmaksızın kesindir. (Roberts ve Varberg, 1973)

İspat: (3.21)’in ispatı tümevarımdan yapılır. n 1 için eşitsizlik doğrudur. Farz edelim ki nk için doğru olsun. Bu durumda nk1 için doğruluğunu göstermemiz gerekir.

1,..., k, k 1

x x x _ I ve ₁₂..._k_k1 olmak üzere 1  ₁, ₂,..., _k, _k1 olsun. 0

1, 2,..., k 1

    ’in en az bir tanesi 1’den küçük olmalıdır. Aksi halde eşitsizlik aşikardır. 1 1 k    ve 1 2 1 2 1 1 1 ... 1 1 1 k k k k k u  x  x  x              (3.22) olsun. 1 1 1 ... 1 1 1 k k k            (3.23) ve

1 1x 2x2 ... kxk k 1xk 1 (1 k 1)u k 1xk 1

             (3.24)

olur. f konveks fonkiyon olduğundan,



(1 k 1) k 1 k 1



(1 k 1) ( ) k 1 ( k 1)

f  _ u _x _   _ f u  _ f x_ (3.25)

bulunur ve tümevarım hipotezinden

1 2 1 2 1 1 1 ( ) ( ) ( ) ... ( ) 1 1 1 k k k k k f u  f x  f x  f x              (3.26)

eşitsizliği vardır. (3.25) ve (3.26) eşitsizliklerinden



1 1 2 2 ... k 1 k 1



1 ( )1 2 ( 2) ... k 1 ( k 1)

f  x  x   _ x _  f x  f x   _ f x_ (3.27)

elde edilir. Böylece eşitsizlik nk1 için kurulmuştur ve böylelikle eşitsizlik herhangi pozitif n tamsayısı için geçerlidir.

Teorem 3.2.15 (Aritmetik-Geometrik Ortalama Eşitsizliği). Eğer x_i 0,_i  ve 0

1 1 n i i   



ise 1 2 1 2 ... 1 1 2 2 ... n n n n x x  x   x  x   x (3.28)

dir. (Roberts ve Varberg, 1973)

İspat: x _i 0 için ispatlamak yeterlidir. y_i logx_i olsun. Bu durumda

log

e e

i i xi i iy

i

x     (3.29)

dir. ( )f t et fonksiyonu (  aralığında konveks olduğundan Jensen eşitsizliği , ) kullanılarak,

1 1 1 1 1 1 e ( ) e n i i i i i n y n i i i i i n n n y i i i i i i i i x f y f y x              _{ }   _{ }     











(3.30) elde edilir.

Teorem 3.2.16. I   açık bir aralık olmak üzere reel değerli bir f fonksiyonunun I ’da konveks olması için gerek ve yeter şart, f ’nin sürekli ve f( )x  olmasıdır. 0 (Niculescu ve Persson, 2006)

Tanım 3.2.17.I   bir aralık olmak üzere eğer log f konveks ise veya her

 

, , 0,1 x yI  için 1 ( (1 ) ) ( ) ( ) f x  y f x f y     (3.31)

ise f I  : fonksiyonuna log-konveks denir. I (0, ) ve f pozitif iken x y,  I

ve 0 1 için

1 1

( ) ( ) ( )

f x y  f x  f y 

 (3.32)

ise çarpımsal konveks denir.

Eğer f çarpımsal konveks ise x f e( x) _{dönüşümü (}  aralığında log-, ) konvekstir. Bunu görmek için 1

2   alınırsa

 













1 1 1 1 1/ 2 1/ 2 2 2 2 2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ln ln 2 2 x y x y xy x y xy x y xy x y xy x y xy x y f x y f x f y e e e e e e e e e e e e e e x y e e xy x y xy    _  _   _                      (3.33)

olur ki, elde edilen son eşitsizlik aritmetik geometrik ortalama eşitsizliğidir ve böylece ( x)

x f e dönüşümünün (  , ) aralığında log-konveks olduğu görülür. exp, sinh, cosh fonksiyonları çarpımsal konvekstir.

(3.31)’in tersi durumuna da log–konkav denir.

Not 3.2.18. f ve g konveks ve g artan ise g f konveks olduğu için f exp log f

olarak yazılabileceğinden log-konveks bir fonksiyon konvekstir. Tersi her zaman doğru değildir. Bu doğrudan (3.28)’den ve (3.31)’den

1

( ) ( ) ( ) (1 ) ( )

f x  f y  f x  f y

   (3.34)

elde edilir. Böylece,





1

(1 ) ( ) ( ) ( ) (1 ) ( )

f x  y f x  f y   f x  f y

      (3.35)

4. MAJORİZASYON VE KONVEKS FONKSİYONLAR

Majorizasyon; öz değer, singüler değer ve matris normlarının matris eşitsizliklerini oluşturmada önemli bir araçtır.



1, 2



x x x ve y



y y₁, ₂



negatif olmayan reel vektörler olsun. Genelliği bozmaksızın, vektörlerin bileşenleri azalan sırada sıralansın. Eğer x₁ y₁ ise x vektörü y ’den büyüktür. Örneğin,



0.8, 0.2

 

 0.6, 0.4



’tür. Fakat bu yaklaşım 3 ya da daha çok bileşen durumuna genişletilemez. Bu bölümde bileşen sayısı ikiden fazla olan vektörler üzerindeki kısmi sıralama ele alınacaktır.

4.1.Temel Gösterimler



1,...,



n n x x x   olsun. x ve x

, sırasıyla azalan ve artan sırada x ’in

koordinatlarının düzenlenmesiyle elde edilen vektörler olsun. Böylece, eğer



1,..., n



x  x x ise x₁ ...x_n ’dir. Benzer şekilde eğer x 



x₁,...,x_n



ise

1 ... n

x  x dir. Not edelim ki,

1, 1

i n i

x x_{ }   i n (4.1)

dir.

Tanım 4.1.1. ,x y n olsun. Eğer

1 1 , 1, 2,..., 1 k k i i i i x y k n     





(4.2) ve 1 1 n n i i i i x y   





(4.3)

Benzer şekilde x₁x₂  x_n 0 ve y₁ y₂  y_n 0 azalan sıralı bileşenli , n

x y  vektörleri için _{x vektörü y vektörünü majorize eder denir ve eğer}

1 1 , 1, 2,..., 1 k k i i i i x y k n     





ve 1 1 n n i i i i x y   





ise x y yazılır. Eğer 1 1 1 1 , 1, 2,..., 1 , 1, 2,..., 1 k k k k i i i i i i i i x y k n x y k n          _    _  









ve 1 1 1 1 i i i i n n n n i i i i x y x y        _  _  









eşitsizlikleri varsa x y, tarafından zayıf majorize

(süper majorize) edilir denir. Sembolle x_w y



xw y



şeklinde gösterilir. Açıktır ki,

w

xyx y’dir.

Örnek 4.1.2. Şekil 4.1.’deki durum göz önüne alınsın. İki farklı vektör görülmektedir. A ve B şemalarında en büyük iki bileşen eşittir (x₁A x₁B ve x₂A x₂B). B şemasındaki en küçük üç bileşen eşittir (x₃B x₄B x₅B), fakat A şemasındaki en küçük üç bileşen eşit değildir.( ₃A ₄A ₅A

x x x ). Buna ek olarak, A ve B şemalarındaki tüm bileşenlerin toplamı eşittir. Tanım 4.1.1.’de verilen sıralama uygulanarak A şemasındaki vektör, B şemasındaki vektörü majorize eder(xAxB).(Jorswieck ve Boche,2006)

Şekil 4.1.Örnek vektörler: xAxB

Örnek 4.1.3. Aşağıdaki vektörler majorizasyon kullanılarak karşılaştırılabilir:





1 1 1 1 1 1 1 1 , ,..., , ,..., , 0 ... , , 0,..., 0 1, 0,..., 0 1 1 1 2 2 n n n n n n                     Teorem 4.1.4. , ,x y z n olsun.

i) x_w yx₁ y₁ ve x yy_n x_i  y₁’dir.

ii) Aşağıdaki ifadeler majorizasyon ve zayıf majorizasyonun geçişli olduğunu gösterir: , ; , w w w x y y z x z x y y z x z         iii) xz y, z pxqyz; p q, 0, pq1. iv) x_w z y, _w z px qy _w z; p q, 0, pq1. v) x yx_w y ve x_w y' dir.

vi) P permütasyon matris olmak üzere x y y, xx yP’dir.

vii) P permütasyon matris olmak üzere x_w y y, _w xx yP’dir.(Zhang,2011) Teorem 4.1.5. Aşağıdaki ifadeler eşdeğerdir:

i) x y , n iken x_w y’dir. ii) z   için n xz ve z ’dir. y

iii) u  n için xu ve uy’dir. (Zhang,2011)

, n

x y  için xy , bileşen toplamını ve x y , x ve y’nin Hadamard çarpımını belirtir. x, negatif koordinatların sıfır ile yer değiştirilmesiyle x ’ten elde

edilen bir vektör ve | |x , tüm koordinatların mutlak değeri alınarak elde edilen bir

vektördür.

Teorem 4.1.6. ,x y n olsun. Bu durumda i) x_w y  t  için









1 1 n n i i i i x t  y t      





(4.4) dır. ii) _xw _{y  t}  _için









1 1 n n i i i i t x  t y      





(4.5) dır.

iii) x y  t  için 1 1 | | | | n n i i i i x t y t     





(4.6) dir. (Bhatia,1997) Teorem 4.1.7. x( ,...,x1 xn), ( ,...,1 ) n n y y y   olmak üzere i) x_w| |x ii) |xy|_w| |x  |y| iii) xy _w xyxy iv) 1 1 1 n n n i i i i i i i i i x y  x y x y      







dir. (Zhang,2011)

Bileşenleri negatif olmayan  üzerindeki tüm vektörlerin kümesi n n_ ile gösterilir. Yani, ui  için 0 ( ,...,1 )

n n u u u  _’dir. Teorem 4.1.8. x( ,...,x₁ x_n), ( ,...,₁ ) n n y y y   olsun. Bu durumda 1 ( ,..., n) n u u u     için 1 1 n n i i i i i i x y x u  y u    

_



_

 ve  u ( ,...,u₁ un) n için 1 1 n n w i i i i i i x y x u  y u    







 dir. (Zhang,2011)

Teorem 4.1.9. x y u v, , ,  n_ olmak üzere i) x_w yx u _w yu

ii) x_w u y, _w vx y _wuv

dir. (Zhang,2011)

Tanım 4.1.10. Satırları ve sütunları toplamı 1 olan, negatif olmayan bir kare matrise

ikili stokastik matris denir. Yani eğer,

, i j  için a _ij 0 (4.7) j  için 1 1 n ij i a  



(4.8)

i  için 1 1 n ij j a  



(4.9)

ise n n bir A

 

a_ij matrisine ikili stokastik matris denir.

Teorem 4.1.11. x y _{olması için gerek ve yeter şart x}Py olacak şekilde ikili stokastik bir P matrisinin olmasıdır. (Bhatia,1997)

Örnek 4.1.12.x



0.6, 0.4

 

 0.8, 0.2



 y olsun. İlgili stokastik matris

2 1 2 1 0.6 _{3 3} 0.8 _{3 3} 0.4 1 2 0.2 1 2 3 3 3 3 P                                      ile verilir.

Teorem 4.1.13. Bir A matrisinin ikili stokastik olması için gerek ve yeter şart her x

vektörü için Ax olmasıdır. (Bhatia,1997) x

Tanım 4.1.14. x  ve _k 0 y  olmak üzere _k 0 x



x₁,...,x_n



ve y



y₁,...,y_n



vektörleri düşünülsün. Eğer k 1,...,n için 1 1 1 k k i i i i x y   





ve 1 1 n n i i i i x y   





ise x , y tarafından

log-majorize edilmiştir denir. Yani, x_log y’dir. Eğer k1,...,n için

1 1 k k i i i i x y   





ise

x , y tarafından zayıf log-majorize edilmiştir denir ve x_wlog y ile gösterilir. Teorem 4.1.15. x y,  n_ olsun. Bu durumda

log w w x yx y (4.10) dir. Yani, 1 1 1 1 , 1, 2,..., , 1, 2,..., k k k k i i i i i i i i x y k n x y k n       

_



_







(4.11) dir. (Zhang, 2011)

4.2. Konveks ve Monoton Fonksiyonlar İçin Majorizasyon

Tanım 4.2.1.  üzerinde tanımlı reel değerli bir  fonksiyonuna n

( ) ( )

x y x  y (4.12)

ise Schur- konveks veya s-konveks denir.

Örneğin, x( ,...,x₁ x_n) olmak üzere ( ) |x  x₁| ... |  x_n| fonksiyonu  n üzerinde Schur-konvekstir. Eğer x ise y A(a_ij), n n ikili stokastik bir matris olmak üzere xAy olarak yazılabilir. Bu durumda

1 1 1 1 1 1 1 1 1 ( ) | | | | | | | | ( ) n n n i ji j i i j n n n n ji j ji j i j i j n j i x x a y a y a y y y                 _{ }    



 



 



 (4.13) dir.

Dikkat edelim ki, x   olmak üzere n f x yazıldığı zaman, ( ) f

fonksiyonunun x ’in tüm bileşenlerini içeren bir aralıkta tanımlı olduğu ve f

fonksiyonunun x ’in tüm bileşenlerine uygulanabileceği anlaşılmalıdır. Yani,



1,..., n



x x x ise f x( )



f x( ),..., (₁ f x_n)



’dir. Teorem 4.2.2. ,x y n olsun. Bu takdirde i) f konveks ise

( ) _w ( ),

xy f x  f y (4.14)

ii) f artan ve konveks ise

( ) ( )

w w

dir. (Zhang,2011) Sonuç 4.2.3. , n x y  olsun. Bu durumda i) x y| |x _w|y|, yani



|x₁|,...,|x_n|



_w



|y₁|,...,|y_n|



’dir. ii) 2 2 w x yx  y , yani









1 1 2 2 2 2 ,..., ,..., n w n x x  y y ’dir.

iii) x yi, i pozitif olmak üzere lnxwlnyxw y’dir.(Zhang,2011)

İspat: | |t ve t2 konveks olduklarından (i) ve (ii) açıktır. et artan ve konveks olduğundan elnx_w elnyx_w y bulunur ki, (iii) elde edilmiş olur.

Teorem 4.2.4. ,x y n olsun. Bu durumda i)

1 1

tüm konveks fonksiyonları için ( ) ( )'dir.

n n i i i i x y f f x f y   

_



_

 ii) 1 1

tüm artan ve konveks fonksiyonları için ( ) ( )'dir.

n n w i i i i x y f f x f y   

_



_



iii) Eğer y, x ’in bir permütasyonu değilse x ve y’nin tüm bileşenlerini içeren herhangi kesin artan ve kesin konveks f fonksiyonu için

1 1 ( ) ( ) n n w i i i i x y f x f y   







 ’dir. (Zhang,2011)

Teorem 4.2.5. ,x y n olsun. Bu durumda

w xy  x y xy (4.16) ve













1 1 1 n n n i i i i i i i i i x y x y x y        







(4.17) dir. (Zhang,2011)

Teorem 4.2.6 (Weyl Majorant Teoremi). A , singüler değerleri s₁...s_n ve öz değerleri |₁| ... |  _n| şeklinde dizilmiş n n bir matris olsun. Bu durumda her t

değeri için ( )et fonksiyonu konveks ve monoton artan olacak şekildeki her :

 _ _ fonksiyonu için











 | 1| ... | n|



w



( ),..., ( )s1  sn



(4.18)

dir. Özel olarak her p  için 0



| 1| ,...,| |





1 ,...,



p p p p

n w s sn

   (4.19)

dir. (Bhatia,1997)

Teorem 4.2.7. ,x y n olsun. Aşağıdaki iki ifade eşdeğerdir: i) x y

ii) : _{konveks fonksiyonları için} iz( )x iz( )y ’dir. (Bhatia,1997)

Teorem 4.2.8. ,x y n olsun. Aşağıdaki iki ifade eşdeğerdir:

i) x_w y

ii) : monoton artan, konveks fonksiyonları için iz( )x iz( )y ’dir. (Bhatia,1997)

4.3. Konveks Fonksiyonlar ve Zayıf Majorizasyon Eşitsizlikleri

, _n

A B   için aşağıdaki 3 sıralama tipi düşünülebilir: i) BA AB pozitif yarı tanımlıdır.

ii) (Öz değer eşitsizlikleri)

( )B ( )A _j( )B _j( )A (j 1, 2,..., )n

     (4.20)

1 1 ( ) ( ) ( ) ( ) ( 1, 2,..., ) k k w j j j j B A B A k n       

_



_

  (4.21)

Buradan BA( )B ( )A ( )B _w ( )A olduğu görülebilir.

Spektrumları I   aralığında bulunan _n üzerindeki tüm Hermityen matrislerin kümesi _n( )I ile belirtilsin. I   üzerinde tanımlı, artan bir f

fonksiyonu için A B,  _n( )I olmak üzere









( )B ( )A f B( ) f A( )

    (4.22)

dır. I üzerinde tanımlı, artan, konveks bir f fonksiyonu için A B,  _n( )I olmak üzere









( )B _w ( )A f B( ) _w f A( )

      (4.23)

dır.

Lemma 4.3.1. A _n( )I ve f I üzerinde konveks bir fonksiyon olsun. , x birim vektörü için



,



( ) ,

f Ax x  f A x x (4.24)

dir.(Bhatia,1997)

Lemma 4.3.2. A _n( )I olsun. Maksimum, u u₁, ₂,...,u_k ortonormal vektörlerinin tüm seçimlerinde geçerli olmak üzere

1 1 ( ) max , ( 1, 2,..., ) k k j j j j j A Au u k n     





(4.25)

dir. Bu ifade “Ky Fan Maksimum Prensibi” olarak bilinir. (Bhatia,1997) Tanım 4.3.3. A 1 ise A_n matrisine kontraksiyon denir.