Grafların yeni çarpımı üzerinde bazı parametrelerin incelenmesi

T.C.

SELÇUK ÜNĠVERSĠTESĠ FEN BĠLĠMLERĠ ENSTĠTÜSÜ

GRAFLARIN YENĠ ÇARPIMI ÜZERĠNDE BAZI PARAMETRELERĠN ĠNCELENMESĠ

Nurettin Talha DĠNÇ YÜKSEK LĠSANS TEZĠ Matematik Anabilim Dalı

ġubat-2014 KONYA Her Hakkı Saklıdır

iv ÖZET

YÜKSEK LĠSANS TEZĠ

GRAFLARIN YENĠ ÇARPIMI ÜZERĠNDE BAZI PARAMETRELERĠN ĠNCELENMESĠ

Nurettin Talha DĠNÇ

Selçuk Üniversitesi Fen Bilimleri Enstitüsü Matematik Anabilim Dalı

DanıĢman: Doç. Dr. A. Dilek MADEN 2014, 40 Sayfa

Jüri

Prof. Dr. A. Sinan ÇEVĠK Doç. Dr. A. Dilek MADEN Doç. Dr. Ahmet ERDOĞAN

Bu çalıĢmada, ilk olarak grafların derece dizisi üzerine inĢa edilmiĢ yeni bir graf çarpımı olan derece çarpım grafı tanımlanmıĢ ve özellikleri incelenmiĢtir. Daha sonra da bu çarpım grafı üzerinde bağımsızlık sayısı, klik sayısı, kromatik sayısı, klik örtü sayısı, diameter, radius, Wiener indeks, Randic indeks gibi graf parametreleri incelenmiĢtir. Son olarak da derece çarpım grafının mükemmel graf olduğu elde edilmiĢtir.

v ABSTRACT

MS THESIS

SOME GRAPH PARAMETERS ON A NEW TYPE OF GRAPH PRODUCT

Nurettin Talha DĠNÇ

THE GRADUATE SCHOOL OF NATURAL AND APPLIED SCIENCE OF SELÇUK UNIVERSITY

THE DEGREE OF MASTER OF SCIENCE IN MATHEMATICS

Advisor: Assoc. Prof. Dr. A. Dilek MADEN 2014, 40 Pages

Jury

Prof. Dr. A. Sinan ÇEVĠK Assoc. Prof. A. Dilek MADEN Assoc. Prof. Ahmet ERDOĞAN

In this study firstly, we define a new type of graph product namely degree product which is based on the degree squence of graphs. Then we examine properties over this new graph. Further we discuss relations among this product and some graph parameters such as independence number, clique number, chromatic number, clique cover number, diameter, radius, Wiener index, Randic index. Finally we show that the degree product of graphs are actually perfect graphs.

vi ÖNSÖZ

Bu çalıĢma Selçuk Üniversitesi Fen Fakültesi Matematik Bölümü Öğretim Üyesi Doç. Dr. A. Dilek MADEN yönetiminde yapılarak, Selçuk Üniversitesi Fen Bilimleri Enstitüsü’ne Yüksek Lisans Tezi olarak sunulmuĢtur.

ÇalıĢma süresince kılavuz olan ve yardımlarını esirgemeyen danıĢman hocam sayın Doç. Dr. A. Dilek MADEN’e, bu tezin ilhamını veren sayın hocam Prof. Dr. A. Sinan ÇEVĠK’e, her zaman yanımda olan ve desteklerini esirgemeyen sevgili aileme teĢekkürü bir borç bilirim.

Nurettin Talha DĠNÇ KONYA-2014

vii ĠÇĠNDEKĠLER ÖZET ... iv ABSTRACT ... v ÖNSÖZ ... vi ĠÇĠNDEKĠLER ... vii

SĠMGELER VE KISALTMALAR ... viii

1. GĠRĠġ ... 1

2. ÖN BĠLGĠLER VE TEMEL TANIMLAR ... 3

2.1. Grafın Tanımı ... 3

2.2. Graflarda Uzaklık ... 5

2.3. Yol ve Devir ... 6

2.4. Bazı Özel Graflar ... 7

2.5. Alt Graf ve ĠndirgenmiĢ Alt Graf ... 9

3. GRAF PARAMETRELERĠ ... 10

3.1. Bağımsızlık Sayısı ... 10

3.2. Klik Sayısı ... 10

3.3. Kromatik Sayısı ... 11

3.4. Klik Örtü Sayısı ... 12

3.5. Eccentricity, Diameter ve Radius ... 12

3.6. Wiener Ġndeks ... 13

3.7. Randic Ġndeks ... 14

3.8. Düzensizlik ve EĢitlik Ġndeksi ... 14

3.9. Mükemmel Graf ... 15

4. GRAF ÇARPIMLARI ... 16

4.1. Kartezyen Çarpım ... 16

4.2. Strong Çarpım ... 17

4.3. Lexicografik Çarpım ... 19

5. GRAFLARIN YENĠ ÇARPIMI ... 22

5.1. Grafların Derece Çarpımı ... 22

6. DERECE ÇARPIM GRAFI ÜZERĠNDE GRAF PARAMETRELERĠ ... 31

7. SONUÇLAR VE ÖNERĠLER ... 37

KAYNAKLAR ... 38

viii SĠMGELER VE KISALTMALAR

SEMBOLLER ANLAMI

A : A kümesinin eleman sayısı

 : altkümesidir

m : boyut (E nin eleman sayısı)

 : büyük ya da eĢittir

 : büyüktür

( )i

der e : e köĢesinin derecesi _i

 : elemanı değildir

 : elemanıdır

 : eĢit değildir

 : eĢittir

( )G

 : G grafının bağımsızlık sayısı

( )

dia G : G grafının diameter sayısı

( )

t G : G grafının düzensizlik indeksi

( )

e G : G grafının eĢitlik indeksi

( )G

 : G grafının klik örtü sayısı

( )

w G : G grafının klik sayısı

( )G

 : G grafının kromatik sayısı

( )

rad G : G grafının radius sayısı

( )

R G : G grafının Randic indeksi

G : G grafının tamamlayıcısı

( )

W G : G grafının Wiener indeksi

G H : G ile Hgrafının derece çarpım grafı

G H : G ile H grafının kartezyen çarpım grafı G H : G ile Hgrafının lexicografik çarpım grafı

G H : G ile Hgrafının strong çarpım grafı

( )G

 : G nin noktalarının derecelerinin maksimumu

( )G

 : G nin noktalarının derecelerinin minimumu

,

r s

K : iki parçalı graf (kümelerin eleman sayısı r ve s)

 : kapsar e : kenar E : kenar kümesi v : köĢe V : köĢe kümesi  : küçük ya da eĢittir  : küçüktür

n : mertebe (V nin eleman sayısı)

n

E : n mertebeli boĢ graf

n

C : n mertebeli devir graf

n

K : n mertebeli tam graf

n

ix

SEMBOLLER ANLAMI

( )G

 : u köĢesinin eccentricity sayısı { , }e ei j veya e e i j : uç köĢeleri e ve i e olan kenar j

,

u v

D : uç köĢeleri u ve v olan yürüme

( , )

d u v : uç köĢeleri u ve v olan yürümenin en kısa

uzunluğu

,

u v

D : uç köĢeleri u ve v olan yürümenin uzunluğu

( , )

G V E : V köĢe kümeli E kenar kümeli bir G grafı

1 2

1. GĠRĠġ

Matematiğin diğer alanlarından farklı olarak Graf Teorisi nin baĢlangıcı 18. yüzyıla uzanır.

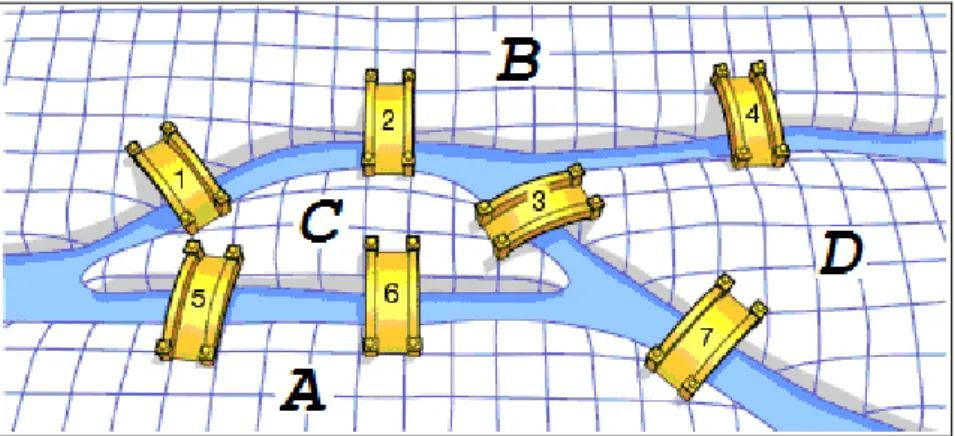
18. yüzyılda Prusya daki Königsberg kasabası Pregel Nehri ile iki bölgeye ayrılmaktaydı ve nehrin içinde iki adacık bulunmaktaydı. Bu nehirdeki adaları kasabaya bağlayan yedi köprüye dair o bölgenin insanları arasında yayılan alıĢagelmeyen bir matematik efsanesi dolaĢmaktaydı. Bu efsane Ģu Ģekildeydi:

ġekil 1.1 Königsberg ün köprüleri

“Kasabanın bir yakasından gezinti yapmak için çıkan biri tüm köprüleri bir kez geçerek baĢladığı noktaya dönebilir”

Bu efsanenin bir yalandan ibaret olduğu Leonhard Euler (1707-1783) tarafından gösterilmiĢtir. Leonhard Euler bu problemin çözümü için uğraĢırken Graf Teorinin ilk adımlarını ve temellerini atmıĢtır.

Ġki nesne arasında daima bir iliĢkiden söz etmek mümkündür. Bu iliĢki nesnelerin boyları, ağırlıkları, renkleri vs. hakkında olabilir.

Söz gelimi yukarıdaki gibi adalar arasındaki köprüleri ele alalım. Adaları bir nokta ile temsil edelim ve eğer iki ada arasında bir köprü varsa bu iki adayı temsil eden noktaları bir çizgi ile birleĢtirelim. Yok, eğer adalar arasında bir köprü yok ise noktaları öylece bırakalım. Örneğin A, B, C ve D adaları için A ile B, A ile D, C ile D, A ile C ve B ile D arasında bir köprü olsun. Bu köprüler ġekil 1.2. deki gibi gösterilebilir.

ġekil 1.2.

Bir graf, iĢte yukarıdaki gibi bir Ģekildir. Nokta sayısı sonsuz olabilir. Bazı noktalar, “... iliĢkisi var” anlamına gelen bir çizgi ile birleĢtirilir. Çizgilerin boyu veya Ģekli hiç önemli değildir, var ya da yok olmaları önemlidir. Noktaların konumu da önemli değildir. Bu özellikleri nedeniyle bir grafın sonsuz farklı Ģeklinin çizilebileceği açıktır.

Grafların uygulama alanları oldukça geniĢ olduğu için 18. yüzyıldan günümüze kadar graflar üzerine çeĢitli çalıĢmalar yapılmıĢtır. Önemli bir yere sahip olan bu çalıĢmalardan biri de graf çarpımlarıdır.

Graf çarpımları basitçe anlatılmak istenilirse herhangi iki graftan yeni bir graf elde etmek graflar üzerinde bir geniĢleme yapmaktır. Örneğin kimyadaki herhangi iki atomdan yeni bir element elde etmeye benzetilebilir.

Klavžar ve Imrich [13] e göre graf çarpımlarının temel öğesi olan “grafların kartezyen çarpımı” ilk olarak 1912 yılında Alfred North Whitehead (1861-1947) ve Bertrand Russell (1872-1970) tarafından tanımlanmıĢtır. Daha sonraları 1960 yılında Gert Sabidussi (1929- ) [21] tarafından tekrar ele alınmıĢ ve yeniden düzenlenmiĢtir. Kartezyen graf çarpımından ilham alınarak günümüze kadar yüzlerce graf çarpımı tanımlanmıĢ ve bunlar üzerine teorem ve uygulamalar kurulmuĢtur. Örnek olarak [11], [17] ve [22] verilebilir.

Bu çalıĢmada da daha önceden tanımlanmıĢ ve üzerine çalıĢmalar yapılmıĢ graf çarpımlarından esinlenerek yeni bir graf çarpımı tanımlanmıĢtır. Bu yeni graf çarpımı üzerinde de graf parametreleri incelenmiĢtir.

ÇalıĢmamızın 2. Bölümünde graf teorinin temel tanım ve teoremlerine; 3. Bölümünde Graf Teori de kullanılan genel parametrelerin tanımları ve örneklerine; 4. Bölümünde önceki graf çarpımları ve teoremlerine yer verilmiĢtir.

5. Bölümde çalıĢmamızın ana konusu olan yeni graf çarpımının tanımı ve özellikleri; 6. Bölümde ise yeni tanımladığımız graf çarpımı üzerinde graf parametreleri incelenmiĢ ve eĢitlikler elde edilmiĢtir.

2. ÖN BĠLGĠLER VE TEMEL TANIMLAR

Bu bölümde Graf Teori de kullanılan bazı temel tanım, teorem ve örnekler verilmiĢtir. Daha detaylı bilgi almak için [1], [2], [9] ve [27] referanslarına bakılabilir.

2.1. Grafın Tanımı

Tanım 2.1.1. V , elemanları köşeler olarak adlandırılan boĢtan farklı bir küme, E de elemanları kenarlar olarak adlandırılan ve V nin bir ya da iki elemanlı alt kümelerinden oluĢan herhangi bir küme olsun. Bu Ģekilde tanımlanan G( , )V E

ikilisine graf adı verilir.

KöĢe kümesi ve kenar kümesi sonlu olan bir graf, sonlu graf olarak adlandırılır. Bu durumda V { , ,v v v_{1 2 3},..., }v_n olmak üzere V n sayısına grafın mertebesi;

1 2 3

{ , , ,..., m}

E e e e e olmak üzere E m sayısına da grafın boyutu denir.

Graflar somut olarak gösterilirken, her bir köĢe bir nokta ile temsil edilir. Her bir

{ , }v v_{i j} kenarı ise v ve _i v_j köĢesine karĢılık gelen noktaları birleĢtiren bir doğru parçası ya da basit bir eğri ile temsil edilir. { , }v v_{i j} kenarında, v ve _i v_j ye kenarın uç noktaları denir. Tek elemanlı bir { }v kenarının uç noktaları, aynı ve v dir. Böyle bir kenara ilmik

adı verilir.

Aynı uç noktalar kümesine sahip olan kenarlar ise katlı kenarlar olarak adlandırılır. Bir

{ , }i j

e v v kenarında v ile i vj köĢeleri için komşudur denir.

Bir kenar yukarıda görüldüğü gibi, kullanılıĢındaki sadelik bakımından ( 1, 2,..., )

i

e i m ile gösterilebilir.

Örnek 2.1.1. KöĢe kümesi V 





e vv, e₄ vw, e₅ wz, e₆ wz olmak üzere E{ ,e e e e e e_{1 2}, ,_{3 4}, , }_{5 6} olarak tanımlanan bir G( , )V E grafının somut gösterimi ġekil 2.1.1. deki gibidir.

ġekil 2.1.1.

ġekil 2.1.1. de dikkat edilirse, bir küme içerisine aynı isimli bir eleman birden fazla yazılamayacağından, grafın kenarları yeniden adlandırılmıĢtır.

Katlı kenarlar bulunduran graflar soyut olarak gösterilirken, böyle bir karıĢıklığa meydan vermemek için grafın kenarlarını yeniden adlandırmak bu nedenle akıllıcadır.

Bir graf, ilmik ya da katlı kenarlar bulundurup bulundurmamasına göre isim alır.

Tanım 2.1.2. Katlı kenarlar ya da ilmik bulunduran graflara pseudo-graf; yalnız katlı kenarlar bulunduran graflara çoğul-graf; katlı kenarlar ve ilmik bulundurmayan graflara ise basit graf adı verilir.

ġekil 2.1.2. de sırasıyla pseudo-graf, çoğul-graf ve basit grafa birer örnek verilmiĢtir.

ġekil 2.1.2. Sırasıyla pseudo-graf, çoğul-graf ve basit graf

Bu çalıĢma basit graflar üzerine olduğundan, bundan böyle “basit graf’ yerine “graf’ ifadesi kullanılacaktır.

Tanım 2.1.3. G bir graf, v V G ( )olsun. v köĢesi ile çakıĢık olan kenarların sayısına

v köşesinin derecesi denir ve der v( ) gösterilir.

Her bir ayrıt komĢu olduğu köĢeye tam olarak 1 derece kazandırırken, bir ilmik ise komĢu olduğu köĢeye 2 derece birden kazandırır. 0 dereceli bir köĢe izole köşe olarak adlandırılır. Derecesi 1 olan köĢeye ise pendant köşe adı verilir. Bir G grafının

en az dereceli köĢesine minimum dereceli denir ve ( )G ile gösterilir. En çok dereceli köĢesine ise maksimum dereceli denir ve ( )G ile gösterilir. Herhangi bir grafın derecelerinin küçükten büyüğe doğru yazılarak oluĢturulan diziye derece dizisi denir. ġekil 2.1.3. de köĢeleri dereceleriyle adlandırılmıĢ G grafında ( ) 1G  ,

( )G 5

  ve derece dizisi (1,1,1, 2, 2,3,3, 4,5) dir.

ġekil 2.1.3. KöĢeleri, dereceleriyle adlandırılmıĢ bir graf

2.2. Graflarda Uzaklık

Tanım 2.2.1. u ve v , bir G grafının herhangi iki köĢesi olsunlar. G nin u köĢesi

ile baĢlayıp v köĢesi ile biten, (uv e v e1, ,1 2, 2,...,e vk, k v) sonlu dizisine bir u-v

yürümesi denir.

Burada i1, 2,...,k olmak üzere e_i v v_{i1 i} dir. u ve v köĢelerine yürümenin

uç köĢeleri adı verilir. Uç köĢeleri u ve v olan bir yürüme Du v, ile gösterilir.

Yürümedeki kenarların sayısı olan k, yürümenin uzunluğu olarak tanımlanır. Herhangi bir D_{u v,} yürümenin uzunluğu D_{u v,} ile gösterilir. BaĢlangıç köĢesi u bitiĢ köĢesi v olan bir yürümenin en kısa uzunluğu d u v( , ) ile gösterilir. Hiç kenar içermeyen, uzunluğu 0 olan bir yürümeye aşikâr yürüme denir.

Bir yürümenin kenarları, köĢelerden kolayca anlaĢılacağı için yürümede sadece köĢeler de gösterilebilir. Au u u0 1 2...uk ve Bv v v0 1 2...vl iki A ve B yürümesi olsunlar. Bu yürümenin eĢit olması için gerekli ve yeterli koĢul, 0 i k, 0 i l için

kl ve u_i v_i, olmasıdır. Aksi halde bu yürümeler farklıdır.

u v yürümesinde eğer uv ise yürüme kapalı, uv ise yürüme açık olarak adlandırılır.

2.3. Yol ve Devir

Tanım 2.3.1. Bir yürümede hiç kenar tekrar etmiyorsa bu yürümeye gezi adı verilir. Hiçbir köĢenin tekrar etmediği bir yürümeye ise yol denir. Herhangi bir G grafın tüm köĢeleri için birbirinden farklı iki köĢeyi bağlayan bir yol bulunabiliyorsa bu G grafına

bağlantılı graf denir. Hiç kenar tekrar etmeyen bir yürümede bazı köĢeler tekrar ediyor olabilir. Tersine; köĢelerin tekrar etmediği bir yürümede hiç kenar tekrar etmeyebilir. Her yol bir gezidir. Ama her gezi bir yol değildir.

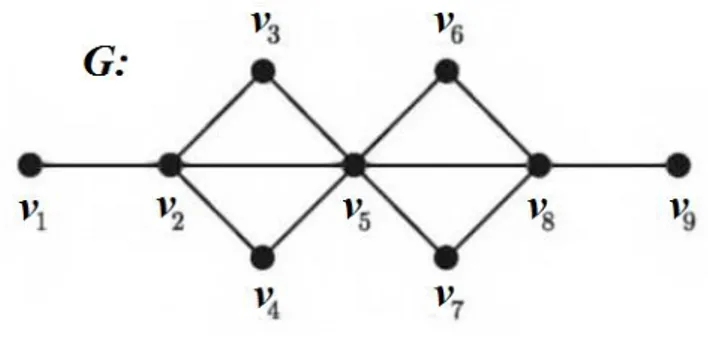
ġekil 2.3.1.

ġekil 2.3.1. deki G grafında ( ,v v v v v v v bir 1 2, ,3 2, , ,5 3 4) v1v4 yürümesi olup bu

yürüme bir gezi değildir. ( ,v v v v v v_{1 2}, , ,_{5 3 2}, ₄) bir v₁v₄ gezisi olup bu gezi bir yol değildir. ( , ,v v v bir _{1 3 4}) v₁v₄ yoludur.

Tanımdan dolayı her yol bir yürümedir. Bu ifadenin tersi doğru değildir.

Tanım 2.3.2. Bir G grafının aĢikâr olmayan bir kapalı gezisi, G nin bir çevresi olarak adlandırılır. n tane farklı v köĢesinden oluĢan i ( ,v v v1 2, ,...,3 v n) n3 çevresi de devir adını alır. n uzunluğunda bir çevrim n devir adını alır. Bir 3-devir, üçgen olarak da

adlandırılır.

Yol ve devir olan n mertebeli bir graf sırasıyla P ve _n C ile gösterilir. ġekil 2.3.2. _n

de ve ġekil 2.3.3. de 4 ya da 4 ten az mertebeli yol ve devir grafları gösterilmiĢtir.

P ₁ P ₂ P ₃ P ₄

ġekil 2.3.3. Mertebesi 4 ya da 4 ten az olan devir graflar

2.4. Bazı Özel Graflar

Tanım 2.4.1. Bir G grafı verilsin. G nin her bir köĢesi r dereceli ise yani G grafı için der v( )_i r i, ( 1, 2,... )n ise, G grafına r-regüler adı verilir.

3-regüler graflar, kübik graf olarak adlandırılırlar. ġekil 2.4.1. de, bütün 4 mertebeli regüler graflar gösterilmiĢtir. G grafı, kübik graftır. Diğer yandan en iyi ₄

bilinen kübik graf muhtemelen ġekil 2.5.2. de gösterilmiĢ olan Petersen grafıdır.

ġekil 2.4.1. 4 mertebeli regüler graflar

ġekil 2.4.2. Petersen Grafı

Tanım 2.4.2. KarĢılıklı olarak tüm köĢeleri birbirine komĢu olan grafa tam graf denir,

n mertebeli bir tam graf, K ile gösterilir. Bir tam graf, köĢe kümesi üzerinde _n

tam graf için ( 1) / 2 2

n

m _{ }n n

  eĢitliği geçerlidir. Bir tam grafın her bir köĢesi n1

dereceli olup bu yüzden regüler bir graftır.

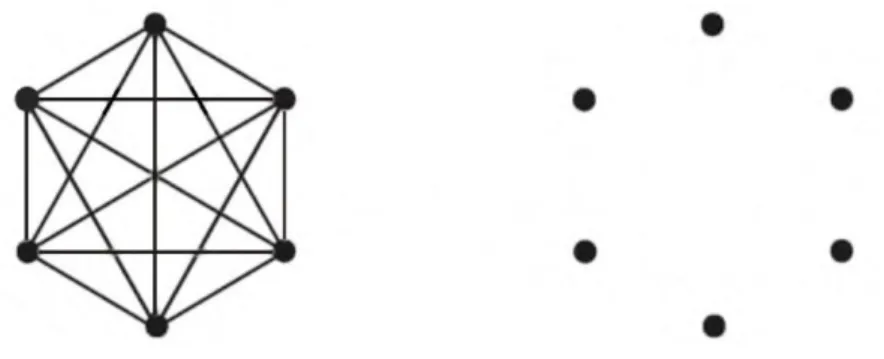
Hiç kenar bulundurmayan graf da boş graf olarak adlandırılır, n mertebeli bir boĢ graf E ile gösterilir. ġekil 2.4.3. de sırasıyla _n K ve ₆ E grafları ₆

gösterilmiĢtir.

ġekil 2.4.3. Sırasıyla 6 mertebeli tam graf ve boĢ graf

Tanım 2.4.3. Bir G grafı verilsin. G ile aynı köĢe kümesine sahip H grafının herhangi iki u ve v köĢenin komĢu olması ancak ve ancak G grafında u ve v köĢesinin komĢu

olmamasına bağlı ise bu H grafı G grafının tamamlayıcısı olarak adlandırılır ve G ile gösterilir.

n köĢeye sahip bir G grafı ile G tamamlayıcısının birleĢmesiyle K tam grafı n oluĢur. K tam grafının tamamlayıcısı _n E boĢ grafıdır. _n

Tanım 2.4.4. Bir G grafı verilsin. Eğer G nin köĢelerini k1 tane, maksimum mertebeli bağımsız ve ayrık kümeye ayırmak mümkünse G ye k-parçalı graf denir, k 2 ise özel olarak G ye iki-parçalı graf adı verilir.

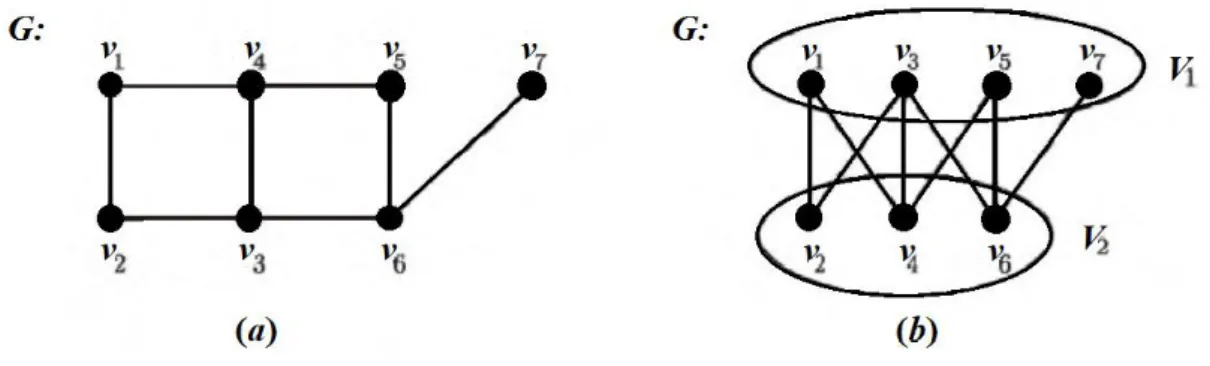
KöĢe kümeleri V ve ₁ V olan iki-parçalı graflar, ₂ V₁r ve V₂ solmak üzere Kr s, ile sembolize edilirler. ġekil 2.4.4. (a) da iki-parçalı bir graf verilmiĢ ve

iki-parçalı oluĢunun kolayca görülebilmesi için ġekil 2.4.4. (b) de yeniden düzenlenmiĢtir. Verilen grafın köĢe kümeleri V1 { , , , }v v v v1 3 5 7 ve V2 { ,v v v2 4, }6

ġekil 2.4.4. Ġki-parçalı bir graf

2.5. Alt Graf ve ĠndirgenmiĢ Alt Graf

Tanım 2.5.1. G ve H iki graf olsun. G grafının köĢe kümesi V G( ), kenar kümesi ( )

E G ; H grafının köĢe kümesi V H( ), kenar kümesi E H( )olmak üzere; eğer

( ) ( )

V G V H ve E G( )E H( ) oluyorsa H grafına G grafının alt grafı denir ve

H G ile gösterilir. ġekil 2.5.1. (b) de verilen graf, (a) grafının alt grafıdır.

Tanım 2.5.2. G ve H iki graf ve G grafının köĢe kümesi V G( ), kenar kümesi E G( );

H grafının köĢe kümesi V H( ), kenar kümesi E H( )olmak üzere V H( )V G( ) ve

( ) ( )

E H E G olsun. Eğer H grafı “H grafındaki her bir u v, köĢe çiftlerinin H

grafında uv kenarını oluĢturabilmesi için gerek ve yeter Ģart uv kenarının G grafında bir kenar olmasıdır.” Ģartını sağlarsa H grafına G grafının indirgenmiş alt grafı denir. Diğer bir deyiĢle H grafındaki köĢelere çakıĢık olan her bir kenar G grafında da aynı köĢelere çakıĢık ise H grafı G grafının indirgenmiĢ alt grafı olur. ġekil 2.5.1. (c) de verilen graf, (a) grafının indirgenmiĢ alt grafıdır.

3. GRAF PARAMETRELERĠ

Bu bölümde Graf Teori de kullanılan bazı temel parametreler verilmiĢtir. Daha detaylı bilgi almak için [1], [2], [9] ve [27] referanslarına bakılabilir.

3.1. Bağımsızlık Sayısı

Tanım 3.1.1. Bir G grafı verilsin. G nin karĢılıklı olarak birbirine komĢu olmayan köĢelerinin kümesine bağımsız küme denir.

Bir G grafının bağımsız kümelerindeki maksimum eleman sayısı, grafın

bağımsızlık sayısı olarak adlandırılır ve bu değer ( )G ile gösterilir. ( )G max{V V bağımsız küme_i : _i }

 

Örnek 3.1.1. ġekil 3.1.1. deki G grafında V₁ { }v₁ , V₂ { , }v v_{1 3} , V₃ { , }v v_{2 8} ,

4 { ,2 7, }9

V  v v v , V₅ { , ,v v v v v v_{1 3 4}, ₆, ₇, }₉ G grafının bağımsız kümelerinden bazılarıdır.

5

V , kümesi G nin bağımsız kümelerinin en geniĢidir. O halde ( )G 6 dır.

ġekil 3.1.1.G grafı için α(G)=6 dır 3.2. Klik Sayısı

Tanım 3.2.1. Bir G grafı verilsin. G nin karĢılıklı olarak birbirine komĢu olan köĢelerinin kümesine klik kümesi denir.

Bir G grafının klik kümelerindeki maksimum eleman sayısı, grafın klik sayısı olarak adlandırılır ve bu değer w G( ) ile gösterilir.

( ) max{ _i : _i }

Örnek 3.2.1. ġekil 3.2.1. deki G grafında V₁ { ,v v v_{1 6}, }₇ , V₂ { , }v v_{2 7} ,

3 { , , , }2 3 5 6

V  v v v v , V₄ { , ,v v v v v_{2 3 4}, , }_{5 6} G grafının klik kümelerinden bazılarıdır. V ₄

kümesi G nin klik kümelerinin en geniĢidir. O halde w G( )5 dir.

ġekil 3.2.1.G grafı için w(G)=5 dir 3.3. Kromatik Sayısı

Tanım 3.3.1. Bir G grafı verilsin. G grafının birbirine komĢu olan köĢelerini farklı renkte boyamak için gerekli olan en az renk sayısı kromatik sayı olarak adlandırılır ve

( )G

 ile gösterilir.

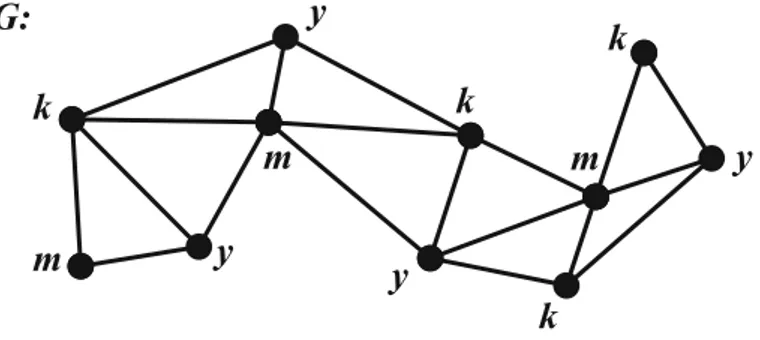
Örnek 3.3.1. ġekil 3.3.1. deki G grafının komĢu köĢelerini farklı renge boyamak için gerekli olan en az renk; kırmızı (k), mavi (m), yeĢil (y) olduğundan ( )G 3 dür.

3.4. Klik Örtü Sayısı

Tanım 3.4.1. Bir G grafı verilsin. V G( ) köĢe kümesini maksimum klik kümeleri ile parçalanmasına G grafının klik örtüsü denir. Bu parçalanmanın minimum sayısı ise

klik örtü sayısı olarak adlandırılır ve ( ) G ile gösterilir. Klik örtü sayısı için 

 

 

Örnek 3.4.1. ġekil 3.4.1. deki G grafında V₁{ , , }v v v_{2 3 4} , V2 { , ,v v v6 9 10}, 3 { ,1 5, 6, 10, 11}

V  v v v v v , V₄ { , ,v v v v_{2 3 4}, }₅ , V₅ { , }v v_{4 7} , V₆ { ,v v v v_{6 7}, , }_{8 9} , 7 { , , }7 8 9

V  v v v G grafının klik kümelerinden bazılarıdır. V₂, V₃, V₇ klik kümeleri ile ( )

V G köĢe kümesini minimum sayıda parçalayabileceğimizden ( )G 3 olarak bulunur.

ġekil 3.4.1.G grafı için θ(G)=3 dür 3.5. Eccentricity, Diameter ve Radius

Tanım 3.5.1. Bir G grafı verilsin. G grafındaki herhangi bir u V G ( ) köĢesinin diğer köĢelere olan en kısa mesafelerinin en büyük değeri; u köĢesinin eccentricity si olarak adlandırılır ve ( )u ile gösterilir.

Tanım 3.5.2. Bir G grafı verilsin. G grafındaki eccentricity lerin maksimum değeri G

grafının diameter ı olarak adlandırılır ve dia G( ) ile gösterilir.

Tanım 3.5.3. Bir G grafı verilsin. G grafındaki eccentricity lerin minimum değeri G

Örnek 3.5.1. ġekil 3.5.1. de G ve H grafının köĢeleri eccentricity değerleri ile adlandırılmıĢtır. G grafı için maksimum eccentricity değeri dört olduğundan

( ) 4

dia G  , minimum eccentricity değeri iki olduğundan rad G( )2 dir. Aynı Ģekilde

H grafı için maksimum eccentricity değeri üç olduğundan dia H( )3, minimum eccentricity değeri iki olduğundan rad H( )2 dir.

ġekil 3.5.1.

3.6. Wiener Ġndeks

Tanım 3.6.1. Bir G grafı ve u v V G,  ( ) verilsin.

, ( ) ( , ) u v V G d u v 



Wiener indeks i olarak adlandırılır ve W G( ) ile gösterilir.

Örnek 3.6.1. ġekil 3.6.1. deki G grafında d x y( , ) 1 , d x t( , ) 1 , d x z( , )2,

( , ) 1

d y z  , d y t( , )2, d z t( , ) 1 olduğuna göre

, ( )

( , ) ( , ) ( , ) ( , ) ( , ) ( , ) ( , )

1 1 2 1 2 1 8 olur. Buradan da ( ) 8 olarak bulunur.

u v V G d u v d x y d x t d x z d y z d y t d z t W G               



3.7. Randic Ġndeks

Tanım 3.7.1. Bir G grafı ve u v V G,  ( ) verilsin. u ile v köĢeleri komĢu olmak

koĢuluyla

, ( )

1 ( ) ( ) u v V G



toplamı G grafının Randic indeks i olarak adlandırılır ve R G( ) ile gösterilir.

Örnek 3.7.1. ġekil 3.7.1. deki G grafında der v( )₁ 2, der v( )₂ 2, der v( )₃ 3,

4

( ) 1

der v  , olduğuna göre

, ( ) _{1 2 1 3 2 3} 3 4 1 1 1 1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 1 1 1 1 olur ( ) ( ) 4 6 6 3 .

u v V G der u der v der v der v der v der v der v der v

der v der v         



ġekil 3.7.1.G grafı için ( ) 3 2 6 2 3 6

R G    dır

3.8. Düzensizlik ve EĢitlik Ġndeksi

Tanım 3.8.1. Bir G grafı verilsin. G grafının birbirinden farklı dereceye sahip köĢe sayısı düzensizlik indeksi olarak adlandırılır ve t G( ) ile gösterilir.

AĢağıdaki eĢitlik indeksi tanımı bizim tarafımızdan tanımlamıĢtır.

Tanım 3.8.2. Bir G grafı verilsin. G grafının aynı dereceye sahip maksimum köĢe sayısı eşitlik indeksi olarak adlandırılır ve e G( ) ile gösterilir.

Herhangi bir G grafının V G( ) köĢe kümesini





  olacak Ģekilde parçalayabiliriz. Bu parçalama sayesinde t G( )k ve

( ) max _i

e G  A olduğu kolaylıkla görülür.

Örnek 3.8.1. ġekil 3.8.1. deki G grafında der v( )₁ 3, der v( )₂ 4, der v( )₃ 3,

4

( ) 2

der v  , der v( )₅ 3, der v( )₆ 4, der v( )₇ 3 olduğuna göre G grafının ( )V G

köĢe kümesini; dereceleri eĢit olan köĢelere sahip A₁{ }v₄ A2 { , , }v v v1 3 5 A3 { , }v v2 6

kümeleriyle parçalayabiliriz. Buradan da t G( )3 ve ( )e G 3 olarak bulunur.

ġekil 3.8.1.G grafı için t(G)=3 ve e(G)=3 dür 3.9. Mükemmel Graf

Tanım 3.9.1. Bir G grafı verilsin. G grafının bütün indirgenmiĢ H alt grafları için

( )G w H( )

  eĢitliği sağlanıyorsa G grafı w-mükemmel graf olarak adlandırılır.

Tanım 3.9.2. Bir G grafı verilsin. G grafının bütün indirgenmiĢ H alt grafları için

( )G (H)

  eĢitliği sağlanıyorsa G grafı -mükemmel graf olarak adlandırılır.

Tanım 3.9.3. Bir G grafı verilsin. G grafı hem “w-mükemmel” hem de “ -mükem- mel” oluyorsa G grafına mükemmel graf denir.

4. GRAF ÇARPIMLARI

Bu bölümde Graf Teori de kullanılan temel graf çarpımları verilmiĢ ve üzerinde bazı graf parametreleri incelenmiĢtir. Daha detaylı bilgi almak için [10], [11] , [17] , [18] ve [22] referanslarına bakılabilir.

4.1. Kartezyen Çarpım

Tanım 4.1.1. G grafının köĢe kümesi V G( ), H grafının köĢe kümesi V H( ) olmak üzere V G( )V H( ) kartezyen kümesinden a( , )u v_{1 1} ile b( ,u v_{2 2}) elemanlarını alalım. Eğer

i) u1u2 ve v v1 2E H( ) veya ii) v1v2 ve u u1 2E G( )

durumlarından biri gerçekleĢiyorsa a( , )u v_{1 1} ile b( ,u v_{2 2}) köĢeleri komĢudur. Bu Ģekilde oluĢan grafa G ile H grafının kartezyen çarpım grafı denir ve G H ile gösterilir. ġekil 4.1.1. de basit iki grafın kartezyen çarpımı verilmiĢtir.

ġekil 4.1.1.Kartezyen çarpım grafı

Teorem 4.1.1. ([19]) G ve H iki graf olmak üzere





   (4.1)

eĢitsizliği geçerlidir.

Teorem 4.1.2. ([5]) G ve H iki graf olmak üzere









w G H  w G w H (4.2)

eĢitsizliği geçerlidir.

Ġspat. Kartezyen çarpım grafı değiĢmeli olduğundan genelliği bozmaksızın





max w G w H( ), ( ) w G( ) alalım. G grafının maksimum elemana sahip klik kümesi

1 2 ( )

{ , ,..., }

G w G

C  u u u ve v V H ( ) için K 





( )

KV G H olsun. 1  i j w G( ) ve i j için u u_{i j}V G H( ) olacağından K kümesi G H çarpım grafının maksimum klik kümesidir.

O halde w G H









Teorem 4.1.3. ([5]) G ve H iki graf ve wmax max{ ( ), ( )}w G w H olmak üzere











Ġspat. [5] de; Teorem 14. den ispatı yapılmıĢtır.

4.2. Strong Çarpım

Tanım 4.2.1. G grafının köĢe kümesi V G( ), H grafının köĢe kümesi V H( ) olmak üzere V G( )V H( ) kartezyen kümesinden a( , )u v_{1 1} ile b( ,u v_{2 2}) elemanlarını alalım.

Eğer

i) u₁u ve v v_{2 1 2}E H( ) veya ii) v₁ v ve u u_{2 1 2}E G( ) veya

iii)u u_{1 2}E G ve v v( ) _{1 2}E H( )

durumlarından biri gerçekleĢiyorsa a( , )u v1 1 ile b( ,u v2 2) köĢeleri komĢudur.

Bu Ģekilde oluĢan grafa G ile H grafının strong çarpım grafı denir ve G H ile gösterilir.

ġekil 4.2.1.Strong çarpım grafı Teorem 4.2.1. ([19]) G ve H iki graf olmak üzere





   (4.4)

eĢitsizliği sağlanır.

Ġspat. [19] da; Lemma 2.7 ve Tablo 1 den ispatı yapılmıĢtır.

Teorem 4.2.2. ([5]) G ve H iki graf olmak üzere





w G H w G w H (4.5)

eĢitliği sağlanır.

Ġspat. Ġlk önce w G





G grafının maksimum elemana sahip klik kümesi CG { ,u u1 2,...,uw G( )} ve H

grafının maksimum elemana sahip klik kümesi CH { ,v v1 2,...,vw H( )} olsun.

1  p r w G( ), 1  q s w H( ) için a(u v_p, _q)C_GC_H, b( ,u v_{r s})C_GC_H

köĢeleri Tanım 4.2.1. e göre i) u_p u_r ise v v_{q s}E H( ), ii) v_q v_s ise u u_{q r}E G( ),

iii)u u_{p r}E G ve v v( ) _{q s}E H( ) durumlarından birini gerçekleĢtirdiğinden a(u v_p, _q)

ve b( ,u vr s) köĢeleri komĢudur. Yani CGCH kümesi G H çarpım grafının maksimum klik kümesidir. Böylece w G





Tersine w G





G H çarpım grafının maksimum klik kümesini nV G( ) , m V H( ) olacak Ģekilde





C u v u v u v u v u v u v u v olarak alalım.

1  p r n için u u_{p r}E G( ) olduğundan mw G( ) ve 1 q  s m için

( )

q s

v v E H olduğundan mw G( ) olacaktır. Böylece nmw G w H( ) ( ) bulunur. Buradan da w G





O halde “w G















Ġspat. [5] de; Teorem 14. den ispatı yapılmıĢtır.

4.3. Lexicografik Çarpım

Tanım 4.3.1. G grafının köĢe kümesi V G( ), H grafının köĢe kümesi V H( ) olmak üzere V G( )V H( ) kartezyen kümesinden a( , )u v_{1 1} ile b( ,u v_{2 2}) elemanlarını alalım.

Eğer

i) u u_{1 2}E G( ) veya ii) u1 u ve v v2 1 2E H( )

durumlarından biri gerçekleĢiyorsa a( , )u v_{1 1} ile b( ,u v_{2 2}) köĢeleri komĢudur. Bu Ģekilde oluĢan grafa G ile H grafının lexicografik çarpım grafı denir ve G H ile gösterilir.

ġekil 4.3.1. Lexicografik çarpım grafı

Teorem 4.3.1. ([19]) G ve H iki graf olmak üzere





    (4.7)

eĢitliği geçerlidir.

Ġspat. [19] de; Lemma 2.7 ve Tablo 1 den ispatı yapılmıĢtır.

Teorem 4.3.2. ([5]) G ve H iki graf olmak üzere





w G H w G w H (4.8)

eĢitliği geçerlidir.

Ġspat. Ġlk önce w G H





G grafının maksimum elemana sahip klik kümesi C_G { ,u u_{1 2},...,u_{w G( )}} ve H

grafının maksimum elemana sahip klik kümesi CH { ,v v1 2,...,vw H( )} olsun

1  p r w G( ), 1  q s w H( ) için a(u v_p, _q)C_GC_H, b( ,u v_{r s})C_GC_H

köĢeleri Tanım 4.2.1. e göre i) g g_{p r}E G ( ) veya ii) g_p g ve h h_{r q s}E H( )

durumlarından birini gerçekleĢtirdiğinden a(u v_p, _q) ve b( , )u v_{r s} köĢeleri

komĢudur. Yani CGCH kümesi G H çarpım grafının maksimum klik kümesidir. Böylece w G H





Tersine w G H





G H çarpım grafının maksimum klik kümesini nV G( ) , mV H( ) olacak Ģekilde





C u v u v u v u v u v u v u v olarak alalım.

1  p r n için u u_{p r}E G( ) olduğundan nw G( ) ve 1 q  s m için

( )

q s

h h E H olduğundan mw G( ) olacaktır. Böylece mnw G w H( ) ( ) bulunur. Buradan da w G H





O halde “w G H















Ġspat. [5] de; Teorem 14. den ispatı yapılmıĢtır.

Bu Ģekilde çarpım grafları üzerinde parametre incelemelerine benzer olarak daha detaylı bilgi almak için [6], [8], [12], [14], [15], [20], [23] ,[24], [28] referanslarına bakılabilir.

5. GRAFLARIN YENĠ ÇARPIMI

4. bölümde graf çarpımlarının en önemli üç tanesi gösterilmiĢtir ve üzerlerinde graf parametrelerinden birkaçı değerlendirilmiĢtir. Bu bölümde bu graf çarpımlarından esinlenerek yeni bir graf çarpımı “derece çarpım” oluĢturulmuĢ ve özellikleri incelenmiĢtir.

5.1. Grafların Derece Çarpımı

Tanım 5.1.1. G grafının köĢe kümesi V G( ), H grafının köĢe kümesi V H( ) ve

1, 2 ( )

u u V G , v v₁, ₂V H( ) olmak üzere V G( )V H( ) kartezyen kümesinden

1 1

( , )

a u v ile b( ,u v2 2) elemanlarını alalım.

Eğer,

i)u₁u ₂  der v( )₁ der v( )₂ veya

ii)v₁ v ₂  der u( )₁ der u( )₂ veya

iii)v₁v₂, u₁ u₂ 





Bu Ģekilde oluĢan grafa G ile H grafının derece çarpım grafı denir ve G H ile gösterilir.

5. ve 6. bölümün tamamında

G grafının köĢe kümesini A_i 





1 k i i A   , _{1 2} 1 ( ) ... k i k i V G A A A A      

H grafının köĢe kümesini B_j  





1 , l j j B    _{1 2} 1 ( ) ... l j l j V H B B B B      

olacak Ģekilde parçalanmıĢtır.

ġekil 5.1.1. P3 yol grafı ile P3 yol grafının derece çarpımı

Önerme 5.1.1. G ve H iki graf ve V G( ) 2, V H( ) 2 olmak üzere G H çarpım grafında pendant köĢe bulunmaz.

Ġspat. Durum 1. Farzedelim ki 1 r k, 1 s l için Ar 1 ve Bs 1 olsun.

1 { }

r r

A  A  u ve B_s  1 B_s { }v alalım. O zaman A_rB_s V G( )V H( ) kümesi sadece tek bir a( , )u v köĢesinden oluĢur. Ayrıca 1 i V G( ) , 1 j V H( )

için b( ,u v_{i j}) köĢesini alalım. der u( )der u( )_i , der v( )der v( )_j olduğu açıktır.

( , )

a u v köĢesiyle b( ,u v_{i j}) köĢeleri Tanım 5.1.1. e göre

i) uu _i  der v( )der v( )_j

ii) vv _j  der u( )der u( )_i

iii) uui , vuj  der u( )der u( ) veya i der v( )der v( )j 

durumlarından birini gerçekleĢtirdiğinden a( , )u v köĢesi G H çarpım grafında hiçbir köĢe ile komĢu değildir. O halde der a( rs)0 olur.

Durum 2. Farzedelim ki 1 r k, 1 s l için A_r 1 ve B_s 2 olsun. { }

r

A  u , B_s { ,v v_{1 2},..., }v_q alalım. O zaman A_rB_s V G( )V H( ) kümesi için 2

r s

A B  olacaktır. a( ,u v_q) A_r B_s köĢelerini ve 1 i V G( ) , 1 j V H( ) için b( ,u v_{i j})V G( )V H( ) köĢelerini alalım.

O halde der u( )der u( )_i , der v( )_q der v( )_j veya der v( )_q der v( )_j olacaktır.

( , _q)

a u v köĢeleriyle b( ,u v_{i j}) köĢeleri Tanım 5.1.1. e göre

i) uu_i  ,v v_{q j}B_s iken der v( )_q der v( ) veya _j der v( )_q der v( )_j

ii) vq v j  der u( )der u( )i

iii) , ( ) ( ) veya , iken ( ) ( ) veya ( ) ( ) i i q j q j s q j q j der u der u u u v v

v v B der v der v der v der v



 

  _{  }

  

 

durumlarından birini gerçekleĢtirdiğinden a( ,u v_q) köĢeleri G H çarpım grafında ya hiçbir köĢe ile komĢu değildir ya da b( ,u v_{i j}) köĢelerinin en az iki tanesiyle komĢudur. O halde der a( rs)0 veya der a( rs)2 olur.

Durum 3. Farzedelim ki 1 r k, 1 s l için Ar 2 ve Bs 2 olsun.

1 2

{ , ,..., }

r p

A  u u u , B_s { ,v v_{1 2},..., }v_q alalım. a(u v_p, _q) A_r B_s köĢelerini ve 1 i V G( ) , 1 j V H( ) için b( ,u v_{i j})V G( )V H( ) köĢelerini alalım.

O halde der u( p)der u( )i veya der u( p)der u( )i ; der v( )q der v( )j veya

( )_q ( )_j

der v der v olacaktır.

( _p, _q)

a u v köĢeleriyle b( ,u v_{i j}) köĢeleri Tanım 5.1.1. e göre

i) u_p u_i  ,v v_{q j}B_s iken der v( )_q der v( ) veya _j der v( )_q der v( )_j

ii) v_q v_j  u v_p, _qA_r iken der u( _p)der u( ) veya _i der u( _p)der u( )_i

iii) , iken ( ) ( ) veya ( ) ( ) veya , , iken ( ) ( ) veya ( ) ( ) p q r p i p i p i q j q j s q j q j

u v A der u der u der u der u

u u v v

v v B der v der v der v der v

         _{  }       

durumlarından birini gerçekleĢtirdiğinden a(u v_p, _q) köĢeleri G H çarpım grafında ya hiçbir köĢe ile komĢu değildir ya da b( ,u v_{i j}) köĢelerinin en az iki tanesiyle komĢudur. O halde der a( _rs)0 veya der a( _rs)2 olur.

Buradan görüldüğü üzere G H çarpım grafında pendant köĢe bulunmaz.

Teorem 5.1.1. G ve H iki graf olmak üzere G H çarpım grafının bağlantılı olması

Ġspat. Farzedelim ki A_r 1 ve B_s 1 olsun. ( 1 r k, 1 s l)

1 { }

r r

A  A  u ve B_s  1 B_s { }v alalım. O zaman A_rB_s V G( )V H( ) kümesi sadece tek bir a( , )u v köĢesinden oluĢur. Ayrıca 1 i V G( ) , 1 j V H( ) için a_ij ( ,g h_{i j}) köĢesini alalım. der u( )der u( )_i , der v( )der v( )_j olduğu açıktır.

( , )

a u v köĢesiyle a_ij ( ,g h_{i j}) köĢeleri Tanım 5.1.1. e göre

i) uu _i  der v( )der v( )_j

ii) vv j  der u( )der u( )i

iii) uu_i , vu_j  _der u( )der u( ) veya _i der v( )der v( )_j _

durumlarından birini gerçekleĢtirdiğinden a( , )u v köĢesi G H çarpım grafında hiçbir köĢe ile komĢu değildir. Böylece G H çarpım grafı bağlantısız olur.

O halde A_i 2 veya B_j 2 ise G H çarpım grafı bağlantılıdır.

Tersine farzedelim ki G H çarpım grafı bağlantısız olsun.

Önerme 2. den a( , )u v V G H(  ) için der a( )0 dır. a( , )u v  A_r B_s ve

( ,i j) i j

b g h  A B olmak üzere a( , )u v köĢesi b( ,g hi j) köĢeleriyle komĢu

olmadığından der u( )der u( )_i ve der v( )der v( )_j olur. Böylece Ar { }u  Ar 1 ve B_s { }v  B_s 1 bulunur.

O halde G H çarpım grafı bağlantılı ise Ai 2 veya Bj 2 dir.

Önerme 5.1.2. G ve H iki graf ve V G( ) n, V H( ) m olmak üzere G H çarpım

grafı içindeki A_rB_s kümesinden oluĢturulan indirgenmiĢ alt graflar tam graftır.

Ġspat. Ar { ,u u_{1 2},...,ug},Bs { ,v v1 2,..., }vh (1 r k , 1 s l) olsun.

1 2

( ) ( ) ... ( )_n

der u der u  der u ve der v( )₁ der v( )₂  ... der v( _m) olduğu açıktır. 1  p i g, 1 q  j h için a(u vp, q) köĢeleriyle b( ,u vi j) köĢeleri Tanım 5.1.1. e göre

i) u_p u _i  der v( )_q der v( )_j

ii) v_q v _j  der u( _p)der u( )_i

iii) u_p u_i , v_q u_j  _der u( _p)der u( ) veya _i der v( )_q der v( )_j _

durumlarından birini gerçekleĢtirdiğinden bütün a(u v_p, _q) köĢeleri tüm

( ,i j)

b u v köĢeleri ile komĢudur. Yani G H çarpım grafı içindeki A_rB_s kümesindeki her bir köĢe birbiriyle komĢudur.

O halde G H çarpım grafı içindeki A_rB_s kümesinden oluĢturulacak indirgenmiĢ alt graflar “ gh ” köĢeye sahip tam graftır.

Teorem 5.1.2. G ve H iki graf olmak üzere G H graf çarpımının tam graf olabilmesi

için gerek ve yeter Ģart G ve H graflarının regüler graf olmasıdır.

Ġspat. Farzedelim ki G ve H grafları regüler iki graf olsun.

1 2 1 2

( ) { , ,..., n}, ( ) , ( ) ( ) ... ( n)

V G  u u u V G n der u der u  der u ,

1 2 1 2

( ) { , ,..., _m}, ( ) , ( ) ( ) ... ( _m)

V H  v v v V H m der v der v  der v olmak üzere

1  p i n, 1 q  j m için a(u v_p, _q) ve b( ,u v_{i j}) köĢeleri Tanım 5.1.1. e göre

i) u_p u _i  der v( )_q der v( )_j

ii) vq v j  der u( p)der u( )i

iii) u_p u_i , v_q u_j  _der u( _p)der u( ) veya _i der v( )_q der v( )_j _

köĢeleri komĢudur. Yani G H çarpım grafı içindeki tüm köĢeler birbirleriyle komĢudur.

O zaman G ve H grafları regüler graf ise G H çarpım grafı tam graftır.

Tersine G H çarpım grafı V G( ) n, V H( ) m olacak Ģekilde nm köĢeye

sahip tam graf ve a(u v_p, _q), b( ,u v_{i j})V G H(  ) olsun. 1  p i n, 1 q  j m

için bütün a(u v_p, _q) köĢeleri tüm b( ,u v_{i j}) köĢeleriyle komĢu olduğundan Tanım 5.1.1. e göre der u( )1 der u( )...2 der u( )n , der v( )1 der v( )2  ... der v( m) olacaktır.

O zaman G H çarpım grafı tam graf ise G ve H grafları regüler graflardır.

O halde “G ve H grafları regüler graftır  G H çarpım grafı tam graftır.”

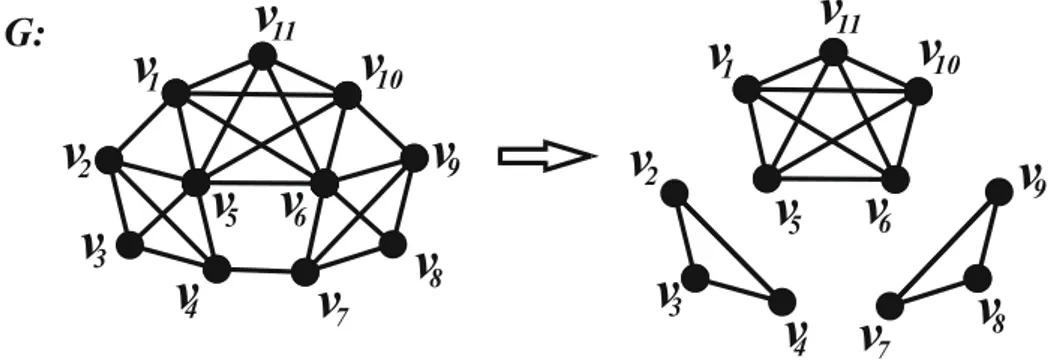
ġekil 5.1.3. de 4-regüler ve 3-regüler iki grafın derece çarpımı K tam grafına izomorf 12

olduğu gösterilmiĢtir.

ġekil 5.1.3. 4-regüler G ile 3-regüler H grafının derece çarpımı.

Önerme 5.1.3. G ve H iki graf olmak üzere G H çarpım grafı içindeki A_iB_j

kümeleri tarafından oluĢturulan indirgenmiĢ tam alt grafdaki köĢelerin dereceleri birbirine eĢittir ve a( , )u v  A_i B_j için der a( ) A_iB_j dir.

Ġspat. V G( ) n, V H( ) m olsun. V G H(  ) kümesini aĢağıdaki gibi ayrı ayrı indirgenmiĢ tam alt grafların köĢe kümelerinin birleĢimi Ģeklinde düĢünebiliriz.

1 1 1 2 1 1 2 1 2 2 2 2 1 2 1 2 ... ... ... ... ( ) ... ... ... ... j l j l i i i j i l k k k j k l A B A B A B A B A B A B A B A B V G H A B A B A B A B A B A B A B A B        _{   }         _{  }                   ( , ) _{i j}

a u v  A B köĢesi Önerme 5.1.2. den A_iB_j kümesindeki bütün köĢelerle komĢudur.

Ayrıca a( , )u v  Ai Bj köĢesi i inci satırdaki

1

i

AB kümesinden









1

i j

AB_ kümesinden









1

i l

AB_ kümesinden









Ayrıca a( , )u v  A_i B_j köĢesi j inci sütundaki

1 j

A B kümesinden









1

i j

A_ B kümesinden









1

k j

A_ B kümesinden









O halde G H çarpım grafı içindeki indirgenmiĢ tam alt graflardaki bütün

köĢelerinin dereceleri birbirine eĢittir ve a( , )u v  A_i B_j için der a( ) A_iB_j

olduğu açıkça görülür.

Sonuç 5.1.1. G ve H iki graf ve V G( ) n, V H( ) m olsun.

G H graf çarpımı içindeki indirgenmiĢ tam alt graflardaki herhangi bir

( , ) _{i j}















































 











O halde der a( ) A m_i (  1) B_j (n 1)





Örnek 5.1.1. ġekil 5.1.4. deki G grafının köĢe kümesini A₁{ , }b c , A₂ { , }a d ; H

grafının köĢe kümesini B1{1, 4}, B2 {2,3} kümeleriyle parçalarsak ( ,1)a  A1 B1

köĢesinin derecesi der a









Önerme 5.1.4. G ve H iki graf x y V G H,  (  ) olmak üzere G H graf çarpımında

( , ) 1

d x y  veya d x y( , )2 dir.

Ġspat. G ve H iki graf olsun. x(u v_p, _q)A_pB_q y( , )u v_{r s}  A_r B_s ve

, ( )

x y V G H  olmak üzere

Farzedelim ki x ile y köĢesi aynı indirgenmiĢ tam alt graf içinde olsun. O halde x ile y köĢesi komĢu olacağından d x y( , ) 1 dir.

Farzedelim ki x ile y köĢesi farklı indirgenmiĢ tam alt grafların içinde ve birbirine komĢu olsun. O halde x ile y köĢesi komĢu olduklarından d x y( , ) 1 dir.

Farzedelim ki x ile y köĢesi farklı indirgenmiĢ tam alt grafların içinde ve birbirine komĢu olmasın. z(u v_p, _j)A_pB_j veya z( ,u v_{i q}) A_i B_s olacak Ģekilde en az bir köĢe bulabiliriz ki xzE G H(  ) ve yzE G H(  ) olacağından d x y( , )2 dir.