Parabolik denklemler için sonlu fark yaklaşımları

T.C.

İNÖNÜ ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ

PARABOLİK DENKLEMLER İÇİN SONLU FARK YAKLAŞIMLARI

Ahmet DEMİRALP

YÜKSEK LİSANS TEZİ MATEMATİK ANABİLİM DALI

MALATYA 2013

Tezin Başlığı: Parabolik Denklemler İçin Sonlu Fark Yaklaşımları Tezi Hazırlayan : Ahmet DEMİRALP

Sınav Tarihi : 02.01.2013

Yukarıda adı geçen tez jürimizce değerlendirilerek Matematik Ana Bilim Dalında Yüksek Lisans Tezi olarak kabul edilmiştir.

Sınav Jürisi Üyeleri

Prof. Dr. Ali ÖZDEŞ(Danışman) ...

Prof. Dr. Alaattin ESEN ...

Doç. Dr. E.Nesligül AKSAN ...

İnönü Üniversitesi Fen Bilimleri Enstitüsü Onayı

Prof. Dr. Mehmet ALPASLAN Enstitü Müdürü

ONUR SÖZÜ

Yüksek Lisans Tezi olarak sunduğum “Parabolik Denklemler İçin Sonlu Fark Yaklaşımları” başlıklı bu çalışmanın bilimsel ahlak ve geleneklere aykırı düşecek bir yardıma başvurmaksızın tarafımdan yazıldığını ve yararlandığım bütün kaynakların, hem metin içinde hem de kaynakçada yöntemine uygun biçimde gösterilenlerden oluştuğunu belirtir, bunu onurumla doğrularım.

Ahmet DEMİRALP

i ÖZET Yüksek Lisans Tezi

PARABOLİK DENKLEMLER İÇİN SONLU FARK YAKLAŞIMLARI

Ahmet DEMĠRALP Ġnönü Üniversitesi Fen Bilimleri Enstitüsü Matematik AnaBilim Dalı

83+xii sayfa 2013

Tez DanıĢmanı : Prof. Dr. Ali ÖZDEġ

Bu Yüksek Lisans tezi beĢ bölümden oluĢmaktadır. Birinci bölümde diğer bölümlerde yapılan çalıĢmalar hakkında kısa bilgi verilmiĢtir.

Ġkinci bölümde sonraki bölümlerde kullanılacak olan temel tanım ve kavramlar verilmiĢtir.

Üçüncü bölümde klasik sonlu fark yöntemlerinden açık, kapalı ve Crank-Nicolson sonlu fark yaklaĢımları çeĢitli sınır Ģartları ile verilen ısı iletim denklemi için incelenmiĢtir.

Dördüncü bölümde çeĢitli sınır Ģartlarındaki ısı iletim denklemi için model problemler ele alınmıĢtır. Nümerik ve analitik çözümler karĢılaĢtırmalı olarak tablolar halinde verilmiĢtir.

BeĢinci bölüm tezin esas kısmını oluĢturmaktadır. Bu bölüm iki kısımdan oluĢmaktadır. Ġlk kısımda 1-boyutlu Burgers’ denklemi için model problemler ele alınarak bu model problemlerin Predictor-Corrector yöntemi için nümerik çözümleri

ii

elde edilmiĢtir ve analitik çözümleriyle karĢılaĢtırmalı olarak tablolar halinde verilmiĢtir. Ġkinci kısımda ise, 2-boyutlu ısı denkleminin verilen model problem için Fractional Step yöntemi ile nümerik çözümleri elde edildi ve analitik çözümleriyle karĢılaĢtırmalı olarak tablolar halinde verildi.

ANAHTAR KELĠMELER : Isı Denklemi, Klasik Sonlu Fark Yöntemleri, Burgers’ Denklemi, Predictor-Corrector(P-C) Yöntemi, Alternating Direction Implicit(ADI) Yöntemi, Fractional Step(FS) Yöntemi.

iii ABSTRACT

MSc. Thesis

FINITE DIFFERENCE APPROXIMATIONS FOR PARABOLIC EQUATION

Ahmet DEMĠRALP Ġnönü University

Graduate School of Natural and Applied Sciences Department of Mathematics

83+xii pages 2013

Supervisor: Prof. Dr. Ali ÖZDEġ

This master thesis consists of five chapters. In the first chapter, brief information has been given about the studies in other sections.

In the second chapter, the fundamental concepts which will be used in the later chapters are presented.

In the third chapter,explicit, implicit and the Crank-Nicolson classical finite difference methods are studied for heat conduction problem with various boundary conditions.

In the fourth chapter, model problems are considered for heat conduction equation with various boundary conditions. The numerical and analytical solutions are presented in tables.

The fifth chapter is the main part of the thesis. This chapter consists of two parts. In the first part, model problems for one-dimensional Burgers’ equation are considered and their numerical solutions are obtained for the Predictor-Corrector method and thenthe numerical solutions of problems are comparatively presented with their

iv

analytical solutions in tables. In the second part, numerical solutions of the two-dimensional heat equation for the given problem with the Fractional Step Method are obtained and are comparatively presented with their analytical solutions in tables.

KEY WORDS: Heat Conduction, The Classical Finite-Difference Methods, Burgers’ Equation, Predictor-Corrector(P-C) Method, Alternating Direction Implicit(ADI) Method, Fractional Step(FS) Method.

v TEŞEKKÜR

Yüksek Lisans çalıĢmamı yöneten ve bu tezin hazırlanması sırasında bana yardımcı olan kıymetli hocam Sayın Prof. Dr. Ali ÖZDEġ’ e, yüksek lisans eğitimim süresince ve tezin hazırlanmasında yardımlarını hiç esirgemeyen Sayın Prof. Dr. Alaattin ESEN’ e, Doç. Dr. Nesligül AKSAN’ a ve Yrd. Doç. Dr. Sibel ÖZER’ e ve program yapımında yardımlarından dolayı Yrd. Doç. Dr. Yusuf UÇAR’ a,AraĢ. Gör. Bilge ĠNAN’ a ve tez ile ilgili düzeltmelerde yardımlarından dolayı Yrd. Doç. Dr. N. Murat YAĞMURLU’ ya ve değerli arkadaĢım ġener YANAN’ a, bana olan desteklerini hiçbir zaman esirgemeyen sevgili aileme teĢekkürü bir borç bilirim.

vi İÇİNDEKİLER ÖZET………i ABSTRACT ………...iii TEŞEKKÜR ………....v İÇİNDEKİLER ………..vi ŞEKİLLER DİZİNİ ...ix TABLOLAR DİZİNİ………..x 1.GİRİŞ ………....1 2. TEMEL KAVRAMLAR………3

3. KLASİK SONLU FARK YÖNTEMLERİ ………...9

3.1. Taylor Seri Açılımı Yardımıyla Sonlu Fark Formülleri………...10

3.2. Açık (Explicit) Sonlu Fark Yöntemi ………...14

3.2.1. Dirichlet Sınır ġartlı Isı Ġletim Problemi………14

3.2.2. Neumann Sınır ġartlı Isı Ġletim Problemi………...15

3.2.3. Robbin Sınır ġartlı Isı Ġletim Problemi………...16

3.3. Kapalı (Ġmplicit) Sonlu Fark Yöntemi ………16

3.3.1. Dirichlet Sınır ġartlı Isı Ġletim Problemi………17

3.3.2. Neumann Sınır ġartlı Isı Ġletim Problemi………...17

3.3.3. Robbin Sınır ġartlı Isı Ġletim Problemi………...18

3.4. Crank-Nicolson Sonlu Fark Yöntemi ………..18

vii

3.4.2. Neumann Sınır ġartlı Isı Ġletim Problemi………..19

3.4.3. Robbin Sınır ġartlı Isı Ġletim Problemi………..20

4. MODEL PROBLEMLER ………...21

4.1. Problem 1 ………21

4.1.1. Problem 1 Ġçin Açık Sonlu Fark YaklaĢımı………..21

4.1.2. Problem 1 Ġçin Kapalı Sonlu Fark YaklaĢımı………22

4.1.3. Problem 1 Ġçin Crank-Nicolson Sonlu Fark YaklaĢımı……….22

4.2. Problem 2 ………31

4.2.1. Problem 2 Ġçin Açık Sonlu Fark YaklaĢımı………..31

4.2.2. Problem 2 Ġçin Kapalı Sonlu Fark YaklaĢımı………32

4.2.3. Problem 2 Ġçin Crank-Nicolson Sonlu Fark YaklaĢımı……….33

4.3. Problem 3 ……….42

4.3.1. Problem 3 Ġçin Açık Sonlu Fark YaklaĢımı………...42

4.3.2. Problem 3 Ġçin Kapalı Sonlu Fark YaklaĢımı………43

4.3.3. Problem 3 Ġçin Crank-Nicolson Sonlu Fark YaklaĢımı……….44

5. PARABOLİK DENKLEMLER İÇİN ALTERNATİF YÖNTEMLER ……...53

5.1. Non-Lineer Parabolik Denklemler Ġçin Predictor-Corrector Yöntemi ……….…...53

5.2. Model Problemler ……….………...54

5.2.1. Problem 1 ……….57

5.2.2. Problem 2 ……….58

5.3. AlternatingDirectionĠmplicit(ADI) Yöntemi………….………...…...70

5.3.1. AlternatingDirectionĠmplicit(ADI) Yönteminin UygulanıĢı………70

viii

5.4.1. Model Problem………74 KAYNAKLAR ………..………...81 ÖZGEÇMİŞ ……….……….83

ix

ŞEKİLLER DİZİNİ

Şekil 3.1 Çözüm Alanının Gridlere Ayrılması

Şekil 5.1 v =1, h =0.1 değerleri için [0,1] aralığında Problem 1’in farklı zamanlarda (p c )nümerik çözümleri

Şekil 5.2t =0.1 , h =0.1 değerleri için Problem 1’in farklı viskosite katsayıları için (p c )nümerik çözümleri

Şekil 5.3 v =0.1 , k =0.0001 ve h =0.0125 değerleri için farklı zamanlardaki Problem 1’in (p c ) nümerik çözümleri

Şekil 5.4 v =1, k =0.0001 ve h =0.0125 değerleri için farklı zamanlarda Problem 1’in nümerik(p c ) çözümleri

Şekil 5.5 v =0.005 , k =0.0001 ve h =0.0125 değerleri için Problem 1’in farklı zamanlardaki nümerik (p c ) çözümleri

Şekil 5.6 v =0.01 , k =0,0001 ve h =0.0125 değerleri için farklı zamanlarda Problem 1’in nümerik (p c ) çözümleri

Şekil 5.7 v =1, h =0.1 değerleri için Problem 2’nin farklı zamanlarda (p c ) nümerik çözümleri

Şekil 5.8 v =1 , h =0.1 değerleri için Problem 2’nin farklı zamanlarda(p c ) nümerik çözümleri

Şekil 5.9t =0.1 , h =0.1 değerlerine karĢılık Problem 2’nin farklı viskosite katsayıları için(p c ) nümerik çözümleri

Şekil 5.10 Ġki boyutlu ısı denkleminin t0 için fractional step metot ile nümerik çözümü

Şekil 5.11 Ġki boyutlu ısı denkleminin t0.1 için fractional step metot ile nümerik çözümü

Şekil 5.12 boyutlu ısı denkleminin t0.05 için fractional step metot ile nümerik çözümü

x

TABLOLAR DİZİNİ

Tablo 4.1.Açık Yöntem : k =0.00001 ve h ’ nin farklı değerleri için t =0.1 zamanında Problem 1’in nümerik ve analitik çözümleri

Tablo 4.2. AçıkYöntem:h =0.01, t =0.1 ve farklı k değerleri için Problem 1’in nümerik sonuçlarının karĢılaĢtırılması

Tablo4.3.Kapalı Yöntem: k =0.00001 ve h ’nin farklı değerleri için t =0.1 zamanında Problem 1’in nümerik ve analitik çözümleri

Tablo4.4. Kapalı Yöntem:h =0.01, t =0.1 ve farklı k değerleri için Problem 1’in nümerik sonuçlarının karĢılaĢtırılması

Tablo 4.5.Crank-Nicolson Yöntemi : k =0.00001 ve h ’nin farklı değerleri için t =0.1 zamanında Problem 1’in nümerik ve analitik çözümleri

Tablo 4.6.Crank-Nicolson Yöntem:h =0.01, t =0.1 ve farklı k değerleri için Problem 1’in nümerik sonuçlarının karĢılaĢtırılması

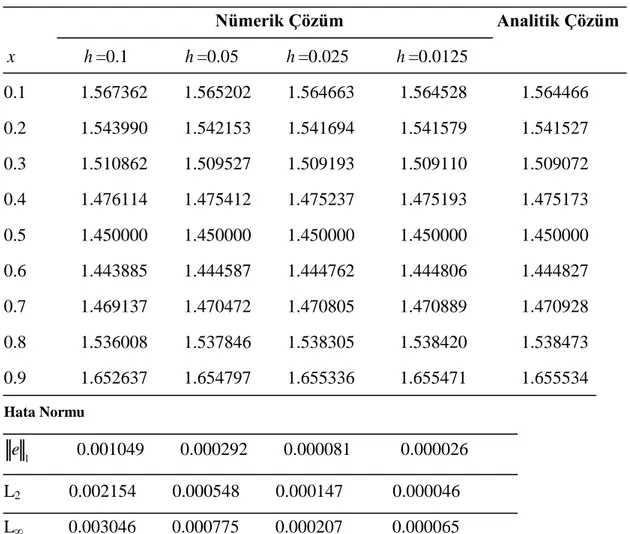
Tablo 4.7.h =0.0125 ve k =0.00001 değerleri için t =0.5 zamanında Problem 1’in nümerik ve analitik çözümleri

Tablo4.8. Açık Yöntem : k =0.00001 ve h ‘nin farklı değerleri için t =0.1 zamanında Problem 2’nin nümerik ve analitik çözümleri

Tablo 4.9. Açık Yöntem:h =0.01, t =0.2 ve farklı k değerleri için Problem 2’ nin nümerik sonuçlarının karĢılaĢtırılması

Tablo 4.10. Kapalı Yöntem : k =0.00001 ve h ’ın farklı değerleri için t =0.1 zamanında Problem 2’nin nümerik ve analitik çözümleri

Tablo 4.11. Kapalı Yöntem:h =0.01, t =0.2 ve farklı k değerleri için Problem 2’nin nümerik sonuçlarının karĢılaĢtırılması

Tablo 4.12.Crank-Nicolson Yöntemi : k =0.00001 ve h ’ın farklı değerleri içi t =0.1 zamanında Problem 2’nin nümerik ve analitik çözümleri

Tablo 4.13. Crank-Nicolson Yöntemi:h =0.01, t =0.2 ve farklı k değerleri için Problem 2’nin nümerik sonuçlarının karĢılaĢtırılması

xi

Tablo 4.14. h =0.1 ve k =0.001 değerleri için t =0.5 zamanında Problem 2’nin nümerik ve analitik çözümleri

Tablo 4.15.Açık Yöntem : k =0.00001 ve h ’ın farklı değerleri için t =0.1 zamanında Problem 3’ün nümerik ve analitik çözümleri

Tablo 4.16. Açık Yöntem:h =0.01, t =0.3 ve farklı k değerleri için Problem 3’ün nümerik sonuçlarının karĢılaĢtırılması

Tablo 4.17.Kapalı Yöntem : k =0.00001 ve h ’ın farklı değerleri için t =0.1 zamanında Problem 3’ün nümerik ve analitik çözümleri

Tablo 4.18. Kapalı Yöntem:h =0.01, t =0.3 ve farklı k değerleri için Problem 3’ün nümerik sonuçlarının karĢılaĢtırılması

Tablo 4.19.Crank-Nicolson Yöntemi: k =0.00001 ve h ’ın farklı değerleri için t =0.1 zamanında Problem 3’ün nümerik ve analitik çözümleri

Tablo 4.20. Crank-Nicolson Yöntemi:h =0.01, t =0.3 ve farklı k değerleri için Problem 3’ün nümerik sonuçlarının karĢılaĢtırılması

Tablo 4.21. h =0.1 ve k =0.001 değerleri için t =0.5 zamanında Problem 3’ün nümerik ve analitik çözümleri

Tablo 5.1.t =0.1, v =1 ve k =0.00001 için Problem 1’in nümerik(p c ) ve tam çözümleri

Tablo 5.2.h =0.0125 , k =0.00001, v =1, v =0.1, v =0.01 için Problem 1’in nümerik (p c )ve tam çözümleri

Tablo 5.3. P-C:h =0.0125, k =0.00001; v =0.005, v =0.001, v =0.0005 ve v =0.0001 için Problem 1’in nümerik sonuçlarının karĢılaĢtırılması

Tablo 5.4.t =0.1 , v =1, k =0.00001 için Problem 2’nin nümerik(p c )ve tam çözümleri

Tablo 5.5.h =0.0125 , v =1, v =0.1, v =0.01 için Problem 2’nin nümerik(p c )ve tam çözümleri

Tablo 5.6.P-C:h =0.0125, k =0.00001; v =0.005, v =0.001, v =0.0005 ve v =0.0001 için Problem 2’nin nümerik sonuçlarının karĢılaĢtırılması

Tablo 5.7. N10, k =0.00001 değerleri için farklı zamanlarda model problemin fractional step metoduyla nümerik çözümü

xii

Tablo 5.8. N20, k =0.00001 değerleri için farklı zamanlarda model problemin fractional step metoduyla nümerik çözümü

Tablo 5.9. N10, k =0.001 değerleri için farklı zamanlarda model problemin fractional step metoduyla nümerik çözümü

Tablo 5.10. N20, k =0.001 değerleri için farklı zamanlarda model problemin fractional step metoduyla nümerik çözümü

1 1.GİRİŞ

Doğadaki olayların modellenmesi genelde lineer olmayan kısmi türevli denklemler ile yapılmaktadır. Ancak lineer olmayan ve karmaşık sınır değerlerine sahip kısmi türevli denklemlerin genelde analitik çözümlerini elde etmek zor veya imkansızdır. Bu nedenle bu tür problemlerin çözümlerinde sıklıkla nümerik yöntemler kullanılır. Kısmi türevli denklemlerin belli başlangıç ve sınır değerleri altında nümerik çözümlerinin elde edilmesi 20. yüzyılın başlarından itibaren oldukça önemli problemler olarak ortaya çıkmıştır. Ayrıca son dönemlerde bilgisayar alanındaki gelişmeler sayesinde çeşitli bilim ve mühendislik alanlarında nümerik yöntemlerin kullanılması yaygınlaşmıştır.

Lineer ve lineer olmayan kısmi türevli denklemlerin çözümünde uygulamasının kolay olasından dolayı, Sonlu fark yöntemi oldukça sık kullanılmaktadır. Ancak kısmi türevli denklemleri içeren problemlerin sonlu fark yöntemleri ile çözümü kolay olmasının yanında ele alınan probleme en uygun sonlu fark yönteminin belirlenmesi aşaması biraz zaman alabilmektedir. En yaygın kullanılan sonlu fark yöntemleri açık, kapalı ve Crank-Nicolson sonlu fark yöntemidir. Bu üç yöntem klasik sonlu fark yöntemi olarak bilinmektedir. Yapılan çalışmalarda öncelikle açık ve kapalı sonlu fark yöntemleri ele alınmıştır. Daha sonra Crank ve Nicolson açık ve kapalı sonlu fark yöntemlerini kullanarak yeni bir kapalı sonlu fark yöntemi olan Crank-Nicolson yöntemini elde etmişlerdir [1].

Biz de bu çalışmamızda parabolik tipten bazı lineer ve lineer olmayan kısmi türevli denklemlerin nümerik çözümlerini inceledik. Öncelikle lineer kısmi türevli denklemlerin genel yapısı, A, B, C, D, E veF; x ,ynin fonksiyonları olmak üzere

2 2 2 2 2 0 u u u u u A B C D E Fu x x y y x y                 

biçimindedir. Eğer bu denklemde:

(i) B24AC>0 ise hiperbolik; (ii) B24AC=0 ise parabolik; (iii) B24AC<0 ise eliptik tiptendir.

2

şeklinde bir sınıflandırma yapılır. Biz bu çalışmada parabolik tipten denklemleri göz önüne alacağız.

Çalışmada ilk olarak ısı iletim denklemi incelendi. Bunun için öncelikle klasik sonlu fark yöntemleri olarak bilinen açık, kapalı ve Crank-Nicolson sonlu fark yaklaşımlarının elde edilişleri verildi ve bu yöntemler kullanılarak farklı sınır şartlarına sahip ısı iletim denklemleri çözüldü. Bu doğrultuda üç model problemin klasik sonlu fark yöntemleri ile elde edilen nümerik sonuçların hem analitik çözümlerle hem de daha önce başka araştırmacıların vermiş olduğu sonuçlar ile karşılaştırılması verildi.

Bu çalışmanın orijinal kısmını oluşturan son bölümde ise bir boyutlu lineer olmayan parabolik denklem ve iki boyutlu lineer parabolik denklemler için sonlu fark teknikleri uygulanarak çözümler elde edildi. Ayrıca lineer olmayan parabolik denklem olarak 1-boyutlu Burgers‟ denklemi ele alındı. Bu denklemin farklı başlangıç değerlerine karşılık gelen nümerik çözümlerini elde etmek için kullanılacak yöntem predictor-corrector yöntemidir. Bu yöntemi ilk olarak Douglas ve Jones birlikte vermişlerdir [2]. Bu çalışmalarında Douglas ve Jones predictor-corrector yöntemini elde etmiş ve 1-boyutlu Burgers‟ denkleminin çözümünü bu yöntemle vermişlerdir. Farklı başlangıç değerlerine karşılık gelen nümerik sonuçlar hem analitik çözümlerle hem de daha önce başka araştırmacıların verdikleri sonuçlarla karşılaştırıldı. İki boyutlu lineer denklem olarak ısı denklemi ele alındı. Bu denklemin çözümünde ise sonlu farkların bir uygulaması olan Fractional Step metot kullanılmıştır. Öncelikle bu yöntemin çıkarılışı ele alınacak olup daha sonra model probleme uygulanması verilecektir. Daha sonra elde edilen nümerik sonuçlar ile analitik çözümlerin karşılaştırılması yapılmıştır.

3 2.TEMEL KAVRAMLAR

Bu bölümde daha sonraki bölümlerde kullanılacak olan bazı temel kavramlar verilmiştir.

Tanım 2.1. Bir veya daha fazla bağımlı değişkenlerin bir veya daha fazla bağımsız değişkenlere göre türevlerini içeren bir denkleme diferansiyel denklem denir [3]. Bir diferansiyel denklem

( , ,dy) 0

f x y

dx 

veya genel olarak

2 2 ( , , , ,..., ) 0 n n dy d y d y f x y dx dx dx 

şeklinde yazılır. Burada y bağımlı değişken, x bağımsız değişkendir. Bir veya daha fazla bağımlı değişkenlerin bir tek bağımsız değişkene göre adi türevlerini içeren bir diferansiyel denkleme adi diferansiyel denklem denir [3].

Bir veya daha fazla bağımlı değişkenlerin birden fazla bağımsız değişkene göre kısmi türevlerini içeren bir diferansiyel denkleme kısmi diferansiyel denklem(KDD) denir [3].

Genel olarak KDD x y, ,...ler bağımsız değişkenler ve u x y( , ,...) bağımlı değişken (bilinmeyen fonksiyon) olmak üzere,

( , ,..., , _x, _y, _xy, _xx, _yy, _xxx,..) 0

f x y u u u u u u u 

şeklinde yazılır. Burada

x u u x    , y u u y    , 2 2 xx u u x    , 2 xy u u x y     , 2 2 yy u u y    , 3 3 xxx u u x    , … dir [3].

Tanım 2.2. Bir diferansiyel denklemde bulunan en yüksek mertebeden türevin mertebesine o diferansiyel denklemin mertebesi denir [4].

4

Tanım 2.3. Bir diferansiyel denklemde bulunan en yüksek mertebeden türevin kuvvetine diferansiyel denklemin derecesi denir [4].

Tanım 2.4. m ve n pozitif tamsayılar olmak üzere, A bir m n _{matrisi mn tane reel} veya kompleks sayının sıralandığı m tane satır, n tane sütundan oluşan bir dikdörtgensel düzendeki yapıya matris denir [4].

Tanım 2.5. Bir matriste satır sayısı sütun sayısına eşit ise o matrise karesel matris denir. m satır m sütundan oluşan bir karesel matrise m . mertebedendir denir [5]. Tanım 2.6. n × n tipindeki bir karesel matriste a₁₁,a₂₂,...,a elemanlarına da karesel _nn matrisin köşegen elemanları denir. Bu elemanların bulunduğu köşegene ise matrisin esas köşegeni denir [5].

Tanım 2.7. Esas köşegen üzerindeki elemanları sıfırdan farklı ve diğer bütün elemanları sıfır olan bir karesel matrise köşegen matris denir [5].

Tanım 2.8. Esas köşegen üzerindeki elemanları eşit fakat 1 olmayan köşegen matrise skaler matris denir [5].

Tanım 2.9. Köşegen üzerindeki elemanları 1 ve köşegen dışındaki elemanları 0 olan n n tipindeki matrise n . mertebeden birim matris denir ve I ile gösterilir [5]. n Tanım 2.10. A, m × n boyutunda bir matris olmak üzere ( , )j i bileşeni A matrisinin

( , )i j bileşeni olan bir n × m boyutundaki matrise A matrisinin transpozu(devriği) denir ve A ile gösterilir [5]. T

Tanım 2.11. Transpozu kendisine eşit olan bir karesel matrise simetrik matris denir. Yani T

A  Aise Akaresel matrisine simetrik matris denir [5].

Tanım 2.12. Tüm terimleri reel olan bir A matrisi için; AT  A oluyor ise A

matrisine ters-simetrik matris denir [5]. Tanım 2.13. (_AT) _A

ise A ya hermityen matris, (_AT) _A

ise A ya anti-hermityen matris denir [5].

Tanım 2.14. Eğer bir A[aij m n]  matrisinde her bir ,i j için aij  0 oluyorsa A matrisine sıfır matris denir [6].

5

Tanım 2.15. A ve B matrisleri ABIve BAI bağıntılarını sağlayan birer n n boyutunda matrisler ise B matrisine A matrisinin tersi(invers) denir ve A1 ile gösterilir [6].

Tanım 2.16. Bir matrisin esas köşegeni ve elemanlarının köşegen etrafında belli bir disipline göre dizilmesinden oluşan matrise bant matris denir [6].

Tanım 2.17. Bir kareselA matrisinin esas köşegeni üstündeki elemanları sıfıra eşit ise bu matrise alt üçgensel matris denir ve benzer şekilde bir B matrisinin esas köşegeni altındaki elemanları sıfıra eşit ise bu matrise de üst üçgensel matris denir [6].

Tanım 2.18. :L V V, nboyutlu bir V vektör uzayından V ‟ nin kendi içine tanımlı bir lineer dönüşüm olsun. Eğer V ‟ nin sıfırdan farklı herhangi bir x vektörü için

( )

L x x

ise, bu durumda  sayısına L‟ nin bir öz değeri denir [7].

( )

L x x denklemini sağlayan sıfırdan farklı her x vektörüne de L‟ nin,  öz değerine karşılık gelen bir öz vektörü denir [7].

Tanım 2.19. n n tipinde bir A matrisi ve  verilsin. Bu durumda ( ) det( n )

P   I A ifadesine A‟ nın karakteristik polinomu denir [7]. Ayrıca

( ) det( _n ) 0 P   I A  denklemine de A‟nın karakteristik denklemi denir [7].

Tanım 2.20. n n tipindeki bir A matrisinin özdeğerlerinin en büyüğüne A matrisinin spektral yarıçapı denir ve ( )A ile gösterilir [7].

Tanım 2.21. n

V olmak üzere

:n   ( )

V  V  V

ifadesine V nin normu denir ve Ѵ sembolü ile gösterilir. V W,  için normun üç n temel özelliği şunlardır [7]:

6

 Ѵ 0 ve ancak eğer V =0 ise sıfıra eşittir.  Herhangi bir c sayısı için 𝑐Ѵ = 𝑐 Ѵ dir.  Ѵ+ 𝑊  Ѵ + 𝑊 . Tanım 2.22. n n A olmak üzere :n_n   ( ) A A  A

olarak tanımlanan dönüşüme n n

 üzerinde bir matris normu denir.

Her A B, nn ve c için matris normunun özellikleri şunlardır:  𝐴 ≥ 0 dır ve ancak eğer A=0 ise sıfırdır.

 𝑐𝐴 = 𝑐 𝐴 dır.

 𝐴 + 𝐵 ≤ 𝐴 + 𝐵 (üçgen eşitsizliği) ve Ѵ vektörü için,

 𝐴Ѵ ≤ 𝐴 Ѵ  𝐴𝐵 ≤ 𝐴 𝐵

şeklindedir [7]. Sıkça kullanılan bazı matris normları aşağıdaki gibi tanımlanır.

1 A = max_𝑗 𝑛_𝑖=1 𝑎𝑖𝑗 , 2 ( ) H A   A A , A _=max_𝑖 𝑛_{𝑗 =1} 𝑎𝑖𝑗 .

Tanım 2.23. f , bir x noktasının komşuluğunda tanımlanmış bir fonksiyon olsun.

0 ( ) ( ) lim x f x x f x x      

7 ( ) ( ) lim f u f x u x _{u x}   _

limiti mevcut ise bu limit değerine f fonksiyonunun x noktasındaki türevi denir ve ( )

f x veya df

dx ile gösterilir [8].

Tanım 2.24. f fonksiyonu a noktasını içeren bir aralıkta her mertebeden türevlenebilir olsun. ( ) ( ) ( ) ( ) ! 0 k f a _k f x x a k k     

serisine a noktasında f fonksiyonu tarafından üretilen Taylor serisi denir [8].

Taylor serisinde sonlu sayıdaki terimden oluşan ( ) 0 ( ) ( ) ( ) ! k n k n k f a P x x a k  



polinomuna n dereceden Taylor polinomu denir [8]. Bu polinom, .

( ) 0 0 0 0 0 0 0 ( ) ( ) ( ) ( ) ( )( ) ( ) ... ( ) ... 2! ! n n n x x x x P x f x f x x x f x f x n           

şeklindedir. f x( ) fonksiyonu için kalan ya da hata terimi,

( ) _n( ) f x P x = R x = _n( ) ( 1) ( ( )) ( 1)! n f x n    1 0 (xx )n

şeklindedir. Burada ( )x , x ile x arasında bir sayıdır [8]. 0

Tanım 2.25. (Lokal Kesme Hatası): ( , )i j incidüğüm noktasında bir kısmi

diferansiyel denkleme yaklaşan fark denklemi, u fark denkleminin tam çözümü olmak üzere,F_{i j,} ( )u 0şeklinde gösterilsin.( , )i j incidüğüm noktasında sonlu fark

yaklaşımının lokal kesme hatası, u kısmi diferansiyel denkleminin tam çözümü olmak üzere, T_{i j,} F_{i j,} ( )U olarak tanımlanır.

8

Lokal kesme hatası, sonlu fark yaklaşımının kısmi diferansiyel denkleme ne derece iyi yaklaştığını veren bir ölçüdür. Taylor seri açılımının kullanılmasıyla lokal kesme hatası, h ve k değerlerinin kuvvetleri ve ( ,ih jk) noktasında kısmi diferansiyel denkleminin tam çözümünün ( )U kısmi türevleri cinsinden kolayca açıklanabilir [9]. Tanım 2.26. (Tutarlılık): h k, 0 olduğunda lokal kesme hatasının limit değeri sıfıra yaklaşıyorsa fark denklemi tutarlıdır. Yani ,

, 0

lim _{i j} 0

h k T  ise fark denklemi tutarlıdır denir [9].

Tanım 2.27. (Kararlılık):Kısmi diferansiyel denkleme karşılık gelen sonlu fark denkleminin çözümünün kısmi diferansiyel denkleminin çözümüne yakın kaldığı durumlarda yöntem kararlıdır denir [9].

Tanım 2.28. (Yakınsaklık): u , fark denkleminin ve U ise kısmi diferansiyel denklemin tam çözümleri olmak üzere

, 0

lim _ij _ij

h k u U ise sonlu fark denkleminin çözümü kısmi diferansiyel denklemin çözümüne yakınsar denir [10].

Tanım 2.29. Bir fark denkleminin hangi şartlar altında kararlı olduğunun araştırılmasına kararlılık analizi denir [10].

Teorem 2.1.( Lax’ ın Denklik Teoremi)Sonlu fark yönteminin yakınsak olması için gerek ve yeter şart yöntemin tutarlı ve kararlı olmasıdır [10].

9 3. KLASİK SONLU FARK YÖNTEMLERİ

Bu bölümde klasik sonlu fark yöntemleri hakkında bilgi verilecek ve çeşitli sınır değerlerine sahip ısı iletim denklemi için sonlu fark formülleri elde edilecektir. Kısmi türevli diferansiyel denklemlerin yaklaşık çözümlerinin bulunmasında değişik yöntemler kullanılır. Bunların arasında en yaygın olan sonlu fark yöntemleridir. Sonlu fark yöntemlerinde, sürekli çözüm alanı diskretize edilerek (alan belli aralıklarda noktalarla temsil edilerek) bağımlı değişkenin sadece bu noktalardaki değeri bulunmaya çalışılır. Bu amaçla denklemde bulunan türevlerin sonlu farklarla ifade edilmesiyle verilen kısmi diferansiyel denklemin (KDD) cebirsel bir denklem veya denklem sistemine dönüşmesi sağlanır. Sonlu farklar yönteminin temeli kısmi diferansiyel denklemlerde görülen türevlerin sonlu ve ayrık noktalarda yaklaşık olarak ifade edilmesi üzerine kuruludur [10].

Şekil 3.1. Çözüm alanının gridlere ayrılması

x

t

j+1

j

j-1

k

h

0

i-1

i

i+1

i-1,j

i,j+1

P(ih,jk)

i,j

i,j-1

i+1,j

10

Sonlu farklar yöntemi kısaca şu şekilde özetlenebilir: u , x ve t değişkenlere bağlı bir fonksiyon olsun. Sonlu fark denkleminin kurulmasındaki ilk adımlardan biri çözüm alanını kafeslere bölmektir. Burada  x h, x -yönündeki konum adım uzunluğu; t k  , t - yönündeki zaman adım uzunluğu olmak üzere, konum ve zaman koordinatları x ve t sırasıyla

0 i

x x  i x ve t_j   t₀ j t

şeklinde gösterilir [10]. Temsili bir P ih jk( , ), düğüm noktası üzerinde u fonksiyonunun noktasal değeri u_Pu ih jk( , )u_ij olarak gösterilir [10]. u fonksiyonunun civar noktalardaki değerleri

1 ( , ) j i i j u  u x t  t 1 ( , ) j i i j u  u x t  t 1 ( , ) j i i j u_ u x  x t 1 ( , ) j i i j u_ u x  x t

şeklinde gösterilecektir. Bir türevin sonlu farklarla ifadesinin temelini türev tanımı oluşturur. u x t( , )fonksiyonunun ( , )x t_{i j} noktasındaki türevi

1 0 ( , ) ( , ) lim j j i j i j i i x u x x t u x t u u u hata x x x       _  _{  }   

olacaktır. Eşitliğin sağ kısmı türevin sonlu farklarla gösterimidir. Sonlu fark gösterimindeki hata, limitin kaldırılmasıyla oluşan hatadır. Sonlu fark gösterimini daha formel bir temele oturtmak için Taylor seri açılımı kullanıldı [10].

3.1.Taylor Seri Açılımı Yardımıyla Sonlu Fark Formülleri

2 2 2 ( ) ( , ) ( , ) ( , ) ( , ) .... 2! i j i j i j i j u u x u x x t u x t x t x x t x x             veya 1 j j i i u_ u + 2 2 2 ( ) ( , ) ( , ) ... 2! i j i j u x x x t x x t x x         (3.1)

11 bu ifade u x   e göre düzenlenirse; ( , )_{i j} u x t x   = 2 1 2 ( , ) ... 2! j j i i i j u u x x x t x x   _  _   (3.1a) ve yüksek mertebeden türevler atılırsa, 1.türevin sonlu fark gösterimi

1 ( , ) j j i i i j u u u x t hata x x    _{ }   (3.2) olarak elde edilir. Birinci türev için bulunan bu ileri sonlu fark ifadesi daha önce bulunan limitli ifade ile aynı olduğu görülmektedir. Atılan terimlere bakıldığında, içlerinde türev mertebesi en düşük olan terimin katsayısı

2

x 

olduğu görülür. Buna göre oluşan kesme hatasının mertebesi O(x) dir.

u x 

 türevinin değişik sonlu fark gösterimleri mevcuttur. Taylor açılımının

2 2 3 3 2 3 ( ) ( ) ( , ) ( , ) ( , ) ( , ) ( , ) ... 2! 3! i j i j i j i j i j u u x u x u x x t u x t x t x x t x t x x x                 şeklinde yazılmasıyla 2 2 3 3 1 2 3 ( ) ( ) ( , ) ( , ) ( , ) .... 2! 3! j j i i i j i j i j u u x u x u u x t x x t x t x x x                (3.3)

elde edilir ve bu ifade u

x   e göre düzenlenirse; 2 1 2 ( , ) ( , ) .... 2 j j i i i j i j u u u u x x t x t x x x    _{ }  _    (3.3a) ifadesi elde edilir ve yüksek mertebeden türevler atılırsa, 1. türevin sonlu fark gösterimi

1 ( , ) ( ) j j i i i j u u u x t O x x x         (3.4) geri sonlu fark türev ifadesi elde edilir.

12 2 2 2 2 3 3 3 3 1 1 2 2 3 3 ( ) ( ) ( ) ( ) .... 2! 2! 3! 3! j j i i u u u x u x u x u x u u x x x x x x x x                             = 3 3 3 ( ) 2 2 .... 3! u x u x x x         (3.5) ve bu ifade u x   e göre düzenlenirse; 2 1 1 ( , ) ( ) 2 j j i i i j u u u x t O x x x     _{  }   (3.6) merkezi sonlu fark ifadesi bulunur. Atılan terimlere bakıldığında bu ifadenin ikinci mertebeden hassasiyete sahip olduğu görülür.

Diğer taraftan denklem (3.1) ve denklem (3.3) taraf tarafa toplanırsa;

2 2 4 4 1 1 2 4 ( ) ( ) 2 2 .... 2 4! j j j i i i u x u x u u u x x              (3.7) ve bu ifade 2 2 u x   e göre düzenlenirse; 2 2 1 1 2 2 2 ( , ) ( ) j j j i i i i j u u u u x t O x x x           (3.8) ikinci mertebeden türev için merkezi sonlu fark ifadesi elde edilir. Kesme hatasına bakıldığında bu ifadenin ikinci mertebeden bir hassasiyete sahip olduğu anlaşılır [12]. Böylece birinci ve ikinci mertebeden kısmi türevler için bazı sonlu fark yaklaşımları:

1 _{( )} j j i i u u u O x x x         (3.9) 1 _{( )} j j i i u u u O x x x         (3.10) 2 1 1 _{( )} 2 j j i i u u u O x x x     _{  }   (3.11) 1 ( ) j j i i u u u O t t t  _  _{  }   (3.12)

13 1 ( ) j j i i u u u O t t t    _{  }   (3.13) 2 1 2 2 2 2 ( ) ( ) j j j i i i u u u u O x x x           (3.14) 2 2 1 2 2 2 ( ) ( ) j j j i i i u u u u O x x x      _{  }   (3.15) 2 2 1 1 2 2 2 [( ) ] ( ) j j j i i i u u u u O x x x      _{  }   (3.16) şeklinde ifade edilebilir. Burada “ O ” ; sonsuz terimli bir eşitliğin sonlu bir terimde kesildiğini, O(x) terimi hatanın  x 0 iken x ile orantılı olduğunu gösterir.

( )

O t ise hatanın t mertebesinde olduğunu gösterir ve böylece t ile orantılı olarak azalacağını göstermektedir. (3.9), (3.10) ve (3.11) ile verilen, x -değişkenine göre birinci mertebeden türev yaklaşımlarına sırasıyla ileri, geri ve merkezi fark formülleri denir. Aynı şekilde (3.12) ve (3.13) ile verilen, t -değişkenine göre birinci mertebeden türev yaklaşımlarına sırasıyla ileri ve geri fak formülleri denir. (3.14), (3.15) ve (3.16) ile verilen , x değişkenine göre ikinci mertebeden türev yaklaşımlarına sırasıyla ileri, geri ve merkezi fark formülleri denir [10].

Şimdi, parabolik denklemlerin tipik bir örneği olan

2 2 u u t  x      , 0<x<l, t>0 (3.17) 1-boyutlu ısı iletim denklemini

1 2 ( , ) ( ), 0 ( , ) ( ), 0 u a t f t t u b t f t t     (Dirichlet sınır şartları) (3.18) 1 0 1 1 ( , ) ( ) ( , ) ( ) u k a t q t x u k b t q t x      _  (Neumann sınır şartları) (3.19)

14 1 0 1 2 1 2 ( , ) ( , ) ( ) ( , ) ( , ) ( ) u k a t p u a t h t x u k b t p u b t h t x       _{ }  (Robbin sınır şartları) (3.20) şeklindeki sınır şartları ve u x( , 0) f x( ),a < x < b (3.21) başlangıç şartı için klasik sonlu fark yaklaşımları oluşturulacaktır. Burada

1, 2, 0, , ,1 1 2

f f q q h h fonksiyonları t nin bilinen fonksiyonları olup k k p p₁, ₂, ₀, ₁, da sabit sayılardır.

3.2. Açık(Explicit) Sonlu Fark Yöntemi

(3.17) denklemindeki u t   ve 2 2 u x 

 türevleri yerine (3.12) ve (3.16) denklemleriyle verilen sonlu fark yaklaşımları hatalar ihmal edilerek yazıldığında ısı iletim denkleminin açık sonlu fark yaklaşımı

1 1 1 2 2 ( ) j j j j j i i i i i u u u u u t  x             _  _ (3.22) veya 1 1 (1 2 ) 1 j j j j i i i i u  ru_   r u ru_ ,i0,1, 2,..., ,m j0,1, 2,...,n _(3.23) olur. Buradar ₂k h 

 olup lokal kesme hatası da [ 2 ( ) ( )

O k O h ].mertebedendir. Burada zaman indisi üst indis olarak yazılmıştır. Ayrıca x b a

m 

  olup m , xyönündeki grid blok sayısıdır. Buna göre x_i   a i x, i0,1, 2,...,m dir.

t

 , zaman adım büyüklüğü olup tj  j tdir [10].(t başlangıç zamanı olup genelde 0

0 0

t  alınır.)

3.2.1. Dirichlet Sınır Şartlı Isı İletim Problemi

15 sonlu fark yaklaşımı,r k₂

h   olmak üzere 1 1 (1 2 ) 1 j j j j i i i i u  ru_   r u ru_ ; i1, 2,...,m1,j0,1,...,n _(3.24)

dir. Buradat_jzaman adımında uij değerleri bilinirsetj1 zaman adımında 1 j i

u  değerleri (3.22) denkleminden bulunur.

3.2.2. Neumann Sınır Şartlı Isı İletim Denklemi

(3.17) de verilen ısı iletim denklemi (3.19) da verilen Neumann sınır şartlarına bağlı olarak dikkate alındığında (3.23) deki açık fark denklemii0(xa) ve

( )

im xb için problemin çözüm bölgesine düşmeyen ( 1, ) j ve (m1, )j düğüm noktalarındaki j₁

u_ veu_mj_1değerlerini içermektedir.( 1, ) j ve (m1, )j düğüm noktalarına

hayali noktalar, j₁

u_ ve j ₁

m

u _ değerlerine de hayali değerler denilmektedir. Bu hayali

değerleri ortadan kaldırmak için sınır şartlarındaki u

x 

 türevi yerine merkezi fark

yaklaşımı kullanılabilir. Bu durumda 0 i için 1 0 1 0 0 1 2 2 (1 2 ) ( ) j j j hr u ru r u q t k  _{   } ve im için ise 1 1 1 1 2 2 (1 2 ) ( ) j j j m m m rh u ru r u q t k      

eşitlikleri bulunur. Sonuç olarak ısı iletim denkleminin açık sonlu fark yaklaşımı

1 0 1 0 0 1 2 2 (1 2 ) ( ) j j j hr u ru r u q t k  _{    ,i0 (3.25)} 1 1 (1 2 ) 1, 1,..., 1 j j j j i i i i u  ru_   r u ru_ i m (3.26) 1 1 1 1 2 2 (1 2 ) ( ) j j j m m m rh u ru r u q t k       im _(3.27)

16 3.2.3. Robbin Sınır Şartlı Isı İletim Denklemi

(3.17) de verilen ısı iletim denklemi (3.20) de verilen Robbin sınır şartlarına bağlı olarak dikkate alındığında (3.23) deki açık fark denkleminde yine i0 ve im

değerleri için problemin çözüm bölgesine düşmeyen j₁

u_ ve u_mj_1 hayali değerleri ortaya çıkacaktır. Bu hayali değerleri ortadan kaldırmak için sınır şartlarındaki u

x 

 türevi

yerine merkezi fark yaklaşımının kullanılmasıyla

1 1 1 0 1 2 ( ( ) (0, )) j j h u u h t p u t k     1 1 2 2 2 ( ( ) ( , )) j j m m l h u u h t p u l t k     

elde edilir. Böylece ısı iletim probleminin açık sonlu fark yaklaşımı

1 0 1 1 0 1 1 2 2 (1 2 ) ( ), 0 j j j rh u ru r u h t i k   _{    } (3.28) 1 1 (1 2 ) 1, 1,..., 1 j j j j i i i i u  ru_   r u ru_ i m (3.29) 1 1 2 2 2 2 2 (1 2 ) ( ), j j j m m m rh u ru r u h t i m k         (3.30) olarak elde edilir. Burada ₁  1 p h k_{0 1} ve ₂  1 p h k_{1 2}dir [13].

3.3. Kapalı(Implicit) Sonlu Fark Yaklaşımı

Bu yöntemde (3.17) ile verilen ısı iletim denklemindeki türevler için 1 ( , ) ( ) j j i i u u u i j O t t t  _    

  (ileri fark formülü)

1 1 1 2 2 1 1 2 2 2 ( , ) [( ) ] ( ) j j j i i i u u u u i j O x x x           

  (merkezi fark formülü)

fark formülü ifadeleri kullanılır. Böylece kısmi diferansiyel denklem için kapalı sonlu fark yaklaşımı

17 1 1 1 1 1 1 2 2 ( ) j j j j j i i i i i u u u u u t  x                _  _ (3.31) bu ifadede r ₂k h   alıp düzenlersek; 1 1 1 1 (1 2 ) 1 j j j j i i i i u  ru_   r u  ru_ , i1, 2,...,m1, j0,1,...,n _(3.32)

şeklini alır ve lokal kesme hatası 2

[ ( )O k O h( )]. mertebedendir [10]. 3.3.1. Dirichlet Sınır Şartlı Isı İletim Problemi

(3.17) deki ısı iletim probleminin (3.18) deki sınır şartlarıyla ve r ₂k h



 den

kapalı sonlu fark yaklaşımı

1 1 1

1 (1 2 ) 1

j j j j

i i i i

u  ru_   r u  ru_ , i1, 2,...,m1, j0,1,...,n (3.33) şeklinde elde edilir.

3.3.2. Neumann Sınır Şartlı Isı İletim Problemi

(3.19) de verilen Neumann sınır şartlarında u

x 

 türevi yerine j1-inci zaman

adımındaki merkezi fark yaklaşım formülü yazılırsa

1 1 1 1 0 1 2 ( ) j j h u u q t k      1 1 1 1 1 1 2 ( ) j j m m h u u q t k      

eşitlikleri elde edilir. Bu durumda verilen ısı denkleminin kapalı sonlu fark yaklaşımı

1 1 0 1 0 0 1 2 2 (1 2 ) ( ), 0 j j j rh u ru r u q t i k         (3.34) 1 1 1 1 (1 2 ) 1, 1,..., 1 j j j j i i i i u  ru_   r u  ru_ i m (3.35) 1 1 1 1 1 2 2 (1 2 ) ( ), j j j m m i rh u ru r u q t i m k          (3.36)

18 olarak elde edilir.

3.3.3. Robbin Sınır Şartlı Isı İletim Problemi

(3.20) de verilen Robbin sınır şartlarında u

x 

 türevi yerine j1-inci zaman

adımındaki merkezi fark yaklaşımı yazılırsa

1 1 1 1 1 1 0 0 1 2 ( ( ) ) j j h j u u h t p u k        (3.37) 1 1 1 1 1 2 1 2 2 ( ( ) ) j j j m m m h u u h t p u k         (3.38) eşitlikleri elde edilir. Bu durumda verilen ısı iletim denkleminin kapalı sonlu fark yaklaşımı 1 1 0 1 1 1 1 2 (1 2 ) 2 ( ), 0 j j j i i rh u r u ru h t i k          (3.39) 1 1 1 1 (1 2 ) 1, 1,..., 1 j j j j i i i i u  ru_   r u  ru_ i m (3.40) 1 1 1 2 2 2 2 2 (1 2 ) ( ), j j j m m m rh u ru r u h t i m k           (3.41) şeklinde elde edilir.

3.4. Crank-Nicolson Sonlu Fark Yöntemi

Bu yöntem John Crank ve Phyllis Nicolson tarafından geliştirilen kapalı bir yöntemdir [10]. Aslında bu yöntem açık ve kapalı yöntemlerin bir karışımıdır. Çünkü bu yöntemde konum türevinin her iki formu da kullanılır. Yani,

1 ( , ) j j i i i j u u u x t t t  _  _   1 1 1 2 1 1 1 1 2 2 2 2 2 1 ( , ) 2 ( ) ( ) j j j j j j i i i i i i i j u u u u u u u x t x x x                _  _  _   _

19 1 1 1 1 1 1 1 1 2 2 2 2 2 ( ) ( ) j j j j j j j j i i i i i i i i u u u u u u u u t x x             _   _      _   _ (3.42) ve r ₂k h   alarak düzenlersek 1 1 1 1 (2 2 ) 1 1 (2 2 ) 1 j j j j j j i i i i i i ru_ r u  ru_ ru_ r u ru_         (3.43)

olarak elde edilir. Burada lokal kesme hatasıO[(t)2 ( x) ]2 .mertebedendir. 3.4.1. Dirichlet Sınır Şartlı Isı İletim Problemi

Isı iletim problemi için herhangi bir jinci ve j 1 inci zaman adımlarındaki

0 j

u , u_mj, u₀j1, u_mj1 değerleri (3.18) deki Dirichlet sınır şartlarından bilindiğinden (3.17) ısı iletim denkleminin Crank-Nicolson sonlu fark yaklaşımı

1, 2,..., 1 i m ve j0,1,...,n için 1 1 1 1 (2 2 ) 1 1 (2 2 ) 1 j j j j j j i i i i i i ru_ r u  ru_ ru_ r u ru_         (3.44) şeklindedir.

3.4.2. Neumann Sınır Şartlı Isı İletim Problemi

(3.19) ile verilen Neumann sınır şartlarında u

x 

 türevi yerine hem j -inci zaman

adımında hem de j1-inci zaman adımındaki merkezi fark formüllerinin yazılmasıyla

1 1 0 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 2 ( ) 2 ( ) 2 ( ) 2 ( ) j j j j j j m m j j m m h u u q t k h u u q t k h u u q t k h u u q t k                  

20

eşitlikleri elde edilir. Bu durumda verilen ısı iletim denkleminin Crank-Nicolson sonlu fark yaklaşımı 1 1 0 1 0 1 0 1 4 (2 2 )r uj 2ruj (2 2 )r uj 2ruj rhq t i( ), 0 k          (3.45) 1 1 1 1 (2 2 ) 1 1 (2 2 ) 1, 1,..., 1 j j j j j j i i i i i i ru_ r u  ru_ ru_ r u ru_ i m           (3.46) 1 1 1 1 1 1 4 2ru_mj (2 2 )r u_mj 2ru_mj (2 2 )r u_mj rhq t i( ), m k             (3.47)

şeklinde elde edilir.

3.4.3. Robbin Sınır Şartlı Isı İletim Problemi

(3.20) de verilen Robbin sınır şartlarında u

x 

 türevi yerine hem j -inci zaman

adımında hem de j1-inci zaman adımındaki merkezi fark yaklaşımları yazılırsa

1 1 1 0 0 1 1 1 2 1 2 1 1 1 1 1 1 0 0 1 1 1 1 1 1 2 1 2 ( ) 2 ( ) 2 ( ) 2 ( ) 2 j j j j j j m m m j j j j j j m m m u u k p u h t h u u k p u h t h u u k p u h t h u u k p u h t h                          

elde edilir. Bu durumda verilen ısı iletim denkleminin Crank-Nicolson sonlu fark yaklaşımı 1 1 1 1 1 0 1 1 0 1 ( ) 2ruj (2 2r )uj 2ruj (2 2r )uj 4rhh t ,i 0 k             (3.48) 1 1 1 1 (2 2 ) 1 1 (2 2 ) 1, 1,..., 1 j j j j j j i i i i i i ru_ r u  ru_ ru_ r u ru_ i m           (3.49) 1 1 2 1 2 1 2 2 ( ) 2ru_mj (2 2r )u_mj 2ru_mj (2 2r )u_mj 4rhh t ,i m k               (3.50)

21 4. MODEL PROBLEMLER

Bu kısımda 3.bölümde verilen ısı iletim denkleminin çeşitli başlangıç ve sınır şartları içinklasik sonlu fark çözümleri elde edilecek ve problemlerin analitik çözümleriyle karşılaştırılacaktır. 4.1. Problem 1: 2 2 u u t x  _   ; 0 x 1, t0 1-boyutlu ısı iletim denklemini

(0, ) 0 u t  ; t0 (1, ) 0 u t  ; t0 sınır şartları ve ( , 0) ( ) u x  f x  2𝑥 ,0 ≤ 𝑥 ≤1₂ 2 1 − 𝑥 ,1₂ ≤ 𝑥 ≤ 1

başlangıç şartı ile birlikte göz önüne alalım. Bu problemin analitik çözümü

2 2 2 2 1 8 1 1 ( , ) sin (sin ) 2 n t n u x t n n x e n 









4.1.1. Problem 1 İçin Açık Sonlu Fark Yaklaşımı

Dirichlet sınır şartlı problemin açık sonlu fark yaklaşımı 1

1 (1 2 ) 1, 1,..., 1, 0,...,

j j j j

i i i i

u  ru_   r u ru_ i m j n

22 1 1 1 2 1 2 1 2 3 1 2 3 2 1 1 1 2 1 (1 2 ) (1 2 ) (1 2 ) (1 2 ) j j j j j j j j j j j m m m m j j j m m m u r u ru u ru r u ru u ru r u ru u ru r u                          

dir. Burada u₀j ve u_mj değerleri sınır şartlarından dolayı sıfıra eşittir. Bu denklem

sisteminin çözümü iteratif bir yapıya sahiptir.

4.1.2. Problem 1 İçin Kapalı Sonlu Fark Yaklaşımı Problem 1 için kapalı sonlu fark yaklaşımı

1 1 1 1 (1 2 ) 1 , 1,..., 1, 0,..., j j j j i i i i ru_ r u  ru_ u i m j n        

şeklindedir. Bu fark yaklaşımı

1 1 1 2 1 1 1 1 1 2 3 2 1 1 1 3 2 1 2 1 1 2 1 1 (1 2 ) (1 2 ) (1 2 ) (1 2 ) j j j j j j j j j j j m m m m j j j m m m r u ru u ru r u ru u ru r u ru u ru r u u                                   

şeklinde bir denklem sistemidir. Burada ₀j

u ve j

m

u değerleri sınır şartlarından dolayı

sıfıra eşittir.

4.1.3. Problem 1 İçin Crank-Nicolson Sonlu Fark Yaklaşımı Problem 1‟in Crank-Nicolson sonlu fark yaklaşımı

1 1 1 1 (2 2 ) 1 1 (2 2 ) 1 j j j j j j i i i i i i ru_ r u  ru_ ru_ r u ru_        

şeklinde olup açık bir şekilde yazarsak ;

1 1 1 0 1 2 0 1 2 1 1 1 1 2 3 1 2 3 1 1 1 3 2 1 3 2 1 1 1 1 2 1 2 1 (2 2 ) (2 2 ) (2 2 ) (2 2 ) (2 2 ) (2 2 ) (2 2 ) (2 2 ) j j j j j j j j j j j j j j j j j j m m m m m m j j j j j m m m m m ru r u ru ru r u ru ru r u ru ru r u ru ru r u ru ru r u ru ru r u ru ru r u                                                       j m ru 

23

denklem sistemi elde edilir. Bu sistem Crout yöntemi kullanılarak çözüldü.

Nümerik Sonuçlar

Elde edilen nümerik çözümlerin analitik çözümlere ne kadar yakın olduğunu göstermek için u x t( , )_{i j} ve u_ij sırasıyla u x t( , ) ve ( , )x t_{i j} noktasındaki analitik ve

nümerik değerleri göstermek üzere hata normları hesaplandı.

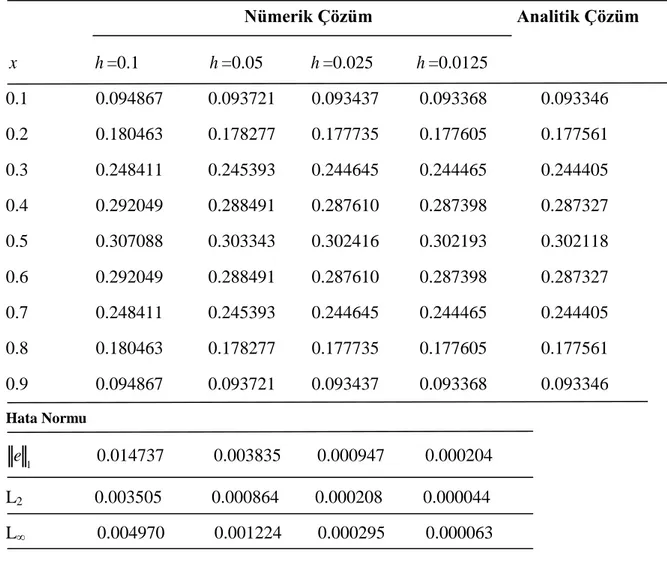
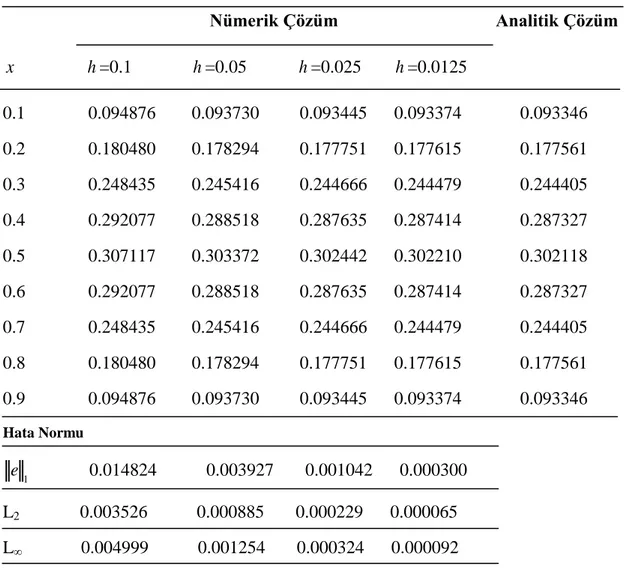
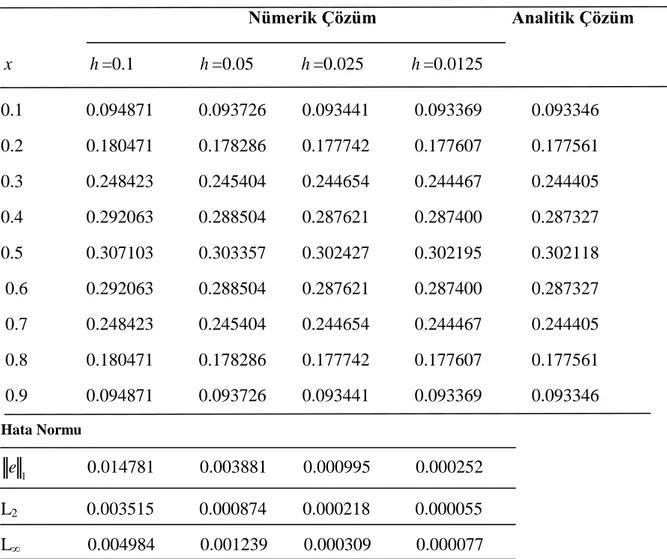
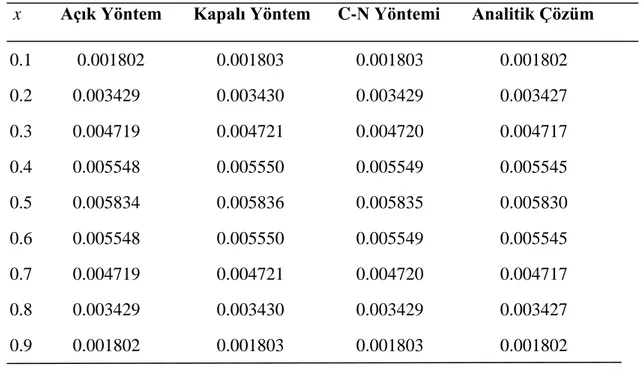
e =1 1 𝑚 1 _{( , )} j i i j u u x t  𝑚−1 𝑖=1 1 2 2 2 1 ( , ) m j i j i i L h u x t u    _  _ 



Problem 1‟in k =0.00001 ve farklı h adım uzunlukları için t =0.1 zamanında açık yöntem ile elde edilen nümerik çözümlerin analitik çözümlerle karşılaştırılması Tablo 4.1 de, kapalı yöntemle elde edilen nümerik çözümlerin analitik çözümlerle karşılaştırılması Tablo 4.3 de ve Crank-Nicolson yöntemiyle elde edilen nümerik çözümlerin analitik çözümlerle karşılaştırılması Tablo 4.5 de verildi. Tablolardan da kolayca görüleceği üzere h adım uzunluğu küçüldükçe nümerik çözümlerin analitik çözümlere yaklaştığı görülmektedir.

Tablo 4.2, Tablo 4.4 ve Tablo 4.6 dah =0.01, t =0.1 ve k =0.000001, k =0.00001, k =0.00004 ve k =0.00005 değerleri için sırasıyla açık, kapalı ve

Crank-Nicolson yöntemleriyle elde edilen nümerik sonuçlar başka araştırmacıların verdikleri sonuçlar ile karşılaştırılması verildi. Tablolardan sonuçların uyum içinde oldukları görülmektedir.

h =0.0125, k =0.00001 ve t =0.5değerleri için Problem 1‟in açık, kapalı ve Crank-Nicolson yöntemleriyle elde edilen nümerik çözümlerin karşılaştırılması Tablo 4.7 de verilmiştir. Tablodan da görüleceği gibi parametrelerin bu değerleri için analitik çözüme en yakın çözümler açık yöntem ile elde edilmiştir.

24

Tablo 4.1 : Açık Yöntem : k =0.00001 ve h ‟ nin farklı değerleri için t =0.1 zamanında Problem 1‟in nümerik ve analitik çözümleri

Nümerik Çözüm Analitik Çözüm x h =0.1 h =0.05 h =0.025 h =0.0125 0.1 0.094867 0.093721 0.093437 0.093368 0.093346 0.2 0.180463 0.178277 0.177735 0.177605 0.177561 0.3 0.248411 0.245393 0.244645 0.244465 0.244405 0.4 0.292049 0.288491 0.287610 0.287398 0.287327 0.5 0.307088 0.303343 0.302416 0.302193 0.302118 0.6 0.292049 0.288491 0.287610 0.287398 0.287327 0.7 0.248411 0.245393 0.244645 0.244465 0.244405 0.8 0.180463 0.178277 0.177735 0.177605 0.177561 0.9 0.094867 0.093721 0.093437 0.093368 0.093346 Hata Normu 1 e 0.014737 0.003835 0.000947 0.000204 L2 0.003505 0.000864 0.000208 0.000044 L∞ 0.004970 0.001224 0.000295 0.000063

25

Tablo 4.2:Açık Yöntem:h =0.01, t =0.1 ve farklı k değerleri için Problem1‟in nümerik sonuçlarının karşılaştırılması [11] Açık Yöntem x k=0.000001 k=0.00001 k=0.000004 k=0.00005 k=0.000001 k=0.00001 k=0.00004 k=0.00005 0.0 0 0 0 0 0 0 0 0 0.1 0.093361 0.093361 0.093363 0.093372 0.093361 0.093365 0.093379 0.093361 0.2 0.177590 0.177591 0.177594 0.177611 0.177591 0.177599 0.177625 0.177591 0.3 0.244445 0.244446 0.244450 0.244473 0.244445 0.244456 0.244493 0.244445 0.4 0.287374 0.287375 0.287380 0.287406 0.287375 0.287388 0.287431 0.287374 0.5 0.302168 0.302169 0.302174 0.302202 0.302169 0.302182 0.302227 0.302168 0.6 0.287374 0.287375 0.287380 0.287406 0.287375 0.287388 0.287431 0.287374 0.7 0.244445 0.244446 0.244450 0.244473 0.244445 0.244456 0.244493 0.244445 0.8 0.177590 0.177591 0.177594 0.177611 0.177591 0.177599 0.177625 0.177591 0.9 0.093361 0.093361 0.093363 0.093372 0.093361 0.093365 0.093379 0.093361 1.0 0 0 0 0 0 0 0 0

26

Tablo 4.3. : Kapalı Yöntem: k =0.00001 ve h ‟nin farklı değerleri için t =0.1 zamanında Problem 1‟in nümerik ve analitik çözümleri

Nümerik Çözüm Analitik Çözüm x h =0.1 h =0.05 h =0.025 h =0.0125 0.1 0.094876 0.093730 0.093445 0.093374 0.093346 0.2 0.180480 0.178294 0.177751 0.177615 0.177561 0.3 0.248435 0.245416 0.244666 0.244479 0.244405 0.4 0.292077 0.288518 0.287635 0.287414 0.287327 0.5 0.307117 0.303372 0.302442 0.302210 0.302118 0.6 0.292077 0.288518 0.287635 0.287414 0.287327 0.7 0.248435 0.245416 0.244666 0.244479 0.244405 0.8 0.180480 0.178294 0.177751 0.177615 0.177561 0.9 0.094876 0.093730 0.093445 0.093374 0.093346 Hata Normu 1 e 0.014824 0.003927 0.001042 0.000300 L2 0.003526 0.000885 0.000229 0.000065 L∞ 0.004999 0.001254 0.000324 0.000092