Özel smarandache eğrileri

ANADOLU ÜNİVERSİTESİ BİLECİK ŞEYH EDEBALİ

ÜNİVERSİTESİ

Fen Bilimleri Enstitüsü

Matematik Anabilim Dalı

ÖZEL SMARANDACHE EĞRİLERİ

Fatih KARAMAN

Yüksek Lisans Tezi

Tez Danışmanı

Yrd. Doç. Dr. Osman Zeki OKUYUCU

Tez İkinci Danışmanı

Prof. Dr. H. Hilmi HACISALİHOĞLU

BİLECİK, 2015

ANADOLU ÜNİVERSİTESİ BİLECİK ŞEYH EDEBALİ

ÜNİVERSİTESİ

Fen Bilimleri Enstitüsü

Matematik Anabilim Dalı

ÖZEL SMARANDACHE EĞRİLERİ

Fatih KARAMAN

Yüksek Lisans Tezi

Tez Danışmanı

Yrd. Doç. Dr. Osman Zeki OKUYUCU

Tez İkinci Danışmanı

Prof. Dr. H. Hilmi HACISALİHOĞLU

ANADOLU UNIVERSITY BILECIK SEYH EDEBALI

UNIVERSITY

Graduate School of Sciences

Department of Mathematics

SPECIAL SMARANDAHE CURVES

Fatih KARAMAN

Master’s Thesis

Thesis Advisor

Yrd.Doç. Dr. Osman Zeki OKUYUCU

Co -Advisor

Prof. Dr. H. Hilmi HACISALİHOĞLU

TEŞEKKÜR

Bu çalışmanın hazırlanması sırasında değerli zamanını ayıran ilgi ve önerileriyle beni yönlendiren Sayın hocam Yrd. Doç. Dr. Osman Zeki OKUYUCU’ ya minnet ve şükranlarımı sunarım.

Ayrıca çalışmam süresince fikirleriyle her konuda desteğini gördüğüm deneyimleri ile bana yol gösteren Sayın hocam Prof. Dr. H. Hilmi HACISALİHOĞLU’ na teşekkürü bir borç bilirim.

Çalışmalarım sırasında birçok fedakarlıklar göstererek beni destekleyen eşim

Tuba KARAMAN’ a ve bana karşı olan inançlarını her zaman hissettiğim aileme sonsuz

ÖZET

Bu tez dört bölümden oluşmaktadır. Birinci bölüm giriş kısmına ayrılmıştır. İkinci bölümde Öklid uzayındaki temel kavramlar ve eğriler konusu tanıtıldı. Ayrıca Frenet Çatıları ve Serret-Frenet formülleri üzerinde duruldu. Üçüncü bölümde 3-boyutlu Öklid Uzayında Frenet çatısına göre Smarandache eğrileri tanıtılmış bu eğrilerin eğrilik ve torsiyonları ayrı ayrı hesaplandı. Dördüncü bölümde eğrinin helis eğrisi olma durumları üzerinde duruldu ve bunun ile ilgili teoremlere yer verildi. Elde edilen bulgular değerlendiriltikten sonra ‘’ Smarandache eğrileri ne zaman helis olur? ‘’ sorusunun cevabı araştırıldı.

Anahtar Kelimeler

ABSTRACT

This thesis consists of four chapters. The first chapter is devoted to the introduction. In the second chapter, basic concepts and curves in Euclidean space subject introduced. Also it is mentioned in the Frenet frame and Serret-Frenet formulas over.- In third chapter, it is introduced the Smarandache curves according to Frenet frame in 3-dimensional Euclidean Space. In the fourth chapter, it is focused on the states being helix of a curve and however was given to the related theorems. The findings were evolated after ‘’ When the curve happens a helix?’’ was investigated in response to the question.

Key Words

İÇİNDEKİLER Sayfa No JÜRİ ONAY SAYFASI TEŞEKKÜR ÖZET………....i ABSTRACT………...ii İÇİNDEKİLER………. iii

SİMGELER VE KISALTMALAR ……….iv

ŞEKİLLER LİSTESİ ………....v

1. GİRİŞ………..1

2. TEMEL KAVRAMLAR……...………2

2.1. 𝚬𝒏_{, n-boyutlu Öklid Uzayında Temel Kavramlar………...2}

2.2. 𝚬𝒏_{, n-boyutlu Öklid Uzayında Eğriler Teorisi……… .5}

3. 𝔼𝟑 3-BOYUTLU ÖKLİD UZAYINDA SMARANDACHE EĞRİLERİ……….11

3.1. TN-Smarandache Eğrisi………..11 3.2. TB-Smarandache Eğrisi………..14 3.3. NB-Smarandache Eğrisi………..16 3.4. TNB-Smarandache Eğrisi………...19 3.5. TC-Smarandache Eğrisi………...23 3.6. NC-Smarandache Eğrisi………..26 3.7. BC-Smarandache Eğrisi………..30 3.8. TNBC-Smarandache Eğrisi……….…33

4. SMARANDACHE EĞRİLERİNDE HELİSLİK………...38

4.1. Helis Eğrisi ve İnvolüt ile İlgili Teoremler………...38

4.2. Smarandache Eğrilerinin Helis Eğrisi Olma Durumları………...41

KAYNAKLAR………...49 ÖZGEÇMİŞ

SİMGELER VE KISALTMALAR

ℝ : Reel Sayılar Cümlesi

𝔼3 _{: 3-boyutlu Öklid uzayı}

‖ ‖ : Norm

〈 , 〉 : İç çarpım

⋀ : 𝔼3 _{de Vektörel çarpım}

𝑘 : Eğrinin eğriliği

𝜏 : Eğrinin burulması (torsiyonu)

{𝕋, ℕ, 𝔹} : Frenet çatısı

𝑊 : Darboux vektörü

C : Birim Darboux vektörü

𝛽 : 𝛽 eğrisi

ŞEKİLLER DİZİNİ

Sayfa No

Şekil 2.1 Eğri………..5

Şekil 2.2 Paramatre Değişimi……….…....6

Şekil 2.3 Frenet vektörleri………..8

1. GİRİŞ

Eğriler teorisi, geometri de çok kapsamlı bir çalışma alanı oluşturur. Eğrinin eğrilik ve burulma değerlerinin hesaplanmasıyla eğrinin biçimini ve uzunluğunu belirleyebiliriz. Özelikle eğrinin Serret-Frenet vektörleri bize eğri hakkında çok önemli bulgular sağlar.

Smarandache eğrisi, regüler bir eğrinin Frenet vektörleri ile üretilen yer vektörüne sahip regüler eğri olarak tanımlanır. Bu konu ile ilgili ilk çalışmalar, A. T. Ali tarafından oluşturuldu. 𝔼3 _{3-boyutlu Öklid uzayında bazı özel Smarandache eğrilerini ifade etmiş}

ve özel bir durumun Serret-Frenet elemanlarını tanıtmıştır. Bu tez çalışmasında ise bu çalışma paralelinde değişik Smarandache eğrilerinin eğrilikleri ve torsiyonları hesaplanmıştır.

𝔼3 _{3-boyutlu Öklid uzayında kuşkusuz en önemli eğrilerden birisi genel}

helislerdir. Helisler günlük hayatımızda en sık karşılaştığımız eğrilerdendir. 𝑘 ve 𝜏 eğriliklerinin ayrı ayrı sabit olmasıyla oluşan eğrilere dairesel helis adı verilir. Genel helisler 𝑘 ve 𝜏 sabit olmadığı halde 𝑘 / 𝜏 oranının sabit olmasıyla oluşur. Bir koni veya bir küre yüzeyi üzerinde çizilebilen helislerin olup olmadığı fikri, bizi helislerin tanımını daha da genelleştirme gereğine sevk etmiştir. Böylece Alman matematikçi E. Müller helisleri ‘’ Her noktada sabit bir doğrultu ile sabit açı yapan eğriler’’ olarak tanımlamış ve bunlara Eğilim çizgileri adını vermiştir.

Bu tez çalışmasında ise Smarandache eğrileri ve onların özel halleri ele alınıp bu özel haller arasındaki eğilim çizgilerinin varlığı araştırıldı. Smarandache eğrileri ne zaman helis olur? Esas eğri helis iken Smarandache eğrisi ne zaman helis olur? sorularının cevabı arandı. Böylece Smarandache eğrilerinin aynı cinsten eğriler olarak ifade edilebileceği bulgusuna varıldı.

2. TEMEL KAVRAMLAR 2.1. 𝚬𝒏, n-boyutlu Öklid Uzayında Temel Kavramlar

Bu bölümde Ε𝑛 _{n-boyutlu Öklid uzayındaki temel kavram ve teoremlerden}

bahsedilecektir.

Tanım 2.1.1. A boş olmayan bir cümle ve bir K cismi üzerindeki vektör uzayı V olsun.

Aşağıdaki önermeleri doğrulayan bir 𝑓; 𝐴 𝑥 𝐴 ⟶ 𝑉 fonksiyonu varsa, A ya V ile birleştirilmiş afin uzay denir(Hacısalihoğlu,1983).

i. ∀ 𝑃, 𝑄 ∈ 𝐴 için 𝑓(𝑃, 𝑄) = 𝑃𝑄⃗⃗⃗⃗⃗ ∈ 𝑉

ii. ∀ 𝑃, 𝑄, 𝑅 ∈ 𝐴 için 𝑓(𝑃, 𝑄) + 𝑓(𝑄, 𝑅) = 𝑓(𝑃, 𝑅)

iii. Bir 𝑃 ∈ 𝐴 ve bir 𝛽 ∈ 𝑉 için 𝑓(𝑃, 𝑄) = 𝛽 olacak şekilde bir tek 𝑄 ∈ 𝐴 noktası vardır.

Tanım 2.1.2. Bir reel afin uzay A ve A ile eşlenen vektör uzayı da V olsun. V vektör

uzayında, boy V = n olmak üzere,

< , > ; 𝑉 𝑥 𝑉 → ℝ

(𝑥, 𝑦) → ∑𝑛𝑖=1𝑥𝑖 𝑦𝑖 {𝑥 = (𝑥1, 𝑥2., … , 𝑥𝑛

) 𝑦 = (𝑦₁, 𝑦₂, … , 𝑦_𝑛)

biçiminde Öklid iç çarpımı tanımlanırsa A afin uzayına n-boyutlu Öklid uzayı denir ve 𝔼𝑛 _{ile gösterilir. 𝔼}𝑛 _{ile eşlenen reel vektör uzayı da ℝ}𝑛 _{ile gösterilir. 𝔼}𝑛 _{in elemanları}

noktalar ve ℝ𝑛 _{in elemanları vektörlerdir(Hacısalihoğlu,1983).}

Tanım 2.1.3. n-boyutlu bir reel iç çarpım uzayı V ve V ile birleşen Öklid uzayı 𝔼𝑛 _olsun.

V vektör uzayı üzerindeki norm ‖ ‖ olmak üzere,

𝑑; 𝔼𝑛 _{𝑥 𝔼}𝑛 _{→ ℝ}

(𝑥, 𝑦) → 𝑑(𝑥, 𝑦) = ‖𝑥𝑦⃗⃗⃗⃗ ‖ = √∑ (𝑦𝑛𝑖=1 𝑖− 𝑥𝑖)2

şeklinde tanımlanan 𝑑 fonksiyonuna 𝔼𝑛_{, n-boyutlu Öklid uzayında uzaklık fonksiyonu}

ve ∀𝑥, 𝑦 ∈ 𝔼𝑛 için 𝑑(𝑥, 𝑦) değerine 𝑥 ile 𝑦 noktaları arasındaki uzaklık denir(Hacısalihoğlu,1983).

Teorem 2.1.1. n-boyutlu Öklid uzayında uzaklık fonksiyonu bir metrik

belirtir(Hacısalihoğlu,1983).

Tanım 2.1.4. , ∈ 𝔼𝑛 olmak üzere,

𝑑; 𝔼𝑛_{𝑥 𝔼}𝑛 _{→ ℝ}

(𝑥, 𝑦) → 𝑑(𝑥, 𝑦) = ‖𝑥𝑦⃗⃗⃗⃗ ‖

biçiminde tanımlanan d fonksiyonunun belirttiği metriğe 𝔼𝑛 _{de Öklid metriği}

denir(Hacısalihoğlu,1983).

Tanım 2.1.5. 𝔼𝑛 _{n-boyutlu Öklid uzayında farklı üç nokta x, y, z olsun.}

𝑥𝑦

⃗⃗⃗⃗ ile 𝑥𝑧⃗⃗⃗⃗ vektörleri arasındaki açı 𝜃 ∈ ℝ , 0 ≤ 𝜃 ≤ 𝜋 olmak üzere,

cos 𝜃 = 〈𝑥𝑦 ⃗⃗⃗⃗⃗ , 𝑥𝑧⃗⃗⃗⃗⃗ 〉 ‖𝑥𝑦⃗⃗⃗⃗ ‖ ‖𝑥𝑧⃗⃗⃗⃗ ‖

ifadesinden hesaplanan 𝜃 reel sayısıdır(Hacısalihoğlu,1983).

Tanım 2.1.6. ℝ𝑛_{, n-boyutlu standart reel iç çarpım uzayı ile eşleşen 𝔼}𝑛 _{Öklid uzayında}

sıralı bir {𝑃⃗⃗⃗⃗⃗⃗⃗⃗ , 𝑃₀𝑃₁ ⃗⃗⃗⃗⃗⃗⃗⃗ , … , 𝑃₀𝑃₂ ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ } vektör sistemi, ℝ₀𝑃_𝑛 𝑛_{, iç çarpım uzayının bir ortonormal bazı}

ise bu nokta (𝑛 + 1)-lisine bir dik çatı veya Öklid çatısı denir(Hacısalihoğlu,1983).

Tanım 2.1.7. ℝ3 _{, 3-boyutlu Öklid uzayı ve 𝑥, 𝑦 ∈ ℝ}3 _olsun.

∧ ; ℝ3 _{𝑥 ℝ}3 _{→ ℝ}3 𝑥 = (𝑥1, 𝑥2, 𝑥3) , 𝑦 = (𝑦1, 𝑦2, 𝑦3) olmak üzere (𝑥 , 𝑦 ) → 𝑥 ∧ 𝑦 = ∑ 𝑑𝑒𝑡(𝑒⃗⃗⃗ , 𝑥𝑖 ⃗⃗ , 𝑦⃗⃗⃗ ) 3 𝑖=1 = |𝑥𝑒⃗⃗⃗ 𝑒1₁ 𝑥⃗⃗⃗ 𝑒2₂ ⃗⃗⃗ 𝑥3₃ 𝑦₁ 𝑦₂ 𝑦₃|

şeklinde tanımlı ∧ işlemine ℝ3 _{üzerinde vektörel çarpım denir. 𝑥 ∧ 𝑦 vektörü hem 𝑥}

hem de 𝑦 vektörüne dik bir vektördür ve

‖𝑥 ∧ 𝑦 ‖ = ‖𝑥 ‖ ‖𝑦 ‖ sin 𝜃

dır(Hacısalihoğlu,1983).

Tanım 2.1.8. ℝ𝑛 _{n-boyutlu Öklid uzayı ve 𝑥 ∈ ℝ}𝑛 _{için 𝑥 vektörünün normu}

‖𝑥 ‖ = √〈𝑥 , 𝑥 〉

biçiminde tanımlanır(Hacısalihoğlu,1983).

Tanım 2.1.9. V vektör uzayı ile eşlenen afin uzay A olsun. P ∈ 𝐴 ve 𝜗 ∈ 𝑉 için (𝑃, 𝜗 ) sıralı ikilisine A afin uzayının P noktasındaki bir tanjant vektörü denir. A afin uzayının P noktasındaki tanjant vektörlerinin cümlesi 𝑇𝐴(𝑃) ile gösterilir(Hacısalihoğlu,1983).

𝑇𝐴(𝑃) de toplama ve skaler ile çarpma işlemleri sırasıyla,

⊕ ; 𝑇𝐴(𝑃) × 𝑇𝐴(𝑃) → 𝑇𝐴(𝑃)

((𝑃, 𝜗 ) , (𝑃, 𝑢⃗ )) → (𝑃, 𝜗 ) ⊕ (𝑃, 𝑢⃗ ) = (𝑃, 𝜗 + 𝑢⃗ ) ⊙ ; ℝ × 𝑇_𝐴(𝑃) → 𝑇𝐴(𝑃)

(𝜆, (𝑃, 𝜗 )) = 𝜆 ⊙ (𝑃, 𝜗 ) = (𝑃, 𝜆𝜗 )

biçiminde tanımlanır. Burada ℝ ile A nın eşlendiği V vektör uzayının cismi gösterilmektedir. {𝑇_𝐴(𝑃), ⊕, ℝ, +, . , ⊙ } vektör uzayına, A afin uzayının P noktasındaki bir tanjant uzayı denir ve kısaca 𝑇𝐴(𝑃) ile gösterilir(Hacısalihoğlu,1983).

Tanım 2.1.10. A⊂ 𝔼𝑛 _{üzerindeki bir vektör alanı}

biçiminde birebir ve örten bir fonksiyondur.

Böylece 𝔼𝑛 _{de bir X vektör alanı, ∀ 𝑃 ∈ 𝔼}𝑛 _{noktasına bir 𝑋} 𝑃

⃗⃗⃗⃗ tanjant vektörü karşılık getiren bir fonksiyon olarak düşünülebilir.

𝔼𝑛 _{de vektör alanlarının cümlesi 𝒳(𝔼}𝑛_{) ile gösterilirse, tanjant uzayına benzer şekilde}

{𝒳(𝔼𝑛_{), ⊕, ℝ, +, . , ⊙ } altılısının da vektör uzayı olduğu gösterilebilir. Bu vektör}

uzayına 𝔼𝑛 _{üzerindeki vektör alanlarının uzayı denir ve kısaca 𝒳(𝔼}𝑛_{) ile}

gösterilir(Hacısalihoğlu,1983).

2.2. 𝚬𝒏, n-boyutlu Öklid Uzayında Eğriler Teorisi Tanım 2.2.1. 𝐼 ⊂ ℝ bir açık aralık ve

𝛼; 𝐼 → Ε𝑛

𝑡 → 𝛼(𝑡) = (𝛼1(𝑡), 𝛼2(𝑡), … , 𝛼𝑛(𝑡))

şeklinde tanımlı 𝛼 fonksiyonu diferensiyellenebilir bir fonksiyon olsun. Bu takdirde 𝛼(𝐼) ⊂ 𝔼𝑛 _{cümlesine 𝔼}𝑛_{, n-boyutlu Öklid uzayında (𝐼, 𝛼) koordinat komşuluğu ile}

verilen bir eğri denir. 𝐼 ⊂ ℝ aralığına 𝛼 eğrisinin parametre aralığı ve 𝑡 ∈ 𝐼 değişkenine de 𝛼(𝑡) eğrisinin parametresi denir(Hacısalihoğlu,1983).

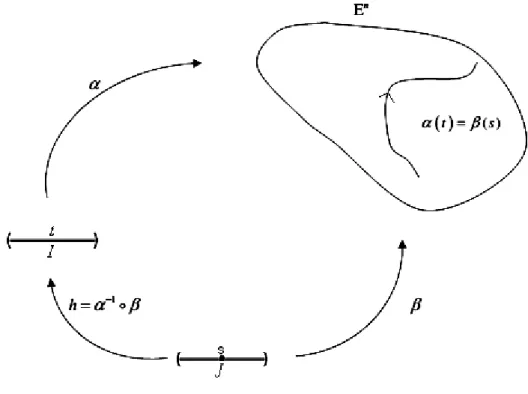
Tanım 2.2.2. 𝔼𝑛 _{de bir M eğrisi (𝐼, 𝛼) ve (𝐽, 𝛽) gibi iki koordinat komşuluğu ile verilsin.}

ℎ = 𝛼−1_{𝜊𝛽; 𝐽 → 𝐼}

diferansiyellenebilir fonksiyonuna M-nin bir parametre değişimi (M-nin I daki parametresinin J deki parametre ile değişimi) denir(Hacısalihoğlu,1983).

Şekil 2.2. Parametre değişimi.

Tanım 2.2.3. 𝔼𝑛 _{de bir M eğrisi (𝐼, 𝛼) koordinat komşuluğu ile verilsin.}

𝑡 → ‖𝛼′‖(𝑡) = ‖𝛼′(𝑡)‖

şeklinde tanımlı ‖𝛼′‖ fonksiyonuna, M eğrisinin (𝐼, 𝛼) koordinat komşuluğuna göre skaler hız fonksiyonu ‖𝛼′(𝑡)‖ reel sayısına da M eğrisinin 𝛼(𝑡) noktasındaki skaler hızı denir.

Eğer ‖𝛼′(𝑡)‖ = 1 ise M eğrisine birim hızlı eğri ve 𝑡 ∈ 𝐼 parametresine de eğrinin yay parametresi denir(Hacısalihoğlu,1983).

Tanım 2.2.4. 𝔼𝑛 _{de bir M eğrisi (𝐼, 𝛼 ) koordinat komşuluğu ile verilsin. 𝛼; 𝐼 → Ε}𝑛

fonksiyonunun Öklid koordinat fonksiyonları {𝛼1, 𝛼2, . . . , 𝛼𝑛} olmak üzere,

𝛼(𝑡) = (𝛼₁(𝑡), 𝛼2(𝑡), … , 𝛼𝑛(𝑡)) 𝑑𝛼 𝑑𝑡 = 𝛼′(𝑡) = ( 𝑑𝛼1 𝑑𝑡 , 𝑑𝛼2 𝑑𝑡 , … , 𝑑𝛼𝑛 𝑑𝑡 ) şeklindedir. (𝛼(𝑡), 𝛼′_{(𝑡)) ∈ 𝑇}

𝔼𝑛(𝑃) tanjant vektörüne, M eğrisinin t ∈ 𝐼 parametre

değerine karşılık gelen 𝛼(t) noktasında (𝐼, 𝛼) koordinat komşuluğuna göre hız vektörü denir(Hacısalihoğlu,1983).

Tanım 2.2.5. Her noktasındaki hız vektörü sıfırdan farklı olan eğriye ( yani ∀ 𝑡 ∈ 𝐼 için 𝛼′_{(𝑡) ≠ 0) regüler eğri denir(Hacısalihoğlu,1983).}

Tanım 2.2.6. 𝔼𝑛 _{de bir M eğrisi (𝐼, 𝛼) koordinat komşuluğu ile verilsin. Bu durumda}

𝜓 = {𝛼′_{, 𝛼}′′_{, … , 𝛼}𝑟_{} sistemi lineer bağımsız ve ∀ 𝛼}𝑘 _{∈ 𝑆𝑝{𝜓} olmak üzere 𝜓 den elde}

edilen {𝑉1, 𝑉2, … , 𝑉𝑟} ortonormal sistemine, M eğrisinin Serret-Frenet r-ayaklı alanı ve

𝑡 ∈ 𝑀 için {𝑉1(𝑡), 𝑉2(𝑡), … , 𝑉𝑟(𝑡)} ye ise 𝑡 ∈ 𝑀noktasındaki Serret-Frenet r-ayaklısı

denir(Hacısalihoğlu,1983).

Tanım 2.2.7. 𝔼𝑛 _{de bir M eğrisi (𝐼, 𝛼) koordinat komşuluğu ile verilsin. 𝑡 ∈ 𝐼 ya}

karşılık gelen 𝛼(t) noktasındaki Serret-Frenet r-ayaklısı {𝑉₁(𝑡), 𝑉₂(𝑡), … , 𝑉_𝑟(𝑡)} olsun. Buna göre;

𝜅_𝑖 ; 𝐼 → ℝ

𝑡 → 𝜅𝑖(𝑡) = 〈𝑉′𝑖(𝑡) , 𝑉′𝑖+1(𝑡)〉 , 1 ≤ 𝑖 < 𝑟

şeklinde tanımlı 𝜅_𝑖 fonksiyonuna M eğrisinin i-yinci eğrilik fonksiyonu ve 𝑡 ∈ 𝐼 için 𝜅𝑖(𝑡) sayısına da 𝛼(𝑡) noktasında M nin i-yinci eğriliği denir(Hacısalihoğlu,1983).

Teorem 2.2.1. 𝔼𝑛 de bir M eğrisi (𝐼, 𝛼) koordinat komşuluğu ile verilsin. 𝑡 ∈ 𝐼 yay

parametresi olmak üzere, 𝛼(t) noktasında M nin i-yinci eğriliği 𝑘𝑖(𝑡) ve Frenet r-ayaklısı

{𝑉1(𝑡), 𝑉2(𝑡), … , 𝑉𝑟(𝑡)} olmak üzere,

i. 𝑉′₁(𝑡) = 𝑘₁(t).𝑉₂(𝑡)

ii. 𝑉′_𝑖(𝑡) = −𝑘_𝑖−1(𝑡). 𝑉_𝑖−1(𝑡) + 𝑘_𝑖(𝑡). 𝑉_𝑖+1(𝑡) , 1 < 𝑖 < 𝑟 iii. 𝑉′_𝑟(𝑡) = −𝑘_𝑟−1(𝑡). 𝑉_𝑟−1(𝑡)

dır. Bu eşitliklere Frenet formülleri denir(Hacısalihoğlu,1983).

Teorem 2.2.2. 𝔼3 de bir M eğrisi (𝐼, 𝛼) koordinat komşuluğu ile verilsin. 𝑠 ∈ 𝐼 yay

parametresi olmak üzere, M eğrisinin {𝕋(𝑠), ℕ(𝑠), 𝔹(𝑠)} Frenet vektörleri

𝕋(𝑠) = 𝛼′(s)

ℕ(𝑠) =_{‖𝛼′′}1_(𝑠)‖. 𝛼′′(𝑠) (2.1) 𝔹(𝑠) = 𝕋(𝑠) ∧ ℕ(𝑠)

şeklindedir(Hacısalihoğlu,1983).

Şekil 2.3. Frenet vektörleri.

Teorem 2.2.3. 𝔼3 de bir M eğrisi (𝐼, 𝛼) koordinat komşuluğu ile verilsin. 𝑡 ∈ 𝐼 herhangi

bir parametre olmak üzere, M eğrisinin 𝛼(𝑡) noktasındaki {𝕋(𝑡), ℕ(𝑡), 𝔹(𝑡)} Frenet vektörleri;

𝕋(𝑡) =

𝛼′(𝑡) ‖𝛼′(𝑡)‖

ℕ(𝑡) = 𝔹(𝑡) ∧ 𝕋(𝑡)

(2.2)

𝔹(𝑡) =

𝛼 ′_{(𝑡) ∧ 𝛼′′(𝑡)} ‖𝛼′_{(𝑡)∧ 𝛼′′(𝑡)‖} şeklinde hesaplanır(Hacısalihoğlu,1983).

Teorem 2.2.4. 𝔼3 de bir M eğrisi (𝐼, 𝛼) koordinat komşuluğu ile verilsin. 𝑡 ∈ 𝐼 herhangi

bir parametre olmak üzere M eğrisinin 𝛼(𝑡) noktasındaki eğriliği ve burulması (torsiyonu), sırasıyla, 𝑘(𝑡) ve 𝜏(𝑡) olmak üzere,

𝑘(𝑡) =

‖𝛼′(𝑡) ∧ 𝛼′′(𝑡)‖

‖𝛼′(𝑡)‖

3

𝜏(𝑡) =

< 𝛼′( 𝑡 ) ∧𝛼_{‖ 𝛼′ (𝑡) ∧ 𝛼}′′( 𝑡 ) , 𝛼_{′′(𝑡) ‖}′′′( 𝑡 ) >₂

(2.3)

formülleri ile hesaplanır(Sabuncuoğlu,2006).

Teorem 2.2.5. 𝛼 ⊂ 𝔼3 eğrisi, 𝑠 ∈ 𝐼 yay parametresi cinsinden verilsin. 𝛼(𝑠) eğrisinin

Frenet 3-ayaklısı {𝕋(𝑠), ℕ(𝑠), 𝔹(𝑠)}; eğrilik ve burulması, sırasıyla, 𝑘(𝑠) ve 𝜏(𝑠) olmak üzere 𝛼(𝑠) eğrisinin frenet formülleri,

𝕋′_{(𝑠) = 𝑘(𝑠)ℕ(𝑠)}

ℕ′_{(𝑠) = −𝑘(𝑠)𝕋(𝑠) + 𝜏(𝑠)𝔹(𝑠) (2.4)}

𝔹′_{(𝑡) = −𝜏(𝑠)ℕ(𝑠)}

dir. Frenet formüllerinin matris olarak gösterimi ise,

[𝕋 ′ ℕ′ 𝔹′ ] = [ −𝑘0 𝑘0 0𝜏 0 −𝜏 0 ] [ℕ𝕋 𝔹 ] (2.5) Şeklindedir(Sabuncuoğlu,2006).

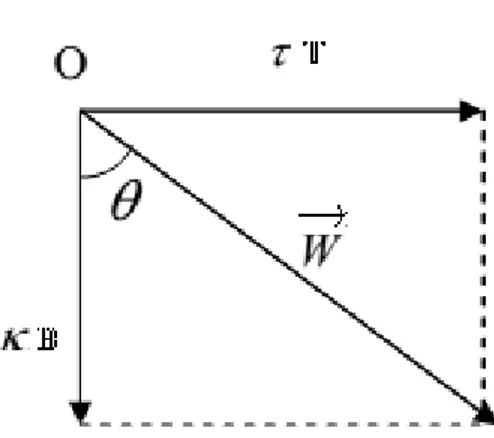
Tanım 2.2.8. 𝛼 ⊂ 𝔼3 _{eğrisinin 𝛼(𝑠) noktasındaki {𝕋(𝑠), ℕ(𝑠), 𝔹(𝑠)} Frenet 3-}

ayaklısının her s anında bir eksen etrafında bir ani helis hareketi yaptığı kabul edilir. Bu eksene eğrinin Darboux ekseni, bu eksenin yön ve doğrultusunu veren vektöre Darboux vektörü denir ve W ile gösterilir. Burada B ile W vektörü arasındaki açı 𝜑 ile gösterilirse,

𝑘 = ‖𝑊‖𝑐𝑜𝑠𝜑

𝜏 = ‖𝑊‖𝑠𝑖𝑛𝜑 (2.6) olur. Darboux vektörü yönündeki birim vektör ise,

𝐶 = 𝑠𝑖𝑛𝜑 𝕋 + 𝑐𝑜𝑠𝜑 𝔹 şeklinde bulunur.

Şekil 2.4. Darboux vektörü.

3. 𝔼𝟑, 3-BOYUTLU ÖKLİD UZAYINDA SMARANDACHE EĞRİLERİ 3.1. TN-Smarandache Eğrisi

Tanım 3.1.1. s yay paramatresi ve 𝛽 = 𝛽(𝑠) eğrisi 𝔼𝟑 _{de birim hızlı regüler bir eğri}

olsun. 𝛽(𝑠) eğrisinin Frenet vektörleri {𝕋(𝑠), ℕ(𝑠), 𝔹(𝑠)} olmak üzere TN-Smarandache eğrisi,

𝛽_𝑇𝑁(𝑠) =_√21 (𝕋(𝑠) + ℕ(𝑠)) (3.1)

şeklinde tanımlanır(Ahmad.T,2010). Bu eğrinin yay parametresini 𝑠𝛽 ile ifade edersek

TN- Smarandache eğrisinin eğrilik ve torsiyonunu hesaplayabiliriz. Bunun için eğrinin türevini alırsak,

𝑑𝛽𝑇𝑁 𝑑𝑠𝛽 𝑑𝑠𝛽 𝑑𝑠

=

1 √2

(−𝑘 𝕋 + 𝑘 ℕ + 𝜏 𝔹)

(3.2)

ifadesini elde ederiz. Bu ifadenin normunu alırsak,

‖𝑑𝛽𝑇𝑁 𝑑𝑠𝛽 ‖ = 1

olduğundan

𝑑𝑠_𝑑𝑠𝛽

= √

2𝑘2₂+𝜏2

(3.3)

bulunur. Buradan 𝛽𝑇𝑁(𝑠) eğrisinin teğet vektör alanı,

𝕋

_𝛽𝑇𝑁

=

(−𝑘 𝕋 + 𝑘 ℕ+ 𝜏 𝔹)

√2𝑘2_+𝜏2 (3.4)

şeklinde bulunur. Bu teğet vektörünün tekrar türevini alırsak,

𝛿

₁

= −[𝑘

2

_(2𝑘

2

_{+ 𝜏}

2

_{) + 𝜏(𝜏𝑘}

′

_{− 𝑘𝜏′)]}

𝛿

₂

= −[𝑘

2

_(2𝑘

2

_{+ 3𝜏}

2

_{) − 𝜏(𝜏}

3

_{+ 𝑘𝜏′ − 𝜏𝑘}

′

_)]

_(3.5)

olmak üzere,

𝕋

′_𝛽𝑇𝑁

=

𝛿1 𝕋 + 𝛿2 ℕ+𝛿3 𝔹

( 2𝑘2 _{+ 𝜏}2 ₎3⁄₂ (3.6)

ifadesini buluruz. O zaman (3.6) ifadesini şu şekilde yazabiliriz;

𝕋

′

𝛽𝑇𝑁

=

√2

(2𝑘2 _{+ 𝜏}2 ₎2

(𝛿

1

𝕋 + 𝛿

2

ℕ+𝛿

3

𝔹)

(3.7)

bu denklemden 𝛽_𝑇𝑁(𝑠) eğrisinin

𝑘

_𝛽𝑇𝑁 eğriliği için,

𝑘

_𝛽𝑇𝑁

= ‖𝕋

′ 𝛽𝑇𝑁

‖ =

√2 (2𝑘2 _{+ 𝜏}2 ₎2

√𝛿

1 2

_{+ 𝛿}

22

+ 𝛿

32 (3. 8)

olur. Diğer taraftan

ℕ

_𝛽𝑇𝑁

=

𝕋

′ 𝛽𝑇𝑁

‖𝕋′

𝛽𝑇𝑁‖ olduğundan

𝛽

𝑇𝑁 eğrisinin asli normal vektör

alanı,

ℕ

_𝛽𝑇𝑁

=

(𝛿1 𝕋+𝛿2 ℕ+𝛿3 𝔹)

√𝛿12+𝛿22+𝛿32

(3.9)

olur

𝔹

_𝛽𝑇𝑁

=

𝕋

_𝛽𝑇𝑁 ∧

ℕ

_𝛽𝑇𝑁 ifadesinden binormal vektör alanı,

𝔹

_𝛽𝑇𝑁

=

1 √2𝑘2 _{+ 𝜏}2_√𝛿12_+𝛿22_+𝛿32

|

𝕋

ℕ

𝔹

−𝑘

𝑘

𝜏

𝛿

₁

𝛿

₂

𝛿

₃

|

(3.10) ve böylece

𝔹

_𝛽𝑇𝑁

=

(𝑘𝛿

3

− 𝜏𝛿

2

)𝕋 + (𝜏𝛿

1

+ 𝑘𝛿

3

)ℕ + (𝑘𝛿

2

+ 𝑘𝛿

1

)𝔹

√2𝑘

2

_{+ 𝜏}

2

_√𝛿

12

+ 𝛿

22

+ 𝛿

32

(3.11)

ifadesi elde edilir. Torsiyonu bulmak için 𝛽_𝑇𝑁 eğrisinin ikinci ve üçüncü türevlerini bulmamız gerekir. Buna göre;

𝛽′′_𝑇𝑁= 1 √2{−(𝑘 2_{+ 𝑘′)𝕋 + (𝑘}′_{− 𝑘}2_{− 𝜏}2_{)ℕ + (𝑘𝜏 + 𝜏′)𝔹}}

_(3.12) ve 𝛽′′′_𝑇𝑁= 1 √2{𝜔1𝕋 + 𝜔2ℕ + 𝜔3𝔹}

(3.13) bulunur. Burada; 𝜔1 = 𝑘3+ 𝑘(𝜏2− 3𝑘′) − 𝑘′′ 𝜔₂ = −𝑘3_{− 𝑘(𝜏}2_{+ 3𝑘}′_{) − 3𝜏𝜏}′_{+ 𝑘}′′

_(3.14) 𝜔₃ = −𝑘2_{𝜏 − 𝜏}3 _{+ 2𝜏𝑘}′_{+ 𝑘𝜏}′_{+ 𝜏′′}

dır. (2.3) bağıntısında (3.2), (3.12), (3.13) ifadeleri yerlerine yazılıp gerekli hesaplamalar yapılırsa

𝛽

_𝑇𝑁 eğrisinin 𝜏_𝛽𝑇𝑁 torsiyonu olarak,

𝜏_𝛽𝑇𝑁 =

√

2

[

(

𝑘2+ 𝜏2 − 𝑘′

)(

𝑘𝜔₃+ 𝜏𝜔₁

)

+ 𝑘

(

𝜏′ + 𝑘𝜏

)(

𝜔₁+ 𝜔₂

)

+

(

𝑘𝜔₃ − 𝜏𝜔₂

)(

𝑘2+ 𝑘′

)

]

[

𝜏

(

2𝑘2 + 𝜏2

₎

_{+ 𝑘𝜏}′ _{− 𝜏𝑘}′

_]

2₊

₍

_𝑘𝜏′ _{− 𝑘}′_𝜏

₎

2 ₊

₍

_2𝑘3 _{+ 𝑘𝜏}2

₎

2 (3.15) olarak bulunur.

Sonuç 3.1. s yay paramatresi ve 𝛽; 𝐼 → 𝔼𝟑 _{eğrisinin Frenet çatısı {𝕋, ℕ, 𝔹} olmak üzere}

TN-Smarandache eğrisinin eğriliği

𝑘

_𝛽𝑇𝑁 ve torsiyonu 𝜏_𝛽𝑇𝑁 aşağıdaki gibidir;

𝑘

_𝛽𝑇𝑁

=

_(2.𝑘2√2 _{+ 𝜏2 )2}

√𝛿

₁2

+ 𝛿

₂2

+ 𝛿

₃2

(3.16)

𝜏_𝛽𝑇𝑁

=

√2[ (𝑘2_+𝜏2_−𝑘′_)(𝑘𝜔 3+𝜏𝜔1)+ 𝑘(𝜏′_{+𝑘𝜏)(𝜔} 1+𝜔2)+ (𝑘𝜔3−𝜏𝜔2)(𝑘2+𝑘′) ] [𝜏(2𝑘2 _{+ 𝜏}2_)+𝑘𝜏′_−𝜏𝑘′_]2_+(𝑘𝜏′_−𝑘′_𝜏)2_+(2𝑘3_+𝑘𝜏2₎2

(3.17)

dır. 3.2. TB-Smarandache Eğrisi

Tanım 3.2.1. s yay paramatresi ve 𝛽 = 𝛽(𝑠) eğrisi 𝔼𝟑 _{de birim hızlı regüler bir eğri}

olsun. 𝛽(𝑠) eğrisinin Frenet vektörleri {𝕋(𝑠), ℕ(𝑠), 𝔹(𝑠)} olmak üzere TB-Smarandache eğrisi,

𝛽𝑇𝐵(𝑠) =_√21 (𝕋(𝑠) + 𝔹(𝑠)) (3.18)

şeklinde tanımlanır(Ahmad.T,2010). Bu eğrinin yay parametresini 𝑠_𝛽 ile ifade edersek TB- Smarandache eğrisinin eğrilik ve torsiyonunu hesaplayabiliriz. Bunun için eğrinin türevini alırsak,

𝑑𝛽_𝑑𝑠𝑇𝐵 𝛽 𝑑𝑠𝛽 𝑑𝑠 = 1 √2((𝑘 − 𝜏)ℕ)

(3.19)

ifadesini elde ederiz. Bu ifadenin normunu alırsak,

‖𝑑𝛽𝑇𝐵 𝑑𝑠_𝛽 ‖ = 1 olduğundan,

𝑑𝑠_𝑑𝑠𝛽

= √

(𝑘−𝜏)₂ 2

=

|𝑘−𝜏|

bulunur. Buradan 𝛽_𝑇𝐵(𝑠) eğrisinin teğet vektör alanı,

𝕋𝛽𝑇𝐵 = {ℕ 𝑘 > 𝜏 _{−ℕ 𝑘 < 𝜏} (3.21)

şeklinde bulunur. Bu teğet vektörünün tekrar türevini alırsak,

𝕋′

𝛽𝑇𝐵 = {−𝑘 𝕋 + 𝜏 𝔹 𝑘 > 𝜏 _{𝑘 𝕋 − 𝜏 𝔹 𝑘 < 𝜏}

(3.22)

ifadesini buluruz. Bu denklemden 𝛽𝑇𝐵(𝑠) eğrisinin

𝑘

𝛽𝑇𝐵 eğriliği,

𝑘𝛽𝑇𝐵 = ‖𝕋′𝛽𝑇𝐵‖ = √𝑘2 + 𝜏2 (3.23)

bulunur. Diğer taraftan

ℕ

_𝛽𝑇𝐵

=

𝕋

′ 𝛽𝑇𝐵

‖𝕋′

𝛽𝑇𝐵‖ olduğundan asli normal vektör alanı,

ℕ_𝛽𝑇𝐵 = 1

√𝑘2 _{+ 𝜏}2{−𝑘 𝕋 + 𝜏 𝔹 𝑘 > 𝜏 _{𝑘 𝕋 − 𝜏 𝔹 𝑘 < 𝜏} (3.24)

olur

.

𝔹

_𝛽𝑇𝐵

=

𝕋

_𝛽𝑇𝐵 ∧

ℕ

_𝛽𝑇𝐵 ifadesinden binormal vektör alanı,

𝔹𝛽𝑇𝐵 = 1 √𝑘2 _{+ 𝜏}2| 𝕋 ℕ 𝔹 0 1 0 𝑘 0 𝜏 | (3.25) ve böylece,

𝔹

_𝛽 𝑇𝐵

=

𝜏 𝕋+𝑘 𝔹 √_𝑘2 _{+ 𝜏}2

(3.26)

ifadesi bulunur. Torsiyonu bulmak için 𝛽_𝑇𝐵 eğrisinin ikinci ve üçüncü türevlerini bulmamız gerekir. Buna göre;

𝛽′′

_𝑇𝐵

=

1

√2

{(−𝑘

ve

𝛽′′′

_𝑇𝐵

=

1 √2

{𝜔

1

𝕋 + 𝜔

2

ℕ + 𝜔

3

𝔹}

(3.28) bulunur. Burada; 𝜔1 = −3𝑘𝑘′+ 2𝑘𝜏′+ 𝑘′𝜏 𝜔₂ = (𝜏 − 𝑘)(𝜏2_{+ 𝑘}2_{) + 𝑘}′′_{− 𝜏′′ (3.29)} 𝜔₃ = −3𝜏𝜏′_{+ 2𝜏𝑘}′_{+ 𝑘𝜏}′

dır. (2.3) bağıntısında (3.19), (3.27), (3.28) ifadeleri yerlerine yazılıp gerekli hesaplamalar yapılırsa,

𝜏

_𝛽 𝑇𝐵

=

[(𝑘2+𝜏2−2𝑘𝜏) (𝑘𝜔₃+ 𝜏 𝜔₁)] 𝜏2_{[𝑘(𝑘− 2𝜏)+𝜏}2_]2_+(𝑘2_+𝜏2_{−2𝑘𝜏)}2 (3.30) olarak bulunur.

Sonuç 3.2. s yay paramatresi ve 𝛽; 𝐼 → 𝔼𝟑 _{eğrisinin Frenet çatısı {𝕋, ℕ, 𝔹} olmak üzere}

TB-Smarandache eğrisinin

𝛽

_𝑇𝐵 eğriliği ve torsiyonu

𝜏

_𝛽

𝑇𝐵 aşağıdaki gibidir;

𝑘

_𝛽𝑇𝐵

= √𝑘

2

_{+ 𝜏}

2

_(3.31)

𝜏

_𝛽 𝑇𝐵

=

[(𝑘2+𝜏2−2𝑘𝜏).(𝑘.𝜔₃+ 𝜏.𝜔₁)] 𝜏2[𝑘(𝑘− 2𝜏)+𝜏2_]2_+(𝑘2_+𝜏2_{−2𝑘𝜏)}2

(3.32) dır.

3.3. NB-Smarandache Eğrisi

Tanım 3.3.1. s yay paramatresi ve 𝛽 = 𝛽(𝑠) eğrisi 𝔼𝟑 _{de birim hızlı regüler bir eğri}

olsun. 𝛽(𝑠) eğrisinin Frenet vektörleri {𝕋(𝑠), ℕ(𝑠), 𝔹(𝑠)} olmak üzere NB-Smarandache eğrisi,

𝛽

_𝑁𝐵

(𝑠) =

1

√2

(

ℕ

(

𝑠

) + 𝔹(𝑠))

(3.33)

şeklinde tanımlanır (Ahmad.T,2010). Bu eğrinin yay parametresini 𝑠_𝛽 ile ifade edelim. O halde NB- Smarandache eğrisinin eğrilik ve torsiyonunu hesaplayabiliriz. Bunun için eğrinin türevini alırsak,

𝑑𝛽𝑁𝐵 𝑑𝑠𝛽 𝑑𝑠𝛽 𝑑𝑠

=

1 √2

(−𝑘𝕋 − 𝜏ℕ + 𝜏𝔹)

(3.34)

ifadesini elde ederiz. Bu ifadenin normunu alırsak,

‖ 𝑑𝛽𝑁𝐵 𝑑𝑠𝛽 ‖ = 1

olduğundan,

𝑑𝑠_𝑑𝑠𝛽

= √

𝑘2+2𝜏₂ 2

(3.35)

bulunur. Buradan 𝛽_𝑁𝐵(𝑠) eğrisinin teğet vektör alanı,

𝕋

_𝛽𝑁𝐵

=

(−𝑘 𝕋−𝜏 ℕ+𝜏 𝔹)

√𝑘2_+𝜏2

(3.36)

şeklinde bulunur. Bu teğet vektörünün tekrar türevini alırsak,

𝛿

₁

= (𝑘

2

_{+ 2𝜏}

2

_{)𝑘𝜏 + 2𝜏(𝑘𝜏}

′

_{− 𝜏𝑘′)}

𝛿

₂

= −(𝑘

2

_{+ 2𝜏}

2

_)(𝑘

2

_{+ 𝜏}

2

_{) + 𝑘(𝑘}

′

_{𝜏 − 𝜏′𝑘)}

_(3.37)

𝛿

₃

= (𝑘

2

_{+ 2𝜏}

2

_)(−𝜏

2

_{) + 𝑘(𝑘𝜏}

′

_{− 𝑘}

′

_𝜏)

olmak üzere,

𝕋

′ 𝛽_𝑁𝐵

=

𝛿1_{( 𝑘} 𝕋 + 𝛿₂ 2 ℕ+𝛿3 𝔹 +2 𝜏2 )3⁄2 (3.38)

ifadesini buluruz. O zaman (3.38) ifadesini şu şekilde yazabiliriz,

𝕋

′

𝛽𝑁𝐵

=

√2

(𝑘2 _{+2 𝜏}2 ₎2

(𝛿

1

𝕋 + 𝛿

2

ℕ+𝛿

3

𝔹)

(3.39)

Bu denklemden 𝛽_𝑁𝐵(𝑠) eğrisinin

𝑘

_𝛽𝑁𝐵 eğriliği,

𝑘

_𝛽𝑁𝐵

= ‖𝕋

′ 𝛽𝑁𝐵

‖ =

√2 (𝑘2 _{+2 𝜏}2 ₎2

√𝛿

1 2

_{+ 𝛿}

22

+ 𝛿

32 (3.40)

bulunur. Diğer taraftan

ℕ

_𝛽𝑁𝐵

=

𝕋

′ 𝛽𝑁𝐵

‖𝕋′

𝛽𝑁𝐵‖ olduğundan asli normal vektör alanı,

ℕ

_𝛽𝑁𝐵

=

(𝛿1 𝕋+𝛿2 ℕ+𝛿3 𝔹)

√𝛿12+𝛿22+𝛿32

(3.41)

olur.

𝔹

_𝛽𝑁𝐵

=

𝕋

_𝛽𝑁𝐵 ∧

ℕ

_𝛽𝑁𝐵 ifadesinden binormal vektör alanı,

𝔹

_𝛽𝑁𝐵

=

1 √𝑘2 _{+ 2𝜏}2 _√𝛿 12+𝛿22+𝛿32

|

−𝑘 −𝜏

𝕋

ℕ

𝔹

𝜏

𝛿

₁

𝛿

₂

𝛿

₃

|

(3.42) ve böylece

𝔹

_𝛽𝑁𝐵

=

(−𝜏 𝛿2−𝜏 𝛿3) 𝕋+(𝜏 𝛿1+𝑘 𝛿3) ℕ+(𝜏 𝛿1−𝑘 𝛿2) 𝔹 √𝑘2 _{+ 2𝜏}2_.√𝛿12_+𝛿22_+𝛿32

(3.43)

ifadesi elde edilir. Torsiyonu bulmak için 𝛽_𝑁𝐵 eğrisinin ikinci ve üçüncü türevlerini bulmamız gerekir. Buna göre;

𝛽′′_𝑁𝐵 = 1

√2{(−𝑘′ + 𝑘𝜏)𝕋 + (−𝑘

2 _{− 𝜏}2_{− 𝜏′)ℕ + (𝜏′ − 𝜏}2_)𝔹}

_(3.44)

𝛽′′′_𝑁𝐵 = 1 √2{𝜔1𝕋 + 𝜔2ℕ + 𝜔3𝔹}

(3.45) bulunur Burada; 𝜔1 = (𝜏2+ 𝑘2)𝑘 + (2𝑘𝜏′− 𝜏𝑘′) − 𝑘′′ 𝜔₂ = (𝜏2_{+ 𝑘}2_{)𝜏 − 3(𝑘𝑘}′_{+ 𝜏𝜏}′_{) (3.46)} 𝜔₃ = (𝜏2_{+ 𝑘}2_{)(−𝜏) − 3𝜏𝜏}′_{+ 𝜏}′′

dır. (2.3) bağıntısında (3.34), (3.44), (3.45) ifadeleri yerlerine yazılıp gerekli hesaplamalar yapılırsa,

𝜏

_𝛽 𝑁𝐵

=

√2[ (𝑘2+2𝜏2) (𝑘𝜔₃+ 𝜏𝜔₁)+ (𝑘𝜏′−𝜏𝑘′)(𝜔₂+𝜔₃)+ 2𝑘𝜏2𝜔₂ ] (2𝜏2_+𝑘2₎2_𝜏2_+(𝑘(2𝜏2_+𝑘2_)+𝑘𝜏′_−𝜏𝑘′₎2_+(𝑘𝜏′_−𝜏𝑘′_+2𝑘𝜏2₎ (3.47) olarak bulunur.

Sonuç 3.3 s yay paramatresi ve 𝛽; 𝐼 → 𝔼𝟑 _{eğrisinin Frenet çatısı {𝕋, ℕ, 𝔹} olmak üzere}

NB-Smarandache eğrisinin

𝑘

_𝛽𝑁𝐵 eğriliği ve torsiyonu

𝜏

_𝛽

𝑁𝐵aşağıdaki gibidir:

𝑘

_𝛽𝑁𝐵

=

_{(𝑘2 +2 𝜏}√2 _{2 )2}

√𝛿

₁2

_{+ 𝛿}

22

+ 𝛿

32

(3.48)

𝜏

_𝛽 𝑁𝐵

=

√2[ (𝑘2+2𝜏2)(𝑘.𝜔₃+ 𝜏.𝜔₁)+ (𝑘𝜏′−𝜏𝑘′)(𝜔₂+𝜔₃)+ 2𝑘𝜏2𝜔₂ ] (2𝜏2_+𝑘2₎2_𝜏2_+(𝑘(2𝜏2_+𝑘2_)+𝑘𝜏′_−𝜏𝑘′₎2_+(𝑘𝜏′_−𝜏𝑘′_+2𝑘𝜏2₎ (3.49) 3.4. TNB-Smarandache Eğrisi

Tanım 3.4.1. s yay paramatresi ve 𝛽 = 𝛽(𝑠) eğrisi 𝔼𝟑 _{de birim hızlı regüler bir eğri}

olsun. 𝛽(𝑠) eğrisinin Frenet vektörleri {𝕋(𝑠), ℕ(𝑠), 𝔹(𝑠)} olmak üzere TNB-Smarandache eğrisi,

𝛽

_𝑇𝑁𝐵

(𝑠) =

1

√3

(𝕋(𝑠) + ℕ(𝑠) + 𝔹(𝑠))

(3.50)

şeklinde tanımlanır(Ahmad.T,2010). Bu eğrinin yay parametresini 𝑠𝛽 ile ifade edersek

TNB- Smarandache eğrisinin eğrilik ve torsiyonunu hesaplayabiliriz. Bunun için eğrinin türevini alırsak ,

𝑑𝛽𝑇𝑁𝐵 𝑑𝑠𝛽 𝑑𝑠𝛽 𝑑𝑠

=

1 √3

(-k

𝕋

+(𝑘 − 𝜏)

ℕ

+τ

𝔹

)

(3.51)

ifadesini elde ederiz. Bu ifadenin normunu alırsak,

‖𝑑𝛽𝑇𝑁𝐵 𝑑𝑠𝛽 ‖ = 1

olduğundan,

𝑑𝑠_𝑑𝑠𝛽

= √

2𝑘2+2𝜏₃2−2𝑘𝜏

(3.52) bulunur. Buradan 𝛽_𝑇𝑁𝐵(𝑠) eğrisinin teğet vektör alanı,

𝕋

_{𝛽𝑇𝑁𝐵}

=

(−𝑘 𝕋 +(𝑘−𝜏) ℕ +τ 𝔹)

√2𝑘2_+2𝜏2_−2𝑘𝜏

(3.53)

şeklinde bulunur. Bu teğet vektörünün tekrar türevini alırsak,

𝛿₁ = 𝑘𝜏[4𝑘(𝑘 − 𝜏) + 2(𝜏′ + 𝜏2_{) + 𝑘′] − 𝑘}2_(2𝑘2 _{+ 𝜏}′_{) − 2𝑘′𝜏}2

𝛿₂ = 2𝑘𝜏[(𝑘 − 𝜏)2_{+ 2𝜏 − 2𝜏′] − 2(𝑘}4_{+ 𝜏}4_{) + 𝑘}′_𝜏2_{− 𝑘}2_{𝜏′ (3.54)}

𝛿₃ = 𝜏[2𝑘(𝑘2_{+ 4𝜏}2 _{− 𝑘}′_{− 𝜏}′_{− 2𝑘𝜏) + (𝜏 𝑘}′_{+ 𝜏}′_{− 2𝜏}3_)]

𝕋

′_{𝛽𝑇𝑁𝐵}

=

𝛿1 𝕋 + 𝛿2 ℕ+𝛿3 𝔹

( 2 𝑘2 _{+ 2𝜏}2_{−2𝑘𝜏 )}3⁄₂ (3.55)

ifadesini buluruz. O zaman (3.55) ifadesini şu şekilde yazabiliriz;

𝕋

′

𝛽_𝑇𝑁𝐵

=

√3(𝛿_(2𝑘12 𝕋+𝛿 _{+2 𝜏}22 ℕ+𝛿_{−2𝑘𝜏)}3 𝔹)2 (3.56)

bu denklemden 𝛽_𝑇𝑁𝐵(𝑠) eğrisinin

𝑘

_{𝛽𝑇𝑁𝐵} eğriliği,

𝑘

_{𝛽𝑇𝑁𝐵}

= ‖𝕋

′

𝛽𝑇𝑁𝐵

‖ =

√3

(2𝑘2 _{+2 𝜏}2_{−2𝑘𝜏)}2

√𝛿

12

+ 𝛿

22

+ 𝛿

32 (3.57)

bulunur. Diğer taraftan

ℕ

_{𝛽𝑇𝑁𝐵}

=

𝕋

′ 𝛽𝑇𝑁𝐵

‖𝕋′

𝛽𝑇𝑁𝐵‖ olduğundan asli normal vektör alanı,

ℕ

_{𝛽𝑇𝑁𝐵}

=

(𝛿1 𝕋+𝛿2 ℕ+𝛿3 𝔹)

√𝛿₁2+𝛿₂2+𝛿₃2

(3.58)

olur

.

𝔹

_{𝛽𝑇𝑁𝐵}

=

𝕋

_{𝛽𝑇𝑁𝐵} ∧

ℕ

_{𝛽𝑇𝑁𝐵} ifadesinden binormal vektör alanı,

𝔹

_{𝛽𝑇𝑁𝐵}

=

1 √_2𝑘2 _{+ 2𝜏}2_−2𝑘𝜏√_𝛿12_+𝛿22_+𝛿32

|

𝕋

ℕ

𝔹

−𝑘 𝑘 − 𝜏

𝜏

𝛿

₁

𝛿

₂

𝛿

₃

|

(3.59) ve böylece,

𝔹

_{𝛽𝑇𝑁𝐵}

=

((𝑘−𝜏)𝛿3−𝜏𝛿2) 𝕋 + (𝜏𝛿1+𝑘𝛿3) ℕ+((𝜏−𝑘)𝛿1−𝑘𝛿2) 𝔹 √2𝑘2 _{+ 2𝜏}2_{−2𝑘𝜏√𝛿1}2_+𝛿22_+𝛿32

(3.60)

ifadesi elde edilir. Torsiyonu bulmak için 𝛽_𝑇𝑁𝐵 eğrisinin ikinci ve üçüncü türevlerini bulmamız gerekir. Buna göre;

𝛽′′_𝑇𝑁𝐵 = 1 √2{−(𝑘 2_{+ 𝑘}′_{+ 𝑘𝜏)𝕋 + (𝑘}′_{− 𝑘}2_{− 𝜏}2 _{− 𝜏′)ℕ + (𝑘𝜏 + 𝜏}′_{− 𝜏}2_{)𝔹} (3.61)} ve

𝛽′′′

_𝑇𝑁𝐵

=

1 √2

{𝜔

1

𝕋 + 𝜔

2

ℕ + 𝜔

3

𝔹}

(3.62) bulunur. Burada, 𝜔₁ = 𝑘(𝑘2_+𝜏2_{− 3𝑘}′_{) − 𝑘}′′_{− 𝑘′𝜏} 𝜔2 = −2𝑘2(𝑘 + 𝜏) + 𝜏2(𝜏 − 𝑘) − 4𝑘𝑘′− 3𝜏𝜏′+ 𝑘′′− 𝜏′′

(3.63)

𝜔3 = −𝜏(𝑘2+𝜏2) − 3𝜏𝜏′+ 2𝑘′𝜏 + 𝑘𝜏′+ 𝜏′′

dır. (2.3) bağıntısında (3.51), (3.61), (3.62) ifadeleri yerlerine yazılıp gerekli hesaplamalar yapılırsa, 𝜏_𝛽 𝑇𝑁𝐵 = 2√3 𝑘[(𝑘𝜏′_{− 𝑘}′_𝜏)(𝜔 3+ 𝜔1+ 𝜔2)𝜏. (𝑘 − 𝜏) + 𝑘(𝑘𝜔3 − 𝜏𝜔2− 𝜏𝜔3)] [2𝑘(𝑘 − 𝜏) + 𝑘𝜏′_{− 𝜏𝑘}′_]2_{+ (−2𝑘𝜏}2 _{+ 𝑘𝜏}′_{− 𝑘}′_𝜏)2_{+ (2𝑘}3_{+ 𝑘𝜏}′_{− 𝑘}′_𝜏)2 (3.64) olarak bulunur.

Sonuç 3.4 s yay parametresi ve 𝛽; 𝐼 → 𝔼𝟑 _{eğrisinin Frenet çatısı {𝕋, ℕ, 𝔹} olmak üzere}

TNB-Smarandache eğrisinin eğriliği ve torsiyonu aşağıdaki gibidir;

𝑘

_{𝛽𝑇𝑁𝐵}

=

√3 (2𝑘2 +2 𝜏2_{−2𝑘𝜏)}2

√

_𝛿

₁2

_{+ 𝛿}

₂2

_{+ 𝛿}

₃2 _(3.65) ve 𝜏_𝛽 𝑇𝑁𝐵 = 2√3𝑘[(𝑘𝜏′_{− 𝑘}′_𝜏)(𝜔 3+ 𝜔1+ 𝜔2)𝜏. (𝑘 − 𝜏) + 𝑘(𝑘𝜔3 − 𝜏𝜔2− 𝜏𝜔3)] [2𝑘(𝑘 − 𝜏) + 𝑘𝜏′_{− 𝜏𝑘}′_]2_{+ (−2𝑘𝜏}2 _{+ 𝑘𝜏}′_{− 𝑘}′_𝜏)2_{+ (2𝑘}3_{+ 𝑘𝜏}′_{− 𝑘}′_𝜏)2 (3.66) dır.

3.5. TC-Smarandache Eğrisi

Tanım 3.5.1. s yay paramatresi ve 𝛽 = 𝛽(𝑠) eğrisi 𝔼𝟑 _{de birim hızlı regüler bir eğri}

olsun. 𝛽(𝑠) eğrisinin Frenet vektörleri {𝕋(𝑠), ℕ(𝑠), 𝔹(𝑠)} ve W, Darboux vektör alanının B Binormal vektör alanı ile yaptığı açı 𝜑 olsun. 𝐶 = 𝑠𝑖𝑛𝜑𝕋 + 𝑐𝑜𝑠𝜑𝔹 vektör alanı birim Darboux vektörü olarak alınırsa,

𝛽_𝑇𝐶(𝑠) =_√21 (𝕋(𝑠) + 𝐶(𝑠)) (3.67)

şeklinde tanımlanan

𝛽

_𝑇𝐶 eğrisine TC-Smarandache eğrisi denir(Ahmad.T,2010).

Bu eğrinin yay parametresini 𝑠_𝛽 ile ifade edersek TC- Smarandache eğrisinin eğrilik ve torsiyonunu hesaplayabiliriz. Bunun için eğrinin türevini alırsak,

𝑑𝛽𝑇𝐶 𝑑𝑠𝛽

.

𝑑𝑠𝛽 𝑑𝑠

=

1 √2

{𝜑

′

_{𝑐𝑜𝑠𝜑𝕋 + 𝑘 ℕ − 𝜑′𝑠𝑖𝑛𝜑 𝔹}}

_(3.68)

ifadesini elde ederiz. Bu ifadenin normunu alırsak,

‖𝑑𝛽𝑇𝐶 𝑑𝑠𝛽‖ = 1

olduğundan,

𝑑𝑠_𝑑𝑠𝛽

=

_√21

√𝑘

2

+ (𝜑′)

2

(3,69)

olarak bulunur. Buradan 𝛽_𝑇𝐶(𝑠) eğrisinin teğet vektör alanı,

𝕋

_𝛽𝑇𝐶

=

(𝜑

′_{𝑐𝑜𝑠𝜑𝕋+ 𝑘 ℕ− 𝜑′𝑠𝑖𝑛𝜑 𝔹)}

√𝑘2+(𝜑′)2 (3.70)

𝛿1 = 𝜑′′𝑐𝑜𝑠𝜑 − (𝜑′)2𝑠𝑖𝑛𝜑 − 𝑘2− 𝑘𝑘′𝜑′𝑐𝑜𝑠𝜑 − 2(𝜑′)2𝜑′′𝑐𝑜𝑠𝜑 𝛿₂ = 𝑘𝜑′_{𝑐𝑜𝑠𝜑 + 𝑘}′_{+ 𝜏𝜑}′_{𝑠𝑖𝑛𝜑 − 𝑘}2_𝑘′_{− 2𝑘𝜑}′_𝜑′′ _(3.71) 𝛿₃ = −𝜑′′_{𝑠𝑖𝑛𝜑 − (𝜑}′₎2_{𝑐𝑜𝑠𝜑 + 𝑘𝜏 + 𝑘𝑘}′_𝜑′_{𝑠𝑖𝑛𝜑 + 2(𝜑}′₎2_𝜑′′_{𝑠𝑖𝑛𝜑}

olmak üzere,

𝕋

′_𝛽𝑇𝐶

=

√2(𝛿1 𝕋+𝛿2 ℕ+𝛿3 𝔹) (𝑘2_+(𝜑′₎2₎2 (3.72)

elde ederiz. O halde 𝛽_𝑇𝐶(𝑠) eğrisinin

𝑘

_𝛽𝑇𝐶 eğriliği,

𝑘

_𝛽𝑇𝐶

= ‖𝕋

′ 𝛽𝑇𝐶

‖ =

√2 (𝑘2_+(𝜑′₎2₎2

√𝛿

1 2

_{+ 𝛿}

22

+ 𝛿

32 (3.73)

bulunur. Diğer taraftan

ℕ

_𝛽𝑇𝐶

=

𝕋

′ 𝛽𝑇𝐶

‖𝕋′

𝛽𝑇𝐶‖ olduğundan asli normal vektör alanı,

ℕ

_𝛽𝑇𝐶

=

(𝛿1 𝕋+𝛿2 ℕ+𝛿3 𝔹)

√𝛿12+𝛿22+𝛿32

(3.74)

olur

.

𝔹

_𝛽𝑇𝐶

(𝑠)= 𝕋

_𝛽𝑇𝐶

(𝑠)

∧

ℕ

_𝛽𝑇𝐶

(𝑠)

ifadesinden binormal vektör alanı,

𝑢 = √𝑘2_{+ (𝜑′)}2

_{𝑣 =}

√

_𝛿 12 + 𝛿22 + 𝛿32

𝔹

_𝛽𝑇𝐶

=

1 𝑢 𝑣

|

𝕋

ℕ

𝔹

𝜑′𝑐𝑜𝑠𝜑

𝑘

−𝜑′𝑠𝑖𝑛𝜑

𝛿

₁

𝛿

₂

𝛿

₃

|

(3.75) şeklinde hesaplanarak,

𝔹

_𝛽𝑇𝐶

=

_{𝑢 𝑣}1

{

(𝑘 𝛿

₃

+ 𝜑′ 𝛿

₂

𝑠𝑖𝑛𝜑)𝕋

−𝜑

′

_(𝛿

1

𝑠𝑖𝑛𝜑 + 𝛿

3

𝑐𝑜𝑠𝜑)ℕ

+(𝛿

₂

𝜑

′

_{𝑐𝑜𝑠𝜑 − 𝑘 𝛿}

1

)𝔹

}

(3.76)

ifadesi bulunur. Torsiyonu bulmak için 𝛽_𝑇𝐶 eğrisinin ikinci ve üçüncü türevlerini bulmamız gerekir. Buna göre;

𝛽′′_𝑇𝐶 = 1 √2{ (𝜑′′_{𝑐𝑜𝑠𝜑 − (𝜑}′₎2_{𝑠𝑖𝑛𝜑 − 𝑘}2_)𝕋 +(𝑘′_{+ 𝑘𝜑}′_{𝑐𝑜𝑠𝜑 + 𝜏𝜑}′_{𝑠𝑖𝑛𝜑)ℕ} +(𝑘𝜏 − 𝜑′′_{𝑠𝑖𝑛𝜑 − (𝜑}′₎2_{𝑐𝑜𝑠𝜑)𝔹} } (3.77) ve 𝛽′′′𝑇𝐶= _√21 {𝜔1𝕋 + 𝜔2ℕ + 𝜔3𝔹}

(3.78)

olarak bulunur. Burada;

𝜔1 = ((𝑘2+ 𝜏2) + (𝜑′)2)(−𝜑′𝑐𝑜𝑠𝜑) + 𝜑′′′𝑐𝑜𝑠𝜑 − 3𝜑′𝜑′′𝑠𝑖𝑛𝜑 − 3𝑘𝑘′

𝜔2 = 2𝜑′′(𝑘𝑐𝑜𝑠𝜑 + 𝜏𝑠𝑖𝑛𝜑) + 𝜑′(𝑘′𝑐𝑜𝑠𝜑 + 𝜏′𝑠𝑖𝑛𝜑) + 𝑘′′− 𝑘2− 𝑘𝜏2

(3.79)

𝜔₃ = (𝑘2_{+ 𝜏}2_)𝜑′_{𝑠𝑖𝑛𝜑 + ((𝜑′)}3_{− 𝜑′′′)𝑠𝑖𝑛𝜑 − 3𝜑}′_𝜑′′_{𝑐𝑜𝑠𝜑 + 2𝑘}′_{𝜏 + 𝜏′𝑘}

dır. (2.3) bağıntısında (3.68), (3.78), (3.79) ifadeleri yerlerine yazılıp gerekli hesaplamalar yapılırsa, 𝜇₁₌(𝑘2_{+ (𝜑}′₎2_{)(𝜏 − 𝑘𝑐𝑜𝑠𝜑) + (𝑘}3_{− 𝜏𝜑′′)𝑐𝑜𝑠𝜑 + 𝑘′𝜑′𝑠𝑖𝑛𝜑} 𝜇2 = (𝜑′)3 (3.80) 𝜇3 = 𝑘(𝑘2+ (𝜑′)2) + 𝑐𝑜𝑠𝜑(𝑘′𝜑′− 𝑘𝜑′′) olmak üzere,

𝜏

_𝛽 𝑇𝐶

=

√2 (𝜔1 𝜇1+𝜔2 𝜇2+𝜔3 𝜇3) 𝜇₁2+ 𝜇₂2+𝜇₃2 (3.81) olarak bulunur.

Sonuç 3.5. s yay paramatresi ve 𝛽; 𝐼 → 𝔼𝟑 _{eğrisinin Frenet çatısı {𝕋, ℕ, 𝔹} olmak üzere}

TC-Smarandache eğrisinin eğriliği ve torsiyonu aşağıdaki gibidir:

𝑘

_𝛽𝑇𝐶

=

_(𝑘2+(𝜑√2_′)2)2

√𝛿

₁2

_{+ 𝛿}

22

+ 𝛿

32

(3.82)

ve

𝜏

_𝛽 𝑇𝐶

=

√2 (𝜔1 𝜇1+𝜔2 𝜇2+𝜔3𝜇3) 𝜇₁2+ 𝜇₂2+𝜇₃2

(3.83) dır. 3.6. NC-Smarandache Eğrisi

Tanım 3.6.1. s yay paramatresi ve 𝛽 = 𝛽(𝑠) eğrisi 𝔼𝟑 _{de birim hızlı regüler bir eğri}

olsun. 𝛽(𝑠) eğrisinin Frenet vektörleri {𝕋(𝑠), ℕ(𝑠), 𝔹(𝑠)} ve W, Darboux vektör alanının B Binormal vektörü ile yaptığı açı 𝜑 olsun. 𝐶 = 𝑠𝑖𝑛𝜑𝕋 + 𝑐𝑜𝑠𝜑𝔹 vektörü birim Darboux vektörü olarak alınırsa,

𝛽𝑁𝐶(𝑠) =_√21 (ℕ(𝑠) + 𝐶(𝑠)) (3.84)

şeklinde tanımlanan

𝛽

_𝑁𝐶 eğrisine NC-Smarandache eğrisi denir(Ahmad.T,2010). Bu eğrinin yay parametresini 𝑠_𝛽 ile ifade edersek NC- Smarandache eğrisinin eğrilik ve torsiyonunu hesaplayabiliriz. Bunun için eğrinin türevini alırsak,

𝑑𝛽𝑁𝐶 𝑑𝑠𝛽 𝑑𝑠𝛽 𝑑𝑠

=

1 √2

{𝜑

′

_{𝑐𝑜𝑠𝜑𝕋 + (𝜏 − 𝜑}

′

_{𝑠𝑖𝑛𝜑 )𝔹}}

_(3.85)

ifadesni elde ederiz. Bu ifadenin normunu alırsak,

‖𝑑𝛽𝑁𝐶

𝑑𝑠_𝛽 ‖=1 olduğundan,

𝑑𝑠𝛽

𝑑𝑠 = 1

√2√(𝜑′)2+ ‖𝑊‖2− 2𝜑′‖𝑊‖

(3.86)

olarak bulunur. Buradan 𝛽_𝑁𝐶(𝑠) eğrisinin teğet vektör alanı,

𝕋

_𝛽𝑁𝐶

=

(𝜑

′_{𝑐𝑜𝑠𝜑−𝑘)𝕋+(𝜏 −𝜑′𝑠𝑖𝑛𝜑 )𝔹)}

√(𝜑′)2_+‖𝑊‖2_{−2𝜑′‖𝑊‖} (3.87)

şeklinde bulunur. Bu teğet vektör alanının tekrar türevini alırsak,

𝛿₁ = 𝜏2_𝜑′′_{𝑐𝑜𝑠𝜑 − 𝑘𝜑′𝜑′′ cos}2_{𝜑 − 𝜏𝜑}′_𝜑′′_{𝑠𝑖𝑛𝜑𝑐𝑜𝑠𝜑 − (𝜑}′₎4_{𝑠𝑖𝑛𝜑 − 𝑘}2_(𝜑′₎2_{𝑠𝑖𝑛𝜑} -𝜏2_(𝜑′₎2_{𝑠𝑖𝑛𝜑 +2k(𝜑}′₎3_{𝑠𝑖𝑛𝜑𝑐𝑜𝑠𝜑 + 2𝜏(𝜑}′₎3_sin2_{𝜑 − 𝑘}′_(𝜑′₎2_{− 𝜏}2_𝑘′_{− 2𝑘𝑘′𝜑′𝑐𝑜𝑠𝜑} -2𝜏𝑘′_𝜑′_{𝑠𝑖𝑛𝜑 − 𝜏𝜏}′_𝜑′_{𝑐𝑜𝑠𝜑 + 𝑘}′_(𝜑′₎2_cos2_{𝜑 + 𝜏}′_(𝜑′₎2_{𝑠𝑖𝑛𝜑𝑐𝑜𝑠𝜑 + 𝑘𝜑}′_𝜑′′_{+ 𝑘𝜏𝜏}′₋ 𝑘𝜏𝜑′′_{𝑠𝑖𝑛𝜑 − 𝜑′𝜏′𝑘𝑠𝑖𝑛𝜑} 𝛿₂ = 𝑘(𝜑′₎3_{𝑐𝑜𝑠𝜑 + 3𝑘}3_𝜑′_{𝑐𝑜𝑠𝜑 + 3𝜏}2_𝑘𝜑′_{𝑐𝑜𝑠𝜑 − 2𝑘}2_(𝜑′₎2_cos2_𝜑-𝑘2_(𝜑′₎2_{− 𝑘}4₋ 2𝑘2_𝜏2_{+ 3𝑘}2_𝜏𝜑′_{𝑠𝑖𝑛𝜑−4𝑘𝜏(𝜑}′₎2_{𝑠𝑖𝑛𝜑𝑐𝑜𝑠𝜑 − 𝜏}2_(𝜑′₎2_+3𝜏3_𝜑′_{𝑠𝑖𝑛𝜑 + 2(𝜏𝜑}′₎2_sin2_𝜑 𝛿₃ = 𝜏′_(𝜑′₎2_{+ 𝑘}2_𝜏′_{− 2𝑘𝜏}′_𝜑′_{𝑐𝑜𝑠𝜑 − 𝑘}2_𝜑′′_{𝑠𝑖𝑛𝜑 + 𝑘𝜑}′_𝜑′′_{𝑠𝑖𝑛𝜑𝑐𝑜𝑠 − 𝜏′(𝜑}′₎2_sin2_𝜑 +𝜏𝜑′_𝜑′′_sin2_{𝜑 − (𝜑}′₎4_{𝑐𝑜𝑠𝜑−𝑘}2_(𝜑′₎2_{𝑐𝑜𝑠𝜑 − (𝜏𝜑}′₎2_{𝑐𝑜𝑠𝜑 + 2𝑘𝜏𝜑}′_𝜑′′_(𝜑′₎3_cos2_𝜑 +2𝜏(𝜑′₎3_{𝑠𝑖𝑛𝜑𝑐𝑜𝑠𝜑 − 𝜏𝑘𝑘}′_{+ 𝜏𝑘𝜑}′′_{𝑐𝑜𝑠𝜑 + 𝜏𝑘}′_𝜑′_{𝑐𝑜𝑠𝜑} (3.88) olmak üzere,

𝕋

′ 𝛽_𝑁𝐶

=

_((𝜑′)√2 (𝛿2 1_{+ ‖𝑊‖} 𝕋 + 𝛿22 _{− 2} ℕ + 𝛿_{𝜑′‖𝑊‖)}3 𝔹 )2 (3.89)

elde ederiz. O halde 𝛽𝑁𝐶(𝑠) eğrisinin

𝑘

𝛽_𝑁𝐶 eğriliği,

𝑘

_𝛽𝑁𝐶

= ‖𝕋

′

𝛽_𝑁𝐶

‖ =

√2 √(𝛿12+𝛿22+𝛿32)

bulunur. Diğer taraftan

ℕ

_𝛽𝑁𝐶

=

𝕋

′ 𝛽𝑁𝐶

‖𝕋′ 𝛽𝑁𝐶‖

olduğundan asli normal vektör alanı,

ℕ

_𝛽𝑁𝐶

=

(𝛿1 𝕋+𝛿2 ℕ+𝛿3 𝔹)

√𝛿₁2+𝛿₂2+𝛿₃2

(3.91)

olur

.

𝔹

_𝛽𝑁𝐶

(𝑠 ) = 𝕋

_𝛽𝑁𝐶

(𝑠)

∧

ℕ

_𝛽𝑁𝐶

(𝑠)

ifadesinden binormal vektör alanı,

𝑢 = √(𝜑′)2_{+ ‖𝑊‖}2_{− 2𝜑′‖𝑊‖ 𝑣 = √𝛿} 12 + 𝛿22+ 𝛿32 olarak alınırsa

𝔹

_𝛽𝑁𝐶

=

1 𝑢 𝑣

|

𝕋

ℕ

𝔹

𝜑

′

_{𝑐𝑜𝑠𝜑 − 𝑘}

_𝑜

_{𝜏 − 𝜑′𝑠𝑖𝑛𝜑}

𝛿

₁

𝛿

₂

𝛿

₃

|

(3.92) şeklinde hesaplanarak, 𝔹𝛽𝑁𝐶 = 1 𝑢 𝑣{ 𝛿₂(𝜑′_{𝑠𝑖𝑛𝜑 − 𝜏)𝕋} +[𝛿1(𝜏 − 𝜑′𝑠𝑖𝑛𝜑) − 𝛿3(𝜑′𝑐𝑜𝑠𝜑 − 𝑘)]ℕ +(𝛿2(𝜑′𝑐𝑜𝑠𝜑 − 𝑘)𝔹 }

(3.93)

ifadesi bulunur. Torsiyonu bulmak için 𝛽_𝑁𝐶 eğrisinin ikinci ve üçüncü türevlerini bulmamız gerekir. Buna göre;

𝛽′′𝑁𝐶 =_√21 { (𝜑′′_{𝑐𝑜𝑠𝜑 − (𝜑}′₎2_{𝑠𝑖𝑛𝜑 − 𝑘′)𝕋} +(−𝑘2_{− 𝜏}2_{+ 𝑘𝜑}′_{𝑐𝑜𝑠𝜑 + 𝜏𝜑}′_{𝑠𝑖𝑛𝜑)ℕ} +(𝜏′ − 𝜑′′_{𝑠𝑖𝑛𝜑 − (𝜑}′₎2_{𝑐𝑜𝑠𝜑)𝔹} } (3.94) ve 𝛽′′′𝑁𝐶 =_√21 {𝜔1𝕋 + 𝜔2ℕ + 𝜔3𝔹}

(3.95)

𝜔1 = (𝑘3+ 𝑘𝜏2− 𝑘′′) − 𝜑′𝑠𝑖𝑛𝜑(𝑘𝜏 + 3𝜑′′) + 𝑐𝑜𝑠𝜑(𝜑′′′− (𝜑′)3− 𝑘2𝜑′)

𝜔₂ = −3𝑘𝑘′_{− 3𝜏𝜏}′_{+ 𝑠𝑖𝑛𝜑(2𝜏𝜑}′′_{+ 𝜏}′_𝜑′_{− 2𝑘(𝜑}′₎2₎

_(3.96)

+𝑐𝑜𝑠𝜑(2𝑘𝜑′′_{+ 𝑘}′_𝜑′_{+ 2𝜏(𝜑}′₎2₎

𝜔₃ = 𝜏′′_{− 𝜏}3 _{− 𝑘}2_{𝜏 + 𝜑}′_{𝑐𝑜𝑠𝜑(𝑘𝜏 − 3𝜑}′′_{) + 𝑠𝑖𝑛𝜑(𝜏}2_𝜑′_{− 𝜑}′′_{+ (𝜑}′₎3₎

dır. (2.3) bağıntısında (3.85), (3.94), (3.95) ifadeleri yerlerine yazılıp gerekli hesaplamalar yapılırsa, 𝜇₁₌(𝑘(𝜑′₎2_{𝑠𝑖𝑛𝜑𝑐𝑜𝑠𝜑 − 𝑘𝜏𝜑′) + (𝜏(𝜑}′₎2_{𝑠𝑖𝑛𝜑 − 𝑘}2_𝜑′_{− 2𝜏}2_{𝜑′)𝑠𝑖𝑛𝜑 + 𝑘}2_{𝜏 − 𝜏}3 𝜇₂ = (𝜏𝜑′′_{− 𝜏}′_𝜑′_{− 𝑘(𝜑}′₎2_{)𝑐𝑜𝑠𝜑 + (−𝜏(𝜑}′₎2_{− 𝑘′𝜑}′_{− 𝑘𝜑′′)𝑠𝑖𝑛𝜑 + (𝜑}′₎3 𝑘𝜏′_{− 𝜏𝑘′ (3.97)} 𝜇₃ = (𝑘(𝜑′₎2_{+ 𝜏(𝜑}′₎2_{𝑠𝑖𝑛𝜑 − 𝜏}2_𝜑′_{− 2𝑘}2_𝜑′_{)𝑐𝑜𝑠𝜑 − 𝑘𝜏𝜑}′_{𝑠𝑖𝑛𝜑 + 𝑘}3_{+ 𝑘𝜏}2 olmak üzere,

𝜏

_𝛽𝑁𝐶

=

√2 ( 𝜔1 𝜇1 + 𝜔2 𝜇2 + 𝜔3 𝜇3) 𝜇₁2+ 𝜇₂2+𝜇₃2 (3.98) olarak bulunur.

Sonuç 3.6. s yay parametresi ve 𝛽; 𝐼 → 𝔼𝟑 _{eğrisinin Frenet çatısı {𝕋, ℕ, 𝔹} olmak üzere}

NC-Smarandache eğrisinin eğriliği ve torsiyonu aşağıdaki gibidir,

𝑘

_𝛽𝑁𝐶

=

_(𝑘2 √2 + (𝜑′₎2 ₎2

√𝛿

1 2

_{+ 𝛿}

22

+ 𝛿

32

(3.99)

ve

𝜏

_𝛽𝑁𝐶

=

√2 (𝜔1 𝜇1+ 𝜔2 𝜇2+ 𝜔3 𝜇3 ) 𝜇₁2+ 𝜇₂2+𝜇₃2

(3.100) dır.

3.7. BC-Smarandache Eğrisi

Tanım 3.7.1. s yay parametresi ve 𝛽 = 𝛽(𝑠) eğrisi 𝔼𝟑 _{de birim hızlı regüler bir eğri}

olsun. 𝛽(𝑠) eğrisinin Frenet vektörleri {𝕋(𝑠), ℕ(𝑠), 𝔹(𝑠)} ve W, Darboux vektör alanının B Binormal vektörü ile yaptığı açı 𝜑 olsun. 𝐶 = 𝑠𝑖𝑛𝜑𝕋 + 𝑐𝑜𝑠𝜑𝔹 vektörü birim Darboux vektörü olarak alınırsa,

𝛽_𝐵𝐶(𝑠) =_√21 (𝔹(𝑠) + 𝐶(𝑠)) (3.101)

şeklinde tanımlanan

𝛽

_𝐵𝐶 eğrisine BC-Smarandache eğrisi denir(Ahmad.T,2010). Bu eğrinin yay parametresini 𝑠_𝛽 ile ifade edersek BC- Smarandache eğrisinin eğrilik ve torsiyonunu hesaplayabiliriz. Bunun için eğrinin türevini alırsak,

𝑑𝛽_𝑑𝑠𝐵𝐶 𝛽 𝑑𝑠_𝛽 𝑑𝑠 = 1 √2{𝜑 ′_{𝑐𝑜𝑠𝜑𝕋 + (−𝜏)ℕ + (−𝜑}′_{𝑠𝑖𝑛𝜑 )𝔹}}

_(3.102)

ifadesni elde ederiz. Bu ifadenin normunu alırsak,

‖𝑑𝛽𝐵𝐶

𝑑𝑠_𝛽 ‖ = 1 olduğundan,

𝑑𝑠_𝑑𝑠𝛽= 1

√2√(𝜑′)2+ 𝜏2

(3,103)

olarak bulunur. Buradan 𝛽𝐵𝐶(𝑠) eğrisinin teğet vektör alanı,

𝕋

_𝛽𝐵𝐶

=

{ 𝜑

′_{𝑐𝑜𝑠𝜑 𝕋 –𝜏 ℕ −𝜑}′_{𝑠𝑖𝑛𝜑 𝔹 }}

√(𝜑′)2 + 𝜏2 (3.104)

𝛿1 = ((𝜑′)2+ 𝜏2)(𝑘𝜏 − (𝜑′)2𝑠𝑖𝑛𝜗) + 𝜏2𝑐𝑜𝑠𝜑(𝜑′′− 𝜏𝜑′) 𝛿₂ = ((𝜑′)2_{+ 𝜏}2_)𝑘𝜑′_{𝑐𝑜𝑠𝜑 + 𝜑′(𝜏𝜑}′′_{− 𝜑′𝜏′) (3.105)} 𝛿₃ = 𝜏2_((𝜑′)2_{𝑐𝑜𝑠𝜑 − 𝜑′′𝑠𝑖𝑛𝜑) + 𝜏𝜏}′_𝜑′_{𝑠𝑖𝑛𝜑 + (𝜑′)}2_((𝜑′)2_{− 𝜏}2_{) − 𝜏}4 olmak üzere,

𝕋

′_𝛽𝐵𝐶

=

√2(𝛿1 𝕋+𝛿2 ℕ+𝛿3 𝔹) ((𝜑′)2_+𝜏2₎2 (3.106)

elde ederiz. O halde 𝛽_𝐵𝐶(𝑠) eğrisinin

𝑘

_𝛽𝐵𝐶 eğriliği,

𝑘

_𝛽𝐵𝐶

= ‖𝕋

′

𝛽_𝐵𝐶

‖ =

√2 √𝛿₁2+𝛿₂2+𝛿₃2

((𝜑′)2_+𝜏2₎2 (3.107)

bulunur. Diğer taraftan

ℕ

_𝛽𝐵𝐶

=

𝕋

′ 𝛽𝐵𝐶

‖𝕋′

𝛽𝐵𝐶‖ olduğundan asli normal vektör alanı,

ℕ

_𝛽𝐵𝐶

=

(𝛿1 𝕋+𝛿2 ℕ+𝛿3 𝔹)

√𝛿12+𝛿22+𝛿32

(3.108)

olur

.

𝔹

_𝛽𝐵𝐶

(𝑠) = 𝕋

_𝛽𝐵𝐶

(𝑠)

∧

ℕ

_𝛽𝐵𝐶

(𝑠)

ifadesinden binormal vektör alanı,

𝑢 = √((𝜑′)2_{+ 𝜏}2_{) 𝑣 = √(𝛿} 12 + 𝛿22+ 𝛿32) olmak üzere

𝔹

_𝛽𝐵𝐶

=

1 𝑢 𝑣

|

𝕋

ℕ

𝔹

𝜑

′

_{𝑐𝑜𝑠𝜑 −𝜏 −𝜑′𝑠𝑖𝑛𝜑}

𝛿

₁

𝛿

₂

𝛿

₃

|

(3.109) şeklinde hesaplanarak,

𝔹_𝛽𝐵𝐶 =_𝑢.𝑣1 {

(𝛿2 𝜑′′𝑠𝑖𝑛𝜑 − 𝜏 𝛿3) 𝕋

−𝜑′[𝛿₁ 𝑠𝑖𝑛𝜑 + 𝛿₃𝑐𝑜𝑠𝜑]ℕ

+(𝛿₁𝜏 + 𝛿₂𝜑′_{𝑐𝑜𝑠𝜑)𝔹} }

(3.110)

ifadesi bulunur. Torsiyonu bulmak için 𝛽_𝐵𝐶 eğrisinin ikinci ve üçüncü türevlerini bulmamız gerekir. Buna göre;

𝛽′′_𝐵𝐶 = 1 √2{ (𝜑′′_{𝑐𝑜𝑠𝜑 − (𝜑}′₎2_{𝑠𝑖𝑛𝜑 + 𝑘𝜏)𝕋} +(−𝜏′ + 𝑘𝜑′_{𝑐𝑜𝑠𝜑 + 𝜏𝜑}′_{𝑠𝑖𝑛𝜑)ℕ} +(−𝜏2_{− 𝜑}′′_{𝑠𝑖𝑛𝜑 − (𝜑}′₎2_{𝑐𝑜𝑠𝜑)𝔹} } (3.111) ve 𝛽′′′_𝐵𝐶 = 1 √2{𝜔1𝕋 + 𝜔2ℕ + 𝜔3𝔹}

(3.112) dır. Burada; 𝜔1 = (𝜑′′′− (𝜑′)3− 𝑘2𝜑′)𝑐𝑜𝑠𝜑 + (−3𝜑′𝜑′′− 𝑘𝜏𝜑′)𝑠𝑖𝑛𝜑 + 2𝑘𝜏′+ 𝑘′𝜏 𝜔₂ = (2𝑘𝜑′′_{+ 𝑘′𝜑′)𝑐𝑜𝑠𝜑 + (2𝜏𝜑}′′_{+ 𝜏}′_𝜑′_{− 2𝑘(𝜑}′₎2_{)𝑠𝑖𝑛𝜑 + 𝑘}2_{𝜏 − 𝜏′′}

_(3.113)

𝜔₃ = 𝜑′_{(𝑘𝜏 − 3𝜑}′′_{)𝑐𝑜𝑠𝜑 + (𝜏}2_𝜑′_{− 𝜑}′′_{+ (𝜑}′₎3_{)𝑠𝑖𝑛𝜑 − 3𝜏𝜏′}

dır. (2.3) bağıntısında (3.102), (3.111), (3.112) ifadeleri yerlerine yazılıp gerekli hesaplamalar yapılırsa,

𝜇₁₌(𝜑′₎2_{(𝜏𝑐𝑜𝑠𝜑 + 𝜏 sin}2_{𝜑 + 𝑘𝑠𝑖𝑛𝜑𝑐𝑜𝑠𝜑) + (𝜏𝜑}′′_{− 𝜏′𝜑′)𝑠𝑖𝑛𝜑 + 𝜏}3

𝜇₂ = (𝜑′₎3_{− 𝜑′(𝑘𝜏 + 𝜑}′′_{𝑐𝑜𝑠𝜑 + 𝜑′′)𝑠𝑖𝑛𝜑 + 𝜑′𝜏}2_{𝑐𝑜𝑠𝜑 (3.114)}

𝜇3 = 𝑘((𝜑′)2− 𝜏2) + (𝜏𝜑′′− 𝜏′𝜑′)𝑐𝑜𝑠𝜑 − 𝜏(𝜑′)2𝑠𝑖𝑛𝜑

olmak üzere torsiyon,

𝜏

_𝛽𝐵𝐶

=

√2 (𝜔1 𝜇1+𝜔2 𝜇2+𝜔3 𝜇3)

𝜇₁2+ 𝜇₂2+𝜇₃2 (3.115)

Sonuç 3.7. s yay parametresi ve 𝛽; 𝐼 → 𝔼𝟑 _{eğrisinin Frenet çatısı {𝕋, ℕ, 𝔹} olmak üzere}

BC-Smarandache eğrisinin eğriliği ve torsiyonu aşağıdaki gibidir.

𝑘

_𝛽𝐵𝐶

=

√

2

√

𝛿12 + 𝛿22 + 𝛿32

((

𝜑′

)

2 _{+ 𝜏}2

)

2 ve

𝜏

_𝛽𝐵𝐶

=

√2(𝜔1 𝜇1+𝜔2 𝜇2+𝜔3 𝜇3) 𝜇₁2_{+ 𝜇2}2_+𝜇32

(3.116)

dır. 3.8. TNBC-Smarandache Eğrisi

Tanım 3.8.1. s yay parametresi ve 𝛽 = 𝛽(𝑠) eğrisi 𝔼𝟑 _{de birim hızlı regüler bir eğri}

olsun. 𝛽(𝑠) eğrisinin Frenet vektörleri {𝕋(𝑠), ℕ(𝑠), 𝔹(𝑠)} ve W, Darboux vektör alanının B Binormal vektörü ile yaptığı açı 𝜑 olsun. 𝐶 = 𝑠𝑖𝑛𝜑𝕋 + 𝑐𝑜𝑠𝜑𝔹 vektörü birim Darboux vektörü olarak alınırsa,

𝛽

_{𝑇𝑁𝐵𝐶}

(𝑠) =

1

2

(

𝕋

(

𝑠

)

+ ℕ

(

𝑠

)

+ 𝔹(𝑠)

+ 𝐶(𝑠))

(3.117)

şeklinde tanımlanan

𝛽

_{𝑇𝑁𝐵𝐶} eğrisine TNBC-Smarandache eğrisi denir(Ahmad.T,2010). Bu eğrinin yay parametresini 𝑠𝛽 ile ifade edersek TNBC- Smarandache eğrisinin eğrilik

ve torsiyonunu hesaplayabiliriz. Bunun için eğrinin türevini alırsak,

𝑑𝛽𝑇𝑁𝐵𝐶 𝑑𝑠𝛽 𝑑𝑠𝛽 𝑑𝑠 = 1 2{(𝜑 ′_{𝑐𝑜𝑠𝜑 − 𝑘)𝕋 + (𝑘 − 𝜏)ℕ + (𝜏 − 𝜑}′_{𝑠𝑖𝑛𝜑 )𝔹}}

_(3.118)