Kesikli k-ardıl δ-şok modeli

(1)

T.C.

SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ

KESİKLİ k-ARDIL δ-ŞOK MODELİ

Havva ARIGÜN YÜKSEK LİSANS TEZİ

İstatistik Anabilim Dalı

(2)

(3)

(4)

ÖZET

YÜKSEK LİSANS TEZİ KESİKLİ k-ARDIL δ-ŞOK MODELİ

Havva ARIGÜN

Selçuk Üniversitesi Fen Bilimleri Enstitüsü İstatistik Anabilim Dalı

Danışman: Doç.Dr. İsmail KINACI 2017, 41 Sayfa

Jüri

Doç.Dr. İsmail KINACI Prof.Dr. Coşkun KUŞ

Yrd.Doç.Dr. Ahmet PEKGÖR

Bir bileşen yada sistemin n=1,2,…anlarında belirli bir olasılıkla şoka maruz kalabileceği düşünülsün. Herhangi bir anda şoka maruz kalınması 1, kalınmaması ise 0 ile gösterilsin. Böylece herhangi bir sistem için zaman içerisinde 0 ve 1’lerden oluşan bir dizi elde edilecektir. Bu dizinin herhangi bir bölümünde, bir şoktan diğer şoka kadar yapılan denemelerin sayısının δ gibi bir eşik değerinden küçük olması o bölümde bir δ-şok olduğu, büyük olması ise o bölümde herhangi bir δ-şok olmadığı anlamına gelmektedir. Literatürde yer alan çalışmalarda ilk δ-şoka yakalanıncaya kadar yapılan denemelerin sayısının olasılık fonksiyonu incelenmiştir. Bu çalışmada sistemin, ardışık olarak k (k>0) kere δ-şok’a maruz kaldığında bozulacağı varsayılmaktadır. Böyle bir sistem, k-ardıl δ-şok modeli olarak adlandırılabilir. Bu varsayım altında sistemin ömrü, ardışık k-kere δ-şok oluncaya kadar yapılan deneme sayısı şeklinde ifade edilebilir. Burada amaç sistem bozuluncaya kadar yapılan deneme sayısının olasılık dağılımını ve bu dağılımın bazı karakteristik özelliklerini elde etmektir. Bu çalışmada Tδ,k rasgele değişkeninin olasılık fonksiyonu elde edilmiş ve ayrıca Tδ,k rasgele değişkeninin bazı özellikleri incelenmiştir.

Anahtar Kelimeler: İki sonuç alan denemeler, Kesikli Dağılımlar, Kombinatorik, Olasılık Üreten Fonksiyonu, Tekrar İstatistiği, δ- Şok Model

(5)

ABSTRACT

MS THESIS

DISCRETE δ-SHOCK MODEL OF ORDER k

Havva ARIGÜN

THE GRADUATE SCHOOL OF NATURAL AND APPLIED SCIENCEOF SELÇUK UNIVERSITY

THE DEGREE OF MASTER OF SCIENCE IN STATISTICS

Advisor:

Assoc.Prof.Dr. İsmail KINACI Jury

Assoc.Prof.Dr. İsmail KINACI Prof.Dr. Coşkun KUŞ

Asst.Prof.Dr. Ahmet PEKGÖR 2017, 41 Pages

Let we think that a component or a system can subject to shock with a probability at time n=1,2,… . Let “1” denotes that there is a shock and “0” denotes that there is no shock. Hence for any system, a sequence which consists of “0” and “1” in time will be obtained. In any part of this sequence, if the number of trials from a shock to next shock is smaller or equal to a threshold value δ then there is a δ-shock in this part. In the literature the probability mass function of the number of trials until the first δ-shock is investigated. In this study, it is assumed that a system will fail with consequtieve k (k>0) δ-shock. Such a system can be called “δ-shock model of order k”. Under this assumption, lifetime of a system , Tδ,k can be expressed as

the number of trials until consequtive k δ-shock is occurred. In this study the probability mass function of randomvariable Tδ,k is obtained and some properties of the Tδ,k is investigated.

Keywords: Binary trials, Combinatorics, Discrete Distributions, Probabity Generating Function, Run

(6)

ÖNSÖZ

Bu tez çalışmasının başından sonuna kadar her aşamasında bilgisini, deneyimini benden esirgemeyen ve çalışmama daima olumlu yönde katkıda bulunan çok değerli danışman hocam Doç. Dr. İsmail KINACI’ya içtenlikle teşekkür ederim.

Hayatımın her döneminde olduğu gibi bu tez çalışmasında da desteklerini eksik etmeyen sevgili aileme sonsuz teşekkürlerimi bir borç bilirim.

Havva ARIGÜN KONYA-2017

(7)

İÇİNDEKİLER ÖZET ... iv ABSTRACT ...v ÖNSÖZ ... vi İÇİNDEKİLER ... vii 1. GİRİŞ ...8

2. KESİKLİ δ-ŞOK MODELİ ... 12

2.1. Model Varsayımları ... 12

2.2. Sistemin Yaşam Zamanı ... 12

2.3. Olasılık Fonksiyonu ... 12

2.4. Olasılık Üreten Fonksiyon, Beklenen Değer ve Varyans ... 14

3. KESİKLİ k-ARDIL δ-ŞOK MODELİ ... 16

3.1. Model Varsayımları ve Bazı Örnekler ... 16

3.2. Olasılık Fonksiyonu ... 18 3.3. Beklenen Değer ... 28 4. SONUÇLAR VE ÖNERİLER ... 31 EKLER ... 32 EK-1: E₄’ün Çözüm Sayısı ... 32 EK-2: E₃’ün Çözüm Sayısı ... 38 ÖZGEÇMİŞ... 40 KAYNAKLAR ... 41

(8)

1. GİRİŞ

Şok modelleri güvenirlik teorisi ve olasılık uygulamaların önemli bir miktarını içine alır. Bir sistem yada bileşenin herhangi bir anda şoka maruz kalması 1, kalmaması ise 0 ile gösterilsin. Böylece herhangi bir sistem için zaman içerisinde 0 ve 1’lerden oluşan bir dizi elde edilecektir. Şok modeller, rasgele büyüklükteki bir şokun rasgele bir zamanda meydana geldiği sistemlerdir. Aslında bu modellerin finans ve sigortacılık gibi güvenirlik ve yaşam analizlerini içeren çeşitli alanlarda da uygulanma olanağına sahip olduğunu düşünebiliriz. Sistem güvenilirliğinde, sistemin rasgele zamanlarda meydana gelen şoklara maruz kaldığı ve sistemin bozulma kriterinin ardışık iki şok arasında geçen zamana bağlı olduğu varsayılmıştır. δ-şok modelleri sadece sistem güvenilirliği

için değil aynı zamanda finans, sigortacılık gibi diğer alanlarda da uygulanabilir. Şok kavramı, bir sigorta şirketinin belli bir portföy ile ilgili hasar talebi olarak düşünülürse ömür, birbirine yakın iki hasar ile karşılaşılıncaya kadar ki bekleme süresi anlamına gelir. Temel olarak üç farklı tür şok model bulunmaktadır. Bunlar tekrar şok modelleri, aşırı şok modeller ve birikimli şok modellerdir. Şok modeller son yıllarda büyük ilgi çeken konular arasında yer almaktadır.(Sumita ve Shanthikumar, 1985), (Gut, 1990), (Mallor ve Omey, 2001) şok modelle ilgili incelemelerde bulunmuşlardır. Bir dizinin herhangi bir bölümünde, bir şoktan diğer şoka kadar yapılan denemelerin sayısının δ gibi bir eşik değerinden küçük olması o bölümde bir δ-şok olduğu, büyük olması ise o bölümde herhangi bir δ-şok olmadığı anlamına gelmektedir ve böyle sistemlere δ-şok model adı verilmektedir. δ-şok model (Li ve Kong, 2007), (Eryılmaz, 2012) tarafından çalışılmıştır. (Eryilmaz, 2013), δ-şok modelindeki şokların n=1,2,… anlarında binomial süreçlere göre meydana geldiği ve şoklar arasında geçen sürenin 1/p ortalamalı geometrik dağılıma sahip olduğu kesikli durum altında δ-şok modellerini incelemiştir. Bu çalışmada kesikli δ-şok modelinde sistemin, ardışık olarak k (k>0) kere δ-şok’a maruz kaldığında bozulacağı varsayılmıştır. Böyle bir sistem, kesikli k-ardıl δ-şok modeli olarak adlandırılabilir. Bu varsayım altında sistemin ömrü, ardışık k-kere δ-şok oluncaya kadar yapılan deneme sayısı şeklinde ifade edilebilir. Burada amaç sistem bozuluncaya kadar yapılan deneme sayısının olasılık dağılımını ve bu dağılımın bazı karakteristik özelliklerini elde etmektir.

İstatistiksel olarak k-ardıl δ-şok modeli şeklinde kurgulanan yapıların gerçek hayatta karşılığı olan pek çok sistem bulunmaktadır. Bu sistemlerin ömürlerinin olasılık

(9)

adına büyük önem taşımaktadır. Örneğin soğutma cihazı olarak kullanılan sistemin her

δ-şoktan sonra ısınması ve ardışık k-tane δ-şoktan sonra bozulması durumunda,

bozuluncaya kadar geçen sürenin (sistemin ömrünün) olasılık dağılımının bulunması sistem kullanıcıları için oldukça önemlidir. Sadece cihazları değil canlıları bile bu sisteme rahatça uyarlanabilir. Örneğin bir bakteri türü için geliştirilen bir ilaç düşünülsün. Bu ilaç için iki kullanım arasındaki geçen sürenin δ’dan büyük olması yani bakterilerin δ-şok’a maruz kalmaması durumunda ilacın önceki dozlarının bakteriler üzerindeki etkisinin yok olduğu düşünülebilir. Bu bakterinin k-kere ardışık δ-şoka (ilaca) maruz kaldıktan sonra öldüğü düşünülürse, ölünceye kadar ki denemelerin sayısının olasılık fonksiyonun bulunması bu canlı üzerinde incelenen bazı durumlar açısından önemlidir. Yukarıda verilen iki örnekte de görüldüğü gibi gerçek hayattaki bazı durumlar kesikli k-ardıl δ-şok modeli ile modellenebilmektedir. Bu açıdan bu modellere ilişkin elde edilecek bulgular büyük öneme sahiptir.

Başarılı-başarısız, sağlam-bozuk, var-yok gibi iki tür sonuç alan denemelere ilişkin Bernoulli, Binom, Geometrik, Negatif Binom gibi çok iyi bilinen olasılık modellerinin yanında daha birçok model önerilmiştir. Bu çalışmalardan bazıları aşağıda sıralanmıştır.

(Aki ve Hirano, 1988): Bu çalışmada Aki ve Hirano, ilk k ardıl başarı elde edilinceye kadar yapılan denemelerin sayısının dağılımını elde etmişlerdir. Ayrıca ilk k ardıl başarı elde edilinceye kadar yapılan denemelerde ki başarıların ve başarısızlıkların dağılımını da elde etmişlerdir.

(Charalambides, 1986): Bu çalışmada Charalambides, k ardıl kesikli dağılımların, kesikli dağılımların genellenmiş hali olduğunu ifade etmiştir. “k ardıl dağılımlar k başarı elde edildikten sonra kesikli dağılımların sağdan budanmış halleridir”. Bu dağılımların olasılık fonksiyonu ve faktöriyel momentlerini Sağdan Budanmış Bell Polinomları ile açıklamıştır.

(Charalambides, 2010): Bu çalışmada Charalambides, Bernstein polinomlarını q-Binom dağılımının olasılık fonksiyonunun tanımlanmasında kullanmıştır. Bu dağılım, önceki bozulma sayısına göre geometrik olarak artan bozulma olasılığına sahip 0 ve 1 değerini alan Bernoulli denemeleri üzerine kurgulanmıştır.

(10)

(Cirillo ve Hüsler, 2009): Urn süreçlerini kullanan genelleştirilen uç şok modellerine yeni bir sezgisel bir yaklaşım ortaya koymuşlardır. Genelleştirilen uç şok modellerinin eşik değerinin her seferinde değiştiğinden bahsetmektedirler.

(Cirillo ve Hüsler, 2011): Gut ve Hüsler rasgele büyüklükte bir şoka rasgele bir zamanda maruz kalan sistemleri uç şok modelleri ile olarak ortaya koymuşlardır. Ortaya konulan bu yapıdaki sistemler dayanıklılık seviyeleri üstünde meydana gelen şoklarda bozulmaktadırlar. Cirillo, Hüsler bu çalışmayı uç şok modelleri yaklaşımına alternatif olarak önermişlerdir.

(Eryılmaz, 2012): Bu çalışmada Eryılmaz ardışık iki şok arasındaki zaman belirlenen bir δ eşik seviyesinden daha az ise sistemin bozulduğundan bahsetmiştir. Bu model çeşitli alanlarda uygulanabilirliğinden söz etmiştir. k ardışık zaman arası δ eşik seviyesinden daha az olduğundan bozulan sistemlerin yaşam fonksiyonları ve sistemlerin ortalama ömürleri zaman aralıkları üstel dağıldığı durumda elde edilmiştir.

(Eryilmaz, 2013): Bu çalışmada Eryılmaz kesikli zaman modellerin için ardışık iki şok arasındaki zamanın kritik bir seviyeden daha az ise sistemin bozulacağını düşünmüş ve sistemlerin ömrünün olasılık fonksiyonunu, olasılık üreten fonksiyonunu elde etmiştir.

(Eryilmaz, 2014): Bu çalışmada Eryılmaz, ödüllü ardıl k Geometrik dağılımını incelemiştir. İkili denemelerin dizisinde, başarı olduğunda rasgele bir ödül verilmektedir. Ardışık ödüllerin toplamı k oluncaya kadar veya k’yı geçene kadar yapılan denemelerin sayısının dağılımı ödüllü ardıl k geometrik dağılım olarak adlandırılmıştır. Bu dağılımın olasılık fonksiyonu bu çalışmada elde edilmiştir.

(Eryilmaz ve Demir, 2007): Bu çalışmada Eryılmaz ve Demir, tekrar istatistiğinin (run) “0” (bozulma) “1” (başarı) değerini alan ξ1,ξ2,…, ξn dizisinin simetrik elemanı olduğu düşünülmüştür. Çeşitli tekrar istatistiklerinin dağılımları her bir tekrar istatistiğinin koşullu dağılımı kullanılarak elde edilmiştir.

(Eryılmaz ve Yalçın, 2011): Bu çalışmada Eryılmaz ve Yalçın, iki sonuç alabilen bağımsız Markov elementlerinin, iki ardışık bozulma arasındaki maksimum uzaklık, minimum uzaklık ve ortalama uzaklıklarından bahsetmişlerdir. Bu rasgele değişen stokastik süreçlerde meydana gelen birtakım problemleri çözmede kullanılabilir. Bu rasgele değişkenin dağılımı kombinatorik tekniği yardımıyla elde edilmiş ve nümerik sonuçlar sunulmuştur.

(11)

(Gut ve Hüsler, 2005): Bu çalışmada Gut ve Hüsler bir şokun sisteme kısmı hasar verebileceğini ve kritik sınırın altındaki bu şokların toplamının sistemi öldürebileceğini düşünmüşler. Sistemi öldüren şokların toplamının durumunu birikimli model olarak ele almışlardır.

(Koutras, 1996): Bu çalışmada Koutras bağımsız ve aynı dağılıma sahip Bernoulli denemelerini kullanarak örtüşmeyen ardışık k başarı elde edilinceye kadar yapılan denemelerin sayısının dağılımını incelemiştir. Ancak bu çalışmadaki farklılık başarı çiftleri arasına en fazla k-2 tane başarısızlık girse de tekrarın sağlanabildiği durumlar olmasıdır. Bu dağılıma ilişkin olasılık fonksiyonu, olasılık üreten fonksiyonu ve momentlerde elde edilmiştir.

(Mohanty, 1994): Bu çalışmada Mohanty, iki sonuçlu Markov denemelerinde k uzunluğundaki başarı elde edilinceye kadar beklenen zaman Geometrik ve Polya-Eggenberge dağılımları olasılık üreten ve kombinatorik yöntem ile elde edilmiştir. Geometrik dağılım için ilk iki moment bulunmuştur.

(Yalcin, 2014): İki sonuçlu n denemelik bir dizide Mn,k (n denemede k uzunluğunda

örtüşen denemelerin sayısı) rasgele değişkenin dağılımı Ling’s Binom dağılımı ya da Tip II Binom dağılımı olarak adlandırılmaktadır. Bu çalışmada Yalçın, Ling’s Binom dağılımı olarak genellemiştir. Bu genelleme yapılırken başarı olasılığı geometrik olarak değişen Bernoulli denemeleri kullanılmıştır. Bu yeni dağılımda q=1 verildiğinde, Ling’s Binom dağılımı elde edilecektir.

Bu tez çalışmasının ikinci bölümünde δ-şok modeller hakkında bilgi verilecek, üçüncü bölümünde ise önerilen kesikli k-ardıl δ-şok modeli ve bazı özellikleri incelenecektir. Dördüncü bölümde ise elde edilen sonuçlar tartışılacaktır.

(12)

2. KESİKLİ δ-ŞOK MODELİ

Bu modelde, sistemin maruz kaldığı ardışık iki şok arasında geçen zamanın δ gibi bir eşik seviyesinin altında olması durumunda sistemin bozulacağı varsayılmaktadır. Sistemin ömrünün, bahsedilen bu olay gerçekleşinceye kadar geçen zaman olarak ifade edilebileceği düşünülürse, bir birleşik rasgele değişken olduğu söylenebilir. δ-şok modellerinin sürekli versiyonu yani şoklar arasında geçen sürenin olasılık dağılımının sürekli olması durumunda sistemin ömrünün davranış özellikleri (Wang* ve Zhang, 2005), (Bai ve ark., 2006), (Li ve Kong, 2007) ve (Li ve Zhao, 2007) tarafından çalışılmıştır. (Eryilmaz, 2013) ise şokların n=1,2,… anlarında binomial süreçlere göre meydana geldiğini ve şoklar arasında geçen sürenin 1/p ortalamalı geometrik dağılıma sahip olduğunu varsaymıştır. Burada bu varsayım altında sistemin ömrünün davranış özellikleri verilecektir.

2.1. Model Varsayımları

Bir sistemin birbiri ardına meydana gelen dış şoklara maruz kaldığı varsayılsın ve şokların n=1,2,… anlarında binomial süreçlere göre meydana geldiği düşünülsün. Yani

n=1,2,… zaman dilimi içinde şokun meydana gelme olasılığı p meydana gelmeme

olasılığı 1-p_{olsun. İlk şok meydana gelene kadar geçen süre}0 ve i1,2,...için i. ve

). 1

(i şoklar arasındaki zaman i ile gösterilsin. Burada 0, 1,… bağımsız ve



 x



 p(1p) 1,x1,2,...

P _i x

şeklindeki aynı olasılık fonksiyonuna sahip rasgele değişkenlerdir. 2.2. Sistemin Yaşam Zamanı

Yukarıdaki varsayımlar altında kesikli δ-şok modelleri ile tanımlanan sistemlerin ömrü



    M i i 0  (1)

şeklinde ifade edilebilir. Burada durdurma rasgele değişkeni olarak adlandırılan M rasgele değişkeni 1   ve m=1,2,… için



1,...,m1 ,m 



ise



M m



olarak tanımlanabilir. 2.3. Olasılık Fonksiyonu

M rasgele değişkeni ₁,₂,...lere bağlı olduğu için (1) eşitliği ile verilen ifade

kullanılarak _ rasgele değişkeninin dağılımını bulmak oldukça zordur. Aşağıda _ rasgele değişkeninin dağılımı, (1) ile verilen sistemin ömrüne denk yeni bir rasgele değişken tanımlanarak ve kombinatorik işlemleri kullanarak elde edilmiştir. Bu yöntem iki sonuçlu dizilerin analizini oldukça kolaylaştıran bir yöntemdir. bkz.(Eryılmaz ve

(13)

Yalçın, 2011). (Eryilmaz, 2013), sistemin ömrü olarak tanımlanan _ rasgele değişkeninin olasılık fonksiyonunu Teorem 1’deki gibi elde etmiştir.

Teorem 1. Meydana gelen şoklar bağımsız ve aynı dağılıma sahip olmak üzere

















2 1 2 2 1 1 1 1 1 1 n n i i i n i n i n p p i i          _    _                _ _   _ _       



şeklindedir. Burada [.] tam değer fonksiyonu, n2,3,... için

ı ş _{ı ş ı} (2) ve



_n



 p 



_n 



 p

 1 , 0 1

olarak tanımlanmaktadır.

İspat. I₁,I₂,...’lerdeki en fazla ‘δ-1’ kadar 0 (şoksuz dönem) ile ayrılmış iki 1 (şoklu dönem) elde edilinceye kadar bekleme zamanı şeklinde bir rasgele değişken tanımlansın

ve W ile gösterilsin._ Bu durumda  1 için _ ve W rasgele değişkenleri dağılımda _

birbirlerine eşit olacaktır.



W_ n



olayının meydana gelmesi yani sistemin n. denemede bozulması olayı için, n denemeden oluşan ve içerisinde tam i tane 1 içeren



i2



yani



W_ n,Q_n i



olayının gerçekleşmesi için bir diziliş

  ...010...010...01...1 10...010...0 0 0 0 2 3 1 1 y y yi yi y . (3)

şeklinde yazılabilir. Böylece n denemedeki 1’lerin sayıları (Q_n) üzerinden

koşullandırma yapılarak



W_ n



olayının olasılığı















 





             2 2 2 1 , , , , i i n i i n i n p p i n C i Q n W P i Q n W P n W P    

olarak yazılabilir. Burada C



n,,i



, iki sonuçlu bir dizinin (3) formuna sahip tüm

mümkün dizilişlerinin sayısını yada buna denk olarak y₁y₂...y_i ni

(14)

çözümlerinin sayısını göstermektedir. z₁  y₁, j2, 3, ,...i1 için z_j  y_j 



ve

i i y

z  şeklinde tanımlansın. O zaman C



n,,i



sayısı, z₁ 0,z₂ 0,…,zi₁ 0,



  z_i

0 koşulları altında z₁...z_i ni



i2



 denkleminin tamsayılı çözümlerinin sayısına eşittir ve



n i



C



n i



C



n i



C ,,  ₁ ,,  ₂ ,, ,

şeklindedir. Burada C₁



n,,i



ve C₂



n,,i



sırasıyla



z_j 0,j1,...,i



ve



z_j 0, j1,...,i1,z_i 





kısıtları altında z₁...z_i ni



i2



 denkleminin

tamsayılı çözümlerinin sayısını göstermektedir.

n z

z₁... _r  denkleminin z_j 0, j 1,...,r kısıtları altında tamsayılı çözümlerinin

sayısı _         1 1 r r n

’dir (Öztürk, 1995).Böylece C₁



n,,i



ve C₂



n,,i



_sayıları









_           1 1 2 , , 1 i i n i n C   ve





 

_           1 1 1 , , 2 i i n i n C  

olarak elde edilebilir.

2.4. Olasılık Üreten Fonksiyon, Beklenen Değer ve Varyans

(Eryilmaz, 2013), T ’nin olasılık üreten fonksiyonunu _ P



_n 1



 p1q olmak üzere

 



 









 



2 1 1 1 pz qz z qz qz pz qz        

şeklinde ve bu olasılık üreten fonksiyona bağlı olarak T_’nin ortalaması ve varyansını

 













1 2 1 1 1 E T p p p           

(15)

 



 







































2 2 1 2 2 2 2 2 1 1 1 2 1 1 2 6 6 6 4 2 1 1 2 1 1 1 2 1 1 1 Var T p p p p p p p p p p p p p p                                        _{ }    _ _{ } _  

(16)

3. KESİKLİ k-ARDIL δ-ŞOK MODELİ

3.1. Model Varsayımları ve Bazı Örnekler

Kesikli zamanlarda şoka maruz kalabilen bir sistem düşünelim. Herhangi bir

t

anında sistemin şoka maruz kalma olasılığı p ve kalmama olasılığı q1 polsun. Sistemin herhangi bir anda şoka maruz kalması 1, kalmaması ise 0ile ifade edilsin. Ayrıca bu sistemin,  olmak üzere maruz kaldığı ardışık iki şok arası sürenin

δ’dan küçük ya da eşit olduğu durum arka arkaya k kere gerçekleştiğinde öldüğünü ya

da bozulduğunu varsayalım. T,k rasgele değişkeni ise bu sistem ölünceye kadar geçen

süreyi göstersin. Aşağıda T__,_k rasgele değişkeninin değerine ilişkin bazı örnekler verilmiştir.

Durum 1:  2, k1

Örnek Örnek diziliş Rasgele değişken

 

T,k 1     1 2 0 3 0 4 0 3 01 001 0001 001 1         k k k k     13 2   1 2 0 3 01 001 01     k k   7 3  1 1 1 001   k  4 4  1 1 1 1   k  2

(17)

Durum 2:  2,k 2

 

T,k 1 _{    } 2 2 1 2 0 3 0 3 1 2 0 3 01 01 001 001 01 001 001             k k k k k k       18 2 _{    } 2 2 1 1 0 3 1 2 0 3 01 1 001 01 001 001           k k k k k      14 3 _{  } 2 2 1 2 0 3 01 01 001 1       k k k    8 4 _{  } 2 2 1 1 0 3 01 1 001 1       k k k    7 5 _{ } 2 1 1 1 1 1 1     k k   3 Durum 3:  3,k 2

 

T,k 1 _ 2 3 1 3 0 4 1 3 001 001 0001 001 01         k k k k     15 2 _{ } 2 2 1 3 0 4 1 3 01 001 0001 001 001         k k k k     15 3 _ 2 3 1 3 001 001 001     k k   9 4 _{ } 2 2 1 2 01 01 01     k k   6 5 _{ } 2 1 1 1 1 1 1     k k   3

(18)

Durum 4:  3,k 3

 

T,k 1  3 3 2 3 1 3 0 4 2 3 1 3 0 4 0 5 0 5 001 001 001 0001 001 001 0001 00001 00001 0001                   k k k k k k k k k            37 2 _{ } 3 3 2 3 1 3 0 4 1 2 0 4 1 3 0 4 001 001 001 0001 01 0001 001 0001 001                 k k k k k k k k         29 3 _{} 3 3 2 3 1 3 0 4 1 3 001 001 001 0001 001 001           k k k k k      19 4 _{  } 3 2 2 2 1 3 01 01 001 001       k k k    10 5 _{  } 3 1 2 2 1 3 1 01 001 001       k k k    9 6 _{  } 3 1 2 1 1 1 1 1 1 001       k k k    6 3.2. Olasılık Fonksiyonu

Burada öncelikli amacımız verilen  ve k değerine bağlı olarak bu T,k rasgele

değişkeninin olasılık fonksiyonunu belirlemektir. Yukarıdaki örneklerden de kolayca anlaşılabileceği gibi T,k, k1,k2,... değerlerini alabilen bir rasgele değişkendir.

k

T__, rasgele değişkeninin olasılık fonksiyonunu belirlemek için



j i

S, {dizilişte tam i tane δ-şoksuz ve tam j tane δ-şoklu dönem olması}

şeklinde bir Si,j olayı tanımlansın. Bu durumda T,k rasgele değişkeninin olasılık

fonksiyonu



T _, n







P



T _, n,S_,



,nk1,k2, P i j j i k k   (4)

şeklinde yazılabilir. Buradaki



T n,S_i,_j



olayı sistemin ömrünün n olması ve n anına kadar tam i tane  şoksuz ve tam j tane  şoklu dönem yaşanması olayıdır. Bu olaya karşılık gelen örnek bir diziliş şekil 1’de verilmiştir. Bu dizilişe ilişkin olasılık





1 2 0 1 1 1 2 0 1 1 2 1 1 , , ... ... ... 0 1 , ,..., 0,0 ,...,0 , ,..., , i s t i wi i i _wi i w i n m k i j x x x j k n n n m m n s t x k x k x k n n n m m m P T_ n S q p q p                                      _ _ _   







 

(5)

(19)

olarak yazılabilir. Elde edilen (5) eşitliği (4)’de yerine yazılarak T,k rasgele

değişkeninin olasılık fonksiyonu

      1 2 0 1 1 1 2 0 1 1 ₂ 1 2 3 1 1 , _{, '} _0, min 1 1 , 0 ... ... ... , ,..., 0,0 ,...,0 , ,..., ( ) i wi i i _wi i n i n k _{lerin dizilişi} i k i k i j k x x x j k n n n m m n x k x k x k n n n E _E m m m E P T n                 _ _ _{ }  _                                  



 

4 1'lerin dizilişi 1 1 0 1 i s t w i n m s t E q  p q  p           







(6)

şeklinde elde edilir.

Yukarıdaki olasılık fonksiyonun içinde yer alan E₁, E₂, E₃, E₄ ifadelerinin açıklaması aşağıda olduğu gibidir.

1

E : Dizilişteki δ-şoksuz dönemlerin toplamı

2

E : Dizilişteki δ-şoklu dönemlerin toplamı

3

E : j tane δ-şoklu dönem var. Bunların k tanesi dizilişin en sonunda, diğer

i

x x

x₁  ₂ ... tanesi ise daha önde bir yerlerde, bu durumda x₁ x₂...x_i  jk

yazılabilir. Burada x_i’ler son k tane ""dan önceki ""ların sayısıdır. E₃ ifadesi de kısıtlar altında, “+” ve “-” lerin mümkün tüm dizilişleri üzerinden toplamı ifade etmektedir.

4

E : Esas dizilişler içindir. n ilk “1” e kadar yani ilk şoklu döneme kadar yapılan ₀

denemelerin sayısı,

i

w

n n

n₁, ₂,..., j tane δ-şoklu dönemdeki deneme sayılarını

göstermektedir. m₁,m₂,...,m_i ise i tane δ-şoksuz dönemdeki deneme sayılarını

göstermektedir. Bu durumda E₄ ifadesi de kısıtlar altında “0” ve “1” lerin mümkün tüm dizilişleri üzerinden toplamı ifade etmektedir. Burada w_i x₁x₂ ...x_i k

(20)

dönem şoklu dönem şoksuz dönem şoklu dönem şoksuz           1 0       0 01 ... 0 0 n              k x n n x         1 1 ... 01 ... 0 ... 01 ... 0 1        1  01 ... 0 m                k x n n_x _x _x           2 1 ... 01 ... 0 ... 01 ... 0 2 1 1        2  01 ... 0 m      3  01 ... 0 m ... ...     _  1  01 ... 0 i m                    k x n n i x x x x i i         _      ... 01 ... 0 ... 01 ... 0 1 ... 1 2 1        i  m 01 ... 0                  k n n _x _x _k i i        _{ }   ... 01 ... 0 ... 01 ... 0 1   j k x x x₁ ₂... _i  

(21)

      1 2 0 1 1 1 2 0 1 1 2 1 1 , min 1 1 1 1 ,k 0 1 0 ... ... ... , ,..., 0,0 ,...,0 , ,..., ( ) s t i j i i j i n i n k j i i k i n m s t i j k x x x j k n n n m m n x k x k x k n n n m m m P T n q p q p                   _ _            _ _                                 _ _   









 

eşitliğindeki toplamların içerisinde yer alan

1 1 0 1 s t j i n m s t q  p q  p          _ _ 







ifadesi



0 1





1 2



1 1 ₁ ₁ ₁ ₁ ₁ ₁ 0 1 ... ... s t j i j i n m _n _n _n _m _m _m s t q  p q  p q  pq  p q  p q  pq  p q  p           _ _ 







                                     i i t t j j s s _p i m q p j n q 0 1 1 1 1 0 1 1           j i j s i t t s p i j m n q  1 1   n j i j i p q

şeklinde yazılabilir. Elde edilen bu ifadeyi (6) eşitliğinde yerine yazarak

        1 2 0 1 1 1 2 0 1 1 2 1 1 , min 1 1 1 1 , 0 ... ... ... , ,..., 0,0 ,...,0 , ,..., ( ) i j i i j i n i n k i k i n j i j i k i j k x x x j k n n n m m n x k x k x k n n n m m m P T n q p                   _ _                                           



 

(7)

eşitliği elde edilir.

(7) eşitliğinde yer alan nji1 ji1

p

q ifadesin₀,n₁,...,n_j,m₁,...,m_i,x₁,...,x_i’lerden bağımsızdır.

(22)

        1 2 0 1 1 1 2 0 1 1 2 1 1 , min 1 1 1 1 , 0 ... ... ... , ,..., 0,0 ,...,0 , ,..., ( ) 1 i j i i j i n i n k i k i n j i j i k i j k x x x j k n n n m m n x k x k x k n n n m m m P T n q p                   _ _                                           



 

₍₈₎

olarak yazılabilir. Burada

0 1 1 0 1 1 2 ... ... 0,0 ,...,0 , ,..., 1 j i j i n n n m m n n n n m m m                    

 

ifadesi, y1y2 ... y_j1... y_j_i1 n denkleminin 1 2 1 2 1 0 y n, 0 y , , 0y_j_  ,  1 y_j_ n, ,  1 y_{j i}_{ } n

kısıtları altında pozitif tam sayılı çözümlerinin sayısına eşittir ve bu çözümlerin sayısı













 





 









0 1 1 0 1 1 2 1 ... ... 0,0 ,...,0 , ,..., 1 1 1 1 1 1, 1 1 1 1, 1 1 1 1, 1 1 1 j i j i n n n m m n n n n m m m j m m i t t G s j i n j i j s j i n j i m m i s j i n j i t n t                                          _{ }              _{ }           

 



(9)

olarak elde edilmiştir. Burada s n k

 

, n 1 k

k

 

 

  

  şeklindedir. Çözüme ilişkin detaylar

EK-1’de verilmiştir. Elde edilen bu ifade (8)’de yerine yazılırsa

        1 2 1 2 1 1 , min 1 1 1 1 , 1 0 ... , ,..., ( ) i i n i n k i k i n j i j i k i j k x x x j k x k x k x k P T n q p G              _ _                            



 

(10)

eşitliği elde edilir. Burada dikkat edilirse G₁ ifadesi x1,x2,...,x_i ifadesinden bağımsızdır.

(23)

        1 2 1 2 1 1 , min 1 1 1 1 , 1 0 ... , ,..., ( ) 1 i i n i n k i k i n j i j i k i j k x x x j k x k x k x k P T n q p G              _ _                            



 

(11)

şeklinde yazılabilir. Burada 1 2 1 2 ... , ,..., 1 i i x x x j k x k x k x k        

 

ifadesi x₁ x₂ ...x_i  jk denkleminin k x k x k

x₁  , ₂  , ..., _i  kısıtları altında pozitif tam sayılı çözümlerinin sayısına eşittir ve bu çözümlerin sayısı





 





1 2 1 2 2 ... , ,..., 1 1 1 , 1 , 1 i i x x x j k x k x k x k i n n G i s i j k s i j n k n                  _  _{ }   _    

 



(12)

olarak elde edilmiştir. Çözüme ilişkin detaylar EK-2’de verilmiştir.

Son olarak elde edilen (12) ifadesi (11) eşitliğinde yerine yazılırsa T__,_k rasgele değişkeninin olasılık fonksiyonu nk1,k2, için

        1 1 , min 1 1 1 1 , 1 2 0 ( ) n i n k i k i n j i j i k i j k P T n q p G G              _ _                   



(13) şeklinde elde edilir. Burada G₁ve G₂ (9) ve (12)’de verildiği gibidir. Aşağıda T,_k rasgele

değişkeninin (13) eşitliği ile verilen olasılık fonksiyonunun çeşitli parametre değerleri için grafikleri Şekil 2-5’de ve değerleri Çizelge 1-4’de verilmiştir.

(24)

Şekil 2. k=2 için P(T,k n) olasılık fonksiyonunun grafikleri

Çizelge 1. k=2 için P(T__,_k n) değerleri

n δ=1 p=0.5 δ=1 p=0.7 δ=1 p= 0.9 δ=2 p= 0.5 δ=2 p=0.7 δ=2 p= 0.9 δ=3 p= 0.5 δ=3 p= 0.7 δ=3 p= 0.9 3 _0,1250 _0,3430 _0,7290 _0,1250 _0,3430 _0,7290 _0,1250 _0,3430 _0,7290 4 _0,0625 _0,1029 _0,0729 _0,3750 _0,6174 _0,4374 _0,3750 _0,6174 _0,4374 5 _0,0625 _0,1029 _0,0729 _0,5000 _0,4939 _0,1166 _0,6563 _0,6483 _0,1531 6 _0,0625 _0,1029 _0,0729 _0,4219 _0,2624 _0,0255 _0,7969 _0,4723 _0,0372 7 _0,0547 _0,0676 _0,0198 _0,2813 _0,1272 _0,0108 _0,7578 _0,2732 _0,0077 8 _0,0508 _0,0570 _0,0144 _0,1758 _0,0649 _0,0037 _0,5938 _0,1348 _0,0019 9 _0,0469 _0,0464 _0,0091 _0,1113 _0,0327 _0,0009 _0,4043 _0,0607 _0,0005 10 _0,0430 _0,0358 _0,0038 _0,0732 _0,0173 _0,0003 _0,2490 _0,0259 _0,0001 11 _0,0396 _0,0289 _0,0024 _0,0518 _0,0109 _0,0001 _0,1450 _0,0108 _0,0000 12 _0,0364 _0,0230 _0,0013 _0,0393 _0,0074 _0,0001 _0,0830 _0,0046 _0,0000 13 _0,0334 _0,0182 _0,0007 _0,0310 _0,0049 _0,0000 _0,0485 _0,0021 _0,0000 14 _0,0308 _0,0146 _0,0004 _0,0249 _0,0031 _0,0000 _0,0297 _0,0011 _0,0000 15 _0,0283 _0,0116 _0,0002 _0,0203 _0,0020 _0,0000 _0,0194 _0,0007 _0,0000 16 _0,0260 _0,0092 _0,0001 _0,0168 _0,0014 _0,0000 _0,0134 _0,0004 _0,0000 17 _0,0239 _0,0073 _0,0001 _0,0141 _0,0009 _0,0000 _0,0096 _0,0002 _0,0000 0 20 40 60 80 0 0.05 0.1 0.15 0.2 n p=0.5, =1 0 20 40 60 80 0 0.1 0.2 0.3 0.4 n p=0.7, =1 0 20 40 60 80 0 0.2 0.4 0.6 0.8 n p=0.9, =1 0 20 40 60 80 0 0.2 0.4 0.6 0.8 n p=0.5, =2 0 20 40 60 80 0 0.2 0.4 0.6 0.8 n p=0.7, =2 0 20 40 60 80 0 0.2 0.4 0.6 0.8 n p=0.9, =2 0 20 40 60 80 0 0.2 0.4 0.6 0.8 n p=0.5, =3 0 20 40 60 80 0 0.2 0.4 0.6 0.8 n p=0.7, =3 0 20 40 60 80 0 0.2 0.4 0.6 0.8 n p=0.9, =3

(25)

Şekil 3. k=3 için P(T__,_k n) olasılık fonksiyonunun grafikleri

Çizelge 2. k=3 için P(T_,_k n) değerleri

(26)

(27)

n δ=1 p=0.5 δ=1 p=0.7 δ=1 p= 0.9 δ=2 p= 0.5 δ=2 p=0.7 δ=2 p= 0.9 δ=3 p= 0.5 δ=3 p= 0.7 δ=3 p= 0.9 6 _0,0156 _0,1176 _0,5314 _0,0156 _0,1176 _0,5314 _0,0156 _0,1176 _0,5314 7 _0,0078 _0,0353 _0,0531 _0,0469 _0,2118 _0,3189 _0,0469 _0,2118 _0,3189 8 _0,0078 _0,0353 _0,0531 _0,0625 _0,1694 _0,0850 _0,0820 _0,2224 _0,1116 9 _0,0078 _0,0353 _0,0531 _0,0527 _0,0900 _0,0186 _0,0996 _0,1620 _0,0271 10 _0,0078 _0,0353 _0,0531 _0,0381 _0,0503 _0,0093 _0,0947 _0,0937 _0,0056 11 _0,0078 _0,0353 _0,0531 _0,0313 _0,0406 _0,0086 _0,0757 _0,0483 _0,0015 12 _0,0078 _0,0353 _0,0531 _0,0298 _0,0394 _0,0086 _0,0559 _0,0269 _0,0010 13 _0,0077 _0,0311 _0,0249 _0,0297 _0,0393 _0,0086 _0,0424 _0,0192 _0,0009 14 _0,0076 _0,0299 _0,0221 _0,0296 _0,0381 _0,0057 _0,0356 _0,0170 _0,0009 15 _0,0076 _0,0287 _0,0193 _0,0293 _0,0340 _0,0026 _0,0330 _0,0162 _0,0006 16 _0,0075 _0,0274 _0,0164 _0,0284 _0,0277 _0,0010 _0,0320 _0,0149 _0,0003 17 _0,0074 _0,0262 _0,0136 _0,0271 _0,0217 _0,0005 _0,0314 _0,0127 _0,0001 18 _0,0074 _0,0249 _0,0108 _0,0255 _0,0174 _0,0004 _0,0303 _0,0099 _0,0000 19 _0,0073 _0,0237 _0,0080 _0,0242 _0,0148 _0,0003 _0,0286 _0,0072 _0,0000 20 _0,0073 _0,0226 _0,0066 _0,0230 _0,0129 _0,0002 _0,0264 _0,0050 _0,0000 0 20 40 60 80 0 0.005 0.01 0.015 0.02 n p=0.5, =1 0 20 40 60 80 0 0.05 0.1 0.15 0.2 n p=0.7, =1 0 20 40 60 80 0 0.2 0.4 0.6 0.8 n p=0.9, =1 0 20 40 60 80 0 0.02 0.04 0.06 0.08 n p=0.5, =2 0 20 40 60 80 0 0.1 0.2 0.3 0.4 n p=0.7, =2 0 20 40 60 80 0 0.2 0.4 0.6 0.8 n p=0.9, =2 0 20 40 60 80 0 0.05 0.1 n p=0.5, =3 0 20 40 60 80 0 0.1 0.2 0.3 0.4 n p=0.7, =3 0 20 40 60 80 0 0.2 0.4 0.6 0.8 n p=0.9, =3

(28)

3.3. Beklenen Değer

k

T__, rasgele değişkeninin olasılık fonksiyonu P T( __,_k n) olmak üzere T__,_k rasgele değişkeninin beklenen değeri

 

        , , 1 1 1 , min 1 1 1 1 1 2 0 1 ( ) k k n k n i n k i k i n j i j i i j k n k E T nP T n n q p G G                  _ _                                 



 



olarak ifade edilir. Ancak bu beklenen değerin daha sade bir ifadesi elde edilememektedir.

k

T__, rasgele değişkeninin beklenen değerinin çeşitli parametre değerleri için grafikleri Şekil 6-9’da verilmiştir.

Şekil 6. k=2 için E(T__,k) beklenen değer grafikleri

0.5 0.6 0.7 0.8 0.9 1 4 6 8 10 12 14 16 18 20 22 p =1 0.5 0.6 0.7 0.8 0.9 1 3 4 5 6 7 8 9 10 11 12 p =2 0.5 0.6 0.7 0.8 0.9 1 3.5 4 4.5 5 5.5 6 6.5 7 7.5 8 p =3

(29)

Şekil 7. k=3 için E(T__,k) beklenen değer grafikleri

Şekil 8. k=4 için E(T,k) beklenen değer grafikleri

0.5 0.6 0.7 0.8 0.9 1 4 6 8 10 12 14 16 18 20 22 p =1 0.5 0.6 0.7 0.8 0.9 1 4 5 6 7 8 9 10 11 12 13 p =2 0.5 0.6 0.7 0.8 0.9 1 4 5 6 7 8 9 10 p =3 0.5 0.6 0.7 0.8 0.9 1 4 6 8 10 12 14 16 18 20 22 p =1 0.5 0.6 0.7 0.8 0.9 1 4 6 8 10 12 14 16 p =2 0.5 0.6 0.7 0.8 0.9 1 4 5 6 7 8 9 10 11 12 13 14 p =3

(30)

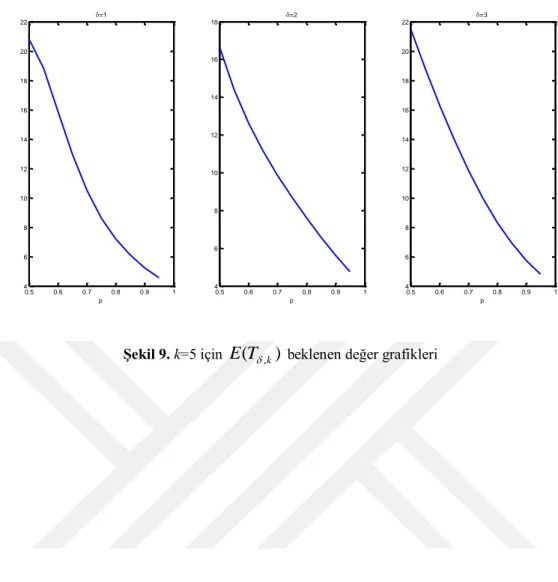
Şekil 9. k=5 için E(T__,k) beklenen değer grafikleri 0.5 0.6 0.7 0.8 0.9 1 4 6 8 10 12 14 16 18 20 22 p =1 0.5 0.6 0.7 0.8 0.9 1 4 6 8 10 12 14 16 18 p =2 0.5 0.6 0.7 0.8 0.9 1 4 6 8 10 12 14 16 18 20 22 p =3

(31)

4. SONUÇLAR VE ÖNERİLER

Bu çalışma ile kesikli δ-şok modellerinin daha genel bir hali olan yeni bir model tanımlanmıştır. Bu modelin olasılık dağılımı ve bu dağılımın bazı karakteristik özellikleri bulunarak literatüre kesikli k-ardıl δ-şok modeli isminde yeni bir olasılık dağılımı kazandırılmıştır. Bu yeni olasılık dağılımı kesikli verilerin modellenmesinde bir alternatif model olarak düşünülebilir. İleriki zamanlarda, elde edilen bu olasılık dağılımına ilişkin sonuç çıkarımı çalışmalarına da yer verilebilir.

(32)

EKLER EK-1: E₄’ün Çözüm Sayısı n y y y y₁ ₂... _j_₁... _j__i_₁  denkleminin 1 2 1 2 1 0 y n, 0 y , , 0y_j  ,  1 y_j n, ,  1 y_{j i}  n

kısıtları altında uygun çözümlerinin sayısını bulmak için

önce kısıtları,    A n y   ₁ 1                B j y y 1, ..., 1 1 1 ₂    _₁                    C i j j n y n y      1 _₂ , ...,  1 __₁  şeklinde yazalım. 1 1 1, 2 2 1,..., j 1 j 1 1 z  y z y  z   y   ,









2 2 1 ,..., 1 1 1 j j j i j i z  y     z    y     dönüşümü sonucu denklem,







1 1



... ... 1 1 2 1z  z   z  n j i  z j j i kısıtlar ise,









1 1, 2 ,..., zj 1 , j 2 1 ,..., zj i 1 1 z  n z    z   n      n   olmaktadır.







1 1



... ... ₁ ₁ 2 1z  z   z  n j i  z _j _j _i









1 1, 2 ,..., zj 1 , j 2 1 ,..., zj i 1 1 z  n z    z   n      n  

(33)

1

1 1z n

A olan çözümlerin kümesi,





 ₂

1 z

B olan çözümlerin kümesi,





 ₃

2 z

. . .    _ 1 j 1 j z

) 1 (

2

1 z  n  

C _j olan çözümlerin kümesi,

. . . ) 1 ( 1    z __ n 

Cj j i olan çözümlerin kümesi,

olsun.

 

_         k k n k n s , 1 olduğundan, 1 A kümesinin çözüm sayısı,

 

A₁ s



ji1, n



j1i



1



(n1)



0 n  dır. (Öztürk, 1995) j B B B₁, ₂,..., kümelerinin çözüm sayısını,

 





 





 



j



j s m j s m j m m j n B n B B nB B B B B B n B n                 







... 1 ... ... 1 2 1 1 1 2 1 şeklinde bulunabilir.

(34)

 

B s



ji1, n



j1i



 1









n m m’den bağımsız



B B



s



ji1, n



j1i



 1



2





n _m _s m’den ve s’den bağımsız

. . .



B B B



s



j i n



j i







j



n 1 2... j   1,  1 1  (Öztürk, 1995)

 





















 





 





1 2 1 1 1 ... 1, 1 1 1 1, 1 1 2 ... 2 1 1, 1 1 1 1, 1 1 j j j m m j n B n B B B s j i n j i j s j i n j i j s j i n j i j j j s j i n j i m m                  _{ }            _{ }               _{ }              _{ }         



olarak elde edilir.

Benzer düşüncelerle C1,C2,...,C_i kümelerinin çözüm sayısı

  



 





  

i

