SELÇUK ÜNĠVERSĠTESĠ FEN BĠLĠMLERĠ ENSTĠTÜSÜ
ÇOK KRĠTERLĠ OPTĠMĠZASYON ĠÇĠN GENETĠK ALGORĠTMA YAKLAġIMLARI
TAHĠR SAĞ YÜKSEK LĠSANS TEZĠ
FEN BĠLĠMLERĠ ENSTĠTÜSÜ
ÇOK KRĠTERLĠ OPTĠMĠZASYON ĠÇĠN GENETĠK ALGORĠTMA YAKLAġIMLARI
TAHĠR SAĞ YÜKSEK LĠSANS TEZĠ
BĠLGĠSAYAR MÜHENDĠSLĠĞĠ ANABĠLĠM DALI
Bu tez 21.01.2008 tarihinde aĢağıdaki jüri tarafından oybirliği / oyçokluğu ile kabul edilmiĢtir. Yrd.Doç.Dr. Mehmet ÇUNKAġ Prof.Dr. Ahmet ARSLAN Prof.Dr. Novruz ALLAHVERDĠ
iii
ÖZET
Yüksek Lisans TeziÇOK KRĠTERLĠ OPTĠMĠZASYON ĠÇĠN GENETĠK ALGORĠTMA YAKLAġIMLARI
Tahir SAĞ
Selçuk Üniversitesi Fen Bilimleri Enstitüsü Bilgisayar Mühendisliği Anabilim Dalı DanıĢman: Yrd. Doç.Dr. Mehmet ÇUNKAġ
2008, 102 sayfa
Jüri: Prof.Dr. Novruz ALLAHVERDĠ Prof.Dr. Ahmet ARSLAN Yrd.Doç.Dr. Mehmet ÇUNKAġ
Gerçek dünya problemleri genelde çok amaçlıdır. Bu problemlerin çözümü birbiriyle çeliĢen çoklu amaçların eĢzamanlı olarak optimizasyonunu gerektirir. Çok amaçlı optimizasyon tek amaçlı optimizasyondan çok farklıdır. Tek-amaçlı optimizasyonda amaç, en iyi olan tek bir tasarım veya kararı elde etmektir. Çok amaçlı optimizasyonda ise birbiriyle çeliĢen amaçlar, içersinde üzerinde uzlaĢma sağlanan bir optimal çözümler kümesi elde edilir. Bu küme genellikle Pareto-Optimal çözümler kümesi olarak adlandırılır. Çok amaçlı optimizasyon problemlerinin çözümü için 1985’ten bu yana evrimsel algoritmaları kullanan çeĢitli yaklaĢımlar önerilmiĢtir. Bu tez çalıĢmasında, baĢlıca sekiz adet çok amaçlı evrimsel algoritma (Vektör Değerlendirmeli Genetik Algoritma, Çok Amaçlı Genetik Algoritma, HücrelendirilmiĢ Pareto Genetik Algoritması, BastırılmamıĢ Sınıflandırmalı Genetik Algoritma, BastırılmamıĢ Sınıflandırmalı Genetik Algoritma II, Kuvvet Pareto Evrim Algoritması, Kuvvet Pareto Evrim Algoritması 2 ve Pareto Zarflama-Temelli Seçim Algoritması) orijinal halleri esas alınarak detaylı olarak incelenmiĢtir. Algoritmaların değerlendirilmesi için bazı performans ölçütleri kullanılmıĢtır. Tüm algoritmalar için C ailesinin son uzantısı olan nesne yönelimli görsel programlama dili C# kullanılarak MOEAT(Multiobjective Evolutionary Algorithms Tool) adı verilen ortak bir arayüzde editör ve simülasyon yazılımı geliĢtirilmiĢtir. Ayrıca, literatürden seçilen sekiz adet test problemi ve iki adet mühendislik problemi aracılığıyla, yazılımın kullanılabilirliği ve iĢlevselliği denenmiĢtir.
Anahtar Kelimeler: Çok amaçlı optimizasyon, Pareto-Optimal Çözümler, evrimsel algoritmalar.
iv
ABSTRACT
Master ThesisGENETIC ALGORITHM APPROACHES FOR MULTIOBJECTIVE OPTIMIZATION
Tahir SAĞ Selcuk University
Graduate School of Natural and Applied Sciences Department of Computer Engineering Supervisor: Asst.Prof. Mehmet ÇUNKAġ
2008, 102 papers
Jury: Prof.Dr. Novruz ALLAHVERDĠ Prof.Dr. Ahmet ARSLAN Asst.Prof. Mehmet ÇUNKAġ
Real world problems are multiobjective in nature. Solution of these problems mostly require the optimization of conflicting objectives each other simultaneously. Multiobjective optimization is principally different from single objective optimization. In single-objective optimization, it is attempted to obtain the best design or decision for an objective. In multiobjective optimization, the objectives which are in competition with each other cause the results to be drifted to not only a solution but to a set of compromise optimal solutions. Such solutions are known as Pareto-Optimal solutions. Various approaches used evolutionary algorithms have been proposed to solve optimization problems since 1985. In this thesis study, mainly eight multiobjective evolutionary algorithms (Vector Evaluated Genetic Algorithm,
Multiobjective Genetic Algorithm, Niched Pareto Genetic Algorithm, Nondominated Sorting Genetic Algorithm, Nondominated Sorting Genetic Algorithm-II, Strength Pareto Evolutionary Algorithm, Strength Pareto Evolutionary Algorithm 2, and Pareto Envelope-based Selection Algorithm) have been examined in detail by taking into consideration original papers published. Some performance metrics to evaluate the algorithms have been observed. And all algorithms have been developed as an editor simulation software called MOEAT (Multiobjective Evolutionary Algorithms Tool) in common interface by using object oriented programming language, C#, which is the final extension of C family. Also the software was run over eight test problems, and two real world engineering problems which were used on this issue and taken from literature, and hopeful results were obtained.
Keywords: Multiobjective optimization, Pareto-Optimal Solutions, Evolutionary Algorithms, MOEAT.
v TEŞEKKÜR
Tez çalıĢmamın gerçekleĢme sürecinde tezime yaptığı katkılardan ve yardımlarından dolayı değerli danıĢman hocam Yrd. Doç. Dr. Mehmet ÇUNKAġ’a teĢekkür ederim.
Tez çalıĢmam boyunca gösterdikleri sabır ve destekten dolayı baĢta annem olmak üzere sevgili aileme teĢekkür ederim.
Bu tez çalıĢması 07101024 proje numarası ile Selçuk Üniversitesi Bilimsel AraĢtırma Projeleri Koordinatörlüğü tarafından desteklenmiĢtir. Katkılarından dolayı teĢekkür ederim.
vi İÇİNDEKİLER ÖZET ... iii ABSTRACT ... iv TEŞEKKÜR ... v İÇİNDEKİLER ... vi ŞEKİL LİSTESİ ... ix TABLO LİSTESİ ... xi 1. GİRİŞ ... 1 1.1. Amaç ... 1 1.2. Kaynak AraĢtırması ... 3 2. OPTİMİZASYON ... 7 2.2. Formülasyonu ... 7
2.3. Optimizasyon Modellerinin Sınıflandırılması... 8
2.4. Genetik Algoritmalar ve Evrimsel Hesaplama ... 9
2.4.1. Genetik algoritmaların avantajları ... 12
2.4.2. Temel algoritması ... 13
3. ÇOK AMAÇLI OPTİMİZASYON ... 15
3.1. Pareto-Optimal Kavramı ... 15
3.2. Çok Amaçlı Optimizasyon Problemleri ... 17
3.3. MOEA’ların Sınıflandırılması ... 18
3.3.1. Toplama fonksiyonları ... 18
3.3.2. Popülâsyon-Temelli YaklaĢımlar ... 19
vii
4. ÇOK AMAÇLI GENETİK ALGORİTMALAR ... 21
4.1. VEGA: Vektör Değerlendirmeli Genetik Algoritma ... 21
4.2. MOGA: Çok Amaçlı Genetik Algoritma ... 23
4.2.1. Seçim süreci ... 25
4.2.2. Seçkinlik stratejisi ... 26
4.2.3. MOGA Algoritması ... 27
4.3. NPGA: HücrelendirilmiĢ Pareto Genetik Algoritması ... 28
4.3.1. Pareto Üstünlük Turnuvası ... 29
4.3.2. BastırılmamıĢ Yüzey Üzerinde PaylaĢım ... 30
4.4. NSGA: BastırılmamıĢ Sınıflandırmalı Genetik Algoritma ... 32
4.5. NSGA-II: BastırılmamıĢ Sınıflandırmalı Genetik Algoritma II ... 35
4.5.1. Hızlı bastırılmamıĢ sınıflandırma yaklaĢımı ... 35
4.5.2. ÇeĢitliliğin sağlanması ... 37
4.5.3. Ana döngü ... 39
4.6. SPEA: Kuvvet Pareto Evrimsel Algoritması ... 41
4.6.1. SPEA Algoritması ... 42
4.6.2. Uygunluk ataması ... 44
4.6.3. Kümeleme algoritması ... 45
4.7. SPEA2: Kuvvet Pareto Evrimsel Algoritması 2 ... 46
4.7.1. SPEA2 Algoritması ... 47
4.7.2. Uygunluk ataması ... 49
4.7.3. Çevresel seçim ... 50
4.8. PESA: Pareto Zarflama-Temelli Seçim Algoritması ... 51
4.8.1. PESA Algoritması ... 52
5. PERFORMANS KRİTERLERİ ... 54
5.1. Yakınsama Metriği ( ) ... 54
5.2. ÇeĢitlilik Metriği (∆) ... 55
6. ÇOK AMAÇLI EVRİMSEL ALGORİTMALAR ARACI ... 57
6.1. Kullanıcı Arayüzleri ... 57
6.1.1. Çok kriterli genetik algoritmalar formu (mgaform.cs)... 58
viii
6.1.3. Performans ölçümü arayüzü (PerformansÖlçümü.cs) ... 62
6.1.4. Öklid mesafesi arayüzü (Euclidean_Mesafesi.cs) ... 65
6.1.5. Grafik arayüzü (Goster.cs) ... 67
6.1.6. Hakkında arayüzü (About.cs): ... 69
6.1.7. Editör arayüzü (Editor.cs) ... 70
6.2. Kodlama ve Algoritmalar... 71
6.2.1. Proje I: multiobjective_genetic_algorithms ... 71
6.2.2. Proje II: Genetic ... 73
6.2.3. Proje III: Problem... 75
7. DENEYSEL ÇALIŞMALAR ... 76
7.1. Test Problemleri ... 76
7.2. Gerçek Mühendislik Problemi Ġncelemeleri ... 91
8. SONUÇ... 96
ix ŞEKİL LİSTESİ
ġekil 2.1: Genetik Algoritma AkıĢ Diyagramı ... 12
ġekil 3.1. BastırılmamıĢ çözümler (kapalı çemberler) ve bastırılmıĢ çözümler (açık çemberler) ... 18
ġekil 4.1: J-Boyutlu bir popülâsyonda I amaç fonksiyonlu bir problem için VEGA Algoritmasının ÇalıĢması (Schaffer 1985)... 22
ġekil 4.2: Schaffer’ın yaklaĢımında arama yönleri (Tadahiko 1994) ... 22
ġekil 4.3: Çok Amaçlı Genetik Algoritmanın Farklı Arama Yönleri (Murata 1997) 23 ġekil 4.4: Sabit Ağırlık Vektörü ile TanımlanmıĢ Arama Yönü (Murata 1997) ... 25
ġekil 4.5: MOGA’da depolanan birey kümelerinin güncellenme süreci (Murata 1997) ... 26
ġekil 4.6: MOGA AkıĢ Diyagramı ... 28
ġekil 4.7: Pareto Üstünlük Turnuvası için Sözde Kod ... 30
ġekil 4.8: EĢdeğer Sınıf PaylaĢımı (Horn, 1994) ... 32
ġekil 4.9: NSGA AkıĢ Diyagramı (Srinivas ve Deb 1993) ... 34
ġekil 4.10: Hızlı BastırılmamıĢ Çözüm Sıralama Metodu Ġçin Sözde Kod (Deb, 2002) ... 36
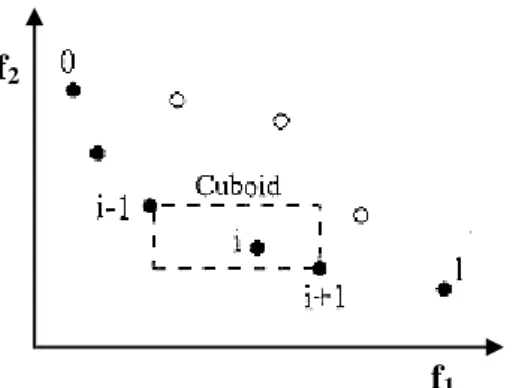
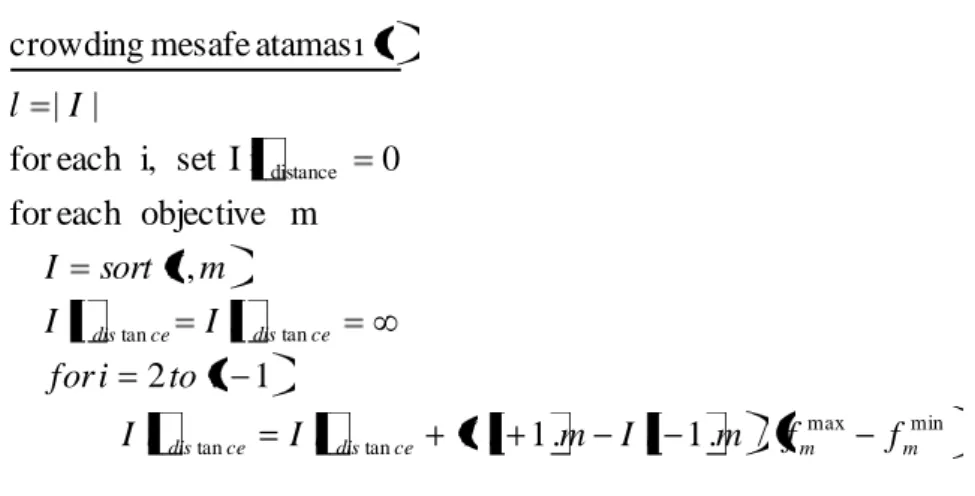
ġekil 4.11: Kalabalık-Mesafe Hesaplaması. Dolu dairelerle iĢaretlenmiĢ noktalar aynı bastırılmamıĢ yüzeydeki çözümlerdir. ... 38
ġekil 4.12: Kalabalık KarĢılaĢtırma Mesafesi (Crowding Mesafesi) için sözde kod . 39 ġekil 4.13: NSGAII Prosedürü (Deb, 2002) ... 40
ġekil 5.1: Performans Metrikleri (a) Yakınsama Metriği (b) ÇeĢitlilik Metriği ... 55
ġekil 6.1: Çok Amaçlı Evrimsel Algoritmalar Aracı Ana Form ... 59
ġekil 6.2: Parametreler Arayüzü ... 60
ġekil 6.3: Performans Ölçümü Arayüzü ... 63
ġekil 6.4: Performan Ölçümü -Sonuç Dosyaları GiriĢ Formu ... 64
ġekil 6.5: Öklid Mesafesi – Orijin Noktası ... 65
ġekil 6.6: Öklid Mesafesi Arayüzü ... 66
ġekil 6.7: Mevcut Grafik Gösterim Arayüzü ... 68
x
ġekil 6.9: Editör Arayüzü ... 70
ġekil 6.10: Proje I – “multiobjective_genetic_algorithms” ... 72
ġekil 6.11: Genetic Projesi Sınıf Diagramaları ve Solution Explorer Penceresi ... 74
ġekil 7.1: OSY problemi için pareto optimal çözümler ... 83
ġekil 7.2: SRN problemi için pareto optimal çözümler ... 84
ġekil 7.3: TNK problemi için pareto optimal çözümler ... 85
ġekil 7.4: CONSTR problemi için pareto optimal çözümler ... 86
ġekil 7.5: FON problemi için pareto optimal çözümler ... 87
ġekil 7.6: SCH problemi için pareto optimal çözümler ... 88
ġekil 7.7: ZDT1 problemi için pareto optimal çözümler ... 89
ġekil 7.8: ZDT4 problemi için pareto optimal çözümler ... 90
ġekil 7.9: Ġndüksiyon Motor EĢdeğer Devresi ... 91
ġekil 7.10: MOEAT’dan elde edilen Pareto-Optimal Çözümler ... 94
ġekil 7.11: I-Kesitli kiriĢ karar değiĢkenlerinin tanımlanması... 95
xi TABLO LİSTESİ
Tablo 7.1: Kısıtlamasız Test Problemleri... 77
Tablo 7.2: Kısıtlamalı Test Problemleri ... 78
Tablo 7.3: Kısıtlamasız Test problemleri için Yakınsama Metriği ( ) ... 79
Tablo 7.4: Kısıtlamasız Test problemleri için ÇeĢitlilik Metriği (∆) ... 80
Tablo 7.5: Kısıtlı test problemleri için Yakınsama Metriği ( ) ... 80
Tablo 7.6: Kısıtlı test problemleri için ÇeĢitlilik Metriği (∆) ... 81
Tablo 7.7: Gerçek Makine Parametreleri ... 93
Tablo 7.8: Parametre Belirleme Sonuçlarının Özeti ... 93
1. GİRİŞ
1.1. Amaç
Optimizasyon, verilen amaç veya amaçlar için belirli kısıtlamaların sağlanarak en uygun çözümün elde edilmesi sürecidir. Optimizasyon problemlerinin çözümü için model arayıĢları sonucunda öncelikle doğrusal ve az sayıda değiĢkenin kullanıldığı matematiksel modellemeler oluĢturulsa da bunun her problem için geçerli olmadığı anlaĢılmıĢ ve doğrusal olmayan modellemeye gidilmiĢtir. Bu noktada, evrim kuramındaki en iyinin korunması ve doğal seçim stratejileri kullanan evrimsel algoritmalar geliĢtirilmiĢtir.
Evrimsel Algoritmalardan olan genetik algoritmalar, geleneksel yöntemlerle çözümü zor veya imkânsız olan problemlerin çözümünde sıklıkla kullanılmaya baĢlanmıĢtır. Genetik algoritmalarda optimize edilecek amaç veya amaçlar sanal olarak evrimden geçirilerek olası çözümler kümesinden en iyi çözüm veya çözümler elde edilmeye çalıĢılır. Tek amaç optimize edilecekse, problem tek-amaçlı optimizasyondur. Eğer birden fazla amaç optimize edilecekse, problemler çok-amaçlı olarak formülize edilmelidir ve bu durumda çok-amaçlı veya vektör optimizasyon problemleri olarak adlandırılırlar. Ġlkesel olarak tek-amaçlı optimizasyon ve çok-amaçlı optimizasyon birbirinden farklıdır. Tek-çok-amaçlı optimizasyonda en iyi olan tek bir çözüm aranırken çok-amaçlı optimizasyonda tüm amaçlara göre en iyi olan tek bir çözüm mevcut olmayabilir. Bu bakımdan her amaç için üzerinde uzlaĢma sağlanan sonlu bir çözüm kümesi aranır. Karar vericiden her biri kabul edilebilir düzeyde olan bu alternatif çözümlerden seçim yapması istenir.
Bu tez çalıĢmasında çok amaçlı genetik algoritmalar (Vektör Değerlendirmeli Genetik Algoritma, Çok Amaçlı Genetik Algoritma, HücrelendirilmiĢ Pareto Genetik Algoritması, BastırılmamıĢ Sınıflandırmalı Genetik Algoritma, BastırılmamıĢ Sınıflandırmalı Genetik Algoritma II, Kuvvet Pareto Evrim Algoritması, Kuvvet Pareto Evrim Algoritması 2 ve Pareto Zarflama-Temelli Seçim Algoritması)
incelendi. Bu algoritmaların performansları test problemleri kullanılarak değerlendirildi. Ayrıca çok amaçlı optimizasyon problemlerinin kolayca tanımlanabildiği ve çözümlerinin elde edilebildiği bir arayüz geliĢtirildi. Elektronik, bilgisayar, inĢaat ve makine gibi bilim dallarına ait optimizasyon problemleri geliĢtirilen, bu arayüz yardımıyla kolayca çözülebilmektedir.
Tez çalıĢması giriĢ bölümü ile beraber toplam sekiz bölümden oluĢmaktadır. Ġkinci bölümde optimizasyon, optimizasyon algoritmaları ve genetik algoritmalar hakkında temel bilgiler verilmektedir. Üçüncü bölümde Pareto-Optimalite kavramı, çok-amaçlı optimizasyonun tanımı çok-amaçlı evrimsel algoritmaların sınıflandırılma yaklaĢımları ele alınmaktadır. Dördüncü bölümde bu alanda yapılmıĢ olan çalıĢmalar üzerinde durularak çok amaçlı genetik algoritmalardan sekiz tanesi incelenmekte ve algoritmaların çok-amaçlı optimizasyon problemlerini çözme yaklaĢımları detaylı olarak açıklanmaktadır. BeĢinci bölümde, incelenen algoritmaların performanslarının karĢılaĢtırılması için kullanılan performans kriterleri açıklanmaktadır. Altıncı bölümde, performans analizlerinin gerçekleĢtirilmesi için geliĢtirilen ve Çok-Amaçlı Evrimsel Algoritmalar Aracı (MOEAT) adı verilen editör simülasyon yazılımı açıklanmaktadır. GeliĢtirilen bu yazılım ile tüm algoritmaların ortak bir arayüzde çalıĢtırma imkânı sağlanmaktadır. Bu bölümde MOEAT’ın kullanımı ve kodlaması iki ayrı alt baĢlıkta ele alınmaktadır. Literatürden seçilen sekiz adet test problemi ve iki adet gerçek dünya problemleri değerlendirilmektedir. Yedinci bölümde elde edilen simülasyon sonuçları tablolar ve grafikler halinde sunulmaktadır. Sonuç bölümünde algoritmaların karĢılaĢtırmalı performans analizleri yapılmaktadır.
1.2. Kaynak Araştırması
Optimizasyon problemleri, evrimsel algoritmalar ve çok amaçlı optimizasyon problemlerinin çözümü ile ilgili bugüne kadar yapılmıĢ pek çok çalıĢma bulunmaktadır. AĢağıda bu çalıĢmaların bazılarına kısaca yer verilmiĢtir.
Dias A.H.F. ve ark. (2002), Evrimsel algoritmalarla çözülen çok-kriterli optimizasyon problemleri tartıĢılmıĢtır. Bu tür problemleri çözecek bastırılmamıĢ sınıflandırmalı genetik algoritma (NSGA) üzerinde durulmuĢtur. Ayrıca performansı diğer dört algoritmadan elde edilen sonuçlarla karĢılaĢtırılmıĢtır.
Andrzej Osyczka, (2002), evrimsel algoritmaların esas bakıĢ açısını içeren bir metin ve özellikle klasik optimizasyon yöntemleri kullanılarak çözülemeyen tasarım optimizasyon problemlerini çözen ileri uygulamalar sunmuĢtur. AraĢtırmacılar ve baĢta makine, inĢaat, endüstri ve bilgisayar mühendislikleri olmak üzere tüm mühendislik bölümlerinin öğrencileri için çalıĢma rehberi niteliğinde bir kitap hazırlanmıĢtır. Konuyu basit tasarım optimizasyon problemlerinin tanıtımından baĢlayarak, daha geliĢmiĢ GA’lar ve evrimsel algoritmalar, evrimsel iĢlemciler; çeĢitli seçim, çaprazlama ve mutasyon türleri; sınırlanmamıĢ-sınırlandırılmıĢ optimizasyon, ceza fonksiyonları ve tarihsel sıralamayla çok-kriterli genetik algoritmalar hakkında çıkarılmıĢ yayınların derlemeleri ve bunlarla ilgili örneklerden, çok-kriterli optimizasyon algoritmalarının diğer yapay zeka teknikleri ile hibritleĢtirilmesi konularına kadar ele almıĢtır.
Gallardo A. ve ark. (2000), hücrelendirilmiĢ genetik algoritmaların temel kavramlarını ve parametrelerini ele almıĢlardır. Ġdeal olarak, bu algoritmalar tasarımcıya daha iyi çözümler bulan birkaç alternatif tasarımlar sunarlar ve paralel olarak çalıĢtırılabilirler.
Sareni ve ark. (2000), sınırlandırılmıĢ optimizasyon problemlerini çözecek birçok Genetik Algoritma Stratejisini tasarlamıĢlardır. Erken yakınsamayı önleyecek çeĢitli genetik iĢlemciler ele almıĢlar ve özellikle, hücrelendirme metotları, her birinin avantajlarını ve sakıncalarını gösteren bir karĢılaĢtırma sunmuĢlardır.
Carlos ve ark. (1992), çok-amaçlı genetik algoritmalar (MOGA) için sıralama-temelli uygunluk ataması yöntemini incelemiĢlerdir. Klasik hücre formasyon metotları, çok-modelli problemler sınıfına geniĢletilerek hücre boyutunu ayarlayan bir teori sunmuĢlardır.
Carlos ve ark. (1994), çok-kriterli evrimsel yaklaĢımlar ve çoklu kriterlerin değerlendirmesini yapmıĢlardır. Ġlerde yapılacak araĢtırma için tavsiyelerde bulunmuĢlardır.
Cheol ve ark. (1999), kısıtlanmıĢ yarıĢmacı seçimi (RCS) kullanan yeni bir hücreleme metodu, çok-modelli bölgede verimli hücreleri (pik noktalarını) tanımlamak ve araĢtırmak için önermiĢlerdir. Geçerliliğini doğrulamak için, bazı klasik matematiksel problemlere ve indüksiyon motor tasarımına uygulanmıĢlardır.
Todd (1999), mühendislik tasarımı ve çalıĢmasında çok kriterli problemler için genetik algoritmaların uygulamalarını araĢtırmıĢtır. GeliĢtirdiği yeni ilerlemeler temel test problemleri üzerinde değerlendirmiĢtir. Pareto Popülasyonu, Uyarlamalı Hücre Boyutlandırma (Adaptive Niche Sizing) ve Sinir Ağı Tercihi (Neural Network Preferencing) gibi kavramlar tanıtmıĢtır.
Goldberg (1989), genetik algoritmalar (GA) – doğal seçim mekanizmasına ve doğal genetiğe dayalı arama iĢlemleri hakkında geniĢ bilgiler vermiĢtir. GA’ların matematiksel temelleri, bilgisayarda gerçekleĢtirim aĢamaları, çeĢitli örnekler, genetik aramada ileri iĢlemci ve teknikler, genetik temelli makine öğrenmesi ve uygulamaları üzerinde detaylı bir Ģekilde incelemiĢtir. Ayrıca bazı dillerde yazılmıĢ kodlarlarla örnekler vermiĢtir.
Huang ve ark. (2007), bir mühendislik tasarım sürecindeki ortak tasarım değiĢkenlerinden ve belirsizliklerden dolayı performans fonksiyonlarının bağlanması, optimizasyon tasarım problemlerinde güçlüklere neden olması ve tasarım amaçları arasındaki zayıf iĢbirliği ve tasarım çeliĢkilerinin zayıf kararlılığı gibi problemleri ortadan kaldırmak için bulanık etkileĢimli çok-kriterli optimizasyon modelini geliĢtirmiĢlerdir. Önerilen metot, maksimum doygunluk dereceli ve ideal çözümden minimum uzaklıkla bir pareto optimal kümeyi üretmede baĢarı sağlamıĢtır.
Horn ve ark. (1994), Pareto optimal kümeyi bulmak için HücrelendirilmiĢ Pareto Genetik Algoritmasını (NPGA) sunmuĢlardır. Ayrıca algoritmanın pareto
optimal popülasyonu bulmadaki ve çeĢitliliği elde etmesindeki yeteneğini göstermek için iki yapay problem ve hidrosistemde bir probleme uygulamıĢlardır.
Deb ve ark. (1999), doğru Pareto-optimal yüzeye yakınsamada çeĢitli problemleri ele almıĢlardır. Tek kriterli optimizasyon problemlerinden oluĢturulan çok kriterli test problemleri geliĢtirilen algoritmaların performans ölçümlerinde kullanılmıĢtır.
Kursawe (1991), çok kriterli optimizasyonda klasik çözüm yöntemleri hakkında kısa bir açıklama yapmıĢ ve evrimsel stratejilerden bahsetmiĢtir.
Srinivas ve Deb (2002), genetik algoritmalarda bir hücrelendirme tekniği ile beraber Golberg’in bastırılmamıĢ çözümleri sınıflandırma düĢüncesini araĢtırmıĢlardır. Sonuçları test problemleri kullanarak değerlendirmiĢlerdir. Bu yöntemin daha büyük boyutlu ve daha zor çok kriterli problemlere geniĢletilebileceğini önermiĢlerdir.
Azar (1999), bazı sorunların üstesinden gelmek için genetik algoritmaları kullanan iki metodu göstermektir. Ġlk metot çok kriterli optimizasyonu ele alırken bazı harici değiĢikliklerle bir genetik algoritma kullanır. Ġkinci metot ise bazı önemli dâhili değiĢiklikli genetik algoritma içinde yürütür. Her iki metodun güçlü ve zayıf yanlarını olarak karĢılaĢtırmıĢtır.
Yang ve ark.(2005), çok amaçlı problemlerin çözümünde Pareto optimal kümeye iyi bir yaklaĢım sağlayan yeni bir evrimsel yaklaĢım – (µ,λ) Çok kriterli Evrimsel Strateji ((µ,λ) MOES) – önermiĢlerdir. Yakınlığın ve bireylerin çeĢitliliğinin nasıl dengelendiği üzerinde durmuĢlardır.
Murata ve Ishibuchi (1995), Çok-kriterli optimizasyon problemlerinin Pareto-optimal çözümlerini araĢtıracak bir genetik algoritma çatısı önermiĢlerdir. Önerilen yaklaĢımın tek-kriterli genetik algoritmalardan ayrılan tarafı, seçim iĢlemi ve seçkini koruma stratejisidir. Önerilen algoritmadaki seçim iĢlemi, çoklu amaç fonksiyonlarının ağırlıklı toplamına dayanan bir çaprazlama iĢlemi ile bireyleri seçer. Seçim iĢleminin karakteristik özelliği, çoklu amaç fonksiyonlarına iliĢtirilen ağırlıkların sabit değil her bir seçim için rasgele bir Ģekilde belirlenmesidir. Seçkini koruma stratejisi; tek bir seçkin çözüm yerine, bir dizi seçkin çözüm kullanır. Belli
sayıda birey Pareto-optimal çözümlerin geçici kümesinden seçilir ve sonraki jenerasyona seçkin bireyler olarak aktarılır.
Murata (1997), öncelikle tek-krtiterli optimizasyon problemlerini GA’lara uygulamıĢtır. GA’ların performansının geliĢtirilmesi için diğer algoritmalarla GA’ların hibritleĢmesi denemiĢtir. Daha sonra, çok-kriterli genetik algoritmalar bazı sezgisel yöntemlerle hibritleĢtirmiĢtir ve çok kriterli hibrit GA’lar zamanlama problemleri ve dilbilimsel karar seçim problemlerine uygulamıĢtır.
Önceki çalıĢmalarda, ele alınan yöntemlerin toplu olarak karĢılaĢtırıldığı, avantajlarının ve sakıncalarının ortaya konulduğu kapsamlı bir değerlendirme görülmemektedir. Ayrıca çok amaçlı optimizasyonda evrimsel algoritmaların farklı problemler için simülasyonu sağlayacak ortak bir yazılım eksikliği tespit edilmiĢtir.
2. OPTİMİZASYON
Optimizasyon, bir problemin çözümünde matematiksel modeller geliĢtirerek, yönetimsel karar üretmeye yardım eden disiplinlerdir (Sarker 2002). Bu bölümde optimizasyonda kullanılan geleneksel teknikler gözden geçirilmektedir. Ayrıca genetik algoritmalar ve evrimsel hesaplamanın temel prensipleri üzerinde durulmaktadır.
2.1. Formülasyonu
Bir tasarım probleminin matematiksel modeli, bir eĢitlikler sistemi ve problemin temelini açıklayan matematiksel ifadelerdir. Eğer hedeflenen n tane karar varsa, bunlar karar değişkenleri x1,x2,...xn olarak temsil edilir. Uygun bir
performans ölçümü, karar değiĢkenlerinin fonksiyonu olarak tanımlanır. Bu fonksiyona amaç fonksiyonu denir. Karar değiĢkenlerinin alabileceği değerlerde sınırlamalar varsa, bu sınırlamalar tipik olarak eĢitsizlikler veya eĢitliklerle açıklanır ve bunlara kısıtlamalar denir. Burada amaç, kısıtlamaların her birini sağlayarak amaç fonksiyonun en iyi değerini elde eden karar değiĢkenlerinin değerlerini belirlemektir.
Örnek olarak, kârı en fazla yapmak için n farklı ürünün üretim seviyelerini seçme problemi ele alınırsa; üretim seviyeleri sınırlı kaynaklardan dolayı m tane kısıta bağlı olacaktır. Bu modelin amacı, aĢağıdaki durumları sağlayacak x1,x2,...xn
parametrelerini belirlemektir. 0 , ... , 0 , 0 ) ,..., , ( ) ,..., , ( ) ,..., , ( ) ,..., , ( 2 1 2 1 2 2 1 2 1 2 1 1 2 1 n m n m n n n x x x ve b x x x g b x x x g b x x x g x x x f Maksimize aşağıdakilere bağlı olarak
Bu modelde, karar değiĢkenleri x1,x2,...xn üretim seviyelerini gösterir, amaç
fonksiyonu f x1,x2,...,xn kârı ölçer ve kısıtlamalar gi x1,x2,...,xn bi m
i 1,..., eĢitsizlikleri ile temsil edilir.
n x x x1, 2,...
değerlerinden herhangi birine çözüm denir. Oysaki tüm
kısıtlamaları sağlayan çözüm uygun çözüm olarak adlandırılır. Tüm uygun çözümlerin kümesine uygun bölge denir. Amaç fonksiyonunu maksimum yapan uygun bölgedeki bir çözüm optimal çözüm olarak adlandırılır.
BaĢka optimizasyon modelleri amaç fonksiyonunu minimize etmeyi amaçlayabilir (maliyetin minimize edilmesi). Ayrıca modeller karıĢık kısıtlamalara sahip olabilir, eĢitlik ve eĢitsizlikler olabilir veya hiç bir kısıtlama olmayabilir.
2.2. Optimizasyon Modellerinin Sınıflandırılması
Bir optimizasyon problemini çözmeden önce, amaç fonksiyonun özellikleri, kısıtlamalar ve karar değiĢkenlerinin durumu önemlidir. Örneğin amaç fonksiyonu lineer veya lineer olmayan, ayrık veya ayrık olmayan, içbükey veya dıĢbükey olabilir. Karar değiĢkenleri sürekli veya ayrık, içbükey veya dıĢbükey olabilir. Bu farklılıklar her bir modelin nasıl çözülebileceğini etkiler ve böylece optimizasyon modelleri bu farklılıklara göre sınıflandırılabilir (Sarker 2002).
Bir çok optimizasyon tekniği lineer fonksiyon kısıtlamalarında amaç fonksiyon veya fonksiyonlarına bağlıdır. Bir fonksiyon, c i değerleri sabit
olduğunda f x1,x2,...,xn c1x1,c2x2,...cnxn Ģeklinde ifade edilebilirse lineerdir. Eğer amaç fonksiyon ve tüm kısıt fonksiyonları, lineer fonksiyonsa, modele lineer programlama modeli denir.
Yukarıda verilen örnekte tek bir amaç vardı (kârın maksimize edilmesi). Bazen tüm yönetimsel amaçları tek bir amaçta ifade etmek mümkün değildir. Kârın maksimize edilmesi ve maliyetin minimize edilmesi gibi. Bu sebeple, birden çok amaç fonksiyonu içeren çok amaçlı optimizasyon modeli ortaya çıkar.
Lineer programlama ve nonlineer programlama tekniklerinde alıĢılagelmiĢ olarak karar değiĢkenlerinin sürekli olduğu varsayılır. BaĢka bir deyiĢle, karar değiĢkenlerinin kısıtlamaları sağlayan, tamsayı olmayan değerler dâhil herhangi bir değer alabilmesine izin verilir. Bununla beraber birçok uygulamada, karar değiĢkenleri sadece tamsayı değerleri için anlamlı olur. Mesela kiĢilere veya teçhizata tamsayı miktarlarında atama yapmak için tamsayı değerler sıklıkla gereklidir. Tüm değiĢkenlerin tamsayı olmasının gerektiği bir model tamsayı
programlama modeli olarak tanımlanır. DeğiĢkenlerden bazıları sürekliyse, ancak
diğerlerinin tamsayı olması gerekiyorsa bu modele de karışık-tamsayı programlama
modeli denir. Modeldeki tüm fonksiyonlar lineerse, lineer tamsayı programlama modeli veya fonksiyonlardan herhangi biri lineer değilse lineer olmayan tamsayı programlama modeli olarak kategorize edilebilir.
Amaç fonksiyonu veya kısıt fonksiyonlarından herhangi biri lineer değilse böyle bir model lineer olmayan programlama modeli olarak adlandırılır. Lineer olmayan programlama problemleri birçok Ģekilde olabilir. Tek bir algoritma tüm bu farklı problem türlerini çözemez. Bu nedenle, optimizasyon algoritmaları değiĢik lineer olmayan programlama problemlerini çözmek için geliĢtirilmiĢtir.
2.3. Genetik Algoritmalar ve Evrimsel Hesaplama
Evrimsel hesaplama, doğal seçim iĢleminden esinlenilerek geliĢtirilmiĢ bir arama ve optimizasyon algoritmasıdır. Doğal seçim iĢlemi, uygunluk değeri en yüksek bireyin seçilmesini sağlar. Böylece, bir evrim algoritması verilen bir probleme en uygun çözüm için olasılıksal bir arama gerçekleĢtirir. Doğada, organizmalar hayatta kalmak ve çoğalmak için yeteneklerini etkileyen belli karakteristiklere sahiptirler. Bu karakteristikler, organizmanın kromozomlarında uzun bilgi stringleri Ģeklinde saklanır. Bu bağlamda evrimsel hesaplama algoritmaları, hayatta kalacak bireylerin yeteneklerini geliĢtirir. Yavru kromozomlar, ebeveyn kromozom çiftlerinin eĢleĢmelerinden oluĢur. Beklenen sonuç, her çiftin en iyi karakteristiklerini içeren yavru kromozomların elde edilmesidir. Evrim doğal
seçim aracılığıyla, popülasyon içinden, rasgele bir Ģekilde seçilmiĢ bireylerden uygun kromozom değerlerinin aranması olarak düĢünülebilir (ÇunkaĢ 2004).
Evrim algoritmaları; genetik algoritmalar (GA), genetik programlama (GP), evrimsel programlama (EP) ve evrimsel strateji (EV) gibi alt bölümlere ayrılabilir.
Genetik Algoritma terminolojisinin anlaĢılması için doğal seçimin anlaĢılması gerekir. Dünya gözlemlenecek olunursa, olup biten olaylarda doğal seçilim göze çarpar. Birbirinden ayrı muazzam organizmalar ve bu organizmalardaki karmaĢıklık, inceleme ve araĢtırma konusudur. Organizmaların niçin böyle olduğu ve nasıl bu aĢamaya geldiği sorgulanabilir. Amaç fonksiyonu, yaĢam mücadelesini temsil eder. Ġnsanoğlu bunu maksimize etmek ister (Grant 1985). Adaptasyon ve uygunluğun seviyesi, dünyada uzun süre yaĢayabilmenin göstergesi haline gelmiĢtir. Evrim süreci, hayat Ģartlarına en uygun olanın yaĢamasını sağlayan büyük bir algoritmadır. Eğer çevreyi değiĢtirme zekâ ve yeteneğine sahip olunursa, hayatta küresel maksimum elde edilebilir (Haupt 1998).
Genetik algoritmalar, ilk defa 1975 yılında John Holland tarafından ortaya konulan, biyolojik süreci modelleyerek fonksiyonları optimize eden evrim algoritmalarıdır. GA parametreleri, biyolojideki genleri temsil ederken, parametrelerin toplu kümesi de kromozomu oluĢturmaktadır. GA’ların her bir ferdi yani her bir aday çözüm kromozom Ģeklinde temsil edilir. Bu aday çözümler kümesi de popülâsyon olarak adlandırılır. Popülâsyonun uygunluğu, belirli kurallar dâhilinde maksimize veya minimize edilir. Her yeni nesil, rasgele bilgi değiĢimi ile oluĢturulan diziler içinde hayatta kalanların birleĢtirilmesi ile elde edilmektedir (Angeline 1995).
Seçim ve Uygunluk Ataması: Hem olasılıklı hem de tamamen belirleyici
olabilen seçim sürecinde, yüksek uygunluğa sahip bireyler yeniden üretilirken, düĢük uygunluklu bireyler popülâsyondan çıkarılır. Burada amaç, arama uzayının özel parçaları üzerinde aramaya odaklanmak ve popülâsyonun ortalama uygunluk değerini yükseltmektir. Optimizasyon iĢlemine göre bir bireyin uygunluğu, sayısal bir değer ile temsil edilir. Uygunluk kavramı, amaç fonksiyonu ve kısıtlamalara bağlı
olduğu için, bu uygunluğu hesaplanmadan önce kodunun1
çözülmesi gerekmektedir. Kodu çözülen bireylerden oluĢturulan karar vektörü, amaç fonksiyonunda kullanılarak amaç vektörü oluĢturulur. Yani uygunluk değerleri hesaplanır.
Çaprazlama ve Mutasyon: Çaprazlama ve mutasyon, amaç uzay içinde mevcut
çözümlerin varyasyonlarıyla yeni çözümler üretmeyi amaçlar. EĢleme sürecinde, seçilen kromozomlardan bir veya birden fazla yeni birey oluĢturma olayına “çaprazlama” denir. En yaygın olarak kullanılanı, iki kromozomdan iki tane yeni birey elde edilmesidir. Bu tip çaprazlamada, öncelikle kromozomun ilk biti ile son biti arasında çaprazlama noktası rasgele seçilir. Birinci kromozomun çaprazlama noktasının solundaki bitlerin hepsi ikinci kromozoma geçerken, benzer tarzda ikinci kromozomun çaprazlama noktasının solundaki bitler de birinci kromozoma geçerler. Sonuçta meydana gelen yeni kromozomlar, her iki kromozomun karakterlerini içermektedirler. Doğal evrimi taklit etmek için kullanılan çaprazlama oranı, bir popülâsyonda ne kadar bireyin çaprazlamaya tabi tutulacağını belirler.
GA operatörlerinin ikincisi olan mutasyon, kromozomdaki bitlerin küçük bir yüzdesini değiĢtirir. Mutasyon ile kromozomdaki bitler “1” ise “0”, “0” ise “1” yapılır. Bir popülasyon matrisinde, mutasyon noktaları rasgele seçilir. Mutasyonun % değeri artırılırsa, algoritma daha geniĢ parametre uzayını tarama yapar.
Ana Döngü: Yukarıdaki kavramlara bağlı olarak, doğal evrim iteratif bir
hesaplama süreci olarak simüle edilir. Öncelikle gerekli parametreler, amaç fonksiyonu ve kısıtlamalar tanılanır ve baĢlangıç popülâsyonu oluĢturulur. Daha sonra bu iĢlemler, belirlenen bir iterasyon sayısınca ya da bir sonlanma kriteri sağlanıncaya kadar, seçim, çaprazlama ve mutasyon sırasıyla tekrarlanır.
1 Bilindiği gibi her biri aday bir çözüm olan bireylerin, kromozom olarak temsil edilebilmeleri için bir karar vektörü ya da uygun bir yapı üzerinde kodlanmıĢ olmaları gerekir. Bu problemin türüne göre bit vektör, reel değerli vektör ya da ağaç kodlaması, permütasyon kodlama Ģeklinde olabilir.
2.3.1. Genetik algoritmaların avantajları
Sürekli ve ayrık parametreleri optimize etmesi Türevsel bilgiler gerektirmemesi
Amaç fonksiyonunu geniĢ bir spektrumda araĢtırması Çok sayıda parametrelerle çalıĢma imkânı olması Paralel PC’ler kullanılarak çalıĢtırılabilmesi
KarmaĢık amaç fonksiyonu parametrelerini, yerel minimum veya maksimumlara takılmadan optimize edebilmesi
Sadece tek çözüm değil, birden fazla parametrelerin optimum çözümlerini elde edebilmesi olarak sıralanabilir (Haupt 1998).
GA lar arama ve optimizasyon için sezgisel yöntemlerdir. Genetik algoritmalar her zaman en iyiyi bulamayabilir. GA’lar Ģartlara uyum sağlayabilir. Bunun anlamı, önceden hiç bilgisi olmamasına karĢın, olayları ve bilgiyi öğrenme ve toplama yeteneğine sahip olmasıdır. ġekil 2.1’de genetik algoritmaların akıĢ diyagramı gösterilmiĢtir. TANIMLA Amaç Fonksiyonu, Parametre ve Sınırlar PARAMETRELERĠN GA’ya UYARLANMASI UYGUNLUK DEĞERĠNĠN HESAPLANMASI SEÇĠM ÇAPRAZLAMA MUTASYON DUR Sonlanma Ölçütü olumlu olumsuz
Her problemin çözümü için GA kullanmak iyi bir yol değildir. Birkaç parametreli analitik fonksiyonun çözümünde klasik metotlar daha hızlıdır. Böyle durumlarda, nümerik metotlar tercih edilmelidir. Paralel bilgisayarlar kullanılırsa GA daha hızlı sonuç verebilir.
2.3.2. Temel algoritması
Girdi: N Popülâsyon boyutu
T jenerasyon sayısı pc çaprazlama olasılığı pm mutasyon olasılığı
Çıktı: A bastırılmamıĢ küme
Adım 1: Başla: P0 ve t 0 For i 1,...,N do
a) Bazı olasılık dağılımlarına göre bir i Iseç.
b) P0 P0 i
Adım 2: Uygunluk Ataması: Her bir i Pt bireyi için hem kodlanan karar vektörü x m(i)hem de y f x amaç vektörünü tanımla ve sayısal uygunluk değeri F i yi hesapla.
Adım 3: Seçim: '
P . For i 1,...,N do
a) Verilen tasarıma ve uygunluk değeri F i ye bağlı olarak bir
t P
i bireyi seç. b) P' P' i
Geçici popülasyon '
P eĢleĢme havuzu olarak adlandırılır. Adım 4: Çaprazlama: '' P . For i N do 2 , ... , 1
a) i,j P' olan iki birey seç ve P'den çıkar.
b) i ve j bireylerini çaprazla. Sonuçta oluĢan çocuklar k,l Idır. c) k,l yi pc olasılığı ile P''ye ekle. Aksi halde i, j bireylerini P''ye
Adım 5: Mutasyon: P''' . For her bir i P'''bireyi için do
a) pm mutasyon oranı ile i bireyine mutasyon uygulanır. OluĢan birey j Idır.
b) P''' P''' i
Adım 6: Bitir: Pt 1 P''' vet t 1. Eğer t T veya herhangi bir sonlanma kriteri sağlanmıĢsa A pmPt aksi halde Adım 2 ye git.
3. ÇOK AMAÇLI OPTİMİZASYON
Doğal seçim ve optimizasyon arasındaki benzerlikler; evrimsel süreci bilgisayar ortamında simüle eden “Evrimsel Algoritmaların” geliĢtirilmesini sağlamıĢtır. Çok amaçlı optimizasyon problemlerinin çözümünde genetik ve evrimsel algoritmaları kullanmanın daha avantajlı olduğu bilinmektedir. Bu yüzden çok amaçlı optimizasyon yöntemlerine dayalı evrimsel algoritmalar son yıllarda yaygın olarak kullanılmaya baĢlanmıĢtır (Osyczka, 2002).
Çok-amaçlı optimizasyon, tek-amaçlı optimizasyondan çok farklıdır. Tek-amaçlı optimizasyonda, bir amaç için en iyi olan tek bir tasarım veya karar elde edilmeye çalıĢılır. Bu, genellikle minimizasyon veya maksimizasyon problemine dayalı olarak küresel minimum veya küresel maksimumun bulunmasıdır.
Gerçek dünyada, tasarımların veya problemlerin tamamına yakını birden fazla ve birbiriyle çeliĢebilen amaçların eĢ zamanlı optimizasyonunu gerektirir. Örneğin; bir köprü inĢası için iyi bir tasarım, düĢük kütle ve yüksek dayanıklılıkla ifade edilir. Uçak tasarımı; yakıt verimliliği, yük ve ağırlığın eĢ zamanlı optimizasyonunu gerektirir. Bir arabanın tavan pencere tasarımı için sürücünün duyacağı gürültünün minimize edilmesi, havalandırmanın ise maksimize edilmesi amaçlanır.
Bu bakımdan, çoklu-amaç durumunda tüm amaçlara göre en iyi olan tek bir çözüm mevcut olmayabilir. Bu durumda karar vericinin, üzerinde uzlaĢma sağlanmıĢ sonlu bir kümeden bir çözüm seçmesi istenir. Uygun çözüm, tüm amaçlar için kabul edilebilir düzeyde bir performans sağlamalıdır.
3.1. Pareto Optimal Kavramı
Pareto Optimal kavramı 1900’lü yılların baĢlarında, esasen Ġtalyan bir iktisatçı ve sosyolog olan Vilfredo Pareto tarafından bulunmuĢ olan ekonomik yeni refah teorisinden gelmektedir. Pareto bir ulusun ekonomisinde olası olan denge
durumlarını araĢtırırken, adını kendisinden alan pareto optimal kavramını buldu. Pareto optimal duruma ulaĢılması halinde insanların yararlı mallara ve hizmetlere olan gereksinimleri, en iyi biçimde tatmin edilmiĢ olur. Bununla modern refah teorisinin temellerini kurmuĢtur. Bu teoriye göre;
1. Herkesin durumunu daha iyi yapan veya kimsenin durumu değiĢtirmediği halde en az bir kiĢinin durumunu daha iyi hale getiren,
2. Herkesin durumunu daha kötü yapan veya kimsenin durumunu değiĢtirmediği halde en az bir kiĢinin durumunu daha kötü yapan değiĢmelerin değerlendirilmesini yaparak Ģu sonuçlara varmıĢtır:
Bazılarının durumunu daha iyi hale getirip bazılarının durumunu daha kötü hale getiren değiĢmelerin refahı ne yönde etkilediği söylenemez. Refah, ancak hiç kimsenin durumunu kötüleĢtirmeden bazı kiĢilerin durumunu iyileĢtirebiliyorsa artmıĢ sayılır ve Ģayet kimsenin durumunu kötüleĢtirmeden bir kiĢinin dahi durumunu iyileĢtirme olanağı yoksa refah maksimuma ulaĢmıĢ sayılır (wikipedia 2007).
Pareto-optimal kavramı, evrimsel algoritmalara uyarlanmasıyla, çok amaçlı evrimsel optimizasyon algoritmaları geliĢtirilmiĢtir. Buna göre, popülâsyondaki bir çözüm amaç değerlerine göre, en iyi, en kötü ve diğer çözümlerden farksız olabilir. En iyi çözüm, amaçların herhangi biri içinde en kötü olmayan ve en azından bir amaç içinde diğerlerinden daha iyi olan çözüm anlamındadır. Optimal çözüm, arama uzayında, herhangi bir diğer çözüm tarafından bastırılmayan çözümdür. Böyle bir optimal çözüme Pareto-Optimal Çözüm ve bütün bu Ģekildeki optimal trade-offs2
çözümlerin kümesi de Pareto-Optimal Küme olarak adlandırılır (Dias 2002, Osyczka 2002, Deb 2002).
Genellikle çok amaçlı evrimsel algoritmaların amacı, tradeoff yüzeyi yani bastırılmamıĢ çözüm noktaları kümesini tespit etmektir. Bu küme, yukarıda tanımlanan Pareto-Optimal yada diğer bilinen ifadeleriyle bastırılmamıĢ (nondominated) yada ikinci dereceden olmayan (noninferior) çözümler kümesi
2 Çok Amaçlı Evrimsel Algoritmalarda Pareto-Optimal Çözümler Kümesi bulunurken doğal olarak genotip uzay dikkate alınarak değerlendirme yapılır. Bulunan bu çözümlerin fenotipik uzayda koordinat sistemindeki gösterimiyle elde edilen eğri yâda yüzey tradeoff yüzey olarak adlandırılır.
olarak adlandırılır. Bu çözümlerden geriye kalanlar ise bastırılmıĢ (dominated) çözümler olarak bilinir. BastırılmamıĢ çözümlerden herhangi birisi çözüm olarak kabul edilebilir. Bir çözümün tercih edilmesi gerekiyorsa problem bilgisi ve bir takım problemle iliĢkili faktörlerin bilinmesine ihtiyaç vardır. Bu yüzden karar verici tarafından seçilen bir çözüm baĢka bir karar vericiye göre veya değiĢik bir çevre içinde uygun olmayabilir. Bu nedenle çok amaçlı optimizasyon problemlerinde, Pareto-Optimal çözümleri değerlendirebilmek için problem hakkında bilgi sahibi olmak önemlidir.
3.2. Çok Amaçlı Optimizasyon Problemleri
Çok-amaçlı optimizasyon problemi birden fazla amaçtan, eĢitlik ve eĢitsizliklerden oluĢur. Bu problemlerin genel matematiksel formülasyonu aĢağıdaki gibi yazılabilir:
Minimize/maksimize fi x = { f1 x,f2 x,...,fn x } i = 1, 2, … , n
AĢağıdakilere bağlı olarak
J j x gi 0 1,2,..., K k x hk 0 1,2,..., (3.1)
x belirlenen bir karar değiĢkenler vektörü ve f1 .,f2 .,...,fn . maksimize/minimize edilecek amaç fonksiyonlardır. AĢağıdaki eĢitsizlikler x ve y çözümleri arasında tutulduğunda, x çözümü y çözümü tarafından bastırılır.
y f x f
i: i i ve j: fj x fj y (3.2)
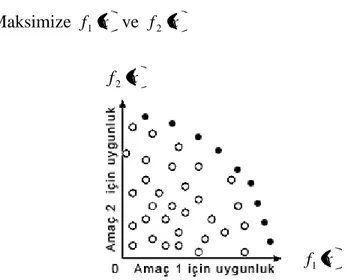
BastırılmamıĢ çözümlerin örnekleri ġekil–3.1’de görülmektedir. BastırılmamıĢ ve bastırılmıĢ çözümler sırasıyla kapalı ve açık çemberlerle iki boyutlu amaç uzayında görülmektedir. ġekil–3.1’deki iki boyutlu amaç uzayı, aĢağıdaki iki amaçlı optimizasyon problemini ifade eder.
Maksimize f1 x ve f2 x (3.3)
Şekil 3.1. BastırılmamıĢ çözümler (kapalı çemberler) ve bastırılmıĢ çözümler (açık çemberler)
3.3. MOEA’ların Sınıflandırılması
Çok Amaçlı Evrimsel Algoritmaların çeĢitli Ģekillerde sınıflandırmasını yapmak mümkündür. Burada seçim mekanizmalarına göre sınıflandırma yapılmıĢtır. Buna göre optimizasyon algoritmaları;
Toplama Fonksiyonları
Popülâsyon-Temelli YaklaĢımlar Pareto-Temelli YaklaĢımlar
olmak üzere 3 grupta toplanabilir. Bunlar hakkındaki kısa açıklamalar aĢağıda verilmektedir (Coello 2005).
3.3.1. Toplama fonksiyonları
Bu konuda, en temel ve en basit olarak nitelendirilebilecek yaklaĢım türüdür. Bu yöntem, çoklu amaçları optimize edebilmek için, amaçların her birini tek bir
x f1
x f2
sayısal değerde birleĢtirdiğinden, toplama fonksiyonları olarak adlandırılır. Genellikle aĢağıdaki gibi bir uygunluk fonksiyonu kullanılarak gerçekleĢtirilir.
k i i if x w 1 min
Burada w (ağırlık katsayısı), her biri sıfırdan büyük eĢit olmak üzere toplam k i
tane amaç fonksiyonundan i. amaç fonksiyonunun ağırlık katsayısını gösterir ve çoğunlukla k i i w 1 1 olduğu varsayılır. 3.3.2. Popülâsyon-Temelli Yaklaşımlar
Bu tür yaklaĢımda evrimsel algoritmanın (EA) popülâsyonu, arama iĢleminin çeĢitlendirilmesi amacıyla kullanılır. Fakat Pareto üstünlük kavramı doğrudan seçim sürecine dâhil edilmez. Bu yaklaĢımın klasik örneği, Schaffer tarafından önerilen Vektör Değerlendirmeli Genetik Algoritma (VEGA)dır. VEGA temel olarak seçim mekanizması değiĢtirilmiĢ basit bir genetik algoritmadan oluĢur. VEGA’da popülâsyon her bir amaç için alt popülasyonlara bölünerek Pareto yüzeyin bulunması hedeflenir. Ancak bu algoritma kısmen baĢarılı sonuçlar üretiyor gibi görünse de oldukça zayıf ve dezavantajları olan bir algoritmadır. VEGA hakkında detaylı bilgi bölüm-3’te verilmektedir.
3.3.3. Pareto temelli yaklaşımlar
Pareto temelli yaklaĢımlarda Pareto-Optimalite kavramı veya diğer bir değiĢle Pareto üstünlüğüne dayalı sınıflandırma kullanılarak bastırılmamıĢ çözümler kümesi elde edilmeye çalıĢılır. Bu yaklaĢımı kullanan algoritmalar, 1989 yılında Golberg’in ortaya koyduğu Pareto derecelendirme metodundan esinlenmiĢlerdir. Goldberg
önerisinde, mevcut popülâsyona göre bastırılmamıĢ olan uygun çözümlerin, bir seçim mekanizması kullanılarak pareto yüzeye yüzeyine doğru popülâsyonun taĢınması gerektiğini söyler. Ayrıca, çeĢitlilik koruma mekanizması olarak uygunluk paylaĢımı ve hücreleme (niching) tekniklerinin kullanılmasını önermektedir. Son yıllarda Pareto-Temelli çok çeĢitli MOEA geliĢtirilmiĢtir. BaĢlıca çok-amaçlı genetik algoritmalar Bölüm-4’te detaylı olarak ele alınmaktadır.
4. ÇOK AMAÇLI GENETİK ALGORİTMALAR
Çok amaçlı optimizasyon problemlerinin çözümünde genetik ve evrimsel algoritmaları kullanmanın avantajlı olduğu bilinmektedir. Bu nedenle çok amaçlı optimizasyon yöntemlerine dayalı genetik algoritmalar son yıllarda yaygın olarak kullanılmaya baĢlanmıĢtır (Osyczka, 2002). Bu bölümde; tez çalıĢmasında ele alınan çok-amaçlı genetik algoritmalar detaylı olarak açıklanacaktır.
4.1. VEGA: Vektör Değerlendirmeli Genetik Algoritma (Vector Evaluated Genetic Algorithm)
Schaffer 1985 yılında bu alanda öncü nitelikte çalıĢmalarda bulundu ve Vektör Değerlendirmeli Genetik Algoritmayı önerdi. VEGA’da sağlanması gereken her amaç ayrı ayrı ele alınır ve tam olarak sağlanan tüm çözümler elde edilmeye çalıĢılır. Bu durum çoğunlukla Pareto-Optimal yüzeyin uç noktaları ve komĢuluklarındaki çözümlerin bulunmasına neden olur.
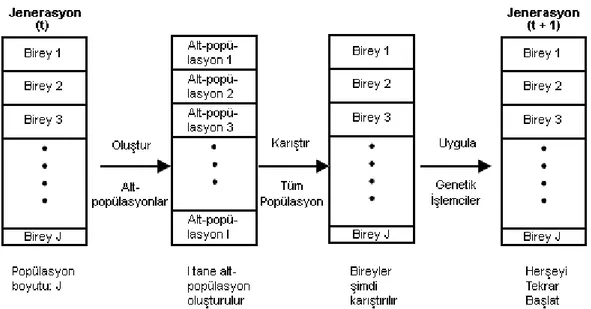
I tane amaç fonksiyonlu bir problemde, her biri J/I boyutlu olan alt
popülasyonlarla birlikte ele alınarak yeni bir J boyutlu popülâsyon elde edilir. Çaprazlama, mutasyon gibi genetik operatörler bu yeni J boyutlu popülâsyon üzerinden uygulanırlar. Bu süreç ġekil-4.1’de görülmektedir (Dias 2002, Osyczka 2002, Schaffer 1985, Schaffer 1984).
ġekil 4.1: J-Boyutlu bir popülâsyonda I amaç fonksiyonlu bir problem için VEGA Algoritmasının ÇalıĢması (Schaffer 1985)
Schaffer tarafından önerilen Vektör Değerlendirmeli Genetik Algoritma popülâsyon temelli yaklaĢımlardan biridir. Çünkü algoritmanın n tane alt popülâsyonunu Ģekillendiren seçim iĢlemi, n tane amacın her birine göre ayrı ayrı gerçekleĢtirilir. Bu yüzden algoritmanın n tane arama yönü vardır. Maksimize edilmesi gereken iki amaçlı bir optimizasyon problemi için arama yönleri ġekil–4.2’de görülmektedir. Bu yaklaĢımda A ve D çözümleri kolaylıkla bulunabilir. Ancak B ve C çözümlerinin bulunması kolay değildir.
Şekil 4.2: Schaffer’ın yaklaĢımında arama yönleri (Tadahiko 1994) Maksimize f1 x ve f2 x
VEGA bazı problemlerde baĢarılı sonuçlara ulaĢabilmesine rağmen, çoğunlukla sadece Pareto-Optimal yüzeyin uç değer çözümlerini bulabildiği görülmüĢtür. Çünkü arama yönleri amaç uzayın eksenlerine paraleldir. Bu sebeple, Schaffer daha sonraları VEGA’yı geliĢtirmek için bazı yeni yaklaĢımlarda bulunmuĢtur. Sonuç olarak VEGA, çok baĢarılı olmayan ancak çok amaçlı optimizasyonda evrimsel algoritmaların kullanılması açısından yol gösterici, öncü çalıĢmaların baĢında gelmektedir.
4.2. MOGA: Çok Amaçlı Genetik Algoritma (Multiobjective Genetic Algorithm)
Çok-Kriterli optimizasyon problemlerinde amaç, birbiriyle çeliĢen çoklu amaç fonksiyonları arasındaki mümkün olan tüm pareto yüzeyin bulunmasıdır. Bu amaçla Tadahiko Murata 1997 yılında çok yönlü bir arama gerçekleĢtirebilmek amacıyla Çok Amaçlı Genetik Algoritmayı önerdi. Bu yaklaĢımı tek-amaçlı genetik algoritmalardan ayıran özellik seçim süreci ve seçkinliği koruma stratejisidir.
n-kriterli optimizasyon problemi için GA’lar kullanıldığında, her bir çözüm
için n tane amaç fonksiyonu değerlendirilmek zorundadır. n tane amaç fonksiyonunun değerleri kullanılarak, her bir bireyin uygunluk değeri tanımlanmalıdır. GA’lar genotip dünyasında tek-amaçlı optimizasyon problemlerindeki gibi en iyi uygunluk değerli bireyi ararlar. Amaç fonksiyonlarının değerlerini, her bir bireyin uygunluk değerine dönüĢtürmek için sıklıkla önerilen yollardan biri sayısal bir fonksiyon içinde birleĢtirmektir (Murata 1997).
(4.1)
x
f x’in uygunluk fonksiyonu ve w1, … , wn n tane amaç için negatif olmayan ağırlıklardır. Bu ağırlıklar aĢağıdaki gibi tanımlanırlar:
için n i wi 0 1,2,..., (4.2) 1 ... 2 1 w wn w (4.3)
Ağırlık değerlerinin sabit seçilmesi arama yönlerini kısıtlar ve VEGA’daki problemi ortaya çıkarır. Optimizasyon problemlerinde, sabit ağırlık değeri yaklaĢımı veya amaçları ayrı ayrı ele alarak tüm yüzeydeki bastırılmamıĢ çözümleri bulma çalıĢmaları baĢarısızdır (ġekil 4.4). Bu yöntemde ise, farklı arama yönlerinin tespit edilmesi için denklem (4.4) gösterildiği gibi rasgele belirlenmiĢ ağırlık değerleri kullanılır (ġekil 4.3). n i random random random wi i/ 1 ... n , 1,2,..., (4.4)
Şekil 4.4: Sabit Ağırlık Vektörü ile TanımlanmıĢ Arama Yönü (Murata 1997)
4.2.1. Seçim süreci
Bir çift ebeveyn birey, mevcut bir ψ popülâsyondan bir çaprazlama iĢlemcisi ile yeni bir birey üretmek için seçildiğinde, öncelikle n tane ağırlık değeri (w1,w2,…,wn) rasgele üretilir. Daha sonra geçerli ψ popülâsyonundaki her bir x
çözümünün uygunluk değeri denklem (4.1)’e uygun bir Ģekilde n tane amacın ağırlıkları toplamı olarak hesaplanır. Doğrusal ölçeklemeye dayalı her bir x bireyinin seçilme olasılığı Ps(xi) rulet tekerleği seçimi ile aĢağıdaki gibi tanımlanır:
(4.5)
fmin(ψ), ψ popülâsyonundaki minimum (en kötü) uygunluk değeridir. Bu seçilme olasılığına göre, ebeveyn bireyler ψ popülâsyonundan seçilir.
Seçilen ebeveyn çiftinden çaprazlama ile yeni bir birey üretilir. Daha sonra bu yeni bireye mutasyon uygulanır. Bir baĢka ebeveyn çifti seçildiğinde, n tane ağırlık değeri (w1, w2, … , wn) rasgele bir Ģekilde yeniden tanımlanır. Yani her bir seçim
için farklı bir ağırlık vektörü kullanılır. Bu sayede, MOGA seçim iĢlemi ġekil–4.4’te gösterildiği gibi farklı arama yönlerine sahip olur.
4.2.2. Seçkinlik stratejisi
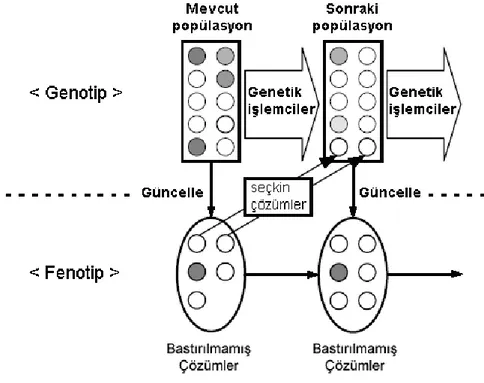
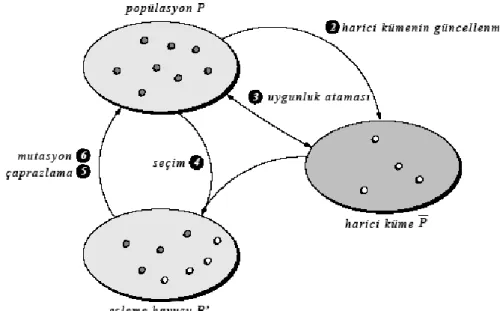
Çok-amaçlı optimizasyonda, iki çözüm kümesi tutulur. Bunlar: geçerli popülâsyon ve geçici bastırılmamıĢ çözümler kümesidir. Geçerli popülasyondaki tüm bireylerin uygunluk değerleri hesaplandıktan sonra, geçici bastırılmamıĢ çözümler kümesi güncellenir. Yani geçerli popülâsyondaki bir birey, bu popülâsyondaki herhangi bir diğer birey tarafından bastırılmıyorsa, bu birey geçici kümeye eklenir. Daha sonra eklenenlerden herhangi birisi tarafından bastırılan tüm çözümler geçici kümeden çıkarılır. Bu Ģekilde, geçici bastırılmamıĢ çözümler kümesi GA’ların çok-kriterli optimizasyonun her jenerasyonunda güncellenir. Geçici bastırılmamıĢ çözümler kümesinden, birkaç çözüm rasgele seçilir ve geçerli popülâsyona eklenir. Rasgele seçilen bastırılmamıĢ çözümler bir tür seçkin çözüm olarak görülür. Çünkü hiçbir genetik operatör uygulanmadan, geçerli popülâsyona eklenirler. Geçerli popülasyonun ve geçici bastırılmamıĢ çözümler kümesinin güncellenmesi ġekil– 4.5’de görülmektedir.
4.2.3. MOGA Algoritması
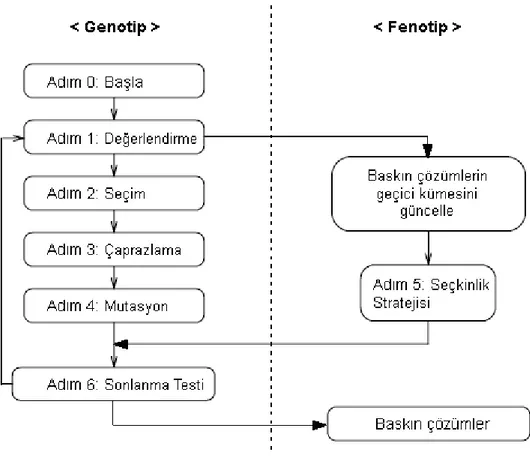
ġekil 4.6’da MOGA’nın akıĢ diyagramı görülmektedir.
Adım 0 (Başlangıç): Npop boyutlu baĢlangıç popülâsyonunun bireyleri rasgele bir Ģekilde üretilir.
Adım 1 (Değerlendirme): Fenotip uzayındaki çözümlere bireyler kodlanır ve her
bir çözüm için n tane amacın değeri hesaplanır. Daha sonra bastırılmamıĢ çözümlerin geçici kümesini güncellenir.
Adım 2 (Seçim): Npop popülâsyon boyutundaki bireyleri üretmek için ebeveyn bireylerini seçecek aĢağıdaki prosedür tekrarlanır.
(i) Rasgele olarak (w1, w2, … , wn) ağırlık değerleri (4.1)’e göre, uygunluk fonksiyonu da (4.4)’ye göre belirlenir.
(ii) Denklem (4.5)’deki seçilme olasılığına göre, bir çift ebeveyn birey seçilir.
Adım 3 (Çaprazlama): Adım 2 de seçilen çiftlerin her birine bir çaprazlama iĢlemcisi uygulanır.
Adım 4 (Mutasyon): Üretilen bireylerin her birine mutasyon olasılığı Pm oranında bir mutasyon iĢlemcisi uygulanır.
Adım 5 (Seçkinlik Stratejisi): Rasgele olarak Nseçkin adet çözüm, Npop boyutunda üretilen popülâsyondan çıkarılır ve bastırılmamıĢ çözümlerin geçici kümesinden rasgele seçilen Nseçkin adet çözüm eklenir.
Adım 6 (Sonlanma Testi): Eğer önceden belirlenmiĢ bir durdurma Ģartı sağlanırsa
Şekil 4.6: MOGA AkıĢ Diyagramı
4.3. NPGA: Hücrelendirilmiş Pareto Genetik Algoritması (Niched Pareto Genetic Algorithm)
HücrelendirilmiĢ Pareto Genetik Algoritması 1993 yılında Jeffrey Horn ve Nicholas Nafpliotis tarafından önerildi. Genetik algoritmalarda seçim iĢlemi; popülâsyondaki bireylerden hangilerinin genotip bilgisinin, sonraki jenerasyona aktarılacağını belirlemek için kullanılır. Seçim süreci için en çok tercih edilen tekniklerden biri turnuva seçimidir. Turnuva seçiminde bireyler kümesi rasgele mevcut popülâsyondan seçilir ve bu seçilen altkümenin en iyisi sonraki popülâsyona aktarılır. Turnuva boyutu belirlenerek, seçim iĢlemi ve yakınsama hızı arttırılabilir. Bu yüzden genellikle en küçük turnuva boyutu olan ikili turnuva, daha geniĢ bir turnuva boyutuna göre daha yavaĢ bir yakınsama gösterir.
NPGA’da yakınsamayı önlemek ve çoklu Pareto-Optimal çözümleri elde etmek için, turnuva seçimi iki Ģekilde değiĢtirilmiĢtir. Bunlar; Pareto Üstünlüklü Turnuvanın (Pareto Domination Tournament) eklenmesi ve bastırılmamıĢ bir turnuva sonucu olduğunda, kazananı belirlemek için PaylaĢım kullanılmasıdır (Horn 1994, Osyczka 2002, www.lania.mx/~ccoello 2007).
4.3.1. Pareto Üstünlük Turnuvası
NPGA’da turnuva seçimi, çoklu amaçları kullanarak Pareto-Optimal yüzeyin elde edebilmesi için değiĢtirilerek Pareto Üstünlük Turnuvasına dönüĢtürülmüĢtür.
Rasgele seçilen iki birey pareto üstünlüklerine göre karĢılaĢtırıldığında doğal olarak ikili bir turnuvaya tabi tutulur. Eğer biri diğerini bastırırsa, kazanan o olur. Ġki aday birey ve bu bireylerin karĢılaĢtırma kümesi mevcut popülâsyondan rasgele alınır. Daha sonra adayların her biri karĢılaĢtırma kümesindeki her bir birey ile kıyaslanır. Eğer bir aday karĢılaĢtırma kümesi tarafından bastırılırsa ve diğer aday bastırılamazsa, diğeri yeniden üretim için seçilir. Her ikisi de bastırılamaz yâda her ikisi de karĢılaĢtırma kümesi tarafından bastırılırsa, kazananı seçmek için paylaĢım kullanılır. Örneğin boyutu: tdom (karĢılaĢtırma kümesinin boyutu) mevcut seçim basıncı üzerindeki kontrolü veya diğer bir değiĢle üstünlük basıncını (domination
pressure) verir. Eğer her iki aday da mevcut bastırılmamıĢ yüzey üzerinde ise iki
aday da bastırılamayacağı için bir problem ortaya çıkacaktır. Küçük bir tdom her ikisinin de bastırılmıĢ görünmediği veya her ikisi de bastırılabileceği anlamına gelebilir. Böyle bir sonuç eĢitliğinde kazanan rasgele seçilirse, genetik sürüklenme popülâsyonun Pareto yüzeyin tek bir bölgesine yakınsamasına yol açar. Bunu önlemek için iki birey arasında bir tercih yapılamadığında, bir tür paylaĢım tekniği uygulanır. ġekil 4.7’de Pareto üstünlük turnuvası için sözde kod görülmektedir.
Şekil 4.7: Pareto Üstünlük Turnuvası için Sözde Kod
4.3.2. Bastırılmamış Yüzey Üzerinde Paylaşım
Pareto-Optimal yüzey boyunca dağılmıĢ bir popülâsyon elde etmek için kararlı bir uygunluk paylaĢım tekniğini uygulanmalıdır. Ġlk olarak Goldberg ve Richardson tarafından önerilen uygunluk paylaĢımının amacı, arama uzayındaki farklı pik noktaları üzerine, pik noktalarının büyüklükleri ile orantılı olarak popülâsyonu Pareto-Optimal yüzey boyunca dağıtmaktır.
Bu dağılımı baĢarmak için paylaşım kullanılarak bir bireyin uygunluk değerinin indirgenmesi sağlanır. Bu indirgeme, basitçe amaç fonksiyonunu (fi) paylaĢılan uygunluğunu bulacak olan mi değerine bölerek bulunur (fi / mi). Hücre boyutu (niche count) mi: i bireyinin komĢuluğunun (niche) ne kadar kalabalık olduğunun bir ölçüsüdür. mi değeri mevcut popülâsyondaki tüm bireyler üzerinden hesaplanır. function seçim begin karıştır(random_pop_index); aday_1 = random_pop_index[1]; aday_2 = random_pop_index[2]; aday_1_dominated = false; aday_2_dominated = false;
for karşılaştırma_kümesi_index = 3 to tdom + 3 do
begin
/* tdom bireylerini S den rasgele seçer*/
karşılaştırılacak_birey =
random_pop_index[karşılatırma_kümesi_index];
if S[karşılaştırılacak_birey] dominates S[aday_1]
then aday_1_dominated = true;
if S[karşılaştırılacak_birey] dominates S[aday_2]
then aday_2_dominated = true; end
if( aday_1_dominated AND !aday_2_dominated )
then return aday_2;
else if( !aday_1_dominated AND aday_2_dominated )
then return aday_1;
else
paylaşım_uygula(); end
pop j i Shd i j m [ , ] ] , [ ji
d i ve j bireyleri arasındaki mesafedir,
d
Sh paylaĢım fonksiyonudur. Shd fonksiyonu, d[ ji, ]nin indirim fonksiyonudur. Öyle ki
1 0
Sh ve Shd share 0
Tipik olarak, üçgensel paylaĢım fonksiyonu kullanılır.
share d d Sh 1 / eğer d share 0 d Sh eğer d share
Burada share hücrenin (niche) yarıçapıdır. share, amaç çözümler arasında istenen veya beklenen bazı minimal sapma tahminlerinde kullanıcı tarafından belirlenir. Birbirinin share mesafesi içindeki bireyler, aynı hücre içinde oldukları için birbirlerinin uygunluk değerlerini azaltırlar. Bu yüzden yakınsama bir hücre içinde meydana gelir. Böylece tüm popülâsyonun yakınsaması önlenir.
Herhangi bir paylaĢım uygulamasında, genotipik paylaĢım gerçekleĢtirilebilir. Çünkü her zaman bir genotip mevcuttur. Fakat yapılan çalıĢmalar genelde fenotipik paylaĢımın, genotipik paylaĢıma göre daha üstün olduğunu gösterir. Fenotipik Pareto-Optimal yüzey boyunca çeĢitliliği elde etmekle ilgilenildiğinden, özellik uzayında paylaĢımın gerçekleĢtirmesi mantıklı olur.
Eşdeğer Sınıf Paylaşımı: Adayların her ikisi de bastırılmıĢ ya da her ikisi de
bastırılmamıĢ olduğunda, muhtemelen aynı denklik sınıfındadırlar. Çünkü yüzey boyunca çeĢitlilik sağlanmaya çalıĢılmaktadır ve bu denklik sınıfındaki bireylerin çoğu eĢit uygunluklu olarak nitelenebilir. Hücre boyutuna göre de herhangi bir uygunluk azaltması yapılmaz. Bunun yerine en uygun aday, kendi hücresi içinde en az sayıda birey olan aday olarak belirlenir ve böylece en küçük hücre boyutu belirlenmiĢ olur. Bu tip paylaĢıma “EĢdeğer Sınıf PaylaĢımı” (Equivalence Class
Şekil 4.8: EĢdeğer Sınıf PaylaĢımı (Horn, 1994)
ġekil–4.8 iki bastırılmamıĢ birey arasında bu paylaĢım tekniğinin çalıĢması görülmektedir. Burada x-ekseni boyunca maksimizasyon ve y-ekseni boyunca minimizasyon yapılmaktadır. Seçim için iki aday, karĢılaĢtırma kümesi tarafından bastırılmaz. Bu durumda bu iki aday, karĢılaĢtırma kümesinin ve adayların birleĢiminin Optimal altkümesindedir (kesik çizgili bölgededir). Pareto-Optimal çözüm açısından bakıldığında, adayların hiçbiri tercih edilmez. Ama faydalı bir çeĢitliliğin elde edilmesi istenildiğinden, daha küçük hücre boyutuna sahip adayı seçmenin en iyisi olacağı açıktır. Bu durumda Ģekilden Aday2 seçilecektir.
4.4. NSGA: Bastırılmamış Sınıflandırmalı Genetik Algoritma (Nondominated Sorting Genetic Algorithm)
BastırılmamıĢ Sınıflandırmalı Genetik Algoritma (NSGA) 1994’te Srinivas ve Deb tarafından önerilmiĢtir. NSGA’nın da basit genetik algoritmadan ayrılan tek yanı diğer çok amaçlı genetik algoritmalarda olduğu gibi seçim iĢlemcisinin uygulanıĢıdır. Çaprazlama ve mutasyon iĢlemcileri alıĢılageldiği Ģekilde uygulanır. Seçim
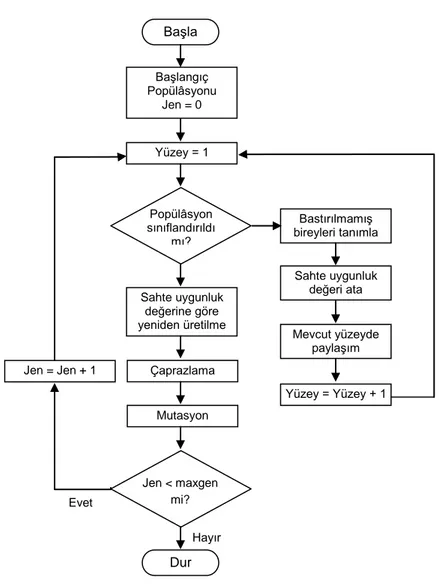
iĢleminden önce, popülâsyon bireylerin Pareto üstünlüklerine göre sıralanır. Öncelikle popülâsyondaki bastırılmamıĢ bireyler, mevcut popülâsyondan tespit edilir ve bu bireylerin ilk Pareto yüzeyi oluĢturduğu varsayılır. Daha sonra bireylere sahte bir uygunluk değeri atanır. Aynı uygunluk değerinin tüm bu bastırılmamıĢ bireylere eĢit üretkenlikte bir potansiyel verdiği varsayılır. Popülâsyondaki çeĢitliliği elde etmek için, bu sınıflandırılmıĢ bireyler daha sonra sahte uygunluk değerleri ile paylaĢılırlar. PaylaĢım; bir bireyin orijinal uygunluk değerinin, bireylerin sayısıyla orantılı bir değere bölünerek elde edilmektedir. Daha sonra bu indirgenmiĢ uygunluk değeri kullanılarak seçim iĢlemi gerçekleĢtirilir. PaylaĢım sürecinden sonra, bastırılmamıĢ bireyler, geçici olarak ihmal edilir. Geriye kalan popülâsyon kullanılarak benzer Ģekilde ikinci bir bastırılmamıĢ yüzey elde edilir. Bu yeni noktalar kümesindeki bireylere, önceki yüzeyin minimum paylaĢılan sahte uygunluğundan daha küçük yeni bir sahte uygunluk değeri atanır. Bu süreç bütün popülâsyonun bireyleri bir yüzey içinde sınıflandırılıncaya kadar devam eder (Srinivas ve Deb, 1993).
Popülâsyon daha sonra sahte uygunluk değerlerine göre yeniden üretilir. Bu çalıĢmada “stochastic remainder proportionate selection” kullanıldı. Ġlk yüzeydeki bireyler maksimum uygunluk değerlerine sahip oldukları için, diğer yüzeylerdeki bireylere oranla her zaman sonraki nesle kopyaları daha fazla alınır. Böylece, bastırılmamıĢ bölgelerin incelenmesi amaçlanır. SınıflandırılmıĢ olan bu çözümler ve paylaĢım tekniği bastırılmamıĢ bölgelere karĢı popülâsyonun daha hızlı yakınsamasına yardımcı olur. NSGA’nın verimliliği, bastırılmamıĢ sıralama prosedürünü kullanılmasından ileri gelmektedir.
Şekil 4.9: NSGA AkıĢ Diyagramı (Srinivas ve Deb 1993)
ġekil–4.9’da algoritmanın akıĢ diyagramı görülmektedir. Her yüzeydeki paylaĢım değeri, aynı yüzeydeki iki birey arasında bir paylaĢım fonksiyon değeri hesaplanarak aĢağıdaki gibi elde edilir:
Aksihalde ise d Eger d d Sh ij share share ij ij , 0 ; , 1 2
Yukarıdaki eĢitlikte; dij parametresi, mevcut yüzeydeki i ve j bireyleri arasındaki fenotipik mesafedir. share bir hücredeki iki birey arasında izin verilen
Başla Başlangıç Popülâsyonu Jen = 0 Yüzey = 1 Popülâsyon sınıflandırıldı mı? Sahte uygunluk değerine göre yeniden üretilme Çaprazlama Mutasyon Jen < maxgen mi? Dur Jen = Jen + 1 Bastırılmamış bireyleri tanımla Sahte uygunluk değeri ata Mevcut yüzeyde paylaşım Yüzey = Yüzey + 1 Hayır Evet