Horadam polinomları ve özellikleri

FEN BİLİMLERİ ENSTİTÜSÜ

HORADAM POLİNOMLARI VE ÖZELLİKLERİ

Tuğba HORZUM

YÜKSEK LİSANS TEZİ İLKÖĞRETİM ANABİLİM DALI

Bu tez 22.08.2008 tarihinde aşağıdaki jüri tarafından oybirliği/oy çokluğu ile kabul edilmiştir.

Yrd. Doç. Dr. E. Gökçen KOÇER Prof.Dr.Eşref HATIR Danışman Jüri

Yrd.Doç.Dr. A.Dilek GÜNGÖR Jüri

iii

Yüksek Lisans Tezi

HORADAM POLİNOMLARI VE ÖZELLİKLERİ

Tuğba HORZUM

Selçuk Üniversitesi Fen Bilimleri Enstitüsü İlköğretim Anabilim Dalı Matematik Öğretmenliği Bilim Dalı

Danışman : Yrd. Doç. Dr. E.Gökçen KOÇER

2008, 43 sayfa

Jüri:

Prof.Dr.Eşref HATIR Yrd.Doç.Dr.E.Gökçen KOÇER Yrd.Doç.Dr.A.Dilek GÜNGÖR

Bu çalışmada Horadam sayılarının bir genelleştirmesi olan Horadam polinomları tanımlanmıştır. Bu polinomun üreteç fonksiyonu ve Binet formülü bulunmuştur. Daha sonra Binet formülünden faydalanarak Horadam polinomları için toplam formülleri ve bazı özdeşlikler elde edilmiştir.

Anahtar Kelimeler: Horadam Polinomu, Binet Formülü, Fibonacci Polinomu, Chebyshev Polinomu.

iv

The Post Graduate Thesis

HORADAM POLYNOMIALS AND PROPERTIES

Tugba HORZUM

Selcuk University

Graduate School of Natural and Applied Science Department of Primary Education

Supervisor: Asist. Prof. Dr. E.Gokcen KOCER

2008, 43 pages

Jury:

Prof.Dr.Eşref HATIR Yrd.Doç.Dr.E.Gökçen KOÇER Yrd.Doç.Dr.A.Dilek GÜNGÖR

In this study, Horadam Polynomials which is generalized Horadam numbers, are defined. The generating function and Binet’s Formula of this polynomial are found. Afterwards, sum formulas and some identities for Horadam polynomials are obtained.

Key Words: Horadam Polynomial, Binet Formula, Fibonacci Polynomial, Chebyshev Polynomial.

v

Fibonacci sayıları doğada birbiriyle ilişkisiz canlı veya cansız sanatın her dalında, görsel, işitsel ve diğer tüm duyulara hitap eden iletişim şekillerinde ve hatta evrenin birçok düzeninde bir oran-orantı olarak karşımıza çıkmaktadır. 13. yüzyılın başlarından bugüne kadar matematik literatürün de önemli bir yer tutan Fibonacci sayılarının bir çok genelleştirmesinden biri olan Horadam sayıları da geniş bir uygulama alanına sahiptir. Biz bu çalışmamızda Horadam sayılarının genelleştirmesi olan Horadam polinomlarını tanımlayarak bu polinomların özelliklerini inceledik.

Çalışmamız üç bölümden oluşmaktadır. Birinci bölümde çalışmamız ile ilgili literatür hakkında inceleme yapılmıştır.

İkinci bölümde Horadam sayıları, özel durumları ve bazı özellikleri hakkında bilgi verilmiştir.

Çalışmamızın esas kısmını üçüncü bölüm oluşturmaktadır. Bu bölümde Horadam polinomları tanımlanarak, üreteç fonksiyonu, Binet formülü bulunmuş ve özel durumları incelenmiştir. Daha sonra Binet formülünden faydalanarak bazı özdeşlikler elde edilmiştir. Ayrıca Horadam polinomları için toplam formülleri elde edilerek özel durumları araştırılmıştır.

Bu tezin oluşmasında büyük katkıları olan Yrd. Doç. Dr. Süleyman SOLAK’a, Yrd. Doç.Dr. Ahmet CİHANGİR’e ve danışman hocam Yrd. Doç.Dr. E.Gökçen KOÇER’e teşekkür ederim.

Tuğba HORZUM Konya, 2008

vi ÖZET………...iii ABSTRACT………iv ÖNSÖZ……….v İÇİNDEKİLER………vi 1. GİRİŞ………1 2. ÖN BİLGİLER……….7

3. HORADAM POLİNOMU VE ÖZELLİKLERİ……….12

3.1. Horadam Polinomunun Üreteç Fonksiyonu ve Binet Formülü………...19

3.2. Horadam Polinomları İçin Toplam Formülleri………25

4. SONUÇ VE ÖNERİLER………41

1. GİRİŞ

İtalyan matematikçi Pisalı Leonardo’nun Liber Abaci isimli kitabında sorduğu bir problemden ortaya çıkan Fibonacci sayılarının sanatta ve bilimde birçok uygulama alanı vardır. Ayrıca Fibonacci sayılarının rekürans bağıntılarına benzer rekürans bağıntılarına sahip birçok sayı dizisi tanımlanmıştır. Bunlar Lucas, Pell,

Pell-Lucas, Jacobsthal ve Jacobsthal-Lucas dizileridir. Doğal olarak tüm bu dizilerin

çeşitli genelleştirmeleri tanımlanmış ve özellikleri araştırılmıştır. Bu genelleştirmelerden biriside Horadam dizisi olup bu diziyi ikinci bölümde inceleyeceğiz. Bunun yanında sayı dizilerinin rekürans bağıntılarına benzer bağıntılar ile polinom dizileri de araştırılmıştır. Bunlardan bazıları Fibonacci, Pell, Pell-Lucas,

Jacobsthal, Jacobsthal-Lucas, birinci ve ikinci çeşit Chebyshev polinomlarıdır.

Belçikalı matematikçi Eugene Charles Catalan ve Alman matematikçi E.

Jacobsthal tarafından 1883 yılında Fibonacci polinomu tanımlanmıştır. Ancak Catalan tarafından yapılan tanım günümüze kadar gelmiştir. O zaman Jacobsthal

tarafından yapılan tanım bugün Jacobsthal polinomu olarak bilinmektedir. Catalan

Fibonacci polinomunu aşağıdaki gibi tanımlamıştır.

Tanım 1.1. n≥3için

F xn

( )

=xFn−1

( )

x +Fn−2

( )

x ; F x1

( )

=1, F x2

( )

=x (1.1) rekürans bağıntısı ve başlangıç şartları ile tanımlanan polinoma Fibonacci Polinomu denir (Lupaş 1999).

Fibonacci polinomunun ilk birkaç elemanı aşağıdaki gibidir.

( )

{

_{1, ,} 2 _1, 3 _{2 ,} 4 ₃ 2 _1, 5 ₄ 3 _{3 ,}

}

n

F x = x x + x + x x + x + x + x + x_K

Eğer (1.1) ifadesinde x=1 alırsak Fibonacci dizisini elde ederiz. Yine dikkat edilirse (1.1) ifadesinde x yerine 2x alınırsa aşağıda tanımı verilen Pell polinomu elde edilir.

Tanım 1.2. n≥3için

P xn

( )

=2xPn−₁

( )

x +Pn−₂

( )

x ; P x₁

( )

=1,P x₂

( )

=2x (1.2) şeklinde tanımlanan polinoma Pell Polinomu denir (Horadam, Mahon 1985).

Pell polinomunun ilk birkaç elemanı aşağıda verilmiştir.

( )

{

_{1, 2 , 4} 2 _1,8 3 _{4 ,16} 4 ₁₂ 2 _1,32 5 ₃₂ 3 _{6 ,}

}

n

P x = x x + x + x x + x + x + x + x_K

Eğer (1.2) ifadesinde x=1 alınırsa Pell sayıları ve x= 1₂ alınırsa Fibonacci sayıları elde edilir.

Tanım 1.3. n≥3için

J x_n

( )

=J_n−1

( )

x +2xJ_n−2

( )

x ; J x₁

( )

=1, J x₂

( )

=1 (1.3) rekürans bağıntısı ve başlangıç şartları ile tanımlanan polinoma Jacobsthal Polinomu denir (Horadam, Flipponi 1997).

Bu tanıma göre Jacobsthal polinomunun ilk birkaç elemanı

( )

{

_{1,1, 2 1, 4 1, 4} 2 _{6 1,12} 2 _{8 1,}

}

n

J x = x+ x+ x + x+ x + x_{+ K}

dir. Burada x=1 alınırsa Jacobsthal sayıları elde edilir. Tanım 1.4. n≥3 için

( )

( )

( )

( )

( )

2 1 2 1 2 2 ; , 2 1 n n n T x = xT₋ x −T₋ x T x =x T x = x − (1.4)

rekürans bağıntısı ve başlangıç şartları ile tanımlanan polinoma birinci çeşit

Chebyshev Polinomu denir (Koshy 2001).

Birinci çeşit Chebyshev polinomunun ilk birkaç elemanı

( )

{

_{, 2} 2 _{1, 4} 3 _{3 ,8} 4 ₈ 2 _1,16 5 ₂₀ 3 _{5 ,}

}

n T x = x x − x − x x − x + x − x + x_K şeklindedir. Tanım 1.5. n≥3 için

( )

( )

( )

( )

( )

2 1 2 1 2 2 ; 2 , 4 1 n n n U x = xU ₋ x −U ₋ x U x = x U x = x − (1.5) rekürans bağıntısı ve başlangıç şartı ile tanımlanan polinoma ikinci çeşit Chebyshev

Polinomu denir (Udrea 1995).

Bu tanıma göre ikinci çeşit Chebyshev polinomunun ilk birkaç elemanı

( )

{

_{2 , 4} 2 _1,8 3 _{4 ,16} 4 ₁₂ 2 _1,32 5 ₃₂ 3 _{6 ,}

}

n

U x = x x − x − x x − x + x − x + x_K

dir.

Şimdiye kadar tanımlarını verdiğimiz polinomlar Fibonacci tipi polinomlar olarak karşımıza çıkmaktadır. Bunun dışında Lucas tipi olarak isimlendirilen polinomların tanımları da aşağıda verilmiştir. Lucas polinomu ilk olarak 1970 yılında

Bicknell tarafından çalışılmıştır. Bicknell tarafından verilen Lucas polinomunun

tanımı aşağıdadır. Tanım 1.6. n≥3 için

( )

( )

( )

( )

( )

2 1 2 ; 1 , 2 2 n n n L x =xL₋ x +L₋ x L x =x L x =x + (1.6) rekürans bağıntısı ve başlangıç şartları ile tanımlanan polinoma Lucas polinomu denir (Koshy 2001).

Lucas polinomunun ilk birkaç elemanı aşağıdaki gibi verilmiştir.

( )

{

_, 2 _2, 3 _{3 ,} 4 ₄ 2 _2, 5 ₅ 3 _{5 ,}

}

n

(1.6) ifadesinde x=1 alınırsa Lucas sayılarının elde edileceği açıktır. Burada dikkat edilirseL x_n

( )

’in katsayılar toplamı Lucas sayılarını vermektedir. Eğer (1.6) ifadesinde x yerine 2x alınırsa aşağıda tanımı verilen Pell-Lucas polinomu elde edilir. Tanım 1.7. n≥3için

( )

( )

( )

( )

( )

2 1 2 1 2 2 ; 2 , 4 2 n n n Q x = xQ₋ x +Q₋ x Q x = x Q x = x + (1.7) rekürans bağıntısı ve başlangıç şartları ile tanımlanan polinoma Pell-Lucas Polinomu denir (Horadam, Mahon 1985).

Pell-Lucas polinomunun ilk birkaç elemanı aşağıda verilmiştir.

( )

{

_{2 , 4} 2 _2,8 3 _{6 ,16} 4 ₁₆ 2 _2,32 5 ₄₀ 3 _{10 ,}

}

n

Q x = x x + x + x x + x + x + x + x_K

Eğer (1.7) ifadesinde x=1 alınırsa Pell-Lucas sayıları elde edilir. Tanım 1.8. n≥3için

j x_n

( )

= j_n−1

( )

x +2xj_n−2

( )

x ; J x₁

( )

=1, J x₂

( )

=4x+1 (1.8) şeklinde tanımlanan polinoma Jacobsthal-Lucas Polinomu denir (Horadam, Flipponi 1997).

Jacobsthal-Lucas polinomunun ilk birkaç elemanı

( )

{

_{1, 4 1,6 1,8} 2 _{8 1, 20} 2 _{10 1,}

}

n

j x = x+ x+ x + x+ x + x_{+ K}

dir. Burada x=1 alınırsa Jacobsthal-Lucas sayıları elde edilir.

Yukarıda tanımlarını verdiğimiz Fibonacci, Lucas, Pell, Pell-Lucas,

Jacobsthal, Jacobsthal-Lucas, birinci ve ikinci çeşit Chebyshev polinomlarının Binet

formülleri sırasıyla

( )

₂1 2 4 2 4 2 2 4 n n n x x x x F x x ⎡_{⎛ + + ⎞ ⎛ − + ⎞} ⎤ ⎢ ⎥ = ⎜_⎜ ⎟_⎟ −⎜_⎜ ⎟_⎟ ⎢ ⎥ + _{⎣⎝ ⎠ ⎝ ⎠ ⎦}

( )

2 4 2 4 2 2 n n n x x x x L x =⎜_⎜⎛ + + ⎞_⎟⎟ +⎛⎜_⎜ − + ⎟⎞_⎟ ⎝ ⎠ ⎝ ⎠

( )

(

2

) (

2

)

2 1 1 1 2 1 n n n P x x x x x x ⎡ ⎤ = _⎢ + + − − + _⎥ ⎣ ⎦ +

( )

(

2 ₁

) (

n 2 ₁

)

n n Q x = x+ x + + x− x +

( )

1 1 8 1 1 8 1 2 2 1 8 n n n x x J x x ⎡_{⎛ + + ⎞ ⎛ − + ⎞} ⎤ ⎢ ⎥ = ⎜_⎜ ⎟_⎟ −⎜_⎜ ⎟_⎟ + ⎢_{⎣⎝ ⎠ ⎝ ⎠} ⎥_⎦

( )

1 1 8 1 1 8 2 2 n n n x x j x =⎜_⎜⎛ + + ⎞_⎟⎟ +⎛⎜_⎜ − + ⎟⎞_⎟ ⎝ ⎠ ⎝ ⎠

( )

(

2

) (

2

)

1 ₂ 1 1 1 2 1 n n n U x x x x x x − = ⎡⎢ + − − − − ⎤⎥ ⎣ ⎦ −

( )

(

) (

)

2 ₁ 2 ₁ 2 n n n x x x x T x = + − + − −

şeklindedir. Aynı zamanda tüm bu polinomları

( )

1 2 2 1 0 1 n n j n j n j F x x j − ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ − − = − − ⎛ ⎞ = _{⎜ ⎟} ⎝ ⎠

∑

,

( )

2 2 0 n n j n j n j n L x x j n j ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ − = − ⎛ ⎞⎛ ⎞ = _{⎜ ⎟⎜ ⎟} − ⎝ ⎠⎝ ⎠

∑

( )

( )

1 2 1 2 0 1 2 n n j n j n j P x x j − ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ _{− −} = − − ⎛ ⎞ = _{⎜ ⎟} ⎝ ⎠

∑

,

( )

2

( )

2 0 2 n n j n j n j n Q x x j n j ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ₋ = − ⎛ ⎞⎛ ⎞ = _{⎜ ⎟⎜ ⎟} − ⎝ ⎠⎝ ⎠

∑

( )

( )

1 2 0 1 2 n j n j n j J x x j − ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ = − − ⎛ ⎞ = _{⎜ ⎟} ⎝ ⎠

∑

,

( )

2

( )

0 2 n j n j n j n j x x j n j ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ = − ⎛ ⎞⎛ ⎞ = _{⎜ ⎟⎜ ⎟} − ⎝ ⎠⎝ ⎠

∑

( )

2

( )

( )

2 0 1 2 n j n j n j n j U x x j ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ₋ = − ⎛ ⎞ = − _{⎜ ⎟} ⎝ ⎠

∑

,

( )

2

( )

( )

2 0 1 2 2 n j n j n j n j n T x x j n j ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ₋ = − − ⎛ ⎞ = _{⎜ ⎟} − ⎝ ⎠

∑

Fibonacci, Lucas, Pell, Pell-Lucas, Jacobsthal, Jacobsthal-Lucas, birinci ve

ikinci çeşit Chebyshev polinomları ile ilgili daha geniş bilgiyi (Koshy 2001, Morgado 1995)’de bulabiliriz.

2. ÖN BİLGİLER

Bugüne kadar Fibonacci ve Lucas sayılarının çeşitli genelleştirmeleri tanımlanmış ve özellikleri araştırılmıştır. Bunlardan biride 1965 yılında

A.F.Horadam tarafından yapılmış ve ismiyle yani Horadam dizisi olarak

anılmaktadır. Horadam dizisi Fibonacci, Lucas, Pell, Pell-Lucas, Jacobsthal,

Jacobsthal-Lucas ve Tagiuri dizilerinin bir genelleştirmesidir. Dolayısıyla Horadam

dizisinin özelliklerinden, yukarıda adı geçen dizilerinde özelliklerini elde etmek mümkündür.

Tanım 2.1. n≥2; , , ,a b p q∈ ve _p2_{+4q≠ olmak üzere; 0}

h_n

(

a b p q, ; ,

)

= ph_n−1

(

a b p q, ; ,

)

+qh_n−2

(

a b p q, ; ,

)

(2.1) rekürans bağıntısı ve

h a b p q₀

(

, ; ,

)

=a, h a b p q₁

(

, ; ,

)

=b (2.2) başlangıç şartları ile tanımlanan diziye Horadam dizisi denir (Horadam 1965).

(2.1) bağıntısının karakteristik denklemi

2 _{p q 0}

λ − λ− = (2.3) olup (2.3) denkleminin kökleri

2 ₄ 2 p p q α = + + ve 2 ₄ 2 p p q β = − + (2.4)

Tablo 2.1. n _{h a b p qn}

(

_{, ; ,}

)

0 a 1 b 2 pb qa+ 3 _{p b pqa qb}2 _{+ +} 4 _{p b p qa}3 ₊ 2 _{+2pqb q a+} 2 5 _{p b p qa}4 ₊ 3 _{+3p qb}2 _{+2pq a q b}2 ₊ 2 6 _{p b p qa}5 ₊ 4 _{+4p qb}3 _{+3p q a}2 2 _{+3pq b q a}2 ₊ 3 7 _{p b p qa}6 ₊ 5 _{+5p qb}4 _{+4p q a}3 2 _{+6p q b}2 2 _{+3pq a q b}3 ₊ 3 8 _{p b p qa}7 ₊ 6 _{+6p qb}5 _{+5p q a}4 2 _{+10p q b}3 2 _{+6p q a}2 3 _{+4pq b q a}3 ₊ 4 M M ( , ; , ) n

h a b p q n. Horadam sayısı olmak üzere, Horadam dizisi için bazı özel durumlar aşağıda verilmiştir.

1) a=0,b=1;p q= = için 1 h_n

(

0,1;1,1

)

=F_n olup F n Fibonacci sayısıdır. _n . 2) a=2,b=1,p q= = için 1 h_n

(

2,1;1,1

)

=L_n dir. L_n n Lucas sayısıdır. . 3) a=0,b=1;p=2,q= için 1 h_n

(

0,1; 2,1

)

=P_n olup P n Pell sayısıdır. _n . 4) a=2,b=2;p=2,q= için 1 h_n

(

2, 2; 2,1

)

=Q_n dir. Q n Pell-Lucas sayısıdır. _n . 5) 0,a= b=1;p=1,q= için 2 h_n

(

0,1;1, 2

)

=J_nolup .J n Jacobsthal sayısıdır. _n

6) 2,a= b=1;p=1,q= için 2 h_n

(

2,1;1, 2

)

= j_nolup j n Jacobsthal-Lucas sayısıdır. _n . 7) p q= = için 1 h a b_n

(

, ;1,1

)

=T_ndir. .T n Tagiuri sayısıdır. _n

Horadam sayılarının özel durumları olan

{ }

F_n Fibonacci,

{ }

L_n Lucas,

{ }

P_n

Pell,

{ }

Q_n Pell-Lucas,

{ }

J_n Jacobsthal,

{ }

j_n Jacobsthal-Lucas ve

{ }

T_n Tagiuri dizilerinin ilk birkaç elemanı aşağıdaki tabloda verilmiştir.

Tablo 2.2. n 0 1 2 3 4 5 6 7 _L n F 0 1 1 2 3 5 8 13 _L n L 2 1 3 4 7 11 18 29 _L n P 0 1 2 5 12 29 70 169 _L n Q 2 2 6 14 34 82 198 478 _L n J 0 1 1 3 5 11 21 43 _L n j 2 1 5 7 17 31 65 127 _L n T a b a b+ a+2b 2a+3b 3a+5b 5a+8b 8a+13b _L

(

)

2 ( ) 1 a t b ap D x pt qt + − = − − (2.5) dir. Üreteç fonksiyonundan faydalanarak Horadam dizisinin Binet formülünü elde edebiliriz. Yani A b a ve B b a= − β = − α olmak üzere Horadam dizisinin Binet formülü k k k A B h α β α β − = − (2.6) olarak bulunur (Mansour 2003).

Horadam sayılarının (2.6) ile verilen Binet formülünden yola çıkarak

Fibonacci, Lucas, Pell, Pell-Lucas, Jacobsthal, Jacobsthal-Lucas sayılarının Binet formülleri sırasıyla aşağıdaki gibidir.

(

0,1;1,1

)

1 1+ 5 1 5 ,

(

2,1;1,1

)

1 5 1 5 2 2 2 2 5 n n n n n n n n F =h = ⎡⎢_⎜⎜⎛ _⎟⎞_⎟ −⎛_⎜⎜ − ⎞_⎟⎟ ⎥⎤ L =h =_⎜⎛_⎜ + _⎟⎟⎞ +_⎜⎜⎛ − _⎟⎞_⎟ ⎢_{⎝ ⎠ ⎝ ⎠} ⎥ _{⎝ ⎠ ⎝ ⎠} ⎣ ⎦

(

0,1; 2,1

)

2 1 2 1 2 ,

(

2, 2; 2,1

)

(

1 2

) (

1 2

)

4 2 2 n n n n n n n n P =h = ⎡⎢_⎜⎛_⎜ + _⎟⎞_⎟ −⎛_⎜⎜ − _⎟⎟⎞ ⎥⎤ Q =h = + + − ⎢_{⎝ ⎠ ⎝ ⎠} ⎥ ⎣ ⎦

(

0,1;1, 2

)

2

( )

1 3 n n n n J =h = − − ,

(

2,1;1, 2

)

2n

( )

1 n n n j =h = + −

Teorem 2.1. n≥1; , , ,a b p q∈ ve h_n n Horadam . sayısı olmak üzere

1 2 2 2 2 0 0 1 n n n k k n k k n k k n k b n k h a p q a p q k p k − ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦ − − = = − − − ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ = _{⎜ ⎟} +_⎜ − _{⎟ ⎜ ⎟} ⎝ ⎠ ⎝ ⎠ ⎝ ⎠

∑

∑

(2.7) dir (Haukkanen 2002).

(2.7) ifadesi Fibonacci, Lucas, Pell, Pell-Lucas, Jacobsthal,

Jacobsthal-Lucas ve Taguri sayıları için sırasıyla

(

)

1 2 0 1 0,1;1,1 n n n k n k F h k − ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ = − − ⎛ ⎞ = = _{⎜ ⎟} ⎝ ⎠

∑

,

(

)

2 0 2,1;1,1 n n n k n k n L h k n k ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ = − ⎛ ⎞ = = _{⎜ ⎟} − ⎝ ⎠

∑

(

)

1 2 1 2 0 1 0,1; 2,1 2 n n k n n k n k P h k − ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ − − = − − ⎛ ⎞ = = _{⎜ ⎟} ⎝ ⎠

∑

,

(

)

1 2 2 0 2, 2; 2,1 2 n n k n n k n k n Q h k n k − ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ − = − ⎛ ⎞ = = _{⎜ ⎟} − ⎝ ⎠

∑

(

)

1 2 0 1 0,1;1, 2 2 n k n n k n k J h k − ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ = − − ⎛ ⎞ = = _{⎜ ⎟} ⎝ ⎠

∑

,

(

)

2 0 2,1;1, 2 2 n k n n k n k n j h k n k ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ = − ⎛ ⎞ = _{⎜ ⎟} − ⎝ ⎠

∑

(

)

(

)

1 2 2 0 0 1 , ;1,1 n n n n k k n k n k h a b a b a k k − ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦ = = − − − ⎛ ⎞ ⎛ ⎞ Τ = = _{⎜ ⎟}+ − _{⎜ ⎟} ⎝ ⎠ ⎝ ⎠

∑

∑

şeklindedir (Koshy 2001).

Teorem 2.2. h k Horadam_k . sayısı ve p q+ ≠ olmak üzere 1

1

(

₁

)

0 1 1 n k n n k h h qh pa a b p q − − = = + + − − + −

∑

(2.8)

3. HORADAM POLİNOMU VE ÖZELLİKLERİ

Bu bölümde Horadam sayılarının genelleştirmesi olan Horadam polinomunu tanımlayarak bu polinomun özelliklerini inceleyeceğiz. Horadam polinomunu

(

; , , ,

)

n

h x a b p q ya da kısaca h x_n

( )

ile göstereceğiz.

Tanım 3.1 n≥3; , , ,a b p q∈ ve _{p x}2 2_{+4q≠ olmak üzere; 0}

h x a b p q_n

(

; , , ,

)

= pxh_n−1

(

x a b p q; , , ,

)

+qh_n−2

(

x a b p q; , , ,

)

(3.1) rekürans bağıntısı ve

h x a b p q₁

(

; , , ,

)

=a h x a b p q, ₂

(

; , , ,

)

=bx (3.2) başlangıç şartları ile tanımlanan polinoma Horadam Polinomu denir.

(3.1) bağıntısının karakteristik denklemi

2 ₀

t −pxt q− = (3.3) olup, (3.3) denkleminin kökleri

2 2 ₄ 2 2 ₄

2 2

px p x q px p x q

ve

α = + + β = − + (3.4)

dir. Horadam polinomunun ilk birkaç elemanını aşağıdaki tabloda verebiliriz.

Tablo 3.1 n _{h x a b p qn}

(

_{; , , ,}

)

1 a 2 bx 3 _bpx2_+aq 4 _{bp x}2 3₊

(

_{apq bq x+}

)

5 _{bp x}3 4₊

(

_{ap q}2 _{+2bpq x}

)

2_+aq2 6 _{bp x}4 5₊

(

_{ap q}3 _{+3bp q x}2

) (

3_{+ 2apq}2_{+bq x}2

)

7 _{bp x}5 6₊

(

_{ap q}4 _{+4bp q x}3

) (

4_{+ 3ap q}2 2_{+3bpq x}2

)

2_+aq3 8 _{bp x}6 7₊

(

_{ap q}5 _{+5bp q x}4

) (

5_{+ 4ap q}3 2_{+6bp q x}2 2

) (

3_{+ 3apq}3_{+bq x}3

)

M M

(

; , , ,

)

n

h x a b p q , n. Horadam polinomu olmak üzere, Horadam polinomu için bazı özel durumlar aşağıda verilmiştir.

1) a b= = = = için Horadam polinomu Fibonacci polinomuna dönüşür. Yani p q 1

(

;1,1,1,1

)

( )

n n

h x =F x

dir.

2) a=2, b= = = için Horadam polinomu Lucas polinomuna dönüşür. Yani p q 1

(

; 2,1,1,1

)

1

( )

n n

dir.

3) 1,a q= = b= =p 2 için Horadam polinomu Pell polinomuna dönüşür. Yani

(

;1, 2, 2,1

)

( )

n n

h x =P x

dir.

4) 2,a b= = =p q= için Horadam polinomu Pell-Lucas polinomuna dönüşür. 1 Yani

(

; 2, 2, 2,1

)

1

( )

n n

h x =Q₋ x

dir.

5) a b= = = =p x 1,q=2y için Horadam polinomu Jacobsthal polinomuna dönüşür. Yani

(

1;1,1,1, 2

)

( )

n n

h y =J y

dir.

6) 2,a= b= = =p x 1,q=2y için Horadam polinomu Jacobsthal-Lucas

polinomuna dönüşür. Yani

(

1; 2,1,1, 2

)

1

( )

n n

h y = j ₋ y

dir.

7) a=1,b=1,p=2,q= − için Horadam polinomu birinci çeşit Chebyshev 1 polinomuna dönüşür. Yani

(

;1,1, 2, 1

)

1

( )

n n

h x − =T₋ x

dir.

8) a=1,b= =p 2,q= − için Horadam polinomu ikinci çeşit Chebyshev 1 polinomuna dönüşür. Yani

(

;1, 2, 2, 1

)

1

( )

n n

h x − =U ₋ x

dir.

9) x=1 için Horadam polinomu Horadam sayılarına dönüşür. Yani

(

1; , , ,

)

1

(

, ; ,

)

n n

h a b p q =h₋ a b p q

dir.

Horadam polinomunun özel durumları olan Fibonacci, Lucas, Pell, Pell-Lucas, Jacobsthal, Jacobsthal-Pell-Lucas, birinci ve ikinci çeşit Chebyshev

polinomlarının ilk birkaç elemanı aşağıdaki tabloda verilmiştir.

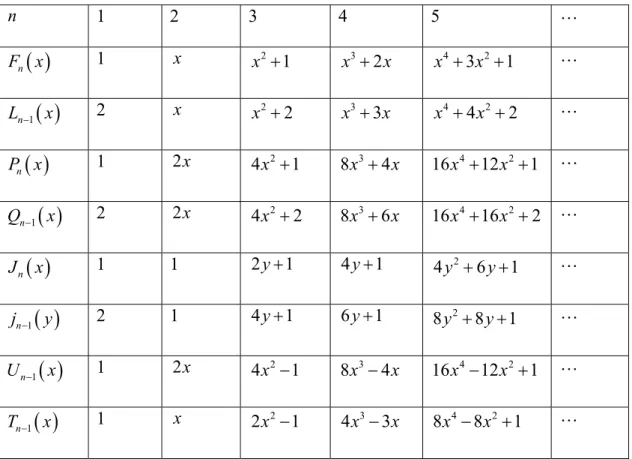
Tablo 3.2 n 1 2 3 4 5 _L

( )

n F x 1 x _x2_{+ 1 x}3_{+2x x}4_+3x2_{+ 1 L}

( )

1 n L ₋ x 2 x _x2_{+ 2 x}3_{+3x x}4_+4x2_{+ 2 L}

( )

n P x 1 2x _4x2_{+ 1 8x}3_{+4x 16x}4_+12x2_{+ 1} L

( )

1 n Q ₋ x 2 2x _4x2_{+ 2 8x}3_{+6x 16x}4_+16x2_{+ 2 L}

( )

n J x 1 1 2y+ 1 4y+ 1 _4y2_{+6y+ 1 L}

( )

1 n j ₋ y 2 1 4y+ 1 6y+ 1 _8y2_{+8y+ 1 L}

( )

1 n U ₋ x 1 2x _4x2_{− 1 8x}3_{−4x 16x}4_−12x2_{+ 1 L}

( )

1 n T₋ x 1 x _2x2_{− 1 4x}3_{−3x 8x}4_−8x2_{+ 1 L}

Teorem 3.1. 1; , , ,n≥ a b p q∈ ve h x n_n

( )

. Horadam polinomu olmak üzere

( )

( )

( )

1 2 2 2 2 1 0 0 1 n n n k k n k k n k k n k b n k h x a px q a px q k p k − ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ₋ ⎣ ⎦ ₋ + = = − − − ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ = _{⎜ ⎟} +_⎜ − _{⎟ ⎜ ⎟} ⎝ ⎠ ⎝ ⎠ ⎝ ⎠

∑

∑

(3.5) dir.

İspat. Tümevarım yöntemi ile ispat açıktır.

Eğer (3.5) ifadesinde x=1alınırsa Teorem 2.1. ile verilen (2.7) ifadesini elde ederiz. (2.7) ifadesi ve

(

)

2 0 2,1;1,1 n n n k n k n L h k n k ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ = − ⎛ ⎞ = = _{⎜ ⎟} − ⎝ ⎠

∑

(

)

1 2 2 0 2, 2; 2,1 2 n n k n n k n k n Q h k n k − ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ − = − ⎛ ⎞ = = _{⎜ ⎟} − ⎝ ⎠

∑

(

)

2 0 2,1;1, 2 2 n k n n k n k n j h k n k ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ = − ⎛ ⎞ = _{⎜ ⎟} − ⎝ ⎠

∑

eşitlikleri göz önüne alındığında polinom dizileri için de aşağıda verilen Lemma 3.1. in var olduğu açıktır.

Lemma 3.1. n≥1 olmak üzere

( )

( )

( )

1 2 2 2 2 2 2 0 0 0 1 2 n n n n k n k n k k k k n k n k n k n x x x k k k n k − ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ₋ ⎣ ⎦ ₋ ⎣ ⎦ ₋ = = = − − − − ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ _{= −} ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ₋ ⎟ ⎝ ⎠⎝ ⎠ ⎝ ⎠ ⎝ ⎠

∑

∑

∑

dir.

Lemma 3.1. den faydalanarak (3.5) ifadesi için bazı özel durumlar aşağıda verilmiştir.

1) a b= = = = için p q 1

( )

2 2 1 0 n n k n k n k F x x k ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ − + = − ⎛ ⎞ = _{⎜ ⎟} ⎝ ⎠

∑

dir (Belbachir, Bencherif 2007). 2) a=2,b= = = için p q 1

( )

2 2 0 n n k n k n k n L x x k n k ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ − = − ⎛ ⎞ ⎛ ⎞ = _{⎜ ⎟⎜ ⎟} − ⎝ ⎠⎝ ⎠

∑

dir (Belbachir, Bencherif 2007). 3) 1,a= b= =p 2, q= için 1

( )

2

( )

2 1 0 2 n n k n k n k P x x k ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ₋ + = − ⎛ ⎞ = _{⎜ ⎟} ⎝ ⎠

∑

dır (Horadam, Mahon 1985). 4) 2,a= = = =b p 2,q= için 1

( )

2

( )

2 0 2 n n k n k n k n Q x x k n k ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ₋ = − ⎛ ⎞ ⎛ ⎞ = _{⎜ ⎟⎜ ⎟} − ⎝ ⎠⎝ ⎠

∑

dir (Horadam, Mahon 1985). 5) a b= = = =p x 1,q=2y için

( )

2

( )

1 0 2 n k n k n k J y y k ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ + = − ⎛ ⎞ = _{⎜ ⎟} ⎝ ⎠

∑

dir (Horadam 1997). 6) 2,a= b= = =p x 1,q=2y için

( )

2

( )

0 2 n k n k n k n j y y k n k ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ = − ⎛ ⎞ ⎛ ⎞ = _{⎜ ⎟⎜ ⎟} − ⎝ ⎠⎝ ⎠

∑

dir (Horadam 1997). 7) 1,a= b= =p 2,q= − için 1

( )

2

( )

( )

2 0 1 2 n k n k n k n k U x x k ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ₋ = − ⎛ ⎞ = − _{⎜ ⎟} ⎝ ⎠

∑

dir (Koshy 2001). 8) a b= =1,p=2,q= − için 1

( )

2

( )

( )

2 0 1 2 2 n k n k n k n k n T x x k n k ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ₋ = − − ⎛ ⎞ = _{⎜ ⎟} − ⎝ ⎠

∑

dir (Koshy 2001).

3.1. Horadam Polinomunun Üreteç Fonksiyonu ve Binet Formülü

Tanım 3.1.1 _{g g g K tek değişkenli fonksiyonların kümesi olmak üzere 1}, , ,_{2 3}

( )

( )

1 1 , n n n G x t ∞ g x t − =

=

∑

ifadesine

{

g x_n

( )

}

dizisininin üreteç fonksiyonu denir (Karlsson 1988).

Teorem 3.1.1

{

h x_n

( )

}

Horadam polinomları dizisinin üreteç fonksiyonu

( )

,

(

₂

)

1 a xt b ap H x t pxt qt + − = − − (3.6) dir.

İspat . Tanım 3.1.1 den

( )

( )

1 1 , n n n H x t ∞ h x t − = =

∑

dir. Bu ifadeyi

( )

( )

1

( )

( )

( )

1 1 2 1 3 , n n n n n n H x t ∞ h x t − h x h x t ∞ h x t − = = =

∑

= + +

∑

şeklinde yazabiliriz. (3.1) ve (3.2) ifadesinden

( )

( )

( )

1 1 2 3 , n n n n H x t a bxt ∞ pxh x qh x t − − − = = + +

∑

⎡_⎣ + ⎤_⎦

elde edilir. Buradan

( )

( )

( )

( )

( )

1 1 1 2 3 3 1 1 1 2 3 3 , n n n n n n n n n n n n H x t a bxt pxh x t qh x t a bxt px h x t q h x t ∞ ∞ − − − − = = ∞ ∞ − − − − = = = + + + = + + +

∑

∑

∑

∑

( )

( )

( )

( )

( )

2 2 3 1 2 3 3 1 2 1 1 1 1 n n n n n n j m j m j m a bxt pxt h x t qt h x t a bxt pxt h x t h x qt h x t ∞ ∞ − − − − = = ∞ ∞ − − = = = + + + ⎡ ⎤ = + + _⎢ − _⎥+ ⎣ ⎦

∑

∑

∑

∑

bulunur. Dolayısıyla

( )

_,

( )

_, 2

( )

_, H x t = +a bxt pxtH x t+ −apxt qt H x t+ dir. Gerekli düzenlemeler yapılırsa

( )

_{, 1} 2

H x t ⎡_⎣ −pxt qt− ⎤_⎦= +a bxt apxt− olur. Buradan Horadam polinomunun üreteç fonksiyonu

( )

, ₁

(

2

)

a xt b ap H x t pxt qt + − = − −

Eğer (3.6) ifadesinde x=1 alınırsa (2.5) ile verilen Horadam dizisinin üreteç fonksiyonu elde edilir.

Teorem 3.1.2 Horadam polinomunun tek ve çift üreteç fonksiyonları sırasıyla;

( )

(

)

(

)(

)

3 1 , ₁ 2 ₁ 2 bxt qxt b ap H x t pxt qt pxt qt − − = − − + − (3.7) ve

( )

(

)

(

)

(

)(

)

2 2 2 2 2 2 1 , 1 1 a qt px t b ap H x t pxt qt pxt qt − + − = − − + − (3.8) dir.

İspat. Eğer H x t₁

( )

, tek fonksiyon ise

( )

(

)

1 , 1 , H x t = −H x t− dir. Buradan

( )

(

)

1 , 1 , 2 H x t −H x t−

ifadesini göz önüne alırsak,

( )

(

)

(

)

(

)

(

(

)

)

(

)

(

)

(

)

(

)

(

)(

)

(

)

(

)(

)

(

)

(

)

1 1 2 2 2 2 2 2 3 3 2 2 3 2 , , 1 2 2 1 1 1 1 1 2 1 1 2 1 2 1 1 1 1 H x t H x t a xt b ap a xt b ap pxt qt pxt qt a xt b ap pxt qt a xt b ap pxt qt pxt qt pxt qt bxt bqxt apqxt pxt qt pxt qt bxt qxt b ap pxt qt ⎡ ⎤ − − + − − − ⎢ ⎥ = − − − + − ⎢ ⎥ ⎣ ⎦ ⎡_⎣⎡ + − _⎦⎤ + − −_⎣⎡ − − _⎦⎤ − − ⎤ ⎢ ⎥ = − − + − ⎢ ⎥ ⎣ ⎦ ⎡ − + ⎤ ⎢ ⎥ = − − + − ⎢ ⎥ ⎣ ⎦ − − = − −

(

_{+ pxt qt−} 2

)

( )

(

)

(

)(

)

3 1 , ₁ 2 ₁ 2 bxt qxt b ap H x t pxt qt pxt qt − − = − − + − dir. Benzer şekilde çift fonksiyonun tanımından

( )

(

)

2 , 2 , H x t =H x t− dir. Buradan

( )

(

)

2 , 2 , 2 H x t +H x t−

ifadesi göz önüne alınırsa;

( )

(

)

(

)

(

)

(

(

)

)

(

)

(

)

(

)

(

)

(

)(

)

2 2 2 2 2 2 2 2 , , 1 2 2 1 1 1 1 1 2 1 1 H x t H x t a xt b ap a xt b ap pxt qt pxt qt a xt b ap pxt qt a xt b ap pxt qt pxt qt pxt qt ⎡ ⎤ + − + − − − ⎢ ⎥ = + − − + − ⎢ ⎥ ⎣ ⎦ ⎡_⎣⎡ + − _⎦⎤ + − +_⎣⎡ − − _⎦⎤ − − ⎤ ⎢ ⎥ = − − + − ⎢ ⎥ ⎣ ⎦

bulunur. Gerekli işlemler yapıldığında

( )

₍

(

₎₍

₎

)

(

)(

)

2 2 2 2 2 2 2 _{2 2} 2 2 2 2 2 2 2 2 2 1 , 2 1 1 1 1 a aqt bpx t ap x t H x t pxt qt pxt qt a aqt bpx t ap x t pxt qt pxt qt ⎡ _{− + −} ⎤ ⎢ ⎥ = − − + − ⎢ ⎥ ⎣ ⎦ ⎡ _{− + −} ⎤ ⎢ ⎥ = − − + − ⎢ ⎥ ⎣ ⎦

elde edilir. Yani Horadam polinomunun çift üreteç fonksiyonu

( )

(

)

(

)

(

)(

)

2 2 2 2 _{2 2} 1 , 1 1 a qt px t b ap H x t pxt qt pxt qt ⎡ − + − ⎤ ⎢ ⎥ = − − + − ⎢ ⎥ ⎣ ⎦ dir.

Horadam polinomunun (3.6) ile verilen üreteç fonksiyonundan faydalanarak Horadam polinomunun Binet formülü elde edilebilir. Horadam polinomunun üreteç

( )

, ₁

(

2

)

a xt b ap H x t pxt qt + − = − − dir. Bu fonksiyonu

( )

,

₍

(

₎₍

)

₎

1 1 a xt b ap H x t t t α β + − = − −

şeklinde yazabiliriz. Bu ifadeyi basit kesirlerine ayırırsak

( )

(

)

(

)(

)

, 1 1 1 1 a xt b ap A B H x t t t t t α β α β + − = = + − − − − (3.9) olur. Gerekli işlemler yapıldığında

(

)

A B a

Aβ Bα x b ap

+ =

+ = − −

lineer denklem sistemi elde edilir. Bu sistem çözülürse

bx a A β α β − = − ve bx a B α α β − = − − elde edilir. Bu değerler (3.9) de yerine yazılırsa

( )

, 1 1 1 1 1 bx a bx a H x t t t bx a bx a t t β α α β α β α β β α α β α β − − − − = − − − ⎡ − − ⎤ = _⎢ − _⎥ − _⎣ − − _⎦ bulunur. 1 1 1 1 n n n a ab x bx ∞ − − = = −

∑

ifadesinden faydalanırsak

( )

( )

(

)

(

)

(

)

(

)

1 1 1 1 1 1 1 1 1 1 1 1 1 , 1 n n n n n n n n n n n n n H x t h x t bx a t bx a t bx a bx a t β α α β α β β α α β α β ∞ ∞ ∞ − − − − − = = = ∞ − − − = ⎡ ⎤ = = _⎢ − − − _⎥ − ⎣ ⎦ ⎡ _{⎡ ⎤} ⎤ = _{⎢ ⎣} − − − _{⎦ ⎥} − ⎣ ⎦

∑

∑

∑

∑

elde edilir. Buradan

( ) (

)

n 1

(

)

n 1 n bx a bx a h x β α α β α β − − − − − = −

olur. Dolayısıyla A₁=bx a− β ve A₂ =bx a− αolmak üzere Horadam polinomunun Binet formülü

( )

1 1 1 2 n n n A A h x α β α β − ₋ − = − (3.10) şeklindedir.

Horadam polinomunun üreteç fonksiyonu ve Binet formülünden yola çıkarak

aşağıdaki özel durumlar verilebilir.

1) (3.6) ve (3.10)’da a b= = = = alırsak Fibonacci polinomunun üreteç p q 1 fonksiyonu ve Binet formülü;

( )

2

( )

₂ 2 2 1 1 4 4 , ; 1 ₄ 2 2 n n n x x x x F x t F x xt t _x ⎡_{⎛ + + ⎞ ⎛ − + ⎞} ⎤ ⎢ ⎥ = = ⎜_⎜ ⎟_⎟ −⎜_⎜ ⎟_⎟ ⎢ ⎥ − − _{+ ⎝ ⎠ ⎝ ⎠} ⎣ ⎦

olarak elde edilir (Lupaş 1999).

2) (3.6) ve (3.10)’da a=2; b= = = alırsak Lucas polinomunun üreteç p q 1 fonksiyonu ve Binet formülü aşağıdaki gibi bulunur (Lupaş 1999).

( )

( )

1 1 2 2 1 2 2 4 4 , ; 1 2 2 n n n xt x x x x L x t L x xt t − − − ⎛ ⎞ ⎛ ⎞ − + + − + = =⎜_⎜ ⎟_⎟ +⎜_⎜ ⎟_⎟ − − _{⎝ ⎠ ⎝ ⎠}

3) (3.6) ve (3.10)’da a=1;b= =p 2; q= alırsak Pell polinomunun üreteç 1 fonksiyonu ve Binet formülü;

( )

( )

(

2

) (

2

)

2 ₂ 1 1 , ; 1 1 1 2 _{2 1} n n n P x t P x x x x x xt t _x ⎡ ⎤ = = _⎢ + + − − + _⎥ − − + ⎣ ⎦

olarak bulunur (Horadam, Mahon 1985).

4) (3.6) ve (3.10)’da a b= = =p 2; q= alırsak Pell-Lucas polinomunun üreteç 1 fonksiyonu ve Binet formülü;

( )

( )

(

2

) (

1 2

)

1 1 2 2 2 , ; 1 1 1 2 n n n xt Q x t Q x x x x x xt t − − − − = = + + + − + − − dır (Horadam, Mahon 1985).

5) (3.6) ve (3.10)’da a b= = = =p x 1; q=2yalırsak Jacobsthal polinomunun üreteç fonksiyonu ve Binet formülü;

( )

2 1 , 1 2 J y t t yt = − − ve

( )

1 8 1 1 8 1 1 2 2 1 8 n n n y y J y y ⎡_{⎛ + + ⎞ ⎛ − + ⎞} ⎤ ⎢ ⎥ = ⎜_⎜ ⎟_⎟ −⎜_⎜ ⎟_⎟ ⎢ ⎥ + _{⎣⎝ ⎠ ⎝ ⎠ ⎦}

dir (Horadam, Flipponi 1997).

6) (3.6) ve (3.10)’da a=2; b= = =p x 1; q=2y alırsak Jacobsthal-Lucas polinomunun üreteç fonksiyonu ve Binet formülü;

( )

2 2 , 1 2 t j y t t yt − = − − ve

( )

1 1 1 1 1 8 1 1 8 2 2 n n n y y j y − − − ⎛ _{+ +} ⎞ ⎛ _{− +} ⎞ =⎜_⎜ ⎟_⎟ +⎜_⎜ ⎟_⎟ ⎝ ⎠ ⎝ ⎠

olarak elde edilir (Horadam, Flipponi 1997).

7) (3.6) ve (3.10)’da a=1; b= =p 2; q= − alırsak ikinci çeşit Chebyshev polinomu-1 nun üreteç fonksiyonu ve Binet formülü;

( )

, 1 ₂ 1 2 U x t xt t = − + ve

( )

(

) (

)

2 2 1 ₂ 1 1 1 2 1 n n n U x x x x x x − = ⎡⎢ + − − − − ⎤⎥ ⎣ ⎦ − dir (Morgado 1995).

8) (3.6) ve (3.10)’da a b= =1;p=2; q= − alırsak birinci çeşit Chebyshev 1

polinomunun üreteç fonksiyonu ve Binet formülü;

( )

, 1 ₂ 1 2 xt T x t xt t − = − + ve

( )

(

) (

1

)

1 2 2 1 1 1 2 n n n x x x x T x − − − + − + − − = dir (Morgado 1995).

3.2. Horadam Polinomları İçin Toplam Formülleri

Horadam polinomunun Binet formülünden faydalanarak önemli toplam

formülleri ve bazı özdeşlikler elde edilebilir ve dikkat edildiğinde bu toplam formüllerinin ve özdeşliklerin Fibonacci, Lucas, Pell-Lucas, Jacobsthal,

Jacobsthal-Lucas, birinci ve ikinci çeşit Chebyshev polinomlarına da indirgenebildiği görülür.

Teorem 3.2.1. h x n_n

( )

, . Horadam polinomu ve n≥0 olmak üzere; 1

( )

( )

1

( )

(

)

1 1 k k k n n h x qh x a x b ap h x px q − − = + − − − = + −

∑

(3.11) dir.

İspat. Horadam polinomunun Binet formülünü kullanırsak

( )

1 1 1 1 1 2 1 1 n n k k n n n A A h x α β α β − − − − = = ⎛ − ⎞ = _{⎜ ⎟} − ⎝ ⎠

∑

∑

dir. Buradan

( )

(

)

(

)

(

)

(

)

(

)(

)

(

)

(

)

1 1 1 1 1 1 2 1 1 1 1 1 1 2 1 1 1 2 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 k k k n n n n n n k k k k k k k k A A h x A A A A A A α β α β α β α β α β α α β β α β β α α β α β β α α β α β αβ α β α β αβ − − − − − = = = − − − − − − − − = − − − ⎛ − ⎞ ⎛ − ⎞ = _{⎜ ⎟}− _{⎜ ⎟} − _⎝ − _⎠ − _⎝ − _⎠ ⎡ − − − − − ⎤ ⎢ ⎥ = − _⎢⎣ − − _⎥⎦ ⎡ − − + − − − + ⎤ ⎢ ⎥ = − _⎢⎣ − − + _⎥⎦

∑

∑

∑

elde edilir. px α β+ = ve αβ = − q

ifadelerini göz önüne alırsak

( )

(

) (

)

(

) (

)

(

) (

)

(

) (

)

1 1 1 1 1 1 1 1 1 2 2 2 2 1 1 1 2 2 1 2 1 2 1 2 1 2 1 1 2 2 1 2 1 2 1 2 1 2 1 1 1 1 1 1 k k k k k n n k k k k k k k k A A A A A A A A h x px q A A A A A A q A A px q A A q A A A A A A px q β α α β α β αβ α β β α α β α β α β α β α β β α α β − − − − − = − − − − − − − − ⎛ − − + − + + − ⎞ = _{⎜ ⎟} − _⎝ − − _⎠ ⎡ − − − − − − − ⎤ ⎢ ⎥ = − _⎢⎣ − − _⎥⎦ ⎡ − + − − − + − ⎤ ⎢ ⎥ = + − _⎢⎣ − _⎥⎦

∑

bulunur. Burada

(

)

(

)

(

)

1 2 2 2 1 2 A A a A A a bx α β β α α β α β − = − − = − − −

dir. Bu ifadeleri ve Horadam polinomunun Binet formülünü kullanırsak

( )

( )

( )

(

)

1 1 1 1 k k k n n h x qh x a x b ap h x px q − − = + − − − = + −

∑

elde edilir.

Eğer (3.11)’de x=1 alınırsa Teorem 2.2. ile verilen (2.8) ifadesi yani

Örnek 3.2.1. k =4 için

( )

( )

( )

(

)

(

)

(

)

(

)

(

)

3 4 3 1 2 3 2 2 2 2 1 1 1 1 1 1 1 n n h x h x qh x a x b ap px q bp x apqx bqx bpqx aq a bx apx px q a px q bx px q bpx aq px q px q a bx bpx aq = = ⎡_⎣ + − − − ⎤_⎦ + − + + + + − − + = + − + − + + − + + + − = + − = + + +

∑

bulunur.

Eğer (3.11) ifadesinden faydalanırsak Fibonacci, Lucas, Pell, Pell-Lucas,

Jacobsthal, Jacobsthal-Lucas, birinci ve ikinci çeşit Chebyshev polinomlarının

toplamları aşağıdaki gibi elde edilir.

1) a b= = = = için p q 1 F x n_n

( )

. Fibonacci polinomu olmak üzere

( )

( )

( )

1 1 1 1 k k k n n F x F x F x x − − = + − =

∑

elde edilir (Lupaş 1999).

2) 2,a= b= = = için p q 1 L_n−1

( ) (

x , n−1 .

)

Lucas polinomu olmak üzere

( )

( )

( )

1 1 2 1 1 2 k k k n n L x L x x L x x − − − − = + + − =

∑

bulunur (Lupaş 1999).

3) a=1,b= =p 2,q= için 1 P x n_n

( )

. Pell polinomu olmak üzere

( )

( )

( )

1 1 1 1 2 k k k n n P x P x P x x − − = + − =

∑

elde edilir (Horadam, Mahon 1985).

( )

( )

( )

1 1 2 1 1 2 2 2 k k k n n Q x Q x x Q x x − − − − = + + − =

∑

dir (Horadam, Mahon 1985).

5) a b= = = =p x 1,q=2y için J y n_n

( )

. Jacobsthal polinomu olmak üzere

1

( )

1

( )

1 1 2 k k n n J y J y y − + = − =

∑

bulunur (Horadam 1997).

6) a=2,b= = =p x 1,q=2y için j_n−1

( ) (

y n−1 .

)

Jacobsthal -Lucas polinomu

olmak üzere 1 ₁

( )

( )

1 1 2 k k n n j y j y y − − = − =

∑

elde edilir (Horadam 1997).

7) a=1,b= =p 2,q= − için 1 U_n−1

( ) (

x , n−1 .

)

ikinci çeşit Chebyshev polinomu olmak üzere 1

( )

1

( )

2

( )

1 1 1 2 2 k k k n n U x U x U x x − − − − = − − = −

∑

dir (Udrea 1996).

8) a b= =1,p=2,q= − için 1 T_n−1

( ) (

x , n−1 .

)

birinci çeşit Chebyshev polinomu olmak üzere 1

( )

1

( )

2

( )

1 1 1 2 2 k k k n n T x T x x T x x − − − − = − + − = −

∑

elde edilir (Udrea 1996).

Teorem 3.2.2. (Cassini Özdeşliği) n≥0ve h x n_n

( )

. Horadam polinomu olmak

( )

( )

2

( )

(

2 2 2 2

)

( )

1 2 1 1 1 n _n n n n h x h x h x b x abpx a q − q − + − − = − − − (3.12) dir.

İspat. Horadam polinomunun Binet formülünü kullanırsak,

( )

( )

2

( )

1 2 1 2 2 2 1 1 2 1 2 1 1 n n n n n n n n n h x h x h x Aα Aβ Aα Aβ Aα Aβ α β α β α β − − − − + − − ⎛ − ⎞⎛ − ⎞ ⎛ − ⎞ =_{⎜ ⎟⎜ ⎟ ⎜}− _⎟ − − − ⎝ ⎠⎝ ⎠ ⎝ ⎠

olur. Burada gerekli işlemler yapıldığında

( )

( )

( )

(

)

(

)

[ ]

(

)

( ) (

)

(

)

( )

2 2 1 1 2 1 2 1 2 1 2 1 1 2 2 2 1 1 1 2 2 1 1 2 2 2 1 1 2 2 2 1 2 2 2 2 n n n n n n n n n n n n n n n n n n A A A A A A h x h x h x A A A A A A q q A A q α β α β α β α β α β α β α β α β α β αβ β α α β α β α β − − − − + − − − − − − − − − − + − − = ⎡ ⎤ − _⎣ + − _⎦ = − ⎡ ⎤ − _⎢ + − _⎥ ⎣ ⎦ = − − − − − = − = − − elde edilir. A₁ =bx a− β, A₂ =bx a− α, 2 2 2 2 1 2 A A =b x −abpx −a q (3.13) olduğu için

( )

( )

2

( )

(

2 2 2 2

)

( )

2 1 1 n n n n h₊ x h₋ x −h x = − b x −abpx −a q −q − bulunur. Dolayısıyla

( )

( )

₂

( )

(

_{2 2 2 2}

)

( ) ( )

2 1 1 1 1 n n n n n h₊ x h₋ x −h x = b x −abpx −a q q − − − dir. Örnek 3.2.2. n=5 için

( ) ( )

( )

(

) (

)

(

)

(

)

(

)

(

)

2 4 5 3 2 3 2 2 2 3 6 4 5 2 3 4 2 2 2 2 2 3 3 2 3 2 2 3 2 2 4 3 2 2 2 2 3 2 2 2 2 h x h x h x bp x ap q bp q x apq bq x bp x apq bq x bp x ap q bpq x aq a p q abpq b q a p q x a q q b x abpx a q ⎡ ⎤ ⎡ ⎤ − =_⎣ + + + + _⎦⎣ + + _⎦ ⎡ ⎤ −_⎣ + + + _⎦ = + + − − = − − dir.

Teorem 3.2.3. (Catalan Özdeşliği) n≥0, n r≥ ve h x n_n

( )

. Horadam polinomu

olmak üzere;

( )

( )

( ) ( )

( )

( )

2 1 1 2 2 2 2 2 2 n r r r n n r n r q bxh x ah x h x h x h x b x abpqx a q − − + + + − − ⎡_⎣ − ⎤_⎦ − = − − (3.14) dir.

İspat. Horadam polinomunun Binet formülünü kullanırsak,

( )

( )

( )

1 1 2 1 1 1 1 2 1 2 1 2 1 2 n n n r n r n r n r n n r n r A A A A A A h x h x h x α β α β α β α β α β α β − − + − + − − − − − + − ⎛ − ⎞ ⎛ − ⎞⎛ − ⎞ − =_{⎜ ⎟} −_{⎜ ⎟⎜ ⎟} − − − ⎝ ⎠ ⎝ ⎠⎝ ⎠

dir. Burada gerekli işlemler yapıldığında

( )

( )

( )

(

)

( )

(

)

( )

(

)

( )

(

)

(

)

1 1 1 1 1 1 2 1 2 1 2 1 2 2 1 1 2 2 2 2 1 1 2 2 2 1 1 2 2 2 2 2 n n n r n r n r n r n n r n r r r n r r r r r r n r r r r n r A A A A A A h x h x h x A A A A q A A q α β α β α β α β α β αβ β α α β α α β β α β α β α β α β − − − − + − + − − − + − − − − − − + + − = − ⎡_{− + +} ⎤ ⎢ ⎥ ⎣ ⎦ = − ⎛ − + ⎞ − _{⎜ ⎟} ⎝ ⎠ = − − = − − bulunur. (3.13) ifadesinden

( )

( )

( )

(

)

( )

1 2 2 2 2 2 2 n r r r n n r n r h x h x h x b x abpx a q q α β α β − − + − ⎛ − ⎞ − = − − − _{⎜ ⎟} − ⎝ ⎠

1

( )

2

( )

2 2 2 2 r r r r bxh x ah x b x abpx a q α β α β + − + − ₌ − − − (3.15) dır. (3.15) ifadesini yukarıda yerine yazarsak

( )

( )

( )

(

)

( )

1 ₁

( )

₂

( )

2 2 2 2 2 2 2 2 2 2 n r _{r r} n n r n r bxh x ah x h x h x h x b x abpx a q q b x abpx a q − − _{+ +} + − − ⎛ ⎞ − = − − − _{⎜ ⎟} − − ⎝ ⎠ olur. Dolayısıyla

( )

( )

( ) ( )

( )

( )

2 1 1 2 2 2 2 2 2 n r r r n n r n r bxh x ah x h x h x h x q b x abpx a q − − + + + − − ⎡ ⎤ ⎣ ⎦ − = − − − bulunur.

Dikkat edilecek olursa (3.14) ile verilen Catalan özdeşliği r= olması 1 durumunda Cassini özdeşliğine dönüşecektir. Yani

( )

( )

( ) ( )

[

]

( )

(

)

( )

( )

2 2 2 3 2 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 _{2 2 2 2} 2 2 2 2 2 _{2 2 2 2} . n n n n n n n q bxh ah h x h x h x b x abpqx a q q bx bx a bpx aq b x abpqx a q q b x abpx a q b x abpqx a q q b x abpqx a q − + − − − − − − − = − − ⎡ ⎤ − _⎣ − − _⎦ = − − ⎡ ⎤ − _⎣ − − _⎦ = − − ⎡ ⎤ = − _⎣ − − _⎦ bulunur. Dolayısıyla

( )

( )

2

( ) ( )

1 2

(

2 2 2 2

)

1 1 1 n n n n n h₊ x h₋ x −h x = − − q − b x −abpqx −a q dir. Örnek 3.2.3. n= ve 4 r= için 2

( )

( ) ( ) ( )

(

)

( )

(

) (

)

( )

(

)

(

)

1 2 3 4 2 4 6 2 2 2 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 n r q bxh ah h x h x h x b x abpqx a q q bx bpx aq a bp x apqx bqx b x abpqx a q q px b x abpqx a q b x abpqx a q p qx b x abpqx a q − − − − − = − − ⎡ ⎤ − _⎣ + − + + _⎦ = − − ⎡ ⎤ − _⎣ − − _⎦ = − − = − − − dir.

Teorem 3.2.4.(D’Ocagne’s Özdeşliği) n≥0, m≥0 ve h x n_n

( )

. Horadam

polinomu olmak üzere;

h x h_m

( )

_n+1

( )

x −h x h_n

( )

_m+1

( ) ( )

x = −q n−1⎡_⎣bxh_{m n− +1}

( )

x −ah_{m n− +2}

( )

x ⎤_⎦ (3.16) dir.

İspat. h x h_m

( )

_n+1

( )

x −h x h_n

( )

_m+1

( )

x =Lolsun. Horadam polinomunun Binet formülünü kullanırsak 2 1 1 1 1 1 1 2 1 2 1 2 n n m m n n _{A A} m m A A A A A A L α β α β α β α β α β α β α β α β − − − − ⎛ ₋ ⎞ ⎛ − ⎞⎛ − ⎞ ⎛ − ⎞ =_{⎜ ⎟⎜ ⎟}− ⎜_⎜ ⎟_{⎟⎜ ⎟} − − − − ⎝ ⎠⎝ ⎠ _{⎝ ⎠}⎝ ⎠

dir. Burada gerekli işlemler yapıldığında

(

)

(

)

(

)

(

)

(

)

1 1 1 1 1 2 2 1 1 1 1 1 2 2 1 1 1 1 1 2 m n n m n m m n m n n m m n n m A A L A A A A α β α β α β α β α β α β α β α β α β α β α β α β α β − − − − − − − − − − − − ⎡− − + + ⎤ ⎣ ⎦ = − ⎡ − + − + ⎤ ⎣ ⎦ = − ⎡ − ⎤ ⎣ ⎦ = − bulunur. Dolayısıyla

( )

1

(

)

1 2 n m n m n A A L αβ α β α β − − ₋ − = −