Kuantum nokta yapıların elektronik özelliklerinin incelenmesi

T.C

SELÇUK ÜNĐVERSĐTESĐ FEN BĐLĐMLERĐ ENSTĐTÜSÜ

KUANTUM NOKTA YAPILARIN

ELEKTRONĐK ÖZELLĐKLERĐNĐN

Đ

NCELENMESĐ

CENGĐZ PEHLĐVANOĞLU

YÜKSEK LĐSANS TEZĐ FĐZĐK ANABĐLĐM DALI

T.C

SELÇUK ÜNĐVERSĐTESĐ FEN BĐLĐMLERĐ ENSTĐTÜSÜ

KUANTUM NOKTA YAPILARIN ELEKTRONĐK ÖZELLĐKLERĐNĐN ĐNCELENMESĐ

Cengiz Pehlivanoğlu

YÜKSEK LĐSANS TEZĐ FĐZĐK ANABĐLĐM DALI

Bu çalışma 26/10/2009 tarihinde aşağıdaki jüri tarafından oy birliği / oy çokluğu ile yüksek lisans tezi olarak kabul edilmiştir.

Prof. Dr. Hüseyin YÜKSEL Prof. Dr. Ayhan ÖZMEN

(Üye) (Üye)

Yrd. Doç. Dr. M. Özgür SEZER (Danışman)

ĐÇĐNDEKĐLER ÖZET ... i ABSTRACT...ii TEŞEKKÜR ... iii ĐÇĐNDEKĐLER ... iv 1. GĐRĐŞ ... 3 2. DÜŞÜK BOYUTLU YAPILAR ... 7 2.1. Kuantum Kuyuları ... 7 2.2. Kuantum Telleri ... 11

2.3. Kartezyen Kuantum Noktaları ... 12

2.4. Küresel Kuantum Noktaları ... 13

2.7. Çok Elektronlu Kuantum Nokta Yapılar ... 15

2.8. Kuantum Noktalarının Deneysel Olarak Elde Edilmesi ... 16

3. KUANTUM NOKTA YAPILARIN ELEKTRONĐK ÖZELLĐKLERĐ ... 18

3.1. Kuantum Nokta Yapılarda adaurum Yoğunluğu ... 18

3.2. Bir Kuantum Noktasının Enerji Düzeyinin Belirlenmesi ... 20

3.3. Fock-Darwın Enerji Spektrumu ... 22

3.4. Kuantum Nokta Yapıların Kabuk Yapıları ve Hund Kuralı ... 23

3.5. Kuantum Nokta Yapıların Sınır Şartları ... 25

3.6. Etkin Kütle ... 27

3.7. Parabolik Potansiyel ... 28

3.8. Harmonik Hapis Potansiyeli ... 31

3.9. Küresel Kuantum Noktasına Manyetik Alan Etkisi ... 32

3.10. Enerji Spektrumu ... 36

4. HESAPLAMA YÖNTEMLERĐ ... 38

4.2. Yoğunluk Fonksiyonel Teori ... 41 4.3. Varyasyon Yöntemi ... 44 4.4. Thomas-Fermi Modeli... 49 5. SONUÇ VE TARTIŞMA ... 52 6. EK ... 53 7. KAYNAKLAR ... 57

ÖZET Yüksek Lisans Tezi

KUANTUM NOKTA YAPILARIN ELEKTRONĐK ÖZELLĐKLERĐNĐN ĐNCELENMESĐ

Cengiz Pehlivanoğlu

Selçuk Üniversitesi Fen Bilimleri Enstitüsü Fizik Anabilim Dalı

Danışman: Yrd. Doç. Dr. M. Özgür SEZER 2009, 60 sayfa

Jüri: Prof. Dr. Hüseyin YÜKSEL Prof.Dr. Ayhan ÖZMEN

Yrd. Doç. Dr. M.Özgür SEZER

Bu çalışmada, kuantum nokta yapıların elektronik özellikleri teorik olarak çalışılmıştır. Bu amaçla, kuantum noktalarına hapsedilen bir elektronun enerji seviyeleri, kabuk yapıları ve manyetik alan içerisindeki davranışları ele alınmıştır. Bir, iki ve üç boyutta sınırlandırılmış kuantum nokta yapıların, kuantum mekaniksel yöntemlerle incelenmiştir. Đlave olarak, bu yapıların elektronik parametrelerinin hesaplanmasında kullanılan yöntemler hakkında bilgi verilmiştir.

ABSTRACT Master Thesis

INVESTIGATION OF ELECTRONIC PROPERTIES OF THE QUANTUM DOT STRUCTURES

Cengiz Pehlivanoğlu

Selçuk Universty Faculty of Science Depertment of Physics

Supervisor

Yrd. Doç. Dr. M. Özgür SEZER 2009, 60 pages

Jury: Prof. Dr. Hüseyin YÜKSEL Prof. Dr. Ayhan ÖZMEN

Ass. Prof. Dr. M. Özgür SEZER

In this study, the electronic properties of quantum dot structures have been studied theoretically. For this purpose, energy levels, shell structures and behaviors within the magnetic fields of electron which confined in the quantum dots have been treated. The quantum dot structures confined with one-, two and three dimensions have been investigated by quantum mechanical methods. In addition, information about the calculation methods of the electronic parameters of these structures were given.

TEŞEKKÜR

Bu çalışma Selçuk üniversitesi Fen-Edebiyat Fakültesi Fizik bölümü öğretim üyesi Sayın Yrd. Doç. Dr. M. Özgür SEZER yönetiminde tamamlanarak S.Ü Fen Bilimleri Enstitüsüne Yüksek Lisans Tezi olarak sunulmuştur.

Tez konusunun seçiminde, araştırmaların yürütülmesinde, bilgi ve önerileriyle beni yönlendiren hocam Sayın Yrd. Doç. Dr. M. Özgür SEZER’ e en içten saygılarımla teşekkür eder şükranlarımı sunarım.

CENGĐZ PEHLĐVANOĞLU Konya, Ekim, 2009

1. GĐRĐŞ

Teknoloji giderek fonksiyonu çok, boyutları küçük olan ürünlere doğru kaymaktadır. En fazla fonksiyonunu en küçük hacimde barındıran teknolojilere nanoteknoloji ile ulaşılabilir. Nanometre bir uzunluk birimidir. Malzemenin olabilecek en küçük boyutudur. Nanometre ölçek olarak metrenin milyarda birini ifade etmektedir. Bir nanometrede yan yana dizilmeyle ortalama 5-10 atom bulunur. Bir kenarı 2,5 nm boyutlu bir küp, yaklaşık 1000 atom ihtiva eder. Nanoboyutlara inildiğinde madde makro-boyutlardan çok farklı fiziksel, kimyasal ve biyolojik özellikler kazanmaktadır. Nano sistemlerin fabrikasyonu ile daha önce varlığı bilinmeyen çeşitli fonksiyonlar çıkartılacak, bunların verimli bir şekilde insanlığın kullanımına sunulması ile de hayat standartlarımızda önemli ilerlemeler kaydedileceği açıktır. Gelişen vakum sistemleri ve malzeme karakterizasyon teknikleri mühendisliğe ve bilime bu seviyede çalışma yapabilirliği sağlamıştır ve gittikçe artan oranlarda sağlamaktadır. Nanosaniyelerde görüntüleme, mekanik kuvvetler uygulayabilme ve mekanik özellik tayini, nanosaniyelerde başlayıp biten çeşitli işlemlerin yakalanabilmesi ve izlenmesi, nanoölçeklerde kimyasal analiz gibi analitik inceleme tekniklerindeki gelişmeler, beraberinde nanoteknoloji bilimini mühendisliğe ve oradan da uygulamalara ulaştırmış ve sensörlerde, hafıza elemanlarında, tıpta etkili yeni cihazların ortaya çıkmasını sağlamıştır. Nanoteknolojide araştıma yönlerini maddeler halinde açıklayabiliriz.

• Nanoteknolojinin kimyasal, biyolojik, radyoaktif patlayıcı tesbiti ve korunmasında kullanımı

• Nano-ölçekte çalışan cihazların üretilmesi

Nanoteknolojinin önemi, atomlar ve moleküller seviyesinde çalışarak, gelişmiş ve tamamen yeni fiziksel, kimyasal, biyolojik özelliklere sahip yapılar elde edilmesine imkân sağlamasından kaynaklanmaktadır. Nanoteknolojinin gelişmesiyle birçok bilim alanlarında yeni boyutlar ve araştırma imkânları doğmuştur. Elektronikte nanoyapılar Moore yasasının sınırlı uzantısı ve klasik araçlardan küçük araçlara geçişini ve kuantum araçları ile yeni işlemci mimarilerinin yapımını mümkün kılar. Safsızlık ve hataların birbirine göre dizilimi çok hassas bir şekilde kontrol edebilme ve mükemmel inorganik ve organik nanoyapılar entegre edebilme

yeteneği tamamen yeni nesil ileri düzey kompozitlerin ortaya çıkmasını sağlayacaktır. Atomların nanoteknoloji yardımıyla öngörülen pozisyonlara yerleştirilmesi bugünkü teknolojide gerçekleştirilmektedir. Nanoteknoloji uygulama alanları:

• Enformasyon teknolojisi, bilgisayar, yazılım ve donanım teknolojileri • Uydu teknolojisi; uydu aracılığı ile bilgi aktarımı.

• Mikro-elektronik teknolojisi; daha hızlı ve hassas birimlerin geliştirilmesine yönelik bilim ve teknolojiler.

• Đletişim teknolojisi(dijital teknoloji, fiber optik, lazer teknolojisi, internet, tele işlem, videotex, telekonferans, CD-Rom, DVD)

• Esnek otomasyon, akıllı imalat teknolojileri • Gelişmiş malzeme teknolojileri

• Biyoteknoloji

• Enerji teknolojileri, Nükleer Enerji • Uzay ve Havacılık

• Bilgisayar teknolojisi, chip, hafıza kartları • Güneş enerjisi, hidrojen üretimi, bataryalar

• Televizyon teknolojisi, elektronik cihazlar, mobil kominikasyon sistemleri • Nanotüp içeren bileşikler, nanopartiküle sahip bileşikler, kimyasal

kaplamalar, alaşımlar, yalıtım akıllı malzemeler • Hücre büyümesini artıran implantasyonlar. • Sensörler, foton üretimi ve dedektörü, lazerler

• Biyo-analiz sistemleri, ayrıştırma teknolojileri, su arıtma sistemleri • Tıp aletleri ve cihazları, tıpta görüntü teknolojisi

• Filtre sistemleri, yapıştırıcılar, patlayıcı maddeler ve boyalar, yakıt patlayıcı maddeler silah endüstrisi

• Tekstil, otomobil endüstrisi, inşaat malzemeleri • Optik sistemler

Yarı iletken aygıtlar üzerine kuantum sınırlandırmasının etkileri ile ilgili tartışmalar 1950 li yıllarda başlar. Schrieffer (1957) bir potansiyel kuyu içerisinde

hapsedilmiş elektronların klasik olarak davranamayacaklarını ve bu elektronların enerji seviyelerinin sınırlandırmanın olduğu boyutta kesikli değerler alacağını öne sürmüştür. 1975 yılında Cho ve Arthur tarafından moleküler demet kaplama (MBE) yönteminin bulunuşu çoklu eklem kuantum yapılarında önemli gelişmelere ışık tutmuştur.

Yarı iletken yapıların en basiti ve en yaygın kullanılanı iki boyutlu elektron gazıdır. Đki farklı yarı iletkenin düzlemsel ara yüzeyinde oluşan potansiyel kuyusu elektronları oldukça ince bir tabakaya hapseder. Uygun tasarlanmış iki boyutlu elektron gazının yapılarında elektronlar, çok az çarpışma yaparak uygun mesafeler kat edebilirler. Öte yandan elektronların dalga boyları yarıiletkenlerin katkılanma miktarı ile belirlendiğinden kuantum büyüklük etkilerini ön plana çıkaracak tasarımlar oldukça kolaydır.

Bugün düşük boyutlu deneylerde çoğunlukla kuantum kuyularından yaralanılıyor. Bu boyutta artık metal tellerin temel görevi bu iki boyutlu elektron gazı içerisinde düşük boyutlu ölçekte devrelerin ve aygıtların oluşturulmasına yardımcı olmaktır. Negatif gerilim uygulanmış metal bir tel iki boyutlu elektron gaz üzerine yerleştirilirse elektron gazı içerisinde telin tam altında elektronlardan arındırılmış yalıtkan bir bölge oluşur. Bu yolla elektron gazı içerisinde aynen metal ince filmlerde olduğu gibi mezoskopik devreler ve aygıtlar oluşturmak olasıdır.

Elektron gazını kırık-kapı adı verilen yöntemle bir doğru boyunca arındırıp iki taraftaki serbest bölgeler arasında elektron dalga boyu mertebesinde dar bir açıklık bırakıldığında bir kuantum nokta bağlantısı elde edilir. Kuantum nokta bağlantısının direnci iletime katkıda bulunan enerji bandı sayısı ile belirlenir ve kuantumlaşmış durumdadır. Bu ilginç özelliğin deneyle gözlenmesi ve ayrıntılı kurumsal açıklaması, mezoskopik fizik çevrelerinde büyük bir heyecanın doğmasına neden olmuştur.

Bilindiği gibi, elektron dalgaları mikroskobik ölçekte anlamlıdır. Öte yandan bir direnç ölçümü için mikroskopik boyutta bir örneği kaynak, voltmetre vb makroskapik büyüklükteki elektronik aletlere bağlamak gerekmektedir. Böyle bir ölçümün kurumsal incelenmesi mikroskopik çokluklarla makroskopik çokluklar arasında bir bağlantı kurulmasını gerektirir. Bu bağlantı mezoskopik fiziğin doğuşundan önce, 1957’de Landauer tarafından önerilmişti. Landauer bağlantısı,

kuantum nokta bağlantıları, üretilene kadar çok duyarlı bir şekilde deneylerle karşılaştırılmamış ve güvenilirliğinden hep kuşkulanılmıştı. Hassas litografi yöntemleri ve iki boyutlu elektron gazı kullanılarak değişik mezoskopik yapılar oluşturmayı başaran deneyciler, sonunda kuantum noktaları elde etmeyi başardılar.

Elektron gazında bir bölgeyi çepeçevre arındırmak suretiyle elektronlar sıfır-boyutlu bir bölgeye hapsedilebilir. Sıfır-sıfır-boyutlu bu adacık kuantum noktası olarak adlandırılır. Bir kuantum noktası, normalde çevresinden yalıtılmış durumdadır. Fakat çeperlerindeki potansiyel eşiği biraz alçaltılırsa çok ilginç bir şey gözlenir. Klasik olarak elektronun nokta dışına çıkması olası değilken, kuantum mekaniğine göre elektron, çok ufak bir olasılıkla da olsa, dışarıya sızabilir. Bu olaya kuatum tünelleme etkisi denir. Bir kuantum noktası elektronların tünellenebileceği birer engelle iki elektron havuzuna bağlanırsa mezoskopik fiziğin yine oldukça ilginç bir başka olgusunu elde edebiliriz. Elektron havuzlarından kuantum noktasına tünelleyen yüksek enerjili elektronlar coulomb etkileşimi nedeniyle, sistemin enerjisini arttıracaklarından düşük enerjili elektronların tünellenmesi engellenir. Ancak adacıkla havuzlar arasına sonlu bir gerilim uygulandığında tünelleme olayını başlatmak mümkündür. Uygulanan gerilim, tünellemenin coulomb engellenmesi denilen eşiği geçtiğinde elektronlar bir musluğun damlasını andıracak şekilde teker teker tünellenmeye başlarlar. Tek-elektron tünellenmesi denilen bu olay 1969’da çok farklı yapıda, metal granülleri içeren bir yalıtkandan inelastik elektron tünellenmesi gözlenirken bulunmuştur (Bozdemir, 2007, Eker,2007).

Tüm boyutlarda güçlü bir sınırlandırma sonucu elde edilen kuantum nokta yapıları kesikli enerji seviyelerine ve kabuk yapısına sahip olduklarından dolayı yapay atom olarak adlandırılırlar. Üretilme aşamasında bu yapıların şekilleri, boyutları, enerji seviyeleri ve sınırlandırdıkları elektron sayıları kontrol edilebilir olduğundan teorik olarakdaha ilgi çekicidir. Kuantum nokta yapıları kullanılarak kızıl ötesi foto dedektörler (QDIP), tek elektron transistorler, hafıza elemanları ve kuantum bilgisayarları gibi cihazlar geliştirilmeye başlanmıştır.

2. DÜŞÜK BOYUTLU YAPILAR

Son yıllarda nano-teknolojideki gelişmeler ve haberleşme, iletişim teknolojisindeki talep ve teorik çalışmalar çok küçük yapıların üretilmesine olanak sağlanmaktadır. Hafıza ve hesaplama sistemlerine aşırı talep, sinyal iletme ve işleme hızlarının yükseltilmesi yönündeki araştırmalar, mikroelektronik ve optoelektronik aygıtların üretilmesine olanak sağlamıştır (Mitin ve ark.1999, Davies 1999). Tabiattaki bütün yapılar makroskobik, mikroskobik ve düşük boyutlu olmak üzere üç gurubta ele alınabilir. Parçacıkların hareketini istatiksel olarak tanımlayan yapılara mikroskobik yapılar denir.

Bu yapıların boyutları 10–1000

0

A arasındadır. Düşük boyutlu yapıların deneysel olarak oluşturulabilmesi için, bu yapılar içindeki taşıyıcıların hareketlerinin potansiyel engeli yardımı ile sınırlandırılması gerekir. Boyuta bağlı olarak taşıyıcı hareketlerinin sınırlandırıldığı nano yapılar, kuantum kuyuları, kuantum telleri ve kuantum noktaları olarak üç ayrı gurupta ele alabiliriz. Kuantum noktaları elektronun üç boyutta sınırlandırılması ile elde edilir. Kuantum noktalarının elektronik ve optoelektronik özellikleri üzerindeki çalışmalar artarak devam etmekte ve yeni elektronik malzemelerin üretiminde kullanılmaktadır.

2.1 KUANTUM KUYUSU

Elektronun hareketinin yalnızca bir boyutta sınırlandırıldığı, diğer iki boyutta serbest hareket edebildiği yapılara kuantum kuyuları denir. Bu yapılar Şekil 2.1’de görüldüğü gibi yasak enerji aralığı küçük olan yarıiletken malzemenin, daha büyük yasak enerji aralığına sahip olan malzeme içine ince bir tabaka şeklinde yerleştirilmesiyle elde edilir. Kuantum kuyusu yüksek iletkenlik bant enerjisine sahip iki yarıiletken tabaka arasına yerleştirilmiş çok ince düz bir yarıiletken tabaka olup, iki malzemenin iletkenlik bandı enerjileri arasındaki fark, elektronları ince bir tabakaya kısıtlar. Genel olarak kuantum kuyuları oluşturmak için kullanılan malzeme GaAs’dır ve bariyer olarak Al

Şekil 2.1. Kuantum kuyusunun bant yapısı

Hareketi y doğrultusunda sınırlandırılmış bir elektron şekilde gösterildiği gibiL_yaralığında hareket edebilsin.

) r (

V Potansiyelini ve toplam enerji E yi, üç koordinattan sadece birinin fonksiyonu olan üç niceliğin fonksiyonu olarak yazılabildiği durumu göz önüne alalım. Buna göre,

) z ( V ) y ( V ) x ( V ) r ( V = + + (2.1a) ve ) z ( E ) y ( E ) x ( E E= + + _(2.1b)

yazılabilir. Burada V potansiyel enerjiyi, E ise toplam enerjiyi ifade eder. Bu duruma karşılık gelen dalga fonksiyonu, bir-boyutlu üç fonksiyonun çarpımı olarak ifade edilebilir. ) z ( ) y ( ) x ( ) r ( =ψ ψ ψ ψ (2.2)

Bu ifadeleri Schrödinger denkleminde yerine yazılırsa ve ψ(r)bölünüp yeniden düzenlenirse, E ) z ( V dz ) z ( d ) z ( 1 m 2 ) y ( V dy ) y ( d ) y ( 1 m 2 ) x ( V dx ) x ( d ) x ( 1 m 2 2 2 2 2 2 2 2 2 2 =       + ψ ψ − +       + ψ ψ − +       + ψ ψ − h h h (2.3) olur. Buradan, ) x ( ) x ( E ) x ( ) x ( V dx ) x ( d m 2 2 2 2 ψ = ψ + ψ − h (2.4) ) y ( ) y ( E ) y ( ) y ( V dy ) y ( d m 2 2 2 2 ψ = ψ + ψ − h (2.5) ) z ( ) z ( E ) z ( ) z ( V dz ) z ( d m 2 2 2 2 ψ = ψ + ψ − h (2.6)

elde edilir. Hareketi y doğrultusunda sınırlandırılmış bir elektron L_y aralığında hareket edebilsin. Bu durumda x ve z doğrultusunda sınırlandırma yapılmadığından

0 ) x ( V = , V(z)=0 olacaktır.      ∞ < < ≤ ≤ − − < < ∞ − = y 2 L V 2 L y 2 L 0 2 L y V ) y ( V y 0 y y y 0

şeklinde olsun. ( 2.5) denklemini ele alalım. ) y ( ) y ( E ) y ( ) y ( V dy ) y ( d m 2 2 2 2 ψ = ψ + ψ − h

denklemi tekrar düzenlersek

[

V(y) E(y)

]

_{(y) 0} m 2 dy ) y ( d 2 2 2 = ψ − + ψ h (2.7) şeklinde bulunur. Kuyunun bölgelerine göre incelersek;

I. bölgede V₀ >E olduğundan dalga fonksiyonu

y k y k 1 y y e B e A ) y ( = + − ψ (2.8) olarak elde edilir. −∞ da yansıyan dalga olmadığından B=0 olmalıdır. I.bölgede dalga fonksiyonu ₁ kyy e A ) y ( = ψ şeklindedir. Burada k_y2 =2m[V₀ −E(y)] h2 olur.

II. bölgede V(y)=0ve E<V0 olması nedeniyle dalga fonksiyonu y i y i 2 y y e D e C ) y ( = −α + α ψ (2.11) y sin ' D y cos ' C ) y ( _{y y} 2 = α + α ψ (2.12) şeklinde olacaktır.

III. bölgede dalga fonksiyonu

y k y k 3 y y e F e E ) y ( = + − ψ (2.13)

şeklinde yazılabilir. Sonsuzdan yansıyan dalga olmaması nedeniyle E =0olacaktır.

     α + α = ψ − ede lg bö . 3 ; e F ede lg bö . 2 ; y sin D y cos C ede lg bö . 1 ; e A ) y ( ky iky (2.14)

Kuyu kenarlarında sınır şartları uygulanırsa y ekseni boyunca dalga vektörü ... , 3 , 2 , 1 n , L n k _y y y y n = π = (2.15)

2 y y 2 L n m 2 ) y ( E _       _π = h (2.16)

olur. Parçacığın toplam enerjisi ise,

                _π + + = 2 y y 2 z 2 x 2 L n k k m 2 E h (2.17)

olarak yazılabilir (Dinçer, Gümüş, 1990).

2.2. KUANTUM TELLERĐ

Elektronların hareketinin iki boyutta sınırlandırıldığı yapıya kuantum telleri denir. Dolayısıyla böyle bir yapıda elektron tek serbestlik derecesi ile karakterize edilecektir. Schrödinger denklemi iki boyutlu olarak yazılırsa,

E ) z ( V dz ) z ( d ) z ( 1 m 2 ) y ( V dy ) y ( d ) y ( 1 m 2 2 2 2 2 2 2 =       + ψ ψ − +       + ψ ψ − h h (2.18) ) y ( ) y ( E ) y ( ) y ( V dy ) y ( d m 2 2 2 2 ψ = ψ + ψ − h ) z ( ) z ( E ) z ( ) z ( V dz ) z ( d m 2 2 2 2 ψ = ψ + ψ − h

olur. y ve z boyunca potansiyeller sonsuz yüksek alınırsa kuyu içerisinde V(y)=0, 0

) z (

V = olur. Sınır şartları uygulanırsa,

y y n L n k y π = , ve z z n L n k z π = (2.19)

ifadeleri elde edilir. Parçacığın hareketini ifade eden dalga fonksiyonları;

        _π = ψ y L n sin L 2 ) y ( y y y (2.20)       _π = ψ z L n sin L 2 ) z ( z z z (2.21) yazılabilir. Bu duruma karşılık gelen enerji,

              _π +         _π = 2 z z 2 y y 2 n L n L n m 2 E z , y h , (2.22)

Bu durumda toplam enerji,

              _π +         _π + = 2 z z 2 y y 2 x 2 L n L n k m 2 E h (2.23)

şeklinde ifade edilebilir.

2.3. KARTEZYEN KUANTUM NOKTALARI

Elektronların hareketinin üç boyutta sınırlandırıldığı yapılara kuantum nokta yapılar denir. Üç boyutlu Schrödinger denklemi,

E ) z ( V dz ) z ( d ) z ( 1 m 2 ) y ( V dy ) y ( d ) y ( 1 m 2 ) x ( V dx ) x ( d ) x ( 1 m 2 2 2 2 2 2 2 2 2 2 =       + ψ ψ − +       + ψ ψ − +       + ψ ψ − h h h

şeklinde olur. Bu ifadeye göre,

) x ( ) x ( E ) x ( ) x ( V dx ) x ( d m 2 2 2 2 ψ = ψ + ψ − h , x- yönünde ) y ( ) y ( E ) y ( ) y ( V dy ) y ( d m 2 2 2 2 ψ = ψ + ψ − h , y- yönünde ) z ( ) z ( E ) z ( ) z ( V dz ) z ( d m 2 2 2 2 ψ = ψ + ψ − h , z- yönünde

yazabiliriz. Üç boyutta potansiyel engelleri sonsuz yüksek alınırsa, kuyu içinde 0

) x (

V = , V(y)=0 ve V(z)=0 olur. Dalga vektörlerini,

x x n L n k x π = , y y n L n k y π = , z z n L n k z π = (2.24)

şeklinde yazabiliriz. Parçacığın hareketini ifade eden dalga fonksiyonları;       _π = ψ x L n sin L 2 ) x ( x x x       _π = ψ z L n sin L 2 ) z ( z z z         _π = ψ y L n sin L 2 ) y ( y y y

olarak yazılabilir. Toplam enerji ise,

              _π +         _π +       _π = 2 z z 2 y y 2 x x 2 L n L n L n m 2 E h (2.25)

ifadesi ile verilir.

2.4. KÜRESEL KUANTUM NOKTALARI

Sınırlandırılan bir elektronun enerji seviyelerinin belirlenmesi ve bu elektronun pozitif bir safsızlığa bağlanma enerjisinin hesaplanabilmesi için Hamiltoniyen işlemcisinin küresel koordinatlara bağlı olarak yazılmalıdır. Schrödinger denklemi küresel koordinatlarda,

ψ = ψ + ψ + ψ       φ ∂ ∂ θ + θ ∂ ∂ θ θ ∂ ∂ θ + ∂ ∂ + ∂ ∂ − V(r) V(r) E sin r 1 ) (sin sin r 1 r r 2 r m 2 2 c 2 2 2 2 2 2 * 2 h (2.26)

şeklinde verilir. Bu şekilde verilen diferansiyel denklemin çözümü açısal momentum öz fonksiyonları ve Legendre polinomları kullanılarak

2 * 2 c * 2 r r m 2 ) 1 ( ) r ( V ) r ( V m 2 P H= + + +h l l+ (2.27)

şeklinde verilir. Bu ifadede P_r kuantum noktası içerisinde sınırlandırılan elektronun momentum operatörü, m* elektronun etkin kütlesi, V elektron ile pozitif yüklü _c safsızlık arasındaki etkileşme potansiyeli, V(r) elektron hareketinin küresel bir

kuantum noktası içerisinde sınırlandırılabilmesi uygulanan potansiyel, l yörünge kuantum sayısı ve r de göz önüne alınan küresel kuantum noktasının yarıçapıdır. (2.27) deki son terim merkezkaç potansiyelidir ve l≠0durumunda önem kazanır. Bu terim küresel kuantum noktası içerisinde sınırlandırılan ve pozitif yüklü safsızlığa bağlı olan elektronun kuvvet merkezine yaklaşmasını engelleyerek yeniden birleşmeyi önler. Toplam potansiyel enerji ifadesi etkin potansiyel olup V_Etk(r) olarak yazılırsa

)

r

(

V

r

m

2

)

1

(

r

r

e

)

r

(

V

2 * 2 0 2 Etk

+

+

+

−

ε

−

=

r

r

h

l

l

_(2.28)

elde edilir. Bu ifadede

ε

yarıiletken malzemenin dielektrik geçirgenlik sabiti, r 0

kuantum noktası merkezine göre pozitif yüklü safsızlığın konumudur. Denklem (2.27) yeniden düzenlenirse ) r ( V r r e r ) 1 ( r r 2 r m 2 H 0 2 2 2 2 * 2 + − ε −       ₊ − ∂ ∂ + ∂ ∂ − = h l l r r (2.29)

ifadesi yazılabilir. ψ(r,θ,φ)=R(r)Y(θ,φ) fonksiyonu yerine yazılıp değişken ayırımı kullanılırsa radyal ve açısal kısım elde edilir. R(r)dalga fonksiyonunun radyal kısmıdır. Serbest parçacık için V=0 alınıp k2 =2mE h2 _{sabiti tanımlanır ise}

0 ) r ( R ) r ) 1 ( k ( ) dr dR r ( dr d r 1 2 2 2 2 = + − + l l (2.30) olarak yazılabilir. ρ=kr gibi boyutsuz değişken olarak tanımlanırsa radyal Shrödinger denklemi 0 R ) 1 ( 1 d dR 2 d R d 2 2 2 =       ρ + − + ρ ρ + ρ l l (2.31) olur. Bu denklem Bessel diferansiyel denklemi olarak bilinir. Bu denklemin küresel Bessel ve küresel Neumann olmak üzere birbirinden bağımsız iki gurup çözümü vardır. Bu denklemin çözümü r k ) r k sin( N ) r ( 1 1 = ψ (2.32)

şeklinde olur ve birinci uyarılmış durum için       − = ψ ) r k ( ) r k cos( ) r k ( ) r k sin( N ) r ( 1 1 2 1 1 _(2.33)

elde edilir (Karaoğlu, 1998). Safsızlığın olmadığı bir durumunda Hamilton denklemi küresel koordinatlarda, ψ = ψ + ψ       ϕ ∂ ∂ θ +       θ ∂ ∂ θ θ ∂ ∂ θ +       ∂ ∂ ∂ ∂ − V(r) E sin r 1 sin sin r 1 r r r r 1 m 2 2 2 2 2 2 2 2 2 h

şeklinde yazılabilir. Bu ifade çözülürse,

2 2 2 2 0 , n ma 2 n E = π h

elde edilir. Burada a kuyunun genişliğidir (Yılmaz, 2004).

2.5. ÇOK ELEKTRONLU KUANTUM NOKTA YAPILAR

Kuantum nokta içerisindeki elektronlar yarıiletkendeki gibi iletkenlik bandına sahiptir. Đletkenlik elektron yoğunluğu düşüktür, ortalama elektron-elektron mesafesi 10 nm dolaylarındadır. Sonuç olarak, örgüde mevcut olan valans ve çekirdek elektronları arasındaki etkileşmeye bağlı olan etkiler, etkin kütle yaklaşımı kullanılarak dikkate alınabilir. Kuantum noktasındaki iletkenlik elektronları m* etkin kütlesine sahip ayrı bir etkileşmeli elektron sistemi oluşturur ve karşılıklı coulomb ekileşimi yarıiletkenin statik dielektrik sabiti ile perdelenir. Bir kuantum nokta yapının çok sayıdaki parçacık hamiltoniyeni H, tek parçacık kısmı ile (kinetik ile potansiyel katkıları) iki parçacık kısmının toplamıdır. Elektronlar arsındaki coulomb etkileşmesini de düşünürsek, hamiltoniyen

∑

∑

< = πεε − +         + = N j i 0 i j 2 N 1 i i * 2 i r r 4 e ) r ( V m 2 p H r r r (2.34)

şeklinde yazılabilir.

2.6. KUANTUM NOKTALARININ DENEYSEL OLARAK ELDE EDĐLMESĐ

Kuantum noktaları, üç boyutta kuantum mekaniksel olarak hapsedilmiş sıfır boyutlu sistemler olarak bilinir. Bu yapılarda doğal uzunluk ölçeği, birkaç nanometre mertebesindedir. Kuantum noktaları, doğal atomlar gibi istenildiğinde değiştirilebilen kesikli elektron sayısı içerir ve enerji seviyeleri kararlı olup kesikli spektruma sahiptir. Bu yüzden kuantum noktaları bazen yapay atomlar olarak anılır. Doğal bir atomdaki gibi, bir kuantum noktasında elektronlar bir merkezi yere doğru çekime uğrar. Başka deyişle, bu kuantum noktasında elektronlar aslında potansiyel bir kuyuda hapsedilmiştir.

Kuantum noktalarına olan ilgi son yirmi yıldır iki sebepten dolayı artarak sürmektedir. Birincisi, bu yapılarda doğal uzunluk ölçeğinin birkaç nanometre mertebesinde olmasıdır. Gerçekte, kuantum noktası, kuantum mekaniğinin çalışıldığı küçük bir laboratuvar gibi düşünülebilir. Bu nedenle kuantum nokta sistemleri kuantum mekaniğini test etmek için mükemmel bir saha sağlayabilir. Đkincisi, belki de daha önemlisi, kuantum nokta sistemleri çok ilginç ve aynı zamanda hacimsel benzerlerinden oldukça farklı birçok yeni fiziksel etkiler göstermektedir.

Kuantum noktaları birçok teknik kullanılarak üretilebilir. Ancak, başlıca amaç elektronları küçük bir bölgeye hapsetmektir. Bu hapsi yapmanın bir yolu, örneğin metal plakayı bir yalıtıcı ile kaplayarak malzemenin sınırlarını kullanmaktır. Aynı zamanda, elektrik alan uygulayarak elektronların hareketini yarıiletken içinde küçük bir bölgeye hapsetmek de mümkündür.

Bir kuantum noktasında elektronlar hiç serbest yöne sahip değildir ve elektronların de Broglie dalga boyu bu sistemlerin kuantum etkilerini şaşırtıcı yapan hapsedilme uzunluğu ile aynı uzunluk mertebesindedir. Bir kuantum noktasının hapsedilme uzunluğu üç yönde de aynı mertebede ise üç boyutlu kuantum noktası olarak adlandırılır. Eğer özel bir yönde hapsedilme uzunluğu diğer iki yön ile karşılaştırıldığında daha küçük olursa bu sistem iki boyutlu kuantum noktası olarak adlandırılır.

Özetle, elektronların ince yarıiletken bir tabakaya hapsedilmesi ile sağlanan boyuttaki azalmanın, elektronların hareketinde önemli değişikliğe yol açtığı görülür. Bu temel kural elektronların etrafındaki boyutu iki boyutlu kuantum kuyusundan bir boyutlu kuantum teline ve en sonunda sıfır boyutlu kuantum noktasına azaltmakla geliştirilebilir. Bu durumda boyut, elektronların momentumunda serbestlik derecesi sayısını gösterir. Genellikle, bir kuantum kuyusunda elektronlar bir yönde hapisli olduğu halde, bir kuantum telinde iki yönde hapislidir ve böylece serbestlik derecesi bire inmiştir. Bir kuantum noktasında ise elektronlar üç yönde de hapislidir ve böylece serbestlik derecesi sıfıra inmiştir (Kervan,2004).

3. KUANTUM NOKTA YAPILARIN ELEKTRONĐK ÖZELLĐKLERĐ

Kuantum noktacıkları ya da nanokristaller büyüklükleri 2–10 nm arasında değişen yarıiletken türüdür. Boyutlarının küçük olmasından dolayı kuantum noktacıklarının özellikleri üzerinde kolayca oynanabilir ve bu parçacıklar yeni uygulamalarda kullanılabilir. Kuantum noktacıklarının özellikleri en çok boyut ve içerdiği atomlara bağlıdır.

Katılarda değerlik bandı mutlak sıfırda elektron bulunan yerlerdeki elektron enerjilerinin oluşturduğu aralıktır. Yarıiletkenlerde ve yalıtkanlarda, iletkenlik bandının üzerinde yasak bant ve bu boşluktan sonra iletkenlik bandı vardır. Yasak bant ise elektronun bulunma olasılığının sıfır olduğu yasak enerji düzeylerinin tümünün adıdır. Metallerde iletkenlik bandı ile yalıtkanlık bandı arasında boşluk yoktur.

Yarıiletkenlerde ve yalıtkanlarda düşük seviyede iletkenlik görülmesi değerlik bandının özelliğinden dolayıdır. Đletim bandı değerlik bandında daha yüksekte olan ve elektrik alan uygulandığında elektronları hızlandırmaya yeten yani elektrik akımı üretmeye yarayan, elektron enerjisi aralığıdır. Kuantum noktacıklarının enerji seviyeleri ayırık olduğu için kuantum noktacığına atom ekleyip, çıkarma yasak bölgenin sınırlarını değiştirir. Kuantum noktacığının yüzey geometrisini değiştirmek de yasak bölge enerjisini değiştirir. Elektron ekleme çıkarma yöntemi ile istenilen renkte kuantum noktacığı oluşturulabilir.

3.1 KUANTUM NOKTALARINDA DURUM YOĞUNLUĞU

Bir kuantum noktası kadar küçük bir alana hapsedilen bir elektronun enerjisi kuantumlu olur. Yani enerji spektrumu farklılaşır. Boyutları 10-100 nm arasında olan yapılar için komşu enerji seviyeleri arasındaki uzaklık birkaç meV kadardır. Bu enerji, 2 2 2 2 n ma 2 n E = π h

şeklinde olur Enerji kuantizasyonu ya da sistemin boyutsallığının azaltılması doğrudan doğruya enerji üzerindeki durum yoğunluğuna bağlıdır. Durum yoğunluğu

birim hacim başına düşen enerji seviyesi sayısıdır ve E ile E+dE enerji aralığında girilebilir mevcut kuantum durumlarının miktarı hakkında bilgi verir. Bu nedenle durum yoğunluğu enerjinin bir fonksiyonudur. Üç boyutlu bir sistem için durum yoğunluğu,

(

)

∑

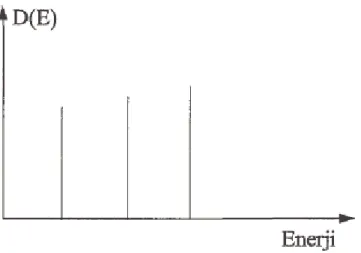
δ − = = z y x z y x n n n n n n z y x E E L L L 2 dE dN ) E ( D (3.1)

şeklinde olur. Enerji ile değişimi şekil 3.1’de gösterilmiştir. Burada δ Dirac-Delta fonksiyonudur (Daragoman, 1999. Mitin ve ark, 1999. Davies, 1999).

Şekil 3.1.Kuantum noktasının durum yoğunluğunun enerji ile değişimi.

Đki boyutlu bir sistem için (kuantum teli) durum yoğunluğu,

∑

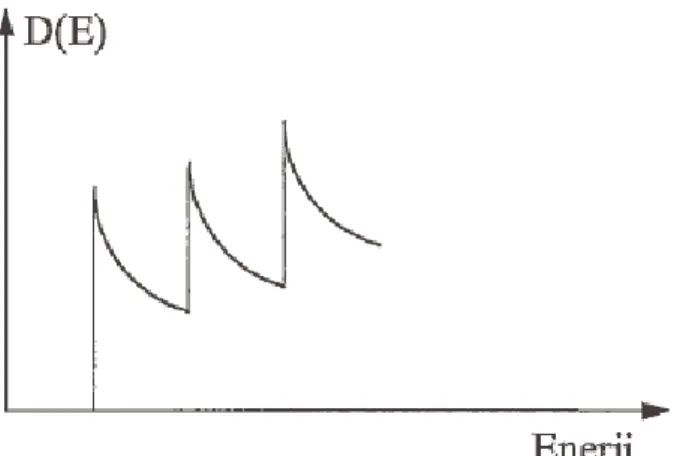
− π = = z , y _y,z n _n 2 z y E E 1 m 2 L L 1 dE dN ) E ( D h (3.2) şeklinde olur. D(E) nin enerji ile değişimi şekil 3,2’de gösterilmiştir. Bir boyutlu bir sistem için yani bir kuantum kuyusu için,

∑

Θ − π = = y y n n y 2 (E E ) L m dE dN ) E ( D h (3.3)

yazılabilir. Burada Θ Heaviside fonksiyonunu gösterir. Kuantum kuyu durum yoğunluğunun enerji ile değişimi şekil 3,3’de gösterilmiştir.

Şekil 3.2. Kuantum telindeki durum yoğunluğunun enerji ile değişimi.

Şekil 3.3. Kuantum kuyu durum yoğunluğunun enerji ile değişimi

3.2. BĐR KUANTUM NOKTASININ ENERJĐ DÜZEYLERĐNĐN

BELĐRLENMESĐ

Bir kuantum noktasının enerji düzeylerinin belirlenmesi demek, bir potansiyel kuyu içerisindeki elektronun enerji düzeylerinin belirlenmesi demektir. Potansiyel kuyu içerisindeki elektronun enerji düzeylerinin bulunabilmesi için öncelikle elektrona ait hamiltoniyeni yazalım

d r e r

V

V

V

m

2

m

2

H

2_{d re rd} d 2 2 e e 2 r r

h

h

−

+

+

+

∇

−

∇

−

=

(3.4)

Yukarıdaki eşitlikte, ilk iki terim elektronun ve deşiğin kinetik enerjisini, sonraki iki terim elektron ve deşiğin potansiyelini ve son terimde elektron ile deşik arasındaki Coulomb potansiyel etkileşimi görülmektedir. Burada me elektronun

bulunduğu potansiyel kuyusunun sınırlarının yüksekliği sonsuz alınırsa elektronun kuyu içindeki potansiyeli sıfır alınabilir. Bu durumda (3.4) eşitliği aşağıdaki gibi yazabiliriz. 2 d d 2 2 e e 2 2m 2m H=− h _∗ ∇ − h _∗ ∇ (3.5) (3.5) eşitliğindeki hamiltoniyen elektronun ve deşiğin kinetik enerjilerinin toplamından oluşmuştur. Elektron ile boşluğun potansiyel enerjilerini ve elektron ile boşluk arasındaki etkileşmeyi ifade eden Coulomb potansiyelini içermez. Elektron ile boşluk arasındaki etkileşim dikkate alınmadığına göre (3.5) eşitliğindeki hamiltoniyen iki parçaya ayrılabilir.

2 e e 2 1 m 2 H =− h _∗ ∇ ve (3.6) 2 d d 2 2 m 2 H =− h _∗ ∇

Sistemin enerji özdeğerini bulmak için, Hamiltoniyen yerine yazılırsa,.

m n m n E Hψ l = ψ l (3.7) m n m n 2 e e 2 E m 2 l l h ψ = ψ         ∇ − _∗ (3.8) nlm nlm nlm 2 2 2 2 2 2 2 2 E ) r ( V sin r 1 sin sin r 1 r r r r 1 m 2 _ψ + ψ = ψ     ϕ ∂ ∂ θ +       θ ∂ ∂ θ θ ∂ ∂ θ +       ∂ ∂ ∂ ∂ −h (3.9)

Denkem küresel koordinatlarda yazılırsa ve denklemin radyal kısmı çözülürse, parçacığın kuyu içerisindeki enerji öz değeri,

2 2 2 2 0 , n ma 2 n E = π h

olarak bulunur. Bu eşitlikte coulomb etkileşmesinin dikkate alınmadığı bir kuantum noktasının enerji düzeyini ifade eder (Allahverdi, 2002).

3.3. FOCK DARWIN ENERJĐ SPEKTRUMU

Homojen bir manyetik alandaki iki boyutlu bir harmonik osilatörün tek parçacık spektrumu Fock ve Darwin tarafından ele alınıp incelenmişti. Fock-Darwin modeli kuantum noktalarındaki tek parçacık etkilerinin analizi için basit ve temel bir kavram olduğu gibi parçacıklar arasındaki etkileşim bakımından da karmaşık ve çok kütleli hesaplamalara esas oluşturmaktadır. Küresel simetrili parabolik hapis ve

      − = Bx,0 2 1 , By 2 1 A r

’li homojen bir manyetik alan için tek parçacık Hamilton Denklemi, 2 2 0 * 2 * m r 2 1 A c e p m 2 1 H  + ω      − = r r (3.10) = c z 2 2 c 2 0 * * 2 2 1 r 4 1 m 2 1 m 2 p l ω −       ω + ω + (3.11)

şeklinde verilir. Burada ω_c =eB m*c siklotron frekansı ve lz ise z-yönündeki

açısal momentum operatörüdür. Sabit manyetik alandaki tek parçacık spektrumu,

c h m , n m 2 1 ) 1 m n 2 ( + + + ω ω = ε h h _(3.12)

olarak yazılabilir. Burada n=1, 2, 3, … radyal kuantum sayısı ve ... , 3 , 2 , 1 , 0

m= ± ± ± azimutal kuantum sayılarıdır. Efektif osilatör frekansı

4 2 c 2 0 2 h =ω +ω

ω ile verilir. Manyetik alandaki ε_n,m, tek parçacık enerjileri şekil 3.4 de şematik olarak gösterilmiştir (Jack, 1998, Manninen ve Reiman,2002).

Şekil 3.4. ωc /ω ’a bağlı olarak Fock-Darwin enerji spektrumları

3.4. KUANTUM NOKTASININ KABUK YAPISI VE HUND KURALI

Bir kuantum noktasında elektronu hapsetmek için potansiyel duvarının olması yeterlidir. Küresel kuantum noktasındaki bir elektronun bağlı durumlar için kabuk yapısı, atomlardaki gibi n baş kuantum sayısı ve ℓ açısal momentum kuantum sayısı ile belirlenir. Atomlardaki elektronlar, çekirdeğin oluşturduğu Coulomb potansiyeli altında hareket ettiklerinden dolayı açısal momentum kuantum sayısı, baş kuantum sayısından büyük olamaz. Yani ℓ en fazla n-1 değerini alabilir. Bundan dolayı atomlardaki kabuk yapısı 1s, 2s, 2p, 3s, 3p,… şeklinde olur (Zhu ve ark.1990). Küresel bir kuantum noktasındaki elektronlar, Coulamb potansiyeli içerisinde hareket etmediklerinden dolayı açısal momentum kuantum sayısında bir sınırlama söz konusu değildir. Bundan dolayı, küresel bir kuantum noktasındaki bağlı durumların kabuk yapısı 1s, 1p, 1d, 2s, 1f, 2p,..şeklindedir. Enerji seviyeleri de Enℓ şeklinde gösterilir (Şahin, 2005).

Bir noktanın disk şeklinde dairesel bir şekli varsa ve sınırlayıcı potansiyeli harmonik ise bu sistem yüksek dereceli bir simetri sistemi demektir. Bu simetri kabuk yapısını oluşturan tek parçacıklı dejenere setler oluşturur. Đki boyutlu

potansiyel için böyle bir kabuk yapısı istikrarlı hesaplamalarla tahmin edilebilir. Atomların kuantum seviyelerini elektronlarla doldurmada, Pauli dışarlama ilkesi yetersiz kalır. Pauli ilkesi ile birlikte fiziğin temel ilkelerinden birisi olan, öncelikle küçük enerjili seviyelerin doldurulması, yani küçük enerjiye öncelik ilkesi de göz önüne alınmalıdır. Sonuç olarak atomun kuantum seviyelerini elektronlarla doldururken bu iki ilke birlikte kullanılmalıdır. Đlkeleri bir defa daha ifade edersek:

1) Bir atomda iki elektron aynı kuantum sayılarına sahip olamazlar.

2) Bir kuantum seviyesinin enerjisi ne kadar negatif ise seviye o kadar kararlıdır.

Atomlarda kuantum seviyelerini elektronlarla doldururken Pauli ilkesi göz önüne alınacağından kuantum sayılarını hatırlayalım.

∞ =1, 2, 3, ..., n ) 1 ( ..., ... , 2 , 1 , 0 − = n l ) 1 2 ( ,.... 0 ,...., m_l =−l +l→ l+ s=1/2 2 ) 1 s 2 ( 2 1 , 2 1 m_s = − → + = farklı değer alır.

Baş kuantum sayısı n aynı olan elektronlar bir kabuk oluştururlar. Baş kuantum sayısı n ile birlikte yörünge kuantum sayısı l_{si de aynı olan elektronlar ise bir alt}

kabuk oluşturur. Kuantum sayılarının yukarda verilen değişim sınırlarını göz önüne alarak, bir alt kabuğa ya da kabuğa kaç elektron yerleşebileceğini belirleyebiliriz. Bir alt kabuğa konabilecek elektron sayısı m ve l m kuantum sayılarının belirledis ği

durum sayılarının çarpımı ile bulunur. Yani m_l →(2l+1),m_s →2 _{farklı durum} olduğundan herhangi bir alt kabuğa 2(2l+1) _{kadar elektron konulabilir. Bir kabuğa} yerleştirilebilecek toplam elektron sayısı N olmak üzere,

[

]

2 1 n 0 n 2 ) 1 n 2 ( ... 5 3 1 2 ) 1 2 ( 2 N=

∑

+ = + + + + − = − = l l

olur. Bir kabuk tam dolu ise dolu kabuk ya da kapalı kabuk denir. Kabuk tam dolu değil ise, açık kabuk ya da kısmen dolu kabuk denir. Hund kuralları bir atomda enerji seviyelerinin s l, ,j kuantum sayılarına bağlı olarak nasıl sıralandığını spektroskopik bir bakış ile açıklar. Bu açıklamada özellikle de nötr bir atomun en düşük enerji seviyesinin spektral gösterimiyle belirlenir. Atomların taban durumunun spektral gösterimli, elektron sralanması ile birlikte değerlendirildiğinde, periyodik cetveldeki tüm bilgileri içerdiği ve özellikle taban enerji durumunun spektral yapısını daha ayrıntılı verdiği görülür. Bir spektral terimin sembolü belirlendiğinde, alt bileşenlerin enerji bakımından sıralanışı Hund kuralları ile belirlenir. Hund Kuralları;

i. Terimler, spin kuantum sayısı s nin değerlerine göre sıralanırlar. s’si büyük olan terim daha kararlıdır. Kararlılık s ile aynı yönde değişir. Buna göre, taban enerji seviyesinin çok katlılığı yani (2s+1) değeri, en büyüktür. (Bunun anlamı =

∑

i i

s s ile belirlenecek.)

ii. Verilen bir s değeri için, çeşitli l değerleri söz konusu olduğundan l’si en büyük olan seviye en kararlıdır yani en aşağıdadır. (Bunun anlamı spektral terimin sembolü =

∑

i i ) m ( l

l _{ile belirlenecek demektir.)}

iii. Verilen bir s ve l çifti için, elektron alt kabuğa yarıdan az dolu ise, j si en küçük olan seviye en kararlı(en altta) olup, alt kabuk yarıdan fazla dolu ise j’si en büyük olan seviye en kararlı(en altta) dır. Yarı dolu alt kabuklar ise yarıdan fazla dolular gibi işlem görür. (Aygün, Zengin,1994)

3.5. KUANTUM NOKTA YAPILARDA SINIR ŞARTLARI

Kuantum nokta yapılar iki boyutlu elektron gazını yarı iletken heteroyapının ara yüzey bölgesinde sınırlandırmak amacıyla metal girişlere elektrostatik potansiyel uygulayarak yapılır. Yarı iletken malzemenin dış yüzeyleri, malzemenin iletkenliğini azaltacak bir başka malzeme ile bileşik yaparsa bu durumda yarıiletken içerisinde oluşturulan küresel kuantum noktası etrafında potansiyel engeli oluşacaktır. Fakat bu potansiyel engeli, küresel kuantum noktası etrafındaki yalıtkan olmamasından dolayı

sonlu olacaktır. Yani küresel kuantum noktası içersindeki bir elektron tünelleme yapabilecek, bundan dolayı elektron kuantum noktası etrafındaki malzeme içerisinde de hareket yeteneğine sahip olacaktır (Yılmaz, 2004). Yarıiletken malzemeler farklı olduğu için bunların etkin kütleleri, dielektrik sabitleri ve örgü sabitleri de farklı olacaktır. Sonlu potansiyel engeline sahip bir kuantum nokta yapısındaki bir elektronun potansiyelini aşması olasılığı vardır. Yani elektron kuyu içinden potansiyel engeli içine geçebilir. Bu durumda elektronun kuyu içinde ve kuyu dışındaki Schrödinger denklemini incelerken, etkin kütle değişimi de hesaba katılmalıdır. Potansiyel engelin yüksekliği V , geni₀ şliği a olan bir kuantum nokta yapısındaki bir elektronun kuyu içindeki etkin kütlesi m₁, kuyu dışındaki etkin kütlesi m₂ olsun. Bu elektronun Schrödinger denklemi

1 1 2 1 2 E m 2 ∇ ψ = ψ − h 0<r<a (3.13) 2 2 0 2 2 2 2 E V m 2 ∇ ψ + ψ = ψ − h r<0 ve r>a (3.14)

şeklinde yazılabilir. Etkin kütle farklılığı olmayan bir sistem için sınır şartı,

a r , 0 r 2 a r , 0 r 1 | = = = ψ | = = ψ a r , 0 r 2 a r , 0 r 1 | dr d | dr d = = = = = ψ ψ (3.15)

şeklinde yazılabilir. Etkin kütle farklılığı olan sistemler için sınır şartı

a r , 0 r 2 a r , 0 r 1 | = = = ψ | = = ψ a r , 0 r 2 2 a r , 0 r 1 1 | dr d m 1 | dr d m 1 = = = = = ψ ψ (3.16)

şeklinde tanımlanır. Böylece etkin kütle farkı hesaba katılmış olur. Bu sınır şartına BenDaniel-Duke şartı denir.

3.6. ETKĐN KÜTLE

Periyodik bir potansiyeldeki bir elektrona elektrik ve manyetik alanın etki etmesinden dolayı, elektronun kütlesi serbest haldeki kütlesinden farklı olacaktır. Bir boyutlu bir kutudaki serbest bir parçacığın momentumu,

k

p=h _(3.17)

ile verilir. Serbest hareket eden parçacığın kinetik enerjisi

m 2 p E 2 = dir. Parçacığın momentumu enerji denkleminde yerine yazılırsa, elektronun kinetik enerjisi

m 2 k E 2 2 h = (3.18) olarak elde edilir. Kristal yapı içerisinde hareket eden elektrona periyodik bir potansiyel etki ettiği için, elektronun momentumu serbest halde iken sahip olduğu momentumundan farklı olacaktır. Buna bağlı olarak elektronun kütlesi, serbest halde iken sahip olduğu kütleden farklıdır. Kristal içerisinde, periyodik potansiyel altında hareket eden elektrona bir dış kuvvet etki ederse elektronun hareket denklemi

dt k d dt v d m a m F F_{dış iç} r h r r r r = = = + (3.19) şeklinde olacaktır. F_dış r

kuvvetide içine alan yeni bir dış kuvvet tanımlanırsa;

a m dt v d m F_Dış r r r ∗ ∗ ₌ = (3.20)

elde edilir. Burada m∗, etkin kütle değeridir (Harrison 1999, Mitin ve ark. 1999, Davies 1999). Parçacığın gurup hızı

dk d

v_g = ω (3.21) olarak verilir. E=hω ifadesinde

h E = ω yerine yazılırsa dk dE 1 E dk d v_g h h_=     = (3.22)

ifadesi elde edilir. Bu ifadenin türevi alınırsa       = = dt dk dk E d 1 dkdt E d 1 dt dv 2 2 g h h (3.23) F dt E d 1 dt dv 2 2 2 g       = h dt dv dk E d F g 2 2 2 h = (3.24) 2 2 2 dk E d m∗ = h olur. Buradan, 2 2 2 dk E d 1 m 1 h = ∗ (3.25)

şeklini alır (Kittel, 1996).

3.7. PARABOLĐK POTANSĐYEL

Etkileşen iki elektron için, parabolik potansiyel m* 2₀r2 2

1

ω olup ve z-yönünde bir manyetik alan uygulanırsa, Hamilton denklemi,

spin 0 2 2 1 i 2 i 2 0 * i 2 i i * i H r 4 e r m 2 1 )) r ( A e P ( m 2 1 H + πεε +       ω + + =

∑

= r r r r (3.26)

şeklinde olur. Burada ri , i. elektronun x-y düzlemindeki koordinatlarıdır. ω0 hapis

frekansıdır ve ε dielektrik sabitidir.

1 2 r r r r r r − = , (r r ) 2 1 R r₁ r₂ r + =

2 2 0 2 R M R 2 1 )) R ( A Q P ( M 2 1 H = + + ω r r r (3.27) r 4 e r 2 1 )) r ( A q p ( 2 1 H 0 2 2 2 0 2 r r r r r πεε + µω + + µ = (3.29)

∑

µ = i z , i B * spin g B S H

şeklinde yazılabilir. Bura da M = 2m*,

2 m* = µ , 2 e q= ve Q=2e. µ_Bve S_i,z Bohr magnetonudur. Denklem (3.27)’un çözümünden,

2 m ) 1 m n 2 ( E c km km km R ω + ω + + =h h _(3.30)

elde edilir. Burada _{c *} m B e = ω siklotronun frekansı, 2 1 2 c 2 0 2 ) ) 2 ( (ω + ω = ω efektif

frekansdır. Yüksek limitlerde ω =µω

h

r , elektron elektron etkileşiminde Hamilton

denklemi r 4 e H 0 2 1 πεε =

dir. Etkileşme olmayan sistemin Hamiltoniyen’i

2 2 0 2 0 r 2 1 )) r ( A q p ( 2 1 H + + µω µ = r r r (3.31) olur. Burada H0 harmonik osilatöre ait hamilton denklemidir. nr =0,m≤0 durumu

için enerji denklemi,

2 m ) 1 m ( E c 0 ω + ω + =h h

2 r im ) 2 1 m ( r 2 2 r km _e e ! m 1 ) r ( ω − φ + ω π = Φ (3.32)

dir. n_r =0, m≤0 durumları için birinci enerji seviyesi E1 yukarıdaki dalga

fonksiyonu kullanılarak aşağıdaki gibi elde edilir.

r 0 2 1 ! m ) 2 1 m ( 4 e E ω + Γ πεε = (3.33)

Buna dayanarak enerji spektrumu,

r 0 2 c r ! m ) 2 1 m ( 4 e 2 m ) 1 m ( E ω + Γ πεε + ω + ω + =h h _(3.34)

yazılabilir. Hamilton Denklemi ise,

) r ( E 2 ) r ( r 2 e i 4 r r 1 r r r 2 1 2 r 0 2 2 c 2 2 r 2 2 2 Φ µ = Φ       εε π µ + φ ∂ ∂ µω + ω φ ∂ ∂ −       ∂ ∂ ∂ ∂ − h h h (3.35) Burada ω =µω h

r dir. Yukarıdaki denklemde ilk terim şu şekilde ifade edilebilir.

2 2 1 2 2 2 1 r 4 ) r ( )) r ( r ( r r r ) r ( r r r 1 _{Φ +}Φ ∂ ∂ =       ∂ Φ ∂ ∂ ∂ −

(3.35) denklemi aşağıdaki gibi düzenlenebilir.

) r ( E 2 ) r ( r 2 e i 4 r r 1 r 4 1 r r r ₂ r 0 2 2 c 2 2 r 2 2 2 2 2 1 2 2 2 1 Φ µ = Φ         εε π µ + φ ∂ ∂ µω + ω + φ ∂ ∂ − −         ∂ ∂ − h h h (3.36) Bu denklem r ve φ koordinatlara ayrılırsa,

2 1 im r 2 ) r ( u e ) r ( π = Φ φ

) r ( u E ) r ( u r 2 2 1 r 1 4 1 m 2 1 dr d 2 1 ' r 2 r 2 2 2 2 =       _α + ω +       − + − (3.37)

halini alır. Burada 2 c 2 r ' r 2 m E E h h ω µ − µ = ve 0 2 2 2 e εε π µ = α h dir.

(3.37) denklemi aşağıdaki gibi yazılabilir. ) r ( u E ) r ( u ) r ( V dr d 2 1 ' r 2 2 =       + − (3.38) Burada r 2 r 1 4 1 m 2 1 r 2 1 ) r ( V 2 2 2 2 r α +       − + ω = (3.39) dir (El-Saıd, 2003).

3.8. HARMONĐK HAPĐS POTANSĐYELĐ

Đki boyutlu harmonik osilatördeki tek elektronun durumunu Fock ve Darwin birbirlerinden bağımsız olarak incelemişlerdir. Fock ve Darwin manyetik alandaki elektronla ilgilendiler. Biz burada manyetik alanı göz ardı edip, hapis potansiyelini

2 2 0 k r 2 1 V ) r (

V =− + olarak ele alacağız. Bu durumda radyal denklem,

) r ( R E ) r ( R V r k 2 1 r 2 m r r r r 2 1 0 2 2 2 2 =         − + +       ∂ ∂ ∂ ∂ − (3.40)

şeklinde olur. Burada radyal kısım çözülürse,

) r k ( L e r A ) r ( R_n,m = _n,m m −kr22 _nm 2 (3.41)

şeklindedir. Burada A_n,m normalizasyon sabitidir, L(_nα)(x) genelleştirilmiş

Laguarre polinomlarıdır. Enerji değerleri,

0 m

,

n k(2n m 1) V

E = + + − (3.42)

3.9. KÜRESEL KUANTUM NOKTASINDA MANYETĐK ALAN ETKĐSĐ

Serbest bir elektronun hareketinin üç boyutta sınırlandırılması ile kuantum nokta yapı elde edilir. Sistemin manyetik alandaki durumunu göz önüne alalım. Manyetik alan parabolik bir fonksiyon olduğundan dolayı, küresel nokta olmasa da elektronun hareketini tek boyutta sınırlayacaktır. Bu ekseni z ekseni alalım.

Manyetik alan etkisi altında Hamilton Denklemi,

) r ( V ) A e p ( m 2 1 H 2 r r r + + = _∗ (3.43)

yazılabilir. (Karaoğlu,1994). Burada A

r

manyetik alan vektörüdür.

A x B r r r ∇ = (3.44) zˆ B B= r

şeklinde bir manyetik alan uygulandığında, manyetik alan vektörü aşağıdaki ifadeden bulunabilir. z y x A A A z y x kˆ jˆ iˆ B ∂ ∂ ∂ ∂ ∂ ∂ = r Bu determinantın açılmasıyla, kˆ y A x A jˆ z A x A iˆ z A y A kˆ B z y z x y x _       ∂ ∂ − ∂ ∂ +       ∂ ∂ − ∂ ∂ −         ∂ ∂ − ∂ ∂ =

ifadesi elde edilir. Burada manyetik alan z yönünde olduğu için iˆ ve jˆ bileşenleri sıfır olacaktır. Manyetik alan vektörünün bileşenlerini eşitliği sağlayacak şekilde seçelim. B y A x Ay _x = ∂ ∂ − ∂ ∂ x B Ay = Ax =0

x B 2 1 A_y = By 2 1 A_x =− 0 Ay = Ax =−By

şeklinde yazılabilir. Manyetik alan vektörünü B yi verecek şekilde istediğimiz gibi seçebiliriz. Önemli olan B xA

r r r ∇ = ifadesinin sağlanmasıdır.       − = Bx,0 2 1 , y B 2 1 A r (3.45) vektör potansiyeli Hamiltoniyen ifadesinde yerine konulursa,

(

p epA eAp e A

)

V(r) m 2 1 H= _∗ 2+ + + 2 2 + r r r r r r (3.46) olur. Burada epA eAp 2eApr r r r r v = + şeklinde yazılırsa p A A p r r r r =

denklemini sağlayacaktır. Bu durumda denklem (3.46) ifadesindeki ilk terimi alırsak

(

2 2 2

)

A e p A e 2 p m 2 1 H r r r r + + = _∗ (3.47) olur. Burada x i p ∂ ∂ = h r veya y i p ∂ ∂ = h r olarak tanımlanır ve ) i ( y Bx 2 1 x By 2 1 p . A r h r −       ∂ ∂ + ∂ ∂ − = (3.48) alınırsa       −       ∂ ∂ + ∂ ∂ = ( i ) x y y x B 2 1 p . A r h r

(

)

[

xpy ypx

]

B 2 1 p . A r= − r

( )

Lz B 2 1 p . A r= r

ifadesi elde edilir. Ayrıca A2

r ifadesi 2 2 2 2 2 x B 4 1 y B 4 1 A = + r

olarak elde edilir. Bu ifade Hamilton denkleminde yerine yazılırsa,

(

x y

)

V(r) m 2 e B 4 1 BL 2 1 m 2 e 2 m 2 p H 2 2 2 2 z 2 + + + + = _{∗ ∗ ∗} (3.49) olarak elde edilir. Burada taban durumu incelendiğ_{inden m = 0 de}ğerini alacaktır bu nedenle Denklem (3.49)’deki ikinci terim düşer. Hamilton denklemi tekrar yazılırsa

(

x y

)

V(r) m 2 e B 4 1 m 2 p H 2 2 2 2 2 + + + = _{∗ ∗} (3.50) olur. p denklemde yerine konursa,

) r ( V m 2 e B 4 1 m 2 H 2 2 2 2 2 + ρ + ∇ − = h _{∗ ∗} (3.51) olur. (3.51) denkleminin birinci terimi Rydberg birim sisteminde yazılırsa,

∗ ∗ ∗ ≈a R m 2 2 2 h

olarak alınabilir. Burada ,

2 0 2 4 2 e m R ε = ∗ ∗ h ve 0₂ 2 e m a∗ = h_∗ε (3.52) dir. Buradan a denklemi düzenlenip ∗ R denkleminde yerine konulursa, ∗

∗ ∗ ∗ =R a m 2 2 h

ifadesi elde edilir. Burada a∗ =1 alındığında

∗ ∗ ₌ m 2 R 2 h (3.53) olarak elde edilir. (3.51) denkleminin ikinci terimi düzenlenirse

2 R m 2 B e γ = ∗ h olur. Buradan, ∗ ∗ = γ R m 2 B e h (3.54) olarak yazılabilir. 2 2 2 2 2 2 R m 4 B e ∗ = γ h (3.55) 2 2 2 2 2 2 m 2 R m 2 B e h ∗ ∗ γ = (3.56) Bu ifade 2 2 a R m 2 ∗ ∗ ∗ = h şeklinde yazılırsa, 2 2 2 2 a R m 2 B e ∗ ∗ ∗ γ = (3.57)

elde edilir. a∗ =1 olarak alınıp ve bulduğumuz ifadeler Hamilton denkleminde yazılırsa, ) r ( V R 4 1 R H=− *∇2+ γ2 ∗ρ2 + (3.58)

Burada denklemi R ’a böler ve ∗ ′ = _∗ R ) r ( V ) r (

V olarak alırsak Hamilton denklemi

) r ( V 4 1 H=−∇2+ γ2ρ2+ ′ (3.59) olarak yazılabilir. 2 2 4 1_{γ ρ}

manyetik alan katkısından gelen ek terimdir. Ayrıca

2 2 2 y x + =

ρ şeklinde yazılır. ρ2 küresel koordinatlarda yazılırsa ρ2 =r2sin2θ

ifadesi elde edilir. Bu ifade Hamilton denkleminde yazılırsa, ) r ( V sin r 4 1 H=−∇2+ γ2 2 2θ+ ′ (3.60) elde edilir (Saften, 2007).

3.10. ENERJĐ SPEKTRUMU

Fock’un çalışmalarını izleyerek Hamilton ifadesi,

) y x ( m 2 1 A c e p m 2 1 H * 2₀ 2 2 2 * _ + ω +     − = r r (3.61)

şeklinde verilir. Simetrik ölçekte vektör potansiyeli Bx,0) 2 1 , By 2 1 ( A= − r ve e

e =− olarak seçilirse Schrödinger denklemi,

0 E r m 2 1 c m 8 r B e c m 2 ieB r 1 r r 1 r m 2 2 2 0 * 2 * 2 2 2 * 2 2 2 2 2 * 2 = ψ         − ω + + θ ∂ ψ ∂ −       θ ∂ ψ ∂ + ∂ ψ ∂ + ∂ ψ ∂ − h h (3.62)

şeklinde yazılabilir. Burada θ

π ψ il e r f − = ( ) 2 1

dir. Denklemin radyal kısmı,

0 f E r m 2 1 c m 8 r B e f c m 2 eB f r dr df r 1 dr f d m 2 2 2 0 * 2 * 2 2 2 * 2 2 2 2 * 2 =       − ω + + −       − + − h l h l (3.63)

olur. Siklotron frekansı

0 * * c m c m eB l h = = ω ve manyetik uzunluk 2 1 0 B e c       ≡ h l

ifadeleri kulanıldığında radyal kısım,

0 f 2 1 r ) 4 ( m 8 1 E f r dr df r 1 dr f d m 2 c 2 2 0 2 c * 2 2 2 2 * 2 =     ω + ω + ω − +       − + l h l h (3.64)

şeklini alır.. Şimdi 2 1 2 c 2 0 ) 4 1 (

b= + ω ω ve yeni bir bağımsız değişken belirleyelim. Buna göre, 2 0 2 2 2 c * 2 br r r 2 b m x l h =α = ω =

olsun. Bu durumda radyal denklem,

0 f b 2 x 4 1 b E x 4 f dr df dr f d x c 2 2 2 =       + − ω + − + l h l (3.65)

b 2 1 / E hω_c + l =

β ve radyal kısımda yerine yazılırsa,

0 f x 4 x 4 1 dr df dr f d x 2 2 2 =       − − β + + l (3.66)

olur. Bu denklemin çözümünden,

[

l l

]

h l = ω b(2n+ +1)− 2 1 E_{n c} = l h h h l c 2 1 2 0 2 2 c 2 2 1 ) 4 1 )( 1 n 2 ( + + ω + ω − ω = _{h c} 2 1 ) 1 n 2 ( +l + hω − lhω _(3.67) olur. Burada       ω + ω = ω 2 0 2 c 2 h 4 1 , n=0,1,2,....ve l=0,±1,,.... _dir. ,... 2 3 E 0 , 1 n 2 1 E , 0 , 0 n 0 B ) 1 n 2 ( E 0 , 0 B c c 0 c 0 , n c ω = ≥ = ω = ≥ = ω >> ω ≠ ω + + = = ω = h l h l h l l

Manyetik alanın düşük değerlerinde manyetik uzunluk, hapis potansiyelinin boyutundan daha yüksektir. Manyetik alanın artmasıyla manyetik uzunluk, hapis potansiyelinin çapından daha küçüktür (Chakraborty, 1999).

4. HESAPLAMA YÖNTEMLERĐ

Fizik çalışmalarında karşılaşılan bazı problemleri çözmek, oldukça karmaşık olabilir ve geleneksel yöntemlerle analitik olarak çözmek mümkün olmayabilir. Bu durumlarda problemi çözülebilir hale getirmek için bazı yaklaşıklıklar yapılması gerekir. Buna örnek olarak Hartree yaklaşımı, varyasyon yöntemi, Thomas-Fermi yaklaşımı ve Yoğunluk fonksiyonel teorisi verilebilir.

Bu yöntemler düşük boyutlu sistemlerin özelliklerinin incelenmesinde başarılı bir şekilde kullanılmaktadır. Şimdi çok elektronlu kuantum noktalarının elektronik özelliklerinin belirlenmesinde kullanılan Hartree yaklaşımı, varyasyon yöntemi, Thomas-Fermi yaklaşımı ve Yoğunluk fonksiyonel yaklaşımlarının ayrıntılarından bahsedilecektir.

4.1. HARTREE-FOCK YÖNTEMĐ

Bu modele göre her elektron, çekirdeğin çekici alanı ve diğer elektronlardan dolayı oluşan itme etkileşimlerinin ortalama etkisini hesaba katan, bir etkin potansiyelde hareket eder. Bu durumda her elektron, kendi dalga fonksiyonu ile tanımlanır. Sezgiye dayanan delilleri kullanarak Hartree, bireysel elektron dalga fonksiyonlarının denklemlerini yazdı. Hartree-Fock yaklaşımında, bağımsız parçacık yaklaşıklığı ve paulinin dışarılama ilkesine uygun olarak, N elektronlu dalga fonksiyonunun bir φ slater determinantı veya başka bir deyişle, bireysel elektron spin-yörüngemsilerinin antisimetrik çarpımı olduğu varsayılır. Sonuç olarak Hartree yaklaşımı çok elektronlu sistemin dalga fonksiyonunu, tek elektron dalga fonksiyonlarının çarpımı olarak yazmaya dayanır (Köksal,1989).

) r ( ) r . ... ,... r , r ( _i N 1 i i N 2 1

∏

= φ = φ r r r (4.1) i. Elektrona etki eden potansiyel,

) r ( V ) r ( V ) r ( V_i r = _iyon r + _H r (4.2)

ile verilebilir. Potansiyel, iyon ve Hartree potansiyelinin toplamıdır.

∑

α _α α − − = ₂ iyon d r Z ) r ( V _r r r r r ) r ( r d ) r ( V_H ′ − ′ ρ ′ − =

_∫

r r r r r (4.3)

şeklinde yazılabilir. i. elektrona etki eden Hartree potansiyelindeki yoğunluk terimi

2 i j j(r ) ) r (

∑

≠ ′ φ = ′ ρ r r (4.4)

ile verilir. Sistemin Hamiltoniyeninin

∑

= + ∇ − = N 1 i i 2 i V(r) 2 1 Hˆ r (4.5) (4.5) ile alınan beklenen değerini (toplam enerjiyi) en küçük yapan tek elektron dalga fonksiyonları Hartree denklemi ile verilir:

) r ( ) r ( r r ) r ( r d ) r ( ) r ( V 2 1 i i i i j 2 j i iyon 2 r r r r r r r r φ =∈ φ ′ − ′ φ ′ + φ     + ∇ −

_∑∫

= (4.6) Denklem (4.6) orbitaller için öz uyumlu çözüldüğünde denklem (4.1) ile sistemin dalga fonksiyonu elde edilmiş olacaktır.

Hartree-Fock yaklaşımında sistemin dalga fonksiyonu, antisimetri özelliğini de sağlayacak şekilde seçilir. Elektronlardan oluşan sistemin dalga fonksiyonu, Pauli dışarılama ilkesi gereği, sistemdeki iki elektronun yer değiştirmesi altında antisimetrik olmalıdır. ) ,... r , ,... r (..., ...) r ., ,... r (..., i j j i r r r r φ − = φ (4.7) Denklem (4.7) i sağlayan en basit dalga fonksiyonu Slater determinantı ile verilir.

) r ( )... r ( ) r ( . . ) r ( .. )... r ( ) r ( ) r ( .. ... ) r ( ) r ( ) r ., ... ,... r , r ( N N 2 N 1 N N 2 2 2 1 2 N 1 2 1 1 1 N 2 1 r r r r r r r r r r r r φ φ φ φ φ φ φ φ φ = φ (4.8)

(4.6) denklemine benzer olan Hartree Fock denklemi de enerjinin beklenen değerini en küçük yapan denklem (4.8) deki tek elektron dalga fonksiyonlarını verir:

) r ( ) r ( r r ) r ( ) r ( r d ) r ( r r ) r ( r d ) r ( ) r ( V 2 1 i i j j i j j i 2 i i iyon 2 j , i r r r r r r r r r r r r r r φ =∈ φ ′ − ′ φ ′ φ ′ δ − φ ′ − ′ φ ′ + φ     + ∇ −

∑

∑

_∫

∗ σσ (4.9) Burada ∈_i i.durum enerjisidir ve son terimise değiş tokuş terimidir. σ_i,σ_j spinleri aynı olduğundan sıfırdan farklıdır. Değiştokuş terimi yerel olmadığından Hartree Fock denkleminin çözümü oldukça zordur. φi fonksiyonuna değişim ilkesi

uygulanırsa Hartree tek parçacık denklemleri elde edilir. ) r ( E ) r ( ) r ( V ) r ( V m 2 i H i i H i dış i 2 r 2 i r r r r h φ = φ       + + ∇ −

∑

(4.10)

Her dolu tek elektron düzeyi i(r)

r

φ için bir tek denklem söz konusu olduğundan (4.10) ifadesi bir denklemler takımını göstermektedir ve “Hartree Denklemleri” olarak bilinir. V_H , Harteree potansiyeli, V_dış dış potansiyel olmak üzere

∑∫

′ φ ₋′_′ = j 2 j 2 H r r ) r ( r d e ) r ( V r r r r r (4.11)

yazılabilir. Toplam enerji ise,

> φ φ − φ φ < + > φ + ∇ − φ < =

∑

∑

≠j i j i i j j i Đ i i dış r i H r r e ) r ( V m E i r r r h r 2 2 2 2 1 2 (4.12) olarak yazılabilir. Hartree denkleminde kullanılan tek elektron ortonormalize dalga fonksiyonu olarak yazılır ise

) S r ( . )... S r ( ) S r ( ) S r ,... S r , S r ( _{N N N N N} r r r r r r r r r r r r φ φ φ = φ _{1 1 2 2 1 1 1 2 2 2} (4.13)

Bu denklemden görüldüğü gibi Hartree denklemi simetrik bir formdadır. Pauli dışarılama ilkesine göre, uzayın aynı noktasında aynı kuantum sayılarına sahip iki fermiyon bulunamaz. Bu ilke açıkça, aynı kuantum setlerine sahip özdeş fermiyon çiftleri arasındaki etkin itmeyi ifade eder ve matematiksel olarak parçacık çiftlerinin değiş tokuşu sırasında antisimetrik olan dalga fonksiyonlarını sağlamak için kullanılır. Sonuç olarak teori Pauli dışarılama ilkesini ihmal etmektedir. Hartree

teorisindeki bu eksiklik Hartree-Fock teorisi ile giderilmiştir. Slater determinantının çözümü ile Hartree-Fock denklemi elde edilir.

) r ( E ) r ( ) r ( V ) r ( V ) r ( V m 2 i HF i i i i ex i H i dış 2 r 2 i r r r r r r h φ = φ       + + + ∇ −

∑

(4.14) dt

V değiş tokuş potansiyeli olmak üzere,

∑

∫

′ ′ − ′ φ ′ φ φ − = φ ∗ j i j j 2 i dt dr r r ) r ( ) r ( ) r ( e ) r ( V r r r r r r (4.15) Hartree-Fock enerjisi, Hartree enerjisine ilave bir terim ile EHF =EH +EEX şeklinde yazılabilir (Devreese ve Camp,1985). Bu teori yalıtkanlar ve yarıiletkenlerin elektronik durumlarını ve temel durum enerjilerini hesaplamada yetersiz kalmıştır. Bu yetersizlik, teoride değiş-tokuş etkileşmesinin perdelemesinin ihmal edilmesinden kaynaklanmaktadır (Deligöz,2007)

4.2.YOĞUNLUK FONKSĐYONEL TEORĐ

Bu teori, 1927 yılında Thomas ve Fermi tarafından yapılmış çalışmaları temel alan Hohenberg ve Kohn (1964) teoremlerine dayanır. Bu teori, fizik ve kimyanın tüm alanlarında yaygın olan bir hesaplama tekniğidir. Teorinin temel ilkesi, birbiri ile etkileşen çok elektronlu bir sistemin taban durumu yoğunluğu olan n(r) ye bağlı olarak sistemin taban durumu özelliklerini belirlemektir. Yoğunluk fonksiyonel teorisi, parçacıklar arasındaki etkileşme ve korelasyon etkilerini de içeren pratik ve kullanışlı bağımsız parçacık yaklaşımlarının geliştirilmesini de olanaklı kılmıştır. Bu nedenle malzemenin elektronik yapısının hesaplanmasında önemli bir araç haline gelmiştir (Erkişi, 2007).

Hohenberg ve Kohn teoremine göre, bir sistemin V(r)potansiyelinin taban durum elektronik özelliklerinin incelenmesi için taban durum elektron yoğunluğunun bilinmesi yeterlidir (Dobson,1999). Bir sistemin taban durum enerjisini yoğunluğun fonksiyonu olarak

şeklinde yazılabilir. Burada F

[ ]

n(r) yoğunluğun evrensel bir fonksiyonelidir. (Hohenberg ve Kohn, 1964. Nagy, 1988). F

[ ]

n(r) ’nin evrenselliği,

) r (

V potansiyeline bağlı olması ve atomlar, moleküller veya katılar gibi tüm sistemler için aynı şekle sahip olması anlamındadır (Harbola ve Banerjee, 2003;

Şahin, 2005). Belirli bir V dı₀ ş potansiyelindeki N elektronlu bir sistemin taban durum enerjisi, bir n~(r)deneme yoğunluğu için her zaman, sistemin taban durum enerjisinden daha büyük veya eşittir. Eşitlik ancak ~n(r) deneme yoğunluğunun, gerçek taban durum yoğunluğu ~n(r)’ye eşit olması ile sağlanır. Yani,

[ ]

n E

[ ]

~n E E o 0 V V 0 ≡ ≤ (4.17)

ilişkisi her zaman geçerlidir. Gerçek taban durum yoğunluğu için, taban durum enerji fonksiyonelinin değişiminin minimum olması gerekir. Dolayısıyla n~(r)≥0 ve

∫

n~(r)d3r=N (4.18) olmak şartıyla, Denk(4.17) ile verilen enerji fonksiyonelinin değişimi

[

]

{

E(n(r)−µ n(r)d3r−N

}

=0 δ

_∫

(4.19) yazılırsa bu durumda

[ ]

[ ]

) r ( n ) r ( n F ) r ( V ) r ( n ) r ( n E δ δ + = δ δ = µ (4.20)

Euler denklemine gider (Şahin, 2005). Burada µ =sistemin kimyasal potansiyelidir ve enerji boyutundadır (Parr ve Yang 1989, Nagy1998; Perdew ve Kurth 2003). Kohn-Sham yaklaşımına göre F

[ ]

n(r) fonksiyoneli

[ ]

[ ]

∫∫

′+

[ ]

′ − ε πε ′ + = d rd r E n(r) r r 4 ) r ( n ) r ( n 2 e ) r ( n T ) r ( n F 3 3 _dt 0 r 2 s (4.21) şeklinde yazılabilir. Burada,