Ölçüm sistemleri analizinde kullanılan istatistiksel yöntemlerin incelenmesi

FEN BİLİMLERİ ENSTİTÜSÜ

ÖLÇÜM SİSTEMLERİ ANALİZİNDE KULLANILAN İSTATİSTİKSEL YÖNTEMLERİN İNCELENMESİ

ÜMİT YAMAN

YÜKSEK LİSANS TEZİ İSTATİSTİK ANABİLİM DALI

Bu çalışma süresince çok değerli görüş ve bilgilerinden yararlandığım, her fırsatta yardımlarını esirgemeyen sevgili hocam Doç.Dr. Coşkun KUŞ’a, çalışmamın uygulama kısmındaki bilgisayar yazılımındaki gerekli çalışmalarda emeğini ve zamanını harcayan sayın Ahmet PEKÖR’e, Tezin biçimlenmesinde değerli katkılarını aldığım Dr. Neslihan YİĞİT’e her konuda destek ve moral veren eşim Keziban Sibel YAMAN ve oğlum Umut Mert YAMAN’a teşekkür ederim.

İÇİNDEKİLER

ÖZET ... i

1. GİRİŞ ... 1

2.TEMEL KAVRAMLAR... 3

2.1. Bazı Özel Fonksiyonlar... 3

2.1.1. Gamma fonksiyonu ... 3

2.1.2. Genelleştirilmiş Hipergeometrik fonksiyon... 3

2.1.3. İndikatör fonksiyon ... 4

2.2. Bazı Dağılımlar ... 4

2.2.1. Normal dağılım ... 4

2.2.2. Ki-kare dağılımı ... 5

2.2.3. F dağılımı... 5

2.2.4. Merkezi olmayan Ki-Kare dağılımı ... 6

2.2.5. Merkezi olmayan F dağılımı ... 7

3. İKİ ETKENLİ VARYANS ANALİZİ MODELLERİ... 8

3.1. Rasgele Etkili Model... 11

3.2. Karma Etkili Model ... 19

4. ÖLÇÜM SİSTEMLERİ ANALİZİ... 26

4.1. Ölçüm Sistemi Yeterliliğinin Analizi için Varyans Analizi Modelleri... 26

4.2. Bazı Ölçüm Yeterlilik Parametreleri ve Tahmin Edicileri... 29

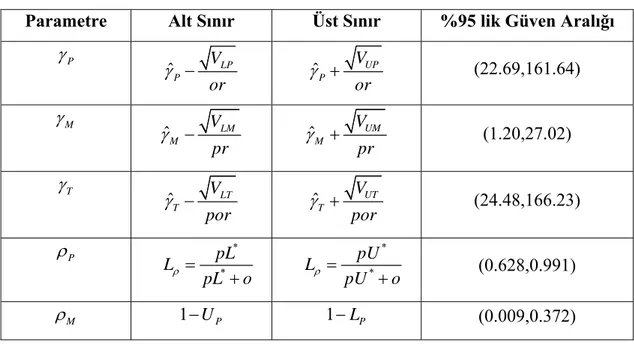
5. ÖLÇÜM YETERLİLİK PARAMETRELERİNİN GÜVEN ARALIKLARI ... 35

5.1. Rasgele Etkili Model Durumu ... 36

5.2. Karma Etkili Model Durumu ... 40

6. SELÇUK STAT, NCSS VE MİNİTAB ÇIKTILARININ İNCELENMESİ... 44

7. SONUÇ VE ÖNERİLER ... 62

ÖZET

Yüksek Lisans Tezi

ÖLÇÜM SİSTEMLERİ ANALİZİNDE KULLANILAN İSTATİSTİKSEL YÖNTEMLERİN İNCELENMESİ

Ümit YAMAN Selçuk Üniversitesi Fen Bilimleri Enstitüsü İstatistik Anabilim Dalı

Danışman: Doç.Dr. Coşkun KUŞ 2009, Sayfa: 65

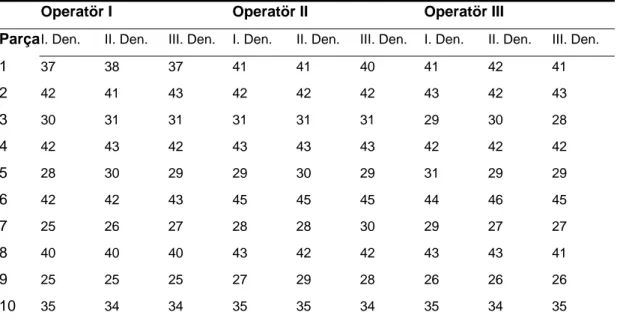
Süreçlerin ve ürünlerin değişkenliğini doğru bir şekilde gözlemlemek için ölçüm değişkenliğini anlamak kaçınılmazdır. Tekrarüretebilirlik ve tekraredilebilirlik (Repeatability&Reproducibility, R&R) çalışması, aynı zamanda ölçüm yeterlilik çalışması olarak adlandırılır. Bir ölçüm prosedürünün, yeterliliğini belirlemede kullanılır. ölçüm prosedürü ile ilgili değişkenliğin, kaynakları varyans analizi(Analyis of Variance, ANOVA) modeli kullanılarak karşılaştırılır. R&R çalışmasında, yaygın olarak kullanılan model iki faktör içerir: parça ve operatörler, süreç sonucunda elde edilen ürünlerde operatörler her bir parça üzerinde tekrarlı ölçüm yaparlar. R&R, Genel olarak operatörlerin bir operatör popülasyonundan rasgele seçildiği varsayılır, kurulan varyans analizi modelinde operatörler, rasgele faktör olarak ele alınır. Ne var ki, genellikle ölçüm prosedürünü yerine getiren operatörler sadece bu iş için, istihdam edilmiş olduğundan, operatörleri özel seçimli faktör olarak ele almak daha gerçekçi olacaktır.

Dolezal, Burdick, Birch (1998), operatörlerin sabit faktör parçaların rasgele faktör olması durumunda, R&R analizi için karma ANOVA modeli ele almışlardır. Bu varsayım altında model parametreleri için, güven aralığı oluşturup, güven aralıkların kapsama olasılıklarının performansı için simülasyon çalışması yapışmışlardır.

Bu tez çalışmasında, rasgele ve karma etkili modellerde ölçüm yeterlilik parametrelerinin tahmin edicileri ve güven aralıkları Selçuk Stat programına monte edilmiştir. Ayrıca Selçuk Stat yazılımının çıktıları, Minitab 15 ve NCSS 2007 yazılım çıktıları ile karşılaştırılmıştır.

Anahtar Kelimeler: Güven aralıkları, ölçüm yeterlilik parametreleri, tekraredilebilirlik, tekrarüretilebilirlik, varyans analizi modelleri.

ABSTRACT Master Thesis

INVESTIGATION OF STATISTICAL METHODS USED IN THE MEASUREMENT SYSTEM ANALYSIS

Ümit YAMAN Selçuk University

Graduate School of Natural and Applied Sciences Department of Statistics

Supervisor: Assoc. Prof. Dr. Coşkun KUŞ 2009, Page: 65

An understanding of measurement variability is necessary to properly monitor the variability of products and processes. A repeatability and reproducibility (R&R) study, also called a gague capability study, is used to determine the capability of a measurement procedure. The sources of variability associated with the measurement procedure are compared using an analysis of variance (ANOVA) model. A common model used in R&R studies involves two factors: parts and operators. Operators make repeated measurements on each part in a sample of process output. It is typically assumed that the operators are a random sample from a population of operators. As such, operators are treated as a random effect. However, the operators used in the study are often the only operators that will be used once the measurement procedure is implemented. In such a case, it is more appropriate to treat operators as a fixed effect.

The mixed effects ANOVA model is considered for R&R analysis by Dolezal et al. (1998) under fixed operators and random part factor assumption. Confidence intervals for several parameters are derived under this assumption. Computer simulation has been performed to evaluate the performance of the confidence intervals.

In this thesis, the estimators and confidence intervals of measurement capability parameters are assembled to Selçuk Stat software under random and mixed effects models. Also outputs of Selçuk Stat are compared with Minitab 15 and NCSS 2007 softwares.

Key Words: Analysis of variance models, confidence interval, mesaurement capability parameters, repeatability, reproducibility.

1. GİRİŞ

Ölçüm değişkenliğinin tespit edilmesi ürün ve süreç değişkenliğini doğru bir biçimde gözlemlemek için gereklidir. Tekraredilebilirlik, operatörlerin ürünleri tekrar tekrar ölçtüğünde hemen hemen aynı değerde ölçebilme kabiliyetini, Terkrarüretilebilirlik, operatörlerin biribiriyle uyum kabiliyetini göstermek üzere Tekraredilebilirlik ve Terkrarüretilebilirlik (Repeatability&Reproducibility, R&R) diğer bir deyişle ölçüm (Gauge, gage) analizi, ölçüm prosedürünün yeterli olup olmadığını belirlemek için kullanılır. Ölçüm prosedürü ile ilgili değişim kaynakları, varyans analizi (Analysis of Variance, ANOVA) kullanılarak tespit edilebilir. R&R analizinde genel olarak kullanılan ANOVA modeli, operatör ve parça olmak üzere iki faktörden(etken) oluşur. R&R analizinden önce operatörler ürünleri tekrar tekrar ölçerler. Genellikle operatörler, operatörler kitlesinden rasgele seçildiği varsayıldığından ANOVA modelindeki faktörler rasgele faktör (random effect) olarak ele alınır. Ne var ki süreç çıktısı ürünleri ölçen operatörler özel seçimli (fix) faktör de olabilir. Örneğin bir fabrikadaki üretilen parçaları ölçmek için önceden istihdam edilmiş üç operatöründe ölçüm yapması durumunda operatör faktörü özel seçimli olarak ele alınmalıdır.

Ölçüm prosesinin yeterli olup olmadığını tespit etmek için Tekraredilebilirlik ve Terkrarüretilebilirlik dışında kullanılan parametrelerden bazıları PTR(Precision-to-Tolerance Ratio), (Burdick, Borror ve Montgomery, 2003), SNR(Signal-to-Noise Ratio), (AIAG, 1995, Sayfa 32) ve DR(Discriminant Ratio), (Meder, 1999 ve Wheeler, 1992) olarak sıralanabilir.

Minitab 15 ve NCSS 2007 yazılımları, R&R analizini performe etmektedir. Minitab 15, R&R analizi için operatörlerin ve parçaların rasgele faktör olarak ele alındığı ANOVA modelini kullanılmasına karşın operatörlerin sabit olarak ele alınması durumunda karma model kullanılması için bir seçenek bulunmamaktadır. Minitab 15 yazılımı, ölçüm değişkenlik parametrelerinin tahmin değerlerini verirken, güven aralıklarını vermemektedir. Ayrıca yukarıda bahsedilen PTR, SNR ve DR

parametrelerinin güven aralıkları Minitab 15 yazılımında hesaplanmamaktadır. NCSS 2007 yazılımında yukarıda bahsedilen güven aralıkları verilmektedir.

Bu tez çalışmasında, İkinci Bölümde ölçüm sistemleri analizinde kullanılacak temel kavramlar, Üçüncü Bölümde, rasgele ve karma iki etkenli ANOVA modeli hakkında genel bilgiler, Dördüncü Bölümde, ölçüm sistemleri analizinde kullanılan parametreler, Beşinci Bölümde, rasgele ve karma etkili modellerde ölçüm sistemi yeterlilik parametrelerinin güven aralıkları, Altıncı Bölümde, Delphi 5 programlama dilinde yazılmakta olan Selçuk Stat programına tez aşamasında monte edilen R&R analiz sonuçlarının doğruluğu, Burdick, Borror ve Montgomery (2003), (Dolezal, Burdick, Birch, 1998) ve Burdick ve Larsen (1997) makalelerdeki nümerik örneklerle karşılaştırılarak kontrol edilmiştir. Ayrıca sonuçları karşılaştırmak için Minitab 15 ve NCSS 2007 çıktıları da bu bölüme eklenmiştir. Yedinci ve son bölümde tez çalışmasının sonuç ve önerilerine yer verilmiştir.

2.TEMEL KAVRAMLAR

Bu bölümde, yapılmış olan çalışma için gerekli olan ilgili tanımlar ve temel bilgiler verilmiştir.

2.1. Bazı Özel Fonksiyonlar

Bu bölümde, tezde ele alınan bazı özel fonksiyonlar hakkında kısa bilgi verilmiştir.

2.1.1. Gamma fonksiyonu

Gama fonksiyonu aşağıdaki gibi tanımlanır.

( )

₌

_∫

∞ −

( )

_{− >} Γ 0 1_{exp , β 0} β β dt t t

β pozitif tam sayı olmak üzere

(

β +1

)

=β! Γ

( )

1.7724538509 exp 2 2 1 0 2 _{= =} − = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Γ

∫

∞ t dt π

( ) ( )

2 ₌ 2 1/222 1/2_Γ

( ) (

_{Γ +}1/2

)

Γ _{β π} − β− _{β β} Stirling formülü

( )

( )

( )

_⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + − Γ − 288 1 12 1 1 2 exp ~ 1/2 1/2 β π β β β β

( )

[

Γ

]

=

(

− −

)

( )

− + −

( )

+ − + + 5 3 1 1 1260 1 360 1 12 1 2 log 2 log 2 log β β β π β β β β

2.1.2. Genelleştirilmiş Hipergeometrik fonksiyon

(

)

( )

_{( )}

1

( )

_{( )}

, 1 1 0 ₁ , , ; , , ; ! k p k k p q p q k _{k q} k a a _z F a a b b z k b b ∞ = × × = × ×

∑

… …

2.1.3. İndikatör fonksiyon A⊂ olmak üzere

{ }

( )

: 0,1 1 , 0 , A A I x A x I x x A → ∈ ⎧ ⎪ → _{= ⎨} ⎪ _∉ ⎩

şeklinde tanımlanan fonksiyona indikatör fonksiyon denir.

2.2. Bazı Dağılımlar

Bu bölümde, tezde ele alınan bazı dağılımlar hakkında kısa bilgi verilmiştir. 2.2.1. Normal dağılım

X rasgele değişkeni, Normal dağılıma sahip olduğunda olasılık yoğunluk fonksiyonu,

( )

2 ₍ , ₎

( )

1 1 exp , 0, 2 2 x f x μ I x σ μ σ πσ −∞ ∞ ⎧ ₋ ⎫ ⎪ ⎛ ⎞ ⎪ = _⎨− _{⎜ ⎟ ⎬} > ∈ ⎝ ⎠ ⎪ ⎪ ⎩ ⎭ (2.1)

şeklindedir, burada I_{( )a b,}

( )

i indikatör fonksiyonudur. X , (2.1) olasılık yoğunluk fonksiyonlu normal dağılıma sahip rasgele değişken olduğunda X in beklenen değer ve varyansı sırasıyla,

( )

E X =μ, Var X

( )

=σ2

biçimindedir. μ ortalamalı, _σ2 _{varyanslı Normal dağılım için}

(

_, 2

)

N μ σ gösterimi kullanılacaktır.

2.2.2. Ki-kare dağılımı

X rasgele değişkeni, r serbestlik dereceli Ki-kare dağılıma sahip olduğunda olasılık yoğunluk fonksiyonu,

( )

{

( )

_{1 2}

}

1 ₂

(

₁

)

_{( )}

( )

0,

2 2r r exp 2 , 0

f x = Γ − r − x − − x I _∞ x r> (2.2)

şeklindedir, burada I_{( )a b,}

( )

i indikatör fonksiyonudur. X , r serbestlik dereceli Ki-kare dağılımına sahip rasgele değişken olduğunda X in beklenen değer ve varyansı sırasıyla,

( )

X r

E = Var

( )

X =2r

biçimindedir. r serbestlik dereceli Ki-kare dağılımı için _{( )}2 r

χ gösterimi kullanılacaktır.

2.2.3. F dağılımı

X rasgele değişkeni, r ve ₁ r serbestlik dereceli F dağılımına sahip ₂ olduğunda olasılık yoğunluk fonksiyonu,

( )

(

)

( )

( )

( ) 1 1 2 1 2 1 1 2 1 2 1 2 2 1 1 1 2 1 2 1 2 2 1 , 0, , 1, 2, 2 2 r r r r r r r r f x x r r x x r r r r − − − + − − ⎡ ⎤ Γ_⎣ + _⎦ ⎡ ⎤ = _⎣ + _⎦ > = ⎛ ⎞ ⎛ ⎞ Γ_{⎜ ⎟ ⎜ ⎟}Γ ⎝ ⎠ ⎝ ⎠ … (2.3)

şeklindedir. X rasgele değişkeni, r ve ₁ r serbestlik dereceli F dağılımına sahip ₂ olduğunda X in beklenen değer ve varyansı sırasıyla,

( )

(

2

)

1, ₂ 2 2 2 − > = − r r r X E

( )

₂

(

)

₁

(

) (

2

)

1

2 2 1 2 2 1

2 1 2 2 4 , 4

Var X = r _⎣⎡ + r − r− ⎤_⎦ r − − r − − r >

biçimindedir. r ve ₁ r serbestlik dereceli ₂ F dağılımı için 2 1,r r

F gösterimi kullanılacaktır.

2.2.4. Merkezi olmayan Ki-Kare dağılımı

1, 2, , n

X X … X bağımız ve sırasıyla N

(

μ_i,1 ,

)

i=1, 2, ,… n dağılımına sahip

rasgele değişkenler olduğunda 2 1 n i i Z X =

=

∑

rasgele değişkenin olasılık yoğunluk fonksiyonu

( )

1 _{( )}

( )

2 0,1 0, 2 1 exp ; exp 2 2 4 2 2 2 n Z n n z z f z F z I z n λ λ − ∞ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ = _⎜− _{⎟ ⎜ ⎟ ⎜}− _⎟ ⎛ ⎞ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ Γ⎜ ⎟_{⎝ ⎠} (2.4) şeklindedir, burada 2 1 n i i λ μ = =

∑

, I_{( )a b,}

( )

i indikatör fonksiyonu ve F_{a b,}

( )

i ,

genelleştirilmiş hipergeometrik fonksiyonudur (Muirhead, 1982). (2.4) de verilen olasılık yoğunluk fonsiyonunlu dağılıma, n serbetlik dereceli, λ merkezsel olmama

parametreli merkezi olmayan Ki-kare dağılımı denir. Z , merkezi olmayan Ki-kare dağılımına sahip olduğunda Z nin beklenen değeri ve varyansı sırasıyla

( )

E Z = +n λ

( )

2 4

Var Z = n+ λ,

şeklindedir (Muirhead, 1982). λ =0 olduğunda dağılıma merkezsel Ki-Kare veya kısaca Ki-Kare dağılımı denir.

2.2.5. Merkezi olmayan F dağılımı

X , n serbetlik dereceli, λ merkezsel olmama parametreli merkezi olmayan ₁ Ki-kare dağılımına sahip, Y ise n serbetlik dereceli Ki-kare dağılımına sahip ₂ bağımız iki rasgele değişken olmak üzere 1

2 / / X n F Y n

= rasgele değişkeninin olasılık yoğunluk fonksiyonu

( )

( )

( )

1 1 1 2 1 1 2 1 2 1,1 1 2 2 1 1 2 1 2 2 0, 1 2 ₂ 1 2 1 2 exp ; ; 2 2 _{2 1} 2 1 2 2 F n n n n n f n n n n f f F n f n n n n _f n I f n n n f n λ λ − ∞ + ⎛ ⎞ ⎜ ₊ ⎟ ⎛ ⎞ _{⎜ ⎟} = _⎜− _⎟ ⎝ ⎠ ⎜ ₊ ⎟ ⎜ ⎟ ⎝ ⎠ ⎛ ⎞ + ⎛ ⎞ Γ_{⎜ ⎟} ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ × ⎛ ⎞ ⎛ ⎞ Γ_{⎜ ⎟ ⎜}Γ _⎟⎛ ⎞ + ⎝ ⎠ ⎝ ⎠ ⎜ ⎟ ⎝ ⎠ (2.5)

şeklindedir, burada I_{( )a b,}

( )

i indikatör fonksiyonu ve Fa b,

( )

i , genelleştirilmiş hipergeometrik fonksiyonudur (Muirhead, 1982). (2.5) de verilen olasılık yoğunluk fonsiyonunlu dağılıma, n ve ₁ n serbetlik dereceli, ₂ λ merkezsel olmama parametreli merkezi olmayan F dağılımı denir. F , merkezi olmayan F dağılımına sahip bir rasgele değişken olduğunda F nin beklenen değeri ve varyansı, sırasıyla,

( )

2

₍

(

1

₎

)

2 1 2 , 0 2 n n E F n n n λ + = > −

( )

(

) (

)(

)

(

) (

)

2 2 1 1 2 2 2 2 1 _{2 2} 2 2 2 , 4 2 4 n n n n Var F n n n n λ λ ⎧ _{+ + + −} ⎫ ⎛ ⎞ ⎪ ⎪ = _{⎜ ⎟ ⎨ ⎬} > − − ⎝ ⎠ ⎪⎩ ⎪⎭ şeklindedir (Muirhead, 1982).

3. İKİ ETKENLİ VARYANS ANALİZİ MODELLERİ

4,5 ve 6. Bölümlerde, R&R çalışmasında iki etkenli varyans analizi (ANOVA) modellerinin önemli bir yeri vardır. Bu sebeple, Öztürk (2009) ün İstatistiksel Deney Tasarımı ders notlarından iki faktörlü ANOVA modelleri konusu bu bölümde ele alınacaktır.

R&R analizinde, iki etkenli (faktörlü) deneylerin iki durumu kullanılmaktadır. Birincisi, her iki etkenin düzeyleri rasgele seçimli olabilir, ikincisi ise etkenlerin birinin düzeyleri özel, diğerinin düzeyleri rasgele seçimli olabilir. Bu durumda modeller: rasgele etkili model (random effects model) ve karma etkili model (mixed effects model) olarak adlandırılır.

İki etkenli dengeli bir deney tasarımında, A etkeninin düzeyleri A A₁, ₂,...,A p ve bu düzeylerin etkileri P P₁, ,...,₂ P ile B etkeninin düzeyleri _p B B₁, ₂,...,B ve bu _o düzeylerin etkileri O O₁, ₂,...,O ile gösterilsin. İki etkenin düzeylerinin _o kombinasyonu olan ortak etkiler

(

PO

)

_ij olmak üzere, iki etkenli çapraz (cross) dengeli (balanced) ANOVA modeli

( ) , 1, 2,..., ; 1, 2,..., ; 1, 2,...,

ijk i j ij ijk

Y = + +μ P O + PO +ε i= p j= o k= r(3.1)

biçiminde tanımlanır. Modeldeki, P P₁, ,...,₂ P , _p O O₁, ₂,...,O düzey etkilerine ana _o etkiler (main effects) ve

(

PO

)

_ij ’lere ise etkileşim (interaction) etkileri denir (Öztürk, 2009).

Rasgele etkili ve karma etkili model için varsayımlar Tablo 1 de verilmiştir (Öztürk, 2009).

Tablo 1. İki faktörlü ANOVA Modeli Varsayımları

Rasgele etkili model Karma model

1, 2,..., ; i= p 1, 2,..., ;j= o k=1, 2,..., r için ijk

ε ’ler bağımsız ve

(

_0, 2

)

N σ dağılımına _ε sahip rasgele değişkenler,

1, ,...,2 p

P P P ler bağımsız ve N

(

0,σ _P2

)

dağılımına sahip rasgele değişkenler,

1, 2,..., o

O O O lar bağımsız N

(

0,σ _O2

)

dağılımına sahip rasgele değişkenler,

1, 2,..., ; i= p j 1, 2,..., = o için

(

PO ’ler

)

_ij bağımsız ve

(

_0, 2

)

PO N σ dağılımına sahip rasgele değişkenler, 1, 2,..., ; i= p j 1, 2,..., ;= o k=1, 2,..., r için

(

)

, , i j ij

P O PO ve ε ’ler bağımsız rasgele _ijk değişkenler. 1, 2,..., ; 1, 2,..., ; 1, 2,..., i= p j= o k= r için ijk ε ’ler bağımsız ve

(

_0, 2

)

N σ dağılımına _ε sahip rasgele değişkenler,

1, 2,..., o O O O ler 1 0 o j j O = =

∑

kısıtını sağla yan sabit sayılar,

(

)

1 0, 1, 2,..., o ij j PO i p = = =

∑

(kısıtsız (unrest

ricted) modelde bu varsayım ele alınmaz),

1, 2,..., ; 1, 2,..., i= p j= o için

(

PO ’ler

)

_ij bağımsız ve

(

_0, 2

)

PO N σ dağılımına sahip rasgele değişkenler, 1, 2,..., ; 1, 2,..., ; 1, 2,..., i= p j= o k= r için

(

)

, j ij

P PO ve ε ’lar bağımsız rasgele _ijk değişkenler.

Karma etkili modellerde

(

)

1 0, 1, 2,..., o ij j PO i p = = =

∑

varsayımı altında (3.1)

modeline kısıtlı (restricted) model,

(

)

1 0 , 1, 2,..., o ij j i p PO = = =

∑

varsayımı ele

alınmadığında (3.1) modeline kısıtsız (unrestricted) model denir (Montgomery, 2001). Modelin kısıtlı ve kısıtsız olmasına göre karma modellerde varyans bileşenlerinin tahmin edicileri ve F hesap değeri değişebilmektedir.

SPSS 13 yazılımı karma modellerde sadece kısıtsız modeli ele almaktadır. Minitab 15 yazılımı ise karma modellerde hem kısıtlı hem de kısıtsız modeli ele alabilmektedir. Genel olarak (Default) Minitab 15, karma modellerde kısıtsız modeli kullanmaktadır. Sırasıyla ANOVA-BALANCED ANOVA-OPTIONS seçilip Use the restricted form of the model seçeneği kullanıldığında Minitab 15’de karma modellerde kısıtlı model ele alınabilir. Bu tez çalışmasında da karma modellerde kısıtsız model ele alınacaktır.

İki etkenli dengeli (balanced) deney tasarımında kitleden alınacak örneklem Tablo 2 deki tablolaştırılabilir.

Tablo 2. İki Etkenli Deney Tasarımı Örneklem Düzeni 1 B B ₂ … B o 1 A Y111,Y112,...,Y11r Y₁₂₁,Y₁₂₂,...,Y_12r … Y1 1o ,Y1 2o ,...,Y 1or 1 1 1 1 o r jk j k Y Y o r = = = ×

∑∑

ii 2 A Y₂₁₁,Y₂₁₂,...,Y_21r Y₂₂₁,Y₂₂₂,...,Y_22r … Y2 1o ,Y2 2o ,...,Y2or 2 1 1 2 o r jk j k Y Y o r = = = ×

∑∑

ii p A Y_p11,Y_p12,...,Y_{p r1} Y_p21,Y_p22,...,Y_{p r2 …} Y_po1,Y_po2,...,Y_por 1 1 o r ijk j k p Y Y o r = = = ×

∑∑

ii 1 1 1 1 p r i k i k Y Y p r = = = ×

∑∑

i i 2 1 1 2 p r i k i k Y Y p r = = = ×

∑∑

i i … 1 1 p r ijk i k o Y Y p r = = = ×

∑∑

i i 1 1 1 p o r ijk i j k Y Y p o r = = = = × ×

∑∑∑

iii i Y_ii, Y_{i ij} , Y_iji ve Y_iii ifadeleri, 1 1 p r ijk j k i Y Y p r = = = ×

∑∑

ii , 1 1 o r ijk i k j Y Y o r = = = ×

∑∑

i i , 1 r ijk k ij Y Y r = =

∑

i ve 1 1 1 p o r ijk i j k Y Y p o r = = = = × ×

∑∑∑

iii

şeklinde tanımlanmak üzere, Y ile Y_ijk iii arasındaki fark,

(

)

(

) (

) (

)

ijk i j ij i j ijk ij

Y −Yiii = Yii−Yiii + Yi i−Yiii + Y i−Yii−Y +Yi i iii + Y −Y i

biçiminde yazılabilir. Yukarıdaki eşitliğin her iki tarafın karesi alınıp ,i j ve k

üzerinden toplam alındığında,

(

)

2

(

)

2

(

)

2 1 1 1 1 1 P O KT_T p o r p o i j ijk i j k i j KT KT Y Y or Y Y pr Y Y = = = = = − = − + −

∑∑∑

iii

∑

ii iii

∑

i i iii

(

)

2

(

)

2 1 1 1 1 1 PO E ij i j ijk ij KT KT p o p o r i j i j k r Y Y Y Y Y Y = = = = = − − + +

∑∑

_{i ii i i iii} +

∑∑∑

− _i

veya sembolik olarak

T P O PO E

KT

=

KT

+

KT

+KT

+

KT

eşitliği elde edilir (Öztürk, 2009). Ayrıca Cochran Teoreminden (Montgomery, 2001: sayfa 69)

KT

_P ,

KT

_O, KT_PO ve

KT

_E ler bağımsızdır.

3.1. Rasgele Etkili Model

Operatörler arasından rasgele seçilen o tane O O₁, ₂,...,O operatör ile _o ürünler arasından rasgele seçilen p tane P P₁, ,...,₂ P ürün kullanılarak, her operatör p her üründe rasgele bir sırada r kez ölçüm yapacak şekilde bir deney tasarlansın.

Etkenler (faktörler):

Operatör etkeni: Düzeyleri O O₁, ₂,...,O rasgele seçimli etken. _o Parça etkeni: DüzeyleriP P₁, ,...,₂ P rasgele seçimli etken. p

İki etkenin düzeylerinin kombinasyonu olan ortak etkiler

(

PO

)

_ij olmak üzere, Rasgele Etkenli Varyans Analizi Modeli

( ) 1, 2,..., ; 1, 2,..., ; 1, 2,...,

ijk i j ij ijk

Y = + +μ P O + PO +ε i= p j= o k= r

biçiminde yazılabilir. Rasgele etkili ANOVA modelinin varsayımları aşağıda verilmiştir.

Varsayım 1. i = 1,2,..., p; j = 1,2,...,o; k = 1,2,...,r için gözlenemeyen rasgele hata terimi olarak adlandırılan ε ’lar bağımsız ve _ijk

(

2

)

N 0,σ dağılıma sahip rasgele _ε değişkenler,

Varsayım 2. P P₁, ,...,₂ P rasgele düzey etkileri bağımsız ve _p N

(

0,σ dağılıma 2_P

)

sahip rasgele değişkenler,

Varsayım 3. O O₁, ₂,...,O rasgele düzey etkileri bağımsız ve o

(

)

2 0, O

N σ dağılıma sahip rasgele değişkenler,

Varsayım 4. i=1, 2,..., ; 1, 2,...,p j= o için

(

)

ij

PO etkileşimleri bağımsız ve

(

_0, 2

)

PO

N σ dağılıma sahip rasgele değişkenler,

Varsayım 5. i = 1,2,..., p; j = 1,2,...,o; k = 1,2,...,r için ε , _ijk P , _i O , _j

(

PO

)

_ij’ler bağımsız rasgele değişkenler olup,

( )

2 2 2 2 ijk P O PO Var Y =σ +σ +σ +σ_ε dır. Oi, Pi,

( )

i PO i,

( )

PO ij,

( )

PO ii, εi ij , εiii, εiji ve εiii ifadeleri

1 1 _, p o j j j i P O O P o p = = =

∑

=

∑

i i ,

( )

( )

1 o ij j i PO PO o = =

∑

i ,

( )

( )

1 p ij i j PO PO p = =

∑

i ,

( )

1 1

( )

p o ij i j PO PO p o = = = ×

∑∑

ii , 1 1 p r ijk i k j p r ε ε ₌ = = ×

∑∑

i i , 1 1 o r ijk j k i o r ε ε ₌ = = ×

∑∑

ii ve 1 r ijk k ij r ε ε ₌

∑

= i , 1 1 1 p o r ijk i j k p o r ε ε ₌ = = = × ×

∑∑∑

iii

şeklinde tanımlanmak üzere yukarıda verilen beş varsayımdan

( )

( )

2

( )

( )

2 2 2 _, 2 P_, 2 2 _, 2 O i P j O E P E P E O E O p o σ σ σ σ = _i = = _i =

( )

_{2 2}

( )

2 2

( )

2 2

( )

2 2 , PO , PO, PO PO ij _{i j} E PO E PO E PO E PO o p po σ σ σ σ ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ ⎡ _{⎤ = = = =} ⎣ ⎦ _⎣⎢ i⎥_⎦ ⎢_⎣ i ⎥_⎦ ⎢_⎣ ii⎥_⎦

yazılabilir (Sahai ve Ageel, 2000).

(

)(

)

2 _{, ,}2 2 1 1 -1 -1 O PO P P O PO KT KT KT S S S p o o p = = = − − ve

(

)

2 1 E E KT S po r = − olmak üzere

( )

2 _,

( )

2 _,

( )

2 P E SP O E SO PO E SPO θ = θ = θ = ve

( )

2 E E SE θ =

şeklinde tanımlansın. Bu durumda Yiii, Yi ij , Yiji ve Yiii ifadeleri (3.1) eşitliğinde verilen model ele alınarak

( )

(

)

( )

1 1 1 1 p r p r ijk i j ij ijk j k j k i i i i Y P O PO Y P O PO p r p r ε μ ε = = = = + + + = = = + + + + × ×

∑∑

∑∑

ii i _i ii (3.2)

( )

(

)

( )

1 1 1 1 o r o r ijk i j _ij ijk i k i k j j j j Y P O PO Y P O PO o r o r ε μ ε = = = = + + + = = = + + + + × ×

∑∑

∑∑

i i i _i i i (3.3)

( )

(

)

( )

1 1 r r ijk i j ij ijk k k ij i j ij ij Y P O PO Y P O PO r r ε μ ε = = + + + =

∑

=

∑

= + + + + i i (3.4)

( )

(

)

( )

1 1 1 1 1 1 p o r p o r ijk i j _ij ijk i j k i j k Y P O PO Y P O PO p o r p o r ε μ ε = = = = = = + + + = = = + + + + × × × ×

∑∑∑

∑∑∑

iii i i _ii iii(3.5)

şeklinde yazılabilir. (3.2) ve (3.5) eşitlikleri kullanılarak KT , _P

(

)

₂

(

( ) ( )

)

2 1 1 1 1 1 1 p o r p o r P i i i i i j k i j k KT Y Y P P PO PO ε ε = = = = = = =

∑∑∑

ii− iii =

∑∑∑

− +i _i− _ii+ ii− iii biçiminde yazılabilir. Yukarıdaki eşitliğinin her iki tarafının beklenen değeri alındığında

( )

(

)

(

( )

( )

)

(

)

(

) (

) (

)

(

)

(

)

(

)

2 2 2 1 1 1 2 2 2 2 2 2 2 2 2 E = = = 1 1 1 p p p P i i i i i i P P PO PO P PO KT or E P P or E PO PO or or p r p p or p r p p ε ε ε ε ε σ σ σ σ σ σ σ σ σ = = = − + − + − − + − + − − + − + −

∑

i

∑

_i ii

∑

ii iii olup θ_P,

(

)

2

(

)

2

(

)

2 2 2 2 1 1 1 1 = P PO P P PO or p r p p p or r ε ε σ σ σ θ σ σ σ − + − + − = − + +

şeklinde elde edilir (Sahai ve Ageel, 2000).

(3.3) ve (3.5) eşitlikleri kullanılarak KT , _O

(

)

2

(

( )

( )

)

2 . 1 1 o o O j j j j j j KT pr Y Y pr O O PO PO ε ε = = =

∑

_{i i}− _iii =

∑

− _i+ − _ii+ _{i i}− _iii i

olarak yazılabilir. Yukarıdaki eşitliğin her iki tarafının beklenen değeri alındığında

( ) ( )

(

)

( )

( )

( )

2 1 2 2 2 2 2 2 2 2 2 ( ) -1 -1 -1 o O j j j j O O PO PO O PO E KT pr E O O PO PO por pr or r o pr o r o o ε ε ε ε ε σ σ σ σ σ σ σ σ σ = = − + − + − = − + − + − = + +

∑

i _{i ii} i i iii olup θ_O,

( )

( )

( )

(

)

2 2 2 2 2 2 -1 -1 -1 1 O PO O O PO pr o r o r o o pr r r ε ε σ σ σ θ σ σ σ + + = − = + + dır (Sahai ve Ageel, 2000). (3.2), (3.3), (3.4) ve (3.5) eşitlikleri kullanılarak KT_PO,

(

)

( )

( ) ( ) ( )

2 1 1 2 1 1 p o PO ij i j i j p o ij i j ij _{i j} i j KT r Y Y Y Y r PO PO PO PO ε ε ε ε = = = = = − − + ⎡ ⎤ = _⎢ − − + + − − + _⎥ ⎣ ⎦

∑∑

∑∑

i ii i i iii i ii i i iii i i ii

şeklinde yazılabilir. Böylece yukarıdaki eşitliğin her iki tarafının beklenen değeri alındığında

(

)

( )

( ) ( ) ( )

2 1 1 2 2 2 2 2 2 2 2 1 1 1 1 1 j p o PO ij _{i j} ij i i j p o p o r PO PO PO PO i j i j k E KT r E PO PO PO PO r p o p o r o r p r p o r ε ε ε ε ε ε ε ε σ σ σ σ σ σ σ σ = = = = = = = ⎡ ⎤ = _⎢ − − + + − − + _⎥ ⎣ ⎦ ⎛ ⎞ ⎛ ⎞ = _⎜ − − + _⎟+ _⎜ − − + _⎟ × × × × × ⎝ ⎠ ⎝ ⎠

∑∑

∑∑

∑∑∑

i i i ii iii i i ii 2 2 2 2 2 2 2 2 PO PO PO PO npoσ noσ npσ nσ poσε pσε oσε σε = − − + + − − + _-1

(

)( )

_-1 2

(

_-1

)( )

_-1 2 PO r p o σ p o σε = + olup θPO,

(

)( )

(

)( )

(

)( )

2 2 2 2 -1 -1 -1 -1 -1 -1 PO PO PO r p o p o p o r ε ε σ σ θ σ σ + = = + dır (Sahai ve Ageel, 2000). (3.1) ve (3.4) eşitlikleri kullanılarak

(

)

2 1 1 1 -p o r E ijk ij i j k KT Y Y = = = =

∑∑∑

i =

(

εijk −εiji

)

2

olarak yazılabilir. Böylece yukarıdaki eşitliğin her iki tarafının beklenen değeri alındığında

eşitliğin her iki tarafın beklenen değeri alındığında

(

)

(

)

(

)

2 1 1 1 2 2 1 1 1 2 2 2 1 p o r E ijk ij i j k p o r i j k E KT E r por po po r ε ε ε ε ε ε ε σ σ σ σ σ = = = = = = = − ⎛ ⎞ = _⎜ − _⎟ ⎝ ⎠ = − = −

∑∑∑

∑∑∑

i olup θE,

(

)

(

)

2 2 1 1 E op r op r ε ε σ θ = − =σ − Dır (Sahai ve Ageel, 2000). 2_, 2_, 2 P O PO σ σ σ ve 2 ε

σ varyans bileşenleri için yansız birer tahmin edici,

2 2 ˆ_ε S_E σ = 2 2 2 ˆ PO E PO S S r σ = − 2 2 2 ˆ P PO P S S p r σ = − × 2 2 2 ˆ O PO O S S o r σ = − ×

şeklinde önerilir (Öztürk, 2009).

Rasgele Etkili Modellerde varyans bileşeninin sıfır olması, normal dağılımlı ve sıfır ortalamalı olan düzey etkilerinin aynı (sıfır) olması demektir. Örneğin, 2

O σ =0 olması, O etkenin seviyelerinin aynı olması (operatör etkeninin düzeyleri arasında fark olmadığı) anlamına gelmektedir (Öztürk, 2009).

İki Etkenli Rasgele Etkili Modelde O etkeni ile ilgili,

2 0: O 0 H σ = 2 1: O 0 H σ >

P etkeni ile ilgili,

2 0: P 0 H σ = 2 1: P 0 H σ >

ve iki etkenin etkileşimi ile ilgili,

2 0: PO 0 H σ = 2 1: PO 0 H σ >

hipotezleri için ANOVA tablosu Tablo 3 de verilmiştir. Beklenen Kareler Ortalamaları (Expected Mean Squares) dikkate alınarak, sıfır hipotezleri altında F değerleri bire eşit olmakta, karşıt hipotez altında birden büyük olmaktadır.

, , P O PO

F F F istatistiklerinin büyük değerleri için ilgili hipotezdeki sıfır hipotezi reddedilmektedir (Öztürk, 2009).

Tablo 3. Varyans Analizi(ANOVA) Tablosu Değişim Kaynağı Serbestlik

Derecesi Hata Kare. Ortalaması Beklenen Kareler Ortalaması F İstatist. Parça

( )

P p− 1 S _P2 θP=orσP2+rσPO2 +σε2 P P PO KT F = KT Operatör

( )

O o−1 S O2 2 2 2 = + + O pr O r PO ε θ σ σ σ O O PO KT F = KT Parça×Operatör

(

P O×

)

( 1)( 1) p− o− S_PO2 θ_PO= rσ_PO2 +σ_ε2 PO PO E KT F KT = Tekraredilebilirlik po r

(

−1

)

S _E2 θ_E =σ_ε2

3.2. Karma Etkili Model

Operatörler arasından özel seçilen o tane O O₁, ₂,...,O operatör ile ürünler _o arasından rasgele seçilen p tane P P₁, ,...,₂ P ürün kullanılarak, her operatör her p üründe rasgele bir sırada r kez ölçüm yapacak şekilde bir deney tasarlansın.

Bağımlı değişken: Y - ürünün ölçüm değeri. Etkenler (faktörler):

Operatör etkeni: Düzeyleri O O₁, ₂,...,O özel seçimli etken. o Parça etkeni: DüzeyleriP P₁, ,...,₂ P rasgele seçimli etken. _p

İki etkenin düzeylerinin kombinasyonu olan ortak etkiler

(

PO

)

_ij olmak üzere, Karma Etkili Varyans Analizi Modeli

( ) 1, 2,..., ; 1, 2,..., ; 1, 2,...,

ijk i j ij ijk

Y = + +μ P O + PO +ε i= p j= o k= r

biçiminde yazılabilir. Karma Etkili ANOVA modelinin varsayımları aşağıda verilmiştir.

Varsayım 1. i = 1,2,..., p; j = 1,2,...,o; k = 1,2,...,r için gözlenemeyen rasgele hata terimi olarak adlandırılan ε ’lar bağımsız ve _ijk N

(

0,σ_ε2

)

dağılıma sahip rasgele değişkenler,

Varsayım 2. O O₁, ₂,...,O özel seçilmiş (sabit) düzey etkileri için _o 1 0 o j j O = =

∑

,

Varsayım 3. P P₁, ,...,₂ P rasgele düzey etkileri bağımsız ve _p N

(

0,σ dağılıma 2P

)

sahip rasgele değişkenler,

Varsayım 4. . i=1, 2,..., ; 1, 2,...,p j= o için

(

PO

)

_ij etkileşimleri bağımsız ve

(

_0, 2

)

PO

N σ dağılıma sahip rasgele değişkenler,

Varsayım 5. i=1, 2,..., ;p j=1, 2,..., ;o k=1, 2,...,r için ε ,_ijk P ,_i

(

PO

)

_ij’ler bağımsız

olup,

( )

2 2 2 ijk P PO Var Y =σ +σ +σ_ε dır. Varsayım 6.

(

)

1 0, 1, 2,..., o ij j PO i p = = =

∑

(Bu varsayım kısıtlı karma model için vardır ancak bu tezde kısıtsız karma modeller kullanılacağından bu varsayım ele alınmayacaktır.) (3.2) ve (3.5) eşitlikleri kullanılarak KT , _P

(

)

₂

(

( )

( )

)

2 1 1 1 1 p o r p P i i i i i j k i KT Y Y or μ P O PO ε μ P O PO ε = = = = =

∑∑∑

_ii− _iii =

∑

+ + _i+ + _ii− − −_{i i}− − _iii i ii =

(

( )

( )

)

2 1 p i i i i or P O PO ε P O PO ε = + + + − − − −

∑

i _i ii i i _ii iii

(

)

(

( )

( )

)

(

)

(

( ) ( )

)

(

)

(

)

(

)

2 1 2 2 2 1 2 2 2 2 2 2 2 2 -1 1 p P i i i i p i i i i PO PO P P P PO E KT or E P PO P PO or E P P E PO PO E

por por por

p o p o o r p o r or p r p ε ε ε ε ε ε σ σ σ σ σ σ σ σ σ = = = + + − − − ⎡ ⎤ = _⎢ − + − + − _⎥ ⎣ ⎦ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ = _⎜ − _⎟+ _⎜ − _⎟+ _⎜ − _⎟ × × × × ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ = + − +

∑

∑

ii i iii i ii i _{i ii} ii iii

(

)

2 ₁ p ε − olup θP,

( )

2

(

-1

)

2

(

1

)

2 2

(

1

)

2 2 2 1 P PO E P P P PO E or p r p p E S or r p σ σ σ θ = = + − + − = σ + σ +σ − dır (Sahai ve Ageel, 2000). (3.3) ve (3.5) eşitlikleri kullanılarak

(

)

₂

(

( )

( )

)

2 1 1 1 1 1 1 p o r p o r j O j j _j i j k i j k KT Y Y O PO ε O PO ε = = = = = = =

∑∑∑

_{i i}− _iii =

∑∑∑

+ + i i− _i− − _iii i ii

olmak üzere her iki tarafın beklenen değeri alındığında

(

)

(

( )

( ) ( )

)

(

)

(

)

(

)

2 1 1 1 2 2 2 2 1 2 2 1 1 1 p o r O j j j i j k o PO O j j o j PO j E KT E O E PO PO E pr O por por p p o p r p o r pr O r o o ε ε ε ε ε σ σ σ σ σ σ = = = = = = + − + − ⎛ ⎞ ⎛ ⎞ = + _⎜ − _⎟+ _⎜ − _⎟ × × × × ⎝ ⎠ ⎝ ⎠ = + − + −

∑∑∑

∑

∑

i i iii i ii olup θ_O,

( )

2

(

)

2 1 2 2 1 -1 1 1 -1 o j PO j O o j PO j pr O r o o o pr O r o ε ε σ σ θ σ σ = = + + − = − = + +

∑

∑

dır (Sahai ve Ageel, 2000). (3.2), (3.3), (3.4) ve (3.5) eşitlikleri kullanılarak

(

)

( )

( ) ( ) ( )

2 1 1 1 2 1 1 1 p o r PO ij i j i j k p o r ij i j ij _{i j} i j k KT Y Y Y Y PO PO PO PO ε ε ε ε = = = = = = = − − + ⎡ ⎤ = _⎢ − − + + − − + _⎥ ⎣ ⎦

∑∑∑

∑∑∑

i ii i i iii i ii i i iii i i ii

olmak üzere yukarıdaki eşitliğin her iki tarafının beklenen değeri alındığında

(

)

(

)

( )

( ) ( ) ( )

2 1 1 1 2 1 1 1 2 2 2 2 2 2 2 2 PO = p o r PO ij i j i j k p o r ij i j ij _{i j} i j k PO PO PO E KT E Y Y Y Y E PO PO PO PO por p o p o r p r o r p o r ε ε ε ε ε ε ε ε σ σ σ σ σ σ σ σ = = = = = = = − − + ⎡ ⎤ = _⎢ − − + + − − + _⎥ ⎣ ⎦ ⎡⎛ ⎞ ⎛ ⎞⎤ − − + + − − + ⎢⎜ _× ⎟ ⎜ _{× × × ×} ⎟⎥ ⎝ ⎠ ⎝ ⎠ ⎣ ⎦

∑∑∑

∑∑∑

i ii i i iii i ii i i iii i i ii

(

)(

)

2

(

)(

)

2 =r p - 1 o - 1 σ_PO + p - 1 o - 1 σε olup θPO,

(

)(

)

(

)(

)

(

)(

)

2 2 2 2 1 PO PO PO r p - 1 o - 1 p o - 1 p - 1 o - 1 r ε ε σ σ θ σ σ + − = = + dır (Sahai ve Ageel, 2000). (3.1) ve (3.4) eşitlikleri kullanılarak

(

)

(

)

( )

2 1 1 1 2 1 1 1 2 2 2 = = -1 p o r E ijk ij i j k p o r ijk ij i j k KT Y Y E por r po r ε ε ε ε ε σ σ σ = = = = = = = − = − ⎛ ⎞ − ⎜ ⎟ ⎝ ⎠

∑∑∑

∑∑∑

i i olup θ_E,

(

)

(

)

2 2 1 E po r - 1 po r ε ε σ θ = =σ − dır (Sahai ve Ageel, 2000).

Karma modelde, μ, ,O O_{1 2},...,O_o parametreleri için yansız birer tahmin edici,

ˆ Y μ= iii , 1, 2,..., j j O =Y_{i i}−Y_iii j= o ve

( )

2 2 E E S =σ_ε

( )

2 2 2 PO PO E S =σ_ε +rσ 2 2 2 2 ( )P PO O E S =σ_ε+rσ +prσ olmak üzere, 2_, 2 P PO σ σ ve 2 ε

σ varyans bileşenleri için yansız birer tahmin edici,

2 2 ˆ_ε S_E σ = 2 2 2 ˆ PO E PO S S r σ = − 2 2 2 ˆ P PO P S S or σ = − dır (Öztürk, 2009).

Karma modelde, P etkeni ile ilgili, 2 0: P 0 H σ = 2 1: P 0 H σ >

O etkeni ile ilgili,

0: 1 2 o 0

H O =O = =O =

1: 1 0 veya 2 0 veya veya o 0

H O ≠ O ≠ O ≠

ve iki etkenin etkileşimi ile ilgili, 2 0: PO 0 H σ = 2 1: PO 0 H σ >

Tablo 4. Varyans Analizi(ANOVA) Tablosu Değişim Kaynağı Serbestlik

Derecesi Hata K.Ort. Beklenen Kareler Ortalaması F İstatist. Parça

( )

P p− 1 S _P2 θ_P= orσ_P2+ rσ_PO2 +σ_ε2 P P PO KT F = KT Operatör

( )

O o−1 S O2 2 2 = o j j=1 2 O PO O pr + r + o - 1 ε θ

∑

σ σ O O PO KT F = KT Parça×Operatör

(

P O×

)

(

p−1

)(

o−1

)

S_PO2 θPO=rσPO2 +σε2 PO PO E KT F KT = Tekraredilebilirlik po r

(

−1

)

S _E2 θ_E =σ_ε2

Burada not edilmelidir ki kısıtlı karma modellerde Tablo 6 daki F , _O O O E KT F KT = olarak alınır.

4. ÖLÇÜM SİSTEMLERİ ANALİZİ

Ölçüm değişkenliğinin tespit edilmesi, ürün ve süreç değişkenliğini doğru bir biçimde gözlemlemek için gereklidir. Tekraredilebilirlik ve Tekrarüretilebilirlik (Repeatability&Reproducibility, R&R) diğer bir deyişle ölçüm (Gauge, gage) analizi ölçüm prosedürünün yeterliliğini belirlemek için kullanılır. Tekraredilebilirlik, ölçüm aletinden kaynaklanan değişimi, tekrarüretilebilirlik, operatörlerin ölçme yönteminden kaynaklanan değişimi temsil eder. Ölçüm prosedürü ile ilgili değişim kaynaklarını elde etmek için iki yöntem kullanılır: Bunlardan ilki, uygun varyans bileşenlerinin tahmin değerinin kullanılmasıyla ANOVA yaklaşımı, diğeri de ölçüm değişkenliğinin bileşenlerinin standart sapmalarının tahmin için genişlik metoduna dayalı çizelge algoritmadır.

Bu tez çalışmasında, kompleks deneylere adapte olabilmesi, Tekraredilebilirlik ve Terkrarüretilebilirlik ve diğer ölçüm yeterlilik parametrelerinin güven aralıklarının elde edilmesine imkan vermesi sebebiyle ANOVA yöntemi ele alınacaktır. R&R analizinde genel olarak kullanılan ANOVA modeli, operatör ve parça olmak üzere iki faktörden oluşur. Genellikle operatörler, operatörler kitlesinden rasgele seçildiği varsayıldığından ANOVA modelinde rasgele faktör (random effect) olarak ele alınır. Operatörler özel seçimli faktör olabilir. Örneğin bir fabrikadaki üretilen parçaları ölçmek için önceden istihdam edilmiş üç operatöründe ölçüm yapması durumunda operatör faktörü özel seçimli olarak düşünülmelidir. Bu durumda ölçüm sistemleri çalışmasında karma (mixed effect) model ele alınmalıdır.

Ölçüm sistemleri analizi ile ilgili ayrıntılı bilgi için (AIAG, 1995, 2002), Horrell (1991) ve Croarkin (2002) kaynaklarına bakılabilir.

4.1. Ölçüm Sistemi Yeterliliğinin Analizi için Varyans Analizi Modelleri

P , parça faktörü, O, operatör faktörü, PO, etkileşim faktörü ve ε hata

( )

, , ijk i j ij ijk

Y = + +μ P O + PO +ε i = 1,2,... p, j = 1,2,...,o k = 1,2,...,r (4.1) şeklinde verilir. Burada p , parça sayısı, o, operatör sayısı ve r , tekrar sayısıdır.

Operatör faktörünün rasgele veya özel seçimli olduğu durumlara göre (4.1) modeli rasgele etkili model veya karma etkili model adını almaktadır.

Rasgele model durumunda P , O , POi j

( )

_ij ve εijk ler 0 ortalamalı ve sırasıyla 2_{, ,} 2 2

P O PO

σ σ σ ve 2

ε

σ varyanslı normal dağılıma sahip bağımsız rasgele değişkenlerdir (Bkz. Tablo 1).

Karma etkili model durumunda (O, operatör faktörü özel seçimli olduğunda)

( )

i _ij

P , PO ve ε_ijk ler 0 ortalamalı ve sırasıyla σ σ_P2, _PO2 ve σ_ε2 varyanslı normal dağılıma sahip bağımsız rasgele değişkenlerdir ve 0

o j j=1

O =

∑

dır (Dolezal, Burdick, Birch, 1998). Ayrıca bu söylenenler için Tablo 1 e bakılabilir.

Rasgele ve Karma modellerde kareler ortalamalarının dağılımları bir istisna dışında aynıdır. Her iki modelde de

(

)

2 1 P P p S θ − ,

(

)(

)

2 1 1 PO PO p o S θ − − ve

(

)

2 1 E E po r S θ − bağımsızdır ve sırasıyla

(

p - 1

)

,

(

p - 1 o - 1

)(

)

ve po r - 1

(

)

serbestlik dereceli

Ki-kare dağılımına sahiptir. Ancak

(

)

2 1 O O o S θ −

, rasgele modelde

(

o - 1

)

serbestlik

dereceli Ki-kare dağılımına sahipken, karma modelde bu durum geçerli değildir.

Karma modelde

(

)

2 1 _O PO o S θ − ,

(

o - 1

)

serbestlik dereceli ve 2 2 o j j=1 PO pr O λ θ =

∑

merkezsel olmama parametreli Ki-kare dağılımına sahiptir (Graybill, 1961). Burada karma modelde

(

)

2 1 _O O o S θ −

Tablo 5 ve Tablo 6 da Rasgele ve Karma model için ANOVA tabloları verilmiştir.

Tablo 5. Rasgele etkili ANOVA modeli için ANOVA Tablosu Değişim Kaynağı Serbestlik

Derecesi Hata K. Ort. Beklenen Kareler Ortalaması F İstatist. Parça

( )

P p−1 S _P2 θ_P =σ_ε2+rσ_PO2 +orσ_P2 P P PO KT F = KT Operatör

( )

O o−1 S O2 2 2 2 O ε r PO pr O θ =σ + σ + σ O O PO KT F = KT Parça×Operatör

(

P O×

)

(

p−1

)(

o−1

)

2 PO S θ_PO =σ_ε2+rσ_PO2 PO PO E KT F KT = Tekraredilebilirlik po r

(

−1

)

S _E2 θ_E =σ_ε2

Tablo 5 de θ_Oile verilen hücrede 2 PO σ yerine 1 o 2 j j=1 O o - 1

∑

yazıldığında kısıtsız karma

model için ANOVA tablosu elde edilir. Buna ilaveten Tablo 5 de

F

_O yerine

E

O O

KT

F =

KT

de alındığında kısıtlı karma model için ANOVA tablosu elde edilir.

Tablo 6. Karma Etkili ANOVA modeli için ANOVA Tablosu Değişim Kaynağı Serbestlik

Derecesi Hata K. Ort. Beklenen Kareler Ortalaması F İstatist. Parça

( )

P p− 1 S _P2 θ_P= orσ_P2+ rσ_PO2 +σ_E2 P P PO KT F = KT Operatör

( )

O o−1 S O2 2 2 1 = o 2 O j PO j=1 pr O + r + o - 1 ε θ

∑

σ σ O O PO KT F = KT Parça×Operatör

(

P O×

)

(

p−1

)(

o−1

)

2 PO S θ_PO=rσ_PO2 +σ_ε2 PO PO E KT F KT = Tekraredilebilirlik po r

(

−1

)

S _E2 θ_E =σ_ε2

Burada not edilmelidir ki kısıtlı karma model durumunda ANOVA tablosu için Tablo 6 daki F yerine _O O O E KT F KT = alınır.

4.2. Bazı Ölçüm Yeterlilik Parametreleri ve Tahmin Edicileri

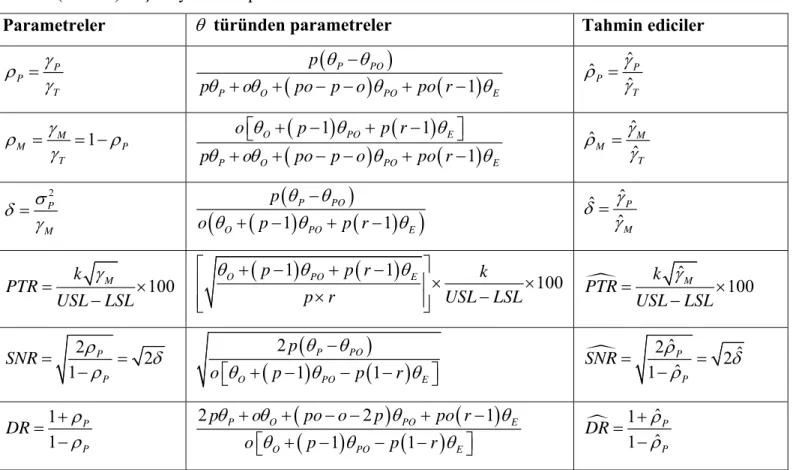
Ölçüm R&R analizinin (Gauge R&R) amacı, ölçüm sisteminin değişkenliğinin ölçülen parçanın değişkenliğine göre daha az olup olamadığını belirlemektir. Literatürde ölçüm sistemleri çalışmasında adı geçen birçok parametre ve bu parametrelerin fonksiyonlarından elde edilmiş parametreler vardır. Bu parametreler Tablo 7 de verilmiştir. Bu parametreler süreç ve ölçüm sistemi değişkenliği hakkında bilgi vermektedir.

Rasgele etkili ANOVA modeli kullanılarak yapılan R&R analizinde tekraredilebilirlik ve tekrarüretilebilirlik, sırasıyla,

2 1 ε γ =σ ve 2 2 2 O PO γ =σ +σ

şeklinde tanımlanır. Bu durumda toplam ölçüm

2 2 2

1 2

M O PO ε

γ = +γ γ =σ +σ +σ

ve toplam süreç varyansı

2 2 2 2

T P M P O PO ε

γ =γ +γ =σ +σ +σ +σ biçiminde tanımlanır.

Karma ANOVA modeli ele alındığında yukarıdaki verilen tanımlarda 2 O σ yerine 2 1 o j j=1 O o−

∑

alınmalıdır.

PTR(Precision-to-Tolerance Ratio) parametresi,

k M %100 PTR USL LSL γ = × −

şeklinde tanımlanır. Burada USL, üst spefikasyon limiti, LSL, alt spefikasyon

limitidir. Ayrıca k =5.15 veya k=6 olarak alınır. Selçuk Stat k =5.15değerini ele

almaktadır. Bu değerler normal dağılım için sırasıyla kitlenin en az %99 unu barındıran %95 lik tolerans aralığı sınırları arasındaki mesafe ve doğal tolerans aralığı arasındaki mesafedir. PTR parametresinin yorumlanmasında faklı görüşler vardır. Montgomery and Runger (1993a) ölçüm sisteminin yeterli olduğunu söyleyebilmek için PTR parametresinin %10 dan az olması gerektiğini vurgulamışlardır. Bu öneri, AIAG Ölçüm Sistemleri Analizi El Kitabı (1995, sayfa 60) nın önerisi ile tutarlıdır. Mader, Prins ve Lambe (1999), Wheeler ve Lyday (1989) ı referans vererek PTR parametresi %20 den fazla olduğu durumda ölçüm sisteminin yetersiz olduğunu ileri sürmüşlerdir. Son olarak Barrentine (1991, sayfa 10) PTR parametresi %30 dan fazla olduğu durumda ölçüm sisteminin yetersiz olduğunu söylemiştir. Bazı özel durumlarda Montgomery and Runger (1993a) ve Mader (1999) PTR parametresinin ölçüm yeterliliği konusunda iyi bir katsayı olamayacağını vurgulamışlardır. Örneğin yüksek yeterliliğe sahip teknoloji, ölçüm sisteminden kaynaklanan değişkenliği tolere edebilir.

Parça hatasının, toplam ölçüm varyansına oranı 2 P M σ δ γ =

şeklinde tanımlanır. Ölçüm prosedürünün yeterliliği hakkında bilgi vermesi bakımından R&R analizinde δ parametresinin önemli bir yeri vardır.

Parça hatasının, toplam süreç hatasına oranı

P P T γ ρ γ = şeklinde tanımlanır.

Toplam ölçüm hatasının, toplam süreç hatasına oranı

1 M M P T γ ρ ρ γ = = − şeklinde tanımlanır.

Toplam ölçüm hatasının toplam süreç hatasına göre oranı %10 dan küçükse ölçüm sistemi yeterli %10 ile %30 arasında ise şartlı yetrli %30 dan büyükse ölçüm sistemi tekrar gözden geçirilmelidir (Kavi ve Elevli, 2008).

(AIAG, 1995, sayfa:32) SNR (Signal-to-Noise Ratio) parametresini δ veya P

ρ parametresine dayalı olarak

2 2 1 P P SNR ρ δ ρ = = −

şeklinde tanımlamıştır. AIAG (1995) ölçüm sisteminin yeterli olduğunu söyleyebilmek için SNR parametresinin 5 den çok olması gerektiğini söylemiştir. Bu parametre kategorilerin farklı seviyelerinin sayısı(the number of distinct levels of categories) olarak da adlandırılır. Not etmek gerekir ki AIAG (1990) ölçüm sisteminin yeterli olduğunu söyleyebilmek için SNR parametresinin 3 den çok olması

gerektiğini söylemiştir (Dolezal, Burdick, Birch, 1998). Ayrıca burada not etmelidir ki (?)SNR = δ olarak tanımlanmıştır. Minitab SNR yi 2δ ve NCSS 2007 SNR

yi δ olarak ele almaktadır.

Bir başka parametre Mader, Prins ve Lampe (1999) ve Wheeler (1992) tarafından önerilen ayırma oranıdır (Discriminant Ratio) ve DR

1 1 P P DR ρ ρ + = −

şeklinde tanımlanır. Mader, Prins ve Lampe (1999), bu oranın dörtten büyük olmasının, ölçüm sisteminin yeterli olduğunu işaret ettiğini ileri sürmüşlerdir. Burada bahsedilen parametrelerin dışındaki parametreler için Vardeman ve VanValkenburg (1999), van den Heuvel ve Trip (2002) ve Larsen (2002) e bakılabilir.

Tablo 7. Ölçüm yeterlilik parametreleri

Parametreler θ türünden parametreler Tahmin ediciler

2 P P γ =σ P PO o r θ −θ × 2 2 P PO P S S o r γ = − × 2 O O γ =σ _{O PO} p r θ −θ × 2 2 O PO O S S p× r γ = − 2 1 ε γ =σ θE γˆ1= 2 E S 2 2 2 O PO γ =σ +σ O

(

p 1

)

PO p E p r θ + − θ − θ ×

(

)

2 2 2 2 1 ˆ SO p SPO pSE p r γ = + − − × 1 2 2 2 2 M O PO ε γ γ γ σ σ σ = + = + +

(

1

)

(

1

)

O p PO p r E p r θ + − θ + − θ ×

(

)

(

)

2 ₁ 2 ₁ 2 O PO E M S p S p r S p r γ = + − + − × 1 2 2 2 2 2 T P P O PO ε γ γ γ γ σ σ σ σ = + + = + + +

(

)

(

1

)

P O PO E p o po p o po r p o r θ + θ + − − θ + − θ × ×

(

)

(

)

2 2 2 ₁ 2 P O PO E T pS oS po p o S po r S p o r γ = + + − − + − × ×

Tablo 7.(Devam) Ölçüm yeterlilik parametreleri

Parametreler θ türünden parametreler Tahmin ediciler

P P T γ ρ γ =

(

)

(

)

(

1

)

P PO P O PO E p p o po p o po r θ θ θ θ θ θ − + + − − + − ˆ ˆ ˆ P P T γ ρ γ = 1 M M P T γ ρ ρ γ = = −

(

)

(

)

(

)

(

)

1 1 1 O PO E P O PO E o p p r p o po p o po r θ θ θ θ θ θ θ + − + − ⎡ ⎤ ⎣ ⎦ + + − − + − ˆ ˆ ˆ M M T γ ρ γ = 2 P M σ δ γ =

₍

₍

(

₎

)

₍

₎

₎

1 1 P PO O PO E p o p p r θ θ θ θ θ − + − + − ˆ ˆ ˆ P M γ δ γ = 100 M k PTR USL LSL γ = × −

(

1

)

(

1

)

100 O p PO p r E k p r USL LSL θ θ θ ⎡ _{+ − + −} ⎤ × × ⎢ ⎥ × − ⎢ ⎥ ⎣ ⎦ ˆ 100 M k PTR USL LSL γ = × − 2 2 1 P P SNR ρ δ ρ = = −

(

)

(

)

(

)

2 1 1 P PO O PO E p o p p r θ θ θ θ θ − + − − − ⎡ ⎤ ⎣ ⎦ ˆ 2 _ˆ 2 ˆ 1 P P SNR ρ δ ρ = = − 1 1 P P DR ρ ρ + = −

(

)

(

)

(

)

(

)

2 2 1 1 1 P O PO E O PO E p o po o p po r o p p r θ θ θ θ θ θ θ + + − − + − + − − − ⎡ ⎤ ⎣ ⎦ ˆ 1 ˆ 1 P P DR ρ ρ + = −