Bitki-otçul fark denklem modellerinin davranışları

(1)

T.C

SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ

BİTKİ- OTÇUL FARK DENKLEM

MODELLERİNİN DAVRANIŞLARI

Düriye KORKMAZ

YÜKSEK LİSANS TEZİ

Matematik Anabilim Dalı

Ağustos-2011 KONYA

(2)

(3)

(4)

iv ÖZET

YÜKSEK LİSANS TEZİ

BİTKİ OTÇUL FARK DENKLEM MODELLERİNİN DAVRANIŞLARI

Düriye KORKMAZ

Selçuk Üniversitesi Fen Bilimleri Enstitüsü Matematik Anabilim Dalı

Danışman: Yrd. Doç. Dr. Kemal USLU

2011, 67 Sayfa

Jüri

Yrd. Doç. Dr. Kemal USLU Prof. Dr. A. Sinan ÇEVİK Yrd. Doç. Dr. Burak SARAÇOĞLU

Bu çalışmada, Biyoloji anabilim dalında görülen bitki-otçul etkileşim fonksiyonları kullanılarak matematiksel modeller oluşturulmuştur. Ayrıca bu modellerin denge noktalarının dinamikleri incelenmiş ve elde edilen sonuçlarla ilgili nümerik örnekler verilmiştir.

Anahtar Kelimeler: Beverton-Holt Fark denklemleri, Bitki-Otçul Modelleri, Lineer olmayan fark denklem sistemi, Denge noktalarının dinamikleri.

(5)

v ABSTRACT

MS THESIS

BEHAVIOURS OF A PLANT-HERBIVORE DISCRETE MODELS

Düriye KORKMAZ

THE GRADUATE SCHOOL OF NATURAL AND APPLIED SCIENCE OF SELÇUK UNIVERSITY

THE DEGREE OF MASTER OF SCIENCE IN MATHEMATICS

Advisor: Asst. Prof. Dr. Kemal USLU

2011, 67 Pages

Agust

Asst. Prof. Dr. Kemal USLU Prof. Dr. A. Sinan ÇEVİK Asst. Prof. Dr. Burak SARAÇOĞLU

In this study, it has been made up mathematical models by using functions of plant-herbivore interaction that appear in Biology. Besides, the dynamics of equilibrium points have been examined and numerical illustrations related to obtained results have been given.

Keywords: Beverton-Holt difference equations, Plant-Herbivore model, Non-linear difference equations, The dynamics of equlibrium points.

(6)

vi ÖNSÖZ

Bu çalışma, Selçuk Üniversitesi Fen Fakültesi Matematik Bölümü Anabilim Dalı Öğretim Üyesi Yrd. Doç. Dr. Kemal USLU yönetiminde hazırlanarak, Selçuk Üniversitesi Fen Bilimleri Enstitüsü’ne Yüksek Lisans Tezi olarak sunulmuştur.

Bu Yüksek Lisans Tezi; birinci bölüm Giriş bölümü, ikinci bölüm Literatür Araştırması, üçüncü bölüm Ön Bilgiler, dördüncü bölüm bazı Bitki-Otçul Fark Denklem Sistemleri, beşinci bölüm Sonuç ve Öneriler olmak üzere toplam beş bölümden oluşmaktadır.

Yüksek Lisans çalışmamı yönetmeyi kabul ederek tezimin hazırlanmasında yardımlarını esirgemeyen danışman hocam Yrd. Doç. Dr. Kemal USLU’ya içtenlikle teşekkür ederim.

Düriye KORKMAZ

KONYA-2011

(7)

vii İÇİNDEKİLER ÖZET ... iv ABSTRACT ...v ÖNSÖZ ... vi İÇİNDEKİLER ... vii SİMGELER VE KISALTMALAR ... ix 1. GİRİŞ ...1 2. LİTERATÜR ARAŞTIRMASI ...3 3. ÖN BİLGİLER ...6

3.1. Fark Denklemleri İle İlgili Ön Bilgiler ...6

3.2. Fark Denklem Sistemleri İle İlgili Ön Bilgiler ... 10

3.3. Popülasyon Biyolojisinde Lineer Olmayan Fark Denklem Modelleri ... 13

3.3.1. Popülasyon Yoğunluğuna Bağlı Tek Tür Modelleri ... 13

3.3.2. Konak-parazit Sistemleri ... 16

4. BAZI BİTKİ OTÇUL FARK DENKLEM SİSTEMLERİ ... 20

4.1. ₁ ₂ - , ₁ 1 - -1 t t aH aH t t t t t rP P e H P e P        Fark Denklem Sistemi ... 22

4.2. - -1 3 , 1 3 1 -1 1 t t aH aH t t t t t t rP rP P e H e P P         Fark Denklem Sistemi ... 27

4.3. ₁ - , ₁ 1 - -1   t t aH aH t t t t t rP P e H P e P        Fark Denklem Sistemi ... 33

4.4. ₁ - , ₁ 1 - -1 ( 1) t t aH aH t t t t r P e H P e r P         Fark Denklem Sistemi ... 40

4.5. - -1 , 1 1 -1 ( 1) t t aH aH t t t t t rP P e H P e r P         Fark Denklem Sistemi ... 47

4.6. 2 - -1 2 , 1 1 -1 ( 1) t t aH aH t t t t t rP P e H P e r P         Fark Denklem Sistemi ... 53

4.7. ₁ - , ₁ 1 - -( 1) t t aH aH t t t t t KrP P e H P e K r P         Fark Denklem Sistemi ... 58

5. SONUÇLAR VE ÖNERİLER ... 64

5.1 Sonuçlar ... 64

(8)

viii

KAYNAKLAR ... 65

(9)

ix

SİMGELER VE KISALTMALAR

Simgeler

: Reel Sayılar



 : Pozitif Reel Sayılar

: Tam Sayılar



 : Pozitif Tam Sayılar x: Denge Noktası

F( , )

(10)

1. GİRİŞ

Dinamik modellerde bir değişkenin dengeye yakınsayıp yakınsamadığını bulmak için zaman faktörü göz önünde bulundurulur. Değişkenlerin zamanlanması sürekli ya da kesikli değişken olarak iki şekilde yapılır. Sürekli zaman, değişken zamanın her noktasında değişime uğrarken, kesikli zaman değişken zamanının bir zaman döneminde yalnızca bir defa değişmeye uğrar. Sürekli değişim oranları arasındaki denklemler diferansiyel denklemlerle, kesikli değişim oranları arasındaki denklemler ise fark denklemleri ile ifade edilir.

20. yüzyılın başlarında, Fizik biliminde incelenen kuantum teorisindeki ilerlemeler ve Biyoloji bilimindeki genetik olayların gelişmelerinden dolayı tüm doğa olaylarının sürekli değişim oranları ile ifade edilemeyeceği görülmüştür. Günümüzde fark denklemleri, Elektrik- Elektronik mühendisliğinde, devrelerin matematiksel ifadesinde, spektrum analizi ve son yıllarda önemi gittikçe artan yapay zekâ konusunda, Ekonomide arz-talep denklemleri, milli gelir, ekonomik dalgalanmalar gibi problemlerde, Sosyoloji ve Psikoloji gibi sosyal bilimlerde de yaygın bir biçimde kullanılmaktadır.

Fark denklem sistemlerinin dinamik modelleri ile gelecekte insan nüfusunun ne olacağı, enerji kaynaklarının kaç yıl yeteceği ve bitki ve otçul popülasyonları incelenerek ekolojik dengenin hangi düzeyde korunacağı gibi soruların yanıtları matematiksel olarak gösterilmektedir.

Biyolojik olaylarda matematiksel sonuçların kullanılması, ileriye yönelik tahminlerde bulunmamızı sağlar. Bu durum doğa problemlerinin çözülmesinde etkin bir rol oynamaktadır. Örneğin orman eko sistemindeki böcek popülasyonun (ağaç güvesi gibi) aşırı bir şekilde büyümesinden dolayı ağaçlarda meydana gelen ciddi tahribatlar orman kayıplarına yol açarak doğal dengeyi bozmaktadır. Böyle bir doğal problemle karşılaşıldığında kimyasal kullanılarak çözüme gitmek hem doğaya hem de insanlara zarar vermektedir. Bu yüzden bu tip doğa problemlerinin matematiksel modelleri incelenerek elde edilen veriler, doğal dengenin hangi düzeyde korunabileceği ya da problemin içinde bulunduğu şartlar altında örneğin 10 yıl veya 100 yıl gibi bir zaman sonra ne kadar büyüyüp azalacağı konusundaki tahminlerde bulunmamızı sağlar. Dolayısıyla bu noktada teorik varsayımların öneminin çok büyük olduğu görülmektedir. Bu çalışmada amacımız; Biyoloji anabilim dalı üzerinde farklı popülasyon modelleri ile ilgili problemlerde matematiğin özelliklede fark denklemlerinin nasıl

(11)

kullanıldığını görebilmek ve elde edilen sonuçların farklı durumlardaki davranışlarını incelemektir. Literatürde bizim çalışmamızı destekleyen pek çok çalışma mevcuttur. Örneğin Henson ve ark. deneysel çalışmalar vasıtasıyla böcek popülasyonun dinamiğini incelemişlerdir. Yine Kang ve ark. ağaç güvesi popülasyon modeli çalışmışlardır.

Bu çalışmanın, birinci bölümünde; çalışmanın içeriği ve amacı hakkında bilgiler verilmiş, ikinci bölümünde; literatürde daha önceden yapılmış örnek makaleler ile ilgili kısa bilgiler verilmiş, üçüncü bölümünde; kullanılan gerekli tanım ve teoremler ile popülasyon modellerinin genel çerçeveleri verilerek daha önce incelemiş örnek modeller gösterilmiş, dördüncü bölümünde; bazı bitki-otçul fark denklem modellerinin dinamiği incelenmiş, elde edilen teorik sonuçlar nümerik örnekler ve grafiklerle desteklenmiş ve beşinci bölümde sonuç ve öneriler verilmiştir.

(12)

2. LİTERATÜR ARAŞTIRMASI

Henson S.M., Costantino R.F., Cushing J.M., Dennis B., Desharnais R.A. (1999) yapmış oldukları çalışmada,

( ) 1 ea t el t c A c L t t L_ bA e  1 (1 ) t l t P   L ( ) 1 (1 ) pa t c A t t a t A_ Pe   A

otonom fark denklem modelinin dinamiğini incelemişlerdir. Doebeli M., Jong G.D. (1999) yaptıkları çalışmada,

1 1 2 1 ( ) ( ) (1 ) ( ) ( ) t t t t t t t t t t N N w N p f N p f N p P w N      

fark denklem sistemini elde ederek, bu modelin dinamiğini ve parametrelerin hassasiyetini incelemişlerdir.

Cushing J.M., Henson S.M. (2001) yaptıkları çalışmada,

1 1 1 ( 1) 1 ( 1) t t t t x r x x r       

monoton fark denklemlerinin periyodikliğini, popülasyon dinamiği uygulamalarını göz önüne alarak çalışmışlardır.

Briggs C.J., Hoopes M.F. (2004) yaptıkları çalışmada,

( )

( ) apt

t

f p e (Nicholson-Bailey fonksiyonu, Nicholson ve Bailey, 1935)

( ) 1 k t t ap f p k    _  _

  (Negatif-Binomiyel fonksiyonu, Mayıs 1978)

 ₍ ₎1  ( ) m t a p t f p e  

(13)

parazitizm fonksiyonları olmak üzere





1 1 ( ) 1 ( ) t t t t t t H H f p p cH f p      

konak-parazitoit (Host-Parasitioid) modelleri üzerine literatür eleştirisi yapmışlardır. Buchanan R.J. (2005) yapmış olduğu çalışmada,

1 1 t t u r av K t t u u e _ _       1 (1 ) t av t t v_ u e

fark denklem sisteminin dinamiğini incelemiştir. Elaydi S., Sacker R.J. (2006) çalışmalarında,

1 ( 1) n n n Kx x K x       , x 0 0, K 0

Beverton-Holt denklemleri gibi otonom olmayan fark denklemleri üzerinde zaman faktörünü ele alan bir metot geliştirmişlerdir. Bu metot, Beverton-Holt denklemleri ile ilişkili Henson ve Cushing varsayımlarını kanıtlamak amacıyla uygulanmıştır.

Deghan M., Nasri M., Douraki M.J. (2005) çalışmalarında ilk olarak,

1 1 _n n n x x b cz     1 1 n n n n y _ dy ex_z 1 1 n n n z _  fz y_

fark denklem sistemini, sürekli HIV enfeksiyon modelinin eş fark denklem modeli olarak elde etmişlerdir. Daha sonra, fark denklem sisteminin dengesinin global ve lokal asimptotik kararlılığı, sınırlılığı, kararlılık ve dallanma gibi dinamikleri araştırmışlardır.

(14)

Kang Y., Armbruster D., Kuang Y. (2008) çalışmalarında a 0, r 0 olmak üzere, 1  1 n n r x ay n n x_ x e   1  1 1 n n r x ay n n y _ x _ e _e 

fark denklem sistemini, belli bir bitki-otçul etkileşimini çalışmak için modellemişlerdir. Elde edilen iki boyutlu fark denklem modelinde durum değişkenleri olarak yaprak ve otçul biyokütlesi kullanılmıştır.

Kang Y., Chesson P. (2010) çalışmalarında,

1 ( , ) t t t t x_ x f x y 1 ( , ) t t t t y_ y g x y

fark denklem sisteminin non-lineerliliğe ilişkin kavramlarını geliştirmişler ve bu kavramları popülasyon dalgalanmalarında türlerin uzun sürede ve düşük yoğunluktaki büyüme oranı etkisinin nasıl olacağını göstermek için kullanmışlardır.

Kang Y., Armbruster D. (2010) çalışmalarında,

1 1 ( ) 1 t t aH t t aH t t P F P e H P e         _  _ ve 1 1 ( ) ( ) 1 t t aH t t aH t t P F P e H F P e         _  _

genel bitki-otçul etkileşim modellerini incelemişler ve genel bitki-otçul modellerinin dinamikleri üzerinde monoton bitki büyüme fonksiyonlarının etkisini çalışmışlardır. Kang Y., Armbruster D., (2011) çalışmalarında,

(1 ) (1 ) 1 I I n n r P a l H I I n n P_ P e    (1 ) (1 ) 1 1 I I n n r P a l H I I n n H P e  e    _  _

bitki-böcek fark zaman model çiftini çalışmışlar ve bu modelin popülasyon dinamiğindeki hem lokal hem de global yayılım etkisinin nasıl yoğunluklarda olduğunu göstermişlerdir.

(15)

3. ÖN BİLGİLER

3.1. Fark Denklemleri İle İlgili Ön Bilgiler

Bu bölümde verilen tanım ve teoremler Kulenovic M. R. S., Merino O., (2002) kitabından alınmıştır.

Tanım 3.1.1. f : tanımlı, sürekli ve diferansiyellenebilen bir fonksiyon olsun. O halde;

1 ( )

n n

x_  f x , n 0,1,... (3.1.1)

denklemine birinci mertebeden fark denklemi denir. x₀ d olmak üzere (3.1.1) denkleminin pozitif yörüngesi

0 1 2

( ) { , ,d x x x ,...} { , ( ), ( ( )),...}d f d f f d



 

dizisidir.

Aşağıda verilen örnekler Keshet L. E., (2005) kitabından alınmıştır. Örnek 3.1.1. (Hücre Bölünmesi)

Farz edelim ki; popülâsyondaki her hücre eş zamanlı olarak bölünsün. M M₁, ₂,...,M _n

sırasıyla birinci, ikinci, … , n. neslin hücre sayısı olsun. O zaman peş peşe nesiller ile ilişkili bir denklem (reküras bağıntısı)

1

n n

M _ aM (3.1.2)

şeklinde kolayca ifade edilebilir. Burada reel bir popülasyon için; 0

a  olması biyolojik olarak anlamlı

0

a  olması ilginç olmayan

0

a  olması gerçek dışı

bir durumdur. Varsayalım ki başlangıçta M hücre olsun. Acaba n nesil sonra ₀

(16)

1 1 ( 1) [ ( 2)] ... 0 n n n n M a aM a a aM a M       

elde edilir. Böylece n . nesil için,

0

n n

M a M

olur. Burada a ’nın mutlak değerce değeri, popülâsyonun zamanla büyüyüp

büyümediğini veya azalıp azalmadığını belirleyecektir. Yani, 1

a  ise M önceki nesle göre artan _n

1

a  ise M önceki nesle göre azalan _n

1

a  İse M sabittir. _n

Örnek 3.1.2. (Böcek Popülasyonu)

n

a .n nesildeki yetişkin dişi yaprak biti sayısı, p ._n n nesildeki yavru sayısı, m genç

yaprak bitlerinin rasyonel ölüm oranı, f dişi yaprak biti başına düşen yavru sayısı, r dişi yaprak bitlerinin tüm yetişkin yaprak bitlerine oranı, a başlangıçtaki dişi yaprak ₀

biti sayısı olmak üzere yavru sayısını ifade eden fark denklemi,

1

n n

p_  fa (3.1.3)

şeklinde oluşturulur. Bu denklemde p_n_₁ (n 1). neslin yavru sayısını, f dişi başına düşen yavru sayısını, a bir önceki neslin dişi sayısını göstermektedir. Hayatta kalmayı _n

başaran ergenler 1 m , büyüyen yavruların da dâhil edilmesinden sonraki r oranı göz

önüne alınırsa,

1 (1 ) 1

n n

a_ r m p_ (3.1.4)

elde edilir. f r m sabit olmak üzere (3.1.3) ve (3.1.4) denklemlerinden, , ,



(1 )



0

n n

(17)

böcek popülâsyonunu ifade eden denklem bulunur.

Tanım 3.1.2. (3.1.1) denklemini ele alalım. Eğer her n 0 değeri için

( )

f x x (3.1.5)

oluyorsa x’e (3.1.1) denkleminin denge noktası veya f sürekli fonksiyonunun bir sabit noktası denir.

Tanım 3.1.3. r  olmak üzere 

*

( )

r

f x x ve fr1( )x* x

ise x ’a (3.1.1) denkleminin er geç (eventually) denge noktası veya f sürekli *

fonksiyonunun er geç sabit noktası denir. Tanım 3.1.4. (Kararlılık)

(i) Eğer her  0 için

0

x x 

eşitsizliğini sağlayan x başlangıç koşulu için, ₀

n

x x 

olacak şekilde  0 sayısı varsa o zaman (3.1.1) denkleminin denge noktası kararlıdır denir.

(ii) Eğer (3.1.1) denkleminin x denge noktası kararlı değil ise, o zaman x denge noktasına kararsızdır denir.

(iii) Eğer x denge noktası kararlı ve  0 için

0

(18)

eşitsizliğini sağlayan x başlangıç değeri için, ₀

lim n

nx x

ise o zaman (3.1.1) denkleminin x denge noktası lokal asimptotik kararlıdır (sink). (iv) I   ve x₀ için I

lim n

nx x

ise, o zaman (3.1.1) denkleminin xdenge noktası global çekicidir denir.

(v) Eğer (3.1.1) denkleminin xdenge noktası hem kararlı hem de global çekici ise, o zaman denge noktasına global asimptotik kararlı denir.

(vi) I   ve x₀ için I

0

0 x x  r

olacak şekilde bir r 0 sayısı varsa, o zaman (3.1.1) denkleminin x denge noktasına kaynak noktası (source) denir ve bu durumda

N

x x  r

olacak şekilde bir N 1 sayısı vardır.

Tanım 3.1.5. f : tanımlı, sürekli ve diferansiyellenebilen bir fonksiyon olsun. O halde

1 ( )

n n

y f x y

  

denklemine (3.1.1) denkleminin x denge noktasındaki lineerleştirilmiş denklemi denir. Teorem 3.1.1. (Lineerleştirilmiş Kararlılık Teoremi)

:

f  tanımlı, sürekli, diferansiyellenebilen bir fonksiyon olsun. O halde aşağıdaki ifadeler doğrudur.

(19)

(i) Eğer f x( )  ise, o zaman (3.1.1) denkleminin 1 x denge noktası lokal asimptotik kararlıdır.

(ii) Eğer f x( )  ise, o zaman (3.1.1) denkleminin 1 x denge noktası kararsızdır. (iii) Eğer f x( )  ise, o zaman (3.1.1) denkleminin 1 x denge noktası hiperboliktir. (iv) Eğer f x( )  ise, o zaman (3.1.1) denkleminin 1 x denge noktası non-hiperboliktir.

3.2. Fark Denklem Sistemleri İle İlgili Ön Bilgiler

Bu bölümde verilen tanım ve teoremler Kulenovic M. R. S., Merino O., (2002) kitabından alınmıştır.

Tanım 3.2.1. f g, :   tanımlı, sürekli, diferansiyellenebilen fonksiyonlar olsun. O halde 1 1 ( , ) ( , ) n n n n n n x f x y y g x y     n 0,1,... (3.2.1)

sistemine birinci mertebeden fark denklem sistemi denir.

Tanım 3.2.2. (3.2.1) fark denklem sistemini göz önüne alalım. Eğer,

( , )

x f x y

( , )

y g x y

olacak şekilde bir ( , )x y noktası varsa, bu noktaya (3.2.1) denklem sisteminin bir

denge noktası denir.

Tanım 3.2.3. ( , ),x y (3.2.1) denklem sisteminin bir denge noktası olsun.

i) Her  0için

0 0

(20)

eşitsizliğini sağlayan her ( ,x y başlangıç koşulu için, ₀ ₀)

( ,x y_n _n) ( , ) x y  

olacak şekilde bir   ( ) varsa, (3.2.1) denklem sisteminin ( , )x y denge noktasına

kararlıdır denir.

ii) ( ,x y₀ ₀) ( , ) x y  r

eşitsizliğini sağlayan tüm ( ,x y başlangıç koşulu için, ₀ ₀)

n   iken ( ,x y_n _n)( , )x y

olacak şekilde bir r 0 sayısı varsa, (3.2.1) denklem sisteminin ( , )x y denge noktası

yerel asimptotik kararlıdır denir.

Tanım 3.2.4. (3.2.1) denklem sistemini göz önüne alalım. ( , ),x y F( , )f g fonksiyonunun bir denge noktası ve ayrıca f ve g fonksiyonları ( , )x y denge noktasında tanımlı, sürekli, diferansiyellenebilen fonksiyonlar olsun. Bu takdirde, F fonksiyonunun

( , )x y denge noktasındaki Jakobiyen matrisi

F ( , ) ( , ) ( , ) ( , ) ( , ) f f x y x y x y J x y g g x y x y x y     _ _         _ _    (3.2.2) dir.

Tanım 3.2.5. J x y_F( , ) :2 2 tanımlı, sürekli, diferansiyellenebilen ve lineer bir fonksiyon olsun. O halde

(21)

















F , , ( , )( , ) , , f f x y x x y y x y J p q x y g g x y x x y y x y      _ _          _ _    (3.2.3)

matrisine F fonksiyonunun ( , )x y denge noktasındaki lineerleştirilmesi denir.

Tanım 3.2.6. ( , ),x y F fonksiyonun denge noktası olmak üzere aşağıdaki ifadeler doğrudur.

i) Eğer J x y_F( , ) Jakobiyen matrisinin birim çember içinde kalan özdeğerleri yoksa o zaman F fonksiyonunun ( , )x y denge noktasına hiperboliktir denir.

ii) Eğer J x y_F( , ) Jakobiyen matrisinin birim çember içinde kalan en az bir tane özdeğeri varsa, o zaman F fonksiyonunun ( , )x y denge noktasına non- hiperboliktir

denir.

Teorem 3.2.1. (Lineerleştirilmiş Kararlılık Teoremi)

F=(f,g) , W   üzerinde tanımlı, sürekli, diferansiyellenebilen bir fonksiyon ve 2

( , )x y , F fonksiyonunun bir denge noktası olsun.

i) Eğer J x y_F( , ) Jakobiyen matrisinin tüm özdeğerlerinin modülü 1’den küçük ise, F fonksiyonunun ( , )x y denge noktası asimptotik kararlıdır.

ii) Eğer J x y_F( , ) Jakobiyen matrisinin özdeğerlerinden en az bir tanesinin modülü 1’den büyük ise, F fonksiyonunun ( , )x y denge noktası kararsızdır.

iii) F fonksiyonunun ( , )x y denge noktasının yerel asimptotik olması için gerek ve yeter

şart

2

F F

izJ x y( , ) detJ x y( , ) 0

    (3.2.4)

karakteristik denkleminin her çözümünün birim çember içinde kalmasıdır. Yani,

F F

iz ( , )J x y  1 detJ x y( , ) 2

(22)

iv) F fonksiyonunun ( , )x y denge noktasının repeller olması için gerek ve yeter şart

(3.2.4) karakteristik denkleminin her çözümünün birim çember dışında kalmasıdır. Yani,

F F

izJ x y( , )  1 detJ ( , )x y ve detJ_F( , )x y 1

olmasıdır.

v) F fonksiyonunun ( , )x y denge noktasının eyer noktası (saddle) olması için gerek ve

yeter koşul (3.2.4) denkleminin bir kökünün birim çemberin içinde ve bir kökünün de birim çemberin dışında kalmasıdır. Yani,

F F

izJ x y( , )  1 detJ ( , )x y ve izJ x y_F( , )24detJ x y_F( , )0

olmasıdır.

vi) F fonksiyonunun ( , )x y denge noktasının non-hiperbolik olması için gerek ve yeter

koşul (3.2.4) karakteristik denkleminin en az bir kökünün birim çember içinde kalmasıdır. Yani,

F F

izJ x y( , )  1 detJ ( , )x y veya detJ x y  ve _F( , ) 1 izJ_F( , )x y 2

olmasıdır.

3.3. Popülasyon Biyolojisinde Lineer Olmayan Fark Denklem Modelleri

Bu bölümde verilen tanım ve teoremler Keshet L. E., (2005) kitabından alınmıştır.

3.3.1. Popülasyon Yoğunluğuna Bağlı Tek Tür Modelleri

Popülasyon yoğunluğu, büyüme oranı, üreme oranı ve ölüm oranı gibi değişkenlere bağlı olsun. Bu durumda

(23)

1 ( )

t t

N_  f N (3.3.1.1)

fark denklemi popülasyon yoğunluğunu ifade eden bir modeldir. Genellikle tek bir türün popülasyon denklemi (örneğin böcekler) (3.3.1.1) denklemi gibi benzer denklemler ile tanımlanır. Burada, (f N popülasyon yoğunluğunun lineer olmayan bir _t) fonksiyonudur. _{f fonksiyonu popülasyondaki peş peşe nesillere ait veriler tarafından} elde edilir.

Tanım 3.3.1.1. ( Varley, Gradwell ve Hassel Modeli, 1973 )

 büyüme oranı, 1 N_t b





yavru döneminden yetişkinlik dönemine kadar geçen süredeki hayatta kalabilme oranı, (N_t) t nesildeki yavru sayısı ve , ,b  olmak üzere 0





1 1 b t t t N N N           (3.1.1.2)

fark denklemi Varley, Grandwell ve Hassel tarafından ortaya koyulmuştur. Bu denklemde hayatta kalanların oranı 1 ve 1’den küçük olabileceği için N_t N₀ olması biyolojik olarak mantıklıdır. (3.1.1.2) denkleminin denge noktası

(1b)

N  N







denkleminin çözümü ile bulunur. Buna göre (3.1.1.2) denkleminin denge noktasının

1 b N          (3.1.1.3) olduğu açıktır.

Teorem 3.3.1.1. (3.1.1.2) denkleminin (3.1.1.3) denge noktasında kararlı olması için gerek ve yeter şart 0  olmasıdır. b 2

Sonuç 3.3.1.1. (3.1.1.2) denkleminde b  durumunda hayatta kalabilme oranı 0 popülasyon yoğunluğuna bağlı değildir. Yani popülasyon   oranında büyür. Buna

(24)

göre b’nin kararlılık değerleri için alt sınır anlamlıdır. b  durumunda popülasyonun 2 ani artış yapabileceği potansiyeli yüzünden popülasyon kararsızdır.

Tanım 3.3.1.2. 1 Nt r K e        

 popülasyonun yoğunluğuna bağlı üreme oranı ve r K , pozitif sabitler olmak üzere,

1 1 t N r K t t N N e          (3.1.1.4)

ifadesi popülasyon biyolojisine uygulanmış bir fark denklemidir. Bu denklemin denge noktası 1 N r K N Ne        

eşitliğinden elde edilir. Açıktır ki, (3.1.1.4) denklemi N K denge noktasına sahiptir. Teorem 3.3.1.2. N K, (3.1.1.4) denkleminin denge noktası olsun. Bu takdirde (3.1.1.4) denkleminin N K denge noktasında kararlı olması için gerek ve yeter şart

0_{  olmasıdır.}r 2

Sonuç 3.3.1.2. (3.1.1.4) denklemi göz önüne alınırsa,

NK olduğu zaman üreme oranı  1

N K olduğu zaman üreme oranı  1 olduğu görülmektedir.

Tanım 3.3.1.3. , ,a b pozitif sabitler olsun. Buna göre,





1 1

b

t t t

N N aN  (3.1.1.5)

fark denklemi Hassel tarafından 1975 yılında ortaya atılmıştır. Bu denklemin denge noktası



1



b N N aN 

(25)

1 1 b N a    (3.1.1.6)

denge noktasına sahip olduğu açıktır.

Teorem 3.3.1.3. (3.1.1.5) denkleminin (3.1.1.6) denge noktasında kararlı olması için gerek ve yeter şart 0b



11b



2 olmasıdır.

3.3.2. Konak-parazit Sistemleri

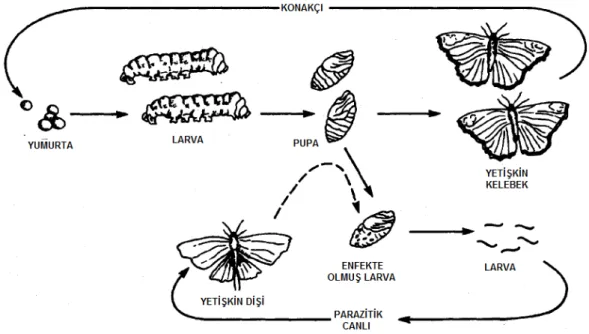
Konak-parazit modelleri en çok böcek popülasyonlarında görülmektedir. Böyle tip bir modelin bazı ayırt edici özellikleri vardır, örneğin böcekleri model alan bir sistemde, her iki türün yaşam döngüsünde de birden fazla safha bulunur. Bunlar yumurta, larva, pupa ve yetişkin dönemleridir. Parazit tür konak olan türden iki şekilde faydalanır. Parazitoit yumurtalarını konağın dış yüzeyine bırakır, bazen de larva ve pupa dönemlerinde olan konağın etenine enjekte eder. Parazitoitin yumurtalarını etene enjekte ettiği durum konağa zarar veren bir durumdur. Bu şekilde larva parazitoit gelişip büyürken konağı tüketerek öldürür. Konak-parazit sisteminin şematik gösterimi aşağıdaki şekildedir.

Şekil 3.1. Yetişkin dişi parazitoit yumurtalarını konağın üzerine ya da larva veya pupa olan konağın içine

depolar. Enfekte olan konak gelişen parazitoit yumurtasından dolayı ölür. Enfekte olmamış konak gelişerek yetişkin olur ve bir sonraki neslin konaklarını oluşturur.

(26)

Bu sistemin basit bir modeli aşağıdaki varsayımlara sahiptir;

 Paratize edilmiş konaklar, bir sonraki neslin parazitoitleri olacaklardır.  Paratize edilmemiş konaklar, kendi yavrularını oluşturacaklardır.

 Paratize edilmiş konakların oranı, iki türün karşılaşma oranına bağlıdır. Genellikle bu oran bir yada iki türün popülasyon yoğunluğuna bağlıdır.

t

N : t nesildeki konak türün yoğunluğu

t

P : t nesildeki Parazit türün yoğunluğu

( _t, )_t

f  f N P : Paratize edilmemiş konakların oranı

 : Konak türün üreme oranı

c : Parazitoitin tek bir konak üzerindeki canlı yumurta sayısı

1

t

N_ : Bir önceki nesildeki konakların sayısı × Paratize edilmemiş konakların oranı × Üreme oranı ( )

1

t

P_ : Bir önceki nesildeki paratize edilmiş konakların sayısı × Paratizoitlerin doğurtkanlık oranı (c )



1 f N P( _t, )_t



: Paratize edilmiş konakların oranı olmak üzere, 1 ( , ) t t t t N N f N P





1 1 ( , ) t t t t P_ cN  f N P

şeklindeki fark denklem sistemi konak-parazit modellerinin genel çerçevesini oluşturmaktadır.

Tanım 3.3.2.1 ( Nicholson-Bailey)

Nicholson ve Bailey, konak-parazit türlerinin karşılaşma sayısı ve paratizizm oranı hakkında şu varsayımı ileri sürmüşlerdir;

 Karşılaşma rasgele meydana gelir. Parazitoitler ile konakların karşılaşma sayısı

e

N , türlerin popülasyon yoğunluğu ile orantılıdır.

Parazitoitler ile konakların karşılaşma sayısı, a parazitoitlerin konak arama

(27)

e t t

N aN P

şeklinde ifade edilir. Av-avcı arasındaki karşılaşmalar gibi rasgele olaylar için tanımlanan olasılık dağılımı poisson dağılımıdır. Konağın yaşam süresi gibi belli bir zaman aralığında meydana gelecek olayların sayısını veren bu olasılık, poisson dağılımındaki peşpeşe terimler tarafından bulunur. Örneğin, r olayın olasılığı;

( ) ! r e P r r _  

dir. Burada  verilen zaman aralığındaki olayların ortalama sayısıdır. Konak tür ile

parazit türün karşılaşması durumunda, birim zaman başına düşen ortalama karşılaşma sayısı; e t t t t t N aP N aP N N    

olarak bulunur. Böylece, konak türün yaşam boyu parazit türle karşılaşmama olasılığı;

0 ( ) ( , ) (0) 0! t t aP aP t t t e aP f N P P e     

şeklinde elde edilir. Buradan a parazitoitlerin konak türü arama verimliliğinin

parametresi olmak üzere, Nicholson-Bailey modeli:

1 1 (1 ) t t aP t t aP t t N N e P cN e         (3.3.2.1)

şeklindedir. Bu sistemin denge noktaları,

ln ln ( , ) , ( 1) N P ac a             (3.3.2.2)

(28)

şeklindedir.

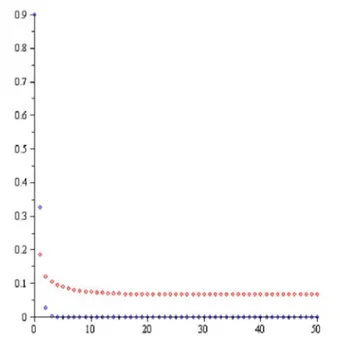
Teorem 3.3.2.1. (3.3.2.1) Nicholson-Bailey modeli, (3.3.2.2) denge noktasında kararsızdır. Bu durum aşağıdaki şekilde açıkça görülmektedir.

Şekil 3.2. Nicholson-Bailey modeli, c1, 2,a1.5

Tanım 3.3.2.2. (Modifiye Edilmiş Nicholson-Bailey Modeli)

Beddington ve ark. konak-parazit modelleri hususunda şu varsayımı ileri sürmüşlerdir;  Parazitoitlerin varlığında, konak popülasyonu belli bir yoğunluk ile sınırlı bir

biçimde büyür.

Böylece, K çevrenin taşıma kapasitesi,

1 Nt r K t N e        

 büyüme oranı olmak üzere;

1 1 1 (1 ) t t t N r aP K t t aP t t N N e P N e _ _               

şeklindeki fark denklem sistemi, Beddington ve ark. (1975) tarafından Nicholson-Bailey modelinin revise edilmesi ile elde edilmiştir. Bu sistemde P 0 olursa, konak popülasyonu N_t K yoğunluğunda büyür, eğer N_t K ise popülasyon azalır.

(29)

4. BAZI BİTKİ OTÇUL FARK DENKLEM SİSTEMLERİ

Bu bölümde, Yun Kang, Dieter Armbruster ve Yang Kuang’ın Nicholson-Bailey modeli üzerine yapmış oldukları çalışmalardan yararlanılmıştır. Buna göre,

t

P : t nesildeki yenilebilir bitki biyokütlesinin yoğunluğu

t

H : t nesildeki otçul popülasyonun yoğunluğu

( , )t

f r P : Bitki başına düşen biyokütle yoğunluğunun büyüme oranını gösteren

fonksiyon ve f r( ,0) r

( , t)

g a H : Bitki popülasyonu büyüme oranı üzerinde otçulun etkisini gösteren fonksiyon

ve g a( ,0) 1

r : Bitkinin maksimum büyüme oranını ifade eden parametre

a : Beslenme gibi otçul tarafından bitkiye verilen zararı ifade eden parametre

( )_t

h P : Popülasyonun bitki yoğunluğu fonksiyonu

( _t)

l H : Popülasyonun lineer olmayan otçul yoğunluğu fonksiyonu

olmak üzere, Kang, Armbruster ve Kuang bitki-otçul fark denklem modeli;

1 1 ( , ) ( , ) ( ) ( ) t t t t t t t P P f r P g a H H h P l H    

şeklindedir. Kang, Armbruster ve Kuang aşağıdaki varsayımlara göre;

 Popülasyonda otçul olmadan, bitki popülasyonunun biyokütlesi monoton bir şekilde arttığı düşünülür. O halde F r P , otçul tüketimi için yeni yaprakların ( , )_t miktarını belirleyici bir fonksiyondur.

 Popülasyonda otçullar bitkiyi rastgele bir biçimde arar. a otçulun tükettiği

toplam biyokütle miktarı ile bağlantılı olan sabit bir parametre olduğuna göre, otçulların ataklarından sonra bitki popülasyonundaki biyokütle _eaHt_oranında

azalacaktır. Bu durumda, ( , ) aHt t g a H e olarak alınırsa ₁ ( , ) aHt t t t P_ P f r P e şeklinde bulunur.

 Bitkilerdeki biyokütlenin, otçul biyokütlesine nasıl dönüştüğünü ifade eden ( )_t

h P fonksiyonudur. Eğer otçul bitki topraktan beslenerek büyümeden önce

(30)

edilir. Otçulun biyokütlesi yediği bitki biyokütlesi kadar olacağından, (l H _t) otçul tarafından tüketilen ( )h P oranını ifade eder. Buna göre _t ( ) 1 aHt

t

l H  e şeklinde olup, otçulun bitkilere atak yapma zamanına göre otçulun biyokütlesi,

1 1 t aH t t H_ P_ e _{ veya} ₁ ( , ) 1 aHt t t t

H_ P f r P _ e _{ olarak elde edilir.} bitki-otçul fark denklem modelini;

Model 1. Eğer otçul bitkiye, bitki topraktan beslenerek büyümeden önce atak yaparsa sistemin modeli; 1 1 ( , ) ( , ) 1 t t t aH aH t t t t aH t t P P f r P e F r P e H P e           _  _

olarak elde etmişlerdir.

Model 2. Şayet otçul bitkiye, bitki topraktan beslenerek büyüdükten sonra atak yaparsa sistemin modeli; 1 1 ( , ) ( , ) ( , ) 1 t t t aH aH t t t t aH t t t P P f r P e F r P e H P f r P e           _  _

olarak elde etmişlerdir. Bu bölümde, ( , ) ₂ 1 t t t rP F r P P   , ( , ) 1 3 t t t rP F r P P   , ( , ) 1 t t t rP F r P P     fonksiyonları göz önüne alınarak elde edilen fark denklem sistemlerinin denge noktalarının kararlılığı incelenerek, elde edilen teorik sonuçlar nümerik örneklerle desteklenmiştir. Ayrıca, Henson ve Cushing tarafından periyodikliği çalışılan ( , ) ,

1 ( 1) t t r F r P r P    ( , ) 1 ( 1) t t t rP F r P r P 

  fonksiyonları, Holling tipindeki

2 2 ( , ) 1 ( 1) t t t rP F r P r P   

fonksiyonu ve Elaydi ve Sacker tarafından çalışılan ( , )

( 1) t t t KrP F r P K r P    fonksiyonu ile elde edilen belirli fark sistemlerinin denge noktalarının da dinamikleri incelenerek, bunlarla ilgili nümerik sonuçlar grafikler ile gösterilmiştir.

(31)

4.1. ₁ ₂ - , ₁ 1 - -1 t t aH aH t t t t t rP P e H P e P      

 Fark Denklem Sistemi

Bu kısımda, P H₀, ₀  başlangıç koşulları için,

1 2 , 1 1 , 0,1,... 1 t t aH aH t t t t t rP P e H P e t P            (4.1.1)

fark denklem sisteminin kararlılığını inceleyeceğiz.

Lemma 4.1.1. r 1 olmak üzere, (4.1.1) denklem sistemi ( ,P H ) (0,0), ( ,P H)( r1,0) ve ( ,P H) ( r1,0) denge noktalarına sahiptir.

İspat. H 0 olsun. Bu takdirde Tanım 3.2.2’ den,

2 1 rP P P   3 (1 ) 0 P  r P 2 ( (1 )) 0 P P  r 

olup, buradan P ₁ 0, P₂  r1, P₃  r1 bulunur. Dolayısıyla ( ,P H ) (0,0), ( ,P H)( r1,0) ve ( ,P H) ( r1,0) denge noktaları elde edilir.

Lemma 4.1.2. r 1 olmak üzere, (4.1.1) denklem sisteminin ( ,P H ) (0,0), ( ,P H)( r1,0) ve ( ,P H) ( r1,0) denge noktalarındaki Jakobiyen matrisleri sırasıyla, F 0 (0,0) 0 0 r J _{ } _   (4.1.2) F 2 ( ) 1 ( 1,0) 0 1 r a r r J r a r                 (4.1.3) F 2 1 ( 1, 0) 0 ( ) 1 r a r r J r a r                  (4.1.4)

(32)

dir.

İspat. F( , )f g , (4.1.1) sisteminin bir fonksiyonu olsun. Buna göre,

2 ( , ) 1 aH rP f P H e P    ve ( , ) 1 aH g P H P_ e _

fonksiyonlarının kısmi türevleri





2 2 2 (1 ) ( , ) 1 aH f r P e P H P _P      _ , ( , ) ( ) 1 2 aH f rP P H a e H P       _ _     ( , ) 1 aH g P H e P     _  _  , ( , ) aH g P H aPe H    

olmak üzere, ( ,P H ) (0,0) denge noktasındaki değerleri





2 0 2 2 (1 0 ) (0,0) 1 0 a f r e r P       _ , 0 2 0 (0,0) ( ) 0 1 0 a f r a e H       _ _     0 (0,0) 1 a 0 g e P     _  _  , 0 (0,0) 0 a 0 g a e H     

bulunur. Buradan Tanım 3.2.4’e göre (4.1.1) sisteminin ( ,P H ) (0,0) denge noktasındaki Jakobiyen matrisi

F 0 (0,0) 0 0 r J _{ } _  

(33)





2 0 2 2 (1 ( 1) ) 2 ( 1,0) 1 ( 1) a f r r e r r P _r r          _ _ 0 2 1 ( 1, 0) ( ) ( ) 1 1 ( 1) a f r r r a e a r H r         _ _    _   _ 0 ( 1,0) 1 a 0 g r e P      _  _  , 0 ( 1, 0) ( 1) a 1 g r a r e a r H        

bulunur. Buradan Tanım 3.2.4’e göre (4.1.1) sisteminin ( ,P H)( r1, 0) denge noktasındaki Jakobiyen matrisi

F 2 ( ) 1 ( 1,0) 0 1 r a r r J r a r                

olarak elde edilir. Benzer şekilde ( ,P H) ( r1,0) denge noktası, elde edilen kısmi türevlerde yerine konulursa,





2 0 2 2 (1 ( 1) ) 2 ( 1,0) 1 ( 1) a f r r e r r P _r r            _{ } _ 0 2 ( 1) ( 1, 0) ( ) 1 1 ( 1) a f r r r a e a r H r           _ _   _    _ 0 ( 1,0) 1 a 0 g r e P       _  _  , 0 ( 1, 0) ( 1) a ( ) 1 g r a r e a r H           

bulunur. Buradan Tanım 3.2.4’e göre (4.1.1) sisteminin ( ,P H) ( r1,0) denge noktasındaki Jakobiyen matrisi

F 2 1 ( 1, 0) 0 ( ) 1 r a r r J r a r                 

(34)

Teorem 4.1.1. ( ,P H ) (0,0), ( ,P H)( r1,0) ve ( ,P H) ( r1,0) noktaları (4.1.1) sisteminin denge noktaları olsun. Buna göre,

(a) (4.1.1) denklem sisteminin, ( ,P H ) (0,0) denge noktası eyer noktasıdır. (b) r 1 ve 1

1

a r



 için (4.1.1) sistemi, ( ,P H)( r1, 0) denge noktasında yerel

asimptotik kararlıdır. (c) r 1 ve 1 1 a r 

 için (4.1.1) sistemi, ( ,P H) ( r1,0) denge noktasında

yerel asimptotik kararlıdır.

İspat. (a) (4.1.2) Jakobiyen matrisinin öz değerleri   ve ₁ r   olup ₂ 0

1

r  olduğundan, Teorem 3.2.1. (v)’e göre öz değerlerden birinin 1’den büyük, diğerinin 1’den küçük olmasından dolayı, (4.1.1) sisteminin ( ,P H ) (0,0) denge noktası eyer noktasıdır.

(b) 1

1

a r



 olması durumunda (4.1.3) Jakobiyen matrisinin öz değerleri 1

2 r

r

  

ve ₂a r olup, 1 r 1 olduğundan her iki öz değerde 1’den küçük olur. O halde Teorem 3.2.1. (i)’ye göre (4.1.1) sistemi, ( ,P H)( r1, 0) denge noktasında yerel asimptotik kararlıdır. (c) 1 1 a r 

 olması halinde (4.1.4) jakobiyen matrisinin öz değerleri 1

2 r

r

   ve

2 ( a) r 1

    olup, r 1 olduğundan her iki öz değerde 1’den küçük olur. O halde Teorem 3.2.1. (i)’ye göre (4.1.1) sistemi, ( ,P H) ( r1,0) denge noktasında yerel asimptotik kararlıdır.

(35)

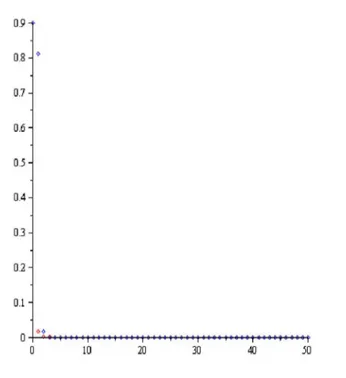
Şekil-1.1 Teorem 4.1.1 (a) şıkkı: a0.5,r1.1,P0 0.9,H0 0.9.

(36)

4.2. ₁ ₃ - , ₁ ₃ 1 - -1 1 t t aH aH t t t t t t rP rP P e H e P P      

  Fark Denklem Sistemi

Bu kısımda, P H₀, ₀  başlangıç koşulları için,

1 3 , 1 3 1 , 0,1,... 1 1 t t aH aH t t t t t t rP rP P e H e t P P             (4.2.1)

fark denklem sisteminin kararlığını inceleyeceğiz.

Lemma 4.2.1. (4.2.1) denklem sistemi ( ,P H ) (0,0) ve _{( ,}_{P H}₎_₍3 _r__1,0)_denge

noktalarına sahiptir.

İspat. H 0 olsun. Buna göre Tanım 3.2.2’ den,

3 1 rP P P   4 (1 ) 0 P  r P 3 ( (1 )) 0 P P  r  olup, buradan P ₁ 0 ve 3 2 1 P  r bulunur. Bu takdirde ( ,P H ) (0,0)_ve 3

( ,P H)( r1,0) denge noktaları elde edilir.

Lemma 4.2.2. (4.2.1) denklem sisteminin ( ,P H ) (0,0) ve _{( ,}_{P H}₎_₍3 _r__1,0)_denge

noktalarındaki Jakobiyen matrisleri sırasıyla,

F 0 (0,0) 0 0 r J _{ } _   (4.2.2) 3 3 F 3 3 2 ( ) 1 ( 1, 0) 0 1 r a r r J r a r                 (4.2.3) dir.

(37)

3 ( , ) 1 aH rP f P H e P    ve ( , ) 1 3 1 aH rP g P H e P     _  _ 





3 2 3 (1 2 ) ( , ) 1 aH f r P e P H P _P      _ , ( , ) ( ) 1 3 aH f rP P H a e H P       _ _    





3 2 3 (1 2 ) ( , ) 1 1 aH g r P P H e P _P       _  _  _ , ( , ) ₁ 3 aH g rP P H ae H P     

olmak üzere, ( ,P H ) (0,0) sıfır denge noktasındaki değerleri





3 0 2 3 (1 20 ) (0,0) 1 0 a f r e r P       _ , 0 3 0 (0,0) ( ) 0 1 0 a f r a e H       _ _    





3 0 2 3 (1 20 ) (0,0) 1 0 1 0 a g r e P       _  _  _ , 0 3 0 (0,0) 0 1 0 a g r ae H      _ _    

F 0 (0,0) 0 0 r J _{ } _  

olarak elde edilir. _{( ,}_{P H}₎_₍3 _r__1,0)_{denge noktası için ise,}





3 0 3 3 2 3 3 (1 2( 1) ) 3 2 ( 1,0) 1 ( 1) a f r r e r r P _r r          _ _ 3 0 3 3 3 3 1 ( 1, 0) ( ) ( ) 1 1 ( 1) a f r r r a e a r H r         _ _    _   _

(38)













3 3 0 3 2 3 3 (1 2 1 ) ( 1,0) 1 0 1 1 a r r g r e P r         _  _    3 0 3 3 3 3 1 ( 1,0) 1 1 ( 1) a g r r r ae a r H r        _ _   _   _

bulunur. Buradan Tanım 3.2.4’e göre (4.2.1) sisteminin 3

( ,P H)( r1, 0) denge noktasındaki Jakobiyen matrisi

3 3 F 3 3 2 ( ) 1 ( 1, 0) 0 1 r a r r J r a r                

olarak elde edilir.

Teorem 4.2.1. ( ,P H ) (0,0)_ve_{( ,}_{P H}₎_₍3_r__1,0)_{(4.2.1) sisteminin denge noktaları}

olsun. Buna göre,

(a) 0  için, (4.2.1) denklem sistemi r 1 ( ,P H ) (0,0) denge noktasında yerel asimptotik kararlıdır. (b) 1r3 ve 3 1 1 a r   için, (4.2.1) sistemi 3 ( ,P H)( r1, 0) denge noktasında yerel asimptotik kararlıdır.

(c) r 3 ve 3 1 1 a r   için, (4.2.1) sisteminin 3

( ,P H)( r1, 0) denge noktası eyer noktasıdır. (d) r 3 ve 3 1 1 a r   için, (4.2.1) sistemi 3 ( ,P H)( r1, 0) denge noktasında kararsızdır.

İspat. (a) 0  olması durumunda (4.2.2) Jakobiyen matrisinin öz değerleri r 1   ₁ r

ve   olup, her iki öz değerde 1’den küçük olur. O halde Teorem 3.2.1. (i)’ye göre ₂ 0

(39)

(b) 1r3 ve 3 1 1 a r 

 olması durumunda, (4.2.3) Jakobiyen matrisinin öz değerleri

1

3 2r

r

   ve 3

2 a r 1

   olup her iki öz değerde 1’den küçük olur. O halde Teorem 3.2.1. (i)’ye göre, (4.2.1) sistemi 3

( ,P H)( r1, 0) denge noktasında yerel asimptotik kararlıdır. (c) r 3 ve 3 1 1 a r 

1

3 2r

r

   ve ₂ a r3  olup, öz değerlerden biri 1’den küçük, diğeri 1’den büyük 1 olur. O halde Teorem 3.2.1. (v)’ye göre, (4.2.1) sisteminin 3

( ,P H)( r1, 0) denge noktası eyer noktasıdır.

(d) r 3 ve 3 1 1 a r 

1

3 2r

r

   ve 3

2 a r 1

   olup, her iki öz değerde 1’den büyük olur. O halde Teorem 3.2.1. (ii)’ye göre, (4.2.1) sistemi 3

( ,P H)( r1, 0) denge noktasında kararsızdır.

(40)

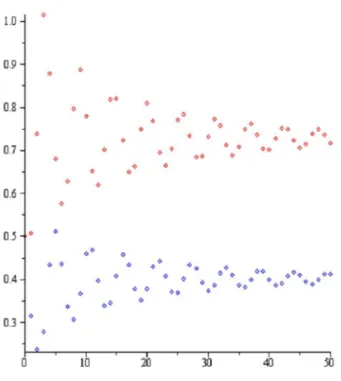
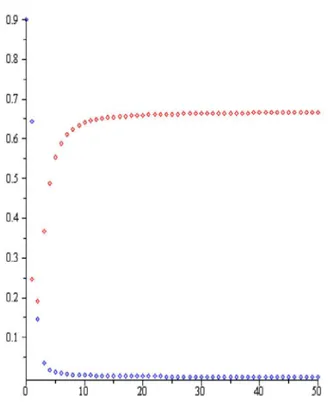
Şekil 2.2. Teorem 4.2.1. (b) şıkkı: a2.14,r1.1,P0 0.5,H0 0.5.

(41)

(42)

4.3. ₁ - , ₁ 1 - -1   t t aH aH t t t t t rP P e H P e P      

 Fark Denklem Sistemi

Bu kısımda, P H₀, ₀  başlangıç koşulları için, 

1 , 1 1 , 0,1,... 1 t t aH aH t t t t t rP P e H P e t P         _  _   (4.3.1)

fark denklem sisteminin kararlığını inceleyeceğiz.

Lemma 4.3.1. (4.3.1) denklem sistemi ( ,P H ) (0,0) ve ( ,P H) r 1,0

         denge noktalarına sahiptir.

İspat. H 0 olsun. Buna göre Tanım 3.2.2’ den,

1 rP P P     2 (1 ) 0 P r P     ( (1 )) 0 P P r  olup, buradan P ₁ 0 ve P₂ r 1    bulunur. Bu takdirde ( ,P H ) (0,0) ve 1 ( ,P H) r ,0         

denge noktaları elde edilir.

Lemma 4.3.1. (4.3.1) denklem sisteminin ( ,P H ) (0,0) ve ( ,P H) r 1,0



  

  

 

denge noktalarındaki Jakobiyen matrisleri sırasıyla,

F 0 (0,0) 0 0 r J _{ } _   (4.3.2) F 1 1 ( ) 1 ,0 1 0 r a r r J r a     _             _  _    _ _       _ _        (4.3.3)

(43)

dir .

İspat. F( , )f g , (4.3.1) sisteminin bir fonksiyonu olsun. Buna göre,

( , ) 1 aH rP f P H e P      ve ( , ) 1 aH g P H P_ e _





2 ( , ) 1 aH f re P H P _P     _   , ( , ) ( ) 1 aH f rP P H a e H P       _ _  _  _   ( , ) 1 aH g P H e P     _  _  , ( , ) aH g P H aPe H    

olmak üzere, ( ,P H ) (0,0) denge noktasındaki değerleri





0 2 (0,0) 1 0 a f re r P          , 0 0 (0, 0) ( ) 0 1 0 a f r a e H         _ _  _  _ 0 (0,0) 1 a 0 g e P     _  _  , 0 (0,0) a 0 0 g ae H     

F 0 (0,0) 0 0 r J _{ } _  

olarak elde edilir. ( ,P H) r 1,0



  

  

 

(44)

0 2 1 1 ,0 1 1 a f r re P _r r    _             _ _ _ _ _     





0 1 1 1 ,0 ( ) 1 1 a r r f r r a e a H r                           _ _ _ _        _ _    _ _    _ _         0 1 ,0 1 a 0 g r e P                    , g r 1_,0 a0 r 1 ae H                   _ _ _ _

bulunur. Buradan Tanım 3.2.4’e göre, (4.3.1) sisteminin ( ,P H) r 1,0 

  

  

 

denge noktasındaki Jakobiyen matrisi

F 1 1 ( ) 1 ,0 1 0 r a r r J r a     _             _  _    _ _       _ _       

olarak elde edilir.

Teorem 4.3.1. ( ,P H ) (0,0) ve ( ,P H) r 1,0 ,          (4.3.1) sisteminin denge noktaları olsun. Buna göre,

(a)   ve 0 r 1 

 için, (4.3.1) denklem sistemi ( ,P H ) (0,0) denge noktasında yerel asimptotik kararlıdır.

(b)   ve 0 r 1



 için, (4.3.1) denklem sisteminin ( ,P H ) (0,0) denge noktası eyer noktasıdır. (c)  0,   , 0 r 1   ve 1 a r     için, (4.3.1) sistemi 1 ( ,P H) r ,0          denge noktasında yerel asimptotik kararlıdır.

(45)

(d)  0,  0, r 1   ve 1 a r     için, (4.3.1) sisteminin 1 ( ,P H) r ,0         

denge noktası eyer noktasıdır. (e)  0,   , 0 r 1   ve 1 a r     için, (4.3.1) sistemi 1 ( ,P H) r ,0          denge noktasında kararsızdır. İspat. (a)   ve 0 r 1 

 olması durumunda, (4.3.2) Jakobiyen matrisinin öz değerleri

1 r

  ve   olup, her iki öz değerde 1’den küçük olur. O halde Teorem 3.2.1. ₂ 0 (i)’ye göre, (4.3.1) sistemi ( ,P H ) (0,0) denge noktasında yerel asimptotik kararlıdır.

(b)   ve 0 r 1



 olması durumunda, (4.3.2) Jakobiyen matrisinin öz değerleri

1 r

  ve   olup, öz değerlerden biri 1’den küçük, diğeri 1’den büyük olur. O ₂ 0 halde Teorem 3.2.1. (v)’ye göre, (4.3.1) sisteminin ( ,P H ) (0,0) denge noktası eyer noktasıdır. (c)  0_, 0_,r 1   ve 1 a r   