Self-consistent theory of localization and Coulomb drag effect
B. TanatarDepartment of Physics, Bilkent University, Bilkent, 06533 Ankara, Turkey A. K. Das
Department of Physics, Dalhousie University, Halifax, Nova Scotia, B3H 3J5, Canada 共Received 3 January 2000兲
We study the Coulomb drag rate for electrons in a double-quantum-well structure in the presence of disorder. The self-consistent theory of localization is used to obtain the frequency dependence of the general-ized diffusion coefficient which influences the response functions. The interplay between screening effects and disorder at low temperature gives rise to an enhanced drag rate as the system goes from a weakly localized to a strongly localized phase with increasing disorder. The change in the interlayer momentum transfer rate may be used as a probe to investigate localization properties of coupled quantum-well systems.
I. INTRODUCTION
There has been extensive theoretical and experimental ac-tivity centered around the frictional drag in coupled quantum-well systems in recent years.1 The so-called drag effect originates2,3in the interlayer Coulomb interactions be-tween two spatially separated electron systems. When a cur-rent I is allowed to pass in only one of the layers, the charge carriers in the second layer are dragged due to the momen-tum transfer process. Here the distance between the layers is large enough so that tunneling effects are not significant. A drag voltage VD is measured under the condition that no current flows in this second layer. Thus, the transresistance
⫽VD/I, or the drag rate drag⫺1⫽ne2/m*, probe the Cou-lomb interaction effects in double-layer electron systems in a transport experiment. The drag effect has been studied ex-perimentally in a variety of setups in which the charge car-riers in the quantum wells are electrons, holes, or one of each.4–9The theoretical efforts have concentrated on calcu-lating the momentum transfer rate due to different mecha-nisms within many-body theory.10–15
In this paper, we study the effects of disorder on the Cou-lomb drag rate in coupled quantum wells in the low tempera-ture regime. In particular, we investigate the changes occur-ring in the drag rate as the system evolves from a weakly disordered metallic state to a strongly disordered insulating state 共Mott insulator兲. There are several motivations for in-vestigating the disorder effects. The issue of localization in two-dimensional共2D兲 disordered electron systems is receiv-ing a renewed interest both experimentally and theoretically16,17due to the intricate interplay between disor-der and interaction effects. In our work we considisor-der only disorder-induced localization and the metal-insulator transi-tion, but not interaction-induced localization effects. Our dis-order is due to nonmagnetic impurities. The experimental results seem to be in agreement with the picture that a me-tallic phase for weak disorder and an insulating phase for strong disorder exist for an interacting two-dimensional elec-tron gas.18The effects of disorder on the Coulomb drag rate for a double-layer system were first considered by Zheng and MacDonald,10 who included disorder in the single-layer
density-density response function in the diffusive domain with a constant diffusion coefficient. For a coupled quantum-wire system we have recently shown19that the drag rate has a nonmonotonic dependence on the amount of disorder. These works are concerned with the metallic phase for weak disorder. Shimshoni20 has suggested that the Coulomb drag rate in double-layer systems offers a possible probe to study the insulating phase for strong disorder. The drag rate is expected to be enhanced at the onset of a metal-insulator transition due to the role played by density fluctuations in both the processes. In the work on coupled quantum-wire systems we used the density-density response function in a number-conserving approximation in order to include weak disorder. This approximation is valid for ranges of q andat the level of the random-phase approximation共RPA兲, but it is not clear if it can account for strong disorder. The latter is the focus of the work presented here. To this end we have used the density-density response function calculated by Vollhardt and Wo¨lfle21,22in a self-consistent scheme that is capable of treating strong disorder. The expression for the single-layer polarizability (q,) that we use is obtained in a general-ized diffusion-pole approximation which is limited to small q and 共i.e., qⰆkF andⰆEF). However, the diffusion co-efficient D() in this calculation is more general than the constant diffusion coefficient used earlier by Zheng and MacDonald10 and by us in our work on quantum-wire systems.19 We determine D() numerically in a self-consistent manner according to the scheme discussed by Vollhardt and Wo¨lfle.22 We employ this self-consistent theory of localization22–24 to obtain a frequency-dependent diffusion coefficient D() in the same spirit. The self-consistent theory of localization has proved useful in predict-ing the same results as the scalpredict-ing theory of localization when the interaction effects are ignored.24
The rest of the paper is organized as follows. We outline the calculation of the total drag rate in terms of contributions from the ballistic and diffusive regimes in Sec. II. The frequency-dependent diffusion coefficient within the self-consistent theory of localization is also introduced. In Sec. III we present our results and discuss the possibility of using drag experiments to probe the transition to an insulating PRB 61
phase in double-layer systems. We also present an estimate of some physical quantities and compare them with existing experimental results.
II. THEORY
We consider two parallel quantum wells of negligible thickness separated by a distance d, which is assumed to be large enough so that interlayer tunneling can be neglected. The bare Coulomb interaction between the electrons is given by Vi j(q)⫽(2e2/⑀0)e⫺qd(1⫺␦i j), in which i and j label the layers, and⑀0is the background dielectric constant. The two-dimensional electron density n is related to the Fermi wave vector by n⫽kF
2
/2. We shall use the dimensionless electron gas parameter rs⫽
冑
2/(kFaB*), in which aB*⫽⑀0/(e2m*) isthe effective Bohr radius in the semiconducting layer with background dielectric constant ⑀0 and electron effective mass m*.
The Coulomb drag rate for double-layer systems has been derived through a variety of theoretical approaches10–15共see also Ref. 1 for a recent review兲. We adopt the expression given by Zheng and MacDonald.10 For simplicity and with-out loss of generality, we consider the same electron density in both the layers. The drag rate is given by
drag⫺1⫽ 1 22m*nT
冕
0 ⬁ dq q3冕
0 ⬁ d冏
W12共q,兲Im共q,兲 sinh共/2T兲冏
2 , 共1兲 where we have assumedប and kB⫽1.drag⫺1 measures the rate of momentum transferred from one quantum well to the other, and includes the drag rate in the ballistic and diffusive regimes 共see below兲. Here, (q,) is the 2D dynamic sus-ceptibility, describing the density-density response function of a single-layer electron system. W12(q,) is thedynami-cally screened effective interaction between electrons in quantum wells 1 and 2. Within the random-phase approxi-mation, it is given by W12(q,)⫽V12(q)/(q,), where
(q,)⫽关1⫺V11(q)(q,)兴2⫺关V12(q)(q,)兴2 is the
screening function for the coupled quantum-well system, which uses the bare intra- and interlayer electron-electron interactions 共ignoring the correlation effects兲. Recent nu-merical calculations15 and experimental results9point to the importance of correlations in coupled quantum-well systems, especially in the high temperature regime, viz., T/EF⬃0.5.
In this work, we retain the wave vector, frequency, disor-der, and temperature dependence of the dynamic susceptibil-ity (q,) that enters the drag rate expression 关Eq. 共1兲兴 as well as the screening function (q,). We account for dis-order by considering an impurity scattering induced damping
␥(⫽1/) which may be regarded as a phenomenological parameter. Here, is an intralayer共transport兲 scattering time for electrons, which may be related to the mobility through
⫽e/m*. The 2D dynamical susceptibility is taken to be the noninteracting disorder-free response function in the bal-listic regime in which the disorder effects are not thought to be important, i.e., for ql⬎1 and /␥⬎1, where l ⫽kF/␥m*is the mean free path. In the diffusive regime, the response function is characterized by the generalized diffu-sion coefficient21,22
D共q,兲⫽N F
D共q,兲q2
D共q,兲q2⫺i, 共2兲 where D(q,) reduces to the commonly used diffusion co-efficient D0⫽l2␥/2 in the limit ql⬍1 and /␥⬍1. In our
work we go beyond a previously used10 constant diffusion coefficient, and consider a D() that retains the full fre-quency dependence within the self-consistent theory of localization,22 the latter being based on a diagrammatic analysis. D() is obtained from the solution of a self-consistent equation21,22 D0 D共兲 ⫽1⫹ 1 NF
兺
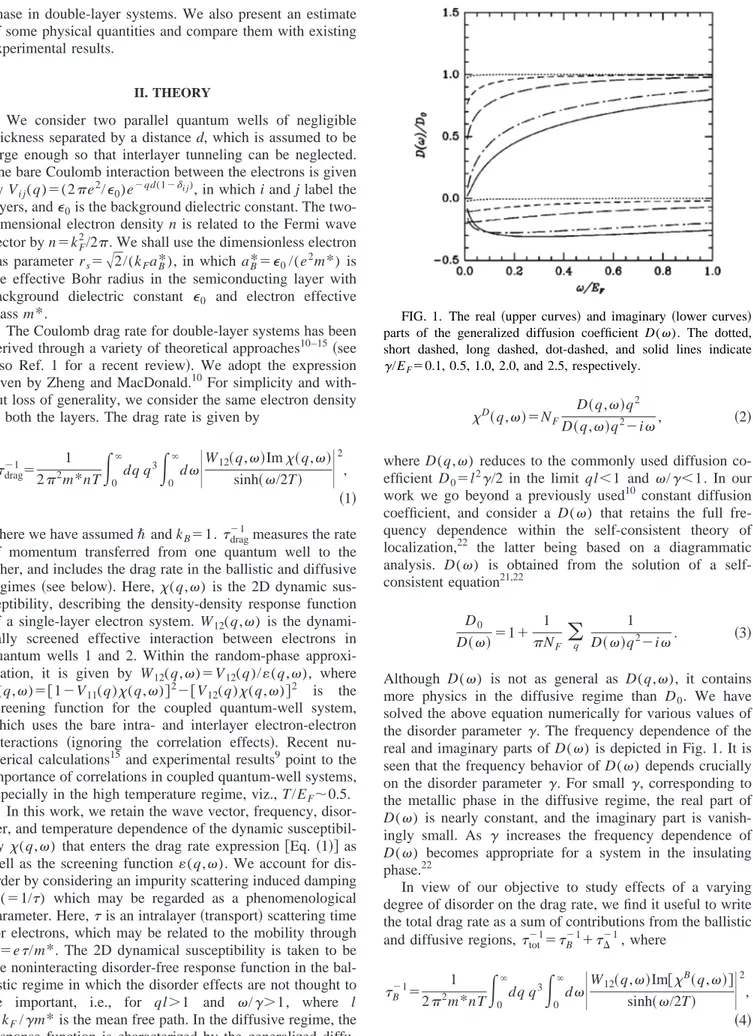
q 1 D共兲q2⫺i. 共3兲 Although D() is not as general as D(q,), it contains more physics in the diffusive regime than D0. We havesolved the above equation numerically for various values of the disorder parameter ␥. The frequency dependence of the real and imaginary parts of D() is depicted in Fig. 1. It is seen that the frequency behavior of D() depends crucially on the disorder parameter ␥. For small␥, corresponding to the metallic phase in the diffusive regime, the real part of D() is nearly constant, and the imaginary part is vanish-ingly small. As ␥ increases the frequency dependence of D() becomes appropriate for a system in the insulating phase.22
In view of our objective to study effects of a varying degree of disorder on the drag rate, we find it useful to write the total drag rate as a sum of contributions from the ballistic and diffusive regions,tot⫺1⫽B⫺1⫹⌬⫺1, where
B⫺1⫽ 1 22m*nT
冕
0 ⬁ dq q3冕
0 ⬁ d冏
W12共q,兲Im关 B共q,兲兴 sinh共/2T兲冏
2 , 共4兲 andFIG. 1. The real 共upper curves兲 and imaginary 共lower curves兲
parts of the generalized diffusion coefficient D(). The dotted, short dashed, long dashed, dot-dashed, and solid lines indicate
⌬⫺1⫽D⫺1⫺ 1 22m*nT
冕
0 1/l dq q3 ⫻冕
0 ␥ d冏
W12共q,兲Im关 B共q,兲兴 sinh共/2T兲冏
2 , 共5兲 with D⫺1⫽ 1 22m*nT冕
0 1/l dq q3 ⫻冕
0 ␥ d冏
W12共q,兲Im关 D共q,兲兴 sinh共/2T兲冏
2 . 共6兲The above decomposition, previously given by Zheng and MacDonald,10expresses the total drag rate as the sum of the disorder-free contributionB⫺1and the correction⌬⫺1 due to disorder-enhanced fluctuations. In Eqs.共4兲 and 共5兲,B(q,) is the disorder-free RPA polarizability of a single-layer elec-tron gas. InD(q,), effects of disorder have been included through the frequency-dependent diffusion coefficient D(). For small values of␥ the system may be considered to be in a weak localization 共or metallic兲 state for which D() re-duces to D0. We would like to mention that disorder in the
drag effect has also been considered19 through a simple number-conserving relaxation-time approximation which gives the response function as
␥共q,兲⫽⫹i共␥⫹i共q,␥兲共q,⫹i␥⫹i兲/␥共q,0兲兲 . 共7兲
This reduces to the well-known diffusion pole which is Eq. 共2兲 with D0 in the regime ql⬍1 and/␥⬍1. Equation 共2兲
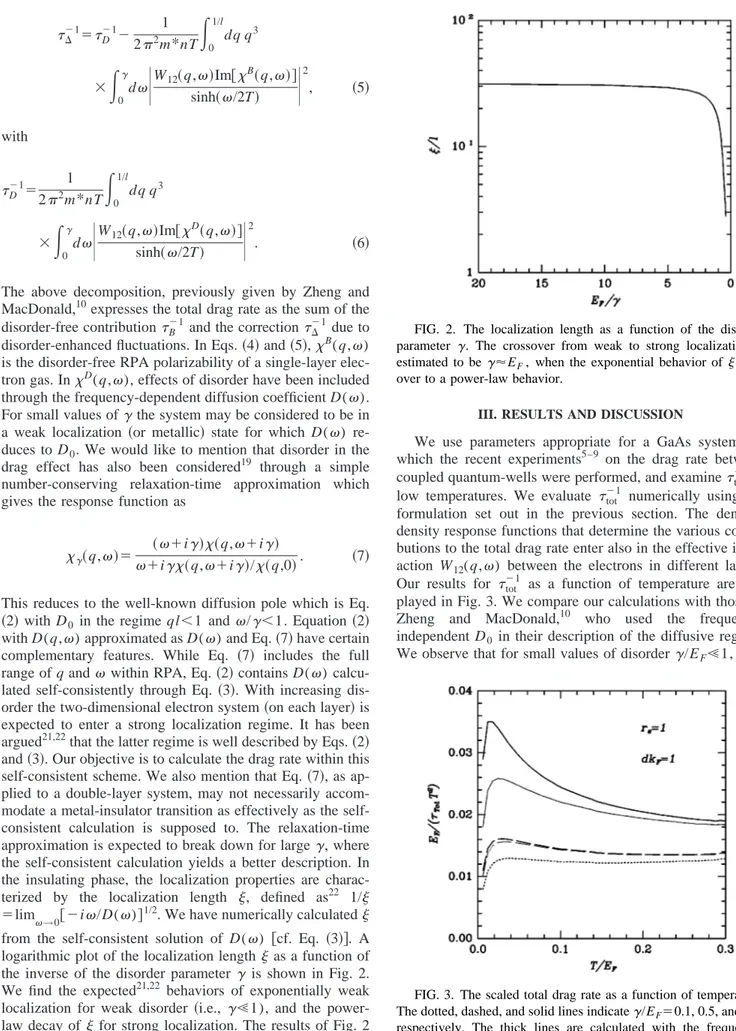
with D(q,) approximated as D() and Eq.共7兲 have certain complementary features. While Eq. 共7兲 includes the full range of q and within RPA, Eq.共2兲 contains D() calcu-lated self-consistently through Eq. 共3兲. With increasing dis-order the two-dimensional electron system共on each layer兲 is expected to enter a strong localization regime. It has been argued21,22that the latter regime is well described by Eqs.共2兲 and共3兲. Our objective is to calculate the drag rate within this self-consistent scheme. We also mention that Eq.共7兲, as ap-plied to a double-layer system, may not necessarily accom-modate a metal-insulator transition as effectively as the self-consistent calculation is supposed to. The relaxation-time approximation is expected to break down for large␥, where the self-consistent calculation yields a better description. In the insulating phase, the localization properties are charac-terized by the localization length , defined as22 1/ ⫽lim→0关⫺i/D()兴1/2. We have numerically calculated from the self-consistent solution of D() 关cf. Eq. 共3兲兴. A logarithmic plot of the localization length as a function of the inverse of the disorder parameter ␥ is shown in Fig. 2. We find the expected21,22 behaviors of exponentially weak localization for weak disorder 共i.e., ␥Ⰶ1), and the power-law decay of for strong localization. The results of Fig. 2 suggest that weak to strong localization crossover occurs around␥⯝EF.
III. RESULTS AND DISCUSSION
We use parameters appropriate for a GaAs system for which the recent experiments5–9 on the drag rate between coupled quantum-wells were performed, and examinetot⫺1at low temperatures. We evaluate tot⫺1 numerically using the formulation set out in the previous section. The density-density response functions that determine the various contri-butions to the total drag rate enter also in the effective inter-action W12(q,) between the electrons in different layers.
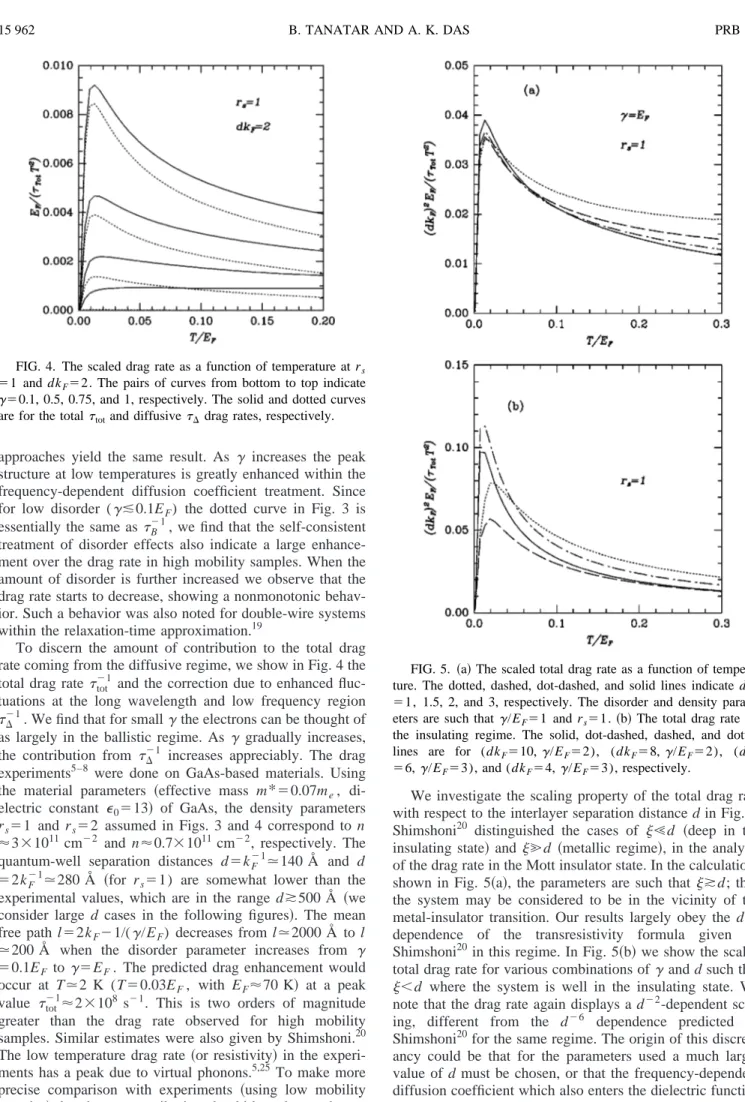
Our results for tot⫺1 as a function of temperature are dis-played in Fig. 3. We compare our calculations with those of Zheng and MacDonald,10 who used the frequency-independent D0 in their description of the diffusive regime. We observe that for small values of disorder ␥/EFⰆ1, both
FIG. 2. The localization length as a function of the disorder
parameter ␥. The crossover from weak to strong localization is
estimated to be ␥⬇EF, when the exponential behavior of goes
over to a power-law behavior.
FIG. 3. The scaled total drag rate as a function of temperature. The dotted, dashed, and solid lines indicate␥/EF⫽0.1, 0.5, and 1.0,
respectively. The thick lines are calculated with the frequency-dependent diffusion coefficient D(), whereas for the thin lines the frequency-independent D0is used.
approaches yield the same result. As ␥ increases the peak structure at low temperatures is greatly enhanced within the frequency-dependent diffusion coefficient treatment. Since for low disorder (␥ⱗ0.1EF) the dotted curve in Fig. 3 is essentially the same as B⫺1, we find that the self-consistent treatment of disorder effects also indicate a large enhance-ment over the drag rate in high mobility samples. When the amount of disorder is further increased we observe that the drag rate starts to decrease, showing a nonmonotonic behav-ior. Such a behavior was also noted for double-wire systems within the relaxation-time approximation.19
To discern the amount of contribution to the total drag rate coming from the diffusive regime, we show in Fig. 4 the total drag ratetot⫺1 and the correction due to enhanced fluc-tuations at the long wavelength and low frequency region
⌬⫺1. We find that for small␥the electrons can be thought of
as largely in the ballistic regime. As ␥ gradually increases, the contribution from ⌬⫺1 increases appreciably. The drag experiments5–8 were done on GaAs-based materials. Using the material parameters 共effective mass m*⫽0.07me, di-electric constant ⑀0⫽13兲 of GaAs, the density parameters rs⫽1 and rs⫽2 assumed in Figs. 3 and 4 correspond to n ⬇3⫻1011 cm⫺2 and n⬇0.7⫻1011cm⫺2, respectively. The
quantum-well separation distances d⫽kF⫺1⯝140 Å and d ⫽2kF⫺1⯝280 Å 共for rs⫽1) are somewhat lower than the experimental values, which are in the range dⲏ500 Å 共we consider large d cases in the following figures兲. The mean free path l⫽2kF⫺1/(␥/EF) decreases from l⯝2000 Å to l ⯝200 Å when the disorder parameter increases from ␥
⫽0.1EF to␥⫽EF. The predicted drag enhancement would occur at T⯝2 K (T⫽0.03EF, with EF⬇70 K兲 at a peak value tot⫺1⬇2⫻108 s⫺1. This is two orders of magnitude greater than the drag rate observed for high mobility samples. Similar estimates were also given by Shimshoni.20 The low temperature drag rate共or resistivity兲 in the experi-ments has a peak due to virtual phonons.5,25To make more precise comparison with experiments 共using low mobility samples兲 the phonon contribution should be subtracted out.
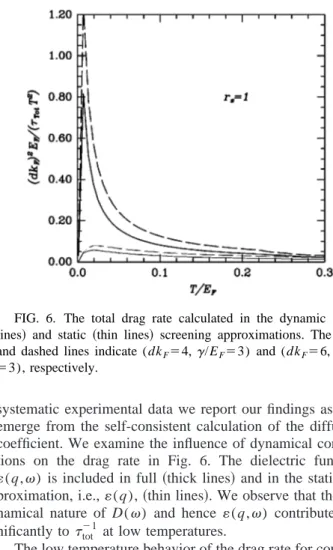
We investigate the scaling property of the total drag rate with respect to the interlayer separation distance d in Fig. 5. Shimshoni20 distinguished the cases of Ⰶd 共deep in the insulating state兲 and Ⰷd 共metallic regime兲, in the analysis of the drag rate in the Mott insulator state. In the calculations shown in Fig. 5共a兲, the parameters are such thatⲏd; thus the system may be considered to be in the vicinity of the metal-insulator transition. Our results largely obey the d⫺2 dependence of the transresistivity formula given by Shimshoni20in this regime. In Fig. 5共b兲 we show the scaled total drag rate for various combinations of␥ and d such that
⬍d where the system is well in the insulating state. We note that the drag rate again displays a d⫺2-dependent scal-ing, different from the d⫺6 dependence predicted by Shimshoni20for the same regime. The origin of this discrep-ancy could be that for the parameters used a much larger value of d must be chosen, or that the frequency-dependent diffusion coefficient which also enters the dielectric function in W12(q,) alters the d dependence. In the absence of any FIG. 4. The scaled drag rate as a function of temperature at rs
⫽1 and dkF⫽2. The pairs of curves from bottom to top indicate
␥⫽0.1, 0.5, 0.75, and 1, respectively. The solid and dotted curves are for the totaltotand diffusive⌬drag rates, respectively.
FIG. 5. 共a兲 The scaled total drag rate as a function of tempera-ture. The dotted, dashed, dot-dashed, and solid lines indicate dkF
⫽1, 1.5, 2, and 3, respectively. The disorder and density param-eters are such that ␥/EF⫽1 and rs⫽1. 共b兲 The total drag rate for
the insulating regime. The solid, dot-dashed, dashed, and dotted
lines are for (dkF⫽10,␥/EF⫽2), (dkF⫽8,␥/EF⫽2), (dkF
systematic experimental data we report our findings as they emerge from the self-consistent calculation of the diffusion coefficient. We examine the influence of dynamical correla-tions on the drag rate in Fig. 6. The dielectric function (q,) is included in full 共thick lines兲 and in the static ap-proximation, i.e.,(q), 共thin lines兲. We observe that the dy-namical nature of D() and hence (q,) contribute sig-nificantly totot⫺1 at low temperatures.
The low temperature behavior of the drag rate for coupled quantum wells has been considered by many researchers. Zheng and MacDonald10 split the contributions of ballistic and diffusive regimes and calculated the correction to the interlayer scattering rate due to disorder-enhanced interac-tions. Our work is similar in spirit, except we include the frequency dependence of the diffusion coefficient. The same enhancement in the drag resistivity was also predicted by Kamenev and Oreg14 using diagrammatic perturbation theory. Gornyi, Yashenkin, and Khveshchenko26studied the effects of correlated disorder in the form of an impurity po-tential in the barrier region between the quantum wells. Such an approach would be relevant to the actual systems if con-trolled experiments can be performed. In a recent paper, Shimshoni20considered the Coulomb drag between two par-allel layers in the Anderson insulating state, examining the Mott and Efros-Shklovskii types separately. In the analysis, Shimshoni20found thatDis suppressed for a Mott insulator with decreasing localization length共i.e., increasing disorder兲. In all these attempts the disorder has the effect of enhancing
drag⫺1 共ortot⫺1) or the transresistance as a function of T for
low to moderate disorder while suppressing drag⫺1 for large disorder. In a Boltzmann-theory-based calculation of the drag rate Flensberg and Hu13 found that charged impurities located a distance s away from the quantum wells influenced
D⫺1 significantly for sⱗ400 Å. Classical simulations to de-termine the influence of ionized impurities on Coulomb drag have also been performed.27Our calculations indicate similar qualitative results without specifying the nature of disorder. We also point out that disorder effects in Coulomb drag problems are gaining attention recently in a variety of related contexts.28
As the electron density is decreased the exchange-correlation effects become significant and the RPA we adopt will be less satisfactory. In studies of drag resistivity and drag rate in double-layer systems it has been found important to include correlation effects beyond those described by the RPA to improve agreement with experimental data at low densities.15 In this work, we have kept the electron gas pa-rameter low (rs⫽1) so that the RPA should be adequate. The interplay between the disorder and correlation effects would have to be taken into account in a more consistent and systematic viewpoint for larger rs values. The interaction effects on the Anderson transition in disordered systems have been discussed by Sadovskii.29
In summary, we have considered the Coulomb drag effect between two parallel quantum wells in the presence of dis-order treated phenomenologically. The temperature depen-dence of the drag rate is known to be significantly enhanced with increasing disorder as the system evolves from a metal-lic state toward an insulating state. Using the self-consistent theory of localization to deduce the frequency dependence of the diffusion coefficient, we account for the influence of dis-order on the density-density correlation function. We find that for small␥ the drag rate is further increased. For larger values of ␥, the density fluctuations are suppressed with a reduced localization length and the drag rate is reduced. Thus, the drag rate drag⫺1 exhibits a nonmonotonic behavior with respect to the strength of disorder, and may be used as a possible probe to understand the localization properties in Coulomb coupled systems. A systematic experimental study with varying degrees of disorder using low mobility samples should be able to test some of our predictions.
ACKNOWLEDGMENTS
This work is partially supported by the Scientific and Technical Research Council of Turkey 共TUBITAK兲 under Grant No. TBAG-1662 and NATO under Grant No. SfP971970. We thank Professor M. V. Sadovskii and Profes-sor I. O. Kulik for fruitful discussions.
1The field was reviewed recently by A.G. Rojo, J. Phys.: Condens.
Matter 11, R31共1999兲.
2M.B. Pogrebinskii, Fiz. Tekh. Poluprovodn. 11, 637共1977兲 关 Sov.
Phys. Semicond. 11, 372共1977兲兴.
3P.J. Price, Physica B & C 117, 750共1983兲.
4P.M. Solomon, P.J. Price, D.J. Frank, and D.C. La Tulipe, Phys.
Rev. Lett. 63, 2508共1989兲.
5T.J. Gramila, J.P. Eisenstein, A.H. MacDonald, L.N. Pfeiffer, and
K.W. West, Phys. Rev. Lett. 66, 1216共1991兲; Phys. Rev. B 47, 12 957共1993兲.
6U. Sivan, P.M. Solomon, and H. Shtrikman, Phys. Rev. Lett. 68,
1196共1992兲.
FIG. 6. The total drag rate calculated in the dynamic 共thick
lines兲 and static 共thin lines兲 screening approximations. The solid and dashed lines indicate (dkF⫽4,␥/EF⫽3) and (dkF⫽6,␥/EF
7H. Rubel, E.H. Linfield, D.A. Ritchie, K.M. Brown, M. Pepper,
and G.A.C. Jones, Semicond. Sci. Technol. 10, 1229共1995兲.
8N.P.R. Hill, J.T. Nicholls, E.H. Linfield, M. Pepper, D.A. Ritchie,
G.A.C. Jones, B.Y.-K. Hu, and K. Flensberg, Phys. Rev. Lett. 78, 2204共1997兲.
9H. Noh, S. Zelakiewicz, X.G. Feng, T.J. Gramila, L.N. Pfeiffer,
and K.W. West, Phys. Rev. B 58, 12 621共1998兲.
10L. Zheng and A.H. MacDonald, Phys. Rev. B 48, 8203共1993兲. 11A.-P. Jauho and H. Smith, Phys. Rev. B 47, 4420共1993兲. 12H.C. Tso, P. Vasilopoulos, and F.M. Peeters, Phys. Rev. Lett. 68,
2516共1992兲; 70, 2146 共1993兲.
13K. Flensberg and B.Y.-K. Hu, Phys. Rev. Lett. 73, 3572共1994兲;
Phys. Rev. B 52, 14 796共1995兲.
14A. Kamenev and Y. Oreg, Phys. Rev. B 52, 7516共1995兲; K.
Flensberg, B.Y.-K. Hu, A.-P. Jauho, and J.M. Kinaret, ibid. 52, 14 761共1995兲.
15L. S´wierkowski, J. Szyman´ski, and Z.W. Gortel, Phys. Rev. B 55,
2280共1997兲; Phys. Rev. Lett. 74, 3245 共1995兲.
16S.V. Kravchenko, G.V. Kravchenko, J.E. Furneaux, V.M.
Pu-dalov, and M. D’Iorio, Phys. Rev. B 50, 8039共1994兲; D. Pop-ovic´, A.B. Fowler, and S. Washburn, Phys. Rev. Lett. 79, 1543 共1997兲.
17C. Castellani, C. Di Castro, and P.A. Lee, Phys. Rev. B 57, 9381
共1998兲; Q. Si and C.M. Varma, Phys. Rev. Lett. 81, 4951
共1998兲; D. Belitz and T.R. Kirkpatrick, Phys. Rev. B 58, 8214 共1998兲.
18A. Gold and W. Go¨tze, Phys. Rev. B 33, 2495共1986兲. 19B. Tanatar, Phys. Rev. B 58, 1154共1998兲.
20E. Shimshoni, Phys. Rev. B 56, 13 301共1997兲.
21D. Vollhardt and P. Wo¨lfle, Phys. Rev. B 22, 4666共1980兲; Phys.
Rev. Lett. 48, 699共1982兲.
22D. Vollhardt and P. Wo¨lfle, in Electronic Phase Transitions,
ed-ited by W. Hanke and Yu.V. Kopaev共North-Holland, Amster-dam, 1990兲.
23
W. Go¨tze, Philos. Mag. B 43, 219共1981兲.
24P.A. Lee and T.V. Ramakrishnan, Rev. Mod. Phys. 57, 287
共1985兲; D. Belitz and T.R. Kirkpatrick, ibid. 66, 261 共1994兲.
25H. Noh, S. Zelakiewicz, T.J. Gramila, L.N. Pfeiffer, and K.W.
West, Phys. Rev. B 59, 13 114共1999兲; S.M. Badalyan and U. Rossleri, ibid. 59, 5643 共1999兲; B.Y.-K. Hu, ibid. 57, 12 345 共1998兲.
26I.V. Gornyi, A.G. Yashenkin, and D.V. Khveshchenko, Phys.
Rev. Lett. 83, 152共1999兲.
27V. Cambel and M. Mosˇko, Semicond. Sci. Technol. 8, 364
共1993兲.
28Y. Oreg and A. Kamenev, Phys. Rev. Lett. 80, 2421共1998兲; A.
Stern and I. Ussishkin, Physica E 1, 176 共1997兲; J. Baker, G. Vignale, and A.G. Rojo, Phys. Rev. B 60, 8804共1999兲.