Galois cisimleri ve en yüksek çözümlü 2k-1 tasarımlarının oluşturulması

statistikçiler Dergisi 3 (2010) 45-53

Galois cisimleri ve en yüksek çözümlü

2

tasar mlar n n olu turulmas

Nazan Danac o lu

Sinop Üniversitesi Fen-Ed. Fak. statistik Bölümü Osmaniye Köyü Yeni Cezaevi Yan

57000 Sinop, Türkiye nazand@sinop.edu.tr

F. Zehra Muluk

Ba(kent Üniversitesi Ticari Bilimler Fak.

Sigortac l k ve Risk Yönetimi Bölümü 06810 Ankara, Türkiye zmuluk@baskent.edu.tr

Özet

Kesirli çok etkenli tasar mlar , uygulamada yayg n olarak kullan lmaktad r. Bu çal mada, sonlu cisim teorisinden, Galois cisimleri üzerindeki polinomlardan yararlanarak, en yüksek çözümlü 2k-1_{tasar mlar n n} nas l olu turulabilece i gösterilmi tir.

Anahtar sözcükler: Çok etkenli tasar mlar; Kesirli çok etkenli tasar mlar; Sonlu cisimler; Galois cismi; Polinomlar.

Abstract

Galois Fields And Construction of 2k-1 _{Designs with Highest Resolution}

Fractional factorialdesigns are commonly used in practice. In this article, the finite flelds theory and polynomials over Galois fields were used to design 2k-1 _{designs with highest resolution.}

Keywords: Factorial designs; Fractional factorial designs; Finite fileds; Galois field; Polynomials.

1. Giri

Çok etkenli ve kesirli çok etkenli (KÇE) (fractional factorial designs) tasar m teorisinde pek çok sorun; geometrik, cebirsel ya da birle imsel (combinatorial) yap ya dönü ür. Sonuç olarak; gruplar, halkalar (rings), cisimler (fields), Öklid ve izdü ümsel (projective) geometri gibi sonlu matematiksel yap lar, çok etkenli ve KÇE tasar mlarla ilgili pek çok sorunun çözümünde, genelle tirilmesinde ve ayd nlat lmas nda ba ar yla kullan lmaktad r.

Çok etkenli tasar mlar olu turma yöntemlerinden literatürde bulunan baz lar ; dikey dizimler (orthogonal arrays), sonlu geometriler (finite geometries), cebirsel ayr ma (algebraic decomposition), etki kar m (confounding), Hadamard matrisleri ve sonlu grafikler olarak s ralanabilir.

KÇE tasar mlar n cebirsel yap s bugüne kadar pek çok çal mada yer alm t r. Shirakura, Suetsugu ve Tsuji [10], Hadamard matris ve Galois cisminden (GF) (Galois field) yaralanarak 2m_{tasar mlar olu turma}

yöntemi önermi ler; Pistone and Rogartin [9], KÇE tasar mlarda, düzey kodlar için cebirsel istatistikleri incelemi , Xu [13], GF, do rusal kodlar ve izdü ümsel geometriden yararlanarak KÇE tasar mlar için bir algoritma olu turmu lard r.

Bu çal mada, katsay lar GF üzerinde bulunan polinomlardan yararlanarak, çok etkenli tasar mlar ve bunlar n en yüksek çözümlü yar kesirlerine nas l ula laca yla ilgilenilmi tir.

2. Genel bilgiler

Bilindi i gibi, etkenlerin p düzeyli oldu u bir KÇE tasar m, p büyüklü ünde GF kullan larak olu turulabilir ve p asal bir say oldu unda, sonlu cisim aritmeti i, p modülünde tam say aritmeti ine e ittir. Bu nedenle modüler aritmetik ile ilgili baz tan mlar üzerinde durulacakt r:

2.1. Denklikler ve Euler fonksiyonu

Tan m 1. n> 0 ve a, b Z olsun. E er n a-b (n, a-b yi böler) ise, a say s n modülüne göre b’ye denktir denir ve a b (mod n) eklinde gösterilir [6].

Tan m 2. x a (mod n) gibi bir denklik ba nt s için n tane denklik s n f vard r ve her biri 0,1,...,n 1

s n flar ndan birine e ittir. Bu denklik s n flar n n aç k olarak yaz l m ;

{

}

{

}

{

}

eklindedir ve n modülüne göre kalan s n flar olarak adland r l r.

{

}

n

Z = 0 , 1, 2,..., n 1

kümesine, n modülüne göre kalan s n flar n n kümesi denir [3].

p asal bir say olmak üzere, Zp’nin p-1 tane s f rdan farkl her ö esi tersinirdir (p asal oldu unda, Zp‘nin

s f rdan farkl her ö esinin Zp içinde bir tersi vard r). Tan m 3, rastgele bir n>1 tam say s için Zn’nin

tersinir ö elerinin say s n bulmaya yöneliktir [6].

Tan m 3. n>1 için, Zn içindeki tersinir ö elerin say s (n) ile gösterilir ve n (n) ba nt s na ya da

k saca (n)’ye Euler fonksiyonu denir [1,6].

(n) ile gösterilen say ; Zn’nin ö elerinden, n’den küçük ya da e it olup, n ile aralar nda asal olan tam

say lar n say s d r. Örne in, (8)=4’tür; çünkü,

1

,

3

,

5

,

7

Özellik 1. (Euler) n, a Z ve n>0 olsun. (n,a)=1 ise, a (n) _{1(mod n)’dir [6].}

Sonuç 1. (Fermat) p, a Z olsun. p asal ve p a (p, a’y bölmez) ise, ap-1 _{1 (mod p)’dir [4].}

2.2.Sonlu cisimler

Gerçel say lar, rasyonel say lar ve kompleks say lar cisimlere örnek olarak verilebilir ve her biri sonsuz say da elemana sahiptir. Sadece, sonlu say da eleman içeren bir cisim, sonlu cisim (finite field) olarak adland r l r. Örne in, n tamsay modülü Zn ile gösterildi inde, mod n’de yap lan standart toplama ve

çarpma i lemlerine göre, Znsonlu bir cisimdir [11,12].

Teorem 1. Znyaln z ve yaln z n asal say ise sonlu bir cisimdir.

Tan m 4. F bir cisim olsun. F cisminin karakteristi i; m

i 1=1 1 1 ... 1 0= + + + = e itli ini sa layan en küçük pozitif m tamsay s d r. E er m yoksa, karakteristik 0 olarak tan mlan r [11].

Teorem 2. F, p karakteristi ine sahip sonlu bir cisimse, bu durumda F, n pozitif tamsay s için, pn

elemanl d r.

F, q elemanl sonlu bir cisimse, genellikle GF(q) ile gösterilir ve q elemanl GF olarak adland r l r. Buradaki q, pn_{biçimindedir ve bir asal say ya da asal say n n kuvvetidir. GF( p}n_{), p karakteristikli bir}

cisimdir ve Zpcismi, GF(p) olarak gösterilir [3, 11].

2.2.1. Galois cismi

p bir asalsa, Fp = <Fp , +p , .p > sistemi, Fp = {0, 1, 2, ..., p-1 } olmak üzere, bir GF’dir ve GF(p) ile

gösterilir. Gerçekte, Fp, en basit GF’dir [3].

Tan m 5. r, xr _{=1 yapan en küçük pozitif tamsay olsun. Bu durumda r, x’in derecesidir ve r en büyük}

de eri, p-1’i ald nda; x’e GF(p)’nin ilkel eleman (primitive element) denir. Her GF(p)’de ilkel bir eleman vard r. x ilkel elemansa, GF(p)’nin s f r olmayan bütün elemanlar , a a daki diziye dahildir [3].

x0_{= 1, x, x}2_{, ..., x}p-2 ₍₂₎

Tan m 6. GF(p)[x], ai} katsay lar GF(p) cisminde olan, rastgele dereceli a0+ a1x +a2x2+ ... + an-1xn-1, ai

{0,1}, polinomlar n n birle imidir [7].

Tan m 7. GF(p)[x]’de dü ük dereceden polinomlar n çarp m eklinde yaz lamayan f(x) fonksiyonuna,

GF(p)’de indirgenemez denir [3,7].

f(x), GF(p)’de indirgenemezse, GF(pn_{)‘nin elemanlar n olu turmak için en küçük fonksiyondur. En}

küçük fonksiyon f(x) uygun olarak seçilirse; x ile gösterilen s n f, GF(pn_{)’nin ilkel eleman olacakt r ve bu}

durumda, GF(pn_{)’nin s f r olmayan bütün elemanlar a a daki gibi ifade edilebilir.}

x0_{= 1, x, x}2_{, ..., p}n 2

x

E itlik (3)’teki ifade, x’in güç döngüsü (power cycle) olarak adland r l r. Baz güç döngüleri Çizelge 1’de verilmektedir [3].

GF(22_{) için güç döngüsü olu turulsun. GF(2}2_{)’nin cisim elemanlar bulunurken, Tan m 6’dan, derecesi}

n=1 olan bir polinomdan yararlan l r.

p(x)= a1x + a0

0 0 0

0 1 1 (4)

1 0 x

1 1 x+1

dir. GF(22_{) için Çizelge 1’de verilen en küçük polinom, 1+x+x}2_{’dir ve Tan m 7’den, ayn zamanda}

indirgenemez bir polinomdur (Bkz. Çiz. 2) olarak gösterilmi tir. E itlik (3)’teki güç döngüsü kullan ld nda;

x0= 1, x, x2, ...,

x

elde edilir. Ancak x2 _{x+1 (mod x}2_{+x+1) oldu undan, güç döngüsü;}

1, x, x+1 (5)

olacakt r. Görüldü ü gibi, cismin 0 d ndaki elemanlar , güç döngüsünü olu turmaktad r.

Çizelge 1. Baz GF(2n_{) cisimleri için en küçük polinomlar ve güç döngüleri}

pn _{En küçük polinom Güç döngüsü}

22 _x2_{+x+1 1,x,x+1}

23 _x3_+x2_{+1 1,x,x}2_{, x}2_{+1, x}2_+x+1,x+1,x2_+x

24 _x4_{+ x}3_{+1 1,x, x}2_{, x}3_{, x}3_{+1, x}3_{+x+1, x}3_+x2_{+x+1, x}2_+x+1,

x3_+x2_{+x, x}2_{+1, x}3_{+x, x}3_+x2_{+1,x+1, x}2_{+x, x}3_+x2

GF(23_{) için güç döngüsü olu turulsun. Tan m 6’dan, GF(2}3_{)’ün elemanlar bulunurken, derecesi n=2 olan}

bir polinomdan yararlan l r. p(x)= a2x2+ a1x +a0, ai Z, i=0,1, a1 0 olmak üzere;

p(x)= a2x2+ a1x + a0 0 0 0 0 0 0 1 1 0 1 0 x 0 1 1 x+1 (6) 1 0 0 x2 1 0 1 x2₊₁ 1 1 0 x2+x 1 1 1 x2_+x+1

elde edilir ki, GF(23_{) için, Çizelge 2.2’de verilen en küçük fonksiyon x}3 _+x2 _{+1 kullan larak, E itlik}

(3)’ten bulunan güç döngüsü; x0_{= 1, x, x}2_{, ..., p}n 2

x

1, x, x2_{, x}2_{+1, x}2_{+x+1, x+1, x}2_{+x (7)}

dir (Bkz. Çiz. 2).

GF(24_{) için güç döngüsü olu turulsun. GF(2}4_{)’ün elemanlar bulunurken, derecesi n=3 olan bir}

p(x)= a3x3+ a2x2+ a1x + a0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 x 0 0 1 1 x+1 0 1 0 0 x2 0 1 0 1 x2₊₁ 0 1 1 0 x2_+x 0 1 1 1 x2_{+x+1 (8)} 1 0 0 0 x3 1 0 0 1 x3₊₁ 1 0 1 0 x3_+x 1 0 1 1 x3_+x+1 1 1 0 0 x3_+x2 1 1 0 1 x3_+x2₊₁ 1 1 1 0 x3_+x2_+x 1 1 1 1 x3_+x2_+x+1

elde edilir. Çizelge 1’deki x4_{+ x}3_{+1 en küçük fonksiyonu kullan larak E itlik (3)’ten güç döngüsü;}

x0_{= 1, x, x}2_{, ..., p}n 2

x

1, x, x2_{, x}3_{, x}3_{+1, x}3_{+x+1, x}3_+x2_{+x+ 1, x}2_{+x+ 1, x}3_+x2_+x,

x2_{+1, x}3_{+x, x}3_+x2_{+ 1, x+1, x}2_{+ x, x}3_+x2 ₍₉₎

dir ve Çizelge 1’den de görülebilir. 2.2.2. ndirgenemez polinomlar

Bilindi i üzere, pn _{elemanl bir cisim olu turmak için, GF(p)[x]’de n. dereceden bir indirgenemez}

polinoma ihtiyaç vard r. As l sorun, GF(p)[x]’de her pozitif n say s için, n. dereceden bir polinomun olup olmad d r. Gerçekte bak lmas gereken, monik bir indirgenemez polinomdur. Monik polinom, x’in en yüksek kuvvetinin s f r olmayan katsay s 1 demektir [13].

Tan m 8. (2 ya da 3. dereceler için indirgenebilirlik testi) F bir cisim olsun. f(x) F[x] ve degf(x)=2 ya da

3 ise; f(x), yaln z ve yaln z F’de s f r de erini al yorsa, F’de indirgenebilirdir [4]. Örne in, 1+x+x3, Z2’de indirgenemezdir; çünkü, Z2’de 03+ 0 + 1 0 ve 13+ 1+ 1 0‘d r.

Sonuç 3. Herhangi bir p 2 asal için,

( )

Q (rasyonel say lar) üzerinde ve dolay s yla Z’de indirgenemezdir [4].

Çizelge 2’de, mod 2 için, dereceleri n=1’den 5’e kadar olan indirgenemez polinomlar listelenmektedir [3].

Çizelge 2. Mod 2’de n. dereceden indirgenemez polinomlar n ndirgenemez polinomlar 1 1+x , x 2 1+x+x2 3 1+x+x3_{, 1+x}2_+x3 4 1+x+x4_{, 1+x+x}2_+x3_+x4_{, 1+x}3_+x4 5 1+x2_+x5_{, 1+x+x}2_+x3_+x5_{, 1+x}3_+x5_{, 1+x+x}3_+x4_+x5_{, 1+x}2_+x3_+x4_+x5_, 1+x+x2_+x4_+x5 2.2.2. En küçük polinom

Tan m 9. F, p karakteristikli bir cisim olsun ve F*_{0 olmayan cisim elemanlar n göstersin. F}*_olsun.

GF(q)’ya göre ’n n en küçük polinomu m(x)’dir ve m( ) = 0’d r [7].

Tan m 10. Bir eleman n n en küçük polinomu tektir [5].

Teorem 3. F*için, ’n n en küçük polinomu m (x) , indirgenemezdir ve m (x) | xq-x‘tir [5,7].

Tan m 11. F için, t, pt _{= yapan en küçük pozitif tamsay olsun. GF(q)’ya göre ’n n çekimler}

(conjugates) kümesi;

{

}

C( )= , , ,..., (11)

ve p karakteristikli F cisminde, bütün i’ler için, C

( )

( )

Teorem 4. F, p karakteristikli bir cisim ve F* _{olsun. C( ), GF(q)’ya göre ’n n çekimler kümesi}

oldu unda,

(

)

( ) C

m (x)= x (12)

katsay lar GF(q) üzerinde ’n n en küçük polinomudur [11].

F=GF(22) cismi olu turulsun. Öncelikle, Z2’de indirgenemez kübik bir polinoma ihtiyaç vard r ve Çizelge

2’den, f(x)= x2 _{+ x +1 al nm t r. F’nin elemanlar ; {[0], [1], [x], [1+x]}(Bkz. E .4) ve karakteristi i de}

2’dir (Bkz. Tan m 4). Elemanlar n çarp mlar f(x) polinom modundad r. x2 _{+ x +1 0 (mod f(x)) ve}

E itlik (1)’den Z2’de 1 -1 oldu undan, x2 -x-1 = x+1(mod f(x))’dir.

=x, F’nin ilkel eleman ya da üretecidir. Gerçekte, Tan m 5’ten, bu cisim için 1 d ndaki 0 olmayan her eleman (Bkz. E .5), cismin üretecidir.

Tan m 11’den pt _{= yapan en küçük eleman; x}2 _{x+1 (mod x}2_{+x+1), x}4_{= x ya da} 22 _{= , oldu undan}

2’dir. E itlik (11)’den çekimler kümesi; _C

( )

{ }

kar kl k olmamas amac yla x yerine y kullan l rsa,

(

)

( ) C

eklinde yaz labilir.

E itlik (4) ve (5)’ten,

(

)

(

)

(

)

(

)

(

) (

)

(

)

Çizelge 3’te GF(23_{)’ün elemanlar n n en küçük polinomlar , 1 üreteç için verilmektedir [2].}

Çizelge 3. En küçük polinomu f(x)=x3_{+ x}2_{+1 al nan GF(2}3_{) cismi}

GF(23_{) cismi için f(x)=x}3_{+ x}2_{+1 ve =x al nd nda}

=(010) = x = 1 =(100) = x2₌ 2 _{m (y)= y}3_{+ y}2₊₁ =(111) = x2_{+x+1 =} 4 =(101) = 1+x2₌ 3 =(011) = x +1= 5 _{m (y)= y}3_{+ y + 1} =(110) = x2_+x= 6

Çizelge 2’de Z2’de indirgenemez di er bir kübik polinom f(x)= x3+x+1 al nd nda, GF (23) elemanlar

ve kar l k gelen en küçük polinomlar da bulunmu tur (Bkz. [2]).

Çizelge 3’te verilen ve GF(23_{)’ü olu tururken kullan lan en küçük polinomlar n her biri, x}8_{-x’i bölmelidir}

ve derecelerinin toplam 8 olmal d r (Bkz. Teo.3). GF(23_{) için,}

x8_{-x= x(x+1)(x}3_+x+1)(x3_+x2_{+1) (14)}

dir. =x oldu unda en küçük polinomlar; x, x+1, (x3_{+x+1), (x}3_+x2_+1)’dir.

3. 2k-1 _{Tasar mlar}

Bilindi i üzere, 2k-p deneme içeren bir 2ktasar m na, 2k tasar m n n 1 / 2pkesiri ya da 2k-p KÇE tasar m denir. Burada; k: etken say s , p: üreteç ya da tan mlay c ba nt say s d r. Bu düzen için tan mlay c ba nt yap s (defining constrast pattern), ba lang çta seçilen p tane üreteç ve bunlar n 2p - p -1 tane genelle tirilmi etkile iminden (generalized interaction) olu ur. p=1 oldu unda, çok etkenli bir tasar m n yar kesrine kar l k gelir [8].

KÇE tasar m n çözümü (resolution) ise, tan mlay c ba nt yap s ndaki en k sa kelime uzunlu u olarak tan mlanabilir ve burada, Romen rakam yla, alt indis olarak gösterilmi tir.

Tan mlay c ba nt s I=ABC olan 3 1 III

2 KÇE tasar m Çizelge 4’te gösterilmektedir.

Çizelge 4. 3 1 III 2 Tasar m (I=ABC) a b c=a+b Denemeler 0 0 0 000 0 1 1 011 1 0 1 101 1 1 0 110

Bu tasar m n tan mlay c ba nt s , I=ABC= x2_{+x+1=(111) olarak da gösterilebilir. x}2_{+x+1 GF(2}3_)’ün

Teorem 3 ve Sonuç 3’ten,

m

(x

)

(

)

(

)

(

)

(

)

oldu u söylenebilir. x2_{+x+1, ayn zamanda en küçük polinomdur. x ve x+1 ise GF(2}3_{)’ün 1. dereceden en}

küçük polinomlar d r.

E itlik (4)’te verilen GF(22_{)’nin elemanlar , Çizelge 4’te a ve b sütunlar yla gösterilen tamamlanm 2}2

çok etkenli tasar m na kar l k gelmektedir. 23-1 _{tasar m na, yani 2}2 _{çok etkenlisinin yar kesrine ula mak}

için, bir anlamda, GF(23_{)’ün yar kesri elde edilmelidir. Bunun için, E itlik (15)’te tan mlay c ba nt y}

gösteren polinom d ndaki x+1 polinomundan yararlan labilir. GF(23_{)’ün yar kesri ya da 2}3-1 _{tasar m}

Çizelge 5’te gösterilmi tir.

Çizelge 5. GF(22_{)’den elde edilen} 3 1 III

2 tasar m GF(22₎

(

)

(

)

3 2

x 1= x 1 x+ + +x 1 Elemanlar n (x+1) polinomuyla _{çarp m} 3 1 III 2 tasar m n n denemeleri 0 0 (0) (x+1) 0.x+1=0 0 0 0 0 1 (1) (x+1) 1. (x+1)=x+1 0 1 1 1 0 (x) (x+1) x(x+1)=x2_{+x 1 1 0} 1 1 (x+1) (x+1) (x+1)(x+1)= x2_{+1 1 0 1}

Çizelge 5’te son sütundaki denemeler polinom derecesine göre s ralan rsa, Çizelge 4’ün son sütunundaki deneme s ras na ula labilir.

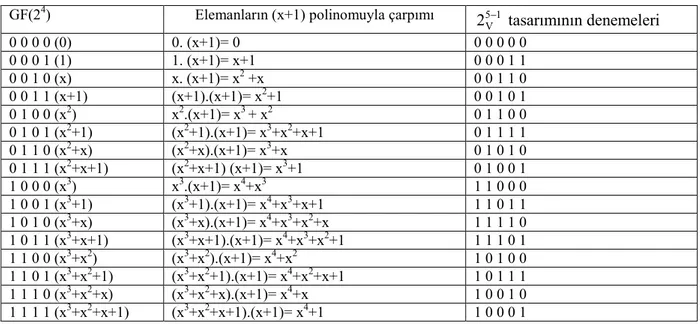
Çizelge 6’da, I=ABCDE=(11111)=x4_+x3_+x2_{+x+1 tan mlay c ba nt l} 5 1 V

2 tasar m n n nas l olu turuldu u gösterilmektedir.

Çizelge 6. GF(24_{)’ten elde edilen} 5 1 V

2 tasar m GF(24) Elemanlar n (x+1) polinomuyla çarp m 5 1

V 2 tasar m n n denemeleri 0 0 0 0 (0) 0. (x+1)= 0 0 0 0 0 0 0 0 0 1 (1) 1. (x+1)= x+1 0 0 0 1 1 0 0 1 0 (x) x. (x+1)= x2_{+x 0 0 1 1 0} 0 0 1 1 (x+1) (x+1).(x+1)= x2_{+1 0 0 1 0 1} 0 1 0 0 (x2_{) x}2_{.(x+1)= x}3_{+ x}2 _{0 1 1 0 0} 0 1 0 1 (x2_{+1) (x}2_{+1).(x+1)= x}3_+x2_{+x+1 0 1 1 1 1} 0 1 1 0 (x2_{+x) (x}2_{+x).(x+1)= x}3_{+x 0 1 0 1 0} 0 1 1 1 (x2_{+x+1) (x}2_{+x+1) (x+1)= x}3_{+1 0 1 0 0 1} 1 0 0 0 (x3_{) x}3_{.(x+1)= x}4_+x3 _{1 1 0 0 0} 1 0 0 1 (x3_{+1) (x}3_{+1).(x+1)= x}4_+x3_{+x+1 1 1 0 1 1} 1 0 1 0 (x3_{+x) (x}3_{+x).(x+1)= x}4_+x3_+x2_{+x 1 1 1 1 0} 1 0 1 1 (x3_{+x+1) (x}3_{+x+1).(x+1)= x}4_+x3_+x2_{+1 1 1 1 0 1} 1 1 0 0 (x3_+x2_{) (x}3_+x2_{).(x+1)= x}4_+x2 _{1 0 1 0 0} 1 1 0 1 (x3_+x2_{+1) (x}3_+x2_{+1).(x+1)= x}4_+x2_{+x+1 1 0 1 1 1} 1 1 1 0 (x3_+x2_{+x) (x}3_+x2_{+x).(x+1)= x}4_{+x 1 0 0 1 0} 1 1 1 1 (x3_+x2_{+x+1) (x}3_+x2_{+x+1).(x+1)= x}4_{+1 1 0 0 0 1}

Sonuç 3’ten x4_+x3_+x2_{+x+1 polinomu indirgenemezdir ve GF(2}5_{)’in eleman d r. Teorem 3’ten,}

_m

_(x

₎

(

)

(

)

5 4 3 2

x 1= x 1 x+ +x +x + +x 1

yaz labilir. Böylelikle, E itlik 8’de verilen GF(24_{) elemanlar n n (x+1) polinomuyla çarp lmas sonucu} 5 1

V

2 tasar m n n denemelerine ula lm t r (Bkz. Çiz. 6).

4. Sonuç ve öneriler

Bilindi i üzere, KÇE, özellikle 2-düzeyli tasar mlar (2k-p_{), belli etkile imlerin olmad -önemsiz oldu}

u-varsay m n n yap labildi i durumlarda; sadece etkenlerden baz lar n n önemli oldu u dü ünülen ön (screening) çal malarda yararl olup, uygulamada yayg n olarak kullan lmaktad r. Bir 2k-p _KÇE

tasar m n n mümkün en yüksek çözüme sahip olmas istenir.

Bu çal mada, 2k-p _{tasar mlar nda p=1 oldu u zaman, en yüksek çözümlü yar kesirli tasar mlara GF}

kullan larak ula lm t r. Burada yer verilmeyen di er yar kesirler de ayn ekilde elde edilebilmektedir. MATLAB program n n GF fonksiyonlar n kullanarak en küçük polinomlara, polinom köklerine veya GF elemanlar na ula mak mümkündür. Polinom çarp mlar n n el ile yap lmas zor oldu unda MATLAB program ndan yararlan labilir. Etken say s çift oldu unda, örne in, 4 1

IV

2 tasar m olu turulmak istenirse, p asal olmad ndan Sonuç 3 sa lanmamaktad r. Bu tasar m için tan mlay c ba nt I=ABCD= x3_+x2_{+x+1’dir ve polinom GF(2}3_{)’te indirgenebilir bir polinomdur (Bkz. Tan m 8). Buna ra men, x}4_-1=

(1+x) (x3_+x2_{+x+1) oldu unda, verilen yöntem kullan larak olu turulabilmektedir. Yar tekrarlar d ndaki}

KÇE tasar mlar için polinomlar n matrislerle gösterimi gerekecektir.

Danac o lu [2], Hamming kodlar nda yer alan, üreteç matrisi (generator matrix) ve denklik-kontrol matrislerini (parity-control matrix) kullanarak, KÇE tasar mlara ula m ve tasar mlar n kod kar l klar n bulmu tur.

Xu [13], r=n-k olmak üzere, GF(2)’deki s f r olmayan (u1, …ur)T r kümeden olu an r×(2r-1) boyutlu G

matris oldu unda; düzenli (regular) her 2n-k _{KÇE tasar m n n n sütununun GF(2)’deki G’nin bütün sat r}

kombinasyonlar ndan olu an bir 2r_×(2r_{-1) matrisi olarak dü ünülebilece ini belirtmi tir.}

Kaynaklar

[1] F. Çall alp, (1999), Say lar Teorisi, Ystanbul.

[2] N. Danac o lu, (2005), Kesirli Çok Etkenli Deneylerde Çözüm ve En Az Sapma Kavram , H.Ü. Ystatistik Bölümü Doktora Tezi.

[3] A. Dey, (1985), Orthogonal Fractional Factorial Designs, New Delhi, Wiley Eastern. [4] J. A. Gallian, (1986), Contemporary Abstract Algebra, D.C.Health and Company.

[5] W. C. Huffman, V. Pless, (2003), Fundemantals of Error Correcting Codes, Cambridge University Pres. [6] A. Kaya, (1988), Say lar Kuram na Giri(, Yzmir.

[7] A. J. Menezes, S. A. Vanstone, P. C. Oorschot van, (1997), Handbook of Applied Cryptography, CRC Pres. [8] D. C. Montgomery, (1984), Design and Analysis of Experiments, Second Edition, John Wiley&Sons, NY. [9] G. Pistone, M. P. Rogartin, (2007), Algebraic Statistics of Level Codings for Fractional Factorial Designs,

Journal of Statistical Plann. and Inf.,138, 234-244.

[10] T. Shirakura, T. Suetsugu, T. Tsuji, (2002), Constructions of Main Effect Plus Two Plans for 2m_Factorials,

Journal of Statistical Plann. and Inf., 105, 405-415.

[11] S. A. Vanstone, P. C. Oorschot van, (1989), An Introduction to Error-Correcting Codes with Application,s Kluwer Academic Publishers.

[12] D. Wiggert, 1978, Error-Control Coding and Applications, Artech House.

[13] H. Xu, (2009), Algorithm construction of efficient fractional factorial designs with large sizes,