STO'lar üzerinden bir ve iki-merkezli kinetik enerji integrallerinin hesaplanması

FEN BİLİMLERİ ENSTİTÜSÜ

STO’LAR ÜZERİNDEN BİR ve İKİ-MERKEZLİ KİNETİK ENERJİ İNTEGRALLERİNİN HESAPLANMASI

Adem KOCAMALCI

YÜKSEK LİSANS TEZİ

FİZİK ANABİLİM DALI

T.C.

SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ

STO’LAR ÜZERİNDEN BİR ve İKİ-MERKEZLİ KİNETİK ENERJİ İNTEGRALLERİNİN HESAPLANMASI

Adem KOCAMALCI

YÜKSEK LİSANS TEZİ

FİZİK ANABİLİM DALI

KONYA, 2010

Bu tez 22/02/2010 tarihinde aşağıdaki jüri tarafından oy birliği ile kabul edilmiştir.

Yrd. Doç. Dr. Erhan AKIN (Danışman)

Doç. Dr. Kemal AYDIN (Üye)

Yrd. Doç. Dr. Gültekin ÇELİK (Üye)

ÖZET

YÜKSEK LİSANS TEZİ

STO’LAR ÜZERİNDEN BİR ve İKİ-MERKEZLİ KİNETİK ENERJİ İNTEGRALLERİNİN HESAPLANMASI

Adem KOCAMALCI

Selçuk Üniversitesi Fen Bilimleri Enstitüsü Fizik Anabilim Dalı

Danışman: Yrd. Doç. Dr. Erhan AKIN 2010, 57 Sayfa

Jüri: Doç. Dr. Kemal AYDIN Yrd. Doç. Dr. Erhan AKIN Yrd. Doç. Dr. Gültekin ÇELİK

Bu çalışmada Slater-tipi atom orbitalleri üzerinden bir ve iki-merkezli kinetik enerji integrallerinin hesaplanması için literatürdeki bir analitik ifadeden yararlanılmıştır. Bu analitik ifade için yalnızca Slater-tipi atom orbitallerinin kuantum sayıları ve perdeleme parametreleri ile çekirdekler arası uzaklığın bilinmesi yeterlidir. Söz konusu analitik ifade literatürde iyi bilinen overlap integralleri cinsinden bir ifadedir. Overlap integrallerinin hesaplanmasında gerekli olan pozitif indisli Q yardımcı fonksiyonlarının hesaplanmasında An(α) ve Bn(α) yardımcı

fonksiyonlarından, negatif indisli Q yardımcı fonksiyonlarının hesaplanmasında ise Jn(α) ve Kn(α) yardımcı fonksiyonlarından yararlanılmıştır. Hesaplamalarda Intel

Fortran Complier ile SUN X2200 Server’da real*16 duyarlıklı aritmetik kullanılmıştır. Keyfi kuantum sayılarına ve perdeleme parametrelerine sahip Slater-tipi atom orbitalleri için yapılan hesaplamalar literatürle karşılaştırılmış ve sonuçların literatürle uyum içinde olduğu görülmüştür.

Anahtar kelimeler: Slater-tipi orbitaller, moleküler integraller, overlap integralleri, kinetik enerji integralleri.

ABSTRACT MS Thesis

Evaluation of One and Two-Center Kinetic Energy Integrals Over STO’s

Adem KOCAMALCI

Selçuk University Graduate School of Natural and Applied Sciences Department of Physics

Supervisor : Assist. Prof. Dr. Erhan AKIN 2010, 57 Pages

Jury : Doç. Dr. Kemal AYDIN Assist Prof. Dr. Erhan AKIN Assist Prof. Dr. Gültekin ÇELİK

In this study, an analytical expression existing in the literature have been used to evaluate the two-center kinetic energy integrals over Slater-type orbitals. This analytical expression needs only quantum numbers and screening parameters of the Slater-type orbitals and internuclear distance.The analytical expression of two-center kinetic energy integrals have been given in terms of overlap integrals well known in the literature. Q functions have been used in the evaluation of overlap integrals. An(α) and Bn(α) auxiliary functions have been used in the evaluation of the Q

functions with positive indice. However, Jn(α) and Kn(α) auxiliary functions have

been used in the evaluation of the Q functions with negative indice. All of the computations have been performed in the real*16 precision arithmetic using Intel Fortran Complier on the SUN X2200 Server. It has been found that the results of calculations carried out in this work for the Slater-type orbitals with arbitrary quantum numbers and screening parameters are in a good aggreement with results given in the literature.

Key words: Slater-type orbitals, molecular integrals, overlap integrals, kinetic energy integrals

ÖNSÖZ

Bu çalışma Selçuk Üniversitesi, Fen Bilimleri Enstitüsü, Fizik Anabilim Dalında yüksek lisans tezi olarak sunulmuştur.

Bu çalışmada Slater-tipi atom orbitalleri üzerinden bir ve iki-merkezli kinetik enerji integralleri için eliptik koordinatlarda literatürde var olan overlap integralleri cinsinden analitik ifadeler verilmiştir. İki-merkezli moleküler integraller, Slater-tipi atom orbitalleri bir çekirdekten başka bir çekirdeğe taşınarak da hesaplanabilir. Ancak taşıma yöntemleri hem uzun hesaplama süresi gerektirdiğinden hem de yüksek duyarlıklı hesaplamalarda tam başarılı olamadığından iki-merkezli integraller yerine üç veya dört-merkezli moleküler integrallerde tercih edilir. Bu şekilde üç veya dört-merkezli integrallerde bir veya iki Slater-tipi atom orbitali diğer Slater-tipi orbitallerin merkezlendiği çekirdeğe taşınarak üç veya dört-merkezli moleküler integral merkezli integrale indirgenerek çözüme ulaşılabilir. Bu nedenle iki-merkezli integraller, üç ve dört-iki-merkezli integrallerin çözümünde de önemli bir rol oynamaktadır.

Çalışmamın konuyla ilgilenen araştırmacılara faydalı olması dileklerimle. Bu çalışmada yardımlarını gördüğüm Sayın hocam Yrd. Doç. Dr. Erhan AKIN’a ve her zaman yanımda olan ve desteğini esirgemeyen sevgili eşim Aynur KOCAMALCI’ya teşekkürlerimi sunarım.

2010

İÇİNDEKİLER ÖZET ……….. iii ABSTRACT ……….. iv ÖNSÖZ ………... v İÇİNDEKİLER ………. vi ŞEKİLLER DİZİNİ ……….. vii TABLOLAR DİZİNİ ……… viii SİMGELER VE KISALTMALAR ………. ix 1. GİRİŞ ……….. 1

1.1. Atomik ve Moleküler Hesaplamaların Kuantum Mekaniksel Temeli 1

1.2. Hidrojen Atomunun Dalga Fonksiyonları ……….... 7

1.3. Hartree-Fock Özuyumlu Alan Dalga Fonksiyonları ………... 22

2. STO’lar ÜZERİNDEN KİNETİK ENERJİ İNTEGRALLERİ 25

2.1. Slater-tipi Atom Orbitalleri Üzerinden Overlap İntegralleri……. 25

2.1.1. Slater-tipi Atom Orbitalleri Üzerinden Bir-Merkezli Overlap İntegralleri……….. 25

2.1.2. Slater-tipi Atom Orbitalleri Üzerinden İki-Merkezli Overlap İntegralleri ……… 26

2.1.2.1 Q Yardımcı Fonksiyonunun Analitik İfadeleri ………... 32

2.2. Bir ve İki-Merkezli Kinetik Enerji İntegralleri ……… 43

2.2.1. STO’lar Üzerinden Bir-Merkezli Kinetik Enerji İntegrallerinin Analitik İfadesi ………. 45

2.2.2. STO’lar Üzerinden İki-Merkezli Kinetik Enerji İntegrallerinin Analitik İfadesi ……….... 47

3. İKİ-MERKEZLİ KİNETİK ENERJİ İNTEGRALLERİNİN BİLGİSAYAR HESAPLAMA SONUÇLARI VE TARTIŞMA …. 48 3.1. Örnek Bir Hesaplama ………. 48

3.2. Keyfi Kuantum Sayıları ve Perdeleme Sabitleri İçin Hesaplama Sonuçları ve Tartışma ………. 49 KAYNAKLAR

ŞEKİLLER DİZİNİ

Şekil 1.1. Hidrojen atomunda bağıl hareketin incelenmesi için koordinat

sistemi ……… 7

ÇİZELGELER DİZİNİ

Çizelge 1.1. l =0,1,2,3 için (1.43) eşitliğinden elde edilen olası küresel

harmonikler ……….. 14

Çizelge 1.2. n=1 ve.2 3 için hidrojen dalga fonksiyonları ………. 21

Çizelge 1.3. Tek bir STO için farklı yöntemlerle elde edilen perdeleme Sabitleri ………. 24

Çizelge 2.1. p=1.6 için bazı An

( )

p değerleri ………. 36

Çizelge 2.2. pt =0.8 için bazı B_n

( )

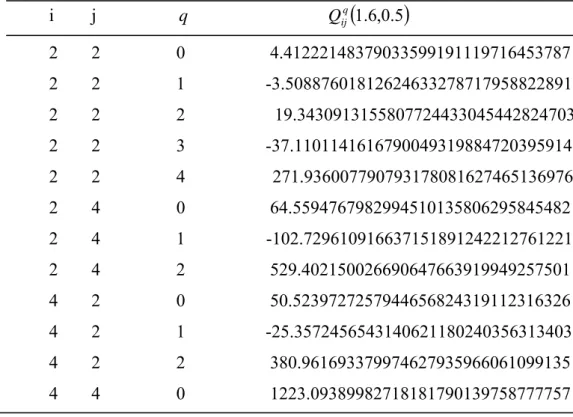
pt değerleri ………. 37

Çizelge 2.3. p=1.6, t =0.5 için bazı Q_ijq

( )

p,t değerleri ……… 38

Çizelge 2.4. p=1.6 için bazı Jn

( )

p değerleri ………. 41

Çizelge 2.5. p=1.6 için bazı K_n

( )

p değerleri ……… 42

Çizelge 2.6. p=1.6, t =0.5 için bazı Q_nq_n′

( )

p,t değerleri ……….. 43

Çizelge 3.1. Keyfi kuantum sayıları ve perdeleme sabitleri için bazı bir-merkezli kinetik enerji integral sonuçları……… 52

Çizelge 3.2. Keyfi kuantum sayıları ve perdeleme sabitleri için bazı iki-merkezli kinetik enerji integral sonuçları ……… 53

SİMGELER ve KISALTMALAR

L Açısal momentum operatörü ark. Arkadaşları

ρ Bağımsız değişken

U Coulomb potansiyel enerjisi k Coulomb sabiti

M Çekirdeğin kütlesi Z Çekirdeğin yükü ψ Dalga fonksiyonu e Elektrik yükü

EFG Elektron Alan Gradyenti r Elektronun çekirdeğe uzaklığı Rr Elektronun konum vektörü H Hamiltonyen operatörü HFR Hartree-Fock Roothan

l Kuantum sayısı

∇ Laplace operatörü

MO-LCAO Moleculer Orbitals Linear Combination of Atomic Orbitals N Normalizasyon katsayısı

SCF Self Consistent Field (özuyumlu alan) STO Slater-Tipi Atom Orbitalleri

1. GİRİŞ

1.1 Atomik ve Moleküler Hesaplamaların Kuantum Mekaniksel Temeli

Klasik mekanikte herhangi bir cismin kütlesi ve konum vektörü rr

( )

t bilinirse bu cismin hızı, ivmesi, çizgisel ve açısal momentumu, kinetik ve potansiyel enerjisi yani cismin durumu tam olarak elde edilebilir. Klasik mekanikteki bu konum vektörü ise kuvvetin bilinmesi durumunda Newton’un II. Kanunundan, kinetik ve potansiyel enerjinin bilinmesi durumunda ise Lagrange denkleminden bulunur. Ancak bilindiği gibi atomik ve moleküler sistemlerde klasik mekanik yetersiz kalmaktadır ve bu sistemlerde parçacıkların hareket durumları günümüzde en iyi olarak kuantum mekaniği ile incelenebilmektedir. Kuantum mekaniksel bakışta klasik mekaniğe göre en önemli fark parçacığın dalga olarak göz önüne alınmasıdır. Kuantum mekaniği ile yapılan hesaplamalarda kuantum mekaniğinin üç postülası kullanılır. Bu postülalar aşağıda verilmiştir (Köksal 1992).

1. Postüla: Bir sistemin durumu tam olarak ψ

(

_r

r

₁,

_r

r

₂,_K,t

)

dalga fonksiyonu ile belirlenir. Burada rr ler seçilen koordinat sistemine göre sistemin her bir parçacığının konum vektörünü ve t zamanı göstermektedir. Dalga fonksiyonu n ,,l m gibi kuantum sayıları ile karakterize edilir. Bu dalga fonksiyonunun karesinin tüm uzay üzerinden integralinin alınabilmesi gerekir. Ayrıca bu dalga fonksiyonunun normalize ya da normalize edilebilir olması, kendisi ve birinci türevinin tek değerli, sürekli ve sonlu olması gerekir.

2. Postüla: Klasik mekanikteki her gözlenebilire bir operatör karşılık getirilir. Aˆ ve Bˆ gibi iki operatör komütasyon bağıntısını sağlıyorsa yani

[ ]

A ˆˆ,B =Aˆ −Bˆ BˆAˆ=0 ise bu operatörlere karşılık gelen gözlenebilirler aynı anda duyarlı bir şekilde ölçülebilir. Aynı zamanda Aˆ ve Bˆ operatörleri komüte ediyorsa aynı öz fonksiyona sahiptirler. Örneğin açısal momentumun karesi ve z bileşenine karşılık gelen operatörler komüte ederler yani

[

L ,2 L_z

]

= 0 dır. Bu nedenle bu

operatörlerin her ikisi de aynı özfonksiyona sahiptir ve bu özfonksiyon küresel harmonikler adı verilen Y lerdir. _lm

3. Postüla: Bir gözlenebilire karşılık gelen Aˆ operatörünün özdeğerleri ψ

ψ a

Aˆ = denkleminden elde edilir. Burada ψ,Aˆ operatörünün özfonksiyonudur ve a özdeğerleri, A gözlemlenebilirinin ölçülebilecek değerlerine karşılık gelir.

Genel olarak bir operatörün tek bir özfonksiyon ve özdeğeri olmaz ve

n n n a

Aˆψ = ψ biçiminde (n=1,2,3_K) bir özfonksiyon ve özdeğerler seti olur. 3. Postülaya göre Aˆ peratörüne karşılık gelen gözlenebilirin ölçüldüğü bir deneyde ancak a₁,a₂,a₃,_K değerleri ölçülebilir. Bu özdeğerler takımına Aˆ işlemcisinin spektrumu denir.

Bir atomik veya moleküler sistemin durumunu anlatan 1. postülada bahsedilen dalga fonksiyonu’nun elde edilmesi için sistemin

ψ ψ ψ U E m∇ + = − 2 2 2 h _(1.1)

ile verilen Schrödinger dalga denkleminin çözülmesi gerekir. Hidrojen atomunda potansiyel enerji fonksiyonu küresel simetrik

(

U ≡U

( )

r

)

olduğundan (1.1) denklemi hidrojen için kolaylıkla çözülebilir. Ancak daha büyük atomlarda veya moleküllerde potansiyel enerji çok sayıda küresel simetrik olmayan terim içerdiğinden (1.1) denkleminin çözümü hemen hemen imkansızdır. Bu nedenle hidrojenden büyük atomik ya da moleküler sistemlerde dalga fonksiyonunu elde etmek için bazı yaklaşımların yapılması gerekir. Başka bir deyişle Hamilton operatörünün çeşitli bileşenlerin toplamı şeklinde yazılabildiği sistemlerde dalga fonksiyonu bu bileşenlerin fonksiyonu olan kısımların çarpımı şeklinde yazılabilir ve Schrödinger denklemi bu bileşenlere ait denklemlerin çözümüne indirgenir. Bununla birlikte kuantum kimyasının konusu olan çok elektronlu atom ve moleküllerde Hamilton operatörünü bileşenlere ayırmak mümkün değildir. Bu durum hidrojen atomundan sonraki en basit sistem olan He atomuna ait Hamilton operatöründe bile görülür. Helyum atomu için Hamilton operatörü atomik birimlerde,

2 1 2 1 2 2 2 1 2 ₁ 2 2 2 ˆ r r r R Z r R Z M H _{r r r r r r} − + − − − − ∇ − ∇ − ∇ − = (1.2)

biçiminde yazılabilir. Burada M, atomik kütle birimi cinsinden çekirdeğin kütlesi,

2 1 2_,∇

∇ ve 2 2

∇ sırasıyla çekirdek ile birinci ve ikinci elektrona ait Laplace operatörleri, Z çekirdeğin yükü, Rr, rr₁ ve rr₂ de sırasıyla çekirdek ile birinci ve ikinci elektronların konum vektörleridir. Görüldüğü gibi ilk üç terim kinetik enerjiye, son üç terim de potansiyel enerjiye aittir. Kinetik enerji terimleri dokuz bileşenin toplamı halinde yazıldığı halde potansiyel enerjiler için aynı şey mümkün değildir. Değişken sayısını üç azaltabilmek için kütle merkezi ve iç koordinatlar kullanılmak istense bile bu defa da kinetik enerji terimleri bunlar cinsinden iki kısma ayrılamamaktadır. Bileşenlerine ayrılamayan sistemin Schrödinger denklemi de tam olarak çözülememektedir.

Çözümün bulunabilmesi için bazı yaklaşık yöntemler denenmiştir. İlk yaklaşım olarak çekirdeğin kinetik enerjisi ihmal edilebilir. Bu ihmal çekirdeğin kütlesi elektronun kütlesinden binlerce defa büyük olduğu için, atomların elektronik yapıları incelenirken düşünülebilecek ötelenme enerjisi ihmal edilmekte ve koordinat merkezi atomun çekirdeğine alınmaktadır. Böylece Hamilton operatörü,

12 2 1 2 2 2 1 1 2 2 ˆ r r Z r Z H =−∇ −∇ − − − (1.3)

şeklinde yazılabilir. Burada r₁ ve r₂ sırasıyla birinci ve ikinci elektronların çekirdeğe uzaklıkları, r₁₂ ise iki elektron arasındaki uzaklıktır.

(1.3) ile verilen Hamilton operatörünün kullanıldığı Schrödinger denklemi de, çözülebilen basit diferansiyel denklemler haline dönüştürülememektedir. Bunun nedeni elektronlar arasındaki Coulomb itme potansiyel enerji ifadesindeki

12

1 r terimidir. Bu terim çok elektronlu atom ve moleküllerin hepsinde bulunacağı için, dalga fonksiyonlarının çarpanlarına ayrılamaması bütün atom ve moleküllerin ortak

özelliği olacaktır. Bu durumda çözümün yapılabilmesi için başka yaklaşım veya ihmaller yapılmalıdır.

İzlenen yaklaşık yollardan birincisinde, sistemin bütün özelliklerini veren dalga fonksiyonunun bulunmasından vazgeçilip, tek bir özelliği genellikle de enerjiyi en iyi verecek dalga fonksiyonu aranmaktadır. İçinde çeşitli parametreler değiştirilerek en iyi enerji değerini veren dalga fonksiyonu bulunduğu için bu yönteme “Varyasyon yöntemi” (Karaoğlu 1993) denir.

İkinci yaklaşık yöntemde ise, gerçek sistem kendine benzeyen ve tam çözümü yapılabilen bir model sistemin pertürbe edilmiş bir hali olarak düşünülmektedir (Karaoğlu 1993). Bu pertürbasyondan gelen düzeltme ve ek etkiler pertürbe edilmemiş sisteme ait fonksiyonlar kullanılarak hesaplanmaktadır. Böylece pertürbe edilmiş sisteme ait özdeğer, pertürbe edilmemiş sistemin özdeğerine ek etkiler katılarak bulunmaktadır. Bu yönteme de “Pertürbasyon yöntemi” (Karaoğlu 1993) denir.

Atom ve moleküllerin yapısının belirlenmesinde kullanılan temel yaklaşımlardan biri de öz uyumlu alan (Self Consistent Field, SCF) yöntemidir. Bu yaklaşımda, molekülün her bir elektronunun, molekülün çekirdeklerinin ve diğer elektronlarının oluşturduğu ortalama alanda hareket ettiği varsayılır ve böylece molekülün her bir elektronu için enerji düzeyleri ve dalga fonksiyonları bulunur. Bir elektron için çok merkezli problemin tam çözümünün mümkün olmamamsı nedeniyle öz uyumlu alan yöntemi içinde yeni bir yaklaşımdan daha yararlanma gereği ortaya çıkar. Öz uyumlu alan yaklaşımı içerisinde yapılması gereken yaklaşımlardan en fazla kullanılanı ise Hartree-Fock-Roothan (HFR) yaklaşımıdır (Roothaan 1951, 1960). HFR yaklaşımına göre her bir elektronun durumu, bir moleküler orbital ile karakterize edilir. Böylece kapalı kabuklu atom ve moleküller için HFR yaklaşımında molekülün dalga fonksiyonu bir elektronlu moleküler spin orbitallerinden oluşturulan

( )

( )

( )

( )

( )

( )

( )

( )

( )

N u N u N u u u u u u u N N N N n n n n n n n n n K K K K K K K K K K K 2 1 2 1 2 1 2 2 2 1 1 1 ! 1 = ψ (1.4)

slater determinantı biçiminde yazılır. Burada n elektronun durumunu karakterize _μ eden kuantum sayıları çokluğu,

s

m i n uu

u _μ = moleküler spin orbitali, u moleküler _i obitalin uzay kısmı,

s

m

u ise elektronun spin fonksiyonudur. Açık kabuklu sistemler için ise sistemin durumunu anlatan dalga fonksiyonu, determinant dalga fonksiyonlarının lineer bileşimi biçiminde alınır (Roothaan 1951, 1960). Uzay koordinatlarına bağlı u moleküler orbitali, i χp ile gösterilen Slater atom

orbitallerinin

∑

= p p ip i c u χ (1.5)

biçiminde lineer bileşimi olarak alınır (Roothan 1960). Burada c , i’inci moleküler ip

orbitalin lineer toplam katsayılarıdır. (1.5) eşitliği MO LCAO (Molecular Orbitals Linear Combination of Atomic Orbitals) yönteminin (Roothaan 1951) temelini oluşturur.

Molekülün dalga fonksiyonu, elemanları (1.5) eşitliği ile verilen (1.4) determinantı biçiminde yazılırsa, varyasyon ilkesinin uygulanması sonucunda aşağıdaki HFR denklemleri bulunur (Roothaan 1951).

(

)

∑

− = q iq pq i pq S c F ε 0 (1.6)

Bu eşitlik kapalı kabuklu sistemler için geçerlidir. Burada ,ε_i i’inci moleküler orbitale sahip elektronun enerjisi; Spq,χp ve χq atom orbitalleri arasındaki overlap

integralleridir ve

∫

= v q p pq dv S χ χ (1.7)

şeklinde tanımlanır. F matrisi _pq

pq pq

pq H G

şeklinde iki elemanlı bir toplamdan ibarettir. Burada

∫

⎜⎜_⎝⎛− ∇ −

∑

⎟⎟_⎠⎞ = v q a a a p pq dv r Z H χ 2 χ 2 1 (1.9) ve

(

)

∑∑

− = j rs psqr pqrs js jr pq c c J J G 2 (1.10) biçimindedir.

( ) ( )

( ) ( )

1 2 12 2 2 1 1 1 dv dv r Jpqrs =

∫

χp χq χr χs (1.11a)

( ) ( )

( ) ( )

1 2 12 2 2 1 1 1 dvdv r J_psqr =

∫

χ_p χ_s χ_r χ_q (1.11b)

olarak verilir. (1.9) eşitliğinde r elektronun _a a çekirdeğine olan uzaklığıdır; toplam ise molekülün çekirdekleri üzerinden alınır. (1.10) ifadesinde j indisi, kapalı moleküler orbitallerin numarasını; sırayla p, q, r ve s ise molekülün atomlarının numaralarını gösterir. (1.11) eşitliğindeki χp, χq,χr ve χs’ler atom orbitalleridir.

Bunlar p, q, r, s atomlarının çekirdeklerinde merkezlenmişlerdir. Bu orbitaller ilgili atomların çekirdeklerinde merkezlendikleri için (1.7), (1.8), (1.9) ve (1.11) integralleri çok merkezli integraller olarak adlandırılır.

(1.6) eşitliğindeki denklemler sistemine karşılık gelen karakteristik denklem yani katsayılar determinantından alınan denklem bilgisayar yardımıyla çözülebilir. Ancak HFR denklemlerinde bulunan çok merkezli integrallerin yani Spq ve F ’ pq

ların hesaplanması, molekülün kuantum mekaniksel olarak en zor çözülebilen problemlerinden biridir. HFR denklemlerindeki çok merkezli integrallerin hesaplanması durumunda, molekülün dalga fonksiyonu kapalı kabuklu moleküller

için tek bir determinant olarak, açık kabuklu moleküller için ise determinantların lineer toplamı olarak elde edilir.

1.2 Hidrojen Atomunun Dalga Fonksiyonları

Şekil 1.1’de görüldüğü gibi hidrojen atomunun çekirdeğini merkez kabul eden bir koordinat sistemi kullanılırsa bu durumda elektronun söz konusu koordinat sistemindeki hareketi hidrojenin çekirdeğinin hareketine bağlı bir hareket olur. Bu bağıl hareket için Schrödinger dalga denklemi

( )

ψ ψ ψ μ∇ +U r =E − 2 2 2 h _(1.12)

biçimindedir (Aygün ve Zengin 1998). Burada _{∇ , Şekil 1.1’ deki koordinat sistemi} 2

için 2 2 2 2 2 2 2 z y x ∂ ∂ + ∂ ∂ + ∂ ∂ = ∇ (1.13)

ile verilen bir operatördür. μ ise indirgenmiş kütledir [μ =m_em_p/

(

m_e +m_p

)

].

( )

r

U , elektrona ait Coulomb potansiyel enerjisidir ve

( )

r Ze r U 2 − = (1.14)

şeklinde ifade edilir. (1.12) denkleminin kartezyen koordinat sisteminde çözümü oldukça karmaşıktır. Bu nedenle (1.12) denklemini çözmek için küresel koordinat sisteminden yararlanılır. Atomik birimler kullanılarak ve _{∇ ’nin küresel} 2

Şekil 1.1: Hidrojen atomunda bağıl hareketin incelenmesi için koordinat sistemi

(

)

0 1 1 1 2 2 2 2 2 2 2 ⎥ − = ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ _ψ ϕ ψ θ θ ψ θ θ θ ψ U E Sin r Sin Sin r r r r r (1.15)

elde edilir. Buradaki U

( )

r , (1.14)’de görüldüğü gibi küresel simetrik olduğundan hidrojen atomu içinde merkezcil bir alan (ya da kuvvet) oluşturur. Bu durumda (1.15)’de verilen Schrödinger denklemi değişkenlerine ayırma yöntemi ile çözülebilir. Bu yönteme göre dalga fonksiyonu ψ,

(

θ ϕ

) ( ) ( )

θ ϕ

ψ r, , =R r Y , (1.16)

biçiminde radyal ve açısal iki fonksiyonun çarpımı şeklinde yazılabilir. Bu fonksiyon (1.15)’de yerine yazılıp düzenleme yapılırsa

(

)

_⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ − = − + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ 2 2 2 2 2 ₂ 1 1 1 1 ϕ θ θ θ θ θ Y Sin Y Sin Sin Y U E r dr dR r dr d R (1.17) θ ϕ θ ϕ θ Cos r z Sin Sin r y Cos Sin r x = = = z y x x ϕ θ r e m y p m z

olur. Görüldüğü gibi bu denklemin sol tarafı yalnızca radyal değişkenleri, sağ tarafı ise yalnızca açısal değişkenleri içermektedir. Bu durumda (1.17) denkleminin sağlanabilmesi için eşitliğin C gibi bir sabite eşit olması gerekir. Bu C sabitine ayırma sabiti adı verilir. Eşitliğin sol tarafı, C’ye eşitlenerek düzenleme yapılırsa

CY Y Sin Y Sin Sin ∂ =− ∂ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ 2 2 2 1 1 ϕ θ θ θ θ θ (1.18)

elde edilir. Bu denklemin çözümü olan Y

( )

θ,ϕ fonksiyonu sabit yarıçaplı bir küre

yüzeyi üzerinde açıların, 0≤θ ≤π ve 0≤ϕ ≤2π aralıklarında harmonik değişimlerini temsil ettiği için küresel harmonik olarak adlandırılır.

(1.18) denklemi de θ ve ϕ bağımsız değişkenlerine göre ayrılabilir. Yani

( )

θ,ϕ

Y fonksiyonu,

( )

θ,ϕ =Θ

( ) ( )

θ Φ ϕ

Y (1.19)

biçiminde yalnızca θ ’ya ve yalnızca ϕ’ye bağlı iki fonksiyonun çarpımı şeklinde yazılabilir. (1.19) eşitliği ile verilen Y

( )

θ,ϕ , (1.18) eşitliğinde yerine yazılıp

düzenleme yapılırsa 2 2 2 1 1 ϕ θ θ θ θ θ d d Sin C d d Sin d d Sin Φ Φ = − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Θ Θ − (1.20)

olur. Görüldüğü gibi bu denklemin sol tarafı yalnızca θ ’ya, sağ tarafı ise yalnızca ϕ’ye bağlıdır. Buna göre böyle bir eşitliğin olabilmesi için denklemin her iki tarafı aynı sabite eşit olmalıdır. Bu sabite 2

m

− denirse, sağ taraf için

2 2 2 1 m d d Φ ₌₋ Φ ϕ (1.21)

( )

ϕ π ϕ im m e 2 1 = Φ (1.22)

dir. Buradaki m, manyetik kuantum sayısı olup m=0,_m1, _m2,_K değerlerini alabilir. (1.22) ile verilen Φ fonksiyonları ortonormal bir küme oluşturur. Yani m

( )

m

( )

mm m Φ d = ′ Φ

∫

π ϕ ϕ ϕ δ 2 0 * _(1.23)

şeklindedir. Şimdi de (1.20) eşitliğinin sol tarafı 2

m

− ’ye eşitlenerek düzenleme yapılırsa 0 1 2 2 = Θ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Θ θ θ θ θ θ Sin m C d d Sin d d Sin (1.24)

diferansiyel denklemi elde edilir. Bu denklemde ζ =Cosθ değişken değişimi yapılarak denklem yeniden düzenlenirse

(

)

0 1 1 ₂ 2 2 _Θ= ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ₋ Θ ζ ζ ζ ζ m C d d d d (1.25)

elde edilir. Bu denklemde m=0, C = ll

( )

+1 ve Θ=P_l kullanılarak düzenleme yapılırsa

(

)

( )

l l l P l l d dP d P d 1 2 1 ₂ 2 2 _{− =− +} − ζ ζ ζ ζ (1.26)

şeklini alır. Buradaki l yörünge kuantum sayısıdır ve l=0,1,2,_K,n−1 değerlerini alabilir. n bu kesimin sonunda karşılaşılacak olan baş kuantum sayısıdır. (1.26) denklemindeki P ’ye normal Legendre polinomu denir ve (1.26) denklemi l

çözüldüğünde

( )

(

)

l l l l l d d l P 1 ! 2 1 2 ₋ = ζ ζ ζ (1.27)

elde edilir. Bu bağıntıya Rodrigues bağıntısı denir.

(1.25) denkleminde m≠0 , c= ll

( )

+1 ve Θ

( )

ζ = P_lm

( )

ζ kullanılarak düzenleme yapıldığında ise

(

)

( )

0 1 1 2 1 ₂ 2 2 2 2 ₌ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − + + − − Plm m l l d d d d ζ ζ ζ ζ ζ (1.28)

elde edilir. Bu diferansiyel denklemin çözümü ise

( )

(

)

l_m

( )

m m lm d P d P ζ ζ ζ ζ = 1− 2 2 (1.29)

ile verilen Asosiye Legendre polinomlarıdır. Burada l≥ m≥0 dır. Asosiye Legendre

polinomları için çok sayıda analitik ifade vardır (Guseinov 1995). Bunlardan birkaçı aşağıda verilmiştir:

(

)

l k l k

k k l

lm Cos a Cos Sin

P 2 2 2 0 2 2 − − + − = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ =

∑

λ λ λ λ θ θ θ (1.30) burada

( )

( ) ( )

l F

( )

l F

( )

l F l F l a l k _{k k} l l k l + − + − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + = _λ λ λ 1 2 2 2 1 2 12 (1.31)

biçiminde tanımlanmıştır ve F’ler

( )

₍

_)!

! ! m n m n n F_m − = (1.32)

biçiminde tanımlanan binom katsayılarıdır. İkinci bir analitik ifade, x=cosθ olmak

üzere

( )

₌

(

₋

)

_∑

− − k k l k l l x x b x P_λ 1 2 λ/2 _λ λ 2 (1.33)

şeklindedir (Guseinov 1995). Burada

( ) (

l F l

) ( ) (

F k

) (

F l k

)

F

(

l k

)

F l b_lk _{l ⎥} − k _k + _{l k} − _{l k} − ⎦ ⎤ ⎢ ⎣ ⎡ + + = 2 _{− − −2} 1 2 2 1 2 1 2 2 1 λ λ λ λ _λ λ (1.34) şeklinde tanımlanmıştır ve

[

( )

]

⎭ ⎬ ⎫ ⎩ ⎨ ⎧ _{− − − −} ≤ ≤ _λ l−λ l k 1 1 2 1 2 1

0 dir. Üçüncü bir analitik

ifade ise

( )

(

)

(

₍

)

(

₎

)

_∑

( )

( )

(

)

( )

= − − + − ₊ − ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + − + − = l s i m l i m l i i l l m lm F l l m F i x m l m l l l x x P 2 2 1 2 2 2 ! 1 ! 2 ! 1 2 ! 2 1 (1.35)

dir (Çetinkaya 2006). Burada l+ m çift sayı ise

2 m l

s= + , tek sayı ise

2 1 + + = l m s dir.

Asosiye Legendre polinomlarının bazı özellikleri aşağıda verilmiştir.

( ) ( )

x P

( )

x P_lλ = −1l−λ _lλ − (1.36)

( ) ( )

2 1 2 1 1 = ± + ± l Plλ l δ >0 (1.37)

( )

∑

= = + + l l x P l 0 2 ₁ 1 2 1 2 2 0 λ δλ λ (1.38)

Asosiye Legendre polinomları aşağıdaki tekrarlama bağıntıları kullanılarak da hesaplanabilir (Arfken ve Weber 1969).

(

)

(

)

(

)

m l m l lm l m P l m P P x l 1 1 _{1 1} 2 + = − + ₊ + + ₋ (1.39)

(

1

)

[

(

1

) (

1

)

]

0 2 1 , , 2 1 2 1 , + + − − = − − ₋ + nm nm n n P n n m m P x mx P (1.40)

(1.27) ile verilen Rodrigues bağıntısından yararlanılarak türetilen Asosiye Legendre polinomları normalize değildir. Asosiye Legendre polinomların normalizasyon katsayısı

( )

( )

(

₍

)

₎

2 1 2 ! ! 2 1 2 1 ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + − + − = + m l m l l N m m lm (1.41)

ile verilir. Bu durumda normalize Θ

( )

θ fonksiyonu

( ) ( )

( )

(

)

(

)

(

θ

)

θ P Cos m l m l l lm m m lm 2 1 2 ! ! 2 1 2 1 ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + − + − = Θ + (1.42)

olarak elde edilir. Bu durumda (1.19) eşitliği ile tanımlanan küresel harmonikler (1.22) ve (1.42) eşitlikleri kullanılarak

( ) ( )

( )

(

)

(

)

(

θ

)

ϕ π ϕ θ im lm m m lm P Cos e m l m l l Y 2 1 2 ! ! 4 1 2 1 , ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + − + − = + _(1.43)

şeklinde elde edilir. Küresel harmoniklerin bazı özellikleri aşağıda verilmiştir.

( ) ( )

θ

,

ϕ

1 *

( )

θ

,

ϕ

lm m m l Y Y₋ = − (1.44)

( ) ( )

lm ll mm lm Y d Y ′ ′ Ω = Ω

∫

* θ,ϕ θ,ϕ δ δ _(1.45) Küresel harmonikler,

( )

θϕ θ

(

_{( )( )}

)(

)

( ) (

θϕ

₍

)(

_{)( )( )}

)(

)

( )

θ,ϕ 3 2 1 1 1 2 , 1 2 1 2 , _2, 2 1 , 1 2 1 m l m l lm Y m l m l l m l m l l Y m l m l l l Cos Y _{− ⎥ −} ⎦ ⎤ ⎢ ⎣ ⎡ − + − − − − + + − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − + = (1.46)

tekrarlama bağıntısından da hesaplanabilir (Weniger ve Steinborn 1982). Bazı küresel harmonikler Çizelge 1.1’de verilmiştir (Aygün ve Zengin 1998).

Çizelge 1.1 l=0,1,2,3 için (1.43) eşitliğinden elde edilen olası küresel harmonikler

θ π π Cos Y Y 2 1 10 00 4 3 0 1 4 1 0 0 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = = ϕ θ π i e Sin Y_± ⎟ ± ⎠ ⎞ ⎜ ⎝ ⎛ = ± 2 1 1 1 8 3 1 _m

(

3 1

)

16 5 0 2 2 2 1 20 ⎟ − ⎠ ⎞ ⎜ ⎝ ⎛ = θ π Cos Y ϕ θ θ π i e Cos Sin Y _± ⎟ ± ⎠ ⎞ ⎜ ⎝ ⎛ = ± 2 1 1 2 8 15 1 _m ϕ θ π i e Sin Y 2 2 2 1 2 2 32 15 2 _± ⎟ ± ⎠ ⎞ ⎜ ⎝ ⎛ = ±

(

θ θ

)

π Cos Cos Y 5 3 16 7 0 3 2 3 1 30 ⎟ − ⎠ ⎞ ⎜ ⎝ ⎛ =

(

_θ

)

ϕ θ π i e Cos Sin Y_± ⎟ − ± ⎠ ⎞ ⎜ ⎝ ⎛ = ± 5 1 64 21 1 2 2 1 1 3 m ϕ θ θ π i e Cos Sin Y 2 2 2 1 2 3 32 105 2 _± ⎟ ± ⎠ ⎞ ⎜ ⎝ ⎛ = ± ϕ θ π i e Sin Y 3 3 2 1 3 3 64 35 3 _± ⎟ ± ⎠ ⎞ ⎜ ⎝ ⎛ = ± _m l m Ylm

( )

θ,ϕ

Hidrojen atomunun dalga fonksiyonlarının radyal kısmını elde etmek için şimdi de (1.17) denkleminin sol tarafı (1.18) denkleminde yapıldığı gibi C = ll

( )

+1

sabitine eşitlenirse atomik birimlerde

( ) (

1

)

( )

0 1 , 2 2 2 ⎥ = ⎦ ⎤ ⎢ ⎣ ⎡ − + + − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ r R U E r l l dr d r dr d r nl (1.47)

elde edilir. Bu denklemde ,U elektronun (1.14) eşitliği ile verilen Coulomb potansiyel enerjisini,

( )

₂1

r l l +

ise ilgili açısal momentumun karesi ile orantılı olan potansiyel enerjiyi temsil etmektedir. Bu iki potansiyel enerjinin toplamına etkin potansiyel enerji denir. Yani

( )

2 1 r l l U Uet + + = (1.48)

biçiminde yazılırsa (1.47) denklemi

( )

(

)

( )

0 1 , 2 2 ⎥ = ⎦ ⎤ ⎢ ⎣ ⎡ − + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ r R r U E dr d r dr d r et nl (1.49) şeklini alır. Bu denklemde (1.14) eşitliği ile verilen Coulomb potansiyel enerjisi de kullanılarak ve α =2 −2Enl tanımlaması yapılırsa

( ) ( ) ( )

2 2 2

( )

( )

( )

12 ,

( )

0 2 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ₊ − + + R r r l l r Z E r d d r r d d l n α α α α α α (1.50)

elde edilir. Bu denklemde de ρ =αr ve Z =γ =n α 2 tanımları kullanılırsa

( )

1

_{( )}

₀ 4 1 2 , 2 2 2 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ _{+ − + −} + _ρ ρ ρ γ ρ ρ ρ Rnl l l d d d d (1.51)

bulunur. Burada ρ, bağımsız değişken, γ ise baş kuantum sayısı

(

γ =n

)

adı verilen bir sabittir.

(1.51) denklemi ρ →∞, 0ρ → ve 0 ile ∞ arasındaki ara bölge için ayrı ayrı çözülür. Bu üç çözümün çarpımı ise Rnl

( )

ρ radyal çözüm fonksiyonunu verir.

∞ → ρ limitinde (1.51) denklemi,

( )

0 4 1 , 2 2 = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ρ ρ Rnl d d (1.52)

biçimini alır. Bu denklemin çözümü ise

(

) (

)

2

, ρ →0 = sabit e±ρ

Rnl (1.53)

dir. Buradaki +ρ2

e durumunda ρ →∞ iken R→∞’ a gider. Kesim 1.1’de verilen kuantum mekaniğinin dalga fonksiyonu ile ilgili olan 1. postülasına göre dalga fonksiyonunun sonlu değer alması gerekir. Bu nedenle ρ →∞ limitinde R→∞’a

gittiğinden bu çözüm fiziksel bir çözüm olamaz. Buna göre başlangıç koşulları uygun seçilerek sabit=1 yapılırsa (1.53) fonksiyonu fiziksel çözüm olarak

(

)

2 , ρ ρ − = ∞ → e R_nl (1.54) halini alır. 0 →

r limitinde

( )

14 ve

(

γ ρ

)

terimleri diğer terimler yanında ihmal edilebilir ve (1.51) denklemi

( )

_{( )}

0 1 2 , 2 2 2 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − + ρ ρ ρ ρ ρ Rnl l l d d d d (1.55)

(

_,

)

( )

₂1

(

_,

)

0 2 2 = + − nl l n R l l R d d _ρ ρ ρ ρ (1.56)

elde edilir. Bu denklemin çözümü ise ρ →0 limitinde

(

)

l

l n

R _, ρ → 0 = ρ (1.57)

olarak elde edilir. Böylece r →∞ ve r→0limitlerinde dalga fonksiyonları elde edilmiş olur. Bu iki durum dışındaki ara bölgedeki radyal fonksiyon da fn,l

( )

ρ

biçiminde düşünülürse bu durumda R_n,l

( )

ρ bu üç fonksiyonun çarpımı olarak

( )

ρ ρ ρ

( )

ρ l n l l n e f R _, = − 2 _, (1.58)

biçiminde bir fonksiyon olmalıdır. Buradaki fn,l nin açık ifadesini elde etmek için

(1.58) ile verilen fonksiyon (1.51) denkleminde yerine yazılırsa

( )

_{( )}

0 1 4 1 2 , 2 2 2 2 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − + − + − ρ ρ ρ ρ γ ρ ρ ρ ρ l n l f e l l d d d d (1.59) olur. Buradan

( )

[

2 1

]

[

( )

1

]

_,

( )

0 2 2 = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + − + − + + γ ρ ρ ρ ρ ρ l f_nl d d l d d (1.60)

bulunur. Bu denklemde j = l2 +1, q=γ +l =n+l ve f_n,l

( )

ρ =L_qj

( )

ρ tanımları kullanılırsa (1.60) denklemi

(

1

)

(

)

( )

0 2 2 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − + + ρ ρ ρ ρ ρ q j Lqj d d j d d (1.61)

şeklini alır. Buradaki L ’ye Asosiye Laguerre polinomları denir. Bu denklemde _qj 0 = j alınırsa denklem

(

1

)

( )

0 2 2 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − + ρ ρ ρ ρ ρ q Lq d d d d (1.62)

halini alır. Bu denklemin çözümü normal Laguerre polinomları olarak adlandırılır ve

( )

ρ

(

_ρ ρ

)

ρ ρ ₌ − e d d e L _q q q q (1.63)

Rodrigues formülünden türetilir (Arfken ve Weber 1995). Kuantum sayısı 0

≠

j olduğu zaman çözüm fonksiyonu (1.61) denkleminden bulunur. (1.61) denkleminin çözümlerine de daha önce de belirtildiği gibi Asosiye Laguerre polinomları denir ve Asosiye Laguerre polinomları, normal Laguerre polinomları kullanılarak

( )

( )

ρ ρ ρ j_{j q} j q L d d L = (1.64)

formülünden türetilir. Bu şekilde elde edilen Asosiye Laguerre polinomları normalize değildir. Asosiye Laguerre polinomlarının normalizasyon katsayıları atomik birimlerde

(

)

(

)

[

]

2 1 3 3 , ! 2 ! 1 2 ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ + − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = l n n l n n Z N_nl (1.65)

ile verilir. Böylece r n

Z 2 =

( )

(

)

(

)

[

]

⎟⎠ ⎞ ⎜ ⎝ ⎛ ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ + − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = − r n Z L e l n n l n n Z r R nr _qj Z l n 2 ! 2 ! 1 2 12 3 3 , (1.66)

olarak elde edilmiş olur. Burada L nin qj

( )

₍

₎

( )

_[

₍

₎

_]

s j q s j s j q r n Z j s q j s s q r n Z L ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − + − = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛

_∑

− = + 2 ! ! ! ! 1 2 2 0 (1.67)

biçimindeki açık ifadesi kullanılarak daha elverişli bir bağıntı elde edilebilir (Arfken ve Weber 1995). (1.67) denkleminde daha önce tanımlanan q=n+l ve j= l2 +1 kullanılır ve bu şekilde elde edilen Asosiye Laguerre polinomu (1.66) ifadesinde yerine yazılırsa

( )

(

_[

_{( )}

)

_]

( )

₍

[

( )

_{) (}

]

₎

⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − − + + + − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − =

∑

−− = − nl s s s r n Z l nl r n Z l s n l s s l n e r n Z l n n l n n Z r R 2 ! 1 ! 1 2 ! ! 1 2 ! 2 ! 1 2 1 2 0 2 1 3 3 (1.68) bulunur. Bu ifade s+l =n′−1, _n n Z _ζ

= tanımları yapılarak yeniden düzenlenirse

( ) (

) (

)

_∑

( )

₍

( )

_{) (}

_{) (}

₎

+ = ′ − − ′ + ′ − − ′ ′ − + ′ − − ′ − ⎥⎦ ⎤ ⎢⎣ ⎡ − − + = n l n r n n n l n l n n e n n l n l n r n l n l n r R 1 1 2 1 1 2 1 , _{1! ! !} 2 1 2 ! ! 1 ζ ζ _(1.69)

elde edilir. İlk kez (1.5) ifadesinde karşılaşılan slater atom orbitalinin radyal kısmının açık ifadesi

(

) ( )

_{( )}

n r n n n n n e r n r R ζ ζ ′− −ζ + ′ ′ ′ = 2 1 1 ! 2 2 , (1.70) (1.69) denkleminde kullanılırsa ve

( )

(

)

(

)

( )

12 1 1 2 1 2 1 1 _⎢⎣⎡ − − + ′ _⎥⎦⎤ − = −− ′−− ′+ ′₊ ′ ′ F n l F n l F n n W_nl_n n l _{n l n l n l} (1.71)

katsayıları tanımlanırsa hidrojene ait dalga fonksiyonunun radyal kısmı

( )

r W R

(

r

)

R n n n l n l n n l n , 1 , ′ ζ + = ′ ′

∑

= (1.72)

olarak elde edilir. Bu durumda hidrojene ait dalga fonksiyonu (1.16) denkleminde R yerine yazılarak

(

θ ϕ

)

(

ζ

)

( )

θ ϕ ψ , , , , 1 lm n l n n n l n n nlm r W R r ⎟Y ⎠ ⎞ ⎜ ⎝ ⎛ =

∑

+ = ′ ′ ′ (1.73)

olarak elde edilir. ψnlm

(

r,θ,ϕ

)

fonksiyonları ortogonâldir. Yani

(

)

nlm

(

)

nn ll mm nlm r ′′ ′ r d = ′ ′ ′

∫

ψ θ ϕ ψ θ ϕ τ δ δ δ τ , , , , * _(1.74)

Bazı hidrojen dalga fonksiyonları Çizelge 1.2’de verilmiştir (Aygün ve Zengin 1998).

Çizelge 1.2 n=1,2 ve 3 için hidrojen dalga fonksiyonları 0 2 3 0 100 1 Zra e a Z − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = π ψ 0 2 0 2 3 0 200 2 2 4 1 Zr a e a Zr a Z − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = π ψ θ π ψ e Cos a r Z a Z Zr2a₀ 0 2 3 0 210 2 4 1 − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ϕ θ π ψ Zr a i e Sin e a r Z a Z − ± ± ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 2 0 0 2 3 0 1 21 8 1 m 0 3 2 0 2 0 2 3 0 300 27 18 2 3 81 1 Zr a e a r Z a r Z a Z − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = π ψ θ π ψ e Cos a r Z a r Z a Z Zr 3a₀ 0 0 2 3 0 310 6 81 2 − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ϕ θ π ψ Zr a i e Sin e a r Z a r Z a Z − ± ± ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 3 0 0 0 2 3 0 1 31 6 81 1 m

(

3 1

)

6 81 1 3 2 2 0 2 2 2 3 0 320 ⎟⎟ 0 − ⎠ ⎞ ⎜⎜ ⎝ ⎛ = − _θ π ψ e Cos a r Z a Z Zr a ϕ θ θ π ψ Zr a i e Cos Sin e a r Z a Z − ± ± ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 3 0 2 0 2 2 2 3 0 1 32 81 1 m ϕ θ π ψ Zr a i e Sin e a r Z a Z 3 _{2 2} 2 0 2 2 2 3 0 2 32 0 162 1 − ± ± ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ =

Daha önce de belirtildiği gibi bu dalga fonksiyonları potansiyel enerji fonksiyonunun küresel simetrik olması durumunda Schrödinger denkleminin çözümünden elde edilen fonksiyonlardır. Hidrojen atomundan büyük atomlarda ve bütün moleküllerde elektronun maruz kaldığı elektriksel potansiyel, küresel simetrik değildir. Bu durumda sistemin dalga fonksiyonunun elde edilmesi için bazı yaklaşımlar yapmak gerekir. Bu yaklaşımlardan en önemlisi Özuyumlu Alan (Self Consistent Field, SCF) yöntemidir. Tek elektron çok merkezli problemlerin tam çözümünün mümkün olmaması nedeniyle özuyumlu alan yaklaşımı içerisinde yeni

bir yaklaşım daha yapmak gerekir. Bu yaklaşım ise Hartree-Fock (HF) yaklaşımıdır (Hartree 1928, Fock 1930) ve bu şekilde elde edilen dalga fonksiyonlarına Hartree-Fock Özuyumlu Alan (HF-SCF) dalga fonksiyonları denir. Bu fonksiyonlar Kesim 1.3’de kısaca anlatılmıştır.

1.3 Hartree-Fock Özuyumlu Alan Dalga Fonksiyonları

Hartree-Fock özuyumlu alan dalga fonksiyonları (HF-SCF) küresel simetrik olan bir etkin potansiyel ile elektronun etkileşimini göz önüne alarak elde edilen bir elektron dalga denkleminin çözümleridir. Bu nedenle HF-SCF dalga fonksiyonlarının açısal kısımları, Kesim 1.2’de elde edilen Hidrojen dalga fonksiyonlarının açısal kısmı

(

Ylm

( )

θ,ϕ

)

ile aynıdır. HF-SCF dalga fonksiyonlarının radyal kısmı ise periyodik tablonun tamamı için yaklaşık olarak, bazı atomlar için ise yüksek hassasiyetle sayısal olarak bilgisayar ile hesaplanabilmektedir. Bu radyal fonksiyon için analitik bir ifade ise Slater tarafından

( ) ( )

( )

n r n e r n r R ζ − −ζ + = 2 1 1 ! 2 2 (1.75)

biçiminde önerilmiştir. Hidrojen atomu dalga fonksiyonunun açısal kısmı da kullanıldığında HF-SCF dalga fonksiyonlarının en önemlisi

( ) ( )

( )

( )

θ ϕ ζ ζ χ ζ _, ! 2 2 , 2 1 1 lm r n n nlm r e Y n r − − + = (1.76)

tek bir fonksiyon biçiminde yazılır. Bu fonksiyonda ζ , Slater kuralları adı verilen kurallardan elde edilirse fonksiyon Slater Atom orbitali olarak, başka yöntemlerle hesaplandığında ise Slater-tipi atom orbitali (STO) yada Slater-tipi fonksiyon olarak adlandırılır. ζ ’nın belirlenmesi için Slater-kuralları aşağıda verilmiştir (Slater 1930);

i) Belirli bir elektron için etkin çekirdek yükü

γ − = Z

Z_nl (1.77) bağıntısından bulunur. Buradaki Z çekirdeğin gerçek yükü, γ ise verilen nl yörüngemsisindeki elektrona ait perdeleme sabitidir.

ii) Perdeleme sabitlerini bulmak için elektronlar aşağıdaki gruplara ayrılırlar:

( ) (

1s, 2s,2p

) (

, 3s,3p

) ( ) (

, 3d , 4s,4p

) ( ) ( ) (

, 4d , 4f , 5s,5p

)

,K

Bu yaklaşık olarak orbitallerin enerji seviyelerine veya elektronların çekirdekten uzaklığına göre yapılan bir sıralamadır ve içten dışa doğru alınmıştır.

iii) Bu grupların perdeleme sabitine katkısı şu şekilde bulunur:

(a) İncelenen elektronun bulunduğu grubun dışındaki gruplarda bulunan elektronların katkısı sıfırdır.

(b) Aynı gruptaki her fazla elektron için katkı 0.35 dir. Eğer incelenen elektron (1s) grubunda ise ikinci elektrondan gelen perdeleme sabiti 0.30 alınır.

(c) İncelenen elektron (s,p) gruplarından birinde ise, bir iç gruptaki her elektron için 0.85, daha iç gruplardaki her elektron için 1.0 katkı alınır. Sonuncu halde “tam perdeleme vardır” denir.

(d) İncelenen elektron d veya f grubunda ise içteki bütün elektronlar için tam perdeleme kabul edilir ve perdeleme sabitinin her birinin katkısı 1.0 olarak alınır.

iv) K, L ve M kabukları için n′=n alınır. N, O ve P kabukları için ise n′ sırasıyla 3.7, 4.0 ve 4.2 olarak alınır.

ζ perdeleme sabitini hesaplama yöntemlerinden biri de özuyumlu alan yöntemidir. Bu yöntemde ζ sabiti varyasyon parametresi olarak göz önüne alınır. Bu amaçla atomun her bir elektronu yalnızca bir tane Slater fonksiyonu ile anlatılır. Bu şekilde varyasyon ilkesi ile elde edilen dalga fonksiyonları en iyi atom orbitali

olarak adlandırılır (Roothaan 1960). Bu şekilde belirlenen Slater fonksiyonlarına Slater-tipi atom orbitali yada Slater-tipi fonksiyon denir. Clementi ve Raimondi (1963, 1967) özuyumlu alan yöntemini kullanarak atom numarası 2’den 86’ya kadar olan atomlar için perdeleme sabitlerini hesaplamışlardır.

ζ ’nın bulunması için başka bir yaklaşım ise Burns (1964) tarafından önerilmiştir ve sistemin önemli bir niceliğini örneğin r’nin veya

r 1

nin ortalama değerini en iyi verecek tek bir Slater –tipi atom orbitalini aramaya dayanır.

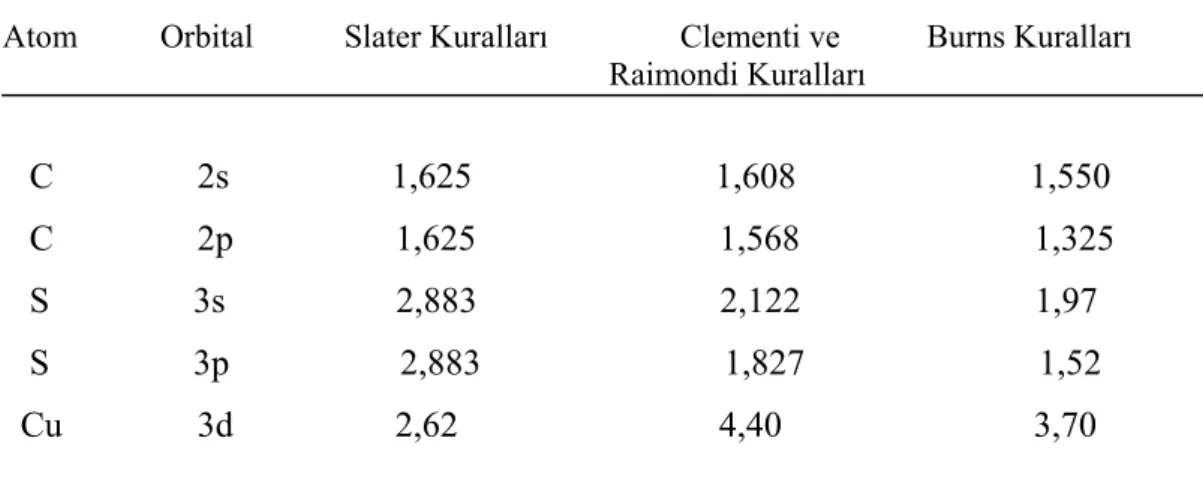
Çizelge 1.3’de karbon atomunun 2s, 2p kükürt atomunun 3s, 3p ve bakır atomunun 3d orbitalleri için perdeleme sabitleri verilmiştir (Burns 1964, Clementi ve Raimondi 1963).

Çizelge 1.3 Tek bir STO için farklı yöntemlerle elde edilen perdeleme sabitleri

Atom Orbital Slater Kuralları Clementi ve Burns Kuralları

Raimondi Kuralları C 2s 1,625 1,608 1,550 C 2p 1,625 1,568 1,325 S 3s 2,883 2,122 1,97 S 3p 2,883 1,827 1,52 Cu 3d 2,62 4,40 3,70

2. STO’lar ÜZERİNDEN KİNETİK ENERJİ İNTEGRALLERİ

Slater-tipi atom orbitalleri üzerinden iki-merkezli kinetik enerji integrallerinin eliptik koordinatlar kullanılarak hesaplanmasında kuantum sayılarının çoğu durumları için overlap integralleri ile karşılaşılır. Bu nedenle Kesim 2.1.1’de slater-tipi atom orbitalleri üzerinden bir-merkezli overlap integrallerinin, Kesim 2.1.2’de ise slater-tipi atom orbitalleri üzerinden iki-merkezli overlap integrallerinin eliptik koordinatlar kullanılarak elde edilen analitik ifadesi (Guseinov ve ark. 1998) incelenecektir.

2.1 Slater-tipi Atom Orbitalleri Üzerinden Overlap İntegralleri

2.1.1 Slater-tipi Atom Orbitalleri Üzerinden Bir-Merkezli Overlap İntegralleri

Slater-tipi atom orbitalleri üzerinden bir-merkezli overlap integralleri

(

ζ ζ

)

χ

( )

ζ χ

(

ζ

)

τ τ d r r S_{nlm,n′l′m′} , ′ =

∫

*_nlm ,r _n′l′m′ ′,r (2.1)

biçiminde tanımlanır. Bu integralde Slater-tipi atom orbitallerinin (1.76) eşitliğinde verilen açık ifadesi yerine yazılırsa

(

) ( ) ( )

( ) ( )

ζ

(

θ ϕ

)

(

θ ϕ

)

τ ζ ζ ζ ζ ζ τ λ λ r e Y r e Y d n n S lm r n lm r n a n n l n nl , , ! 2 ! 2 2 2 , 2 1 * 1 1 2 1 , ′′ ′ − − ′ − − + ′ + ′ ′

∫

′ ′ = ′ (2.2)

elde edilir. Bu integralin çözümü, küresel harmoniklerin (1.45) eşitliği ile verilen ortogonallik bağıntısı ve Gama fonksiyonları kullanılarak

(

) ( ) ( )

(

)

n n

( ) ( )

(

)

ll mm n n l n nl n n n n S _{+′+ ′ ′} + ′ + ′ ′ ′ ′ + ′ + ′ = ′ δ δ ζ ζ ζ ζ ζ ζ λ λ ! 2 ! 2 ! 2 2 , ₁2 1 2 1 , (2.3)

2.1.2 Slater-Tipi Atom Orbitalleri Üzerinden İki-Merkezli Overlap İntegralleri

Slater atom orbitallerini içeren overlap integralleri,

(

ζ ζ

)

χ

(

ζ

)

χ

(

ζ

)

τ τ d r r R S_{nlm,n′l′m′} , ′, r_ab =

∫

_nlm* ,r_{a n′l′m′} ′,r_b (2.4)

biçiminde tanımlanır. Burada χ_nlm

(

ζ,rv_a

)

herhangi bir a atomunun, χ_n′l′m′

(

ζ′,rv_b

)

’de herhangi bir b atomunun çekirdeğinde merkezlenmiş Slater-tipi atom orbitalleridir. Overlap integrallerinin hesaplanması için literatürde bir çok çalışma bulunmaktadır. Bu çalışmalardan biri Jones (1981) tarafından yapılmıştır. Bu çalışmada Jones overlap integrallerini hesaplamak için Taylor seri açılımından yararlanmıştır. Jones tarafından yapılan başka bir çalışmada (1992) overlap integrallerinin çözümü için Löwdin’in α fonksiyonu (Löwdin 1953) kullanılarak b çekirdeğinde merkezlenmiş Slater-tipi atom orbitalleri a merkezine taşınmış ve böylelikle ortaya çıkan tek merkezli integral için analitik ifadeler bulunmuştur. Ayrıca Bhattacharya ve Dhabal (1986), bu integrallerin çözümü için Fourier dönüşüm yönteminden yararlanmışlardır.

Guseinov ve ark. (1998) overlap integrallerini hesaplamak için eliptik koordinatlardan yararlanmışlardır. Overlap integrallerinin çözümünde eliptik koordinatlardan yararlanılması, yukarıda sözü edilen yöntemlere göre daha yararlıdır. Çünkü yukarıda sözü edilen yöntemler her ζ değeri için kararlı sonuçlar vermemektedir. Örneğin Jones (1987) overlap integrallerini hesaplamak için ζ ’nın küçük ve büyük değerlerine göre farklı analitik ifadeler kullanmıştır.

Küresel koordinatlardan eliptik koordinatlara geçmek için Şekil 2.1’de gösterildiği gibi z eksenleri birbirinin zıttı yönde yönelmiş iki kartezyen koordinat sistemi göz önüne alınır. Buradaki

(

x_ay_az_a

)

kartezyen koordinat sisteminin merkezinde a atomunun çekirdeği,

(

xbybzb

)

kartezyen koordinat sistemenin

merkezinde ise b atomunun çekirdeği bulunmaktadır. Elektronun a çekirdeğine olan uzaklığı r , b çekirdeğine olan uzaklığı ise _a r dir. _b R ise a ile b çekirdeği arasındaki _ab

uzaklıktır.

( )

xyz kartezyen koordinat sistemi ise

(

x_ay_az_a

)

ile

(

x_by_bz_b

)

kartezyen koordinat sistemlerinin ortasında merkezlenmiş genel koordinat sistemidir.

Şekil 2.1: Eliptik koordinatlar

R/2 R/2 a y b y y b z b z a z O θ b θ r b r a r a θ a ϕ b x x a x

(2.4) eşitliği ile verilen integrali çözmek için

( )

rθϕ küresel koordinatlarından

(

μvϕ

)

eliptik koordinatlarına geçmek gerekir. Elektronun eliptik koordinatları,

ab b a R r r + = μ ab b a R r r v= − ϕ =ϕ_a −ϕ_b (2.5)

dönüşüm formülleri yardımıyla bulunur. Burada 1≤μ ≤∞, −1≤v≤+1, 0≤ϕ≤2π

şeklindedir.

(

xayaza

)

,

(

xbybzb

)

,

( )

xyz kartezyen koordinatlarından

(

μvϕ

)

eliptik

koordinatlarına

(

)(

)

[

μ 1 1

]

cosϕ 2 2 1 2 2 v R x x x ab b a = = − − = (2.6)

(

)(

)

[

μ 1 1

]

sinϕ 2 2 1 2 2 v R y y y ab b a = = − − = (2.7)

(

v

)

R za = ab 1+μ 2 (2.8)

(

v

)

R z ab b = 1−μ 2 (2.9) v R z ab μ 2 = (2.10)

dönüşüm bağıntılarıyla geçildiğini görmek kolaydır. Ayrıca eliptik koordinatlarda hacim elemanı,

(

μ v

)

dμdvdϕ R dV ab 2 2 3 8 − = (2.11)

v v a + + = μ μ θ 1 cos

[

(

)(

)

]

v v a + − − = μ μ θ 2 1 2 2 _{1 1} sin (2.12) v v b − − = μ μ θ 1 cos

[

(

)(

)

]

v v b − − − = μ μ θ 2 1 2 2 _{1 1} sin (2.13)

biçiminde bulunur. (2.5) eşitliğinden elektronun a ve b çekirdeklerine olan uzaklıkları eliptik koordinatlarda

(

v

)

R r ab a = μ+ 2 (2.14)

(

v

)

R r ab b = μ− 2 (2.15)

olarak elde edilir.

Slater atom orbitallerinin (1.76) eşitliğindeki açık şekli m= m′=λ durumu

için (2.4)’de yerine yazılırsa

(

ζ ζ

)

( ) ( )

ζ

_{( ) ( )}

ζ ζ λ

(

θ ϕ

)

ζ λ

(

θ ϕ

)

τ τ λ λ r e S r e S d n n R S l b b r n b a a l r n a n n ab l n nl b a ′ ′ − − ′ − − + ′ + ′ ′

∫

′ ′ = ′ 2 1 1 1 2 1 , ! 2 ! 2 2 2 , , r (2.16)

bulunur. (2.13)’de S_lλ

( )

θϕ ’nin (1.43) eşitliği ile verilen açık ifadesi yazılarak eliptik koordinatlara geçilirse

(

)

( ) ( )

_{( ) ( )}

(

)

( )

(

)

( )

(

)

(2.17) 8 0 sin 0 cos 1 1 2 2 2 1 ! 2 ! 2 2 2 , , 2 2 3 2 2 1 1 2 0 2 1 2 1 2 1 2 1 , ϕ ν μ ν μ λ ϕ λ λ ϕ λ ν μ μν ν μ μν μ μ π ζ ζ ζ ζ λ λ λ π _{ζ μ ζ μ} λ λ d d d R P P e v R e v R n n R S l l v R n v R n n n ab l n nl − ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ < ≥ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + × ⎥⎦ ⎤ ⎢⎣ ⎡ ₋ ⎥⎦ ⎤ ⎢⎣ ⎡ ₊ ′ ′ = ′ ′ ∞ − − ′ − − ′ + − − + ′ + ′ ′

∫∫ ∫

r

elde edilir. Burada ( ) ( )

(

)

( )

(

) (

α

)

β β α αβ λ β λ α λ λ _{μ ν μ ν} μν λ λ ν μ μν ν μ μν − + ′ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + +

∑

∑

∑

+ = ′ = − = ′ q q q l l l l P g l l P 1 1 , 0 2 2 _(2.18)

şeklinde yazılabilir. (2.18) ifadesindeki q

g_αβ,

(

)

(

) ( ) ( )

λ β λ λ α λ αβ λ λ α λ β λ k λ l k l k k q q D D F F l l g _{+ −} ′ =

∑

− − + = ′ _{2 2} 0 1 , , (2.19)

ile verilir (Guseinov 1995). Burada

( )

( )

(

)

( )

λ ( β)

( )

β λ

(

β

)

λ β ε λ β ⎥ + ⎦ ⎤ ⎢ ⎣ ⎡ + + − = − _{− −} l F l F l F l F l D l l l l 2 2 1 2 2 1 2 1 2 1 (2.20)

şeklinde tanımlanır. (2.16) ifadesindeki F_i( sk, ) katsayıları genelleştirilmiş binom katsayıları olarak adlandırılır. Genelleştirilmiş binom katsayıları ise

( )

_∑

( ) ( )

( )

= − − = s j j i j j i k s F s F k F 0 1 , (2.21)

şeklinde tanımlanır. Burada s=min

(

i,s,k−i

)

dir. (2.17) ifadesinde (2.18) kullanılır ve ϕ üzerinden integral alınırsa

(

)

( )

( ) ( )

(

)

( ) (

) (

)

(

)

∫ ∫

∑

∑

∑

∞ − − − − ′ − + = ′ = − = ′ ′ ′ − + × ′ = ′ 1 1 1 0 2 2 , 22 . 2 , , , , dv d e e v v v l l g t p N R S ptv p n n q q q l l n n ab l n nl μ μ μ μ λ λ ζ ζ μ β α β α αβ λ β λ α λ λ

( )

[

( )

_{( ) ( )!}

]

[

( )

]

2 ! 2 1 1 , 2 1 2 1 n n t p t p t p N n n n n ′ − + = + ′ + ′ (2.23)

(

ζ +ζ′

)

= 2 ab R p (2.24)

(

)

(

ζ ζ

)

ζ ζ ′ + ′ − = t (2.25)

( )

∞

_{∫ ∫}

( ) (

) (

)

− − − − + = 1 1 1 ,t μν μ ν μ ν e μe νdμdν p Q_ik_j k i j p pt (2.26)

tanımı kullanılırsa (2.22) denklemi

( )

_{P t N}

( )

_{p t} ( ) ( ) _g

(

_{l l}

)

_Q

( )

_{P t} S _nq _n q q l l n n l n nl , , , , , 0 2 2 , α β β α αβ λ β λ α λ λ λ λ − ′− + = ′ = − = ′ ′ ′ =

∑

∑

∑

′ (2.27)

şeklini alır. Bu ifadedeki

(

n−α

)

ve

(

n′−β

)

nın daima pozitif olduğuna dikkat

edilmelidir. Ancak STO lar üzerinden iki-merkezli kinetik enerji integralleri hesaplanırken karşılaşılan overlap integrallerinde n′ 2− <l′ durumunda

(

n′−β

)

negatif değer alır. Bu durumda ise Q yardımcı fonksiyonunun analitik çözümü farklıdır.

Bu çalışmada

(

n′−β

)

’nın pozitif olması durumunda Guseinov ve

arkadaşlarının (1998) Q için A ve B yardımcı fonksiyonları cinsinden verdikleri analitik ifade,

(

n′−β

)

nın negatif olması durumunda ise Özmen ve arkadaşlarının

(2003) Q için J ve K yardımcı fonksiyonları cinsinden verdikleri analitik ifadeler kullanılacaktır.