Kuadratik sayı cisimlerinde çarpanlara ayırma, ideal sınıf grubu ve L-fonksiyonları

YILDIZ TEKNİK ÜNİVERSİTESİ

FEN BİLİMLERİ ENSTİTÜSÜ

KUADRATİK SAYI CİSİMLERİNDE ÇARPANLARA

AYIRMA, İDEAL SINIF GRUBU ve L-FONKSİYONLARI

Matematikçi Bülent KÖKLÜCE

FBE Matematik Anabilim Dalı Matematik Programında Hazırlanan

DOKTORA TEZİ

Tez Savunma Tarihi: 8 Aralık 2005

Tez Danışmanı : Doç. Dr. Ömer GÖK (YTÜ)

Jüri Üyeleri : Prof. Dr. Göksel AĞARGÜN (YTÜ)

: Doç. Dr. Mustafa BAYRAM (YTÜ) : Prof. Dr. Mehmet BAYRAMOĞLU(YTÜ) : Prof. Dr. Elimhan MAHMUDOV (İÜ)

ii

Sayfa

SİMGE LİSTESİ ...iv

KISALTMA LİSTESİ ...vi

ÇİZELGE LİSTESİ ...vii

ÖNSÖZ...viii

ÖZET...ix

ABSTRACT ... x

1. GİRİŞ... 1

2. CEBİRSEL SAYI CİSİMLERİ ve KUADRATİK SAYI CİSİMLERİ ... 6

2.1 Cebirsel Sayı Cisimleri... 6

2.2 Kuadratik Sayı Cisimlerine Giriş ... 10

2.3 Kuadratik Sayı Cisimlerinin Tamlık Halkası ve Diskriminantı ... 13

2.4 Kuadratik Sayı Cisimlerinde Birimseller Grubu ... 17

2.5 Bölümle İlgili Pari Komut ve Programları ... 31

3. KUADRATİK SAYI CİSİMLERİNDE ÇARPANLARA AYIRMA ve İDEALLER... 35

3.1 Tek Türlü Çarpanlara Ayrılabilme Özelliği Üzerine... 35

3.2 Euclid Bölgeleri... 42

3.3 Kuadratik sayı Cisimlerinin İdealleri ... 45

3.4 İdeal Sınıf Grubu ... 53

3.5 Asalların Parçalanışı ... 58

3.5.1 Bölümle İlgili Pari Komut ve Programları ... 75

3.5.2 Bölümle İlgili Maple Komut ve Programları ... 77

4. İKİLİ KUADRATİK FORMLAR ve KUADRATİK SAYI CİSİMLERİYLE BAĞLANTISI ... 81

4.1 İkili Kuadratik Formlar... 81

4.2 İkili Kuadratik Formlar ve Kuadratik Sayı Cisimlerinin İdealleri Arasındaki Bağlantı... 87

4.3 Bölümle İlgili Pari Komut ve Programları ... 93

5. ZETA ve L-FONKSİYONLARI ... 98

5.1 Dirichlet Karakterleri... 98

5.2 Zeta ve L-Fonksiyonları ... 104

5.3 Kuadratik Sayı Cisimlerinin Zeta ve L-Fonksiyonları ... 108

iii

KAYNAKLAR... 128 ÖZGEÇMİŞ... 130

b a a böler b ) (mod n b a≡ a denktir mod b n ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ p a Legendre sembolü ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ n a Kronecker sembolü

(

α,β

)

a= O_K’nın α ve β tarafından üretilen ideali

a′ a’nın eşleniği b

a aideali ’yı böler veya b b⊆a

1 −

a akesirsel idealinin tersi b

a~ a ve b idealleri denk idealler

[ ]

a a’nın denklik sınıfı n B n. Bernoulli sayısı C Kompleks sayılar Cl K’nın ideal sınıf grubu f

çek f'nin çekirdeği

) , ( x

derP_F α α’nın üzerindeki derecesi F

( )

a,b

ebob a,bideallerinin en büyük ortak böleni

( )

a,b

ekok a,bideallerinin en küçük ortak katı

K

d K’nın diskriminantı

Q

d Q ikili kuadratik formunun diskriminantı

K

F K’nın sıfırdan farklı kesirsel ideallerinin kümesi

K

h K’nın sınıf sayısı

[

K:Q

]

K sayı cisminin Q rasyonel sayı cismi üzerindeki boyutu

) ( d

K =Q d kare-bağımsız tamsayı olmak üzere, d ’yi içeren kuadratik sayı cismi

) , (s χ

L χ Dirichlet karakteri ile ’de Dirichlet L-fonksiyonu s

) , 1 ( χ

L χ Dirichlet karakteri ile 1’de Dirichlet L-fonksiyonu

K

M Minkowski sınırı

N Doğal sayılar kümesi

( )

α

N α’nın normu

( )

a

N a idealinin normu

K

O K =Q

( )

d nin tamlık halkası

) , ( x

P_F α α∈E cebirsel sayısının p(x)∈F[X] minimal polinomu

q

p, O_K’nınasal idealleri

P O_K’nın temel kesirsel ideallerinin kümesi

Q Rasyonel sayılar kümesi

( )

x y

Q , x,y değişkenli ikili kuadratik form Q

Q~ ′ Denk kuadratik formlar

R Regülatör

R Reel sayılar kümesi

1

r K →Creel otomorfizmaların sayısı

2

r K →Csanalotomorfizmaların yarı sayısı )

(

2 R

SL 2×2’lik determinantı ’dan farklı olan reel sayı bileşenli matrislerin kümesi 0 )

(

2 Z

SL 2×2’lik determinantı 1 olan tamsayı bileşenli matrislerin oluşturduğu grup

( )

α

Tr α’nın izi

u O_K’ nın birimsel elemanı

K

U O_K’nın birimsel elemanlarının grubu

[ ]

x

Z Z halkası üzerinde polinom halkası

Z Tamsayılar kümesi

{

1,ωd

}

OK’nın tamlık tabanı

( )

α α tarafından üretilen temel ideal

α′ α’nın eşleniği

) (n

χ Dirichlet karakteri K

ε K =Q

( )

d ’nin temel birimi

) (α

σi K’dan ’ye C σi :K →C otomorfizması d

ω Kuadratik sayı cismi K =Q

( )

d ’de d ≡2,3(mod4 )iseω_d = d;

ise 1(mod4) d≡ 2 1 d d + =

ω biçiminde tanımlanan kompleks sayı w K sanal kuadratik sayı cismindeki birimsellerin sayısı

n

ζ 1’in dereceden kökü n.

) (s

ζ Riemann zeta fonksiyonu )

(s K

ζ K sayı cismi üzerindeki zeta fonksiyonu

(

α1,...αn

)

∆ α₁,...α_n∈K’nın diskriminantı

vi ALP Ayrık Logaritma Problemi

DB Dedekind Bölgesi

EB Euclid Bölgesi

FST Fermat’ın Son Teoremi İKF İkili Kuadratik Form

İTS İndirgenmiş Tam Temsilciler Sistemi TB Tamlık Bölgesi

TÇAB Tek Türlü Çarpanlara Ayrılabilen Bölge

Çizelge 2.1 K =_Q

( )

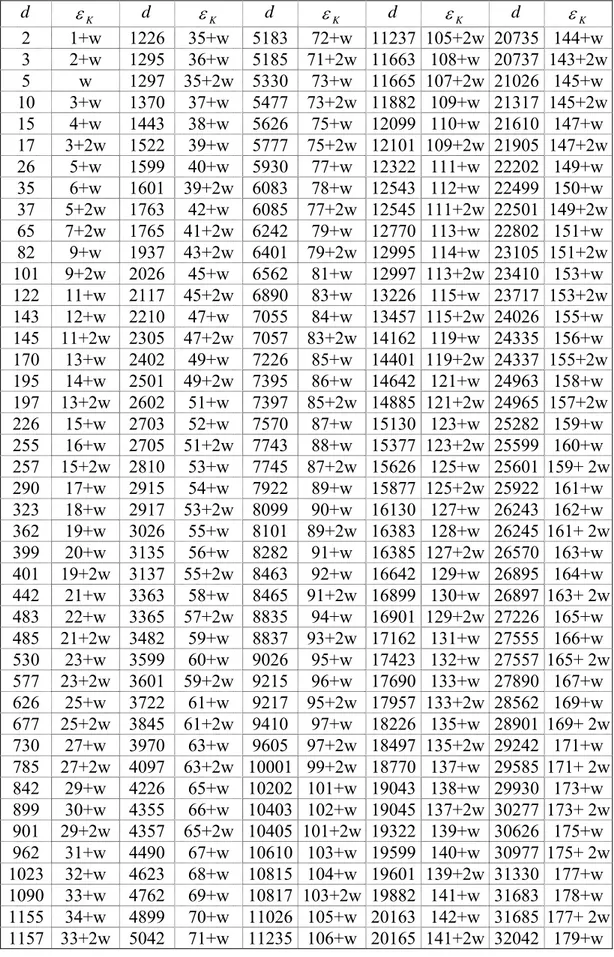
34 ’de temel birimin hesaplanması... 24

Çizelge 2.2 Sürekli kesirler kullanılarak temel birimin bulunması ... 25 Çizelge 2.3 Bazı reel kuadratik sayı cisimlerinin temel birimleri ... 27

kare-bağımsız d ler için,

370 ,... 2 , 1 =

d K =Q

( )

d reel kuadratik sayı

cisimlerinde temel birimlerin,

(

ε_K =a+bω_d

)

listesi... 27 Çizelge 2.4 d =2,...,32050 için temel birimi küçük olan bazı K =Q

( )

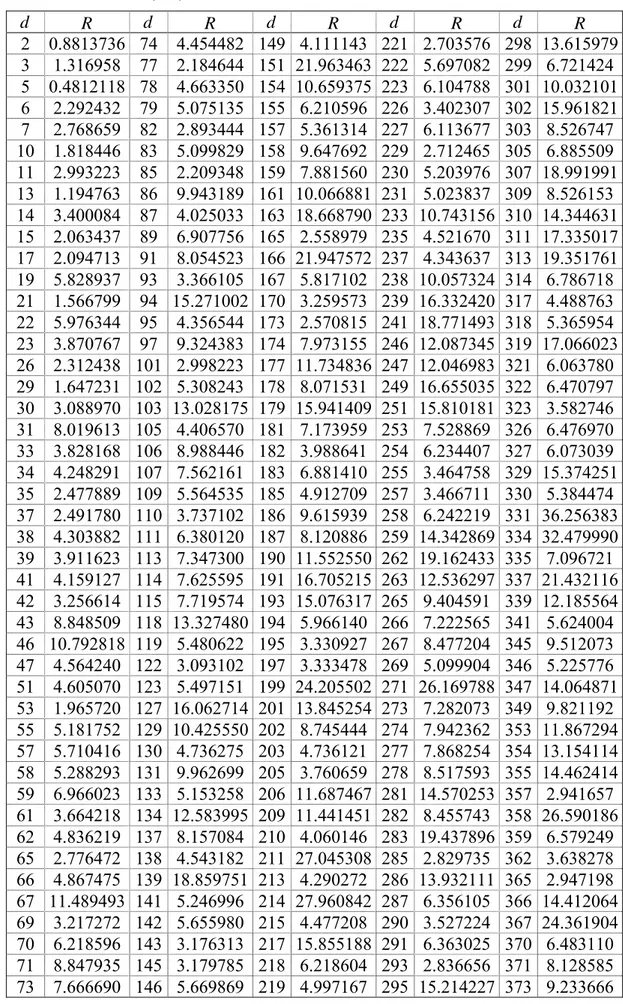
d reel kuadratik sayı

cisimlerinde temel birimlerin örnek bir listesi... 29 Çizelge 2.5 Bazı K =Q

( )

d reel kuadratik sayı cisimlerinin regülatörleri (R=log

(

ε_K

)

). . 30 Çizelge 3.1 TÇAB olmayan tamlık halkası bazı Z

[ ]

ω_d ’lerde çarpanlara ayrılmanın tek türlü

olmadığına dair örnekler (Stewart ve Tall, 2002)... 40 Çizelge 3.2. d ≤70 olan kare bağımsız ’ler için d K =Q

( )

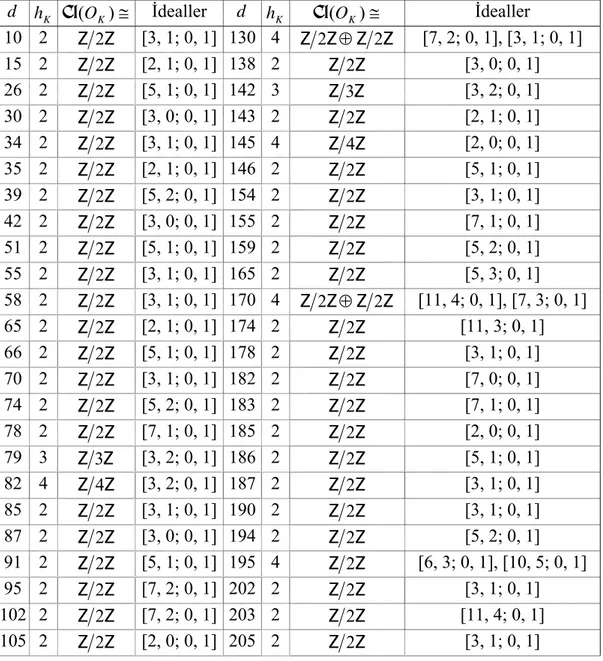
d kuadratik sayı cisimlerine

karşılık gelen Minkowski sınırlarının (M_K)değerleri... 57 Çizelge 3.3 d =1,2,...226 için TİB olmayan reel kuadratik sayı cisimlerinde

( )

d

K =Q ’nin ideal sınıf gruplarının yapıları... 71

Çizelge 3.4 Kare-bağımsız (d d <870) değerleri için K =Q

( )

d reel kuadratik sayı

cisimlerinin sınıf sayıları

(

h=h_K

)

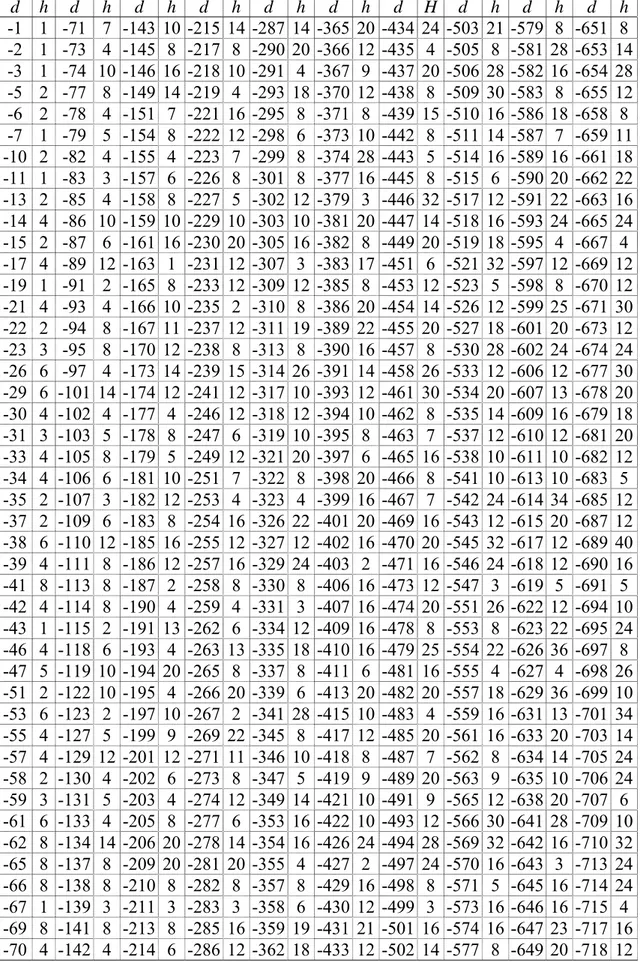
... 73 Çizelge 3.5 Kare-bağımsız d =−1,−2,...,−718 değerleri için K =Q

( )

d sanal kuadratik

sayı cisimlerinin sınıf sayıları

(

h=h_K

)

... 74 Çizelge 4.1 K =_Q

(

−119

)

sanal kuadratik sayı cismi için indirgenmiş kuadratik formlar. 87

Çizelge 4.2 K =_Q

(

−71

)

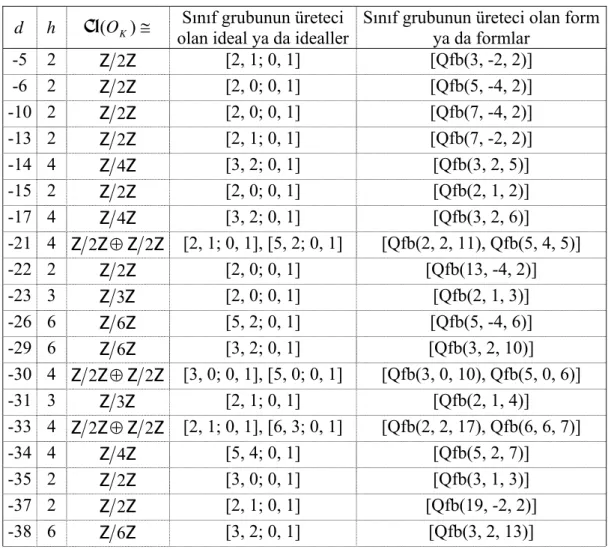
sanal kuadratik sayı cismi için indirgenmiş kuadratik formlar... 89

Çizelge 4.3 d =−1,−2,...−100 için, TİB olmayan sanal kuadratik sayı cisimleri

( )

d

K =Q ’lerde ideal sınıf gruplarının yapıları. ... 91

Çizelge 5.1 mod5 Dirichlet karakterleri... 101 Çizelge 5.2 d <12 ve 1≤ n≤45 için χ

( )

n ’nin değerleri. Eğer d ≡1(mod4) iseχ ,

d

mod Dirichlet karakteri, d ≡2,3(mod4) ise χ , mod4d Dirichlet

karakteridir... 103 Çizelge 5.3 n=0,1,2,...,50 için Bernoulli sayıları ... 107 Çizelge 5.4 Zeta fonksiyonunun bazı tamsayı değerleri... 108 Çizelge 5.5 d =2...443 için K =Q

( )

d ’lere karşılık gelen L

( )

1,χ fonksiyonlarının

değerleri ... 121 Çizelge 5.6 d =−1...−443 için K =Q

( )

d sanal kuadratik sayı cisimlerine karşılık gelen

( )

1,χ

L fonksiyonlarının değerleri ... 122

viii

Bu tez çalışması sırasında yaptığı değerli katkılarından ötürü öncelikle danışman hocam Doç. Dr. Ömer Gök’e sonsuz teşekkür ederim.

Beni, sayılar teorisiyle ve özellikle de kuadratik sayı cisimleriyle tanıştıran Fatih Üniversitesi Öğretim Üyesi Prof. Dr. Barış Kendirli’ye teşekkürlerimi belirtmek istiyorum.

Ayrıca tez izleme komitemin diğer değerli üyelerinden Prof. Dr. Göksel Ağargün’e değerli tavsiyeleriyle yol göstermesinden dolayı ve Doç. Dr. Mustafa Bayram’a tezimi dikkatli bir şekilde okuyup onun gelişmesi konusunda faydalı tavsiyelerde bulunmasından dolayı çok teşekkür ederim.

Son olarak, doktora çalışmalarım boyunca büyük bir sabırla benden sevgi ve desteklerini hiç esirgemeyen ve beni sürekli cesaretlendiren başta ailem olmak üzere dost, akraba, arkadaşlarım ve ümidimi yitirdiğim anlarda beni hayat dolu sözleriyle ümitlendiren ama bugün aramızda olmayan sevgili ablama sonsuz şükranlarımı belirtmek istiyorum.

) ( d

K =Q kuadratik sayı cisminin tamsayılar halkası TÇAB olduğunda sayılar

teorisinde tamsayılar için yapılan birçok işlem bu tamlık halkalarına transfer edilebilir. Fakat maalesef cebirsel sayı cisimlerinin tamlık halkalarında her zaman çarpanlara ayrılma tamsayılardaki gibi tek türlü olmayabiliyor. Bu özelliğin yokluğunun ölçüsü sınıf sayısı olarak adlandırılır. Sayılar teorisiyle uğraşanların bu özelliğin olmayabileceğini fark etmesinden sonra bu problemin üstesinden gelebilmek için epeyce çaba harcamışlardır. Bu çalışmalar yeni bir alanı, ideal teorisini doğurmuştur. Ondan beri ideal teorisi ve sınıf sayısı hesaplama problemi üzerine çok sayıda çalışmalar yapılmıştır. Sınıf sayısının hesaplanmasının zorluğu kriptografik uygulamalarda kuadratik sayı cisimlerinin kullanılmasını sonuç vermiştir.

K

O

Bu tezde K =Q( d) kuadratik sayı cisimlerinde çarpanlara ayırma ve ideal teorisi genişçe

ele alınmıştır. İdeal sınıf gruplarının yapısı ve sınıf sayısı diye adlandırılan mertebeleri incelenmiştir. İkisi cebirsel birisi analitik olan üç farklı sınıf sayı bulma metodu ele alınmıştır. Dirichlet karakterleri ve bir kuadratik sayı cismine karşılık gelen kuadratik formlar, ζ ve L-fonksiyonları çalışılmış ve kuadratik sayı cisimleriyle bağlantılarına dair sonuçlar elde edilmiştir. Pari programının cebirsel sayı cisimleri paketinin geniş bir kısmını kaplayan kuadratik sayı cisimleriyle ilgili bölümü tanıtıldı. Her bir bölümün sonunda bölümle ilgili Pari kodları ve tezde çözülen problemlerde ve çizelgelerin oluşturulmasında kullanılan Pari programları verildi.

Anahtar kelimeler: Kuadratik sayı cisimleri, tamsayılar halkası, temel birim, Euclid bölgesi, tek türlü çarpanlara ayrılabilen bölge, idealler, temel ideal bölgesi, ideal sınıf grubu, ikili kuadratik formlar, indirgenmiş formlar, sınıf sayısı, Dirichlet karakterleri, zeta fonksiyonları, L-fonksiyonları, Pari GP.

ABSTRACT

When the ring of integers O_K of a quadratic number field K =Q( d) is UFD, then most of

the applications can be transferred from ordinary integers to this rings which can be done in ordinary number theory. But unfortunately the factorization is not always unique for the ring of integers of an algebraic number field as in the case of ordinary integers. The size of non-existence of this property is called the class number. After realizing the failure of unique factorization property in most of such rings, number theorists has been expended a great amount of effort to overcome this problem. Such works has given rise to a new field, the ideal theory. Since then there has been done so many works on ideal theory and the class number computation problem. The difficulty of computing the class number has given rise to cryptographic algorithms based on arithmetic in quadratic fields.

In this thesis the factorization and ideal theory in a quadratic field K =Q( d) has been

studied, widely. The structure and index of ideal class groups is investigated. Three different class number computation method has been studied, two of which are based on algebraic and one is on analytic methods. The Dirichlet characters, binary quadratic forms, ζ and L-functions of quadratic number fields has been studied and some results are obtained from this subjects. Quadratic number fields part of the algebraic number fields package of Pari program is introduced. At the end of each chapter related Pari codes and scripts are given which are used for solving some problems and preparing the figures in the thesis.

Keywords: Quadratic fields, ring of integers, fundamental unit, Euclidean domain, unique factorization domain, ideals, principal ideal domain, ideal class group, binary quadratic forms, reduced forms, class number, Dirichlet characters, zeta functions, L-functions, Pari GP.

1. GİRİŞ

Fermat’ın(1601-1665) Son Teoremi (FST) kısaca; n n n

z y

x + = denkleminin n>2 için tamsayı çözümünün olmadığını ifade eder. Yaklaşık 350 yıl aradan sonra 1994 yılında Andrew Wiles(1953-) tarafından ispatlanan bu teorem üzerinde yapılan çalışmalar sayılar teorisinin gelişmesine önemli katkıda bulunmuştur. Kummer’ın(1810-1893) FST üzerindeki çalışmalarından beri sayılar teorisi birçok matematikçi için büyük bir ilgi alanı olmuştur. Cebirsel sayı cisimleri ve özellikle de kuadratik sayı cisimleri üzerinde o tarihlerden bu yana epeyce çaba sarf edilmiştir. Kuadratik sayı cisimleri Kummer, Dedekind (1831-1916) ve diğerleri tarafından sonraları daha yüksek dereceli sayı cisimlerine genişletilmiştir. Onların başarılı çalışmaları matematiğin önemli branşlarından olan cebirsel sayılar teorisinin temelini de oluşturmaktadır. Kummer’ın cebirsel sayı cisimleri ile ilgili çalışmaları onun FST üzerindeki en başarılı sonuçları elde etmesinde rol oynamıştır öyle ki, onun kullandığı metotlar modern matematiğin yapıtaşları haline gelmiştir.

Cebirsel sayı cisimlerinin iyi bilinen örneklerinden bazıları; ζn, 1’in n dereceden kökü . olmak üzere _Q

( )

ζ_n biçiminde gösterilen cyclotomikcisimler, θ, .3 dereceden indirgenemez bir polinomun kökü olmak üzere Q biçiminde gösterilen kübik sayı cisimleri ve d kare-

( )

θ bağımsız bir tamsayı olmak üzere Q

( )

d biçiminde gösterilen ve tezimin konusu olan

kuadratik sayı cisimleridir. Genel olarak θ, n dereceden tamsayı katsayılı bir minimal . polinomun kökü ise Q(θ) cismi n dereceden bir cebirsel sayı cismi diye adlandırılır. Bu . bağlamda ikinci dereceden bir indirgenemez polinomun kökü olan θ’nın Q ’ya katılmasıyla oluşturulan kuadratik sayı cisimleri Q( d), .2 dereceden cebirsel sayı cisimleridir. Burada eğer d >0 ise Q( d)’yi reel, d <0 ise Q( d)’yi sanal kuadratik sayı cismi diye isimlendirerek ayırt ederiz. Her iki tür sayı cisminde çalışma da Gauss’un tanıttığı

Z ∈ +

+bxy cy a b c

ax2 2: , , biçimindeki ikili kuadratik formların teorisiyle oldukça yakından bağlantılıdır.

K sayı cismindeki monik, tamsayı katsayılı bir polinomun kökü olan sayılar (cebirsel

tamsayılar) bir halka oluşturur, bu halkaya K’nın tamlık halkası adı verilir ve O_K biçiminde gösterilir.

K

O ’da terslenebilir elemanların oluşturduğu K ’ın alt grubu olan × U_K birim grubu şeklinde isimlendirilir. Q

( )

d kuadratik sayı cisminin birim grubu d <0 iken sonlu, d >0 olduğunda

ise sonsuz devirli bir gruptur. Kübik sayı cisimlerinde ise birim grubu, rankın 1 veya 2

olmasına bağlı olarak değişir.

FST’nin n=3 ve n=5 gibi özel haller için ispatında kullanılan yöntem ve malzemeler kuadratik sayı cisimlerinin rasyonel tamsayılar teorisi üzerine ilk uygulamalarını oluşturmaktadır. Euler 1770’te K =_Q

( )

−3 sanal kuadratik sayı cisminin tamlık halkası

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − = 2 3 1 Z K

O ’yi FST’nin n=3 özel hali, Dirichlet(1805-1859) ve

Legendre(1752-1833)’de 1825’te, K =Q

( )

5 reel kuadratik sayı cisminin tamlık halkası _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + = 2 5 1 Z K O ’yi 5 =

n özel hali için teoremin doğru olduğunu ispatlamada kullanmışlardır. Ama bu alanda ilk önemli adımlar 1830’larda Gauss’un(1777-1855) bikuadratik rezidüler üzerinde çalışmaları sırasında Z için sayılar teorisi geliştirmekle başlamıştır. Bugün

[ ]

i Z halkası Gauss’un

[ ]

i kuadratik sayı cisimlerinde öncü çalışmalarından ötürü onun onuruna Gauss tamsayıları diye adlandırılmaktadır. Gauss’un ardından, onun gözde öğrencisi Eisenstein(1823-1852),

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − 2 3 1

Z ’yi kübik rezidülerle ilgili sayılar teorisiyle bağlantılı sonuçlar elde etmek için kullanmıştır. O yüzden bu sayılar da Eisenstein sayıları olarak isimlendirilirler.

Kummer, cebirsel sayı cisimleri üzerinde çalışmaları sırasında FST’ni ispatladığını zannetmiştir ama cyclotomic cisimlerde tamsayılardan farklı olarak tek türlü çarpanlara ayrılma özelliğinin olmayabileceği gerçeğini göz ardı etmiştir. O yüzden bu problem üzerindeki çalışmaları başarısızlıkla sonuçlanmıştır. Daha sonraları tek türlü çarpanlara ayrılma özelliğinin olabilmesi için gerek ve yeter şartın K sayı cisminin sınıf sayısının 1

olması gerektiği sonucuna varacaktır. Kummer tek türlü çarpanlara ayrılma özelliğinin eksikliği probleminin üstesinden gelebilmek için de ideal kompleks sayıları geliştirerek yeni bir çığır açmıştır. İlerleyen yıllarda FST’nin bütün düzgün asal sayılar ( p: p, k =Q(ζp) sayı cisminin sınıf sayısını bölmez şartını sağlayan asal sayı) için doğru olduğunu ispatlamıştır. Kummer’dan sonra Dedekind, onun ideal kompleks sayılarında karşılaştığı problemlerin üstesinden gelebilmek için onların üzerine ideal teorisini geliştirmiş ve Kummer’ın ideal kompleks sayılar diye tarif ettiği sayıların ismini idealler diye değiştirmiştir. Sonuç olarak 1800’lerin sonlarına doğru Kronecker(1823-1891)’in de katkısıyla cebirsel sayılar için bir bütün teori ortaya çıkmıştır.

K

O ’nın bütün ideallerinin kümesi, idealler arası tanımlanan çarpma işlemi altında bir yarı-grup oluşturur. Bu yarı grubu gruba çevirmek için kesirsel idealleri hesaba katmak gereklidir.

K’nın bütün kesirsel ideallerinin grubu F, O_K’nın idealleri tarafından üretilen serbest değişmeli bir gruptur. F’nin bütün temel kesirsel idealleri onun bir P alt grubunu oluşturur.

P

F bölüm grubu K sayı cisminin sınıf grubu diye adlandırılır ve Cl=Cl

( )

O_K biçiminde gösterilir. Minkowsky teoremi bu grubun eleman sayısının sonlu olduğunu belirtir. Bu sonlu grubun derecesi K’nın sınıf sayısı olarak isimlendirilir ve h_K ile gösterilir.

İkili kuadratik formlarla bağlantılı olan kuadratik sayı cisimleri, cebirsel sayı cisimleriyle uğraşanlar için her zaman iyi bir test alanı olmuştur. Kuadratik sayı cisimleri, cebirsel sayı cisimleri arasında en anlaşılır teoriye sahip olmasına rağmen hala çok sayıda zor ve çözülmemiş problem vardır. Mesela sınıf sayısı 1 olan reel kuadratik sayı cisimlerinin sonlu olup olmadığı henüz çözülmemiş bir problemdir. Zengin geçmişi ile birlikte hala cebirsel sayılar teorisinde kayda değer önemli çalışmalar yapılmaktadır. Bunlardan birisi 1966’da H. M. Stark’ın TÇAB olan sanal kuadratik sayı cisimlerinin 9 taneden ibaret olduğunu göstermesiyle bu problemin çözümüne son noktayı koymasıdır. Günümüzde sınıf sayısı problemi, sınıf sayısının belli sayılar tarafından bölünebilirliği ve kriptografik uygulamalar üzerinde çok sayıda yeni çalışmalar yapılmaktadır.

Gauss, aynı ( 2 4 ) ac b

d

d = − diskriminantlı kuadratik formları hesaba katarak formların denkliğini tanımladı. Belli bir diskriminanta sahip formların sınıf sayılarını onların denklik sınıflarının sayısı olarak tanımladı. Bu sınıf sayısı ile aynı diskriminantlı kuadratik sayı cisimlerinin sınıf sayıları arasında basit bir bağlantı vardır. Aslında K’nın içindeki ideal

sınıfları ile ikili kuadratik formların denklik sınıfları arasında birebir bir eşleme vardır. Bu bize d <0 iken sınıf sayısının hesaplanmasında en kolay metotlardan birini verir. Kuadratik formların bileşkesi diyebileceğimiz bir bileşke kuralı vardır ve bu kural ideal sınıflarının çarpımı işlemine karşılık gelir.

2 2

cy bxy

ax + + İKF’una karşılık gelen ideal sınıf sayısını hesaplamak için b ’nin

3 d b≤ − şartını sağlayan bütün idealleri dolaşmasını ve d ’ye bağlı olarak onun da tek veya çift sayı olmasını isteriz. Bu tipte her b için ac=

(

b2 −d

)

4 1

yi çarpanlarına ayırırız ve a≥b>−a,

a

c≥ ve a= ise c b≥0 şartını sağlayan

(

a,b,c

)

üçlülerini hesaplarız. Burada, h , K’nın

Hem reel hem de sanal kuadratik sayı cisimlerinin sınıf grubu ve sınıf sayılarının belirlenmesi çoğu zaman zor olabilmektedir. Kuadratik sayı cisimlerinde sınıf sayılarının hesaplanmasında kullanılan metot ve materyaller oldukça karmaşık olmasına rağmen sınıf grubu ve sayısının hesaplanmasının zorluğu kriptografik protokollerin güvenliğinde pratik kullanımından dolayı bu alanda kriptografik çalışmaların başlamasını beraberinde getirmiştir. Örneğin, anahtar değişim protokolleri hem sanal hem de reel sayı cisimlerinin kullanımlarını içermektedir. Bu projelerde güvenlik cismin seçimine bağlıdır, dolayısıyla kuadratik sayı cisminin yapısının bilinmesine ihtiyaç vardır.

Günümüz popüler kripto sistemleri genellikle tamsayılar üzerinde ya çarpanlara ayırmanın ya da Ayrık Logaritma Problemi (ALP)’nin çözümünün zorluğu üzerine inşa edilmiştir. Modulo n tamsayılar üzerine inşa edilmeyen bir anahtar değişim problemi tamsayı sistemi kırıldığında hala güvenli kalabileceği için daha kullanışlı hale gelir. İşte bu maksatla Buchmann ve Hugh Williams sanal kuadratik sayı cisimlerinin sınıf grubu üzerine kurulu bir anahtar değişim tanımlamışlardır. Bu çalışma daha sonra reel kuadratik sayı cisimlerine, kübik sayı cisimlerine ve fonksiyon cisimlerine de genişletilmiştir.

Çalışmamızın birinci ve ikinci bölümü kuadratik sayı cisimleri ile ilgili temel tanım ve teoremlere ayılmıştır. Üçüncü bölümde, kuadratik sayı cisimlerinde çarpanlara ayırma üzerinde duruldu. Çarpanlara ayırmanın tek türlü olmadığı durumlarda ideallerin nasıl bu problemin üstesinden gelmede kullanılabileceği anlatıldı ve ideal teorisi geniş bir şekilde ele alındı. Dördüncü bölümde öncelikle kuadratik formlar tanıtıldı daha sonra ideallerle kuadratik formlar arasındaki bağlantı üzerinde duruldu. Her ikisi için de ideal sınıf grubunun yapısı ve mertebesi değişik tanım ve teoremlerle ele alındı. Bu grupların mertebelerinin hesaplanması için iki cebirsel metot gösterilmiş ve grubun üretecinin elde edilmesi örneklerle açıklanmıştır. Beşinci bölümde öncelikle genel manada Dirichlet karakterleri tanıtılarak bir kuadratik sayı cismine karşılık gelen Dirichlet karakterleri ele alındı. Daha sonra Riemann ζ ve L fonksiyonları tanıtılarak kuadratik sayı cisimlerine karşılık gelen ζ ve L fonksiyonları ele alındı. Bazı kuadratik sayı cisimlerine karşılık gelen Dirichlet karakterleri hesaplanarak

( )

1,χ

L fonksiyonlarının değerleri elde edildi. Bu fonksiyonların değerleriyle sınıf sayısı arasındaki bağlantı üzerinde duruldu. L

( )

1,χ fonksiyonun değerlerinin hesaplanması için farklı metotlar verildi ve gösterilen bu metotlarla sınıf sayısının analitik yolla hesaplanmasının ne kadar kolay olduğu örneklerle gösterildi. Hemen her bölümle bağlantılı olarak oldukça yeni olan ayrıca henüz kullanımı çok yaygınlaşmayan ve cebirsel sayılar

teorisi üzerine geniş bir altyapısı olan Pari programı kullanıldı. Bölüm sonlarına, ilgili bölümlerle bağlantılı Pari komutları eklenmiş, açıklamaları yapılmış ve örnek olarak verilen problemlerin çözümü ve tabloların hazırlanmasında kullanılan Pari programları eklenmiştir.

2. CEBİRSEL SAYI CİSİMLERİ ve KUADRATİK SAYI CİSİMLERİ

2.1 Cebirsel Sayı Cisimleri

Tanım 2.1. E ve F iki cisim olmak üzere F ≤ (Yani F , E ’nin bir alt cismi) ise E ’ye E F ’nin bir genişlemesi adı verilir.

Tanım 2.2. E , F ’nin bir genişlemesi olmak üzere eğer

[

E :F

]

sonlu ise E ’ye sonlu genişleme denir.

Tanım 2.3. E , F ’nin bir genişlemesi olsun. Eğer α∈E için f(α)=0 olacak şekilde sıfırdan farklı bir f(x) a₀ a₁x ... a Xn F[X]

n ∈

+ + +

= polinomu varsa α ’ya F üzerinde

cebirsel eleman denir. α , F üzerinde cebirsel değilse α ’ya transandantal eleman denir. Örnek 2.1. _C (kompleks sayılar kümesi) ve _{Q ’nun (rasyonel sayılar kümesi) her ikisi de} toplama ve çarpma işlemi altında birer cisimdirler. Q ⊂ olduğu için C C, Q ’nun bir cisim genişlemesidir. − 5∈C sayısı Q üzerinde cebirseldir. Çünkü kolayca görüleceği üzere

5

− , ]_f(_x)_=x2 ₊5_∈Q[_{X polinomunun bir köküdür.}

Örnek 2.2. π sayısı Q rasyonel sayı cismi üzerinde transandanttır ama R (reel sayılar cismi) üzerinde cebirseldir. Çünkü Q[X]’te π ’yi kök kabul eden herhangi bir polinom bulunmamasına rağmen π sayısı, ]f(x)= x−π∈R[X polinomunun bir köküdür.

Tanım 2.4. _C’nin _{Q üzerindeki cebirsel olan elemanlarına cebirsel sayı denir. C}’nin _Q üzerinde cebirsel olmayan elemanlarına da transandantal sayı denir.

Örnek 2.3. 3 ₂−i∈C _sayısı Q üzerinde cebirseldir. Çünkü eğer α ₌3 _{2−i alırsak} α

sayısı,

(

_{α + i}

)

3 ₌2

denkleminin bir kökü olduğu açıktır. Buradan 3_i(_α2 ₋1)₌2₊3_{α −α}3. Her iki tarafın karesi alınırsa 3 ₂−i_{’nin ]x}6 _+3x4 _−4x3 _+3x2 _{+12x+5∈Q[X polinomunun}

bir kökü olduğu görülür.

Benzer şekilde 3− 11, ]_x2 ₋6_x−2_∈Q[_{X polinomunun kökü, i+ 2 de} ]

[ 9 2 2

4 _{x x}

x − + ∈Q polinomunun kökü olduğu için cebirsel sayıdırlar.

Tanım 2.5. Eğer α∈E cebirsel ise aşağıdaki şartları sağlayan bir p(x)∈F[X] polinomu vardır ve bu polinoma α ’nın sağladığı minimal polinom (minipol) denir. α ’nın F

üzerindeki minimal polinomu P_F( xα, ) biçiminde gösterilir. • p≠0 ve p(α)=0,

• p(x) monik (baş katsayısı 1 olan) polinomdur, • p(x), F[x]’in indirgenemez polinomudur.

Diğer yandan bu p(x) polinomu α ’yı kök kabul eden muhtemel diğer bütün polinomları da böler.

Tanım 2.6. Tanım 2.5 ile tanımlanan polinomun derecesine α ’nın F üzerindeki derecesi denir ve derP_F(α,x) biçiminde gösterilir.

Tanım 2.7. F ≤ ve E α∈E olmak üzere F(α), F ≤ F(α) ve α∈F(α) şartlarını sağlayan en küçük cisim olarak tanımlanır. F(α) cismine F ’ye α katmakla elde edilen basit cisim denir.

Teorem 2.1. Eğer α∈E cebirsel ve n=derP_F(α,x) ise

[

F(α):F

]

:n’dir . Ayrıca

{

_1,α,α2_,...αn−1

}

_{, F(α)/F’nin bir bazıdır.}

Örnek 2.4. [Q(311):Q]=derP_Q(3 11,x)’dir. Burada P_Q(311,x)= x3−11’dir ve p=11 alınırsa Eisenstein kriterine göre _x3 ₋11 _{polinomu indirgenemezdir. Bu durumda}

{

_1,3_11,(3₁₁₎2

}

_{, Q(}3 _{11) cismi için bir bazdır. O halde Q(}3_{11)’nın elemanları}

Q ∈ + + 3 2 _{0 1 2} 2 3 1 0 a ( 11) a ( 11) :a ,a ,a a biçiminde sayılardır.

Tanım 2.8. E , F ’nin bir genişlemesi ve eğer ∀α∈E sayısı F üzerinde cebirsel ise E ’ye F’nin bir cebirsel genişlemesi adı verilir.

Teorem 2.2. Eğer

[

E :F

]

<∞⇒ E/F cebirseldir.

Teorem 2.3. α₁,α₂ ∈E cebirsel iseler α₁ ±α₂,α₁.α₂ sayıları da cebirseldirler. Ayrıca eğer,

⇒ ≠ 0

2

α α₁/α₂’de F üzerinde cebirseldir.

Tanım 2.9. Q rasyonel sayılar cisminin sonlu genişlemelerine cebirsel sayı cismi denir. Örnek 2.5. Cebirsel sayı cisimlerinin en bilinen örneklerinden bazıları;

cisimleri,

ii-)ζn, 1’in n. dereceden kökü olmak üzere Q

( )

ζn biçiminde gösterilen cyclotomikcisimler ve

iii-) θ , 3. dereceden indirgenemez bir polinomun kökü olmak üzere Q

( )

θ biçiminde gösterilen kübik sayı cisimleridir.

Örnek 2.4’te verdiğimiz Q(311) _cismi Q ’nun bir sonlu genişlemesidir ve bir kübik sayı cismidir.

Tanım 2.10. Özel olarak eğer α∈C, katsayıları tamsayı olan bir monik polinomun kökü ise α ’ya cebirsel tamsayı denir. Bir cebirsel sayı cisminde cebirsel tamsayıların kümesi bir halka oluşturur. Bu halkaya tamlık halkası denir ve OK sembolü ile gösterilir.

Örnek 2.6.

2 3 3+ − =

θ sayısı tamsayı katsayılı

( )

₌ 2 ₋3 ₊3 x x x

f monik polinomun kökü

olduğu için cebirsel bir tamsayıdır. Buna rağmen γ =13/5 cebirsel tamsayı değildir. 13/5

sayısı, f

( )

x = x5 −13 polinomunun bir köküdür fakat bu polinom monik değildir. Öte yandan 5

/

13 , g

( )

x = x−13/5 monik polinomunun bir köküdür ama bu polinomun da katsayıları

tamsayı değildir. Aslında 5γ =13/ ’in kökü olduğu tamsayı katsayılı bir polinom bulunamaz . Dolayısıyla bir cebirsel tamsayı değildir fakat cebirsel sayıdır. Her cebirsel tamsayının bir cebirsel sayı olduğu açıktır. Ama tersi doğru değildir.

Bölüm 2.3’te Q

( )

d ’nin tamlık halkasının d ≡1(mod4) olduğunda _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + 2 1 d Z ve ) 4 (mod 3 , 2 ≡

d olduğunda ise Z

[ ]

d olduğu ispatlayacağız. Q

( )

ζ_n cisminin tamlık halkası ise Z

[ ]

ζn dir.

Teorem 2.4. K =Q(α), Q üzerinde n. dereceden bir sayı cismi olsun. Bu durumda α∈K

olmak üzere K ’dan _C’ye n-tane faklı σ_i :K →C,σ_i(α)=α_i :,(i=1...n) olacak şekilde otomorfizma vardır. Burada

∏

= − = n i i x x P 1 ) ( ) , (α α

Q , α ’nın minimal polinomunun kompleks

sayılar üzerindeki parçalanışını göstermek üzere, σi(α)=αi’ler, PQ( xα, )’in C’deki n -farklı köküdür.

) , ( x

P_Q α ’in reel köklerinin sayısı için r₁, kompleks kök çiftlerinin sayısı için r₂ sembolleri kullanılır. Burada n=r₁ +2r₂ eşitliği mevcuttur.

Tanım 2.11. Teorem 2.4’te verilen α_i’lerin her birine α ∈K’nın eşlenikleri denir. Bu i

α ’lerin her biri cebirsel sayılardır ve her birinin minimal polinomları P_Q( xα, )’tir . ∀α∈K

için kendisi ile birlikte n farklı eşlenik vardır.

Örnek 2.7. α =4 3 ve K =Q(α) olsun. α ’nın minimal polinomu 4. dereceden

( )

,_{x = x}4 ₋3

P_Q α polinomudur. Bu polinom iki tane reel köke (_±4 _{3), iki tane de kompleks}

köke (_±i4 _{3) sahiptir. Buradan 2, 1} 2 1 = r =

r olduğu anlaşılmaktadır. σ_i :K →C omorfizmalar aşağıdaki gibidir.

( )

( )

( )

( )

4 4 4 3 4 2 4 1 3 3 3 3 i i − = = − = = α σ α σ α σ α σ

Tanım 2.12. K =Q(α), Q üzerinde n. dereceden bir sayı cismi ve σ₁,σ₂,...σ_n, K ’dan C’ye otomorfizmalar olmak üzere, β∈K’nın normu ve iz(trace)’i sırasıyla aşağıdaki gibi tanımlanır.

∏

= = n i i Q K N 1 / (β) σ (β), (2.1)

∑

= = n i i Q K Tr 1 / (β) σ (β). (2.2)

Tanım 2.13. K , n. dereceden bir sayı cismi olmak üzere α₁,α₂,α₃,...α_n∈K’ların diskriminantı,

(

)

(

(

( )

)

)

2 3 2 1,α ,α ,...αn detσi αj α = ∆ biçiminde verilir.

Örnek 2.8. K =Q

( )

3 , olmak üzere P_Q(α,x)= P_Q( 3,x)= x2 −3. Bu polinomun kökleri 3

- ve ,

3 ) 3 ( , 3 ) 3 ( ₂ 1 = σ =− σ

şeklinde iki tanedir. α₁ =3,α₂ =2+ 3 olmak üzere,

(

)

(

3(2 3) 3(2 3)

)

108. 3 2 3 2 3 3 3 2 , 3 2 2 = + − − = − + = + ∆

Teorem 2.5. K , n. dereceden bir sayı cismi ve α₁,α₂,α₃,...α_n∈K olmak üzere K

n∈

α α α

α₁, ₂, ₃,... ’nın diskriminantı ∆

(

α1,α2,α3,...αn

)

=det

(

TrK/Q

(

αiαj

)

)

şeklindedir.

Teorem 2.6. ∆

(

α1,α2,α3,...αn

)

∈Q dur. Özel olarak eğer αi’ler cebirsel tamsayı ise

(

)

∈Z

∆α₁,α₂,α₃,...α_n ’dir.

Tanım 2.14. K sayı cisminin diskriminantı, O_K’nın bir tamlık tabanı α₁,α₂,...α_n

diskriminantı ∆

(

α₁,α₂,...,α_n

)

olarak tanımlanır.

Tanım 2.15. Bir cebirsel sayı cismi K ’da O_K’nın bütün idealleri ideal çarpma işlemine göre

bir semi-grup oluşturmaktadır. Bu semi-grubu, gruba dönüştürmek için kesirsel idealler hesaba katılabilir. Bir kesirsel a ideali α∈O_K için αa⊂O_Kşartını sağlayan O_K’nın bir alt

modülüdür. K ’nın bütün kesirsel ideallerin grubu F, O_K’nın asal idealleri tarafından

üretilmiş olan serbest değişmeli gruptur. F’nin bütün temel kesirsel ideallerinin kümesi P

ile gösterilen F’nin bir alt grubudur. Cl= F P kesrine K ’nın sınıf grubu adı verilir, bu

grubun mertebesi Cl ’ye ise K sayı cisminin sınıf sayısı adı verilir bu da h_K sembolüyle

gösterilir.

Bu bölümde cebirsel sayılar ve cebirsel sayı cisimlerinin bazı temel tanım ve özellikleri verildi. Sonraki bölümden itibaren tezin esas konusu olan kuadratik sayı cisimleri ele alındı.

2.2 Kuadratik Sayı Cisimlerine Giriş

Tanım 2.16. K/_Q bir cebirsel genişleme olmak üzere özel olarak,

[

K :Q

]

=2 ise K

cebirsel sayı cismine kuadratik sayı cismi denir.

Teorem 2.7. d, kare-bağımsız (bölenleri arasında 1’den başka tam-kare içermeyen) bir

İspat:K bir kuadratik sayı cismi ve

{ }

1,α , K ’nın Q üzerindeki bir bazı olsun. Bu durumda ) (α Q = K ve ∃ ,b c∈Z:α2 =c+bα _{dır. α ,} c bx x x f_{( )}= 2 − − _(2.3)

polinomunun bir köküdür. Diğer taraftan (2.3) denklemiyle verilen f ’nin kökleri

2 4

2 _c b b± +

’dir. d kare-bağımsız bir tamsayı olmak üzere b2 ₊₄c₌a2d _{olacak şekilde}

Q ∈ a vardır. Böylece b b c b a d 2 2 2 4 2 ± = + ± dir. Dolayısıyla α∈Q

( )

d ve d ∈Q

( )

α . Yani d kare-bağımsız bir sayı olmak üzere K =Q

( )

α =Q

( )

d .

{ }

1, d bir baz olduğu için

( )

d

Q ’nin elemanları p+q d : p,q∈Q şeklindedir. Böylece d, kare-bağımsız olmak üzere,

( ) {

Q

}

Q d = p+q d : p,q∈ . (2.4)

biçiminde verilir.

Tanım 2.17. K =Q

( )

d bir kuadratik sayı cismi olmak üzere eğer d >0 ise K ’ya reel kuadratik sayı cismi, d <0 ise K ’ya sanal (imajiner) kuadratik sayı cismi denir.

Örnek 2.9. Q

( )

105 reel, _Q

(

−23

)

ise sanal kuadratik sayı cisimleridir. Bununla birlikte (2.4)’ten

(

23

)

fakat

(

23

)

2 23 2− − _{∈ − ∉ −} Q Q i olduğu da anlaşılmaktadır.

Teorem 2.8. Kuadratik sayı cisimlerinde iki tane otomorfizma σ₁,σ₂ :Q

( )

d →C vardır. Bu otomorfizmalar α =a+b d ∈Q

( )

d olmak üzere; σ₁(a+b d)=a+b d özdeşlik dönüşümü ve σ₂(a+b d)=a−b d şeklinde verilen dönüşümlerden oluşan otomorfizmalardır.

İspat: P_Q

(

d_,x

)

= f₍x₎= x2 −d _{olduğu açıktır. f}

( )

_{x ’in C’deki kökleri ise d ve − d} olmak üzere iki tanedir. Buradan otomorfizmaların σ₁: d → d,σ₂ : d →− d olduğu görülmektedir. O halde α =a+b d ∈Q

( )

d olmak σ₁(a+b d)=a+b d özdeşlik dönüşümü ve σ₂(a+b d)=a−b d dönüşümleri mevcuttur.

Diğer yandan eğer, K reel kuadratik sayı cismi ise r₁ = r2, ₂ =0, sanal kuadratik sayı cismi ise r₁ = r0, ₂ =1 olduğu da açıktır.

Tanım 2.18. K =Q

( )

d bir kuadratik sayı cismi olsun. α =a+b d ∈Q

( )

d ’nin eşleniği (α′), normu (N_K/Q(α)) ve iz’i (Tr_K/Q(α)) sırasıyla aşağıdaki gibi tanımlanır.

• α′=a−b d , • N a b d a b d a b d a b d a b d i i K 1 2 2 2 2 1 / ( )=

∏

( )= ( + ) ( + )=( + )( − )= − = σ σ α σ α Q , • Tr

( )

( )

a b d a b d a b d a b d a i i K 1( ) 2( ) ( ) ( ) 2 2 1 / =

∑

= + + + = + + − = = σ σ α σ α Q .

Bu tanımda (2.1) ve (2.2) denklemleri kullanılarak norm ve iz tanımları verilmiş daha sonra formüller kuadratik sayı cisimleri için daha basit hale getirilmiştir. Bundan böyle α ’nın normu ve iz’i için genel kullanıma uyarak sırasıyla kısaca N

( )

α ve Tr

( )

α sembollerini kullanacağız. N

( )

α =αα′ ve Tr

( )

α =α +α′ olduğu açıktır. İlerde görüleceği üzere norm,

( )

d

Q ’deki çarpma ve bölünebilme ile ilgili problemleri Z ’ye transfer etmede oldukça yarayışlıdır.

Örnek 2.10. _Q

(

−11

)

’de α =3−2 −11 alalım. Bu durumda;

11 2 3+ − = ′ α , 53 11 . 4 9 ) 11 2 3 )( 11 2 3 ( ) (α = − − + − = + = N ,

( )

α =(3−2 −11)+(3+2 −11)=2.3=6 Tr elde edilir.

Teorem 2.9. α,β∈_Q

( )

d olmak üzere norm ve iz’in aşağıdaki özellikleri vardır. i-)

(

α ±β

)

′ =α′±β′,

( )

αβ ′ =α′β′,

ii)N(α.β)= N

( ) ( )

α .N β , iii-)Tr

(

α ±β

)

=Tr

( )

α ±Tr

( )

β ,

iv-)N

( ) ( )

α ,Tr α ∈_Q, v-)α∈Q

( )

d , f₍x₎= x2 −Tr

( )

α x+N

( )

α _{polinomunun bir köküdür.} İspat:α =a+b d,β =e+ f d olsun. i-)

(

α ±β

)

′ =

(

a+b d ±e+ f d

)

′ =

(

(

a±e

) (

+ b± f

)

d

)

′ =

(

a±e

) (

− b± f

)

d

(

−

) (

± −

)

=α′±β′ = a b d e f d

( )

αβ ′ =

(

(

a+b d

)(

e+ f d

)

)

′ =

(

(

ae+bfd

) (

+ af +eb

)

d

)

′ =

(

(

ae+bfd

) (

− af +eb

)

d

)

(

−

)(

−

) (

= +

) (

′ +

)

′ =α′β′. = a b d e f d a b d e f d

ii-)Özellik (i) kullanılırsa, N

( ) ( )( )

α.β = αβ αβ ′ =αβα′β′=αα′ββ′=N

( ) ( )

α N β elde edilir. iii)Benzer şekilde;

(

α β

) (

α β

) (

α β

)

α β α β

(

α α

) (

β β

)

Tr

( )

α Tr

( )

β

Tr ± = ± + ± ′ = ± + ′± ′= + ′ ± ± ′ = ± . iv-)a,b∈Q ∈,d Z olduğu için N

( )

_α =a2 −b2d∈Q _{ve Tr}

( )

_{a = a2 ∈Q olduğu açıktır.} v-) _f

( )

_{α =α}2 _−Tr

( )

_{α α +N}

( )

_{α =α}2 ₋(_{α +α′})_{α −αα′=α}2 _−α2 _{−α′α +αα′=}0 _olduğu için aşikardır.

2.3 Kuadratik Sayı Cisimlerinin Tamlık Halkası ve Diskriminantı

( )

d

K =Q bir kuadratik sayı cismi olmak üzere, K ’da bulunan cebirsel tamsayıların kümesini O_K ile göstereceğiz. Herhangi bir kuadratik sayı cismi K ’da O_K ⊂K olacak şekilde Q ’nun Z ile ilişkisine benzer bir ilişki kurabileceğimiz bir tamsayılar kümesi vardır. Eğer a ve b birer tamsayı iseler N

(

a₊b d

)

₌a2 ₋b2d _{ve Tr}

(

_{a+b d}

)

_{=2a değerleri} tamsayı oldukları için a+b d sayısı tamsayı katsayılı, f

( )

x = x2 −Tr

( )

x x+N

( )

x _monik polinomunun bir kökü olduğunu Teorem 2.9’un beşinci özelliğinden dolayı biliyoruz. Dolayısıyla, eğer a,b∈Z ise α =a+b d sayısı cebirsel bir tamsayıdır. Yani O_K’nın bir elemanıdır. Fakat K’da başka cebirsel sayılar da vardır. Aşağıdaki teoremle K ’da cebirsel sayıları içeren en geniş kümeyi elde edeceğiz.

Teorem 2.10. ⎪⎩ ⎪ ⎨ ⎧ ≡ + ≡ = 1(mod4) d ; 2 1 ) 4 (mod 3 , 2 ; d d d d ω (2.5) olmak üzere,

{

+ ∈Z

}

= m n m n O_K ω_d : , (2.6) dir. İspat: α =m+n d ∈Q

( )

d :m,n∈Qolsun.

Eğer n=0 ise α = m∈Q cebirsel tamsayıdır ⇔ m∈_Z’dir.

0 ≠

n olduğunu varsayalım. α ’nın Q üzerindeki minimal polinomu X2 −Tr

( )

α X +N

( )

α _, yani _X2 _{−2mX +m}2 _−dn2_{’dir. O halde,}

⇔ ∈ + =m n d O_K α 2m∈Z ve _m2 −_dn2∈Z _(2.7) olmalıdır. ⇒ ∈_Z m 2 2 :m a a∈ =

∃ _Z ’dir. Diğer taraftan (2.6)’dan

( )

2∈Z 2n d elde edilir. Çünkü Z Z⇒ ∈ ∈ ₄ 2 2m m ve

(

)

Z

( )

Z Z⇒ − = − ∈ ⇒ = ∈ ∈ − 2 2 2 2 2 2 2 2 _{dn 4m dn 4m 4dn 4dn d 2n}

m elde edilir. Fakat d

kare-bağımsız olduğu için

( )

2n 2 ∈Z. Dolayısıyla 2n∈Z’dir. O halde

2 :n b b∈ =

∃ _Z ’dir.

Dolayısıyla )_m2 _−dn2_∈Z⇔a2 _−db2 _≡0(mod4 _{’tür. Fakat tam kare sayıların mod4’e göre} 0 veya 1’e denk oldukları göz önüne alınırsa iki durum ortaya çıkar;

Eğer, ) 4 (mod 0 ) 4 (mod 3 , 2 _⇒ 2 _≡ 2 _≡ ≡ a b

d . Yani a ve b çift sayılardır.

dir. ' , sayı çift , ) 4 (mod 0 2 2 _{≡b ≡ ⇒a b ⇒m n∈Z} a , ) 4 (mod 1 2 2 _{b a b}

a ≡ ≡ ⇒ tek sayı olacakları için

2 1 , , : + ∈ ∃s Z m n s tipindedir.

Bu sonuçlar birleştirilirse istenen elde edilmiş olur.

(2.6) ile belirtilen O_K’yı aşağıdaki gibi yazmakta mümkündür.

[ ]

⎪ ⎩ ⎪ ⎨ ⎧ ≡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ≡ = ) 4 (mod 1 , 2 1 ) 4 (mod 3 , 2 , d d d d O_K Z Z (2.8)

İlerleyen kısımlarda K kuadratik sayı cisminin cebirsel tamsayılarını ifade etmek için O_K, veya ω =ω_d (2.5)’te belirtildiği gibi olmak üzereZ

[ ]

ω sembollerinden birini kullanacağız. Örnek 2.11. K =_Q

(

−79

)

alınırsa −79≡1(mod4)olduğundan (2.5)’ten dolayı

2 79 1 79 − + = −

ω ’dir. Dolayısıyla K ’nın cebirsel tamsayılarının kümesi (2.6)’dan

⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ∈ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − + = − m n m n Z O : , 2 79 1

79 olduğu kolayca görülür. Örnek olarak;

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − − = − − 2 79 1 . 1 2 2 79 3

ve 2,1∈Z olduğu için K =_Q

(

−79

)

cisminin cebirsel bir tamsayısıdır. Fakat 3 3 2 1 n m+ =

+ olacak şekilde m,n∈Z bulunamayacağı için

( )

3 3 2 1 Q ∈

+ olduğu halde cebirsel bir tamsayı değildir.

Teorem 2.11. O_K cebirsel tamsayılar kümesi K =Q

( )

d ’nin bir alt halkasıdır.

İspat: O_K’nın K ’nın alt halkası olduğunu göstermek için ∀α,β∈O_K için α -β,α.β∈O_K

olduğunu göstermeliyiz. α =m₁ +n₁ω_d,β =m₂ +n₂ω_d olmak üzere;

K d O n n m m − + − ∈ = −β ω α ( _{1 2}) ( _{1 2}) ’dır, çünkü (m₁ −m₂),(n₁−n₂)∈Z’dir.

(

)

d K d d d d mm nn d mn m n O d ≡ ⇒ω = ⇒ω 2 = ⇒αβ = _{1 2} + _{1 2} + _{1 2} + _{2 1} ω ∈ . ) 4 (mod 3 , 2 ’dır.

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − _∈ − + = ⇒ ≡ _Z 4 1 : 4 1 ) 4 (mod 1 2 d d d ω_d ω_d ’dir. ⇒ m m nn d ⎟+

(

mn +m n +nn

)

_d ∈O_K ⎠ ⎞ ⎜ ⎝ ⎛ − + = ω αβ _{1 2 1 2 1 2 2 1 1 2} 4 1 ’dır.

Dolayısıyla O_K bir alt halkadır.

Ayrıca α =m₁ +n₁ω_d ∈O_K için eğer d ≡2,3(mod4)⇒ω_d = d olduğundan

K d O n m d n m − = − ∈ = ′ ω α _{1 1 1 1} dır. Yine, eğer 2 1 ) 4 (mod 1 d d ≡ ⇒ω_d = + olur ki bu durumda da α′=m₁+n₁ − d = m₁ +n₁ −n₁ + d =(m₁+n₁)−n₁ω_d ∈O_K 2 1 ) ( 2 1 ’dır. Yani

her iki durumda da α′∈O_K elde ederiz.

Özel olarak Z

[ ]

i tamlık halkasına Gauss sayıları, _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ _{+ −} 2 3 1

Z tamlık halkasına da Eisenstein

sayıları adı verilir.

Tanım 2.19.O_K’ya Q

( )

d ’nin tamlık halkası denir, ve

{

1,ω_d

}

’ye de O_K tamlık halkasının tamlık tabanı adı verilir.

{

1,ω_d

}

tamlık tabanı olduğu için a,b∈Z olmak üzere O_K’nın her bir elemanı a.1+b.ω_d biçiminde ifade edilebilir.

Bölüm 1’de bir K sayı cisminin diskriminantını onun tamlık halkasının tamlık tabanının diskriminantı olarak tanımlamıştık. O halde Q

( )

d ’nin diskriminantını artık belirleyebiliriz. Teorem 2.12. K =Q

( )

d bir kuadratik sayı cismi olmak üzere K ’nın diskriminantı;

(

)

(

)

⎩ ⎨ ⎧ ≡ ≡ = 4 mod 1 , 4 4 mod 3 , 2 , d d d d d_K (2.9) dir.

İspat: d ≡2,3

(

mod4

)

olsun. Bu durumda O_K’nın tamlık tabanı

{ }

1, d ’dir. Dolayısıyla;

( )

(

d d

) (

d

)

d d d d d_K 1, 1 1 2 2 2 4 2 = − = − − = − = ∆ = ,

(

mod4

)

1 ≡

d olsun. O_K’nın tamlık tabanı

⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + 2 1 , 1 d ’dir. O halde;

( )

d d d d_K d d d d _⎟⎟ = − = ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ₊ ∆ = + − − + 2 2 2 2 1 2 1 2 1 2 1 1 1 2 1 , 1 .

2.4 Kuadratik Sayı Cisimlerinde Birimseller Grubu Tanım 2.20. u∈O_K olmak üzere eğer u−1∈O_{K ise u’ya}

K

O ’da birimsel eleman veya kısaca birimsel denir. K sayı cisminin tamlık halkası O_K’daki birimsel elemanların kümesini

K

U ile göstereceğiz. Bazı kaynaklarda U_K yerine O kullanılmıştır. _K× Teorem 2.13. u∈O_K olsun. u∈U_K ⇔ N

( )

u =±1’dir.

İspat:⇒ u birimsel ise u−1∈O_K’dır, dolayısıyla N

( )

u ,N

( )

u−1 ∈Z’dir. Diğer yandan

( )

₁

( )

1

( )

( )

1

1_{= N =N uu}− _{=N u N u}− _{’dir. '1 in bölenleri 1}

m ’den ibaret olduğu için N

( )

u =±1’dir. ⇐ N

( )

u =±1 ise uu′=±1dir. Dolayısıyla u−1 =±u′_{. Teorem 2.11 in sonucunda gösterildiği} üzere eğer u∈O_K ise u′∈O_K olacağı açıktır. Böylece u−1∈O_{K’dır. O halde}

K U u∈ . Örnek 2.12. O_K =

{ }

1, 3 alırsak 2+ 3∈U_K dır. Çünkü; K O u = − ∈ + = − _{2 3} 3 2 1 1 _{’dır. Fakat ,} K O ∉ − = − = + 6 3 2 1 6 3 3 3 3 1 olacağından 3+ 3∉U_K’dır.

Teorem 2.14. u= x+ yω_d :x,y∈Z olmak üzere u∈U_K ‘dır ancak ve ancak

ise ) 4 (mod 1 , 1 4 1 ise ) 4 (mod 3 , 2 , 1 2 2 2 2 ≡ ± = − + + ≡ ± = − d y d xy x d dy x .

⎪⎩ ⎪ ⎨ ⎧ ≡ + ≡ = ) 4 (mod 1 , 2 1 ) 4 (mod 3 , 2 , d d d d d ω

olduğu göz önüne alınıp Teorem 2.13 ile birleştirildiğinde istenen elde edilmiş olur.

Teorem 2.15. d <0 ise O_K’da sadece sonlu sayıda birimsel vardır ve d =−1 ,d =−3 halleri dışında birimseller 1± olmak üzere iki taneden ibarettir.

• d =−1 ise birimseller ± ,1 ±i olmak üzere dört tanedir.

• d =−3 ise birimseller 2 3 1 , 1 ± ± −

± olmak üzere altı tanedir.

İspat: α =m+n d ∈O_K’nın birimsel olması için N

( )

α =±1 olmalıdır. Fakat d <0

olduğunda N

( )

α ≥0 olur. O halde d <0 durumunda α∈O_K’nın birimsel olması için

( )

α =1

N olmalıdır.

(2.6)’dan )d ≡2,3(mod4 ise α∈O_K’nın m+n d :m,n∈_Z biçiminde olduğunu biliyoruz. Dolayısıyla _N

(

_{m+n d}

)

_=m2 _−dn2 _=m2 _{+ dn}2_’dir. Eğer d =−1 ise 1 2 2 _{+ n =} m (2.10)

denkleminin çözümleri Z

[]

i ’nin(Gauss Sayılarının) birimsellerini verir. Kolayca gösterileceği üzere (2.10) ile belirtilen denklemin tamsayı çözümleri

(

m,n

) (

= ±1,0

) (

, 0,±1

)

olmak üzere dört taneden ibarettir. Bunlara karşılık gelen m+ n −1’ler ise ± ,1 ±i’dir. O halde;K =_Q

( )

−1 ise U_K =

{

±1,±i

}

.

Eğer )d ≡2,3(mod4 ve _{d <−}1_⇒m2 _{+ dn}2 ₌1 _{denkleminin bütün çözümleri}

(

_±1,0

)

_den

ibarettir. Çünkü, _m2 _{+ nd} 2 _≥0 _{olduğundan n=0 olmalıdır. Eğer n=0 alınırsa 1m}2 ₌

elde edilir ki bu da m=±1 demektir. Dolayısıyla da birimseller 1± olmak üzere iki tanedir.

Şimdi, d ≡1

(

mod4

)

olduğunu varsayalım. α∈O_K , m+n + d :m,n∈Z 2

1

2 2 2 2 4 1 4 1 2 1 n d mn m n d mn m n m N d _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + + = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + + = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + (2.11) dir.

Burada d ≡3(mod4) olduğundan + ∈Z 4 1 d ’dir. Şimdi _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = 4 1 d r alalım, bu durumda (2.11) denklemi, 1 2 2 _{+mn+rn =} m (2.12)

denklemine dönüşür. Bu denklemi negatif olmayan

(

m−n

)

2 ve

(

m+n

)

2 terimleri cinsinden yazarsak;

(

₋

)

2 ₌1₋3 ₋( ₋1) 2 _≥0 n r mn n m (2.13)

(

₊

)

2 ₌1_{+ −}

(

₋1

)

2 _≥0 n r mn n m (2.14)

denklemlerini elde ederiz.

Özel olarak d =−3 ise r=1 olur. Bu durumda (2.13) ve (2.14) yerine 1− mn3 ≥0 ve

0

1+ mn≥ denklemleri gelir ki, bunları bir tek denk denklemde birleştirirsek

3 1 1≤ ≤

− mn

elde ederiz. Bu şartı ve (2.12)’yi sağlayan )(m,n ikilileri ise,

(

m,n

)

=(1,0),(0,1),(−1,0),(0,−1),(1,−1),(−1,1)’dir. Bunlar _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = + 2 1 d n m

α ’de yerine yazılırsa,

2 3 1 ,

1 ± ± −

± olmak üzere altı tane birimsel

elde edilir. Özetle; K =_Q

( )

−3 ise ⎭ ⎬ ⎫ ⎩ ⎨ ⎧_± ± ± − = 2 3 1 , 1 K U ’dir.

Eğer d <−3⇒r >1’dir. Bu durumda da n=0 ise m=±1’dir. n>0 ise (2.13) ve (2.14)’ten 1

) 1

(_{r− n}2 _{≥ ’dir ve − mn3 ≥0 ve mn≥0 elde ederiz ki bu durumda çözüm olmadığı açıktır.}

teori oldukça farklıdır. Bu durumda O_K’daki birimsellerin sayısı sonlu değildir ve bunların belirlenmesi her zaman kolay olmayabilir.

Teorem 2.16. d >0 ise O_K’nın sonsuz sayıda birimsel elemanı vardır.

İspat: Öncelikle ∀ yx, ∈Z için u=x+ y d ∈O_K olduğunu gösterelim. (2.5) ve (2.6)’dan ) 4 (mod 3 , 2 ≡

d ise ω_d = d dir ve u =x+ y d ∈O_K olduğu açıktır. Eğer )d ≡1(mod4 ise yine x+ y d =(x−y)+(2y)ω_d biçiminde yazılabilir. O halde her iki durumda da

K

O d y x

u= + ∈ ’dır. u= x+y d ∈U_K olması içinse _N

( )

_{u =x}2 _−dy2 _=±1 _olmalıdır. Diğer yandan bilindiği üzere eğer d >0 kare-bağımsız ise,

( )

_{u =x}2 _−dy2 ₌1

N (2.15)

Pell(1611-1683) denkleminin her zaman çözümü vardır ve sonsuz sayıdadır, (Silverman, 2001).

Eğer )( yx, ikilisi (2.15) denklemin bir çözümü ise u =x+y d ∈U_K birimsel elemandır. Ayrıca ∀n∈Z için un ₌₍x₊ y d₎n ₌ x_{n +}y_n d _{olmak üzere ( , )}

n n y

x ikilileri de bu Pell denkleminin çözümüdür, dolayısıyla _un_{∈UK’dır. Bu durumda sonsuz sayıda birimsel vardır} ve anlaşılacağı üzere bunların saptanması (2.15) ile verilen Pell denkleminin çözümü ile doğrudan bağlantılıdır.

Teorem 2.17. (Adams ve Goldstein, 1976) u∈O_K birimsel ise −u ve u 1

birimseldirler. Ayrıca u₁,u₂ ∈U_K ise u₁.u₂ ∈U_K’dır.

İspat: u birimsel ise N

( )

u =±1 dir. Normun çarpımsallık özelliğinden

( )

−u = N

( ) ( )

−1N u =±1 N ve

_{( )}

( )

1 1 1 1 1 ± = ± = = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ u N N u N olduğundan U_K u u ∈ − ,1 olduğu açıktır.

Yine u₁,u₂ ∈U_K ise N

( )

u₁ =±1 ve N

( )

u₂ =±1 dir. O halde N

(

u₁u₂

)

= N

( ) ( )

u₁ N u₂ =±1. Yani u₁u₂∈U_K.

Birimsellerin kümesi çarpma işlemi altında grup özelliklerini sağladığı için bir grup oluşturur. Bu gruba K kuadratik sayı cisminin birim grubu adı verilir.

Teorem 2.18. (Adams ve Goldstein, 1976) B>1 olmak üzere 1<u<B şartını sağlayan

sadece sonlu sayıda u∈OK vardır.

İspat: u∈O_K bir birimsel olsun. O_K’nın herhangi bir elemanı u’nun, tamsayı katsayılı

0 ) ( ) ( 2 _{− + =} u N X u Tr

X denkleminin kökü olduğunu biliyoruz. u, birimsel olduğundan

( )

u =±1 N ’dir, dolayısıyla; 0 1 ) ( 2 _{− ± =} X u Tr X ’dır. >1,

( )

= ′=±1⇒ ′ = 1 <1 u u u u u N u ’dir. Böylece, Tr

( )

u = u+u′ ≤ u + u′ <B+1’dir.

Bu durumda a ≤ B+1 olmak üzere u, X2 + aX ±1=0 denklem çiftinden birinin köküdür. Bu şekilde sadece sonlu sayıda denklem vardır ve bu denklemler kuadratik olduğundan her biri en fazla iki tane çözüme sahiptir. Dolayısıyla sadece sonlu sayıda 1<u<B şartını

sağlayan u∈OK vardır.

Bunu sağlayan sonlu sayıda eleman olduğundan bunların en küçüğünden rahatlıkla söz edebiliriz.

Tanım 2.21. OK’nın 1’den büyük en küçük birimsel elemanına temel birim denir ve εK ile gösterilir.

Teorem 2.19. d >0 ve OK =

{

1,ωd

}

olsun. Bu durumda;

{

± ∈Z

}

= n

UK εKn : (2.16)

dir

İspat: u≥1 O_K’nın bir birimseli olsun. ε_K >1 olduğundan n→∞ iken ε_Kn →∞ dir. O

halde n≥0 olacak şekilde ∃n∈Z bulunabilir öyle ki,

1 + < ≤ n K n K u ε ε (2.17)

dir. (2.17) ile verilen eşitsizliğin her iki yanı n K ε ile bölünürse K n K uε <ε ≤ − 1 elde edilir. Fakat ε ’nın tanımından onun K 1’den büyük en küçük birimsel olduğunu biliyoruz. O halde

1 =

−n

K