Ground-state properties, vortices, and collective excitations in a two-dimensional Bose-Einstein
condensate with gravitylike interatomic attraction
A. Keleş, S. Sevinçli,
*
and B. TanatarDepartment of Physics, Bilkent University, 06800 Ankara, Turkey
共Received 21 November 2007; published 9 May 2008兲
We study the ground-state properties of a Bose-Einstein condensate with short-range repulsion and gravity-like 1/r interatomic attraction in two-dimensions 共2D兲. Using the variational approach we obtain the ground-state energy and analyze the stability of the condensate for a range of interaction strengths in 2D. We also determine the collective excitations at zero temperature using the time-dependent variational method. We analyze the properties of the Thomas-Fermi-gravity and gravity regimes, and we examine the vortex states, finding the coherence length and monopole mode frequency for these regimes. Our results are compared and contrasted with those in 3D condensates.
DOI:10.1103/PhysRevA.77.053604 PACS number共s兲: 03.75.Kk, 04.40.⫺b, 34.20.Cf
I. INTRODUCTION
Investigations of Bose-Einstein condensates 共BECs兲 have mostly concentrated on systems with two-body short-ranged interaction which is characterized by the s-wave scattering length 关1兴. Recently, O’Dell et al. 关2兴 proposed a configura-tion for the occurrence of 1/r interaction which is a totally new regime for cold gases that have a long-range attractive interaction. They showed that a particular spatial configura-tion of external electromagnetic fields causes a 1/r potential in the near zone. The analysis of this configuration is also important since it suggests a new way to examine the stellar 1/r interaction in the laboratory. Apart from this possibility, it is interesting that such a system results in stable conden-sates even in the absence of an external trap potential 关3兴. Recent experiments关4兴 on polar molecules and condensates with dipole-dipole interactions have started to probe the properties of such systems.
The gravitylike interaction of atoms in a condensate is mostly a result of dipole-dipole interactions关2,5兴. By adjust-ment of the configuration of intense off-resonant laser beams, the r−3 term in the dipole-dipole interaction is made to vanish, and one can obtain an interaction of the form
U共r兲=−u/r in which u is related to the material parameters
and laser intensity. In this system, two new regimes appear where the kinetic energy, contact interaction energy, and gravitylike attractive interaction form a stable configuration without a trap potential 关2,5兴, i.e., the condensate is self-bound. Self-bound condensates have been examined exten-sively in the literature in the context of laser-induced gravi-tation 关6兴 and other systems 关3兴. Ghosh 关7兴 has studied the collective excitation frequencies of this system in three-dimensions 共3D兲 within the time-dependent variational method. He showed that variational analysis agrees very well with the results of Ref.关5兴, in which the sum-rule approach was used. Recently it has been shown that numerical solu-tions are in very good agreement with variational solusolu-tions for 3D systems关8兴.
There is a growing interest in condensates with long-range interactions, especially in those with dipole-dipole
in-teractions 关9,10兴. After the realization of Bose-Einstein con-densation with 52Cr atoms 关11兴, many theoretical and experimental studies on systems with dipolar interaction ap-peared关12兴. The recent progress in the cooling and trapping of neutral atomic gases with an electromagnetic field has also made it possible to study 2D Bose gases关13兴. The 2D atomic BECs have many interesting properties as revealed by ex-periments and theoretical predictions. The excitation spec-trum and vortex states of ordinary 2D BECs 关14,15兴 and BECs with dipole-dipole interaction关16兴 have also been in-vestigated.
In this paper we study a 2D condensate with attractive 1/r interaction. We calculate the ground-state properties using a variational approach and show that the condensate is stable without the external potential. We also consider the dynamics of the condensate within the time-dependent variational method and calculate the monopole and quadrupole mode frequencies. We examine the excitation spectrum for the Thomas-Fermi–gravity and gravity regimes, analyze the vor-tex states, and calculate the coherence length as well as the critical angular frequency to create a vortex. Our work par-allels a similar consideration for 3D condensates 关7兴 which allows for a comparison of the effects of dimensionality. II. GROUND-STATE PROPERTIES AND COLLECTIVE
EXCITATIONS
We will make use of the mean-field theory together with the variational method to investigate the ground-state prop-erties. For a dilute gas of bosonic atoms, we can write the equation of motion for the system,
iប共r,t兲 t =
冉
− ប2 2mⵜ 2+ V ext共r兲 + VH共r兲冊
共r,t兲, 共1兲in which Vext= m02r2/2 is the external harmonic potential
and VHis the Hartree potential, consisting of hard sphere and gravity interactions, respectively, in the form
VH共r兲 = g兩⌿共r兲兩2− u
冕
d2r⬘
兩⌿共r⬘
兲兩 2兩r
⬘
− r兩 , 共2兲 where g = 2冑
2ប2a/maz is the interaction strength with a being the 2D s-wave scattering length, and azis the harmonic *sevilay@fen.bilkent.edu.troscillator length in the tightly confined direction. We con-sider a highly anisotropic condensate, i.e., zⰇ⬜, and use the quasi-three-dimensional scattering model. In this model, if azⰇa, atoms experience collisions in 3D and the contact interaction parameter can be written in terms of the same parameter in 3D 关17–19兴. One must remember that we can write the Hartree potential in this form if the −u/r potential is sufficiently weak and does not affect the short-range scat-tering. We use the variational wave function in the form ⌿共r,兲=
冑
N/2l 0 2exp共−r2/22l 0 2兲, where l 0=冑
ប/m0, andthis form satisfies the normalization condition with total number of particles N. Using this function in the energy functional, the energy per particle can be obtained as
E共兲 Nប0
=1 2共
−2+2+ s˜−2− 2u˜−1兲, 共3兲
where we choose the dimensionless interaction parameters as
s
˜ =
冑
2/Na/az and u˜ =冑
/2uN/共2l0ប0兲. Equation 共3兲im-plies that the scattering interaction 共third term兲 in 2D shifts the kinetic energy by s˜. Minimizing the energy with respect
to the variational parameter, we obtain
1 −共1 + s˜兲−4+ u˜−3= 0. 共4兲
One can obtain the virial relation as −T + Vext− Es− Eu/2=0 from a scaling analysis, which is equivalent to the above relation, where T and Vextare the kinetic and trap potential
energies and Es and Eu are the interaction energies. It is worth mentioning here that variational calculations have
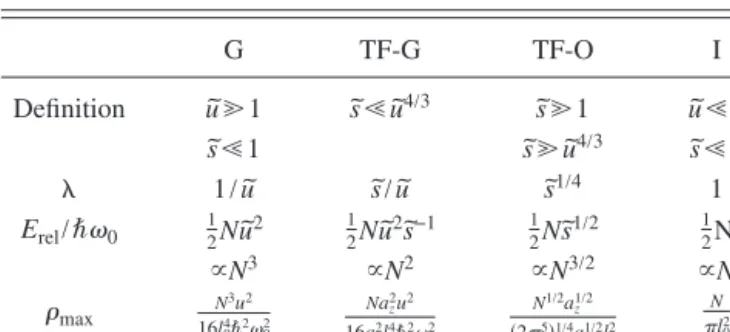
been shown 关8兴 to be quite accurate for a large range of parameters in the case of 3D condensates with gravitylike interaction. Based on our variational results, TableIgives a comparison of the four asymptotic regions on some experi-mental quantities such as the condensate radius, release en-ergy, and peak density. The radius and release energy are experimentally important quantities since they are the signa-tures of 1/r interaction 关2兴. As can be seen from the phase diagram in Fig. 1共a兲, there are four regions, as in 3D. The ideal noninteracting region 共I兲 and ordinary Thomas-Fermi region 共TF-O兲 are well known from the study of ordinary condensates 共with short-range interaction only兲. The gravity 共G兲 and Thomas-Fermi–gravity 共TF-G兲 regions are related to the balance of the gravitylike potential with the kinetic en-ergy and the contact interaction, respectively. Because these regions are not sensitive to the external potential, it can be adiabatically turned off. The gravitylike attraction does not induce the collapse of the condensate, unlike the contact in-teraction. Unlike the 3D system 关2兴, a 2D condensate is stable for negative scattering lengths if s˜⬎−1 irrespective of
the value of u˜, whereas there is a sudden collapse for s˜ⱕ
−1. In 3D, the condition below which there is no stable con-densate becomes s˜u˜ⱕ1/4 关2兴. From Fig.1共b兲, one can
con-clude that self-bound condensate is stable without the exter-nal trap. This can be seen from Eq.共3兲, which reveals that for small radii gravitylike attraction is always weaker than the kinetic energy; thus the stability of the condensate depends on the balance between the kinetic energy and contact inter-action.
We use the time-dependent variational approach to obtain the dynamics of the condensate. The Lagrangian density can be written as关20兴 L =iប 2
冉
ⴱ t − ⴱ t冊
− ប2 2m兩ⵜ兩 2+VH共r兲 2 兩兩 2, 共5兲in which the external potential is set to zero. Oscillation fre-quencies in 3D obtained by a Gaussian ansatz are compatible with the exact calculations 关5兴. Thus, we choose the trial function
TABLE I. Comparison of four asymptotic regions.
G TF-G TF-O I Definition ˜uⰇ1 ˜sⰆu˜4/3 ˜sⰇ1 ˜uⰆ1 s ˜Ⰶ1 ˜sⰇu˜4/3 ˜sⰆ1 1/u˜ ˜s/u˜ ˜s1/4 1 Erel/ប0 12Nu˜2 21Nu˜2˜s−1 21Ns˜1/2 12N ⬀N3 ⬀N2 ⬀N3/2 ⬀N max N 3u2 16l04ប202 Naz2u2 16a2l 0 4ប2 0 2 N1/2az1/2 共25兲1/4a1/2l 0 2 N l02 −2 0 2 4 6 8 −5 0 5 10 ln(u)~ ln(s) ~ 0 0.02 0.04 0.06 0.08 0.1 −3000 −2000 −1000 0 1000 2000 3000 λ E/Nh −ω 0 I TF−O TF−G G (a) (b) 20 5 −10 −20
FIG. 1.共Color online兲 共a兲 Con-tour plot of the logarithm of the condensate radius as a function of ln u˜ and ln s˜; darker shade
corre-sponds to smaller radius. Four asymptotic regions can be seen from the plot.共b兲 Ground-state en-ergy of the condensate for differ-ent values of the variational pa-rameter s˜u˜ as a function of, the
condensate radius, for large u˜. The
energy is scaled by Nប0and the radius by l0, the harmonic
oscilla-tor length. For s˜ⱕ−1, there is no
共x,y,t兲 =
冑
N␣11
exp
冉
−1 2关␣共t兲x2+共t兲y2兴
冊
, 共6兲where the wave function is normalized to N, x and y are variables in units of l0=
冑
ប/mg, and g= mu2N2/ប3 is the gravitational frequency. ␣共t兲=1/␣12+ i␣2 and 共t兲=1/12+ i2 are the dimensionless time-dependent variational pa-rameters, and ␣1 and1 are condensate widths along the x and y directions, respectively. The complex parts of the variational parameters are necessary for an accurate descrip-tion of the condensate dynamics关21兴. Substituting this wave function into the Lagrangian density and integrating over 2D spatial coordinates, we obtain the following Lagrangian:
L =SN 2u2 g
冋
1 2共␣1 2␣˙ 2+1 2˙ 2兲 − 1 2冉
1 ␣12 +␣12␣22冊
−1 2冉
1 1 2+1222冊
− 1 S ␣11 +冑
2 2F1共
1 2, 1 2;1;1 −1 2/␣ 1 2兲
␣1册
, 共7兲where S = gmN/2ប2 is a dimensionless scattering parameter
and 2F1共1/2,1/2;1;1−12/␣12兲 is the hypergeometric
func-tion. Note that the scattering parameter S in this part is re-lated to the earlier s˜ by S =˜.s
The ground-state energy as a function of the variational parameter in an isotropic system is found to be
E =SN 2u2 g
冉
1 ␣2+ 1 S ␣2−冑
2 1 ␣冊
. 共8兲Minimizing the energy functional with respect to the varia-tional parameter, the equilibrium point is obtained as =共2/兲1/2共2+2S/兲. The chemical potential =E/N and
sound velocity cs
2
=/m can be calculated from Eq. 共8兲. Us-ing the Euler-Lagrange equations, the time evolutions of the widths are ␣¨1= 1 ␣13 +
冑
2冉
S ˜ ␣121 + F␣ 1冊
, 共9兲 ¨ 1= 1 1 3+冑
2冉
S ˜ ␣11 2+ F1冊
, 共10兲 where S˜ =冑
2/3S, and F␣1 and F1 are the derivatives of
2F1共1/2,1/2;1;1−12/␣21兲/␣1with respect to␣1 and1,
re-spectively. We are looking for low-energy excitations which correspond to small oscillations around the equilibrium point. Thus, we perform an expansion around the equilibrium width by letting␣1=+␦␣1and1=+␦1for the isotropic
system. The time evolution of the widths is given by
␦␣¨1=
冋
− 3 4+冑
2冉
− 2S˜ 4+ 5 83冊
册
␦␣1 +冑
2冉
− S 4+ 3 83冊
␦1, 共11兲 ␦¨ 1=冑
2冉
− S ˜ 4+ 3 83冊
␦␣1 +冋
− 3 4+冑
2冉
− 2S˜ 4+ 5 83冊
册
␦1. 共12兲 Substituting eit-type solutions in the above set of equations, we obtain the following excitation frequencies:+ 2 = 3 4+
冑
2冉
3S˜ 4− 1 3冊
, 共13兲 − 2 = 3 4+冑
2冉
S ˜ 4− 1 43冊
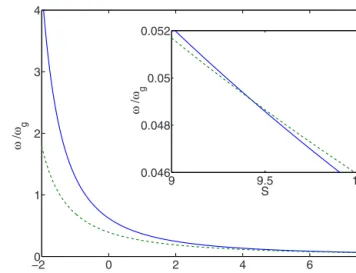
. 共14兲The excitation spectrum for a 2D condensate with gravitylike interaction is plotted in Fig.2as a function of the dimension-less scattering parameter. We observe that, in contrast to 3D, the 2D system can bear the negative scattering parameter down to S = −. For large values of the scattering parameter, the pseudopotential term dominates the gravitational energy and the monopole mode is more energetic than the quadru-pole mode. At S = 9.42, there is an intersection of the two modes which can be seen from the inset of Fig.2, where it is not possible to distinguish two modes experimentally. A similar crossing occurs in 3D at a larger value of S 关7兴.
TF-G regime. When the gravitylike potential is balanced
by the contact interaction i.e., for large s-wave scattering lengths, the kinetic energy can be neglected. The total energy of the ground state becomes E0= −0.62共N2u2/g兲. The
ground-state energy per particle varies with N as in 3D. In this regime, monopole and quadrupole frequencies are ob-tained as Q= 1.5462gS−3/2 and M= 2.1867gS−3/2. Their ratio isM/Q= 1.42, which is 1.58 in 3D. Note also that the dependence of QandMon S in 3D is⬃S−3/4, which is a distinctive feature. The facility with which the s-wave scat-tering length can be tuned through the Feshbach resonance
−20 0 2 4 6 8 1 2 3 4 S ω /ω g 9 9.5 10 0.046 0.048 0.05 0.052 S ω /ω g
FIG. 2. 共Color online兲 Monopole 共dashed line兲 and quadrupole mode 共solid line兲 frequencies 共M and Q, respectively兲 as func-tions of the dimensionless scattering parameter S. Inset shows the intersection of two modes.
makes the results of our calculation amenable to experimen-tal investigations. The identification of the 2D nature of con-densates is thus possible from the study of collective excita-tions.
G regime. In this regime we neglect the contact
interac-tion; this is the analog of the nonrelativistic boson star关22兴. The ground-state energy per particle varies with N similarly to the case in the TF-G regime. Quadrupole and monopole mode frequencies are calculated as Q= 0.6269g and M = 0.3927g, respectively, in terms of the gravitational fre-quencyg. Their ratio isM/Q= 0.63 in this regime, which is to be compared with 0.60 in 3D.
We now discuss the experimental feasibility of 2D con-densates with 1/r interaction against losses. The main sources of depletion in a gravitylike interacting gas, in the TF-G and G regions, are losses due to 1/r3oscillating
inter-fering terms and those due to incoherent phonon scattering, namely, Rayleigh scattering. The conditions necessary to ob-serve the transition from external trapping to self-binding have been analyzed by O’Dell et al.关2兴 and Giovanazzi et al. 关6兴 in the case of 3D condensates. They have shown that the Rayleigh scattering rate is reduced by a factor 共qRrms兲2 for
sample sizes smaller than the laser wavelength关2,6兴. Here q is the wave vector associated with the laser wavelength共i.e.,
q = 2/L兲 and Rrms is the root mean square of the
conden-sate size proportional to the variational width parameter. Our numerical calculations for the TF-G region give Rrms ⬃0.46L for the values a⬃3 nm, aⴱ⬃10 cm, and L = 10.6 m, which means that this region is experimentally accessible.
We calculate the temporal characteristics in relation to Rayleigh scattering rate by adopting the approach of Gio-vanazzi et al. 关6兴 to a 2D condensate. In the TF-G and G regimes, the characteristic time scale for the dynamics of the system can be estimated from the plasma frequency, which has the form
p 2 =4 2u peak mL 共15兲
in 2D关23兴, wherepeakis the peak density andLis the laser wavelength. The Rayleigh scattering rate can be expressed as 关6兴 ⌫Ray= 20 11 u បL. 共16兲
Using Eq. 共16兲 and recoil energy ER=ប2q2/2m, one can
write the plasma frequency pas
p= 0.72 ⌫Ray 3/2N3/2 共ER/ប兲1/2 1 1 + s˜. 共17兲
For a 2D condensate, azⰇa and the last quotient in the above expression goes to unity since s˜→0. Thus, for the
param-eters given in Ref. 关6兴, namely, N=40 atoms, ⌫Ray= 1.58
⫻104 s−1, and recoil energy E
R/ប=1.57⫻105 s−1, we find
p⬇57⌫Ray, which is about three times the value in the 3D
case关23兴. This estimation shows that even for a small num-ber of atoms the proposed laser characteristics and two-dimensional nature of the condensate allow for several
oscil-lations of the self-bound gas within the Rayleigh lifetime. One may also compare the monopole and quadrupole mode frequencies in the TF-G regime to the Rayleigh scat-tering rate. Recalling, for instance, that Q= 1.5462gS−3/2, the ratio of the TF-G quadrupole mode to⌫Rayis
Q ⌫Ray = 0.94ប⌫RayN 2S−3/2 ER . 共18兲
For the parameters given above, we find that Q/⌫Ray⬍53 for S⬍2 and Q/⌫Ray⬍1 for S⬎28. Our estimation again
shows that excitations can be observed experimentally within the Rayleigh lifetime.
III. VORTICES
Vortices in Bose-Einstein condensed systems are impor-tant as they experimentally reveal the macroscopic phase co-herence properties. To study the vortex states we again use the time-dependent variational analysis and choose the varia-tional wave function for the self-bound gas as
共r,t兲 =
冑
N q !␣2q+2r qexp冉
−r 2 2关1/␣共t兲 2 + i共t兲兴冊
exp共iq兲, 共19兲 where q is the vortex quantum number. By using the same Lagrangian density in Eq. 共5兲, we obtain the LagrangianL =SN 2u2 g
冋
共q + 1兲␣ 2˙ − 共q + 1兲冉
1 ␣2+␣ 22冊
−gq S ␣2+冑
2 cq ␣册
, 共20兲 where gq=共2q兲! /22q共q!兲2, c 1= 7/16, and c2= 321/1024.Then, one can find the energy of the vortex state as
Eq= SN2u2 g
冉
共q + 1兲 1 ␣2+ gq S ␣2−冑
2 cq ␣冊
. 共21兲The equilibrium point is found by minimizing the energy
q=
冑
2 冉
2共q + 1兲 + 共2/兲gqS cq冊
. 共22兲The balance between the kinetic energy and the interaction energy terms fixes the structure of the vortex core. The co-herence lengthis a measure of the superfluid characteristics of the system, which is obtained by equating these three energies: ប2 2m= gN 2R2− uN , 共23兲
where R = g
冑
F/2uS is the radius of the condensed state and F = −共12+ S 2−冑
2 1兲, in which is the equilibrium width
R=
冑
F +冑
F + 2S2S . 共24兲
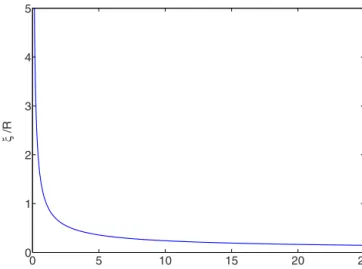
The coherence length as a function of the scattering param-eter S is shown in Fig. 3. For small values of the scattering parameter, /R is seen to be very large, which implies that superfluidity is destroyed. As the scattering length increases, the coherence length is getting much smaller, i.e., the system keeps displaying superfluidity.
The critical angular frequency to create a vortex is found by using the energies of the vortex and vortex-free states as
⍀q=g 2
冋
2 q 2− 1 2+ S 2冉
1 2q 2− 1 22冊
−冑
2冉
7 16q − 1 冊
册
. 共25兲 In Fig. 4, we present the behavior of the critical angular frequency for one vortex. From the inset one can see that⍀1increases for negative S, i.e., for attractive interaction it is
harder to create a vortex, and it decreases as the scattering parameter increases.
The frequency of the monopole mode for the vortex state is obtained as q 2 =
冉
3 q 4+ 3gqS 共q + 1兲q 4−冑
2 cq 共q + 1兲q 3冊
, 共26兲whereqis defined in Eq.共22兲. In the presence of vortices, the system collapses at S = −共q+1兲/gq.
TF-G regime. When the s-wave scattering length is very
large, the kinetic energy contribution can be neglected. Using Eq. 共24兲, the superfluid coherence length is obtained as
/R=0.7071S−1/2 where F = 1.23S−1. As S increases, the
co-herence length gets smaller compared to the size of the con-densate, i.e., superfluid properties are observed in the TF-G regime. The critical angular frequencies needed to create vor-tices are ⍀1= 0.3808gS−1 and ⍀2= 0.2277gS−1 for q = 1 and 2, respectively. Unlike in the 3D case, these two frequen-cies are larger than the chemical potentials1 and2; thus the condensate state with a vortex is unbounded in this re-gime.
G regime. In this regime the s-wave interaction energy is
very small, so it is neglected. The radius of the condensate is
Rg= g
冑
F/2uS and the superfluid coherence length is = 0.798Rg, close to the radius of the condensate, which means that superfluidity disappears. This ratio is larger in the 3D system 关7兴. The critical angular frequencies are ⍀1= 0.1776g and ⍀2= 0.095g for q = 1 and 2, respectively, and⍀2is much less than⍀1. The chemical potentials in the
rotating frame are 兩1兩/ប=0.0188g and 兩2兩/ប=0.0065g.
In this regime, only one monopole mode is stable: 1 = 0.0188g. For q = 2, the monopole mode frequency 2
= 0.0096g⬎−/ប, which means that this oscillation is un-stable and particles can escape from the condensate.
A recent paper by Giovanazzi, Santos, and Pfau关12兴 dis-cusses the way in which accurate determination of the
s-wave scattering length can be made using the collective
oscillation frequencies in a dipolar BEC. We surmise that a similar idea may be developed in the present context of gravitylike 1/r interaction.
IV. CONCLUSIONS
In this paper, we have shown that a laser-induced attrac-tive 1/r interaction gives rise to a stable condensate in 2D without a trap as in the 3D case. Unlike the 3D case, there is no collapse till s˜ = −1. We have calculated experimental
quantities such as the release energy, the peak velocity, and the condensate radius for the I, TF-O, TF-G, and G regions. We have also studied the dynamics of the system and calcu-lated the monopole and quadrupole frequencies and analyzed them within the TF-G and G regimes. These modes depend on the scattering length a in the TF-G regime, unlike the case in the ordinary TF regime. We have shown that the monopole mode exists not only for positive S values but also for nega-tive values down to S = −, in contrast to the situation in 3D 关7兴 where the monopole mode exists for S⬎0 only. Our es-timate of the main loss mechanism, namely, the Rayleigh
0 5 10 15 20 25 0 1 2 3 4 5 S ξ /R
FIG. 3. 共Color online兲 Coherence length as a function of the dimensionless scattering parameter S.
0 100 200 300 400 500 0 0.02 0.04 0.06 S Ω1 /ωg −50 0 5 0.2 0.4 0.6 S Ω1 /ωg
FIG. 4. 共Color online兲 Critical angular frequency for q=1 as a function of the dimensionless scattering parameter S. Inset is a zoom plot for negative S values.
scattering, shows that these collective oscillations may be observed in 2D condensates for reasonable parameters.
We have also investigated the vortex states and calculated the energy, the coherence length, the critical angular frequen-cies, and the monopole mode frequencies for q = 1 , 2. The presence of vortices in the condensate extends the range of S in which the condensate is stable. As the scattering parameter increases, the system keeps displaying superfluidity since the coherence length is getting smaller. We have examined the TF-G and G regimes and have shown that in the TF-G re-gime the condensate state is unbounded. In the G rere-gime, superfluidity disappears and only the monopole mode for the vortex state for q = 1 is stable.
It would be interesting to study the collective excitations of the present system within the sum-rule approach 关5兴.
Comparison of the time-dependent variational method and the sum-rule approach has yielded a very good agreement in 3D condensates with gravitylike attraction. A similar com-parison would provide a further assessment of the reliability of our results. Finally, the results of our calculations should be useful in analyzing experiments performed on 2D conden-sates. The distinctive features of collective modes may help in the identification of the 2D nature of condensates in vari-ous regimes compared to the 3D case.
ACKNOWLEDGMENTS
This work is supported by TUBITAK 共Grant No. 106T052兲 and TUBA. We thank M. Ö. Oktel for fruitful discussions.
关1兴 F. Dalfovo, S. Giorgini, L. P. Pitaevskii, and S. Stringari, Rev. Mod. Phys. 71, 463共1999兲.
关2兴 D. O’Dell, S. Giovanazzi, G. Kurizki, and V. M. Akulin, Phys. Rev. Lett. 84, 5687共2000兲.
关3兴 H. Saito and M. Ueda, Phys. Rev. Lett. 90, 040403 共2003兲; P. G. Kevrekidis, G. Theocharis, D. J. Frantzeskakis, and B. A. Malomed, ibid. 90, 230401 共2003兲; G. D. Montesinos, V. M. Perez-Garcia, and H. Michinel, ibid. 92, 133901 共2004兲; M. Matuszewski, E. Infeld, B. A. Malomed, and M. Trippenbach,
ibid. 95, 050403共2005兲.
关4兴 J. Stuhler, A. Griesmaier, T. Koch, M. Fattori, T. Pfau, S. Giovanazzi, P. Pedri, and L. Santos, Phys. Rev. Lett. 95, 150406共2005兲.
关5兴 S. Giovanazzi, G. Kurizki, I. E. Mazets, and S. Stringari, Eu-rophys. Lett. 56, 1共2001兲.
关6兴 S. Giovanazzi, D. O’Dell, and G. Kurizki, Phys. Rev. A 63, 031603共R兲 共2001兲.
关7兴 T. K. Ghosh, Phys. Rev. A 65, 053616 共2002兲.
关8兴 I. Papadopoulos, P. Wagner, G. Wunner, and J. Main, Phys. Rev. A 76, 053604共2007兲.
关9兴 K. Goral and L. Santos, Phys. Rev. A 66, 023613 共2002兲. 关10兴 L. Santos, G. V. Shlyapnikov, and M. Lewenstein, Phys. Rev.
Lett. 90, 250403共2003兲.
关11兴 A. Griesmaier, J. Werner, S. Hensler, J. Stuhler, and T. Pfau, Phys. Rev. Lett. 94, 160401共2005兲.
关12兴 S. Giovanazzi, L. Santos, and T. Pfau, Phys. Rev. A 75, 015604共2007兲.
关13兴 A. Posazhennikova, Rev. Mod. Phys. 78, 1111 共2006兲. 关14兴 L. Pricoupenko, Phys. Rev. A 70, 013601 共2004兲.
关15兴 L. D. Carr and C. W. Clark, Phys. Rev. Lett. 97, 010403 共2006兲.
关16兴 U. R. Fischer, Phys. Rev. A 73, 031602共R兲 共2006兲.
关17兴 M. D. Lee, S. A. Morgan, M. J. Davis, and K. Burnett, Phys. Rev. A 65, 043617共2002兲.
关18兴 L. Salasnich, A. Parola, and L. Reatto, Phys. Rev. A 65, 043614共2002兲.
关19兴 B. Tanatar, A. Minguzzi, P. Vignolo, and M. P. Tosi, Phys. Lett. A 302, 131共2002兲.
关20兴 L. Salasnich, Int. J. Mod. Phys. B 14, 1 共2000兲.
关21兴 V. M. Perez-Garcia, H. Michinel, J. I. Cirac, M. Lewenstein, and P. Zoller, Phys. Rev. Lett. 77, 5320共1996兲.
关22兴 X. Z. Wang, Phys. Rev. D 64, 124009 共2001兲.
关23兴 C. I. Um, W. H. Kahng, E. S. Yim, and T. F. George, Phys. Rev. B 41, 259共1990兲.