Matematiksel Modelleme Etkinliklerinin Ortaokul Öğrencilerinin PISA Matematik Başarı Düzeylerine Etkisi

(1)

(2)

(3)

MATEMATİKSEL MODELLEME ETKİNLİKLERİNİN ORTAOKUL

ÖĞRENCİLERİNİN PISA MATEMATİK BAŞARI DÜZEYLERİNE

ETKİSİ

CANSU BAKIRCI

YÜKSEK LİSANS TEZİ

İLKÖĞRETİM MATEMATİK EĞİTİMİ BİLİM DALI

GAZİ ÜNİVERSİTESİ

EĞİTİM BİLİMLERİ ENSTİTÜSÜ

(4)

i

TELİF HAKKI VE TEZ FOTOKOPİ İZİN FORMU

YAZARIN

Adı : Cansu Soyadı : BAKIRCI Bölümü : İlköğretim İmza : Teslim Tarihi :

TEZİN

Türkçe Adı : Matematiksel Modelleme Etkinliklerinin Ortaokul Öğrencilerinin PISA Matematik Başarı Düzeylerine Etkisi

İngilizce Adı : The Effects of the Mathematical Modelling Activities on Secondary School Students’ Mathematics Achievement Level on the PISA.

(5)

ii

ETİK İLKELERE UYGUNLUK BEYANI

Tez yazma sürecinde bilimsel ve etik ilkelere uyduğumu, yararlandığım tüm kaynakları kaynak gösterme ilkelerine uygun olarak kaynakçada belirttiğimi ve bu bölümler dışındaki tüm ifadelerin şahsıma ait olduğunu beyan ederim.

Yazar Adı Soyadı: Cansu BAKIRCI İmza:

(6)

iii

JÜRİ ONAY SAYFASI

Cansu BAKIRCI tarafından hazırlanan “Matematiksel Modelleme Etkinliklerinin Ortaokul Öğrencilerinin PISA Matematik Başarı Düzeylerine Etkisi” adlı tez çalışması aşağıdaki jüri tarafından oy birliği / oy çokluğu ile Gazi Üniversitesi Matematik ve Fen Bilimleri Eğitimi Dalı’nda Yüksek Lisans tezi olarak kabul edilmiştir.

Danışman: Yrd. Doç. Dr. Neslihan Bulut ... Matematik Eğitimi Anabilim Dalı, Gazi Üniversitesi

Başkan: Yrd. Doç Dr. Hasan Es ... Matematik Eğitimi Anabilim Dalı, Gazi Üniversitesi

Üye: Yrd. Doç Dr. Mesture Kayhan Altay ... İlköğretim Matematik Eğitimi Anabilim Dalı, Hacettepe Üniversitesi

Tez Savunma Tarihi: 17/08/2016

Bu tezin Matematik ve Fen Bilimleri Eğitimi Anabilim Dalı’nda Yüksek Lisans tezi olması için şartları yerine getirdiğini onaylıyorum.

Prof. Dr. Ülkü ESER ÜNALDI ………

(7)

iv

TEŞEKKÜR

İlk olarak, bu araştırmaya beni yönlendiren, çalışmalarım sırasında bana bilgisiyle yol gösteren, her türlü desteği sağlayan değerli danışmanım Sayın Yrd. Doç. Dr. Neslihan BULUT’a teşekkürü bir borç bilirim.

Bu çalışmanın uygulanmasında ve yürütülmesinde bana okulun tüm imkanlarını sunan Çankaya Talatpaşa Ortaokulu Müdürü’ne, matematik öğretmeni Işılay ŞENGİL’e ve 7. sınıf öğrencilerine çok teşekkür ediyorum.

Değerli araştırma görevlisi arkadaşlarım Birnaz KANBUR ve Pınar AKYILDIZ’a çalışmalarım sırasındaki katkılarından dolayı çok teşekkür ediyorum.

Yüksek Lisans eğitimim boyunca sağladığı maddi ve manevi desteklerden dolayı Türkiye Bilimsel ve Teknolojik Araştırma Kurumu’na (TUBİTAK) çok teşekkür ediyorum.

Son olarak, eğitimimin her aşamasında olduğu gibi burada da yanımda olan beni hep cesaretlendiren ve destekleyen değerli annem ve babam Zahide ve Mehmet Hanifi BAKIRCI’ya çok teşekkür ediyorum.

(8)

v

MATEMATİKSEL MODELLEME ETKİNLİKLERİNİN ORTAOKUL

ÖĞRENCİLERİNİN PISA MATEMATİK BAŞARI DÜZEYLERİNE

ETKİSİ

(Yüksek Lisans Tezi)

Cansu Bakırcı

GAZİ ÜNİVERSİTESİ

EĞİTİM BİLİMLERİ ENSTİTÜSÜ

AĞUSTOS 2016

ÖZ

Geleneksel yöntemlerin ve problem çözme etkinliklerinin öğrencilerin problem çözme becerisini geliştirmede yetersiz kaldığı düşüncesi “Öğrencilerin gerçek hayatta kullanabilecekleri matematiksel bilgi ve matematiksel düşünme becerisine sahip olabilmeleri için nasıl bir matematik eğitimi yapılmalıdır?” sorusunu beraberinde getirmiştir (Kertil, 2008). Matematik eğitiminde matematiksel modelleme ile ilgili araştırmalar incelendiğinde matematiksel modelleme etkinliklerinin, günümüz dünyasının gereksinimine karşılık verebilecek yapıda olduğu anlaşılmaktadır. Bu araştırma matematiksel modelleme etkinliklerinin ortaokul öğrencilerinin PISA matematik başarı düzeylerine etkisini incelemek amacıyla yapılmıştır. Çalışmada hem nicel hem nitel yöntemlerin birlikte kullanıldığı karma araştırma deseni araştırma modeli olarak kullanılmıştır. Araştırma, problem durumunun araştırılması için “ön test-son test kontrol gruplu yarı deneysel desen”e göre düzenlenmiştir. Araştırma, 2015-2016 öğretim yılında bir devlet ortaokulunun 7.sınıf Seçmeli Matematik Uygulamaları dersinin iki şubesindeki toplam 44 öğrenci ile gerçekleştirilmiştir. Bu öğrencilerin 24’ü deney grubunda, 20’si kontrol grubunda yer almıştır. Deney grubunda “Matematiksel Modelleme Etkinlikleri” kontrol grubunda ise Milli Eğitim Bakanlığı’nın belirlediği ders kitabındaki veya öğretmenin kendi oluşturduğu problemler ve etkinlikler kullanılmıştır. Araştırmada veriler,

(9)

vi

açıklanan PISA sorularından oluşan PISA Matematik Başarı Testi, Matematiksel Modelleme Etkinlikleri ve yarı yapılandırılmış görüşmelerden elde edilmiştir. Nicel verilerin analizinde bağımsız t-testi, bağımlı t-testi, mann-whitney U ve wilcoxon testi gibi parametrik ve parametrik olmayan testler kullanılmıştır. Elde edilen nitel verilerin içerik analizi yapılmıştır. Araştırmada elde edilen verilerin analizi sonucunda; hem deney grubunda hem de kontrol grubunda PISA Matematik Başarı Testi ortalamalarına göre öğrencilerin PISA matematik başarı düzeylerinde anlamlı bir artış olduğu ancak deney ve kontrol gruplarının son testleri karşılaştırıldığında, deney grubunun kontrol grubuna göre PISA Matematik Başarı düzeyinin daha yüksek olduğu görülmüştür. Nitel verilerin analizi sonucunda matematiksel modelleme etkinliklerinin uygulanması sürecinde öğrencilerin ve öğretmenin karşılaştığı zorluklar tespit edilmeye çalışılmıştır. Ayrıca yapılan görüşmelerde öğrencilerin matematiksel modelleme etkinliklerine ilişkin görüşlerinin olumlu olduğu görülmüştür. Araştırmada elde edilen yukarıdaki bulgular ayrıntılı bir şekilde yorumlanmış ve çalışmanın sonunda çeşitli önerilere yer verilmiştir.

Anahtar Kelimeler : Matematiksel Modelleme Etkinlikleri, PISA, Matematik Öğretimi Sayfa Adedi : 195

(10)

vii

: THE EFFECTS OF THE MATHEMATİCAL MODELLİNG

ACTİVİTİES ON SECONDARY SCHOOL STUDENTS’

MATHEMATİCS ACHİEVEMENT LEVEL ON THE PISA.

(M.S. Thesis)

Cansu Bakırcı

GAZI UNIVERSITY

GRADUATE SCHOOL OF EDUCATIONAL SCIENCES

August 2016

ABSTRACT

The thought of traditional methods and problem solving activities remain incapable on developing problem solving abilities of students, accompanies the question “How to provide education for mathematics to make students have mathematical knowledge and mathematical thinking abilllities which they could use on their real life?” (Kertil, 2008). When analyzing researches about mathematical modelling on mathematics education, it is seen that mathematical modelling activities meet the necessities of today’s world. This study aims investigating effects of mathematical modelling activities on secondary school student’s mathematics achievement level on the PISA. The researcher employed an mixed method which a quantitative method was nested within a qualitative method. “Pretest-post-test design with control group” was used to investigate the problem status. The research was conducted with 44 seventh grade students from a state secondary school during 2015-2016 academic years. Two groups of students were investigated. The experiment group consisted of 24 and the control group consisted of 20 students. Mathematical modeling activities and traditional instruction methods were used in the experiment group and the control group respectively. PISA Mathematics Achievement Test, Mathematical Modeling Activities and Semi-structured interview were used in the research. In the analysis of research data, for quantitative data Independent Samples t-test, Paired Samples t-test,

(11)

viii

Mann-Whitney U test and Wilcoxon test were used. In the analysis of qualitative data content analysis was used. As a result of the collected data analyses in the research; it has been observed that using mathematical modeling activities in mathematics education increased students’mathematics achievement level on the PISA. By means of appreciating qualitative data results, difficulties that students and teachers faced with were tried to be determined. Also it was found that students have positive opinions about mathematical modelling activities. Results were implemented and there were different recommendations at the end of the study.

Key Words : Mathematical Modeling Activities, PISA, Mathematics Teaching Page Number : 195

(12)

ix

İÇİNDEKİLER

ÖZ ... v

ABSTRACT ... vii

İÇİNDEKİLER ... ix

TABLOLAR LİSTESİ... xiii

ŞEKİLLER LİSTESİ ... xiv

BÖLÜM 1 ... 1 GİRİŞ ... 1 1.1. Problem Durumu ... 1 1.2. Araştırmanın Amacı ... 5 1.3. Araştırmanın Problemi ... 5 1.4 Alt Problemler ... 5 1.5 Araştırmanın Önemi ... 5 1.6 Sınırlılıklar... 7 1.7 Varsayımlar ... 7 1.8 Tanımlar ... 7 BÖLÜM 2 ... 9 KURAMSAL ÇERÇEVE ... 9 2.1. Model ve Modelleme ... 9 2.2. Matematiksel Modelleme ... 13

(13)

x

2.3. Modelleme Süreci ... 18

2.4. Matematiksel Modelleme Yaklaşımları ... 23

2.5. Matematiksel Modelleme Sürecinde Ortaya Çıkan Bazı Zorluklar ... 25

2.6. Matematiksel Modelleme ve Problem Çözme Arasındaki İlişki ... 26

2.7. Model Oluşturma/ Modelleme Etkinlikleri ... 27

2.8. Modelleme Etkinlikleri ve Geleneksel Sözel Problemler ... 31

2.9. Matematiksel Modelleme Etkinliklerinde Grup Çalışmasının ve Öğretmenin Rolü ... 34

2.10. PISA ve Matematiksel Modelleme ... 36

2.11. İlgili Araştırmalar ... 39

2.11.1. Matematiksel Modelleme İle İlgili Çalışmalar ... 39

2.11.2. Uluslararası Öğrenci Değerlendirme Programı (PISA) İle İlgili Çalışmalar ... 48

BÖLÜM 3 ... 51

YÖNTEM... 51

3.1 Araştırmanın Modeli ... 51

3.2. Araştırma Grubu ... 52

3.3. Veri Toplama Araçları ... 53

3.3.1. PISA Matematik Başarı Testi ... 53

3.3.2. Matematiksel Modelleme Etkinlikleri... 56

3.3.3. Görüşmeler ... 60

3.4. Uygulama Süreci ... 61

3.4.1. Deney Grubundaki Uygulama Süreci ... 61

3.4.2. Kontrol Grubundaki Uygulama Süreci ... 61

3.5. Verilerin Toplanması ... 62

(14)

xi

BÖLÜM 4 ... 65

BULGULAR ... 65

4.1. Birinci Alt Probleme İlişkin Bulgular ... 65

4.2. İkinci Alt Probleme İlişkin Bulgular ... 69

4.2.1 Birinci Modelleme Etkinliğine Dayalı Bulgular ... 69

4.2.2 İkinci Modelleme Etkinliğine Dayalı Bulgular... 73

4.2.3. Üçüncü Modelleme Etkinliğine Dayalı Bulgular ... 77

4.2.4. Dördüncü Modelleme Etkinliğine Dayalı Bulgular ... 79

4.2.5. Beşinci Modelleme Etkinliğine Dayalı Bulgular ... 84

4.2.6. Altıncı Modelleme Etkinliğine Dayalı Bulgular ... 88

4.2.7. Yedinci Modelleme Etkinliğine Dayalı Bulgular ... 91

4.2.8. Sekizinci Modelleme Etkinliğine Dayalı Bulgular ... 94

4.3. Görüşmelere Dayalı Bulgular ... 97

4.3.1. Kullanılan Modelleme Etkinliklerinin Amacına Yönelik Görüşler ... 97

4.3.2. Modelleme Etkinliklerinin Rutin Problemler ile Karşılaştırılmasına Yönelik Görüşler ... 100

4.3.3. Matematiğin Günlük Hayatta Kullanımına Yönelik Görüşler ... 103

4.3.4. Modelleme Etkinliklerinin Aktiflik ve Başarıya Etkisine Yönelik Görüşler ... 104

BÖLÜM 5 ... 107

SONUÇ, TARTIŞMA VE ÖNERİLER ... 107

5.1. Tartışma ve Sonuç... 107

5.1.1. Modelleme Etkinliklerinin PISA Matematik Başarı Düzeyine Etkisi ... 107

5.1.2. Modelleme Etkinliklerinin Uygulanması Sürecinde Öğretmenin ve Öğrencilerin Yaşadığı Zorluklar ... 109

(15)

xii

5.2. Öneriler ... 114

5.2.1. Araştırmacılara Yönelik Öneriler ... 114

5.2.2. Öğretmenlere Yönelik Öneriler ... 115

5.2.3. Milli Eğitim Kurumları’na ve Üniversitelere Yönelik Öneriler ... 115

KAYNAKLAR ... 117

EKLER... 129

Ek 1: Belirtke Tablosu ... 130

EK 2: PISA Matematik Başarı Testi ve Rubrik ... 133

(16)

xiii

TABLOLAR LİSTESİ

Tablo 1 Modelleme Yaklaşımlarının Sınıflandırılması ... 24

Tablo 2 Problem Çözme ve Matematiksel Modelleme Bir Karşılaştırılması ... 33

Tablo 3 Araştırmanın Deneysel Deseni ... 52

Tablo 4 Deney ve Kontrol Grubundaki Öğrencilerin Cinsiyete Göre Dağılımları ... 53

Tablo 5 Modelleme Problemi’nin Prensiplere İlişkin Değerlendirme İçerikleri ... 56

Tablo 6 Deney ve Kontrol Grubunda Yer Alan Öğrencilerin PISA Matematik Başarı Ön Test Puanlarının Karşılaştırılmasına İlişkin Bağımsız Gruplar T-testi ... 66

Tablo 7 Deney ve Kontrol Grubunda Yer Alan Öğrencilerin PISA Matematik Başarı Son Test Puanlarının Karşılaştırılasına İlişkin Mann Whitney-U Testi ... 66

Tablo 8 Deney grubunun PISA Matematik Başarı Ön Test - Son Test Puanları İçin Wilcoxon İşaretli Sıralar Testi Sonuçları ... 67

Tablo 9 Kontrol grubunun PISA Matematik Başarı Ön Test - Son Test Puanları İçin Bağımlı Gruplar T-Testi Sonuçları ... 68

Tablo 10 Birinci Görüşme Sorusunun Analizi ... 98

Tablo 11 İkinci Görüşme Sorusunun Analizi ... 100

Tablo 12 Üçüncü Görüşme Sorusunun Analizi ... 103

Tablo 13 Dördüncü Görüşme Sorusunun Analizi ... 104

Tablo 14Belirtke Tablosu 1 ... 130

(17)

xiv

ŞEKİLLER LİSTESİ

Şekil 1. Matematiksel modellemenin basit bir görünümü. ... 19

Şekil 2. Matematiksel modelleme döngüsü. ... 20

Şekil 3. Süreç modeli... 21

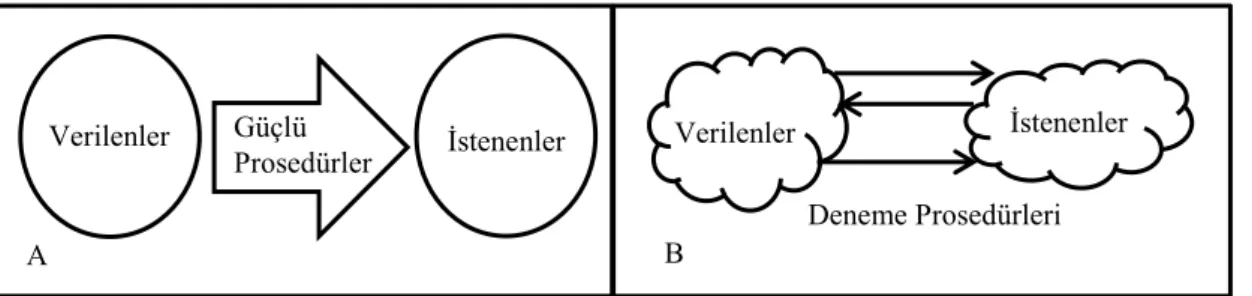
Şekil 4. Problem çözmede geleneksel yaklaşım (A) ve modelleme yaklaşımı (B). ... 32

Şekil 5 Örnek PISA problemi ve puanlaması ... 55

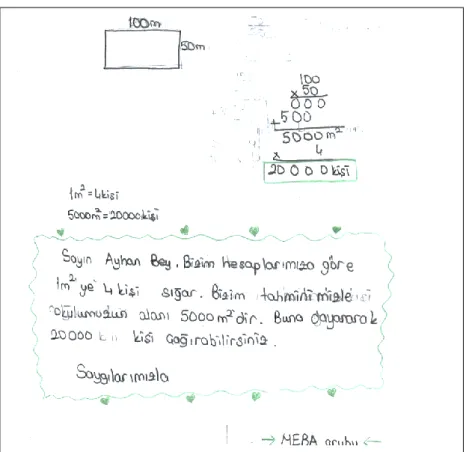
Şekil 6 İsimsizler grubu etkinlik işlem ve rapor kağıdı... 71

Şekil 7. Yıldızlar grubu etkinlik işlem ve rapor kağıdı. ... 71

Şekil 8. Meba grubu etkinlik işlem ve rapor kağıdı. ... 72

Şekil 9. Meba grubu etkinlik işlem ve rapor kağıdı. ... 75

Şekil 10. Yıldızlar grubu etkinlik rapor kağıdı... 75

Şekil 11. Beyin fırtınası grubu etkinlik işlem ve rapor kağıdı. ... 76

Şekil 12. Biz biliriz grubu etkinlik işlem ve rapor kağıdı. ... 78

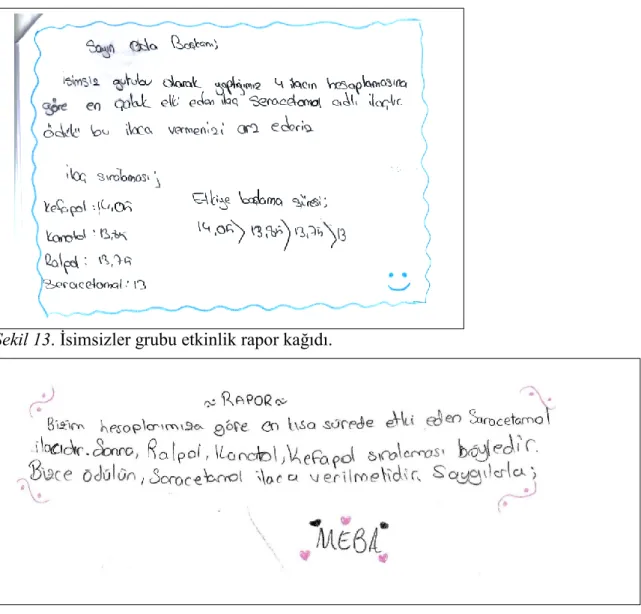
Şekil 13. İsimsizler grubu etkinlik rapor kağıdı. ... 79

Şekil 18. Meba grubu etkinlik rapor kağıdı. ... 83

(18)

xv

Şekil 20. Süper 4’lü grubu etkinlik rapor kağıdı. ... 83

Şekil 22 Meba grubu etkinlik işlem ve rapor kağıdı. ... 86

Şekil 23. Yıldızlar grubu etkinlik işlem ve rapor kağıdı. ... 87

Şekil 24. Süper 4’lü grubu etkinlik işlem ve rapor kağıdı... 87

Şekil 27. Meba grubu etkinlik rapor kağıdı. ... 93

Şekil 29. Yıldızlar grubu etkinlik rapor kağıdı... 95

(19)

xvi

SİMGELER VE KISALTMALAR LİSTESİ

MEB Milli Eğitim Bakanlığı

PISA Programme for International Student Assessment SPSS Statistical Package for the Social Sciences

NCTM National Council of Teachers of Mathematics

OECD Organisation for Economic Co-operation and Development

MOE Model Oluşturma Etkinlikleri

p Önem Derecesi

𝑋 Ortalama

(20)

1

BÖLÜM 1

GİRİŞ

Bu bölümde, “Problem Durumu”, “Problem Cümlesi”, “Alt Problemler”, “Araştırmanın Amacı”, “Sayıltılar”, “Sınırlılıklar” ve “Tanımlar” üzerinde durulmaktadır.

1.1. Problem Durumu

Bilginin ve teknolojinin hızlı gelişimi toplumun eğitim dünyasından beklentilerini de değiştirmekte, matematik eğitimcilerinden gerçek problem durumlarında etkili çözümler üretebilen, öğrendiği matematiği günlük yaşamında etkili bir şekilde kullanabilen, matematiğin gerçek dünya ile olan sıkı ilişkisinin farkında olan ve böylece matematikten korkmak yerine ondan zevk alan ve onu seven bireylerin yetiştirilmesini beklemektedir (Doruk ve Umay, 2011). Matematik öğretiminin genel olarak kabul gören amaçlarından biri, bireylere günlük hayatında matematiği kullanabilme yeteneği ve yeterliği kazandırılmasıdır (Kaiser,2005).

Dünya genelinde insanların çoğu matematiğin gerçek yaşamla ilgisi olmadığını düşünmekte, toplum ve sosyal yaşamla büyük ilgisi olan temel bir bilim olduğu halde, birçok insan için soyut ve yaşamla teması olmayan bir bilim olarak görülmektedir (Maaß’dan aktaran Doruk, 2011). Matematik gerçek hayattan uzak sadece okullarda yapılan bir bilim olarak görülmesine rağmen gerçek dünya problemlerine çözüm getiren sistematik bir bilim dalıdır. Matematik günümüzde yaşamımızın birçok alanında yer almasına rağmen bunun farkına ancak çok az kişi varabilmektedir. Günlük yaşamı insanların günlük aktivitelerinin veya günlük işlerinin gerektirdiği eylemler olarak tanımlayabiliriz. Taksi ücretinin hesabını kontrol ederken, salon için ne kadar boya

(21)

2

gerektiğini hesaplamaya çalışırken, değişik sayıdaki kişi için yemek tarifini yeniden ayarlarken, bir kitaplık kurmaya veya taşımaya çalışırken, uygun boyutta bir halı satın alırken, pokerde bir miktar para kazanırken veya domates dikerken, günlük yaşamımızda sürekli matematik kullanırız (Pollak, 1969).

Öğrenciler matematiği çok soyut bulmakta ve matematikten korkmaktadırlar. Aynı zamanda sınıfta öğrendikleri bilgileri günlük yaşama transfer etmede güçlük çekmektedirler. Öğrenme ortamlarının öğretmen merkezli ve tek düze olması öğrencilerin bilgileri günlük yaşantılarında nerede ve nasıl uygulayacakları konusunda zorluk çekmelerinin nedenlerinden biri olabilir. Bu anlamda öğrencilere derste öğretilen konuların, daha anlamlı ve günlük yaşamla ilişkili şekilde farklı uygulama ve etkinliklerle öğretilmesi gerekmektedir. Bu etkinliklerden biri olan matematiksel modelleme etkinliklerinin öğrencilere matematiğin gerçek yaşamla ilişkisini ve gerçek hayata uygulanabilirliğini gösterdiğini söyleyebiliriz.

Ülkemizde son yıllarda yaşanan öğretim programlarındaki değişimler ve iyileştirmeler matematik derslerinde programın felsefesinin değişmesine bağlı olarak öğretmenin ve öğrencinin değişen görevleri, öğrencilerin yeni becerilerle donatılması gerekliliği, öğrenme ortamının yapısındaki farklılaşma, matematiksel öğrenmelerin ölçülmesindeki yaklaşımların zenginleşmesini de beraberinde getirmiştir. Matematiksel düşünme ve anlamanın gittikçe karmaşıklaştığı günümüz dünyasında matematiksel kavramları ve kavram sistemlerini hipotez etmeyi öğrenmek, ilişkileri anlamak, anlatmak, yeniden inşa etmek ve analiz etmeyi öğrenmek öğrenciler için kritik öneme sahip bir durum haline gelmiştir (Thomas & Hart, 2010). İçinde bulunduğumuz çağda geleneksel eğitimden uzaklaşılarak öğrenenin merkezde olduğu ve eleştirel düşünme ve yaratıcı düşünme becerileri gibi kavramların daha fazla değer kazandığı görülmektedir. Bu becerilere sahip nitelikli insanlardan ise gerçek problem durumlarında etkili çözümler üretmeleri, öğrendiği matematiği günlük yaşamında etkili bir şekilde kullanabilmeleri, matematiğin gerçek yaşam ile ilişkisinin farkında olmaları beklenmektedir. Ancak araştırmacılara göre öğrenciler matematik yaparken gerçek hayatla matematik arasındaki ilişkiyi göz ardı etmektedirler ve bunda sözel probemlerin payı büyüktür (Greer, 1997). Günümüzde sadece matematiksel işlem süreçlerini ezberlemek ve buna benzer problem durumlarına uygulamak yeterli değildir. Bu bağlamda öğrencilerin sınıf ortamında öğrendikleri bilgileri ve kavramları daha anlamlı bir hale getirilmesi için farklı uygulama alanlarına gereksinim

(22)

3

duyulmaktadır. Bu farklı uygulama alanlarından biri de matematiksel modellemedir. Öğrencinin gerçek hayat problemleri ile matematik arasındaki ilişkiyi kurabilmesinde matematiksel modellemenin önemli bir rolü vardır.

Günümüzde matematik eğitiminde kâğıt-kalem ile hesaplamaların önemi azalırken tahmin edebilme, problem çözme gibi beceriler önem kazanmıştır (Güder, 2013). Matematik eğitiminin temel amaçlarından biri öğrencilerin problem çözme becerilerini geliştirmektir. Matematik öğretiminde problem çözme becerisi önemli bir beceri olarak görülmekte problem çözmeye dayalı öğretim yaklaşımlarının bu becerinin öğrencilere kazandırılmasındaki önemine dikkat çekilmektedir. Bu nedenle, problem çözme, öğretim programı içerisinde yer alan her konu için geliştirilmesi beklenen temel bir beceri olarak ele alınmaktadır (Milli Eğitim Bakanlığı [MEB], 2013).

İster alışılmış ve sıradan ister farklı ve sıra dışı problemler ele alınarak öğrencilere bu beceriyi kazandırmak hedeflensin çözümün daima tek olması matematikte öne çıkan esneklik değeri ile uyuşmamaktadır (Bishop & Clarkson’dan Aktaran Durmuş, 2011). Bu bağlamda öğrencilerin problem çözme becerilerini geliştirmek için onlara araştırma yapabilecekleri, iletişim kurabilecekleri, eleştirel düşünebilecekleri, farklı çözüm yöntemlerini sunabilecekleri açık uçlu sorular ve etkinliklere yer verilmelidir. Öğrencilerin seviyesine ve ilgilerine uygun, aktif katılımlarını sağlayacak gerçekçi problem çözme etkinliklerine dayalı öğrenme ortamları tercih edilmelidir (MEB, 2013). Bu öğrenme ortamlarıyla birçok matematiksel kavramın öğrenciler için daha anlamlı hale getirilmesi amacıyla bazı farklı uygulamalar ve bağlamlara başvurulmalıdır. Bu bağlamlardan biri de matematiksel modelleme etkinlikleridir. Matematiksel modelleme sürecinde gerçek yaşamdan doğan bir konu alınır ve matematiksel olarak ifade edilir. Modelleme sınıf ortamında öğrenciler tarafından yapılır. Matematiksel modelleme etkinlikleri, öğrenciler için matematiği öğrenmenin yanında matematiğin gerçek yaşamda çok farklı yönlerini fark etme açısından mükemmel bir yoldur (Lingefjard & Holmquist, 2005).

Matematiğin çok çeşitli değerleri içinde barındırması sınıf içi uygulamalarda da yeni yaklaşımların düşünülmesine neden olmuş, hazırlanan yeni matematik öğretim programında kazandırılacak beceriler arasında matematiksel modelleme yapabilme becerisine yer verilmiş ve önemine vurgu yapılmıştır. Ayrıca modellemeyi öğretim programının temel öğelerinden biri olarak ele alarak, vizyonunu yaşamında matematiği gerektiği şekilde kullanabilen, gerçek yaşam durumlarıyla matematik arasındaki ilişkiyi

(23)

4

kurabilen, karşılaştığı problemlere farklı çözüm yolları üretebilen, analitik düşünceye sahip, akıl yürütme ve ilişkilendirme gibi becerilere sahip bireyler yetiştirmek olarak yeniden ifade etmiştir (MEB, 2005). Bu durumun temel nedeni dünyada matematiksel modellemenin pek çok ülkenin öğretim programlarında yer alması olarak değerlendirilebilir (ör. Australian Curriculum, Assessment and Reporting Authority, 2009; NCTM, 1989; English version of the Swedish Curriculum for the Gymnasium’dan Aktaran Lingefjard, 2007, The New German Educational Strandards and Curricula’dan Aktaran Maaβ, 2007). Öğretim programındaki bu yeniliklere rağmen Türk Eğitim sisteminde öğrencilerin modelleme becerilerini ve dolayısı ile matematik bilgilerini farklı bağlamlarda uygulama becerilerini geliştirmeye yönelik ilköğretim ve ortaokul düzeyinde bir eğitimin (en azından geçmiş yıllarda) verilmediği müfredat ve uygulamalarında görülebilir (Kertil, 2008). Ülkemizde matematiksel modelleme üzerine yapılan çalışmalarda ise (Çiltaş 2011; Taşova 2011; Kertil, 2008; Keskin, 2008; Sandalcı, 2013) yükseköğretim ve ortaokul 2.kademe düzeyinde yoğunlaşıldığı ancak ortaokul 1.kademe düzeyinde yapılan çalışmaların yetersiz kaldığı görülmektedir.

Türk öğrencilerin PISA sınavında derste öğrendikleri matematiksel bilgileri gerçek yaşamda karşılaştıkları problem durumlarına uygulayamadıkları ve matematiğin dünyadaki rolünü kavrayamadıkları görülmüştür; bu nedenle de ülkemiz PISA sınav başarısında alt sıralarda bulunmaktadır. Avrupa’daki Türkiye gibi başarı sıralamasında alt sıralarda yer alan ülkeler, öğrencilerin matematiği günlük yaşama uygulamakta güçlük çektiklerini ve matematiksel modelleme etkinliklerinin bu güçlüğü yenebileceğini tartışmışlardır. Fakat matematiksel modelleme etkinliklerinin PISA matematik başarı düzeylerini ne derece etkileyeceğine yönelik deneysel çalışmalara pek rastlanılmamaktadır. Geçmiş yıllarda PISA uygulamalarındaki düşük başarı düzeyinin altında yatan nedenleri çeşitli faktörler yönünden araştıran çalışmalar vardır (İş, 2003; Berberoğlu ve Kalender, 2005; Berberoğlu, 2007; Özer, 2009).

Bu çalışmanın problem durumu yukarıda verilen bilgilerden yola çıkarak matematiksel modelleme etkinliklerinin ortaokul 7. sınıf öğrencilerinin PISA matematik başarı düzeylerine etkisini incelemektir.

(24)

5 1.2. Araştırmanın Amacı

Bu araştırmada, matematiksel modelleme etkinliklerinin ortaokul 7. sınıf öğrencilerinin PISA matematik başarı düzeylerine etkisini ve öğrencilerin matematiksel modelleme etkinlikleri hakkındaki görüşlerini belirlemek amaçlanmıştır.

1.3. Araştırmanın Problemi

Matematiksel modelleme etkinliklerinin ortaokul 7. sınıf öğrencilerinin PISA matematik başarı düzeylerine etkisi nedir?

1.4 Alt Problemler

1. Matematiksel modelleme etkinliklerinin kullanıldığı deney grubu ile matematiksel modelleme etkinliklerinin kullanılmadığı kontrol grubunın PISA Matematik Başarı Testi puan ortalamaları arasında anlamlı bir fark var mıdır?

2. Modelleme etkinliklerinin uygulanışı sürecinde öğretmenin ve öğrencilerin karşılaştıkları zorluklar nelerdir?

3. Ortaokul 7. sınıf öğrencilerinin matematiksel modelleme etkinlikleri hakkındaki görüşleri nelerdir?

1.5 Araştırmanın Önemi

“Günlük hayatımızda matematik var mıdır?” şeklinde bir soruya verilen cevaplara dikkat edildiğinde cevapların belli konularda yoğunlaştığı görülür.

Sayılar, günlük hayat ve matematik ilişkisinin en fazla kurulabildiği konudur. Sayma, markette para ödeme ve üstüne ödenmesi gereken parayı hesaplama, yolun kaç kilometre olduğunu, kaç saatte gidileceğini bulma gibi konular herkesin kurabildiği temel ilişkiler olarak göze çarpmaktadır. Daha farklı ilişkilerin kurulabilmesi matematik derslerinde öğrenilen konuların günlük hayata ne kadar taşındığı ile ilişkili olarak değişmektedir (Erturan, 2007).

(25)

6

Matematik eğitimi üzerine yapılan çalışmalar incelendiğinde büyük çoğunluğunun matematiksel kavramların öğretilmesi ve öğrencilerin matematiği nasıl yorumladığı üzerine odaklanmakdığı görülmektedir. Farklı ortamlarda farklı becerileri geliştirmeye yönelik farklı eğitim öğretim yöntemleri üzerine yapılan çalışmalar ise yetersiz görünmektedir.

Geleneksel yöntemlerin ve problem çözme etkinliklerinin öğrencilerin problem çözme becerisini geliştirmede yetersiz kaldığı düşüncesi “Öğrencilerin gerçek hayatta kullanabilecekleri matematiksel bilgi ve matematiksel düşünme becerisine sahip olabilmeleri için nasıl bir matematik eğitimi yapılmalıdır?” sorusunu beraberinde getirmiştir (Kertil, 2008).

Gerçek hayat problemleri karmaşık ve kendine has olduğu için öğrenciler okullarda belirli bir bağlamda öğrendikleri problemi farklı bir bağlamda çözmekte zorluk çekmektedirler. Öğrenciler sınıf ortamında öğrendikleri bilgileri gerçek hayatta uygulayamamaktadır. Örneğin, Brezilya’da sokaklarda satış yapan çocukların satış esnasında gereken matematiksel hesaplamaları hızlı ve doğru bir şekilde yaptıkları halde, aynı öğrencilerin aynı tür problemleri sınıf ortamında çözemedikleri gözlemlenmiştir (Carraher, 1986; Carraher, Carraher ve Schlieman, 1985). Bu bağlamda matematiksel modelleme etkinlikleri öğrencilere gerçek hayat problemlerini farklı bağlamlarda sunması bakımından önem arz etmektedir. Gerçek yaşamımızda karşılaştığımız karmaşık problemlere matematikçi gözüyle bakmak, bu problemleri çözmemizde önemli yere sahiptir. Bireyler bu matematikçi bakış açısını matematiksel modelleme ile kazanabilirler.

Matematik eğitiminde matematiksel modelleme ile ilgili araştırmalar incelendiğinde matematiksel modelleme etkinliklerinin, günümüz dünyasının gereksinimine karşılık verebilecek yapıda olduğu anlaşılmaktadır. Matematik eğitiminde matematiksel modelleme yaklaşımı çok önemli bir konu olmasına ve dünyada son yıllarda üzerinde sıklıkla çalışılmasına karşın ülkemizde bu konuda yapılmış çalışmaların sınırlı oluşunun araştırmaya ayrı bir önem kazandıracağı düşünülmektedir. Ülkemizde matematiksel modelleme üzerine yapılan çalışmalarda (Çiltaş 2011; Taşova 2010; Kertil, 2008; Keskin, 2008) yükseköğretim ve ortaokul 2. kademe düzeyinde yoğunlaşıldığı görülmektedir. İlköğretim düzeyinde yapılan çalışmaların yetersiz kaldığı görülmektedir. İlköğretim düzeyindeki çalışmalarda ise literatürde bulunan veya uyarlanan modelleme etkinlikleri kullanılmış, hep aynı modelleme etkinlikleri kullanıldığı için tekrara düşülmüştür. Bu

(26)

7

yüzden çalışma, ilkokul ve ortaokul düzeyinde yapılan çalışmalarda kullanılan modelleme etkinliklerinin çeşitlendirilmesi bakımından önem arz etmektedir. Geçmiş yıllardaki PISA uygulamalarındaki düşük başarı düzeyinin altında yatan nedenleri çeşitli faktörler yönünden araştıran çalışmalar olmasına rağmen (İş, 2003; Berberoğlu ve Kalender, 2005; Berberoğlu, 2007; Özer, 2009), PISA matematik başarı düzeyini artırmaya yönelik deneysel çalışmalara pek rastlanılmamaktadır. Bu yüzden çalışma aynı zamanda, PISA matematik başarı düzeyini artırmaya yönelik deneysel bir çalışma olması bakımından da önem arz etmektedir.

1.6 Sınırlılıklar Araştırma,

1. Örneklem olarak İç Anadolu Bölgesi'ndeki bir devlet ortaokulunda öğrenim gören 44 yedinci sınıf öğrencisi ile sınırlıdır.

2. Zaman açısından 2015-2016 eğitim-öğretim yılı ile sınırlıdır.

3. Konu olarak Sayılar ve İşlemler, Cebirsel İfadeler ve Denklemler konuları ile sınırlıdır.

4. Veri toplama araçları açısından, “PISA Matematik Başarı Testi” , “Modelleme Etkinlikleri” ve “Görüşmeler” ile sınırlıdır.

1.7 Varsayımlar

Araştırma için deney ve kontrol grubundaki öğrencilere yapılan uygulamaların ardından öğrenciler arasında araştırma konusu ile ilgili bir etkileşimin olmadığı, deney ve kontrol gruplarının kontrol altına alınamayan değişkenlerden eşit şekilde etkilendiği, öğrencilerin mülakat sorularına samimi cevaplar verdiği varsayılmıştır.

1.8 Tanımlar

Matematiksel Modelleme; Gerçek hayattan veya gerçek hayat durumlarından alınan bir problemin matematiksel yöntemler kullanarak analiz edilmesi sürecidir. Gerçek hayat durumlarından alınan problemler matematize edilerek bir matematiksel modele ulaşılır ve model üzerinde çalışılarak çözüm bulunur. Daha sonra çözüm yorumlanır ve doğruluğu

(27)

8

gösterilir. Öğrenciler gerçek hayat veya problem durumlarının modellerinden matematiksel modellere ulaşırlar.

Matematiksel Modelleme Etkinlikleri; Modelleme etkinliklerinde öğrenciler gerçek yaşamdan alınan problem durumlarını bir araştırmacı gibi çözümleyip benzer durumlar için de uygulanabilecek bir bağıntıya ulaşmaya çalışırlar. Matematiksel modelleme etkinlikleriyle, öğrenciler sınıf ortamında küçük gruplar halinde matematiksel modelleme yaparlar. Arkadaşları ve öğretmenleriyle etkileşim içinde olup verimli tartışmalarla aktif olarak katılım sağlarlar. Verilen gerçek yaşam durumunu grup içerisinde etkileşimli olarak tartışırlar ve ürettikleri matematiksel düşünceleri birbirlerine iletirler.

PISA (Programme for International Student Assessment), Açılımı Uluslararası Öğrenci Değerlendirme Programı olan ve Ekonomik İşbirliği ve Kalkınma Örgütü (OECD) tarafından üçer yıllık dönemler hâlinde öğrencilerin kazanmış oldukları bilgi ve becerileri değerlendiren bir araştırma projesidir.

(28)

9

BÖLÜM 2

KURAMSAL ÇERÇEVE

2.1. Model ve Modelleme

Alan yazın incelendiğinde model ve modelleme kavramlarının farklı şekillerde tanımlandığı görülmektedir. Model ve modelleme arasındaki ilişkiyi süreç ve ürün arasındaki ilişkiye benzetebiliriz. Model, sürecin sonundaki ürünü ifade ederken, modelleme bir durumun fiziksel, sembolik ya da soyut modelini oluşturma sürecini ifade etmektedir (Sriraman, 2006). Başka bir ifadeyle model, modelleme sonucunda ortaya çıkan bir ürünü ifade ederken modelleme bir süreci ifade etmektedir (Sağırlı-Özturan, 2010). Lesh ve Doerr’a (2003a) göre ise model, karmaşık sistemleri ve yapıları yorumlamak, anlamak ve düzenlemek için zihinde var olan kavramsal yapılar ile bunların dış gösterimleridir. İnsanlar gerçek hayat durumlarını anlayıp yorumlamak için modelleri kullanırlar. Doğası ve hangi durumlarda kullanıldığı ile ilgili olarak şunlar belirtilmiştir:

1) Havacılık mühendisliğinde, bilim adamları gerçek uçakları (ya da doğada kendiliğinden oluşamayan diğer karmaşık sistemleri) geliştirmeye ve tasarımlamaya kılavuzluk etmek için model uçaklar oluşturabilirler. Bu gibi durumlarda modellere ihtiyaç duyulabilir çünkü gerçek sistemleri kullanmayı denemek hem çok tehlikeli hem de çok pahalı olabilir.

2) Tarım alanında veya yer ve atmosfer bilimlerinde bilim adamları doğal oluşan karmaşık fenomenleri araştırmak için bilgisayar tabanlı simülasyonlar (modeller) oluşturabilirler. Bu durumda modellere gerçek sistemleri basitleştirmek için gereksinim duyulabilir. Ya da bu sistemlerde ileride ortaya çıkabilecek zorlukları

(29)

10

araştırmak (tahmin etmek, önlemek, manipule etmek ya da kontrol etmek) için kullanılabilirler.

3) Ekonomi veya iş yönetimi gibi alanlarda istatistiksel modeller, direk olarak ulaşılamayan karmaşık düzen ve numunelerin tanımlarını basitleştirmeyi sağlayabilecek grafik ve denklemlerle somutlaştırabilirler.

4) Psikologlar, problem çözme durumlarında insan davranışlarını taklit etmek için bilgisayar programları geliştirebilirler.

5) Günlük deneyimlere dayanarak öğrenciler elektrik, ışık gölgeleri veya diğer benzer durumları içeren olguları açıklamak için çeşitli analojiler, metaforlar, diyagramlar, modeller ve hikayeler kullanabilirler. Örneğin; elektrik devreleri borulardan akan suya benzetilerek tanımlanabilir. (Lesh ve Doerr’den Aktaran Deniz, 2014)

Model, karmaşık bir nesne veya sürecin basitleştirilmiş gösterimi veya sunumudur ve bir bir nesnenin nasıl oluştuğunu veya sürecin nasıl meydana geldiğini anlamamızı sağlamaktadır (Kinnear and Martin, 1992). Modelleme ise birçok etkinliği içeren karmaşık bir süreçtir (Justi & Gilbert, 2002).

Van Driel ve Verloop (1999), bilimsel modellerin ortak özelliklerini şu şekilde belirtmiştir: 1) Bir model, her zaman modelin temsil ettiği hedef veya hedeflerle ilişkilidir. Hedef

bir sistem, bir nesne, bir olgu veya bir süreç olabilir.

2) Bir model, doğrudan gözlenemeyen veya ölçülemeyen bir hedef hakkında bilgi elde etmek için kullanılan bir araştırma aracıdır. Bu nedenle ölçeklendirme modelleri ki bu modeller bir nesnenin başka bir ölçekteki kopyasıdır (ev, köprü maketleri gibi), bilimsel model olarak kabul edilmez.

3) Bir model temsil ettiği hedef ile doğrudan etkileşmez. Bu nedenle bir fotoğraf veya spektrum bir model olarak nitelendirilmez.

4) Bir model hedefe uygun benzetmelere dayanır ve bu nedenle araştırmacıların modellenen hedef kavramla ilgili çalışmaları süresince test edilebilir hipotezler üretebilmelerine imkân verir. Bu hipotezlerin test edilmesi hedef hakkında yeni bilgiler ortaya çıkarır.

5) Bir model her zaman hedeften belirgin ayrıntılarla farklılık gösterir. Genel olarak bir model olabildiğince basite indirgenir. Yapılacak araştırmanın özel amaçlarına bağlı olarak hedefin bazı ayrıntıları kasıtlı olarak model dışında bırakılabilir.

(30)

11

6) Bir model oluşturulurken, hedef ile model arasındaki benzerlik ve farklılıklar, araştırmacılara modelin temsil ettikleriyle ilgili tahminler yapabilme imkânı sağlayabilmelidir. Oluşturulacak modelin bu boyutu araştırma soruları ile yönlendirilir.

7) Bir model karşılıklı olarak birbirini etkileyen süreçler sonucunda geliştirilir ve hedefle ilgili yeni çalışmalar ortaya çıktıkça modellerde revizyona gidilebilir (Van Driel ve Verloop’dan Aktaran Güneş, Gülçiçek ve Bağcı, 2004).

Modellerin sınıflandırılmasına yönelik çalışmalarda modellemeler, bilimsel olan/bilimsel olmayan modeller, görünüş bakımından modeller (somut-soyut modeller), işlevleri bakımından modeller (tanımlayıcı-açıklayıcı-betimleyici modeller) olarak sınıflandırılmıştır. Derslerde öğrenci ve öğretmenlerin gözlemlenmesiyle ve onlarla yapılan mülakatlarla ayrıntılı bir sınıflandırma yapan Harrison ve Treagust (2000) elde ettikleri verileri literatür araştırmaları ile desteklemiş ve modelleri aşağıdaki şekilde sınıflandırmışlardır.

1) Ölçeklendirme modelleri: Hayvanların, bitkilerin, arabaların ve binaların ölçeklendirilmiş modelleri; renkleri, dış şekilleri ve yapısal özellikleri tanımlamakta kullanılır. Ölçeklendirme modelleri ayrıntılı bir şekilde dış görünüşü yansıtmasına rağmen nadiren iç yapıyı, işlevleri ve kullanımı yansıtır. Ölçeklendirme modelleri genellikle oyuncaktır veya oyuncak gibidir. Bu nedenle, model ile hedef arasındaki paylaşılmayan farklılıkların saklı kalmasına yol açabilir. 2) Pedagojik analojik modeller: Bunların analojik olarak isimlendirilmesinin nedeni,

modelin bilgiyi hedefle paylaşmasından ileri gelir. Pedagojik olarak isimlendirilmesinin nedeni ise, atom ve molekül gibi gözlenemeyen varlıkları öğrenciler için ulaşılabilir yapmak üzere öğretmenler tarafından açıklayıcı olarak geliştirilmelerinden kaynaklanmaktadır. Analojinin yapısına bir veya birden fazla özellik hükmeder, örnek olarak molekül modellerindeki top ve çubuk temsili verilebilir. Çünkü analojik modeller hedefle analoji arasındaki uyumu kesin özellikler için tek tek yansıtırlar. Analojik özellikler kavramsal niteliklere dikkat çekmek için genellikle aşırı basitleştirilmiş veya genişletilmiştir.

3) Simgesel veya sembolik modeller: Kimyasal formüller veya eşitlikler sembolik modellerle anlamlı hale getirilmiştir. Formüller ve eşitlikler bu şekilde kimya diline yerleşmiştir. Örnek olarak CO2 (karbon dioksit) gösterimi verilebilir.

(31)

12

4) Matematiksel modeller: Fiziksel özellikler ve süreçler, kavramsal ilişkileri ortaya çıkaran matematiksel eşitliklerle ve grafiklerle temsil edilebilir. Örnek olarak, Boyle-Mariotte Kanunu, üstel eğriler veya Newton’un ikinci hareket kanununun temsili olan 𝐹⃗ = 𝑚. 𝑎⃗ eşitliği verilebilir.

5) Teorik modeller: Elektromanyetik alan çizgileri ve fotonlar teorik modellerdir, çünkü bu modeller iyi yapılandırılmış ve insanlar tarafından oluşturulan teorik temellerle tanımlanmıştır. Kinetik teorinin gaz basıncını açıklaması, ısı ve basınç bu kategoriye girer.

6) Haritalar, diyagramlar ve tablolar: Bu modeller öğrenciler tarafından kolaylıkla canlandırılabilen yolları, örnekleri ve ilişkileri temsil eder. Bu modellere örnek olarak periyodik tablo, soy ağaçları, hava durumunu gösteren haritalar, devre şemaları, kan dolaşımı sistemi ve beslenme zinciri gösterimleri verilebilir.

7) Kavram-süreç modelleri: Birçok fen kavramı nesneden ziyade süreçten ibarettir. Örnek olarak kimyasal denge veya asit-baz reaksiyon modelleri verilebilir.

8) Simülasyonlar: Simülasyonlar global ısınma, uçuşlar, nükleer reaksiyonlar, trafik kazaları gibi karmaşık süreçleri temsil etmede kullanılır.

9) Zihinsel modeller: Zihinsel modeller özel bir çeşit zihinsel temsildir ve bireyler tarafından bilişsel işlemler sonucunda üretilir. Öğrenciler tarafından üretilen ve kullanılan zihinsel modeller tamamlanmamıştır ve kararlı değildir yani değişebilir. (Harrison ve Treagust’dan Aktaran Güneş vd., 2004)

Van de Walle, Karp ve Bay-Williams’ın (2012, s.28-29) 6 farklı kavram için önerdiği 6 farklı model ve modellerin çeşitliğini göstermektedir. Bunlar;

1) Sayma ile ilgili modeller: Sayma pulları, çubuklar, abaküsler gibi sayılabilir nesneler “sayı” kavramını ve “bir fazlası” gibi sayı kavramına bağlı fikirleri modellemek için kullanılabilir.

2) Uzunluk kavramı ile ilgili modeller: “Uzunluk” farklı nesnelerin uzunluk niteliklerinin kıyaslanmasını içerir. Çubuklar uzunluk ölçümünde kullanılabilir. 3) Ondalık kavramı: Onluk sayı sistemine dair kavramlar (birlik, onluk, yüzlük)

çoğunlukla şerit ve karelerle modellenir. Çubuk ve çubuk desteleri de ayrıca bu amaçla kullanılmaktadır.

(32)

13

5) Dikdörtgen kavramı: “Dikdörtgenler” noktalı kağıt üzerinde modellenebilir. Dikdörtgenler uzunluk ve uzamsal ilişkileri içerir.

6) Negatif/pozitif kavramı: “Pozitif” ve “negaif” tam sayılar, sayı doğrusunda yönlerle, farklı yön ve uzunlukta oklarla ve termometredeki sıcaklık arasındaki ilişki ile modellenebilir.

Modelleme ise, gerçek dünyada karşılaşılan bir durumun özünde var olan bir ilişkinin belirgin hâle getirilerek bir temsilinin bulunmasıdır. Bu temsil, söz, resim, diyagram, çizim, tablo biçiminde olabileceği gibi grafik ve denklem biçiminde de olabilir (Kaput’dan Aktaran Durmuş, 2011). Günümüzde modelleme sadece matematikte değil tıp, mühendislik, teknoloji ve diğer birçok alanda da kullanılmakta, modellemenin farklı alanlarda da kullanılması bu kavramın önemini açıkça ortaya koymaktadır. Örneğin e=m.c2 denklemi ışık hızı, kütle ve enerji arasındaki ilişkiyi modeller. Ya da deprem ve gün uzunlukları gibi durumları açıklamak için trigonometrik fonksiyonlar da matematiksel model olarak düşünülebilir. Matematiksel bir düşüncenin teknoloji ortamında oluşturulmuş animasyonu, geometrik kavramların temsili için kullanılan katı cisimler (küp, üçgen prizma, koni, vs.), değişkenler arasındaki ilişkileri izah etmek için kullanılan grafikler, güncel yaşam koşullarını çağrıştıran yapılar ve analojiler gibi sözel betimlemeler ile bunların anlaşılmasında sergilenen düşünce ve yaklaşımlar da birer model olarak kabul edilebilir (Bayazit, Aksoy ve Kırnap, 2011). Bunlara ek olarak havacılık mühendisliğinde, bilim adamları tarafından gerçek uçakları geliştirmeye ve tasarımlamaya yol göstermesi için geliştirilen model uçaklar, tarım alanında veya yer ve atmosfer biliminde bilim adamları doğal olarak ortaya çıkan karmaşık fenomenleri araştırmak için geliştirilen bilgisayar tabanlı simülasyonlar (modeller), ekonomi veya iş yönetimi gibi alanlarda istatistiksel modeller, psikologların verilen bir problem durumları koleksiyonunda olası insan davranışlarını modelleyen bilgisayar programları gerçek hayatta kullanılan modellere örnek olarak gösterilebilir.

2.2. Matematiksel Modelleme

Matematiksel modelleme genel anlamda gerçek hayattan veya gerçek hayat durumlarından alınan bir problemin matematiksel yöntemler kullanarak analiz edilmesi sürecidir. Yani başka bir deyişle gerçek hayat durumlarının matematiğin sembolik diline aktarılarak ifade

(33)

14

edilmesi sürecidir (Gravemeijer, 2002). Bilim adamları gerçekleri matematiksel tekniklerle ifade ederler. Matematiksel modelleme de gerçeği matematiksel tekniklerle analiz etmeye ve yorumlamaya yardım eder. Matematiksel teknikler gerçek hayat durumlarına ışık tutmak için kullanılırlar.

Lesh ve Doerr’e (2003a) göre matematiksel modeller gerçek yaşam durumunun yorumlanmasına, çözümlenmesine olanak sağlayan zihindeki yapıların matematiksel forma dönüştürülmüş dış temsilleridir. Bu tanıma göre zihinsel modelleme sürecini gerektiren bir süreç de denilebilir. Keskin (2008)’e göre ise matematiksel modelleme günlük hayat problemlerinin üstesinden gelme sürecidir. Bu süreçte öğrenciler verilenleri kullanarak bir sonuca ulaşırken, bu çözümü gerçek hayat durumuyla karşılaştırıp, çözümün yetersizliğine göre çözümü geliştirir veya farklı bir çözüm geliştirirler.

Matematiksel modelleme, bir gerçek yaşam durumunun fiziksel, sembolik ya da soyut modelini oluşturma sürecidir (Sriraman, 2006). İlköğretimde matematiksel modelleme somut materyaller olarak algılanmakta, bazı matematiksel kavramlar için birileri tarafından oluşturulan hazır ve statik modellerin matematiksel modeller olduğu düşünülmektedir. Oysaki matematiksel modelleme daha genel bir kavram olmakla birlikte birileri tarafından oluşturulan bu soyut materyallerin öğrencilerin kendi zihinsel yapılandırma sürecinden geçmediği noktasında eleştirilmektedir (Gravemeijer’den Aktaran Erbaş vd., 2014).

Lingefjard (2006) ise matematiksel modellemenin orijinal durum göz önüne alınarak yorımlanabilen bir sonuca ulaşmak için, genellikle gerçek yaşamdan bir durum alınarak, duruma uygun bir kaç değişken ve basit işlemler kullanmaktan çok daha fazlasını içeren bir süreç olduğunu vurgulamıştır.

Matematiksel modelleme gerçek hayat problemlerinin matematik dünyasına taşınarak matematik dilinde ifade edilmesini içeren bir süreçtir (Bukova-Güzel ve Uğurel, 2010). Bu bağlamda gerçek hayat durumunu etkili bir şekilde matematize etmek için öğrencilerin işlemsel ve aritmetik bilgilerin ötesinde uzamsal düşünme, yorumlama, tahmin etme gibi matematiksel donanımlara sahip olmaları gerekmektedir (Lehrer ve Schauble, 2003). Matematiksel modeller tanımladıkları sistemin fiziksel, biyolojik, esteik özelliklerinden ziyade yapısal özellikleri üzerinde odaklanması bakımından model ve modelleme konusunda sunulmuş olan diğer model kategorilerden oldukça farklıdır (Sağırlı-Özturan, 2010).

(34)

15

Berry and Houstan (1995)’e göre dört çeşit matematiksel modellemeden söz edebiliriz: 1) Deneysel Modelleme: Uygun deneylerle elde edilen veriler veya hazır verilerle

grafik ya da bir eşitlik elde edilerek kolayca yapılabilen modellemeye deneysel modelleme denir. Fakat bu problem çözme sürecinde grafiklerden elde edilen yorumlamaların geçerliliğinde ciddi sınırlılıklar söz konusudur.

2) Teorik Modelleme: Matematiksel modellemeyi formüle ederken problemin önemli özelliklerindeki değişimleri içermesi için farklı problem çözme süreçleri gereklidir. Veriden daha çok teoriye dayanan bu problem çözme sürecine ise teorik modelleme denir.

3) Simülasyon Modelleme (Simulating Modelling): Genellikle matematiksel modellerin formüle edilmesinde cebir kullanılır. Bazı problem çözme durumlarında bu yolla analitik olarak modelleme yapmak ya da verileri elde etmek kolay değildir. Bu gibi durumlarda uygun verilerle, genellikle bilgisayar kullanılarak istatistikleri ve olasılıkları simule etmeye simulasyon modelleme denir.

4) Boyutsal Analiz Modelleme (Dimensiol Analysis Modelling): ‘Boyut’olarak adlandırılan fiziğin temel özelliği kullanılarak ve bu boyutlarla bir method araştırarak etkili değişken grubu bulunmasını içeren modellemeye boyutsal analiz modelleme denir.

Matematiksel model ile matematiksel modelleme de çok sık karıştırılan kavramlardır. Matematiksel modeller, bireylerin karşılaştıkları problemleri matematiksel olarak yorumlayabilmeleri için gerekli olan kavramsal araçlardır (Kertil, 2008). Örneğin Matematiksel bir düşüncenin teknoloji ortamında oluşturulmuş animasyonu, geometrik kavramların temsili için kullanılan katı cisimler (küp, üçgen prizma, koni, vs.), değişkenler arasındaki ilişkileri izah etmek için kullanılan grafikler, değişken, sabit, fonksiyon, eşitlik, eşitsizlik ve formül gibi matematiksel kavram parçaları, nüfus artışı, arz- talep, düşen bir nesnenin hızı, bir bebeğin yaşam süresinin tahmini gibi olayların fonksiyonlar veya eşitlikler şeklindeki matematiksel ifadeleri matematiksel modeller olarak gösterebiliriz. Matematiksel modelleme ise gerçek hayat problemlerinin soyutlandığı, matematikleştirildiği, çözüldüğü ve değerlendirildiği periyodik bir döngü olarak tanımlanır (Deniz, 2014). Gerçek hayat durumlarından alınan problemler matematize edilerek bir matematiksel modele ulaşılır ve model üzerinde çalışılarak çözüm bulunur. Daha sonra

(35)

16

çözüm yorumlanır ve doğruluğu gösterilir. Öğrenciler gerçek hayat veya problem durumlarının modellerinden matematiksel modellere ulaşırlar.

Modeller matematik eğitiminde çok eski zamandan beri kullanılan araçlar olmasına rağmen teknolojinin gelişmesiyle birlikte model kullanımı ve modelleme etkinlikleri çok daha erişilebilir bir hale gelmiştir. Böylece sosyo-ekonomik ve kültürel olarak gelişmiş birçok ülke öğretim programlarında müfredatlara model kullanımlarına ve matematiksel modelleme etkinliklerine yer vermeye başlamışlardır. Bu ülkelerin matematiksel modelleme ve matematiksel modelleme etkinliklerine bu denli önem vermelerinin nedeni olarak modellemenin, matematiksel kavramların öğrenilmesine katkı sağlaması, bilgileri zihinde tutmayı kolaylaştırması, gerçek yaşam ile matematik arasındaki ilişkiyi kurmayı sağlaması ve öğrencilerde matematiğe karşı olumlu tutum geliştirmelerine yardımcı olması olarak ifade edebiliriz.

Dünyada olduğu gibi ülkemizde de değişim ve gelişim hızlı bir şekilde devam etmekte ve günlük hayatta matematiği kullanabilmenin önemi Türkiye’deki matematik öğretim programlarına da yansımaktadır. Geçmiş yıllardaki ilköğretim ve ortaokul müfredatları incelendiğinde geleneksel sözel problemlere yer verilip, matematiksel modelleme yapma becerisini kazandırmaya yönelik gerçek hayat durumlarından oluşan problemlere ise çok az yer verilse de; Talim Terbiye Kurulu’nun 2009 yılında yayımladığı Matematik Dersi Öğretim Programı’nda ise günlük yaşamda matematiği kullanabilme ve anlayabilme gereksinimi önem kazanmakta ve sürekli arttığı vurgulanmakta, değişimlerle birlikte matematiğin ve matematik eğitiminin belirlenen ihtiyaçlar doğrultusunda yeniden tanımlanması ve gözden geçirilmesi gerektiği ifade edilmektedir (MEB, 2009). Nitekim 2013 yılında yayımlanan Matematik Dersi Öğretim Programı’nda, öğrencilerin matematiksel modelleme yaparak problem çözme, iletişim kurma, akıl yürütme gibi becerilerinin geliştirilmesine yönelik ortamlar hazırlanması gerektiği vurgulanmıştır (MEB, 2013). Bu programlarda her ne kadar okullarda matematiksel modellemeye daha fazla yer verilmesi gerektiği vurgulansa da alan yazında modellemenin anlamı ve kullanımına yönelik ortak bir anlayıştan ise söz etmek pek mümkün değildir (Aztekin ve Şener, 2015).

Ulusal Matematik Öğretmenleri Konseyi’nin yayınladığı Okul Matematiğinin Prensipleri ve Standartları’nda (NCTM, 2000), öğrencilerin modellemelerin ve matematiğin günlük yaşam olaylarını tahmin etmedeki gücünü anlamasını sağlayacak tecrübeler içermesi

(36)

17

gerektiği vurgulanmakta, matematiğin en önemli kullanımlarından birinin de olguların matematiksel modellemesinin yapılabilmesi olduğu belirtilmektedir. Ayrıca, ilk sınıflarda öğrencilerin nesneleri, resimleri ve simgeleri toplama ve çıkarmayı modellemek için kullanabilirken, 3-5. Sınıflarda öğrencilerin modelleri kestirimde bulunmak, sonuç çıkarmak ya da sayısal durumları daha iyi anlamak için kullanabilecekleri, lise öğrencilerinin ise fonksiyonlar bilgisine sahip olduklarından birçok model geliştirebilecekleri vurgulanmıştır.

Son yıllarda yurt dışında matematiksel modellemeye odaklanan çok sayıda araştırma yapılmıştır (English ve Watters, 2004; Kaiser, 2006; Mousolides, Sriroman ve Christou, 2007; Blum ve Borromeo Ferri, 2009). Yapılan çalışmalar modelleme etkinlikleriyle çalışan öğrencilerin düşünceyi ortaya çıkaran çok bileşenli karmaşık problemlerin üstesinden başarı ile gelebildiklerini ve var olan anlayışlarını geliştirdiklerini ortaya koymuştur (English, 2006). Çalışmaların yanı sıra matematiksel modelleme ve uygulamaları alanında İngiltere, ABD, Almanya, Danimarka, Hollanda, İrlanda, Avusturya, Portekiz, Çin ve Avustralya da dergiler ve sempozyumlar düzenlenmektedir. Bu dergilere örnekler verilecek olunursa; Journal of Mathematical Modeling and Application, Journal of Mathematical Modelling and Algorithms, Teaching Mathematics and its Applications, Applied Mathematical Modelling, Mathematical and Computer Modelling, Mathematical Modelling and Applied Computing, International Journal of Mathematical Modelling, Simulation and Applications (Çiltaş, 2011). Türkiye’deki matematik eğitimi araştırmalarında da matematiksel modellemeyle ilgili yapılan çalışmaların artarak devam ettiği görülmektedir. Öğrencilerin matematiği daha anlamlı ve gerçek hayatla ilişkili öğrenmelerine yardımcı olacağı düşüncesi ve mevcut problem türlerinin bu hedefi gerçekleştirmede yetersiz kalması, araştırmacıların ilgilerinin matematiksel modellemeye yönelmesinin temel sebeplerindendir. Matematiksel modelleme öğrencilerin matematiği sadece okuldaki bir ders olarak değil, yaşamlarının her döneminde kullanabilecekleri bilgi ve becerileri kazandıran bir alan olarak görmelerini sağlar.

Matematiksel modelleme uygulamaları karmaşık ve zor bir süreç gibi görünse de gerçek hayat problemleri matematiksel modeller yardımıyla sunulduğunda problemin karmaşıklığı giderilmekte ve anlamlandırma kolaylaşmaktadır. Böylece matematiksel modeller öğrencilerin matematiksel bilgi ve becerilerini gerçek hayat problemlerine uygulayabilme

(37)

18

yeteneğini kazanmalarını hızlandırmaktadır (MEB’den Aktaran Biber ve Yapıcıoğlu-Ulaş, 2013).

Niss (1989) matematiksel modelleme ve uygulamalarının neden matematik dersi öğretim programının bir parçası olması gerektiğini, aşağıda sunulan beş özellik açısından açıklamıştır.

1) Öğreniciler arasında genel yaratıcılık ve problem çözme davranışlarını, aktivitelerini ve becerilerini geliştirmek.

2) Matematik dışındaki alanlarda da matematiğin kullanımı sayesinde öğrencilerde eleştirel bir potansiyel oluşturmak, geliştirmek ve nitelendirmek.

3) Öğrencileri şu anda, gelecekte veya gelecekteki meslek hayatlarındaki konuların öğretiminde modelleme ve uygulamalarını yapabilecek pratiğe sahip bireyler ve vatandaşlar olarak hazırlamak.

4) Dengeli ve görsel bir matematik resmi oluşturmak ve onun özelliklerini ve dünyadaki yerini tanıtmak.

5) Öğrencilerin matematiksel kavramları, bilgileri, metotları, sonuçları ve konuları anlamasında yardımcı olmak.

2.3. Modelleme Süreci

Matematiksel modelleme süreci uygun değişkenleri seçme, değişkenler arasındaki bağıntıyı ortaya çıkarma, değişken ve bağlantılara bağlı olarak matematiksel bir model ortaya koyma ve modeli ve uygulamalarını test etme olarak tanımlanmaktadır (Kapur’dan Aktaran Hıdıroğlu ve Bukova-Güzel, 2013). Matematiksel modelleme sürecinde gerçek yaşamdan, pür matematiğin dışından bir konu alınır ve bu konu matematiksel olarak ifade edilir; böylece matematiksel çözümü yapılır. Bu anlamda modelleme, gerçek yaşamdan alınan durumun matematikselleştirildiği bir problem çözme sürecidir (Blum ve Niss, 1991).

Berry ve Houston’a (1995) göre, matematiksel modelleme gerçek yaşam problemlerini çözmek için gerekli adımları kullanma sürecidir ve bu süreç 3 aşamada gerçekleşir. Birinci aşamada, grafik, denklemler, eşitsizlikler veya dikkatlice yaptığımız varsayımlar gibi matematiksel yapılarla matematiksel model gerçek yaşamı temsil ederek formüle edilir. İkinci aşamada ortaya çıkabilecek tüm denklemler çözülür. Üçüncü aşamada ise modelin

(38)

19

gerçek yaşama uyumluluğunu test etmek için uygun veriler kullanılır ve matematiksel analiz sonuçları yorumlarınır. Bu süreçte yaşam durumunun formüle edilmesi için matematiğe geçiş, elde edilen matematiksel sonuçların yorumlanması için de gerçek yaşama geçiş yapılmalıdır. Diğer bir ifadeyle, gerçek yaşam problemini matematiksel sembollerle formüle edip, matematiksel modeli ortaya çıkarılırken, çözülen problemden elde edilen matematiksel sonuçlar gerçek yaşam durumu kapsamında yorumlanır.

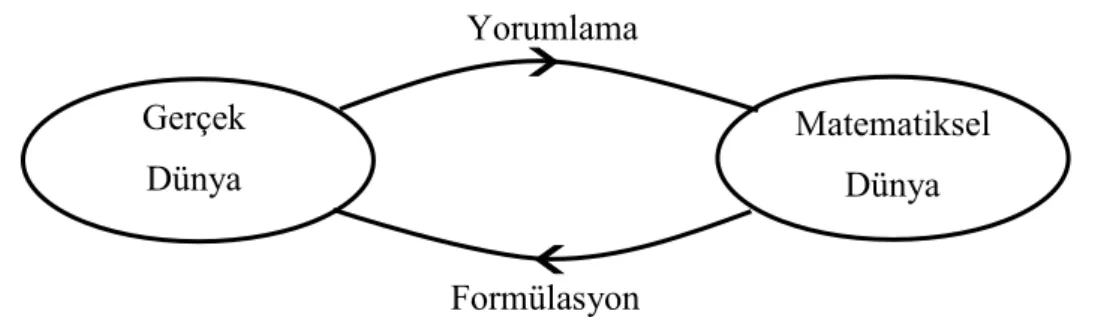
Şekil 1. Matematiksel modellemenin basit bir görünümü. “Mathematical modeling”, Berry,

J., Houston, K. (1995), London: Edward Arnold kaynağından alınmıştır.

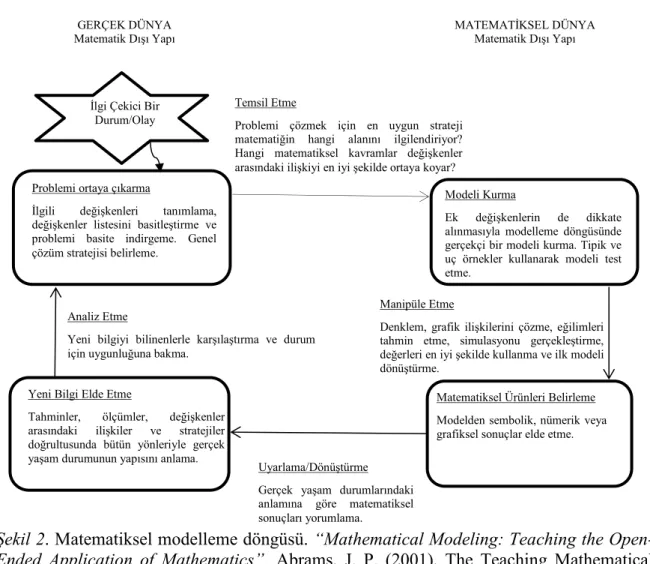
Matematiksel modellemenin aşamalı döngüsel bir süreç olmasıyla birlikte verilen problem durumuna bulunan çözüm yolundan her zaman daha verimli bir çözüm yolu vardır. Eğer problem durumuna bulunan çözüm tatmin edici değil olarak yorumlanırsa yeni bir matematiksel modelleme döngüsü başlar. Bazı durumlarda ise tanımlanan modelin gerçeğe uygun olduğu düşünülse de modelden elde edilen matematiksel sonuçların gerçek yaşam durumlarına dönüşmediği görülebilir; böyle durumlarda Modeli Doğrulama basamağından tekrar Matematiksel Modeli Tanımlamak basamağına geçerek tekrar yeni bir model geliştirilmesi gerekir (Mason’dan Aktaran Hıdıroğlu ve Bukova-Güzel, 2013). Abrams (2001), matematiksel modellemenin matematiksel düşünmenin ortaya çıkması ve uygulanması için güçlü bir süreci yarattığını ifade etmektedir. Öğrencilerin söz konusu problemi çözmek için ihtiyaç duydukları etkenlerin başında ise, probleme dair sahip oldukları deneyimler gelmektedir (Bkz. Şekil 2).

Gerçek Dünya Matematiksel Dünya Yorumlama Formülasyon

(39)

20

Şekil 2. Matematiksel modelleme döngüsü. “Mathematical Modeling: Teaching the Open-Ended Application of Mathematics”, Abrams, J. P. (2001), The Teaching Mathematical

Modeling and the of Representation, http://www.meaningfulmath.org/modelingcycle.pdf sayfasından erişilmiştir.

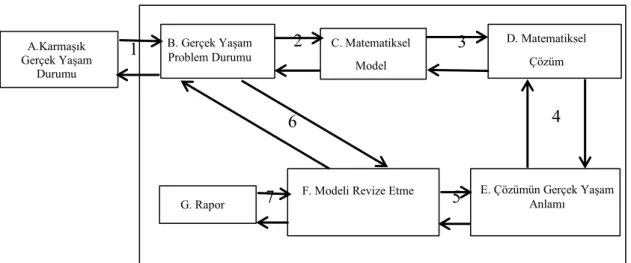
Stillman, Galbraith, Brown ve Edward (2007) tarafından gerçekleştirilen modelleme uygulamalarına dayanarak geliştirilen modelleme sürecindeki aşamalar Şekil 3’te verilmiştir.

GERÇEK DÜNYA

Matematik Dışı Yapı MATEMATİKSEL DÜNYA Matematik Dışı Yapı

İlgi Çekici Bir Durum/Olay

Problemi ortaya çıkarma

İlgili değişkenleri tanımlama, değişkenler listesini basitleştirme ve problemi basite indirgeme. Genel çözüm stratejisi belirleme.

Temsil Etme

Problemi çözmek için en uygun strateji matematiğin hangi alanını ilgilendiriyor? Hangi matematiksel kavramlar değişkenler arasındaki ilişkiyi en iyi şekilde ortaya koyar?

Modeli Kurma

Ek değişkenlerin de dikkate alınmasıyla modelleme döngüsünde gerçekçi bir modeli kurma. Tipik ve uç örnekler kullanarak modeli test etme.

Analiz Etme

Yeni bilgiyi bilinenlerle karşılaştırma ve durum için uygunluğuna bakma.

Yeni Bilgi Elde Etme

Tahminler, ölçümler, değişkenler arasındaki ilişkiler ve stratejiler doğrultusunda bütün yönleriyle gerçek yaşam durumunun yapısını anlama.

Uyarlama/Dönüştürme Gerçek yaşam durumlarındaki anlamına göre matematiksel sonuçları yorumlama.

Manipüle Etme

Denklem, grafik ilişkilerini çözme, eğilimleri tahmin etme, simulasyonu gerçekleştirme, değerleri en iyi şekilde kullanma ve ilk modeli dönüştürme.

Matematiksel Ürünleri Belirleme Modelden sembolik, nümerik veya grafiksel sonuçlar elde etme.

(40)

21

Şekil 3. Süreç modeli. “A Framework for Success in Implementing Mathematical Modelling in the Secondary Classroom”, Stillman, G., Galbraith, P., Brown, J. ve

Edwards, I., 2007, Mathematics: Essential Research, Essential Practice kaynağından erişilmiştir.

1. Anlama, yapılandırma, basitleştirme, içeriği yorumlama. 2. Varsayımda bulunma, formüle etme, matematikselleştirme. 3. Matematiksel çalışma yapma.

4. Matematiksel çıktıları yorumlama. 5. Birleştirme, eleştirme, doğrulama.

6. İletişim, çözümü savunma (eğer model tatmin edici olarak kabul edildiyse).

7. Modelleme sürecinin tekrar edilmesi (eğer model tatmin edici olarak kabul edilmediyse)

Yukarıda gösterilen matematiksel modelleme süreçlerinin gösterimlerine ek olarak farklı gösterimler ve modeller de mevcuttur (Siller ve Greefrad, 2010; Voskoglou, 2006; Blomhøj ve Jensen, 2006; Borromeo Ferri, 2006). Bu gösterimler öğrencilerin modelleme sürecinden geçtiği aşamaların idealleştirilmiş tanımlarından ibarettir (Erbaş vd., 2014). Fakat bu gösterimler ve modeller, öğretmenlerin modelleme etkinliklerinde öğrencilerin hangi aşamalardan geçtiğini ve hangi aşamalarda problemle karşılaşacaklarını anlamaları açısından yardımcı olabilir.

Modelleme sürecinin sürdürebilirliği için bazı yeterlilikler vardır. Blum ve Kaiser (1997) modelleme yeterliliklerini aşağıdaki gibi açıklamışlardır :

A. Gerçek problemi anlayabilme ve gerçeğe dayalı model kurma yeterliliği A1) Problem ile ilgili varsayımlar yapmak ve problem durumunu basitleştirmek

A.Karmaşık Gerçek Yaşam Durumu B. Gerçek Yaşam Problem Durumu C. Matematiksel Model D. Matematiksel Çözüm E. Çözümün Gerçek Yaşam Anlamı G. Rapor

F. Modeli Revize Etme veya Çözümü Kabul Etme

1 6 7 5 4 3 2

(41)

22

A2) Durumu etkileyen nicelikleri tanımak, isimlendirmek ve anahtar değişkenleri belirlemek.

A3) Değişkenler arasında ilişkiler kurmak

A4) Mevcut bilgileri aramak ve ilgili/ilgisiz bilgileri ayırt etmek.

B. Gerçek modelden matematiksel model oluşturma yeterliliği B1) İlgili nicelikleri ve aralarındaki ilişkiyi matematikselleştirmek

B2) İlgili nicelikleri ve aralarındaki ilişkiyi (eğer gerekliyse) basitleştirmek ve bunların sayısını ve karmaşıklığını azaltmak.

B3) Uygun matematiksel gösterimleri/formülleri seçme ve durumların grafiksel gösterimlerini yapma

C. Matematiksel model yardımıyla matematiksel problem çözebilme yeterliliği C1) Problemi küçük problemlere bölme, benzer veya analog problemlerle ilişki kurma, problemi başka bir şekilde ifade etme veya farklı bir biçimde inceleme, eldeki verileri ve nicelikleri çeşitlendirme gibi buluşsal stratejileri kullanma

C2) Problemi çözmek için matematiksel bilgiyi kullanma

D. Matematiksel sonuçları gerçek durumlarda yorumlayabilme yeterliliği D1) Matematiksel sonuçları matematik dışı bağlamlarda yorumlayabilme D2) Özel bir durum için geliştirilen çözümleri genelleyebilme

D3) Uygun matematiksel dil kullanarak veya çözümler hakkında iletişim kurarak probleme çözümler sunma

E. Çözümü doğrulayabilme yeterliliği

E1) Eleştirel ve derinlemesine düşünerek çözümleri kontrol etme

E2) Çözümler durumla uyuşmuyorsa modelin bazı bölümlerini gözden geçirme veya modelleme sürecini tekrar geçme

E3) Çözümler farklı bir şekilde geliştirilebilirse diğer problem çözme yollarını düşünme

(42)

23

Modelleme yeterlilikleri, modelleme sürecini uygun bir şekilde sürdürebilmeyi içerir. Bu yüzden modelleme yeterlilikleri modelleme süreçleri ile yakından ilgilidir.

2.4. Matematiksel Modelleme Yaklaşımları

Matematik eğitimi alan yazınında öğretimde matematiksel modellemenin anlamı, amacı, öğrencilere sunuluş biçimi, öğretim programına entegre edilme biçimleri ve öğretmenlerin sahip olması gereken mesleki donanımlar gibi konularda araştırmalarda ele alınan farklı yaklaşımlardan da görüldüğü gibi kabul görmüş ortak bir yaklaşımdan söz etmek mümkün değildir (Erbaş vd., 2014).

Matematiksel modellemenin öğretim sürecinde kullanımı bakımında iki ayrı yaklaşımdan bahsetmek mümkündür (Gravemeijer, Niss ve ark.’dan Aktaran Erbaş vd.). Bunlardan birincisi derste hazır olarak verilen bilgilerin gerçek hayat durumlarının analizinde uyarlanmasıdır. Bu tür yaklaşımda öğrencinin modelleri hangi gerçek yaşam durumlarında uyarlayacağı hazır bilgi olarak verilmektedir. Diğer yaklaşımda ise öğrenciler gerçek yaşam durumlarını analiz ederken kendi modellerini geliştirirler.

Matematiksel modellemenin öğrenimi ve öğretimi ile ilgili tüm dünyada kabul gören bir teoriden bahsetmek mümkün olmasa da literatürde var olan modelleme perspektifleri, Kaiser ve Sriraman (2006) tarafından ise Tablo 1’de görüldüğü gibi sınıflandırılmıştır.