Regresyonda alternatıf metolar

İÇİNDEKİLER   İÇİNDEKİLER ... i ÖZET ... iv ABSTRACT... v TEŞEKKÜR ... vi TABLO DİZİNİ ... vii 1. GİRİŞ ... 1 2. REGRESYON ANALİZİ ... 3 2.1. Model Kontrolü... 4 3. EN KÜÇÜK KARELER REGRESYONU ... 5 3.1. Regresyon Tahmini... 5 3.2. Testi ... 6 3.2.1. Tahmini ... 7 3.3. Normalite Kontrolü ... 7

3.4. Regresyon Katsayılarının Tahmini ... 7

3.4.1. Matris Gösterimi... 8

3.5. Regresyon Katsayılarının Testi ... 8

3.5.1. Test İstatistiği ... 8

3.5.2. Tahmini ... 9

3.5.3. p Değeri ... 9

3.6. Testi... 9

3.7. Çoklu Belirleyicilik Katsayısının Hesaplanması... 10

3.8. Basit Regresyon Örneği... 10

3.9. Çoklu Regresyon Örneği ... 13

4. EN KÜÇÜK MUTLAK SAPMA (LAD) REGRESYONU ... 15

4.1. Regresyon Tahmini... 15

4.2. β =0 Testi... 17

4.2.1. LAD ve EKK yöntemlerinin karşılaştırılması... 18

4.2.2.τ parametresi ... 18

4.3. Regresyon Katsayılarının Tahmini ... 19

4.3.1. Algoritmanın taslağı ... 19

4.3.2. d yönündeki tahminlerin en iyi vektörünün bulunması... 20

4.3.3. Uygun yön vektörünün bulunması... 20

4.3.4. Algoritma... 21

4.3.5. Algoritmanın tekrarlanması ... 21

4.4. βq+1 =L= βp =0 _{Testi ... 22}

4.5. Basit Regresyon Örneği... 23

4.6. Çoklu Regresyon Örneği ... 26

5. M- REGRESYON ... 32

5.1. Regresyon Tahmini... 32

5.1.1. Huber M- tahminin tanımı... 32

5.1.2. Algoritma... 33

5.1.3. Algoritmanın Gerçekleşmesi... 33

5.2. Testi ... 36

5.3. Regresyon Katsayısının Tahmini ... 37

5.3.1. Algoritma... 37

5.4. Testi... 37

5.5. Basit Regresyon Örneği... 38

5.6. Çoklu Regresyon Örneği ... 41

6. PARAMETRİK OLMAYAN REGRESYON ... 46

6.1. Regresyon Tahmini... 46

6.1.1. Ağırlıklı Medyanlar ... 46

6.1.2. nın Parametrik Olmayan Tahminleri ... 47

6.1.3. nın Ranklar Açısından Tanımı... 47

6.2. Testi ... 48

6.2.2. EKK Testine Benzerliği... 49

6.3. Regresyon Katsayılarının Tahmini ... 49

6.3.1. Algoritmanın Gerçekleştirilmesi ... 50

6.4. Testi... 51

6.5. Basit Regresyon Örneği... 52

6.6. Çoklu Regresyon Örneği ... 55

7. BAYES REGRESYON... 59

7.1. Bayes Yaklaşımı ... 59

7.2. Regresyon Tahmini... 59

7.2.1. Bilgi vermeyen önsel dağılımının kullanımı ... 60

7.2.2. Ortak Önsel Dağılımın Kullanımı ... 60

7.2.3. Bayes Tahmini... 61

7.3. Sonsal Dağılım ve p Değeri ... 62

7.3.1. Önsel Dağılım ... 62

7.3.3. Testin Tanımı ... 63

7.4. Regresyon Katsayısının Tahmini ... 64

7.4.1. Bilgisi Olmayan Önsel Dağılım Kullanımı ... 64

7.4.2. Bayes Tahmini... 64

7.4.3. Ortak Önsel Dağılımın Kullanımı ... 65

7.4.4. Bayes Tahmini... 65

7.5. Testi ... 66

7.5.1. Testin Tanımı ... 66

7.6. Basit Regresyon Örneği... 66

7.7. Çoklu Regresyon Örneği ... 68

8. UYGULAMA ... 71

8.1. Basit Regresyon Analizi Uygulaması ... 71

8.2. Çoklu Regresyon Analizi Uygulaması... 80

9. SONUÇ VE ÖNERİLER... 101

ÖZET

YÜKSEK LİSANS TEZİ

REGRESYONDA ALTERNATİF METODLAR

Fatma ÇİFTCİ

Selçuk Üniversitesi Fen Bilimleri Enstitüsü İSTATİSTİK Anabilim Dalı

Danışman: Doç.Dr. Aşır GENÇ Yıl: 2009

Jüri: Doç.Dr. Aşır Genç

Jüri: Yrd.Doç.Dr.Nimet Yapıcı PEHİVAN

ABSTRACT

MASTER OF SCIENCE THESIS

ALTERNATIF METODS OF REGRESSION

Fatma ÇİFTCİ

Selçuk University

Graduate School of Natural and Applied Sciences

Department of STATİSTİCS

Supervisor: Assoc, Doç. Dr. Aşır GENÇ

2009,….Page

Assize : Doç.Dr. Aşır Genç

Assize: Yrd.Doç.Dr.Nimet Yapıcı PEHİVAN Assize: Yrd. Doç. Dr. Hasan KÖSE

TEŞEKKÜR

Bu çalışmasın yapılmasında bana her türlü imkanı sağlayan ve beni her konuda yönlendiren değerli danışman hocam Doç.Dr. Aşır GENÇ’ e sonsuz teşekkürlerimi sunarım.

Bu tezin hazırlanmasında bana maddi ve manevi destek olan eşim İsmail ÇİFTCİ ve oğlum Mahmut Sirac ÇİFTCİ ye sonsuz teşekkürlerimi sunarım.

TABLO DİZİNİ

Tablo 2. 1. n Bağımlı ve p Bağımsız Değişkenli Veri Seti... 3

Tablo 3. 1. Asit Ölçüm Verisi... 11

Tablo 3. 2. Şalgam Verisi ... 13

Tablo 4. 1. Doğum Oranı Verisi………...24

Tablo 4. 2. Canada veri noktası hariç eğimler ... 24

Tablo 4. 3. Artan düzende doğum oranı verisinin LAD regresyon analizindeki sıfır olmayan artıkları ... 25

Tablo 4.4. Yangın Verisi... 26

Tablo 4. 5. t=0 olduğunda Eşitlik (4.10) nun Elle Hesaplanması... 29

Tablo 5. 1. Raf Ömrü Verisi ... 38

Tablo 5. 2. Raf Ömrü Verisi için M tahminin 1. İterasyonu... 39

Tablo 5. 3. Aerobik Verisi ... 42

Tablo 5. 4. Aerobik Verisi için M tahminin 1. İterasyonu... 43

Tablo 6. 1. Kol Uzunluğu Verisi………...53

Tablo 6. 2. Ağırlıkların Kümülatif Toplamı ... 54

Tablo 6. 3. Eğitime Harcanan Para Verisi ... 56

Tablo 7. 1. Yağış Miktarı Verisi………...67

Tablo 7. 2. Kaldırım Verisi... 69

Tablo 8. 1. TEFE Verisi………71

Tablo 8. 2. Basit Regresyon Sonuç Tablosu... 78

Tablo 8. 3. Bezostaja Verisi... 81

1. GİRİŞ

Legendre 1805 yılında gezegenlerin yörüngelerini belirlemek amacıyla En Küçük Kareler (EKK) olarak bilinen tekniği oluşturmuştur. Yöntem ilk olarak astro-nomide kullanılmıştır. Bilinen değişkenlerden yola çıkarak regresyon modeli kurulur. Regresyon analizi bağımlı değişkenle bağımsız değişkenler arasındaki fonksi-yonel ilişkiyi belirlemede kullanılan tekniklerden bir tanesidir.

Yule (1899), araştırmaların sonucunda bir regresyon denklemi hesaplamıştır. Yule’ nin bu yaklaşımı özellikle sosyal bilimler ve tıp alanlarında sıklıkla kullanılmış-tır. Regresyon analizinde yapılan çalışmalar Neyman (1923) tarafından devam ettiril-miştir. Freedman (1999) ın yaptığı inceleme sonucunda, Neyman ın çalışmalarının Rubin (1974) ve Holland (1988) tarafından devam ettirildiği söylenebilir.

Regresyon modeli oluşturulurken, gözlem değerlerinin ve etkilenilen olayların bir matematiksel gösterimle yani bir fonksiyon yardımıyla ifade edilmesi gerekmekte-dir.

Regresyon modelinin amacı, elde edilen gözlem değerlerini kullanarak bir denklem elde etmektir. Kullanılan en yaygın yöntem EKK yöntemidir.

EKK yöntemi ile parametre tahminlerinin yapıla bilmesi için hata terimi normal dağılıma sahip olmalıdır. Farklı gözlemlerin hataları birbirinden ba-ğımsız olmalı ve varyansları sabit olmalıdır. hata terimleri ile baba-ğımsız değiş-kenleri bağımsız olmalıdır. Bu varsayımların sağlanmadığı durumlarda tutarlı olma-yan ve olma-yanlı tahminler ortaya çıkmaktadır(Tukey, 1977).

Gözlem değerlerinin normallik varsayımını bozan en önemli etken büyük hata terimi olarak nitelendirilen aykırı değerlerdir. Aykırı değerler, istatistiksel tekniğe ve kurulan regresyon modeline zarar verirler. Bununla birlikte, aykırı değerin modeli açıklayan bir değer olması olasılığı çok düşüktür. Eğer model değiştirilirse, bu aykırı değerin etkisi de büyük ölçüde azalmaktadır. Robust regresyon yöntemleri, aykırı de-ğere sahip gözlem değerini güncelleyerek, analizi bu yeni güncellenmiş değer ile yapmaktır. Hata terimlerinin normal dağılmaması EKK tekniğinin uygulanmasını zor-laştırır. Bu durumda alternatif regresyon teknikleri daha uygun sonuçlar vermekte-dir(Ergül, 2006).

Hata terimlerinin normal dağılmaması, aykırı gözlemlerin olması gibi durum-lar EKK yönteminin kullanılmasını zorlaştırmaktadır. Bu yüzden alternatif regresyon yöntemleri kullanılmaktadır.

Bu çalışmanın ikinci bölümü, tez çalışmasının altyapısı için gerekli görülen temel tanım ve kavramları içermektedir.

Çalışmanın üçüncü bölümünde EKK yöntemi ile parametre tahminleri konu alınmıştır. Dördüncü bölümde LAD yöntemi hakkında bilgi verilmiştir. LAD tekniği, EKK tekniğinden çok daha önce bulunmasına karşın LAD yönteminin yapısı ve algo-ritması uzun süren işlemler gerektirdiğinden dolayı uygulama alanı bulamamıştır. Veri seti içerisinde x-yönünde aykırı değerlerin varlığında yönteminin performansı oldukça azalmaktadır (Öztürk, 2003). Beşinci bölümde M regresyon yöntemi ile aykırı gözlem değerlerin tespitine yönelik çalışmalar irdelenmiştir. Altıncı bölüm parametrik olma-yan regresyon yöntemini içermektedir. Parametrik olmaolma-yan regresyon aykırı gözlem-lerin bulunduğu veri seti için önemli bir analizdir. Aykırı gözlemleri etkigözlem-lerini farklı biçimlerde ele alan güçlü M regresyon yöntemleri vardır. Ama aykırı gözlemlerinde dolaylı yoldan parametreleri bozduğu için güçlü yöntemler bile uygun çözümler ver-meyebilir. Bu durumda parametrik olmayan regresyon ön bilgi sağlamaktadır. Yedinci bölümde Bayes regresyon çalışılmıştır. Analiz edilen veri hakkında eksik bir bilgiye sahip ise Bayes metodunu kullanarak bu bilgiyi kapsamak mümkündür. Son bölümde ise uygulama ile beraber sonuçlar ve öneriler yer almaktadır. Literatürde benzer alan-da çalışılan makalelerin hemen hemen hepsi doğrusal regresyonla ilgilidir.

Bu çalışmada Minitab ve SPSS istatistik paket programlarından yararlanılarak tahmin edicileri elde etmek için literatürdeki algoritmalardan faydalanılmıştır.

2. REGRESYON ANALİZİ

Regresyon analizi, değişkenler arasındaki sebep sonuç ilişkisini bağımlı ve ğımsız değişkenler yardımıyla açıklamaktır. Regresyon analizi uygulanırken bir ba-ğımlı bir ya da birden fazla bağımsız değişken kullanılır. Kurulacak modelde bağımsız değişken sayısı bir tane ise basit regresyon analizi, birden fazla ise çoklu regresyon analizi denilmektedir.

n gözlemden oluşan p tane bağımsız değişken ve Y bağımlı de-ğişkenli veri olsun. Genel model, Tablo 2.1 deki düzenlenen veri setidir. Bu set reg-resyon modeli olarak da adlandırılır. Lineer regreg-resyon modelinin denklemi,

(2.1) ya da ,

(2.2) dır. Modelde tahmin edilen rastgele hatalar olmaktadır.

Tablo 2. 1. n Bağımlı ve p Bağımsız Değişkenli Veri Seti

Sıra Y 1 2 N

Lineer regresyon fonksiyonunun temel özelliği ’nın bilinmeyen parametre vektörü ve ’nın verilerden elde edilen bilinen değer olan terimlerinin topla-mıdır. Verilerden elde edilen ’nın durumu önemli değildir. Örneğin yaş (Y) ve ara-cın çapları (X) olan bir veri setine sahip olsak, bu veri seti için lineer regresyon modeli

dır. Diğer regresyon modeli ise lineer

modelden ziyade 2. dereceden model olmaktadır. Çünkü teriminiiçermektedir. Bu

gösterimde basit değişimler yaparsak ve model

Lineer regresyon model hakkında bazı varsayımlar vardır. Bu varsayımlar, ba-ğımsız değişkenlerin fonksiyonunun lineer olması, rastgele hataların baba-ğımsızlığını ve rastgele hataların varyanslarının eşitliğini içermektedir. Bu varsayımların geçerliliği-nin kontrolü için yöntemler geliştirilmektedir.

Önerilen modelin geçerli olup olmadığı, gerekli varsayımları sağlayıp sağla-madığına bağlıdır.

(2.3) =1,2, n için varsayımlar:

i) rastgele değişken olsun. Beklenen değeri açıklayıcı değiş-kenlerin bir fonksiyonudur ve fonksiyon tüm i ler için aynıdır.

ii) katsayıları için, regresyon fonksiyonu lineerdir, yani nin ortalaması dir.

iii) Hata terimleri birbirinden bağımsızdır . Ortalaması sıfır ve varyans sabittir.

2.1. Model Kontrolü

Eşitlik (2.2) de varsayılan model ele alınsın. Her bir için gözlem noktaları dır. Noktalar kümesi eğri biçiminde ise, (ii) varsayımındaki regresyon fonksiyonu lineer olmayandır. Varsayımın ihlalini göster-mektedir. Küme dağınık biçimde ise bu durum (iii) varsayımının ihlalini gösterir. Hataların tahmini yani artıkların hesaplanması

3. EN KÜÇÜK KARELER REGRESYONU 3.1. Regresyon Tahmini

Eşitlik (2.2) de verilen lineer regresyon modeli ele alınsın. p nın değeri 1 dir. Sadece bir açıklayıcı değişkenli modele basit lineer regresyon model denir. Eşitlik (2.2), şeklinde yazılabilir. Ya da model,

(3.1) şeklindedir.

ve parametrelerini tahmin etmek için birçok yöntem bulunmaktadır. Bu bölümde en küçük kareler yöntemi anlatılmaktadır.

Tanımlanan regresyon doğrusu dır. Artıklar

şeklinde bulunur. Artıklar , veri noktasına regresyon modelinden hesaplanan uzaklıktadır. Artıkların kareleri toplamını minimum yapan ve yi seçilir.

Regresyonun EKK yönteminde,    artıklarının toplam büyüklüğü ölçülür.

ve nın en küçük kareler tahmin edicileri, nın en küçük değeri olarak verilen , ve değerleri ile tanımlanır. Yani,

(3.2) bulunur (David, 1981). Burada ve sırası ile ve gözlemlerinin ortalamasını ifade etmektedir.

için formül,

dır.

Bu, veri noktalarının merkezi olarak kabul edilen ) noktasından geçen tahmin edilen regresyon modelidir.

için formül,

,

veri noktaları ve orta noktasından geçen doğrunun eğimi arasın-daki modelin eğimi dir. Böylece tahmin edilen regresyon modelinin

eğimi bu eğimlerin ortalamasının en iyisidir.

ağırlıkları negatif değildir ve toplamları 1dir. (Ortalama, bütün ağırlıkları 1/n’ e eşit olan ağırlıklı ortalamanın özel durumudur). ve şeklinde-dir.

3.2. Testi

X ile kurulan tüm model ve X, indirgenen mo-deli karşılaştırıldığında tüm momo-delin sonucu indirgenmiş momo-delin sonucundan daha iyi ise X ve Y arasında ilişkinin olduğu söylenir.

İki modelin ilişkisinin ölçülmesi için diğer bir yol hipotezinin test edildiği yoldur. Eşitlik (3.2) de kullanılan hesabı ile test edilir,

Burada , hataların standart sapmasını ifade eder. Test istatistiği;

Testin p değeri, n-2 serbestlik derecesi ile t dağılımından elde edilir. Mutlak değer ile bu dağılımın büyük ya da büyük eşit olma olasılığı hesaplanır.

ise olup model anlamlıdır.

3.2.1. Tahmini

Standart sapmanın tahmini, hata terimlerinin basit standart sapmasıdır. Artıklar

olduğundan bu tahmin dır.

3.3. Normalite Kontrolü

Hataların olasılık dağılımı normal dağılım kabul edilirse EKK testi ve tahmini yeterlidir. Normallik sağlanamazsa EKK yöntemi sağlamdır ama tahminler optimal-lıktan uzaktır.

3.4. Regresyon Katsayılarının Tahmini

Çok değişkenli regresyon modeli parametreleri nın EKK

tahmin-leri dır. Artıkların kareleri toplamı olarak verilmektedir. Burada

3.4.1. Matris Gösterimi

n gözlemli p bağımsız değişkenli veri seti Tablo 2.1 de gösterilmiştir. y, boyutlu ve X de den oluşan matrisi göstermektedir. Matris gösterimiyle,

, , ,

olmak üzere,

(3.9) Şeklinde elde ederiz (Dodge, 1993).

3.5. Regresyon Katsayılarının Testi

Regresyon analizinde kullanılan ilk test, bağımsız değişkenlerin önemli dü-zeyde açıklayıcı bilgiye sahip olup olmadığını test etmektedir. p tane değişkeni içeren tüm model ile hiç bağımsız değişken içermeyen indirgenmiş model karşı-laştırılmak istenir. Diğer bir deyişle hipotezine karşı

hipotezi anlam düzeyinde test edilmek istenir.

3.5.1. Test İstatistiği

Artıkların kareleri toplamı en küçük yapan model en iyisidir. EKK yöntemi ile artıkların kareleri toplamı alınarak artıkların büyüklüğü verilmektedir. Modelde artık-larının karelerinin toplamı SSR dır. Bütün model ve indirgenmiş model için ve

ile gösterilsin. p=4 için hipotezini test etmede kullanılan test istatistiği,

Burada rastgele hataların dağılımının tahminidir.

3.5.2. Tahmini

Artıklar dir. nin tahmin edicisi,

(3.11) şeklinde hesaplanır.

3.5.3. p Değeri

p değeri, incelenen F değerinden daha büyük ya da büyük eşit olan F rastgele değeridir. Bağımsız değişkenler için hesaplanan F değeri, test istatistiğinin değeridir. p değerini hesaplamak için alternatif hipotez doğru olduğu zaman rastgele değişkenin dağılımının bilinmesi gerekir.

3.6. Testi

Lineer regresyon modelinin genel formu düşünülsün,

. Açıklayıcı değişkenlerle oluşmuş tüm model ile

indir-genmiş model karşılaştırılır.

Artıkların karelerinin toplamı iki model için ve şek-linde gösterilmektedir. , nın tarafsız tahminini ifade etmektedir.

Hataların dağılımının normal olduğu varsayılsın, F, alternatif hipotez doğru olduğu zaman p-q ve n-p-1 serbestlik derecesi ile F dağılımına sahiptir.

3.7. Çoklu Belirleyicilik Katsayısının Hesaplanması

Çoklu belirleyicilik katsayısı, bağımsız değişkenlerin bağımlı değişkeni ne ka-dar iyi açıkladığının ölçüsüdür.

(3.14) Eşitliğinden hesaplanır (Gujarati, 1999).

Sapma iki kısma bölünmektedir. Birinci kısım =( dır.

İkinci kısım asıl sapmanın kısmıdır, yani bağımsız değişkenler ile bağımlı

değişkenle-rin ilişkisi, tarafından açıklanır. toplamı

bağımlı değişkendeki bütün değişimi dikkate almaktadır. , bağımsız değişkenler tarafından açıklanan kısmın bağımlı değişkendeki değişme oranıdır.

Çoklu belirleyicilik katsayısı, testi için F test istatistiğine bağlıdır. Aslında , , F nın fonksiyonudur. Basit regresyon durumunda , X ve Y arasındaki korelasyonun karesine eşittir.

3.8. Basit Regresyon Örneği

Deney, kimyasal asit içeriğini belirtmek için farklı iki yöntemi arasındaki iliş-kiyi hesaplamaktadır. İki metot, farklı şekilde ölçüm içerir. Kimyasal örneğin organik asit içeriği, pahalı olan ağırlık ve çıkarma metoduyla belirlenebilir ama asit numarası-nı titrasyon metodu ile bulmak çok daha ucuzdur. Kullanumarası-nılan regresyonda organik asit miktarında pahalı model yerine ucuz model kullanılması beklenir. Her iki yöntem 20 kimyasal örnek üzerinde uygulandı. Veriler Tablo 3.1 de gösterilmektedir. Bu verileri kullanarak asit içeriği ölçümünün kesin fonksiyonu olarak organik asit içeriği ölçü-münü ifade eden bir eşitliği elde eder. (Dodge, 1993)

Tablo 3. 1. Asit Ölçüm Verisi

Organik asit Pahalı ölçüm Ucuz ölçüm ölçümü sırası (Y) (X) 1 76 123 2 70 109 3 55 62 4 71 104 5 55 57 6 48 37 7 50 44 8 66 100 9 41 16 10 43 28 11 82 138 12 68 105 13 88 159 14 58 75 15 64 88 16 88 164 17 89 169 18 88 167 19 84 149 20 88 167 Gösterim,

Kimyasal örneğin pahalı organik asit ölçümü Kimyasal örneğin ucuz asit numarası

Veri noktaları Tablo 3.1 de gösterilmektedir. X ve Y arasındaki ilişki yaklaşık olarak lineerdir. Eşitlik (2.1) de verilen lineer regresyon modeli göz önüne alınsın. Bu örnek için p nın değeri 1 dir. Sadece bir açıklayıcı değişkenli mode-le basit lineer regresyon model denir. Regresyon doğrusu eşitlik (2.1) deki gibi,

olarak ya da şeklinde yazılabilir.

Buradan ve tahmin edilir. Böylece X asit numarasına sahip örnek için, organik asit içeriği olarak tahmin edilebilir.

Tablo 3.1 deki verilerden elde edilen tahmin ediciler =35.46 ve ’

dır. Regresyon modeli şeklindedir. =0.0056 dır.

Basit EKK regresyondan dir. Asit içeriği verisi için bu şeklinde bulunur. Eşitlik (2.6) daki 0.0000203944 de-ğeri matrisin sol köşesini göstermektedir.

Asit verisi için serbestlik derecesi 18 dir. = 57 dir. p değeri için t tablo de-ğerine bakarız. Tabloya baktığımızda 18 dede-ğerine karşılık 1.33, 1.73, 2.10, 2.58, 3.92 değerleri gösterilmektedir. olduğu zaman rasgele değişkenin olasılığı 3.29 dan büyüktür.

Asit verisi için testin p değeri 0.001den küçüktür. p=1 için eşitlik ( 3.9) hesaplanır,

3.9. Çoklu Regresyon Örneği

Basit regresyon, bağımsız değişken bir tanedir, çoklu regresyonda birden faz-ladır. Tablo 3.2 deki veri şalgamdaki B2 vitamini çalışması için derlenmiştir. Üç

faktö-rün B2 vitamini miktarını etkilediği düşünülmektedir. Bunlar güneş ışığı, toprak nemi

ve hava sıcaklığıdır. 27 farklı durumda araştırmacılar şalgam bitkisi topladılar. B2

vitaminin konsantrasyonunu, güneş ışığının yarım gün süresindeki radyasyon miktarı-nı, nemin ortalama gerilimini ve hava sıcaklığını ölçmüşlerdir. Bu veri ile şalgam yap-rağındaki B2 vitaminin ne kadarının toprak nemine, hava sıcaklığına ve güneş ışığına

bağlı olduğu öğrenilmek istendi. (Dodge, 1993)

Tablo 3. 2. Şalgam Verisi

Sıra B2 Vitamini Güneş ışığı Toprak nemi Hava sıcaklığı

(Y) (X1) ( X2) (X3) 1 110,4 176 7,0 78 2 102,8 155 7,0 89 3 101,0 273 7,0 89 4 108,4 273 7,0 72 5 100,7 256 7,0 84 6 100,3 280 7,0 87 7 102,0 280 7,0 74 8 93,7 184 7,0 87 9 98,9 216 7,0 88 10 96,6 198 2,0 76 11 99,4 59 2,0 65 12 96,2 80 2,0 67 13 99,0 80 2,0 62 14 88,4 105 2,0 70 15 75,3 180 2,0 73 16 92,0 180 2,0 65 17 82,4 177 2,0 76 18 77,1 230 2,0 82 19 74,0 203 47,4 76 20 65,7 191 47,4 83 21 56,8 191 47,4 82 22 62,1 191 47,4 69 23 61,0 76 47,4 74 24 53,2 213 47,4 76 25 59,4 213 47,4 69 26 58,7 151 47,4 75 27 58,0 205 47,4 76

Gösterim,

bölgedeki bitki için vitaminin toplamı bölgedeki bitki için güneş ışığının ölçümü bölgedeki bitki için toprak neminin ölçümü bölgedeki bitki için hava sıcaklığı

Verinin toplandığı belirli bir bitkiden bahsedildiği zaman , , , gösterimleri kullanılacaktır. Belirlenmemiş bir bitkiden genel olarak konuşulduğu zaman , , , gösterimi kullanılır. Diğer değişkenlere bağlı olduğu düşünülen Y değişkeni, bağımlı değişken ya da tepkime değişkeni olarak adlandırılır. Diğer de-ğişkenler , , bağımsız ya da açıklayıcı değişkenler olarak adlandırılır.

Örnekteki veriyi analiz etmek için şalgam yapraklarındaki miktarının toplamının (Y) yaklaşık olarak, güneş ışığı ( ), toprak nemi ( ) ve hava sıcaklığı ) değişkenlerinden etkilendiği göz önüne alınılacaktır. X ler tarafından açıklanan

Y nin ’nu yazılsın. denklemi regresyon modelidir.

regresyon fonksiyonu ve rasgele hatadır. Lineer regresyon modeli, regresyon fonksiyonunun lineer olduğu bir regresyon modelidir.

Örnek için regresyon modeli

şeklinde kurulur.

olarak bulunur.

Regresyon modeli yapmak

dır. (Eğer bunu birden fazla değişken için yapmak istersek bilgisayar kullanırız. Hesap makinesi kullanmak (3.8) eşitliğini hesaplamada p=1 elverişlidir ama p=3 için zor-dur).

4. EN KÜÇÜK MUTLAK SAPMA (LAD) REGRESYONU

LAD tekniğinin amacı, mutlak sapmaların toplamını minimum yapan regres-yon modelinin seçimidir. Bu model, herhangi bir ( ) gözlem noktasından geçen doğrular arasından en iyi sonucu veren doğru olacaktır (Ergün, 2006).

4.1. Regresyon Tahmini

EKK metodunda ve tahmin değerleri bulunur ve artıklarının kareleri toplamının minimum olması istenir. LAD metodunda ve tahmin değerleri bulu-nur ve artıkların mutlak değerde toplamının minimum olması istenir (Tasker, 2000).

ve tahmin değerleri,

(4.1) İfadesini minimum yapan a ve b değerlerinin tahminidir.

farkı, ( noktalarının sapmasıdır. Model dır. Tahmin hesabında, LAD metodu çok karmaşıktır. Tahminleri hesaplamak için bir al-goritma verilebilmesine rağmen LAD tahmini için bir formül yoktur. (Dodge, 1993).

4.1.1. LAD Algoritması

Algoritmada amaç noktasından geçen en iyi modele ulaşmaktır. Algoritma ilk olarak veri noktaların ilki olan ile başlar ve en iyi model bulunur. Bu mo-del vasıtası ile diğer veri noktaların gidilmektedir. Diğer veri noktası ile göste-rilmektedir. En iyi model vasıtası ile bulunacaktır. Bu model de, diğer bir veri noktasına götürmektedir. Diğer veri noktasını göstermektedir. Algoritma, mo-deller içinden en iyi olanı bulunca son bulmaktadır. Sonuç olarak elde edilen en son model bir önceki ile aynıdır. Bu hangi noktalardan geçtiğine bakmaksızın modeller arasında en iyi modeldir. Bu LAD regresyon modelidir.

Her bir için gözlemi ve noktaları ile modelin eğimi

(4.2) durumunu sağlayan k değeri belirlenir.

noktasından geçen en iyi doğru dır. Burada

(4.3)

bulunur (Dodge, 1993).

4.1.2. Algoritmanın Oluşumu

dan geçen en iyi modeli bulmak için süreç aşağıdaki gibi tanımlan-mıştır. dan geçen modeline göre şeklindedir.

den geçen bütün modeller arasından (4.1) deki modeli minimum yapanı bulmak

iste-nir. sapması şeklinde yazılabilir. b değerinin

(4.4) ifadesini minimum yapması istenmektedir.

b nın fonksiyonu olarak eşitlik (4.4) e bakalım. mutlak değer t=0 fonksiyo-nu dışında türevlenebilir. Bu durumda için eşitlik (4.2) belirtilen eşitsizliğin (4.4) deki türevi negatiftir ve için pozitiftir. (4.4) ifadesi sürekli bir fonksiyondur. (4.4) fonksiyonu olduğunda azalır ve olduğunda artandır.

dan geçen en iyi model olarak adlandırılan diğer bir gözlem noktasından geçer. Bunu kontrol etmek için ve nın eşitlik (4.3) de gösterilen tanımları kullanılır. Bu da, bu verilerden geçen en iyi modelin aynı zamanda diğerinden de geçtiğini doğrulamaktadır.

Eğim , olduğunda tanımlı değildir. Bunun nedeni in eşitlik (4.4) deki toplama katkısının bütün b’ ler için nın aynı değerde olmasıdır.

LAD yöntemi için regresyon model belirlenmesinde kullanılan algoritma,

1. Gözlem değerlerinden bir tanesi rastgele seçilir. Seçilen bu gözlem değeri

genellikle ilk sırada olandır.

2. Seçilen gözlem değeri kullanılarak tek tek her gözlem değeri için eğimleri

ve bu eğimlere karşılık gelen değerleri hesaplanır.

3. Eğimler küçükten büyüğe sıraya konularak, bunlara karşılık gelen

değerlerinin mutlak değeri alınır.

4. Bulunan değerlerinin birikimli toplamı hesaplanır.

5. T değeri bulunur. Bu değer bir önceki adımda elde edilen birikimli toplamın

yarına eşittir.

6. T değerine karşılık gelen eğim değerinin tespiti için 3. adımdaki gözlem

değerlerine bakılır. T değerinden büyük olan ilk değer aranan nokta olmaktadır.

7. Bu eğim değerini veren noktanın sırası tespit edilir. Bu değer sonraki

adım-da yeni başlangıç değeridir.

8. Yeni gözlem değeri kullanılarak yukarıdaki adımlar tekrar edilir.

Algorit-ma sonucunda ayrı ayrı iki tane aynı eğim değeri bulununca algoritAlgorit-ma durdurulur.

4.2. β =0 Testi

İlk olarak LAD regresyon tahminleri ve ve artıklarını e_i = y_i −(αˆ+βˆx_i) ar-tan sıraya koyarak hesaplanır. Sıfır olmayan artıklar sıralanırsa; ˆe en küçük artık ola-₁ rak ifade edilmekte, ˆe ondan sonraki en küçük, …, ₂ eˆ en büyüktür. m (m+1)/2− m değerine en yakın tamsayı k ve ₁ (m+1)/2+ m değerine en yakın tamsayı k olmak ₂ üzere,

[

]

∑

Testin p değeri Prob

[

]

β =0 olup olmadığını test etmek için (4.7) de ki test istatistiğini kullanılmak-tadır. β ve βˆ _{arasındaki uzaklık bir veya iki standart sapma SD}

( )

bir tahmin değildir. Eğer t büyükse βˆ ve 0 arasındaki uzaklığı ölçen bu değer

) ˆ (

.SD β

est den daha büyüktür ve β ≠ 0 ile sonuca varılır.

4.2.1. LAD ve EKK yöntemlerinin karşılaştırılması

Tanımlanan LAD testi EKK testine benzemektedir. Formül (4.7) formül (3.6) nın tamamen aynısıdır. βˆ _{ve est.SD(}βˆ_{) farklı şekilde hesaplanır. LAD regresyonunda}

( )

SD için kesin formül bulunmamaktadır. est.SD(βˆ) için iki formüldeki fark EKK formülünden elde edilen σˆ ve LAD formülünden elde edilen τˆ dır .

4.2.2.τ parametresi

EKK regresyonunda , tahmini LAD regresyondaki τ parametresinin tah-mini (4.5) deki τˆ ya benzemektedir. βˆ_{EKK nın standart sapması}

(

)

/

∑

σ dır

halbuki βˆ_{LAD ın standart sapması}

∑

ikisi de rastgele hataların çapının ölçüsüdür. τ ,1/2θ ya eşittir. (LAD regresyonu var-sayımlarında, hataların ortalaması bazen sıfırdır eğer dağılım simetrikse medyanı rast-geledir.) Eğer σ büyükse hatalar dışa doğru yayılır, medyanın etrafındaki yoğunluk azdır. Bundan dolayı τ nun büyük olması θ nın küçük olduğunu gösterir.

σ büyük olduğu zaman τ büyüktür. σ küçük olduğu zaman τ de küçüktür. σ

τ/ oranı hataların dağılımının biçimine bağlıdır. Eğer hatalar normal dağılıyor ise σ

τ/ =1.253> 1 dir. Böylece büyük örnekler için LAD regresyon tahminleri EKK reg-resyon tahminlerinden daha küçüktür. Eğer hatalar Laplace dağılımına sahipse

σ

τ/ =0,707<1 dir.

4.3. Regresyon Katsayılarının Tahmini

βˆ0,βˆ1,βˆ2,βˆ3 tahmin değerleri hesaplanacaktır. Artık tahminlerin mutlak top-lamının

∑

∑

4.3.1. Algoritmanın taslağı

Algoritma için vektör gösterimi kullanmaktadır.

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 3 2 1 0 b b b b b ve ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 3 2 1 1 i i i x x x i x

mutlak sapma toplamı olan eşitlik (4.8) şu şekilde yazılmaktadır,

∑

Basit LAD regresyon için bir algoritma uygulanır. Bir değer ile başlanır, böy-lece bütün modelller içinden en iyi model seçilir. Benzer şekilde çoklu LAD regres-yonu için bir algoritma uygulanır. Her basamakta bir b tahmin vektörü bulunarak daha

iyi bir vektörü elde edilir. Bunun için uygun bir d yön vektörü bulunur ve için en uygun t değeri elde edilmeye çalışılır.

4.3.2. d yönündeki tahminlerin en iyi vektörünün bulunması

t değerini bulmak için (4.10) daki denklem minimize edilir,

∑

∑

Bu, en küçük b yi bulma problemi ile aynıdır. z / oranları bulunur ve artan _i w_i sırada sıralanır. z ve w yeniden bu sıraya göre indekslenir,

w w wk 2T 1 1 2 1 + +L+ − < w w wk wk 2T 1 1 2 1 + +L+ − + >

Burada T =

∑

4.3.3. Uygun yön vektörünün bulunması

Dört yön vektörü d₁,d₂,d₃,d₄ olsun. ( p bağımsız değişkene sahip model için p+1 tane yön vektörü düşünülür). Her dj vektörü için -dj negatif vektörü de alındığı için sekiz tane yön vektörü elde edilir. Bu sekiz yön vektörü arasında en iyi yön vektö-rü (4.10) ifadesini minimum yapan değerlerden biridir. Bu değer t=0 olarak düşünül-düğünde. W−+W0−W+ , W , − Wi lerin toplamıdır. Burada z / nin negatif olduğu i wi durumdaki toplam W , 0 zi =0 için wi nın toplamı ve. W , + z / pozitif olduğunda i wi

i

W toplamıdır. Bu türev sekiz yönün her biri için hesaplanmaktadır. Türevleri nega-tif olduğunda en uygun yön seçilmektedir. Bütün türevler pozinega-tif ise b vektörü en iyi

4.3.4. Algoritma

Basit LAD regresyon modeli iki veri noktasından geçer. Benzer şekilde p ba-ğımsız değişken ile kurulan çoklu regresyonda LAD regresyon doğrusu p+1 gözlem noktasını sağlar. Örnekte, p=3 dür. Böylece p+1=4 olur. Algoritma için dört veri nok-tası örneğin i=1,2,3,4 seçilerek başlamaktadır ve b tahmin vektörünün ilk basamağı için i=1,2,3,4 yi =b′xi olarak tanımlanır. Ab= olarak yazılabilir, burada c

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ′ ′ ′ ′ = 4 3 2 x x x x A 1 ve ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 4 3 2 1 y y y y c dır. Bu nedenle b₌ A-1c_. 4 3 2 1,d ,d ,d

d vektörleri yönünde ilk dizi A ın dört kolo--1 nudur.

4.3.5. Algoritmanın tekrarlanması

Her bir basamakta b tahminleri dört veri noktası ile tahmin edilir. Bu noktalar 4 3 2 1,i ,i ,i i tarafından gösterilir. ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ′ ′ ′ ′ = i4 i3 i2 x x x x A 1 i

Yön vektörleri A ın dört kolonudur. Aşağıdaki tanımlanan sekiz türev hesap--1 lanır. Dört yön vektörü ve onların negatiflerinden en çok negatif türeve sahip olan yön seçilir. Örnekte tahmin edilen bu yön d dur. Tahmin edilen vektör, ₃ b∗ =b+t∗d3

olarak açıklanan b nin iyileştirilmiş halidir. Burada t , (4.10) ifadesini minimum ya-∗ pan t değeridir. Bazı k değerlei için ∗ =₍ −b′x_k)/d′₃x_k

k y

A nın üçüncü kolonu, x′ ile değiştirilir. Bu matris _k A olarak adlandırılır. Yön vek-∗ törlerinin yeni dizisi A∗'£1 ın dört kolonudur.

p=3 ve gözlem noktalarının x1,x2,x3,x4 olduğu düşünülsün,

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ′ ′ ′ ′ = 4 3 2 x x x x A 1 ve ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 4 3 2 1 y y y y c

Katsayı vektörü b₌ A-1c _{dır. Eğer}

3

x veri noktası yerine x gözlemi konursa, _k yeni katsayı vektörü _b∗ _=A∗-1_c∗_{olur. Burada,}

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ′ ′ ′ ′ = ∗ 4 k 2 x x x x A 1 ve ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ∗ 4 3 2 1 y y y y c 3

d yön vektörü kullanılarak t∗ =(yk −b′xk)/d′3xk _{elde edilir. Çünkü} ∗

∗

∗ ₌

+ d A c

b t ₃ -1 dır (Dodge, 1993).

Tabii ki (4.10) için en küçük negatif sapmayı veren vektörü seçmek mantıklı-dır çünkü bütün hataların toplamı en azmantıklı-dır. Bulunan t için yöntem bölüm 4.2 de ta-∗ nımlanmaktadır.

4.4. βq+1 =L=βp =0 _Testi

Genel lineer regresyon modeli Y = β0+β1X1+L+βpXp +e dır. EKK test

istatistiği βq+1 =L=βp =0 testi için,

(p q)σˆ2 SSR SSR F_EKK indirgenmiş tüm − − = dır.

Burada SSR, artıkların karelerin toplamıdır. =

∑

SSR . Benzer bir test ista-tistiği LAD regresyonda kullanılmaktadır.

(p q)(τˆ/2) SAR SAR F indirgenmiş tüm Lad ₋ − = (4.12)

Burada SAR, artıkların mutlak değerinin toplamıdır. SAR = eˆ_i . τˆ değeri (4.5)ile hesaplanır. m=n-(p+1) şeklinde verilmektedir (Dodge, 1993).

Rastgele hatalar normal dağılıma sahip ve sıfır hipotezi doğru olduğu zaman

EKK

F test istatistiği F dağılımdır. Rastgele hataların dağılımı belirtilmediği zaman

EKK

F , F dağılımına yaklaşmaktadır. Bu F_LAD test istatistiği için de aynıdır. Büyük n için değeri testin p değeri Prob

[

]

p değeri Prob

[

]

[

]

∞ =

n G nın dağılımına benzemektedir. Ortalama n büyüklüğü için, G ye bağlı p değeri daha kesin olarak belirlenebilmektedir.

4.5. Basit Regresyon Örneği

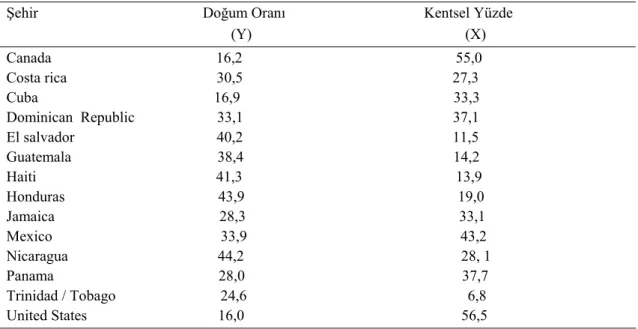
Tablo 4.1 deki Kuzey ve Orta Amerika’daki 14 ülkede doğum oranı ve kentsel yüzdelerden oluşan veri seti düşünülsün. (Dodge, 1993)

Tablo 4. 1. Doğum Oranı Verisi

Şehir Doğum Oranı Kentsel Yüzde (Y) (X) Canada 16,2 55,0 Costa rica 30,5 27,3 Cuba 16,9 33,3 Dominican Republic 33,1 37,1 El salvador 40,2 11,5 Guatemala 38,4 14,2 Haiti 41,3 13,9 Honduras 43,9 19,0 Jamaica 28,3 33,1 Mexico 33,9 43,2 Nicaragua 44,2 28, 1 Panama 28,0 37,7 Trinidad / Tobago 24,6 6,8 United States 16,0 56,5

ve regresyon katsayıları LAD regresyon yöntemi ile tahmin edilsin. elde edilir.

Tablo 4.1 deki doğum oranı verisi için basit LAD regresyon algoritması elde alınsın. 1. bölümde Canada’ya ait veri noktası (58,0,16,2) ilk değer olarak seçilmiştir. Eğimi dır . Örneğin Costa Rica . 13 olarak bulunur. Ülke için eğim Canada hariç Tablo 4.2 de gösterilmektedir.

Tablo 4. 2. Canada veri noktası hariç eğimler

Ülke Kümülatif Toplam

Mexico -1,5000 11,8 11,8 Nicaragua -1,0566 26,5 38,3 Dominican Repuplic -0,9441 17,9 56,2 Honduras -0,7694 36,0 92,2 Panama -0,6821 17,3 109,5 Haiti -0,6107 41,1 150,6 Jamaica -0,5525 21,9 172,5 El Salvador -0,5517 43,5 216,0 Guatemala -0,5447 40,8 256,8 Costa Rica -0,5162 27,7 284,5 Trinidad / Tobago -0,1743 48,2 332,7 United States -0,1333 1,5 334,2 Cuba -0,0323 21,7 355,9

dır. Bu değer 2 ye bölündüğünde 355,9/2=177,95 elde edilir ve Tablo 4.1 ın 4 kolonundaki kümülatif toplamına bakılarak ülke seçilmektedir. 172,5<177,95 ve 216,0>177,95 olduğundan El Salvador noktası belirlenir. =-0,5517 ve =16,2-(-0,5517)(55,0)=46,54 olarak bulunur. El Salvador ve Canada veri noktalarından geçen en iyi modeli belirlenmiş olur.

El Salvador gözlemi ile diğer gözlemlerin eğimi hesaplanır. oluşturu-lur ve sıralanır. Tablo (3.2) ye benzer bir tablo oluşturuoluşturu-lursa kümülatif toplamı 265.5 olur ve 1. 265,/2=13,5 olarak United States noktası bulunur. ABD ve El Salvador veri noktasından geçen en iyi model bulunmuş olur.

United States gözlemi içinde Tablo 4.2 dekine benzer bir tablo oluşturulur ve kümü-latif toplama bakıldığında United States verisinden geçen modelin aynı zamanda El Salva-dor veri noktasından da geçtiğini görülür. Bu, gecen basamakta elde edilen modelin aynısı-dır. Böylece algoritma durur. LAD regresyon modeli El Salvador veri değerinden gecen

modeldir. Eğimi ve dır.

LAD regresyon modeli, olur.

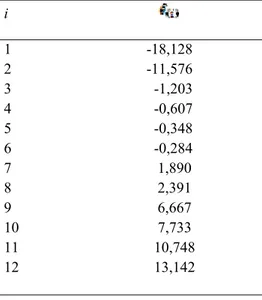
Tablo 4. 3. Artan düzende doğum oranı verisinin LAD regresyon analizindeki

sıfır olmayan artıkları i 1 -18,128 2 -11,576 3 -1,203 4 -0,607 5 -0,348 6 -0,284 7 1,890 8 2,391 9 6,667 10 7,733 11 10,748 12 13,142

Tablo 4.3 de sıfır olmayan artıklar listelenmektedir. m=n-2=12 ve

04 , 3 12 2 / 13 2 / ) 1 (m+ − m = − = , k₁ =3 ve k₂ =10dır.τˆ = 12

[

]

dolayı τˆ =7,739 ve

∑

i dır. est.SD(βˆ)=7,739/ 3151=0,1379 dur. p değerini hesaplamada t dağılımı n–2=12 serbestlik derecesi ile kullanılır. t tablosun-da, bulunan p değeri 0.001 ve 0.01 arasındadır. Regresyon modelinin eğiminin gerçek-ten negatif olduğu sonucuna varılır. EKK testi bu veri setine uygulandığı zaman, p değeri 0.018 bulunur. Bu da β ≠0 olduğunu gösterir.

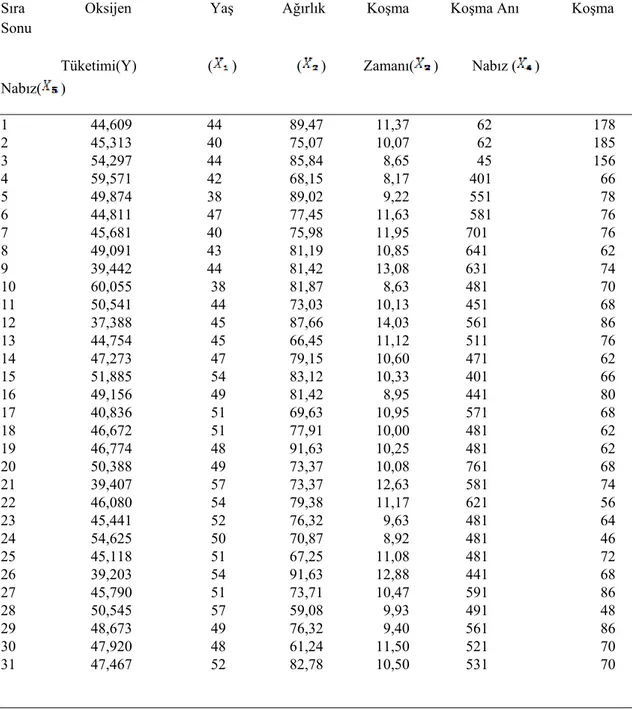
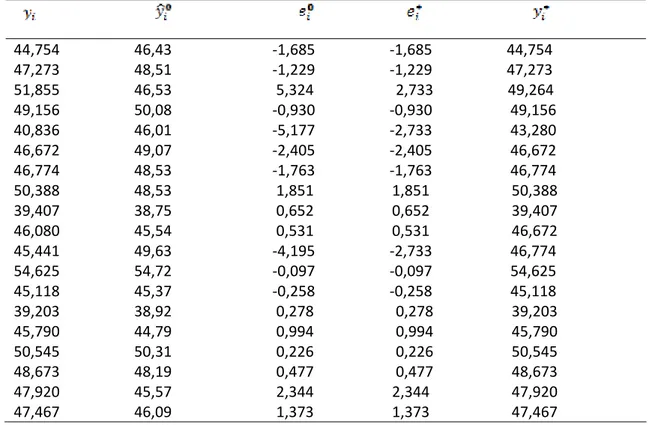
4.6. Çoklu Regresyon Örneği

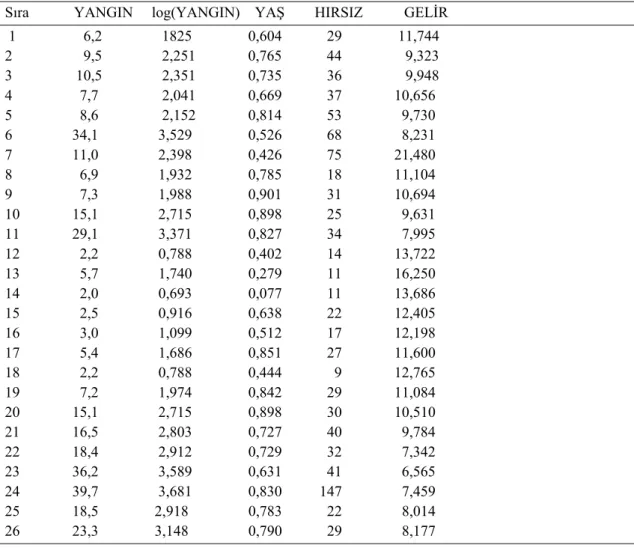
Bu veri 1975 yılında Chicago’da 45 yerleşim alanından alınmıştır. YANGIN sü-tunu o bölgede 1000 evde meydana gelen yangın sayısıdır. YAŞ kolonu 1940 dan önce yapılan evlerin oranıdır. HIRSIZ lık sütunu, hırsızlık sayısını ve GELİR sütunu da aile-lerin ortalama gelirini $1000 olarak gösterilmektedir. Bu veri seti için LAD regresyon yöntemi uygulanarak. YANGIN sayısının bu bölgenin üç karakteristiğine (YAŞ, HIR-SIZ ve GELİR) nasıl bağlı olduğu ortaya çıkarılmak isteniyor. (Dodge, 1993)

Tablo 4.4. Yangın Verisi

Sıra YANGIN log(YANGIN) YAŞ HIRSIZ GELİR

1 6,2 1825 0,604 29 11,744 2 9,5 2,251 0,765 44 9,323 3 10,5 2,351 0,735 36 9,948 4 7,7 2,041 0,669 37 10,656 5 8,6 2,152 0,814 53 9,730 6 34,1 3,529 0,526 68 8,231 7 11,0 2,398 0,426 75 21,480 8 6,9 1,932 0,785 18 11,104 9 7,3 1,988 0,901 31 10,694 10 15,1 2,715 0,898 25 9,631 11 29,1 3,371 0,827 34 7,995 12 2,2 0,788 0,402 14 13,722 13 5,7 1,740 0,279 11 16,250 14 2,0 0,693 0,077 11 13,686 15 2,5 0,916 0,638 22 12,405 16 3,0 1,099 0,512 17 12,198 17 5,4 1,686 0,851 27 11,600 18 2,2 0,788 0,444 9 12,765 19 7,2 1,974 0,842 29 11,084 20 15,1 2,715 0,898 30 10,510 21 16,5 2,803 0,727 40 9,784 22 18,4 2,912 0,729 32 7,342 23 36,2 3,589 0,631 41 6,565 24 39,7 3,681 0,830 147 7,459 25 18,5 2,918 0,783 22 8,014 26 23,3 3,148 0,790 29 8,177

Tablo 4.4 Yangın Verisi Devamı

Sıra YANGIN log(YANGIN) YAŞ HIRSIZ GELİR

27 12,2 2,501 0,480 46 8,212 28 5,6 1,723 0,715 23 11,230 29 21,8 3,082 0,731 4 8,330 30 21,6 3,073 0,650 31 5,583 31 9,0 2,197 0,754 39 8,564 32 3,6 1,281 0,208 15 12,102 33 5,0 1,609 0,618 32 11,876 34 28,6 3,353 0,781 27 9,742 35 17,4 2,856 0,686 32 7,520 36 11,3 2,425 0,734 34 7,388 37 3,4 1,224 0,020 17 13,842 38 11,9 2,477 0,750 46 11,040 39 10,5 2,351 0,559 42 10,332 40 10,7 2,370 0,675 43 10,908 41 10,8 2,380 0,580 34 11,156 42 4,8 5,690 0,152 19 13,323 43 10,4 2,342 0,408 25 12,960 44 15,6 2,747 0,578 28 11,260 45 7,0 1,946 0,114 3 10,080 46 7,1 1,960 0,492 23 11,428 47 4,9 1,589 0,466 27 13,731

Yangın değişkeni logaritması alınarak modele dahil edilmiştir. . Model şu şekil-de yazılır:

Burada Y=log(YANGIN), X =YAŞ, ₁ X =HIRSIZ ve ₂ X =GELİR ₃ dir.

İlk dört gözlem alınarak algoritmaya başlanır.

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 656 , 10 37 669 , 0 1 948 , 9 36 735 , 0 1 323 , 9 44 765 , 0 1 744 , 11 29 604 , 0 1 A ve ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 041 , 2 351 , 2 251 , 2 825 , 1 c

dir. İlk tahmin vektörü

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = = 443 , 2 1161 , 0 26 , 23 93 , 47 -c A b -1

Yön vektörlerinin ilk matrisi, ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − − − − = 91 , 21 185 , 8 51 , 15 59 , 14 7321 , 0 4656 , 0 6744 , 0 5233 , 0 3 , 261 71 , 79 6 , 176 5 , 164 4 , 436 8 , 157 3 , 308 9 , 284 1 -A şeklindedir.

Yeni tahmin edilen değerin b den daha iyi olması istenir. Bu, _{A nın dört ko-}-1

lonu tarafından gösterilen dört yön ve onların negatifleri için hesaplayarak yapılır. A -1

in birinci kolonu d i göstermektedir. Tablo 4.4 de gösterilmektedir. Modelde 7. ve ₁

24. gözlemler ihmal edilmektedir. z_i = y_i−b′x_i ve w_i =d′₁x_i olduğuna dikkat edilir. Örneğin,

[

]

[

]

Tablo 4. 5. t=0 olduğunda Eşitlik (4.10) nun Elle Hesaplanması Sıra işaret 1 0 1 0 1 2 0 0 * 0 3 0 0 * 0 4 0 0 * 0 5 3,08 18,71 + 18,71 6 -4,16 -42,68 + 48,68 8 1,48 15,67 + 15,67 9 4,74 35,67 + 35,67 10 2,10 16,43 + 16,43 11 -1,84 -14,42 + 14,42 12 -2,65 -11,21 + 11,21 13 1,27 3,88 + 3,88 14 -10,74 -66,75 + 66,75 15 0,68 12,57 + 12,57 16 -3,15 -13,78 + 13,78 17 5,02 38,48 + 38,48 18 -4,59 -20,88 + 20,88 19 4,07 30,51 + 30,51 20 4,83 31,87 + 31,87 21 0,33 -1,62 - 1,62 22 -6,41 -41,11 + 41,11 23 -8,87 -63,85 + 63,85 25 -4,67 -27,65 + 27,65 26 -3,06 -20,46 + 20,46 27 -8,86 -62,04 + 62,04 28 0,53 8,62 + 8,62 29 -7,03 -41,01 + 41,01 30 -12,50 -80,29 + 80,29 31 -2,74 -15,50 + 15,50 32 -10,51 -66,23 + 66,23 33 0,78 6,80 + 6,80 34 0,52 -0,15 - 0,15 35 -7,03 -45,58 + 45,58 36 -6,44 -38,57 + 38,57 37 -10,46 -70,71 + 70,71

_{Tahminin ilk vektörü i =1,2,3,4 için yi =b′xi seçilmektedir. Bu}

0 4 3 2

1 = z = z = z =

z durumu açıklanır. A nın i sırası xi′dir ve -1

A ın birinci kolo-nu d dir. Böylece ₁

( )

i

w ‘yi veren x ′_i d₁ ifadesi olur. _{AA nın} -1

z ve i w hesabından sonra i z / in işareti tanımlanmaktadır. Eğer i wi wi =0 ise bu oran tanımlanmamaktadır. Ama bu önemli değildir çünkü örnek veri noktası sap-maya w_i =0_{dan dolayı katkıda bulunmamaktadır.} z / ’nin işretinin negatif veya _i w_i değerinin sıfır olması durumunda wi ’ ler toplanır ve pozitif olduğunda wi ’ler çıka-rılarak tüm i’ ler için hesaplanır.

1

d için hesap yapıldığında, -d yönündeki sapma hesabı için kısa bir yol var-₁ dır. z nin değeri ve i wi benzer şekilde kalmakta ama w in işareti değişmekte ve bu i yüzden z / işaretleri i wi zi =0 noktaları dışında aynı kalmaktadır. zi =0 olan dört veri noktası vardır, biri w_i =1 ve diğeri w_i =0 dır. -d yönündeki sapmayı ima eden ₁ bu değer –(-1221-1)+1=1223 dur. Genel olarak d ve d- yönündeki sapma 2 ile top-lanarak diğer yönün büyüklüğü bulunur.

A in dört kolonu için sapmalar ve bunların negatifleri -1221, 1223, -1323, -1 1325, 645, -652, 1903 ve -1901 dır. Bunlardan − yönündeki -1901 en küçük nega-d₄ tif değerdir. Böylece en iyi vektör b t+ d₄ biçiminde olur.

Bu algoritmada (0,0) dan geçen en iyi doğruyu (w₁₄,z₁₄) verir. A nın dördün-cü satırı yerine 14. gözlem alınacaktır. Yani bir sonraki adım,

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 686 . 13 11 077 . 0 1 948 . 9 36 735 . 0 1 323 . 9 44 765 . 0 1 744 . 11 29 604 . 0 1 A ve ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 693 0 351 2 251 2 825 1 . . . . c bulunur.

Her bir adımda dört veri noktası gerekli regresyon eşitliğini tanımlamaktadır. Bunlar temel olarak adlandırılır. Her bir badımda, veri noktalarından biri temeldeki yerine konulmaktadır. 1, 2, 3, 4 veri noktaları ile ilk temel olarak başlanmaktadır. Bi-rinci adımda, 4. nokta, 14. nokta ile yer değiştirir. Algoritma şu şekilde ilerlemektedir,

39. tarafından, 10., 19. tarafından, 14., 45. tarafından ve 23., 37. tarafından temelden çıkarılır. Sonra bu en son adımda, temel 37, 19, 39 ve 45 noktalarından oluşmaktadır. Sekiz yön için sapmalar bu adımda hesaplandığı zaman, hepsi pozitif bulunmaktadır. Böylece algoritma sona erer. LAD regresyon eşitliği 37, 19, 39, 45 veri noktaları tara-fından tanımlanır, ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = − 2425 . 0 01299 . 0 09098 . 0 362 . 4 946 . 1 351 . 2 974 . 1 224 . 1 080 . 10 3 114 . 0 1 332 . 10 42 559 . 0 1 084 . 11 29 842 . 0 1 842 . 13 17 020 . 0 1 ˆ 1 β Yˆ =4.362−0.09098X1+0.01299X2−0.2425X3

Eşitlik (4.12) deki F_LAD hesaplansın. Artıklar

) 2425 . 0 01299 . 0 09098 . 0 362 . 4 ( ˆ_i y_i x_i1 x_i2 x_i3

e = − − + − Tablo 4.5 de verilmiştir.

Mut-lak değerlerinin toplamı SAR_tüm =15.78 dir. m=41 ve sıfır olmayan artıklar τˆ ‘yi hesaplamada kullanılmıştır. Böylece (41+1)/2- 41 =14.60 elde edilir. k₁ =15 ve

27 2 = k dır. Tablo 4.5 te de eˆ(15) =−0.1492 ve eˆ( )27 =0.2488 dır. Bu yüzden 6371 . 0 4 / ) 1492 . 0 2488 . 0 ( 41 ˆ= + =

τ olarak bulunur. İndirgenmiş model Y = β₀+e

dir. β0 in LAD tahmini bu modelde basit örnek ortalaması y , yangın verisi için 2.251 dır. SARindirgenmiş=

∑

04 . 12 ) 2 / 6371 . 0 ( 3 / ) 78 . 15 29 . 27 ( − = = LAD F dır.

p değerine bakıldığında, (p−q)(1−(p−q)/n)FLAD =3(1−3/45)(12.04)=33.71olur. p

değeri Prob

[

]

[

]

5. M- REGRESYON 5.1. Regresyon Tahmini

EKK tahmininde , yi minimum yapan

α

LAD tahmininde

∑

α

_α

_∑

_{( )}

i eˆ

ρ yı minimum yapan tahminlerdir. Burada ρ

( )

5.1.1. Huber M- tahminin tanımı

Huber M tahmini olarak adlandırılan M tahminleri ρ

( )

e yı bulmaktadır. EKK tahminine göre LAD tahmininin avantajı aykırı gözlemlere karşı daha duyarlı olmasıdır.

(5.1)

biçiminde dönüşür (Jabr, 2005). k =1.5σˆ dır. Burada σˆ rastgele hataların standart sapmasıdır. σ nın tahmini σˆ =1.483MAD olarak alınır burada MAD, e mutlak sapmanın ortalamasıdır. Eğer rastgele hatanın dağılımı normal ise, Huber M tahmini αˆ ve βˆ_{, a ve b yi minimum yapan değerlerdir.}

∑

(

)

5.1.2. Algoritma

Algoritmaya başlarken α ve β nın ilk tahminler için EKK tahminleri alınır. Bunlar σ nın tahmini ve sapmaların hesaplanmasında kullanılır. Algoritma bu şekilde tekrarlanır, önceki tekrarlara benzeyen tahminler araştırılır.

Algoritmanın her basamağında ve , α ve β nın tahminleridir. Sapmaları ve hesaplanır. değeri büyük sapmaları atarak düzenlenir. nın sapması regresyon modeli tahmininde dır.

Böylece olur. tanımlanır, ayarlanmış

sapmadır ve dan elde edilmiştir. Sapmaların hiçbiri mutlak değerdeki dan büyük değildir. Yani , ve arasında ise dır, , dan küçük ise dır ve , den büyük ise dır. ve nın yeni tahminleri, olarak düzenlenen veride ele alınan EKK tahminidir.

5.1.3. Algoritmanın Gerçekleşmesi

Eşitlik (5.2) de a ve b nın türevleri alınıp sıfıra eşitlenip minimum hale getiri-lir,

(5.3)

nın türevi için değeridir ve , her için de-ğerine eşittir. Eşitlik (5.3) de çözümler sapmalara göre aynı kalmaktadır. Eğer

sapma-lar , ve 1 arasında ise seçilen dir. ,

dan küçük ise dır ve den büyük ise dır.

Eşitlik (5.3) çözümünü değiştirmeden düzenlenmiş değeri ile yer değiştirilir(Dodge, 1993).

dır. ifadesinin en

M- regresyon yöntemi için regresyon model belirlenmesinde kullanılan algo-ritma özetle (Yorulmaz, 2003);

1. ve tahmin değerleri EKK yöntemi ile hesaplanır.

2. MAD ve değerleri bulunur.

3. Bulunan değerleri üzerinden fonksiyonu kullanılarak düzeltilmiş

değerleri bulunur.

4. değerleri kullanılarak bulunur ve EKK ile ve tahmin

değer-leri hesaplanır.

5. ve için güncellenen tahminler ile bir önceki tahmin değerleri karşı-laştırılır.

6. Tahminler arasındaki fark 0.001 den küçükse işlem bitirilir.

7. Aksi halde ve değerleri ve olarak atanır ve Adım 2 ye

dö-nülür.

Ağırlıklandırılmış EKK yöntemi, regresyon analizinde kullanılan bazı gözlem değerlerinin diğerlerine göre oldukça farklı olmasından yola çıkarak bulunmuştur. Ağırlıklar hata teriminin ters bir fonksiyonudur ve aşağıdaki özellikleri sağlar (Gujarati, 1999);

1. Gözlem değerleri ağırlıklı fonksiyonu tarafından belirlenen aralık içerisinde ise

ağırlıklı değer 1 olacaktır.

2. Gözlem değerleri ağırlıklı fonksiyonu tarafından belirlenen aralık içerisinde

değil ise ağırlıklı değer 1 değerinden farklıdır.

3. değerlerinin toplamı EKK ile minimize edilecektir. hata teriminin bir fonksiyonudur. Ve,

Parametreler şu şekilde bulunur (Gujarati, 1999); (5.5) Burada ve (5.6) olarak bulunur.

EKK yönteminde hata kareler toplamını minimize ederken tüm değerlerine ağırlıklı değer olarak 1 değeri verilir. M regresyon yönteminde hata kareler topla-mını minimum yapmak yerine hata terimlerinin fonksiyonun minimize edilir.

olarak tanımlanır. Standartlaştırılmış hata terimlerinin fonksiyonu,

(5.7)

şeklindedir. k=1,5dır. Bu fonksiyonun türevi alınarak,

elde edilir. Ağırlıklı fonksiyon ise,

dır. Ağırlık değeridir (Şanlı, 2005).

(5.9)

şeklindedir.

M ağırlıklı regresyon yöntemin algoritması şu şekildedir (Fox, 2002),

1. ve tahmin değerleri EKK yöntemi ile hesaplanır.

2. değerleri bulunur. 3. MAD değeri bulunur.

4. Ağırlıklı değerleri hesaplanır.

5. Ağırlıklı EKK yöntemi ile ve tahmin değerleri hesaplanır.

6. ve değerleri ve değerleri karşılaştırılır.

7. Tahminler arasındaki fark 0.001 den küçükse işlem bitirilir, aksi halde Adım

2 ye dönülür.

5.2. Testi

Kesim 5.4 de çoklu lineer regresyon modelinde testinin nasıl tanımlandığı gösterildi. testi p=1 ve q=0 için özel bir durumdur. Test istatistiği, Eşitlik (5.11) deki dır. p değeri olarak hesaplanır. , 1 ve n-2 serbestlik derecesi ile dağılımına sahip rastgele değişkeni göstermektedir.

olmak üzere burada ve t, n-2 serbestlik derecesi ile t dağı-lımına sahip rastgele değişkeni göstermektedir.

5.3. Regresyon Katsayısının Tahmini

Bu yöntem basit regresyondaki M tahmininin bulunması için kesim 5.1 de tanımlanan yöntemin genel şeklidir. Huber M tahmini,

(5.10) ifadesini minimum yapan değerleridir. , eşitlik (5.1) de tanımlanan fonksiyondur.

Matris gösterimi ile;

ve

Biçiminde verilir. Huber M tahmini; vektörü yi minimize eden b vektörü olarak tanımlanır (Dodge, 1993).

5.3.1. Algoritma

Regresyon katsayısı vektörü ilk olarak EKK ile tahmin edilir. nın tah-mini, tahmini ve sapmaların hesaplanmasında kullanılır. nın ilk tahminine ula-şana kadar bu algoritma tekrar eder. Sapmalar ve hesap-lanır. Büyük sapmalardan kurtulmak için y değerlerinin ayarlaması yapılır. Regresyon

tahminindeki nin sapması dır. + şeklindedir ve

denkleminde , den elde edilmiş ayarlanmış sapmadır. Hiçbir sapma mutlak değerce 1.5 den büyük değildir. (Dodge, 1993).

5.4. Testi

Genel lineer regresyon modeli deki

Artıkların toplamı için STR sabit olmaktadır. ve olarak verilir. fonksiyonu eşitlik (5.1) de ki gibidir. Hesaplanan tüm modeldeki artıklarda kullanılır. Testteki yaklaşık p değeri EKK testine benzer yolla olarak hesaplanır. , p-q ve n-p-1 serbestlik derecesi ile dağı-lımına sahip rastgele değişkeni göstermektedir.

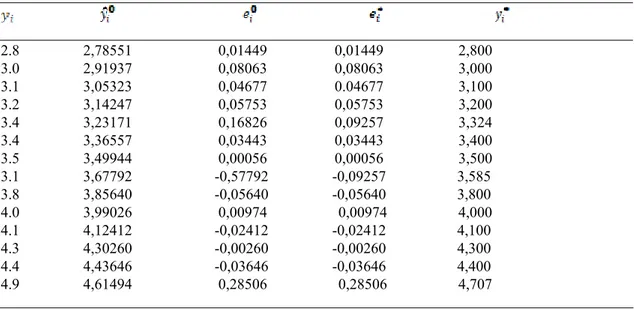
5.5. Basit Regresyon Örneği

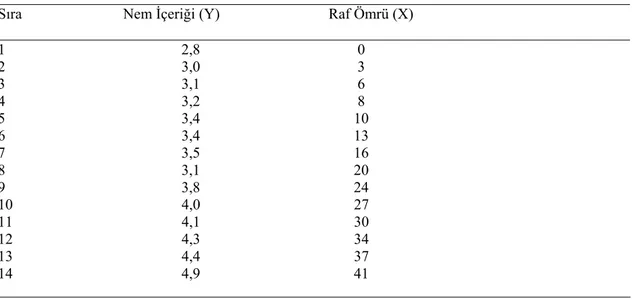
Bir gıda ürünün son kullanım süresi üzerine yapılan çalışma Tablo 5.1 de gös-terilmiştir. Raftaki zamana bağlı nem içeriğinin görüldüğü bu veri seti kullanılacak-tır.(Dodge, 1993)

Tablo 5. 1. Raf Ömrü Verisi

Sıra Nem İçeriği (Y) Raf Ömrü (X) 1 2,8 0 2 3,0 3 3 3,1 6 4 3,2 8 5 3,4 10 6 3,4 13 7 3,5 16 8 3,1 20 9 3,8 24 10 4,0 27 11 4,1 30 12 4,3 34 13 4,4 37 14 4,9 41

İlk olarak X= Raftaki günler ve Y= Nem içeriği ile verinin doğrusu oluşturulur. Basit lineer regresyon modeli Y =α+βx+e nin en iyi model olduğu görülmektedir.