Yeni kesikli dağılımlar ve özellikleri

T.C.

SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ

YENİ KESİKLİ DAĞILIMLAR VE ÖZELLİKLERİ

Kadir KARAKAYA YÜKSEK LİSANS TEZİ İstatistik Anabilim Dalını

AĞUSTOS-2015 KONYA Her Hakkı Saklıdır

TEZ BİLDİRİMİ

Bu tezdeki bütün bilgilerin etik davranış ve akademik kurallar çerçevesinde elde edildiğini ve tez yazım kurallarına uygun olarak hazırlanan bu çalışmada bana ait olmayan her türlü ifade ve bilginin kaynağına eksiksiz atıf yapıldığını bildiririm.

DECLARATION PAGE

I hereby declare that all information in this document has been obtained and presented in accordance with academic rules and ethical conduct. I also declare that, as required by these rules and conduct, I have fully cited and referenced all material and results that are not original to this work.

Kadir KARAKAYA Tarih: 18/08/2015

iv

YÜKSEK LİSANS TEZİ

YENİ KESİKLİ DAĞILIMLAR VE ÖZELLİKLERİ

Kadir KARAKAYA

Selçuk Üniversitesi Fen Bilimleri Enstitüsü İstatistik Anabilim Dalı

Danışman: Doç.Dr. İsmail KINACI 2015, 51 Sayfa

Jüri Doç.Dr. İsmail KINACI

Prof.Dr. Mehmet Fedai KAYA Yrd.Doç.Dr. Ahmet PEKGÖR

Bu tez çalışmasında, k-ardıl q-Binom dağılımının genellemesi yapılmıştır. , , q n k l

N ; n uzunluğundaki iki sonuçlu deneme dizilerinde l-örtüşen ardışık k başarı sayılarını temsil etmek üzere,

, , q n k l

N rasgele değişkenine ilişkin dağılım fonksiyonu ve ilk iki moment elde edilmiştir. Ayrıca i-1 ile i. şoklar arasında geçen zamanın 1/pi ortalamalı geometrik dağılıma sahip olduğu varsayılarak yeni bir şok model önerilmiştir. Önerilen bu modele ilişkin olasılık fonksiyonu, olasılık üreten fonksiyonu, beklenen değeri ve varyansı elde edilmiştir. Yeni dağılımın gerçek veri modellemesini göstermek için ayrıca sayısal bir değerlendirme yapılmıştır.

Anahtar Kelimeler: İki sonuç alan denemeler, Kesikli Dağılımlar, Olasılık Üreten Fonksiyonu, Tekrar İstatistiği, q-Dağılımlar, δ- Şok Model

v MS THESIS

NEW DISCRETE DISRIBUTION AND THEIR PROPERTIES

Kadir KARAKAYA

THE GRADUATE SCHOOL OF NATURAL AND APPLIED SCIENCE OF SELÇUK UNIVERSITY

THE DEGREE OF MASTER OF SCIENCE IN STATISTICS

Advisor:

Assoc. Prof. Dr. İsmail KINACI Jury

Assoc. Prof. Dr. İsmail KINACI Prof.Dr. Mehmet Fedai KAYA

Assist.Prof.Dr. Ahmet PEKGÖR 2015, 51 Pages

In this study, we consider a generalization of a q-Binomial distribution of order k. Nn k lq, , denote the number of l-overlapping success runs of lenght k in n Bernoulli trials under q-sequence of binary trials. The probabilty mass function, first and second moment of , ,

q n k l

N random variables are obtained. Also we think a shock model. We assume that the interarrival times between two consecutive shocks follow a geometric distribution with mean 1/pi.The pmfprobabity generating function, mean and variance

of the system are obtained. A numerical example is also given to show the capacity of new distribution for modelling any real data.

Keywords: Binary trials, Discrete Distributions, Probabity Generating Function, Run Statistic, q-Distributions, δ-Shock Model

vi

Bu çalışmada büyük emeği geçen, yol göstericiliği ve bilgisiyle yönlendiren değerli danışmanım Doç. Dr. İsmail KINACI’ ya, bu tez çalışmasındaki katkılarından dolayı Prof. Dr. Coşkun KUŞ Hocama, değerli arkadaşlarım Arş. Gör. Yunus AKDOĞAN ve Fatih ŞAHİN’ e teşekkürü bir borç bilirim. Ayrıca her zaman yanımda olan eşim Emine KARAKAYA’ ya ve bütün aileme teşekkür ederim. TÜBİTAK 2211 Yurt İçi Lisansüstü Burs Programına desteğinden dolayı teşekkür ederim.

Kadir KARAKAYA KONYA-2015

vii İÇİNDEKİLER ÖZET ... iv  ABSTRACT... v  ÖNSÖZ ... vi  İÇİNDEKİLER ...vii  1.  GİRİŞ ... 1  2.  TEMEL KAVRAMLAR ... 3 

2.1. q-Sayılar İlişkin Bazı Bilgiler ... 3 

2.2. Momentler... 4 

2.3. Olasılık Üreten Fonksiyon ... 4 

2.4. Oran Tahmini... 4 

3.  BAZI TEKRAR İSTATİSTİKLERİ VE DAĞILIMLARI... 6 

3.1. q-Binom Dağılımı ... 6 

3.2. k-ardıl Binom Dağılımı... 7 

3.3. k-ardıl q-Binom Dağılımı... 7 

3.4. k-ardıl Geometrik Dağılımı... 8 

3.5. k-ardıl q- Geometrik Dağılımı ... 9 

3.6. Ling’s Binom Dağılımı... 10 

3.7. q-Ling’s Binom Dağılımı... 11 

4. q_{, ,} n k l N RASGELE DEĞİŞKENİNİN DAĞILIMI VE BAZI ÖZELLİKLERİ... 12 

4.1. q_{, ,} n k l N rasgele değişkenin dağılımı ... 12 

4.2. q_{, ,} n k l N rasgele değişkenin beklenen değeri ... 17 

5. YENİ BİR δ-ŞOK MODELİ... 25 

5.1. Tanımlanan Sistem ve Sistemin Olasılık Fonksiyonu ... 25 

5.2. Olasılık Üreten Fonksiyonu ve Momentler ... 31 

5.3. Oran Tahmini... 34 

5.4. Sayısal Bir Örnek... 37 

6. SONUÇLAR VE ÖNERİLER ... 39 

KAYNAKLAR ... 40 

1. GİRİŞ

İki sonuçlu denemeler (binary trials), Başarı-Başarısız, Sağlam-Bozuk gibi sonuçlar alan ve genellikle “1” ve “0” elemanları ile gösterilen denemelerdir. İki sonuç alan denemeler kullanılarak birçok tanım ortaya atılmıştır. İki sonuç alan denemelerin üst üste gelen aynı tür elemanlarının (1 veya 0) diğer türden elemanla sonlanması ile oluşan alt dizilere tekrar (run) adı verilmektedir. İki değer alabilen tekrar istatistikleri birçok uygulama alanında kullanılmaktadır. Bu uygulama alanlarından bazıları rasgelelik testleri, istatistiksel süreç kontrolü, güvenirlik ve moleküler biyoloji olarak sıralanabilir.

İlk olarak De Moivre (1738) yılında yazmış olduğu kitabında tekrar istatistikleri ile alakalı problemler ortaya koymuştur. 1940’ lı yıllarda tekrar istatistikleri ile alakalı çalışmalara olan ilgi ortaya çıkmaya başlamıştır. İlk olarak bir dizinin rasgele dizilip dizilmediğinin test edilmesi amacıyla run testi kullanılmıştır. Bu testteki test istatistiğine ilişkin bazı sonuç çıkarımlar Mood (1940) ve Wald ve Wolfowitz (1940) çalışmalarında incelenmiştir. Daha sonraki yıllarda birçok tekrar istatistiği tanımlanmış ve tanımlanan tekrar istatistiklerine ilişkin bazı sonuç çıkarımları yapılmıştır. Literatürde tanımlanmış olan tekrar istatistiklerine ilişkin dağılım fonksiyonlarının elde edilmesinde kombinatorik yaklaşım, olasılık üreten fonksiyonu yaklaşımı ve Markov zinciri yaklaşımı yöntemleri kullanılmaktadır. Mood (1940), Wald ve Wolfowitz (1940), Monsteller (1941) ve Wolfowitz (1943) tekrar istatistiklerinin temelini teşkil eden toplam tekrar sayısını (Rn) ve toplam

tekrar başarı sayısını (Rn(1)) temel alan çalışmalarını yapmışlardır. Philippou ve

Makri (1986), Hirano (1986) iki sonuç alabilen n uzunluğundaki denemedeki k uzunluğuna sahip başarı tekrarlarının sayısını gösteren En,k tekrar istatistiği

üzerinde, Muselli (1996) yine n uzunluğundaki denemedeki k ve k’ dan büyük uzunluğuna sahip başarı tekrarların sayısını gösteren Gn,k tekrar istatistiği üzerinde,

Hirano(1986), Aki ve Hirano (1988), Phillippou ve Makri (1986), Godbole (1992) n uzunluğuna sahip bir denemede örtüşmeyen (non-overlapping) ardıl olarak k tane başarı sayısını gösteren Nn,k üzerine, Ling (1988), Ling (1989), Hirano ve

ark.(1991), Koutras ve Alexandrou (1997) n uzunluğuna sahip bir denemede örtüşen (overlapping) ardıl olarak k tane başarı sayısını gösteren Mn,k üzerine

çalışmalar yapmışlardır. Tekrar istatistikleri kullanılarak Geometrik, Binom, Negatif Binom gibi bilinen bazı dağılımları genellemiştir. Philippou ve ark. (1983) geometrik dağılımını, Yalçın (2013) Ling’s Binom dağılımını, Philippou (1984)

Negatif Binom dağılmını, Yalçın ve Eryılmaz (2014) k-ardıl geometrik ve k-ardıl binom dağılımlarını genellemişlerdir.

Yine 0 ve 1 değerlerini alabilen iki sonuçlu denemeleri göz önüne alalım. Ancak buradaki 0 ve 1 değerlerine yükleyeceğimiz anlam “0: şok” “1: şok değil” şeklinde olsun. Temelde iki sonuç alan denemeler üzerine kurulu olarak şok modeller tanımlanabilir. Şok modeller, rasgele büyüklükteki bir şokun rasgele bir zamanda meydana geldiği sistemlerdir. Üç farklı tür şok model bulunmaktadır. Bunlar tekrar şok modelleri, aşırı şok modeller ve birikimli şok modellerdir. Şok model son yıllarda büyük ilgi çeken konular arasında yer almaktadır. Sumita ve Shanthikumar (1985), Gut (1990), Mallor ve Omey (2001) şok modelle ilgili incelemelerde bulunmuşlardır. Bir sistemde iki ardışık şok arasındaki süre belirli bir δ değerinin altında ise böyle sistemlere δ-şok model adı verilmektedir. δ-şok model Li ve Kong (2007), Eryılmaz (2012) tarafından çalışılmıştır. Eryılmaz (2013) çalışmasında, iki şok arasındaki geçen sürenin 1/p ortalamalı geometrik dağılıma sahip olduğu bir binom süreci olduğunu ele almış ve δ-şok modelin kesikli versiyonunu incelemiştir.

Bu çalışmada herbir başarısızlıktan sonra başarı olasılığı geometrik olarak azalan n tane Bernoulli denemesindeki l tanesi örtüşen k-ardıl başarıların sayısı şeklinde yeni bir rasgele değişken tanımlanmıştır. Ayrıca iki şok arasında geçen zamanın(yani yapılan deneme sayısının) 1/ p_i ortalamalı geometrik dağılıma sahip olduğu varsayılarak yeni bir δ-şok model önerilmiştir.

Bu tez çalışmasının ikinci bölümünde genel tanımlar verilmiştir.

Çalışmanın üçüncü bölümünde belirli varsayımlar altında literatürde tanımlı çeşitli tekrar istatistiklerine ilişkin olasılık dağılımları ve bazı özellikleri verilmiştir.

Çalışmanın dördüncü bölümünde ise yeni tanımlanmış olan Nq

n,k,l rasgele

değişkenine ilişkin dağılım fonksiyonu, ilk iki momenti ele alınmıştır. Ayrıca bazı nümerik sonuçlar verilmiştir.

Çalışmanın beşinci bölümünde ise yeni bir δ-Şok model tanımlanacaktır. Tanımlanacak olan modelin olasılık fonksiyonu, olasılık üreten fonksiyonu, ortalama ve varyans değerleri verilmiştir. Yeni dağlımın gerçek veri modelleme performansını görmek için ayrıca sayısal bir değerlendirme yapılmıştır.

2. TEMEL KAVRAMLAR

2.1. q-Sayılar İlişkin Bazı Bilgiler

x ve q reel sayılar (q≠1) ve k bir tamsayı olsun.

[ ]

x

(

qx

)

(

q

)

q = 1− /1− q-sayısı

olarak adlandırılır.

[ ]

k q ise q-tamsayı olarak adlandırılır.

[ ]

xq q-sayısının k. sıra

faktöriyeli

[ ]

x _{k q,} =

[ ] [

x _q x−1 ...

] [

_q x k− +1 ,

]

_q k=0,1, (2.1) olarak ifade edilir ve x’ in k -ardıl q-faktöriyeli olarak adlandırılır. q-Binom katsayısı (ya da Gaussian Polinomu)

[ ]

[ ]

! , 0,1,... , ₌ = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ k k x k x q q k q

olarak ifade edilir(Charalambides (2010)).

Phillips (1997) çalışmasında, [0,1] aralığında değer alabilen herhangi bir sürekli fonksiyonun n -ardıl q-Bernstein polinomunu

,... 2 , 1 , ) 1 ( ) ( ) ; ), ( ( 0 1 1 ₌ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ =

∑

∏

= − = − _n xq x r n t f x q t f B n r r n i i r q r n

olarak ifade etmiştir. Burada 0<x<1,q>0vetr =

[ ] [ ]

r q / n q,r=0,1,...,nşeklindedir.

q=1 olması durumunda ise bu polinom bilinen k-ardıl Bernstein polinomuna

( )

0 ( ( ); ) n ( ) r(1 ) ,n r 1, 2, 2.2 n r r n B f t x f t x x n r − = ⎛ ⎞ = _{⎜ ⎟} − = ⎝ ⎠

∑

… dönüşmektedir. 1 , 1 ( , ) rn r (1 i ), 0,1,..., 0 1, 0 1 n r i q n P x q x xq r n x q r − − = ⎡ ⎤ =_{⎢ ⎥} − = < < < < ⎣ ⎦

∏

(2.3)

formu ise Basis q-Bernstein olarak adlandırılır.

II’inskii ve Ostrovska (2002) ve Ostrovska(2003) çalışmalarında q-Berntein Polinomunun yakınsaması üzerine çalışmalar yapmışlardır. Ostrovska (2003) çalışmasında Eşitlik 2.3’ te verilen B_n(f(t),q;x),n→∞ _{q-Bernstein polinomunun} yakınsamasını _x=_q−m, _q>1 _{ve m pozitif tamsayı olması özel durumları altında}

[ ]

1 1 1 , 1 ( ) 1 , ( , ) (1 ) (1 ) , 0,1,..., n r m rm m i n r i q r m n r n r n r q q n P q q q q r n q q m r n r − − − − − − + − = − − + − − − ⎡ ⎤ =_{⎢ ⎥} − ⎣ ⎦ ⎡ ⎤ =_{⎢ ⎥} − = ⎣ ⎦

∏

(2.4)

şeklinde elde etmiştir.

2.2. Momentler

X bir rasgele değişken ve k pozitif bir tamsayı olmak üzere _{E X}

( )

k _{değerine X}

rasgele değişkeninin k. momenti, E X

(

( )k

)

=E X X

(

( −1) (X k− +1)

)

değerine X rasgele değişkeninin k. faktoriyel momenti adı verilmektedir.

2.3. Olasılık Üreten Fonksiyon

X kesikli bir rasgele değişken olmak üzere

( )

0 ( X) ( ) x x z E z p x z

ψ

∞ = = =

∑

değeri olasılık üreten fonksiyonu olarak adlandırılmaktadır. Burada p, X rasgele değişkeninin olasılık fonksiyonudur. Bu seri z ≤1 için mutlak yakınsaktır (Shahbazov (2005)).

Olasılık üreten fonksiyonu kullanılarak X rasgele değişkeninin beklenen değeri ve varyansı ( ) ( ) ( ) ( ) ( ) ( ) 2 1 , 1 1 1 . E X Var X ψ ψ ψ ψ ′ = ′′ ′ ′ = + − ⎡_⎣ ⎤_⎦ şeklinde elde edilir.

2.4. Oran Tahmini

Khan ve ark. 1989 yılında kesikli Weibull dağılımının parametrelerinin tahmini için bir yöntem önermişlerdir. Yöntemin daha iyi anlaşılması için teorisi düzgün geometrik dağılımı üzerinden anlatılmaya çalışılacaktır.

n

X X

X₁, ₂,…, Düzgün-Geometrik dağılımından alınmış rasgele örneklem olmak üzere, i=1 …,2, ,n için (.)ν indikatör fonksiyonu

Xi  1, Xi  1 0, Xi  1 şeklindedir. n

( )

_i i n X

Y =1∑₌₁ν _{, örneklemde bulunan 1 değerinin örneklemdeki oranını} gösterir. Y oranı, P

(

X =1

)

olasılığının yansız ve tutarlı bir tahminidir.

( ) ( 1)

E Y =P X =

Böylece, düzgün geometrik dağılımının p parametresinin oran tahmin edicisi p~

( )

(

p

)

p p y − − = 1 log

3. BAZI TEKRAR İSTATİSTİKLERİ VE DAĞILIMLARI

k-ardıl kesikli dağılımlar istatistiksel kalite kontrol süreci ve güvenilirlik alanlarında

sıkça kullanılmaktadır. Örneğin, ardışık k tane nokta kontrol limitinin dışına düşünüyorsa üretim sürecinin kontrol dışında olduğu söylenebilir. İlk kontrol sinyali dışına düşen bir parçadan önceki toplanan örneklemin sayısı k-ardıl geometrik dağılıma sahip bir rasgele değişkendir. k uzunluğunda tekrarların sayısı ile veya ilk k uzunluğundaki tekrar oluncaya kadar beklenen zaman ile ilgileniliyorsa k-ardıl kesikli dağılımlar uygun birer modeldir (Yalçın ve Eryılmaz (2014)). Aşağıda literatürde yer alan bu modellerden bazıları verilmiştir.

3.1. q-Binom Dağılımı

q-Binom dağılım Charalambides’ in 2010 çalışmasında incelenmiştir.

Bu çalışmada q-Binom dağılımı başarı olasılığı geometrik olarak değişen Bernolli denemeleri üzerine kurulmuştur. (i-1). ile i. başarısızlık arasındaki denemelerde başarısızlık olasılığı

1

1 i , 1, 2, , 0 1,0 1 (3.1)

i

q = −

θ

q− i = < <

θ

< ≤q

eşitliğine göre değişmektedir.

n

Z : n tane iki sonuç alan denemedeki başarıların sayısı olarak tanımlanan bir rasgele

değişken olduğunda bu rasgele değişkenin olasılık fonksiyonu

{

}

1 1 (1 ), 0 1, 0 1, 0,1, , n r r i n i q n P Z r q q r n r θ θ θ − − = ⎡ ⎤ = =_{⎢ ⎥} − < < < < = ⎣ ⎦

∏

(3.2) şeklindedir.

Bu dağılıma ilişkin faktöriyel momentler

[ ]

[ ]

_{[ ]}

, 1 1 (1 ) 1 n j q j j n j _q n E Z q q = j θ = − −

∑

ve

[

]

(

)

[ ]

[ ] [ ]

1 , 2 2 2 1 2 ( ) (1 ) 1 j n j q j j n j i _{q q} n E Z q i j q θ − = = = − −

∑∑

şeklinde ifade edilmiştir.

3.2. k-ardıl Binom Dağılımı

k-ardıl Binom dağılım Philippou ve Makri (1986) çalışmasında incelenmiştir. Bu

dağılım Binom dağılımının bir genellemesidir. Bu dağılımın genellemesi olan k-ardıl q-Binom dağılımı ise Yalçın ve Eryılmaz (2014) tarafından çalışılmıştır.

,

n k

N : n denemedeki k uzunluğunda örtüşmeyen başarıların sayısı olarak tanımlanan bir

rasgele değişken olmak üzere bu rasgele değişkene ilişkin olasılık fonksiyonu

{

}

1 1 1 1 , 0 , , 1 , 0,1, , , , , k k x x k k n n k i x x k x x x q n P N x p x x x x p k + + − = + + + ⎛ ⎞ ⎛ ⎞ ⎡ ⎤ = = _{⎜ ⎟ ⎜ ⎟} = _{⎢ ⎥} ⎣ ⎦ ⎝ ⎠ ⎝ ⎠

∑ ∑

(3.3) şeklindedir. Burada

[ ]

x , x değerinini tam kısmını göstermekte ve x₁, ,x _k

1 2 2 k

x + x + +kx = − −n i kx eşitliğini sağlayan negatif olmayan tamsayılardır.

3.3. k-ardıl q-Binom Dağılımı

k-ardıl q-Binom dağılım Yalçın ve Eryılmaz (2014) tarafından incelenmiştir.

Bu dağılımın olasılık fonksiyonunun elde edilmesinde aşağıdaki Lemma’ dan yararlanılacaktır. Lemma 3.1. 0< ≤ için q 1 2 3 1 1 1 2 ( 1) 0, , 0 ( , , ) r r r r y y r y q y y s y y t k k y y A r s t q + + + − + + = ⎡ ⎤_{+ +}⎡ ⎤₌ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦ ≥ ≥ =

∑ ∑

şeklinde tanımsın. Burada

[ ]

x ‘ler x ’lerin tam kısmını göstermekte ve _i y ’ler _i

tamsayıdır. Ayrıca A r s t için _q( , , )

( 1) 0 ( 1, , ), 1, 0, 0 ( , , ) 1, 1, 0, 0, . . s r j q j q j q A r s j t r s t k s A r s t r s t k d y − = ⎧ _{− − −}⎡ ⎤ _{> ≥ ≥} ⎪ ⎢ ⎥_{⎣ ⎦} ⎪ ⎪⎪ ⎡ ⎤ =_⎨ = ≥ _{⎢ ⎥}= ⎣ ⎦ ⎪ ⎪ ⎪ ⎪⎩

∑

(i-1). ile i. başarısızlık arasındaki denemelerde başarısızlık olasılığı

1

1 i , 1, 2, ,0 1,0 1

i

q _{= −}θq− i_{= < <}θ _{< ≤}q

eşitliğine göre değişen n tane Bernoulli denemesi göz önüne alınsın.

,

q n k

N : n denemedeki k uzunluğunda örtüşmeyen başarıların sayısı olarak tanımlanan bir

rasgele değişken olmak üzere bu rasgele değişkene ilişkin olasılık fonksiyonu 0< ≤ için q 1

{

}

1 , 0 1 (1 ) ( 1, , ), 0,1, , i n kx q n i j n k q i j n P N x q A i n i x x k θ θ − − − = = ⎡ ⎤ = = − + − = _{⎢ ⎥} ⎣ ⎦

∑ ∏

(3.4) şeklindedir.

k-ardıl q-Binom dağılımının olasılık fonksiyonunda q=1 alındığında k-ardıl Binom

dağılımının olasılık fonksiyonu

{

,

}

(

)

1 0 1 ( 1, , ), 0,1, , n kx i q n i n k i n P N x A i n i x x k θ θ − − = ⎡ ⎤ = = − + − = _{⎢ ⎥} ⎣ ⎦

∑

(3.5) elde edilmiş olur.

3.4. k-ardıl Geometrik Dağılımı

k-ardıl Geometrik dağılım Philippou ve ark. (1983) tarafından incelenmiştir. Bu

dağılım Binom dağılımının bir genellemesidir. Bu dağılımın genellemesi olan k-ardıl q-Geometrik dağılım Yalçın ve Eryılmaz (2014) tarafından çalışılmıştır.

k

T : İlk ardışık k başarı elde edilinceye kadar yapılan denemelerin sayısı olarak

tanımlanan bir rasgele değişken olmak üzere bu rasgele değişkene ilişkin olasılık fonksiyonu

{

}

1 1 1 , , 1 , , , k k x x k x k x x k x x q P T x p x k x x p + + + + ⎛ ⎞ ⎛ ⎞ = = _{⎜ ⎟ ⎜ ⎟} ≥ ⎝ ⎠ ⎝ ⎠

∑

(3.6) şeklindedir. Burada x₁, ,x _k x₁+2x₂+ +kx_k = − eşitliğini sağlamayan negatif x k

k

T rasgele değişkeninin olasılık üreten fonksiyonu

( )

_{z p z}k k

(

_{1 pz}

)

_{/ 1}

(

_{z qp z}k k 1

)

_{, z 1}

ψ

_{= − − +} + _≤

şeklindedir.

k

T rasgele değişkeninin beklenen değeri ve varyansı sırasıyla

( )

(

1 k

)

/ k k E T = −p qp ve

( )

₁

(

_{2 1}

)

k 2k 1 _/

(

2 2k

)

k Var T = −⎡_⎣ k+ qp −p + ⎤_⎦ q p olarak verilmiştir.

k=1 alındığı zaman k-ardıl Geometrik dağılım bilinen Geometrik dağılıma gitmektedir.

3.5. k-ardıl q- Geometrik Dağılımı

k-ardıl q-geometrik dağılım Yalçın ve Eryılmaz (2014) tarafından incelenmiştir.

Bu dağılımın olasılık fonksiyonunun elde edilmesinde kullanılan aşağıdaki Lemma’ dan faydalanılacaktır. Lemma 3.2. 2 3 1 1 2 ( 1) 0 , ,0 ( , ) r r r x x r x q x x s x k x k C r s q + + + − + = ≤ < ≤ < =

∑ ∑

burada 0< ≤ ve q 1 x ’ler tamsayıdır. Ayrıca _i C r s için _q( , )

1 ( 1) 0 ( 1, ), 1,0 ( 1) ( , ) 1, 1,0 0, . . k t r q t q q C r s t r s k r C r s r s k d y − − = ⎧ _{− − > ≤ ≤ −} ⎪ ⎪⎪ =_⎨ = ≤ ≤ ⎪ ⎪ ⎪⎩

∑

(i-1). ile i. başarısızlık arasındaki denemelerde başarısızlık olasılığı

1

1 i , 1, 2, ,0 1,0 1

i

q = −θq− i= < <θ < ≤q _{eşitliğine göre değişen Bernoulli denemeleri}

göz önüne alınsın. 0< ≤ için q 1

q k

T : Ardışık ilk k başarı elde edilinceye kadar yapılan denemelerin sayısı olarak tanımlanan bir rasgele değişken olmak üzere bu rasgele değişkene ilişkin olasılık fonksiyonu

{

}

1 1 1 (1 ) ( , ), 1 , 0, . . i x k ik x i i q i j q k _k q q C i x i k x k P T x x k d y θ θ θ − − − = = ⎧ _{− − − ≥ +} ⎪ ⎪ = _{= ⎨} = ⎪ ⎪⎩

∑

∏

(3.7) şeklindedir.

k-ardıl geometrik dağılımın olasılık fonksiyonunda q=1 alındığında başarı olasılığı θ olan Bernoulli denemelerinde ilk ardışık k başarı elde edilinceye kadar yapılan denemelerin sayısının dağılımı yani k-ardıl geometrik dağılım elde edilmiş olur.

3.6. Ling’s Binom Dağılımı

Ling’s Binom dağılımı Ling (1988) tarafından incelenmiştir. Bu dağılımın aynı zamanda k-ardıl Tip II Binom dağılımı olarak da adlandırılmaktadır. Başarı olasılığı p olan bağımsız ve aynı dağılıma sahip n tane Bernoulli denemesini göz önüne alalım.

,

n k

M : n denemedeki k uzunluğunda örtüşen başarıların sayısı olarak tanımlanan bir

rasgele değişken olmak üzere bu rasgele değişkene ilişkin olasılık fonksiyonu

{

}

{

}

1 , 1 , 1 , 1 2 , ( 0) max(0, ) , 0 n n n k x k j n j k j p x n k P M x p q x n k p qP M x j k x n k − + − − = ⎧ ⎪ _{= − +} ⎪⎪ = =_⎨ = − > ⎪ ⎪ = − − ≤ ≤ − ⎪⎩

∑

(3.8)

şeklindedir. Ayrıca M rasgele değişkeninin olasılık fonksiyonu _{n k,}

{

}

1 1 2 1 1 2 , 2 0 1 2 max(0, 1) ( ) , , , n i i n n j j k x n n n n k x x nx i n i n i k i j x x x x x _q P M x p x x x p = = + + + + + = = − + + − = ∑ + + + ⎛ ⎞ ⎛ ⎞ = = _{⎜ ⎟ ⎜ ⎟} ⎝ ⎠ ⎝ ⎠ ∑

∑

∑

(3.9)

3.7. q-Ling’s Binom Dağılımı

q-Ling’s Binom dağılım Yalçın (2013) tarafından incelenmiştir. Bu dağılımın olasılık fonksiyonunun elde edilmesinde aşağıdaki Lemma’ dan yararlanılacaktır.

Lemma 3.3. 0< ≤ için q 1 2 3 1 1 1 1 1 2 ( 1) ( 1)( ) 0, , 0 ( , , ) r r r r r r y y r y q y y s I y I y k I I t y y B r s t q + + + − + + = + + − − + + = ≥ ≥ =

∑ ∑

şeklinde tanımlansın. Burada 1, 0, . . j j y k I d y ≥ ⎧ = ⎨ ⎩

ve (y j_j =1, 2, , )r ’ler negatif olmayan tamsayılardır. Ayrıca ( , , )B r s t için _q 1 ( 1) ( 1) 0 ( 1, , ) ( 1, , 1), 1, 0, 0 ( , , ) 1, 1, , 1 1,0 , 0 0, . . k s r j r j q q j j k q q B r s j t q B r s j t j k r s t B r s t r s k t s k ya da r s k t d y − − − = = ⎧ _{− − + − − − + − > ≥ ≥} ⎪ ⎪⎪ =_⎨ = ≥ = − + = ≤ < = ⎪ ⎪ ⎪⎩

∑

∑

indirgeme bağıntısı yazılabilir.

(i-1). ile i. başarısızlık arasındaki denemelerde başarısızlık olasılığı

1

1 i , 1, 2, ,0 1,0 1

i

q _{= −}θq− i_{= < <}θ _{< ≤ eşitliğine göre değişen n tane Bernoulli} q

denemesi göz önüne alınsın.

,

n k

M : n denemedeki k uzunluğunda örtüşen başarıların sayısı olarak tanımlanan bir

rasgele değişken olmak üzere bu rasgele değişkene ilişkin olasılık fonksiyonu 0< ≤ için q 1

{

}

1 , 0 1 (1 ) ( 1, , ), 0,1, , 1 i n n i j n k q i j P M x θ − θq − B i n i x x n k = = = =

∑ ∏

− + − = − + (3.10) şeklindedir.

Bu dağılımda q=1 alındığında Ling’s Binom dağılımının olasılık fonksiyonu elde edilmiş olur.

4. q_{, ,} n k l

N RASGELE DEĞİŞKENİNİN DAĞILIMI VE BAZI ÖZELLİKLERİ

Tez çalışmasının bu bölümünde, her bir başarısızlıktan sonra başarı olasılığı geometrik olarak azalan n tane Bernoulli denemesindeki l tanesi örtüşen k-ardıl başarıların sayısı şeklinde bir rasgele değişken tanımlanmıştır. Tanımlanan bu rasgele değişken q

l k n

N _{, ,} ile gösterilmiştir. Örneğin n=15 için Bernoulli denemelerinin dizisi aşağıdaki gibi olsun.

1 1 1 0 1 1 1 1 0 1 1 1 1 1 0 Bu durumda l=2 ve k=3 olduğu zaman _Nq

2 , 3 ,

15 = 6 olarak belirlenir. Başarı tekrarları ise

şu şekildedir; 1 2 3, 5 6 7, 6 7 8, 10 11 12, 11 12 13, 12 13 14 l=1 ve k=3 için ise _Nq 1 , 3 ,

15 =4 olarak belirlenir. Başarı tekrarları ise şu şekildedir;

1 2 3, 5 6 7, 10 11 12, 12 13 14

4.1. q_{, ,} n k l

N rasgele değişkenin dağılımı

, ,

q n k l

N rasgele değişkeninin dağılımına geçmeden önce bize yardımcı olacak aşağıdaki lemma verilsin.

Lemma 4.1. 0<q≤1 için,

(

_{, ,}

)

y2 2y3 ( )r 1yr_, B q r s t q A =

∑

∑

+ + + − olsun. Burada

{

: ₁+ ₂+ + = , ₁+ ₂+ + = , ₁≥0, , ≥0

}

, = y y y_r s c c c_r t y y_r B y … , 0 . . j y l j k l j y k c d y − − ⎧⎡ ⎤ _≥ ⎪⎣ ⎦ = ⎨ ⎪⎩

(

y1,y2,…,yr

)

=

y şeklindedir.

[ ]

x , x ’in tam kısımlarını göstermektedir ve y ’ lerin _i

(

)

( )

(

)

(

)

(

)

1 0 1, , , 1, 0, 0 , , 1, , 1, 1,0 , 0 0, . ., s r j q j j s l q k l q A r s j t d r s t A r s t r s k t veya r s k t d y − = − − ⎧ − − − > ≥ ≥ ⎪ ⎪ ⎪ ⎪ =⎨ = ≥ = ⎪ _{= ≤ < =} ⎪ ⎪ ⎪ ⎩

∑

indirgeme bağıntısı yazılabilir. Burada j=0, 1, . . ., s için , 0 . . j l k l j j k d d y − − ⎧⎡ ⎤ ≥ ⎪⎣ ⎦ = ⎨ ⎪⎩ şeklindedir.

İspat. r >1 için y ‘nın alabileceği değerler _r

(

)

( ) ( ) ( ) ( ) ( ) ( )

(

)

(

)

( )

₍

₎

( )

(

_{1, ,}

)

_, , 0 , 1 , 1 , 1 , , 1 , , 1 0 1 1 1 0 2 2 1 2 2 1 2 2 2 1 2 2 1 3 2 1 3 2 2 1 3 2 1 1 3 2 0 j q j r s j s q r s q r q y r y y B r s y r y y B r y r y y B r y r y y B q d t j s r A q d t r A q d t s r A q d t s r A q q q q q q q t s r A r s r r r − − − = − − + + − − − + − − = + + + + = − = − − − + + + − − + + + − − + + + − − + + +

∑

∑

∑

∑

∑

∑

∑

∑

∑

− − − −

olarak yazılabilir. Burada

{

: 1+ 2+ + 1= − , 1+ 2 + + 1 = − , 1≥0, , 1≥0

}

= r₋ r₋ j r₋ j y y y s j c c c t d y y B y … , j=0, 1, . . ., s ve 1 s j j B B =

= ∪ şeklindedir. Eşitliğin diğer parçaları oldukça açıktır. Teorem 4.1. q

l k n

N _{, ,} her bir başarısızlıktan sonra başarı olasılığı geometrik olarak azalan

n tane Bernoulli denemesindeki l tanesi örtüşen k-ardıl başarıların sayısını göstersin. Bu

durumda 0<q≤1 için q l k n

N _{, ,} rasgele değişkeninin olasılık fonksiyonu;

{

}

( )

(

1

)

(

)

, , 0 1 1 1, , , 0,1, , v x i q n i j n l n k l q k l i j P N x θ − θq − A i n i x x − − = = = =

∑ ∏

− + − = … ⎡ ⎤_{⎣ ⎦} (4.1) şeklindedir. Burada

( )

x n

₍

₍

₎

₎

,_, x_{. .}0

n x k l l d y

ν _{= ⎨ −}⎧⎪ =

− + ⎪⎩

ve Aq

(

r,s,t

)

Lemma 4.1. deki tanımlandığı gibidir.

İspat. S , _n n denemedeki sıfırların sayısını göstersin. O zaman

{

, ,

}

{

, , ,

}

q q

n k l n k l n

i

P N =x =

∑

P N =x S =i

şeklinde yazılabilir. Burada

{

Nq x S_n i

}

l k

n, , = , = olayı tam i tane sıfırdan oluşan n

denemelik 1 2 1 1 1 0 1 1 0 0 1 1 0 1 1 + i i y y y y … … … … …

şeklindeki bir dizilişte yj ≥0, j=1,2,…,i+1, olmak üzere

x c c c i n y y y i i = + + + − = + + + + + 1 2 1 1 2 1

olmasına karşılık gelmektedir. Ayrıca i değerinin en az 0 ve en çok ν

( )

x değerini alacağı açıktır. Buna göre Charalambides (2010) modeli altında,

{

}

( )

( ) (

)

( ) (

)

(

) (

)( )

( )

(

)

( ) ( ) 1 ₂ 1 1 1 1 1 1 1 2 3 1 1 1 1 1 1 1 , , 0 0 1 1 0 0, , 0 2 1 1 0 1 0, , 0 0 1 1 1 1 1 1 i i i j j i j j i i i i j j i j j i q n k l x y y _i y _{i i} y i y n i c x y y x i y y i y iy n i j i j y n i c x y y x i n i i j P N x q q q q q q q q q ν ν ν θ θ θ θ θ θ θ θ θ θ + + = + = + + + = + = + − − = = − = ≥ ≥ + + + − + − − = = _{∑ = −} ∑ = ≥ ≥ − = = = = − − × × − ∑ ∑ = − =

∑ ∑ ∑

∑ ∏

∑ ∑

∑ ∏

…

(

1

)

(

)

1, , . j q q A i n i x θ − − + −

olarak yazılabilir. Böylece ispat tamamlanmış q l k n

N _{, ,} rasgele değişkininin olasılık fonksiyonu elde edilmiştir.

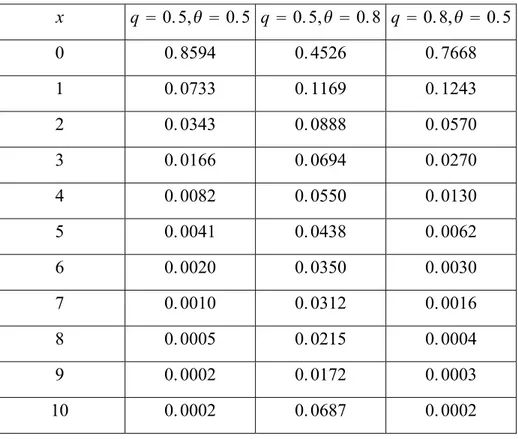
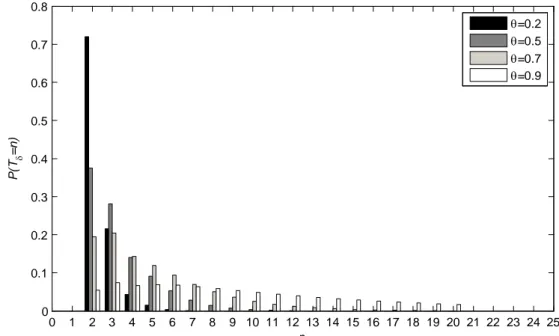
Aşağıdaki tabloda q ve θ‘nın farklı değerleri için _N12,3,2q _{olasılık fonksiyonun aldığı}

Tablo 4.1._Nq 2 , 3 , 12 ’ nın olasılık fonksiyonu x q  0. 5,   0. 5 q  0. 5,   0. 8 q  0. 8,   0. 5 0 0. 8594 0. 4526 0. 7668 1 0. 0733 0. 1169 0. 1243 2 0. 0343 0. 0888 0. 0570 3 0. 0166 0. 0694 0. 0270 4 0. 0082 0. 0550 0. 0130 5 0. 0041 0. 0438 0. 0062 6 0. 0020 0. 0350 0. 0030 7 0. 0010 0. 0312 0. 0016 8 0. 0005 0. 0215 0. 0004 9 0. 0002 0. 0172 0. 0003 10 0. 0002 0. 0687 0. 0002

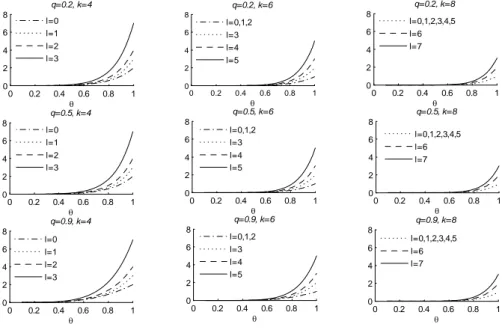
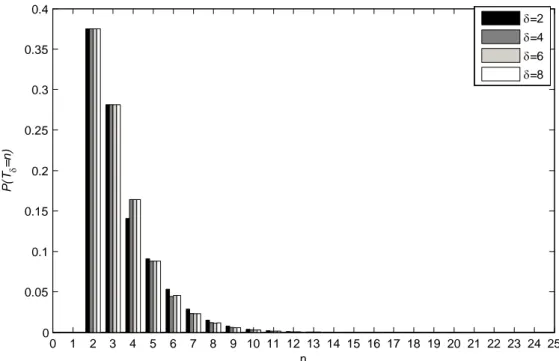
Aşağıda farklı k,l,q,θ değerleri için q l k

N_{12, ,} rasgele değişkeninin olasılık fonksiyonun grafiği verilmiştir.

k=2,3,4 durumu için çizilen grafikte n=12, l=2, q=0.5 ve θ=0.5 l=2,3,4 durumu için çizilen grafikte n=12, k=5, q=0.5 ve θ=0.5 q=0.2, 0.5, 0.8 durumu için çizilen grafikte n=12, k=3, l=2 ve θ=0.5 θ=0.2, 0.5, 0.8 durumu için çizilen grafikte n=12, k=3, l=2 ve q=0.5

0 1 2 3 4 5 6 7 8 9 10 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 x k=2 0 1 2 3 4 5 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 x k=3 0 1 2 3 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 x k=4 0 1 2 3 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 x l=2 0 1 2 3 4 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 x l=3 0 1 2 3 4 5 6 7 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 x l=4 0 1 2 3 4 5 6 7 8 9 10 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 x q=0.2 0 1 2 3 4 5 6 7 8 9 10 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 x q=0.5 0 1 2 3 4 5 6 7 8 9 10 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 x q=0.8 0 1 2 3 4 5 6 7 8 9 10 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 x θ=0.2 0 1 2 3 4 5 6 7 8 9 10 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 x θ=0.5 0 1 2 3 4 5 6 7 8 9 10 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 x θ=0.8

Şekil 4.1. Farklı durumlar için q l k

N_{12, ,} ’ nin olasılık fonksiyonun grafiği

q l k n

N _{, ,} rasgele değişkeninin dağılımı bazı özel durumlarda tezin üçüncü bölümünde söz edilen dağılımlara dönüşmektedir.

• q→1 iken Makri ve Phillippou(2005)’ deki N_n,k,l rasgele değişkeninin dağılımına

• l=k-1 iken Eşitlik 3.10’ da verilen dağılımına • q→1 ve l=k-1 iken Eşitlik 3.8’ te verilen dağılımına • l=0 iken Eşitlik 3.4’ te verilen dağılıma

4.2. q_{, ,} n k l

N rasgele değişkenin beklenen değeri

q l k n

N _{, ,} rasgele değişkeninin beklenen değerin aşağıdaki teoremde verilmiştir. Teorem 4.2. n≤ k−1için

(

q_{, ,}

)

=0 l k n N E ve n≥k >l≥0 _için

(

)

(

)

(

_s

)(

_s

)

k j(k l) s l k i j k n i k i A i k q l k n j i j i j i j i q q s Z P N E − −+ + − = ⎥⎦ ⎤ ⎢⎣ ⎡ − − = + − = − + ∈ − = + + =

∑

∑

∑

∑

1 0 2 0 1 2 1 , , , , , , 2 1 ν ν ν ν θ θ θ θ şeklindedir. Burada νi,j =i− j

(

k−l

)

−2 ve PZy  s  n s q s



i1 n−s 1 − qi−1_

şeklinde başarı olasılığı θ olan q-binom dağılımının olasılık fonksiyonudur.

İspat. X₁,X₂,…,X_n başarı olasılığı geometrik olarak değişen Bernoulli rasgele değişkenleri olsun. _i=1,_k−_l+1,2

(

_k−_l

)

+1, ,

[ ]

−₋

(

_k−_l

)

+1 l k k n … için _{E olayı i} “X X_{1 2} X_{i k+ −1}= ”olarak ve 1 i=2,…,n−k+1 ve _j

[ ]

_ki _l − − =_{0 …,1, ,} 2 _için j i E, olayı

“Xi−j₍k−l₎−1 =0,Xi−j₍k−l₎× ×Xi+k−1 =1” olarak tanımlansın. A1,A2,A3ise

{

1,2, , − +1

}

= n k I … indis kümesinin

{}

(

)

[ ]

(

)

{

}

(

)

. , 1 , , 1 2 , 1 , 1 2 1 3 2 1 A A I A l k l k l k A A l k k n ∪ − = + − + − + − = = − − …

şeklinde bir parçalanması olsun

1

1≤i≤n−k+ için Y rasgele değişkenleri aşağıdaki gibi tanımlansın. _i

⎩ ⎨ ⎧ = . . , 0 gelirse meydana olayı , 1 ₁ 1 y d E Y 2 A i∈ için [ ] ⎪ ⎩ ⎪ ⎨ ⎧ ∪ = − − = . . , 0 gelirse meydana olayı , 1 _, 0 2 y d E E Y i j j i i l k i

∪

3 A i∈ için [ ] ⎪ ⎩ ⎪ ⎨ ⎧ = − − = .. . , 0 gelirse meydana olayı , 1 _, 0 2 y d E Y i j j i l k i

∪

Bu durumda q l k n

N _{, ,} rasgele değişkeni Yirasgele değişkenleri cinsinden

1 , , 1 n k q n k l i i N − +Y = =

∑

olarak yazılabilir (Makri ve Philippou(2005)). Bu durumda

(

)

(

)

(

)

(

)

2 3 , , 1 1 1 1 q n k l i i i A i A E N P Y P Y P Y ∈ ∈ = = +

∑

= +

∑

= (4.2)

şeklinde yazılabilir. Bu eşitlikte üç parça halinde yer alan olasılıklar aşağıdaki gibi elde edilmektedir.

(

1 1

)

( . . .1 2 k 1) ( 1 1, 2 1, , k 1) k P Y = =P X X X = =P X = X = X = =θ (4.3) 2 A i∈ için

(

)

(

_{[ ]}

)

( ) ( )

i i

( )

i_{[ ]}

( )

i i i i i i E P E P E P E P E E E E P Y P l k i l k i + + + + = ∪ ∪ ∪ ∪ = = − − − − 2 2 , 1 , 0 , , 1 , 0 , 1 (4.4) ve

( )

(

( ) ( )

)

(

)

(

)(

)

( )

_{[ ]}

, , , 1 , 0 , 1 1 , 0 2 1 0 1 1 , , , , , l k i l k j k s s s k i l k j i l k j i j i j q q s Z P X X X P E P j i j i j i j i − − − + + − − = − + − − − − − = − = = = × × = =

∑

_ν ν ν … ν θ θ (4.5)

( )

(

1

)

1. 1 1 − + − + = = × × = i k k i i P X X E P θ (4.6)

olarak yazılabilir. i∈A₂ için, Eşitlik (4.5) ve Eşitlik (4.6), Eşitlik (4.4)’ te yerine yazılırsa

(

1

)

(

)

(

1

)(

1

)

( ) 1. 0 2 0 , , , , − + − + + − − = ⎥⎦ ⎤ ⎢⎣ ⎡ − − = + − = = =

∑

∑

s s k jk l i k s l k i j i j i j i j i j i q q s Z P Y P _ν θ ν θ ν θ ν (4.7) Benzer şekilde i∈ A₃

(

1

)

(

)

(

1

)(

1

)

( ). 0 2 0 , , , , l k j k s s s l k i j i j i j i j i j i q q s Z P Y P − −+ + − = ⎥⎦ ⎤ ⎢⎣ ⎡ − − = − = = =

∑

∑

_ν ν ν ν θ θ (4.8)

olarak yazılabilir. İspat Eşitlik (4.3), Eşitlik (4.7) ve Eşitlik (4.8), Eşitlik (4.2)’ te yerine yazılarak tamamlanabilir.

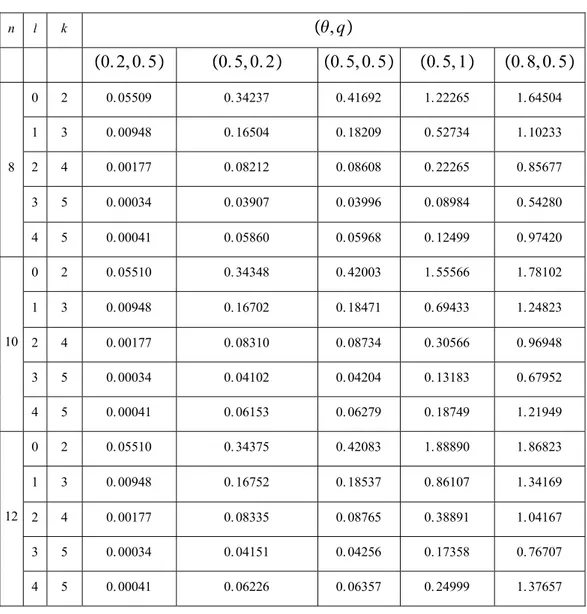
Aşağıdaki Tablo 4.2’ de farklı θ, , , ,q n k l _{değerleri için} q_{, ,} n k l

N rasgele değişkeninin beklenen değerlerine aldığı değerler verilmiştir. Yine Şekil 4.2’ de ise beklenen değere ilişkin grafikler verilmiştir.

Tablo 4.2. Farklı θ,q,n,k ve l değerleri için

(

q

)

l k n N E _{, ,} n l k , q 0.2, 0. 5 0. 5, 0. 2 0.5, 0. 5 0. 5, 1 0.8, 0. 5 0 2 0. 05509 0. 34237 0. 41692 1. 22265 1. 64504 1 3 0. 00948 0. 16504 0. 18209 0. 52734 1. 10233 2 4 0. 00177 0. 08212 0. 08608 0. 22265 0. 85677 3 5 0. 00034 0. 03907 0. 03996 0. 08984 0. 54280 8 4 5 0. 00041 0. 05860 0. 05968 0. 12499 0. 97420 0 2 0. 05510 0. 34348 0. 42003 1. 55566 1. 78102 1 3 0. 00948 0. 16702 0. 18471 0. 69433 1. 24823 2 4 0. 00177 0. 08310 0. 08734 0. 30566 0. 96948 3 5 0. 00034 0. 04102 0. 04204 0. 13183 0. 67952 10 4 5 0. 00041 0. 06153 0. 06279 0. 18749 1. 21949 0 2 0. 05510 0. 34375 0. 42083 1. 88890 1. 86823 1 3 0. 00948 0. 16752 0. 18537 0. 86107 1. 34169 2 4 0. 00177 0. 08335 0. 08765 0. 38891 1. 04167 3 5 0. 00034 0. 04151 0. 04256 0. 17358 0. 76707 12 4 5 0. 00041 0. 06226 0. 06357 0. 24999 1. 37657

0 0.2 0.4 0.6 0.8 1 0 2 4 6 8 θ q=0.2, k=4 0 0.2 0.4 0.6 0.8 1 0 2 4 6 8 θ q=0.2, k=6 0 0.2 0.4 0.6 0.8 1 0 2 4 6 8 θ q=0.2, k=8 0 0.2 0.4 0.6 0.8 1 0 2 4 6 8 θ q=0.5, k=4 0 0.2 0.4 0.6 0.8 1 0 2 4 6 8 θ q=0.5, k=6 0 0.2 0.4 0.6 0.8 1 0 2 4 6 8 θ q=0.5, k=8 0 0.2 0.4 0.6 0.8 1 0 2 4 6 8 θ q=0.9, k=4 0 0.2 0.4 0.6 0.8 1 0 2 4 6 8 θ q=0.9, k=6 0 0.2 0.4 0.6 0.8 1 0 2 4 6 8 θ q=0.9, k=8 l=0 l=1 l=2 l=3 l=0 l=1 l=2 l=3 l=0 l=1 l=2 l=3 l=0,1,2,3,4,5 l=6 l=7 l=0,1,2 l=3 l=4 l=5 l=0,1,2 l=3 l=4 l=5 l=0,1,2,3,4,5 l=6 l=7 l=0,1,2,3,4,5 l=6 l=7 l=0,1,2 l=3 l=4 l=5

Şekil 4.2. Farklı θ,q,n,k ve l değerleri için

(

q

)

l k n N E _{, ,} ’ nin grafiği Teorem 4.3. n≤ k−1için

(

q_{, ,}

)

2 =0 l k n N E ve n≥k >l≥0için

(

)

2

(

)

(

)

, , , , 2 1 2 q q n k l n k l E N =E N + I +I şeklindedir. Burada

(

)

(

)(

)

( )

(

)(

)(

)

( )

(

)

(

( )

)

(

( )

)

( )

(

)(

)(

)

( )

(

) (

)(

)

( ) , 1 1 1 1 , 1 1 1 1 0 1 0 1 1 1 1 0 2 1 2 1 1 0 0 1 0 2 0 1 1 2 2 1 1 0 2 0 1 2 1 2 2 2 2 , , 2 , , 2 , , 2 , , 2 2 1 1 1 , 1 1 , 1 , 1 , 1 2 2 1 2 , , 1 , 2 1 2 , , 1 , 2 , , 1 1 1 , 1 1 , 1 , 2 , , 2 1 , 1 2 1 2 , , 1 , , 1 , , 1 , , 1 − + > ∈ ∈ − + + − − − + = ⎥⎦ ⎤ ⎢⎣ ⎡ − − − − = + − + = ∈ − + − + + − − = − + + + − + + + − + − + + − − = = ⎥⎦ ⎤ ⎢⎣ ⎡ − − − − = ⎥⎦ ⎤ ⎢⎣ ⎡ − − = + − + = − = − + ∈ − + + − − = ⎥⎦ ⎤ ⎢⎣ ⎡ − − − = + − =

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

+ − = + ⎪⎭ ⎪ ⎬ ⎫ − = + ⎟ ⎠ ⎞ ⎥⎦ ⎤ − = × ⎪ ⎩ ⎪ ⎨ ⎧ ⎜ ⎜ ⎜ ⎝ ⎛ ⎢ ⎢ ⎣ ⎡ − = = + − = = k r i r A r A i l k t k s s k i s l k k i r t k n i r A i l k t i k r s s s l k t k s s s s l k t k s s s s l k k i r t l k i t k n i r k n i k r A r l k j k s s k s l k k r j k n r t r i t r i t r i t r i t r t r t r t r t r i t i t r i t i t r i t i t i t i t r i t i j r j r j r j r q q s Z P q q s Z P q q s W P q q s Z P I q q s Z P I θ θ θ θ θ θ δ θ θ θ θ θ θ θ θ η η η η ν ν ν ν η ν η ν η ν ν ν η ν η η η η ( ) ⎩ ⎨ ⎧ = − − + − . . , 0 , 1 1 y d ise tamsayı l k l k t i r δ

(

)

2, , ,

(

)

1 ,j =i− j k−l − ir j =r−i−k− j k−l − i η ν şeklindedir. Ayrıca

(

Z s1

)

dağılımının olasılık fonksiyonlarını göstermektedir. İspat.

(

)

2 , , q n k l

N rasgele değişkeninin Bölüm 4.2’de tanımlanan ,Y i_i =1, 2,...,n k− + rasgele 1 değişkenleri cinsinden

(

)

₂ 1 2 1 1 2 , , 1 1 1 1 2 n k n k n k n k q n k l i i i r i i i r i N − +Y − +Y − − +YY = = = = + ⎛ ⎞ =_{⎜ ⎟} = + ⎝

∑

⎠

∑

∑ ∑

olarak yazılabileceği gayet açıktır. Ayrıca Y rasgele değişkenleri 0 yada 1 değerlerini _i

alabildiğinden 2 q_{, ,} i i n k l Y = Y =N

∑

∑

olacak ve

(

)

2

(

)

1

(

)

, , , , 1 1 2 . n k n k q q n k l n k l i r i r i E N E N − − +E YY = = + = +

∑ ∑

(4.9)

olarak yazılabilecektir. Eşitlik (4.9)’ un sağ tarafı

( )

(

)

(

1

)

(

1

)

, 1 1 1 2 1 1 2 1 1 1 1 1 1 = + = = = =

∑

∑

∑

∑

∑

∑

∑

+ − + = − = + − = + − + = − = + − + = − = r i k n i r k n i r k n r r i k n i r k n i r i k n i r k n i Y Y P Y Y P Y Y P Y Y E

olarak elde edilebilir. Burada

(

)

[ ] [ ] [ ]

(

)

(

)(

)

( ) [ ]

(

)

(

)(

)

( ) , , 1 , 1 , , 1 3 1 0 0 2 1 1 0 0 3 , 0 1 2 , 0 1 1 , , 1 , , 1 , , 1 , , 1 2 , , 1 , , 1 , , 1 , , 1 2 2 2 ⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧ ∈ − = ∑ ∑ ∈ + − = ∑ ∑ = ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ∈ ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∩ ∈ ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∪ ∩ = = − + + − − = = − + − + + − − = = = = −− − −− − − − − − A r q q s Z P A r q q s Z P A r E E P A r E E E P Y Y P l k j k s s k s j k r l k j k s s k s j j r j r j r j r j r j r j r j r l k k r j r j r j r j r l k k r l k r l k r η η η η η η η η θ θ θ θ θ θ θ ∪ ∪

(

)

2 2 1 2 1 2 2 2 1 2 1 2 2 1 1 , , 2 0 0 , , 2 3 0 0 , 0 , , , , 1 i r k l k l i r k l k l i k l i t i r t r t t i t i r t t t i r i t t P E E E E i r A P E E E i A r A P YY P E − − − − − − − − − − ⎡ ⎤ ⎡ ⎤ ⎣ ⎦ ⎣ ⎦ = = ⎡ ⎤ ⎡ ⎤ ⎣ ⎦ ⎣ ⎦ = = ⎡ ⎤ ⎣ ⎦ = ⎧⎛ ⎞ ⎛ ⎞⎫ ⎪ _{∪ ∩ ∪} ⎪ _∈ ⎜ ⎟ ⎜ ⎟ ⎨_{⎜ ⎟ ⎜ ⎟}⎬ ⎪⎝ ⎠ ⎝ ⎠⎪ ⎩ ⎭ ⎧⎛ ⎞ ⎛ ⎞⎫ ⎪ _{∪ ∩} ⎪ _{∈ ∈} ⎜ ⎟ ⎜ ⎟ ⎨_{⎜ ⎟ ⎜ ⎟}⎬ ⎪⎝ ⎠ ⎝ ⎠⎪ ⎩ ⎭ = = ⎛ ⎞ ∩ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ∪ ∪ ∪ ∪ ∪ 2 2 2 2 2 1 2 1 2 , 3 2 0 , , 3 0 0 , , , , r k l i r k l k l r t r t i t r t t t E E i A r A P E E i r A − − − − − − ⎡ ⎤ ⎣ ⎦ = ⎡ ⎤ ⎡ ⎤ ⎣ ⎦ ⎣ ⎦ = = ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ ⎛ ⎞⎫ ⎪ ⎪ _∪ ⎪ _{∈ ∈} ⎜ ⎟ ⎨ ⎬ ⎪ _{⎜ ⎟} ⎪ ⎝ ⎠⎪ ⎪ ⎩ ⎭ ⎪ _{⎧⎛ ⎞ ⎛ ⎞⎫} ⎪ ⎪ ⎪ _{⎜ ⎟ ⎜∩ ⎟ ∈} ⎨ ⎬ ⎪ _⎪⎜_⎝ ⎟ ⎜_{⎠ ⎝} ⎟_⎠⎪ ⎩ ⎭ ⎩ ∪ ∪ ∪

(

)

(

( )

)

(

)

(

)

(

)

( ) 2 1 1 1 2 1 2 1 2 2 2 1 1 1 2 1 2 , , _, 0 0 2 2 , 0 , , _, 0 0 , , i r i k k l k l r i t k l k l r i k k l i r i k k l k l r i t k l k i t r t _r t t i r t i r t i t r t _r t t P E E P E i A r A P E E P E E P E E P E δ δ − − − − − − − + − − − − − − − − − − − − − + − − ⎡ ⎤ ⎡ ⎤ ⎣ ⎦ ⎣ ⎦ = = ⎡ ⎤ ⎣ ⎦ = ⎡ ⎤ ⎡ ⎤ ⎣ ⎦ ⎣ ⎦ = = ⎧⎛ ⎞ ⎫ ⎪ ⎪ ∑ ⎨⎜_⎜ ∑ ∩ ⎟_⎟+ ⎬ ⎪⎝ ⎠ ⎪ ⎩ ⎭ _{∈ ∈} + ∑ ∩ + ∩ ⎛ ⎞ ∑ ⎜_⎜ ∑ ∩ ⎟_⎟+ ⎝ ⎠ =

(

)

(

)

(

)

(

( )

)

1 2 2 2 1 1 1 2 1 2 2 3 , 0 , , _, 3 2 3 0 0 , , , , l r i k k l i r i k k l k l r i t k l k l i r t t i t r t _r t t i A r A P E E P E E δP E i A r A A − − − − − − − − − − − + − − ⎡ ⎤ ⎣ ⎦ = ⎡ ⎤ ⎡ ⎤ ⎣ ⎦ ⎣ ⎦ = = ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ ⎫ ⎪ _{⎪ ⎪} ⎪ ⎨ ⎬ ⎪ _{⎪⎩ ⎪⎭ ∈ ∈} ⎨ ⎪ + ∑ ∩ ⎪ ⎪ ⎪ _{⎧⎪⎛ ⎞ ⎫⎪} ⎪ ∑ ⎨⎜_⎜ ∑ ∩ ⎟_⎟+ ⎬ ∈ ∈ ∪ ⎪ _{⎪⎩⎝ ⎠ ⎪⎭} ⎪ ⎪ ⎪ ⎩

(

)

(

)

(

) (

)(

)

( ) , 1 , 2 2 , , 2 , , 2 , , 2 , , 2 1 1 0 , 1 l k t k s s k i s t r i k r r i t r i t r i t r i t r i q q s Z P E E P E E P − + + − − − + = − + − = = ∩ = ∩

∑

η η η η θ θ θ θ

(

)

(

)(

)(

)

( )

(

)

(

( )

)

(

( )

)

( ) ( )

(

)(

)(

)

( ) , 1 , 1 1 1 1 1 , 1 1 , 1 , 1 , 1 1 2 2 1 2 , , 1 , 2 1 2 , , 1 , 2 , , 1 1 1 , 1 1 , 1 , 2 , , 2 1 , 1 2 1 1 1 0 , 2 1 2 1 1 0 0 , , l k t i k r s s s r l k t k s s s s l k t k s s s s t r t i t r t r t r t r l k l k t i r t r i t i t r i t i t r i t i t i t i t r i t i q q s Z P E P q q s W P q q s Z P E E P − + − + + − − = − + + + − + + + − + − + + − − = = − = = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = × − = = ∩

∑

∑

∑

− − + − ν ν ν ν η ν η ν η ν ν ν η ν θ θ θ θ θ θ

şeklindedir. Ayrıca P

(

Z_a =s₁

)

ve P W

(

b =s2

)

sırasıyla başlangıç olasılıkları θ ve 1

1+ −s

a

q

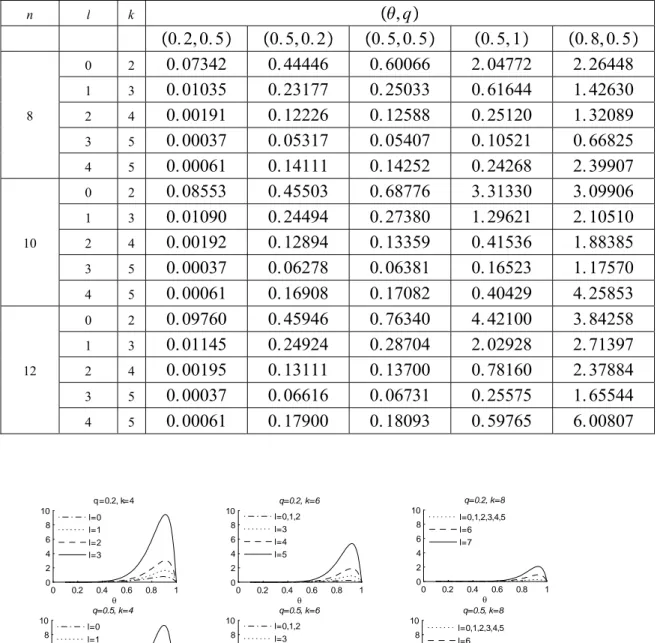
Aşağıdaki Tablo 4.3’te ve Şekil 4.3’ te farklıθ, , , ,q n k l _{değerleri için} q_{, ,} n k l

N rasgele değişkeninin varyans değerlerine ilişkin değerler ve grafikler verilmiştir.

Tablo 4.3. Farklı θ,q,n,k ve l değerleri için

(

q

)

l k n N Var _{, ,} n l k , q 0. 2, 0. 5 0.5, 0. 2 0.5, 0. 5 0. 5, 1 0.8, 0. 5 0 2 0. 07342 0. 44446 0. 60066 2. 04772 2. 26448 1 3 0. 01035 0. 23177 0. 25033 0. 61644 1. 42630 2 4 0. 00191 0. 12226 0. 12588 0. 25120 1. 32089 3 5 0. 00037 0. 05317 0. 05407 0. 10521 0. 66825 8 4 5 0. 00061 0. 14111 0. 14252 0. 24268 2. 39907 0 2 0. 08553 0. 45503 0. 68776 3. 31330 3. 09906 1 3 0. 01090 0. 24494 0. 27380 1. 29621 2. 10510 2 4 0. 00192 0. 12894 0. 13359 0. 41536 1. 88385 3 5 0. 00037 0. 06278 0. 06381 0. 16523 1. 17570 10 4 5 0. 00061 0. 16908 0. 17082 0. 40429 4. 25853 0 2 0. 09760 0. 45946 0. 76340 4. 42100 3. 84258 1 3 0. 01145 0. 24924 0. 28704 2. 02928 2. 71397 2 4 0. 00195 0. 13111 0. 13700 0. 78160 2. 37884 3 5 0. 00037 0. 06616 0. 06731 0. 25575 1. 65544 12 4 5 0. 00061 0. 17900 0. 18093 0. 59765 6. 00807 0 0.2 0.4 0.6 0.8 1 0 2 4 6 8 10 θ q =0.2, k=4 0 0.2 0.4 0.6 0.8 1 0 2 4 6 8 10 θ q=0.2, k=6 0 0.2 0.4 0.6 0.8 1 0 2 4 6 8 10 θ q=0.2, k=8 0 0.2 0.4 0.6 0.8 1 0 2 4 6 8 10 θ q=0.5, k=4 0 0.2 0.4 0.6 0.8 1 0 2 4 6 8 10 θ q=0.5, k=6 0 0.2 0.4 0.6 0.8 1 0 2 4 6 8 10 θ q=0.5, k=8 0 0.2 0.4 0.6 0.8 1 0 2 4 6 8 10 θ q=0.9, k=4 0 0.2 0.4 0.6 0.8 1 0 2 4 6 8 10 θ q=0.9, k=6 0 0.2 0.4 0.6 0.8 1 0 2 4 6 8 10 θ q=0.9, k=8 l=0 l=1 l=2 l=3 l=0,1,2 l=3 l=4 l=5 l=0,1,2,3,4,5 l=6 l=7 l=0 l=1 l=2 l=3 l=0,1,2 l=3 l=4 l=5 l=0,1,2,3,4,5 l=6 l=7 l=0 l=1 l=2 l=3 l=0,1,2 l=3 l=4 l=5 l=0,1,2,3,4,5 l=6 l=7

Şekil 4.3. Farklı θ,q,n,k ve l değerleri için

(

q

)

l k n

N

Tablo 4.3 ve Şekil 4.3’ten de görülebileceği gibi • l arttığında,

(

q

)

l k n N E _{, ,} ve

(

q

)

l k n N

Var _{, ,} değerleri artmaktadır. • k arttığında,

(

q

)

l k n N E _{, ,} ve

(

q

)

l k n N

Var _{, ,} değerleri azalmaktadır. • q veya θ değeri arttığında,

(

q

)

l k n N E _{, ,} değeri artarken,

(

q

)

l k n N Var _{, ,} değeri monoton bir hareket sergilememektedir.

5. YENİ BİR δ-ŞOK MODELİ

Şok modeller güvenilirlik teorisinde büyük ilgi çeken bir konu haline gelmiştir. Şok modeller, rasgele büyüklükteki şokların rasgele bir zamanda meydana geldiği sistemlerdir. Üç farklı türde şok model mevcuttur. Bunlar tekrar şok modeli, aşırı şok model ve birikimli şok modellerdir. Tekrar şok modellerinde, belirlenmiş sayıda ardışık şok olması, aşırı şok modelde şokun belli bir eşik değerinden daha büyük olması, birikimli şok modelde ise maruz kalınan şok büyüklüklerinin toplamının belli bir eşik değerinden büyük olması bozulma kriteri olarak düşünülür.

Eğer bir sistem, maruz kaldığı iki ardışık şok arasındaki geçen süre belirli bir δ değerinin altında iken ölüyor ise böyle sistemler δ-şok model adını almaktadır. δ-şok modelde iki şok arasındaki şokların büyüklük yerine zaman dikkate alındığında bu modeller dördüncü tür şok modeller olarak düşünülebilir. Li ve Kong (2007) δ-şok modeller üzerine çalışılmıştır. Eryılmaz (2013), δ-şok modelin kesikli versiyonunu çalışmıştır. Bu model, iki şok arasındaki geçen sürenin 1/p ortalamalı geometrik dağılıma sahip olduğu bir binom süreci olarak düşünülmüştür.

Tez çalışmasının bu bölümünde, i−1 ile i. şoklar arasında geçen zamanın (yani yapılan deneme sayısının) 1/p_i ortalamalı geometrik dağılıma sahip olduğu varsayılmıştır. Burada _{p = q}i−1,_i=1,2,...,0_{< <}1,0_{< p≤}1

i θ θ şeklindedir.

5.1. Tanımlanan Sistem ve Sistemin Olasılık Fonksiyonu

Aşağıda tanımlanacak olan bir şok dizisine maruz kalan bir sistem düşünülsün. 0 (Şok) ve 1 (Şok Değil) ‘lerden oluşan bir I ...,1, In iki sonuç alabilen Bernoulli

denemelerini göz önüne alalım. Bu denemelerden i-1. şoktan i. şoka kadar olan denemeler bağımsız ve bozulma olasılığı 1

1 i , 1, 2,..., 0 1, 0 1

i

q = −θq− i= < <θ < ≤p _olan

Bernoulli dağılıma sahiptir. Bu süreç Charalambides (2010) tarafından çalışılmıştır. Bu süreçle anlatılmak istenileni şu şekilde özetleyebiliriz. i. şokun olması olasılığı q_i−1 ve olmaması olasılığı 1−q_i−1 şeklindedir. Ve _{X ilk şoka kadar geçen zamanı, , 1,2,..0} X i_i =

i. ile i−1. şok arasındaki zamanı göstersin. Bu durumda bağısız fakat aynı dağılıma sahip olmayan X₀,X₁,... rasgele değişkenlerinin olasılık fonksiyonu;

,... 2 , 1 , ) 1 ( } {_{X =x =q −q} −1 _x= P x i i i

şeklinde olacaktır. Yukarıdaki varsayımlar altında, incelenecek model kısaca qδ-şok modeli olarak gösterilecektir. Bu durumda qδ-şok modeli üzerine kurulu sistemin yaşam zamanı

T 

∑

i0

M

Xi

olarak tanımlanabilir (Eryılmaz (2013)). Buradaki durdurma rasgele değişkeni M aşağıdaki gibi tanımlanabilir.

,... 2 , 1 , 1 }, , ,..., { } {M =m ⇔ X₁ >δ X_m−1 >δ X_m ≤δ δ ≥ m= Lemma 5.1. 0< q ≤1olmak üzere

( )

2 3 4 ( ) 1 1 , 2 , , 2 , 0 1 1 , 2 1 2 3 2 , − ≥ − ≥ − ≥ ≥ + −= + − + + + + ∑ ∑ = r r y r y y y y yr s y y r y y y q r s q B … … … … δ δ δ

şeklinde tanımlansın burada y ’ ler tamsayıdır. Buradaki _i B_q

( )

r,s için ( ) _{( )}

(

)

⎪

⎪

⎩

⎪

⎪

⎨

⎧

≥

=

−

≥

≥

−

−

∑

=

− − − =

.

.

,

0

0

,

2

,

1

2

,

3

,

)

,

1

(

)

,

(

2 3

y

d

s

r

r

s

r

w

s

r

B

q

s

r

B

q w r r s w q

δ

δ δ

indirgeme bağıntısı yazılabilir.

İspat. r ≥ 3 ve s ≥ r − 2. değerleri için

Bqr, s 

y 1y2yr−1s y 1≥0,y2≥,…,yr−2≥,yr−1≥

∑

…

∑

qy22y33y4r−2yr−1



∑

w s−r−3  qr−2 w y 1y2yr−2s−w y 1≥0,y2≥,…,yr−2≥

∑

…

∑

qy22y33y4r−3 yr−2



∑

w

s−r−3 

qr−2 w_B

qr − 1, s − w.