Grafların normalized laplacian matrisinin hızı ve diğer bazı parametreler ile olan bağıntıları

T.C.

SELÇUK ÜNĠVERSĠTESĠ FEN BĠLĠMLERĠ ENSTĠTÜSÜ

GRAFLARIN NORMALĠZED LAPLACĠAN MATRĠSĠNĠN HIZI VE DĠĞER BAZI PARAMETRELER ĠLE OLAN BAĞINTILARI

Aydan Zeynep AYDIN YÜKSEK LĠSANS TEZĠ MatematikAnabilim Dalı

12-2013 KONYA Her Hakkı Saklıdır

iv ÖZET

YÜKSEK LĠSANS TEZĠ

GRAFLARIN NORMALĠZED LAPLACĠAN MATRĠSĠNĠN HIZI VE DĠĞER BAZI PARAMETRELER ĠLE OLAN BAĞINTILARI

Aydan Zeynep AYDIN

Selçuk Üniversitesi Fen Bilimleri Enstitüsü Matematik Anabilim Dalı

DanıĢman: Doç. Dr. AyĢe Dilek MADEN 2013, 45 Sayfa

Jüri

Doç. Dr. AyĢe Dilek MADEN Prof. Dr. Ahmet Sinan ÇEVĠK

Doç. Dr. Bünyamin AYDIN

Bu çalışmada basit bağlantılı bir grafın normalize edilmiş Laplacian matrisinin en büyük özdeğeri ile sıfırdan farklı en küçük özdeğeri arasındaki fark normalize edilmiş Laplacian hız olarak tanımlanmıştır ve

SL G şeklinde gösterilmiştir. Daha sonra ise SL G değeri için bazı sınır elde edilmiş ve bazı graf parametreleri ile bağlantılar sağlanmıştır. (Klik sayısı, Bağımsızlık sayısı, Randik indeks). Ayrıca iki grafın tensor çarpımlarının normalize edilmiş Laplacian hızı için sınırlar elde edilmiştir. Özel olarak seçilmiş bir ağaç ve bir tek devir içeren graf içinde normalize edilmiş Laplacian hızları bulduktan sonra son olarak normalize edilmiş Laplacian matrisin özdeğerlerine bağlı olarak derece Kirchhoff indeks için sınırlar bulacağız.

Anahtar Kelimeler:Bağımsızlık sayısı, klik sayısı, normalize edilmiş Laplacian hız, Randić indeks, tensor çarpım.

v ABSTRACT

MS THESIS

THE NORMALIZED LAPLACIAN SPREAD OF GRAPHS AND RELATIONS WITH OTHER SOME PARAMETERS

Aydan Zeynep AYDIN

THE GRADUATE SCHOOL OF NATURAL AND APPLIED SCIENCEOF SELÇUK UNIVERSITY

THE DEGREE OF MASTER OF SCIENCE IN MATHEMATĠCS

Advisor: Assoc. Prof. Dr. AyĢe Dilek MADEN 2013, 44Pages

Jury

Assoc. Prof. Dr. AyĢe Dilek MADEN Prof. Dr. Ahmet Sinan ÇEVĠK Assoc. Prof. Dr. Bünyamin AYDIN

In this study, we define the normalized Laplacian spread of a simple graph as the difference between the largest eigenvalue and the second smallest eigenvalue of the normalized Laplacian matrix of the graph and denote bySL( )G . Then we present some bounds for SL( )G andrelatedwith graph parameterssuch asRandić index, clique and independent number. Moreover, as extendent approximation of the theory, we obtain lower and upper bounds for the normalized Laplacian spread of tensor product of any two simple graphs. We calculate normalized Laplacian spread for specially selected in a tree and unicyclic graph after finally, we find upper and lower bounds for the degree-Kirchhoff index depending on eigenvalues of normalized Laplacian matrix.

Keywords:Clique number, independent number, normalized Laplacian spread, Randić index,

vi ÖNSÖZ

Bu çalışma Selçuk Üniversitesi Fen Fakültesi Matematik Bölümü Öğretim Üyesi Doç. Dr. Ayşe Dilek MADEN danışmanlığında yapılarak, Selçuk Üniversitesi Fen Bilimleri Enstitüsü‟ne yüksek lisans tezi olarak sunulmuştur.

Bu çalışma yedi bölümden oluşmaktadır. Çalışmanın birinci bölümünde, graf teorinin ve spektral graf teorinin tarihçesi ve literatür özetlerinden bahsedilmiştir. İkinci bölüm, giriş bölümü olup, ileriki bölümlerde kullanacağımız temel bilgiler verilmiştir. Geriye kalan bölümler çalışmanın ana bölümleri olup öncelikle basit bağlantılı bir grafın normalize edilmiş Laplacian matrisinin hızıtanımlanıp bunun için bir üst sınır bulunmuştur. Daha sonra ise bazı parametreler ile normalize edilmiş Laplacian hız arasında çeşitli bağıntılar kurulup grafların tensor çarpımları ve bazı özel seçilmiş graflar için normalize edilmiş hız ile ilgili bağıntılar bulunmuştur. Son olarak ise derece Kirchhoff indeks için normalize edilmiş Laplacian matrisin öz değerleri türünden sınırlar bulunmuştur.

Bu çalışma süresince emeği geçen değerli hocam Doç. Dr. Ayşe Dilek MADEN‟e ve sevgili aileme en içten teşekkürlerimi sunarım.

Aydan Zeynep AYDIN KONYA-2013

vii ĠÇĠNDEKĠLER ÖZET ... iv ABSTRACT ... v ÖNSÖZ ... vi ĠÇĠNDEKĠLER ... vii

SĠMGELER VE KISALTMALAR ... viii

1. GĠRĠġ ... 1

2. GENEL TANIM VE TEOREMLER ... 4

2.1. Graf Tanımları ... 4

2.1.1. Özel Graflar ... 8

2.2. Grafların Matris Gösterimleri ... 10

2.3. Lineer Cebir Bilgileri ... 13

2.3.1 Matrislerin Tensor Çarpımları ... 15

2.4. Normalize EdilmişLaplacian Matrisin Özdeğerleri ... 16

3. NORMALIZE EDĠLMĠġ LAPLACIAN HIZ ... 18

3.1. Hız Tanımı ve Özellikleri ... 18

3.2. Normalize Edilmiş Laplacian Hız ... 18

4. NORMALĠZE EDĠLMĠġ LAPLACĠAN HIZIN KLĠK VE BAĞIMSIZLIK SAYILARI ĠLE ĠLĠġKĠSĠ ... 21

5. GRAFLARIN TENSOR ÇARPIMININ NORMALĠZE EDĠLMĠġ LAPLACĠAN HIZI ... 25

6. AĞAÇLARIN ve TEK DEVĠRLĠ GRAFLARIN NORMALIZE EDĠLMĠġ LAPLACIAN HIZI ... 31

6.1. T n p, - Tipindeki Ağaçların Normalize Edilmiş Laplacian Hızı ... 31

6.2. G n₁( 3, 0; )n - Tipindeki (n 5)Tek Devir İçeren Grafların Normalize Edilmiş Laplacian Hızı ... 33

7. GRAFLARIN DERECE KIRCHHOFF ĠNDEKSĠ ... 35

viii SĠMGELER VE KISALTMALAR Simgeler elemanıdır elemanı değildir eşittir eşit değildir altkümesidir kapsar büyüktür küçüktür büyük ya da eşittir küçük ya da eşittir

( )G G grafının bağımsızlık sayısı

( )G G grafının klik sayısı

( )G G nin noktalarının derecelerinin minimumu

( )G G nin noktalarının derecelerinin maksimumu

A A kümesinin eleman sayısı

( )i

der e einoktasınınderecesi

E kenar kümesi

e kenar

{ ,e e_{i j}}veyae e_{i j} uç noktaları e_i ve e_j olan kenar ( , )

G V E Vnokta kümeli E kenar kümeli bir G grafı

G

1 2

G G G₁ileG₂grafının tensor çarpım grafı ( )

Kf G G grafının Kirchhoff indeksi

ij

r i ve j noktaları arasındaki direnç mesafesi

( )

S M M matrisinin hızı

m boyut (E nin eleman sayısı)

n mertebe (Vnin eleman sayısı)

n

B nmertebeli boş graf

n

C nmertebeli devir graf

n

P nmertebeli yol graf

n

K nmertebeli tam graf

, r s

K iki parçalı graf (kümelerin eleman sayısı r ve s)

V nokta kümesi

v nokta

1 2

V V V1kümesi ile V2 kümesinin kartezyen çarpımı

1. GĠRĠġ

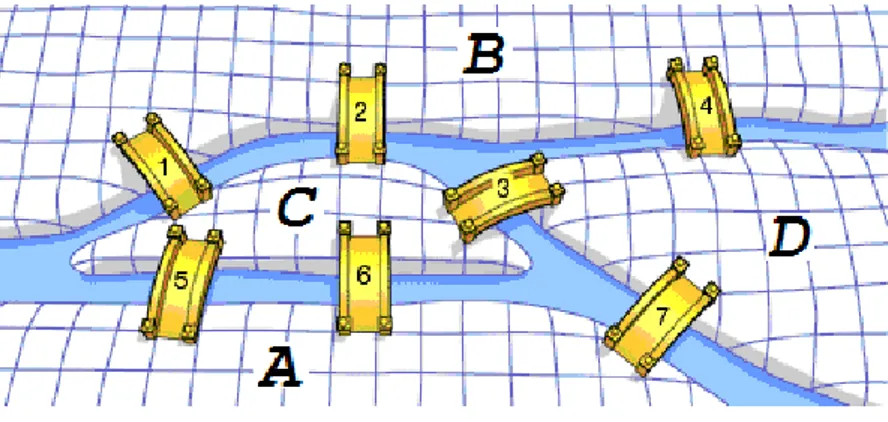
Graf teorisinin temeli olan köprü problemi,18. yüzyılda,Prusya‟daki Königsberg kasabasının Pregel Nehri ile dört bölgeye ayrılmasıyla ilgilidir. Bu dört bölgeyi birbirine bağlayan yedi köprü bulunmaktadır (Şekil 1.1).Kasabanın bu karmaşık yapısı üzerine “Kasabanın bir yakasından gezinti yapmak için çıkan biri tüm köprüleri bir kez

geçerek başladığı noktaya dönebilir mi? ”sorusu ortaya çıkmıştır.Bu soru ünlü

matematikçi Leonhard Euler‟e (1707-1783) kadar ulaşmıştır ve 1736 yılındabu problemin çözümü olmadığı Leonhard Euler tarafından gösterilmiştir. Leonhard Euler, bu problemin çözümü için uğraşırken Graf Teorinin ilk adımlarını da atmıştır.

ġekil 1.1.Königsberg Köprüsü

Sonraki yüzyıl boyunca üzerinde herhangi bir çalışma yapılmayan teori, 1847 yılında G. R. Kirchhoff‟ un (1824 – 1887) “Ağaç Teorisinin Elektrik Devrelerine

Uygulanması” başlıklı çalışması ile yeniden gündeme geldi. Bundan on yıl kadar sonra

A. Cayley (1821 – 1895) “CnH2n+2 Doymuş Hidrokarbon İzomerlerinin Sınıflaması” çalışması sırasında ağaç kavramını keşfetti.

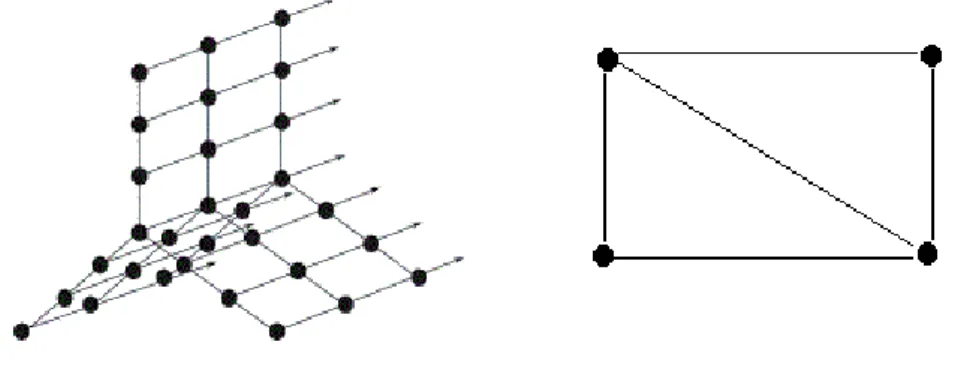
İki nesne arasında daima bir ilişkiden söz etmek mümkündür. Bu ilişki nesnelerin boyları, ağırlıkları, renkleri vs. hakkında olabilir. Söz gelimi kişiler arası tanışıklık ilişkisini ele alalım. Bu tanışıklıkilişkisinde, her bir kişiyi nokta ile temsil edelim. Eğer herhangi iki kişi tanışıyor ise bu iki kişiyi temsil eden noktaları bir çizgi ile birleştirelim, aksi halde noktaları öylece bırakalım.

Örneğin; Mahmut, Gökçen ve Yalçın isimli üç öğrenci düşünelim. Eğer Mahmut; Gökçen ve Yalçın‟ı tanıyorsa fakat Gökçen ve Yalçın birbirini tanımıyorsa bu ilişki şekil 1.2. deki gibi gösterilebilir.

ġekil 1.2.

Bir graf, işte yukarıdaki gibi bir şekildir. Nokta sayısı sonsuz olabilir. Bazı noktalar, “... ilişkisi var” anlamına gelen bir çizgi ile birleştirilir. Çizgilerin boyu veya şekli hiç önemlideğildir, var ya da yok olmaları önemlidir. Noktaların konumu da önemli değildir. Bu özellikleri nedeniyle bir grafın sonsuz farklı şeklinin çizilebileceği açıktır.

Graf teorinin önemli alt dallarından biride spektral graf teoridir. Spektral graf teorinin temeli ise 1950‟li yıllara dayanmakla birlikte daha eskilere kadar uzanmaktadır. Bu alan bilgisayar bilimleri, kimya ve kodlama teorisi gibi birçok alanda uygulanabilir olması açısından ayrık matematiğin önemli bir parçasıdır. Bu alanda, grafın bazı matrislerinin özdeğerleri ve özvektörleri üzerine çalışılır. Bu çalışmada en önemli amaç; grafın matrislerden elde edilen spektral bilgiler vasıtası ile belli başlı özellikleri hakkında bilgi edinmektir. Kuantum kimyada Hückel‟in 1931‟deki makalesinde belirli elektronların enerji sınıflarını bulurken spektral graf teoriden yararlandığını görüyoruz.

Matris-Ağaç Teorisi ise, spektral graf teori sonucunda ortaya çıkmakla birlikteilk olarak Kirchhoff‟un 1847‟deki makalesinde belirtilmektedir.

Collatz ve Sinogowitz in 1957‟deki çalışmalarından buyana spektral graf teori kavramına matematik literatüründe sıklıkla rastlanmaktadır. Genellikle graf teoriye, grafın derece-özdeğer ilişkisi anlamında yaklaşılmıştır. Fakat Cvetković, Rowlinson ve Simić 1980 de grafların spektral ve yapısal özelliklerini incelediler. (Bunun için;Biggs N., 1993, Biggs N., Lloyd E. ve Wilson R., 1986, Brouwer A. ve Haemers W., 2010 gibi çalışmalara bakılabilir.)

Spektral graf teorinin temel problemi, grafların matris gösterimlerinin özdeğerleri ile graf yapılarının nasıl bağdaştırılacağıdır. Bunun için sadece graf teori değil lineer cebirede ihtiyaç duyarız. Bu nedenle öncelikle bizim için gerekli olan graf tanımlarını verdikten sonra lineer cebir tanımlarına da değineceğiz.

Şimdi çalışmamızla ilgili birkaç literatür hakkında bilgi verelim.

A.D. Maden ve arkadaşları (2013)çalışmalarında,işaretsiz Laplacian matrisin hızı için bir alt sınır ve iki grafın tensor çarpımının hızı için bir üst sınır elde etmişlerdir. A.D. Maden ve A. S. Çevik (2012) çalışmalarında, işaretsiz Laplacian matrisin hızı için klik sayısına ve bağımsızlık sayısına bağlı bir alt ve bir üst sınır elde etmişlerdir.

Y.Z. Fan ve arkadaşları (2008) çalışmalarında,T n p, tipindeki bir ağaçlar için 5

n ve 6 , 2 4

2

n

n p n olmak üzere Laplacian hız hesaplamışlardır.

Y.H. Bao ve arkadaşları (2009) çalışmalarında, özel seçilmiş tek devir içeren bir grafın Laplacian hızı hakkında çalışmalar yapmışlardır.

Ş. B. Bozkurt ve D.Bozkurt(2012) çalışmalarında, bir grafın direnç mesafesi ve derece Kirchhoff indeksinin o grafın normalize edilmiş Laplacian matrisinin özdeğerleri ile eşitini bulmuşlardır.

K. C. Das (2013) çalışmasında, Bir grafın Kirchhoff indeksini, o grafın Laplacian matrisinin özdeğerleri ile üstten ve alttan sınırlamıştır.

2. GENEL TANIM VE TEOREMLER

Bu bölümün ilk kısmında graflarla ilgili temel tanımlar verilmiştir. İkinci kısmında ise matrislerle ilgili ihtiyacımız olan genel bilgiler ve grafların matris gösterimleri ile ilgili bilgiler yer almaktadır.

2.1. Graf Tanımları

Tanım2.1.1.V , boş olmayan bir küme ve E , her elemanı V nin farklı elemanlarının oluşturduğu sıralı olmayan çiftlerden oluşan küme olmak üzere V ve E kümelerinden oluşanG V E, şeklinde ki yapıya graf denir.

V kümesinin elemanlarına nokta, E kümesinin elemanlarına ise kenar denir.

,

u v Volmak üzere kenarlar,e u v, formundaki kümelerle daha da basit olarak e uv şeklinde gösterilir. ,u vise bu kenarın uç noktaları olarak ifade edilir.

Tanım 2.1.2.Bir G V E, grafı için v_G n V_G gösterimine grafın mertebesi,

G m EG gösterimine ise grafın boyutu denir. Kısaca n grafın nokta sayısını, m

ise grafın kenar sayısını gösterir.

Tanım 2.1.3. G grafı, noktalar kümesi V G v v₁, ₂,...,vn olan bir graf olmak üzere i

v ve v_j noktaları kenar oluşturuyor ise bu noktalara komşudur denir ve v_i v_j şeklinde gösterilir.Aksi takdirde komşu değildir denir ve v_i v_j şeklinde gösterilir. Herhangi bir v_i noktasının derecesi v_i ye komşu olan noktaların sayısı olup d_i ile gösterilir. Derecesi 0 (sıfır) olan noktaya izole nokta, derecesi 1 (bir) olan noktaya ise pendant nokta denir.

Bir G grafının en az komşuya sahip olan noktasına minimum dereceli nokta denir ve bu noktanın derecesi G ile gösterilir. En çok komşuya sahip noktaya ise maksimum dereceli noktadenir ve bu noktanın derecesi G ile gösterilir.

Bir grafta aynı nokta çiftini birleştiren iki ya da daha fazla kenara katlı kenar denir. Bir noktayı kendisi ile birleştiren kenara ilmek denir. Katlı kenar ya da ilmeği olmayan grafa ise basit graf denir.

Örneğin; aşağıdaki grafta,v₂ noktası v₃ ve v₆ noktaları ile komşudur fakat diğer noktalar ile komşu değildir. Bu grafın noktalarının dereceleri d1 1, d2 4,

3 4

d , d4 2, d5 0, d6 3 olup G 0, G 4. Grafın v5 noktası izole

nokta,v₁ noktası ise pendant noktadır.

ġekil 2.1.1

Bir G grafının m tane kenarı ve v v₁, ₂, ... ,v_nile gösterilen n tane noktası olsun. Her bir kenar başlangıç ve bitiş noktaları olmak üzere iki nokta ile temsil edileceğinden

1 2 n i i d v m

şeklinde ifade edilebilir (Euler teoremi).

Tanım 2.1.4.G ve H iki graf olmak üzere H grafının noktaları ve kenarları G grafının yeniden adlandırılması ile oluşuyorsa bu graflaraizomorf graflar denir. Daha açık olarak

, ( )

u v V G için uv E G( ) u v E H olacak şekilde :V G V H

birebir ve örten fonksiyonu varsa,G ve Hgrafları izomorfiktir denir. Örneğin; Şekil 2.1.1

deki iki graf izomorftur.

Tanım 2.1.5.Graflar, sayılabilirliklerine göre sonlu ve sonsuz graflar olmak üzere ikiye ayrılır. Nokta ve kenar kümeleri, sonsuz kümeler alınarak oluşturulan yapılara sonsuz graf denir. Sonlu kenar ve nokta kümelerinin oluşturduğu graflara ise sonlu graf denir.

ġekil 2.1.3. Sonsuz ve sonlu graf örnekleri

Tanım2.1.6. Bir G grafının nokta kümesi V G u v w x, , , ,..., ,y z olsun. Ardı ardına

k kenarın dizilmesi ile elde edilen

, , ,...,

k

uv vw wx yz

formuna G de k uzunluğunda bir yürüme denir. Bu şekildeki bir yürüme uvwx yz ... şeklinde gösterilir.

Herhangi bir G grafında; aynı noktada başlayan ve biten yürümeye G de bir kapalı yürümedenir.Bütün noktaları ve kenarları birbirinden farklı olan yürümeye G de bir yoldenir. Bütün kenarları ile başlangıç ve bitiş noktaları hariç, bütün noktaları farklı olan kapalı bir yürümeye ise G de bir devir denir.Nokta sayılarına göre, nnoktalı bir yolPn, devir Cnile gösterilir.

G grafı, nokta kümesi V G v v₁, ₂,...,v_n olan bir graf olsun. G nin vi ve vj

noktaları arasında bir yol varsa bu takdirde bu noktalara bağlantılıdırdenir. Bağlantılılık bağıntısı V üzerinde bir denklik bağıntısıdır. V V1, 2,...,Vrdenklik sınıfları olmak üzere

1 , 2 ,..., r

G V G V G V alt graflarına G nin birleşenleridenir. r 1olması durumunda graf bağlantılıdır, aksi taktirde

r

Tanım 2.1.7. G ve H iki graf olmak üzere V_H V_G ve E_H E_G olacak şekildeki H grafına G grafının alt grafı denir ve H G ile gösterilir. H , G grafının alt grafı ise

Ggrafına H grafınınsüper grafı denir.

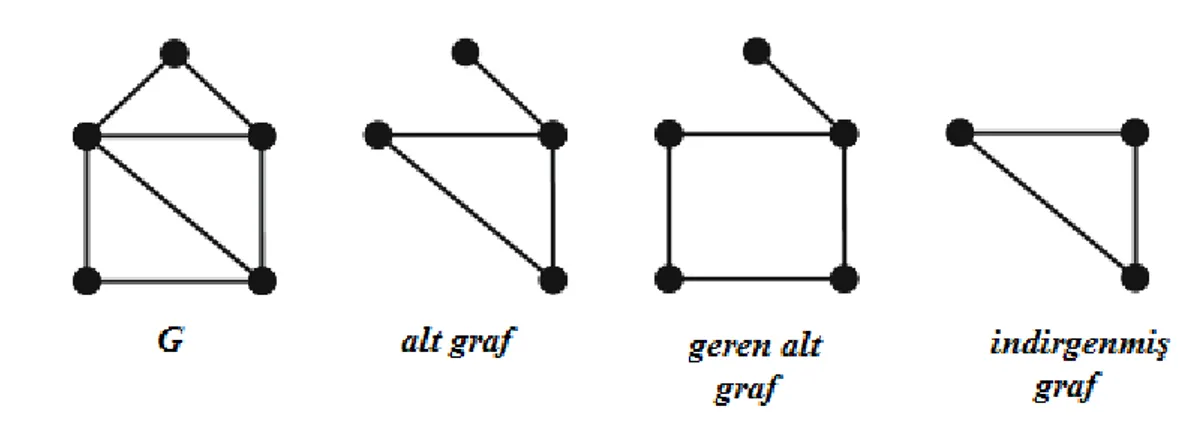
H , G grafının alt grafı ve VH VG ya da EH EG ise H grafına G grafının

özalt grafı denir. EğerV_H V_G ise H, G’ nin geren alt grafıdır.

Eğer, E_H E_G E V_H ise H ‟ye G ‟nin indirgenmişalt grafı (induced subgraph) denir.

ġekil 2.1.4. BirGgrafın sırası ile alt, geren ve indirgenmiş alt grafları.

Tanım 2.1.8. Bir G grafı verilsin. G nin ikişerli komşu olmayan noktalarının bir kümesine bağımsız küme (independent sets)denir.

Bir G grafının,maksimum eleman sayısına sahip olanbağımsız kümelerinin eleman sayısına grafın bağımsızlık sayısı (independence number)denir ve bu sayı

G

( )ile gösterilir. Yani,

( ) max{

G

V V bağımsız küme

:

}

dir.

Tanım 2.1.9.Bir G grafı verilsin. G nin alt graflarından tam graf olanların kümesine klik kümesi (clique sets) denir.

Bir G grafının klik kümeleri içinde en çok noktaya sahip olanın nokta sayısına, grafın klik sayısı (cliquenumber) denir ve ( )G ile gösterilir.

max _i : _{i i}, _i

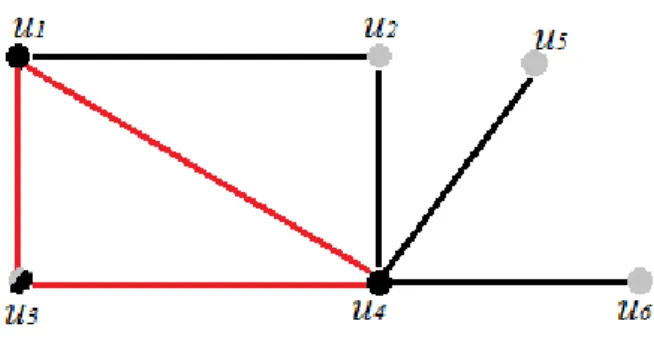
Şekil 2.1.5. Klik ve bağımsızlık sayılarını gösteren bir graf örneği

Şekil 2.1.5 daki grafta bağımsızlık sayısı, açık renk ile belirtilen noktaların sayısı olup α(G)=4, ve klik sayısı ise koyu ile belirtilen noktaların sayısı yani ω(G)=3 dür. Tanım 2.1.10. G nnoktalı bir graf olmak üzeregenel randić indeks,

( ) _{u v}

uv E

R G d d

biçiminde tanımlanır .

Biz çalışmamız da genel olarak 1 alınarak elde edilen ₁( ) 1

uv E u v

R G

d d ifadesini kullanacağız.

2.1.1. Özel Graflar

Şimdi çalışmamızda adı geçen bazı özel grafların tanımlarını verelim.

Tanım 2.1.1.1.Her bir nokta çifti birbirine komşu olan Ggrafına birtam grafdenir. n noktalı bir tam graf K_n ile gösterilir.Bir tam graf, nokta kümesi üzerinde tanımlanabilecek bütün kenarları bulundurur. Bu nedenle nmertebeli ve m boyutlu

bir tam graf için ( 1)

2 2

n n n

m eşitliği geçerlidir.

Nokta kümesi X ve Y gibi iki alt kümeye ayrılmış olan ve kenarları da X deki bir noktaylaYdeki bir noktanın birleştirilmesi ile elde edilen, G grafına iki parçalı graf ve

X Y

,

Y

q

Aşağıda iki parçalı graf ve star graf örneği verilmiştir.

ġekil 2.1.1.1. İki parçalı tam graf ve yıldız örneği

Tanım 2.1.1.2.Hiç deviri olmayan bağlantılı grafa ağaç denir, T ( , )V E şeklinde gösterilir. Bizim çalışmamızda sıklıkla kullanacağımız özel T n p( , ) grafı ise Bölüm 6.1 de tanımlandı.

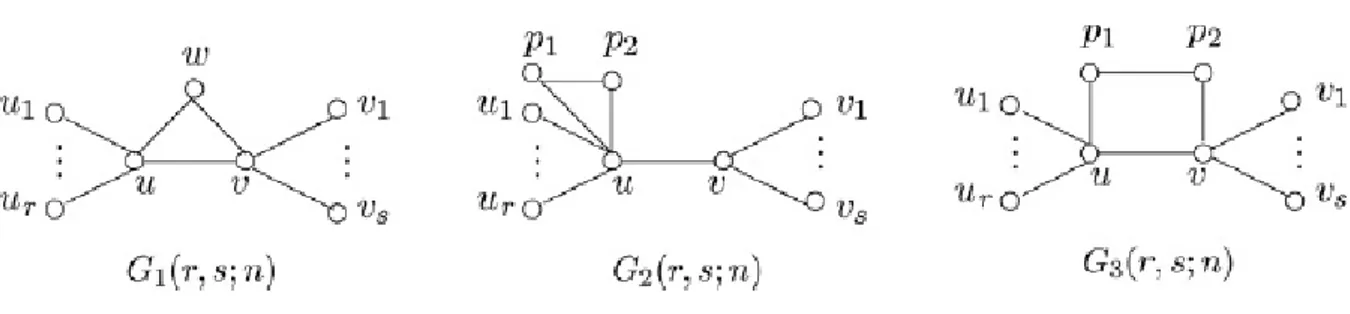
Tanım 2.1.1.3.Bir devir ve bir ya da birkaç ağaçın birleşmesi ile oluşan graflaraTekdevir içeren graflardenir. Bu graflar pek çok şekilde oluşturulabilirler. Fakat spektral graf teoride genel olarak üç sınıf altında inceleme yapılmıştır. Bunlar şekil 2.1.1.2 da gösterilmiştir.

ġekil 2.1.1.2. Tek devir içeren graf örnekleri

Tanım 2.1.1.4.Tek bir noktaya sahip olan hiç kenarı olmayan grafa trivial graf denir.Hiç kenarı olmayan sadece noktalardan oluşan grafa boş (null)grafdenir.

Tanım 2.1.1.5.Bir G grafında tüm noktaların dereceleri birbirine eşit yani vi VG için i

ġekil 2.1.1.4.Petersen grafı

Tanım 2.1.1.6.G (V EG, G) şeklinde bir graf ve EG e E V e E G olmak

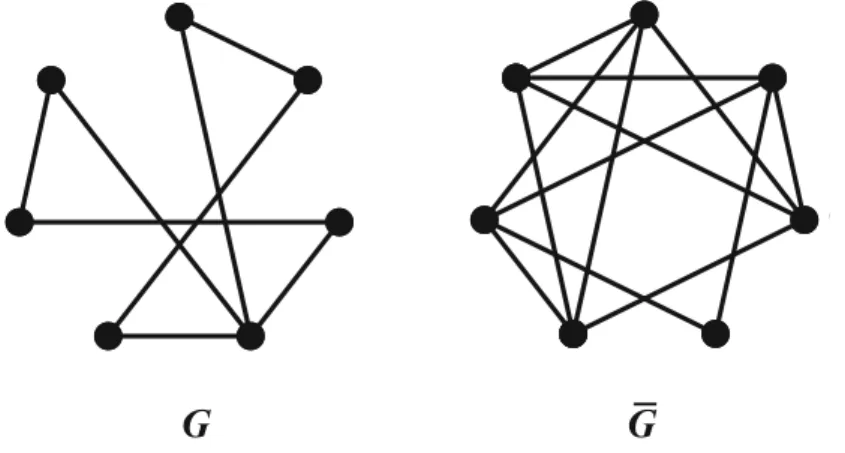
üzere G (V_G,E_G) şeklindeki grafa G grafının tamamlayıcısı (complement)denir.

ġekil 2.1.1.5.G grafı ve tamamlayıcısı

2.2. Grafların Matris Gösterimleri

Bir G grafı verilsin, grafın yapısı hakkındaki bazı bilgileri kullanarak bu grafı matris şekline getirebiliriz. Grafların matris gösterimleri hakkındaki çalışmaların çoğu komşuluk matrisi (adjacency matrix),kombinatoryal Laplacian matris (combinatorial

Laplacian matrix), işaretsiz Laplacian matris ve normalize edilmiş Laplacian

matrisüzerinedir.

Bir G V E, grafının komşuluk matrisi(adjacencymatrix, A G ),satır ve sütunları G grafının noktaları ile adlandırılarak aşağıdaki şekilde tanımlanır.

1 , ( ) . 0 , i j ij v v A G a aksi halde

Bir G V E, grafınınDerece matrisi (degreematrix,D G ),satır ve sütunları

G grafının noktaları ile adlandırılarak aşağıdaki şekilde tanımlanır.

, ( ) ( ) . 0 , i i j ij d v v D G d aksi halde

Bir G V E, grafınınKombinatoryal Laplacian matrisi(combinatorial

Laplacian matrix,L G( )),satır ve sütunları G grafının noktaları ile adlandırılarak aşağıdaki şekilde tanımlanır.

, 1 , . 0 , i i j ij i j d v v L G l v v aksi halde

Bir G V E, grafınınİşaretsiz Laplacian matris(signless Laplacian matrix,

Q G ), satır ve sütunları G grafının noktaları ile adlandırılarak aşağıdaki şekilde

tanımlanır. , 1 , . 0 , i i j ij i j d v v Q G q v v aksi halde

Bir G V E, grafınınNormalize Edilmiş Laplacian matris(normalized

Laplacian matrix, L G ), satır ve sütunları G grafının noktaları ile adlandırılarak aşağıdaki şekilde tanımlanır.

1 , 0 1 , . 0 , i j i ij i j i j v v ve d G v v d d aksi halde L

ġekil 2.2.1. Basit bağlantılı G grafı Komşuluk matrisi; 0 1 0 0 1 0 1 0 1 1 1 0 0 1 0 0 0 1 0 1 0 0 1 0 1 1 0 1 0 1 0 0 1 0 1 0 A G . Derece matrisi; 2 0 0 0 0 0 0 4 0 0 0 0 0 0 2 0 0 0 0 0 0 2 0 0 0 0 0 0 4 0 0 0 0 0 0 2 D G .

Kombinatoryal Laplacian matris;

2 1 0 0 1 0 1 4 1 1 1 0 0 1 2 0 0 1 0 1 0 2 1 0 1 1 0 1 4 1 0 0 1 0 1 2 L G .

İşaretsiz Laplacian matrisi; 2 1 0 0 1 0 1 4 1 1 1 0 0 1 2 0 0 1 0 1 0 2 1 0 1 1 0 1 4 1 0 0 1 0 1 2 Q G .

Normalize edilmiş Laplacian matrisi;

1 1 1 0 0 0 8 8 1 1 1 1 1 0 4 8 8 8 1 1 0 1 0 0 2 8 1 1 0 0 1 0 8 8 1 1 1 1 0 1 4 8 8 8 1 1 0 0 0 1 2 8 G L şeklindedir.

2.3. Lineer Cebir Bilgileri

Bu bölümde çalışmamızda kullanacağımız bazı Lineer Cebir bilgilerini hatırlayacağız ve kullanacağımız notasyonları açıklayacağız.

n

I ; n boyutlu birim matrisi, 0_{m n} ise m n boyutlu sıfır matrisi göstermektedir.

0_n; n boyutlu sıfır vektör, e_n, n boyutlu her bir elemanı bir olan vektör olarak kabul edilir.

M ,n mertebeli reel matris olarak ele alınacaktır. M , M nin transpozesini T gösterirken,det I M 0fonksiyonuna matrisin karekteristik polinomu, bu polinomun köklerine ise matrisin özdeğerleri denir. Bir matrisin özdeğerlerinin kümesi ise o matrisin spektrumu olarak adlandırılır. Bir matrisin özdeğerleri , , q gibi notasyonlarla gösterilirken, Mx x denklemini sağlayan sıfırdan farklıx değerlerine matrisin özvektörleri denir.Matrsinözvektörleri ise u v x gibi notasyonlarla , , göstereceğiz.

,

u vsıfırdan farklı boyutlarıuygun herhangi iki vektör olsun, Mu u ve

T

M v v denklemlerini sağlayan değerine M nin tekil (singular) değeri denir. Bir reel matrisin transpozesi kendisine eşit T

M M ise o matrise simetrik matris denir.

Reel simetrik ve n boyutlu bir M matrisi, her nboyutlu xvektörü için

0

T

x M x şartını sağlıyorsa bu matrise pozitif yarı tanımlı matris denir.

Teorem 2.3.1. (Cvetković ve ark., 1980, Horn ve ark., 1985) M n boyutlu reel simetrik bir matris olmak üzere

i) M matrisinin özdeğerleri reel sayılardır.

ii) M matrisinin özdeğerlerinincebirsel ve geometrik katlılıkları eşittir. iii) M matrisinin singüler değerleri, özdeğerlerinin mutlak değerine eşittir.

Teorem 2.3.2. (Fan, 1951) M ve N n- boyutlu iki kare matris olmak üzere;

1 1 1 n n n i i i i i i A B A A şartını sağlar.

Teorem 2.3.3.(Horn ve ark., 1985) M n boyutlu reel simetrik bir matris olmak üzere aşağıdakiler özdeştir.

i) n

x için x M xT 0 şartını sağlıyorsa M matrisi pozitif yarı tanımlıdır.

ii) M matrisinin her bir özdeğerleri pozitif yada sıfırdır. iii)M S STolacak şekilde bir S matrisi vardır.

M nboyutlu kare matrisinin esas köşegen elemanları toplamına o matrisin izi denir ve iz M ile gösterilir,

1 n i i iz M M eşitliği vardır.

M nboyutlu matris ve a b, olmak üzere aM bIn matrisinin özdeğerleri;

1( ) , 2( ) ,..., n( )

a M b a M b a M b şeklindedir.

2.3.1 Matrislerin Tensor Çarpımları

Tanım 2.3.1.1.A m n, tipinde B p q, tipinde iki matris olmak üzere A ve B matrislerinin tensor (kronecker ya da direkt) çarpımı

11 1n

m1 mn mp nq

a B a B

A B

a B a B

biçiminde tanımlanır. Tensor çarpım değişmeli değildir.

Örneğin;A 2 1 1 3 ve 4 1 B 3 1 olsun. 8 2 4 1 2B B 6 2 3 1 A B B 3B 4 1 12 3 3 1 9 3 , 8 4 2 1 4 A A 4 12 1 3 B A 3A A 6 3 2 1 3 9 1 3 olup, A B B Adır.

ŞimdiKronecker çarpım ile ilgili bazı teoremleri verelim.

Teorem 2.3.1.1.(Belmann, 1970) A ve B reel değerli iki kare matris olmak üzere

i) 0 A A 0 0 .

Teorem 2.3.1.2(Belmann, 1970) A₁ve A₂ aynı boyutlu matrisler ve B herhangi bir matris olmak üzere , için

i) A₁ A₂ B A₁ B A₂ B . ii)B A₁ A₂ B A₁ B A₂ . iii) A B A B . eşitlikleri sağlanır. Teorem 2.3.1.3.(Belmann, 1970) _{ij ij ij ij} m n p q n r q s A a ,B b ,C c , D d

şeklindeki reel değerli matrisler olmak üzere

A B C D AC BD , eşitliği vardır.

Teorem 2.3.1.4.(Belmann, 1970) A ,B,C reel değerli üç matris olmak üzere A B C A B C

dir.

Teorem 2.3.1.5.(Belmann, 1970) A ve B tekil olmayan iki matris olmak üzere

1 _{1 1}

A B A B dir.

Teorem 2.3.1.6.(Belmann, 1970) _{ij ij}

n n m m

A a ,B b reel değerli iki matris, A

nınözdeğerleri 1, 2,..., nve B nin özdeğerleri ise 1, 2,..., m olmak üzere A B nin

özdeğerleri _{1 1}, _{1 2},..., _{1 m},..., _{n 1}, _{n 2},..., _{n m} şeklindedir.

2.4. Normalize EdilmiĢLaplacian Matrisin Özdeğerleri

G , n noktalı bir graf ve L( )G , G nin normalize edilmiş Laplacian matrisi olmak üzere,L( )G reel, simetrik ve pozitif yarı tanımlıbir matristir. Böylece özdeğerleri pozitif reel sayılardır.

S , satır ve sütunları G grafının noktaları ile adlandırılmış bir matris olmak

1 , 1 , , 0 , x x e xy ve u x d S u e e xy ve u y d aksi halde

şeklinde seçeceğimiz S matrisi L( )G SST şartını sağlar. Böylece Teorem 2.3.3 den ( )

L G matrisinin özdeğerleri pozitif yada sıfırdır.

Ayrıca izole nokta içermeyen her graf için normalize edilmiş Laplacian matris ile derece matrisi, komşuluk matrisi ve kombinatoryal Laplacian matris arasındaki ilişki

1/ 2 1/ 2 1/ 2 1/ 2 1/ 2 1/ 2 D L D D D A D I D A D L şeklindedir.

Lemma 2.4.1. (Chung, 1997) G , n 2 noktalı izole nokta içermeyen bir graf ve normalize edilmiş Laplacian spektrumu;

1( )G 2( )G ... n 1( )G n( )G 0 olsun. Bu özdeğerler, i) 1 L n i i n ii) 1 1 n n

n eşitlik şartı sadece n noktalı tam graflarda geçerlidir.

iii) 1

1

n

n eşitlik şartı sadece n noktalı tam graflarda geçerlidir.

iv) Eğer G tam graf değilse, _{n 1} 1 şartını sağlar.

v) G bağlantılı, kenar sayısı m ve diameter D olan bir graf ise; 1

1 0 2 n mD dır. vi) 1 i n için i L 0, 2

vii) ₁ 2 eşitlik şartı sadece iki parçalı tam graflar için geçerlidir. şartlarını sağlar.

3. NORMALIZE EDĠLMĠġ LAPLACIAN HIZ

Bu bölümde, öncelikle reel matrisler için hız tanımı ve özellikleri verildi. Daha sonra basit bağlantılı grafların normalize edilmiş Laplacian matrislerinin hızlarına dair bir üst sınır elde edildi.

3.1. Hız Tanımı ve Özellikleri

ŞimdiTeorem 3.2.1 de kullanacağımız, literatürdeyer alan temel tanım ve ifadeleri verelim. [Johnson ve ark., 1985; Mirsky, 1956; Nylen ve Tam, 1994; Thompson, 1992]

Tanım 3.1.1.M m_ij , n n tipinde reel bir matris ve herhangi iki özdeğeri i ve j

olsun. M matrisinin özdeğerlerininfarkının maksimum değerine matrisin hızı (spread) denir ve aşağıdaki şekilde ifade edilir.

,

max _{i j}

i j S M

MHermityen matris olduğundanözdeğerleri _{i i} M şeklindeki reel sayılardır.

Mmatrisininözdeğerlerinin artmayan sırayla dizilişi _{1 2} ... _n olsun. M matrisinin hızı;

1

( ) n

S M

dir. M Hermityen matrisi ve x y, n için

* *

1 x Mx , n y My

olup bunları hız tanımında yerine koyarsak;

* * , , , max max _{ij i j i j} x y x y i j S M x Mx y My m x x y y elde edilir.

3.2. Normalize EdilmiĢ Laplacian Hız

Literatürde grafların kombinatoryal Laplacian ve işaretsiz Laplacian matrislerinin hız değerleri üzerine pek çok çalışma mevcuttur. Örneğin; Liu M. ve Liu B., 2010;Maden ve ark., 2013;Zhai ve ark., 2011.Bizde bu çalışmalara ek olarak normalize edilmiş Laplacian matrisin hızı tanımlayarak bazı sınır elde edeceğiz. Öncelikle bu hesaplama için bize gerekli olan tanımları verelim

G basit bağlantılı bir graf olmak üzere, G grafının normalize edilmiş Laplacian matrisinin 1 , 0 1 , 0 , i j i ij i j i j v v ve d G v v d d aksi halde L

şeklinde tanımlandığını biliyoruz. Simetrik L( )G matrisinin özdeğerleri

1( )L 2( )L ... n 1( )L n( )L 0

şeklindeartmayan sırada sıralansın. Bu tanımlardan yararlanarak bir G grafının normalize edilmiş Laplacian matrisinin hızını

1 1

( ) _n

SL G şeklinde tanımlayabiliriz.

Şimdi SL( )G nin üst sınırını hesaplamak için aşağıdaki bilinen eşitlikleri kullanacağız. 1 ( ( )) n i i iz L G n , 2 1 1 (L ( )) 2 2 ( ) uv E u v iz G n n R G d d . (3.2.1)

Teorem 3.2.1. G, n noktalı basit bağlantılı graf olmak üzere, G grafının normalize edilmiş Laplacian matrisinin hızı için aşağıdaki eşitsizlik geçerlidir.

2 1 1 1 1 ( ) ( ) 2 ( ) 2 ( ) 2 L n S G G n R G R G . (3.2.2)

Ġspat.(3.2.1) eşitliğini kullanarak,

2 2

1 n 1 n 2R1( )G

eşitsizliğini yazabiliriz. Bu eşitsizliği normalize edilmiş Laplacian hız tanımında yerine yazarsak 2 1 1 1 1 1 ( ) ( ) 2 ( ) L _n S G G n R G (3.2.3)

elde edilir. Burada ₁ e bağlı ₁ n 2R₁( )G ₁2 fonksiyonu, 1 1

( )

2

n

R G

( )

2

n

R G

(3.2.3) de 1 1

( )

2

n

R G

2

1

( )

2

( )

2

( )

2

n

G

n

R

G

R

G

ifadesini elde etmiş oluruz. Böylece (3.2.2) eşitsizliğini sağlatırız.

Bazı bilinen özel grafların normalize edilmiş Laplacian hızlarını hesaplayalım, n

K tam grafının normalize edilmiş Laplacian matrisi ;

1 , 1 , 1 n K u v aksi halde n L

şeklindedir. Bu matrisin özdeğerleri ise

1 1 , 0 1 n n

n olup, normalize edilmiş

Laplacian hızı ise SL( )G _{1 n 1} formülünden, ( ) 0 L _n

S K

olarak elde edilir. Benzer olarak; p,q

K iki parçalı grafının normalize edilmiş Laplacian matrisinin özdeğerleri ,

1 2 1 2 ,1p q , 0 olup, , ( ) 1 L _{p q} S K dir.

Petersen grafının normalize edilmiş Laplacian matrisinin özdeğerleri ise ;

4 5 1 5 2 , , 0 3 3 olup

1

S

L

G

4. NORMALĠZE EDĠLMĠġ LAPLACĠAN HIZIN KLĠK VE BAĞIMSIZLIK SAYILARI ĠLE ĠLĠġKĠSĠ

Bu bölümde normalize edilmiş Laplacian hız için klik ve bağımsızlık sayılarına bağlı olarak alt ve üst sınırlar elde edildi. Buradaki temel tanımlar ve ifadeler için ana kaynak olarak Motzkin ve Strauss, 1965 ve Maden ve Çevik, 2012 çalışmaları kullanıldı.

S, n_de

(n 1)-boyutlu birim simpleks olsun. Yani S x n:e xT 1, x 1 Klik sayısının ve bağımsızlık sayısının , komşuluk matrisi A ile arasında

1 1 max , x S x Ax (4.1) 1 min , x S x I A x

şeklinde bir bağıntı vardır.

( )G

L nin 1( )G 2( )G ... n 1( )G n( )G 0 şeklindeki özdeğerlerine ait

özvektörler 1 2

0, ,..., n olmak üzere y_i ui 1 2 1u n olacak şekilde bir birim vektör ailesi oluşturulabilir. i 1, 2,...,n , ( 1, 1) . Buradan i 2 3, ,...,n için 1 2 2 : 0 ₁ max 0 i j j i j u _i j j u l u u ve 1 2 2 : 0 ₁ min 0 i j j i j u _i j j u u u u

olmak üzere l u_i, _i için, (4.1) denkleminin olası çözümü, ( ) (1 / T ( )) / ( )

i i i

z e y y

olarak elde edilir. T i i s e u olmak üzere , 2 2 1 2 , ₂ 1 max ( ) ( ) (1 ) max 1 i i i i T i i i l u i l u i g z Az s s

olsun. *

1,2,..., max i

i n

g g biçiminde gösterirsek (4.1)denkleminden dolayı

*

1 1 g

elde edilir. Şimdi bu bilgileri kullanarak, klik ve bağımsızlık sayısı için normalize edilmiş Laplacian matrisin özdeğerlerine bağlı sınırlar bulmaya çalışalım.

Teorem 4.1. G bir graf ve minimum derecesi olmak üzere

2 1,2,..., 1 1 max ( ( ) 1) i n i n n (4.2) ( 1, 1) eşitsizliği mevcuttur.

Ġspat.L( )G nin özdeğerleri 1( )G 2( )G ... n 1( )G n( )G 0, bu özdeğerlere

içinözvektörler 1 2 0, ,..., n olmak üzere 1/ 2 1/ 2 1/ 2 1/ 2 1 1 ( ) , ( ) ( ) , ( ) ( ) ( ) , ( ) ( ) , ( ) ( ) , ( ) ( ) , ( ) 1 ( ) , ( ) i i i i i i i i n n i i i i u v _{u v} i i i z z z D AD z z z z D AD z z Az z z d d z z g L (4.3) (4.3) eşitsizliğinde, 2 2 1 2 2 1 (1 ) ( ) , ( ) 1 i i i i z z s s

eşitliğini yerine koyarsak,

2 2 2 2 1 2 2 2 2 1 1 (1 ) (1 ) 1 1 ( 1) 1 1 i i i s s s s (4.4)

eşitsizliğini elde ederiz ve 2 2 1 1

i

s s n olduğunu biliyoruz(Maden ve Çevik, 2012). Buna göre (4.4) eşitsizliğini düzenlersek,

2 2 1 1 1 1 2 2 1 2 1 1 2 1 1 1 1 1 1 (1 ) , 1 1 1 (1 ) , 1 1 1 i i i i i n s s n n

elde edilir. Buradan (4.2) eşitsizliğinin sağlandığı açıktır.

Teorem 4.2.G bir graf ve maksimum derecesi ve U_i s_i 1 2s olmak üzere ₁

2 2 2 1,2,..., 1 1 max ( ( ) 1) i i n i i U U ( 1, 1) eşitsizliği mevcuttur.

Ġspat.Teorem 4.1 ve (4.1) denkleminden ispat açıktır.

Şimdi Teorem 4.1 ve Teorem 4.2 için bazı sonuçlar verelim.

Sonuç 4.1. G n noktalı ve minimum derecesi olan bir graf olmak üzere klik sayısı ile normalize edilmiş Laplacian hız arasına,

1 2 1 (1 ) 1 ( ) n SL G eşitsizliği vardır. Ġspat. 2 1 1 ( ( _i) 1) n n 1 i n için çözüm yapılırsa, 2 1 ( ( ( )) 1) n n SL G ve 2 1 1 (SL( ))G 1 n(1 )

elde edilir. Böylece ispat tamamlanmış olur.

Sonuç 4.2. G n noktalı ve maksimum derecesi olan bir graf olmak üzere bağımsızlık sayısı ile normalize edilmiş Laplacian hız arasında,

2 1 1 2 1 1 1 ( ) n U SL G

şeklinde bir bağıntı vardır. 2

(1 i n U, _i s_i s_i 1 )

Sonuç 4.3. Normalize edilmiş Laplacian hızın klik sayısı ve bağımsızlık sayısına bağlı bağlı olarak alt ve üst sınırları

2 1 1 ₁ 2 2 1 ₁ 1 1 _{(1 ) 1} ( ) n n U SL G şeklindedir.

5. GRAFLARIN TENSOR ÇARPIMININ NORMALĠZE EDĠLMĠġ LAPLACĠAN HIZI

Bu bölümde basit bağlantılı grafların tensor çarpımının normalize edilmiş Laplacian matrisin hızı için bir alt ve bir üst sınır elde edildi. Matrislerin tensor çarpımları ile ilgili daha genel bilgiler Bölüm 2.3.1. de bulunmakla birlikte bazı önemli tanımlardan bu bölümde bahsedeceğiz.

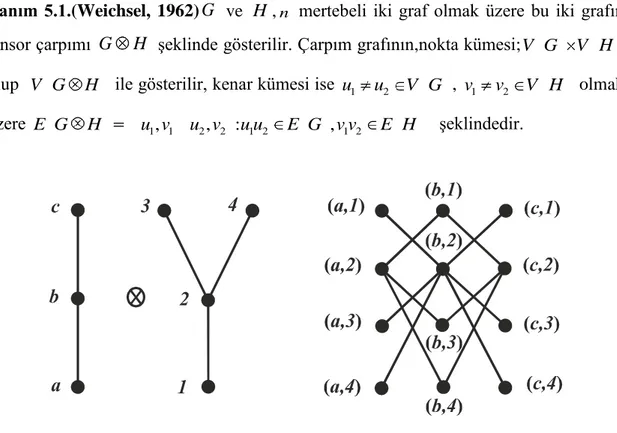
Tanım 5.1.(Weichsel, 1962) G ve H ,n mertebeli iki graf olmak üzere bu iki grafın tensor çarpımı G H şeklinde gösterilir. Çarpım grafının,nokta kümesi;V G V H olup V G H ile gösterilir, kenar kümesi ise u₁ u₂ V G , v₁ v₂ V H olmak üzere E G H u v₁, ₁ u v₂, ₂ :u u_{1 2} E G v v, _{1 2} E H şeklindedir.

ġekil 5.1.1İki grafın tensor çarpımı

Lemma 5.1. (Cvetković ve ark.,2010;Weichsel, 1962) G ve H graflarını ele alalım. Bu grafların komşuluk matrisleri sırası ile A G( ) veA H( )olsun. G H grafının

komşuluk matrisi ise A G( H) olup, bu matrisler arasında

( ) ( ) ( )

A G H A G A H (5.1) eşitliği vardır.Benzer olarak derece matrisleri için,

( ) ( ) ( )

D G H D G D H (5.2) eşitliği vardır.

Tanım 5.2. _ij

m n

A a ve _kl

p q

B b iki matris olmak üzere bu iki matrisin tensor

çarpımı ise A B a Bij _{mp nq} şeklindedir ve X Y Z, , ve T herhangi reel matrisler

olmak üzere

(X Y) (Z T) (X Z) (X T) (Y Z) (Y T) eşitliği verdır.

Lemma 5.2. G ve H basit bağlantılı iki graf olmak üzere

G H G H G H G H

L L L L L (5.3)

eşitliği vardır.

Ġspat. 1/2 1/2

D AD

L olduğunu biliyoruz. G H grafı için bu eşitliği yazalım.

1/2 1/2 G H G H D G H A G H D G H L olup (5.1) ve (5.2) eşitliklerden, 1/2 1/2 1/2 1/2 G H G H D G D H A G A H D G D H L

olur. Bu eşitliği düzenlersek,

1/ 2 1/ 2 1/ 2 1/ 2 L L L L L L L G H G H D G A G D G D H A H D H G H G G H H G H G H G H G H G H

sonuç olarak (5.3) eşitliği elde edilir.

Örnek 5.1.Şekil 5.1.1daki grafın normalize edilmiş Laplacian matrisleri için lemma 5.2. nin doğruluğunu gösterelim.

-1 1 0 0 -1 3 1 0 -1 -1 -1 2 1 -1 -1 3 3 3 1 , -1 2 2 0 1 0 -1 3 0 1 -1 2 0 0 1 3 G H L L

olupL G H G L H L G H L G L H eşitliğinde yerlerine yazarsak, -1 1 0 0 -1 3 1 0 1 0 0 0 -1 -1 -1 2 1 0 0 1 0 1 0 0 -1 -1 3 3 3 0 1 0 1 -1 2 2 0 0 1 0 0 1 0 0 0 1 -1 3 0 0 0 1 0 1 -1 2 0 0 1 3 -1 1 0 0 -1 3 1 0 -1 -1 -1 2 1 -1 -1 3 3 3 1 -1 2 2 0 1 -1 3 0 1 2 G H L 0 -1 0 0 1 3

1 1 0 0 0 0 0 0 0 0 0 0 6 1 1 1 0 1 0 0 0 0 0 0 0 6 6 6 1 0 0 1 0 0 0 0 0 0 0 0 6 1 0 0 0 1 0 0 0 0 0 0 0 6 1 1 0 0 0 1 0 0 0 0 0 0 6 6 1 1 1 1 1 1 0 0 1 0 0 0 6 6 6 6 6 6 1 1 0 0 0 0 0 1 0 0 0 0 6 6 1 1 0 0 0 0 0 0 1 0 0 0 6 6 1 0 0 0 0 0 0 0 1 0 0 0 6 1 1 1 0 0 0 0 0 0 1 0 0 6 6 6 1 0 0 0 0 0 0 0 0 0 1 0 6 1 0 0 0 0 0 0 0 0 0 0 1 6 G H L

olarak elde edilir.

Önerme 5.1.(Kaveh ve Alinejad, 2009)Ai ve Bi

1 i n

1 i j n için A A_{i j} A A_{j i} ve B B_{i j} B B_{j i} ise, aşağıdaki eşitlik mevcuttur.

1

n

i i i i

i

eig A B eig A B

Teorem 5.1G ve H sırası ile n ve m mertebeli iki basit bağlantılı graf olmak üzere SL G H SL G SL H S L G L H

eşitsizliği vardır. Eşitlik şartı ise sadece G ve H tam graf olduğu taktirde geçerlidir.

max eig L G H max eig G L H L G H L G L H ve

min eig L G H min eig G L H L G H L G L H olup bu eşitlikleri düzenlersek,

max max max

min

L L L L

L L

eig G H eig G H eig G H

eig G H

ve

min min min

max

eig G H eig G H eig G H

eig G H

L L L

L L

olarak elde edilir. Bu eşitsizlikleri normalize edilmiş Laplacian hız formülünde yerine yazarsak,

max min max min

max min

max min

L L L L

L L

L L L L

eig G H eig G H eig G H eig G H

eig G H eig G H

eig G H eig G H

elde edilir. Normalize edilmiş hız tanımına göre ispat açıktır.

Teorem 5.2. G ve H sırası ile n ve m mertebeli iki basit bağlantılı graf ve n 1( )G

ve _{m 1}(H)sırasıyla G ve H nin normalize edilmiş Laplacian matrisininözdeğerleriolmak üzere

1 1

1 m 1 n

SL G H SL G SL H SL G SL G (5.4)

eşitsizliği vardır, eşitlik şartı ise sadece tam graflar için geçerlidir.

Ġspat.Lemma 5.2. den, 1

G

H

H

G

G

H

L

L

L

L

L

L

G

H

L

H

L

G

L

G

L

H

1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 nm m n n m n m m n n m m n G H G H H H G G G H G H G G H H H H G G G H H H G G L L L L L L L L L L L L L L L L L L L L L L L L

olarak elde edilir. Böylece ispat tamamlanmış olur.

Şimdi grafların tensor çarpımının normalize edilmiş Laplacian hızı için bulduğumuz sınırları bir örnek üzerinde inceleyelim.

Örnek 5.2.örnek 5.1 de ki matrisler için; G

L için;özdeğerler kümesi, 2 1 0, , olupSL G 1dir.L H için;özdeğerler kümesi, 2 1 1 0, , , olup SL H 1dir.L G H için; özdeğerlerkümesi,

, , , , , , , , , , ,

2 2 1 1 1 1 1 1 1 1 0 0 olup SL G H 1olup, bu değerlerin, Teorem 5.1 ve Teorem 5.2 deki eşitsizlikleri sağladığı açıkça görülür.

6. AĞAÇLARIN ve TEK DEVĠRLĠ GRAFLARIN NORMALIZE EDĠLMĠġ LAPLACIAN HIZI

Bu bölümdeözel T n p, ve G n( 3, 0; )n (n 5)graflarının normalize edilmiş Laplacian hızlarını hesaplayacağız.

6.1. T n p, - Tipindeki Ağaçların Normalize EdilmiĢ Laplacian Hızı

Öncelikle T n p, tipindeki ağaçların tanımını verip bu grafların normalize edilmiş Laplacian matrisinin karakteristik polinomunu hesaplayalım.

,

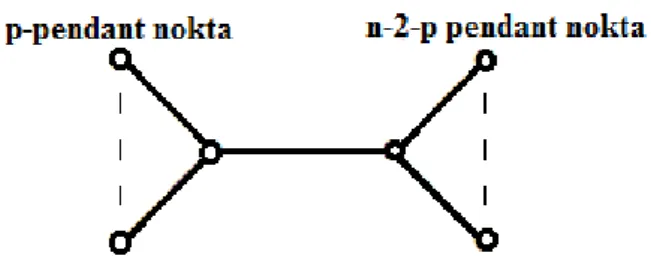
T n p tipindeki ağaçlarK_{1, p} ve K_{1,n 2 p} şeklindeki iki yıldızın birleştirilmesi ile oluşurve şekil 6.1.1 deki gibi gösterilir.

ġekil 6.1.1T n p, - tipindeki ağaç

Şimdi bu grafın normalize edilmiş Laplacian matrisinin karakteristik polinomunu hesaplayalım.

Teorem 6.1.1. q n p 2 olmak üzere L T n p, karakteristik polinomu

2 det , 1 2 1 1 1 p q pq T n p p q L (6.1) dir. Ġspat.M T n p, olsun,

1 0 0 1 0 1 0 1 1 0 1 1 1 1 1 0 1 1 1 1 p p q q p q e p e q M e p p q e q p q

olup bu matrisini soldan

2 0 1 , 1 1 p q T T p q e e B diag p q

matrisi ile çarparsak,

1 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 1 1 1 p p q q e p e q BM p q p q (6.2)

matrisini elde ederiz. Eşitlik 6.2 deki matrisin determinantı,

2 . 1. ( ( , )) 1 2 1 1 1 p q pq BM B M T n p p q L ve 2 ( ( , )) 1 2 1 1 1 p q pq M T n p p q L

elde edilir. Böylece ispat tamamlanmış olur.

Yukarıda elde ettiğimizkarakteristik polinomunun kökleri T n p, -tipi ağacın normalize edilmiş Laplacian özdeğerleri denir ve bu özdeğerlerin en büyüğü ile sıfırdan

farklı en küçüğü arasındaki farka T n p, tipindeki grafların normalize edilmiş Laplacian hızı denir. Şimdi bu hızı hesaplayalım.

Teorem 6.1.2. T n p, tipindeki grafların normalize edilmiş Laplacian hızı için 2 q n p olmak üzere , 1 1 1 pq S T n p p q L eşitliği vardır.

Ġspat. Teorem 6.1.1 de L T n p( ( , )) matrisinin karakteristik polinomunu

2 det ( ( , )) 1 2 1 1 1 p q pq T n p p q L

biçiminde hesaplamıştık. Bu eşitlikten L T n p, matrisinin özdeğerleri;

1 2, 2,3 1 , 4 0

1 1

pq

p q şeklindedir. Sonuç olarak hız tanımından;

, 1 1 1 pq S T n p p q L elde edilir.

6.2. G n₁( 3, 0; )n - Tipindeki (n 5)Tek Devir Ġçeren Grafların Normalize

EdilmiĢ Laplacian Hızı

Bu bölümdetek devir içerengrafalardan özel olarak Şekil 6.2.1görülen (n 5) 1( 3, 0; )

Şekil 6.2.1. G n₁( 3, 0; )n - tipi(n 5) tek devir içeren graf

Teorem 6.2.1.G n1( 3, 0; )n , (n 5)tipindeki grafların normalize edilmiş Laplacian hızı

1 3 ( 3, 0; ) 1 L n S G n n n (6.3) dır. Ġspat.Öncelikle M L G n₁( 3, 0; )n olsun. 3 3 3 1 0 0 1 1 1 1 1 2 1 2 1 1 1 0 1 2 2 1 1 1 0 1 2 2 1 n n T n e n e n n n M n n

olur. Elementer satır işlemi uygulayarak

3 3 1 0 0 1 2 1 1 0 1 1 _{2 1 2 1} 1 1 0 1 2 2 1 1 1 0 1 2 2 1 n n e n n _{n n} M n n

elde edilir. Buradan

3 1 3 3 det ( 3, 0; ) 1 2 2 1 n n G n n n L

olur. n 5için

( )

3

2

1

x

f x

x

3

2

1

n

n

Normalize edilmiş Laplacian hız tanımını kullanarak (6.3) eşitliğini kolaylıkla elde edelir.

7. GRAFLARIN DERECE KIRCHHOFF ĠNDEKSĠ

Bu bölümde derece Kirchhoff indeksi içingrafın normalize edilmiş Laplacian matrisinin özdeğerlerine, kenar ve nokta parametrelerine bağlı alt ve üst sınırlar bulundu. Şimdi bu sınırları bulmak için kullandığımız bazı tanım ve teoremleri verelim.

Tanım 7.1. (Chen ve Zhang, 2007)Direnç mesafesi (resistancedistance, r_ij) elektrik ağlarının herhangi iki kenarı arasındaki mesafe olarak bilinir ve kombinatoryal Laplacian matris ve normalize edilmiş Laplacian matrisin özdeğerleri ve özvektörleri ile ifade edilebilir.

Bir G grafının tüm noktaları ve bazı kenarları ile oluşan devir içermeyen alt grafına geren ağaç denir. Bir grafın içerdiği tüm geren ağaçların sayısı t G( )ile gösterilir. Biz çalışmamız sırasında bu değeri kısaca

t

Tanım7.2. (Xiou ve Gutman, 2003;Klein ve Randić 1993; Das, 2013)G basit bağlantılı bir graf olmak üzere G nin herhangi iki noktası v_i ve v_j olsun. Bu noktalar arasındaki direnç mesafesi (resistancedistance)r_ij ile ifade edilmek üzere bir G moleküler grafının tüm noktaları arasındaki direnç mesafeleri toplamına Kirchhoff indeks denir. Kısaca

( )

i j

Kf G

r

şeklinde gösterilir.

Tanım7.3.(Xiou ve Gutman, 2003; Das, 2013) Bir n noktalı,m kenarlı G grafının Laplacian matrisi, derece matrisi ile komşuluk matrisinin farkına eşittir. Yani

( ) ( ) ( )

L G D G A G dir. Laplacian matrisinözdeğerleri 1 2 ... n 0olmak

üzere Kichhoffindex için Xiouve Gutman ( 2003) aşağıdaki bağıntıyı elde etmiştir. 1 1

1

( )

.

Kf G

n

Tanım 7.4. Chen ve Zang (2007) Kirchhoff indeks tanımından yolla çıkarak,

i j ij i j

Kf

G

d d r

şeklinde derece Kirchhoff indeksi tanımladılar.Yine aynı çalışmada grafın, kenar sayısına ve normalize edilmiş Laplacian matrisin özdeğerlerine

1( )L 2( )L ... n1( )L n( )L 0 bağlı olarak derece Kirchhoff indeks için

1 1

1

2

Kf

G

m

Şimdi ise çalışmamızın bu bölümünde kullanacağımız lemmaları verelim.

Lemma 7.1. (Cvetković ve ark., 1980)Geren ağaç sayısı, normalize edilmiş Laplacian matrisin özdeğerlerine bağlı olarak

1 1 2 n i i t m şeklinde elde edilmiştir.

Lemma7.2.(Maclaurin’sSymmetricMeanInequality)a a₁, ₂,...,a_rpozitif reel sayıları içina_inin k tanesinin çarpımının ortalaması P_k ile gösterilsin. Bu taktirde

1 2 1 ... _r a a a P r 1 2 1 3 1 2 ... 1 1 2 r a a a a a a P r r 1 2 1 1 2 2 2 3 1 1 ... _r ... _{r r} ... ... _{r r} r a a a a a a a a a a a P r 1 2... r r P a a a olmak üzere 1/ 2 1/3 1/ 1 2 3 ... r r P P P P sağlanır.

Şimdi derece Kirchhoff indeks için elde ettiğimiz ilk ana sonucumuzu verelim. Teorem 7.1. G ;n noktalı, m kenarlı bir graf olsun. Bu grafın maksimum derecesi ve geren ağaç sayısı t olmak üzere, derece Kirchhoff indeks için,

2 1 2 ₂ 2 * 1 1 1 1 2 ( ) 2 2 ( 2) 2 2( 1)( 2) n n m n n n G m n Kf G mt t n n eşitsizlikleri sağlanır.

Ġspat. Alt sınır için Tanım 7.4.‟daki (7.2) eşitliğini düzenlersek,

1 2 1 1 1 2 n i i Kf G m

elde edilir. Lemma7.2.‟der n 2 ve ai i, i 2,3,...,n 1 olarak kabul edersek, 1 2 2 3 1 2 ... n n n i i P ve 1 1 1 1 2 2 1 1 2 2 3 2 1 1 1 2 2 2 2 2 n n n n j j j i j n j n i j j n i i m P Kf G n n n m elde edilir.

Lemma 7.2.‟deki eşitsizliğe göre, 1/ 2 1/ 3

2 3

n n

n n

P P olduğundan yukarıda bulduklarımızı yerine yazarsak;

ve böylece

elde edilir. Buradan

alt sınırına ulaşılır. Üst sınır için öncelikle,

1 2 3 1 1 ... , 0 n i n n n i n , 2 2 1 n i i n 2 1 1 (L ( )) 2 2 ( ) uv E u v iz G n n R G d d 1 3/ 2 1 2 2 1 1 2 2 2 n n n j n j i i m Kf G n m 1/ 2 1 2 1 2 2 ( 2) n n i i m m n Kf G 1/ 2 1 2 1 2 2 ( 2) n n i i m m n Kf G

eşitliklerini hatırlayalım. Lemma 7.1.‟deki eşitliği düzenlersek, 1 1 2 n i i mt olduğu açıktır. Lemma 7.2. „de r n 1 ve a_{i i}, i 1, 2,...,n 1 olarak kabul edersek,

2 1 1 1 1 2 2 1 1 1 1 1 1 1 2 1 2 n m n n i j i i i j i i i j P n n n n

eşitliğini daha sade hale getirirsek

2 2 1 1 2 1 2 P n n R n n

olarak elde edilir ve

1 1 1 1 1 1 1 1 2 1 1 1 1 n m n i j j i j n j n i j n i i P n n

daha sade şekilde

* 2 2 ( ) 1 2 n mt Kf G P n m

olarak elde edilir. Lemma7.2.‟deki eşitsizlikten 1/ 2 1/ 2 2/ 2

2 2 , 2 2

n n

n n

P P P P olduğunu

biliyoruz. Yukarıda bulduğumuz P₂ ve P_{n 2} değerlerini bu eşitsizliklerde yerine yazarsak, 2 /2 * 2 1 ( ) 2 1 2 2 1 1 2 n Kf G mt n n R m n n n ve buradan 2 / 2 * 2 1 1 1 ( ) 2 1 2 n n Kf G n n R t n n

olarak üst sınır elde edilir.

Bu sınırları, ağaçlar ve tek devir içeren graflar için uygularsak aşağıdaki sonuçları elde ederiz.

Sonuç 7.1. T ,n noktalı bir ağaç ve bu ağacın en büyük derecesi Δ olmak üzere, T ağacının derece Kirchhoff indeksi için

2 1 2 ₂ 2 * 1 1 1 2 ( ) 2 2 ( 2) 1 2 2( 1)( 2) n n m n n T m n Kf T n m n n eşitsizlikleri sağlanır.

Ġspat. Ağaçlar için t 1 olup Teorem 7.1 den sonuç açıktır.

Sonuç 7.2. U , n noktalı tek devir içeren bir graf olmak üzere bu grafın en büyük derecesi olarak Δ alınırsa tek devir içerenU grafının derece Kirchhoff indeksi için alt ve üst sınırlar 2 1 2 ₂ 2 * 1 1 1 1 2 ( ) 2 2 ( 2) 2 3 2( 1)( 2) n n _m n _{n n U} m n Kf U mn n n şeklindedir.

Ġspat. Tek devir içeren graflar için 3 t n olmak üzere Teorem 7.1 den ispat açıktır. Lemma 7.3. Reel sayılar kümesinde tanımlı, , ,...,

2 1 n a a a 0, n i i 1 p 1olacak şekildeki, , ,..., 2 1 n p p p 0 ve min , ,..., 2 1 n p p p olmak üzere, i n n n n p 1 n i i i i i i 1 i 1 i 1 i 1 p a a n a a

eşitsizliği mevcuttur. Eşitlik şartı ancak ve ancak ...

2

1 n

a a a için geçerlidir.

Şimdi bu lemmadan yararlanarak derece Kirchhoff indeks için bir alt sınır bulalım.

Teorem7.2. G n noktalı, maksimum derecesi Δ , geren ağaç sayısı

t

* 1 2n 3 1 2 n 2 2 n 1 n 2 n 1 n n 2mt 1 2mt Kf G 2m 4m n 2 n 1 n 1 2 eşitsizliği vardır.

Ġspat. Lemma 7.3 deki eşitsizlikte a_{i i}, i 1 2, ,...,n 1 ve p₁ 1

2 n 1 ,

i

2n 3 p

2 n 1 n 2 , i 2 3, ,...,n 1 olarak alınırsa, min p1,p2,...,pn p olup 1