MODELING OF SEMICONDUCTOR
DEVICES BASED ON QUANTUM WELLS:
QUANTUM CASCADE LASER AS AN
EXAMPLE
a thesis submitted to
the graduate school of engineering and science
of bilkent university
in partial fulfillment of the requirements for
the degree of
master of science
in
physics
By
Hamed Abbasian
February 2018
Modeling of semiconductor devices based on quantum wells: Quantum cascade laser as an example
By Hamed Abbasian February 2018
We certify that we have read this thesis and that in our opinion it is fully adequate, in scope and in quality, as a thesis for the degree of Master of Science.
O˘guz G¨ulseren(Advisor)
Ceyhun Bulutay
Mehmet Emre Ta¸sgın
Approved for the Graduate School of Engineering and Science:
Ezhan Kara¸san
ABSTRACT
MODELING OF SEMICONDUCTOR DEVICES BASED
ON QUANTUM WELLS: QUANTUM CASCADE
LASER AS AN EXAMPLE
Hamed Abbasian M.S. in Physics Advisor: O˘guz G¨ulseren
February 2018
It has been two decades since the quantum-cascade lasers (QCLs) have emerged in 1994 for the first time. As time goes on, QCLs reach to higher points sci-entifically and economically and the usage of QCLs devices continually grows in optoelectronic device market because of their potential applications in vari-ous areas in mid- and far-infrared regions. Moreover, their performance is still improving. QCLs lase based on electron transition between intersubbands and tunneling through potential barriers where electron transition causes photon emis-sion. This takes place in conduction band; that is why QCLs are considered as unipolar semiconductor lasers. The frequencies of emitted photons depend on the location of the allowed energy levels which can be controlled by carefully choos-ing consecutive wells and barriers with suitable widths. In the present thesis, the transfer matrix method is employed to obtain transmission coefficient and wave functions of electron inside an arbitrary potential profile which is crucial for characterizing semiconductor devices based on quantum well. The obtained wave functions are used to get quantities necessary for characterizing QCL resulted from the potential profile.
Keywords: Quantum cascade laser, Transfer matrix method, Nanostructured de-vice, Quantum well.
¨
OZET
KUVANTUM KUYULARINA DAYANAN YARI
˙ILETKEN AYGITLARIN MODELLENMES˙I:
KUANTUM ARDIL LAZER ¨
ORNE ˘
G˙I
Hamed Abbasian Fizik, Y¨uksek Lisans Tez Danı¸smanı: O˘guz G¨ulseren
S¸ubat 2018
Kuvantum-ardıl lazerlerin (KAL) 1994’te ortaya ¸cıkı¸sının ¨uzerinden 20 yıldan fazla ge¸cti. Zaman ge¸ctik¸ce KAL’lar hem bilimsel hemde ekonomik olarak ¸cok geli¸sti. Performansının halen artırılmakta oldu˘gu orta- ve uzak-kızıl¨otesi b¨olgedeki ¸ce¸sitli uygulama potansiyellerinden ¨ot¨ur¨u KAL aygıtların optoelek-tronik pazarında de˘gerleri arttı. Elektron ge¸ci¸sinin sadece iletkenlik enerji bantında olmasından ve bu ge¸ci¸sin foton salınımından dolay KAL lazerleme. Tek-kutuplu yarı iletken lazerler olarak de˘gerlendirilir. Salınan fotonların frekansları geni¸slikleri dikkatlice se¸cilen ard arda kuyuların ve bariyerler ile kontrol edilme-sidir. Bu tezde, iletkenlik katsayısını (transmission coefficient) ve elektronların kuvantum kuyular temel alınarak ¨uretilen yarı iletken cihazların karakterizasyonu i¸cin ¨onemli olan rastgele potansiyel ¸sekillerindeki dalga fonksiyonlarını elde etmek i¸cin ’transfer matriks’ metodu uygulandı. Elde edilen dalga fonksiyonları, potan-siyel profillerinden sonu¸clanan KAL’ların karakterizasyonu i¸cin gerekli ifadelerin hesaplanmasında kullanıldı.
Anahtar s¨ozc¨ukler : Kuvantum Ardıl Lazer, transfer matrisi metodu, nano-yapılı aygitlar, kuvantum kuyusu.
Acknowledgement
I would like to demonstrate my appreciation to my helpful friends Murod Baho-vadinov, Mohammad Yahyavi, Sina Golizadeh and Mohammad Ali Saberi
I would also like to thank my dear parents for being supportive throughout my studies particularly graduate studies where I was miles away from home.
Contents
1 Introduction 1
1.1 Organization of thesis . . . 2
2 A brief review on quantum cascade laser devices 3 2.1 Semiconductor laser devices . . . 3
2.2 Why are we interested in quantum cascade lasers? . . . 5
2.3 Intersubband transition . . . 7
2.4 Tsu-Esaki model . . . 10
3 Numerical solution of Schr¨odinger equation 12 3.1 Transfer matrix method . . . 13
3.2 Evaluation of the employed mathematical formalism in transfer matrix method . . . 16
3.2.1 Example I: semi-analytical graphical method versus trans-fer matrix approach . . . 19
CONTENTS viii
3.2.2 Example II: applying transfer matrix method to a simple
potential profile . . . 24
4 Modeling of QCL 26 4.1 Solving Schr¨odinger equation in QCLs potential profile . . . 27
4.1.1 Example I . . . 27
4.1.2 Example II . . . 33
4.1.3 Example III . . . 36
List of Figures
2.1 Interband versus intersubband transitions which occur in regular diode lasers and quantum cascade lasers respectively (from Ref 4). 4 2.2 One stage of a potential profile of a mid-IR QCL. Squared wave
functions of four involved band states are shown. Bold solid lines stand for upper and lower laser levels and depopulation and injec-tor states are demonstrated with dashed line and thin solid line respectively (from Ref 8). . . 7 2.3 The first and second picture from left show DT and FNT processes
respectively and the one in the rightmost demonstrates TE (from Ref 31). . . 11
3.1 Energy versus quantum well’s width for well of 1 eV depth, ob-tained from graphical method. . . 19 3.2 Energy versus quantum wells width for well of 5 eV depth, obtained
from graphical method. . . 20 3.3 Energy versus quantum wells width for well of 10 eV depth,
ob-tained from graphical method. . . 20 3.4 Energy versus quantum well’s width for well of 25 eV depth,
LIST OF FIGURES x
3.5 Energy versus quantum well’s width for well of 1 eV depth, results from graphical and transfer matrix method. . . 22 3.6 Energy versus quantum well’s width for well of 5 eV depth, results
from graphical and transfer matrix method. . . 22 3.7 Energy versus quantum well’s width for well of 10 eV depth, results
from graphical and transfer matrix method. . . 23 3.8 Energy versus quantum well’s width for well of 25 eV depth, results
from graphical and transfer matrix method. . . 23 3.9 Transmission coefficient versus energy for an electron with an
ef-fective mass of 7 percent of electron’ rest mass. . . 24 3.10 Bound states (ground and first excited) wave functions, localized
in the potential profile. . . 25 3.11 Transmission coefficient versus energy for an electron with an
ef-fective mass of 7 percent of electron’ rest mass while there is an applied bias across the potential profile. . . 25
4.1 Schematic potential profile diagram employed by Hugi to make a quantum cascade laser emitting at 11.5 µm with an applied poten-tial difference equal to 60 kV per cm. . . 28 4.2 Transmission coefficient versus energy for potential profile
em-ployed by Hugi et al. The peaks in the graphs exhibit the allowed energy levels. . . 29 4.3 Our results on the potential profile used by Hugi et al where the
bound state energies are E1 = 0.2051 eV, E2 = 0.2207 eV, E3 = 0.2425 eV, E4 = 0.2563 eV, E5 = 0.2886 eV, E6 = 0.3151 eV, E7 = 0.3466 eV and E8 = 0.463 eV. . . 30
LIST OF FIGURES xi
4.4 Hugi’s potential profile with two added contacts. . . 31 4.5 Supply function versus electron’s energies for the system; applied
bias is 1.5 V. . . 32 4.6 The red graph displays current density at 100 Kelvin while blue
and orange show the system at 200 and 300 K respectively. . . 33 4.7 Strupirchonski’ device and the related modulus squared wave
func-tions. . . 34 4.8 Transmission coefficient versus energy for potential profile
em-ployed by Strupirchonski et al. . . 35 4.9 Modulus squared wave functions, the reproduction of
Strupirchon-ski’ work. . . 36 4.10 Bound state wave functions (modulus squared) done by
Milo-vanovic where the applied bias is 10 kV/cm. . . 37 4.11 Modulus squared wave functions coming from transfer matrix
Chapter 1
Introduction
Devices based on quantum well have attracted plenty of attention from both scientific and industrial communities for their potential applications. Also the-oretically interesting features make them an appealing topic for research. It is well known that quantum devices emerged, for the first time, when Tsu and Esaki suggested that structures made of alternating thin films of semiconductor with different band gaps can lead to devices with novel features [1]. Now the question arises here is, why this kind of structures have the potential of showing novel physical properties. The critical point is in this sort of structures, where the thicknesses of layers are of the order of nano-meter, the electron mean free path and its wavelength can exceed the sum of the thicknesses of layers in the structure [2]. As mentioned, quantum well based semiconductor devices consist of semiconductor thin films; actually, they are made of at least one well layer sandwiched between two barrier layers where layers are crystalline thin semicon-ductors with different band gaps laminated alternatively. Therefore, molecular beam epitaxy (MBE) technique as a method of growing ultrathin films, is a vital tool in paving the way for the flourishing of the quantum well devices industry. The industry contains many devices of this kind and always there is a chance of new sort of devices to be added to the list. Let’s start with transistors which were introduced as a heterostructure in 1980 while it keeps appearing in new
kinds (e.g. TEGFET, MODFET, SDFET, HFET) and basically must be consid-ered as quantum well device. Since quantum well devices possess tunable band structures, they are very suitable as photo detector e.g. widely used as infrared photodetector (QWIP). Likewise, devices that employ quantum- confined Stark effect (QCSE) are actually quantum well devices which are used for the modu-lation of light. Quantum well lasers are also among quantum well devices which have well-known applications in various fields [2].
In the investigation of all the mentioned quantum well devices, the electron wave functions and also bound energy levels formed within their potential profiles are the key points which are necessarily needed to be obtained. Having that in mind, we numerically solve the Schr¨odinger equation inside an arbitrary potential profile. To concentrate on just one specific quantum well we take quantum cascade lasers as the case of study.
1.1
Organization of thesis
The thesis begins with an introduction to quantum wells and devices that exploit quantum wells for their operation where the principles of electronic devices be-longing to the class are explained. Chapter two is a brief summary on quantum cascade lasers that are the main case of study here, also, Tsu Esaki model as the major tool in investigating tunneling current has been introduced. Chapter three presents models and methods used for solving Schr¨odinger equation in QCLs po-tential profiles. Also, at this chapter, transfer matrix method has been derived and evaluated by solving two examples. Chapter four exhibits the solutions of Schr¨odinger equation in three different QCLs potential profiles. Finally, chapter five summarizes the conclusion of the thesis.
Chapter 2
A brief review on quantum
cascade laser devices
2.1
Semiconductor laser devices
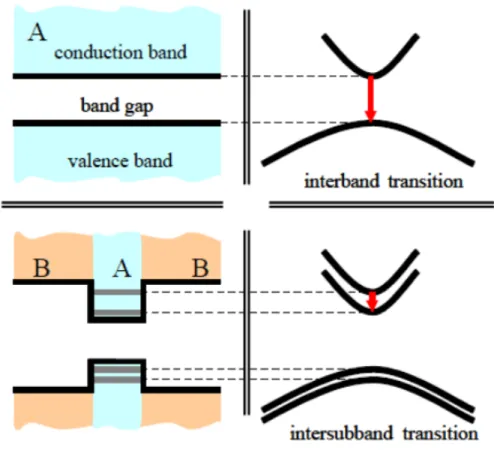
In regular semiconductor lasers devices, the recombination of electron-hole in conduction and valence under population inversion band leads to lasing action whereby the wavelength of the emitted photon depends on the band gap of the utilized material in the device. For instance, these kinds of semiconductor lasers are usually constructed from group III and V in the periodic table and called III-V compound semiconductors which are made by combining group III elements (Al, Ga, In) with group V elements (N, P, As, Sb). Lasing at the mentioned semiconductor lasers are based on interband radiative transitions. Of these types of lasers, GaAs-based laser diode (LD) was for the first time reported by Rup-precht et al in 1963 [3]. In contrast, transitions at quantum cascade lasers, take place between the states of the same band; actually, that is why quantum cascade lasers are considered as unipolar semiconductor lasers; where the lasing action takes place as a result of electron transition between existing subbands within conduction band. Therefore, the emission wavelength of the laser light is deter-mined by the width of wells and barriers in its potential profile; figure (1) of this
chapter [4] illustrates a simple schematic of what happens.
Figure 2.1: Interband versus intersubband transitions which occur in regular diode lasers and quantum cascade lasers respectively (from Ref 4).
As mentioned, quantum cascade lasers (QCLs) are typically classified among semiconductor laser where they lase due to intersubband transitions in a sequence of wells and barriers which have been alternatively grown by utilizing molecular beam epitaxy (MBE) technique. Since here lasing is originated from intersubband transitions, it is then independent of the materials the laser is built from, which allows us to make these kinds of lasers from industrially well-developed materials. In other words, the frequencies of emitted photons do not depend on materials rather depend on the quantum well and barriers thickness, that thanks to MBE, are totally under control. Actually, the main idea in QCLs structures is that different conduction band edges of the materials in two sides of junction, form
barrier and well where electron confines. To make a lasing device, there should be applied bias as well in order to have electronic pumping. It was Kazarinov who suggested for the first time to make use of intersubband transitions for gen-erating laser light in 1971 [5] he predicted that there must be the possibility of transitions between subbands. He published his work in a scientific paper which was later called a diagonal or photon-assisted tunneling transition. However, it took two decades until the first experimental prototype of mid-infrared QCL de-vice emerged which was constructed by Faist et al [6]. It took even more for first THz QCL introduced by Kohler [7]. Fig (2) reproduced from Ref[8] shows how QCLs basically work, electron transits between upper and lower laser level through stimulated emission. Considering the figure as a special case, the tran-sition leads to mid-infrared radiation at a wavelength of 5µm. In addition to upper and lower laser levels, depopulation and injector levels are also involved in the process. The energy difference between lower and depopulation level is equal to longitudinal optical phonon energy which is around 30 meV in InGaAs, for example. Depopulation level’s role is significant in creating population inversion. As for injector level, it is placed between two neighboring stages whereby electron is able to transfer to the upper laser level at the next stage. The same occurs in the following stages, that is why this kind of laser device has been called quantum cascade lasers. Actually, cascading nature of QCLs allow an electron to generate tens of photons during its journey in the active regions; therefore, these kinds of lasers have the potential to cause laser with high-power capabilities.
2.2
Why are we interested in quantum cascade
lasers?
The answer lies in the importance of mid-infrared (mid-IR) and far infrared (far-IR) radiations. Mid-IR covers 3 µm to 30 µm and far-IR covers 30 µm to 1000 µm wavelengths; frequency counterparts range from 0.3 to 10 THz which is the reason why it is also called terahertz radiation. To produce mid and far infrared radiation using conventional semiconductor laser one needs a narrow gap semiconductor
suitable for generating the mentioned wavelength; however, there is no such bulk semiconductor. QCLs because of their engineered-band structure nature, have the potential to be a high-performance, compact and reliable laser source for those radiations [9]. Potential applications are the motivation for the high demand for mid and far infrared radiations. Let’s have a look at their applications. Terahertz radiation is of great interest because of its various applications particularly in security [10, 11] and medical imaging [12, 13, 14, 15, 16]. It can be used in medical imaging because of its absorption by water molecules whereby healthy tissues can be identified versus unhealthy tissues and also non-ionizing feature of terahertz makes it safer and provides faster results than X-ray. On the other hand, terahertz radiation is useful in security issues since it is transparent to dielectric materials including plastic, clothing, wood, paper, masonry, cardboard, and ceramics which allows security staff to discover forbidden objects where it is necessary. In addition to the mentioned cases, terahertz radiation has applications in spectroscopy since many materials have terahertz fingerprints which are very important in chemical spectroscopy and help to identify materials.
Todays’ terahertz sources are not capable of producing this kind of light with high enough power suitable for being employed for above applications [17, 18, 19, 20, 21]. In fact, industry waits for technology to produce terahertz rays that are bright enough to be employed in its potential applications. Evidently, industry considers QCLs as reliable candidates for meeting the mentioned needs. The first built QCL was of type mid-infrared that has been going through great progress since its first experimental illustration. In contrast to the first prototype, recent QCL are covering a wider spectral zone ranging from 2.6 µm to above 400 µm that has been achieved exploiting an external magnetic field. Moreover, recently built QCLs at mid-infrared region are able to be operated under continuous wave regime at room temperature while their output powers are around several watts. However, terahertz QCL did not experience the same progress; it was devised for the first time in 2002 and it needs more time to mature, as it still needs cryogenic temperature to work. And when it is to work at room temperature its output power becomes very low just about few microwatts. Even with the help of an external magnetic field, the operating temperature cannot exceed 225K [22, 23].
Evidently, there are still challenges and problems to be solved and the ulti-mate point is to make QCLs with higher output that can be operated in room temperature and cover a wider range of mid-IR or terahertz radiations.
Figure 2.2: One stage of a potential profile of a mid-IR QCL. Squared wave functions of four involved band states are shown. Bold solid lines stand for upper and lower laser levels and depopulation and injector states are demonstrated with dashed line and thin solid line respectively (from Ref 8).
2.3
Intersubband transition
The concept of subband and intersubband transition are significant for realizing involved physics in QCLs, so it is worth spending some time to discuss them. In QCLs, subbands are created because of size confinement in the growth direction of heterolayers. The layers’ low thickness qualifies them as quantum wells; speaking
more precisely, the thickness of layers must be smaller than electron-decoherence-length to create quantized energy levels for electrons. In other words, they can be considered as quantum wells if their low dimensions in thickness cause physically observable effects which here are discrete allowed energy levels that lead to cer-tain emission and absorption spectrum. In QCLs structures, electrons and holes are confined in conduction and valence band respectively where relative band off-sets of two embedded semiconductors give rise to consecutive wells and barriers and the confined holes and electrons are distributed in the certain energy levels called subbands. There are three main assumptions for electron’s distribution within subbands. Firstly, the distribution of electrons are thermalized then they are distributed according to Fermi-Dirac formula; secondly, in a subband, the temperature of all electrons are the same; finally, the lattice and electrons are at the same temperature [24].
Energy levels within quantum wells are one-dimensional subbands which have two-dimensional dispersion relation so that the energy of a particle can be ex-pressed as follows. En(kx, ky) = Ec+ n2εz + ~2(k2x+ ky2) 2mc (2.1) Where n is an integer, εz = π 2 ~2
2mcL2z, Lz stands for well’s width and kz =
nπ Lz
which means momentum is quantized along Z direction while it is continuous in X and Y directions [25]. In the described hetero-structures, the possible opti-cal transitions between two-dimensional electronic states are opti-called inter-subband transitions where Fermi golden rule governs all possible transitions. Let’s consider a transition to final state f from initial state i subject to an external electromag-netic field, according to Fermi golden rule, the transition rate will be as follows:
Wif = 2π ~ | < ψi|H 0|ψ f > | 2 δ(Ef − Ei− ~ω) (2.2)
Where H0 describes the interaction of electron in an electromagnetic field. Solving the problem for a single electronic band, using envelope function approach, ex-hibiting the function as ψi(r) = fi(r)uυ(r) where i shows quantum number, uυ(r) is the lattice periodic Bloch function of band υ in an extremum point in the Bril-louin zone, and also using dipole approximation, the rate equation according to
Fermi rule can be written as follows: Wif = 2π ~ e2E◦2 4m∗2ω2| < ψi| → ee.→p |ψf > | 2 δ(Ef − Ei− ~ω) (2.3) Where E◦ stands for the amplitude of the electric field of emitted photon,
→ ee is the polarization vector of emitted photon and →p is the momentum of electron. To obtain a more clear view of the derived formula it would be useful to split up its matrix elements as follows.
< ψi| → ee.→p |ψf > = → ee. < uυ| → p |un0 >< fn|fn0 > + → ee. < uν|uυ0 >< fn| → p |fn0 > (2.4) where n0, n and υ0, υ are subband and band indices of the final and initial states respectively. The above equation consists of two terms the first one explains inter-band transitions; it cancels out when the final and initial states are in the same band, which is the case in QCLs. In contrast, intersubband transition is described by the second term where there is an overlap integral of Bloch functions which will be unity or zero when υ0 = υ or υ0 6= υ respectively. Therefore, the only remaining term is a dipole matrix element of overlap function which can be calculated as follows: < fnk⊥|ee.p|fn0k⊥0 >= 1 A Z d3re−ik⊥.rϕ n∗(z)[eexpx+ eeypy+ eezpz]e−ik 0 ⊥.rϕ n0(z) (2.5) At the above equation the only non zero elements are the terms which are at eez direction while terms at eex and eey directions vanish except for cases at which n = n0 and k⊥ = k0⊥. Therefore the only contributing terms in the matrix element of equation (2.4) will be as follows.
< n|pz|n0 >= Z
dzϕ∗(z)pzϕn0(z) (2.6)
Substituting the above formula, in Fermi relation will make it easy to calculate the transition rate between subbands. Transitions are not allowed between two arbitrary subbands but there is selection rule e.g. in a potential profile with inversion symmetry with respect to the quantum well center, only parity changing transitions can take place. The rule is not valid (i.e. transitions can occur between
all the existing subbands) once the symmetry is broken, the following three ways can be employed for reaching asymmetric quantum wells.
1. Establishing step quantum wells by using different alloy compositions in the structure
2. Employing electrical potential across the structure.
3. Utilizing asymmetric coupled quantum wells, that is to say, constructing two quantum wells with a thin barrier in between.
To end up true band structure engineering, each or all of the mentioned ways at the same time can be utilized as it is so in quantum cascade lasers structures.
2.4
Tsu-Esaki model
Tsu-Esaki model was introduced for the first time by Tsu and Esaki [26] to de-scribe the tunneling current density in superlattices. They derived below formula for density of tunneling current flowing through layered nano-structures:
J = em ∗k BT 2π2 ~3 Z ∞ eV dEZT c ln ( 1 + exp[(EF + eV − EZ)/kBT ] 1 + exp[(EF − EZ)/kBT ] ) (2.7)
Where EZ stands for electron’s kinetic energy along growth direction, m∗ is electrons’ effective mass, T is temperature, Tcis transmission coefficient and V is applied bias voltage.
What is tunneling phenomenon? By definition, once an electron with kinetic energy less than the height of a potential barrier passes through it, the phe-nomenon is called quantum mechanical tunneling. Tunneling can take place in different mechanisms, it is called direct tunneling (DT) where electron passes through the whole width of barrier, it is called Fowler-Nordheim (FNT) tunnel-ing when it passes a reduced-path through the barrier because of electric field,
or the ”tunneling” can be thermionic emission (TE) [27]. The mentioned three main mechanisms for tunneling process have been schematically presented in the following figure.
Figure 2.3: The first and second picture from left show DT and FNT processes respectively and the one in the rightmost demonstrates TE (from Ref 31).
In the current research project, we deal with tunneling phenomenon by ob-taining transmission coefficient or tunneling probability in consecutive wells and barriers by using transfer matrix technique. In order to make a quantum me-chanical tunneling current flow in a potential profile, the applied electric field has to be huge around million volts per meter; actually, at low bias, Fermi energy is lower than available energy level in the given potential profile, hence there is no tendency for ”tunneling” while the current originating from thermal emission is negligibly low. The applied bias should cause E1 (the lowest energy level of the bound states inside potential profile) to drop below Ef; therefore, once a small bias is applied (for example applied across layered nano-structure) there is no immediate increase in the current; however, by increasing the applied bias to a certain amount, there would be a quick increase in the current which means E1 drops below Ef and then there is tunneling current through barriers. As the bias keeps increasing the current decreases till the situation again meets the necessary condition for tunneling current which is once the second allowed state drops below Ef and so on. It is worth mentioning that the potential interval at which potential increases while current in response decreases, is called negative differential resistance which is also of interest to investigate.
Chapter 3
Numerical solution of
Schr¨
odinger equation
There are several numerical methods for solving Schr¨odinger equation, including density matrix method (DM), non equilibrium green function method and finite difference method etc. For solving Schr¨odinger equation each having its pros and cons. For instance, applying Schr¨odinger-poisson solver in finite difference method, it would be possible to take into account the electron-electron interac-tion. In density matrix method, depending on the demanding level of detail, basis sets of wave function localized at two sides of a barrier have to be chosen. Then each design has to have its own DM which means the solution is not portable to different designs. Among various approaches, transfer matrix method is eas-ier to be implemented for including non-parabolicity and also to treat potential steps located between wells and barriers more precisely. It is also well-known that transfer matrix method is computationally less expensive compared to oth-ers so that it can be performed using non-expensive computoth-ers. In this thesis, we used the transfer matrix approach and we also benchmark its results for special potential profile against semi-analytical approach.
3.1
Transfer matrix method
Transfer matrix method is a simple way to study and model quantum phenom-ena in devices built based on quantum wells. It has been widely utilized to get the solution of Schr¨odinger equation [28, 29, 30, 31, 32, 33] since it is not ex-pensive computationally, there is no complex mathematics involved and also it is easy to employ. The method is particularly a well-matched approach for devices based on heterostructures. In this method, in one dimension the wave function is considered as two linear independent wave functions which move the opposite directions, the two wave functions have coefficients which have to be assigned:
Ψj = ajeikjx+ bje−ikjx (3.1)
Ψj+1 = cj+1eikj+1x+ dj+1e−ikj+1x (3.2) Where a and c represent coefficients for wave functions propagating from left to right while b and d are coefficients for wave functions traveling the opposite direction. In above wave functions k is defined as
ki =
(2m(E − eVj)) 1/2 ~
(3.3)
The coefficients should be achieved by two boundary conditions which require wave functions and their derivatives to be continuous in the boundaries.
Ψj|x=xj+1 = Ψj+1|x=xj+1 (3.4) dΨj dx x=xj+1 = dΨj+1 dx x=xj+1 (3.5)
Therefore, boundary conditions require that ajeikjx+ bje−ikj+1x = cj+1eikj+1x+ dj+1e−ikj+1x (3.6) ajeikjx− bje−ikj+1x = kj+1 kj cj+1eikj+1x− kj+1 kj dj+1e−ikj+1x (3.7) It should be highlighted that in semiconductor heterostructures the difference in effective mass has to be considered so that in the above equation all factors
kj+1
kj must be replaced with
mjkj+1
mj+1kj.
In transfer matrix method, in order to define an arbitrary potential profile, the potential profile has to be considered a combination of small segments so that in each segment the potential is constant and at each segment, the coefficients of the wave functions are specified by applying transfer matrix on those of neighbor-ing segments. Employneighbor-ing continuity boundary condition, we reach the followneighbor-ing expression 1 1 1 −1 ! aj bj ! = k1 1 j+1 kj − kj+1 kj ! cj+1 dj+1 ! (3.8)
We can change the above equation in a simple and preferred form by eliminat-ing the first matrix from the left side as follows
aj bj ! = Pjstep cj+1 dj+1 ! (3.9)
Where Pjstepis called step matrix and can be used to obtain the coefficients of wave functions at an adjacent region when it confronts a step potential.
Pjstep= 12 1 + kj+1 kj 1 − kj+1 kj 1 −kj+1 kj 1 + kj+1 kj ! (3.10)
By making the arbitrary potential profile a combination of segments, we will have small step potential coming together and make the potential profile in a
whole. Having step matrix, we can get wave function in the next step; however, the job is not still complete as we should also consider the propagation between steps as well. Let’s assume that the length between two successive steps is Lj then what would happen is Ψaje
ikjLj = Ψ
cj and Ψbje
−ikjLj = Ψ
dj. Actually, the
wave function gets a phase difference traveling L at the same step. This phase difference can be formulated as follows
cj+1 dj+1 ! = e ikjLj 0 0 e−ikjLj ! aj bj ! (3.11)
Calling the first matrix from the right side of the above equation as Pjf ree, the final formulation for transfer matrix turns as follows.
aj bj ! = Pjf ree cj+1 dj+1 ! (3.12)
To reach final form of the transfer matrix formulation, the last two matrix expression should be multiplied as follows, they will give us the propagation matrix at j-th section. Pj = Pjf reePjstep (3.13) Pj = (kj+1 kj + 1)e −ikjLj (−kj+1 kj + 1)e −ikjLj (−kj+1 kj + 1)e ikjLj (kj+1 kj + 1)e ikjLj ! (3.14)
One can observe from the above matrix that there is symmetry in it as P11 = P22∗ and P21 = P12∗. It turns out that this kind of symmetry stems from time-reversal symmetry. Discussing time-time-reversal symmetry is not in the scope of this thesis. In short, there is time-reversal symmetry in a system when its potential is real and remains unchanged in time. As it has been already mentioned, in transfer matrix method the potential profile has to be segmented which leads to a potential profile with N (the number of segments) potential steps. To obtain the total propagation matrix, the propagation matrix of each segment has to be
multiplied to that of the adjacent segment as follows P = P1P2P3....Pj...PN = j=N Π Pj j=1 (3.15) Assuming the particle coming from the left side, one can consider a=1 and also since there is no reflected wave at the rightmost side then d=0; therefore, the relationship among coefficients can be summarized as follows
1 b ! = P11 P12 P21 P22 ! c 0 ! (3.16) Applying the definition of transmission probability, we can get an expression for that according to propagation matrix elements as follows
|T |2 = | 1 P11
| 2
(3.17)
Transmission coefficient or probability is crucial in finding the energies of bound states of a certain quantum well or an arbitrary potential profile by transfer matrix method. Actually, the maximum points in the transmission-coefficient-versus-energy-graph show the energies that electrons with those energies are able to tunnel through barriers. Because those energies coincide with allowed energy levels of the well and that is the point that has been used to get the allowed energy levels of a potential profile using transfer matrix method.
3.2
Evaluation of the employed mathematical
formalism in transfer matrix method
At this section, the solution of Schr¨odinger equation in a finite one-dimensional square well is going to be obtained employing a semi-analytical method (i.e. graphical method). It would be helpful in assessing the solution of Schr¨odinger equation obtained from transfer matrix method. Then, we solve one-dimensional finite well using graphical method as example number one and simple potential
profile as second example. Let’s consider time-independent solving Schr¨odinger equation in a potential profile for a given square well as follows:
HΨ(z) = − ~ 2d2 2mdx2Ψ(z) + V (z)Ψ(z) = EΨ(z) (3.18) V (z) = −V0 f or − l ≤ Z ≤ l 0 f or |Z| < l (3.19)
The solution of the problem is pretty well-known and can be found in many quantum mechanic books. Since we want to obtain just bound state of quantum well then energy should be limited to 0 < E < V0. For region |Z| < l where potential is zero, the equation turns to
− ~ 2d2 2mdx2Ψ(z) = EΨ(z) −→ κ 2Ψ(z) = d 2Ψ dx2 (3.20)
where κ stands for √
−2mE
~ . The solution for this will be
Ψ(z) = aeκz+ be−κz (3.21)
Considering boundary conditions for region z < −l , ”a” has to be zero to prevent wave function from diverging when z goes to mines infinity, similarly ”b” needs to be zero so that the wave function does not go to infinity when z goes to plus infinity. So, the final solution will be as follows
Ψ(z) = ae−κz f or z > l beκz f or z < −l (3.22)
for region where |z| < l Schr¨odinger equation changes its form to d2ψ
dx2 = −K
2Ψ (3.23)
where K stands for √
2m(E+V0)
~ the equation gives solution as follows
Considering Ψ(−z) = −Ψ(z) for odd-parity state and Ψ(−z) = Ψ(z) for even-parity state, the solution can be split into two parts where clearly d is zero for odd-parity solution while c = 0 gives rise to even-parity solution. Therefore, the complete solution can be presented as follows
odd − parity → Ψ(z) = ae−κz f or z > l dsin(Kz) f or − l < z < −l −aeκz f or z < −l (3.25) even − parity → Ψ(z) = ae−κz f or z > l ccos(Kz) f or − l < z < −l aeκz f or z < −l (3.26)
Now it is the time to impose boundary condition so that wave equations and their derivative be continuous at two sides of boundaries.
Continuity in wave functions gives rise to
ae−κl = dsin(Kl) (3.27)
Similarly, continuity in derivative gives rise to
−κae−κl = dKcos(Kl) (3.28)
Considering two previous questions lead to
κ = −Kcot(Kl) (3.29)
Following the same approach for even-parity state leads to
κ = Ktan(Kl) (3.30)
In order to obtain allowed energies of bound states, both sides of recent equa-tions have to be plotted in the same coordinate where their intercepts give the energies, the energy of odd-parity states are obtained from the first equation and the energy of even-parity states from the second one.
3.2.1
Example I: semi-analytical graphical method versus
transfer matrix approach
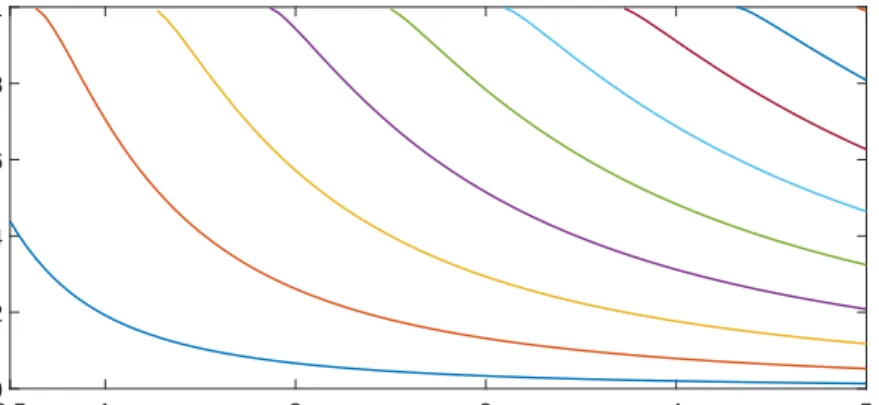
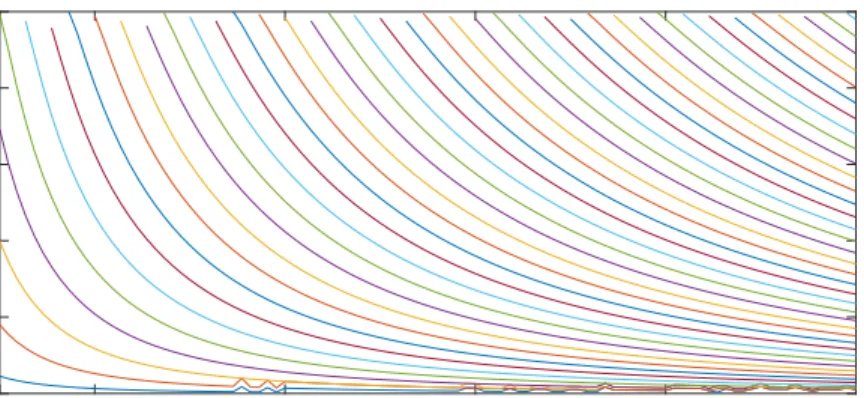
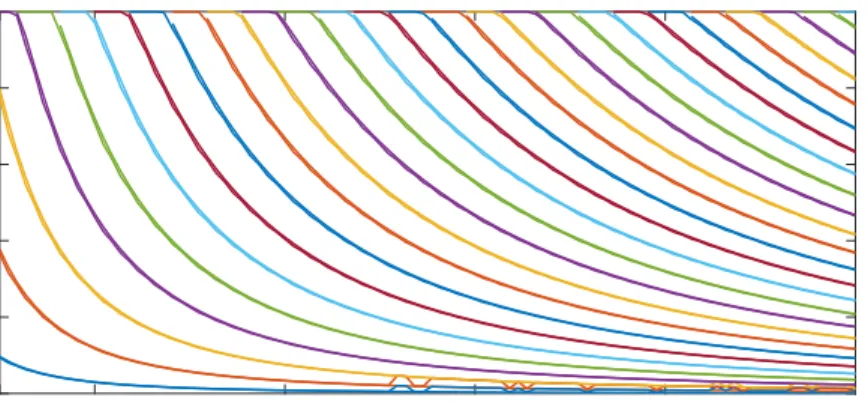
For benchmarking the results, there should be solutions coming from a method other than transfer matrix method. Graphical approach as a basic and already tested one was employed. The results have been presented in energy versus well’s width graphs where the width changes from 0.5 nanometer to 5 nanometer and depth of well changes from 1 eV to 25 eV. Putting light spot on ground state, it seems after 3 nanometer the graphs get flat which means that quantum confine-ment effect is going to decrease after wells’ width exceed 3 nanometer. To get an idea of how many bound states exist in a well with a certain width, one can consider a line, parallel to the energy axis crossing to a certain width point at the perpendicular axis. The number of points at which the line intersects graphs equal to the bound state number.
0.5 1 2 3 4 5
Width of quantum well (nm)
0 0.2 0.4 0.6 0.8 1 Energy(eV)
Figure 3.1: Energy versus quantum well’s width for well of 1 eV depth, obtained from graphical method.
0.5 1 2 3 4 5
Width of quantum well (nm)
0 1 2 3 4 5 Energy (eV)
Figure 3.2: Energy versus quantum wells width for well of 5 eV depth, obtained from graphical method.
0.5 1 2 3 4 5
Width of quantum well (nm)
0 2 4 6 8 10 Energy (eV)
Figure 3.3: Energy versus quantum wells width for well of 10 eV depth, obtained from graphical method.
0.5 1 2 3 4 5
Width of quantum well (nm)
0 5 10 15 20 25 Energy (eV)
Figure 3.4: Energy versus quantum well’s width for well of 25 eV depth, obtained from graphical method.
From these plots it is clear that density of bound state get denser moving from left to right which means that the energy differences between states decrease when well gets wider that results in more bound states. For instance, the well 1 eV deep has just one bound state shown at the leftmost side of the plot when its width is just one-half nanometer; however, the number of bound states increase to nine as its width increases to five nanometer.
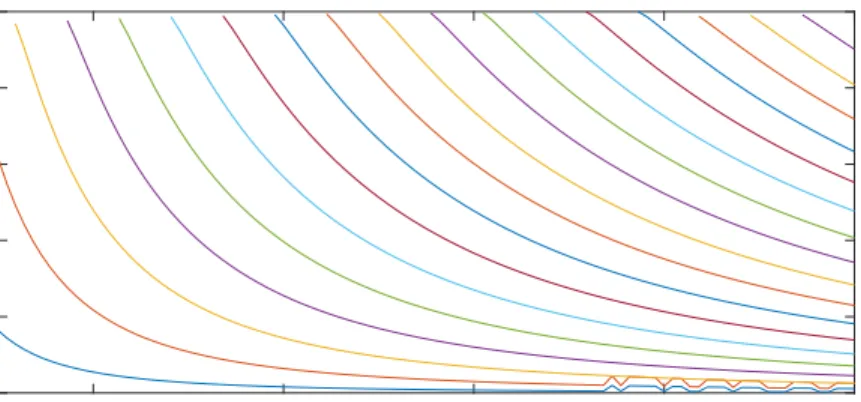
To make sure that our used formulas in transfer matrix method are correct; transfer matrix method was utilized to plot energy versus well’s width graphs for five wells with different depths similar to the arrangement of the results of graphical method. The following graphs show the results of two methods in the same frame.
0.5 1 2 3 4 5
Width of quantum well (nm)
0 0.2 0.4 0.6 0.8 1 Energy(eV)
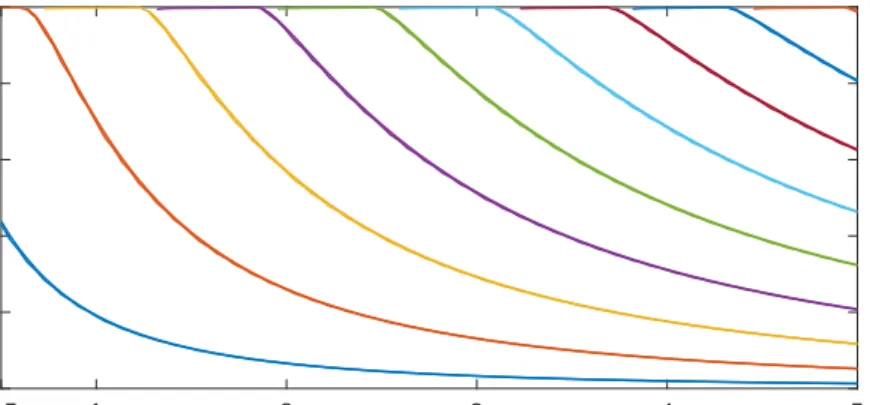
Figure 3.5: Energy versus quantum well’s width for well of 1 eV depth, results from graphical and transfer matrix method.
0.5 1 2 3 4 5
Width of quantum well (nm)
0 1 2 3 4 5 Energy (eV)
Figure 3.6: Energy versus quantum well’s width for well of 5 eV depth, results from graphical and transfer matrix method.
0.5 1 2 3 4 5
Width of quantum well (nm)
0 2 4 6 8 10 Energy(eV)
Figure 3.7: Energy versus quantum well’s width for well of 10 eV depth, results from graphical and transfer matrix method.
0.5 1 2 3 4 5
Width of quantum well (nm)
0 5 10 15 20 25 Energy (eV)
Figure 3.8: Energy versus quantum well’s width for well of 25 eV depth, results from graphical and transfer matrix method.
Examining both graphs plotted in the same frame illustrates that there is an exact coincidence between graphs coming from two different methods.
3.2.2
Example II: applying transfer matrix method to a
simple potential profile
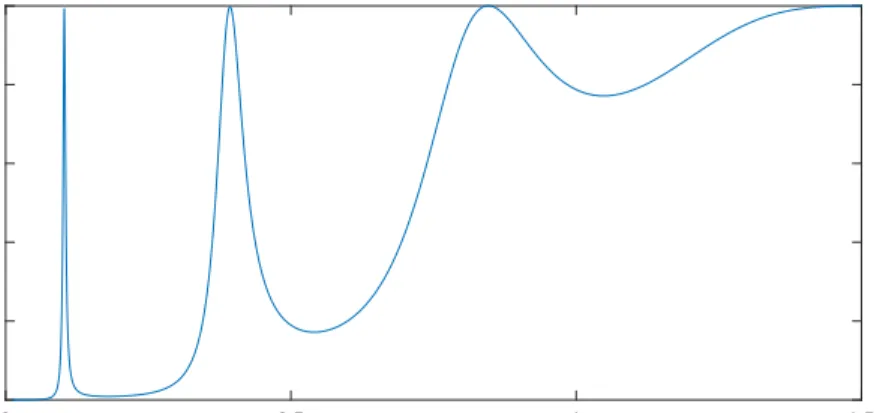
Let’s now apply the transfer matrix method on a simple potential profile shown in Fig 3.10. Figure 3.9 shows transmission coefficient versus energy for a potential profile, the next figure, where the height of barrier is 0.5 eV and the mass of the particle is chosen to be 0.07 of the rest mass of electron which is close to electron mass in GaAs lattice. As it is clear from the graph, there are two bound states where transmission coefficients are maximum. The graph shows that a particle can pass through barriers when it possesses specific amount of energies. According to the graph, the probability of transmission is hundred percent in four energy points whereas two of them are lower than barrier’s height while the other two are greater than that. Passing through a potential barrier which energetically is in a higher position and also the behavior of transmission coefficient graph when the particle’s energy is higher than barrier height, clearly, demonstrate the wavy aspect of the particle.
0 0.5 1 1.5 Energy(eV) 0 0.2 0.4 0.6 0.8 1 Transmission Coefficient
Figure 3.9: Transmission coefficient versus energy for an electron with an effective mass of 7 percent of electron’ rest mass.
0 5 10 15 20 Distance (nm) 0 0.2 0.4 0.6 0.8 1 Energy (eV)
Figure 3.10: Bound states (ground and first excited) wave functions, localized in the potential profile.
It is of interest to know about the same graph when there is an applied bias across it. For instance, the transmission-energy graph of the above potential profile will change to Fig (3.11) when there is 0.5 V applied bias.
0 0.5 1 1.5 Energy(eV) 0 0.2 0.4 0.6 0.8 1 Transmission Coefficient
Figure 3.11: Transmission coefficient versus energy for an electron with an effec-tive mass of 7 percent of electron’ rest mass while there is an applied bias across the potential profile.
Chapter 4
Modeling of QCL
Now that it is verified that our mathematical formalism in transfer matrix method works well for a single well, the method can be extended to solve Schr¨odinger equation in an arbitrary number of consecutive wells and barriers. As a matter of fact, in quantum cascade lasers, electrons move inside semiconductor layers which have crystalline structures so they should be affected by the surrounding envi-ronment. To take this into consideration, it should be considered that electrons’ energies and masses depend on their velocities and motion directions inside the crystal. The parabolic approximation is a conventional method to estimate the effective mass of electrons where one or few bands can be employed. Nonetheless, to keep things simple, what we consider as effective mass here, is the one extracted from conduction band valley. Here, two different effective masses correspond to wells and barriers are implemented. The wave function we are looking for, is the product of pseudo-free electron wave function in x and y direction, envelop Bloch function and the eigenfunction of the hamiltonian of a one-dimensional potential in the growth direction. The explained terms can be expressed as follows
< r|ψ >=< x|ψ >< y|ψ >< z|ψ >= B(x, y, z)√1 Lx eikx 1 pLy eikyψ n(z) (4.1)
Where ψn(z) is the part that we get through numerical approach. It should be noted that in the x and y directions, the wave function can be considered similar to a free particle wave function (within effective mass approximation) since the
structure is assumed to be uniform along those directions. In the above expression the Bloch function can be dropped since it actually comprises the effects related to the non-uniformity of the crystal potential in atomic scale.
4.1
Solving Schr¨
odinger equation in QCLs
po-tential profile
At this part, we choose three potential profile of quantum cascade lasers and solve them using transfer matrix method. The chosen examples are not the outputs of the same methods (e.g. first example has been done using density matrix method while the wave functions in the third example are the result of Schr¨odinger-Possion solver).
4.1.1
Example I
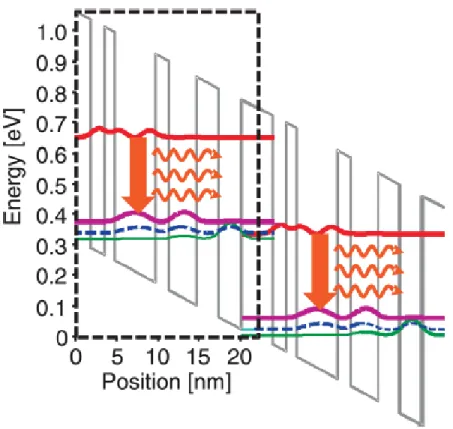
To start, a potential profile employed by Hugi et al [34] was considered. The potential profile they have designed is shown at the figure below. It consists of 8 wells where the sequence of layers in one cascade are 3.9, 2.18, 0.46, 5.93, 0.62, 5.46, 0.62, 4.34, 1.1, 3.9, 0.93, 3.9, 1.56, 3.75, 2.34, 3.43 (all in nanometer). Their device is made of 74 stages which means the shown potential profile is repeated 74 times in the real device. As it is clear from the figure, their structure has 8 bound states inside the potential profile and the applied bias is 60 kV/cm their expectation is that the potential profile will emit at λ= 11.5 micrometer. They used density matrix method to characterize their device. We followed the designed potential profile by them, using transfer matrix method and presented our results in three graphs namely transmission coefficient versus energy, electron’s squared modulus wave functions versus position and also current versus applied bias.
Figure 4.1: Schematic potential profile diagram employed by Hugi to make a quantum cascade laser emitting at 11.5 µm with an applied potential difference equal to 60 kV per cm.
Fig (4.2) displays a semi-logarithmic plot corresponding to transmission co-efficient versus energy for example number one where the energy changes from zero to the height of the barrier. By definition, a group of close peaks is called mini band whereas the interval with no peak between them and the next peak is called mini gap. The formed band structure is totally dependent on the potential profile and consequently to the width of wells and barriers as the term of band structure engineering was coined to describe this kind of structures.
0 0.1 0.2 0.3 0.4 0.5
Energy (eV)
10-40 10-30 10-20 10-10 100Transmission Coefficient
Figure 4.2: Transmission coefficient versus energy for potential profile employed by Hugi et al. The peaks in the graphs exhibit the allowed energy levels.
The below figure shows the obtained wave functions where they have been shifted according to their energy levels (extracted from transmission coefficient graph). Comparing our graph with the one in Hugi’ work convinces us that our results are in good agreement with Hugi’ work. As it is clear from the graph, there is gap-like between the highest state and its lower neighbor where lasing happens between these two states, so that electron scatters from upper level to the lower level then it transfers through other states to the highest level of the next stage. This cascading motion of electron keeps happening till it reaches the last stage.
10 20 30 40 50
Distance (nm)
0 0.2 0.4 0.6 0.8Energy (eV)
Figure 4.3: Our results on the potential profile used by Hugi et al where the bound state energies are E1 = 0.2051 eV, E2 = 0.2207 eV, E3 = 0.2425 eV, E4 = 0.2563 eV, E5 = 0.2886 eV, E6 = 0.3151 eV, E7 = 0.3466 eV and E8 = 0.463 eV.
To get an idea about the behavior of current density versus applied bias across the structure, we consider the structure as Fig (4.4) and implement Tsu Esaki model. The model has been explained in chapter two; it describes tunneling current in a potential profile between two contacts. The figure presented below is the same as Hugi work except for the two contacts we have added to.
10 20 30 40 50
Distance (nm)
0 0.1 0.2 0.3 0.4 0.5Energy(eV)
Figure 4.4: Hugi’s potential profile with two added contacts.
As mentioned, Tsu-Esaki model can suitably describe tunneling current. Let’s write it down as follows
J = constant Z ∞
eV
dEZT cN E (4.2)
where Tcis transmission coefficient and N E = kBT emp ln (1+exp[(E1+exp[(EF+eV −EF−EZ)/kZ)/kBT ]BT ]) called supply function. By definition, the difference in the supply of the carrier on the surface of the dielectric layer (between two contacts), is called supply function. To have a better understanding of it, we present supply function of the system in applied bias of 1.5 V and three different temperatures. According to the model, the current density is the area between the product of transmission coefficient and supply function and the energy axis.
As it is clear from the graph, three supply functions have the same behavior, they decrease as the energy increases and they turn to zero when the energy exceeds a certain value.
0
0.2
0.4
0.6
0.8
1
Energy (eV)
0
0.5
1
1.5
Supply function
10
-20 T=300K & Bias=1.5 V T=200K & Bias=1.5 V T=100K & Bias=1.5 VFigure 4.5: Supply function versus electron’s energies for the system; applied bias is 1.5 V.
The current density versus biased voltage has been displayed in the below graph. The behavior of the current in three different temperatures are more or less the same. Following the graphs from the origin, currents increase as voltage increases thereafter in three of them the current experience a sharp increase to reach a peak. However, after the peak, the currents decrease as voltage increases which is called negative differential resistance and is a conventional behavior in this sort of structures. No need to mention, the peak in three graphs happens at the same bias, although the temperatures are different.
0 0.5 1 1.5
Applied bias
0 2 4 6 8Current density (kA/cm
2
)
T=200KT=300KT=100K
Figure 4.6: The red graph displays current density at 100 Kelvin while blue and orange show the system at 200 and 300 K respectively.
4.1.2
Example II
Strupirchonski et al [35] has employed Al0.25 Ga0.75As/GaAs as barriers and wells of their QCL device where the sequence of layers in one cascade are 3, 3.2, 17.3, 3.2, 9.4, 1.7, 9.4 (all in nanometer). Their target electromagnetic spectrum area was terahertz region. They used the below potential profile for this purpose. However, in real devices, which has been experimentally synthesized, there are 20 periods.
Figure 4.7: Strupirchonski’ device and the related modulus squared wave func-tions.
We numerically solved Schr¨odinger equation in their potential profile. The transmission coefficient has been presented in the figure below. Mini band and mini gap are clear in the graph.
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4
Energy (eV)
10-50 10-40 10-30 10-20 10-10 100Transmission Coefficient
Figure 4.8: Transmission coefficient versus energy for potential profile employed by Strupirchonski et al.
Our results on bound state energies are shown in the below graph. As it is obvious from the arranged wave functions, the lower laser level is the third wave function from the bottom while the next higher one is the upper laser level.
20
40
60
80
100
Distance (nm)
0
0.1
0.2
0.3
0.4
Energy (eV)
Figure 4.9: Modulus squared wave functions, the reproduction of Strupirchonski’ work.
4.1.3
Example III
The third example that we have solved, is the potential profile representing GaAs/Al15 Ga85As thin films as well and barrier respectively. The thicknesses of grown layers in nanometer are 5.5, 9.2, 3, 15.5, 4.1, 6.6, 2.7, 8. It is three stages of a QCL potential profile done by Milovanovic [36] using Monte Carlo simulation. We followed their potential profile and got the steady-state carrier distribution using transfer matrix method. As it is shown in the below figure it consists of three similar stages. The corresponding graph from our results has been shown in the next coming picture.
Figure 4.10: Bound state wave functions (modulus squared) done by Milovanovic where the applied bias is 10 kV/cm.
Figure 4.11: Modulus squared wave functions coming from transfer matrix method.
It is worth reminding that the real devices contain several periods of the dis-played potential profiles. The third example clearly demonstrates that the found wave functions repeat themselves at the other stages then, one needs to find them in just one period. However, it is still advised to consider a three-stage potential profile and obtain the results in the central stage.
Chapter 5
Conclusion
In this thesis, we did a comprehensive study on devices built based on quan-tum wells orienting our study toward quanquan-tum cascade lasers. We examined the methods and models implemented for studying this sort of devices. Among those approaches, we chose to go with transfer matrix technique where MATLAB programming was employed for utilizing transfer matrix approach. To evaluate our formalism, the code was tested by solving Schr¨odinger equation in a sin-gle quantum well and the results were compared with those of semi-analytical method. Then we developed our code to be able to solve consecutive wells and barriers which are representative for potential profiles of quantum devices. We selected three quantum cascade lasers to investigate, then we successfully solved Schr¨odinger equation and finally got the steady-state electron distributions inside their potential profile. We also employed Tsu-Esaki model to obtain current-voltage characteristics of the structures. At the end, it is worth mentioning transfer matrix method is a simpler technique to research on QCLs comparing to other methods; at the same time it is very easy to be implemented for investigat-ing an arbitrary potential profile of various materials; nonetheless, its results are precise enough to evaluate a certain potential profile to see if that is applicable as a QCL. Therefore, the technique can be considered as a trustworthy technique at the forefront of the ongoing research upon designing innovative potential profile for QCLs.
Bibliography
[1] L. Esaki and R. Tsu, “Superlattice and negative differential conductivity in semiconductors,” IBM Journal of Research and Development, vol. 14, no. 1, pp. 61–65, 1970.
[2] B. R. Nag, Physics of quantum well devices, vol. 7. Springer Science & Business Media, 2001.
[3] M. Pilkuhn, H. Rupprecht, and J. Woodall, “Continuos stimulated emission from gaas diodes at 77 k,” Proceedings of the IEEE, vol. 51, no. 9, pp. 1243– 1243, 1963.
[4] M. Razeghi, Technology of quantum devices. Springer, 2010.
[5] R. Kazarinov, “Possibility of amplification of electromagnetic waves in a semiconductor with superlattice,” Sov. Phys.-Semicond., vol. 5, no. 4, pp. 707–709, 1971.
[6] J. Faist, F. Capasso, D. L. Sivco, C. Sirtori, A. L. Hutchinson, A. Y. Cho, et al., “Quantum cascade laser,” Science-AAAS-Weekly Paper Edition-including Guide to Scientific Information, vol. 264, no. 5158, pp. 553–555, 1994.
[7] R. K¨ohler, A. Tredicucci, F. Beltram, H. E. Beere, E. H. Linfield, A. G. Davies, D. A. Ritchie, R. C. Iotti, and F. Rossi, “Terahertz semiconductor-heterostructure laser,” Nature, vol. 417, no. 6885, pp. 156–159, 2002.
[8] C. Jirauschek and T. Kubis, “Modeling techniques for quantum cascade lasers,” Applied Physics Reviews, vol. 1, no. 1, p. 011307, 2014.
[9] R. F. Curl, F. Capasso, C. Gmachl, A. A. Kosterev, B. McManus, R. Lewicki, M. Pusharsky, G. Wysocki, and F. K. Tittel, “Quantum cascade lasers in chemical physics,” Chemical Physics Letters, vol. 487, no. 1, pp. 1–18, 2010. [10] J. Bjarnason, T. Chan, A. Lee, M. Celis, and E. Brown, “Millimeter-wave, terahertz, and mid-infrared transmissionthrough common clothing,” Applied Physics Letters, vol. 85, no. 4, pp. 519–521, 2004.
[11] J. C. Dickinson, T. M. Goyette, A. J. Gatesman, C. S. Joseph, Z. G. Root, R. H. Giles, J. Waldman, and W. E. Nixon, “Terahertz imaging of subjects with concealed weapons,” tech. rep., MASSACHUSETTS UNIV LOWELL, 2006.
[12] P. H. Siegel, “Terahertz technology in biology and medicine,” IEEE trans-actions on microwave theory and techniques, vol. 52, no. 10, pp. 2438–2447, 2004.
[13] H.-T. Chen, R. Kersting, and G. C. Cho, “Terahertz imaging with nanometer resolution,” Applied Physics Letters, vol. 83, no. 15, pp. 3009–3011, 2003. [14] P. Han, G. Cho, and X.-C. Zhang, “Time-domain transillumination of
biolog-ical tissues with terahertz pulses,” Optics Letters, vol. 25, no. 4, pp. 242–244, 2000.
[15] K. Humphreys, J. Loughran, M. Gradziel, W. Lanigan, T. Ward, J. Murphy, and C. O’sullivan, “Medical applications of terahertz imaging: a review of current technology and potential applications in biomedical engineering,” in Engineering in Medicine and Biology Society, 2004. IEMBS’04. 26th Annual International Conference of the IEEE, vol. 1, pp. 1302–1305, IEEE, 2004. [16] C. S. Joseph, A. N. Yaroslavsky, J. L. Lagraves, T. M. Goyette, and R. H.
Giles, “Dual-frequency continuous-wave terahertz transmission imaging of nonmelanoma skin cancers,” in Proc SPIE, vol. 7601, pp. 760104–760104, 2010.
[17] P. H. Siegel, “Terahertz technology,” IEEE Transactions on microwave the-ory and techniques, vol. 50, no. 3, pp. 910–928, 2002.
[18] B. S. Williams, “Terahertz quantum-cascade lasers,” Nature photonics, vol. 1, no. 9, pp. 517–525, 2007.
[19] D. L. Woolard, R. Brown, M. Pepper, and M. Kemp, “Terahertz frequency sensing and imaging: A time of reckoning future applications?,” Proceedings of the IEEE, vol. 93, no. 10, pp. 1722–1743, 2005.
[20] I. Mehdi, G. Chattopadhyay, E. Schlecht, J. Ward, J. Gill, F. Maiwald, and A. Maestrini, “Terahertz multiplier circuits,” in Microwave Symposium Digest, 2006. IEEE MTT-S International, pp. 341–344, IEEE, 2006.
[21] A. Maestrini, J. Ward, J. Gill, H. Javadi, E. Schlecht, G. Chattopadhyay, F. Maiwald, N. R. Erickson, and I. Mehdi, “A 1.7-1.9 thz local oscillator source,” IEEE Microwave and Wireless Components Letters, vol. 14, no. 6, pp. 253–255, 2004.
[22] Q. Lu, N. Bandyopadhyay, S. Slivken, Y. Bai, and M. Razeghi, “High per-formance terahertz quantum cascade laser sources based on intracavity dif-ference frequency generation,” Optics express, vol. 21, no. 1, pp. 968–973, 2013.
[23] K. Vijayraghavan, Y. Jiang, M. Jang, A. Jiang, K. Choutagunta, A. Vizbaras, F. Demmerle, G. Boehm, M. C. Amann, and M. A. Belkin, “Broadly tunable terahertz generation in mid-infrared quantum cascade lasers,” Nature communications, vol. 4, p. 2021, 2013.
[24] P. Harrison, “The nature of the electron distribution functions in quantum cascade lasers,” Applied physics letters, vol. 75, no. 18, pp. 2800–2802, 1999. [25] S. Datta, Quantum transport: atom to transistor. Cambridge University
Press, 2005.
[26] R. Tsu and L. Esaki, “Tunneling in a finite superlattice,” Applied Physics Letters, vol. 22, no. 11, pp. 562–564, 1973.
[27] N. Tuomisto, A. Zugarramurdi, and M. J. Puska, “Modeling of electron tunneling through a tilted potential barrier,” Journal of Applied Physics, vol. 121, no. 13, p. 134304, 2017.
[28] B. Jonsson and S. T. Eng, “Solving the schrodinger equation in arbitrary quantum-well potential profiles using the transfer matrix method,” IEEE journal of quantum electronics, vol. 26, no. 11, pp. 2025–2035, 1990.
[29] C. Jirauschek, “Accuracy of transfer matrix approaches for solving the ef-fective mass schr¨odinger equation,” IEEE Journal of Quantum Electronics, vol. 45, no. 9, pp. 1059–1067, 2009.
[30] W. W. Lui and M. Fukuma, “Exact solution of the schrodinger equation across an arbitrary one-dimensional piecewise-linear potential barrier,” Jour-nal of Applied Physics, vol. 60, no. 5, pp. 1555–1559, 1986.
[31] S. L. Chuang, “Efficient band-structure calculations of strained quantum wells,” Physical Review B, vol. 43, no. 12, p. 9649, 1991.
[32] J. Singh, Quantum mechanics: fundamentals and applications to technology. John Wiley & Sons, 2008.
[33] S. L. Chuang, “Physics of optoelectronic devices,” 1995.
[34] A. Hugi, R. Terazzi, Y. Bonetti, A. Wittmann, M. Fischer, M. Beck, J. Faist, and E. Gini, “External cavity quantum cascade laser tunable from 7.6 to 11.4 µ m,” Applied Physics Letters, vol. 95, no. 6, p. 061103, 2009.
[35] E. Strupiechonski, H. Galinski, M. Gonzalez, R. Blanchard, D. C. Bell, E. H. Linfield, and F. Capasso, “Modeling and design of al 0.25 ga 0.75 as/gaas ter-ahertz quantum cascade lasers with a realistic band structure,” in Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), 2017 42nd International Conference on, pp. 1–2, IEEE, 2017.